Prerpints.org logo
Preprint
Brief Report

Pion-Argon Inclusive Cross-Section Measurement on ProtoDUNE-SP

Altmetrics

Downloads

100

Views

20

Comments

0

This version is not peer-reviewed

Submitted:

07 June 2023

Posted:

07 June 2023

You are already at the latest version

Alerts
Abstract
The pion-argon cross-section measurement is crucial to understand effects such as final-state interactions, which account for a large source of systematic uncertainty in neutrino oscillation experiments. ProtoDUNE-SP, with its charged particle beam data, can provide such experimental constraints. This paper elaborates the methodology to measure the cross-section on large-scale LArTPCs like ProtoDUNE-SP. We use the 1 GeV MC sample to demonstrate the analysis procedures. The cross-sections for pion kinetic energy ranging from 350 MeV to 950 MeV are measured on the MC. The consistency of the MC results with its input values serves as validation of the method and the procedures, which we will later use to perform measurements on the data sample.
Keywords: 
Subject: Physical Sciences  -   Nuclear and High Energy Physics

1. Introduction

The liquid Argon Time Projection Chamber (LArTPC) is a promising technology used by many modern neutrino experiments, including the future Deep Underground Neutrino Experiment (DUNE) [1]. Knowledge on the pion-argon cross-section is important for us to understand and explain the data collected in the LArTPC. For one thing, neutrinos are detected by their interaction with argon atoms, which can produce hadronic particles, and these features will be used to identify the neutrino. For another, when a neutrino interacts with an argon atom, the initially produced pions can also interact within the nucleus, which will change the kinematics of particles emitted from the atom. This is called the hadronic final-state interactions (FSI) effect. These effects account for a major source of systematic uncertainty in neutrino oscillation analyses, which need constraints from the pion-argon cross-section.
Currently, the pion-argon cross-section is predicted mainly by interpolating data from lighter and heavier nuclei [2], while the experimental measurements are scarce. Only the LADS collaboration [3] and the LArIAT collaboration [4] have performed such measurements. ProtoDUNE-SP [5], which contains 770 tons of LAr, is a prototype for one of DUNE’s far detectors. Charged particles, including pions with various momentum modes ranging from 300 MeV to 7 GeV, are delivered into the TPC through a beam plug, making it a good place to measure the pion-argon cross-section.
In this paper, we first introduce the energy-slicing method in Section 2, which is used to extract the cross-section. After that, we describe the analysis procedures in Section 3, including selections, background subtraction, and unfolding. Finally, in Section 4, we use a subset of the 1 GeV MC as a fake data sample to exemplify using the method and the procedures to measure the cross-section and compare to the input cross-sections as validation. A few discussions towards measuring real data are given in Section 5.

2. Energy-slicing method

Based on the idea of the thin-slice method proposed by the LArIAT collaboration [4], we develop the energy-slicing method [6]. Figure 1 shows one TPC of ProtoDUNE-SP. A beam pion is shown as the dashed orange track with some possible daughter particles originating from the end vertex. The initial kinetic energy of the beam pion at the front-face of the TPC is denoted as E ini , and the kinetic energy at the end vertex is denoted as E end . Given these two energies, the track can be divided into several energy slices by pre-defined energy bins, determined according to the energy resolution and the statistics on a case-by-case basis. In this analysis, the energy bins are chosen to be [0, 350, 450, 500, 550, 600, 650, 700, 750, 800, 850, 950, ∞) MeV. The bin edges are indicated by red bars in Figure 1, where the last bar is dashed because the beam pion stops before it reaches that energy. The first complete energy slice is referred to as the initial slice; the slice where the track stops is called the end slice. If the signal interaction occurs at the end vertex, then the end slice is also called an interaction slice.
It is worth noting that E ini is larger than the energy in the initial slice, and the piece of track before the initial slice is referred to as an incomplete slice, which is not usable. On the contrary, E end is inside the end slice. For convenience, we define the slice ID from 1 to the number of energy bins, N, starting with the bin with the highest energy. For example, energy bin [950, ∞) has slice ID 1, and [0, 350] has slice ID 12. Therefore, for each event which has a beam pion track in the TPC, there is an initial slice ID, an end slice ID, as well as an interaction slice ID, which is assigned as null if the interaction occurring at the end vertex is not the signal interaction. However, if the beam pion stops inside the incomplete slice, the whole track is not usable, so all three slice IDs will be assigned as null.
For all events with a beam pion track in the TPC, the distribution of initial slice ID is called the initial histogram  N ini , and similarly we have the end histogram N end and the interaction histogram N int . The number of incident events, where the beam pion goes through the whole range of the energy bin, forms the incident histogram N inc , and it can be calculated as
N inc ( i ) = ∑ j = i N N end ( j ) − ∑ j = i + 1 N N ini ( j ) .
Finally, the cross-section in each energy bin can be given by
σ ( E ) = M Ar ρ N A Δ E d E d x ( E ) ln N inc ( i ( E ) ) N inc ( i ( E ) ) − N int ( i ( E ) ) ,
where M Ar is the molar mass of argon, ρ is the density of LAr, N A is the Avogadro constant, and Δ E is the energy bin width. The stopping power of pion in LAr, d E d x ( E ) , is evaluated from theory at the midpoint of each bin using the Bethe-Bloch formula [7] and is assumed to be a constant within each energy bin.

3. Analysis procedures

The whole MC sample is divided into two halves: one is used as fake data, and the other is referred to as truth MC. Using slice ID histograms derived from its truth energy information, we can extract the truth cross-section of the fake data sample, which can then be used to validate the slicing method. On the other hand, we can also treat fake data the same as real data and perform the same procedures to measure the cross-section using reconstruction information. The results can be used to validate the procedures, which will later be applied to measuring real data. The reconstructed E ini is derived from the measured beamline instrumented kinetic energy minus a constant upstream energy loss, the value of which is estimated using MC. E end is calculated from E ini and the reconstructed track length based on the theoretical Bethe-Bloch formula as
E end = E ini − ∫ d E d x d x reco .
To conduct the energy-slicing method, we need to select beam pion tracks. Based on machine learning, Pandora [8] selects one track in each event which is most likely to be the beam track. The information of this track and its daughters will then be used for further selections. In addition to technical cuts ensuring useful information from the track, we also perform some specific cuts to veto certain types of backgrounds. The beam particle enters the TPC through the beam plug, and we know approximately where the particle enters the TPC as well as its direction. Thus, we set cuts on the start position as well as the angle of the detected beam track in order to reduce non-beam tracks caused by mis-identification. Proton tracks have a very different d E / d x curve compared to pions and muons [5], so this feature can be used to reduce proton background. In order to mitigate muon background, a CNN-based Michel electron identifier is built [9] and gives the detected beam track a daughter Michel score that can be used to distinguish pions from stopping muons. After full selections, we have 80.1% pion inelastic events, which are the signal events for the inclusive measurement. The remaining backgrounds, estimated using the truth MC, are given in Table 1.
Next, we subtract the background histograms, estimated by truth MC, from the reconstructed histogram after selections, N reco , which represents N ini , N end , or N int . However, to account for difference of background fractions f between the (fake) data sample and the truth MC, we perform a data-driven method by introducing a scale factor α i for each background type i. Thus, the reconstructed signal histogram is
N reco sig = N reco · 1 − ∑ i f i data = N reco · 1 − ∑ i f i MC · α i .
In practice, we only consider α i ≠ 1 for the three major backgrounds, which are muon, non-beam proton, and non-beam pion. α i is fitted for the best agreement between data and truth MC in the sideband of a variable distribution used in data selection, where background i dominates. For the fake data sample, the fitted results of the three α i are all consistent with unity, which is reasonable since the fake data is statistically the same with the truth MC. However, this may not be the case for real data.
Finally, we perform unfolding [10] to transform reconstructed histograms into true histograms, expressed as
N true sig = M unfolding · N reco sig .
The response matrix R i j = P ( x ∈ reco bin i | y ∈ true bin j ) is estimated using true beam pion tracks in the truth MC sample. We use the d’Agostini method [11] implemented in the RooUnfold package [12] to model the unfolding matrix M unfolding . To take into account the correlations among the three histograms, N ini , N end , and N int , we combine them as one variable ( N ini , N end , N int ) and perform 3-D unfolding. The index of the combined variable is N 2 · ID ini + N · ID end + ID int . To be conservative, the number of iterations in the d’Agostini method is chosen to be as large as 20 to obtain the results in Section 4, but this parameter should be optimized based on further studies.

4. Validation results

The true histograms derived after unfolding can be plugged into Equation 1 and then Equation 2 to calculate the cross-section. Figure 2 shows the 1 GeV fake data cross-section results. The red curve is the Geant4 input, which is used to the generate the MC. The green points are derived using the truth information from the fake data sample, and their consistency with the red curve suggests the feasibility of the energy-slicing method. The black points are the measured results for the fake data sample. They also agree with the red curve, which validates the procedures described in Section 3. Cross-sections in the underflow and the overflow energy bins are not calculated. The horizontal error bars indicate the bin width, and the vertical error bars are purely statistical.

5. Conclusions and outlook

In this paper, we introduce the energy-slicing method and measure the pion-argon inclusive cross-section using a 1 GeV fake data sample for validation. When applying these procedures to measuring real data, we first need to study the differences between data and MC. We will reweight MC accordingly in order to make it more consistent with real data, since both the background estimations and the response matrix rely on MC to model. The differences between real data and MC will also be included in studies of systematic uncertainties.

References

  1. Abi, B.; others. Deep Underground Neutrino Experiment (DUNE), Far Detector Technical Design Report, Volume II: DUNE Physics 2020. [arXiv:hep-ex/2002.03005]. arXiv:hep-ex/2002.03005].
  2. Carroll, A.S.; Chiang, I.H.; Dover, C.B.; Kycia, T.F.; Li, K.K.; Mazur, P.O.; Michael, D.N.; Mockett, P.M.; Rahm, D.C.; Rubinstein, R. Pion-Nucleus Total Cross-Sections in the (3,3) Resonance Region. Phys. Rev. C 1976, 14, 635–638. [Google Scholar] [CrossRef]
  3. Rowntree, D.; others. pi+ absorption on N and Ar. Phys. Rev. C 1999, 60, 054610. [Google Scholar] [CrossRef]
  4. Gramellini, E.; others. Measurement of the π–Ar total hadronic cross section at the LArIAT experiment. Phys. Rev. D 2022, arXiv:hep-ex/2108.00040]106, 052009. [Google Scholar] [CrossRef]
  5. Abi, B.; others. First results on ProtoDUNE-SP liquid argon time projection chamber performance from a beam test at the CERN Neutrino Platform. JINST 2020, arXiv:physics.ins-det/2007.06722]15, P12004. [Google Scholar] [CrossRef]
  6. Stocker, F. Measurement of the Pion Absorption Cross-Section with the ProtoDUNE Experiment. PhD thesis, University of Bern, 2021.
  7. Workman, R.L.; others. Review of Particle Physics. PTEP 2022, 2022, 083C01. [Google Scholar] [CrossRef]
  8. Marshall, J.S.; Thomson, M.A. The Pandora Software Development Kit for Pattern Recognition. Eur. Phys. J. C 2015, arXiv:physics.data-an/1506.05348]75, 439. [Google Scholar] [CrossRef]
  9. Abed Abud, A.; others. Separation of track- and shower-like energy deposits in ProtoDUNE-SP using a convolutional neural network. Eur. Phys. J. C 2022, arXiv:physics.ins-det/2203.17053]82, 903. [Google Scholar] [CrossRef]
  10. Cowan, G. A survey of unfolding methods for particle physics. Conf. Proc. C 2002, 0203181, 248–257. [Google Scholar]
  11. D’Agostini, G. A Multidimensional unfolding method based on Bayes’ theorem. Nucl. Instrum. Meth. A 1995, 362, 487–498. [Google Scholar] [CrossRef]
  12. Brenner, L.; Balasubramanian, R.; Burgard, C.; Verkerke, W.; Cowan, G.; Verschuuren, P.; Croft, V. Comparison of unfolding methods using RooFitUnfold. Int. J. Mod. Phys. A 2020, arXiv:physics.data-an/1910.14654]35, 2050145. [Google Scholar] [CrossRef]
Preprints 75911 g001
Figure 1. Demonstration of the energy-slicing method. In this example, E ini = 866 MeV, E end = 627 MeV.
Figure 1. Demonstration of the energy-slicing method. In this example, E ini = 866 MeV, E end = 627 MeV.
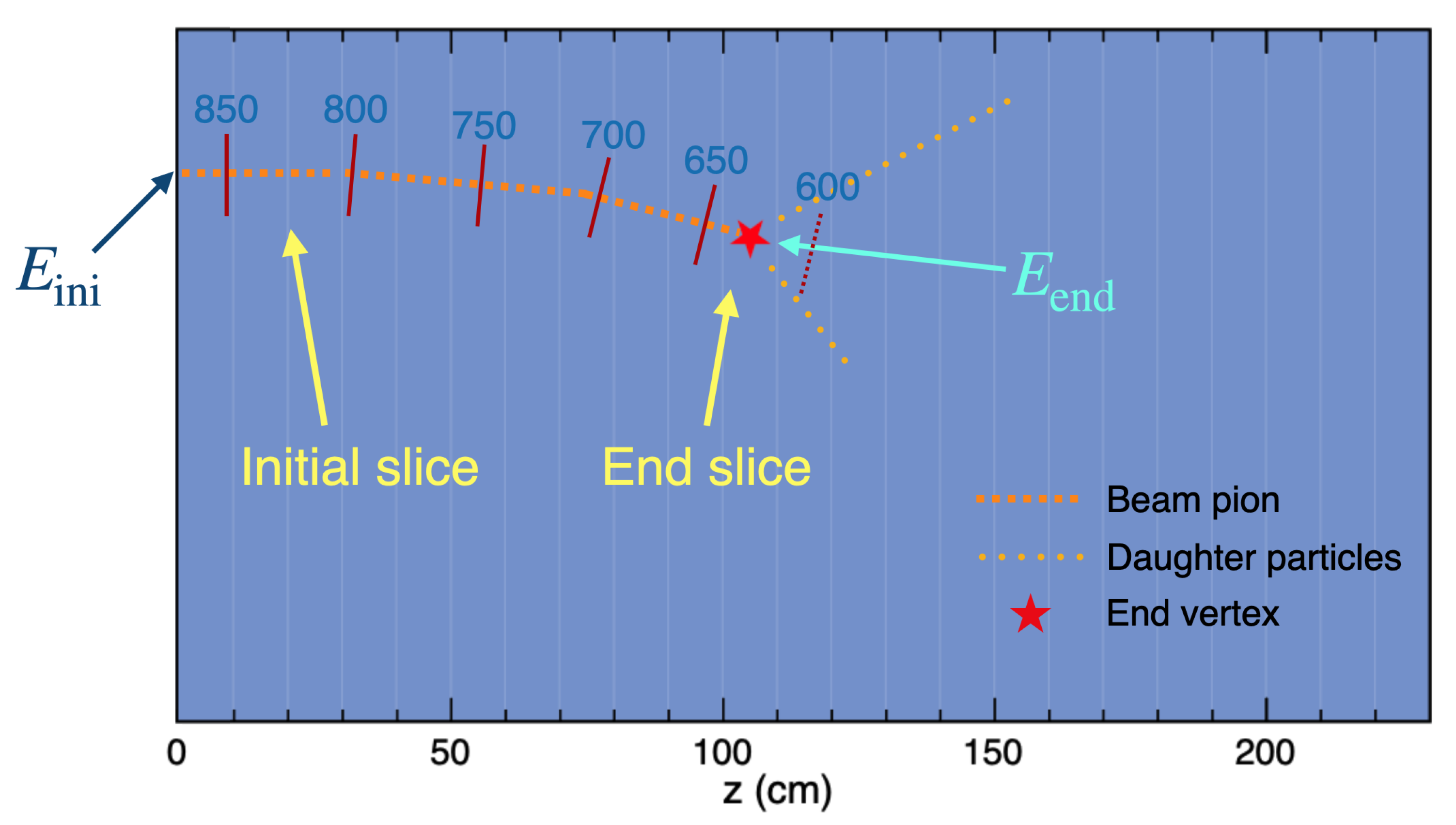
Preprints 75911 g001
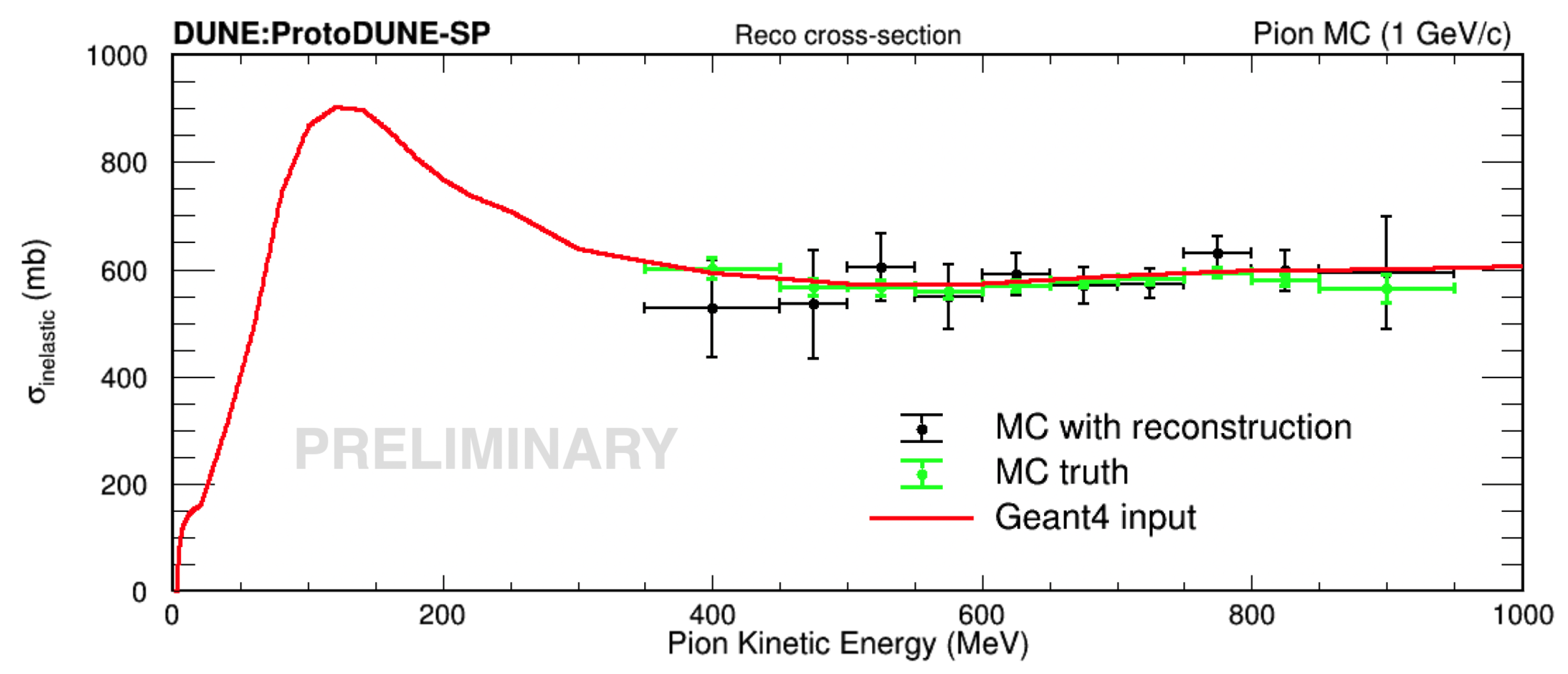
Preprints 75911 g002
Figure 2. Pion-argon inclusive cross-section results for the 1 GeV fake data sample.
Figure 2. Pion-argon inclusive cross-section results for the 1 GeV fake data sample.
Preprints 75911 g002
Table 1. The number of events of each type after full selections.
Table 1. The number of events of each type after full selections.
Total truth MC 39970 Pion inelastic 32014 Pion decay 298 Muon 3237 Cosmic origin 12
Non-beam proton 1590 Non-beam pion 1520 Non-beam muon 892 Shower 212 Other non-beam 195
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated