Prerpints.org logo
Preprint
Article

Propagation of Terahertz Surface Plasmon Pulses in a Plasmonic Fiber

Altmetrics

Downloads

110

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

07 June 2023

Posted:

08 June 2023

You are already at the latest version

Alerts
Abstract
The dispersion properties of surface plasmon polaritons during propagation on metal wires with a dielectric coating in the terahertz frequency range are investigated theoretically. An analytical expression is obtained for a pulsed electric field from the solution of Maxwell equations taking into account high-order dispersion terms. The effect of the dielectric coating on the distortion of the pulse shape is analyzed. Unlike uncoated wire, the propagation of a surface plasmon pulses along a coated wire is highly dispersive. It is shown that the coating leads to the appearance of a long-chirped signal with a propagation of only a few millimeters, i.e. when a terahertz pulse propagates along a coated wire, it acquires a long oscillatory tail, the frequency of which depends on time.
Keywords: 
Subject: Physical Sciences  -   Applied Physics

1. Introduction

Efficient transmission of terahertz radiation is one of the challenges for the new generation of terahertz systems. To transmit terahertz pulses, waveguides with low losses and low dispersion are needed. Conventional dielectric fibers for visible light and metal waveguides for microwave radiation are unsuitable for use in the THz range. It is well known that the surface plasmon polaritons (SPP’s) in the terahertz frequency range have very low losses and low dispersion [1,2,3,4]. Therefore, metal wire waveguides are very important for use in imaging, sensing and spectroscopy. Unlike SPP’s in the visible and infrared frequency ranges, the behavior of SPPs in the terahertz frequency range is different [2]. It was shown in [2], that the behavior of SPPs on cylindrical metal surfaces in the terahertz frequency range is dispersive and differs from the behavior of surface plasmon waves on a flat surface. The spectral and spatial distributions of the SPP’s field over the gold surface was measured in [3]. It was found that a thin dielectric film on top of the metal leads to strong confinement of the SPP’s field to the surface. In [4], the effect of a dielectric coating on THz surface plasmon pulse propagation along copper wire was studied. Usually THz surface plasmon waves (SPWs) propagate at the boundary between a metal and a dielectric layer. Recent studies show that THz surface plasmon waves can propagate along line-guided metallic structures, such as grooves, stripes, gratings, and gaps [5,6,7,8,9,10]. Reviews on terahertz technology and SPWs in the THz regime are presented in [11,12,13]. Various THz optical fiber types including solid core fibers, tube fibers, porous-core fibers, anti-resonant fibers, metamaterial-based fibers, and their guiding mechanisms are examined in [14,15]. In [16] the propagation characteristics of SPPs in the THz frequency range in cylindrical metal wires with a dielectric coating were studied by solving Maxwell equations. The phase velocities and attenuation lengths of SPPs were determined as function of the conductivity and frequency for different wire radii. It was shown that the phase velocities and attenuation lengths increase with increasing conductivity and radius of the wire. It was shown that the coating leads to a decrease in the phase velocity and an increase in the propagation length of SPWs.
The group velocity dispersion is a significant obstacle that limits the application of waveguides in terahertz communication systems and spectroscopy. The fact is that the various frequency components of a wide spectrum of THz radiation propagate at different group velocities, which leads to distortion of the pulse shape.
In this paper, we investigate the dispersive propagation of surface plasmon-polariton pulses along a coated metal wire in the terahertz frequency range. The effect of a dielectric coating made of a non-dispersive material on the dispersion of pulses is investigated. Analytical expressions for the electric field are obtained, which make it possible to carry out time-saving calculations of the characteristics of the pulse when propagating along a coated wire.

2. Problem Formulation

The dielectric fibers are widely used to transmit the electromagnetic beams in optical regimes through the dielectric fibers [17,18]. Even though dielectric fibers for visible light cannot be used to transmit terahertz electromagnetic waves, the methods used to solve Maxwell's equations in the optical regime can also be applied to consider terahertz radiation.
Consider a cylindrical plasmonic fiber (Figure 1), where a metal wire with radius r 0 is embedded in a dielectric fiber with radius R f ≫ r 0 .
It is well known that the surface electromagnetic waves can propagate along the conducting wire. A detailed theoretical analysis of surface waves propagating along a metal wire was carried out a long time ago by Sommerfeld [19].
For the cylindrical structure of a dielectric fiber with a metal wire core the guided modes may be determined from the Helmholtz equations for the longitudinal field component Ez [20]:
∇ ⊥ 2 + k 0 2 ε m − β 2 E z = 0 ,   0 < r < r 0 ∇ ⊥ 2 + k 0 2 ε d − β 2 E z = 0 ,   r > r 0 ,
where ∇ ⊥ 2 = 1 r ∂ ∂ r r ∂ ∂ r + 1 r 2 ∂ 2 ∂ φ 2 , k 0 = ω c is the wavenumber in free space, β is the longitudinal component of the wavenumber, r 0 is the metal wire radius, ε m = ε ' + i σ ω ε 0 is the complex dielectric constant, where σ = 1 R l π r 0 2 is the electric conductivity of the wire, R l is the resistance per unit length, ε d is the dielectric constant of dielectric cover and ε 0 is the dielectric constant of free space.
Solutions of the equations (1) are the Bessel functions:
E z ( z ) = A 1 I 0 ( η r ) , r ≤ r 0 A 2 K 0 ( η 0 r ) , r ≥ r 0 e i β z
where A1 and A2 are the amplitude coefficients, I 0 and K 0 are the modified Bessel functions of the first and second kind, η 2 = ω 2 c 2 ε p − β 2 , η 0 2 = ω 2 c 2 ε d − β 2 .
The behavior of the electromagnetic field in the considered structure is described by the dispersion equation, which follows from the Maxwell equations. The dispersion equation for surface electromagnetic waves follows from the boundary condition of continuity for the tangential components of the field at r = r 0 = a :
ε p η a I 0 ' ( η a ) I 0 ( η a ) = 1 η 0 a K 0 ' ( η 0 a ) K 0 ( η 0 a )
where I 0 and K 0 are the modified Bessel functions of the first and second kind, accordingly, I 0 ' and K 0 ' are the derivatives of the Bessel functions.
The propagation of waves of a given frequency ω is determined by the propagation constant β, i.e. the spatial distribution of the electric field in the transverse plane is preserved when propagating along the wire. However, when the pulses propagate, noticeable changes occur. The fact is that the dependence of the speed and attenuation length on the frequency leads to the dispersive propagation of the pulse.
Consider an input pulse in the form:
E ( z = 0 , t ) = A 0 E ( r ) exp ⁡ ( − t 2 τ 0 2 + i ω 0 t ) = A 0 E ( r ) e i ω 0 t ∫ F ( Ω ~ ) e i Ω ~ t d Ω ~
where F ( Ω ~ ) is the spectrum of the incident pulse, Ω ~ = ω − ω 0 is the detuning from the carrier frequency of the pulse ω 0 .
The frequency spectrum of this pulse is determined by
F ω − ω 0 = 1 2 π ∫ − ∞ ∞ f ( t ) e − i ω t d t = τ 2 π e x p − ω − ω 0 2 τ 2 / 2
The evolution of the spatial distribution of the field at r ≥ r 0 can be expressed as an expansion in terms of plane waves
E r , z , ω − ω 0 = A 2 ∫ 0 η 0 m a x η 0 K 0 ( η 0 r ) F ( ω − ω 0 ) e i β ω z d η 0
The inverse Fourier transform of (6) gives an expression for the electric field in the time domain:
E r , z , t = 1 2 π ∫ − ∞ ∞ E r , z , ω − ω 0 e x p − i ω − ω 0 t d ω
Expand β ( ω ) in a Taylor series in the neighbourhood of ω 0 :
β ω = ∑ m = 0 ω − ω 0 m m ! γ m = γ 0 + ω − ω 0 γ 1 + ω − ω 0 2 2 ! γ 2 + ω − ω 0 3 3 ! γ 3 …
where γ m = d m d ω m β ( ω ) ω = ω 0 = ω 0 , γ 1 = d β d ω ω = ω 0 .
Substituting (6) into (7) we obtain for the electric field
E r , z , t = τ 2 π ∫ 0 η 0 m a x η 0 K 0 η 0 r e i γ 0 z f t , z , τ d η 0
where f t , z , τ = 2 π τ 2 − i z γ 2 e x p − t − z γ 1 2 2 τ 2 − i z γ 2 .
Here the second order dispersion term γ 2 is taken into account.
Taking into account the higher order dispersion term γ 3 (third order correction from (8)) we have
f t , z , τ = 2 π γ 3 z / 2 3 e x p 1 γ 3 z γ 1 z − t τ 2 − i γ 2 z + 1 3 γ 3 z 2 τ 2 − i γ 2 z 3 A i ( x ) ,
where A i x = 1 2 π ∫ − ∞ ∞ exp ⁡ i t 3 3 + i x t d t is the Airy function,
x = i γ 3 z / 2 3 γ 1 z − t + 1 4 γ 3 z / 2 4 / 3 τ 2 − i γ 2 z 2
The dispersion determined by the value of γ 2 leads to an increase in the pulse duration. A higher-order dispersion determined by the contribution of the γ 3 leads to a distortion of the pulse shape. The pulse acquires an asymmetric shape and has an oscillatory structure on the tail. Indeed, expression (10) for the electric field includes the Airy function, which is characterized by oscillatory behavior.
Note that the higher order dispersion effects become significant if the dispersion length L 3 = τ 3 / γ 3 is less than the dispersion length L 2 = τ 2 / γ 2 , i.e. when τ γ 2 / γ 3 < 1 . Usually, the contribution of the dispersion term γ 3 is small in comparison with the dispersion term γ 2 . However, for the picosecond pulses in the terahertz range the effect of the term γ 3 can be significant.

3. Pulse Velocity and Dispersion

Phase and group velocities of the surface wave can be determined from the dispersion equation (3). The real part β ' defines the phase velocity V p h = ω β ' of the wave, and the group velocity is determined by V g = d ω d β ' . The imaginary part β ″ defines the attenuation length z 0 = 1 β ″ of the surface wave propagating along the plasmonic fiber.
Figure 2 shows the velocity and attenuation length depending on the frequency. The velocity increases, and the propagation length decreases with increasing frequency.
The physical origin of the increase of dissipation with frequency is the skin effect. The thickness of the skin layer decreases with frequency, and the resistance of the wire increases with frequency, thereby causing an increase in losses. Simulations show that the propagation distance in the coated metal wire increases in comparison with the metal-air boundary. An increase in the propagation length in the presence of a dielectric coating has also been shown experimentally in [21].
Calculations show that the propagation length increases with the increase of the radius of a wire. The velocities of surface waves in metal wires with a dielectric coating decrease as v p = c / ε d , where c is the speed of light in free space, ε d is the dielectric permittivity of a cladding.
Note that the conductivity of metal wires depends on the plasmon frequency of free electrons. It follows from a Drude formula for copper [22], that ε m = − 6.3 · 10 5 + i 2.77 · 10 6 for the frequency of 0.5 THz. The conductivity of copper wire is σ = 1.23 · 10 7   Ω − 1 m − 1 , and silver and gold wires have slightly higher conductivities.
In Figure 3 the pulse intensities I z , t , τ = E ( z , t , τ ) 2 for different lengths of bare wires are presented in an offset time scale t + T 0 , where T 0 = z / v p − 8 · τ , z is the distance, at which the pulse is recorded.
It can be seen that the shape of the pulse changes with distance, acquiring an asymmetric distribution.

3.1. Effect of a dielectric coating

Consider the effect of the dielectric coating on the velocity and attenuation length of SPPs. Different glass and polymer materials were studied for terahertz fibers [14, 15}. It follows from recent terahertz studies that polymers have lower absorption coefficients. In [23] the dielectric properties of polymers were characterized by transmission terahertz time-domain spectroscopy in the frequency range extending from 0.2 to 3.0 THz. In the calculations below, we use a constant refractive index n = 1.6 + 0.03i in the frequency ranges under consideration, which is consistent with the value for polyurethane given in [24]. The influence of the imaginary part of the refractive index of a dielectric coating on the velocity and attenuation length is also considered.
In Figure 4 the pulse intensity profiles at various distances for a given pulse duration and carrier frequency are presented.
Unlike a bare wire, propagation along a coated wire is highly dispersive. The coating leads to the appearance of a long-chirped signal with a propagation of only a few millimeters. The appearance of the oscillatory tail in the pulse is caused by the third-order term γ 3 in (8). When only the second-order term γ 2 is taken into account, the pulse shape remains Gaussian. Note that such an oscillatory behavior was also observed experimentally during the propagation of a terahertz pulse along a coated copper wire in [4].

Effect of a pulse duration

Consider the effect of the pulse duration on the shape of the pulse propagating along the coated wire. Figure 5 shows the pulse shapes for different duration of the incident pulse at a propagation distance of z = 0.5 cm.
It follows from the simulation that the chirped output signal is observed when the pulse duration decreases. The oscillation depth increases as the pulse duration decreases. This indicates that the contribution of the dispersion term of the third order becomes significant with a decrease in the pulse duration. For a wide pulse, the third-order dispersion effect is negligible, and the oscillating tail disappears (Figure 5a).

4. Discussion

Thus, the effect of a dielectric coating on the dispersion of pulses propagating along a metal wire is investigated. The nondispersive coating material leads to highly dispersive propagation along the wire, which is expressed in the appearance of a chirped output signal. Results obtained are consistent with the experimental data presented in [4], where the chirped signal was observed on the propagation of terahertz pulses over copper wire with a polyurethane coating.
The physical origin of the long-chirped tail is associated with a third-order dispersion term in the propagation constant (8). The oscillations at the tail of the pulse weaken with an increase in the duration of the incident pulse. This is due to the fact that as the pulse duration increases, the contribution of the dispersion term γ 2 becomes greater than the contribution of the dispersion term γ 3 . There is no oscillatory tail if the third-order dispersion term is neglected during modeling.
Note that the change in the shape of the pulse during propagation can be obtained from the time-consuming numerical solution of Maxwell's equations. Here we used an analytical approach that allowed us to consider the effects of high-order dispersion leading to the appearance of a chirped signal observed in experiments [4].
Losses in the dielectric coating are the main limitations to the transmission of a THz signal over long distances. Therefore, the search for materials with low absorption is an important task. Currently, porous core photonic crystal fibers with a very low level of material loss have been proposed for pulse propagation [25,26,27,28]. These fibers have an effective material loss of less than 0.1 cm-1 at an operating frequency of f = 1 THz. In [27], a low-loss THz waveguide based on a photonic crystal structure with an average power loss of 0.02 cm-1 was designed and manufactured by 3D printing.
Future research may be related to the consideration of pulse propagation taking into account higher-order dispersion terms and structured vector vortex modes of SPPs in a plasmonic fiber. Of particular interest is the consideration of structured vortex beams with orbital angular momentum [24,29,30,31,32,33] and the effects of the Goos-Hanchen shift [34,35,36,37]. Tunable resonance Goos-Hanchen and Imbert-Fedorov shifts for THz beams reflected from graphene plasmonic metasurfaces were investigated in [34].

5. Conclusions

In conclusion, the characteristics of propagation of SPP pulses in the THz frequency range in cylindrical metal wires with a dielectric coating were studied by analytical solution of Maxwell's equations. An expression is obtained for a pulsed electric field taking into account high-order dispersion terms. This allows time-saving calculations of pulse propagation along a coated wire.
It is shown that significant distortions of the terahertz pulse occur due to the dispersive propagation of SPPs along the coated wire. The coating results in a long-chirped signal for short incident pulses. The depth of the oscillations strongly depends on the pulse duration, and the intensity can drop to zero between adjacent periods.
It follows from the study that coated metal wires can be used as sensitive sensors of the characteristics of dielectric materials at terahertz frequencies.
The results obtained can be applied in the field of THz spectroscopy and imaging, communications, plasmon fibers and in the development of various sensors.

Funding

This research was funded by the Ministry of Science and Higher Education of the Russian Federation under the State contract No. FFNS-2022-0009. .

Data Availability Statement

Not applicable.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Wang, K.; Mittleman, D.M. Metal wires for terahertz wave guiding. Nature 2004, 432, 376–379. [Google Scholar] [CrossRef]
  2. Wang, K.; Mittleman, D.M. Dispersion of surface plasmon polaritons on metal wires in the terahertz frequency range. Phys. Rev. Lett. 2006, 96, 157401. [Google Scholar] [CrossRef] [PubMed]
  3. Saxler, J.; Rivas, J.G.; Janke, C.; Pellemans, H.P.M.; Bolivar, P.H.; and Kurz, H. Time-domain measurements of surface plasmon polaritons in the terahertz frequency range. Phys. Rev. B 2004, 69, 155427. [Google Scholar] [CrossRef]
  4. Van der Valk, N.C.J.; and Planken, P.C.M. Effect of a dielectric coating on terahertz surface plasmon polaritons on metal wires. Appl. Phys. Lett. 2005, 87, 071106. [Google Scholar] [CrossRef]
  5. Mitrofanov, O.; Harrington, J.A. Dielectric-lined cylindrical metallic THz waveguides: Mode structure and dispersion. Opt. Express 2010, 18, 1898–1903. [Google Scholar] [CrossRef]
  6. Chen, Y.; Song, Z.; Li, Y.; Hu, M.; Xing, Q.; Zhang, Z.; Chai, L.; Wang, C.Y. Effective surface plasmon polaritons on the metal wire with arrays of subwavelength grooves. Opt. Express 2006, 14, 13021–13029. [Google Scholar] [CrossRef] [PubMed]
  7. Williams, C.R.; Andrews, S.R.; Maier, S.; Fernandez-Dominguez, A.I.; Martín-Moreno, L.; Garcia-Vidal, F. Highly confined guiding of terahertz surface plasmon polaritons on structured metal surfaces. Nat. Photonics 2008, 2, 175–179. [Google Scholar] [CrossRef]
  8. Rivas, J.G.; Kuttge, M.; Bolivar, P.H.; Kurz, H.; Sánchez-Gil, J.A. Propagation of surface plasmon polaritons on semiconductor gratings. Phys. Rev. Lett. 2004, 93, 256804. [Google Scholar] [CrossRef]
  9. Gan, C.H.; Chu, H.S.; Li, E.P. Synthesis of highly confined surface plasmon modes with doped graphene sheets in the midinfrared and terahertz frequencies. Phys. Rev. B 2012, 85, 125431. [Google Scholar] [CrossRef]
  10. Bulgakova, V.V.; Gerasimov, V.V.; Goldenberg, B.G.; Lemzyakov, A.G.; Malkin, A.M. Study of terahertz spoof surface plasmons on subwavelength gratings with dielectric substance in grooves. Phys. Procedia 2017, 201, 14–23. [Google Scholar] [CrossRef]
  11. Dhillon, S.S.; Vitiello, M.S.; Linfield, E.H.; Davies, A.; Hoffmann, M.; Booske, J.; Paoloni, C.; Gensch, M.; Weightman, P.; Williams, G.P.; et al. The 2017 terahertz science and technology roadmap. J. Phys. D Appl. Phys. 2017, 50, 043001. [Google Scholar] [CrossRef]
  12. Chen, S.H.; Chen, K.W.; Chu, K.R. A comparative study of single-wire and hollow metallic waveguides for terahertz waves. AIP Adv. 2018, 8, 115028. [Google Scholar] [CrossRef]
  13. Zhang, X.; Xu, Q.; Xia, L.; Li, Y.; Gu, J.; Tian, Z.; Ouyang, C.; Han, J.; Zhang, W. Terahertz surface plasmonic waves: A review. Adv. Photonics 2020, 2, 014001. [Google Scholar] [CrossRef]
  14. Atakaramians, A.; Afshar, S.V.; Monro, T.M.; Abbott, D. Terahertz dielectric waveguides. Adv. Opt. Photon. 2013, 5, 169–215. [Google Scholar] [CrossRef]
  15. Islam, M.S.; Cordeiro, C.M.B.; Franco, M.A.R.; Sultana, J.; Cruz, A.L.S.; Abbott, D. Terahertz optical fibers [Invited]. Opt. Express 2020, 28, 16089–16117. [Google Scholar] [CrossRef]
  16. Petrov, N.I. Propagation of Terahertz Surface Plasmon Polaritons in a Dielectric Fiber with a Metal Wire Core. Fibers 2022, 10, 89. [Google Scholar] [CrossRef]
  17. Marcuse, D. Light transmission Optics. Van Nostrand Reinhold, 1982.
  18. Snyder, A.W.; Love, J. Optical Waveguide Theory; Chapman and Hall: New York, NY, USA, 1983. [Google Scholar]
  19. Sommerfeld, A. Ueber die Fortpflanzung elektrodynamischer Wellen längs eines Drahtes. Ann. Phys. 1899, 303(2), 233–290. [Google Scholar] [CrossRef]
  20. Petrov, N.I. Synchrotron mechanism of X-ray and gamma-ray emissions in lightning and spark discharges. Sci. Rep. 2021, 11, 19824. [Google Scholar] [CrossRef] [PubMed]
  21. Gerasimov, V.V.; Knyazev, B.A.; Lemzyakov, A.G.; Nikitin, A.K.; Zhizhin, G.N. Growth of terahertz surface plasmon propagation length due to thin-layer dielectric coating. J. Opt. Soc. Am. B 2016, 33, 2196–2203. [Google Scholar] [CrossRef]
  22. Ordal, M. A.; Bell, R. J.; Alexander, R. W.; Long, L. L.; and Querry, M. R. Optical properties of fourteen metals in the infrared and far infrared: Al, Co, Cu, Au, Fe, Pb, Mo, Ni, Pd, Pt, Ag, Ti, V, and W. Appl. Opt. 1985, 24, 4493–4499. [Google Scholar] [CrossRef] [PubMed]
  23. Jin, Y.S.; Kim, G.J.; Jeon, S.G. Terahertz Dielectric Properties of Polymers. J. Korean Phys. Soc. 2006, 49, 513–517. [Google Scholar]
  24. Stefani, A.; Fleming, S.C.; and Kuhlmey, B.T. Terahertz orbital angular momentum modes with flexible twisted hollow core antiresonant fiber. APL Photonics 2018, 3(5), 051708. [Google Scholar] [CrossRef]
  25. Hassani, A.; Dupuis, A.; and Skorobogatiy, M. Porous polymer fibers for low-loss Terahertz guiding. Opt. Express 2008, 16, 6340–6351. [Google Scholar] [CrossRef] [PubMed]
  26. Paul, B.K.; Bhuiyan, T.; Abdulrazak, L.F.; Sarker, K.; Hassan, M.M.; Shariful, S.; Ahmed, K. Extremely low loss optical waveguide for terahertz pulse guidance. Results Phys. 2019, 15, 102666. [Google Scholar] [CrossRef]
  27. Yang, J.; Zhao, J.; Gong, C.; Tian, H.; Sun, L.; Chen, P.; Lin, L.; Liu, W. 3D printed low-loss THz waveguide based on Kagome photonic crystal structure. Opt. Express 2016, 24, 22454–22460. [Google Scholar] [CrossRef]
  28. Stefani, A.; Skelton, J.H.; and Tuniz, A. Bend losses in flexible polyurethane antiresonant terahertz waveguides. Opt. Exp. 2021, 29, 28692–28703. [Google Scholar] [CrossRef]
  29. Petrov, N.I. Splitting of levels in a cylindrical dielectric waveguide. Opt. Lett. 2013, 38, 2020–2022. [Google Scholar] [CrossRef] [PubMed]
  30. Petrov, N.I. Vector Laguerre–Gauss beams with polarization-orbital angular momentum entanglement in a graded-index medium. J. Opt. Soc. Am. A 2016, 33, 1363–1369. [Google Scholar] [CrossRef]
  31. Petrov, N.I. Depolarization of vector light beams on propagation in free space. Photonics 2022, 9, 162. [Google Scholar] [CrossRef]
  32. Petrov, N.I. Speed of structured light pulses in free space. Sci. Rep. 2019, 9, 18332. [Google Scholar] [CrossRef]
  33. Petrov, N. I. Nonparaxial Propagation of Bessel Correlated Vortex Beams in Free Space. Micromachines 2023, 14, 38. [CrossRef]
  34. Farmani, A.; Miri, M.; Sheikhi, M.H. Tunable resonant Goos–Hänchen and Imbert–Fedorov shifts in total reflection of terahertz beams from graphene plasmonic metasurfaces. J. Opt. Soc. Am. B 2017, 34, 1097–1106. [Google Scholar] [CrossRef]
  35. Petrov, N.I.; Danilov, V.A.; Popov, V.V.; Usievich, B.A. Large positive and negative Goos-Hänchen shifts near the surface plasmon resonance in subwavelength grating. Opt. Express 2020, 28, 7552–7564. [Google Scholar] [CrossRef]
  36. Petrov, N.I.; Sokolov, Y.M.; Stoiakin, V.V.; Danilov, V.A.; Popov, V.V.; Usievich, B.A. Observation of Giant Angular Goos-Hanchen Shifts Enhanced by Surface Plasmon Resonance in Subwavelength Grating. Photonics 2023, 10, 180. /. [CrossRef]
  37. Kan, X.F.; Zou, Z.X.; Yin, C.; Xu, H.P.; Wang, X.P.; Han, Q.B.; Cao, Z.Q. Continuous Goos-Hänchen Shift of Vortex Beam via Symmetric Metal-Cladding Waveguide. Materials 2022, 15, 4267. [Google Scholar] [CrossRef]
Preprints 76001 g001
Figure 1. Schematic view of a dielectric fiber with a metal wire core (a) and its cross section (b).
Figure 1. Schematic view of a dielectric fiber with a metal wire core (a) and its cross section (b).
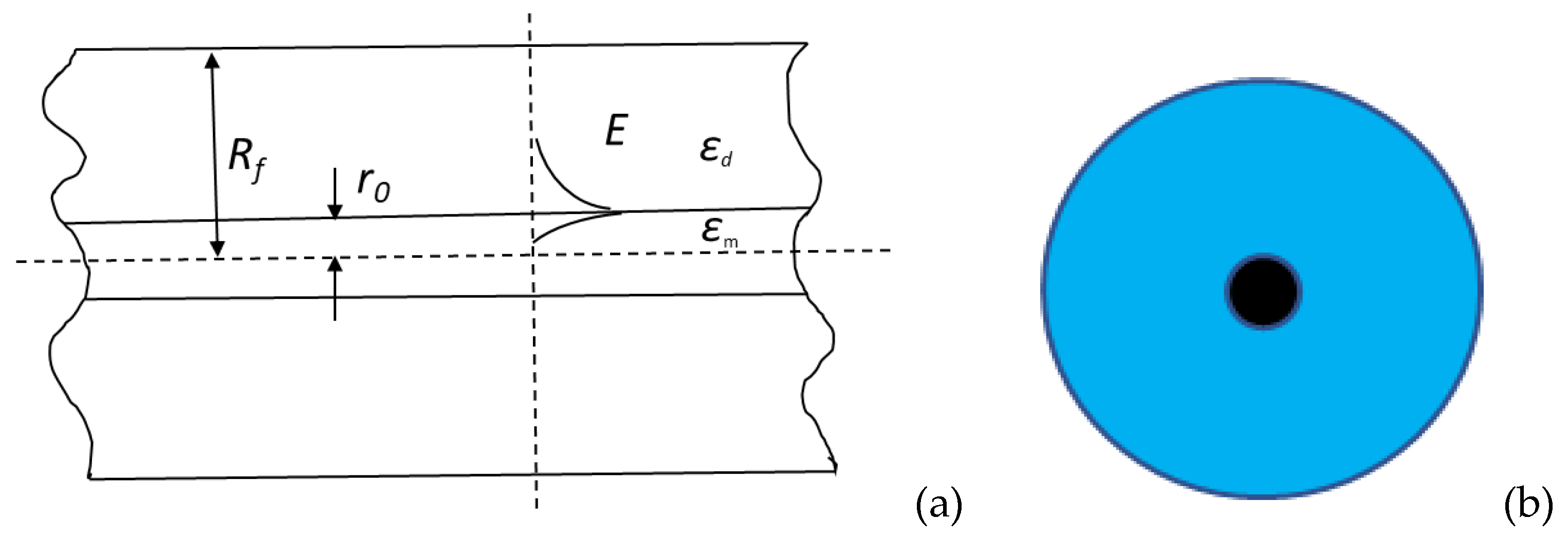
Preprints 76001 g001
Preprints 76001 g002
Figure 2. Phase velocity (a, c) and attenuation length (b, d) as function of frequency. r 0 = 10   μ m ,   σ = 1.23 · 10 7   Ω − 1 m − 1 . ε d = 1.0 (a, b); ε d = 2.56 (c, d).
Figure 2. Phase velocity (a, c) and attenuation length (b, d) as function of frequency. r 0 = 10   μ m ,   σ = 1.23 · 10 7   Ω − 1 m − 1 . ε d = 1.0 (a, b); ε d = 2.56 (c, d).
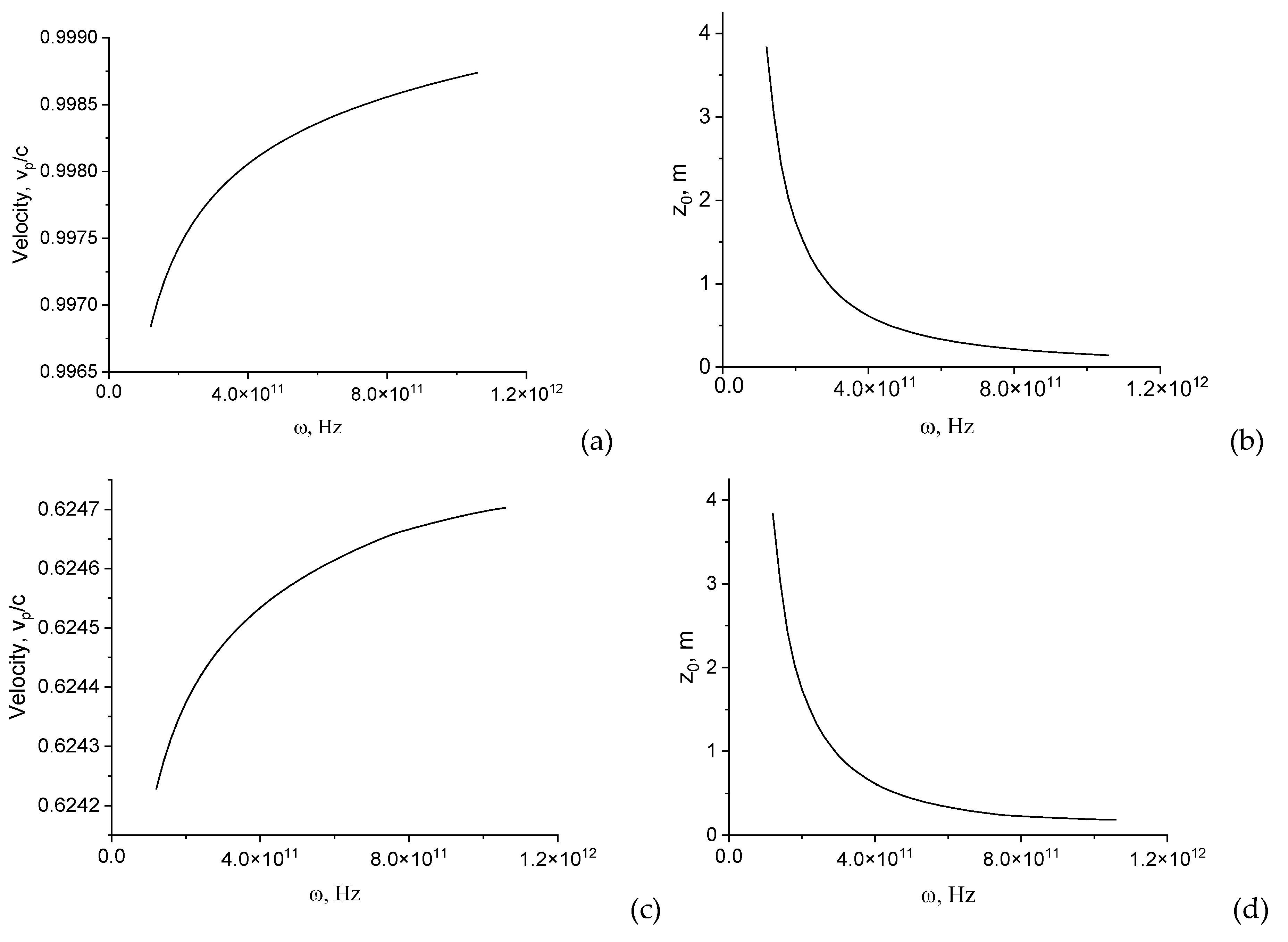
Preprints 76001 g002
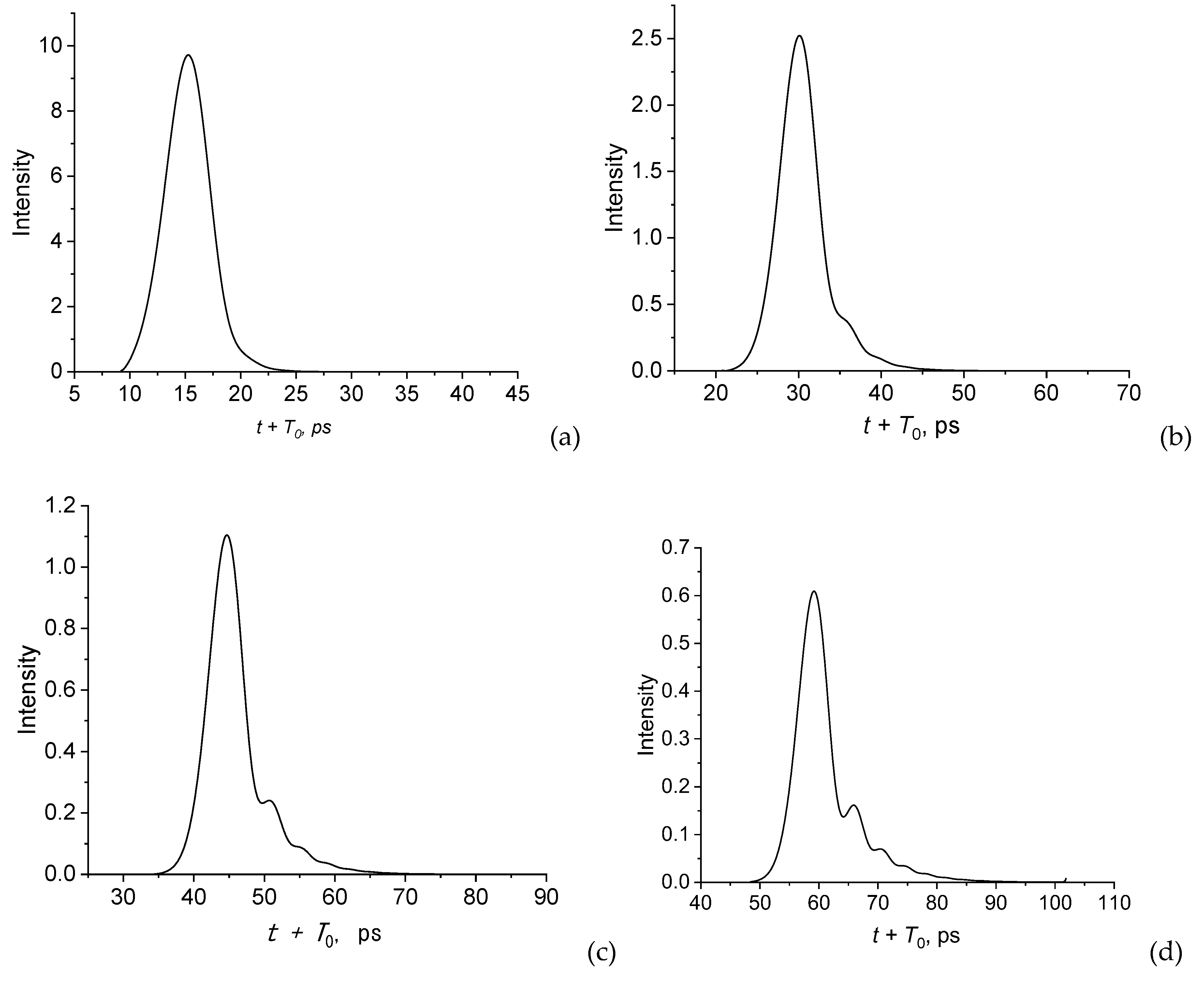
Preprints 76001 g003
Figure 3. Intensity profiles of pulses at different lengths of bare wires. z = 0.5 cm (a), 1.0 cm (b), 1.5 cm (c) and 2.0 cm (d). r 0 = 100 μm. ω 0 = 0.8 THz, τ = 2.3   p s ,   ε d = 1.0 , T 0 = z / v p − 8 · τ .
Figure 3. Intensity profiles of pulses at different lengths of bare wires. z = 0.5 cm (a), 1.0 cm (b), 1.5 cm (c) and 2.0 cm (d). r 0 = 100 μm. ω 0 = 0.8 THz, τ = 2.3   p s ,   ε d = 1.0 , T 0 = z / v p − 8 · τ .
Preprints 76001 g003
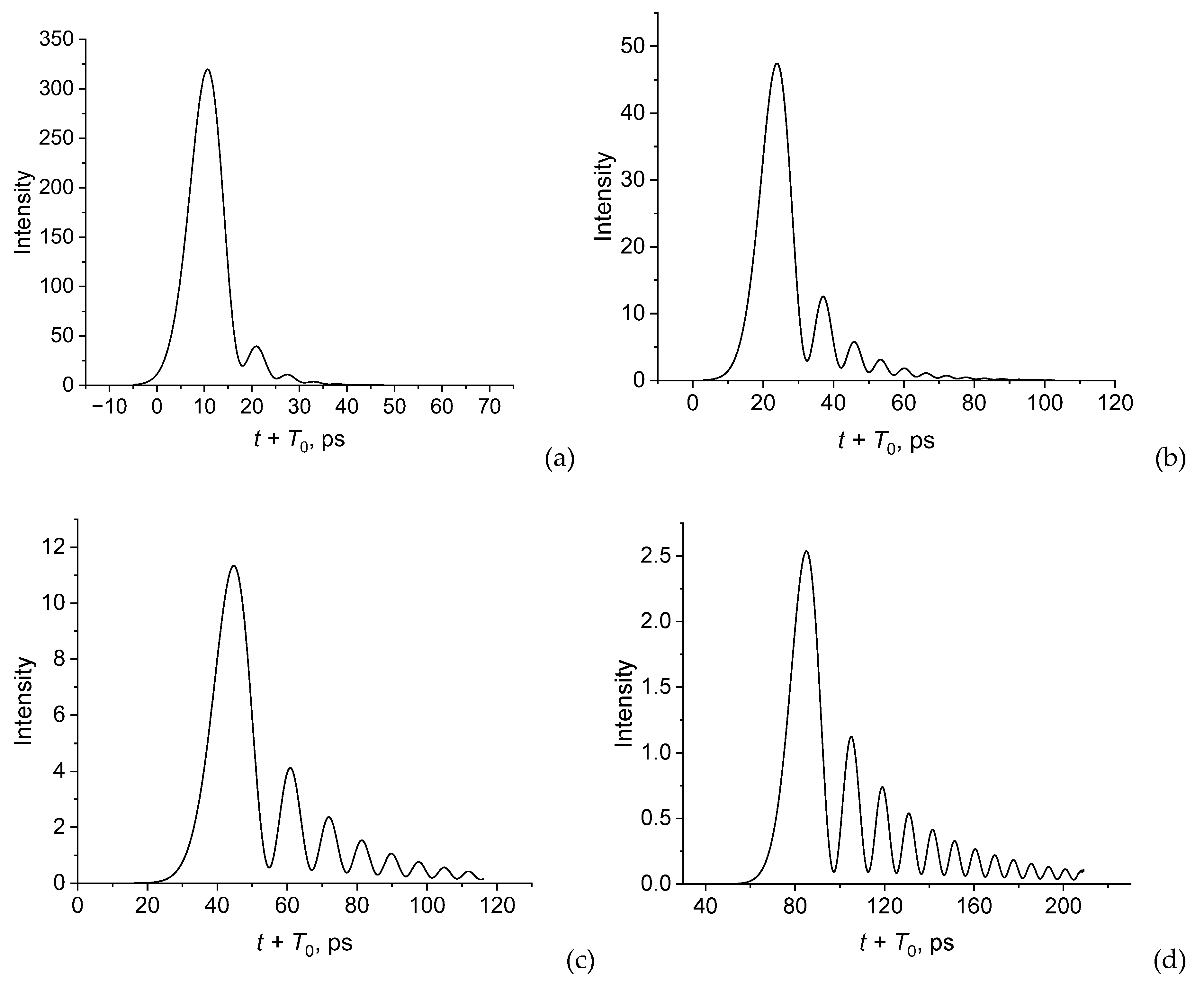
Preprints 76001 g004
Figure 4. Intensity profiles of pulses at different distances. z = 0.1 cm (a), 0.25 cm (b), 0.5 cm (c) and 1.0 cm (d); r 0 = 100 μm, ω 0 = 0.9 THz, τ = 3.5   p s ,   ε d = 2.56 , T 0 = z / v p − 3 τ .
Figure 4. Intensity profiles of pulses at different distances. z = 0.1 cm (a), 0.25 cm (b), 0.5 cm (c) and 1.0 cm (d); r 0 = 100 μm, ω 0 = 0.9 THz, τ = 3.5   p s ,   ε d = 2.56 , T 0 = z / v p − 3 τ .
Preprints 76001 g004
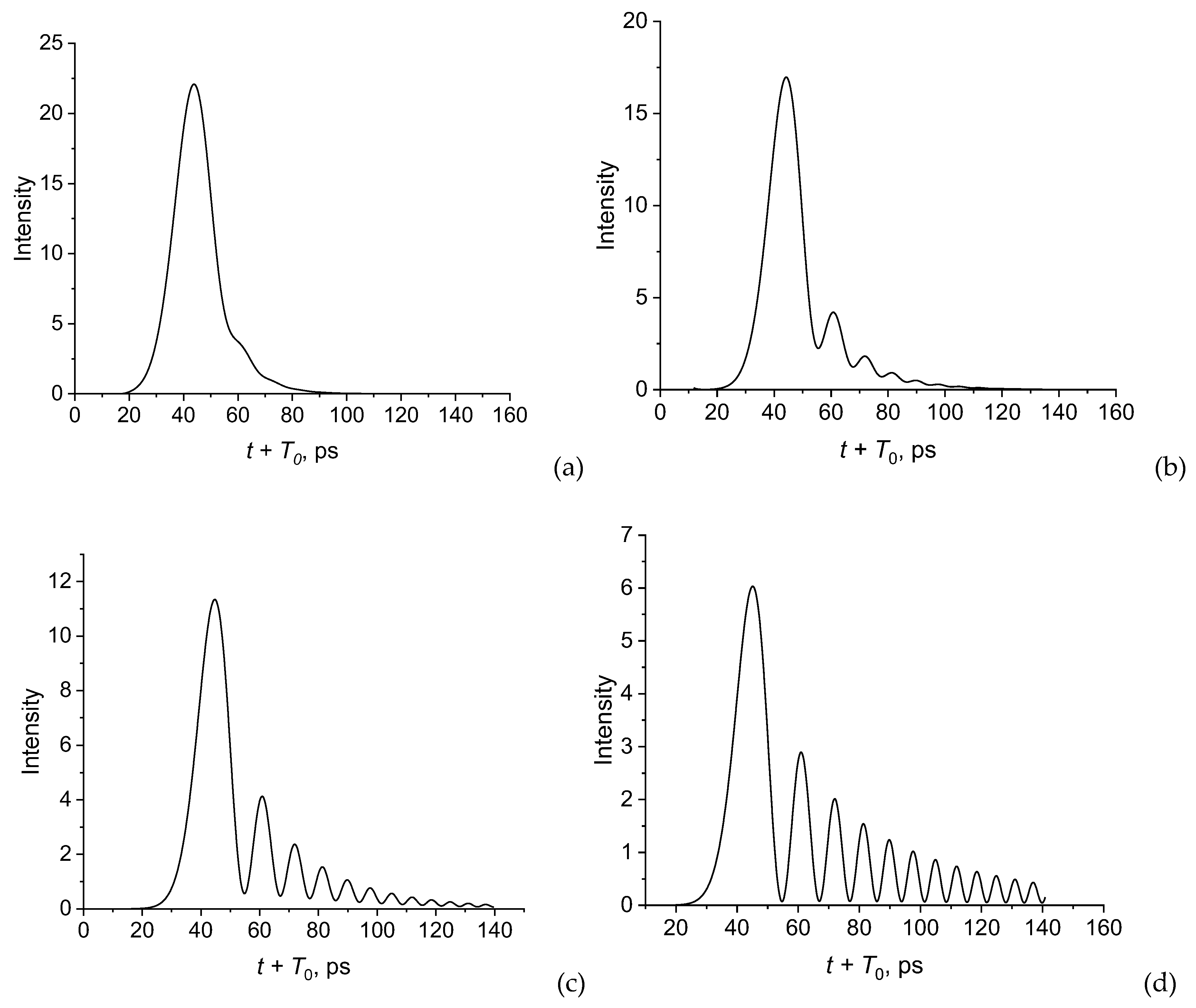
Preprints 76001 g005
Figure 5. Intensity profiles of pulses for different incident pulse durations at z = 0.5 cm. τ = 7.0   p s (a), τ = 5.0   p s   b ,   τ = 3.5   p s   ( c ) , τ = 2.3   p s   ( d ) . r 0 = 100 μm, ω 0 = 0.9 THz, ε d = 2.56 , T 0 = z / v p − 3 τ .
Figure 5. Intensity profiles of pulses for different incident pulse durations at z = 0.5 cm. τ = 7.0   p s (a), τ = 5.0   p s   b ,   τ = 3.5   p s   ( c ) , τ = 2.3   p s   ( d ) . r 0 = 100 μm, ω 0 = 0.9 THz, ε d = 2.56 , T 0 = z / v p − 3 τ .
Preprints 76001 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated