Preprint
Article
Cumulative Residual Entropy of the Residual Lifetime of a Mixed System at the System Level
Altmetrics
Downloads
180
Views
22
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
07 June 2023
Posted:
08 June 2023
You are already at the latest version
Alerts
Abstract
Recently, there has been growing interest in alternative measures of uncertainty, including
cumulative residual entropy. In this paper, we consider a mixed system consisting of n components,
assuming that all components are operational at time t. We use the system signature to calculate
the cumulative residual entropy of the mixed system’s remaining lifetime. This measure is a useful
criterion for assessing the predictability of a system’s lifetime. We study several results related to the
cumulative residual entropy of mixed systems, including expressions, limits, and order properties.
These results shed light on the behavior of the measure and provide insights into the predictability
of mixed systems. In addition, we propose a criterion for selecting a preferred system based on
the relative residual cumulative entropy. This criterion is closely related to the parallel system and
provides a practical way to choose the best system configuration. Overall, the present study of
cumulative residual entropy and the proposed selection criterion provide valuable insights into the
predictability of mixed systems and can be applied in various fields.
Keywords:
Subject: Physical Sciences - Mathematical Physics
1. Introduction
The analysis of distribution functions based on partial information involves several relevant activities, such as model selection, estimation, hypothesis testing, inequality/poverty assessment, and portfolio analysis. The entropy measure of a probability distribution has found diverse applications in various fields, including information science, physics, probability, statistics, communication theory, and economics. Its comprehensive introduction dates back to Shannon’s extensive article [1]. If X is an absolutely continuous, non-negative random variable with probability density function (pdf) , Shannon differential entropy can be defined as provided the expected value exists. This measure is used in many areas of research due to its versatility and usefulness.
Despite the many advantages of differential entropy, Rao et al. [2] proposed an alternative measure, cumulative residual entropy (CRE). This measure is obtained by replacing the pdf with the survival function , and is defined as follows:
The CRE is particularly useful for describing information dispersion in problems related to the aging properties of reliability theory. This measure has been used in several studies, including by Asadi and Zohrevand [3], Baratpour [4], Baratpour and Habibi Rad [5], Navarro et al. [6], Rao [7], and Toomaj et al. [8] and many others cited therein. For example, Asadi and Zohrevand [3] have shown that the CRE is the expected value of the mean residual life (MRL) function , which can be expressed as .
It is critical for engineers to identify and quantify uncertainty during the life of a system. This is because system reliability decreases as uncertainty increases, and systems with longer lives and lower uncertainty are considered better systems. This concept has been studied extensively, as shown by Ebrahimi and Pellery [9]. In situations where operators have some knowledge of the current age of the system, measuring the uncertainty in the remaining life of the system may be of interest. In such cases, the dynamic cumulative residual entropy (DCRE) is a more appropriate measure than , where X denotes the lifetime of a new system. The DCRE is defined as follows:
where is the survival function of , and is the quantile function of . The function is used to define the DCRE. In this paper, we assume a mixed system consisting of n components having the property that, at time all components of the system are alive. We then apply the system signature to determine the CRE of a coherent system’s residual lifetime.
Therefore, the result of this paper is structured as follows: In Section 2, we derive an expression for the CRE lifetime of a mixed system, assuming that all components of the system have survived to time t. We introduce the concept of system signature and use it when the lifetimes of the components in a mixed system are independent and identically distributed. We also show that the dynamic CRE can be ordered based on some ordering properties of system signatures without requiring extensive computations. In Section 3, we introduce some useful bounds for CRE. These bounds provide insights into the behavior of CRE and can be used to assess the predictability of mixed systems. Moreover, in Section 4, we propose a new criterion for selecting a preferred mixed system based on the relative CRE. This criterion considers the ordering properties of system signatures and can be applied in practice to choose the best system configuration. We conclude the paper in Section 5 with some concluding remarks and suggestions for future research.
“ Throughout the paper, “" and “" stand for stochastic and dispersive orders, respectively; for more details on these orderings, we refer the reader to Shaked and Shanthikumar [10]. ”
2. CRE of the residual lifetime
In this section, we introduce the concept of system signature to define the CRE of the remaining lifetime of a mixed system with any system-level structure, assuming that all components of the system are operational at time t. A mixed system is a stochastic mixture of coherent systems, while a coherent system is a system that has no irrelevant components and has a monotonic structure function. The signature of such a system is represented by an n-dimensional vector , where for , as defined in [11]. Consider a mixed system with independent and identically distributed (i.i.d.) component lifetimes and a known signature vector . Let denote the remaining lifetime of the system under the condition that all components are operational at time t. From the results of [12], the survival function of can be expressed as follows:
where for . This function denotes the survival function of the residual lifetime of an i-out-of-n system under the condition that all components are operational at time t. The survival function of can be written as follows:
In what follows, we focus on the study of the CRE of the random variable , which measures the degree of uncertainty contained in the density of regarding the predictability of the remaining lifetime of the system. For this purpose, we use the probability integral transformation , which plays a crucial role in our analysis. It is clear that the transform follows a beta distribution with parameters and i, and its distribution function can be expressed as follows
In the following theorem, we provide an expression for the CRE of using the probability integral transformation and the beta distribution.
Theorem 2.1.
The CRE of can be expressed as follows:
where for all and
is the distribution function of denotes the lifetime of the system with i.i.d. uniform distribution.
Proof.
In the special case where we consider an i-out-of-n system with the system signature for , then (6) reduces to
for all . The next theorem follows immediately from Theorem 2.1 and is expressed in terms of the aging properties of the components. Recall that a random variable X has increasing failure rate (IFR) (decreasing failure rate (DFR)) if its survival function is decreasing (increasing) in x for all .
Theorem 2.2.
If X is IFR (DFR), then is decreasing (increasing) in t.
Proof.
From the definition of the hazard function, we have for By substituting this expression into (6), we obtain the following alternative expression for the CRE of
for all One can show that for If , then and so when X is IFR(DFR), we have
Using (9), we conclude that for all , which completes the proof. □
The following example demonstrates how Theorems 2.1 and 2.2 can be applied in practice to analyze the CRE a coherent system at the system level and the aging properties of a system.
Example 2.1.
We consider a coherent system with the system signature , as shown in Figure 1.
Assume that the component lifetimes are i.i.d. having the common Weibull distribution with the survival function given by
After some manipulation, we can express the cumulative residual entropy of as
for Unfortunately, an explicit expression for this relation is not available, and numerical methods must be used to evaluate it. We plotted the CRE of as a function of time t for various values of k in Figure 2. It is well-known that X is DFR when and IFR when As expected from Theorem 2.2, we observe that is increasing in t for and decreasing for
The following theorem shows that the cumulative residual entropy of a mixed system lifetime, assuming that all components of the system are in operation at time t, is dominated by the cumulative residual entropy of a new system lifetime.
Theorem 2.3.
Consider a mixed system with i.i.d. IFR(DFR) component lifetimes. Then, for all , we have .
Proof.
In engineering reliability, the concept of duality is useful for reducing the computations of signatures of all coherent systems of a given size by about half (see, e.g., Kochar et al. [13]). Specifically, if is the signature of a given mixed system with lifetime , then the signature of its dual system with lifetime is . In the following theorem, we use the concept of duality to reduce the computation of the residual CRE of mixed systems.
Theorem 2.4.
Let be the lifetime of a mixed system with signature consisting of n i.i.d. components. If for all and t, then for all and n.
Proof.
Note that for all and . Assuming for all and using (6), we have
This completes the proof. □
Next, we study the partial order of the conditional lifetimes of two mixed systems, taking into account their uncertainties. We study the CRE order of the residual lifetimes of the two systems based on different existing orders between the component lifetimes and their signature vectors. The following theorem compares the CREs of the residual lifetimes of two mixed systems.
Theorem 2.5.
Consider two mixed systems with the same signatures and n i.i.d component lifetimes and , with residual lifetimes denoted as and , respectively. If and X or Y is IFR, then we have for all t.
Proof.
The next example gives an application of Theorem 2.5.
Example 2.2.
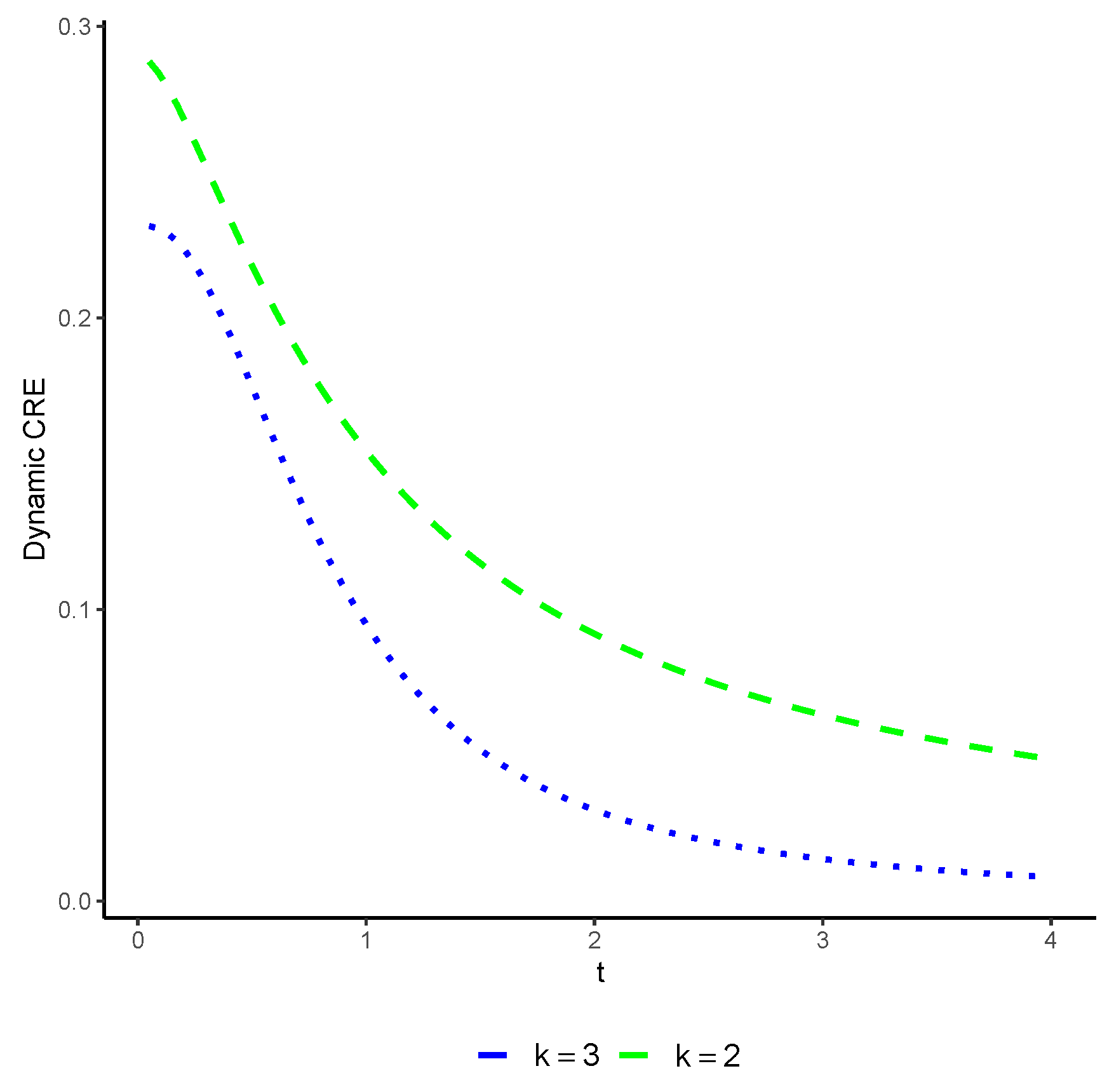
Consider two coherent systems characterized by their residual lifetimes, denoted by and , respectively, which share the common signature . Let X and Y follow the Weibull distributions with shape and scale parameters and , respectively. It is noteworthy that , and both distributions belong to the class of increasing failure rate distributions. Consequently, invoking Theorem 2.5 leads to the conclusion that for all . The associated dynamic CRE measure for these systems are depicted in Figure 3.
3. Bounds for CRE of the residual lifetime
When dealing with highly complex systems with a large number of components, calculating the cumulative residual entropy of a mixed system can be challenging. This is a common practical problem that arises in many applications. To address this challenge, researchers have recently developed bounds on the uncertainty of the lifetimes of mixed systems, as discussed in studies such as [15] and the related references. In the following theorem, we provide bounds on the cumulative residual entropy of the lifetime of a mixed system in terms of the residual entropy of the parent distribution . These bounds can be useful for estimating the lifetime of a mixed system, especially in cases where the exact computation of the cumulative residual entropy is difficult.
Proposition 3.1.
Consider a mixed system with the same signature and n i.i.d component lifetimes with residual lifetime denoted as Then
where , and .
Proof.
We can obtain an upper bound for of a mixed system with n i.i.d. component lifetimes by using (6). Specifically, we have
where is a constant that depends on the distribution of V. Similarly, we can obtain a lower bound for using the same approach. □
In the above theorem, the lower bound is determined by the minimum value of the ratio , evaluated at . The upper bound is determined by the maximum value of the same ratio, evaluated at . These bounds provide a useful tool for estimating the residual cumulative residual entropy of a mixed system based on the cumulative residual entropy of its component lifetimes.
Remark 3.1.
We remark that the lower bound in Proposition 3.1 is zero for all the mixed systems with i.i.d. components and signature satisfying or . In particular, it is zero for all the coherent systems with i.i.d. components; (see [8]).
Now, we obtain a general lower bound for the CRE of which can be obtained from the system signature and CRE of k-out-of-n systems.
Proposition 3.2.
If denotes the lifetime of a mixed system with signature based on n i.i.d. components, then
where
Proof.
Using Samaniego’s representation, we can express the distortion function associated with the signature vector and the component lifetimes as , where is the distortion function associated with the ith order statistic . By applying (6) and the concavity of the distortion function , we obtain the lower bound:
where is the cumulative residual entropy of . □
This bound shows that the cumulative residual entropy of the mixed system is bounded downward by a linear combination of the cumulative residual entropies of the component lifetimes, whose weights are given by the signature vector. This result can be particularly useful when the signature vector is known and the component lifetimes have a monotonic hazard rate function, as it provides a direct estimate of the cumulative residual entropy of the mixed system without requiring complex calculations. Note that the equality in (12) holds for i-out-of-n systems in the sense that we have for and for and then . If the lower bounds in both parts of the theorems 3.1 and 3.2 can be computed, one can use the maximum of the two lower bounds.
Example 3.1.
Consider a coherent system with the signature , consisting of i.i.d. component lifetimes with a uniform distribution in the interval . Let denote the residual lifetime of this system, defined as . Remarkably, due to Remark 3.1, we have , while and Utilizing Theorem 3.1, we conclude that the conditional residual entropy of is bounded as follows:
In addition, since the lower bound given in (12) can be expressed as:
for all By combining the lower bound in (14) and the upper bound in (13), we obtain the following inequality for the conditional CRE of :
for all This provides a tight bound on the conditional CRE of for all values of t in the interval .
4. Preferable system
In pairwise comparisons, the physical nature of certain system structures often makes it impossible to use the usual stochastic arrangement. There are many pairs of systems that are not comparable under any of the usual stochastic indices. We explore several metrics for comparing system performance with respect to this type of constraint. In what follows, we present an innovative approach to comparing information measures. In general, engineers agree that a system that performs over time is best. It is important that the characteristics of the competing systems be similar. Thus, given the same characteristics, it can be seen that the parallel system design is more suitable because it has better performance and longer remaining life among all the systems. As for reliability, from (4) we have the following property:
for all So instead of comparing systems pairwise, we can find a system whose structure or distribution is more similar to that of the parallel system. In other words, we are looking for an answer to the following question: which of these systems is more similar (or closer) to the configuration of the parallel system and more distant from the configuration of the serial system? To answer this question, we use relative CRE discrimination. To proceed with our results, we use the following measure of the distance between two distributions considered by Toomaj et al. [8].
Definition 4.1.
If X and Y are two nonnegative RVs with a common support and CDFs F and G, respectively, then SCKL is defined as follows:
The measure (15) proposed is nonnegative, symmetric, and satisfies if and only if the survival functions and are almost everywhere equal. This result is due to [8], and it is summarized in Lemma 1.
Lemma 4.1.
Let and Z be random variables with CDFs F, G and H, respectively. If , then and .
Using the stochastic order relation , which holds for any system based on , we can establish the following result.
Proposition 4.1.
If is the lifetime of a mixed system based on component lifetimes with signature , then , for .
We now introduce the dynamic distance symmetric measure (DDSM) for , denoted by .
From Proposition 4.1, we have . One can see that if and only if and if and only if . In other words, one can say that if is closer to 1, the distribution of is closer to the distribution of the parallel system, and if is closer to , the distribution of is closer to the distribution of the series system. Now, we propose the following definition.
Definition 4.2.
Let and be residual lifetimes of two mixed systems with n i.i.d. component lifetimes and dynamic signatures and , respectively. We say that is more preferable than in terms of the Dynamic Distance Symmetric Measure, denoted by , at time t, denoted by , if and only if for all
We should note here that does not imply . Under the conditions of Definition 4.2, we define If the components are i.d., expression (15) and the above transformations imply that
for . Then, from (16), we get
and
If the components are i.i.d., then and . As an application of the proposed measure, consider the following example.
Example 4.1.
Consider two systems with signatures and , denoted and , respectively. Suppose that the component lifetimes follow an i.i.d. standard exponential distribution with a survival function for . Although the two systems are not comparable in the usual stochastic order when all components are in operation, we can use the symmetric measure of dynamical distance to compare which of these systems is more similar (or closer) to the configuration of the parallel system and which is more distant from the configuration of the series system. We find that and , indicating that is more predictable than . Based on the DDSM, we conclude that is closer to the parallel system than and therefore is the preferable system.
5. Conclusion
In recent years, there has been increasing interest in measuring the uncertainty associated with the lifetime of engineering systems. An assessment of predictability over the lifetime of a system can be determined by this criterion. The measure CRE as an extension of Shannon entropy is very attractive in such situations. In this work, we have found an expression for the CRE of the system lifetime under the condition that all system components are functioning at time t. Various properties of the proposed measure were also investigated. Some limits have been obtained and partial orderings between the remaining lifetimes of two mixed systems have been studied in terms of their CRE uncertainties using the concept of system signature. Several examples are also given to illustrate the results. Finally, based on the relative CRE, we introduced a criterion for selecting a preferred system that is closely related to the parallel system.
Author Contributions
Conceptualization, M.K.; methodology, M.K.; software, M.A.A.; validation, M.A.A.; formal analysis, M.K.; investigation, M.S.; resources, M.A.A.; writing—original draft preparation, M.K.; writing—review and editing, M.A.A.; visualization, M.A.A.; supervision, M.S.; project administration, M.K.; funding acquisition, M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by Researchers Supporting Project number (RSP2023R392), King Saud University, Riyadh, Saudi Arabia.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors acknowledge financial support from King Saud University. This work was supported by Researchers Supporting Project number (RSP2023R392), King Saud University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shannon, C.E. A mathematical theory of communication. The Bell system technical journal 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Rao, M.; Chen, Y.; Vemuri, B.C.; Wang, F. Cumulative residual entropy: a new measure of information. IEEE transactions on Information Theory 2004, 50, 1220–1228. [Google Scholar] [CrossRef]
- Asadi, M.; Zohrevand, Y. On the dynamic cumulative residual entropy. Journal of Statistical Planning and Inference 2007, 137, 1931–1941. [Google Scholar] [CrossRef]
- Baratpour, S. Characterizations based on cumulative residual entropy of first-order statistics. Communications in Statistics—Theory and Methods 2010, 39, 3645–3651. [Google Scholar] [CrossRef]
- Baratpour, S.; Rad, A.H. Testing goodness-of-fit for exponential distribution based on cumulative residual entropy. Communications in Statistics-Theory and Methods 2012, 41, 1387–1396. [Google Scholar] [CrossRef]
- Navarro, J.; del Aguila, Y.; Asadi, M. Some new results on the cumulative residual entropy. Journal of Statistical Planning and Inference 2010, 140, 310–322. [Google Scholar] [CrossRef]
- Rao, M. More on a new concept of entropy and information. Journal of Theoretical Probability 2005, 18, 967–981. [Google Scholar] [CrossRef]
- Toomaj, A.; Zarei, R. Some new results on information properties of mixture distributions. Filomat 2017, 31, 4225–4230. [Google Scholar] [CrossRef]
- Ebrahimi, N.; Pellerey, F. New partial ordering of survival functions based on the notion of uncertainty. Journal of applied probability 1995, 32, 202–211. [Google Scholar] [CrossRef]
- Shaked, M.; Shanthikumar, J.G. Stochastic orders; Springer Science & Business Media, 2007.
- Samaniego, F.J. System signatures and their applications in engineering reliability; Vol. 110, Springer Science & Business Media, 2007.
- Khaledi, B.E.; Shaked, M. Ordering conditional lifetimes of coherent systems. Journal of Statistical Planning and Inference 2007, 137, 1173–1184. [Google Scholar] [CrossRef]
- Kochar, S.; Mukerjee, H.; Samaniego, F.J. The “signature” of a coherent system and its application to comparisons among systems. Naval Research Logistics (NRL) 1999, 46, 507–523. [Google Scholar] [CrossRef]
- Ebrahimi, N.; Kirmani, S. Some results on ordering of survival functions through uncertainty. Statistics & probability letters 1996, 29, 167–176. [Google Scholar]
- Toomaj, A.; Chahkandi, M.; Balakrishnan, N. On the information properties of working used systems using dynamic signature. Applied Stochastic Models in Business and Industry 2021, 37, 318–341. [Google Scholar] [CrossRef]
Figure 1.
A coherent system with signature
Figure 2.
The exact values of with respect to t for the Weibull distribution for various values of
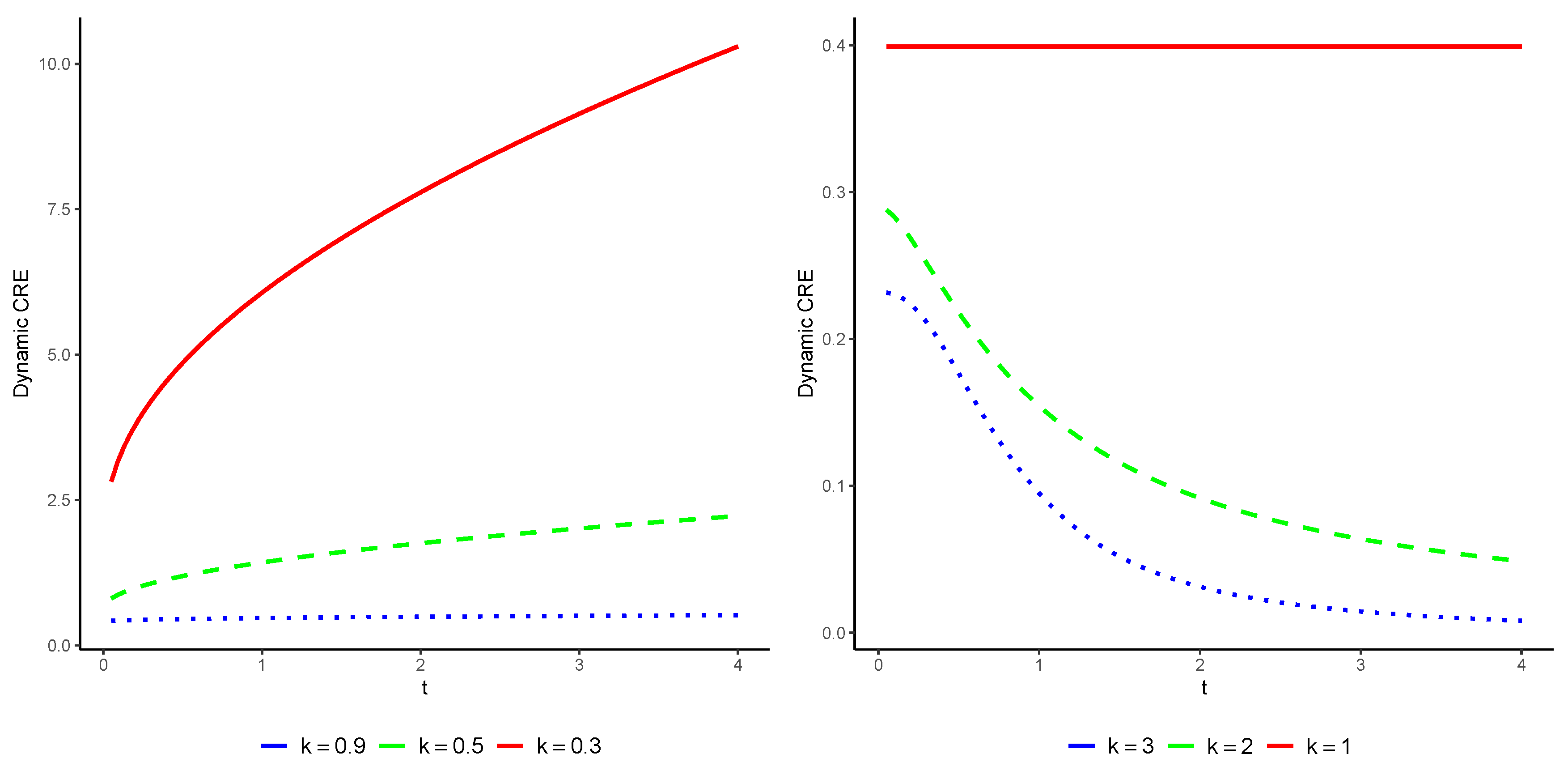
Figure 3.
The exact values of (blue color) and (green color) with respect to
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






