Prerpints.org logo
Preprint
Article

Simultaneous Tracking and Recognizing Drone Targets with Millimeter-Wave Radar and Convolutional Neural Network

Altmetrics

Downloads

204

Views

100

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

08 June 2023

Posted:

08 June 2023

You are already at the latest version

Alerts
Abstract
In this paper, a framework for simultaneous tracking and recognizing drone targets using a low-cost and small-sized millimeter-wave radar is presented. The radar collects the reflected signals of multiple targets in the field of view including drone and non-drone targets. The analysis of the received signals allows multiple targets to be distinguished because of the different reflection patterns. The proposed framework consists of four processes including signal processing, cloud points clustering, target tracking, and target recognition. Signal processing translates the raw signals into spare cloud points. These points are merged into several clusters, each representing a single target. Target tracking estimates the new locations of each detected target. A novel convolutional neural network model is developed for drone and/or non-drone targets feature extraction and recognition. For performance evaluation, a dataset collected with an IWR6843ISK mmWave sensor by Texas Instruments is used for training and testing the convolutional neural network. The proposed recognition model achieves an accuracy of 98.4% for one target and 98.1% for two targets.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Networks and Communications

1. Introduction

Motivation. In recent years, unmanned aerial vehicles, such as drones, have received significant attention for performing tasks in different domains. This is due to their low cost, high coverage, and vast mobility, as well as their capability of performing different operations using small-scale sensors (Kanellakis and Nikolakopoulos 2017). Technological development has allowed drones to be operated using smartphones rather than traditional remote controllers. In addition, drone technology can provide live video streaming and image capturing as well as make autonomous decisions based on these data. As a result, it has gained the focus of attention by utilizing artificial intelligence techniques in the provisioning of civilian and military services (Fu et al. 2021). In this context, drones have been adopted for express shipping and delivery (Doole, Ellerbroek, and Hoekstra 2020)(Brahim et al. 2022)(Sinhababu and Pramanik 2022), natural disaster prevention (Cheng et al. 2022)(Rizk et al. 2022), geographical mapping (Nath, Cheng, and Behzadan 2022), search and rescue operations (Mishra et al. 2020), aerial photography for journalism and film making (Jacob, Kaushik, and Velavan 2022), providing essential materials (Chechushkov et al. 2022), providing border control surveillance (Molnar 2022) and building safety inspection (Sharma et al. 2022). Even though drone technology offers a multitude of benefits, it raises mixed concerns when it comes to how it will be used in the future. Drones pose many potential threats including invasion of privacy, smuggling, espionage, flight disruption, human injury, and even terrorist attacks. These threats compromise aviation operations and public safety. However, it has become increasingly necessary to detect, track, and recognize drone targets, and to take decisions in certain situations, such as detonating or jamming unwanted drone targets.
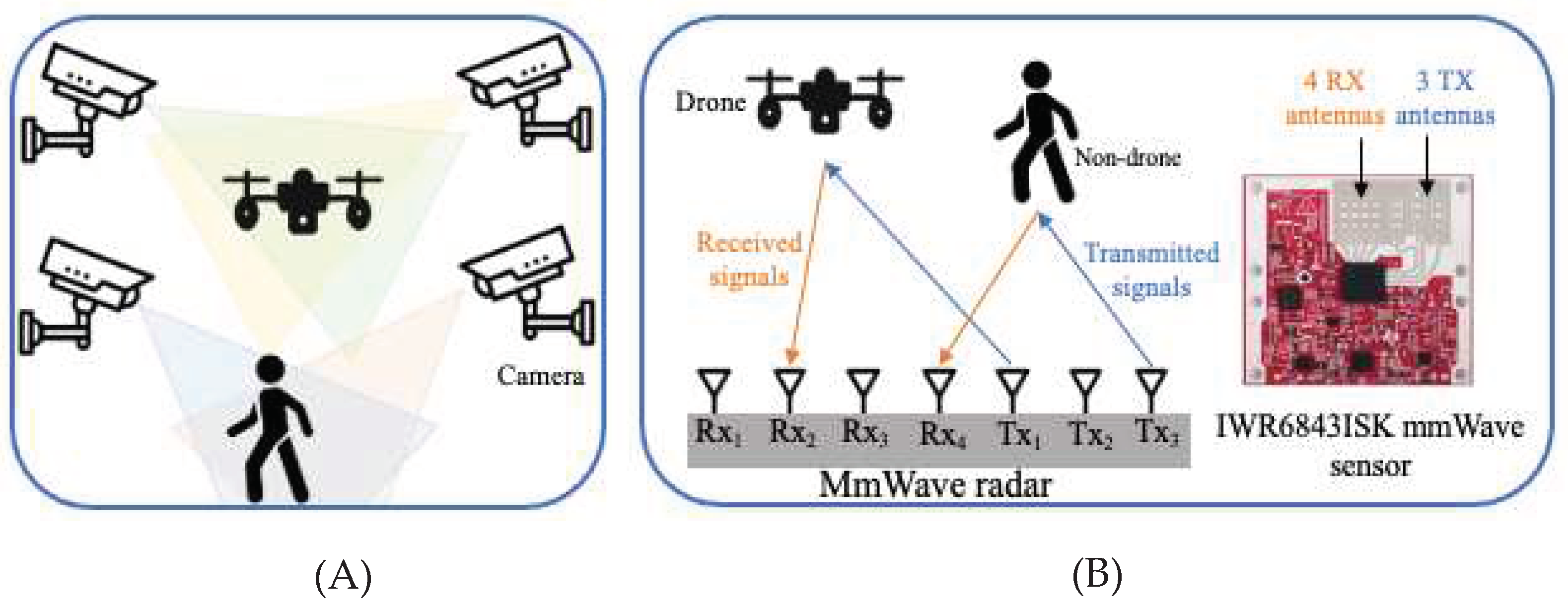
Challenges. The detection of unwanted drones poses heavy challenges to observation systems, especially in urban areas as drones are tiny and move at different rates and heights compared to other moving targets (Fu et al. 2021). For target recognition, optic-based systems that rely on cameras provide more detailed information compared to Radio Frequency (RF)-based systems, but these require a clear, frontal view as well as ideal light and weather conditions (Bhatia et al. 2021) (Huang et al. 2021), as shown in Figure 1A. Using cameras for target recognition is intrusive in nature, which increases privacy concerns and leads to poor social acceptance in both residential and business environments (Beringer et al. 2011). Although using RF-based systems is less intrusive, the signals received from RF devices are not as expressive or intuitive as those from images. Humans are often unable to interpret RF signals directly. Thus, preprocessing RF signals is a challenging process that requires translating raw data into intuitive information for target recognition. It has been proven that RF-based systems such as WiFi, ultrasound sensors, and Millimeter-Wave (mmWave) radar can be useful for a variety of observation applications that are not affected by light or weather conditions (Ferris Jr and Currie 1998). WiFi signals require a delicate transmitter and receiver and are limited to situations in which targets must move between the transmitter and receiver (Zhao et al. 2019). Since ultrasound signals are short-range, they are usually used to detect close targets, and they are affected by blocking or interference from other nearby transmitters (Bhatia et al. 2021).
The large bandwidth of mmWave allows high distance-independent resolution, which not only facilitates the detection and tracking of moving targets but also their recognition. Furthermore, mmWave radar requires at least two antennas for transmitting and receiving signals and thus the collected signals can be used in multiple observation operations (Zhao et al. 2019). Rather than true-color image representation, mmWave signals can represent multiple targets using reflected Three-Dimensional (3D) cloud points, micro-Doppler signatures, RF intensity-based spatial heat maps, or range-Doppler localizations (Sengupta et al. 2020).
MmWave-based systems frequently use conventional neural networks (CNN) to extract representative features from micro-Doppler signatures to recognize objects (Zhao et al. 2019) (Yang et al. 2019) (Tripathi et al. 2017) but examining micro-Doppler signals is computationally complex as they deal with images, and they only distinguish moving targets based on translational motion. Employing CNN to extract representative features from cloud points is becoming the tool of choice for developing mathematical modeling underlying dynamic environments and leveraging spatiotemporal information processed from range, velocity, and angle information, thereby improving robustness, reliability, and detection accuracy, and reducing computing complexity to achieve a simultaneous performance of mmWave radar operations (Wang et al. 2016).
Our Solution. To solve these challenges, a novel framework for simultaneous tracking and recognizing drone targets using mmWave radar is proposed. The proposed framework is based on installing a low-cost and small-sized mmWave sensor for transmitting and receiving signals, as shown in Figure 1B. Our main objective is to utilize 3D point clouds generated by a mmWave radar to detect, track, and recognize multiple moving targets including drone and non-drone targets. When raw analog to digital conversion data from antenna arrays is converted into 3D point clouds, the data size is reduced from tens of gigabytes to a few megabytes (Palipana et al. 2021). This allows faster data transfer, processing, and applying complex machine learning algorithms. Unlike the micro-Doppler signature, the spatiotemporal features of cloud points are more representative and easily interpretable because movements occur in 3D space. For performance evaluation, a dataset1 collected with an IWR6843ISK mmWave sensor by Texas Instruments (TI) is used for training and testing the convolutional neural network. In summary, our key contributions can be summarized as follows:
A signal processing algorithm is proposed to generate 3D point clouds of moving targets in the FoV, considering both static and dynamic reflections of mmWave radar signals.
A multi-target tracking algorithm is developed that integrates a density-based clustering algorithm to merge related point clouds into clusters, Extended Kalman Filters (EKF) to estimate the new position of the targets, and the Hungarian algorithm to match each new estimated track with its target cluster.
A novel CNN model is proposed f feature extraction and identification of drone and non-drone targets from clustered 3D cloud points.
The performance of the proposed tracking and recognition algorithms is evaluated, demonstrating clustering accuracy achieves 88.2% for one target and 68.8% for two targets, tracking Root Mean Square Error (RMSE) of 0.21, and identification accuracy of 98.4% for one target and 98.1% for two targets.
The rest of the paper is organized as follows. Section 2 reviews existing literature. Section 3 presents the proposed framework. Section 4 describes the signal preprocessing. Section 5 describes the clustering processing. Section 6 describes the tracking process. Section 7 describes the recognition process. Section 8 discusses performance evaluation. Section 9 presents the conclusion and future work.

2. Related Works

In the literature, several techniques have been developed to detect and recognize drones, including visual (Srigrarom et al. 2021), audio (Al-Emadi, Al-Ali, and Al-Ali 2021), WiFi (Alsoliman et al. 2021)(Rzewuski et al. 2021), infrared camera (Svanström, Englund, and Alonso-Fernandez 2021), and radar (Yoo et al. 2021). Drone audio detection relies on detecting propeller sounds and separating them from background noise. A high-resolution daylight camera and a low-resolution infrared camera were used for visual assessment (Dogru, Baptista, and Marques 2019). Good weather and a reasonable distance between the drone and the cameras are still required for visual assessment. Fixed visual detection methods cannot estimate the drone’s continuance track. Infrared cameras detect heat sources on drones, like batteries, motors, and motor driver boards. MmWave radar is less impacted by external circumstances, and it has long been the most popular means for military troops to detect airborne vehicles. Traditional military radars, on the other hand, are designed to recognize huge targets and have trouble detecting small drones. Furthermore, target discrimination may not be a simple matter. When the target is multiple times the wavelength, better radar detection is accomplished (Dogru, Baptista, and Marques 2019). As a result, radars with shorter wavelengths may offer better results for small drones.
This subsection discusses various recent drone classifications through machine learning and deep learning models. Radar Cross-Section (RCS) signatures of different drones with different frequency levels have been discussed in several papers, including (Fu et al. 2021) (Semkin et al. 2021). The method proposed in (Fu et al. 2021) relied on converting RCS into images and then using a CNN to perform drone classification, which required a lot of computation. As a result, they introduced a weight optimization model that reduces computation overhead, resulting in improved Long Short-Term Memory Networks (LSTM). The authors showed how a database of mmWave radar RCS signatures can be utilized to recognize and categorize drones in (Semkin et al. 2021). They demonstrated RCS measurements at 28 GHz for a carbon fiber drone model. The measurements were collected in an anechoic chamber and provided significant information about the drone’s RCS signature. The author aided RCS-based detection probability and range accuracy by performing simulations in metropolitan environments. The drones were placed at different distances ranging from 30 to 90 meters, and the RCS signatures used for detection and classification were developed by trial and error.
The authors proposed a novel drone localization and activity classification method using mmWave radar antennas oriented vertically to measure the drone’s elevation angle from the ground station in (Rai et al. 2021). The measured radial distance and elevation angle are used to estimate the drone’s height and horizontal distance from the radar station. A machine learning model is used to classify the drone’s activity based on micro-Doppler signatures extracted from radar measurements taken in an outdoor environment.
The system architecture and performance of the FAROS-E 77 GHz radar at the University of St Andrews were reported by the authors in (Rahman and Robertson 2021) for detecting and classifying drones. The goal of the system was to show that a highly reliable drone classification sensor could be used for security surveillance in a small, low-cost, and possibly portable package. To enable robust micro-Doppler signature analysis and classification, the low phase noise, coherent architecture took advantage of the high Doppler sensitivity available at mmWave frequencies. Even when a drone was hovering stationary, the classification algorithm was able to classify its presence. In (Jokanovic, Amin, and Ahmad 2016), the authors employed a vector network analyzer that functioned as a continuous wave radar with a carrier frequency of 6 GHz to gather Doppler patterns from test data and then recognize the motions using a neural network.

3. The Proposed Framework

The proposed framework for simultaneous tracking and recognizing drone targets using mmWave radar is presented in this section. A front-end mmWave radar system with three transmitting (Tx) and four receiving antennas (Rx) is shown in Figure 1. Mmwave radar transmits multiple frequency-modulated continuous waveform (FMCW) chirps. These signals are received by the receiving antennas after they have reflected from multiple targets in the FoV. The radar then combines the Tx and Rx signals to demodulate the FMCW signals and generate Intermediate Frequency (IF) signals, creating a time-stamped snapshot of the FoV (Molchanov et al. 2015). The collected sequence of IF signals is insufficiently informative and hence applied to preliminary preprocessing to extract some features of the target such as range, velocity, and angle (Molchanov et al. 2015) (Yang et al. 2019). 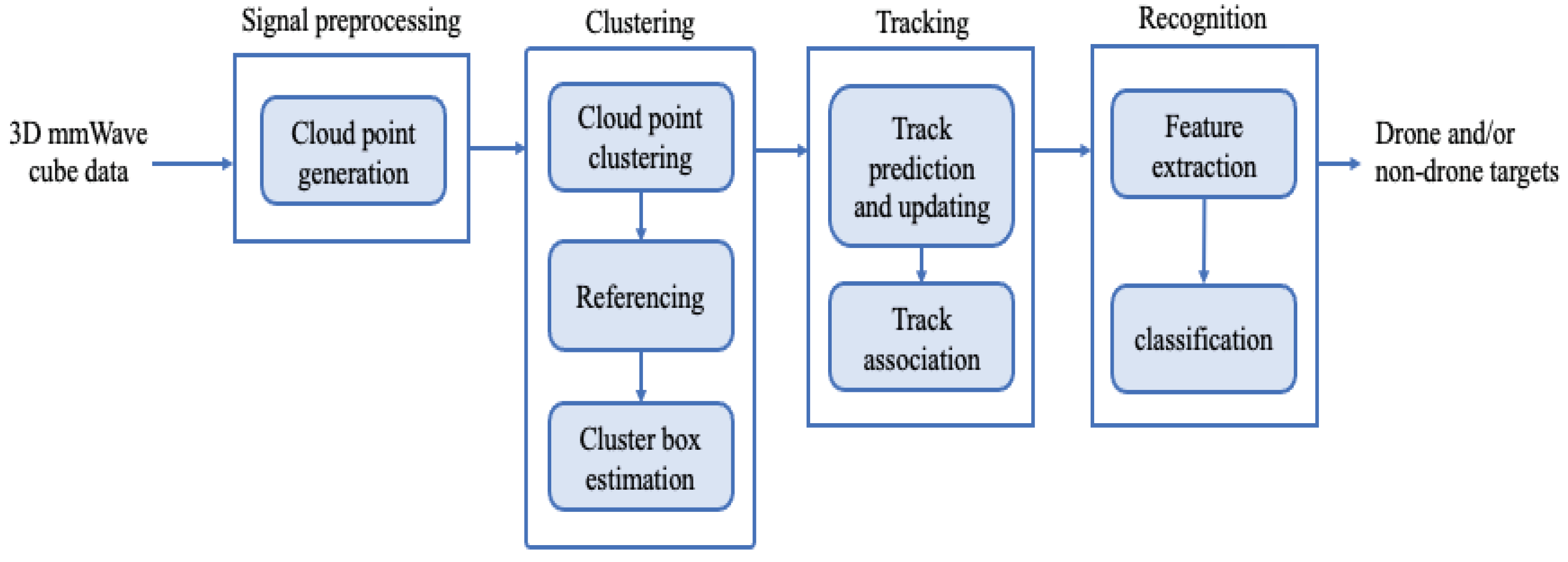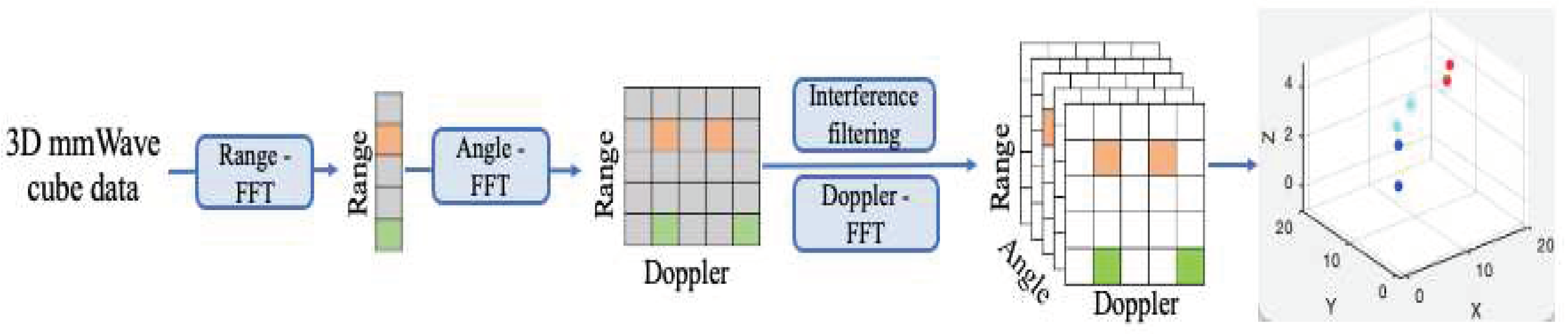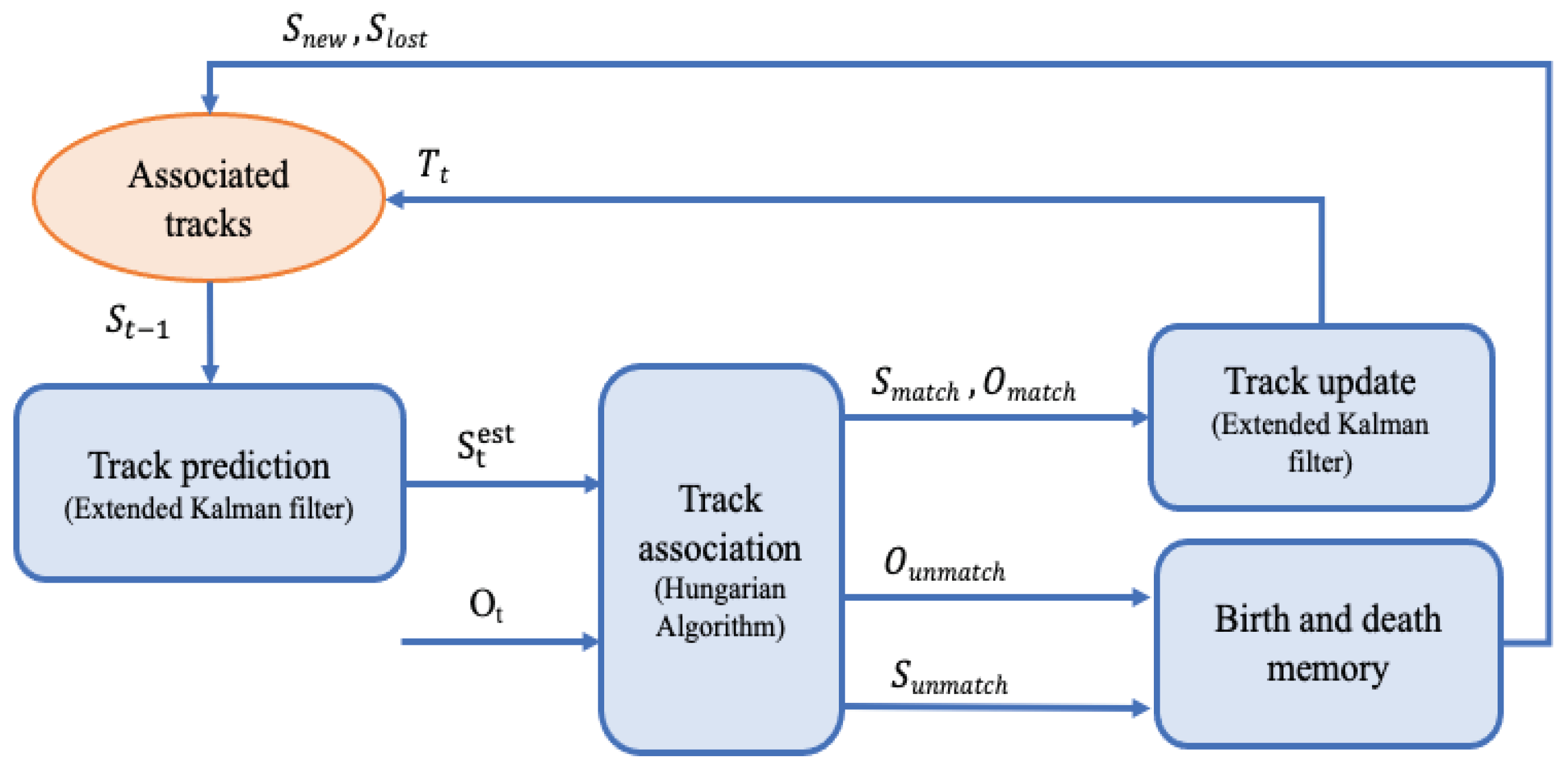Figure 2 shows the proposed framework which is made up of four modules that operate in a pipelined approach as follows:
Signal preprocessing. This module translates the raw information collected by mmWave radar into sparse point clouds and eliminates the points associated with interference noises and static objects (i.e., points that appeared in the previous frame), which reveal the existence and movement of targets.
Clustering. This module detects different moving targets and merges related point clouds into clusters, each cluster represents a single moving target.
Tracking. This module estimates a target track in successive frames and applies an association algorithm to keep track of multiple targets’ paths.
Recognition. This module utilizes a CNN model to extract representative spatiotemporal features from cloud points and then classify the detected targets as drone and/or non-drone targets.
The four modules of the proposed framework are explored in further depth in the following section.
Preprints 76046 g002
Figure 2. The proposed framework.
Figure 2. The proposed framework.
Preprints 76046 g002

4. Signal Preprocessing

The raw IF signals are collected in the form of 3D cube data (time, chirp, and antenna). Fast Fourier transformations are performed on IF signals to estimate the moving target’s range, velocity, and Angle of Arrival (AoA) (Bhatia et al. 2021) (Janakaraj et al. 2019). Cloud point is a 3D model composed of a set of points used in the literature to describe a list of detected targets provided by radar signals processing (Mafukidze et al. 2022). Figure 3 illustrates a four-step signal preprocessing workflow to generate a series of cloud points, each comprising 3D spatial position, velocity, and AoA (Shuai et al. 2021).

4.1. Range Fast Fourier Transform (Range-FFT)

FMCW transmitted chirps are characterized by frequency f , bandwidth b , and duration T c h i r p . The reflected IF single is parsed to determine the radial range between the radar and the target. The frequency of IF signal f I F is proportional to the radial distance r , which is denoted as:
f I F = s . 2 r c   ,
However, the radial distance between the target and the radar is estimated by:
r = f I F . c 2 s ,
where c represents the light speed 3 × 10 8 m/s, and s is the chirp frequency slope, which is calculated by ( s = b T c h i r p ). Range-FFT is applied to each chirp of radar cube data to convert the time-domain IF signal into the frequency-domain. The peak of the resulting frequency spectrum determines the range of each target. The distance can be calculated by averaging the distance collected by all chips in a frame and the number of chirps in the frame.

4.2. Doppler Fast Fourier Transform (Doppler-FFT)

A slight change in the target’s distance results in a significant shift in the IF signal phase. To determine the target velocity, two or more time-separated chirps by duration T c h i r p are required. Then, a Doppler-FFT is applied across the phases received from these chirps. Therefore, target radial velocity can be estimated by comparing the phase differences of the two received signals. If the target is moving, the phase difference ω can be calculated as:
ω = 4 π   .     T c h i r p   . υ λ ,
This approach can discriminate between targets moving at various velocities at the same distance. The target velocity v for each moving target be calculated as:
υ = λ ω 4 π   T c h i r p ,
where λ is the wavelength.
The phase difference between two chirps at the range-FFT peak is proportional to the detected target’s radial velocity. Applying Doppler-FFT to the signal range spectrum yields 2D range-Doppler localizations.

4.3. Interference filtering

Interference filtering is responsible for removing interference scattering points reflected from unwanted objects in FoV. Reflections from a noisy background, such as reflections from walls, must be removed, as well as reflections from clutters of static (non-moving) objects, such as trees. Because drone targets are in continuous movement, reflections from drone targets would be combined with such inferences, causing significant issues in the clustering, tracking, and recognition processes of drones. The interference is filtered by applying Constant False Alarm Rate (CFAR) and Moving Target Indication (MTI).

4.3.1. CFAR algorithm

The received signal X r t from the FoV can be expressed as:
X r t =   X s t + g t ,
where   X s t is the target reflection and g t is the white Gaussian noise at a certain frame t .
From the received signal, the CFAR algorithm (Richards, Holm, and Scheer 2010) is applied to detect the presence or absence of a target. A fixed threshold value is used in traditional detectors such as the Neyman-Pearson detector (Mafukidze et al. 2022). The assumption is that interference (noise or clutter) is spread similarly across the test range bins, such that if the signal in the test bin exceeds a specific threshold γ , the bin contains a target. This results in False Alarm conditions, as shown in the following equations:
  X s t   + g t   ≥   γ ,   True   Detection
g t ≥   γ ,   False   Alarm
CFAR detectors rely on maintaining a constant false alarm rate, thereby altering the detection threshold within range bins, which are created to address false alarms, and missed detections caused by a set threshold. The detector calculates the noise level inside a sliding window and utilizes this estimate to assess the presence or absence of a target in the test bin in this manner. If a target is found in a bin, the algorithm returns the target’s range-Doppler localizations (Mafukidze et al. 2022). Finally, all CFAR-identified targets are organized into groups based on their position on a 3D matrix. In certain cases, this assumption might be deceptive, such as when the target returns only contain interference that surpasses the detection threshold. Therefore, additional filters with clustering are applied as shown in Section 5.

4.3.2. MTI algorithm

In this step, the MTI algorithm is applied to exclude the static clutter points. This process necessitates the use of range and velocity information since it filters out static targets from the FoV and removes those points corresponding to static targets (i.e., points that appeared in the previous frame). To remove those points, the static targets are mapped onto a vertical line that corresponds to the velocity of 0 m/s, and the Doppler channels associated with negligible velocities are removed from range-Doppler localization.
By adjusting the CFAR threshold, most non-target dynamic interference can also be removed. However, there might still be dynamic interference that is difficult to remove. It is because some distractors are moving at high or low speeds, while others are moving at close speeds to drones, such as when humans are walking. A threshold that is too small results in too much dynamic interference, while a threshold that is too large results in part of the drone and non-drone targets not being detected.

4.4. Angle Fourier Transform (Angle-FFT)

AOA estimation necessitates the use of at least two receiving antennas. The reflected signal from the target is received by both antennas, but it must travel an additional distance β to reach the second antenna. A minor movement in the target location causes a phase shift across receiving antennas. The phase difference between two receiving antennas along the elevation dimension φEL and the azimuth dimension φAZ are determined as follows (Tripathi et al. 2017) (Pegoraro and Rossi 2021):
φ E L = 2 π β   s i n ( θ ) λ ,
φ A Z = 2 π β   c o s θ s i n ⁡ ( ∅ ) λ ,
where θ and ∅ are the elevation and azimuth angles of a reflecting target. β is the distance between two receiving antennas, λ is the wavelength of the signal. Due to slight differences in the phase of the received signals, θ and ∅ can be calculated as:
θ = s i n − 1 ( λ φ E L 2 π β ) ,
∅ = sin − 1 ⁡ ( c o s θ λ φ E L 2 π β ) ,
Angle-FFT is applied on 2D range-Doppler localization resulting 3D range-Doppler-angle cube. Considering a point cloud P = { P 1 ,   . . . ,   P n   } where n is the number of detected targets, and each point P i t is represented by a feature set at a certain time t is denoted by P i t = [ x , y , z , v , ∅ , θ ] i t , where x, y, z are the Cartesian coordinate in 3D apace.

5. Clustering

5.1. Cloud point clustering

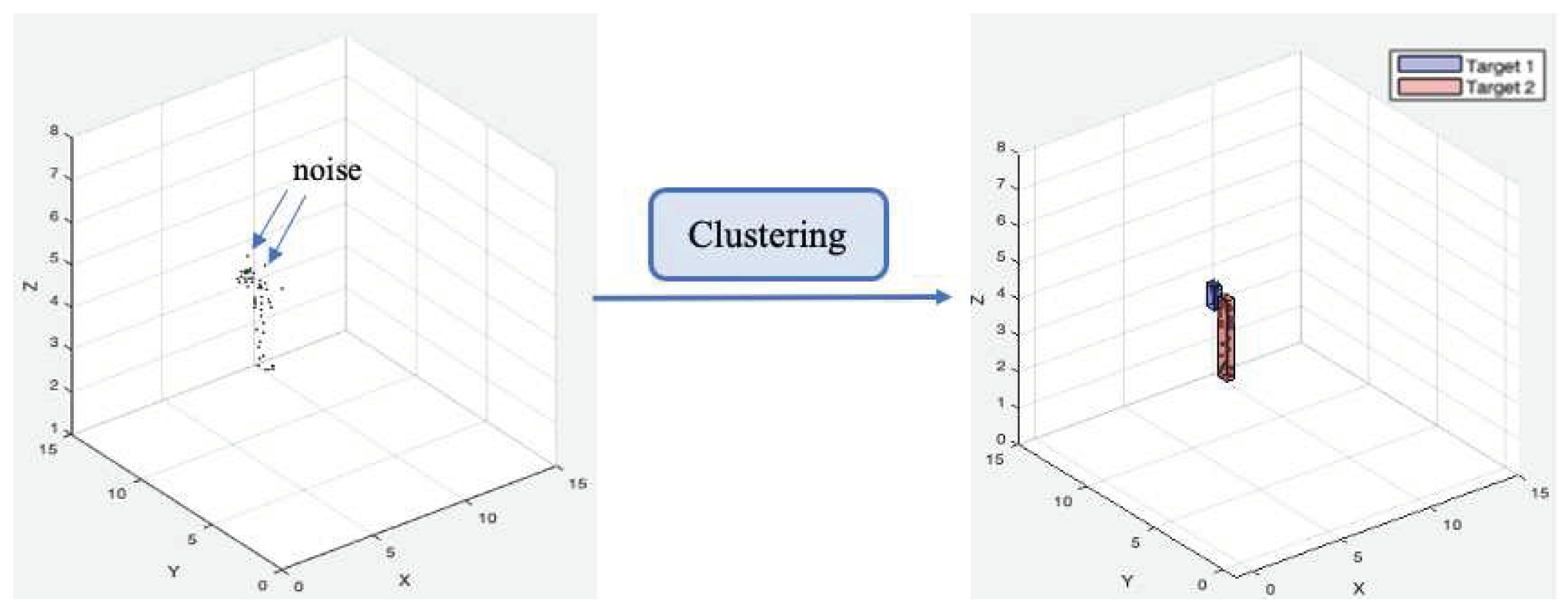
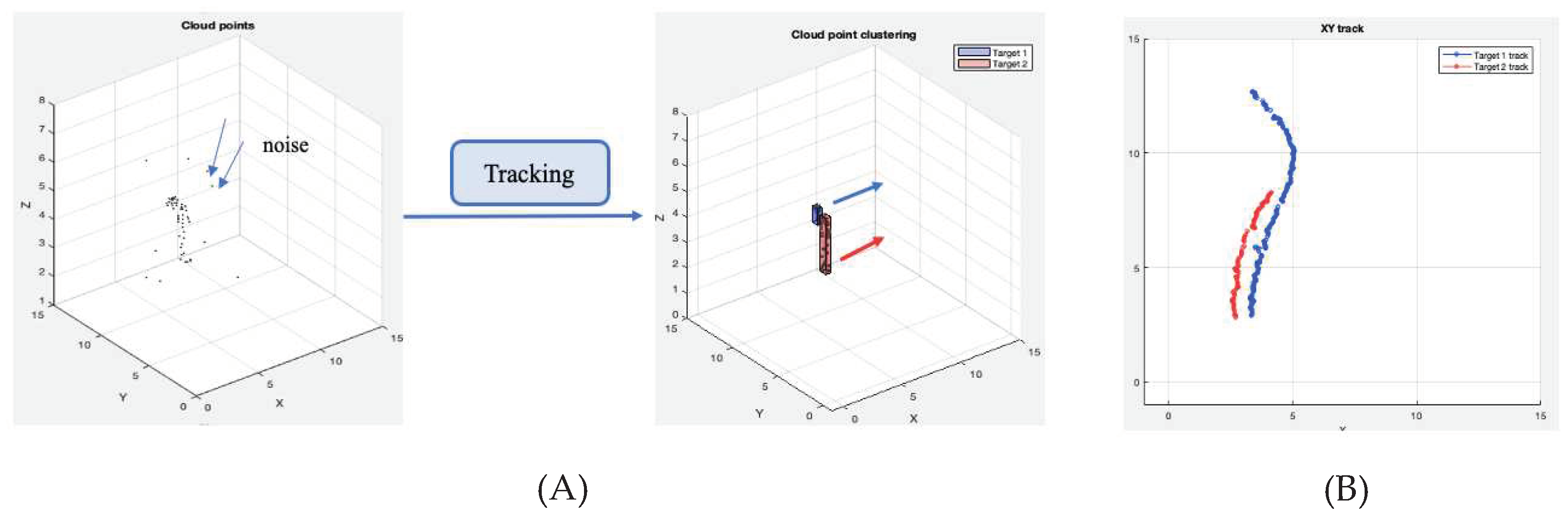
The generated point clouds are sparse and insufficiently informative to recognize distinct targets in the FoV. Furthermore, while static targets and noisy background reflections are removed through interference filtering as shown in Section 4, the remaining points are not always reflected by the targets. As shown in Figure 4, these interference points can be significant and lead to confusion with points from nearby target targets. Therefore, in this module, a clustering algorithm is applied to remove the noise points in the point cloud, besides grouping sparse point clouds into several clusters, each corresponding to a single target present in the FoV.
The Density-Based Spatial Clustering of Applications with Noise (DBScan) algorithm is applied as a clustering algorithm (Birant and Kut 2007), which is a density-aware clustering method that separates cloud points based on the Euclidean distance in the 3D space. DBScan groups several points in high-density regions into clusters, whereas interference points are typically spread in low-density regions and are thus removed. In each frame, DBScan scans all points sequentially, enlarging a cluster until a certain density connectivity criterion is no longer met. Unlike K-means, DBScan does not require previous knowledge of the number of clusters and is hence well-suited for target detection problems with an arbitrary number of targets.
The distance between two points is used as the distance metric in DBSCAN for density-connection checking and is defined as follows:
d t ( i , j )   : = α x ( x i t − x j t ) 2 + α y ( y i t − y j t ) 2 + α z ( z i t − z j t ) 2 + α v ( v i t − v j t ) 2   ,
where α = [ α x , α y , α z , α v ] is the weight vector used to balance the contributions of each element. Velocity information is applied during the clustering phase to distinguish two nearby targets with varying speeds, such as when two targets pass by face-to-face. The clustering algorithm is illustrated in Table 1.

5.2. Referencing

After clustering, each point is identified by index of the cluster or a noise point flag. For each clustered target, a reference point must be determined. This reference point will eventually be utilized for tracking and retrieving track information. A cluster’s centroid can be used as the reference point. The algorithms can determine a cluster’s centroid location with a low misclassification rate, as illustrated in Table 2.

5.3. Cluster box estimation

All detected targets are enclosed by cluster boxes. The outermost points of each cluster are scanned, and these points are used to approximate the size of the 3D bounding box. The result after applying cluster box estimation at frame t is a collection of detected targets O t = [ O 1 ,   O 2 ,   … O n ] T where n is the number of detected targets that might differ across frames. Each target O i t , is represented as a 6-dimensional vector comprising of centroid Cartesian coordinates x , y , z ; and length, height, and width of the 3D bounding box l , h , and w . Specifically, the i t h point is denoted by O i t = [ x , y , z , v , ∅ , θ , l , h , w ] i t .
Preprints 76046 g005
Figure 5. Tracking process input and output. (A) The estimation of the track at a certain frame. (B). The continuous track estimation.
Figure 5. Tracking process input and output. (A) The estimation of the track at a certain frame. (B). The continuous track estimation.
Preprints 76046 g005
Table 1. Clustering algorithm. Table 2. Centroid determining algorithm.
Preprints 76046 i001 Preprints 76046 i002

6. Tracking

During the tracking phase, the new position of the detected target is estimated sequentially as shown in Figure 5A, followed by temporal association of the new estimated track and the target cluster to create a continuous target track as shown in Figure 5B. A workflow of the proposed multiple targets tracking algorithm is shown in Figure 6. The components of the proposed target tracker are explored in further depth below.

6.1. Track estimation and updating

At track estimation, the EKF (Kalman 1960) (Fujii 2013) is adopted to predict the state tracks S t − 1 to current frame t , which is denoted as S t e s t .
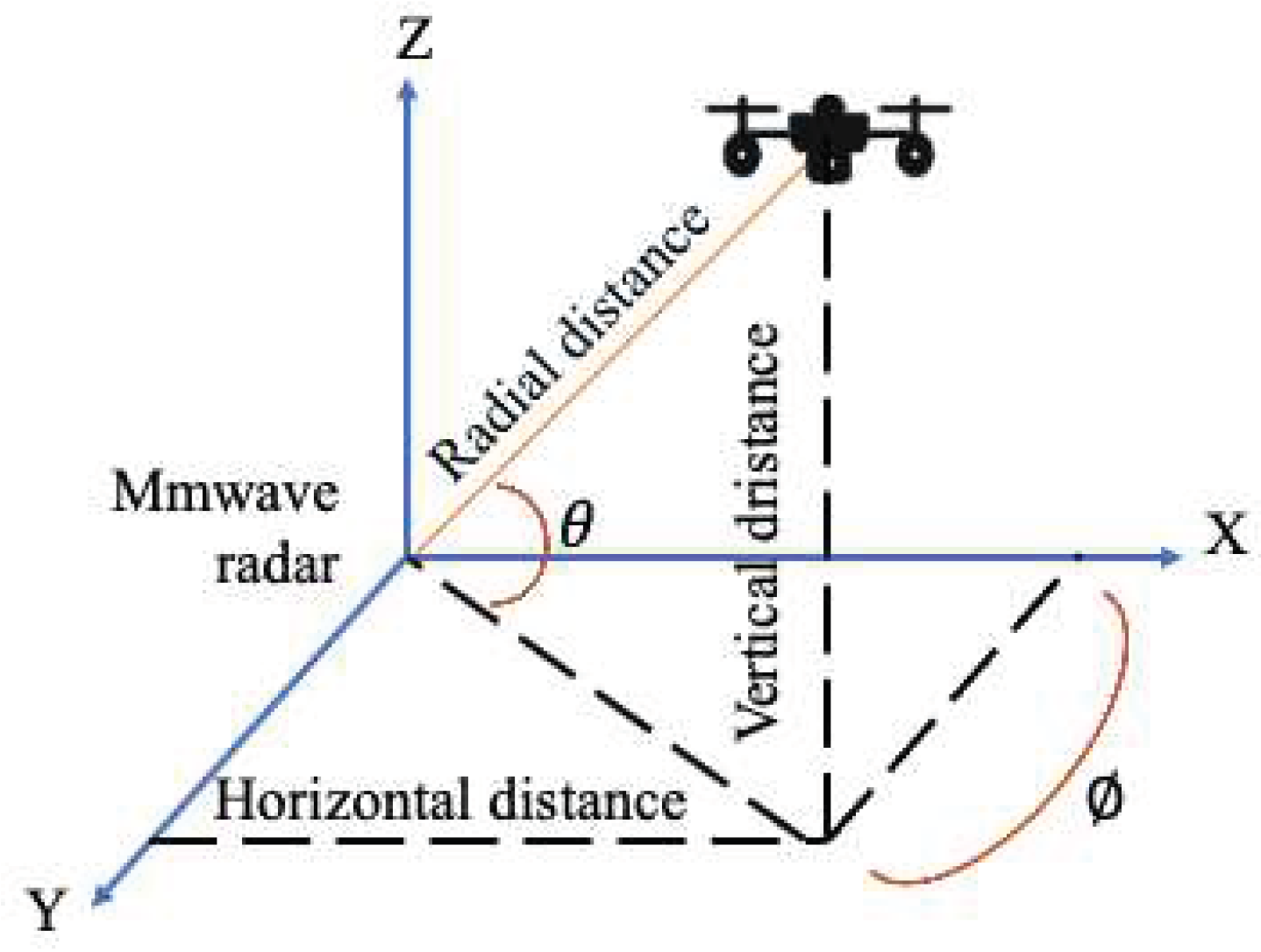
An EKF is a recursive linear filter that is used to determine the state of a dynamic system based on the time series of noisy observations. In addition, it features a low computational complexity, and a recursive structure, and is resistant to measurement errors and correlations when dealing with multiple targets. As a result, the radar community uses the KF-based tracking technique most frequently (Blackman 1986). Using EKF when tracking a moving target will allow the system to detect the target even if it remains stationary, as well as follow the target wherever it travels. In this paper, target tracking is performed utilizing distance and azimuth angle observations rather than radial velocity observations. Most investigations in the literature included radial velocity observations into the model, which caused the system to become too non-linear to produce meaningful estimates using KF. Moreover, observing only the distance limits the ability to locate a target in 3D space; this limitation can be overcome by observing the angular positions of moving targets and eventually reconstructing the full track of the target.
Therefore, the KF model observations vector consists of the detected target’s radial distance and azimuth angle at frame t is defined as m   t = [ r   ,   ∅   ] t . The graphical representation of the radial distance and the azimuth angle of a target from the ground station is shown in Figure 7. The current track state of the detected target at frame t is defined as,   S t : = x , y , z , v , ∅ , θ , l , h , w t .
The typical state-space representation of a nonlinear time-discrete model is as follows:
S t = A S t − 1 + u t ,  
M t = h ( T t ) + q t ,
where Equation (13) is responsible for explaining the evolution of the target states through t ; Equation (14) is responsible for matching the target’s state to the measurements. u t and q t are white Gaussian process noise and measurements noise, respectively. h S t = x 2 + y 2 + z 2   ,   t a n − 1 y x t represents the non-linear measurement process. A is the state transition matrix given in time-discrete by:
A = 1 0 0 0 1 0 0 0 1         ∆ t 0 0 0 ∆ t 0 0 0 ∆ t 0 0 0 0 0 0 0 0 0           1     0   0   0   1     0   0   0   1   ,
To solve this non-linearly measurement, a modified observation vector M ´ t = [ r   c o s   θ ,   r   s i n   θ ] is obtained to Equation (13) and Equation (14). The EKF is used to estimate the new position of the detected targets in two steps. In the first step, the new track state is predicted by the mean S e s t t and covariance P t at time t and defined as:
S e s t t = A S t − 1 + u t   ,
P T = A P t − 1 A T + q t   ,
In the second step, the filter updates the first step state estimations using the Kalman gain K t , which is denoted as:
K t = P t   H t T ( H t P t H t T + U ) − 1
S t = S t − 1 + K t ( M t − h ( P t ) ) ,
P t = I − K t   H t P t − 1 ,
where H t is the Jacobian matrix of partial derivatives of h ( ⋅ ) , U is the noise covariance, and I is the identity matrix.

6.2. Track association

Several successful single target tracking systems have been explored in the literature, but tracking becomes difficult in the presence of multiple targets. The task of matching new tracks with target clusters from frame to frame in each input sequence has proven complicated.
During track association, the detected targets O t and predicted track state S t e s t are associated at each frame. The Hungarian algorithm (Kuhn 1955) is adopted here to solve this many-to-many assignment problem with the objective of minimizing the combined distance loss. The procedure consists of two steps, in the first step, the actual cost matrix with the dimension of O t × S t − 1 is constructed using the squared Mahalanobis distance between the centroid of target detection O t and the predicted track S t e s t for each frame t .
The cost matrix C t i j for the association between the predicted track i at t − 1 and the detected target j at the frame t is calculated as:
C i j t = ( M i t − H S i t ) T   ( D t ) − 1   M i t − H S i t ,
where M i t − H S i t is the innovation process, D t is the covariance matrix calculated as H P t H + R , and are both obtained as part of the KF update step.
The outputs of the track association module are a collection of detections O m a t c h = { O m a t c h 1 , O m a t c h 2 , ⋯ , O m a t c h w } matched with tracks S m a t c h = { S m a t c h 1 , S m a t c h 2 , ⋯ , S m a t c h w } , along with the unmatched tracks S u n m a t c h = { S u n m a t c h 1 , S u n m a t c h   2 , ⋯ , S u n m a t c h m − w } and unmatched detected targets O u n m a t c h = { O m a t c h 1 , O m a t c h 2 , ⋯ , O u n m a t c h n − w } , where w , m , and n are the number of matches, predicted tracks and detected target, respectively.

6.3. Birth and death

This module manages the newly appearing and disappearing tracks when existing targets disappear, and new ones arise. In this work, all unmatched detections O u n m a t c h are considered as potential targets entering the FoV. To avoid tracking false positives, a new track S n e w i will not be created for O u n m a t c h i unless it has continually matched in the next few frames. All unmatched tracks, on the other hand, are considered potential targets when leaving the FoV. To avoid deleting true positive tracks with missing detection at specific frames, each unmatched track is kept for a few frames before being deleted.

7. Recognition

7.1. CNN model for feature extraction and classification

In this section, the proposed CNN model for multiple targets features extraction and classification is presented to recognize drone or non-drone targets. To overcome non-uniformity in the number of points per frame and ensure a consistent length of input data, the data are processed before training and testing the CNN model. No matter how many points are in each frame, the point clouds in a 3D point cloud grid are converted into 2D occupancy grids. In particular, the cluster that encloses the points of a potential drone target is used to determine discriminative spatiotemporal patterns for each target individually.
However, a CNN model is developed for spatiotemporal feature extraction throughout the 2D occupancy grids periodically. In order to reduce network consumption and enhance training speed, the features of the point cloud data are directly used as input data for the CNN rather than mapping the point cloud to images. Features extracted from 2D occupancy grids of the cluster cloud points include distance, velocity, and angle, as shown in Section 4. Additional discriminative features were extracted such as the height of the target and the size of clusters.
The most distinguishing feature of drones is their ability to reach higher altitudes and tiny sizes than pedestrians and other on-ground moving vehicles. The target altitude is determined by calculating the vertical distance as:
λ = r   ∗ c o s θ ,
where λ the height of the target from the ground.
In addition, the target size is determined by calculating the area of the clustered box as follows:
a = 2 l w   ∗   2 l h   ∗   2 w h ,
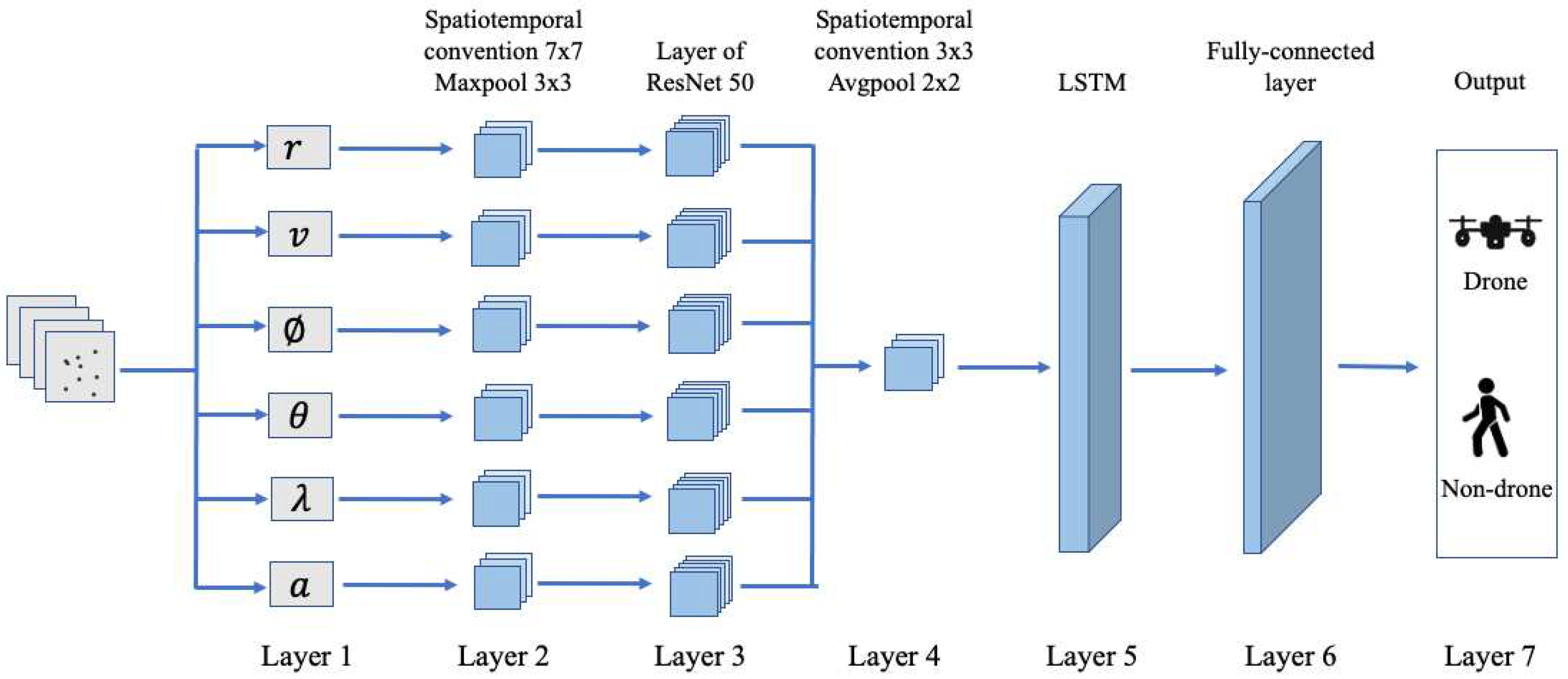
The CNN model consists of seven layers, as shown in Figure 8. Layer 1 is the input layer containing the six attributes: radial distance in meters, velocity in meters/second, azimuth angle in degrees, elevation angle in degrees, height in meters, and area in m e t e r 2 . Layer 2 is made up of six distinct modules, each of which is made up of a spatiotemporal convolution with kernel size 7 × 7 , maximum pooling composition with a sum size 3 × 3 , Rectified Linear Unit (ReLU) activation functions, and maximum pooling with pooling area size 3 × 3 and a stride of 2. Layer 3 is made up of six separated ResNet50. Layer 4 is made up of spatiotemporal convolution with kernel size 3 × 3 and average pooling with a pooling area of size 2 × 2 to fuse the six features. Layer 5 is made of an LSTM layer with an input size of 256 and a 128-cell hidden layer and a dropout of probability 0.5. Layer 6 is made of two fully connected (FC) layers and a ReLU activation function hidden layer to determine the output of the nodes in FC. The final output layer would have three nodes, corresponding to the three classes of drone, non-drone, and (drone and non-drone).
The CNN loss function L o s s is calculated as:
L o s s s c r , t = − s c r t l o g ⁡ ( ∑ j e x p ⁡ ( s c r [ j ] ) ) ,
where s c r is the classification score.
The context flow of local and global time and space is designed using LSTM, which fuses local and global spatiotemporal features. The six attributes of the point cloud served as input independently, and the spatiotemporal convolution kernels are applied to extract the point cloud’s spatiotemporal features. However, it is impossible for six distinct drone and non-drone target identification to adequately capture the intrinsic features, hence these six attributes must be fused. As a result, the fusion network is developed on the Layer 4 to fuse the six features. After fusion, the features are more extensive and may more thoroughly describe a target dimension, speed, altitude, and spatial position correspondence.
Preprints 76046 g008
Figure 8. The proposed CNN model for drone target recognition.
Figure 8. The proposed CNN model for drone target recognition.
Preprints 76046 g008

8. Performance Evaluation

To evaluate the performance of the proposed framework, we used a dataset collected with an IWR6843ISK by Texas TI Single-chip 60-GHz to 64-GHz intelligent mmWave radar sensors (Texas Instruments 2022) for training and testing the CNN. In addition, the data are divided into training set and test set according to a 5:1 ratio. In this context, the accuracy of the proposed algorithms for clustering, tracking, and recognition is determined as follows:

8.1. Clustering

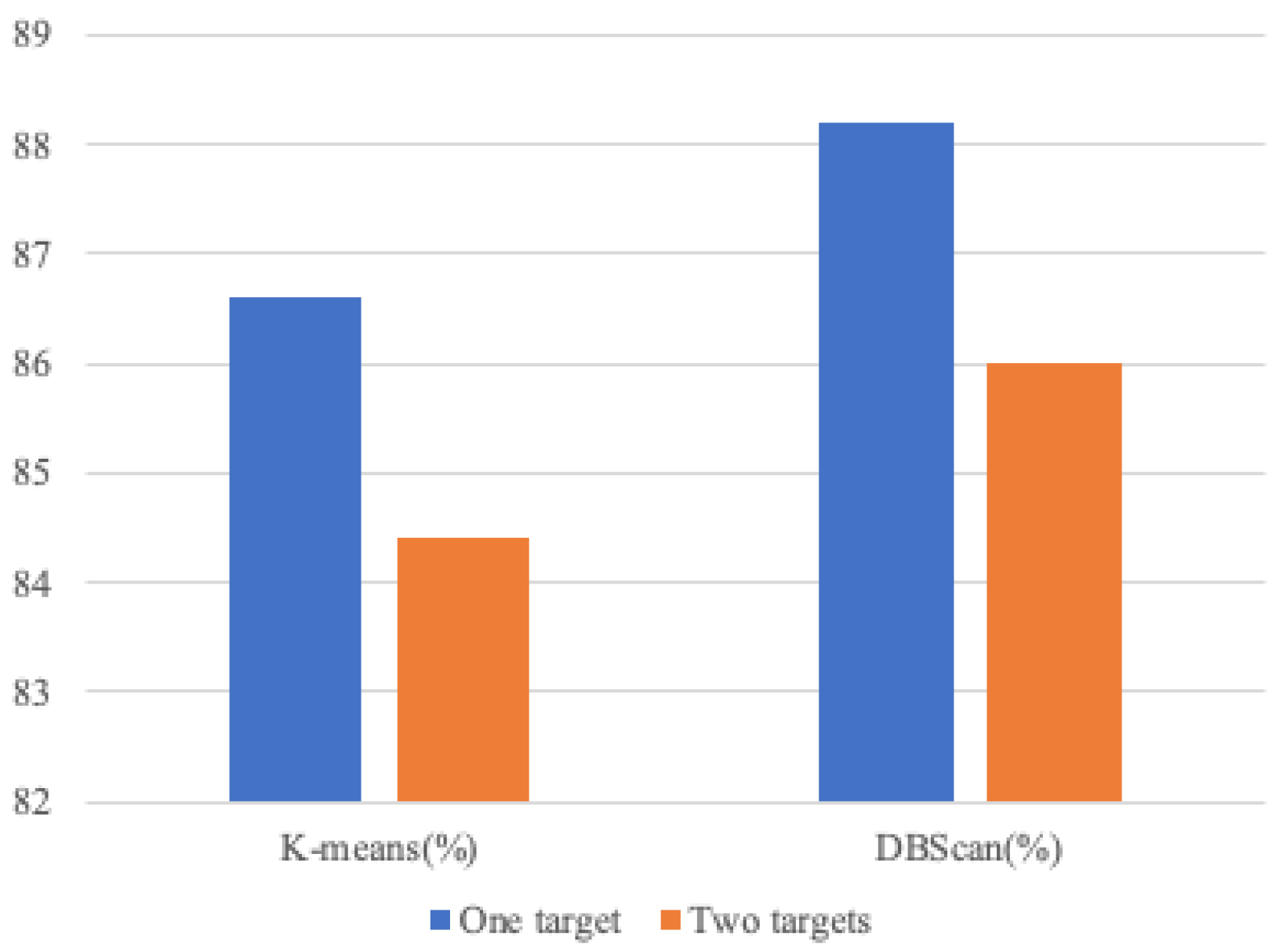
The proposed clustering algorithm based on DBScan is compared to the well-known K-means clustering algorithm as shown in Figure 9. The clustering accuracy achieves 88.2% for one target and 68.8% for two targets. Our proposed clustering algorithm is more accurate than the K-means algorithm. To improve DBScan performance, the weighting parameter α in Equation (12) must be defined. Practically, we discovered that α = 0.25 yields better clustering performance. Outliers are blended into the cluster when α = 0 . Points relating to a certain target are divided into two groups when = 1 (standard Euclidean distance).

8.2. Tracking

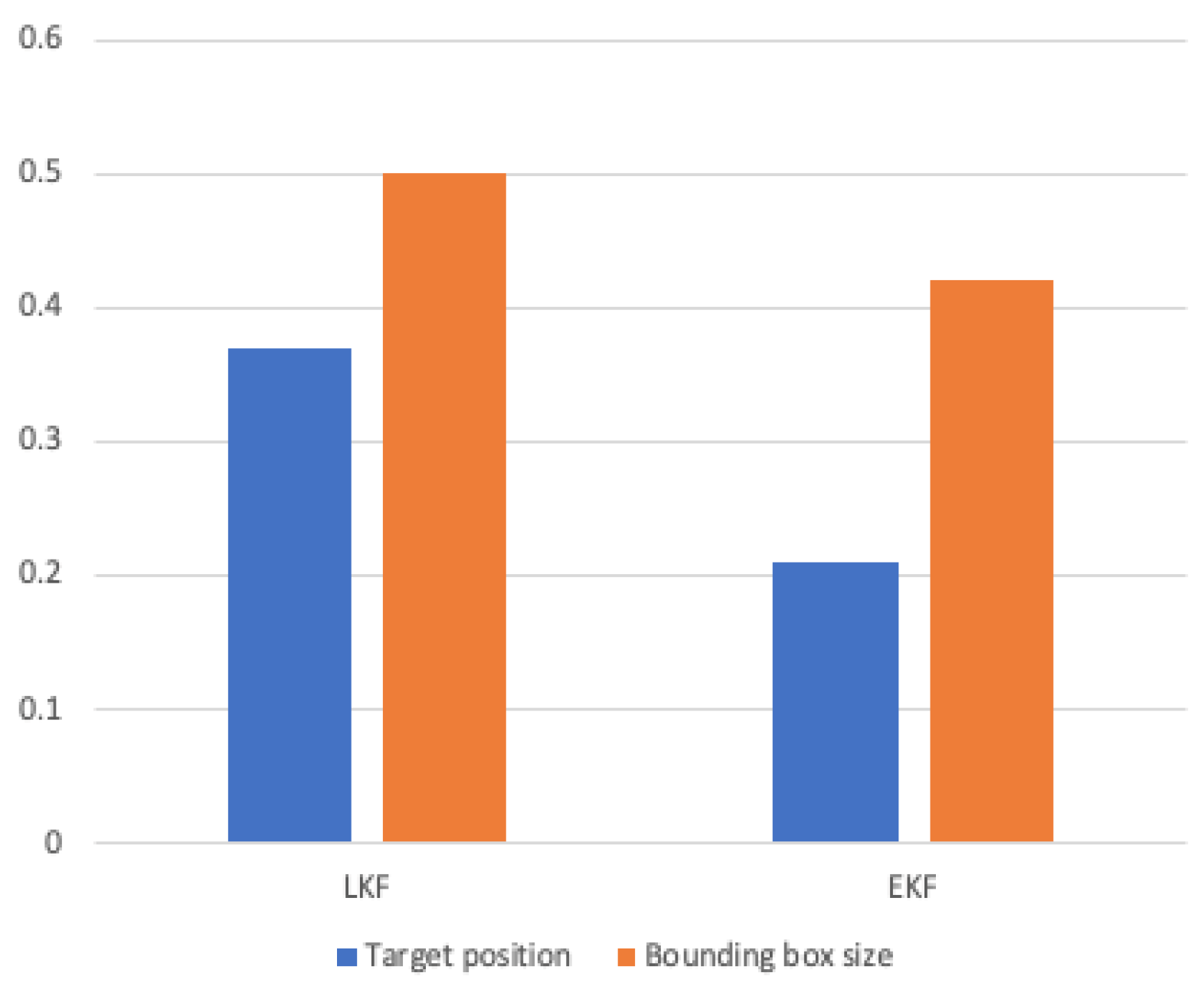
The estimated track accuracy is measured based on RMSE in Figure 10. RMSE value of EKF for target position is 0.21, whereas RMSE value of Linear Kalman Filter (LKF) is 0.36. Based on RMSE analysis, the EKF is more accurate than the LKF. This is because the EKF approximates a non-linear system using a first-order derivative and produces acceptable results in a slightly non-linear dynamic environment.
The RMSE for the target position is less than that for the bounding box size. The bounding box size is determined after cloud point clustering which is used to extract the predicted track. In rare circumstances, the algorithm fails to extract the precise bounding box of the tracked object when noise points are not filtered from the FoV. In addition, EKF has a shorter computational time since transition matrices are not required for the calculation due to the linearization effect.
Preprints 76046 g009
Figure 9. Clustering accuracy results.
Figure 9. Clustering accuracy results.
Preprints 76046 g009
Preprints 76046 g010
Figure 10. Tracking accuracy results.
Figure 10. Tracking accuracy results.
Preprints 76046 g010

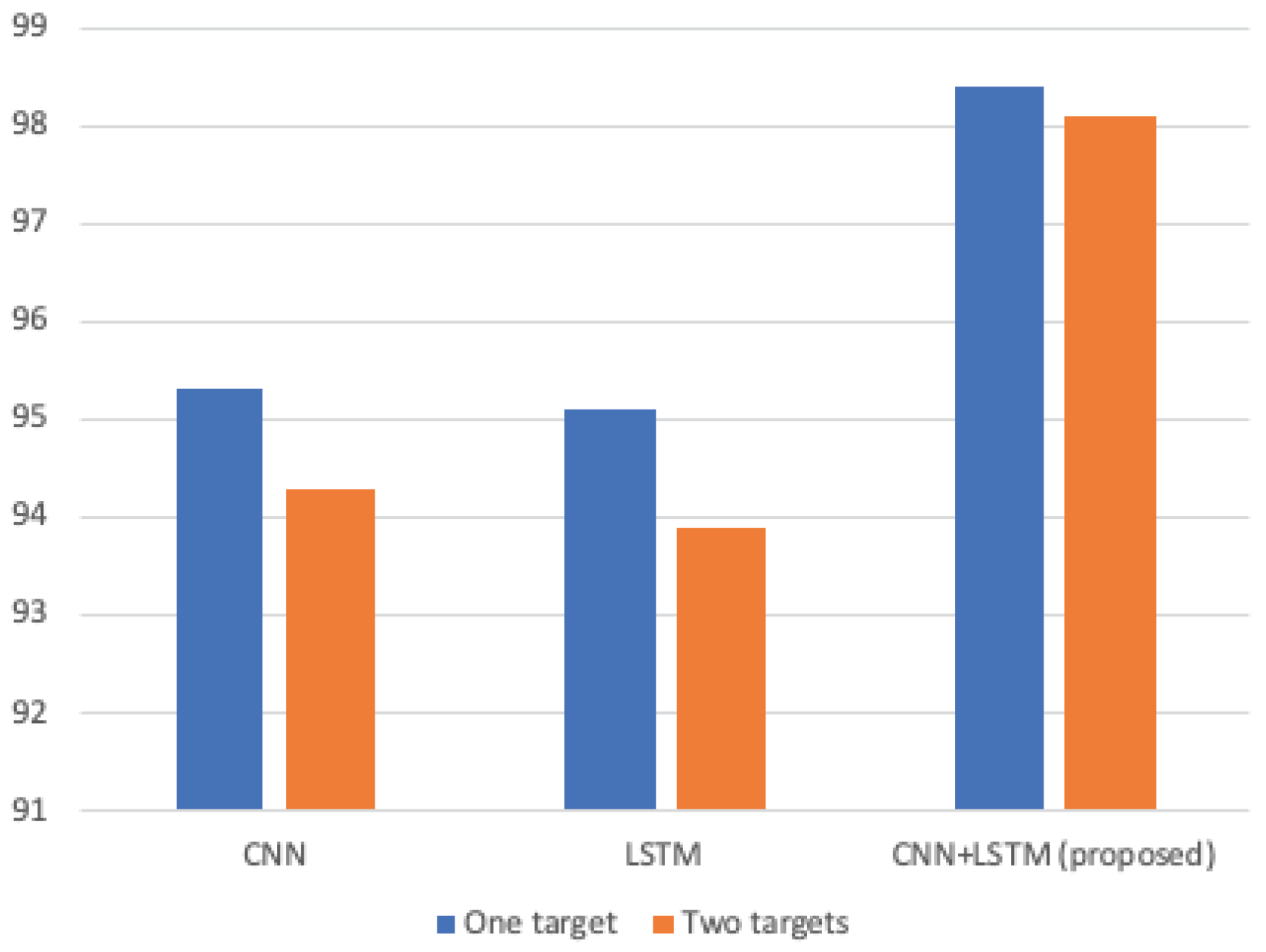
8.3. Recognition

To validate the proposed recognition model, the accuracy of two network modes: CNN and LSTM are compared to the proposed CNN+LSTM model. CNN and LSTM make up the first and second parts of our network, respectively. It can be observed from Figure 11 that the proposed model provides the best accuracy of 98.4% for one target and 98.1% for two targets.

9. Conclusion and Future Work

In this work, we proposed a novel framework that performs simultaneous drone tracking and resignification using sparse cloud points generated from a low-cost small-sized mmWave radar sensor. Following detection, clustering, and Kalman filtering for location estimates in the 2D space plane, the raw data is processed further with a designed CNN classifier based on a cloud point spatiotemporal feature extractor. Our framework surpasses previous solutions in the literature in terms of recognizing accuracy of 98.4% for one target and 98.1% for two targets with tracking RMSE of 0.21.
As there is no dataset containing drones or targets closely similar to drones, our framework recognizes three classes of targets: drone, non-drone, and (drone and non-drone), with a pedestrian as the non-drone targets. As part of future research, the proposed framework will be developed, and the dataset will be expanded to include drone-like targets such as birds.

Notes

1
https://github.com/00Nave198/MSU-ECE480-13-mmWave/tree/main/data

References

  1. Al-Emadi, S.; Al-Ali, A.; Al-Ali, A. Audio-Based Drone Detection and Identification Using Deep Learning Techniques with Dataset Enhancement through Generative Adversarial Networks. Sensors 2021, 21, 4953. [Google Scholar] [CrossRef]
  2. Alsoliman, A.; et al. COTS Drone Detection Using Video Streaming Characteristics. In International Conference on Distributed Computing and Networking; 2021; pp. 166–175. [Google Scholar]
  3. Beringer, R.; et al. The ‘Acceptance’ of Ambient Assisted Living: Developing an Alternate Methodology to This Limited Research Lens. In International Conference on Smart Homes and Health Telematics; Springer, 2011; pp. 161–167. [Google Scholar]
  4. Bhatia, J.; et al. Object Classification Technique for MmWave FMCW Radars Using Range-FFT Features. In 2021 International Conference on COMmunication Systems & NETworkS (COMSNETS); IEEE, 2021; pp. 111–115. [Google Scholar]
  5. Birant, D.; Kut, A. ST-DBSCAN: An Algorithm for Clustering Spatial–Temporal Data. Data & knowledge engineering 2007, 60, 208–221. [Google Scholar]
  6. Blackman, S.S. Multiple-Target Tracking with Radar Applications. Dedham 1986. [Google Scholar]
  7. Ben Brahim, I.; Addouche, S.-A.; El Mhamedi, A.; Boujelbene, Y. Cluster-Based WSA Method to Elicit Expert Knowledge for Bayesian Reasoning—Case of Parcel Delivery with Drone. Expert Systems with Applications 2022, 191, 116160. [Google Scholar] [CrossRef]
  8. Chechushkov, I.V.; et al. Assessment of Excavated Volume and Labor Investment at the Novotemirsky Copper Ore Mining Site. In Geoarchaeology and Archaeological Mineralogy; Springer, 2022; pp. 199–205. [Google Scholar]
  9. Cheng, M.-L.; Matsuoka, M.; Liu, W.; Yamazaki, F. Near-Real-Time Gradually Expanding 3D Land Surface Reconstruction in Disaster Areas by Sequential Drone Imagery. Automation in Construction 2022, 135, 104105. [Google Scholar] [CrossRef]
  10. Dogru, S.; Baptista, R.; Marques, L. Tracking Drones with Drones Using Millimeter Wave Radar. In Iberian Robotics Conference; Springer, 2019; pp. 392–402. [Google Scholar]
  11. Doole, M.; Ellerbroek, J.; Hoekstra, J. Estimation of Traffic Density from Drone-Based Delivery in Very Low Level Urban Airspace. Journal of Air Transport Management 2020, 88, 101862. [Google Scholar] [CrossRef]
  12. Ferris, D.D., Jr.; Currie, N.C. Microwave and Millimeter-Wave Systems for Wall Penetration. In Targets and Backgrounds: Characterization and Representation IV; International Society for Optics and Photonics, 1998; pp. 269–279. [Google Scholar]
  13. Fu, R.; et al. Deep Learning-Based Drone Classification Using Radar Cross Section Signatures at MmWave Frequencies. IEEE Access 2021, 9, 161431–161444. [Google Scholar] [CrossRef]
  14. Fujii, K. Extended Kalman Filter. Refernce Manual 2013, 14. [Google Scholar]
  15. Huang, X.; Cheena, H.; Thomas, A.; Tsoi, J.K.P. Indoor Detection and Tracking of People Using MmWave Sensor. Journal of Sensors 2021, 2021, 1–14. [Google Scholar] [CrossRef]
  16. Jacob, B.; Kaushik, A.; Velavan, P. Autonomous Navigation of Drones Using Reinforcement Learning. In Advances in Augmented Reality and Virtual Reality; Springer, 2022; pp. 159–176. [Google Scholar]
  17. Janakaraj, P.; et al. STAR: Simultaneous Tracking and Recognition through Millimeter Waves and Deep Learning. In 2019 12th IFIP Wireless and Mobile Networking Conference (WMNC); IEEE, 2019; pp. 211–218. [Google Scholar]
  18. Jokanovic, B.; Amin, M.G.; Ahmad, F. Effect of Data Representations on Deep Learning in Fall Detection. In 2016 IEEE Sensor Array and Multichannel Signal Processing Workshop (SAM); IEEE, 2016; pp. 1–5. [Google Scholar]
  19. Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. 1960.
  20. Kanellakis, C.; Nikolakopoulos, G. Survey on Computer Vision for UAVs: Current Developments and Trends. Journal of Intelligent & Robotic Systems 2017, 87, 141–168. [Google Scholar]
  21. Kuhn, H.W. The Hungarian Method for the Assignment Problem. Naval research logistics quarterly 1955, 2, 83–97. [Google Scholar] [CrossRef]
  22. Mafukidze, H.D.; Mishra, A.K.; Pidanic, J.; Francois, S.W.P. Scattering Centers to Point Clouds: A Review of MmWave Radars for Non-Radar-Engineers. IEEE Access 2022. [Google Scholar] [CrossRef]
  23. Mishra, B.; Garg, D.; Narang, P.; Mishra, V. Drone-Surveillance for Search and Rescue in Natural Disaster. Computer Communications 2020, 156, 1–10. [Google Scholar] [CrossRef]
  24. Molchanov, P.; Gupta, S.; Kim, K.; Pulli, K. Short-Range FMCW Monopulse Radar for Hand-Gesture Sensing. In 2015 IEEE Radar Conference (RadarCon); IEEE, 2015; pp. 1491–1496. [Google Scholar]
  25. Molnar, P. Territorial and Digital Borders and Migrant Vulnerability Under a Pandemic Crisis. In Migration and Pandemics; Springer: Cham, 2022; pp. 45–64. [Google Scholar]
  26. Nath, N.D.; Cheng, C.-S.; Behzadan, A.H. Drone Mapping of Damage Information in GPS-Denied Disaster Sites. Advanced Engineering Informatics 2022, 51, 101450. [Google Scholar] [CrossRef]
  27. Palipana, S.; Salami, D.; Leiva, L.A.; Sigg, S. Pantomime: Mid-Air Gesture Recognition with Sparse Millimeter-Wave Radar Point Clouds. Proceedings of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies 2021, 5, 1–27. [Google Scholar] [CrossRef]
  28. Pegoraro, J.; Rossi, M. Real-Time People Tracking and Identification from Sparse Mm-Wave Radar Point-Clouds. IEEE Access 2021, 9, 78504–78520. [Google Scholar] [CrossRef]
  29. Rahman, S.; Robertson, D.A. FAROS-E: A Compact and Low-Cost Millimeter Wave Surveillance Radar for Real Time Drone Detection and Classification. In 2021 21st International Radar Symposium (IRS); IEEE, 2021; pp. 1–6. [Google Scholar]
  30. Rai, P.K.; et al. Localization and Activity Classification of Unmanned Aerial Vehicle Using MmWave FMCW Radars. IEEE Sensors Journal 2021. [Google Scholar] [CrossRef]
  31. Richards, M.; Holm, W.; Scheer, J. Principles of Modern Radar: Basic Principles. Ser. Electromagnetics and Radar. Institution of Engineering and Technology 2010, 6, 47. [Google Scholar]
  32. Rizk, H.; Nishimur, Y.; Yamaguchi, H.; Higashino, T. Drone-Based Water Level Detection in Flood Disasters. International Journal of Environmental Research and Public Health 2022, 19, 237. [Google Scholar] [CrossRef]
  33. Rzewuski, S.; et al. Drone Detectability Feasibility Study Using Passive Radars Operating in WIFI and DVB-T Band; The Institute of Electronic Systems, 2021. [Google Scholar]
  34. Semkin, V.; et al. Drone Detection and Classification Based on Radar Cross Section Signatures. In 2020 International Symposium on Antennas and Propagation (ISAP); IEEE, 2021; pp. 223–224. [Google Scholar]
  35. Sengupta, A.; Jin, F.; Zhang, R.; Cao, S. Mm-Pose: Real-Time Human Skeletal Posture Estimation Using MmWave Radars and CNNs. IEEE Sensors Journal 2020, 20, 10032–10044. [Google Scholar] [CrossRef]
  36. Sharma, N.; Saqib, M.; Scully-Power, P.; Blumenstein, M. SharkSpotter: Shark Detection with Drones for Human Safety and Environmental Protection. In Humanity Driven AI; Springer, 2022; pp. 223–237. [Google Scholar]
  37. Shuai, X.; et al. Millieye: A Lightweight Mmwave Radar and Camera Fusion System for Robust Object Detection. In Proceedings of the International Conference on Internet-of-Things Design and Implementation; 2021; pp. 145–157. [Google Scholar]
  38. Sinhababu, N.; Pramanik, P.K.D. An Efficient Obstacle Detection Scheme for Low-Altitude UAVs Using Google Maps. In Data Management, Analytics and Innovation; Springer, 2022; pp. 455–470. [Google Scholar]
  39. Srigrarom, S.; et al. Multi-Camera Multi-Drone Detection, Tracking and Localization with Trajectory-Based Re-Identification. In 2021 Second International Symposium on Instrumentation, Control, Artificial Intelligence, and Robotics (ICA-SYMP); IEEE, 2021; pp. 1–6. [Google Scholar]
  40. Svanström, F.; Englund, C.; Alonso-Fernandez, F. Real-Time Drone Detection and Tracking With Visible, Thermal and Acoustic Sensors. In 2020 25th International Conference on Pattern Recognition (ICPR); IEEE, 2021; pp. 7265–7272. [Google Scholar]
  41. Texas Instruments. Single-Chip 60-GHz to 64-GHz Intelligent MmWave Sensor Integrating Processing Capability. 2022, 1. [Google Scholar]
  42. Tripathi, S.; Kang, B.; Dane, G.; Nguyen, T. Low-Complexity Object Detection with Deep Convolutional Neural Network for Embedded Systems. In Applications of Digital Image Processing XL; International Society for Optics and Photonics, 2017; 103961M. [Google Scholar]
  43. Wang, S.; et al. Interacting with Soli: Exploring Fine-Grained Dynamic Gesture Recognition in the Radio-Frequency Spectrum. In Proceedings of the 29th Annual Symposium on User Interface Software and Technology; 2016; pp. 851–860. [Google Scholar]
  44. Yang, Y.; et al. Person Identification Using Micro-Doppler Signatures of Human Motions and UWB Radar. IEEE Microwave and Wireless Components Letters 2019, 29, 366–368. [Google Scholar] [CrossRef]
  45. Yoo, L.-S.; et al. Application of a Drone Magnetometer System to Military Mine Detection in the Demilitarized Zone. Sensors 2021, 21, 3175. [Google Scholar] [CrossRef] [PubMed]
  46. Zhao, P.; et al. MID: Tracking and Identifying People with Millimeter Wave Radar. In 2019 15th International Conference on Distributed Computing in Sensor Systems (DCOSS); IEEE, 2019; pp. 33–40. [Google Scholar]
Preprints 76046 g001
Figure 1. In contrast to (A) an optic-based system, (B) the proposed framework is based on mmWave radar that consists of three transmitting and four receiving antennas.
Figure 1. In contrast to (A) an optic-based system, (B) the proposed framework is based on mmWave radar that consists of three transmitting and four receiving antennas.
Preprints 76046 g001
Preprints 76046 g003
Figure 3. The workflow of signal processing and cloud point generation.
Figure 3. The workflow of signal processing and cloud point generation.
Preprints 76046 g003
Preprints 76046 g004
Figure 4. Clustering process input and output.
Figure 4. Clustering process input and output.
Preprints 76046 g004
Preprints 76046 g006
Figure 6. The workflow of the proposed target tracker.
Figure 6. The workflow of the proposed target tracker.
Preprints 76046 g006
Preprints 76046 g007
Figure 7. The radial distance and the angular position of the detected target.
Figure 7. The radial distance and the angular position of the detected target.
Preprints 76046 g007
Preprints 76046 g011
Figure 11. Tracking accuracy results.
Figure 11. Tracking accuracy results.
Preprints 76046 g011
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated