Prerpints.org logo
Preprint
Article

Simulation of the Damage and Failure Characteristics of Coal under True Triaxial Static-Dynamic Loads

Altmetrics

Downloads

102

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

08 June 2023

Posted:

09 June 2023

You are already at the latest version

Alerts
Abstract
The damage evolution rules of coal under true triaxial combined static-dynamic loads are important to understand and reveal the mechanism of rockburst in coal mines. The numerical simulation was carried out using FLAC3D to explore the coupling effect of static and dynamic stress, especially the influence of dynamic load parameters. The results show that the increase of dynamic load amplitude not only makes the plastic zone grow exponentially and shorten the damage development time, but also decreases the residual strength of the coal sample, which leads to a much more violent of the dynamic failure. The stress wave can propagate more stable in the coal sample with the increase of dynamic load frequency and the development time of the plastic zone also show synchronous fluctuating features, and when the frequency is like the intrinsic frequency of the coal sample, the dynamic load has a significant stimulate effect. The static and dynamic loads have different damage effect to the coal sample under true triaxial stress path, the weight decreases in order of the minimum principal stress, the maximum principal, the amplitude of the dynamic load and at last the dynamic stress frequency by the entropy weight method analysis.
Keywords: 
Subject: Engineering  -   Mining and Mineral Processing

1. Introduction

Rockburst, also called coal burst, is among the most frequent dynamic disasters occurring in coal mines across China. According to statistics compiled by The National Mine Safety Administration of China, there are 138 rockburst-prone coal mines under production in 13 provinces (regions) of China and main coal-producing bases have all suffered from rockburst disasters [1]. In recent years, catastrophic accidents induced by rockburst have occurred repeatedly in China, threatening the safety and efficient coal mining and causing severe casualties and economic losses [2,3,4]. The mechanical failure modes of coal are closely related to the stress conditions and stress paths [5,6]. Theoretical research and in-situ microseismic monitoring demonstrate that the failure locations of rockburst are usually not the same with the focus but with a considerable distance which mainly in the range of 150 m and can reach to a maximum of 500 m [7]. The appearance area of rockbusrt mainly located in the roadways ahead the workface about 50 m, where the abutment stress most concentrated, and the coal seam bears biaxial or triaxial stress state. So, the process of rockburst shows a static-dynamic combined loads characteristics [8,9,10,11,12]. Numerous scholars have studied the rockburst mechanism from the perspective of static-dynamic combined loads [13,14,15,16,17,18] and proposed theories including disturbance response theory of rockburst, theory of rockburst induced by superimposed dynamic and static loads, and rockburst initiation theory [19,20,21,22,23].
The damage of coal or rock under true triaxial static and dynamic loads is key to reveal the mechanism of rockburst. Researchers across the world have conducted numerous studies on the mechanical property, damage and failure mechanism of coal and rock under true triaxial stress condition [24,25,26,27,28,29,30,31,32,33,34]. Various triaxial presses have been developed by Mogi [35], Li [17], Wen [36], and Yin [37] et al, and some of these presses have the function of applying dynamic load, which provided convenient conditions for the experiments under complex stress path. On the basis of the laboratory experiments, numerical simulation has also been extensively used to explore the damage and failure of coal or rock material under static and dynamic stress path and more extra information could be obtained [38,39,40,41,42]. Li et al. [43,44,45] simulated rock failure under static and dynamic loading using FDEM as well as FEM code. Zhu et al. [46,47] carried out simulations using RFPA software and pointed out that dynamic disturbance brought about the greater influences on the stability of underground opening with its increasing magnitude and prolonged duration, and the effects of axial static stress and dynamic stress on the damage and failure process of rock were also examined. There have been many achievements in simulations of failure and rockburst of roadway surrounding rock under static–dynamic combined loads, the quasi-dynamic loads were set as sinusoidal waves in most cases and the different roles of the in-situ stress, the direction of the dynamic stress, the distance between the dynamic source and the roadway, the amplitude of the dynamic, etc., were all thoroughly discussed [47,48,49,50,51,52,53]. Li et al. [54] proposed a grain-based discrete element method (GB-DEM) modelling to explore the behaviors of fracturing and damage evolution of rock materials under dynamic loading. Aziznejad et al. [55] reported a numerical investigation to address the responses of jointed rock masses subjected to impact loading using PFC2D model. Gao et al. [56] developed a distinct-element bonded block method to simulate strain bursts, instead of triggering failure by an assumed dynamic disturbance, a seismic event was generated by self-initiated rock mass fracturing. Yang et al. [57] presented stress initialization methods for dynamic numerical simulation of rock mass with high in-situ stress. Li et al. [58] conducted numerical studies on the elastic deformation and the stress field of brittle rocks under harmonic dynamic load, the position on the rock, the frequency and the amplitude of dynamic load, the type of indenter and the loading conditions (static and static-dynamic) were taken into account. Asadi et al. [59] utilized the CA3 bonded particle - finite element computer program to examine the combined influence of loading rate and particle size on the compressive and tensile strengths of rock. Feng et al. [60] investigated the mechanical properties and the cracking behaviors of rock specimens with both parallel and unparallel flaws under different coupled static-dynamic loads. Yang et al. [61] made some suggestion on boundary settings for the seismic dynamic response analysis of rock masses using the numerical manifold method. Resende et al. [62] simulated the interaction of stress waves and rock fractures in a particle micromechanical model.
There are various different sources of dynamic load in coal mines, which form different stress waves. The damage to coal under combinations of dynamic loads with different characteristics and stress in the true triaxial path has not been well studied. This paper focused on the influences of static load and different parameters of dynamic load on the damage of coal under true triaxial path. This research attempts to provide support for revealing the mechanism of rockburst disasters and prevention engineering design for rockburst induced by dynamic load.

2. Test Model and Parameters

2.1. Strength parameters of coal

Zhangshuanglou coal mine located in the city of Xuzhou, Jiangsu Province in China, is a typical kilometer-deep mine, and also encounters rockburst risk during excavation. The coal samples were collected from No. 9 coal seam at a roadway in No. 24 panel with a burial depth of 850 m. The No. 9 coal seam has bursting liability tested based on the national standards of “Methods for test, monitoring and prevention of rock burst-part 2: Classification and laboratory test method on bursting liability of coal”. The results are shown in Table 1. The coal blocks were processed into 16 cuboidal specimens measuring 50 mm × 50 mm × 100 mm. Uniaxial compression tests were conducted on these coal specimens on the MTS electro-hydraulic servo test system to calibrate physical mechanical parameters of the model. 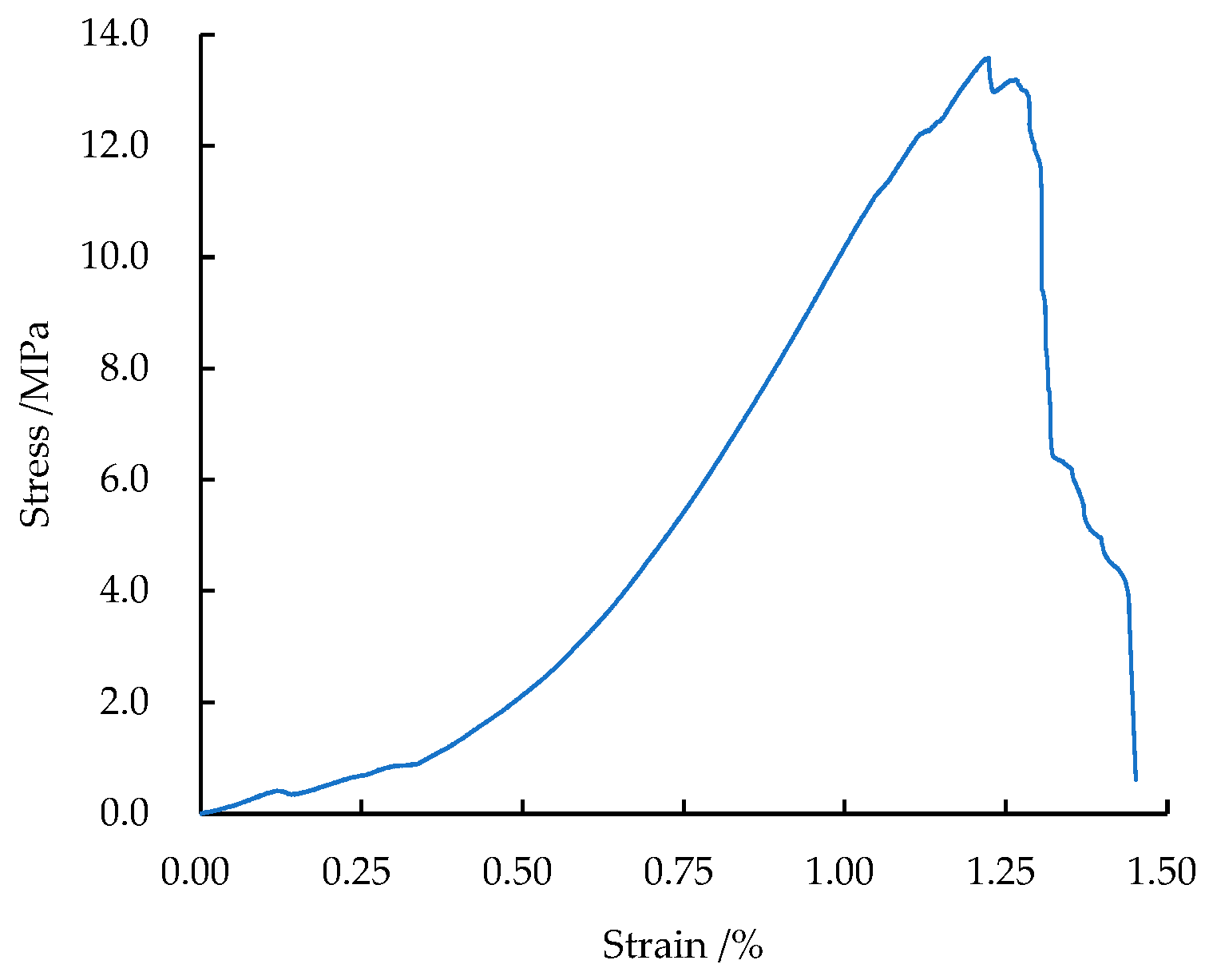The basic results are listed in Table 2 and the stress-strain curve of a typical coal specimen is illustrated in Figure 1.
True triaxial tests were conducted using a test system for dynamic rockburst during coal mining customized by staff at China University of Mining and Technology. The test machine comprises a host, oil source, oil cooler, electric control cabinet, control system, an air gun, hydraulic sub-stations, and supporting accessories (including hydraulic hoses and fixtures), the design structure diagram and physical image are shown in Figure 2. The value ranges of loads applied in three directions are shown as follows: 0 ~ 2500 kN, 0 ~ 1500 kN, and 0 ~ 1500 kN for static loads along the X, Y, and Z-axes. This realized horizontal static servo-motor-controlled loading in three directions and the measurement precision met the national standard required for mechanical testing of rocks. 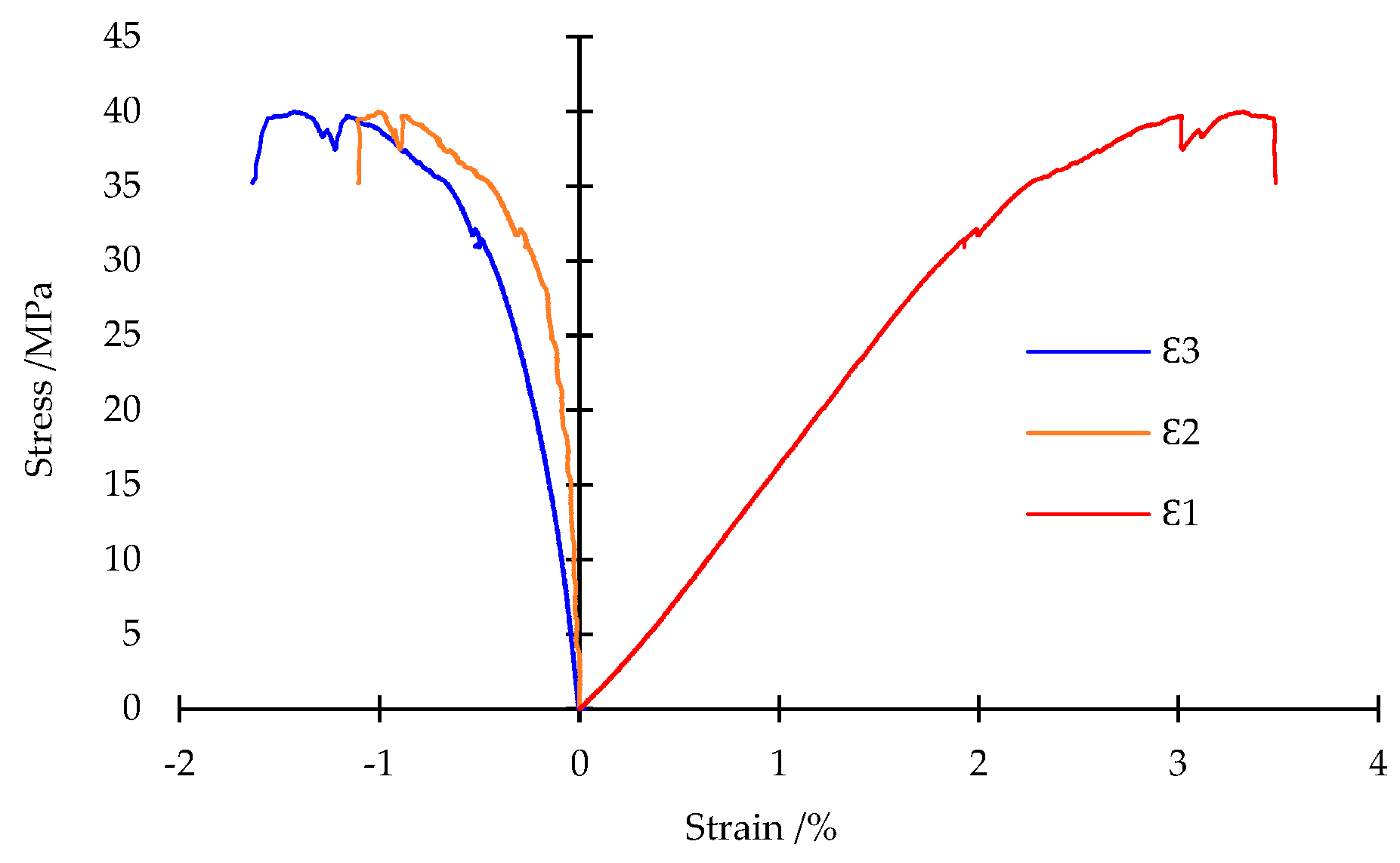A total of six specimens in two groups were tested and triaxial strengths of coal under different confining pressures are listed in Table 3. The triaxial stress-strain curves of typical specimens are shown in Figure 3.
Numerical simulation software FLAC3D was adopted for simulation. The strain softening model was used as the constitutive model. In the strain softening model, the values of cohesion, internal frictional angle, and dilatancy angle of the coal model all change albeit following different trends at yield in the coal model, so it is necessary to calibrate these parameters.
According to previous research [62], the internal frictional angle does not fluctuate to any great extent during the failure process of rocks, so it is kept constant in the present simulation process. The cohesion can be set according to the following piecewise function:
c = − c max − c min ε p ε s + c max ε s ＜ ε p c min ε s ＞ ε p
where, c max and c min separately represent the maximum and minimum cohesion; ε s is the plastic strain in coal, ε p is the strain at which the coal enters the residual deformation stage.
According to previous research results [63], the function describing changes in the dilatancy angle with the plastic strain is shown as Eq. (2):
ψ = 1000 ψ 0.001 ε s ε s ＜ 0.001 ψ 0.01 − ψ 0.001 − ψ 0.01 0.009 ε s 0.001 ≤ ε s ＜ 0.01 ψ 0.01 − ψ 0.01 − ψ 0.03 0.002 ε s 0.01 ≤ ε s ＜ 0.03 ψ 0.03 ε s ＜ 0.001
where, ψ 0.01 , ψ 0.03 , and ψ 0.001 separately correspond to dilatancy angles when the coal has 1%, 3%, and 0.1% of plastic shear deformation.
To simulate the propagation of stress waves in the model, it requires that the grid size Δ l should not exceed 1/8 to 1/10 of the wavelength corresponding to the maximum frequency of waves.
Δ l ≤ ( 1 8 ~ 1 10 ) λ
where, λ is the wavelength corresponding to the maximum frequency, and
λ = C 0 · T = C 0 f
where, C 0 is the average wave velocity (4000 to 6000 m/s in most types of rock); T is the period (s); f is the frequency (Hz).
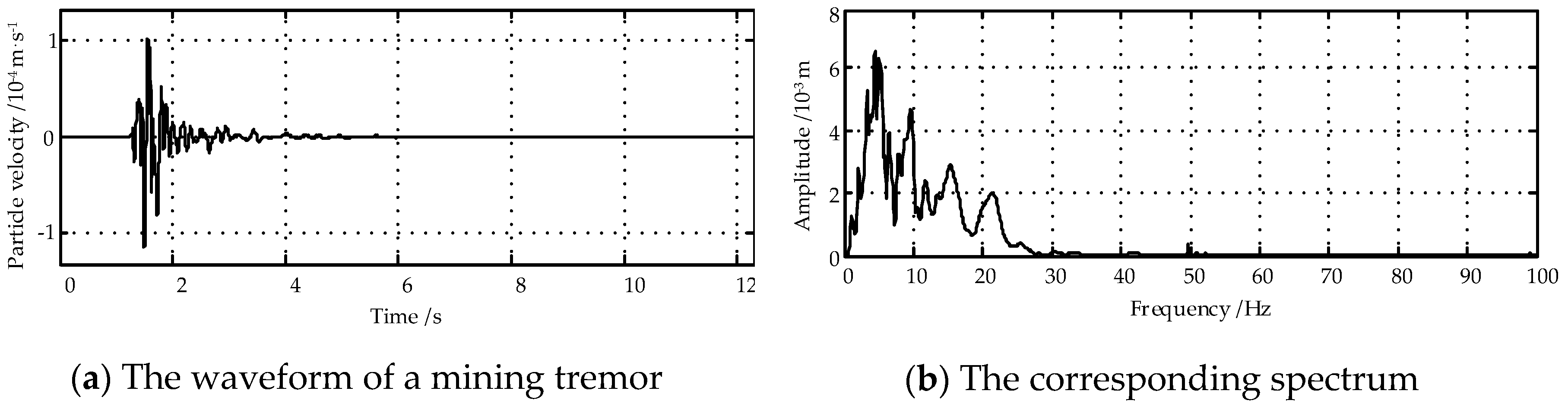
By using a microseismic monitoring system, the frequency of underground dynamic load is found to be lower than 70 Hz, typical waveform is shown in Figure 4. To study damage characteristics of coal at different frequencies, the frequency was set to 5, 20, 40, and 60 Hz in simulation. During numerical simulation, the stress amplitude of dynamic load was generally set to 1 to 10 MPa.
Based on the above analysis, a model measuring 1 m × 1 m × 1 m, containing 20 × 20 × 20 elements (each measuring 5 mm × 5 mm × 5 mm) was established, which met the requirements for precision. The strain softening model was adopted, and the dynamic load was applied to the top face of static boundaries of the model as a sinusoidal function.

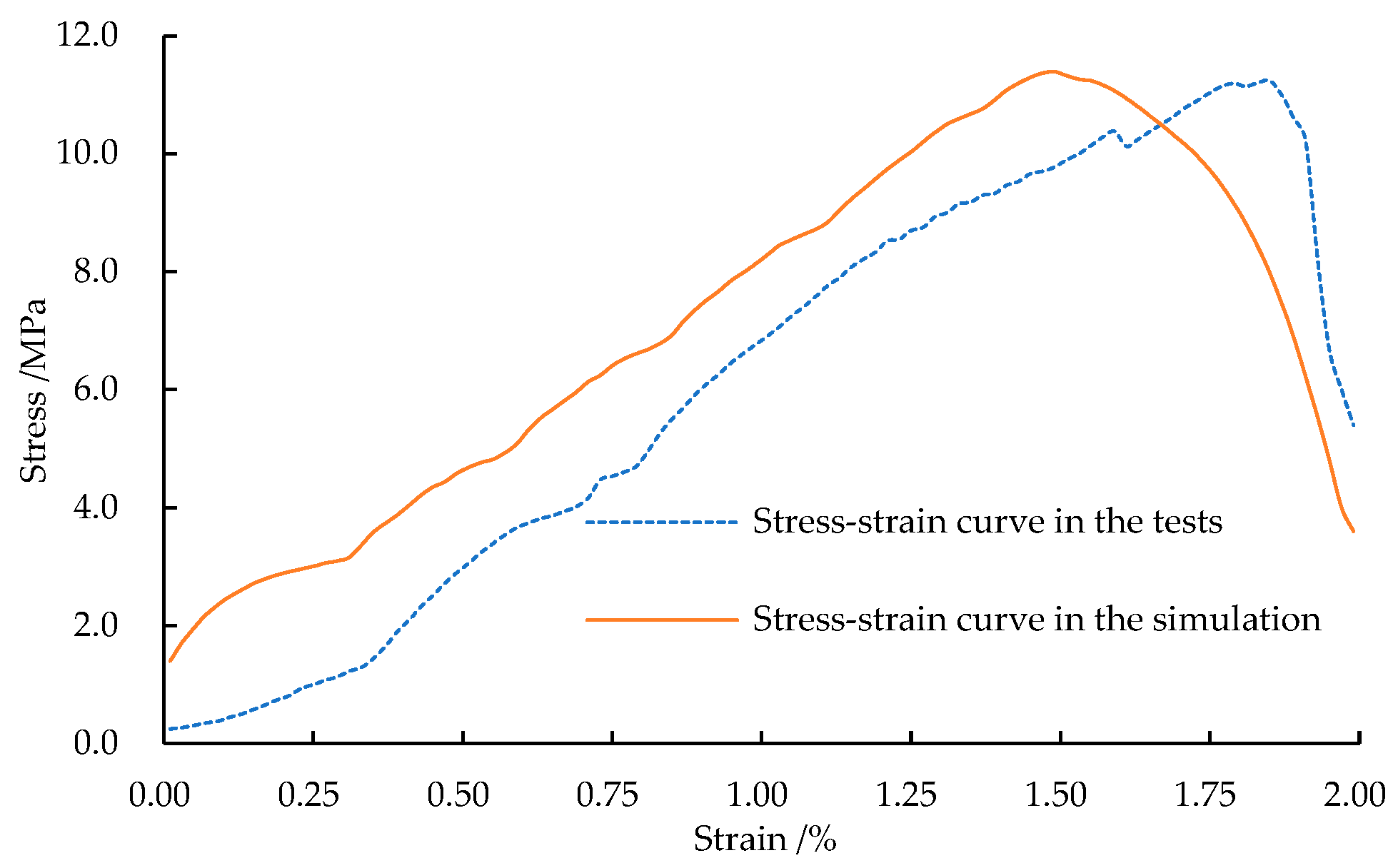
2.2. Model verification

Figure 5 illustrates the stress-strain curves of standard specimens obtained under uniaxial compression in laboratory tests and numerical simulation. The two stress-strain curves macroscopically remain the same shape. The elastic modulus, peak strength, and residual strength obtained in the simulation basically have the same values with those from experiments. The difference lies in that the strain in the numerical simulation is slightly lower than that in laboratory tests which is mainly because there is no compaction stage in the numerical model, so strain induced by compaction is absent in the whole process. The verification results indicate that the model parameters are set appropriately.

2.3. Scheme for the test model

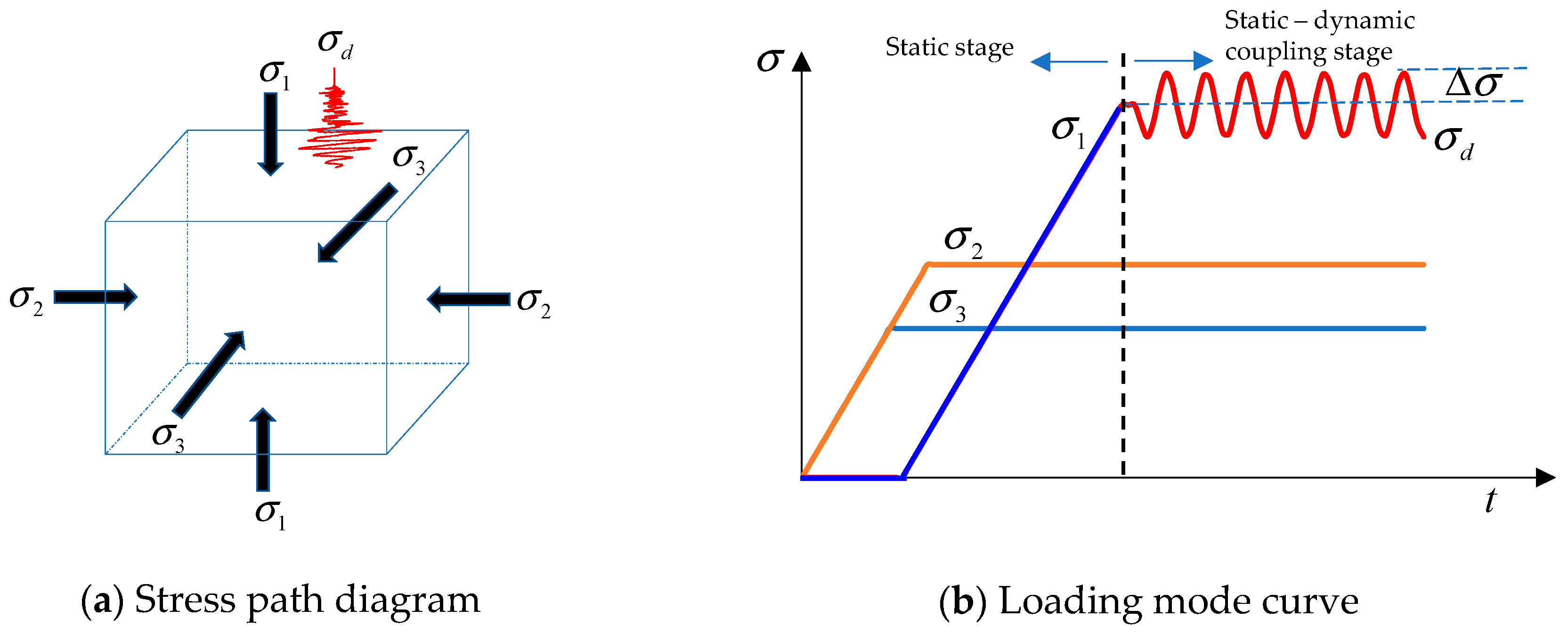
Based on the mechanical properties of coal obtained in the laboratory, the FLAC3D numerical model was adopted to simulate damage and failure trends of coal subjected to true triaxial stress path, as shown in Figure 6. In the research, the static loads parallel and vertical to the direction for applying dynamic load were called the axial static load and static confining pressure, respectively. The test scheme can be described as follows: the initial static load was applied to the model; after computation reached equilibrium, the dynamic load was applied together with axial loading to failure. Three conditions were studied (Table 4), wherein the influences of static loads on damage to coal were mainly studied under Conditions 1 and 2; damage to coal under different parameters of dynamic load was mainly investigated under Condition 3.
In FLAC3D, the fish programming language is used to calculate the volume of plastic zones in the model. The degree of damage is represented by the volume of plastic zones and the damage variable D is expressed as follows:
D = V s n V s z
where V s n is the current volume of plastic zones in the model; V s z denotes the volume of plastic zones in the model after disturbance and failure of the model.

3. Influences of static loads on damage to coal

3.1. Influences of axial static load on damage to coal

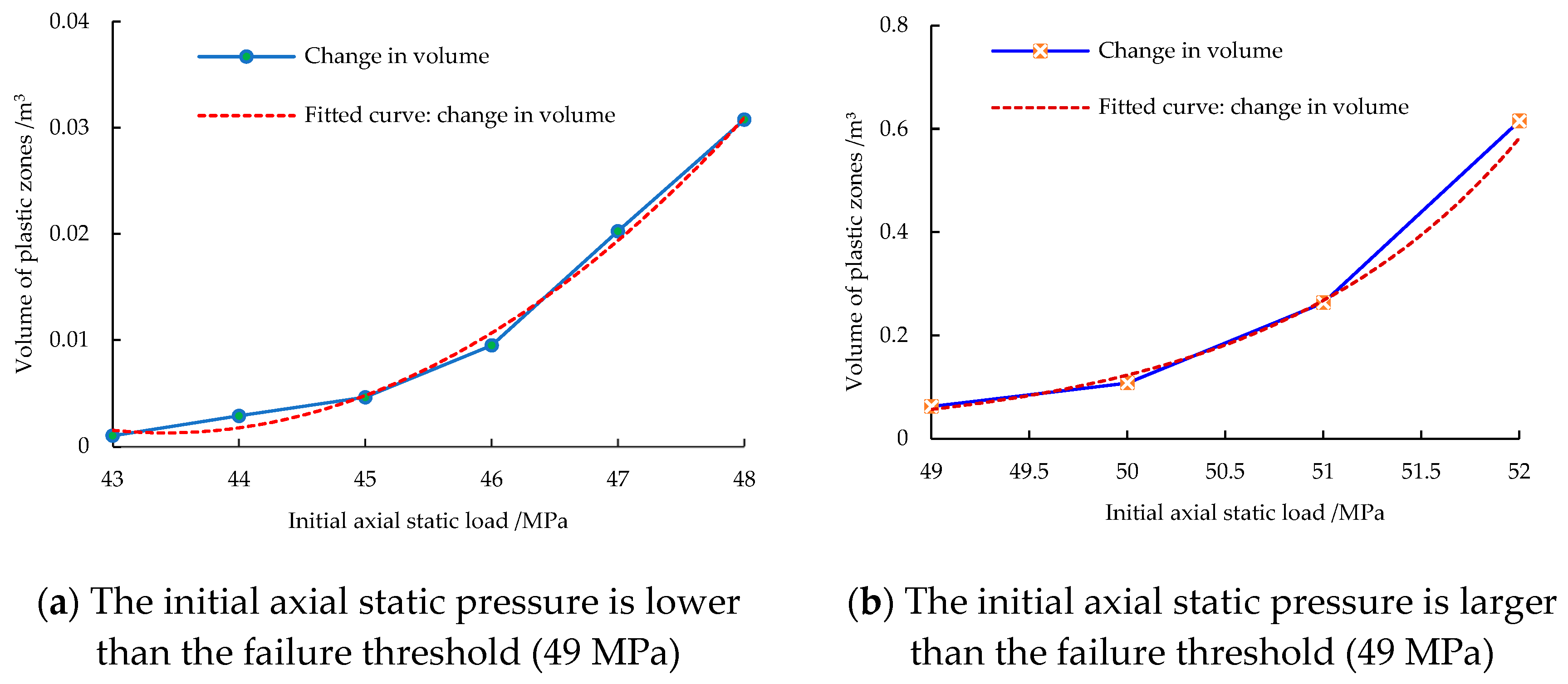
Following Condition 1 in Table 4, different initial axial static pressures from 42 MPa (according to Table 3, which is about 75% of the strength of the coal under the applied confining pressure) to 52 MPa were applied to the coal specimens, followed by application of dynamic load with an amplitude of 4 MPa at a frequency of 20 Hz, under the fixed confining pressures (8 and 12 MPa). Model tests show that when the initial axial static pressure reaches 77% of the compressive strength, namely, 43 MPa, the coal yields and plastic zones develop therein under the dynamic load, while it is not damaged sufficiently to cause failure. Only when the initial axial static pressure reaches 89% of the compressive strength, that is, 49 MPa, the coal is disturbed and damaged under the dynamic load. This indicates that the coal has a yield threshold and a disturbance threshold of the initial axial static pressure under dynamic load, which are separately 43 and 49 MPa under the test conditions.
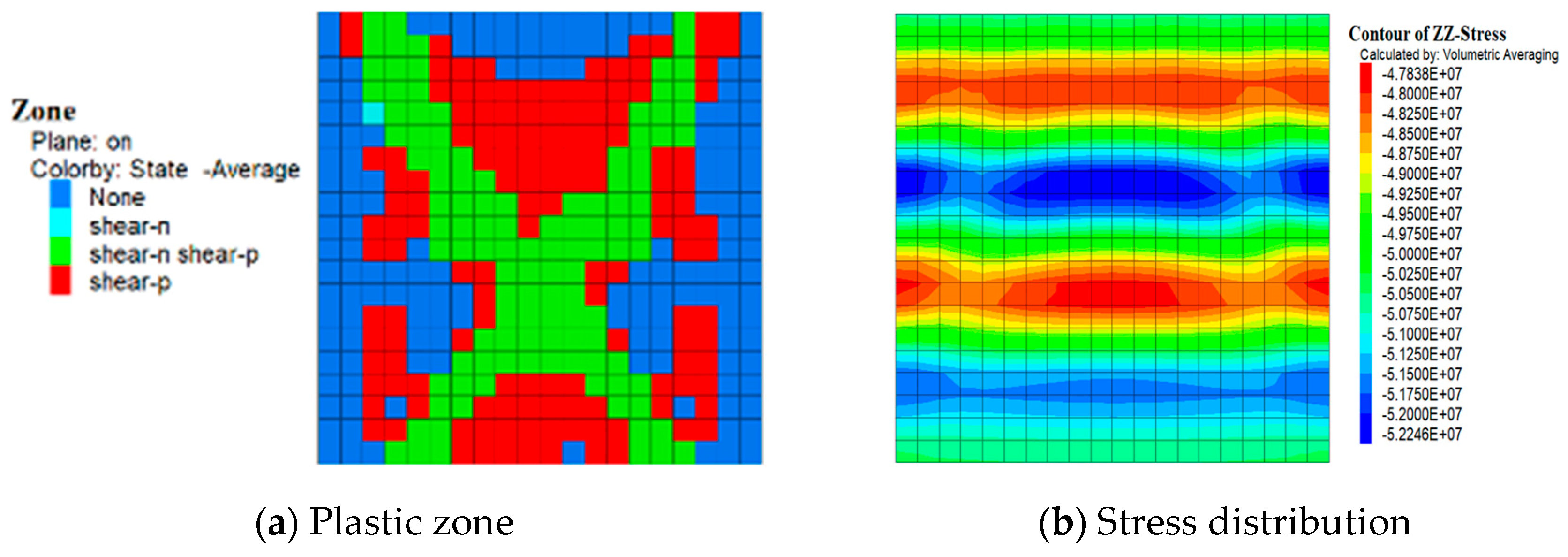
The evolution of plastic zones during dynamic-static loading until failure of the coal under different initial axial static loads is illustrated in Figure 7. As the initial axial static load grows, the volume of plastic zones in the coal after acting the dynamic load also tend to increase. When the initial axial static load is lower than the failure threshold, the fitting curve for the volume of plastic zones is a quadratic function; as the initial axial static load exceeds the failure threshold, the fitting curve becomes an exponential function. That is, total volume and volume increment of plastic zones in the coal both increase when increasing the initial axial static pressure. Typical stress distribution and plastic zones are shown in Figure 8.
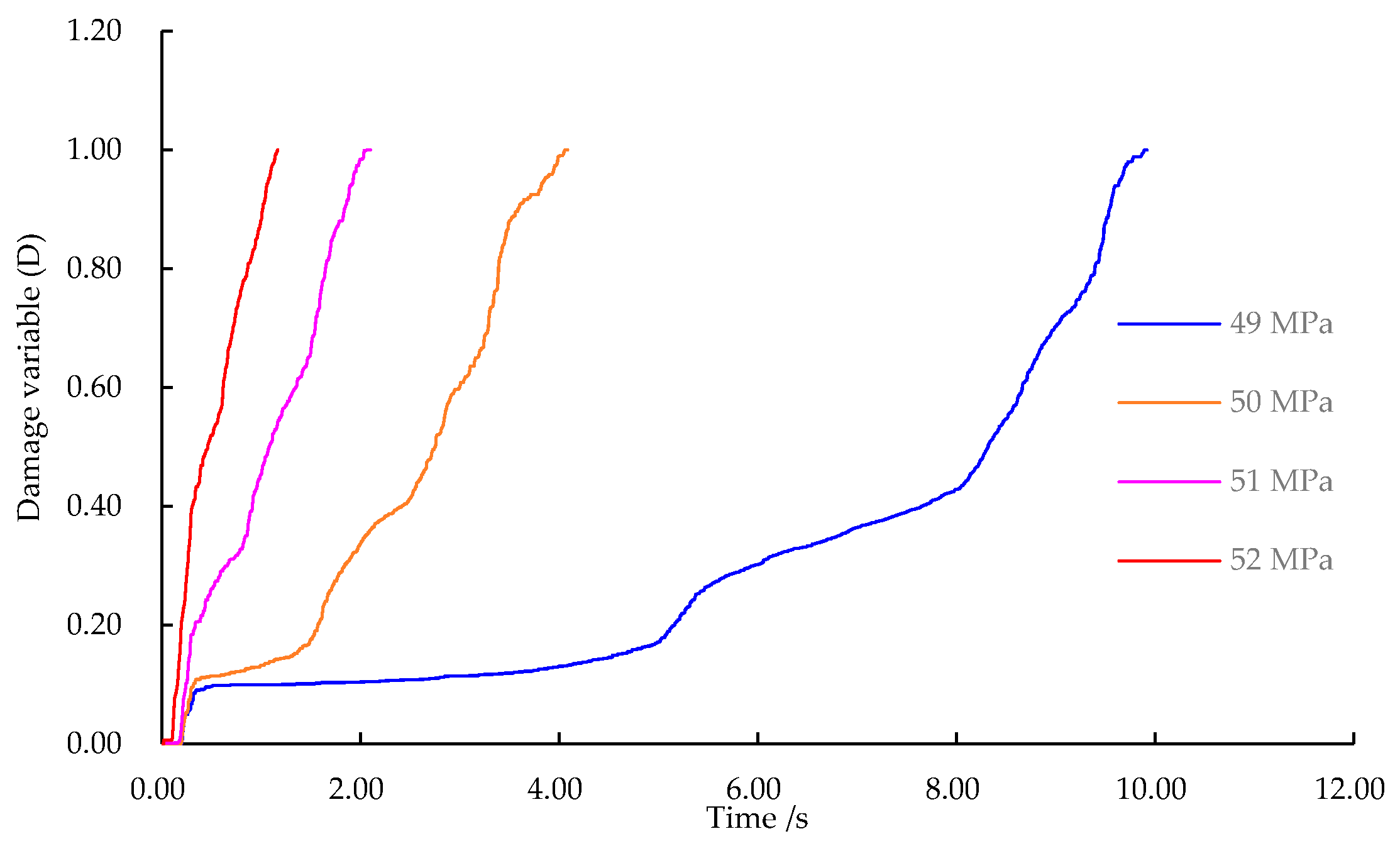
Under different axial static loads, the damage evolution is displayed in Figure 9, the damage variable shows step-like growth when the strain begins to increase. In addition, the larger the initial axial static load is, the more the elastic energy stored in the sample before dynamic load applied, the greater the energy released during failure, and the faster the growth of the damage variable. When the initial axial static pressure is 49 MPa, the growth of the damage variable is 0.08 while reaches 0.4 at 52 MPa. Thereafter, the rate of growth of damage variable gradually decreases as the strain increases. The larger the initial axial static pressure, the smaller the strain at failure in the coal. As the initial axial static load is increased from 49 to 52 MPa, the strain at failure of coal reduces from 0.9% to 0.3%, that is, the dynamic load renders the coal more prone to brittle failure under the high static load.

3.2. Influences of confining pressure on damage to coal

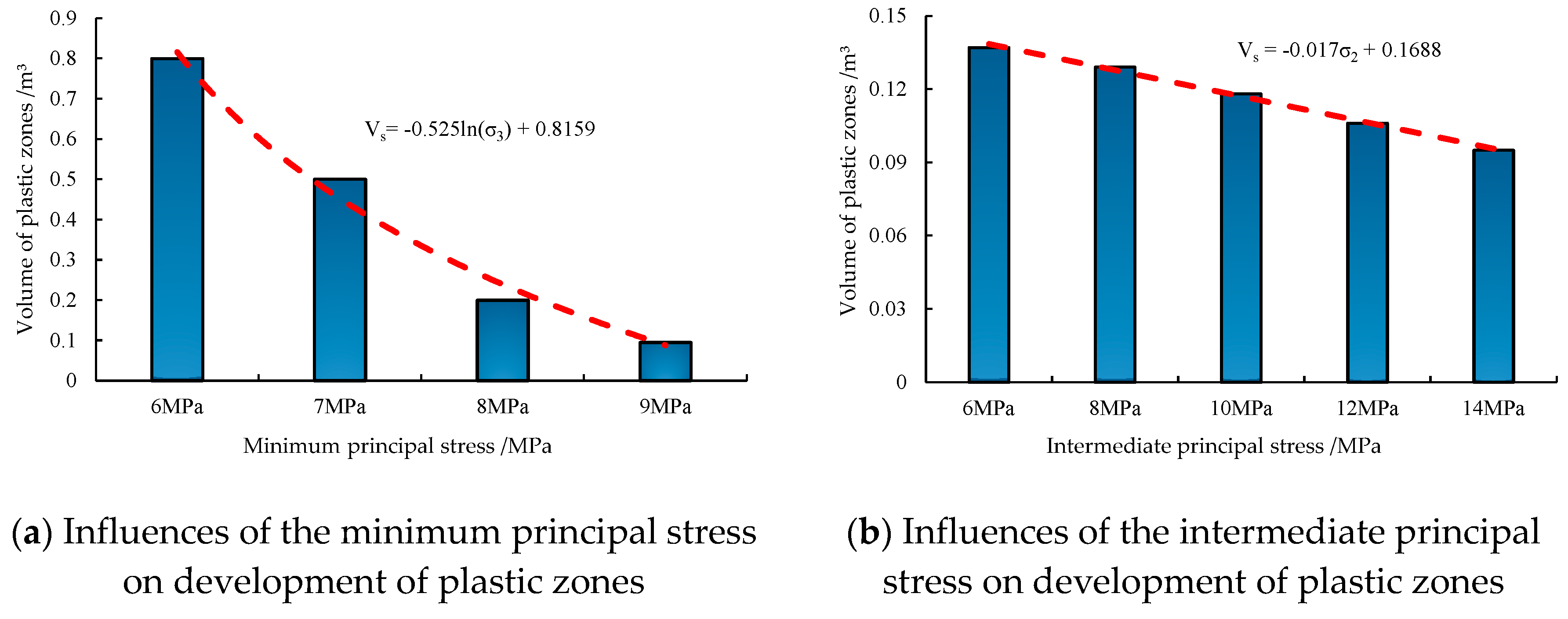
Combinations of different confining pressures were applied along the X and Y-axes of the coal model. The dynamic load was applied on the top face and the yield threshold and failure threshold of the model under different conditions were recorded. Figure 10 illustrates influences of the minimum and intermediate principal stresses on the plastic zones. The figure shows that as the minimum principal stress increases, the damage caused by dynamic load is weakened, appearance time of plastic zones gradually delay, and the fitting curve for the volume of plastic zones is a logarithmic function. This indicates that the minimum principal stress can significantly inhibit the damage caused by the dynamic load. In comparison, as the intermediate principal stress increases, the volume of plastic zones in the coal reduces but the attenuation amplitude is small, the fitting curve is a linear function, and the volume of plastic zones changes uniformly with the intermediate principal stress. Comparison reveals that the damage caused by the dynamic load is weakened ether the minimum or intermediate principal stress on the coal is increased, and the minimum principal stress inhibits the damage to a greater extent.

4. Damage caused by dynamic load

4.1. Influences of the amplitude of dynamic load on damage evolution

Based on aforementioned simulations, coal is damaged much more significantly under dynamic-static combined loading with high static loads. Therefore, when studying influences of dynamic load on damage, the confining pressures were set to 16 and 18 MPa, under which the strength of coal is about 99 MPa, as revealed by numerical model tests. Changes in the amplitude of dynamic load are separately set to 2.5% (2.475 MPa), 5% (4.95 MPa), 7.5% (7.425 MPa), and 10% (9.9 MPa) of the peak strength, while keeping the frequency of dynamic load constant at 20 Hz.
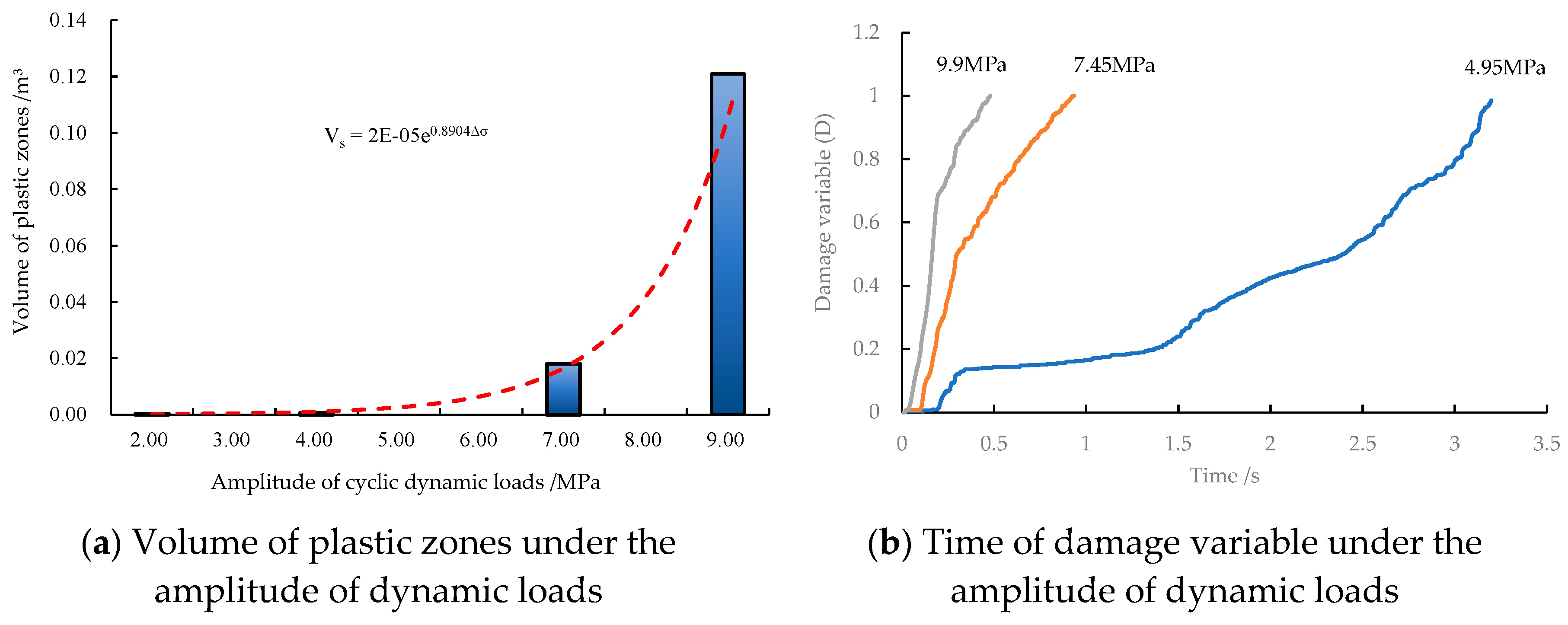
After the same period of dynamic loading with different amplitudes, the variation of plastic zones and its fitting curve are illustrated in Figure 11. With the increasing amplitude of dynamic load, the volume of plastic zones enlarges after the same time, the curve representing the variation of volume of plastic zones with the amplitude is exponential, i.e., when increasing the dynamic load by a given amount, the greater the original amplitude of dynamic load, the more severe the damage of the model. When the amplitude of dynamic load exceeds 7.5% of the compressive strength, the damage caused by the dynamic load is more severe.
The result shows that the larger the amplitude of the dynamic load, the more intense the damage of the coal and the shorter the time required to cause that damage. In the meantime, the development time and volume of plastic zones are interlocked: the larger the volume of the plastic zones, the shorter the development time. The rapid expansion of plastic zones is generally accompanied by a rockburst, therefore, if there are ultra-thick hard roofs and dynamic load sources of large-scale active faults in coal mines, weakening or eliminating dynamic load sources has become the primary measure to prevent rockburst.
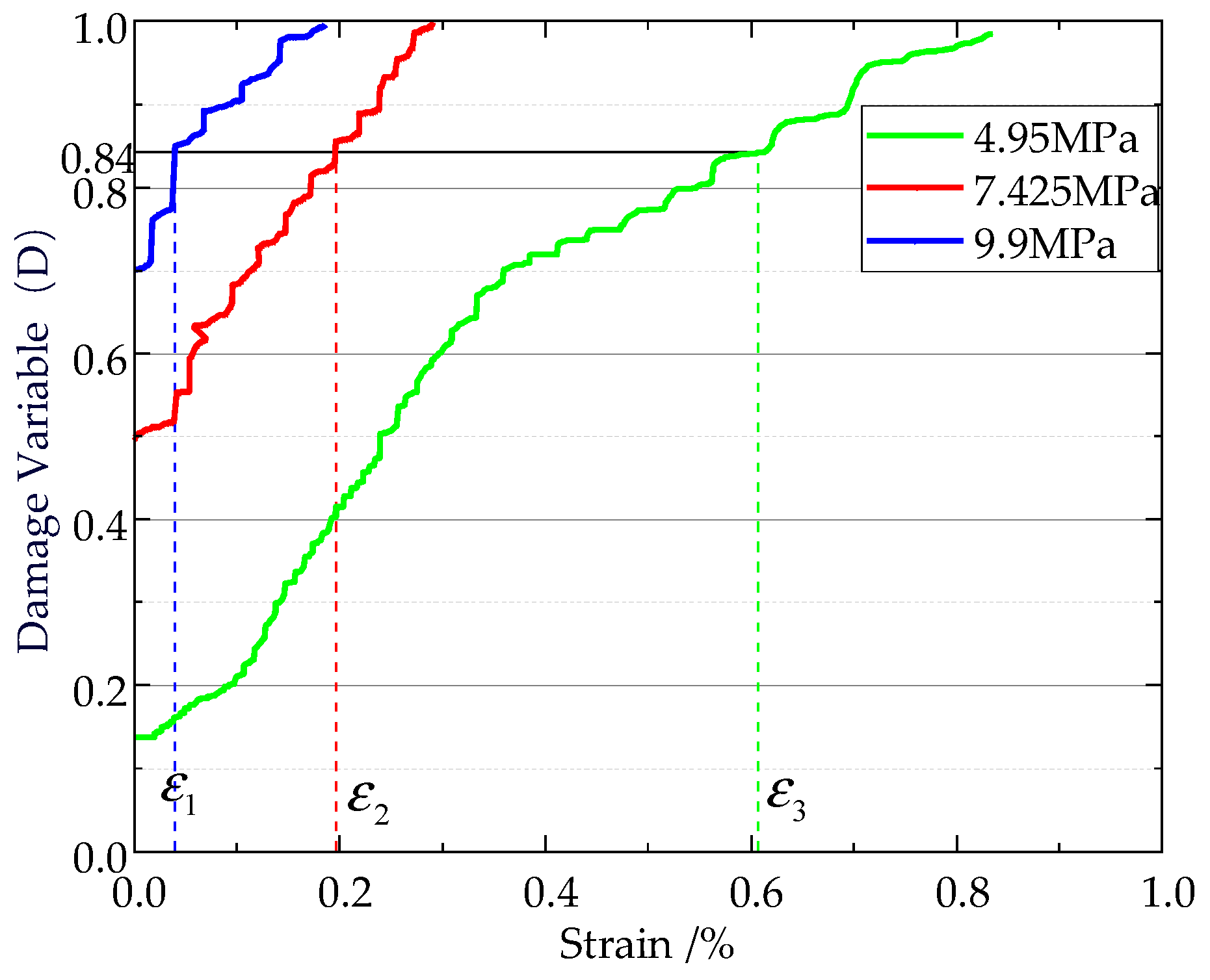
Figure 12 shows the relationships of the damage variable and strain of coal under dynamic load with different amplitudes. The figure reveals that, with increasing amplitude, the initial damage variable constantly increases and the strain corresponding to complete damage decreases. This is because the greater the amplitude is, the more intense the damage effect of dynamic load and the smaller time of dynamic loads that can be borne by the model. The strain when damage factor is about 84% can be used as the residual strain, expressed by ε 1 , ε 2 , and ε 3 . It can be seen that ε 1 < ε 2 < ε 3 , which indicates that the residual strain of coal constantly decreases with increasing amplitude. This is because the strength is reduced by a greater amount and the residual strength is also lower after microstructural units are subjected to the damage caused by the stress waves with greater energy. In the roadway of a coal mine, if the coal seam undergoes rockburst failure triggered by dynamic load, the kinetic energy of coal blocks would increase with the raise of the amplitude of dynamic load, similar rules also evinced by previous research results [64].

4.2. Amplitude attenuation of dynamic load with changes in the frequency of dynamic load

The confining pressures on the model were set to 18 and 16 MPa, while the dynamic load had an amplitude of 4.95 MPa and frequencies of 5, 20, 40, and 60 Hz, and only the frequency of the dynamic load was changed.
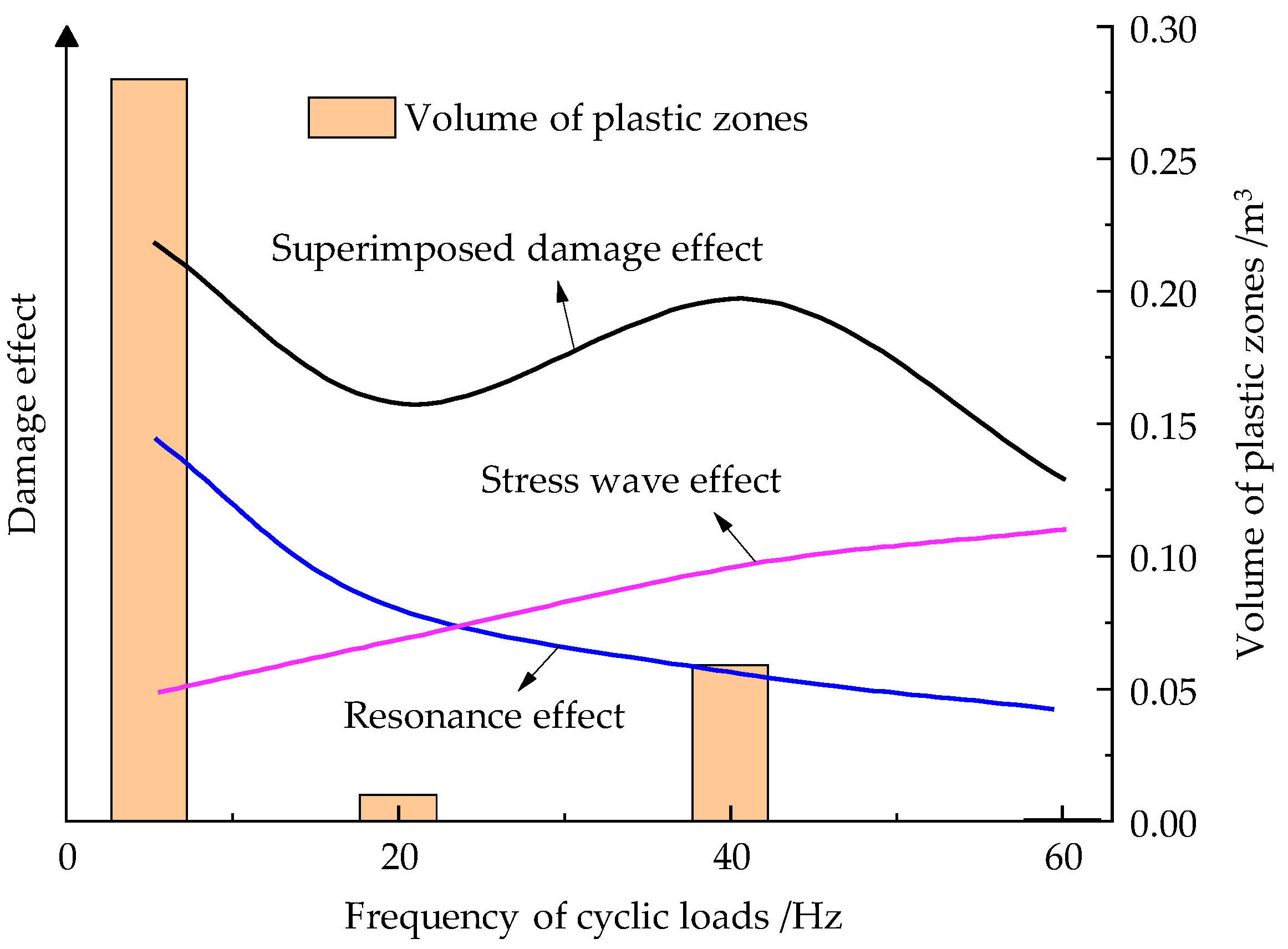
As the frequency increases from 5 to 60 Hz, the volume of plastic zones fluctuates (first decreasing, then increasing, and reducing again), which indicates that the damage under dynamic load fluctuates as the frequency increases. It is worth noting that when the frequency is 5 Hz, the volume of plastic zones is largest. This is because 5 Hz approximates to the intrinsic frequency of the model, at which the dynamic load exerts significant damage and excitation effects on the grid. As a result, static grids in the model change to dynamic ones, accompanied by high speed synchronous vibration, which facilitates the development and propagation of damage in the model.
Figure 13 shows a schematic diagram of the damage caused by dynamic load at different frequencies. The damage caused by resonance is reduced as the frequency increases. This is because the higher the frequency, the greater the difference from the resonant frequency and therefore the weaker the damage and excitation effects induced by resonance. Moreover, the damage caused by stress waves is enhanced with increasing frequency because the higher the frequency, the more stable the stress propagation and the greater the stress on the coal. The superimposed damage effect on coal fluctuates due to the asynchronous variation of the two factors, this explains why the volume of plastic zones in the model (Figure 11) are subject to fluctuations with increasing frequency.
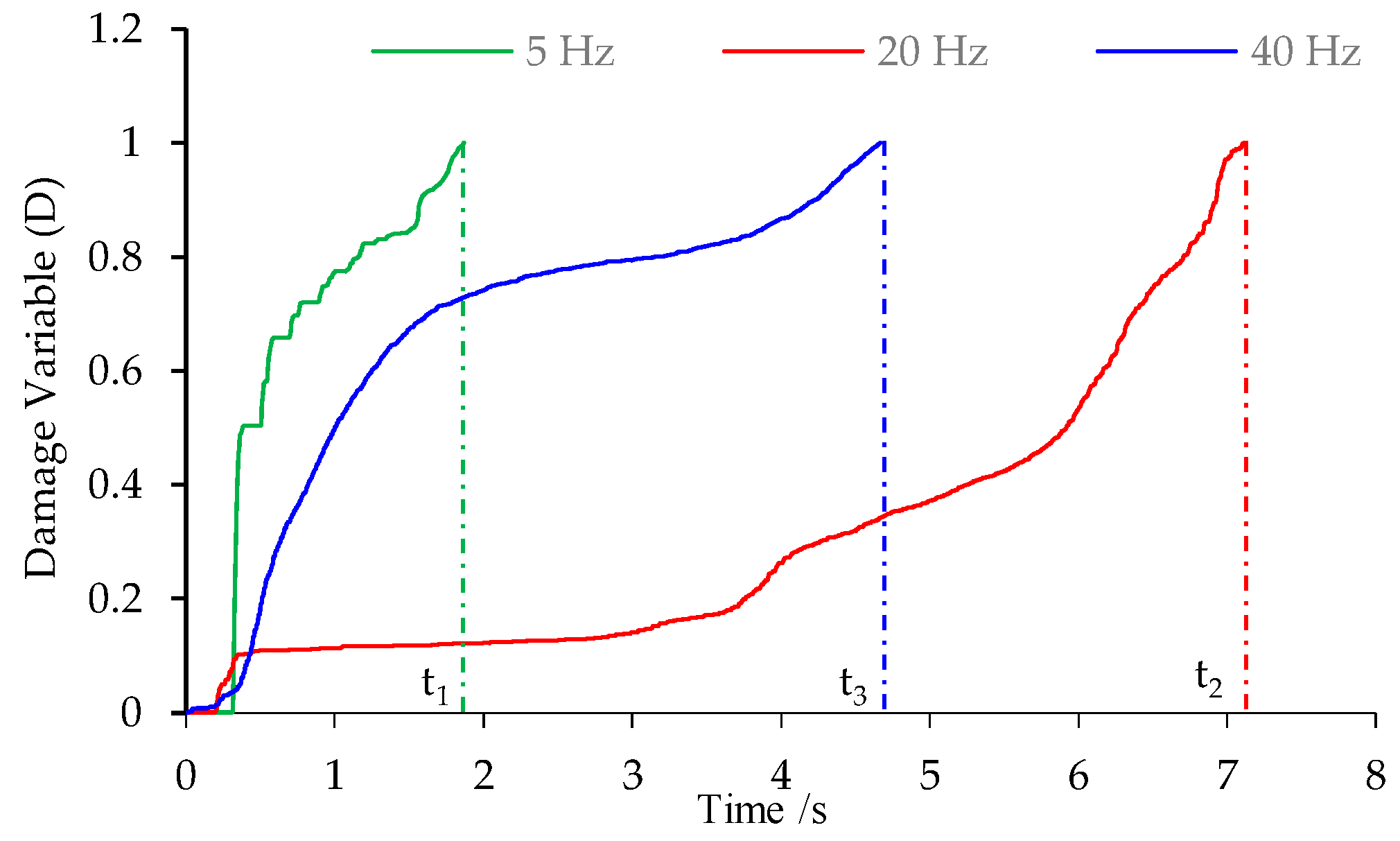
Figure 14 shows the relationship between the damage variable of coal and time at different frequencies: at a frequency of 5 Hz, the curves rise near-vertically in the initial stage, while the slopes remain relatively high even though reduce to some extent in the mid and late stages. This suggests that the plastic zones enlarge explosively in the initial development stage under dynamic load at a frequency of 5 Hz, and remain subject to rapid expansion throughout. At a frequency of 20 Hz, the curves are shallow in the early stage of development, and the slopes are relatively low in the late stage, despite increasing somewhat. This means that plastic zones are mainly formed in the late stage and their development is slow under the frequency of 20 Hz. As the frequency increases to 40 Hz, the damage variable increases in a step-like, manner indicating that plastic zones are mainly formed in the early and late stages. Meanwhile, t 1 , t 2 , and t 3 in the figure correspond to the total development time of plastic zones in the model under dynamic loads at frequencies of 5, 20, and 40 Hz. It can be seen that t 1 < t 3 < t 2 , which suggests that the development time of plastic zones is interlocked with the volume of plastic zones, that is, the larger the plastic zones, the faster their development.
If plastic zones in coal are formed statically or quasi-statically, they will not trigger dynamic rockburst disasters in the surrounding rock; if plastic zones expand and develop rapidly, they may generate rockburst in the coal. The above analysis reveals that when coal is resonant under dynamic load, more plastic zones develop in the coal (and they do so rapidly), providing favorable conditions for the development of impact disasters therein.

4.3. Mechanism of influence of dynamic load parameters on the damage to coal

The damage and failure of coal under static – dynamic combined stress condition are mainly related to the stress state. Assuming that the static principal stress at a certain particle is σ s and the dynamic stress is σ d , expressed as equation (6) and (7), respectively.
σ s = σ s 1 0 0 σ s 2
σ d = σ ( t ) d 1 τ d ( t ) τ d ( t ) σ d 2 ( t )
So, the stress state can be obtained as equation (8),
σ d = σ s 1 + σ ( t ) d 1 τ d ( t ) τ d ( t ) σ s 2 + σ d 2 ( t )
and the principal stress at this point becomes,
σ p 1 , p 2 = σ s 1 + σ s 2 + σ d 1 ( t ) + σ d 2 ( t ) 2 ± [ σ s 1 − σ s 2 + σ d 1 ( t ) − σ d 2 ( t ) ] 2 4 + τ d ( t ) 2
one can obtain the rotation angle for the axis of principal stress under static - dynamic combination as equation (10),
θ p = 1 2 arctan 2 τ d ( t ) σ 1 − σ 3 + σ d 1 ( t ) − σ d 3 ( t )
where τ d t is the shear stress component formed by dynamic load; σ d 1 t and σ d 3 t separately represent normal stress components of dynamic load.
Under dynamic load, the direction of principal stress constantly rotates with time and the change is mainly related to the principal stress difference between static and dynamic loads. The greater and the wider the range of dynamic load, the larger range of rotation of the axes of principal stresses. Therefore, under dynamic-static combined loading, dynamic load plays a role in changing the stress (in terms of both magnitude and direction). When the magnitude of the stress is changed, cracks over a wider range of angles can reach the critical stress and therefore propagate. With the rotation of the principal stress axes, the dominant direction also rotates, so that cracks propagate in more directions, thus damaging the coal. After the action of dynamic load, many cracks in the coal have propagated and their length has increased, the critical stress for propagation decreases. In the meantime, because the increase of damage factor, the critical crack length decreases, therefore, after dynamic load, cracks in the coal will further propagate under static load to damage the coal until dynamic failure. It can be concluded that static loads lay the stress foundation while dynamic load triggers crack propagation under the combination of dynamic and static loads.

5. Weights of different load parameters for damage to coal

5.1. Entropy weight method and its weight assignment process

The simulation results can only determine influences of a single factor on damage to coal, while hard to determine weights of each factor in influencing damage and deterioration of coal. The entropy weight method has been applied to predict rockburst, so it was used to calculate the weights of the minimum principal stress, maximum principal stress, amplitude of dynamic load, and frequency of dynamic load. Due to the low influences of intermediate principal stress on damage to coal, its weight was not calculated.
The first step of the entropy weight method is data normalization. At first, data are classified as either positive or negative indices (factors that facilitate the damage effect of dynamic load are taken as positive factors) and the normalization equation is expressed as
x i j = x i j − min ( x i j ) max ( x i j ) − min ( x i j ) ( Positive   indicators ) x i j = max ( x i j ) − x i j max ( x i j ) − min ( x i j ) ( Negative   indicators )
step 2 entails calculation of the weights of the j t h index under the i t h condition using the following formula:
Y i j = x i j ∑ i m x i j
step 3 entails calculation of the information entropy of indices using the following formula:
e j = − k ∑ i = 1 m Y i j ln Y i j
where m is the number of data sets used for assessment; k is expressed as follows:
k = 1 / ln m
step 4 entails calculation of the redundancy of information entropy using the following formula:
d j = 1 − e j
step 5 entails calculation of the weights of indices using the following formula:
W j = d j / ∑ j = 1 n d j
where n represents the number of indices.

5.2. Weight calculation results

A total of 24 data sets at failure of the established model due to dynamic load were selected and the aforementioned formulae were used to calculate weights using the entropy weight method, as shown in Table 5.
Table 5 shows that various factors are listed in a descending order as the minimum principal stress, maximum principal stress, amplitude of dynamic load, and frequency of dynamic load according to their weights. When reserving one decimal fraction, their weights are 29.1%, 28.9%, 24.3%, and 17.7%, respectively. The weights of the minimum and maximum principal stresses differ slightly. This indicates that although the vibration effect of dynamic load may exacerbate the damage, the most important factor remains the static load. Damage caused by dynamic load is significant or not determined whether it exceed the failure threshold. And the threshold values are also to a large extent determined by values of the confining pressure and axial static load. Therefore, the static load has a greater weight in terms of its damaging effect on coal. The research shows that altering the frequency of dynamic load will cause fluctuating changes in the damaging effect. However, it is difficult to control the natural frequency and predict frequencies of load sources in practice. Considering this, the following measures were proposed to inhibit rockburst induced by superimposed dynamic and static loads:
1) The measures to prevent rockburst should be prioritized as follows: increasing the minimum principal stress, reducing the maximum principal stress, and decreasing the amplitude of dynamic load;
2) Dynamic load induced rockburst can be avoided by either effective stress relief to reduce abutment pressures on surrounding rocks or reasonable support to increase the minimum principal stress on the surrounding rock.
For artificial dynamic load sources including excavation and blasting, measures including decelerating the rate of mining of coal seams and using low-charge multi-hole blasting can be used to reduce the rockburst risk.

6. Discussion and Conclusion

1) The larger the initial axial static load (the maximum principal stress), the faster the increase in the damage variable under dynamic load and the greater the tendency to brittle failure. The confining pressures (intermediate and minimum principal stresses) inhibit the dynamic disturbance to the coal.
2) With increasing amplitude of dynamic load, the volume of plastic zones in coal grows exponentially while the residual strength of the coal constantly decreases, which would increase the risk of rockburst and enhance the intensity of a rockburst.
3) The damage and deterioration effects of dynamic load on coal fluctuate with the rising frequency. In addition, when the dynamic load is applied to coal to induce resonance, the damage variable increases in a quasi-linear manner with time: dynamic load exerts the strongest damage, and is most likely to induce a rockburst.
4) Under dynamic load, the time taken for the development of plastic zones is interlocked with the volume of plastic zones, that is, the greater the volume of the plastic zones, the faster their development.
5) For the minimum principal stress, maximum principal stress, amplitude of dynamic load, and frequency of dynamic load, their weights on the deterioration and damage effects on coal decrease in succession. Increasing the confining pressure on the rock surrounding the roadways and reducing the abutment pressure can prevent impact failure of the rock surrounding a roadway.

Author Contributions

Conceptualization, Hu He; methodology, Siyuan Gong; data curation, Xuwei Li; software, Zonglong Mu. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the State Key Research Development Program of China (Grant No. 2022YFC3004605), the National Natural Science Foundation of China (No. 51974302; 52274147) and the Fundamental Research Funds for the Central Universities (No. 2013QNB30).

Data Availability Statement

The data used for conducting classifications are available from the corresponding author upon request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Dou, L.M.; Tian, X.X.; Cao, A.Y.; Gong, S.Y.; He, H.; He, J.; Cai, W.; Li, X.W. Present situation and problems of coal mine rock burst prevention and control in China. Journal of China Coal Society. 2022, 47, 152–171. [Google Scholar]
  2. Zhang, C.; Canbulat, I.; Hebblewhite, B.; Ward, C.R. Assessing coal burst phenomena in mining and insights into directions for future research. Int. J. Coal Geol. 2017, 179, 28–44. [Google Scholar] [CrossRef]
  3. Wu, M.; Ye, Y.; Wang, Q.; Hu, N. Development of Rockburst Research: A Comprehensive Review. Applied Sciences. 2022, 12, 974. [Google Scholar] [CrossRef]
  4. Yuan, L. Risk identification, monitoring and early warning of typical coal mine dynamic disasters during the 13th Five-Year Plan period. Journal of Mining Science and Technology, 2021, 6, 1–8. [Google Scholar]
  5. He, M.; Ren, F.; Liu, D. Rockburst mechanism research and its control. Int. J. Min. Sci. Technol. 2018, 28, 829–837. [Google Scholar] [CrossRef]
  6. Xie, H.; Lu, J.; Li, C.; Li, M.; Gao, M. Experimental study on the mechanical and failure behaviors of deep rock subjected to true triaxial stress: A review. Int J Min Sci Techno 2022, 32, 915–950. [Google Scholar] [CrossRef]
  7. He, H.; Dou, L.; Gong, S.; He, J.; Zheng, Y.; Zhang, X. Microseismic and electromagnetic coupling method for coal bump risk assessment based on dynamic static energy principles. Safety Sci 2019, 114, 30–39. [Google Scholar] [CrossRef]
  8. Alexeev, A.D.; Revva, V.N.; Alyshev, N.A.; Zhitlyonok, D.M. True triaxial loading apparatus and its application to coal outburst prediction. Int J Coal Geol 2004, 58, 245–250. [Google Scholar] [CrossRef]
  9. Du, K.; Tao, M.; Li, X.; Zhou, J. Experimental Study of Slabbing and Rockburst Induced by True-Triaxial Unloading and Local Dynamic Disturbance. Rock Mech Rock Eng 2016, 49, 3437–3453. [Google Scholar] [CrossRef]
  10. Li, X.; Gong, F.; Tao, M.; Dong, L.; Du, K.; Ma, C.; Zhou, Z.; Yin, T. Failure mechanism and coupled static-dynamic loading theory in deep hard rock mining: A review. J Rock Mech Geotech 2017, 9, 767–782. [Google Scholar] [CrossRef]
  11. Weng, L.; Huang, L.; Taheri, A.; Li, X. Rockburst characteristics and numerical simulation based on a strain energy density index: A case study of a roadway in Linglong gold mine, China. Tunn Undergr Sp Tech 2017, 69, 223–232. [Google Scholar] [CrossRef]
  12. Ren, F.; Zhu, C.; He, M.; Shang, J.; Feng, G.; Bai, J. Characteristics and Precursor of Static and Dynamic Triggered Rockburst: Insight from Multifractal. Rock Mech Rock Eng. 2023, 56, 1945–1967. [Google Scholar] [CrossRef]
  13. Ma, Z.; Yan, P.; Cheng, S.; Gong, P.; Qi, F.; Wang, J. Experimental study of the dynamic mechanical responses and failure characteristics of coal under true triaxial confinements. Int J Min Sci Techno 2023. [CrossRef]
  14. Liu, C.; Zhao, G.; Xu, W.; Meng, X.; Liu, Z.; Cheng, X.; Lin, G. Experimental study on failure characteristics of single-sided unloading rock under different intermediate principal stress conditions. Int J Min Sci Techno 2023, 33, 275–287. [Google Scholar] [CrossRef]
  15. Zhou, Y.; Sheng, Q.; Li, N.; Fu, X. The Dynamic Mechanical Properties of a Hard Rock Under True Triaxial Damage-Controlled Dynamic Cyclic Loading with Different Loading Rates: A Case Study. Rock Mech Rock Eng 2022, 55, 2471–2492. [Google Scholar] [CrossRef]
  16. Deng, J. Analytical and numerical investigations on pillar rockbursts induced by triangular blasting waves. Int J Rock Mech Min 2021, 138, 104518. [Google Scholar] [CrossRef]
  17. Li, X.; Gong, F. Research progress and prospect of deep mining rock mechanics based on coupled static-dynamic loading testing. Journal of China Coal Society. 2021, 46, 846–866. [Google Scholar]
  18. Feng, X.; Ding, Z.; Ju, Y.; Zhang, Q.; Ali, M. “Double Peak” of Dynamic Strengths and Acoustic Emission Responses of Coal Masses Under Dynamic Loading. Nat Resour Res. 2022, 31, 1705–1720. [Google Scholar] [CrossRef]
  19. Dou, L.; Bai, J.; Li, X.; He, H. Study on prevention and control technology of rockburst disaster based on theory of dynamic and static load. Coal Science and Technology. 2018, 46, 1–8. [Google Scholar]
  20. Cai, W.; Dou, L.; Si, G.; Hu, Y. Fault-Induced Coal Burst Mechanism under Mining-Induced Static and Dynamic Stresses. Engineering. 2021, 7, 687–700. [Google Scholar] [CrossRef]
  21. Zhou, Z.; Cai, X.; Li, X.; Cao, W.; Du, X. Dynamic Response and Energy Evolution of Sandstone Under Coupled Static–Dynamic Compression: Insights from Experimental Study into Deep Rock Engineering Applications. Rock Mech Rock Eng. 2020, 53, 1305–1331. [Google Scholar] [CrossRef]
  22. Wang, C.; Cao, A.; Zhang, C.; Canbulat, I. A New Method to Assess Coal Burst Risks Using Dynamic and Static Loading Analysis. Rock Mech Rock Eng. 2020, 53, 1113–1128. [Google Scholar] [CrossRef]
  23. Cai, W.; Bai, X.; Si, G.; Cao, W.; Gong, S.; Dou, L. A Monitoring Investigation into Rock Burst Mechanism Based on the Coupled Theory of Static and Dynamic Stresses. Rock Mech Rock Eng. 2020, 53, 5451–5471. [Google Scholar] [CrossRef]
  24. Haimson, B. True Triaxial Stresses and the Brittle Fracture of Rock. Pure Appl Geophys 2006, 163, 1101–1130. [Google Scholar] [CrossRef]
  25. Alexeev, A.D.; Revva, V.N.; Bachurin, L.L.; Prokhorov, I.Y. The effect of stress state factor on fracture of sandstones under true triaxial loading. Int J Fracture 2008, 149, 1–10. [Google Scholar] [CrossRef]
  26. Lee, H.; Haimson, B.C. True triaxial strength, deformability, and brittle failure of granodiorite from the San Andreas Fault Observatory at Depth. Int J Rock Mech Min 2011, 48, 1199–1207. [Google Scholar] [CrossRef]
  27. Kwaśniewski, M. Comments on the ISRM Suggested Method “A Failure Criterion for Rocks Based on True Triaxial Testing”. Rock Mech Rock Eng 2013, 46, 917–919. [Google Scholar] [CrossRef]
  28. Baizhanov, B.; Katsuki, D.; Tutuncu, A.N.; Mese, A.I. Experimental Investigation of Coupled Geomechanical, Acoustic, and Permeability Characterization of Berea Sandstone Using a Novel True Triaxial Assembly. Rock Mech Rock Eng 2019, 52, 2491–2503. [Google Scholar] [CrossRef]
  29. Liu, K.; Zhang, Q.B.; Wu, G.; Li, J.C.; Zhao, J. Dynamic Mechanical and Fracture Behaviour of Sandstone Under Multiaxial Loads Using a Triaxial Hopkinson Bar. Rock Mech Rock Eng 2019, 52, 2175–2195. [Google Scholar] [CrossRef]
  30. Shirani Faradonbeh, R.; Taheri, A.; Ribeiro E Sousa, L.; Karakus, M. Rockburst assessment in deep geotechnical conditions using true-triaxial tests and data-driven approaches. Int J Rock Mech Min 2020, 128, 104279. [Google Scholar] [CrossRef]
  31. Minaeian, V.; Dewhurst, D.N.; Rasouli, V. An Investigation on Failure Behaviour of a Porous Sandstone Using Single-Stage and Multi-stage True Triaxial Stress Tests. Rock Mech Rock Eng 2020, 53, 3543–3562. [Google Scholar] [CrossRef]
  32. Duan, M.; Jiang, C.; Yin, W.; Yang, K.; Li, J.; Liu, Q. Experimental study on mechanical and damage characteristics of coal under true triaxial cyclic disturbance. Eng Geol 2021, 295, 106445. [Google Scholar] [CrossRef]
  33. He, M.; Ren, F.; Liu, D.; Zhang, S. Experimental Study on Strain Burst Characteristics of Sandstone Under True Triaxial Loading and Double Faces Unloading in One Direction. Rock Mech Rock Eng 2021, 54, 149–171. [Google Scholar] [CrossRef]
  34. Meng, Q.; Liu, J.; Ren, L.; Pu, H.; Chen, Y. Experimental Study on Rock Strength and Deformation Characteristics Under Triaxial Cyclic Loading and Unloading Conditions. Rock Mech Rock Eng 2021, 54, 777–797. [Google Scholar] [CrossRef]
  35. Mogi, K. How I developed a true triaxial rock testing machine. In TRUE TRIAXIAL TESTING OF ROCKS, Kwasniewski, M.; Li, X.; Takahashi, M., Eds. International Workshop on the True Triaxial Testing of Rocks (TTT), 2012; Vol. 4, pp 139-157.
  36. Wen, Z.; Huang, J.; Jiang, Y.; Zhu, Z.; Xiao, P. Development and experiment of a coupled static-dynamic cyclic loading test system. Journal of Central South University (Science and Technology). 2021, 52, 2817–2827. [Google Scholar]
  37. Yin, G.; Li, M.; Xu, J.; Wang, W.; Li, W.; Li, X.; Song, Z.; Deng, B. A New Multi-Functional True Triaxial Fluid-Solid Coupling Experiment System and Its Application. Chinese Journal of Rock Mechanics and Engineering. 2015, 34, 2436–2445. [Google Scholar]
  38. Tao, M.; Li, X.; Wu, C. 3D numerical model for dynamic loading-induced multiple fracture zones around underground cavity faces. Comput Geotech 2013, 54, 33–45. [Google Scholar] [CrossRef]
  39. Li, X.; Weng, L. Numerical investigation on fracturing behaviors of deep-buried opening under dynamic disturbance. Tunn Undergr Sp Tech 2016, 54, 61–72. [Google Scholar] [CrossRef]
  40. Yoshida, S. Numerical Simulations of Earthquake Triggering by Dynamic and Static Stress Changes Based on a Revised Friction Law. Journal of Geophysical Research: Solid Earth 2018, 123, 4109–4122. [Google Scholar] [CrossRef]
  41. Wu, X.; Jiang, L.; Xu, X.; Guo, T.; Zhang, P.; Huang, W. Numerical analysis of deformation and failure characteristics of deep roadway surrounding rock under static-dynamic coupling stress. J Cent South Univ 2021, 28, 543–555. [Google Scholar] [CrossRef]
  42. Foroutan, T.; Mirghasemi, A.A. Use of CFD-DEM to evaluate the effect of intermediate stress ratio on the undrained behaviour of granular materials. Adv Powder Technol 2022, 33, 103507. [Google Scholar] [CrossRef]
  43. Li, X.; Weng, L. Numerical investigation on fracturing behaviors of deep-buried opening under dynamic disturbance. Tunn Undergr Sp Tech 2016, 54, 61–72. [Google Scholar] [CrossRef]
  44. Li, X.; Feng, F.; Li, D. Numerical simulation of rock failure under static and dynamic loading by splitting test of circular ring. Eng Fract Mech 2018, 188, 184–201. [Google Scholar] [CrossRef]
  45. Weng, L.; Wu, Z.; Li, X. Mesodamage Characteristics of Rock with a Pre-cut Opening Under Combined Static–Dynamic Loads: A Nuclear Magnetic Resonance (NMR) Investigation. Rock Mech Rock Eng 2018, 51, 2339–2354. [Google Scholar] [CrossRef]
  46. Zhu, W.C.; Li, Z.H.; Zhu, L.; Tang, C.A. Numerical simulation on rockburst of underground opening triggered by dynamic disturbance. Tunn Undergr Sp Tech 2010, 25, 587–599. [Google Scholar] [CrossRef]
  47. Zhu, W.C.; Bai, Y.; Li, X.B.; Niu, L.L. Numerical simulation on rock failure under combined static and dynamic loading during SHPB tests. Int J Impact Eng 2012, 49, 142–157. [Google Scholar] [CrossRef]
  48. Zhou, X.; Zhang, D.; Nowamooz, H.; Jiang, C.; Ye, C. Investigation on Damage and Failure Mechanisms of Roadway Surrounding Rock Triggered by Dynamic–Static Combined Loads. Rock Mech Rock Eng 2022, 55, 5639–5657. [Google Scholar] [CrossRef]
  49. Yang, J.H.; Yao, C.; Jiang, Q.H.; Lu, W.B.; Jiang, S.H. 2D numerical analysis of rock damage induced by dynamic in-situ stress redistribution and blast loading in underground blasting excavation. Tunn Undergr Sp Tech 2017, 70, 221–232. [Google Scholar] [CrossRef]
  50. Wu, X.; Jiang, L.; Xu, X.; Guo, T.; Zhang, P.; Huang, W. Numerical analysis of deformation and failure characteristics of deep roadway surrounding rock under static-dynamic coupling stress. J Cent South Univ 2021, 28, 543–555. [Google Scholar] [CrossRef]
  51. Wang, L.; Cao, A.; Dou, L.; Guo, W.; Zhang, Z.; Zhi, S.; Zhao, Y. Numerical simulation on failure effect of mining-induced dynamic loading and its influential factors. Safety Sci 2019, 113, 372–381. [Google Scholar] [CrossRef]
  52. Manouchehrian, A.; Cai, M. Analysis of rockburst in tunnels subjected to static and dynamic loads. J Rock Mech Geotech 2017, 9, 1031–1040. [Google Scholar] [CrossRef]
  53. Hu, L.; Ma, K.; Liang, X.; Tang, C.; Wang, Z.; Yan, L. Experimental and numerical study on rockburst triggered by tangential weak cyclic dynamic disturbance under true triaxial conditions. Tunn Undergr Sp Tech 2018, 81, 602–618. [Google Scholar] [CrossRef]
  54. Li, X.F.; Zhang, Q.B.; Li, H.B.; Zhao, J. Grain-Based Discrete Element Method (GB-DEM) Modelling of Multi-scale Fracturing in Rocks Under Dynamic Loading. Rock Mech Rock Eng 2018, 51, 3785–3817. [Google Scholar] [CrossRef]
  55. Aziznejad, S.; Esmaieli, K.; Hadjigeorgiou, J.; Labrie, D. Responses of jointed rock masses subjected to impact loading. J Rock Mech Geotech 2018, 10, 624–634. [Google Scholar] [CrossRef]
  56. Gao, F.; Kaiser, P.K.; Stead, D.; Eberhardt, E.; Elmo, D. Strainburst phenomena and numerical simulation of self-initiated brittle rock failure. Int J Rock Mech Min 2019, 116, 52–63. [Google Scholar] [CrossRef]
  57. Yang, J.; Liu, K.; Li, X.; Liu, Z. Stress initialization methods for dynamic numerical simulation of rock mass with high in-situ stress. J Cent South Univ 2020, 27, 3149–3162. [Google Scholar] [CrossRef]
  58. Li, S.; Chen, Z.; Li, W.; Yan, T.; Bi, F.; Tong, Y. An FE Simulation of the Fracture Characteristics of Blunt Rock Indenter Under Static and Harmonic Dynamic Loadings Using Cohesive Elements. Rock Mech Rock Eng 2023, 56, 2935–2947. [Google Scholar] [CrossRef]
  59. Asadi, P.; Fakhimi, A. Bonded particle modeling of grain size effect on tensile and compressive strengths of rock under static and dynamic loading. Adv Powder Technol 2023, 34, 104013. [Google Scholar] [CrossRef]
  60. Feng, P.; Wei, M.; Dai, F.; Tang, R.; Qiu, H.; Gong, J. DEM investigation on the mechanical behaviors of flawed specimens subjected to coupled static-dynamic loads. Soil Dyn Earthq Eng 2020, 135, 106220. [Google Scholar] [CrossRef]
  61. Yang, Y.; Guo, H.; Fu, X.; Zheng, H. Boundary settings for the seismic dynamic response analysis of rock masses using the numerical manifold method. Int J Numer Anal Met 2018, 42, 1095–1122. [Google Scholar] [CrossRef]
  62. Jin, J.; She, C.; Shang, P. Study on strength parameters and dilation angle evolution models in hard rock elastic-plastic deformation and failure process. Rock and Soil Mechanics. 2019, 40, 4401–4411. [Google Scholar]
  63. Wang, Y.; Gong, J.; Chen, Z. Deformation characteristics and dilatancy model of coal rock under different confining pressures. Hydrogeology and Engineering Geology 2015, 42, 106–111. [Google Scholar]
  64. Gong, F.; Si, X.; Li, X.; Wang, S. Dynamic triaxial compression tests on sandstone at high strain rates and low confining pressures with split Hopkinson pressure bar. Int J Rock Mech Min 2019, 113, 211–219. [Google Scholar] [CrossRef]
Preprints 76056 g001
Figure 1. Stress-strain curve of a typical coal specimen.
Figure 1. Stress-strain curve of a typical coal specimen.
Preprints 76056 g001
Preprints 76056 g002
Figure 2. The design structure diagram and realistic image of the testing system.
Figure 2. The design structure diagram and realistic image of the testing system.
Preprints 76056 g002
Preprints 76056 g003
Figure 3. Stress-strain curves of typical coal specimens in true triaxial tests.
Figure 3. Stress-strain curves of typical coal specimens in true triaxial tests.
Preprints 76056 g003
Preprints 76056 g004
Figure 4. Waveform and spectrum of a typical mining tremor
Figure 4. Waveform and spectrum of a typical mining tremor
Preprints 76056 g004
Preprints 76056 g005
Figure 5. Comparison between numerical simulation and laboratory test.
Figure 5. Comparison between numerical simulation and laboratory test.
Preprints 76056 g005
Preprints 76056 g006
Figure 6. Stress path of the simulation model
Figure 6. Stress path of the simulation model
Preprints 76056 g006
Preprints 76056 g007
Figure 7. Influences of the initial axial static stress on the evolution of plastic zones.
Figure 7. Influences of the initial axial static stress on the evolution of plastic zones.
Preprints 76056 g007
Preprints 76056 g008
Figure 8. Typical stress distribution and plastic zones.
Figure 8. Typical stress distribution and plastic zones.
Preprints 76056 g008
Preprints 76056 g009
Figure 9. Influences of the initial axial static load on the evolution of damage.
Figure 9. Influences of the initial axial static load on the evolution of damage.
Preprints 76056 g009
Preprints 76056 g010
Figure 10. Influences of the confining pressures on the evolution of plastic zones.
Figure 10. Influences of the confining pressures on the evolution of plastic zones.
Preprints 76056 g010
Preprints 76056 g011
Figure 11. Influences of the amplitude of dynamic load on damage evolution.
Figure 11. Influences of the amplitude of dynamic load on damage evolution.
Preprints 76056 g011
Preprints 76056 g012
Figure 12. Relationship between strain and damage variable.
Figure 12. Relationship between strain and damage variable.
Preprints 76056 g012
Preprints 76056 g013
Figure 13. Schematic representation of the damage under dynamic load at different frequencies.
Figure 13. Schematic representation of the damage under dynamic load at different frequencies.
Preprints 76056 g013
Preprints 76056 g014
Figure 14. Relationship between damage variable and time at different dynamic frequencies.
Figure 14. Relationship between damage variable and time at different dynamic frequencies.
Preprints 76056 g014
Table 1. Results of bursting liability of No.9 coal seam.
Table 1. Results of bursting liability of No.9 coal seam.
Index Testing result
Duration of dynamic fracture
DT / ms		 Elastic strain energy index
WET 		Bursting energy index
KE 		Uniaxial compressive strength
Rc / MPa		 Category Level
570 4.923 4.596 14.82 II Weak
Table 2. Mechanical parameters of coal specimens.
Table 2. Mechanical parameters of coal specimens.
Uniaxial compressive strength/ MPa Poisson’s ratio Elastic modulus/ GPa Cohesion/ MPa Internal frictional angle/ °
8.40 0.21 0.88 2.4 40
Table 3. True triaxial compressive strengths of coal specimens.
Table 3. True triaxial compressive strengths of coal specimens.
Serial numbers σ 3 σ 2 Mean peak strength/ MPa
1 4 6 41.13
2 8 12 55.6
Table 4. Simulation experiments.
Table 4. Simulation experiments.
Conditions Initial static loads Dynamic load
σ3/ MPa σ2/ MPa σ1/ MPa Amplitude/ MPa Frequency/ Hz
1 8 12 42-52 4 20
2 4-20 4-20 Loading to failure 2-10 20
3 4-20 4-20 Loading to failure 1-10 5-60
Table 5. Calculation results of the entropy weight method.
Table 5. Calculation results of the entropy weight method.
Indices σ 1 (MPa) σ 3 (MPa) Δ σ (MPa) Frequency (Hz)
Conditions 1 (positive) -1 (negative) 1 (positive) -1 (negative)
S-1 37 6 2.15 5
S-2 41 8 2.15 20
S-3 41 6 2.15 40
S-4 42 6 2.15 60
S-5 84 12 4.95 5
S-6 94 14 4.95 20
S-7 94 16 4.95 40
S-8 95 16 4.95 60
S-9 43 6 1.075 20
S-10 41 8 2.15 40
S-11 39 10 3.225 20
S-12 37 6 4.3 20
S-13 99 16 2.475 40
S-14 94 16 4.95 60
S-15 91 14 7.45 20
S-16 88 16 9.9 20
S-17 29 4 2.3 20
S-18 39 6 3.17 40
S-19 49 8 4 60
S-20 59 10 4.95 20
S-21 69 12 5.8 20
S-22 80 14 6.57 20
S-23 91 16 7.4 40
S-24 101 18 8.3 20
Information entropy 0.913055423 0.912274886 0.926943146 0.946807107
Information redundancy 0.086944577 0.087725114 0.073056854 0.053192893
Weight 0.288929746 0.291523586 0.24277878 0.176767887
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated