Preprint
Article
Soil Moisture Retrieval in Bare Agricultural Areas using Sentinel-1 Images
Altmetrics
Downloads
140
Views
86
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
08 June 2023
Posted:
09 June 2023
You are already at the latest version
Alerts
Abstract
Soil moisture maps are essential for hydrological, agricultural and risk assessment applications. To best meet these requirements, it is essential to develop soil moisture products at high spatial resolution which is now made possible using the free Sentinel-1 (S1) SAR (Synthetic Aperture Radar) data. Some soil moisture retrieval techniques using S1 data relied on the use of a priori weather information in order to increase the precision of soil moisture estimates, which required access to a weather forecasting framework. This paper presents an improved and fully automated solution for high-resolution soil moisture mapping in bare agricultural areas. The proposed solution derives a priori weather information directly from the original Sentinel images, thus bypassing the need for a weather forecasting framework. For soil moisture estimation, the neural network technique was implemented to ensure the optimum integration of radar information. The neural networks were trained using synthetic data generated by the modified Integral Equation Model (IEM) model and validated on real data from two study sites in France and Tunisia. Main findings showed that the use of radar signal averaged over grids of a few km2 in addition to radar signal at plot scale instead of a priori weather information, provides good soil moisture estimations. The accuracy is even slightly better comparatively to the accuracy obtained using a priori weather information.
Keywords:
Subject: Environmental and Earth Sciences - Remote Sensing
1. Introduction
Understanding the water cycle is crucial for various natural phenomena, such as floods, landslides, and droughts, which pose significant risks to human lives [1]. Soil surface characteristics, particularly moisture content and surface roughness, play a vital role in water cycle monitoring [2,3,4,5,6]. While ground measurements can accurately estimate these parameters, they are often time-consuming, labor-intensive, and limited in spatial representation [7]. Observations collected through remote sensing from space provide effective resources for tracking and mapping changes across vast regions both spatially and over time which is needed for reliable predictions of water cycle behaviors [8]. In the case of plot scale soil surface characteristics estimation, low spatial resolution measurements provided by sensors like SMOS, SMAP, and ASCAT are unsuitable [9]. To overcome this low spatial resolution limitation, the open source and free-of-charge Sentinel-1A and -1B Synthetic Aperture Radar (SAR) sensors operating in the C-band have been introduced, offering high spatial resolution soil surface characteristics mapping [10].
In areas with sparse vegetation cover, Synthetic Aperture Radar (SAR) data operating in the C-band has emerged as a valuable tool for estimating soil moisture. Among the models employed to simulate the SAR signal, the Integral Equation Model (IEM), a physical model developed by Fung [11], has gained considerable attention. Fung’s IEM possesses the advantage of not requiring site-specific calibration, as it can consistently be used to simulate backscattering coefficients based on radar configuration (frequency, polarization, and incidence angle) and soil parameters (soil moisture and soil roughness). However, Fung’s IEM has shown discrepancies between simulated and observed SAR data [12]. The IEM accurately replicates radar scatter on smooth surfaces. However, it under-performs on rough surfaces, where it predicts a more uniform response with incidence angle than what is observed in C and X bands signals. Baghdadi et al. [13,14] addressed this challenge by proposing a semi-empirical calibration for the IEM. This calibration was designed to enhance the precision of simulated backscattering values by accounting for the difficulties in measuring the correlation length input parameter. Furthermore, it has been shown that for bare soil fields and at high incidence angles, surface roughness has a more significant impact on the radar signal in the C-band than soil surface moisture (SSM) [15]. Consequently, estimating soil moisture from SAR data without considering the contribution of the root mean surface height (HRMS) would lead to imprecise soil moisture estimations, with underestimation for low HRMS values and overestimation for higher values [16].
One of the prevailing approaches currently being employed to estimate surface soil moisture from SAR data involves the inversion of backscatter simulation models using machine learning algorithms, specifically neural networks [7,17]. The backscatter models are used to build a synthetic database of simulated backscattering coefficients for various soil conditions and sensor attributes, then, neural networks are trained to estimate soil moisture on this synthetic database [14]. A key enhancement to this approach has been the use of a priori weather information in order to partition the estimation domain into dry or wet conditions, leading to the application of one of two distinct neural networks, each specifically trained for either dry to wet (between 4 vol.% and 30 vol.%) or very wet (between 20 vol.% and 40 vol.%) soil conditions [16].
Our study builds upon the approach introduced by El Hajj et al. [16] and presents a fully automated solution to overcome the need for a priori weather information. By utilizing the backscattering coefficients at the grid scale (a few ), we can deduce the weather conditions used for the estimation domain partitioning, without the need for a priori weather information. The hypothesis behind this new approach relies on the fact that dry or wet conditions can be deduced for each grid cell from the average backscatter coefficient of the whole grid. The second main objective is to study the potential of incorporating soil roughness estimates into the soil moisture estimation procedure, thereby analyzing the accuracy of surface soil moisture estimation when accounting for the influence of surface roughness on radar backscattering. The added value of using grid data and soil roughness estimates was studied in comparison to the previous models on the synthetic dataset generated by the calibrated IEM [13] and on a real dataset taken from two study sites where in situ soil moisture and soil roughness measurements are available.
2. Dataset description and problem statement
In this section, we provide a detailed description of the two datasets used in our study. The first is the synthetic dataset obtained from the well-calibrated radar backscattering model IEM (Integral Equation Model). The second dataset is a real dataset obtained from field measurements conducted in Montpellier, France, and Kairouan, Tunisia. The performance of different neural network configurations using these two datasets are then compared in order to identify the strengths and limitations of each configuration.
2.1. Synthetic dataset
The synthetic dataset is a collection of generated backscattering coefficients obtained from the calibrated IEM. The primary goal is to utilize a part of this dataset for training different machine learning configurations. The second part of this dataset will be used in the evaluation phase of our radar signal inversion approaches, providing a reliable benchmark for performance comparison.
2.1.1. Calibrated radar backscattering IEM
For bare agricultural areas, the IEM calculates the backscattering coefficient () by incorporating the sensor’s attributes (incidence angle, polarization, and radar wavelength) along with the soil’s parameters (soil moisture and soil roughness). The radar backscattering coefficient for a bare agricultural soil can be formulated as follows:
Where, the sensor attributes are:
- is the radar backscatter coefficient (no unit)
- is the incidence angle (°)
- is the radar wavelength (cm)
- is the polarization (VV or VH; Sentinel-1 configuration)
The soil parameters:
- is the soil Moisture Value (vol.%)
- is the Height Root Mean Square of soil roughness (cm)
In our study, we estimate the soil moisture from the radar backscattering coefficients (single or dual polarization) and HRMS (measured or otherwise estimated). Thus, this inverse problem can be formulated as follows:
In the case where the soil roughness is unknown, the inputs to the neural networks are the SAR data:
Thus, inversion of the radar signal to estimate soil moisture does not necessarily require knowledge of the roughness. Inaccurate estimates of soil moisture would be obtained, however, in the case where the roughness value is unknown.
2.1.2. Range of input parameters
The input parameter values needed to build a relevant synthetic dataset were chosen to represent the same range of values as the parameters of real sensors and soils in agricultural areas. These inputs were used to generate backscattering coefficients using the calibrated IEM. The radar wavelength was set to 5.5 cm representing the Sentinel-1 radar wavelength. The incidence angle () ranged from 20° to 45° with a step size of 1°. For each incidence angle, soil roughness (HRMS) was considered from a generated list of values, ranging from 0.5 to 3.8 cm with a step size of 0.1 (34 values). For each (, ) combination, the soil moisture spanned from 4 to 40 vol.% with a step size of 2 vol.%.
Given that the SAR signal can show a strong increase with changes in soil moisture, especially after heavy rainfall [17], calculating the average radar signal over large areas (watershed or a given grid of several km²) using bare agricultural soils is useful as is represents the general soil moisture conditions over the study area (very wet, wet to dry). In this study, as input to our soil moisture estimation algorithm, we use information at the plot level (marked with a "p", VVp and VHp) and information at the grid level (marked with a "g", VVg and VHg). For grid synthetic data we followed the following scheme: We start by fixing the grid soil moisture MVg between 4 and 40 vol.%). Next, for a given MVg value and each combination of incidence angle, soil roughness within the chosen ranges, 100 samples of soil moisture at plot scale were generated using a bounded normal distribution with a mean value equal to the soil moisture at grid scale and a standard deviation of 10 vol.%. The generated MVp samples were constrained within the range [MVg -10, MVg+10] and the soil moisture at the plot scale was filtered to retain only those between 4 and 40 vol.%. Thus, in addition to MVp values, we can also have MVg values as input in our inversion algorithm.
2.1.3. Synthetic dataset generation
Once the synthetic inputs are generated, we run the calibrated IEM to generate the backscatter coefficients for the grid level using the grid soil moisture values (, ) or for the plot level using the soil moisture at plot scale (, ). Then an absolute error corresponding to the SAR observation accuracy was added to the simulated backscattering coefficients to obtain a more realistic synthetic dataset. For Sentinel-1, this error is defined by the absolute radiometric accuracy, which is equal to 0.70 dB and 1.0 dB for VV and VH polarizations respectively [10]. Accordingly, for each element of our dataset, 5 noise samples were randomly selected from the zero-mean Gaussian noise distribution with a standard deviation of 0.7 and 1.0 dB, respectively for VV and VH. The randomly selected noise values were then added to the IEM’s simulated at both scales (plot and grid). Finally, our noisy synthetic dataset, in VV and VH polarizations is composed of about 8 million elements.
Table 1 shows an example of the possible combinations of our input parameters in an 8-column data format. Each row represents a unique data combination defined by a given radar incidence angle (), surface roughness, and soil moisture at plot and grid scales. and were simulated using (, , ) while and were simulated using (, , ).
Table 1.
Example of synthetic data generated by the calibrated IEM using Sentinel-1 wavelength.
| IEM inputs | IEM outputs | ||||||
|---|---|---|---|---|---|---|---|
| HRMS | MVg | MVp | |||||
| 20.0 | 0.5 | 4.0 | 6.56 | -12.16 | -27.58 | -9.30 | -21.21 |
| 20.0 | 0.5 | 4.0 | 6.45 | -10.72 | -24.56 | -9.06 | -19.27 |
| 20.0 | 0.5 | 4.0 | 10.76 | -10.21 | -24.82 | -8.77 | -20.32 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 45.0 | 3.8 | 40.0 | 36.98 | -6.04 | -15.49 | -7.67 | -17.01 |
| 45.0 | 3.8 | 40.0 | 32.38 | -6.36 | -17.66 | -8.60 | -17.55 |
| 45.0 | 3.8 | 40.0 | 38.40 | -4.78 | -15.53 | -6.40 | -17.39 |
In this study half of the synthetic dataset is used for training the neural networks and the other half for their evaluation, the evaluation half is referred to as the validation dataset.
2.2. Real dataset
In this part, we introduce our real dataset from two distinct study areas in Montpellier, France, and Kairouan, Tunisia. This dataset offers diverse environmental conditions with associated satellite data and field measurements. The satellite data contain the backscatter coefficients in VV and VH polarizations calculated from Sentinel-1 images. In addition, fields measurements provide measured soil moisture (MVp) and surface roughness (HRMS) collected at reference fields. The proposed machine learning configurations for soil moisture estimations are evaluated using the in situ measured soil moisture in the two study sites.
2.2.1. Montpellier dataset
Study area
The first real dataset is collected in a study site located in the Occitanie region of France as shown in Figure 1. With a relatively flat terrain topography, it is composed mainly of forest, vineyards, grasslands, and agricultural fields (mainly wheat). The climate of the study site is Mediterranean with a rainy season between mid-October and March and an average annual cumulative rainfall of approximately 750 mm. The average air temperature varies between 2.9 °C and 29.3 °C. The topsoil texture of the agricultural fields is loam.
Sentinel-1 images
Over the French study site, 28 Sentinel-1 images (S1) acquired between 15/04/2016 and 26/06/2018 were used. The Sentinel-1 (S1) images are downloadable from the Copernicus website (https://scihub.copernicus.eu/dhus/#/home). The 28 S1 images used were acquired in IW imaging mode with the VV and VH polarizations. The S1 images were calibrated using the S1 toolbox developed by ESA (European Spatial Agency). The calibration aims to convert the digital number values of S1 images into backscattering coefficients () in a linear unit. Thus, for each polarization, the average signal of all pixels in each plot is computed to obtain a single representative value for each reference plot (). Then, to build real SAR signals at grid scale (), for each S1 acquisition and polarization the average backscatter coefficient is computed using all agricultural pixels with low NDVI values (below 0.4).
In situ measurements
In situ measurements of soil moisture and surface roughness were collected during 28 field surveys between 15/04/2016 and 26/06/2018. These fields correspond to bare or partially vegetated soils (NDVI lower than 0.4). Soil moisture at plot scale (MVp) was measured within a window of 2 h with respect to the Sentinel-1 acquisition date. For each reference plot, 20 to 30 measurements of volumetric soil moisture were conducted in the top 5 cm of soil by means of a calibrated TDR (Time Domain Reflectometry) probe. All soil moisture measurements within each plot were averaged to provide a mean value for each plot. The range of the soil moisture value is between 4.5 and 32.5 vol.%. In addition, the soil roughness parameter HRMS was determined using a needle profilometer with a length of 1 m and a needle spacing of 1 cm. For each reference plot, five parallel roughness profiles along the SAR line of sight were recorded and another five perpendicular to the line. Thus, by processing the roughness profile, the HRMS was derived. In our study, the recorded HRMS values of the reference plots varied between 0.5 and 4.0 cm. It is important to note that the parcels are not irrigated.
Finally, our French dataset is composed of 198 elements with radar backscattering coefficients (in VV and VH) and in situ measurements of soil moisture (MVp) and surface roughness (HRMS). Each element of this real dataset represents a reference plot with an associated MVp value, incidence angle and mean backscattering coefficients in VV and VH. The incidence angles of our reference plots vary from 39° to 41°. This dataset was only used to validate our soil moisture estimates.
2.2.2. Kairouan dataset
Study area
The second real dataset was collected over a study area located in the Kairouan Governorate of Tunisia as shown in Figure 2, in central Tunisia. The climate in this region is semi-arid, with an average annual rainfall of approximately 300 mm/year, characterized by a rainy season lasting from October to May, with the two rainiest months being October and March. The mean temperature in Kairouan City is 19.2 °C (minimum of 10.7 °C in January and maximum of 38.6 °C in August). The landscape is mainly flat, and the vegetation is dominated by agricultural production (cereals, olive groves, fruit trees, market gardens and bare soils).
Sentinel-1 images
17 Sentinel-1 images were acquired between 06/12/2015 and 30/03/2017 over this study area. The same processing of S1 images was performed as that for the Montpellier study site.
In situ measurements
Ground campaigns were carried out at the same time as the 17 Sentinel-1 acquisitions. The ground measurements made on the reference fields involved the characterization of the soil moisture using a theta-probe instrument. On average 35 bare soil reference fields were selected at each Sentinel-1 visit. For each reference field, approximately 20 handheld theta-probe measurements were made at a depth of 5 cm. The samples were taken from various locations in each reference field, within a two-hour time frame between 15:40 and 17:40, coinciding with the time of each S1 acquisition. The volumetric moisture ranged between 4.0 vol.% and 32.0 vol.%. Soil roughness measurements were not available for the Kairouan dataset as opposed to the Montpellier dataset. It is important to note that the Kairouan parcels are frequently irrigated. Finally, our Tunisian dataset is composed of 201 elements with radar backscattering coefficients (in VV and VH) and in situ measurements of soil moisture (MVp) and surface roughness (HRMS). The incidence angles of our reference plots vary from 39.5° to 39.9°. This dataset was only used to validate our soil moisture estimates.
In summary, the synthetic dataset will serve as a benchmark for training and evaluating various machine learning configurations through a wide range of backscattering coefficients obtained from the calibrated IEM. Additionally, the real dataset offers a comprehensive and diverse set of environmental conditions, satellite data, and field measurements from two distinct study areas in Montpellier, France, and Kairouan, Tunisia. By comparing the soil moisture estimated from the sensor attributes and the in situ soil moisture, our study can evaluate the machine learning configurations on veritable data. The field measurements obtained from both study areas provide us with real data on soil attributes, enabling us to ensure that the satellite data analysis is grounded in reality and is providing an accurate representation of the soil attributes being studied.
3. Methodology
In this section, we introduce our experimental setups for inverting Sentinel-1 signals in order to estimate soil moisture. First, inversion models are described. Then, the model architecture and the process of model training and optimization are presented. Finally, the different input/output configurations of the inversion model as well as the precision metrics used for the models evaluation are detailed.
3.1. Inversion algorithm
This study focuses on estimating soil moisture content using radar backscattering coefficients as input data (inverse equations 2 and 3). Therefore, the problem is formulated as developing a model that can effectively estimate soil moisture levels based on the provided radar backscattering coefficients, enabling a better understanding and monitoring of soil moisture dynamics. In fact, the inversion model uses the neural network technique trained on the synthetic dataset described in the previous section in order to inverse the radar signal. The trained neural networks are then used to estimate soil moisture using the real Backscatter computed from Sentinel-1 images.
Given an input vector of S1 radar measurements, we want to learn the function that maps the radar measurements to soil moisture values MV. This problem can be formulated as:
where the the inputs are the radar backscatter coefficient (dB) at VV and VH polarizations (Sentinel-1 configuration) provided by the satellite images and spatially averaged at plot (VVp and VHp) or grid scales (VVg and VHg), the associated incidence angle (°), and the soil roughness value (if available). The vector denotes the weights and the bias of the neural network . denotes the estimation error. One of the objectives of this study is to find the best attribute configuration, with the minimum .
The adopted neural network architecture is composed of two hidden layers. The first layer is associated with a linear activation function while the second hidden layer uses a tangent sigmoid activation function. Both hidden layers contain 20 neurons each [16]. In fact, after comparing this neural network with other machine learning models (gradient-boosted decision tree and multi-layer perceptron), we found that the added value of changing the machine learning model can be ignored in relation to the added value of changing the machine learning model’s attributes. Let and be the weight matrices of dimensions and , respectively, and and be the bias vectors of dimensions and , respectively. For the first hidden layer, we use a linear transfer function, denoted as , and for the second hidden layer, we use a tangent sigmoid transfer function, denoted as . The forward pass can be formulated as:
a) First hidden layer (linear transfer function):
b) Second hidden layer (tangent sigmoid transfer function):
c) Output layer:
Where x is the input vector containing the sensor attributes values and is the estimated output.
The optimization problem aims to minimize a loss function , where is the estimated output and y is the observed output. We want to find the optimal weight matrices and bias vectors that minimize the loss function:
with .
This is typically achieved through an iterative process such as gradient descent, which updates the weights and biases based on the gradients of the loss function with respect to the model parameters. In our case the optimization technique used is the Levenberg-Marquardt (LM) algorithm [18]. The Levenberg-Marquardt (LM) algorithm is a popular optimization technique that combines the features of gradient descent and the Gauss-Newton method, making it particularly suitable for solving nonlinear least-squares problems (see appendix). The LM algorithm is applied to our neural networks () for training by minimizing the sum of squared errors (SSE) loss function.
3.2. Evaluated Sentinel-1 configurations
Various configurations aimed at optimizing soil moisture estimation accuracy were evaluated. These configurations involve the integration of Sentinel-1 polarizations, partitioning the estimation domain into dry and wet conditions, incorporating a Sentinel-1 large-scale signal thanks to the grid backscatter coefficients, and training neural networks with soil roughness estimates.
-
Configuration 1: Analyze the effect of Sentinel-1 polarizationsThree inversion Sentinel-1 configurations were tested: (1) VV polarization alone; (2) VH polarization alone; and (3) both VV and VH polarizations. In this configuration the soil roughness parameter HRMS is ignored. They can be formulated as:
-
Configuration 2: Separate the MVp estimation domain into two separate domains one for dry to slightly wet and one for very wetUsing the same polarizations as in the previous configuration, we separate our MVp solution search domain into two domains: one with a search for a solution for dry to slightly wet soil conditions and one for a solution for wet to very wet soil conditions. This configuration needs a priori information on MVp (a priori dry to slightly wet or very wet). Partitioning the estimation domain into distinct dry and wet conditions and training dedicated neural networks for each domain may significantly enhance soil moisture estimation accuracy [16]. By focusing on domain-specific patterns and relationships, the specialized neural networks can capture the complexities associated with soil moisture variations more effectively. In the case of a priori dry to slightly wet soil, will be built up using the synthetic training dataset elements with MVp between 4 and 30 vol.%. Contrarily, in the case of a priori very wet soil conditions, will be developed using the synthetic training dataset elements with MVp between 20 and 40 vol.%. An overlap of 10 vol.% on MVp is considered between the dry to slightly wet and the very wet training datasets of . During the evaluation, the dry is applied on attributes with MVp < 25, while the wet is applied on attributes with MVp ≥ 25. In an operational context, the choice between or is determined by meteorological data, primarily focusing on precipitation. For example, if there has been significant rainfall one or two days before the S1 acquisition, the would be used; otherwise, the is applied. In this configuration the soil roughness parameter HRMS is ignored.This is formulated as:
-
Configuration 3: Assess the added value of using the grid information in addition to plot scaleIn this configuration, we hypothesize that incorporating backscatter coefficients at the grid scale into the soil moisture estimation process, in addition to backscatter coefficients at the plot scale, can improve the accuracy of MVp estimation, potentially offering an alternative to the domain-separated approach which necessitates weather data for selecting the appropriate neural network (dry to slightly wet or very wet). This hypothesis assumes that integrating grid coefficients can inform about the soil moisture status in the study area, enabling the inversion model to adapt to both dry and wet soil characteristics. We also chose to use both polarizations as its the most precise configurations. There are two subcases of configuration 3, formulated as:Equations (11) give a detailed presentation of the neural networks and their inputs used in configuration 3. In only was used, this network was trained using the backscatter coefficients for VV and VH polarizations on the grid and plot scales. In three were used, is trained to estimate using the backscatter coefficients for VV and VH on the grid scale, the estimated from will serve as dry/wet domain separator if estimated vol.% the config will use in order to estimate otherwise it will use . The second and third were trained using the backscatter coefficients for VV and VH polarizations on the grid and plot scales, uses backscatter coefficients on vol.% and uses backscatter coefficients on vol.%. In this configuration the soil roughness parameter HRMS is ignored.
-
Configuration 4: Analyze the added value of using soil roughness estimatesIn this last configuration, we hypothesize that training neural networks with soil roughness estimates, in conjunction with incorporating grid backscatter coefficients and partitioning estimation domains, can potentially improve soil moisture estimation accuracy. This hypothesis suggests that by accounting for the complex relationships between soil moisture, surface roughness, and backscatter signals, neural networks can better capture the intricacies of soil moisture variations across various surface conditions. There are two subcases of configuration 4, formulated as:In two were used. was trained to estimate the soil roughness using the backscatter coefficients for VV and VH polarizations on the grid and plot scales, while was trained to estimate the soil moisture using the backscatter coefficients for VV and VH polarizations on the grid and plot scales in addition to soil roughness. Further, to account for the uncertainties on HRMS estimated from SAR images [7] in the training phase, a zero-mean Gaussian noise was added to HRMS with a standard deviation of 0.5. Estimated from is used to estimates .In five were used, like in , is used to separate the estimation domain of and into two domains dry-wet/very wet using the same thresholds on as . Then, is estimated according to dry or wet conditions ( or ) and then this estimate of HRMS is used in the network to estimate MVp ( or ).
Note that configurations 1 and 2 have already been tested by El Hajj & al. [16] and that in our study they serve as benchmarks for configurations 3 and 4.
3.3. Evaluation metrics
The first evaluation metric used is the Root Mean Squared Error (RMSE). RMSE is a valuable metric in soil moisture estimation due to its comprehensive assessment of accuracy, emphasis on larger errors, and clear interpretability. Its consideration of larger discrepancies ensures significant errors are addressed. It can be formulated as:
with N representing the number of data, denoting the observed value for the i-th data point, and denoting the estimated value for the i-th data point.
The second evaluation metric used is Bias. The Bias metric serves as an important evaluation tool due to its interpretability and ability to quantify systematic error. By measuring the average difference between estimated and observed values, the Bias metric offers valuable insights into the model’s overall performance. This metric enables us to identify and understand the extent to which a model consistently overestimates or underestimates the target variable:
The third evaluation metric used is the Mean Absolute Percentage Error (MAPE). MAPE is an essential evaluation metric that provides a clear understanding of a model’s prediction accuracy in terms of relative error. It computes the average percentage differences between estimated and observed values:
4. Result analysis
In this section, the effectiveness of the configurations described in the section « Methodology » will be compared on both the synthetic validation set (half the dataset that wasn’t used for training) and the real dataset. This comprehensive evaluation will allow us to assess the performance of each configuration under controlled and real-world conditions, thereby providing a better understanding of their applicability and potential limitations. By examining the outcomes of these configurations, we aim to determine the most effective configurations for optimizing soil moisture estimation accuracy.
4.1. Using synthetic validation set
All the configurations previously discussed are ranked using the three mentioned metrics and displayed as a bar plot leaderboard in Figure 3. For configuration 1, which focused on the effect of Sentinel-1 polarization, the combined use of VV and VH polarizations yielded a more accurate estimation compared to using either polarization individually, with an RMSE decrease of about 0.7 vol.% for VH and 0.35 vol.% for VV as shown in Figure 3. In configuration 2 (with a priori information on MVp), which involved separating the estimation domain into dry and wet conditions using a weather forecasting framework, improved accuracy was observed in comparison to configuration 1, particularly when both VV and VH polarizations were utilized, with an RMSE decrease of 0.4 vol.%. For configuration 3, which assessed the added value of using the radar signal computed at the grid scale, the two subcases (Config_3_grid and Config_3_grid_MVg) show that directly estimating MVp with grid information produces the same performance as estimating MVg and then partitioning the MVp to dry and wet using the MVg estimated. However, the three precision metrics show a clear improvement in accuracy using the grid scale information compared to configurations 1 and 2 except for configuration 2 when both polarizations are used, where we get an RMSE that improves only of about 0.2 vol.%. Lastly, in configuration 4, which analyzed the added value of using soil roughness estimates, the integration of soil roughness estimates did not improve the estimation accuracy in comparison to configuration 3. Figure 3 shows that we get the same order of magnitude on all three precision metrics between configurations 3 and 4, about 3.5 vol.% on RMSE and 14% on MAPE.
Thus, the evaluation of these configurations suggests that the combined use of VV and VH polarizations, separating the MVp estimation domain into dry and wet conditions yields better results than the configuration without a priori information on MVp (configuration 1). The incorporation of radar signal computed at grid scale using the bare agricultural soils included in each grid cell replaces the priori information on the soil moisture conditions, extracted in general using expert knowledge from meteorological data [16]. The added value of soil roughness estimates is negligible compared to other configurations without the use of roughness information.
4.1.1. Performance of used as a function of the soil moisture
In this part, model sensitivities to soil moisture are analyzed on the synthetic validation set. Figure 4 shows the three precision metrics (Bias, RMSE and MAPE) calculated for intervals of soil moisture values as boxplots. In configurations 1 and 2, the percentile values reveal a general increase in RMSE values as the MVp level increases. The RMSE passes of about 2 vol.% for MVp in the range 4 to 7.5 vol.% to about 5 vol.% for MVp in the range 37.5 to 40 vol.%, indicating a decline in soil moisture estimation accuracy as the soil moisture levels increase, as shown in Figure 4. However, the MAPE shows that despite the increase in the RMSE, the performance of the soil moisture estimations is improved as the soil moisture level increase. For example, the MAPE for the level [32.5,37.5[ was about 10% less than that for low soil moisture values between 4 vol% and 7.5 vol%. This suggests that soil moisture estimation accuracy is influenced by the soil moisture levels. In configurations 3 and 4, without a priori information on MVp in order to estimate the soil moisture, the percentile values demonstrate an improvement in soil moisture estimation accuracy compared to configurations 1 and 2. In fact, for seven of the eight MVp ranges, the difference between 25% and 75% percentiles is smaller for configurations 3 and 4 than for configurations 1 and 2 on all metrics, showing that not only configurations 3 and 4 are more precise but also more stable. Finally, in configuration 4 where estimated HRMS is used to optimize the MVp estimates, the percentile values reveal a very slight improvement in soil moisture estimation accuracy than the other configurations. The bias metric shows that all configurations tend to overestimate soil moisture for MVp under 32.5 vol.% and start to underestimate soil moisture values above 32.5 vol.%.
4.1.2. Performance of used as a function of the soil roughness value
In this section, we evaluate how the best subcase of each configuration reacts to soil roughness variations on the synthetic validation dataset. The precision metrics computed over diverse soil roughness ranges are presented as boxplots in Figure 5. For all configurations, the percentile values show high RMSE and MAPE values for low (HRMS < 1.5 cm) and high soil roughnesses (HRMS ≥ 2.5 cm), they also show the lowest scores for HRMS range between 1.5 and 2.5 cm Figure 5. The bias shows that all configurations tend to underestimate MVp for low roughnesses (HRMS < 1.5 cm) and overestimate MVp for high roughnesses (HRMS ≥ 2.5), this suggests that soil moisture estimation accuracy is influenced by soil roughness and that the best HRMS range for estimating MVp is between 1.5 and 2.5 cm as shown in Figure 5. In configurations 3 and 4 without a priori information on MVp, the percentile values demonstrate an improvement in soil moisture estimation accuracy compared to configurations 1 and 2, especially for HRMS ≥ 1.5. Finally, in configuration 4, the percentile values reveal a slightly greater improvement in soil moisture estimation accuracy than in other configurations, thus affirming that might benefit from training using soil roughness estimates.
4.2. Using real Dataset
In this section, we present the results of our evaluation on the real dataset, which originates from the Kairouan region in Tunisia and the Occitanie region in France. The bar chart, referenced as Figure 6, displays the rankings for the previously discussed configurations, using data from the real dataset. The results of configurations 1 and 2 align with our findings from the synthetic dataset, where the combination of both polarizations significantly improves estimation accuracy compared to using each polarization individually (Figure 6). The use of both polarization reduces the RMSE on MVp estimates of about 0.5.vol% in the case of configuration 1 and of about 0.35 vol.% for configuration 2. In addition, the use of two polarizations considerably reduces bias as shown in Figure 6. Results of configuration 3 suggest that incorporating grid information optimizes soil moisture estimation accuracy compared to the first configuration. The accuracy analysis on the MVp estimates obtained by configuration 3 shows the same accuracy gain compared to configuration 1 as in configuration 2, confirming that we can achieve higher accuracy using grid information without the need for a priori weather. The integration of roughness estimates (configuration 4) shows a relatively minor improvement in soil moisture estimates compared to configurations 2 and 3. These results are consistent with the synthetic dataset results.
4.2.1. Performance of used as a function of the soil moisture
In this part, model sensitivities to soil moisture are analyzed on real data. Figure 7 presents Bias, RMSE and MAPE scores as percentile values for our better configurations (conf_1_VV_VH, conf_2_VV_VH, conf_3_grid_MVg, and conf_4_grid) across various soil moisture levels ranging from very dry to very wet conditions. For all configurations, the percentile values reveal a general decrease in RMSE and MAPE values as MVp increases in the MVp range lower than 17.5 vol.% (from very dry to slightly wet soils). Then we observe a change in trend as the MVp level increases from 17.5 vol.% (slightly wet) to 32.5 (wet), as shown in Figure 7. Furthermore, the BIAS percentile values show that our model is prone to slight overestimation in dry soil conditions and high underestimation in wet soil conditions (bias reaches 10 vol.% for MVp higher than 32.5 vol.%). Separately, Figure 7 shows that configurations 3 and 4 give better scores from very dry to wet conditions (best overall percentiles on all scores) and that configuration 1 gives the best scores on very wet conditions.
4.2.2. Performance of used as a function of the soil roughness
This part focuses on examining the sensitivities of the model to soil roughness using real data. Figure 8 displays percentile values of Bias, RMSE, and MAPE scores for the best 4 configurations across different soil moisture levels. Soil moisture estimates appear to be unaffected by variations in soil roughness since the BIAS metric demonstrates relatively balanced bias scores across all soil roughness ranges as shown in Figure 8. This observation holds true for every configuration tested. Consequently, soil roughness does not introduce any significant bias into soil moisture assessment. The dependence between the accuracy on the estimation of MVp and the soil roughness is less well marked with the real data because only a few measurements have roughnesses lower than 1 cm or higher than 3 cm. Indeed, it is only on the small and strong roughnesses that we could observe a strong dependence on the radar signal in C-band [19].
5. Discussion
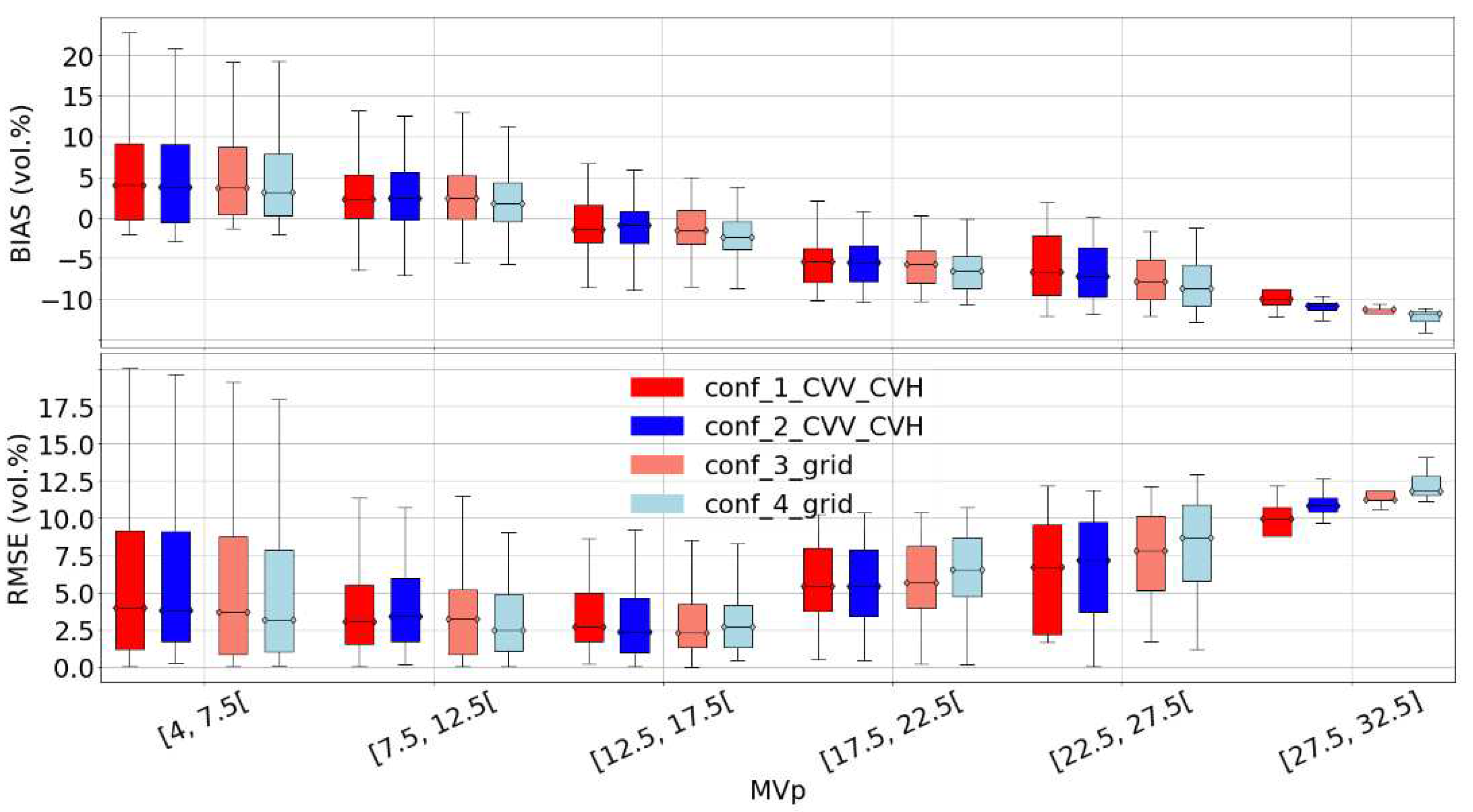
In this part, we discuss the limitations of our S1 signal inversion procedures. The first limitation concerns the accuracy of our model results, which may be due to an incorrect choice to use dry network instead of wet network or vice versa (configurations 2, 3 and 4). This issue arises in cases where some fields are irrigated, such as in the Kairouan study site, as opposed to the non-irrigated fields in the Montpellier site. Indeed, for a given S1 date where the soils are mostly dry (lack of rainfall since a long time), the dry network will be used in configurations 2, 3 and 4 in order to estimate the soil moisture even if some fields are very wet after a recent irrigation event. Similarly, for the configurations 3 and 4 with the use of MVg estimates in input to for estimating MVp, the low and medium values of estimated MVg corresponding to dry to slightly wet soil conditions even with some irrigated fields in each grid cell will inform the network that will estimate MVp that overall we are in dry to moderately wet soil conditions (at grid scale), while for some fields the moisture content can be very high because they have been irrigated very recently. Thus, the presence of irrigated fields could lead to a strong underestimation of MVp for irrigated fields. The Bias values in Figure 9 and Figure 10 are stronger for Kairouan (irrigated site). For example, MVP is underestimated by about 10 vol.% in very wet conditions (MVP between 27.5 and 32.5 vol.%) for Kairouan against 7 vol.% for Montpellier (non irrigated site). In addition, Figure 10 shows that the configurations 2, 3 and 4 demonstrate better performance on non-irrigated parcels (lower Bias and RMSE).
The second limitation pertains to the generation of our dataset. The data generation process involves fixing grid soil moisture (MVg) values between 4 and 40 vol.%, and then generating 100 samples of soil moisture at the plot scale (MVp) for each combination of incidence angle and soil roughness. These samples are created using a bounded normal distribution, with a mean value equal to the grid soil moisture and a standard deviation of 10 vol.%. The generated MVp samples are constrained within the range [MVg -10, MVg+10], and soil moisture at the plot scale is filtered to retain only values between 4 and 40 vol.%. Capping the values in this manner can lead to an unbalanced dataset, as MVg values below 14 and above 30 do not have MVp samples centered on MVg with a standard deviation of 10. This constraint results in a limited representation of soil moisture variability for these particular MVg ranges. Consequently, the dataset becomes skewed, with certain soil moisture ranges being underrepresented. This imbalance negatively impacts the model’s performance, particularly in scenarios where soil moisture values fall within the underrepresented ranges, potentially leading to biased or inaccurate results.
The results obtained with configuration 4 which uses an estimation of the roughness in input to to estimate the soil moisture are not very conclusive because of the limiting Sentinel-1 sensor’s instrumental characteristics for mapping the soil roughness (C-band, VV and VH polarizations, incidence angles between 25° and 45°). Numerous results show that the radar signal in the C-band is strongly dependent on surface roughness mainly for low levels of roughness [11,13,19]. The studies showed that the sensitivity of radar signal to surface roughness increases with incidence angle. Baghdadi et al [13] have shown that high incidence angles (45°) are best suited to the discrimination between smooth and rough areas. Furthermore, when the incidence angle is low (between 20° and 35°), the backscattering coefficient rapidly attains its maximum value for roughness values around 1 cm (HRMS of less than 1 cm are rare in agricultural areas). Therefore, for agricultural applications, soil-roughness mapping is not feasible using C-band SAR data at a low incidence angle due to the rapid saturation of the radar signal. Concerning polarization effect, we observe theoretically and from experimental studies a higher dynamic to soil roughness for HH and VH than with VV polarization [5,11,12]. All this literature review shows that Sentinel-1 data are not optimal for a good estimation of soil roughness. Thus, an unreliable estimate of roughness in does not provide an improvement in moisture estimation compared to the case where soil roughness is not considered a parameter of .
The radar signal, which depends on various radar parameters (polarization, incidence angle, and frequency), is also correlated, for bare soils, with soil surface roughness and moisture content [11]. In an inversion approach, we are led to estimate the two soil parameters MV and HRMS or only one of the two parameters if we have information on the second parameter. Estimating both soil parameters requires two input channels. The ideal way would be to have at least two decorrelated channels, for example two different incidence angles (one low 25° and one high 45°) or two different radar frequencies (C and L for example). This is not possible because the available SAR sensors are mono-wavelength and acquire, on a given date, a backscattered signal at a single incidence angle. However, on a given date, Sentinel-1 acquires data at C-band and at only one incidence (the incidence angle value depends on the position of the pixel in the image) but with two polarizations VV and VH. As VV and VH are not completely decorrelated for the estimation of soil parameters, the use of both VV and VH in the inversion approach of SAR images does not always allow a good optimization of the estimated values of MVp and HRMS. This ambiguity in the estimation of the couple (MVp, HRMS) can sometimes occur mainly in the case of soils with low HRMS value and high MVp value or vice versa.
In this study, as in previous studies before it, the incorporation of coarse soil moisture information over a given site is of great interest to improve the estimation of soil moisture. In [16,20], the introduction of expert knowledge on the soil moisture (dry to wet soils or very wet soils) using meteorological data (e.g. precipitations, temperature) reduced the errors on the soil moisture estimates by one third. By adding a priori information on the humidity, the inversion of the radar signal is done on half of the space (MVp, HRMS) thus reducing the ambiguity in the retrieval problem. This paper has successfully tested the use of a feature computed from Sentinel-1 input data instead of using meteorological data which is not always free, open access, and available in real-time, thus making the inversion chain completely independent. This feature highly correlated with rainfall, corresponds to the average of the Sentinel-1 signal at large scale (grid cells of 5 km x 5 km). In fact, Bazzi et al [17,21]) showed that the S1 backscattering signal averaged over a few (using the bare agricultural pixels) is strongly correlated with rainfall and can be used as an indicator for the soil moisture content at the date of passage of S1.
6. Conclusions
This study aimed to develop a fully automated solution for high-resolution soil moisture mapping in bare agricultural areas using Sentinel-1 data, while eliminating the need for a priori weather information, sometimes required for better accuracy on soil moisture estimates. Algorithms based on neural networks were trained on a synthetic dataset generated by the radar backscattering model IEM and validated using real data from two study sites in Montpellier, France, and Kairouan, Tunisia. The results showed that our proposed algorithms were able to estimate soil moisture with high accuracy. The use of the backscattering coefficients at plot scale as well as those at grid scale defined by the average of all bare soil pixel values within each grid cell allowed for the inference of global soil moisture conditions at a large scale.
Combining VV and VH polarizations (Configuration 1) consistently improves accuracy compared to using either polarizations individually. Separating the estimation domain into dry and wet conditions (Configuration 2) highlights the importance of using a priori information on the global soil moisture state in the study site, yielding even better results when both VV and VH polarizations are used, with about 14% gain on the synthetic dataset and 5% gain on the real dataset in RMSE compared to the best configuration without domain separation. Incorporating grid information (Configuration 3) optimizes accuracy without the need for weather information with about an 18% gain on the synthetic dataset (slightly better than the configuration that separates the estimation domain using weather information) and a 5% gain on the real dataset in RMSE compared to the first configuration. Finally, while integrating soil roughness estimates (Configuration 4) does slightly enhance estimation accuracy, the improvements are negligible as to the complexity of the architecture (5 NNs compared to just 1). Overall, the combined use of VV and VH polarizations and incorporating grid information offers the most significant improvements in soil moisture estimation accuracy, with soil roughness estimates providing a marginal additional contribution to the process.
Our Sentinel-1 signal inversion procedures have revealed limitations. Firstly, the accuracy of the inversion model based on the use of grid information or incorporating a priori information on soil moisture (dry to slightly wet condition or very wet condition) can be compromised due to the inappropriate choice of dry or wet network for estimating soil moisture, especially in areas with irrigation practices. Secondly, the results from Configuration 4, which estimates soil roughness, are inconclusive due to the instrumental characteristics of the Sentinel-1 sensor. Indeed, the C-band of Sentinel-1 is not the optimum wavelength for soil roughness mapping as well as the incidence angles which are lower than 40°-45° for a wide part of Sentinel-1 images. Lastly, the high dependence of the radar signal on both soil roughness and moisture content leads to an ambiguity in the estimation of soil moisture when the inversion model estimates only the soil moisture without taking into account roughness or when the inversion model can’t estimate correctly both soil roughness and moisture content (SAR layers in the input are insufficient). Despite these limitations, integrating coarse soil moisture information (average moisture over large areas) has been demonstrated to improve soil moisture estimation at plot scale.
Author Contributions
M.E. and N.B. conceived and designed the experiments; M.E. performed the experiments; M.E. and N.B. analyzed the data; N.B., H.B., P.A.G, E.F., and M.Z. revised the manuscript; M.E. wrote the article.
Funding
This research received funding from the European Space Agency’s Climate Change Initiative Plus for Soil Moisture (ESRIN Contract No: 4000126684/19/I-NB: ”ESA CCI+ Phase 1 New R&D on CCI ECVS Soil Moisture”), and the company Aiway.
Acknowledgments
The authors wish also to thank the European Space Agency for the Sentinel-1 and Sentinel-2 data. Finally, the authors would like to thank Zohra Lili Chabaane for generously providing the in situ data over the Kairouan study area.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
Appendix 7.1. Levenberg-Marquardt algorithm
The Levenberg-Marquardt algorithm [18] is used to optimize the parameters of our neural network and writes as follows:
- Initialize the parameters: Set the weight matrices and bias vectors to initial values and choose an initial damping factor .
- Compute the Jacobian matrix J: For each input-output pair , compute the Jacobian matrix , which contains the partial derivatives of the loss function with respect to the model parameters for that specific input-output pair. Then, compute the combined Jacobian matrix J by stacking vertically for all input-output pairs in the dataset.
- Compute the gradient vector g: Calculate the gradient vector g by multiplying the transpose of the Jacobian matrix J with the error vector e (the difference between the predicted output and the true output) for all input-output pairs in the dataset.
- Update the parameters: Solve the following linear equation for the parameter update vector :where represents a diagonal matrix with the diagonal elements of the matrix , and is the damping factor.
- Update the parameters by adding the parameter update vector :
- Evaluate the new parameters: Calculate the new loss function value using the updated parameters. If is smaller than the current loss function value L, accept the updated parameters, decrease the damping factor (e.g., by multiplying it by a factor between 0.1 and 0.5), and proceed to the next iteration. If is not smaller than the current loss function value L, reject the updated parameters, increase the damping factor (e.g., by multiplying it by a factor between 2 and 10), and repeat the parameter update step.
- Convergence check: Repeat steps 2-6 until a stopping criterion is met, such as reaching a maximum number of iterations, a minimum change in the loss function, or a minimum change in the model parameters.
The Levenberg-Marquardt algorithm adjusts the damping factor to balance between gradient descent and Gauss-Newton method behavior, resulting in a more efficient convergence to the optimal solution. References
References
- Chaudhary M.T., Piracha A. 2021. Natural Disasters-Origins, Impacts, Management. Encyclopedia 2021, 1, 1101-1131. [CrossRef]
- Baghdadi N., Zribi M. 2016. Characterization of Soil Surface Properties Using Radar Remote Sensing. Land Surface Remote Sensing in Continental Hydrology, 1-39. [CrossRef]
- Ulaby F.T., Moore R.K., Fung A.K. Microwave Remote Sensing: Active and Passive. Volume I: Microwave Remote Sensing Fundamentals and Radiometry. International Microwave Remote Sensing Fundamentals and Radiometry; Artech House: Norwood, MA, USA, 1981.
- Dubois P.C., van Zyl J., Engman T. 1995. Measuring Soil Moisture with Imaging Radars. International IEEE Transactions on Geoscience and Remote Sensing, 33(4), 915-926.
- Holah N., Baghdadi N., Zribi M., Bruand A., and King C., 2005. Potential of ASAR/ENVISAT for the characterization of soil surface parameters over bare agricultural fields. Remote sensing of environment, Vol. 96, no. 1, 78-86. [CrossRef]
- Mattia F., Satalino G., Pauwels V.R.N., Loew A. 2009. Soil moisture retrieval through a merging of multi-temporal L-band SAR data and hydrologic modelling. Hydrology and Earth System Sciences, 13(3), 343-356. [CrossRef]
- Hamze M., Baghdadi N., El Hajj M., Zribi M., Bazzi H., Cheviron B., Faour G. Integration of L-Band Derived Soil Roughness into a Bare Soil Moisture Retrieval Approach from C-Band SAR Data. Remote Sens. 2021, 13, 2102. [CrossRef]
- QH, Tang & Gao, Huilin & Lu, Hui & Lettenmaier, Dennis. 2009. Remote sensing: Hydrology. Progress in Physical Geography. 33. 490-509. [CrossRef]
- Knipper K.R., Hogue T.S., Franz K.J., Scott R.L. Downscaling SMAP and SMOS soil moisture with moderate-resolution imaging spectroradiometer visible and infrared products over southern Arizona. International Journal of Applied Remote Sensing 2017, 11, 026021. [CrossRef]
- Schwerdt M., Schmidt K., Ramon N.T., Klenk P., Yague-Martinez N., Prats Iraola P., Zink M., Geudtner D., Independent System Calibration of Sentinel-1B.Remote. Sens. 2017, 9, 511.. [CrossRef]
- Fung A.K. 1994. Microwave scattering and emission models and their applications, Artech House:Boston, MA.
- Zribi M., Taconet O., Le Hégarat-Mascle S., Vidal-Madjar D., Emblanch C., Loumagne C., and Normand M., 1997. Backscattering behavior and simulation comparison over bare soils using SIRC/XSAR and ERASME 1994 data over Orgeval. Remote Sensing of Environment, vol. 59, no. 2, 256-266. [CrossRef]
- Baghdadi N., King C., Chanzy A., and Wingneron J.-P., 2002. An empirical calibration of IEM model based on SAR data and measurements of soil moisture and surface roughness over bare soils. International Journal of Remote Sensing, vol. 23, no. 20, pp. 4325-4340. [CrossRef]
- Baghdadi N., Gherboudj I., Zribi M., Sahebi M., Bonn F., and King C., 2004. Semi-empirical calibration of the IEM backscattering model using radar images and moisture and roughness field measurements. International Journal of Remote Sensing, vol. 25, no. 18, pp. 3593-3623. [CrossRef]
- Chen K.-S., Wu T.-D., Tsang L., Li Q., Shi J., Fung A.K. 2003. Emission of rough surfaces calculated by the integral equation method with comparison to three-dimensional moment method simulations. IEEE Trans. Geosci. Remote Sens., 41, 90–101. [CrossRef]
- El Hajj M., Baghdadi N., Zribi M., Bazzi H., 2017. Synergic use of Sentinel-1 and Sentinel-2 images for operational soil moisture mapping at high spatial resolution over agricultural areas. Remote Sensing, 2017, 9, 1292. [CrossRef]
- Bazzi H., Baghdadi N., El Hajj M., Zribi M., 2019. Potential of Sentinel-1 Surface Soil Moisture Product for Detecting Heavy Rainfall in the South of France. Sensors, 2019, 19, 802; doi:10.3390/s19040802. [CrossRef]
- Levenberg K., 1994. A Method for the Solution of Certain Non-linear Problems in Least Squares. Quarterly of Applied Mathematics, Vol. 2, No. 2 (JULY, 1944), pp. 164-168. [CrossRef]
- Aubert M., Baghdadi N., Zribi M., Douaoui A., Loumagne C., Baup F., El Hajj M., Garrigues S., 2011. Characterization of soil surface by TerraSAR-X imagery. Remote Sensing of Environment, 115, 1801–1810, 2011.
- Baghdadi N., Gaultier S., and King C., 2002. Retrieving surface roughness and soil moisture from SAR data using neural network. Canadian Journal of Remote Sensing, vol. 28, no. 5, pp. 701-711. [CrossRef]
- Bazzi H., Baghdadi N., Fayad I., Zribi M., Belhouchette H., Demarez V., 2020. Near Real- Time Irrigation Detection at Plot Scale Using Sentinel-1 Data. Remote Sensing, 12, 1456. [CrossRef]
- Baghdadi N., King C., Bourguignon A., and Remond A., 2002. Potential of ERS and RADARSAT data for surface roughness monitoring over bare agricultural fields: application to catchments in Northern France. International Journal of Remote Sensing, vol. 23, no. 17, pp. 3427-3442. [CrossRef]
Figure 1.
Locator map of the Montpellier study area in the Occitanie region of France. In green are the reference fields on which soil moisture and roughness measurements were collected.
Figure 1.
Locator map of the Montpellier study area in the Occitanie region of France. In green are the reference fields on which soil moisture and roughness measurements were collected.
Figure 2.
Locator map of the Kairouan study area in the Kairouan Governorate of Tunisia. In green are the reference fields on which soil moisture measurements are collected.
Figure 2.
Locator map of the Kairouan study area in the Kairouan Governorate of Tunisia. In green are the reference fields on which soil moisture measurements are collected.
Figure 3.
Accuracy metrics (BIAS, RMSE and MAPE) on soil moisture estimates of the 4 configurations using the synthetic validation set.
Figure 3.
Accuracy metrics (BIAS, RMSE and MAPE) on soil moisture estimates of the 4 configurations using the synthetic validation set.
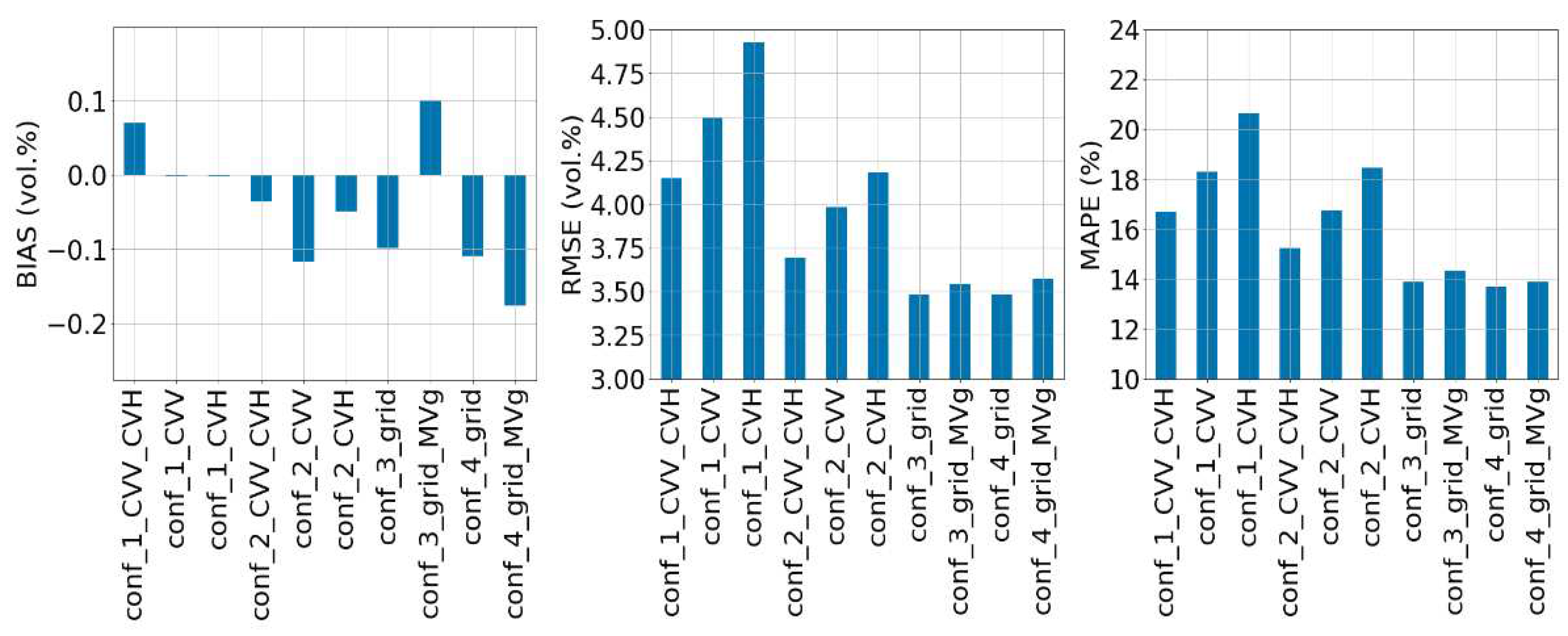
Figure 4.
sensitivities on soil moisture ranges for the synthetic validation set. Only the best subcase of each configuration is plotted, conf_3_grid and conf_4_grid were plotted without a priori information on MVp.
Figure 4.
sensitivities on soil moisture ranges for the synthetic validation set. Only the best subcase of each configuration is plotted, conf_3_grid and conf_4_grid were plotted without a priori information on MVp.
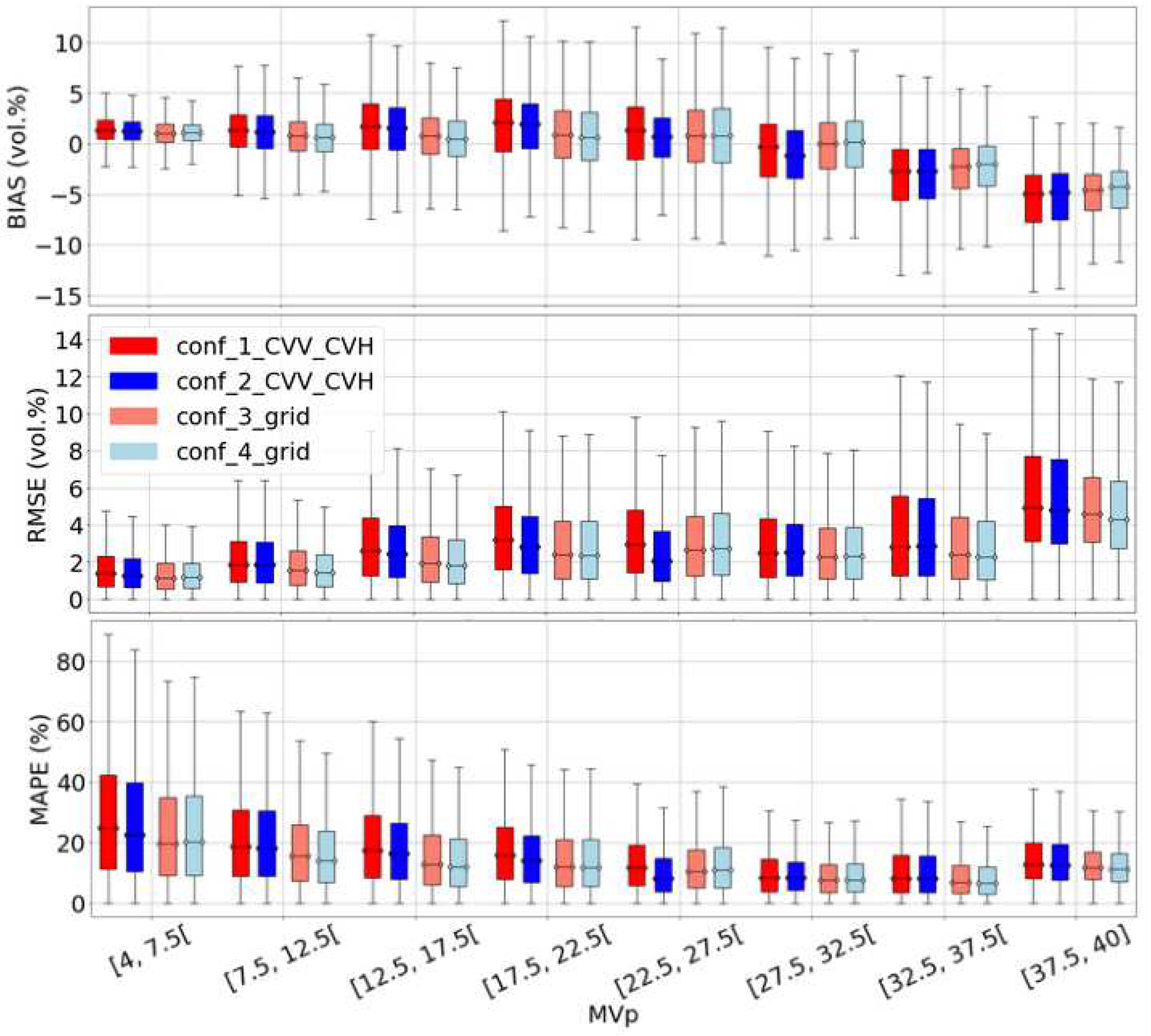
Figure 5.
sensitivities on soil roughness (HRMS) for the synthetic validation set. Only the best subcase of each configuration is plotted, conf_3_grid and conf_4_grid were plotted without a priori information on MVp.
Figure 5.
sensitivities on soil roughness (HRMS) for the synthetic validation set. Only the best subcase of each configuration is plotted, conf_3_grid and conf_4_grid were plotted without a priori information on MVp.
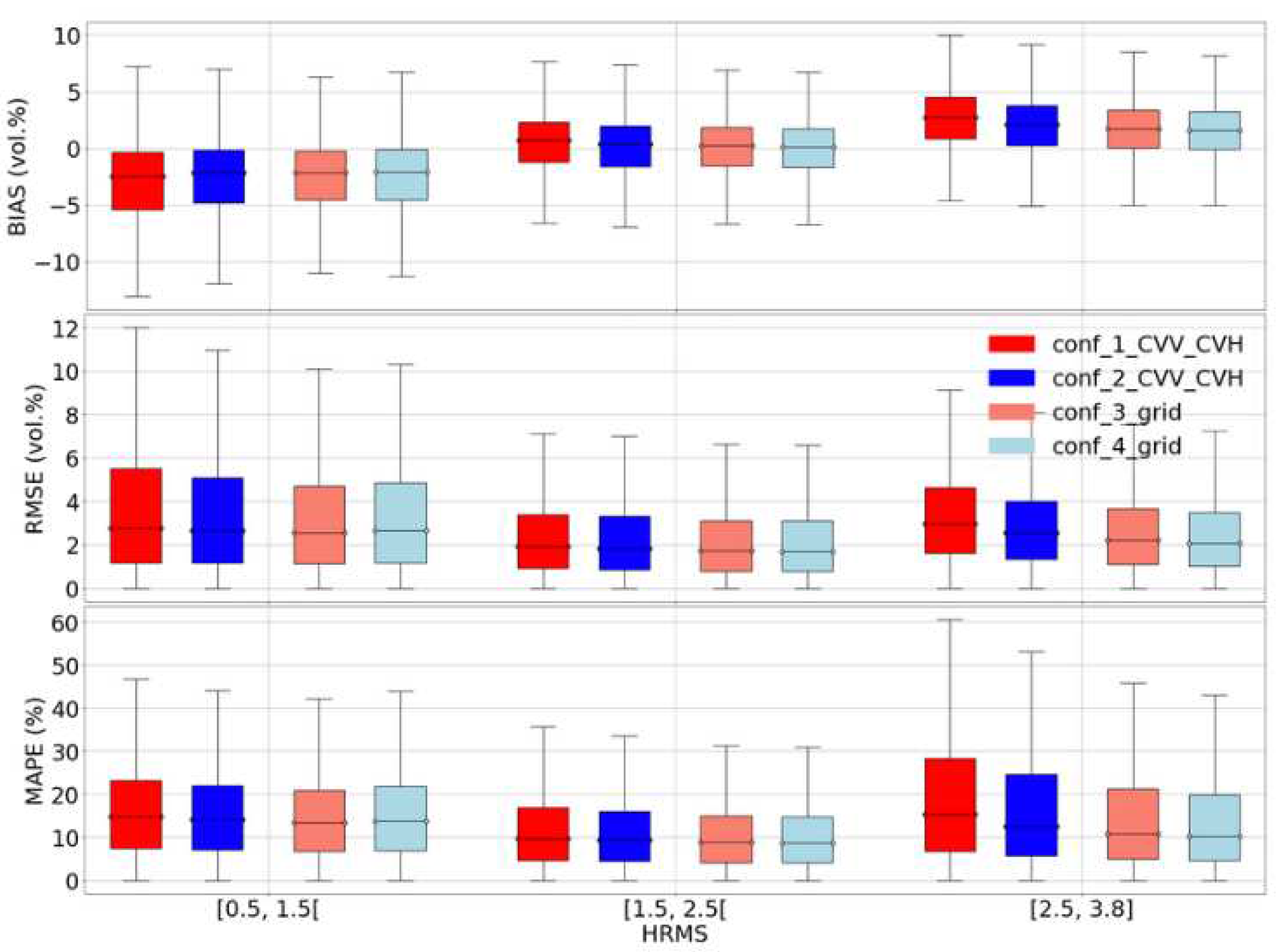
Figure 6.
Accuracy metrics (BIAS, RMSE and MAPE) on soil moisture estimates of the 4 configurations using the real dataset.
Figure 6.
Accuracy metrics (BIAS, RMSE and MAPE) on soil moisture estimates of the 4 configurations using the real dataset.
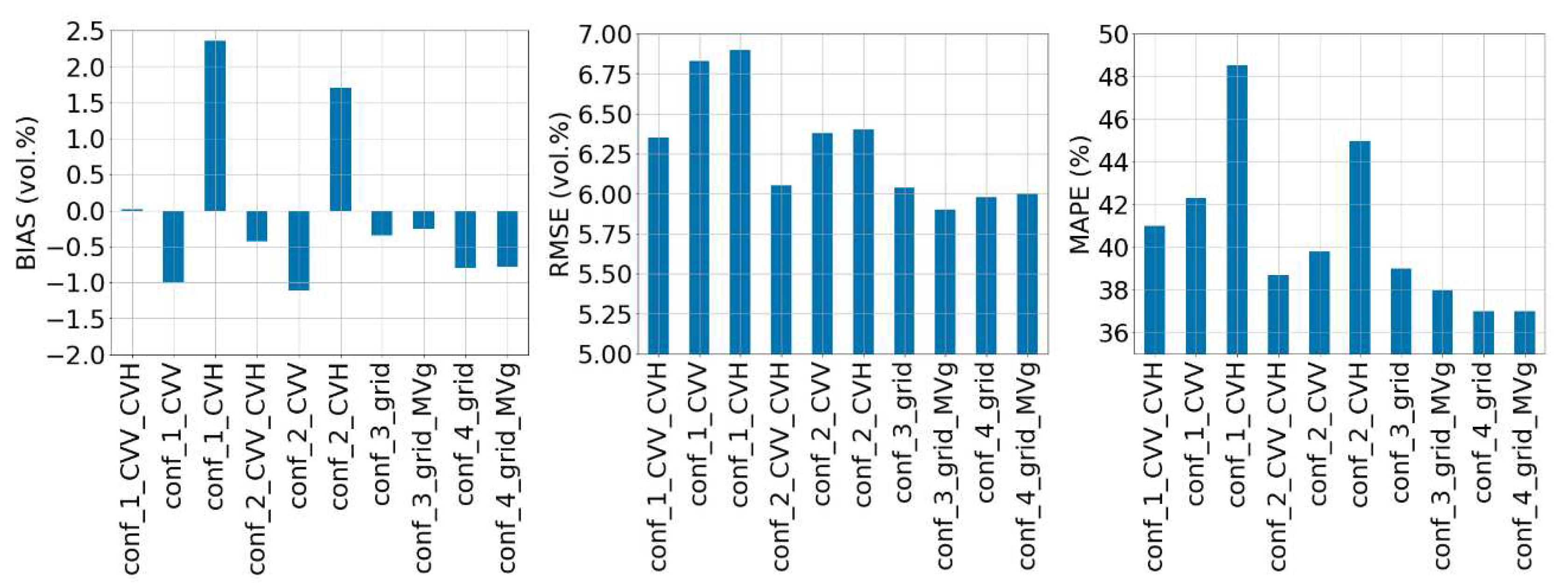
Figure 7.
Model sensitivity on soil moisture for the real dataset. Only the best subcase of each configuration is plotted, case_3_grid_MVg and conf_4_grid were plotted without a priori information on MVp.
Figure 7.
Model sensitivity on soil moisture for the real dataset. Only the best subcase of each configuration is plotted, case_3_grid_MVg and conf_4_grid were plotted without a priori information on MVp.
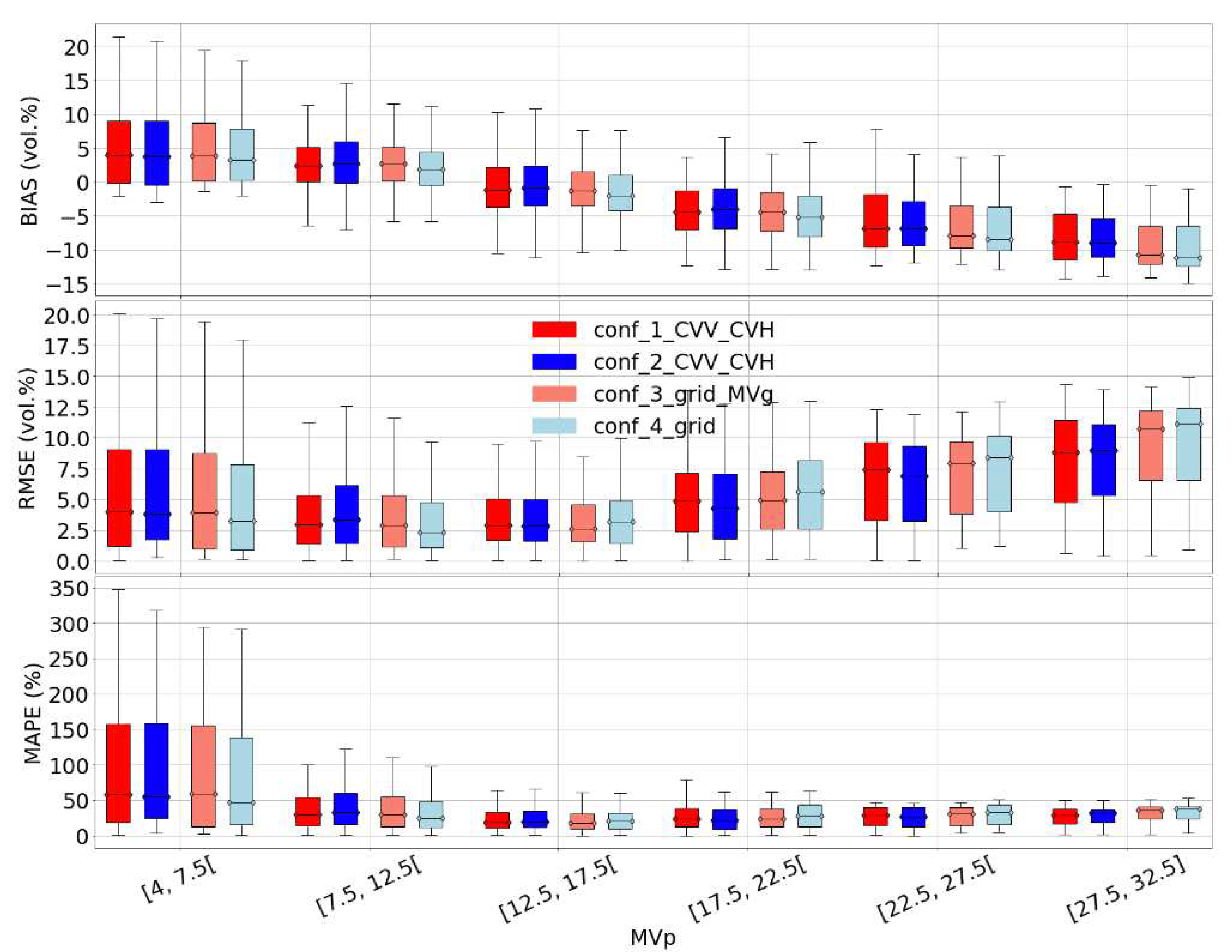
Figure 8.
Model sensitivity across different soil roughness ranges for the real dataset. Only the best subcase of each configuration is plotted, case_3_grid_MVg and conf_4_grid were plotted without a priori information on MVp.
Figure 8.
Model sensitivity across different soil roughness ranges for the real dataset. Only the best subcase of each configuration is plotted, case_3_grid_MVg and conf_4_grid were plotted without a priori information on MVp.
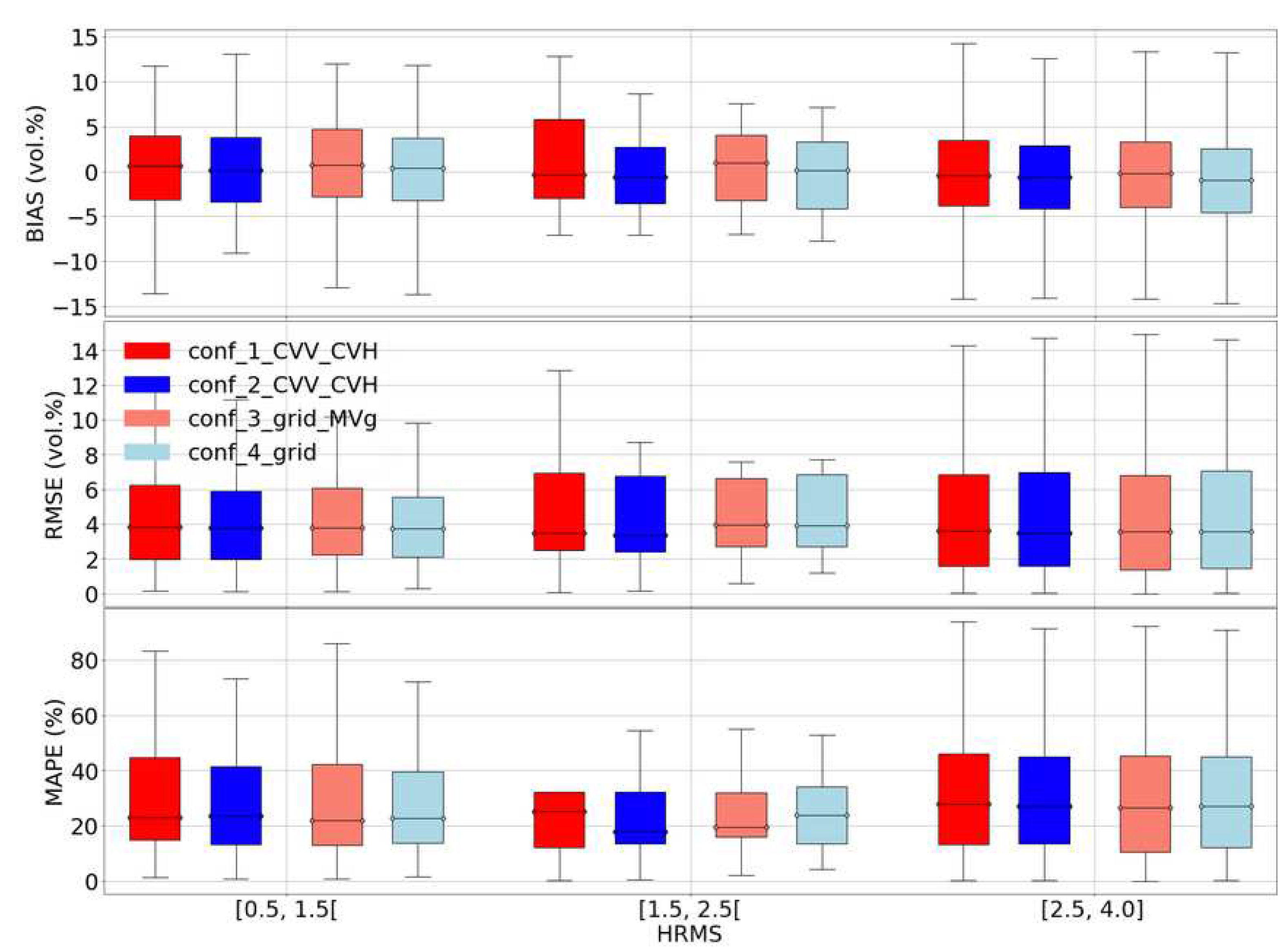
Figure 9.
Model sensitivity on soil moisture for the Montpellier dataset. Only the best subcase of each configuration is plotted, case_3_grid_MVg and conf_4_grid were plotted without a priori information on MVp.
Figure 9.
Model sensitivity on soil moisture for the Montpellier dataset. Only the best subcase of each configuration is plotted, case_3_grid_MVg and conf_4_grid were plotted without a priori information on MVp.
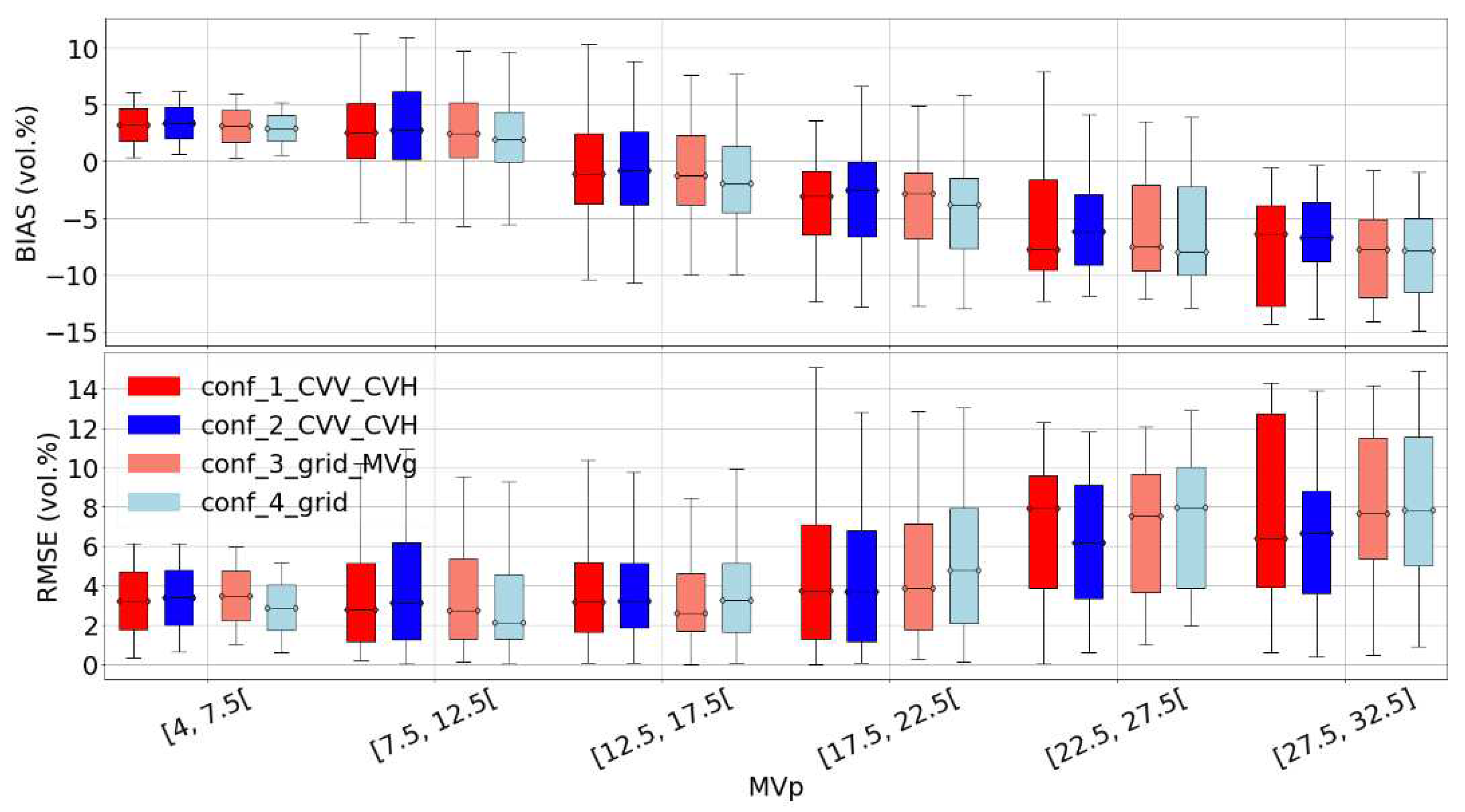
Figure 10.
Model sensitivity on soil moisture for the Kairouan dataset. Only the best subcase of each configuration is plotted, case_3_grid and conf_4_grid were plotted without a priori information on MVp.
Figure 10.
Model sensitivity on soil moisture for the Kairouan dataset. Only the best subcase of each configuration is plotted, case_3_grid and conf_4_grid were plotted without a priori information on MVp.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








