Prerpints.org logo
Preprint
Article

Vegetation Identification in Hyperspectral Images Using Distance/Correlation Metrics

Altmetrics

Downloads

142

Views

44

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

08 June 2023

Posted:

09 June 2023

You are already at the latest version

Alerts
Abstract
Vegetation identification using remote sensing is essential for understanding terrestrial ecosystems and monitoring climate change. This technology by providing high-resolution images of the Earth's surface from satellites, aircraft, and drones has revolutionized the way scientists study and un-derstand vegetation patterns, providing information on the distribution, structure, and health of plant communities in different regions and biomes. However, identifying vegetation in multi and hyperspectral images remains a difficult, time-consuming, and costly process. Traditional methods for vegetation mapping involve the in-terpretation of spectral indices such as the Normalized Difference Vegetation Index (NDVI), alt-hough they often suffer from limitations such as manual interpretation and limited spatial resolution of satellite images. Furthermore, machine learning techniques, artificial neural networks, decision trees, support vector machines, and random forests have shown promising results in identifying and classifying vegetation cover from hyperspectral images. However, due to the need for per-son-nel with specialized expertise, their application on a large scale is still challenging. On the other hand, correlation methods between curves have emerged as powerful and simplified tool for comparing spectral signatures of hyperspectral image pixels and efficiently classifying vegetation in a study area. Pearson's correlation coefficient and spectral angle mapper are among the most common correlation methods used in vegetation mapping. These correlation methods, among many others available, offer an easily implemented and computationally efficient approach, making them particularly useful for applications in developing countries or regions with limited resources. In this article, a comparative study of correlation/distance metrics was conducted for the detection of vegetation pixels in hyperspectral images. The study allowed for the comparison of five distance and/or correlation metrics: direct correlation, cosine similarity, normalized Euclidean distance, Bray-Curtis’s distance, and Pearson correlation. The two metrics that yielded the best accuracy results in vegetation pixel detection were direct correlation and Pearson correlation. Based on the selected methods, a vegetation detection algorithm was implemented and validated on a hyper-spectral image of the Manga neighborhood in Cartagena de Indias, Colombia. The spectral library was utilized for image processing, while the numpy and scipy libraries in the Python programming language were used for the mathematical calculation of correlations. Both the study's approach and the implemented algorithm aim to serve as a reference for conducting detection studies of various material types in hyperspectral images using open-access programming platforms.
Keywords: 
Subject: Environmental and Earth Sciences  -   Environmental Science

1. Introduction

Remote sensing technology has revolutionized the field of vegetation mapping and monitoring, providing a powerful tool for scientists and researchers to study and understand complex terrestrial ecosystems, [1,2,3,4]. The ability to obtain high-resolution images of the Earth’s surface from satellites, aircraft, and drones has transformed the way humans perceive and analyze vegetation patterns, providing insights into the distribution, structure, and health of plant communities across different regions and biomes, [1,5,6,7,8,9,10].
Despite the significant advances in remote sensing technology over the past few decades, the identification of vegetation in multi and hyperspectral images remains a challenging task due to the complex spectral signatures of different plant species, as well as the influence of environmental factors such as soil, water, and atmospheric conditions, [11]. Traditional methods for vegetation mapping using remote sensing involve the interpretation of spectral indices, such as the Normalized Difference Vegetation Index (NDVI), which provide a measure of the vegetation cover based on the contrast between the red and near-infrared bands of the electromagnetic spectrum, [9,12,13,14,15,16,17,18,19,20,21].
While these methods have proven to be effective in many applications, they suffer from several limitations, including the need for manual interpretation and the limited spatial resolution of satellite images. Moreover, traditional methods are often time-consuming and high cost, requiring extensive field surveys and ground truth data to calibrate and validate the results, [11,22,23].
To overcome these challenges, machine learning techniques have emerged as a promising approach for vegetation mapping and classification, offering a cost-effective and accurate solution for remote sensing applications, especially in developing countries. Machine learning algorithms can analyze vast amounts of hyperspectral data and identify patterns and features that are difficult or impossible to discern through human interpretation, allowing for the automated and objective detection of vegetation cover. The use of machine learning applications in vegetation mapping has been on the rise in recent years [24,25,26], driven by the availability of large hyperspectral datasets and the development of advanced algorithms and computational tools. Machine learning techniques such as artificial neural networks [27,28,29], decision trees [30,31], support vector machines [32], and random forests [33,34], have shown promising results in identifying and classifying vegetation cover from hyperspectral images, offering a more robust, reliable and cost-effective solution for remote sensing applications.
In addition to machine learning techniques, correlation methods between curves have emerged as another powerful tool for comparing spectral signatures of hyperspectral image pixels and efficiently classifying vegetation in a study area. Spectral signatures are graphical representations of the reflectance values of an object or material across the electromagnetic spectrum. In the context of vegetation mapping, spectral signatures can be used to identify different plant species or vegetation types based on their unique spectral properties, [35]. Correlation methods between curves can be used to compare the spectral signatures of different pixels in a hyperspectral image and identify similarities or differences in their spectral properties. Among the most common correlation methods used in vegetation mapping are include Pearson’s correlation coefficient and spectral angle mapper among many other methos available [30,36]
Pearson’s correlation coefficient measures the linear relationship between two sets of data and ranges from -1 to 1, with values closer to 1 indicating a strong positive correlation between the two sets of data. In vegetation mapping, Pearson’s correlation coefficient can be used to compare the spectral signatures of different pixels and identify areas with similar vegetation cover, [37,38].
The spectral angle mapper, on the other hand, measures the angular similarity between two spectral signatures and ranges from 0 to 1, with values closer to 1 indicating a high degree of spectral similarity between the two signatures. The spectral angle mapper can be used to compare the spectral signatures of different pixels and identify areas with similar vegetation, [30,39,40].
These correlations offer a complementary approach to machine learning techniques. Moreover, these correlation methods can be easily implemented and computationally efficient, making them particularly useful for applications in developing countries or regions with limited resources.
The need to efficiently classify vegetation in a study area using remote sensing technology has led to the development of various methods for comparing spectral signatures of hyperspectral image pixels. The focus of the present work is to determine the best distance/correlation-based method for vegetation detection in hyperspectral images with 380 bands from 400nm to 2400 nm in an urban area through five different Correlation Methods named as “Correlation methos”, “Cosine” “Euclidean”, “Bray Curtis” and “Pearson”, [41,42,43,44,45]. The paper is organized as follows: In Section 2 the authors present an overview of the correlation method used for vegetation mapping in the present work, including the key features and parameters of different algorithms. In Section 3, results are presented discussing their effectiveness and potential for future research. Finally, in Section 4, the authors provide concluding remarks and highlight the key challenges and opportunities of using these methods for vegetation mapping and classification.

2. Methodology

For the development of this research, the following 5 methodological phases were considered (Figure 1): identification of reference pixels, obtaining the average or characteristic pixel, determination of distance/correlation metrics, selection of the best metrics and detection of vegetation in the reference image.
In phase 1 of the methodology, a set of 100 coordinates corresponding to vegetation pixels and a set of 100 coordinates corresponding to non-vegetation pixels (roofs, road, sea, containers) were obtained manually from the reference image. The aforementioned, to compare the accuracy of the different distance and correlation metrics in both sets. In phase 2 of the methodology, an average pixel or characteristic pixel was obtained from the 100 vegetation pixels, which was determined by averaging the arrays of 380 positions of each vegetation pixel. Once the characteristic pixel is obtained, in phase 3 of the methodology, the calculation of the distance/correlation metrics between the average pixel and the vegetation and non-vegetation sets is performed, in order to determine the precision of each metric. The 5 distance/correlation metrics used in this phase were: direct correlation (correlation distance), similarity or cosine distance, normalized Euclidean distance, Bray-Curtis distance (also known as Normalized Manhattan distance) and Pearson’s correlation coefficient. The mathematical description of each of these metrics is presented below.
Direct correlation: It is a measure of dependence between two paired random variables (vectors) of arbitrary dimension, not necessarily equal. That is, it calculates the correlation distance between two one-dimensional arrays. The correlation distance between two vectors u → and v → , is defined as [41], (1):
d ( u → , v → ) = 1 − ( u → − u → ¯ ) · ( v → − v → ¯ ) ( u → − u → ¯ ) 2 ( v → − v → ¯ ) 2
where u → ¯ and v → ¯ are the means of the elements of u → and v → , ( u → − u → ¯ ) · ( v → − v → ¯ ) is the scalar product and ( u → − u → ¯ ) 2 is its norm or variance.
Similarity or cosine distance: It is a measure of similarity between two non-zero vectors defined in an inner product space. The cosine distance is the cosine of the angle between the vectors. It is the scalar product of the vectors divided by the product of their lengths. It differs from direct correlation as it circumvents the utilization of the arithmetic mean or average of the vectors under examination. The cosine distance, ascribed as the disparity between two vectors u → and v → u ⃗ and v ⃗, is rigorously delineated as, [45], (2):
d ( u → , v → ) = 1 − u → · v → u → 2 v → 2
where u → · v → is the scalar product and u → 2 is its norm.
Normalized Euclidean Distance: It gives the squared distance between two vectors where the lengths have been scaled to have a unit norm. This is useful when the direction of the vector is significant but the magnitude is not [43]. According to [43] the normalized Euclidean distance of two vectors is defined by (3):
N E D ( u → , v → ) 2 = 1 2 · u → − u → ¯ − v → − v → ¯ 2 ( u → − u → ¯ 2 + v → − v → ¯ 2 ) = 0.5 v a r ( u → − v → ) v a r u → + v a r ( v → )
where u → ¯ and v → ¯ are the means of the elements of u → and v → and   2 is the variance.
Bray-Curtis distance: The Bray-Curtis distance is a normalization method commonly used in the field of botany, ecology and environmental sciences [44]. It is a statistic used to quantify the compositional dissimilarity between two different sites, based on counts at each site. It is defined by equation [44], (4):
d ( u → , v → ) = ∑ i = 1 n ( u i − v i ) ∑ i = 1 n ( u i + v i )
where n is the size of the vectors or sample. The Bray-Curtis distance is in the range [0, 1] if all coordinates are positive and is undefined if the entries are of length zero.
Pearson correlation coefficient: It is a measure of linear dependence between two quantitative random variables (vectors). Unlike covariance, Pearson’s correlation is independent of the scale of measurement of the variables [41]. Pearson’s population correlation coefficient (also denoted by r ( u → , v → ) ) is defined as [43], (5).
r ( u → , v → ) = σ ( u → , v → ) σ u → · σ v → = ∑ i = 1 n ( u i − u → ¯ ) · ( v i − v → ¯ ) ∑ i = 1 n ( u i − u → ¯ ) 2 · ∑ i = 1 n ( v i − v → ¯ ) 2
where n is the sample size, σ ( u → , v → ) is the covariance of ( u → , v → ) , σ u → is the standard deviation of vector u → ,, σ v → is the standard deviation of vector v → , and u → ¯ and v → ¯ are the means of u → and v → respectively.
Based on the previous equations corresponding to correlation metrics and considering that these metrics have values close to 0 when the correlation is high, Equation (6) was proposed to obtain a percentage of correlation or similarity
p o r c _ c o r r = ( 1 − a b s ( c o r r ) ) · 100
In phase 4 of the methodology, the results obtained by calculating the correlations and similarities described in phase 3 were consolidated in relation to vegetation and non-vegetation pixels. The aim was to determine the precision thresholds for the correlation percentages of each metric in both cases, in order to identify the best metrics to be used in vegetation detection. These metrics are the ones that best classify a pixel as vegetation. Finally, in phase 5, the vegetation detection process was performed on the entire hyperspectral reference image using the selected similarity and/or correlation metrics.

3. Results and Discussion

Firstly, starting from a hyperspectral image obtained from the Manga neighborhood in the city of Cartagena de Indias, Colombia, measuring 1500 x 1500 pixels with 380 bands per pixel ranging from 400 nm to 2400 nm (see Figure 2), a total of 100 arbitrary vegetation pixels were extracted from various locations across the image. The purpose was to obtain a representative or characteristic pixel by averaging the corresponding spectral signatures of the 100 pixels. This representative pixel was used to compare the correlation and similarity metrics described in the methodology (section 2).
In Figure 3a, the spectral signatures of the selected 100 pixels and their distribution across 380 bands can be observed. It is possible to appreciate that although the reflectance values exhibit variations, the shape of the 100 curves remains the same. They possess a set of peaks that are repeated in a similar manner across the different pixels. Similarly, in Figure 3b, the spectral signature corresponding to the characteristic or average pixel can be observed. This pixel is obtained by averaging the curves of the 100 pixels, incorporating the representative maximum and minimum values of the considered sample. The image reading and processing of the different pixels that compose it were performed using the functionalities provided by the Python spectral library.
Based on the above, initially, the representative or average pixel was correlated with each of the 100 selected vegetation pixels using the five metrics considered in Section 2. This was done to determine both the average and the thresholds obtained for each metric, which helps identify the most accurate and effective method for identifying the vegetation’s spectral signature. For this purpose, the authors started with the idea that each pixel in the image is a vector representation in space. In other words, each pixel is a vector with 380 positions corresponding to the 380 bands, each of which stores a reflectance value. By performing vector operations using the numpy library and the statistical tool from scipy between the average pixel and the 100 vegetation pixels, the bar chart presented in Figure 4 displays the average, minimum, and maximum values obtained for each of the five metrics considered.
In Figure 4, it is possible to observe that Pearson correlation, cosine distance, and direct correlation are the metrics that respectively present the highest average values of correlation percentage between the average pixel and the 100 vegetation pixels, with respective values of 99.54%, 99.47%, and 99.09%. Similarly, it can be appreciated that these same three metrics, in the same order, present the highest minimum percentage values of correlation between the average pixel and the 100 vegetation pixels, with respective values of 92.77%, 92.55%, and 85.53%. On the other hand, upon consolidating and comparing the threshold values of these three top metrics, it is possible to observe in Table 1 that the metric with the smallest difference between the maximum and minimum thresholds is Pearson correlation with a difference of 7.2%, followed by cosine distance with a difference of 7.41%.
Once the 100 vegetation pixels were studied, the correlation between the average pixel and the 100 randomly selected non-vegetation pixels was performed using the same five metrics and following a similar procedure as with the vegetation pixels. Hence, by conducting vector operations using the same Python libraries between the average pixel and the 100 non-vegetation pixels, the bar chart in Figure 5 presents the average, minimum, and maximum values for the five studied metrics.
According to Figure 5, it is possible to observe that direct correlation, Bray-Curtis distance (Bc), and Pearson correlation are the metrics that respectively present the lowest average values of correlation percentage between the average pixel and the 100 non-vegetation pixels, with respective values of 31.24%, 56.81%, and 65.62%. Similarly, in Figure 5, it can be appreciated that Bray-Curtis distance (Bc), direct correlation, and Euclidean distance (Eu) are the metrics that respectively present the lowest maximum values of correlation percentage between the average pixel and the 100 non-vegetation pixels, with respective values of 74.24%, 78.52%, and 82.09%. It is also important to mention that cosine distance and Pearson correlation, which showed the two best results for vegetation pixels in this case, have the two highest maximum percentages for non-vegetation pixels with values of 90.12% and 89.26% respectively. Although these values do not surpass the minimum threshold detected with vegetation pixels, they are close to a difference of 2.43% and 3.51% from the minimum threshold in vegetation pixels.
Continuing with the comparison between the results of correlation in vegetation and non-vegetation pixels, Figure 6 presents a comparative graph that shows, for each of the five considered metrics, the minimum correlation percentage value for vegetation and the maximum correlation percentage value for non-vegetation. It can be observed initially that Euclidean distance (Eu) and Bray-Curtis distance (Bc) metrics exhibit an overlap between these thresholds (the maximum value is greater than the minimum value, indicating a negative difference). This implies that applying these methods to the image may lead to confusion between vegetation and non-vegetation pixels. On the other hand, it is evident that the three metrics without overlap between the thresholds are direct correlation, cosine distance, and Pearson correlation. Among them, direct correlation shows the greatest difference between the thresholds (limits), with a percentage difference value of 7.01%.
The specification of the differences in thresholds shown in Figure 6 is presented in Table 2, which includes the percentage differences for each of the five metrics when comparing the lowest correlation with vegetation pixels to the highest correlation with non-vegetation pixels.
In Table 2, it is possible to verify how the overlap of thresholds in the Euclidean distance and Bray-Curtis distance metrics is evidenced by the negative difference between the minimum correlation percentage in vegetation pixels and the maximum correlation percentage in non-vegetation pixels. Similarly, it can be observed that the best results are respectively obtained for the direct correlation and Pearson correlation metrics, with percentage difference values of 7.01% and 3.51%. It is worth mentioning that these metrics are also among the top three metrics with the highest average correlation percentage in vegetation pixels. Therefore, based on the results, they represent the best options for vegetation detection in hyperspectral images.
According to the previous analysis, Figure 7 presents the results of applying the direct correlation and Pearson correlation methods to the hyperspectral image of the Manga neighborhood in Cartagena. This was done using the spectral library in Python and considering a threshold correlation percentage of 95%. In this regard, the implemented vegetation detection algorithm traverses each pixel of the image matrix, correlating each pixel of the image (a 380 positions vector) with the average vegetation pixel (380 positions) using direct correlation and Pearson correlation to determine the correlation percentage. If the correlation percentage is greater than 98%, the corresponding pixel in the displayed image is colored blue. Visually, it can be observed that in both cases, the detection algorithm adequately identifies the regions where vegetation is present, and the density of the detected vegetation pixels depends on the threshold adjustment for each correlation.
Finally, by performing a count on the vegetation pixels of the hyperspectral image of the Manga neighborhood that were detected by the algorithm based on correlation metrics, Pearson correlation, and cosine distance, with a 95% threshold, the percentages of detected vegetation were obtained, as presented in Figure 8. It can be observed that, according to the results obtained by the considered metrics, between 15% and 17% of the pixels correspond to vegetation within the hyperspectral image.
The present study introduces a novel approach to identify vegetation in hyperspectral images. This research offers valuable insights into the field of remote sensing and image analysis by utilizing distance and correlation metrics. The significance of this study is particularly relevant for developing countries, as it highlights the importance of open-access programming platforms for analyzing hyperspectral images. Accessible tools enable these countries to harness the potential of hyperspectral data, aiding in land monitoring, agricultural management, and environmental conservation efforts.

4. Conclusions

The purpose of this study was to propose a comparative approach to evaluate the accuracy of various distance and correlation metrics in the identification of vegetation in hyperspectral images of an urban area of the Manga neighborhood of Cartagena, Colombia. 100 pixels of vegetation and non-vegetation were selected from the hyperspectral image to create a reference pixel or average pixel. Then, correlations were made using five different metrics, and it was found that the direct correlation and Pearson metrics had the best precision and discrimination of vegetation pixels and were more efficient than the methods based on supervised learning.
Although these two metrics are different, a similar approach was used by randomly selecting 100 pixels of vegetation for training and creating an average pixel that includes the particular spectral signature of the vegetation. Afterwards, the correlations were validated using the average pixel and the five metrics considered. In addition, it was found that the Euclidean and Bray-Curtis distance metrics present greater difficulties in classifying pixels as vegetation or non-vegetation.
In general, the method proposed in this study, based on the use of correlation and/or vector distance metrics, proved to be effective for the differentiation of spectral signatures in the context of hyperspectral images. A visual inspection was carried out on the image to confirm that the detection algorithm based on both metrics allowed us to determine the vegetation in the correct areas, although the number of pixels detected can be adjusted according to the minimum thresholds for each correlation.
The algorithm implemented from the best correlation metrics can be used to carry out studies related to the determination of the spatial distribution of vegetation in different latitudes. In addition, the algorithm can be used as a reference for the detection of different types of objects or surfaces, such as water, asphalt, containers, roofs, among others.
An innovative aspect of the present study is the use of open-source software tools for the access, processing, and analysis of hyperspectral images. The spectral library was used to access, read, and obtain the pixels of the hyperspectral image in vector representation. The Python numpy and scipy libraries were also used to handle vector operations and calculate correlations. Finally, the Python matplotlib library was used to manage and display the spectral signatures of pixels and hyperspectral images. These tools can serve as a reference for testing and validating detection algorithms in the context of hyperspectral imaging.
In the future, it is intended to use machine learning models and specific classification models for the detection of vegetation pixels in hyperspectral images. It is also planned to test and calibrate the metrics considered in the detection of asbestos-cement on roofs in urban areas.

Supplementary Materials

Available upon reasonable request

Author Contributions

Conceptualization, G.E.C.G and M.A.O.A; methodology, G.E.C.G; software, G.E.C.G; validation, G.E.C.G. and M.A.O.A.; formal analysis, G.E.C.G.; investigation, G.E.C.G.; resources, M.S.; data curation, M.A.O.A.; writing—original draft preparation, G.E.C.G.; writing—review and editing, M.A.O.A. and M.S.; visualization, M.A.O.A.; supervision, M.S.; project administration, M.S.; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.

Funding

This article is considered a product in the framework of the project “Formulation of an integral strategy to reduce the impact on public and environmental health due to the presence of asbestos in the territory of the Department of Bolivar”, financed by the General System of Royalties of Colombia (SGR) and identified with the code BPIN 2020000100366. This project was executed by the University of Cartagena, Colombia, and the Asbestos-Free Colombia Foundation.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors thank David Enrique Valdelamar Martinez.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. F. Pérez-Cabello, R. Montorio, and D. B. Alves, “Remote sensing techniques to assess post-fire vegetation recovery,” Curr. Opin. Environ. Sci. Heal., vol. 21, p. 100251, Jun. 2021. https://doi.org/10.1016/J.COESH.2021.100251. [CrossRef]
  2. D. Andreatta, D. Gianelle, M. Scotton, and M. Dalponte, “Estimating grassland vegetation cover with remote sensing: A comparison between Landsat-8, Sentinel-2 and PlanetScope imagery,” Ecol. Indic., vol. 141, p. 109102, 2022. https://doi.org/10.1016/j.ecolind.2022.109102. [CrossRef]
  3. R. P. Sripada, “Determining In-Season Nitrogen Requirements for Corn Using Aerial Color-Infrared Photography,” North Carolina State University, 2005.
  4. L. Shikwambana, K. Xongo, M. Mashalane, and P. Mhangara, “Climatic and Vegetation Response Patterns over South Africa during the 2010/2011 and 2015/2016 Strong ENSO Phases,” Atmosphere (Basel)., vol. 14, no. 2, pp. 1–14, 2023. https://doi.org/10.3390/atmos14020416. [CrossRef]
  5. K. A. García-Pardo, D. Moreno-Rangel, S. Domínguez-Amarillo, and J. R. García-Chávez, “Remote sensing for the assessment of ecosystem services provided by urban vegetation: A review of the methods applied,” Urban For. Urban Green., vol. 74, p. 127636, Aug. 2022. https://doi.org/10.1016/J.UFUG.2022.127636. [CrossRef]
  6. E. Neinavaz, M. Schlerf, R. Darvishzadeh, M. Gerhards, and A. K. Skidmore, “Thermal infrared remote sensing of vegetation: Current status and perspectives,” Int. J. Appl. Earth Obs. Geoinf., vol. 102, p. 102415, Oct. 2021. https://doi.org/10.1016/J.JAG.2021.102415. [CrossRef]
  7. K. Meusburger, D. Bänninger, and C. Alewell, “Estimating vegetation parameter for soil erosion assessment in an alpine catchment by means of QuickBird imagery,” Int. J. Appl. Earth Obs. Geoinf., vol. 12, no. 3, pp. 201–207, Jun. 2010. https://doi.org/10.1016/J.JAG.2010.02.009. [CrossRef]
  8. V. Henrich, G. Krauss, C. Götze, and C. Sandow, “Index DataBase. A database for remote sensing indices,” 2012. https://www.indexdatabase.de/db/s-single.php?id=9 (accessed Sep. 29, 2022).
  9. S. Huang, L. Tang, J. P. Hupy, Y. Wang, and G. Shao, “A commentary review on the use of normalized difference vegetation index (NDVI) in the era of popular remote sensing,” J. For. Res., vol. 32, no. 1, pp. 1–6, 2021. https://doi.org/10.1007/s11676-020-01155-1. [CrossRef]
  10. D. H. Beltrán Hernández, “Aplicación de índices de vegetación para evaluar procesos de restauración ecológica en el Parque Forestal Embalse del Neusa,” Universidad Militar Nueva Granada, Neusa, Colombia, 2017.
  11. L. K. Torres Gil, D. Valdelamar Martínez, and M. Saba, “The Widespread Use of Remote Sensing in Asbestos, Vegetation, Oil and Gas, and Geology Applications,” Atmosphere (Basel)., vol. 14, no. 1, p. 172, 2023. https://doi.org/10.3390/atmos14010172. [CrossRef]
  12. G. S. Birth and G. R. McVey, “Measuring the Color of Growing Turf with a Reflectance Spectrophotometer,” Agron. J., vol. 60, no. 6, pp. 640–643, Nov. 1968. https://doi.org/10.2134/AGRONJ1968.00021962006000060016X. [CrossRef]
  13. A. F. Wolf, “Using WorldView-2 Vis-NIR multispectral imagery to support land mapping and feature extraction using normalized difference index ratios,” https://doi.org/10.1117/12.917717, vol. 8390, pp. 188–195, May 2012. https://doi.org/10.1117/12.917717.
  14. J. W. . J. Rouse et al., “Monitoring vegetation systems in the great plains with erts,” 1974.
  15. R. J. Kauth and G. S. P. Thomas, “The tasselled cap - A graphic description of the spectral-temporal development of agricultural crops as seen by Landsat,” 1976.
  16. C. J. Tucker, “Red and photographic infrared linear combinations for monitoring vegetation,” Remote Sens. Environ., vol. 8, no. 2, pp. 127–150, May 1979. https://doi.org/10.1016/0034-4257(79)90013-0. [CrossRef]
  17. A. R. Huete, “A soil-adjusted vegetation index (SAVI),” Remote Sens. Environ., vol. 25, no. 3, pp. 295–309, Aug. 1988. https://doi.org/10.1016/0034-4257(88)90106-X. [CrossRef]
  18. R. E. Crippen, “Calculating the vegetation index faster,” Remote Sens. Environ., vol. 34, no. 1, pp. 71–73, Oct. 1990. https://doi.org/10.1016/0034-4257(90)90085-Z. [CrossRef]
  19. A. A. Gitelson and M. N. Merzlyak, “Remote sensing of chlorophyll concentration in higher plant leaves,” Adv. Sp. Res., vol. 22, no. 5, pp. 689–692, Jan. 1998. https://doi.org/10.1016/S0273-1177(97)01133-2. [CrossRef]
  20. A. Bannari, H. Asalhi, and P. M. Teillet, “Transformed difference vegetation index (TDVI) for vegetation cover mapping,” in IEEE International Geoscience and Remote Sensing Symposium, 2002, vol. 5, pp. 3053–3055 vol.5. https://doi.org/10.1109/IGARSS.2002.1026867. [CrossRef]
  21. MaxMax, “Enhanced Normalized Difference Vegetation Index (ENDVI),” 2015. https://www.maxmax.com/endvi.htm (accessed Sep. 26, 2022).
  22. T. Adão et al., “Hyperspectral Imaging: A Review on UAV-Based Sensors, Data Processing and Applications for Agriculture and Forestry,” Remote Sens. 2017, Vol. 9, Page 1110, vol. 9, no. 11, p. 1110, Oct. 2017. https://doi.org/10.3390/RS9111110. [CrossRef]
  23. L. Wan, H. Li, C. Li, A. Wang, Y. Yang, and P. Wang, “Hyperspectral Sensing of Plant Diseases: Principle and Methods,” Agronomy, vol. 12, no. 6, pp. 1–19, 2022. https://doi.org/10.3390/agronomy12061451. [CrossRef]
  24. S. Wang et al., “Airborne hyperspectral imaging of cover crops through radiative transfer process-guided machine learning,” Remote Sens. Environ., vol. 285, p. 113386, 2023. https://doi.org/10.1016/j.rse.2022.113386. [CrossRef]
  25. A. Khan, A. D. Vibhute, S. Mali, and C. H. Patil, “A systematic review on hyperspectral imaging technology with a machine and deep learning methodology for agricultural applications,” Ecol. Inform., vol. 69, p. 101678, 2022. https://doi.org/10.1016/j.ecoinf.2022.101678. [CrossRef]
  26. D.Chen et al., “Improved Na+ estimation from hyperspectral data of saline vegetation by machine learning,” Comput. Electron. Agric., vol. 196, p. 106862, 2022. https://doi.org/10.1016/j.compag.2022.106862. [CrossRef]
  27. S. Gakhar and K. Chandra Tiwari, “Spectral – spatial urban target detection for hyperspectral remote sensing data using artificial neural network,” Egypt. J. Remote Sens. Sp. Sci., vol. 24, no. 2, pp. 173–180, 2021. https://doi.org/10.1016/j.ejrs.2021.01.002. [CrossRef]
  28. B. Ma, W. Zeng, G. Hu, R. Cao, D. Cui, and T. Zhang, “Normalized difference vegetation index prediction based on the delta downscaling method and back-propagation artificial neural network under climate change in the Sanjiangyuan region, China,” Ecol. Inform., vol. 72, p. 101883, 2022. https://doi.org/10.1016/j.ecoinf.2022.101883. [CrossRef]
  29. M. Trombetti, D. Riaño, M. A. Rubio, Y. B. Cheng, and S. L. Ustin, “Multi-temporal vegetation canopy water content retrieval and interpretation using artificial neural networks for the continental USA,” Remote Sens. Environ., vol. 112, no. 1, pp. 203–215, 2008. https://doi.org/10.1016/j.rse.2007.04.013. [CrossRef]
  30. B. F. R. Davies et al., “Multi- and hyperspectral classification of soft-bottom intertidal vegetation using a spectral library for coastal biodiversity remote sensing,” Remote Sens. Environ., vol. 290, p. 113554, 2023. https://doi.org/10.1016/j.rse.2023.113554. [CrossRef]
  31. A. Badola, S. K. Panda, D. A. Roberts, C. F. Waigl, R. R. Jandt, and U. S. Bhatt, “A novel method to simulate AVIRIS-NG hyperspectral image from Sentinel-2 image for improved vegetation/wildfire fuel mapping, boreal Alaska,” Int. J. Appl. Earth Obs. Geoinf., vol. 112, p. 102891, 2022. https://doi.org/10.1016/j.jag.2022.102891. [CrossRef]
  32. T. Rumpf, A.-K. Mahlein, U. Steiner, E.-C. Oerke, H.-W. Dehne, and L. Plümer, “Early detection and classification of plant diseases with Support Vector Machines based on hyperspectral reflectance,” Comput. Electron. Agric., vol. 74, no. 1, pp. 91–99, 2010. https://doi.org/10.1016/j.compag.2010.06.009. [CrossRef]
  33. L. Wang and Q. Wang, “Fast spatial-spectral random forests for thick cloud removal of hyperspectral images,” Int. J. Appl. Earth Obs. Geoinf., vol. 112, p. 102916, 2022. https://doi.org/10.1016/j.jag.2022.102916. [CrossRef]
  34. X. Ding, Q. Wang, and X. Tong, “Integrating 250 m MODIS data in spectral unmixing for 500 m fractional vegetation cover estimation,” Int. J. Appl. Earth Obs. Geoinf., vol. 111, p. 102860, 2022. https://doi.org/10.1016/j.jag.2022.102860. [CrossRef]
  35. S. N. Shore, “Astrochemistry,” Encycl. Phys. Sci. Technol., pp. 665–678, 2003. https://doi.org/10.1016/B0-12-227410-5/00032-6. [CrossRef]
  36. N. J. Galle et al., “Correlation of WorldView-3 spectral vegetation indices and soil health indicators of individual urban trees with exceptions to topsoil disturbance,” City Environ. Interact., vol. 11, p. 100068, 2021. https://doi.org/10.1016/j.cacint.2021.100068. [CrossRef]
  37. K. R. Thorp, A. N. French, and A. Rango, “Effect of image spatial and spectral characteristics on mapping semi-arid rangeland vegetation using multiple endmember spectral mixture analysis (MESMA),” Remote Sens. Environ., vol. 132, pp. 120–130, 2013. https://doi.org/10.1016/j.rse.2013.01.008. [CrossRef]
  38. Y. Zhu et al., “Converted vegetation type regulates the vegetation greening effects on land surface albedo in arid regions of China,” Agric. For. Meteorol., vol. 324, p. 109119, 2022. https://doi.org/10.1016/j.agrformet.2022.109119. [CrossRef]
  39. T. A. G. Smyth, R. Wilson, P. Rooney, and K. L. Yates, “Extent, accuracy and repeatability of bare sand and vegetation cover in dunes mapped from aerial imagery is highly variable,” Aeolian Res., vol. 56, p. 100799, 2022. https://doi.org/10.1016/j.aeolia.2022.100799. [CrossRef]
  40. J. Tian et al., “Simultaneous estimation of fractional cover of photosynthetic and non-photosynthetic vegetation using visible-near infrared satellite imagery,” Remote Sens. Environ., vol. 290, p. 113549, 2023. https://doi.org/10.1016/j.rse.2023.113549. [CrossRef]
  41. R. Lyons, “Distance covariance in metric spaces,” Ann. Probab., vol. 41, no. 5, pp. 3284–3305, 2013. https://doi.org/10.1214/12-AOP803. [CrossRef]
  42. G. J. Székely and M. L. Rizzo, “Brownian distance covariance,” Ann. Appl. Stat., vol. 3, no. 4, pp. 1236–1265, 2009. https://doi.org/10.1214/09-AOAS312. [CrossRef]
  43. R. Connor, “A tale of four metrics,” Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics), vol. 9939 LNCS, pp. 210–217, 2016. https://doi.org/10.1007/978-3-319-46759-7_16. [CrossRef]
  44. J. R. Bray and J. T. Curtis, “An Ordination of the Upland Forest Communities of Southern Wisconsin,” Source Ecol. Monogr., vol. 27, no. 4, pp. 325–349, 1957. https://doi.org/10.2307/1942268. [CrossRef]
  45. V. t. Novotn, “Implementation notes for the soft cosine measure,” Int. Conf. Inf. Knowl. Manag. Proc., pp. 1639–1642, 2018. https://doi.org/10.1145/3269206.3269317. [CrossRef]
Preprints 76092 g001
Figure 1. Methodology considered.
Figure 1. Methodology considered.
Preprints 76092 g001
Preprints 76092 g002
Figure 2. Reference hyperspectral image.
Figure 2. Reference hyperspectral image.
Preprints 76092 g002
Preprints 76092 g003
Figure 3. Pixels selected for comparative study (a) and mean pixel (b).
Figure 3. Pixels selected for comparative study (a) and mean pixel (b).
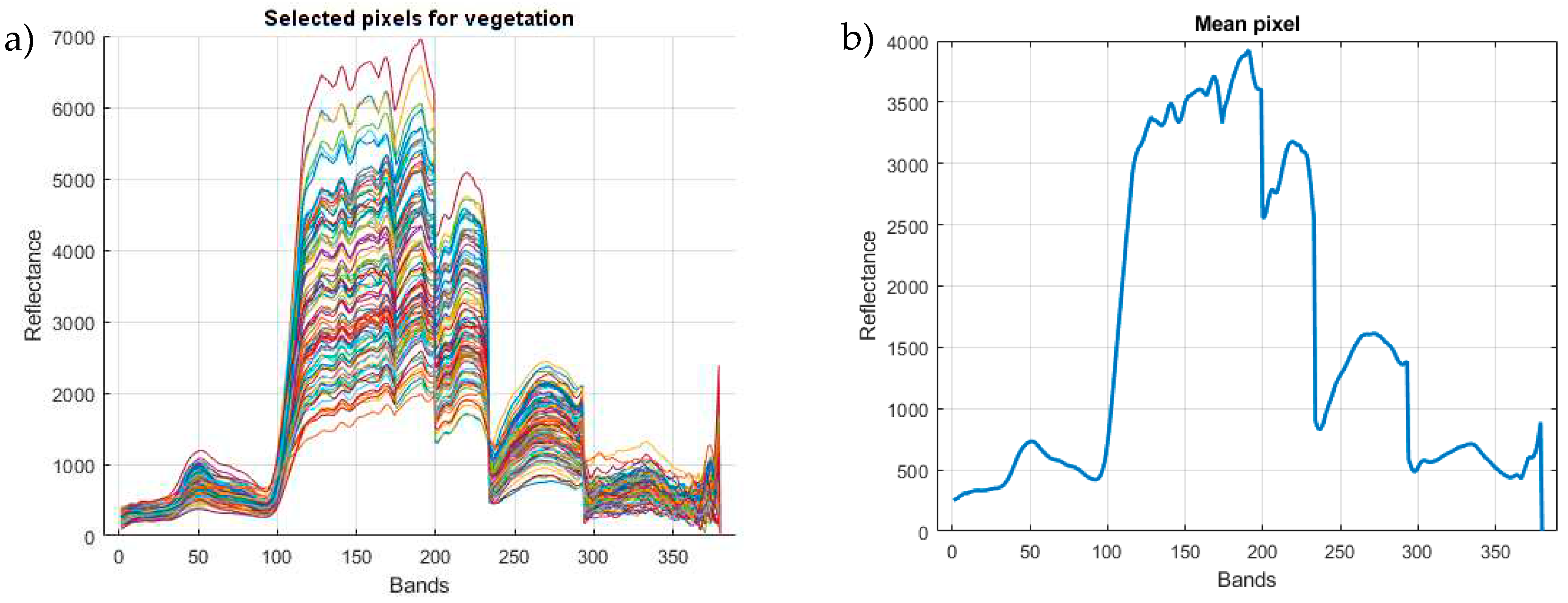
Preprints 76092 g003
Preprints 76092 g004
Figure 4. Result of the comparative study of similarity or correlation methods in vegetation pixels.
Figure 4. Result of the comparative study of similarity or correlation methods in vegetation pixels.
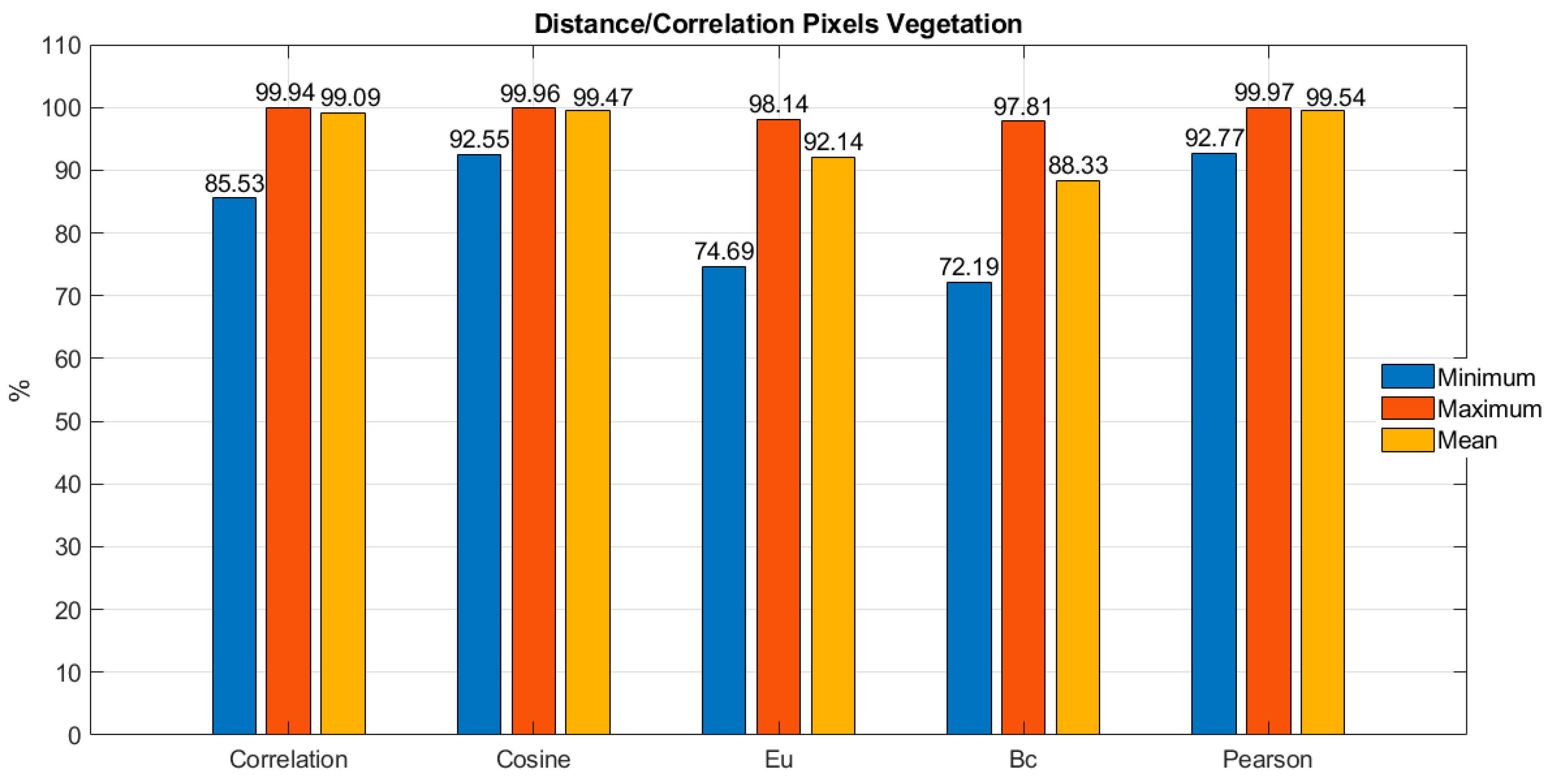
Preprints 76092 g004
Preprints 76092 g005
Figure 5. Result of the comparative study of similarity or correlation methods in non-vegetation pixels.
Figure 5. Result of the comparative study of similarity or correlation methods in non-vegetation pixels.
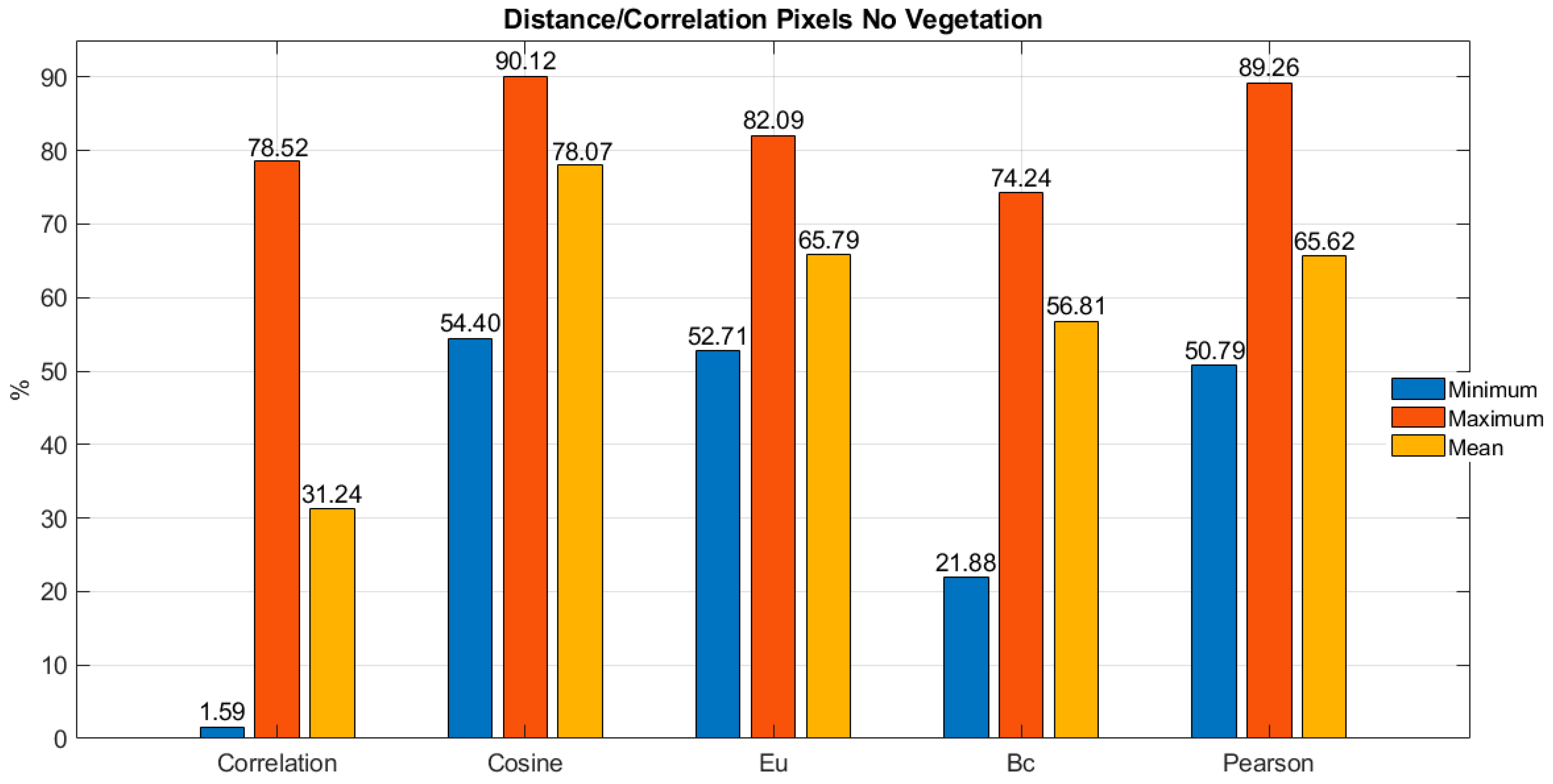
Preprints 76092 g005
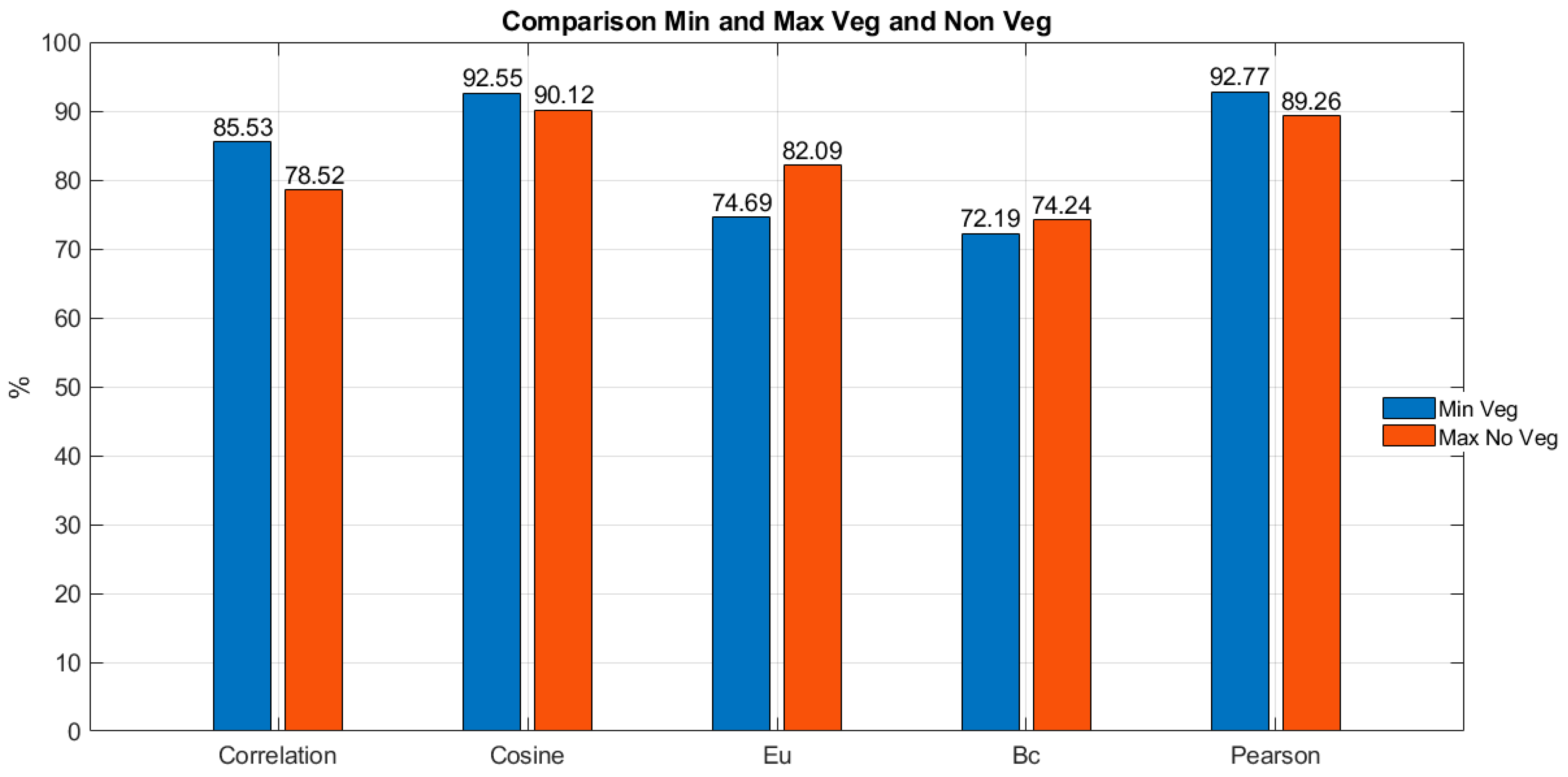
Preprints 76092 g006
Figure 6. Comparison between minimum and maximum thresholds in vegetation and non-vegetation pixels.
Figure 6. Comparison between minimum and maximum thresholds in vegetation and non-vegetation pixels.
Preprints 76092 g006
Preprints 76092 g007
Figure 7. Application of direct correlation and Pearson correlation metrics on the hyperspectral test image.
Figure 7. Application of direct correlation and Pearson correlation metrics on the hyperspectral test image.
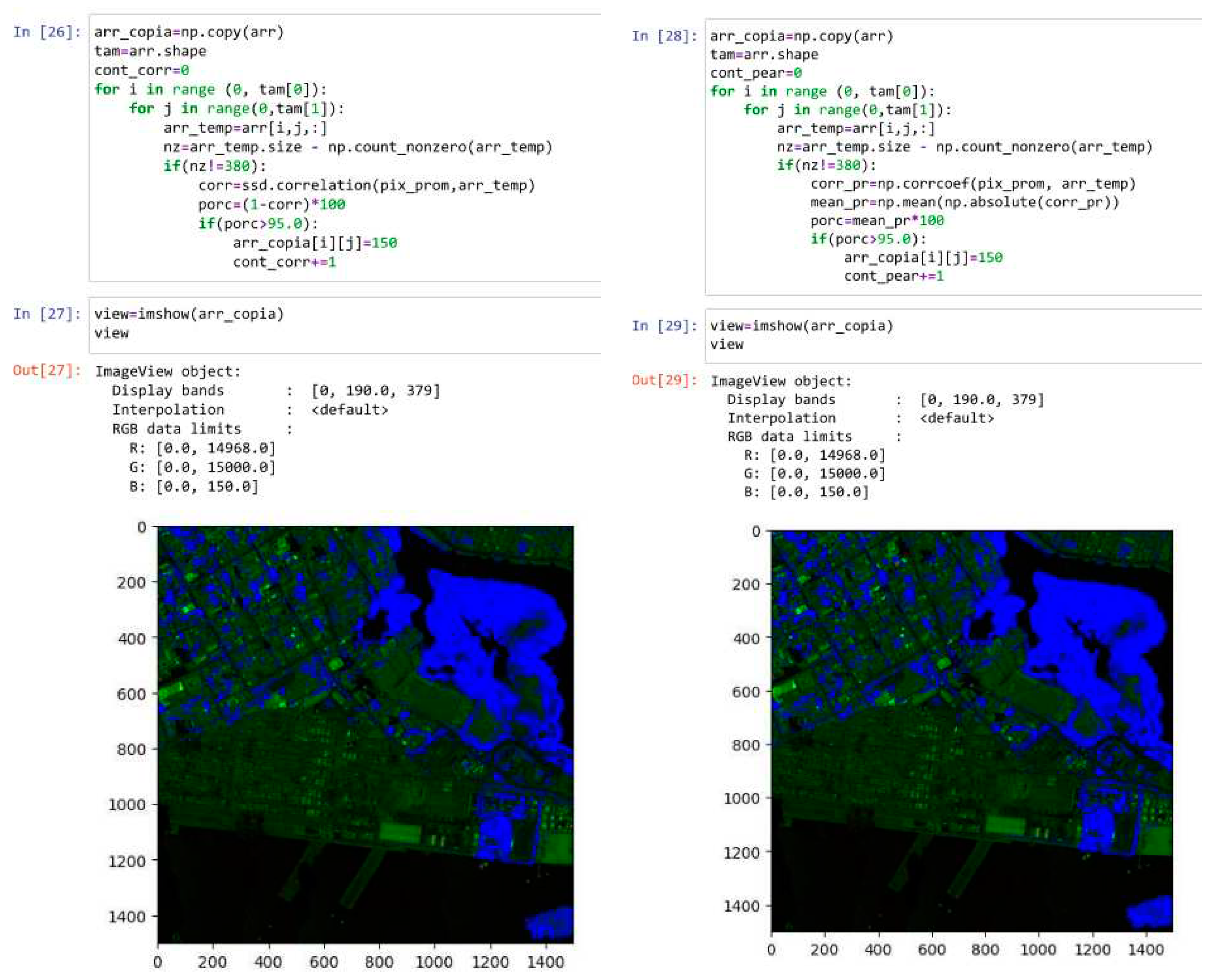
Preprints 76092 g007
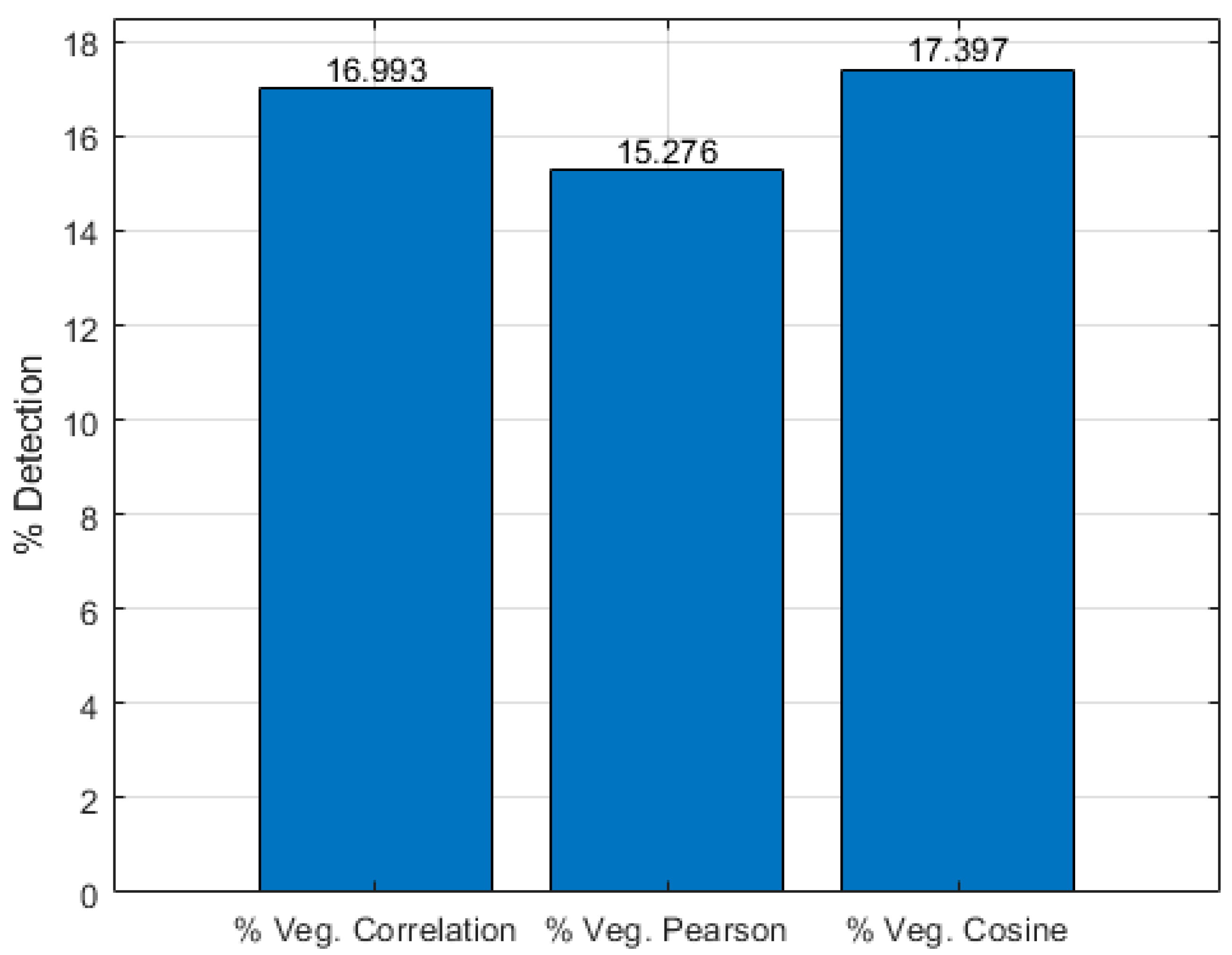
Preprints 76092 g008
Figure 8. % Vegetation Detection.
Figure 8. % Vegetation Detection.
Preprints 76092 g008
Table 1. Thresholds (Limits) of the top three metrics in vegetation pixels.
Table 1. Thresholds (Limits) of the top three metrics in vegetation pixels.
Metrics Thresholds
Pearson correlation Maximum percentage: 99.97%
Minimum percentage: 92.77%
Difference percentages: 7.2%
Cosine distance Maximum percentage: 99.96%
Minimum percentage: 92.55%
Difference percentages: 7.41%
Direct correlation Maximum percentage: 99.94%
Minimum percentage: 85.53%
Difference percentages: 14.41%
Table 2. Difference in correlation percentages in vegetation and non-vegetation pixels.
Table 2. Difference in correlation percentages in vegetation and non-vegetation pixels.
Metrics Correlation Percentage Difference
Direct correlation % Minimum Veg: 85.53%
% Maximum Non Veg: 78.52%
Difference percentages: 7.01%
Cosine distance % Minimum Veg: 92.55%
% Maximum Non Veg: 90.12%
Difference percentages: 2.43%
Euclidean distance % Minimum Veg: 74.69%
% Maximum Non Veg: 82.09%
Difference percentages: -7.4%
Bray–Curtis distance % Minimum Veg: 72.19%
% Maximum Non Veg: 74.24%
Difference percentages: -2.05%
Pearson correlation % Minimum Veg: 92.77%
% Maximum Non Veg: 89.26%
Difference percentages: 3.51%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated