Preprint
Article
Earthquake Prediction for The Marmara Region of Düzce Province Using Artificial Intelligence
Altmetrics
Downloads
118
Views
55
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
08 June 2023
Posted:
09 June 2023
You are already at the latest version
Alerts
Abstract
An earthquake is a natural event by its general definition. This natural event is a disaster that causes significant damage, loss of life, and other economic effects that will damage the state. The possibility of predicting a natural event such as an earthquake will minimize the reasons mentioned. Data collection, data processing, and data evaluation were carried out in this study. Earthquake forecasting was performed using the data and the RNN (Recurrent Neural Network) method. The study was carried out on seismic data with a magnitude of 3.0 and above belonging to Düzce Province between 1990 and 2022. In order to increase the learning potential of the method, the b and d values of the earthquake were calculated and included in the data set, except for the earthquake magnitude. The determination of earthquakes in a specific time interval in regions of Turkey, the classification of earthquake-related seismic data using artificial neural networks, and the production of predictions for the future reveal the importance of this study.
Keywords:
Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning
1. Introduction
Natural phenomena are in a constant state of change. The centers monitor the control of these changes, and the data obtained is recorded. One of the natural events is an earthquake [1]. From the past to the present, many large and small earthquakes have occurred in every corner of the world. These earthquake data are recorded in the earthquake monitoring center with the station's signals [2]. The recorded data is analyzed and scaled by seismologists [3]. However, after the earthquake has occurred, the magnitude can be calculated precisely. If aftershocks occur after the earthquake, the magnitude can be measured similarly after the calculation process [4].
There still needs to be a straightforward method for earthquake prediction and pre-scaling. It is because it is tough to predict an earthquake due to the uncertainty of the event and its sudden occurrence [5]. Many methods, probability calculations, algorithms, and analysis techniques have been used to predict earthquakes. Artificial intelligence methods and machine learning are most commonly used in earthquake prediction [6]. However, in engineering, as in many other fields, artificial intelligence is used effectively on excess data [7]. When research in recent years is examined, it is seen that artificial intelligence is used to predict human or natural events and solve problems in different fields [8]. The distribution of the data to be used during the estimation according to time and the classification of the data are essential. Time distributions are a technique primarily used in data classification. We can call it a “time series,” a data collection in chronological order [9]. It provides an opportunity to evaluate and analyze the data generated using this series [10].
2. Related Stduies
Many methods, analyses, and results were encountered when studies on earthquake prediction were examined. Some of these results approached the goal, and some still need to reach it. As a result of the literature study, the study analyses that most closely approach the goal are listed:
E.I. In a study by Alves in 2006, he was one of the first to propose artificial neural networks for earthquake prediction [11]. The author, E.I. Alves, was inspired by the successful application of similar approaches to financial forecasting tasks, similar to seismic activity in their chaotic nature. He tested this method on seismic data from the Azores region,
Portugal. E. I. Alves scientifically stated that he predicted the earthquakes in July 1998 (MMI = 8) and January 2004 (MMI = 5) correctly. However, it was not calculated using any statistical measurement. Therefore, the performance of this approach has yet to be evaluated objectively.
In the studies of Panakkat and H. Adeli in 2007 and H. Adeli and A. Panakkat in 2009, the problem of earthquake prediction was organized in terms of output classes with the largest seismic magnitude ranges in a predefined time series [12]. He used this dataset to estimate the magnitude of the largest earthquake in a predefined region for the next month. In the study, they prepared eight mathematically calculated “seismicity indicators” that can be used to evaluate the seismic potential of a region [13]. The authors proposed the architecture of a Probabilistic Neural Network (PNN) for prediction using the formulas they created. The model has been tested on data for the Southern California seismic region (33.8–35.4 N° and 114.75–119.25 W°) and has proven to give good prediction accuracy for earthquakes of magnitude 4.5–6.0. However, PNN did not perform satisfactorily for earthquakes greater than magnitude 6.0.
M. Moustra et al. in 2011, a study conducted, it was desired to evaluate the accuracy of the neural network for earthquake prediction using different inputs [14]:
- The first case study for estimating the next day's biggest seismic event using only time series earthquake magnitude data,
- The latter study focuses on the use of Seismic Electrical Signals (SES) to predict the magnitude of the next seismic event.
For the first case, a feedforward backpropagation neural network is used. An input file contains the maximum size value for each day. The accuracy rate resulting from the model was stated as 58.02%. In the second case, ANN was used to generate loss data using magnitude time series. The accuracy of the size estimation was stated to be just over 60% in the initial dataset.
Handan Çam and Osman Duman reminded the reader in their 2016 study. “Earthquake Prediction with Artificial Neural Network Method: Turkey West Anatolian Fault Line Application,” a generalized method that knows for sure about earthquakes that will occur beforehand, has not yet been discovered [15]. In this study, a feedforward backpropagation artificial neural network based on the b value, based on the Gutenberg-Richter relationship and used in earthquake predictions, has been developed. The artificial neural network was trained using earthquake data from four regions with intense seismic activity in western Turkey. After the training phase, earthquake data from later dates for the same regions were used for testing, and the network's success was demonstrated.
In his 2011 study titled “Earthquake Probability Estimates for Kostamonu and Its Surroundings,” Özmen, B. examined the city of Kastamonu, which is located in the 1st-degree earthquake zone [16]. The seismicity of Kastamonu was investigated using earthquake data with a magnitude of M ≥ 4.0 that occurred between 1900 and 2011, which fell within the region drawn 150 km from the city center.
Most earthquakes occurred on the North Anatolian Fault Zone, the Dodurga fault, the Eldivan - Elmadağ tectonic wedge, the Merzifon fault, and the Taşova - Çorum fault zone in the south of Kastamonu. The study used earthquake data with M >= 4.0, which occurred in circular areas drawn to surround the Kastamonu city center for 50, 100, and 150 km and accepted as seismotectonic zones. It aims to find the a and b parameters in the Gutenberg—Richter Magnitude—Frequency relation for each region. Using these parameters and the Poisson model, it is possible to predict the probability of earthquakes of different magnitudes and their return periods. The earthquake probabilities of each region are calculated for earthquakes in 10, 20, 30, 40, 50, 75, and 100 years and with magnitudes of 5.0, 5.5, 6.0, 6.5, 7.0, and 7.5. The results were found to be satisfactory.
Florios, K., Contopoulos, I., Tatsis, G., Christofilakis, V., Chronopoulos, S., Repapis, C., and Tritakis, V. In a study conducted in 2021 for earthquake prediction in a limited period, an extended time series of Schumann Resonance records were analyzed using two multiparametric statistical methods, generalized linear Logistic Regression (LogReg) and nonlinear Random Forest (R.F.), to test their potential [17]. The analysis examined events with a 48-hour magnitude window at least 250 km from the observatory and a magnitude more fantastic than four on the Richter scale. The LogReg method defines the magnitude of the signal within 10 minutes of the recording intervals as the main seismic reporter parameter. The method R.F. has been shown to produce promising results, which will be improved by continuously enriching the operational data with new data.
Many classifications, data sets, locations, and approaches have been used in earthquake prediction. In this study, Düzce province, geographically located in the Marmara Region of Turkey, was selected with GPS coordinates of 40° 49' 59” North and 31° 10' 0” East. Düzce province was selected as the study area because it is a province in the Marmara region with intense earthquake activity.
The purpose of this study is to determine the earthquake magnitude and occurrence in the future by using the earthquake magnitude data, including the Moon's distance of the Moon from the Earth, the b-value and d-value of the earthquake, the depth and time information of the region between the years 1990 and 2022, and by applying the RNN method to estimate the probability.
3. Materials and Method
This section contains information about the research model, research variables, data collection instruments, experimental process, data preparation and analysis, estimation instrument, and data interpretation.
3.1. Calculation of Earthquake Magnitude
To calculate the earthquake Magnitude, Primary - (P) and Secondary - (S) waves are evaluated using formulas, and the magnitude of the earthquake is scientifically derived [18]. In P or compressional waves, the vibration of the rock occurs in the direction of propagation. P waves are the fastest propagating waves in the ground and the first to be detected by seismometers [19].
The P-wave velocity is calculated according to the following formula [19]:
In S or shear waves, the rock vibrates perpendicular to the direction of wave propagation. In rock, S waves usually propagate about 60% as fast as P waves, and the S wave always follows the P wave [20]:
In the first phase, the time from the beginning of the P waves to the beginning of the S waves is calculated, the nomogram is marked, and the corresponding km value is read. It is the distance of the station from the epicenter.
In the second step, the amplitude of the strongest S-wave is measured and plotted on the nomogram. The first two signs are combined linearly. The earthquake's magnitude is where the line connecting these two signs crosses the scale.
This method calculated the earthquake magnitudes of 3 and above (M > =3) that occurred in Düzce province between 1990 and 2022. The 1-year data set for 1990 is shown in (Table 1).
The 32-year histogram distribution showing the number corresponding to the size of the earthquake data set is shown in Figure 1.
The earthquake's time, location, and depth were added to the record. The Kandilli Observatory Earthquake Research Institute provided seismic data.
3.2. Distance of the Moon from Earth
The formula for calculating the distance of the Moon from the Earth is used to calculate the varying distance along the axes of the Moon's orbit around the Earth. This formula refers to the fact that the Moon's orbit around the Earth is elliptical and is related to the varying distance of the Moon along the axes of its orbit around the Earth [21]. It can be expressed as the Moon's orbit around the Earth is elliptical and is used to calculate the Moon's average distance around the Earth. This formula refers to the orbit of the Moon around the Earth and is used to calculate the average distance of the Moon from the Earth [22]. The formula is: “Average distance of the Moon from the Earth = small length of the axes of the Moon's orbit around the Earth x large length of the axes of the Moon's orbit around the Earth.”
The average distance of the Moon from the Earth, based on the dates and locations of earthquakes in Düzce Province between 1990 and 2022, can be found on the website timeanddate.com [23].
3.3. B-Value and D-Value Calculation
The earthquake b-value indicates the average intensity of earthquakes occurring in an earthquake area during a measurement period. The earthquake d-value, on the other hand, indicates the total intensity of earthquakes occurring in an earthquake area [24].
The difference between the earthquake values b and d is the difference between the number of earthquakes occurring in the earthquake zone and the total intensity of the earthquakes. If the number of earthquakes in the earthquake zone is high, the value for earthquake b may be high, and the value for earthquake d may be low. In this case, earthquakes of low intensity were frequent in the earthquake zone. If the total intensity of earthquakes occurring in the earthquake zone is high, the value for earthquake d may be high, while the value for earthquake b may be low [25]. In this case, rare but high-intensity earthquakes occur in the earthquake zone.
The earthquake b value is a parameter used to measure the intensity of earthquakes occurring in an earthquake zone. The earthquake b value was calculated using the formula [26]:
b = log10 (N + C)
Where N is the number of earthquakes occurring in the earthquake zone and C is a constant value. A high value for earthquake b means frequent earthquakes of high intensity in the earthquake zone. A low value for earthquake b means earthquakes in the earthquake zone are rare and of low intensity.
To calculate the earthquake value b, first, the number of earthquakes (N) occurring in the earthquake zone was determined. Then the constant value (C) was added, and the earthquake b value was calculated using the formula. The calculated b-values were included in the study as a data set.
The formula was used to calculate the earthquake d value [27]:
d = log10 (D + C)
Where D is the total intensity of earthquakes occurring in the earthquake zone and C is a constant value. A high value for earthquake d means that the earthquakes occurring in the earthquake zone are generally of high intensity. A low earthquake d value means earthquakes occurring in the earthquake zone are generally low intensity.
The d-values from earthquakes and the total intensity (D) of the earthquakes occurring in the zone were first calculated. Then, the earthquake d-value was calculated by adding the constant value (C) and using the formula. The calculated d-values were added to the study as a data set.
3.4. RNN (Recurrent Neural Network)
RNN is an Artificial Intelligence (A.I.) method. RNN is an artificial neural network that considers the order and timing of input data. RNN is an artificial neural network that considers input data's order and timing and is very good at estimating the relationship between data. Due to this property, RNN is widely used in machine learning applications and gives the correct results [28].
The RNN working algorithm includes the following steps:
- a)
- The input data is entered into the input layer.
- b)
- The input data is processed in the hidden layers, and the weights are learned.
- c)
- The hidden layers process the data and generate the output data.
- d)
- The output data is sent to the output layer.
- e)
- The output data is generated.
The primary purpose of this study is to predict future earthquakes with the RNN model, using past earthquakes and other data as inputs to build an earthquake prediction model. The data used in the study include the magnitude, location, time, depth, b and d values of the earthquakes, and the distance of the Moon from the Earth. By processing these sequential data, the RNN model will predict the when, location, and probability of possible earthquakes in the future.
A 32-year data set was used to train the RNN model and test its predictions.
4. Experimental Datasets
Based on previous studies, adjustments and additions were made to the data set. The seismic data (earthquake magnitude, latitude, longitude, and depth) were provided by the Kandilli Observatory. The seismic data are records of magnitude 3 and above that occurred between 1990 and 2022 in Düzce province in the Marmara region.
In the estimation phase, the seismic data are used to train and test the model. RNN was used as the model. To increase the robustness of the model, the distance of the Moon from the Earth, which is assumed to be effective in the formation of the earthquake, was added. As another data set, the b-value and d-value of the earthquake were calculated for each earthquake that occurred within 32 years and had a magnitude greater than 3.0. The calculated b and d values are included in the model.
To test the accuracy of the model, earthquakes that occurred in November and December 2022 were compared to the data predicted by the model. Second, the August 1999 earthquakes with high earthquake intensity and the data estimated by the model were compared.
5. Results and Discussion
This section contains the results of the estimation of earthquake probability and magnitude between 1990 and 2022 for Düzce province. The first study was conducted for the earthquakes in November and December 2022 in Düzce province. Seven hundred fifty-six earthquakes with magnitudes between 1.0 and 6.1 occurred in the indicated period. Of the earthquakes that occurred, 16 earthquakes with magnitudes of 3.0 and above are shown in Figure 2.
According to the RNN method, the earthquake magnitude, depth, location, time, the distance of the Moon from the Earth, b-value, and d-value were used in the training and testing phase. The estimation phase was studied using earthquakes with magnitude three and above that occurred in Düzce province in November and December. The estimated magnitudes and probability values were compared with the actual data.
The estimated earthquake magnitudes are shown in Figure 3.
Examination of the results shows that the highest probability of 75.3% and the lowest probability of 58.9% for an earthquake are between the actual data and the estimated data. Compared to the actual earthquake magnitudes and the estimated earthquake magnitudes, the actual earthquake magnitudes were estimated with a maximum error rate of 0.5% and a minimum error rate of 0.4%. The actual sizes and the probable and prospective sizes are shown in (Table 3).
The second study was conducted for the August 19 earthquake that occurred in Düzce in 1999 and caused great destruction. In order to evaluate the period before and after the earthquake, the months of July, August, and September were studied. An earthquake magnitude estimation study was conducted in August. A total of 295 earthquakes with magnitudes of 3.0 and above occurred within the specified 3-month period. Of the earthquakes experienced, 141 earthquakes occurred in August. The diurnal distribution of earthquakes in August is shown in Figure 4.
The estimation phase was carried out using the RNN method for earthquakes with magnitude three and above in August 1999 in Düzce. The estimated magnitude and probability values were compared with the actual data.
The estimated earthquake magnitudes are shown in Figure 5.
Examination of the obtained results shows that the highest probability of an earthquake is 74.3% and the lowest is 68.3% between the real data and the estimated data. In the month of August, a minimum of 6 and a maximum of 14 earthquakes occurred per day. The average earthquake magnitude per day is given in (Table 4).
When comparing the earthquake magnitude that occurred on a given day and the estimated earthquake magnitude, the actual earthquake magnitudes were estimated with a maximum error rate of 0.6% and a minimum error rate of 0.1%.
The actual magnitude data, probability, and predicted magnitudes are shown in (Table 4).
6. Conclusions and Future Work
In this study, earthquake prediction and prediction rates were investigated using the RNN method for Düzce province, which is geographically located in the Marmara Region of Turkey and has GPS coordinates of 40° 49' 59” North and 31° 10' 0” East between the years 1990-2022. The data set used was earthquake magnitude, depth, the distance of the Moon from the Earth, b-value, and d-value. Although different methods are used in the studies, it can be seen that it is challenging to estimate 100% of the seismic data due to the irregular data structure.
The study found that the magnitude values estimated by the data set created according to the research results and the applied method are close to the actual earthquake magnitude.
It is expected that the study will be helpful for future prediction studies.
References
- Al-Baghdadi, J. A., Mozahim Hamdoon, R., & Janan Yosief, F. (2020). Prediction the Locations of Future Earthquakes in Eastern Part of Iraq Using GIS Techniques. MS&E, 745(1), 012134. [CrossRef]
- Deschamps, A., Iannaccone, G., & Scarpa, R. (1984). The umbrian earthquake (Italy) of 19 september 1979. Ann. Geophys, 2(1), 29-36.
- Ishibashi, K. (2004). Status of historical seismology in Japan. Annals of Geophysics, 47(2-3). [CrossRef]
- Van der Elst, N. J., & Shaw, B. E. (2015). Larger aftershocks happen farther away: Nonseparability of magnitude and spatial distributions of aftershocks. Geophysical Research Letters, 42(14), 5771-5778.
- Purnomo, M. R. A. (2020). A Bayesian Reasoning for Earthquake Prediction Based on IoT System. JPhCS, 1471(1), 012022. [CrossRef]
- Azam, F., Sharif, M., Yasmin, M., & Mohsin, S. (2014). Artificial intelligence based techniques for earthquake prediction: a review. Sci Int, 26(4), 1495-1502.
- Nez, J. L. M. N., & Lantada, A. S. D. (2020). Artificial Intelligence Aided Engineering Education: State of the Art, Potentials and Challenges.
- Brykov, M. N., Petryshynets, I., Pruncu, C. I., Efremenko, V. G., Pimenov, D. Y., Giasin, K.,... & Wojciechowski, S. (2020). Machine learning modelling and feature engineering in seismology experiment. Sensors, 20(15), 4228. [CrossRef]
- Faouzi, J., & Janati, H. (2020). pyts: A Python Package for Time Series Classification. Journal of Machine Learning Research, 21(46), 1-6.
- Krischer, L., Megies, T., Barsch, R., Beyreuther, M., Lecocq, T., Caudron, C., & Wassermann, J. (2015). ObsPy: A bridge for seismology into the scientific Python ecosystem. Computational Science & Discovery, 8(1), 014003. [CrossRef]
- Alves, E. I. (2006). Earthquake forecasting using neural networks: results and future work. Nonlinear Dynamics, 44(1), 341-349. [CrossRef]
- Panakkat, A., & Adeli, H. (2007). Neural network models for earthquake magnitude prediction using multiple seismicity indicators. International journal of neural systems, 17(01), 13-33. [CrossRef]
- Adeli, H., & Panakkat, A. (2009). A probabilistic neural network for earthquake magnitude prediction. Neural networks, 22(7), 1018-1024. [CrossRef]
- Moustra, M., Avraamides, M., & Christodoulou, C. (2011). Artificial neural networks for earthquake prediction using time series magnitude data or seismic electric signals. Expert systems with applications, 38(12), 15032-15039. [CrossRef]
- Çam, H., & Duman, O. (2016). Yapay Sinir Ağı Yöntemiyle Deprem Tahmini: Türkiye Batı Anadolu Fay Hattı Uygulaması. Gümüshane University Electronic Journal of the Institute of Social Science/Gümüshane Üniversitesi Sosyal Bilimler Enstitüsü Elektronik Dergisi, 7(17).
- Özmen, B. (2011). Kastamonu ve yakın çevresi için deprem olasılığı tahminleri. Türkiye Jeoloji Bülteni, 54(3), 109-122.
- Florios, K., Contopoulos, I., Tatsis, G., Christofilakis, V., Chronopoulos, S., Repapis, C., & Tritakis, V. (2021). Possible earthquake forecasting in a narrow space-time-magnitude window. Earth Science Informatics, 14(1), 349-364. [CrossRef]
- Wu, Y. M., & Zhao, L. (2006). Magnitude estimation using the first three seconds P-wave amplitude in earthquake early warning. Geophysical research letters, 33(16). [CrossRef]
- Yamasaki, E. (2012). What we can learn from Japan's early earthquake warning system. Momentum, 1(1), 2.
- Nuttli, O. (1961). The effect of the Earth's surface on the S wave particle motion. Bulletin of the Seismological Society of America, 51(2), 237-246. [CrossRef]
- Yılmaz, O., & Misli, Ç. (2016). Aristarchus Yöntemi ile Ay ve Güneş. Fizik Dünyası Dergisi, 1(3).
- Gimsa, A. (2020). Development of the Distance Earth-Moon. International Journal of Scientific Research and Management, 8(03).
- Moon Distance Calculator, https://www.timeanddate.com/astronomy/moon/distance.html Accessed 07 January 2022.
- Ceylan, S. (2008). Marmara depremlerinin kaotik özellikleri ve fraktal analizi (Doctoral dissertation, Yüksek Lisans Tezi, İstanbul Teknik Üniversitesi, Fen Bilimleri Enstitüsü, İstanbul, 90).
- Öztürk, S. (2015). Depremselliğin fraktal boyutu ve beklenen güçlü depremlerin orta vadede bölgesel olarak tahmini üzerine bir modelleme: Doğu Anadolu Bölgesi, Türkiye. Gümüşhane Üniversitesi Fen Bilimleri Dergisi, 5(1), 1-23.
- Öztürk, S. (2017) Elazığ Depremleri İçin Gutenberg-Rıchter B-Değeri Ve Fraktal Boyut Dc-Değerinin İstatistiksel Bir Analizi.
- Polat, O., Goek, E., & Yilmaz, D. (2008). Earthquake hazard of the Aegean extension region (West Turkey). Turkish Journal of Earth Sciences, 17(3), 593-614.
- Sherstinsky, A. (2020). Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Physica D: Nonlinear Phenomena, 404, 132306. [CrossRef]
- Gao, Y., & Glowacka, D. (2016, November). Deep gate recurrent neural network. In Asian conference on machine learning (pp. 350-365).
Figure 1.
Earthquake magnitude distribution.
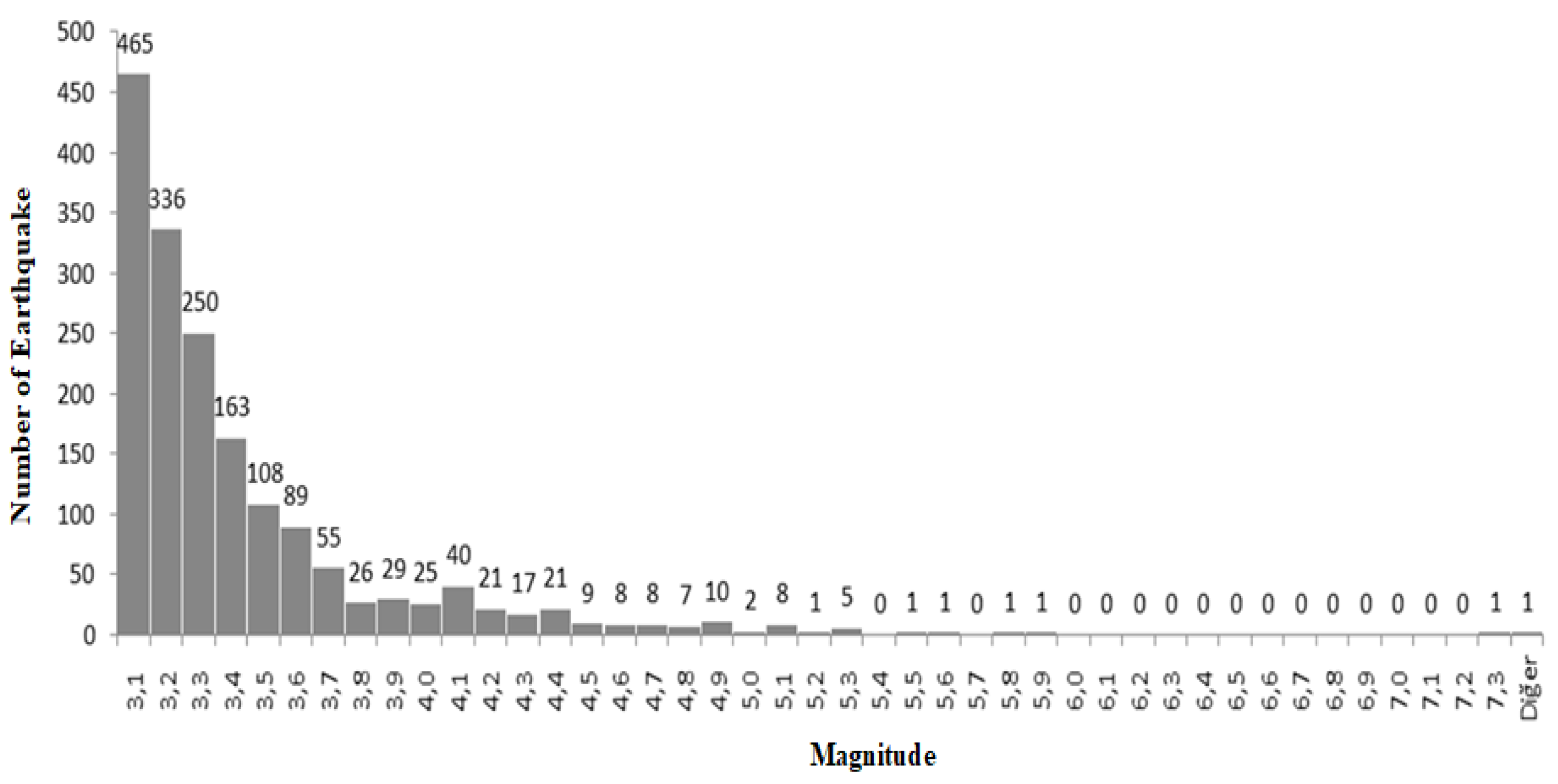
Figure 2.
Düzce November and December earthquake distribution.
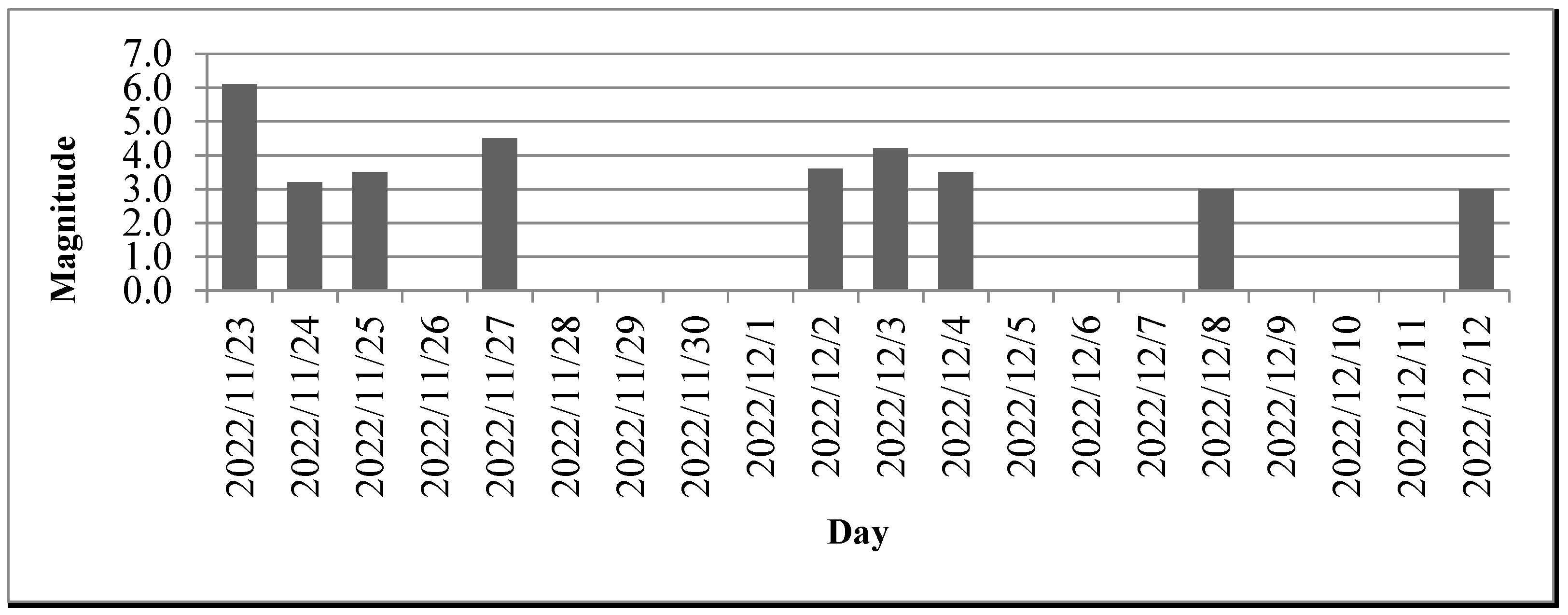
Figure 3.
Estimated distribution of earthquake magnitudes.
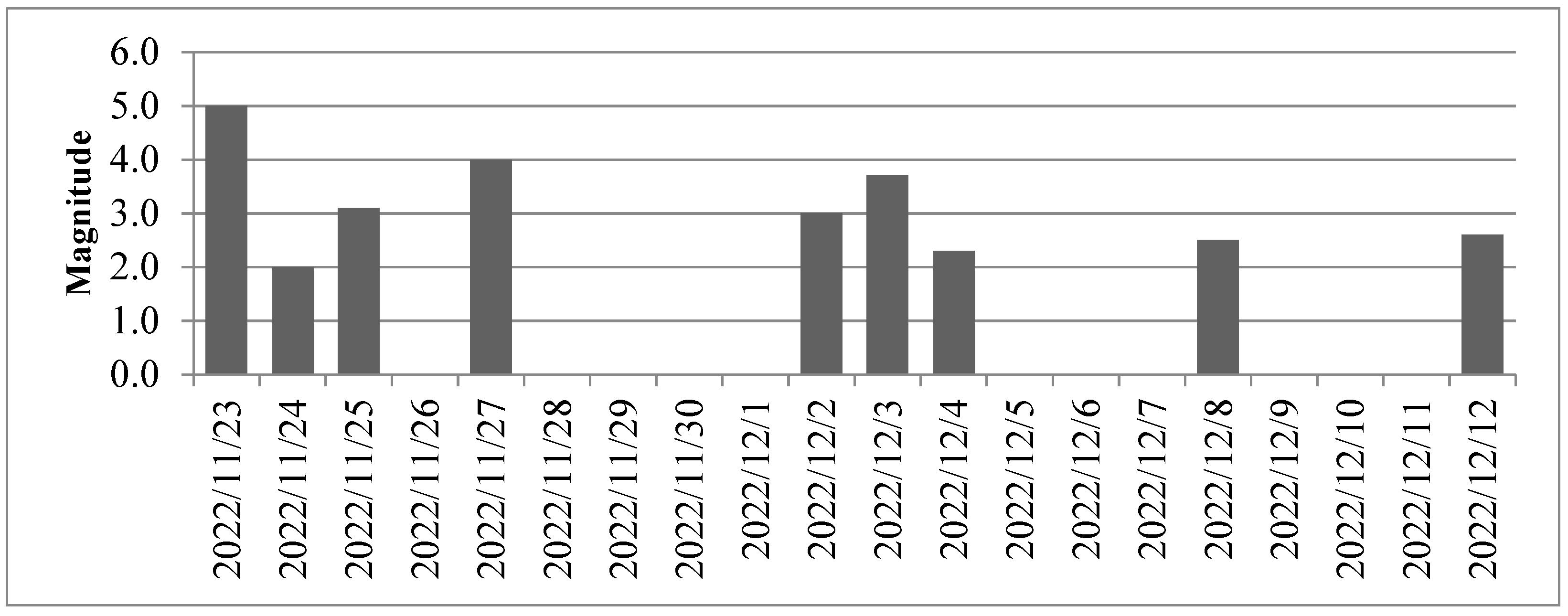
Figure 4.
Düzce 1999-August earthquake distribution.
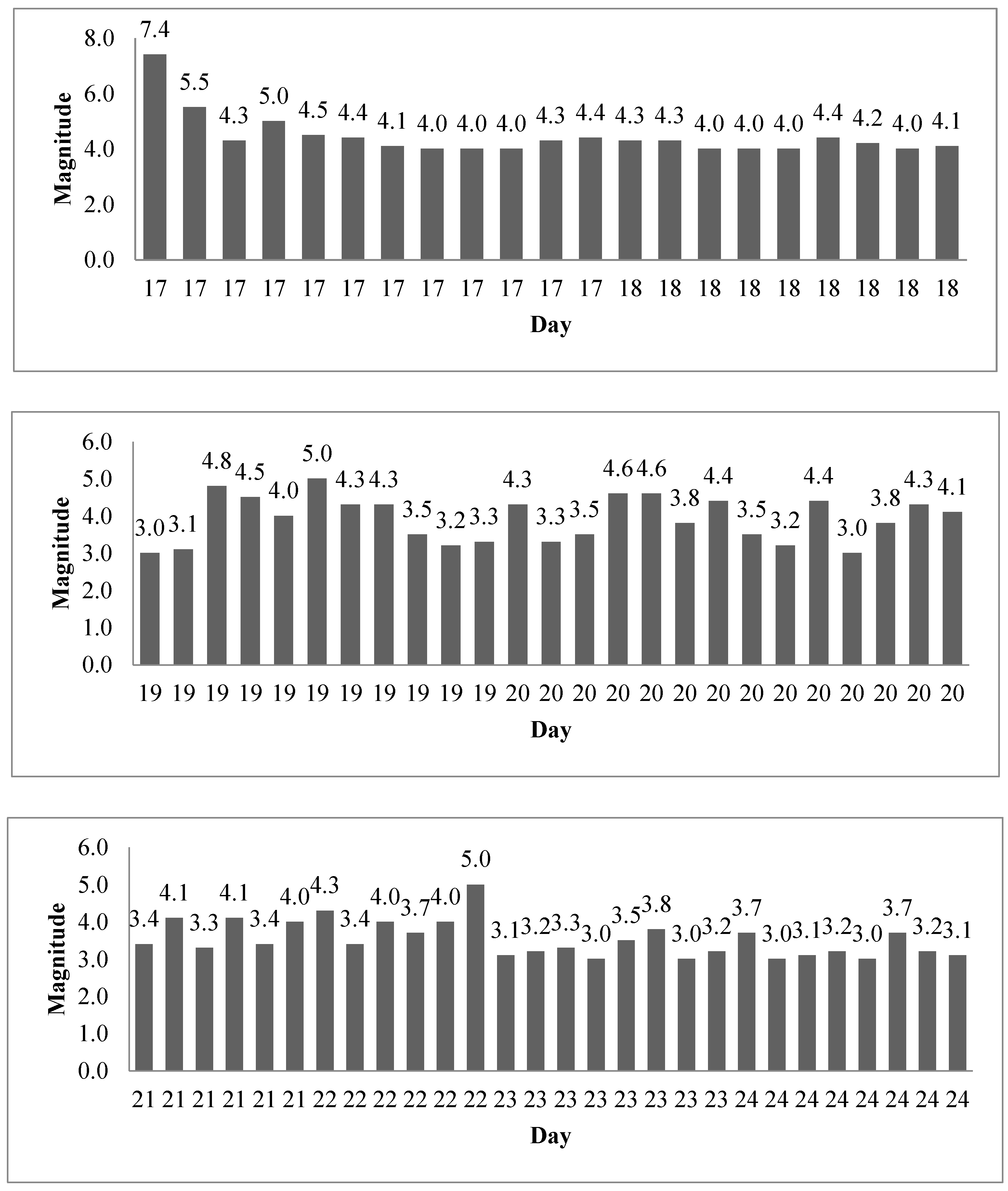
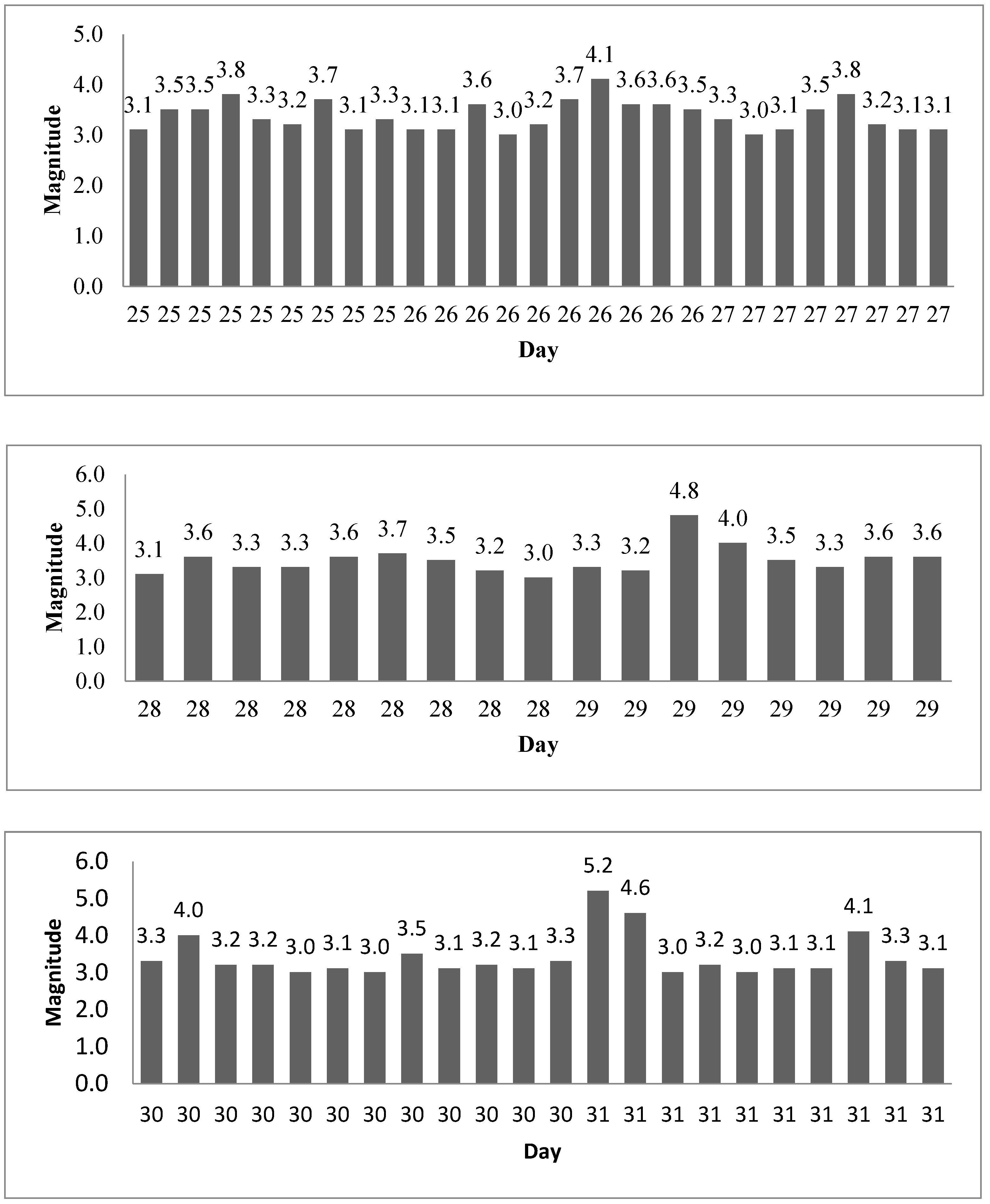
Figure 5.
Estimated magnitude data.
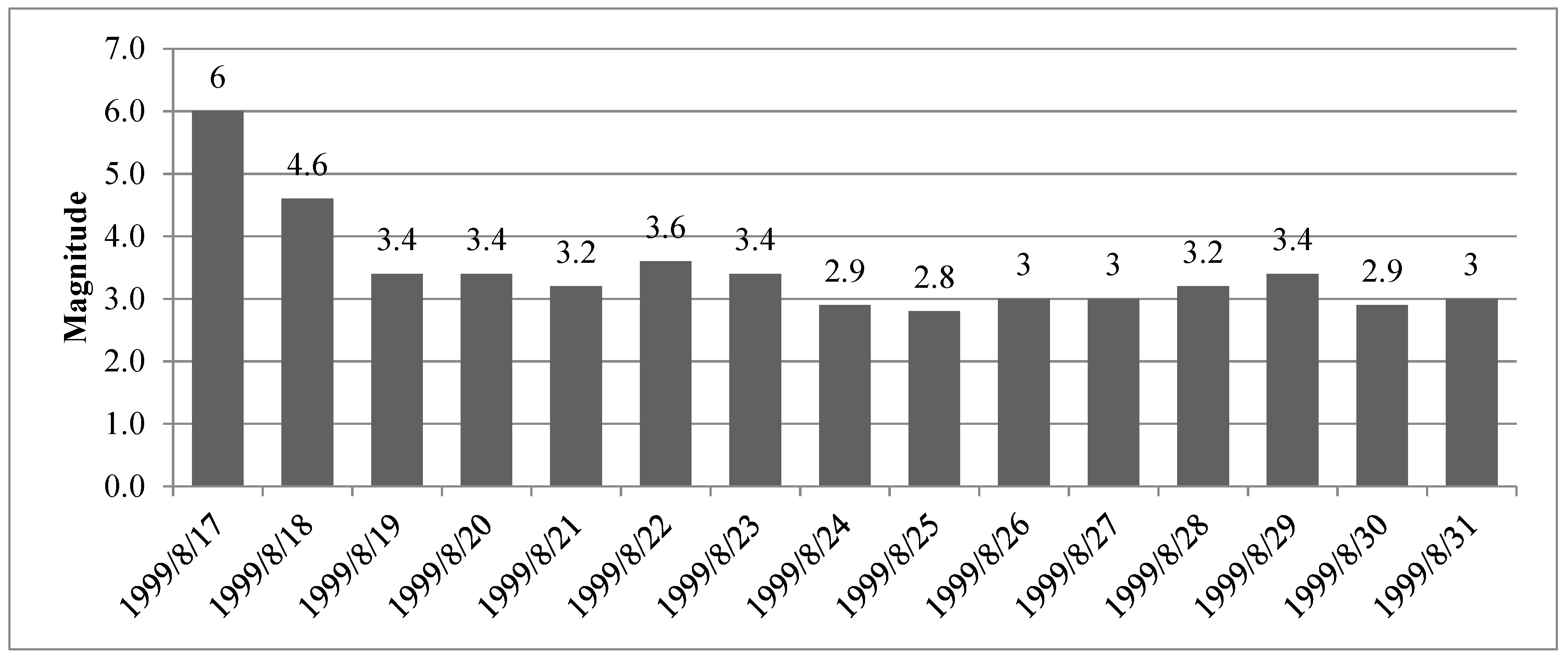
Table 1.
Earthquakes in Düzce province between 1990 and 2022 (M > =3).
| Date | Month | Day | Time | Latitude | Longitude | Depth | Magnitude |
|---|---|---|---|---|---|---|---|
| 1990 | 02 | 09 | 18:20:00.00 | 41.0000 | 31.9000 | 10 | 3.7 |
| 1990 | 02 | 14 | 12:17:01.40 | 40.7400 | 29.1000 | 7 | 3.0 |
| 1990 | 04 | 11 | 08:02:08.00 | 40.7000 | 29.9000 | 7 | 3.0 |
| 1990 | 05 | 06 | 22:09:13.60 | 40.7200 | 29.7000 | 13 | 3.1 |
| 1990 | 05 | 07 | 10:36:02.70 | 40.5800 | 30.2000 | 5 | 3.5 |
| 1990 | 06 | 07 | 23:28:30.00 | 40.7400 | 29.2000 | 10 | 3.3 |
| 1990 | 06 | 08 | 01:47:56.00 | 40.5400 | 30.1400 | 3 | 3.9 |
| 1990 | 06 | 18 | 19:27:08.00 | 40.5100 | 30.5000 | 5 | 3.3 |
| 1990 | 07 | 21 | 17:56:49.00 | 40.7000 | 30.3000 | 22 | 3.1 |
| 1990 | 08 | 22 | 13:02:34.00 | 41.0000 | 29.9000 | 3 | 3.1 |
| 1990 | 09 | 01 | 17:27:37.00 | 40.7000 | 30.0000 | 8 | 3.0 |
| 1990 | 09 | 29 | 00:02:17.00 | 40.7000 | 29.8000 | 12 | 3.0 |
| 1990 | 10 | 03 | 01:51:29.00 | 40.6900 | 30.0000 | 5 | 3.0 |
| 1990 | 10 | 05 | 10:16:45.00 | 40.7000 | 30.0000 | 7 | 3.0 |
| 1990 | 10 | 08 | 05:50:14.00 | 40.7000 | 30.2000 | 4 | 3.1 |
| 1990 | 10 | 19 | 05:28:11.00 | 40.6800 | 30.0000 | 7 | 3.0 |
| 1990 | 11 | 04 | 08:07:49.70 | 40.7800 | 30.0300 | 9 | 3.1 |
| 1990 | 11 | 11 | 22:06:00.10 | 40.6000 | 31.7400 | 14 | 3.2 |
Table 2.
RNN formulas.
| Formulas | Explanation |
|---|---|
| ht=f(h t-1,Xt) | h_t: current value of h h_t-1: the previous h value x_t: current input vector |
| ht=tanh(Whhh t-1 + WxhXt) | W: weight h: hidden layer W_hh: weight of the previous hidden layer W_hx: weight of the current hidden layer tanh: activation function |
| yt= Whyh t | W_hy: weighting value of the output layer y_t: output |
Table 3.
Predicted and current earthquake data.
| Date | Magnitude (M>=3) |
Depth (km) |
Probability (%) |
Prediction (M) |
|---|---|---|---|---|
| 23.11.2022 | 6.1 | 8.3 | 73.0 | 5.6 |
| 23.11.2022 | 4.4 | 5 | 75.3 | 4.0 |
| 23.11.2022 | 3.8 | 5.3 | 73.2 | 3.1 |
| 24.11.2022 | 3.2 | 3.8 | 60.7 | 2.7 |
| 25.11.2022 | 3.5 | 5 | 65.4 | 3.1 |
| 25.11.2022 | 3.4 | 5 | 60.2 | 2.9 |
| 25.11.2022 | 3 | 6.5 | 63.4 | 2.6 |
| 27.11.2022 | 4.5 | 17.5 | 73.2 | 4.0 |
| 2.12.2022 | 3.6 | 9.9 | 74.1 | 3.1 |
| 2.12.2022 | 3.6 | 5.1 | 72.2 | 3.1 |
| 2.12.2022 | 3.3 | 8.3 | 73.4 | 2.8 |
| 3.12.2022 | 4.2 | 10.6 | 69.2 | 3.7 |
| 3.12.2022 | 3.6 | 14.1 | 71.3 | 3.1 |
| 4.12.2022 | 3.5 | 6.3 | 58.9 | 3.0 |
| 8.12.2022 | 3 | 5.4 | 63.4 | 2.5 |
| 12.12.2022 | 3 | 4.5 | 66.9 | 2.6 |
Table 4.
Actual and estimated magnitude data.
| Date | Depth (km) |
Magnitude (M>=3) |
Average Magnitude (M>=3) |
Probability (%) |
Prediction (M) |
||
|---|---|---|---|---|---|---|---|
| 1999 | 08 | 17 | 18 | 7.4 | 4.7 | 74.3 | 6.8 |
| 1999 | 08 | 17 | 15 | 5.5 | |||
| 1999 | 08 | 17 | 5 | 4.3 | |||
| 1999 | 08 | 17 | 16 | 5.0 | |||
| 1999 | 08 | 17 | 16 | 4.5 | |||
| 1999 | 08 | 17 | 17 | 4.4 | |||
| 1999 | 08 | 17 | 10 | 4.1 | |||
| 1999 | 08 | 17 | 11 | 4.0 | |||
| 1999 | 08 | 17 | 6 | 4.0 | |||
| 1999 | 08 | 17 | 13 | 4.0 | |||
| 1999 | 08 | 17 | 16 | 4.3 | |||
| 1999 | 08 | 17 | 16 | 4.4 | |||
| 1999 | 08 | 18 | 14 | 4.3 | 4.2 | 74.0 | 4.6 |
| 1999 | 08 | 18 | 5 | 4.3 | |||
| 1999 | 08 | 18 | 5 | 4.0 | |||
| 1999 | 08 | 18 | 9 | 4.0 | |||
| 1999 | 08 | 18 | 8 | 4.0 | |||
| 1999 | 08 | 18 | 11 | 4.4 | |||
| 1999 | 08 | 18 | 9 | 4.2 | |||
| 1999 | 08 | 18 | 1 | 4.0 | |||
| 1999 | 08 | 18 | 24 | 4.1 | |||
| 1999 | 08 | 19 | 10 | 3.0 | 3.9 | 72.2 | 3.4 |
| 1999 | 08 | 19 | 3 | 3.1 | |||
| 1999 | 08 | 19 | 6 | 4.8 | |||
| 1999 | 08 | 19 | 12 | 4.5 | |||
| 1999 | 08 | 19 | 14 | 4.0 | |||
| 1999 | 08 | 19 | 11 | 5.0 | |||
| 1999 | 08 | 19 | 12 | 4.3 | |||
| 1999 | 08 | 19 | 1 | 4.3 | |||
| 1999 | 08 | 19 | 9 | 3.5 | |||
| 1999 | 08 | 19 | 28 | 3.2 | |||
| 1999 | 08 | 19 | 7 | 3.3 | |||
| 1999 | 08 | 20 | 11 | 4.3 | 3.9 | 70.4 | 3.4 |
| 1999 | 08 | 20 | 5 | 3.3 | |||
| 1999 | 08 | 20 | 14 | 3.5 | |||
| 1999 | 08 | 20 | 8 | 4.6 | |||
| 1999 | 08 | 20 | 17 | 4.6 | |||
| 1999 | 08 | 20 | 12 | 3.8 | |||
| 1999 | 08 | 20 | 7 | 4.4 | |||
| 1999 | 08 | 20 | 5 | 3.5 | |||
| 1999 | 08 | 20 | 9 | 3.2 | |||
| 1999 | 08 | 20 | 16 | 4.4 | |||
| 1999 | 08 | 20 | 21 | 3.0 | |||
| 1999 | 08 | 20 | 8 | 3.8 | |||
| 1999 | 08 | 20 | 9 | 4.3 | |||
| 1999 | 08 | 20 | 1 | 4.1 | |||
| 1999 | 08 | 21 | 8 | 3.4 | 3.7 | 71.5 | 3.2 |
| 1999 | 08 | 21 | 8 | 4.1 | |||
| 1999 | 08 | 21 | 7 | 3.3 | |||
| 1999 | 08 | 21 | 1 | 4.1 | |||
| 1999 | 08 | 21 | 1 | 3.4 | |||
| 1999 | 08 | 21 | 23 | 4.0 | |||
| 1999 | 08 | 22 | 10 | 4.3 | 4.1 | 73.0 | 3.6 |
| 1999 | 08 | 22 | 9 | 3.4 | |||
| 1999 | 08 | 22 | 9 | 4.0 | |||
| 1999 | 08 | 22 | 5 | 3.7 | |||
| 1999 | 08 | 22 | 1 | 4.0 | |||
| 1999 | 08 | 22 | 5 | 5.0 | |||
| 1999 | 08 | 23 | 1 | 3.1 | 3.3 | 69.4 | 3.4 |
| 1999 | 08 | 23 | 6 | 3.2 | |||
| 1999 | 08 | 23 | 4 | 3.3 | |||
| 1999 | 08 | 23 | 11 | 3.0 | |||
| 1999 | 08 | 23 | 23 | 3.5 | |||
| 1999 | 08 | 23 | 5 | 3.8 | |||
| 1999 | 08 | 23 | 7 | 3.0 | |||
| 1999 | 08 | 23 | 4 | 3.2 | |||
| 1999 | 08 | 24 | 5 | 3.7 | 3.3 | 69.6 | 2.9 |
| 1999 | 08 | 24 | 9 | 3.0 | |||
| 1999 | 08 | 24 | 8 | 3.1 | |||
| 1999 | 08 | 24 | 6 | 3.2 | |||
| 1999 | 08 | 24 | 7 | 3.0 | |||
| 1999 | 08 | 24 | 16 | 3.7 | |||
| 1999 | 08 | 24 | 1 | 3.2 | |||
| 1999 | 08 | 24 | 1 | 3.1 | |||
| 1999 | 08 | 25 | 1 | 3.1 | 3.4 | 70.1 | 2.8 |
| 1999 | 08 | 25 | 1 | 3.5 | |||
| 1999 | 08 | 25 | 14 | 3.5 | |||
| 1999 | 08 | 25 | 12 | 3.8 | |||
| 1999 | 08 | 25 | 7 | 3.3 | |||
| 1999 | 08 | 25 | 14 | 3.2 | |||
| 1999 | 08 | 25 | 13 | 3.7 | |||
| 1999 | 08 | 25 | 5 | 3.1 | |||
| 1999 | 08 | 25 | 5 | 3.3 | |||
| 1999 | 08 | 26 | 9 | 3.1 | 3.5 | 68.9 | 3.0 |
| 1999 | 08 | 26 | 2 | 3.1 | |||
| 1999 | 08 | 26 | 1 | 3.6 | |||
| 1999 | 08 | 26 | 7 | 3.0 | |||
| 1999 | 08 | 26 | 5 | 3.2 | |||
| 1999 | 08 | 26 | 6 | 3.7 | |||
| 1999 | 08 | 26 | 3 | 4.1 | |||
| 1999 | 08 | 26 | 5 | 3.6 | |||
| 1999 | 08 | 26 | 5 | 3.6 | |||
| 1999 | 08 | 26 | 5 | 3.5 | |||
| 1999 | 08 | 27 | 9 | 3.3 | 3.3 | 71.1 | 3.0 |
| 1999 | 08 | 27 | 15 | 3.0 | |||
| 1999 | 08 | 27 | 16 | 3.1 | |||
| 1999 | 08 | 27 | 7 | 3.5 | |||
| 1999 | 08 | 27 | 10 | 3.8 | |||
| 1999 | 08 | 27 | 10 | 3.2 | |||
| 1999 | 08 | 27 | 5 | 3.1 | |||
| 1999 | 08 | 27 | 10 | 3.1 | |||
| 1999 | 08 | 28 | 7 | 3.1 | 3.4 | 68.3 | 3.2 |
| 1999 | 08 | 28 | 5 | 3.6 | |||
| 1999 | 08 | 28 | 5 | 3.3 | |||
| 1999 | 08 | 28 | 22 | 3.3 | |||
| 1999 | 08 | 28 | 9 | 3.6 | |||
| 1999 | 08 | 28 | 5 | 3.7 | |||
| 1999 | 08 | 28 | 9 | 3.5 | |||
| 1999 | 08 | 28 | 9 | 3.2 | |||
| 1999 | 08 | 28 | 9 | 3.0 | |||
| 1999 | 08 | 29 | 5 | 3.3 | 3.7 | 70.3 | 3.4 |
| 1999 | 08 | 29 | 5 | 3.2 | |||
| 1999 | 08 | 29 | 7 | 4.8 | |||
| 1999 | 08 | 29 | 16 | 4.0 | |||
| 1999 | 08 | 29 | 5 | 3.5 | |||
| 1999 | 08 | 29 | 12 | 3.3 | |||
| 1999 | 08 | 29 | 4 | 3.6 | |||
| 1999 | 08 | 29 | 7 | 3.6 | |||
| 1999 | 08 | 30 | 9 | 3.3 | 3.3 | 69.8 | 2.9 |
| 1999 | 08 | 30 | 4 | 4.0 | |||
| 1999 | 08 | 30 | 5 | 3.2 | |||
| 1999 | 08 | 30 | 8 | 3.2 | |||
| 1999 | 08 | 30 | 1 | 3.0 | |||
| 1999 | 08 | 30 | 5 | 3.1 | |||
| 1999 | 08 | 30 | 5 | 3.0 | |||
| 1999 | 08 | 30 | 8 | 3.5 | |||
| 1999 | 08 | 30 | 10 | 3.1 | |||
| 1999 | 08 | 30 | 5 | 3.2 | |||
| 1999 | 08 | 30 | 13 | 3.1 | |||
| 1999 | 08 | 30 | 4 | 3.3 | |||
| 1999 | 08 | 31 | 17 | 5.2 | 3.5 | 70.3 | 3.0 |
| 1999 | 08 | 31 | 10 | 4.6 | |||
| 1999 | 08 | 31 | 4 | 3.0 | |||
| 1999 | 08 | 31 | 20 | 3.2 | |||
| 1999 | 08 | 31 | 1 | 3.0 | |||
| 1999 | 08 | 31 | 5 | 3.1 | |||
| 1999 | 08 | 31 | 7 | 3.1 | |||
| 1999 | 08 | 31 | 19 | 4.1 | |||
| 1999 | 08 | 31 | 10 | 3.3 | |||
| 1999 | 08 | 31 | 7 | 3.1 | |||
| 1999 | 08 | 31 | 14 | 3.2 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






