Preprint
Article
Electromagnetic Waves’ Impact on Hydraulic Conductivity of Granular Soils
Altmetrics
Downloads
91
Views
13
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
09 June 2023
Posted:
09 June 2023
You are already at the latest version
Alerts
Abstract
Electromagnetic (EM) waves, used for purposes such as geophysical characterization, impact properties to be measured. This paper describes the effects of radio frequency (RF) waves on the hydraulic conductivity of glass beads and natural sand. A series of tests were conducted using a customized, rigid-wall, cylindrical permeameter inside a resonant cavity made of Plexiglas covered with electrically conductive transparent films. Constant head ASTM-D2434 [1] tests were performed to measure the samples’ hydraulic conductivity. RF stimulation was performed using a magnetically coupled loop antenna at a constant frequency of 726 MHz and input power levels of 10, 25, 40, and 50 Watts. The hydraulic conductivity of both natural sand and glass-bead samples increased with RF stimulation. Furthermore, measurement of the electric-field component of RF waves was also performed to illustrate the pattern of the electric field as well as evaluate the RF impact on the hydraulic conductivity tests. The electric field was numerically simulated and validated against experimentally measured electric fields. A finite-difference numerical model was developed in MATLAB to analyze the seepage flow, which was then validated against the experimental results. An optimization scheme was then used to develop a governing equation for the RF impact on hydraulic conductivity.
Keywords:
Subject: Engineering - Civil Engineering
1. Introduction
Seismic-induced liquefaction is a result of a sudden increase in the excess pore-water pressure (EPWP) in loose, water-saturated noncohesive soils. This phenomenon has been observed in many different earthquakes such as the 1964 Niigata, Japan [2], 1999 Adapazari, Turkey [3], and 2011 Christchurch, New Zealand [4] earthquakes. Liquefaction leads to a reduction of effective stress and a decrease in contact force between the soil grains, often resulting in the loss of shear strength, thus, lateral spreading, slope instability, and foundation and building damage.
Research on soils susceptible to liquefaction, such as sand and silty sand, demonstrated that liquefaction depends upon parameters such as peak acceleration, groundwater level, and soil’s grain size, relative density, cyclic shear strength, soil’s plasticity, and degree of water saturation [2]. All these parameters, however, are linked to the water dissipation rate. The inability of fluids to fully dissipate in a short period of an earthquake leads to a rapid buildup of excess pore-water pressure (EPWP), resulting in liquefaction. Nonetheless, if all soil properties remain constant, liquefaction depends upon fluid properties. Using a viscous fluid (k = 0.0021 cm/s) in a centrifuge test, Sharp et. al. [5] successfully demonstrated a decrease in the thickness of the liquified layer and settlement with an increase in permeability. Ganainy et al. [6] obtained a lower EPWP ratio (), which is a ratio between the excess pore-water pressure and initial effective stress and a smaller thickness of liquefied soil and shear strain when the tests were conducted using water than the one that was conducted using more viscous fluids (hydraulic conductivity was 25 times lower than water).
Electromagnetic waves have traditionally been used for radar-based geophysical detection and characterization, and even remediation [7,8] as electrostatic sources can align individual water molecules, and magnetic fields can float droplets of water [9]. By the same token, water dipoles oscillate in alternating electromagnetic (EM) fields. The vibration of water molecules enhances different transport mechanisms inside the soil; therefore, altering hydraulic conductivity. Azad et al. [10] conducted a study using radio frequency (RF) waves to alter hydraulic conductivity. In sandy soils, hydraulic conductivity increased as much as 14% when an RF test was conducted on natural sand at a frequency of 153 MHz with an RF-power input of 20 Watts. The increase in hydraulic conductivity was justified by the RF energy absorbed by the water molecules, which decreased viscosity and led to an increase in hydraulic conductivity. This is important because using electromagnetic waves can reduce soil susceptibility to liquefaction by reducing hydraulic conductivity related to liquefaction. A reduction of even the slightest amount of generated EPWP can mitigate liquefaction. Therefore, the objectives of this study were to investigate (1) RF waves on the hydraulic conductivity of sandy soils and (2) determine whether this could be sufficiently large and fast enough to reduce excessive pore-water pressure (EPWP) during earthquakes to mitigate liquefaction. During earthquakes, EPWP is generated within fine sands or silty sands due to a low dissipation rate. To achieve these stated goals, the effect of RF waves at varying powering levels and frequencies on the hydraulic conductivity of noncohesive soils was studied as well as measuring the increase in the EPWP within non-cohesive soils during unstimulated and RF-stimulated tests at different RF waves’ frequencies and power levels.
2. Theoretical Background
2.1. Hydraulic conductivity
Water seeps through the void space between soil grains that form interconnected paths. Seepage flow and its velocity are measured by and depend on hydraulic conductivity. Water flows through the soil from one point to another when there is a difference in the total head (also known as hydraulic head). In this paper, Darcy’s Law (Equation 1) was considered as the governing equation of seepage flow,
where Q = discharge (m3/s), h = total head (m), dL = flow-path length (m), A = cross-sectional area of the soil specimen (m2), k = hydraulic conductivity of soil (m/s), v = discharge or Darcy’s velocity (m/s), and = hydraulic gradient.
The hydraulic conductivity of soils is a function (Equation 2) of the property of both the porous medium (i.e., intrinsic permeability) and fluid (unit weight and viscosity) [11].
where K = intrinsic permeability of a soil medium (m2), which depends on the shape of openings and the mean-pore diameter [12] of the soil; g = gravitational acceleration (m/s2); = unit weight of water (N/m3); = absolute or dynamic viscosity of water (Pa·s); = kinematic viscosity (m2/s); ρ = density of water (kg/m3). Typical values of intrinsic permeability and hydraulic conductivity of silty sands range from 10-3 to 1 Darcy’s and from 10-6 to 10-3 cm/s, respectively.
This research work hypothesizes that by impacting the permeating fluid, in this case, water, the hydraulic conductivity can be altered without the need to change the intrinsic permeability via costly and permanent methods of changing the soil environment, e.g., compaction.
2.2. Liquefaction
Liquefaction occurs when the shear strength of saturated loose soils is lost due to the sudden increase in the pore-water pressure (PWP, u) beyond the hydrostatic PWP—referred to as excess pore-water pressure (EPWP, ue)— due to a rapid dynamic load of an earthquake. During rapid loading, there is a sudden increase in EPWP, thus decreasing the amount of time for PWP to dissipate. As a result, the effective vertical stress of the soil decreases to zero, leading to liquefaction. The vanishing effective vertical stress leads to the loss of friction, the sole source of shear strength in noncohesive soils, such as sand.
Liquefaction susceptibility depends upon a number of factors, including geologic and compositional properties as well as the state of the soil, since volume-change behavior influences the rise of EPWP. Liquefaction has been dominant in soils that have shallow groundwater depths. Moreover, reclaimed lands with loose soil are prone to liquefaction [2]. Liquefaction is not common in all types of soils. Fine-grained soils such as clay have cohesion, and very coarse-grained soils, though frictional, are highly permeable, hence, both are less susceptible to liquefaction. However, liquefaction of nonplastic silts has been observed [2]. Nonplastic and cohesionless silts having dimensions equal in all directions (bulk shape) are prone to liquefaction [2]. In the case of the Adalpazari earthquake, the layer of sand containing 30% nonplastic fines and classified as silty sand (SM) was considered liquefiable under moderate levels of ground shaking [3] and liquefied in areas where soil treatment was not completed. Liquefaction of soil also depends upon the gradation of soil. Well-graded soils are less prone to any increase in EPWP than poorly graded or uniformly graded soils. An increase in the pore-water pressure during earthquakes also depends upon the density of the soil and its initial stress condition [2] .
An EPWP ratio parameter, , has been defined to illustrate the path toward liquefaction, where = initial effective stress, and = EPWP increase during an earthquake. When ru = 1, liquefaction occurs, and when ru = 0.25 to 0.70, partial liquefaction occurs [6].
The EPWP generation has a significant effect on the shear strength, stability, and settlement characteristics of soil deposits, even if the soil does not completely liquefy [13]. Therefore, an even small decrease in the EPWP can reduce the potentially hazardous effects of liquefaction.
2.3. Electromagnetic Waves
Alternating electric fields generate magnetic fields, and vice versa, alternating magnetic fields generate electric fields. Electromagnetic (EM) waves are formed when an electric and magnetic field alternate perpendicular to each other and the direction of wave propagation. These orthogonal oscillations are governed by Maxwell’s equations. Maxwell’s equations (Equations 3 through 6) are a set of four equations, written in either integral or differential form, stating the relationship between the fundamental electromagnetic quantities. The fundamental quantities are the electric flux density, (C/m2), the magnetic flux density, (Wb/m2), the electric field intensity, (V/m), the magnetic field intensity, (A/m), the current density, (A/m2), and the electric charge density, (C/m3) [14]. For general time-varying fields, Maxwell’s equation can be written as follows.
2.3.1. EM Waves Impact on Soil Media
Soils have three phases: (i) solid grains with voids filled with (ii) air and/or (iii) fluids that have different physical and dielectric properties. A dielectric is a material that can be polarized by an EM wave. Water has a high dielectric permittivity (≈ 80). Oscillations of individual water molecules can induce a net change in the movement and flow of water through a porous medium without altering the properties of the medium itself [10]. When under the influence of an electric field, water molecules can start to reorient parallel to the direction of the electrostatic field [15]. As reorientation occurs, the hydrogen bond starts weakening, thus decreasing the viscosity of the molecule. A decrease in viscosity could result in an increase in hydraulic conductivity.
3. Materials and Methods
3.1. Experimental Setup and Testing Procedures
The following are the details of a series of tests that evaluated the impact of RF stimulation on the hydraulic conductivity of granular soils, which includes details of seepage RF wave generation and hydraulic conductivity measurements.
3.1.1. Seepage Measurements
The flow is simulated experimentally using a rigid-wall constant-head test, according to ASTM D2434 [1], where the flow rate of water is high, and a constant head can be maintained by a continuous supply of water. For a homogeneous soil sample, if there are no EM waves, then hydraulic conductivity can be assumed spatially constant and found as follows (Equation 7).
where, h = hL = hydraulic head loss across the soil medium (m), A = cross-sectional area of soil specimen (m2), L = length of soil specimen (m), t = time of water collection (s), and V = volume of water collected (m3).
3.1.2. RF Wave Setup
To supply the power and RF electric field intensity for these tests, a magnetically coupled loop antenna, inserted into the cavity parallel to the magnetic lines, was used. The loop antenna was made of an RG-8 coaxial cable. The RF signal was generated using the Agilent Model #E4400B signal generator. An amplifier was used to amplify the generated signal. To maximize power output and reduce harmful reflections back into the amplifier, the impedance of the load (setup) should match that of the source (50Ω). The impedance was measured using an Agilent N9320A, vector network analyzer (VNA), and matched to the 50Ω impedance of the RF source using a matching network made of a series of variable capacitors. Two dual-directional couplers were also used in the network to monitor the forward power into the device under testing (DUT) and the reflected power back into the amplifier. Figure 1 shows the schematic of the setup used for launching RF into the DUT.
All these tests were performed on a resonant cavity filled with two types of medium, one filled with glass beads and the other filled with a natural sand sample. The saturated glass-bead specimen was prepared using the wet-pluviation method [16]. Glass beads for this study are Class-A Ballotini impact beads with a specific gravity of 2.46 g/cm3. Table 1 displays the properties of the beads.
A customized experimental setup to measure RF-stimulated hydraulic conductivity was developed here. Glass beads and natural sand were used as the coarse-grained samples in this test. The natural sand was classified as SW, according to the USCS classification system.
To perform the hydraulic conductivity tests, a customized, rigid-wall, cylindrical permeameter was constructed using acrylic material. However, prior to performing the test using the customized permeameter, the customized device needed to be calibrated. Hence, the unstimulated tests were performed using both a standard permeameter (2.5-inch diameter and 12-inch height) as suggested by D2434 [1] and the customized (152-mm diameter and 140-mm height) permeameter to calibrate the customized permeameter. Figure 2(a) displays the schematic of the customized, rigid-wall, cylindrical permeameter setup. The glass beads used in this test were prepared by dry-pluviation. The total density of the glass-bead sample was measured to be 14.72 kN/m3. In the case of natural sand, natural sand was poured into the permeameter in three layers. Each layer was compacted using 50 blows with a standard compaction hammer. The density of the natural sand was measured to be 18.25 kN/m3. The depth of the soil specimen in the customized permeameter was 110 mm. Figure 2(a) shows the schematic of the setup and its dimensions, and Figure 2(b) shows the setup for the RF-stimulated hydraulic conductivity test. The customized permeameter was placed inside a resonant cavity. RF stimulation was performed on both the glass-bead and natural sand samples at a frequency of 726 MHz and power levels of 10, 25, and 40 Watts.
3.1.3. Electric Field Mapping
Using a vertical monopole probe, the electric field inside the cavity was measured. Using an RG-58, 18 GHz precision-test cable, the monopole probe was connected to a spectrum analyzer to measure the electric field at the corresponding location of the probe inside the cavity. The probe was moved to various locations throughout the specimen as a number of holes were drilled through the top plate of the resonant cavity on a grid in the X-Y plane. The monopole was placed inside a glass tube casing and inserted vertically into the cavity. The location of the probe on the top decided the respective X- and Y-coordinates of the probe and its depth decided the Z-coordinate.
Electric-field measurements for the RF-stimulated hydraulic conductivity tests were performed at frequencies of 710 MHz and 726 MHz. The location of the measurement probe along the X-direction was fixed at distances of 2cm and 4cm from the centrally placed source (monopole antenna). A total of seven measurement points along the Y-axis were selected, which were separated at 2cm intervals. Figure 3 presents the schematic top view of the customized permeameter with the location of the depth slices. Measurements were recorded in dBm using the spectrum analyzer at the frequency generated by the signal generator. The electric field was also numerically simulated using the RF module of COMSOL Multiphysics and validated against the experimentally measured electric field.
3.2. Three-dimensional Numerical Forward Model of Seepage simulated by RF waves
To study the impact of EM waves on hydraulic conductivity, spatial and temporal relations between seepage and electric fields need to be studied. Experimental measurements do not provide a complete three-dimensional image of the two. To acquire a complete picture, experimentally validated numerical models are needed. The following is an explanation of how the numerical simulations were generated and experimentally validated.
3.2.1. Unstimulated Seepage
The 3D numerical model of seepage flow developed in this research simulates a saturated medium where flow is governed by the conservation of mass and—if water density is constant—volume (Equation 8).
where ρ = fluid density (m3/s), t = time (s), and = seepage flow velocity vector (m/s). In the case of incompressible fluids, the density of the fluid is constant. Therefore, the conservation of mass equation (Equation 8) can be simplified to the conservation of volume equation (Equation 9).
Applying Darcy’s law, where in 3D, , Equation 9 can now be rewritten in the matrix form as shown in Equation 10.
where, is the hydraulic conductivity tensor.
A 3D numerical model of seepage flow was then developed in the MATLAB interface using the finite-difference method. The water-saturated soil specimens were 15 cm in diameter and 11 cm in height. The entire grid used to model the flow was a rectangular-cubical specimen with the dimensions of . This rectangular-cubical domain was discretized into 15 nodes along both the X and Y axes. The top view of the discretized domain has a circular cross-section and rectangular mesh, which is illustrated in Figure 4. The top and bottom surfaces of the cylindrical specimen were modeled as Dirichlet boundary conditions with known hydraulic heads. However, the circumference of the permeameter was an impermeable boundary and modeled using the Neuman boundary conditions.
The computational code was developed based on the central finite-difference method and then used to calculate the spatial variation of the hydraulic head within the soil using the hydraulic conductivity values obtained for the unstimulated tests. Equation 10 was used, and the flow through the soils was considered at the steady state for the unstimulated tests. Furthermore, the flow and discharge rates were also calculated. However, this only solved the hydraulic head inside the specimen while the test was performed in the unstimulated condition.
3.2.2. RF-stimulated Seepage
The hydraulic head under RF stimulation was assumed to be k’, and for flow was rewritten as Equation 11.
where, is the RF-stimulated hydraulic conductivity tensor.
Since the application of RF waves had demonstrated altering hydraulic conductivity, it was proposed that RF-stimulated hydraulic conductivity (k’) and the flow discharge (Qst) in the RF-stimulated tests are functions of the electric field, E. Hence,
Additionally,
where, s = RF-power density (W/m2), Zo = characteristic impedance of the free space (Ω), P = RF power (Watts), and a = area enclosing each node (m2).
From Equations 12, 13, and 14, it was proposed that the hydraulic conductivity and the flow discharge in the RF-stimulated tests are functions of the power density, and hence power. The results showed an increase in hydraulic conductivity with the increase of RF-power level in coarse-grained media. A nonlinear, but proportional, relation was assumed between the RF-stimulated hydraulic conductivity, k’, and RF power, P. Based on Equations 12, 13, and 14, the RF-stimulated hydraulic conductivity and RF-power can be correlated as Equation 15.
where β is a constant value, and k is the unstimulated hydraulic conductivity (cm/s). Therefore, the increase in k’ at each discretized node in the soil specimen domain could be correlated to the increase in the RF power at that node, while calculating the hydraulic head at the specific node. Equation 15 can be redefined as Equation 16.
A similar computational code in the MATLAB interface was developed to solve Equations 11 and 16. The RF-power density at each node was obtained from the RF forward model generated using COMSOL Multiphysics. The RF-power densities in the form of a 3D matrix were exported from the COMSOL model into the MATLAB interface. Afterward, an optimization scheme was implemented to find by minimizing a cost function equal to the difference between the numerically simulated and experimentally measured values of the RF-stimulated discharge, i.e., Qsim,st Qexp,st, respectively. The COMSOL code was used to export the RF-power densities at a frequency of 726 MHz at the power levels of 10, 25, and 40 Watts to be imported into the optimization scheme.
4. Results
4.1. Electric-Field Measurement and Validation of Numerical Simulation
The electric-field pattern within the cavity numerically simulated using COMSOL was validated against experimentally measured values of the Z component of the electric field. This was because the vertically located monopole probe was vertically polarized, i.e., its measurement was dominated by the Z component of the electric field. The experimental measurements were performed at two frequencies, 498 MHz, and 632 MHz. As seen in Figure 5, the experimental measurements were performed near where the pore-pressure transducer was installed within the sample. The location of Slice 1 is +4 cm away from the transducer along the X-axis, and Slice 2 is -4 cm along the X-axis. Electric-field measurements were performed using a glass-cased monopole probe inserted into the cavity through the top plate down to the desired depth. Figure 6 shows the maps of the numerically simulated (left) experimentally measured (right) electric field, Ez, on Slices 1 and 2, respectively. Electric-field measurements are normalized to the maximum electric field measured on the corresponding slice.
Figure 6 shows a reasonable agreement between the experimentally measured and numerically simulated electric fields on each slice. Since the monopole probe is not calibrated, the experimentally measured electric field does not represent the actual strength of the electric field within the cavity and just represents the electric field pattern. Both numerically simulated and experimentally measured electric-field patterns have their maximum at similar depths, i.e., the predesigned location of the pore-pressure transducer. As mentioned, the strength of the electric field at any specific location depends on the frequency of RF waves launched. Effects of RF waves on physical properties such as the viscosity of water may not be linear due to having different field patterns at different frequencies. Hence, a change in any physical property may or may not be linearly correlated with an increase or decrease in frequency.
3.3. Hydraulic Conductivity Tests
RF waves’ effect on hydraulic conductivity at different combinations of powers and frequencies needs to be studied. Figure 7 shows the measurement of the unstimulated hydraulic conductivity of the glass-bead sample performed using a standard permeameter. The test was continued for four hours. Hydraulic conductivity values remained fairly constant during the entire run of the test. The average unstimulated hydraulic conductivity of the glass-bead sample was measured to be cm/s.
A series of RF-stimulated hydraulic conductivity tests were conducted on the glass-bead sample in the customized permeameter. There was a discrepancy of 3.5% between the customized permeameter and the standard permeameter. The discrepancy was calibrated. To calibrate the customized permeameter, the hydraulic conductivity measurements obtained were multiplied with a multiplication factor of 1.035.
The RF-stimulated tests were then conducted at a frequency of 726 MHz and RF-power levels of 10, 25, and 40 Watts. Figure 8 shows the hydraulic conductivity measurements at different RF-power levels. There was no sharp increase in the hydraulic conductivity with the RF stimulation. However, the hydraulic conductivity started to increase gradually with time and eventually attained a peak value. As seen in Figure 8, at an RF-power level of 10 Watts, hydraulic conductivity started to increase from cm/s to a peak value of cm/s after two hours and 30 minutes and remained constant thereafter. Similar changes were observed at the other RF-power levels of 25 Watts and 40 Watts (Figure 8). At the RF-power level of 25 Watts, the RF stimulation was terminated once the RF- stimulated hydraulic conductivity reached its maximum. After the termination of RF waves, the hydraulic conductivity slightly decreased with time and then stabilized at a smaller value but was still larger than the unstimulated value. Even though the increase in hydraulic conductivity is larger at higher RF power levels, the slope of the increase is on average 0.0225% per hour and even seems higher for 10 Watts of power. The average unstimulated hydraulic conductivity before the start of RF stimulation and the peak value of the RF-stimulated hydraulic conductivity are compared in Table 2. As seen in Table 3, the hydraulic conductivity increased with the increase in the RF input power. The increase in the hydraulic conductivity was, however, small compared to the result obtained by [18].
The effect of RF waves on hydraulic conductivity was smaller in glass beads than those in natural sand [10]. Hence, a new set of RF-stimulated hydraulic conductivity tests were performed on the natural sand sample. Unstimulated hydraulic conductivity tests were first performed on the natural sand sample in the standard permeameter for calibration purposes.
Figure 9 shows the measurement of unstimulated hydraulic conductivity of the natural sand sample performed using the standard permeameter. The average unstimulated hydraulic conductivity of the natural sand sample was measured to be cm/s. A series of RF-stimulated hydraulic conductivity tests were then conducted on the natural sand sample in the customized permeameter. There was a discrepancy of 5.1% between the customized and standard permeameters, which was later calibrated. RF-stimulated tests were performed at a frequency of 726 MHz and power levels of 10, 25, and 40 Watts. The conducted tests were similar to the RF-stimulated hydraulic conductivity tests out on glass beads. Figure 10 shows the hydraulic conductivity measurements at different RF-power levels. The results show a similar pattern of change in hydraulic conductivity. After RF stimulation started, the hydraulic conductivity of the sand sample started to increase gradually with time and attained a peak value. At an RF-power level of 10 Watts, the hydraulic conductivity started to increase from cm/s reached a peak value of cm/s after four hours and remained constant thereafter. Similar changes were observed at other input powers of 25 and 40 Watts. At 25 Watts, RF stimulation was terminated once the RF-stimulated hydraulic conductivity of sand decreased with time and then stabilized at a slightly smaller value, yet much larger than the original unstimulated one. In the case of natural sand, not only is the increase in hydraulic conductivity larger at higher RF power levels, but the slope of the increase is also slightly larger for higher RF power levels, increasing from 0.02% per hour for 10W to 0.03 and 0.033% per hour and even at 25 and 40 W.
Moreover, the percent change in the hydraulic conductivity of natural sand due to RF stimulation is larger than that of the glass bead for all input RF-power levels. The results: however, show a similar pattern of increase and decrease in the hydraulic conductivity of both sand and glass beads during the application and termination of the RF stimulation, respectively (Table 3). The increase in hydraulic conductivity was also slow and gradual. With a test setup that can only provide up to 40 Watts of RF power, RF stimulation would not be high enough to change the hydraulic conductivity promptly, even for natural sand.
4.3. Electric-Field
4.3.1. Measurement and Comparison
The experimental measurements of the electric-field pattern for the RF-stimulated tests were performed at two frequencies, 710 MHz, and 726 MHz. As seen in Figure 11, the patterns of both numerically simulated and experimentally measured electric fields matched each other. As mentioned, since the monopole was not calibrated, the experimentally measured electric-field measurements do not represent the actual intensity of the electric field within the cavity. The intensity of the electric field at any specific location depends on the frequency of RF waves launched. The effect of RF waves on physical properties, such as the viscosity of water, may not be linear due to having different electric-field patterns at different frequencies. Hence, the change in any physical property may not be linearly correlated with the change in frequency.
4.4. Seepage Flow Numerical Simulation
The unstimulated seepage-flow model was developed based on the hydraulic conductivity value of the unstimulated test performed in the lab. The model in MATLAB interface was used to compute the spatial variations of the hydraulic head within the soil. Figure 12 shows the contour maps of the hydraulic head on fifteen vertical slices within the sandy sample obtained using the forward model for the unstimulated test. The hydraulic head decreased gradually and uniformly from the bottom (inlet) to the top (outlet), indicating the existence of a uniform gradient along the length of the soil specimen and an upward uniform flow within the homogeneous sand sample.
The experimentally measured flow discharge in the natural sand sample during unstimulated tests was . Additionally, the finite-difference forward model computed the flow discharge to be . There is a small discrepancy of 1.18% between the experimental and numerical values, and the difference is due to the approximation of the cylindrical walls of the permeameter using a stepwise rectangular cubical wall.
To better understand the RF stimulation effect on hydraulic conductivity, the increase in hydraulic conductivity due to RF waves was correlated with the RF-power level. The RF-power density at each node was obtained from the RF forward model generated using COMSOL Multiphysics. Table 4 shows the experimental flow discharge, numerically computed flow discharge, and slope () at a frequency of 726 MHz and RF-power levels of 10, 25, and 40 Watts.
Similarly, the experimentally measured and numerically computed flow discharge with respect to the RF-power levels were plotted in Figure 13. Using the optimization scheme, the cost function was minimized to less than 3%, indicating the numerically computed values reasonably matched the experimental values. In addition, the β-value at all three power levels was nearly constant.
As the optimization was completed, optimized flow discharge, optimized hydraulic conductivity, and optimized hydraulic heads were obtained. Figure 14 displays the contour/color maps of the hydraulic heads obtained from the inverse model at a frequency of 726 MHz and an RF-power level of 25 Watts. Similar to the unstimulated case, the contour/color maps show a uniform decrease in the hydraulic head from the bottom (inlet) to the top (outlet), indicating an upward flow. There was a spatially variable alteration in the hydraulic conductivity in X, Y, and Z directions, which is a function of the spatially variable electric-field power density. This resulted in a change in the hydraulic head within the soil specimen due to the RF-waves application, which is uniform along the X and Y directions and only varies along the Z direction However, the change is uniform and does not manifest as a distortion in the contour/color maps of the hydraulic head.
As mentioned, the value of hydraulic conductivity and flow discharge changed due to RF stimulation. The model assumed that the scalar value of the RF power governs the alteration in the hydraulic conductivity. Hence, the variation will be the same for all components of the hydraulic conductivity tensor (i.e., the same slope, , in all directions). Figure 15 shows the contour/color map for (Z-component of the RF-stimulated hydraulic conductivity) computed using the inverse model on Slice 7 at a frequency of 726 MHz and RF-power level of 25 Watts. Other components on the k’ tensor can also be plotted. However, the hydraulic conductivity of the soil was assumed isotropic, and was assumed the same in all directions. Therefore, k’ will be isotropic. Figure 16 shows the contour/color map of the RF-power density at a frequency of 726 MHz and RF-power level of 25 Watts on Slice 7. The RF-power density at each node was obtained from the RF forward model generated using COMSOL Multiphysics.
As seen in Figure 15 and Figure 16, the hydraulic conductivity along the Z-direction changed due to the application of RF waves. Additionally, the contour plot of the hydraulic conductivity corresponds to the variation in the power densities due to the linear relationship between the power densities at each node and RF-stimulated hydraulic conductivity.
5. Conclusions
The work outlined in this paper demonstrates the changes in the hydraulic conductivity of glass beads and a natural sand sample due to RF waves of various frequencies.
The electric field inside the cavity was measured at various resonant frequencies and then validated against the numerically simulated electric field using COMSOL Multiphysics. The measured and numerically simulated electric fields reasonably agreed.
At all RF-power levels, for both the glass beads and natural sand, RF waves increased the hydraulic conductivity. The increase in the hydraulic conductivity was gradual with time. Additionally, for both glass-bead and natural sand samples, RF-stimulated hydraulic conductivity increased with increasing RF-power levels. However, this percentage increase was observed more in the natural sand sample than the glass-bead. This could be due to the influence of the silt content within the natural sand. When RF stimulation was terminated, the hydraulic conductivity initially stabilized at its peak value. However, as time increased after termination, hydraulic conductivity slightly decreased and stabilized at a smaller value but still larger than the initial unstimulated value. The tests were not continued long enough to observe any further decrease.
The measured hydraulic conductivity was then correlated to a numerically simulated hydraulic conductivity using MATLAB interface. Results from the numerical model for the seepage flow showed a uniform decrease of the hydraulic head from the bottom (flow inlet) to the top (flow outlet) due to upward seepage flow through the sample. In the case of RF-stimulated tests, hydraulic heads were computed using an inverse model based on an optimization scheme. After optimization, the optimized RF-stimulated numerically computed hydraulic conductivity showed a similar spatially variable pattern to that of the RF-power density.
6. Patents
An invention disclosure has been submitted and is pending.
Funding
This research was supported by the National Science Foundation through the Interdisciplinary Research (IDR) program, CBET Award No. 0928703 as well as DUE Program, Award No. 1930464. The authors appreciate the support by the NSF and its IDR and DUE programs.
Data Availability Statement
Data availability No need for any data besides the figures presented in this paper.
Acknowledgments
The authors would also like to express appreciation toward the Boise State University Instrumentation office for the fabrication and machining support of the experimental setup.
References
- American Standard and Testing Materials (ASTM). ASTM D2434: Standard test methods for measurement of hydraulic conductivity of coarse-grained soils. In ASTM International, 2022, 6p.,.
- Kramer, S. L. Geotechnical Earthquake Engineering. Pearson, 2013.
- Martin, J. R., Olgun, C.G., Mitchell, J.K., and Durgunoglu, H.T. High-Modulus Columns for Liquefaction Mitigation. Journal of Geotechnical and Geoenvironmental Engineering. 2004, Volume 130, Issue 6, pp. 561. [CrossRef]
- Cole, G. L., Rajesh P.D., and Fred M.T. Building Pounding Damage Observed in the 2011 Christchurch Earthquake. Earthquake Engineering & Structural Dynamics, 2012, Volume 41, Issue 5, pp. 893–913. [CrossRef]
- Sharp, M. K., Dobry, R., and Abdoun, T. Liquefaction Centrifuge Modeling of Sands of Different Permeability. Journal of Geotechnical and Geoenvironmental Engineering. 2004, Volume 129, Issue 12, 9p. [CrossRef]
- Ganainy, H.E., Abdoun, T., and Dobry, R. Centrifuge Study of the Effect of Permeability and Other Soil Properties on the Liquefaction and Lateral Spreading of Dense Sand.” In Proceedings of GeoCongress, Oakland, CA, USA, 2012.
- Farid, A., Najafi, A., Browning, J., and Barney Smith, E. Electromagnetic Waves’ Effect on Airflow during Air Sparging. Elsevier Journal of Contaminant Hydrology, 2019, Volume 220, pp. 49-58. [CrossRef]
- Azad, S., Farid, A., and Browning, J. Consequence of EM stimulation on Hydraulic Conductivity of a Bentonite Clayey Sample. Environmental Geotechnics Journal, 2015, Volume 2, Issue 4, pp. 211-223, August.
- Ikezoe, Y., Hirota, N., Nakagawa, J., Kitazawa, K. Making Water Levitate. Nature, 1998, Volume 393, Issue 6687, pp. 749. [CrossRef]
- Azad, S; Najafi, A.; Farid, A.; Browning, J.; Barney Smith, E. “Study of Mechanisms Governing Electromagnetic Alteration of Hydraulic Conductivity of Soils.” In Geotechnical Special Publication, American Society of Civil Engineers (ASCE), Arlington, VA, USA. 2014, pp. 1693–1702. [CrossRef]
- Hubbert, M. Darcy’s law and the field equations of the flow of underground fluids. International Association of Scientific Hydrology. Bulletin. 1957, pp. 23-59. [CrossRef]
- Fetter, C.W. Applied Hydrogeology. 4th ed. Pearson, 2001.
- Hazirbaba, K. and Rathje. E.M. 2009. Pore Pressure Generation of Silty Sands due to Induced Cyclic Shear Strains. Journal of Geotechnical and Geoenvironmental Engineering. 2009, Volume 135, Issue 12. [CrossRef]
- Santamarina, J. Carlos, et al. Electromagnetism: Soils and Waves. John Wiley & Sons, Chichester, USA, 2001, pp. 303–327.
- Sun, W., Xu, X., Xu, C. Effects of H2O Dipole Polarization on Ice Formation Process under Electrostatic Field. Journal of Cryobiology, 2007, Volume 56, Issue 1, pp. 93-99.
- Vaid, Y. P. and Negussey, D., Preparation of Reconstituted Sand Specimens. Advanced triaxial testing of soil and rock, ASTM STP 977, Philadelphia, 1988, pp. 405-417.
- Farid, A., Najafi, A.*, Browning, J., & Barney Smith, E. Electromagnetic Waves’ Effect on Airflow during Air Sparging. Elsevier Journal of Contaminant Hydrology, 2019, Vol. 220, pp. 49-58.
- Azad, S. Electromagnetic alteration of hydraulic conductivity of soils. MS thesis, Boise State University. 2013.
- Azad, M. Analysis of electromagnetic stimulation of transport in water for geoenvironmental applications. MS Thesis, Boise State University. 2012.
Figure 1.
Schematic of launching RF setup into the DUT.
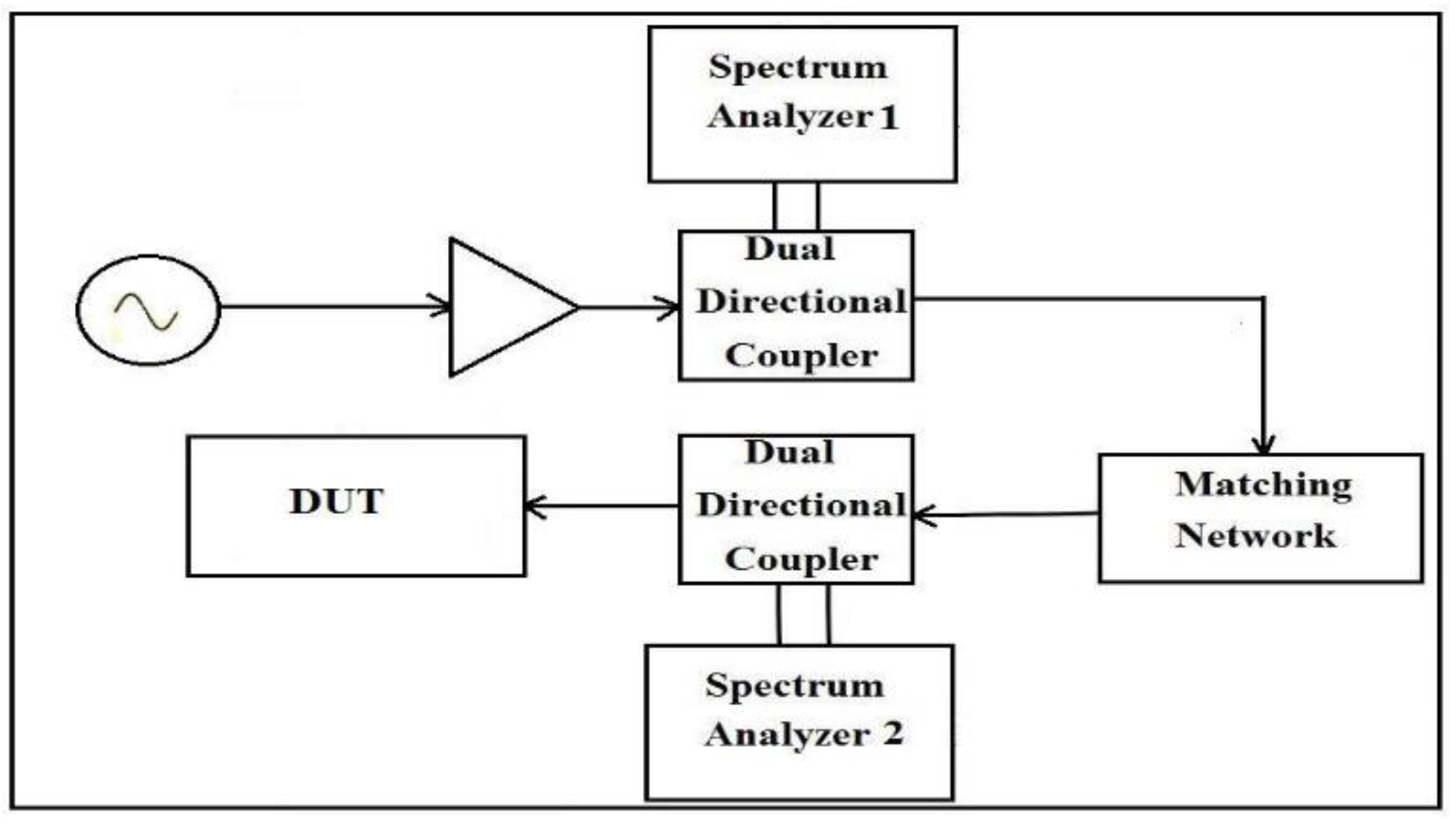
Figure 2.
Schematics of (a) customized, rigid-wall cylindrical permeameter designed to conduct RF-stimulated hydraulic conductivity tests on sand; (b) RF-stimulation setup [18].
Figure 2.
Schematics of (a) customized, rigid-wall cylindrical permeameter designed to conduct RF-stimulated hydraulic conductivity tests on sand; (b) RF-stimulation setup [18].
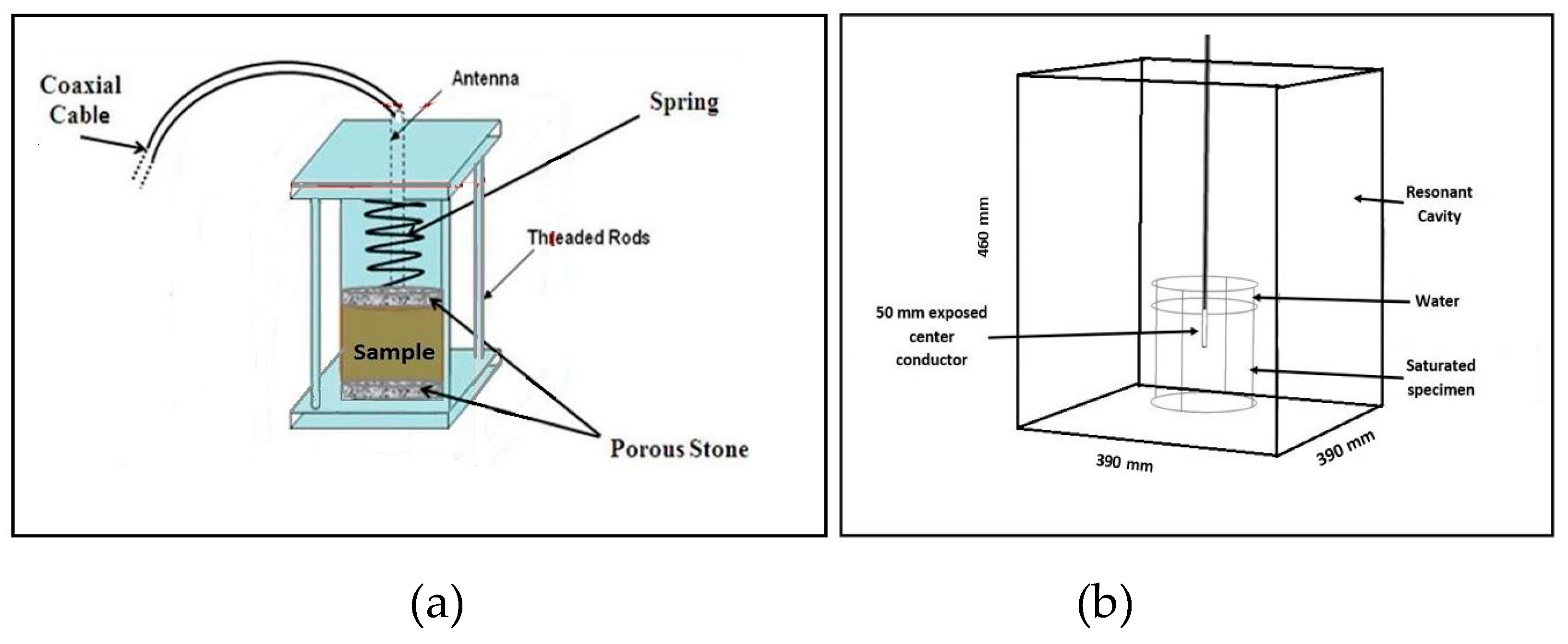
Figure 3.
Schematic top view of customized permeameter with location of depth slices for hydraulic conductivity tests.
Figure 3.
Schematic top view of customized permeameter with location of depth slices for hydraulic conductivity tests.
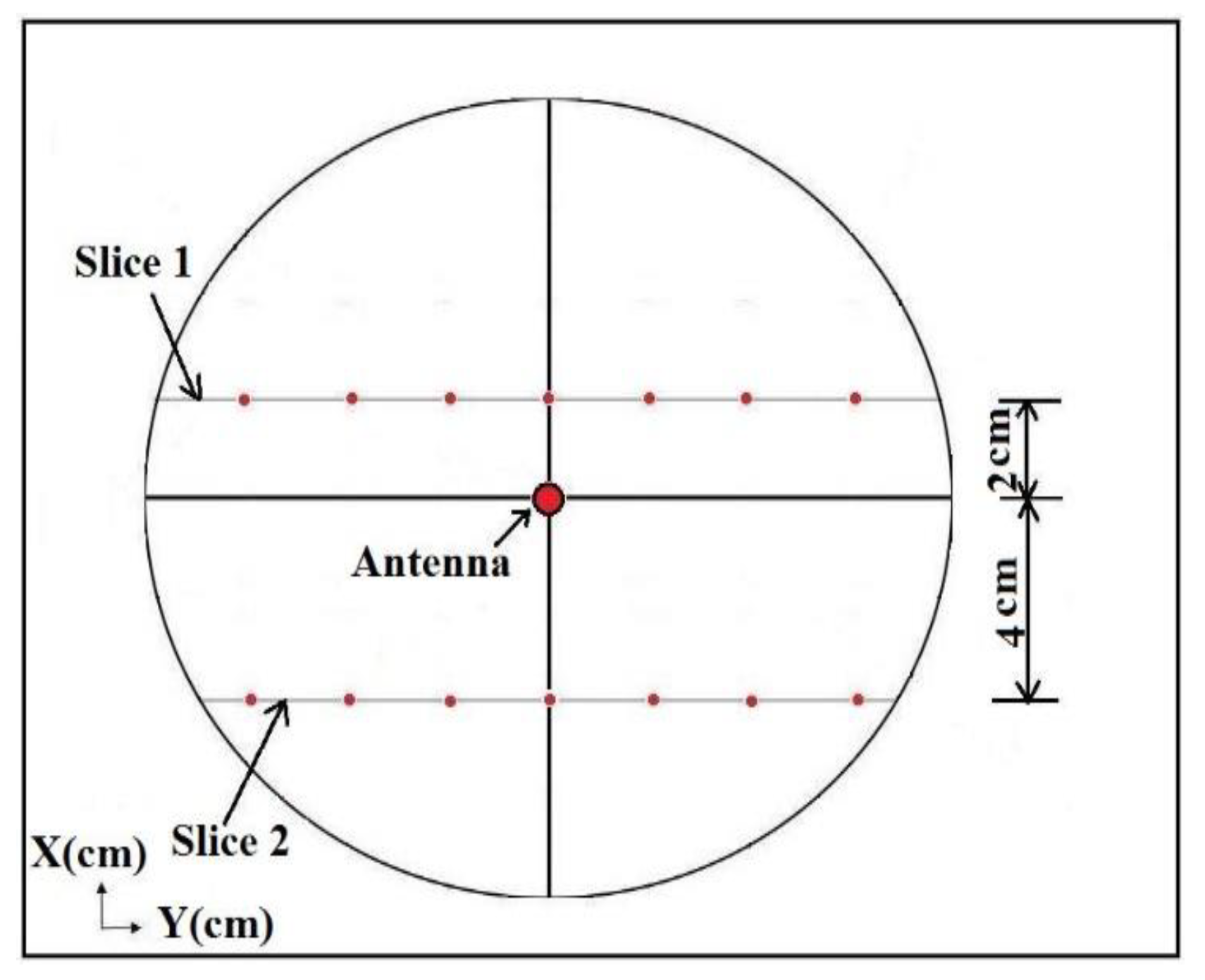
Figure 4.
Schematic of (a) top view of discretized rectangular-cubical domain with circular cross-section; (b) 3D view of rectangular-cubical domain and cylindrical region within sample.
Figure 4.
Schematic of (a) top view of discretized rectangular-cubical domain with circular cross-section; (b) 3D view of rectangular-cubical domain and cylindrical region within sample.
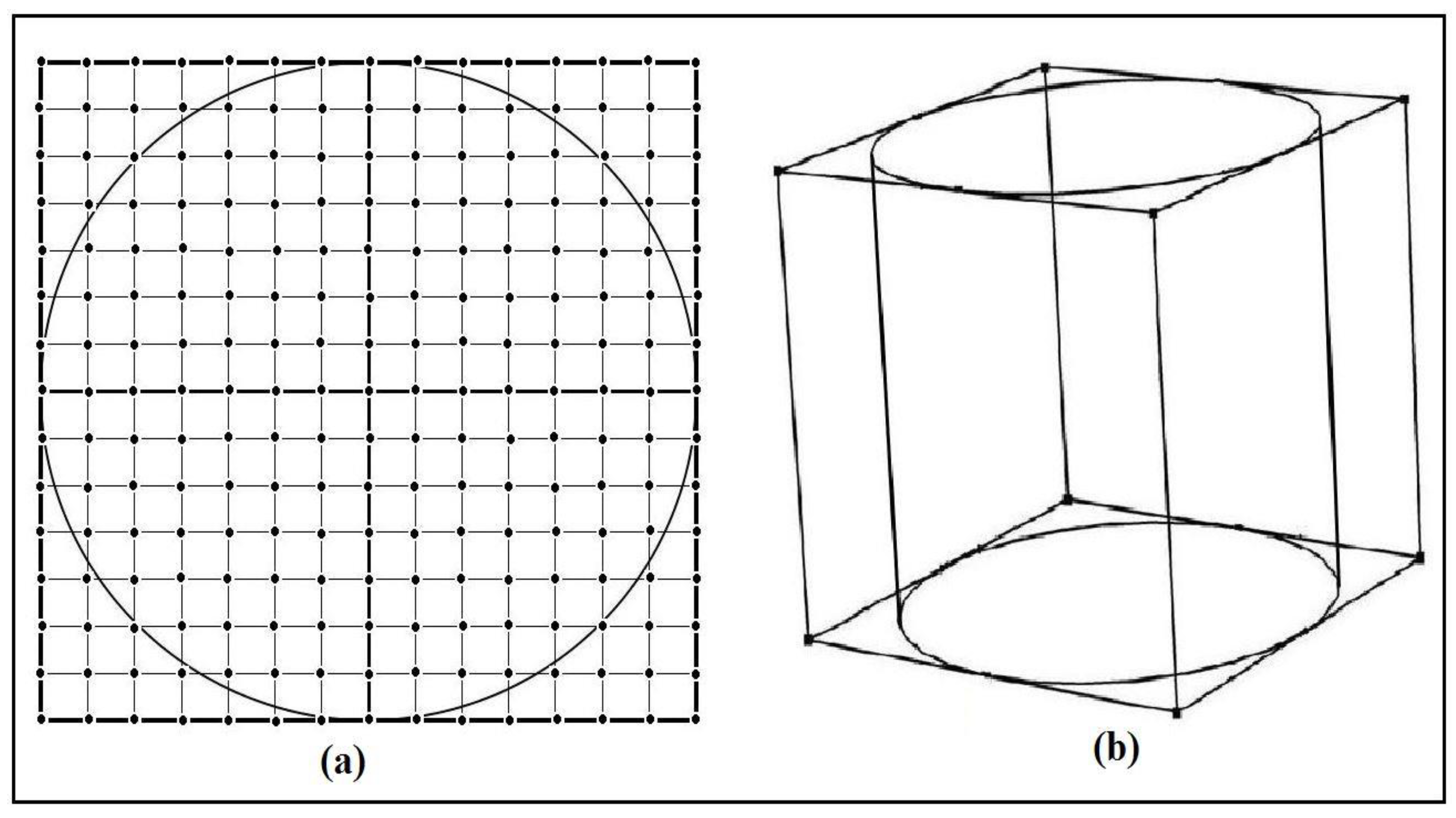
Figure 5.
Schematic of the location of depth (i.e., vertical) slices in 3D view.
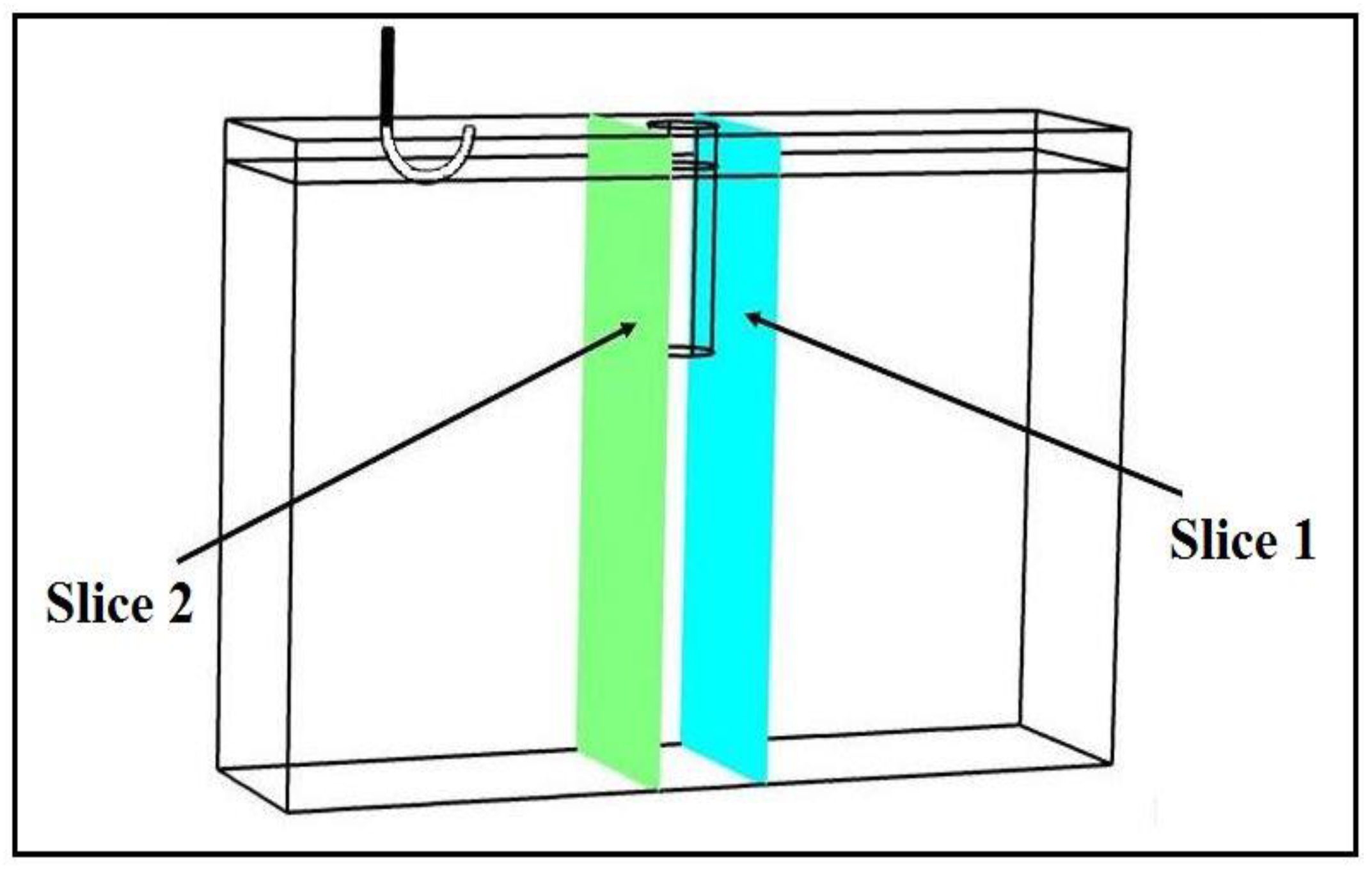
Figure 6.
Electric field: numerically simulated using COMSOL Multiphysics (left) and experimentally measured (right) within the glass-bead sample: a) Depth Slice 1 at 498 MHz; b) Depth Slice 2 at 498 MHz; c) Depth Slice 1 at frequency 632 MHz; and d) Depth Slice 2 at frequency 632 MHz.
Figure 6.
Electric field: numerically simulated using COMSOL Multiphysics (left) and experimentally measured (right) within the glass-bead sample: a) Depth Slice 1 at 498 MHz; b) Depth Slice 2 at 498 MHz; c) Depth Slice 1 at frequency 632 MHz; and d) Depth Slice 2 at frequency 632 MHz.
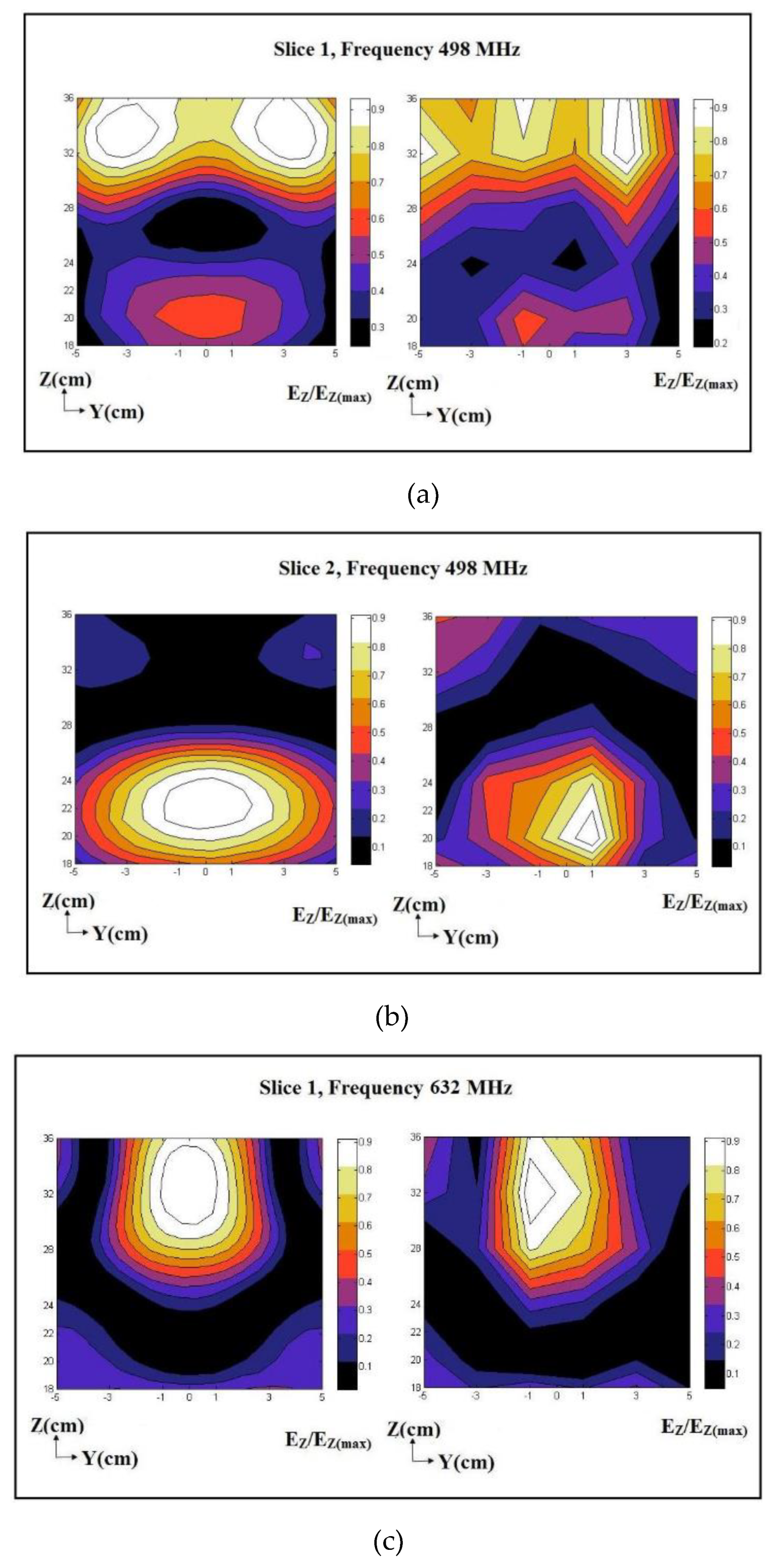
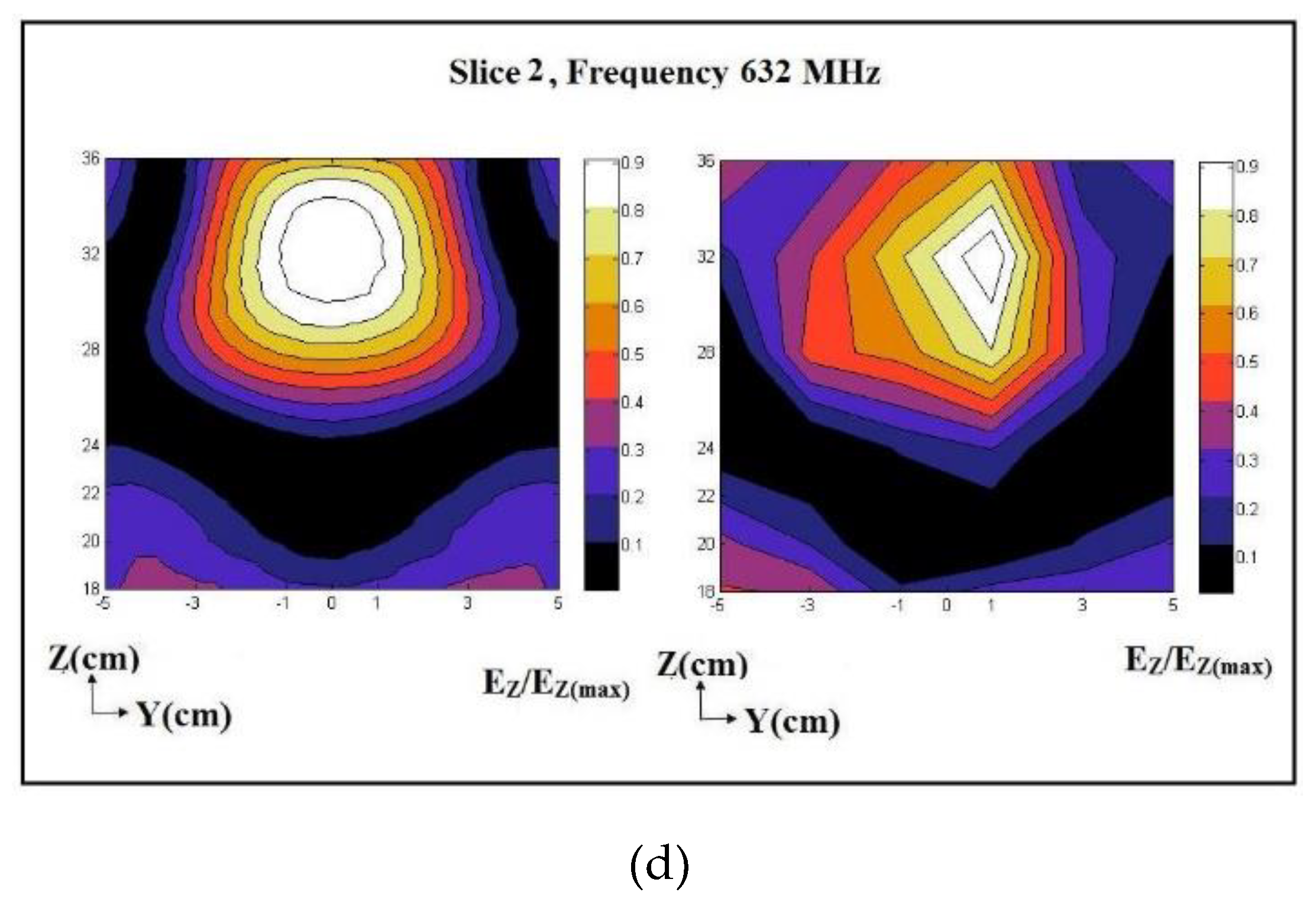
Figure 7.
Measured unstimulated hydraulic conductivity of the glass-bead sample.
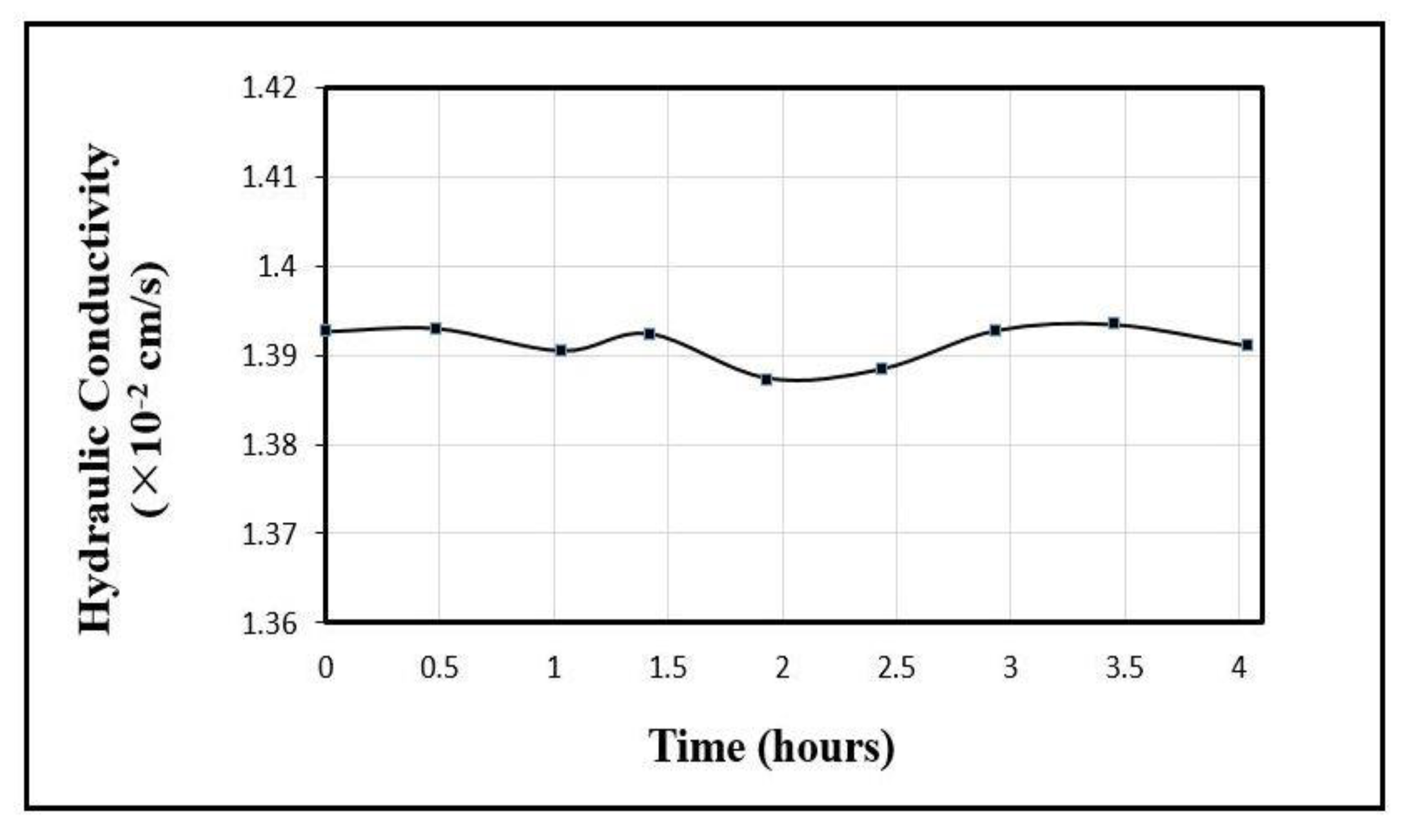
Figure 8.
Measured RF-stimulated hydraulic conductivity of glass-bead sample at a frequency of 726 MHz and RF-power levels of: a) 10 Watts; b) 25 Watts; and c) 40 Watts.
Figure 8.
Measured RF-stimulated hydraulic conductivity of glass-bead sample at a frequency of 726 MHz and RF-power levels of: a) 10 Watts; b) 25 Watts; and c) 40 Watts.
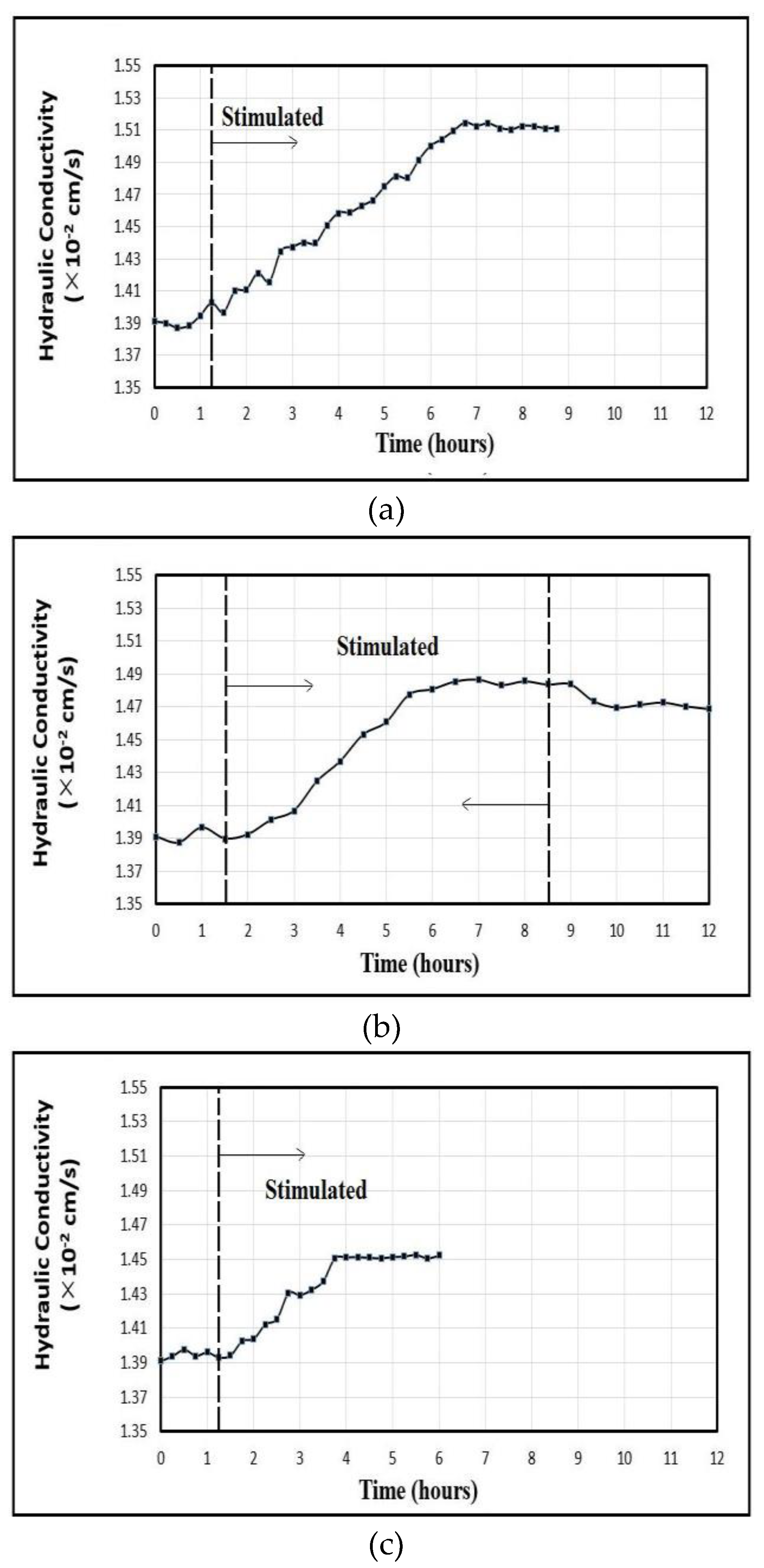
Figure 9.
Measured unstimulated hydraulic conductivity of the natural sand sample.
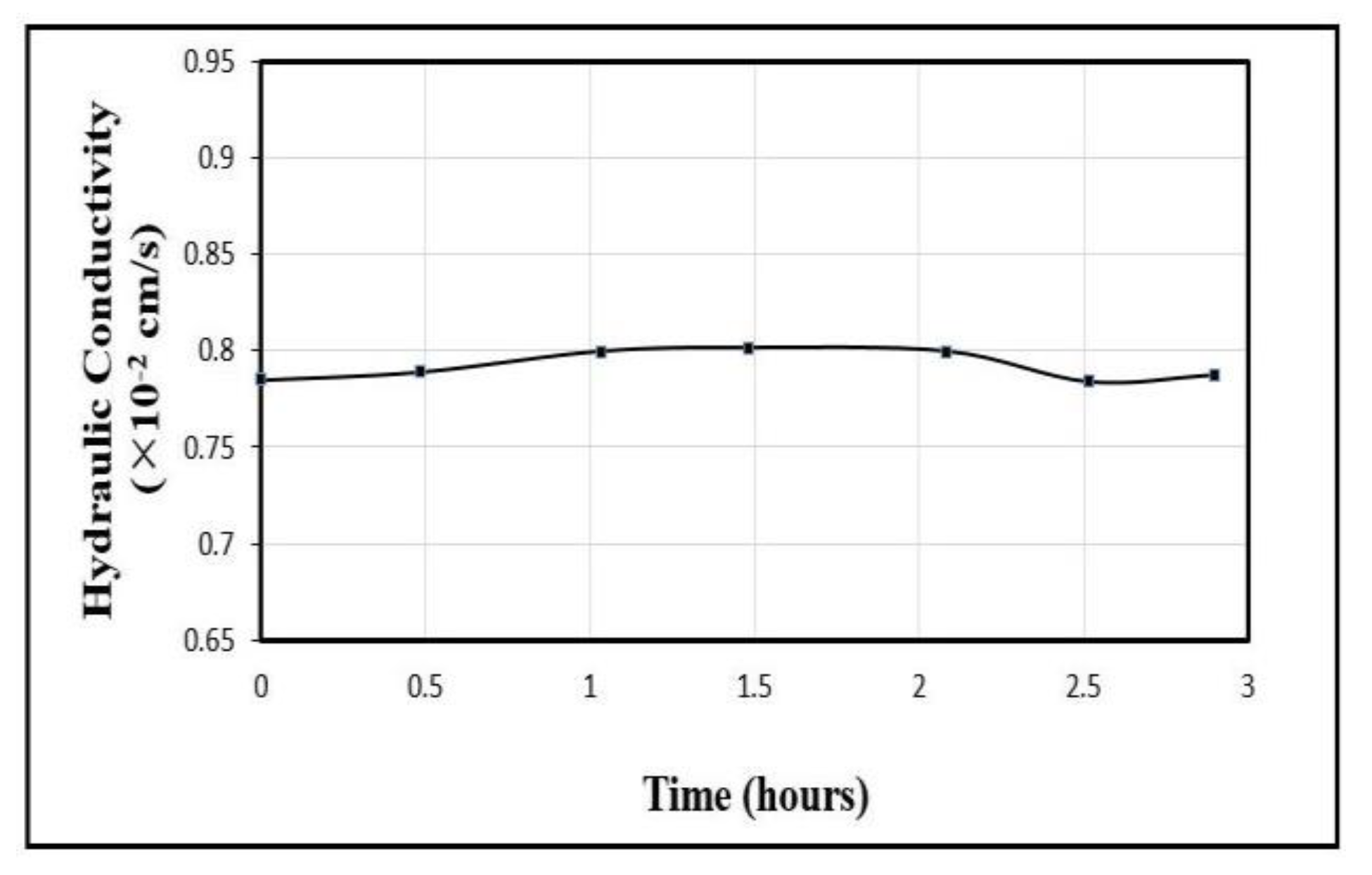
Figure 10.
Measured RF-stimulated hydraulic conductivity of natural sand samples at a frequency of 726 MHz and RF-power levels of a) 10 Watts; b) 25 Watts; and c) 40 Watts.
Figure 10.
Measured RF-stimulated hydraulic conductivity of natural sand samples at a frequency of 726 MHz and RF-power levels of a) 10 Watts; b) 25 Watts; and c) 40 Watts.
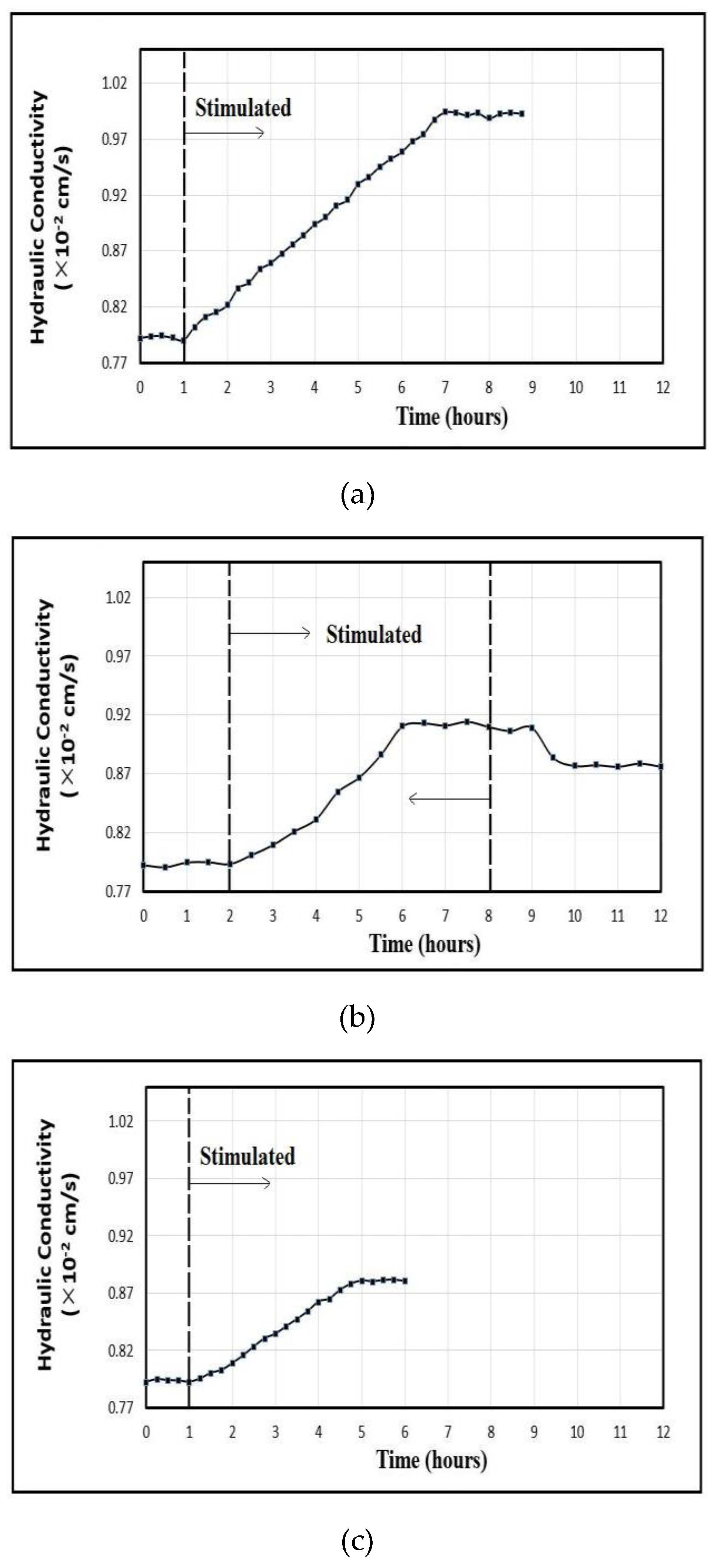
Figure 11.
Electric field, numerically simulated using COMSOL Multiphysics (left) and experimentally measured (right) within the glass-bead sample on a) Depth Slice 1, frequency = 710 MHz; b) Depth Slice 2, frequency = 710 MHz; c) Depth Slice 1, frequency = 726 MHz; and d) Depth Slice 2, frequency = 726 MHz.
Figure 11.
Electric field, numerically simulated using COMSOL Multiphysics (left) and experimentally measured (right) within the glass-bead sample on a) Depth Slice 1, frequency = 710 MHz; b) Depth Slice 2, frequency = 710 MHz; c) Depth Slice 1, frequency = 726 MHz; and d) Depth Slice 2, frequency = 726 MHz.
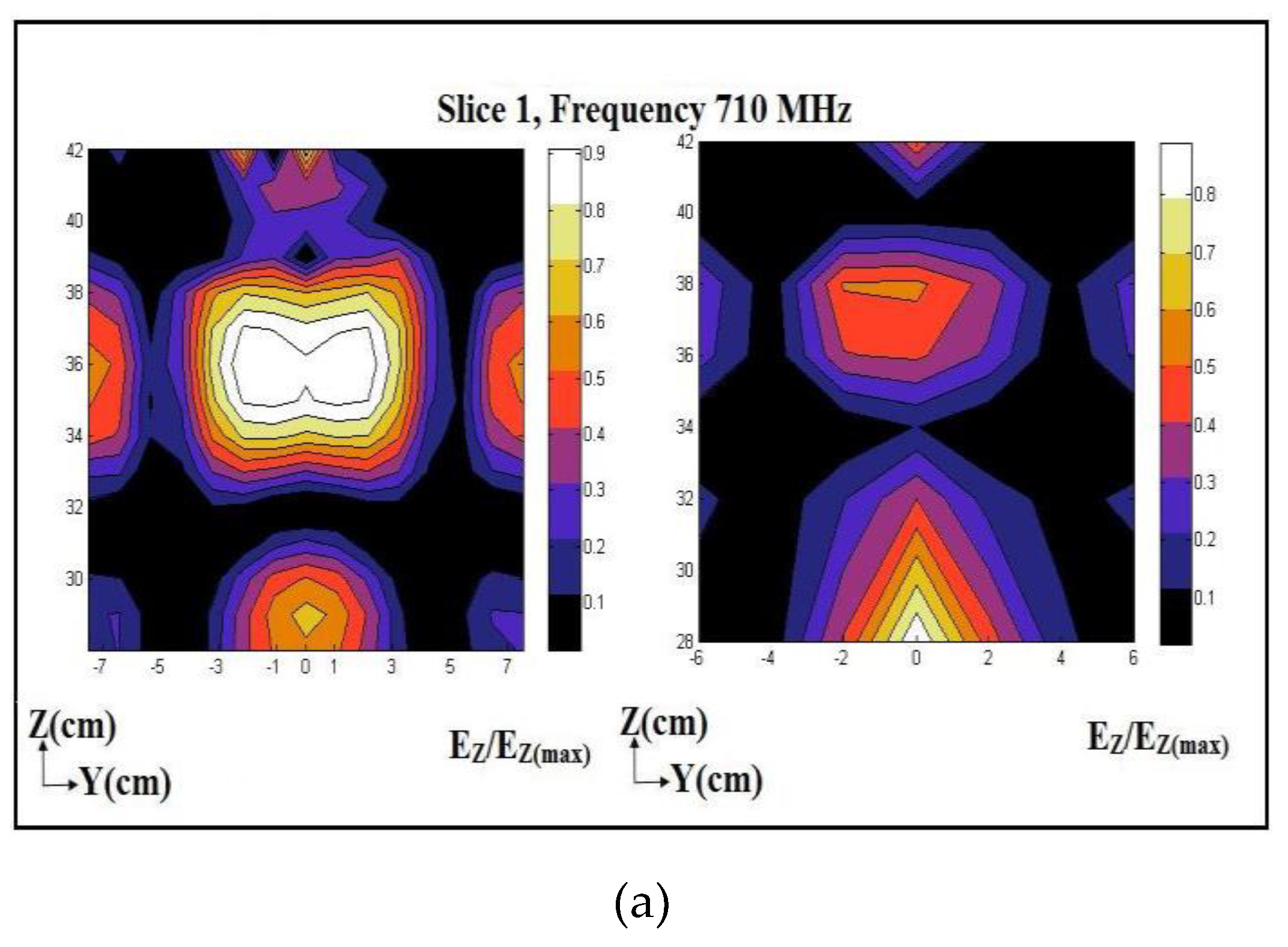
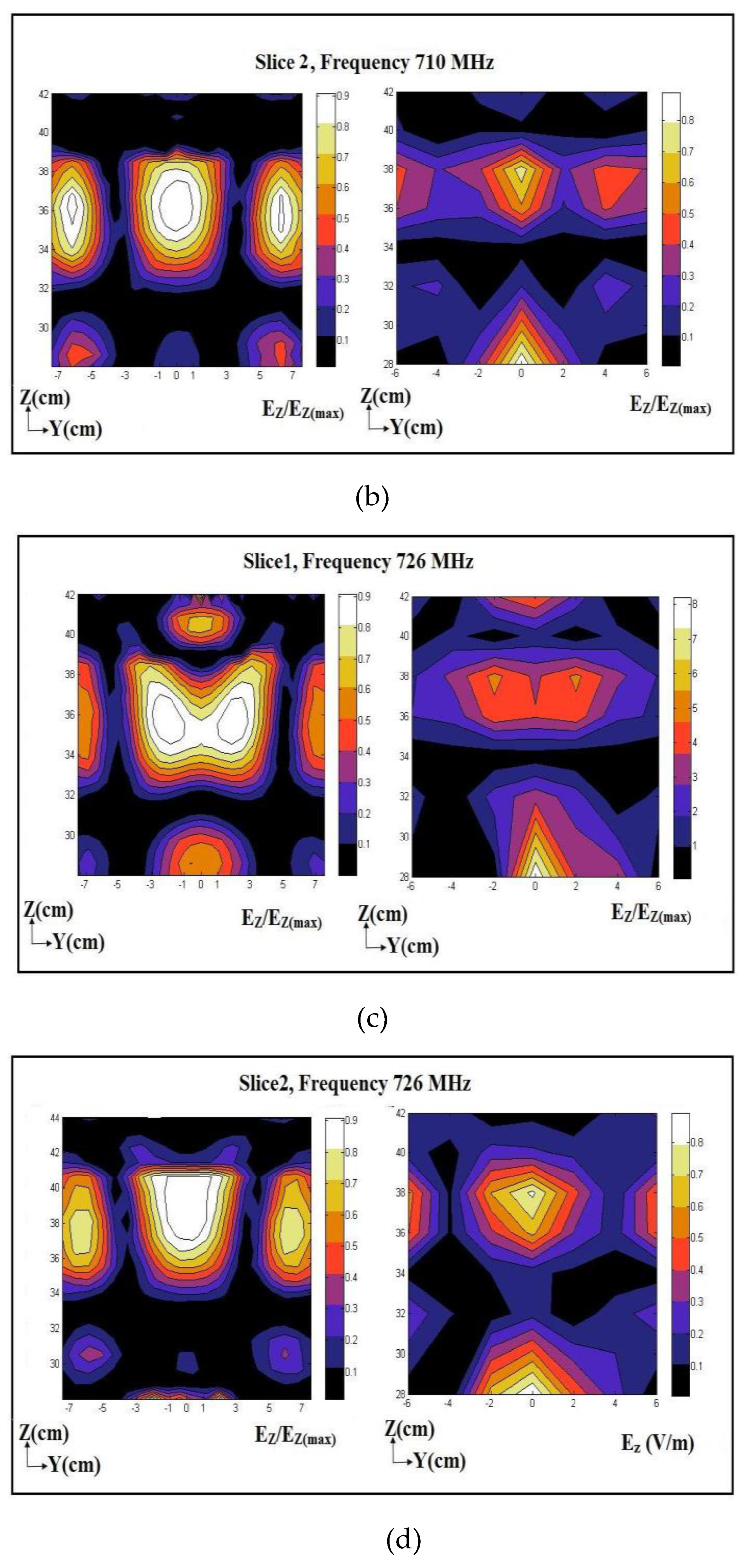
Figure 12.
Contour/color maps of the hydraulic head (m) for natural sand specimen on a) Depth Slices 1 and 15, and Depth Slices 2 and 14; b) Depth Slices 3 and 13, and Depth Slices 4 and 12; c) Depth Slices 5 and 11, and Depth Slices 6 and 10; d) Depth Slices 7 and Depth Slice 8.
Figure 12.
Contour/color maps of the hydraulic head (m) for natural sand specimen on a) Depth Slices 1 and 15, and Depth Slices 2 and 14; b) Depth Slices 3 and 13, and Depth Slices 4 and 12; c) Depth Slices 5 and 11, and Depth Slices 6 and 10; d) Depth Slices 7 and Depth Slice 8.
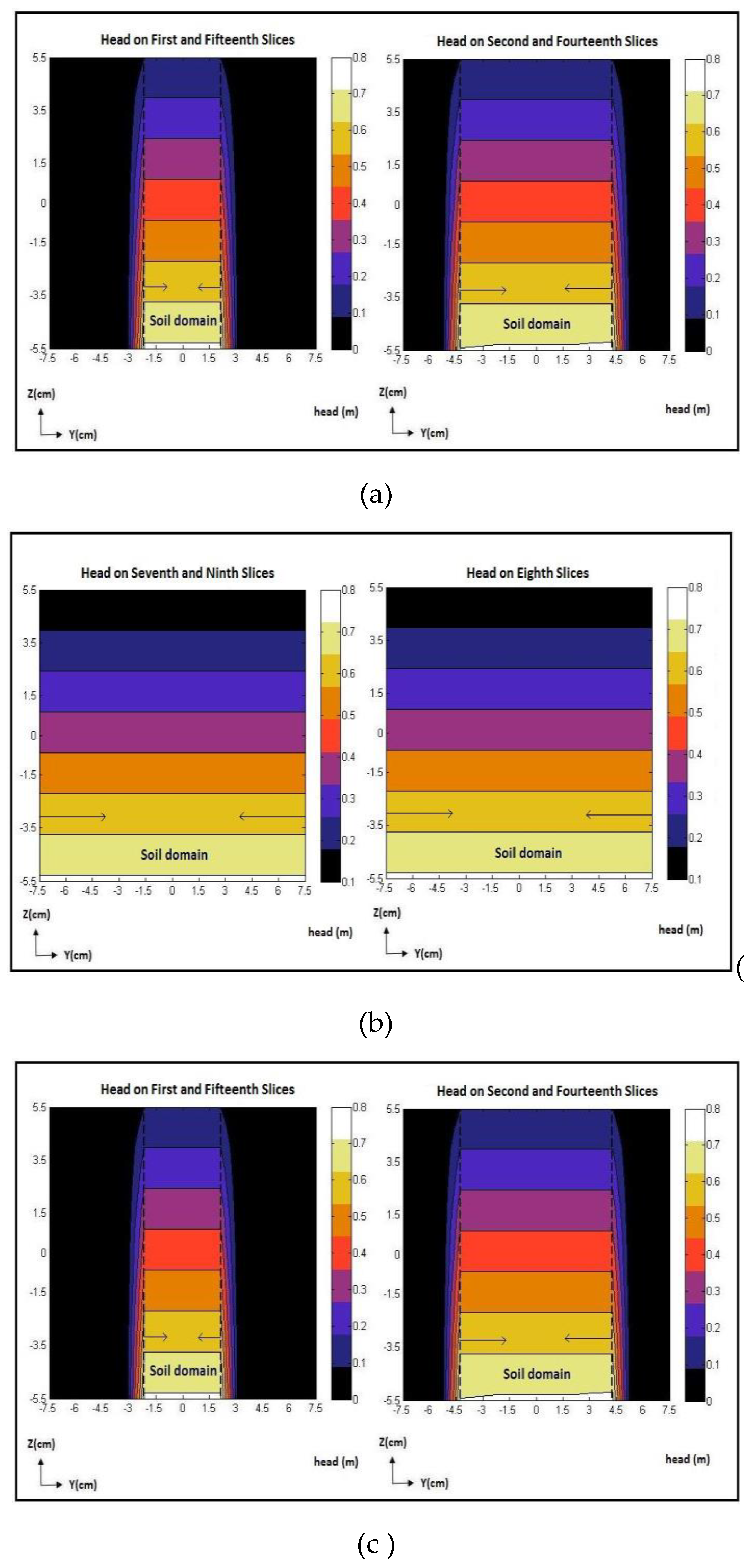
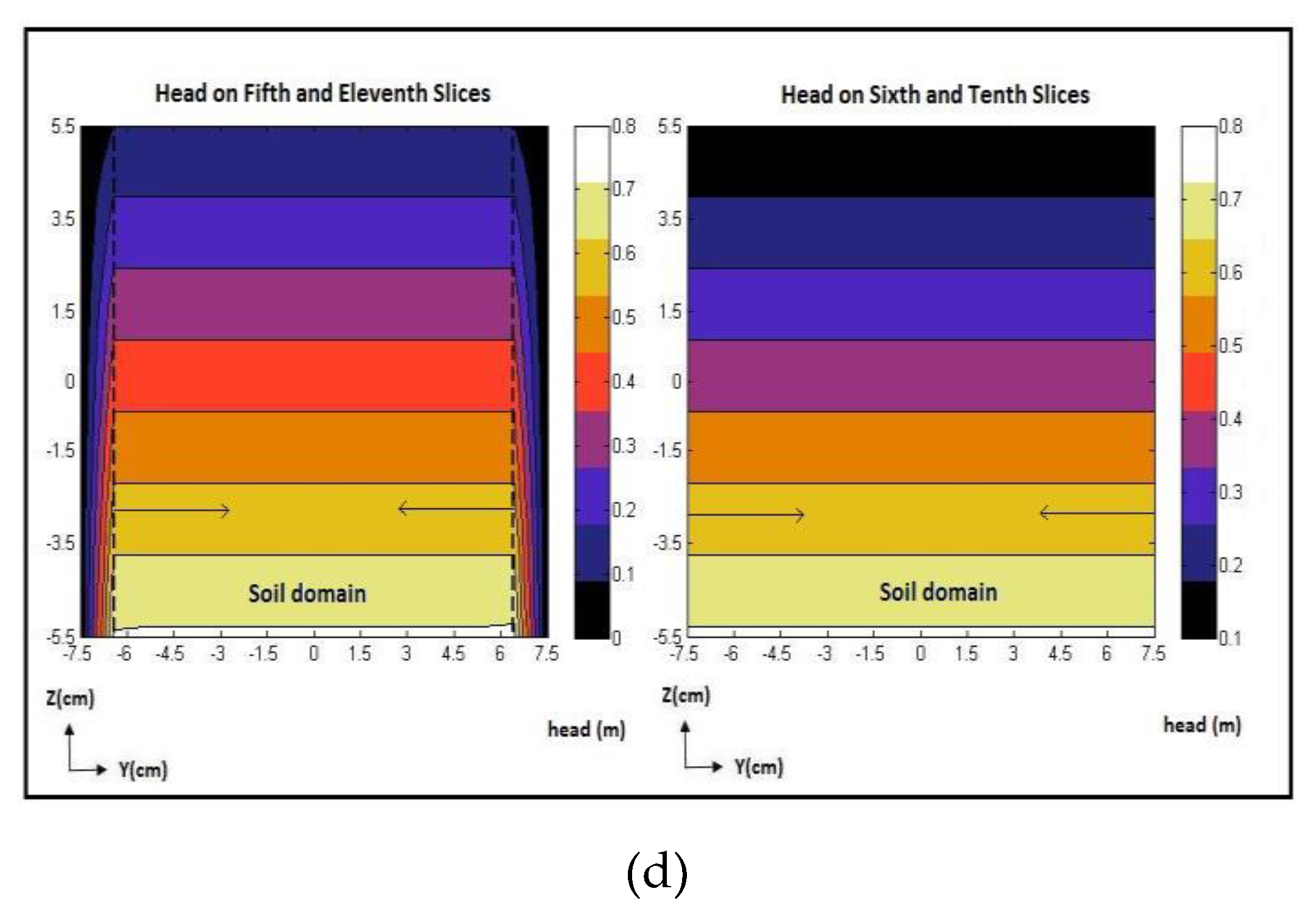
Figure 13.
RF-stimulation flow rate v. RF-power for natural sand specimen.

Figure 14.
Contour/color maps of hydraulic head (m) on: a) Depth Slices 1 and 15, and Depth Slices 2 and 14, at a frequency of 726 MHz and RF-power level of 25 Watts; b) Depth Slices 3 and 13, and Depth Slices 4 and 12, at a frequency of 726 MHz and RF-power25 Watts; c) Depth Slices 5 and 11, and Depth Slices 6 and 10, at a frequency of 726 MHz and RF-power level of 25 Watts; d) Depth Slices 7 and 9, and Depth Slice 8, at a frequency of 726 MHz and RF-power level of 25 Watts for natural sand specimen.
Figure 14.
Contour/color maps of hydraulic head (m) on: a) Depth Slices 1 and 15, and Depth Slices 2 and 14, at a frequency of 726 MHz and RF-power level of 25 Watts; b) Depth Slices 3 and 13, and Depth Slices 4 and 12, at a frequency of 726 MHz and RF-power25 Watts; c) Depth Slices 5 and 11, and Depth Slices 6 and 10, at a frequency of 726 MHz and RF-power level of 25 Watts; d) Depth Slices 7 and 9, and Depth Slice 8, at a frequency of 726 MHz and RF-power level of 25 Watts for natural sand specimen.
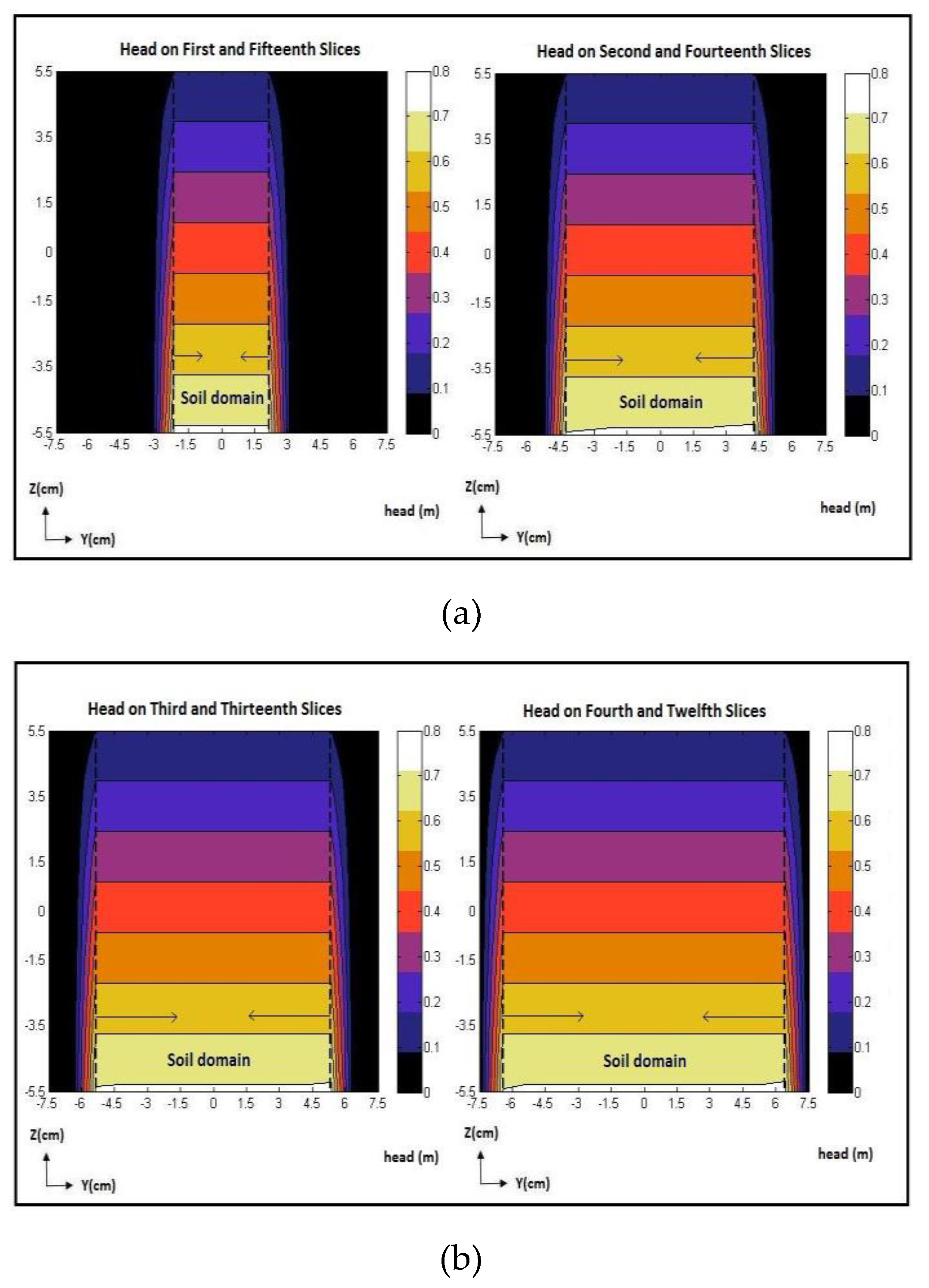
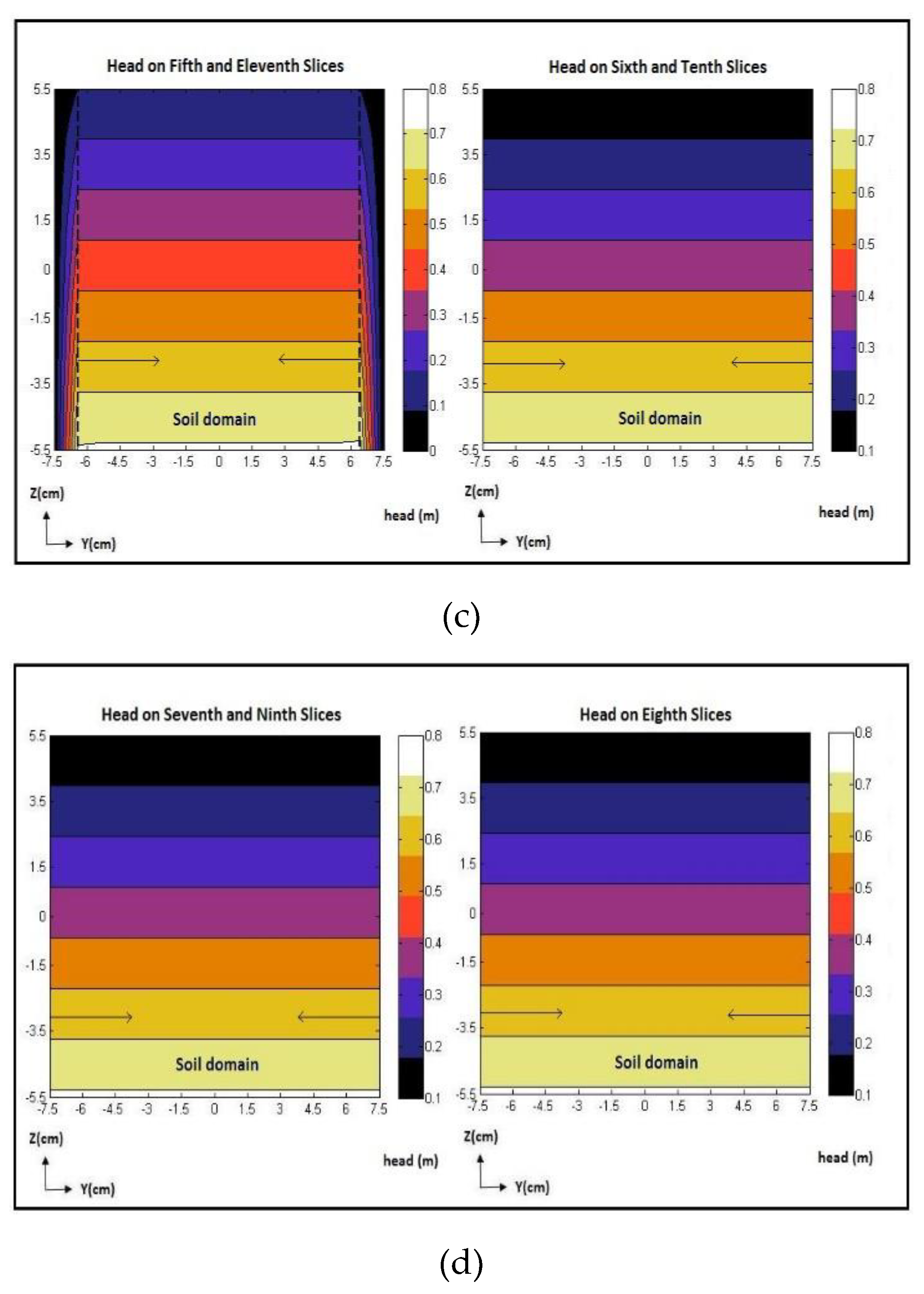
Figure 15.
Contour/color map of normalized difference between RF-stimulated hydraulic conductivity computed and unstimulated hydraulic conductivity for natural sand specimen along the vertical (Z) direction on Slice 7.
Figure 15.
Contour/color map of normalized difference between RF-stimulated hydraulic conductivity computed and unstimulated hydraulic conductivity for natural sand specimen along the vertical (Z) direction on Slice 7.
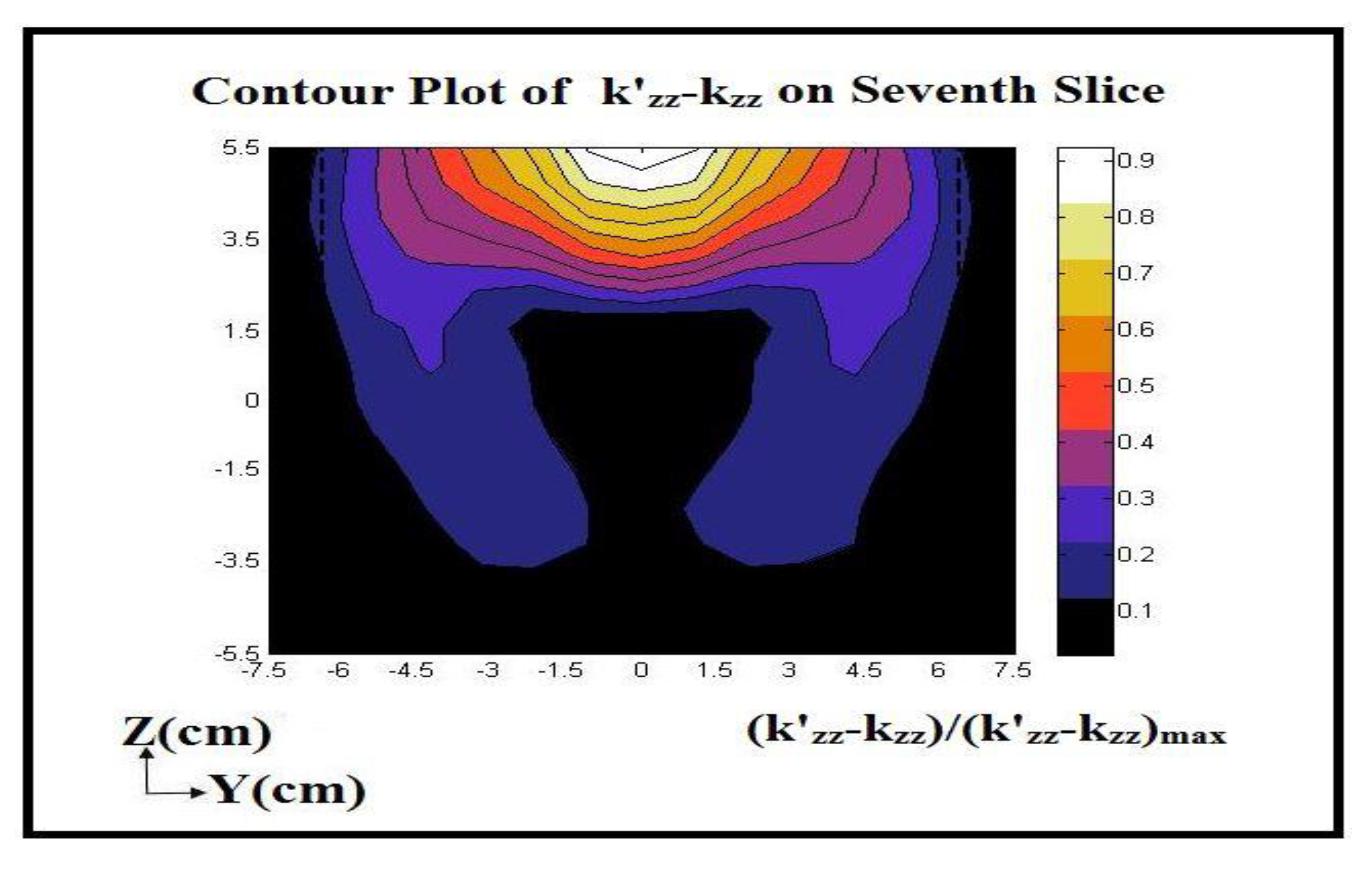
Figure 16.
Contour/color map of normalized power density for natural sand specimen along the vertical (Z) direction on Slice 7.
Figure 16.
Contour/color map of normalized power density for natural sand specimen along the vertical (Z) direction on Slice 7.

Table 1.
Properties of Glass Beads [17].
Table 1.
Properties of Glass Beads [17].
| Potters Designation | U.S. Sieve Number | Maximum Size (in.) | Minimum Size (in.) | Maximum Size (µm) | Minimum Size (µm) | Minimum % of Round Beads |
| Class A | 20-30 | 0.0331 | 0.0234 | 850 | 600 | 65 |
Table 2.
Hydraulic conductivity measurements of the glass-bead sample at a frequency of 726 MHz and various RF-power levels.
Table 2.
Hydraulic conductivity measurements of the glass-bead sample at a frequency of 726 MHz and various RF-power levels.
| Power (Watts) | Average of Unstimulated Hydraulic Conductivity Measured Before RF-stimulation, k (cm/s) | RF-stimulated Hydraulic Conductivity, Peak Value, k’ (cm/s) | Percent Change (%) |
| 10 | 1.3942 ×10-2 | 1.452×10-2 | (+) 4.190% |
| 25 | 1.3911×10-2 | 1.482×10-2 | (+) 6.864% |
| 40 | 1.3923×10-2 | 1.514 ×10-2 | (+) 8.774% |
Table 3.
Hydraulic conductivity measurements of the natural sand sample at a frequency of 726 MHz and various RF-power levels.
Table 3.
Hydraulic conductivity measurements of the natural sand sample at a frequency of 726 MHz and various RF-power levels.
| RF-Power (Watts) | Average of Measured Unstimulated Hydraulic Conductivity Values, k (cm/s) | RF-stimulated Hydraulic Conductivity, Peak Value, k’ (cm/s) | Percent Change (%) |
| 10 | 0.7933 Í10-2 | 0.881Í10-2 | (+) 11.091% |
| 25 | 0.7932Í10-2 | 0.915Í10-2 | (+) 15.287% |
| 40 | 0.7928Í10-2 | 0.994 Í10-2 | (+) 25.386% |
Table 4.
Experimentally measured and numerically computed flow discharge in the natural sand sample at various RF-power levels.
Table 4.
Experimentally measured and numerically computed flow discharge in the natural sand sample at various RF-power levels.
| RF Input Power (Watts) | (Experimental) | Slope () (Numerical Stimulation) | (Numerical value based on optimized k’) | Cost Function |
| 0 | 9.34Í10-6 | None | 9.23Í10-6 | 1.18% |
| 10 | 10.39Í10-6 | 3.65Í10-8 | 10.11Í10-6 | 2.77% |
| 25 | 10.78Í10-6 | 3.25Í10-8 | 10.52Í10-6 | 2.47% |
| 40 | 11.71Í10-6 | 3.25Í10-8 | 11.42Í10-6 | 2.54% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






