Preprint
Article
Numerical Simulation and Experiment of Stress Relief and Processing Deformation of 2219 Aluminum Alloy Ring
Altmetrics
Downloads
89
Views
32
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
09 June 2023
Posted:
09 June 2023
You are already at the latest version
Alerts
Abstract
Large aluminum alloy ring forgings are the core components of heavy-duty rocket fuel storage tanks, and the large residual stress inside the rings leads to poor shape accuracy of large thin-walled parts. The initial stress of the 2219 aluminum alloy ring blank was tested using the drilling method, and the creep constitutive coefficient of the 2219 aluminum alloy was determined through stress relaxation tests. The numerical simulation processes of thermal stress relief (TSR), vibration stress relief (VSR), and thermal-vibration stress relief (TVSR) were compared and established. Through the correlation analysis between the actual measurement results of residual stress and the simulation results, it can be seen that the strong correlation in three directions at each measurement point accounts for over 37.5%, and the moderate correlation accounts for over 62.5%. This indicates that the numerical simulation model of 2219 aluminum alloy ring containing initial residual stress can accurately reflect the size and distribution of residual stress inside the actual ring. The simulation results show that the derived constitutive model can describe the stress relaxation process of TVSR by combining a single thermal time effect stress relaxation constitutive theory with a VSR plastic deformation material model. The simulation models established above were used to calculate the residual stress homogenization ability of three types of aging. The results showed that VSR, TSR, and TVSR can homogenize and reduce the residual stress field inside the ring, improve the distribution of residual stress inside the ring, and have a better overall homogenization ability of TVSR. The VSR control has a certain effect on reducing and homogenizing residual stress, but compared with TSR and TVSR, the reduction and homogenization ability of residual stress control is limited. The homogenization control effect TVSR>TSR>VSR, and the maximum equivalent stress homogenization rates of VSR, TSR, and TVSR are 52.8%, 80.6%, and 82.2%, respectively. Then, numerical simulation technology is used to study how the initial residual stress in the blank will cause the deformation of the ring during the thin-walled machining process. The roundness error theory of the minimum containment area method is applied to evaluate the deformation degree during the thin-walled numerical machining process, and the TVSR method is used for stress regulation. The deformation law of the thin-walled machining of the ring under different aging parameters is studied.
Keywords:
Subject: Engineering - Mechanical Engineering
1. Introduction
During processes such as machining, heat treatment, and electroplating, parts can directly or indirectly introduce residual stress. Residual stress exists in various machining processes of the ring, and the excessive and unevenly distributed residual stress inside the ring may be an important factor in component failure and scrapping, especially when the ring is thin-walled cutting and forming process, as well as when the formed ring is subjected to large loads, complex external vibration environment, and intense high-temperature friction heat generation environment during rocket launch, residual stress becomes a factor that cannot be ignored.
Aluminum alloy ring rolling forming involves material nonlinearity and boundary conditions (such as temperature and load) nonlinearity. Under the coupling of temperature and processing environment, residual stress is inevitably generated. With the increase of ring rolling size, the uneven distribution of residual stress and local stress are more obvious. In addition, after ring rolling forming, the quality of the connecting ring used for rocket storage tanks is required, and it needs to be processed into an aviation thin-walled ring, which is prone to deformation during the manufacturing process. Residual stress not only reduces the ability of aluminum alloy to resist stress corrosion cracking, but also significantly reduces its strength, stability and fatigue resistance. Moreover, various research results show that the main factor causing machining deformation is the initial residual stress in the blank, which has the greatest impact on machining deformation [1,2,3]. With the continuous thinning of rough forgings, the initial residual stress is released and redistributed, resulting in deformation during the processing and use of parts, low forming accuracy, and noncircular shapes. Therefore, in order to effectively control and reduce the structural deformation that occurs during the use of 2219 aluminum alloy rings, it is necessary to minimize the residual stress in the blank ring forging as much as possible. In addition, in response to the deformation caused by out of roundness during the use of rough ring forgings, it is also necessary to ensure that the residual stress in the rough ring forgings is evenly distributed along the circumference as much as possible.
Integral thin-walled parts are widely used in aviation and aerospace production due to their high specific stiffness and strength. The largest integral rolling ring has a diameter of nearly 10 meters and a wall thickness of about 0.2 meters. When processing large thin-walled rolling ring parts, they are prone to machining deformation caused by residual stress [4]. In addition, thin-walled parts are manufactured through turning and milling, in which more than 90% of the material is removed from the billet. The appropriate distribution of residual stress can significantly reduce machining deformation [5]. Therefore, as the main blank forging of aviation storage tank parts, the removal of residual stress in 2219 aluminum alloy rings is an important link to ensure the dimensional stability of the parts, improve the assembly accuracy, performance, and reliability of the storage tank [6]. The homogenization of initial residual stress has become more important for solving machining deformation.
At present, the method of reducing or eliminating residual internal stress in metal at home and abroad to stabilize the dimensional accuracy of metal workpieces is called "aging". The use of aging technology is the most common method for controlling residual stress. In the ring rolling process, the blank forming process inevitably generates high and uneven residual stress. Research by experts [7] suggests that the decrease in peak residual stress changes the internal stress field, causing the internal stress of the component to decrease and redistribute, achieving equilibrium at lower stress levels. Therefore, after the ring blank forming process, aging techniques (such as natural aging, TSR, VSR, and TVSR) are generally used to eliminate or reduce the adverse effects of residual stress on the workpiece. The basic idea of either method is to intervene in the micro defects or dislocation of lattice molecules within metal components, enabling them to undergo plastic deformation or lattice movement at the micro level, eliminating the imbalanced dislocation caused by such lattice molecules, and thereby reducing or eliminating internal stress [8].
The natural aging method utilizes the "slow release" characteristic of residual stress inside the workpiece over a sufficiently long period of time. Although this method is simple and easy to implement, with high and stable dimensional accuracy, it has a long cycle and low efficiency, and is no longer sufficient to meet the needs of modern production. Under the modern industrial system, it has been basically phased out.
The thermal stress relief (TSR) method, which eliminates or reduces residual stress due to the elastic-plastic deformation caused by the thermal relaxation effect under temperature, is relatively reliable and the process is relatively mature. Research has shown that different aging heat treatments will have a significant impact on the final properties of alloy materials [9]. Researchers from various countries have analyzed various TSR processes for aluminum alloy parts, and found that TSR at the aging temperature of aluminum alloy can not only ensure the performance of the parts does not decrease, but also meet the requirement that the residual stress level is at a lower level, which is better than natural aging. This ensures the reliability of the parts and improves their lifespan, and makes the mechanical properties of the materials better [10, 11]. In recent years, researchers from various countries have continuously explored the mechanism of TSR. Some researchers [12] believe that most aluminum alloy components undergo aging treatment after quenching, and the residual stress of the components changes due to material creep during this process. Therefore, on the basis of quenching stress research, Gao et al. [13] have extended the study of residual stress evolution to the aging stage based on creep behavior research. Dong et al. [14] studied the evolution behavior of quenching residual stress in 2024 aluminum alloy during aging. This study showed that the quenching residual stress of components gradually decreases with time when aged at 140~170 ℃. With the rapid development of science and technology and in-depth research on TSR technology, the theory of creep behavior can better describe the residual stress process of parts controlled by TSR technology.
Vibration stress relief (VSR) is an energy saving, environmentally friendly, and efficient stress relief process. The ordinary vibration generated by mechanical and other methods (such as vibration exciters) repeatedly applies cyclic loads to the workpiece with residual stress, causing a certain plastic deformation of the workpiece. As a result, the residual stress is relaxed and reduced, thereby stabilizing the size of the workpiece. VSR is a supplement and development of TSR, replacing TSR within a certain range [15, 16]. Many researchers [17-21] have studied the VSR during part resonance through experimental or numerical analysis. The larger amplitude generated by excitation can more effectively eliminate residual stress. In engineering, excitation at zero amplitude can be used to meet the requirements of relatively small vibration intensity and good stress relaxation. This technology is almost applicable to all types of part shapes and sizes, whether it is thin-walled parts, welded parts, or square plates, this technology can improve the dimensional stability of parts, and the residual stress distribution is more uniform after VSR treatment.
Thermal-vibration stress relief (TVSR), as the temperature increases to the aging temperature, the elastic modulus of the material decreases, which not only helps to increase the amplitude but also reduces the yield strength. Dynamic stress is generated at the natural frequency of the part and under external vibration loads, resulting in greater yield and relaxation of residual stress. The residual stress homogenization method first proposed by Zhang et al. [22] achieves residual stress relief under lower strain conditions under the combined action of high temperature and vibration. Improved delamination method experiments and numerical simulations were used to verify that the stress homogenization effect of TVSR on 7075 aluminum alloy is better than that of VSR. TVSR technology is a new research direction on workpiece aging technology in recent years. As a new type of stress homogenization process, TVSR is gradually receiving attention from scholars. Gao et al. [23] studied the residual stress and microstructure differences of Ti6Al4V titanium alloy under three different aging techniques: TSR, VSR, and TVSR. The results showed that TVSR and TSR were able to eliminate more than 90% of residual stress, but the removal efficiency of TVSR was 4.2 times that of TSR; Meanwhile, the elimination efficiency of TVSR is 45.04% higher than that of VSR. Chen et al. [24] studied three aging techniques: TSR, VSR, and TVSR, and compared the residual stress homogenization effect of 2219 aluminum alloy welded parts. The results showed that after the three aging treatments, the stress of 2219 aluminum alloy welded samples was relatively small and uniform, and TVSR performed better in overall homogenization of stress at the weld seam. Li et al. [25] studied the TVSR process on the control of the residual stress and machining deformation before finish machining. It can be concluded that the final maximum deformation of specimen can be reduced by 38.33%. Kasim et al. [26] combined VSR and heat treatment after welding, and found that the resonance frequency and higher vibration amplitude of VSR are more effective for stress homogenization after welding heat treatment. Chen et al. [27] optimized the TVSR process based on aluminum alloy rings by studying the effects of different amplitudes, vibration times, vibration frequencies, heating times, holding times, and cooling times on TVSR treatment. The results show that the optimized process parameters can reduce the maximum residual stress of the aluminum alloy ring by 93.6%.
TVSR can significantly eliminate residual stress inside aluminum alloys and effectively reduce the residual stress of 7075 aluminum alloy. Due to the unique shape of ring shaped parts during quenching, residual stress is introduced into the 2219 aluminum alloy ring during the quenching experiment, resulting in a complex distribution of residual stress field. During multiple stages of heating, insulation, and rapid cooling, the radial stress, circumferential stress, and shear stress inside the ring are constantly changing.
Therefore, in order to study the homogenization and regulation of residual stress inside the 2219 aluminum alloy ring of the new generation rocket storage tank by VSR, TSR, and TVSR. In response to the problem of large and uneven distribution of residual stress inside the ring, stress aging homogenization and regulation research were conducted on 2219 aluminum alloy ring after obtaining the initial residual stress. By establishing a finite element numerical model of the ring component and assigning initial residual stress during quenching, the numerical simulation results of TVSR technology, VSR technology, and TSR technology are used to verify the homogenization and control effect of residual stress inside the aluminum alloy ring component before and after the process. Then, numerical simulation technology was used to study how the initial residual stress in the blank during the thin-walled machining process of the ring will cause the deformation of the ring, and the deformation law of the thin-walled machining of the ring was studied.
2. Simulation modeling description
2.1. Aging simulation modeling
2.1.1. Quenching Experiment and Residual Stress Testing Experiment of Aluminum Alloy Ring Parts
2.1.1.1. Thermal parameters of 2219 aluminum alloy material
The research object of this article is 2219 aluminum alloy, and the thermal physical properties of aluminum alloy materials are greatly affected by temperature. The numerical simulation process of TSR and TVSR also needs to consider the material's thermal physical properties and mechanical performance parameters that vary with temperature. According to literature [28,29], the average density of 2219 aluminum alloy is 2840 kg/m3, and the Poisson's ratio is 0.3. According to reference [30], the quenching temperature of 2219 aluminum alloy is 535 ℃. Therefore, the temperature range for the thermal properties of the material is between 20 ℃ and 700 ℃. The fitting curve of material properties related to temperature of 2219 aluminum alloy is shown in Figure A1 [27]. Figure A1 includes such thermophysical property parameters as elastic modulus, specific heat capacity, density, thermal conductivity, coefficient of thermal expansion and yield stress of 2219 aluminum alloy material.
2.1.1.2 Experimental Process Route for Quenching Aluminum Alloy Rings
The connecting part blank of the rocket fuel storage tank studied in this article is a circular part, with an outer diameter of 450 mm, an inner diameter of 366 mm, and a height of 105 mm. The 2219 sample aluminum alloy ring is placed in a heating furnace and heated from room temperature of 25 ℃ to 535 ℃ for insulation. The heating time is 120 minutes, the insulation time is 150 minutes, and the temperature is controlled within ± 3 ℃. After the insulation is completed, the sample is placed in a 25 ℃ water tank for cooling treatment, with a transfer time of less than 10 seconds, resulting in a large amount of residual stress generated by the temperature gradient caused by rapid water quenching. The quenching process route of 2219 aluminum alloy ring components is shown in Figure 1a.
a) Process route of 2219 aluminum alloy quenching ring, b) Quenching experimental equipment
In order to evaluate the numerical simulation results of stress aging, the initial residual quenching experimental stress is introduced into the stress aging numerical simulation process. Design an aluminum alloy ring quenching experiment based on Figure 1a aluminum alloy quenching process roadmap, using an electronic temperature control unit with timing function, which can control the temperature within ±3 ℃, accurately adjust the quenching temperature, and ensure the minimum temperature error between the experimental temperature value of the ring and the theoretically designed quenching process route. The on-site quenching experimental equipment and cooling pool are shown in Figure 1b.
2.1.1.3 Residual stress testing of aluminum alloy ring after quenching
In order to investigate the distribution status of residual stress in the ring blank and evaluate the magnitude of residual stress inside the ring, it is necessary to conduct residual stress testing on the experimental ring before numerical simulation of stress aging.
The initial residual stress is one of the main factors causing the deformation of the workpiece during processing. Due to the presence of residual stress in any part of the ring, precise multi point measurement is not yet feasible, and as of now, there is no universal and accurate residual stress testing technology due to the imperfect theory of residual stress testing for parts and the limitations of measuring equipment. The sample size of this experiment is relatively large. In order to more comprehensively and accurately reflect the stress distribution law of the ring rolled piece, 1 point was taken every 90 ° along the circumferential direction in the axial direction, and a total of 8 measurement points were taken. The actual photos of residual stress measurement points for 2219 aluminum alloy ring pieces at the experimental site are shown in Figure A2a.
Due to the fact that the measured component is a ring component, in order to evaluate the residual stress of the ring component as much as possible, combined with existing experimental conditions, the multi-point drilling method was used for residual stress measurement.
The drilling method is an early developed, low-cost, widely used, and most mature residual stress testing method. It has the advantages of high measurement accuracy, convenient operation, and cheap equipment, and has been determined as the standard residual stress measurement method by ASTM. The basic principle of the drilling method is to drill a small hole on the surface of the workpiece that generates residual stress. The stress in the vicinity of the hole is released, resulting in the corresponding strain. By measuring the magnitude of the strain, the average residual stress in the depth direction of the drilling can be obtained through calculation. The measurement principle is shown in Figure A2b.
The drilling method used in this article to measure the residual stress of 2219 aluminum alloy rings is based on the American Material Testing Standard E-837-13a [31]. As mentioned earlier, residual stress cannot be directly measured. Typically, the elastic strain generated by the initial release stress at the hole location is directly measured, and then residual stress can be calculated using mathematical relationships. In the experiment, firstly, according to the requirements of sticking strain gauge to measure residual stress by drilling method, stick strain rosettes, connect the measuring bridge circuit (this experiment uses a half bridge measuring circuit), and record the output value of the bridge when the hole is not drilled. The drilling device is used to drill holes at the drilling position to release the residual stress inside the workpiece. At this time, the resistance of the working strain gauge will change, and the output of the bridge circuit will change. Record the output result at this time to obtain the change value of the output voltage. The residual stress measurement system of the ring using the drilling method is shown in Figure 2a, and the on-site clamping is shown in Figure 2b.
When measuring, the measuring points should be polished and polished first to ensure a bright, flat, and scratch free surface, avoiding slight vibration of the pasted three-dimensional strain pattern during drilling and increasing measurement error. After the three-dimensional strain pattern is pasted, it is welded to the strain measuring instrument for wiring, and then the 2219 aluminum alloy experimental sample and drilling fixing seat are fixed to prevent the sample from slipping and swinging, and to avoid the phenomenon of drilling and milling cutter breakage. Through the built-in eyepiece, the fine-tuning drilling and milling cutter is located at the center of the three-dimensional strain pattern. The drilling method equipment uses high-pressure nitrogen gas cylinders to provide high-speed drilling and milling power for the drilling and milling cutter. Each measuring point measures a depth of 1.0 mm, starting from the surface and measuring residual stress every 0.1 mm. This means that each measuring point takes 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1.0 mm in the radial depth direction of the ring as a group, totaling 8 sets of residual stress measurement results. According to the principle of drilling method, the measurement results are two main stress directions and main stress direction angles. Usually, the residual stress on the surface of the structure is in a plane stress state, and the two main stresses and main stress direction angles are unknown [32]. Therefore, it is necessary to use a three-dimensional strain pattern for measurement. As the residual stress test sample in this article is an aluminum alloy ring, uneven and smooth polishing will prevent the correct adhesion of the three-dimensional strain pattern, leading to significant measurement errors. Derive the strain values before and after drilling through mathematical formulas and measure the three-dimensional strain pattern ε1, ε2 and ε3. Using strain to deduce stress, the calculation relationship is shown in equation (2-1).
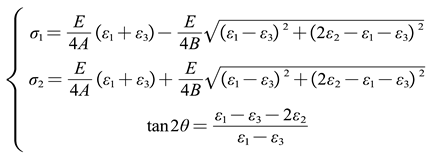 where , ——Two directions of principal stress;
where , ——Two directions of principal stress;
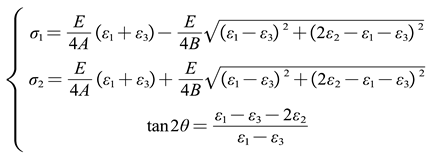
——The angle between the main stress and the sensitive grid ;
——Elastic modulus;
, , ——Three direction strain value of three direction strain flower;
, ——Strain release (correction) coefficient.
As the result value of residual stress of the ring measured by the drilling method is the reference result value in the plane Cartesian coordinate system. Therefore, it is necessary to transform the Cartesian coordinate system stress component into the polar coordinate stress component characterizing the cylindrical coordinate system of the ring piece [33] through the balance method of micro elements in elasticity. The conversion principle is shown in Figure 3.
According to the calculation program H-DRILL manual for residual stress in drilling, the recorded strain values will be ε1, ε2 and ε3 After inputs, specify the type of three-dimensional strain pattern to calculate the principal stress in both directions σ1, σ2 and plane shear stress τ12. Based on the stress situation of the triangular micro element and the geometric relationship of each side in Figure 3, the residual stress measurement results are transformed to obtain the radial, circumferential, and shear residual stresses of the ring at the measurement point. For the convenience of rapid calculation, it is rewritten in matrix form, and the results are shown in Equation (2-2).
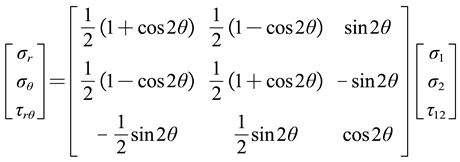 where ——Radial stress;
where ——Radial stress;
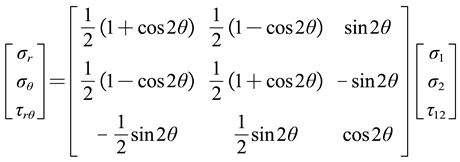
——The angle between the main stress and the sensitive grid;
——hoop stress;
and ——shearing stress.
2.1.2. Stress relaxation test for aluminum alloy ring components
Before the stress relaxation test, solid solution treatment should be carried out in a resistance heating furnace, with a solution temperature of 535 ℃ and a insulation time of no less than 35 minutes. The potentiometer is used to control the furnace temperature, and the error is controlled within ±3 ℃; Room temperature water quenching, with a quenching transfer time of less than 35 seconds. Perform stress relaxation tests immediately after solution treatment.
Process standard stress relaxation test specimens according to the metal stress relaxation test standard, with a sample size of 4. Subsequently, stress relaxation tests were conducted on an electronic high-temperature creep endurance strength testing machine. After completing the sample preparation, stress relaxation tests were conducted on the RD-50 electronic creep endurance testing machine at the National Non ferrous Metals and Electronic Materials Analysis and Testing Center in Beijing, China. The equipment prototype is shown in Figure A3. In addition, the aging heat treatment temperature range of aluminum alloy materials is generally 120~200 ℃, while the artificial aging heat treatment temperature of 2219 aluminum alloy materials is generally around 175 ℃. After correctly installing the card, set the test temperature to 175 ℃ and the test time to 18 hours. Based on the stress measurement results of the blank ring, set four different stress levels to conduct stress relaxation tests under stress conditions of 50 MPa, 150 MPa, 250 MPa, and 350 MPa, and obtain the test data. After data processing, obtain the stress relaxation curves at each stress level.
There are many constitutive equations to describe the stress relaxation behavior of metals. Different empirical formulas are used to fit data to obtain constitutive parameters, such as logarithmic, exponential and Maxwell equations. Accurate stress relaxation equations are helpful in calculating stress relaxation at any initial stress and at any time, with the most important being exponential equations. Compared to exponential equations, delay functions have the characteristics of high accuracy, high applicability, and flexibility [34]. The delay function equation is shown in equations (2-3).
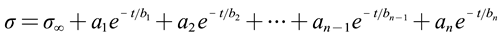 where -instantaneous stress;
where -instantaneous stress;
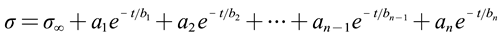
-Stress relaxation time;
-Residual stress after prolonged stress relaxation;
, , ... , , -Determine the shape of the curve, indicating the speed of stress relaxation.
Based on actual data, this article uses quadratic and cubic delay functions to fit the stress relaxation curves of 2219 aluminum alloy under various experimental stress levels. The fitting results are shown in Table 1.
The curve fitting adopts an improved optimization algorithm Levenberg Marquardt, with an allowable error of 1E-6, and retains three decimal places of the stress relaxation curve fitting parameters. The experimental values and fitting results are shown in Figure 4. The correlation coefficients for stress levels of 50 MPa, 150 MPa, 250 MPa, and 350 MPa were 0.9976, 0.9933, 0.9996, and 0.9988, respectively. The closer the correlation coefficient of the fitting curve equation is to 1, the better the curve fitting effect.
The raw data and fitting results of the stress relaxation test shown in Figure 4. Based on experimental data and corresponding fitting curve equations, a set of nonlinear equations containing unknown creep parameters of C1~C4 materials was established. The creep results of 7075-T6 aluminum alloy material were obtained by solving the equations, as shown in Table 2.
2.1.3. Stress Aging Simulation Modeling of Aluminum Alloy Ring Parts
In order to study the stress control effect of thermal vibration composite on the internal stress of large aluminum alloy ring blanks, 2219 material was selected for rolling aluminum alloy rings in this paper, and the geometric dimensions of the rings were consistent with the actual situation. Apply ANSYS for finite element modeling and solving to complete the research on residual stress regulation and deformation control of 2219 aluminum alloy ring components. Select an 8-node Solid185 element for grid division, which has the ability of plasticity, hyperelasticity, stress stiffening, creep, large deflection, and large strain. Generally, the vibration response of small parts adopts a platform type excitation mode, and the parts are fixedly connected to the excitation platform. In order to reduce the impact of external constraints on the calculation results of the numerical simulation model, the platform is considered as an elastic constraint. In order to avoid external constraints affecting the simulation calculation results, Song et al. [35] implemented the constraint points at the bottom of the workpiece through a large number of spring elements, which not only ensured the convergence of the calculation but also limited the rigid body displacement of the workpiece in three directions, which is closer to the actual surface contact. Therefore, the surface nodes of the ring are covered with spring element Combin14 with smaller element stiffness, with a stiffness value of 1E-4 mm/N.
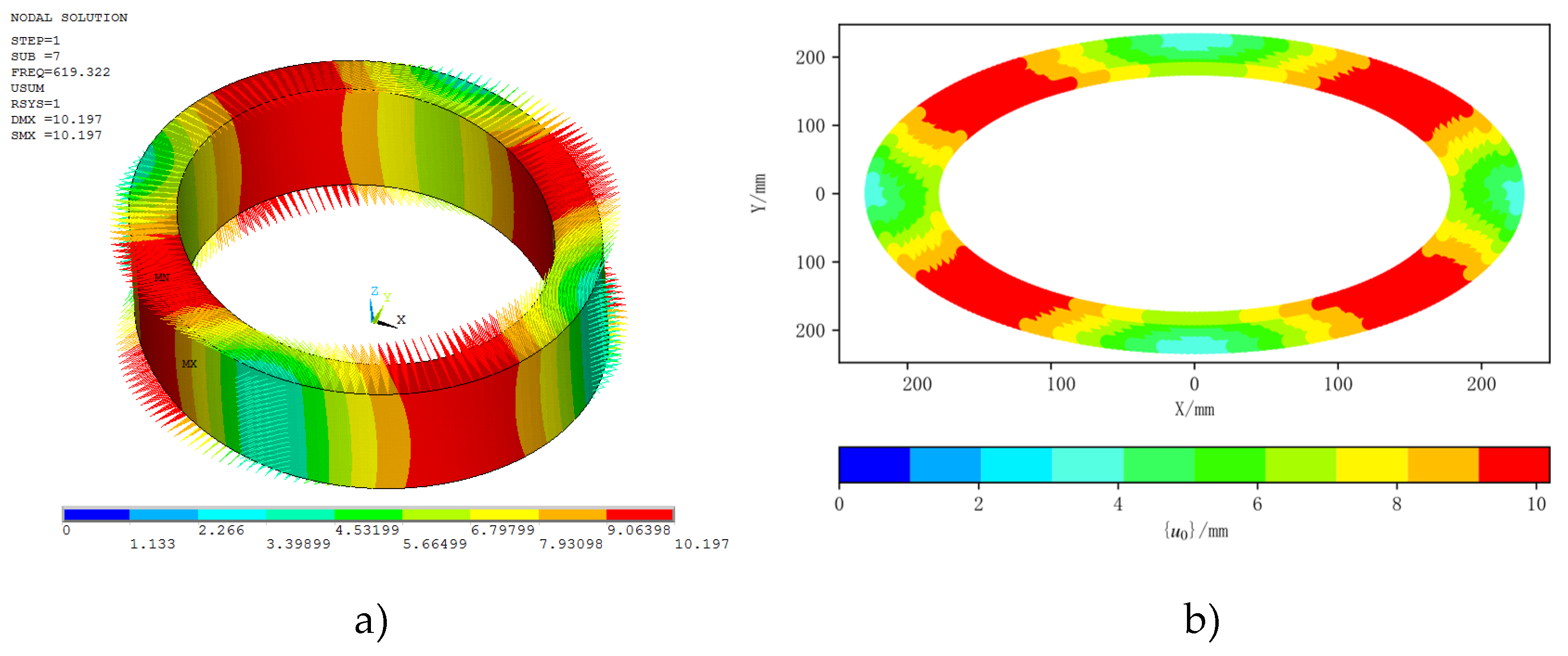
Similarly, before numerical simulation using thermal or VSR methods, modal analysis is required to obtain the vibration frequencies and modes of each order of 2219 aluminum alloy ring, and the first 10 modes are solved. The results are shown in Figure 5. From Figure 5, it can be obtained that the first natural frequency (i.e. the seventh natural frequency in this article) of the ring is the excitation frequency of the 2219 aluminum alloy ring, with a frequency amplitude of 619.32Hz. The relative total deformation results of the seventh mode are shown in Figure A4a, and for the ring, the vibration has symmetry.
Most vibration relief equipment uses a rotating eccentric mass, which causes forced vibration of the components under the rotation of the eccentric wheel. The vibration equation of the components is shown in equations (2-4) [36].
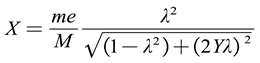 where - vibration displacement;
where - vibration displacement;
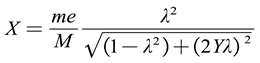
- Total vibration mass;
- Rotor eccentricity mass;
- Eccentricity;
- The ratio of vibration frequency k to natural frequency k0;
- Damping ratio.
From the above analysis, it can be seen that at the natural frequency of the component, in equations (2-4) λ= 1. From this, the vibration equation amplitude A shown in equation (2-4) can be obtained as shown in equation (2-5).
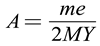
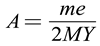
In general, loading at the peak of a component is more likely to reach the yield limit of the material, thereby reducing residual stress. This article selects the relative total deformation of the surface nodes on the ring based on the 7th order vibration mode of the ring, as shown in Figure A4b, and then multiplies it by a proportional coefficient p to replace the amplitude A. Considering the vibration situation of wave peaks and valleys, which is used to achieve the numerical simulation process of VSR, the vibration equation in this paper is shown in equations (2-6).
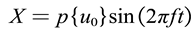 where - scale factor;
where - scale factor;
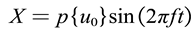
- The relative total deformation of the 7th order vibration mode node on the upper surface of the ring;
- Hz 7th natural frequency, unit: Hz;
- Time, in units of s.
Through the TVSR numerical simulation and experiment of 7075 aluminum alloy plate, the research results show that the finite element model considering stress relaxation effect and bilinear strengthening criterion has good consistency with the experimental results [13]. The TSR creep constitutive equation of 7075 aluminum alloy material and the bilinear strengthening criterion (BISO) of cyclic stress and strain obey [37, 38] are taken as the numerical simulation constitutive model, and the transient dynamic numerical simulation analysis is carried out in the form of equation (2-6) in the finite element software to realize the numerical simulation of thermal vibration combined aging process.
During the TSR process, due to stress relaxation and the reduction of elastic modulus and yield limit, the residual stress inside the part is released and homogenized. In finite element numerical simulation, the implicit creep equation with strain hardening can be used to simulate the stress relaxation process. Through the stress relaxation test of 7075-T6 aluminum alloy in Section 2.1.1, the test data can be fitted and a set of nonlinear equations can be solved to obtain the material creep constitutive parameters shown in Table 2.
Therefore, using the ANSYS APDL script language, the modeling process of the thermal mechanical coupling finite element model for the TVSR process of 2219 aluminum alloy ring samples is as follows:
(1) The unit type is defined as Solid185, and the material is 2219 aluminum alloy. The chemical composition of the material is shown in Table 3. Then, by consulting literature [27], some relevant mechanical parameters of 2219 aluminum alloy within the range of 25-200 ℃ were obtained. Adopting bilinear isotropic hardening model as the material plastic constitutive model.
(2) Establish outer diameter 450× internal diameter 366× high 105 mm circular ring geometry. The diameter and height of the inner and outer rings of the finite element model are consistent with the size of the sample in the experiment. The geometric modeling is divided into 40 layers along the height direction and 12 layers along the radial direction. The grid is generated by sweeping method, which is convenient to extract the residual stress results in different directions and analyze the aging effect.
(3) Establish a spring element with a lower normal stiffness around the solid element, with a normal stiffness set at 10mm/N to constrain displacement while allowing the specimen to deform freely.
(4) Based on the stress measurement test results, define the initial residual stress field in layers using the "inistate" command.
(5) Define transient thermal loads. Apply heating load according to the temperature time curve measured in the experiment. Defined periodic displacement boundary conditions and simulated the vibration of the workbench and specimen. The finite element model was solved through transient analysis and the data was processed during post-processing. The numerical simulation process of 2219 aluminum alloy ring TVSR is shown in Figure 5.
Therefore, according to the numerical simulation process of TVSR in Figure 5, the residual stress evolution during the stress release process can be obtained by solving the established finite element model of TVSR.
2.2. Modeling of machining deformation simulation
Rolling is an important step in the initial forming of aluminum alloy ring processing and manufacturing, and the high-precision machining and forming process of thin-walled ring parts is an important part. Residual stress is inevitably introduced into the ring during multiple machining processes, which is coupled with the initial residual stress contained in the blank, resulting in large and uneven distribution of residual stress inside the formed ring. This stress that cannot be completely eliminated is the main reason for deformation during ring machining.
This chapter implements the numerical simulation process of 2219 aluminum alloy ring thin-wall machining using the "unit life and death" technology. Establish a typical/optimal numerical simulation model for thermal vibration parameter aging, and compare the deformation of aluminum alloy rings during thin-walled processing. In actual situations, the ring is generally processed into a certain shape. After multiple cutting processes, the thin-walled ring is finally processed into a shape of "r", with the thinnest part being 2 mm, as shown in Figure 6a. Different processing sequences can affect the degree of residual stress release and also affect the accuracy of ring cutting and forming. As mentioned earlier, different TVSR parameters can affect the magnitude of residual stress inside the ring, and residual stress is an important factor affecting the deformation of thin-walled ring processing. Therefore, in order to study the influence of residual stress on ring processing deformation after aging and reduce the simulation time, the wall thickness is divided into six layers. Because the section shape of simulation cutting is "r", the "unit to be killed" is defined as a set through APDL. This simulation establishes eight groups of unit sets, that is, eight simulation milling processes are performed for simulation. The sequence of the simulation machining process is shown in Figure 6b.
In the finite element numerical simulation, the density of the model grid is related to the length of the finite Metacomputing time and the solution accuracy. This chapter sets the size of the complex cross-section grid unit to 2, and the ring section is divided into grids as shown in Figure 7.
Before dividing the grid, a numerical simulation machining route has been defined. To reduce simulation calculations, the wall thickness of the ring is divided into 6 layers, as shown in Figure 6b. Select the solid element in ANSYS software, assign the material attribute to 2219 aluminum alloy, and then transform the surface mesh shown in Figure 7 into a three-dimensional finite element mesh of the ring entity to complete the mesh division of the finite element numerical model of the ring. Using the finite element "life and death element" numerical simulation technology, the solution process and data reading and writing operations are established in APDL language to complete the numerical simulation process of thin-walled ring machining.
In addition, considering the influence of thermal vibration combined aging on the deformation law of ring processing, the number of coordinates required for evaluating roundness error using the minimum envelope area method, and the impact of complex cross-sectional mesh of the ring on the accuracy of the numerical model, the model constructed in this paper has the same size as the actual model, and numerical simulation is conducted on the thin-walled processing process of the ring after aging with two different thermal vibration parameters, To verify the influence of optimal and typical thermal vibration parameters on the processing deformation of aluminum alloy rings.
The roundness error of finished rings is an important standard for evaluating the quality and dimensional accuracy of finished products. Roundness error can conveniently evaluate the degree of deformation caused by the continuous release and balance of residual stress inside the aluminum alloy ring during the machining process. The material removal process in numerical simulation is similar to the actual machining process. In order to improve the simulation running speed and reduce the amount of data, the thickness of each cutting metal layer in the simulation is 7 mm, and the entire layer is removed 8 times from the inside out direction. Using the "life and death element method" numerical simulation to remove the inner wall material of the ring layer by layer, record the coordinates of the inner circle of the ring after each cutting process of the inner wall. The measurement of coordinate data during the material removal process of the ring is shown in Figure 8. From Figure 8, it can be seen that in the first few simulation processing sessions, the inner circle coordinates of the upper surface of the ring were taken, while in the later few simulation processing sessions, the inner circle coordinates of the "r" shaped upper surface were taken. Firstly, record the inner circle coordinate values of the upper surface of the ring before the TVSR. After the TVSR, perform thin-wall cutting of the 2219 aluminum alloy ring, and then record the inner circle coordinate values of each upper surface according to Figure 8. The numerical model of the ring has 160 units in the circumferential direction. After each simulation machining, there are a total of 161 sets of node coordinate values. In order to quickly adopt the roundness error evaluation method and improve the calculation speed, node coordinates are taken every 10 sets to calculate the roundness error and evaluate the deformation of the ring after simulation machining.
3. Results and Discussion
3.1. Correlation analysis between initial residual stress experiment and numerical simulation
The Pearson correlation coefficient is commonly used in statistics to describe whether there is a correlation between continuous variables and the magnitude of the correlation between variables. Although this article only used the drilling method to obtain the residual stress at 8 different drilling depths of the ring, the residual stress varies continuously on the surface and inside of the ring, and the measurement results can be considered both continuous and relevant. In finite element analysis, there are often errors between numerical simulation results and experiments, let alone measurement errors in the experiments themselves. Therefore, to characterize the correlation between the experimental measurement results of the initial residual stress of the ring and the numerical simulation results of the initial residual stress, the correlation coefficient (R) of the correlation concept in statistics can be used to measure [39, 40]. The correlation expression is shown in equations (3-1). The approximate calculation formula for Pearson correlation coefficient in this article can conveniently implement equation (3-1), and the calculation formula is shown in equation (3-2).
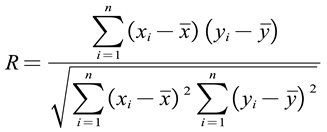
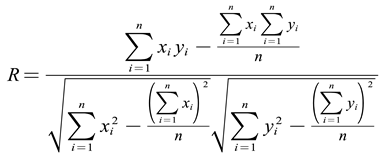 where ——Number of drilling depths;
where ——Number of drilling depths;
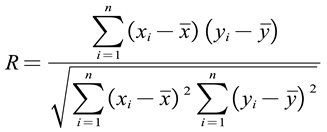
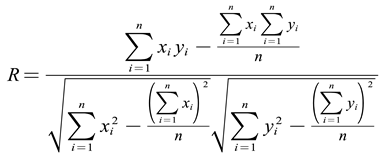
——Initial residual stress experimental data;
——Average of data of ;
——Numerical simulation data of initial residual stress;
——Average of data of .
When |R| approaches 0, it indicates that there is no correlation between experimental data and numerical simulation data, and the correlation becomes weaker; Generally, when | R | is above 0.5, it indicates a direct linear correlation between the data. The closer it is to 1, the stronger the data correlation. This article takes experimental results and numerical simulation data of drilling depths of 0.2, 0.4, 0.6, 0.8, and 1.0 mm at each measurement point, and calculates residual stress correlation coefficients in different directions based on the approximate calculation formula of Pearson correlation coefficients. The results are shown in Figure 9.
From Figure 9, it can be seen that the strong correlation in three directions of each measurement point accounts for over 37.5%, and the moderate correlation accounts for over 62.5%. Although a higher value of |R| does not necessarily indicate a higher accuracy of the numerical simulation model containing initial residual stress, the correlation between the measured residual stress in the overall experiment of 2219 aluminum alloy ring and the numerical simulation model shows a moderate to strong correlation between the initial residual stress in three directions. This indicates that the numerical simulation model of 2219 aluminum alloy ring containing initial residual stress can accurately reflect the size and distribution of residual stress inside the actual ring.
3.2. Numerical simulation results and analysis of residual stress field during stress aging process
This chapter takes the ring formed from high-strength 2219 aluminum alloy material as the research object, and establishes a numerical simulation model for the stress aging process. Based on temperature related material parameters and fitted creep constitutive parameters, the transient dynamic analysis of the complete method is used to solve the displacement, strain, stress, and force of the structure over time under the combined action of transient dynamic load and temperature load. Develop an APDL script to explore the effects of VSR, TSR, and TVSR aging on the homogenization and regulation of residual stress inside 2219 aluminum alloy rings. The numerical simulation process routes for VSR, TSR, and TVSR aging are shown in Figure 10.
In order to intuitively compare the numerical simulation results of TSR, VSR and TVSR, the X direction, Y direction, XY direction and the maximum equivalent residual stress of the ring under the cylindrical coordinate system are extracted respectively. The results are shown in Figure 11. To verify the simulation effect of TSR, VSR, and TVSR aging techniques on reducing initial residual stress in the blank. Calculate the residual stress relief rate in each direction before and after aging using equations (3-3) η, the results of the maximum residual stress relief rate in each direction are shown in Figure 12.
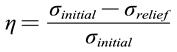 where - Initial residual stress;
where - Initial residual stress;

- Residual stress after aging.
From Figure 11, it can be seen that TSR, VSR, and TVSR can all reduce the three-dimensional residual stress of 2219 aluminum alloy rings. Among them, TSR and TVSR have a significant effect on regulating and reducing residual stress inside the ring, while VSR has a less effective regulation and homogenization effect than TSR and TVSR.
The three types of aging TSR, VSR, and TVSR have different effects on the homogenization and regulation of residual stress inside the ring. The maximum equivalent stress relief rates of VSR, TSR, and TVSR are 52.8%, 80.6%, and 82.2%, respectively. The relief effect TVSR>TSR>VSR indicates that VSR, TSR, and TVSR can effectively reduce and homogenize the residual stress inside the ring. Research has shown that the limited effectiveness of VSR is due to the dynamic stress generated by external excitation superimposed on the compressive stress on the material surface, making it difficult to reach the yield limit of the material. Based on Figure 11 and Figure 12, it can be seen that the fact that VSR affects the stress release of ring components indicates that due to the movement and change of internal grains under external loads, there is local micro yielding of the material on the surface. Therefore, the ability of VSR homogenization to regulate residual stress inside the ring is not as good as TSR and TVSR.
In addition, from Figure 12, it can be seen that the elimination rate of residual stress inside the control ring of TSR and TVSR is not significantly different in each direction, and the effect of reducing the ability of aging control is roughly equivalent. Therefore, in order to improve the ability of TVSR regulation and homogenization of residual stress inside the ring, the next chapter will conduct optimization simulation for identifying key parameters of thermal vibration, and obtain the optimal TVSR process parameters and aging plan.
3.3. Analysis of machining deformation simulation results
3.3.1. Evaluation Results of Roundness Error of Rough Ring Parts
The initial residual stress experimental results of 2219 aluminum alloy ring indicate that the distribution of residual stress inside the ring is uneven and large. The magnitude of initial residual stress is the key factor affecting the deformation of thin-walled machining. Therefore, in order to study the deformation patterns of 2219 aluminum alloy rings during thin-walled machining before and after TVSR, the minimum inclusion area method was used to evaluate and calculate the simulation coordinate data. The thin-walled numerical simulation machining process results of the blank ring are shown in Table 4 and Table 5. The evaluation results of roundness error and the maximum equivalent stress results during the machining process are shown in Figure 13.
From Figure 13, it can be seen that the residual stress inside the blank ring is relatively high before and during processing. As the thin-walled processing of the ring parts progresses, due to the significant removal of the ring material during different processing processes, residual stress is partially released and continuously balanced, causing further deformation of the thin-walled ring parts. The roundness error changes from 0.8833 mm during aging to 1.0527 mm after final processing, with a growth rate of 19.18% for the roundness error of the ring parts. From the evaluation results of roundness error in Table 5-1, it can be seen that the average roundness error during the processing is 0.9661 mm, with a maximum value of 1.0959 mm, indicating significant deformation of the ring during processing. During the thin-walled machining process, the residual stress inside the ring is constantly changing and decreasing, with the maximum equivalent stress decreasing from the initial 332.06 MPa to the final processed 233.49 MPa. The maximum equivalent residual stress release amplitude rate is 29.68%.
Overall, the thin-walled processing of rough rings under high residual stress has low precision and high degree of deformation. Subsequently, a study was conducted on the deformation control of thin-walled machining after typical and optimal thermal vibration parameter aging, to verify the effectiveness of TVSR technology in controlling the deformation of 2219 aluminum alloy ring thin-walled machining.
3.3.2. Evaluation Results of Roundness Error of Typical Thermal Vibration Parameters
In order to study the effect of TVSR with different thermal vibration parameters on the deformation of ring processing. The typical thermal vibration parameters selected in this section are shown in Table 6.
As mentioned earlier, the minimum containment area method is also used to evaluate and calculate the simulation coordinate data. The evaluation results of ring roundness error are shown in Table 7, and the simulation data of maximum equivalent stress results are shown in Table 8.
The evaluation results of roundness error and the maximum equivalent stress during the machining process are shown in Figure 14.
From the variation relationship diagram shown in Figure 14, it can be seen that the maximum equivalent stress and roundness error of the ring before aging. Before numerical simulation processing, the initial residual stress of the ring blank is very large, and the roundness error evaluated by the minimum inclusion area method is close to 0.9 mm, indicating that the ring is very "elliptical". The large residual stress can cause significant deformation of the ring and reduce the machining deformation accuracy.
The 1-8th numerical simulation process of thin-walled machining of ring components after TVSR. From Tables 7, 8, and Figure 14 above, it can be seen that after TVSR, the residual stress inside the ring is homogenized and regulated, and the maximum equivalent stress amplitude decreases from 332.06 MPa to 62.44 MPa, with a reduction rate of 81.2%. As thin-walled processing progresses, the maximum equivalent stress decreases as well as increases. The maximum equivalent stress amplitude before and after thin-walled processing ranges from 1.2 to 18.2 MPa. The maximum equivalent stress increased from 46.57 MPa before aging to 62.44 MPa, with an amplitude rate of 34.01%. From Table 7, it can be observed that the maximum equivalent stress values increased in a changing pattern during the 7th and 8th thin-wall machining processes, indicating that in the final stage of thin-wall machining, the degree of deformation increased, leading to an increase in residual stress. This indicates that a large amount of material has been removed around the "r" shape of the ring, resulting in large elliptical deformation during the machining process, leading to an increase in overall size and an increase in residual stress.
From Figure 14, it can be seen that the processing stages with the most significant changes in roundness error of the ring are the 7th and 8th stages. As the thin-walled processing of the ring parts progresses, the section "r" of the ring parts gradually takes shape. As the 7th and 8th stages are the last two stages of the thin-walled processing of the ring parts, a large amount of material is removed, causing the residual stress balance to be disrupted during processing, resulting in greater deformation of the thin-walled formed parts. The roundness error of the final cutting formed parts rapidly increases. Compared with the 6th machining stage, the roundness error increased from 0.0889 mm to 0.2948 mm and 0.5236 mm, with an increase rate of 231.4% and 488.6%, respectively, showing significant changes.
Therefore, in the final stage of forming thin-walled ring parts, the processing plan should be adjusted to avoid increased deformation of thin-walled forming parts and improve the forming accuracy of thin-walled ring parts after TVSR.
3.3.3. Evaluation results of roundness error of optimal thermal vibration parameters
The thermal vibration parameter is a key parameter for homogenizing and reducing residual stress inside the ring. Based on the optimization results of thermal vibration parameters in Literature [27] and combined with the characteristics of the ring thin-walled machining model, as mentioned earlier, the optimal thermal vibration parameters are selected as shown in Table 9.
In this simulation of thin-walled cutting of ring components, the minimum containment area method was used to evaluate and calculate the simulation coordinate data. The roundness error and maximum equivalent stress results during the thin-walled processing of ring components are shown in Table 10 and Table 11, respectively. The numerical simulation results of the thin-walled machining process of 2219 aluminum alloy rings are shown in Figure 15.
Similarly, from Table 10 and Table 11, it can be seen that after TVSR, the residual stress in the 2219 aluminum alloy ring is homogenized and regulated, the degree of processing deformation is improved, and the thin-walled processing deformation is smaller. The maximum equivalent stress amplitude decreased from 332.06 MPa to 51.77 MPa, with a reduction rate of 84.4%. During the thin-walled machining process, the maximum equivalent stress variation amplitude is between 0.9 and 11.1 MPa. The optimal thermal vibration parameter regulation of 2219 aluminum alloy ring internal residual stress regulation is better, which is more effective for controlling the thin-walled machining of ring parts and improving the forming accuracy of thin-walled parts. The maximum equivalent stress decreased from 55.36 MPa before aging to 51.77 MPa during the forming of thin-walled "r" parts, with a decrease amplitude rate of 6.5%. The optimal thermal vibration parameters have a better control effect on residual stress compared to the thin-walled machining results under typical thermal vibration parameters. From Table 11, it can be observed that the maximum equivalent stress value increased in a variable manner during the 8th thin-wall machining process. This also indicates that in the final stage of thin-wall machining forming, the degree of deformation will increase, but instead there will be an increase in residual stress.
From Table 10 and Figure 15, it can be seen that during the thin-walled forming process of ring parts, the thin-walled parts gradually form, and the calculated roundness error of the ring parts also gradually increases. The most obvious changes are in the 7th and 8th processing stages. As the thin-walled processing of the ring progresses, the cross-section "r" of the thin-walled ring gradually takes shape. As shown in Figure 4, the 7th and 8th stages are the last two stages of the thin-walled processing of the ring. A large amount of material is removed, causing the residual stress balance to be disrupted during processing, resulting in greater deformation of the thin-walled formed part. The roundness error of the final cutting formed part rapidly increases. Compared with the sixth processing stage, the roundness error increased from 0.0798 mm to 0.2454 mm and 0.4341 mm, with an increase rate of 207.4% and 443.9%, respectively. Compared with the increase rates of 231.4% and 488.6% under typical thermal vibration parameters, the TVSR control ring with optimal thermal vibration parameters has better ability to control the deformation of thin-walled processing.
In order to facilitate the comparison of the thin-walled numerical simulation processing deformation of the blank ring without aging, typical thermal vibration parameter aging, and optimal thermal vibration parameter aging, the roundness error evaluation results and maximum equivalent stress data during the thin-walled machining process of the ring in Figures 13, 14, and 15 are synthesized, and the results are shown in Figure 16.
From Figure 16, it can be seen that whether the residual stress is homogenized and regulated during the thin-walled processing and forming process of the ring is an important factor affecting the deformation of the part during processing. After rolling and forming, the quenched blank ring has a large residual stress inside. During the thin-walled processing and forming process, the deformation degree of the ring has not been improved, and continuous thinning and material removal have intensified the deformation of the ring, causing the thin-walled forming of "r" parts to deform and twist, exceeding the allowable range of processing accuracy.
After thermal vibration combined aging, the residual stress inside the ring is homogenized and regulated, and the maximum equivalent stress peak amplitude significantly decreases. In the first six processing processes, the maximum equivalent stress of the ring is smaller than before aging, and the residual stress release degree is controlled. The stress change amplitude is evenly released, ensuring that the deformation degree of the ring remains consistent during the thin-walled processing of the ring, ensuring that the processing degree is controllable. Moreover, the roundness error is smaller than before aging, indicating that the deformation of the thin-walled processing of the ring has been improved. Specifically, the roundness error of the ring gradually increases with the increase of material removal thickness, with a slower increase in the early stage. As the stress is gradually released, the stress decreases, and the thin-walled ring gradually forms, becoming more "elliptical", and the increasing trend becomes faster.
The optimal thermal vibration parameters in this chapter are based on the results of the optimization of thermal vibration parameters in Literature [27]. In order to compare the deformation results of thin-walled machining after aging with different thermal vibration parameters, typical thermal vibration parameters were selected. From Figure 16, it can be seen that TVSR can significantly homogenize and regulate the large stresses existing inside the ring, reducing residual stresses. At the same time, the roundness error during the numerical processing after two different types of TVSR has accumulated and increased, and the forming accuracy of the thin-walled processing ring after aging is better than before aging.
In addition, the roundness error and maximum equivalent stress results of the thin-walled numerical machining process of the ring after aging with different thermal vibration parameters are different. Among them, compared with the results before aging, the optimal thermal vibration parameters have a decrease amplitude rate of 84.4% in the maximum equivalent stress after aging, and a decrease rate of 50.8% in roundness error; The maximum equivalent stress reduction amplitude rate of typical thermal vibration parameters after aging is 81.2%, and the roundness error reduction rate is 40.7%. The optimal thermal vibration parameters of the thin-walled machining numerical model have better aging effect, and the thin-walled machining deformation is effectively controlled. This is because the optimization of thermal vibration parameters mentioned in Literature [27] is summarized by range analysis and grey correlation analysis of orthogonal test tables. Although it is a result within a local finite number of times, different mesh element numbers and boundary conditions can also affect the results. The residual stress layering assignment of different finite element models will further introduce errors. However, the numerical model for thin-walled ring machining in this chapter is consistent with the actual ring size, the reasonable setting of unit size is crucial for the reliable numerical simulation results of thin-walled ring machining.
Based on the above conclusions, it can be concluded that residual stress inside the ring is an important factor affecting the forming accuracy of thin-walled ring machining. From the deformation results of thin-walled machining of rough ring parts, it can be seen that large residual stress will lead to greater machining deformation, reducing the accuracy of the final thin-walled part forming. Different TVSR parameters have different effects on stress homogenization control of 2219 aluminum alloy rings. Ring after aging with two different TVSR parameters.
4. Conclusion
This paper takes 2219 aluminum alloy rings as the research object, combines constitutive theories related to TSR and VSR, and establishes a finite element model using ANSYS numerical simulation software. In order to explore the effect of stress aging technology on the regulation and homogenization of residual stress inside the ring, the initial stress of the ring blank was measured using drilling method experiments. At the same time, the creep constitutive coefficient of 2219 aluminum alloy was determined through stress relaxation experiments, and the numerical simulation calculation processes of VSR, TSR, and TVSR were compared and established. The simulation results show that VSR, TSR, and TVSR can homogenize and reduce the residual stress field inside the ring, improve the distribution of residual stress inside the ring, and achieve a homogenization control effect of TVSR>TSR>VSR. The TVSR method is an optimal method for eliminating and homogenizing residual stress in the ring. Then, using numerical simulation technology to study how the initial residual stress in the blank will cause the deformation of the ring during thin-walled machining process. The minimum inclusion zone method roundness error theory is applied to evaluate the deformation degree during thin-walled numerical machining process, and the TVSR method is used for stress regulation. The deformation law of thin-walled machining of the ring under different aging parameters is studied. The conclusion of this simulation result is as follows:
(1) Based on the creep mechanism of TSR and the principle of VSR, this paper conducted a simulation of residual stress control of 2219 aluminum alloy rings during TVSR using ANSYS. The simulation results show that the derived constitutive model can describe the stress relaxation process of TVSR by combining a single thermal time effect stress relaxation constitutive theory with a VSR plastic deformation material model.
(2) Analyze the correlation between the experimental measurement results of initial residual stress and the established numerical simulation results of the ring containing initial residual stress. It can be seen that the strong correlation in three directions of each measurement point accounts for over 37.5%, and the moderate correlation accounts for over 62.5%. Compared with the numerical simulation model, the measurement values of residual stress in the overall experiment of 2219 aluminum alloy ring show a moderate and strong correlation with the initial residual stress in three directions. This indicates that the numerical simulation model of 2219 aluminum alloy ring containing initial residual stress can accurately reflect the size and distribution of residual stress inside the actual ring.
(3) VSR, TSR, and TVSR can all regulate and reduce the residual stress of 2219 aluminum alloy rings. The VSR homogenization rate is the smallest, and the radial direction of the ring is only 12.5%. The maximum equivalent residual stress relief rate of ring TSR and TVSR can reach over 80%, and the residual stress relief effect of ring components is very effective after aging. The VSR control has a certain effect on reducing and homogenizing the residual stress of 2219 aluminum alloy rings, but compared with TSR and TVSR, the residual stress control reduction and homogenization ability are limited.
(4) VSR, TSR, and TVSR can all homogenize residual stresses inside and on the surface of the ring, and the overall homogenization ability of TVSR is good. Regardless of whether the residual stress inside the ring is large or small, the maximum equivalent stress homogenization rate for all three aging treatments is at least 40%. But when the residual stress is large, the TVSR is more effective in homogenizing the stress of the ring, and the maximum stress homogenization rate in the circumferential direction can reach 90.0%. The maximum equivalent stress homogenization rates of VSR, TSR, and TVSR are 52.8%, 80.6%, and 82.2%, respectively. It can be seen that the effect of homogenization and regulation of residual stress inside the 2219 aluminum alloy ring is more effective for TVSR than VSR and TSR.
(5) Different TVSR parameters can cause different residual stress homogenization effects inside the ring. Among them, compared with the results before aging, the optimal thermal vibration parameters have a decrease amplitude rate of 84.4% in the maximum equivalent stress after aging, and a decrease rate of 50.8% in roundness error; The maximum equivalent stress reduction amplitude rate of typical thermal vibration parameters after aging is 81.2%, and the roundness error reduction rate is 40.7%. The optimal thermal vibration parameters of the thin-walled machining numerical model have better aging effect. It can be seen that appropriate TVSR parameters are the key to homogenizing the residual stress inside the ring and improving the machining deformation accuracy. The optimal thermal vibration parameters have a better effect on controlling the deformation of thin-walled processing of ring components than typical thermal vibration parameters.
(6) The deformation degree of thin-walled ring components with a "r" shaped cross-section will increase in the final processing stage (7th and 8th times in this article). Under the optimal thermal vibration parameters, the roundness error in the 7th and 8th processing stages increased from 0.0798 mm to 0.2454 mm and 0.4341 mm, respectively, compared to the 6th processing stage, with an increase rate of 207.4% and 443.9%, respectively. Under typical thermal vibration parameters, the roundness error in the 7th and 8th processing stages increased from 0.0889 mm to 0.2948 mm and 0.5236 mm compared to the 6th processing stage, with an increase rate of 231.4% and 488.6%, respectively. Therefore, in the final stage of thin-walled ring processing and forming, the processing process plan should be adjusted to improve the accuracy of thin-walled ring processing and forming after TVSR.
Author Contributions
Bianhong Li supervision, writing—review & editing, conceptualization, investigation, writing—original draft; Yushuang Dong conceptualization, experiments; Yang Ouyang proofread the manuscript; Hanjun Gao validation. All authors have read and agreed to the published version of the manuscript.
Funding
The work is financially support by the Defense Industrial Technology Development Program [grant number JCKY2020601C004].
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Appendix A
Figure A1.
Thermo-physical parameters of 2219 aluminum alloy material [27].
Figure A1.
Thermo-physical parameters of 2219 aluminum alloy material [27].
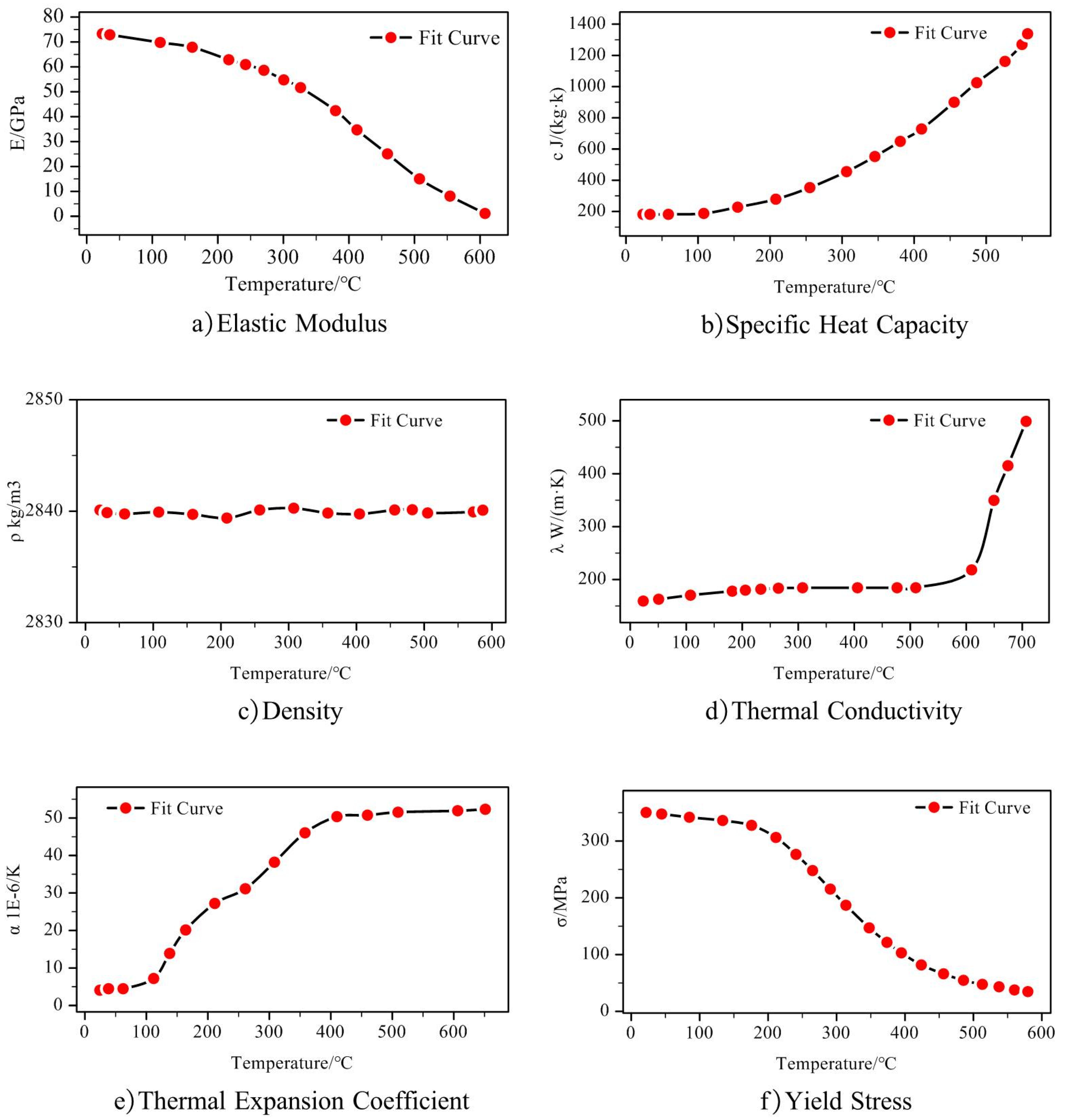
Figure A2.
residual stress measurement. a) Measurement point scheme of residual stress experiment; b) Residual stress measurement by hole-drilling method.
Figure A2.
residual stress measurement. a) Measurement point scheme of residual stress experiment; b) Residual stress measurement by hole-drilling method.
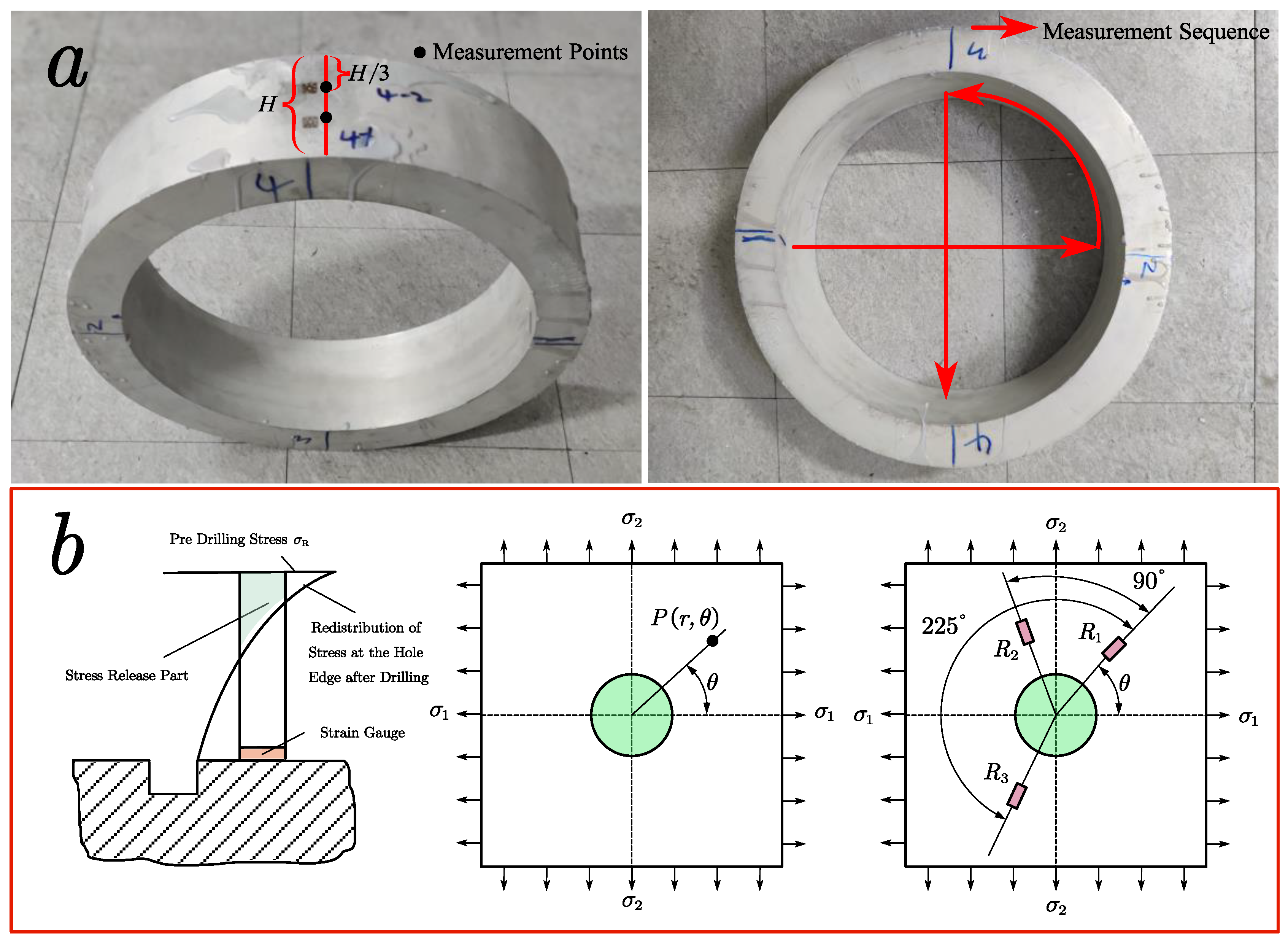
Figure A3.
Stress relaxation test equipment.

Figure A4.
Relative total deformation of a) the 7th order modal analysis, b) the upper surface node of the ring part at the 7th mode {u0}.
Figure A4.
Relative total deformation of a) the 7th order modal analysis, b) the upper surface node of the ring part at the 7th mode {u0}.
References
- C. Garcia, T. Lotz, M. Martinez, et al. Fatigue crack growth in residual stress fields. International Journal of Fatigue, 2016, 87. [CrossRef]
- Gao, H., Zhang, Y., Wu, Q. et al. An analytical model for predicting the machining deformation of a plate blank considers biaxial initial residual stresses. Int J Adv Manuf Technol 93, 1473–1486 (2017). [CrossRef]
- Li, B., Deng, H., Hui, D. et al. A semi-analytical model for predicting the machining deformation of thin-walled parts considering machining-induced and blank initial residual stress. Int J Adv Manuf Technol 110, 139–161 (2020). [CrossRef]
- Ma, Y. , Xue, N., Wu, Q. , Gao, H. , & Wu, J. .(2020). Residual stress analysis of a 2219 aluminum alloy ring using the indentation strain-gauge method. Metals - Open Access Metallurgy Journal, 10(7), 979. [CrossRef]
- Li, B., Gao, H., Deng, H. et al. A machining deformation control method of thin-walled part based on enhancing the equivalent bending stiffness. Int J Adv Manuf Technol 108, 2775–2790 (2020). [CrossRef]
- Hechuan Song, Hanjun Gao, Qiong Wu, Yidu Zhang, Effects of segmented thermal-vibration stress relief process on residual stresses, mechanical properties and microstructures of large 2219 Al alloy rings, Journal of Alloys and Compounds, Volume 886, 2021, 161269, ISSN 0925-8388. [CrossRef]
- Gong, H.; Sun, X.; Zhang, T.; Tang, H. Effects of Cold Expansion on Residual Stress of 7050 Aluminium Alloy Frame Forging. Metals 2023, 13, 732. [CrossRef]
- Hanjun Gao, Xin Li, Bianhong Li, Qiong Wu, Yandong Ma, Xiaojun Jian, Hechuan Song, Shuguang Chen, Residual stress and microstructure of Ti6Al4V treated by thermal-vibratory stress relief process, Journal of Materials Research and Technology, Volume 18, 2022, Pages 5161-5181, ISSN 2238-7854. [CrossRef]
- Wan Li, Deng Yunlai, Fan Shitong. Effects of aging on microstructures, properties and residual stress of 7050 aluminum alloy. Transactions of nonferrous metals society of China, 2018, 028(007): 1277-1283. [CrossRef]
- Martucci, A.; Marchese, G.; Bassini, E.; Lombardi, M. Effects of Stress-Relieving Temperature on Residual Stresses, Microstructure and Mechanical Behaviour of Inconel 625 Processed by PBF-LB/M. Metals 2023, 13, 796. [CrossRef]
- Araghchi M, Mansouri H, Vafaei R, et al. Optimization of the Mechanical Properties and Residual Stresses in 2024 Aluminum Alloy Through Heat Treatment. Journal of Materials Engineering and Performance, 2018(12): 1-5. [CrossRef]
- Song H, Gao H , Wu Q , et al. Residual stress relief mechanisms of 2219 Al–Cu alloy by thermal stress relief method. REVIEWS ON ADVANCED MATERIALS SCIENCE, 2022(61): 102-116. [CrossRef]
- Gao, H., Wu, S., Wu, Q., Li, B., & Mo, S. Experimental and simulation investigation on thermal-vibratory stress relief process for 7075 aluminium alloy. Materials & design, 2020(195):108954. [CrossRef]
- Y.-B. Dong, W.-Z. Shao, J.-T. Jiang, D.-Y. Chao & L. Zhen. Influence of quenching rate on microstructure and dimensional stability of Al–Cu–Mg–Si alloy, Materials Science and Technology, 2016(32:18):1861-1868. [CrossRef]
- Hanjun Gao, Yidu Zhang, Qiong Wu, Jing Song, Kai Wen, Fatigue life of 7075-T651 aluminium alloy treated with vibratory stress relief, International Journal of Fatigue, 2018(108): 62-67, ISSN 0142-1123. [CrossRef]
- Gao, H.-J.; Zhang, Y.-D.; Wu, Q.; Song, J. Experimental Investigation on the Fatigue Life of Ti-6Al-4V Treated by Vibratory Stress Relief. Metals 2017, 7, 158. [CrossRef]
- Gong, H.; Sun, Y.; Liu, Y.; Wu, Y.; He, Y.; Sun, X.; Zhang, M. Effect of Vibration Stress Relief on the Shape Stability of Aluminum Alloy 7075 Thin-Walled Parts. Metals 2019, 9, 27. [CrossRef]
- Tian L, Zhang Y. Dynamic stress analysis for vibratory stress relief through the vibration platform. 2014 IEEE Workshop on Electronics, Computer and Applications (IWECA). IEEE, 2014. [CrossRef]
- Jing S, Zhang Y , Ke S. The Numerical Simulation for Effect of Vibratory Stress Relief on Titanium Alloy Ti-6Al-4V Fatigue Life. Springer Singapore, 2016. [CrossRef]
- Gong H, Sun Y, Liu Y, et al. Effect of Vibration Stress Relief on the Shape Stability of Aluminum Alloy 7075 Thin-Walled Parts. Metals, 2018, 9(1). [CrossRef]
- G H Xiong, K Liao, X Y Chang, et al. Deformation Control by VSR Technique on Al alloy Thin-Walled Components. IOP Conference Series: Materials Science and Engineering, 2017, 269(1). [CrossRef]
- Tian Lv, Yidu Zhang. A combined method of thermal and vibratory stress relief. Journal of Vibroengineering, 2015, 17(6).
- Hanjun Gao, Xin Li, Bianhong Li, Qiong Wu, Yandong Ma, Xiaojun Jian, Hechuan Song, Shuguang Chen, Residual stress and microstructure of Ti6Al4V treated by thermal-vibratory stress relief process, Journal of Materials Research and Technology, Volume 18, 2022, Pages 5161-5181, ISSN 2238-7854. [CrossRef]
- Chen S G, Zhang Y D, Wu Q, et al. Residual Stress Relief for 2219 Aluminum Alloy Weldments: A Comparative Study on Three Stress Relief Methods. Metals - Open Access Metallurgy Journal, 2019, 9(4): 419. [CrossRef]
- Xu Y, Shi Z, Li B, et al. Effects of TVSR process on the dimensional stability and residual stress of 7075 aluminum alloy parts. Reviews on Advanced Materials Science, 2021, 60: 631–642. [CrossRef]
- Kasim S Y, Ab Tt An N S. Experimental Comparison Study on Stress Relief for Welded Low Carbon Steel (St 37) Bar by Vibration Mechanism and Heat Treatment Process. IOP Conference Series Materials Science and Engineering, 2018, 454. [CrossRef]
- Chen, S., Gao, H., Lin, M., Wu, S. and Wu, Q. Research on process optimization and rapid prediction method of thermal vibration stress relief for 2219 aluminum alloy rings. REVIEWS ON ADVANCED MATERIALS SCIENCE, 2022(61):292-305. [CrossRef]
- Ahmad, Abdulrahaman, Wu Yunxin, et al. Determination of the Effect of Cold Working Compression on Residual Stress Reduction in Quenched Aluminum Alloy 2219 Block. Journal of Mechanical Engineering, 2019, 65(5): 311-318. [CrossRef]
- Ahmad A S , Wu Y , Gong H , et al. Numerical Simulation of Thermal and Residual Stress Field Induced by Three-Pass TIG Welding of Al 2219 Considering the Effect of Interpass Cooling. International Journal of Precision Engineering and Manufacturing, 2020, 21(8):1501-1518. [CrossRef]
- Hu Deyou, Li Jiguang, Zhang Jiegang, et al. Research on performance of typical specification 2219 aluminum alloy sheet under different heat treatment conditions for rocket tank. Forging Technology, 2020, 45(10): 53-58. [CrossRef]
- Michal Švantner, Jiří Skála. Uncertainties of the Evaluation of the Hole Drilling Residual Stress Measurement According to the ASTM E837 Standard. Applied Mechanics and Materials, 2015, 3825. [CrossRef]
- HUANG Gang, ZHANG Qingdong, WANG Chunhai, et al. Experimental research on the blind hole-drilling method for measuring residual stress of steel plate. Journal of Welding, 2020, 41(09): 49-598099-100. [CrossRef]
- Meng Longhui, He Ning, Yang Yinfei, et al. Measurement of residual stress on the surface of Ti6Al4V pipe fittings using FEM correction method. Journal of Harbin Institute of Technology, 2015, 47(05): 71-75.
- Bi Jing, Cui Xuexue, Zhang Yanling, et al Study on Stress Relaxation Behavior of Ti-6Al-4V Titanium Alloy Thin Plate. Journal of Mechanical Engineering, 2019, 55 (18): 43-52+62. [CrossRef]
- Song H C , Zhang Y D , Wu Q , et al. Low-stiffness spring element constraint boundary condition method for machining deformation simulation. Journal of Mechanical Science and Technology, 2020, 34(10):4117-4128. [CrossRef]
- Li Qiang, Peng Jingqi. Theory and Method of Eliminating Residual Stress in Components by Vibration Aging. Journal of North China Institute of Technology, 2001, 22(3): 186-189. [CrossRef]
- Jiang Z, Li G, Zhao L, et al. Generation mechanism of stress wave while milling aluminium 2219. Australian Journal of Mechanical Engineering, 2020: 1-10. [CrossRef]
- Sudula P, Sai V. Bilinear Isotropic and Bilinear Kinematic Hardening of AZ31 Magnesium Alloy. International Journal of Advanced Research in Engineering and Technology, 2020, 11(8). [CrossRef]
- Guo-zheng Quan, Zhen-yu Zou, Tong Wang, et al. Modeling the Hot Deformation Behaviors of As-Extruded 7075 Aluminum Alloy by an Artificial Neural Network with Back-Propagation Algorithm. High Temperature Materials and Processes, 2017, 36(1): 1-13. [CrossRef]
- Nayak, Dhondapure, Singh, et al. Assessment of constitutive models to predict high temperature flow behaviour of Ti-6Al-4V preform. Advances in Materials and Processing Technologies, 2020, 6(2): 244-258. [CrossRef]
Figure 1.
ring quenching process.
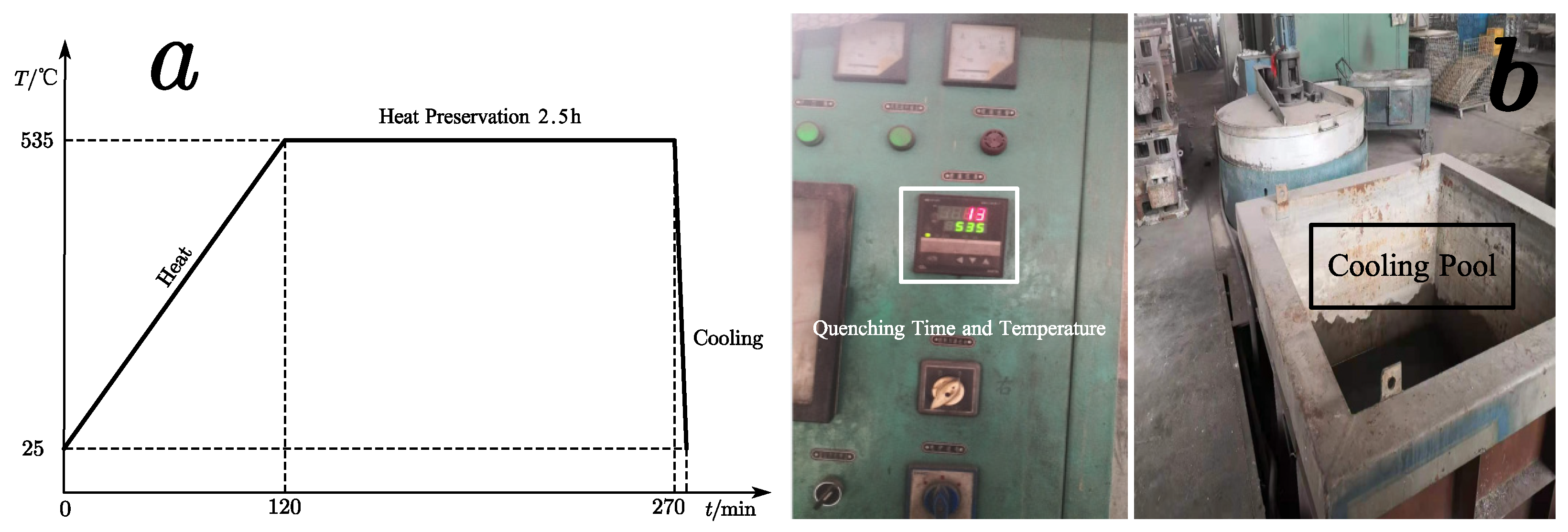
Figure 2.
residual stress measurement. a) System of measuring residual stress of ring by hole-drilling method, b) Experimental clamping scheme for 2219 aluminum alloy ring.
Figure 2.
residual stress measurement. a) System of measuring residual stress of ring by hole-drilling method, b) Experimental clamping scheme for 2219 aluminum alloy ring.
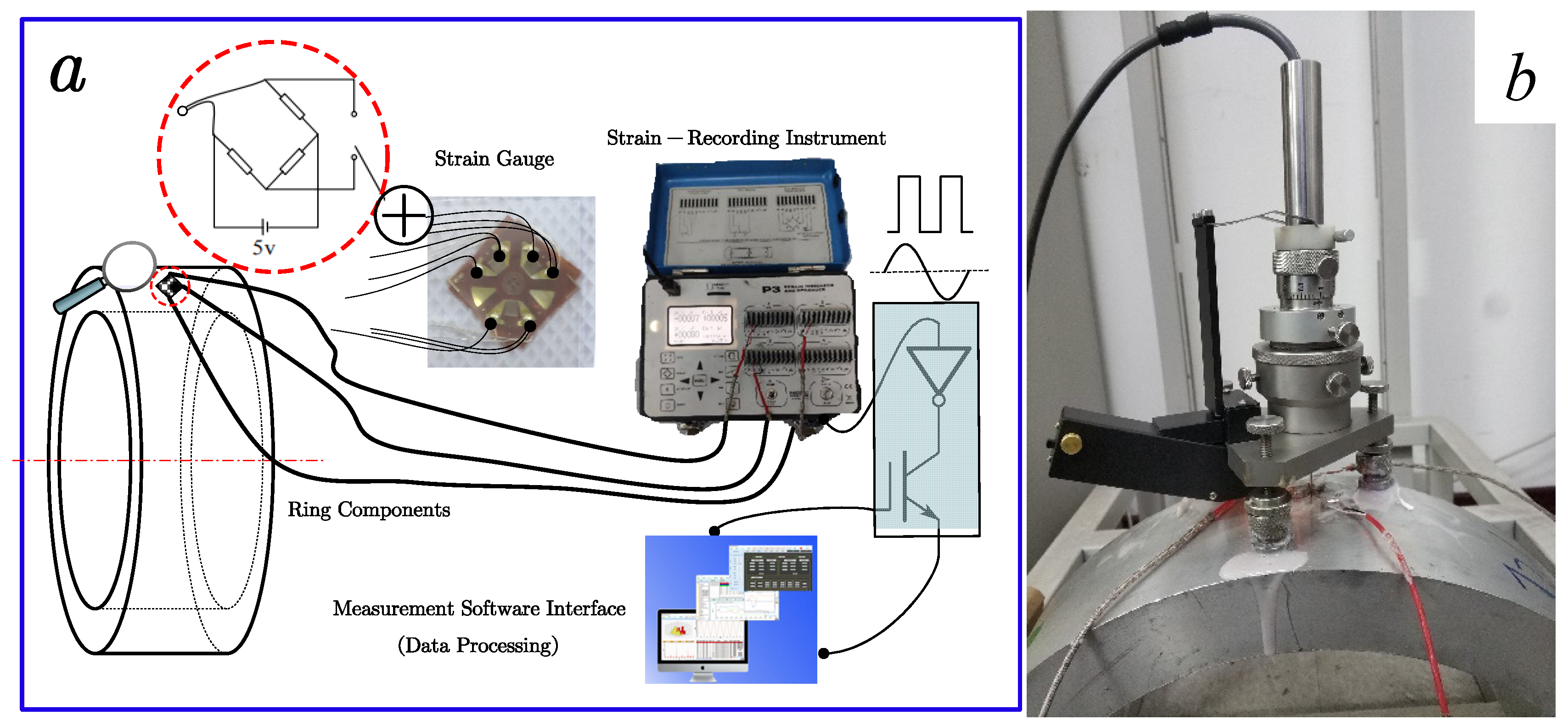
Figure 3.
Equilibrium of micro-element.
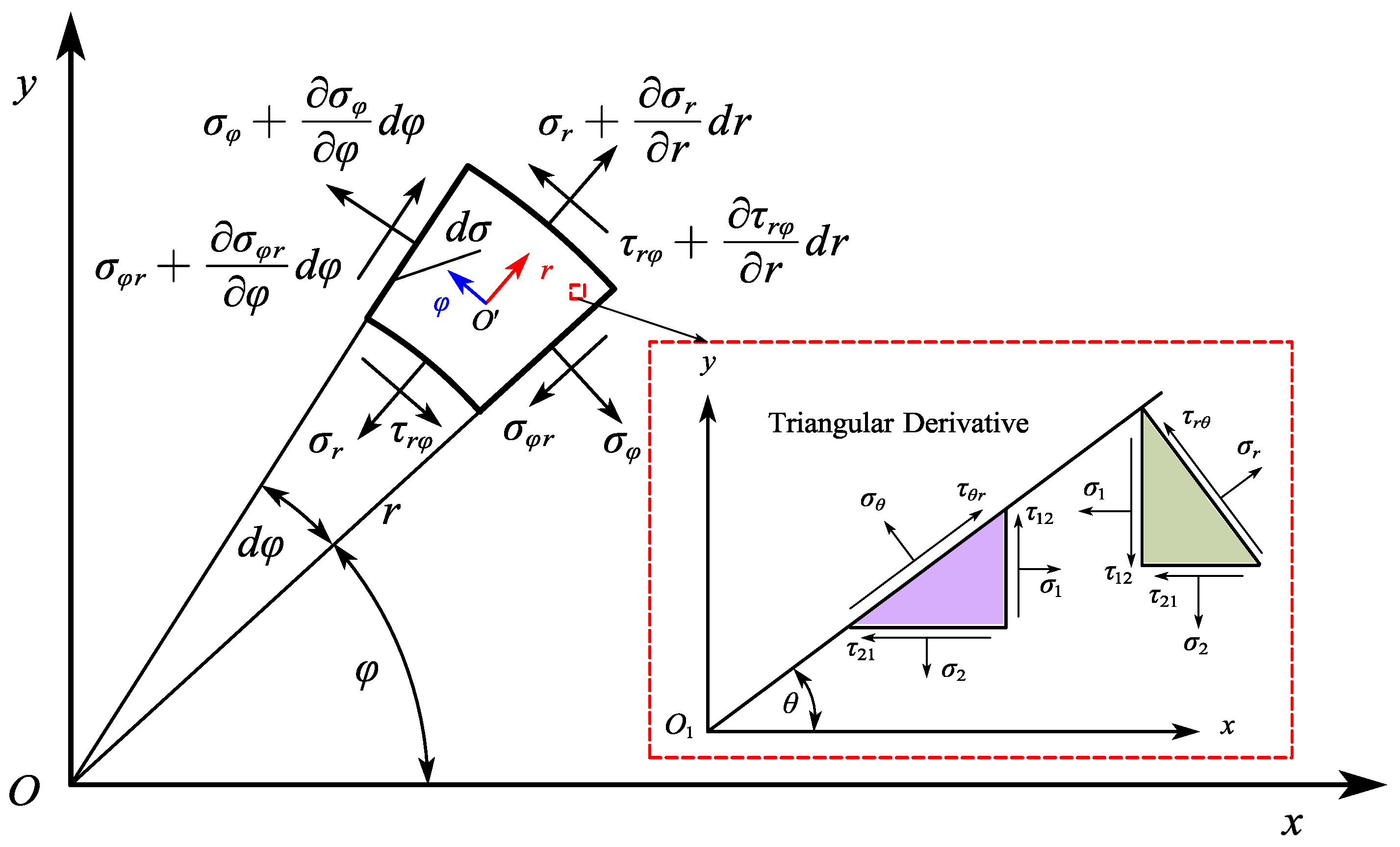
Figure 4.
Fitting diagram of four groups of 7075-T6 aluminum alloy stress relaxation curve.
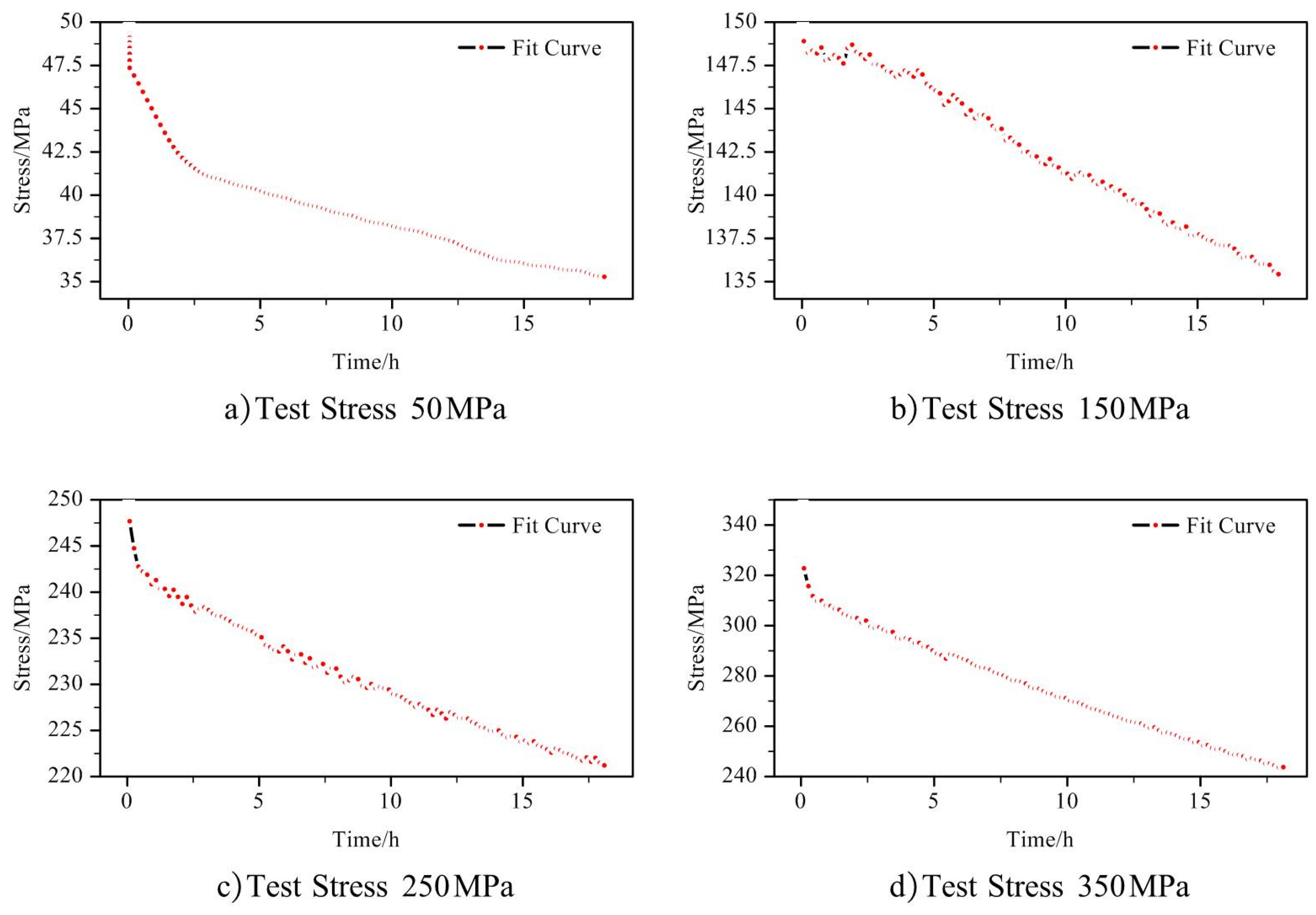
Figure 5.
Numerical simulation process of thermal-vibration stress relief for 2219 aluminum alloy ring.
Figure 5.
Numerical simulation process of thermal-vibration stress relief for 2219 aluminum alloy ring.
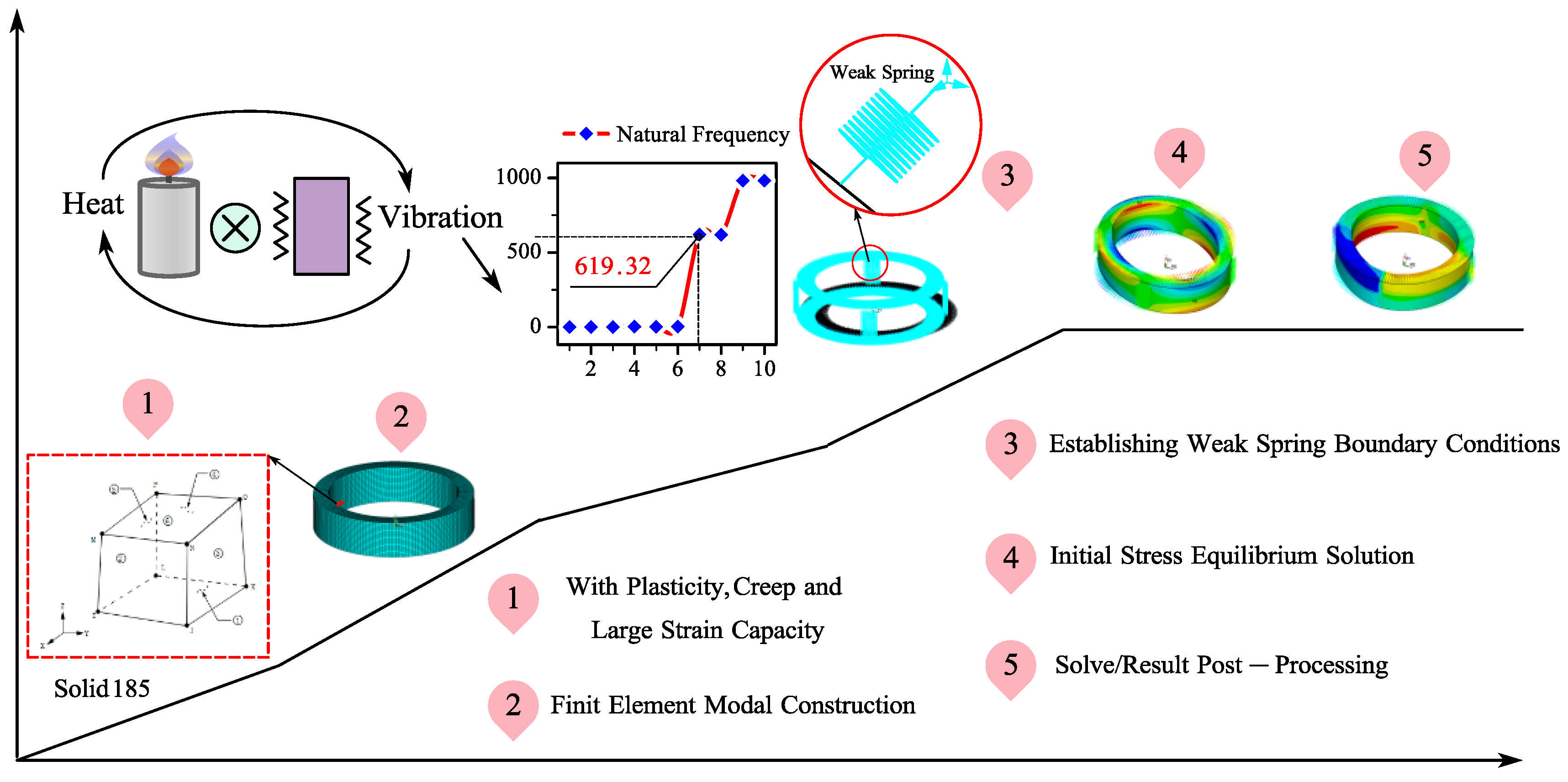
Figure 6.
Thin-walled ring a) machining shapes of rings, b) processing sequence of thin-walled ring.
Figure 6.
Thin-walled ring a) machining shapes of rings, b) processing sequence of thin-walled ring.
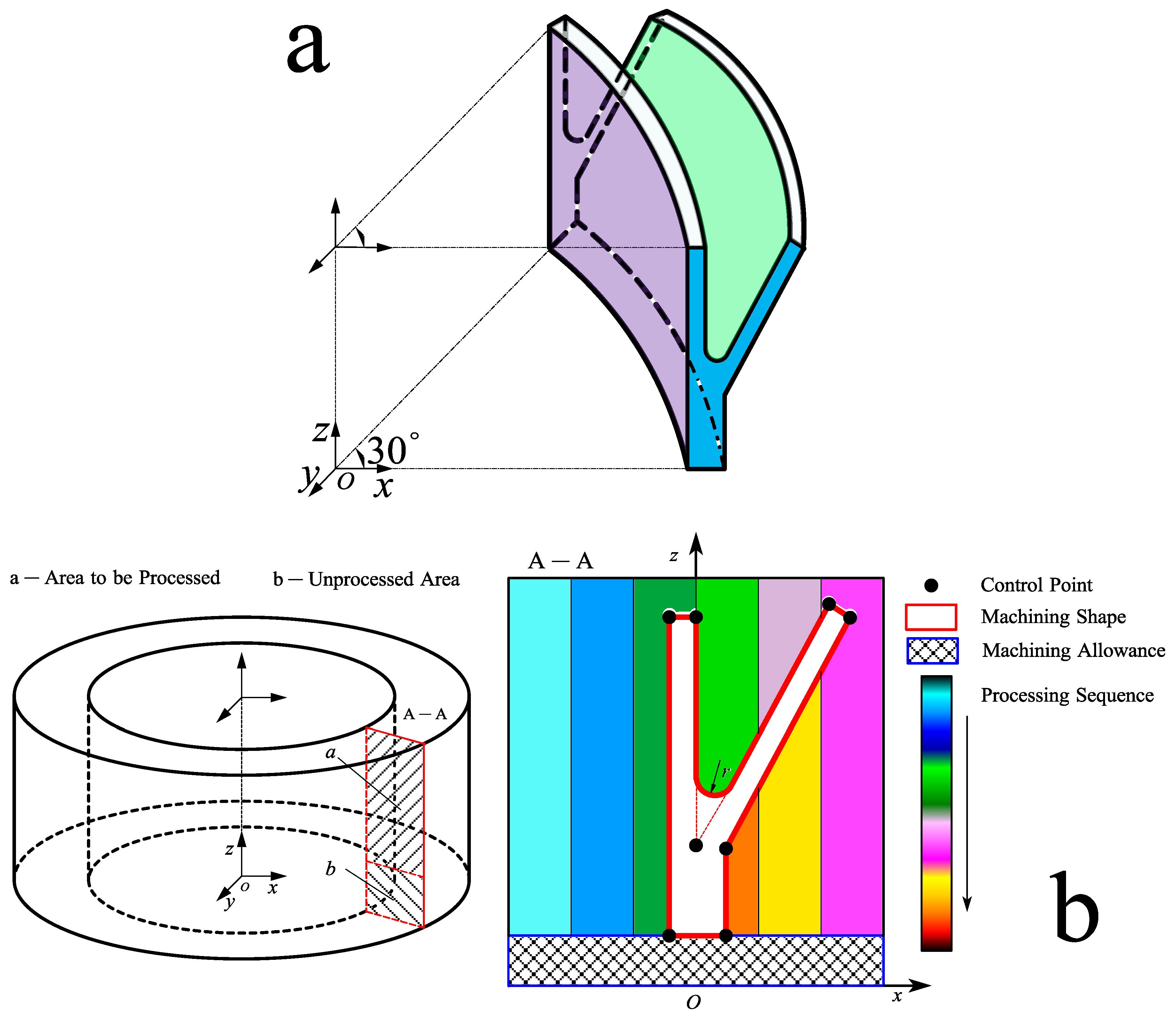
Figure 7.
Cross-section grid of rings.
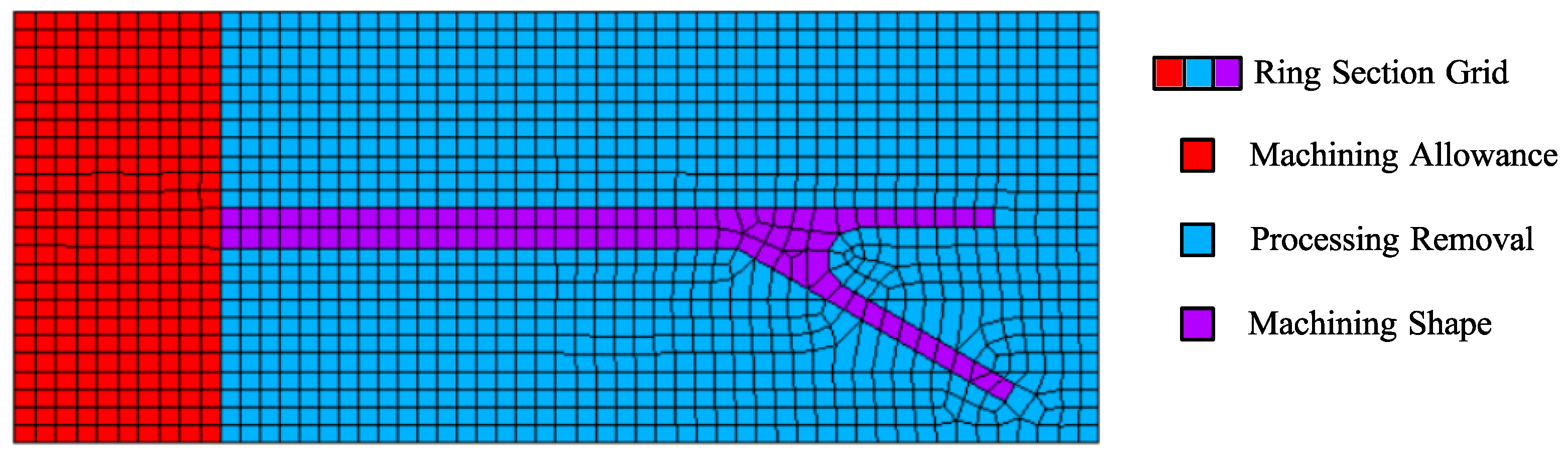
Figure 8.
Schematic diagram of coordinate measurement in ring machining process.
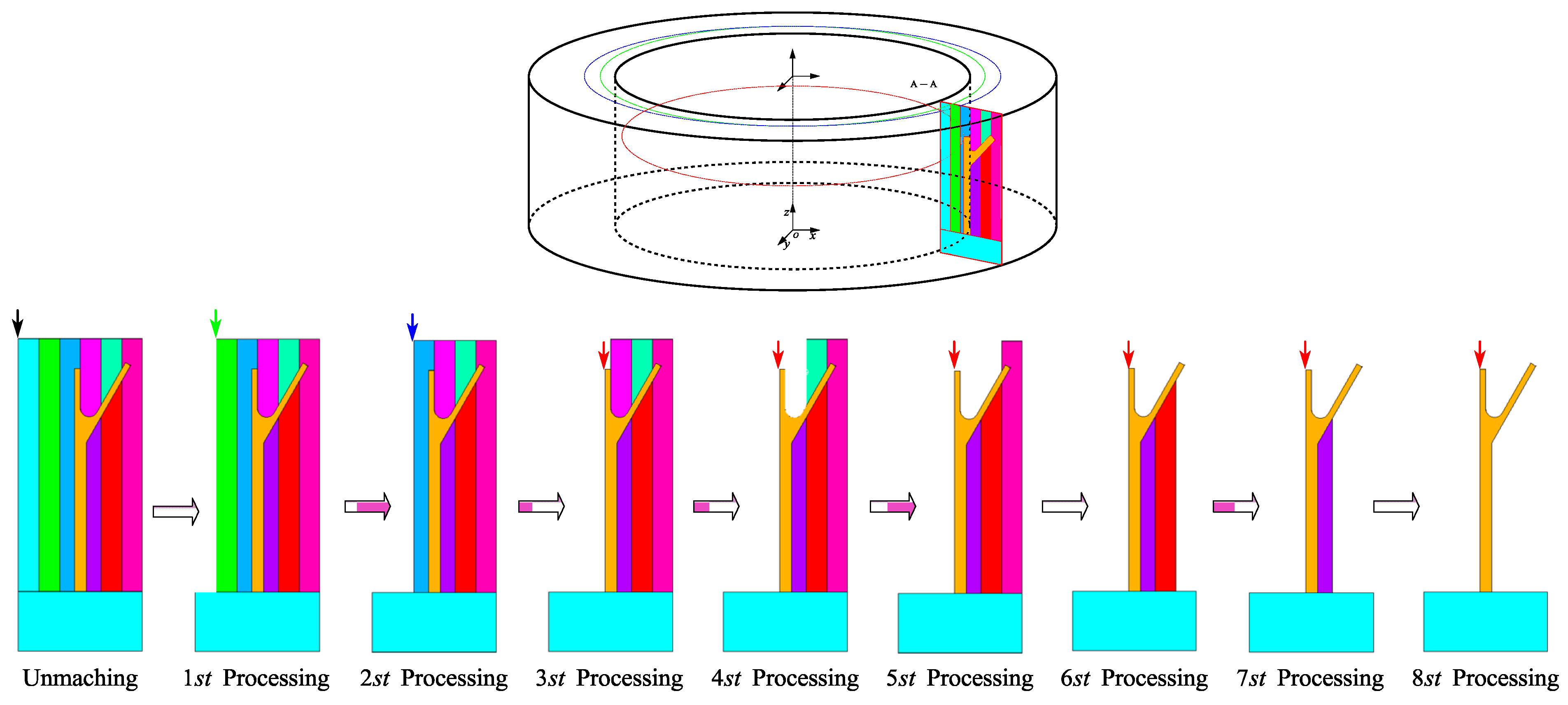
Figure 9.
Correlation analysis between experimental measurement and numerical simulation results of initial residual stress.
Figure 9.
Correlation analysis between experimental measurement and numerical simulation results of initial residual stress.
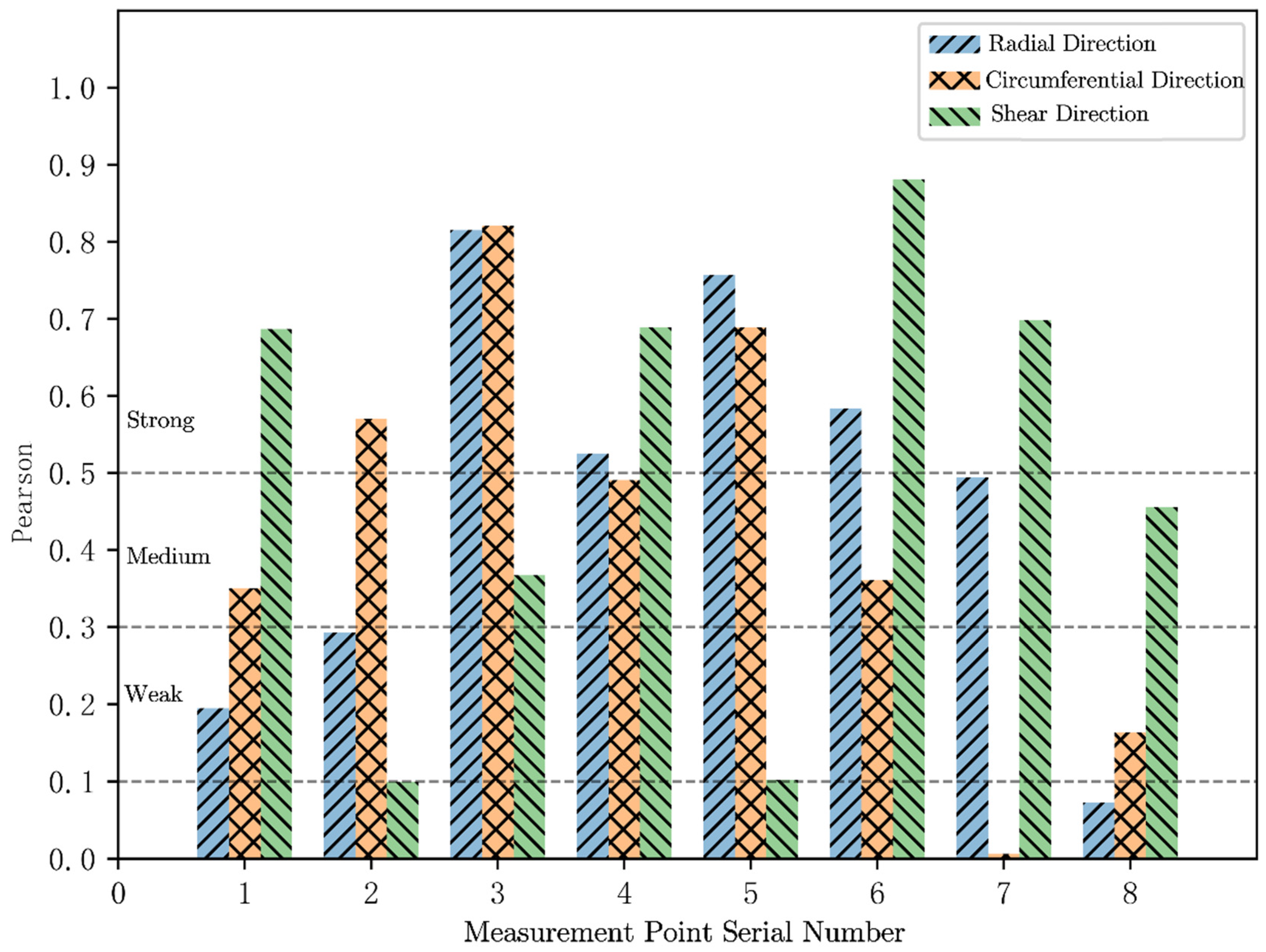
Figure 10.
Numerical simulation process for stress relief of 2219 aluminum alloy ring.
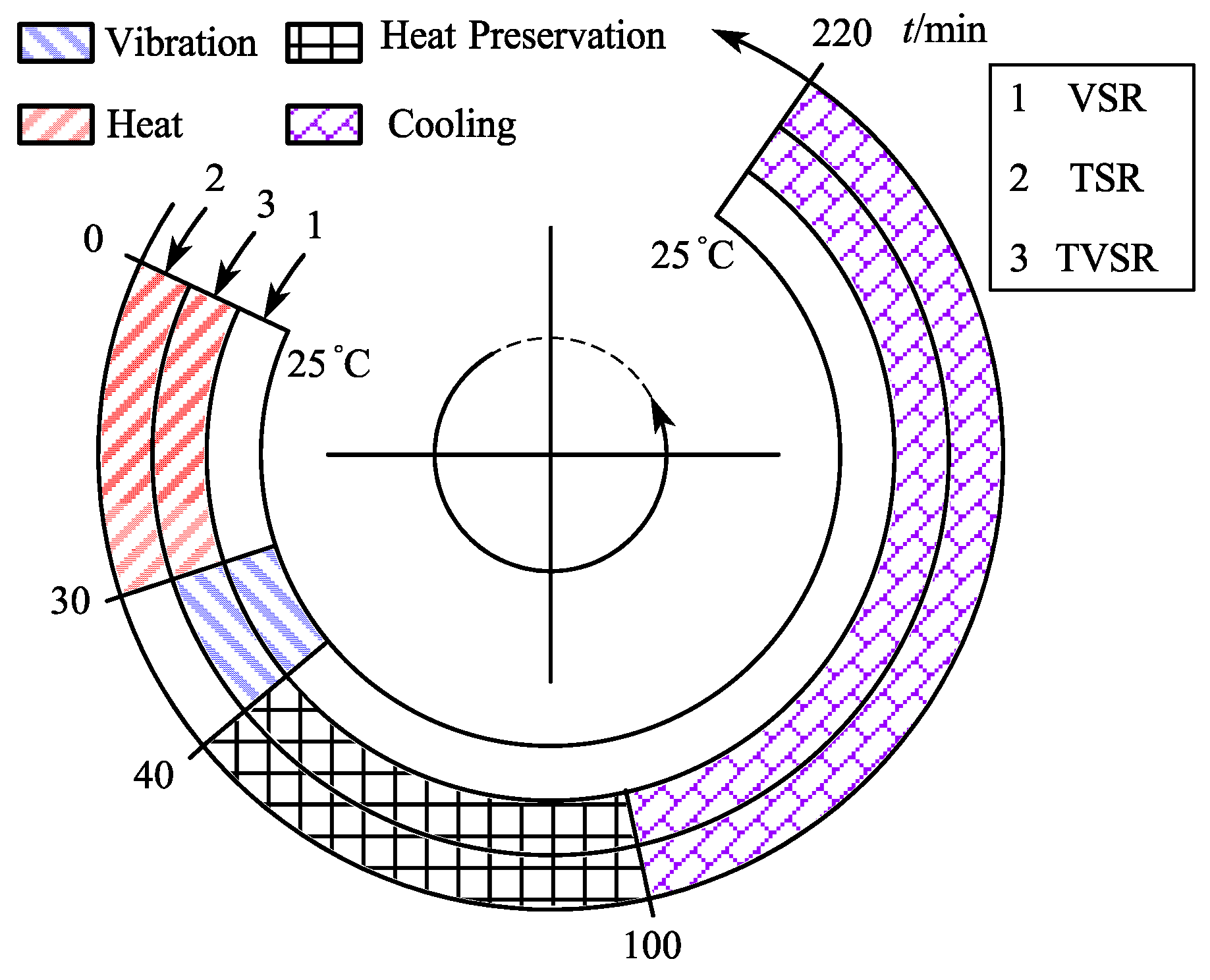
Figure 11.
Residual stress of 2219 aluminum alloy ring before and after stress relief.
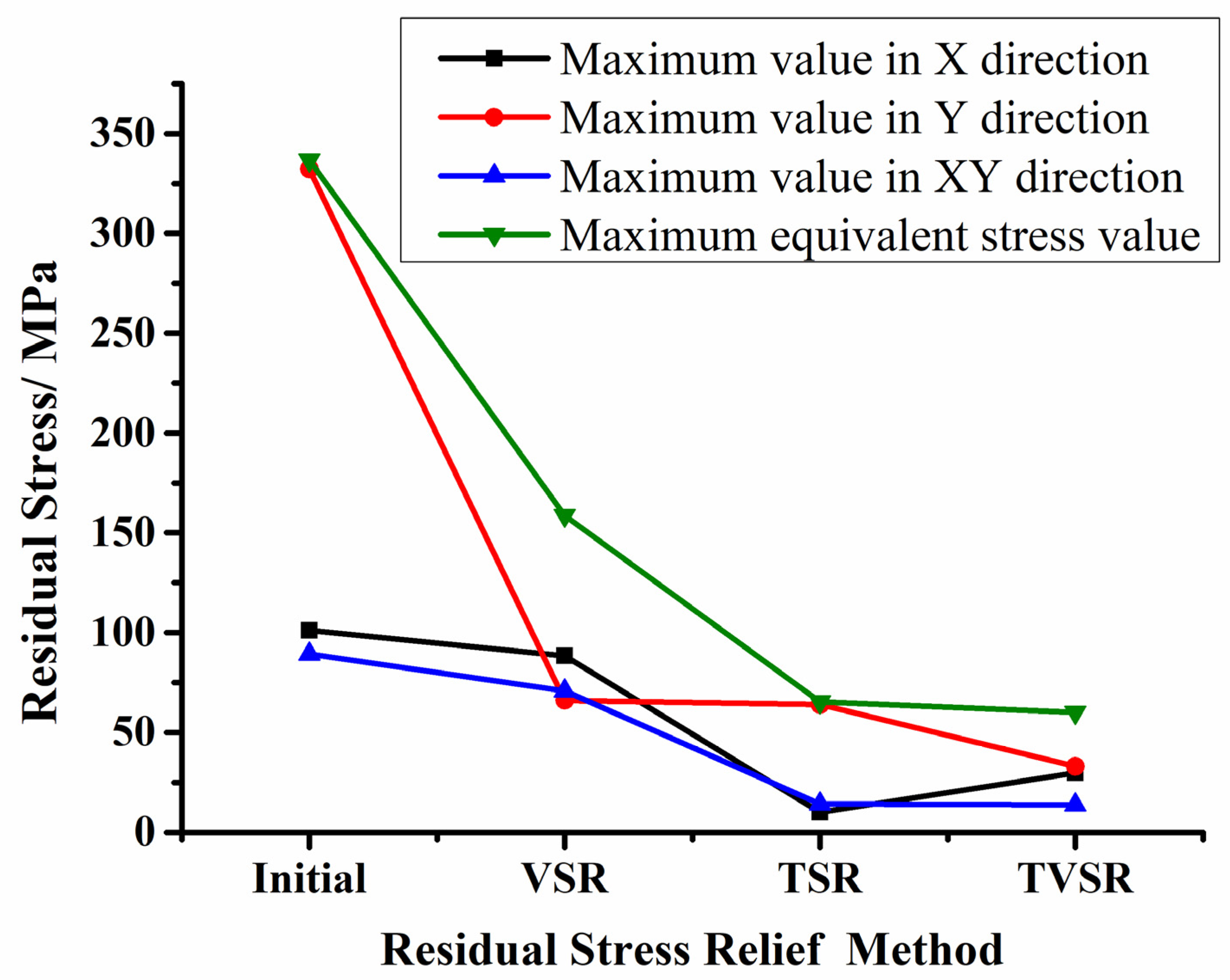
Figure 12.
Residual stress homogenization rate of 2219 aluminum alloy ring after stress relief.
Figure 13.
Roundness error and maximum equivalent stress in thin-walled blank ring machining.
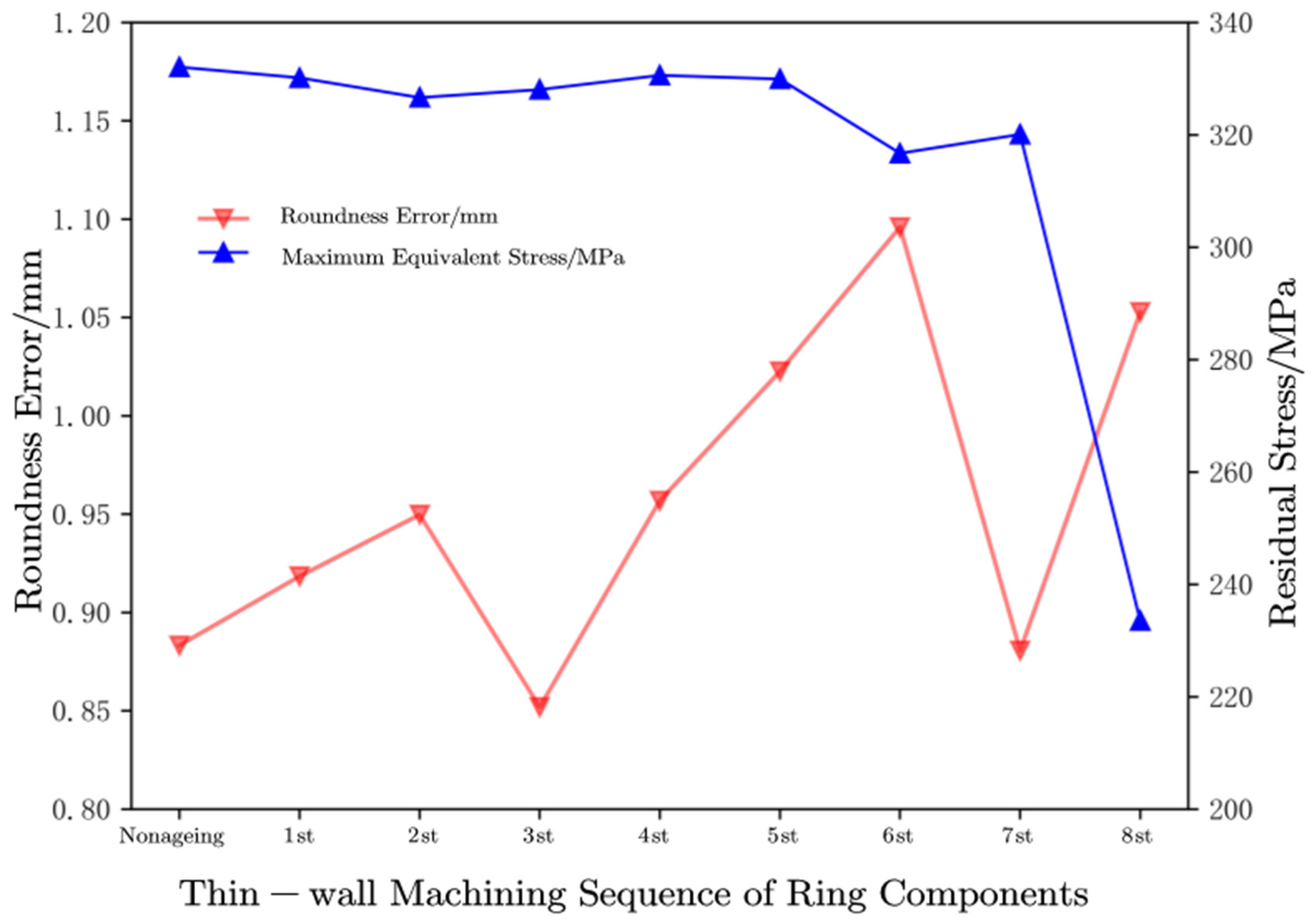
Figure 14.
Roundness error and maximum equivalent stress in thin-wall machining of ring parts.
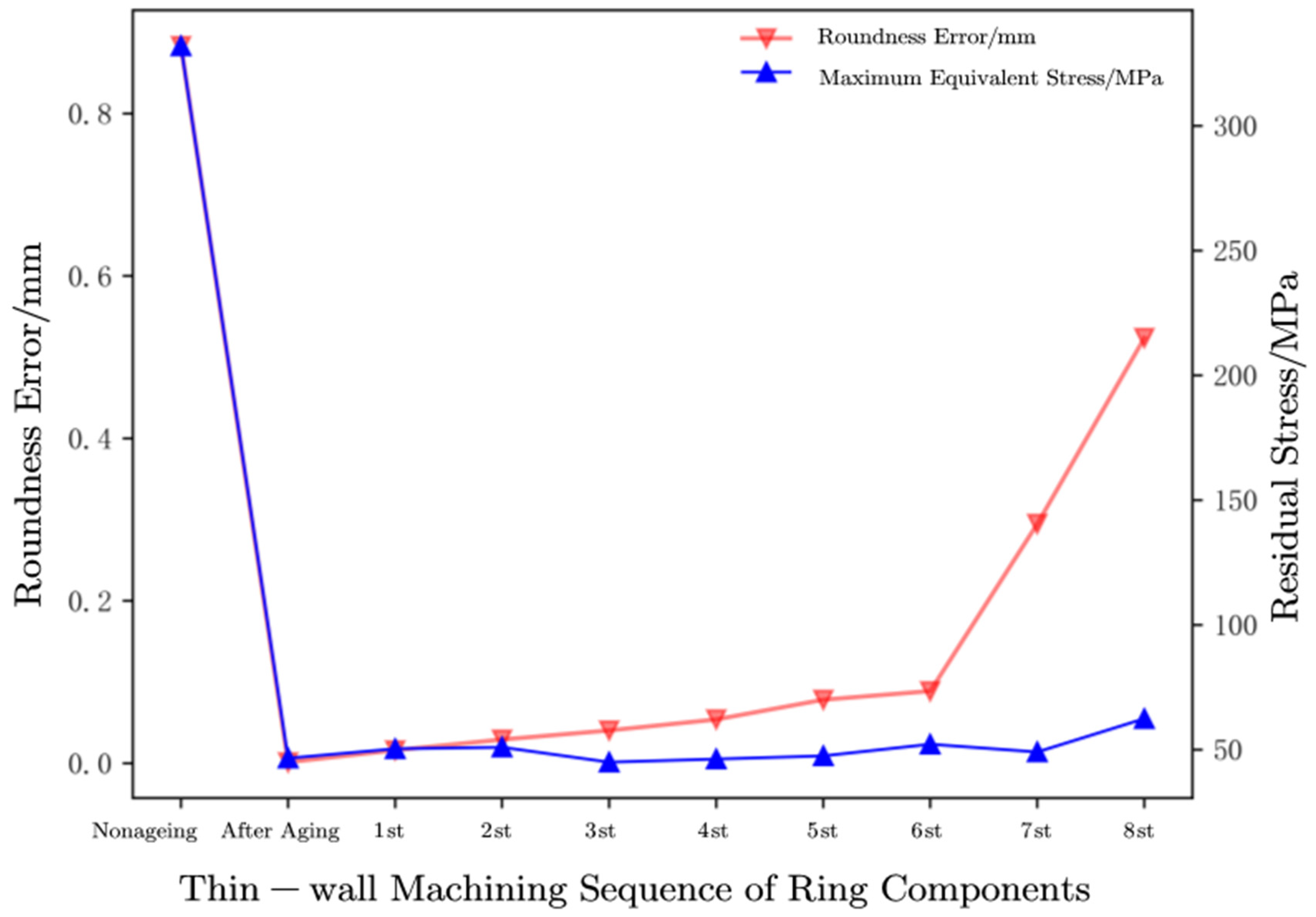
Figure 15.
Roundness error and maximum equivalent stress in thin-wall machining of ring parts.
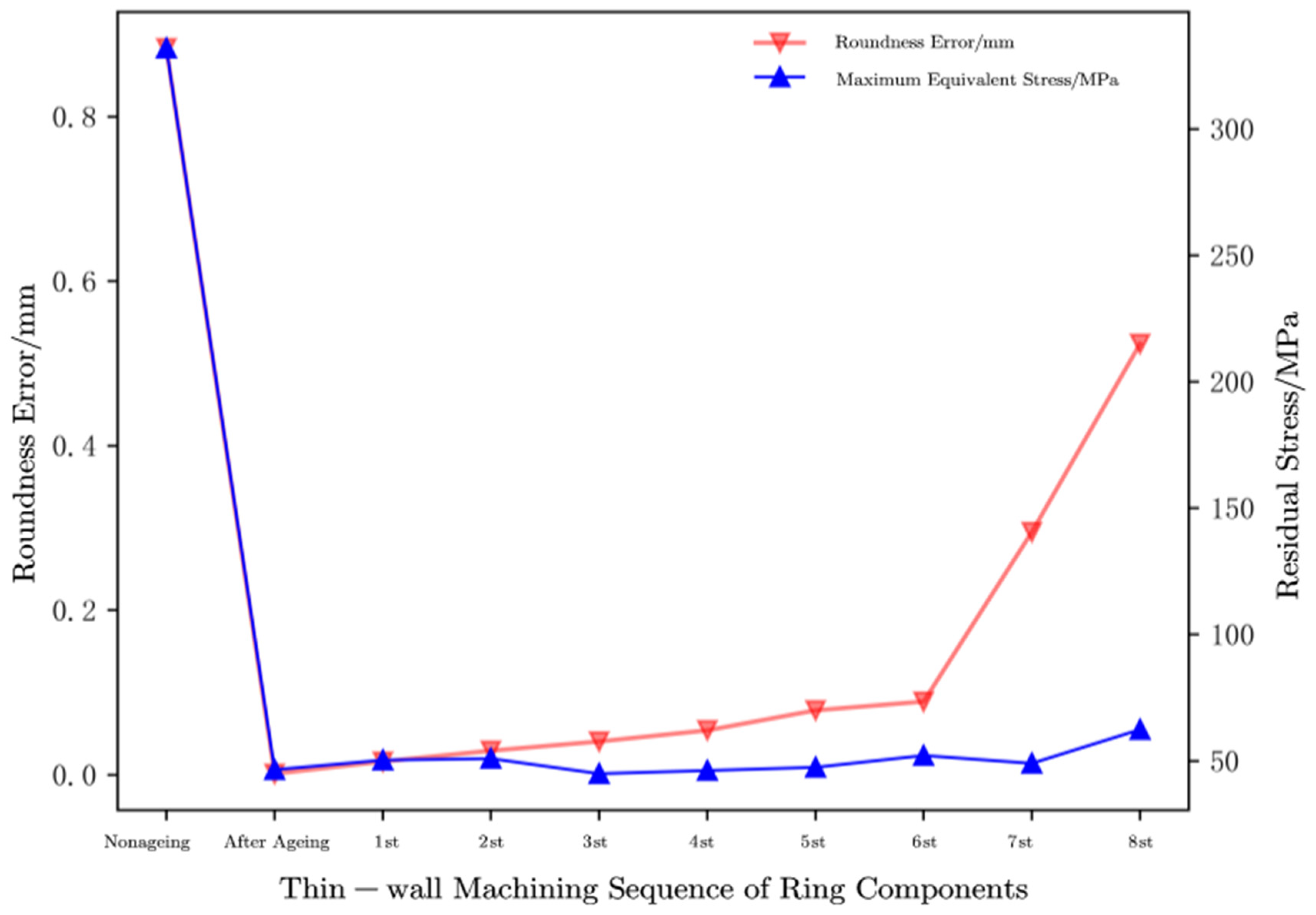
Figure 16.
Comparison results of roundness error and maximum equivalent stress in different machining processes.
Figure 16.
Comparison results of roundness error and maximum equivalent stress in different machining processes.
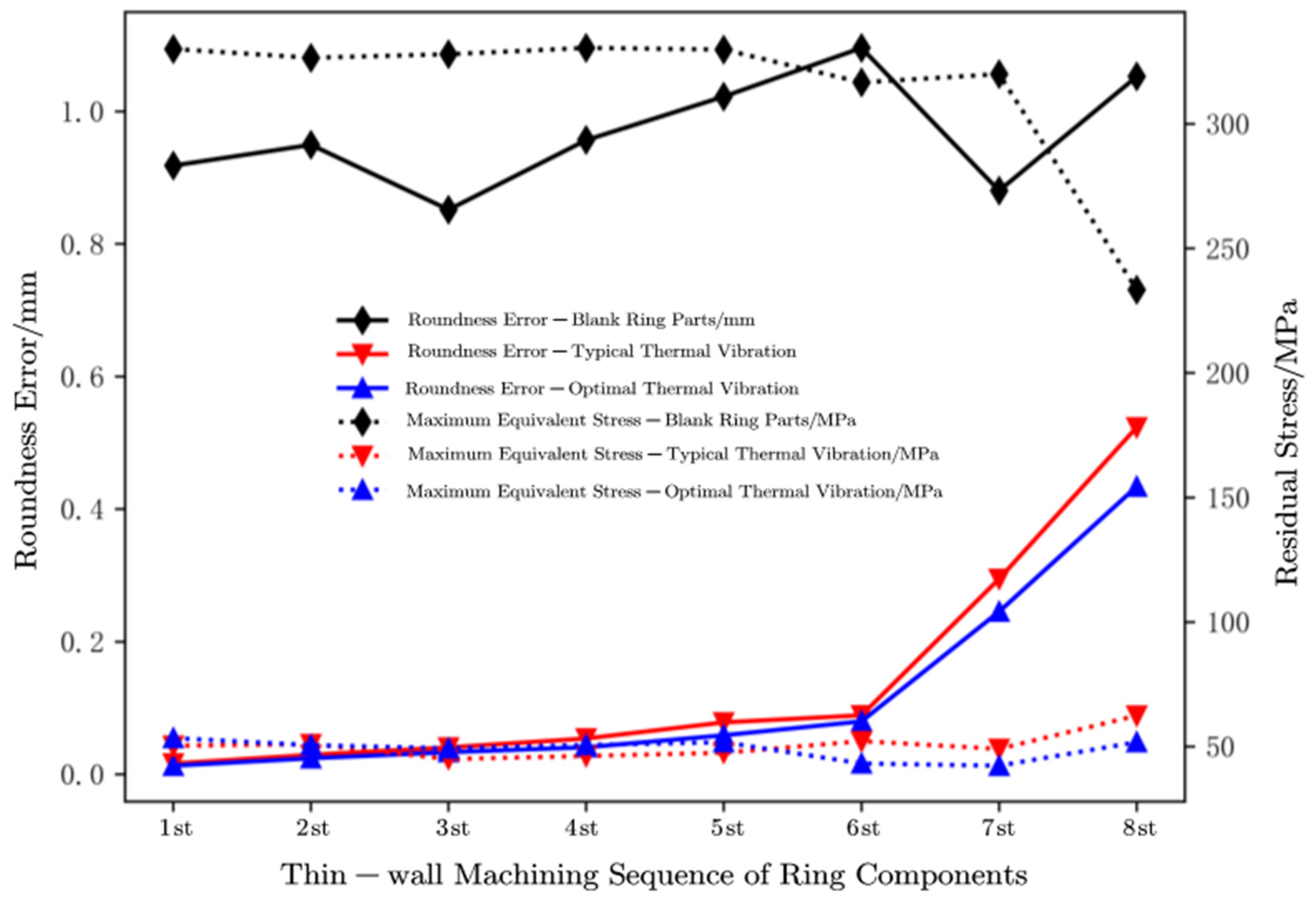
Table 1.
Curve fitting results of stress relaxation of 2219 aluminum alloy.
| Stress level /MPa | Iterations | Parameter | ||||||
| σ∞ | a1 | b1 | a2 | b2 | a3 | b3 | ||
| 50 | 99 | 15.859 | 13.841 | 55.640 | 12.801 | 55.641 | 7.487 | 0.832 |
| 150 | 208 | 220.261 | -23.666 | -100.164 | -23.669 | -100.164 | -23.667 | -100.164 |
| 250 | 87 | 202.553 | 5.541 | 0.263 | 40.062 | 23.894 | 10.292 | 0.045 |
| 350 | 68 | 154.149 | 1096.787 | 0.022 | 160.053 | 31.214 | - | - |
Table 2.
Creep parameters of 2219 aluminum alloy.
| Creep Parameters | C1 | C2 | C3 | C4 |
| Solution Results | 1.1518E-12 | 3.40 | -0.14 | 409.75 |
Table 3.
2219 aluminum alloy chemical composition table.
| Component | Cu | Fe | Mn | Si | Zn | Zr | Ti | V | Al |
| ωt% | 5.5-6.8 | 0.3 | 0.2-0.4 | 0.2 | 0.1 | 0.1-0.25 | 0.02-0.1 | 0.05-0.15 | the rest |
Table 4.
Roundness error evaluation results of thin-walled blank ring machining.
| Machining Sequences | Fitted Concentric Circle Center | Fitted Concentric Circle Radius | Roundness Error /mm | |||
| X/mm | Y/mm | Inside Diameter /mm | Outside Diameter /mm | |||
| After Aging | 0.7912 | -0.2892 | 182.6999 | 183.5832 | 0.8833 | |
| 1st | 0.8262 | -0.3017 | 189.6878 | 190.6062 | 0.91841 | |
| 2st | 0.8602 | -0.3115 | 196.6782 | 197.6279 | 0.9497 | |
| 3st | 0.8832 | -0.2829 | 201.7049 | 202.5568 | 0.8519 | |
| 4st | 0.8594 | -0.3251 | 201.6824 | 202.6393 | 0.9569 | |
| 5st | 0.8440 | -0.3493 | 201.6651 | 202.6877 | 1.0226 | |
| 6st | 0.9699 | -0.0901 | 201.6085 | 202.7045 | 1.0959 | |
| 7st | 0.8169 | 0.1903 | 201.7445 | 202.6252 | 0.8806 | |
| 8st | 0.6648 | 0.3158 | 201.5538 | 202.6066 | 1.0527 | |
Table 5.
Maximum equivalent stress results of thin-walled blank ring machining.
| Machining Sequences | Nonageing | 1st | 2st | 3st | 4st | 5st | 6st | 7st | 8st |
| Maximum Equivalent Stress /MPa | 332.06 | 330.15 | 326.63 | 328.05 | 330.59 | 329.94 | 316.72 | 320.08 | 233.49 |
Table 6.
Typical thermal-vibration parameters.
| Vibration Amplitude ratio | Vibrating Time /min | Vibration Frequency /Hz | Heating Time /h | Holding Time /h | Cooling Time /h |
| 1 | 2 | 619.096 | 0.5 | 1 | 1 |
Table 7.
Roundness error evaluation results of ring thin-walled machining.
| Machining Sequences | Fitted Concentric Circle Center | Fitted Concentric Circle Radius | Roundness Error /mm | ||
| X/mm | Y/mm | Inside Diameter /mm | Outside Diameter /mm | ||
| After Aging | -0.1323 | -0.0002 | 182.9993 | 183.0007 | 0.0014 |
| 1st | -0.1291 | -0.0027 | 189.9919 | 190.0081 | 0.0162 |
| 2st | -0.1291 | -0.0074 | 196.9884 | 197.0177 | 0.0293 |
| 3st | -0.1238 | -0.0071 | 201.9820 | 202.0225 | 0.0405 |
| 4st | -0.1238 | -0.0091 | 201.9815 | 202.0355 | 0.0540 |
| 5st | -0.1096 | -0.0086 | 201.9697 | 202.0480 | 0.0783 |
| 6st | -0.1274 | 0.0154 | 201.9561 | 202.0450 | 0.0889 |
| 7st | -0.1351 | 0.05043 | 201.8588 | 202.1536 | 0.2948 |
| 8st | -0.1284 | 0.11065 | 201.7239 | 202.2475 | 0.5236 |
Table 8.
Maximum equivalent stress in thin-wall machining of ring parts.
| Machining Sequences | After Aging | 1st | 2st | 3st | 4st | 5st | 6st | 7st | 8st |
| Maximum Equivalent Stress /MPa | 46.57 | 50.35 | 50.96 | 44.99 | 46.24 | 47.51 | 52.18 | 49.07 | 62.44 |
Table 9.
Optimum thermal-vibration parameters.
| Vibration Amplitude ratio | Vibrating Time /min | Vibration Frequency /Hz | Heating Time /h | Holding Time /h | Cooling Time /h |
| 1 | 5 | 619.096 | 1 | 1.5 | 2 |
Table 10.
Roundness error evaluation results of ring thin-walled machining.
| Machining Sequence | Fitted Concentric Circle Center | Fitted Concentric Circle Radius | Roundness Error /mm | ||
| X/mm | Y/mm | Inside Diameter /mm | Outside Diameter /mm | ||
| After aging | -0.1323 | -0.0001 | 182.9994 | 183.0006 | 0.0013 |
| 1st | -0.1299 | -0.0019 | 189.9934 | 190.0063 | 0.0129 |
| 2st | -0.1292 | -0.0054 | 196.9900 | 197.0141 | 0.0241 |
| 3st | -0.1244 | -0.005 | 201.9851 | 202.0184 | 0.0333 |
| 4st | -0.1259 | -0.0062 | 201.9856 | 202.0263 | 0.0407 |
| 5st | -0.1158 | -0.0066 | 201.9775 | 202.0363 | 0.0589 |
| 6st | -0.1274 | 0.0142 | 201.9604 | 202.0402 | 0.0798 |
| 7st | -0.1353 | 0.0429 | 201.8817 | 202.1271 | 0.2454 |
| 8st | -0.1269 | 0.0926 | 201.7694 | 202.2036 | 0.4342 |
Table 11.
Maximum equivalent stress in thin-wall machining of ring parts.
| Machining Sequence | After aging | 1st | 2st | 3st | 4st | 5st | 6st | 7st | 8st |
| Maximum Equivalent Stress/MPa | 55.36 | 53.41 | 50.59 | 49.30 | 50.61 | 51.75 | 43.22 | 42.32 | 51.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





