Preprint
Article
Enhancing Decomposition Approach for Solving Multi-Objective Dynamic Non-Linear Programming Problems Involving Fuzziness
Altmetrics
Downloads
103
Views
466
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
08 June 2023
Posted:
09 June 2023
You are already at the latest version
Alerts
Abstract
In real-life scenario, there are many mathematical tools to handle the incomplete and imprecise data. One of them is the fuzzy approach. This article aims to contribute to the literature of fuzzy multi-objective dynamic programming issues involving the fuzzy objective functions. The piecewise quadratic fuzzy numbers characterize these fuzzy parameters. Some basic notions in the problem under the α-pareto optimal solution concept is redefined and analyzed to study the stability of the problem. Furthermore, a technique, named as enhancing decomposition approach, is presented for achieving a subset for the parametric space that contains the sameα-pareto optimal solution. For a better understanding and comprehension of the suggested concept, a numerical example is provided.
Keywords:
Subject: Computer Science and Mathematics - Mathematics
1. Introduction
One of the most essential methodologies for solving optimization problems is dynamic programming (DP), where the so-called principle of optimality, as defined by Bellman [1] in 1957, is used to create its methods. The multi-objective dynamic programming (MODP) is a method for resolving problems with competing objective functions that follows the DP properties (Mine and Fukushima [2], 1979; Carraway et al. [3]; Abo- Sinna and Hussein [4]; Abo-Sinna and Hussein [5]).
Osman [6-7] introduces the ideas of solvability set, the stability sets of first-kind and second-kind, as well as the analysis of these terms for parametric convex non-linear programming problem. In order to a certain class of multi-objective convex programming problems, Osman and Dauer [8] dedicated themselves to the discovering of the first-kind stability set. In addition, they provided a technique to compute this set and the related pareto optimum solution.
First and foremost, Zadeh [9] presented the philosophy of fuzziness in literature, which can be applied to deal with the issues in real-life scenario where the information is in the form of ambiguousness and incompleteness. Bellman and Zadeh [10] created a method for solving decision-making problems involving fuzziness that improved and aided managerial decision-making. Linear programming along with fuzzy programming involving numerous objective functions were presented by Zimmermann [11] in 1978. Several people afterwards worked in the field of fuzziness. As a result of the convenience, the piecewise linear fuzzy numbers such as interval, triangular, trapezoidal, pentagonal, hexagonal fuzzy numbers, etc. have been applied in the literature [12-16]. Many authors have investigated the solution methodology as well as their applications involving fuzziness, fuzzy systems, and fuzzy mathematical programming problems [17-18].
In the literature, fuzzy dynamic programming models in particular have gotten a lot of attention (see, Bellman and Zadeh [10]; Zimmermann [19]; Esogbue [20]; Esogbue and Bellman [21]; Hussein and Abo- Sinna [22]). Tanaka and Asai [23] introduced fuzzy parameters to multi-objective linear programming (MOLP) problems. General fuzzy multi-objective non-linear programming (MONLP) models were formulated by Orlovski [24] in 1984. Sakawa and Yano [25-26] developed the idea of pareto optimum optimality and proposed a new interactive fuzzy approach for MOLP and MONLP issues with fuzzy parameters. For fuzzy MONLP situations, Osman and El-Banna [27], in 1993, proposed a qualitative analysis and stability. There are enormous researches, who developed the MODP (for instance, Moghaddam and Ghoseiri [28]; Muruganantham et al. [29]; Li et al. [30]; Deng et al. [31]; Besheli et al. [32]; Peraza et al. [33]; Azevedo et al. [34]; Ni et al. [35]; Wu et al. [36]; Liu et al. [37]; Zou et al. [38]; and Zhang et al. [39]).
Based on aforesaid literature survey, in this article, the parameters of the model are re-defined and further studied for MODP problems involving the fuzzy parameters in objective functions, as a result of the above literature.
The main contribution of this article is as follows:
- (i)
- For the core terminology associated with the stability in non-linear programming problem, the parameters are rearranged to study in case of MODP.
- (ii)
- An algorithm for computing the subset of the parametric space that possesses the same associated pareto optimal solution, is developed.
The remainder of this article is organized as in Figure 1 below:
2. Preliminaries
In this section, we recall some basic concepts.
Definition 1
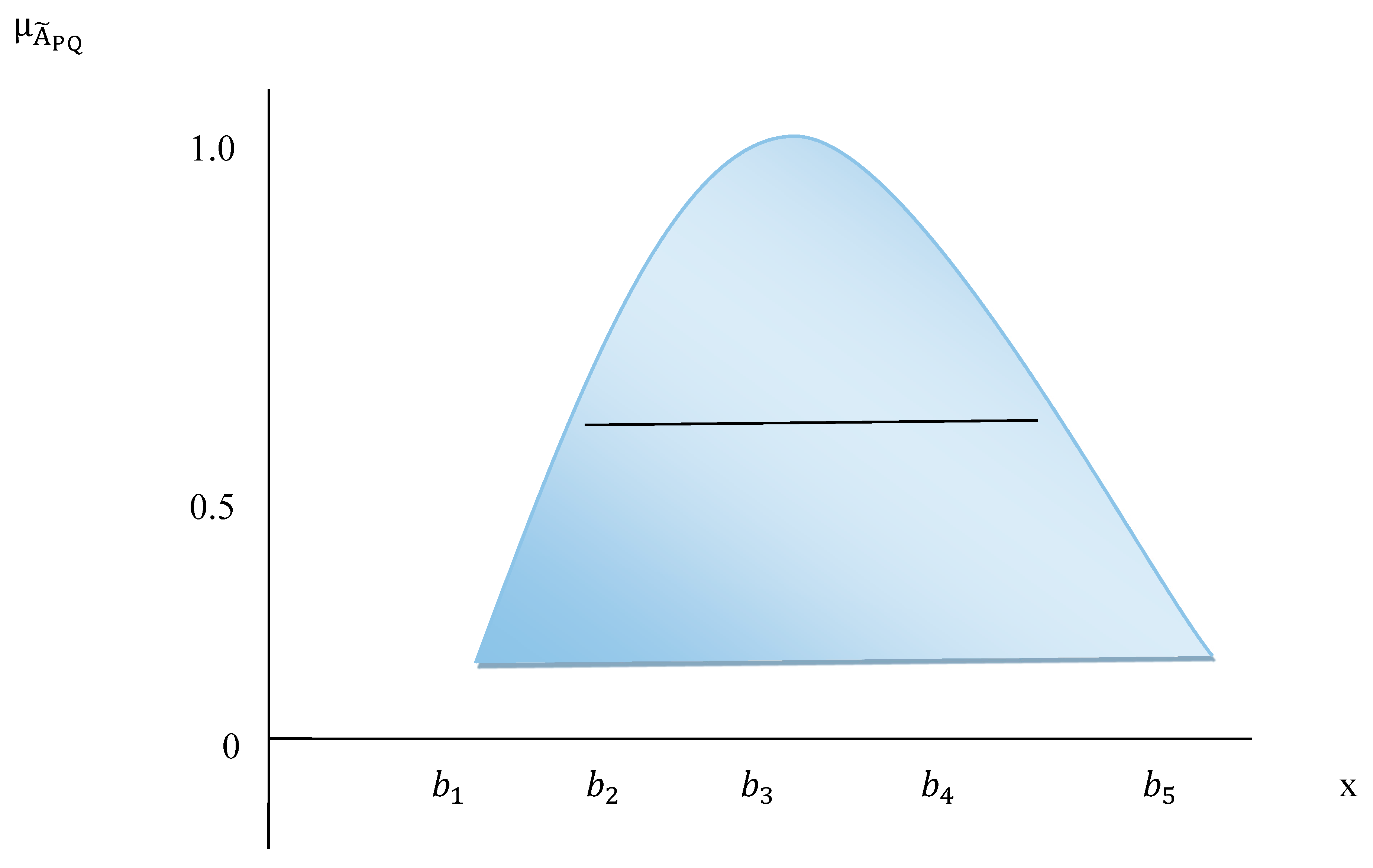
(Jain, 2010). A piecewise quadratic fuzzy number (PQFN) is designated by , where are real numbers, and its membership function is given by (see, Figure 2)
Definition 2.
(Jain [41]). For a given PQFN , the interval approximation, denoted by , is called the closed interval approximation, when the below mentioned condition is satisfied:
Definition 3.
(Jain [41]). Suppose that and be two P.Q.F.N.s. Then
- (i)
- Addition: .
- (ii)
- Subtraction:
- (iii)
- Scalar multiplication:
Definition 4.
(Jain [41]). Suppose , and are two inexact interval for the PQFN. Then, the arithmetic rules are presented as follows:
- (i)
- ,
- (ii)
- (iii)
- (iv)
- (v)
Definition 5.
(Jain [41]). The order relations for the intervals and is designated as follows:
- (i)
- iff and
- (i)
- iff and or
- (iii)
- iff and or
3. PROBLEM STATEMENT
A minimization type problem involving the fuzzy parameters within the objective functions is formulated as follows
(PQF-VMP) s. t.
.
Here, is a vector, and are convex real function of class on and are real-valued functions on , and represent the fuzzy parameters in vector form, in It is assumed that the aforesaid fuzzy parameters are designated as per the reference Jain [41], as well as the PQF-VMP is stable (Rockafellar [44]).
Definition 6.
([17]). The level set of the fuzzy numbers refers the usual set where the degree of the membership function is grater that the level as described below:
For a certain value of the aforesaid PQF-VMP problem is converted into the following problem (Sakawa and Yano [25])
(-VMP)
s. t.
Since PQF-VMP problem becomes stable, therefore the -VMP would also be stable.
Definition 7.
(Mine and Fukushima [2]). The objective function is called separable provided that there would exist functions defined on and functions designated on satisfies, for .
Similarly, it can be illustrated that
In a situation when all the objectives as well as the constraints become separable, we claim that the -VMP problem would also be separable. In addition, the functions, designated by and , are referred as the separating functions for the set as well as for the set .
Consequently, the separation of the -VMP is termed as monotone provided that all and are strictly increasing functions relative to the first argument for each constant second argument for each ,
Definition 8.
(pareto optimal solution). The feasible solution to the –VMP, is referred as pareto optimal solution provided that we do not find the feasible such that
and
for minimum one index
Assumption 1: The -VMP problem possesses the reparability property. In addition, the separation property refers to monotonicity.
Assumption 2. For each is assumed to be compact and . Also, we assume that are continuous functions of and .
Based on the weighting method (Chankong and Haimes [40]), -VMP problem can be treated as presented below:
s. t.
Consider that each follows the addition rule, i. e., for , we have
.
So, the objective function in -VMPw attaints the following form:
Now, let us define:
The recursive relation, for is presented as follows:
where, Assuming the monotonicity of , let be defined as
Theorem 1. Let the assumptions 1 and 2 be satisfied. Also, suppose is an pareto optimal solution of for some . Then would be an pareto optimal solution for
Proof (see, Mine and Fukushima [2]).
4. Stability Set of the First Kind
Definition 9. Given a particular containing the corresponding pareto optimal solution. The stability set of first kind of relative to is designated as follows:
4.1. Computation of first kind stability set
Let a point be an pareto optimal solution for . Therefore, we can find a point so that becomes an pareto optimal solution of (-VMPw). Based on the stability for (-VMPw), it refers that we can find a point and so that the below mentioned Kuhn- Tucker conditions are hold (Mangasarian [42]; Khalifa and Kumar [43]).
Let the two sets and be defined by
, and
As a result, we get the two linear independent systems of equations below.
(13)The system (13) can be rewritten as presented below
where, is matrix, is an matrix, and . Here, is the cardinality of , and is the cardinality of Consider that . Here, the cardinality of is (). Therefore, let us consider the below mentioned system in matrix form:
Here, is a matrix of order .
is a matrix of order .
Consequently, system (11) along with the equation , provides another system (14) that, in turn, becomes equivalent to the previous system (11).
Proposition 1. (Zeleny [45]). If , then
where, and are matrices of order and , respectively.
Proposition 2. (Zeleny [45]). If , then we have
5. An Algorithm
In this section, an algorithm for determining the is presented in the below steps:
Step 1: Start at
Step 2: Define the membership grades of the fuzzy number as per definition 2.
Step 3: Formulate the piecewise quadratic fuzzy dynamic multi-objective problem,
i. e., (PQF-VMP)
Step 4: Choose, that is by using the relation (2) to achieve the pareto optimal solution of (-VMPw).
Step 5: Putting the value of the in the Kuhn- Tucker conditions, we have systems (11) as well as (15). In addition, we can use the Gauss Elimination method for solving system (12).
Step 6: Based on the Lagrange multipliers values, we obtain
- (i)
- When , we have
- (ii)
- When , we have that is provided by (16),
- (iii)
- When , we have that is provided by (17).
Step 7: Set . Then, move to step 1.
Step 8: Repeat the interval at the steps of the proposed algorithm until the is completely nullified.
6. A Numerical Example
Take into account the following (PQF-VMP)
s. t.
Here, The close intervals approximation for , and are as follows:
The -VMP) can be written as
s. t.
By applying the weighting method (Chankong and Haimes [40]), we have
s. t. (23)
Constraints in (22).
At the point , the dynamic programming approach steps arise.
Firstly,
The pareto optimal solution isSecondly,
The pareto optimal solution isThirdly,
The pareto optimal solution is summarized as follows:
Now, let us determine as described below
Systems (11) and (12) allowed
Then
.
Thus, we obtain
7. Conclusions and Future Works
The dynamic multi-objective programming issue with piecewise quadratic fuzzy parameters has been investigated in this study. The first kind stability set has been identified, and the algorithm allows the problem solver for the decomposition of the parametric w- space. There are various future research directions to work on the proposed paper. One of them is to extend further this study to other fuzzy-type uncertainties, for example, Intuitionistic fuzzy sets, Pythagorean fuzzy sets, etc. Another possible scope is to include the spherical fuzzy sets, and neutrosophic sets considering wide coverage of decision-making problems in real-life situations.
Funding
This research received no funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bellman, R. E. Dynamic Programming, Princeton University Press, Princeton, N. J., 1957.
- Mine, H., and Fukushima, M. (1979). Decomposition of multiple criteria mathematical programming by dynamic programming. International Journal of Systems Science, 10(5): 557- 566. [CrossRef]
- Carraway, R. L., Morin, Th.., and Moskowitz, H. (1990). Generalized dynamic programming for multicritera optimization. European Journal of Operational Research, 44(1): 95-104. [CrossRef]
- Abo- Sinna, M. A., Hussein, M. L. (1994). An algorithm for decomposing the parametric space in multiobjective dynamic programming problems. European Journal of Operational Research, 73(3): 532-538. [CrossRef]
- Abo- Sinna, M. A., Hussein, M. L. (1995). An algorithm for generating efficient solutions of multiobjective dynamic programming problems. European Journal of Operational Research, 80(1): 156-165.
- Osman, M. S. A, (1977a). Qualitative analysis of basic notions in parametric convex programming, I (parameters in the constraints), Aplikace Matematiky, 22(5): 318-332.
- Osman, M. S. A, (1977b). Qualitative analysis of basic notions in parametric convex programming, II (parameters in the objective functions), Aplikace Matematiky, 22(5): 333-348.
- Osman, M.S. A., and Dauer, J. P. Characterization of Basic Notations in Multiobjective Convex Programming Problems. Technical Report, Lincoln, University of Nebraska, USA, 1983.
- Zadeh, L. A. (1965). Fuzzy sets. Information Control, 8(1): 338-353. [CrossRef]
- Bellmann, R., and Zadeh, L. (1970). Decision making in a fuzzy environment. Management Science, 17(4): 141-164. [CrossRef]
- Zimmermann, H. J. (1978). Fuzzy programming and linear programming with several objective functions. Fuzzy Sets and System, 1(1): 45–55. [CrossRef]
- Khalifa, H. A., Kumar, P., and Majed, G. A. (2021). On characterizing solution for multi-objective fractional two-stage solid transportation problem under fuzzy environment. Journal of Intelligent Systems, 30(1): 620-635. [CrossRef]
- Prameela, K. U., and Kumar, P. (2020). Conceptualization of finite capacity single-server queuing model with triangular, trapezoidal and hexagonal fuzzy numbers using α-cuts. In: Dutta D., Mahanty B. (eds) Numerical Optimization in Engineering and Sciences. Advances in Intelligent Systems and Computing, vol 979. pp. 201-212. Springer, Singapore. ISSN: 2194-5357. [CrossRef]
- Kumar, P. (2021). Optimal policies for an inventory model with shortages, time-varying holding and ordering costs in trapezoidal fuzzy environment. Independent Journal of Management & Production, 12(2): 557-574. [CrossRef]
- Kumar P. (2022). Solution of extended multi-objective portfolio selection problem in uncertain environment using weighted Tchebycheff method. Computers- MDPI. 11(10):144. [CrossRef]
- Prameela, K. U., and Kumar, P. (2019). Execution proportions of multi-server queuing model with pentagonal fuzzy number: DSW algorithm approach. International Journal of Innovative Technology and Exploring Engineering. 8(7): 1047-1051.
- Dubois, D., and Prade, H. Fuzzy Sets and Systems; Theory and Applications, Academic Press, New York, 1980.
- Kaufmann, A., and Gupta, M.M. Fuzzy Mathematical Models in Engineering and Management Science, Elsevier Science Publishing Company INC, New York, 1988.
- Zimmermann, H. J. Fuzzy Set Theory and its Applications, (International Series in Management Science/ Operations Research), Kluwer- Nijhoff Publishing, Dordrecht, 1985.
- Esogbue, A. O. (1983). Dynamic programming, fuzzy set, and the modeling of R& D management control system. IEEE Transaction on Systems Management and Cybernetics, SMC, 13(1): 18-30.
- Esogbue, A. O., and Bellman, R. E. (1984). Fuzzy dynamic programming and it is extensions, in H- J. Zimmermann et al., Eds, Times/ Studies in the Management Sciences, 200(1): 147-167.
- Hussein, M. L., and Abo- Sinna, M. A. (1993). Decomposition of multiobjective programming problems by hybrid fuzzy- dynamic programming. Fuzzy Sets and Systems, 60(1): 25-32.
- Tanaka, H., and Asai, K. (1984). Fuzzy linear programming with fuzzy numbers. Fuzzy Sets and Systems, 13(1): 1-10. [CrossRef]
- Orlovski, S. (1984). Multiobjective programming problems with fuzzy parameters. Control Cybernetic, 13(3): 175-183.
- Sakawa, M., and Yano, H. (1989). Interactive decision making for multiobjective nonlinear programming problems with fuzzy parameters, Fuzzy Sets and Systems, 29(3): 315-326. [CrossRef]
- Sakawa, M., and Yano, H. (1990). An interactive fuzzy satisficing method for multiobjective nonlinear programming problems with fuzzy parameters. Fuzzy Sets and Systems, 30(1): 221-238.
- Osman, M. S. A., and El- Banna, A. H. (1993). Stability of multiobjective nonlinear programming problems with fuzzy parameters'', Mathematics and Computers in Simulation, 35(1): 321-326.
- Moghaddam- J, A. R., and Ghoseiri, K. (2011). Fuzzy dynamic multi- objective Data Envelopment Analysis model. Expert Systems with Applications, 38(1): 850-855. [CrossRef]
- Muruganantham, A., Zhao, Y., Gee, S. B., Qiu, X., and Tan, K. C. (2013). Dynamic multiobjective optimization using evolutionary algorithm with Kalman Filter. Procedia Computer Science, 24(1): 66-75. [CrossRef]
- Li, Z., Chen, H., Xie, Z., Chen, C., and Sallam. A. (2014). Dynamic multiobjective optimization algorithm based on average distance linear predication model. The Scientific World Journal, Vol. 2014, Article ID389742, 9 pages. [CrossRef]
- Deng, X., Xu, W- J., and Wang, Z- Q. (2016). Dynamic multi- objective fuzzy portfolio model that considers corporate social responsibility and background risk. Journal of Interdisciplinary Mathematics, 19(2): 413-432. [CrossRef]
- Besheli, S. F., Keshteli, R. N., Emami, S., and Rasoluli, S. M. (2017). A fuzzy dynamic multi- objective multi- item model by considering customer satisfaction in a supply chain. Scientia Iranica E, 24(5): 2623-2639. /: https. [CrossRef]
- Peraza, C., Valdez, F., Castro, J. R., and Castillo, O. (2018). Fuzzy dynamic parameter Adaptation in the harmony search algorithm for the optimization of the ball and beam controller. Advances in Operations Research, Vol. 2018, Article ID 3092872, 16 pages. [CrossRef]
- Azevedo, M. M., Crispim, J. A., and de Sousa,J. P. (2019). A dynamic multiobjective model for designing machine layouts. IFAC- PapersOnLine, 52(13): 1896- 1901. [CrossRef]
- Ni, P., Gao, J., Song, Y., Quan, W., and Xing, Q. (2020). A new method for dynamic multi- objective optimization based on segment and cloud prediction. Symmetry, (12): 465-477. [CrossRef]
- Wu, Y., Shi, L., and Liu, X. (2020). A new dynamic strategy for dynamic multiobjective optimization. Information Sciences, 529(1): 116-131. [CrossRef]
- Liu, R., Yang, P., and Liu, J. (2021). A dynamic multi- objective optimization evolutionary algorithm for complex environmental changes. Knowledge- Based Systems, 216: 106612. [CrossRef]
- Zou, F., Yen, G. G., and Zhao, C. (2021). Dynamic multiobjective optimization driven by inverse reinforcement learning. Information Sciences, 575: 468-484. [CrossRef]
- Zhang, Q., Jiang, S., Yang, S., and Song, H. (2021). Solving dynamic multi- objective problems with a new prediction- based optimization algorithm. PloS One, 16(8): e0254839. eCollection 2021. [CrossRef]
- Chankong, V., and Haimes, Y. Y. Multiobjective Decision Making Theory and Methodology, North- Holland, New York, 1983.
- Jain, S. (2010). Close interval approximation of piecewise quadratic fuzzy numbers for fuzzy fractional program. Iranian Journal of Operations Research, 2(1): 77-88.
- Mangasarian, O. L. Nonlinear Programming, McGraw- Hill, New York, 1969.
- Khalifa, H. A., and Kumar, P. (2023). Multi-objective optimization for solving cooperative continuous static games using Karush-Kuhn-Tucker conditions. International Journal of Operational Research, 46(1), 133-147. [CrossRef]
- Rockafellar, R. (1967). Duality and stability in extremal problems involving convex functions. Pacific Journal of Mathematics, 21(1): 167-181. [CrossRef]
- Zeleny, M. Linear Multiobjective Programming, Lecture Notes in Economics and Mathematical Systems, Vol. 95, Springer- Verlag, New York, 1974. [CrossRef]
Figure 1.
Layout of Remaining Paper.

Figure 2.
Graph Illustration of a PQFN.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






