Prerpints.org logo
Preprint
Article

Solder Alloy Design: Investigation of Predictive Models for Tensile Properties Based on Different Alloy Compositions and Microstructures

Altmetrics

Downloads

160

Views

99

Comments

0

Submitted:

10 June 2023

Posted:

12 June 2023

You are already at the latest version

Alerts
Abstract
In this study, an extensive data set was based on existing literature records in order to enable the suitability of several predictive models, from Multiple Linear Regression (MLR) to Neural Networks (NN). The main objective was to, through regression analyses, generate model computations to correlate tensile properties (UTS- Ultimate Tensile Strength, YTS – Yield Tensile Strength and EF – Elongation-to-Fracture) to a given alloy composition and microstructural spacing. This investigation led to positive results, as the highest accuracies of the trained modules (in 80% of the database) were found to be above ~82% (UTS and EF) and a maximum of ~98% (YTS), when analyzing the results to a test data set. Later, these models were used to define trends for possible next solder alloy commercial compositions. Overall, using the standard model’s setup, the Random Forest and Decision Tree models showed the highest accuracy results, with 0.958 for YTS as opposed to 0.907 for MLR. Moreover, Multilayer Perceptron (MLP)-optimized models yielded the best results for each variable, with the highest increases in accuracy associated with the YTS and EF. The present contribution might imply an important milestone towards alloy design research based on data science guidelines to unlock the full potential of former experiments and their extensive set of results.
Keywords: 
Subject: Engineering  -   Metallurgy and Metallurgical Engineering

1. Introduction

In light of his findings, Gordon E. Moore claimed that component density and performance of integrated circuits would double every two years [1]. Although this statement was based on empirical observations regarding available components at the time, it remained to be unabated for more than 40 years [2] and became known as Moore’s law”. However, with such progress in microelectronics size evolution in last years, effective heat dissipation became critical to ensure reliable operation as well as increasing the average lifetime of these devices [3]. In face of this challenge, it became common to employ Cu-based heat sinks in an effort to maximize heat dissipation.
Most of the systems work with two copper pieces that are physically attached composing a heat sink. Only a very restrict mechanical contact between the solder and the copper plate is created due to irregularities in the micro-scale surface roughness [4]. Actually, Razeeb et al. pointed out in their studies that the total surface mechanical copper/alloy junction might be around 1-2% [3]. Consequently, researchers started to investigate filler materials with a higher thermal conductivity value and reasonable mechanical properties to fulfill these gaps. The materials used in such applications became known as thermal interface material” (TIM), in which solder alloys are well-thought-out as the most suitable for challenging applications based on their high thermal conductivity values, i.e., 20-80 W/(mK) [4]
Notably, Sn-based solder alloys gained tremendous importance, in the microelectronics assemblies due to their great properties found when alloyed with lead. However, due to Pb toxicity, several other alloy systems were investigated, in which Sn-Ag-Cu (SAC) turns into the most prominent one [5], even though other systems are still worthy of further investigations, such as Sn-Bi [6]. This is mainly because the SAC alloys have the disadvantage of coarse Cu-Sn intermetallics formation at the solder/copper reaction interface, which damages both the mechanical properties and the overall interface thermal conductivity [7].
Despite the alloy composition importance, soldering operations depend significantly on the process conditions (i.e., solidification cooling rates) as these parameters influence the phases formed (eutectics, dendrites and etc.) as well as their characteristics, such as the interdendritic spacing [8]. These microstructural data have proven to have a direct inter-relation with the solder alloy mechanical properties, for which Hall-Petch-type equations are considered as the most significant correlations [9]. Although based on Simple Linear Regression (SLR) with good estimates for binary systems (such as Sn-Cu and Sn-Ag), recent explorations highlight the need for deeper investigation of more elaborated predictive models due to the intricate complexity of the alloy microstructures [5]. With this in mind, it seems that one of the knowledge gaps still necessary to be fulfilled is a more systematic and data-oriented approach to propose models towards a connection of both alloy design concepts and theoretical considerations of statistical data science.
In the context presented above, in this study, a data set was investigated considering several predictive models from Multiple Linear Regression (MLR) model to Neural Networks for solder tensile properties based on various alloy compositions, process parameters, and microstructural spacing. The outcome was not only a comprehensive dataset with multiple compositions and microstructural parameters from available research, but also a first systematic investigation which allowed surprisingly considerable accuracy models (above ~82% and a maximum of ~98%) to be developed. These models might then be used to identify trends for potential new commercial compositions for solder alloys. In this work, the strengths and weaknesses of these models and their main characteristics are discussed.

2. Materials and Methods

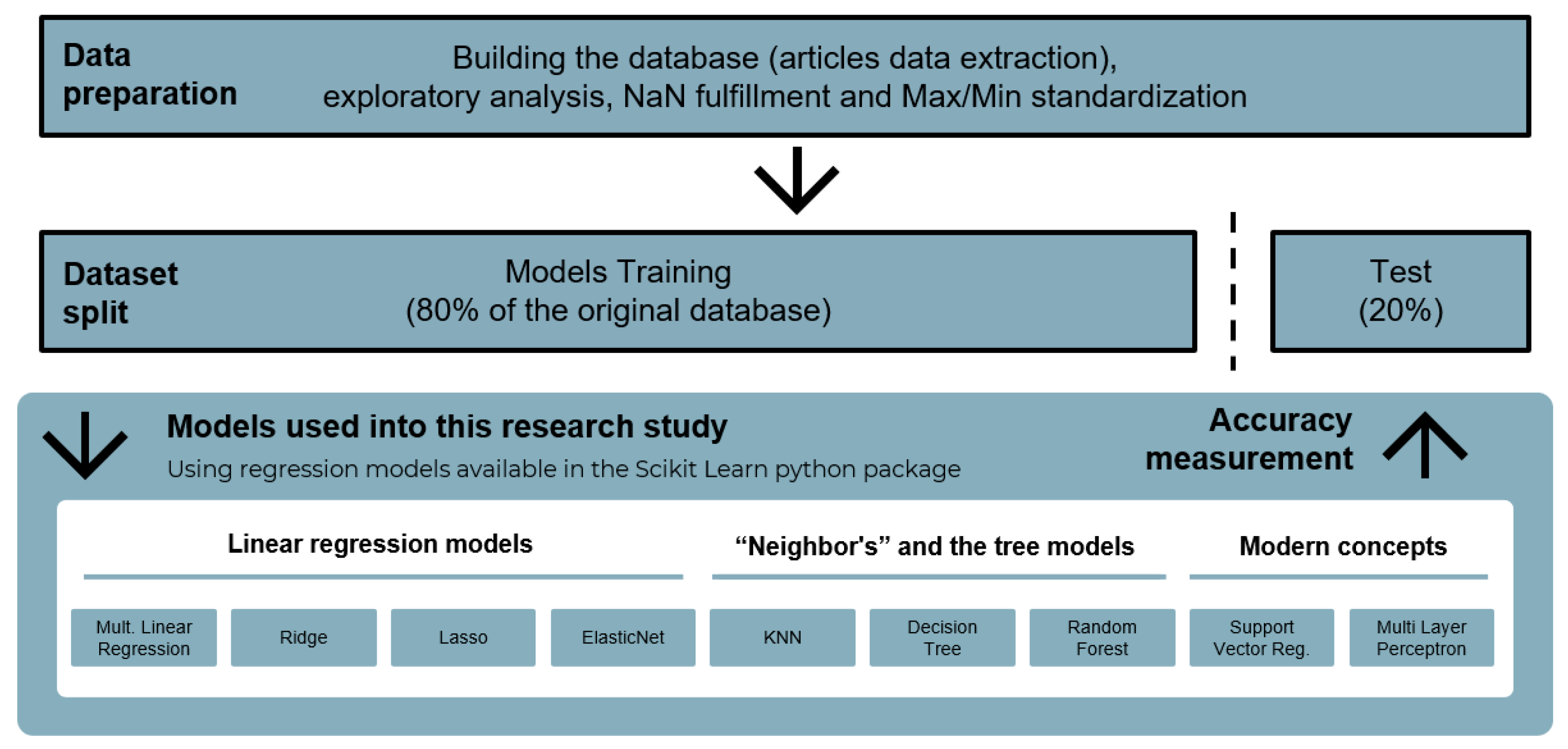
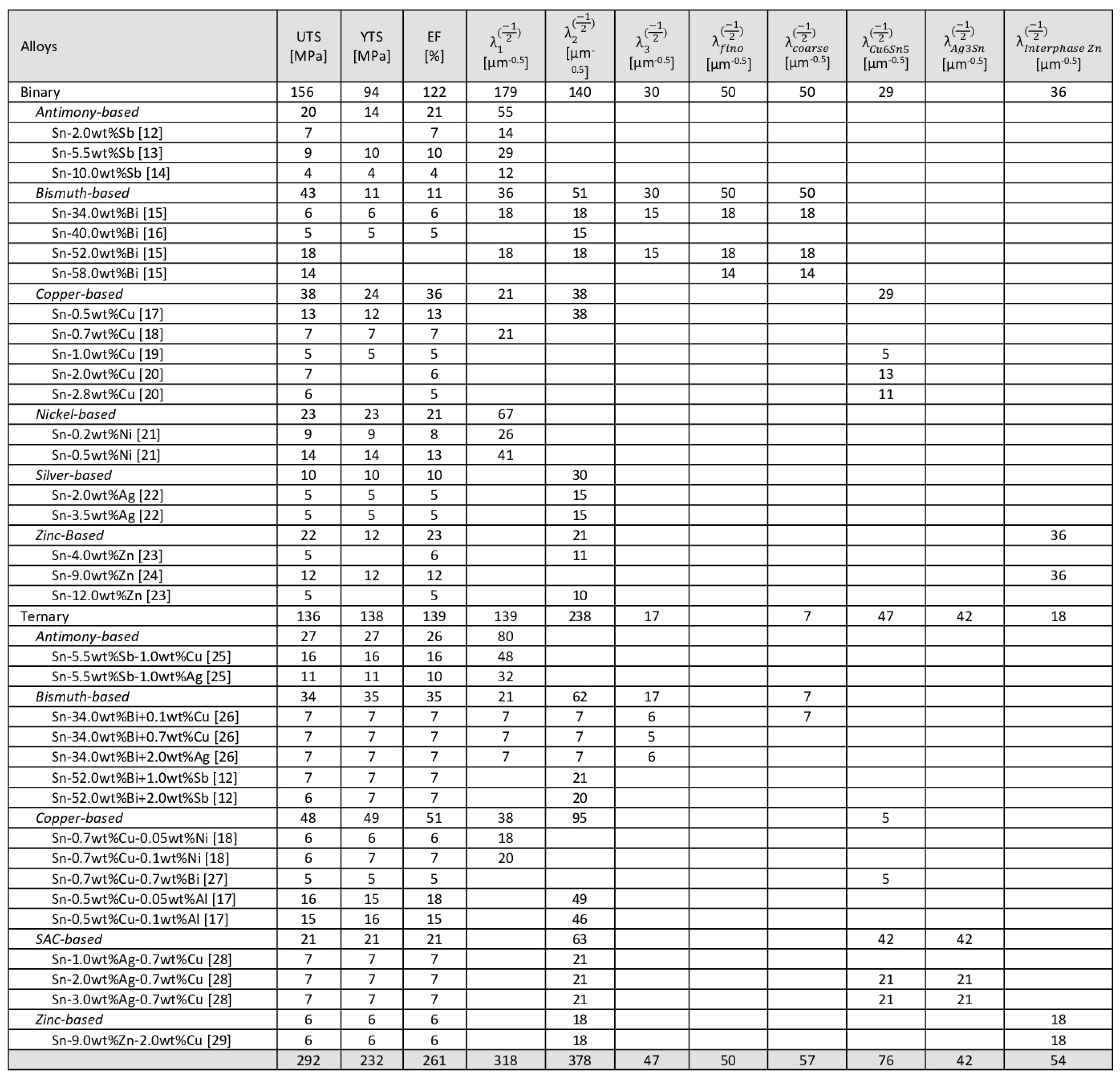
2.1. Database Generation

As mentioned in the Section above, previously published studies on the effect of the alloy composition and the microstructure in solder alloys have not systematically developing approaches with a data-oriented mindset. Therefore, in order to enable the possibility to apply alloy design concepts based on predictive models, the first step in this study was to address this issue. The data for the present study come from a compilation of several research articles published focused on specific alloy/systems. These were previously developed works mostly by two international Research Teams devoted to solidification investigation of several alternative Sn-based solders, i.e., the M2PS (Microstructure and Properties in Solidification Processes)/UFSCar, Brazil and the GPS (Solidification Research Team)/Unicamp, Brazil, as well as some minor contributions from other groups.
A summary of the resultant compiled database with an overview of the number of registers per expected results (UTS, YTS, and EF) and attributes (alloy composition and microstructural features), also referencing the research paper where the data was extracted, is summarized in the Table 1. After all, data from a total of 35 alloys either ternary or binary chemistries from different systems were gathered. An exploratory analysis was carried out to better evaluate the consistency of the database, based on Panda’s data frame package’s resources [10] and Sweetviz [11].
Most of the studies [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29] employed directional solidification systems to allow microstructural and tensile data to be assessed. After solidifying the casting, transverse (perpendicular to the solidification direction) and longitudinal samples (at various sections from the cooled bottom of the castings) were removed of alloy casting for the metallographic procedure using optical microscopy.
To measure λ1, the cross sections were considered, as well as the neighborhood criterion, which considers the spacing value equal to the average distance between the geometric centers of the primary dendritic trunks in question, as defined by the triangle method. The secondary (λ2) and tertiary (λ3) dendritic arm spacings were measured by using the linear intercept method using longitudinal sections (parallel to the extraction direction of heat) and transversal, respectively. The same linear intercept method was adopted in some of the studies [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29] for determining λfino, λcoarse, λcu6Sn5, λAg3Sn and λZn. Moreover, the tensile properties of the alloys were determined through tensile tests at different positions in the castings with strain rates in the order of 10-3 s-1.

2.2. Regression Models

This Section presents a brief description of the main concept of all the regression models used in this study, focusing on how the key parameters could be used in order to enhance the model quality. Most of the equations and descriptions were based on James et al. [30], whose book is indeed a great review of the statistical learning concepts. On the other hand, some other concepts such as ElasticNet and Multilayer Perceptron (MLP) had better analysis and description in Morettin and Singer [31], which, therefore, can be considered the basis for these specific topics. Regarding the content organization itself, the present Section evolutes from more simple concepts, such as Linear Regression, up to more modern concepts, that is, Neural Networks.
The regression models are widely used in statistical learning and supervised learning. They aim to predict a response variable (Y) based on predictor variable (X) [30], as represented in the Equation 1. Multiple regression models are basically an extension of simple linear regression, which is a basic method for supervised learning. In multiple regression, there are multiple predictor variables, and the model aims to find the relationship between these variables and the response variable, as shown in Equation 2. The model is represented by an equation that includes intercept and slopes for each predictor variable. The model is estimated using the least squares method, which minimizes the Residual Sum of Squares - RSS (Equation 3). In this study, the model applied was based on Scikit Learn Linear Regression [32], where further description about the algorithm can be found.
Y = β 0 + β 1 X + ϵ ,
Y = β 0 + β 1 X 1 + β 2 X 2 + … + β p X p + ϵ ,
R S S = ∑ i = 1 n Y i −   Y ^ i 2 = ∑ i = 1 n Y i −   β ^ 0 + β ^ 1 X i 1 + β ^ 2 X i 2 + … + β ^ p X i p 2 ,
where: X represents the predictor variable, Y is the answer variable that one is trying to predict. On top of these two, to compose a linear model, it is also important to mention that β 0 and β 1 are unknown constants that represents the intercept with the y-axis and slopes with regard to the x-axis, respectively [30]. Finally, the ϵ can be defined as a mean-zero random error term, added to represent the deviations that cannot be explained by the linear model. Regarding Equation 2, each pair of β p X p represent a linear function with its own slope, having p as an integer from 1 to the number of considered predictor variables. Finally, in Equation 3, RSS” means the Residual Sum of Squares and, one might also notice Y ^ i , which means the predicted value based in the MLR formula with a vector of coefficients β ^ 0 and β ^ .
James et al. [30] pointed out that linear regression models can be surprisingly competitive even when compared to more sophisticated non-linear models [30]. For this reason, these authors also brought up in their work analysis about methods to improve the linear method in terms of prediction accuracy and interpretability. The prediction accuracy is an important factor to avoid overfitting (Figure 1), in which later the predictive model might have poor predictions. This is a big concern especially when the number of predictor variables is similar in magnitude to the number of n samples itself. Concerning interpretability, this concept was developed as an attempt to reduce the complexity of the model by removing irrelevant variables for the prediction [30].
To enhance the linear regression model, several regularization techniques have been introduced. Ridge regression is one method that adds a shrinkage penalty term to the least squares’ equation, as shown in Equation 4. This penalty term helps reduce the coefficients of irrelevant variables, leading to a more interpretable model. Lasso regression, on the other hand, imposes a penalty that forces some coefficients to be exactly zero, effectively performing variable selection (Equation 5). Finally, Elastic-net regression combines the penalties of both Ridge and Lasso regressions, providing a trade-off between the two approaches (Equation 6). Further description of the concept can be found in James et al. [30] work, especially for Ridge and Lasso, whereas ElasticNet was better developed in the work by Morettin and Singer [31]. In any case, all three models used are available in the Scikit Learn package. [34,35,36].
R S S + λ ∑ i = 1 p   β ^ i 2  
R S S + λ ∑ i = 1 p   β ^ i
∑ i n Y − X i β ^ 2 2 n + λ 1 − α 2   ∑ i = 1 p     β ^ i 2 +   α ∑ i = 1 p   β ^ i ,
where: in Equation 4, the term " λ " is the Rigde’s shrinkage factor, which gets smaller when the estimated coefficients β ^ " get closer to zero. The same reasoning is applied in Equation 5, where there is also a modular penalty. Finally, in Equation 6, the final formula basically shows a balance regarding both penalties, which is given based on the value of α".
In addition to the linear regression, other regression models have been developed to capture different characteristics of the data. Two concepts could be mentioned in this work, which were the spatial and the tree-based ones. Concerning the first one, the most prominent model related to this method is the K-nearest neighbors (KNN). James et al. [30] demonstrated this model, especially regarding its function as a classifier. The KNN model is a non-parametric approach that predicts a value based on the average of the K closest neighbors. The number of neighbors and the weighting of distances can be adjusted to improve performance. Equation 7 depicts the formula, whereas the algorithm applied description can be found within the Scikit Learn package description [37].
Y ^ = 1 K ∑ i = 1 N Y i ,
where Y i is the Y” value for the i neighbor within the K ones decided by the user.
Similar to the KNN model, other regression models were later created to further sophisticate the usage of the predictor space. Already aforementioned, the tree-based models are included in this scenario, where the model basically tries to stratify or segment the X values into simple regions for calculation performing [30]. Once this is done, to issue a prediction, the model calculates the mean average based on the region into the model determined by referencing the given attributes of the respective register. Decision trees and random forests are tree-based models that segment the predictor space into regions and predict the response variable based on the average of the samples within each region. Random forests combine multiple decision trees to reduce variance and improve prediction accuracy. Figure 2 depicts the Random Forest regression concept, where the output of several decision outputs is collected to later issue the final prediction figure. In the present study, both regression model algorithms were based in the Scikit Learn package functions [38,39].
As mentioned by James et al. [30]. the support vector regression (SVR) concept was introduced back in the 1990s and has its popularity growing ever since. When analyzing this approach as a classifier, it can be understood as a generalization of an intuitive concept of the maximal margin classifier”. As a classifier, the most common use terminology is support vector machine (SVM). In summary, the SVM method tries to find the best hyperplane to separate groups based on the maximum error we are willing to accept its margins and certain degrees of freedom. This method sometimes might require changes in remapping the data entry into higher space dimensions. Morettin and Singer [31] described that, in the case of linear functions, in which the goal was to determine α and β in which f X i = α + β T X i ≤ ϵ + ξ i . ϵ was considered the total acceptable error and ξ represent a certain degree of freedom that can be added to the model. Adding the contact C as a positive figure means a commitment to flattening the function. Considering a linear model, the function to define a prediction for a register with predictor variables is given by a vector X 0 . In this formula, a ^ is equal to y i − ε − β ^ T X i , with ∑ i = 1 n λ ^ i X i . Finally, the other components are: λ ^ i as a Lagrange multiplier, and K X 0 , X i as a Kernel [31]. Although complex, the model can be easily applied using Scikit learn algorithm [41], and are summarized in Equations 8 and 9.
m i n i m i z e   1 2 β 2 + ∑ i = 1 n C ξ + ξ *   s u b j e c t   t o   Y i − β T X i − α ≤   ϵ + ξ i   α + β T X i − Y i   ≤   ϵ + ξ i *
f X 0 = ∑ i = 1 n λ ^ i K X 0 , X i + a ^
One might ponder that the final model considered in this study is the least evident of all others discussed so far. The method, Multi-Layer Perceptron (MLP), was named as such based on the human brain structure concept [31]. In brief, the brain can be considered a three-dimensional pack of neurons. Each neuron receives input signals from other neurons in its surroundings through its dendrites and then processes them based on its own manner, issuing later through its axons output signals for other neurons. In 1958, Rosenblatt introduced the concept of the perceptron as a new for supervised learning [31]. Basically, the perceptron would be a parallel of the neuron, receiving inputs which a later process by it based on an activation function. With respect to this last point, several functions can be considered. Although very interesting, discussions regarding each type of activation function impact fall out of the scope of this work. Once added into a layer with other perceptron and later packed with other layers, the model runs an exercise to balance layers based on the batch of the predictor variable, in an effort to the define the weights of each perceptron activation based in the inputs of their input layers. Therefore, one might point out that the main parameters to be investigated within this method are: the number of layers, perceptrons per layer, and, finally, the number of training sessions. [42].
Each regression model applied here has its own strengths and weaknesses, and the choice of model depends on the characteristics of the data and the specific goals of the analysis. What is key to point out is that understanding these models and their parameters may enhance the quality of the predictive models and make more informed interpretations of the results.

2.3. Database Split and Model Accuracy Measurement

There might be no dissenters to the view that one should always need to quantify the quality of a certain model prediction. On the other hand, as mentioned by James et al. [30], some researchers have disregarded a more modern concept with regard to this crucial issue. For instance, previous projects have largely overlooked the general concept of Mean Square Error (MSE) as presented in the Equation 10 below. In this formula, the MSE will be smaller as the MSE gets closer to the n” true responses in the training data set.
M S E = 1 n ∑ i = 1 n ( Y i − Y ^ i ) 2
Most statistical learning scholars seem to agree [30] that this can led to the wrong assumption about the model quality. For instance, one might understand the smallest MSE as the most precise model, without understanding that this analysis does reference only the training dataset. James et al [30] are explicit in their work that the best way to determine a given model accuracy is to analyze its predicted values in comparison to previously unseen test data. In this context, one should use [30] calculating the average squared prediction error for the test true response.
M S E = A v e r a g e   ( Y i − Y ^ i ) 2 ,
where Y i is the real predictor variable of the register i of the test data set, and Y ^ i is the given predicted value based on the register attributes.
Figure 3 illustrates the concept of the overfitting occurrence, where the increase in the flexibility of the models applied managed to increase the training MSE calculation, whereas decreasing the test MSE prediction accuracy. In the current study, the method to create unseen” data for the trained model was based on the sklearn.model_selection.train_test_split” using a 80% training / 20% test ratio [43]. The data was also prepared in terms of standardization [44], which shall be explained after the analysis shown in the next Section. Finally, each model prediction was evaluated using the Scikit Learn score method [45], which uses the test MSE formula, scaling the number versus the maximum error possible, i.e., normalizing the figure between 0 to 1. All details considered, the overview of all the methods and process within were summarized in the workflow in Figure 4.

3. Results and Discussion

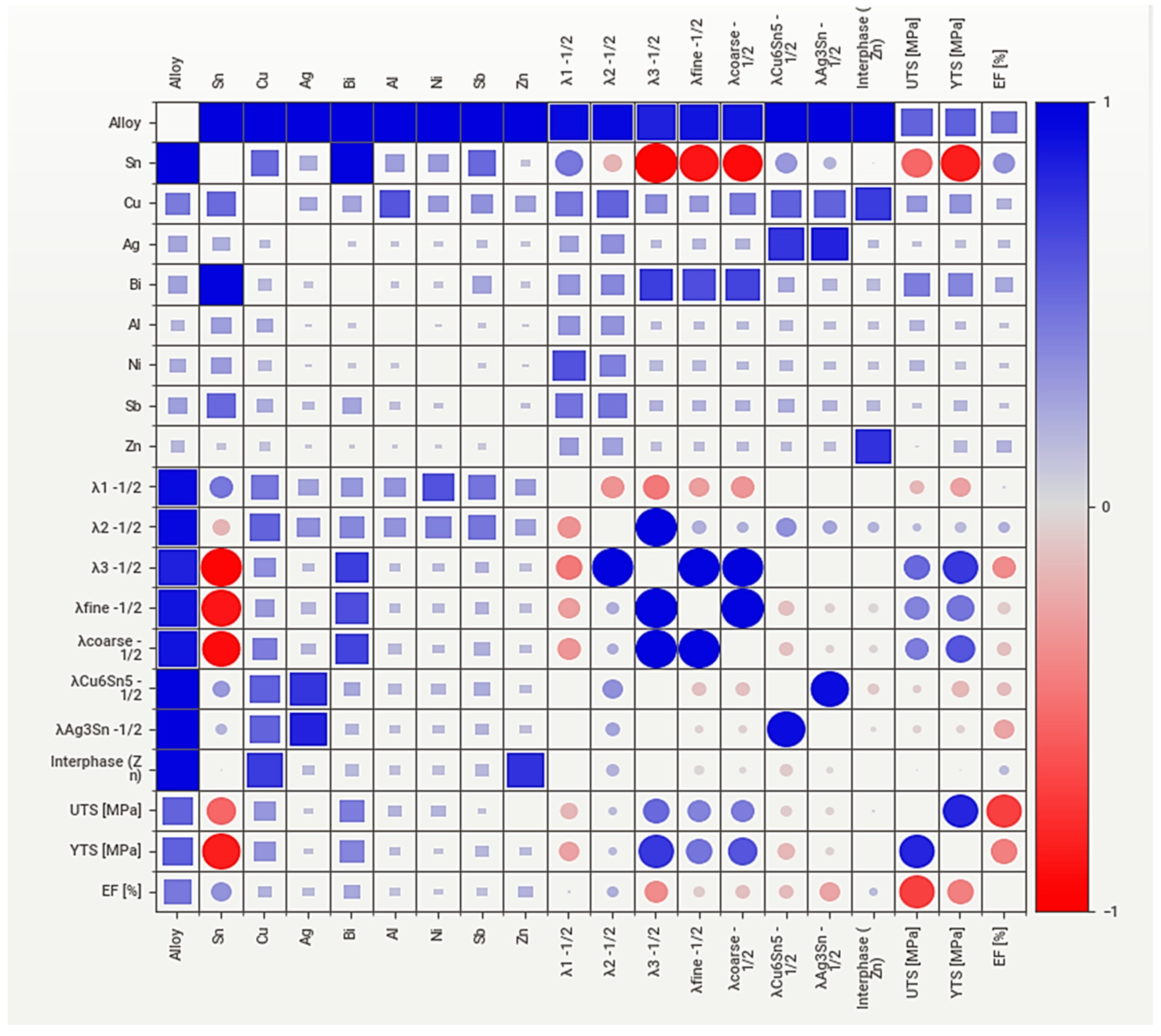
3.1. Database Exploratory Analysis

Once the database was finalized, Python [46] was used to investigate its main characteristics. Table 2 shows the 5 first registers of a certain pandas’ data frame” (denominated here by DF) [10] created object. In summary, each register as shown in the DF index relates to a certain composition (given by the amount of the elements) alloy, which had its microstructure determined through metallographic measurements (as per a variety of λ spacing columns) and its tested tensile properties (final 3 columns). The final database shape had 735 registers within 20 columns. However, in Table 2 is already possible to notice that some attributes were added NaN”. As mentioned, most of these registers were extracted based on single correlation plots for a specific alloy composition. Although not available, this reference could not be set to zero, as this could lead the models to a wrong definition.
To put it in another way, a parallel thinking can be done based on Figure 5, where a grey puzzle has one missing piece, which turns out to be blue. Considering for a moment that the available data in the report was the grey puzzles, while the missing blue piece was not available, one could easily argue that the missing piece’s color should be grey as well. If it is possible to guess” the missing information, this could lead to a wrong modeling of the process, as the missing information is also a piece of information to be used for a variable prediction. Therefore, in cases that the missing information could be reasonably supposed”, such as setting to zero Cu6Sn5 spacing, this was adopted indeed. On the other hand, the NaN” figure replacement was set as one key parameter to understand its impact on the final model accuracy.
To begin with the attribute relations, evaluating the many relationships each alloy component has with the tensile properties may arouse some curiosity about each attribute impacting these numbers. A fascinating way to indicate this is based on an association/correlation matrix, such as that in Figure 6. This matrix was based on the Sweetviz package association function, which shows circles for symmetrical numerical correlations from -1 to 1, whereas squares are added to indicate categorical associations from 0 to 1. In this sense, one point to be highlighted is the correlation for the microstructural parameters. For sure, one might argue that this is straightforward, as these should be fundamentally based on the local solidification rates occurring during the phase growth. Anyway, it is still interesting to notice some correlation among different length-scale parameters such as: tertiary dendrite arm spacing, fine/coarse eutectic lamellar spacing, and the Cu6Sn5 and Ag3Sn intermetallic spacing values.
On top of this, for sure the most noteworthy points should be placed in the last three columns/lines in Table 2. When analyzing the UTS and YTS, the most relevant impacting features according to the specialized literature are related to the tertiary dendrite arm and eutectic spacing values [48], as well as the categorical relations of Cu and Bi. However, it is fair to argue that part of this stronger relation might come from the higher number of available compositions data. Finally, the Sn content, which is available in all registers shows a strong negative correlation with these tensile properties. This aspect shows that this analysis might indirectly capture theoretical concepts, for instance, the solute alloying impact on the crystalline structure, and increase in the resistance for the dislocation to move through the slip planes during loading [49]. With regards to the EF, the hypothesis that EF and UTS/YTS do not behave in similar ways might be confirmed by noticing the different results comparing EF and UTS rows. Key aspects to underline are primary dendrite arm spacing positive relation, similar to those for Sn, Cu, Zn, and Bi categorical relations. Taking these reflections under consideration, Bi alloying shows a very good balance with the increase in tensile strength without a negative impact on ductility, which can be seen as a suitable behavior.

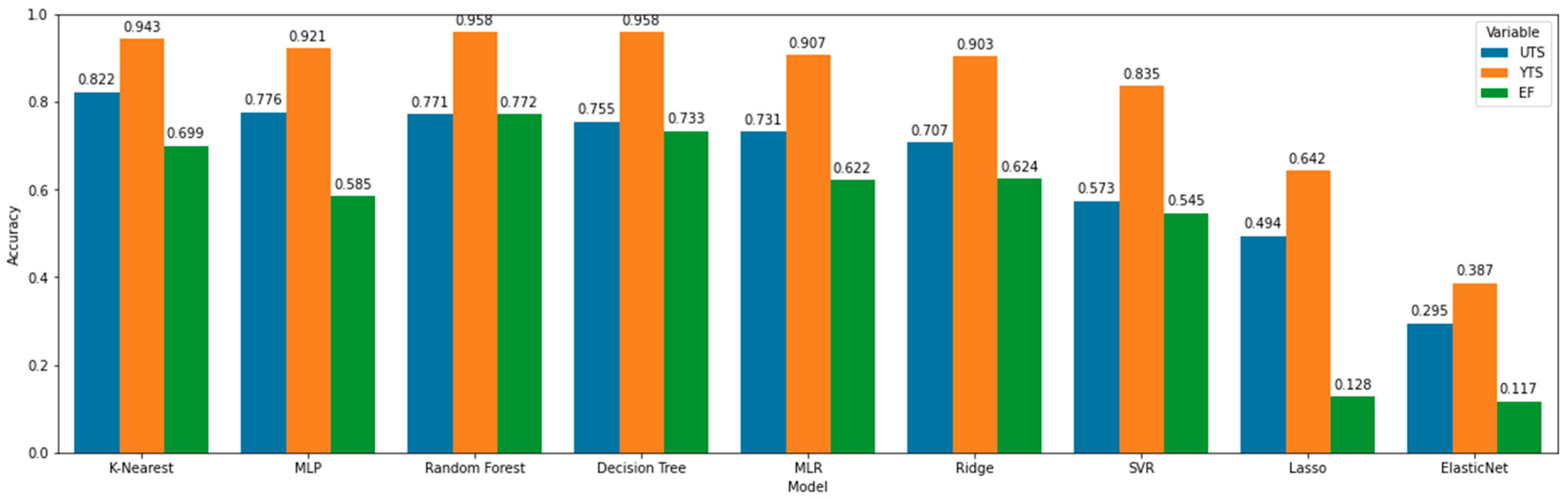
3.2. A First Glance in the Predictive Models’ Application

As mentioned before, the fulfillment of the missing pieces” of the collected information could play a major role in the accurate definition of the models. The results shown in Figure 7 demonstrate how the NaN” fulfillment parameter would influence differently each model. All mentioned models were applied for the database considering UTS as the value to be predicted using different arbitrary NaN” fulfillment parameters. Before deep diving into which model had the best results, it is important noting that this single value definition can change for instance the MLR accuracy from 0.4 to 0.73, almost doubling it. Apart from this last parameter, all other models’ parameters were kept as the standard ones proposed in the Scikit Learn [50]
Another key point to highlight was that this parameter variation had a similar impact on the same family” models. For example, all traditional” regression models show the same pattern of increasing the accuracy to a peak at NA filled” equal to 2.0”, and then reducing till the highest parameter value. The same family model similarity is noticed by analyzing the Decision tree and Random Forest results, which in these cases had the highest accuracies for 0” and 0.5” insertions. The reason behind this probably varies based on the characteristic of each model. For instance, one may argue that when the inserted values become too large, it does not influence the tree” division models. Therefore, these may be values as low as possible to avoid impact on how the model uses these attributes. On the other hand, for the regression models, the peak accuracy related to the 2.0” NA might mean that, at first, the increase helps the regression to differentiate this information from the given 0.0” in the database. However, as the NaN parameters get bigger, it influences the standardization in a way it might get the actual attributes compacted, impacting the coefficient calculation and, therefore, the accuracy.
Figure 8 consolidates is a single plot all the highest accuracies achieved by each model for each predictive variable. It is also significant the fact the fixed accuracy relation shows YTS > UTS > EF”. One hypothesis that could be used as an explanation is related to the own metallurgical concept of each variable. The yield strength, as the first” phenomenon related to edge movement start [49] during the tensile test, is maybe the simplest” tensile parameter to determine and may be more related to the microstructural characteristics (given by attributes). Although UTS and EF also have significant dependencies on the alloy/microstructure attributes, those might not be the only ones to influence them. For instance, the sample machining quality and random cracks can ease up both necks start during tensile tests as well as crack propagation, engendering a more random factor” that was not captured by the attributes in the database. All things considered, it is possible to notice that a standard predictive model application on a crafted” database built upon research available data had interesting results, which could support the scientific evolution of this challenge in materials engineering.

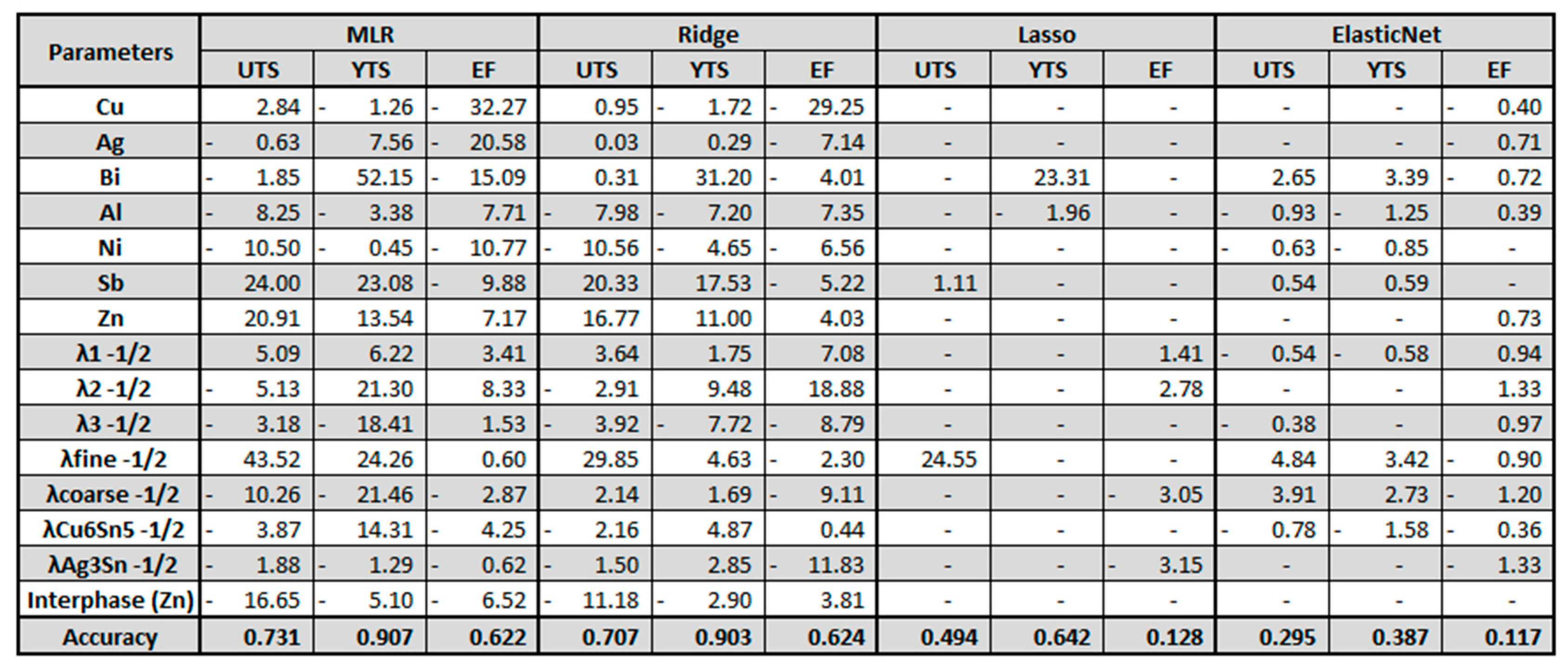
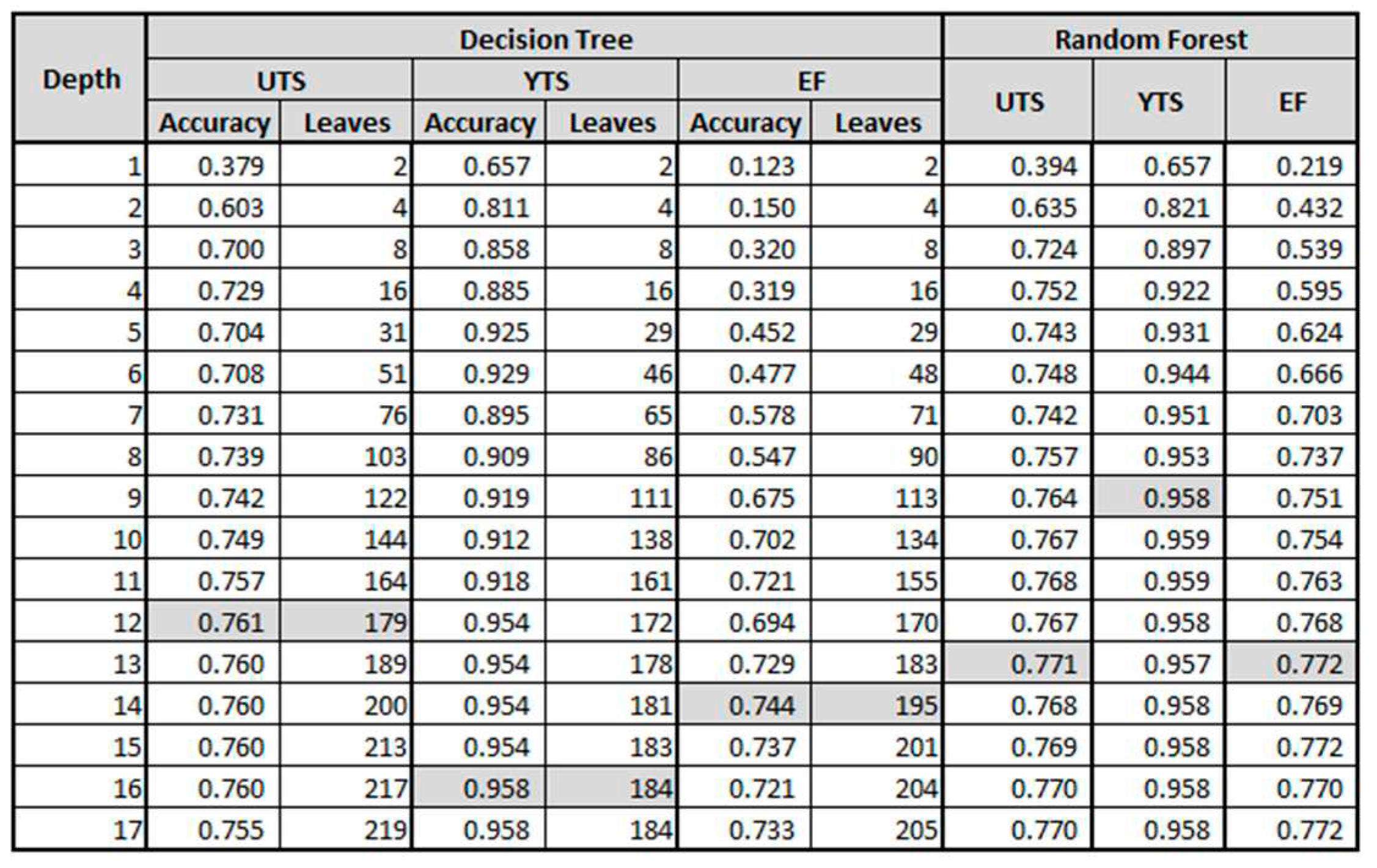
3.3. Deep Diving into Each Predictive Model Group

In the analysis of the linear regression models for predicting tensile properties in alloy systems, the coefficients obtained for the MLR, Ridge, Lasso, and ElasticNet models reveal some key insights, as can be seen in Table 3. In particular, the presence of "zeros" in the Lasso and ElasticNet columns indicates that these models effectively penalize certain coefficients to avoid overfitting. However, this penalization strategy negatively affects the overall accuracy of the models, suggesting that no parameter should be disregarded entirely. This, somehow, accounts for a very general and beneficial metallurgists’ perception that even small details might matter for the final tensile properties. Additionally, a comparison between MLR and Ridge models shows a reduction in overall coefficient values from MLR to Ridge, which can be a sign of the penalization method.
For sure, some comparisons using the metallurgical concepts can be performed. This is one of the key reasons why researchers prefer linear models over MLP, for example, because the relationships are more obvious. However, this would tremendously increase the overall description of results within this article. In any case, for the ones basing their analysis with this information, it is important to bear in mind the accuracy that each formula presented. Moreover, the key point to consider within this analysis is that any of the methodologies presented to increase accuracy through the overall overfitting reduction when compared to the traditional MLR model.
Surprisingly, the sometimes here mentioned spatial” models showed a very consistently better performance than the other models. The only exception was in the case of the UTS-related results, where MLP had a higher accuracy value than Random Forest and Decision Tree. In any case, these two also presented the highest accuracy figures comparing with the standard models’ setup, with an outstanding 0.958”. Even though this was a good result, this might also indicate a problem concerning the database itself. For instance, one might argue that there is not a broad distribution of the measured properties (e.g., from 14 MPa to 60 MPa for YTS) on top of a small number of registers (YTS with only 232 registers). On the other hand, one might argue that this was the modeling concept that had the best fit considering a behavior that has only discrete variations based on each attribute and, therefore, the closest references are reasonable estimators.
In any case, another question that may be considered when analyzing the KNN model is the number of neighbors that might lead to the best possible fit. Based on the Scikit KNN model description [37], the standard configuration was set to having N equal to 5. Table 4 shows a ceteris paribus analysis considering the highest NaN fulfillment. As it can be perceived, all models found even a small change in their accuracy. The most significant variations ended up with EF and YTS variables, which smaller number of neighbors enabling better predictions.
Interestingly, KNN is not the only model that has such a key parameter to be explored. Among all the important inputs for the Decision Tree [38] and Random Forest [39] models, one of the most impactful is the tree depth limitation. In order to this parameter become more visual, one might consider analyzing the tree shown in Figure 9. The given figure is the UTS model tree resulting from the fit using the standard setup, which has no depth limitation. In this case, the tree has a depth of 17”, counting 219” leaves. Concerning the depth parameter, it defines the limit for the lower side of the model ramification. Table 5 demonstrates the accuracy values obtained by limiting the depth size into these models. It is interesting to notice that the highest accuracy was not necessarily obtained for the highest depths.
As formerly explained, the support vector regression model can be understood as a generalization of the maximal margin classifier” concept. This method simply tries to find the best hyperplane for different groups based on the maximum accepted error in its margins, also based on some degrees of freedom. Also, it was mentioned that this method sometimes might require changes in remapping the data entry into higher space dimensions. Based only on this explanation, it is easy to notice that the SVR method would certainly present several parameters to deal with. The most interesting as described in the Scikit Learn [41] package remains the Kernel type (which can be set as linear”, poly”, rbf”, and sigmoid”), the degree of the polynomial kernel function, the regularization parameter C (which must be a positive figure) and the epsilon (which specifies the epsilon-tube within which no penalty is associated in the training loss function). The Scikit Learn model [41] has a set of predefined parameters which are based on a rbf” Kernel, therefore ignoring the polynomial degree, with an epsilon equal to 0.1” and a C parameter equal to 1.0”.
The SVR was always appearing on the lower performer side by using the standard setup, as can be seen in Figure 10. However, such is the impact the parameters might have in the overall accuracy, that even exploring only the kernel function could already lead to a considerable accuracy increase, putting it over the range of the highest accuracy models. Even though all kernel functions respective accuracies grew to a certain extent, the one that achieved the highest value in all cases was the rbf” one. Concerning the polynomial degree, a figure equivalent to 9” was the one that lead to the most optimized result. Finally, the highest values were found by using a C equal to 90”, while epsilon was set to a value of 5”.
The MLP is not only the most currently popular concept but also the one with the widest range of parameters. For instance, based on the Scikit learn model [42], one might cite: the number of elements per layer (positive figure), the number of layers (positive figure), the perceptron activation formula (ReLu”, ’ identity”, tanh” or logistic”), the solver for weight optimization (lbfgs”, sgd” or adam”), the batch size (positive figure), the learning rate scheduled for weight updates (constant”, invscaling” or adaptive”), the learning rate initialization value (positive figure) and the number of maximum iterations (positive number).
Although a very systematic variation of these parameters would be the most recommended way to find the best optimized set of parameters, the processing computer set up some limitations for a very first deep investigation using this model. Anyway, loop was generated to investigate a group of predefined parameters based on evidences from several empirical testing. The main parameters analyzed were the perceptron activation for identity” and ReLu”, the solver using lbfgs” and sgd, the learning rate scheduler as invscaling” and adaptative”, as well a maximum interaction of 200 and 3000. Such empirical clarifications also leaded to a usage for higher initial learning rate, such as 0.1”. Figure 11 shows the highest accuracy values found in comparison with the ones formerly presented, based on the standard parameters, whereas Table 6 shows the adopted parameters that led to the optimized accuracy values. Finally, in order to illustrate actual predictions from these models, Table 7 depicts different test data the given predicted values. The small difference analyzing different data demonstrate the overall positive perception associated with the models.

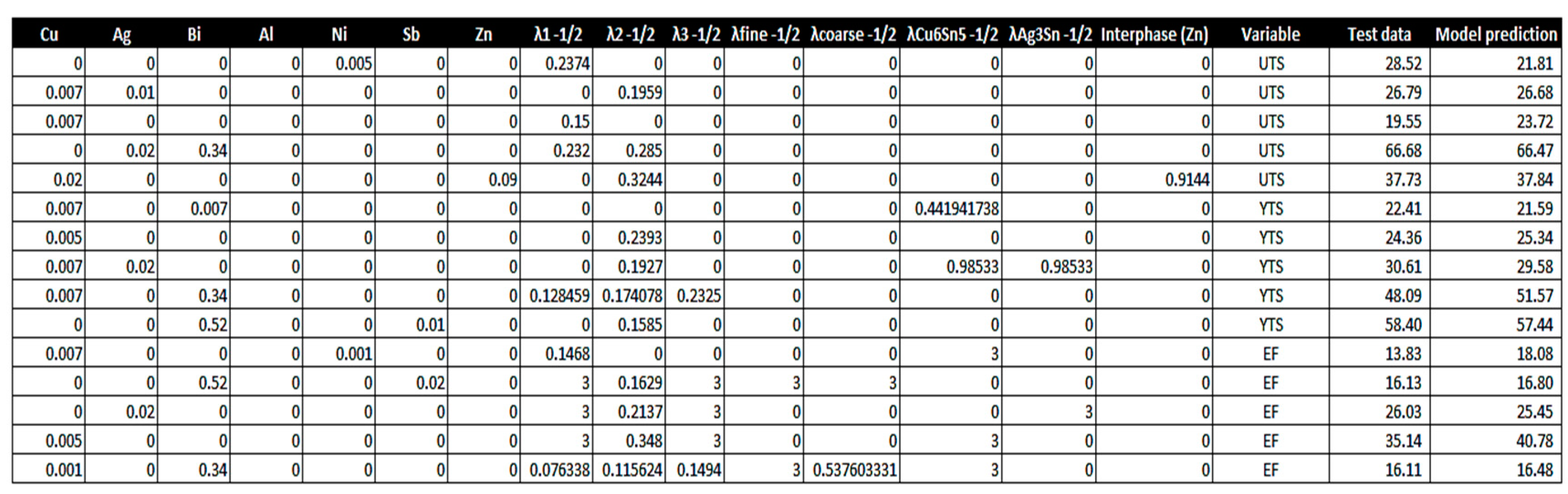
3.4. Final Models Outcome and Alloy Design Application

Finally, with the alloy design goal in mind, these high-accuracy models were applied to an exploratory” database, which had several values within the maximum and minimum ranges of the training database. Based on that, one might be able to determine the set of attributes that have the highest prediction for each variable. These findings are shown in Table 8 and can be used to indicate tendencies that should be further investigated. The most interesting ones are related to the possible improved UTS values based on the addition of Ag and Sb alloying elements, as well as the interesting YTS trends for Bi-containing alloys with Sb additions.

4. Conclusions

Throughout the present alloy design based on applying data science concepts and models in a more systematic fashion for solder alloys, the following conclusions could be drawn:
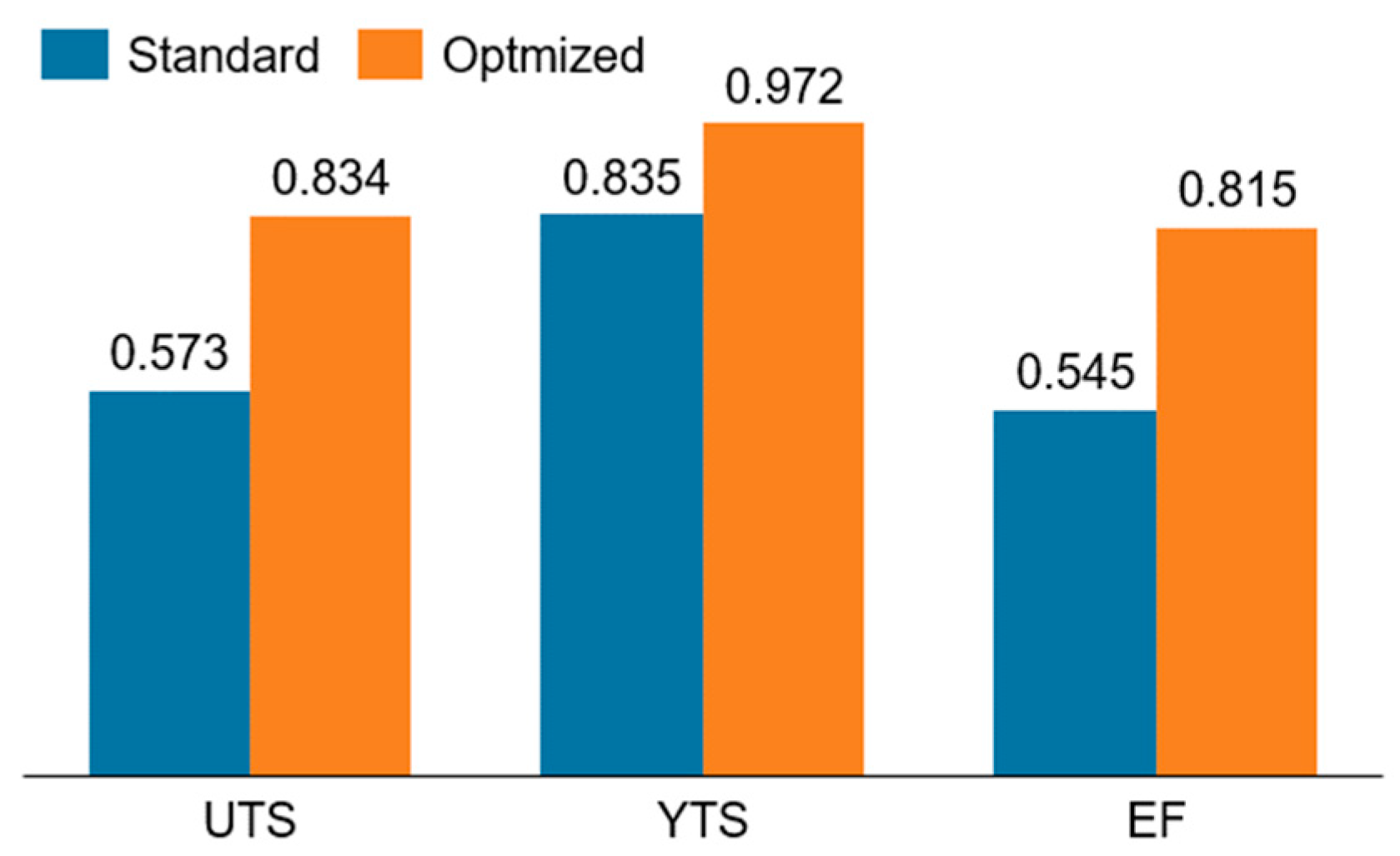
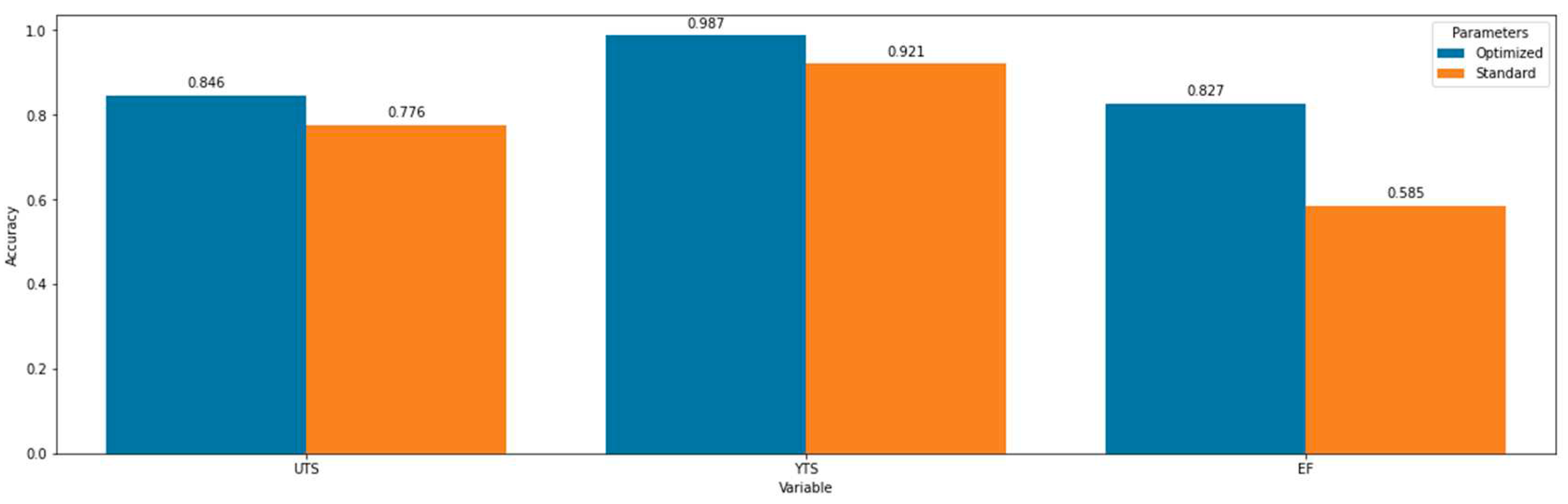
  • Although all MLP-optimized models became the best performance found for each variable, the highest increases were related to the YTS and EF. While the first case might be highlighted because of the high accuracy value found, the EF accuracy showed an increase of 0.242, attaining 0.827. This evolution placed the EF predictions in a comparable scenario to the UTS ones, which was first indicated to be a more suitable case.
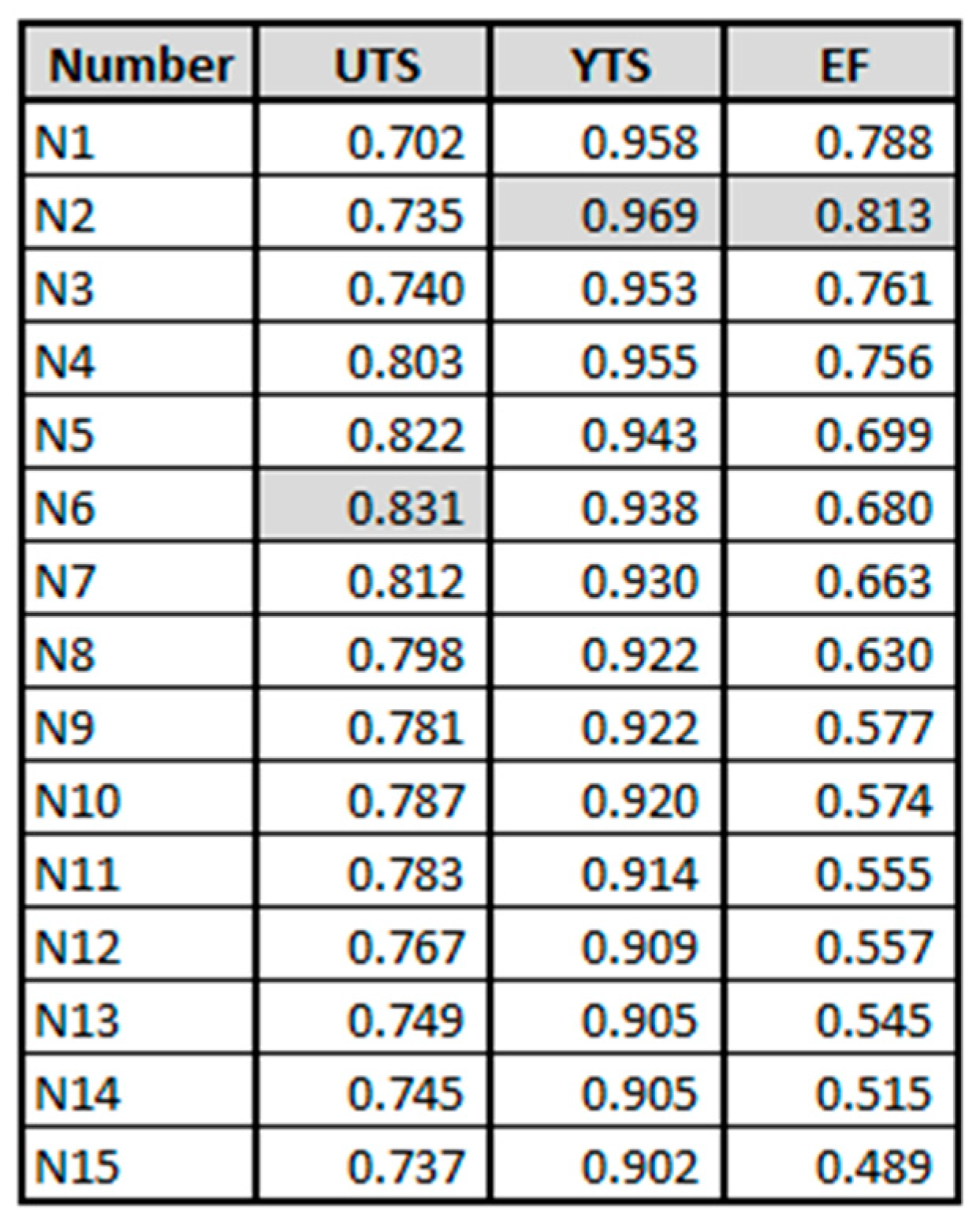
  • The KNN-optimized model results were also satisfactory and could be improved from 0.943 to 0.969 for YTS and from 0.699 to 0.813 for EF, with higher performance for smaller number of neighbors.
  • It was noted that the alloy design predictions shall not be perfect, but they can be used for sure to indicate a trend. In this sense, the most interesting ones were related to the possible improved UTS based on the Ag and Sb additions, as well as the interesting YTS trends related to Bi-containing alloys modified with Sb.
  • Although results could be considered positive, a future study could deep dive into the phase fraction relations of the alloys and investigate a way to enhance the geometrical/spatial” relation behind the attributes. For example, one could use the theoretical models to estimate the non-equilibrium phase fractions forming the alloy microstructures.

Author Contributions

Conceptualization, V.C.E.S., J.E.S, V.L.D.T.; methodology, V.C.E.S., J.E.S, V.L.D.T., B.L.S.; formal analysis, V.C.E.S., V.L.D.T.; investigation, V.C.E.S.; resources, J.E.S, V.L.D.T.; data curation, B.L.S., G.G., V.C.E.S.; writing, V.C.E.S., J.E.S; writing—review and editing, V.C.E.S., J.E.S; visualization, V.C.E.S.; supervision, V.L.D.T.; project administration, V.C.E.S. V.L.D.T.; funding acquisition, J.E.S.

Data Availability Statement

All the data used in the analysis are available within the link: https://docs.google.com/spreadsheets/d/1rjcBGvZryca1KQFpEArwlRPAKzA0hqqT/edit?usp=sharing&ouid=106630229905855410714&rtpof=true&sd=true

Acknowledgments

The authors acknowledge FAPESP (grants #2019/23673-7 and #2021/08436-9) and CNPq. This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001.

Conflicts of Interest

The authors declare no conflict of interest.”

References

  1. 1. G. E. Moore, Progress In Digital Integrated Electronics. IEDM Tech. Digest.
  2. Thompson, S.E.; Parthasarathy, E.S. Moore’s law: The future of Si microelectronics. Materials Today 2006, 9, 20–25. [Google Scholar] [CrossRef]
  3. KRazeeb, M.; Dalton, E.; Cross, G.L.W.; Robinson, A.J. Present and future thermal interface materials for electronic devices. International Materials Reviews 2018, 63, 1–21. [Google Scholar] [CrossRef]
  4. Sarvar, F.; Whalley, D.; Conway, E. Thermal Interface Materials - A Review of the State of the Art. 1st Electronic Systemintegration Technology Conference, 1292. [Google Scholar]
  5. Schon, A.F.; Castro, N.A.; Barros, A.D.S.; Spinelli, J.E.; Garcia, A.; Silva, N.C. Multiple linear regression approach to predict tensile properties of Sn-Ag-Cu (SAC) alloys. Materials Letters 2021, 304, 130587. [Google Scholar] [CrossRef]
  6. Jiang, N.; Zhang, L.; Gao, L.-L.; Song, X.-G. Recent advances on SnBi low-temperature solder for electronic interconnections. J Mater Sci: Mater Electron 2021, 32, 22731–22759. [Google Scholar] [CrossRef]
  7. Skuriat, R.; Li, J.; Agyakwa, N.; Johnson, C. Degradation of thermal interface materials for high-temperature power electronics applications. Microelectronics Reliability 2013, 53, 1933–1942. [Google Scholar] [CrossRef]
  8. Garcia, A. Solidificação: Fundamentos e Aplicações, Editora Unicamp, 2007.
  9. Callister, W.D.; Rethwisch, E.D.G. Materials Science and Engineering: An Introduction, Wiley, 2013.
  10. Pandas Pydata, pandas DataFrame. Available online: https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.html (accessed on 21 Dcember 2022).
  11. PyPI, SweetViz. PyPI. Available online: https://pypi.org/project/sweetviz/ (accessed on 21 Dcember 2023).
  12. Schon, A.F.; Reyes, R.V.; Spinelli, J.E.; Garcia, A.; Silva, B.L. Assessing microstructure and mechanical behavior changes in a Sn-Sb solder alloy induced by cooling rate. J Alloys Compd 2019, 809, 151780. [Google Scholar] [CrossRef]
  13. Dias, M.; Costa, T.A.; Rocha, O.F.L.; Spinelli, J.; Cheung, N.; Garcia, A. Interconnection of thermal parameters, microstructure and mechanical properties in directionally solidified Sn-Sb lead-free solder alloys. Materials Characterization 2015, 106, 52–61. [Google Scholar] [CrossRef]
  14. Dias, M.; Costa, T.A.; Silva, B.; Spinelli, J.; Cheung, N.; Garcia, A. A comparative analysis of microstructural features, tensile properties and wettability of hypoperitectic and peritectic Sn-Sb solder alloys. Microelectronics Reliability 2018, 81, 150–158. [Google Scholar] [CrossRef]
  15. Silva, B.L.; Silva, V.C.E.D.; Garcia, A.; Spinelli, J.E. Effects of solidification thermal parameters on microstructure and mechanical properties of Sn-Bi solder alloys. Journal of Electronic Materials 2017, 46, 1754–1769. [Google Scholar] [CrossRef]
  16. Osório, W.R.; Peixoto, L.C.; Garcia, L.R.; Mangelinck-Noël, N.; Garcia, A. Microstructure and mechanical properties of Sn–Bi, Sn–Ag and Sn–Zn lead-free solder alloys. Journal of Alloys and Compounds 2013, 572, 97–106. [Google Scholar] [CrossRef]
  17. Soares, T.; Gouveia, G.L.; Septimio, U.S.; Cruz, C.B.; Silva, B.; Brito, C.; Spinelli, J.; Cheung, N. Sn-0.5Cu(-x)Al solder alloys: microstructure-related aspects and tensile properties responses. Metals 2019, 9, 241–241. [Google Scholar]
  18. Silva, B.L.; Cheung, N.; Garcia, A.; Spinelli, J.E. Sn–0.7wt%Cu–(xNi) alloys: Microstructure–mechanical properties correlations with solder/substrate interfacial heat transfer coefficient. Journal of Alloys and Compounds 2015, 632, 274–285. [Google Scholar] [CrossRef]
  19. Hu, X.; Chen, W.; Wu, B.; Hu, X.; Chen, W.; Wu, B. Materials Science and Engineering: A 2012, 556, 816-823.
  20. Spinelli, J.E.; Garcia, A. Microstructural development and mechanical properties of hypereutectic Sn–Cu solderalloys. Microstructural development and mechanical properties of hypereutectic Sn–Cu solderalloys 2013, 568, 195–201. [Google Scholar] [CrossRef]
  21. Cruz, C.B.; Kakitani, R.; Silva, B.; Xavier, M.G.C.; Garcia, A.; Cheung, N.; Spinelli, J. Transient Unidirectional Solidification, Microstructure and Intermetallics in Sn-Ni Alloys. Materials Research 2018, 21, 2018. [Google Scholar] [CrossRef]
  22. Osório, W.R.; Leiva, D.R.; Peixoto, L.C.; Garcia, L.R.; Garcia, A. Mechanical properties of Sn–Ag lead-free solder alloys based on the dendritic array and Ag3Sn morphology. Journal of Alloys and Compounds 2013, 562, 194–204. [Google Scholar] [CrossRef]
  23. Garcia, L.R.; Osório, W.R.; Peixoto, L.C.; Garcia, A. Mechanical properties of Sn–Zn lead-free solder alloys based on the microstructure array. Mechanical 2010, 61, 212–220. [Google Scholar] [CrossRef]
  24. Ramos, L.; Reyes, R.V.; Gomes, L.F.; Garcia, A.; Spinelli, J.; Silva, B. The role of eutectic colonies in the tensile properties of a Sn-Zn eutectic solder alloy. Materials Science and Engineering A 2020, 776, 138959. [Google Scholar] [CrossRef]
  25. Dias, M.; Costa, T.A.; Soares, T.; Silva, B.L.; Cheung, N.; Spinelli, J.E.; Garcia, A. Tailoring Morphology and Size of Microstructure and Tensile Properties of Sn-5.5 wt.%Sb-1 wt.%(Cu,Ag) Solder Alloys. Journal of Electronic Materials 2018, 47, 1647–1657. [Google Scholar] [CrossRef]
  26. Silva, B.; Xavier, M.G.C.; Garcia, A.; Spinelli, J. Cu and Ag additions affecting the solidification microstructure and tensile properties of Sn-Bi lead-free solder alloys. Materials Science and Engineering A 2017, 705, 325–334. [Google Scholar] [CrossRef]
  27. Hu, X.; Li, K.; Min, Z. Microstructure evolution and mechanical properties of Sn0.7Cu0.7Bi lead-free solders produced by directional solidification. Journal of Alloys and Compounds 2013, 566, 239–245. [Google Scholar] [CrossRef]
  28. Spinelli, J.E.; Silva, B.L.; Garcia, A. Assessment of Tertiary Dendritic Growth and Its Effects on Mechanical Properties of Directionally Solidified Sn-0.7Cu-xAg Solder Alloys. J. Electron. Mater 2014, 43, 1347–1361. [Google Scholar] [CrossRef]
  29. Silva, B.L.; Spinelli, J.E. Correlations of microstructure and mechanical properties of the ternary Sn-9wt%Zn-2wt%Cu solder alloy. Materials Research 2018, 21, e20170877. [Google Scholar] [CrossRef]
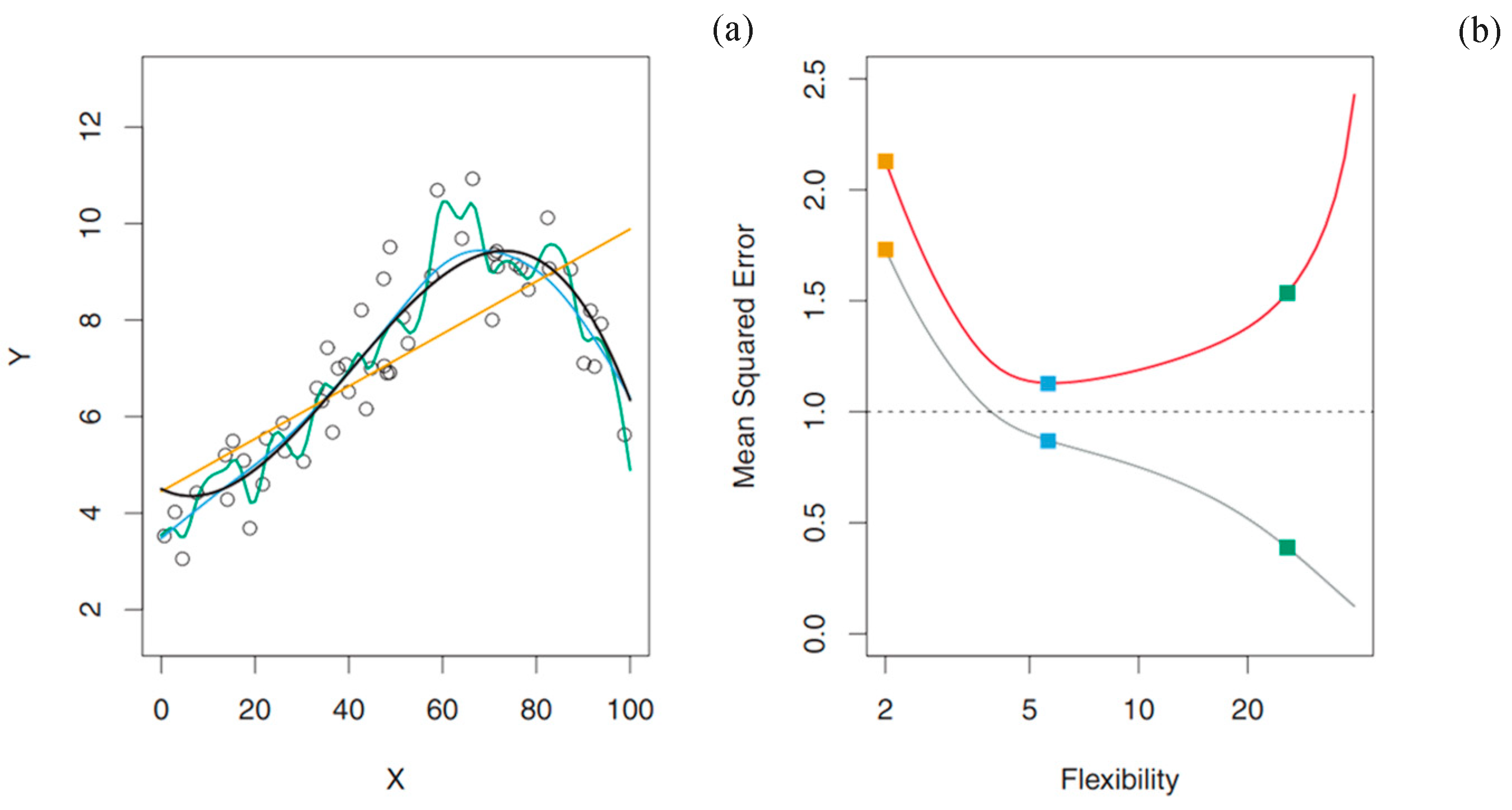
  30. James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning with Applications in R, New York: Springer, 2013.
  31. Morettin, A.; Singer, J.M. Estatística e Ciência de Dados - Versão Preliminar, São Paulo, 2021.
  32. Scikit Learn, sklearn.linear_model.LinearRegression. Scikit Leanr. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html# (accessed on 21 May 2023).
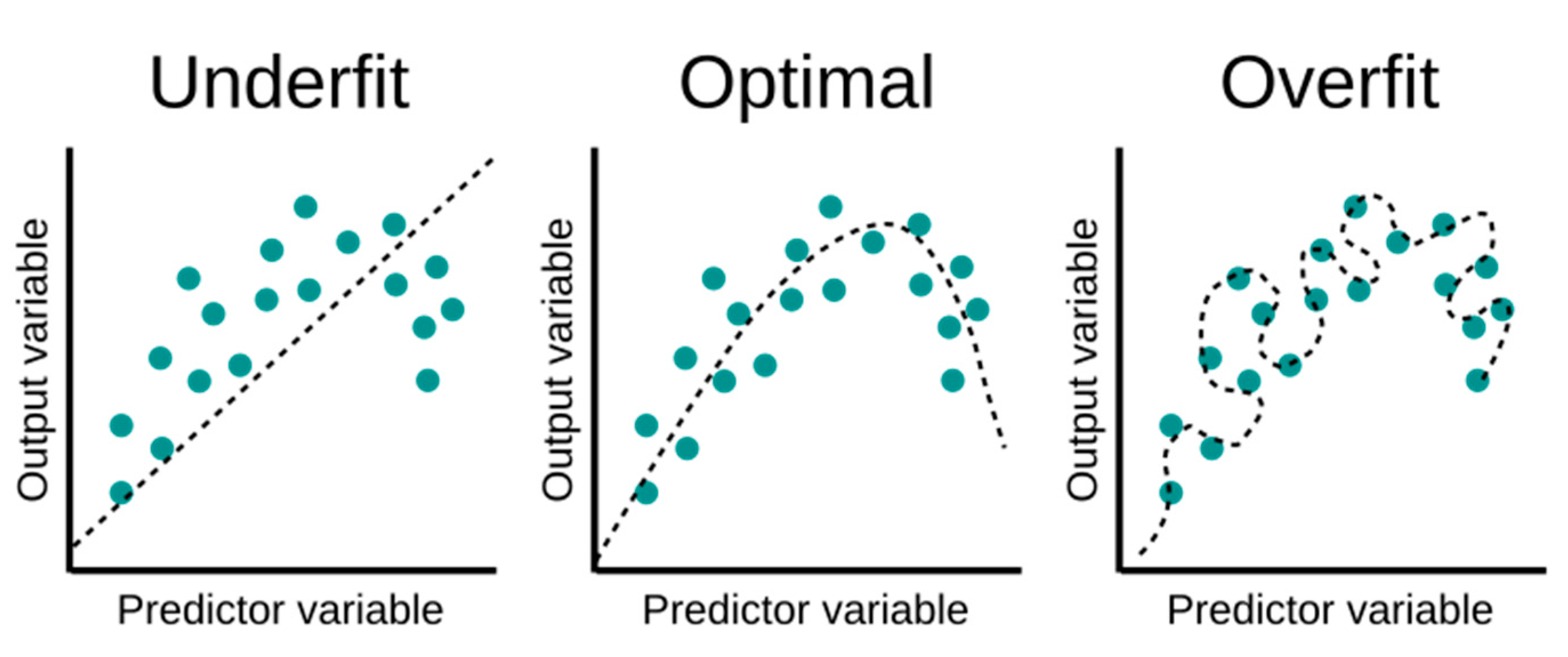
  33. Educative, Inc, Educative.io. Educative, Inc. Available online: https://www.educative.io/answers/overfitting-and-underfitting (accessed on 1 October 2022).
  34. Scikit Learn, sklearn.linear_model.Ridge. Scikit Learn. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Ridge.html (accessed on 21 May 2023).
  35. Scikit Learn, sklearn.linear_model.Lasso. Scikit Learn. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Lasso.html (accessed on 21 May 2023).
  36. Scikit Learn, sklearn.linear_model.ElasticNet. Scikit Learn. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.ElasticNet.html (accessed on 21 May 2023).
  37. Scikit Learn, sklearn.neighbors.KNeighborsRegressor. Scikit Learn. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsRegressor.html (accessed on 1 October 2022).
  38. Scikit Learn, sklearn.tree.DecisionTreeRegressor. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeRegressor.html#sklearn.tree.DecisionTreeRegressor (accessed on 13 January 2023).
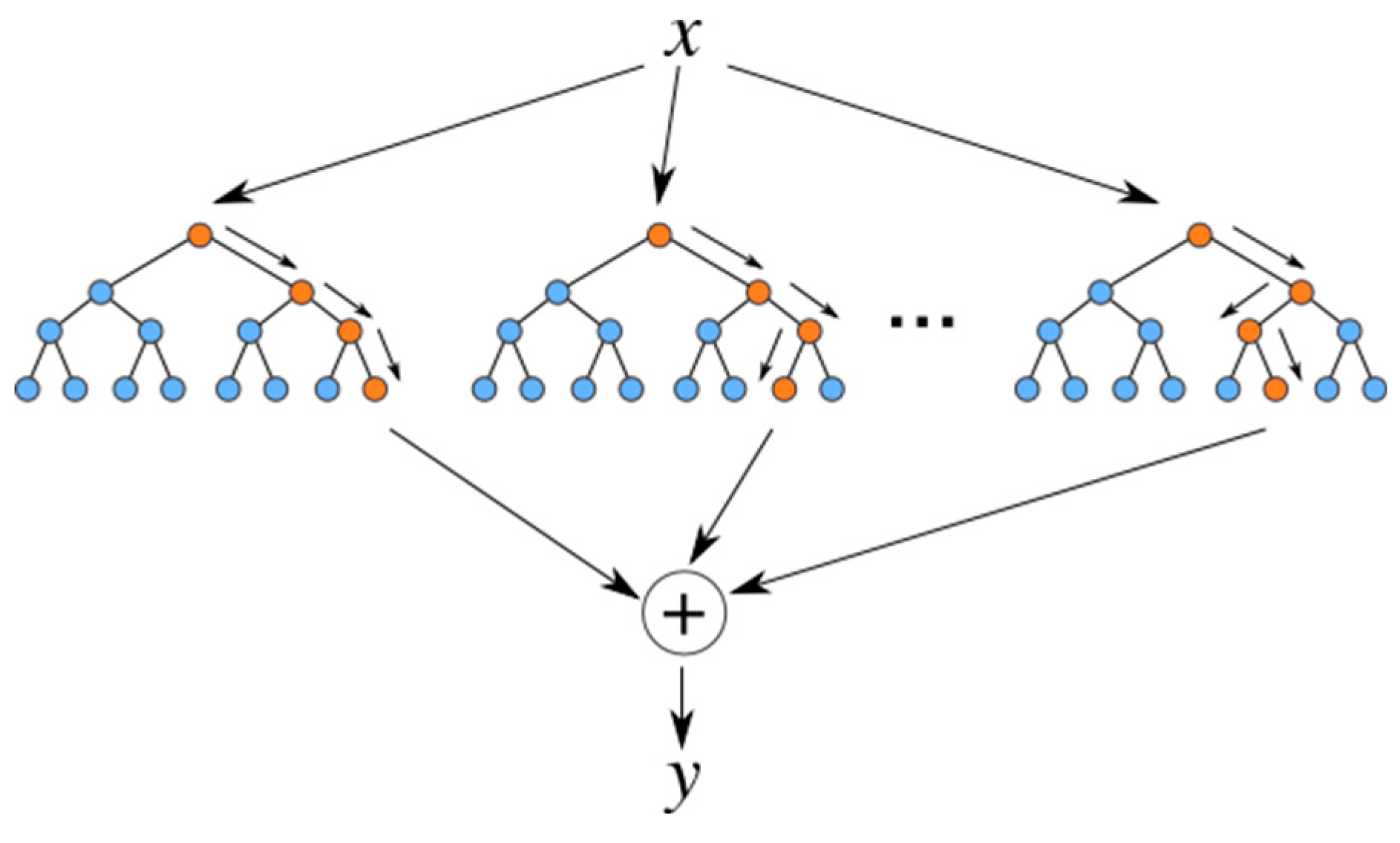
  39. Scikit Learn, sklearn.ensemble.RandomForestRegressor. Available online: https://sklearn.ensemble.RandomForestRegressor (accessed on 13 January 2023).
  40. Bakshi, C.; Random Forest Regression. Levelup.gitconnected. Available online: https://levelup.gitconnected.com/random-forest-regression-209c0f354c84 (accessed on 1 October 2022).
  41. Scikit Learn, sklearn.svm.SVR. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVR.html (accessed on 13 January 2023).
  42. Scikit Learn, sklearn.neural_network.MLPRegressor. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.neural_network.MLPRegressor.html (accessed on 13 January 2023).
  43. Scikit Learn, sklearn.model_selection.train_test_split. Scikit Learn. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html (accessed on 13 January 2023).
  44. Scikit Learn, sklearn.preprocessing.MinMaxScaler. Scikit Learn. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html (accessed on 13 January 2023).
  45. Scikit Learn, 3.3. Metrics and scoring: quantifying the quality of predictions. Scikit Learn. Available online: https://scikit-learn.org/stable/modules/model_evaluation.html (accessed on 13 January 2023).
  46. Python Software Foundation, Python Org. Available online: https://www.python.org/ (accessed on 13 January 2023).
  47. Clipartmax, Clipartmax. Available online: https://www.clipartmax.com/middle/m2H7i8d3b1m2N4i8_blue-piece-missing-missing-puzzle-piece-clip-art/ (accessed on 13 January 2023).
  48. Campbell, J. Complete Casting Handbook (Second Edition), Butterworth-Heinemann, 2015, Page 639, ISBN 9780444635099.
  49. Dieter, G.E. Mechanical Metallurgy, SI Metrics Edition, 1989.
  50. Scikit Learn. Available online: https://scikit-learn.org/stable/ (accessed on 13 January 2023).
Preprints 76266 g001
Figure 1. Underfitting and overfitting concept [33].
Figure 1. Underfitting and overfitting concept [33].
Preprints 76266 g001
Preprints 76266 g002
Figure 2. Random Forest regression concept [40].
Figure 2. Random Forest regression concept [40].
Preprints 76266 g002
Preprints 76266 g003
Figure 3. Illustration of the overfitting occurrence where in image (a) three models are applied to one training data (black circles) based on the black curve with random error addition. The models tested were a single linear regression line (yellow curve), and two smoothing line fits (blue and green curves). In the image (b), one might notice the training MSE (grey curve) and test MSE (red curve), plotted versus the model flexibility applied [30].
Figure 3. Illustration of the overfitting occurrence where in image (a) three models are applied to one training data (black circles) based on the black curve with random error addition. The models tested were a single linear regression line (yellow curve), and two smoothing line fits (blue and green curves). In the image (b), one might notice the training MSE (grey curve) and test MSE (red curve), plotted versus the model flexibility applied [30].
Preprints 76266 g003
Preprints 76266 g004
Figure 4. Overview of the applied methodology in this study.
Figure 4. Overview of the applied methodology in this study.
Preprints 76266 g004
Preprints 76266 g005
Figure 5. A general grey puzzle with a blue missing piece [47].
Figure 5. A general grey puzzle with a blue missing piece [47].
Preprints 76266 g005
Preprints 76266 g006
Figure 6. Sweetviz association matrix with all attributes employed in this study.
Figure 6. Sweetviz association matrix with all attributes employed in this study.
Preprints 76266 g006
Preprints 76266 g007
Figure 7. Models’ accuracy for the UTS variable comparing the impact of several NaN” artificially inserted values.
Figure 7. Models’ accuracy for the UTS variable comparing the impact of several NaN” artificially inserted values.
Preprints 76266 g007
Preprints 76266 g008
Figure 8. Consolidated maximum accuracy value obtained per model and per predictor variable (UTS, YTS, and EF) based on standard model`s setup.
Figure 8. Consolidated maximum accuracy value obtained per model and per predictor variable (UTS, YTS, and EF) based on standard model`s setup.
Preprints 76266 g008
Preprints 76266 g009
Figure 9. UTS Decision tree resultant model without no depth limitation (standard setup).
Figure 9. UTS Decision tree resultant model without no depth limitation (standard setup).
Preprints 76266 g009
Preprints 76266 g010
Figure 10. SVR accuracy increase from the standard parameters versus optimized ones.
Figure 10. SVR accuracy increase from the standard parameters versus optimized ones.
Preprints 76266 g010
Preprints 76266 g011
Figure 11. MLP accuracy results after optimization for all variables.
Figure 11. MLP accuracy results after optimization for all variables.
Preprints 76266 g011
Table 1. Solder alloy register dataset and given referenced articles.
Table 1. Solder alloy register dataset and given referenced articles.
Preprints 76266 i001
Table 2. Head of the raw final database and examples of some registers for the solder alloys.
Table 2. Head of the raw final database and examples of some registers for the solder alloys.
Preprints 76266 i002
Table 3. Linear regression models’ coefficients for the UTS, YTS, and EF variables.
Table 3. Linear regression models’ coefficients for the UTS, YTS, and EF variables.
Preprints 76266 i003
Table 4. KNN accuracy based on the number of neighbors considered for UTS, YTS, and EF.
Table 4. KNN accuracy based on the number of neighbors considered for UTS, YTS, and EF.
Preprints 76266 i004
Table 5. Decision tree and random forest accuracies and the number of leaves based on the maximum depth of the models for the UTS, YTS, and EF.
Table 5. Decision tree and random forest accuracies and the number of leaves based on the maximum depth of the models for the UTS, YTS, and EF.
Preprints 76266 i005
Table 6. Highest accuracy model parameters for the MLP model.
Table 6. Highest accuracy model parameters for the MLP model.
Preprints 76266 i006
Table 7. Example of different predictions compared to the given test data using the highest accuracy parameters on the MLP models.
Table 7. Example of different predictions compared to the given test data using the highest accuracy parameters on the MLP models.
Preprints 76266 i007
Table 8. Final scheme based on the highest model accuracy.
Table 8. Final scheme based on the highest model accuracy.
Preprints 76266 i008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated