Prerpints.org logo
Preprint
Article

Application of Bilinear Softening Laws and Fracture Toughness of Foamed Concrete

Altmetrics

Downloads

138

Views

40

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

11 June 2023

Posted:

13 June 2023

You are already at the latest version

Alerts
Abstract
Fracture and failure performance of foamed concrete materials were conducted using three methods, i.e., inverse analysis, digital image correlation (DIC) and finite element modelling (FEM) from tested normalized notched beams under three-point bending. From this study, several characteristics both experimental and FEM are discussed. However inverse analysis is only well applicable for series GF-30. The bilinear softening of the testing beam was estimated to identify fracture energy (GF), critical crack length (ac) and elastic modulus (E) with values of 0.015 N/mm, 54.5 mm, and 13 GPa, respectively. Additionally, fracture toughness was calculated by adopting double-K (initiation fracture of 6.907 MPa.mm0.5, unstable fracture of 23.186 MPa.mm0.5 and cohesive fracture of 16.278 MPa.mm0.5). Two-dimensional FEA Modelling of fracture was carried out using a Traction Separation Law (TSL), incorporating extended finite element method (XFEM) and cohesive zone (CZM) techniques. A sensitivity study was carried out, global mesh size of two and damage stabilization cohesive with the value of 1 × 10-5 showed good convergence and were used in other models. Furthermore, by comparing experimental observation using DIC, reliability FEM was validated and showed good acceptance to simulating the crack propagation.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Building structural design entails determining the best way to transmit loads to the ground. However, utilization of concrete is inevitable for construction due to its moldability, impermeability and favorable compression condition; somehow, the weight of normal concrete is relatively hefty and creates a huge dead load for the upper structure. Regarding sub-structure such as the foundation, a massive load, which is transferred, impacts foundation design more than if the soil bearing capacity is low. This becomes a high cost. Introducing lightweight materials such as foamed concrete is promising as a solution to counter this problem. Nevertheless, incorporating void into concrete limits the strength properties but still, has potential as a structural material. Incorporating pozzolanic material as cement replacement not only reduces the production of CO2 but also enhances the strength material properties of foamed concrete. Several studies utilized silica fume as pozzolanic materials by: Lee et al. (2018)[1], Gökçe et al. (2019)[2], Ahmad et al. (2019)[3] and Wang et al. (2020)[4] with density 1700, 1424, 1300 and 1400 kg/m3 have compression strength with 27.12, 26.8, 24.3 and 20 MPa, respectively.
In conventional theory (stress-strain equilibrium), concrete tensile resistance is negligible, however knowing the fracture behavior of brittle material which can lead to catastrophic failure is essential, especially in critical buildings such as dam, tunnel and nuke power plant. The drawback of conventional theory is not able to predict the fracture behavior of material especially after it reached the material’s resistance. The characteristic of fracture process zone (FPZ) ahead of a crack tip prior to fracture[5], the shape and dimension within concrete material result in improper methods of predicting failure process using Linear Elastic Fracture Mechanic (LEFM)[6]. The stress-transfer capability of the material, sometimes referred to as the softening features of concrete, is compromised by the presence of FPZ. Various studies on fundamental models were approached, such as the fictitious crack model (also known as a cohesive crack model)[5], crack band model[7], two-parameters fracture model, effective crack band model[8], size-effect model[9] and double-K fracture model[10].
Fracture energy is the amount of energy used to open a unit area of a crack surface, and this is one of the parameters governing the damage and fracture mechanism. A study conducted by Jaini et al. (2015)[11] investigated fracture energy on foamed concrete with different densities (1400-1600 kg/m3). A similar investigation by Kozlowski et al. (2015)[12] with density (488-1024 kg/m3). Both studies showed that an increased density of foamed concrete density results in increased fracture energy. According to Falliano et al. (2019)[13], fracture energy in foamed concrete is influenced by curing method selections. While Xu et al. (2018)[14] investigated fracture energy considering the boundary effect. It was found that the smaller the local fracture energy was, the closer it was to the element boundary. Ding et al. (2020)[15] observe fracture energy on slag-based geopolymer (SG) and Portland cement (PC) with various compressive strengths. Similar to the compressive strength, SG developed higher fracture energy compared to PC.
Non-contact monitoring methods, including acoustic emission (AE) and digital image correlation (DIC), have become widely employed to better understand the fracture process occurring before the crack tip [16], [17] and [18]. Ohno et al. (2014)[19] investigated FPZ in a notched concrete beam under three-point bending (3PBT) with various-size aggregates by applying acoustic emission (AE). It found that the fracture energy correlates with the width of the AE cluster, as the energy increase when the width of FPZ expands. Alam et al. (2014) [20] observed FPZ of the notched beam under 3PBT by using DIC and AE. It concluded that DIC is better compared to AE due to DIC is based on crack opening, while AE may cause a loss of information as it is not possible to know exactly the crack tip. While Wu et al. (2011)[21] observed FPZ by DIC and stated the length of FPZ increased during crack propagation and decreased after FPZ is fully developed.
Finite element (FE) has been extensively utilized in previous studies to investigate the damage and fracture mechanisms in structural engineering [22], [23], [24], [25] and [26]. There are three well-known methods within Traction Separation Law (TSL): Extended Finite Element Method (XFEM), Cohesive Zone Model (CZM) and Virtual Crack Closure Technique (VCCT). However, the selection method within TSL will determine the behavior and structural response [27]. An investigation by Yu et al. (2021) [28] observed a notched graphite nuclear beam using XFEM, CZM and VCCT. The result showed VCCT is more sensitive compared to XFEM and CZM. While Omar et al. (2021) [29] worked on foam concrete beams using XFEM and CZM and found that there was less agreement within CZM due to the simplification of adopting a failure path. However, the LEFM theory adopted within ABAQUS software is only well applicable for materials that have a relatively small plastic process zone [30].
The novelty within this study is that the material constituent of foamed concrete is different compared to normal concrete, such as no coarse aggregate, and a more void presence, which affects in fracture process zone length (or critical crack). As far as our best knowledge, there has been no previous study done before. The inverse analysis is adopted to estimate critical crack length, which will describe in the following section. DIC was also carried out to observe critical crack length at the ultimate load. In addition, TSL incorporated with XFEM and CZM within two-dimensional (2D) FEA Modelling is adopted. Later crack propagation at ultimate load and predicted results were also observed.

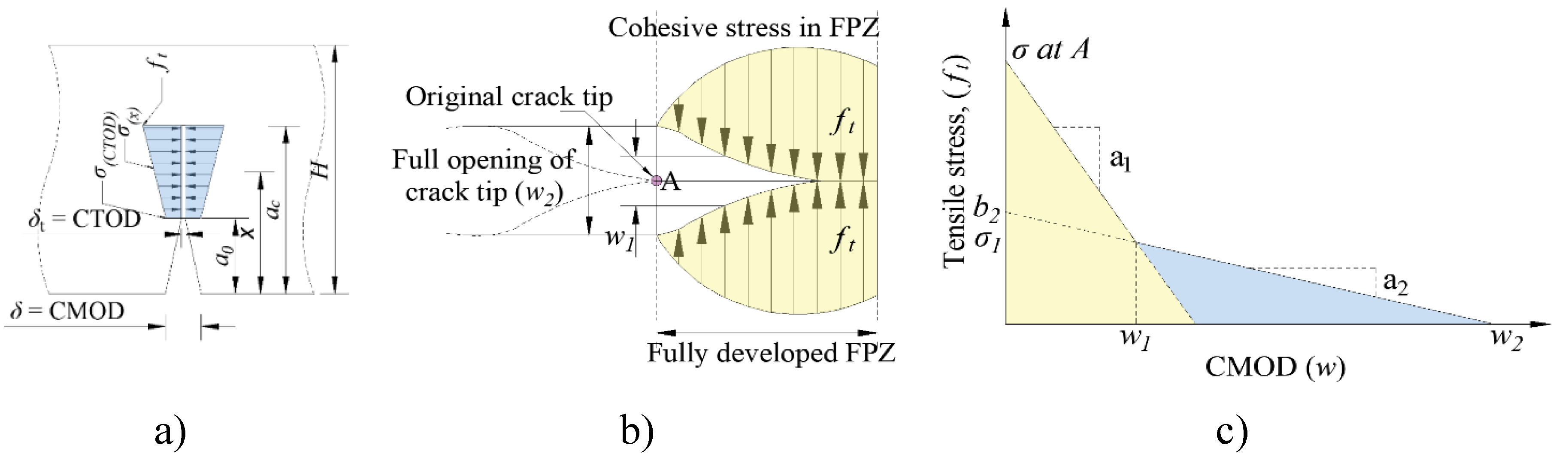
1.1. Bilinear Softening Law

The classical bilinear softening law is extensively used in fracture mechanics and used as a cohesive zone model [5], [31] and [32]. The model is based on the idea that concrete softens gradually owing to microcracking and other energy dissipation processes in an extended fracture process zone (FPZ) prior to a real traction-free crack. As with a real traction-free crack, this portion of the crack cannot be continuous with complete separation of its faces. The fictitious crack faces have certain residual stress that can be transferred across them that are not consistent along their length. An investigation by S. Hu & Fan (2019) [33], as depicted in Figure 1 a) stated that when critical tip opening displacement reaches its value ( C T O D c ) , σ C T O D c , which is the cohesive stress at the fracture tip is reached. Figure 1 b) is a condition where crack is already formed. This condition is described in Figure 1 c). Meanwhile, according to Roelfstra & Wittmann (1986)[34] emphasized that the determined kink point (σ1, w1) of bilinear softening law is the most essential.

1.2. Fracture Toughness

Prior to reaching the ultimate load, crack initiation is already formed within the concrete material[33]. However, this condition of crack propagation under applied load can be explained by utilized fracture toughness (K). Since using LEFM theory is not relevant due to FPZ presence, the double-K method was adopted by several researchers [35], [36], [37], [38] and [17]. The important parameters of fracture toughness are Kini and Kun, which are the initial cracking and unstable cracking toughness, respectively. From this case, it is clear that in quasi-brittle, the fracture crack developed in three stages: initial cracking, stable development and failure development. The corresponding fracture criteria are that when K < K I C i n i no crack appears. When K I C i n i ≤ K < K I C u n the crack developed stably and when K ≥ K I C u n the crack develops unstably, the specimen is in the failure stage. These parameters have the following relationship: K I C u n = K I C i n + K I C C , Δ a c = a c − a 0 . K I C i n i and K I C u n can be calculated using Eqs. 1 and 3, respectively.
K I C i n i = 3 P i n i S a 0 2 H 2 B F a 0 H
F a 0 H = 1.99 − a 0 H 1 − a 0 H 2.15 − 3.93 a 0 H + 2.7 a 0 H 2 1 + 2 a 0 H 1 − a 0 H 1.5
K I C u n = 3 P u l t S a c 2 H 2 B F a c H
F a c H = 1.99 − a c H 1 − a c H 2.15 − 3.93 a c H + 2.7 a c H 2 1 + 2 a c H 1 − a c H 1.5
a c = 2 π H + H 0 a r c t a n B . E 32.6 P u l t C M O D c − 0.1135 − H 0
E = 6 S a 0 C i B H 2 0.76 − 2.28 α 0 + 3.87 α 0 2 − 2.04 α 0 2 + 0.66 1 − α 0 2
C T O D c = C M O D c 1 − a 0 a c 2 + 1.081 − 1.14 a c H a 0 a c − a 0 a c 2 1 / 2
Where Pult is the ultimate load, and Pini was obtained through the initial point of non-linearity in the P-CMOD curve. B, H and S are the width, height and span of the beam, respectively; H0 is clip gauge holder thickness (this study is 2 mm). In addition, elastic modulus can be predicted using inverse analysis from the P-CMOD curve. Where α 0 = ( a 0 + H 0 ) / ( H + H 0 ) and Ci is the initial compliance of the P-CMOD. The sum of the initial pre-cut crack length ( a 0 ) and fictitious crack extension length ( Δ a c ) equals the critical crack length ( a c ).

2. Experimental Investigations

2.1. Experimental Testing

A specific gravity mix design was utilized for batching the lightweight foamed concrete. The component of lightweight foam concrete was river sand with a maximum 3 mm grain size, Portland Cement I-42.5R, superplasticizer (SP), water pH 7, and silica fume (SF). SF was manufactured by Shinjiang Shengping Minerals Co. Ltd as a partial cement replacement. A synthetic-based foaming agent Sika Aer 50/50, with a ratio of 1:20 was used to generate foam. According to Table 1, water to binder, sand to binder, and SP to binder ratio, SF replacement were 0.42, 3, 0.01 and 5%, respectively. Prior to foam addition, the base mix density was measured to be 1995 kg/m3, and the addition of foam was intended to achieve a density of 1820 kg/m3. Casting was carried out when concrete achieved desired density. The concrete was set for 24 hours before demold and water cured for 28 days.
Preprints 76268 g002
Figure 2. Fabrication of foamed concrete and density checking each stage.
Figure 2. Fabrication of foamed concrete and density checking each stage.
Preprints 76268 g002
After reaching the 28th day, to obtain dry conditions, specimens were put inside the oven for 24 hours. Prior to testing, painting and marking were conducted. Contrast color white and black spackles, smooth surface, were applied in order for DIC software (GOM Suite) able to detect. Three specimens of each notched beam and cylinder were tested and recorded by two configured cameras (camera 1 was to detect deformation, and camera 2 was to show applied load, Figure 3 (d)). Un-notched concrete beams were tested under a four-point bending test following ASTM-C78-02 [39]. The purpose of an un-notched beam is to determine tensile strength without being affected by stress concentration (or un-notched strength) which this value is required in FEM later. While notched beams were tested under a three-point bending test based on JCI-S-001[40] standard with a speed rate of 0.1 mm/min. The purpose of this notched beam is to observe fracture characteristics and fracture energy (GF). The schematic test and geometry of specimens for the un-notched and notched concrete beam are shown in Figure 3. While cylinder specimens were tested under compression test following ASTM C469-02 [41] standard, which is to determine elastic modulus and poison’s ratio required for FEM. Table 2 shows the testing series for each specimen
Preprints 76268 g003
Figure 3. (a) Un-notched beam, (b) Notched beam, (c) Cylinder of foamed concrete and (d) UTM testing.
Figure 3. (a) Un-notched beam, (b) Notched beam, (c) Cylinder of foamed concrete and (d) UTM testing.
Preprints 76268 g003
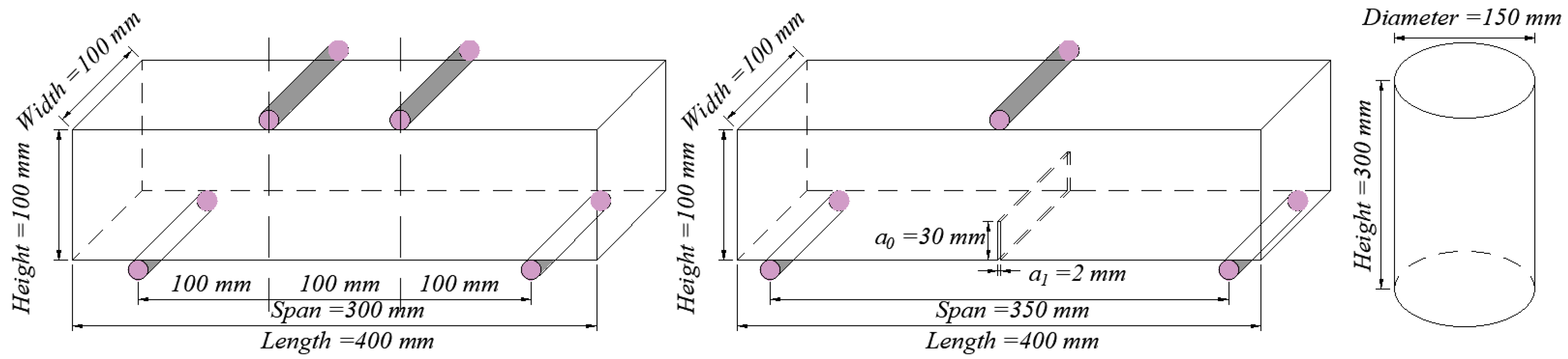
Preprints 76268 g004
Figure 4. Schematic test of (a) Un-notched beam, (b) Notched beam (with GF-30) and (c) Cylinder of foamed.
Figure 4. Schematic test of (a) Un-notched beam, (b) Notched beam (with GF-30) and (c) Cylinder of foamed.
Preprints 76268 g004

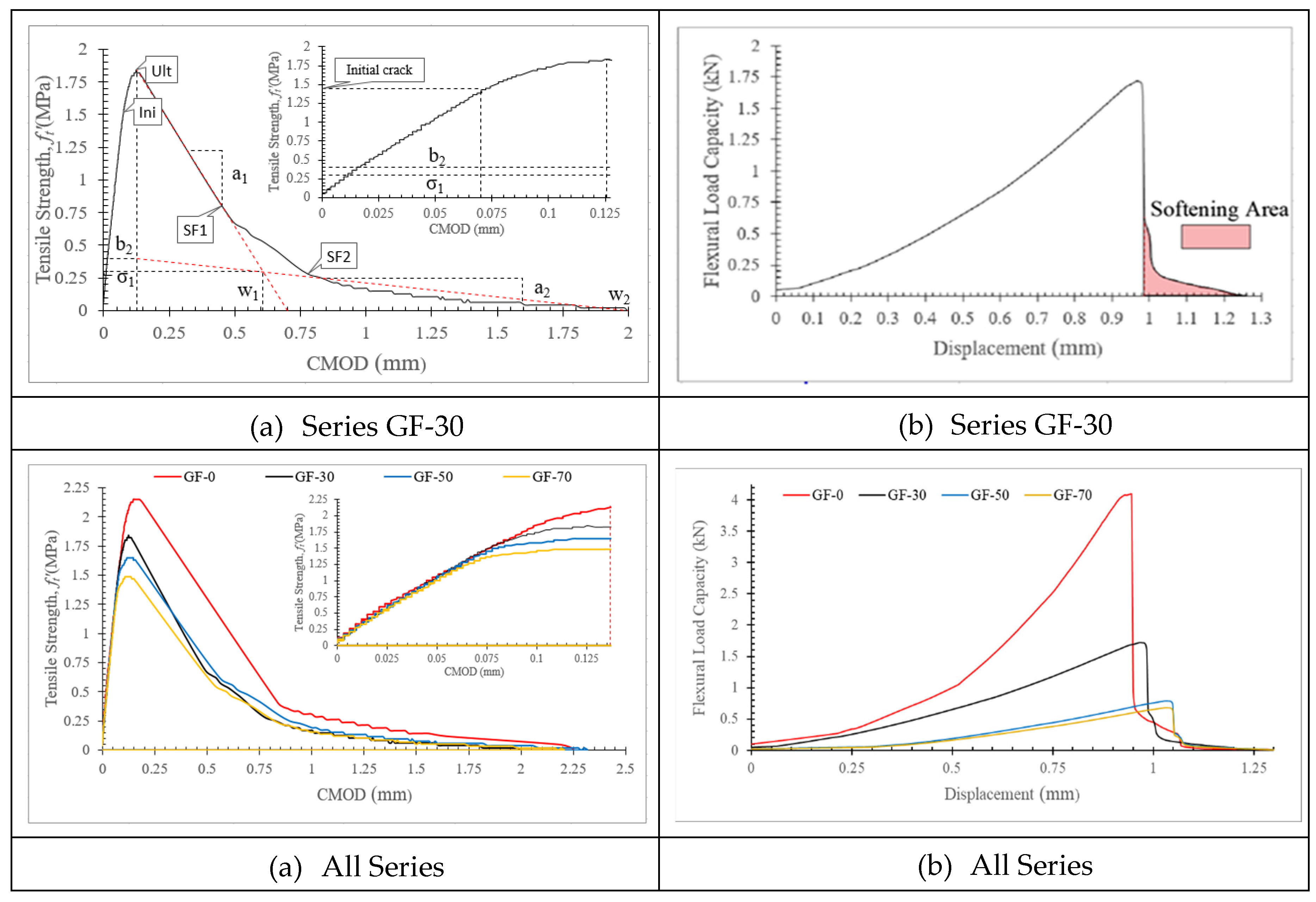
2.2. Experimental Output

The shape of the bilinear softening law is determined by four parameters ft, σ1, w1, w2 (see. Figure 3 (a)). Compared to the previous study [15], this study obtained different kink points (σ1, w1) and zero stress points (w2) in the expression of cohesive law (see Table 3). Regarding kink point (σ1, w1), according to [42], it was assumed to occur at 0.15-0.33 and are similar within this study. Nevertheless, zero stress point (w2) was compared to other studies[15,33] (with values 0.284 and 0.239 mm, respectively) on normal concrete, but foamed concrete developed a value of more than 2.0 mm. This condition was due to void presence, which allowed to arrest of the crack. Regards to an initiation crack obtained from a second non-linear load-CMOD [16], [33], the initiation within foamed concrete is relatively close to the ultimate load. This is because the foamed concrete does not contain coarse aggregate to provide bridging. Stress concentration such as notch influenced height of FPZ above crack tip (Figure 10 (a)) which reduces tensile strength (ft) and also at kink point (σ1, w1) see Table 3.
Preprints 76268 g005
Figure 5. a) Bilinear softening law and (b) P-d curve within 3PBT.
Figure 5. a) Bilinear softening law and (b) P-d curve within 3PBT.
Preprints 76268 g005
In this study, fracture energy (GF) was estimated using the classical Hillerborg [43] model (based on load-displacement) (Eq 8). The previous study used the Hillerborg model to estimate fracture energy of foamed concrete material [11], [12] with values 0.018-0.025 N/mm for density 1400-1600 kg/m3 and 0.001-0.012 N/mm for density 488-1024 kg/m3, respectively. While Falliano et al. (2019) [13] estimated the fracture energy according to JCI-S-001[40] equation (based on load-CMOD) with a value of 0.003-0.010 N/mm for density 800 kg/m3. Figure 3(b) depicts the softening area (U0) within this model, while mg is specimen weight, do is deflection at the failure, W is specimen width, H is specimen height, and a0 is notch height. Compared to other studies working on normal concrete, foamed concrete fracture energy exhibited relatively lower. In addition, inverse analysis (from the notched beam) and conventional analysis (from the cylinder) are carried out; however, both analyses showed good agreement in terms of elastic modulus (E), as mentioned in Table 4. Double-K was used to observe fracture toughness in this study, and critical tip opening displacement (CTODc) was computed from critical mouth opening displacement (CMODc) at ultimate load.
G F = U 0 + m g d 0 W ( H − a 0 )

2.3. Digital Image Correlation

In this observation, the deformation represented by micro-crack was analyzed using the DIC software GOM Suit. Figure 4 (a) depicts the deformation of each stage within foamed concrete by referring to Figure 3. During the initiation crack, the micro-crack above the notch tip is started. The microcrack develops and gets longer until at ultimate load. At this stage, the length of the micro-crack is assumed to be a critical crack. However, both inverse analyses and the DIC method showed good agreement. After reaching the ultimate load, the crack starts visibly with the naked eye within softening phase (SF). During the first softening (SF1), the traction starts losing from the notched tip. The traction disappears along the crack propagation, as seen during the second softening (SF2). Nevertheless, the traction length gets shorter when the crack is propagated until fully separated. Figure 4 (b) shows the opening distance along the notch height. This figure can be as a verification related to inverse analysis (or superposition method) for CTODc. The value of CTODc from DIC observation was slightly lower (see Figure 4 (b) at ultimate load = 0.07 mm) compared to CTODc from inverse analysis (see Table 3 = 0.075 mm). In addition, the value from CMODc from experimental observation (Table 3 = 0.123 mm) is slightly higher compared to DIC (Figure 4 (b) at ultimate = 0.120 mm).
Preprints 76268 g006
Figure 6. Deformation observation using DIC (with testing series GF-30).
Figure 6. Deformation observation using DIC (with testing series GF-30).
Preprints 76268 g006

3. Finite Element Works

In this study, XFEM and CZM are adopted to perform strength prediction and crack propagation at ultimate load, which will be described in the following section. In this study, ABAQUS software is utilized to carry out FEM. Table 5 describes the material (elastic modulus (E), Poisson’s ratio (v), un-notched strength (σ0), fracture energy mode I (GI)) and geometry properties of foam concrete beam used in FEA Modelling. While Figure 5 shows the implementation of the XFEM and CZM area (red zone) within the notched concrete beam.
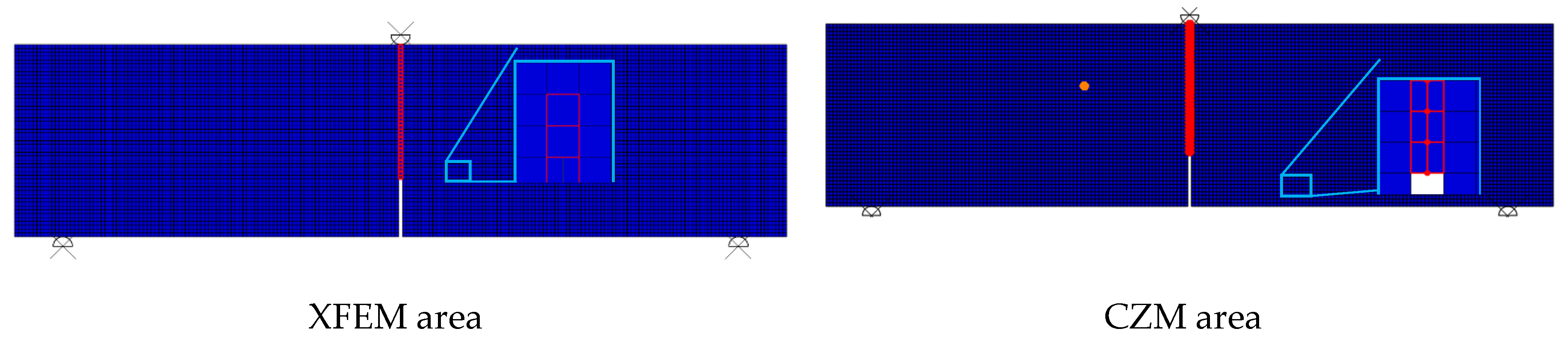
Preprints 76268 g007
Figure 7. Schematic and implementation of XFEM and CZM in FEM.
Figure 7. Schematic and implementation of XFEM and CZM in FEM.
Preprints 76268 g007

3.1. Sensitivity Study

Sensitivity analysis was carried out to evaluate the effects of mesh and damage stabilization cohesive dependence on FEA Modelling. Munjiza et al. (2001) [44] stated that the size of a finite element near the crack tip needs to be smaller than the actual plastic zone size. Nevertheless, shell-based formulation within this study is modelled using a 4-noded shell element named CPE4R. More & Bindu., (2015) [45] stated that an FE model with a larger mesh might lead to less accurate results but faster computational time. Finer mesh yields high accuracy but takes more computational effort. Therefore in this study, the global mesh size range from coarse to fine mesh size (i.e., mesh density 5-0.5) was observed. Figure 6 shows the global mesh size 2 and damage stabilization cohesive with a value 1 × 10-5. The model showed good consistency at ultimate load for both XFEM and CZM methods. Similar findings with global mesh size 2 were also reported in [46], while [47], [48] and [49] with global mesh sizes 0.01mm, 0.125 mm and 1-0.5 mm, respectively. Meanwhile, damage stabilization cohesive with a value of 1 × 10-5 was also reported in [28], [50] and [51].
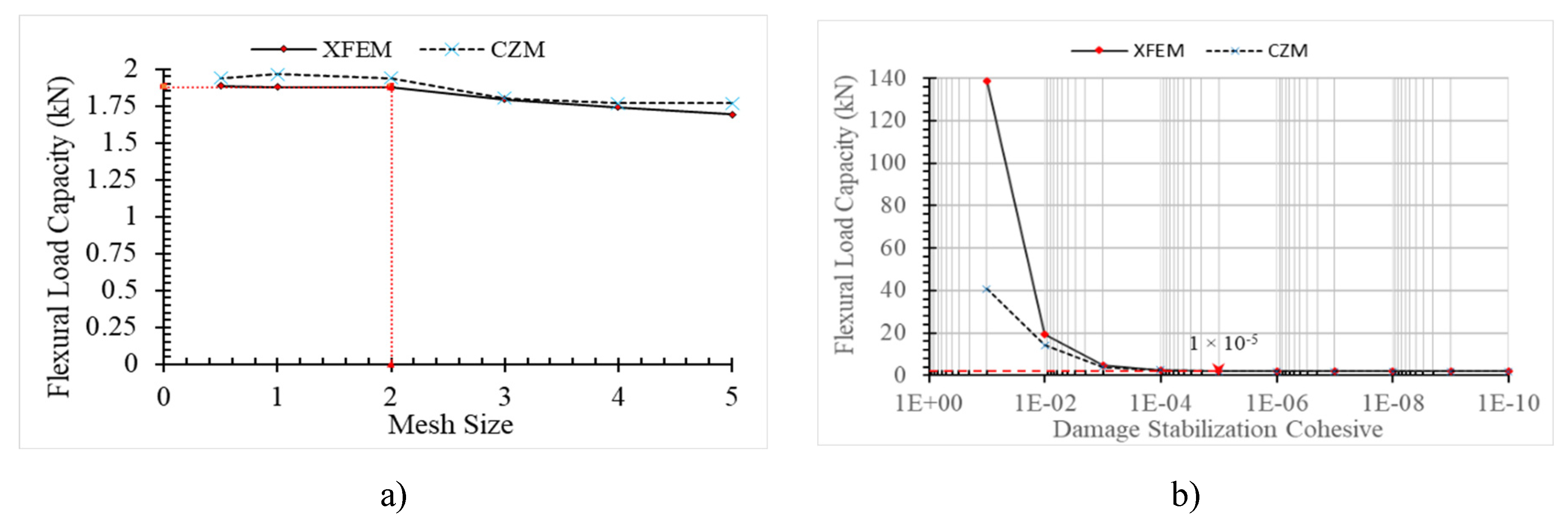
Preprints 76268 g008
Figure 8. A sensitivity study on (a) Global mesh size, (b) Damage stabilization cohesive.
Figure 8. A sensitivity study on (a) Global mesh size, (b) Damage stabilization cohesive.
Preprints 76268 g008

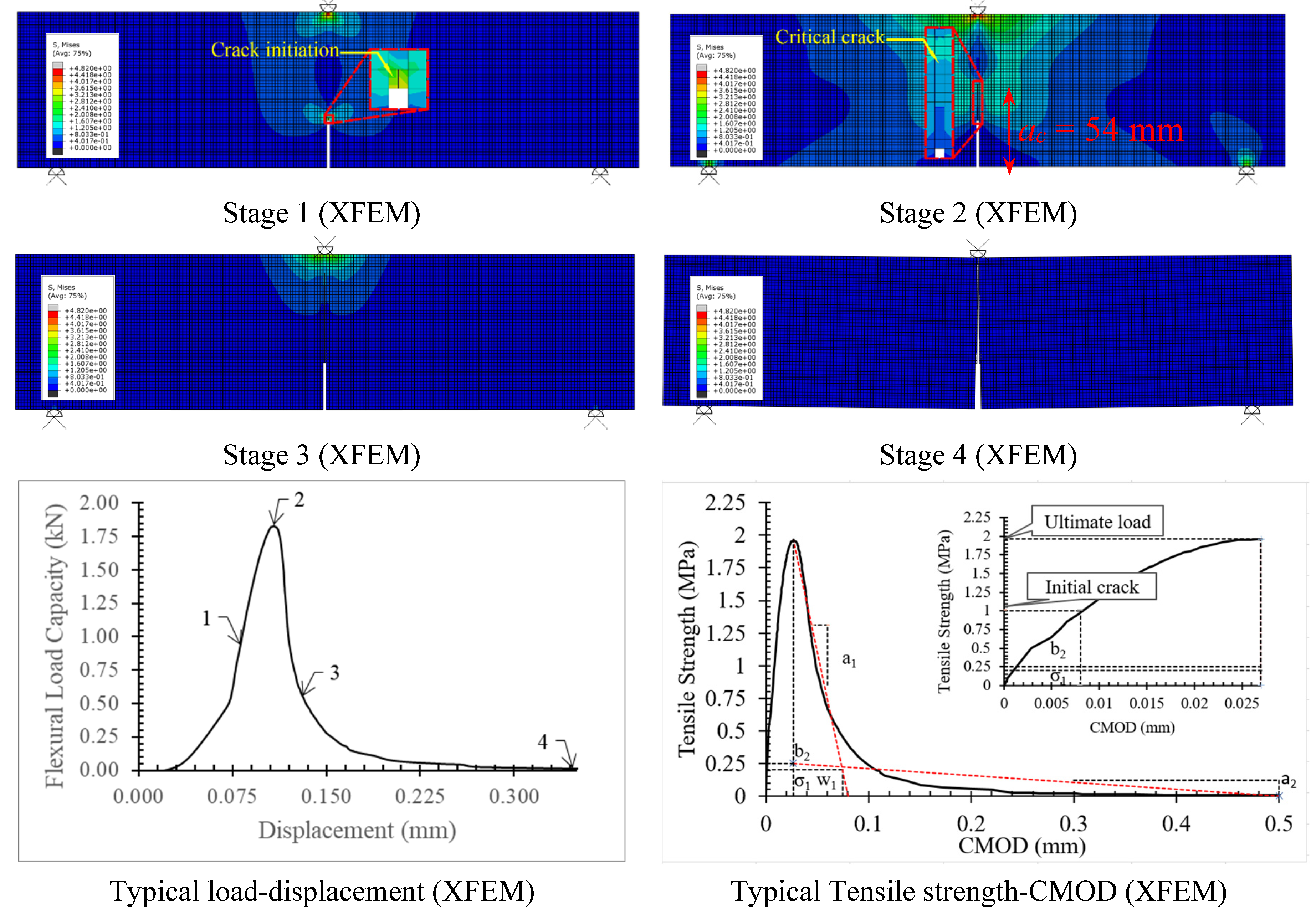
3.2. Damage Plot

Figure 7 depicts a schematic damage plot of each stage of damage from the beginning until it completely failed. At Stage 1 the crack starts to initiate after reaching its maximum principal tensile stress of the material. Nevertheless, compared to crack initiation exhibited in the experiment, FEM results indicate propagation at a lower load. By increasing the load, the crack is propagated until Stage 2, where the ultimate load is reached. At this stage, the length of the crack is named a critical crack. However, compared to experimental (DIC observation) or inverse analysis, within FEM, results showed shorter. In Stage 3, the beam is under softening conditions, and the crack still propagates until the beam is fully separated, as shown in Stage 4. While Table 6 shows the bilinear parameter from FEM (referred to as load-CMOD in Figure 6). Compared to the experimental output in Table 2, it was found that the characters within FEM were not able fully to represent the experimental. Nevertheless, related to critical crack length (ac) at the ultimate load both experimental (DIC and FEM) showed a good agreement. It can be seen the presence of notch height influenced the height of critical crack length (known as fracture process zone at ultimate load). However, CZM provides better agreement with the experimental compared to XFEM related to critical crack length. Again, the LEFM theory adopted within ABAQUS software is only well applicable for materials with relatively small plastic process zones [30] while concrete material has a large plastic process zone or commonly named as fracture process zone.
Preprints 76268 g009
Figure 9. Damage plot (a) Load-displacement, (b) Tensile-CMOD.
Figure 9. Damage plot (a) Load-displacement, (b) Tensile-CMOD.
Preprints 76268 g009
Preprints 76268 g010
Figure 10. Critical crack at ultimate load between (a) DIC deformation and (b) XFEM deformation.
Figure 10. Critical crack at ultimate load between (a) DIC deformation and (b) XFEM deformation.
Preprints 76268 g010
Figure 11 showed output FEM for both XFEM and CZM related to load prediction and opening crack. It showed that in terms of load prediction compared to CZM, XFEM exhibited better (see Table 6). Both experimental and FEM (XFEM and CZM) exhibited a similar trend in terms of tensile strength, in which the higher notch, the less material to resist the load due to stress concentration. This stress concentration is the outcome of fracture process zone length which is influenced by notch height. Meanwhile, during softening after reaching ultimate load, CZM is more representing experimental compared to XFEM in the crack opening. Regards to kink points (σ1, w1) in Table 6, CZM provides relatively higher (for σ1) and larger (for w1). Nevertheless, zero stress point (w2) compare to experimental, both XFEM and CZM provide a good agreement for series GF-0 and GF-30.
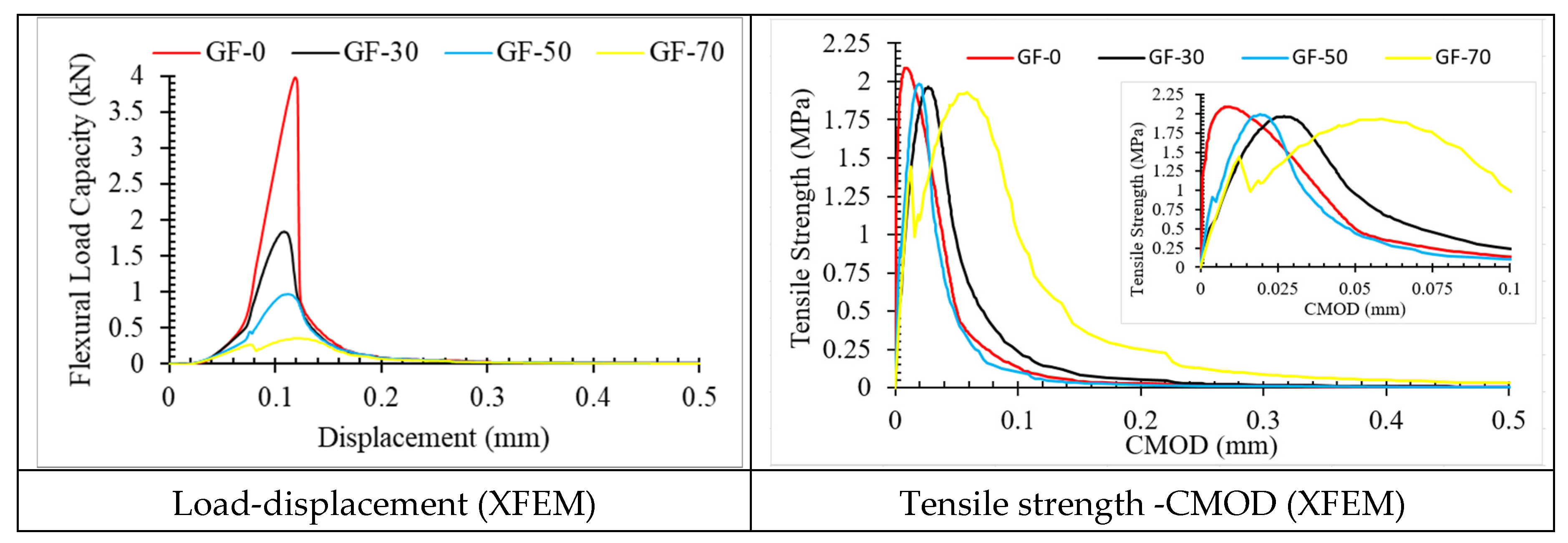
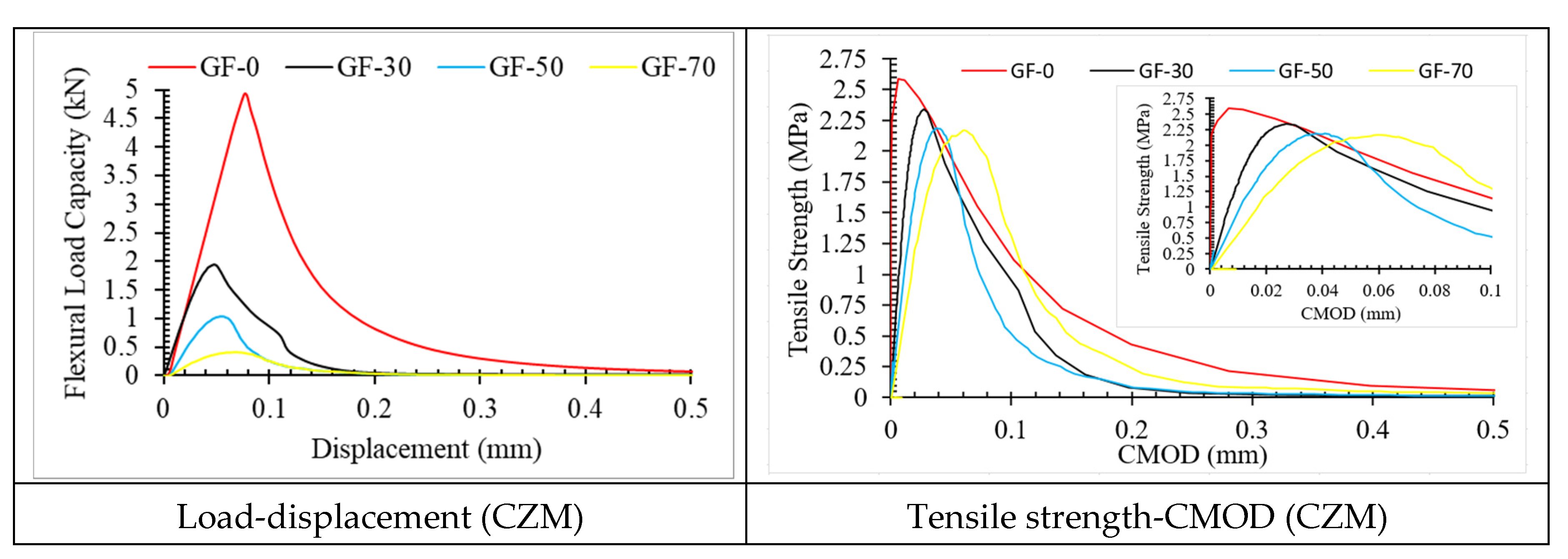
Preprints 76268 g011aPreprints 76268 g011b
Figure 11. Load-displacement and Tensile strength (a) XFEM and (b) CZM.
Figure 11. Load-displacement and Tensile strength (a) XFEM and (b) CZM.
Preprints 76268 g011aPreprints 76268 g011b

4. Conclusions

In this study, three specimens each of un-notched beams, normalized notched beams and cylinders of foamed concrete material, were experimentally and numerically investigated. According to investigations, there are several conclusions. The inverse analysis is only well applicable for notched height of 30 mm. However, All of the methods (DIC, XFEM and CZM) have a good agreement in terms of predicting critical crack length (ac) and P-CMOD at ultimate load (Series GF-30 with value Inverse analysis = 54.45 mm, DIC = 55 mm, FEM XFEM = 54 mm, and FEM CZM = 56 mm). Elastic modulus obtained from both the P-CMOD and Conventional method showed good agreement with a value of 13 GPa. In terms of softening, by comparing previous studies on normal concrete, foam concrete exhibited longer openings in zero stress points (w2) up to 2 mm. The model showed independence from sensitivity with global mesh size 2 and damage stabilization cohesive with 1 × 10-5. Fracture toughness for initiation, unstable and cohesive are 6.907, 23.186 and 16.278 MPa.mm0.5, respectively. Prior to the ultimate load, the traction length (known as FPZ) increases but decreases after the ultimate load. Fracture energy (GF) from the Hillerborg model (with a value of 0.015 N/mm) can be adopted within FEM for foamed concrete materials. Whether fracture energy of foamed concrete is relatively lower compare to normal concrete, however this material has better resistance during fracture (in terms of flexibility and zero stress point (w2)) .

Author Contributions

Investigation, Data curation, Writing—original draft, M.R.M; H.A; S.S. Methodology, Writing, Review and editing, M.R.M; H.A; S.S. Conceptualization, Funding acquisition, Supervision, H.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

This research was financially supported by the Ministry of Higher Education Malaysia (MOHE) through Fundamental Research Grant Scheme (FRGS/1/2020/TK01/UTHM/02/4). We also want to thank Research Management Centre (RMC), University Tun Hussein Oon Malaysia (UTHM) for sponsoring this work under Postgraduate Research Grant (GPPS) (Research Grant No.H706).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Lee, Y. L. ; Tan, C. S. ; Lim, S. K., Mohammad, S.; Lim, J. H. Strength Performance on Different Mix of Cement-Sand Ratio and Sand Condition for Lightweight Foamed Concrete. E3S Web of Conferences. 2018; 65, 1–10. [CrossRef]
  2. Gökçe, H. S.; Hatungimana, D.; Ramyar, K. Effect of Fly Ash and Silica Fume on Hardened Properties of Foam Concrete. Construction and Building Materials. 2019, 194(8), 1-11. [CrossRef]
  3. Ahmad, M. R.; Chen, B.; Farasat Ali Shah, S. Ahmad, M. R.; Chen, B.; Farasat Ali Shah, S. Investigate the Influence of Expanded Clay Aggregate and Silica Fume on the Properties of Lightweight Concrete. Construction and Building Materials. 2019, 220(6), 253-266. [CrossRef]
  4. Wang, X.; Huang, J.; Dai, S.; Ma, B.; Jiang, Q. Investigation of Silica Fume as Foam Cell Stabilizer for Foamed Concrete. Construction and Building Materials. 2020, 237(10), 117514. [CrossRef]
  5. Hillerborg, A.; Modéer, M.; Petersson, P. E. Analysis of Crack Formation and Crack Growth in Concrete by Means of Fracture Mechanics and Finite Elements. Cement and Concrete Research. 1976, 6(6), 773-781. [CrossRef]
  6. Bažant, Z. P. Size Effect in Blunt Fracture: Concrete, Rock, Metal. Journal of Engineering Mechanics. 1984 110(4), 518-53. [CrossRef]
  7. Bažant, Z. P.; Oh, B. H. Crack Band Theory for Fracture of Concrete. Matériaux et Constructions. 1983 16(3), 155-177. [CrossRef]
  8. Nallathambi, P.; Karihaloo, B. L. Determination of Specimen-Size Independent Fracture Toughness of Plain Concrete. Magazine of Concrete Research. 1986, 38((135)), 67–76. [Google Scholar] [CrossRef]
  9. Bazant, Z. P.; Kazemi, M. T. Determination of fracture energy, process zone longth and brittleness number from size effect, with application to rock and conerete. International Journal of Fracture. 1990, 44((2)), 111–131. [Google Scholar] [CrossRef]
  10. Xu, S.; Reinhardt, H. W. Determination of Double-K Criterion for Crack Propagation in Quasi-brittle fracture, Part II: Experimental investigation of crack propagation. International Journal of Fracture. 1999, 98((2)), 111–149. [Google Scholar] [CrossRef]
  11. Rahman, N. A.; Jaini, Z. M. An Experimental Study on the Fracture Energy of Foamed Concrete Using V-Notched Beams. InCIEC 2014. 2015, (3), 1-13. [CrossRef]
  12. Kozłowski, M; Kadela, M; Kukiełka, A. Fracture Energy of Foamed Concrete Based on Three-Point Bending Test on Notched Beams. Procedia Engineering. 2015, 108(10), 349-354. [CrossRef]
  13. Falliano, D.; De Domenico, D.; Sciarrone, A.; Ricciardi, G.; Restuccia, L.; Tulliani, J. M. C.; Gugliandolo, E. Fracture Behavior of Lightweight Foamed Concrete: The Crucial Role of Curing Conditions. Theoretical and Applied Fracture Mechanics. 2019, 103((4)), 102297. [Google Scholar] [CrossRef]
  14. Xu, P.; Ma, J.; Zhang, M.; Ding, Y.; Meng, L. Fracture Energy Analysis of Concrete Considering the Boundary Effect of Single-Edge Notched Beams. Advances in Civil Engineering. 2018, 2018(10), 10. [Google Scholar] [CrossRef]
  15. Ding, Bai, Y.; Dai, J.; Shi, C. An Investigation of Softening Laws and Fracture Toughness of Slag-Based Geopolymer Concrete. 2020, 10(10), 1-14. [CrossRef]
  16. Bu, J.; Chen, X.; Hu, L.; Yang, H.; Liu, S. Experimental Study on Crack Propagation of Concrete Under Various Loading Rates with Digital Image Correlation Method. International Journal of Concrete Structures and Materials. 2020, 14((1)). [Google Scholar] [CrossRef]
  17. Qing, L.; Su, Y.; Dong, M.; Cheng, Y.; Li, Y. Size effect on double-K fracture parameters of concrete based on fracture extreme theory. Archive of Applied Mechanics. 2021, 91((1)), 427–442. [Google Scholar] [CrossRef]
  18. Skarzyński, Kozicki, J.; Tejchman, J. Application of DIC Technique to Concrete-Study on Objectivity of Measured Surface Displacements. Experimental Mechanics. 2013, 53(9), 1545–1559. [CrossRef]
  19. Ohno, K.; Uji, K.; Ueno, A.; Ohtsu, M. Fracture Process Zone in Notched Concrete Beam under Three-Point Bending by Acoustic Emission. Construction and Building Materials. 2014, 67(PART B), 139–145. [Google Scholar] [CrossRef]
  20. Alam, S. Y.; Saliba, J.; & Loukili, A. Fracture Examination in Concrete Through Combined Digital Image Correlation and Acoustic Emission Techniques. Construction and Building Materials. 2014, 69, 232–242. [CrossRef]
  21. Wu, Z. M.; Rong, H.; Zheng, J. J.; Xu, F.; Dong, W. An Experimental Investigation on the FPZ Properties in Concrete Using Digital Image Correlation Technique. Engineering Fracture Mechanics. 2011, 78((17)), 2978–2990. [Google Scholar] [CrossRef]
  22. Park, K.; Choi, H.; Paulino, G. H. Assessment of Cohesive Traction-Separation Relationships in ABAQUS: A Comparative Study. Mechanics Research Communications. 2016, 78, 71–78. [Google Scholar] [CrossRef]
  23. Elices, M.; Guinea, G. V.; Gómez, J.; Planas, J. The cohesive zone model: Advantages, limitations and challenges. Engineering Fracture Mechanics. 2001, 69((2)), pp.137–163. [Google Scholar] [CrossRef]
  24. Freed, Y.; Banks-Sills, L. A New Cohesive Zone Model for Mixed Mode Interface Fracture in Bimaterials. Engineering Fracture Mechanics. 2008, 75((15)), pp.4583–4593. [Google Scholar] [CrossRef]
  25. McGarry, J. P.; Ó Máirtín, É.; Parry, G.; Beltz, G. E. Potential-based and non-potential-based cohesive zone formulations under mixed-mode separation and over-closure. Part I: Theoretical analysis. Journal of the Mechanics and Physics of Solids. 2014, 63(1), pp.336-362. 2014; 63, pp.336–362. [Google Scholar] [CrossRef]
  26. Faron, A.; Rombach, G. A. Simulation of Crack Growth in Reinforced Concrete Beams Using Extended Finite Element Method. Engineering Failure Analysis. 2020, 116((1)), 104698. [Google Scholar] [CrossRef]
  27. Campilho, R. D. S. G.; Banea, M. D.; Neto, J. A. B. P.; Da Silva, L. F. M. Modelling adhesive joints with cohesive zone models: Effect of the cohesive law shape of the adhesive layer. International Journal of Adhesion and Adhesives. 2013, 44, 48–56. [Google Scholar] [CrossRef]
  28. Yu, Z.; Zhang, J.; Shen, J.; Chen, H. Simulation of Crack Propagation Behavior of Nuclear Graphite by Using XFEM, VCCT and CZM Methods. Nuclear Materials and Energy. 2021, 29((2)). [Google Scholar] [CrossRef]
  29. Ahmad, H.; Sugiman, S.; Jaini, Z. M.; Omar, A. Z. Numerical Modelling of Foamed Concrete Beam under Flexural Using Traction-Separation Relationship. 2021, 18(5), 1–13. [CrossRef]
  30. Park, K.; Paulino, G. H.; Roesler, J. R. Determination of the Kink Point in the Bilinear Softening Model for Concrete. 2008, 75(2), 3806-3818. [CrossRef]
  31. Petersson, P. E. Crack Growth and Development of Fracture Zones in Plain Concrete and Similar Materials. Ph.D Thesis. Lund University. 1981.
  32. Wittmann, F. H.; Rokugo, K.; Brühwiler, E.; Mihashi, H.; Simonin, P. Fracture Energy and Strain Softening of Concrete as Determined by Means of Compact Tension Specimens. Materials and Structures. 1988, 21((1)), 21–32. [Google Scholar] [CrossRef]
  33. Hu, S.; Fan, B. Study on the Bilinear Softening Mode and Fracture Parameters of Concrete in Low Temperature Environments. Engineering Fracture Mechanics. 2019, 211((2)), 1–16. [Google Scholar] [CrossRef]
  34. Roelfstra, P.E.; Wittmann, F. Numerical Method to Link Strain Softening with Failure of Concrete. In Fracture Toughness and Fracture Energy of Concrete. 1986, 163-175.
  35. Kumar, S.; Barai, S. V. Effect of loading condition, specimen geometry, size-effect and softening function on double-K fracture parameters of concrete. Sadhana - Academy Proceedings in Engineering Sciences. 2012, 37((1)), 3–15. [Google Scholar] [CrossRef]
  36. Zhang, X.; Xu, S.; Zheng, S. Experimental measurement of double-K fracture parameters of concrete with small-size aggregates. Frontiers of Architecture and Civil Engineering in China. 2007, 1((4)), 448–457. [Google Scholar] [CrossRef]
  37. Yu, K.; Lu, Z. Determining residual double-K fracture toughness of post-fire concrete using analytical and weight function method. Materials and Structures/Materiaux et Constructions. 2014, 47((5)), 839–852. [Google Scholar] [CrossRef]
  38. Kumar, S.; Barai, S. V. Influence of specimen geometry on determination of double-K fracture parameters of concrete: A comparative study. International Journal of Fracture. 2008, 149((1)), 47–66. [Google Scholar] [CrossRef]
  39. American Society Testing and Materials. Standard Test Method for Flexural Strength of Concrete (Using Simple Beam with Third-Point Loading)1. America. ASTM-C78-02. 2002.
  40. Japan Concrete Institute Standard. Method of Test for Fracture Energy of Concrete by Use of Notched Beam. Tokyo. JCI-S-001.2003.
  41. >American Society Testing and Materials. Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression. America. ASTM C469-02.2002.
  42. Bažant, Z. P. Concrete Fracture Models : Testing and Practice. 2002, 69(3), 165-205. [CrossRef]
  43. Hillerborg. The Theoretical Basis of a Method to Determine the Fracture Energy GF of Concrete. Mater. Struct. 1985, 21(4), pp.162. [CrossRef]
  44. Munjiza, A.; John, N. W. M. Mesh Size Sensitivity of the Combined FEM/DEM Fracture and Fragmentation Algorithms. Engineering Fracture Mechanics. 2001, 69(2), pp.281-295. [CrossRef]
  45. More, S. T., & Bindu, R. S. (2015). Effect of Mesh Size on Finite Element Analysis of Plate Structure. International Journal of Engineering Science and Innovative Technology, 4(3), pp.181-185.
  46. Maulana, M. R.; Sugiman, S.; Ahmad, H.; Jaini, Z. M.; Mansor, H. XFEM Modelling and Experimental Observations of Foam Concrete Beam Externally-Bonded with KFRP Sheet. Latin American Journal of Solids and Structures. 2022, 19(6), 1–12. [CrossRef]
  47. Shen, W.; Liang, G.; Lei, J.; Li, C. Thin-Walled Structures Singular Intensity Factor Method to Estimate Notch Stress and N-SIF in Double Edge V-Notched Plate. Thin-Walled Structures, 2021, 169((9)), 108387. [Google Scholar] [CrossRef]
  48. Ye, J.; Gong, Y.; Tao, J.; Cao, T.; Zhao, L.; Zhang, J.; Hu, N. Efficiently Determining the R-Curve and Bridging Traction-Separation Relation of Mode I Delamination in a Simple Way. Composite Structures. 2022, 288((1)), 115388. [Google Scholar] [CrossRef]
  49. Koslan, M. F. S.; Zaidi, A. M. A.; Othman, M. Z.; Abdullah, S.; Thanakodi, S. The Effect of Mesh Sizing Toward Deformation Result in Computational Dynamic Simulation for Blast Loading Application. Modern Applied Science. 2013, 7((7)), 23–28. [Google Scholar] [CrossRef]
  50. Supar, K.; Ahmad, H. Multi-Holes Configurations of Woven Fabric Kenaf Composite Plates: Experimental Works and 2-D Modelling. Journal of Mechanical Engineering and Sciences. 2018, 12((2)), 3539–3547. [Google Scholar] [CrossRef]
  51. Ahmad, H.; Crocombe, A. D.; & Smith, P. A. Strength prediction in CFRP woven laminate bolted double-lap joints under quasi-static loading using XFEM. Composites Part A: Applied Science and Manufacturing. 2014, 56, 192–202. [CrossRef]
Preprints 76268 g001
Figure 1. (a) Cohesive softening stress distribution at the maximum applied load, (b) Traction-free crack near the tip, (c) Bilinear stress crack opening relationship.
Figure 1. (a) Cohesive softening stress distribution at the maximum applied load, (b) Traction-free crack near the tip, (c) Bilinear stress crack opening relationship.
Preprints 76268 g001
Table 1. Mix design of foamed concrete for 1 m3.
Table 1. Mix design of foamed concrete for 1 m3.
Binder (kg/m3) Sand (kg/m3) SP
(kg/m3)		 Water
(kg/m3)		 Foam (liter/m3) f'c
(MPa)
Cement SF
1043.91 54.94 366.28 10.99 461.52 105 42.3
Table 2. Testing series of each specimen.
Table 2. Testing series of each specimen.
Testing Series Dimension (mm)
(l × b × h)		 Notch height (mm) Standard Speed rate
Control 400 × 100 × 100 Un-notched ASTM-C78-02 [39] 0.5 mm/min
GF-0 400 × 100 × 100 0 JCI-S-001[40] 0.1 mm/min
GF-30 30
GF-50 50
GF-70 70
E D150 × 300 - ASTM C469-02 [41] 3 kN/sec
Table 3. Parameter of the bilinear softening curve for experimental observation.
Table 3. Parameter of the bilinear softening curve for experimental observation.
Testing Series Pini
(kN)		 Pult
(kN)		 ft
(MPa)		 σ1
(MPa)		 w1
(mm)		 w2
(mm)		 a1
(mm-1)		 a2
(mm-1)		 b2
(MPa)
GF-0 3.333 4.101 2.153 0.380 0.820 2.250 2.623 0.214 0.550
± 0.075 ± 0.089 ± 0.105 ± 0.034 ± 0.098 ± 0.052 ± 0.398 ± 0.025 ± 0.104
GF-30 1.384 1.752 1.877 0.317 0.650 2.000 2.612 0.240 0.433
± 0.135 ± 0.142 ± 0.159 ± 0.057 ± 0.153 ± 0.288 ± 0.398 ± 0.038 ± 0.088
GF-50 0.595 0.786 1.650 0.270 0.700 2.310 2.118 0.187 0.350
± 0.075 ± 0.052 ± 0.095 ± 0.045 ± 0.115 ± 0.288 ± 0.086 ± 0.045 ± 0.093
GF-70 0.244 0.254 1.303 0.270 0.670 2.203 2.082 0.200 0.345
± 0.021 ± 0.015 ± 0.058 ± 0.031 ± 0.124 ± 0.288 ± 0.152 ± 0.018 ± 0.101
Table 5. Material and geometry properties.
Table 5. Material and geometry properties.
E
(GPa)		 v σ0
(MPa)		 GI
(N/mm)		 TSL
13.0 0.28 1.652 0.015 MaxPS
Table 6. Parameter of the bilinear softening curve for FEM.
Table 6. Parameter of the bilinear softening curve for FEM.
TSL Pini
(kN)		 Pult
(kN)		 ft
(MPa)		 σ1
(MPa)		 w1
(mm)		 w2
(mm)		 a1
(mm-1)		 a2
(mm-1)		 b2
(MPa)
GF-0 XFEM 2.563 3.974 2.086 0.230 0.070 2.217 33.030 0.424 0.250
CZM 2.985 4.928 2.587 0.350 0.150 2.274 15.830 0.467 0.500
GF-30 XFEM 0.938 1.832 1.963 0.220 0.080 2.215 22.956 0.350 0.241
CZM 1.125 2.455 2.338 0.250 0.140 2.341 33.973 0.452 0.300
GF-50 XFEM 0.552 0.945 1.985 0.210 0.090 1.659 21.562 0.325 0.236
CZM 0.589 1.040 2.185 0.240 0.130 2.547 22.867 0.441 0.280
GF-70 XFEM 0.215 0.330 1.928 0.200 0.190 1.348 21.795 0.375 0.268
CZM 0.258 0.340 2.166 0.235 0.160 2.942 22.207 0.410 0.410
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated