Preprint
Communication
Exploring the Potential Energy Surface of Medium-Sized Aromatic Polycyclic Systems with Embedded Planar Tetracoordinate Carbons: A Guided Approach
Altmetrics
Downloads
174
Views
102
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.pdf (7.16MB )
This version is not peer-reviewed
Submitted:
12 June 2023
Posted:
13 June 2023
You are already at the latest version
Alerts
Abstract
This study scrutinizes the complexities of designing and exploring the potential energy surface (PES) of systems containing more than twenty atoms with planar tetracoordinate carbons (ptCs). To tackle this issue, we utilized an established design rule to design a Naphtho [1,2-b:4,3-b′:5,6-b′′:8,7-b′′′]tetrathiophene derivative computationally. This process began with substituting S atoms with CH– units, then replacing three sequential protons with two Si2+ units in the resultant polycyclic aromatic hydrocarbon polyanion. Despite not representing the global minimum, the newly designed Si8C22 system with four ptCs provided valuable insights into strategic design and PES exploration. Our results underscore the importance of employing adequate methodologies to confirm the stability of newly designed molecular structures containing planar hypercoordinate carbons.
Keywords:
Subject: Chemistry and Materials Science - Theoretical Chemistry
1. Introduction
In the past five decades, the scientific community has witnessed remarkable progress in understanding and exploring compounds containing planar hypercoordinate carbons (p-hyp-Cs) [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. These intriguing compounds are characterized by carbon atoms connected to a minimum of four in-plane atoms. Despite initial skepticism due to their violation of the van't Hoff and Le Bel's rules, which favor the tetrahedral configuration of tetracoordinate carbon compounds [24,25], researchers have made significant strides in this field.
The exploration of compounds with p-hyp-Cs can be traced back to 1968 when Monkhorst first proposed the CH4 transition state planar structure involved in the stereomutation of methane [26]. In 1970, Hoffmann and his team showed that the stability of the planar tetracoordinate carbon (ptC) structure could be enhanced electronically[27]. This was achieved by substituting the planar methane H atoms with either σ electron donors, which improved their involvement in electron-deficient σ bonds, or π acceptors, which helped distribute the unfavorable lone pair of the central atom. This led to the conceptualization of various molecular prototype architectures. In 1976, Collins and his colleagues theoretically introduced the first ptC-containing molecule, 1,1-dilithiocyclopropane[1]. This was followed by the unintentional synthesis of the first ptC-containing molecule by Cotton and Millar a year later [28], marking a significant milestone in this field. These studies began a journey leading to numerous discoveries and advancements.
Inspired by the concepts offered by Hoffman and coworkers, our group proposed a method to construct planar tetracoordinate carbon (ptC) global minima (GM). This method centered around substituting three consecutive protons from an aromatic hydrocarbon with two E2+ dications, where E represents elements from Silicon (Si) to Lead (Pb) [29]. This substitution was designed to preserve the π-aromatic circuits inherent in the parent aromatic hydrocarbons. This strategy was initially tested on derivatives of small aromatic hydrocarbons, each featuring one or two ptCs [23,29,30,31,32,33,34,35]. A striking feature of these ptC systems is their global π-aromaticity and three-center, two-electron (3c-2e) E-ptC-E σ- bonds that display localized σ-aromaticity.
Exploring the potential energy surfaces (PES) of p-hyp-Cs species is essential to ensuring them as GM structures [21,23,30,34], thus supporting their experimental viability (at least in gas phase experiments) [14,36]. Consequently, devising methods to assist PES exploration is vital for discovering new viable p-hyp-C species [37,38,39,40,41,42]. Experimentally, gaseous species are spectroscopically characterized; however, theoretical research remains indispensable in gaining insights into these compounds' structural and electronic structures, especially for identifying the lowest energy structure (GM) and other relevant structures for matching between the computed and experimental spectrum, thus allowing the structural elucidation of the compound identified in the gas cloud [43].
In the study of p-hypC systems, the employment of stochastic and evolutionary algorithms is common to locate the lowest energy structures amongst the plethora of structural possibilities, thereby improving our understanding of the stability and reactivity of p-hyp-Cs compounds [21,23,29,44,45]. Numerous GM structures have been reported, including planar tetracoordinate, pentacoordinate, and hexacoordinate carbon structures [14,19,20,22,46,47]. However, the efficiency of search algorithms decreases with increasing system size due to the exponential growth of local minima to be visited [48,49]. Systems exceeding 20 atoms could present substantial challenges, and these difficulties are further amplified when they comprise more than two elements, such as Si, C, and H, in the current study. Therefore, an important question arises, how to explore the PES of candidates for GMs with p-hyp-Cs with more than 20 atoms?
In this study, we apply the design rule for systems with ptCs, as mentioned above, to the design of a Naphtho[1,2-b:3,4-b′:5,6-b′′:7,8-b′′′]tetrathiophene derivative, chosen for their aromatic peripheral pentagonal rings. Moreover, a similar strategy was employed last year, beginning with the [6]radialene benzo[1,2-c:3,4-c0:5,6-c00 ]trithiophene, which enabled us to design a GM harboring three ptCs [29]. The system we design here, Si8C22, has an isomer with four ptCs that exhibits aromaticity but does not correspond to the GM. Nevertheless, examining this system has been beneficial for testing the design rule and a guided strategy for exploring its PES, given the complexity of this task for such a large system using conventional techniques.
Consequently, our results emphasize the importance of employing appropriate methodologies to validate the thermodynamic and kinetic stability of newly computationally designed structures containing p-hyp-Cs.
2. Computational Details
Our guided exploration of the PES of the Si8C22 started using the coronene (C24H12) as a starting structural template, applying a dual-stage atomic exchange process. Initially, a hydrogen-to-silicon atomic substitution was executed, succeeded by a swap where four silicon and two carbon atoms were removed to achieve the intended stoichiometry (Refer to Figure 3). Employing the AM1 method [50], we methodically scrutinized an exhaustive set of 993 structures through single-point computations to pinpoint energy-favored structures. Isomers displaying energies beneath 50 kcal·mol-1 underwent subsequent geometric optimization at the PBE0 [51]/SDDAll [52,53,54,55,56] level. Then, structures maintaining energies below 30 kcal·mol-1 were refined at the PBE0-D3 [57]/Def2-TZVP [58] level, complemented by vibrational frequency assessments to affirm their status as true PES minima (Figure S1). All these calculations were performed with the Gaussian16 (Revision B.01) program [59].
We computed current densities utilizing the GIMIC program [60,61] that implements the gauge-included atomic orbital (GIAO) method [62] at the PBE0-D3/Def2-TZVP level, considering an external magnetic field oriented perpendicular to the molecular plane. In our analysis, diatropic (aromatic) and paratropic (antiaromatic) ring currents circulate clockwise and counterclockwise, respectively. Visualization of these currents was performed with Paraview 5.10.0 software [63,64], and ring current strength (RCS) was determined after considering various rectangular integration planes that intersected the bonds of interest, originating from the center of the rings (Refer to Figures S2 and S3). The GIMIC program's integration process employs the two-dimensional Gauss-Lobatto algorithm [65]. Positive and negative RCS values represent diatropic (aromatic) and paratropic (antiaromatic) ring currents, respectively, while values near zero indicate a non-aromatic character [66]. The different ring current circuits have been determined by analyzing the current strength profiles across the integration planes (see Figures S2 and S3), following the strategy previously proposed elsewhere [66,67,68].
Chemical bonding analyses employed several methods: Wiberg bond indices (WBI) [69], natural population analysis (NPA) [70], and the adaptive natural density partitioning method (AdNDP) [71,72]. These methodologies are anchored in the natural bond orbital (NBO) method and were executed using the wavefunction derived at the PBE0-D3/Def2-TZVP level. WBI and NPA computations were facilitated with the NBO 6.0 code[73], while the AdNDP analysis was carried out with Multiwfn 3.8 [74]. Molecular structure and AdNDP orbitals were visualized using CYLview 2.0[75] and VMD 1.9.3 [76].
3. Results and Discussion
3.1. Design of the Si8C22 Cluster Incorporating Four ptCs
This research delves into the intricate processes of designing and examining the PES of polycyclic systems comprising over twenty atoms featuring ptCs. To address this challenge, we employed a proven design principle [23,29,30,31,32,33,34,35], to computationally formulate a derivative of Naphtho[1,2-b:4,3-b′:5,6-b′′:8,7-b′′′′]tetrathiophene. This design procedure initiated substituting sulfur atoms with CH– units. Then a sequential triplet of protons is replaced with a pair of Si2+ units within the resulting polycyclic aromatic hydrocarbon polyanion (see Scheme 1).
Despite not achieving the global minimum (GM), the resultant cluster (1) is a local minimum on the PES. It allowed us to assess a simple but effective strategy to explore its PES (see below). Our findings accentuate the necessity of rigorous methodologies to validate the stability of novel structures featuring p-hyp-Cs.
A crucial prerequisite for the design of ptC embedded aromatic rings is their inherent aromatic character. A recurring trait among the previously reported global minima (GMs) of these systems includes global, semilocal, and local π-aromaticity, the latter two present in fused rings, supplemented by local σ-aromaticity provided by the delocalization of two electrons in the E-ptC-E delocalized bond, where E represents Si in this study. Thus, our analysis necessitates an in-depth evaluation of this aromaticity. To accomplish this, we assessed the magnetically induced current density. We employed current strength profiles to identify the ring current circuits and their respective strengths (nA/T), as depicted in Figure 1, following a strategy established previously [66,67,68].
For comparative purposes, Figure 1 also presents analyses for two formerly reported systems, one derived from benzene (Si2C6H2+) and another from cyclopentadienyl anion (Si3C5). Notably, these monocyclic rings display a pronounced diatropic ring current (15.3 and 12.0 nA/T) distributed predominantly around carbon rings. Local diatropic ring currents around ptC (8.2 and 6.1 nA/T), possibly linked with local Si-ptC-Si delocalization, and paratropic ring currents at the molecular rings' center, albeit less intense, are also discernible. These observations align with those reported earlier for these systems [30,31,32,33]. System 1's current density analysis reveals a strong diatropic global ring current (12.7 nA/T) and much fainter local diatropic ring currents (2.3 and 2.5 nA/T). Local currents around the ptCs, and weak paratropic local currents within the local rings, are also identified. These findings, therefore, affirm the robust aromatic character of System 1 following our design strategy.
However, affirming System 1 as the most stable structure for the Si8C22 combination requires further verification. This validation can only be achieved by comprehensively scanning the PES of the Si8C22 cluster, as elucidated in the subsequent section.
Our previous analysis revealed that the magnetic response analysis of compound 1 identified it as an aromatic system. However, what can we infer about this system from the perspective of its chemical bonding? The Adaptive Natural Density Partitioning (AdNDP) analysis offers an instructive portrayal of the chemical bonding within this species. As depicted in Figure 2, the AdNDP technique uncovers the lone-electron pairs on each Si atom, the C-C σ-bonds forming the C22 backbone, and the C-Si σ-bonds linking the C-periphery with Si atoms. Additionally, it unveils the delocalized Si-ptC-Si three-center two-electron (3c-2e) σ-bonds, a defining feature of these species.
Moreover, 13 delocalized π-bonds accounting for 26 π-electrons are spread across the system. If one were to draw parallels with the current analysis, these could be partitioned into local and global groups, in both cases adhering to Hückel's 4n+2 rule for aromatic systems, demonstrating their aromaticity. Thus, the AdNDP analysis confirms that compound 1 maintains the bonding patterns observed in its predecessors, featuring ptCs integrated into an aromatic ring. This interpretation of chemical bonding also agrees with the Wiberg bond index (WBI) analysis, as reported in Figure S4.
3.2. Potential Energy Surface Exploration of the Si8C22 Cluster
As commented in the introduction, exploring the PES of medium-sized clusters using commonly implemented methods such as genetic algorithms or stochastic procedures is challenging due to the computational resources required, which many research groups might find prohibitive. This is because many candidate structures need to be evaluated and optimized locally, i.e., using density functional theory (DFT) methods and an adequate basis set.
To overcome these hurdles, we leveraged what is commonly referred to as "chemical intuition," using structural and chemical bonding information from prior studies on analogous systems to generate our candidate population. However, the success of strategies based on chemical intuition to explore the PES of atomic clusters depends on the information used as a guide. In the past, we used the best minima derived from a stochastic search or evolutionary methods, which were subsequently slightly altered (moving atoms to generate a new structure) [77]. With this approximation, we enriched the variety of local minima close in energy to the GM by identifying missing structures in the evolutive or stochastic search. Besides, in the case of systems featuring p-hyp-Cs embedded in polycyclic aromatic hydrocarbons, we succeeded by performing substitutions and permutations on related and well-characterized polycyclic hydrocarbon structures to the system under study [29]. This method allowed the sampling of a wide range of polycyclic structures with randomness introduced by the permutations and substitutions. Thus, we will employ this strategy here.
It is crucial to mention that the used approach is successful only when we ensure that we sample the correct region of the PES, i.e., where the global minimum should ideally be found. While we cannot guarantee this 100%, our prior studies suggest it is an adequate method for this system. Building on these considerations, we illustrate the procedure employed for the PES exploration of Si8C22 in Figure 3. We selected coronene (C24H12) as the starting template and stochastically removed two carbon atoms. As the figure represents, we replaced H atoms with Si, resulting in 12 Si atoms, from which we randomly removed four. To fulfill the carbon atoms in the interest system. By this procedure, we generated 993 structures whose energy was computed using a semiempirical method; then, the best structures in a range of 50 kcal·mol-1 were optimized via a DFT method using a small basis set. Finally, we refined the best structures within a 30 kcal·mol-1 range at a higher level (for more details on the used methods, refer to the computational methods section). Figure 3 displays the best structures identified through our exploration. This approach allowed for a thorough yet resource-conscious exploration of the PES of Si8C22, offering valuable insights into the energetically preferred structures for this combination. Regrettably, Structure 1 exhibits considerably higher energy than the best-identified structure for the Si8C22 combination. Nevertheless, this study underscores the essentiality of employing suitable techniques to ascertain that the designed cluster corresponds to the global minimum. This prerequisite critically influences its potential viability in the gas phase.
An intriguing question that persists is why 1 is not a good minimum on the potential energy surface (PES). A plausible explanation may be uncovered by examining its computationally designed structural counterpart, the C22H124– tetra-anion, which is stabilized by four Li+ counterions. As reported in Cartesian coordinates (in Table S1), the C22 skeleton in Li4C22H12 does not lay flat, in contrast to the planar configuration in System 1, possibly due to the rigidity imparted by the bridged Si-C bonds. Consequently, this flatness could strain the C22 skeleton, ultimately rendering the structure of 1 with four ptCs energetically unfavorable.
3. Conclusions
In this research, we have utilized a previously suggested strategy to design a cluster, termed 1, with the formula Si8C22 featuring four planar tetracoordinate carbons (ptCs). We adopted Naft[1,2-b:3,4-b':5,6-b'':7,8-b'']tetrathiophene as the base structure, wherein sulfur atoms were initially replaced with CH– units. Subsequently, two Si2+ units replaced three sequential protons. Although this strategy has proven successful in designing global minima featuring ptCs in the past, our findings demonstrate that 1 does not represent the global minimum. Instead, it is a local minimum, positioned over 30 kcal/mol above the lowest energy structure identified in this study.
An essential contribution of our work lies in assessing a novel yet straightforward methodology for exploring such systems' potential energy surface (PES) using known polycyclic hydrocarbons as template structures. Specifically, we used coronene, which facilitated evaluating a series of designs through substitution, elimination, and permutation of atoms.
The reliability of the minima identified through this approach is corroborated by earlier studies where it was compared with evolutionary methods. Our findings underscore the significance of employing appropriate ways to navigate the PES when designing structures with planar hypercoordinate carbons, particularly pertinent for intermediate-sized forms, like 1, where conventional stochastic or evolutionary methods can be challenging to implement. Note that the manual approach may be subject to biases that obstruct identifying the best structures.
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Figure S1: Minimum energy isomers of Si8C22 and their respective point group symmetries and spectroscopic states. Relative energies are shown in kcal·mol-1 at PBE0-D3/Def2-TZVP levels including zero-point energy (ZPE) corrections. Figure S2: Vector plots visualization of the current density in diverse planes of the Si3C5, Si2C6H3+ and Si8C22 cluster. Diatropic currents are assumed to circle clockwise. Figure S3: Top view of integration planes considered to average the profile RCS for Si3C5, Si2C6H3+ and Si8C22 (up) and the RCS pro-files along the different integration planes (down). Figure S4: Bond length in (black), natural charges (red and blue) and Wiberg bond indices (green) for Si8C22 at the PBE0-D3/Def2-TZVP level of theory. Table S1: Cartesian coordinate of the C22H124– and Si8C22 systems calculated at the PBE0-D3/Def2-TZVP level of theory.
Author Contributions
Conceptualization, W.T., V.S.T., L.L-P. and D.I.; methodology, D.I., O.Y. and V.S.T.; software, D.I., O.Y.; validation, W.T., V.S.T., L.L-P.; formal analysis, W.T., A.C., and L.L-P.; investigation, W.T., V.S.T., A.C., D.I.; resources, W.T., V.S.T, A.C.; data curation, V.S.T., L.L-P.,D.I. and O.Y.; writing—original draft preparation, W.T., L.L-P., and D.I.; writing—review and editing, all authors.; visualization, W.T., O.Y., L.L-P. and D.I.; supervision, W.T., V.S.T.; project administration, W.T. and D.I.; funding acquisition, W.T.. All authors have read and agreed to the published version of the manuscript.
Acknowledgments
We thank the financial support of National Agency for Research and Development (ANID) through FONDECYT project 1211128 (W.T.) and National Agency for Research and Development (ANID)/Scholarship Program/BECAS DOCTORADO NACIONAL/2019-21190427 (D.I.). National Agency for Research and Development (ANID)/Scholarship Program/BECAS DOCTORADO NACIONAL/2020-21201177 (L.L-P.). Powered@NLHPC: This research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02). Computational support provided at SDSU (for V.S.T) is gratefully acknowledged. Computational support provided at the SDSU by DURIP Grant W911NF-10-1-0157 from the U.S. Department of Defense and by NSF CRIF Grant CHE-0947087 is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Collins, J.B.; Dill, J.D.; Jemmis, E.D.; Apeloig, Y.; Schleyer, P.V.; Seeger, R.; Pople, J.A. Stabilization of Planar Tetracoordinate Carbon. Journal of the American Chemical Society 1976, 98, 5419–5427. [Google Scholar] [CrossRef]
- Erker, G. Planar-Tetracoordinate Carbon: Making Stable Anti-van′t Hoff/LeBel Compounds. Comments on Inorganic Chemistry 1992, 13, 111–131. [Google Scholar] [CrossRef]
- Rottger, D.; Erker, G. Compounds containing planar-tetracoordinate carbon. Angew Chem Int Edit 1997, 36, 813–827. [Google Scholar] [CrossRef]
- Siebert, W.; Gunale, A. Compounds containing a planar-tetracoordinate carbon atom as analogues of planar methane. Chemical Society Reviews 1999, 28, 367–371. [Google Scholar] [CrossRef]
- Exner, K.; Schleyer, P. v. R. Planar hexacoordinate carbon: A viable possibility. Science 2000, 290, 1937–1940. [Google Scholar] [CrossRef]
- Merino, G.; Méndez-Rojas, M.A.; Beltrán, H.I.; Corminboeuf, C.; Heine, T.; Vela, A. Theoretical analysis of the smallest carbon cluster containing a planar tetracoordinate carbon. J Am Chem Soc 2004, 126, 16160–16169. [Google Scholar] [CrossRef] [PubMed]
- Perez, N.; Heine, T.; Barthel, R.; Seifert, G.; Vela, A.; Mendez-Rojas, M.A.; Merino, G. Planar tetracoordinate carbons in cyclic hydrocarbons. Organic Letters 2005, 7, 1509–1512. [Google Scholar] [CrossRef]
- Keese, R. Carbon flatland: planar tetracoordinate carbon and fenestranes. Chemical reviews 2006, 106, 4787–4808. [Google Scholar] [CrossRef]
- Merino, G.; Méndez-Rojas, M.A.; Vela, A.; Heine, T. Recent advances in planar tetracoordinate carbon chemistry. Journal of Computational Chemistry 2007, 28, 362–372. [Google Scholar] [CrossRef]
- Vela, A.; Méndez-Rojas, M.A.; Merino, G. Theoretical design of electronically stabilized molecules containing planar tetracoordinate carbons. In Theoretical and Computational Chemistry, Elsevier: 2007; Vol. 19, pp 251-267.
- Pei, Y.; An, W.; Ito, K.; Schleyer, P.V.R.; Zeng, X.C. Planar pentacoordinate carbon in CAl5+: a global minimum. J Am Chem Soc 2008, 130, 10394–10400. [Google Scholar] [CrossRef]
- Perez-Peralta, N.; Sanchez, M.; Martin-Polo, J.; Islas, R.; Vela, A.; Merino, G. Planar tetracoordinate carbons in cyclic semisaturated hydrocarbons. The Journal of Organic Chemistry 2008, 73, 7037–7044. [Google Scholar] [CrossRef]
- Li, Y.; Liao, Y.; Chen, Z. Be2C monolayer with quasi-planar hexacoordinate carbons: a global minimum structure. Angewandte Chemie International Edition 2014, 53, 7248–7252. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.M.; Ganz, E.; Chen, Z.; Wang, Z.X.; Schleyer, P. v. R. Four decades of the chemistry of planar hypercoordinate compounds. Angewandte Chemie International Edition 2015, 54, 9468–9501. [Google Scholar] [CrossRef]
- Wang, Y.; Li, F.; Li, Y.; Chen, Z. Semi-metallic Be5C2 monolayer global minimum with quasi-planar pentacoordinate carbons and negative Poisson’s ratio. Nature communications 2016, 7, 11488. [Google Scholar] [CrossRef] [PubMed]
- Cui, Z.-h.; Vassilev-Galindo, V.; Cabellos, J.L.; Osorio, E.; Orozco, M.; Pan, S.; Ding, Y.-h.; Merino, G. Planar pentacoordinate carbon atoms embedded in a metallocene framework. Chemical Communications 2017, 53, 138–141. [Google Scholar] [CrossRef]
- Liu, C.-S.; Zhu, H.-H.; Ye, X.-J.; Yan, X.-H. Prediction of a new BeC monolayer with perfectly planar tetracoordinate carbons. Nanoscale 2017, 9, 5854–5858. [Google Scholar] [CrossRef]
- Pan, S.; Cabellos, J.L.; Orozco-Ic, M.; Chattaraj, P.K.; Zhao, L.; Merino, G. Planar pentacoordinate carbon in CGa 5+ derivatives. Physical Chemistry Chemical Physics 2018, 20, 12350–12355. [Google Scholar] [CrossRef]
- Vassilev-Galindo, V.; Pan, S.; Donald, K.J.; Merino, G. Planar pentacoordinate carbons. Nature Reviews Chemistry 2018, 2, 0114. [Google Scholar] [CrossRef]
- Guo, J.-C.; Feng, L.-Y.; Barroso, J.; Merino, G.; Zhai, H.-J. Planar or tetrahedral? A ternary 17-electron CBe 5 H 4+ cluster with planar pentacoordinate carbon. Chemical Communications 2020, 56, 8305–8308. [Google Scholar] [CrossRef]
- Wang, M.-h.; Dong, X.; Ding, Y.-h.; Cui, Z.-h. Avoided spin coupling: an unexpected σ–σ diradical in global planar pentacoordinate carbon. Chemical Communications 2020, 56, 7285–7288. [Google Scholar] [CrossRef]
- Leyva-Parra, L.; Diego, L.; Yañez, O.; Inostroza, D.; Barroso, J.; Vásquez-Espinal, A.; Merino, G.; Tiznado, W. Planar hexacoordinate carbons: half covalent, half ionic. Angewandte Chemie International Edition 2021, 60, 8700–8704. [Google Scholar] [CrossRef] [PubMed]
- Leyva-Parra, L.; Inostroza, D.; Yañez, O.; Cruz, J.C.; Garza, J.; García, V.; Tiznado, W. Persistent planar tetracoordinate carbon in global minima structures of silicon-carbon clusters. Atoms 2022, 10, 27. [Google Scholar] [CrossRef]
- van't Hoff, J. Arch. Neerl. Sci. Exactes Nat. 1874.
- Le Bel, J.A. Sur les relations qui existent entre les formules atomiques des corps organiques et le pouvoir rotatoire de leurs dissolutions. Bull. Soc. Chim. Fr 1874, 22, 337–347. [Google Scholar]
- Monkhorst, H. Activation energy for interconversion of enantiomers containing an asymmetric carbon atom without breaking bonds. Chemical Communications (London) 1968, 18, 1111–1112. [Google Scholar] [CrossRef]
- Hoffmann, R.; Alder, R.W.; Wilcox, C.F. Planar Tetracoordinate Carbon. J Am Chem Soc 1970, 92, 4992. [Google Scholar] [CrossRef]
- Cotton, F.A.; Millar, M. Probable Existence of a Triple Bond between 2 Vanadium Atoms. Journal of the American Chemical Society 1977, 99, 7886–7891. [Google Scholar] [CrossRef]
- Inostroza, D.; Leyva-Parra, L.; Vásquez-Espinal, A.; Contreras-García, J.; Cui, Z.-H.; Pan, S.; Thimmakondu, V.S.; Tiznado, W. E 6 C 15 (E= Si–Pb): polycyclic aromatic compounds with three planar tetracoordinate carbons. Chemical Communications 2022, 58, 13075–13078. [Google Scholar] [CrossRef]
- Yañez, O.; Vásquez-Espinal, A.; Pino-Rios, R.; Ferraro, F.; Pan, S.; Osorio, E.; Merino, G.; Tiznado, W. Exploiting electronic strategies to stabilize a planar tetracoordinate carbon in cyclic aromatic hydrocarbons. Chemical Communications 2017, 53, 12112–12115. [Google Scholar] [CrossRef]
- Thimmakondu, V.S. Comment on “Exploiting electronic strategies to stabilize a planar tetracoordinate carbon in cyclic aromatic hydrocarbons” by O. Yañez et al. Chem. Commun. 2017, 53, 12112. Chemical Communications 2019, 55, 12719–12720. [Google Scholar] [CrossRef]
- Yanez, O.; Vasquez-Espinal, A.; Pino-Rios, R.; Ferraro, F.; Pan, S.; Osorio, E.; Merino, G.; Tiznado, W. Reply to the 'Comment on "Exploiting electronic strategies to stabilize a planar tetracoordinate carbon in cyclic aromatic hydrocarbons"' by V. S. Thimmakondu, Chem. Commun., 2019, DOI: 10.1039/c9cc04639a. Chem. Commun. 2019, 55, 12721–12722. [Google Scholar]
- Yañez, O.; Vásquez-Espinal, A.; Báez-Grez, R.; Rabanal-León, W.A.; Osorio, E.; Ruiz, L.; Tiznado, W. Carbon rings decorated with group 14 elements: New aromatic clusters containing planar tetracoordinate carbon. New Journal of Chemistry 2019, 43, 6781–6785. [Google Scholar] [CrossRef]
- Yañez, O.; Báez-Grez, R.; Garza, J.; Pan, S.; Barroso, J.; Vásquez-Espinal, A.; Merino, G.; Tiznado, W. Embedding a Planar Hypercoordinate Carbon Atom into a [4n+ 2] π-System. ChemPhysChem 2020, 21, 145–148. [Google Scholar] [CrossRef] [PubMed]
- Inostroza, D.; Leyva-Parra, L.; Yañez, O.; Cruz, J.C.; Garza, J.; García, V.; Thimmakondu, V.S.; Ceron, M.L.; Tiznado, W. Si6C18: A bispentalene derivative with two planar tetracoordinate carbons. International Journal of Quantum Chemistry 2022, 123, e27008. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.F.; Wang, L.S.; Geske, G.D.; Boldyrev, A.I. Pentaatomic tetracoordinate planar carbon,[CAl4] 2−: a new structural unit and its salt complexes. Angewandte Chemie 2000, 112, 3776–3778. [Google Scholar] [CrossRef]
- Curtarolo, S.; Morgan, D.; Persson, K.; Rodgers, J.; Ceder, G. Predicting crystal structures with data mining of quantum calculations. Physical review letters 2003, 91, 135503. [Google Scholar] [CrossRef]
- Addicoat, M.A.; Metha, G.F. Kick: constraining a stochastic search procedure with molecular fragments. Journal of computational chemistry 2009, 30, 57–64. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Crystal structure prediction via particle-swarm optimization. Physical Review B 2010, 82, 094116. [Google Scholar] [CrossRef]
- Yanez, O.; Baez-Grez, R.; Inostroza, D.; Rabanal-Leon, W.A.; Pino-Rios, R.; Garza, J.; Tiznado, W. AUTOMATON: A Program That Combines a Probabilistic Cellular Automata and a Genetic Algorithm for Global Minimum Search of Clusters and Molecules. J Chem Theory Comput 2019, 15, 1463–1475. [Google Scholar] [CrossRef]
- Yañez, O.; Inostroza, D.; Usuga-Acevedo, B.; Vásquez-Espinal, A.; Pino-Rios, R.; Tabilo-Sepulveda, M.; Garza, J.; Barroso, J.; Merino, G.; Tiznado, W. Evaluation of restricted probabilistic cellular automata on the exploration of the potential energy surface of Be6B11−. Theoretical Chemistry Accounts 2020, 139, 1–8. [Google Scholar] [CrossRef]
- Yañez, O.; Báez-Grez, R.; Inostroza, D.; Pino-Rios, R.; Rabanal-León, W.A.; Contreras-García, J.; Cardenas, C.; Tiznado, W. Kick–Fukui: A Fukui Function-Guided Method for Molecular Structure Prediction. Journal of Chemical Information and Modeling 2021, 61, 3955–3963. [Google Scholar] [CrossRef]
- Boldyrev, A.I.; Wang, L.-S. All-Metal Aromaticity and Antiaromaticity. Chemical Reviews 2005, 105, 3716–3757. [Google Scholar] [CrossRef]
- Guo, J.C.; Feng, L.Y.; Zhang, X.Y.; Zhai, H.J. Star-Like CBe5Au5+ Cluster: Planar Pentacoordinate Carbon, Superalkali Cation, and Multifold (pi and sigma) Aromaticity. J. Phys. Chem. A 2018, 122, 1138–1145. [Google Scholar] [CrossRef] [PubMed]
- Kalita, A.J.; Rohman, S.S.; Kashyap, C.; Ullah, S.S.; Guha, A.K. Double aromaticity in a BBe6H6+ cluster with a planar hexacoordinate boron structure. Chem. Commun. 2020, 56, 12597–12599. [Google Scholar] [CrossRef]
- Averkiev, B.B.; Zubarev, D.Y.; Wang, L.M.; Huang, W.; Wang, L.S.; Boldyrev, A.I. Planar Pentacoordinate Carbon in CAl5+: A Global Minimum. J. Am. Chem. Soc. 2008, 130, 9248–9250. [Google Scholar] [CrossRef] [PubMed]
- Leyva-Parra, L.; Diego, L.; Inostroza, D.; Yañez, O.; Pumachagua-Huertas, R.; Barroso, J.; Vásquez-Espinal, A.; Merino, G.; Tiznado, W. Planar Hypercoordinate Carbons in Alkali Metal Decorated CE32− and CE22− Dianions. Chemistry–A European Journal 2021, 27, 16701–16706. [Google Scholar] [CrossRef] [PubMed]
- Stillinger, F.H. Exponential multiplicity of inherent structures. Physical Review E 1999, 59, 48. [Google Scholar] [CrossRef]
- Rossi, G.; Ferrando, R. Searching for low-energy structures of nanoparticles: a comparison of different methods and algorithms. Journal of Physics: Condensed Matter 2009, 21, 084208. [Google Scholar] [CrossRef]
- Dewar, M.J.; Zoebisch, E.G.; Healy, E.F.; Stewart, J.J. Development and use of quantum mechanical molecular models. 76. AM1: a new general purpose quantum mechanical molecular model. Journal of the American Chemical Society 1985, 107, 3902–3909. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. The Journal of chemical physics 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Fuentealba, P.; Preuss, H.; Stoll, H.; Von Szentpály, L. A proper account of core-polarization with pseudopotentials: single valence-electron alkali compounds. Chemical Physics Letters 1982, 89, 418–422. [Google Scholar] [CrossRef]
- Fuentealba, P.; Von Szentpaly, L.; Preuss, H.; Stoll, H. Pseudopotential calculations for alkaline-earth atoms. Journal of Physics B: Atomic and Molecular Physics (1968-1987) 1985, 18, 1287. [Google Scholar] [CrossRef]
- Küchle, W.; Dolg, M.; Stoll, H.; Preuss, H. Ab initio pseudopotentials for Hg through Rn: I. Parameter sets and atomic calculations. Molecular Physics 1991, 74, 1245–1263. [Google Scholar] [CrossRef]
- Bergner, A.; Dolg, M.; Küchle, W.; Stoll, H.; Preuß, H. Ab initio energy-adjusted pseudopotentials for elements of groups 13–17. Molecular Physics 1993, 80, 1431–1441. [Google Scholar] [CrossRef]
- Küchle, W.; Dolg, M.; Stoll, H.; Preuss, H. Energy-adjusted pseudopotentials for the actinides. Parameter sets and test calculations for thorium and thorium monoxide. The Journal of chemical physics 1994, 100, 7535–7542. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J Chem Phys 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Physical Chemistry Chemical Physics 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. B.01, Wallingford, CT, 2016.
- Jusélius, J.; Sundholm, D.; Gauss, J. Calculation of current densities using gauge-including atomic orbitals. The Journal of chemical physics 2004, 121, 3952–3963. [Google Scholar] [CrossRef]
- Fliegl, H.; Taubert, S.; Lehtonen, O.; Sundholm, D. The gauge including magnetically induced current method. Physical Chemistry Chemical Physics 2011, 13, 20500–20518. [Google Scholar] [CrossRef]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. Journal of the American Chemical Society 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Ayachit, U.; Geveci, B.; Moreland, K.; Patchett, J.; Ahrens, J. The ParaView Visualization Application. 2012.
- Ayachit, U. The paraview guide: a parallel visualization application. Kitware, Inc.: 2015.
- Abramowitz, M. Handbook of Mathematical Functions, with Formulas, Graphs, and Mathematical Tables. New York, NY, USA, 1974.
- Sundholm, D.; Fliegl, H.; Berger, R.J. Calculations of magnetically induced current densities: theory and applications. Wiley Interdisciplinary Reviews: Computational Molecular Science 2016, 6, 639–678. [Google Scholar] [CrossRef]
- Sundholm, D.; Berger, R.J.; Fliegl, H. Analysis of the magnetically induced current density of molecules consisting of annelated aromatic and antiaromatic hydrocarbon rings. Physical Chemistry Chemical Physics 2016, 18, 15934–15942. [Google Scholar] [CrossRef]
- Inostroza, D.; García, V.; Yañez, O.; Torres-Vega, J.J.; Vásquez-Espinal, A.; Pino-Rios, R.; Báez-Grez, R.; Tiznado, W. On the NICS limitations to predict local and global current pathways in polycyclic systems. New Journal of Chemistry 2021, 45, 8345–8351. [Google Scholar] [CrossRef]
- Wiberg, K.B. Application of the pople-santry-segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane. Tetrahedron 1968, 24, 1083–1096. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural population analysis. The Journal of Chemical Physics 1985, 83, 735–746. [Google Scholar] [CrossRef]
- Zubarev, D.Y.; Boldyrev, A.I. Developing paradigms of chemical bonding: adaptive natural density partitioning. Physical chemistry chemical physics 2008, 10, 5207–5217. [Google Scholar] [CrossRef] [PubMed]
- Zubarev, D.Y.; Boldyrev, A.I. Revealing intuitively assessable chemical bonding patterns in organic aromatic molecules via adaptive natural density partitioning. The Journal of Organic Chemistry 2008, 73, 9251–9258. [Google Scholar] [CrossRef] [PubMed]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. NBO 6.0: natural bond orbital analysis program. J Comput Chem 2013, 34, 1429–1437. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: a multifunctional wavefunction analyzer. Journal of computational chemistry 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Legault, C.Y. CYLview20, Université de Sherbrooke: 2020.
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: visual molecular dynamics. J Mol Graph 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Thimmakondu, V.S.; Sinjari, A.; Inostroza, D.; Vairaprakash, P.; Thirumoorthy, K.; Roy, S.; Anoop, A.; Tiznado, W. Why an integrated approach between search algorithms and chemical intuition is necessary? Physical Chemistry Chemical Physics 2022, 24, 11680–11686. [Google Scholar] [CrossRef]
Scheme 1.
Design of Si8C22 ptC system starting from the Naphtho[1,2-b:3,4-b’:5,6-b’’:7,8-b´´]tetrathiophene (left) to build C22H124– and finally the ptC candidate (right).
Scheme 1.
Design of Si8C22 ptC system starting from the Naphtho[1,2-b:3,4-b’:5,6-b’’:7,8-b´´]tetrathiophene (left) to build C22H124– and finally the ptC candidate (right).
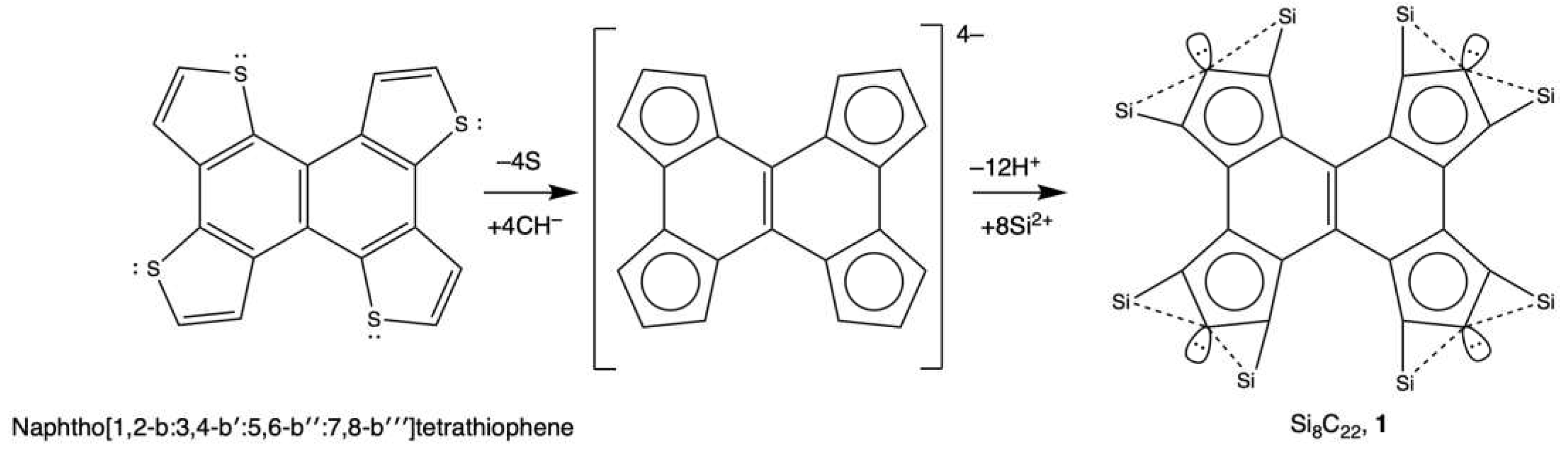
Figure 1.
Schematic depiction of the identified ring current circuits (noted with their corresponding strengths in nA/T) for aromatic hydrocarbon derivatives featuring ptCs. Subfigures include: a) benzene derivative (Si2C6H3+), b) cyclopentadienyl anion derivative (Si3C5), c) Naphtho[1,2-b:3,4-b′:5,6-b′′:7,8-b′′′′]tetrathiophene derivative(S8C22).
Figure 1.
Schematic depiction of the identified ring current circuits (noted with their corresponding strengths in nA/T) for aromatic hydrocarbon derivatives featuring ptCs. Subfigures include: a) benzene derivative (Si2C6H3+), b) cyclopentadienyl anion derivative (Si3C5), c) Naphtho[1,2-b:3,4-b′:5,6-b′′:7,8-b′′′′]tetrathiophene derivative(S8C22).
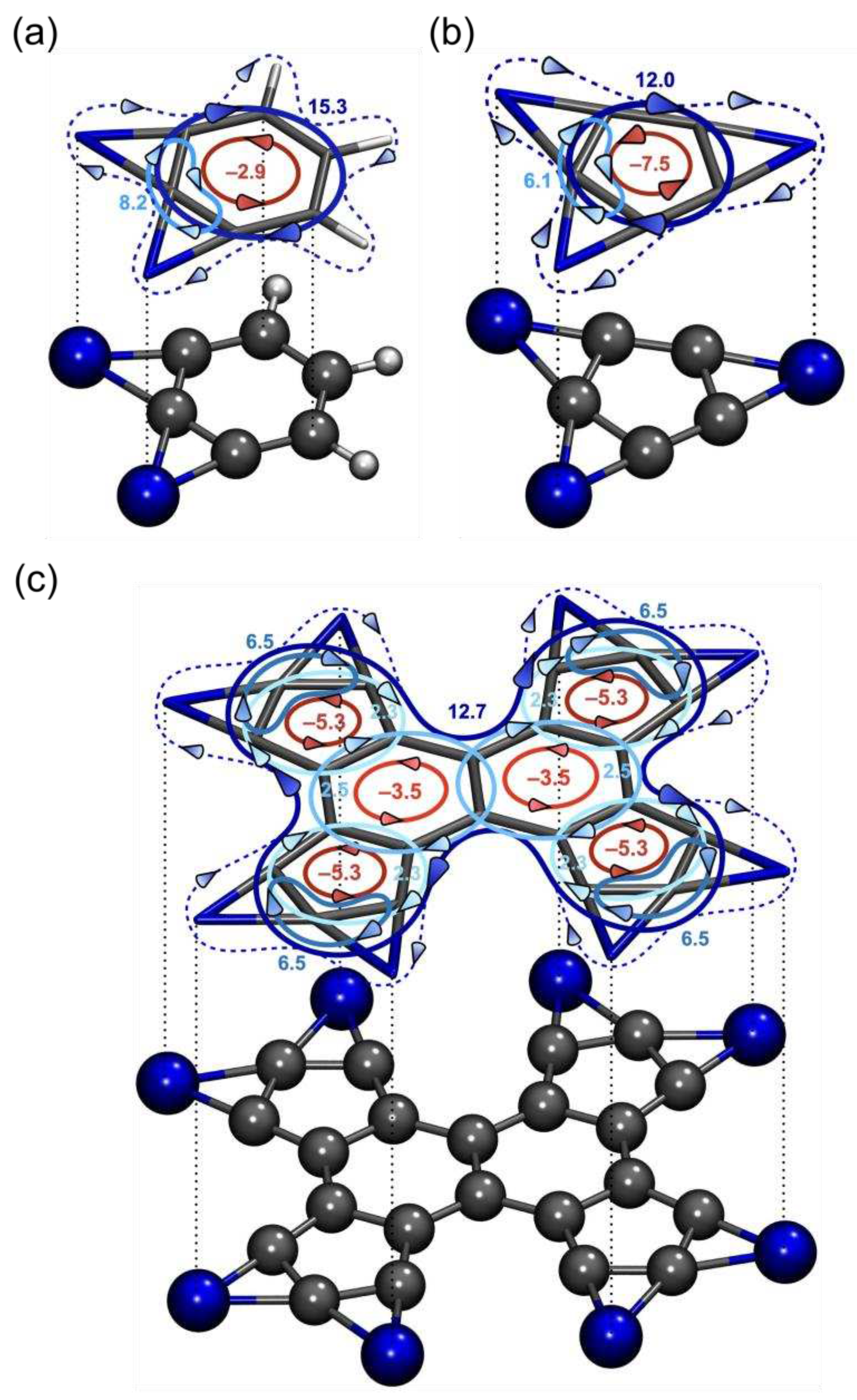
Figure 2.
AdNDP analysis of 1 at the PBE0-D3/Def2-TZVP level. ON stands for occupation number. Carbon=gray, silicon=blue.
Figure 2.
AdNDP analysis of 1 at the PBE0-D3/Def2-TZVP level. ON stands for occupation number. Carbon=gray, silicon=blue.
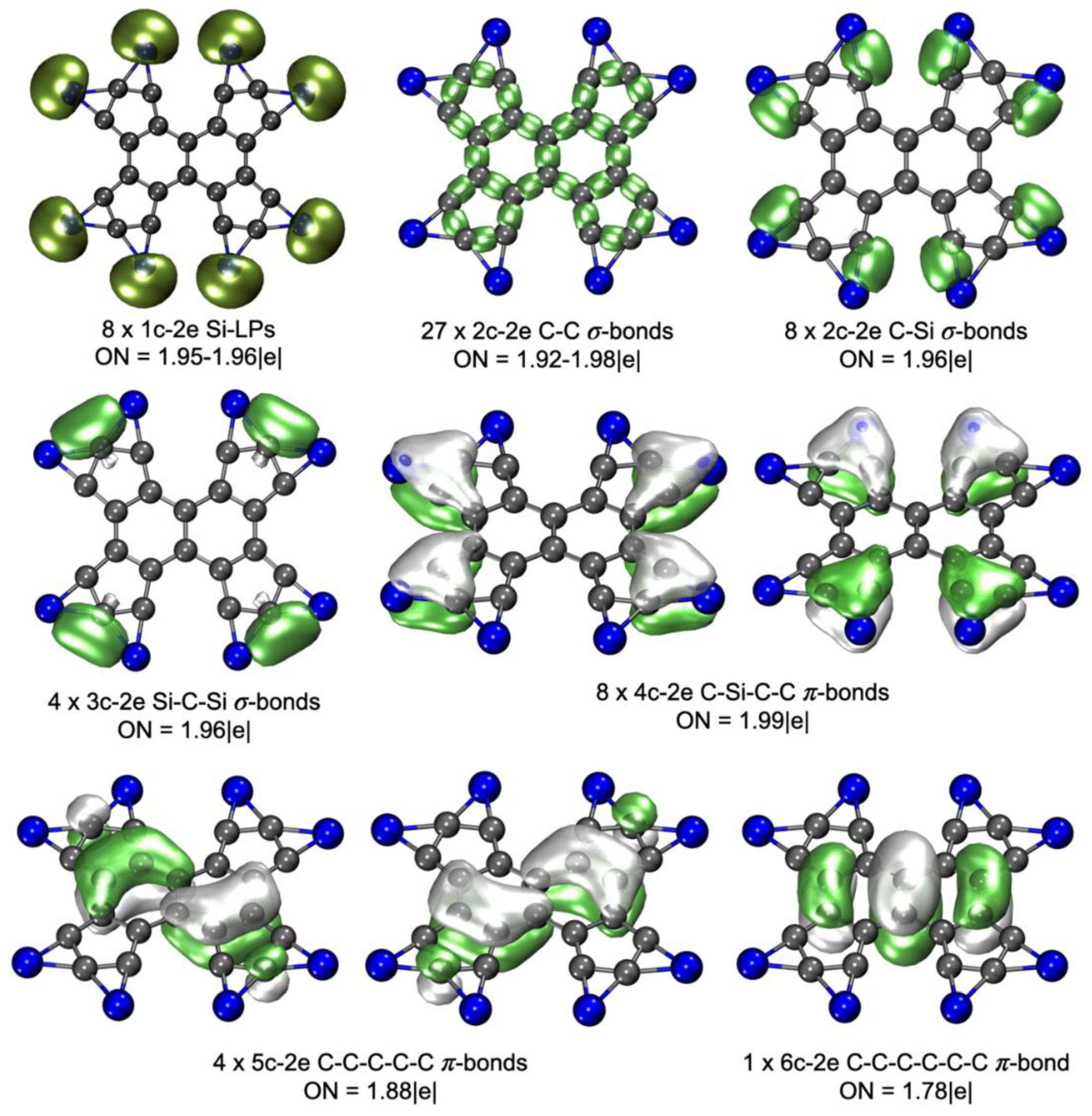
Figure 3.
Schematic representation of the strategic approach for exploring the Si8C22 cluster's potential energy surface.
Figure 3.
Schematic representation of the strategic approach for exploring the Si8C22 cluster's potential energy surface.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






