Prerpints.org logo
Preprint
Article

Wavelet Transforms and Machine Learning Methods for the Study of Turbulence

Altmetrics

Downloads

153

Views

101

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

08 June 2023

Posted:

13 June 2023

You are already at the latest version

Alerts
Abstract
This article examines the wavelet transforms and the machine learning methods in accelerating large eddy simulations of turbulent flows. An overarching challenge of large eddy simulations is to accurately represent the cascade of kinetic energy across the cut-off length scale. Taylor hypothesis suggests that the energy cascade occurs through the process of vortex stretching. However, Richardson hypothesis assumes the self-amplification of the strain field and a hierarchical break down of large eddies lead the energy cascade. The large eddy simulations typically employs the self-amplification of the strain in formulating subgrid models. However, several studies also proposed subgrid models based on vortex stretching. The wavelet-based coherent vortex simulation of turbulence directly accounts for vortex stretching in overall forward scatter of energy, while allowing local backscatter. The wavelet-based large eddy simulation adapts the grid to capture the creation of small-scale eddies, while adopting subgrid models based on the self-amplification of strain. The advancement of artificial intelligence in turbulence modelling is currently evolving around accelerating the numerical simulations of turbulent flow. However, there is a clear connection between the application of wavelet transfroms and neural networks for directly solving the Navier-Stokes equation, indicating some potential benefits of wavelet methods over the neural networks.
Keywords: 
Subject: Physical Sciences  -   Fluids and Plasmas Physics

1. Introduction

Turbulence is a multiscale process consisting of localized coherent vortices that coexist at a wide range of length and time scales [1,2,3]. Therefore, identifying and capturing the localized flow features in turbulence are crucial to understanding and controlling turbulence [4,5]. Recent advances in wavelet method (e.g. [6,7]) and machine learning (e.g. [8,9]) aim to address these issues and complement the existing turbulence modeling approaches [10]. This article reviews the recent progresses in applications of machine learning and wavelet transforms in turbulence modeling. These two approaches have great promise and potential to become the methodological portfolio of turbulent fluid dynamics.
Machine learning and turbulence modeling are two distinct fields that offer fertile ground to the data-driven paradigm [8]. Both fields exploit the coherence property underlying high-dimensional systems. Machine learning leverages the coherence of data to improve performance on some sets of tasks. It uses optimization algorithms to learn a set of parameters and gradually enhance its learning rates. Machine learning methods are an essential part of the methodological portfolio of the growing field of data science. Researchers have recently applied machine learning methods to fluid mechanics ranging from flow control to turbulence modeling [11,12,13,14]. As machine learning continues to augment traditional methods, the demand of dedicated algorithms for solving the Navier-Stokes equations has also grown simultaneously.
The Navier-Stokes equations characterize turbulence at large Reynolds numbers ( R e ). Solving these equations at high R e remains daunting. The study of the Naiver-Stokes equations and turbulence plays a significant role in all technologies involving fluids. For instance, turbulence-induced drag causes vehicles to emit 2 Gigatons of CO 2 annually, about 5% of the world’s energy usage. Capturing a turbulent flow at typical values of R e ∼ 10 8 requires millions of terabytes of data. The growth of turbulence data from experiments, field measurements, and numerical simulations is remarkable. Moreover, the growth of methods in handling such a fluid data have put current generation researchers at the confluence of vast and increasing volumes of data and algorithms. The wavelet method aims to optimize such algorithms. Using wavelet-based algorithms in turbulence modeling, our goal is to optimize first-principle conservation laws by predicting the evolution of the coherent structures of turbulent fluid flows.
In the early 1990, Farge [3] reviewed the application of wavelet transforms to study turbulence, covering a general presentation of both the continuous wavelet transform and the discrete wavelet transform. In 2010, Schneider and Vasilyev [6] reviewed the application of wavelet transforms in computational fluid dynamics (CFD). Recently, Mehta et al. [15] documented the new developments of the adaptive wavelet collocation method (AWCM) as a technique for solving partial differential equations (PDEs). Brunton et al. [8] documented the concept of machine learning in fluid dynamics. In this article, we outline recent progresses in classical turbulence modelling, focus on the application of machine learning in turbulence modeling, and finally, discuss the potential route to address current turbulence modelling issues by combining wavelet method with machine learning.

Outline

Section 2 provides an overview of turbulence modeling in the context of large eddy simulation (LES). Section 3 summarizes current trends in advancements of machine learning algorithms in CFD and turbulence modeling. Section 4 summarizes the wavelet-based turbulence modelling strategy.

2. Turbulence Modeling Background

The direct numerical simulation (DNS) uses a fine grid to capture the entire spectrum of turbulence eddies. In contrast, the Reynolds averaged Navier-Stokes simulation (RANS) uses a coarse to represent the full range of turbulence eddies through the closure approximation scheme. LES is intermediate to DNS and RANS, which resolves a significant fraction of turbulent eddies and uses a subgrid model for the unresolved eddies. We see from the following discussion that the primary difference between LES and RANS comes from the turbulence closure models for the partially unresolved and entirely unresolved turbulent motions, respectively.

2.1. Filtering

The first step in formulating LES is the convolution of the velocity u ( x , t ) : [ a , b ] × [ 0 , T ] → R with a kernel G ( r ) such that
u ¯ ( x , t ) = ∫ − ∞ ∞ u ( x − r , t ) G ( r ) d t .
In the following, we say that u ¯ i ( x , t ) is the i-th component of the wavelet-filtered velocity if G ( r ) is a wavelet; otherwise, it is called filtered velocity. We use bold-faced symbols to denote a quantity in the 3D Euclidean space and subscript i (or j and k) to denote standard tensorial representations considered in fluid dynamics. We remind readers that the discretization technique serves as an implicit filter G ( r ) unless an explicit filter is mentioned. Moreover, the wavelet filter is a special form of the explicit filter.

2.2. The Filtered Navier-Stokes System

The temporal evolution of the large-scale dynamics of a fluid system is given by filtered Navier-Stokes equations:
∂ u i ¯ ∂ x i = 0 ,
∂ u i ¯ ∂ t + u j ¯ ∂ u i ¯ ∂ x j = − 1 ρ ∂ P ¯ ∂ x i + ∂ ∂ x j 2 ν S i j − τ i j ,
and
τ i j − 1 3 τ k k δ i j = − 2 ν τ S i j .
The filtering operator ( · ) ¯ extracts the energy containing significant motion. The effect of discarding residual motion is represented by the subfilter-scale turbulence stress τ i j s = u i u ¯ j − u ¯ i u ¯ j . In Eqs (2-3), the subgrid scale stress τ i j is an approximation of the subfilter scale stress τ i j s . We keep this notation to clarify that subgrid scale stresses are not the same as the true subfilter scale stresses. The divergence of the symmetric part of the velocity gradient tensor, S i j = ( 1 / 2 ) ( ∂ u i / ∂ u j + ∂ u j / ∂ u i ) , becomes a Laplacian due to Eq (1), and thus, Eq (3) is an ideal candidate to model turbulence, where ν τ ( x , t ) = c s ( x , t ) Δ 2 2 S i j S i j . The amplification of the strain-rate tensor S i j plays a direct role in the classical subgrid models of LES.

2.3. Classical LES

In classical LES, we treat a coarse-grid approximation of the fluid velocity u ¯ i ( x , t ) as a filtered representation of the ground truth u i ( x , t ) and employ the closure scheme to model the subfilter-scale stress τ i j s [10,16]. Over the last three decades, there have been promising progresses in LES of turbulence [16]. Various developments of subgrid-scale models have been an integral part of the LES of turbulence. In general, LES finds an approximation of the subfilter-scale stress τ i j s as a function of the symmetric part of the velocity gradient tensor and a dynamic parameter c s ( x , t ) , such as
τ i j s ≈ τ i j ≡ Π ( c s , S i j ) .
Note that
∂ u i ∂ x j = 1 2 ∂ u i ∂ x j + ∂ u j ∂ x i ︷ strain , S i j + 1 2 ∂ u i ∂ x j − ∂ u j ∂ x i ︸ vorticity , R i j .
Clearly, the subgrid model Eq (3) excludes the vorticity. Also, the dynamic evaluation of c s ( x , t ) has been a major focus in turbulence modeling. This is one of the most challenging and computationally intensive elements of LES.
A principal open challenge is to represent the eddy viscosity ν τ in Eq (3) when the discretization of Eqs (1-2) becomes sufficient to capture a major proportion of large eddies (i.e. about 80% of the kinetic energy [10]). Each of the commonly used models differs depending on how we calculate c s ( x , t ) to dynamically adapt the eddy viscosity ν τ to the multiscale nature of the problem. A fine grid that is sufficient to resolve most of the eddies at a particular time in a region may become insufficient at another time. The range of grid resolution in which turbulence is insufficiently resolved in some part of the domain and becomes full resolved is other parts called the grey zone of atmospheric turbulence. For instance, in the atmospheric boundary layer turbulence, the energy-containing eddies’ size is locally reduced by both the frictional effects of the earth’s surface and the thermal stratification. Honnert et al. [17] reviewed the current state-of-the-art in ‘grey-zone’ turbulence modelling, where neither the LES nor the RANS model is appropriate [18].
For LES of wall-bounded turbulent flows, specialized treatments of the eddy viscosity ν τ become essential, which is called wall-modelled LES. Bose and Park [19] recently reviewed various formulations of the wall-modelled LES. Readers interested in other developments of the eddy viscosity ν τ may consider the recent work of Moser et al. [16]. An interesting open question is whether the existing LES techniques adequately capture a number of geometric and statistical phenomena, such as the alignment of vorticity with respect to the strain rate eigenvectors, non-Gaussian statistics, and intermittency [20,21,22]. Another question is whether the dynamic adaption of c s in formulating the eddy viscosity by Eq (3) can account for the subgrid scale production via vortex stretching [22,23].
Recent developments in machine learning and wavelet methods aim to address some of the above questions. Kurz et al. [24] covers the recent progresses, challenges and promises of machine learning methods applied to large eddy simulation (LES) of turbulence (see also [25]). Schneider and Vasilyev [6], and De Stefano and Vasilyev [26] have thoroughly covered the promise of wavelet methods in addressing the above questions. In the atmosphere and oceans, turbulence is heterogenous, anisotropic, and scale-dependent. Scale-aware subgrid models automatically adjust their effects according to the changes of grid resolution, grid orientation, and fraction of resolved flow.

2.4. Scale-Adaptive LES

Recently, we have developed the scale-adaptive LES methodology to formulate the eddy viscosity ν τ in Eq (3) via the idea of energy casecade by vortex stretching. Menter and Egorov [27] presented a scale-adaptive simulation, which adapts the RANS model with the LES model. For example, RANS model is applied in a particular region, where the grid is locally insufficient to capture energetic fluctuations (such as in a close proximity of walls), and switches off to LES model otherwise. In the atmospheric boundary layer simulations, such hybrid RANS/LES methods are applied at O ( 100 ) m to O ( 1000 ) m horizontal grid spacing. If we achieve the scale adaptivity by blending two models, the turbulence dissipation from RANS model may also suppress the generation of LES content in the RANS/LES interface [28,29].
The scale-adaptive LES may address such a problem by considering that turbulence consists of vortices in nonlinear interactions. However, we do not have a sufficient knowledge of the vorticity production by nonlinear instabilities, e.g., in boundary layers due to the duality between physical localization and spectral localization. To account for the vorticity dynamics in scale-adaptive LES of atmospheric turbulence over complex terrain, Bhuiyan and Alam [30] considered the scale-similarity assumption [31], which states that the subfilter scale stress τ i j s equals the resolved stresses τ i j L = u ¯ i u ¯ ˜ j − u ¯ ˜ i u ¯ ˜ j at scales between Δ and α Δ (with α ≥ 1 ) [32,33]. Here, we apply an explicit filtering in addition to the implicit filtering, where Δ and α Δ refer to the resolved length scales of implicit and explicit LES filtering, respectively.
Using the Taylor expansion of u i ( x , t ) surrounding an arbitrary point in the flow the Leonard (resolved) stress is analytically equivalent to τ i j L = Δ 2 G i k G k j , where G i j = ∂ u i / ∂ x j [33,34]. That is to say, the second invariant of the Leonard stress, as it can be expressed in the following form
Q L = − 1 4 S i j ω j S i k ω k + 1 3 ( G i j G i j ) 2
accounts for vortex stretching S i j ω j S i k ω k and the relative significance of the vorticity over the strain. Here, Q = − ( 1 / 2 ) ( G i j G i j ) 2 is the Q-criterion for vortex identification. Further, the energy flux associated with the Leonard stress
− S i j τ i j L = c k Δ 2 − S i j S j k S k i + 1 4 ω i ω j S i j
indicates that a negative skewness of the strain − S i j S j k S k i along with a positive value of the enstrophy production by vorticity stretching ω i ω j S i j would extract energy by small-scale vortex stretching when the large-scale strain is enhanced. This observation suggest the existence of a functional of τ i j L , which may be in the form of its second invariant, and represents the local rate of dissipation in turbulent flows. Based on the dimensional reasoning, we form a functional that maps the space of the velocity gradient tensor to that of turbulence kinetic energy, which takes the following form:
k sgs ( x , t ) = Δ 2 1 2 S i j ω j S i k ω k + 1 6 ( G i j G i j ) 2 3 ( S i j S i j ) 5 / 2 + 1 2 S i j ω j S i k ω k + 1 6 ( G i j G i j ) 2 5 / 4 2 .
To further extend the aforementioned discussion, we follow Deardorff [35] to form the following subgrid scale model:
τ i j − 1 3 τ k k δ i j = − c k Δ k sgs S i j .
In Eq (4), the consideration of vorticity is important from a dynamical point of view because Helmholtz and Kelvin theorems have set vorticity as the essential field that triggers the fluctuations of velocity. This view shares that of Farge [3] and Chorin [36] who advocate for vorticity as the computational element of turbulent flows.

2.5. Remark

In this section, we show that the turbulence energy cascade occurs through the process of vortex stretching, but vortex stretching is not the main elements of the commonly used subgrid models in LES. We illustrate one way of incorporating vortex stretching in scale-adaptive LES. We have considered an explicit form the Leonard stresses to lay a vortex stretching-based LES framework. We show in the later section that the wavelet transforms and the proper orthogonal decomposition (POD) method are two promising and attractive tools to explicitly compute the Leonard stresses for scale-adaptive LES. Machine learning of suibgrid models provide one possible route to the evarlasting problem of turbulence given the availabiblity of high-resolution taining data.

3. Machine Learnig in Computational Fluid Dynamics

Machine learning is a modeling framework for artificial intelligence, which has recently become a core technology in data science [37]. In fluid dynamics, we are interested in adopting some of the advantages of machine learning to accelerate CFD/DNS calculations [5], improve subgrid-scale modeling [13], or derive reduced order models of fluid flows [38]. CFD/DNS caculations are often computationally demanding but highly accurate. In contrast, machine learning models may run faster than CFD models [8]. For instance, solving the Poisson equation for pressure is one of the computationally extensive step of CFD/DNS, which can be accelerated by adopting a machine learning algorithm [39]. Thus, our parsimonious objectives are twofold. First, we want to employ machine learning to extract a compact latent representation of high-dimensional dynamics, while accounting for the underlying non-linearity into a low-dimensional manifold [40]. In other words, we need to learn both the (nonlinear) differential operator underlying a data and the associated forces, e.g., if the data represents some fluid-structure interactions. Second, we want an optimal reconstruction/prediction of the high-dimensional data in a low-dimensional manifold. Thus, to accelerate CFD calculations, we look for solutions from a low-dimensional manifold, while penalizing the size of the solution vector [41].
A machine learning algorithm finds an approximation ϕ ( x , y , w ) that assigns an input x to an output y with respect to a set of parameters w. Given a set of observations y ( x ) , we look for parameters w to formulate an approximation y ( x ) ≈ ϕ ( x , y , w ) . The approximation is weighted by some probability distribution σ ( x , y ) that constrains the parameter w with respect to observations y ( x ) . The expected loss or the residual of such approximation is given by
R [ w ] = ∫ L ( y , ϕ ( x , y , w ) ) σ ( x , y ) d x d y
where L ( · ) is a measure of some objectives such as accuracy, smoothness, cost, etc. The precise form of ϕ ( x , y , w ) is found during the learning (aka training) phase. In other words, a set of parameters w is determined to minimize the expected loss R [ w ] . Once the model is learned, it can determine the best match of a new input x to a target output y. Various algorithms of machine learning are grouped into three main catagories.
Unsupervised learning is an algorithm that finds an approximation ϕ ( x , y , w ) to represent the self-organization of input x to groups of output y. Examples of unsupervised learning in data science include clustering, anomaly detection, etc. In fluid mechanics, the energy spectrum is a low-dimensional projection of turbulent flows, which clusters turbulence kinetic energy in spherical shells of wavenumbers. The POD method organizes the variability of turbulent flow to recognize coherent patterns of turbulence.
Supervised machine learning is the process that comprises some existing observations of the target output corresponding to the approximate model ϕ ( x , y , w ) . For instance, neural networks can approximate the underlying functional between observations and targets. The observations allow to explicitly define the loss, e.g., R [ w ] = | | y − ϕ ( x , y , w ) | | 2 , which may be regularized, such as R [ w ] = | | y − ϕ ( x , y , w ) | | 2 + ( λ / 2 ) | | w | | 2 . The direct numerical simulation (DNS) of turbulent flows observes velocity and pressure and minimizes the loss of mapping the observations to the solution (i.e. target) of Navier-Stokes equations. DNS of incompressible flows employs various regularization algorithms to minimize additional pressure loss. Researchers have extensively utilized the DNS algorithm to learn fluids and control various machines that operate through fluids. The potential for artificial intelligence in aerospace and fluid machinary evolved several new numerical optimization schemes through the developments in CFD in the early 1980s.
Reinforcement learning finds suitable actions to take in a given situation to maximize a reward. The idea is that a learning algorithm would discover the optimal model for a target by trial and error. For instance, in LES of turbulence, each grid point is an agent that learns the subgrid-scale turbulent environment receiving rewards in the form of dissipation rates or eddy viscosity.
The brief discussion above has set the common CFD portfolio in the machine learning framework. It is necessary to understand the algorithmic framework if we want to develop machine learning techniques in fluid dynamics. Machine learning can undoubtedly become a critical tool in several other aspects of CFD and flow modeling, which have not been discussed above. Developing and adapting machine learning algorithms that accelerate a CFD approach is crucial. Fluid dynamics presents additional challenges from its underlying physics and dynamics, which differs from those in data science. CFD utilizes centuries-old developments in fluid dynamics, which are based on first principles. Combining first principles with data-driven algorithms has the potential to impact both CFD and machine learning.

3.1. Neural Networks and LES

To improve the performance of LES, such as in atmospheric boundary layer flows, the SGS quantity c s ( x , t ) and the wall shear stress τ w ( x 1 , x 2 , 0 , t ) are computed dynamically as the calculation progresses. This step of LES is computationally expensive, and strictly related to the local conditions of the flow [19,42]. The Reynolds number scaling for LES of such wall-bounded turbulent flows is in the range of R e 9 / 5 to R e 13 / 7 . Resolving the relevant detail of the flow phenomena requires trillions of grid points.
Machine learning of c s ( x , t ) and/or τ w ( x 1 , x 2 , 0 , t ) can significantly reduce the computational cost of LES. Here, we consider data-driven turbulence closure models based on supervised machine learning by neural network (NN) [43,44]. The artificial NNs are parameterized class of nonlinear maps, ϕ ( x , y , w ) . The application of NNs in subgrid scale turbulence modelling is a very innovative idea [45]. It is important to note that NNs provide universal approximations of nonlinear maps, albeit the same could be achieved by conventional orthogonal bases. In the following discussion, we consider 9 components of the velocity gradient tensor and 6 components of the resolved Reynolds stress to define the subgrid scale quantity c s ( x , t ) . NNs are trained to learn the following nonlinear map
c s ( x , t ) = Π ∂ u i ∂ x j , τ i j .
Thus, for a subset of grid points, we need to find the best weight vector w of 15 elements so that the bias between c s and Π are minimized. Sarghini et al. [45] observed that the LES data for a duration of two eddy turn over time units were sufficient to model c s ( x , t ) for turbulent channel flow at Taylor scale Reynolds number 180. We also highlight the work of Novati et al. [46] regarding reinforcement learning of c s ( x , t ) for homogeneous isotropic turbulence at moderate Reynolds numbers. Several recent investigations have applied NNs to predict a “perfect” SGS stress tensor that accelerates the LES of turbulent flows [13,47,48,49,50].
Note that reinforcement learning is a type of machine learning framework that employs artificial intelligence in complex applications, such as self-driving cars, and more. Bae and Koumoutsakos [9] proposed the multi-agent reinforcement learning method to approximate the subgrid scale quantity c s ( x , t ) . To briefly illustrate the NN-based reinforcement learning of the near-wall turbulence, we illustrate the conceptual framework in Figure 1. In this approach, we consider several fluid parcels to act like agents learning the flow environment at each time step. Each agent performs an action according to a desired wall-modelled LES (see [19]) and receives a scalar reward to update the wall shear stress. In order for the reinforcement learning of agents to be universally applicable, the machine learning algorithm establishes a relationship between the wall friction velocity and the wall shear stress (see [9]).

3.2. Solving PDEs with Neural Networks

The application of NNs to construct numerical solution methods for PDEs date back to the early 1990s [51,52,53]. Recently, physics-informed neural networks (PINN) [54] have initiated a surge of ensuing research activity in the deep learning of nonlinear PDEs. The PINN approach employs NNs to solve PDEs in the simultaneous space-time domain. Here, we illustrate the PINN method for approximating the solution u : [ 0 , T ] × Ω → R of the following evolutionary PDE [55] :
∂ u ∂ t + N ( u ) = 0 ( x , t ) ∈ Ω × [ 0 , T ]
subject to boundary condtions u ( x , t ) = u b ( x , t ) for ( x , t ) ∈ ( 0 , T ) × ∂ Ω and initial conditions u ( x , 0 ) = u 0 : Ω → R . Using the neural network approach, we find the best parameter w for the approximation u w ( x , t ) ≈ u ( x , t ) , where the initial condition and the boundary conditions provide training data. Then, we minimize the residual (or loss) R [ u w ] : = ∂ t u w − N [ u w ] over a set of scattered grid points in the simultaneous space-time domain. To construct a solution by a purely data-driven approach, PINN considers a set of N state-value pairs { ( x i , t i , u i ) } i = 1 N , where u i : = u ( x i , t i ) is unknown. Then, we seek for a neural network approximation u w ( x i , t i ) and find the best fit parameter w such that u w ( x i , t i ) = u ( x i , t i ) for i = 1 , … , N . Finally, u w ( x , t ) : Ω × [ 0 , T ] → R denotes a solution realized by the neural network using the optimal values of the parameter w. Note that the PINN approach does not require past solution as training data. Instead of minimizing the standard error | u w ( x i , t i ) − u ( x i , t i ) | , the PINN method takes the PDE as the underlying physics and minimizes the least square residual | | R [ u w ] | | 2 2 to find the optimal values of the parameter w. Several publications [56] reviewed the application of the PINN method to solve the Navier-Stokes equations. For incompressible flows, PINNs form the neural network approximation of each velocity components and pressure by minimizing the residual of Navier-Stokes equations on a set of space-time collocation points.

3.3. Remark

In this section, we have briefly reviewed machine learning framework to accelerate the LES of turbulent flows. Machine learning of new subgrid models from high-resolution flow field is a promising approach, but such an artificial inteligence have been prone to instabilities and their performance on different grid spacing has not been investigated. We illustrate the neural network pathway to turbulence modelling. The universal approximation theorem implies that neural networks can find appropriate weights w and minimizes the bias b to represent a wide variety of interesting functions, such that [57]
y = f ( x ) ≈ w x + b .
The NN approach is a powerful framework that we can adapt to the computation of various turbulent quantities.
We show that the PINN approach can directly solve a nonlinear PDE. Nevertheless, solving the Navier-Stokes equations at very large Reynolds number require PINNs to incorporate a suitable turbulence modelling scheme, which is currently a work-in-progress. For solving Eq (8), the PINN approach has the flexibility of incorporating subgrid scale terms through supervised or reinforcement learning approaches. Note that a principle of machine learning is to provide a probability distribution σ ( x , y ) of input-output pair, while minimizing the loss function (6). Thus, we have enough flexibility “to inform” the underlying “physics” as we construct universal approximation of fluid flows by neural networks.

4. Wavelets in Computational Fluid Dynamics

4.1. Background

The wavelet method evolved as a nonlinear approximation of the critical information in high-dimensional systems. The wavelet-based CFD techniques are efficient algorithms that map a high-dimensional fluid dynamics phenomena onto a low-dimensional manifold. Our classical CFD approach is not suitable to deal with the large number of the degrees of freedom of turbulent flows. The wavelet method projects the turbulent flow onto a low-dimensional manifold to capture the energy containing motion with a relatively small number of the wavelet modes (or grid points). The wavelet transform is a convolution with wavelets, which is translation covariant. It is thus suitable to extract multiscale energy containing eddies of turbulent motions [58].
In the late 1980s, FARGE and RABREAU [59] introduced for the first time the novel idea of wavelet-based turbulence modeling (see [3,60,61,62]). Over the last decade, a number of new developments have been made. The wavelet method in CFD has evolved in two directions. First, the coherent vortex simulation (CVS) methodology is based on the idea that vortex stretching drives the energy cascade phenomena in turbulent flows [63,64,65,66]. Since nonlinear terms of the Navier-Stokes equations represent vortex stretching, the vorticity is an appealing candidate for turbulence modelling. Farge et al. [60] have discussed more details in this direction. The second approach is the adaptive wavelet collocation method (AWCM) that generalizes the classical turbulence modelling toward a new direction of the wavelet-based CFD techniques. AWCM follows the hypothesis that the energy cascade occurs through a hierarchical breakdown of eddies in a localized manner [67]. Many of the recent developments of AWCM include wavelet adaptive DNS (WA-DNS), wavelet adaptive LES (WA-LES), wavelet adaptive RANS (WA-RANS), wavelet adaptive DES (WA-DES), and wavelet adaptive climate model (WAVTRISK) [26,68,69,70,71].
Here, we want to highlight the fundamental differences between the CVS and AWCM in the context of turbulent flows. CVS treats vortex tubes as ‘sinews’ of turbulence [4]. Vortex tubes with diameters between Kolmogorov micro scale and Taylor micro scale are usually surrounded by the strain field [4]. When a vortex tube is stretched, its circulation is conserved and it exerts a tensile stress onto the surrounding strain, which cascades energy toward smaller scales. Since the tube-like vortices occupy a relatively small fraction ( ∼ 1 % ) of the total volume, a relatively small number of grid points is necessary to account for a much larger fraction ( 10 % − 20 % ) of the turbulence energy dissipation. The main strategy of CVS is thus to employ wavelets for projecting coherent vortices onto a low-dimensional manifold, and solve the Navier-Stokes equations on a wavelet basis.
The AWCM is based on the assumption that the energy dissipation is confined to high wavenumber Fourier modes that are highly localized, whereas the injection of energy is confined to the low wavenumber Fourier modes. Thus, AWCM employs wavelets to dynamically adapt the computational grid to capture the localized energy dissipation rates. AWCM requires a subgrid scale model (e.g. WA-LES) unless the smallest resolved scale is about the same as the dissipation scale (e.g. WA-DNS). This approach is not compatible with the local production of small-scale vorticity in boundary layers or shear layers. Nevertheless, simulations of homogeneous isotropic turbulence show that the Reynolds number scaling of CVS, O ( R e 3 ) , is slightly higher than that of AWCM (specifically WA-LES), O ( R e 2.75 ) . Recently, Mehta et al. [15], Ge et al. [7], and De Stefano and Vasilyev [26] covered a detailed review of turbulence modelling by the AWCM approach. Such studies primarily focused on the promise of wavelet compression and grid adaptation. Below, we provide a technical overview of the above discussion regarding vortex stretching. Readers interested in more details are referred to (in particular chapter 5 of) Davidson [4].

4.2. Coherent Structure Extraction by the CVS and the AWCM Methods

Considering that the velocity u as a diagnostic variable via vorticity ω = ∇ × u , three-dimensional Navier-Stokes equations read:
∂ ω ∂ t + u · ∇ ω = ω · ∇ u + 1 R e ∇ 2 ω .
Using the wavelet-based solution ω ¯ of Eq (9) in ω ¯ = ∇ × u ¯ , we find a wavelet filtered velocity u ¯ , which is an approximation to the solution of the wavelet filtered Navier-Stokes equations, Eqs (1-2).
To extract coherent structures by the CVS approach, we split each snapshot of a turbulent flow into two parts. The wavelet filtered vorticity ω ¯ ( x ) is given by the inverse wavelet transform applied to wavelet coefficients whose modulus is larger than the threshold ε opt = 4 Z ln N / 3 , where Z = ( 1 / 2 ) ∫ | ω | 2 d x is the total enstrophy. The residual part ω ′ = ω ( x ) − ω ¯ ( x ) represents the incoherent background. It is worth mentioning that the CVS decomposition follows one of the best known mathematical results, due to Foias and Temam [72], that the regularity and uniqueness of the velocity are guaranteed up to a finite time if the enstrophy (Z) of the flow remains bounded. According to Donoho [73], the optimal wavelet thresholding corresponds to negligible subfilter scale stresses (via Leonard decomposition). By the Helmholtz vortex theorem, the vortex-flux through a vortex tube is conserved as the tube is stretched, and the strength of a stretched vortex increases in direct proportion to its length [4].
Taylor [74] considered experimental data to analyze the production of enstrophy in decaying turbulence generated from wind-tunnel measurements of the velocity. Based upon the equation for enstrophy production, Taylor [74] argued that enstrophy will be created when the mean rate of vortex stretching is positive and exceeds the mean destruction of enstrophy by viscosity. In the AWCM approach, we consider the wavelet filtered velocity u ¯ to extract coherent vortices ω ¯ = ∇ × u ¯ and solve the wavelet filtered momentum equations (1-2), instead of directly solving Eq (9). Here, the cumulative effect of discarding all wavelet modes is associated with the total energy E = ( 1 / 2 ) ∫ | u | 2 d x instead of the total enstrophy, Z [70,75]. Note also that AWCM solves the momentum equations (1-2) considering the subfilter scale stress terms [7,70], where the effects of the subfilter-scale stress τ s = [ u i u ¯ j − u ¯ i u ¯ j ] is not negligible [75,76]. A comparison of the evolution of enstrophy between CVS and AWCM approaches is crucial in the context of enstrophy production by vortex stretching.
Applying the curl operator onto Eq (2), we get the vorticity equation associated with the AWCM approach, which leads to the following form of the wavelet filtered enstrophy equation:
∂ ∂ t 1 2 | ω ¯ | 2 = ω ¯ T S ω ¯ − 1 R e | ∇ ω ¯ | 2 − ∇ · τ s − 1 3 tr τ s · ( ∇ × ω ¯ ) ︸ subgrid enstrophy .
The first term on the righthand side of Eq (10) represents inertial-range vortex-stretching. The last term in Eq (10) (denoted by ‘subgrid enstrophy’) represents the enstrophy flux to unresolved scales, which is due to the subgrid-scale turbulence modelling because the AWCM solves Eq (2). Removing the last term from Eq (10) provided the enstrophy evolution of the CVS method. Clearly, in Eq (10), the last term accounts for the enstrophy production associated with the subgrid model (3). In other word, Eq (10) suggests that a primary role of the subgrid model (in WA-LES) is to dissipate the subgrid-scale production of enstrophy [72]. Moreover, CVS method directly accounts for the conservation of circulations, which is essential to ensure that the mean rate of positive vortex-stretching cause the forward energy cascade to small-scales.

4.2.1. CVS Modes of Near-Wall Dynamics

The CVS method employs a nonlinear approximation that designs a good nonlinear dictionary, and finds the optimal approximation as a linear combination of N elements of the dictionary. The main goal is to identify the CVS modes leading to the best N -term approximation of a turbulent flow. CVS is a two stage process. First, we identify the dictionary of wavelets extracting hidden information of the vorticity field. Second, we extract the CVS modes by finding the best wavelets associated with the dominant vortical structures.
Here, we briefly illustrate the CVS method for capturing the near-wall vortices from the DNS data of a turbulent channel flow. The technical details of the channel flow simulation is given by Sakurai et al. [77]. Applying the CVS method onto vorticity field, we extract the coherent flow structure in the near-wall region. It is worth mentioning that standard techniques, such as the Q-criteria identifies the region where vorticity dominates over the strain. A region of negative λ 2 , the second largest eigenvalue of the tensor S i k S k j + R i k R k j , captures the vortical flow structures. Standard vortex identification criteria uses the velocity gradient tensor in physical space. In contrast, the CVS modes extracts the hidden patterns of the vorticity field in Fourier space.
On the top of Figure 2, we show the total vorticity | ω ¯ | (green) of the DNS of 256 × 256 × 2048 (i.e. ≈ 130 millions) grid points. Then, wavelet decomposition was applied to the total vorticity. On the middle of Figure 2, we show the vorticity | ω ¯ | (red) of the CVS modes. We observe that these vortices have been captured by about 7 × 10 6 of the CVS modes (Figure 2, red). This number of CVS degrees of freedom is only about 0.55 % of the original number of grid points. The incoherent vorticity is the residual | ω − ω ¯ | , which is shown at the bottom of Figure 2 (blue). The CVS modes captures the coherent flow, which retains 99.9 % of the total energy and 99.7 % of the total enstrophy.

4.2.2. The POD Modes of Coherent Structures

In the late 1960’s, Lumley [2] introduced the POD method, which is an orthogonal decomposition of a function, u ( x , t ) : [ a , b ] × [ 0 , T ] → R , given by
u ( x , t ) = ∑ k = 0 ∞ c k ( t ) φ k ( x ) .
The decomposition (11) is said to be complete if it converges to all u ( x , t ) ∈ L 2 [ a , b ] for all t ∈ [ 0 , T ] 1. The Bessel’s inequality and the Parseval’s equality
∑ k = 0 ∞ c k 2 | | φ k ( x ) | | 2 ≤ | | u | | 2 < ∞ and | | u | | 2 = ∑ k = 0 ∞ c k 2 | | φ k ( x ) | | 2 ≤ | | u | | 2 , respectively ,
guarantee that a finite number of coefficients c k = 〈 u , φ k 〉 / | | φ k | | 2 is sufficient for the best approximation of all u ∈ L 2 [ a , b ] for all t ∈ [ 0 , T ] . The same decomposition, Eq (11), is applied to three-dimensional flow field. The coherent structures detected by the POD modes ϕ k ( x ) represent statistical correlation of the dynamics at various time snapshots.
The POD is a widely used unsupervised machine learning technique in fluid dynamics to study turbulent flows, but it’s application to turbulence modelling is relatively new. For 3D turbulent flows, the POD method constructs a data-driven basis { φ k ( x ) } k = 1 N with a near-optimal dimension N , which represents the spatial coherence of the flow kinematics, while the time evolution of the coefficients { c k ( t ) } k = 1 N captures the low-dimensional coherent dynamics. Thus, the POD method essentially offers an optimal low-dimensional approximations of high-dimensional fluid data using an orthogonal basis in a certain least-squares optimal sense.
Here, we employ the best approximation by the POD modes to formulate the Leonard decomposition of a turbulent flow. Let us consider the POD of velocity snapshots, U , toward a decomposition of the form U = U ¯ + U ′ ′ , where U ¯ contains most of the turbulence kinetic energy if | | U ′ ′ | | 1 is minimized. Such a decomposition is obtained by minimizing the following Lagrangian
L ( U ¯ , U ′ ′ ] , V ) = | | U ¯ | | * + λ | | U ′ ′ | | 1 + V T ( U − U ¯ − U ′ ′ ) + η 2 | | U − U ¯ − U ′ ′ | | F 2
to extract the energy containing motion captured by the POD modes. Note that minimizing the nuclear norm | | · | | * ensures to maximize the TKE over a low-dimensional subspace. Also, minimizing the norm | | U ′ ′ | | 1 aims to capture the intermittency of turbulence fluctuations. Based on the POD method, we have the Leonard stress τ i j L = u ˜ i u ˜ ¯ j − u ˜ ¯ i u ˜ ¯ j . Here, we have considered the ensemble average of the low-dimensional POD reconstructions to form the Leonard stress. The POD method captures the most energy containing coherent structures, thereby leading to a residual stress to account for the spatio temporal variability of turbulent flows (see Shinde [78]). Combining a spatial filtering process with the POD method, we get
u i u j ˜ ¯ − u ˜ ¯ i u ˜ ¯ j = u ¯ i u ¯ ¯ j − u ˜ ¯ i u ˜ ¯ j ︸ τ i j L + u i u j ˜ ¯ − u ¯ i u ¯ ¯ j ︸ τ i j .
Eq (13) takes the standard form of a mixed model [79], where the Leonard stress τ i j L is obtained through the POD method and subgrid scale stress τ i j is obtained through a classical approach. The linear combination of the Leonard (resolved) stress ( τ i j L ) with the subgrid scale stress ( τ i j ) improves the prediction of the true subfilter scale stress ( τ i j s ). Kang et al. [80] proposed a mixed subgrid scale model using the NN approach and tested the performance by simulating isotropic turbulence and turbulent channel flow. In the context of the present article, we suggest to use the POD method for the resolved stress and the wavelet method for the subgrid scale stress.
Let us now briefly review the wavelet method and the POD method for dimensionality reduction while extracting coherent structures. Here, we consider the velocity snapshots U for a two-dimensional flow past a circular cylinder at R e = 14 440 [81]. A column of U ∈ R 2 N × M consists of two velocity components [ u ( x i , y j , t n ) , v ( x i , y j , t n ) ] T at N grid points ( i , j ) and n-th time step. Consider the one-dimensional wavelet transform of each row of U . The wavelet transform produces coefficients that contain energetic information of the relative local contribution of various frequency bandwidth at each level of wavelet transform. Figure 3a shows the energy distribution of wavelet components. The cumulative energy at each successive level of wavelet decomposition is also show.
We have compared the relative energy per wavelet modes with that of the POD modes. Figure 3b shows the energy distribution of POD modes. Figure 3 compares the energy distribution of wavelet modes (Figure 3a) and POD modes (Figure 3b). The first four wavelet components contain 88 % of the total kinetic energy. The wavelet components of levels 1 and 2 makes the largest contribution, accounting for 32 % and 45 % energy, respectively. The first four POD modes are the most energetic, containing 80 % of the total kinetic energy. The first and the second POD modes contribute 41 % and 32 % energy, respectively). The energy distribution of first two wavelet components is similar with first two POD modes [82].

4.3. Space-Time Wavelet and Neural Networks

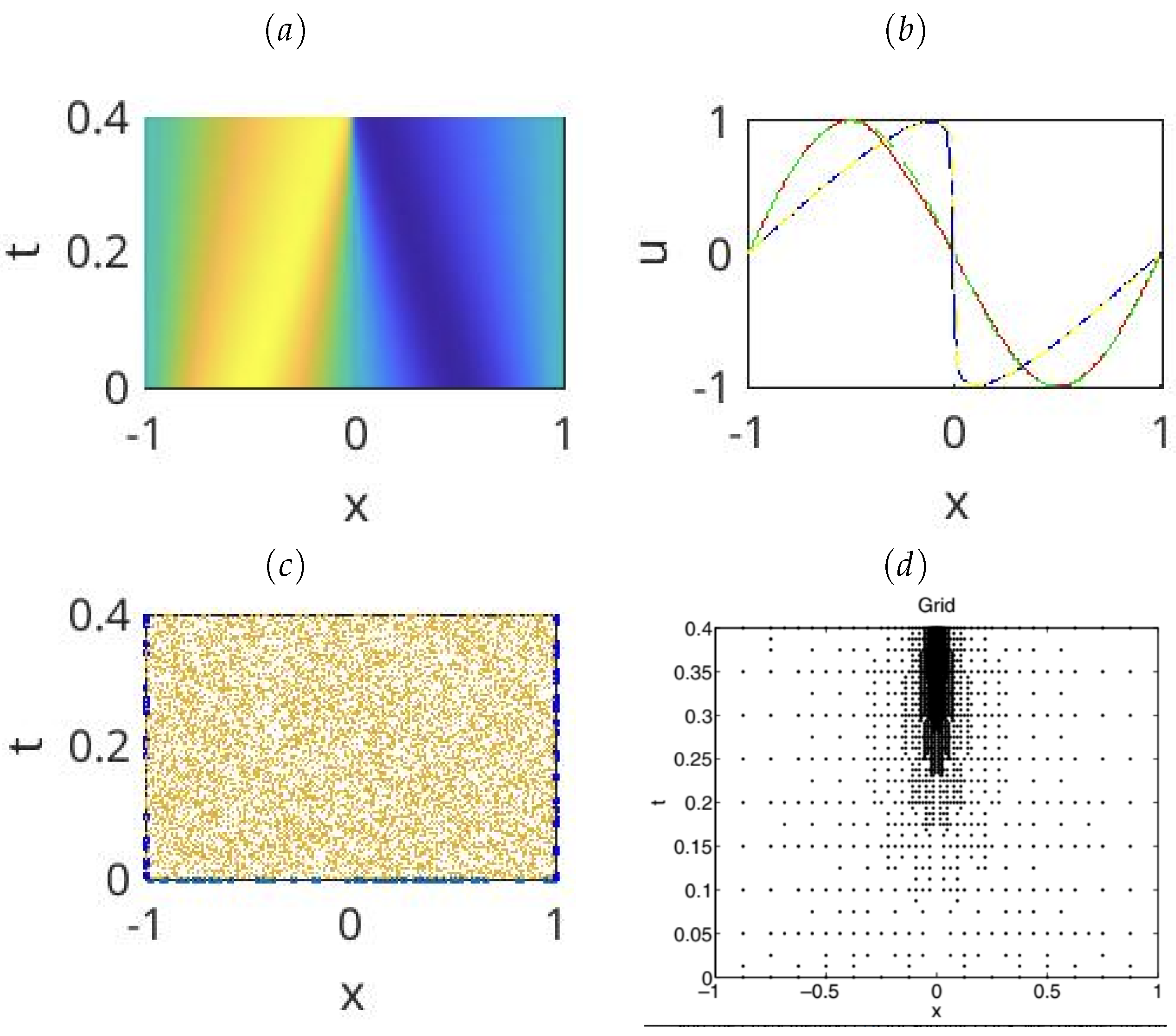
Here, we solve the one-dimensional Burgers equation to illustrate both the space-time adaptive wavelet method [83] and the PINN method [55] for solving PDEs. The wavelet method finds the optimal number of the wavelet modes to formulate the best approximation u w ( x , t ) ≈ u ( x , t ) of the solution. Each wavelet mode is associated with a grid point. Thus, discarding a wavelet mode discards the corresponding grid point. Interested readers may find a technical details of the space-time wavelet method given by Alam et al. [83].
This work has implemented the PINN method in Python using the TensorFlow environment. Our code has been adapted from Raissi et al. [55]. Note that the PINN method finds the best approximation u w ( x , t ) ≈ u ( x , t ) of the solution by finding the optimal values of the parameter w. Both methods minimize the residual R [ u w ] given by Eq (6), and capture the solution on a set of collocation points in the simultaneous space-time domain.
Figure 4 a , b compares the solution u ( x , t ) between the two methods. We see from Figure 4c that PINNs aim to optimize the values of the parameter w on a set of collocation points. There is no requirement to adjust the location or the number of grid points. Moreover, PINN seeks for a linear approximation of the form y = w x + b , where the activation through hidden layers accounts for the underlying nonlinearity.

5. Conclusions and Future Direction

Wavelet-based turbulence modelling is only over a 30 years old research topic. While many researchers have thoroughly investigated the AWCM and the CVS methods, their applicability remains limited by the underlying mathematical complexity of wavelet transforms [26,84]. The CVS method has evolved under the assumption that vortex-stretching is a primary mechanism for the energy cascade. CVS does not require to solve a turbulence closure problem. The computational complexity of the CVS method is about the same as that of the wavelet-based LES method [15]. In contrast, the AWCM assumes that the fidelity of subgrid models depends on the local grid refinement to ensure that subgrid scales are approximately isotropic. Thus, the AWCM can drastically reduce the computational complexity of the LES method. A substantial number of articles demonstrated wavelet-based RANS, DES, and LES techniques for numerical simulation of compressible and incompressible flows [15].
The applications of wavelet transforms and artificial intelligence in turbulence modelling are relatively new areas of research. This review clearly identifies two overarching challenges in the development of artificial intelligence in subgrid models of turbulence. In turbulence modelling, we first need an optimal low-dimensional representation of nonlinear dynamics and the large-scale turbulent motion. This is a principal hypothesis of LES, where (implicit) filtering captures the low-dimensional, coarse-grained flow features. A comparison of PINNs solution of Burgers equation with that for space-time wavelet indicate that neural networks are efficient to learn the dynamics; however, wavelets are efficient for a compressed representation of the dynamics. Thus, neural networks may provide a good approximation to the turbulence closure problem. In contrast, the wavelet-based LES learns the physics of turbulence.
Recent developments in the applications of neural networks in turbulence modelling aims to speed-up the computational cost of solving the Navier-Stokes equations. A formal description of the speed-up of CFD calculations by neural networks is not available from the literature. Some studies indicate a 20% speed-up of CFD calculations if machine learning takes care of some of the costly elements of turbulence modelling. The space-time adaptive wavelet collocation method developed by Alam et al. [83] is similar to the recent developments of physics informed neural networks proposed by Raissi et al. [55]. There are potential new research directions on the applications of neural networks and wavelet transfroms in understanding many unresolved problems of fluid’s turbulence.

Author Contributions

Conceptualization, J.A.; methodology, J. A.; formal analysis, J.A.; writing—original draft preparation, J.A.; writing—review and editing, J.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research was partially funded by NSERC and The APC was funded by MDPI and NSERC.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Kolmogorov, A.N. The Local Structure of Turbulence in the Incompressible Viscous Fluid for very Large Reynolds Number. C. R. Acad. Sci. U.S.S.R. 1941, 30, 301–306. [Google Scholar]
  2. Lumley, J.L. The structure of inhomogeneous turbulent flows. Atmospheric Turbulence and Radio Wave Propagation 1967. [Google Scholar]
  3. Farge, M. Wavelet transforms and their application to turbulence. Annu. Rev. Fluid Mech. 1992, 24. [Google Scholar] [CrossRef]
  4. Davidson, P.A. Turbulence - An Introduction for Scientists and Engineers; Oxford University Press, 2004.
  5. Vinuesa, R.; Brunton, S. Enhancing computational fluid dynamics with machine learning. Nature Computational Science 2022, 2, 358–366. [Google Scholar] [CrossRef] [PubMed]
  6. Schneider, K.; Vasilyev, O.V. Wavelet Methods in Computational Fluid Dynamics. Annu. Rev. Fluid Mech. 2010, 42, 473–503. [Google Scholar] [CrossRef]
  7. Ge, X.; De Stefano, G.; Hussaini, M.Y.; Vasilyev, O.V. Wavelet-Based Adaptive Eddy-Resolving Methods for Modeling and Simulation of Complex Wall-Bounded Compressible Turbulent Flows. Fluids 2021, 6. [Google Scholar] [CrossRef]
  8. Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine Learning for Fluid Mechanics. Annual Review of Fluid Mechanics 2020, 52, 477–508. [Google Scholar] [CrossRef]
  9. Bae, H.J.; Koumoutsakos, P. Scientific multi-agent reinforcement learning for wall-models of turbulent flows. Nature Communications 2022, 13, 1–9. [Google Scholar] [CrossRef]
  10. Pope, S.B. Turbulent Flows; Cambridge University Press, 2000.
  11. Wang, J.X.; Wu, J.L.; Xiao, H. Physics-informed machine learning approach for reconstructing Reynolds stress modeling discrepancies based on DNS data. Phys. Rev. Fluids 2017, 2, 034603. [Google Scholar] [CrossRef]
  12. Singh, A.P.; Medida, S.; Duraisamy, K. Machine-Learning-Augmented Predictive Modeling of Turbulent Separated Flows over Airfoils. AIAA Journal 2017, 55, 2215–2227. [Google Scholar] [CrossRef]
  13. Maulik, R.; San, O.; Rasheed, A.; Vedula, P. Subgrid modelling for two-dimensional turbulence using neural networks. Journal of Fluid Mechanics 2019, 858, 122–144. [Google Scholar] [CrossRef]
  14. Jin, X.; Cai, S.; Li, H.; Karniadakis, G.E. NSFnets (Navier-Stokes flow nets): Physics-informed neural networks for the incompressible Navier-Stokes equations. Journal of Computational Physics 2021, 426, 109951. [Google Scholar] [CrossRef]
  15. Mehta, Y.; Nejadmalayeri, A.; Regele, J.D. Computational Fluid Dynamics Using the Adaptive Wavelet-Collocation Method. Fluids 2021, 6. [Google Scholar] [CrossRef]
  16. Moser, R.D.; Haering, S.W.; Yalla, G.R. Statistical Properties of Subgrid-Scale Turbulence Models. Annual Review of Fluid Mechanics 2021, 53, 255–286. [Google Scholar] [CrossRef]
  17. Honnert, R.; Efstathiou, G.A.; Beare, R.J.; Ito, J.; Lock, A.; Neggers, R.; Plant, R.S.; Shin, H.H.; Tomassini, L.; Zhou, B. The Atmospheric Boundary Layer and the “Gray Zone” of Turbulence: A Critical Review. Journal of Geophysical Research: Atmospheres 2020, 125, e2019JD030317. [Google Scholar] [CrossRef]
  18. Wyngaard, J.C. Toward Numerical Modeling in the ”Terra Incognita”. Journal of the atmospheric sciences 2004, 3, 1816–1826. [Google Scholar] [CrossRef]
  19. Bose, S.T.; Park, G.I. Wall-Modeled Large-Eddy Simulation for Complex Turbulent Flows. Annual Review of Fluid Mechanics 2018, 50, 535–561. [Google Scholar] [CrossRef] [PubMed]
  20. Meneveau, C. Lagrangian Dynamics and Models of the Velocity Gradient Tensor in Turbulent Flows. Annual Review of Fluid Mechanics 2011, 43, 219–245. [Google Scholar] [CrossRef]
  21. Danish, M.; Meneveau, C. Multiscale analysis of the invariants of the velocity gradient tensor in isotropic turbulence. Phys. Rev. Fluids 2018, 3, 044604. [Google Scholar] [CrossRef]
  22. Hossen, M.K.; Mulayath Variyath, A.; Alam, J.M. Statistical Analysis of Dynamic Subgrid Modeling Approaches in Large Eddy Simulation. Aerospace 2021, 8. [Google Scholar] [CrossRef]
  23. Carbone, M.; Bragg, A.D. Is vortex stretching the main cause of the turbulent energy cascade? Journal of Fluid Mechanics 2020, 883, R2. [Google Scholar] [CrossRef]
  24. Kurz, M.; Offenhäuser, P.; Beck, A. Deep reinforcement learning for turbulence modeling in large eddy simulations. International Journal of Heat and Fluid Flow 2023, 99, 109094. [Google Scholar] [CrossRef]
  25. Kim, J.; Kim, H.; Kim, J.; Lee, C. Deep reinforcement learning for large-eddy simulation modeling in wall-bounded turbulence, 2022.
  26. De Stefano, G.; Vasilyev, O.V. Hierarchical Adaptive Eddy-Capturing Approach for Modeling and Simulation of Turbulent Flows. Fluids 2021, 6. [Google Scholar] [CrossRef]
  27. Menter, F.R.; Egorov, Y. The Scale-Adaptive Simulation Method for Unsteady Turbulent Flow Predictions. Part 1: Theory and Model Description. Flow, Turbulence and Combustion 2010, 85, 113–138. [Google Scholar] [CrossRef]
  28. Talbot, C.; Bou-Zeid, E.; Smith, J. Nested Mesoscale Large-Eddy Simulations with WRF: Performance in Real Test Cases. Journal of Hydrometeorology 2012, 13, 1421–1441. [Google Scholar] [CrossRef]
  29. Heinz, S. A review of hybrid RANS-LES methods for turbulent flows: Concepts and applications. Progress in Aerospace Sciences 2020, 114, 100597. [Google Scholar] [CrossRef]
  30. Bhuiyan, M.A.S.; Alam, J.M. Scale-adaptive turbulence modeling for LES over complex terrain. Engineering with Computers 2020, pp. 1–13.
  31. Leonard, A. Energy cascade in large-eddy simulations of turbulent fluid flows. Adv. in Geophys 1974, 18, 237–248. [Google Scholar]
  32. Meneveau, C. Statistics of turbulence subgrid-scale stresses: Necessary conditions and experimental tests. Physics of Fluids 1994, 6, 815–833. [Google Scholar] [CrossRef]
  33. Borue, V.; Orszag, S.A. Local energy flux and subgrid-scale statistics in three-dimensional turbulence. Journal of Fluid Mechanics 1998, 366, 1–31. [Google Scholar] [CrossRef]
  34. Alam, J. Interaction of vortex stretching with wind power fluctuations. Physics of Fluids 2022, 34, 075132. [Google Scholar] [CrossRef]
  35. Deardorff, J.W. Numerical Investigation of Nutral and Unstable Planetary Boundary Layer. J. Atmospheric Science 1972, 29, 91–115. [Google Scholar] [CrossRef]
  36. Chorin, A.J. Vorticity and turbulence; springer, 1994.
  37. Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer-Verlag: Berlin, Heidelberg, 2006. [Google Scholar]
  38. Debnath, M.; Santoni, C.; Leonardi, S.; Iungo, G.V. Towards reduced order modelling for predicting the dynamics of coherent vorticity structures within wind turbine wakes. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2017, 375, 20160108. [Google Scholar] [CrossRef]
  39. Calzolari, G.; Liu, W. Deep learning to replace, improve, or aid CFD analysis in built environment applications: A review. Building and Environment 2021, 206, 108315. [Google Scholar] [CrossRef]
  40. Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proceedings of the National Academy of Sciences 2016, 113, 3932–3937. [Google Scholar] [CrossRef]
  41. Kochkov, D.; Smith, J.A.; Alieva, A.; Wang, Q.; Brenner, M.P.; Hoyer, S. Machine learning–accelerated computational fluid dynamics. Proceedings of the National Academy of Sciences 2021, 118, e2101784118. [Google Scholar] [CrossRef]
  42. Schumann, U. Subgrid scale model for finite difference simulations of turbulent flows in plane channels and annuli. Journal of Computational Physics 1975, 18, 376–404. [Google Scholar] [CrossRef]
  43. Beck, A.; Flad, D.; Munz, C.D. Deep neural networks for data-driven LES closure models. Journal of Computational Physics 2019, 398, 108910. [Google Scholar] [CrossRef]
  44. Lapeyre, C.J.; Misdariis, A.; Cazard, N.; Veynante, D.; Poinsot, T. Training convolutional neural networks to estimate turbulent sub-grid scale reaction rates. Combustion and Flame 2019, 203, 255–264. [Google Scholar] [CrossRef]
  45. Sarghini, F.; de Felice, G.; Santini, S. Neural networks based subgrid scale modeling in large eddy simulations. Computers & Fluids 2003, 32, 97–108. [Google Scholar]
  46. Novati, G.; de Laroussilhe, H.L.; Koumoutsakos, P. Automating Turbulence Modeling by Multi-Agent Reinforcement Learning. Nature machine learning 2021, 3, 87–96. [Google Scholar]
  47. Maulik, R.; San, O. A neural network approach for the blind deconvolution of turbulent flows. Journal of Fluid Mechanics 2017, 831, 151–181. [Google Scholar] [CrossRef]
  48. Vollant, A.; Balarac, G.; Corre, C. Subgrid-scale scalar flux modelling based on optimal estimation theory and machine-learning procedures. Journal of Turbulence 2017, 18, 854–878. [Google Scholar] [CrossRef]
  49. Gamahara, M.; Hattori, Y. Searching for turbulence models by artificial neural network. Phys. Rev. Fluids 2017, 2, 054604. [Google Scholar] [CrossRef]
  50. Reissmann, M.; Hasslberger, J.; Sandberg, R.D.; Klein, M. Application of Gene Expression Programming to a-posteriori LES modeling of a Taylor Green Vortex. Journal of Computational Physics 2021, 424, 109859. [Google Scholar] [CrossRef]
  51. Lagaris, I.; Likas, A.; Fotiadis, D. Artificial neural networks for solving ordinary and partial differential equations. IEEE Transactions on Neural Networks 1998, 9, 987–1000. [Google Scholar] [CrossRef]
  52. Lagaris, I.; Likas, A.; Papageorgiou, D. Neural-network methods for boundary value problems with irregular boundaries. IEEE Transactions on Neural Networks 2000, 11, 1041–1049. [Google Scholar] [CrossRef] [PubMed]
  53. Lee, H.; Kang, I.S. Neural algorithm for solving differential equations. Journal of Computational Physics 1990, 91, 110–131. [Google Scholar] [CrossRef]
  54. Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations. ArXiv, 2017, abs/1711.10561. [Google Scholar]
  55. Raissi, M.; Perdikaris, P.; Karniadakis, G. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics 2019, 378, 686–707. [Google Scholar] [CrossRef]
  56. Sharma, P.; Chung, W.T.; Akoush, B.; Ihme, M. A Review of Physics-Informed Machine Learning in Fluid Mechanics. Energies 2023, 16. [Google Scholar] [CrossRef]
  57. Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Networks 1989, 2, 359–366. [Google Scholar] [CrossRef]
  58. Mallat, S. A wavelet tour of signal processing; Academic Press, 2009.
  59. FARGE, M.; RABREAU, G. Transformée en ondelettes pour détecter et analyser les structures cohérentes dans les écoulements turbulents bidimensionnels. Comptes rendus de l’Académie des sciences. Série 2, Mécanique, Physique, Chimie, Sciences de l’univers, Sciences de la Terre 1988, 307, 1479–1486. [Google Scholar]
  60. Farge, M.; Kevlahan, N.R.; Perrier, V.; Schneider, K. Turbulence analysis, modelling and computing using wavelets. In Wavelets and Physics; Cambrige University Press, 1999.
  61. Farge, M.; Schneider, K. Coherent Vortex Simulation (CVS), A Semi-Deterministic Turbulence Model Using Wavelets. Flow, Turbulence and Combustion 2001, 66, 393–426. [Google Scholar] [CrossRef]
  62. Farge, M.; Schneider, K.; Kevlahan, N.R. Non-gaussianity and coherent vortex simulation for two-dimensional turbulence using an adaptive orthogonal wavelet basis. Phys. Fluids. 1999, 11, 2187–2201. [Google Scholar] [CrossRef]
  63. Taylor, G.I. The transport of vorticity and heat through fluids in turbulent motion. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 1932, 135, 685–702. [Google Scholar]
  64. Taylor, G.I. The Spectrum of Turbulence. Proceedings of the Royal Society of London. Series A - Mathematical and Physical Sciences 1938, 164, 476–490. [Google Scholar] [CrossRef]
  65. Tennekes, H.; Lumley, J.L. A First Course in Turbulence.; MIT Press, 1976.
  66. Doan, N.A.K.; Swaminathan, N.; Davidson, P.A.; Tanahashi, M. Scale locality of the energy cascade using real space quantities. Phys. Rev. Fluids 2018, 3, 084601. [Google Scholar] [CrossRef]
  67. Richardson, L.F. Weather prediction by numerical process; Cambridge University Press, 1922.
  68. Aechtner, M.; Kevlahan, N.K.R.; Dubos, T. A conservative adaptive wavelet method for the shallow-water equations on the sphere. Quarterly Journal of the Royal Meteorological Society, 2015, pp. 1712–1726. [Google Scholar]
  69. Ge, X.; Vasilyev, O.V.; Hussaini, M.Y. Wavelet-based adaptive delayed detached eddy simulations for wall-bounded compressible turbulent flows. Journal of Fluid Mechanics 2019, 873, 1116–1157. [Google Scholar] [CrossRef]
  70. De Stefano, G.; Brown-Dymkoski, E.; Vasilyev, O.V. Wavelet-based adaptive large-eddy simulation of supersonic channel flow. Journal of Fluid Mechanics 2020, 901, A13–27. [Google Scholar] [CrossRef]
  71. Kevlahan, N.K.R.; Lemarié, F. wavetrisk-2.1: an adaptive dynamical core for ocean modelling. Geoscientific Model Development 2022, 15, 6521–6539. [Google Scholar] [CrossRef]
  72. Foias, C.; Temam, R. Determination of the solutions of the Navier-Stokes equations by a set of nodal values. Math. Comput. 1984, 43, 117–133. [Google Scholar] [CrossRef]
  73. Donoho, D.L. Compressed Sensing. IEEE Trans. Inf. Theor. 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
  74. Taylor, G.I. Production and dissipation of vorticity in a turbulent fluid. Proceedings of the Royal Society of London. Series A - Mathematical and Physical Sciences 1938, 164, 15–23. [Google Scholar]
  75. De Stefano, G.; Vasilyev, O.V. Stochastic coherent adaptive large eddy simulation of forced isotropic turbulence. J. Fluid Mech. 2010, 646, 453–470. [Google Scholar] [CrossRef]
  76. Alam, J.; Islam, M.R. A multiscale eddy simulation methodology for the atmospheric Ekman boundary layer. Geophysical & Astrophysical Fluid Dynamics 2015, 109, 1–20. [Google Scholar]
  77. Sakurai, T.; Yoshimatsu, K.; Schneider, K.; Farge, M.; Morishita, K.; Ishihara, T. Coherent structure extraction in turbulent channel flow using boundary adapted wavelets. Journal of Turbulence 2017, 18, 352–372. [Google Scholar] [CrossRef]
  78. Shinde, V. Proper orthogonal decomposition assisted subfilter-scale model of turbulence for large eddy simulation. Phys. Rev. Fluids 2020, 5, 014605. [Google Scholar] [CrossRef]
  79. Bardina, J.; Ferziger, J.; Reynolds, W. Improved subgrid-scale models for large-eddy simulation. 13th Fluid and PlasmaDynamics Conference, 1980.
  80. Kang, M.; Jeon, Y.; You, D. Neural-network-based mixed subgrid-scale model for turbulent flow. Journal of Fluid Mechanics 2023, 962, A38. [Google Scholar] [CrossRef]
  81. Zheng, Y.; Fujimoto, S.; Rinoshika, A. Combining wavelet transform and POD to analyze wake flow. Journal of Visualization 2016, 19, 193–210. [Google Scholar] [CrossRef]
  82. Krah, P.; Engels, T.; Schneider, K.; Reiss, J. Wavelet Adaptive Proper Orthogonal Decomposition for Large Scale Flow Data. Advances in Computational Mathematics 2022, 48. [Google Scholar] [CrossRef]
  83. Alam, J.; Kevlahan, N.K.R.; Vasilyev, O. Simultaneous space–time adaptive solution of nonlinear parabolic differential equations. Journal of Computational Physics 2006, 214, 829–857. [Google Scholar] [CrossRef]
  84. De Stefano, G. Wavelet-based adaptive large-eddy simulation of supersonic channel flow with different thermal boundary conditions. Physics of Fluids 2023, 35. 035138. [Google Scholar] [CrossRef]
1
Some texts refer to this a generalized Fourier series of functions satisfying periodic boundary conditions.
Preprints 76074 g001
Figure 1. Distribution of agents, where each agent obtains state information at a distance of h m from the wall, computes the reward at the wall, and executes the policy π to obtain actions for the next time step. Reproduced with permission from [9].
Figure 1. Distribution of agents, where each agent obtains state information at a distance of h m from the wall, computes the reward at the wall, and executes the policy π to obtain actions for the next time step. Reproduced with permission from [9].
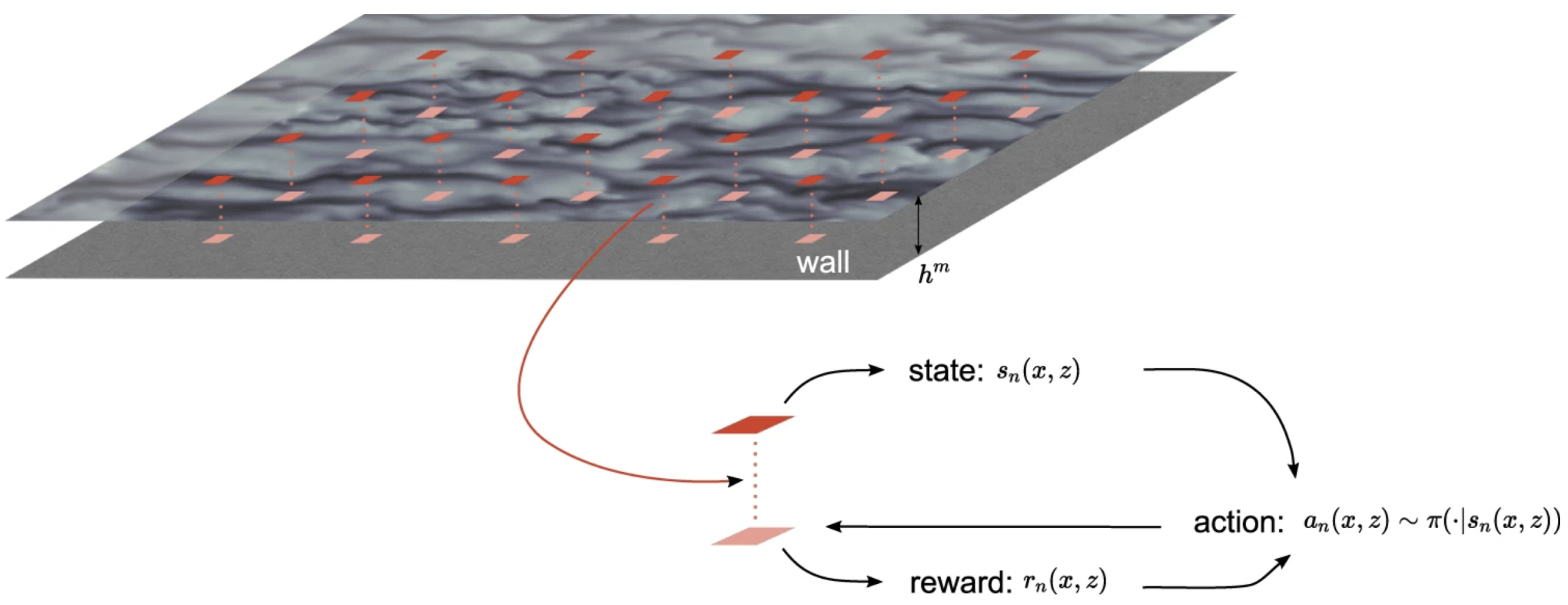
Preprints 76074 g001
Preprints 76074 g002
Figure 2. Visualization of total vorticity | ω | (green), coherent vorticity | ω c | (red) and incoherent vorticity ω i (blue). Reproduced with permission from [77].
Figure 2. Visualization of total vorticity | ω | (green), coherent vorticity | ω c | (red) and incoherent vorticity ω i (blue). Reproduced with permission from [77].
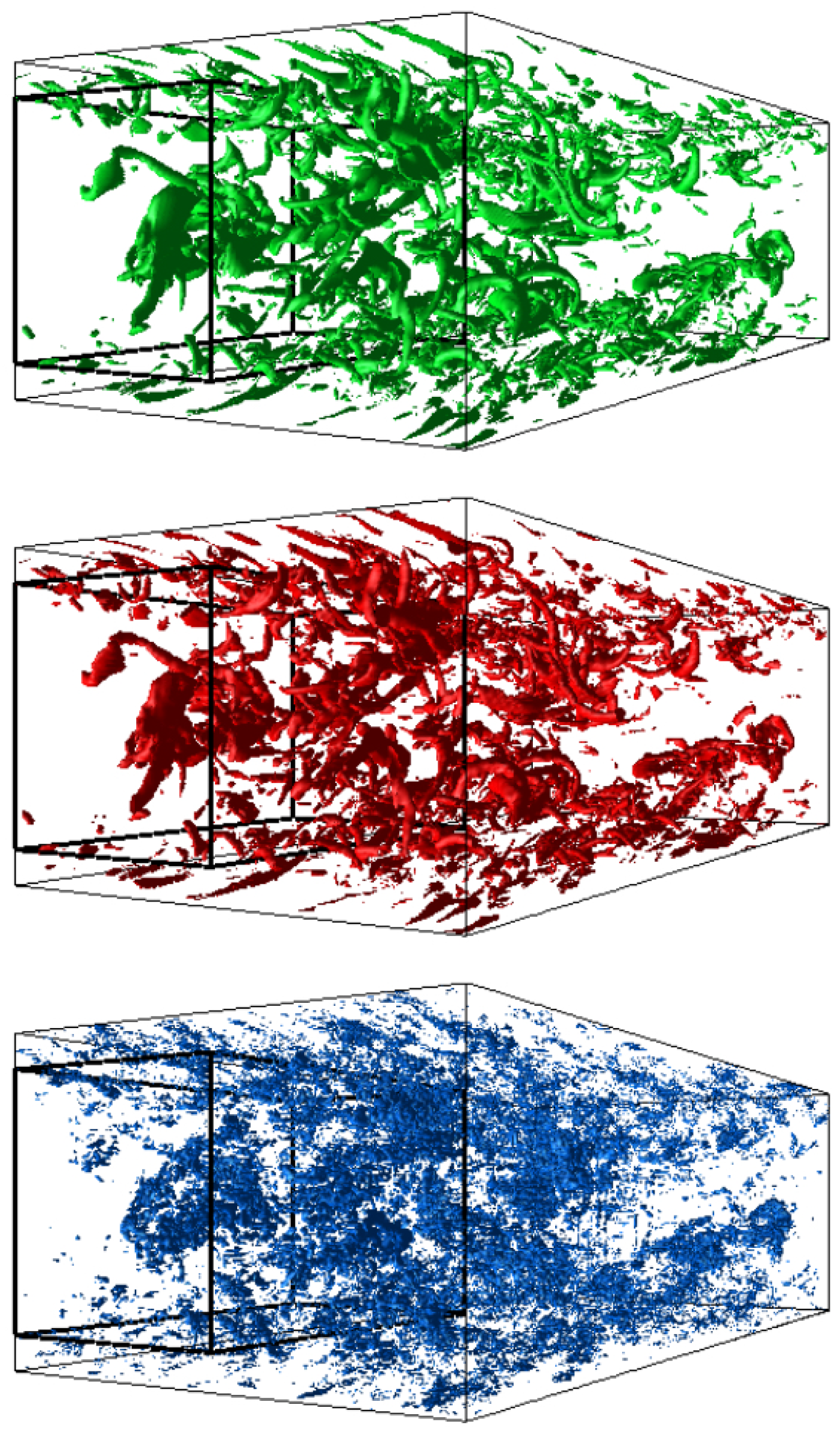
Preprints 76074 g002
Preprints 76074 g003
Figure 3. The distribution of energy a) in wavelet modes and b) POD modes. Reproduced with permission from [81].
Figure 3. The distribution of energy a) in wavelet modes and b) POD modes. Reproduced with permission from [81].
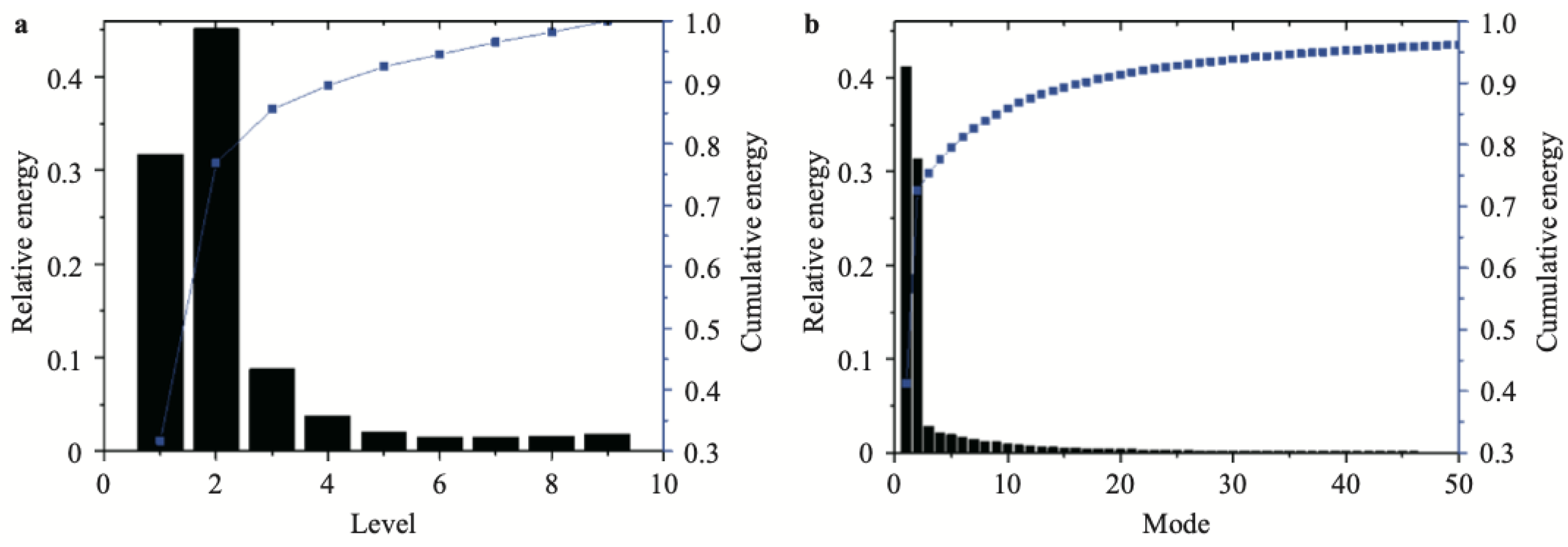
Preprints 76074 g003
Preprints 76074 g004
Figure 4. ( a ) The approximate solution u ( x , t ) by the PINN method. ( b ) A comparison of u ( x , t ) at t = 0 and t = 0.4 between the PINN method and the wavelet method. ( c ) The grid used by the PINN method. ( d ) The grid used by the wavelet method (reproduced with permission from [83].
Figure 4. ( a ) The approximate solution u ( x , t ) by the PINN method. ( b ) A comparison of u ( x , t ) at t = 0 and t = 0.4 between the PINN method and the wavelet method. ( c ) The grid used by the PINN method. ( d ) The grid used by the wavelet method (reproduced with permission from [83].
Preprints 76074 g004

( a ) ( b )
( c ) ( d )
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated