Preprint
Article
Structural Equation Modeling of the Marine Ecological System in Nan Wan Bay using SPSS Amos
Altmetrics
Downloads
149
Views
66
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
12 June 2023
Posted:
13 June 2023
You are already at the latest version
Alerts
Abstract
In order to sustain the marine environment relationship between the environmental factors and marine biota must be investigated. This study aims to study such a correlation in the adjacent waters of Nan Wan Bay, Kenting, Taiwan, and to explore the covariance of environmental factors on marine life (whether they enhance or diminish it). To achieve these objectives, factor analysis was used to identify potential latent variables that could affect the water quality of the adjacent waters, including phytoplankton (quantity), zooplankton (quantity), and fish (quantity and species). These potential variables were named based on the results of past studies and related literature. Finally, a structural equation model (SEM) was constructed to establish a marine ecological model among the potential variables. The factor analysis results revealed that nutrients, upwelling, and primary productivity are the primary factors affecting the environmental changes in the adjacent waters of Nan Wan Bay. The comprehensive SEM showed that nutrients and primary productivity significantly impact plankton. Path analysis indicated that primary productivity has the highest direct effect on the phytoplankton cluster. However, the upwelling has a low significance in its effect on phytoplankton, zooplankton, and fish clusters. Compared to the results of past related studies, the SEM proposed in this study can reflect a considerable degree of change in the waters.
Keywords:
Subject: Environmental and Earth Sciences - Ecology
1. Introduction
In marine ecosystems, changes in water temperature reflect the heat balance of seawater and its temporal variation and are also important factors affecting the survival of marine organisms. To support national economic development and industrial growth, many countries have chosen to build nuclear power plants in coastal areas to supply electricity for daily life and industry. However, the phenomenon of local seawater temperature increase caused by a large amount discharge of warm water from the cooled heated seawater by nuclear power plants may affect marine organisms, and the extent of the impact on different trophic level organisms in the local area may be related to site characteristics and environmental background [1]. Previous studies have shown that environmental factors can affect changes in marine organisms [2,3]. Phytoplankton is the primary producer in marine ecosystems where water temperature, light, and nutrient concentration often affect the aggregation structure of phytoplankton in specific times and spaces [32]. The increase in water temperature caused by discharged heated water may affect the photosynthetic efficiency and species composition of phytoplankton, and may also affect the metabolism of zooplankton, reducing their abundance [4,5,6]. Changes in prey organisms and water temperature may cause differences in the distribution of fish [7].
This study has been conducted in a semi-enclosed Nanwan Bay, Taiwan where about ten million tons of cooling seawater are drawn and discharged every day due to the operation of a nuclear power plant started operation in May 1984. Long-term water quality monitoring data indicates that the water temperature changes in the Bay are mainly affected by weather, seasonality, and large-scale ocean events, and are not directly related to the discharge of heated water [8,9]. To fully investigate the factors of environmental change in this marine area and the possible correlation between environmental and biological factors, this study used Structural Equation Models (SEM), which integrates Factor Analysis and Path Analysis, to analyze the data [10,11]. This methodology not only serves as an approach for theoretical verification but also incorporates multiple environmental and biological factors into one model. The goal is to explore the extent of the impact of natural and anthropogenic interference on the accumulation of marine organisms through appropriate models and quantitative analysis.
2. Materials and Methods
This study analyzed a total of 223 valid water quality and marine biological data surveyed at 4 stations in the Nanwan Bay, Kenting, Taiwan in the same season and month in 16 years from the summer of 2000 to the spring of 2016 (Figure 1). The present study employed a multi-stage approach to examine the interrelationships among various factors in the marine environment, with the aim of constructing a Structural Equation Model (SEM) for marine ecology. In the first stage, Pearson Correlation Analysis was used to evaluate the linear association between the variables. Then, Factor Analysis was conducted to identify common factors among the variables, with these factors subsequently serving as measurement models in the SEM.
One issue that can compromise the validity of Factor Analysis is excessively high or low correlations between variables. To address this, the Kaiser-Meyer-Olkin (KMO) measure, a statistic that compares the magnitude of observed correlation coefficients to the magnitude of partial correlation coefficients, was utilized [12]. In conjunction, Bartlett’s test of sphericity, which checks the overall significance of all the correlations within the correlation matrix, was used. Both tests helped ensure adequate sampling (Table 1) and sufficient correlation matrices, respectively.
To ensure the validity of the measurement models, we assessed construct validity. Construct validity encompasses convergent validity, which confirms whether measures that theoretically should be related are indeed correlated with corresponding factors, and discriminant validity, which measures how much a construct is distinct from other constructs. We used factor loadings of 0.5 and above as a benchmark for convergent validity and specified cross-loading of below 0.5 to ensure discriminant validity, as suggested by Chen (2005) [13]. After validating these measurements, environmental-related literature and ecological knowledge were incorporated to assign meanings to each extracted factor.
Finally, potential SEMs were created based on previous studies and the results of our Factor Analysis (Figure 2). Relationships between marine ecology factors were determined using analytical findings from Ramdani et al. (2009) [3]. Each factor was assigned a composite score, representing the intensity of the variables it represented.
We assessed the performance of the model using absolute fit indices, incremental fit indices, and parsimonious fit indices. The absolute fit indices, such as the Chi-square Index and Goodness of Fit Index, measured the degree to which the observed covariance or correlation matrix matched the predicted theoretical model. Incremental fit indices, like the Non-Normed Fit Index, compared the fit of the theoretical model to a baseline or null model. Parsimonious fit indices, such as the Parsimonious Normed Fit Index and Hoelter’s Critical N, favored models that achieved a good fit with fewer parameters. Table 2 provides a summary of the model's adequacy evaluation.
| GPS of sampling stations of water quality and plankton | GPS of sampling stations of fish | ||||
| No. | N | E | No. | N | E |
| 22 | 21°57'18" | 120°45'44" | 1 | 21°56'37" | 120°45'00" |
| 23 | 21°56'45" | 120°45'29" | 2 | 21°56'18" | 120°44'47" |
| 24 | 21°55'47" | 120°44'56" | 3 | 21°55'37" | 120°44'37" |
| 12 | 21°54'53" | 120°44'57" | 5 | 21°55'17" | 120°44'27" |
Figure 1.
The location of research geography and sampling stations. ●Sampling station of water quality and plankton ▲Sampling station of fish.
Figure 1.
The location of research geography and sampling stations. ●Sampling station of water quality and plankton ▲Sampling station of fish.
Table 1.
KMO measurement sampling adequacy criteria (Kaiser, 1974) [12].
Table 1.
KMO measurement sampling adequacy criteria (Kaiser, 1974) [12].
| KMO value | Applicability of factor analysis |
|---|---|
| 0.9≦KMO | Marvelous |
| 0.8≦KMO≦0.9 | Meritorious |
| 0.7≦KMO≦0.8 | Middling |
| 0.6≦KMO≦0.7 | Mediocre |
| 0.5≦KMO≦0.6 | Miserable |
| KMO≦0.5 | Unacceptable |
Figure 2.
The construction process of SEM.
Table 2.
The indices’ thresholds for SEM evaluation.
| Key metrics | Guidelines | Reference | ||
|---|---|---|---|---|
| Preliminary fit criteria | Factor loading | 0.50~0.95 | Chen, 2005 [13] | |
| Overall model fit | absolute fit indices | χ2 | the lower the better | Hwang, 2004,2009 [14,15] |
| χ2/df | <5 (<3 better fit) | Hair et al., 1998 [16] Carmines et al., 1981 [17] |
||
| GFI | >0.9 | Joreskog & Sorbom, 1996 [18] | ||
| AGFI | >0.9 (>0.8 acceptable fit) | Hair et al., 1998 [16] Joreskog & Sorbom, 1996 [18] |
||
| RMSEA | <0.05, good fit |
Hair et al., 2006 [19] Browne & Cudeck, 1993 [20] |
||
| 0.05~0.08, reasonable fit | ||||
| 0.08~0.10, medium fit | ||||
| >0.10, poor fit | ||||
| SRMR | ≦0.08 | Hu & Bentler, 1999 [21] | ||
| incremental fit indices | NNFI | >0.9 | Tucker & Lewis, 1973 [22] | |
| parsimonious fit indices | PNFI | ≧0.5 | Tucker & Lewis, 1973 [22] | |
| PGFI | ≧0.5 | Mulaik et al., 1989 [23] | ||
| CN | ≧200 | Mulaik et al., 1989 [23] | ||
3. Results and Discussions
3.1. Pearson Correlation Coefficient
The statistics of each measurement variable are shown in Table 3 and Table 4. The initial investigation relied on simple correlation analysis (Table 5) due to the variance in measurement units between water quality parameters and biometric parameters. The standardized correlation coefficient (r) is utilized to evaluate the level of linear correlation between each measurement variable and is employed as a benchmark for the development and refinement of subsequent models.
The standardized correlation coefficient (r) ranges between -1 and +1, with a value closer to -1 or +1 indicating a stronger correlation between the two random variables, and a value closer to 0 indicating a weaker correlation. In Table 5, it is evident that a majority of the measurement variables under investigation in this study exhibit a substantial degree of linear relationship, while the remaining variables cannot be determined as having a linear relationship (potentially due to a non-linear relationship or lack of correlation).
As correlation analysis only reveals the existence of linear relationships between variables, it does not imply the establishment of a causal relationship. Thus, in order to identify any potential variables and investigate the common variance between each variable, further factor analysis must be conducted.
3.2. Factor Analysis of Environmental Variables
Before conducting factor analysis, it is necessary to determine the suitability of each measurement variable by checking if the Kaiser-Meyer-Olkin (KMO) value is greater than 0.6 and if Bartlett's sphericity test is significant (p ≦ 0.05). This study hypothesizes that environmental variables, such as nitrate, silicate, phosphate, nitrite, temperature, salinity, pH, dissolved oxygen, transparency, and chlorophyll a, have effects on biological variables, such as the number of zooplankton, crab larvae, shrimp larvae, fish eggs, larvae, fish species, and fish abundance. Therefore, potential factors were first extracted from all the environmental and biological variables. Among the observed variables related to phytoplankton, only the "number of phytoplankton" was included in the analysis of biological variables as it can explain the variation in phytoplankton community structure, hence it is reserved in the SEM but excluded from factor analysis of the biological variables.
3.2.1. First Factor Analysis
The result of the first factor analysis of the environmental variables indicated a KMO value of 0.642. As per Kaiser's suggested criteria, a value between 0.6 and 0.7 is considered to have "normal" applicability. Furthermore, Bartlett's sphericity test was significant (p<0.001), implying that the water quality measurement variables investigated in this study are appropriate for factor analysis.
In this study, the principal component method of extraction was employed to extract factors. Following Kaiser's Criterion, only factors with eigenvalues greater than or equal to 1 were retained. The scree plot was also used to observe the slope of the cumulative explanatory power. When the slope is significantly flattened, the extraction process can be stopped. The results indicated that three factors have eigenvalues greater than 1 and can explain 61.075% of the total variation. With the determined principal components, factor rotation was then conducted.
The purpose of factor rotation is to make the data conform to the assumptions of the statistical model and to convert the data. By rotating the axis in the “maximum space covering range”, associated with different factor loading to increase the differences. In other words, it sets to achieve the greatest amount of variation. Through rotation, both positive and negative correlations between each factor (axis) and variables are strengthened, thus variables that were initially relevant will maintain a high factor loading, which is conducive to naming and interpreting the factors (latent variable).
In this study, the varimax method of orthogonal rotation made each variable have only one factor producing a large factor loading and avoiding duplication. The orthogonal rotations allow the axes to maintain a 90-degree angle, and the varimax method allows a set of variables with high factor loading and the rest with low factor loading, making the factor easy to interpret.
Ensuring construct validity, which refers to the degree to which a measurement variable effectively captures the abstract concept it's intended to measure, necessitates that all elements of the variable exhibit both convergent and discriminant validity. Convergence validity refers to the degree to which variables on the same factor component axis correlate with each other. Additionally, a variable that can be assigned to multiple factors simultaneously does not demonstrate discriminant validity, which refers to the degree to which variables on different factor axes correlate with each other.
After rotation, factor 1 (nitrate, silicate, phosphate, nitrite) can explain 24.528% of the variance; factor 2 (temperature, dissolved oxygen, salinity) can explain 18.505% of the variance; factor 3 (transparency, chlorophyll a) can explain 18.042% of the variance. The findings of the study indicated that the pH environmental variable did not demonstrate adequate convergence validity in the construct validity, as none of the three different rotations produced factor loading values above 0.5.
Communality is a measure that indicates the extent to which a variable contributes to a factor. It ranges from 0 to 1, with higher values indicating that the variable is more closely related to the common factor and has lower uniqueness. Thus, a variable with higher communality is considered a more appropriate measurement variable. The communality of pH is 0.359, the lowest value among all measurement variables. According to Chen (2005), a factor loading of greater than 0.5 and a communality of greater than 0.5 are significant criteria [13]. Therefore, since pH does not have convergent validity, it has been removed, and a second factor analysis was conducted. Note that when deleting variables, it is essential to remove only one at a time and consider the importance of each variable to the research.
3.2.2. Second Factor Analysis
The second attempt resulted in a KMO value of 0.632 indicating normal applicability. Additionally, Bartlett’s sphericity test was significant with p < 0.001. The results showed that after removing pH, the remaining environmental variables are still suitable for factor analysis.
In the second step, the scree plot diagram revealed that three factors had eigenvalues greater than 1, resulting in a cumulative total variation of 65.360%. These factors were further processed in factor rotation.
After the rotation, factor 1 (nitrate, silicate, phosphate, nitrite) can explain 25.860% of the variance; Factor 2 (temperature, dissolved oxygen, salinity) can explain 20.347% of the variance; factor 3 (chlorophyll a, transparency) can explain 19.153% of the variance. It is evident that the "salinity" environmental variables can be observed in both factor composition axes 2 and 3, with both exceeding a factor loading of 0.5. This indicated that salinity lacks discriminant validity. However, none of the other environmental variables from factors 1 to 3 exhibited factor loadings of 0.5 and above simultaneously, implying that these variables possessed discriminant validity. Moreover, none of the environmental variables in factors 1 to 3 have all factor loadings below 0.5, indicating that variables from factor 1 to 3 possessed convergent validity. Lastly, it is essential to examine whether the communality of the environmental variables is greater than or equal to 0.5. As illustrated in Table 7, "nitrite" exhibits a communality of 0.427, which is lower than 0.5, rendering it the smallest of the other environmental variables. Therefore, it was eliminated, and the third factor analysis was executed.
3.2.3. Third Factor Analysis
The third factor analysis yielded a KMO value of 0.579 which is deemed as "not a good fit". However, Bartlett's sphericity test was significant (p<0.001), indicating the presence of sufficient correlation among the variables. Nonetheless, given the low effect of extracting common factors as revealed by KMO, it is not advisable to proceed with further analysis of the remaining environmental variables if nitrite is eliminated.
The sea area of the present study exists interrelationships among various water quality environmental measurement variables. Specifically, the study examined the relationship between phosphate and nitrate, which serve as raw materials for the synthesis of organic matter by photosynthesis of marine plants, and silicates, which are the primary constituent materials of phytoplankton cell wall. These interrelationships arise from the interaction between environmental and biological variables. However, given the dynamic nature of marine environments, it was challenging to identify the precise nature of these relationships. Furthermore, deleting any variable may result in interpretational errors. Hence, the researchers chose to exclude only the pH variable. The remaining environmental variables were retained and named based on the outcomes of the second factor analysis as shown in Table 6 and Table 7.
Table 6.
The component matrix of environmental variables in each factor after rotation (pH excluded).
Table 6.
The component matrix of environmental variables in each factor after rotation (pH excluded).
| measured variable | factor loading(N=223) | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| nitrate | 0.828 | 0.191 | -0.019 |
| silicate | 0.811 | -0.113 | 0.084 |
| phosphate | 0.693 | 0.090 | 0.193 |
| nitrite | 0.584 | 0.290 | -0.053 |
| temperature | -0.297 | -0.836 | 0.051 |
| dissolved oxygen | -0.082 | 0.737 | 0.428 |
| salinity | 0.198 | 0.639 | -0.563 |
| chlorophyll a | 0.158 | -0.088 | 0.777 |
| transparency | -0.066 | -0.180 | 0.754 |
| eigenvalue | 2.237 | 1.831 | 1.724 |
| variance % | 25.860 | 20.347 | 19.153 |
| cumulated variance % | 25.860 | 46.207 | 65.360 |
Table 7.
The communality of environmental variables (pH excluded).
| environmental variables | total variance extracted % |
|---|---|
| temperature | .789 |
| salinity | .765 |
| dissolved oxygen | .733 |
| transparency | .606 |
| chlorophyll a | .637 |
| nitrate | .722 |
| nitrite | .427 |
| phosphate | .525 |
| silicate | .678 |
3.2.4. Factor Naming
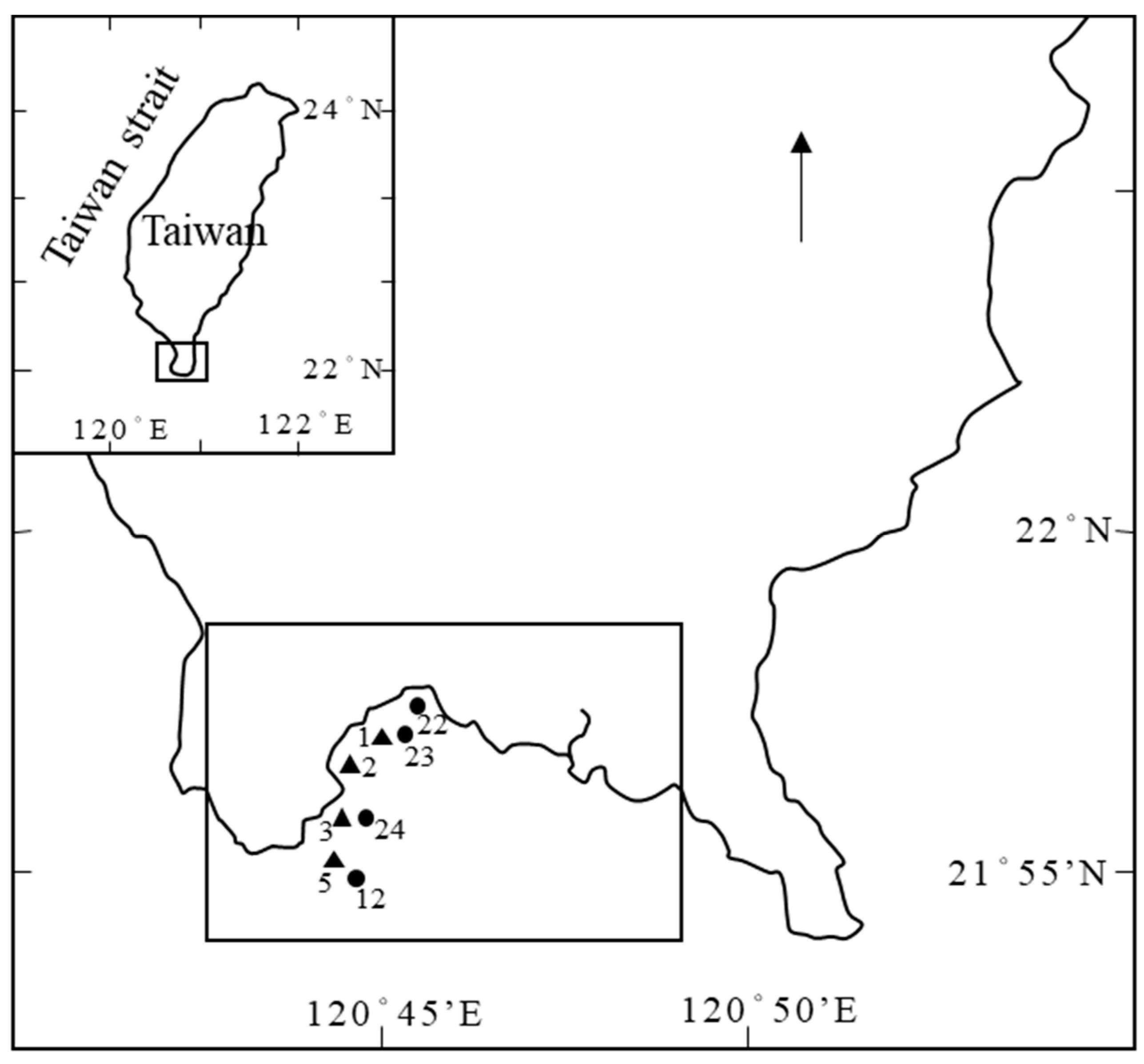
In the field of factor analysis, each variable possesses a distinct meaning, and the extracted factors themselves hold unique significance. Typically, factors are labeled after variables that display high factor loading, and their collective meaning is synthesized to name the factor. In the present study, water quality samples were obtained from the adjacent sea area of Nan Wan Bay, Kenting, Taiwan. Previous research has indicated that the hydrological environment in the nearby waters is intricate, and the occurrence of upwelling in the bay has been established. As a result, the factors were named after Nan Wan Bay's ocean-environmental variations.
Based on the accumulated findings from various studies conducted in the sea area over the years, and the factor analysis outcomes displayed in Table 6, three component axes were extracted from the component matrix following rotation. These axes are described below.3.3. Factor analysis on biological variables
The first component axis in the present study encompasses nitrate (0.828), silicate (0.811), phosphate (0.693), and nitrite (0.584), which can account for 25.860% of the variation. The factor loading is positive, indicating a positive correlation among the variables. It is noteworthy that in this study, the majority of the water quality measurement parameters were collected from the water surface. The occurrence of sea surges elevates the nutrient salt from the deep ocean to the surface, leading to a concurrent increase in nutrients. Therefore, this component axis was aptly named "Nutrients."
The second component axis in the current study comprises temperature (-0.836), dissolved oxygen (0.737), and salinity (0.639), accounting for 20.347% variation. The results showed a negative factor loading for temperature, while dissolved oxygen and salinity exhibited positive factor loading, indicating a negative correlation between temperature and dissolved oxygen, and temperature and salinity, but a positive correlation between dissolved oxygen and salinity.
Taiwan is located in subtropical, and the surface of seawater is influenced by solar radiation and is typically warmer. Additionally, the evaporation rate exceeds the rainfall rate, leading to an increase in seawater salinity. The waters near Nan Wan Bay are impacted by surges, which transport colder water from deep mid-levels to the surface. As deep mid-level waters lack light and photosynthesis, dissolved oxygen is not saturated, resulting in an overall decrease in dissolved oxygen and temperature when such water surfaces. However, other studies have suggested that Nan Wan Bay is also influenced by internal ocean waves, which cause intense water agglomeration at the seabed and increase dissolved oxygen at the surface. Considering the location of the study in an inland bay and the highest correlation coefficient between temperature drop in the component axis and factor 2 (-0.836), the component axis was named "upwelling current."
3.3. Factor Analysis of Environmental Variables
After factor analysis for environmental variables, the next step is to factor analyze biological variables.3.3.1. First factor analysis
3.3.1. First Factor Analysis
With a KMO value of 0.73, it was considered a "fairly acceptable" fit. Furthermore, the Bartlett's sphericity test was significant at p<0.001, indicating the appropriateness of performing factor analysis on the biological variables of interest. The results of factor extraction revealed two eigenvalues greater than 1, which together explained 54.507% of the total variance.
The second step involves performing a factor rotation using the varimax method of orthogonal rotation. After the rotation, factor 1 (shrimp, number of zooplankton, larvae, crabs) can explain 36.064% of the variance; factor 2 (number of fish, number of fish species, fish eggs) can explain 18.444% of the variation. Based on the findings, it appears that the biological variables related to the "fish eggs" exhibit factor loadings of less than 0.5 in both component axes 1 and 2, indicating a lack of convergent validity. To determine the adequacy of the remaining variables, the communality values of factors 1 and 2 were examined, with a threshold of 0.5 or greater. The communality value for "fish eggs" is only 0.162, the lowest among all the biological variables. Therefore, "fish eggs" is removed for the second round of factor analysis.
3.3.2. Second Factor Analysis
The results of the second factor analysis presented a KMO value of 0.749 indicating a "fair" fit. Moreover, Bartlett's sphericity test was significant (p<0.001), suggesting that the biological variables were appropriate for factor analysis after the removal of the "fish eggs" variable.
After the factor extraction, only two components were reserved for the factor rotation process. The rotation factor 1 (shrimp, number of zooplankton, juvenile larvae, crabs) can explain 42.180% variation; factor 2 (number of fish, number of fish species) can explain 20.377% variation while none of the factor loadings in factors 1 and 2 are greater than 0.5 simultaneously, which suggests that factors 1 and 2 have discriminant validity. Hence, the results from the second factor analysis were preserved for further analysis as shown in Table 8.
3.3.3. Factor Naming
Based on the results of the previous studies in the sea area and the analysis of the factor extraction in Table 8, the two factors were named as described below.
The first principal component axis, comprised four biological variables, namely shrimp larvae (0.886), number of zooplankton (0.855), fish larvae (0.773), and juvenile crabs (0.634), which collectively account for 42.180% of the total variation. The factor loading for each variable was positive, implying a positive correlation between them. Zooplankton, in particular, is widely distributed and has a larger number of species, including copepods. Fish larvae and juvenile crabs are also ecologically significant in terms of fishery resources. Previous studies have shown that the intersection of Kuroshio and upwelling currents support diverse flora and fauna[24,25]. The number of juvenile shrimp (0.886) and zooplankton (0.855) in the first component axis exhibited a higher correlation coefficient with factor 1, indicating that the sea during the previous sampling period had a higher abundance of zooplankton, especially crustaceans, which are the main food source for fish larvae. Consequently, this component axis was termed “zooplankton cluster”.
The second component axis was composed of two variables, namely the number of fish (0.779) and the number of fish species (0.759), which can explain 42.180% of the variation. The factor loadings of both variables were positive, suggesting a positive correlation between them. The phenomenon of fish migration in groups during foraging season and the formation of fishery in areas with abundant zooplankton can lead to a higher number of fish [26]. Thus, the name "fish cluster" was given to this component axis.
3.4. Structural Equation
Given the different units of measurements among the variables in the proposed structure, factor analysis was utilized to extract potential factors, namely nutrient, upwelling, primary productivity, zooplankton cluster, and fish cluster, to investigate the interplay between water quality and plankton assemblage, as well as plankton clustering and fish clustering. To test the hypothesis model, this study employed the sampling data assuming a normal distribution. The estimation model assumed that the measured variables of the latent factors were consistent with those presented in Table 6 and Table 8. Notably, the sign of coefficients of the latent factor “upwelling current” differed from the factor loading in Table 6 where the negative values was denoted by the [-] symbol in the model.
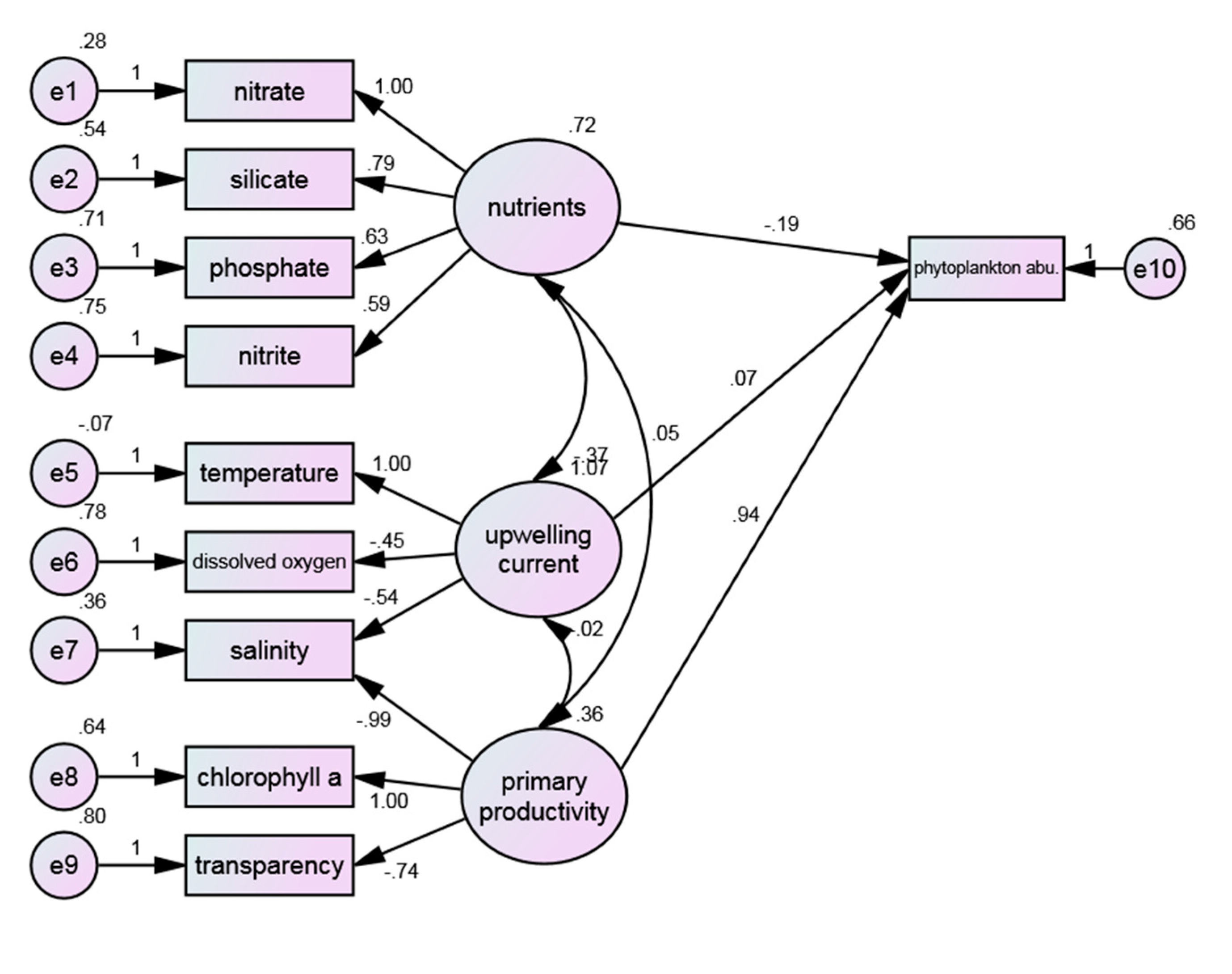
3.4.1. Water Quality Environmental Factors and Phytoplankton Cluster
Figure 3 shows the structure pattern between water quality environments and phytoplankton cluster. The RMSEA (0.113) is in the range of “bad fit”, indicating that the setting of the study model cannot be effectively matched with the sampling data, and the rest of the indicators are not up to the reference criteria. The overall model has not passed the test.
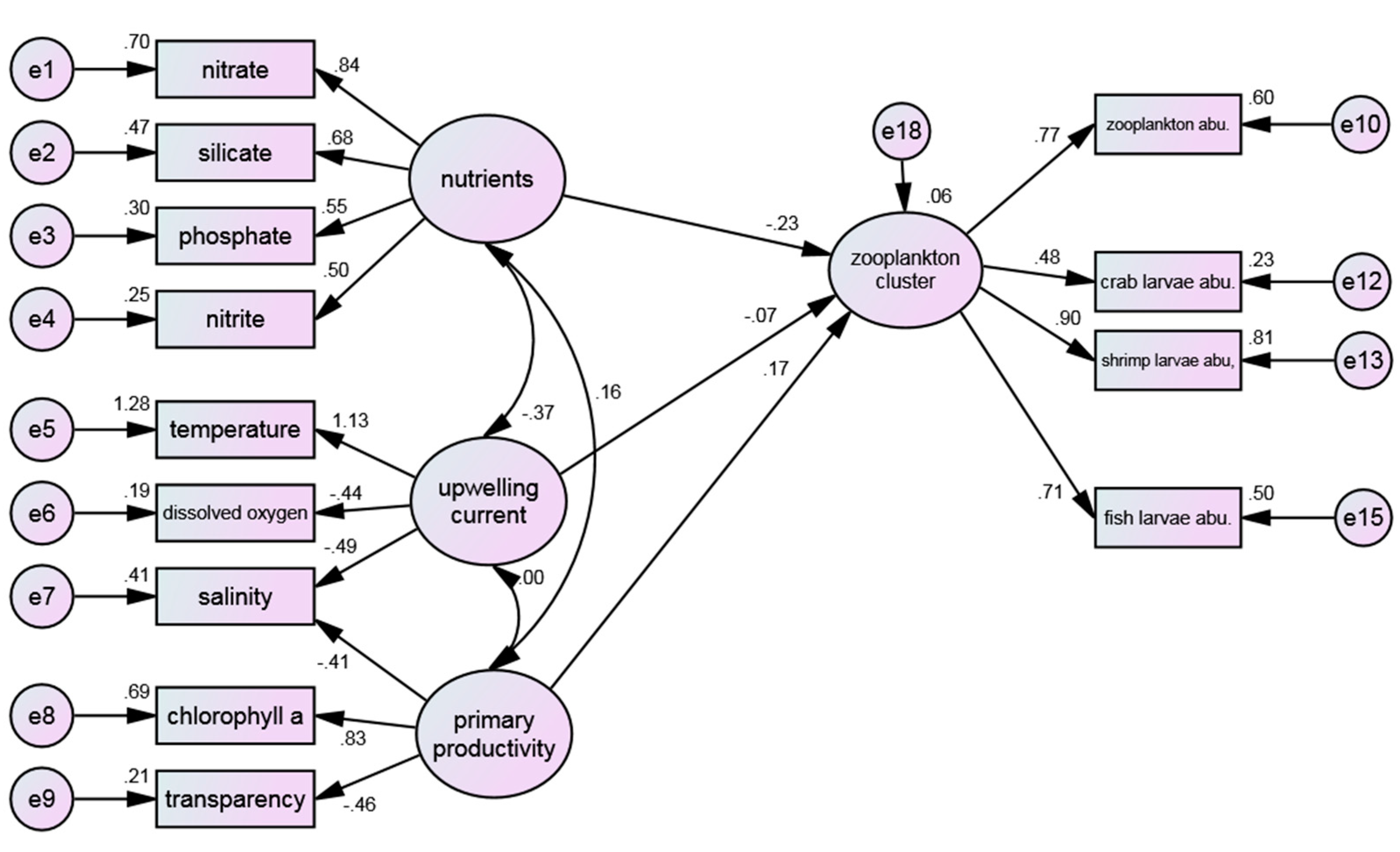
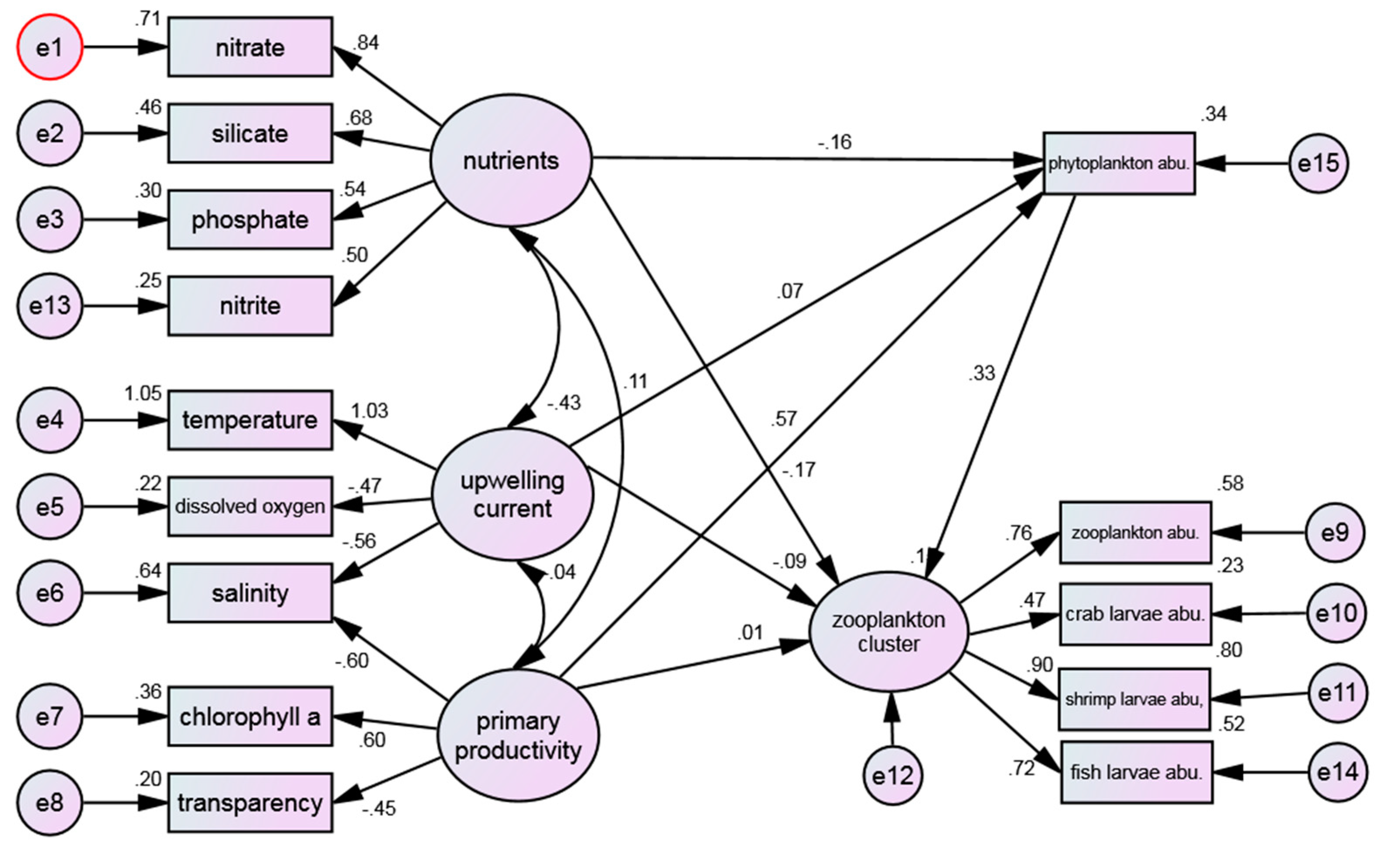
3.4.2. Water Quality Environmental Factors and Zooplankton Cluster
Figure 4 shows the structure pattern between water quality environments and zooplankton cluster. The RMSEA (0.085) value obtained from the model fit analysis (0.085) falls within the range of "moderately fit", albeit falling short of the optimal reference value of less than 0.05. However, the obtained value is still considered acceptable, indicating that the conceptual model proposed is in line with the empirical data obtained. Meanwhile, the non-normed fit index (NNFI) value (0.842) does not meet the reference criteria, which was used to assess the degree of association between the research model and the observed variables and to identify areas for model improvement. Hence, adjustment is needed for covariate relationships.
3.4.3. Water Quality Environmental Factors and Plankton Cluster
Figure 5 shows the structure pattern between water quality environments and both phytoplankton and zooplankton clusters. The index shows that the RMSEA value (0.097) is indicative of a "moderate" fit, although it is close to the threshold of a poor fit. This suggests that the model and the sampling data had only a low degree of probability event and couldn’t effectively explain the results. Furthermore, the NNFI value (0.787) did not meet the reference criteria. The GFI value (0.892) also did not meet the reference criteria. GFI is primarily used to test the proportion between the variance of the explainable observed variables before model adjustment and covariance. However, AGFI (0.831) met the criteria. It was hypothesized that the model must provide more observational data to enhance the degree of interpretation of the observed variables for the potential variables.
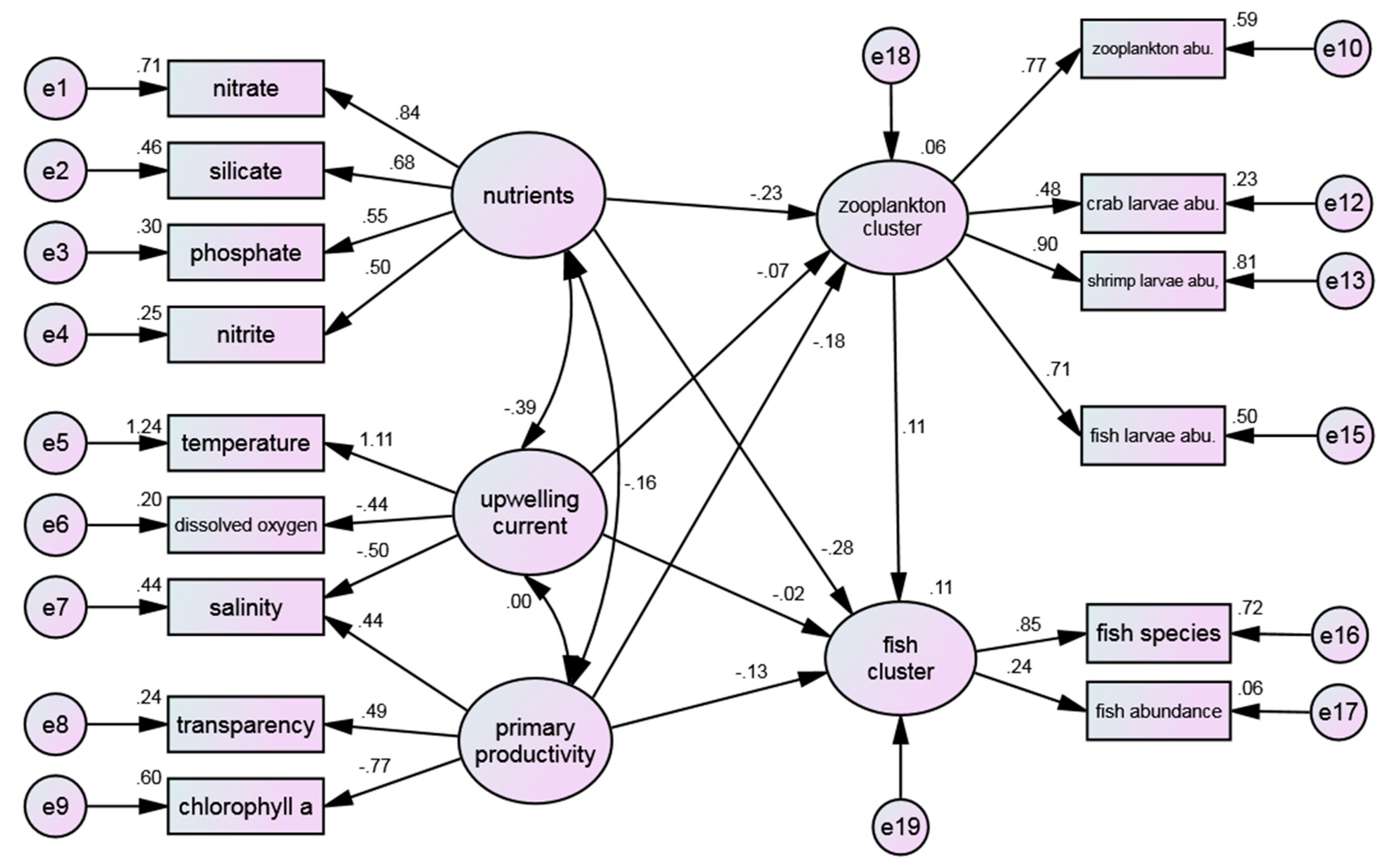
3.4.4. Water Quality Environmental Factors and Marine Life Cluster
The structure that included all three clusters was also considered. However, due to the high correlation between chlorophyll a and the phytoplankton cluster, the model reserves chlorophyll a to represent the primary productivity and dropped phytoplankton cluster.
Figure 6 shows the comprehensive structure pattern between water quality environments and both zooplankton and fish clusters. Of all the indices utilized, only NNFI (0.840) falls short of meeting the reference value and therefore requires further refinement of the model. The remaining indices have successfully passed the test, with RMSEA (0.074) reaching a level of good fit. This suggested that the model has the potential to effectively explicate marine-ecological phenomena to a significant extent.
In the present study, the proposed hypothesis model examining the relationship between environmental factors and marine-life clusters failed to meet the NNFI criteria. This may be due to several factors, including the nature of the sample itself, environmental changes, such as seasonal and weekly-daily fluctuations, and the accuracy and stability of the measuring instrument, which may result in a higher probability of standard errors (non-normal distribution) in the measurement variables. Furthermore, various potential environmental factors, such as sea tide and internal wave phenomena, in the Nan Wan Bay were not included in the statistical analysis. As a result, the proposed model is limited to explaining ecological phenomena only in the sampling waters and may not be applicable to other waters.
3.5. Model Modification
Continuing with the results of the model verification, the next step involves model modification. Due to the covariant relationship between observed variables in the model, parameters in the Modification Index (MI) provided in the Amos Graphics software can be used to modify the model. The main objective of model modification is to improve its simplicity, model fit, explanatory power, and reduce measurement error and structural residuals. However, there is a risk of losing the characteristic of verification and converting the model into an exploratory tool. In the context of the measurement model, one way to modify the model is to allow correlation between measurement variables when supported by theory or literature.
The objective of this study is to explore the correlation between the variables presented in Figure 5 and Figure 6. During the model verification phase, the Root Mean Square Error of Approximation (RMSEA) for the models shown in Figure 4, Figure 5 and Figure 6 are all in the moderate fit range (0.08 to 0.10). Notably, the model depicted in Figure 6 achieved a better fit range (0.05 to 0.08). As the correlation of the variables in the model of Figure 4 is included in the model of Figure 5, only the models in Figure 5 and Figure 6 were considered for revision.
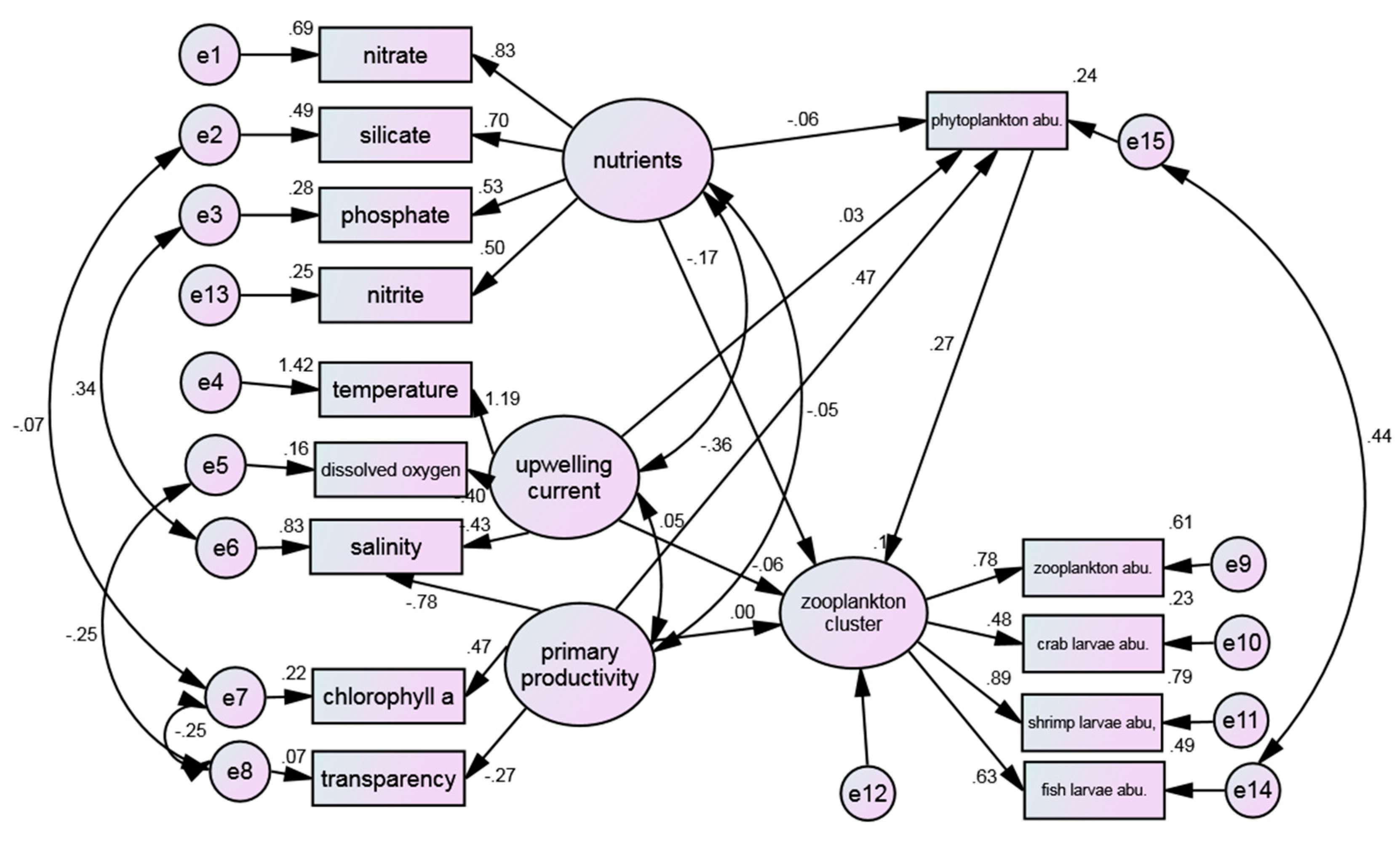
The model in Figure 5 was modified based on the MI value provided in the Amos report by establishing the correlation between residuals of measured variables. Specifically, the correlation between measured variable residuals was increased to reduce the chi-square value, following the principle of modifying one parameter at a time. The revised model is shown in Figure 7. After the revision, the NNFI (0.939) was in accordance with the reference criteria, and the rest of the indexes also provided validation for the model, especially RMSEA (0.052) reached the range of well fit, indicating that the model and observed data achieved the desired fitting (Table 9).
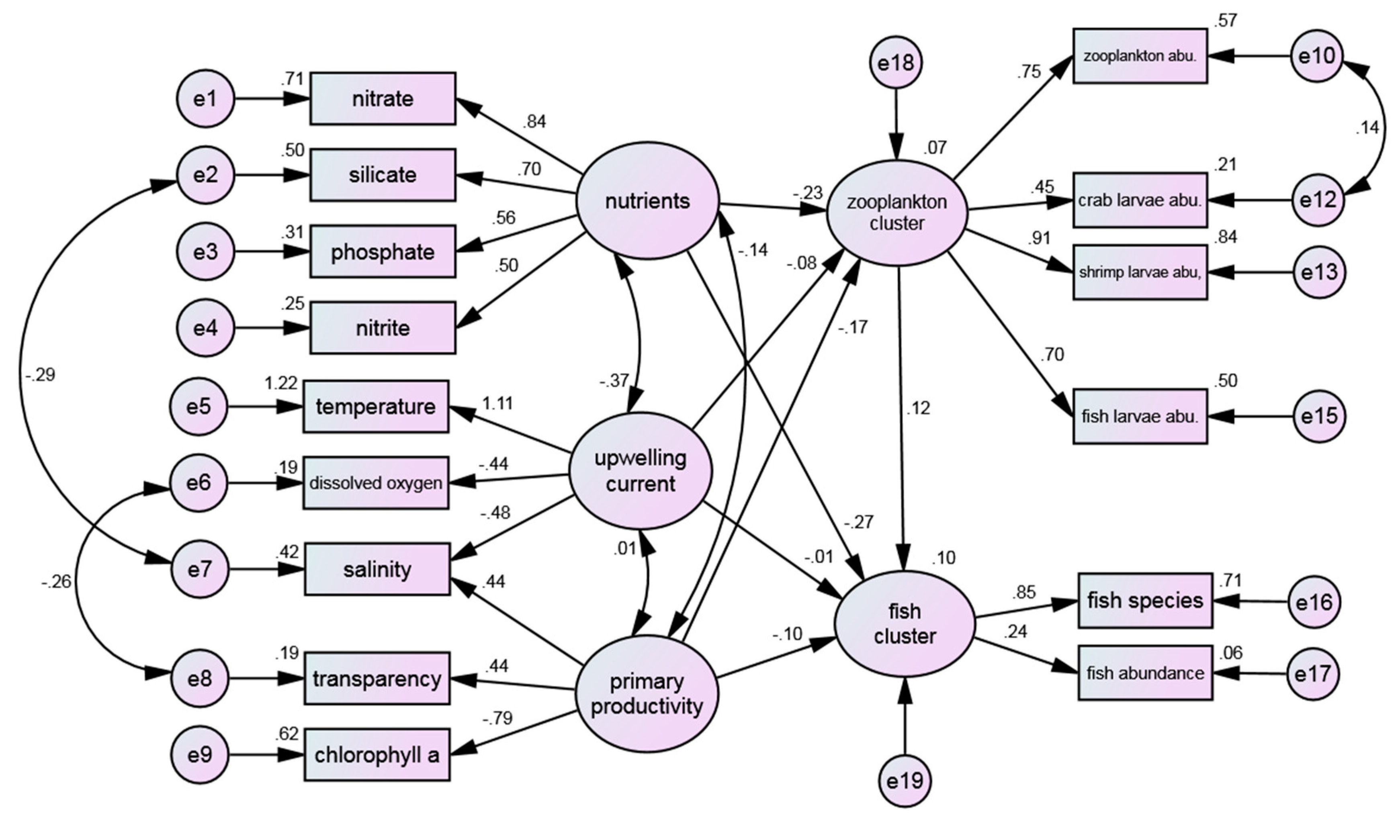
Figure 8 is the revision of Figure 6, and the results are shown in Table 10. It can be observed that the Normalized Fit Index (NNFI) attained a value of 0.912, which met the established reference criteria. Furthermore, the other indices also provided validation of the model, with particular emphasis on the Root Mean Square Error of Approximation (RMSEA) which fell within the well-fit range at 0.055. This indicated that the model and the observed data achieved the desired level of fit.
Upon completion of the model revision, subsequent path analysis and the effect between variables were conducted to verify the assumptions made in this study.
3.6. Path Analysis
In addition to evaluating the overall fitness of the model modification and the intrinsic quality of the test, further examination is required to comprehend the linear association between the latent variables. This can be achieved through the observed direct effects and indirect effects to determine the direct and indirect impacts, as well as overall impacts (direct and indirect effects) among the latent variables.
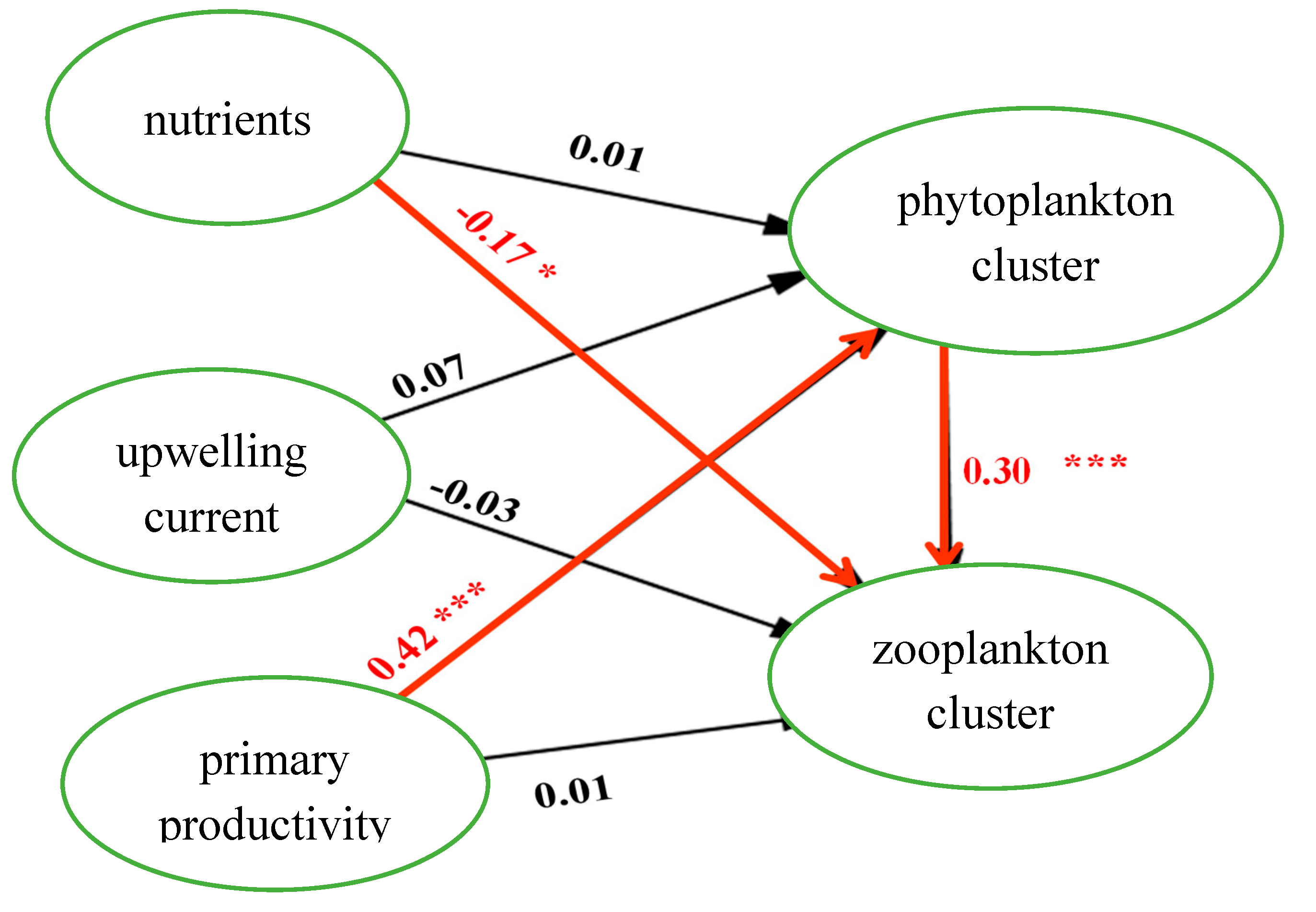
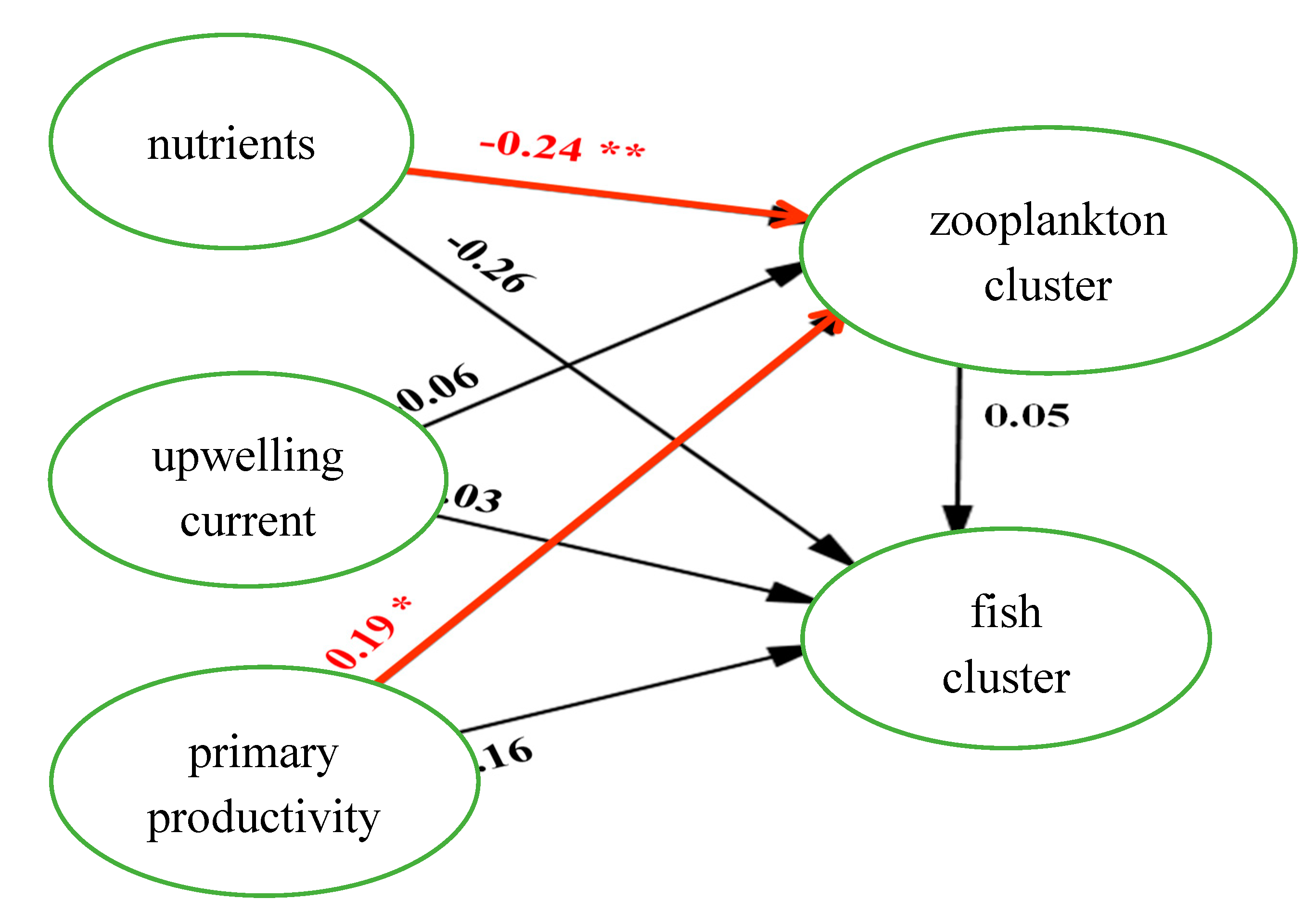
The path relations between the facets were estimated by the structural equation model. The standardized coefficients were used to determine the relationship between the latent variables in the model, as depicted in Figure 7 and Figure 8. In Figure 9, the path effects of "nutrient on zooplankton clustering," "primary productivity on phytoplankton clustering," and "phytoplankton clustering on zooplankton clustering" were found to be statistically significant. Similarly, in Figure 10, the path effects of "nutrient on zooplankton clustering" and "primary productivity on zooplankton clustering" were also significant, indicating that both models possess considerable predictive capabilities for assessing direct and indirect effects (enhancement or offset) on environmental and biological factors.
The path analysis provides empirical evidence of the direct and indirect effects. The direct effects of nutrients on the zooplankton cluster, primary productivity on the phytoplankton cluster, and phytoplankton cluster on the zooplankton cluster were found to be statistically significant (H2, H5, and H7, respectively). Additionally, the direct effects of nutrients on the zooplankton cluster and primary productivity on the zooplankton cluster were also statistically significant (H8 and H12, respectively). Among the significant direct effects, the effect of primary productivity on the phytoplankton cluster (H5) is the strongest (0.421).
In addition to the direct effects, the study also examined the indirect effects of the predictor variables on the zooplankton cluster. The results in Table 11 and Table 12 indicated that, except for the path of primary productivity on the zooplankton cluster, which has a rather higher coefficient of 0.122, the remaining paths have lower coefficients. Therefore, the direct effects were found to be more significant than the indirect effects.
Overall, the study suggests that the marine environment is subject to various factors that may influence the relationships among nutrient salt, primary productivity, phytoplankton cluster, and zooplankton cluster. This may explain why the indirect effects were not significant in this study. It is also possible that there are other intermediary variables or relationships that were not included in the structural statistics, or that the data itself had a high degree of variation.
4. Conclusions
The Nanwan Bay is a semi-closed water with a variety of coral reef organisms. Due to the discharge of cooling water from nuclear power plants, it is discussed to affect the sustainability of marine ecology. This study analysis 223 valid survey data in 16 years and employed Structural Equation Modeling (SEM) to construct the linear relationships between environmental factors and marine organisms, specifically water quality, plankton quantity, and fish species and quantity. The results of the analysis revealed 3 important findings.
First, based on the two revised models in this study- “Modification of environmental factors and plankton clusters” and “Modification of environmental factors and marine life clusters”. The main environmental change factors in this water are “primary productivity” and “nutrient”, the two factors have a considerable degree of impact on “plankton”, in which primary productivity has the highest direct effect.
Secondly, in the current study, two revised models were developed to explore the relationship between the upwelling current and the phytoplankton cluster, the zooplankton cluster, and the fish cluster. The results of the analysis revealed that the effect of upwelling current on these variables was not statistically significant. One possible explanation for this finding is that the upwelling current represents a medium through which deep seawater is transported to the surface layer of the ocean. As such, it may not have a direct impact on the marine organisms under investigation in this study. Rather, it may indirectly influence other environmental factors, such as nutrient availability and primary productivity, which in turn may affect the distribution and abundance of phytoplankton, zooplankton, and fish in the study area.
Finally, this study compared the phenomena presented in previous related surveys and used structural equation modeling to illustrate how the upwelling current phenomenon affects the nutrient content in the water of Nanwan Bay, thereby influencing the quantity of surface plankton.
Author Contributions
All authors have contributed to the designed research, analyzed the data, and wrote up the paper. All authors have read and approved the final manuscript.
Acknowledgments
This research was supported by Taipower, Taiwan. (Grant Nos. 061090002101)
Conflicts of Interest
All authors have no conflict of interests to any other parties.
References
- Wei, X. -Y.; Wang, Y. -C.; Zhang, K.; Dang, Y. -Q.; Xiong, X. -W.; Shang, Z. Review of assessment of thermal discharges from power plants on aquatic biota. Journal of Hydroecology 2018, 39, 1–10. [Google Scholar]
- Colebrook, J. M. Continuous plankton records: seasonal variations in the distribution and abundance of plankton in the North Atlantic Ocean and the North Sea. Journal of Plankton Research. 1982, 4, 435–462. [Google Scholar] [CrossRef]
- Ramdani, M.; Elkhiati, N.; Flower, R. J.; Thompson, J. R.; Chouba, L.; Kraiem, M. M.; Ayache, F.; Ahmed, M. H. Environmental influences on the qualitative and quantitative composition of phytoplankton and zooplankton in North African coastal lagoons. Hydrobiologia. 2009, 622, 113–131. [Google Scholar] [CrossRef]
- Poornima, E. H.; Rajadurai, M.; Rao, T. S. Impact of thermal discharge from a tropical coastal power plant on phytoplankton. Journal of Thermal Biology. 2005, 30, 307–316. [Google Scholar] [CrossRef]
- Jiang, Z. B.; Zeng, J. N.; Chen Q., Z. Potential impact of rising seawater temperature on copepods due to coastal power plants in subtropical areas. Journal of Experimental Marine Biology and Ecology. 2009, 368, 196–201. [Google Scholar] [CrossRef]
- Marrasse, C.; Lim, E.; Caron, D. Seasonal and daily changes in bacterivory in a coastal plankton community. Marine Ecology Progress Series. 1992, 82, 281–289. [Google Scholar] [CrossRef]
- Cooke, S. J.; Bunt, C. M.; Schreer, J. F. Understanding fish behavior, distribution, and survival in thermal effluents using fixed telemetry arrays: a case study of smallmouth bass in a discharge canal during winter. Journal Environment Management. 2004, 33, 140–150. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.-T. A.; Tsai, H. -S.; Lin, W. -H.; Wang, B. -J. Lui, H. -K. Hydrology and water chemistry around the Third Nuclear Power Plant dominated by large scale environmental changes. Monthly Journal of Taipower’s Engineering. 2016, 810, 64–71. [Google Scholar]
- Chen, C.-T. A.; Jan, S.; Chen, M.-H.; Liu, L.-L.; Huang, J.-F.; Yang, Y.-J. Far-field influences shadow the effects of a nuclear power plant’s discharger in a semi-enclosed bay. Sustainability. 2023, 15, 9092. [Google Scholar] [CrossRef]
- Pugesek, B. H.; Tomer, A.; von Eye, A. Structural Equation Modeling: Applications in Ecological and Evolutionary Biology. Cambridge University Press, Cambridge, UK. 2003, 336 pp.
- Jia, L.; Shen, L.; Shuai, C.; He, B. A novel approach for assessing the performance of sustainable urbanization based on structural equation modeling: A China case study. Sustainability. 2016, 8, 910. [Google Scholar] [CrossRef]
- Kaiser, H. F. An index of factorial simplicity, Psychometrika. 1974, 39, 31–36.
- Chen, S.-Y. Multivariate analysis, Fourth edition. Huatai Book Company, Taipei. 2005, 710 pp.
- Hwang, F.-M. The statistical methodology for social science-structural equation modeling. Wunan Bookstore, Taipei. 2004, 477 pp.
- Hwang, F.-M. Structural Equation Modeling. Wunan Bookstore, Taipei. 2009, 496 pp.
- Hair, J. F. Jr.; Anderson, R. E.; Tatham, R. L.; Black, W. C. Multivariate Data Analysis (5th ed.), Englewood Cliffs, Prentice-Hall, NJ. 1998, 730 pp.
- Carmines, E. G.; McIver, J. P. Analyzing models with observable variables. In G.W. Bohrnstedt, & E. F. Borgatta(Eds.). Social measurement. Beverly Hills:Sage. 1981, 65-115.
- Joreskog, K. G.; Sorbom, D. LISREL 8: User’s reference guide. Chicago Scientific Software International. 1996, 378 pp.
- Hair, J. F.; Black, W. C.; Babin, B. J.; Anderson, R. E.; Tatham, R. L. Multivariate Date Analysis, Pearson Education, Inc. 6th. 2006, 899 pp.
- Browne, M.W.; Cudeck, R. Alternative ways of assessing model fit. In K.A. Bollen, & J.S. Long(Eds.). Testing structural equation models. 1993, 136-162.
- Hu, L.; Bentler, P. M. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling. 1999, 6, 1–55. [Google Scholar] [CrossRef]
- Tucker, L. R.; Lewis, C. A reliability coefficient for maximum likelihood factor analysis. Psychometrika, 1973, 38, 1–10. [Google Scholar] [CrossRef]
- Mulaik, S. A.; James, L.R.; Van Alstine, J.; Bennet, N.; Lind, S.; Stilwell, C. D. Evaluation of Goodness-of-Fit Indices for Structural Equation Models. Psychological Bulletin. 1989, 105, 430–445. [Google Scholar] [CrossRef]
- Walsh, J. J.; Whitledge, T. E.; Esaias, W. E.; Smith, R. L.; Huntsman, S. A.; Santander, H.; De Mendiola, B. R. The spawning habits of the Peruvian anchovy, Engraulis ringens. Deep-Sea Research 1980, 27, 1–27. [Google Scholar] [CrossRef]
- Armstrong, D. A.; Mitchell-Innes, B. A.; Verheye-Dua, F.; Waldron, H.; Hutchings, L. Physical and biological features across an upwelling front in the southern Benguela. South African Journal of Marine Science. 1987, 5, 171–190. [Google Scholar] [CrossRef]
- Longhurst, A. R.; Pauly, D. Ecology of tropical oceans. Academic Press, London. 1987, 407 pp.
Figure 3.
SEM of environmental variables and the phytoplankton cluster.
Figure 4.
SEM of environmental variables and the zooplankton cluster.
Figure 5.
SEM of environmental variables and the plankton clusters.
Figure 6.
SEM of environmental variables and marine life.
Figure 7.
Modified SEM of environmental variables and plankton clusters.
Figure 8.
Modified SEM of environmental variables and marine life.
Figure 9.
The path analysis of environmental variables and plankton clusters.
Figure 10.
The path analysis of environmental variables and marine life.
Table 3.
Statistical summary of environmental variables.
| Environment variable N=223 | unit | maximum | minimum | mean | standard deviation | variance |
|---|---|---|---|---|---|---|
| temperature | ℃ | 17.200 | 31.100 | 26.744 | 2.078 | 4.316 |
| salinity | psu | 32.111 | 35.741 | 34.114 | 0.498 | 0.248 |
| pH | - | 7.953 | 8.195 | 8.077 | 0.036 | 0.001 |
| dissolved oxygen | mg/L | 5.168 | 7.560 | 6.521 | 0.281 | 0.079 |
| transparency | m | 0.000 | 20.000 | 11.486 | 3.129 | 9.792 |
| chlorophyll a | μg/L | 0.005 | 1.223 | 0.212 | 0.200 | 0.040 |
| nitrate | μM | 0.000 | 2.957 | 0.616 | 0.518 | 0.268 |
| nitrite | μM | 0.000 | 0.244 | 0.066 | 0.041 | 0.002 |
| phosphate | μM | 0.006 | 0.780 | 0.093 | 0.067 | 0.005 |
| silicate | μM | 0.913 | 5.630 | 2.258 | 0.756 | 0.571 |
Table 4.
Statistical summary of biological variables.
| Biological variable N=223 | unit | maximum | minimum | mean | standard deviation | variance |
|---|---|---|---|---|---|---|
| fish species | Species | 15 | 67 | 39.776 | 8.699 | 75.670 |
| fish abundance | ind./station | 51 | 3,082 | 299.170 | 275.870 | 76104.016 |
| zooplankton | ind./1000m3 | 22,590 | 2,329,724 | 410051.466 | 380477.250 | 1.45E+11 |
| phytoplankton | ind./1000m3 | 10 | 120,600 | 2390.063 | 13069.235 | 1.71E+08 |
| crab larvae | ind./1000m3 | 0 | 111,962 | 2496.565 | 7862.203 | 6.18E+07 |
| shrimp larvae | ind./1000m3 | 19 | 51,510 | 5938.323 | 8541.610 | 7.30E+07 |
| fish eggs | ind./1000m3 | 0 | 81,596 | 10418.305 | 14776.330 | 2.18E+08 |
| fish larvae | ind./1000m3 | 0 | 3,551 | 318.350 | 457.812 | 209591.670 |
Table 5.
Correlation analysis results of measurement variables.
| temperature | salinity | pH | dissolved oxygen | transparency | chlorophyll a | nitrate | nitrite | phosphate | silicate | zooplankton abu. | phytoplankton abu. | crab larvae abu. | shrimp larvae abu, | fish egg abu. | fish larvae abu. | fish species | fish abundance | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| temperature | 1.000 | |||||||||||||||||
| salinity | -0.586** | 1.000 | ||||||||||||||||
| pH | 0.444** | -0.128 | 1.000 | |||||||||||||||
| dissolved oxygen | -0.550** | 0.239** | -0.014 | 1.000 | ||||||||||||||
| transparency | 0.074 | 0.088 | -0.074 | -0.325** | 1.000 | |||||||||||||
| chlorophyll a | -0.126 | -0.273** | 0.051 | 0.233** | -0.395** | 1.000 | ||||||||||||
| nitrate | -0.432** | 0.268** | -0.384** | 0.064 | -0.030 | 0.109 | 1.000 | |||||||||||
| nitrite | -0.307** | 0.321** | -0.163* | 0.170* | -0.122 | 0.065 | 0.285** | 1.000 | ||||||||||
| phosphate | -0.396** | 0.264** | -0.280** | 0.208** | -0.209** | 0.199** | 0.547** | 0.376** | 1.000 | |||||||||
| silicate | -0.190** | -0.101 | -0.248** | 0.086 | -0.029 | 0.104 | 0.438** | 0.215** | 0.351** | 1.000 | ||||||||
| zooplankton abu. | 0.124 | -0.191** | -0.236** | 0.016 | 0.041 | 0.047 | -0.245** | -0.164* | -0.177** | -0.183** | 1.000 | |||||||
| phytoplankton abu. | 0.237** | -0.143* | 0.093 | -0.010 | -0.107 | -0.060 | -0.216** | -0.038 | -0.139* | -0.029 | 0.079 | 1.000 | ||||||
| crab larvae abu. | 0.285** | -0.314** | 0.044 | -0.126 | -0.184** | 0.099 | -0.192** | -0.157* | -0.093 | -0.090 | 0.385** | 0.066 | 1.000 | |||||
| shrimp larvae abu, | -0.041 | -0.109 | -0.180** | 0.140* | -0.123 | 0.083 | -0.138* | -0.132* | -0.067 | -0.203** | 0.634** | 0.111 | 0.474** | 1.000 | ||||
| fish egg abu. | 0.550** | -0.346** | -0.020 | -0.392** | 0.176** | -0.076 | -0.172* | -0.141* | -0.113 | 0.045 | 0.301** | 0.228** | 0.375** | 0.107 | 1.000 | |||
| fish larvae abu. | 0.254** | -0.091 | 0.019 | -0.093 | 0.020 | -0.047 | -0.137* | -0.130 | -0.148* | -0.213** | 0.476** | 0.143* | 0.396** | 0.501** | 0.347** | 1.000 | ||
| fish species | 0.084 | -0.175** | -0.077 | 0.078 | -0.085 | -0.081 | -0.212** | -0.061 | -0.172* | -0.050 | 0.120 | 0.176** | 0.133* | 0.167* | 0.004 | 0.118 | 1.000 | |
| fish abundance | 0.049 | 0.006 | 0.173** | 0.032 | -0.021 | 0.018 | -0.201** | -0.071 | -0.103 | -0.026 | -0.017 | 0.039 | 0.017 | 0.016 | -0.029 | 0.069 | 0.460** | 1.000 |
Table 8.
The component matrix of biological variables in each factor after rotation (fish eggs excluded).
Table 8.
The component matrix of biological variables in each factor after rotation (fish eggs excluded).
| measured variable | factor loading(N=223) | |
|---|---|---|
| 1 | 2 | |
| shrimp larvae abundance | 0.886 | 0.073 |
| Zooplankton abundance | 0.855 | -0.004 |
| fish larvae abundance | 0.773 | 0.174 |
| crab larvae abundance | 0.634 | -0.053 |
| fish abundance | -0.039 | 0.779 |
| fish species | 0.114 | 0.759 |
| eigenvalue | 2.531 | 1.223 |
| variance % | 42.180 | 20.377 |
| cumulated variance % | 42.180 | 62.557 |
Table 9.
The model evaluation result of the modified SEM of environmental variables and the plankton clusters.
Table 9.
The model evaluation result of the modified SEM of environmental variables and the plankton clusters.
| Key metrics | Reference guidelines | Model validation | Test result |
|---|---|---|---|
| χ2 | the lower the better | 97.663 | |
| χ2/df | <5(<3 better fit) | 1.601 | compliant |
| GFI | >0.9 | 0.941 | compliant |
| AGFI | >0.9(>0.8 acceptable fit) | 0.898 | compliant |
| RMSEA | <0.05，good fit | 0.052 | reasonable fit |
| 0.05~0.08，reasonable fit | |||
| 0.08~0.10，medium fit | |||
| >0.10，poor fit | |||
| SRMR | ≦0.08 | 0.0634 | compliant |
| NNFI | >0.9 | 0.939 | compliant |
| PNFI | ≧0.5 | 0.604 | compliant |
| PGFI | ≧0.5 | 0.547 | compliant |
| GN | ≧200 | 223 | compliant |
Table 10.
The model evaluation result of the modified SEM of environmental variables and marine life.
Table 10.
The model evaluation result of the modified SEM of environmental variables and marine life.
| Key metrics | Reference guidelines | Model validation | Test result |
|---|---|---|---|
| χ2 | the lower the better | 127.053 | |
| χ2/df | <5(<3 better fit) | 1.672 | compliant |
| GFI | >0.9 | 0.931 | compliant |
| AGFI | >0.9(>0.8 acceptable fit) | 0.891 | compliant |
| RMSEA | <0.05，good fit | 0.055 | reasonable fit |
| 0.05~0.08，reasonable fit | |||
| 0.08~0.10，medium fit | |||
| >0.10，poor fit | |||
| SRMR | ≦0.08 | 0.0621 | compliant |
| NNFI | >0.9 | 0.912 | compliant |
| PNFI | ≧0.5 | 0.623 | compliant |
| PGFI | ≧0.5 | 0.589 | compliant |
| GN | ≧200 | 223 | compliant |
Table 11.
The effects between environmental factors and plankton cluster.
| phytoplankton | zooplankton | ||
|---|---|---|---|
| nutrients | direct effect | 0.009 (H1) | -0.172* (H2) |
| indirect effect | - | 0.003 | |
| total effect | 0.009 | -0.169 | |
| upwelling current | direct effect | 0.072 (H3) | -0.033 (H4) |
| indirect effect | - | 0.0231 | |
| total effect | 0.072 | -0.012 | |
| primary productivity | direct effect | 0.421*** (H5) | 0.012 (H6) |
| indirect effect | - | 0.122 | |
| total effect | 0.421 | 0.135 | |
| phytoplankton | direct effect | - | 0.290*** (H7) |
| indirect effect | - | - | |
| total effect | - | 0.290 |
*p<0.05；**p<0.01；***p<0.001 Different superscripts indicate significant difference.
Table 12.
The effects between environmental factors and marine life.
| zooplankton | fish species | ||
|---|---|---|---|
| nutrients | direct effect | -0.239** (H8) | -0.265 (H9) |
| indirect effect | - | -0.011 | |
| total effect | -0.239 | -0.276 | |
| upwelling current | direct effect | -0.056 (H10) | -0.034 (H11) |
| indirect effect | - | -0.003 | |
| total effect | -0.056 | -0.036 | |
| primary productivity | direct effect | 0.192* (H12) | 0.159 (H13) |
| indirect effect | - | 0.006 | |
| total effect | 0.192 | 0.168 | |
| zooplankton | direct effect | - | 0.048 (H14) |
| indirect effect | - | - | |
| total effect | - | 0.048 |
*p<0.05；**p<0.01；***p<0.001 Different superscripts indicate significant difference.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated