1. Introduction

2. Results and Discussion

2.1. N₂ Adsorption-Desorption Isotherms

Figure 1a shows the N₂ adsorption-desorption isotherms at -196 °C and Figure 1b shows the pore size distributions of the two home-made carbons. The porous carbons presented type I(b) adsorption/desorption isotherm according to IUPAC classification [46,47] indicating the pore size distributions (PSD) are mainly composed by micropores [48] as can be seen in Figure 1b. The cumulative pore volume trend observed inset Figure 1b suggest that MPB-CO₂ sample possess a close topology, with a main proportion of supermicropores (< 1.0 nm). On the contrary, the sample submitted to chemical activation (MPB-P50) shows an important contribution of large micropores (1.0 – 2.0 nm), and small mesopores (2.0 – 3.0 nm), even when the hysteresis loop is negligible. Table 1 shows a summary of the textural parameters and the activation yields. For the sake of comparison, the commercial activated carbons [49] are also included.

Figure 1. (a): N₂ adsorption-desorption isotherms at -196 °C; (b): Pore size distributions. The figure inset shows the cumulative pore volume on the activated carbons.

Figure 1. (a): N₂ adsorption-desorption isotherms at -196 °C; (b): Pore size distributions. The figure inset shows the cumulative pore volume on the activated carbons.

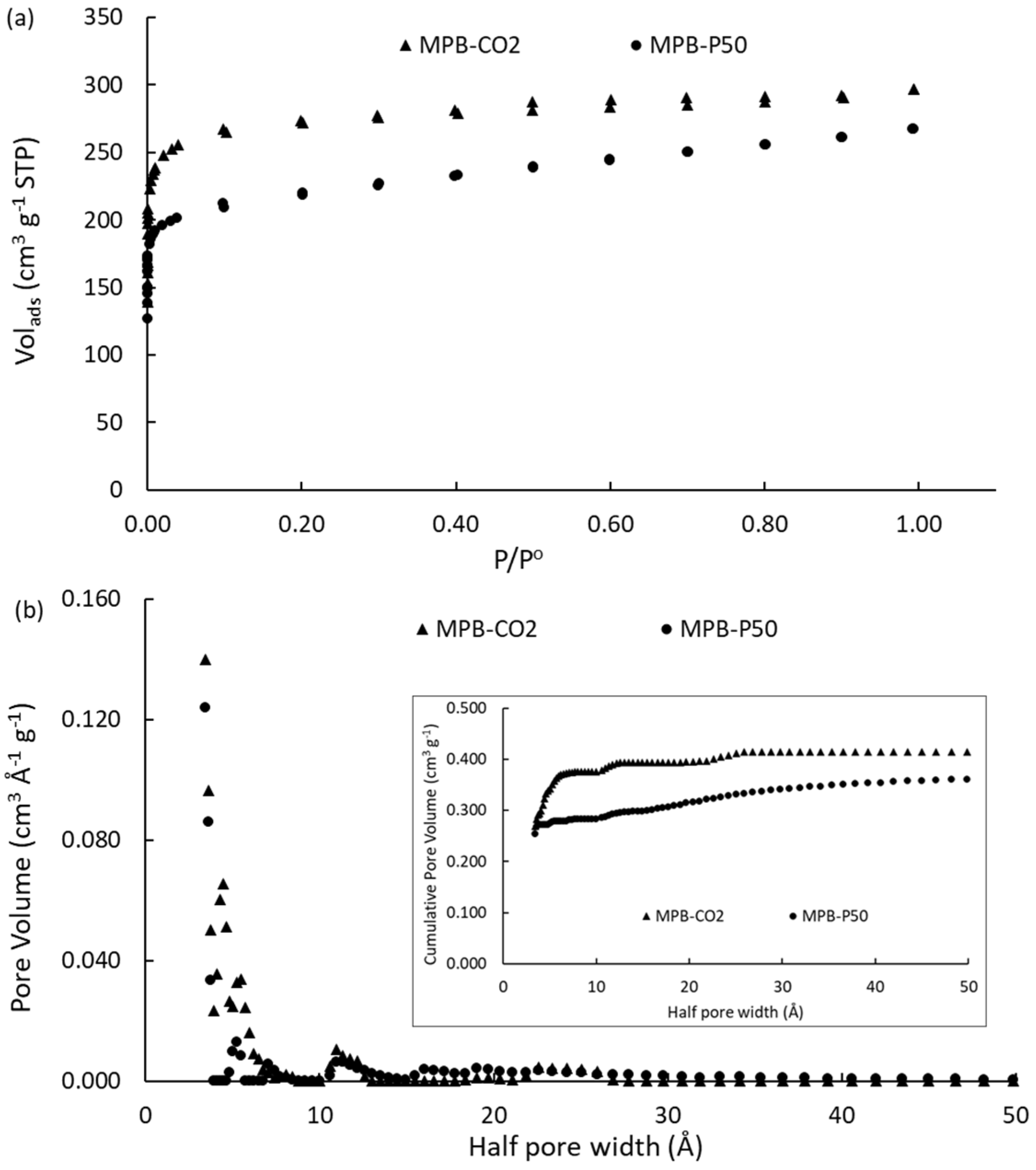
Table 1. Summary of burn-off and textural properties of the mangosteen-derived char, home-made activated carbons, and commercial activated carbons (AC_M and AC_PC).

Table 1. Summary of burn-off and textural properties of the mangosteen-derived char, home-made activated carbons, and commercial activated carbons (AC_M and AC_PC).

Samples	Yield (%) a	SBET (m2.g-1) b	Vmic (cm3.g-1) c	W (nm) c	Vtot (cm3 g-1) d	Vmic/Vtot (%) e
MPB	35	20	0.001	--	0.030	0.03
MPB-CO2	24	1080	0.420	0.72	0.459	0.92
MPB-P50	32	847	0322	1.38	0.414	0.78
ACM f	--	775	0.402	0.96	0.495	0.81
ACPC f	--	1240	0.390	1.98	0.650	0.60

^a Yields estimated from the initial and final weight (after activation). The pyrolysis yield is reported for MPB while for the other samples, the final yield is the product of the two process. ^b S_BET is the BET specific surface area [46,47]. ^c V_mic and W are the volume of micropores and the mean pore width according to Dubinin-Astakhov model [48]. ^d V_Tot is the total volume of pores estimated at P/P_o ≈ 0.99. ^e V_mic/V_tot is the micropore contribution to the pore framework. ^f Values taken from reference [49].

The low yield found in both cases suggests a high reactivity of the char during the activation [50,51]. For physical activation, a direct gasification occurred under CO₂ flow (pressure ca. 1 atm, flow ca. 100 mL·min^-1) according to Eq. (2).

C + CO₂ → 2CO

Eq. (2)

Chemical activation is characterized by an indirect gasification by steam according to Eq. (3) formed from the thermal degradation of H₃PO₄ according to Eq. (4).

C + H₂O → CO + H₂

Eq. (3)

2H₃PO₄ → P₂O₅ + 3H₂O

Eq. (4)

It is clear S_BET and V_tot for the char (MPB) are negligible compared to the other carbons. The higher value of S_BET was observed for the physical activation (ca. 982 m²·g^-1) instead of chemical activation (ca. 847 m²·g^-1) suggesting a more efficient interaction between the char and CO₂ in agreement with a higher burn-off of ca. 76%. The present results are consistent with the experimental conditions used. In physical activation, 0.07 mols of CO₂ flowed in 1 h activation at 800°C, while only ca. 0.03 mols H₂O were formed from H₃PO₄. Thus, keeping in mind the initial mols of MPB char (for 100% C content) is ca. 0.083 mols, it is clear that physical activation should be more effective in the present conditions.

The PSD (Figure 1b) of the porous carbons is characterized by a large contribution to the porosity in the range of 0.4 to 1.0 nm with the highest contribution in the ultramicropores range from 0.4 to 0.7 nm for MPB-CO₂. For MPB-P50, small mesopores have a low contribution in the range between 2 – 3 nm. The maxima contribution of micropore volume to the total volume of pores (V_mic/V_tot = 0.92) was observed for MPB-CO₂ sample with a mean pore width ca. 0.72 nm, which is ca. 52 % lower than MPB-P50 (ca. 1.38 nm). It is interesting to highlight that the commercial carbons were selected for the present study due to the similarities with the carbons prepared from mangosteen peels-derived char. For instance, AC_M is mainly characterized by a micropore framework with ca. 81% micropores and 0.96 nm of mean pore width while AC_PC presents only 60% microporosity and a mean pore width of ca. 1.98 nm, which corresponds to the double of AC_M.

2.2. Scanning Electron Microscopy (SEM) and Surface Analysis

Figure 2 shows SEM images of the activated carbons. It is clear the two materials are amorphous with an important roughness on the surface. Nevertheless, micro- or mesopores are not visible by low-resolution SEM, it is evident the formation of macropores in the two samples. The pore framework in the MPB-CO₂ sample (Figure 2a) seems to be more ordered along the surface, while the images from Figure 2b suggest a less porosity for MPB-P50 sample. This observation could be associated with a lower reactivity in the chemical activation due to the low quantity of steam formed from the degradation of the activator.

Figure 2. SEM images of the home-made carbons. (a): MPB-CO₂; (b): MPB-P50.

Figure 2. SEM images of the home-made carbons. (a): MPB-CO₂; (b): MPB-P50.

On the other hand, Figure 3 shows the evolution of pH of aqueous solution in contact with the activated carbons as a function of time. The surface pH or zero-point charge pH (pH_PZC) of carbon materials can be estimated from the extrapolation of the plot at steady-state conditions [45]. For the sake of comparison, the two commercial activated carbons have also been included in Figure 3. After ca. 75 min, the steady-state condition is achieved. It is clear both commercial carbons and home-made nanoporous carbons show opposite surface pH. It can be observed a surface pH of ca. 10.1, 3.9, 9.7, and 5.4 for AC_M, AC_PC, MPB-CO₂, and MPB-P50. It means, that the surface pH of the activated carbons can be modulated as those of commercial activated carbons. Table 2 shows a summary of the surface pH (pH_PZC) and the results obtained from Boehm´s titration. It is clear that the sample activated under CO₂ flow shows more lactone´s like groups (0.532 mmol·g^-1) than acidic groups including a low proportion of carboxylic acids (0.053 mmol·g^-1) and phenol (0.360 mmol·g^-1).

Figure 3. Evolution of pH of activated carbons as a function of contact time.

Figure 3. Evolution of pH of activated carbons as a function of contact time.

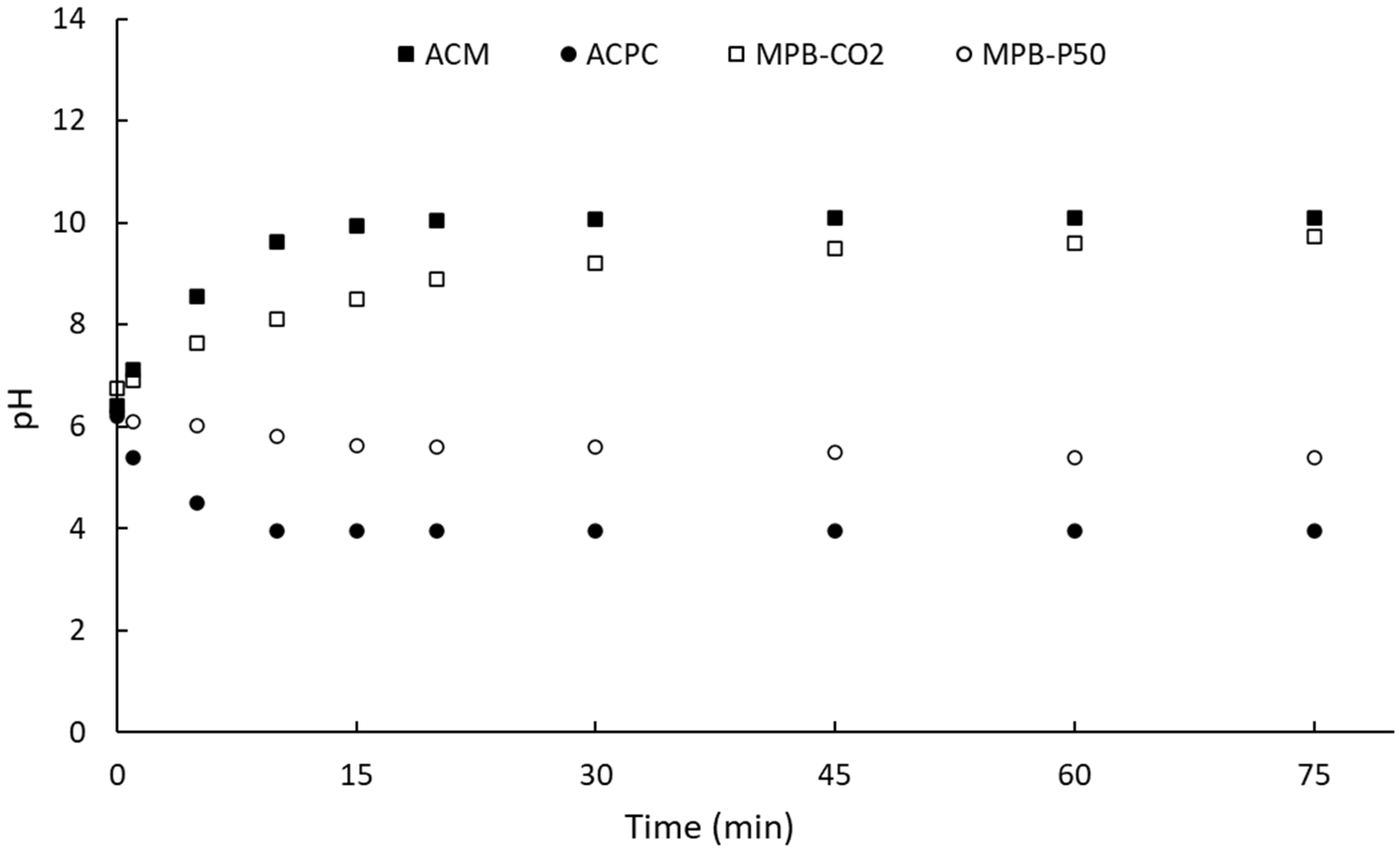
Since phenol is a weaker Brönsted acid than carboxylic acid [52] while lactone is a strong Lewis´s base, and therefore, a basic surface pH for MPB-CO₂ activated carbon is expected in agreement with the surface pH obtained from the drift method (Figure 3). On the contrary, both carboxylic acids and phenolic groups are much higher for MPB-P50. It can be seen from Table 2 that MPB-P50 is characterized by a total acid groups of ca. 6.063 mmol·g-1 which is ca. 15 times higher than MPB-CO₂. This result agrees with the surface pH detected for MPB-P50-800 carbon in Figure 3. Our group have previously reported [44,49] the surface chemistry of the two commercial activated carbons.

Table 2. Summary of surface functional groups of home-made activated carbons evaluated by Boehm´s titrations and surface pH (pH_PZC).

Table 2. Summary of surface functional groups of home-made activated carbons evaluated by Boehm´s titrations and surface pH (pH_PZC).

Sample	Carboxylic	Lactones	Phenol	Total acid	Total basic	Total	pHPZC
	(mmol·g-1)	(mmol·g-1)	(mmol·g-1)	(mmol·g-1)	(mmol·g-1)	(mmol·g-1)
MPB-CO2	0.053	0.532	0.360	0.413	0.532	0.945	9.7
MPB-P50	0.619	0.137	5.444	6.063	0.137	6.200	5.4

AC_M is characterized by low phenolic groups and mainly lactone and pyrone groups in agreement with its basic surface pH. It means both the surface pH (almost similar pH_PZC) and the porosimetry discussed above (Table 1, 92% against 85% micropores) of ACM can be compared MPB-CO₂. On the contrary, AC_PC is mainly characterized by an important proportion of carboxylic and phenolic groups, accordingly, it shows an acidic pH. In a similar way, MPB-P50 posses an acid surface comparable to that observed on AC_PC and in addition, MPB-P50 is characterized by an important proportion of mesopores (Table 1, 22% mesopores) which can permit a reasonable comparison with that of AC_PC (Table 1, 40% mesopores).

2.3. Atrazine Adsorption

2.3.1. Kinetic Studies

Figure 4 shows the kinetics of ATZ adsorption for different initial concentration (0.5 – 5.0 ppm). Table 3 contains a summary of atrazine adsorbed at equilibrium condition (after 120 min) and different kinetics parameters of adsorption. The two commercial carbons showed the highest ATZ uptake for all the initial concentrations. This result is ascribed to a combination of a high surface area and high total volume of pores (Table 1). However, in spite of AC_PC is characterized by a higher surface area and total volume of pores than AC_M (Table 1), it is clear that AC_PC removes less ATZ (Table 3). For instance, AC_PC adsorbs ca. 15% and ca. 34% less ATZ than AC_M for 0.5 ppm and 5.0 ppm. This results suggest that the diffusion of ATZ molecules from the bulk of solution to the pores of adsorbents is more efficient for low concentration of herbicide. This result seems to be contradictory with the dynamics of adsorption described by the intraparticle diffusion model (IPD) [53,54,55] since AC_PC has a higher mesopore contribution than that of AC_M (Table 1). It cannot be discarded that the acidic functional groups of AC_PC inhibit the diffusion of ATZ molecules to the pore framework. This inference seems to be reinforced by comparing the ATZ adsorbed on MPB-CO₂ against MPB-P50. In spite of the surface area and total volume of pores of MPB-CO₂ does not differ much from the values for MPB-P50, it is clear that atrazine adsorption is remarkable different. For instance, increasing the initial concentration from 0.5 - 5.0 ppm, the ATZ adsorbed on MPB-CO₂ was ca. 8.9, 7.1, 6.7, and 6.5 higher than that adsorbed on MPB-P50. It suggests the acidic surface functional groups (mainly carboxylic acids and phenol) of MPB-P50 inhibit the diffusion to the pore framework.

Figure 4. Kinetics of atrazine adsorption (q_t) as a function of the initial concentration. (a): AC_M; (b): AC_PC; (c): MPB-CO₂; (d): MPB-P50.

Figure 4. Kinetics of atrazine adsorption (q_t) as a function of the initial concentration. (a): AC_M; (b): AC_PC; (c): MPB-CO₂; (d): MPB-P50.

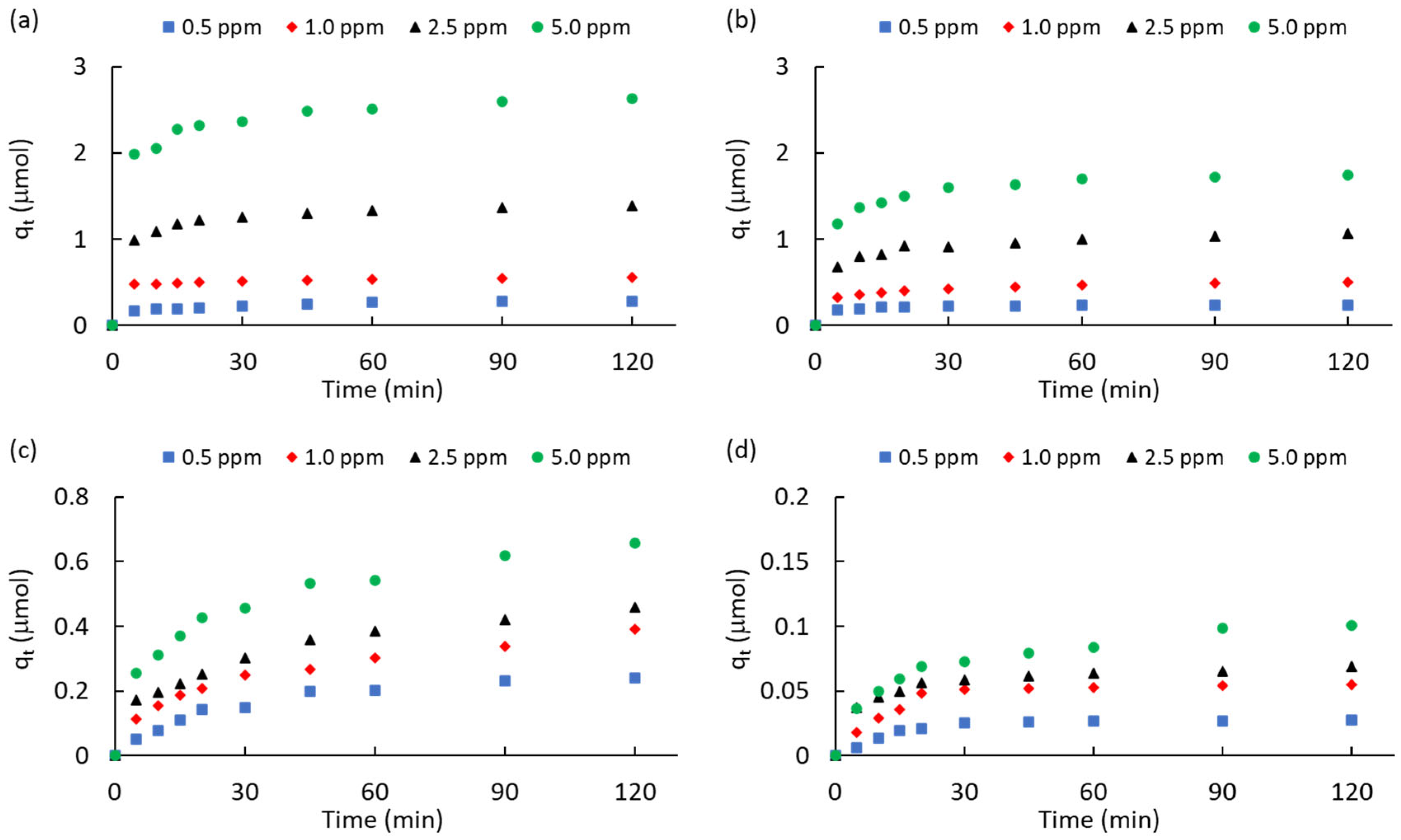
Table 3. Summary of kinetic parameters for the atrazine removal on porous carbons.

Table 3. Summary of kinetic parameters for the atrazine removal on porous carbons.

Carbon	ATZ (ppm)	qeq a (μmol)	k1 b (min-1)	R2k1 c	k2 d (μmol-1·min-1)	R2k2 e	kp f (μmol-1·min-0.5)	C g (μmol)	R2kp h
ACM	0.5	0.282	0.032	0.997	0.743	0.928	0.014	0.146	0.954
	1	0.556	0.024	0.996	0.638	0.966	0.009	0.458	0.981
	2.5	1.385	0.033	0.985	0.285	0.963	0.042	0.981	0.863
	5	2.632	0.021	0.906	0.130	0.979	0.073	1.921	0.889
ACPC	0.5	0.241	0.053	0.972	1.956	0.966	0.006	0.181	0.852
	1	0.503	0.028	0.996	0.394	0.950	0.020	0.299	0.955
	2.5	1.064	0.028	0.965	0.227	0.949	0.039	0.675	0.879
	5	1.742	0.041	0.985	0.349	0.846	0.060	1.181	0.844
MPB-CO2	0.5	0.241	0.033	0.977	0.378	0.944	0.022	0.023	0.931
	1	0.391	0.019	0.987	0.133	0.983	0.030	0.063	0.984
	2.5	0.459	0.024	0.996	0.185	0.971	0.035	0.099	0.977
	5	0.658	0.026	0.980	0.124	0.980	0.046	0.189	0.963
MPB-P50	0.5	0.027	0.052	0.919	18.796	0.911	0.002	0.014	0.698
	1	0.055	0.042	0.872	8.395	0.972	0.003	0.029	0.643
	2.5	0.069	0.023	0.900	2.684	0.993	0.003	0.041	0.875
	5	0.101	0.035	0.919	0.818	0.992	0.006	0.035	0.958

^a ATZ adsorbed after 120 min. ^b k₁ is the pseudo-first-order rate constant. ^c R²_k1 is the quadratic linear factor for k₁. ^d k₂ is the pseudo-second-order rate constant. ^e R²_k2 is the quadratic linear factor for k₂. ^f k_p is the intraparticle diffusion model (IPD) rate constant. ^g C is the boundary layer thickness constant for the IPD model. ^h R²_kp is the quadratic linear factor for the k_p.

The molecular interactions associated with the mechanism of ATZ adsorption on the present porous carbons can be also interpreted in terms of the kinetics parameters of adsorption were obtained for the pseudo-first order [53,56], the pseudo-second order [53,57], and the intraparticle diffusion [53,54,55] models. Table S1 (Supplementary) shows a summary of the kinetic expressions and parameters obtained from the pseudo-first-order rate constant (k₁), the pseudo-second-order rate constant (k₂), the intraparticle (IPD) rate constant (k_p) and the C constant attributed to the extension of the boundary layer thickness. The pseudo-first order kinetics is associated with the reversible physisorption of molecules [58] while a pseudo-second order kinetics is associated with chemisorption phenomena [59] where strong interactions and bond formation may occur between the adsorbate and adsorbent. Figure 5 shows the plots for the atrazine adsorption on AC_M and MPB-CO₂ at 0.5 and 5.0 ppm, respectively, in terms of the pseudo-first order, pseudo-second order and the intraparticle diffusion models. It can be seen from Figure 5 and the regression values from Table 3 that both AC_M and MPB-CO₂ have fitted very-well with the pseudo first-order and pseudo second-order showing R² > 0.95 in most of cases. The average values for R²_k1 and R²_k2 were ca. 0.971 and 0.959 for AC_M while 0.985 and 0.969 were estimated for MPB-CO₂.

It can be suggested that a mixture of physisorption and chemisorption mechanisms governs ATZ adsorption on carbons characterized by a basic surface and micropore framework. It is important to highlight that AC_M does not fit well with the intraparticle model with an average R²_kp values of ca. 0.921 while a value of ca. 0.964 was obtained for MPB-CO₂. It can be seen from Table 3 that at low ATZ concentration (0.5 ppm), ATZ adsorbed at equilibrium conditions (q_eq) is similar in both commercial carbons (0.282 μmol against 0.241 μmol).

Figure 5. Kinetics treatments for ATZ adsorption on AC_M (a,b,c,g,h,i) and MPB-CO₂ (d,e,f,j,k,l). 0.5 ppm: (a,b,c,d,e,f); 5.0 ppm: (g,h,i,j,k,l). Pseudo first-order: (a,d,g,j); Pseudo second-order: (b,e,h,k); Intraparticle diffusion model: (c,f,i,l).

Figure 5. Kinetics treatments for ATZ adsorption on AC_M (a,b,c,g,h,i) and MPB-CO₂ (d,e,f,j,k,l). 0.5 ppm: (a,b,c,d,e,f); 5.0 ppm: (g,h,i,j,k,l). Pseudo first-order: (a,d,g,j); Pseudo second-order: (b,e,h,k); Intraparticle diffusion model: (c,f,i,l).

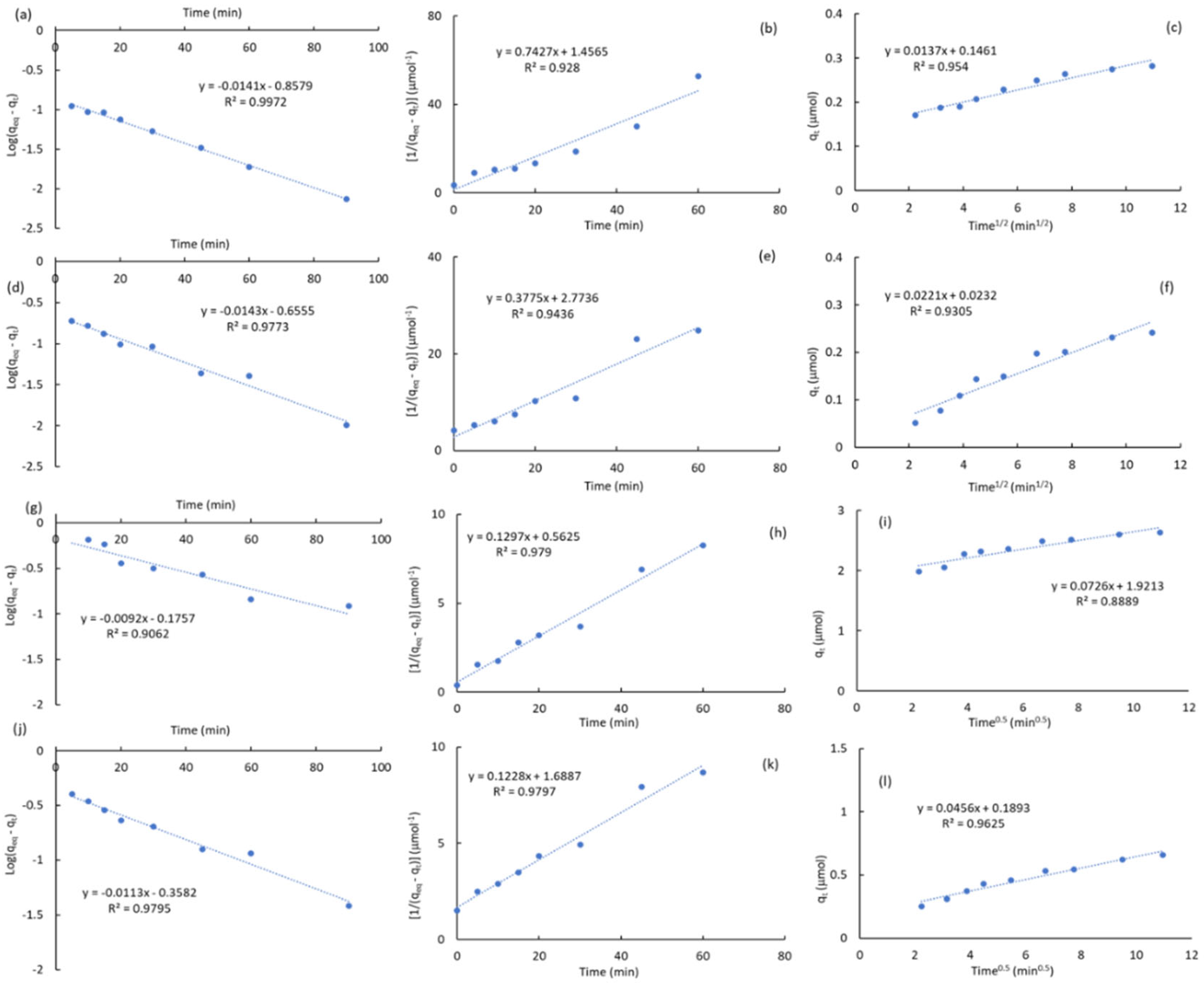
On the contrary, at high initial concentrations (5.0 ppm), q_eq is higher on AC_M than AC_PC and ca. 4 times higher than MPB-CO₂ (2.632 μmol against 0.658 μmol). It suggests that in spite of the micropore contribution and the surface pH of AC_M is almost similar to that of MPB-CO₂, AC_M permits a better diffusion of molecules from the bulk of solution to the pore framework. This ability is stronger at high initial concentrations. This inference is reinforced when the values of C constant from IPD model are compared between both carbons. Table 3 shows C values monotonically increases as a function of the initial concentrations from 0.146 up to 1.921 μmols (13.2 times higher) for AC_M while for MPB-CO₂ increased from 0.023 μmol up to 0.189 μmol (8.2 times higher). In other words, high adsorption capacities for the ATZ removal drives to high values of C constant. According to the IPD model, C is a measure of the boundary layer thickness of molecules approaching or in the vicinity of the adsorbent.

A similar analysis can be performed for AC_PC and MPB-P50. Figure 6 shows the plots for the ATZ adsorption on AC_PC and MPB-P50 at 0.5 and 5.0 ppm, respectively. The regression values observed in Figure 6 shows that AC_PC fitted very-well with the pseudo first-order model (R²_k1 of ca. 0.980).

Figure 6. Kinetics treatments for ATZ adsorption on AC_PC (a,b,c,g,h,i) and MPB-P50 (d,e,f,j,k,l). 0.5 ppm: (a,b,c,d,e,f); 5.0 ppm: (g,h,i,j,k,l). Pseudo first-order: (a,d,g,j); Pseudo second-order: (b,e,h,k); Intraparticle diffusion model: (c,f,i,l).

Figure 6. Kinetics treatments for ATZ adsorption on AC_PC (a,b,c,g,h,i) and MPB-P50 (d,e,f,j,k,l). 0.5 ppm: (a,b,c,d,e,f); 5.0 ppm: (g,h,i,j,k,l). Pseudo first-order: (a,d,g,j); Pseudo second-order: (b,e,h,k); Intraparticle diffusion model: (c,f,i,l).

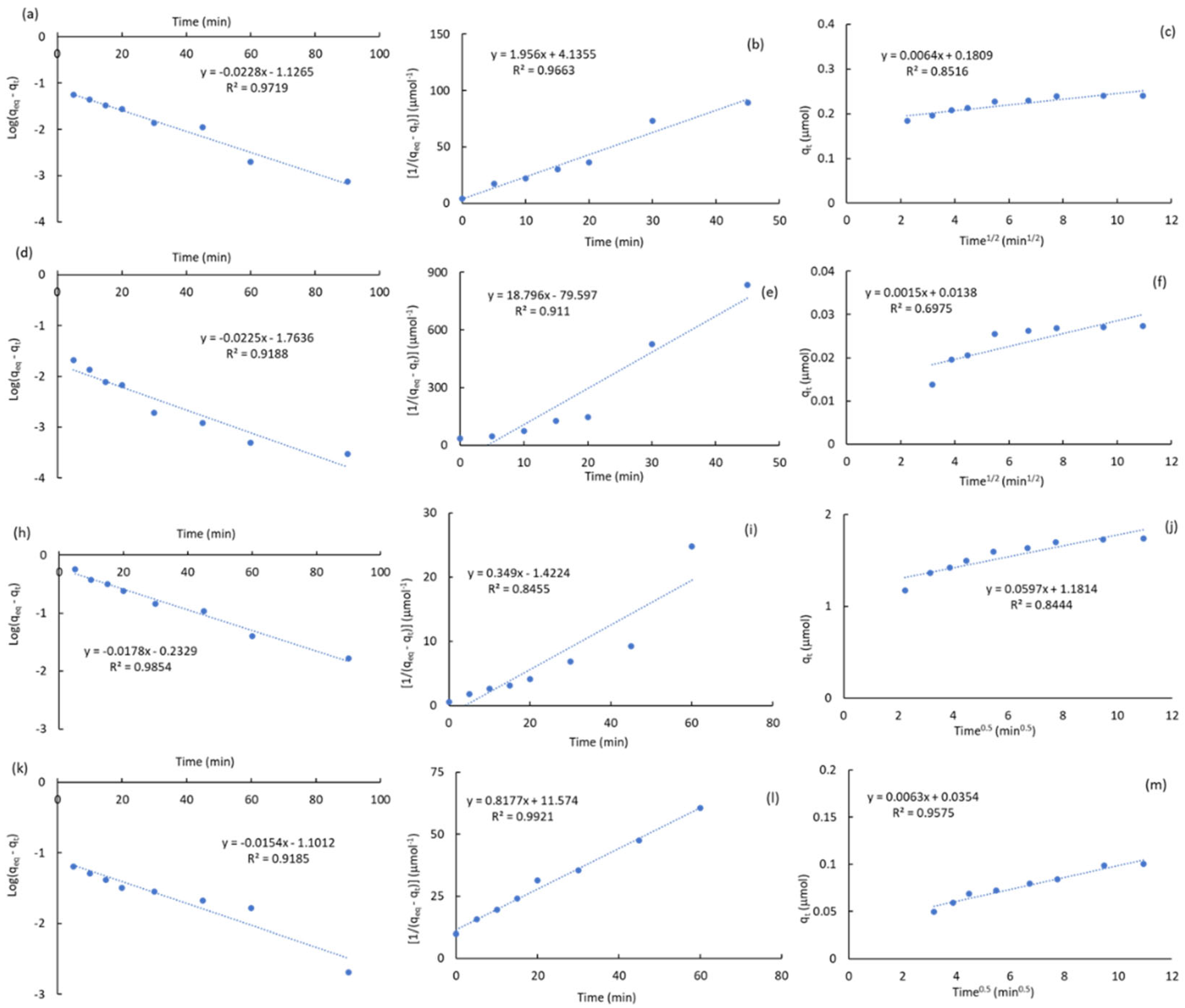
On the contrary, this commercial carbon does not fit well with the pseudo second-order showing an average R²_k1 of ca. 0.927. In other words, in spite of the surface of AC_PC is acidic, ATZ prefers to be adsorbed by a physisorption mechanism probably due to a high contribution of mesopores (Table 1). On the contrary, ATZ is preferentially adsorbed by a chemisorption mechanism. This suggestion can be inferred from R²_k2 values in Table 3 which are clearly higher than R²_k1 values. At the same time, it can be seen from Table 3 that the C constants are clearly higher on AC_PC than on MPB-P50. For instance, C values increased from 0.181 μmol up to 1.181 μmol (6.5 times higher) on AC_PC while for MPB-P50 only increased from 0.014 μmol up to 0.035 μmol when ATZ concentration increased from 0.5 up top 5.0 ppm.

Finally, with the exception of MPB-P50, k₁ and k₂ rate constants observed in MPB-CO₂ and the commercial nanoporous carbons are in the same order of magnitude than values reported by Tan and coworkers [60] using corn straw-derived porous carbons. In general, it is interesting to remark that k₁ and k₂ trends to decrease their values with the increase of concentration. This is remarkable for k₂ in most of carbons studied in the present work. This results permits to suggest that chemisorption mechanism is favored at low concentration while at higher concentration, physisorption and IPD model control the mechanism of adsorption. This result suggests that atrazine adsorption is highly dependent on the concentration of ATZ according to the intraparticle diffusion model [61]. In other words, at high concentration the energy required for the formation of bonds leading to chemisorption is higher since the number of surface interactions between ATZ molecules and the surface sites of adsorption decrease. This suggestions will be discussed in the following two sections using the equilibrium parameters obtained from Langmuir and Freundlich isotherms as well as the theoretical estimations.

2.3.2. Adsorption Isotherms of Atrazine

Table S2 (SM) shows a summary of the mathematical expressions used for the equilibrium studies of atrazine adsorption according to Langmuir [62], and Freundlich [63] models. Figure 7 shows the experimental results obtained on the two commercial activated carbons (AC_M and AC_PC). Table 4 contains a summary of the equilibrium adsorption parameters obtained, including the maximum capacity for the atrazine adsorption in the monolayer (q_T, μmol); the adsorption constant according to Langmuir model (K_L, L·μmol^-1); the adsorption constant according to Freundlich model (K_F, mg·g^-1); and the Freundlich´s heterogeneity factor (n). The linear regression factors according to Freundlich model fit much better than Langmuir model for the commercial carbons (AC_M and AC_PC). However, this trend is opposite in the mangosteen-derived carbons. Figure 7a shows AC_M adsorbs more ATZ than AC_PC (Figure 7d) at initial concentrations higher than 1.0 ppm (Table 3). The maximum capacity for ATZ adsorption in the monolayer for AC_PC is higher (2.937 μmol) than that obtained for AC_M (1.573 μmol). This result agrees with the higher specific surface area of AC_PC than that of AC_M (Table 1) and a higher mesopore structure that will permit to inhibit the diffusion of ATZ molecules from the bulk of solution to the pore framework as suggested by lower values of C constant from IPD model on AC_PC than AC_M (Table 3) when ATZ is higher than 1 ppm. However, it can be proposes that in the present range of study (0.5 – 5.0 ppm) AC_M adsorb more than one monolayer of atrazine molecules. This is inferred from the fact that the maximum capacity for ATZ adsorption in the monolayer (q_T) according to Langmuir model for AC_M is clearly lower (1.573 μmol, Table 4) than the value adsorbed at equilibrium (q_eq) when the initial concentration of ATZ is 5.0 ppm (2.632 μmol, Table 3).

Figure 7. Adsorption isotherms of atrazine for the commercial activated carbons. (a,b,c): AC_M; (d,e,f): AC_PC. (a,b,d,e): Langmuir model. (c,f): Freundlich model.

Figure 7. Adsorption isotherms of atrazine for the commercial activated carbons. (a,b,c): AC_M; (d,e,f): AC_PC. (a,b,d,e): Langmuir model. (c,f): Freundlich model.

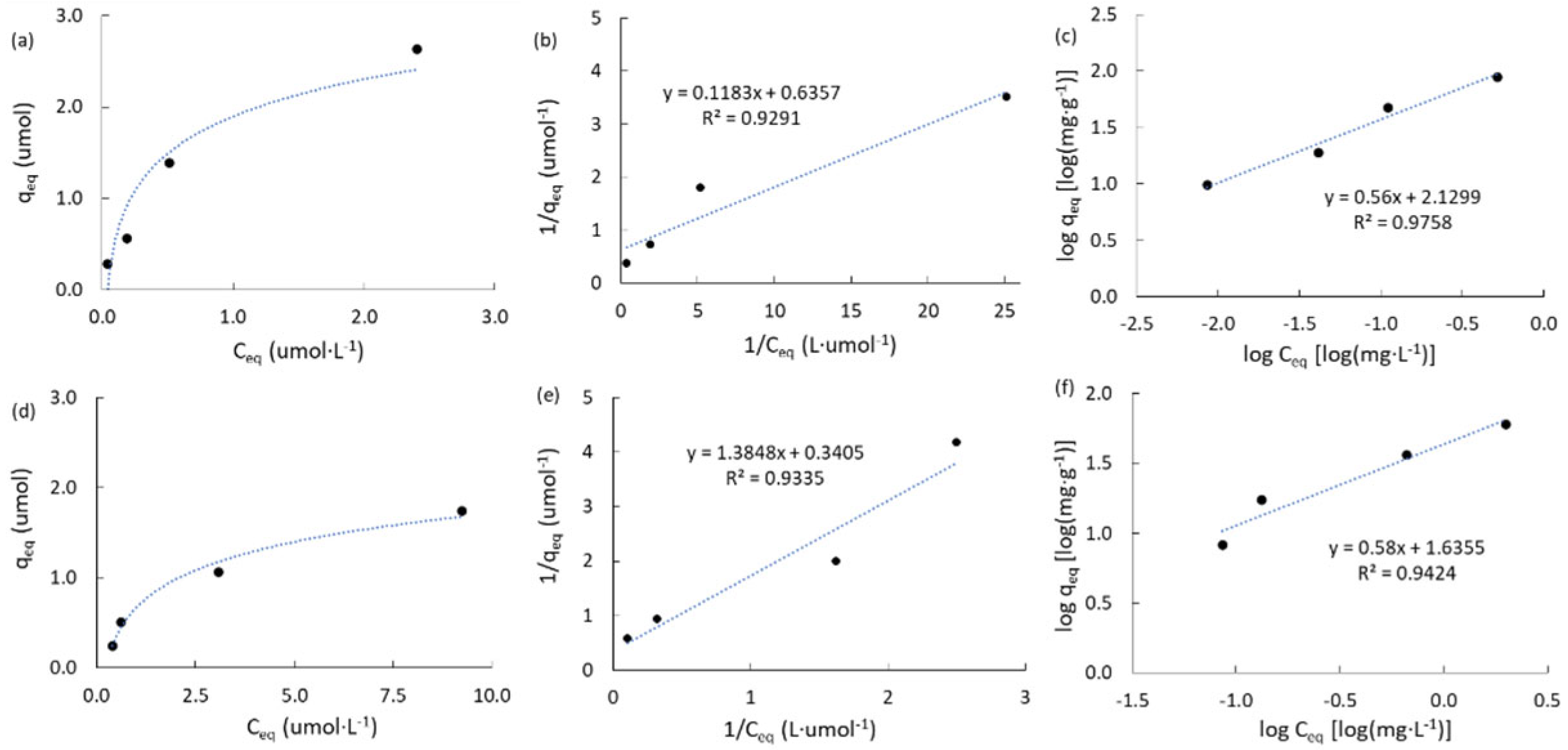
On the other hand, Freundlich isotherm assumed that the surface of the adsorbent is energetically heterogeneous, where the adsorption sites have similar characteristic energies. It is also considered that there are no lateral interactions between the adsorbed molecules and therefore, only a monolayer is adsorbed. The heterogeneity factor of Freundlich (n_F) is similar in both commercial carbons (1.8 and 1.9 for AC_M and AC_PC) which suggests that only one monolayer should be adsorbed which is contrary to ATZ adsorption observed on AC_M.

Table 4. Summary of the equilibrium parameters obtained for atrazine adsorption.

Table 4. Summary of the equilibrium parameters obtained for atrazine adsorption.

Carbon	qT (μmol) a	KL (L·μmol-1) b	R2L c	KF d (mg·g-1)	nF e	R2F f
ACM	1.573	5.374	0.929	134.9	1.79	0.976
ACPC	2.937	0.246	0.934	43.2	1.72	0.942
MPB-CO2	0.565	1.574	0.952	15.3	4.12	0.923
MPB-P50	0.139	0.120	0.964	1.59	1.99	0.921

^a q_T is the maximum capacity for ATZ adsorption in the monolayer; ^b K_L is the adsorption constant according to Langmuir; ^c Linear regression factor according to Langmuir; ^d K_F is the adsorption constant according to Freundlich; ^e n_F is the Freundlich´s heterogeneity factor; ^f Linear regression factor according to Freundlich.

On the other hand, it is clear from data in Table 4 that the adsorption constant according to Langmuir model (K_L) observed on AC_M is ca. 22 times higher than observed on AC_PC (5.374 L·mmol^-1 against 0.246 L·mmol^-1). This result indicates that AC_M is characterized by a higher thermodynamic trend to adsorb ATZ than that of AC_PC, in spite of the S_BET of the latter is higher. This trend is reinforced by the adsorption constant values obtained from the Freundlich model (K_F) which is ca. 3 times higher on AC_M than on AC_PC (134.9 mg·g^-1 against 43.2 mg·g^-1). Accordingly, it can be suggested that the surface chemistry of AC_M plays the main role in the adsorption of ATZ.

Figure 8 shows the results obtained on the mangosteen-derived porous carbons (MPB-CO₂ and MPB-P50) and the summary of equilibrium results obtained from Langmuir and Freundlich isotherms are summarized in Table 4.

Figure 8. Adsorption isotherms of atrazine for the mangosteen-derived porous carbons. (a,b,c): MPB-CO₂; (d,e,f): MPB-P50. (a,b,d,e): Langmuir model. (c,f): Freundlich model.

Figure 8. Adsorption isotherms of atrazine for the mangosteen-derived porous carbons. (a,b,c): MPB-CO₂; (d,e,f): MPB-P50. (a,b,d,e): Langmuir model. (c,f): Freundlich model.

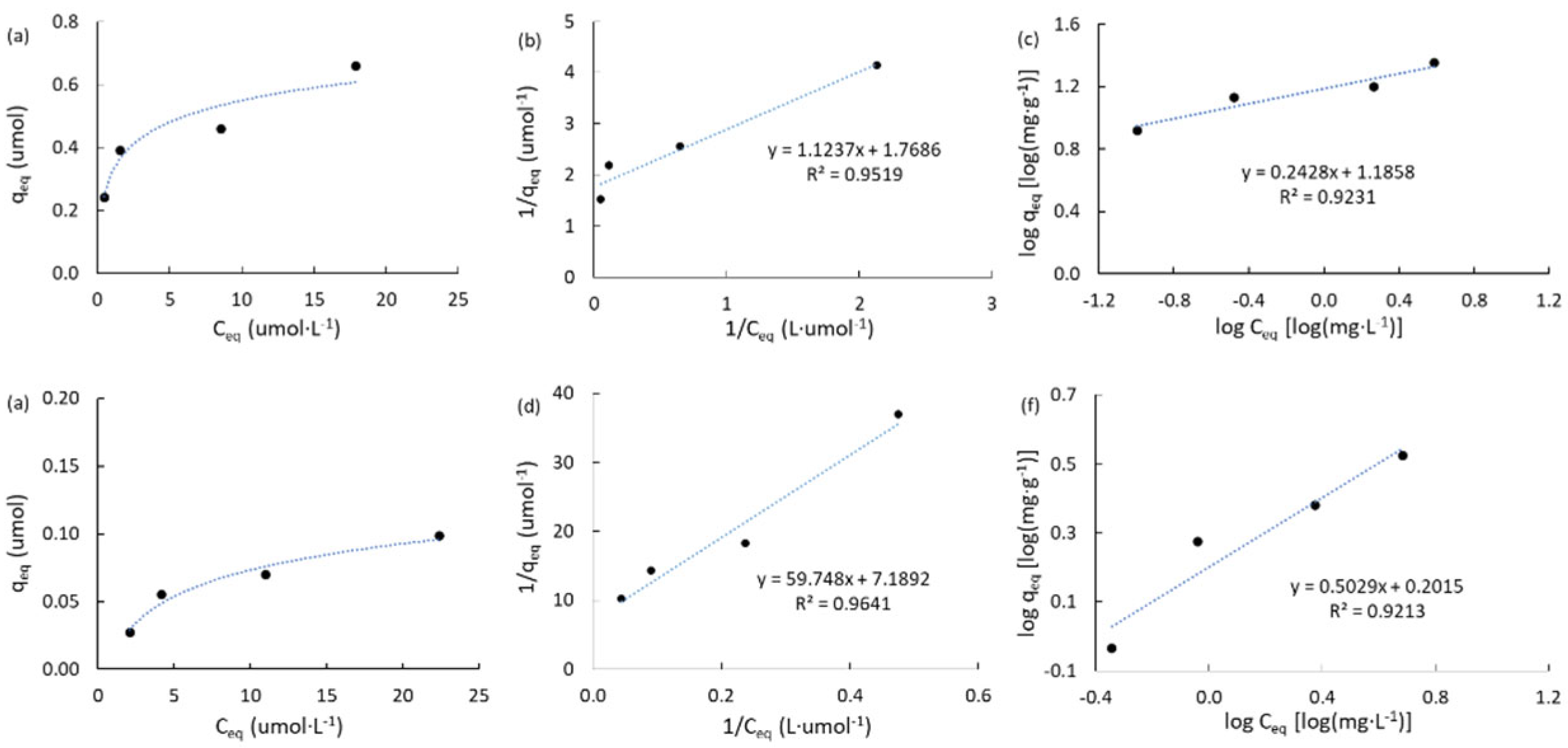
For instance, q_T, K_L, K_F and n_F parameters are ca. 4.0, 13.1, 9.6, and 2.1 times higher on MPB-CO₂ than on MPB-P50. It is clear that MPB-CO₂ possesses a higher capacity than MPB-P50 to adsorb atrazine and this fact can be attributed to superior textural and porosimetry properties, mainly a higher BET surface area and a higher total volume of pores (Table 1). In addition, MPB-CO₂ is characterized by a basic surface with a high surface pH instead of acidic groups and acid surface pH for MPB-P50 (10.1 against 3.9, Table 1) which could be responsible for an important electrostatic attraction for hydrated atrazine molecules.

This fact will be discussed in the next section. It is interesting to highlight that the adsorption parameters observed in the mangosteen-derived carbons were remarkably lower in comparison to those observed on the commercial activated carbons. For MPB-CO₂ carbon, this fact can be attributed to the high value of the heterogeneity factor according to Freundlich model (n_F) which mainly indicates both the material is characterized by different types of adsorption sites and more importantly, it has a high thermodynamic trend to adsorb ATZ. However, this is not the case for MPB-P50 with a value of n_F ca. 2.0, lightly higher than those observed for the commercial carbons. It can be suggested that the high micropore proportion of the mangosteen-derived porous carbons, up to 92% and 78% for MPB-CO₂ and MPB-P50, can be responsible for the low ATZ adsorption parameters. However, AC_M and MPB-P50 possess comparable surface areas and pore frameworks (Table 1). Thus, it is clear that thermodynamic trend to adsorb atrazine is favored by the presence of strong basic functional groups on the surface of the carbons. In addition, it should be highlighted that the average particle size of the mangosteen-derived carbons was ca. 350 μm which is ca. 5 times higher than values observed for the commercial nanoporous carbons (ca. 75 μm). It a previous work we have shown [45] that the lower the size of particles the higher the capacity of atrazine´s adsorption. Thus, the equilibrium studies can be summarized in the following aspects. At low concentration of atrazine, the pore framework of the adsorbent plays the most important role being mesopores the driven-force inhibiting intraparticle pore diffusion limitations. However, at high concentration of ATZ, the surface chemistry seems to be the driving-force for the adsorption of the herbicide. Accordingly, it can be concluded that Langmuir and Freundlich models can be used to explain both the uptake and thermodynamic trends of atrazine adsorption on the present commercial nanoporous carbons. For instance, q_T values were ca. 38.1 mg·g^-1, 100.6 mg·g^-1, 19.3 mg·g^-1, and 4.8 mg·g^-1 for AC_M, AC_PC, MPB-CO₂, and MPB-P50, respectively. These values are clearly higher, even for MPB-P50, than that reported by Tan and coworkers [64] for a porous carbon prepared from corn straw, with a q_T of ca. 4.6 mg·g^-1. The loading used in the present work is ca. 0.05 g·L^-1 is similar to that reported by Tan and coworkers [64]. In spite of the commercial carbons are characterized by superior capabilities to adsorb atrazine, it can be noted that the mangosteen-derived porous carbon prepared by physical activation under CO₂ flow (MPB-CO₂) is a potential adsorbent, mainly due to its high BET surface area of ca. 1080 m²·g^-1 instead of 466 m²·g^-1 for the corn straw-derived carbon [64]. In addition, K_L values were ca. 24.9 mg·g^-1, 1.14 mg·g^-1, 7.3 mg·g^-1, and 0.56 mg·g^-1 for AC_M, AC_PC, MPB-CO₂, and MPB-P50, respectively, which are remarkable higher than ca. 0.04 L mg^-1 reported for the corn straw-derived carbons [64] characterized by basic surface and an important contribution of mesopores to the total volume of pores. Accordingly, the superior thermodynamic trend of AC_M and MPB-CO₂ to adsorb ATZ can be attributed to the combination of the basic surface and the low contribution of mesopores (Table 1). On the contrary, the present commercial and mangosteen peels-derived nanoporous carbons showed lower q_T but higher K_L (in most cases) than carbons prepared from hemp stem [65] with values of ca. 227 mg·g^-1 and ca. 0.64 L·mg^-1, respectively. The higher q_T can be attributed to a higher surface area (2135 m²·g^-1) and to a much higher loading of adsorbent of ca. 3.0 g·L^-1 (ca. 60 times higher) than that used in the present study. It should be highlighted that the K_L value obtained on MPB-CO₂ porous carbons is ca. 11.4 times higher than that reported for hemp stem [70]. This comparison suggests that a basic surface chemistry plays the most important role for ATZ adsorption, mainly at high concentrations. This suggestion is discussed as follows by using DFT estimations.

2.4. General Discussion and Theoretical Estimations

It is well-known that Langmuir model [62] considers all adsorption sites similar and finite. This model also assumes that interactions do not take place between adsorbed molecules. It means that the molecular density (ρ_surf) also called surface density [66,67] can be estimated using the Eq. (5):

ρ_surf = [(q_T/S_BET)·F]

(5)

where q_T is the maxima capacity of adsorption of atrazine obtained from Langmuir´s adsorption isotherms (Table 4), S_BET is the specific surface area (Table 1), and F is a correction factor (F = 95.6) including Avogadro´s number, the weight of carbons (6.3 mg) and conversion factors to adjust the units of ρ_surf to adsorbed molecules·nm^-2.

The surface density of ATZ molecules adsorbed in the maxima capacity of adsorption (q_eq = q_T = 1) were ca. 0.194, 0.226, 0.050, and 0.015 molecules·nm^-2 for AC_M, AC_PC, MPB-CO₂, and MPB-P50, respectively. Accordingly, the reciprocal of the surface density corresponds to the experimental value of the cross-sectional area (σ_ATZ = 1/(ρ_surf) of atrazine adsorbed obtained for the maxima coverage of adsorption according to the Langmuir model. The σ_ATZ values were ca. 5.2, 4.4, 20.0, and 66.7 nm²·molecule^-1 for AC_M, AC_PC, MPB-CO₂, and MPB-P50, respectively. Accordingly In other words, the higher q_T and the lower S_BET, the higher ρ_surf and accordingly, the lower the cross-sectional area of one atrazine molecule. It means, the present values of surface density suggest the commercial activated carbons (AC_M and AC_PC) are characterized by low repulsions forces among ATZ molecules than mangosteen peels-derived carbons (MPB-CO₂ and MPB-P50) are characterized by high repulsions forces. For instance, AC_M adsorbs ca. 4 times more ATZ molecules than MPB-CO₂. At the same time, AC_PC adsorbs ca. 15 times more ATZ molecules. It means, the electrostatic repulsion among atrazine molecules is the driven-force for the adsorption of the pollutant. It is interesting to point out that the values so obtained for σ_AT are much higher than that reported by Borisover and Graber [68], ca. 0.544 nm² molecule^-1 suggesting that more than one atrazine molecules are being adsorbed by each adsorption site. In a previous work, our group reported [45] the formation of clusters of atrazine molecules adsorbed on the surface of porous carbons.

In the lowest adsorption capacity observed in this work (q_eq values obtained from 0.5 ppm of ATZ, Table 3), the surface density values were ca. 0.035, 0.019, 0.021, and 0.003 molecules·nm^-2 for AC_M, AC_PC, MPB-CO₂, and MPB-P50, respectively. It can be seen that both AC_M and MPB-CO₂ showed higher surface density than AC_PC suggesting that strong basic groups of carbons led the adsorption at low initial concentration of ATZ; however, at high concentration, both surface chemistry and porosimetry are responsible for the adsorption of ATZ.

According to this analysis, the adsorption energy of atrazine (E_ads-ATZ) has been evaluated on the pristine graphene (G_Pristine) and after the introduction of different oxygen-containing functional groups. The periodic calculations were performed using the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional [69]. This functional has proven to be trustable in the evaluation of adsorption energies of N-doped and Al-doped graphene [70] and carboxyl and hydroxyl decorated holes in graphene oxide [71]. Herein, the theoretical calculations were limited to oxygen-functionalized graphene with pyrone (G_Pyrone), ketone (G_Ketone), phenol (G_PhOH), and carboxylic acid (G_COOH) groups. These groups were selected since they were identified from the Boehm´s titrations study discussed above (Table 2). Figure 9 shows the optimized geometry for the atrazine adsorbed on the selected functionalized graphene.

Figure 9. Optimized geometries of adsorbed systems in 1/1 monolayer using one atrazine molecule on a 5x5 graphene surface unit cell. O, N, Cl, and H atoms correspond to red, blue, green, and grey spheres, respectively.

Figure 9. Optimized geometries of adsorbed systems in 1/1 monolayer using one atrazine molecule on a 5x5 graphene surface unit cell. O, N, Cl, and H atoms correspond to red, blue, green, and grey spheres, respectively.

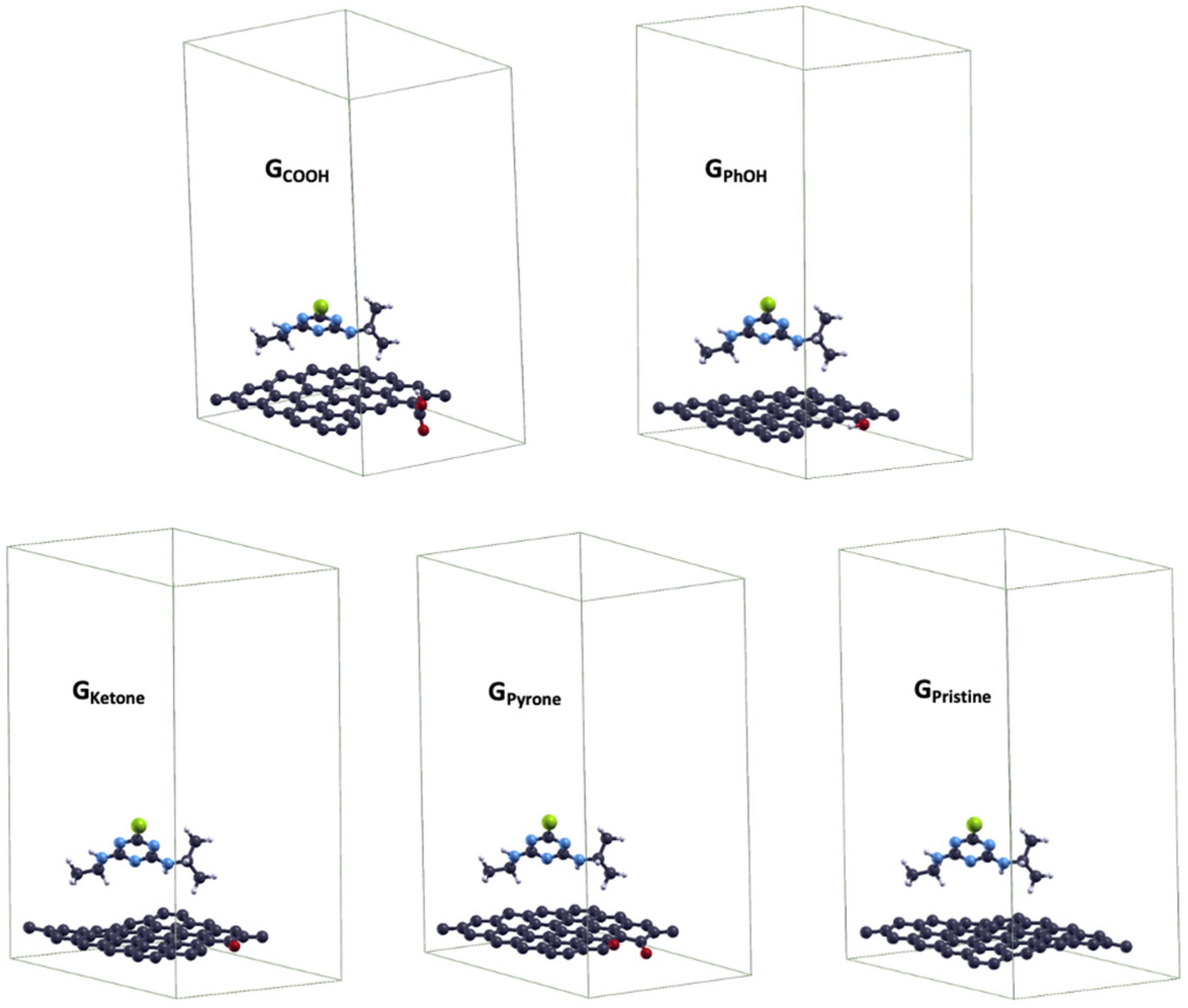
Figure 9 was constructed on the basis of a highest adsorbate coverage, corresponding to a surface coverage of 1/1 monolayer using one atrazine molecule on a 5x5 graphene surface unit cell. Adsorption energies of atrazine (E_ads-ATZ) were calculated by the Eq. (6).

(E_ads-ATZ) = [(E_Az-G) - (E_G + E_Az)]

(6)

According to Eq. (6), E_ads-ATZ can be estimated from the difference between the energy of the adsorbed system (E_Az-G) containing both graphene and adsorbed atrazine, and the sum of energies of a clean graphene surface (E_G), and an isolated atrazine molecule (E_Az).

Table 5 shows the theoretically predicted adsorption energies ranging from -0.169 eV for G_Pristine to -0.024 eV for G_PhOH. The energy of adsorption is a thermodynamic potential that measures the spontaneous trend to adsorb molecules. Accordingly, it is clear that the higher and negative is E_ads-ATZ, the more spontaneous is the atrazine adsorption.

Table 5. Summary of adsorption energies of atrazine (E_ads-ATZ) and dipolar moment (µ) obtained on pristine and oxygen-containing groups on graphene layers.

Table 5. Summary of adsorption energies of atrazine (E_ads-ATZ) and dipolar moment (µ) obtained on pristine and oxygen-containing groups on graphene layers.

System	GPhOH	GCOOH	GKetone	GPyrone	GPristine
Eads-ATZ (eV)	-0.024	-0.048	-0.063	-0.099	-0.169
µ (D)	1.103	3.290	1.917	1.791	0.001

For instance, the lowest thermodynamic susceptibility to adsorb atrazine corresponds to the functionalization of graphene with acidic groups such as G_PhOH (-0.024 eV) and G_COOH (- 0.048 eV). On the contrary, the highest corresponds to the functionalization of basic groups such as G_Ketone (- 0.063 eV) and G_Pyrone (-0.099 eV). Pristine graphene showed the highest susceptibility to remove atrazine (- 0.169 eV). Such trend can be explained in terms of electron density; the polarization of the electronic density is smaller in G_Ketone, G_Pyrone, and as expected G_Pristine is the least polarized system. It is worth noting that the adsorption energies decrease with the dipole moment (µ) of clean graphene surfaces, except for G_PhOH. In this system the amplitude of µ is not as significant as in G_COOH due to the attenuation of the electronic delocalization in the whole layer, which is likely caused by the weak resonance of sp³ C atoms bonded to O atom in the -OH group. Instead, in G_COOH, the attenuation is mostly caused by the orientation of -COOH group respect to the carbon surface, and hence the charge is polarized towards the -COOH moiety. In fact, G_COOH showed a high dipole moment. In summary, systems with larger electron delocalization led to large E_ads-ATZ values.

Figure 10. DOS (black line) and projected DOS on the pristine G_Pristine graphene (green line) and atrazine (blue line) with the PBE functional.

Figure 10. DOS (black line) and projected DOS on the pristine G_Pristine graphene (green line) and atrazine (blue line) with the PBE functional.

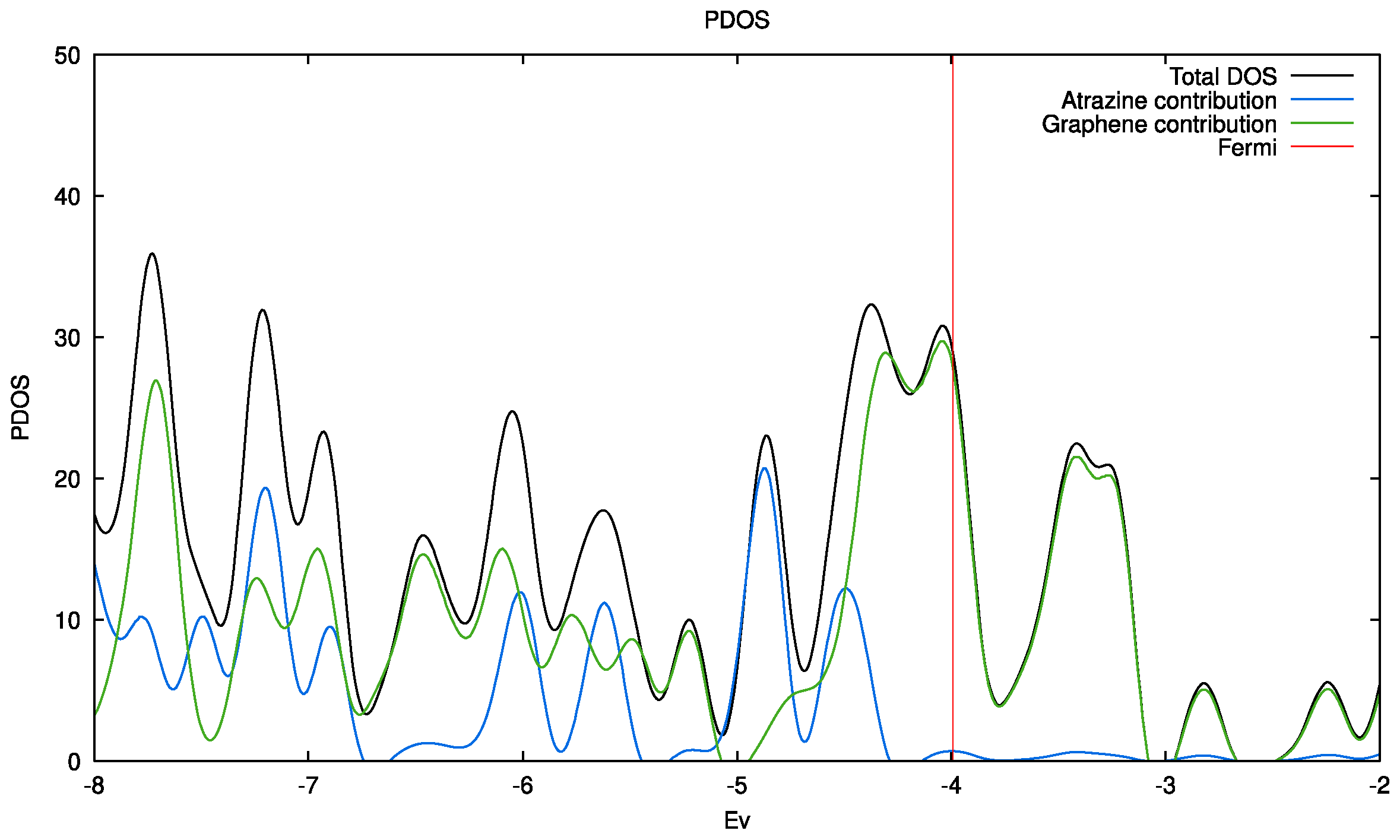
The density of states (DOS), and the projected density of states (PDOS), resulting from periodic calculations in the atrazine adsorbed systems (Figure 10). These calculations predict a conductor-like behavior for all systems, namely there is no bandgap. Notoriously, the lack of bandgap between the conduction and valence bands is associated to the graphene, which has a continuous electronic density around the Fermi level. As can be seen in Figure S1 (Supplementary Material), after adsorption the materials remain almost unchanged in its conductivity pattern independently of the type of oxygen-containing functional groups. In summary, on the basis of the results from the kinetics and equilibrium of adsorption, the density values discussed above permits to suggest two possibilities for the atrazine adsorption on nanoporous carbons. Figure 11 shows a schematic model for the situation of low and high concentration of atrazine´s adsorption within slit-like pores of carbons.

For instance, Figure 11a shows the first case when atrazine is physically adsorbed in a parallel mode forming a pseudo layer within the carbon layers. In this case, the surface density is very low with values of ca. 0.050 and 0.015 molecules·nm^-2 and with a high cross-sectional area of ca. 20.0 nm²·molecule^-1 and 66.7 nm²·molecule^-1 observed on MPB-CO₂ and MPB-P50, respectively. However, the present experimental values are remarkable higher than the theoretical calculated and reported by Borisover and Graber [68] of ca. 0.544 nm² molecule^-1. On the contrary, at high ATZ concentration, (Figure 11b) the molecules are cumulated within the slit pores, and consequently, some of them are forced to rotate and adopted a vertical geometry mode leading to high surface density values and low cross-sectional areas.

Figure 11. Schematic model for the atrazine adsorption on porous carbons. a): Low ATZ concentration. b): High ATZ concentration.

Figure 11. Schematic model for the atrazine adsorption on porous carbons. a): Low ATZ concentration. b): High ATZ concentration.

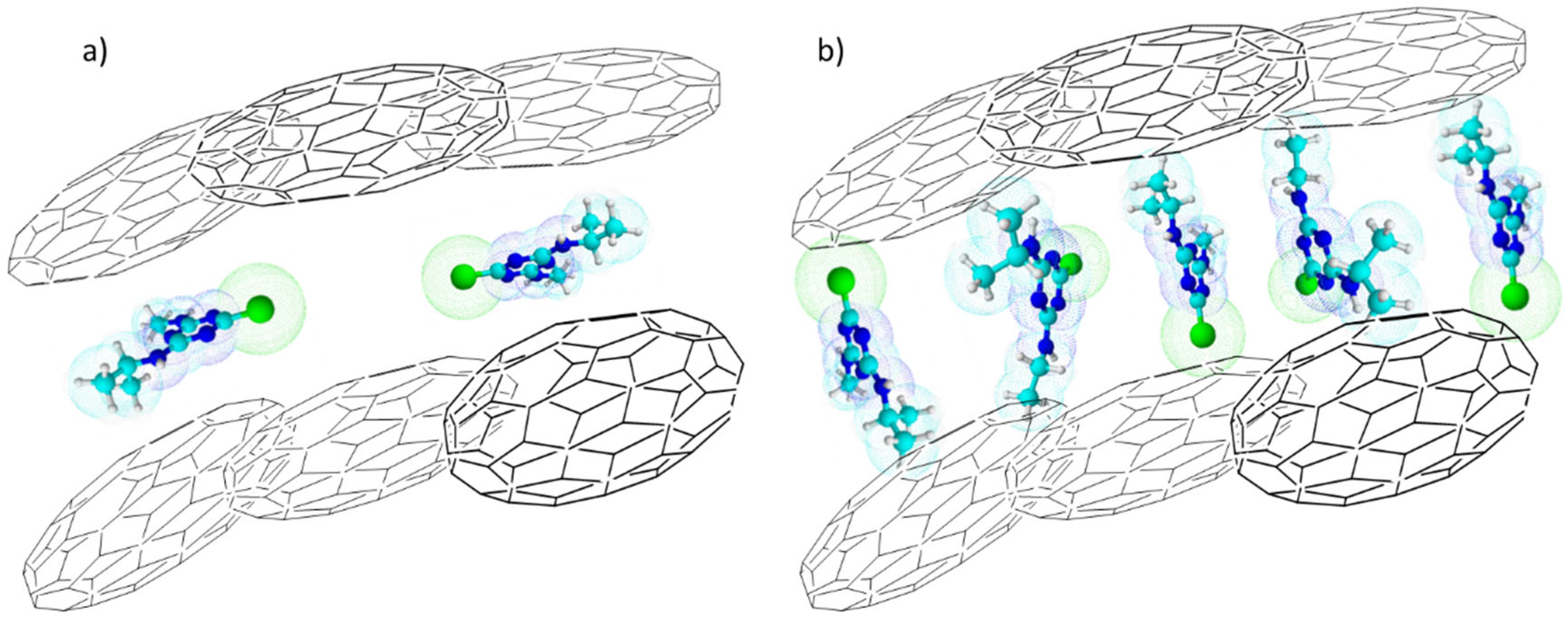
In addition, this configuration led to high values of C constants (Table 3) according to IPD model. This is the specific case of AC_M and AC_PC with values of surface density of ca. 0.194 and ca. 0.226 molecules·nm^-2, respectively. Accordingly, the cross-sectional area (σ_ATZ = 1/ρ_surf) of atrazine adsorbed obtained for the maxima coverage of adsorption were ca. 5.2 and ca. 4.4 nm²·molecule^-1 for AC_M and AC_PC, respectively. These values are close to one order magnitude lower than those obtained on MPB-CO₂ and MPB-P50 but still higher than the theoretical reported [68] concluding that more than one adsorption site is required for the atrazine adsorption on the present nanoporous carbons.

3. Experimental

4. Conclusions

References

1. D.D. Ratnayaka, M.J. Brandt, K.M. Johnson. Specialized and advanced water treatment processes. In D. Ratnayaka, M. J. Brandt, & K. M. Johnson. (Eds.), Water Supply. Elsevier (2009) 6^th Ed., pp. 365–423.
2. J.C. Crittenden, R.R. Trussell, D.W. Hand, K.J. Howe, G. Tchobanoglous. Granular filtration. In MWH’s Water Treatment: Principles and Design Wiley & Sons, Inc (2012) pp. 727–818.
3. S. Sauvé, M. Desrosiers, A review of what is an emerging contaminant. Chemistry Central Journal 8 (2014) 1-7. [CrossRef]
4. T.A. Ternes, M. Meisenheimer, D. McDowell, F. Sacher, H.-J. Brauch, B. Haistgulde, N. Zulei-Seibert, Removal of pharmaceuticals during drinking water treatment. Environmental Science & Technology 36 (2002) 3855–3863. [CrossRef]
5. G.A. Loraine, M.E. Pettigrove, Seasonal variations in concentrations of pharmaceuticals and personal care products in drinking water and reclaimed wastewater in southern California. Environmental Science & Technology 40 (2006) 687–695. [CrossRef]
6. J. Gibs, P.E. Stackelberg, E.T. Furlong, M. Meyer, S.D. Zaugg, R.L. Lippincott, Persistence of pharmaceuticals and other organic compounds in chlorinated drinking water as a function of time. Science of The Total Environment 373 (2007) 240–249. [CrossRef]
7. P.E. Stackelberg, J. Gibs, E.T. Furlong, M. Meyer, S.D. Zaugg, R. Lippincott (2007). Efficiency of conventional drinking-water-treatment processes in removal of pharmaceuticals and other organic compounds. Science of The Total Environment 377 (2007) 255–272. [CrossRef]
8. M. Syafrudin, R.A. Kristanti, A. Yuniarto, T. Hadibarata, J. Rhee, W.A. Al-Onazi, T.S. Algarni, A.H. Almarri, A.M. Al-Mohaimeed, Pesticides in drinking water—A review. Int. J. Environ. Res. Public Health 18 (2021) 468. [CrossRef]
9. I. Buchanan, H.C. Liang, W. Khan, Z. Liu, R. Singh, K. Ikehata, P. Chelme-Ayala. Pesticides and Herbicides Water Environment Research 81 (2009) 1731-1815.
10. Agency for Toxic Substances and Disease Registry (ATSDR). ATRAZINE, CAS # 1912-24-9, September 2003.
11. United States Environmental Protection Agency (USEPA), Washington, D.C., 2003. https://www3.epa.gov/pesticides/chem_search/reg_actions/reregistration/ired_PC-080803_1-Jan-03.pdf.
12. T.K. James, H. Ghanizadeh, K.C. Harrington, N.S. Bolan, Degradation of atrazine and bromacil in two forestry waste products. Sci. Rep. 11 (2021) 3284. [CrossRef]
13. M. Graymore, F. Stagnitti, G. Allinson, Impacts of atrazine in aquatic ecosystems. Environment International 26 (2001) 483–495.
14. A. Mudhoo, V.K. Garg, Sorption, Transport and transformation of atrazine in soils, minerals and composts: A review. Pedosphere 21 (2011) 11–25. [CrossRef]
15. K. Nödler, T. Licha, D. Voutsa, Twenty years later – Atrazine concentrations in selected coastal waters of the Mediterranean and the Baltic Sea. Marine Pollution Bulletin 70 (2013) 112–118. [CrossRef]
16. S. Singh, V. Kumar, A. Chauhan, S. Datta, A.B. Wani, N. Singh, J. Singh, Toxicity, degradation and analysis of the herbicide atrazine. Environ. Chem. Lett. 16 (2018) 211–237. [CrossRef]
17. L. Spanò, C.R. Tyler C.R, R. van Aerle, P. Devos, S.N. Mandiki, F. Silvestre, J.P. Thomé, P. Kestemont. Effects of atrazine on sex steroid dynamics, plasma vitellogenin concentration and gonad development in adult goldfish (Carassius auratus). Aquat. Toxicol. 66 (2004) 369-379. [CrossRef]
18. T.B. Hayes, A. Collins, M. Lee, M. Mendoza, N. Noriega, A. Stuart, A. Vonk, Hermaphroditic, demasculinized frogs after exposure to the herbicide atrazine at low ecologically relevant doses. PNAS 99 (2002) 5476-5480. [CrossRef]
19. F.P. Albuquerque, J.L. de Oliveira, V. Moschini-Carlos, L.F. Fraceto, An overview of the potential impacts of atrazine in aquatic environments: perspectives for tailored solutions based on nanotechnology, Science of the Total Environment 700 (2019) 134868.
20. W. Fan, T. Yanase, H. Morinaga, S. Gondo, T. Okabe, M. Nomura, T. Komatsu, K. Morohashi, T.B. Hayes, R. Takayanagi, H. Nawata, Atrazine-induced aromatase expression is SF-1 dependent: implications for endocrine disruption in wildlife and reproductive cancers in humans. Environ Health Perspect. 115 (2017) 720. [CrossRef]
21. J.L. Rinsky, C. Hopenhayn, V. Golla, S. Browning, H. Bush, Atrazine exposure in public drinking water and preterm birth. Public Health Reports 127 (2012), 72–80. [CrossRef]
22. K.S. Almberg, M.E. Turyk, R.M. Jones, K. Rankin, S. Freels, L.T. Stayner, Atrazine contamination of drinking water and adverse birth outcomes in community water systems with elevated atrazine in Ohio, 2006–2008. Int. J. Environ. Res. Public Health 15 (2018) 1889. [CrossRef]
23. V. Galbiati, E. Buoso, B. d’Emmanuele di Villa Bianca, R.D. Paola, F. Morroni, G. Nocentini, M. Racchi, B. Viviani, E. Corsini, Immune and nervous systems interaction in endocrine disruptors toxicity: The case of atrazine. Front. Toxicol. 3 (2021) 649024. [CrossRef]
24. Commission decision concerning the non-inclusion of atrazine in Annex I to Council Directive 91/414/EEC and the withdrawal of authorizations for plant protection products containing this active substance. Official J. European Union (2004) 3. https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:52020SC0087&rid=1.
25. Directive 2000/60/EC of the European Parliament and of the Council of 23 October 2000 establishing a framework for Community action in the field of water policy. Official Journal of the European Communities (2000) 72. https://www.eea.europa.eu/policy-documents/directive-2000-60-ec-of.
26. PAN International. The Consolidated List of Banned Pesticides, 6^th Edition, May 2022 Pesticide Action Network International, Penang (2022). https://pan-international.org/pan-international-consolidated-list-of-banned-pesticides/.
27. World Health Organization (WHO). 2011. Guidelines for Drinking Water Quality. http://whqlibdoc.who.int/publications/2011/9789241548151_eng.pdf.
28. C.M. Villanueva, G. Durand, M.B. Coutté, C. Chevrier, S. Cordier, Atrazine in municipal drinking water and risk of low birth weight, preterm delivery, and small-for-gestational-age status. Occupational and environmental medicine, 62 (2005) 400-405. [CrossRef]
29. A. Hildebrandt, M. Guillamon, S. Lacorte, R. Tauler, D. Barcelo, Impact of pesticides used in agriculture and vineyards to surface and groundwater quality (NorthSpain). Water Res., 42 (2008) 3315-3326.
30. T. Bohn, E. Cocco, L. Gourdol, C. Guignard, L. Hoffmann, Determination of atrazine and degradation products in Luxembourgish drinking water: origin and fate of potential endocrine disrupting pesticides. Food Additives & Contaminants 28 (2011) 1041-1054. [CrossRef]
31. A.I. Gómez-Gutiérrez, E. Jover, L. Bodineau, J. Albaigés, J.M. Bayona, Organic contaminant loads into the Western Mediterranean Sea: Estimate of Ebro river inputs. Chemosphere 65 (2006) 224-236. [CrossRef]
32. R. Carafa, J. Wollgast, E. Canuti, J. Ligthart, S. Dueri, G. Hanke, S.J. Eisenreich, P. Viaroli, J.M. Zaldívar, Seasonal variations of selected herbicides and related metabolites in water, sediment, seaweed and clams in the Sacca di Goro coastal lagoon (Northern Adriatic). Chemosphere 69 (2007) 1625-1637. [CrossRef]
33. Ministerio de Ambiente, Vivienda y Desarrollo Territorial. Resolución 2115 (2017). https://www.minsalud.gov.co/sites/rid/Lists/BibliotecaDigital/RIDE/DE/DIJ/Resoluci%C3%B3n_2115_de_2007.pdf.
34. United Nations Environment Program (UNEP), Central America, and the Caribbean Regional Report. Regionally based assessment of persistent toxic substances. (2002). http://www.oas.org/dsd/Quimicos/Central%20America%20Caribbean%20Report%20UNEP.pdf.
35. A. Hernandez-Antonio. Modelo conceptual de contaminación de aguas superficiales por uso de atrazina en zonas agrícolas. PhD Thesis. Universidad Nacional Autónoma de México, Morelos, México (2013). https://repositorio.unam.mx/contenidos/modelo-conceptual-de-contaminacion-de-aguas-superficiales-por-uso-de-atrazina-en-zonas-agricolas-74101?c=r1gbgE&d=false&q=*:*&i=2&v=1&t=search_0&as=0.
36. M.P. Ormad, N. Miguel, A. Claver, J.M. Matesanz, J.L. Ovelleiro, Pesticides removal in the process of drinking water production. Chemosphere 71 (2008), 97–106. [CrossRef]
37. K. Ignatowicz, Selection of sorbent for removing pesticides during water treatment. Journal of Hazardous Materials 169 (2009) 953–957. [CrossRef]
38. Y. Chen, B. Huang, M. Huang, B. Cai, On the preparation and characterization of activated carbon from mangosteen shell, J. Taiwan Inst. Chem. Eng. 42 (2011) 837–842. [CrossRef]
39. M.I. Yusufu, C.C. Ariahu, B.D. Igbabul, Production and characterization of activated carbon from selected local raw materials Afr. J. Pure Appl. Chem. 6 (2012) 123–131.
40. V.K. Gupta, I. Ali, Water treatment for organic pollutants by adsorption technology. In V. K. Gupta & I. Ali (Eds.), Environmental Water: Advances in Treatment, Remediation and Recycling. Elsevier (2013) 29–91.
41. M.A. Yahya, Z. Al-Qodah, C.W.Z. Ngah, Agricultural bio-waste materials as potential sustainable precursors used for activated carbon production: A review. Renewable and Sustainable Energy Reviews, 46 (2015) 218–235. [CrossRef]
42. I. Lupul, J. Yperman, R. Carleer, G. Gryglewicz, Adsorption of atrazine on hemp stem-based activated carbons with different surface chemistry. Adsorption 21 (2015) 489–498. [CrossRef]
43. Y. Li, X. Wang, M. Cao, Three-dimensional porous carbon frameworks derived from mangosteen peel waste as promising materials for CO₂ capture and supercapacitors. J. CO₂ Utilization 27 (2018) 204-216. [CrossRef]
44. A. Dasgupta, J. Matos, H. Muramatsu, Y. Ono, V. González, H. Liu, C. Rotella, K. Fujizawa, R. Cruz-Silva, Y. Hashimoto, M. Endo, K. Kaneko, L. Radovic, M. Terrones. Nanostructured carbon materials for enhanced nitrobenzene adsorption: Physical vs. Chemical surface properties. Carbon 139 (2018) 833-844.
45. C.P. Amézquita-Marroquín, P. Torres-Lozada, L. Giraldo, P.D. Húmpola, E. Rivero, P.S. Poon, J. Matos, J.C. Moreno-Piraján. Sustainable production of nanoporous carbons: Kinetics and equilibrium studies in the removal of atrazine. J. Coll. Inter. Science. 562 (2020) 252-267. [CrossRef]
46. J. Rouquerol, P. Llewellyn, F. Rouquerol. Characterization of porous solids VII. Stud. Surf. Sci. Catal. 160 (2007) 49–56.
47. M. Thommes, K.A. Cychosz. Physical adsorption characterization of nanoporous materials: progress and challenges. Adsorption 20 (2014) 233–250. [CrossRef]
48. M.M. Dubinin. Description of adsorption equilibria of vapors on zeolites over wide ranges of temperature and pressure. Adv. Chem. Ser. 102 (1971) 69–85.
49. J. Matos, J. Laine. Ethylene Conversion on Activated Carbon Supported NiMo Catalysts: Effect of the Support. Applied Catalysis A: General, 241, 1-2 (2003) 25-38. [CrossRef]
50. J. Matos, M. Labady, A. Albornoz, J. Laine, J.L. Brito. Topological organization and textural changes of carbon macro-networks submitted to activation with N₂ and CO₂. J. Mater. Science 39 (2004) 3705-3716. [CrossRef]
51. J. Matos, M. Labady, A. Albornoz, J. Laine, J.L. Brito. Catalytic Effect of KOH on textural changes of carbon macronetworks by physical activation. J. Molec. Catal. A: Chemical 228 (2005) 189-194. [CrossRef]
52. L.A. Alves, A.H. de Castro, F.G. de Mendonça, J.P. de Mesquita. Characterization of acid functional groups of carbon dots by nonlinear regression data fitting of potentiometric titration curves. Appl. Surf. Sci. 370 (2016) 486–495.
53. J. Matos, J. Arcibar-Orozco, P.S. Poon, G. Pecchi, J.R. Rangel-Mendez. Influence of phosphorous upon the formation of DMPO-•OH and POBN-O₂•¯ spin-trapping adducts in carbon-supported P-promoted Fe-based photocatalysts. J. Photochem. Photobiol. A: Chem. 391 (2020) 112362. [CrossRef]
54. F.-C. Wu, R.-L. Tseng, R.-S. Juang, Initial behavior of intraparticle diffusion model used in the description of adsorption kinetics, Chem. Eng. J. 153 (2009) 1-8. [CrossRef]
55. G. McKay, M.S. Otterburn, A.G. Sweeney, The removal of color from effluent using various adsorbents—III. Silica: Rate processes, Water Res. 14 (1980) 15-20.
56. Y.S. Ho, G. McKay, A Comparison of Chemisorption Kinetic Models Applied to Pollutant Removal on Various Sorbents, Process Saf. Environ. Prot. 76 (1998) 332-340. [CrossRef]
57. F.-C. Wu, R.-L. Tseng, R.-S. Juang, Kinetic modeling of liquid-phase adsorption of reactive dyes and metal ions on chitosan, Water Res. 35 (2001) 613-618. [CrossRef]
58. S. Lagergren. Zur theorie der sogenannten adsorption geloster stoffe, K. Sven. Vetenskapsakademiens. Handl. 24 (1898) 1–39.
59. Y. Ho, G. McKay. Pseudo-second order model for sorption processes. Process Biochem. 34 (1999) 451–465. [CrossRef]
60. G. Tan, W. Sun, Y. Xu, H. Wang, N. Xu. Sorption of mercury (II) and atrazine by biochar, modified biochars and biochar based activated carbon in aqueous solution. Bioresour. Technol. 211 (2016) 727–735. [CrossRef]
61. R. Leyva-Ramos, R. Ocampo-Perez, J. Mendoza-Barrón. External mass transfer and hindered diffusion of organic compounds in the adsorption on activated carbon cloth. Chem. Eng. J. 183 (2012) 141-151. [CrossRef]
62. I. Langmuir. The constitution and fundamental properties of solids and liquids. Part I. Solids. J. Am. Chem. Soc. 38 (1916) 2221–2295. [CrossRef]
63. H. Freundlich, Über die adsorption in Lösungen, Zeitschrift für Physikalische Chemie – Stöchiometrie und Verwandschaftslehre 57 (1907) 385–470.
64. G. Tan, W. Sun, Y. Xu, H. Wang, N. Xu. Sorption of mercury (II) and atrazine by biochar, modified biochars and biochar based activated carbon in aqueous solution. Bioresource Technol. 211 (2016) 727–735. [CrossRef]
65. I. Lupul, J. Yperman, R. Carleer, G. Gryglewicz. Adsorption of atrazine on hemp stem-based activated carbons with different surface chemistry. Adsorption 21 (2015) 489–498. [CrossRef]
66. J. Matos, V. Fierro, R. Montaña, E. Rivero, A. Martínez de Yuso, W. Zhao, A. Celzard. High surface area microporous carbons as photoreactors for the catalytic photodegradation of methylene blue under UV-vis irradiation. Appl. Catal. A: Gen. 517 (2016) 1-11.
67. J. Matos, J. Ocares-Riquelme, P.S. Poon, R. Montaña, X. García, K. Campos, J.C. Hernández-Garrido, M.M. Titirici. C-doped anatase TiO₂: Adsorption kinetics and photocatalytic degradation of methylene blue and phenol, and correlations with DFT estimations. J. Colloid Inter. Science 547 (2019) 14-29.
68. M.D. Borisover, E.R. Graber, Comment on competitive sorption between atrazine and other organic compounds in soils and model sorbents. Environ. Sci. Technol. 31 (1997) 1577. [CrossRef]
69. J.P. Perdew, K. Burke, M. Ernzerhof, Generalized gradient approximation made simple. Physical Review Letters 78 (1997) 1396. [CrossRef]
70. Wang, W.; Zhang, Y.; Shen, C.; Chai, Y., Adsorption of CO molecules on doped graphene: A first-principles study. AIP Advances 2016, 6 (2), 025317. [CrossRef]
71. Bagri, A.; Grantab, R.; Medhekar, N. V.; Shenoy, V. B., Stability and Formation Mechanisms of Carbonyl- and Hydroxyl-Decorated Holes in Graphene Oxide. The Journal of Physical Chemistry C 2010, 114 (28), 12053-12061. [CrossRef]
72. H.P. Boehm, Surface oxides on carbon and their analysis: a critical assessment. Carbon 40 (2002) 145–149. [CrossRef]
73. M.C. Fernández de Cordoba, J. Matos, R. Montaña, P.S. Poon, S. Lanfredi, F.R. Praxedes, J.C. Hernández-Garrido, J.J. Calvino, E. Rodríguez-Aguado, E. Rodríguez-Castellón, C.O. Ania. Sunlight photoactivity of rice husks-derived biogenic silica. Catalysis Today 328 (2019) 125-135.
74. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G.L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A.P. Seitsonen, A. Smogunov, P. Umari, R.M. Wentzcovitch, Quantum Espresso: a modular and open-source software project for quantum simulations of materials. J. Physics: Condensed Matter 21 (2009) 395502.
75. http://pseudopotentials.quantum-espresso.org/legacy_tables/ps-library/o.