Prerpints.org logo
Preprint
Article

Structural Stability of γ-Boron under High Pressure up to 126 GPa with Fine Pressure Increment

Altmetrics

Downloads

131

Views

25

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

12 June 2023

Posted:

14 June 2023

You are already at the latest version

Alerts
Abstract
The structural stability of γ-boron is investigated using Raman spectra under high pressures up to 126 GPa at ambient temperature. The pressure dependence of all the Raman-active modes of the γ-boron is reported. We also observe amusing changes within the B3g and B1g Raman-active vibrational modes, which results in the phenomenon of merging first and then separating of the Raman peaks. In addition to the Raman measurements, the changes in crystal structure and force constants are calculated to reasonably explain the discrepancy between the two Raman modes in response to pressure. The results of the continuous shifts for all Raman modes with increasing pressure indicate that γ-boron remains stable below this pressure value, with no changes in either symmetry or structure.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

Introduction

Boron, one of the most fundamental elements in nature, often exists in the form of boron-rich solids due to its high chemical activity. The first nonmetallic solid in the Periodic Table under ambient conditions makes boron an extraordinarily attractive topic in terms of its physical and chemical properties, such as boron-rich solids are one of the most important members of non-metallic superhard materials. However, pure boron has rarely been studied due to its difficult preparation.
Although the literature suggests that boron exists in many polymorphs [1], only three pure phases are well characterized with definite structures. They are α-B12 [1], β-B106 [2] and γ-B28 [3], all of which have complicated structures dominated by B12 icosahedron clusters. The only three valence electrons sufficiently localized result in boron nonmetallization. However, several theoretical studies have reported that α-B12 and β-B106 should undergo a transformation from non-metal to metal under compression [4，5，6]. It was confirmed that the β-B106 transforms from a nonmetal to a superconductor at about 160 GPa [7]. The high-pressure resistance measurements of α-B12 also demonstrated its pressure-induced superconductivity [8,9]. Nevertheless, from the structural viewpoint, focusing on the phase stability of boron under high pressure is indispensable. The structural stability of α-B12 and β-B106 under pressure has been investigated experimentally and theoretically [10,11,12,13,14,15,16,17,18,19,20]. Unfortunately, the structural stability of γ-B28 at high pressures is still experimentally unsolved, while many previous studies have concentrated on the synthesis and phase diagram at high pressure and high temperature (HPHT) [21,22,23,24,25].
Wentorf firstly observed γ-B28 at HPHT in 1965 [26]. In 2009, Oganov et al. determined its structure, as shown in Figure 1[3]. They concluded that γ-B28 remained stable up to 89 GPa and then transformed into the α-Ga-type phase, which was predicted to be a possible good candidate for the high-pressure metallic phase of boron via ab initio evolutionary crystal structure predictions [27]. Several theoretical and experimental studies have been devoted to the structural stability of γ-B28 under pressure. However, there are contradictions and controversies in these results. Jiang et al. suggested that the structure of γ-B28 was excepted to remain stable up to 40 GPa using first-principles density functional calculations [28]. At the same time, the γ-B28 phase was demonstrated to be stable up to at least 65 GPa as a result of high-pressure x-ray diffraction (XRD) measurements with Ne or He as a pressure-transmitting medium [29,30,31]. However, Zarechnaya et al. claimed that γ-B28 undergoes an isostructural phase transformation around 40 GPa based on their Raman spectra and XRD data under high pressure. They reported that both Raman modes of Ag at 380 cm−1 and B3g at 470 cm−1 undergo hardening and then softening with increasing pressure, and the modes at 480 cm−1 and 810 cm−1 split at approximately 40 GPa [32]. However, Oganov et al. considered insufficient evidence to be responsible for such a transition [33].
Boron is a light element and a very poor scatterer because of the low scattering cross-section of boron atoms. Thus, it is very difficult to measure XRD of boron at high pressure. This makes studying the behavior of boron under high pressure extremely difficult. γ-B28 has an extraordinary complicated structure with an utterly unique and easily distinguishable Raman spectrum [34]. Moreover, phase transitions are often associated with changes in crystal structure and symmetry, which can be directly demonstrated by Raman spectroscopy. Therefore, Raman spectroscopy is the most convenient and powerful method to research the properties of γ-B28 under high pressure. However, experimental information about the high-pressure Raman spectra of γ-B28 is limited. Here we present the results of the high-pressure Raman spectroscopy of γ-B28 up to 126 GPa at room temperature.

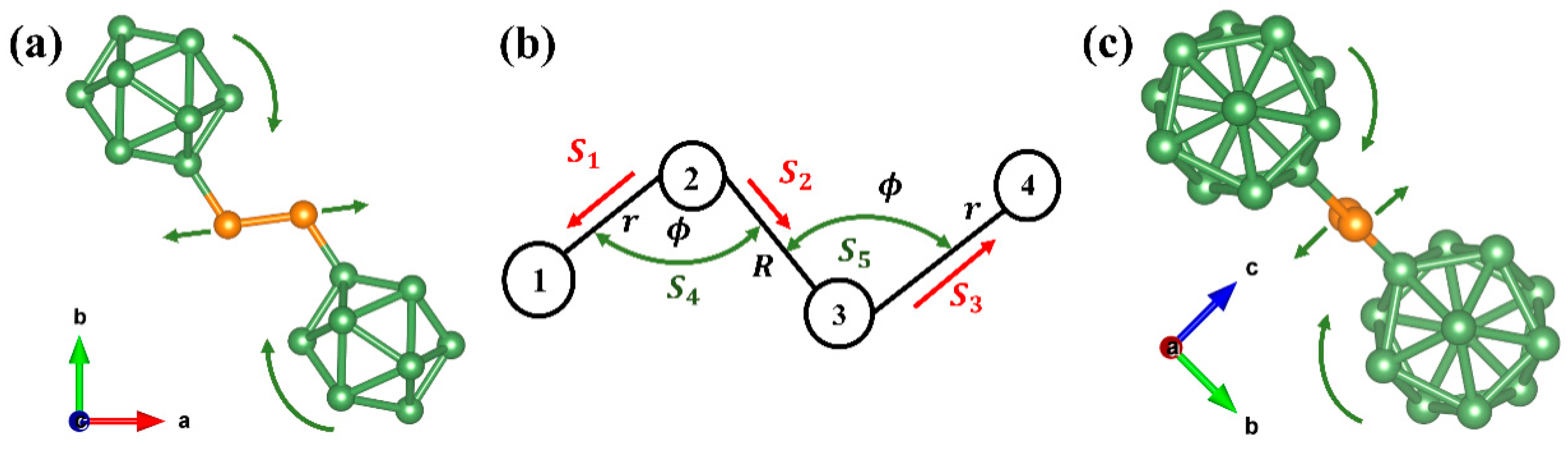
Experimental details

β-boron (β-B106, rhombohedral, space group R-3m; purity at. 99.9999%) is employed as the raw material to synthesize a polycrystalline aggregates of gamma phase boron (γ-B28, orthorhombic with space group Pnnm) at 10 GPa and high temperatures above 2000 K.
High-pressure experiments were carried out using a diamond-anvil-cell (DAC) with 100 μm diameter culets. Rhenium was used as gasket between the diamonds, which was preindented to a thickness of 20 μm; then, a hole with diameter of 70 μm was dilled in the center as sample chamber. The β-boron and ruby particles were packed into the chamber. Ruby served as pressure sensors while pressure was measured in situ from the calibrated shift of the ruby R1 fluorescent line. Neon was loaded as a pressure-transmitting medium (PTM). A one-side laser-heating device was employed to provide a high-temperature environment for boron during the experiment. A near-infrared laser (YAG,1064nm) was utilized to heat the sample at a maximum powder of 11W. In the experiment, we used a confocal microscope Raman spectrometer system equipped with a stigmatic spectrometer and a multichannel air-cooled CCD detector to collect the Raman scattering spectra. A He-Ne laser (632.8 nm, power of 7 mW) was used for an excitation source. After laser heating, the pressure stabilized at 13.5 GPa. Then, pressure in the cell was pressurized to 126.2 GPa at room temperature. The Raman spectra was measured at each pressure step.

First principle calculations

Crystal structures under high pressure were performed using the periodic plane-wave density functional theory (DFT) method with the projected-augmented wave (PAW) method implemented in the VASP code. The Perdew-Burke-Ernzerhof (PBE) was used for the exchange-correlation potentials. The energy cutoff for the plane-wave basis was set to 500 eV and the Brillouin zone was sampled by a Monkhorst-Pack grid of 12×12×12. The self-consistent convergence criteria of energy were set to 1×10-6 for ionic relaxations, and all atoms were relaxed until the forces was less than 0.01 eV/ Å.

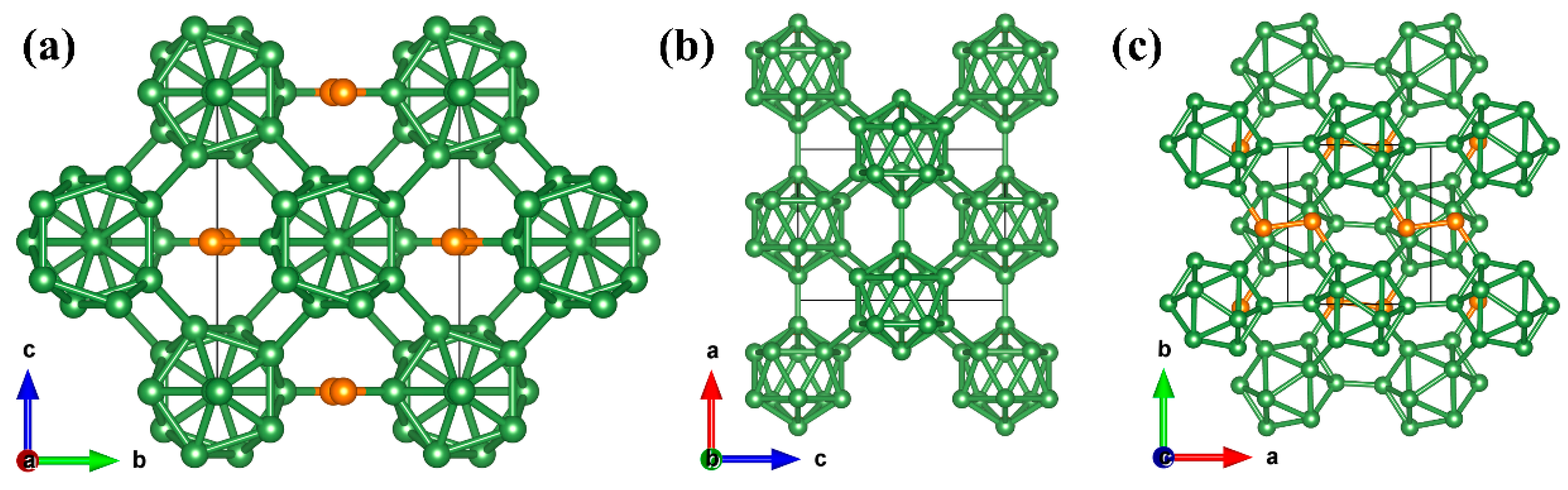
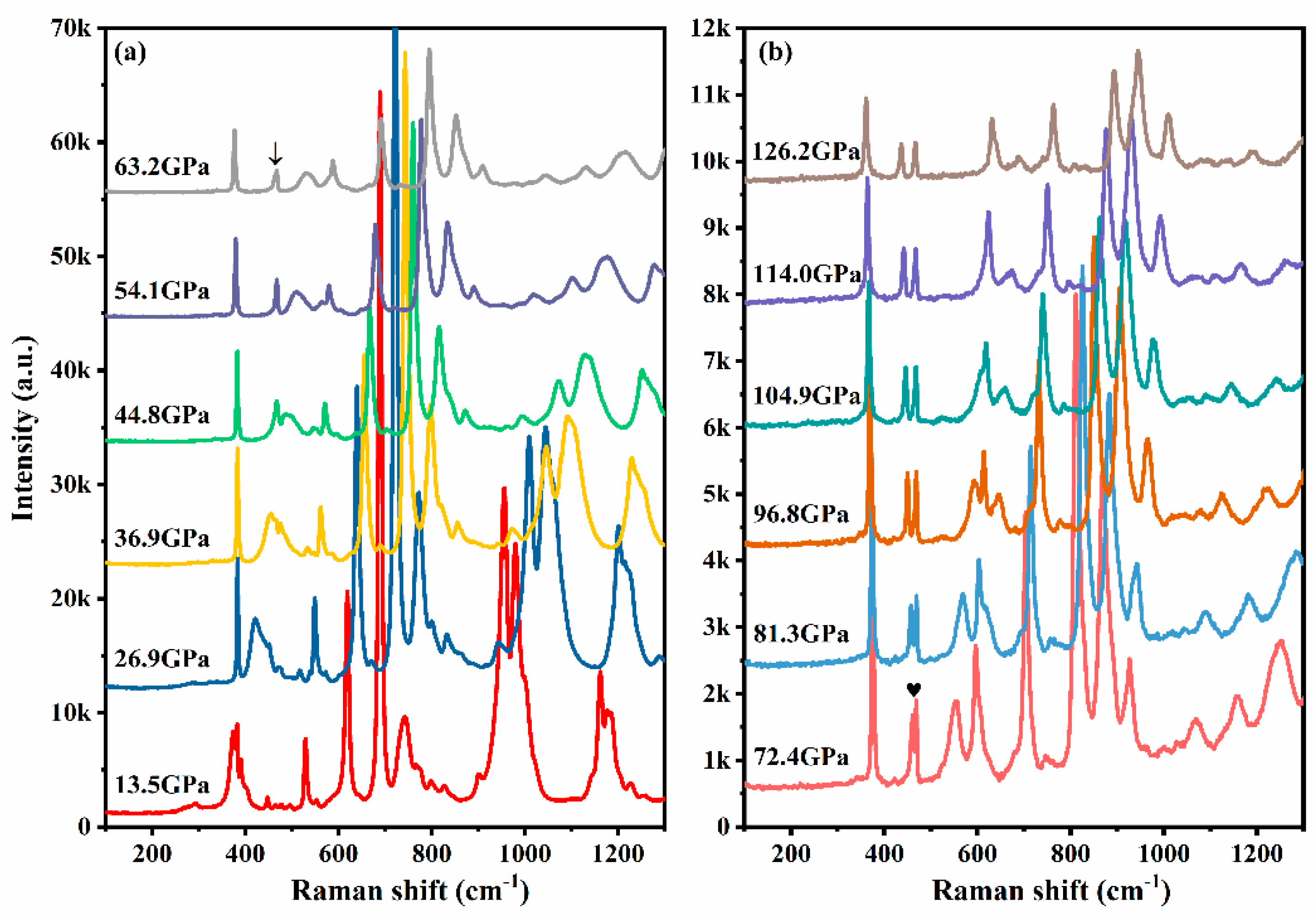
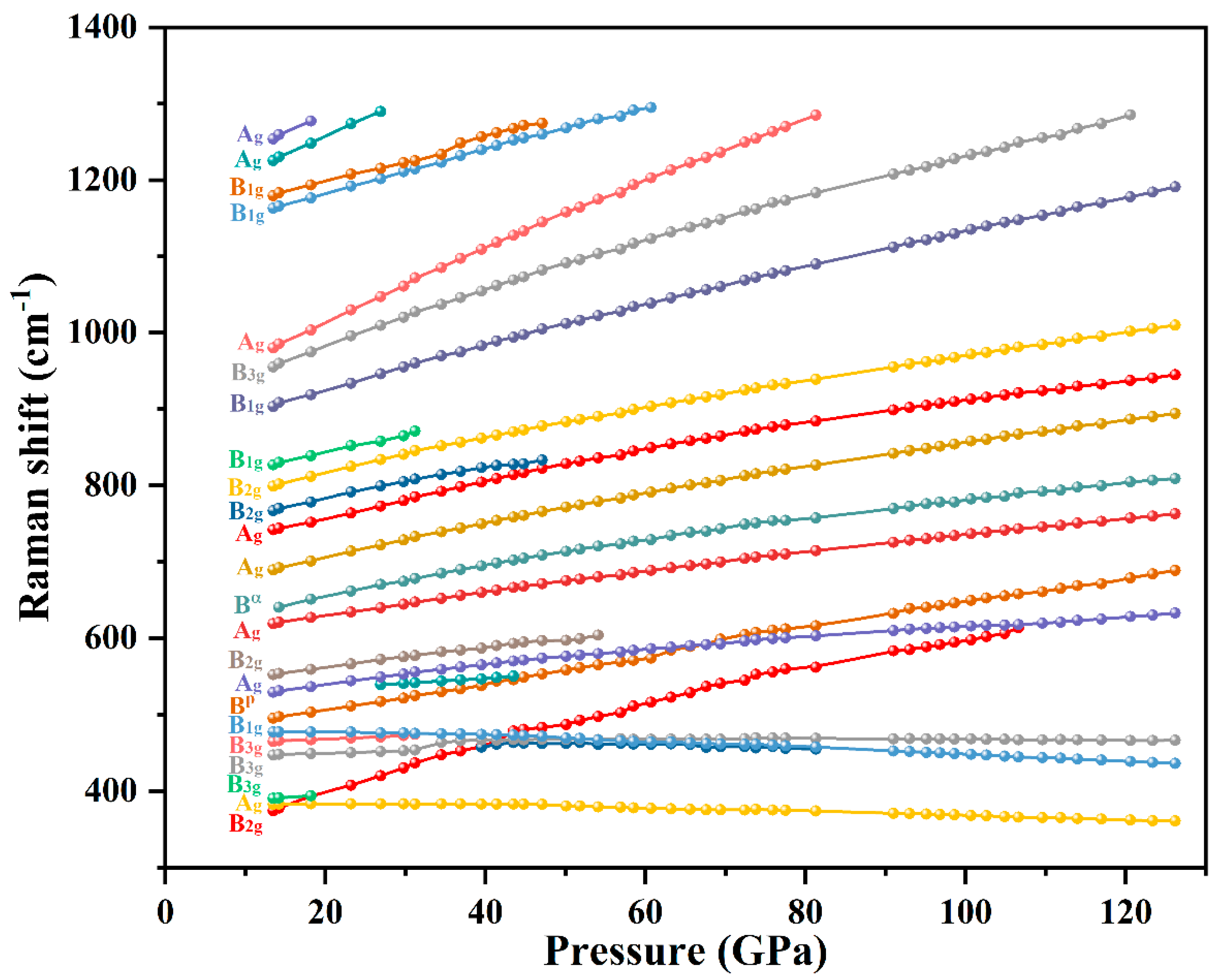
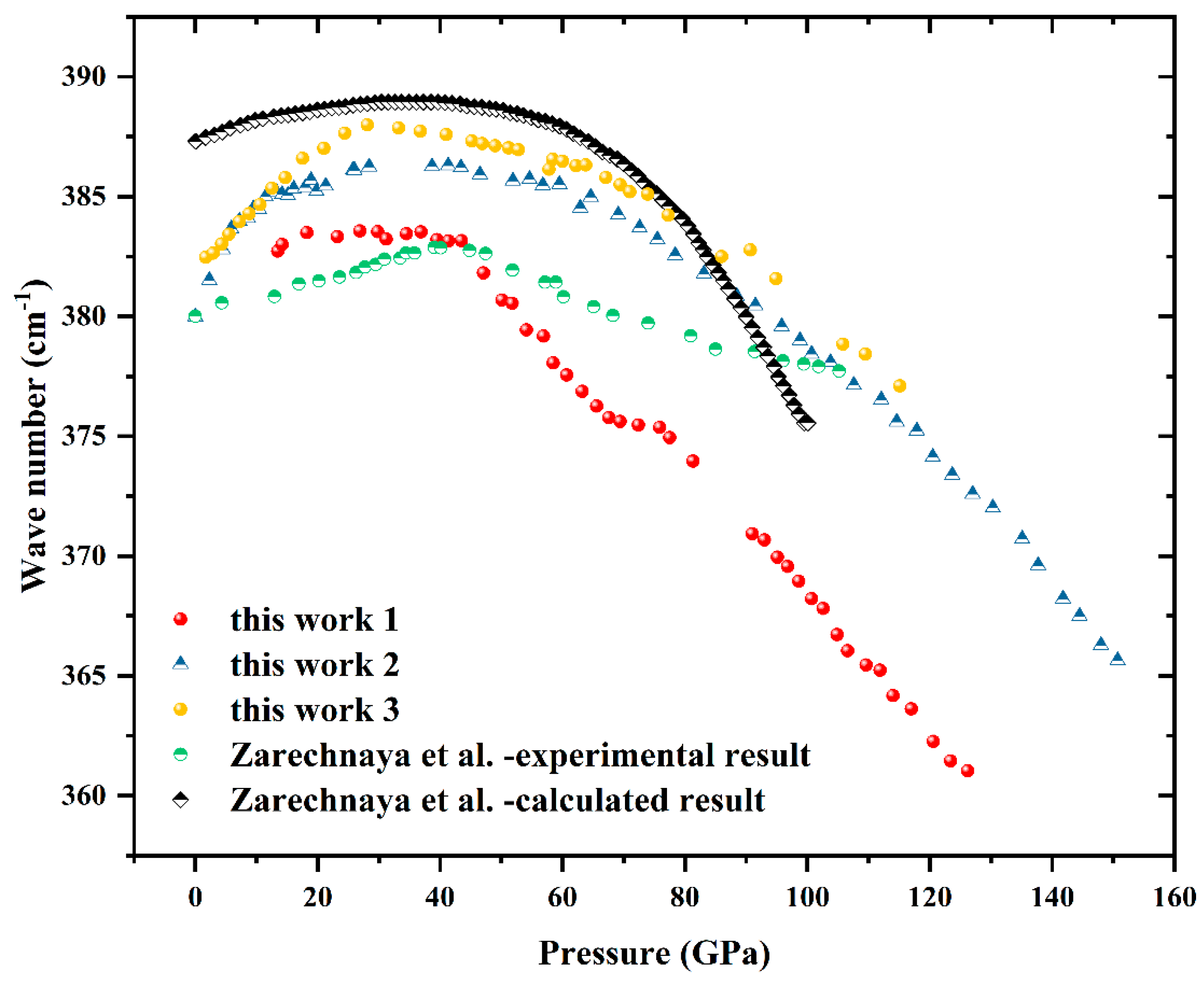
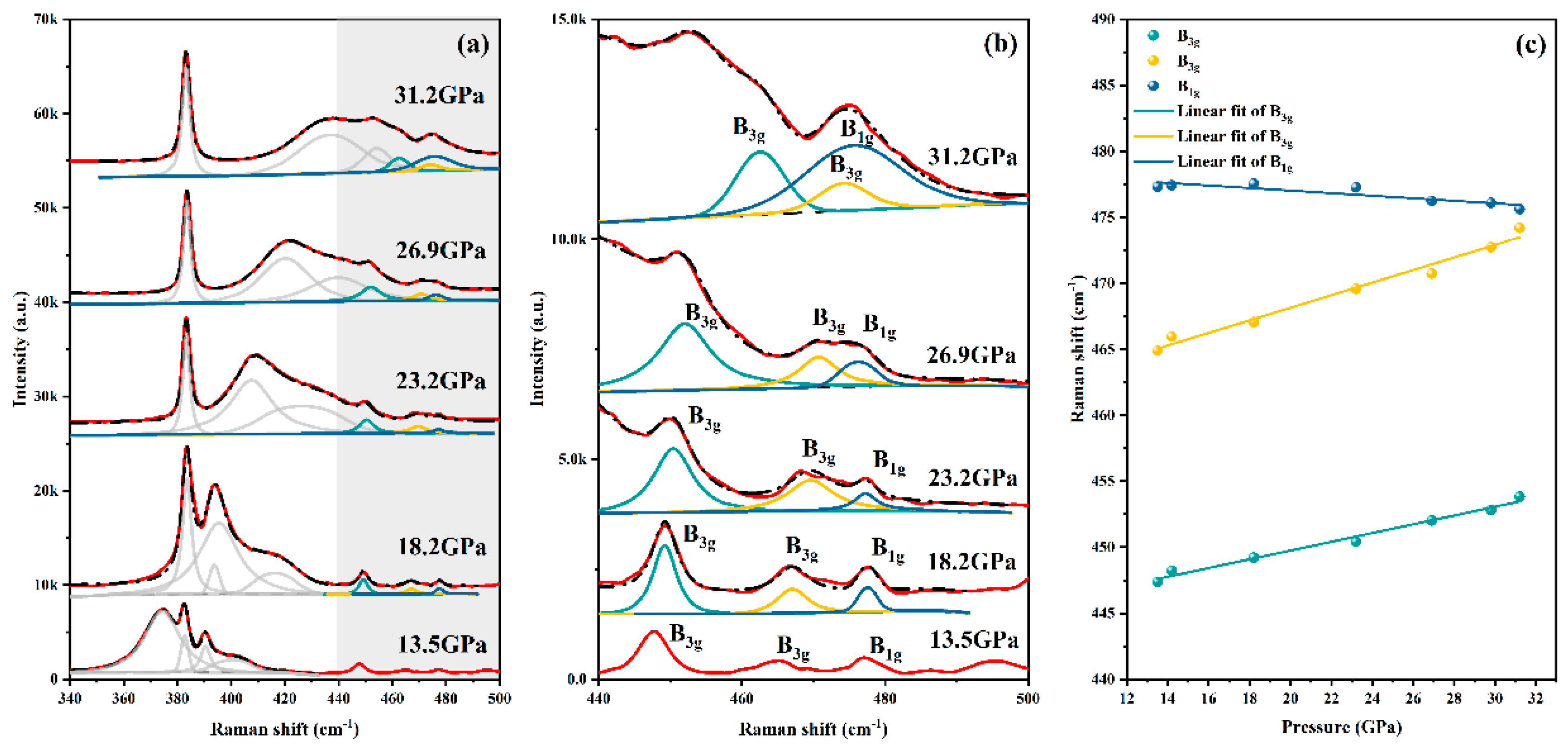
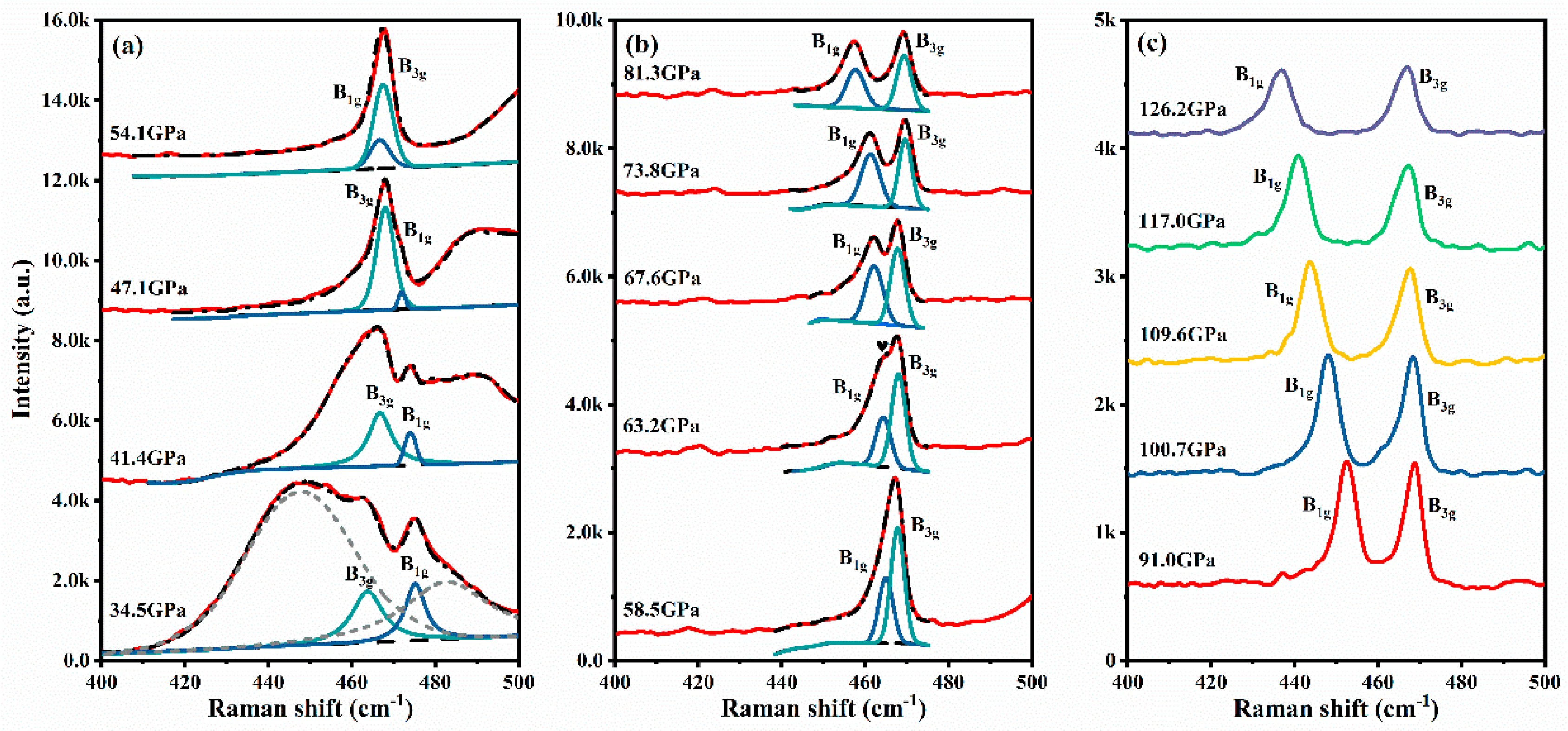
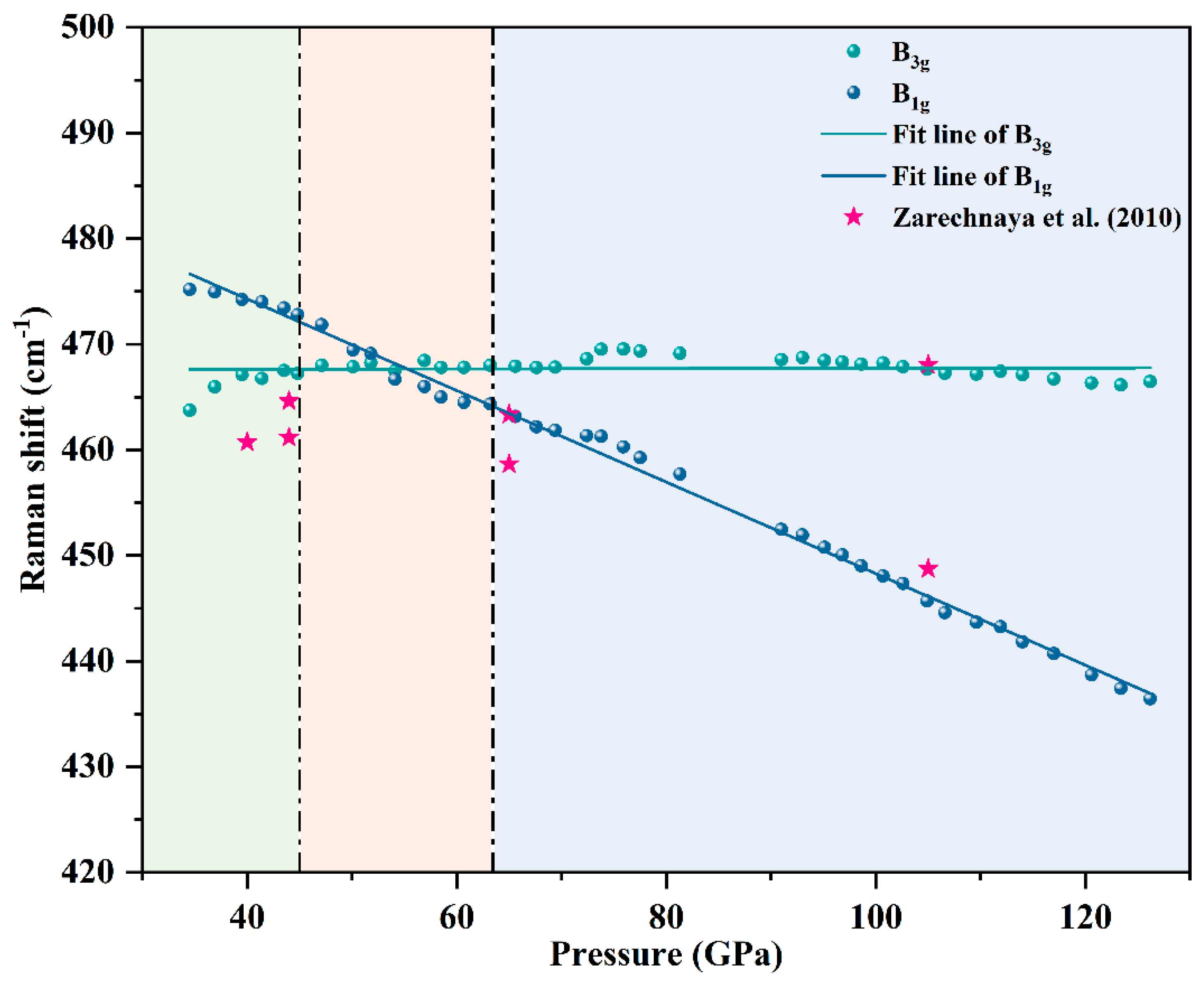
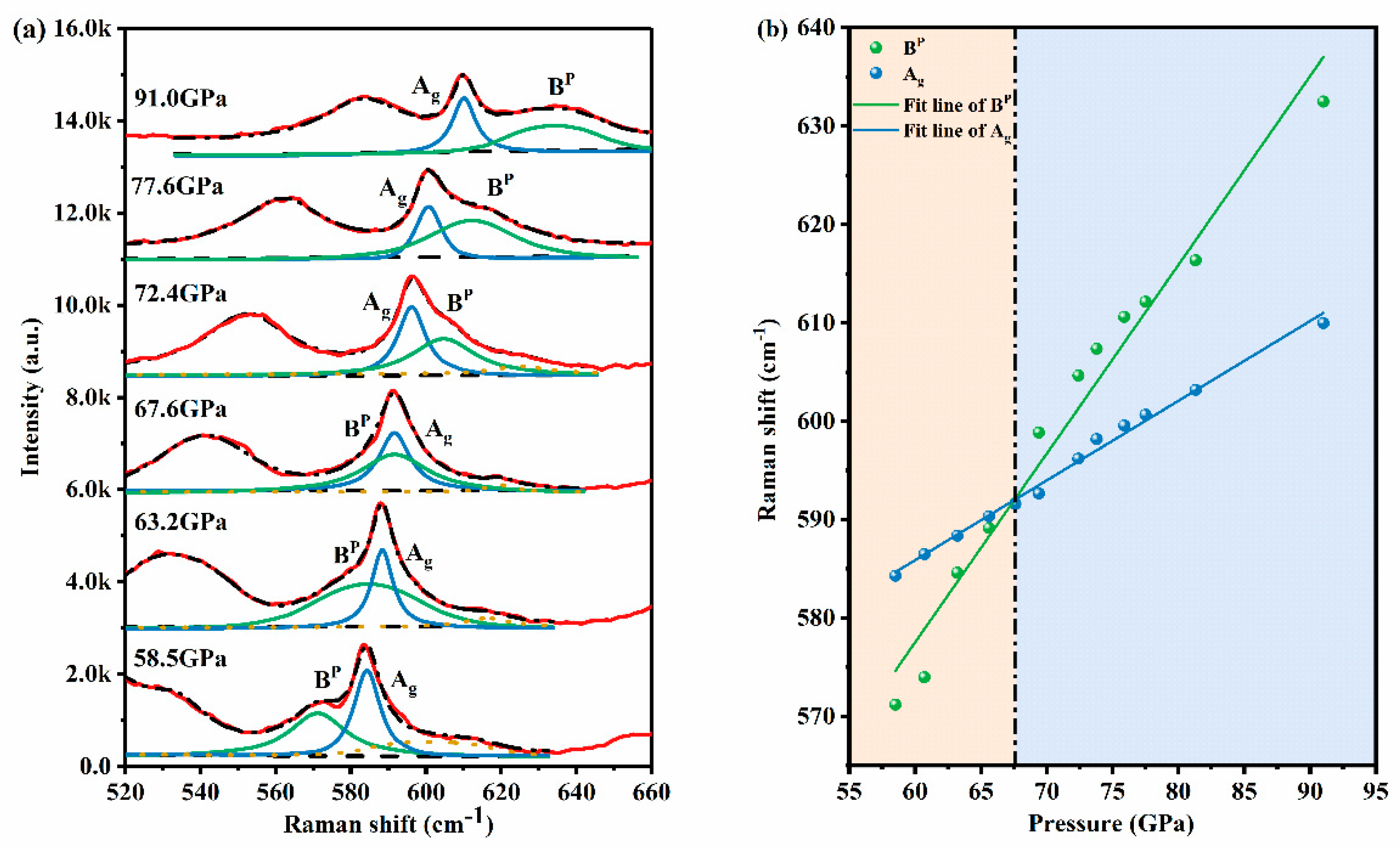
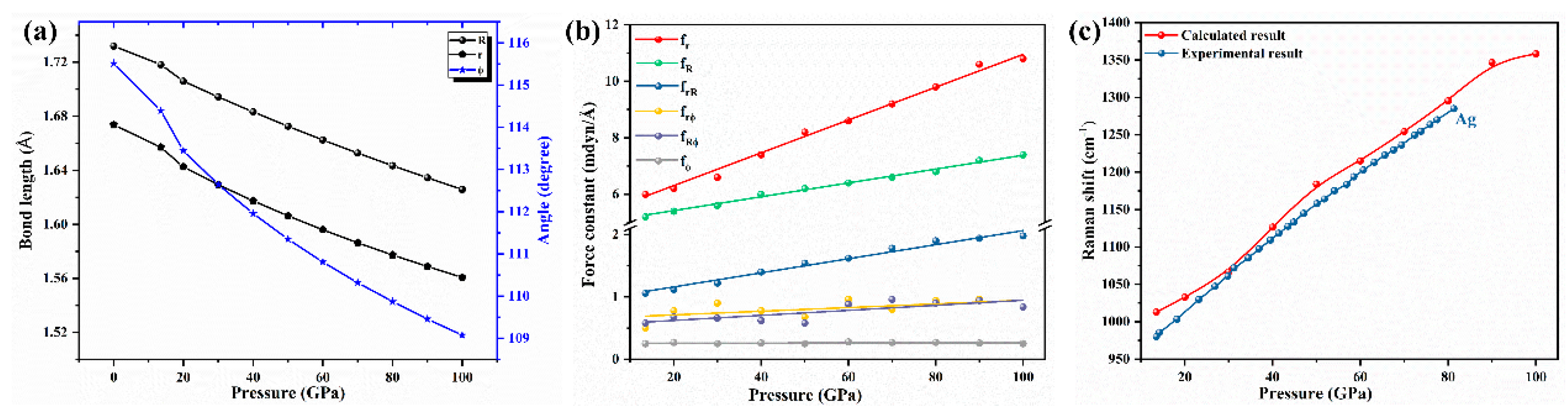
Results and Discussion

To investigate the structural stability of γ-boron under high pressure, we performed in-situ Raman spectroscopy measurements under high pressure up to 126 GPa at ambient temperature. The pre-synthesized γ-boron samples demonstrate high quality and consequently many weak Raman modes could also be detected. Figure 2 shows the evolution of the Raman modes of γ-boron between 100 cm-1 and 1300 cm-1 under high pressure up to 126 GPa at room temperature. Moreover, the pressure dependence of the frequencies of different Raman-active modes is displayed in Figure 3. We measured the pressure dependence of 23 Raman modes. Compared to previous works [32,35], one mode at approximately 500 cm-1 marked as “BP” at high pressure could not be assigned; another mode could not be determined, and its type (B2g or B3g) was noted as “Bα”, as shown in Figure 3. All Raman modes of γ-boron smoothly shift with increasing pressure. With loading compression, all Raman modes above 500 cm-1 remain in blueshift. However, the Ag mode at 380 cm-1 first shifts towards higher frequencies and then becomes soft at high pressures, as shown in Figure 4. The agreement between our results and those previously published [32] is quite good.
Preprints 76370 g001
Figure 1. Structure of γ-B28 from different directions.
Figure 1. Structure of γ-B28 from different directions.
Preprints 76370 g001
Next, we concentrate on detailed variations of some Raman modes, especially the Raman modes between 400 cm-1 and 500 cm-1 in which some peaks “split” intuitively at 63 GPa, marked by an arrow in Figure 2(a). Figure 5 shows the evolution process of Raman modes between 340 cm-1 and 500 cm-1 during compression. As observed in Figure 5(a), the lattice mode at 374 cm-1 displays a broad peak and a fast blueshift with increasing pressure, overlapping with the B3g mode at 23.2 GPa and then lifts the background of B3g and B1g modes with the further loading as shown in Figure 5(b). Below the pressure of 18 GPa, the three Raman modes of B3g (447 cm-1), B3g (465 cm-1) and B1g (477 cm-1) are obviously distinguishable as seen in the Raman spectra of Figure 5(b). In the process of pressurization from 13.5 GPa, the Raman modes B3g (447 cm-1) and B3g (465 cm-1) move to high wavenumbers, while B1g (477 cm-1) shifts in the opposite direction. Above 23GPa, the B3g (465 cm-1) begins to merge into the B1g (477 cm-1). When pressure reaches approximately 31GPa, B3g (465 cm-1) and B1g (477 cm-1) are completely degenerate, causing the relative strength of B1g (477 cm-1) to increase, while B3g (465 cm-1) becomes no longer measurable. At this pressure, the intensity of B1g (477 cm-1) is stronger than that of B3g (447 cm-1). Figure 5(c) displays the pressure dependence of the three Raman modes frequencies up to 30 GPa.
Figure 6 shows the evolution of the B3g and B1g modes between 400 cm-1 and 500 cm-1 from 30 GPa to 126 GPa. For this wavenumber region, in addition to the two broad peaks of the B2g and Ag modes fast sweep, only the B3g and B1g modes remain in the pressure region. The relationship between the shifts of these two modes with pressure up to 126 GPa is shown in the Figure 7. Under compression, B3g and B1g modes keep the blueshift and redshift respectively and cross at 54 GPa. Around the pressure at 54 GPa, a single Raman peak is observed due to overlap of the two modes, but they are distinguishable based on the decomposition of the spectrum, as displayed in Figure 6(a, b). At a pressure of 91GPa, B3g and B1g are completely separated. With further loading compression, the B3g and B1g modes continue to move monotonously.
Similar phenomena to B3g and B1g can also be discovered in other Raman modes, such as BP (495 cm-1) and Ag (529 cm-1) at 58.5 GPa, as shown in Figure 8. Both peaks remain blueshifted under pressure at very different rates. At the same time, BP is more sensitive to pressure, and BP merges into Ag above 60 GPa. Starting from 68 GPa, the relative position of BP and Ag will be reversed. BP could only be recognized again on the Raman spectrum once the pressure had been loaded to 91GPa.
Our results indicate that no new peaks appear, and all Raman modes are continuously shifted up to 126 GPa. In this pressure range, neither the symmetry nor the structure change was detected. It is controversial that Zarechnaya et al. regard the softening of the Ag Raman mode at 380 cm-1 under high pressure as evidence of an isostructural phase transition. In the work of Isaac F. Silvera and S.J. Jeon in 1992 [36], they used an established theory of Raman-active modes to investigate the high-pressure softening of the Raman-active vibron of hydrogen and deuterium. They showed that the Raman frequency is affected by both the density-dependent intramolecular potential in the solid and the intermolecular potential, and the softening of the Raman mode is due to the intermolecular potential. Therefore, the softening of Ag Raman mode under high pressure is potentially caused by the intermolecular potential varying with pressure rather than the isostructural phase transition. In previous work [32], the Raman mode splitting observed at approximately 40-45 GPa was considered as characteristic of the isostructural phase transition. This is due to the different shift rates of the two Raman modes of B3g (447 cm-1) and B1g (477 cm-1) with increasing pressure, which results in the phenomenon of merging first and then separating. This fact suggests that γ-boron remains stable under pressures up to 126 GPa, and no new high-pressure phase is generated.
Despite the complicated structure of γ-boron, we proposed a model to explain the above amusing phenomenon. The Raman modes B1g and B3g correspond to the tilts of the B12 icosahedron around the c-axis and a-axis, respectively [32]. As displayed in Figure 9(a), two B12 icosahedrons are connected by a B2 dumbbell. When two B12 icosahedrons tilt around the c-axis, they will drive the two boron atoms of the B2 dumbbell to stretch along the bond direction. Figure 9(c) displays the tilt of the B12 icosahedron around the a-axis, which responds to the B3g mode. In contrast, the inclination of B12 icosahedron makes the B2 dumbbell swing in a direction perpendicular to its plane, which is very difficult. The B2 dumbbell limits the tilt of the B12 icosahedron and even makes it less affected by compression. Therefore, the B3g mode has a very weak response to pressure, with only a slight and negligible blueshift. If B12-icosahedron is equivalent to an atom, the complex structure in Figure 9(a) can be simplified to a four-atom system, as shown in Figure 9(b).
In this four-atom system, atoms 1 and 4 are icosahedrons, while atoms 2 and 3 are single boron atoms. The lengths of the bonds between 1 and 2, 3 and 4 are the same, which is r. The bond between 2 and 3 is longer, which is R. The bond angles (123) and (234) are also the same, which is 𝜙. The dihedral angle between the planes of atoms (123) and (234) is zero because four atoms are located in one plane.
To make it easier to investigate the amusing behavior of the B1g mode, the internal coordinates were used to analyze the vibration of the 4-atom system. For a system of N atoms, the distance between atoms, the bond angle between chemical bonds, or the change of both, can be used as a set of 3N-6 (for linear molecules, 3N-5) internal coordinates. That is, the coordinates are not affected by the translational and rotational motion of the molecule as a whole, so it is a more advanced method for studying vibration. In the above 4-atom system, in addition to the dihedral angle (no change), there are five internal coordinates, which are S t (t=1,2,3,4,5), as shown in Fig.9b.
The internal coordinates S t can be expressed in the following form[37]
S t = ∑ α = 1 N s t α ⋅ ρ α
where the point in the formula represent the scalar product of two vectors. The physical meaning of the vector s t α is that only the α atom deviates from the equilibrium position; the direction of s t α is a given position shift of the α atom, which is the direction of the maximum increase of S t ; and the value of s t α is equal to the increase of S t of the atom due to the unit displacement in the most effective direction. In this way a given internal coordinate S t is characterized by a set of vectors s t α , one for each atom t.
In the 4-atom system, s t α can be expressed[38]:
s t α = ( e 21 − e 21 0 0 0 − e 23 e 23 0 0 0 − e 34 e 34 cos ϕ 123 e 21 − e 23 r 12 sin ϕ 123 [ ( r 12 − r 23 cos ϕ 123 ) e 21 + ( r 23 − r 12 cos ϕ 123 ) e 23 ] r 12 r 23 sin ϕ 123 cos ϕ 123 e 23 − e 21 r 23 sin ϕ 123 0 0 cos ϕ 234 e 32 − e 34 r 23 sin ϕ 234 [ ( r 23 − r 34 cos ϕ 234 ) e 32 + ( r 34 − r 23 cos ϕ 234 ) e 34 ] r 23 r 34 sin ϕ 234 cos ϕ 234 e 34 − e 32 r 34 sin ϕ 234 )
The potential energy of vibration can be expressed as[39]
2 T = ∑ t t ' ( G − 1 ) t t ' S · t S · t '
∑ t ' ( G − 1 ) t t ' G t ' t ' ' = δ t ' t ' '
The kinetic energy matrix G t t ' can be given by[38]
G t t ' = ∑ α = 1 N μ α s t α ⋅ s t ' α
where the point in the formula represent the scalar product of two vectors, μ α = 1 / m α is the reciprocal of the mass of the atom to which α refers. Each pair of internal coordinates S t and S t ' have an element G t t ' , and this form has the advantage that it requires no coordinate system.
According to the above equation, the G matrix of the 4-atom system can be obtained:
G = M + m m * c 0 − m * s R − m * s R m * c M + m m * c − m * s r − m * s r 0 m * c M + m − m * s R − m * s r − m * s R − m * s r − m * s R M r 2 + m R 2 + m * ( r 2 + R 2 − 2 R * r * c ) ( r * R ) 2 2 m * ( r − R * c ) r * R 2 − m * s R − m * s r − m * s r 2 m * ( r − R * c ) r * R 2 M r 2 + m R 2 + m * ( r 2 + R 2 − 2 R * r * c ) ( r * R ) 2
where μ 1 = μ 4 = M , μ 2 = μ 3 = m , r 12 = r 34 = r , r 23 = R , c o s ϕ = c , s i n ϕ = s .
If the potential energy is also expressed by the same internal coordinates, then [39]
2 V = ∑ t t ' F t t ' S t S t '
where F t t ' is the force constant, therefore, it has the form
F = f r f r R 0 r f r ∅ 0 f r R f R f r R R f R ∅ R f R ∅ 0 f r R f r 0 r f r ∅ r f r ∅ R f R ∅ 0 R r f ∅ R r f ∅ 0 R f R ∅ r f r ∅ R r f ∅ R r f ∅
where fr is the r bond-stretching force constant; fR is the R bond-stretching force constant; frR is the force constant for the interaction between bonds r and R; fr𝜙 is the force constant for the interaction between bond r and bond angle 𝜙123 or 𝜙234; fR𝜙 is the force constant for the interaction between the bond R and bond angle 𝜙123 or 𝜙234; and f𝜙 is the force constant for the interaction between bond angle 𝜙123 and 𝜙234.
The secular equation can be obtained from the vibration problem and Newton's equation of motion[39]:
G F − E λ = 0
where E is the unit matrix, λ = 4 π c 2 ν 2 , and ν is the vibration frequency:
ν = λ 2 π c = 1302.8 λ
Crystal structures of γ-B28 under high pressure were performed via first principles. Therefore, the structural parameters r, R and 𝜙 under high pressures could be obtained. Figure 10(a) displays the decrease in r, R and 𝜙 with pressure up to 100 GPa. Under certain pressure, the matrix G is a constant matrix because of the known r, R, 𝜙, m and M. Iterate repeatedly the force constants fr, fR, frR, fr𝜙, fR𝜙 and f𝜙. According to equations (6) and (7), the vibration frequency under this pressure could be calculated. Equal the calculated value to the experimental frequency value to achieve convergence to obtain a set of force constants under pressure. Moreover, the force constants under pressures could be obtained. Figure 10(b) shows the force constants as a function of pressure. All force constants increase with increasing pressure, except that f𝜙 remains basically unchanged. To verify the accuracy of the calculated results, another Raman mode was simulated with the calculated force constants. The result was consistent with the experimentally obtained Ag mode, as shown in Figure 10(c). In conclusion, the abnormal behavior of the B1g Raman mode under pressure is caused by changes in the crystal structure and force constants. During the process of pressurization, the reduced bond length and bond angle with increased force constants make it more difficult for two B12 icosahedrons to drive the two boron atoms of the B2 dumbbell to stretch along the bond direction, resulting in the redshift of the B1g mode with increasing pressure.

Conclusion

We synthesized γ-boron at HPHT and reported its Raman spectra at pressures up to 126 GPa at room temperature. The details of the evolution of the Raman spectrum with pressure were investigated, especially the Raman modes between 400cm-1 and 500 cm-1, in which some peaks “split” intuitively at 63GPa. All Raman modes changed continuously under high pressure, which indicated that the γ-boron remained stable under pressures up to 126GPa, and no new high-pressure phase was generated. The Raman mode “splitting” observed at high pressure was actually due to the different direction and rate of shift of the two Raman modes B1g and B3g under pressure, which results in the phenomenon of merging first and then separating. Then we proposed a model to explain the above amusing phenomenon. B1g and B3g correspond to the tilts of the B12 icosahedron around the c-axis and a-axis, respectively. Crystal structures of γ-B28 under high pressure were calculated via first principles. The response of the force constants to pressures was calculated by the method of internal coordinates, which results in the redshift of the B1g mode with increasing pressure. However, the influence of pressure on the B3g mode is limited, with only a negligible blueshift.

Acknowledgements

This work is supported by the Frontier Scientific Research Program of Deep Space Exploration Laboratory under grant No. 2022-QYKYJH-HXYF-019, the National Natural Science Foundation of China (No. 12074360), and the project of National Key Laboratory of Shock Wave and Detonation Physics (No. JCKYS2022212008)

References

  1. Douglas, B.; Shih-MingHo. Structure and Chemistry of Crystalline Solids; Springer: New York, NY, USA, 2016. [Google Scholar]
  2. Hughes, R.E.; Kennard, C.H.L.; Sullenger, D.B.; Weakliem, H.A.; Sands, D.E.; Hoard, J.L. The Structure of β-Rhombohedral Boron. J. Am. Chem. Soc. 1963, 85, 361–362. [Google Scholar] [CrossRef]
  3. Oganov, A.R.; Chen, J.; Gatti, C.; Ma, Y.; Ma, Y.; Glass, C.W.; Liu, Z.; Yu, T.; Kurakevych, O.O.; Solozhenko, V.L. Ionic high-pressure form of elemental boron. Nature 2009, 457, 863–867. [Google Scholar] [CrossRef] [PubMed]
  4. Zhao, J.; Lu, J.P. Pressure-induced metallization in solid boron. Phys. Rev. B 2002, 66. [Google Scholar] [CrossRef]
  5. Haussermann, U.; Simak, S.I.; Ahuja, R.; Johansson, B. Metal-nonmetal transition in the boron group elements. Phys Rev Lett 2003, 90, 065701. [Google Scholar] [CrossRef]
  6. Shirai, K.; Dekura, H.; Yanase, A. Electronic Structure and Electrical Resistivity of α-Boron under High Pressure. J. Phys. Soc. Jpn. 2009, 78. [Google Scholar] [CrossRef]
  7. Eremets, M.I.; Struzhkin, V.V.; Mao, H.; Hemley, R.J. Superconductivity in boron. Science 2001, 293, 272–274. [Google Scholar] [CrossRef]
  8. Kaneshige, M.; Hirayama, S.; Yabuuchi, T.; Matsuoka, T.; Shimizu, K.; Mita, Y.; Hyoudo, H.; Kimura, K. Measurement of Electrical Resistance and Raman Spectrum of α-Boron under High Pressure. J. Phys. Soc. Jpn. 2007, 76, 19–20. [Google Scholar] [CrossRef]
  9. Shimizu, K.; Kaneshige, M.; Hashimoto, Y.; Nagatochi, T.; Hyodo, H.; Kimura, K. Superconductivity in α-boron at Mbar pressure. Phys. C Supercond. Its Appl. 2010, 470, S631–S632. [Google Scholar] [CrossRef]
  10. Vast, N.; Baroni, S.; Zerah, G.; Besson, J.M.; Polian, A.; Grimsditch, M.; Chervin, J.C. Lattice Dynamics of Icosahedralα-Boron under Pressure. Phys. Rev. Lett. 1997, 78, 693–696. [Google Scholar] [CrossRef]
  11. Masago, A.; Shirai, K.; Katayama-Yoshida, H. Crystal stability ofα- andβ-boron. Phys. Rev. B 2006, 73. [Google Scholar] [CrossRef]
  12. Shang, S.; Wang, Y.; Arroyave, R.; Liu, Z.-K. Phase stability inα- andβ-rhombohedral boron. Phys. Rev. B 2007, 75. [Google Scholar] [CrossRef]
  13. Polian, A.; Chervin, J.C.; Munsch, P.; Gauthier, M. α-boron at very high pressure: structural and vibrational properties. J. Phys. Conf. Ser. 2008, 121. [Google Scholar] [CrossRef]
  14. Parakhonskiy, G.; Vtech, V.; Dubrovinskaia, N.; Caracas, R.; Dubrovinsky, L. Raman spectroscopy investigation of alpha boron at elevated pressures and temperatures. Solid State Commun. 2013, 154, 34–39. [Google Scholar] [CrossRef]
  15. Chuvashova, I.; Bykova, E.; Bykov, M.; Svitlyk, V.; Gasharova, B.; Mathis, Y.-L.; Caracas, R.; Dubrovinsky, L.; Dubrovinskaia, N. High-pressure behavior of α-boron studied on single crystals by X-ray diffraction, Raman and IR spectroscopy. J. Solid State Chem. 2017, 245, 50–60. [Google Scholar] [CrossRef]
  16. Pokatashkin, P.A.; Korotaev, P.Y.; Yanilkin, A.V. Amorphization inα-boron: A molecular dynamics study. Phys. Rev. B 2017, 95. [Google Scholar] [CrossRef]
  17. Sanz, D.N.; Loubeyre, P.; Mezouar, M. Equation of state and pressure induced amorphization of beta-boron from X-ray measurements up to 100 GPa. Phys Rev Lett 2002, 89, 245501. [Google Scholar] [CrossRef]
  18. Ma, Y.; Prewitt, C.T.; Zou, G.; Mao, H.-k.; Hemley, R.J. High-pressure high-temperature x-ray diffraction of β-boron to 30 GPa. Phys. Rev. B 2003, 67. [Google Scholar] [CrossRef]
  19. Siberchicot, B. Ab initioequation of state ofα- andβ-boron: Possible amorphization ofβ-boron under high pressure. Phys. Rev. B 2009, 79. [Google Scholar] [CrossRef]
  20. An, Q.; Morozov, S.I. Brittle failure of β- and τ-boron: Amorphization under high pressure. Phys. Rev. B 2017, 95. [Google Scholar] [CrossRef]
  21. Shirai, K.; Masago, A.; Katayama-Yoshida, H. High-pressure properties and phase diagram of boron. physica status solidi (b) 2007, 244, 303–308. [Google Scholar] [CrossRef]
  22. Parakhonskiy, G.; Dubrovinskaia, N.; Bykova, E.; Wirth, R.; Dubrovinsky, L. Experimental pressure-temperature phase diagram of boron: resolving the long-standing enigma. Sci Rep 2011, 1, 96. [Google Scholar] [CrossRef]
  23. Qin, J.; Irifune, T.; Dekura, H.; Ohfuji, H.; Nishiyama, N.; Lei, L.; Shinmei, T. Phase relations in boron at pressures up to 18 GPa and temperatures up to 2200∘C. Phys. Rev. B 2012, 85. [Google Scholar] [CrossRef]
  24. Solozhenko, V.L.; Kurakevych, O.O. Equilibrium p-T phase diagram of boron: experimental study and thermodynamic analysis. Sci Rep 2013, 3, 2351. [Google Scholar] [CrossRef] [PubMed]
  25. Shirai, K. Phase diagram of boron crystals. Jpn. J. Appl. Phys. 2017, 56. [Google Scholar] [CrossRef]
  26. Wentorf, R.H., Jr. Boron: Another Form. Science 1965, 147, 49–50. [Google Scholar] [CrossRef]
  27. Ma, Y.; Tse, J.S.; Klug, D.D.; Ahuja, R. Electron-phonon coupling ofα−Gaboron. Phys. Rev. B 2004, 70. [Google Scholar] [CrossRef]
  28. Jiang, C.; Lin, Z.; Zhang, J.; Zhao, Y. First-principles prediction of mechanical properties of gamma-boron. Appl. Phys. Lett. 2009, 94. [Google Scholar] [CrossRef]
  29. Zarechnaya, E.Y.; Dubrovinsky, L.; Dubrovinskaia, N.; Filinchuk, Y.; Chernyshov, D.; Dmitriev, V.; Miyajima, N.; El Goresy, A.; Braun, H.F.; Van Smaalen, S.; et al. Superhard semiconducting optically transparent high pressure phase of boron. Phys Rev Lett 2009, 102, 185501. [Google Scholar] [CrossRef]
  30. Isaev, E.I.; Simak, S.I.; Mikhaylushkin, A.S.; Vekilov, Y.K.; Zarechnaya, E.Y.; Dubrovinsky, L.; Dubrovinskaia, N.; Merlini, M.; Hanfland, M.; Abrikosov, I.A. Impact of lattice vibrations on equation of state of the hardest boron phase. Phys. Rev. B 2011, 83. [Google Scholar] [CrossRef]
  31. Godec, Y.L.; Kurakevych, O.O.; Munsch, P.; Garbarino, G.; Solozhenko, V.L. Equation of state of orthorhombic boron, -B28. Solid State Commun. 2009, 149, 1356–1358. [Google Scholar] [CrossRef]
  32. Zarechnaya, E.; Dubrovinskaia, N.; Caracas, R.; Merlini, M.; Hanfland, M.; Filinchuk, Y.; Chernyshov, D.; Dmitriev, V.; Dubrovinsky, L. Pressure-induced isostructural phase transformation inγ-B28. Phys. Rev. B 2010, 82. [Google Scholar] [CrossRef]
  33. Oganov, A.R.; Solozhenko, V.L.; Gatti, C.; Kurakevych, O.O.; Le Godec, Y. The high-pressure phase of boron, γ-B28: Disputes and conclusions of 5 years after discovery. J. Superhard Mater. 2011, 33, 363–379. [Google Scholar] [CrossRef]
  34. Yu Zarechnaya, E.; Dubrovinsky, L.; Dubrovinskaia, N.; Miyajima, N.; Filinchuk, Y.; Chernyshov, D.; Dmitriev, V. Synthesis of an orthorhombic high pressure boron phase. Sci Technol Adv Mater 2008, 9, 044209. [Google Scholar] [CrossRef] [PubMed]
  35. Zarechnaya, E.Y.; Dubrovinskaia, N.; Dubrovinsky, L. Polarized Raman spectroscopy of high-pressure orthorhombic boron phase. High Press. Res. 2009, 29, 530–535. [Google Scholar] [CrossRef]
  36. Silvera, I.F.; Jeon, S.J.; Lorenzana, H.E. Pressure dependence of the vibron modes in solid hydrogen and deuterium. Phys Rev B Condens Matter 1992, 46, 5791–5794. [Google Scholar] [CrossRef]
  37. Wilson, E.B. Some Mathematical Methods for the Study of Molecular Vibrations. J. Chem. Phys. 1941, 9, 76–84. [Google Scholar] [CrossRef]
  38. Decius, J.C. A Tabulation of General Formulas for Inverse Kinetic Energy Matrix Elements in Acyclic Molecules. J. Chem. Phys. 1948, 16, 1025–1034. [Google Scholar] [CrossRef]
  39. Wilson, E.B. A Method of Obtaining the Expanded Secular Equation for the Vibration Frequencies of a Molecule. J. Chem. Phys. 1939, 7, 1047–1052. [Google Scholar] [CrossRef]
Preprints 76370 g002
Figure 2. Raman spectra of γ-B28 compressed in a neon pressure transmitting medium in a diamond anvil cell.
Figure 2. Raman spectra of γ-B28 compressed in a neon pressure transmitting medium in a diamond anvil cell.
Preprints 76370 g002
Preprints 76370 g003
Figure 3. Variation in the positions of Raman peaks of γ-B28 as a function of pressure.
Figure 3. Variation in the positions of Raman peaks of γ-B28 as a function of pressure.
Preprints 76370 g003
Preprints 76370 g004
Figure 4. Pressure dependence of the Ag Raman mode, the results of this work and Zarechnaya et al. are represented by scatters of different colors and shapes.
Figure 4. Pressure dependence of the Ag Raman mode, the results of this work and Zarechnaya et al. are represented by scatters of different colors and shapes.
Preprints 76370 g004
Preprints 76370 g005
Figure 5. (a)The evolution process during compression, (b) is the gray area in (a), and (c)the positions of these three modes (B3g, B3g and B1g) as a function of pressure up to 30 GPa.
Figure 5. (a)The evolution process during compression, (b) is the gray area in (a), and (c)the positions of these three modes (B3g, B3g and B1g) as a function of pressure up to 30 GPa.
Preprints 76370 g005
Preprints 76370 g006
Figure 6. The process of merging first and then separating of B3g and B1g modes with pressure from 30 GPa to 126 GPa.
Figure 6. The process of merging first and then separating of B3g and B1g modes with pressure from 30 GPa to 126 GPa.
Preprints 76370 g006
Preprints 76370 g007
Figure 7. The relationship between the displacements of these two modes (B3g and B1g) with pressure from 30 GPa to 126 GPa. The green, pink and blue areas are the pressure ranges where the two peaks begin to merge, have been merged and finally begin to separate respectively.
Figure 7. The relationship between the displacements of these two modes (B3g and B1g) with pressure from 30 GPa to 126 GPa. The green, pink and blue areas are the pressure ranges where the two peaks begin to merge, have been merged and finally begin to separate respectively.
Preprints 76370 g007
Preprints 76370 g008
Figure 8. (a) Raman spectra taken at pressures and (b) positions as a function of pressure of BP and Ag modes from 58.5 GPa to 91 GPa.
Figure 8. (a) Raman spectra taken at pressures and (b) positions as a function of pressure of BP and Ag modes from 58.5 GPa to 91 GPa.
Preprints 76370 g008
Preprints 76370 g009
Figure 9. The tilts of the B12 icosahedron around the c-axis (a) and a-axis (c), which respond to the B1g and B3g mode respectively. (b) displays the four-atom system.
Figure 9. The tilts of the B12 icosahedron around the c-axis (a) and a-axis (c), which respond to the B1g and B3g mode respectively. (b) displays the four-atom system.
Preprints 76370 g009
Preprints 76370 g010
Figure 10. The (a)bond length R and r, bond angle 𝜙, and (b)force constants varies as functions of pressure. (c)Comparison of the calculated Raman mode and the experimental Ag mode.
Figure 10. The (a)bond length R and r, bond angle 𝜙, and (b)force constants varies as functions of pressure. (c)Comparison of the calculated Raman mode and the experimental Ag mode.
Preprints 76370 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated