Prerpints.org logo
Preprint
Article

Insuring Alpine Grasslands Against Drought-Related Yield Losses by Sentinel-2 Satellite Data

Altmetrics

Downloads

128

Views

88

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.pdf (1.73MB )

Submitted:

13 June 2023

Posted:

14 June 2023

You are already at the latest version

Alerts
Abstract
This work estimates yield losses due to drought events in mountain grasslands in north-eastern Italy, laying the groundwork for index-based insurance. Given the high correlation between Leaf Area Index (LAI) and grassland yield, we exploit LAI as a proxy for yield. We estimate LAI by the Sentinel-2 biophysical processor and we compare different gap-filling methods, including time-series interpolation and fusion with Sentinel-1 SAR data. We derive a Forage Production Index (FPI) as the growing season cumulate of the daily product between LAI and a meteorological water stress coefficient. Finally, we calculate the drought index as the anomaly of FPI. The validation of Sentinel-2 LAI with ground measurements showed RMSE of 0.92 [m2 m-2] and R2 of 0.81, on average over all the measurement sites. The comparison between FPI and yield showed R2 of 0.56 at the pixel scale and R2 of 0.74 at the parcel scale. The developed prototype FPI index was used at the end of the growing season of the year 2022 for calculating the payments of an experimental insurance scheme that was proposed to a group of farmers in Trentino-South Tyrol.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Mountain grasslands in the European Alps have an important economic function because they are the major source of forage for livestock farming, and a place of recreation for tourism [1,2]. In addition, they play a crucial role in climate regulation, biodiversity safeguarding, landscape conservation, soil quality preservation, and soil stabilization and protection from erosion [3,4,5].
Alpine grasslands are more exposed to climate change compared to other parts or Europe [2,6,7,8]. Despite water being abundant in the past in the Alps, its scarcity has started to raise concerns because droughts events are becoming more and more frequent [9,10,11,12], altering mainly grassland productivity [13], and thus endangering income stability for mountain farmers. According to climate observations, mean annual temperature in the Alps has increased of about 1.8° C from 1880, which is almost twice the mean global warming, with a strong acceleration over the recent decades [14,15]. Regional climate projections predict a further temperature increase by the end of the 21st century up to +4 °C with respect to 1981-2010 under the worst-case emission scenario [15,16]. Precipitation, in contrast, is predicted to decrease in summer, especially in the southern Alps, and increase in winter during the 21st century [15].
These changes in climate will not only cause changes in the species composition and warming-related upward shifts of many grasses’ communities [17], but will also affect the productivity of grasslands [18] and its predictability, with more economic instability and possible losses for the farmers [19]. This is especially likely in case of combined extreme events, like drought and heat waves [20]. Accordingly, it is urgent to plan the necessary strategies and adaptation pathways.
Risk management instruments, like insurances, can help grassland-based mountain agricultural systems to overcome production shortcomings, and thus increase their economic robustness and resilience, prevent land abandonment, and maintain their functioning over time. Traditional insurance schemes, the so-called indemnity insurance, require physical inspections by insurance appraisers to assess damages, but this approach is not economically sustainable for grassland due to its high cost compared to the low value of the production. In addition, it is difficult to obtain reliable site-specific reference values of the expected normal yield to estimate forage losses, because the yield of a specific year depends on the management (e.g., fertilization, cut frequency), which could differ from that of the previous years. Furthermore, damage evaluations based on physical inspections are subjective as they depend on expert's experience and can lead to unfair assessments. Index-based insurances are not exposed to these issues because payoffs depend on an index related to grassland production that does not require physical checks and provides site-specific reference values for yield over time. In this context, freely available high-resolution satellite data from the Sentinel constellations of the Copernicus Program allow the development of accurate and low-cost tools to support risk management. Despite some high-resolution large-scale products are now freely available, for example from the Copernicus Land Monitoring Service [21], they lack the co-design with stakeholders, adaptation of processing chains to the local conditions, including land use, topography, and meteorology, and near-real-time production and dissemination, which are crucial to facilitate the exploitation of satellite-based products for agricultural insurance.
It is worthwhile mentioning that index insurances based on satellite data are subject to basis risk [22] due to the possible discrepancy between the index-derived payout and actual losses. Basis risk could hinder the attractiveness of these new insurance schemes for the farmers or the insuring companies. One important challenge to minimize the basis risk associated to index insurances is a proper selection of the parameters which are related to drought occurrence and drought impact. Currently operational index insurances for pasture and rangeland use as parameter for estimating yield losses greenness indices, like the Normalized Difference Vegetation Index (NDVI) [23,24], or meteorological drought indices derived from weather station data [25,26]. These parameters present some criticalities. As to NDVI, it can be affected by soil effects, geometry of illumination, and atmospheric conditions. Furthermore, it is subjected to saturation under high production values. As to weather station data, they often lack the spatial density that is needed to correctly represent extreme weather conditions, like drought. In addition, the impact of meteorological drought conditions on yield depends on land management, topography, and soil type.
In this work we develop an index of grassland production (Forage Production Index, FPI) based on leaf area index (LAI), a biophysical parameter which is directly related to grassland yield. In the formulation of the FPI, we include a coefficient of water stress derived from gridded meteorological data at high spatial resolution. The aim is to lay the foundation for an index-based insurance for mountain grasslands, in which the insurance payments depend on yield losses estimated from the FPI anomalies at parcel scale. One noteworthy part of the work is the involvement of the local agricultural stakeholders in the design of the index.
To verify that S2 LAI is a reliable parameter for the derivation of an index-based insurance, we perform a systematic validation of LAI and an evaluation of the derived FPI. To this aim, we collect ground measurements of LAI and yield at selected plots within grassland farms which are representative of the target of the new insurance scheme under development.
We assume that LAI is a valid parameter for estimating the impact of drought on grassland productivity, considering the high correlation that we observed between LAI and yield, and the simple retrieval algorithms, compared to other variables related to the carbon and water cycle, like biomass and evapotranspiration. LAI can be estimated from Sentinel-2A/B (S2) multispectral data at a spatial resolution up to 10 m. This resolution allows a proper characterization of the management practices and of the vegetation conditions within the single parcels [27,28,29,30].
On the other side, LAI from S2 might not be sufficient to characterize the temporal evolution of vegetation, because there is an overpass of S2 every 5 days, and because within each acquisition entire images or portions of them can be unusable due to the presence of clouds. It is thus necessary to implement gap-filling methods to increase the frequency of available LAI estimates [31,32]. Here, we investigate three gap-filling strategies:
  • LAI temporal interpolation at pixel level by linear interpolation between two S2 overpasses,
  • LAI timeseries spatial-temporal interpolation, which exploits the spatial and temporal correlation of close LAI values to derive an estimate of missing values, providing at the same time a unique aggregated estimate for the parcel of interest,
  • LAI timeseries enrichment by Synthetic Aperture Radar (SAR) data from Sentinel-1A/B (S1), based on the SAR data sensitivity to vegetation structural changes.
The first two interpolation techniques, without the addition of other ancillary data, are easy to implement and computationally light, and thus worth to test in view of an operationalization of the method to derive the FPI, while the enrichment of S2 LAI by S1 SAR is preliminarily tested here to start to design a future enhanced version of the FPI.
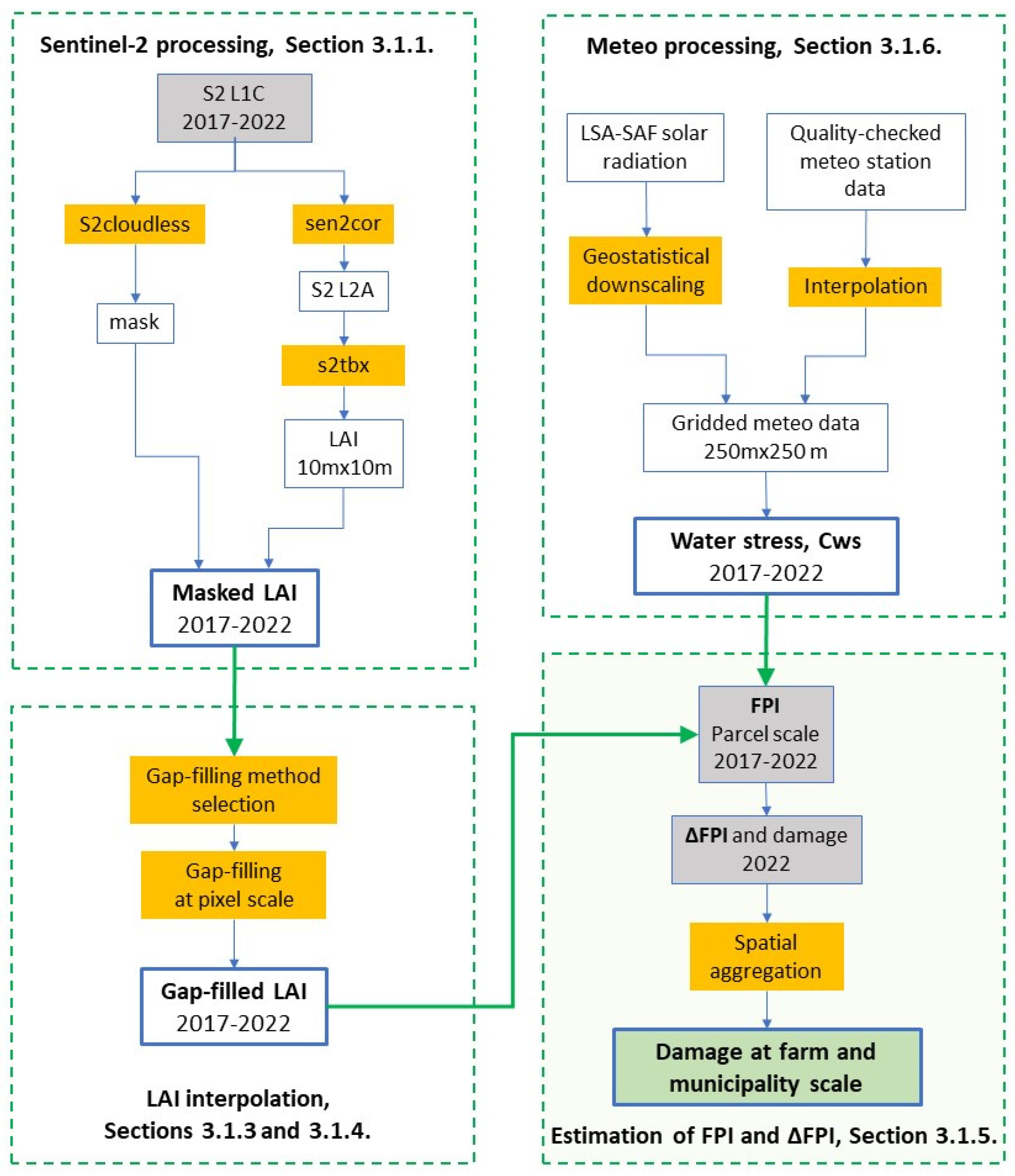
After providing a description of the study area and of the ground data collection (Section 2), we summarize the methods used to derive the FPI and its anomalies (Section 3.1.), and to evaluate LAI and FPI against ground measurements of LAI and yield (Section 3.2.). In Section 3.3. we describe the experiment of fusion between S1 SAR and S2 optical data. The results of the comparison between in situ LAI and yield (Section 4.1.) and the validation of S2 LAI (Section 4.2.) support the choice of LAI as a proxy of grassland productivity, while the comparison between different LAI interpolation techniques (Section 4.3.) justifies the choice of the method adopted in the first version of the FPI. The comparison between FPI and yield measurements helps to identify the main factors affecting the ability of FPI to predict yield variations (Section 4.4.). Yield losses estimated for the year 2022 from FPI anomalies are summarized in Section 4.5. The preliminary results of the S1-S2 data fusion (Section 4.6.) set the basis for the future enhancement of the FPI. Strengths and limitations of the proposed index are discussed in Section 5.

2. Study Area and Ground Data Collection

2.1. Study Area

The region Trentino-South Tyrol, including the autonomous provinces of Trento and Bolzano/Bozen, is located in north-eastern Italy and covers an area of 13605 km2. Its mountainous territory, covering a large portion of the Dolomites and southern Alps, is characterized by a strong topographic complexity. Its climate is highly variable, being influenced by humid air masses from the Atlantic, dry air masses from the continental east, and warm air from the Mediterranean region [33], and is characterized by cold and humid winters, and warm and dry summers.
20.83% of the area of South Tyrol is covered by agricultural areas [34], 70.02% of which is covered by grasslands [35]. Similarly, 15.32% of the area of the Trentino is used as agricultural area [34], 83.06% of which consists in meadows and pastures [35].
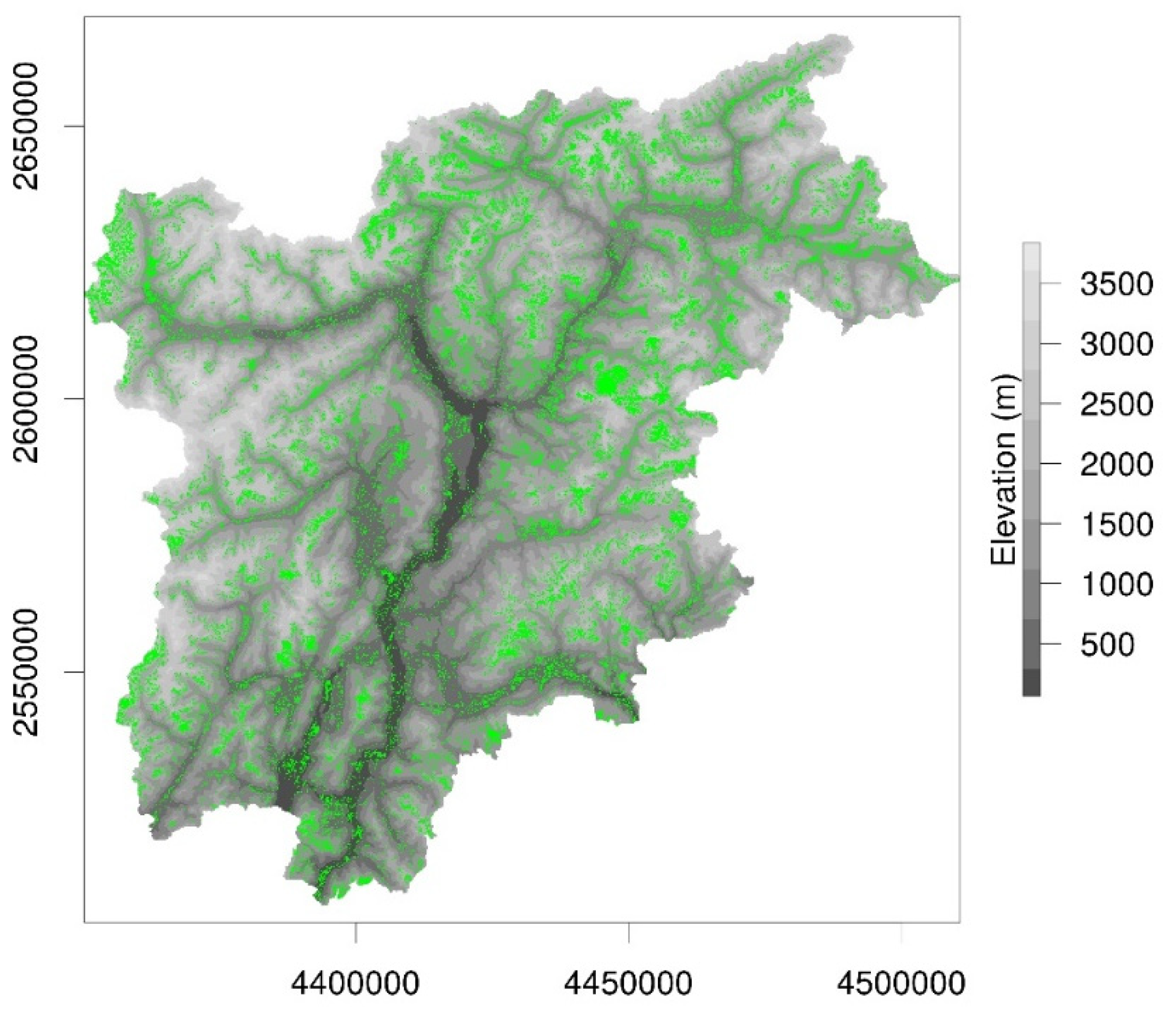
The index-based insurance which is the target of the present study is potentially applicable to all the meadows primarily aimed at forage production and natural pastures, which cover around 1870 km2 (Figure 1). The management intensity of meadows in this region mostly ranges between one and four cuts per year. They are mainly fertilized with organic manures (farmyard manure combined with manure effluent, slurry and biogas slurry). The botanical composition varies according to the site characteristics and to the management intensity [36,37].

2.2. Ground Data Collection

The main criteria for test site selection were i) to be representative of the most frequent situations in the local agriculture being the subject of the new insurance system, ii) to minimize logistic efforts for sampling, and iii) to guarantee a good reliability of the communication with the farm owners.
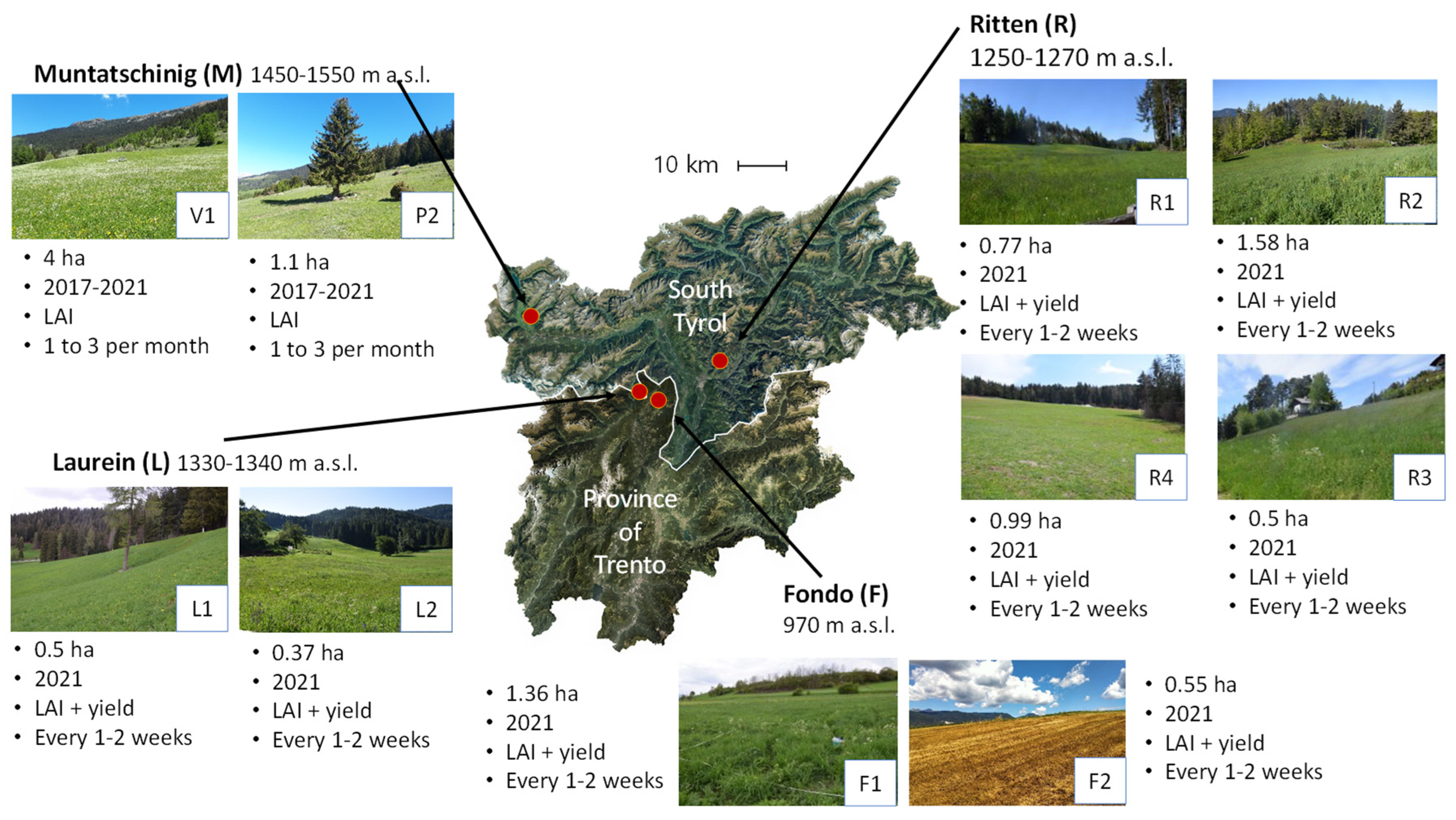
The chosen test sites are eight differently managed meadows at four farms located in three different municipalities: Ritten (R), Laurein (L) and Fondo (F) (Figure 2, Table 1). They cover an elevation range of about 600 m (970 to 1550 m a.s.l.), have a cut frequency of two to four cuts per year, with additional grazing of the last regrowth and total N-inputs ranging between 112 and 189 kg ha-1 year-1, exclusively provided by means of organic manures. Information about the botanical composition was obtained prior to the first cut by means of visual estimates of the yield proportion [40] of species and of the functional groups of grasses (including also graminoids), legumes and forbs in two sampling areas of 5x5 m in each meadow (mean values are reported). The investigated parcels are extremely to quite poor in species (9 to 19 species), except for L1 and L2 (27 and 24 species respectively). All meadows are rich in grasses (69 to 99% yield proportion), with dominant species being typical of intensive management like Alopecurus pratensis, Dactylis glomerata, Lolium perenne and Elymus repens (see Table S1).
The sampling campaign started on the 9th of April 2021 and continued until the 29th of October 2021. At each sampling event and for each sampling site, four plots corresponding to different pixels of the S2 grid were sampled. In each plot three LAI measurements were collected by LAI 2200C [39] as five replicates per LAI measurement, and one grass sample was taken by means of electric scissors within a metal frame of 0.25 m2 at a stubble height of 4-5 cm, in order to obtain a realistic estimate of the forage yield. The samples were dried at 60°C until weight constancy and weighted to determine the dry matter yield. In addition, complementary visual assessments were taken of lodging (estimated on a four-level-scale: no lodging, light lodging, medium lodging, heavy lodging).
Samples were collected every two weeks for the first growth cycle until begin of stem elongation and then once per week until the first cut, taking care to perform the last measurement as close as possible to the mowing event. For the regrowth, sampling occurred about every two weeks, taking care also in this case to perform the last measurement as close as possible to the mowing event. Over the whole 2021 field campaign season, 1615 LAI measurements and 558 yield samples were taken.
In addition to the field campaigns described above, a further dataset was used for LAI validation, including timeseries of LAI collected at the long-term socio-ecological research site installed by Institute for Alpine Environment of Eurac Research at Muntatschinig, in the Vinschgau valley in the Autonomous Province of Bolzano/Bozen (Muntatschinig site, Figure 2 and Table 1). At this site, a meadow (V1) and a pasture (P2) parcels were sampled from 2017 to 2021 throughout the vegetation-growing season. Having multiannual observations of biophysical variables is important to understand the dynamics of vegetation growth for two sites with very different management forms [40,41]. The meadow is mown twice a year (end of June, begin of September) and its dominant species is Trisetum flavescens. The pasture is lightly grazed by livestock from mid-June to mid-October and its dominant species is Festuca valesiaca. At each measurement event three replicates of LAI measurements were acquired by LAI2200C at three to five plots corresponding to different pixels of the S2 grid. The sampling campaign over the whole period resulted in 910 LAI measurements.

3. Methods

3.1. Estimation of Yield Losses for the Year 2022

3.1.1. Estimation of LAI from S2

LAI was estimated by the S2 Toolbox Biophysical processor (s2tbx) [42] for the years 2017-2022 (Figure 3). S2 imagery was preprocesses to L2A by Sen2Cor [43], and specific revisions to the processing chain were implemented to adapt the retrieval to the high heterogeneity of the alpine environment. In particular:
  • S2 L2 reflectance 20 m imagery was resampled to 10 m spatial resolution, to fully exploit the highest spatial resolution available from the MSI sensor and maintain at the same time the full spectral information required by the LAI biophysical processor to perform robust estimates. A preliminary comparison with ground measurements motivated this choice, as it showed that using only the 10 m bands, as in [44], performs worse over our study area.
  • An additional cloud mask layer was generated by sen2cloudless [45] and integrated, together with LAI Biophysical processor quality flags, in the LAI maps masking process, to minimize the occurrence of bad quality LAI values and their impact on the final drought index calculation.

3.1.2. Gaussian Process Regression (GPR) Models

GPR models were explored to interpolate cloudy LAI retrievals at parcel level (section 3.1.3.), and to enrich S2 LAI timeseries with S1 SAR imagery (section 3.3.). GPR models [46] allow non-parametric regression and function approximation, also providing an estimation of the uncertainty in the prediction. In recent years, GPR models have been often used to estimate biophysical parameters from optical and radar remote sensing data [31,47,48,49]. Hereafter follows a short summary of how GPR models can be used for solving regression problems, while a complete mathematical description can be found in [46].
Given a training set D of N observations, with D = x i ,     y i   i = 1 ,   … , N } , where x is an input vector, and y is an output scalar, the purpose is to estimate a function that is able to predict y for new inputs, x * , for which there are no observations. To estimate this function, GPR uses a Bayesian approach. f ( x ) is assumed to be a Gaussian-distributed random vector with zero mean and covariance matrix K ( x , x ) , f x = N ( 0 ,   K ) . The elements of the covariance matrix are calculated by a kernel function [46], k ( x i , x j ) , which describes the similarity between vectors x i and x j . According to the Bayes’ theorem, the posterior distribution of f   at the test point x * , conditioned on training data and hyperparameters, can be expressed as:
p y * x * , D = N ( y * | μ G P x * , σ G P 2 x * )
with predictive mean and predictive variance given by:
f x * = μ G P x * = k * T K + σ n 2   I N   y σ f 2 x * = σ G P 2 x * = k x * ,   x * + σ n 2 − k * T K + σ n 2   I N − 1 k *
where k * = [ k x * ,   x 1 ,   … ,   k x * ,   x N ]T contains the similarities between the test point and the training points, K is the N × N kernel covariance matrix containing the similarities between the training points, y = [ y 1 , … , y N ] T, k x * ,   x * is a scalar with the self-similarity of x * , and σ n 2 is a hyperparameter describing noise variance. The covariance function has an associated set of hyperparameters which are estimated during the model training phase, by maximizing the marginal likelihood of the model.

3.1.3. Interpolation of S2 LAI at Pixel and Parcel Level

The simplest gap-filling method that was tested is the linear interpolation of LAI for each S2 MSI pixel. As an alternative to pixel-based gap-filling, two spatial-temporal interpolation techniques were assessed to exploit all the information available for each parcel while minimizing the data storage:
  • Parcel-based linear interpolation, which consists in extrapolating the mean values from the good quality pixels within a given parcel followed by a linear interpolation between two subsequent dates. The interpolated LAI values can thus be easily computed from the parcel specific linear functions at the desired temporal sampling interval. This approach is appealing due to its simplicity and fast interpretability. At the same time, it could be affected by noisy data or large temporal gaps between the available input LAI maps. The average LAI for a parcel p at the time ti, when there is no observation available, is estimated as:
    L A I p , t i = L A I p , t 1 + t i − t 1 t 2 − t 1 ( L A I p , t 2 − L A I p , t 1 )
  • Where L A I p ,   t 1 and L A I p ,   t 2 are the average values of LAI over the parcel at time t1 and t2, before and after ti.
  • Non-parametric non-linear interpolation, based on the use of GPR models to infer the most suitable continuous function from available timeseries data. In this case, the output model is not constrained to a given set of points as in the case of the linear method, thus possibly limiting the effect of noisy data. According to this method, the mean and variance of the function estimating LAI for a parcel at the time t * , when there is no S2 imagery available, are estimated as:
    f t * = k t * T K t + σ n t 2 I N t − 1 y σ f 2 t * = k t * ,   t * + σ n 2 − k t * T K t + σ n 2   I N − 1 k t *
  • where k t * = [ k t * ,   t 1 ,   … ,   k t * ,   t N ] T is the array of the similarities of the test point t * with the training points, K t is the covariance matrix with the similarities between the training points, y is the LAI timeseries derived from S2, and σ n t 2 is the variance of the timeseries additive noise. The covariance matrix K t is calculated by the Matern 3/2 kernel function [46,50]:
    K t = σ s t 2 1 + 3 ( t J 1 , N t − J N t , 1 t T ) σ t e x p − 3 ( t J 1 , N t − J N t , 1 t T ) σ t
  • with σ t the length scale along the time dimension, and σ s t 2 the timeseries signal variance.

3.1.4. Filling Missing LAI Values at the Beginning and End of the Growing Season

A further gap-filling technique was applied in all those instances showing LAI gaps at the head and tail of the time-series. That is, for those pixels or parcels where the time-series showed missing values at the beginning and end of the growing season. Such situations prevented from linearly gap-filling the values at the extremes of the growing season as there were no LAI values available to be used for the interpolation. An Extreme Gradient Boosting (XGB) regression model [51] was trained to predict any missing LAI value within the first 15 days and the last 15 days of the growing season. Elevation, daily mean temperature, month, and year were considered as predictors. After performing Bayesian Optimization hyperparameter fine-tuning [52], LAI was estimated with an average RMSE of 0.33 [m2 m-2], assessed by a 5-fold cross validation.

3.1.5. Estimation of the FPI and of Its Anomalies

Based on the daily LAI gap-filled by pixel-based linear interpolation, FPI was calculated as in [53], as the growing season cumulate of the daily product between LAI and a Coefficient of Water Stress, C w s :
F P I n = ∑ i = S O S i = E O S ( L A I g r a s s l a n d i × C w s i )
where C w s is defined as in Section 3.1.6. The start (SOS) and end (EOS) of the growing season were assumed to correspond to the 1st of April and the 31st of October, or to vary with elevation (Table 2). This corresponds to the specifications of the insurance system currently implemented in Trentino-South Tyrol and was determined by the agricultural consortia based on knowledge of the local agricultural practices. In this way, the insurance systems aim at accounting for the reduction of the growing season length occurring with increasing altitude [2].
Finally, the drought index was calculated as the anomaly of the FPI based on the preceding five years [54]:
∆ F P I n = F P I n O l y m p i c a v e r a g e ( F P I n − 1 ; … ; F P I n − 5 )
Based on the indications of the agricultural consortia, and on the conditions for the facilitation of the insurance policy [55], the final drought index that is used to estimate yield losses and insurance payments was averaged among the parcels with the same land use and belonging to the same farm and municipality. This reduces the risk of conflicts due to unequal payments within the same administrative unit. Furthermore, this spatial aggregation procedure excludes from FPI calculation polygons with low availability of high-quality S2 data which could prevent a robust gap-filling.

3.1.6. Estimation of the Meteorological Coefficient of Water Stress

The motivation behind including a meteorological water stress coefficient derives from [53] who tested different FPI formulations and demonstrated that the water stress coefficient significantly improved the performances of the index. Those results were based on the application of moderate resolution satellite data over homogeneous grasslands in France, thus their validity over our heterogeneous Alpine study area is to be verified.
C w s is defined as:
C w s = 0.5 + 0.5   A W
where A W is the available water, i.e., the ratio between cumulated precipitation, P, and potential evapotranspiration E T 0 over a certain time interval. Daily C w s was computed considering a running window of 30 days over which daily values of P and E T 0 were cumulated. A W was set to 1 when P exceeded E T 0 so that C w s can only vary between 0.5, when the water shortage is maximum, and 1, when no water stress conditions occur.
C w s was computed on a 250-m resolution grid covering Trentino-South Tyrol from the year 2004 to the year 2021. E T 0 was estimated by means of the Jensen-Haise equation [56], based on mean temperature T (°C) and solar radiation Rs (MJ m-2):
E T 0 = 0.025 T + 0.078 0.408 R s
Daily time series of T and P were derived from the 250-m gridded dataset obtained by interpolating the quality-checked and homogenized database of station observations of the regional meteorological networks [57].
Daily Rs grids at 250 m resolution were derived by applying a geostatistical downscaling to the daily Downward Surface Shortwave Flux (DSSF) product available on the LSA-SAF system (https://landsaf.ipma.pt). In particular, the sharpening of daily DSSF was performed by Regression Kriging (RK) based on elevation, slope steepness and its orientation [58].

3.2. Evaluation of LAI and FPI as Proxies for Forage Yield

The measurement campaigns described in Section 2.2 were specifically designed to cover the spatial heterogeneity of the study area and the temporal variability of LAI and yield, and were used for the following analyses:
  • To verify whether LAI is a good proxy for grassland yield in our study area, we compared ground measurements of LAI and yield by regression analysis, also considering the effect of lodging.
  • To evaluate the accuracy of S2 LAI, we validated it against ground measurements of LAI.
  • We compared the performances of different interpolation methods against parcel scale LAI measurements.
  • We evaluated FPI against yield measurements.

3.2.1. S2 LAI Validation

The S2 LAI dataset was compared with ground observations of LAI by means of Mean Absolute Error (MAE), Mean Bias (MB), Root Mean Squared Error (RMSE), and coefficient of determination (R²), with MAE, MB, and RMSE calculated as follows:
M A E = 1 N ∑ i = 1 N Y i − X i
M B = 1 N ∑ i = 1 N Y i − X i
R M S E = ∑ i = 1 N Y i − X i 2 N
where Xi and Yi are the observed and estimated LAI at the ith time step, where the estimated LAI consists in the original retrievals, before the gap-filling.
A 5 m buffer was applied to select the pixels corresponding to each sampled plot, to account for the absolute geolocation uncertainty of S2 and of the handheld Global Navigation Satellite System (GNSS) used during the field campaigns. The standard deviation and weighted predicted mean for each plot were calculated based on the pixels intersecting the buffer.

3.2.2. Relationship of Daily S2 LAI and FPI with Physical Yield Measurements

The relationship between remote sensing-estimates of LAI or FPI with ground measurements of forage yield was performed by ANOVA using different subsets of data, depending on i) the LAI interpolation method, ii) the use of LAI or FPI, being the daily value of LAI corrected by means of Cws, iii) the use of remote-sensing estimates obtained at S2-pixel or parcel scale with the respective yield measurements (single measurements obtained within a single S2-pixel or their mean at parcel level), iv) the use of the exact yield sampling date or a conventional date of two days before as reference date for extracting LAI or FPI. This aims at preventing large discrepancies between LAI/FPI and yield due to satellite overpass occurring on the mowing date with the cut being performed after yield sampling and before the satellite overpass, v) the inclusion or exclusion of the ground measurements performed just before or after the mowing dates. The analysis was performed for each possible combination of the levels of these factors. Adjusted R² was used to assess the fit of each model. The effect of these factors on R² was separately analyzed for each factor by means of linear mixed models accounting also for the paired observations given by the combination of the levels of all other factors and differing only by the level of the factor in question, which were considered to be repeated measurements. The covariance structure was adjusted using the Akaike Information criteria as an indicator of model fit. The most suitable interpolation method (factor i) was identified first, and then all remaining analysis (factors ii to v) were performed with the values obtained by this interpolation method.

3.3. Pilot Experiment of S2 LAI Time Series Enrichment by S1 SAR Data

SAR data are not affected by cloud coverage; therefore, they can be used to reduce the time gap between two subsequent LAI estimates. SAR imagery is influenced by many factors, including vegetation water content, undercover soil moisture, and terrain roughness, and can thus be difficult to interpret, especially over grasslands [31,32]. Consequently, the relationship between SAR data and the target biophysical parameter is strongly nonlinear and depends on external ancillary information. To overcome these issues, here nonlinear machine learning regression was exploited. The rationale behind such techniques is the inference of a generic non-parametric and potentially non-linear relationship between the input features (the SAR signal and possibly ancillary data) and the output target variable (LAI) exploiting a set of representative training examples. In particular, the use of the GPR technique was investigated, because of its good generalization ability also when the number of available training data is limited, and the promising performance achieved in similar application contexts [32,33].

3.3.1. S1 Data Preprocessing

S1 SAR imagery time series consists of 34 scenes acquired over the Muntatschinig test site (relative orbit 168) in the period April 2017 - October 2017. This interval of time was chosen based on the availability of ready-to-use soil moisture data derived from S1, which are needed to perform the experiments described in Section 3.3.2. Only the descending pass direction was used because the ascending orbit was affected by layover effects over the study area and thus was not usable. S1 images were downloaded from the Copernicus Open Access Hub as Level 1 Interferometric Wide Swath Ground Range Detected (GRD) High Resolution mode, VV+VH dual polarization mode. Level 1 GRD consists of focused SAR data that have been detected, multi-looked and projected to ground range using an Earth ellipsoid model. Pixel spacing is 10x10 m in High Resolution mode. An additional preprocessing of S1 VH and VV bands was performed by the SNAP S1 toolbox [46], consisting in spatial speckle filtering with a 7x7 pixel window Lee-Sigma spatial filter, bad acquisition pixel masking by means of extreme low and high backscattering values exclusion according to a statistic performed over the test area, and co-registering with S2 LAI timeseries. Finally, for each S1 acquisition, two indices representative of the sensitivity of SAR backscattering to vegetation development were generated, including the VH/VV simple ratio and the dual-pol Radar Vegetation Index [47] (RVI), calculated as:
R V I = 4 V H V H + V V

3.3.2. S1 and S2 Data Fusion by GPR

A pilot assessment of GPR to fuse S1 and S2 timeseries data was performed, to enrich the LAI timeseries retrieved from S2 optical data with S1 SAR data. This test was performed for the growing season of the year 2017 over a subset of the study area including 118 parcels (Figure S2, Table 3). The temporal extent is based on the availability of ready-to-use input features, while the spatial extent includes samples of all land uses where the proposed drought index in Trentino-South Tyrol is potentially applicable.
The target variable was LAI derived from S2. As input features, different combinations of the following variables were considered, which were normalized by scaling between 0 and 1:
  • VV and VH polarization bands from the S1 dual polarization StrimMap product,
  • Simple ratio and RVI, which have proven to enhance the sensitivity of SAR data to the vegetation characteristics [59,60,61],
  • Soil moisture content maps (SM), produced by Eurac Research from S1 imagery [62], with the aim to provide an information on the soil water content status to the regression algorithm to help disentangling the intrinsic ambiguity of SAR data,
  • Day of year (DOY).
The selection of the input features was performed based on a 5-fold cross validation, testing all possible combinations of input features across the 118 parcels.
The training of the GPR model, consisting in the optimization of the hyperparameters through maximization of the marginal likelihood, was performed at different scales: a) land use specific, and b) parcel specific. The trained models were used to estimate LAI and its uncertainty from the selected input features at the test point x * ∈ R D , where D is the number of input features. For this application, the squared exponential covariance function was used [46]:
k x i , x j = σ f 2 e x p − 1 2 ( x i − x j ) T ( x i − x j ) σ l 2
where σ f 2 is the signal variance and σ l is the scale length.
After the feature selection, two different experiments were performed, i.e., “spatial sampling”, to verify the ability of the GPR model to predict missing pixels values due to cloudiness, and “temporal sampling”, to verify the ability of the GPR model to predict pixels values on missing acquisition dates. In the first case, 30%, 50%, or 70% of randomly selected pixels within each S1 acquisition date were excluded from the training set and used as test set. In the “temporal sampling” experiment, 3, 6, or 9 acquisition dates within the entire growing season were excluded from the training set and used as test set. Both experiments were performed on the individual parcels and on clusters of parcels with the same land cover type. To avoid biased results, the random sampling was performed 5 times, then the GPR model performances were averaged.

4. Results

4.1. Comparison between Ground Measurements of LAI and Yield

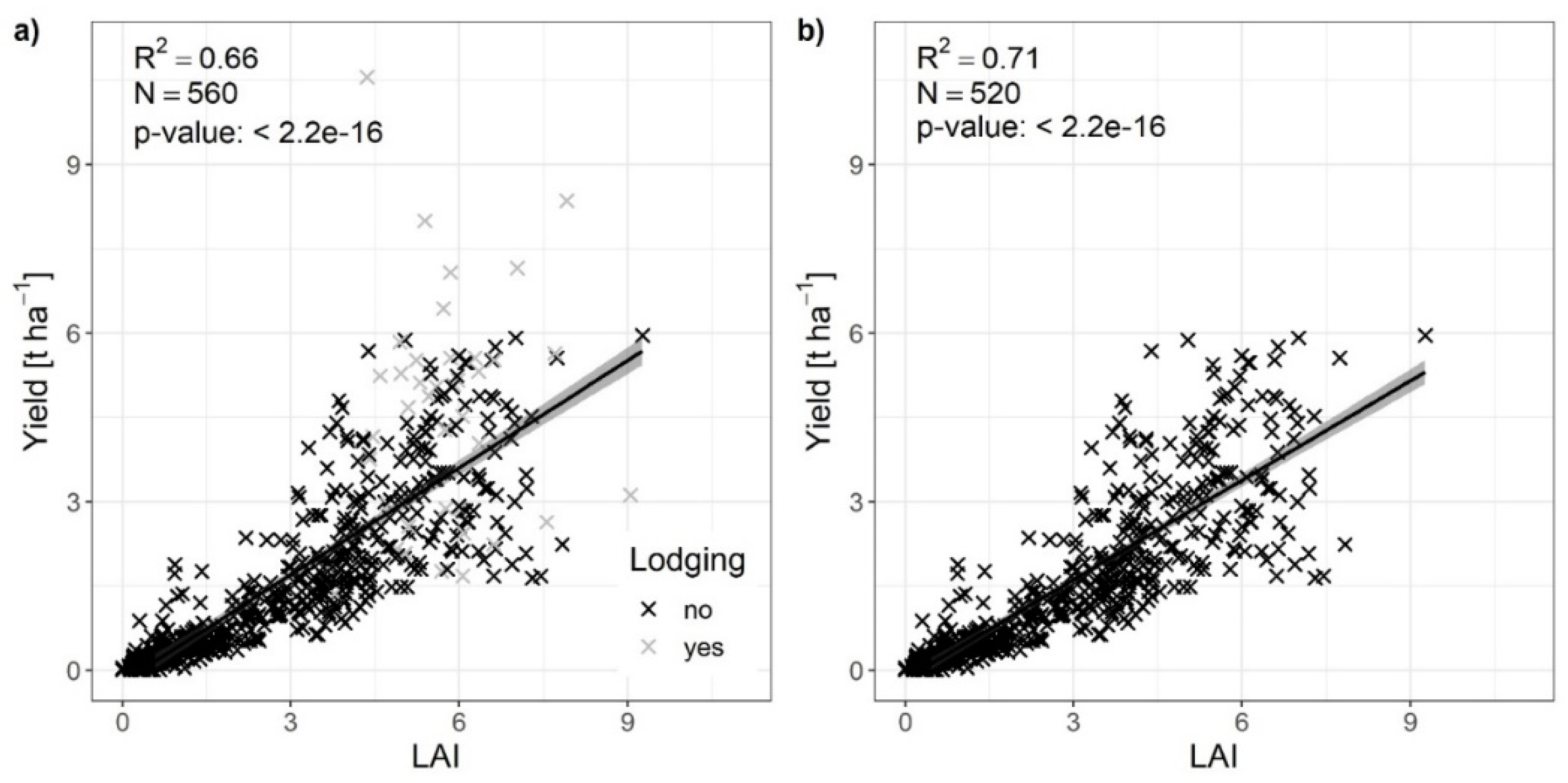
As first part of the FPI assessment, we verified the relationship between LAI, which is the variable selected for the calculation of the index, and yield, which is the target variable, for the year 2021, when ground measurements of both variables were collected (Table 1). Based on all the available observations, an R² = 0.66 between ground measurements of LAI and yield was found. LAI tends to increase faster than yield for low yield values, with an overestimation of lower yield values (Figure 4), and most of the strongly underestimated yield values are observations affected by medium or heavy lodging of the vegetation at the time of the measurement (Figure 4a). Indeed, dropping these observations (40 cases, 20 of which were affected by heavy lodging) from the investigated dataset resulted in an improvement of R² to 0.71 with a slight reduction of the slope and of its standard error from 0.64 ± 0.020 to 0.59 ± 0.017 (Figure 4b).

4.2. Validation of LAI Derived from S2

As a second part of the FPI assessment, we verified the performance of the LAI estimated from satellite imagery against ground measurements of LAI performed in the year 2021 over four sites, and in the years 2017-2021 over one sites (Table 1). S2 LAI showed a R2 between 0.48 and 0.88 and RMSE between 0.71 and 1.2 [m2 m-2] with respect to ground measurements of LAI for all the monitored meadows (Table 4). Only at the pasture site P2 the performances were worse (Table 4), with R2 = 0.12. 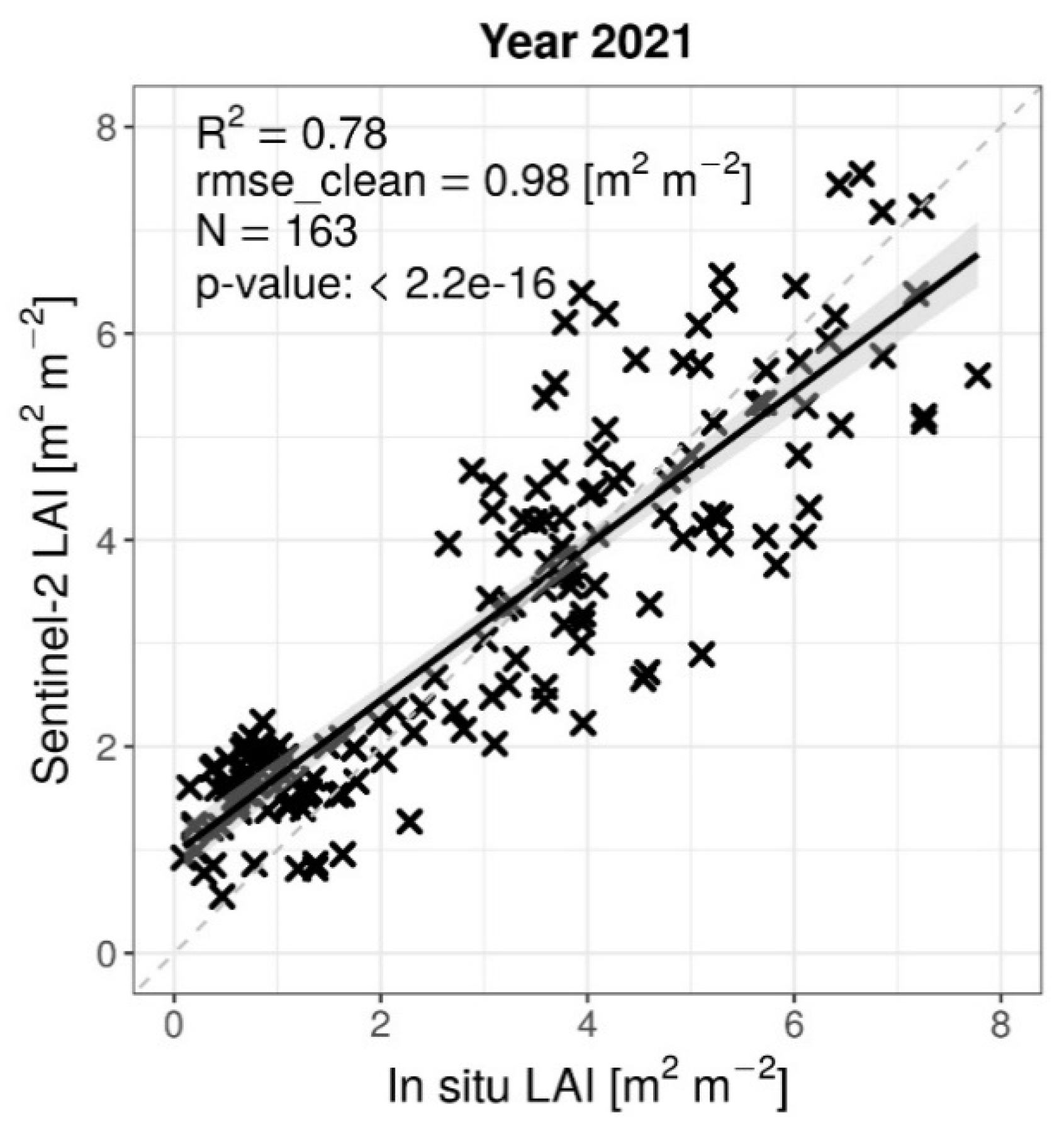A tendency to overestimate low LAI values is observable (Figure 5 and Figure 6). In the year 2021 (Figure 5), R2 = 0.78 and RMSE = 0.98 [m2 m-2], based on measurements from all the sites. 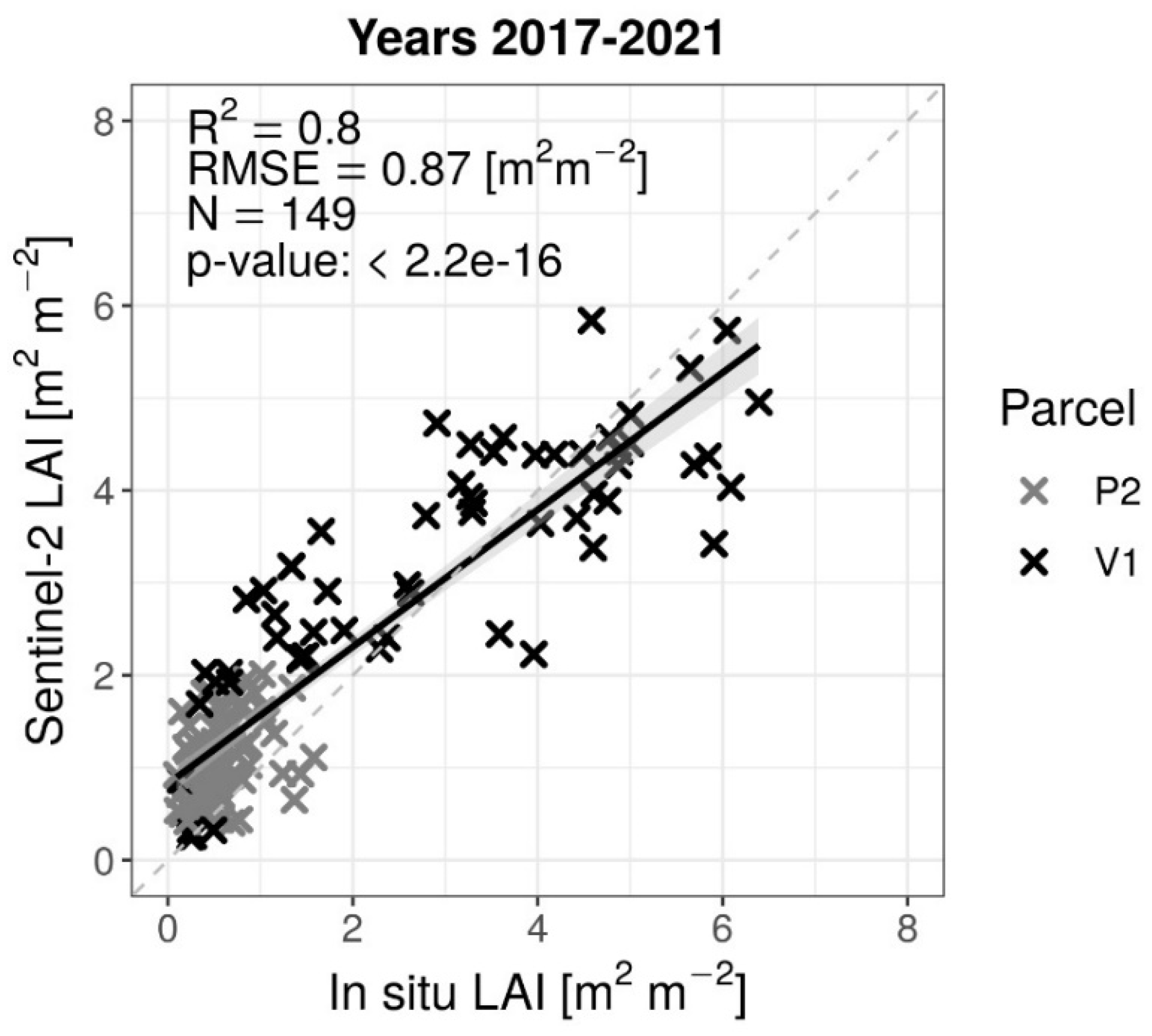In the period 2017-2021 (Figure 6), R2 = 0.80 and RMSE = 0.87 [m2 m-2], based on measurements from the two Muntatschinig parcels.

4.3. Assessment of Three LAI Interpolation Methods

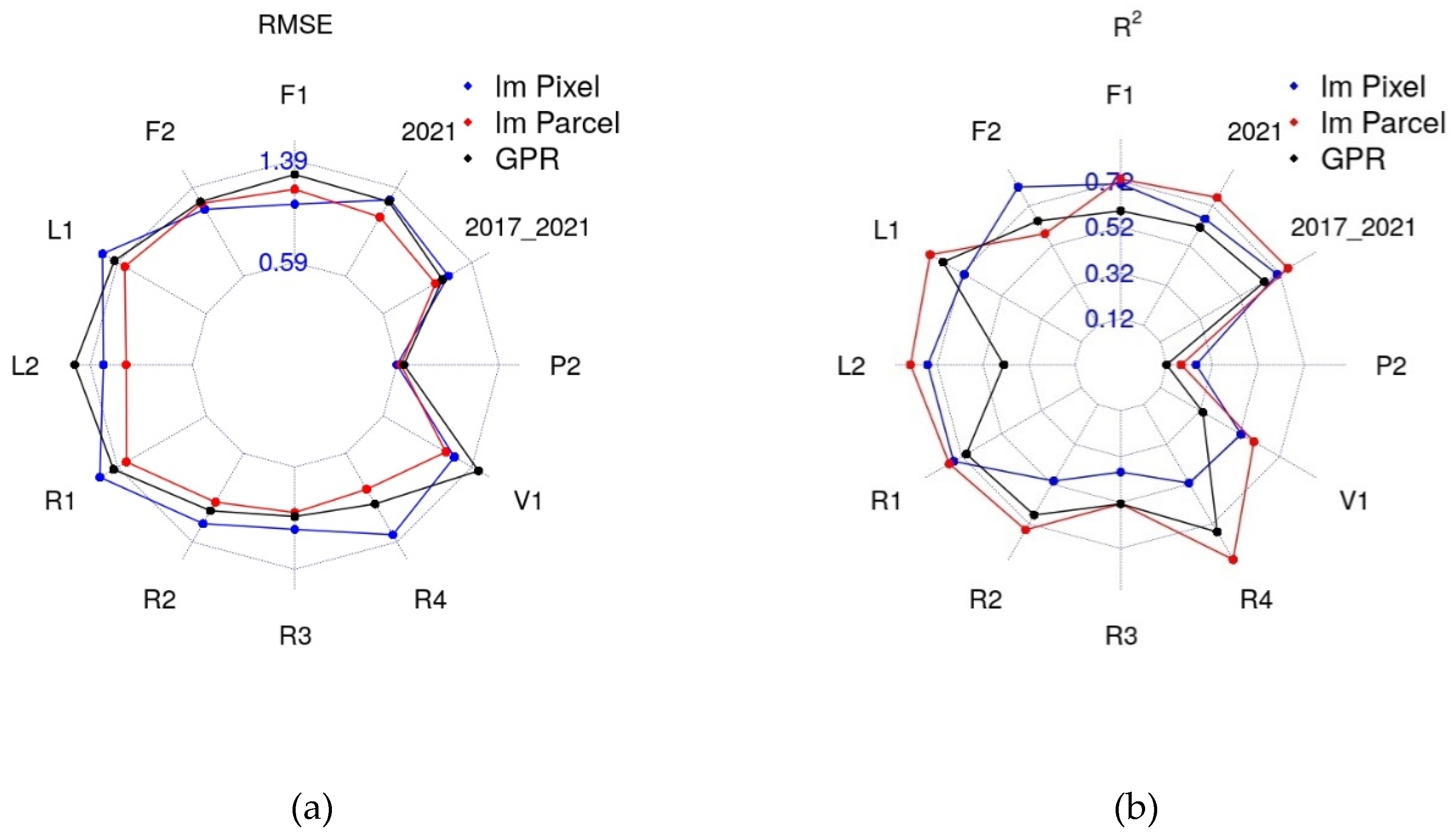
The performance of the different interpolation approaches was assessed by comparison with field measurements of LAI aggregated at parcel level (Figure 7). The comparison was performed when and where ground data were available, i.e., in the year 2021 over 4 sites, and in the years 2017-2021 over one sites (Table 1). On average, considering all the stations and all the available data, for the parcel-based linear interpolation RMSE = 1.2 [m2 m-2] and R2 = 0.72, for the pixel-based interpolation RMSE = 1.35 [m2 m-2] and R2 = 0.67, and for the GPR interpolation RMSE = 1.28 [m2 m-2] and R2 = 0.61. Considering the higher R2, only the first two methods were applied for the comparison between LAI/FPI and yield (Section 4.4.).

4.4. Comparison between LAI/FPI from Remote Sensing and Ground Yield Measurements

As a third and last part of the FPI assessment, we compared LAI and FPI estimated from satellite imagery against ground measurements of yield performed in the year 2021 over four sites including eight parcels (Table 1).
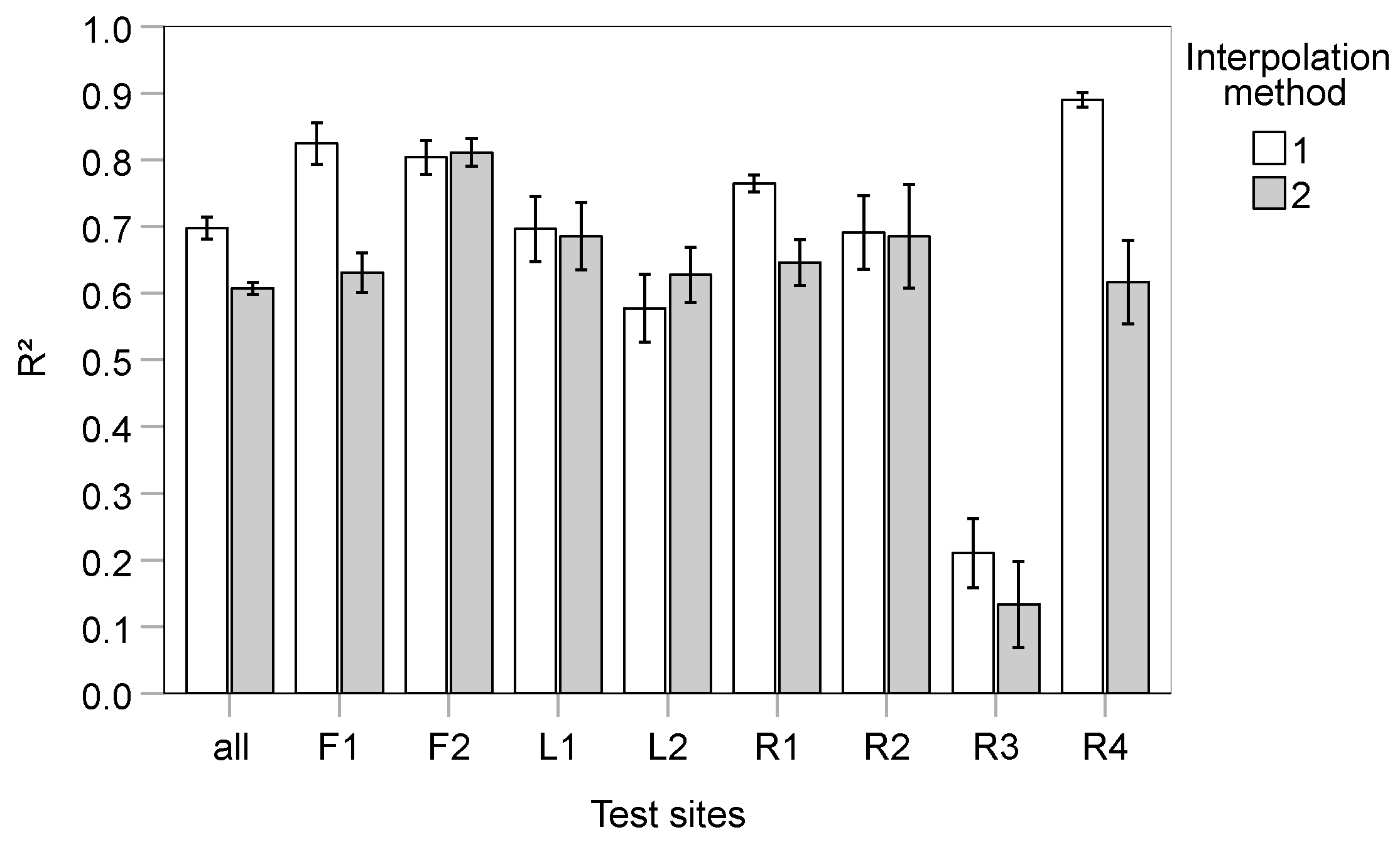
The use of LAI gap-filled by pixel-based linear interpolation (method 1), resulted in higher mean R² values in comparison to parcel-based linear interpolation (method 2), with a mean difference of about 0.1; this was apparently caused by the notably higher R² values obtained with this method at the sites F1, R1 and R4, whilst similar results were observed using the two methods at the remaining sites (Figure 8). For this reason, all further analyses were performed using method 1.
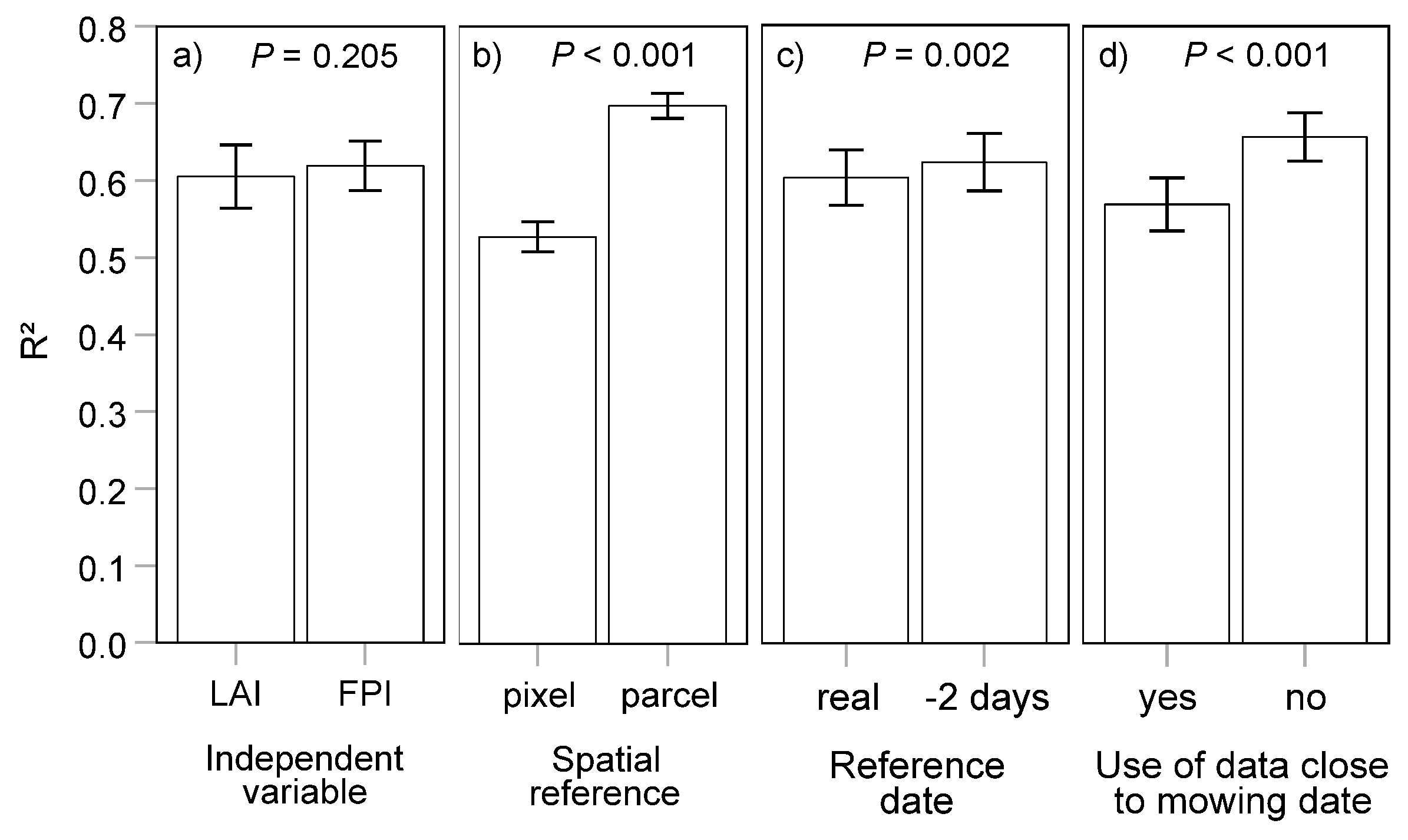
The analysis of the relationship between the remote sensing-based LAI or FPI and yield showed that model fit (assessed by R² of the linear regression) greatly varied depending on the combination of factor levels used in the models and it ranged from a minimum of 0.45 to a maximum of 0.75 (Figure 10, Figures from S6 to S8). When averaged over the levels of all other factors and considering the effect of the paired observations given by the combination of the levels of all other factors and differing only by the level of the factor in question, systematic patterns of the model fit were detected (Figure 9). The use of data averaged at parcel level instead of at pixel level resulted in the most relevant improvement of model fit, with a mean difference in R² of 0.17 (Figure 9b). The inclusion of the measurements taken on dates close in time to the mowing event (the last one preceding it and the first one following it) proved to negatively affect the model fit. The removal of these measurements increased indeed R² from 0.57 to 0.66 (Figure 9d). A significant, but small improvement of R² from 0.60 to 0.62 resulted from the use of satellite imagery of two days prior to the sampling event, compared to the use of that of the real sampling events (Figure 9c). In contrast, it was observed that the use of FPI instead of LAI did not result in a significant improvement of model fit (Figure 9a).
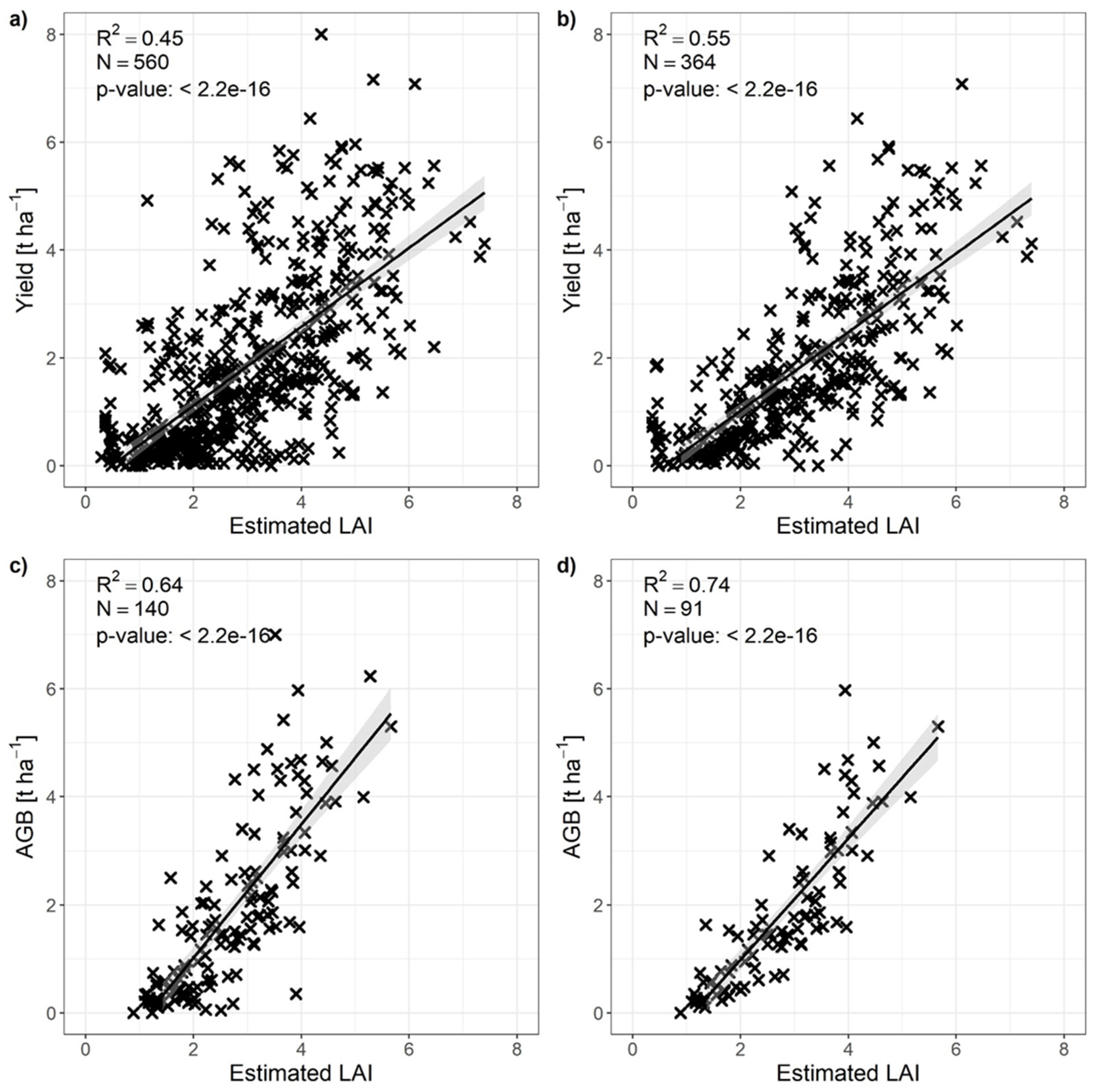
The impact of operating at parcel vs. pixel level and of excluding observations close to the mowing events is exemplified in Figure 10 for the relationship between remote sensing-estimated LAI and the respective ground measurements of yield by using the real mowing dates as a reference. Operating at plot level improved R² from 0.45 to 0.64 when using all data, and from 0.55 to 0.74 when excluding the data close to the mowing date. At both pixel and parcel level, the exclusion of the observations close to the mowing events led to an R² improvement of 0.10.
The same pattern was detected for all other analyses by using a date of two days before the mowing event for LAI extraction and of all other analyses addressing FPI as a dependent variable (Figures from S6 to S8).
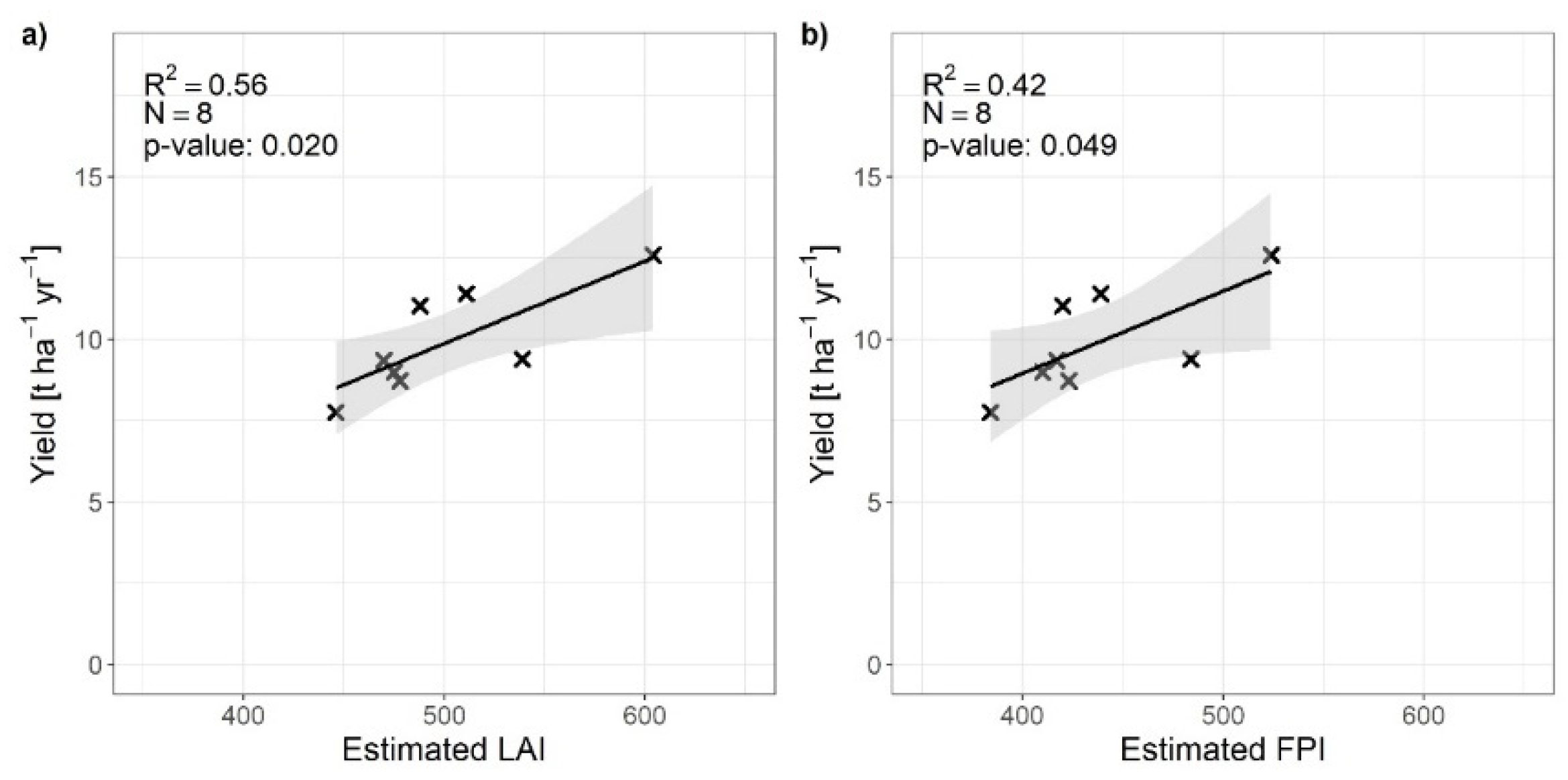
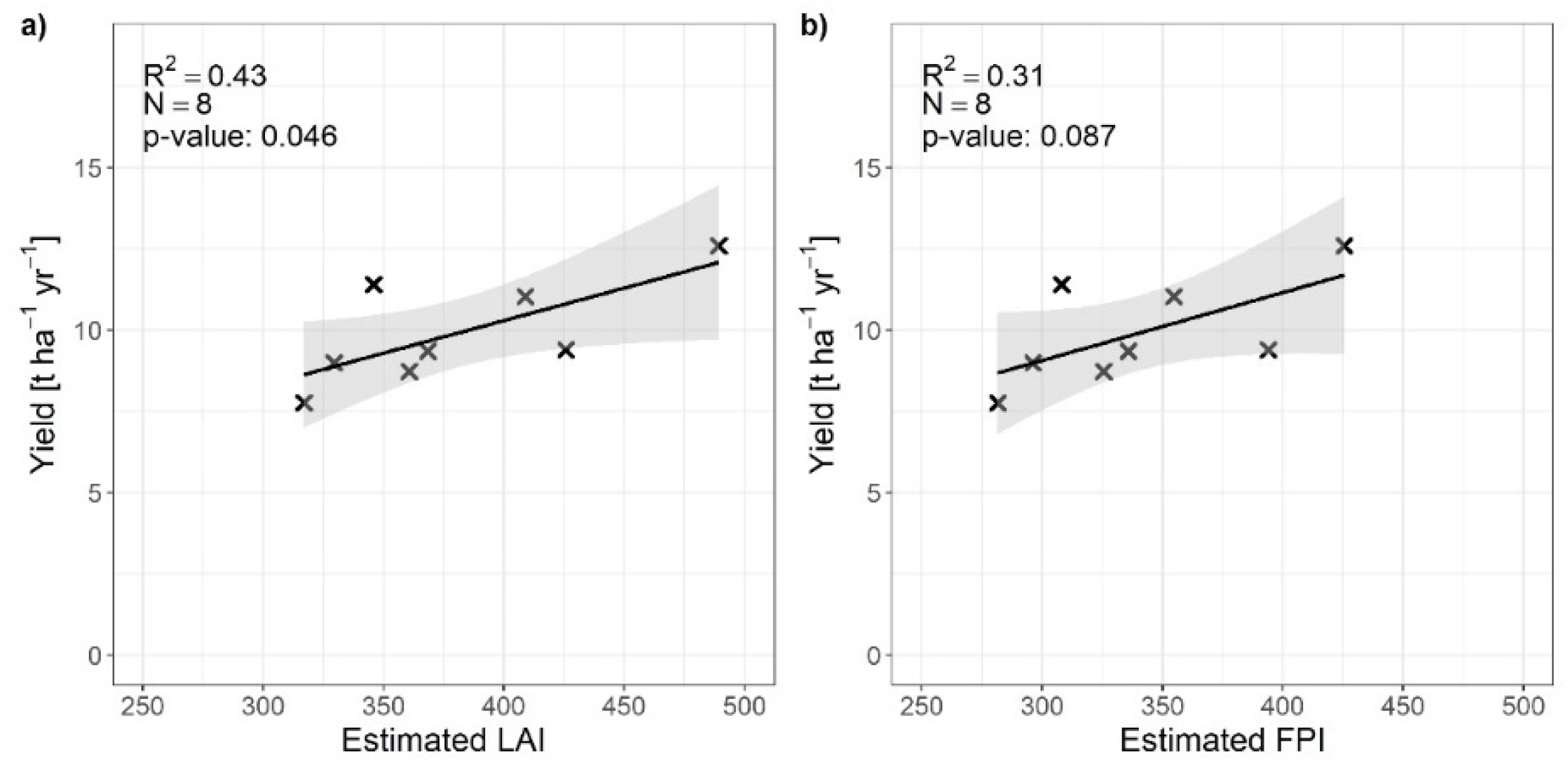
Only 8 yearly yield values at parcel scale were available from the test sites. The analysis of their correlation with yearly cumulated LAI and FPI showed a strong linear relationship between LAI and yield (Figure 11a), and a moderate correlation between FPI and yield (Figure 11b) when a fixed length of the growing season was assumed. When the growing season length was assumed to vary with elevation, R² between LAI and yield decreased from 0.56 to 0.43 (Figure 12a), and that of FPI from 0.42 to 0.31 (Figure 12b). Moreover, the P-value of the relationship between FPI and yield increased from 0.049 to 0.087.

4.5. Estimated Yield Losses for the Year 2022

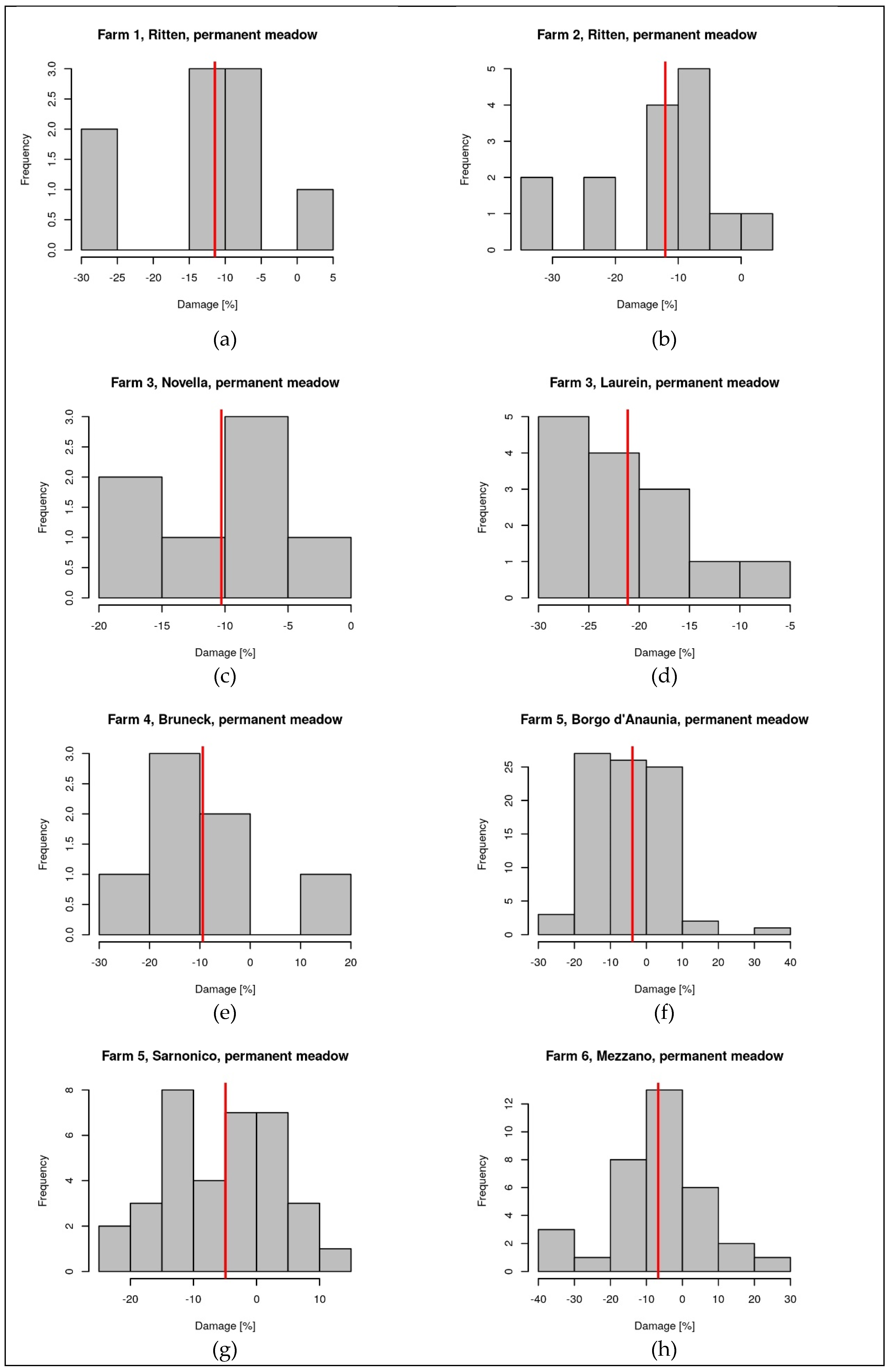
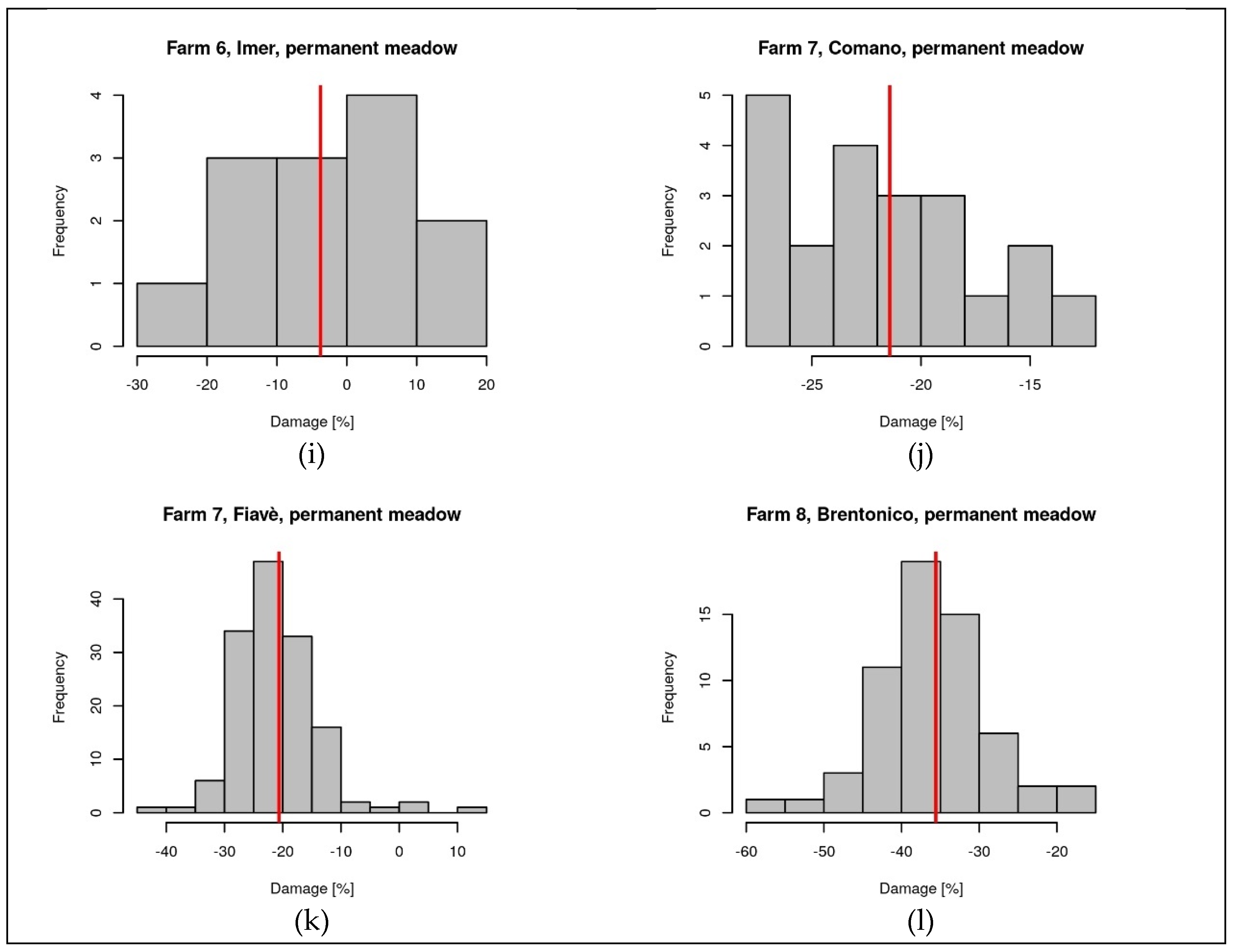
In the year 2022, yield losses were estimated using ΔFPI for 8 farms. ΔFPI was calculated for all the insured parcels of each farm and was averaged for all the parcels of a farm located in the same municipality and with the same land use. The damage was calculated as (ΔFPI-1) × 100, with negative values representing a reduction of the production with respect to the average of the preceding years.
For several parcels the estimated damage was high (Figure 13), however, when averaged by farm, municipality, and land use, only in one case (Figure 13l, Farm 8 located in Brentonico, used as permanent meadow) the average damage exceeded the threshold of 30%, which is set by the Italian agricultural risk management plan [63] as the minimum value of damage that can be refunded for index-based insurance policies.

4.6. Evaluation of the GPR Model Potential to Enrich S2 LAI Time Series by S1 SAR Data

S1-S2 data fusion by GPR model was tested over a subset of the study area for the year 2017, as described in Section 3.3.. Here the results of the feature selection and of the model validation are summarized.

4.6.1. Feature Selection

The 5-fold cross validation encompassing all the possible combinations of input features showed, on average, that the best predictors are VH, SM and DOY. By this combination, LAI was estimated from S1 with R2 = 0.83 and RMSE = 0.25 [m2 m-2] with respect to LAI estimated from S2. The performances depend on the land use (Figure S3, which includes only the best combinations of features). The training over the individual parcels performed better than the training over clusters of parcels with the same land use, especially for “permanent meadow” (AP2).
The combination VH, SM and DOY, globally providing the best performances, was used for the analyses presented hereafter.

4.6.2. Temporal and Spatial Gap-Filling Experiments

For all the land uses, when the dimension of the temporal gaps in the LAI timeseries increased, RMSE increased (Figure S4). R2 decreased with increasing number of missing acquisition dates for the parcel-based training, while the experiment with 3 missing dates provided worst results for the training based on land-use classes (Figure S4, d).
For the parcel-based models, on average considering all the parcels, R2 = 0.44, 0.40, and 0.28, and RMSE = 0.55, 0.65 and 0.91 [m2 m-2] with 3, 6, and 9 missing acquisition dates. For the land-use based models, on average based on all the land uses, R2 = 0.20, 0.26, and 0.19, and RMSE = 0.69, 0.87, and 0.98 [m2 m-2] with 3, 6, and 9 missing acquisition dates.
The dimension of the spatial gaps in the LAI images derived from S2 did not influence the average results (Figure S5). Specifically, when artificial gaps of 30%, 50%, and 70% of the pixels were introduced, the comparison between S1 and S2 LAI showed, respectively, R2 = 0.53, 0.53 and 0.52, and RMSE = 0.66, 0.67, and 0.68 [m2 m-2].

5. Discussion

This work derives a forage production index for mountain grasslands, the FPI, based on S2 LAI. The choice of LAI as biophysical indicator of grassland productivity is motivated by its strong correlation with measured yield over our study area. In addition, the calculation of LAI is relatively simple, thus providing FPI immediately after the end of the growing season, which is a requirement for a timely calculation of the insurance payments.
In the definition and development of FPI, we took appropriate measures to minimize basis risk usually associated to index insurance systems, i.e., the difference between the index value and the derived payoffs, and the actual yield variations [64]. Specifically, considering the three main components of basis risk identified by [65]:
  • Design risk, deriving from the possibility that the index does not correctly describe the variable of interest, i.e., yield, was minimized by studying the correlation between LAI and yield, verifying the accuracy of LAI derived from satellite data, and assessing the ability of the FPI to explain yield variability.
  • Temporal basis risk, emerging from the mismatch between the temporal aggregation of the index and the temporal scale of interest for grassland growth, was reduced by estimating the FPI as the growing season cumulate of daily values of LAI.
  • Spatial risk, due to the distance between the insured farm and the point where the index is estimated, is partially solved thanks to the high spatial resolution of S2 data which allows to estimate FPI by aggregating pixels within the parcels belonging to the insured farms. However, when parcels are aggregated by municipality, as foreseen by the Italian regulations [63], the variability from one parcel to another is lost, and the farmers are not rewarded for the parcels where high losses are estimated. Yet by aggregation it is possible to exclude from the calculation of the damage the parcels that lack the requirements for the calculation of ΔFPI, i.e., dense tree cover, recent changes in the land use, and extremely small size.
In the analysis of the relationship between in situ LAI and yield, the fit improvement obtained by disregarding the yield observations affected by lodging suggests that lodging can be regarded as a source of inaccuracy and a possible critical point if LAI retrievals from remote sensing are used in insurance systems to assess the yield in the field. As lodging is favored by the occurrence of large amounts of yield, this noise is mainly expected to occur in situations of high forage availability, thus leading to an underestimation of very high yield values.
The validation of S2 LAI showed that the S2 Biophysical processor can estimate LAI at a satisfactory level of accuracy for grasslands of Trentino/South Tyrol. Despite our study area is rather challenging due to land cover heterogeneity and topographic complexity, results were in line with other large scale validation studies performed over homogeneous sites [66,67]. We observed a tendency to overestimate low yield values by LAI. Indeed, at the pasture site, characterized by very low productivity and LAI values, the worst performances were observed, suggesting that the index we developed is appropriate for estimating yield losses in meadows, but further improvements are needed for pastures or, more in general, for extensively managed grassland with low yield potential.
In the comparison between daily S2 LAI/FPI and in situ yield, the model fit improvement observed when moving from the pixel to the parcel level suggests that averaging data at parcel level potentially reduces the effect of single outliers. This is a positive outcome because the insurance payments are estimated based on FPI at parcel scale.
Differently from what observed by [53] and [68] which used moderate resolution remote sensing data, no improvement of model fit could be achieved by taking into account the meteorological component (i.e. the water stress coefficient Cws). This may be caused by the fact that at the higher spatial resolution provided by the data from the S2 mission, the correction provided by the meteorological component becomes irrelevant.
In the comparison between S2 LAI/FPI cumulated during the growing season and yearly in situ yield, the correlation was slightly reduced when we assumed a length of the growing season which varies with elevation. Although an ultimate evaluation of this approach is very difficult based on 8 observations only, some considerations are possible. On one hand, discrepancies might be attributable to the fact that there can be yield accumulation beyond the empirically determined growing season start and end. On the other hand, as LAI was found to overestimate low yield values, this approach could prevent wrongly accumulating yield in times in which plant growth did not really start yet. Moreover, it is a common practice letting young cattle returning to the home farms from the summer pastures graze the last regrowth of meadows from late Summer to Autumn. This prevents a reliable estimation of the productivity during the last part of the growing season based on remote sensing observations. Considering a shorter length of the growing season can help to avoid these cases and to include only the period in which grassland is mown and there is no grazing.
In this work we accumulated LAI values over the entire growing season to have an estimate of yield. One alternative method that could be tested is the accumulation of LAI estimations immediately before mowing events. In the near future, approaches to identify mowing events from S1 and S2 satellite data [69,70] can be incorporated in our algorithm for the calculation of FPI. In particular, there is one method under development focusing on the Alpine region, where our study area is located [71]. In the use of these approaches, on one hand it is still challenging to get exactly the date of the mowing over heterogeneous agricultural areas from earth observation sensors, and on the other hand, it is difficult to obtain good LAI retrievals from S2 in correspondence of the mowing due to cloudiness. So far, the yearly cumulation is, in our study setup, the best solution to get a reasonable quantitative assessment of the production over the growing season. Nevertheless, the correct identification of the mowing dates could be useful to refine and constrain S2 LAI gap-filling approaches. For example, it would avoid the use of images acquired before and after a mowing event to estimate a missing LAI value in between.
We preliminarily assessed the potential of the fusion of optical and radar data for estimating grassland LAI. This exploratory analysis showed promising results especially for the spatial gap-filling, suggesting that the fusion with S1 could help to reduce gaps due to cloudiness in LAI maps obtained from S2. In particular, the VH polarization (in combination with ancillary data) showed better predictive capacity than VV or SAR vegetation indices in our specific test case. This could be ascribed to the increased sensitivity of VH polarization to grassland structure and to the less pronounced saturation tendency while increasing grassland height (and thus LAI) [72]. The GPR model training performed by aggregating all the parcels with the same land use gave worse results for permanent meadows. This class includes parcels with very different size and agricultural management. A different way of aggregating the parcels for model training should be tested for this land use class, considering the heterogeneity of agricultural practices. In the future we plan to perform the GPR model training based on a more extended dataset. In addition, a more thorough exploration, with comparison of different machine learning models, is required before including this technique in the production of the FPI.

6. Conclusions and Outlook

This study supports the development of an insurance instrument to mitigate the consequences of drought for grassland farming in the Alps. An innovative index-based insurance was developed in codesign with local agricultural stakeholders, accounting for the characteristics of the region in terms of meteorology, topography, and land use and management. A thorough comparison of the satellite-based LAI and FPI with extensive ground measurements of LAI and yield proved the robustness of the drought index.
For the growing season of the year 2022 the agricultural consortia of Trentino and South Tyrol have estimated yield losses due to drought at 8 farms including around 700 agricultural parcels by the anomalies of the FPI developed in this paper. The first version of the FPI included pixel-based linear interpolation of LAI, meteorological Cws coefficient, and adjustment of the growing season length depending on elevation.
The accuracy of the FPI can be improved by enriching the LAI timeseries based on optical S2 data with radar S1 data, because gaps in S2 data due to cloudiness might last several days. The synergistic exploitation of S1 and S2 was tested in this paper and will be developed as a next step.
The agricultural consortia of Trentino and South Tyrol, which are cutting-edge in offering innovative solutions for the management of agricultural risk to their associates farmers and to their partner insurance companies, have greatly appreciated the developed FPI index and are interested in proposing an FPI-based insurance to several grassland farmers starting from the year 2024, possibly based on an enhanced FPI by optical and SAR data fusion.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Additional information is provided in the file Supplementary_Materials.pdf. Reference [73] is cited in the Supplementary Materials.

Author Contributions

Conceptualization, Mariapina Castelli, Giovanni Peratoner, Roberto Monsorno and Claudia Notarnicola; Data curation, Mariapina Castelli, Giovanni Peratoner, Luca Pasolli, Giulia Molisse, Alexander Dovas, Gabriel Sicher, Alice Crespi, Mattia Rossi, Mohammad Alasawedah and Evelyn Soini; Formal analysis, Mariapina Castelli, Giovanni Peratoner, Luca Pasolli, Giulia Molisse and Alexander Dovas; Funding acquisition, Mariapina Castelli, Giovanni Peratoner and Roberto Monsorno; Investigation, Mariapina Castelli, Giovanni Peratoner, Alexander Dovas and Gabriel Sicher; Methodology, Mariapina Castelli, Giovanni Peratoner, Luca Pasolli, Alexander Dovas, Gabriel Sicher, Alice Crespi and Mattia Rossi; Project administration, Mariapina Castelli; Resources, Mariapina Castelli; Software, Mariapina Castelli, Giovanni Peratoner, Luca Pasolli, Giulia Molisse, Alexander Dovas, Alice Crespi and Mohammad Alasawedah; Supervision, Mariapina Castelli, Giovanni Peratoner and Claudia Notarnicola; Validation, Mariapina Castelli, Giovanni Peratoner, Luca Pasolli, Giulia Molisse and Alexander Dovas; Visualization, Mariapina Castelli and Giovanni Peratoner; Writing – original draft, Mariapina Castelli and Giovanni Peratoner.

Funding

This study was funded by the project DRI2 (2021-2022): Development of an innovative approach for the derivation of a drought index for alpine grassland by combining satellite data, physical models, and meteorological information, funded by the Autonomous Province of Bolzano/Bozen (Ufficio Ricerca), and by the Action Plan 2016-2022 for Research and Training in the Fields of Mountain Agriculture and Food Science of the Autonomous Province of Bolzano/Bozen.

Data availability statement

Publicly available satellite and meteorological datasets were processed in this study. These datasets can be found at the following links:.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Flury, C.; Huber, R.; Tasser, E. Future of Mountain Agriculture in the Alps. Springer Geogr. 2013, 105–126. [Google Scholar] [CrossRef]
  2. Jäger, H.; Peratoner, G.; Tappeiner, U.; Tasser, E. Grassland biomass balance in the European Alps: current and future ecosystem service perspectives. Ecosyst. Serv. 2020, 45, 101163. [Google Scholar] [CrossRef]
  3. Sala, O.E.; Yahdjian, L.; Havstad, K.; Aguiar, M.R. Rangeland Ecosystem Services: Nature’s Supply and Humans’ Demand. In Rangeland Systems: Processes, Management and Challenges; New York, NY, 2017; pp. 467–489. Available online: https://link.springer.com/chapter/10.1007/978-3-319-46709-2_14 (accessed on March 20, 2023).
  4. Zimmermann, P.; Tasser, E.; Leitinger, G.; Tappeiner, U. Effects of land-use and land-cover pattern on landscape-scale biodiversity in the European Alps. Agric. Ecosyst. Environ. 2010, 139, 13–22. [Google Scholar] [CrossRef]
  5. Zhao, Y.; Liu, Z.; Wu, Á.J. Grassland ecosystem services: a systematic review of research advances and future directions. Landscape Ecology 2020, 35, 793–814. [Google Scholar] [CrossRef]
  6. Schirpke, U.; Wang, G.; Padoa-Schioppa, E. Editorial: Mountain landscapes: Protected areas, ecosystem services, and future challenges. Ecosyst. Serv. 2021, 49, 101302. [Google Scholar] [CrossRef]
  7. Bahn, M.; Rodeghiero, M.; Anderson-Dunn, M.; Dore, S.; Gimeno, C.; Drösler, M.; Williams, M.; Ammann, C.; Berninger, F.; Flechard, C.; et al. Soil Respiration in European Grasslands in Relation to Climate and Assimilate Supply. Ecosyst. 2008 118 2008, 11, 1352–1367. [Google Scholar] [CrossRef] [PubMed]
  8. Neuwirth, C.; Hofer, B. Spatial sensitivity of grassland yields to weather variations in Austria and its implications for the future. Appl. Geogr. 2013, 45, 332–341. [Google Scholar] [CrossRef]
  9. Baronetti, A.; Provenzale, A.; Fratianni, S. Future droughts in northern Italy: high resolution projections using EURO-CORDEX and MED-CORDEX ensembles. Climatic Change 2022, 172, 22. [Google Scholar] [CrossRef]
  10. Stephan, R.; Erfurt, M.; Terzi, S.; Zun, M.; Kristan, B.; Haslinger, K.; Stahl, K. An inventory of Alpine drought impact reports to explore past droughts in a mountain region. Nat. Hazards Earth Syst. Sci. 2021, 21, 2485–2501. [Google Scholar] [CrossRef]
  11. Spinoni, J.; Vogt, J. V.; Naumann, G.; Barbosa, P.; Dosio, A. Will drought events become more frequent and severe in Europe? Int. J. Climatol. 2018, 38, 1718–1736. [Google Scholar] [CrossRef]
  12. Böhnisch, A.; Mittermeier, M.; Leduc, M.; Ludwig, R. Hot Spots and Climate Trends of Meteorological Droughts in Europe–Assessing the Percent of Normal Index in a Single-Model Initial-Condition Large Ensemble. Front. Water 2021, 3, 107. [Google Scholar] [CrossRef]
  13. Dibari, C.; Pulina, A.; Argenti, G.; Aglietti, C.; Bindi, M.; Moriondo, M.; Mula, L.; Pasqui, M.; Seddaiu, G.; Roggero, P.P. Climate change impacts on the Alpine, Continental and Mediterranean grassland systems of Italy: A review. Ital. J. Agron. 2021, 16. [Google Scholar] [CrossRef]
  14. Begert, M.; Frei, C. Long-term area-mean temperature series for Switzerland—Combining homogenized station data and high resolution grid data. Int. J. Climatol. 2018, 38, 2792–2807. [Google Scholar] [CrossRef]
  15. Kotlarski, S.; Gobiet, A.; Morin, S.; Olefs, M.; Rajczak, J.; Samacoïts, R. 21st Century alpine climate change. Clim. Dyn. 2023, 60, 65–86. [Google Scholar] [CrossRef]
  16. ENSEMBLES: Climate Change and its Impacts: Summary of research and results from the ENSEMBLES project. van der Linden P., and J.F.B. Mitchell (eds.): Met Office Hadley Centre, FitzRoy Road, Exeter EX1 3PB, UK. 160pp, 2009. Available online: http://ensembles-eu.metoffice.com/docs/Ensembles_final_report_Nov09.pdf (accessed on March 20, 2023).
  17. Dibari, C.; Costafreda-Aumedes, S.; Argenti, G.; Bindi, M.; Carotenuto, F.; Moriondo, M.; Padovan, G.; Pardini, A.; Staglianò, N.; Vagnoli, C.; et al. Expected Changes to Alpine Pastures in Extent and Composition under Future Climate Conditions. Agron. 2020, Vol. 10, Page 926 2020, 10, 926. [Google Scholar] [CrossRef]
  18. Schirpke, U.; Kohler, M.; Leitinger, G.; Fontana, V.; Tasser, E.; Tappeiner, U. Future impacts of changing land-use and climate on ecosystem services of mountain grassland and their resilience. Ecosyst. Serv. 2017, 26, 79–94. [Google Scholar] [CrossRef]
  19. Herzog, F.; Seidl, I. Swiss alpine summer farming: current status and future development under climate change. The Rangeland Journal. 2018, 40(5), 501–511. [Google Scholar] [CrossRef]
  20. De Boeck, H.J.; Bassin, S.; Verlinden, M.; Zeiter, M.; Hiltbrunner, E. Simulated heat waves affected alpine grassland only in combination with drought. New Phytol. 2016, 209, 531–541. [Google Scholar] [CrossRef]
  21. Smets, B.; Cai, Z.; Eklundh, L.; Tian, F.; Bonte, K.; Van Hoost, R.; De Roo, B.; Jacobs, T.; Camacho, F.; Sánchez-Zapero, J.; et al. HIGH RESOLUTION VEGETATION PHENOLOGY AND PRODUCTIVITY (HR-VPP), Seasonal Trajectories and VPP parameters; Copernicus Land Monitoring Service, 2022. Available online: https://land.copernicus.eu/user-corner/technical-library/product-user-manual-of-seasonal-trajectories (accesses on March 20, 2023).
  22. Clement, K.Y.; Wouter Botzen, W.J.; Brouwer, R.; Aerts, J.C.J.H. A global review of the impact of basis risk on the functioning of and demand for index insurance. Int. J. Disaster Risk Reduct. 2018, 28, 845–853. [Google Scholar] [CrossRef]
  23. Keller, J.B.; Saitone, T.L. Basis risk in the pasture, rangeland, and forage insurance program: Evidence from California. American Journal of Agricultural Economics 2022, 104, 1203–1223. [Google Scholar] [CrossRef]
  24. Martín-Sotoca, J.J.; Saa-Requejo, A.; Moratiel, R.; Dalezios, N.; Faraslis, I.; María Tarquis, A. Statistical analysis for satellite-index-based insurance to define damaged pasture thresholds. Nat. Hazards Earth Syst. Sci. 2019, 19, 1685–1702. [Google Scholar] [CrossRef]
  25. Goodrich, B.; Yu, J.; Vandeveer, M. Participation patterns of the rainfall index insurance for pasture, rangeland and forage programme. Geneva Pap. Risk Insur. Issues Pract. 2020, 45, 29–51. [Google Scholar] [CrossRef]
  26. Williams, T.M.; Travis, W.R. Evaluating Alternative Drought Indicators in a Weather Index Insurance Instrument. Weather. Clim. Soc. 2019, 11, 629–649. [Google Scholar] [CrossRef]
  27. Sawyer, G.; Oligschläger, C.; Khabarov, N.; A Case Study Growing Potatoes in Belgium. ESA, Sentinels Benefits Study (SeBS). 2019. Available online: https://earsc.org/sebs/wp-content/uploads/2019/08/1_full-report-Growing-Potatoes-in-Belgium.pdf (accessed online on May 5, 2023).
  28. Echeverría, A.; Urmeneta, A.; González-Audícana, M.; González, E.M. Monitoring Rainfed Alfalfa Growth in Semiarid Agrosystems Using Sentinel-2 Imagery. Remote Sens. 2021, Vol. 13, Page 4719 2021, 13, 4719. [Google Scholar] [CrossRef]
  29. Vajsová, B.; Fasbender, D.; Wirnhardt, C.; Lemajic, S.; Devos, W. Assessing Spatial Limits of Sentinel-2 Data on Arable Crops in the Context of Checks by Monitoring. Remote Sens. 2020, Vol. 12, Page 2195 2020, 12, 2195. [Google Scholar] [CrossRef]
  30. Defourny, P.; Bontemps, S.; Bellemans, N.; Cara, C.; Dedieu, G.; Guzzonato, E.; Hagolle, O.; Inglada, J.; Nicola, L.; Rabaute, T.; et al. Near real-time agriculture monitoring at national scale at parcel resolution: Performance assessment of the Sen2-Agri automated system in various cropping systems around the world. Remote Sens. Environ. 2019, 221, 551–568. [Google Scholar] [CrossRef]
  31. Pipia, L.; Muñoz-Marí, J.; Amin, E.; Belda, S.; Camps-Valls, G.; Verrelst, J. Fusing optical and SAR time series for LAI gap filling with multioutput Gaussian processes. Remote Sens. Environ. 2019, 235, 111452. [Google Scholar] [CrossRef]
  32. Kandasamy, S.; Baret, F.; Verger, A.; Neveux, P.; Weiss, M. A comparison of methods for smoothing and gap filling time series of remote sensing observations - application to MODIS LAI products. Biogeosciences 2013, 10, 4055–4071. [Google Scholar] [CrossRef]
  33. Adler, S., Chimani, B., Drechsel, S., Haslinger, K., Hiebl, J.; Meyer, V., Resch, G., Rudolph, J., Vergeiner, J., Z.; C., Marigo, G., Fischer, A., and Seiser, B. DAS KLIMA VON TIROL-SÜDTIROL-BELLUNO; 2015. Available online: http://www.alpenklima.eu/images/Das_Klima_von_Tirol-Suedtirol-Belluno.pdf (accessed on May 5, 2023).
  34. CORINE Land Cover — Copernicus Land Monitoring Service. Available online: https://land.copernicus.eu/pan-european/corine-land-cover (accessed on Mar 17, 2023).
  35. Grassland — Copernicus Land Monitoring Service. Available online: https://land.copernicus.eu/pan-european/high-resolution-layers/grassland (accessed on Mar 17, 2023).
  36. Kasal, A., Zelli, E., Cassar, A., Mair, V., Dallagiacoma, E. Futterertrag auf Naturwiesen in Südtirol. Laimbg. J. 2004, 1, 86–94. [Google Scholar]
  37. Scotton, M.; Sicher, L.; Kasal, A. Semi-natural grasslands of the Non Valley (Eastern Italian Alps): Agronomic and environmental value of traditional and new Alpine hay-meadow types. Agric. Ecosyst. Environ. 2014, 197, 243–254. [Google Scholar] [CrossRef]
  38. Peratoner, G.; Pötsch, E.M. Methods to describe the botanical composition of vegetation in grassland research. Bodenkultur 2019, 70, 1–18. [Google Scholar] [CrossRef]
  39. LI-2200C Plant Canopy Analyzer. Available online: https://www.licor.com/env/products/leaf_area/LAI-2200C/?gclid=CjwKCAjw682TBhATEiwA9crl3-0bom1ZoJNNYbVlVUn9eZyD4-UcfkZVSTNzA2zi95HyiiqwV_hTFRoCzUoQAvD_BwE (accessed on May 5, 2022).
  40. Rossi, M.; Niedrist, G.; Asam, S.; Tonon, G.; Tomelleri, E.; Zebisch, M. A Comparison of the Signal from Diverse Optical Sensors for Monitoring Alpine Grassland Dynamics. Remote Sens. 2019, Vol. 11, Page 296 2019, 11, 296. [Google Scholar] [CrossRef]
  41. Chiarito, E.; Cigna, F.; Cuozzo, G.; Fontanelli, G.; Mejia Aguilar, A.; Paloscia, S.; Rossi, M.; Santi, E.; Tapete, D.; Notarnicola, C. Biomass retrieval based on genetic algorithm feature selection and support vector regression in Alpine grassland using ground-based hyperspectral and Sentinel-1 SAR data. https://doi.org/10.1080/22797254.2021.1901063 2021, 54, 209–225. [Google Scholar] [CrossRef]
  42. Gascon, F.; Ramoino, F.; Deanos, Y.-L. Sentinel-2 data exploitation with ESA’s Sentinel-2 Toolbox; 2017; 19th EGU General Assembly, EGU2017, proceedings from the conference held 23-28 April, 2017 in Vienna, Austria., p.19548. Bibcode: 2017EGUGA..1919548G.
  43. Main-Knorn, M.; Pflug, B.; Louis, J.; Debaecker, V.; Müller-Wilm, U.; Gascon, F. Sen2Cor for Sentinel-2. https://doi.org/10.1117/12.2278218 2017, 10427, 37–48. [Google Scholar] [CrossRef]
  44. Vegetation Indices — Copernicus Land Monitoring Service. Available online: https://land.copernicus.eu/pan-european/biophysical-parameters/high-resolution-vegetation-phenology-and-productivity/vegetation-indices (accessed on Mar 31, 2022).
  45. GitHub - sentinel-hub/sentinel2-cloud-detector: Sentinel Hub Cloud Detector for Sentinel-2 images in Python. Available online: https://github.com/sentinel-hub/sentinel2-cloud-detector (accessed on February 9, 2022).
  46. Rasmussen, C.E. Gaussian Processes in Machine Learning. Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics) 2004, 3176, 63–71. [Google Scholar] [CrossRef]
  47. Verrelst, J.; Rivera, J.P.; Moreno, J.; Camps-Valls, G. Gaussian processes uncertainty estimates in experimental Sentinel-2 LAI and leaf chlorophyll content retrieval. ISPRS J. Photogramm. Remote Sens. 2013, 86, 157–167. [Google Scholar] [CrossRef]
  48. Pipia, L.; Amin, E.; Belda, S.; Salinero-Delgado, M.; Verrelst, J. Green LAI Mapping and Cloud Gap-Filling Using Gaussian Process Regression in Google Earth Engine. Remote Sens. 2021, Vol. 13, Page 403 2021, 13, 403. [Google Scholar] [CrossRef]
  49. Camps-Valls, G.; Verrelst, J.; Munoz-Mari, J.; Laparra, V.; Mateo-Jimenez, F.; Gomez-Dans, J. A survey on Gaussian processes for earth-observation data analysis: A comprehensive investigation. IEEE Geosci. Remote Sens. Mag. 2016, 4, 58–78. [Google Scholar] [CrossRef]
  50. Stein, M.L. Interpolation of Spatial Data. Springer Science & Business Media 1999. [Google Scholar] [CrossRef]
  51. Python API Reference — xgboost 1.7.4 documentation. Available online: https://xgboost.readthedocs.io/en/stable/python/python_api.html (accessed on March 21, 2023).
  52. GitHub - fmfn/BayesianOptimization: A Python implementation of global optimization with gaussian processes. Available online: https://github.com/fmfn/BayesianOptimization (accessed on March 21, 2023).
  53. Roumiguié, A.; Sigel, G.; Poilvé, H.; Bouchard, B.; Vrieling, A.; Jacquin, A. Insuring forage through satellites: testing alternative indices against grassland production estimates for France. International Journal of Remote Sensing 2016, 38, 1912–1939. [Google Scholar] [CrossRef]
  54. EUR-Lex - 32020R2220 - EN - EUR-Lex. Available online: https://eur-lex.europa.eu/legal-content/IT/TXT/?uri=celex%3A32020R2220 (accessed on February 8, 2022).
  55. Mipaaf - DM n.9402305 del 29/12/2020 - Piano di gestione dei rischi in agricoltura 2021. Available online: https://www.politicheagricole.it/flex/cm/pages/ServeBLOB.php/L/IT/IDPagina/16490 (accessed on February 9, 2022).
  56. Jensen, M.E.; Haise, H.R. Estimating Evapotranspiration from Solar Radiation. J. Irrig. Drain. Div. 1963, 89, 15–41. [Google Scholar] [CrossRef]
  57. Crespi, A.; Matiu, M.; Bertoldi, G.; Petitta, M.; Zebisch, M. A high-resolution gridded dataset of daily temperature and precipitation records (1980–2018) for Trentino – South Tyrol (north-eastern Italian Alps). Earth Syst. Sci. Data 2021, 13, 2801–2818. [Google Scholar] [CrossRef]
  58. Bartkowiak, P.; Castelli, M.; Crespi, A.; Niedrist, G.; Zanotelli, D.; Colombo, R.; Notarnicola, C. Land Surface Temperature Reconstruction Under Long-Term Cloudy-Sky Conditions at 250 m Spatial Resolution: Case Study of Vinschgau/Venosta Valley in the European Alps. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 2037–2057. [Google Scholar] [CrossRef]
  59. Mandal, D.; Kumar, V.; Ratha, D.; Dey, S.; Bhattacharya, A.; Lopez-Sanchez, J.M.; McNairn, H.; Rao, Y.S. Dual polarimetric radar vegetation index for crop growth monitoring using sentinel-1 SAR data. Remote Sens. Environ. 2020, 247, 111954. [Google Scholar] [CrossRef]
  60. Nasirzadehdizaji, R.; Sanli, F.B.; Abdikan, S.; Cakir, Z.; Sekertekin, A.; Ustuner, M. Sensitivity analysis of multi-temporal Sentinel-1 SAR parameters to crop height and canopy coverage. Appl. Sci. 2019, 9. [Google Scholar] [CrossRef]
  61. Veloso, A.; Mermoz, S.; Bouvet, A.; Le Toan, T.; Planells, M.; Dejoux, J.F.; Ceschia, E. Understanding the temporal behavior of crops using Sentinel-1 and Sentinel-2-like data for agricultural applications. Remote Sens. Environ. 2017, 199, 415–426. [Google Scholar] [CrossRef]
  62. Greifeneder, F.; Notarnicola, C.; Wagner, W. A Machine Learning-Based Approach for Surface Soil Moisture Estimations with Google Earth Engine. Remote Sens. 2021, Vol. 13, Page 2099 2021, 13, 2099. [Google Scholar] [CrossRef]
  63. Ministero dell’agricoltura, della sovranità alimentare e delle foreste Piano di gestione dei rischi in agricoltura 2022. DM n. 148418 del 31/03/2022 - Piano di gestione dei rischi in agricoltura 2022. Available online: https://www.politicheagricole.it/flex/cm/pages/ServeBLOB.php/L/IT/IDPagina/17999 (accessed on November 8, 2022).
  64. Vroege, W.; Dalhaus, T.; Finger, R. Index insurances for grasslands – A review for Europe and North-America. Agric. Syst. 2019, 168, 101–111. [Google Scholar] [CrossRef]
  65. Dalhaus, T.; Finger, R. Can gridded precipitation data and phenological observations reduce basis risk of weather index-based insurance? Weather. Clim. Soc. 2016, 8, 409–419. [Google Scholar] [CrossRef]
  66. Brown, L.A.; Fernandes, R.; Djamai, N.; Meier, C.; Gobron, N.; Morris, H.; Canisius, F.; Bai, G.; Lerebourg, C.; Lanconelli, C.; et al. Validation of baseline and modified Sentinel-2 Level 2 Prototype Processor leaf area index retrievals over the United States. ISPRS J. Photogramm. Remote Sens. 2021, 175, 71–87. [Google Scholar] [CrossRef]
  67. Sánchez-Zapero, J.; Camacho, F.; Swinnen, E.; Bonte, K.; Martinez-Sánchez, E. Validation Report. Copernicus Land Monitoring Service. HIGH RESOLUTION VEGETATION PHENOLOGY AND PRODUCTIVITY (HRVPP), Daily Raw Vegetation Indices. Available online: https://land.copernicus.eu/user-corner/technical-library/validation-report-of-vegetation-indices (accessed on March 20, 2023).
  68. Velpuri, N.M.; Senay, G.B.; Singh, R.K.; Bohms, S.; Verdin, J.P. A comprehensive evaluation of two MODIS evapotranspiration products over the conterminous United States: Using point and gridded FLUXNET and water balance ET. Remote Sens. Environ. 2013, 139, 35–49. [Google Scholar] [CrossRef]
  69. De Vroey, M.; Radoux, J.; Defourny, P. Grassland Mowing Detection Using Sentinel-1 Time Series: Potential and Limitations. Remote Sens. 2021, Vol. 13, Page 348 2021, 13, 348. [Google Scholar] [CrossRef]
  70. Reinermann, S.; Gessner, U.; Asam, S.; Ullmann, T.; Schucknecht, A.; Kuenzer, C. Detection of Grassland Mowing Events for Germany by Combining Sentinel-1 and Sentinel-2 Time Series. Remote Sens. 2022, Vol. 14, Page 1647 2022, 14, 1647. [Google Scholar] [CrossRef]
  71. Earth Observation for Alpine ecosystems – Alps regional initiative. Available online: https://www.eurac.edu/en/institutes-centers/institute-for-earth-observation/projects/eco4alps. (accessed on June 5, 2023).
  72. Bériaux, E.; Waldner, F.; Collienne, F.; Bogaert, P.; Defourny, P. Maize Leaf Area Index Retrieval from Synthetic Quad Pol SAR Time Series Using the Water Cloud Model. Remote Sens. 2015, 7, 16204–16225. [Google Scholar] [CrossRef]
  73. Peratoner, G.; Sicher, G.; Matteazzi, A. Richtwerte des Nährstoffgehalts von Wirtschaftsdüngern in Südtirol. Tabellenwerk 2022. Pfatten/Vadena: Versuchszentrum Laimburg. 2022. Available online: https://t1p.de/kmm9 (accessed on March 20, 2023).
Preprints 76491 g001
Figure 1. Map of the study area, Trentino-South Tyrol, with elevation (m) and extension of the grassland area in which the proposed index-based insurance is potentially applicable (areas highlighted in green, derived from [35]).
Figure 1. Map of the study area, Trentino-South Tyrol, with elevation (m) and extension of the grassland area in which the proposed index-based insurance is potentially applicable (areas highlighted in green, derived from [35]).
Preprints 76491 g001
Preprints 76491 g002
Figure 2. Location, elevation, parcel size, observation years, type and frequency of measurement at the test sites for ground measurements of LAI and yield.
Figure 2. Location, elevation, parcel size, observation years, type and frequency of measurement at the test sites for ground measurements of LAI and yield.
Preprints 76491 g002
Preprints 76491 g003
Figure 3. Flowchart of the methods for the estimation of yield losses for the year 2022.
Figure 3. Flowchart of the methods for the estimation of yield losses for the year 2022.
Preprints 76491 g003
Preprints 76491 g004
Figure 4. Scatterplot of ground measurements of LAI and yield in 2021 at the sites L1, L2, R1, R2, R3, R4, F1, and F2. a) all yield observations, b) only yield observations without medium and heavy lodging (observations in grey color in Figure 4a). The grey shaded area shows the 95% confidence interval of the slope of the regression line.
Figure 4. Scatterplot of ground measurements of LAI and yield in 2021 at the sites L1, L2, R1, R2, R3, R4, F1, and F2. a) all yield observations, b) only yield observations without medium and heavy lodging (observations in grey color in Figure 4a). The grey shaded area shows the 95% confidence interval of the slope of the regression line.
Preprints 76491 g004
Preprints 76491 g005
Figure 5. Scatterplot between LAI estimated from S2 and ground measurements of LAI performed in the year 2021. All the sites monitored in 2021 are included. The grey shaded area shows the 95% confidence interval of the slope of the regression line.
Figure 5. Scatterplot between LAI estimated from S2 and ground measurements of LAI performed in the year 2021. All the sites monitored in 2021 are included. The grey shaded area shows the 95% confidence interval of the slope of the regression line.
Preprints 76491 g005
Preprints 76491 g006
Figure 6. Scatterplot between LAI estimated from S2 and ground measurements of LAI performed in the years 2017-2021 at the sites V1 (meadow) and P2 (pasture) in Muntatschinig. The grey shaded area shows the 95% confidence interval of the slope of the regression line.
Figure 6. Scatterplot between LAI estimated from S2 and ground measurements of LAI performed in the years 2017-2021 at the sites V1 (meadow) and P2 (pasture) in Muntatschinig. The grey shaded area shows the 95% confidence interval of the slope of the regression line.
Preprints 76491 g006
Preprints 76491 g007
Figure 7. Performances of different LAI gap-filling approaches against the daily average of LAI measurements for the site of interest in terms of RMSE [m2 m-2] (a) and R2 (b). We used black lines for the GPR interpolation at parcel scale, blue lines for the linear interpolation at parcel scale, and red lines for the linear interpolation at pixel scale. F1 to P2, counterclockwise, represent the single parcels, as in Table 1. 2017_2021 and 2021 summarize, respectively, the results for all available parcels in the years from 2017 to 2021 (2 parcels), and in the year 2021 (10 parcels).
Figure 7. Performances of different LAI gap-filling approaches against the daily average of LAI measurements for the site of interest in terms of RMSE [m2 m-2] (a) and R2 (b). We used black lines for the GPR interpolation at parcel scale, blue lines for the linear interpolation at parcel scale, and red lines for the linear interpolation at pixel scale. F1 to P2, counterclockwise, represent the single parcels, as in Table 1. 2017_2021 and 2021 summarize, respectively, the results for all available parcels in the years from 2017 to 2021 (2 parcels), and in the year 2021 (10 parcels).
Preprints 76491 g007
Preprints 76491 g008
Figure 8. Mean R² values ± SE between LAI or FPI and ground measurements of yield in 2021 over all sites (all) and at the single sites L1, L2, R1, R2, R3, R4, F1, and F2 depending on the method for interpolating LAI and FPI. 1 = pixel-based linear interpolation, 2 = parcel-based linear interpolation.
Figure 8. Mean R² values ± SE between LAI or FPI and ground measurements of yield in 2021 over all sites (all) and at the single sites L1, L2, R1, R2, R3, R4, F1, and F2 depending on the method for interpolating LAI and FPI. 1 = pixel-based linear interpolation, 2 = parcel-based linear interpolation.
Preprints 76491 g008
Preprints 76491 g009
Figure 9. Mean R² values ± SE depending on a) the use of LAI or FPI, b) the use of remote-sensing estimates obtained at pixel or parcel scale, c) the use of the real yield sampling date or a conventional date of two days before the mowing event as reference date, and d) the inclusion or exclusion of the ground measurements performed just before or after the mowing dates in the field. The P-values refer to the effect of the respective factor by mixed models analysis.
Figure 9. Mean R² values ± SE depending on a) the use of LAI or FPI, b) the use of remote-sensing estimates obtained at pixel or parcel scale, c) the use of the real yield sampling date or a conventional date of two days before the mowing event as reference date, and d) the inclusion or exclusion of the ground measurements performed just before or after the mowing dates in the field. The P-values refer to the effect of the respective factor by mixed models analysis.
Preprints 76491 g009
Preprints 76491 g010
Figure 10. Scatterplots of estimated LAI and ground measurements of yield (a) at pixel level considering all observations, (b) at pixel level without the observations close to the mowing dates, (c) at parcel level considering all observations, and (d) at parcel level without the observations close to the mowing dates. The grey shaded area shows the 95% confidence interval of the slope of the regression line.
Figure 10. Scatterplots of estimated LAI and ground measurements of yield (a) at pixel level considering all observations, (b) at pixel level without the observations close to the mowing dates, (c) at parcel level considering all observations, and (d) at parcel level without the observations close to the mowing dates. The grey shaded area shows the 95% confidence interval of the slope of the regression line.
Preprints 76491 g010
Preprints 76491 g011
Figure 11. Scatterplots of annual values of a) estimated LAI or b) FPI and ground measurements of yield. The grey shaded areas represent the 95% confidence intervals of the slope of the regression line. The growing season length is assumed fix, from the beginning of April to the end of October.
Figure 11. Scatterplots of annual values of a) estimated LAI or b) FPI and ground measurements of yield. The grey shaded areas represent the 95% confidence intervals of the slope of the regression line. The growing season length is assumed fix, from the beginning of April to the end of October.
Preprints 76491 g011
Preprints 76491 g012
Figure 12. Scatterplots of annual values of a) estimated LAI or b) FPI and ground measurements of yield. The grey shaded areas represent the 95% confidence intervals of the slope of the regression line. The growing season length is assumed to vary with elevation, following Table 3.
Figure 12. Scatterplots of annual values of a) estimated LAI or b) FPI and ground measurements of yield. The grey shaded areas represent the 95% confidence intervals of the slope of the regression line. The growing season length is assumed to vary with elevation, following Table 3.
Preprints 76491 g012
Preprints 76491 g013aPreprints 76491 g013b
Figure 13. Histogram of the distribution of the estimated damage among all the parcels of the 8 insured farms for the year 2022, grouped by municipality. The vertical red lines represent the average value of the estimated damage over the parcels belonging to the farm and municipality of interest.
Figure 13. Histogram of the distribution of the estimated damage among all the parcels of the 8 insured farms for the year 2022, grouped by municipality. The vertical red lines represent the average value of the estimated damage over the parcels belonging to the farm and municipality of interest.
Preprints 76491 g013aPreprints 76491 g013b
Table 1. Information on the sites where ground measurements were collected.
Table 1. Information on the sites where ground measurements were collected.
Site Parcels Codes Elevation
[m a.s.l.]		 Years Type of
measurement		 Frequency of
measurement
Laurein/Lauregno (BZ) L1, L2 1330-1340 2021 LAI and yield Every 1-2 weeks
Ritten/Renon (BZ) R1, R2, R3, R4 1250-1270 2021 LAI and yield Every 1-2 weeks
Muntatschinig/
Monteschino (BZ)		 V1, P2 1490, 1549 2017-2021 LAI 1 to 3 per month
Fondo (TN) F1, F2 970 2021 LAI and yield Every 1-2 weeks
Table 2. Definition of the growing season length according to elevation.
Table 2. Definition of the growing season length according to elevation.
Elevation [m a.s.l.] Start of the growing season (SOS) End of the growing season (EOS)
< 500 20/03 30/9
500 - 699 25/03 20/9
700 - 899 01/04 15/9
900 - 1099 10/04 10/9
1100 - 1299 15/04 5/9
1300 - 1500 01/05 30/8
Table 3. Characteristics of the parcels used to train the GPR model to estimate LAI from S1, aggregated by land use.
Table 3. Characteristics of the parcels used to train the GPR model to estimate LAI from S1, aggregated by land use.
Land use Number of parcels Parcel area (min - max) [m2]
Wooded summer pasture, tare 20% 21 64 - 154924
Wooded summer pasture, tare 50% 12 397 - 42743
Summer pasture 4 4602- 11346
Pasture 5 958 - 16428
Wooded pasture, tare 20% 8 507 – 2131
Permanent meadow 64 28 - 72467
Meadow, special area 4 981 - 4844
Table 4. Metrics of the validation of LAI estimated from S2 with ground measurements of LAI. n is the number of pairs used for the comparison.
Table 4. Metrics of the validation of LAI estimated from S2 with ground measurements of LAI. n is the number of pairs used for the comparison.
Parcel Years MAE
[m2 m-2]		 RMSE
[m2 m-2]		 MB
[m2 m-2]		 R2
 n
F1 2021 0.58 0.71 -0.39 0.88 21
F2 2021 0.69 0.87 -0.69 0.85 8
L1 2021 0.98 1.10 0.18 0.83 11
L2 2021 0.58 0.81 -0.11 0.83 11
R1 2021 0.82 1.01 0.08 0.85 25
R2 2021 0.96 1.20 0.81 0.74 19
R3 2021 0.72 0.98 0.20 0.48 25
R4 2021 0.86 0.95 0.67 0.83 20
V1 2017-2021 0.92 1.10 0.30 0.69 60
P2 2017-2021 0.59 0.67 0.53 0.12 89
V1, P2 (Figure 6) 2017-2021 0.72 0.87 0.44 0.80 149
All (Figure 5) 2021 0.78 0.98 -0.19 0.78 163
All 2017-2021 0.80 0.92 -0.31 0.81 289
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated