Prerpints.org logo
Preprint
Article

Effect of Tree Size Heterogeneity on the Overall Growth Trend of Trees in Coniferous Forests of the Tibetan Plateau

Altmetrics

Downloads

115

Views

79

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

14 June 2023

Posted:

14 June 2023

You are already at the latest version

Alerts
Abstract
Tree growth is under the combined influence of abiotic and biotic factors. Trees with different sizes may respond differently to these factors, implying that tree heterogeneity in tree size may also modulate the overall growth trend. To test this hypothesis, we focused on the radial growth trends of natural subalpine forests on the Tibetan Plateau. We first extended the iterative growth model (IGM) to the tree-ring scale (IGMR) to test the applicability of the generalized metabolic growth theory to tree growth. As predicted by the IGMR, the radial growth of trees at the aggregate scale is constrained by a unimodal pattern. Using the IGMR, we reconstructed the historical best growth trajectory (HBGT) of trees within the same community based on the tree with the largest radius and/or longest age in the community. From the average difference between the HBGT and the current radial growth rate of trees with different sizes, we constructed an indicator that can measure the overall variation in tree radial growth. Based on this indicator, we found a negative effect of tree size heterogeneity on the overall variability of tree growth across elevations. Further analysis also revealed that the radial growth rate of trees on the Tibetan Plateau has increased significantly compared to the past, where growing season average temperature and annual minimum temperature were negatively and positively correlated with tree growth below and above the treeline, respectively. Our study not only confirmed that the overall variability of tree growth depends on tree size heterogeneity but also proposed an indicator that reveals net changes in tree radial growth rate relative to the past. These theoretical advances facilitate the understanding of changes in the extent of subalpine forests.
Keywords: 
Subject: Biology and Life Sciences  -   Forestry

1. Introduction

It has been widely accepted that plant growth follows a 'rise-and-fall' unimodal curve (Ryan et al. 1997; Karadavut et al. 2008; Shi et al. 2013). However, some studies have suggested that very old trees may continue to increase their biomass (Johnson & Abrams 2009; Sillett et al. 2010; Stephenson et al. 2014), which appears to contradict the classical unimodal growth hypothesis. Although further studies have suggested that this may be related to heterogeneity in tree growth and the mitigation of growth limits (Sheil et al. 2017; Begović et al. 2023), it is still unclear what pattern the growth trend follows at the community scale and what its variation mechanism is. Furthermore, most growth models assume stable state variables (Marshall & White 2019), which limits our ability to predict the effects of abiotic and biotic factors on tree growth.
Tree radial growth is an important indicator of tree growth that captures both climate change and intrinsic growth trends. However, it is challenging to determine the overall radial growth trends followed by trees in natural forests. On the one hand, climate, competition, disturbance, and functional traits regulate the unimodal growth trajectory and fluctuate or change over time (Hérault et al. 2011). On the other hand, trees with different sizes may respond differently to these influence factors, and shape different growth trajectories (Yao et al. 2023). Metabolic growth theory (Hou et al. 2008; Zuo et al. 2012) provides a promising basis for understanding tree growth. However, there is still insufficient evidence to support its applicability to plant growth (Shi et al. 2013). We found that this may be related to the incompleteness of its core assumptions. To this end, we introduced the concept of unit tissue "formation time" (T) and thus derived a more comprehensive iterative growth model (IGM) (Shu et al. 2021; Yao et al. 2023). This improvement highlights the second law of thermodynamics constraint on organism growth and reveals the range to which growth trajectories occur (Shu et al. 2021; Yao et al. 2023). Not only that, evidence from plantations with similar tree size and stand age supports this unimodal growth model and suggests that climate can induce changes in the height and length of unimodal radial growth curves (Yao et al. 2023). We hypothesize that tree growth trajectories in natural forests are still constrained by the single-peaked model and can be described by the IGM.
Compared to planted forests, natural forests tend to have greater tree size heterogeneity. This means that the overall radial growth trend of trees in natural forests cannot be considered as a simple scale-up of individual growth. In multi-aged stands, the causes of size heterogeneity are related to repeated disturbances or silvicultural interventions that regenerate these new age classes (Nepstad et al. 2007; O'Hara & Ramage 2013; Shu et al. 2019). In single-aged stands, competition directly drives tree size differentiation (Forrester 2019). Obviously, to a large extent, tree size heterogeneity may mediate the effects of competition and disturbance on tree growth. Under different climatic conditions, how tree size heterogeneity influences the overall radial growth trend of trees is still unknown.
Ongoing climate warming in mountain areas is amplified with elevation, and its impact on forest distribution is still a major question in global change biology (Wang et al. 2017). Range shifts caused by warming have already been observed in some biomes, particularly those subalpine forests close to the treeline (Pepin et al. 2015). Tree radial growth consists of age-dependent low-frequency and climate-sensitive high-frequency signals. Although the high-frequency signal is a result of the rapid response of tree radial growth to climate, the age effects and sampling strategies still affect the accuracy of tree growth assessments and climate responses (Wang et al. 2017). In fact, studies have found that trees along elevation gradients respond divergently to warming (Fan et al. 2009; Dang et al. 2013; Lyu et al. 2016), and the age or size effect profoundly affects tree growth. Exploring the age effect, particularly the radial growth trajectory and its variability at the community scale, will undoubtedly enhance the understanding of forest distribution across different elevations.
The subalpine ecosystem occupies elevations just below tree-line between 2,700 and 3,500 m. They are not only widely distributed but also sensitive to global climate change (Shu et al. 2019; Shi et al. 2021). The Hengduan and southern Qinghai mountains, which run north‒south across the southeastern and northeastern Tibetan Plateau (TP), are rich in natural subalpine forests, providing invaluable opportunities to study tree growth patterns and variability in natural forests.
The aim of this study was to determine the effect of tree size heterogeneity on the overall radial growth trend of trees in natural forests. The experiment consisted of three steps. First, we extended the IGM to the tree-ring scale (IGMR) and evaluated its constraints on community-scale tree growth trends. Second, we developed a model-based measure to assess the overall radial growth variability of trees. Finally, we focused on the effect of tree size heterogeneity in communities under different climatic conditions on this variability across elevations.

2. Materials and Methods

2.1. Study Area and Data Collection

The study focused on coniferous forests in the Hengduan Mountains and South Qinghai Mountains on the Tibetan Plateau (Figure 1). The Hengduan Mountains experience the typical monsoonal climate, influenced by both the South Asian monsoon and the East Asian monsoon (Shi et al. 2021). The southern Qinghai Mountains experience a continental climate with large temperature fluctuations from day to night. The sample sites ranged in altitude from 2500-4136 m, with an average annual temperature of 5.04 °C and an average annual precipitation of 486.98 mm. Raw tree-ring width data for 7 species were collected from 45 natural forest sample sites distributed throughout the Tibetan Plateau region through the International Tree-Ring Data Bank (https://www.ncdc.noaa.gov/data-access/paleoclimatologydata/datasets/tree-ring), involving a total of 2500 tree cores (Figure 1 and Table 1).

2.2. Quantification of Tree Radial Growth Pattern and Its Overall Variability

We have extended the IGM to the tree-ring scale (IGMR) (Yao et al. 2023) (See Appendix A and Appendix B). Assuming that f(r)T is the ring width formed during time T, the relationships between tree growth rate (f(r)), metabolic exponent (b), current radius (r), and potential maximum radius (R) can be expressed as follows:
f ( r ) = 1 T ( ( T m r g r r 2 / b ( ( R r ) 2 / b - 2 - 1 ) + r 2 / b ) b / 2 − r )
where gr is the relatively stable respiration cost required to produce a unit of tissue and mr is the variable maintenance respiration rate per unit of tissue (Thornley & Cannell 2000). The value of T is related to the thermodynamic significance of respiration and ranges between 0 and gr/mr (Shu et al. 2021). To counteract natural degradation (entropy increase), organisms must continuously use negative entropy to maintain the complexity, variety, and order of their components. During time T, the growth energy proportional to gr decreases the entropy of a new unit tissue relative to that of their free precursor monomers (Clarke 2019). Meanwhile, maintenance energy, which is proportional to Tmr, maintains a low entropy state of an existing unit tissue and indicates its entropy accumulation during this time. Assuming the old and new units of tissue are identical, synthesis of a new unit of tissue is possible only if Tmr is less than gr; that is, T < gr/mr.
Mathematically, the limits T → 0 and gr/mr provide us with upper and lower boundaries for f(r). Usually, b is considered equal to 0.75 (West et al. 1999; Mori et al. 2010), but some evidence suggests that it may be equal to 0.85 (Cheng et al. 2010). Since the following results support the former, we give here only two growth boundaries at b = 0.75:
f ( r ) = 3 8 m r g r ( R 2 / 3 r 1 / 3 − r )  
f ( r ) = m r g r ( R 1 / 4 r 3 / 4 − r )
In theory, the more rapidly a unit of tissue grows (T → 0), the closer f(r) approaches Equation (1-b). Otherwise, (T → gr/mr), the closer f(r) is to Equation (1-c) (Shu et al. 2021). We termed Equations (1-b) and (1-c) as the thermodynamic lower (IGMR-L) and upper (IGMR-U) boundaries of the IGMR.
On the basis of Equations (1-b) and (1-c), we can establish a historical best growth trajectory (HBGT) based on the maximum radius and age of trees in the community, which can be expressed as:
f ( r ) H B G T = 2 k + 2 1 − k 1 T G T ( R 1 − k r k − r )
where 1/3 < k < 3/4. Moreover, according to the IGM, the total growth time (TGT) of an organism is gr/mr × (2b + 2)/(1 − b). However, the TGT for Equation (1-b) is 32/3 × gr/mr. It is also likely that the pattern that tree radial growth follows would shift from Equation (1-b) to Equation (1-c) over time, therefore ensuring that the TGT of tree radial growth is consistent with that of biomass growth. We speculated that the k value is closer to 3/4 due to T → gr/mr. Note that the other case is when b = 0.85 and T → gr/mr with k = 0.85.
Assuming that trees with the largest radius (R) and age (TGT) have the best growth trajectory and are more determined by historical factors, we can further quantify the overall average growth variability (OVG) relative to HBGT for the same community based on Equation (2) as follows:
O V G = ∑ ( c ( r i ) − f ( r i ) H B G T ) ∑ f ( r i ) H B G T
where c(ri) and f(ri)HBGT denote the current average growth rate over the past five years and estimated historical best growth rate, respectively, for tree i. When the OVG is greater than 0, it means that the overall growth trend of trees is better than historical; otherwise, this trend may decline or maintain the status quo.

2.3. Data Processing and Analysis

We conducted statistics on growth information for each chronology, including the current diameter (rc), age (L), and average growth rate over the past five years (f(r)c) for each tree core. Additionally, we extracted the average tree ring growth rate (f(r)m) for trees of the same species within each site. To ensure the robustness of our findings, we only analyzed chronologies with a minimum of 30 samples. We assumed that tree TGT is the 95th percentile of the L values of all trees of the same species within that site. However, this estimation tends to overestimate TGT for most trees because of growth heterogeneity. Mathematically, we can still assume that TGT is accurate, but f(r)m is overestimated. Therefore, the actual relationship between the normalized tree diameter (r/R) and the normalized growth rate (f(r)c/f(r)m) should be lower than the normalized Equation (2). Note that R here is equal to TGT × f(r)m. The normalized Equation (2) is obtained by assuming R = 1 and mr/gr = 1. Afterwards, we calculated the coefficient of variation of tree radius (CVR) at each site and performed a unimodal growth trajectory test for trees in sites classified as having low and high tree size variability. Based on the results of the test, we estimated the HBGT and CVR of each site using Equations (2) and (3).
After obtaining the current CVR value for each site, we analyzed its relationship with tree size heterogeneity and climate. Tree size heterogeneity is characterized by CVR, and the meteorological factors used, such as the mean annual temperature (MAT) and the mean annual precipitation (MAP), were extracted from WorldClim (2.5 min) (https://www.worldclim.org/data/worldclim21.html#). These meteorological factors are annual averages from 1970 to 2000. The hierarchical partitioning method was employed to determine the individual contribution of climate variables, CVR, and elevation to OVG via the rdacca.hp package in R (Lai et al. 2022). To analyze the direct and indirect effects of CVR and meteorological factors on OVG, we fitted a structural equation model (SEM). The sample size used here is 45. Since structural equation modeling requires a sample size of at least ten times the number of observed variables (Jackson 2003), we only included five observational variables in this study. The overall fit of the SEM was evaluated using the p value, GIF and RMSEA in the SEM package. In addition, we analyzed the differences between the best historical growth rates and the current growth rates of trees at different elevation ranges. Wilcox tests were chosen because the distribution of the data was not known.

3. Results

3.1. Tree Radial Growth Follows the IGMR-U

We first determined the distribution of CVR and tested whether the radial growth of trees within different CVR ranges was constrained by the IGMR. The results showed that CVR conforms to a normal distribution with a mean value of 0.375 and a variance of 0.143. We found that the estimated r/R mostly ranged from 0 to 1. Not only that r/R was normally distributed under CVR < 0.375 (gray bars in Figure 2A) (Figure A1). This means that a smaller CVR can filter the effects of competition and interference. When CVR < 0.375, the boundary (95th percentile) of the normalized radial growth rate conforms to the normalized Equation (1-c), where the fitted value of k is 0.736 ± 0.10, which supports our theoretical prediction, i.e., k = b = 0.75. On the other hand, when CVR is large (CVR > 0.375, white bars in Figure 2A), this boundary still falls below the normalized Equation (1-c). From our results, it is evident that unimodal patterns limit tree radial growth, following the IGMR-U.
The test samples in (B) and (C) are from data belonging to the gray and white bars in (A), respectively. The green curve in (C) is obtained from the 0.95 quantile fit of the data by Equation (2), where b = k = 0.736 ± 0.10. The curve in (B) is consistent with (C). B and C: The dot density is shown by different colors, with warmer hues representing higher density and cooler hues representing lower density.

3.2. Effect of Tree Size Heterogeneity on Overall Growth Variability

Using the IGMR-U, we reconstructed the HBGT for each site and assessed the overall variation in current radial tree growth. The results indicated a significant negative correlation between CVR and OVG (R2 = 0.24, p < 0.01), as presented in Figure 3A. Furthermore, hierarchical partitioning analysis suggested that CVR had a higher independent contribution to OVG than climate factors (Figure 3B). To further clarify the direct and indirect effects of climatic variability and/or CVR on OVG, we used SEM to fit the data, as shown in Figure 3C. The SEM indicates that, except for annual precipitation and the ratio of tree average to maximum age, which have certain direct positive and negative effects on OVG (0.33 and -0.52), OVG is mainly mediated by CVR. The precipitation of the warmest quarter and the ratio of tree average to maximum age can indirectly affect OVG through CVR, but they could only explain 31% of the variation in OVG. Most of the variations in OVG are independent of climate and forest age, and directly affect OVG. The standardized direct effects of climate, forest development, and CVR on OVG are 0.335, -0.521, and -0.672, respectively. Standardized indirect effects were 0.193, 0.301 and 0, respectively. Collectively, they could explain 61% of the variation in OVG.

3.3. Tree Radial Growth Assessment

On the basis of OVG, we further assessed tree radial growth at different elevations. We found that the current growth rate is generally higher than the historical best, calculated by HBGT, when the growth rate was small. However, the opposite was true when the growth rate is large, as shown in Figure 4A. This difference may be related to elevation, as shown in Figure 4B and 4C. Tree radial growth rates greatly increased at lower elevations. Conversely, the current growth rate of trees situated above the treeline was generally lower than the historical best value. If we assumed that the average radial growth rate is only half of the ideal, then we can calculate the historical average growth rate. We defined the difference between the current average growth rate and the historical average growth rate as the net increase in radial growth rate. In the low elevation region, there was a strong negative correlation between this net increase rate and the mean temperature of the wettest quarter (Figure 4D). On the other hand, at the upper treeline, the minimum temperature of the coldest month was positively correlated with this net change (Figure 4E).

4. Discussion

4.1. Tree Size or Radius Constrains Its Radial Growth and Growth- Climate Sensitivity

Radial growth of trees is usually considered to be influenced by age (or size) and climatic factors, showing an age-dependent low frequency (with a stable trend) and a climate-sensitive high frequency (rapid change) signal (Wilmking et al. 2017; Peltier & Ogle 2020; Yao et al. 2023). After removing the modulations of the age effect trend, this signal typically exhibits stable climate sensitivity, termed stationarity assumptions or uniformity principles (Wilmking et al. 2017; Peltier & Ogle 2020). Based on this principle, it is possible to obtain high-resolution global information on tree species’ responses to global change, forest carbon and water dynamics, and past climate variability and extremes from tree ring dynamics (Wilmking et al. 2020). However, our research indicated that there is no essential difference between high-frequency and low-frequency growth signals. Mathematically, the high-frequency signal is the limited fluctuation of the low-frequency signal, and both are mediated by tree size or radius, mr/gr, and potential maximum size or radius, where environmental and resource intake could significantly affect mr and the maximum size or radius.. Some evidence supports this conclusion. For example, age effects and sampling strategy affect the accuracy of tree growth assessment and its climate response (Wu et al. 2013; Sun & Liu 2015; Wang et al. 2017). Moreover, changes in tree physiological status (Peltier & Ogle 2020) result in different climate-growth relationships (Wu et al. 2013; Sun & Liu 2015) and inevitably feed back to the size-to-growth constraint (Coomes et al. 2012; Pillet et al. 2018; Shu et al. 2019). In fact, size has a greater effect than cellular senescence on age-related declines in relative growth and net assimilation rates (Mencuccini et al. 2005). Our model highlights that tree size, specifically the radius, determines the radial growth trend and climate sensitivity (Figure 5). That is, the variation coefficient of radial growth rate still shows a single-peaked pattern on the radius gradient.
Along the radius gradient, the variation coefficient of tree-ring width in the past five years follows a similar unimodal distribution. The green curve is consistent with Figure 2B. The dot density is shown by different colors, with warmer hues representing higher density and cooler hues representing lower density.

4.2. Limited Influence of Climate on Tree Size Heterogeneity of Subalpine Forests

Overall, warm season precipitation contributed to size convergence of trees in subalpine forests (Figure 3C). Concurrently, forest growth or development can also spontaneously reduce tree size heterogeneity. At lower elevations, increased precipitation can promote radial growth by reducing water stress and accelerating xylem activity during the growing season (Vieira et al. 2021). This boost will be more pronounced for smaller trees that grow faster, thus reducing CVR. However, at higher elevations with lower temperatures, increased precipitation may cause trees to experience more snowfall events and physical disturbances, resulting in increased CVR. Thus, significant negative (r = -0.79, p < 0.01) and positive (r = 0.44, p < 0.01) correlations were observed between CVR and the precipitation of coldest quarter at low and high elevations, respectively (see Appendix B, Figure A2). However, the role of precipitation and forest growth or development in regulating size heterogeneity is relatively limited, suggesting the repeated effects of disturbance and competition on forests. These results suggest that precipitation plays a key role in shaping the location and structure of the treeline (Lloyd & Graumlich 1997; Sigdel et al. 2018).

4.3. Forest Range Response to Tree Size Heterogeneity and Climate Change

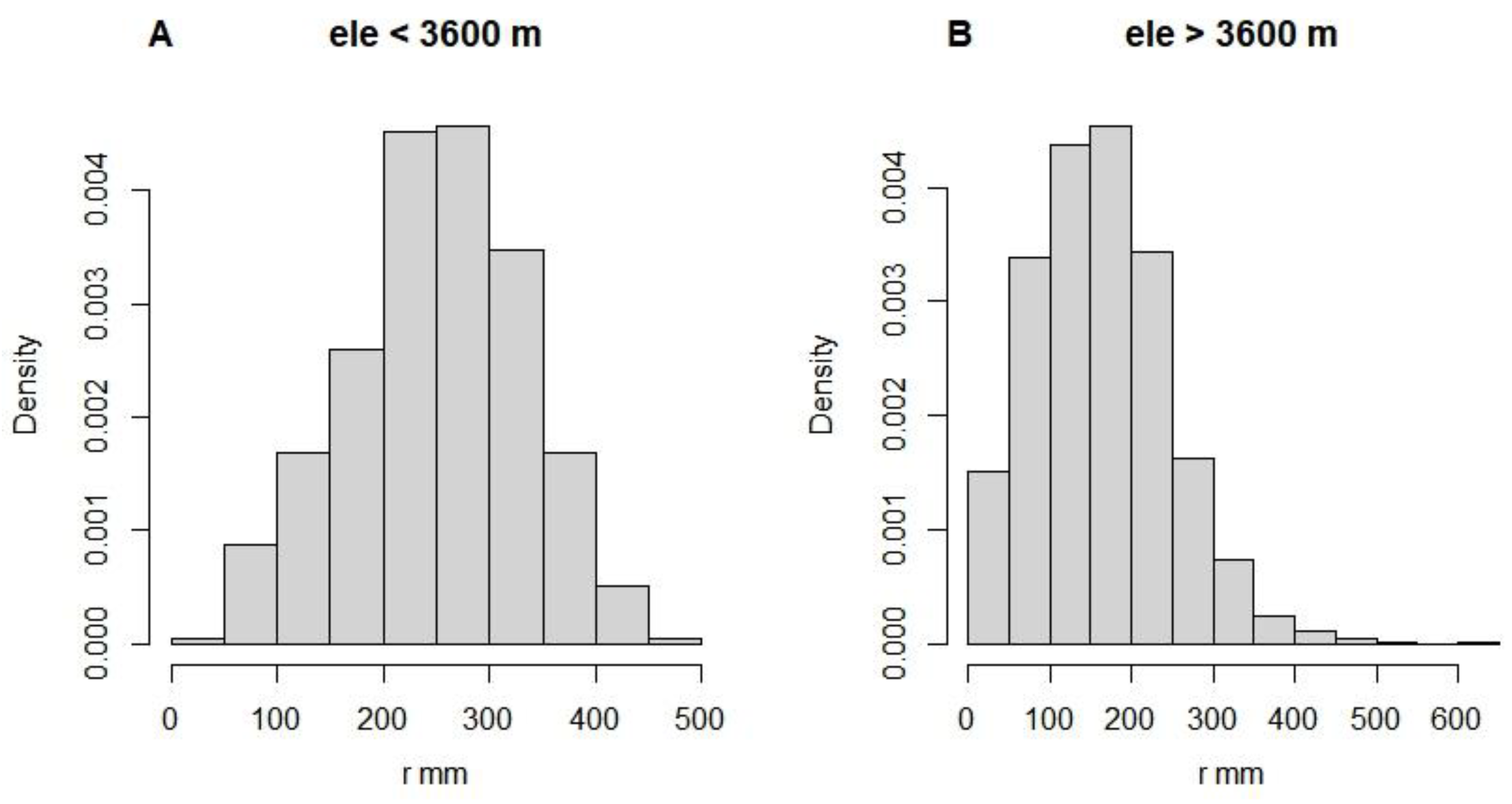
Our research suggests that treeline expansion may be related to both tree size heterogeneity and temperature in different seasons. On the one hand, size inequality may cause an overall decrease in tree growth. We found that tree CVR was significantly lower in the low elevation region (< 3600 m) than in the high elevation region (> 3600 m) (see Appendix B, Figure A3), while the radial growth rate of low elevation trees was also overall higher than the estimated historical best value (Figs. 4B and 4C). This difference can be attributed to the negative effect of CVR on OVG (Figure 3). We speculated that competition and disturbance may be the main causes of increased CVR and decreased OVG. Usually, in natural forests, smaller trees are more vulnerable to asymmetric competition, whereas larger trees are prone to being affected by disturbance (Coomes et al. 2012; Pillet et al. 2018; Shu et al. 2019). For subalpine forests, this pattern also broadly applies, but the proportion of large individuals decreases significantly with increasing elevation (see Appendix B, Figure A4), implying that disturbance may be related to treeline formation. On the other hand, net changes in tree radial growth rates at low and high elevations may be differentially affected by temperature in different seasons. In the subalpine forest belts, precipitation tends to be more abundant during the growing season. Nevertheless, rising temperatures may lead to an increase in respiration rates, which can lead to a decrease in the allocation of photosynthetic product to growth (Peng et al. 2013). Consequently, we can observe a significant negative correlation between net changes in tree radial growth rates and the mean temperature of the wettest quarter (Figure 4D). At higher elevations, low temperatures limited tree growth, showing a positive correlation between minimum temperature and this change (Figure 4E). These results imply that global warming affects tree growth variability differently in the high and low elevation ranges of subalpine.

4.4. Tree Growth Assessment Based on Generalized Metabolic Growth Theory

Understanding how abiotic and biotic factors contribute to tree growth has been a longstanding challenge in global ecology. Our study introduces a new indicator for measuring radial growth variability based on a generalized metabolic growth theory. The theoretical framework underlying this indicator not only considers variability in state variables, such as b but also incorporates an iterative growth mechanism, making it highly suitable for modeling and predicting plant growth (Shu et al. 2019). The differences in tree lifespan and average growth rate under different environments will be captured by the growth model (Yao et al. 2023). Therefore, our method of measuring overall tree growth variability is highly applicable. However, sampling strategies can affect the accuracy of tree growth assessments and the response to climate (Wu et al. 2013; Sun & Liu 2015). Traditional sampling methods may introduce bias into the growth trend (Nehrbass-Ahles et al. 2014). Therefore, in future studies, it is worth considering the different age classes of the trees at the time of sampling. We recommend choosing as many trees of different sizes as possible so that the overall fit appears as a unimodal trajectory in theory.

5. Conclusions

We revealed a single-peak pattern of radial growth in natural forest trees by expanding the IGM, thereby quantifying the overall average difference in radial growth of trees in subalpine forests relative to history best estimate. Further analysis showed that precipitation and tree size heterogeneity have positive and negative effects on this difference, respectively. At lower elevations, precipitation can reduce tree size heterogeneity, but with increasing elevation, precipitation evolves into snowfall disturbance and increases size heterogeneity. In addition, our results suggest a constraining effect of tree size on growth-climate sensitivity.

Author Contributions

Conceptualization: Y.W. and S.S.; Methodology: S.S.; Visualization: Y.W.; Funding acquisition: S.S. and X.W.; Project administration: X.W.; Supervision: X.W.; Writing—original draft: Y.W. and S.S.; Writing—review & editing: S.S., X.W. and W.C. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No: 32201374) and by the Second Tibetan Plateau Scientific Expedition and Research Program (Grant No: 2019QZKK0404).

Data Availability Statement

Tree radial growth data are available at https://www.ncei.noaa.gov/products/paleoclimatology/tree-ring.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Glossary

Symbol Meaning Unit
f(r) tree ring growth rate mm/y
T The formation time of unit tissue is primarily controlled genetically and by physiological activities, with the intrinsic or developmental growth rate independent of organism size y
R Tree maximum radius mm
r Tree current radius mm
mr Rate of maintenance respiration per unit of tissue mg g−1 y−1
gr Cost of respiration needed to produce a unit of tissue mg g−1
b Metabolic exponent, taken here as 0.75 1
TGT Total growth time y
f(r)HGBT Growth rate of historical best growth trajectory mm/y
OVG overall average growth variability 1
c(ri) current average growth rate over the past five years, for tree i. mm/y
f(ri)HBGT Estimated historical best growth rate for tree i mm/y
f(r)c average growth rate over the past five years mm/y
rc Statistical current diameter mm
L Statistical tree age y
f(r)m Statistical average tree ring growth rate mm/y
k Pending parameter 1
CVR coefficient of variation of tree radius 1

Appendix A

Appendix A.1. Iterative Growth Model (IGM)

Tree respiration involves the transport, release, and use of energy stored in photosynthetic carbohydrate products. This supports tree growth, maintenance, and longevity. These energy-demanding processes also follow the first and second laws of thermodynamics and the allometric scaling laws of metabolism. Based on these rules, we constructed a general kinetic framework for organism growth (Shu et al. 2021)
f ( m ) T = m r g r ( M 1 − b ( m − o ) b − m + o )
where f(m) is the total biomass of new tissue created during the formation time T of a unit of tissue and hence f(m)/T represents the average growth rate over this formation time, as well as the growth rate; b is the metabolic scaling exponent, related to a space-filling fractal (self-similar)-like network; gr is the cost of respiration needed to produce a new unit of tissue; and mr is a unit of tissue's rate of maintenance respiration (per unit of time). Generally, gr is stable, and mr is sensitive to the environment and is driven by temperature, with its trend following the Arrhenius equation. Mathematically, Equation (A1) highlights a growth iterative mechanism. Namely, growth can be described as a series of spontaneously iterated feedbacks - each of length T. At each iteration the organism moves from the initial biomass m0 (slightly larger than the threshold biomass for growth, o) and approaches the final mass M. Thus, we refer to Equation (1) as an iterative growth model (IGM).
Moreover, the IGM contains two implicit thermodynamic and mathematical constraints. The first constraint is that T < gr/mr. We derive this from the thermodynamic significance of respiration. To counteract natural degradation (entropy increase), organisms must continuously use negative entropy to maintain the complexity, variety, and order of their components. Usually, organisms obtain useful energy (e.g., chemical energy stored in photosynthetic products or food) from the environment and return equivalent amounts of energy to the environment in less useful forms, such as dissipated energy or heat. In this process, energy provides negative entropy or the required order to organisms. Thus, from an entropy perspective, during time T, the growth energy proportional to gr decreases the entropy of a new unit of tissue relative to that of their free precursor monomers (Clarke 2019), causing free monomers to achieve an appropriate ordered state. At the same time, the maintenance energy proportional to Tmr contributes the negative entropy to maintain the low entropy state of a unit of old tissue, and mr and Tmr are also proportional to the entropy increase rate and entropy accumulation of a unit of old tissue during time T, respectively. Assuming there is no difference between the new and old units of tissue, the new-unit tissue can be synthesized only when Tmr must be less than gr, i.e., T < gr/mr. When T → 0 and gr/mr, integrating or iterating Equation (1) will produce two smooth functions driven by time (t), i.e., the Richards and Gompertz equations (Shu et al. 2021).
m = M ( 1 − L exp ( − r t ) ) 1 / 1 − b
m = M ⋅ ( m 0 / M ) b n
where L = 1-Mb−1×m01-b, r = mr/gr(1-b), m0 is the first biomass observed, and n is the number of iterations and is equal to t•mr/gr. These results indicate that actual growth dynamics lie somewhere between these equations (Equations (A2-a) and (A2-b)) and may not be an explicit analytic solution in most cases.
Second, from a mathematical perspective, M maintains a strict relationship with other parameters.
M = D T g r m r 2 b + 2 1 − b
where D is the average f(m), mainly determined by the ability of plants to absorb resources and the supply of resources, and TM/D or gr/mr×(2b+2)/(1-b) represents the total growth time. The basis for this equation is an integral transform from f(m) to M (Shu et al. 2021).
Due to tree radius (r) ∝ mb/2 (West et al. 1999), we can then derive Equation (1-a).

Appendix B

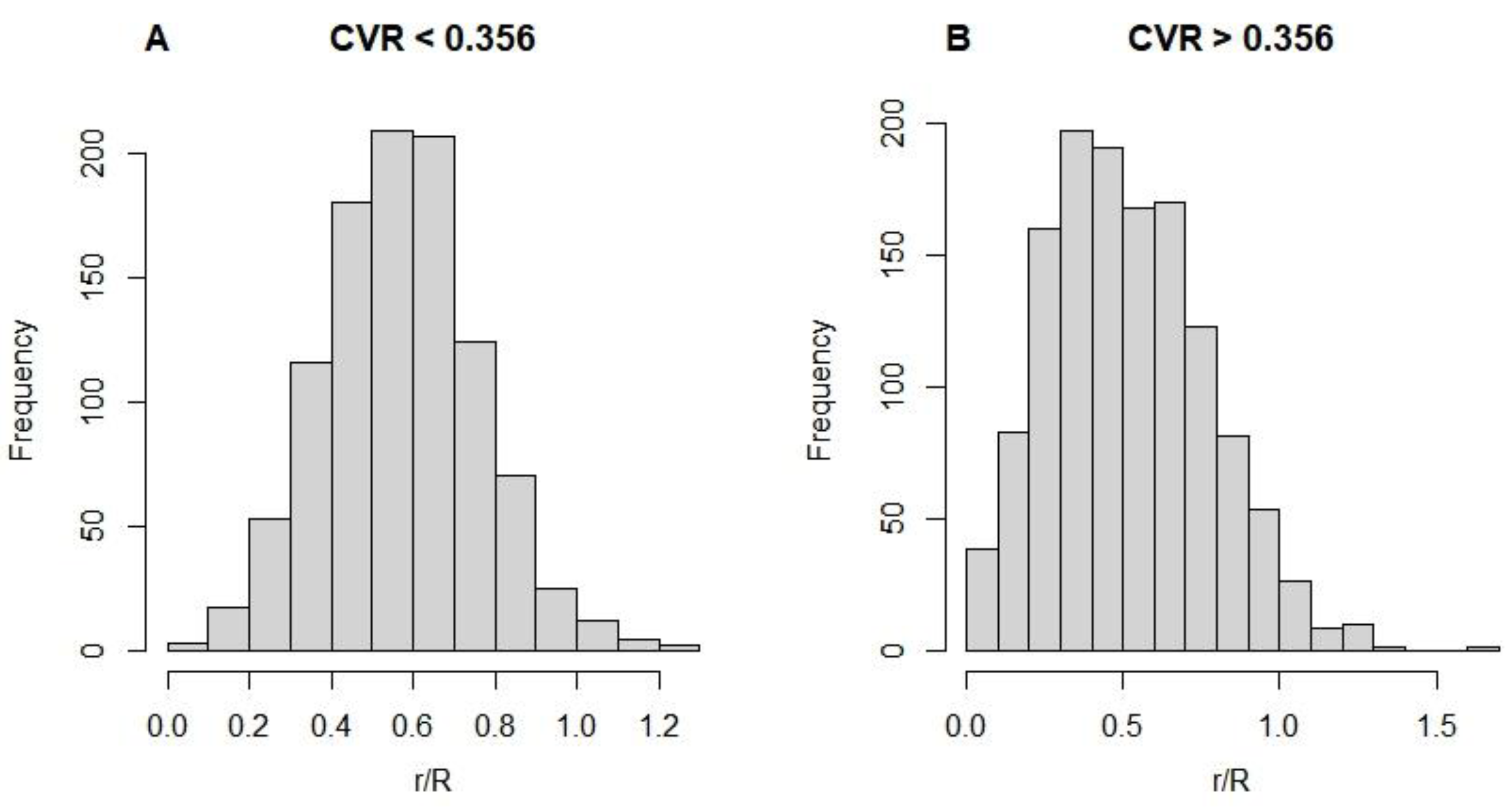
Preprints 76591 g0a1
Figure A1. Distribution of r/R over different CVR intervals. CVR: the coefficient of variation of tree radius.
Figure A1. Distribution of r/R over different CVR intervals. CVR: the coefficient of variation of tree radius.
Preprints 76591 g0a1
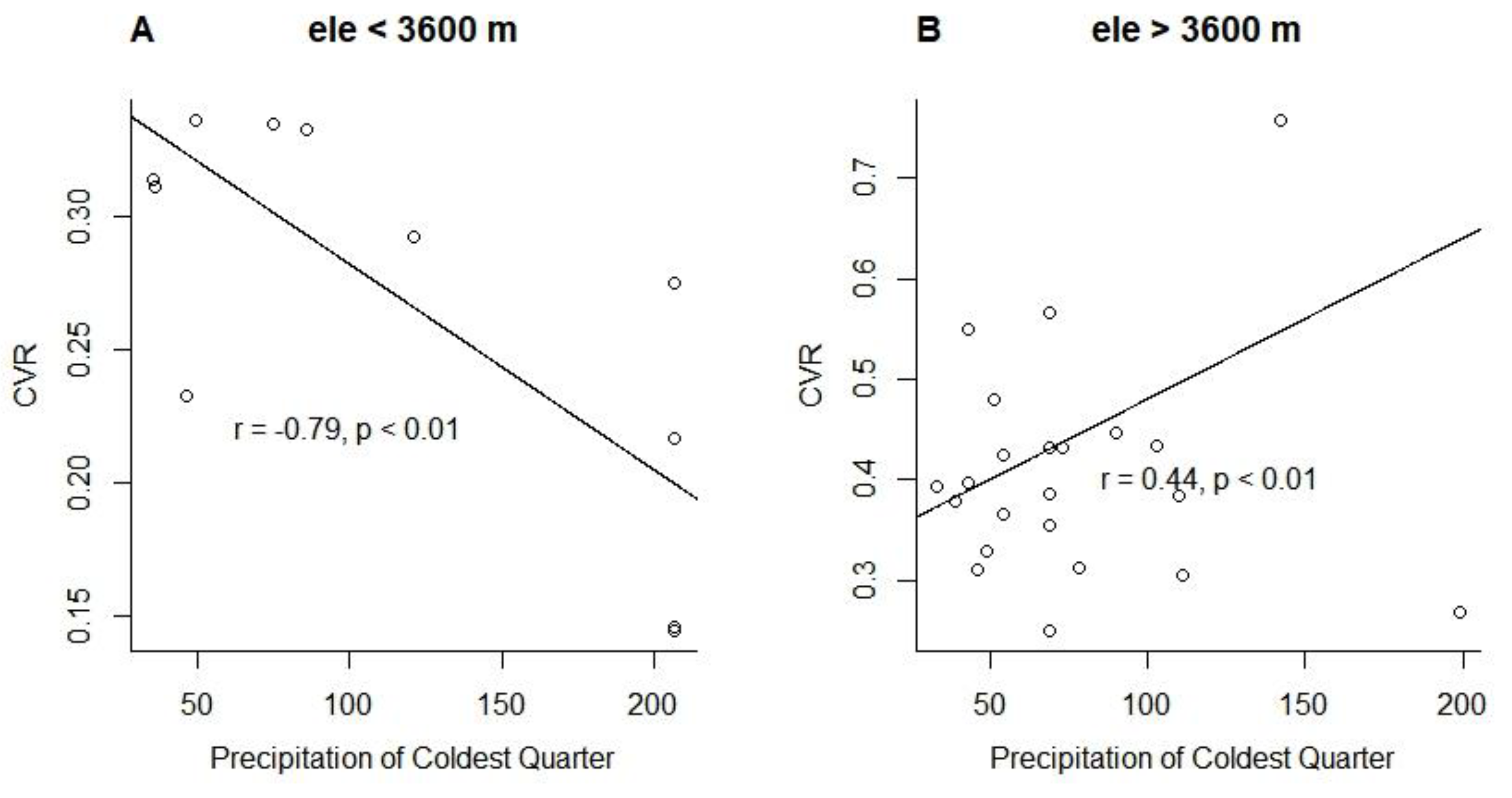
Preprints 76591 g0a2
Figure A2. Correlation of precipitation of coldest quarter with coefficient of variation of tree radius (CVR) at different elevation ranges.
Figure A2. Correlation of precipitation of coldest quarter with coefficient of variation of tree radius (CVR) at different elevation ranges.
Preprints 76591 g0a2
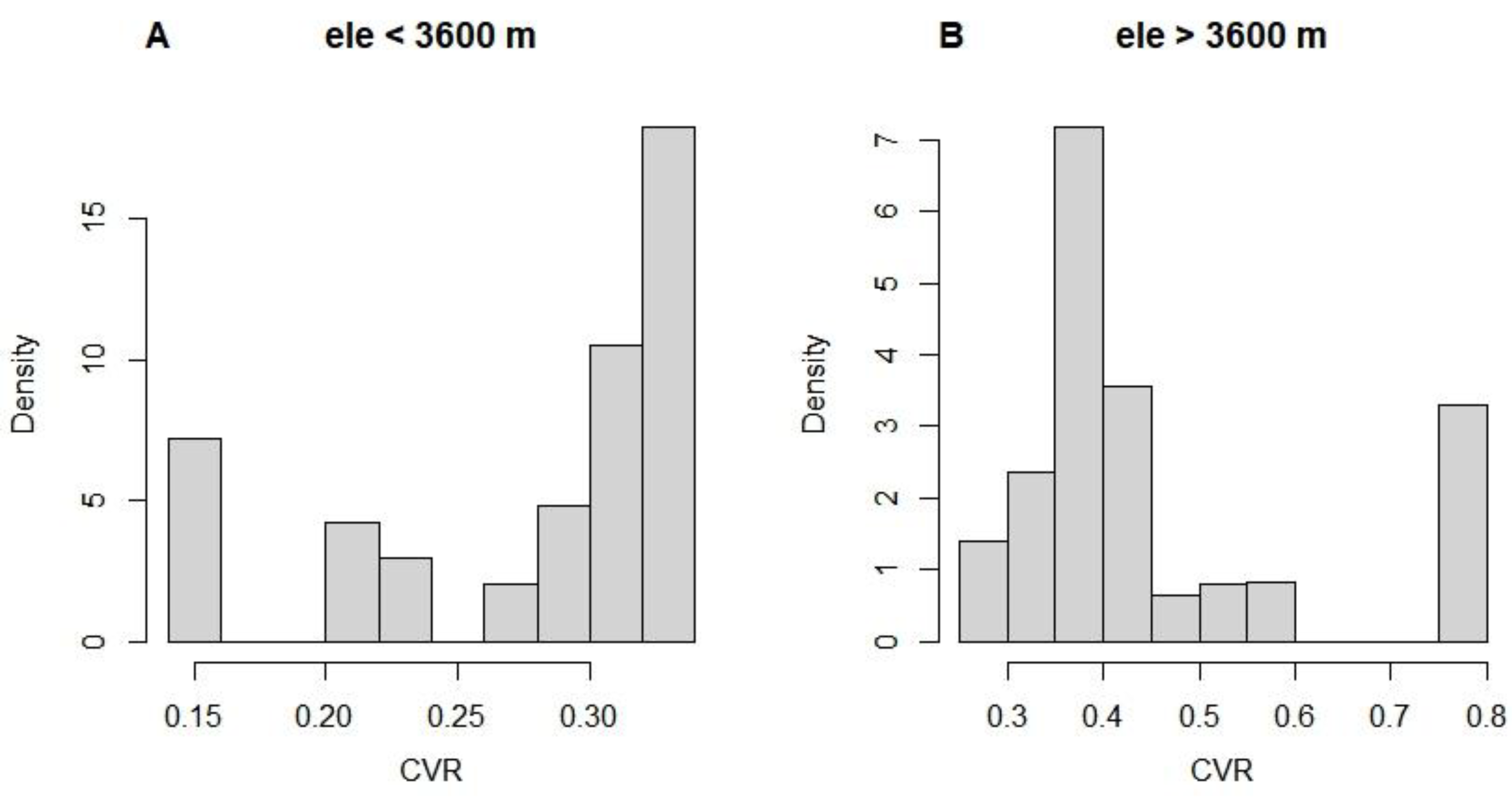
Preprints 76591 g0a3
Figure A3. Coefficient of variation of tree radius (CVR) at different elevation ranges.
Figure A3. Coefficient of variation of tree radius (CVR) at different elevation ranges.
Preprints 76591 g0a3
Preprints 76591 g0a4
Figure A4. Radius distribution of trees at different elevation ranges.
Figure A4. Radius distribution of trees at different elevation ranges.
Preprints 76591 g0a4

References

  1. Begović, K., Schurman, J.S., Svitok, M., Pavlin, J., Langbehn, T., Svobodová, K. et al. (2023). Large old trees increase growth under shifting climatic constraints: Aligning tree longevity and individual growth dynamics in primary mountain spruce forests. Global Change Biology, 29, 143-164. [CrossRef]
  2. Cheng, D.L., Li, T., Zhong, Q.L. & Wang, G.X. (2010). Scaling relationship between tree respiration rates and biomass. Biology letters, 6, 715-717. [CrossRef]
  3. Clarke, A. (2019). Energy Flow in Growth and Production. Trends in Ecology & Evolution, 34, 502-509. [CrossRef]
  4. Coomes, D.A., Holdaway, R.J., Kobe, R.K., Lines, E.R. & Allen, R.B. (2012). A general integrative framework for modelling woody biomass production and carbon sequestration rates in forests. Journal of Ecology, 100, 42-64. [CrossRef]
  5. Dang, H., Zhang, Y., Zhang, K., Jiang, M. & Zhang, Q. (2013). Climate-growth relationships of subalpine fir (Abies fargesii) across the altitudinal range in the Shennongjia Mountains, central China. Climatic Change, 117, 903-917. [CrossRef]
  6. Fan, Z.-X., Braeuning, A., Cao, K.-F. & Zhu, S.-D. (2009). Growth-climate responses of high-elevation conifers in the central Hengduan Mountains, southwestern China. Forest Ecology and Management, 258, 306-313.
  7. Forrester, D.I. (2019). Linking forest growth with stand structure: Tree size inequality, tree growth or resource partitioning and the asymmetry of competition. Forest Ecology and Management, 447, 139-157. [CrossRef]
  8. Hérault, B., Bachelot, B., Poorter, L., Rossi, V., Bongers, F., Chave, J. et al. (2011). Functional traits shape ontogenetic growth trajectories of rain forest tree species. Journal of Ecology, 99, 1431-1440. [CrossRef]
  9. Hou, C., Zuo, W., Moses, M.E., Woodruff, W.H., Brown, J.H. & West, G.B. (2008). Energy Uptake and Allocation During Ontogeny. Science, 322, 736-739. [CrossRef]
  10. Jackson, D.L. (2003). Revisiting Sample Size and Number of Parameter Estimates: Some Support for the N:q Hypothesis. Structural Equation Modeling: A Multidisciplinary Journal, 10, 128-141. [CrossRef]
  11. Johnson, S.E. & Abrams, M.D. (2009). Age class, longevity and growth rate relationships: protracted growth increases in old trees in the eastern United States. Tree Physiology, 29, 1317-1328. [CrossRef]
  12. Karadavut, U., Kayis, S. & Okur, O. (2008). A Growth Curve Application to Compare Plant Heights and Dry Weights of Some Wheat Varieties. American-Eurasian Journal of Agricultural & Environmental Sciences, 3.
  13. Lai, J., Zou, Y., Zhang, J. & Peres-Neto, P.R. (2022). Generalizing hierarchical and variation partitioning in multiple regression and canonical analyses using the rdacca.hp R package. Methods in Ecology and Evolution, 13, 782-788.
  14. Lloyd, A.H. & Graumlich, L.J. (1997). HOLOCENE DYNAMICS OF TREELINE FORESTS IN THE SIERRA NEVADA. Ecology, 78, 1199-1210.
  15. Lyu, L., Deng, X. & Zhang, Q.-B. (2016). Elevation Pattern in Growth Coherency on the Southeastern Tibetan Plateau. Plos One, 11. [CrossRef]
  16. Marshall, D.J. & White, C.R. (2019). Have We Outgrown the Existing Models of Growth? Trends in Ecology & Evolution, 34, 102-111.
  17. Mencuccini, M., Martínez-Vilalta, J., Vanderklein, D., Hamid, H.A., Korakaki, E., Lee, S. et al. (2005). Size-mediated ageing reduces vigour in trees. Ecology Letters, 8, 1183-1190. [CrossRef]
  18. Mori, S., Yamaji, K., Ishida, A., Prokushkin, S.G., Masyagina, O.V., Hagihara, A. et al. (2010). Mixed-power scaling of whole-plant respiration from seedlings to giant trees. Proceedings of the National Academy of Sciences of the United States of America, 107, 1447-1451.
  19. Nehrbass-Ahles, C., Babst, F., Klesse, S., Nötzli, M., Bouriaud, O., Neukom, R. et al. (2014). The influence of sampling design on tree-ring-based quantification of forest growth. Global Change Biology, 20, 2867-2885. [CrossRef]
  20. Nepstad, D.C., Tohver, I.M., Ray, D., Moutinho, P. & Cardinot, G. (2007). MORTALITY OF LARGE TREES AND LIANAS FOLLOWING EXPERIMENTAL DROUGHT IN AN AMAZON FOREST. Ecology, 88, 2259-2269. [CrossRef]
  21. O'Hara, K.L. & Ramage, B.S. (2013). Silviculture in an uncertain world: utilizing multi-aged management systems to integrate disturbance†. Forestry: An International Journal of Forest Research, 86, 401-410. [CrossRef]
  22. Peltier, D.M.P. & Ogle, K. (2020). Tree growth sensitivity to climate is temporally variable. Ecology Letters, 23, 1561-1572. [CrossRef]
  23. Peng, S., Piao, S., Ciais, P., Myneni, R.B., Chen, A., Chevallier, F. et al. (2013). Asymmetric effects of daytime and night-time warming on Northern Hemisphere vegetation. Nature, 501, 88-92. [CrossRef]
  24. Pepin, N., Bradley, R.S., Diaz, H.F., Baraer, M., Caceres, E.B., Forsythe, N. et al. (2015). Elevation-dependent warming in mountain regions of the world. Nature Climate Change, 5, 424-430. [CrossRef]
  25. Pillet, M., Joetzjer, E., Belmin, C., Chave, J., Ciais, P., Dourdain, A. et al. (2018). Disentangling competitive vs. climatic drivers of tropical forest mortality. Journal of Ecology, 106, 1165-1179. [CrossRef]
  26. Ryan, M.G., Binkley, D. & Fownes, J.H. (1997). Age-Related Decline in Forest Productivity: Pattern and Process. In: Advances in Ecological Research (eds. Begon, M & Fitter, AH). Academic Press, pp. 213-262. [CrossRef]
  27. Sheil, D., Eastaugh, C.S., Vlam, M., Zuidema, P.A., Groenendijk, P., van der Sleen, P. et al. (2017). Does biomass growth increase in the largest trees? Flaws, fallacies and alternative analyses. Functional Ecology, 31, 568-581. [CrossRef]
  28. Shi, P.-J., Men, X.-Y., Sandhu, H.S., Chakraborty, A., Li, B.-L., Ou-Yang, F. et al. (2013). The “general” ontogenetic growth model is inapplicable to crop growth. Ecological Modelling, 266, 1-9.
  29. Shi, S., Liu, G., Li, Z. & Ye, X. (2021). Elevation-dependent growth trends of forests as affected by climate warming in the southeastern Tibetan Plateau. Forest Ecology and Management, 498, 119551. [CrossRef]
  30. Shu, S.-m., Zhu, W.-z., Kontsevich, G., Zhao, Y.-y., Wang, W.-z., Zhao, X.-x. et al. (2021). A discrete model of ontogenetic growth. Ecological Modelling, 460, 109752. [CrossRef]
  31. Shu, S.-m., Zhu, W.-z., Wang, W.-z., Jia, M., Zhang, Y.-y. & Sheng, Z.-l. (2019). Effects of tree size heterogeneity on carbon sink in old forests. Forest Ecology and Management, 432, 637-648. [CrossRef]
  32. Sigdel, S.R., Wang, Y., Camarero, J.J., Zhu, H., Liang, E. & Peñuelas, J. (2018). Moisture-mediated responsiveness of treeline shifts to global warming in the Himalayas. Glob Chang Biol, 24, 5549-5559. [CrossRef]
  33. Sillett, S.C., Van Pelt, R., Koch, G.W., Ambrose, A.R., Carroll, A.L., Antoine, M.E. et al. (2010). Increasing wood production through old age in tall trees. Forest Ecology and Management, 259, 976-994. [CrossRef]
  34. Stephenson, N.L., Das, A.J., Condit, R., Russo, S.E., Baker, P.J., Beckman, N.G. et al. (2014). Rate of tree carbon accumulation increases continuously with tree size. Nature, 507, 90-93. [CrossRef]
  35. Sun, J. & Liu, Y. (2015). Age-independent climate-growth response of Chinese pine (Pinus tabulaeformis Carrière) in North China. Trees, 29, 397-406. [CrossRef]
  36. Thornley, J.H.M. & Cannell, M.G.R. (2000). Modelling the Components of Plant Respiration: Representation and Realism. Annals of Botany, 85, 55-67. [CrossRef]
  37. Vieira, J., Nabais, C. & Campelo, F. (2021). Extreme Growth Increments Reveal Local and Regional Climatic Signals in Two Pinus pinaster Populations. Frontiers in Plant Science, 12. [CrossRef]
  38. Wang, W., Jia, M., Wang, G., Zhu, W. & McDowell, N.G. (2017). Rapid warming forces contrasting growth trends of subalpine fir (Abies fabri) at higher- and lower-elevations in the eastern Tibetan Plateau. Forest Ecology and Management, 402, 135-144. [CrossRef]
  39. West, G.B., Brown, J.H. & Enquist, B.J. (1999). A general model for the structure and allometry of plant vascular systems. Nature, 400, 664-667. [CrossRef]
  40. Wilmking, M., Scharnweber, T., van der Maaten-Theunissen, M. & van der Maaten, E. (2017). Reconciling the community with a concept—The uniformitarian principle in the dendro-sciences. Dendrochronologia, 44, 211-214.
  41. Wilmking, M., van der Maaten-Theunissen, M., van der Maaten, E., Scharnweber, T., Buras, A., Biermann, C. et al. (2020). Global assessment of relationships between climate and tree growth. Global Change Biology, 26, 3212-3220. [CrossRef]
  42. Wu, G. , Xu, G., Chen, T., Liu, X., Zhang, Y., An, W. et al. (2013). Age-dependent tree-ring growth responses of Schrenk spruce (Picea schrenkiana) to climate—A case study in the Tianshan Mountain, China. Dendrochronologia, 31, 318-326. [CrossRef]
  43. Yao, Y., Shu, S., Wang, W., Liu, R., Wang, Y., Wang, X. et al. (2023). Growth and carbon sequestration of poplar plantations on the Tibetan Plateau. Ecological Indicators, 147, 109930. [CrossRef]
  44. Zuo, W., Moses, M.E., West, G.B., Hou, C. & Brown, J.H. (2012). A general model for effects of temperature on ectotherm ontogenetic growth and development. Proceedings of the Royal Society B: Biological Sciences, 279, 1840-1846. [CrossRef]
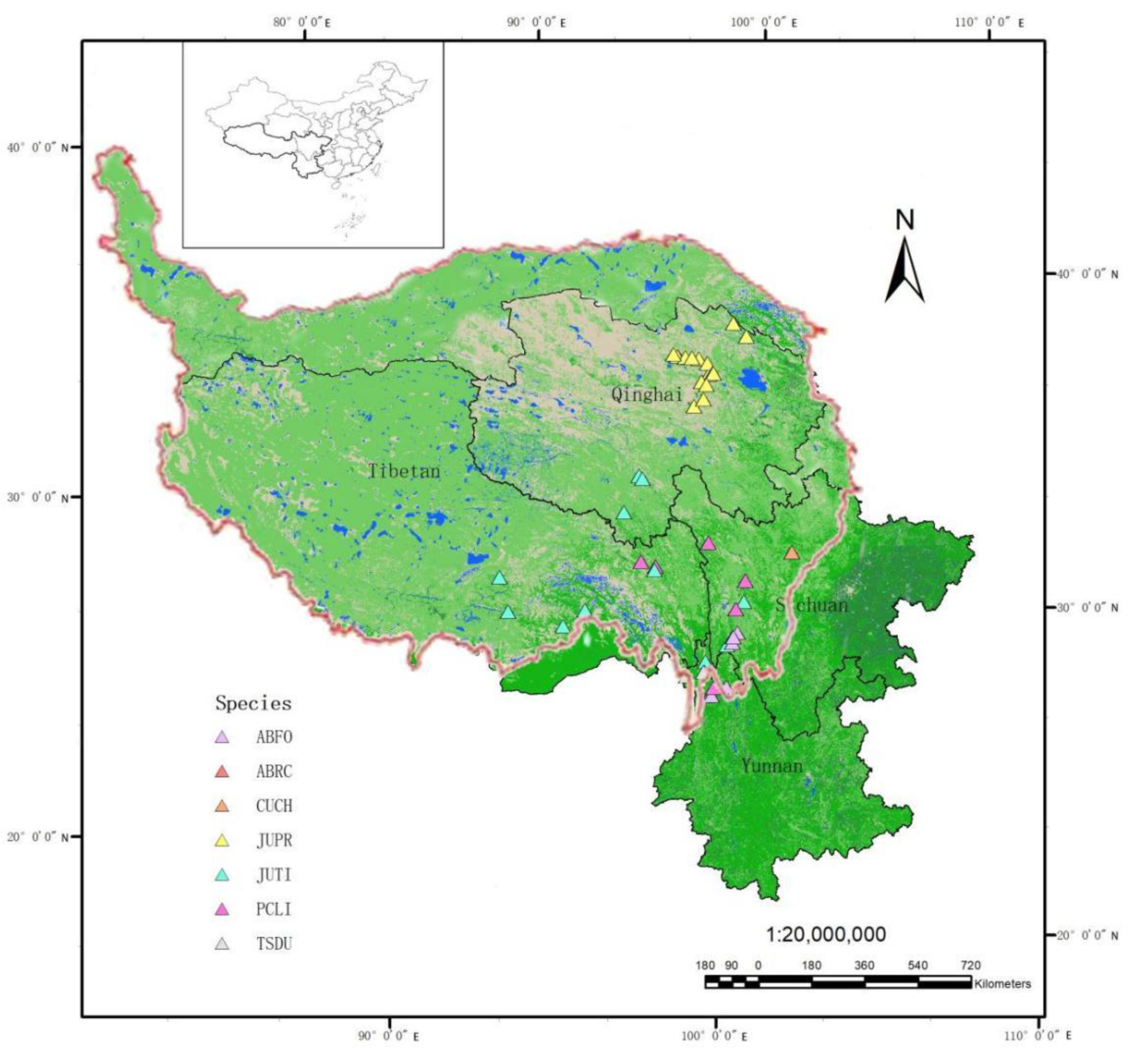
Preprints 76591 g001
Figure 1. Map of the research area, Tibetan Plateau.
Figure 1. Map of the research area, Tibetan Plateau.
Preprints 76591 g001
Preprints 76591 g002
Figure 2. Distribution of the coefficient of variation in the tree radius (A) and the distribution of the normalized growth rate on the relative radius (B and C).
Figure 2. Distribution of the coefficient of variation in the tree radius (A) and the distribution of the normalized growth rate on the relative radius (B and C).
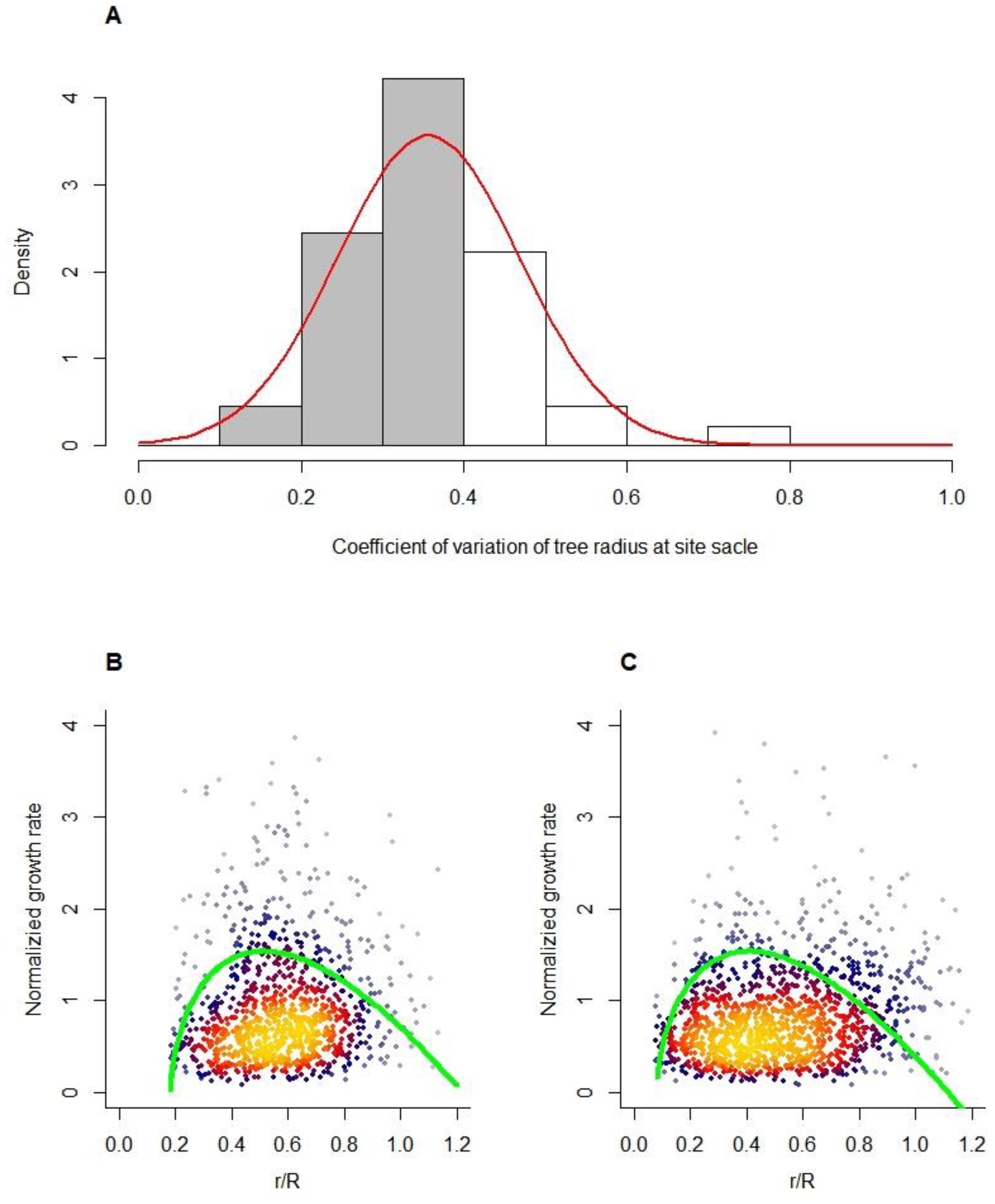
Preprints 76591 g002
Preprints 76591 g003aPreprints 76591 g003b
Figure 3. Correlation (A), hierarchical partitioning (B), and structural equation model analyses (C) between explanatory variables and OVG. A: Normalized growth rate: ratio of the average growth rate of tree cores over the past five years to the average growth rate of all tree cores (f(r)c/f(r)m). B: ele: elevation; Temp: mean annual temperature; Maxtwm: max temperature of warmest month; Mentwq: mean temperature of warmest quarter; Mentcq: mean temperature of coldest quarter; Ap: annual precipitation; Pwq: precipitation of wettest quarter, Pcq: precipitation of driest quarter. C: Solid red and green arrows represent significant (p < 0.05) positive and negative paths, respectively; double arrow solid lines indicate correlation. The numbers near the lines indicate the standard path coefficients or correlation coefficients. R2 represents the amount of variation of the variable explained by corresponding paths. The red and green lines indicate negative and positive effects, respectively.
Figure 3. Correlation (A), hierarchical partitioning (B), and structural equation model analyses (C) between explanatory variables and OVG. A: Normalized growth rate: ratio of the average growth rate of tree cores over the past five years to the average growth rate of all tree cores (f(r)c/f(r)m). B: ele: elevation; Temp: mean annual temperature; Maxtwm: max temperature of warmest month; Mentwq: mean temperature of warmest quarter; Mentcq: mean temperature of coldest quarter; Ap: annual precipitation; Pwq: precipitation of wettest quarter, Pcq: precipitation of driest quarter. C: Solid red and green arrows represent significant (p < 0.05) positive and negative paths, respectively; double arrow solid lines indicate correlation. The numbers near the lines indicate the standard path coefficients or correlation coefficients. R2 represents the amount of variation of the variable explained by corresponding paths. The red and green lines indicate negative and positive effects, respectively.
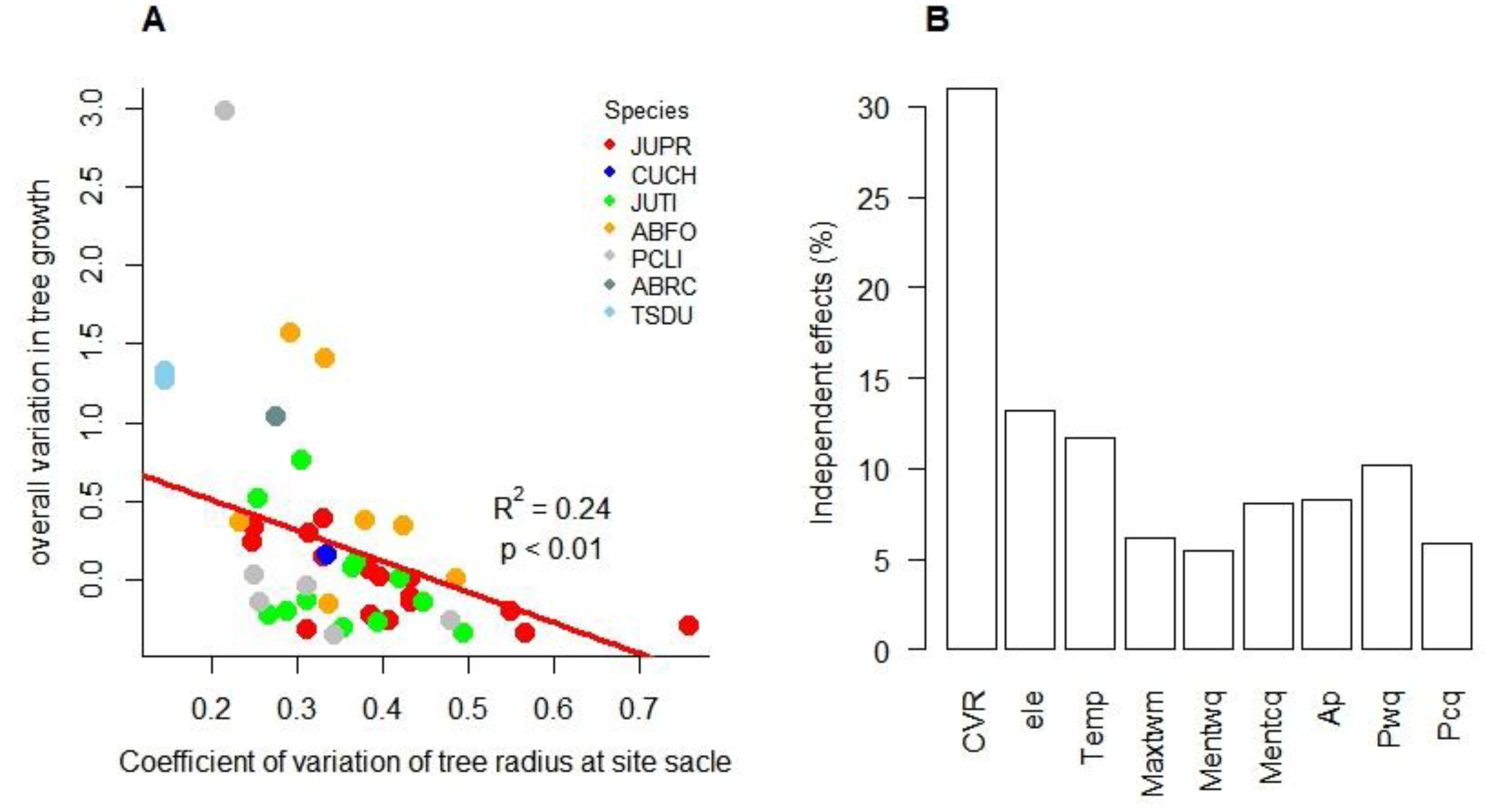
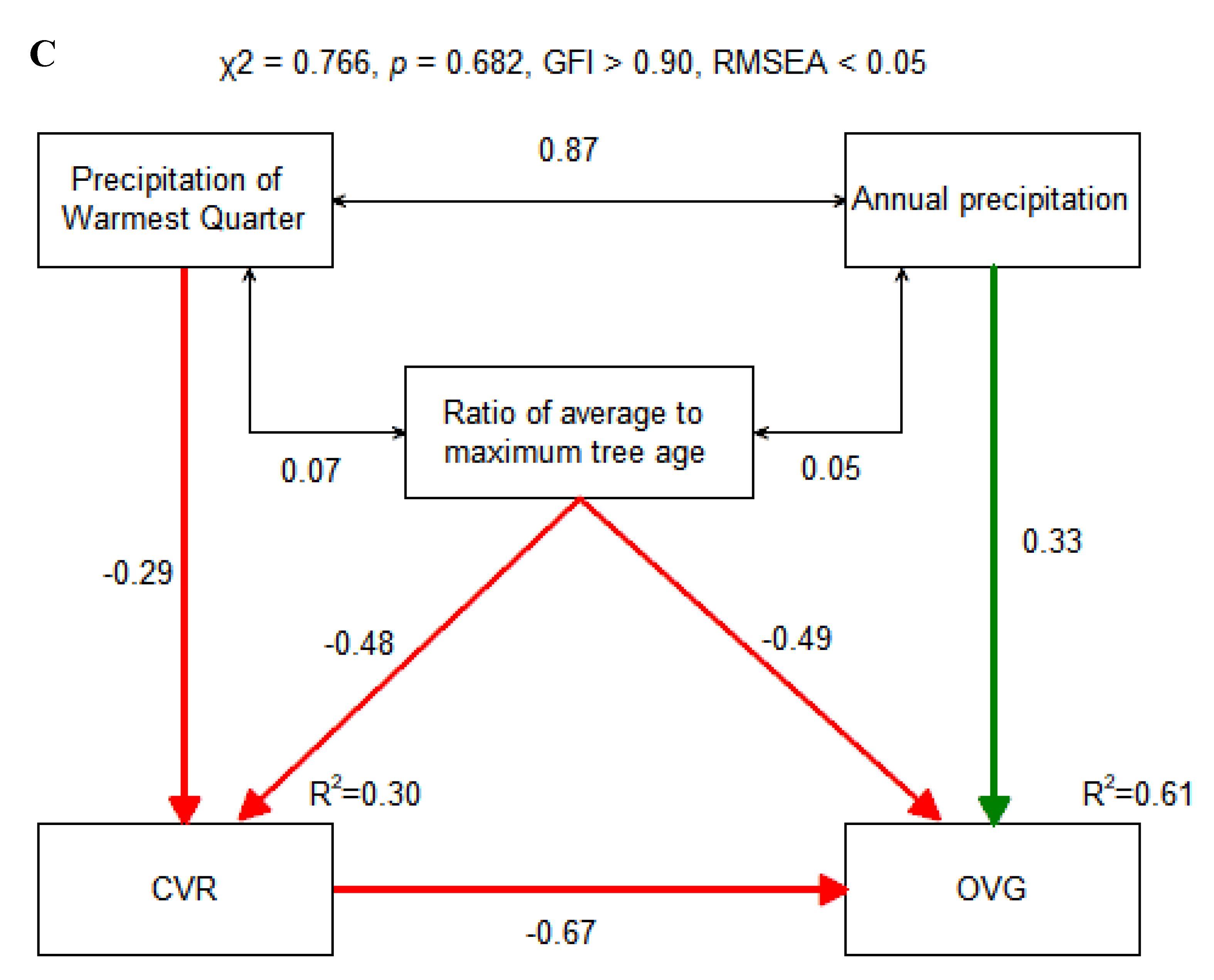
Preprints 76591 g003aPreprints 76591 g003b
Preprints 76591 g004
Figure 4. Radial growth rates at current tree radii vs. model-estimated historical best radial growth rates at same radii (A) (n =2500), comparison of their differences at different elevations (B and C) (W-test, ***P<0.001), and the correlation of this difference with climatic factors (D and E).
Figure 4. Radial growth rates at current tree radii vs. model-estimated historical best radial growth rates at same radii (A) (n =2500), comparison of their differences at different elevations (B and C) (W-test, ***P<0.001), and the correlation of this difference with climatic factors (D and E).
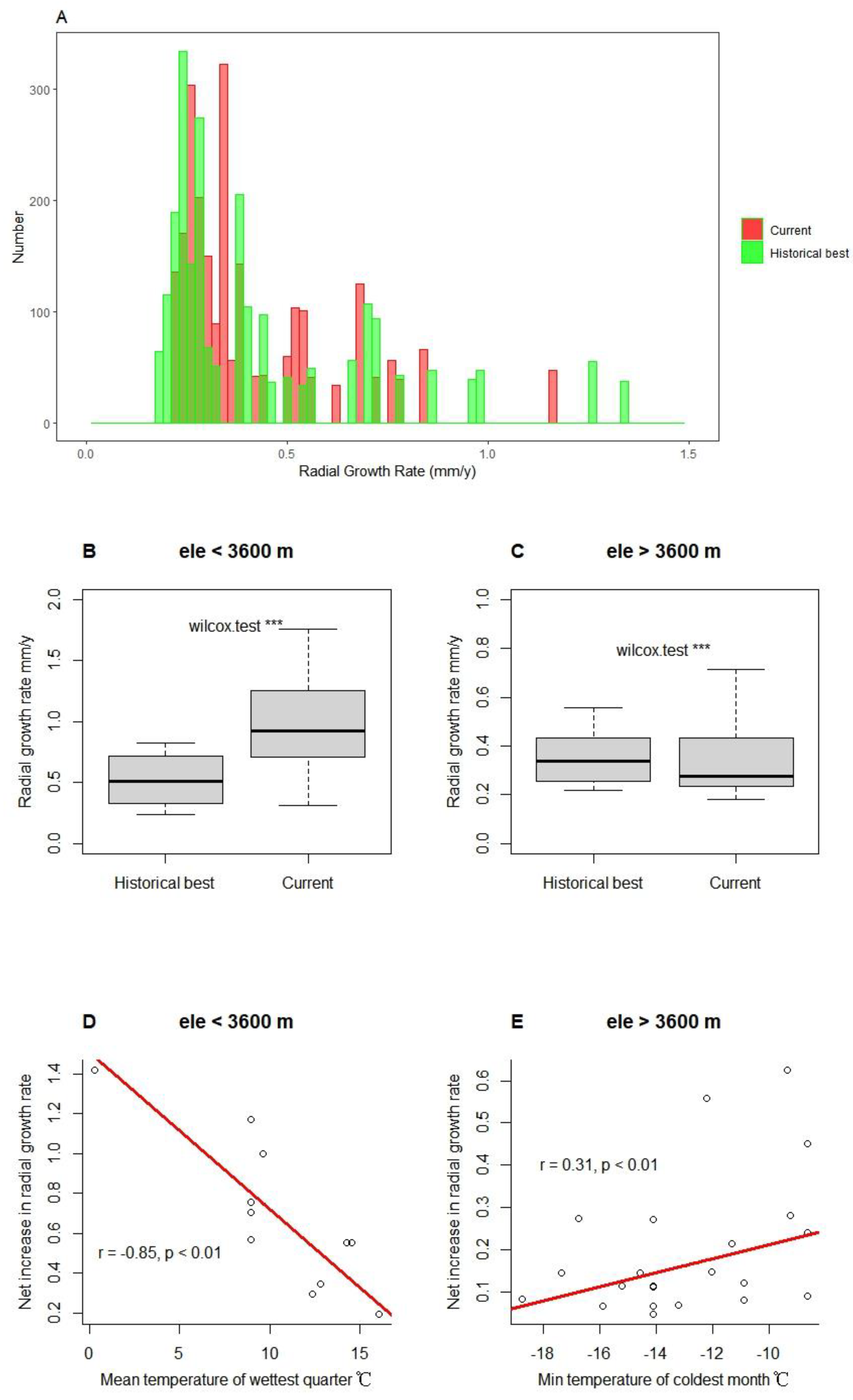
Preprints 76591 g004
Preprints 76591 g005
Figure 5. Distribution of the coefficient of variation in the tree ring growth rate along the relative radius in the past 5 years.
Figure 5. Distribution of the coefficient of variation in the tree ring growth rate along the relative radius in the past 5 years.
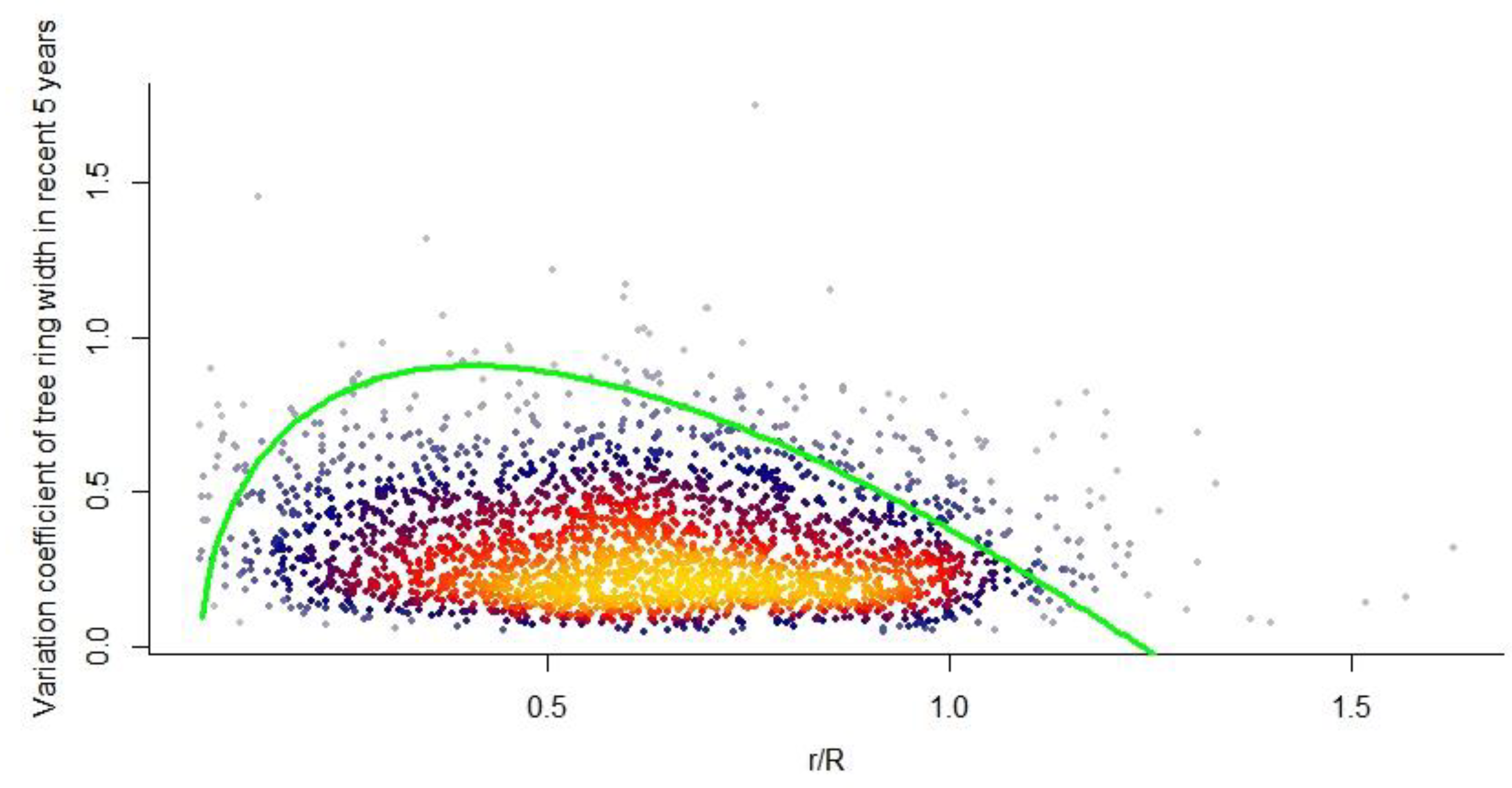
Preprints 76591 g005
Table 1. Geographic description of the sample sites.
Table 1. Geographic description of the sample sites.
Species Name Abbreviated Name Latitude Longitude Average Elevation (m) Number Of Sample Sites/Tree Cores Species Composition Age Structure Average ±SD/Maximum DBH (mm) Average ±SD/Maximum Age (y)
Abies forestii Rogers ABFO 27.33-29.28 99.27-100.08 3521 7/345 single species Single/mixed age 202 ± 94/386 261 ± 121/463
Abies recurvata Mast ABRC 28.04 99.02 3200 1/18 - Single age 276 ± 76/394 272 ± 88/394
Cupressus chengiana S.Y.Hu CUCH 31.78 101.9167 2500 1/39 single species - 218 ± 73/330 210 ± 88/358
Juniperus przewalskii Komarov JUPR 36.00-38.57 97.06-99.87 3741 16/1256 - Single/mixed age 162 ± 80/294 552 ± 288/1046
Juniperus tibetica Kom. JUTI 28.37-33.80 91.52-100.27 4136 12/549 single species Single/mixed age 178 ± 81/323 407 ± 200/795
Picea likiangensis (Franchet) Pritzel PCLI 27.58-31.95 96.48-100.28 3520 6/195 - - 212 ± 83/341 232 ± 102/439
Tsuga dumosa (D. Don) Eichler TSDU 27.88-28.04 98.40-98.98 3125 2/63 - Single age 310 ± 44/362 293 ± 82/460
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated