Prerpints.org logo
Preprint
Article

A Method to Fast Ab Initio Cryo-Electron Microscopy Initial Volume Reconstruction

Altmetrics

Downloads

146

Views

65

Comments

0

This version is not peer-reviewed

Submitted:

14 June 2023

Posted:

14 June 2023

You are already at the latest version

Alerts
Abstract
Single particle analysis with cryogenic electron microscopy (cryo-EM) can determine high resolution structures of macromolecular assemblies. To reconstruct final three-dimension(3D) density map, a reliable initial model is essential and ab-initio reconstruction usually can avoid model bias. The grand challenge for ab-initio reconstruction is to alignment two-dimension(2D) low signal-to-noise ratio(SNR) of particle images with random and unknown parameters. Here we formulate a fast ab initio reconstruction method(named AlignFM) based on Fourier Mellin transform and particle-swarm intelligence optimization(PSO) algorithm. It enables simultaneous 2D alignment and 3D refinement, which can fast generate a reliable 3D map. After experiments on several real datasets. AlignFM shows high performance on fast ab initio reconstruction with a small amount of data.
Keywords: 
Subject: Biology and Life Sciences  -   Biochemistry and Molecular Biology

1. Introduction

As a powerful tool, cryo-EM provides near-atomic resolution structure of biological macromolecules to understand their molecular mechanisms. Data analysis of thousands of images contained 2D projections of macromolecular objects called single particle, to find parameters to describe those projections, often adopts a model-based approach[1-6]. This process often begins with an initial model, directly from the images or indirectly from related or simulated data[7]. As a starting model, it should not be bias the final structure[8].
To address model bias, ab-initio reconstruction[6, 7, 9-12] directly from images is necessary. In cryo-EM, frozen biologic molecules are imaged with a low electron dose and multiple sources of noise. Those images maintain the information of atomic structures but with a low SNR. The orientation described by five parameters, (two translations (x,y) and three rotational Euler angles(θ,φ,ω) ) of the particle in each image is unknown and random. Due to above effect, it full of challenge to produce a reliable 3d reconstruction directly from noisy 2D projection images. Basically, 3D reconstruction is considered as an optimization problem to find a 3D structure to describe the observed images. It equals to find the best orientation of particles to reconstruct a 3D map of the object. To estimate a set of high-dimensional parameters, maximum-likelihood (ML)-based algorithms[5, 6] and correlation-based projection matching algorithms[1], run gridding[5] and gradient-descent algorithms[1] or its variant[6] version in iterative alignment of 3D reconstruction. Monte Carlo method[12, 13] and stochastic hill climbing[11, 14] also are introduced to search space exploration and assign parameters to each image. Those optimization schemes make studying particles by random model (RM) method become reality. AUTO3DEM[15] study icosahedral virus from random model[7] and search parameters by polar Fourier transform[16]. Weighted orientation assignment in SIMPLE[11] built several initial model with different symmetry. cryoSPARC[6] can obtain fast low-resolution model initialization for heterogeneous structure determination. A particle-filter algorithm in THUNDER[12] obtains optimal Bayesian estimations to process ab initio reconstruction. CisTEM[17] has ab-initio method by performing a user-specified number of global alignment parameter searches. In summary, those methods fall into two categories, first 2D alignment(in-plane search) and then 3D refinement(out-of-plane search) and simultaneous 2D alignment and 3D refinement(SAR). Numerous 2D alignment kernels have been proposed for in-plane search, including mathematical computation method[16, 18-22] and optimization search method[5, 14, 17, 23, 24]. When 2D alignment kernels can obtain good performance for in-plane parameters and optimization search method can achieve good convergence to global optimal, ab initio reconstruction can be produced.
We recently developed an ab initio reconstruction algorithm based on the formulation of SAR as Object optimization problem(OOP). We applied a variant version of particle-swarm optimization(PSO)[25-28] to estimate all parameters subject to optimization. With known (θ,φ) and in-plane parameters(ω,x,y) calculated by Fourier Mellin transform[29-31], multi-grid points are selected as initial point to start search, which refer to ‘particles’ in PSO algorithm. More accurate in-plane computation and high performance of optimization search to achieve good convergence make ab initio reconstruction generate a reliable initial 3d model for several real homogeneous dataset with different symmetry. And the ultimate resolution of serval datasets can achieve near atom resolution with limited particles. The implemented algorithm is just so called AlignFM(Alignment based on Fourier-Mellin transform).

2. Materials and Methods

Basically, structure determination by cryo-EM is to find a set of unknown variables which describes CTF, in-plane and out-of-plane parameters for each particle image, and those variables can be used to reconstruct a 3D map from which the re-projection, projected with those variables, can best explain the observed images. The process can be formalized as a OOP:
a r g m i n   F ( Θ , V ) = ∑ i = 1 N f ( Θ i , V ) S . T .           Θ = Θ 1 , Θ 2 , Θ 3 , ⋯ , Θ N           f ( Θ i , V ) = i m g i − C T F i * P ( Θ i , V )           Θ i = { θ i , φ i , ω i , x i , y i   }           θ i ∈ θ m i n , θ m a x ，     φ i ∈ φ m i n , φ m a x ，   ω i ∈ ω m i n , ω m a x           x i ∈ x m i n , x m a x ，     y i ∈ y m i n , y m a x         g ( x i , y i ) = e − ( x i − x ¯ ) 2 + ( y i − y ¯ ) 2 2 ζ x y 2 < = 1  
Assumed that the translations of all particle images N obey a gaussian distribution[32] with mean x ¯ , y ¯ and standard deviations ζ x y 2 , the aim of the optimization is to find the parameters Θi in high-dimensional space of each observed image imgi to recontruct a 3D map V and then minimize the difference between images and its re-projection from the 3D map with related parameters. Objective function to measure similarity between images and its re-projection often use likelihood function[5, 32-34] or cross-correlation function[1, 4, 16].

2.1. Fast in-plane parameter computation

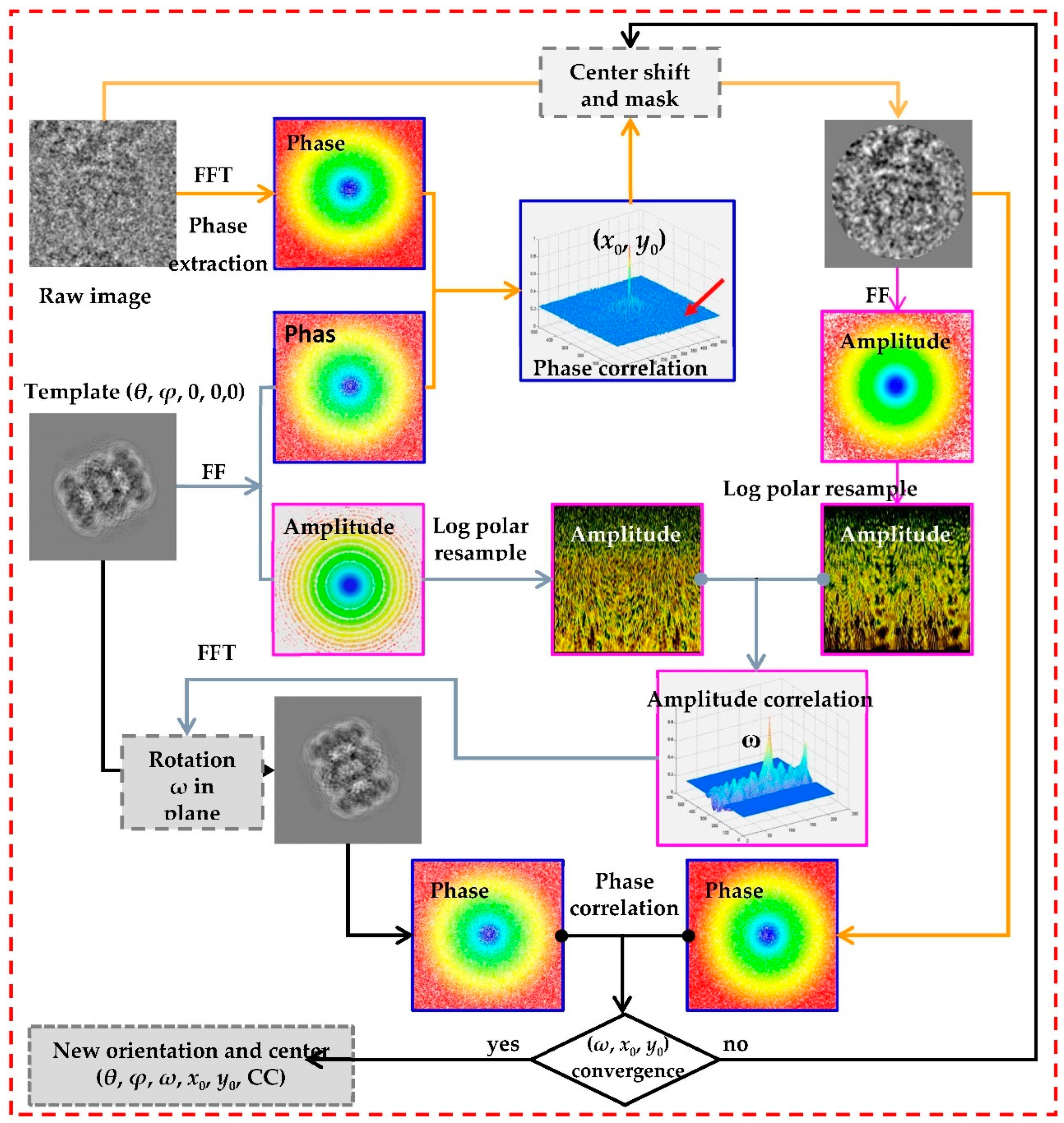
For a particle image I and its reprojection T with in-plane rotation ω0 and translation (x0,y0), their relationship is indicated as follow:
I ( x , y ) = T ( x cos ω 0 + y sin ω 0 − x 0 , − x sin ω 0 + y cos ω 0 − y 0 )
After Fourier transform(FT), their relationship can be formalized as:
I F T ( ξ , η ) = e − i 2 π ( ξ x 0 + η y 0 ) T F T ( ξ cos ω 0 + η sin ϖ 0 , − ξ sin ω 0 + η cos ω 0 )
From above equation, the relationship of amplitude information between image I and its re-projection T refer to the in-plane rotation angle, and the relation of phase information between them refer to translation. According Fourier-Mellin transform[30], log-polar transform of amplitude information can translate rotational relationship to translation relationship(see Figure 1) which can be solved by Fourier shift theory. Also the shift relationship can be resolved directly with phase information by phase correlation or normalized cross correlation[29].

2.2. Objective function

Objective function is to measure similarity between images and its reprojection and choose the best parameters. In theory, a perfect objective function should be a convex function which can make the search achieve convergence fast. In cryo-EM, an amount of random parameters in high-dimensional space, noise in each particle image, incorrect initial 3d model, etc. make search achieve convergence difficultly. We divide ab initio reconstruction algorithm into three parts, global search(mode 1,resolution usually equal 60Å),low resolution refinement (mode 2,resolution usually more than 10Å) and high resolution refinement(mode 3). And three parts use different forms of objective functions which are all maximized and given by cross correlation function CC(Θi,V) minus punish function O(Θi).
C C ( Θ i , V ) = I F T ( ξ , η ) T F T ( ξ , η ) ∗ I F T ( ξ , η ) T F T ( ξ , η ) ∗                                         m o d e   1 ∑ r = 1 R e − r 2 2 R 2 • ∑ x 2 + y 2 < r ± ε I F T ( ξ , η ) T F T ( ξ , η ) ∗ ∑ x 2 + y 2 < r ± ε I F T ( ξ , η ) ∑ x 2 + y 2 < r ± ε T F T ( ξ , η ) ∗             m o d e   2 ∑ r = 1 R e r 2 2 R 2 • ∑ x 2 + y 2 < r ± ε I F T ( ξ , η ) T F T ( ξ , η ) ∗ ∑ x 2 + y 2 < r ± ε I F T ( ξ , η ) ∑ x 2 + y 2 < r ± ε T F T ( ξ , η ) ∗             m o d e   3                                    
O ( Θ i ) = ( x i − x ¯ ) 2 + ( y i − y ¯ ) 2 2 ζ x y 2
In mode 1, the Fourier matrix of cross-correlation must do inverse Fourier transform(IFT) to obtain translation parameters. The result of phase correlation is a delta function and able to provide strong and clearly identifiable correlation between particle image and its matched templates[30], which makes the objective function be convex and the process of search achieve convergence fast. To speed up search, a weighted Fourier ring correlation(FRC)[17] on each resolution r with a certain interval ε is calculated without IFT to obtain similarity after global search.

2.3. The procedure of ab initio reconstruction

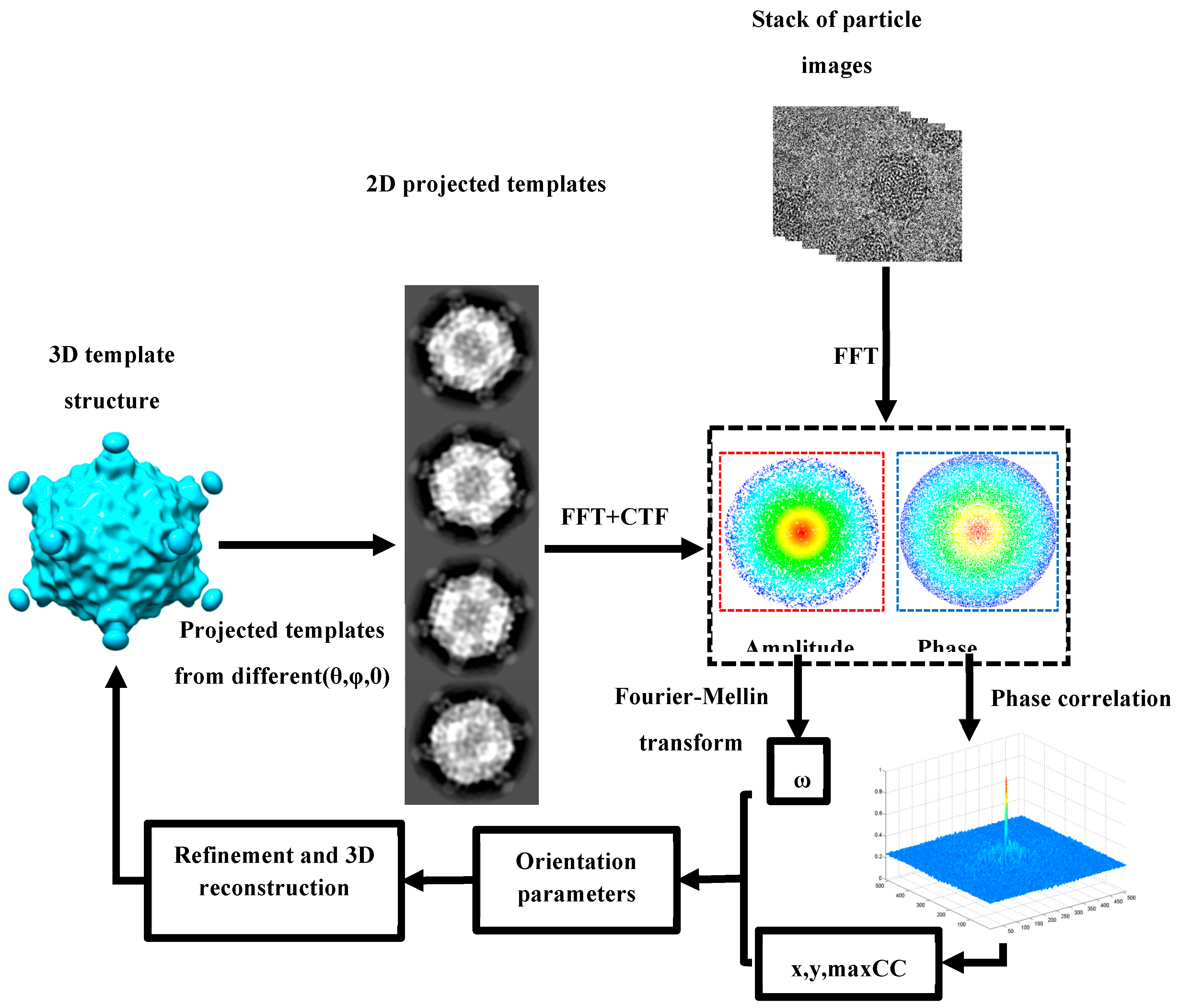
The ab initio reconstruction begins with a random model generated from original image directly[7]. Global search(shown in Figure 2) generates heuristic points according (θ,φ) parameters with given interval in quasi-even distribution on Ewald sphere. For each heuristic point (θ,φ), in-plane parameters(ω,x,y) is calculated by FMT(shown in Figure 3). A template is projected from given 3D map with out-of-plane parameter(θ,φ) and translation parameters(x,y) are calculated by phase correlation. After that particle image shift its center to (x,y), a soft mask is done to remove noise. And then the amplitude information of particle image and its projected template are abstracted and log-polar transformation is done to them. Rotational parameter ω can be calculated by phase correlation of two log-polar amplitude images. A certain heuristic points with high score are selected as “particles” in PSO algorithm[35] and the search based on template matching is launched. After the search is finished, the result of orientation parameters can generate a new 3D model and an iterative reconstruction is processing until a reliable initial 3D mode is generated. After that, global search can generate heuristic points within asymmetrical unit according symmetry of the reliable initial 3D mode, and local refinement push the model to achieve expected high resolution. The whole procedure is summarized as follows:
  • A random model is generated directly from particle image with random orientation parameters.
  • For a given 3D model, global search(mode 1 and 2) is launched to find rough orientation parameters near global optimization and generate a new 3D model.
  • For a given 3D model and old orientation parameters, local refinement(mode 2 and 3) search is launched to find better orientation parameters near local optimization and then generate a new 3D model.
  • Repeating steps 2–3 until convergence or expected resolution are achieved.

3. Results

We program our ab initio reconstruction algorithm with parallel CPU code and implement it on several real data from asymmetry(C1-symmetric) to high symmetry( D2-symmetric, D7-symmetric and icosahedral symmetry). We used three high-resolution datasets(EMPIAR-10028, EMPIAR-10012, EMPIAR-10025) from the Electron Microscopy Public Image Archive (EMPIAR). All initial random models are generated directly from real data without imposed symmetry.
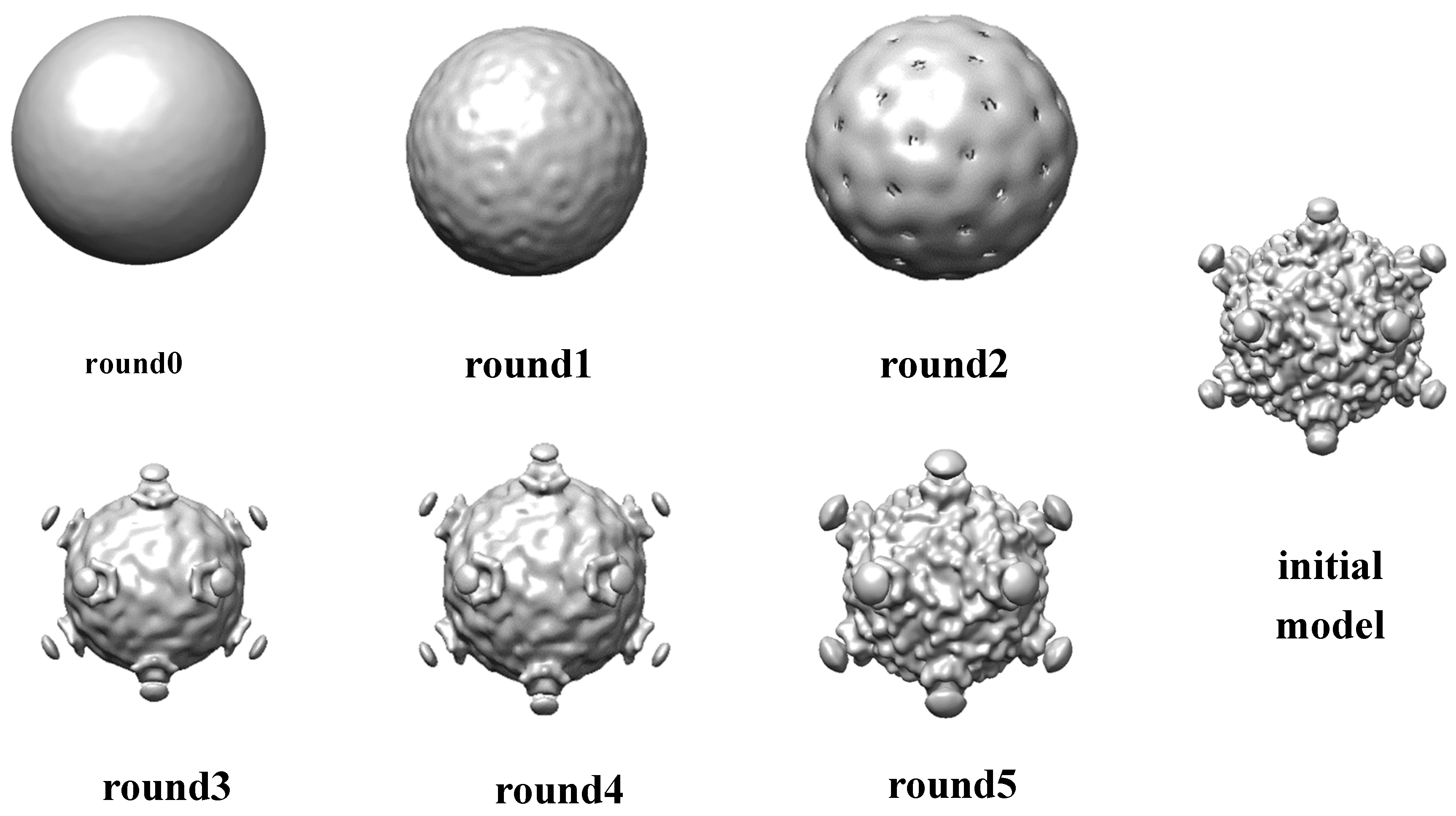
A set of 5000 Cytoplasmic polyhedrosis virus(CPV) particles[36, 37] with icosahedral symmetry are randomly selected. A random model is generated without assuming any point-group symmetry from selected data. After the alignment was initialized with this random model, the feature of 5-fold is clear after three rounds and the feature of 3-fold and 2-fold are clear after 5 rounds(in Figure 4). The resolution of CPV data set is not pushed and this dataset is only for functional test.
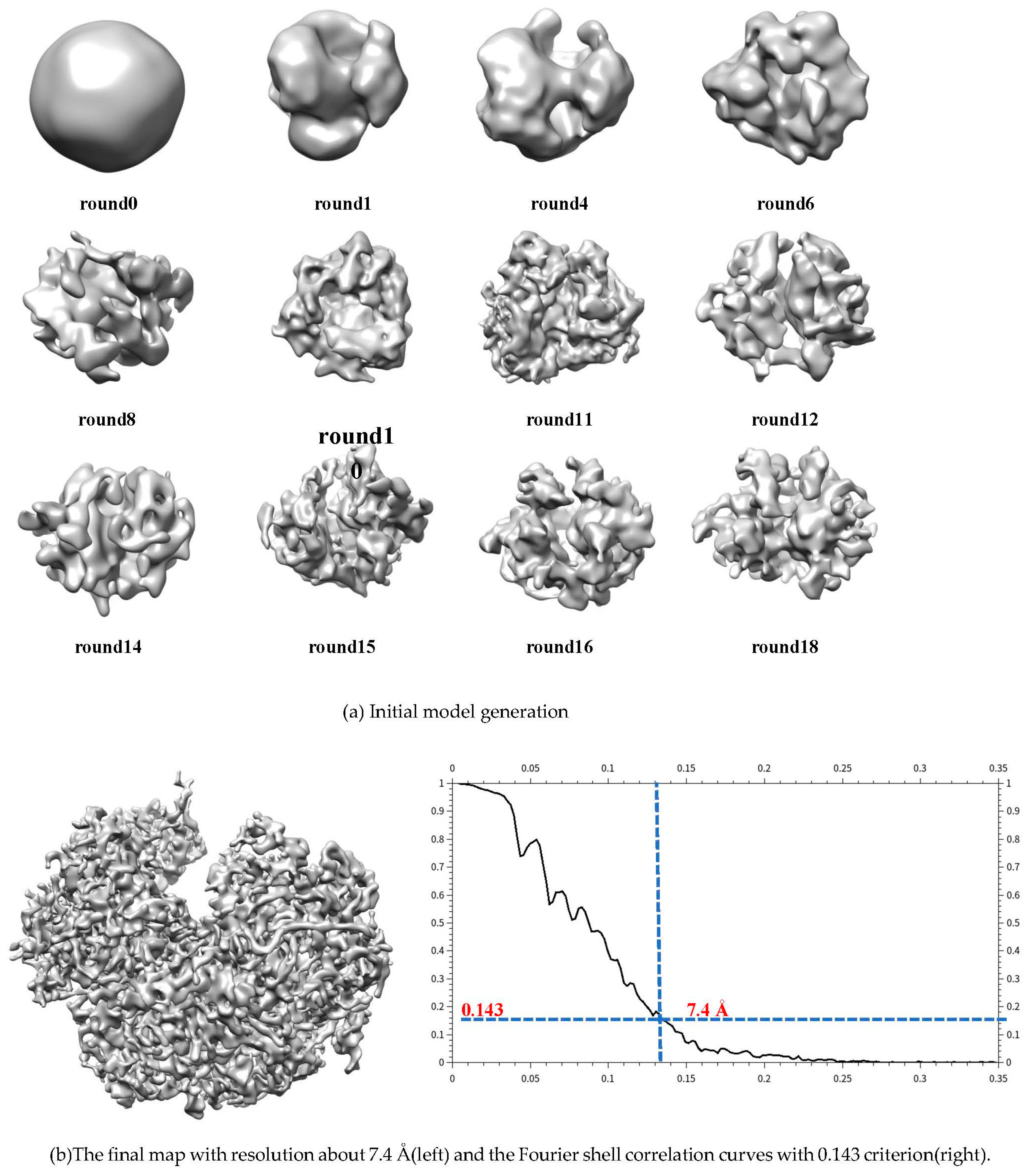
A set of 5000 Plasmodium Falciparum 80S Ribosome particles[38] with C1 symmetry(EMPIAR-10028) are randomly selected. A random model is generated without assuming any point-group symmetry from selected data. Due to its asymmetry, the process is converged until 18 rounds. And the ultimate resolution is 7.4 Å according Fourier shell correlation curves with 0.143 criterion (in Figure 5).
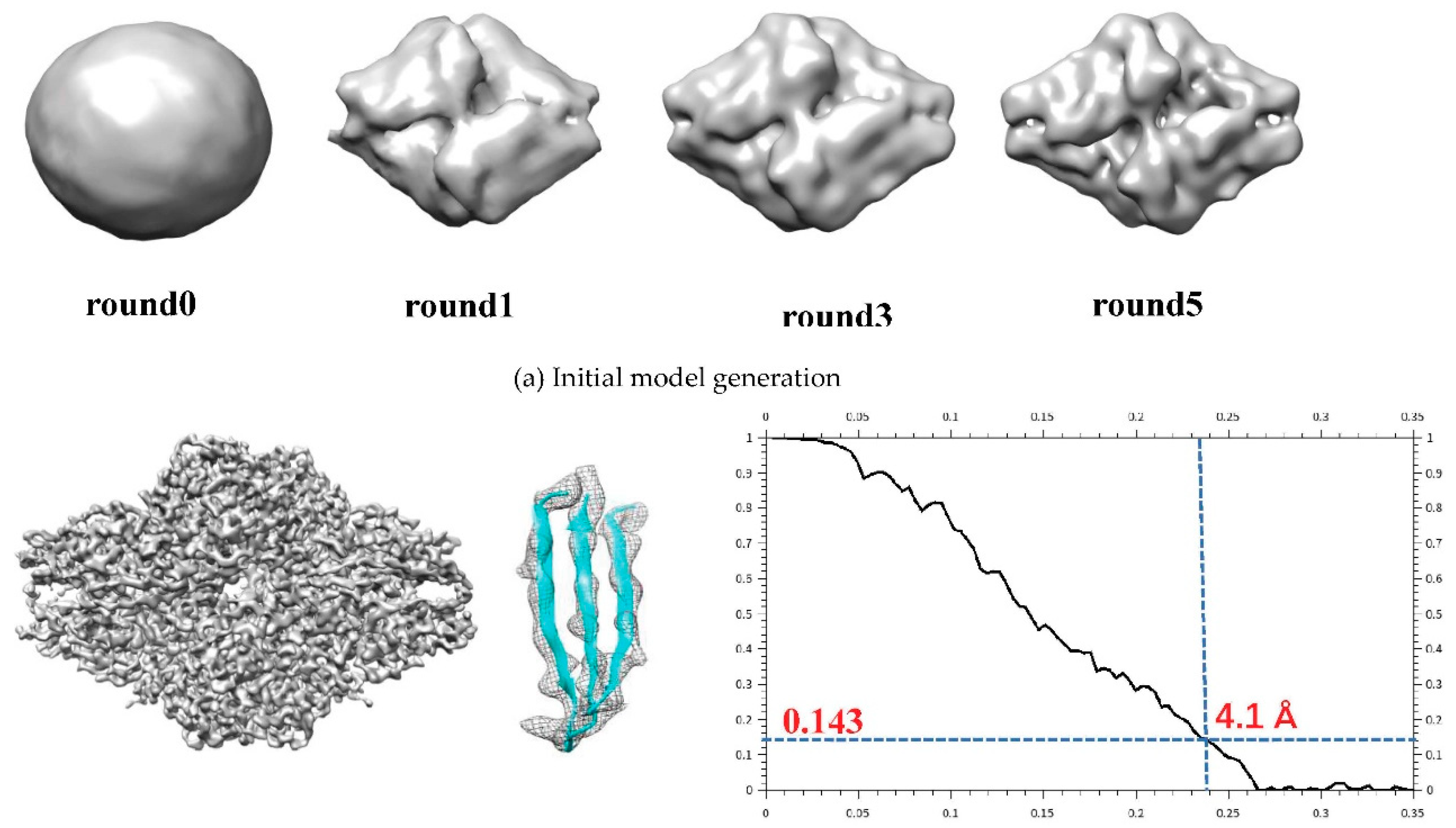
A set of 5000 β-galactosidase particles[39] with D2 symmetry(EMPIAR-10012) are randomly selected. A random model is generated without assuming any point-group symmetry from selected data. After five rounds, the axis of symmetry is clear and then D2 symmetry is added to the map. And the ultimate resolution is 4.1 Å according Fourier shell correlation curves with 0.143 criterion (in Figure 6).
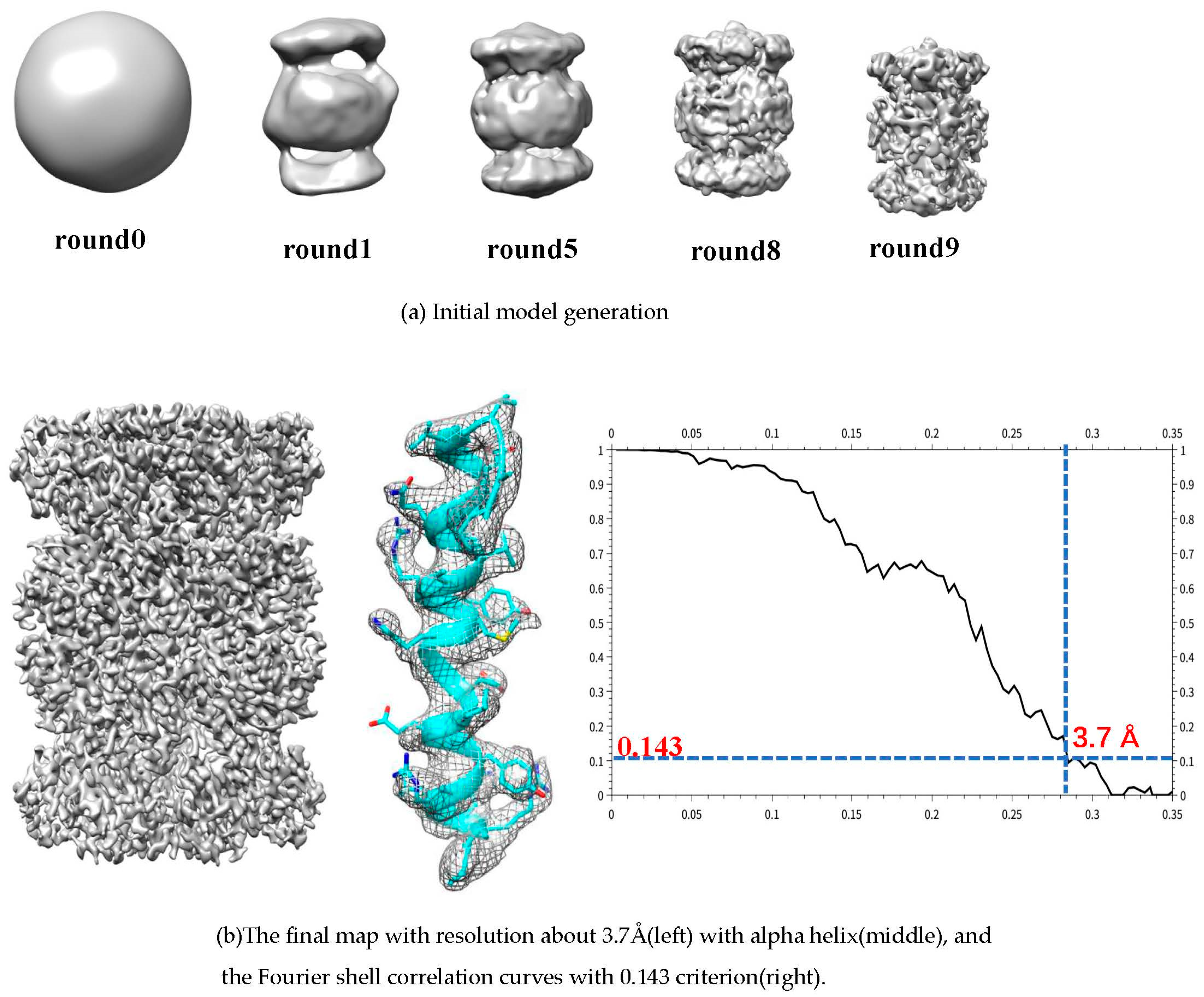
A set of 5000 Thermoplasma acidophilum 20S proteasome [40] with D7 symmetry(EMPIAR-10025) are randomly selected. A random model is generated without assuming any point-group symmetry from selected data. After ten rounds, the axis of symmetry is clear and then D7 symmetry is added to the map. And the final resolution is 3.7 Å according Fourier shell correlation curves with 0.143 criterion (in Figure 7).

4. Discussion

Standard projection matching for alignment is an exhaustive procedure for global search and greedy procedure for local search. In global search, it is computationally intractable to launch systematic search by scanning through the entire high-dimensional space. In practice, heuristic search often sets a set of possible parameters and feasible subset is selected according their score. And then local search explores the neighborhood of the feasible subset separately to guarantee convergence to a local optimum. A sensitive problem is how many feasible parameters kept in the subset. Small subset means fast but just local optimum and large subset need more computational time but get more chance to global optimum. Here, we adopt Fourier Mellin transform to calculate in-plane parameters and heuristic search only focus on out-of-plane parameters. The low SNR of cryo-EM images often cause objective function nonconvex and may give risk to search trapped in a single best parameter. The result of phase correlation is a delta function which can make objective function convex. Out-of-plane parameters search means feasible subset can contain more possible parameters and more ‘particles’ in PSO can enhance performance of search. Different from the other optimization algorithm, particle-swarm optimization take advantage of global and local information to explore the search space. In global search, more feasible parameters, referred to as ‘particles’ in PSO, share global optimum and drive search to the direction toward the combination with its local optimum and global optimum. It can achieve fast better convergence which provide better parameters for 3D reconstruction. The above advantage benefits to improve our algorithm to fast ad initio reconstruction.

5. Conclusions

In all tested cases, AlignFM generates accurate 3D maps without a priori assumptions about the structure or its symmetry directly from the noisy cryo-EM images, which pass the process of 2D image alignment and clustering. From generated accurate inital 3D maps, AlignFM can push the maps to the desired resolution with limited number of particle images.

Author Contributions

The authors have equal contributions.

Funding

This research was supported by the National Natural Science Foundation of China (12034006, 32071209).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Grigorieff, N. FREALIGN: high-resolution refinement of single particle structures. Journal of structural biology 2007, 157, 117–125. [Google Scholar] [CrossRef]
  2. Hohn, M.; Tang, G.; Goodyear, G.; Baldwin, P.R.; Huang, Z.; Penczek, P.A.; Yang, C.; Glaeser, R.M.; Adams, P.D.; Ludtke, S.J. SPARX, a new environment for Cryo-EM image processing. Journal of structural biology 2007, 157, 47–55. [Google Scholar] [CrossRef]
  3. Tang, G.; Peng, L.; Baldwin, P.R.; Mann, D.S.; Jiang, W.; Rees, I.; Ludtke, S.J. EMAN2: an extensible image processing suite for electron microscopy. Journal of structural biology 2007, 157, 38–46. [Google Scholar] [CrossRef]
  4. Elmlund, D.; Elmlund, H. SIMPLE: Software for ab initio reconstruction of heterogeneous single-particles. Journal of structural biology 2012, 180, 420–7. [Google Scholar] [CrossRef] [PubMed]
  5. Scheres, S.H. RELION: implementation of a Bayesian approach to cryo-EM structure determination. Journal of structural biology 2012, 180, 519–30. [Google Scholar] [CrossRef]
  6. Punjani, A.; Rubinstein, J.L. cryoSPARC: algorithms for rapid unsupervised cryo-EM structure determination. Nature methods 2017, 14, 290–296. [Google Scholar] [CrossRef]
  7. Yan, X.; Dryden, K.A.; Tang, J.; Baker, T.S. Ab initio random model method facilitates 3D reconstruction of icosahedral particles. Journal of structural biology 2007, 157, 211–25. [Google Scholar] [CrossRef] [PubMed]
  8. Sigworth, F.J. Principles of cryo-EM single-particle image processing. Microscopy (Oxford, England) 2016, 65, 57–67. [Google Scholar] [CrossRef]
  9. Elmlund, D.; Davis, R.; Elmlund, H. Ab initio structure determination from electron microscopic images of single molecules coexisting in different functional states. Structure 2010, 18, 777–86. [Google Scholar] [CrossRef]
  10. Lyumkis, D.; Vinterbo, S.; Potter, C.S.; Carragher, B. Optimod--an automated approach for constructing and optimizing initial models for single-particle electron microscopy. Journal of structural biology 2013, 184, 417–26. [Google Scholar] [CrossRef] [PubMed]
  11. Elmlund, H.; Elmlund, D.; Bengio, S. PRIME: probabilistic initial 3D model generation for single-particle cryo-electron microscopy. Structure 2013, 21, 1299–306. [Google Scholar] [CrossRef]
  12. Hu, M.; Yu, H. A particle-filter framework for robust cryo-EM 3D reconstruction. Nature methods 2018, 15, 1083–1089. [Google Scholar] [CrossRef]
  13. Liu, X.; Jiang, W.; Jakana, J.; Chiu, W. Averaging tens to hundreds of icosahedral particle images to resolve protein secondary structure elements using a Multi-Path Simulated Annealing optimization algorithm. Journal of structural biology 2007, 160, 11–27. [Google Scholar] [CrossRef]
  14. Reboul, C.F.; Bonnet, F.; Elmlund, D.; Elmlund, H. A Stochastic Hill Climbing Approach for Simultaneous 2D Alignment and Clustering of Cryogenic Electron Microscopy Images. Structure 2016, 24, 988–96. [Google Scholar] [CrossRef] [PubMed]
  15. Yan, X.; Sinkovits, R.S.; Baker, T.S. AUTO3DEM--an automated and high throughput program for image reconstruction of icosahedral particles. Journal of structural biology 2007, 157, 73–82. [Google Scholar] [CrossRef] [PubMed]
  16. Baker, T.S.; Cheng, R.H. A model-based approach for determining orientations of biological macromolecules imaged by cryoelectron microscopy. Journal of structural biology 1996, 116, 120–30. [Google Scholar] [CrossRef] [PubMed]
  17. Grant, T.; Rohou, A.; Grigorieff, N. cisTEM, user-friendly software for single-particle image processing. Elife 2018, 7. [Google Scholar] [CrossRef] [PubMed]
  18. Cong, Y.; Kovacs, J.A.; Wriggers, W. 2D fast rotational matching for image processing of biophysical data. Journal of structural biology 2003, 144, 51–60. [Google Scholar] [CrossRef]
  19. Frank, J.; Verschoor, A.; Boublik, M. Computer averaging of electron micrographs of 40S ribosomal subunits. Science 1981, 214, 1353–5. [Google Scholar] [CrossRef]
  20. Joyeux, L.; Penczek, P.A. Efficiency of 2D alignment methods. Ultramicroscopy 2002, 92, 33–46. [Google Scholar] [CrossRef] [PubMed]
  21. Penczek, P.; Radermacher, M.; Frank, J. Three-dimensional reconstruction of single particles embedded in ice. Ultramicroscopy 1992, 40, 33–53. [Google Scholar] [CrossRef] [PubMed]
  22. Van Heel, M.; Schatz, M.; Orlova, E. Correlation functions revisited. Ultramicroscopy 1992, 46, 307–316. [Google Scholar] [CrossRef]
  23. Bracewell, R.N.; Bracewell, R.N. The Fourier transform and its applications., 3rd ed.; McGraw-Hill: New York, 1986. [Google Scholar]
  24. Reboul, C.F.; Eager, M.; Elmlund, D.; Elmlund, H. Single-particle cryo-EM-Improved ab initio 3D reconstruction with SIMPLE/PRIME. Protein science 2018, 27, 51–61. [Google Scholar] [CrossRef] [PubMed]
  25. Eberhart, R.; Kennedy, J. In A new optimizer using particle swarm theory, Micro Machine and Human Science, Proceedings of the Sixth International Symposium on, 1995; IEEE: 1995; pp 39-43.
  26. Suganthan, P.N. Particle swarm optimiser with neighbourhood operator, Proceedings of the 1999 Congress on Evolutionary Computation-CEC99; IEEE: 1999; pp 1958-1962.
  27. Mendes, R.; Cortez, P.; Rocha, M.; Neves, J. In Particle swarms for feedforward neural network training, Neural Networks, 2002. Proceedings of the 2002 International Joint Conference on, 2002; IEEE: 2002; pp 1895-1899.
  28. Robinson, J.; Sinton, S.; Rahmat-Samii, Y. Particle swarm, genetic algorithm, and their hybrids: optimization of a profiled corrugated horn antenna, IEEE Antennas and Propagation Society International Symposium. IEEE, 2002; pp 314-317.
  29. Chen, Q.-s.; Defrise, M.; Deconinck, F. Symmetric phase-only matched filtering of Fourier-Mellin transforms for image registration and recognition. IEEE Transactions on pattern analysis and machine intelligence 1994, 16, 1156–1168. [Google Scholar] [CrossRef]
  30. Reddy, B.S.; Chatterji, B.N. An FFT-based technique for translation, rotation, and scale-invariant image registration. IEEE transactions on image processing 1996, 5, 1266–1271. [Google Scholar] [CrossRef] [PubMed]
  31. Lehmann, T.M. In A two-stage algorithm for model-based registration of medical images, Pattern Recognition, 1998. Proceedings. Fourteenth International Conference on, 1998; IEEE: 1998; pp 344-351.
  32. Lyumkis, D.; Brilot, A.F.; Theobald, D.L.; Grigorieff, N. Likelihood-based classification of cryo-EM images using FREALIGN. Journal of structural biology 2013, 183, 377–88. [Google Scholar] [CrossRef] [PubMed]
  33. Sigworth, F.J. A maximum-likelihood approach to single-particle image refinement. Journal of structural biology 1998, 122, 328–39. [Google Scholar] [CrossRef]
  34. Scheres, S.H.; Valle, M.; Nunez, R.; Sorzano, C.O.; Marabini, R.; Herman, G.T.; Carazo, J.M. Maximum-likelihood multi-reference refinement for electron microscopy images. Journal of molecular biology 2005, 348, 139–49. [Google Scholar] [CrossRef]
  35. Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intelligence 2007, 1, 33–57. [Google Scholar] [CrossRef]
  36. Zhu, B.; Yang, C.; Liu, H.; Cheng, L.; Song, F.; Zeng, S.; Huang, X.; Ji, G.; Zhu, P. Identification of the active sites in the methyltransferases of a transcribing dsRNA virus. Journal of molecular biology 2014, 426, 2167–74. [Google Scholar] [CrossRef] [PubMed]
  37. Liu, H.; Cheng, L. Cryo-EM shows the polymerase structures and a nonspooled genome within a dsRNA virus. Science 2015, 349, 1347–50. [Google Scholar] [CrossRef] [PubMed]
  38. Wong, W.; Bai, X.-c.; Brown, A.; Fernandez, I.S.; Hanssen, E.; Condron, M.; Tan, Y.H.; Baum, J.; Scheres, S.H. Cryo-EM structure of the Plasmodium falciparum 80S ribosome bound to the anti-protozoan drug emetine. eLife 2014, 3, e03080. [Google Scholar] [CrossRef] [PubMed]
  39. Bartesaghi, A.; Matthies, D.; Banerjee, S.; Merk, A.; Subramaniam, S. Structure of beta-galactosidase at 3. 2-A resolution obtained by cryo-electron microscopy. Proceedings of the National Academy of Sciences of the United States of America 2014, 111, 11709–14. [Google Scholar] [PubMed]
  40. Campbell, M.G.; Veesler, D.; Cheng, A.; Potter, C.S.; Carragher, B. 2.8 Å resolution reconstruction of the Thermoplasma acidophilum 20S proteasome using cryo-electron microscopy. eLife 2015, 4, e06380. [Google Scholar] [CrossRef]
Preprints 76594 g001
Figure 1. Rotational relationship indicated by translation relationship between amplitude information resampling with log polar coordination.
Figure 1. Rotational relationship indicated by translation relationship between amplitude information resampling with log polar coordination.
Preprints 76594 g001
Preprints 76594 g002
Figure 2. Process of global search. Several heuristic points on Ewald sphere are uniformly sampled and related projections are projected from a given 3D model. For each partice image, the in-plane parameters are cacluated by FMT with all heuristic points. A certain number of heuristic points with high correlation are selected and refinemnet are launched around them until convergence. Finally, a new 3D model is generated. .
Figure 2. Process of global search. Several heuristic points on Ewald sphere are uniformly sampled and related projections are projected from a given 3D model. For each partice image, the in-plane parameters are cacluated by FMT with all heuristic points. A certain number of heuristic points with high correlation are selected and refinemnet are launched around them until convergence. Finally, a new 3D model is generated. .
Preprints 76594 g002
Preprints 76594 g003
Figure 3. Process of in-plane parameters calcualted by FMT. For particle image and its matched template, Amplitude and phase information are detached after FFT. Amplitude imformation is resampled with log-polar coordinate. Phase correlation is calcualted with log-polar amplitude information and phase information to obtain in-plane rotational angle,translation and correlation.
Figure 3. Process of in-plane parameters calcualted by FMT. For particle image and its matched template, Amplitude and phase information are detached after FFT. Amplitude imformation is resampled with log-polar coordinate. Phase correlation is calcualted with log-polar amplitude information and phase information to obtain in-plane rotational angle,translation and correlation.
Preprints 76594 g003
Preprints 76594 g004
Figure 4. Initial model generation of CPV symmetry imposed. The process begins from a random model. The total cycle are six rounds. Each round include one global search which is followed six or seven local refinement.
Figure 4. Initial model generation of CPV symmetry imposed. The process begins from a random model. The total cycle are six rounds. Each round include one global search which is followed six or seven local refinement.
Preprints 76594 g004
Preprints 76594 g005
Figure 5. Initial model of plasmodium falciparum 80S ribosome. The process begins from a random model. The total cycle are eighteen rounds. Each round include one global search which is followed six or seven local refinement. After the model is stable, the high resolution is pushed to 7.4 Å.
Figure 5. Initial model of plasmodium falciparum 80S ribosome. The process begins from a random model. The total cycle are eighteen rounds. Each round include one global search which is followed six or seven local refinement. After the model is stable, the high resolution is pushed to 7.4 Å.
Preprints 76594 g005
Preprints 76594 g006
Figure 6. Initial model of β-galactosidase. The process begins from a random model. The total cycle are five rounds. Each round include one global search which is followed six or seven local refinement. After the model is stable, the high resolution is pushed to 4.1 Å. Under this resolution, β sheet is clear.
Figure 6. Initial model of β-galactosidase. The process begins from a random model. The total cycle are five rounds. Each round include one global search which is followed six or seven local refinement. After the model is stable, the high resolution is pushed to 4.1 Å. Under this resolution, β sheet is clear.
Preprints 76594 g006
Preprints 76594 g007
Figure 7. Initial model of Thermoplasma acidophilum 20S proteasome. The process begins from a random model. The total cycle are ten rounds. Each round include one global search which is followed six or seven local refinement. After the model is stable, the high resolution is pushed to 3.7 Å. Under this resolution, side chain is clear.
Figure 7. Initial model of Thermoplasma acidophilum 20S proteasome. The process begins from a random model. The total cycle are ten rounds. Each round include one global search which is followed six or seven local refinement. After the model is stable, the high resolution is pushed to 3.7 Å. Under this resolution, side chain is clear.
Preprints 76594 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated