Design and Simulation of Soft Decision Decoding Based on Chaotic M-ary Spread Spectrum System

Preprint

Article

Design and Simulation of Soft Decision Decoding Based on Chaotic M-ary Spread Spectrum System

Altmetrics

Downloads

138

Views

Comments

A peer-reviewed article of this preprint also exists.

Ruopeng Liu,Pengyi Wang,

Xiduo Wang^*

Ruopeng Liu,Pengyi Wang,

Xiduo Wang^*

This version is not peer-reviewed

Submitted:

13 June 2023

Posted:

14 June 2023

You are already at the latest version

Alerts

Abstract

In this paper, chaos sequence is used to replace the traditional Spread Spectrum sequence. From the perspective of the communication partner, a new method of generating the initial value of chaotic sequence is proposed, which is more suitable for the multi-base Spread Spectrum System and easy to extract. In order to further improve the error performance of the system and ensure the integrity of the system, an improved suboptimal soft information extraction method based on log-likelihood ratio (LLR) is proposed in the channel coding module, which can further improve the error performance of the system. On this basis, we choose the synchronization mode of multiple transmission of one reference signal to solve the problem that chaotic sequence is difficult to obtain synchronization because of its aperiodic characteristics. Finally, the system is simulated in the channel with low SNR. The simulation results show that chaotic sequence as Spread Spectrum code can make the signal transmit accurately in the worse channel environment. The performance gain of applying soft information decoding decision in the M-ary Spread Spectrum System with chaotic sequence as Spread Spectrum code can reach 5.2dB compared with the traditional Direct Spread Spectrum System.

Keywords:

Subject: Computer Science and Mathematics - Signal Processing

1. Introduction

The multi-base spread spectrum system transmits multiple bits per spread spectrum sequence, so the transmission efficiency is improved. Secondly, the multi-base spread spectrum system occupies less bandwidth, which is suitable for the environment with strict bandwidth limitation and high data rate. At the same time, the multi-base spread spectrum system extends the information sequence by the form of block coding, and obtains the coding gain as well as the spread spectrum gain. Under certain conditions, the multi-base spread spectrum system has better bit error performance than the direct spread spectrum system. Because of these advantages, multi-base spread spectrum technology has been widely used [1]. But with the development of information science and digital signal processing theory and technology, the detection methods of existing spread spectrum communication signals also appear, which will lead to serious deterioration of system performance.

In order to improve the anti-jamming and anti-deciphering ability of communication system, it is necessary to find new spread spectrum codes. Chaotic sequence is widely concerned by the industry because of its characteristics such as large number, high confidentiality, good randomness and excellent correlation performance [2], and is expected to become an ideal spread spectrum code in spread spectrum communication. It is worth mentioning (It is worth mentioning,) that in a large number of papers on chaotic DSSS, synchronization is ignored or it is assumed that synchronization has been completed at the signal receiving end [3]. In order to overcome the difficulty of synchronization of chaotic MSSS, it is allowed to use spread spectrum code as an independent branch to transmit in the channel. If this synchronization mode appears in DSSS, it will take a lot of computation to synchronize the chaotic sequence to obtain the code sequence and track it due to the characteristics of chaotic sequence [4,5,6]. However, in this paper, the system is built based on the communication partner. In the generation of the spread spectrum code block, an iterative method is proposed to generate the whole spread spectrum code block by using the last value of the former unquantized spread spectrum code as the initial value of the latter spread spectrum code block, which not only maintains the excellent correlation and randomness of the chaotic sequence itself, but also reduces the difficulty of the communication partner to obtain the code sequence. Therefore, this paper will follow the synchronization mode of the transmission of the reference signal.

In order to combat external interference, the current anti-interference technologies mainly include: error correcting coding technology, spread spectrum technology, beamforming technology and diversity technology [7]. In this paper, the channel coding technology and spread spectrum technology are studied in order to resist the interference in the bad channel environment and realize the reliable transmission of information under the condition of ensuring a certain transmission rate.

In order to ensure the reliability of signal transmission, channel coding technology is a crucial technology in modern communication systems [8]. According to the way the signal is received and processed, the channel coding includes two categories: Hard Decision decoding (Hard Decision) and Soft decision decoding (Soft Decision), at the same bit rate and code length, the performance of soft decision decoding is much higher than that of hard decision decoding. In order to reach the Shannon limit, the log-likelihood ratio (LLR) should be used to extract soft information [9], but its complexity is high and the computation is huge, which is basically impossible to implement in engineering. In this paper, an improved soft information extraction method based on the log-likelihood ratio (LLR) is proposed, which greatly reduces the computational complexity and is easier to implement in hardware.

The structure of this paper is as follows: Firstly, the whole system model of the multi-base spread spectrum system is introduced, then the generation mode of chaotic sequence spread spectrum code block in this paper is introduced, the basic principle of reference signal branch synchronization is introduced, including the two steps of capture and tracking, and the sub-optimal soft information extraction algorithm based on LLR is introduced, which is combined with channel encoding and decoding to optimize the system. The error performance of the whole system in the channel is analyzed, and finally the full text is summarized.

2. M-ary Spread Spectrum communication system model

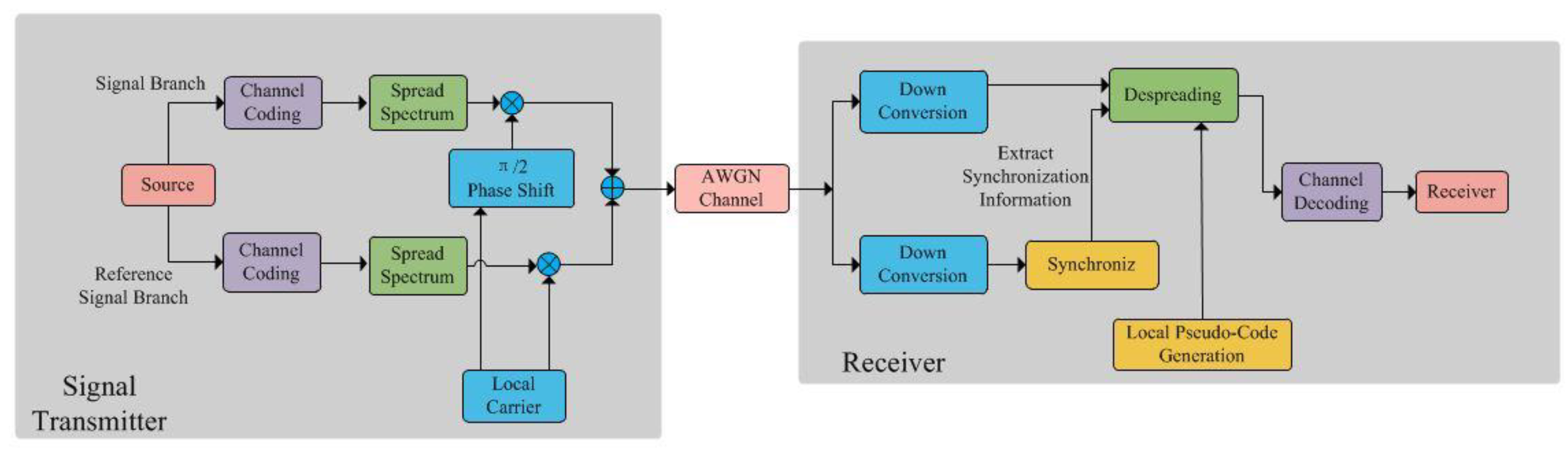
Figure 1 shows the system model considered in this paper. At the sending end, the binary message sequence is encoded by (2,1,7) convolution coding to map 1 bit to 2 bit encoded signal. This signal continues to undergo spread spectrum modulation in the channel.

M-ary Spread Spectrum can actually be seen as a (N,k) encoding, where continuous K-bit information is mapped to the symbol Ci(i=0,1,…,M-1), and the system model of multi-base spread spectrum is shown in Figure 1. The K-bit information code corresponds to M states,

M = 2^{k}

, so the system is also called M-base spread spectrum system. The K-bit information code is represented by a spread spectrum code of length N. In the M-base spread spectrum system, the K-bit information code has M different states, which requires a spread spectrum code of length N Ci(i=0,1,…,M-1), to represent M different states. Ci can be expressed as:

C^{i} (t) = \sum_{n = 0}^{N - 1} C_{n}^{i} g_{c} (t - {nT}_{c})

(1)

g_{c} (t)

is a gate function, which is 1 when 0≤t

<

Tc, and is obtained by dividing an by k bits,

a (t) = \sum_{i = 0}^{\infty} a_{n} g_{b} (t - {nT}_{b})

(2)

a_{k} (t) = \sum_{m = 0}^{k - 1} a_{m} g_{b} (t - {mT}_{b})

(3)

Where T=kTa=NTc is the pseudo-code period, Tc is the width of the pseudo-code chip, and N is the length of the pseudo-code. The corresponding method of information code and spread spectrum code adopted in this paper is: weighted value j of K-bit information code,

j = \sum_{i = 0}^{k - 1} a_{i} 2^{k - 1 - i}

(4)

Pseudo-code Cj(t)(j=01,…,M-1) with corresponding subscript to complete the M-ary information expansion. The sending signal is:

S (t) = \sum_{n = 0}^{\infty} C_{j} (t - nT)

(5)

QPSK modulation is performed on the signal

S (t)

which is the Spread spectrum modulated signal:

S_{I} (t) = S (t) {\cos ω}_{c} t - iS (t) {\sin ω}_{c} t

(6)

Gaussian additive noise will be increased when the modulated signal enters the AWGN channel:

S_{n} (t) = S (t) {\cos ω}_{c} t - iS (t) {\sin ω}_{c} t + n_{0} (t)

(7)

At the demodulation end, the signal receiving frequency changes due to the relative motion between the signal transmitting end and the receiving end, the received signal frequency is no longer

f_{c} (f_{c} = ω_{c} / 2 π)

but

f_{r} = f_{c} + f_{d}

Where

f_{d}

is called Doppler shift, this phenomenon because the signal frequency changes with the relative motion between the transmitting source and the receiver is called Doppler effect. The phase of the spread spectrum code copied at the receiving end is also different from that of the received signal. The received signal cannot be demodulated and demodulated directly.

The carrier and pseudo-code are captured and tracked by the synchronization module, and the synchronization information is obtained to dissociate the signal. In this system, considering the non-periodicity and complexity of chaotic code, a short reference signal branch is adopted to obtain synchronization information through this branch and then compensate to the information path to complete synchronization. Because the two signals are transmitted in parallel, the two signals are relatively synchronous, which is also the premise of applying this method.

After the synchronization is completed, the sent signal is recovered and then the convolutional encoding and decoding of it can completely strip the sent binary sequence.

In the hard decision receiver, the receiver makes the best decision for the modulation input signal according to the ratio of the output signal of the multi-channel matching filter, and the maximum output value of the matched filter is sent to the decoder as the decision result, and the decoder then makes a judgment on it to correct the wrong decision that may occur in the demodulator. However, the waveform information is wasted and the decoding performance is not high. Soft decision decoding can provide almost the best decoding, which is the reason why I choose soft decision decoding. However, soft decision decoding based on LLR is not easy to implement in engineering because of its high complexity. In this paper, a sub-optimal soft information extraction algorithm based on LLR is proposed to improve system performance with less complexity increase.

3. Generate chaotic spread spectrum code

This system is a (1024, 10) M-ary Spread Spectrum System. Due to the high number of base numbers in the system and the large number of spread spectrum codes required, it is very difficult to find 1024 pseudo-code sequences with excellent correlation performance for traditional pseudo-code sequences, such as M sequence and Gold sequence, while chaotic sequence is extremely sensitive to initial values. The characteristics of continuous wideband spectrum and huge amount of spectrum meet the requirement of spread spectrum code in M-ary Spread Spectrum System very well.

However, because of the non-periodicity of chaotic sequences, it brings new difficulties to the process of synchronization and local recovery of pseudo-codes. Therefore, according to the extreme sensitivity of chaotic sequences to initial values, a method of generating pseudo-code sequences using the last value of the previous sequence as the initial value of the latter sequence is proposed, which greatly reduces the difficulty of extracting local pseudo-code as a communication partner.

Before introducing the specific generation mode of chaotic sequence, the author thinks it is necessary to briefly introduce the concept of chaos. According to the Li-Yorke definition of chaos, first proposed by Chinese American scholar Li Tianyan (Li.T.Y) and American mathematician Yorke J A in 1975, chaos can be understood: Chaos is an unpredictable random phenomenon of a certain macroscopic nonlinear system under certain deterministic conditions, and its unpredictable characteristics come from its internal nonlinear cross-coupling mechanism rather than external stimuli. The extreme sensitivity to the initial value is also due to this nonlinear cross-coupling effect, which can show chaotic phenomenon under certain critical conditions.Chaotic sequences have the following characteristics:

1) Chaotic sequences are generated by deterministic equations, and the reception and generation can be controlled by users;

2) Chaos can only be generated in nonlinear systems, because the motion state of chaos is formed by repeated separation and folding, so its mapping relationship is not one-to-one correspondence;

3) In nonlinear motion, only a certain parameter space corresponds to the chaotic state, because the chaotic state is related to the parameters of the system equation in addition to its mapping form;

4) In chaotic motion, the motion state of the system is extremely sensitive to the initial value;

5) Sequences generated by chaotic systems have good autocorrelation performance, and even two different sequences in a unified sequence have almost zero correlation.

Among them, the fourth and fifth characteristics are also the basis for the design of chaotic spread spectrum sequences in this paper.

In this paper, Full-Logistic mapping is selected to generate chaotic sequences, and the Logistic mapping is defined as follows:

X_{n + 1} = f (X_{n}) = 1 - {aX}_{n}^{2}, 1.40115518909205 \dots < a \leq 2

(8)

When the argument a=2 is taken, the entire (-1, 1) interval will be filled. Therefore, it is called Full mapping, and full-logistic mapping can be concretely expressed as:

X_{n + 1} = 1 - 2 X_{n}^{2}, - 1 < X_{n} \leq 1

(9)

A series of discrete values are generated by equation 9, and quantized by threshold. In this system, the threshold is set to th=0, and then the spread spectrum sequence is generated by T-bit truncation method. The author chose to discard the first 20 bits of a series of discrete values and then intercepted 1024 bits to generate a pseudo-code sequence, and stored the last quantized value of the previous pseudo-code sequence in the register as the initial value of the next pseudo-code sequence, and generated 1024 pseudo-code sequences in this way.

4. Synchronization module

The synchronization module can be divided into two parts, capture and tracking. In order for the receiver tracking loop to track the signal successfully, the carrier and pseudo-code copied inside the initial receiver must match the received signal to a certain extent, otherwise the tracking loop will lose the signal lock because the difference between the two exceeds the pull-in range of the loop. This is where the capture module comes in before tracing. It can also be more roughly understood as “coarse synchronization” and “fine synchronization”.

4.1. Signal Capture

In order to estimate the two parameter values of carrier frequency and code phase of a signal, the signal capture process is generally completed by two-dimensional scanning search of the carrier and phase of the signal, until the signal is found and confirmed, marking the completion of capture.

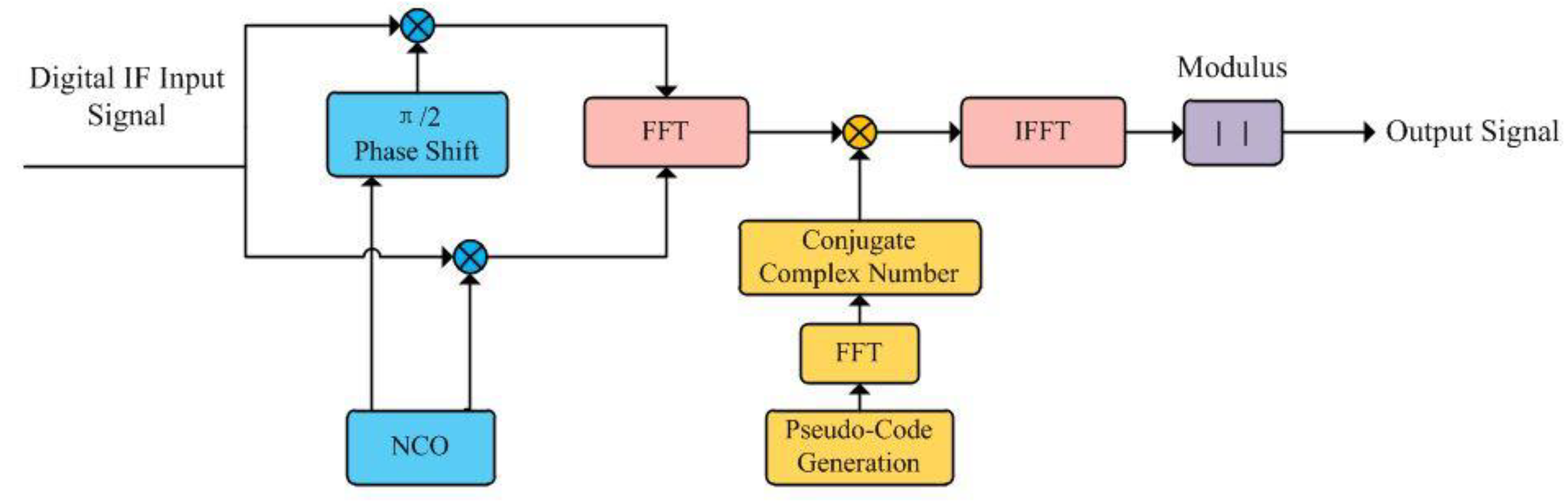
As mentioned above, due to Doppler effect and actual receiver crystal oscillation, clock frequency drift and other factors, the center frequency of the carrier signal received by the receiver is generally different from the nominal frequency at the time of transmission, so it is necessary to search the signal carrier frequency in one dimension. At the same time, because the distance of the receiver changes from time to time, the pseudo-code phase of the received signal also changes from time to time, so the receiver needs to search the code phase in one dimension. The carrier frequency is a one-dimensional search in frequency, and the code phase is a one-dimensional search in time, so the capture of the signal can be called a two-dimensional search in the two-dimensional space composed of time domain and frequency domain. The main operation of search is correlation operation. In this paper, the parallel code phase capture method is adopted, and 2048 times code phase search can be completed by Fourier transform at one time, so the two-dimensional search is simplified to one-dimensional search in the frequency domain. So it can be seen that the correlation technique based on FFT is equivalent to parallel correlators.

As shown in Figure 2, after the digital IF signal is mixed with the sine and cosine signals copied at a certain frequency on the I and Q branches respectively, the phase search of parallel code is to make the mixing result i+jq in the complex form Fourier transform, multiply it with the Fourier transform conjugate value of the copied pseudo-code, and then detect the value of the inverse Fourier transform. Instead of having the mixing results i and q directly correlated with the copied pseudo-code via a digital correlator. After completing the search and detection of the current frequency band, the above calculation is repeated by changing the frequency value of the replicated carrier through the numerical control oscillator (NCO)

Next, the author will prove the correctness of the correlation operation using the Fourier transform instead of the correlator.

Assuming that two sequences of length N and their correlation values are, the correlation definition gives:

z (n) = \frac{1}{N} \sum_{m = 0}^{N - 1} x (m) y (m - n)

(10)

Applying the Fourier transform to z(n) yields Z(f):

Z (f) = \sum_{n = 0}^{N - 1} z (n) e^{- i 2 π fn / N}

(11)

Substituting formula 10 into formula 11 yields:

Z (f) = \frac{1}{N} X (f) Y^{*} (f)

(12)

Where is the conjugate of

Y^{*} (f)

complex number

Y (f)

, thus proved.

4.2. Signal Tracking

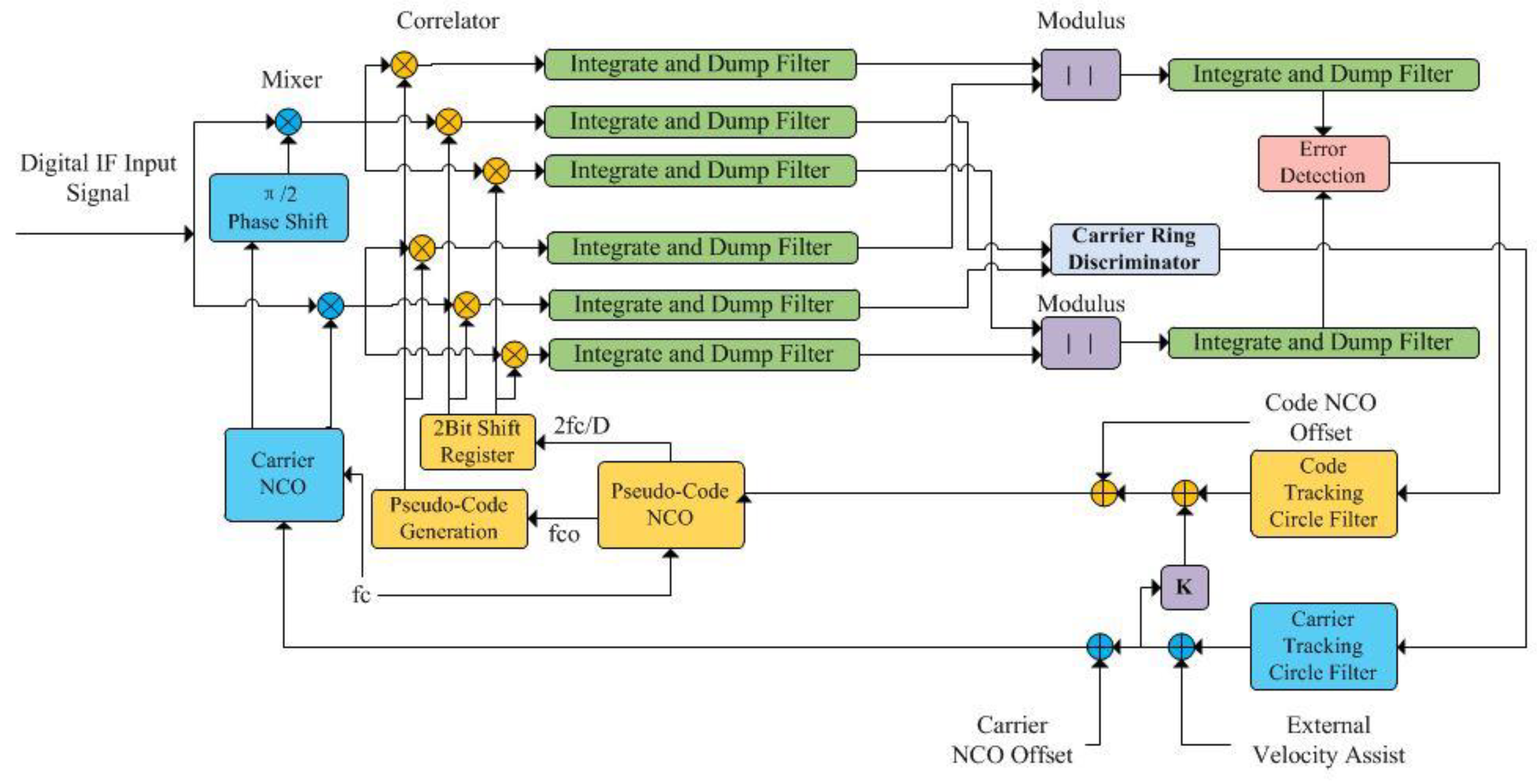
After the signal is captured, and the error can be controlled within half of the chip, the tracking loop is entered to further detect the carrier frequency and the code phase offset more finely.

The tracking loop of the signal is actually composed of two loops, carrier tracking ring and code tracking ring, respectively tracking the carrier and the pseudo-code in the received signal. The purpose of the carrier ring is to make the copied carrier signal consistent with the received carrier signal, and the carrier can be stripped after mixing to obtain the baseband signal. In contrast, if the copied carrier is not exactly the same as the received carrier, it cannot be completely stripped off, and the relevant value obtained after entering the code ring will also be weakened.

Code ring through its internal correlator to copy the pseudo-code and the received signal to do correlation operations, the purpose is to strip the pseudo-code, only the phase of the copied pseudo-code and the pseudo-code phase of the received signal is exactly the same, the correlation value has a maximum, and the relative phase is still deviated, the correlation value will be weakened.

Through analysis, it can be seen that the ultimate purpose of synchronization is to restore the received signal into a baseband signal without pseudo code, the carrier ring strips the carrier, the code ring strips the pseudo code, and the correlation value is still used to determine whether the tracking is on. The specific process is shown in Figure 3.

4.2.1. Phase locking loop

Hereinafter referred to as phase-locked loop. The phase-locked loop (PLL) is a carrier loop that targets the phase of the carrier signal. When the phase of the input and output signals is basically consistent, it is judged to be locked. At this time, the PLL shows steady-state characteristics. There are some key parameters in PLL that need to be determined, which will be analyzed by the author.

The system function of the PLL obtained by definition is:

H (s) = \frac{KF (s)}{s + KF (s)}

(13)

Where K is the loop gain and F(s) is the transfer function of the loop filter. In this system, a second-order loop filter is selected, where F(s) is

F (s) = \frac{τ_{2} s + 1}{τ_{1} s}

(14)

Substituting formula 14 into formula 13 yields:

H (s) = \frac{2 {ξ ω}_{n} s + ω_{n}^{2}}{s^{2} + 2 {ξ ω}_{n} s + ω_{n}^{2}}

(15)

In Formula 15,

ω_{n}

is called the characteristic frequency and

ξ

is called the damping coefficient, which completely determine the performance of the second-order PLL, and the relationship is as follows:

{\begin{matrix} ω_{n} = \sqrt{\frac{K}{τ_{1}}} \\ ξ = \frac{ω_{n} τ_{2}}{2} \end{matrix}

(16)

When the damping coefficient is

0 < ξ < 1

, the system responds flexibly but oscillates violently. When

ξ > 1

, the stability of PLL is relatively high but the system reaction is relatively slow. Noise bandwidth is defined as:

B_{L} = \frac{ω_{n}}{4} = \frac{ω_{n}}{2} (ξ + \frac{1}{4 ξ})

(17)

It controls the amount of noise entering the loop, the narrower the noise bandwidth, the better the loop filtering effect, but it is not infinitely small, because the high dynamic stress will cause the received signal carrier frequency and phase of the violent oscillation, hope to allow such fluctuations as small as possible under the premise.

Therefore, there are:

{\begin{matrix} ξ = 0.707 \\ B_{L} = 0.53 ω_{n} \end{matrix}

(18)

Phase discriminator module, this paper selects the arctangent function:

φ_{e} (t) = \arctan (\frac{Q (t)}{I (t)})

(19)

What gets

φ_{e} (t)

is the phase difference at time t, and

Q (t)

and

I (t)

are the output results of integration-eliminator I and Q respectively.

NCO is used to copy the carrier. The work of NCO is divided into two steps: first, the carrier numerical control oscillator outputs a stepped periodic signal, and then the sine and cosine lookup table converts the stepped signal into the digital sine and cosine carrier copy signal respectively. From the above two processes, it can be seen that the CNC oscillator can be simplified into two parts: “accumulation” and “accumulation after overflow and reverse zero”. For an n-bit CNC oscillator, the frequency of the step signal is defined as:

f_{o} = \frac{{Mf}_{c}}{2^{N}}

(20)

Where M is the phase increment of the carrier CNC oscillator, which makes the carrier CNC oscillator output an IF frequency including Doppler shift, when the loop filter output is 0, it can be considered that the output frequency is equal to the nominal IF frequency, and the offset value can be derived from this.

Since the Doppler change rate is also considered in addition to the Doppler frequency shift, that is, the receiving end and the transmitting end are always moving relative to each other at a fixed rate. In this system, a second-order loop is adopted, so the obtained frequency tracking steady state has a certain slope, and when the phase reaches a steady state, it oscillates around 0.

4.2.2. Code tracking loop

The code tracking loop is based on the good correlation characteristics of the pseudo-code sequence. If the two-bit code sequence is different or there are still phase differences, the correlation becomes low or even close to 0, and the correlation peak is reached only when the two sequences are the same pseudo-code.

Similar to the carrier ring, the code ring estimates the phase difference between the copied and received pseudo-codes based on the correlation values, and uses the filtered phase difference as the input to the pseudo-code numerical control oscillator for phase adjustment.

The difference is that the code ring copies three copies of the pseudo-code of different phases at each moment, that is, the pseudo-code of leading, immediate and delayed replication, as shown in Figure 3 for comparison. Otherwise, it will be difficult to determine whether the correlation value reaches the maximum.

The low-pass filter after mixing is replaced by an integral-cleaning module in this system, because considering the complexity of the system and the reality of subsequent engineering implementation, the integral-cleaning module is less difficult to achieve and can also filter out the effect of high-frequency components and noise through integral operation in a certain time, and improve the carrier-to-noise ratio. This process is coherent integration, and the corresponding integration time

T_{coh}

is called the pre-detection coherent integration time.

To ensure that the data level does not jump within

T_{coh}

, the system samples 10 sampling points per data point, so each

T_{coh}

in the system contains 5 sampling points. The principle of the pseudo-code numerical control oscillator is the same as that of the carrier numerical control oscillator, which will not be detailed here.

5. Soft decision decoding algorithm

The receiver makes the best decision for the modulation input signal according to the ratio of the output signal of the multi-channel matching filter, and the maximum output value of the matched filter is sent to the decoder as the decision result, and the decoder then makes a decision on it to correct the wrong decision that may occur in the demodulator. A judgment in this way is called a hard judgment. The demodulation end is shown in Figure 1.

The advantage of hard decision method is that it is easy to engineering implementation, but the disadvantage is that a part of useful information is wasted, making the decoding performance is not high, and the performance is to lose the coding gain of 2 ~ 3dB, especially in the case of the channel original bit error rate is not high.

Soft decision decoding can provide almost the best decoding, and the performance is far superior to hard decision decoding.

It is assumed that the transmission code word is equal probability, the wireless channel is AWGN channel, and

n (t)

is Gaussian white noise with power spectral density

N_{0} / 2

. M-base spread spectrum communication system, each code word has k bits,

k = \log_{2} M

, each bit is denoted by

d_{j} (j = 0, 1, \dots, k - 1)

. The code word composed of

d_{j}

is denoted

{D}

, the spread spectrum code

{C_{i}} (i = 0, 1, \dots, M - 1)

d_{j} = 0

is denoted by

G_{j}^{0}

, is donated as

C_{0}^{i}

, and the spread spectrum code

{C_{i}}

d_{j} = 1

is denoted by

G_{j}^{1}

, is donated as

C_{1}^{i}

and the soft information extracted by LLR can be written as:

\land_{j} = \land (d_{j}) = \ln \frac{\sum_{C_{i} \in G_{j}^{1}} P ({RC}_{i})}{\sum_{C_{i} \in G_{j}^{0}} P ({RC}_{i})}

(21)

In this formula:

P ({RC}_{i}) = {(\frac{1}{\sqrt{{π N}_{0}}})}^{N} \exp (- \frac{∣ R - C_{i} ∣^{2}}{N_{0}})

(22)

If the log-likelihood ratio is adopted for soft information extraction, the calculation of the algorithm is complicated and the circuit implementation is difficult, a sub-optimal algorithm for soft information extraction will be adopted by using the approximation relation of equation (22), which greatly reduces the complexity and has good effect.

\ln [\sum_{k = 1}^{N} ε_{k}] \approx \ln [\max_{k \in 1, 2, \dots, N} {ε_{k}}]

(23)

According to the approximate relation (21) of equation (23), it becomes:

\land_{j} \approx \ln [\max_{C_{i} \in G_{j}^{1}} P ({RC}_{i})] - \ln [\max_{C_{i} \in G_{j}^{0}} P ({RC}_{i})]

(24)

Substitute equation (22) into equation (24) :

\land_{j} = \frac{1}{N_{0}} (\max_{C_{i} \in G_{j}^{0}} ∣ R - C_{0}^{i} ∣ - \max_{C_{i} \in G_{j}^{1}} ∣ R - C_{0}^{i} ∣) - \frac{N}{2} \ln ({π N}_{0}) = \land_{j}^{'} + A_{const}

(25)

Where

A_{const} = - \frac{N}{2} \ln ({π N}_{0})

is a constant;

\land_{j}^{'} = \frac{1}{N_{0}} (\max_{C_{i} \in G_{j}^{0}} ∣ R - C_{0}^{i} ∣ - \max_{C_{i} \in G_{j}^{1}} ∣ R - C_{0}^{i} ∣)

. In the AWGN channel, each signal has the same energy, that is,

∣ C_{0}^{i} ∣^{2} = ∣ C_{1}^{i} ∣^{2}

, then there are:

\land_{j}^{'} = \frac{2}{N_{0}} (\max_{C_{i} \in G_{j}^{1}} R \cdot C_{1}^{i} - \max_{C_{i} \in G_{j}^{0}} R \cdot C_{0}^{i})

(26)

Where

R \cdot C_{1}^{i}

and

R \cdot C_{0}^{i}

are the output of the matching filter whose JTH bit is 1 or 0 of the code word D.D is grouped as follows:

g_{j}^{1} = {\forall D, d_{j} = 1} g_{j}^{0} = {\forall D, d_{j} = 0}

(27)

The j-bit soft information is obtained as follows:

S_{j} \approx \max_{D \in g_{j}^{1}} ∣ R \cdot C_{1}^{i} ∣ - \max_{D \in g_{j}^{0}} ∣ R \cdot C_{0}^{i} ∣

(28)

Normalization to:

S_{j} \approx (\max_{D \in g_{j}^{1}} ∣ R \cdot C_{1}^{i} ∣ - \max_{D \in g_{j}^{0}} ∣ R \cdot C_{0}^{i} ∣) / {MAX}_{j}

(29)

{MAX}_{j} = \max (\max_{D \in g_{j}^{1}} ∣ R \cdot C_{1}^{i} ∣, \max_{D \in g_{j}^{0}} ∣ R \cdot C_{0}^{i} ∣)

(30)

6. Bit error performance analysis

When the signal between K users in the system is assumed to have a random time delay, and the signal power of each user is equal, considering white Gaussian noise (AWGN) and multiple access interference (MAI), the bit error rate formula of the M-base spread spectrum system is as follows:

P_{r} = (M - 1) Q [{(\frac{N_{0}}{E_{s}} + \frac{2 (K - 1) M_{ε}}{{NT}_{c}^{3}})}^{- \frac{1}{2}}]

(31)

In formula (31), K is the number of users, M is the number of bases,

E_{b}

is the energy of information bits,

E_{s}

is the energy of multibase symbols,

E_{s} = E_{b} \log_{2} M

, N is the length of the spread spectrum code,

M_{ε}

is the integral of the square of the autocorrelation function of the waveform function in a chip.

Q (x) = \frac{1}{\sqrt{2 π}} \int_{x}^{\infty} \exp (- t^{2} / 2) dt

, the waveform function is known to be a gate function, equation (31) can be written as:

P_{r} = (M - 1) Q [{(\frac{N_{0}}{E_{b} \log_{2} M} + \frac{2 (K - 1)}{3 N})}^{- \frac{1}{2}}]

(32)

Each M decimal symbol of the multi-base spread spectrum corresponds to

\log_{2} M

bit, and the decoder miscalculates the error corresponding to

\log_{2} M

bit once. The bit error rate of the multi-base spread spectrum system is obtained as follows:

P_{b} = \frac{M \log_{2} M}{2 (M - 1)} P_{r}

(33)

When considering AWGN and MAI, the bit error rate formula of direct spread spectrum system is:

P_{b} = Q [{(\frac{K - 1}{3 N} + \frac{N_{0}}{2 E_{b}})}^{- \frac{1}{2}}]

(34)

The reduction of the bit error rate of multibase spread spectrum system is obtained by coding gain. According to formula (33) and formula (34), when the base number M is small, the error performance of the traditional direct spread spectrum system and the multi-base spread spectrum system is not much different, and in a certain signal-to-noise ratio range, the increase of M corresponds to the error performance of the multi-base spread spectrum system is better than that of the traditional direct spread spectrum system.

7. Simulation results and analysis

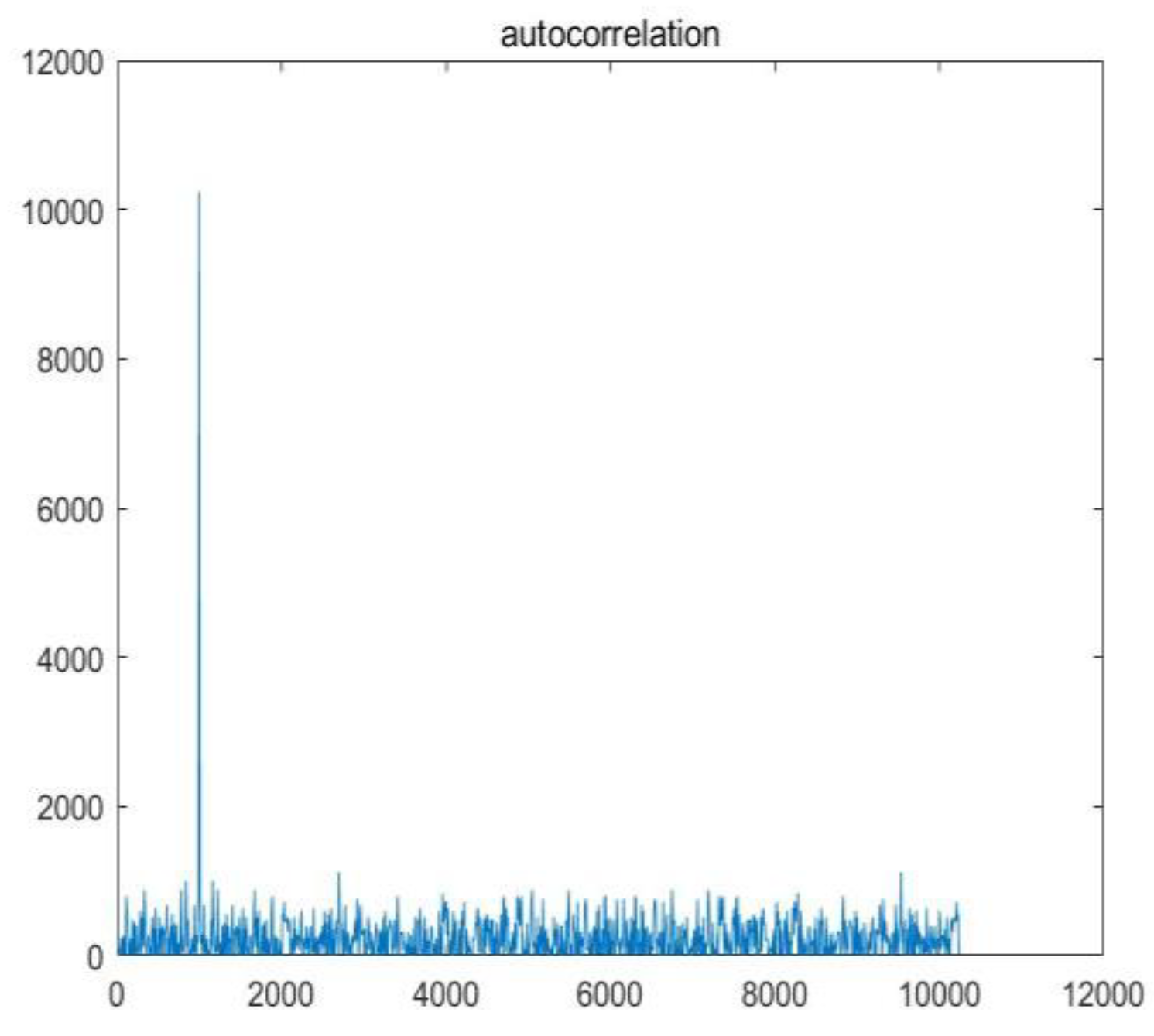
Firstly, the correlation of chaotic sequences is tested. The autocorrelation images and cross-correlation images of chaotic sequences are shown in Figure 4 and Figure 5.

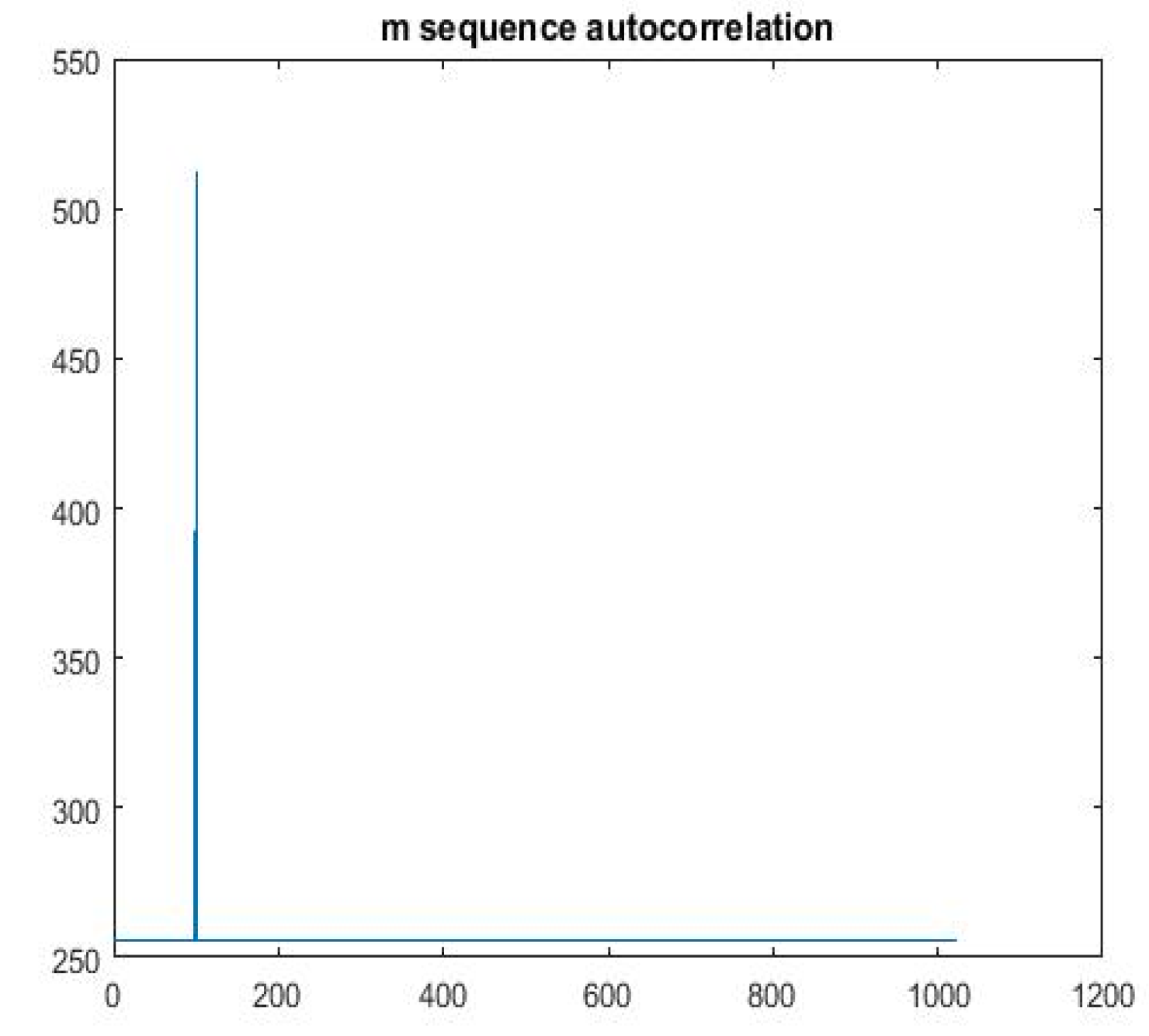
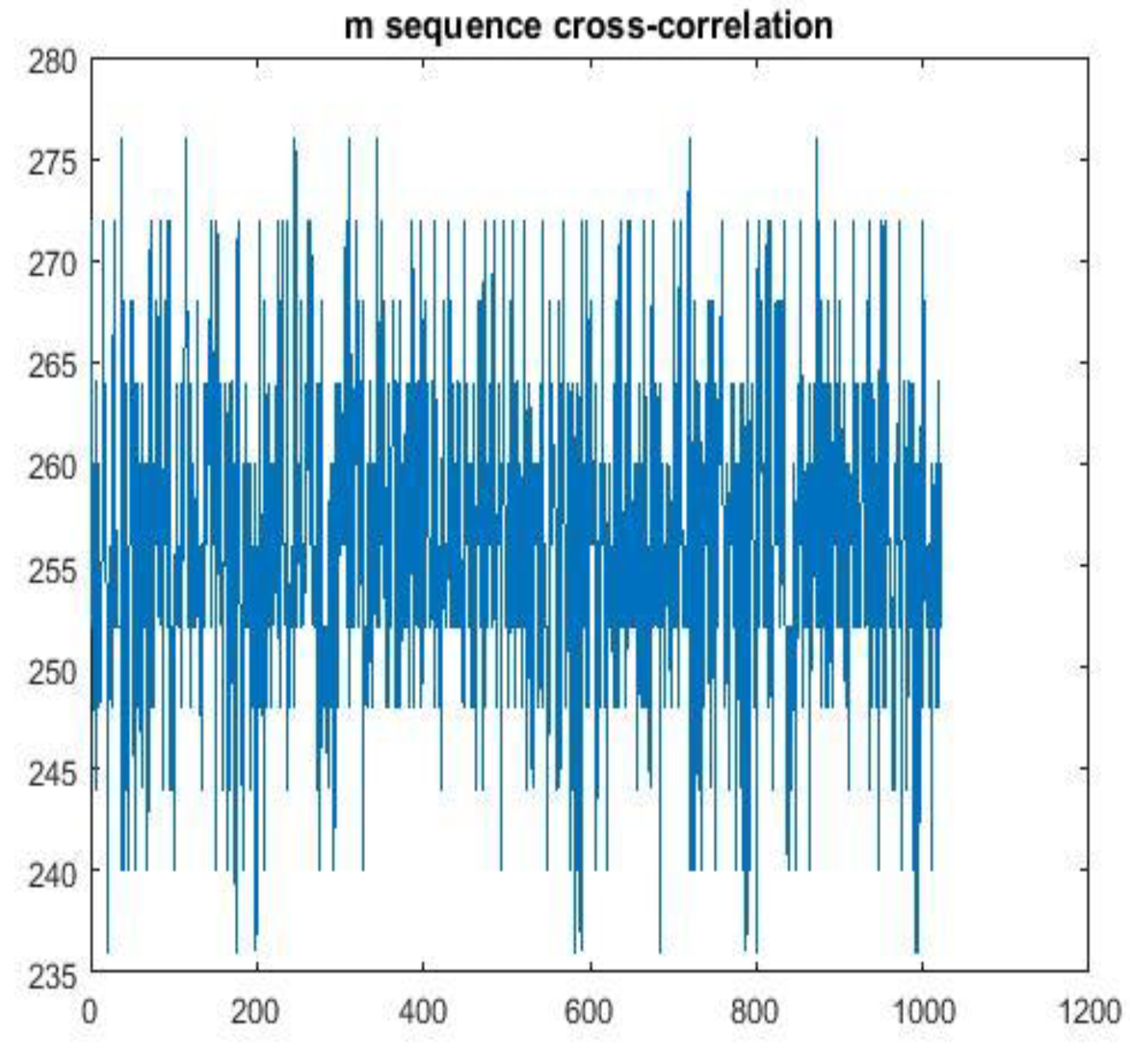
The autocorrelation and cross-correlation images of m-sequence are shown in Figure 6 and Figure 7. By comparison, the correlation characteristics of chaotic sequence are better than those of m-sequence.

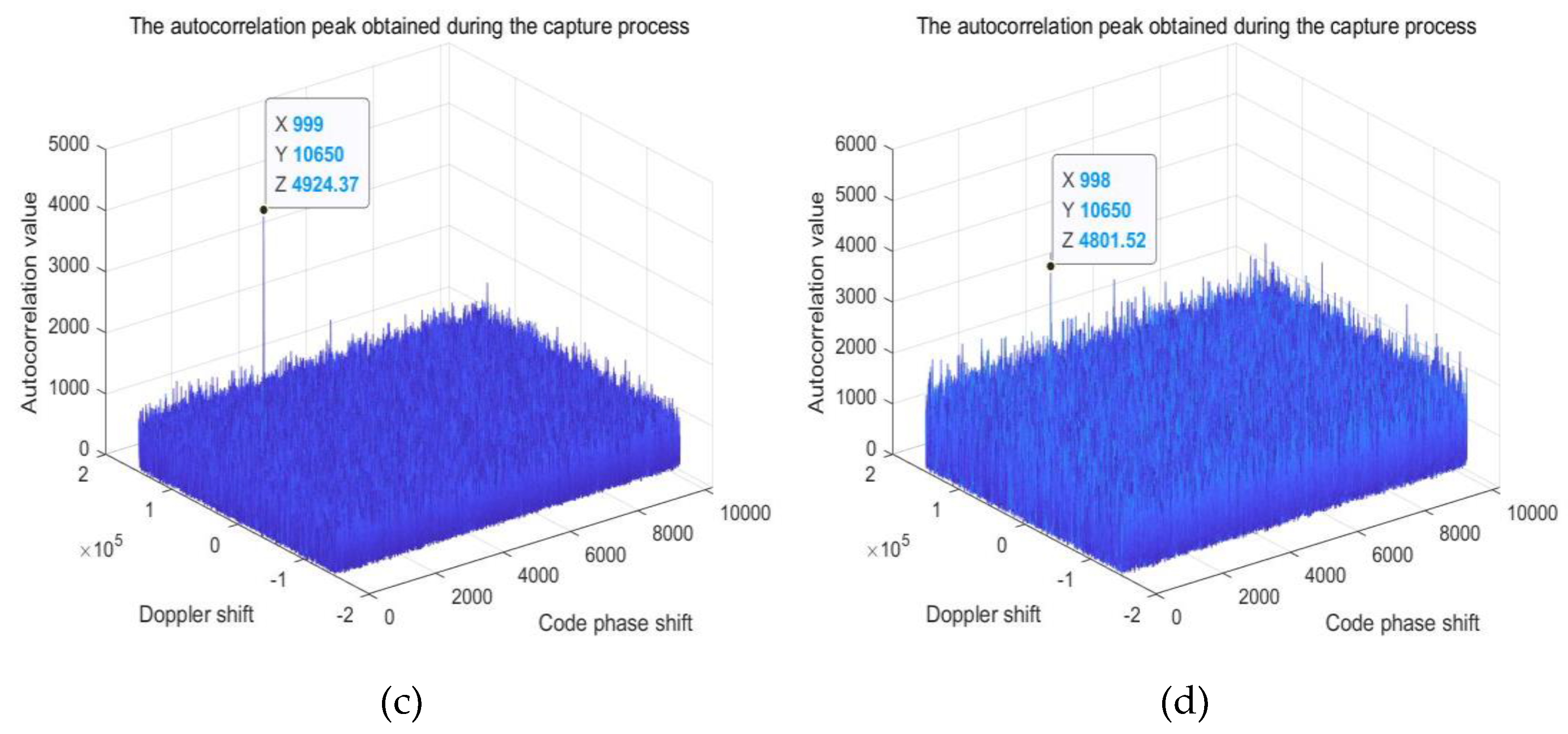
Figure 8 shows the images captured in Gaussian channels with different SNR. The Doppler frequency offset set is 10.5KHz, the Doppler change rate is 2KHz/s, and the code phase offset is 100. Search and capture are carried out in the range of -15KHz to 15KHz. The SNR of Figure (a) to Figure (d) is 8dB, -1dB, -5dB and -20dB, respectively. From the figure, it can be seen that in the case of poor channel environment, the spread spectrum system using chaotic sequence as pseudo-code can still see sharp correlation peaks, and the error is far less than the length of half a chip.

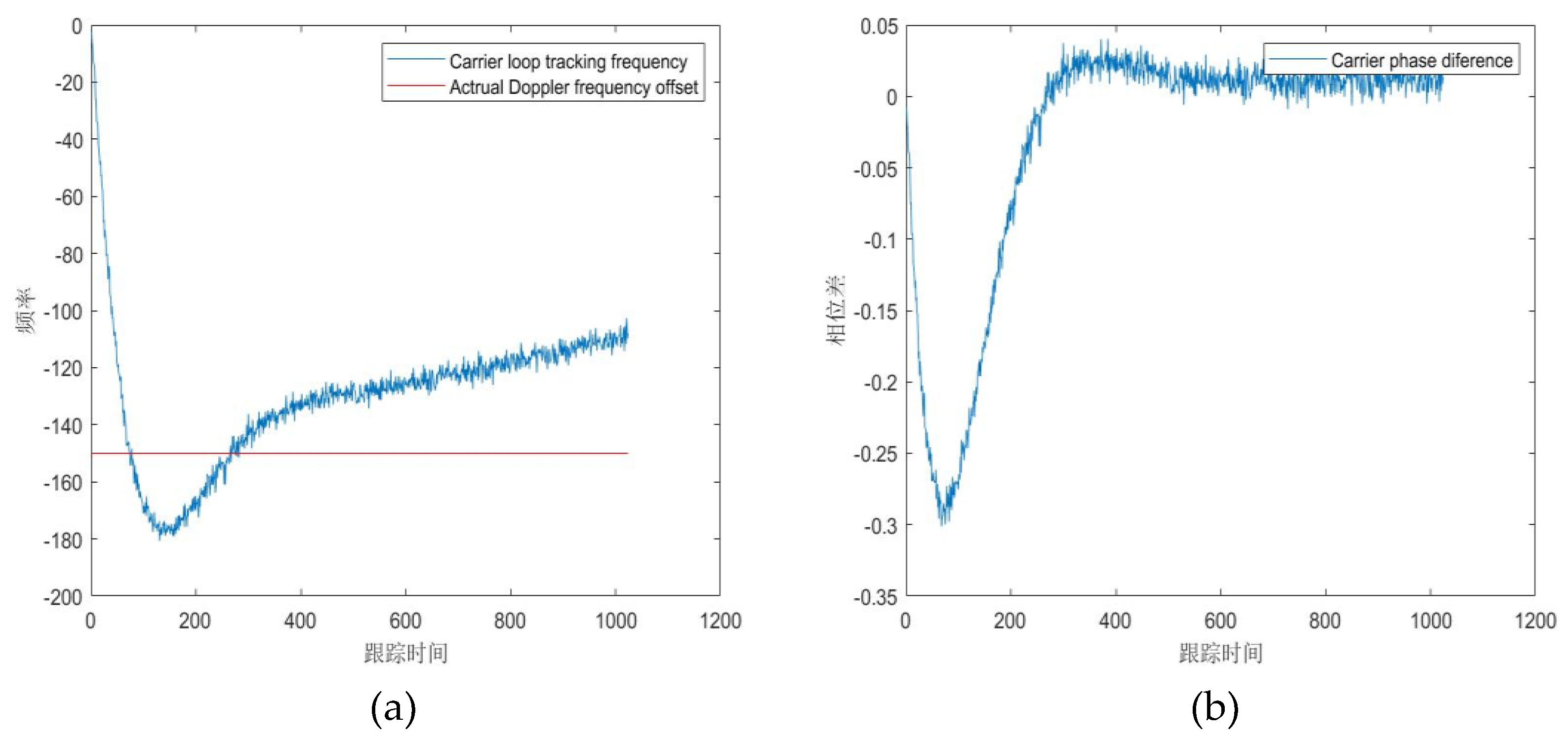
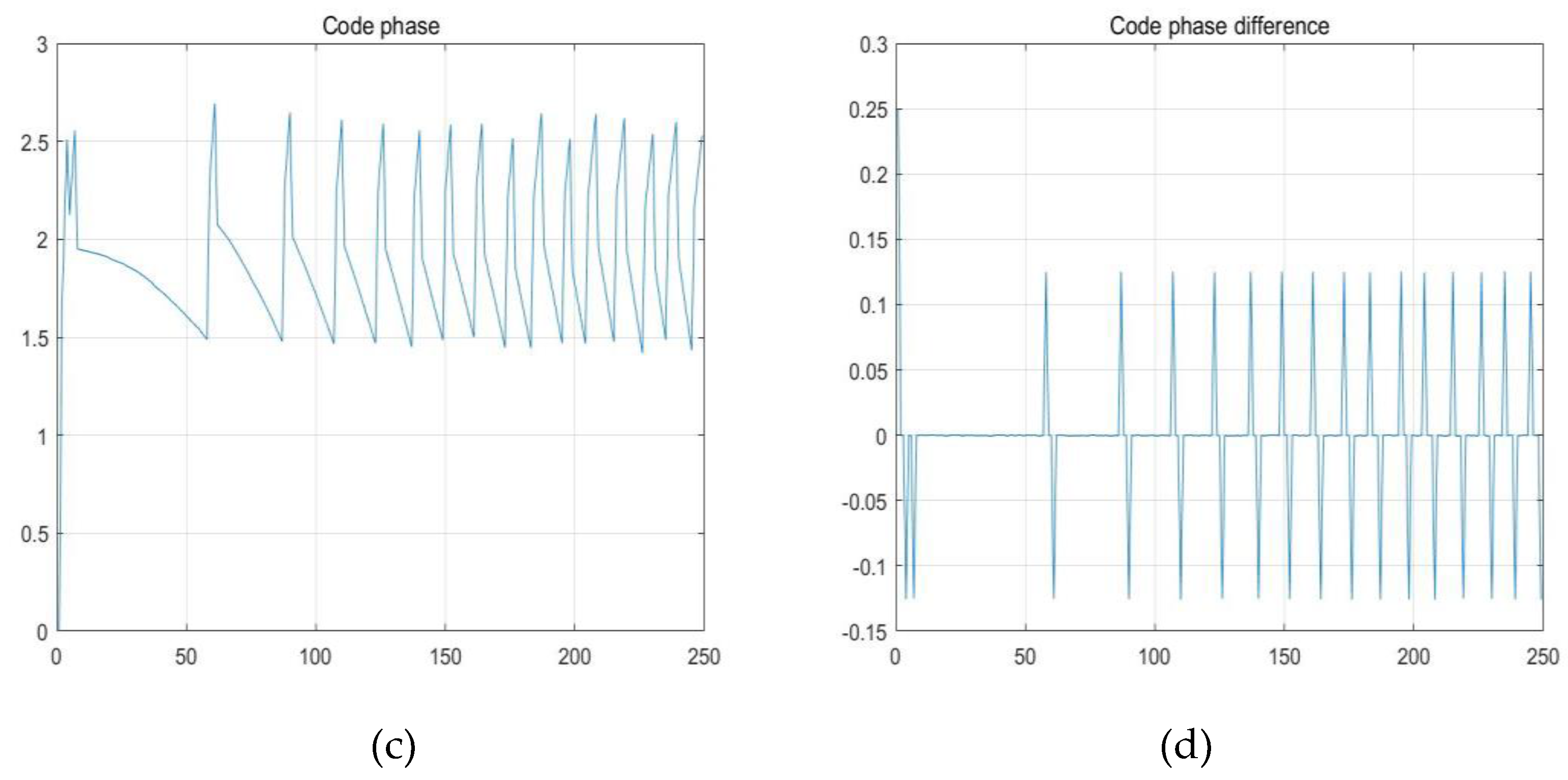
After compensating the captured chip offset and carrier offset, the tracking loop is entered, and the carrier exchange tracking image and code ring tracking image obtained are shown in Figure 9. Since the Doppler change rate is set, the carrier frequency image after the carrier tracking ring is tracked does not fluctuate in a fixed frequency range, but increases at a fixed rate. By calculating the slope of the image, it can be seen that the Doppler change rate on the tracking is 2KHz/s, which is the same as the set rate, and the phase difference always oscillates around 0, which also proves that the target has been tracked. (c) and (d) are tracking images of the code ring and enter the tracking loop after compensating the tracked code bias. Figure (c) indicates that the code bias that still exists is captured and oscillates around this area, while Figure (d) indicates that the code phase difference oscillates around 0. The combination of the two indicates that the tracking of the pseudo-code enters a steady state and is consistent with the set code bias.

After the coarse synchronization process of capture, it enters the tracking loop for further fine synchronization process. Both steps are completed, and complete synchronization can be obtained through the simulation diagram, which proves that the design method used in this paper is completely feasible and has excellent effect.

Then the error performance of the system is simulated. The parameter design is shown in Table 1. In order to clearly compare the impact of different synchronization modes, whether to add channel coding and soft and hard decision modes on the system error performance, MATLAB is used to compare and simulate the system performance in AWGN channel. Simulation parameters are shown in Table 1. Matlab will be used for simulation. The channel coding adopted is (2,1,7) convolution coding, and the multibase spread spectrum system (1024, 10) is adopted.

The bit error rate of multibase spread spectrum system is better than that of traditional direct spread spectrum under certain SNR condition, which can be seen from the formula in Section 5.

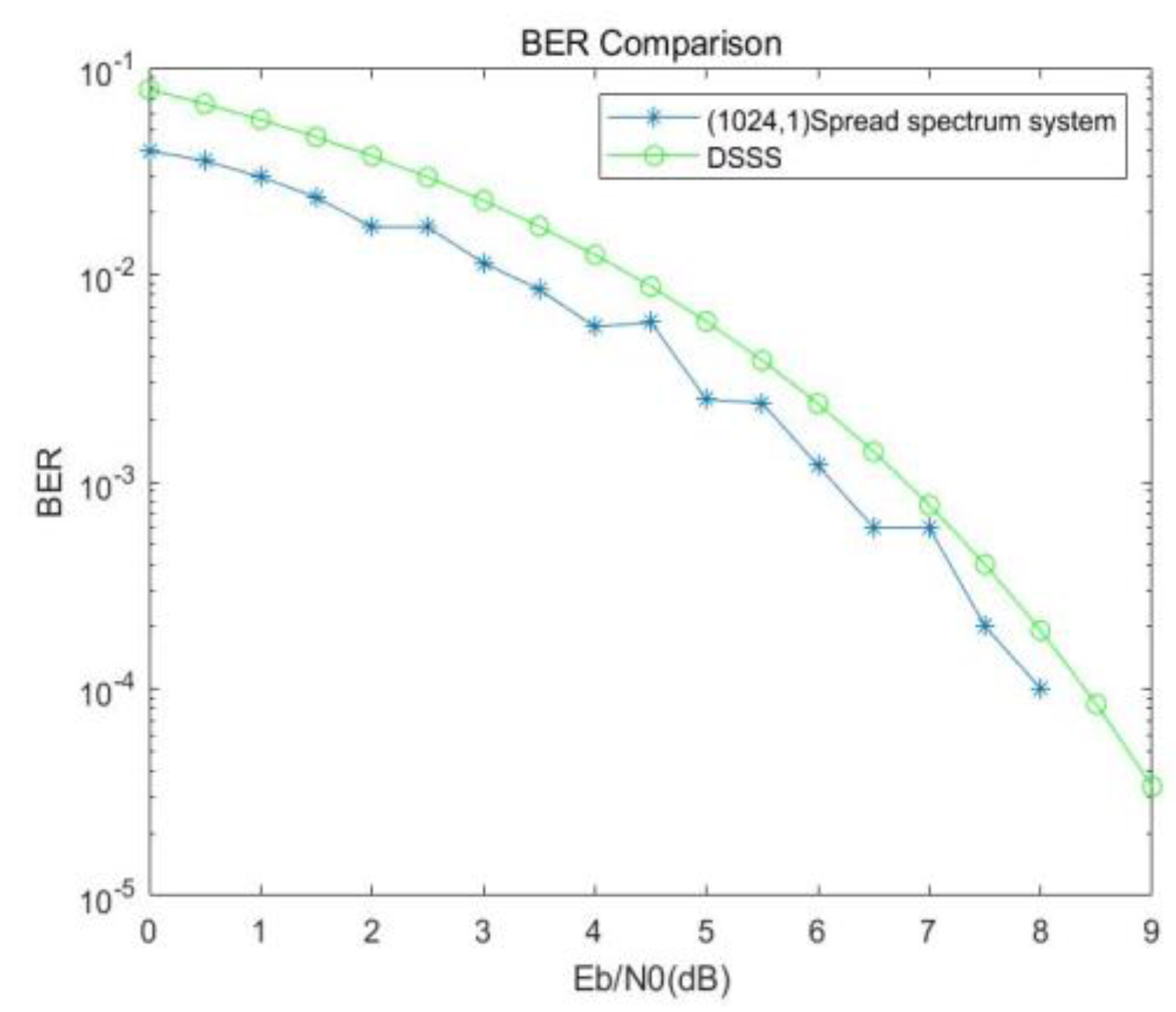
As can be seen from Figure 10, when the bit error rate

BER = 1 \times 10^{- 3}

, the (1024, 1) system outperforms the traditional direct spread spectrum system by about 0.7dB.

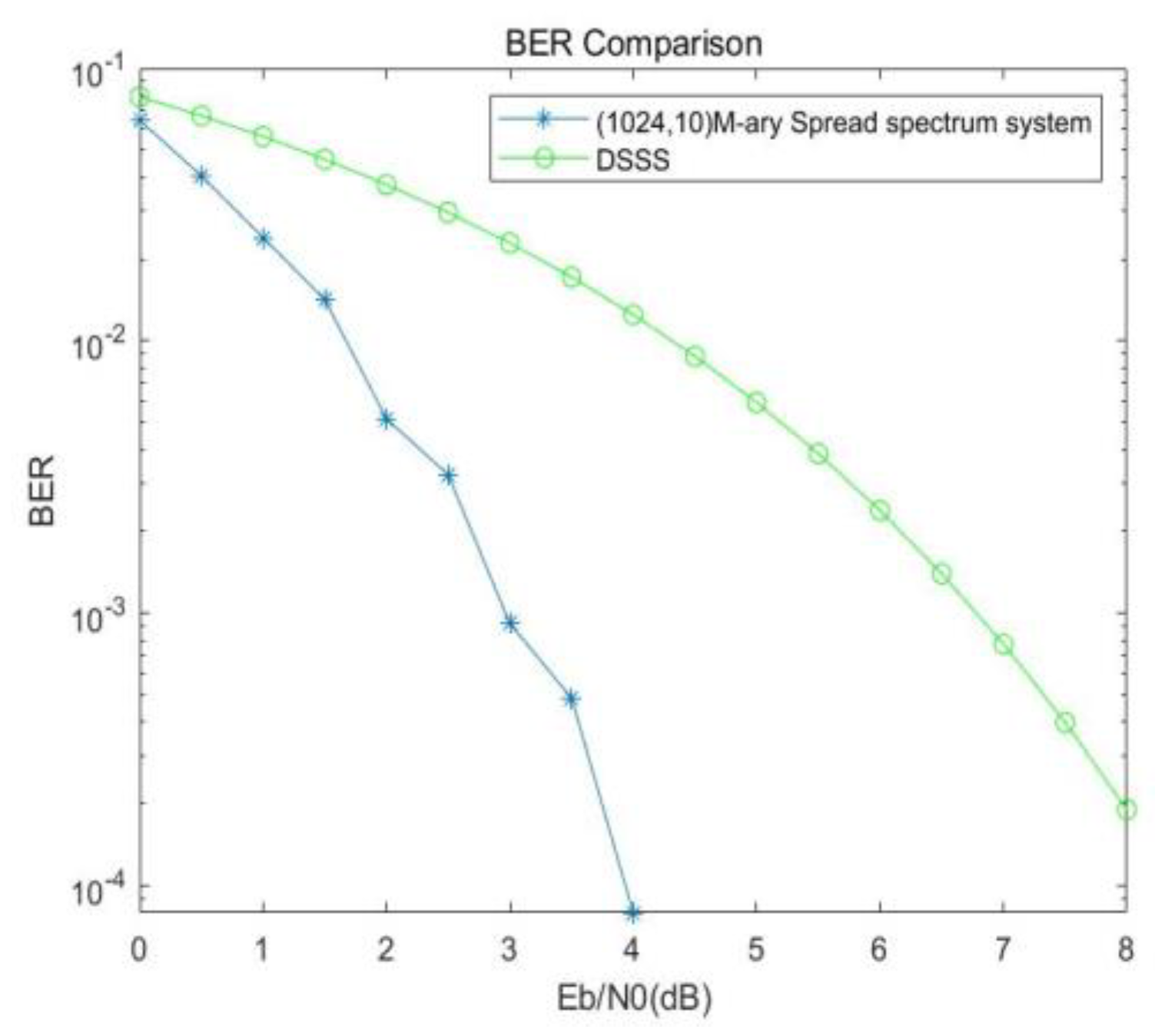
Comparing Figure 11 with Figure 10, when the bit error rate is s

BER = 1 \times 10^{- 3}

, the (1024, 10) multi-base spread spectrum system has a gain of about 4.2dB compared with the DSSS system, and the (1024, 10) compared with the (1024, 1) system has a gain of about 3.5dB, which is the coding gain.

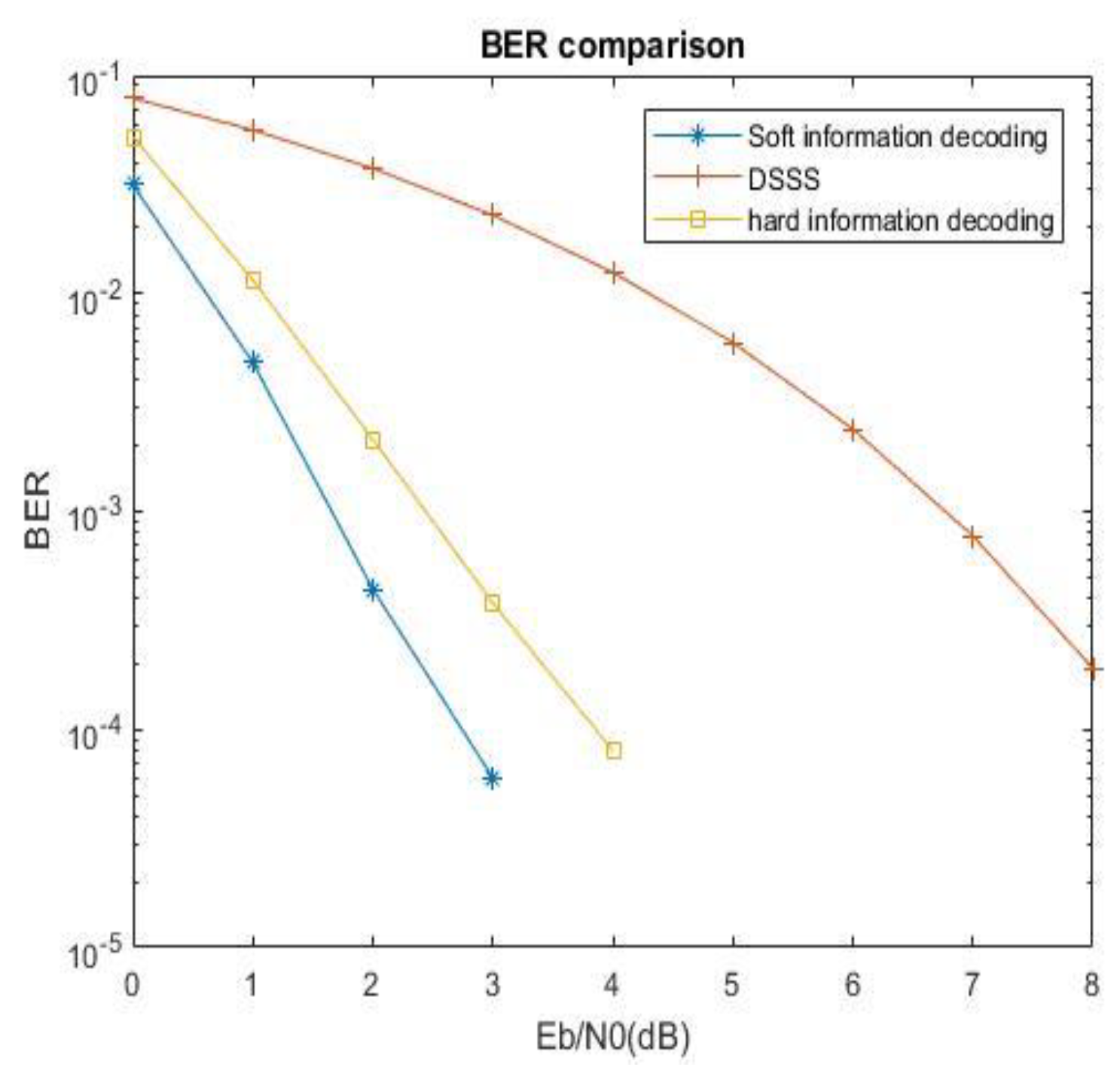
There is no significant difference in error performance between the two methods of hard decision unexpanding directly on the received signal and hard decision unexpanding after extracting soft information from the received signal. The method of hard decision after extracting soft information does not make full use of the feature of “possibility information” contained in the soft information, so the performance is not well improved, as shown in Figure 12. Therefore, convolutional coding and soft decision decoding continue to be combined.

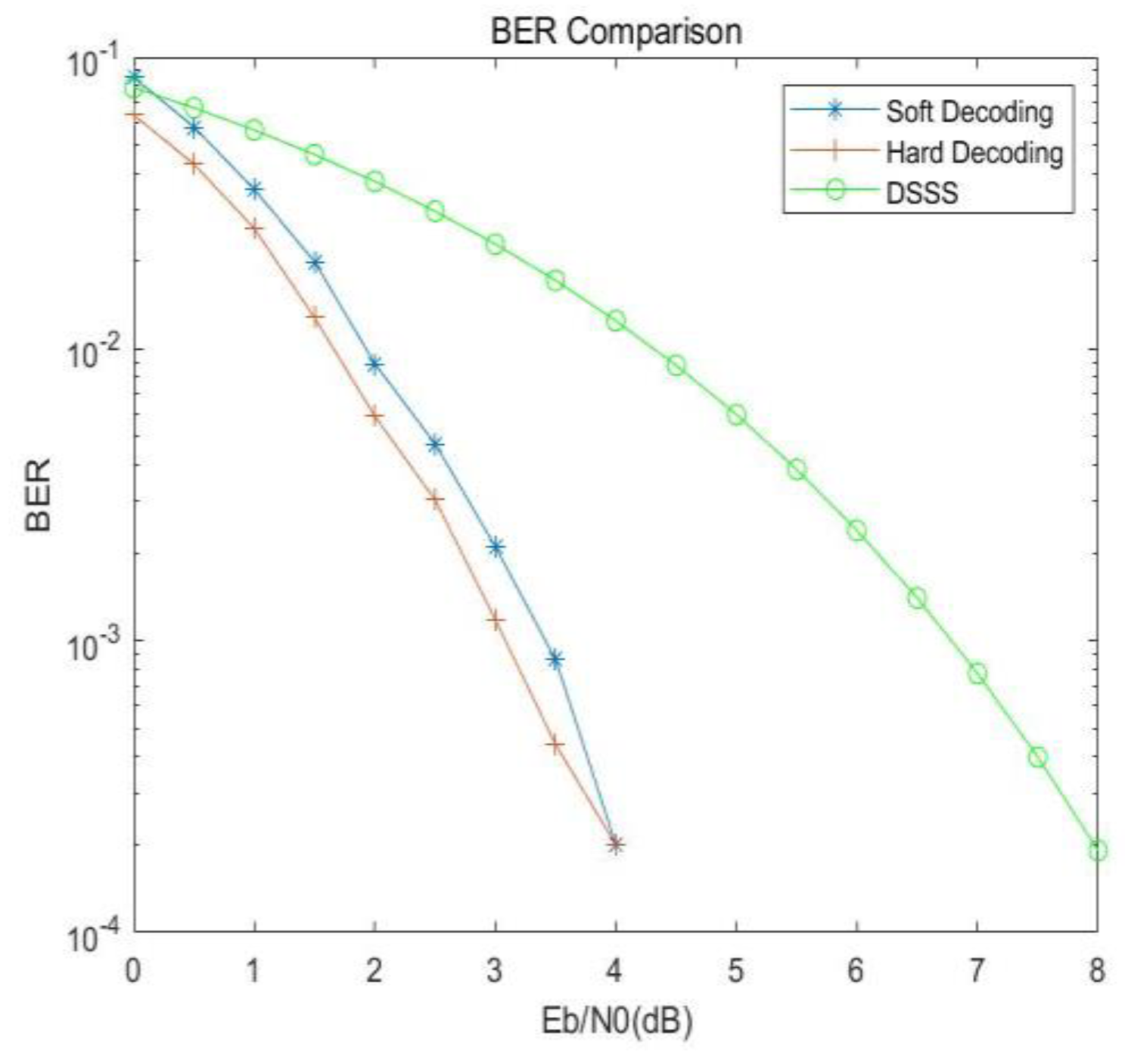
When (2,1,7) convolutional coding is added to the system, the performance is greatly improved. The comparison of error performance of hard decision or soft decision when the channel decoding mode is selected is shown in Figure 13. It can be seen from Figure 13 that the error performance of the whole system after convolutional coding is better than that of the multi-base spread spectrum system, with a gain of about 5.2dB, while the performance of soft-decision decoding is about 1dB higher than that of hard decision decoding.

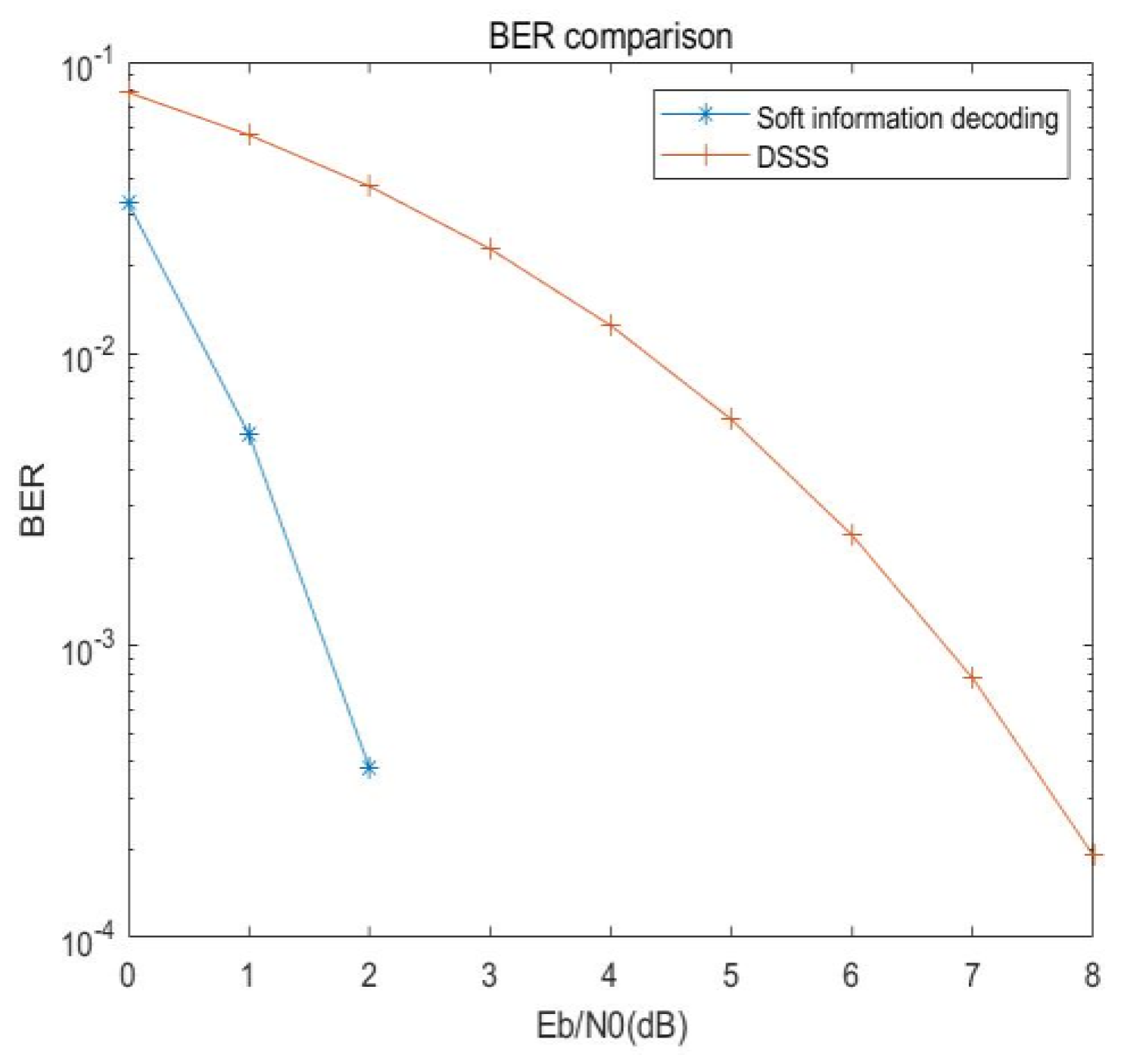
It can be intuitively seen from Figure 14 that the error performance of the system using soft decision decoding and multi-base spread spectrum is greatly improved than that of the DSSS system. When the bit error rate is high, the error performance of the system is improved by about 5.2dB.

8. Conclusions

A suboptimal soft information extraction algorithm based on LLR is proposed based on multi-base spread spectrum system, considering the practical conditions of application in engineering, which can significantly improve system performance with less complexity. In this paper, the anti-interference ability of the multi-base spread spectrum system is studied from the perspective of the communication partner. In addition to preventing the enemy from detecting the spread spectrum code, it is also necessary to consider how to make the partner obtain the local pseudo-code as quickly and accurately as possible. Therefore, based on the initial value sensitivity and aperiodicity of chaotic sequence, an iterative method is proposed to obtain spread spectrum code with the last value of the unquantized chaotic sequence as the initial value of the latter sequence. The simulation results show that the correlation performance of chaotic code as a spread spectrum sequence is better than that of traditional spread spectrum code, and it can be captured in the channel environment with lower signal-to-noise ratio during synchronous capture. In the test of acquisition performance, the correlation peak is still sharp in the channel with the SNR of -20, which is much better than that with the traditional spread spectrum code, and the captured Doppler frequency offset and chip offset error can be controlled within a small range. When the bit error rate is high, the system can gain 5.2dB and 1.8dB respectively in AWGN compared with DSSS and common (1024, 10) multibase spread spectrum system. From the above experimental results, it can be concluded that the proposed scheme is of great significance in realizing reliable signal transmission under bad channel environment, improving anti-jamming and anti-interception performance in secure communication, and practical engineering implementation.

References

Zeng. X; Yin. W; Liu. N. Performance Analysis of Soft Spread Spectrum System (In Chinese). Journal on Communications, China, Proceedings of Academic Communication, 1997.
Ling. C; Wu. X; Sun. S. A General Efficient Method of Chaotic Signal Estimation. IEEE Trans. on Signal Processing, 1999, 47(5): 1424-1428.
Sun. K; Zhou. J; Mou. J. Design and Performance Analysis of Multi-user Chaotic Sequence Spread-Spectrum Communication System(In Chinese). Journal of Electronics & Information Technology,2007(10): 2436-2440.
Luca, M.B.; Azou, S.; Burel, G.; Serbanescu, A. A complete receiver solution for a chaotic direct-sequence spread spectrum communication system. In Proceedings of the Proceedings—IEEE International Symposium on Circuits and Systems, Kobe, Japan, 23–26 May 2005; pp. 3813–3816.
Volkovskii, A.R.; Tsimring, L.S.; Rulkov, N.F.; Langmore, I. Spread spectrum communication system with chaotic frequency modulation. Chaos 2005, 15, 033101. [CrossRef]
Kaddoum, G.; Roviras, D.; Chargé, P.; Fournier-Prunaret, D. Robust synchronization for asynchronous multi-user chaos-based DS-CDMA. Signal Process. 2009, 89, 807–818. [CrossRef]
Arturs. A; Nikolajs. T. Software-Defined Radio Implementation and Performance Evaluation of Frequency-Modulated Antipodal Chaos Shift Keying Communication System. Electronics 2023, 12, 1240.
Bernard. S.Translated by Xu. P; Song. T et al. Digital Communication – Fundamentals and Applications, 2nd ed; Publishing House of Electronics Industry: Beijing, China, 2002.9: 547-561.
Fan. C; Cao. L. Principles of Communications (In Chinese), 7th ed; National Defense Industry Press: Beijing, China, 2012: 4-20.
FOSSORIER. M. P. C; Burkert. F; Shu. L. On the Equivalence Between SOVA and Max-log-MAP Decodingd. IEEE Communications Letters, 1998,2(5): 137-139.
Kis, G. Performance Analysis of Chaotic Communications Systems. Ph.D. Thesis, Budapest University of Technology and Economics, Budapest, Hungary, 2003.
Li. D. Research on the Key Technology of M-ary Spread Spectrum System. Xi’an, Shanxi, China: Master Thesis, Xi ’an University of Electronic Science and Technology, 2001: 4-9.
Xia. G; Luo. Y; Jin. Z. Performance Analysis and Simulation of Multidigit Direct Spread Spectrum Sequences(In Chinese). Avionics Technology,2015,46(2): 12-15,20.
Michaels, A.J. Digital Chaotic Communications. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2009.
Wang. L. Reasearch on Application of Chaotic Spreading Spectrum Technology to CDMA Communication System. Ph.D. Thesis, University of Electronic Science and Technology, 2001.
Heidari-Bateni. G , Mcgillem. C. D .Chaotic direct-sequence spread-spectrum communication system.IEEE Transactions on Communications, 1994, 42(234):1524-1527. [CrossRef]
Sascha. M; Weher. C. L. A Unified Approach to Serial Search Spread Spectrum Code Acquisition, Part I/II. IEEE Trans. Commun, 1984, vol.COM-32, No.5: 549-560.
Oppenheim. A. V; Schafer. R. W; Buck. J. R. Translated by Liu. S; Huang. J. Discrete-Time Signal Processing, 3^rd ed; Publishing House of Electronics Industry,2015,9: 588-598.
Yu. X; Bi. G. Algorithms of Long Sequence Fast Correlation and Convolution. Journal of Circuits and Systems, 2001(04): 78-83.
Xie. G. Principles of GPS and Receiver Design. Beijing, China: Publishing House of Electronics Industry, 2011.
Wang. L; Wang. J; Wang. Y. Analysis of Performance of M-ary Orthogonal Code Spread Spectrum System with Convolutional Code(In Chinese). Radio Engineering, 2008,No. 233(10): 20-22.

Figure 1. Whole System Diagram.

Figure 2. Acquisition Algorithm Flow.

Figure 3. Tracking Algorithm Loop.

Figure 4. Chaotic sequence Autocorrelation.

Figure 5. Chaotic sequence cross correlation

Figure 6. Chaotic sequence Autocorrelation.

Figure 7. Chaotic sequence cross correlation

Figure 8. The autocorrelation peak obtained during the capture process.

Figure 9. Tracking loop.

Figure 10. (1024,1) compared with the bit error rate of DSSS.

Figure 11. (1024,10) compared with the bit error rate of DSSS.

Figure 12. (1024,10) System hard decision and Comparison of hard performance decision error rate of soft information extracted.

Figure 13. Convolutional coding system error.

Figure 14. (1024,10) System (2,1,7) soft decision decoding bit error performance.

Table 1. Simulation parameters of M-ary Spread Spectrum communication system.

M	R_b(b/s)	f_c(Hz)
1024	100K	50M
R_c	codelength	Eb/N0(dB)
10.24M	1M	0-8

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Design and Simulation of Soft Decision Decoding Based on Chaotic M-ary Spread Spectrum System

Abstract

1. Introduction

2. M-ary Spread Spectrum communication system model

3. Generate chaotic spread spectrum code

4. Synchronization module

4.1. Signal Capture

4.2. Signal Tracking

4.2.1. Phase locking loop

4.2.2. Code tracking loop

5. Soft decision decoding algorithm

6. Bit error performance analysis

7. Simulation results and analysis

8. Conclusions

References

MDPI Initiatives

Important Links

Subscribe