Prerpints.org logo
Preprint
Article

Impact of a Thermally Stratified Energy Source in a Supersonic Flow past a Pointed Cylinder Aerodynamic Model on the Pressure Signatures and PLdB Effect on the Ground

This version is not peer-reviewed.

Submitted:

13 June 2023

Posted:

14 June 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
The research is devoted to the problem of noise generation during flights of supersonic civil aircrafts. The effect of a thermally stratified energy source used to control the flow past a pointed cylinder aerodynamic models on the nearfield and ground pressure signatures, as well as on the perceived loudness in decibels (PLdB) on the ground is evaluated. The fields of parameters and the dynamics of the drag forces are studied for different values of temperature in the layers of the thermally stratified energy source and for different number of layers in it. It has been shown that when performing the flow control at freestream Mach numbers 1.5-2 using thermally stratified energy sources with the number of layers from 2.5 to 7.5 and rarefaction parameters in the layers from 0.15 to 0.3, no additional noise impact on the ground is introduced. Thus, the simulations showed that changing the surface pressure signature due to drag reduction does not necessarily imply a change in the PLdB on the ground.
Keywords: 
Subject: 
Engineering  -   Aerospace Engineering

1. Introduction

The problem of high-speed flow control using non-mechanical tools, in particular, remote energy deposition, currently occupies a leading position among studies of flow/flight control [1]. Recently, the control of supersonic flows with the help of electric discharges, microwave and laser energy deposition is a fairly developed area of aerospace technology (see reviews in [1,2,3]). A historical review of ideas that arose several decades ago about controlling a supersonic flow by supplying energy to various points in the flow and on the surface of an aerodynamic (AD) body is presented in [4]. In [5], the study is conducted of a sonic boom effect using continuous energy deposition consists of two and three longitudinal heated filaments. The flow case was considered when one of the filaments is located upper the sharpen AD body. Due to the impact of such an energy deposition on the flow, a decrease in the perceived loudness in decibels (PLdB) on the ground was obtained, although this was shown to require a significant energy consumption. An overview of studies of noise generation (the Sonic Boom problem) in the field of supersonic flows/flights is presented in [6] where a summary is provided of the researches conducted in the framework of the Second AIAA Sonic Boom Workshop.
Previously, the efficiency of energy supply in the form of longitudinal filaments for reduction of aerodynamic drag was established theoretically and experimentally [7,8,9]. At present, researchers are paying attention to the influence of spatially inhomogeneous plasma structures on the flow. The effect of layered plasma on the reflected shock wave in a supersonic flow was studied in [10]. In [11], an array of surface plasma actuators was used to control the interaction of a shock wave with a boundary layer in a flow. As a result, the disappearance of a fragment of the shock wave in the regions of stratified inhomogeneities was established [10,11]. In experiments [12], thermal and density inhomogeneities were generated using a set of heated thin wires, which, when interacting with a shock wave, led to the generation of the Richtmyer-Meshkov instability and the formation of a vortex line due to the Kelvin-Helmholtz instability.
The influence of the region of ionization instability of a glow gas discharge, which is accompanied by the formation of a layered structure of the ionization strata, on an initially flat plane shock wave was studied in [13]. In these experiments, it was shown that the stratification of the electron temperature field leads to the stratification of the gas temperature, and the impact of an inhomogeneous plasma medium caused distortion and, in some cases, complete disappearance of the shock wave front. Theoretically, the numerical experiment showed the generation of Richtmyer-Meshkov instabilities at many points, under the action of which the shock wave front was smeared (in the density field), which explained the results of the experiment [13].
In [14], the effect of a combined energy source on the supersonic flow is considered and a double-vortex mechanism of its effect on the AD body is proposed, which explains the additional effect on the frontal drag force. Besides, it was shown that the generation of double vortices is the result of the manifestation of the Richtmyer-Meshkov instabilities in two points in the flow. A natural continuation of this idea was the study of the effect of a thermally stratified energy source (TSS) on the supersonic flow past an AD body [15], where a new multi-vortex mechanism of the TSS action on the surface of an AD body connected with multiple manifestation of the Richtmyer-Meshkov instabilities was established. In [16,17], the basic principles of non-stationary and stationary control of a high-speed flow using TSSs were obtained. A possibility of controlling the bow shock wave (BSW) and the aerodynamic characteristics of a streamlined body, such as parameters at the stagnation point, drag and lift forces, location and shape of the BSW etc., by using a TSS in front of the BSW has been shown.
The present paper is devoted to the study of the problem of noise generation during flights of supersonic civil aircrafts (Sonic Boom problem) (M∞=1.5-2). The fields of the flow parameters and the dynamics of the drag forces of a pointed cylinder aerodynamic model by means of a TSS with a different number of layers and different temperatures in the layers are studied. The influence of the TSS used for the flow control on the nearfield pressure signature and the ground pressure signature is considered, and the impact of the perceived loudness in decibels (PLdB) is estimated. It has been shown that when controlling the flow with the help of TSS of the considered parameters, no additional noise impact on the ground is introduced.

2. Statement of the Problem and Methodology

The impact of an area of thermally stratified energy deposition (which for short, hereinafter referred to as thermally stratified energy source - TSS) on a supersonic flow past a sharpen cylinder body is considered. Freestream Mach number M∞=1.5 and 2 (Figure 1). It should be noted that the shapes of AD bodies considered in the article were chosen from the considerations that an attached BSW was formed in the surrounding flow and do not apply to any existing aircraft shape.
The simulation of the flow for evaluating the nearfield pressure signature is based on the Euler system of equations in a cylinder form for perfect inviscid gas with the ratio of specific heats γ=1.4:
( U r ) t + ( F r ) x + ( G r ) r = H ,
U = ( ρ , ρ u , ρ v , E ) T , F = ( ρ u , p + ρ u 2 , ρ u v , u ( E + p ) ) T ,
G = ( ρ v , ρ u v , p + ρ v 2 , v ( E + p ) ) T , H = ( 0,0 , p , 0 ) T ,
E = ρ ( ε + 0.5 ( u 2 + v 2 ) ) .
The state equation for a perfect gas is used:
ε = p / ( ρ ( γ − 1 ) ) .
Here ρ, p, u, v are the gas density, pressure and velocity x- and y-components, ε is the specific internal energy. The following normalizing values for the parameters are accepted:
ρ n = ρ ∞ , p n = 5 p ∞ , l n = k l − 1 R , T n = T ∞ , u n = ( p ∞ / ρ ∞ ) 0.5 , t n = l n / u n .
where kl is the dimensionless value of R.
The thermally stratified energy source (TSS) was given as a set of rarefied gas layers located in front of the BSW (Figure 1). The layers in TSS were suggested to have the same width; distances between them were equal to half the layer’s width. Inside every j- layer, gas density was given to be reduced, ρj=αjρ∞, with the rarefaction coefficient αj<1, j=1÷N, N is a number of layers in TSS in the calculation area taking to account the cylinder symmetry of the problem (for example, in the TSS in Figure 1 N=3.5). The pressure and velocity in the domain of TSS were set equal to their freestream values, pj=p∞, uj=u∞, vj=0. So, the temperature inside the layers was increased compared to its freestream value, Tj=αj-1T∞. The flow cases are considered when the r-coordinate of the upper boundary of the TSS is not greater than 1.1R, where R is the radius of the cylinder part of the AD body.
For evaluation of the nearfield pressure signature we used our own software package based on the complex conservative difference schemes [18]. When constructing these schemes, differential consequences of (1) are used, which makes it possible to obtain the second order of approximation in space and time on the minimal stencil, which is the stencil of the well-known Lax scheme. So, the grids used are Cartesian and staggered. The boundaries of the body are included in the computational domain without violating the conservation laws in space and time. For this purpose, discrete conservation laws were written for each emerging grid configuration in the vicinity of the boundary. The construction of complex conservative schemes in the computational domain and near the boundaries of an AD body, as well as numerous test examples, are presented in [18]. The position of the conical part of the body on the difference grid is shown in an enlarged view in Figure 2. In the calculations, the distance between the stencil nodes at each time level was assumed to be 2hx, 2hr (where hx, hr are the space steps in the x- and r-directions).

3. Analysis of the Grid Convergence

For the analysis of the grid convergence, the calculations of flow dynamics up to the establishment of the steady flow mode for three difference grids were conducted (Table 1, t=0.5). Here for the grid convergence test, the computational domain was cut off in x- and in r- directions, and the flow near the body was considered. Figure 3 demonstrates the flow fields in isochores (Figure 3a) and the dynamics of the parameters at the apex of the body (Figure 3b) obtained using these three difference grids. The numbers of nodes of Grid1 and Grid3 differ approximately by 9 times, of Grid1 and Grid2 differ by 4 times, but nevertheless, the isochores of the flow near the body and shapes of the BSWs almost coincide (see Figure 3a) and the values at the apex of the body differ only at the initial stage (where the solution is not smooth) and are practically the same at the steady flow mode (Figure 3b). So, all these test variants show the presence of the grid convergence in the used numerical methods.

4. Results

4.1. The Effect of TSS on the BSW, Nearfield Pressure Signature And aerodynamic Characteristics of a Body, L/R=10

First, let us consider the effect of TSS on the BSW and the aerodynamic characteristics of a pointed AD body for a fairly short body. The angle at the apex of the body is 16.6o fore and aft, L/R=10. The dimensional length of the body is presumably 5m. The defining flow parameters and normalizing values used in the simulations are presented in Table 2. TSS is supposed to occur at the initial stage of the process, at the time ti=0.001, and it is assumed that it has an unlimited duration in time. The axis of symmetry of TSS is supposed to coincide with the axis of symmetry of the body (see Figure 1). In Part 4.1, for the simulations we used Grid2 (hx=0.004, hr=0.002) on the computation domains which was extended to the entire calculation area and contained 18×106 nodes (counting the middle point of the stencil).
The dynamics of the density fields at M∞=2 in isochores under the action of TSS containing 2.5 layers with the equal rarefaction parameters in the layers αj=0.3 is presented in red in Figure 4. Here the r-coordinate of the upper boundary of the TSS is Rs=0.35R. For comparison, the dynamics of the density fields without the impact of the TSS is also shown (blue). Here, the density fields are presented for two different time moments, t=9.0 and t=20.0, which reflect unsteady and steady flow modes relative to the flow at the level of r=4.0 (Figure 4a,b). Figure 4c shows the density field during the interaction of TSS with the BSW in an enlarged view.
Dynamics of the according profiles of relative pressure Δp/p for r=4.0 are presented in Figure 5. Here Δp/p=(p(x) - p∞)/p(x). Next, we study the pressure profiles for t=20.0 at the level of r=4.0 (nearfield signatures) when these pressure profiles are stationary in time.
The relative pressure profiles Δp/p at the level r=4.0 (nearfield signatures) for TSS with different values αj are presented in Figure 6a. It can be seen from the enlarged image (Figure 6b) that the smaller αjin the TSS (the higher the temperature in the layers) the greater the effect of this TSS on the BSW front. One can also conclude that this effect causes decrease in pressure at the front.
Density fields of the steady flows at t=20 and αj=0.15 under the action of the TSSs with the number of layers N= 3.5 (Rs=0.5R), N=5.5 (Rs=0.8R), and N=7.5 (Rs=1.1R) are presented in Figure 7, Figure 8 and Figure 9 (in red), accordingly. The corresponding enlarged images of the density fields during the interaction of different TSSs with the BSW are also shown there. For comparison, the according dynamics of the density fields without the impact of the TSS is shown (in blue), as well.
The enlarged images in Figure 4c, Figures 7b–9b show that the front of the BSW in the TSS region is almost completely blurred (see the red contours). This is taken place due to the influence of three factors that distinguish the effect of TSS from the effect of a homogeneous energy source. Firstly, this is a manifestation of the Richtmyer-Meshkov instability in multiple points at the initial stage of interaction, which smears the front of the shock wave [15,16]. Secondly, the action of heated layers interspersed with cold gaps between them changes the shape of the BSW and gives it a wavy appearance, which also contributes to the blurring of its front. The third one is, of course, that the BSW also weakens simply due to a change in the Mach number inside the heated layers. This smearing of the front under the action of the TSS is further influenced the pressure amplitudes in the nearfield signature, and finally may possibly affect the pressure amplitudes in the ground signature, and the PLdB on the ground.
Possibility of flow control using heated filaments has been well proven both experimentally and theoretically (see [1,2,3,4]). Figure 10 and Figure 11 demonstrate the possibility of flow control for the considered shape of the body at M∞=1.5 and M∞=2 using the considered TSSs, in particular, controlling the drag force F. Here
F = ∫ 0 R p b r d r ,
where pb is the pressure on the conical surface. For comparison, the corresponding dynamics of F is also shown in the absence of the influence of TSS (in blue). It can be seen that the smaller αjin the TSS (the higher the temperature in the layers) the greater the influence of this TSS on the stationary value of the drag force F (Figure 10). The greatest effect ε for αj=0.15 is 10.8% (from the value of F 0 without the impact of TSS) at M∞=2 and 11.1% at M∞=1.5. Here
ε = ( F − F 0 ) / F 0 × 100 % .
In Figure 11, the dynamics of F is presented at M∞=1.5 and M∞=2 for αj=0.15 under the action of the TSSs with 3.5, 5.5 and 7.5 layers. One can see that the greater the number of layers N in TSS in the TSS the stronger the effect of this TSS on the steady value of the drag force F (Figure 11). The greatest effect (for N=7.5) is 15.1% of the value of F without the impact of TSS at M∞=2 and 12.3% at M∞=1.5.
At the same time, analyzing the corresponding relative pressure profiles (nearfield signatures) at the level of r=4.0 (t=20), it can be concluded that the considered TSSs decrease the pressure at the BSW front (for example, by 2.8% of p for the best case of the TSS with N=7.5 for M∞=2 and 7.4% for M∞=1.5, using the same criterion as for F) (Figure 12). Thus, when controlling the flow with the help of TSS under the considered parameters at M∞=1.5 - 2, the nearfield pressure signature does not show an increase in the amplitudes of the BSW front values in the near-field region to the AD body.

4.2. The Effect of TSS on the BSW and Nearfield Pressure Signature, L/R=12.5; Energetic Considerations

In order to evaluate the impact of the PLdB during the implementation of flow control using the TSS, calculations of the relative pressure Δp/p in the near field (nearfield signatures) for a longer body (L=10) at the level of r=16.8 were carried out. The angle at the apex of the body is 24o, L/R=12.5. The dimensional length of the body is presumably 80m. The defining flow parameters and normalizing values used have the order of real parameters of aircraft (see Table 3). In Part 4.2, the calculations were carried out on a grid of 9600×4500 (43.2×106 nodes, counting the middle node of the stencil) with hx=0.005, hr=0.004.
Dynamics of density fields for αj=0.25 under the action of the TSS with the number of layers N=7.5 (Rs=1.1R) compared with that in the absence of TSS at M∞=1.5, 2 is presented in Figure 13. In Figure 14, the dynamics of F is presented at M∞=1.5 and M∞=2 for αj=0.25 under the action of the TSSs with 7.5 layers (of the greatest effect). The effect in the reduction of the drag force F is 20.7% at M∞=2 and 19.0% at M∞=1.5. Figure 15 shows a comparison of the relative pressure profiles Δp/p at r=16.8 in a case of the absence of TSS (blue) and in the presence of TSS with αj=0.25, N=7.5 (orange) at t=40. One can see that the action of TSS does not increase the amplitude of the BSW in the nearfield pressure signature in spite of the presence of the effect of drag reduction. The reason of this is that the TSS impact on the BSW is concentrated in the area closest to the body.
Using the formulas (20) and (25) from [5] it is possible to evaluate the effective power P required for creation of the considered stratified energy sources. Taken into account that the half width of the layers in considered TSSs rs=10hr and the coordinates of the centers of layers rc in these simulations can be calculated as r c = 30 ( N − 0.5 ) h r the effective power P can be evaluated as follows:
P = π / 4 γ γ − 1 β u ∞ p ∞ r s 2 / 4 1 − α j + 4 π ( N − 0.5 ) γ γ − 1 β u ∞ p ∞ r c r s 1 − α j =
= π γ γ − 1 β M ∞ c ∞ p ∞ 100 h r 2 1 − α j ( 1 / 16 + 12 ( N − 0.5 ) 2 ) ,
where a constant β=0.1 [5]. The values of the effective power for the parameters of the simulations from Parts 4.2, 4.3 αj=0.25, N=7.5 using the obtained expression for P are 591.27 MW for M∞=1.5 and 788.37 MW for M∞=2 which are large and likely impractical. Nevertheless, we examine the maximal possible effect from the considered TSS to evaluate the perceived level in decibels (PLdB) impact on the ground during the implementation of the flow control using TSS.

4.3. The Effect of TSS on the Ground Pressure Signature and PLdB on the Ground, L/R=12.5

To assess the PLdB impact on the ground, we were guided by the approach proposed in [19,20]. The profiles from Figure 14 were processed with the use of the software packages from [19] to simulate the passage of a signal through the atmosphere. We evaluated the impact of only the "N-wave" in the profiles; besides, the profiles were shifted to the coordinate origin. Figure 15 shows the processing of the profiles and the final ground signatures resulting after using the numerical code from [19]. The ground pressure signatures are expressed in pounds per square foot. A comparison is shown at M∞=2 and M∞=1.5 for the cases of the absent of the TSS action (blue) and of the maximal effect of the TSS on the nearfield pressure signatures (N=7.5) (orange) at the level of r=16.8. The flight altitude was supposed to be equal to 10000 m or 32808.4 ft.
The according values of the PLdB impact on the ground evaluated using the open source package PyLdB [21] are presented in Table 4. The PyLdB code implements the perceived loudness level calculation determined using the algorithm from [22]. One can see that at M∞=1.5 - 2 the TSS which has the maximum effect on the front of the BSW (and on the nearfield pressure signature, as well) does not increase the impact of the ground sound pressure. Thus, it can be concluded that the controlling of the flow (past an AD body of the considered shape) using the TSSs with the considered parameters, does not increase the PLdB impact on the ground.

5. Conclusions

A study was made of the effect of a thermally stratified energy source on the supersonic flow past a pointed cylindrical body "cone-cylinder-cone" at M∞=1.5, 2.0. Density fields under the influence of the stratified energy sources (TSS) with different temperatures in their layers and different number of layers are investigated. A comparison is made with the density fields for steady supersonic flow in the absence of the external influence. It was shown that the higher the temperature in the layers in the TSS and the greater the number of layers in it, the greater the influence of such a TSS on the amplitude of the BSW and the value of the frontal drag force of the AD body.
Pressure signatures in the near field, and on the ground, as well as the sonic boom impact on the ground (in decibels) have been studied at freestream Mach numbers 1.5, 2. The number of layers in TSS varied from 2.5 to 7.5 and the rarefaction parameters in the layers were set from 0.15 to 0.3. It was found that when controlling the flow by changing the temperature in the layers of the TSS and changing the number of layers in TSS, the pressure amplitudes in the nearfield signature and in the ground signature do not exceed their values for the flow without a TSS. In other words, it has been shown that when performing the flow control using considered thermally stratified energy sources, no additional noise is introduced on the ground. Besides, in a broad sense, the simulations showed that changing the surface pressure signature due to drag reduction does not necessarily imply a change in the perceived loudness in decibels (PLdB) on the ground.

Author Contributions

Conceptualization, D. Knight; Data curation, O. Kravchenko, O. Azarova and D. Knight; Formal analysis, O. Kravchenko, O. Azarova and D. Knight; Methodology, O. Azarova and D. Knight; Software, O. Kravchenko and O. Azarova; Supervision, D. Knight; Validation, O. Kravchenko, O. Azarova and D. Knight; Visualization, O. Kravchenko and O. Azarova; Writing – original draft, O. Azarova and D. Knight. All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author, [O.A.], upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

R = radius of a cylinder part of the aerodynamic body
M∞ = the freestream Mach number
p, ρ, u, v = pressure, density, and velocity components of a gas
pb = the pressure on the conical surface of an AD body
t = time
αj = rarefaction parameter in a j-layer of the stratified energy source
N = a number of layers in the stratified energy source
rs = the half width of a j-layer in the energy source
rc = r-coordinate of the center of a j-layer in the energy source
Rs = r-coordinate of the upper boundary of the thermally stratified energy source
γ = ratio of specific heats

Indices

j = parameters in the layers of the stratified energy source
n = normalizing parameters
t = parameters in the front central point of the body
∞ = freestream parameters

Abbreviations

AD – aerodynamic
TSS – thermally stratified energy source
BSW – bow shock wave
PLdB – perceived loudness in decibels

References

  1. Knight, D.D. Review of Energy Deposition for High-Speed Flow Control. Energies 2022, 15, 24, 9645. [CrossRef]
  2. Ahmed. M.Y.M.; Qin, N. Forebody shock control devices for drag and aero-heating reduction: A comprehensive survey with a practical perspective. Prog. Aerosp. Sci. 2020, 112, 100585. [CrossRef]
  3. Leonov, S.B. Review of plasma-based methods for high-speed flow control. In Proceedings of the Sixth International Conference on Fluid Mechanics AIP Conf. Proc., Guangzhou, China, 30 June – 3 July, 2011. [CrossRef]
  4. Fomin, V.M.; Tretyakov, P.K.; Taran, J.-P. Flow control using various plasma and aerodynamic approaches (short review). Aerosp. Sci. Technol. 2004, 8, 411-421. [CrossRef]
  5. Knight, D. Reduction of Sonic Boom Signature Using Energy Deposition. In Proceedings of AIAA SciTech Forum, US, San Diego, January 3-7, 2022. [CrossRef]
  6. Park, M.A.; Nemec, M. Nearfield summary and statistical analysis of the Second AIAA Sonic Boom Prediction Workshop. 2018. American Institute of Aeronautics and Astronautics, pp. 1-61. [CrossRef]
  7. Georgievsky, P.Y.; Levin, V.A. Supersonic flow over bodies in the presence of external energy release. Pis’ma v Zh. Tekh. Fiz. 1988, 14, 684–687. (In Russian). URL: http://journals.ioffe.ru/articles/viewPDF/31216.
  8. Artem’ev, V.I.; Bergel’son, V.I.; Nemchinov, I.V.; Orlova, T.I.; Smirnov, V.A.; Hazins, V.M. Changing the regime of supersonic streamlining obstacles via raising the thin channel of low density. Izv. Akad. Nauk SSSR, Meh. Židk. Gaza. 1989, 5, 146–151. (In Russian).
  9. Kolesnichenko, Yu.F.; Brovkin, V.G.; Azarova, O.A.; Grudnitsky, V.G.; Lashkov, V.A.; Mashek, I.Ch. Microwave energy release regimes for drag reduction in supersonic flows. AIAA 2002-0353. In Proceedings of the 40th Aerospace Sciences Meeting and Exhibit, Reno, Nevada, USA, 14–17 January, 2002. [CrossRef]
  10. Leonov, S.B.; Carter, C.D.; Hedlund, B.E.; Houpt, A.W.; Ombrello, T.; Firsov, A.A. Control of amplitude and position of reflected shock wave by stripwise plasma. AIAA 2018-0683. In Proceedings of the Aerospace Sciences Meeting, Kissimmee, Florida, USA, 8–12 January, 2018. [CrossRef]
  11. Gan, T.; Wu, Y.; Sun, Z.; Jin, D.; Song, H.; Jia, M. Shock wave boundary layer interaction controlled by surface arc plasma actuators. Phys. Fluids 2018, 30, 055107. [CrossRef]
  12. Apazidis, N.; Sembian, S.; Liverts, M. Blast wave interaction with thermal and density inhomogeneities in air. In Proceeding of the 32nd International Symposium on Shock Waves, Singapore, 14-19 July 2019. [CrossRef]
  13. Lapushkina, T.A.; Erofeev, A.V.; Azarova, O.A.; Kravchenko, O.V. Interaction of a plane shock wave with an area of ionization instability of discharge plasma in air. Aerosp. Sci. Technol. 2019, 85, 347-358. [CrossRef]
  14. Azarova, O.A. Supersonic flow control using combined energy deposition. Aerospace. 2015, 2, 118-134.. [CrossRef]
  15. Azarova, O.A.; Kravchenko, O.V. Impact of a thermally stratified energy source on the bow shock wave and aerodynamic characteristics of a body. J. Phys. Conf. Ser. 2021, 1891, 012025. [CrossRef]
  16. Azarova, O.A.; Kravchenko, O.V. Principles of unsteady high-speed flow control using a time-limited thermally stratified energy source. Fluids. 2022, 7, 10, 326, pp. 1-22. [CrossRef]
  17. Azarova, O.A. Basics of control of the bow shock wave, drag and lift forces, and stability in a steady supersonic flow past an AD Body using permanently operating thermally stratified energy deposition. Energies. 2022, 15, 22, 8627, pp. 1-31. [CrossRef]
  18. Azarova, O.A. Complex conservative difference schemes for computing supersonic flows past simple aerodynamic forms. J. Comp. Math. Math. Phys. 2015, 55, pp. 2025-2049. [CrossRef]
  19. Thomas, C.L. Extrapolation of sonic boom pressure signatures by the waveform parameter method. NASA tehnical note D-6832. 1972, pp. 1-31. URL: https://archive.org/details/NASA_NTRS_Archive_19720018354/mode/2up.
  20. Munguia, B.C.; Economon, T.D.; Alonso, J.J. A Discrete Adjoint Framework for Low-Boom Supersonic Aircraft Shape Optimization. 18th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, 5-9 June 2017, Denver, Colorado, AIAA 2017-3326, pp. 1-11. [CrossRef]
  21. Pyldb, 2019, “PyLdB”, accessed Apr. 20, 2023. https://github.com/usuaero/PyLdB.
  22. Stevens, S. S. Perceived level of noise by Mark VII and decibels (E). The Journal of the Acoustical Society of America. 1972, 51, pp. 575-601. [CrossRef]
Preprints 76547 g001
Figure 1. Statement of the problem (schematic).
Figure 1. Statement of the problem (schematic).
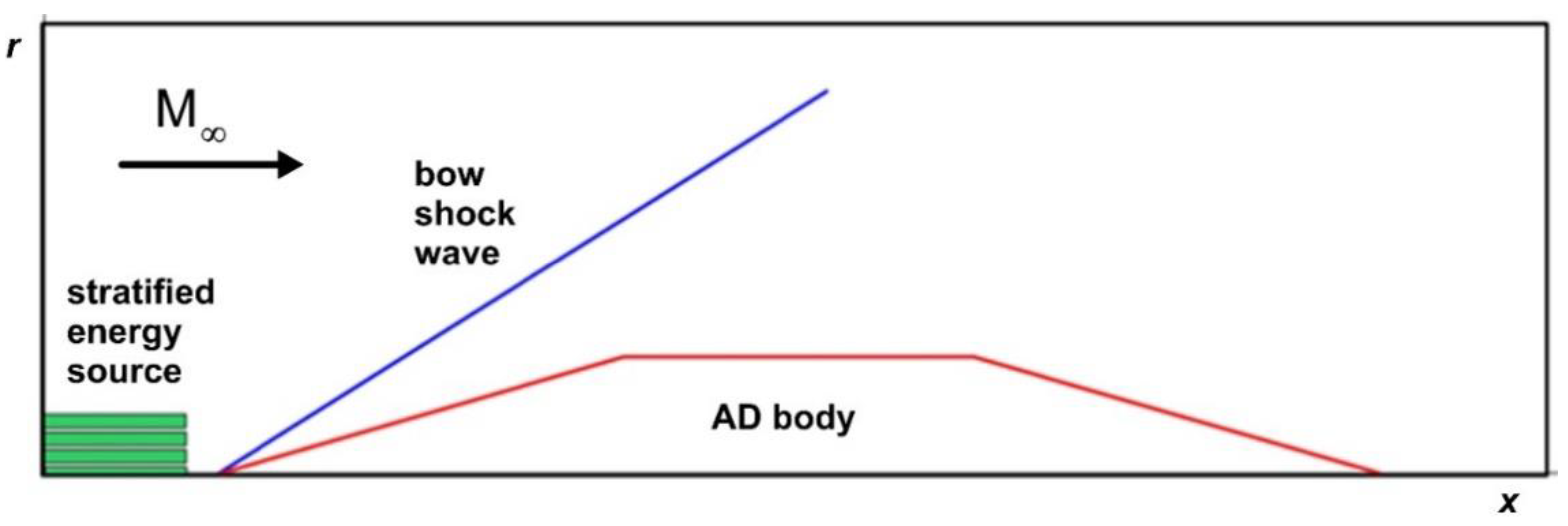
Preprints 76547 g001
Preprints 76547 g002
Figure 2. The position of the sharpen part of the body on a computational grid (enlarged):a) each node in x and r is shown; b) every second node in x and every fourth node in r is shown.
Figure 2. The position of the sharpen part of the body on a computational grid (enlarged):a) each node in x and r is shown; b) every second node in x and every fourth node in r is shown.
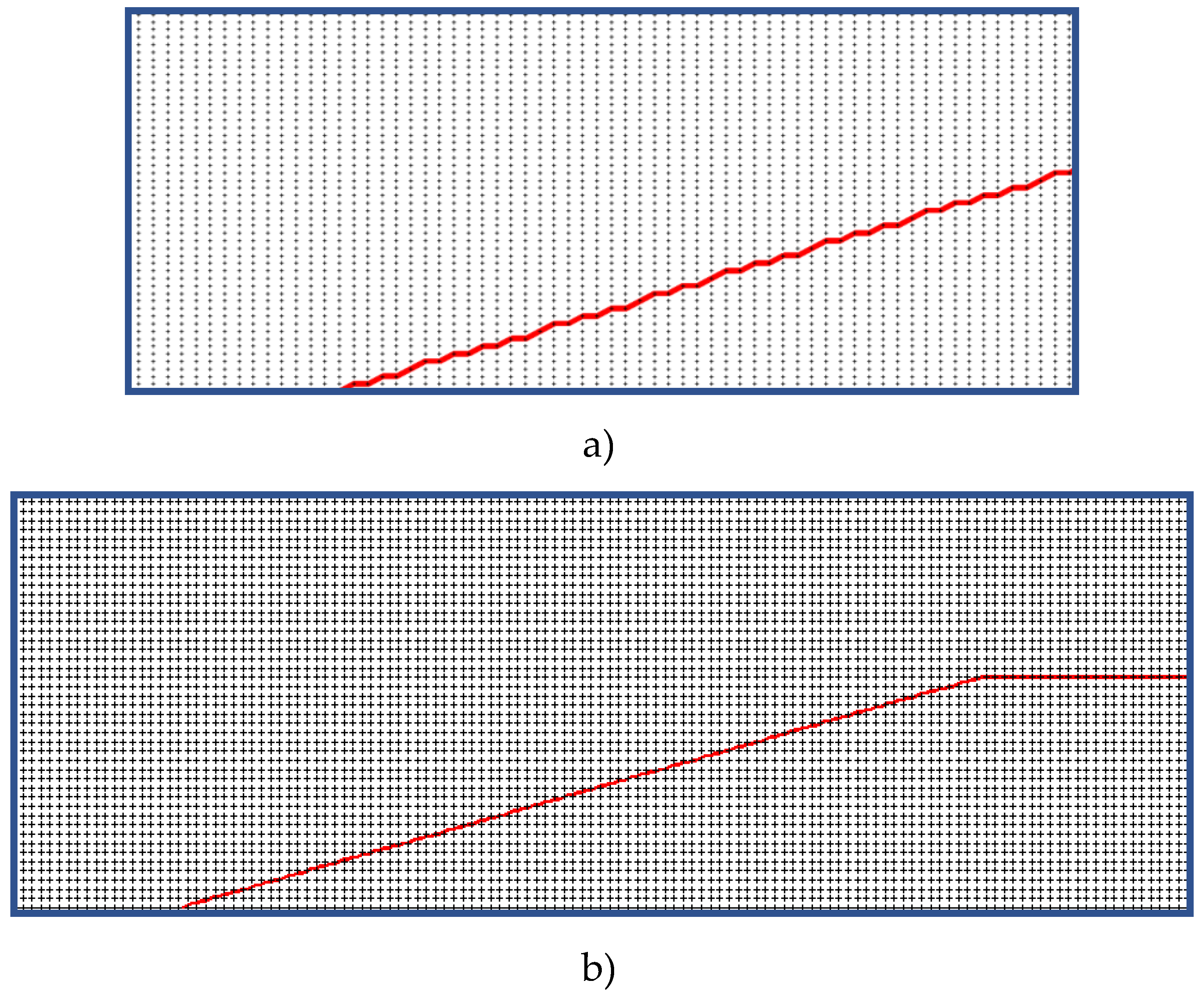
Preprints 76547 g002
Preprints 76547 g003
Figure 3. Analysis of the grid convergence using three different grids: a) - density fields, t=0.5 (superposed); b) – dynamics of the pressure pt and density ρt at the apex of the body.
Figure 3. Analysis of the grid convergence using three different grids: a) - density fields, t=0.5 (superposed); b) – dynamics of the pressure pt and density ρt at the apex of the body.
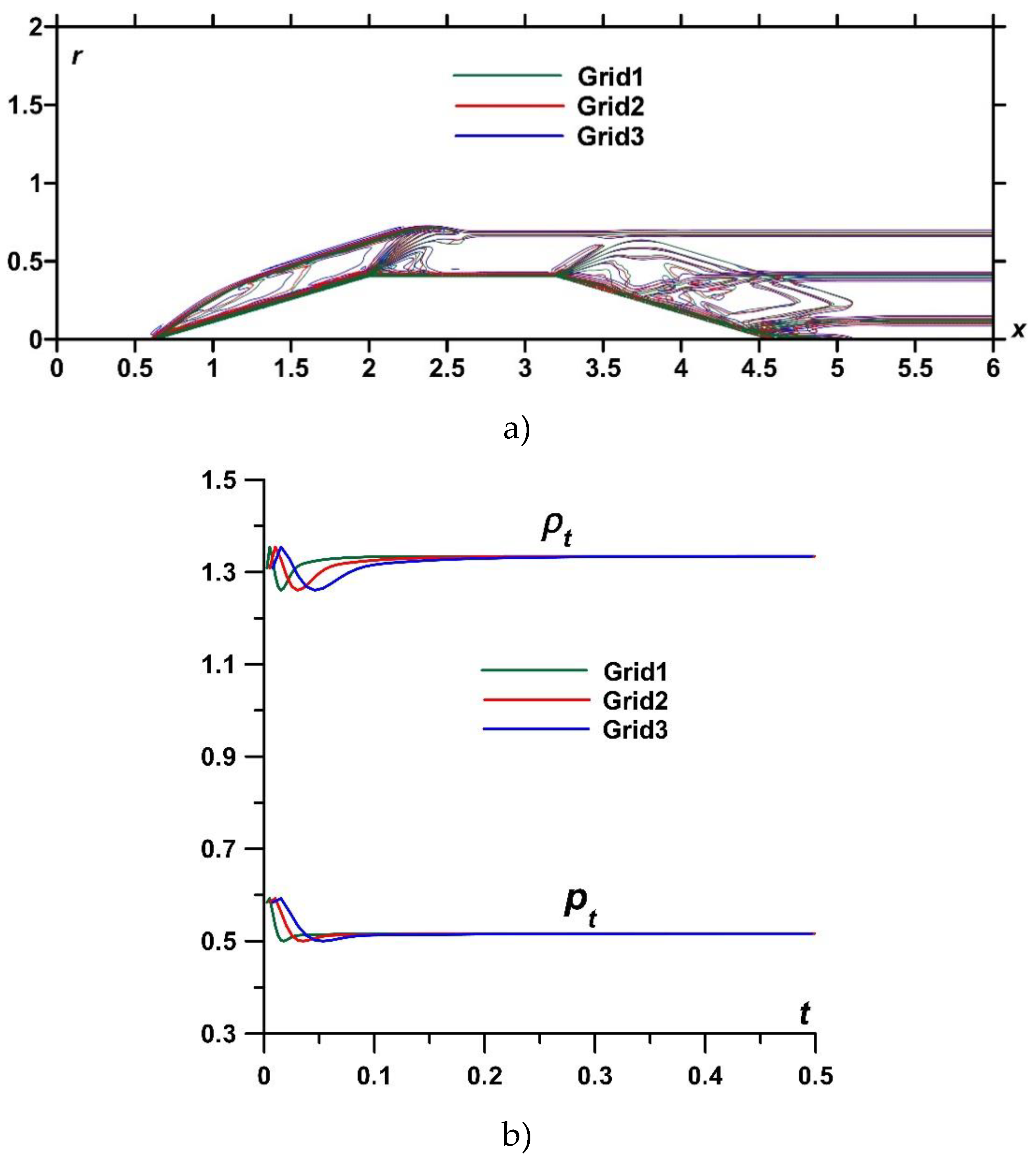
Preprints 76547 g003
Preprints 76547 g004aPreprints 76547 g004b
Figure 4. Impact of TSS on the flow past the body: dynamics of the density fields,.without energy source - blue, with TSS, M∞=2, αj=0.3; N=2.5 - red; a) t=9.0; b) t=20.0; c) interaction of TSS with the BSW (enlarged).
Figure 4. Impact of TSS on the flow past the body: dynamics of the density fields,.without energy source - blue, with TSS, M∞=2, αj=0.3; N=2.5 - red; a) t=9.0; b) t=20.0; c) interaction of TSS with the BSW (enlarged).
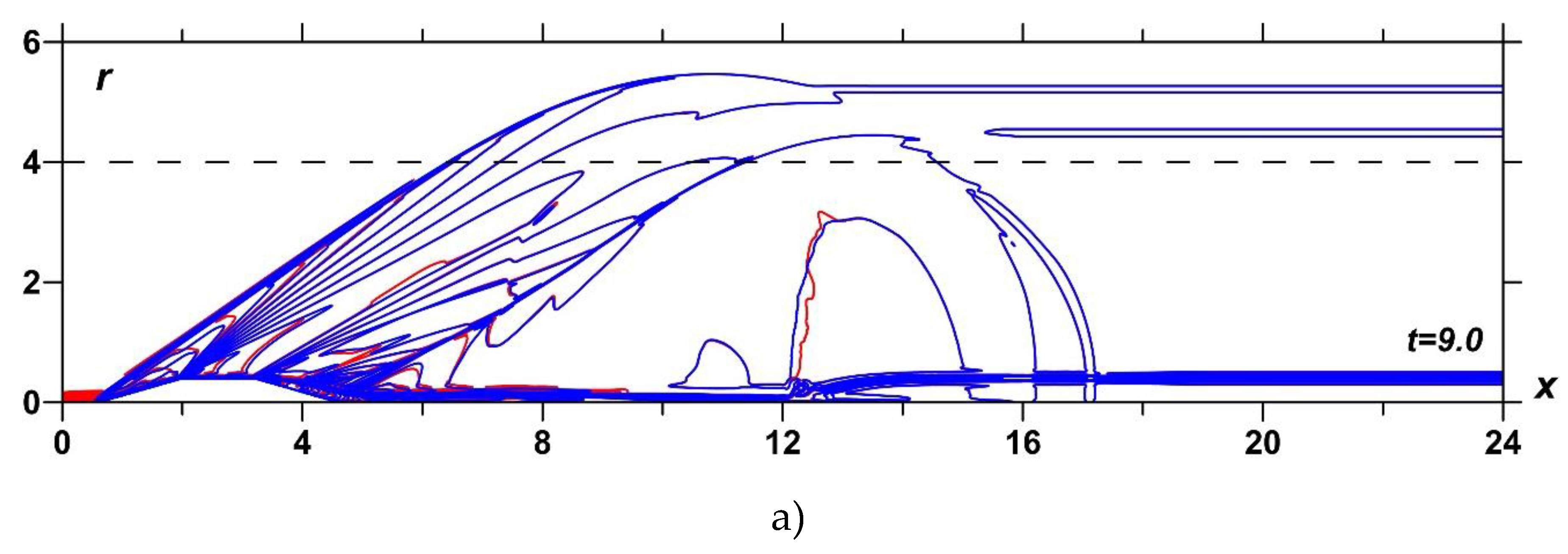
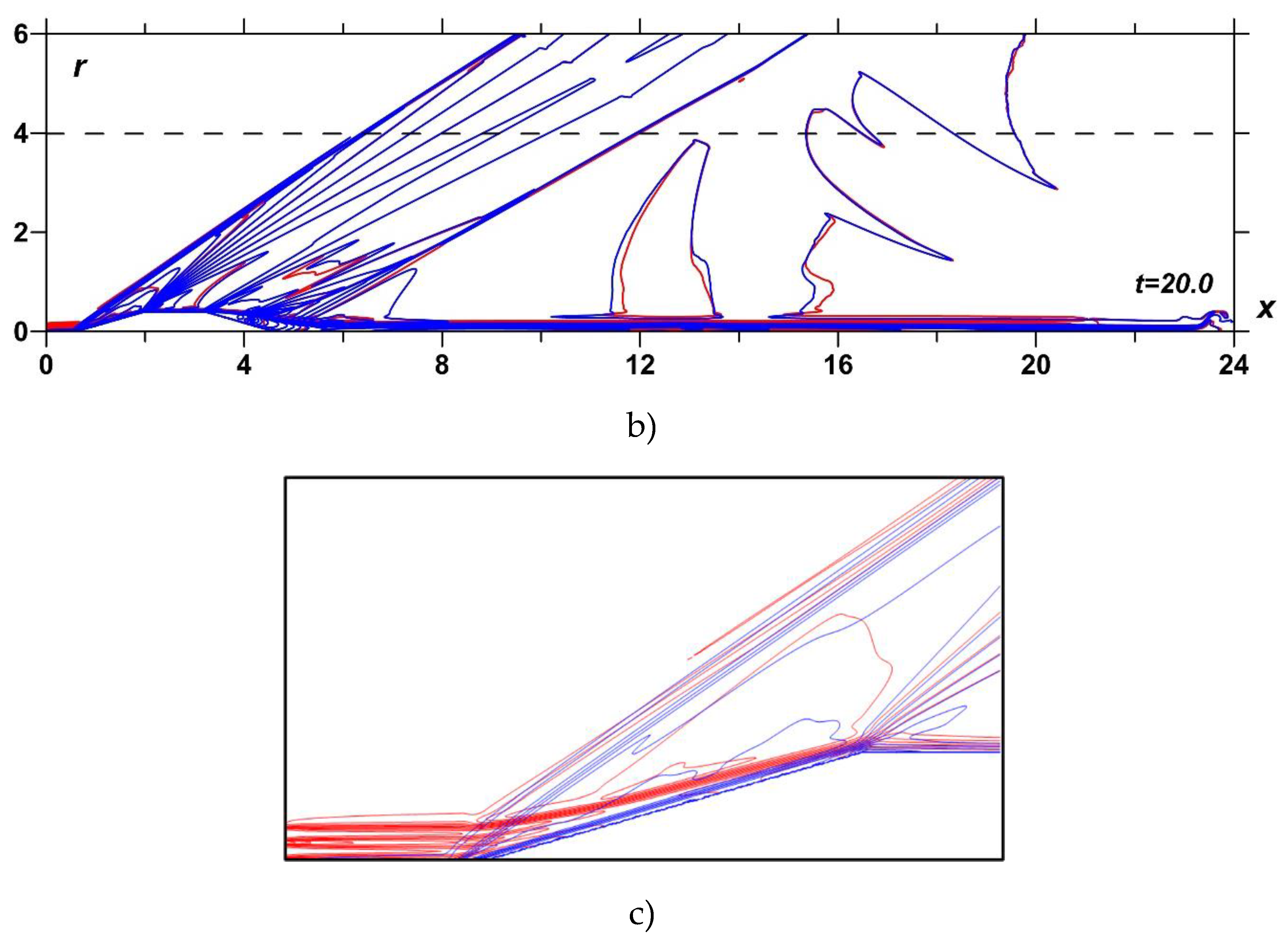
Preprints 76547 g004aPreprints 76547 g004b
Preprints 76547 g005
Figure 5. Dynamics of profiles of relative pressure Δp/p for r=4.0, M∞=2, in TSS αj=0.3, N=2.5, t=20.
Figure 5. Dynamics of profiles of relative pressure Δp/p for r=4.0, M∞=2, in TSS αj=0.3, N=2.5, t=20.
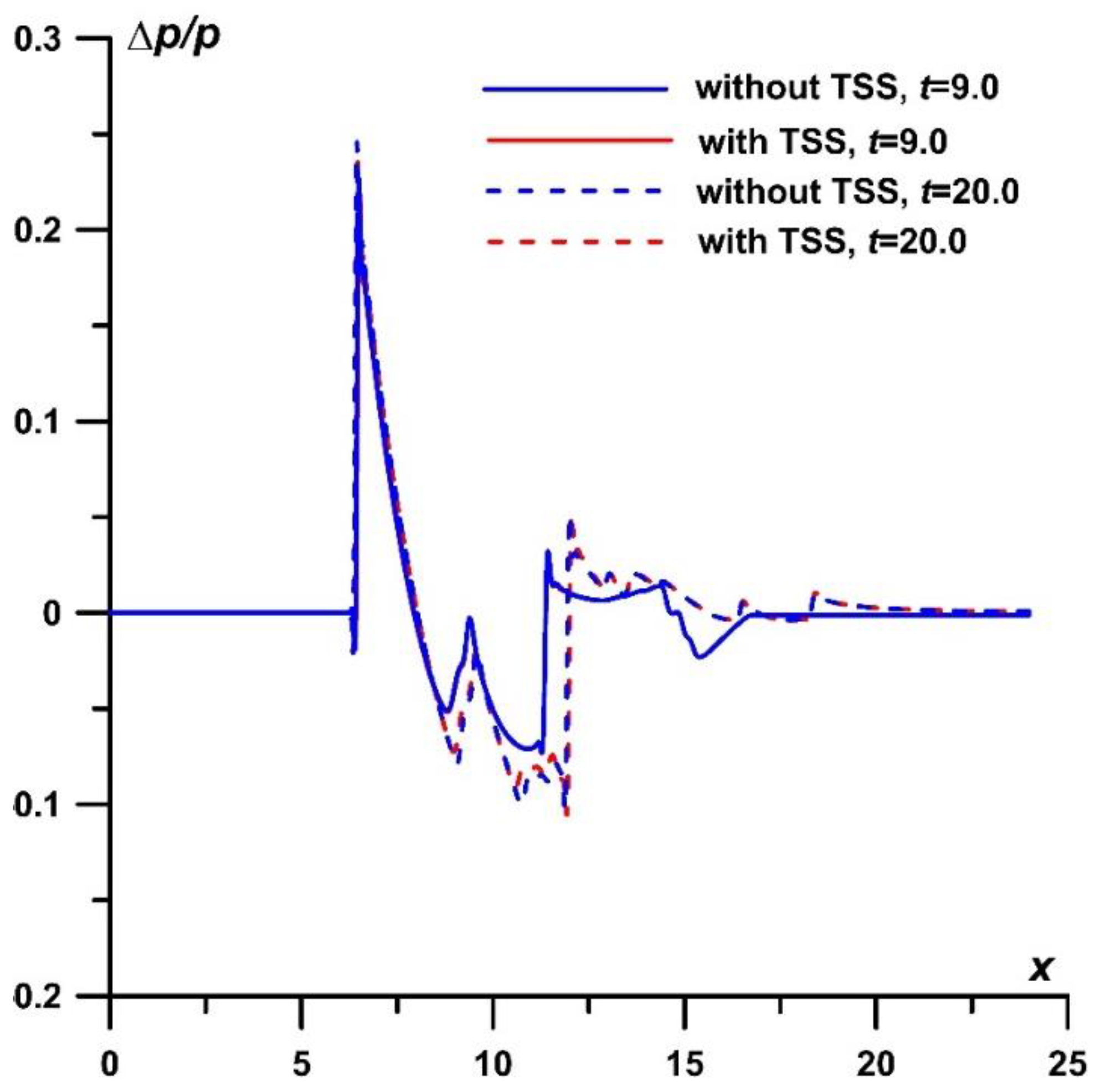
Preprints 76547 g005
Preprints 76547 g006
Figure 6. Profiles of relative pressure Δp/p for r=4.0, different αj, N=2.5, t=20 (left); impact on the BSW, enlarged (right): a) M∞=2; b) M∞=1.5.
Figure 6. Profiles of relative pressure Δp/p for r=4.0, different αj, N=2.5, t=20 (left); impact on the BSW, enlarged (right): a) M∞=2; b) M∞=1.5.
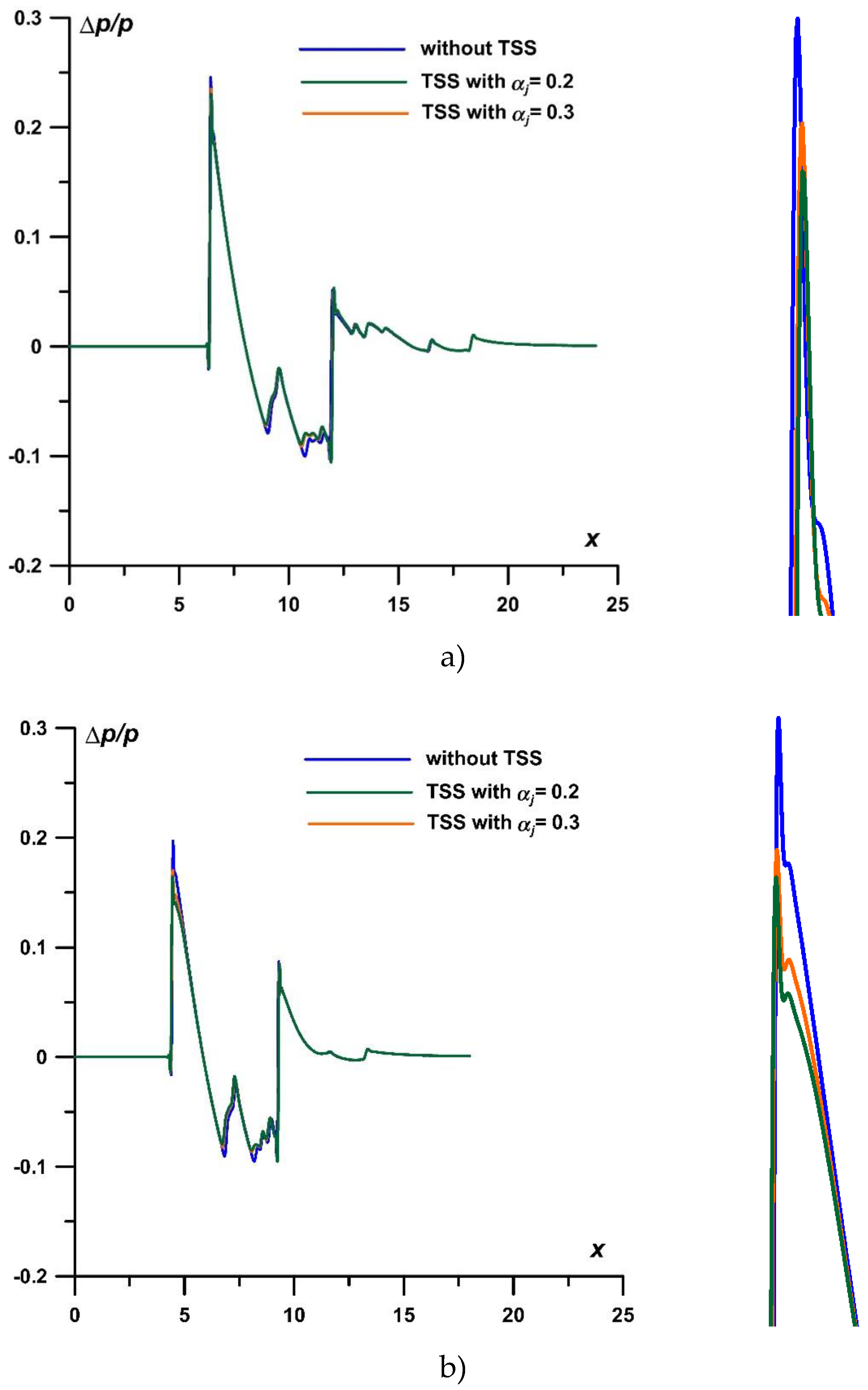
Preprints 76547 g006
Preprints 76547 g007
Figure 7. Density field, M∞=2: without energy source (blue), with TSS, αj=0.15, N=3.5 (red); a) full calculation area, t=20.0; b) interaction of TSS with the BSW (enlarged).
Figure 7. Density field, M∞=2: without energy source (blue), with TSS, αj=0.15, N=3.5 (red); a) full calculation area, t=20.0; b) interaction of TSS with the BSW (enlarged).
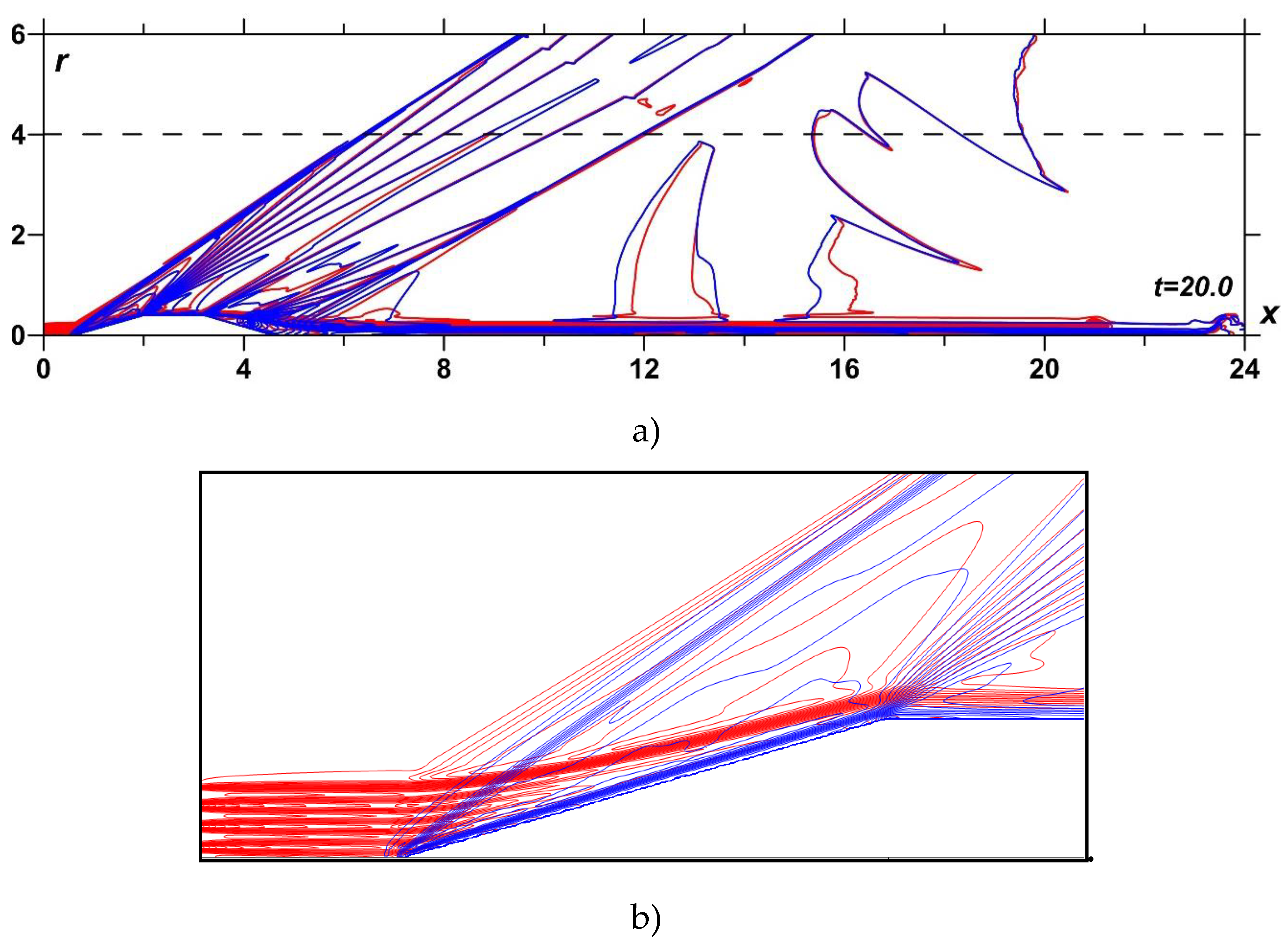
Preprints 76547 g007
Preprints 76547 g008aPreprints 76547 g008b
Figure 8. Density field, M∞=2: without energy source (blue), with TSS, αj=0.15, N=5.5 (red); a) full calculation area, t=20.0; b) interaction of TSS with the BSW (enlarged).
Figure 8. Density field, M∞=2: without energy source (blue), with TSS, αj=0.15, N=5.5 (red); a) full calculation area, t=20.0; b) interaction of TSS with the BSW (enlarged).
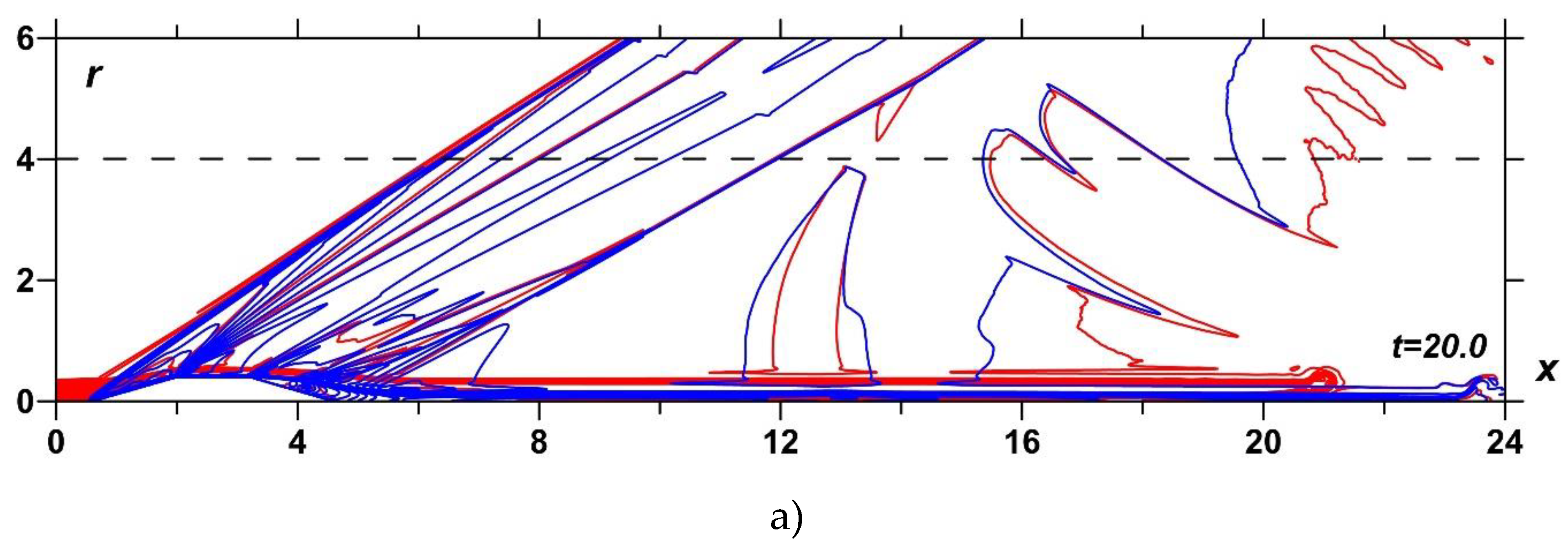
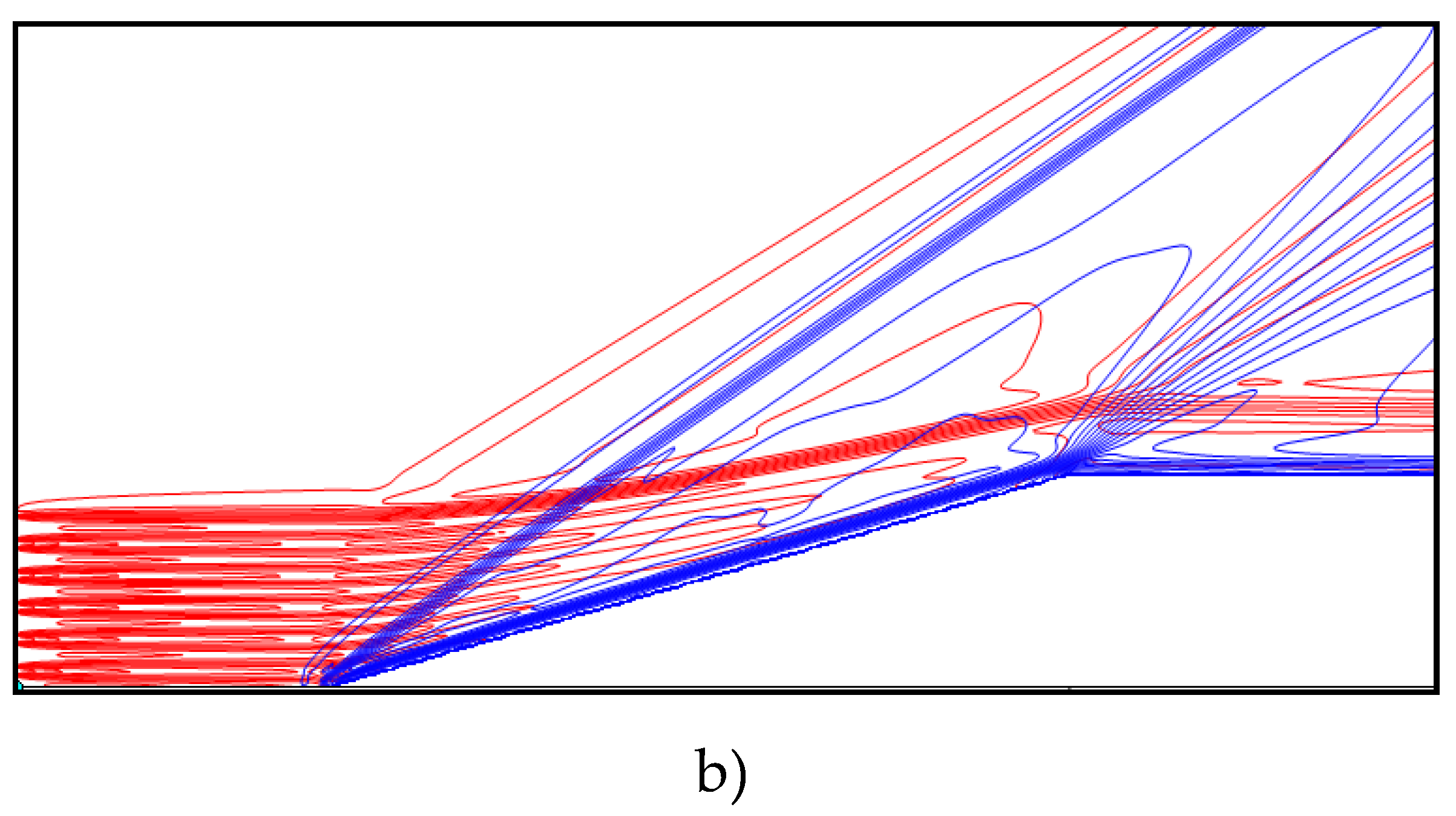
Preprints 76547 g008aPreprints 76547 g008b
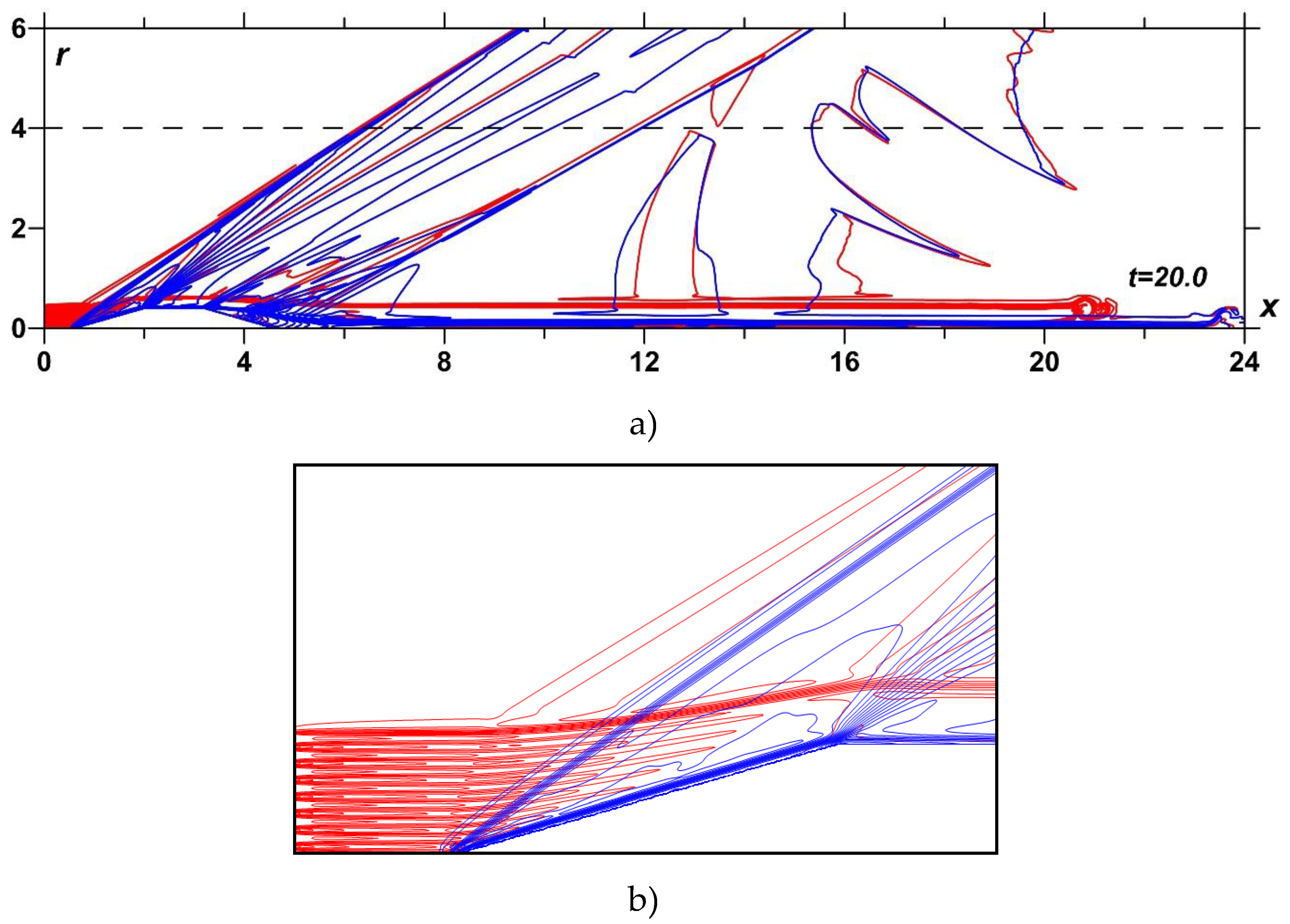
Preprints 76547 g009
Figure 9. Density field, M∞=2: without energy source (blue), with TSS, αj=0.15, N=7.5 (red); a) full calculation area, t=20.0; b) interaction of TSS with the BSW (enlarged).
Figure 9. Density field, M∞=2: without energy source (blue), with TSS, αj=0.15, N=7.5 (red); a) full calculation area, t=20.0; b) interaction of TSS with the BSW (enlarged).
Preprints 76547 g009
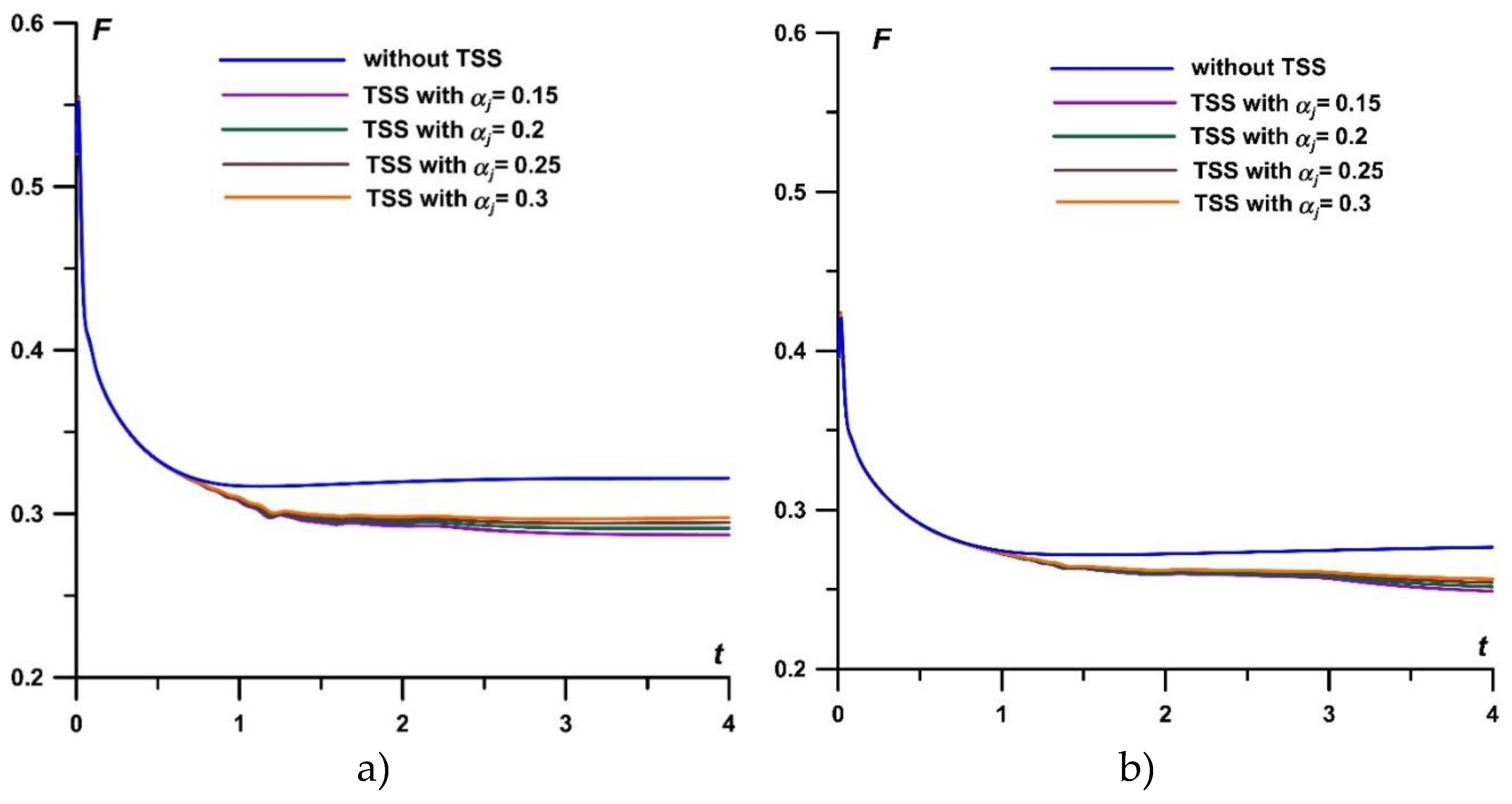
Preprints 76547 g010
Figure 10. Dynamics of the drag force for TSS with different αj, N=5.5: a) M∞=2; b) M∞=1.5.
Figure 10. Dynamics of the drag force for TSS with different αj, N=5.5: a) M∞=2; b) M∞=1.5.
Preprints 76547 g010
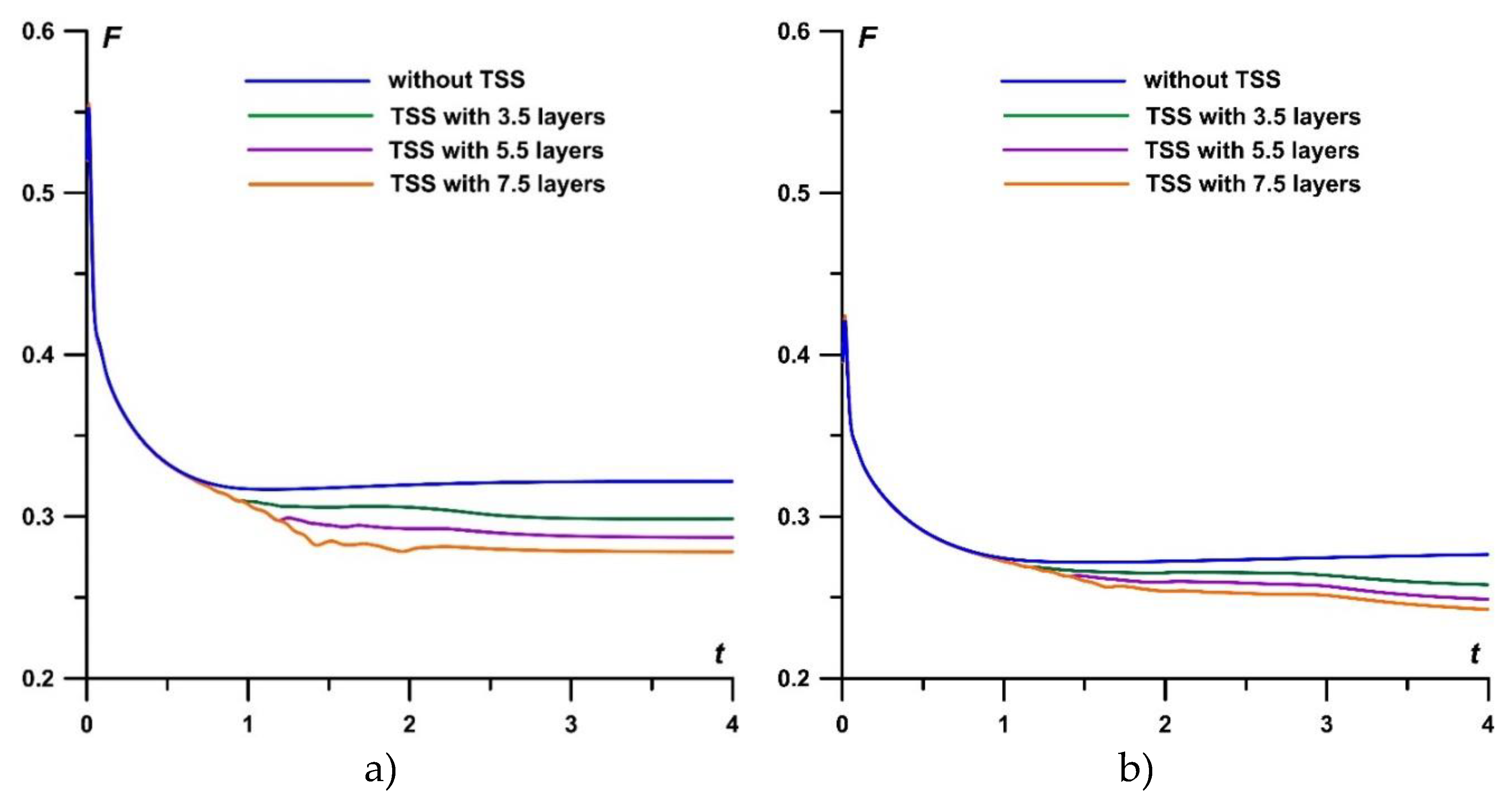
Preprints 76547 g011
Figure 11. Dynamics of the drag force for TSS with different N, αj=0.15: a) M∞=2; b) M∞=1.5 .
Figure 11. Dynamics of the drag force for TSS with different N, αj=0.15: a) M∞=2; b) M∞=1.5 .
Preprints 76547 g011
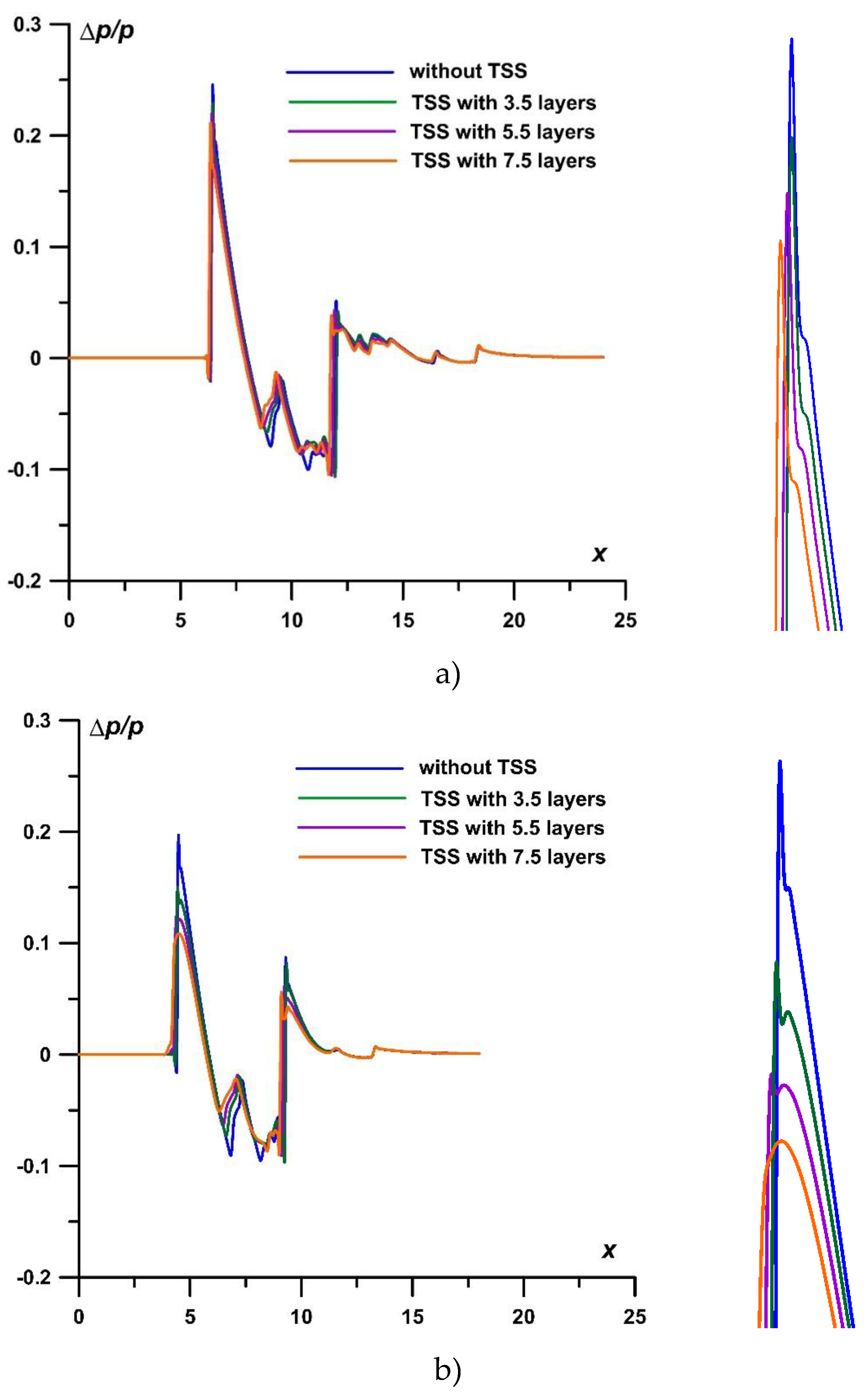
Preprints 76547 g012
Figure 12. Profiles of relative pressure Δp/p for r=4.0, αj=0.15, different N, t=20 (left);.impact on the BSW, enlarged (right): a) M∞=2; b) M∞=1.5.
Figure 12. Profiles of relative pressure Δp/p for r=4.0, αj=0.15, different N, t=20 (left);.impact on the BSW, enlarged (right): a) M∞=2; b) M∞=1.5.
Preprints 76547 g012
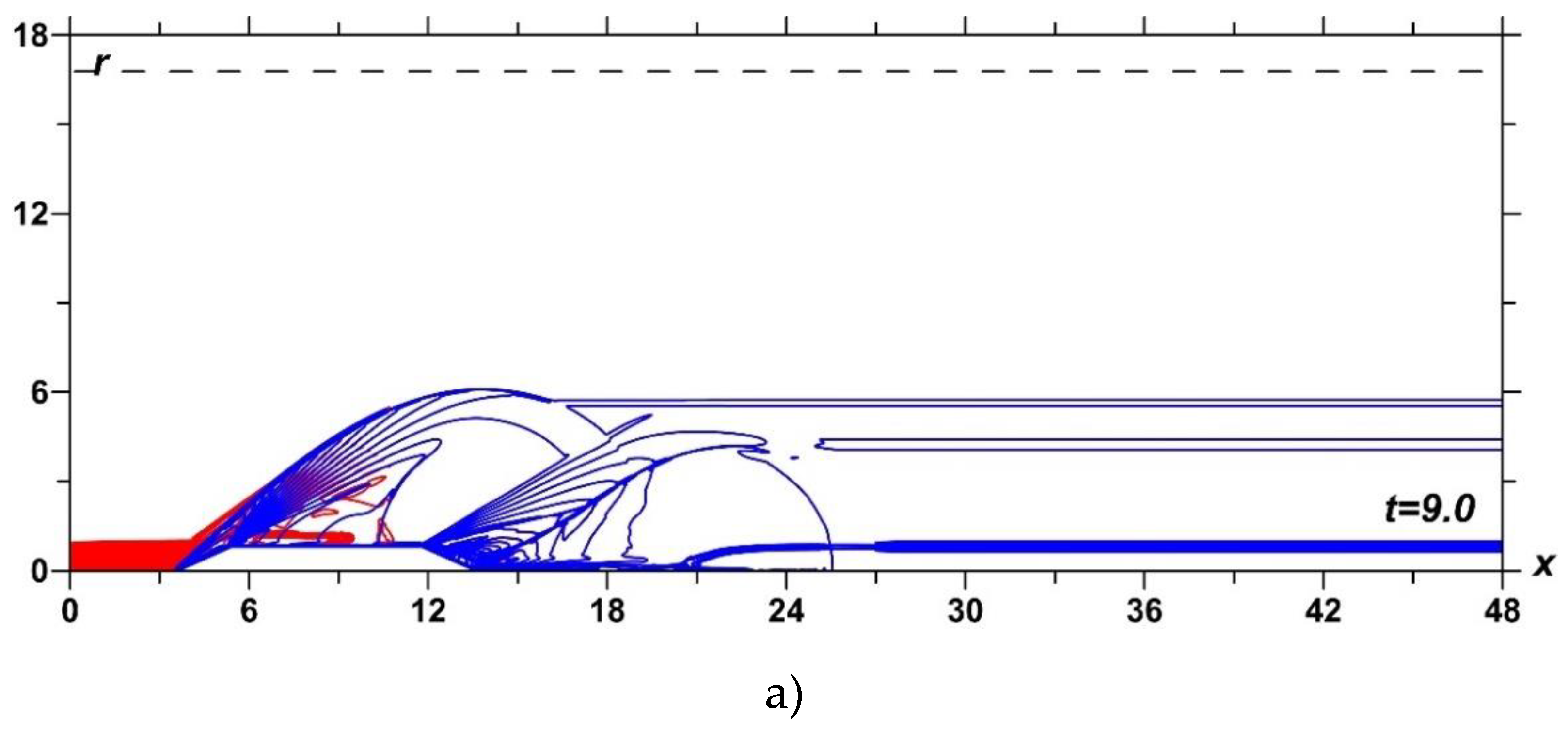
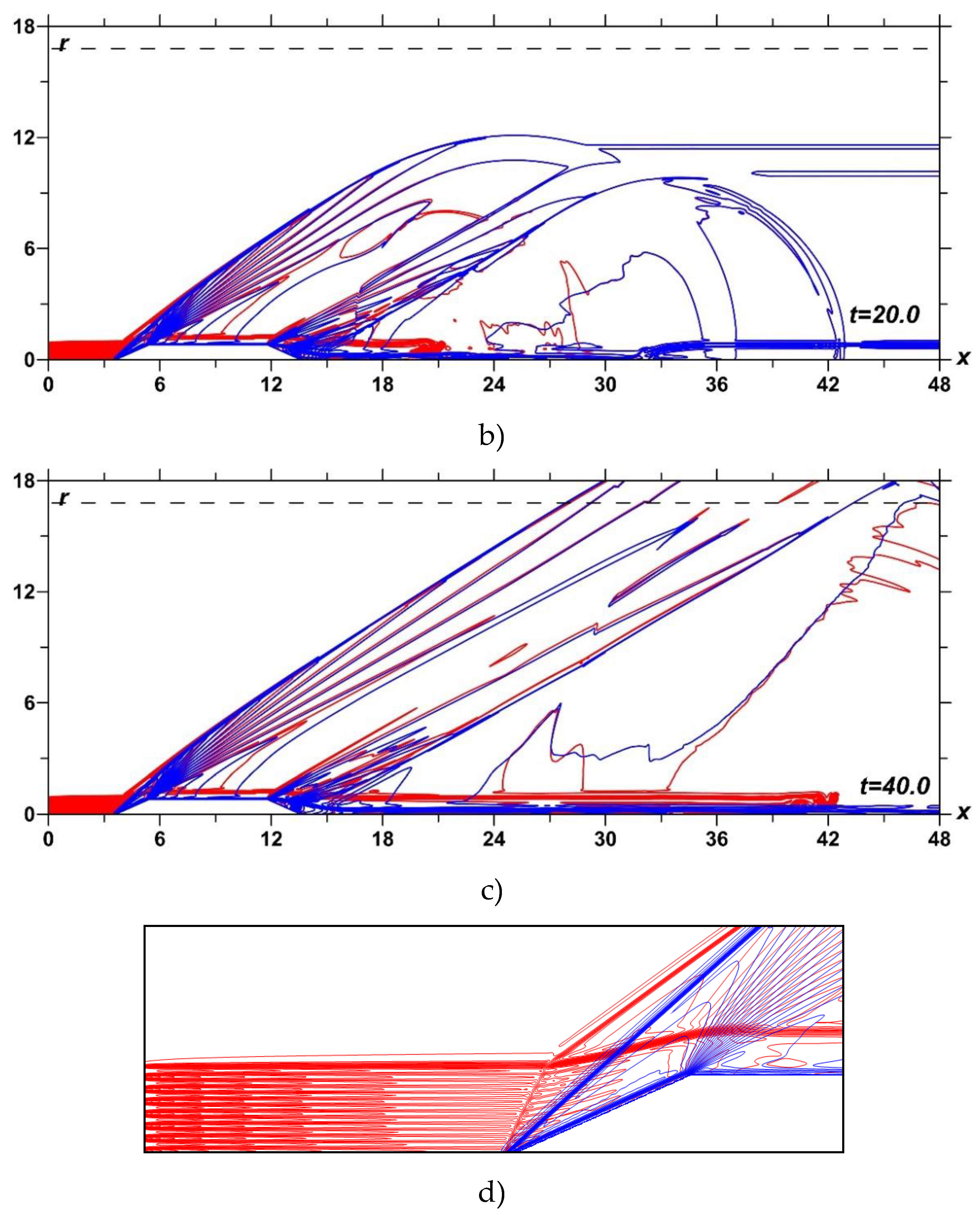
Preprints 76547 g013aPreprints 76547 g013b
Figure 13. Impact of TSS on the flow past the body: dynamics of the density fields, without energy source - blue, with TSS, M∞=2, αj=0.25; N=7.5 - red; a) t=9.0; b) t=20.0; c) t=40.0; b) interaction of TSS with the BSW (enlarged).
Figure 13. Impact of TSS on the flow past the body: dynamics of the density fields, without energy source - blue, with TSS, M∞=2, αj=0.25; N=7.5 - red; a) t=9.0; b) t=20.0; c) t=40.0; b) interaction of TSS with the BSW (enlarged).
Preprints 76547 g013aPreprints 76547 g013b
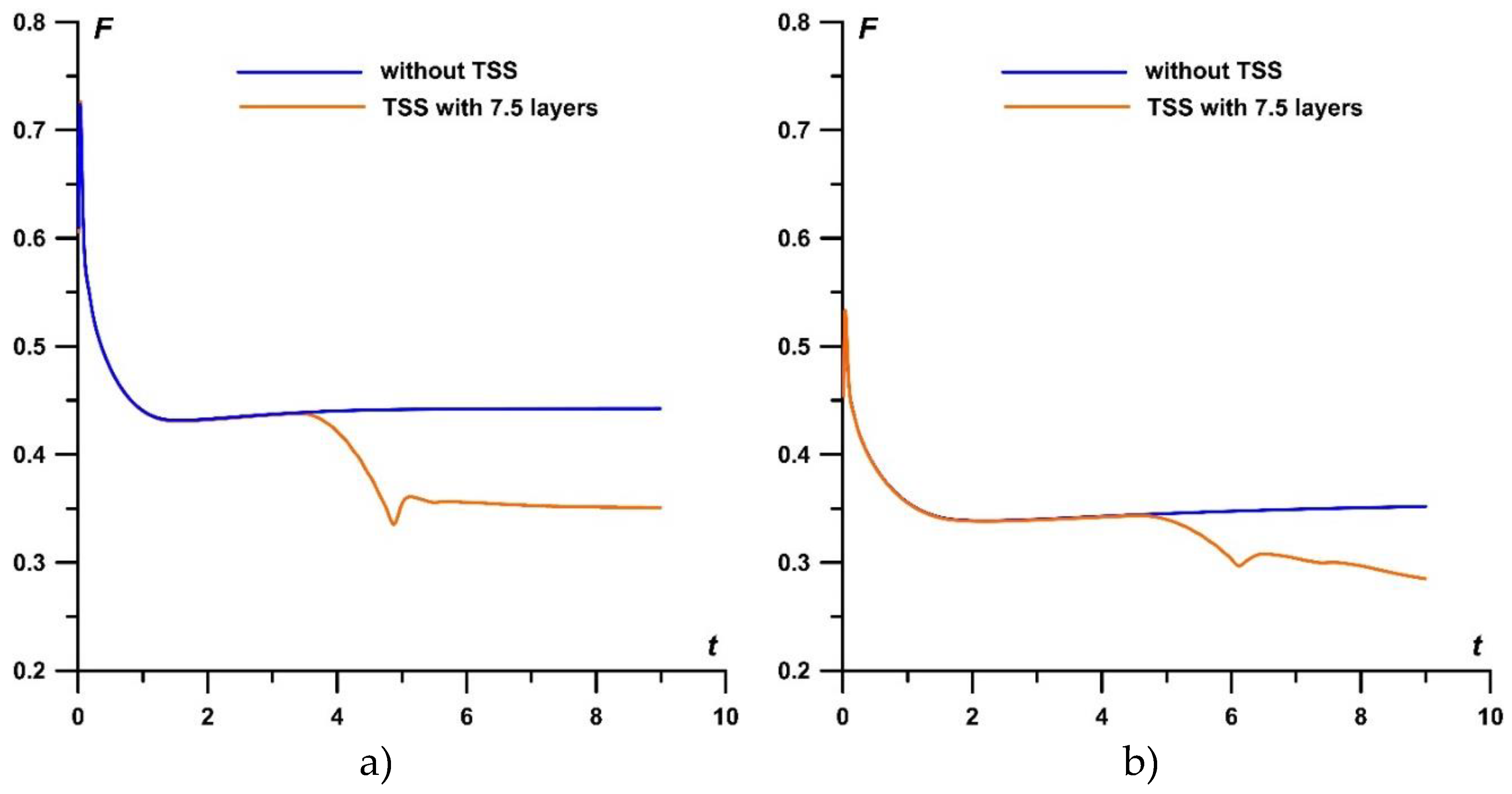
Preprints 76547 g014
Figure 14. Dynamics of the drag force for TSS with N=7.5, αj=0.25 in comparison with the undisturbed flow case: a) M∞=2; b) M∞=1.5 .
Figure 14. Dynamics of the drag force for TSS with N=7.5, αj=0.25 in comparison with the undisturbed flow case: a) M∞=2; b) M∞=1.5 .
Preprints 76547 g014
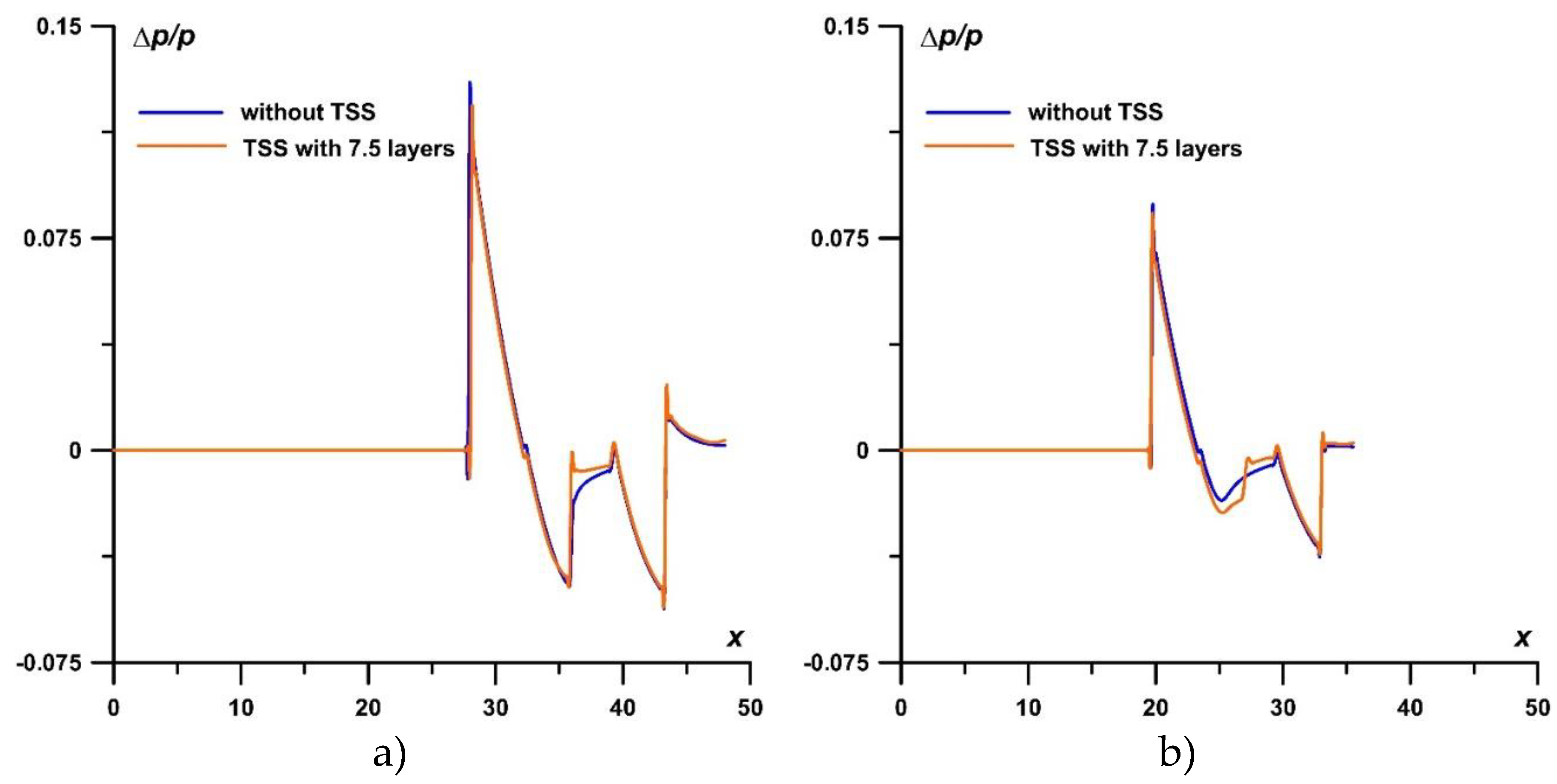
Preprints 76547 g015
Figure 15. Profiles of relative pressure Δp/p for r=16.8, αj=0.25, N=7.5, t=40: a) M∞=2; b) M∞=1.5.
Figure 15. Profiles of relative pressure Δp/p for r=16.8, αj=0.25, N=7.5, t=40: a) M∞=2; b) M∞=1.5.
Preprints 76547 g015
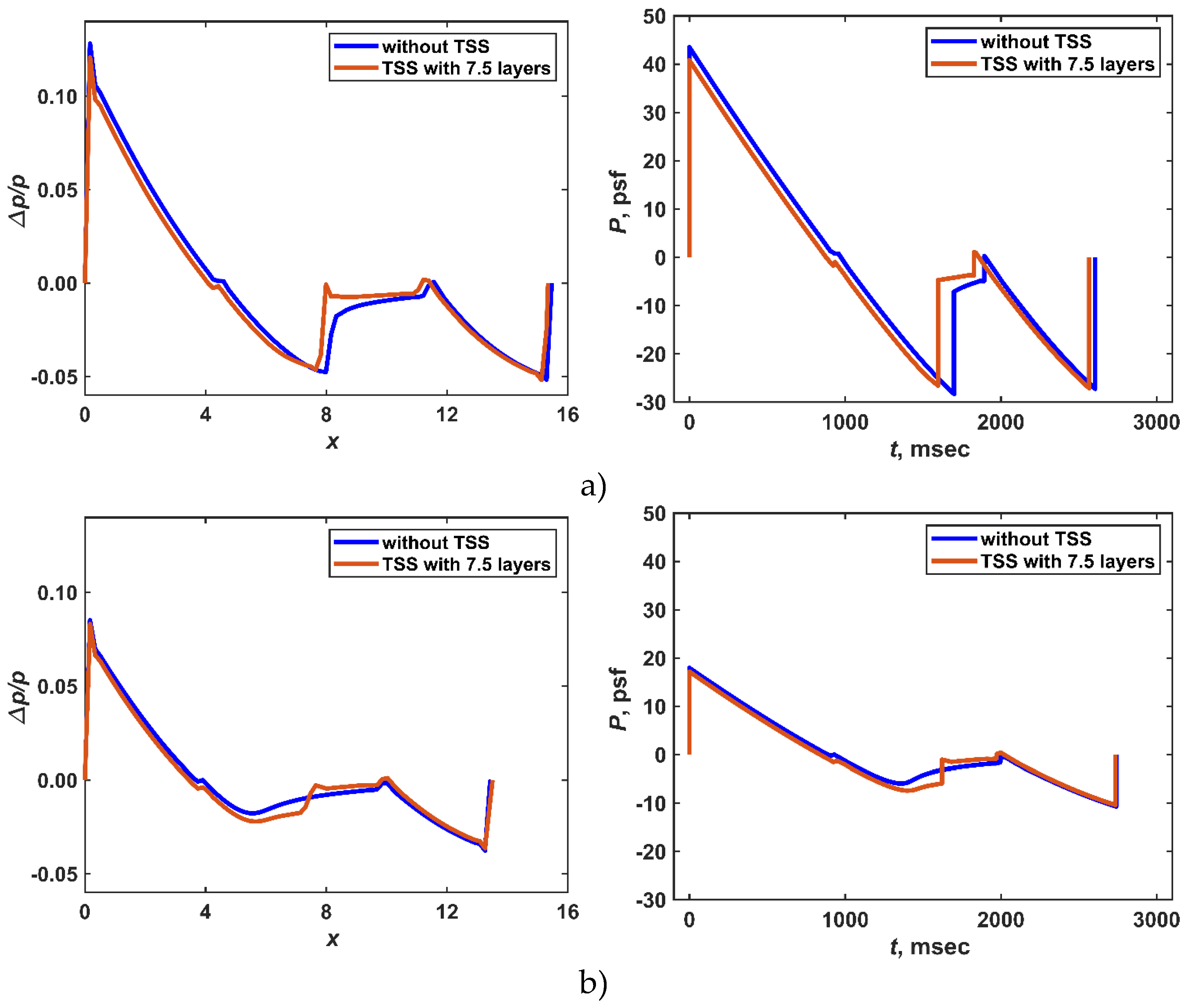
Preprints 76547 g016
Figure 16. Profiles of relative pressure Δp/p for r=16.8, t=40, M∞=1.5, αj=0.25, N=7.5, profile processing (left), ground signatures (right): a) M∞=2; b) M∞=1.5.
Figure 16. Profiles of relative pressure Δp/p for r=16.8, t=40, M∞=1.5, αj=0.25, N=7.5, profile processing (left), ground signatures (right): a) M∞=2; b) M∞=1.5.
Preprints 76547 g016
Table 1. Characteristics of the difference grids.
Table 1. Characteristics of the difference grids.
Grid Steps hx, hr Sizes
Grid1 hx=0.002
hr=0.001		 3000×2000
Grid2 hx=0.004
hr=0.002		 1500×1000
Grid3 hx=0.00606060606
hr=0.00303030303		 990×660
Table 2. Parameters of the freestream flow, aerodynamic body, and the energy source.
Table 2. Parameters of the freestream flow, aerodynamic body, and the energy source.
Description Definition Non-dimensional value Dimensional value Normalizing value
Freestream Max number M∞ 2.0; 1.5
Freestream pressure p∞ 0.2 26.5kPa pn=132.5kPa
Ratio of specific heats   1.4
Radius of a cylinder part of the AD body R 0.4 0.5m ln=1.25m
Length of the AD body L 4.0 0.5m ln=1.25m
The width of the layers in considered TSSs rs 0.04 0.05m ln=1.25m
Number of layers in different TSSs 2.5; 3.5; 5.5; 7.5
Rarefaction parameter in the layer j in different TSSs j 0.15; 0.2; 0.25; 0.3
Table 3. Parameters of the freestream flow, aerodynamic body, and the energy source.
Table 3. Parameters of the freestream flow, aerodynamic body, and the energy source.
Description Definition Non-Dimensional Value Dimensional Value Normalizing Value
Freestream Max number M∞ 2.0; 1.5
Freestream pressure p∞ 0.2 26.5kPa pn=132.5kPa
Ratio of specific heats   1.4
Radius of a cylinder part of the AD body R 0.8 6.4m ln=8m
Length of the AD body L 10.0 80m ln=8m
The half width of the layers in considered TSSs rs 0.04 0.32m ln=8m
Number of layers in different TSSs 7.5
Rarefaction parameter in the layer j in different TSSs j 0.25
Table 4. PLdB impact on the ground for different nearfield signatures at M∞=1.5 and 2.
Table 4. PLdB impact on the ground for different nearfield signatures at M∞=1.5 and 2.
Nearfield Signatures Δp/p Ground Sound Pressure Impact,
M∞=1.5		 Ground Sound Pressure Impact,
M∞=2
Without TSS 163.62 dB 166.11 dB
With TSS 163.26 dB 165.60 dB
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated