Prerpints.org logo
Preprint
Article

Maturation Stress and Wood Properties of Poplar (Populus × euramericana ‘Zhonglin46’) Tension Wood

Altmetrics

Downloads

131

Views

44

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

15 June 2023

Posted:

15 June 2023

You are already at the latest version

Alerts
Abstract
Understanding maturation stress and wood properties of poplar tension wood are critical for improving lumber yields and utilization ratio. In this study, Released Longitudinal Maturation Strains (RLMS), anatomical features, physical and mechanical properties, and nano-mechanical properties of the cell wall were analyzed at different peripheral positions and heights in nine inclined, 12-year-old poplar (Populus×euramericana ‘Zhonglin46’) trees. The correlations between RLMS and wood properties were determined. The results showed that there were mixed effects of artificial inclination on wood quality and properties. The upper sides of inclined stems had higher RLMS, proportion of G-layer, bending modulus of elasticity, and elastic modulus of cell wall but lower microfibril angle than the lower sides. At heights between 0.7 m and 2.2 m, only the double wall thickness increased with height, RLMS and other wood properties such as fiber length and basic density fluctuated or changed little with height. RLMS was a good indicator of wood properties in the tension wood area and at heights between 0.7 m and 1.5 m. The results of this study present opportunities to identify and select better quality wood in poplar trees.
Keywords: 
Subject: Biology and Life Sciences  -   Forestry

1. Introduction

Tree growth stress is a result of cell wall maturation during growth, helping keep trees up-right against disturbance by gravity or wind [1]. ‘Abnormal’ cell growth enhances the strength of tree trunks and controls their growth orientation [2,3]. Growth stress also act as a pre-stressing system which can reduce the risk of axial buckling of fiber [4].
The thickening in the secondary cell wall generates mechanical stresses at the periphery of the trunk mostly along the stem axis [5]. When reaction wood is produced in inclined stems and/or branches, the distribution of stress across the cross section is heterogeneous [6,7,8] whereby greater stress on one side generates a bending moment to facilitate gravitropism in stems [9]. Eccentric growth and stiffness heterogeneity help to optimize this process [10]. In angiosperms, tension wood is generated on the upper side to restore the trunk to the upright position [11]. Some temperate-zone hardwood species such as P. euramericana contain a gelatinous (G) layer with the characteristics of high tensile growth stresses and low microfibril angle (MFA) values [12] which in turn affects wood strength properties and quality.
Growth stress affects timber production, causing problems such as radial splitting at the log edges and bowed/twisted sawn planks [13,14]. Reaction wood can cause serious defects which can cause economic losses across the lumber industry [3]. Understanding tree growth stresses and reaction wood, their distribution, wood properties are interesting not only for ecophysiology but also necessary in the field of wood quality, timber conversion and engineering.
Numerous studies have highlighted the influence of growth stress levels on the properties of tension wood in Poplar [15], Beech [16], Eucalyptus [17], and Chestnut [18], with most focusing on the microscopic and macroscopic level. Very few studies were reported on the relationship between growth stress and properties of wood at the nanometer level of tension wood. Nanoindentation can be used to characterize mechanical properties of wood such as elastic modulus and stiffness of cell wall [19,20,21].
Poplars (Populus sp.) are the most common in commercially important hardwoods in China [22], several species such as P. euramericana ‘Zhonglin46’ are commonly used in the plywood, solid wood, and paper industries [23,24]. But their stems are susceptible to tension wood formation [15,25]. It is therefore necessary to assess the levels and distribution of growth stresses to increase sawn lumber yields and utilization ratio. Growth stress can be easily measured experimentally using the release method [26]. In this study the Released Longitudinal Maturation Strains (RLMS), anatomical features, physical and mechanical properties, and nano-mechanical properties of the cell wall were examined in leaning trees of P. euramericana ‘Zhonglin46’. The objectives of this research were to (1) Identify the changes in maturation stresses and related wood properties along peripheral and vertical positions, (2) Determine and discuss the correlations between RLMS and wood properties.

2. Materials and Methods

2.1. Study site and tree information

The experimental site was located at Anhui Agricultural University in Hefei City, Anhui province, China (31°87’ N, 117°26’ E), with a subtropical humid climate and monsoon influence. The site is 20 m–40 m ASL, annual temperature range of 13°C–22°C, average annual temperature of 15.7°C, annual rainfall range of 794 mm–1523 mm, and average annual rainfall of 1000 mm. The sampled P. euramericana ‘Zhonglin46’ trees were spaced in a 3 m × 3 m configuration in a monoculture planted on a north-facing slope with soil type being yellow-brown soil.
In January 2021, a total of nine well-developed 12-year-old trees were selected for sampling. Figure 1 shows typical trees sampled. The trees were planted in 2009 and were artificially inclined to 15–60° for about one year to test the growth stress of seedings for another experiment. After the first year, the trees were allowed to grow naturally. The average tree height, DBH, and tilted angle of sampled trees are listed in Table 1.

2.2. Released Longitudinal Maturation Strains

RLMS was estimate using strain gauges [26,27] on seven measuring points of the leaning tree at three different heights vis. 0.7 m, 1.5 m, and 2.2 m from the ground (Figure 1a). In each sampled tree, the uppermost side was set as position 0°, seven positions were numbered in clockwise sequence at 50–60° intervals as 0°, 50°, 100°, 150°, -160°, -110°, and -60° around the trunk (Figure 2).
Before testing, bark and cambium was removed using a knife and axe to expose fresh and smooth xylem zone with a size of about 5 cm × 5 cm. A 10 mm long electric-wire strain gauge (Sigmar Co., BSF120-6AA-T, Jinan, China) was glued securely to the exposed zone and was connected to a strain meter (Sigmar Co., ASMB2-16, Jinan, China). Then grooves with 5 mm depth were cut with a saw above and below gauges 5 mm (Figure 1b), RLMS values were recorded until the changed strain values remain stable.

2.3. Sampling of felled trees

After RLMS measurement all sample trees were felled for wood properties sampling. Eccentricity in diameter was calculated as:
Eccentricity = T T W − T O W T T W + T O W
Where T T W was the radius of the TW area, T O W was the radius of the OW area.
Seven locations beneath the RLMS measurement positions at three different heights were marked on the trunk surfaces for further studies with 21 wood properties samples cut from each tree. Rectangular wood strips measuring 380 mm (longitudinal direction, L) × 20 mm (radial direction, R) × 20 mm (tangential direction, T) were cut along the axial of the stem. Specimens measured for standard physical and mechanical properties according to Chinese National Standard GB/T 1929-2009 [28]. Bending modulus of rupture (MOR) and bending modulus of elasticity (MOE) was measured on specimens measuring 300 mm (L) × 20 mm (R) × 20 mm (T) and basic density (BD) specimens were 20 mm (L) × 20 mm (R) × 20 mm (T). Two 30 mm (L) × 20 mm (R) × 20 mm (T) samples were cut to test compressive strength (CS) and anatomical features of the wood at each location.

2.4. Anatomical features

Fiber length (FL) was determined from 30 measurements of macerated fibers at each location. The specimens used to assess wood anatomical features measured 20 mm (L) × 10 mm (R) × 10 mm (T) and were pre-softened by microwaving for 5–10 min. Transverse sections 20 μm in thickness were sliced using a rotary microtome (Leica, RM 2265, Wetzlar, Germany) and double-stained with safranine and Astra-blue. This double-stained method can detect G fibers in tension wood (Figure 3). Sections were observed and thirty measurements each for double wall thickness (2WT) were made on each transverse section. The proportion of G-layer (PG) were counted and calculated on 20 randomly selected areas.
MFA were measured through X-ray diffraction, with the size of 30 mm (L) × 0.5 mm (R) × 10 mm (T). The recorded data were then processed using the 0.6 T method [29].

2.5. Physical and mechanical properties

BD of wood specimens (20 × 20 × 20 mm3) was measured following Chinese National Standard GB/T 1933-2009 [30].
MOR and MOE were tested on specimens measuring 300 × 20 × 20 mm3 according to Chinese National Standard GB/T 1936.1, 1936.2-2009 [31,32]. Specimens measuring 30 × 20 × 20 mm3 (LRT) were tested for CS according to Chinese National Standard GB/T 1935-2009 [33]. The mechanical properties were tested using a universal mechanical testing machine (Instron, 68TM-5, Boston, USA).

2.6. Nanoindentation test

The elastic modulus of cell walls (EC) was tested at different areas and heights. Three peripheral position specimens were chosen at a height of 1.5 m: TW specimen from position 0°, LW specimen from position 100°, and OW specimen from position -160°. Positions 0° was sampled at three heights: 0.7 m, 1.5 m, and 2.2 m.
Small wood blocks measuring 3 mm × 1 mm × 1 mm (LRT) were cut and equilibrated to -12% MC [21]. The blocks were then embedded in Spurr resin (SPI-Chem, USA). Then the blocks were cut to a pyramid shape and the top portion was polished by a semi-thin microtome (Leica, RM 2265, Wetzlar, Germany) using a glass knife and a diamond knife (SYM6050H, Japan). The nanoindenter (Bruker, Dimension ICON, Massachusetts, USA) and the Peak Force Quantitative Nanomechanical Mapping (PF-QNM) mode was used. A load-shift curve was obtained using the Derjaguin-Muller-Toporov (DMT) contact model [34]. The elastic modulus distribution of S1, S2, and G layers were obtained using Nanoscope Analysis software.

2.7. Statistical analyses

Statistical software SPSS 19.0 (IBM, NY, USA) was used to conduct ANOVA to determine significant differences in wood properties among peripheral positions and tree heights, followed by Duncan’s means comparison tests at the 5% significance level. Correlation coefficients between RLMS and wood properties were calculated by correlation analysis.

3. Results

3.1. Released Longitudinal Maturation Strains

The RLMS values in all nine trees were negative meaning that longitudinal maturation stress was always tensile (Table 2). From Table 2 average RLMS values for positions and heights ranged from -0.16% and 0.00% with an overall mean of -0.04% (±0.03SD). Variation between peripheral positions and heights was large with an overall CV of 75%. ANOVA analysis detected significant differences in the RLMS among different peripheral positions (p<0.001), but no significant differences among different heights (p>0.05). Distribution of RLMS with peripheral positions and heights is shown in Figure 4. The upper sides (0° locations) had the largest RLMS, and the lower sides (corresponding to 150° or -160°) had the smallest values. Mean RLMS values changed little with height in trees.

3.2. Anatomical properties

The anatomical parameters from the nine sampled trees are listed in Table 2. The minimum value of MFA was 0.1° which was much lower than the average values. CV for MFA was 45.8%. The mean values of PG ranged between 0.0% and 68.8%, with highest CV of 110.9%. There was significant variation in FL, 2WT, MFA, and PG (p<0.001) with peripheral position around the trunk (Figure 5). MFA was significantly lower on the upper side of the trunk than the underside. The upper side of the trunk showed a high proportion of PG. FL and 2WT did not show any specific trends with position.
There was significant variation in FL and 2WT (p<0.01) with height except in MFA and PG (p>0.05). At heights between 0.7 m and 2.2 m, 2WT increased with height, but other anatomical parameters fluctuated or changed little with height.

3.3. Physical and mechanical properties

The physical and mechanical properties of wood from the sampled trees are listed in Table 2. There were significant differences in MOE among positions (p<0.001) but no significant differences in BD, MOR, and CS (p>0.05). MOE values were significantly higher on the upper sides of the stem (Figure 6). BD, MOR and CS fluctuated or showed little change with positions. With the increase of height, BD, MOE, MOR, and CS showed little variation. There were no significant differences in BD, MOE, MOR, and CS among heights (p>0.05).

3.4. Elastic modulus of cell wall

The elastic modulus of each wall layer in wood fiber cells in the TW-tension wood area, LW-lateral wood area, and OW-opposite wood area was characterized by AFM using the PF-QNM mode. As can be seen in Figure 7, the fibers of TW and LW contained a G-layer, but no G-layer was found in OW cells. There were clear differences in elastic modulus among three layers (Table 3, Figure 7). In TW and LW areas the average elastic modulus of the G-layer was higher than S2 and S1 layer. In the OW where the G-layer was absent the average elastic modulus of the S2 layer was larger than the S1 layer. The average elastic modulus of TW area was higher (13.9 GPa) than LW area (13.3 GPa) and the OW area (10.4 GPa). Cell wall elastic modulus was significantly different between TW, LW and OW areas (p<0.05).
The elastic modulus of the cell walls at different heights: 0.7 m, 1.5 m, and 2.2 m are shown in Figure 8, and the elastic modulus values for each wall layer are summarized in Table 4. Since these samples were chosen from position 0° the G-layers could be observed. There was variation among S1, S2, and G-layer, and average elastic modulus of cell walls at 0.7 m was slightly higher than 1.5 m and 2.2 m, but the difference was not significant between heights (p>0.05).

3.5. Relationships between Released Longitudinal Maturation Strains and wood properties

Pearson correlation coefficients between RLMS and wood properties for peripheral positions were calculated and listed in Table 5. In the TW zone a positive correlation was found between RLMS and PG, BD, MOE, MOR and EC and a significant negative correlation was found between RLMS and MFA. In the LW zone a significant positive correlation was found between RLMS and FL and BD and a significant negative correlation was found between RLMS and CS. In the OW zone a significant positive correlation was found between RLMS and MFA and a significant negative correlation was found between RLMS and PG. There were no significant correlations between RLMS and other wood properties.
Pearson correlation coefficients between RLMS and wood properties at different heights were calculated and listed in Table 6. At the height of 0.7 m, a significant positive correlation was found between RLMS and 2WT, PG, BD, MOE, and MOR, and a significant negative correlation was found between RLMS and MFA. At the height of 1.5 m, a significant positive correlation was found between RLMS and FL, PG, BD, MOE, and MOR. At the height of 2.2 m, a significant positive correlation was found between RLMS and MOE, a significant negative correlation was found between RLMS and EC. There were no significant correlations between RLMS and other wood properties.

4. Discussion

Wilson and Gartner [35] reported that growth stress increased with lean on the top side and Yoshida et al. [36] found growth stress increased from 0° (vertical) to 20°. As shown in Figure 9a the effect of inclination angle on maturation stress in artificially inclined poplar trees is limited (p>0.05), which was in contrast to previous studies. Analysis of the relationship between the mean RLMS on a tree and its eccentricity reveals significant relationships (p<0.05), as shown in Figure 9b. This means that eccentric growth increases the magnitude and heterogeneity of tensile RLMS. Eccentric growth, rigidity, and growth stress all increase the efficiency of controlling the orientation of tree axes [8,36]. Our results support the idea that gravitropism (ability to restore upright growth) in poplar trees is caused by synergistic effects of increased tensile growth stress and promotion of secondary growth on the upper side of the inclined stem [37]. The mean values of RLMS (-0.16%–0.00%) here are similar to those found in other studies on Populus×euramericana [15] and Eucalyptus grandis-urophylla [38].
RLMS were significantly different between peripheral positions, which is interpreted as an adaption enabling them to re-orient the stem to vertical growth [37]. The effect of sampling height was not significant which consistent with findings by Li et al. [25] for Populus × euramericana cv. ‘74/76’ trees. Huang et al. [39] also found no obvious relationship between height in tree and measured surface strains in the axial direction in Zelkova serrata. Other studies suggest growth stresses do vary with sampling height e.g., Omonte and Valenzuela [40] found that growth stress indicators at different height were highly variable in the case of Eucalyptus nitens. Naghizadeh and Wessels [38] reported that growth strains decreased from 1.4 m to 11.4 m in Eucalyptus grandis-urophylla trees.
Results from this study found no significant difference in fiber length between tension wood and normal wood, in accord with findings by Scurfield and Wardrop [41]. Fang et al. [15] reported the cell wall thickness increased in mild and severe tension wood areas. However, in this study, 2WT in the upper side tension wood were similar to those in wood cells from the other positions. MFAs range from 15°–30° in S2 layer, and 0°–2.5° in G-layer [42]. Our results accordingly showed low MFAs on the upper side and larger MFAs on the lower side of the poplar trunks. The smaller the microfibril angle, the larger the longitudinal tensile stress [7,43,44]. PG has been shown to be greater on the upper side, which can trigger big tensile stress for the vertical recovery of stems [2,45].
In accord with previous works, our findings showed BD remains unchanged between tension and normal wood [46]. Higher MOE, MOR, and CS on the upper side has been observed in Picea asperata, Cecropia sciadophylla [19,44]. In this study only MOE followed the same trend but MOR and CS showed minimal change. The higher wood MOE and elastic modulus of the cell wall in TW area are believed to be related to the characteristics of the G-layer which include higher cellulose content and crystallinity, and lower microfibril angles [21].
Li et al. [47] found that with the axial height from 0 m to 11.3 m in Catalpa bungei trees, fiber wall thickness decreased. Wu et al. [20] found in triploid hybrids of Populus tomentosa that fiber length decreased with height between 2 m and 6 m. De Boever et al. [48] observed an increase in MOE, MOR, and density with tree height in hybrid poplar from 1.2 m, 6.5 m and 11.5 m which they attributed to changes in the ratio of heartwood to tension wood. Kijidani and Kitahara [49] found the MOE of Cryptomeria japonica wood to be greater and the MFA lower at 5 m height compared to at 1.5 m, while the wood BD and latewood tracheid length did not change with height. Lima Jr. et al. [50] found that MOE of Eucalyptus grandis wood increases with height of 3 m, 6 m and 9 m from the base. Himes et al. [51] found density, MOR and MOE of hybrid poplar lumber samples generally increased with height from 0 m to 10 m. In this study, lower heights (0.7 m, 1.5 m, and 2.2 m from the ground) were selected for RLMS and wood properties than other studies due to restricted electric-wire length and operational safety of measuring RLMS in living trees. Here only 2WT was found to increase with height, while FL and MOE fluctuated with no particular relationship with height, while RLMS, MFA, PG, BD, MOR, CS, and elastic modulus of cell wall did not change with sampling height in tree. Increased 2WT with height may be attributed to the thinning treatment over the 12-year growth period [52].
Many researchers have reported the correlations between growth stress/growth strain and wood properties [25,53], but the effects and correlations among different peripheral positions and heights are seldom reported or discussed. Correlations in the TW zone were stronger than in other zones. It should also be noted that the correlations at the different heights were quite different, there were significant correlations between RLMS and wood properties at 0.7 m and 1.5 m, while at 2.2 m correlations weakened considerably. Therefore, RLMS could be considered a good indicator of wood properties in the TW area of the bole below 1.5 m height.

5. Conclusions

The influence of peripheral positions and heights on Released Longitudinal Maturation Strains (RLMS), anatomical features, physical and mechanical properties, and nano-mechanical properties of the cell wall were assessed in this work. Correlations between RLMS and wood properties were also analyzed. The results showed that upper sides of the inclined trunks had higher RLMS, proportion of G-layer, bending modulus of elasticity, and elastic modulus of cell wall but lower microfibril angle than the other sides. These differences may be related to the existence of the G-layer in tension wood area. Sampling height in trunk had little effect on measured wood and cell characteristics, except for double wall thickness which tended to be lower closer to the base of trees (0.7 m, 1.5 m, and 2.2 m from the ground). RLMS showed strong correlations with wood characteristics in the tension wood zone and with height up to around 1.5 m.
In general, the artificial inclination in the trees had mixed effects on wood properties and quality. The variation observed in this study could be used to improve the conversion value of poplar logs by identifying which parts of the lower trunk produce better wood quality suitable for higher value or higher demand products such as plywood, solid lumber or certain paper products when isolated from the rest of the tree. Additional studies are required to evaluate the variability in longitudinal maturation strains and wood characteristics higher up in the trunk for appropriate selection strategies.

Author Contributions

Conceptualization, Y.L. and X.W.; methodology, Y.L.; software, J.Z.; validation, C.D. and S.L.; formal analysis, Y.L.; investigation, X.W.; resources, S.L.; data curation, X.W.; writing—original draft preparation, Y.L.; writing—review and editing, K.S.; visualization, J.Z.; supervision, K.S. and C.D.; project administration, X.W.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the China Scholarship Council (202008775007) and Engineering Research Council of Canada (RGPIN-2020-06097).

Acknowledgments

We acknowledge N.P., S.F, M.Z. and X.W. for technical assistance.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Thibaut, B.; Gril, J. Growth stresses: in Wood quality and its biological basis. Blackwell: Oxford, UK, 2003; pp. 137-156.
  2. Alméras, T.; Clair, B. Critical review on the mechanisms of maturation stress generation in trees. J R Soc Interface. 2016, 13, 20160550. [Google Scholar] [CrossRef] [PubMed]
  3. Gril, J.; Jullien, D.; Bardet, S.; Yamamoto, H. Tree growth stress and related problems. J Wood Sci. 2017, 63, 411–432. [Google Scholar] [CrossRef]
  4. Mattheck, C.; Kubler, H. Wood: the internal optimization of trees. Arboricultural Journal: The International Journal of Urban Forestry. 1995, 19, 97–110. [Google Scholar] [CrossRef]
  5. Clair, B.; Alteyrac, J.; Gronvold, A.; Espejo, J.; Chanson, B.; Alméras, T. Patterns of longitudinal and tangential maturation stresses in Eucalyptus nitens plantation trees. Ann Forest Sci. 2013, 70, 801–811. [Google Scholar] [CrossRef]
  6. Yamamoto, H.; Yoshida, M.; Okuvama, T. Growth stress controls negative gravitropism in woody plant stems. Planta. 2002, 216, 280–292. [Google Scholar] [CrossRef] [PubMed]
  7. Huang, Y.; Chen, S.; Kuo-Huang, L.; Lee, C. Growth strain in the trunk and branches of Chamaecyparis formosensis and its influence on tree form. Tree Physiol. 2005, 25, 1119–1126. [Google Scholar] [CrossRef]
  8. Alméras, T.; Thibaut, A.; Gril, J. Effect of circumferential heterogeneity of wood maturation strain, modulus of elasticity and radial growth on the regulation of stem orientation in trees. Trees. 2005, 19, 457–467. [Google Scholar] [CrossRef]
  9. Alméras, T.; Fournier, M. Biomechanical design and long-term stability of trees: morphological and wood traits involved in the balance between weight increase and the gravitropic reaction. J Theor Biol. 2009, 256, 370–381. [Google Scholar] [CrossRef]
  10. Alméras, T.; Derycke, M.; Jaouen, G.; Beauchêne, J.; Fournier, M. Functional diversity in gravitropic reaction among tropical seedlings in relation to ecological and developmental traits. J Exp Bot. 2009, 60, 4397–4410. [Google Scholar] [CrossRef]
  11. Yoshida, M.; Ohta, H.; Yamamoto, H.; Okuyama, T. Tensile growth stress and lignin distribution in the cell walls of yellow poplar, Liriodendron tulipifera Linn. Trees. 2002, 16, 457–464. [Google Scholar] [CrossRef]
  12. Ruelle, J.; Clair, B.; Beauchene, J.; Prevost, M.F.; Fournier, M. Tension wood and opposite wood in 21 tropical rain forest species. 2. Comparison of some anatomical and ultrastructural criteria. IAWA J. 2006, 27, 341–376. [Google Scholar] [CrossRef]
  13. Nistal França, F.J.; Filgueira Amorim França, T.S.; Vidaurre, G.B. Effect of growth stress and interlocked grain on splitting of seven different hybrid clones of Eucalyptus grandis × Eucalyptus urophylla wood. Holzforschung. 2020, 74, 917–926. [Google Scholar] [CrossRef]
  14. Moya, R.; Tenorio, C.; de Ingeniería Forestal, E.; Rica, C. Reduction of effect of growth stress presence using endless screw during kiln drying and steaming and heating treatment in log before sawing. Wood Res-Slovakia. 2022, 67, 157–169. [Google Scholar] [CrossRef]
  15. Fang, C.; Guibal, D.; Clair, B.; Gril, J.; Liu, Y.; Liu, S. Relationships between growth stress and wood properties in poplar I-69 (Populus deltoides Bartr. Cv. “lux” ex i-69/55). Ann For Res. 2008, 65, 307. [Google Scholar] [CrossRef]
  16. Yoshida, M.; Ikawa, M.; Kaneda, K.; Okayama, T. Stem tangential strain on the tension wood side of Fagus crenata saplings. J Wood Sci. 2003, 49, 475–478. [Google Scholar] [CrossRef]
  17. Washusen, R.; Ilic, J.; Waugh, G. The relationship between longitudinal growth strain and the occurrence of gelatinous fibers in 10 and 11-year-old Eucalyptus globulus Labill. Holz Als Roh-Und Werkstoff. 2003, 61, 299–303. [Google Scholar] [CrossRef]
  18. Clair, B.; Ruelle, J.; Thibaut, B. Relationship between growth stresses, mechano-physical properties and proportion of fibre with gelatinous layer in chestnut (Castanea sativa Mill.). Holzforschung. 2003, 57, 189–195. [Google Scholar] [CrossRef]
  19. Gindl, W.; Schöberl, T. The significance of the elastic modulus of wood cell walls obtained from nanoindentation measurements. Compos Part A-Appl S. 2004, 35, 1345–1349. [Google Scholar] [CrossRef]
  20. Wu, Y.; Wang, S.; Zhou, D.; Xing, C.; Zhang, Y. Use of nanoindentation and silviscan to determine the mechanical properties of 10 hardwood species. Wood Fiber Sci. 2009, 41, 64–73. [Google Scholar]
  21. Liang, R.; Zhu, Y.; Yang, X.; Gao, J.; Zhang, Y.; Cai, L. Study on the ultrastructure and properties of gelatinous layer in poplar. J Mater Sci. 2021, 56, 415–427. [Google Scholar] [CrossRef]
  22. Liu, Y.; Zhou, L.; Zhu, Y.; Liu, S. Anatomical Features and Its Radial Variations among Different Catalpa bungei Clones. Forests. 2020, 11, 824. [Google Scholar] [CrossRef]
  23. Ahmed, A.K.M.; Fu, Z.; Ding, C.; Jiang, L.; Han, X.; Yang, A.; Ma, Y.; Zhao, X. Growth and wood properties of a 38-year-old Populus simonii × P. Nigra plantation established with different densities in semi-arid areas of northeastern China. J Forestry Res. 2019, 31, 497–506. [Google Scholar] [CrossRef]
  24. Zhang, L.; Liu, B.; Zhang, J.; Hu, J. Insights of molecular mechanism of xylem development in five black poplar cultivars. Front Plant Sci. 2020, 11, 620. [Google Scholar] [CrossRef]
  25. Li, J.; Liu, S.; Zhou, L.; Liu, Y. Growth strain in straight and inclined Populus × euramericana cv. ‘74/76’ trees, and its relationship with selected wood properties. Eur J Wood Wood Prod. 2018, 76, 1715–1723. [Google Scholar] [CrossRef]
  26. Archer, R.R. Growth stresses and strains in trees. Springer-Verlag: Berlin, Germany, 1987.
  27. Yoshida, M.; Yamamoto, H.; Okuyama, T.; Nakamura, T. Negative gravitropism and growth stress in GA3-treated branches of Prunus spachiana kitamura f. spachiana cv. Plenarosea. J Wood Sci. 1999, 45, 368. [Google Scholar] [CrossRef]
  28. 28. Research Institute of Wood Industry, Chinese Academy of Forestry. Method of sample logs sawing and test specimens selection for physical and mechanical tests of wood, Standard GB/T 1929-2009, Standards Press of China, Beijing, 2009.
  29. Cave, I.D. Theory of x-ray measurement of microfibril angle in wood. Forest Prod J. 1966, 16, 37–42. [Google Scholar]
  30. Research Institute of Wood Industry, Chinese Academy of Forestry. Method for determination of the density of wood. Standard GB/T 1933-2009, Standards Press of China, Beijing, 2009.
  31. Research Institute of Wood Industry, Chinese Academy of Forestry. Method of testing in bending strength of wood. Standard GB/T 1936.1-2009, Standards Press of China, Beijing, 2009.
  32. Research Institute of Wood Industry, Chinese Academy of Forestry. Method for determination of the modulus of elasticity in static bending of wood. Standard GB/T 1936.2-2009, Standards Press of China, Beijing, 2009.
  33. Research Institute of Wood Industry, Chinese Academy of Forestry. Method of testing in compressive strength parallel to grain of wood. Standard GB/T 1935-2009, Standards Press of China, Beijing, 2009.
  34. Zhang, Y. Transitions Between Different Contact Models. J Adhes Sci Technol. 2008, 22, 699–715. [Google Scholar]
  35. Wilson, B.F.; Gartner, B.L. Lean in red alder (Alnus rubra): Growth stress, tension wood, and righting response. Can. J. For. Res. 1996, 26, 1951–1956. [Google Scholar] [CrossRef]
  36. Yoshida, M.; Okuda, T.; Okuyam, T. Tension wood and growth stress induced by artificial inclination in Liriodendron tulipifera Linn. and Prunus spachiana kitamura f. ascendens Kitamura. Ann Forest Sci. 2000, 57, 739–746. [Google Scholar] [CrossRef]
  37. Shirai, T.; Yamamoto, H.; Yoshida, M.; Inatsugu, M.; Ko, C.; Fukushima, K.; Matsushita, Y.; Yagami, S.; Lahjie, A.M.; Sawada, M.; Kule, A. Eccentric growth and growth stress in inclined stems of Gnetum gnemon. IAWA J. 2015, 36, 365–377. [Google Scholar] [CrossRef]
  38. Naghizadeh, Z.; Wessels, C.B. The effect of water availability on growth strain in Eucalyptus grandis-urophylla trees. Forest Ecol Manag. 2021, 483, 118926. [Google Scholar] [CrossRef]
  39. Huang, Y.S.; Chen, S.S.; Kuo-Huang, L.L.; Lee, M.C. Growth stress of Zelkova serrata and its reduction by heat treatment. Forest Prod J. 2005, 55, 88–93. [Google Scholar]
  40. Omonte, M.; Valenzuela, L. Longitudinal growth stresses in Eucalyptus nitens trees with sawable dimensions. Maderas-Cienc Tecnol 2015, 17, 673–684. [Google Scholar] [CrossRef]
  41. Scurfield, G.; Wardrop, A.B. The nature of reaction wood. Ⅵ. The reaction anatomy of seedlings of woody perennials. Aust J Bot. 1962, 10, 93–105. [Google Scholar] [CrossRef]
  42. Baba, K.; Park, Y.W.; Kaku, T.; Kaida, R.; Takeuchi, M.; Yoshida, M.; Hosoo, Y.; Ojio, Y.; Okuyama, T.; Taniguchi, T.; Ohmiya, Y.; Kondo, T.; Shani, Z.; Shoseyov, O.; Awano, T.; Serada, S.; Norioka, N.; Norioka, S.; Hayashi, T. Xyloglucan for generating tensile stress to bend tree stem. Mol Plant. 2009, 2, 893–903. [Google Scholar] [CrossRef] [PubMed]
  43. Okuyama, T.; Yamamoto, H.; Yoshida, M.; Hattori, Y.; Archer, R.R. Growth stresses in tension wood: role of microfbrils and lignifcation. Ann Sci For. 1994, 51, 291–300. [Google Scholar] [CrossRef]
  44. Ruelle, J.; Beauchene, J.; Thibaut, A.; Thibaut, B. Comparison of physical and mechanical properties of tension and opposite wood from ten tropical rainforest trees from different species. Ann Forest Sci. 2007, 64, 503–510. [Google Scholar] [CrossRef]
  45. Chang, S.; Quignard, F.; Alméras, T.; Clair, B. Mesoporosity changes from cambium to mature tension wood: a new step toward the understanding of maturation stress generation in trees. New Phytol. 2015, 205, 1277–1287. [Google Scholar] [CrossRef]
  46. Lowell, E.C.; Krahmer, R.L. Effects of lean in red alder trees on wood shrinkage and density. Wood Fiber Sci. 1993, 25, 2–7. [Google Scholar]
  47. Li, S.; Li, X.; Link, R.; Li, R.; Deng, L.; Schuldt, B.; Jiang, X.; Zhao, R.; Zheng, J.; Li, S.; Yin, Y. Influence of cambial age and axial height on the spatial patterns of xylem traits in Catalpa bungei, a Ring-Porous tree species native to China. Forests. 2019, 10, 662. [Google Scholar] [CrossRef]
  48. De Boever, L.; Vansteenkiste, D.; Van Acker, J.; Stevens, M. End-use related physical and mechanical properties of selected fast-growing poplar hybrids (Populus trichocarpa x P. deltoides). Ann Forest Sci. 2007, 64, 621–630. [Google Scholar] [CrossRef]
  49. Kijidani, Y.M.U.J.; Kitahara, R. Variation of wood properties with height position in the stems of obi-sugi [Cryptomeria japonica] cultivars. Mokuzai Gakkaishi. 2009, 55, 198–206. [Google Scholar] [CrossRef]
  50. Lima Junior, M.P.D.; Biazzon, J.C.; De Araujo, V.A.; Munis, R.A.; Martins, J.C.; Cortez-Barbosa, J.; Gava, M.; Valarelli, I.D.D.; Morales, E.A.M. Mechanical properties evaluation of Eucalyptus grandis wood at three different heights by impulse excitation technique (iet). BioResources. 2018, 13, 3377–3385. [Google Scholar] [CrossRef]
  51. Himes, A.; Leavengood, S.; Polinko, A. Variation in wood properties of hybrid poplar lumber by radial and vertical position in stem: a case study from Boardman, Oregon. Wood Fiber Sci. 2021, 53, 161–177. [Google Scholar] [CrossRef]
  52. Jeong, G. Y.; Zink-Sharp, A. Technical note: anatomical variability within a loblolly pine tree under thinning management. Wood Fiber Sci. 2013, 45, 119–122. [Google Scholar]
  53. Gilbero, D.M.; Abasolo, W.P.; Matsuo-Ueda, M.; Yamamoto, H. Surface growth stress and wood properties of 8-year-old planted big-leaf mahogany (Swietenia macrophylla King) from different landrace provenances and trial sites in the Philippines. J Wood Sci. 2019, 65, 35. [Google Scholar] [CrossRef]
Preprints 76704 g001
Figure 1. Image of sampled trees. a. Measuring points at three different heights of tree 5; b. Maturation strains released by strain gauges of tree 6.
Figure 1. Image of sampled trees. a. Measuring points at three different heights of tree 5; b. Maturation strains released by strain gauges of tree 6.
Preprints 76704 g001
Preprints 76704 g002
Figure 2. Schematic of measurement positions. TW: tension wood area (0°, 50°, and -60°); LW: lateral wood area (100° and -110°); OW: opposite wood area (150° and -160°).
Figure 2. Schematic of measurement positions. TW: tension wood area (0°, 50°, and -60°); LW: lateral wood area (100° and -110°); OW: opposite wood area (150° and -160°).
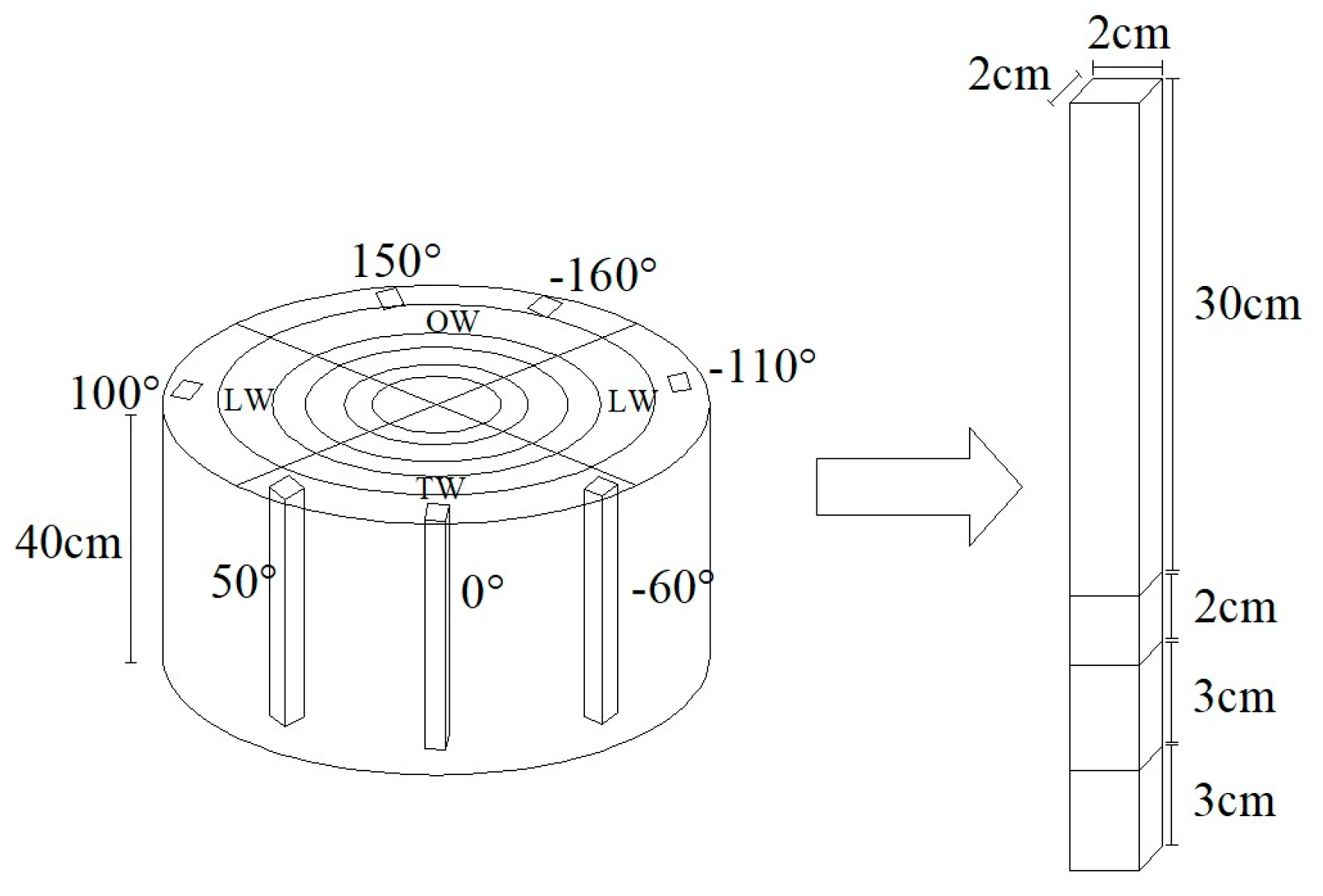
Preprints 76704 g002
Preprints 76704 g003
Figure 3. Light microscope view of anatomical sections of poplar tension wood. a. TW area; b. LW area; c. OW area.
Figure 3. Light microscope view of anatomical sections of poplar tension wood. a. TW area; b. LW area; c. OW area.
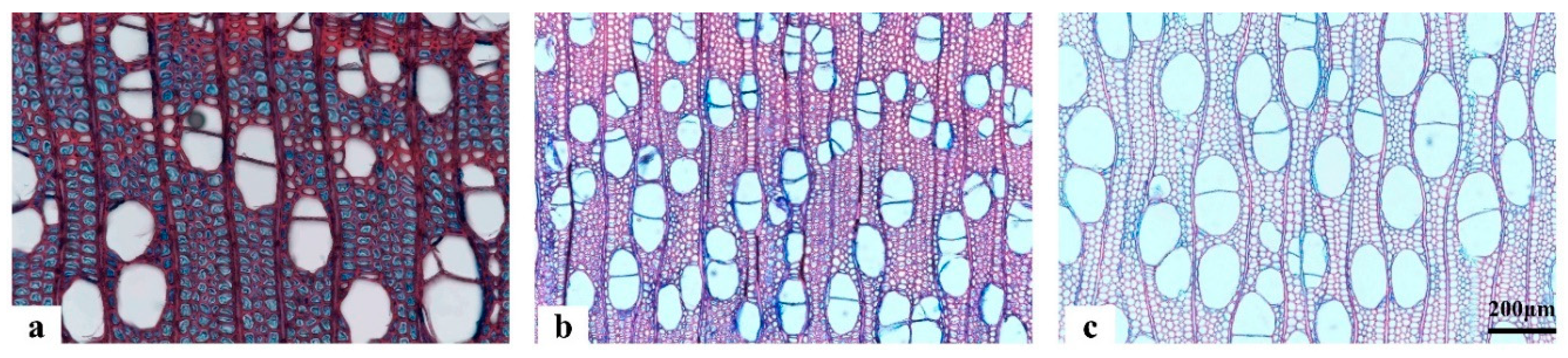
Preprints 76704 g003
Preprints 76704 g004
Figure 4. Distributions of RLMS with peripheral positions (a) and heights (b). Different letters indicate significant differences according to Duncan’s means comparison tests in p<0.05. RLMS: Released Longitudinal Maturation Strains.
Figure 4. Distributions of RLMS with peripheral positions (a) and heights (b). Different letters indicate significant differences according to Duncan’s means comparison tests in p<0.05. RLMS: Released Longitudinal Maturation Strains.
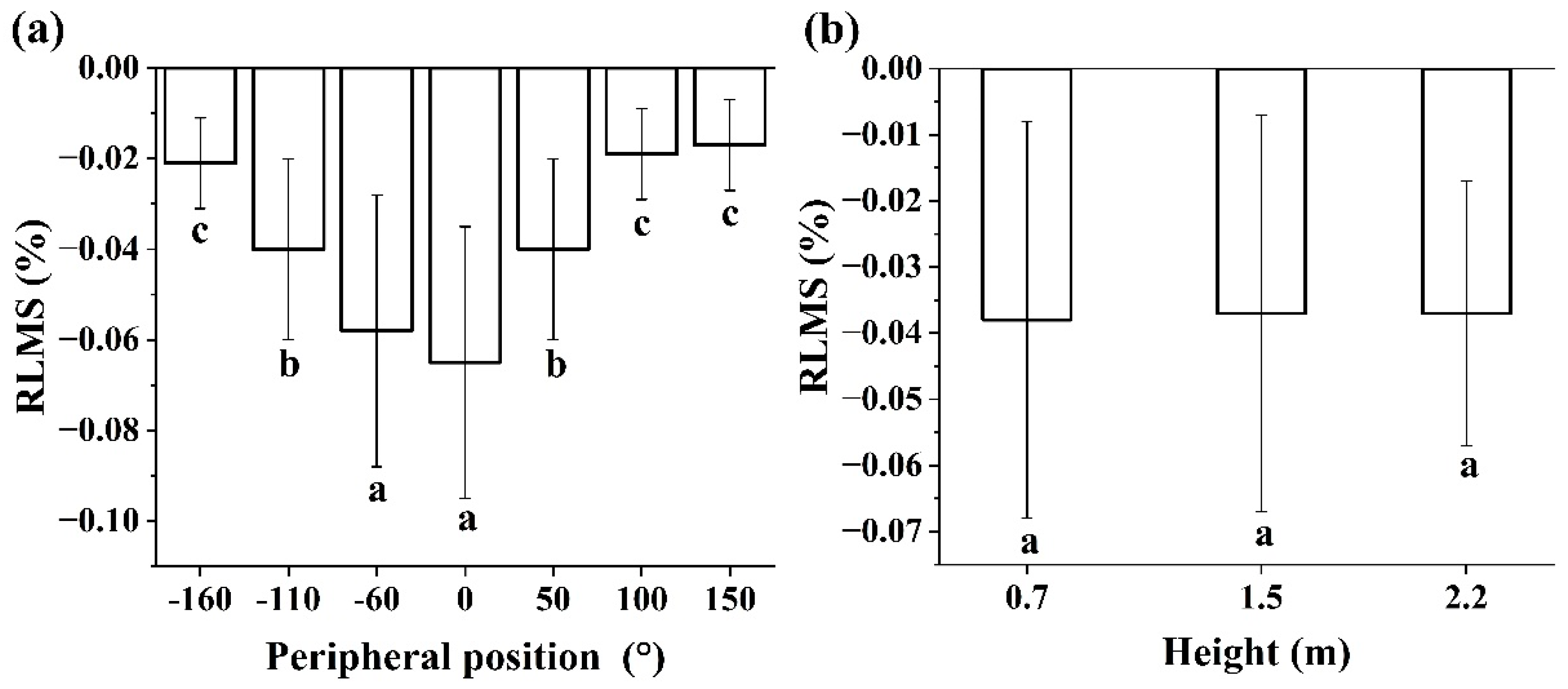
Preprints 76704 g004
Preprints 76704 g005
Figure 5. Distributions of anatomical measured parameters with peripheral positions (a) and heights (b). Different letters indicate significant differences according to Duncan’s means comparison tests in p<0.05. FL: fiber length; 2WT: double wall thickness; MFA: microfibril angle; PG: proportion of G-layer.
Figure 5. Distributions of anatomical measured parameters with peripheral positions (a) and heights (b). Different letters indicate significant differences according to Duncan’s means comparison tests in p<0.05. FL: fiber length; 2WT: double wall thickness; MFA: microfibril angle; PG: proportion of G-layer.
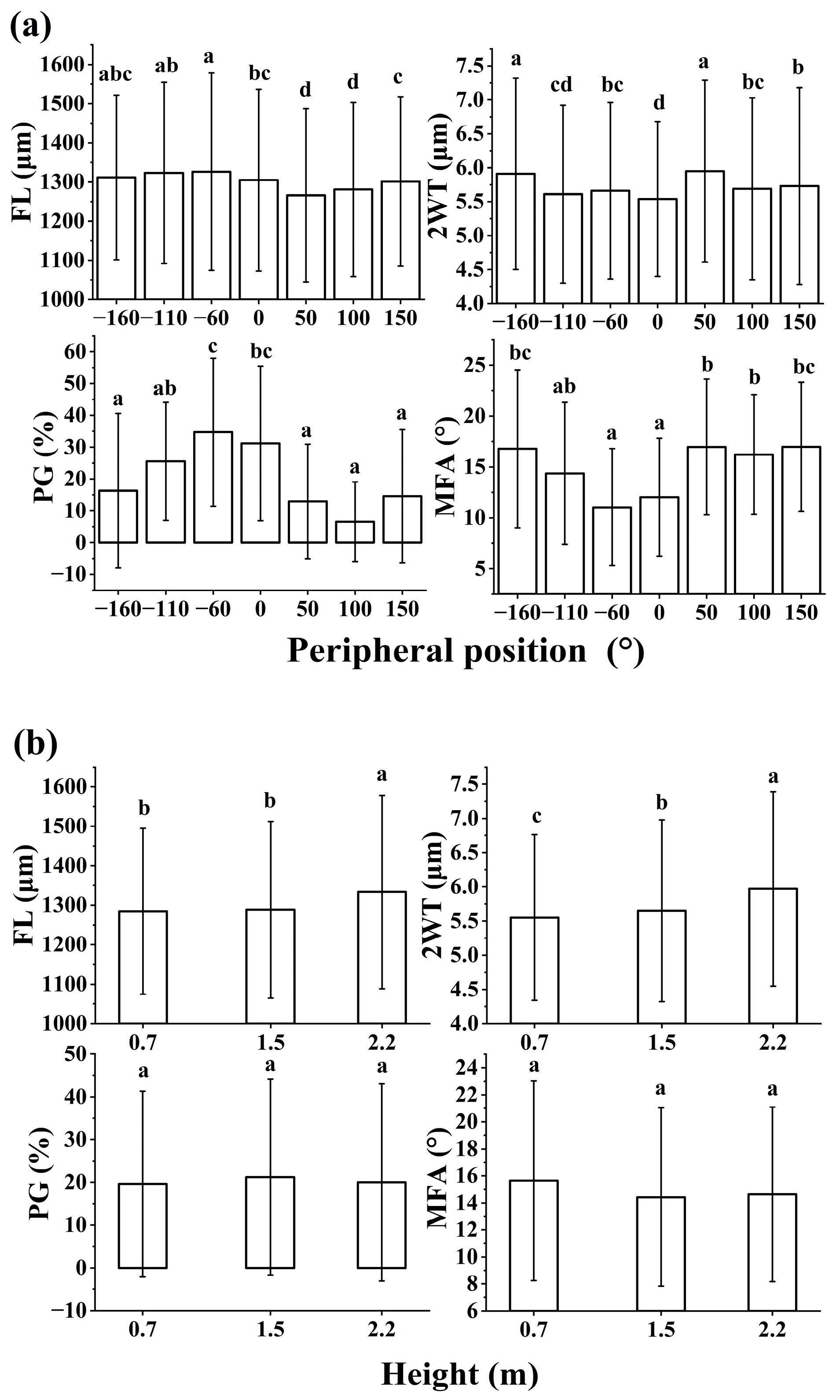
Preprints 76704 g005
Preprints 76704 g006
Figure 6. Distributions of physical and mechanical properties with peripheral positions (a) and heights (b). Different letters indicate significant differences according to Duncan’s means comparison tests in p<0.05. BD: basic density; MOE: bending modulus of elasticity; MOR: bending modulus of rupture; CS: compressive strength.
Figure 6. Distributions of physical and mechanical properties with peripheral positions (a) and heights (b). Different letters indicate significant differences according to Duncan’s means comparison tests in p<0.05. BD: basic density; MOE: bending modulus of elasticity; MOR: bending modulus of rupture; CS: compressive strength.
Preprints 76704 g006
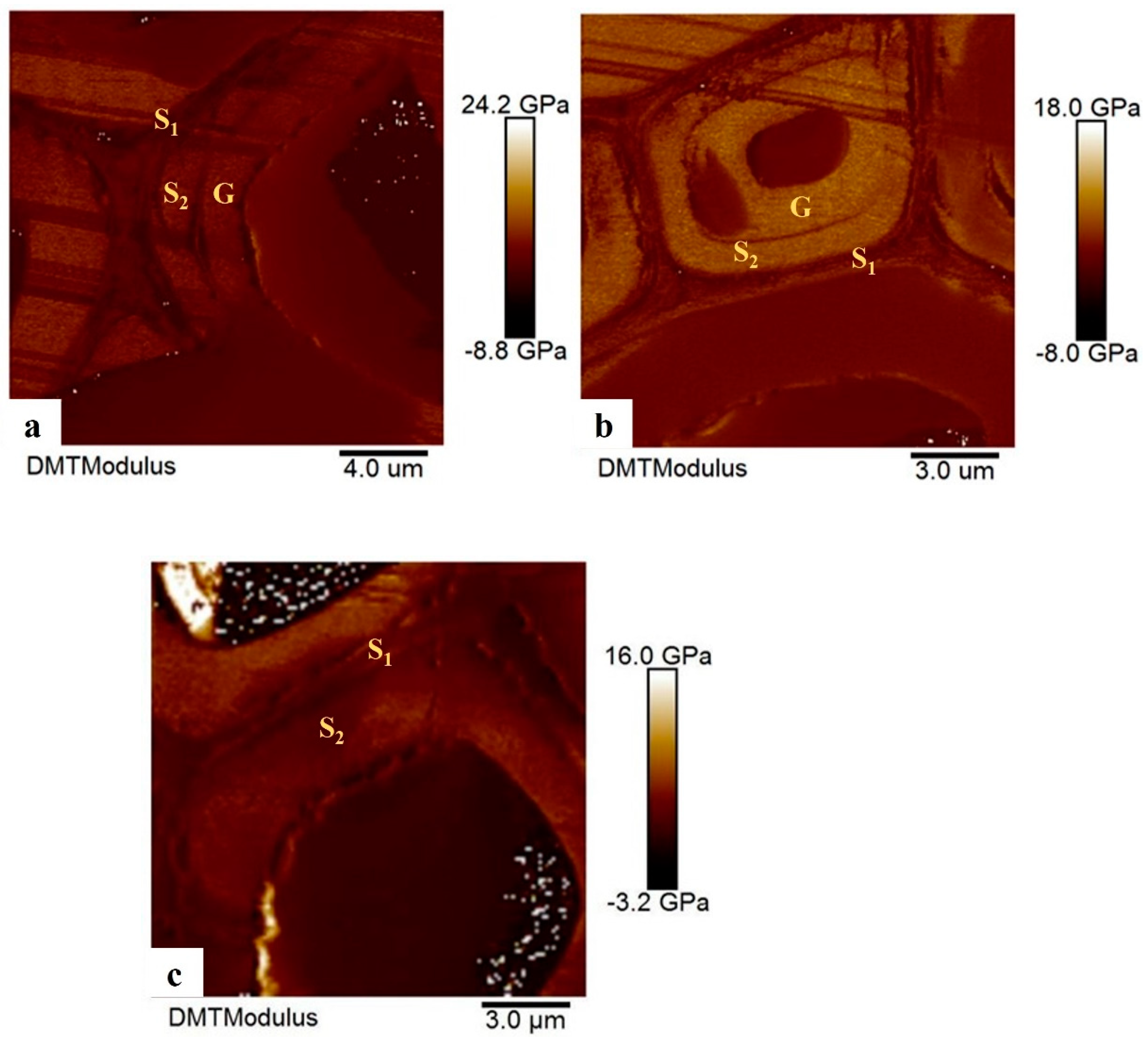
Preprints 76704 g007
Figure 7. Elastic modulus of cell wall layer in DMT mode. a. TW area, b. LW area, c. OW area.
Figure 7. Elastic modulus of cell wall layer in DMT mode. a. TW area, b. LW area, c. OW area.
Preprints 76704 g007
Preprints 76704 g008
Figure 8. Elastic modulus of cell wall layer in DMT mode. a. 0.7 m, b. 1.5 m, c. 2.2 m.
Figure 8. Elastic modulus of cell wall layer in DMT mode. a. 0.7 m, b. 1.5 m, c. 2.2 m.
Preprints 76704 g008
Preprints 76704 g009
Figure 9. (a) Relationship of RLMS to lean angle in inclined trees, regression coefficients were not significant (p=0.53). Mean lean angle and SD=17.9°±5.11. (b) Relationship of RLMS to eccentricity in leaning trees, regression coefficients were significant (p=0.01). Mean eccentricity and SD=16.3%±6.90.
Figure 9. (a) Relationship of RLMS to lean angle in inclined trees, regression coefficients were not significant (p=0.53). Mean lean angle and SD=17.9°±5.11. (b) Relationship of RLMS to eccentricity in leaning trees, regression coefficients were significant (p=0.01). Mean eccentricity and SD=16.3%±6.90.
Preprints 76704 g009
Table 1. Sample information of nine studied trees.
Table 1. Sample information of nine studied trees.
Tree number Tree height
(m)		 DBH (cm) Tilt angle from
vertical position (°)
1 19.6 38.8 27
2 21.7 51.2 11
3 18.5 35.6 17
4 16.5 23.8 15
5 15.9 18.4 24
6 14.3 15.2 18
7 16.2 21.0 13
8 14.1 14.7 16
9 15.8 19.1 20
DBH: diameter at breast height.
Table 2. Basic statistics for measured parameters
Table 2. Basic statistics for measured parameters
Parameters n Average SD Max Min CV%
RLMS (%) 189 -0.04 0.03 -0.16 0.00 75.0
FL (μm) 7990 1302 227.71 2343 508 17.5
2WT (μm) 8698 5.73 1.34 11.69 2.50 23.4
MFA (°) 294 14.90 6.83 34.10 0.10 45.8
PG (%) 189 20.3 22.5 68.8 0.0 110.9
BD (g/cm3) 189 0.37 0.03 0.50 0.31 8.1
MOE (MPa) 189 4224 444.80 5776 3273 10.5
MOR (MPa) 189 49.42 5.47 64 24 11.1
CS (MPa) 189 35.52 4.29 47 22 12.1
n: number of samples; SD: standard deviations; Max: maximum value; Min: minimum value; CV%: coefficient of variation. RLMS: Released Longitudinal Maturation Strains; FL: fiber length; 2WT: double wall thickness; PG: proportion of G-layer; MFA: microfibril angle; BD: basic density; MOE: bending modulus of elasticity; MOR: bending modulus of rupture; CS: compressive strength.
Table 3. Means and standard deviations of elastic modulus (in GPa) of cell wall at different areas.
Table 3. Means and standard deviations of elastic modulus (in GPa) of cell wall at different areas.
TW LW OW
S1 9.5±1.41 a 9.4±1.24 b 8.6±1.52 c
S2 15.6±2.51 a 15.1±2.53 b 12.2±2.60 c
G 16.6±3.15 a 15.5±2.98 b N.A.
Different letters indicate significant differences according to Duncan’s means comparison tests in p<0.05.
Table 4. Means and standard deviations of elastic modulus (in GPa) of cell wall at different heights.
Table 4. Means and standard deviations of elastic modulus (in GPa) of cell wall at different heights.
0.7 m 1.5 m 2.2 m
S1 9.4+1.98 a 9.3+1.59 a 9.2+1.43 a
S2 12.1+2.35 a 11.3+2.44 a 11.6+2.53 a
G 13.1+3.21 a 12.8+2.38 a 13.0+2.57 a
Different letters indicate significant differences according to Duncan’s means comparison tests in p<0.05.
Table 5. Results of correlation analysis between RLMS and wood properties among different peripheral positions.
Table 5. Results of correlation analysis between RLMS and wood properties among different peripheral positions.
TW (0°, 50°, -60°) LW (100°, -110°) OW (150°, -160°)
p Sig. df p Sig. df p Sig. df
FL -0.071 ns 81 0.270 * 54 0.185 ns 54
2WT 0.14 ns 81 0.146 ns 54 0.176 ns 54
PG 0.386 ** 81 0.234 ns 54 -0.290 * 54
MFA -0.482 ** 81 -0.078 ns 54 0.323 * 54
BD 0.267 * 81 0.340 * 54 -0.169 ns 54
MOE 0.322 ** 81 0.205 ns 54 0.144 ns 54
MOR 0.303 ** 81 0.144 ns 54 0.159 ns 54
CS 0.027 ns 81 -0.269 * 54 -0.137 ns 54
EC 0.955 ** 9 0.523 ns 9 0.643 ns 9
RLMS: Released Longitudinal Maturation Strains; FL: fiber length; 2WT: double wall thickness; PG: proportion of G-layer; MFA: microfibril angle; BD: basic density; MOE: bending modulus of elasticity; MOR: bending modulus of rupture; CS: compressive strength; EC: elastic modulus of cell wall; ns: Non-significant; *: Significant at 0.05 level; **: Significant at 0.01 level.
Table 6. Results of correlation analysis between RLMS and wood properties among different heights.
Table 6. Results of correlation analysis between RLMS and wood properties among different heights.
0.7 m 1.5 m 2.2 m
p Sig. df p Sig. df p Sig. df
FL -0.081 ns 63 0.265 * 63 -0.059 ns 63
2WT 0.345 ** 63 0.065 ns 63 0.023 ns 63
PG 0.312 * 63 0.393 ** 63 0.24 ns 63
MFA -0.393 ** 63 -0.179 ns 63 -0.075 ns 63
BD 0.258 * 63 0.338 ** 63 0.159 ns 63
MOE 0.429 ** 63 0.497 ** 63 0.352 ** 63
MOR 0.444 ** 63 0.252 * 63 0.066 ns 63
CS -0.109 ns 63 -0.105 ns 63 -0.04 ns 63
EC 0.647 ns 9 0.005 ns 9 -0.773 * 9
RLMS: Released Longitudinal Maturation Strains; FL: fiber length; 2WT: double wall thickness; PG: proportion of G-layer; MFA: microfibril angle; BD: basic density; MOE: bending modulus of elasticity; MOR: bending modulus of rupture; CS: compressive strength; EC: elastic modulus of cell wall; ns: Non-significant; *: Significant at 0.05 level; **: Significant at 0.01 level.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated