Preprint
Article
Convex Stochastic Approaches for the Optimal Allocation of Distributed Energy Resources in AC Distribution Networks with Measurements Fitted to a Continuous Probability Distribution Function
This version is not peer-reviewed.
Submitted:
14 June 2023
Posted:
16 June 2023
You are already at the latest version
A peer-reviewed article of this preprint also exists.
Abstract
This paper addresses the optimal stochastic allocation of Distributed Energy Resources in distribution Networks. Typically, uncertain problems are analyzed in multi-stage formulations including case generation routines, resulting in computationally exhaustive programs. In this article, two probabilistic approaches are proposed resulting in a single-stage, convex, stochastic optimal power flow problem: The Range-Probability Optimization (RPO) and Value-Probability Optimization (VPO). The RPO maximizes probabilities within a range of uncertainty, whilst the VPO optimizes the values of the random variables and maximizes their probabilities. Random variables are modeled with hourly measurements fitted to the logistic distribution. These formulations were tested on two systems and compared against the deterministic case built from expected values. Results indicate that assuming deterministic conditions ends in highly underestimated losses. The RPO showed that by including a ±10 % uncertainty, the losses can be increased up to 40 % with up to −72 % photovoltaic capacity, depending on the system, whereas the VPO resulted in up to 85 % increases in power losses despite PV installations, with 20 % greater probabilities in average. By implementing any of the proposed approaches, it was possible to obtain more probable upper envelopes in the objective, avoiding case generation stages and heuristic methods.
Keywords:
Subject:
Engineering - Electrical and Electronic Engineering1. Introduction
The Optimal Power Flow problem (AC-OPF) has been an extensively used tool to find optimal operative set points in the planning and operation of power systems. This analysis has been transforming from a rigid, centralized framework, to a more flexible one by including new economic agents and operational strategies. For instance, with the introduction of Peer-To-Peer trading schemes, a consumer-producer (prosumer) is integrated into energy communities and the overall welfare of the community is optimized by coordinating resources and energy transactions with conventional grids [1], or the aggregation of Distributed Energy Resources (DER) into multi-energy virtual power plants, whose operation is economically optimized to provide services such as upstream reactive power support or frequency control [2]. Similarly, the problem of planning virtual microgrids (optimal partitions of a larger conventional distribution network) with the allocation of Distributed Energy Resources (DER) can be addressed with an integrated approach (instead of separating the problem) with the very same constraints imposed by the original AC-OPF [3]. Although the AC-OPF formulates properly a balanced steady state problem for conventional networks, it has been also modified for the design of microgrids with Photovoltaic (PV) units and storage systems to overcome power intermittence from the utility to supply critical loads[4]. This increase in the number of applications for the AC-OPF has been boosted by more efficient and cheaper technologies in the production of electricity (allowing consumers to meet part of their demand and sell surpluses), the integration of information technologies (IT) advancements in the operation within energy supply chain, and data science analyses (e.g., the implementation of IoT solutions for energy management in microgrids[5], the aggregation of Distributed Energy Resources (DER) via IT[6], the demand charcterization for infrastructure planning[7], the statistical characterization of solar irradiation[8] or solar predictions based on Artificial Neural Networks[9]), requiring grid operators, especially in the distribution, to operate considering uncertainties and multi-directional flows of power, currency and information. Under these conditions, network planners and operators implement the AC-OPF to optimize either individual or in a combination, technical, economical or environmental objectives, such as power losses minimization [10], voltage regulation[11], emissions reduction [12], operational and infrastructure investment cost reductions [13,14], or a combination resulting in techno-economic-environmental multi-objective formulations [15]. This requires the study of newer methodologies involving Active Distribution Network modeling [16], adequate mathematical formulation of optimization problems aiming to increase efficiency and solution quality [17] and proper implementation of optimization techniques to solve the problem [18]. Additionally, recent multidisciplinary research has been directed to increase computational efficiency in the solution of the OPF problem [18], showing results particularly in newer meta-heuristic techniques (e.g., Arithmetic Optimization Algorithm (AOA) [19], hybrid Harris Hawks Optimizer-AOA (hHHO-AOA) [20], Mutation Improved Grey Wolf Optimizer (MIGWO) [21]), and in the convexification of the problem with relaxations based on Second-Order Cones [22,23] or Positive Semi-definite expressions [24]. This is relevant since AC-OPF formulations are more complex than the original power balance problem: it might include non-linear cost functions (in addition to the quadratic expression for the losses found in the original AC-OPF fomulation), Mixed-Integer expressions (as in a reconfiguration [25] or resource allocation problem [26]), and/or uncertainty, which individually or all together aren’t necessarily convex when included to the problem (in addition to the non-convex quadratic constraints in the original AC-Power Flow problem), thus limiting the quality of the solutions and the scope of results. Nevertheless, if the necessary effort is made to make the problem convex, the solution is ensured to be optimal, unique, exact (if feasible), and solvable in polynomial time (if not combinatorial). If convex is not possible, sub-optimal solutions are always obtainable with other tools (meta-heuristics), although the solution can´t be guaranteed to be exact or unique. However, such tools are particularly useful in such cases and in multi-objective Pareto optimization [10].
Uncertainty has become relevant in the analysis of power systems since most common DER technologies and demand have stochastic behavior. Uncertainty is typically included in optimization problems by implementing case analysis [11,27], Montecarlo simulations [28], sensitivity analysis [29,30], or typically by using expected value reductions and treating the stochastic problem deterministically. Depending on the model used to describe uncertainty, the stochastic optimization problem can be formulated as a chance-constrained OPF, in which the knowledge of random variables is expressed by distribution functions, and their associated probabilities are constrained to comply operational constraints, e.g., in [31] demand and PV are modeled to with the normal distribution, and the probabilities constraint the problem to avoid voltage, line power flow, and storage power violations. In [32], the probability of frequency deviation violations constraints the primary frequency control problem. On the other hand, the optimization problem can be formulated in multi-stage approaches, by generating representative cases that follow the distributions of random variables, and solving a deterministic problem for each case. For instance, in [16], a two-stage stochastic program is defined for load restoration in distributed microgrids, whose first stage generates the cases with Monte-Carlo simulations, and reduce them using hierarchical clustering. This information is fed to the second stage that implements the AC-OPF to retrieve the solution set for each case. Similarly, in [33] two optimization stages are proposed, but for the first stage uncertainty is modeled by implementing probability distributions, scenarios are generated with the scenario tree method and reduced with the Kantorovich distance method. A different approach for the two-stage stochastic optimization can be seen in [34], in which for both stages, Monte-Carlo sampling is implemented individually. See also [35] for a review in multiple techniques to handle uncertainty.
In contrast to the two stage stochastic programs, in this paper two single stage approaches are proposed to formulate convex stochastic AC-OPF problems regarding DER sizing and location. The allocation problem aims to install a single DER unit (photovoltaic PV) to minimize power losses in the system, considering demand and irradiance random variables that are modeled from measured data fitted to the logistic continuous distribution. The main contributions of this work are summarized as follows:
- The implementation of single-stage convex stochastic programs, that require no additional software implementations, whose results are expected to be global optimum.
- The uncertainty is modeled using a probabilistic approach, based on data available. Its implementation in the optimization problem is done with continuous logistic distribution functions. With this approach, other distribution functions can be used to calculate probabilities, as long as they can be formulated as concave expressions. With this, the formulation of the optimization problem is more flexible to different probability distributions that might fit better the data.
- The implementation of mathematical expressions for probabilities are tailored to follow the sense of the optimization and the nature of the random variable.
- The results show that the deterministic case (based on expected values) represent a less likely case. On the other hand, both proposed approaches are more likely, thus estimating better the long-term expected behavior.
After this introduction, the rest of the manuscript is organized to present the notation first, followed by the formulation of the proposed optimization problems, an overview of the test systems (one of the systems implements a real-world model from a distribution network in San Andres Island in Colombia), and a summary of the resulting AC-OPF problems (Deterministic and Stochastic) with the computational implementation. Then the results, the discussion, and the conclusions are presented.
2. Methods
In this section, the notation used throughout the article is firstly described, followed by the formulation of non-convex AC-OPF and a convex reformulation. Then, the proposed definition of the objective function regarding power losses and probabilities and, subsequently, constraints regarding the formulated PV-Capacity-Irradiance interface are defined. Finally, an overview of the deterministic and the proposed stochastic problems is shown together with the specifications in the computational implementation.
2.1. Notation
A distribution network consisting in the nodes set , and the set of lines whose elements consist in a pair of nodes , can be represented as an undirected graph . The reference parameters and are defined for the first node (busbar) of the system, that also hosts the main generator injecting the apparent power to supply the demand and cover the losses. A node is a neighbour of node if the pair are connected through a line whose complex admittance, , remains constant. The neighbourhood of the node , is the set of neighbouring nodes . The admittance matrix (size is ) of the network is composed of each line admittance in the neighbourhood . Its diagonal elements are calculated with , while the off-diagonal elements are calculated with . The ∗ operator stands for the complex conjugate. The complex voltage is denoted with v. The squared magnitude of the voltage is represented with the variable u, while for two adjacent nodes the product between and is represented with . The Euclidean norm is represented with the operator . The symbols and stand for the upper and lower bound respectively. For multiperiod analyses the set is introduced to extend the size of affected variables, i.e., for the h period of analysis. In this paper, multiperiod analyses are carried out in hourly steps within a day. Probabilities are assigned to the letter p. In the optimization problems, stands for the objective function. Additional variables and symbols are presented throughout the paper and are explained as they appear. The bolded expression represents a row vector of ones, whereas represents the transpose of the row-vector of ones (column vector of ones). The functions and extract the real and imaginary components of the complex input argument.
2.2. AC-OPF formulations
The AC-OPF problem is, as originally formulated by Carpentier, a non-convex Quadratically Constrained Quadratic Program QCQP [36] (omitting objective function definition) since the admittance matrix is not Hermitian. The balance of power can be expressed as in Equation 1.
An alternative formulation can be implemented by taking advantage of the sparsity in the incidence matrix of radial networks. The Bus Injection Model (BIM) considers the current flow through each line (sending and receiving flows) connected to the node as can be observed in Equation 2 [37]. This formulation continues being non-convex.
As can be observed, in Equation 1 the sum takes into account each element within the admittance matrix, whereas in Equation 2 the summation is only done for each line in the neighborhood of the node with its respective admittance (it does not consider the admittance matrix, but single element admittance).
To convexify the problem, as proposed in [38] (See [22,39] for more comprehensive information regarding convex relaxations), a linearization is implemented by substituting quadratic expressions with affine ones, and relaxing the equivalent term to form Second Order Conic constraints. The linearization takes place by introducing a new complex variable that replaces quadratic voltage terms, as seen in Equation 3. From these relaxations, convexity can be ensured as long as the convex feasible set lies within the non-convex feasible set.
If one builds a matrix W with every element, it is possible to see that W must be hermitian, and the diagonal elements correspond to each node’s squared voltage magnitude. To the diagonal elements of W, a new variable u is assigned. These transformations can be observed in Equations 4,5,6,7 and 8, where the index i is replaced by the index k to leave the i as the imaginary unit.
These transformations are used to create a set of conic constraints (one for each line) taking advantage of the Euclidean norm of complex numbers (Equation 9) and creating a separated expression for the term (Equation 10). Combining those equalities, and relaxing them into inequalities, the set of convex conic constraints, namely Second Order Conic Constraints (SOC), is expressed as in Equation 11.
The basic convex AC-OPF based on the BIM is then formulated as in Equation 12.
If a multi-period analysis is carried out, the relaxed AC-OPF formulation changes to the expressions in Equation 13.
Additional operational constraints can be included in the formulation, i.e., voltage limits, generator capacity, and line power flow limits, but in this paper, such restrictions are not considered because uncertainties could make the problem infeasible. Nevertheless, the generation in the reference node is only bounded to be non-negative, as expressed in Equation 14.
2.3. Objective function
Now that the AC-OPF is constrained to convex terms, the objective function must be defined with convex expressions as well. Therefore, a single objective function is defined for two objectives: Minimize power losses and Maximize probabilities.
2.3.1. Energy Losses
The expression for Energy losses is typically non-convex, but by using the aforementioned transformations, it is now convex (affine), as shown in Equation 15.
2.3.2. Probabilities
In this paper, the maximization of probabilities for the logistic probability distribution is carried out. The continuous logistic distribution is a two-parameter distribution and has both probability density (pdf) , and cumulative probability (cdf) functions, whose definitions are shown in Equations 16 and 17 respectively.
The first proposed approach to handle uncertainty is called Range Probability Optimization (hereafter named RPO), and is defined to find the value x of the random variable X within an uncertainty range by maximizing its probability of occurrence. Therefore, the maximization of this probability is included in the objective function. To calculate the probability for the random variable following the RPO approach, the cdf is implemented as depicted in Equation 18.
Where and define the uncertainty range in which the probability is evaluated, and is the parameter that establishes the half width of the allowed uncertainty. The expression in Equation 19 results from the simplification of Equation 18, and after natural logarithm is applied, it is converted into a sum of concave expressions, as it is shown in equation 20, which are convenient for maximization. The natural logarithm is a monotonically increasing function, thus the maximization of the probability’s logarithm, represents the maximization of the probability itself.
Besides the RPO, a different approach named Value-Probability Optimization (hereafter called VPO) is proposed. It includes in the objective function the maximization of the random variable value and its probability of being greater than the value, as described in Equations 21,22 and 23, and the minimization of the value with the maximization of the variable’s probability of being less or equal than its value, as described in Equations 24 and 25.
After simplifications in Equation 23 and by applying the natural logarithm to it and to Equation 25, the resultant concave expressions are shown in Equation 26 and 27.
Since the aim of these formulations is to increase probabilities and decrease power losses, the random variables and the calculation of their probabilities must be assigned properly when considering VPO analyses. Generally speaking, if one is determined to reduce power losses, the demand is to be reduced either by managing it directly with demand response schemes or curtailment, or by supplying it with distributed resources. Consequently, and to avoid trivialityin the solution, the demand coefficient is to be minimized and its probability maximized following Equation 25, while the irradiance coefficient and its probability (Equation 22) are both to be maximized. Calculating probabilities otherwise, would end in trivial solutions: if the probability for the demand coefficient is calculated with Equation 22, the maximum probability is obtained when the variable reaches its lower bound while minimizing variable’s value, and if the probability for the irradiance coefficient is calculated with Equation 25, the maximum probability is obtained when the variable reaches its upper bound, while maximizing the variable’s value. Therefore, the demand minimization and its probability maximization are included in the objective function with Equation 27, whereas the maximization of the irradiance coefficient and its probability is included with Equation 26.
2.4. DER and Demand modelling
In this article, the generation through Photovoltaic DER (PV) and the demand are modeled as stochastic processes from real data. The research group Electric Machines and Drives (EM&D) at the National University in Bogotá, Colombia, worked on demand characterization from data collected from Distribution Companies. The collected data for demand was measured hourly from 2018 until 2020. Whereas, the Irradiance (Global Solar Irradiance) hourly measurements were provided by the Colombian Institute of Hydrology, Meteorology, and Environmental Studies (IDEAM) for the period 2015-2018.
To obtain the distribution parameters for both variables, the data were fitted hourly to a Logistic distribution. In Figure 1, the fitted parameters are illustrated (See Table A1 in the appendix for mean and scale parameter values).
Consequently, irradiance () and demand coefficients () replace the random variable X seen through Equations 16-27, and modulate the behavior of the PV generation and the demand respectively. Although the demand is typically defined constant for each node in Power Flow Analysis , in this article the demand through every node is regulated evenly by the random coefficient as it is described in Equation 28.
2.4.1. PV Location modelling
The optimization problem in this article includes the allocation (size and locate) of a PV unit in the system. The location is represented by a boolean variable that indicates if a PV unit is to be installed in a node or not (Equation 29), whereas the size of the PV unit is modeled to deliver active power modulated linearly by the irradiance coefficient () with a constrained capacity. The rated capacity of the PV unit can be fully utilized if the irradiance measures (in per unit this would be the base value), although such level was not registered in the measurements. The linearized expression for the power delivered by the PV unit including its location is shown in Equations 30, 31, and 32.
Where the variables and represent the location of the PV, the modulated power and the effective power of the located PV unit, respectively, and the parameters and stand for the maximum number of PV units to be installed and their maximum capacity, respectively.
2.4.2. PV-Capacity-Irradiance interface
The interface between the PV unit power , its capacity and the irradiance is expressed in Equation 33. This interface is named hereafter PCI.
This non-linear expression is linearized using piece-wise linear approximations. The variables and are sectioned in k and m equidistant points from their minimum until their maximum values, giving place to coefficients interpolating the sectioned values in each variable, as it is shown in Equations 34, 35 and 36.
Where and are the set of sectioned values for the PV capacity, Irradiance and the resulting modulated power, respectively. The set of is a Special Ordered Set 2 (SOS2), for which only two adjacent values (in rows and columns) can be non-zero and its whole sum is 1 (Equation 37). To ensure that only two adjacent rows and columns can be non-zero two additional SOS2 sets are defined (one set for rows, the other for columns) such that the sum of their values is also 1, as observed in equations 38 and 39.
2.5. Test systems
For this article, the data of two distribution systems parameterize the AC-OPF formulations: The IEEE33-bus system (hereafter named I33) and the modelled distribution network for the neighborhood "Juan 23" (hereafter named J23) located in San Andres Island (Colombia). J23 system was modelled from data provided by the EM&D research group. The I33 system has a total demand of 3715 and 2300 with 210.9876 power losses (see system data in [40]) with a rated voltage of 12.66 , whereas the J23 system, with 13.6 rated voltage, totals 1302 and 593 in demand and 31.30 in power losses (see system data in Table A3 in the Appendix). Each respective rated voltage and 1 (for both systems) are used as base values. If a multi-period Power Flow Analysis (see Equation 13) is carried out with the demand following the mean averaged hourly profile ( in Table 1), then the losses sum up 1.51 for the I33 system and 337.25 for the J23 system. As can be observed in Figure 2, the I33 and J23 systems have radial and radial/ring configurations respectively.
2.6. Deterministic AC-OPF model
To set reference OPF results, the problem of locating and sizing a PV unit will be also considered deterministically. To do so, the mean profiles for irradiance and demand coeficients () will be included in the formulation to modulate demand and PV power injections. This model is much simpler than the stochastic one since the AC-OPF would not include the probability expressions in the objective function nor the PV-Irradiance-Capacity interface defined before, but only the PV location modelling. This model is described in Equation 44.
2.7. Stochastic AC-OPF model
The formulation including objective function with Equation 20 (RPO) is intended to obtain the maximum probability values within a 10 % range, whereas the AC-OPF with Equations 26 and 27 in the objective (VPO) is intended to find an operating point by minimizing the demand, and maximizing DER injections while maximizing probabilities in both random variables. Therefore, two OPF problems are defined (RPO and VPO), for two test systems (I33 and J23). The complete OPF considering each case’s objective function and some additional operational constraints is detailed in Equation 45.
2.8. Computational Implementation
The optimization problems defined in this article are implemented in CVXPY [41,42] through Anaconda’s Python distribution [43] and solved with MOSEK [44]. The following parameters (expressed in per unit) were implemented for the applicable simulation: , , , for , for . Solver parameters were kept in their default values.
3. Results
In this section the main results obtained from the defined optimization problems are shown. For each system, the results for the deterministic AC-OPF problem are first outlined, followed by the results for the stochastic formulations (RPO and VPO) respectively. The RPO and VPO probabilities for the mean coefficients are available in Table A5 in the Appendix.
3.1. Results for the I33 system
3.1.1. Deterministic AC-OPF
3.1.2. Stochastic OPF
Simulation results for the I33 test system under RPO (Eq. 19 in the objective function) are summarized in Table 2. The demand coefficients profile and their probabilities are depicted in Figure 3 while the irradiance coefficients profile and their probabilities are shown in Figure 4 (See Table A6 in the appendix for detailed hourly modulating coefficients and their associated probabilities).
For simulations under VPO (Equations 24 and 21 for demand and irradiance respectively in the objective function), results are summarized in Table 3 and detailed with coefficients and probabilities in Table A7. Demand coefficients profile and their probabilities are illustrated in Figure 5 while Irradiance coefficients profile and their probabilities are depicted in Figure 6.
3.2. Results for the J23 system
3.2.1. Deterministic AC-OPF
3.2.2. Stochastic OPF
Simulation results for the J23 test system under RPO (Eq. 19 in the objective function) are summarized in Table 5. The profiles outlined by Demand coefficients and their probabilities are depicted in Figure 7 while the profiles for irradiance and probabilities are shown in Figure 8 (See Table A8 in the appendix for detailed hourly modulating coefficients and their associated probabilities).
For simulations under VPO (Equations 24 and 21 for demand and irradiance respectively in the objective function), results are summarized in Table 6 and detailed with coefficients and probabilities in Table A9. Profiles shaped from Demand coefficients and their probabilities are illustrated in Figure 9 while the profiles constructed from Irradiance coefficients and their probabilities are shown in Figure 10.
4. Discussion
For the I33 system, it could be observed from results that the averaged probabilities during the day are increased by around 1.4 % (RPO) and 35 % (VPO) for demand and by around 1.1 % (RPO) and 20 % (VPO) for irradiance compared to the deterministic case. The location of the PV unit changed from node 8 to nodes 17 and 12 under RPO and VPO respectively. Its capacity was kept near the upper bound in the deterministic and VPO cases, while it suffered an reduction with the RPO, suggesting that, even under uncertainty, DER units should be located in the most congested branch (the active power load is distributed to in branch 2-6, in branch 7-18, in branch 19-22, in branch 23-25 and in branch 26-33). The minimum power loss was achieved in the deterministic case, followed by a increase for the RPO and a increase for the VPO, approximately, showing how sensitive can be the analysis to uncertain values: Although demand and irradiance profiles suffered small deviations compared to the expected values, the system losses were affected much more negatively compared to the improvements gained in probabilities, even when deploying DER optimally. The results for the VPO can be interpreted as an approximation to the worst-case scenario since, as observed in Figure 5 and Figure 6, the obtained demand and irradiance coefficients are considerably higher and lower than the mean values, respectively, and both probabilities (to have lower demand and greater irradiance coefficients) are very high ( for demand and for irradiance on average). In other words, the probability of the losses being lesser than is on an hourly average greater than , compared to the on hourly average resulted from estimating the random variables to the mean values. In contrast to the RPO analysis, a drastic increase in power losses was accompanied with increases in probabilities comparing with the deterministic case. These results allow also the analysis of other operating constraints, such as voltage magnitudes. It could be observed, that the operational voltage limit constraint might be violated (especially the lower bound) if considering scenarios with worsened conditions, as in VPO, i.e., if the demand coefficients from VPO were considered for power flow analysis (without PV), the lower bound would not be complied (see Table 3). However, the installation of the PV unit kept voltage magnitudes within the lower bound. Evidently, tighter bounds in voltages might take the problem to infeasibility regions or, in a practical scenario, make the grid non-compliant of operative constraints under uncertainty, which might represent economic losses due to penalties. For the J23 system, results were somewhat similar to the I33 ones. RPO and VPO probabilities increased by and for demand and by and for irradiance respectively compared to the deterministic case. This indicates that probabilities are not very affected by the system even though the random variables affect directly the power losses, which at the same time depends on the grid’s configuration and its parameters (size, redundancy, line impedances, load distribution, voltage level). As in the I33, the PV units were located in the most congested branch, in contrast to the deterministic case that located it in the second most congested branch (the active power load is distributed to in branch 2-11, in branch 12-25, in branch 26-43 and in branch 28-32). Regarding PV capacity, an important reduction happened when comparing both systems. In the I33 system the PV capacity was kept capped but in the RPO case when it was reduced , yet in the J23, PV capacity reached near the of the maximum capacity in the deterministic case, and decreased under uncertainty to the of the maximum with both RPO and VPO approaches. Similar to the results for the I33 system, the J23 system gathered the minimum energy losses from the deterministic case, and were progressively worsening under uncertainty ( and increases for the RPO and VPO respectively). Probabilities were increased likewise as in the analyses for the I33. Regarding voltages, the J23 system has significantly lower losses than the I33 system in the power flow analysis (PF). This is also reflected in the voltage envelopes shown in the different OPF analysis, where the minimum voltage remained almost unaltered within the range even in cases with greater demand and lower irradiance (VPO). This explains that the J23 grid has the capability to sustain greater loads under uncertainty, possibly with greater hosting capacities, while operating safely. In Figure A1 and Figure A2 for the I33, and Figure A3 and Figure A4 for the J23 on the Appendix, it is possible to observe how the probability of coefficient profiles under RPO and VPO is compared to the probability under the opposite approach, i.e. the probability of the demand and irradiance profiles obtained from RPO compared to the probability of those profiles under VPO and vice-versa. Those illustrations show that probabilities are greater when calculated with the profiles obtained from their respective analysis than with the opposite. However, for irradiance profiles, the differences between the probabilities are noticeable, especially when comparing VPO probabilities, indicating that RPO irradiance coefficients and mean values are overestimated. Whereas, the VPO profiles show lower RPO probabilities but establish a case with higher probabilities of being more favorable, since the range in which the random variable could fall is much wider. To summarize, mean value estimations have lower probabilities, resulting in important power loss underestimations, whereas, under the RPO approach, a better estimation is obtained even though the irradiance is clearly overestimated. Under the VPO approach, an even more probable case is defined by estimating worsened conditions for the objective, showing that both Deterministic and RPO approaches underestimate the losses with less likely conditions. Finally, the formulation of the proposed convex stochastic programs, allowed to obtain global optimal solutions. Although most of the variables in the proposed stochastic programs are integer, the problem size (directly related to the grid’s size) hadn’t had any considerable impact on the solving time. On the contrary, for the I33 stochastic AC-OPFs, it took longer to find the solution. An explanation for this is that variations in the variables within the PCI (which contains the majority of integer variables and has the same dimensions for each test case), produce greater effects in power losses due to line lengths (impedance) and distribution of greater demands, requiring more intensive Branch-and-Bound steps until the difference between the objective upper and lower bounds, respectively set by the improvements in root relaxation and the incumbent solution, lies within the parameterized relative gap.
5. Conclusions
In this article, two alternatives are proposed to handle uncertainties on convex AC-OPF formulations, whose random variables are based on real measurements of demand and irradiance fitted to the logistic distribution. The effective PV power capability is related to the irradiance and to its capacity, by means of a non-linear expression. To linearize it, a PV-Capacity-Irradiance (PCI) interface was implemented using piece-wise linear approximations. One of the proposed approaches is called Range-Probability Optimization (RPO), and intends to maximize the probability of occurrence for random variables within a range of uncertainty, which is defined as a parameter (). The second approach is called Value-Probability Optimization (VPO), in which the values of the random variables are optimized along with the maximization of their probabilities. For the VPO to have sense, and to avoid trivial solutions, random variables and the probability functions are assigned following the sense of the main objective (minimize power losses). Thus, The demand is minimized while maximizing the probability of having lower or equal demand and the irradiance is to be maximized while maximizing the probability of having greater irradiance. The proposed approaches were implemented for two distribution networks: The IEEE 33-bus test system and the modelled distribution network in the "Juan 23" neighborhood in San Andres Island (Colombia), and tested against the deterministic case whose parameters follow the expected values of the distribution. The problem of allocating DER in distribution networks was modified to include uncertainty under RPO and VPO approaches, and as a result, it was possible to observe the problem’s sensitivity to uncertainty. With the RPO, although the variation in the averaged probabilities for demand and irradiance coefficients is very small and the location of the PV unit remained in the most congested branch, the capacity of the PV unit was decreased due to overestimated irradiance and underestimated demand, resulting in increased losses compared to the deterministic case. Meanwhile, with the VPO approach, by increasing the probabilities, the resulting profiles for demand and irradiance coefficients showed negative behaviors towards the minimization of power losses, suggesting that VPO approximates the problem to an scenario with worsened conditions without being the worst-case scenario, which provides robust information for stochastic decision making without underestimating (or overestimating) random variables, or over-sizing DER installations, as the worst-case scenario would suggest. Regarding computational efficiency, the proposed stochastic formulations resulted in the collection of global optimal solutions due to convexity, and the inclusion of mixed-integer expressions hadn’t the expected impact on computation times for combinatorial problems, since systems with bigger size, i.e. J23, were actually solved faster, which is explained by a greater sensitivity of the objectives to the integer variables in systems with greater base losses and deviations in bus voltages, such as in the I33. As future work, it is proposed to perform different RPO analyses varying the range width (), and test the VPO probability of the resulting irradiance profiles to see if the differences between both approaches can be narrowed. Considering that Energy Storage Systems (ESS) are usually implemented in power systems to overcome uncertainties in DER, it is proposed to test both VPO and RPO approaches in the allocation of DER and ESS resources, and test if ESS has effects on probabilities. Additionally, it can be interesting to assign different demand profiles following geographic demand characteristics in the network and to fit the demand and irradiance measured data to other distribution functions to see its impact on the convexity of the formulations and on results themselves. Since the proposed formulations are convex MI-SOCP formulations, it can be interesting to find solutions using meta-heuristic techniques for each system, with convex and non-convex formulations, and see the differences in solution quality and computation times.
Author Contributions
Conceptualization, D.M.O and J.R.G.; Methodology, D.M.O and J.R.G.; investigation, D.M.O;writing—original draft preparation, D.M.O; writing—review and editing, D.M.O and J.R.G.; funding acquisition, J.R.G.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Colombian Ministerio de Ciencia y Tecnología and Universidad Nacional de Colombia under grant “Becas del bicentenario, Corte 1: Formación de capital humano de alto nivel Universidad Nacional de Colombia” [BPIN:2019000100026] and Electrical Machines and Drives (EM&D) from Universidad Nacional de Colombia and Project Think Green on the island of San Andres [BPIN: 2016000100002 EEDAS ESP].
Data Availability Statement
Additional data can be available on request, by contacting the corresponding author of this manuscript.
Acknowledgments
The authors would like to aknowledge the contributions of the EM&D group to this article, particularly Alvaro Zambrano and Santiago Toledo for providing the San Andres demand characterization data and the J23 data for its modelling. We would like to thank PhD. Gustavo Bula and PhD. Eduardo Mojica at Universidad Nacional for the insightful conversations regarding convex optimization.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AC-OPF | AC-Optimal Power Flow |
| AOA | Arithmetic Optimization Algorithm |
| BIM | Bus-Injection Model |
| CDF | Cumulative Probability Function |
| DER | Distributed Energy Resources |
| EM&D | Electrical Machines And Drives |
| GWO | Grey Wolf Optimizer |
| HHO | Harris Hawks Optimizer |
| hHHO-AOA | Hybrid HHO-AOA |
| I33 | IEEE 33-bus system |
| IDEAM | Instituto de Hidrología, Meteorología y Estudios Ambientales |
| IoT | Internet of Things |
| IT | Information Technologies |
| J23 | Juan 23 Distribution Network |
| MIGWO | Mutation Improved Grey Wolf Optimizer |
| MI-SOCP | Mixed-Integer Second Order Conic Program |
| PCI | PV-Capacity-Irradiance interface |
| Probability Density Function | |
| PF | Power Flow |
| PV | Photovoltaic Energy |
| QCQP | Quadratically Constrained Quadratic Problem |
| RPO | Range Probability Optimization |
| SOC | Second Order Conic |
| SOS2 | Special Ordered Set 2 |
| VPO | Value-Probability Optimization |
Appendix A
Appendix A.1
Table A1.
Fitted parameters of logistic Distribution for Demand and Irradiance
| h | ||||
|---|---|---|---|---|
| 1 | 0.1196 | 0.0567 | 0 | 0 |
| 2 | 0.1165 | 0.0551 | 0 | 0 |
| 3 | 0.1152 | 0.0541 | 0 | 0 |
| 4 | 0.1138 | 0.0534 | 0 | 0 |
| 5 | 0.1151 | 0.0541 | 0 | 0 |
| 6 | 0.1181 | 0.0573 | 0 | 0 |
| 7 | 0.1321 | 0.0704 | 0 | 0 |
| 8 | 0.2111 | 0.1248 | 0.0197 | 0.0082 |
| 9 | 0.4919 | 0.2152 | 0.1228 | 0.0311 |
| 10 | 0.8634 | 0.1519 | 0.3214 | 0.0646 |
| 11 | 1.0000 | 0.1208 | 0.5064 | 0.0963 |
| 12 | 0.9578 | 0.1064 | 0.6537 | 0.1102 |
| 13 | 0.7464 | 0.1427 | 0.7540 | 0.1243 |
| 14 | 0.5029 | 0.1902 | 0.7804 | 0.1315 |
| 15 | 0.6278 | 0.1950 | 0.7478 | 0.1304 |
| 16 | 0.8580 | 0.1220 | 0.6398 | 0.1256 |
| 17 | 0.8989 | 0.1170 | 0.4761 | 0.1060 |
| 18 | 0.8428 | 0.1346 | 0.2965 | 0.0713 |
| 19 | 0.6953 | 0.1918 | 0.1180 | 0.0370 |
| 20 | 0.5249 | 0.1938 | 0.0135 | 0.0068 |
| 21 | 0.2884 | 0.1268 | 0 | 0 |
| 22 | 0.1706 | 0.0833 | 0 | 0 |
| 23 | 0.1397 | 0.0669 | 0 | 0 |
| 24 | 0.1237 | 0.0592 | 0 | 0 |
Table A3.
J23 distribution network model data.
| i | j | ||||
|---|---|---|---|---|---|
| 1 | 2 | 0.16715 | 0.10971 | 0.03129 | 0.01425 |
| 2 | 3 | 0.03768 | 0.02472 | 0.03129 | 0.01425 |
| 3 | 4 | 0.01704 | 0.01118 | 0.03129 | 0.01425 |
| 4 | 5 | 0.02891 | 0.01897 | 0.02086 | 0.00950 |
| 5 | 6 | 0.01808 | 0.01186 | 0.03129 | 0.01425 |
| 6 | 7 | 0.02551 | 0.01674 | 0 | 0 |
| 7 | 8 | 0.01723 | 0.01130 | 0.04694 | 0.02138 |
| 8 | 9 | 0.02391 | 0.01569 | 0.03129 | 0.01425 |
| 11 | 10 | 0.01067 | 0.00700 | 0 | 0 |
| 7 | 11 | 0.02905 | 0.01906 | 0.03129 | 0.01425 |
| 10 | 12 | 0.01181 | 0.00775 | 0.03129 | 0.01425 |
| 12 | 13 | 0.01027 | 0.00674 | 0.04694 | 0.02138 |
| 13 | 14 | 0.01506 | 0.00988 | 0.04694 | 0.02138 |
| 14 | 15 | 0.02613 | 0.01715 | 0.03129 | 0.01425 |
| 15 | 16 | 0.00610 | 0.00400 | 0 | 0 |
| 16 | 17 | 0.00528 | 0.00346 | 0.03129 | 0.01425 |
| 17 | 18 | 0.00278 | 0.00182 | 0 | 0 |
| 18 | 19 | 0.01193 | 0.00783 | 0.04694 | 0.02138 |
| 19 | 20 | 0.00741 | 0.00486 | 0.04694 | 0.02138 |
| 16 | 21 | 0.00827 | 0.00543 | 0.04694 | 0.02138 |
| 23 | 22 | 0.21027 | 0.13798 | 0.04694 | 0.02138 |
| 18 | 23 | 0.03503 | 0.02298 | 0.04694 | 0.02138 |
| 23 | 24 | 0.01012 | 0.00664 | 0.03129 | 0.01425 |
| 24 | 25 | 0.00371 | 0.00243 | 0 | 0 |
| 25 | 26 | 0.02282 | 0.01497 | 0.02086 | 0.00950 |
| 26 | 27 | 0.01808 | 0.01186 | 0 | 0 |
| 25 | 28 | 0.01047 | 0.00687 | 0.04694 | 0.02138 |
| 28 | 29 | 0.01921 | 0.01261 | 0.04694 | 0.02138 |
| 29 | 30 | 0.00544 | 0.00357 | 0.01877 | 0.00855 |
| 29 | 31 | 0.00751 | 0.00493 | 0.06259 | 0.02850 |
| 31 | 32 | 0.00699 | 0.00459 | 0.04694 | 0.02138 |
| 27 | 33 | 0.00699 | 0.00459 | 0.04694 | 0.02138 |
| 27 | 34 | 0.03341 | 0.02193 | 0.03129 | 0.01425 |
| 37 | 35 | 0.00931 | 0.00611 | 0.03129 | 0.01425 |
| 35 | 36 | 0.01037 | 0.00680 | 0.03129 | 0.01425 |
| 34 | 37 | 0.01782 | 0.01169 | 0 | 0 |
| 37 | 38 | 0.00618 | 0.00405 | 0.03129 | 0.01425 |
| 38 | 39 | 0.01395 | 0.00915 | 0.02086 | 0.00950 |
| 39 | 40 | 0.00917 | 0.00602 | 0.04694 | 0.02138 |
| 40 | 41 | 0.02503 | 0.01643 | 0 | 0 |
| 41 | 42 | 0.01629 | 0.01069 | 0.04694 | 0.02138 |
| 41 | 43 | 0.01463 | 0.00960 | 0.03129 | 0.01425 |
| 10 | 43 | 0.01384 | 0.00908 | 0.03129 | 0.01425 |
Table A5.
Operation coefficients and Probabilities for mean profiles (Table A1) according to Equations 19 and 22 for demand and irradiance respectively.
| h |
|
|
|
|
|---|---|---|---|---|
| 1 | 0.1050 | 0.5000 | 1.0000 | 1.0000 |
| 2 | 0.1052 | 0.5000 | 1.0000 | 1.0000 |
| 3 | 0.1060 | 0.5000 | 1.0000 | 1.0000 |
| 4 | 0.1061 | 0.5000 | 1.0000 | 1.0000 |
| 5 | 0.1059 | 0.5000 | 1.0000 | 1.0000 |
| 6 | 0.1026 | 0.5000 | 1.0000 | 1.0000 |
| 7 | 0.0935 | 0.5000 | 1.0000 | 1.0000 |
| 8 | 0.0843 | 0.5000 | 0.1195 | 0.5000 |
| 9 | 0.1137 | 0.5000 | 0.1950 | 0.5000 |
| 10 | 0.2766 | 0.5000 | 0.2436 | 0.5000 |
| 11 | 0.3915 | 0.5000 | 0.2570 | 0.5000 |
| 12 | 0.4219 | 0.5000 | 0.2882 | 0.5000 |
| 13 | 0.2556 | 0.5000 | 0.2943 | 0.5000 |
| 14 | 0.1314 | 0.5000 | 0.2888 | 0.5000 |
| 15 | 0.1596 | 0.5000 | 0.2790 | 0.5000 |
| 16 | 0.3375 | 0.5000 | 0.2493 | 0.5000 |
| 17 | 0.3662 | 0.5000 | 0.2209 | 0.5000 |
| 18 | 0.3031 | 0.5000 | 0.2050 | 0.5000 |
| 19 | 0.1792 | 0.5000 | 0.1580 | 0.5000 |
| 20 | 0.1346 | 0.5000 | 0.0990 | 0.5000 |
| 21 | 0.1131 | 0.5000 | 1.0000 | 1.0000 |
| 22 | 0.1020 | 0.5000 | 1.0000 | 1.0000 |
| 23 | 0.1040 | 0.5000 | 1.0000 | 1.0000 |
| 24 | 0.1040 | 0.5000 | 1.0000 | 1.0000 |
| 4.3037 | 12.0000 | 2.8975* | 6.5* | |
| 0.1793 | 0.5000 | 0.2228* | 0.5* |
* When irradiance is zero, its probability is not accounted in the sum or the average.
Table A6.
Operation coefficients and Probabilities according Equation 19 obtained from the RPO-OPF on the I33.
Table A6.
Operation coefficients and Probabilities according Equation 19 obtained from the RPO-OPF on the I33.
| h |
|
|
||
|---|---|---|---|---|
| 1 | 0.1613 | 0.1240 | 0 | 1 |
| 2 | 0.1570 | 0.1242 | 0 | 1 |
| 3 | 0.1547 | 0.1248 | 0 | 1 |
| 4 | 0.1528 | 0.1249 | 0 | 1 |
| 5 | 0.1546 | 0.1248 | 0 | 1 |
| 6 | 0.1608 | 0.1219 | 0 | 1 |
| 7 | 0.1875 | 0.1141 | 0 | 1 |
| 8 | 0.310 | 0.1063 | 0.0253 | 0.1368 |
| 9 | 0.6238 | 0.1314 | 0.1375 | 0.2064 |
| 10 | 0.9001 | 0.2839 | 0.3473 | 0.2528 |
| 11 | 1.0184 | 0.3960 | 0.5436 | 0.2656 |
| 12 | 0.9745 | 0.4262 | 0.6917 | 0.2958 |
| 13 | 0.7914 | 0.2642 | 0.7946 | 0.3018 |
| 14 | 0.6166 | 0.1474 | 0.8229 | 0.2959 |
| 15 | 0.7236 | 0.1731 | 0.7921 | 0.2869 |
| 16 | 0.8848 | 0.3436 | 0.6886 | 0.2583 |
| 17 | 0.9207 | 0.3714 | 0.5224 | 0.2310 |
| 18 | 0.8734 | 0.3097 | 0.3333 | 0.2157 |
| 19 | 0.7701 | 0.1910 | 0.1388 | 0.1718 |
| 20 | 0.6282 | 0.1500 | 0.0186 | 0.1188 |
| 21 | 0.3736 | 0.1311 | 0 | 1 |
| 22 | 0.2323 | 0.1214 | 0 | 1 |
| 23 | 0.1890 | 0.1232 | 0 | 1 |
| 24 | 0.1674 | 0.1232 | 0 | 1 |
| 4.6529 | 3.0383* | |||
| 0.1938 | 0.2337* |
* When irradiance is zero, its probability is not accounted in the sum or the average.
Table A7.
Operation coefficients and Probabilities according Equations 25 and 22 (for demand and irradiance respectively) from the VPO-OPF on the I33
| h | ||||
|---|---|---|---|---|
| 1 | 0.2731 | 0.9373 | 0 | 1 |
| 2 | 0.2675 | 0.9391 | 0 | 1 |
| 3 | 0.2645 | 0.9403 | 0 | 1 |
| 4 | 0.2620 | 0.9411 | 0 | 1 |
| 5 | 0.2644 | 0.9404 | 0 | 1 |
| 6 | 0.2726 | 0.9366 | 0 | 1 |
| 7 | 0.3054 | 0.9212 | 0 | 1 |
| 8 | 0.4319 | 0.8542 | 0.0181 | 0.5472 |
| 9 | 0.7025 | 0.7268 | 0.0990 | 0.6821 |
| 10 | 1.0613 | 0.7862 | 0.2553 | 0.7355 |
| 11 | 1.1890 | 0.8269 | 0.4025 | 0.7462 |
| 12 | 1.1455 | 0.8537 | 0.5164 | 0.7765 |
| 13 | 0.9625 | 0.8196 | 0.5910 | 0.7876 |
| 14 | 0.7426 | 0.7790 | 0.6072 | 0.7885 |
| 15 | 0.8557 | 0.7628 | 0.5844 | 0.7776 |
| 16 | 1.0581 | 0.8373 | 0.5064 | 0.7430 |
| 17 | 1.0912 | 0.8380 | 0.3819 | 0.7086 |
| 18 | 1.0395 | 0.8115 | 0.2395 | 0.6899 |
| 19 | 0.8941 | 0.7381 | 0.0996 | 0.6214 |
| 20 | 0.7339 | 0.7461 | 0.0135 | 0.4977 |
| 21 | 0.5057 | 0.8471 | 0 | 1 |
| 22 | 0.3584 | 0.9049 | 0 | 1 |
| 23 | 0.3079 | 0.9251 | 0 | 1 |
| 24 | 0.2810 | 0.9343 | 0 | 1 |
| 20.5486 | 9.1023* | |||
| 0.8561 | 0.7001* |
* When irradiance is zero, its probability is not accounted in the sum or the average.
Table A8.
Operation coefficients and Probabilities according Equation 19 obtained from the RPO-OPF on the J23
Table A8.
Operation coefficients and Probabilities according Equation 19 obtained from the RPO-OPF on the J23
| h |
|
|
||
|---|---|---|---|---|
| 1 | 0.1615 | 0.1240 | 0 | 1 |
| 2 | 0.1572 | 0.1242 | 0 | 1 |
| 3 | 0.1549 | 0.1248 | 0 | 1 |
| 4 | 0.1530 | 0.1249 | 0 | 1 |
| 5 | 0.1548 | 0.1248 | 0 | 1 |
| 6 | 0.1611 | 0.1219 | 0 | 1 |
| 7 | 0.1879 | 0.1141 | 0 | 1 |
| 8 | 0.3157 | 0.1063 | 0.0253 | 0.1368 |
| 9 | 0.6415 | 0.1317 | 0.1374 | 0.2064 |
| 10 | 0.9149 | 0.2846 | 0.3333 | 0.2503 |
| 11 | 1.0295 | 0.3968 | 0.5419 | 0.2657 |
| 12 | 0.9820 | 0.4267 | 0.6904 | 0.2958 |
| 13 | 0.7985 | 0.2644 | 0.7946 | 0.3018 |
| 14 | 0.7209 | 0.1383 | 0.8888 | 0.2804 |
| 15 | 0.7338 | 0.1733 | 0.7777 | 0.2861 |
| 16 | 0.8925 | 0.3439 | 0.6666 | 0.2566 |
| 17 | 0.9294 | 0.3720 | 0.5208 | 0.2310 |
| 18 | 0.8849 | 0.3103 | 0.3286 | 0.2159 |
| 19 | 0.7902 | 0.1916 | 0.1385 | 0.1718 |
| 20 | 0.6448 | 0.1503 | 0.0186 | 0.1188 |
| 21 | 0.3773 | 0.1312 | 0 | 1 |
| 22 | 0.2332 | 0.1214 | 0 | 1 |
| 23 | 0.1894 | 0.1232 | 0 | 1 |
| 24 | 0.1677 | 0.1232 | 0 | 1 |
| 4.6490 | 3.0180* | |||
| 0.1937 | 0.2321* |
* When irradiance is zero, its probability is not accounted in the sum or the average.
Table A9.
Operation coefficients and Probabilities according Equations 25 and 22 (for demand and irradiance respectively) from the VPO-OPF on the J23
| h | ||||
|---|---|---|---|---|
| 1 | 0.2790 | 0.9431 | 0 | 1 |
| 2 | 0.2732 | 0.9447 | 0 | 1 |
| 3 | 0.2700 | 0.9457 | 0 | 1 |
| 4 | 0.2673 | 0.9464 | 0 | 1 |
| 5 | 0.2698 | 0.9458 | 0 | 1 |
| 6 | 0.2786 | 0.9425 | 0 | 1 |
| 7 | 0.3137 | 0.9293 | 0 | 1 |
| 8 | 0.4536 | 0.8745 | 0.0181 | 0.5477 |
| 9 | 0.7675 | 0.7825 | 0.0986 | 0.6850 |
| 10 | 1.1220 | 0.8457 | 0.2221 | 0.8227 |
| 11 | 1.2378 | 0.8773 | 0.3968 | 0.7572 |
| 12 | 1.1827 | 0.8922 | 0.4444 | 0.8698 |
| 13 | 1.0004 | 0.8556 | 0.5554 | 0.8316 |
| 14 | 0.7765 | 0.8081 | 0.6667 | 0.7035 |
| 15 | 0.9014 | 0.8026 | 0.5850 | 0.7769 |
| 16 | 1.0970 | 0.8762 | 0.5019 | 0.7498 |
| 17 | 1.1335 | 0.8813 | 0.3767 | 0.7186 |
| 18 | 1.0912 | 0.8634 | 0.2221 | 0.7395 |
| 19 | 0.9682 | 0.8057 | 0.0989 | 0.6259 |
| 20 | 0.7985 | 0.8040 | 0.0135 | 0.4983 |
| 21 | 0.5322 | 0.8722 | 0 | 1 |
| 22 | 0.3701 | 0.9163 | 0 | 1 |
| 23 | 0.3159 | 0.9329 | 0 | 1 |
| 24 | 0.2874 | 0.9406 | 0 | 1 |
| 21.2298 | 9.3271* | |||
| 0.8845 | 0.7174* |
* When irradiance is zero, its probability is not accounted in the sum or the average.
Figure A1.
RPO probabilities for profiles obtained from RPO and VPO analyses for the I33. Left: Demand. Right: Irradiance. system
Figure A1.
RPO probabilities for profiles obtained from RPO and VPO analyses for the I33. Left: Demand. Right: Irradiance. system
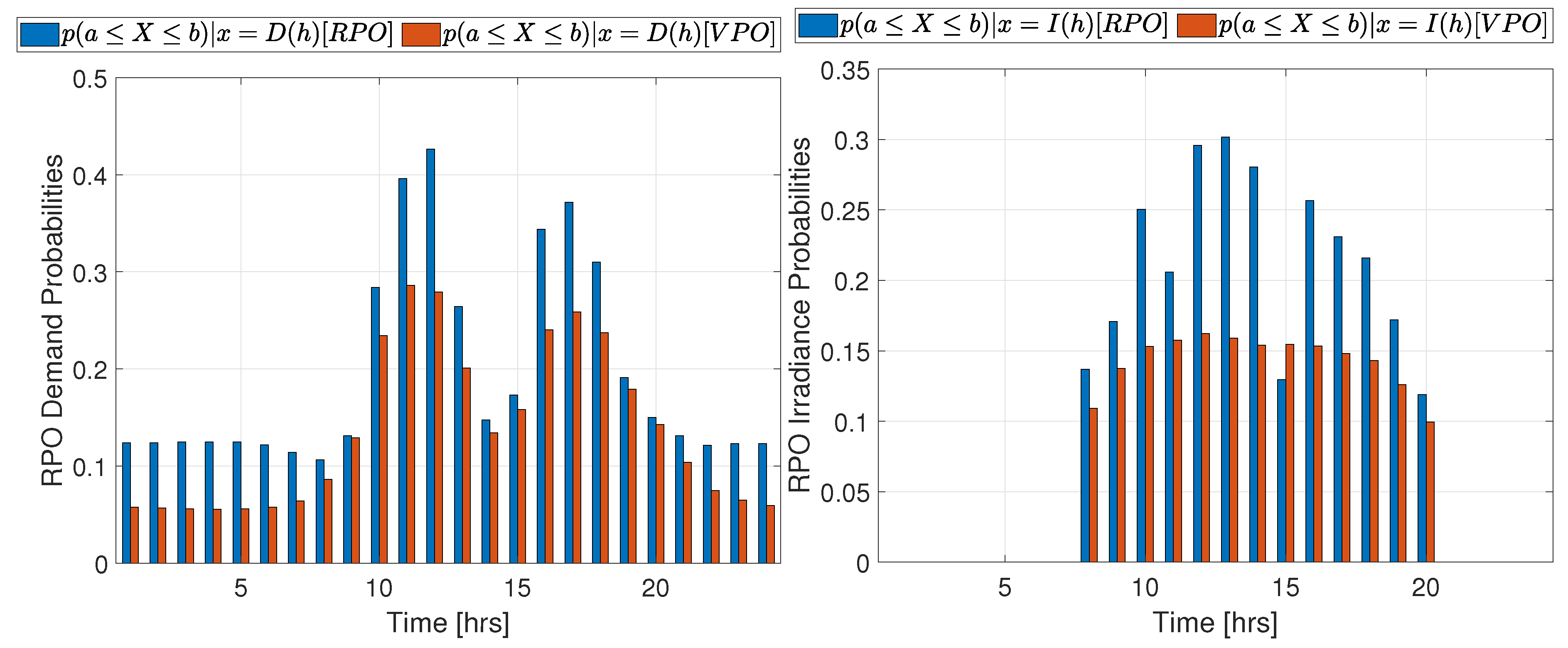
Figure A2.
VPO probabilities for profiles obtained from RPO and VPO analyses for the I33 system. Left: Demand. Right: Irradiance.
Figure A2.
VPO probabilities for profiles obtained from RPO and VPO analyses for the I33 system. Left: Demand. Right: Irradiance.
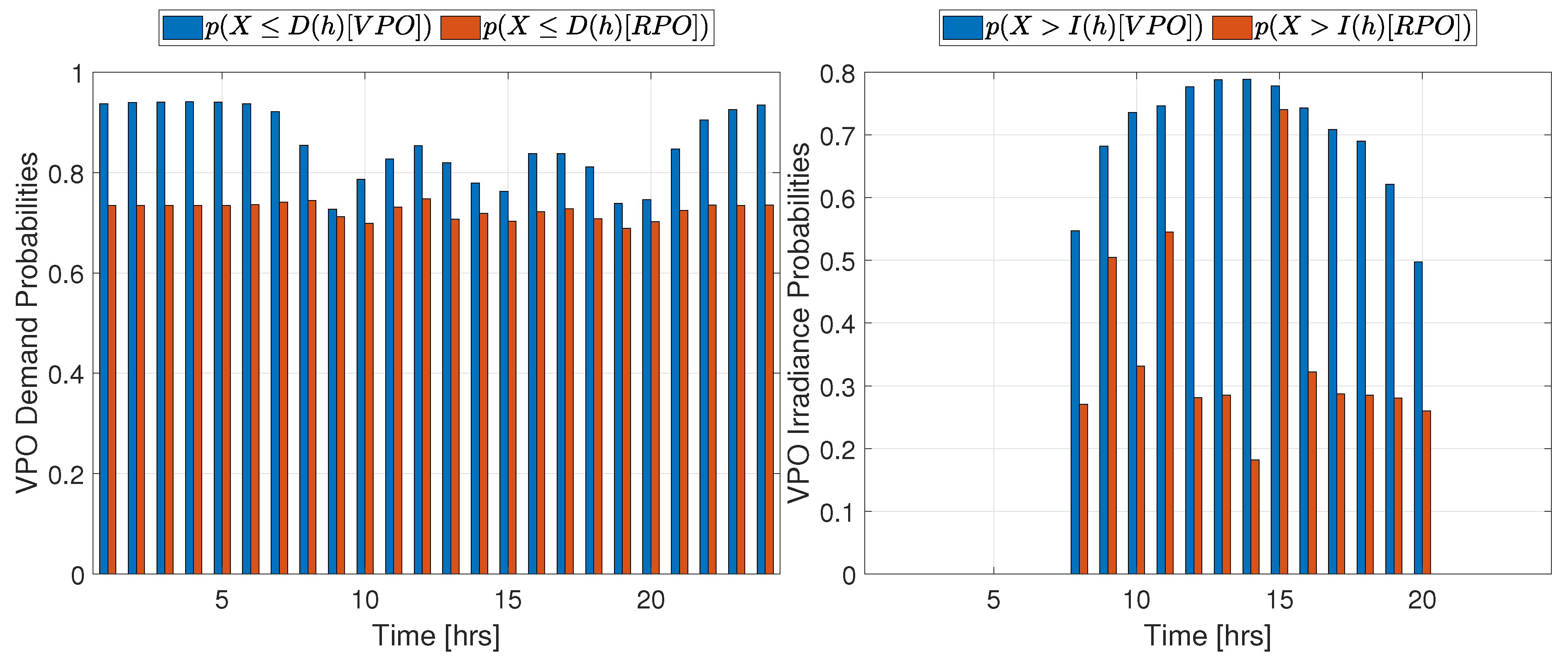
Figure A3.
RPO probabilities for profiles obtained from RPO and VPO analyses for the J23. Left:Demand. Right: Irradiance. system
Figure A3.
RPO probabilities for profiles obtained from RPO and VPO analyses for the J23. Left:Demand. Right: Irradiance. system
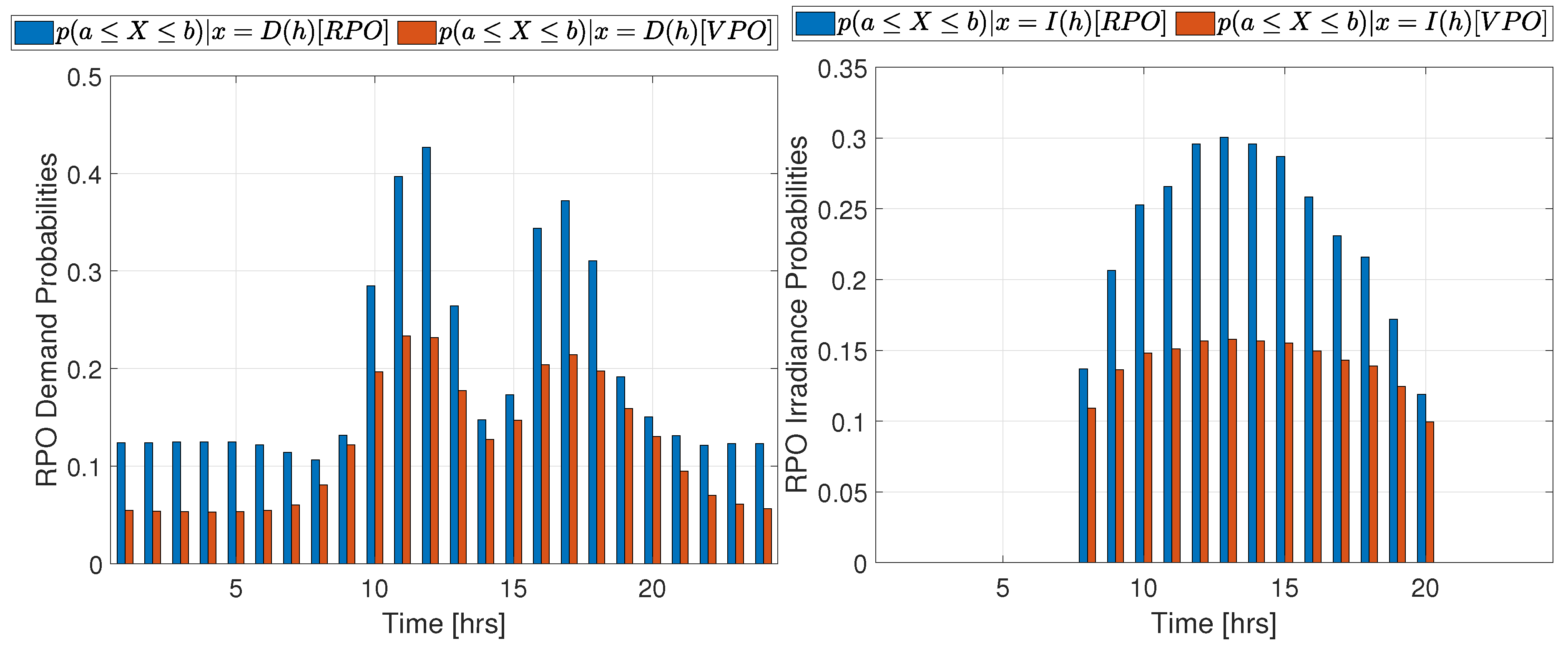
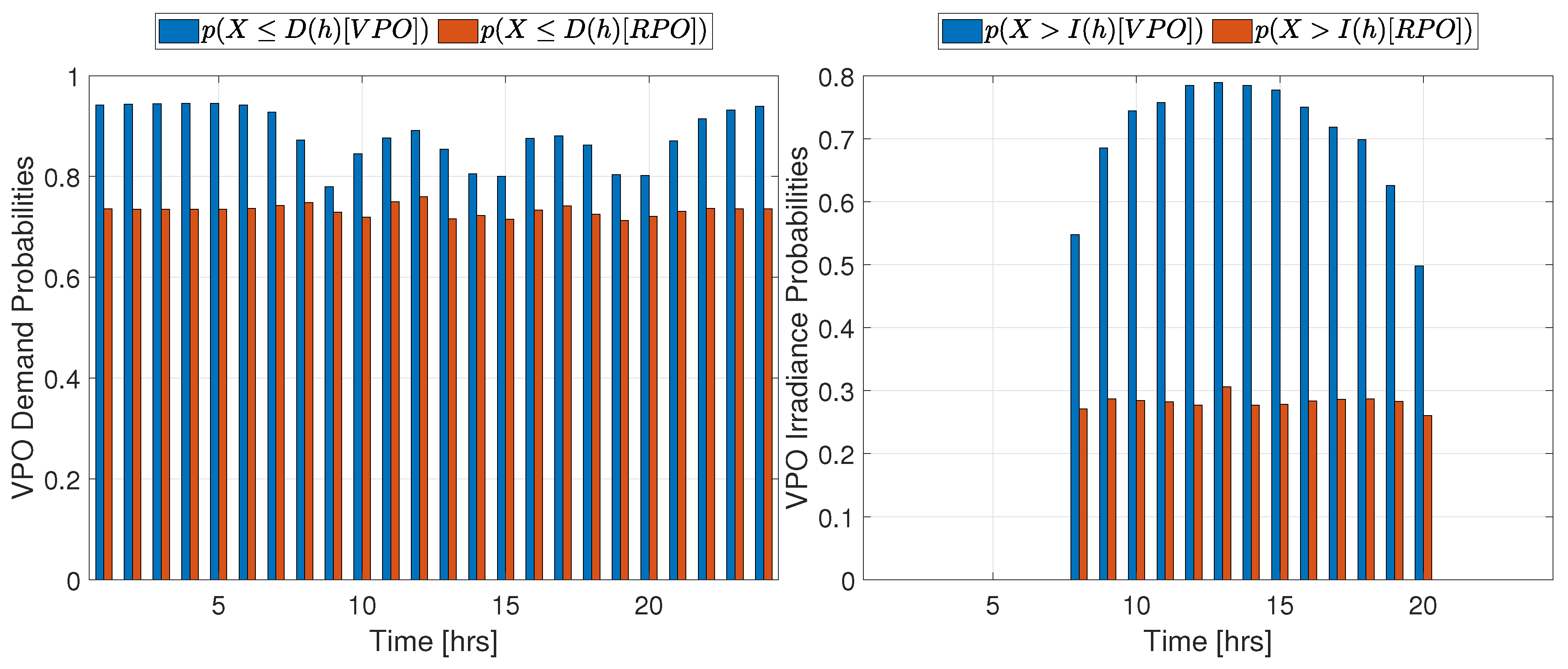
Figure A4.
VPO probabilities for profiles obtained from RPO and VPO analyses for the J23 system. Left: Demand. Right: Irradiance.
Figure A4.
VPO probabilities for profiles obtained from RPO and VPO analyses for the J23 system. Left: Demand. Right: Irradiance.
References
- Kazacos Winter, D.; Khatri, R.; Schmidt, M. Decentralized Prosumer-Centric P2P Electricity Market Coordination with Grid Security. Energies 2021, 14. [Google Scholar] [CrossRef]
- Naughton, J.; Wang, H.; Riaz, S.; Cantoni, M.; Mancarella, P. Optimization of multi-energy virtual power plants for providing multiple market and local network services. Electric Power Systems Research 2020, 189, 106775. [Google Scholar] [CrossRef]
- Wu, Q.; Xue, F.; Lu, S.; Jiang, L.; Huang, T.; Wang, X.; Sang, Y. Integrated network partitioning and DERs allocation for planning of Virtual Microgrids. Electric Power Systems Research 2023, 216, 109024. [Google Scholar] [CrossRef]
- León, L.M.; Romero-Quete, D.; Merchán, N.; Cortés, C.A. Optimal design of PV and hybrid storage based microgrids for healthcare and government facilities connected to highly intermittent utility grids. Applied Energy 2023, 335, 120709. [Google Scholar] [CrossRef]
- Silva, J.A.A.; López, J.C.; Guzman, C.P.; Arias, N.B.; Rider, M.J.; da Silva, L.C. An IoT-based energy management system for AC microgrids with grid and security constraints. Applied Energy 2023, 337, 120904. [Google Scholar] [CrossRef]
- Stekli, J.; Bai, L.; Cali, U.; Halden, U.; Dynge, M.F. Distributed energy resource participation in electricity markets: A review of approaches, modeling, and enabling information and communication technologies. Energy Strategy Reviews 2022, 43, 100940. [Google Scholar] [CrossRef]
- Sánchez, S.B.; Franco, J.F.G.; Agudelo, J.P.; Lemoine, C.A.; Quintero, S.X.C. Methodology for characterization and planning of electricity demand in an isolated zone: Mitú Approach. Transactions on Energy Systems and Engineering Applications 2022, 3, 1–11. [Google Scholar] [CrossRef]
- Bouhorma, N.; Martín, H.; de la Hoz, J.; Coronas, S. A Comprehensive Methodology for the Statistical Characterization of Solar Irradiation: Application to the Case of Morocco. Applied Sciences (Switzerland) 2023, 13. [Google Scholar] [CrossRef]
- Alassery, F.; Alzahrani, A.; Khan, A.I.; Irshad, K.; Kshirsagar, S.R. An artificial intelligence-based solar radiation prophesy model for green energy utilization in energy management system. Sustainable Energy Technologies and Assessments 2022, 52, 102060. [Google Scholar] [CrossRef]
- Mendoza, D.; Garcia, J.R. Multi-Objective Optimization of a Microgrid Considering MBESS Efficiencies, the Initial State of Charge, and Storage Capacity. International Review of Electrical Engineering (IREE) 2022, 17, 273. [Google Scholar] [CrossRef]
- Noori, S.M.; Scott, P.; Mahmoodi, M.; Attarha, A. Data-driven adjustable robust solution to voltage-regulation problem in PV-rich distribution systems. International Journal of Electrical Power and Energy Systems 2022, 141, 108118. [Google Scholar] [CrossRef]
- Tarife, R.; Nakanishi, Y.; Chen, Y.; Zhou, Y.; Estoperez, N.; Tahud, A. Optimization of Hybrid Renewable Energy Microgrid for Rural Agricultural Area in Southern Philippines. Energies 2022, 15, 2251. [Google Scholar] [CrossRef]
- Anestis, A.; Georgios, V. Economic benefits of Smart Microgrids with penetration of DER and mCHP units for non-interconnected islands. Renewable Energy 2019, 142, 478–486. [Google Scholar] [CrossRef]
- Pham, A.T.; Lovdal, L.; Zhang, T.; Craig, M.T. A techno-economic analysis of distributed energy resources versus wholesale electricity purchases for fueling decarbonized heavy duty vehicles. Applied Energy 2022, 322. [Google Scholar] [CrossRef]
- Saini, P.; Gidwani, L. An environmental based techno-economic assessment for battery energy storage system allocation in distribution system using new node voltage deviation sensitivity approach. International Journal of Electrical Power and Energy Systems 2021, 128. [Google Scholar] [CrossRef]
- Wang, Y.; Rousis, A.O.; Qiu, D.; Strbac, G. A stochastic distributed control approach for load restoration of networked microgrids with mobile energy storage systems. International Journal of Electrical Power and Energy Systems 2023, 148, 108999. [Google Scholar] [CrossRef]
- Osorio, D.M.; Garcia, J.R. Optimization of Distributed Energy Resources in Distribution Networks: Applications of Convex Optimal Power Flow Formulations in Distribution Networks. International Transactions on Electrical Energy Systems 2023, 2023, 1–16. [Google Scholar] [CrossRef]
- Mendoza, D. A Review in Bess Optimization for Power Systems. TecnoLógicas 2023, 26. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Elaziz, M.A.; Gandomi, A.H. The Arithmetic Optimization Algorithm. Computer Methods in Applied Mechanics and Engineering 2021, 376, 113609. [Google Scholar] [CrossRef]
- Cetinbas, I.; Tamyurek, B.; Demirtas, M. The Hybrid Harris Hawks Optimizer-Arithmetic Optimization Algorithm: A New Hybrid Algorithm for Sizing Optimization and Design of Microgrids. IEEE Access 2022, 10, 19254–19283. [Google Scholar] [CrossRef]
- Sidea, D.; Picioroaga, I.; Bulac, C. Optimal Battery Energy Storage System Scheduling Based on Mutation-Improved Grey Wolf Optimizer Using GPU-Accelerated Load Flow in Active Distribution Networks. IEEE Access 2021, 9, 13922–13937. [Google Scholar] [CrossRef]
- Huang, S.; Filonenko, K.; Veje, C.T. A Review of The Convexification Methods for AC Optimal Power Flow; A Review of The Convexification Methods for AC Optimal Power Flow. 2019 IEEE Electrical Power and Energy Conference (EPEC) 2019. [Google Scholar]
- Chen, Y.; Xia, B.; Xu, C.; Chen, Q.; Shi, Z.; Huang, S. A Second-Order Cone Relaxation Based Method for Optimal Power Flow of Meshed Networks. 2022 5th International Conference on Energy, Electrical and Power Engineering (CEEPE) 2022, pp. 280–285. [Google Scholar] [CrossRef]
- Ma, M.; Fan, L.; Miao, Z.; Zeng, B.; Ghassempour, H. A sparse convex AC OPF solver and convex iteration implementation based on 3-node cycles. Electric Power Systems Research 2020, 180. [Google Scholar] [CrossRef]
- Rahiminejad, A.; Ghafouri, M.; Atallah, R.; Lucia, W.; Debbabi, M.; Mohammadi, A. Resilience enhancement of Islanded Microgrid by diversification, reconfiguration, and DER placement/sizing. International Journal of Electrical Power and Energy Systems 2023, 147. [Google Scholar] [CrossRef]
- García-Muñoz, F.; Díaz-González, F.; Corchero, C. A novel algorithm based on the combination of AC-OPF and GA for the optimal sizing and location of DERs into distribution networks. Sustainable Energy, Grids and Networks 2021, 27. [Google Scholar] [CrossRef]
- Chen, C.; Shen, X.; Guo, Q.; Sun, H. Robust planning-operation co-optimization of energy hub considering precise model of batteries’ economic efficiency. Energy Procedia 2019, 158, 6496–6501. [Google Scholar] [CrossRef]
- Mahmood, D.; Javaid, N.; Ahmed, G.; Khan, S.; Monteiro, V. A review on optimization strategies integrating renewable energy sources focusing uncertainty factor – Paving path to eco-friendly smart cities. Sustainable Computing: Informatics and Systems 2021, 30, 100559. [Google Scholar] [CrossRef]
- Liao, X.; Liu, K.; Le, J.; Zhu, S.; Huai, Q.; Li, B.; Zhang, Y. Extended affine arithmetic-based global sensitivity analysis for power flow with uncertainties. International Journal of Electrical Power and Energy Systems 2020, 115, 105440. [Google Scholar] [CrossRef]
- Yu, X.; Dong, X.; Pang, S.; Zhou, L.; Zang, H. Energy storage sizing optimization and sensitivity analysis based on wind power forecast error compensation. Energies 2019, 12. [Google Scholar] [CrossRef]
- Yi, Y.; Verbič, G. Fair operating envelopes under uncertainty using chance constrained optimal power flow. Electric Power Systems Research 2022, 213. [Google Scholar] [CrossRef]
- Claessens, B.; Engels, J.; Deconinck, G. Combined stochastic optimization of frequency control and self-consumption with a battery. IEEE Transactions on Smart Grid 2019, 10, 1971–1981. [Google Scholar] [CrossRef]
- Vahid-Ghavidel, M.; Shafie-khah, M.; Javadi, M.S.; Santos, S.F.; Gough, M.; Quijano, D.A.; Catalao, J.P. Hybrid IGDT-stochastic self-scheduling of a distributed energy resources aggregator in a multi-energy system. Energy 2023, 265. [Google Scholar] [CrossRef]
- Moradi, S.; Zizzo, G.; Favuzza, S.; Massaro, F. A stochastic approach for self-healing capability evaluation in active islanded AC/DC hybrid microgrids. Sustainable Energy, Grids and Networks 2023, 33, 100982. [Google Scholar] [CrossRef]
- Singh, V.; Moger, T.; Jena, D. Uncertainty handling techniques in power systems: A critical review. Electric Power Systems Research 2022, 203, 107633. [Google Scholar] [CrossRef]
- Gil-González, W.; Garces, A.; Montoya, O.D.; Hernández, J.C. A mixed-integer convex model for the optimal placement and sizing of distributed generators in power distribution networks. Applied Sciences (Switzerland) 2021, 11, 1–15. [Google Scholar] [CrossRef]
- Ding, T.; Lu, R.; Yang, Y.; Blaabjerg, F. A Condition of Equivalence between Bus Injection and Branch Flow Models in Radial Networks. IEEE Transactions on Circuits and Systems II: Express Briefs 2020, 67, 536–540. [Google Scholar] [CrossRef]
- Low, S.H. Convex relaxation of optimal power flow: A tutorial. Proceedings of IREP Symposium: Bulk Power System Dynamics and Control - IX Optimization, Security and Control of the Emerging Power Grid, IREP 2013 2013, pp. 1–15. [Google Scholar] [CrossRef]
- Venzke, A.; Chatzivasileiadis, S.; Molzahn, D.K. Inexact convex relaxations for AC optimal power flow: Towards AC feasibility. Electric Power Systems Research 2020, 187. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L.F. An exact MINLP model for optimal location and sizing of DGs in distribution networks: A general algebraic modeling system approach. Ain Shams Engineering Journal 2020, 11, 409–418. [Google Scholar] [CrossRef]
- Diamond, S.; Boyd, S. CVXPY: A Python-Embedded Modeling Language for Convex Optimization, 2016.
- Agrawal, A.; Verschueren, R.; Diamond, S.; Boyd, S. A rewriting system for convex optimization problems. Journal of Control and Decision 2018, 5, 42–60. [Google Scholar] [CrossRef]
- Anaconda Software Distribution, 2016.
- ApS, M. MOSEK Optimizer API for Python manual. Version 10.0.40, 2023.
Figure 1.
Logistic distribution fitted parameters
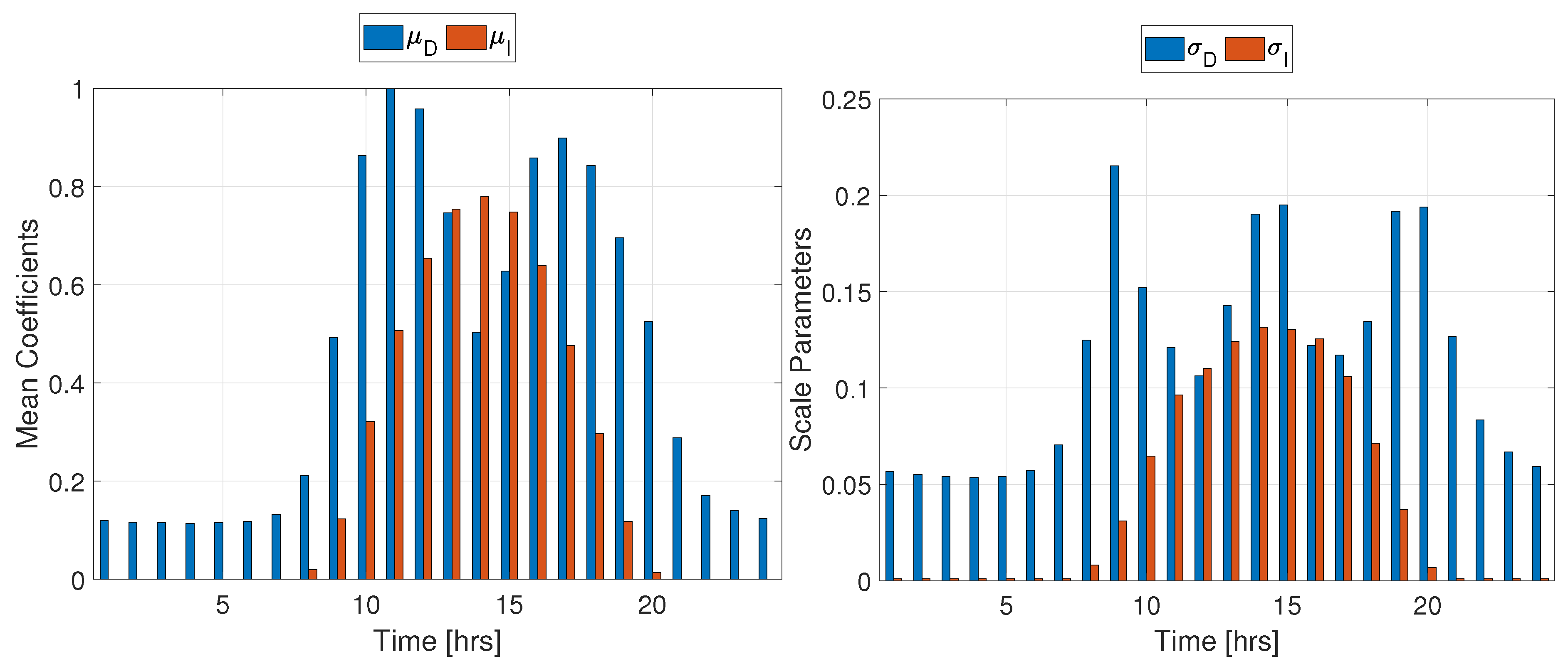
Figure 2.
Grid configuration of test cases: Left I33, right J23.
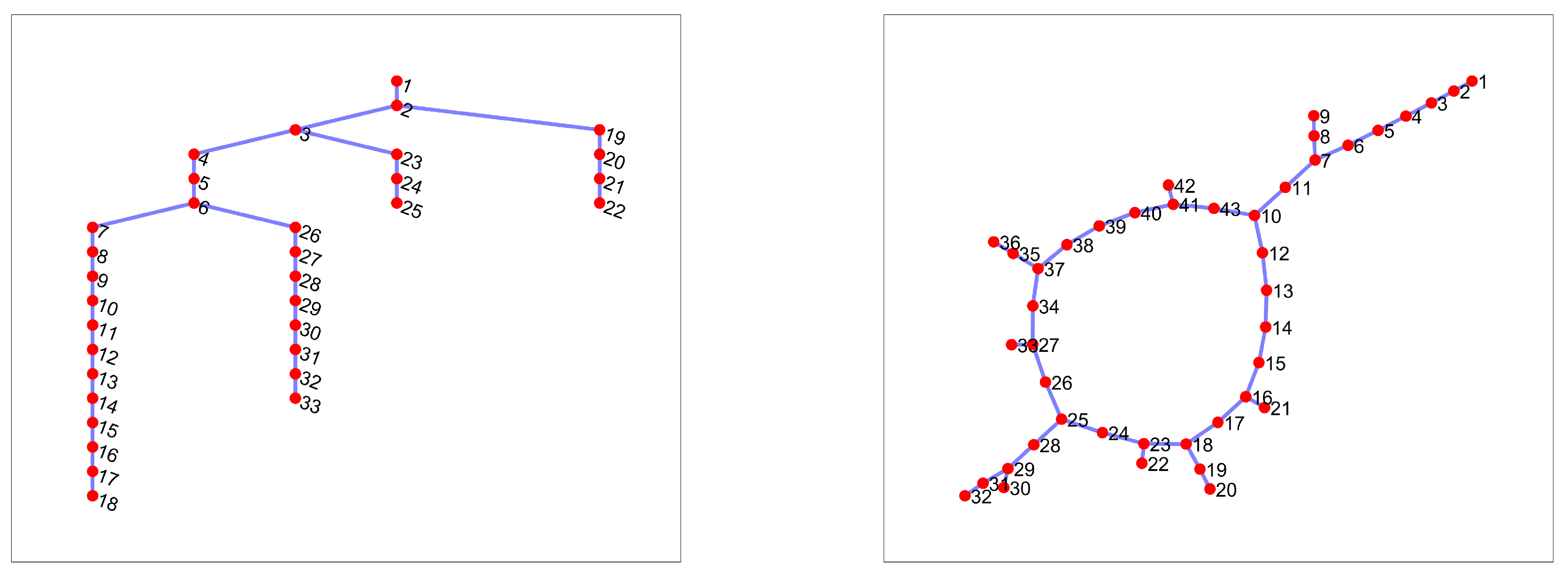
Figure 3.
Demand coefficients and mean values with RPO probabilities.
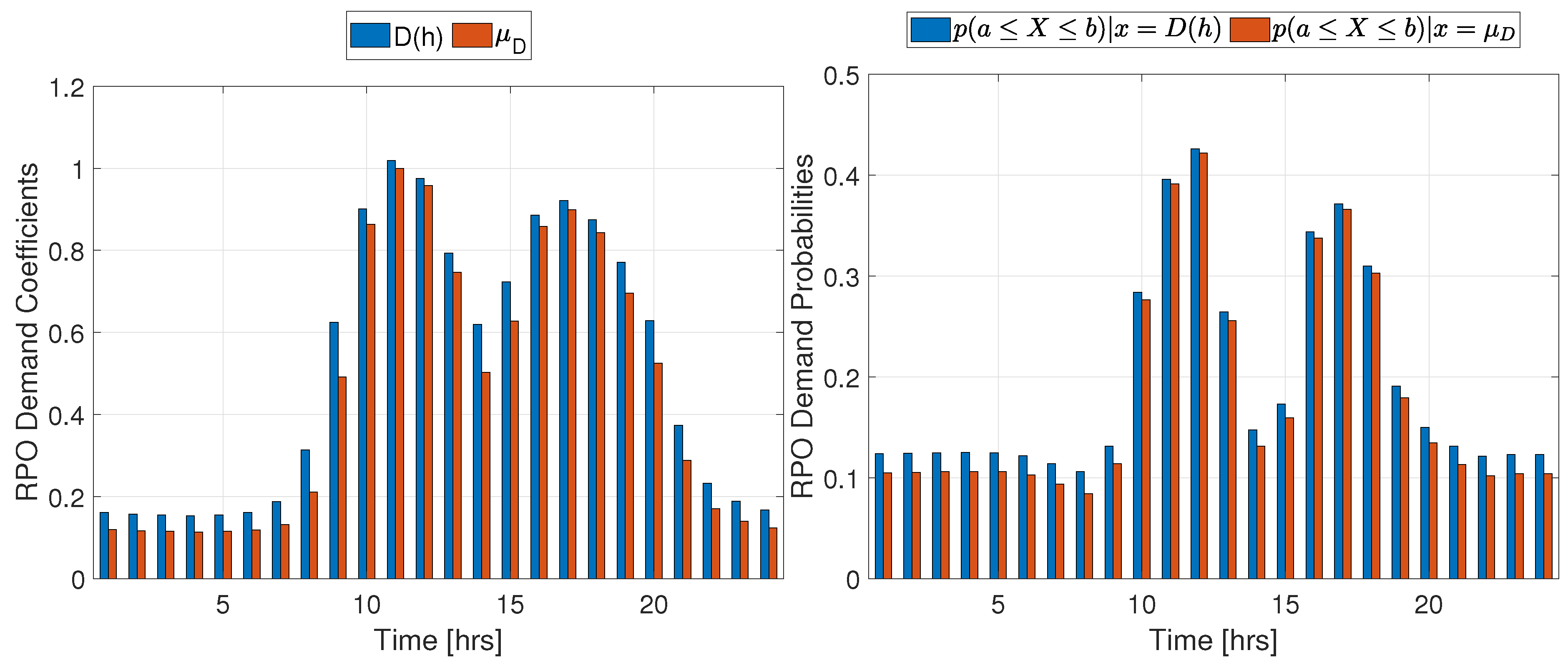
Figure 4.
Irradiance coefficients and mean values with RPO probabilities.
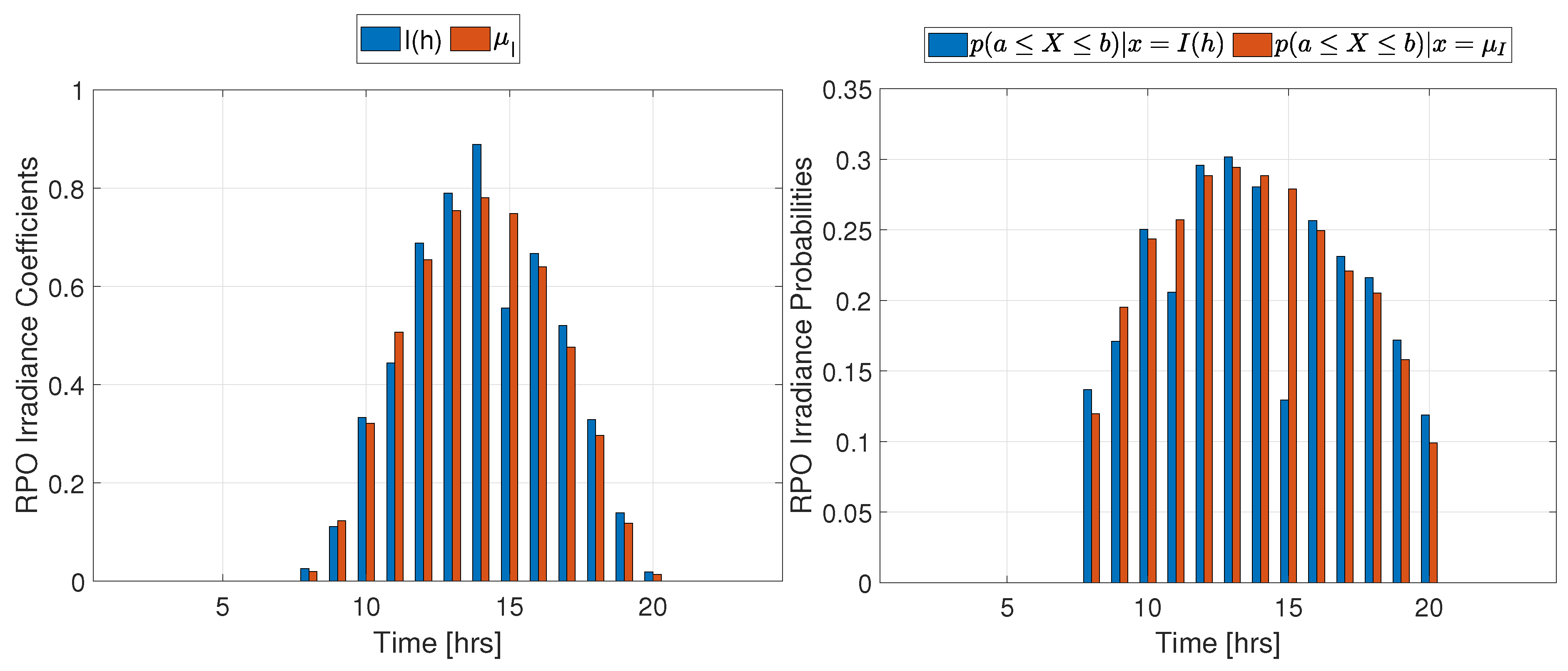
Figure 5.
Demand coefficients and mean values with VPO probabilities
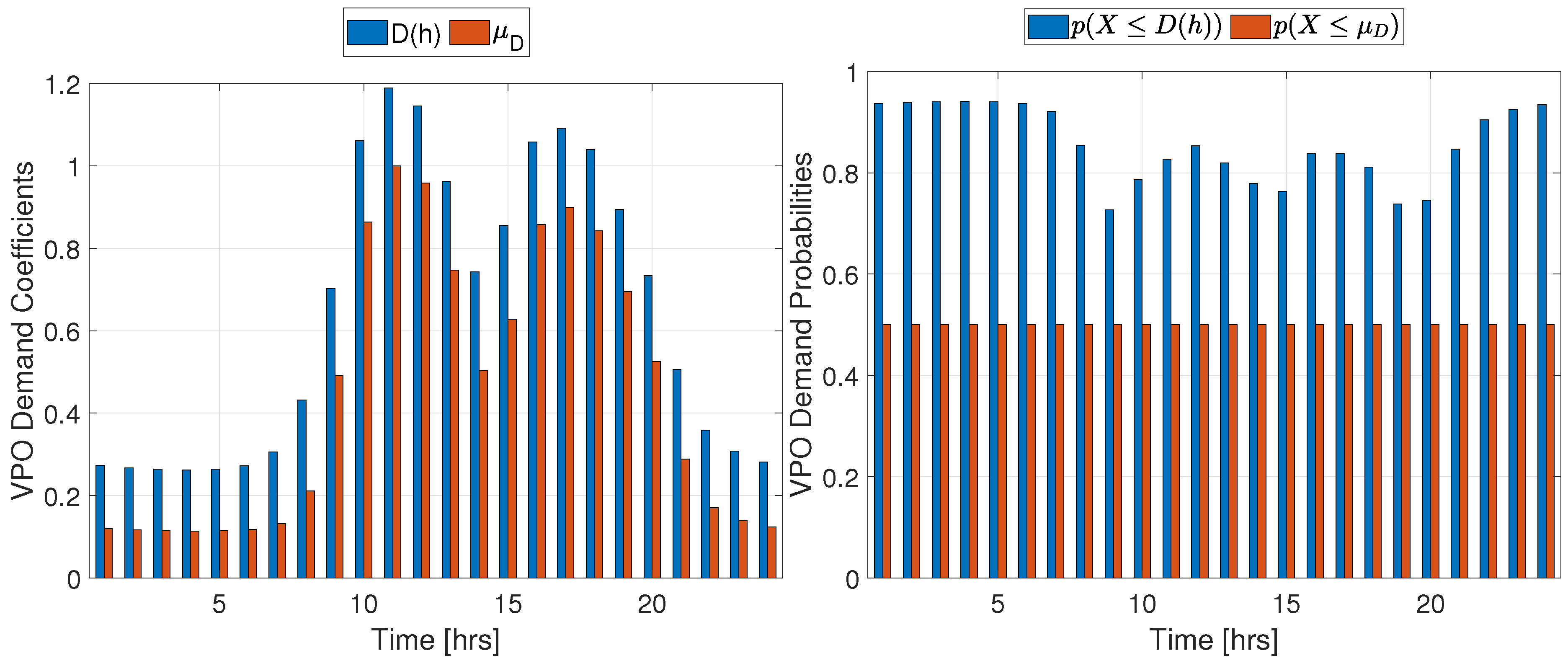
Figure 6.
Irradiance coefficients and mean values with VPO probabilities
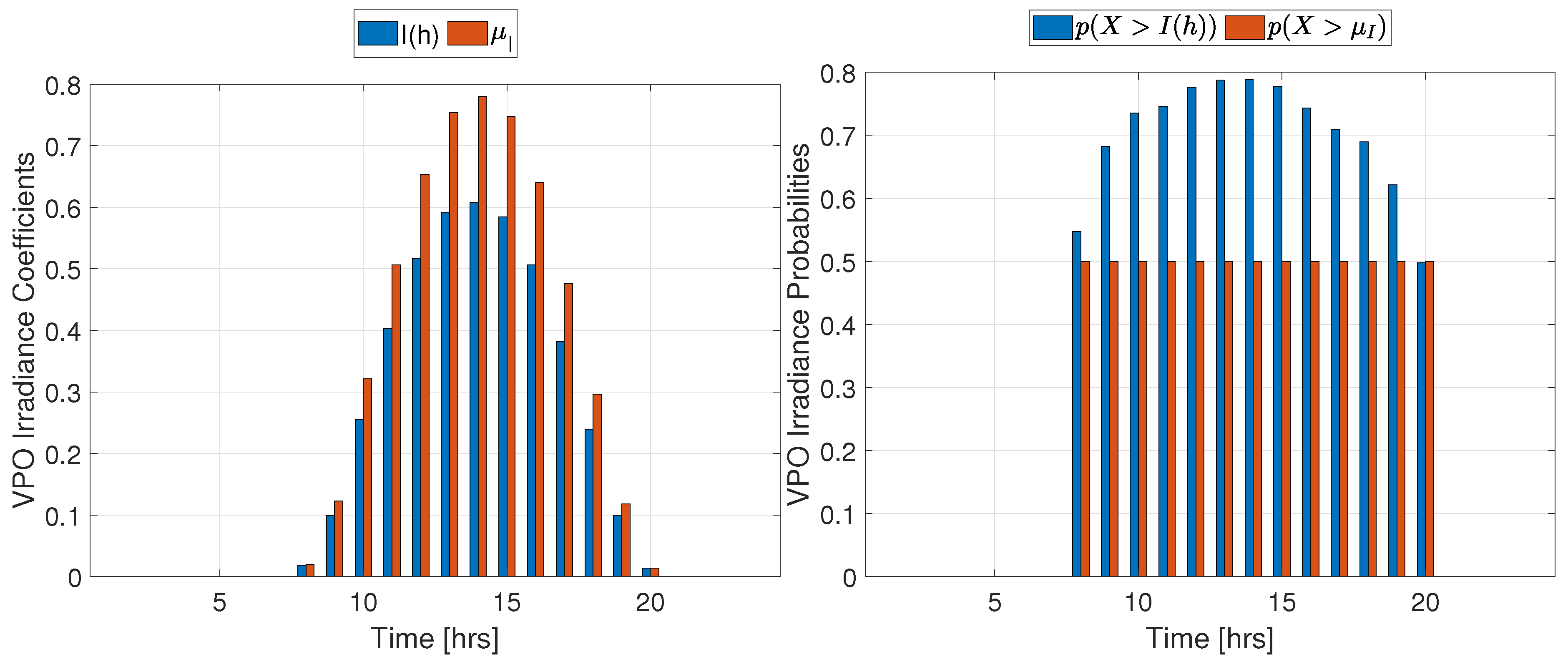
Figure 7.
Demand coefficients and mean values with RPO probabilities.
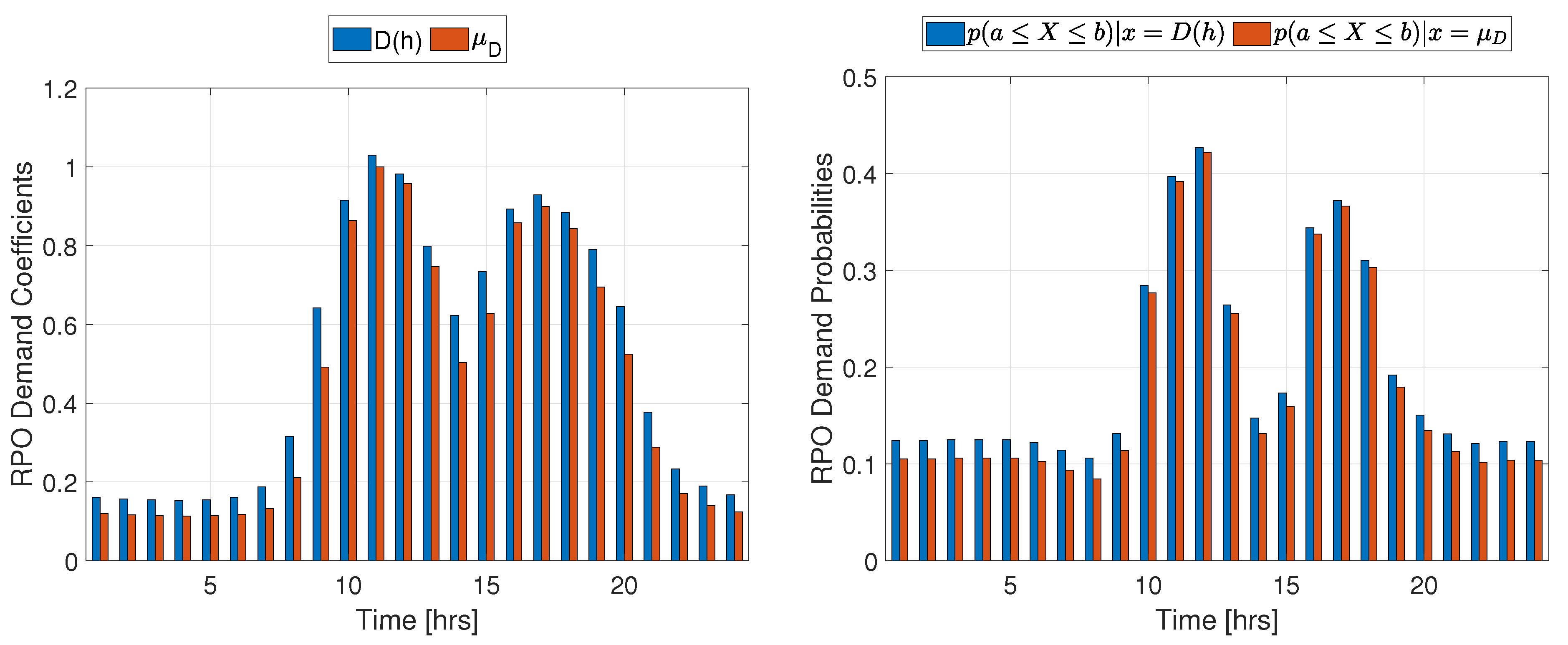
Figure 8.
Irradiance coefficients and mean values with RPO probabilities.
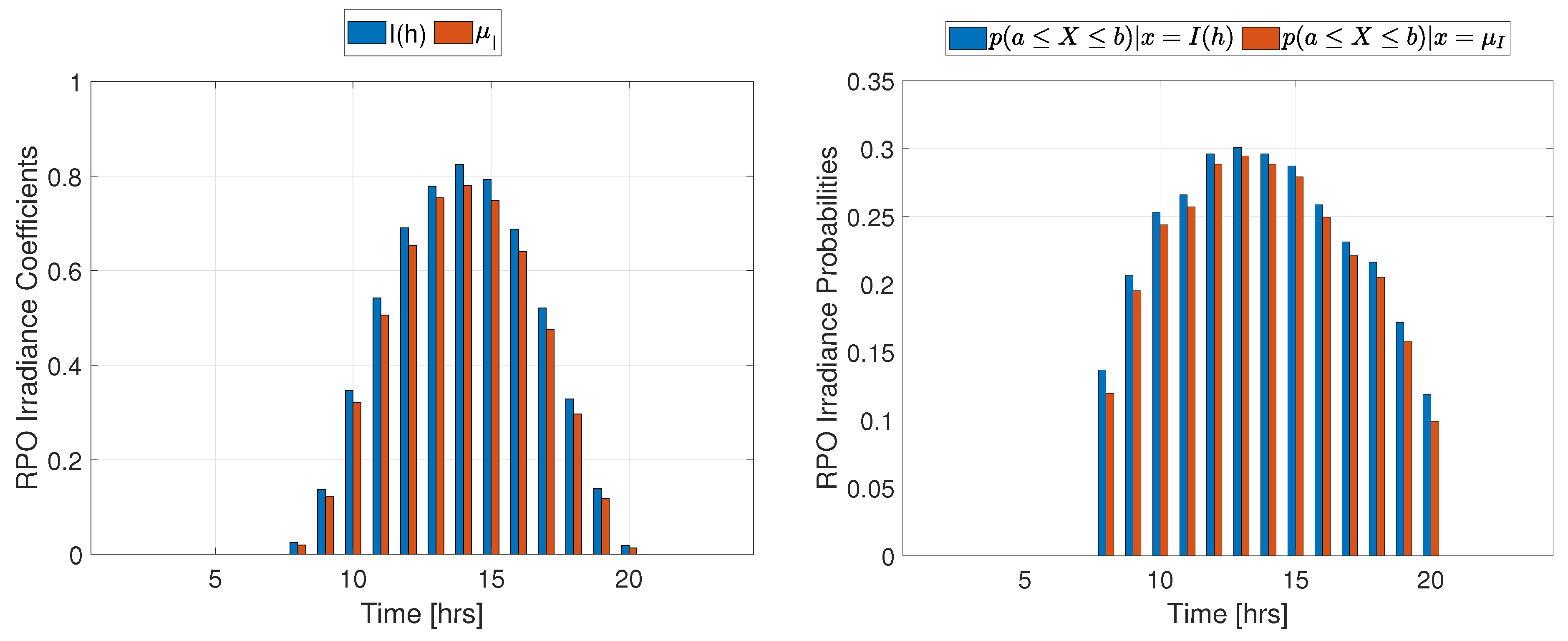
Figure 9.
Demand coefficients and mean values with VPO probabilities
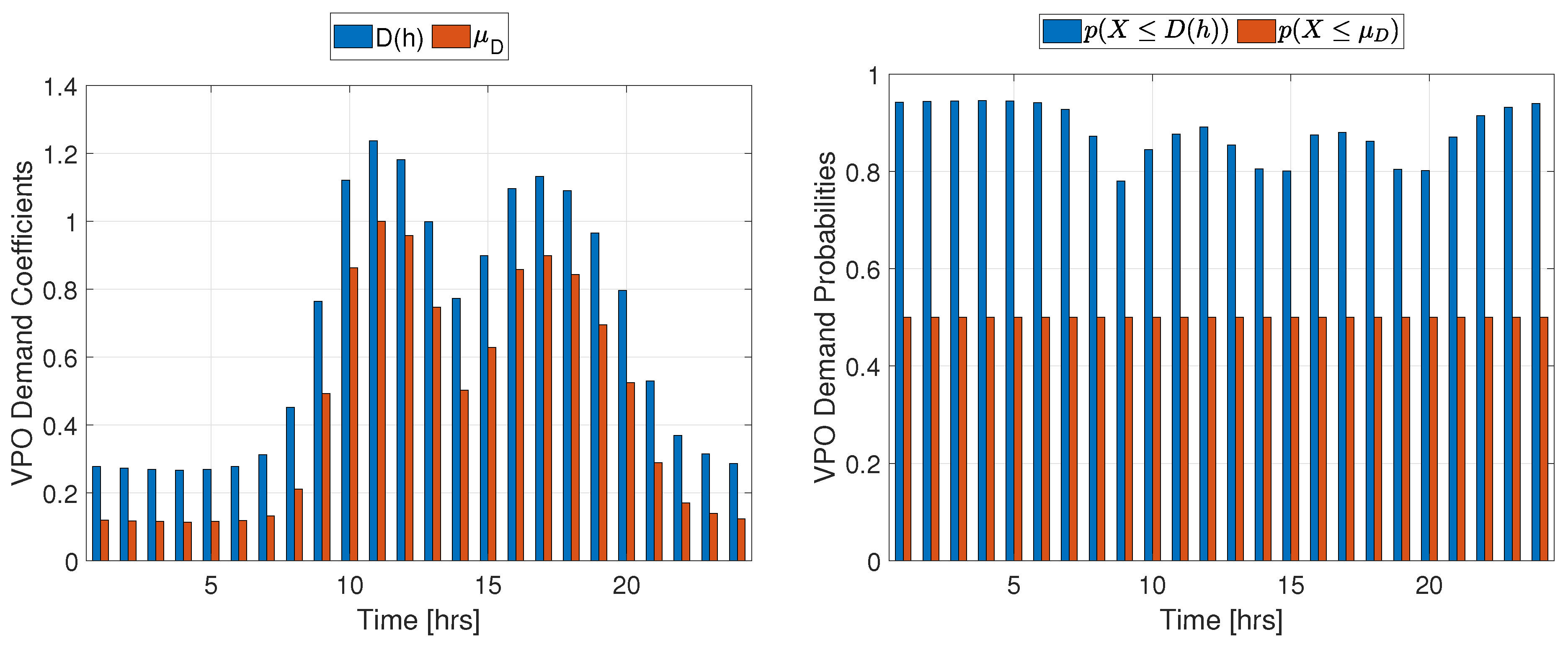
Figure 10.
Irradiance coefficients and mean values with VPO probabilities
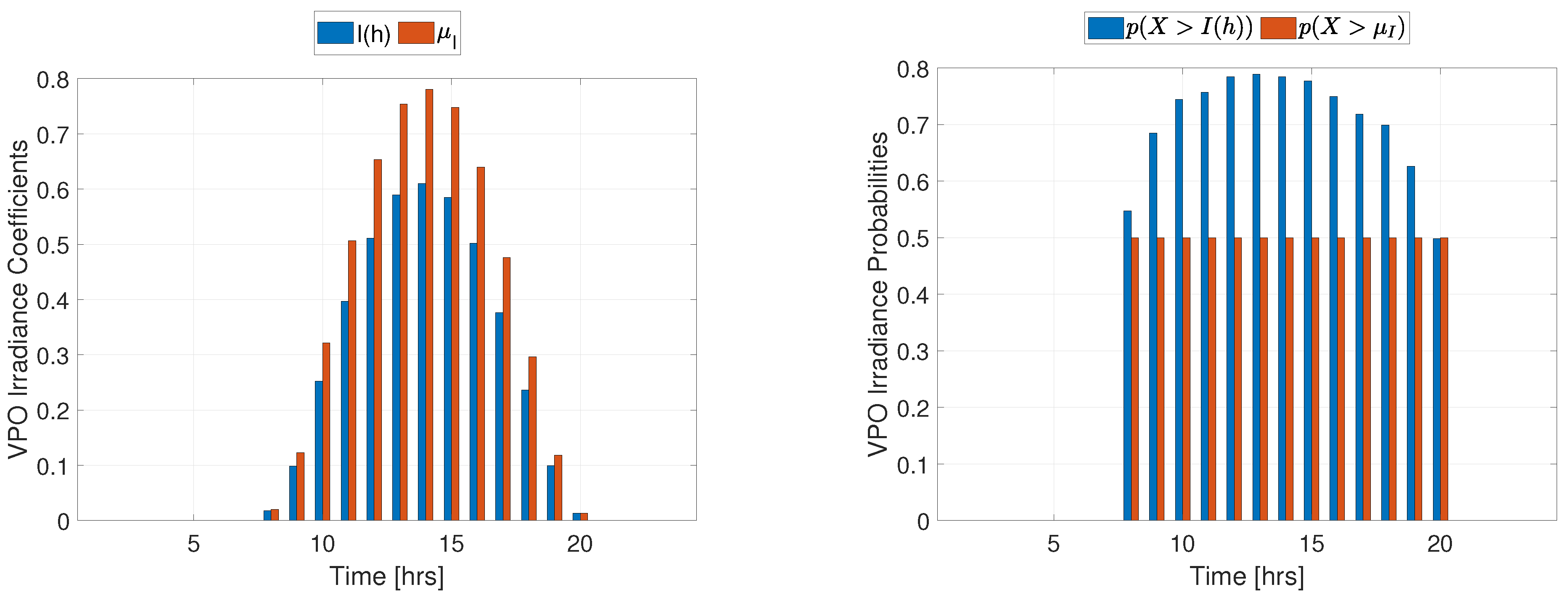
Table 1.
Overall results of the deterministic OPF compared to multiperiod PF results for the I33 system
Table 1.
Overall results of the deterministic OPF compared to multiperiod PF results for the I33 system
| Analysis | [MW] | [MWh/day] | [p.u.] | [p.u.] | |
|---|---|---|---|---|---|
| PF () | - | - | 1.5155 | 0.9037 | 1.0000 |
| OPF | 8 | 1.9999 | 1.0325 | 0.9319 | 1.0070 |
Table 2.
Overall results from the RPO-OPF compared to multiperiod PF results for the I33 system
| Analysis | [MW] | [MWh/day] | [p.u.] | [p.u.] | |
|---|---|---|---|---|---|
| PF () | - | - | 1.5155 | 0.9037 | 1.0000 |
| PF () | - | - | 1.7702 | 0.9018 | 1.0000 |
| RPO-OPF | 17 | 1.7777 | 1.4168 | 0.9270 | 1.0487 |
Table 3.
Overall results from the VPO-OPF compared to multiperiod PF results for the I33 system
| Analysis | [MW] | [MWh/day] | [p.u.] | [p.u.] | |
|---|---|---|---|---|---|
| PF () | - | - | 1.5155 | 0.9037 | 1.0000 |
| PF () | - | - | 2.6283 | 0.8834 | 1.0000 |
| VPO-OPF | 12 | 1.9992 | 1.9124 | 0.9121 | 1.0000 |
Table 4.
Overall results of the deterministic OPF compared to multi-period PF results for the J23 system
Table 4.
Overall results of the deterministic OPF compared to multi-period PF results for the J23 system
| Analysis | [MW] | [MWh/day] | [p.u.] | [p.u.] | |
|---|---|---|---|---|---|
| PF () | - | - | 0.3372 | 0.9964 | 1.0000 |
| OPF | 36 | 0.7992 | 0.2344 | 0.9973 | 1.0000 |
Table 5.
Overall results from the RPO-OPF compared to multi-period PF results for the J23 system
| Analysis | [MW] | [MWh/day] | [p.u.] | [p.u.] | |
|---|---|---|---|---|---|
| PF () | - | - | 0.3372 | 0.9964 | 1.0000 |
| PF () | - | - | 0.3874 | 0.9963 | 1.0000 |
| RPO-OPF | 20 | 0.2222 | 0.2668 | 0.9967 | 1.0000 |
Table 6.
Overall results from the VPO-OPF compared to multiperiod PF results for the J23 system
| Analysis | [MW] | [MWh/day] | [p.u.] | [p.u.] | |
|---|---|---|---|---|---|
| PF () | - | - | 0.3372 | 0.9964 | 1.0000 |
| PF () | - | - | 0.5004 | 0.9956 | 1.0000 |
| VPO-OPF | 25 | 0.2222 | 0.3479 | 0.9959 | 1.0000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
MDPI Initiatives
Important Links
© 2025 MDPI (Basel, Switzerland) unless otherwise stated






