Prerpints.org logo
Preprint
Communication

Extreme Droughts and Their Relationship with the Interdecadal Pacific Oscillation over the Peruvian Altiplano Region during the Last 100 Years

Altmetrics

Downloads

126

Views

132

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

15 June 2023

Posted:

15 June 2023

You are already at the latest version

Alerts
Abstract
Empirical Orthogonal Functions (EOF) analysis between the anomalies of Lake Titicaca water levels (WLs) and the Pacific Interdecadal Oscillation (IPO) reveals a correlation coefficient of 0.71 between the WLs and the principal component (PC1). These findings demonstrate the high accuracy of the IPO in representing the positive and negative phases of the water levels. By utilizing wavelet functions, we identified multi-decadal variability with periods ranging between 20 and 30 years. The statistical techniques employed indicate a relationship between IPO and ENSO; however, they operate on different timescales of climate variability. The IPO exhibits longer-term variability, typically spanning 20-30 years, while ENSO events occur on average every 2-7 years. Nevertheless, the IPO has the ability to modulate the strength and frequency of El Niño and La Niña events, and vice versa. During the positive phase of the IPO, there is a tendency for more frequent and intense El Niño events, accompanied by fewer La Niña events. This can be attributed to warmer sea surface temperatures in the central and eastern Pacific, which create favorable conditions for El Niño development. Conversely, during the negative phase of the IPO, there is a tendency for more frequent and intense La Niña events, with fewer occurrences of El Niño events, due to cooler sea surface temperatures in the central and eastern Pacific.
Keywords: 
Subject: Environmental and Earth Sciences  -   Atmospheric Science and Meteorology

1. Introduction

The Peruvian Altiplano Region (RAP) [1] is a high plateau geographical area located above 3,810 meters of altitude (Figure 1). It is surrounded by the Western and Eastern Andes mountain ranges, and its drainage is primarily through a large river system that includes Lake Titicaca (LT), as well as the Poopó, Coipasa, and Uyuni basins. The precipitation patterns in the RAP exhibit tendencies of decreasing trends, but there are no clearly defined patterns [2,3]. However [4], observed trends indicate systematic increases in precipitation on the western slope of the RAP, while decreases are observed in the eastern, southern, and central parts of the slope. According to Garreaud (2000) and Garreaud and Aceituno (2001) [5,6], the temporal and spatial variability of precipitation in the Altiplano region is influenced by the easterly moisture flux and the interaction between the El Niño Southern Oscillation (ENSO) and below-average values. The influence of ENSO on the reduction of precipitation in the Altiplano region during the rainy season has been identified [7,8]. Previous studies [9,10,11,12,13,14] have shown the interaction between ENSO events (La Niña/El Niño) and the precipitation regime (positive/negative) in the Altiplano region. For the southern region of Lake Titicaca [15,16], the temporal and spatial variability of precipitation in the southeast to southwest direction of the Altiplano basin has been demonstrated, establishing its relationship with equatorial sea surface temperature (SST). Additionally, studies [17,18,19,20] have indicated the strong influence of the South American Monsoon (SMAS) on precipitation at a large scale.

1.1. Interdecadal Pacific Oscillation (IPO)

Research has revealed the relationship between the Interdecadal Pacific Oscillation (IPO) and the interdecadal variability of sea surface temperature (SST) [21,22,23,24,25,26,27,28]. Historical SST records indicate periods of cold regimes during 1909-1925, 1944-1976, and from 1998 onwards, as well as warm regimes during 1925-1944 and 1976-1998 [29].
The linkage between ENSO and the low-frequency modulation of the IPO has been explored in studies [30,31,32,33,34], which demonstrate that the warm (positive)/cool (negative) phase of the IPO can strengthen El Niño events and weaken La Niña events. Similarly, [35] associated the cold (negative) phase of the IPO with reduced rainfall on the northern coast of Chile (18°S - 30°S).
On the other hand, [36] observed a warm (positive) phase in the IPO series from 1970 to 2000, coinciding with extreme El Niño events in 1982-1983 and 1997-1998 [37,38,39,40], which resulted in severe droughts in the PAR and a reduction in water levels of Lake Titicaca. Despite extensive studies on the influence of ENSO and IPO on the spatial-temporal distribution of rainfall in the Altiplano region, the gradual decrease in water levels of Lake Titicaca in recent years is a significant concern. According to SENAMHI-PERU statistics and [8,41], the water level of Lake Titicaca exhibited substantial variations throughout the 20th century (Figure 2), with a difference of up to 5 meters between the extremes of 1944 (3806.7m) and 1986 (3811.6m).

2. Data sets and Methods

In this study, we used monthly data on water levels of Lake Titicaca from 1914 to 2015. The data were obtained from the Servicio Nacional de Meteorología e Hidrología del Perú (SENAMHI). Additionally, the Pacific Interdecadal Oscillation (IPO) data for the same period as the water levels were acquired from the Hadley Center, Meteorological Office, UK (http://cola.gmu.edu/c20c/).

2.1. Wavelet Transform

The variability of positive and negative water levels in Lake Titicaca directly corresponds to the presence or absence of precipitation in the region. To study the smooth or abrupt temporal variations and the symmetric or asymmetric distribution of precipitation, the Morlet wavelet [42,43,44] can be utilized. The Wavelet Transform (WT) decomposes the time series into different levels of time-frequency resolution, thereby allowing the identification of dominant variability components within the series [45]. According Andreoli et al, 2004 [46] show a complex exponential modulated by a Gaussian (Equation 1) where 𝜼 = 𝒕⁄𝒔where 𝒕 is the time and 𝒔 is the wavelet scale as a function of time (= 𝟐⁄𝒅𝒕) e 𝒘𝟎 is a non-dimensional frequency (𝒍𝒂𝒈𝟏 = 𝟎. 𝟕). In this study this value was chosen Andreoli et al, 2004.
ψ t = e i w 0 η e − η 2 / 2

2.2. Empirical Orthogonal Function (EOF)

Empirical Orthogonal Function (EOF) analysis, also known as Principal Component Analysis (PCA), is a widely used statistical technique in climate and atmospheric sciences for examining spatiotemporal patterns in data. The concept of EOF analysis was initially introduced [47] to decompose complex atmospheric fields into orthogonal patterns associated with different temporal variability. On the other hand, [48,49] provided a mathematical framework for EOF analysis, clarifying its mathematical properties and its relationship with the eigen decomposition of covariance matrices. Hannachi et al. (2007) [50] emphasized the application of EOF analysis in climate studies, particularly for model evaluation and comparison. Wilks (2019) [51] explored the utilization of EOFs in weather and climate forecasting, demonstrating their potential as predictors for long-range predictions. For the analysis of EOFs between water levels (WLs) and Pacific Interdecadal Oscillation (IPO), the period considered was from September 1914 to July 2018 on a monthly scale.

3. Results

3.1. Wavelet Transform Analysis of WLs

The WLs were analyzed using the wavelet transform at a monthly scale from 1914 to 2017. The results obtained from the TW technique reveal variability on a multidecadal time scale of 20 to 30 years. In Figure 3, the negative phase (decrease) of the WLs is depicted by the red contours, which exhibit the highest energy in the Wavelet Power Spectrum (EPO). According to the period axis, this energy is concentrated in the multidecadal variability associated with El Niño/La Niña events.
During the period from 1934 to 1943, the WLs experienced a negative phase, resulting in a decrease of 4.816 meters of water, equivalent to 455 million m3. Similarly, for the period from 1986 to 1996, the WLs decreased by 4.430 meters (424 million m3). Both periods are represented in the IPO (highlighted as the red-colored region in Figure 1) on the multidecadal time scale, which suggests an association with the IPO climate index. According to [52], mega-drought events (prolonged droughts lasting several decades) are linked to persistent time-scale SST anomalies in the tropical Pacific, specifically negative anomalies of the IPO. The negative phase of the WLs during the driest period (1934 to 1943) coincides with the strongest phase of the IPO (Figure 1).

3.2. EOFs between WLs and IPO index

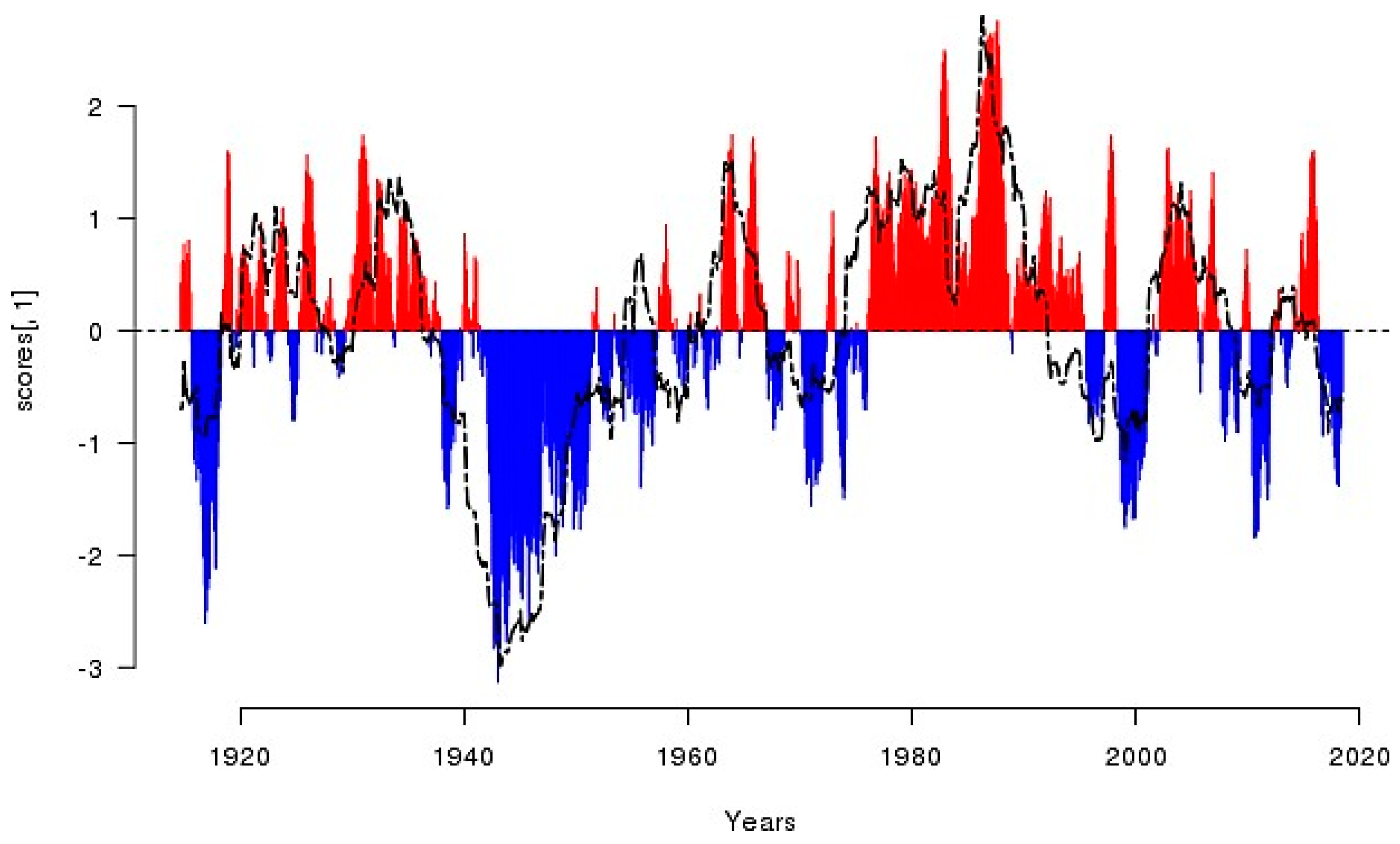
The correlation coefficients of EOF1 for the WL data and the IPO for the period 1914/09 to 2018/07 were: CP1 (0.55) and CP2 (0.45). The first component would explain the 55% of the total variance and the coefficients of the eigenvector primer, 0.7071068 and 0.7071068 (CP1) are equal and both positive which would show that they have strong correlation, indicating that for the primer PC, Z1 is a weighted average of both variables related to the variability the WLs and IPO have in common. Figure 2, represents the time series of the PC1 and the WLs for the period from 1914/09 to 2018/07. The positive (negative) values of PC1 represent the warm (cold) phase of the IPO and the increase (decrease) of the WLs. In the warm phase of the IPO (1979 to 1999) there were extreme El Niño events and some weak La Niña events, which would be related to the absence/presence of precipitation in the region. Similar results were obtained by [31,36,53]

4. Discussion

WLs in the region experienced a negative phase during the periods from 1934 to 1943 and from 1986 to 1996. These negative phases resulted in significant decreases in water levels, equivalent to 455 million m3 and 424 million m3, respectively.
The negative phase of WLs during the driest period (1934 to 1943) coincided with the strongest phase of the IPO, suggesting an association between the IPO climate index and extreme droughts.
Mega-drought events, which are prolonged droughts lasting several decades, have been linked to persistent time-scale sea surface temperature (SST) anomalies in the tropical Pacific, specifically negative anomalies of the IPO.
The correlation coefficients between the dominant mode of variability in WLs (represented by EOF1) and the IPO for the period 1914/09 to 2018/07 were 0.55 and 0.45 for two components (CP1 and CP2) of the EOF analysis. These coefficients indicate a moderate positive correlation between WLs and the IPO.
The time series of the first principal component (PC1) and WLs from 1914/09 to 2018/07 show that positive values of PC1 correspond to the warm phase of the IPO and an increase in WLs, while negative values represent the cold phase of the IPO and a decrease in WLs.
The warm phase of the IPO from 1979 to 1999 coincided with extreme El Niño events and some weak La Niña events, which could be related to the absence or presence of precipitation in the region.
The findings presented in the passage are consistent with previous studies [31,36,51,53] which also suggest a connection between the IPO, SST anomalies in the tropical Pacific, and drought events in the South American Altiplano region.

5. Conclusions

The results of the Empirical Orthogonal Function (EOF) analysis between the time series of water level anomalies (WLs) of Lake Titicaca and the IPO (Pacific Interdecadal Oscillation) climate index show a correlation coefficient of 0.71 between the WLs and the principal component (PC1).
With the aid of Wavelet analysis, multi-decadal variability (periods between 20 and 30 years) can be identified in the study.
Based on the results of multiple analysis techniques, we could establish an association between WLs and the IPO climate index. Thus, during the negative/positive phase (1916-1925, 1946-1975, and 1999-2013)/(1926-1941 and 1978-1998) of the IPO, there were El Niño/La Niña events that could be associated with the increase/decrease of Lake Titicaca water levels. Although there is this possible association between WLs and the IPO, other atmospheric conditions that influence precipitation [54,55,56,57] exist, such as the Bolivian High (AB) and its relation with the Intertropical Convergence Zone (ITCZ), the Northeast Trough, or Northeast Bight (NEB).
The IPO and ENSO are related, but they represent different timescales of climate variability. The IPO has a longer period of variability, typically around 20-30 years, while ENSO events occur on average every 2-7 years. However, the IPO can modulate the strength and frequency of El Niño and La Niña events, and vice versa.
During the positive phase of the IPO, there is a tendency for more frequent and stronger El Niño events and fewer La Niña events. This is because a positive IPO phase is associated with warmer sea surface temperatures in the central and eastern Pacific, which can create favorable conditions for the development of El Niño events. In contrast, during the negative phase of the IPO, there is a tendency for more frequent and stronger La Niña events and fewer El Niño events due to cooler sea surface temperatures in the central and eastern Pacific.
Negative phases of the Interdecadal Pacific Oscillation (IPO) index, characterized by persistent time-scale sea surface temperature (SST) anomalies in the tropical Pacific, are associated with mega-drought events (prolonged droughts lasting several decades) in the region.
The negative phase of the water levels (WLs) in the study area during the driest periods (1934-1943 and 1986-1996) coincided with the strongest phase of the IPO. This suggests a relationship between the IPO and the decrease in water levels in the region.
The correlation coefficients between the dominant mode of variability in WL data (EOF1) and the IPO for the period 1914-2018 were 0.55 and 0.45 for two components (CP1 and CP2). CP1, which explained 55% of the total variance, showed a strong positive correlation between WLs and the IPO.
The time series analysis of the first principal component (PC1) and WLs showed that positive (negative) values of PC1 corresponded to the warm (cold) phase of the IPO and an increase (decrease) in WLs. The warm phase of the IPO from 1979 to 1999 coincided with extreme El Niño events and some weak La Niña events, which may be related to precipitation patterns in the region.
The referenced studies [36,51,53] support similar findings regarding the association between IPO, El Niño events, and precipitation variability in the study area.
HoweRver, it is important to note that the relationship between the IPO and ENSO is not always consistent, and there are other factors that can also influence the occurrence and intensity of El Niño and La Niña events. Therefore, the IPO and ENSO should be studied and analyzed together in order to fully understand their impacts on climate variability and weather patterns.

Author Contributions

E.C.A. and A.J.P.F. analyzed the data; A.J.P.F. contributed materials and analysis tools; E.C.A. wrote the article. All authors have read and agreed to the published version of the manuscript.

Funding

This research publication was sponsored by PROEX/CAPE The second author is supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) under grant 302349/2017-6.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Is excluded.

Acknowledgments

The present work was the result of the master’s thesis financed by Capes (Coordination of Improvement of Higher-Level Personnel), foundation of the Ministry of Education of Brazil.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
WLs Water levels
WT Wavelet Transform
IPO Interdecadal Pacific Oscillation
EOF Empirical Orthogonal Functions
ENSO El Niño Southern Oscillation
SST Sea Surface Temperature
RAP Peruvian Altiplano Region
LT Titicaca Lake

References

  1. Choquehuanca, H. A. Lago Titicaca: maravilla del mundo. Universidad Nacional del Altiplano. 2013.
  2. IPCC. Climate Change 2001: The Physical Science Basis. Working Group 1 Contribution to the Third Assessment Report of the Intergovernmental Panel on Climate Change. 2001. Available online: https://www.ipcc.ch/site/assets/uploads/2018/03/WGI_TAR_full_report.
  3. Sanabria, J.; Marengo, J.; Valverde, M.; Paulo, S. Escenarios de Cambio Climático con modelos regionales sobre el Altiplano Peruano Departamento de Puno. Revista Peruana GeoAtmosférica. 2009, 149(1), 134-149. Available online: https://repositorio.senamhi.gob.pe/bitstream/handle/20.500.12542/1076/Escenarios-de-cambio-clim%C3%A1tico-con-modelos-regionales-sobre-el-Altiplano-Peruano.pdf?sequence=1.
  4. Servicio Nacional de Meteorología e Hidrología del Perú. Escenarios Climáticos en el Perú para el año 2030, 2009, 35. Available online: https://repositorio.senamhi.gob.pe/handle/20.500.12542/141.
  5. Garreaud, R. D. Intraseasonal Variability of Moisture and Rainfall over the South American Altiplano. American Meteorological Society. 2000, 128, 3337–3346. [Google Scholar] [CrossRef]
  6. Garreaud R., D.; Aceituno, P. Interannual Rainfall Variability over the South American Altiplano. American Meteorological Society. 2001, 14, 2779–2789. [Google Scholar] [CrossRef]
  7. Villue, M. Atmospheric circulation over the Bolivian Altiplano during dry and wet periods and extreme phases of the Southern Oscillation. Int. J. Climatol. 1999, 1579–16000. [Google Scholar] [CrossRef]
  8. Angulo, E. C.; Pereira Filho, A. J. Ocean Forcing on Titicaca Lake Water Volume. Open Journal Modern Hydrology. 2022, 12, 1–10. [Google Scholar] [CrossRef]
  9. Lagos, P.; Silva, Y.; Nickl, E.; Mosquera, K. El Niño-related precipitation variability in Peru. Advances in Geosciences. 2008, 14, 231–237. [Google Scholar] [CrossRef]
  10. Lavado-Casimiro, W.S.; Espinoza, J.C.; Guyot, J.L.; Labat, D. Basin-scale analysis of rainfall and runoff in Peru (1969-2004): Pacific, Titicaca and Amazonas dranaiges. Hydrological Sciences Journal. 2012, 57, 625–642. [Google Scholar] [CrossRef]
  11. Lavado-Casimiro, W.; Espinoza, J. C. Impactos de El Niño y La Niña en las lluvias del Perú. Rev. Bras. Meteorol. 2014, 29 (2).
  12. Rau, P.; Bourrel, L.; Labat, D.; Melo, P.; Dewitte, B.; Frappart, F.; Lavado-Casimiro, W. ; Oscar Felipe. Regionalization of rainfall over the Peruvian Pacific slope an coast. Int. J. Climatol. 2016, 37, 143–258. [Google Scholar] [CrossRef]
  13. Sulca, J.; Takahashi, K.; Espinoza, J. C.; Villue, M.; Lavado-Casimiro, W. Int. J. Climatol. 2017, 38, 420–435. [CrossRef]
  14. Imfeld, N.; Schuler, C. B.; Marrou, K. M. C.; Jaques-Cooper, M.; Sedlmeier, K.; Gubler, S.; Huerta, H.; Brönnimann, S. Summertime precipitation deficits in the southern Peruvian highlands since 1964. Int. J. Climatol. 2019, 39, 4497–5413. [Google Scholar] [CrossRef]
  15. Ronchail, J.; Gallaire, R. ENSO and rainfall along the Zongo Valley (Bolivia) from the Altiplano to the Amazon Basin. Int. J. Climatol. 2006, 26, 1223–1236. [Google Scholar] [CrossRef]
  16. Huerta, A.; Lavado, C. W. Trends and variabity of precipitation extremes in the Peruvian Altiplano (1971-2013). Int. J. Climatol. 2020, 1–16. [Google Scholar] [CrossRef]
  17. Vera, C.; Silvestre, G.; Liebmann, B.; Gonzáles, P. Climate change scenarios for seasonal precipitation in South America from IPCC-AR4 models. Geophysical Research Letters. 2006, 33, 13. [Google Scholar] [CrossRef]
  18. Garreaud, R. D. The Andes climate and weather. Adv. Geosci., 2009, 7, 1–9 wwwadv. [Google Scholar] [CrossRef]
  19. Marengo, J. A.; Liebman, B.; Grimm, A. M.; Misra., V.; Silva Dias, P. L.; Cavalcanti, I. F. A.; Carvalho, L. M. V.; Berbery, E. H.; Ambrizzi, T.; Vera, C. S.; et al. Recent developments on the South American moonson system. Inter. J. Climatol. 2010, 32, 1–21. [Google Scholar] [CrossRef]
  20. Jara I., A., Maldonado A. Gonzáles L., Hernández A., Sáez A., Giralt S., Bao R., Valero-Garcés B. (2019). Centennial-scale precipitation anomalies in the southern Altiplano (18°S) suggest an extratropical driver for the South American summer monsoon during the late Holocene. Clim. Past. 15, 1845-1859. [CrossRef]
  21. Muntua N. J., Hare S. R., Zhang Y. Wallace J. M., Francis R. C. A Pacific interdecadal climate oscillation with impacts on salmon production. Bull. Am. Meteorol. Soc. 1997, 78, 1069–1079. [Google Scholar] [CrossRef]
  22. Muntua N., J.; Hare S., R. The Pacific decadal oscillation. J. Ocean. 2002, 58, 35–44. [Google Scholar] [CrossRef]
  23. Deser, C. , Phillips A. S., & Hurrel J. W. (2004). Pacific interdecadal variability: linkages between the tropics and the North Pacific during boreal winter since 1900. J. Clim. 17, 3190-3124. [CrossRef]
  24. Shen, C. , Whang, W. C., Gong, W., & Hao, Z. (2006). A pacific decadal oscillation record since 1470 AD reconstructed from proxy data of summer rainfall over eastern China. Geophys. Res. Lett. 33. [CrossRef]
  25. Mohino, E. , Janicot S., Bader J. (2011a). Sahel Rainfall and decadal to multi- decadal sea surface temperature variability. Clim. Dyn. 37, 419-440. [CrossRef]
  26. Dai, A. (2013). The influence of the inter-decadal Pacific oscillation on US precipitation during 1923-2010. Clim. Dyn. 41, 633-646. [CrossRef]
  27. Jacquer-Coper, M.; Garreaud R., D. Characterization of the 1970s climate shift in South America. Int. J. Climatol. 2014, 35(8), 2164–2179. [Google Scholar] [CrossRef]
  28. Villamayor, J. (2020). Influence of the Sea Surface Temperature Decadal Variability on Tropical Precipitation: West African an South American Monsoon. Springer Theses. Chapter 5. [CrossRef]
  29. Folland C., K.; Parker, D. E.; Colman, A. W.; Washington, R. (1999). Large- scale modes of ocean surface temperature since the late nineteenth century. In Beyond El Niño: Decadal and Interdecadal Climate Variability. Springer, 73-102. Available online: https://link.springer.com/book/10.1007/978-3-642-58369-8.
  30. Salinger, M.J.; Renwick J., A.; Mullan A., B. Interdecadal Pacific Oscillation and South Pacific Climate. Int. J. Climatol. 2001, 21, 1705–1721. [Google Scholar] [CrossRef]
  31. Andreoli, R. V. & Kayano, M. T. (2004). Multi-scale variability of the sea surface temperature in the Tropical Atlantic. Journal of Geophysical Research. 109, C05009. [CrossRef]
  32. Cai, W. , McPhaen, M. J., Grimm, A. M., Rodrigues, R. R., Taschetto, A. S., Garreaud, R. D., Dewitte, B., Poveda, G., Ham, Y., Santoso, A., Ng B., Anderson, W., Wang, G., Geng, T., Jo H., Marengo, J. A., Alves, L. M., Osman, M., Li S., Wu L., Karamperidou, C., Takahashi, K., & Vera C. (2020). Climate impacts of the El Niño-Sothern Oscillation on South America. Nat Rev Earth Environ 1, 215- 231. [CrossRef]
  33. Tao Gao., Fuqiang Cao., Dan Li., Ming Li., Gong Xiang & Junjie Zhan. (2021). The precipitation variability of the wet and dry season at the interannual and decadal scales over Eastern China (1901-2016): the impacts of the Pacific Ocean. Hydrol. Earth Syst. Sci., 25, 1467-1481. [CrossRef]
  34. Souza I., P. , Andreoli R. V., Kayano M. T., Cerón W. L., Souza R. A. F., Roy I. (2023). Interdecadal Pacific Oscillation modulation of ENSO teleconnections in its decaying stages: Relations with Indian Ocean basin-wide mode and South American precipitation. Int. J. Climatol. [CrossRef]
  35. Schulz, N. , Boisier J. P., Aceituno G. P. (2011). Climate change along the arid coast of northern Chile. Available online: https://repositorio.uchile.cl/handle/2250/126105.
  36. Flantua, G.; Hooghiemstra, H.; Vuille, M.; Behling, H.; Carson, F.; Gosling, D.; Hoyos, I.; Ledru, M.; Montoya, E.; Mayle, F.; Maldonado, A.; Rull, A.; Tonello, S.; Whitney, B.; Gonzáles-Arango, C. (2016). Climate variability and human impact in South America durign the last 2000 years: synthesis and perspectives from pollen records. Open Acces the European Geosciencies Union. Clim. Past, 12, 483-523. [CrossRef]
  37. Garreaud, R.; Vuille, M. & Clement, A. C. (2003). The climate of the Altiplano: observed current conditions and mechanisms of past changes. Palaeogeography, Palaeocimatology, Palaeoecology 194, 5-22. [CrossRef]
  38. Poveda, G. , Espinoza J. C., Zuluaga M. D., Solman S. A., Garreaud R., Oevelen P. J. (2020). High Impact Weather Events in the Andes. Frot. Earth Sci. 8: 162. [CrossRef]
  39. Canedo-Rosso, C. , Hochrainer-Stigler S., Pflug G., Condori B., Berndtsson R. (2021). Drought impact in the Boliviam Altiplano agriculture associated with the El Niño-Southern Oscillation using satellite imagery data. Nat. Hazards Earth Syst. Sci. 21, 995-1010. [CrossRef]
  40. Morales, M. S. , Crispin-DelaCruz, D. B., Álvarez C., Christie, D. A., Ferrero, M. E., Andreu-Hayles, L., Villalba, R., Guerra, A., Ticse-Otarola, G., Rodríguez- Ramírez, E. C., Llocclla-Martínez, R., Sanchez-Ferrer, J., & Requena-Rojas, E. (2023). Drougth increase since the mid-20th century in the northern South American Altiplano revealed by a 389-year precipitation record. Clim. Past. 19, 457-476. [CrossRef]
  41. Ronchail, J. , Espinoza J., Labat D., Callède, J., Lavado, W. (2014). Evolución del nivel del Lago Titicaca durante el siglo XX. Línea base de conocimientos sobre los recursos hídricos y hidrobiológicos en el sistema TDPS con enfoque en la Cuenca del lago Titicaca. Available online: https://horizon.documentation.ird.fr/exl-doc/pleins_textes/divers14-09/010062839.pdf.
  42. Andreoli, R. , & Kayano M. T. (2005). ENSO-related rainfall anomalies in South America and associated circulation features during warm and cold Pacific decadal oscillation regimes. Int. J. Climatol. 25, 2017-2030. [CrossRef]
  43. Alves, J. M. B.; Souza, E. B.; Costa, A. A.; Martins, E. S. P. R. &; Silva, E.M. (2012). On the signal of a dynamic donwscaling the Intraseasonal oscillations of precipitation in the northern sector of northeastern Brazil. Ver. bras. Meteorol. 27, 219-228. [CrossRef]
  44. Da Silva (2017). Application of Wavelet Analysis for Detection of Rainfall Cycles and Extremes in Eastern Northeastern Brazil. Rev. Bras. Meteorol. 32(2). [CrossRef]
  45. Torrence, C.; Compo, G. P. A. (1998). A practical guide to wavelet analysis. Bull. Am. Meteor. Soc. 79, 61-78. [CrossRef]
  46. Andreoli, R. V.; Kayano, M. T.; Guedes, R. L.; Oyama, M. D. & Alves, M. A. S. (2004). The influence of sea surface temperature of the Pacific and Atlantic Oceans on precipitation variability in Fortaleza. Revista Brasileira de Meteorologia. 19, 337-344. Available online: http://urlib.net/ibi/x6e6X3pFwXQZ3DUS8rS5/BGHFb.
  47. Lorenz, E. N. (1956). Empirical Orthogonal Functions and Statistical Weather Prediction. Scientific Report No. 1, Statistical Forecasting Project, Department of Meteorology, Massachusetts Institute of Technology.
  48. Hotelling, H. (1993). Analysis of a complex of statistical variables into principal components. Journal of Educational Psychology, 24(6), 417-441. [CrossRef]
  49. Hotelling, H. (1995). Empirical Orthogonal Functions and Statistical Weather Prediction. Mathematical Monographs, 23, 159-166.
  50. Hannachi, A. , Jolliffe, I. T., & Stephenson, D. B. (2007). Empirical orthogonal functions and related techniques in atmospheric science: A review. International Journal of Climatology, 27(9), 1119-1152. [CrossRef]
  51. Wilks, D. S. Statistical methods in the atmospheric sciences (4th ed.). Academic Press, 2019. [Google Scholar]
  52. Meehl, G. A.; Hu, A. (2006). Megadroughts in the Indian monsoon region and southwest North America and a mechanism for associated multidecadal Pacific sea surface temperature anomalies. Journal of Climate, 19(9), 1605-1623. [CrossRef]
  53. Weir Tony, Kumar Ravind, & Ngari Arona (2021). Interdecadal modulation of the effect of ENSO on rainfall in the southwestern Pacific. Journal of Southern Hemisphere Earth Systems Science. 71, 53-65. [CrossRef]
  54. Lavado-Casimiro, W. , Vuille, M., Hardy, D. R., Bradley, R. S., & Thompson, L. G. (2012). Recent warming trends in the Andes of southern Peru, derived from temperature records from tropical ice cores. Journal of Geophysical Research: Atmospheres, 117(D2), D02117. [CrossRef]
  55. Espinoza, J. C. , Guyot, J. L., Ronchail, J., Cochonneau, G., Filizola, N., Fraizy, P., De Oliveira, E., & Pombosa, R. (2011). Spatio-temporal rainfall variability in the Amazon basin countries (Brazil, Peru, Bolivia, Colombia, and Ecuador). International Journal of Climatology, 31(12), 1645-1665. [CrossRef]
  56. Espinoza, J. C. , Ronchail, J., Guyot, J. L., Cochonneau, G., Naziano, F., Lavado, W., & De Oliveira, E. (2009). Contrasting regional discharge evolutions in the Amazon basin (1974-2004). Journal of Hydrology, 375(3-4), 297-311. [CrossRef]
  57. Silva, Y. (2008). Hydrometeorological variability in the Titicaca Lake basin (South America) and its relationship with large-scale atmospheric circulation. Journal of Climate, 21(9), 1795-1806.
Preprints 76709 g001
Figure 1. Wavelet transform analysis for the WLs series after removing trend and seasonality from the data. Period 1914 - 2017. The color scale represents the global energy spectrum.
Figure 1. Wavelet transform analysis for the WLs series after removing trend and seasonality from the data. Period 1914 - 2017. The color scale represents the global energy spectrum.
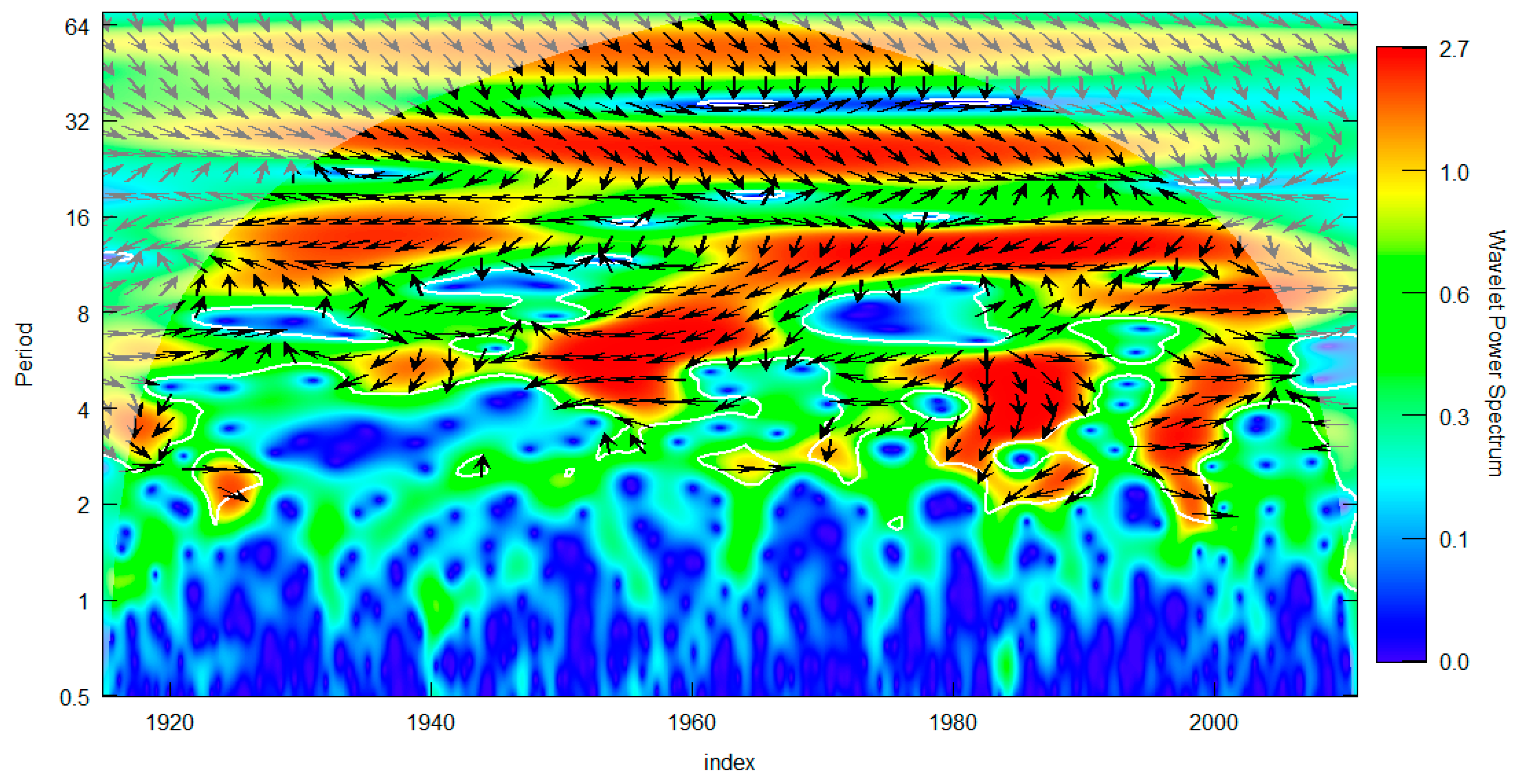
Preprints 76709 g001
Preprints 76709 g002
Figure 2. Water level anomalies (black dotted line) and the PC1 time series for the period 1914/09 to 2018/07. The correlation coefficient between WLs and the IPO was 0.71, the positive (negative) values are associated with the warm (cold) phase of the IPO and directly related to the decrease (increase) of WLs.
Figure 2. Water level anomalies (black dotted line) and the PC1 time series for the period 1914/09 to 2018/07. The correlation coefficient between WLs and the IPO was 0.71, the positive (negative) values are associated with the warm (cold) phase of the IPO and directly related to the decrease (increase) of WLs.
Preprints 76709 g002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated