Preprint
Communication
The Put-Call Parity Certainty Equivalent Rate and the Implied Put-Call Parity Certainty Equivalent Rate Surface
Altmetrics
Downloads
93
Views
30
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
14 June 2023
Posted:
15 June 2023
You are already at the latest version
Alerts
Abstract
In real financial markets, the certainty equivalent rate is an important factor for investors to consider. From the value of a specific company’s certainty equivalent rate, investors can judge if this company is worth investing in. In this paper, we will explore how to obtain the value of the certainty equivalent rate so that we can evaluate a given company. First, we will introduce the theoretical support of this paper, which is put-call parity. From put-call parity, we will derive the mathematical expression for the certainty equivalent rate. Second, we will use the mathematical expression for the certainty equivalent rate to perform an empirical study. We will consider some extreme examples, including some of the best- and worst-performing stocks up to this point in 2023. Based on these stocks’ data, we will visualize the performance of these stocks and explain the meaning of the data. Finally, we will apply the results to a very popular industry—the electric vehicle industry—to explore the current electric vehicle market situation in the U.S.A.
Keywords:
Subject: Business, Economics and Management - Finance
1. Introduction
The certainty equivalent rate is a measure derived from the certainty equivalent, and it is quite important in financial markets. Investors will refer to the value of a specific company’s certainty equivalent rate to determine if this company is worth investing in. In this paper, we will derive the value of the certainty equivalent rate by using put-call parity, and then we will find the relationship between time and the maturity, the moneyness, and the implied certainty equivalent rate calculated using the put-call parity by visualizing the data we collected. Using the data visualization, we will explain the meaning of the data and obtain a general conclusion.
2. Theoretical Support
The key theorem we will use is put-call parity. A detailed explanation of put-call parity can be found in [4]. [4] considers interest and dividends to be paid in accordance with continuous compounding, but in a real financial market, interest and dividends are more likely to be paid at specific points in time rather than every second. Thus, we prefer to use the discrete-compounding version of put-call parity when we consider problems in a real financial market. Hence, the following is the detailed mathematical expression of put-call parity that we will use in this paper:
where
Based on , we can obtain the mathematical expression for
In the following sections, we will mainly use to explore the relationship between time and the maturity , the moneyness , and the implied company-specific put-call parity certainty equivalent rate .
3. Empirical Research
3.1. Preparation
Before continuing our empirical research, we must do some preparation to figure out how to obtain the values of the arguments in :
- We can find the values of the arguments t and in every stock’s “historical data” section on Yahoo Finance.
- For the argument , we will consider the value of the “forward annual dividend yield”; the relevant data can be found in the “statistics” section on Yahoo Finance.
- We can find the arguments T and on CBOE.
- For the arguments and , although we cannot obtain the values of these arguments directly from CBOE, we can obtain the “bid” and “ask” of every option. Here, we can calculate the mid-price of the bid and ask, and we consider it to be the corresponding call option price and put option price.
Since we want to explore the best- and worst-performing stocks up to this point in 2023, without loss of generality, we can consider the start date t as January 3, 2023, which is the first date that the financial market was open in 2023. Thus, represents the stock price of a given company on January 3, 2023.
3.2. Data Visualization and Explanation
Based on financial news from [1,2,3,5], we can select three of the best-performing stocks, which come from Apple, Nvidia, and Meta, respectively. On the other hand, the three worst-performing stocks that we select are from First Republic Bank, Signature Bank, and Charles Schwab, respectively. Next, we will create graphs that describe the relationship between time and the maturity , the moneyness , and the implied put-call parity certainty equivalent rate r for the companies we selected, and we will explain some key values from these graphs.
Figure 1.
Implied put-call parity certainty equivalent surface (best-performing companies).
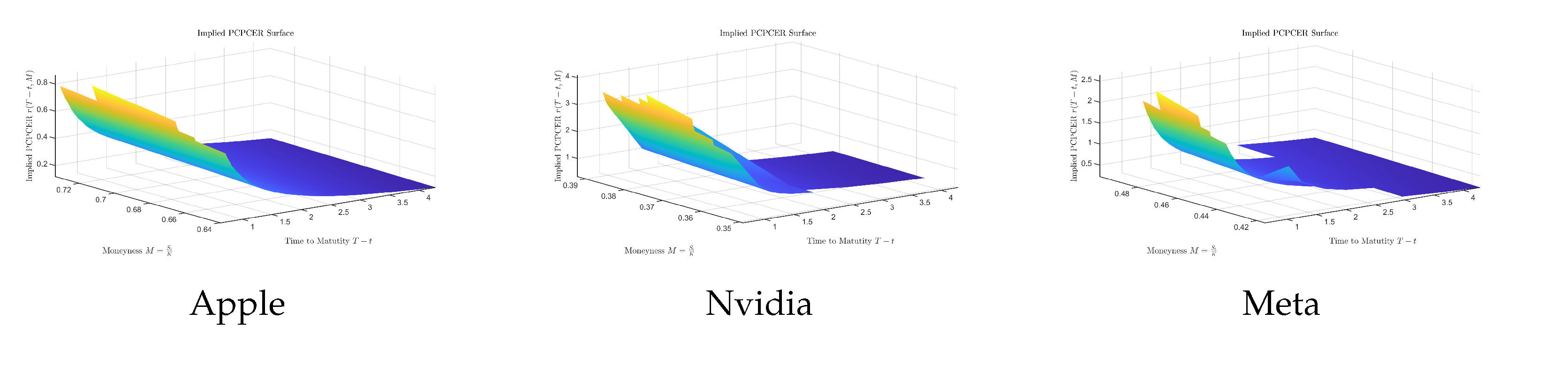
Figure 2.
Implied put-call parity certainty equivalent surface (worst-performing companies).
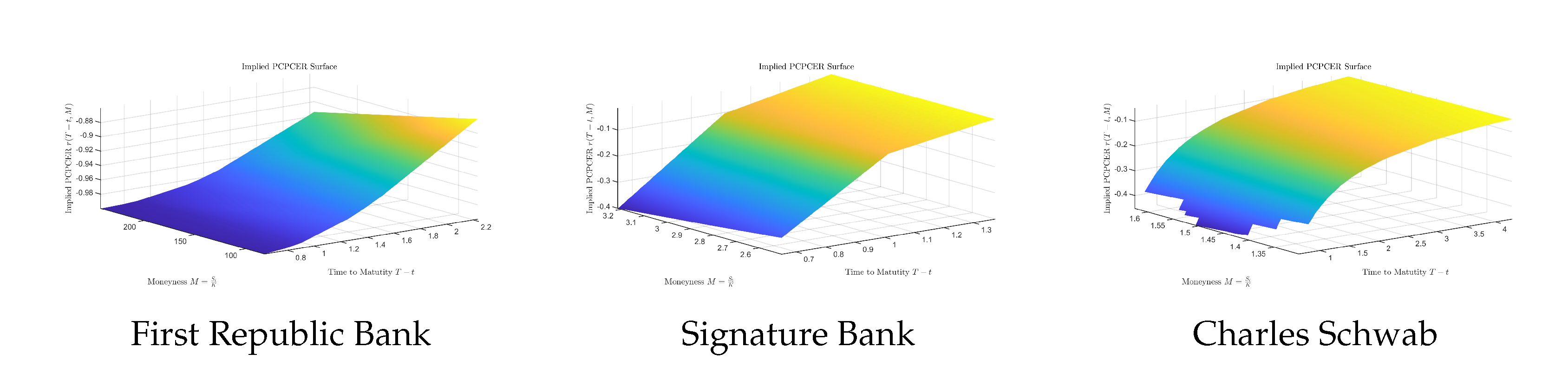
From Table 1, it is clear that the best-performing companies have strictly positive implied put-call parity certainty equivalent rates, regardless of the maximum value, minimum value, or mean value. On the other hand, the worst-performing companies have strictly negative implied put-call parity certainty equivalent rates.
A positive rate means that investors have a high probability of obtaining a return if they invest in the company’s stock, while a negative rate means that investors may lose their money if they try to invest in the company’s stock. By combining the data and the financial news, we find that the implied put-call parity certainty equivalent rate is quite useful; it can help investors determine which company’s stock option is worth investing in.
Now, let us consider the shape of the graph. For the best-performing companies, we can observe that when the time to maturity is small, the corresponding rate is high, which means that in the near future, the return of the stock option is quite high, so that investors may make money by investing in the option. Of course, they may have to take on some amount of risk. In this case, we are suggesting that the investor consider Apple first, then Meta, and finally Nvidia. A high rate represents a high risk, and normal investors definitely do not want to take on a high risk when they decide to invest in something.
As time goes by, i.e., as the value of the time to maturity becomes larger, the implied put-call parity certainty equivalent rate will become smaller because it is reasonable to consider the long-term rate as the riskless rate of the financial market. Additionally, it is clear that the riskless rate of the financial market should be lower than the near-future implied put-call parity certainty equivalent rates of the best-performing companies.
Finally, let us consider the worst-performing companies. We can see that the values of the certainty equivalent rates of these companies are negative, which means that investors have a high risk of losing money if they decide to invest in these companies’ stock options.
4. Application: Electric Vehicle Industry
Today, more and more people are paying attention to environmental issues. To reduce the pollution released by vehicles, people are considering driving electric vehicles instead of traditional oil-powered vehicles. In the U.S.A., there are several well-known companies that make electric vehicles, such as Tesla, General Motors, and Ford Motor Company. We can apply the results we obtained in the previous section to these electric vehicle companies. The following figure visualizes the data of these companies, and the key values derived from the graphs are given in the following table.
Based on the shapes of the graphs shown in Figure 3, we can see that these three companies are all doing well. In the near future, we recommend that investors invest in these companies’ stock options. According to the data from Table 2, we can see that if we plot the three surfaces on the same coordinate axis, the relative positions of these three surfaces from top to bottom are Tesla, Ford Motor Company, and General Motors, respectively. Based on the positional relationships, we can see that investors should prefer to invest in General Motors, then Ford Motor Company, and finally Tesla.
5. Summary
In this paper, we have used put-call parity to derive the implied put-call parity certainty equivalent rate. We have also considered the meaning of positive rates and negative rates. Then, we utilized the idea of the implied volatility surface to construct the implied put-call parity certainty equivalent rate. From the relative positions of these surfaces, we can determine which stock option we should consider investing in first.
However, the certainty equivalent rate is only one factor that should be considered in investing. It is obvious that investors cannot just consider this factor. When deciding to invest in a product, investors should also consider other factors so that they can make optimal decisions.
Author Contributions
Conceptualization, S.R.; methodology, S.R.; software, Y.H.; formal analysis, Y.H. and S.R.; investigation, Y.H. and S.R.; resources, Y.H. and S.R.; data curation, Y.H.; writing—original draft preparation, Y.H.; writing—review and editing, Y.H. and S.R.; visualization, Y.H.; supervision, S.R.; project administration, S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Derek Saul. 2023. These are the best (and worst) performing stocks of 2023. In Forbes. Available online: https://www.forbes.com/sites/dereksaul/2023/02/20/these-are-the-best-and-worst-performing-stocks-of-2023/?sh=39a59b3d85a6 (accessed on 20 February 2023).
- Henry Khederian. 2023. Why Charles Schwab (SCHW) stock is falling sharply? In BENZINGA. Available online: https://www.benzinga.com/news/23/05/32168058/why-charles-schwab-schw-stock-is-falling-sharply (accessed on 2 May 2023).
- Hugh Son. 2023. JPMorgan Chase takes over First Republic after biggest U.S. bank failure since 2008. In CNBC. Available online: https://www.cnbc.com/2023/05/01/first-republic-bank-failure.html (accessed on 1 May 2023).
- John, C. Hull. 2022. Put-call parity. In Options, Futures and Other Derivatives, 11th ed. New York, NY, U.S.A.: Pearson, p. 368.
- Lora Shinn and Vikki Velasquez. 2023. What happened to Signature Bank? In Investopedia. Available online: https://www.investopedia.com/what-happened-to-signature-bank-7370710 (accessed on 1 May 2023).
Figure 3.
Implied put-call parity certainty equivalent surface (electric vehicle companies in the U.S.A.).
Figure 3.
Implied put-call parity certainty equivalent surface (electric vehicle companies in the U.S.A.).
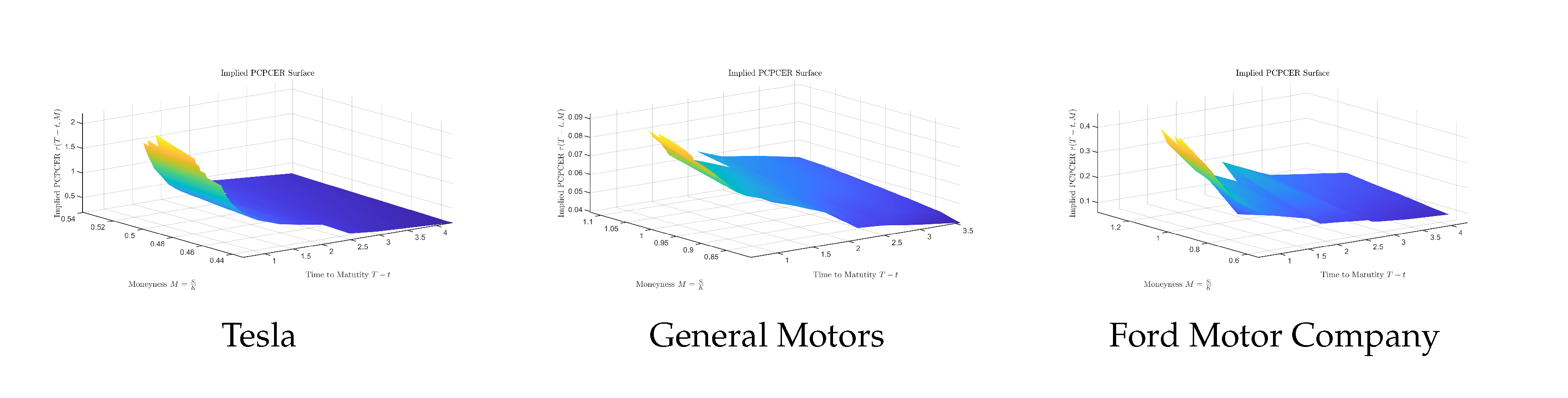
Table 1.
Implied put-call parity certainty equivalent rate (best- and worst-performing companies).
| Company | Maximum value | Minimum value | Mean value |
|---|---|---|---|
| Apple | 0.8644 | 0.1181 | 0.4437 |
| Nvidia | 4.0908 | 0.3308 | 1.8897 |
| Meta | 2.6418 | 0.2238 | 1.2135 |
| First Republic Bank | -0.8600 | -0.9998 | -0.9731 |
| Signature Bank | -0.0166 | -0.4008 | -0.1601 |
| Charles Schwab | -0.0481 | -0.4523 | -0.2625 |
Table 2.
Implied put-call parity certainty equivalent rate (electric vehicle companies).
| Company | Maximum value | Minimum value | Mean value |
|---|---|---|---|
| Tesla | 2.1970 | 0.1994 | 1.0320 |
| General Motors | 0.0927 | 0.0395 | 0.0708 |
| Ford Motor Company | 0.4549 | 0.0615 | 0.2626 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







