Prerpints.org logo
Preprint
Article

Mathematical Modeling and Computational Simulation Applied to the Study of Glycerol and/or Molasses Anaerobic Co-digestion Processes

Altmetrics

Downloads

140

Views

54

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

14 June 2023

Posted:

15 June 2023

You are already at the latest version

Alerts
Abstract
Abstract: An attractive application of crude glycerol is in the generation of biomethane by means of anaerobic co-digestion, involving the decomposition of the organic matter in two or more substrates by bacteria and archaea, in the absence of oxygen. Thus, the objective of this work was to evaluate the potential of neural networks and fuzzy logic to predict the production of biomethane from the anaerobic co-digestion of glycerol and/or sugarcane molasses. Firstly, a reactor model was implemented using Scilab, with Monod kinetics involving two substrates and an intermediate (M2SI model), to generate a database for subsequent fitting and evaluation of neural and fuzzy models. The neural network package of Matlab was used. Fuzzy modeling was applied using the Takagi-Sugeno approach available in the ANFIS package of Matlab. The biomethane production results simulated by M2SI were used in neural network modeling, firstly employing a “generic” network applicable to all 8 scenarios. A very good fit was obtained (R²>0.99). Excellent performance was also observed for specific artificial neural networks (one for each condition). The parameters of the M2SI model for the 8 different conditions were also mapped using a neural network, as a function of the organic material composition. A fit with R²>0.99 was obtained using 25 neurons. In the case of the fuzzy logic, RMSE of 18.88 mL of methane was obtained with 216 rules, which was a value lower than 0.5% of the order of magnitude of the accumulated methane. It could be concluded from the results that fuzzy logic and artificial neural networks offer excellent ability to predict methane production, as well as to parameterize the M2SI kinetic model (using neural networks).
Keywords: 
Subject: Engineering  -   Chemical Engineering

1. Introduction

Since the Stockholm Conference in Sweden, in 1972, many efforts have been made and public policies have been created aiming to minimize the impacts of anthropogenic activities on the environment [1]. The use of biofuels is a clean energy option that can replace fossil fuels and contribute to reducing greenhouse gas emissions. Biofuels are usually produced from renewable sources of plant origin, but can also be obtained from byproducts and domestic and agro-industrial wastes. This makes them highly appropriate in the circular economy and provides a use for materials that would otherwise be improperly discarded in the environment.
Brazil can be highlighted in the global policy of production and marketing of bio-fuels, since the country was a pioneer in the production of ethanol. In 2004, the Federal Government published a National Policy for the Use and Production of Biodiesel, stipulating the increasing incorporation of biodiesel in diesel, to reach 15% in 2023 [2]. Most of Brazilian biodiesel production uses soybean oil, although waste frying oil and animal fat may also be used [3,4]
In 2018, the Federal Government established a National Biofuels Policy, with de-carbonization targets to be met by 2030, linked to incentivizing the production of ethanol and biodiesel. Hence, it is expected that the production of these biofuels in the country will increase during the next ten years [5]. One consequence of increased biodiesel production is the large quantity of glycerol generated. However, the market demand for this product has not grown at the same rate, which has led to depreciation of the glycerol price. Furthermore, the glycerol formed in the process contains many impurities, so it needs to be purified before it can be sold. Due to the low glycerol price, its treatment has not been economically feasible, especially for small and medium sized biodiesel producers. Glycerol has high polluting potential, so it should not be discharged into the environment in effluents. As an alternative, one emerging use for crude glycerol is as a substrate in anaerobic digestion for the production of biogas and application in energy processes [6].
Anaerobic digestion consists of the degradation of organic matter by bacteria and archaea, in the absence of oxygen. However, maintaining the metabolic processes of these microorganisms requires nutrients (such as nitrogen, phosphorus, potassium, sodium, and iron, among others) and favorable environmental conditions [7]. Glycerol is a compound rich in carbon, so it can provide a source of energy for the process. However, it does not contain the macro and micronutrients required to support fermentation. Therefore, to make the process feasible, it is necessary to add synthetic nutrients or a co-substrate that contains the main nutrients in its composition.
Sugarcane molasses, a byproduct from the crystallization step of sugar production, contains nutrients (including calcium, nitrogen, phosphorus, iron, and sulfur) that can assist microbial growth [8]. Predictions for the Brazilian sugar and ethanol sector indicate the continued generation of molasses on a large scale, with widespread availability and low prices [9]
The literature contains many experimental studies, such as those by Costa [10], Paranhos and Silva [11], Freitas [12] and Pereyra et al. [13], aimed at exploring the energy potentials of these two substrates (glycerol and sugarcane molasses) and finding optimal conditions for the production of hydrogen, methane, and value-added metabolites. Anaerobic digestion is a complex process requiring the evaluation of many different parameters (such as temperature, organic load, pH, alkalinity, and retention time, among others), with kinetic studies being essential for maximizing bioenergy production and optimizing the variables. One approach is to use the Monod two-substrate with an intermediate kinetic model, proposed by Rakmak et al. [14], which allows calculation of the accumulated methane production in anaerobic co-digestion.
On the other hand, when a database is available, an attractive approach is to use artificial intelligence for rapid, precise, and inexpensive prediction of the behavior of the process. Artificial intelligence uses mathematical approaches based on the way that humans think and learn. The main methods involve the use of artificial neural networks and fuzzy logic. As the name suggests, artificial neural networks were inspired by biological neural networks and are structured in layers, with the results of mathematical calculations flowing from one layer to another, simulating nerve synapses. Fuzzy logic, on the other hand, is based on the relative and nebulous way of human thinking when quantifying situations, with the solving of problems using a series of rules elaborated using non-numerical variables [15].
Considering the above background, the aim of the present work was to evaluate the potential of artificial neural networks and fuzzy logic to predict methane production and the kinetic parameters for co-digestion of glycerol and sugarcane molasses.

2. Bibliographic review

2.1. Substrates used and their importance

2.1.1. Glycerol

The glycerol molecule can be formed in biological processes, chemical synthesis of petrochemical compounds, ethanol production, hydrogenation of the sucrose molecule in the presence of a catalyst, at high temperature and pressure, and as a byproduct of soap or biodiesel production [16]. According to Quispe et al., [6], until the 1950s, all the global glycerol production was from the saponification reaction, while today glycerol is also produced by the transesterification reaction and from glycerides. The crude glycerol obtained from the transesterification reaction has around 70% purity, with the other components being impurities such as water (8-30%), salts (0-10%), alcohols (<0.5%), and residual oils (~0.5%).
Ayoub and Abdullah [17] described how the physicochemical properties of glycerol result in it having many applications in the pharmaceutical, cosmetics, chemical, and food industries. There are different types of crude glycerol refining, which consider the degree of purity required for the intended application [6,16].
Given the increasing global demand for biodiesel, the quantity of glycerol generated will also increase. A volume of 8-10% of glycerol is generated during transesterification, with an estimated 41.9 million cubic meters of glycerol produced worldwide in 2020 [18,19]. According to Abiquim [20], in 2008 the Brazilian market had an annual demand of around 30 thousand cubic meters of glycerol, while the production capacity was ap-proximately 117 thousand cubic meters of double-distilled glycerol from transesterification. Industrial applications require high-purity glycerol, but the purification process is expensive, while at the same time the increased supply has reduced the market price. The recovery of alcohols (usually methanol) requires distillation or evaporation processes, where the recovery process may be more expensive than using new methanol, making reuse unfeasible. Therefore, it is important to develop new applications for crude glycerol, in order to make biodiesel production more competitive and viable, in addition to ensuring that all the glycerol generated can be absorbed by the market in some way. The high chemical oxygen demand (COD) of glycerol means that it has high polluting potential if released into water bodies in the environment [11].

2.1.2. Sugarcane molasses

Molasses, a byproduct of the sugar crystallization process, has a low market value, wide availability, and biodegradability. The nutrient content of molasses makes it a good co-substrate for optimizing the production of biohydrogen and biomethane by dark fermentation. Exploiting the energy potential of sugarcane molasses and diversifying the production of biofuels could be a more competitive strategy, compared to only producing bioethanol [21].

2.2. Anaerobic co-digestion

Co-digestion refers to processes where the organic matter consists of two or more different substrates. The use of different substrates can enhance fermentation and increase biogas yield, if the combination is performed strategically. Co-digestion can assist in regulating pH, improving carbon/nitrogen and carbon/phosphorus ratios, and increasing the availability of micro and macronutrients required for the metabolism of the microbial community.
Preliminary batch studies of the co-digestion of glycerol and a second substrate were performed by Aguilar et al., [22], using swine waste, with the results showing that biogas production and COD removal were favored by co-digestion.
The anaerobic process usually has four distinct stages [7]: Hydrolysis; Acidogenesis; Acetogenesis and Methanogenesis. Acidogenesis and acetogenesis are also known as primary fermentation, while methanogenesis is secondary fermentation. In the presence of nitrate or sulfate, the hydrogen formed in the acidogenesis step acts as an electron donor for the reducing bacteria, producing sulfides and ammonia [7].
Temperature is an important factor in the digestion process. Microorganisms are unable to regulate their internal temperature, which is therefore determined by the environment. The production of methane can occur in a wide temperature range up to 97 °C, while hydrogen formation occurs from 15 to 85 °C, and it is not possible to produce H2 under psychrophilic conditions [7,23]. According to Chernicharo [7], the best temperatures for microbial growth and biogas production are in the mesophilic (30-35 °C) and thermophilic (50-55 °C) ranges, with thermophilic conditions generally providing higher hydrogen and methane production rates. Operating at around 55 °C requires the consumption of energy to transfer heat, which can make the process economically unfeasible. Therefore, most anaerobic digesters are operated under mesophilic conditions, which are easy to provide in tropical countries, such as Brazil [7,23]. Controlled fermentation processes can be performed in different types of reactors, which may be operated continuously or in batch mode [7].

2.3. Artificial Neural Networks

Different artificial neural network architectures are described in the literature, although the most common is the multilayer perceptron (MLP), often incorrectly used as a neural network synonym. Other architectures include convolutional neural networks and recurrent neural networks, among others. According to Nelles [15], the MLP can approximate any smooth function, with a degree of precision that varies with increase of the number of neurons in the hidden layer. Increasing the number of hidden layers makes the method more powerful, albeit more complex.
The structure of an MLP network can be described by Equation 1. There are “n” inputs (x), with each input being accompanied by a weighting (wij) that is a network adjustment parameter. In addition, there is a bias (wi0) that provides a further degree of freedom for fitting the network response to experimental data, which can be considered an independent weighting (not associated with any input variable). All these parameters compose the “m” neurons of the hidden layer. The hidden layer neurons are usually composed of sigmoid (ϕi) logistic (Equation 2) and hyperbolic tangent (Equation 3) functions. These neurons are arranged in parallel and send signals to the neurons of the next layer, until reaching the output layer (in practice, one or two hidden layers are sufficient). In the output layer, the neurons are usually composed of linear functions (a linear combination) for adjusting the amplitude and the point of operation. This mathematical structure enables the MLP to be applied to different problems, demonstrating the universality of the method [15].
y = ∑ i = 0 m w i φ i ∑ j = 0 n w i j x j ,     φ 0 = 1   a n d   x 0 = 1
making u= wij xj:
L o g i s t i c   f u n c t i o n :   φ i u = 1 1 + e x p ⁡ ( − u )
H y p e r b o l i c   t a n g e n t :   φ i u = exp ⁡ u − e x p ⁡ ( − u ) e x p ⁡ ( u ) + e x p ⁡ ( − u ) = 1 − e x p ⁡ ( − 2 u ) 1 + e x p ⁡ ( − 2 u )

2.3.1. Application of Neural Networks in biogas production

In order to optimize the development of bioenergy and make it attractive from both environmental and economic perspectives, different areas of research and technology have encouraged the use of artificial neural network resources for the prediction of biogas production scenarios using the co-digestion of different substrates. This methodology can assist in solving problems that are complicated to model, predicting outcomes in a more simplified way.
Jaroenpoj et al., [24] used a multilayer feedforward model to predict the production of biogas from co-digestion of leachate and pineapple peel. In comparison with experimental data, the simulation results had a squared error of 0.0267 and R2 of 0.9942, showing the effectiveness of this approach and its versatility in prediction applied to nonlinear problems.
Ghatak and Ghatak [25] used artificial neural networks to model and optimize the production of biogas from co-digestion of cattle manure combined with bamboo dust, sugarcane bagasse, or sawdust, under mesophilic and thermophilic conditions. The results for biogas specific production presented R2 of 0.997 and accuracy of ±0.01, compared to experimental values. The simulations were performed using different temperatures of the substrates. The best biogas production was obtained using the co-digestion of cattle manure with sugarcane bagasse.
Özarslan et al., [26] used artificial neural networks to predict the production of methane from co-digestion of tea factory wastes and spent tea waste, comparing the results to experimental data from the co-digestion of these substrates for 49 days, in batch mode, under mesophilic conditions. The coefficient of determination (R2) value obtained for the fit was 0.9982 and the best mixture for methane production was 65% tea production waste and 35% spent tea. The accumulated production of biogas obtained in the co-digestion was 183% higher than for anaerobic digestion of the substrates separately.
Gonçalves Neto et al., [27] investigated the digestion and co-digestion of food wastes (including fruits, vegetables, meats, and dairy products) using experiments in batch mode, under mesophilic conditions and with different organic loadings. In addition to the experimental values, the database included literature data that acted as a basis for implementing the logic of artificial neural networks. The input variables were the substrate mixture composition, reactor feed flow rate, reactor type, organic loading, pH, hydraulic retention time, volatile solids, temperature, and reactor volume. The output variable was the accumulated biogas production. The network provided R2 values of 0.9929 for training, 0.8486 for testing, and 0.6167 for validation. It was found that the biogas pro-duction volume was higher under thermophilic conditions, with a local maximum for mesophilic temperatures. It was also concluded that the isolated digestion of fruits and vegetables produced a greater accumulated quantity of biogas, compared to the co-digestion of food wastes.

2.4. Fuzzy Logic

An alternative to artificial neural networks is the use of fuzzy logic, developed in 1965 by Lotfi A. Zadeh. The methodology was inspired by the vague and uncertain way in which human beings think and communicate, absorbing semiquantitative information in the description of a process [15].
This approach is especially useful for complex systems. Advantages are that fuzzy logic is conceptually easy to understand and that the mathematical equations employed are relatively simple. Recent years have seen increasing use of fuzzy logic in the development of cameras, washing machines, microwaves, and industrial process control systems [28].
The main concepts on which fuzzy logic is based are presented below.
  • Linguistic variable and linguistic value
In fuzzy logic, linguistic variables are non-numerical, being represented qualitatively by linguistic values (high, medium, and low). Consequently, they have a degree of uncertainty, since the numerical input data will be subdivided into linguistic values with a certain degree of adherence.
  • Membership functions
In fuzzy logic, membership functions (MF) describe the linguistic value intervals and the degree of belonging (degree of membership) of an element to these values. The membership functions can present different standard or customized curves, depending on the situation, with the most common being Gaussian, triangular, and trapezoidal.
A linguistic variable can have more than one linguistic value, with each linguistic value having its own function.
  • Heuristic rules
Based on the behavior of human thought, the heuristic rules of fuzzy logic are formulated according to the concept of cause and effect: “IF” there is a given input condition “THEN” there is a consequent specific response. The number of rules is a com-bination of the inputs and depends on the granularity (degree of detail) of the linguistic variables. Like artificial neural networks, fuzzy logic is a universal variable estimation tool [15]
There are two different approaches that structure the “IF”...“THEN” rules. The Mamdani approach uses linguistic variables for the input (antecedent, “IF”) and the output (consequent, “THEN”), while the Takagi-Sugeno approach uses linguistic variables for the input and numerical variables for the output. In the Takagi-Sugeno approach, the numerical variables are normally calculated using a linear function. Examples of the approaches are as follows:
IF long period THEN high volume of CH4 (Mamdani)
IF long period THEN 5000 mL volume of CH4 (Takagi-Sugeno)
  • Logical operators
In cases of more than one linguistic variable in the antecedent of the rules, then these variables are combined using logical operators, typically “AND” and “OR”. The “AND” operator is applied when the two antecedent conditions need to occur, in order for the consequent action to be performed. The “OR” operator is used when only one of the antecedent conditions needs to occur, in order for the consequent action to be performed.
Each operator performs specific calculations combining the degrees of membership of the linguistic variables in the antecedent. According to Nelles [15], this combination is called the degree of rule fulfillment or the triggering force of the rule, reflecting how well a created premise reflects the specific input value. If the combination of membership degrees (MDs) is equal to zero, then the rule is not active. The step where these operators are applied is denoted aggregation.
The “AND” operator combines MDs using the minimum or product methods (other methods exist, but these are the most common). The “OR” operator can also combine MDs in different ways, although the most common are the maximum and probabilistic OR methods.
After calculation of the degree of compliance with the rule, evaluation is made of the consequent of the rule. The commonest implication methods are truncation (using the minimum function) and scale reduction (using the product function). Use of a single rule is normally ineffective in solving the problem; therefore, it is necessary to evaluate the implication of the consequent for each rule, after which all the consequents are accumulated [15,28]. The commonest accumulation methods are the maximum, probabilistic, and weighted average methods. The maximum function evaluates the MFs point by point, selecting the highest value. The probabilistic function is indicated when there are only two rules, with calculation of the sum minus the product of each point of the MFs. The weighted average method performs the sum of all the points of the MFs and applies a weight to each value based on the MD.
In the Takagi-Sugeno approach, the combination of all the consequents provides the final result (output variable) of the problem. In the Mamdani approach, there is a final defuzzification step.
An excellent strategy that has increased the possible applications of fuzzy logic is its combination with neurocomputing and/or genetic algorithms. The ANFIS (Adaptive-Network-Based Fuzzy Inference System) methodology, developed by Jyh-Shing Roger Jang in 1993, functions in a similar way as artificial neural networks. It involves defining the parameters of a Takagi-Sugeno model, which enables the inference system to perform a mapping of the relationship between the inputs and the outputs, using im-plication rules. The parameters are adjusted using the backpropagation algorithm in combination with a statistical least squares method [28].

2.4.1. Application of fuzzy logic in biogas production

Among the many applications for fuzzy logic, recent reports have described its use in the prediction of biogas production from the anaerobic digestion of different substrates.
Khayum et al., [29] used the Mamdani fuzzy logic approach to predict the performance of co-digestion of spent tea waste and cattle manure. The simulation employed a triangular membership function and five layers, with a total of 125 “IF”...“THEN” rules being inferred. The input variables were digestion time, pH, and carbon/nitrogen ratio. Comparison of the experimental and predicted values resulted in R² of 0.994, demonstrating the precision of the fuzzy logic data. It was found that the highest biogas pro-duction was achieved using a mixture of 70% cattle manure and 30% spent tea waste.
Heydari et al., [30] investigated the production of biogas from the anaerobic digestion of mint essential oil wastewater, under mesophilic conditions in a UASB reactor, adopting the Takagi-Sugeno approach and the ANFIS methodology. The simulations were per-formed using Matlab R2017b, with 19 samples and 10 input variables (influent COD, pH, suspended solids, volatile solids, oil and grease removal, turbidity removal, COD removal, phenol removal, effluent volatile acids, and alkalinity). For prediction of methane production, the data were grouped in pairs in the first layer and the model was divided into eight sub-networks, employing five layers. The model provided a satisfactory fit, with R² of 0.956 and low mean relative error of 0.315%.

3. Objectives

3.1. General Objective

The main objective of this work was to explore the potential of computational intelligence (fuzzy logic and neural networks) for predicting methane production from co-digestion of glycerol and molasses in wastewater.

3.2. Specific Objectives

  • Obtain a database from computer simulation employing the Monod two-substrate with an intermediate (M2SI) simple kinetic model;
  • Train neural networks to predict methane production based on the database created;
  • Train a neural network to provide the kinetic parameters of the M2SI model;
  • Evaluate the quality of the results provided by artificial neural networks;
  • Specify a membership function type for fuzzy logic;
  • Define ranges of linguistic values for the linguistic variables of the fuzzy inference system;
  • Apply a neuro-fuzzy methodology for parameterization of the fuzzy model;
  • Evaluate the effectiveness of the fuzzy logic approach;
  • Compare the results obtained using the artificial neural network and fuzzy logic approaches.

4. Materials and Methods

4.1. Monod two-substrate with an intermediate (M2SI) kinetic simulation model

For generation of a database of biomethane production from the co-digestion of wastewaters containing glycerol or molasses, the Monod two-substrate with an inter-mediate (M2SI) kinetic model proposed by Rakmak et al., [14] was considered, with parameters as reported by Phayungphan et al., [31]. In this work, the generation of a database by using the M2SI Model has methodological importance only, to allow the assessment of computational intelligence models. Obviously, this step is not necessary in a practical situation where an experimental database is already available.
The M2SI model adopts the following hypotheses:
  • Endogenous metabolism is present in the process.
  • An intermediate substrate (Si) is added in the hydrolysis step. This substrate is obtained from slow degradation (Ss). The Si is consumed by a specific group of microorganisms (Xe).
  • There are two groups of microorganisms: Xe (degrades Se and Si) and Xs (grows on Ss)
Assuming these hypotheses, the M2SI model was produced using the ordinary differential equations shown below, where X is the concentration of microorganisms, S is the concentration of substrate, and P is the concentration of biogas. The subscripts “e”, “s”, and “i” indicate substrates with fast degradation (Se), slow degradation (Ss), and intermediate (Si); µ and µm are the specific and maximum microbial growth rates, respectively; kd is the specific microbial death rate; K is the saturation constant; YX is the yield of microorganisms; and YP is the biogas production yield from each substrate. The factors fSsX and fisX correspond to the conversion of X to Ss and of Ss to Si, respectively.
d X e d t = X e μ e + μ i − k d e ,   μ e = μ m e S e K e + S e
d X s d t = X s μ s − k d s ,   μ s = g ( P ) μ m s S s K s + S s
d S e d t = − μ e X e Y X e S e
d S i d t = f i s X μ s X s 1 − Y X s S s Y X s S s − μ i X e Y X e S i ,   μ i = μ m i S i K i + S i
d S s d t = f S s X k d e X e + k d s X s − μ s X s Y X s S s
d P d t = μ e X e Y P S e Y X e S e + μ i X e Y P S i Y X e S i
The function g(P) is a commutation or preference function, given by Equation 10. The variables α, Pc, fc, and fSs are the amplification factor, critical biogas concentration, critical factor, and fraction of Ss in the initial substrate concentration (S0), respectively.
g P = 1 π t a n − 1 α P − P c + π 2 ,   P c = S 0 Y P S e f c ( 1 − f S s )
Equations 4-10 were implemented in Scilab (v. 6.1.1), using the “ode” function to solve the system of ODEs and obtain the biogas concentrations for the conditions shown in Table 1. The final concentrations were compared with the values reported by Phayungphan et al., [31]. The results that showed good agreement were saved as .csv files.

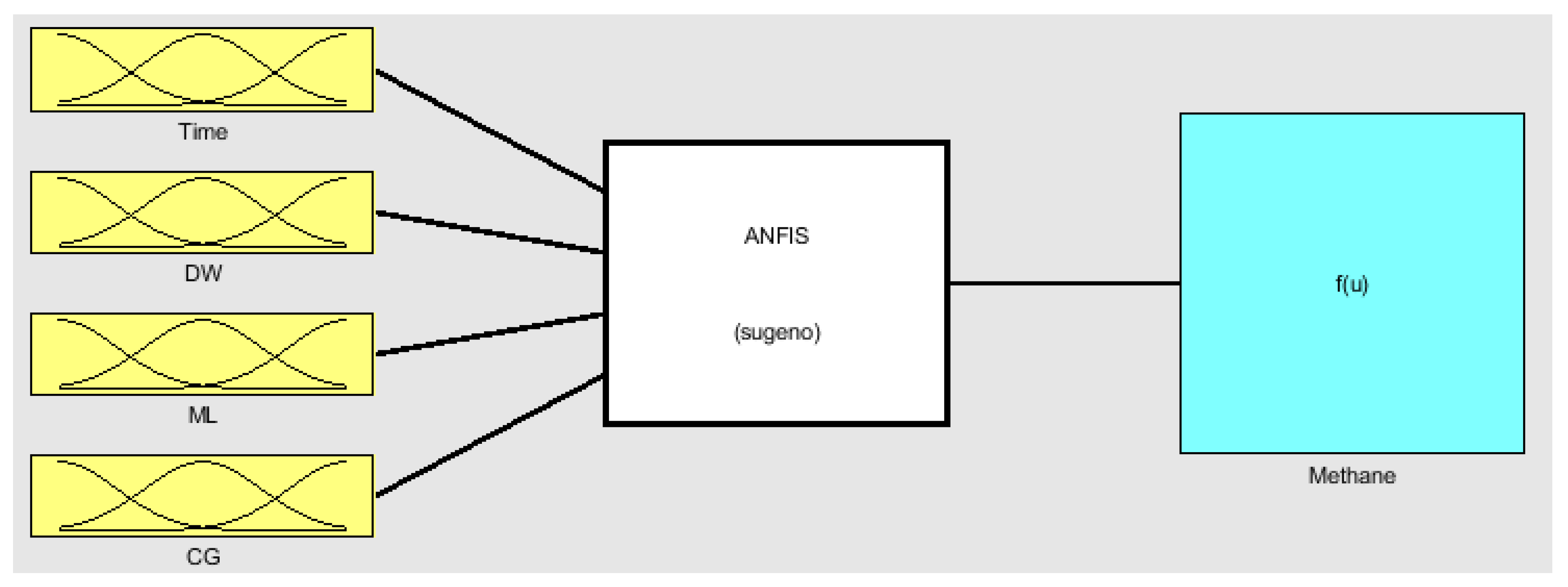
4.2. Application of the neural networks

Implementation of the neural networks was performed using the Neural Network package of Matlab v. R2018a, based on the review by Beale et al., [32]. Firstly, network training was performed, with simulations to predict the production of biogas according to time, considering different substrate compositions, followed by network training to predict the Monod parameters as a function of substrate composition.
All the training employed the Levenberg-Marquardt backpropagation algorithm.

4.2.1. Training of the neural network for obtaining biomethane

In elaboration of the training of a “generic” neural network (a single network, incorporating all the different substrate composition conditions), four inputs were considered, constituting a matrix of 4x688 elements. The first row of the matrix corresponds to the time variable (0 to 45 days), the second row to the normalized percentage of distillery wastewater (DW) in the substrate (95 to 100%, i.e., 0.95 to 1), the third row to the normalized percentage of molasses (ML) in the substrate composition (0 to 5%, i.e., 0 to 0.05), and the fourth line to the normalized percentage of crude glycerol (CG) in the substrate (0 and 5%, i.e., 0 to 0.05), as shown in Figure 1.
The output data of the generic neural network consisted of a 1x688 matrix, with a single line containing the methane production values (in mL) for each day and specific substrate composition. Hence, the network had four inputs and one output. The effect of the quantity of neurons in the hidden layer was tested until obtaining the minimum value that led to a good fit.
For simulation of specific neural networks (one for each composition condition) only the time variable was considered as input for each condition, with a 1x25 matrix for the 100% DW condition and 1x45 matrices for the other conditions. The output of each specific neural network was the methane production (in mL) for that condition, according to time. The network structure consisted of one input and one output, and 10 neurons were used in the hidden layer.
For both types of networks (generic and specific), the distribution of the data was 70% for training, 15% for validation, and 15% for testing.

4.2.2. Network training for prediction of the monod parameters

In agreement with the work of Phayungphan et al., [31], the Monod parameters were as follows:
  • Maximum microbial growth rate of Xe (µme);
  • Maximum microbial growth rate of Xs (µms);
  • Methane production yield from consumption of Se (YPSe);
  • Fraction of Ss in the total substrate composition (fSs);
  • Amplification factor (α).
These parameters constituted the 5 outputs of the network, associated with a 5x8 matrix (since there were 8 substrate composition conditions). The input matrix was 3x8, where the 3 inputs were the percentages of distillery wastewater, molasses, and glycerol in the substrate composition for the 8 different configurations.

4.3. Fuzzy Logic

The fuzzy logic was implemented using the ANFIS package of Matlab R2018a and the database generated in the M2SI simulation based on the work by Phayungphan et al., [31].
The data were divided into 628 points for training and 60 points for testing. The files were converted to text, with the data arranged in columns, where the last column corresponded to the output and the other columns corresponded to the input variables, as shown in Figure 2 (noticing that Figure 2 is not the same as Figure 1). The text file was loaded into the ANFIS program.
In the generation of the FIS, evaluation was made of the granularity of the input variables, in order to find the one that produced the lowest root mean square error. The Gaussian membership function (gaussmf) was employed (Equation 11), which uses the standard deviation (σ) and mean (x ̅) of the input values (x) [28]. This function was chosen based on the positive results observed in earlier tests.
F P x = exp ⁡ − x − x ¯ 2 2 σ 2
The ANFIS generated a Takagi-Sugeno type FIS, with four fuzzified input variables and an output variable calculated using a linear function (Figure 3), with parameter adjustment based on neural network concepts. A hybrid training algorithm was selected, combining backpropagation and the least squares method.

5. Results and Discussion

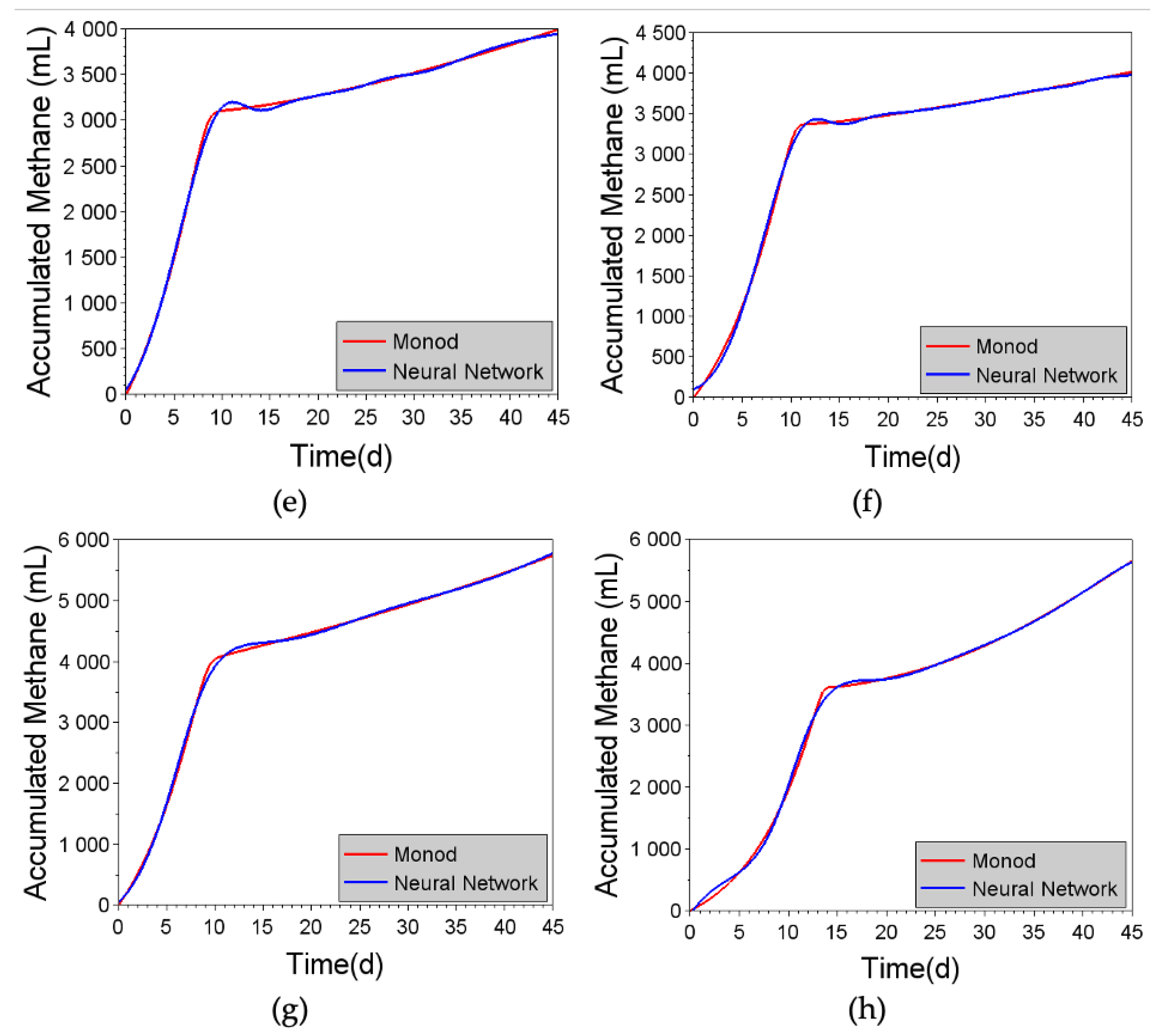
5.1. Biomethane production using monod kinetics

Based on the values and ranges for the Monod kinetic parameters published by Phayungphan et al., [31] and the M2SI model proposed by Rakmak et al., [14], the ac-cumulation of methane over time was estimated for the co-digestion of molasses (ML) or crude glycerol (CG) and distillery wastewater (DW). Comparison of the results of the M2SI model with the experimental results reported by Phayungphan et al., [31] indicated very satisfactory agreement, with low divergence, for compositions containing 100% DW, 99% DW / 1% ML, 98% DW / 2% ML, 97% DW / 3% ML, 96% DW / 4% ML, 95% DW / 5% ML, 99% DW / 1% CG, and 95% DW / 5% CG, which composed the database directly used to train the neural networks and the fuzzy model. Biogas production rates were similar to those presented by Phayungphan et al., [31]. The majority of the substrate degradation occurred in the first 10 days, after which there was a substantial decrease in methane production, indicative of possible inhibition of microbial activity. Total accumulated methane at the end of each batch is summarized in Table 2. In general, it was evident that the addition of glycerol to the distillery wastewater led to greater production of methane, compared to the addition of molasses.
The region of compositions containing about 98% DW / 2% CG and 97% DW / 3% CG, in turn, was posteriorly considered for additional assessment of the predictive capability of hybrid M2SI-Neural Network model (as will be seen in Section 5.5.1.) and analysis of the response surface generated by the fuzzy model (as will be seen in Section 5.6.1.).

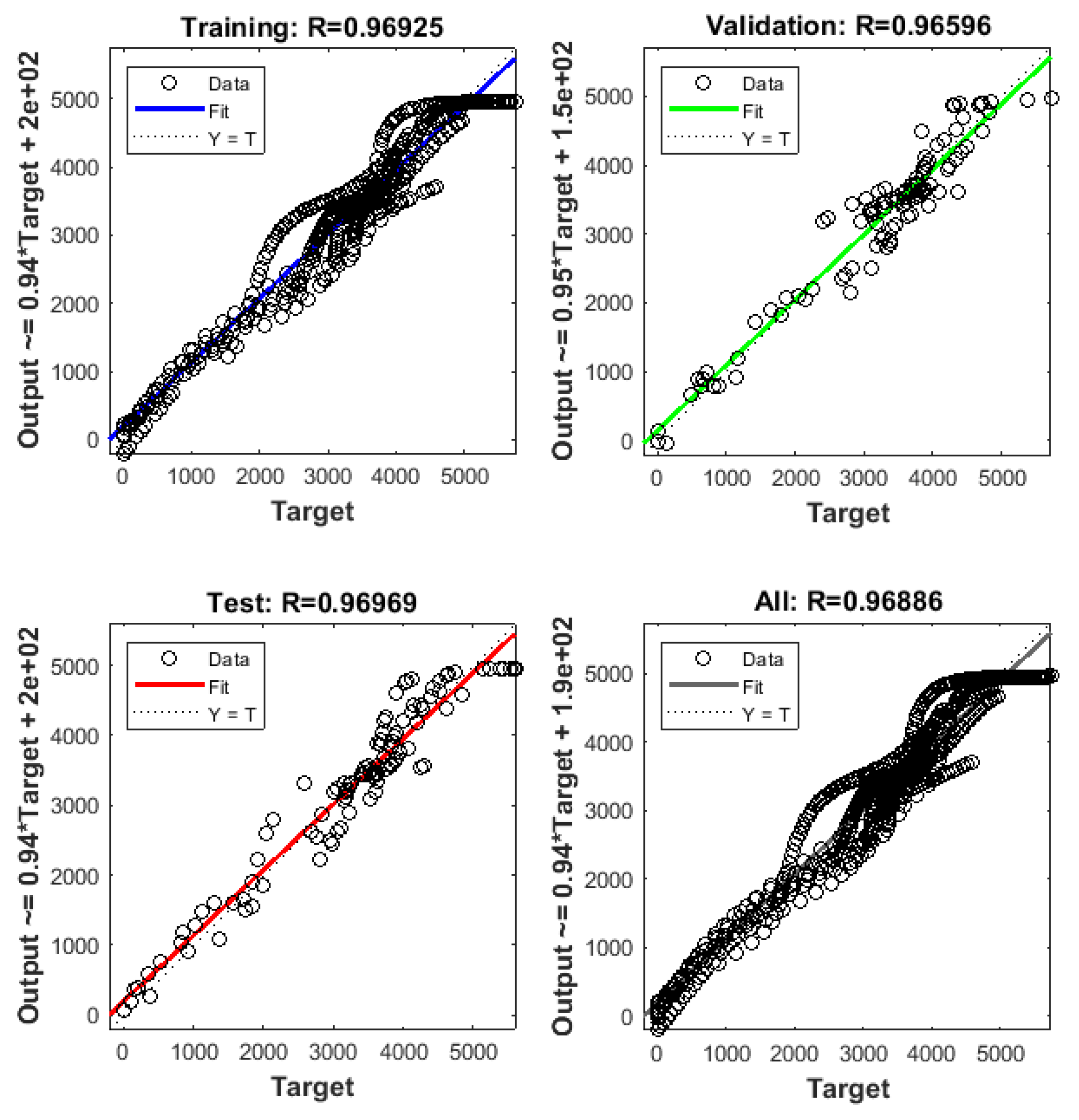
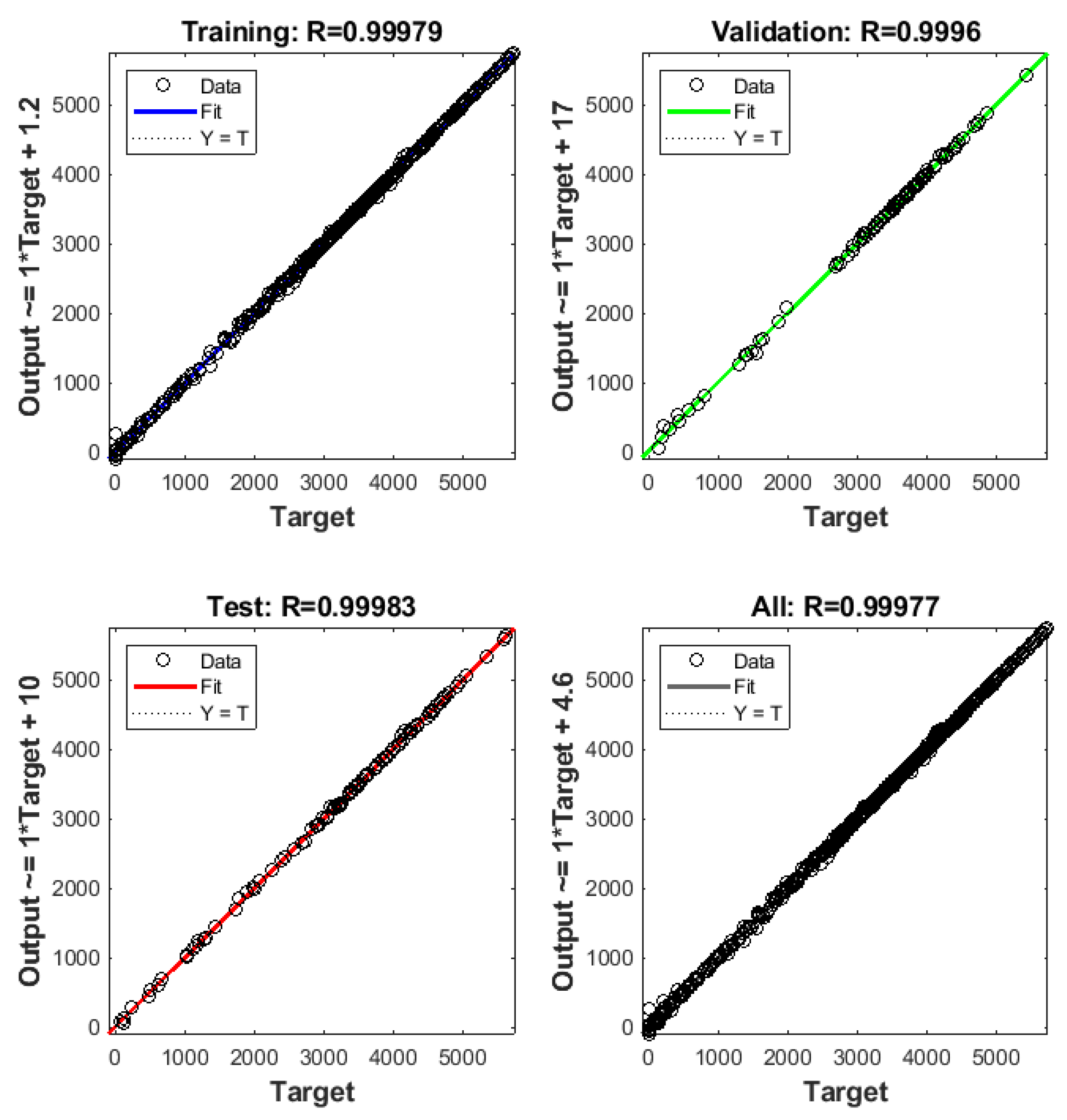
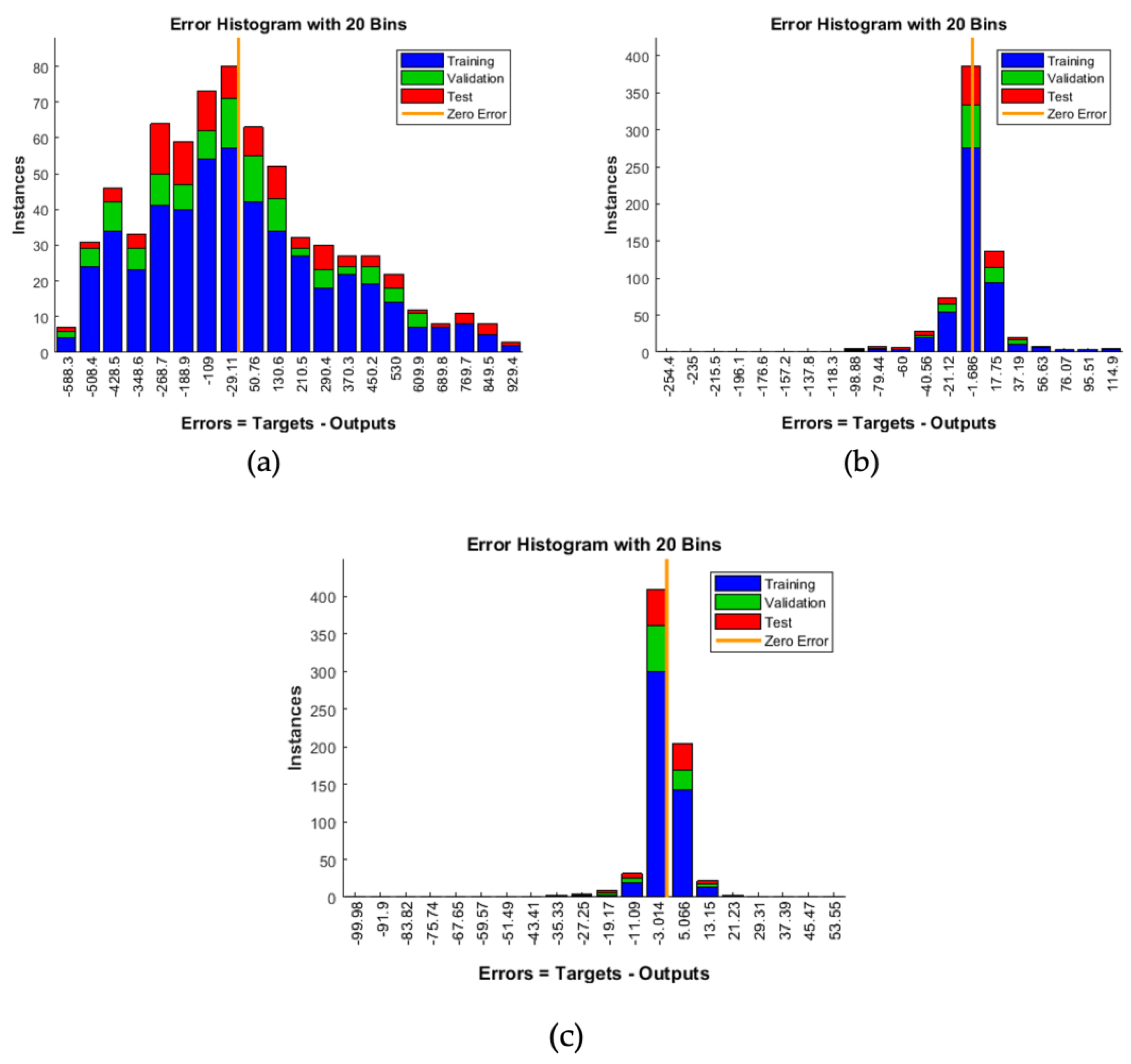
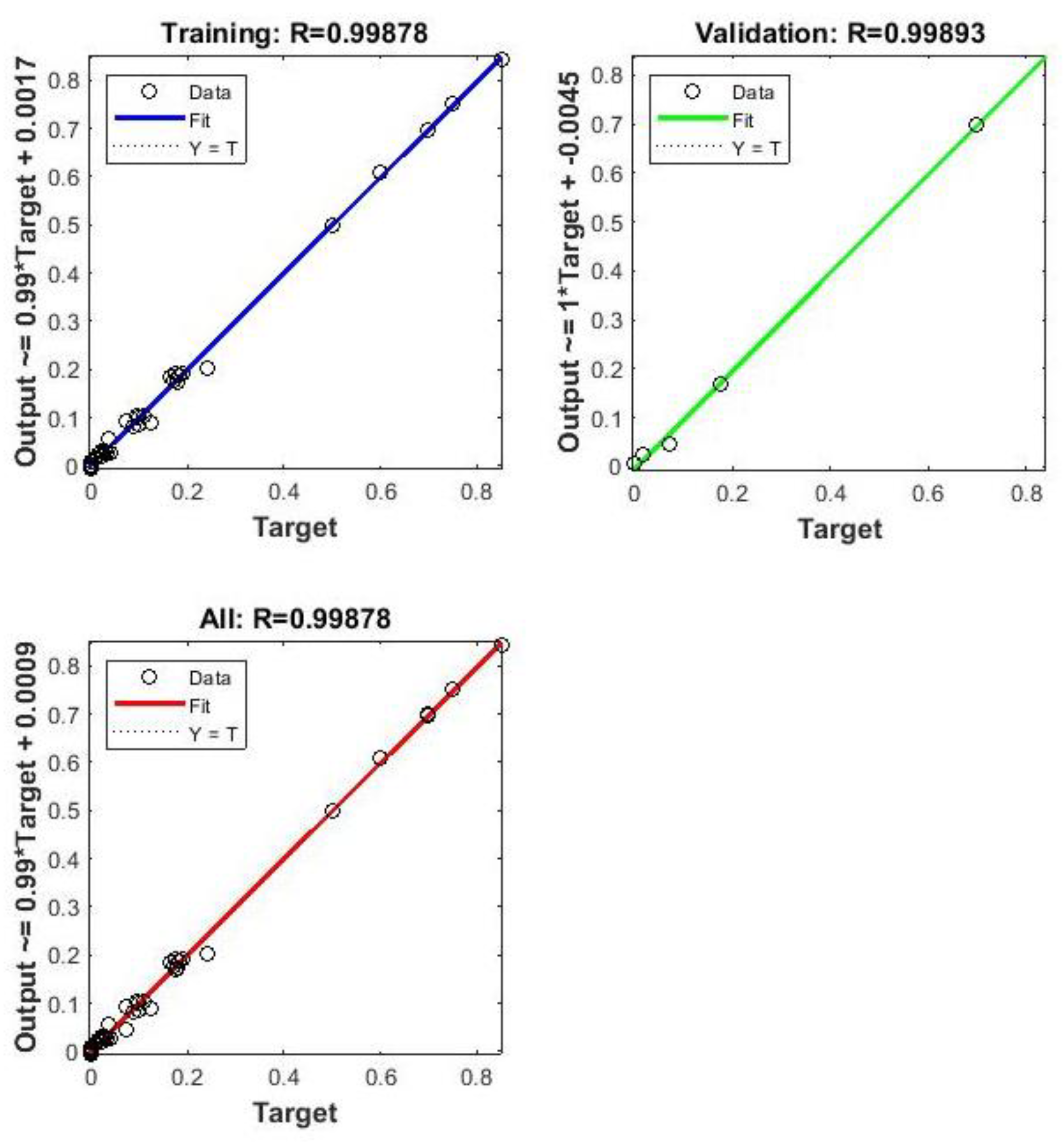
5.2. Training of the neural network for biomethane production

The training of the artificial neural network for methane production according to time, varying the substrate composition (Section 4.2.1), was made testing various quantities of neurons to find the minimum quantity of neurons in the hidden layer that provided a good fit between the intended output value and the value provided by the neural network. A lower number of neurons means that there is a lower number of “synapses” to be incorporated, resulting in faster processing of information by the network. The results obtained for “n” of 2, 14, and 60 are shown in Figure 4, Figure 5, Figure 6 and Figure 7. It is straightforward to see that 2 neurons are not enough, with low R2 values. The minimum number of neurons in the hidden layer required to obtain satisfactory results was 14.
As can be seen in Figure 4, Figure 5, Figure 6 and Figure 7, the fitting improved substantially when the number of neurons was increased from 2 to 14 neurons, while further increase to 60 neurons had a more subtle effect. Hence, increasing the number of neurons progressively improved the fit of the model, although the improvement was not significant after 60 neurons, so further testing was unnecessary. In addition, indiscriminate increase of the number of neurons (above 60) would make the model unnecessarily complex, with possible computational overload during data processing.
No previous studies were found in the literature that used neural networks for the prediction of methane production from the co-digestion of molasses and glycerol. Yetilmezsoy et al., [33] used neural networks in an investigation of the production of biogas and methane from the digestion of molasses wastewater in a UASB reactor, under mesophilic conditions. The input variables considered in the simulation were the organic loading, influent and effluent pH and alkalinity, temperature, volatile acids concentration, and COD. Three hidden layers with sigmoid tangent functions were applied, with optimal numbers of nine and twelve neurons obtained for the production of biogas and methane, respectively. Eleven types of network training algorithms were evaluated, with the best results obtained using the SCG (scaled conjugate gradient) algorithm, which provided coefficients of determination in the testing stage of 0.935 for biogas and 0.924 for methane. The fit of the model for methane production was poorer than found in the present work (R² = 0.99983 for 14 neurons), but it was considered satisfactory by the authors, considering the greater complexity of the system that was modeled.

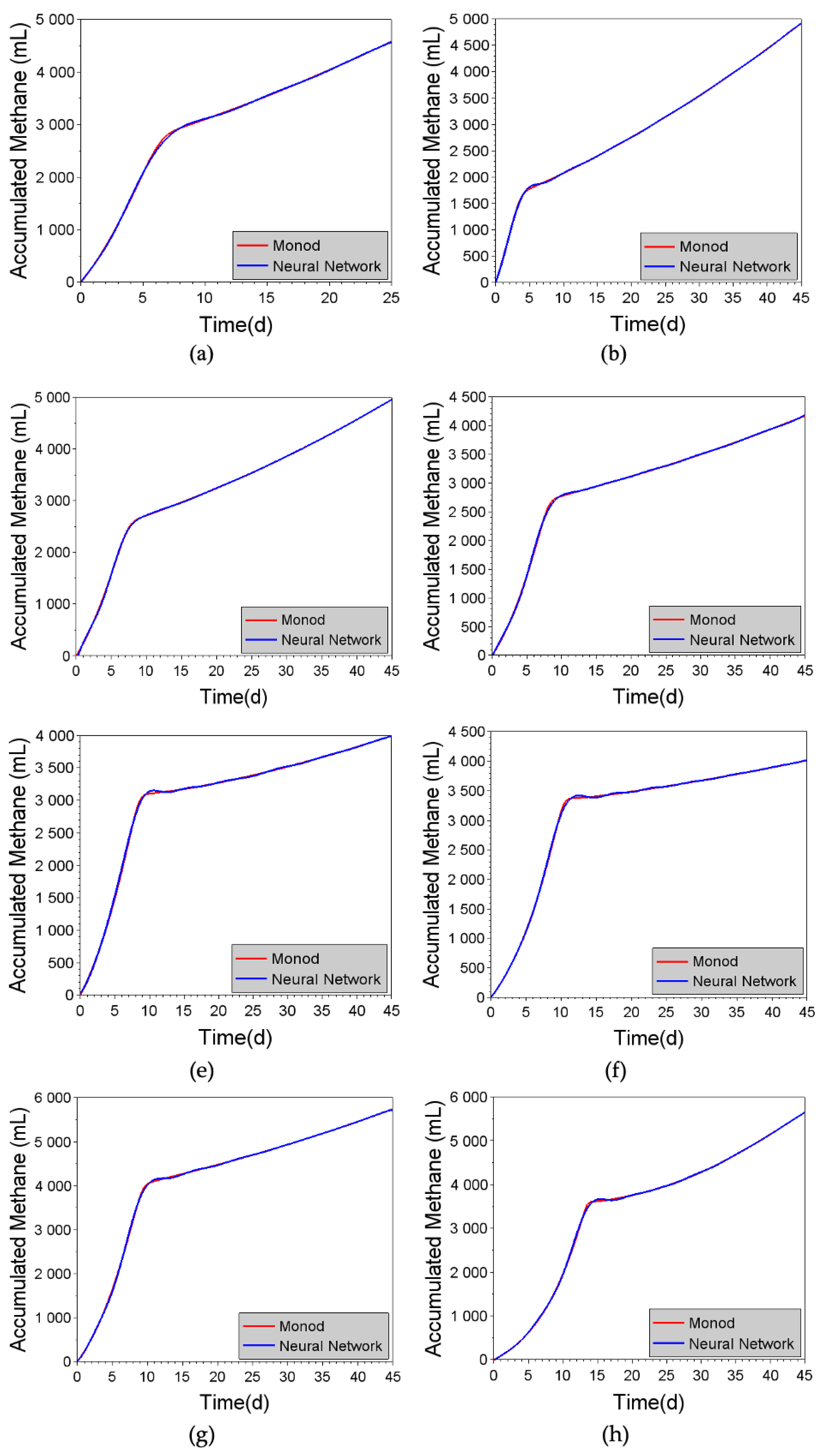
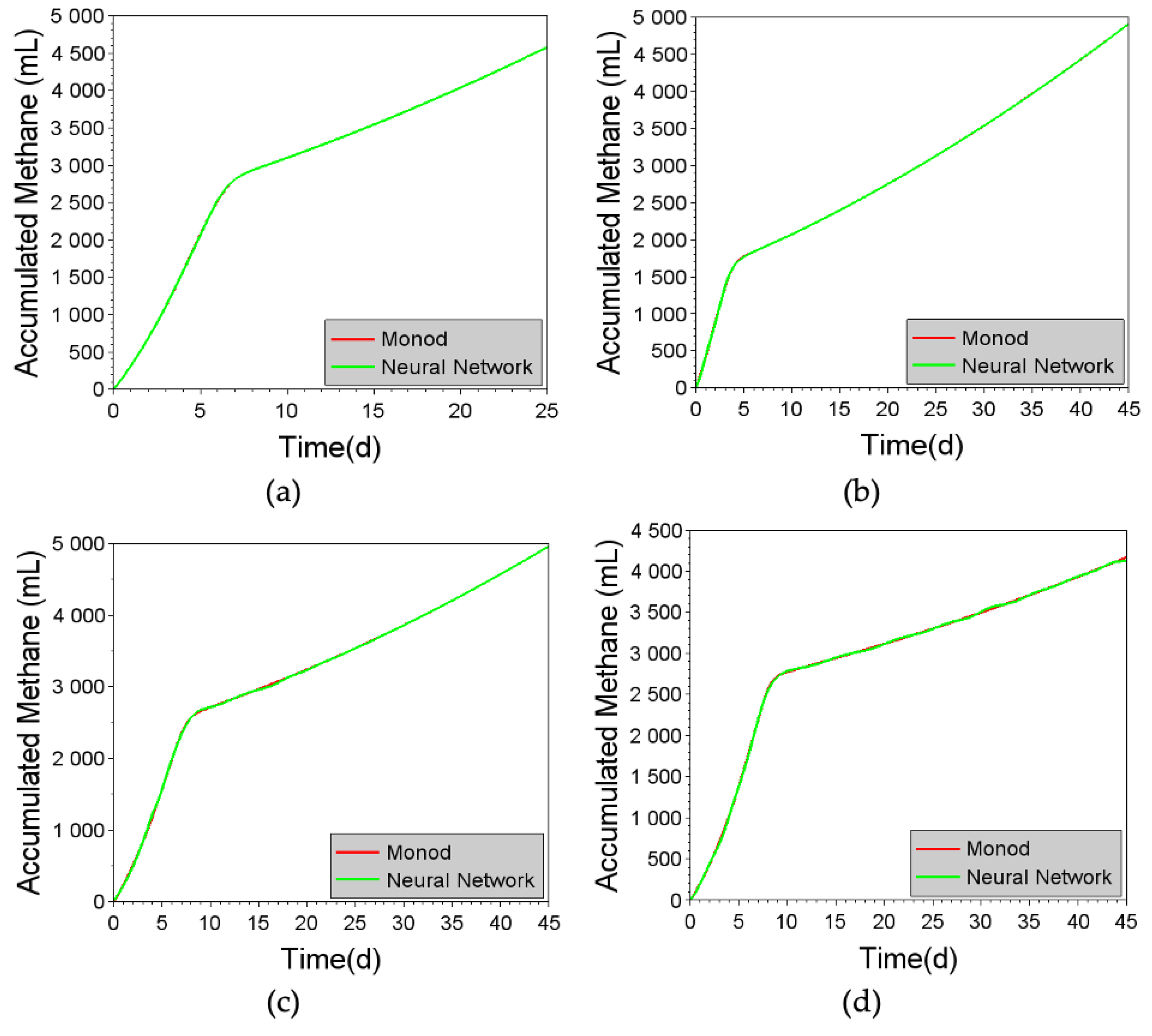
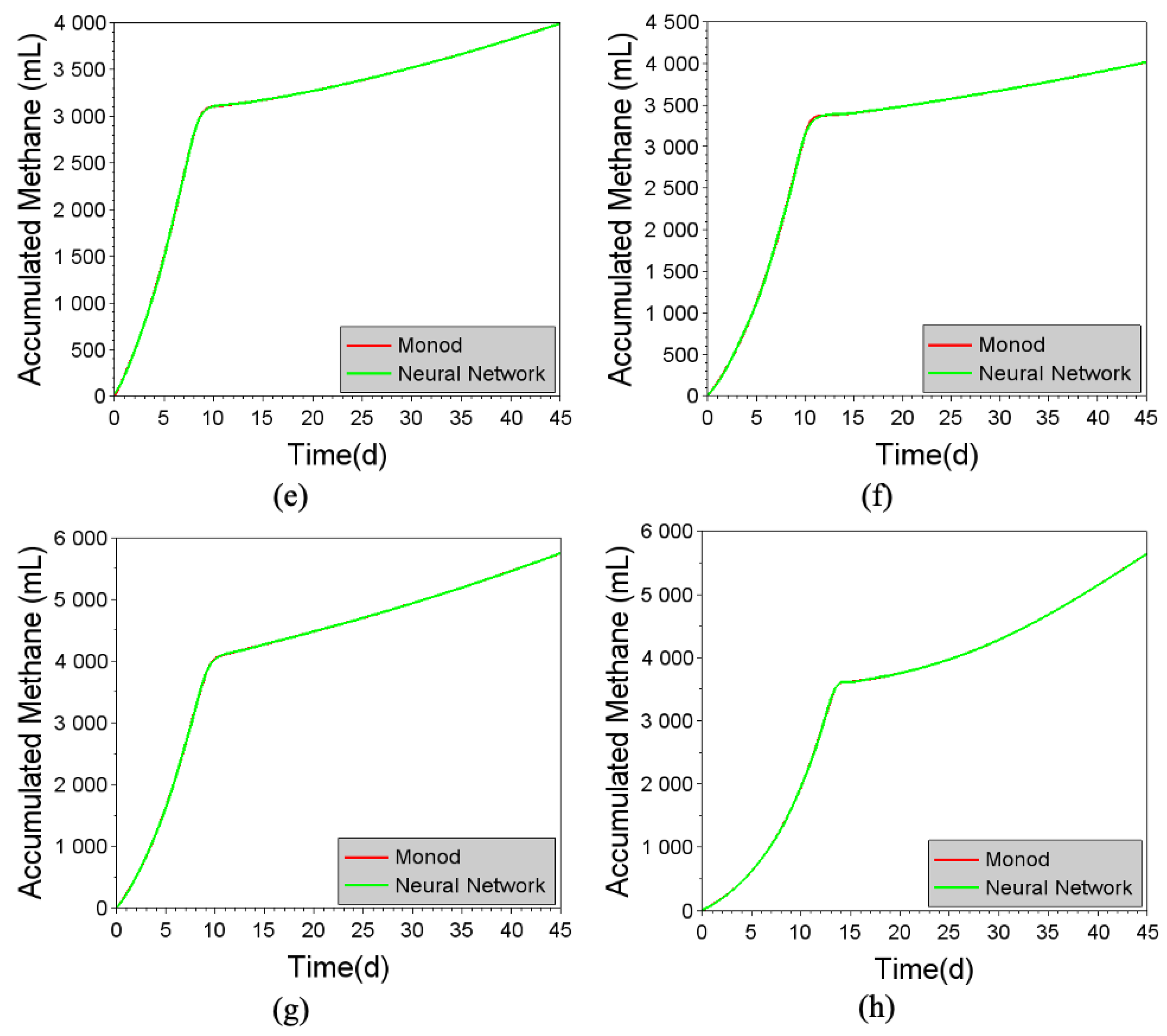
5.3. Comparison of prediction of methane production using the M2SI model and the generic neural network

After training the neural network, comparison was made of the predicted methane production obtained using the M2SI model and the artificial neural network (Figure 8).
As shown in Figure 8, good agreement was obtained between the predicted biomethane production curves for the M2SI model and the generic neural network, for the different conditions. Nonetheless, it should be noted that the predictions could be improved further by increasing the number of neurons in the hidden layer (to 60, for example), without risk of overfitting (see Figure 9).

5.4. Prediction of methane production using specific neural networks

Figure 10 shows a comparison of the predicted methane production using the M2SI model and the specific artificial neural networks. The results demonstrated the excellent predictive capacity of these artificial neural networks, which could therefore be used as an alternative strategy. In comparison with generic networks, the latter allow the use of interpolations of different values for the substrate composition, as well as the testing of hypothetical scenarios for methane production, which can generate an optimized combination, using a single network. However, it is possible to create a set of specific neural networks, where their combination in a committee would also allow interpolations of different values for the substrate composition. In a similar way, Horta et al., [34] proposed a committee of neural networks for identifying Streptococcus pneumoniae growth phases, used for on-line state inference.

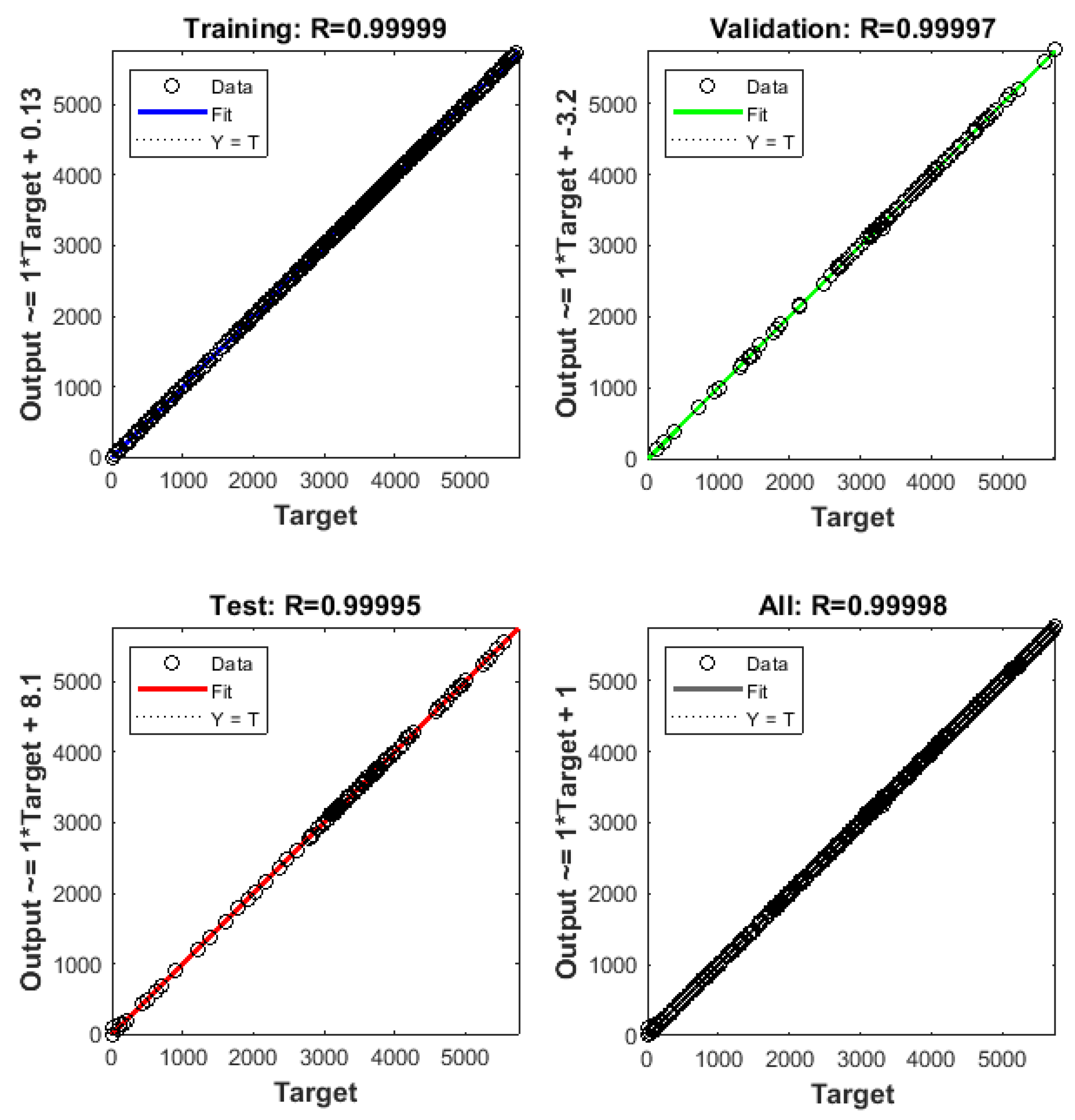
5.5. Neural network training to predict monod kinetic parameters

A neural network was trained to provide the kinetic parameters of the M2SI model, with the best fit obtained using 25 neurons (Figure 11). In order to achieve satisfactory prediction of the data, the testing step was eliminated, with 90% of the data being used in the training step and 10% in the validation step. This enabled consistent results to be obtained in the simulations, with fits presenting R² values higher than 0.99. Therefore, the neural network could be used in a hybrid M2SI-neural network approach. This enabled simulation of alternative compositions, obtaining the kinetic parameters for application in the M2SI model considered to predict methane production.

5.5.1. Assessment of the predictive capability of hybrid M2SI-Neural Network approach

By applying the neural network to predict Monod's parameters at 97% DW - 3% CG condition, it was possible to evaluate the predictive capability of the hybrid model. Experimental data from Phayungphan et al., [31] was considered for comparison purposes. The predicted methane production reached 4,766.39 mL of accumulated CH4 (as shown in Figure 12) compared to the experimental value of 4,464.64 mL of CH4, which represents a minor divergence of 6.7%.
In the training phase, no data on this composition was presented to the neural network. Despite that, the hybrid M2SI-neural network predicted a downward trend in accumulated methane with substrate containing 97% DW and 3% CG, which is in agreement with the experimental behavior.

5.6. Application of fuzzy logic

The simulations were performed with alteration of the granularity of the fuzzy system. As a standard procedure, Matlab R2018a recommends dividing the variables into three ranges of linguistic values. However, since the time variable had a greater range (0 to 45 days), it was initially divided into five linguistic values, while the other variables (concentrations of distillery wastewater, molasses, and glycerol) were divided into three values. Using this granularity, the model generated 135 “IF”...“THEN” rules and provided a root mean square error of 43.10 mL. When the granularity was changed to six linguistic values for the time variable, while keeping the other variables at three linguistic values, 162 rules were obtained, with root mean square error of 36.33 mL. Finally, when eight linguistic values were defined for time, while keeping the other variables at three values, a root mean square error of 18.88 mL was obtained, with 216 rules. Considering that the order of magnitude of the accumulated methane was around 5x10³, the error was very small (less than 0.5%). This could be considered a very satisfactory result. Increasing granularity progressively improved the capacity of the model, although granularity higher than eight for the time variable resulted in improvements that were less significant. Therefore, higher values were considered unnecessary. Besides, here it is possible to point out that concerns (to analyze and validate models) are not only based on R2 value. Furthermore, granularity higher than eight for the time variable would lead to greater difficulty in labeling its linguistic values, or even the loss of practical meaning for the labels applied.
Table 3 lists the parameters of the membership functions fitted using the ANFIS model.
The effectiveness of the neuro-fuzzy training was evidenced by the good agreement between the responses of the fuzzy model and the data from the M2SI model, as shown in Figure 13.
Turkdogan-Aydinol and Yetilmezsoy [35] investigated the production of methane from anaerobic digestion of molasses wastewater, under mesophilic conditions, applying the Mamdani fuzzy logic approach. This resulted in generation of 134 “IF”...“THEN” rules, with five input variables (organic load, COD removal, alkalinity, and influent and effluent pH) divided into 8 linguistic values. A trapezoidal type curve was selected for generation of the membership functions. The fuzzy model provided satisfactory results, with R² of 0.96, demonstrating the effectiveness of using a simple method, without complex mathematical equations, for accurate prediction of methane production.

5.6.1. Analysis of the response surface generated by the fuzzy model

From the fuzzy modeling, it was possible to build a response surface and evaluate the global effect of the composition of distillery wastewater, glycerol, and molasses on methane production. The time was set at 25 days as it was the maximum time for which information was available for the specific case of 100% distillery wastewater composition. Sugarcane molasses was fixed at 2.5%. Glycerol ranged from 0 to 5% and distillery wastewater from 95 to 100%.
In the scenario presented in Figure 14, the region with an amount of distillery wastewater greater than 97.5% is a non-feasible region (even with 0% of glycerol), since the composition of the substrates would exceed 100%. The same reasoning applies to the case of a glycerol amount greater than 2.5% (even with 95% still water).
Still, in Figure 14, it is possible to note the accuracy of the results, since for 0% glycerol, the volume of accumulated methane is around 3000 mL, which is consistent with the predictions for the compositions containing 2 and 3 % molasses (and 98 and 97% distillery wastewater, respectively). In addition, the volume of accumulated methane followed the expected behavior for glycerol, with a downward trend in methane production for glycerol composition increasing from zero to about 2.5% (95% distillery wastewater), as discussed in an analogous way in the application of hybrid M2SI-neural modeling. Actually, this was an important objective here: apply simple methodologies that can assist in solving problems that are complicated to model, predicting outcomes such as methane production as a function of mixing ratios of substrates in a more simplified way. Of course, it is supposed that the individual substrates maintain, in average, their main own basic characteristics.

6. Conclusions

From the results of the modeling and simulation using artificial neural networks, a good fit was obtained in the network training step (R² > 0.99). A minimum of 14 neurons were required in the hidden layer of the generic neural network for prediction of methane production. Good agreement was obtained between the methane production curves generated by the M2SI model and the generic neural network, under various conditions. Besides, a hybrid model provided satisfactory prediction of the kinetic parameters for the M2SI model. The number of neurons in the hidden layer of the neural network for prediction of the kinetic parameters of the M2SI model was 25.
The training of the fuzzy model with 216 rules had a mean square error of 18.88 mL of methane, which was less than 0.5% of the order of magnitude of the accumulated methane. Good agreement was obtained between the M2SI model methane production points and the fuzzy model simulation.
Even after phenomenological models (and some of them much more complex than M2SI) have been created to clarify the digestion process, their drawbacks have compelled many researchers to develop simplified alternatives. This way, artificial intelligence approaches can be used to solve engineering problems such as modeling, prediction and optimization of co-digestion based on artificial neural networks and fuzzy modeling (as presented in this work, which of course can be extended to the study of co-digestion from other substrates).

Author Contributions

Conceptualization, Carolina Ferreira and Ruy de Sousa Júnior; Formal analysis, Carolina Ferreira and Ruy de Sousa Júnior; Funding acquisition, Ruy de Sousa Júnior; Investigation, Carolina Ferreira; Methodology, Carolina Ferreira, Rafael Akisue and Ruy de Sousa Júnior; Project administration, Ruy de Sousa Júnior; Resources, Ruy de Sousa Júnior; Software, Carolina Ferreira, Rafael Akisue and Ruy de Sousa Júnior; Validation, Carolina Ferreira and Ruy de Sousa Júnior; Visualization, Carolina Ferreira and Rafael Akisue; Writing – original draft, Carolina Ferreira and Ruy de Sousa Júnior; Writing – review & editing, Ruy de Sousa Júnior.

Funding

This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001, and CNPq.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript
DW Distillery wastewater
ANFIS Adaptive-Network-Based Fuzzy Inference System
ANP Agência Nacional de Petróleo, Gás Natural e Biocombustíveis
CH4 Methane
CH3COOH Acetate
CO2 Carbon dioxide
COD Chemical oxygen demand
FIS Fuzzy inference system
MF Membership function
ML Molasses
CG Crude glycerol
MD Membership degree
H2 Hydrogen gas
H2O Water
M2SI Monod two-substrate with an intermediate model
MLP Multilayer perceptron
pH Hydrogen ion potential
RMSE Root mean squared error
R² Coefficient of determination
SCG Scaled conjugate gradient
UASB Upflow anaerobic sludge blanket

References

  1. UN – United Nations. United Nations Conference in the Human Environment, 5-16 June 1972, Stockholm. Available online: https://www.un.org/en/conferences/environment/stockholm1972 (access on 13 april 2022a).
  2. ANP – Agência Nacional de Petróleo, Gás Natural e Biocombustíveis. Biodiesel. Available online: https://www.gov.br/anp/pt-br/assuntos/producao-e-fornecimento-de-biocombustiveis/biodiesel (access on 14 april 2022a).
  3. ANP – Agência Nacional de Petróleo, Gás Natural e Biocombustíveis. Painel Dinâmico de Produtores de Biodiesel. Available online: https://www.gov.br/anp/pt-br/centrais-de-conteudo/paineis-dinamicos-da-anp/paineis-e-mapa-dinamicos-de-produtores-de-combustiveis-e-derivados/painel-dinamico-de-produtores-de-biodiesel (access on 14 april 2022b).
  4. Leung, D. Y.C.; Wu, X.; Leung, M. K.H. A review on biodiesel production using catalyzed transesterification. Applied Energy, 2010, 87, 1083–1095. [CrossRef]
  5. ANP – Agência Nacional de Petróleo, Gás Natural e Biocombustíveis. RenovaBio. Available online: https://www.gov.br/anp/pt-br/assuntos/renovabio (access on 14 april 2022c).
  6. Quispe, C. A.G.; Coronado, C. J.R.; Carvalho, J. A. Glycerol: Production, consumption, prices, characterization and new trends in combustion. Renewable and Sustainable Energy Reviews, 2013, 27, 475–493. [CrossRef]
  7. Chernicharo, C. A. L. Anaerobic Reactors. Vol 4 - Biological Wastewater Treatment. IWA Publishing: London, UK, 2007.
  8. Gabra, F. A.; Abd-alla, M. H.; Danial, A. W.; et al. Production of biofuel from sugarcane molasses by diazotrophic Bacillus and recycle of spent bacterial biomass as biofertilizer inoculants for oil crops. Biocatalysis and Agricultural Biotechnology, 2019, 19. [CrossRef]
  9. UN – United Nations. FAO: América Latina e Caribe vão responder por mais de 25% das exportações agrícolas globais até 2028. Available online: https://brasil.un.org/pt-br/83643-fao-america-latina-e-caribe-vao-responder-por-mais-de-25-das-exportacoes-agricolas-globais (access on 13 april 2022b).
  10. Costa, T. B. Produção de hidrogênio e metano a partir de glicerol bruto e cultura mista em reatores anaeróbios de leito fluidizado termofílicos; Federal University of São Carlos. Master Thesis, São Carlos, Brazil, 2017.
  11. Paranhos, A.G.O., Silva, E. L. Optimized 1,3-propanediol production from crude glycerol using mixed cultures in batch and continuous reactors. Bioprocess Biosystems Engineering, 2018, 41, 1807–1816. [CrossRef]
  12. Freitas, I. B. F. Produção de hidrogênio e metabólitos com valor biotecnológico a partir de melaço da cana-de-açucar utilizando reatores de leito granular expandido mesofílicos. University of São Paulo – São Carlos School of Engineering. Master Thesis, São Carlos, Brazil, 2018.
  13. Pereyra, D. A. D.; Rueger, I. B.; Barbosa, P. A. M. A.; Peiter, F. S.; Freitas, D. M. S.; Amorim, E. L. C. Co-fermentation of glycerol and molasses for obtaining biofuels and value-added products. Brazilian Journal of Chemical Engineering, 2020, 37, 653-660. [CrossRef]
  14. Rakmak, N.; Noynoo, L.; Jijai, S.; Siripatana, C. Monod-Type Two-Substrate Models for Batch Anaerobic Co-Digestion. In Lecture Notes in Applied Mathematics and Applied Science in Engineering. Melaka, Malaysia, p. 11–20, 2019.
  15. Nelles, O. Nonlinear System Identification: from classical approaches to neural networks and fuzzy models. Springer: New York, USA, 2001; 785 p.
  16. Viana, M B; Freitas, A V; Leitão, R C; Pinto, G. A. S.; Santaella, S. T. Anaerobic digestion of crude glycerol: a review. Environmental Technology Reviews, 2012, 1, 81–92. [CrossRef]
  17. Ayoub, M.; Abdullah, A. Z. Critical review on the current scenario and significance of crude glycerol resulting from biodiesel industry towards more sustainable renewable energy industry. Renewable and Sustainable Energy Reviews, 2012, 16, 2671–2686. [CrossRef]
  18. Santibáñez, C.; Vernero, M. T.; Bustamante, M. Residual glycerol from biodiesel manufacturing, waste or potential source of bioenergy: a review. Chilean Journal of Agricultural Research, 2011, 71, 469–475. [CrossRef]
  19. Rezania, S.; Oryani, B.; Park, J.; Hashemi, B.; Yadav, K. K.; Kwon, E. E.; Hur, J.; Cho, J. Review on transesterification of non-edible sources for biodiesel production with a focus on economic aspects, fuel properties and by-product applications. Energy Conversion and Management, 2019, 201, 112-155. [CrossRef]
  20. ABIQUIM - ASSOCIAÇÃO BRASILEIRA DA INDÚSTRIA QUÍMICA. Report of Dynamic system of statistical information. São Paulo, Brazil, 2008. 36 p.
  21. Oliveira, C. A.; Fuess, L. T.; Soares, L. A.; et al. Thermophilic biomethanation of sugarcane molasses comparing single and two-stage systems: Process performance and energetic potential. Bioresource Technology Reports, 2020, 12. [CrossRef]
  22. Aguilar, F. A.; Nelson, D L.; Pantoja, L. A.; Santos, A. S. Study of anaerobic co-digestion of crude glycerol and swine manure for the production of biogas. Revista Virtual de Quimica, 2017, 9, 2384–2403. [CrossRef]
  23. Menezes, C. A.; Beike, K. et al. Biohydrogen Production in Fluidized Bed Reactors: An Environmental Approach. In Fluidized Bed Reactors: Principles and Applications. 1st edition; Nova Science Publishers: New York, 2020; pp 1-39.
  24. Jaroenpoj, S.; Yu, Q. J.; Ness, J. Development of Artificial Neural Network Models for Biogas Production from Co-Digestion of Leachate and Pineapple Peel. The Global Environmental Engineers, 2014, 1, 42-47. [CrossRef]
  25. Ghatak, M.; Ghatak, A. Artificial neural network model to predict behavior of biogas production curve from mixed lignocellulosic co-substrates. Fuel, 2018, 232, 178–189. [CrossRef]
  26. Özarslan, S.; Abut, S.; Atelge, M.R.; Kaya, M.; Unalan, S. Modeling and simulation of co-digestion performance with artificial neural network for prediction of methane production from tea factory waste with co-substrate of spent tea waste. Fuel, 2021, 306. [CrossRef]
  27. Gonçalves Neto, J.; Ozorio, L. V.; Abreu, T. C. C.; Santos, B. F.; Pradelle, F. Modeling of biogas production from food, fruits and vegetables wastes using artificial neural network (ANN). Fuel, 2021, 285. [CrossRef]
  28. MathWorks. Fuzzy Logic ToolboxTM User’s Guide R2018a. MathWorks: Natick, MA, USA, 2018.
  29. Khayum, N.; Rout, A.; Deepak, B. B. V. L.; Anbarasu, S.; Murugan, S. Application of Fuzzy Regression Analysis in Predicting the Performance of the Anaerobic Reactor Co-digesting Spent Tea Waste with Cow Manure. Waste And Biomass Valorization, 2019, 11, 5665-5678. [CrossRef]
  30. Heydari, B.; Sharghi, E. A.; Rafiee, S.; Mohtasebi, S. S. Use of artificial neural network and adaptive neuro-fuzzy inference system for prediction of biogas production from spearmint essential oil wastewater treatment in up-flow anaerobic sludge blanket reactor. Fuel, 2021, 306. [CrossRef]
  31. Phayungphan, K.; Rakmak, N.; Promraksa, A. Application of monod two-substrate kinetics with an intermediate for anaerobic co-digestion of distillery wastewater and molasses/glycerol waste in batch experiments. Water Practice and Technology, 2020, 15, 1068-1082. [CrossRef]
  32. Beale, M. H.; Hagan, M. T.; Demuth, H. B. Neural Network Toolbox: user's guide. 7th ed. Natick, MA, USA, 2010.
  33. Yetilmezsoy, K.; Turkdogan, F. I.; Temizel, I.; Gunay, A. Development of Ann-Based Models to Predict Biogas and Methane Productions in Anaerobic Treatment of Molasses Wastewater. International Journal of Green Energy, 2013, 10, 885-907. [CrossRef]
  34. Horta, A. C. L.; Zangirolami, T. C.; Nicoletti, M. C.; Montera, L.; Carmo, T. S.; Gonçalves, V. M. An Empirical Investigation of the Use of a Neural Network Committee for Identifying the Streptococcus pneumoniae Growth Phases in Batch Cultivations. Lecture Notes in Computer Science, 2008, 5027, 215-224. [CrossRef]
  35. Turkdogan-Aydinol, F. I.; Yetilmezsoy, K. A fuzzy-logic-based model to predict biogas and methane production rates in a pilot-scale mesophilic UASB reactor treating molasses wastewater. Journal of Hazardous Materials, 2010; 182, 460-471. [CrossRef]
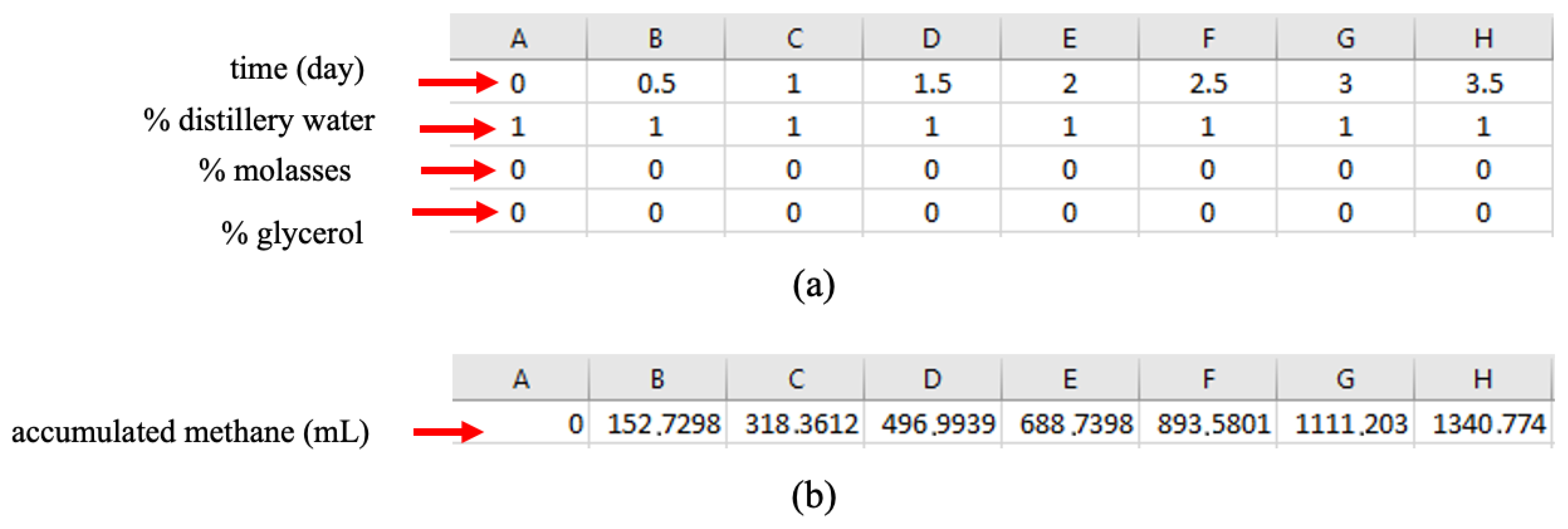
Preprints 76674 g001
Figure 1. Representation of the database for training of the generic neural network: (a) input variables and (b) output variable.
Figure 1. Representation of the database for training of the generic neural network: (a) input variables and (b) output variable.
Preprints 76674 g001
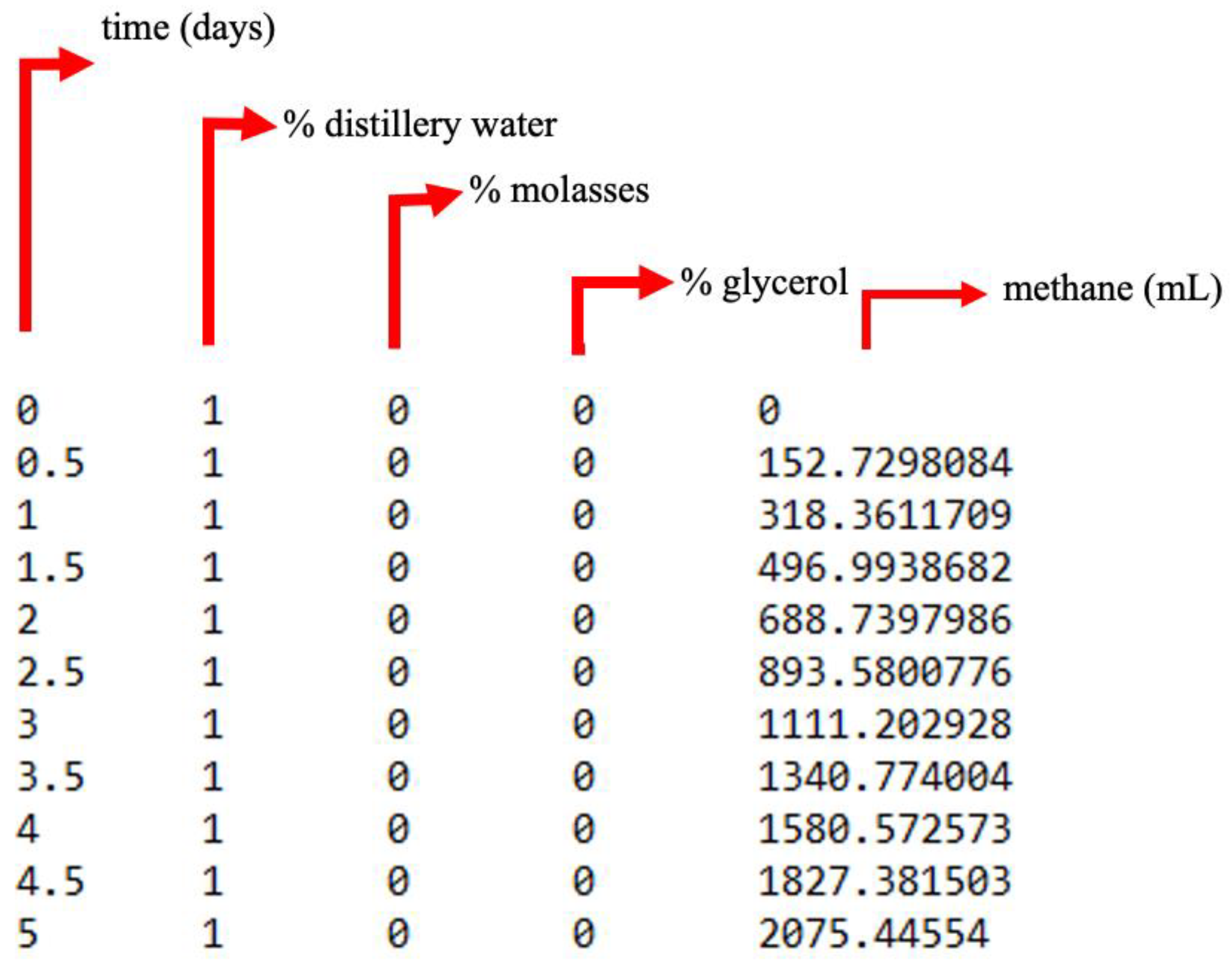
Preprints 76674 g002
Figure 2. Representation of the database for training the FIS.
Figure 2. Representation of the database for training the FIS.
Preprints 76674 g002
Preprints 76674 g003
Figure 3. Representation of the fuzzy model structure.
Figure 3. Representation of the fuzzy model structure.
Preprints 76674 g003
Preprints 76674 g004
Figure 4. Linear regression fits of the network output values for 2 neurons.
Figure 4. Linear regression fits of the network output values for 2 neurons.
Preprints 76674 g004
Preprints 76674 g005
Figure 5. Linear regression fits of the network output values for 14 neurons.
Figure 5. Linear regression fits of the network output values for 14 neurons.
Preprints 76674 g005
Preprints 76674 g006
Figure 6. Linear regression fits of the network output values for 60 neurons.
Figure 6. Linear regression fits of the network output values for 60 neurons.
Preprints 76674 g006
Preprints 76674 g007
Figure 7. Differences between the expected and network output values for (a) 2 neurons, (b) 14 neurons, and (c) 60 neurons.
Figure 7. Differences between the expected and network output values for (a) 2 neurons, (b) 14 neurons, and (c) 60 neurons.
Preprints 76674 g007
Preprints 76674 g008aPreprints 76674 g008b
Figure 8. Comparison of cumulative methane production predicted using the Monod kinetic model and the generic neural network (with 14 neurons), for the different substrates: (a) 100% DW, (b) 99% DW and 1% ML, (c) 98% DW and 2% ML, (d) 97% DW and 3% ML, (e) 96% DW and 4% ML, (f) 95% DW and 5% ML, (g) 99% DW and 1% CG, and (h) 95% DW and 5% CG.
Figure 8. Comparison of cumulative methane production predicted using the Monod kinetic model and the generic neural network (with 14 neurons), for the different substrates: (a) 100% DW, (b) 99% DW and 1% ML, (c) 98% DW and 2% ML, (d) 97% DW and 3% ML, (e) 96% DW and 4% ML, (f) 95% DW and 5% ML, (g) 99% DW and 1% CG, and (h) 95% DW and 5% CG.
Preprints 76674 g008aPreprints 76674 g008b
Preprints 76674 g009
Figure 9. Comparison of cumulative methane production predicted using the Monod kinetic model and the generic neural network (with 14 neurons), for the different substrates: (a) 100% DW, (b) 99% DW and 1% ML, (c) 98% DW and 2% ML, (d) 97% DW and 3% ML, (e) 96% DW and 4% ML, (f) 95% DW and 5% ML, (g) 99% DW and 1% CG, and (h) 95% DW and 5% CG.
Figure 9. Comparison of cumulative methane production predicted using the Monod kinetic model and the generic neural network (with 14 neurons), for the different substrates: (a) 100% DW, (b) 99% DW and 1% ML, (c) 98% DW and 2% ML, (d) 97% DW and 3% ML, (e) 96% DW and 4% ML, (f) 95% DW and 5% ML, (g) 99% DW and 1% CG, and (h) 95% DW and 5% CG.
Preprints 76674 g009
Preprints 76674 g010aPreprints 76674 g010b
Figure 10. Comparison of cumulative methane production predicted using the Monod kinetic model and the specific neural networks, for the different substrates: (a) 100% DW, (b) 99% DW and 1% ML, (c) 98% DW and 2% ML, (d) 97% DW and 3% ML, (e) 96% DW and 4% ML, (f) 95% DW and 5% ML, (g) 99% DW and 1% CG, and (h) 95% DW and 5% CG.
Figure 10. Comparison of cumulative methane production predicted using the Monod kinetic model and the specific neural networks, for the different substrates: (a) 100% DW, (b) 99% DW and 1% ML, (c) 98% DW and 2% ML, (d) 97% DW and 3% ML, (e) 96% DW and 4% ML, (f) 95% DW and 5% ML, (g) 99% DW and 1% CG, and (h) 95% DW and 5% CG.
Preprints 76674 g010aPreprints 76674 g010b
Preprints 76674 g011
Figure 11. Linear regression fits of the output values obtained using the neural network with 25 neurons.
Figure 11. Linear regression fits of the output values obtained using the neural network with 25 neurons.
Preprints 76674 g011
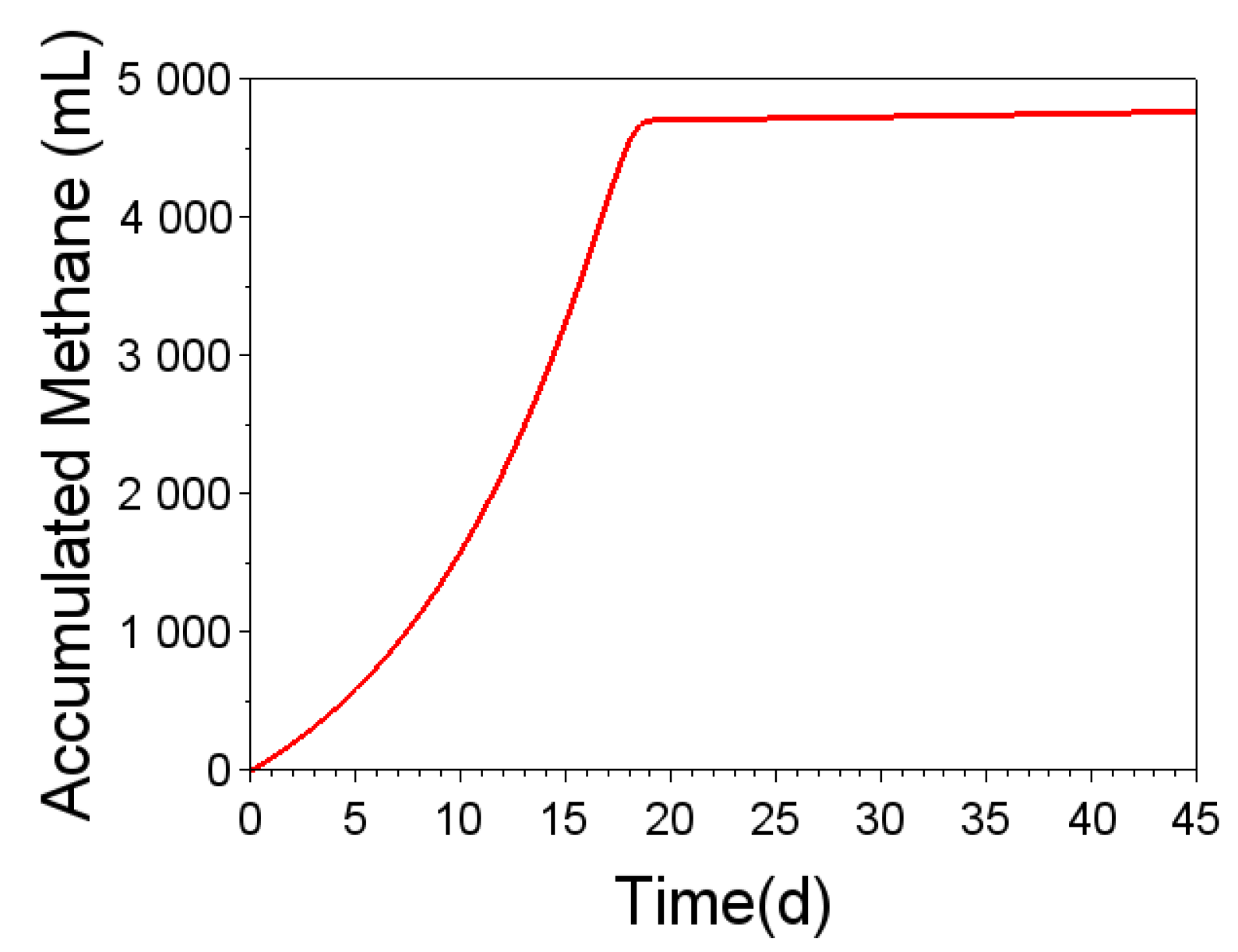
Preprints 76674 g012
Figure 12. Prediction of hybrid M2SI-neural approach at 97% DW-3% CG condition.
Figure 12. Prediction of hybrid M2SI-neural approach at 97% DW-3% CG condition.
Preprints 76674 g012
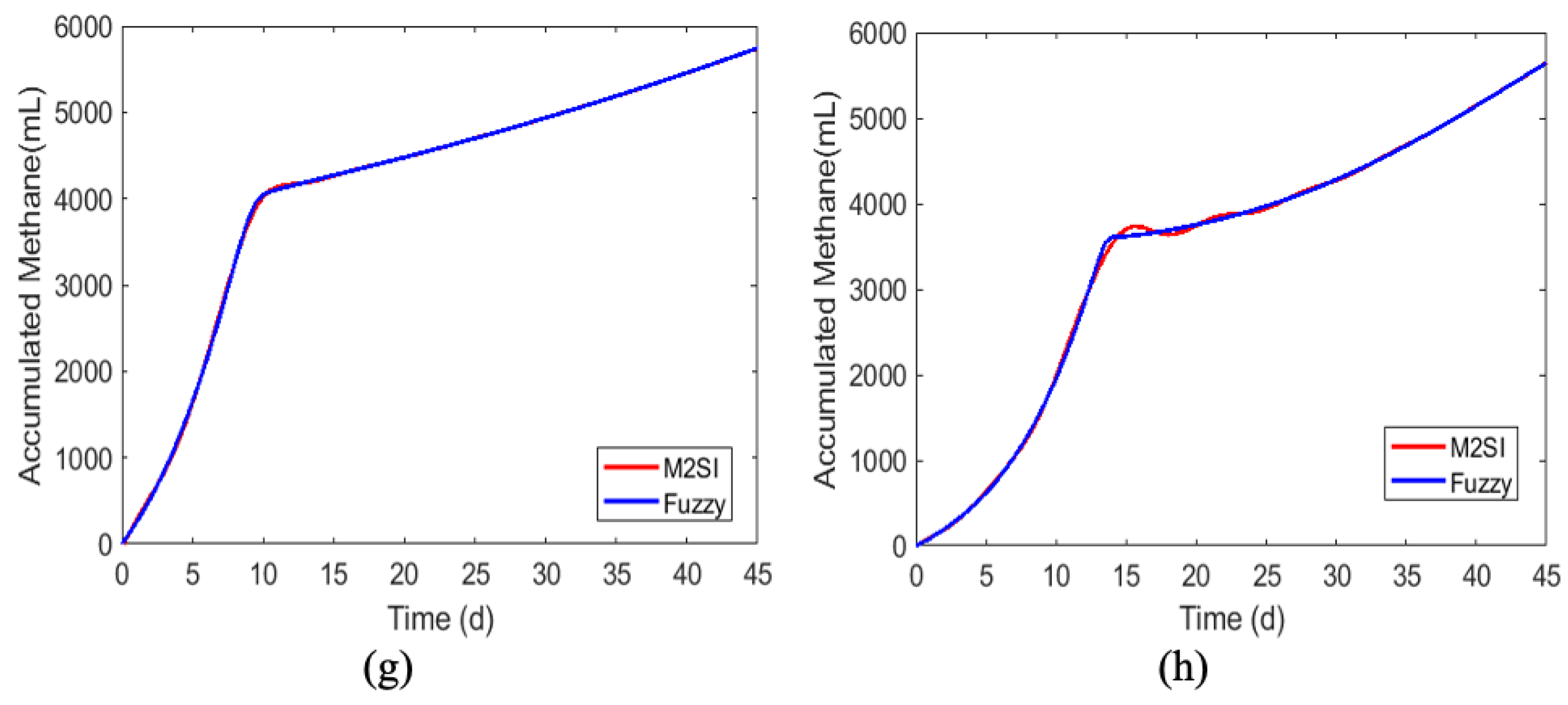
Preprints 76674 g013aPreprints 76674 g013b
Figure 13. Comparison of the responses of the fuzzy model and the M2SI model for the different substrates: (a) 100% DW, (b) 99% DW and 1% ML, (c) 98% DW and 2% ML, (d) 97% DW and 3% ML, (e) 96% DW and 4% ML, (f) 95% DW and 5% ML, (g) 99% DW and 1% CG, and (h) 95% DW and 5% CG.
Figure 13. Comparison of the responses of the fuzzy model and the M2SI model for the different substrates: (a) 100% DW, (b) 99% DW and 1% ML, (c) 98% DW and 2% ML, (d) 97% DW and 3% ML, (e) 96% DW and 4% ML, (f) 95% DW and 5% ML, (g) 99% DW and 1% CG, and (h) 95% DW and 5% CG.
Preprints 76674 g013aPreprints 76674 g013b
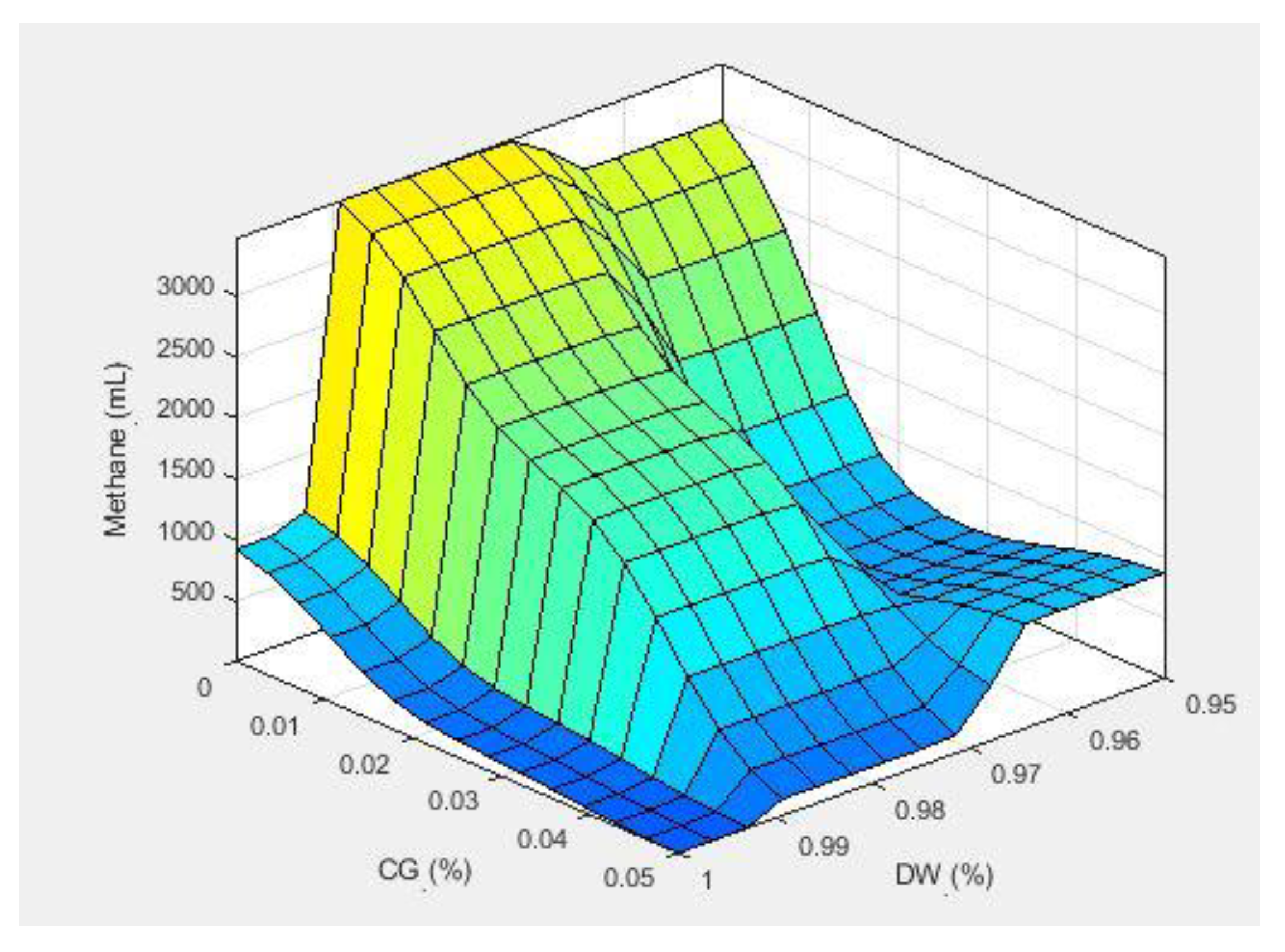
Preprints 76674 g014
Figure 14. Response surface with 2.5% ML and time at 25 days (percentage values of CG and DW were normalized to a range between 0 and 1).
Figure 14. Response surface with 2.5% ML and time at 25 days (percentage values of CG and DW were normalized to a range between 0 and 1).
Preprints 76674 g014
Table 1. Percentage composition (by volume) of the substrate.
Table 1. Percentage composition (by volume) of the substrate.
Assay Distillery wastewater (%) Molasses (%) Glycerol (%)
1 100 0 0
2 99 1 0
3 98 2 0
4 97 3 0
5 96 4 0
6 95 5 0
7 99 0 1
8 98 0 2
9 97 0 3
10 96 0 4
11 95 0 5
Table 2. Accumulated methane for each composition of the substrate.
Table 2. Accumulated methane for each composition of the substrate.
Assay1 Composition (%) Accumulated Methane (mL)
1 100 DW 4580.44
2 99 DW + 1 ML 4918.50
3 98 DW + 2 ML 4963.33
4 97 DW + 3 ML 4168.67
5 96 DW + 4 ML 3992.97
6 95 DW + 5 ML 4014.97
7 99 DW + 1 CG 5744.64
8 95 DW + 5 CG 5647.33
1total digestion time of 45 days, except for Assay 1, whose digestion time was 25 days.
Table 3. Parameters of the membership functions fitted using the ANFIS model.
Table 3. Parameters of the membership functions fitted using the ANFIS model.
Linguistic variable Linguistic value Standard deviation (σ) Input   mean   ( x ¯ )
Time Initial 2.731 0.00077
Very short 2.730 6.428
Short 2.730 12.860
Low medium 2.731 19.280
Medium 2.730 25.710
High medium 2.730 32.140
Long 2.730 38.570
Very long 2.730 45.000
DW Low 0.0073 0.9483
Medium 0.0034 0.9768
High 0.0029 1.0040
ML Low 0.0091 -0.0016
Medium 0.0145 0.0250
High 0.0163 0.0480
CG Low 0.0094 -0.0013
Medium 0.0116 0.0238
High 0.0106 0.0500
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated