Generating Renewable Energy Based on the Circuit Approach

Preprint

Article

Generating Renewable Energy Based on the Circuit Approach

Altmetrics

Downloads

136

Views

111

Comments

Shinichi Ishiguri^*

This version is not peer-reviewed

Submitted:

14 June 2023

Posted:

15 June 2023

You are already at the latest version

Alerts

Abstract

In this study, a new methodology based on the circuit approach is employed to obtain renewable electric energy. Although a voltage source and a current source generate voltage and current, respectively, they work only when they receive electric power, which is the product of voltage and current. However, this paper proposes a circuit with a voltage source, a current source and a super-condenser connected in series, in which the voltage source provides voltage for the current source and the current source provides current for the voltage source. Resultantly, electric power is generated both at the voltage and current sources, and the energy (i.e., the electric power) from the current source is converted to the charging energy in the super-condenser. Herein, we describe the method for charging the super-condenser using a voltage source and a current source. To confirm the abovementioned concept, we conducted experiments, and the energy was successfully produced, with high reproducibility. Finally, the brief mechanism for the energy conversion, a schematic method for reducing the capacitances of stored batteries, and the significance of this study are described.

Keywords:

Subject: Physical Sciences - Applied Physics

1. Introduction

There are two reasons to introduce renewable and sustainable energies [1,2,3,4] (specifically, solar and wind energies are famous [5]). One is related to economic problems, which stem from the high costs of crude oils [6]. The other is the reduction of the CO₂ concentration in the atmosphere, considering the global environment [7]. For the introduction of renewable energy, it is imperative to consider both views of economy and technology. Specifically, it is very important to achieve high efficiency with low cost [8,9].

Considering the safety of the global environment and the reduction of the concentration of CO₂ in addition to abolishing atomic power stations, distributed power supplies, such as solar cells or wind power, are significantly exploited. However, frequency and voltage are unstable when the distributed power supplies are introduced to the existing power system. Specifically, it is necessary to employ a storage battery to maintain the quality of the power generated from the distributed power supplies, i.e., solar cells or wind power. On days when cloudy weather is maintained, a large storage buttery is needed, which implies an increase in cost.

A simulation system, DNE21+ [10] has calculated the potential to introduce renewable energy and determined whether or not our country can achieve net carbon neutrality by 2050. However, it mentions that, without some breakthroughs in technology, it might be impossible to completely achieve it.

Here, let us summarize the problems of the existing renewable energy and nuclear power generation.

1): Crucially, the outputs of renewable energies are considerably unstable depending on climate change. As mentioned, this defect implies that large storage batteries must be introduced, which are expensive. Moreover, if large amounts of renewable energies are introduced, the unstable outputs inevitably result in instability in the existing power system.
2): DNE 21+ calculated the potential, including nuclear power generation. However, we cannot forget the Fukushima nuclear accident in Japan in 2011.

Considering the above, naturally, our research motivation is to propose a new system to generate the right amount of energy at the right time, i.e., a stable energy supply that satisfies the demands.

As a brief description of our system, first, a voltage source and a current source are prepared. These two sources and a super-condenser (i.e., electric double-layer capacitor) are connected in series. Generally, electric power (i.e., energy) is defined as the product of a voltage and a current, and power supply sources, such as the voltage source or the current source, can work only when receiving electric power from the outside. However, because these sources are connected in series with a super-condenser, they interact; therefore, voltage is provided for the current source, and current is provided for the voltage source. Thus, new electric power (i.e., energy) is provided, and the electric power in the current source is stored in the super-condenser. Resultantly, with no input energy from the outside, new renewable energy is provided. This paper will describe this proposed system using the experiments.

Let us review the contents of this paper:

Before the main street, we briefly review the voltage and current sources, which are parts of our present system. Next, the principle (i.e., the methodology) of our system is described. First, the functions of a current source are explained with in-depth views. Thereafter, a more concrete method for the experiments will be provided. Next, the result of the experiment will be presented. Furthermore, the reduction method of storage batteries, a more detailed interpretation of the experiment, the energy conversion, and the significance of this paper will be presented. Finally, we conclude the entire contents in Section 7.

2. Review of a voltage source and current source

In this study, a voltage source and a current source, which are parts of an electric circuit, are employed. Notably, both sources generate a specific type of power. The voltage source generates voltage regardless of the load, whereas the current source generates current. The symbols of these sources are shown in Figure 1. In this study, two stabilized power supply sources will be employed. One is used as the voltage source in a cv mode, whereas the other is used as the current source in a cc mode.

3. Principle

As shown in Figure 2, a voltage source, current source, and super-condenser are connected in series. As will be described, in this circuit, the voltage source generates only voltage without a current and the current source generates only current without a voltage. Generally, electric power is defined as the product of voltage and current. In this system, the voltage source provides voltage for the current source, which forms electric power (i.e., energy), and the current source provides current for the voltage source, which also forms electric power. Therefore, both the voltage and current sources do not need external electric power to work. The generated energy in the current source is charged to the super-condenser. Consequently, although the net input energy is zero, the output energy is generated and stored in the super-condenser.

4. Method

4.1. Instruction of this section

1): The necessity to input a voltage in the current source when it charges a super-condenser

As shown in Figure 3, let us consider a case where a current source simply charges a super-condenser. Initially, using the input from the current source, the voltage of the condenser increases. However, at what voltage level is the condenser completely charged? A stabilized power supply source should be used as the current source, and a voltage, V₀, must be input in advance. When the current source charges the condenser up to V₀, the condenser is completely charged. In other words, when a current source works to generate a current (I₀), the current source inputs the electric power (V₀I₀) (i.e., the energy) into the condenser. Notably, this case is applied only to a super-condenser whose internal impedance is significantly small and not to a normal ceramic condenser; this is because a current source cannot provide current because of the extremely high impedance of the normal ceramic condenser.

2): The necessity to input a voltage in the current source when it generates current to load

Next, let us consider a case where a current source is connected to a normal resistance, as shown in Figure 4. In this case, owing to the energy conservation, the following equation is formed:

V I = R I^{2},

(1)

where V, I, and R denote the voltage of the current source, the circuit current, and the resistance, respectively.

This equation implies that the generated electric power (VI) (i.e., the generated energy) from the current source is transmitted to the Joule heating (RI²) in the load. Notably, the voltage (V) here is that of the current source. Thus, the higher the (R) or (I) is required, the higher the (V) we need to input into the current source. If this condition is not followed, the cc mode of the current source automatically changes to the cv mode.

To conclude, although a current source generates a current, it transmits electric power. Thus, depending on the stabilized power supply as the cc mode of the current source, it is necessary to input a voltage in the cc mode of the current source.

4.2. Main body of this section

In Figure 2, the circuit of the system is presented. As shown in this figure, two stabilized power supply sources and a super-condenser are employed. Among the two stabilized power supply sources, one is for a voltage source (i.e., the cv mode) and the other is for a current source (i.e., the cc mode). Importantly, the adjustments of the current source must not be increased, i.e., the zero voltage generation from the current source should remain constant. Moreover, current must not be generated from the voltage source. These imply that energy is not externally consumed by the two stabilized power supply sources.

In this system, the voltage (V_α) from the voltage source is added until the current is not generated. For example, according to our system, V_α

\approx

0.4 V is allowed to be added because, up to 0.4 V, current is not generated in the system. This is owing to the input impedance for the voltage source of the system. When the voltage source generates a voltage of 0.4 V, approximately 0.4 V is applied to the current source for the following reasons:

The impedance of the current source is relatively high.
The input impedance of the super-condenser is considerably low.

Resultantly, the (V_α) of the voltage source should be applied to the current source. Thus, when the current source applies current, electric power is generated. This generated electric power is transmitted to the super-condenser, and the condenser is automatically charged.

Table 1, Table 2 and Table 3 show the energy conversions. Details are presented in the discussion section. Notably, as is described later, this method is explained by each stage in which the charging of the condenser is partially achieved. That is, because the input voltage (V_α) must be provided gradually, the condenser must be also charged gradually.

(The first stage)

Table 1 indicates the initial states of the system. As shown, electric power is generated in both the voltage and current sources. Table 2 shows the transient state of the system. At this time, the electric power (p) from the current source is transmitted to the super-condenser.

The p is defined as

p = {〈V〉}_{c v} 〈I〉,

(2)

where

〈I〉

is the time average of the current from the cc mode of the current source, and

{〈V〉}_{c v}

is the time average of the voltage in the cc mode from the cv mode.

In Table 3, the steady and final state of the system is shown. Notably, the cc mode of the stabilized power supply of the current source automatically changes to the cv mode.

Resultantly, the following equation holds:

\int_{0}^{t_{0}} {〈V〉}_{c v} 〈I〉 d t = \frac{1}{2} C_{s} V_{α}^{2},

(3)

where C_s is the capacitance of the super-condenser, and t₀ is the steady time.

(The second stage)

Using the above equation, the first stage is achieved, and by resetting the cv mode of the current source to the cc mode, the initial state of the system is revived.

Next, let us consider the method for further charging the condenser.

First, the voltage source of the cv mode is set to

2 \times V_{α}

, up to which a current is not generated. This is because, as shown in Figure 5, considering the distribution of voltages, the net input voltage is equal to the V_α, which is related to the input impedance for the voltage source of the system. For example, in our system, as the input voltage in the cv mode of the voltage source,

2 \times V_{α} \approx 0.8 [V]

, is applied.

The next step is the iteration of the first stage. Let us review the conductions:

After setting the voltage of the voltage source of the cv mode, a current is supplied by the current source of the cc mode.
The voltage/current of the cc mode of the current source varies (0.0/0.0, respectively).
Resultantly, more energy is given to the super-condenser:

\int_{0}^{t_{0}} {〈V〉}_{c v} 〈I〉 d t = \frac{1}{2} C_{s} {(2 \times V_{α})}^{2}

(4)

4.: The cc mode of the current source changes to the cv mode.
5.: The cv mode of the current source is reset to the cc mode to proceed to the third stage.

(The third stage)

Initially, the voltage of

3 \times V_{α}

is input, up to which a current does not flow. Afterward, the procedure is the same as the second stage or the first stage. Resultantly, the condenser is charged as

\int_{0}^{t_{0}} {〈V〉}_{c v} 〈I〉 d t = \frac{1}{2} C_{s} {(3 \times V_{α})}^{2} .

(5)

Consequently, the fourth stage is the iteration of the above. That is, the first stage → the second stage → the third stage → the fourth stage → the fifth stage, and so on. The only difference between each stage is that the initial input voltage of the cv mode of the voltage source differs. By this iteration, we can charge the super-condenser up to the standard voltage.

In the Result section, these abovementioned phenomena will be confirmed.

5. Result

In Figure 6, the employed super-condenser (i.e., electric double-layer capacitor) is shown. This condenser capacitance is 3.3 F, and the standard voltage is 2.5 V.

Figure 7 shows the results with time. Notably, because of the limitation of the number of photographs, these results only indicate the first stage. Except for the initial input voltage (V_α), the further stages are iterations.

Figure 7. The complete view of the system. In this figure, the left stabilized power supply (i.e., red character) is a cv mode, and the center device is a voltmeter for the super-condenser, and the right stabilized power supply (i.e., green character) is a cc mode. Notably, the super-condenser is blue and located below.

Figure 7. First, the voltage of the voltage source in the cv mode is set to V_α. Up to V_α, current does not flow because of the input impedance for the voltage source. In this experiment, the voltage V_α is approximately 0.4 V.

Figure 7. After setting the V_α of the cv mode, the current source of the cc mode receives the same voltage, which becomes a part of the product of electric power. Although a small current slightly flows from the voltage source of the cv mode, it is negligible. Notably, the voltage adjustments in the current source are fixed at the zero point using the black tapes. This will be clarified later.

Figure 7. A current from the cc mode of the current source is supplied to the system.

Figure 7. Resultantly, approximately 0.25 A was supplied to the system. Notably, the voltmeter for the super-condenser is now measuring.

Figure 7. The right-hand power supply changes from the cc mode to the cv mode, and the voltage of the super-condenser was charged to approximately 0.49 V. Notably, when the right power supply changes from the cc mode to the cv mode, its voltage is 0.0V. This implies that the input of the voltage to the cc mode of the current source is zero. For details, see the main body in this paper.

Figure 7. For the next stage, the cv mode of the right power supply is again set to the cc mode.

Figure 7. The next initial mode has been achieved. For the second stage, the voltage of the cv mode is set to 2V_a ≈ 0.8 V. The other procedures are the same as the first stage.

6. Discussion

6.1. Feed-back to operate the power supplies

As mentioned, our system provides net energy (E₀). As mentioned many times, the voltage source and current source do not require energy to work. However, these sources are electrical devices, which work using an outlet and require considerably low energy (E_s) to work. How should we consider that? As the E_s is significantly lower than the E₀ (i.e.,

E_{0} ≫ E_{s}

), the E₀ is fed back to these sources.

6.2. The reduction of the cost of storage battery when operating our system

The existing renewable energy requires high cost and capacitance of the storage battery because the output of the existing renewable energy is not stable owing to its dependence on climate change, which is not stable. However, our presented system can provide energy independent of climate change. That is, we can provide the right amount of energy at the right time, which is equal to the demand for energy. Thus, the capacitance of a super-condenser can be reduced, as shown in Figure 8.

Figure 8. The principle of successive charging, successive discharging, and successive supply to a load. In this figure,

U_{β}

U_{α}

, and

U_{0}

imply the generated energy, condenser’s stored energy, and consumer energy. The small arrows imply the energy conversion. Two paired and identical systems are prepared. Note that

U_{0}

is common between systems 1 and 2. 1) When system 1 is generating the energy, system 2 discharges the condenser energy to the consumer. 2) In turn, when system 2 is generating the energy, system 1 discharges the condenser energy to the consumer. Therefore, it is possible to charge and discharge simultaneously. Conclusively, tep 1) ⇄ step 2) is iterated N times. Thus it is interpreted that

{N U}_{β, 0} \to U_{β}

N U_{α, 0} \to U_{α}

and

N U_{0,0} \to U_{0}

Figure 8. The principle of successive charging, successive discharging, and successive supply to a load. In this figure,

U_{β}

U_{α}

, and

U_{0}

imply the generated energy, condenser’s stored energy, and consumer energy. The small arrows imply the energy conversion. Two paired and identical systems are prepared. Note that

U_{0}

{N U}_{β, 0} \to U_{β}

N U_{α, 0} \to U_{α}

and

N U_{0,0} \to U_{0}

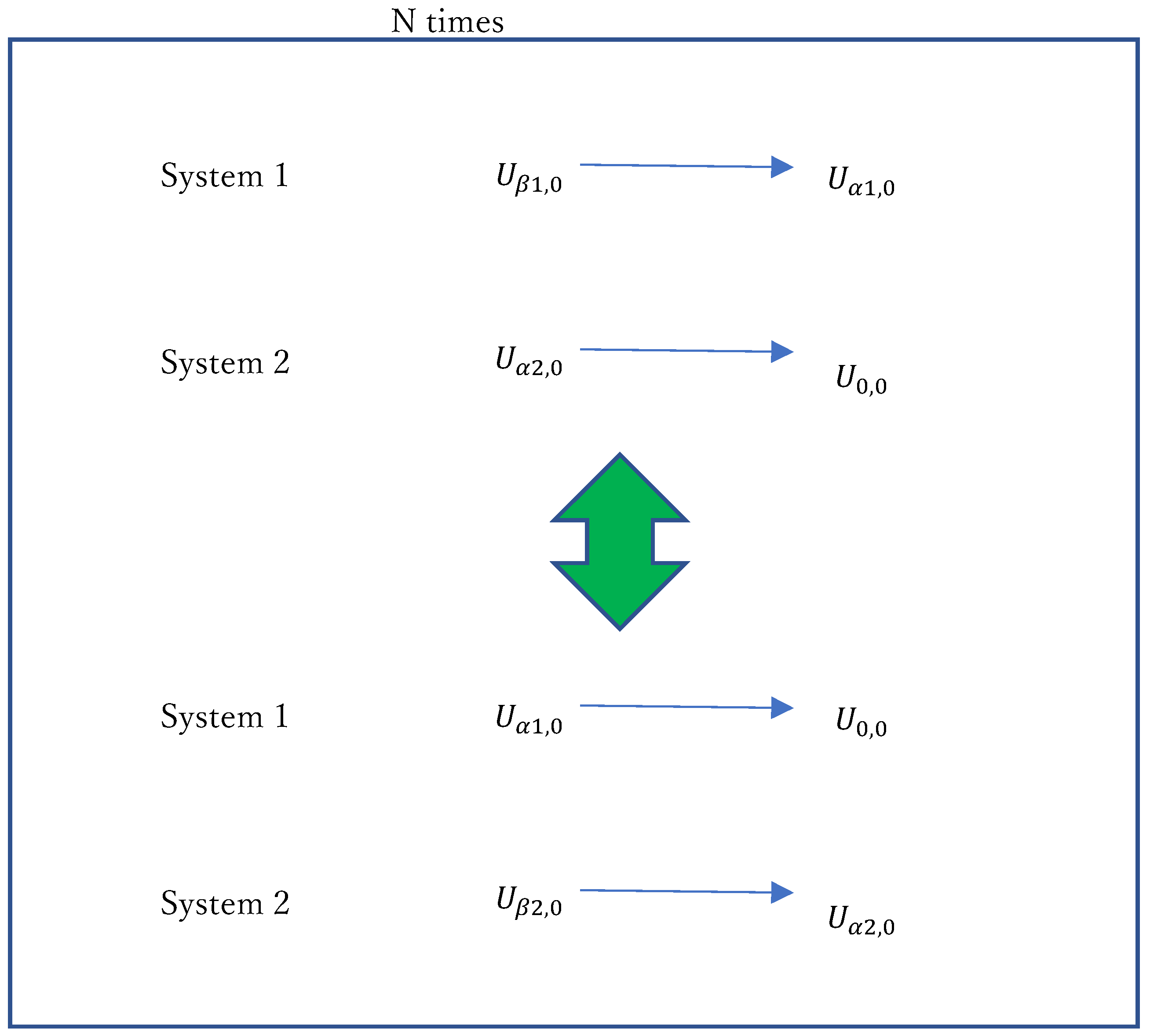
Figure 8 shows that, independent of climate changes, using our system, we can provide equal energy (U_β,₀) to the demand energy (U_0,0), mediating the energy stored in the condenser (U_α,0). Further, in Figure 8, U_β,₀→U_α,0 implies the conversion of the energy, for example. More concretely, paired and identical systems, system 1 and system 2, are prepared. When system 1 provides energy (U_β1,₀) to the condenser energy (U_α1,0), system 2 discharges the condenser energy (U_α2,0) to the demand energy (U_0,0). Further, when system 2 provides the energy (U_β2,₀) to the condenser energy (U_α2,0), system 1 discharges the condenser energy (U_α1,0) to the demand energy (U_0,0). Concisely, using systems 1 and 2, charging and discharging are conducted simultaneously. Notably, between systems 1 and 2, the demand energy (U_0,0) is common. By the many iterations of the above process (N times), we can provide the net energy to a consumer. Thus, we can reduce the capacitance of the super-condenser. Similarly, if other storage batteries are employed in our system, the same logic can be formed. Consequently, our presented system can reduce the cost and the capacitance of the storage battery.

6.3. The evidence that the input voltage in the current source had been zero

Let us review the procedure of the experiments for each stage:

Among the two stabilized power supplies, one is set to the cv mode as the voltage source and the other is set to the cc mode as the current source.
The initial voltage from the voltage source, V_α, is applied.
A current is applied from the cc mode of the current source to the system.
The voltage/current of the current source in the cc mode varies (0.0/0.0, respectively).
Simultaneously, the charging of the super-condenser is achieved.
The cc mode of the current source automatically changes to the cv mode.
The cv mode of the current source is reset to the cc mode to proceed to the next stage.

In the above procedures, step 6 is important, where the cc mode temporally changes to the cv mode. The voltage of this cv mode, which is not 0.0 V, would be displayed if a voltage was initially input in the cc mode. However, as shown in the experiment, the voltage of the power supply that changes temporally from the cc mode to the cv mode became 0.0 V, which implies no voltage was input to the cc mode and the net input electric power from the cc mode was zero.

6.4. Discussion of the conversion of energy

In this section, let us consider the conversion of the energy, based on Table 2.

According to this table, we can introduce the vectors of voltage and current:

\vec{v} = (V_{α}, {〈V〉}_{c v}),

(6-1)

\vec{i} = ({〈I〉}_{c c}, 〈I〉),

(6-2)

where

{〈V〉}_{c v}

implies the average voltage of the cc mode from the voltage source (i.e., the cv mode), and

{〈I〉}_{c c}

implies the average current from the cc mode of the current source.

Thus, the net input electric power (p_i) and input energy (U_i) are

p_{i} = \vec{v} \cdot \vec{i} = V_{α} {〈I〉}_{c c} + 〈I〉 {〈V〉}_{c v},

(7)

U_{i} = \int_{0}^{t_{0}} (V_{α} {〈I〉}_{c c} + 〈I〉 {〈V〉}_{c v}) d t .

(8)

Our system does not consider the energy input, and thus, U_i = 0.

- \int_{0}^{t_{0}} V_{α} {〈I〉}_{c c} d t = \int_{0}^{t_{0}} 〈I〉 {〈V〉}_{c v} d t .

(9)

That is,

\int_{t_{0}}^{0} V_{α} {〈I〉}_{c c} d t = \int_{0}^{t_{0}} 〈I〉 {〈V〉}_{c v} d t .

(10)

The above equation implies that, in our system, energy in terms of time-reverse symmetry is conserved.

Moreover, at the steady state (t = t₀), because

〈I〉 \to 0

and

{〈V〉}_{c v} \to 0

, the above-conserved energy must be transformed into the condenser’s stored energy:

\int_{0}^{t_{0}} 〈I〉 {〈V〉}_{c v} d t \to \frac{1}{2} C_{s} V_{α}^{2} .

(11)

6.5. Significance of this paper

In our system, a voltage source, current source, and super-condenser are connected in series. In this circuit, the voltage source generates only voltage without a current and the current source generates only current without a voltage. Generally, electric power is defined as the product of voltage and current. That is, both sources do not consume energy. In this system, the voltage source provides voltage to the current source, which forms electric power (i.e., energy), and the current source provides current to the voltage source, which also forms electric power. The generated energy in the current source is used to charge the super-condenser. To conclude, although the net input and consumed energy in our system are almost zero, a high output energy is stored in the super-condenser.

Employing our system, it is possible to provide the right amount of energy at the right place at the right time, and it is considerably stable compared with the existing renewable energy systems. Our system does not generate hazardous substances or CO₂. Therefore, by applying our energy system, our global environmental problems can be solved.

7. Conclusions

Herein, we propose a new energy system for circuit-based energy generation, which is confirmed by the experimental results. This proposed system can provide the right amount of energy at the right time at the right place, and thus, the energy generating cost can be significantly reduced compared with the existing renewable energy systems. As a follow-up, it is necessary to automate the steps of each stage in operating the system. Moreover, it is needed to experimentally achieve the mentioned schematic method shown in Figure 8.

Acknowledgments

We thank Enago (www.enago.jp) for English language reviews.

Additional information

This paper is not related to any competing interests such as funding, employment, and personal financial interests. Moreover, this paper is not related to non-financial competing interesting.

References

P. Anand et al. Insights Reg.Dev. 2022, 4, 96–109.
A. Tyo et al, Entrep. Sustain. 2019, 7, 1514–1524.
L. EI Iyaouy et al. Insights Reg. Dev. 2019, 1, 259–271.
M.R. Chehabeddine et al. Insights Reg. Dev. 2022, 4, 22–40.
H. Obane et al. Renewable Energy 2021, 160, 842–851.
O. Sabishchenko et al. Energies 2020, 13.
M. Wierzbowski et al. Renew. Sustain. Energy Rev. 2017, 74, 51–70.
C.-W. Wang et al, Energies 2020, 13, 2629.
T. Radavicius et al, Insights Reg. Dev. 2021, 3, 10–30.
K. Akimoto et al. Energy and Climate Change 2021, 2, 100057.

Figure 1. Electric circuit symbols of the voltage and current sources.

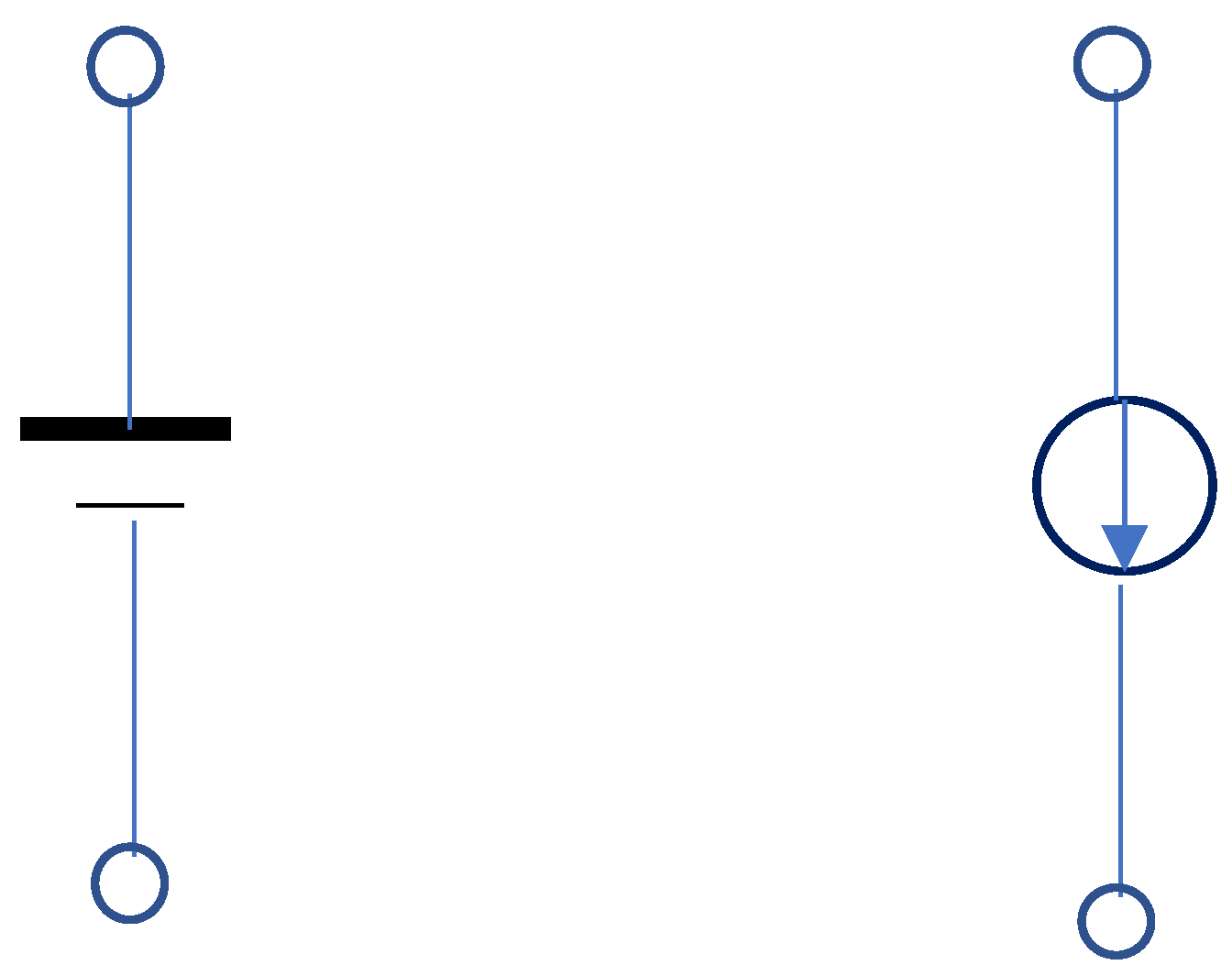
Figure 2. The circuit of our system; the single voltage source and the single current source do not require electric power to work; however, as a result of the interaction, outputs appear as electric power and are stored in the super-condenser.

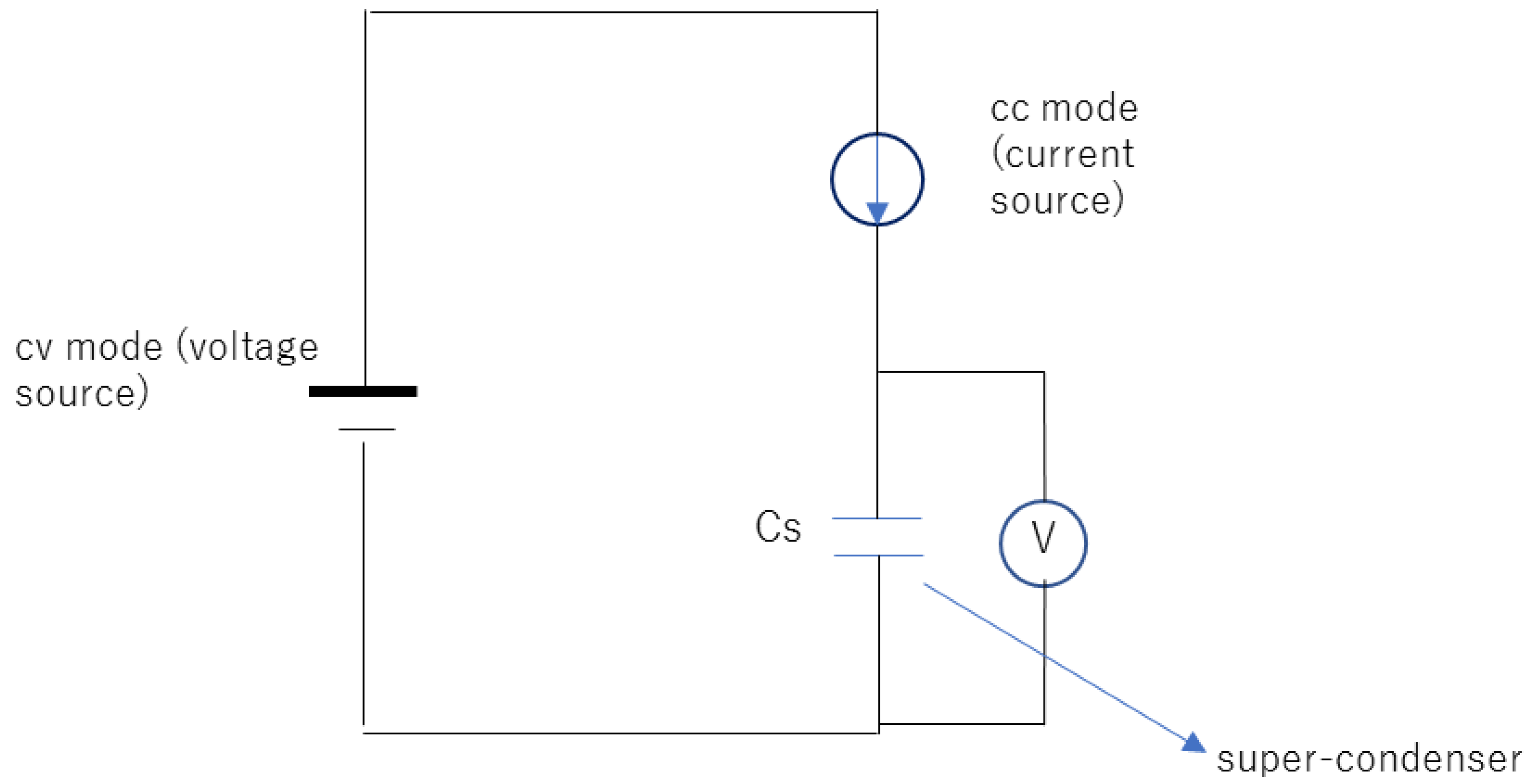
Figure 3. An ordinary circuit of a super-condenser and a current source.

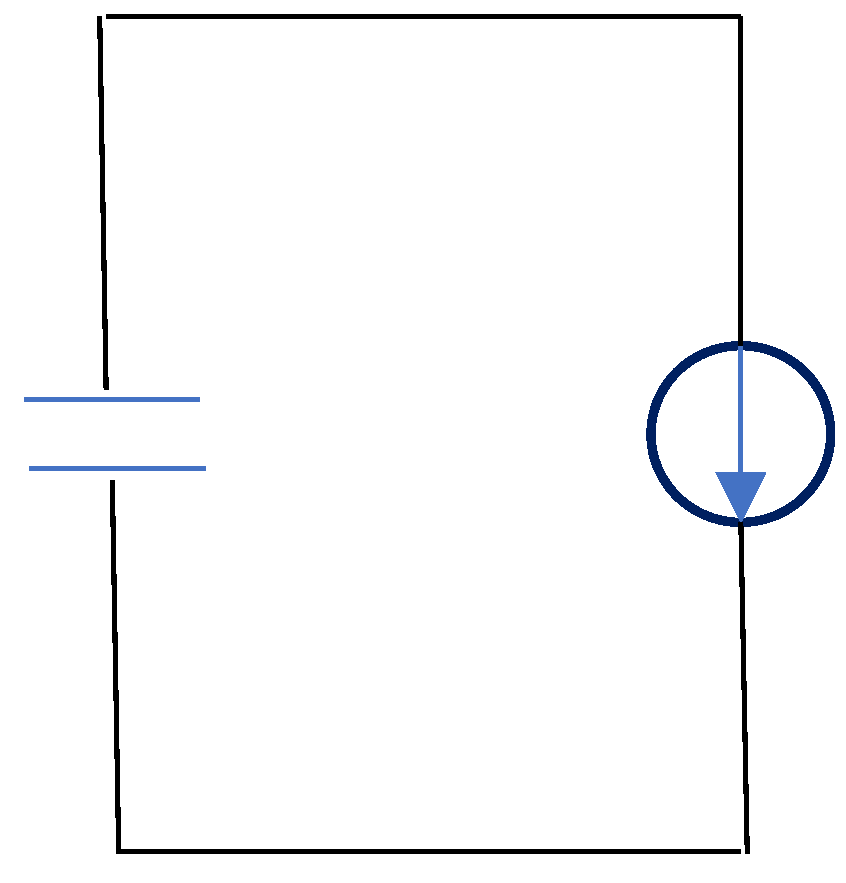
Figure 4. An ordinary circuit of a resistance and current source.

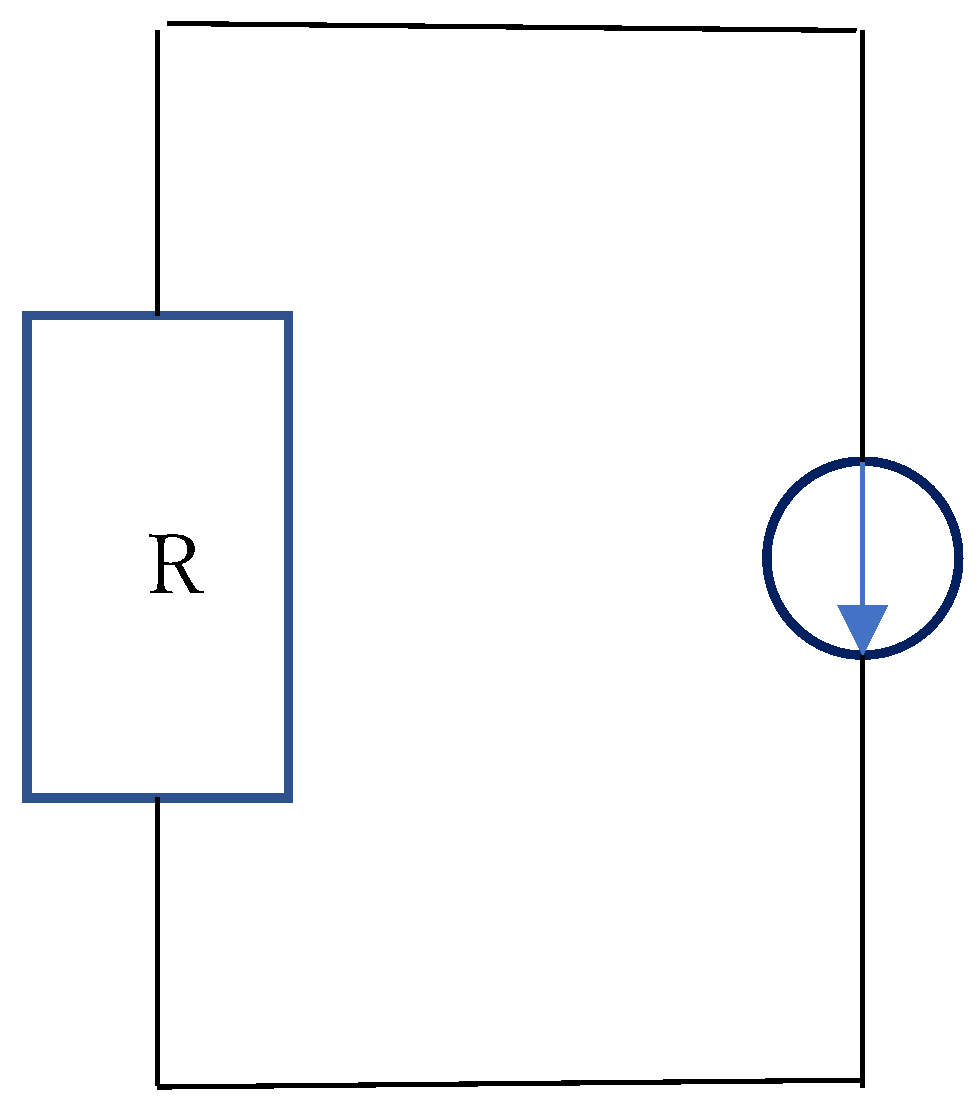
Figure 5. Distribution of voltages. The left panel is the state of a completely charged super-condenser through the first stage. The right panel implies the initial voltage distribution at the second stage. Considering the total voltage of the current source and the super-condenser, the related voltage of the input impedance for the cv mode of the voltage source is still V_α, which implies that the right panel does not generate a current.

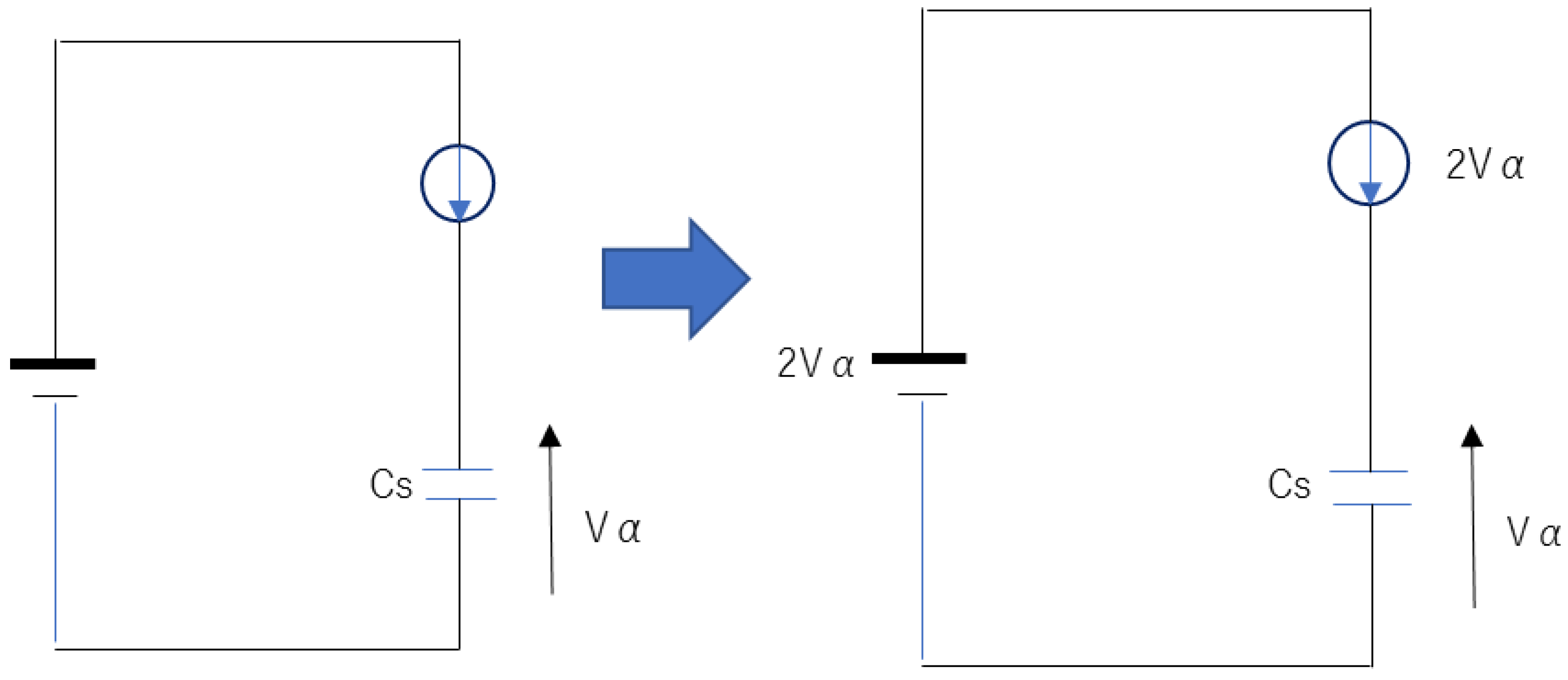
Figure 6. The employed super-condenser. The capacitance is 3.3 F, and the standard voltage is 2.5 V.

Table 1. The initial states of the system.

	Voltage [V]	Current [A]
cv mode	V_α	I_α from cc mode
cc mode	V_α from cv mode	I_α

Table 2. The transient state of the system.

	Voltage [V]	Current [A]
cv mode	V_α	$〈I〉$ from cc mode
cc mode	$〈V〉$ from cv mode	$〈I〉$

Table 3. The steady state of the system.

	Voltage [V]	Current [A]
cv mode	V_α	0
cc mode → cv mode	0	0

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Generating Renewable Energy Based on the Circuit Approach

Abstract

1. Introduction

2. Review of a voltage source and current source

3. Principle

4. Method

4.1. Instruction of this section

4.2. Main body of this section

5. Result

6. Discussion

6.1. Feed-back to operate the power supplies

6.2. The reduction of the cost of storage battery when operating our system

6.3. The evidence that the input voltage in the current source had been zero

6.4. Discussion of the conversion of energy

6.5. Significance of this paper

7. Conclusions

Acknowledgments

Additional information

References

MDPI Initiatives

Important Links

Subscribe