Prerpints.org logo
Preprint
Article

A new approach for DVHOP localization algorithm improvement in Wireless Sensor Network

Altmetrics

Downloads

139

Views

74

Comments

0

Submitted:

14 June 2023

Posted:

15 June 2023

You are already at the latest version

Alerts
Abstract
Wireless sensor networks (WSN) are mostly utilized in many applications. Indeed, WSN is composed of sensors to evaluate some physical phenomena. However, the information brought by the sensor still missed if we don't know the exact location of the event. Several localization algorithms have been proposed in order to locate the nodes in WSN. The localization algorithms are categorized into range-based and range-free techniques. The range-based techniques use either distance or time to calculate the coordinates of unknown nodes. Nevertheless, those kinds of techniques need some additional material in computation purpose. Therefore, range-based techniques present an expensive solution for positioning in WSN. Alternatively, range-free techniques may do the same task without involving additional material. But they don’t offer a high precision of localization in comparison with range-based techniques. DVHOP is the most popular range-free technique that uses the hop count method in the localization process. In this work, we propose an improvement of DVHOP localization algorithm to create three improved versions of this algorithm and we have achieved that by adopting two meta-heuristic (simulated annealing, particle swarm optimization) and FMINCON solver dedicated to the optimization in the field of WSN nodes localization. The experimental results obtained in this work show clearly the gain and the good impact of our proposition.
Keywords: 
Subject: Engineering  -   Telecommunications

1. Introduction

Nowadays, with the continuous development of Micro electro-mechanical systems (MEMS), there is a significant interest by researchers in wireless sensor network (WSN), because the latter has shown an efficiency in different applications. However, localization is an important part of WSN [1], indeed without location’s information, messages will be missed. At this point, the most used solution to locate the sensor node in WSN is Global Positioning System (GPS). Therefore, this positioning solution is not practicable in all cases, because GPS cannot be used in indoor areas. Besides that, it consumes a lot of energy. In order to mitigate the two issues caused by GPS, some alternative solutions have been invented to the localization problem, in which we equip just a few sensor nodes with GPS named anchors and those anchors help the other unknown nodes to be aware of their positions by using network connectivity and some additional calculations. By opting for alternative localization solutions, we avoid the high energy consumption of the localization process.
The localization techniques can be classified into two classes: range-based and range-free techniques [2,3,4]. However, range-free methods are based on the connectivity of the network, the advantages of those methods that they don’t need any additional hardware, making them more efficient in terms of low cost. In the field of research, the most used range-free techniques include APIT [5], Centroid [6], Distance Vector-Hop (DVHOP) [7,8,9] and Amorphous [10] algorithm. On the other hand, range-based techniques [11] make the localization by using Time of Arrival (TOA) [12], Angle of Arrival (AOA) [13], Time Difference of Arrival (TDOA) [14] and Received Signal Strength Indicator (RSSI) [15]. In general, those methods require extra material but they offer a high level of accuracy, making them more precise and expensive than range-free techniques. Moreover, in some cases, the leak of deployed anchors in WSN may lead to a weak coverage of the network. To mitigate this issue, multi-hop localization algorithms can be used. The specificity of those algorithms that sensor nodes may be located despite they aren’t in communication range with anchors. The most known multi-hop localization algorithm is DVHOP. The advantages of DVHOP reside in its simplicity in implementation, also this algorithm gives the results in a short duration of time. Besides that, DVHOP can offer good coverage of localization in comparison with other localization algorithms. Their drawbacks reside in the low accuracy that it can offer, especially when the network becomes small. Therefore, many improvements have been proposed to enhance the precision of the traditional DVHOP. In our approach, we create three improved versions of DVHOP in order to avoid the least square method adopted by the traditional algorithm because it’s the main reason for locating the sensor node imprecisely.
In fact, in uniform deployment, it’s been found that DVHOP is a suitable algorithm in terms of coverage of localization and can also offer an acceptable level of accuracy. However, when the network becomes anisotropic; presence of an irregularity in the distribution of nodes, the accuracy of the algorithm becomes worse because the hop-size calculation done by DVHOP in a non-uniform network leads to a big inaccuracy in the distance calculation step. Consequently, the Average Localization Error (ALE) of the algorithm is characterized by insufficiency. Aiming to enhance the localization accuracy of DVHOP in non-uniform networks, the research community has invented Amorphous localization algorithm that makes the distance calculation using an offline method. Indeed, Amorphous uses Kleinrock and Silvester formula [16] in order to calculate hop-size for reducing the localization error. In our contribution, we bring DVHOP for improvement in both cases of the distribution (uniform, no-uniform) in order to correct the issue of resolving the non-linear equations presented in the multilateration process.
The main contributions of this paper are as follows:
  • The importance of WSN has led the research community to investigate more about the problem of localization in WSN. DVHOP belongs to range-free localization techniques; its last step is judged to be the main reason for the imprecision of DVHOP. Furthermore, the traditional formula equation used to retrieve the locations causes an error. Hence, the latter can be reformulated as an optimization problem.
  • The resolution of the least square method adopted by DVHOP may be interpreted as a minimizing problem that has the ability to be resolved either by simulated annealing, particle swarm optimization and FMINCON solver dedicated to mathematical optimization under MATLAB. The purpose of those modifications is to enhance the accuracy of the traditional DVHOP.
  • The performance comparison of SA-DVHOP, FMINCON-DVHOP, PSO-DVHOP and DVHOP is carried out under two different network environments. The experimental results prove that the proposed SA-DVHOP has a smaller localization error. Also, it’s shown that the improved method is not dependent on the additional anchors to give the best result.
The remainder of the paper is as follows: in Section 2, we mention a definition of WSN, highlighting its different use cases and its problem of localization. Then, in Section 3, we define DVHOP in detail by citing its advantages and drawbacks. In Section 4, we introduce the improved versions of DVHOP. Simulation is done and discussed in Section 5. Finally, we conclude the paper and present future works in Section 6.
Research methodology
Our research methodology is as follows: Firstly, we study DVHOP deeply by analyzing the reason behind its huge error. Secondly, we formulate the last step of DVHOP into an optimization problem in which we minimize the fitness function. That means we minimize the sum of errors accumulated during the multilateration process, obviously to reach the convenient locations of unknown nodes. For that purpose, we have adopted simulated annealing algorithm, particle swarm optimization and FMINCON solver dedicated to mathematical optimization under MATLAB to replace the step of resolution done by DVHOP localization algorithm. Finally, our experience is split into two phases. In the first step, we prepare an experimental environment by fixing the number of nodes. Then, we compare the performance of our improved version of DVHOP and the traditional DVHOP by varying the percentage of anchors. In the second step, we re-make the comparison by varying the number of nodes and keeping the percentage of anchors at 30%.

2. Wireless Sensor Network

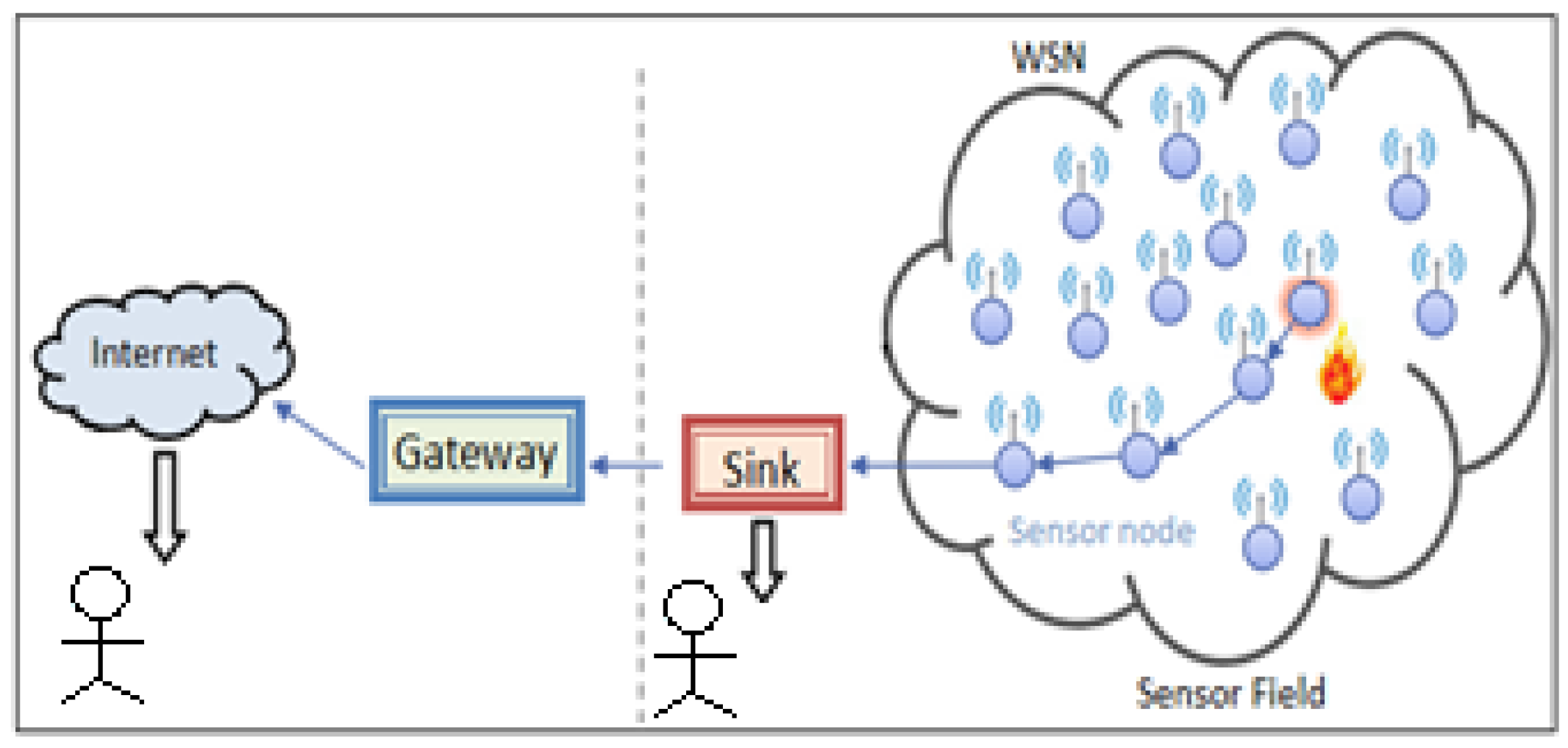
The sensor nodes are usually distributed in a field of sensing as shown in Figure 1. Each of these distributed sensors may gather the data and disseminate it back to the final user. In Figure 1, it’s illustrated a set of sensors scattered throughout a forest; when a specified sensor records the triggering of fire, the location of the event should be routed to the firefighter as fast as possible for making the necessary interventions.
Wireless sensor networks (WSNs) are considered and used in a wide range of applications, such as military sensing [17], smart environmental [18], vehicule adhoc network (VANET) [19], healthcare [20], agriculture [21], industry [22], multimedia [23], etc. Briefly, the sensor may do a complicated computational task similar to one done by a real computer. Besides that, WSN is able to respond to some critical issues encountered in nature and even in the industry. For example, the necessity of pertinent measurement in high-risk places where humans cannot seriously be there to take a manual measure or even to diagnose the status of the scattered sensors. That is to say, the most critical issue that confronts the sensor is the exhaustion of the battery. Hence, the concept of different mechanisms (transmission, synchronization, localization) to guarantee the long lifetime of sensors has become a hot research topic. Seeing that in our contribution we shall tackle localization in WSN, we shall study range-free techniques due to their reliability in terms of energy consumption.
Range-free techniques are the process of determining the position of an unknown node based on the known node position and some algorithms. Indeed, they’re vital to many applications, such as battlefield surveillance [24], environmental monitoring [25] and target tracking [26]. However, hop-based algorithms are judged to be the most practical solution for locating nodes in WSN. DVHOP belongs to hop-based algorithms. Indeed, it’s known for its simplicity and high coverage of localization. Nevertheless, the latter suffers from a leak of accuracy that’s caused by the least square method adopted to extract the solutions in the multilateration process. As we know, the multilateration is the intersection of the circles with the purpose of locating the target. However, more circles are required to calculate the coordinates of the unknown node more precisely. That means more equations are devoted to resolution purposes. In addition to that, those equations are presented in non-linear form. As a consequence, we are facing a huge and complicated problem. Our aim was to transform the cited issue into an optimization problem. Indeed, it was seen that simulated annealing [27,28,29], PSO [30,33], FMINCON [31,32,33] the convenient methods for resolving the cited problem.

3. Related works

In fact, there are two factors contributing to the imprecision of DVHOP. Firstly, by the least squares method used to solve the non-linear equations. Secondly, by the manner adopted in averaging hop-size. During our research, we find that the research community focuses on resolving DVHOP by replacing the least squares method because the error introduced in the distance calculation step has a slight impact on the accuracy of DVHOP. In general, many scientists adopt nature-inspired meta-heuristic algorithms [34] to enhance the precision of DVHOP. For example, we find that particle swarm optimization (PSO) is mostly used to mitigate this issue. In [35], the author adopts PSO and he uses Linear Decreasing Inertia Weight (LDIW) [36] to have a balance between the exploration and exploitation phases of PSO in order to minimize the cost function and reach the global solution. Then, the solution extracted by PSO presents the optimal location of the unknown node. In [37], the study of localization is extended to three dimensions. In addition to that, the genetic algorithm has been used in order to improve DVHOP. In detail, the process of positioning is summarized in six steps: flooding phase, hop-size calculation, population initialization, crossover, selection and mutation. Briefly, GA-DVHOP [38] changes the last phase of the traditional DVHOP to genetic steps, aiming to reach a better solution. Although that method gives a high degree of accuracy, its drawback resides in its high complexity in comparison with PSO-DVHOP. In [39], the authors attempt to resolve the premature convergence caused by PSO-DVHOP. For that purpose, they use Quantum Particle Swarm optimization (QPSO) in order to reach the global solution of the localizing problem. In general, the purpose of QPSO-DVHOP is to enhance the precision of positioning in WSN. In addition, QPSO-DVHOP satisfied a good time of calculation in comparison with the traditional PSO-DVHOP.
In [40], it’s shown that Amorphous outperforms DVHOP in terms of accuracy by varying the number of nodes and the percentage of anchors. This study also proves the efficiency of Amorphous in terms of energy consumption. According to the experimental results, it’s confirmed that Amorphous reach a satisfactory precision in WSN with a few anchors. However, DVHOP requires more anchors to perform better. In [41], the authors highlight the importance of locating a node in a wireless sensor network. Also, they present different localization algorithms that exist. According to their results, it’s shown that Amorphous outperforms both Centroid and DVHOP by varying the proportion of anchors, communication range and number of nodes in a network with an irregular distribution of nodes. In [42], a performance comparison of Amorphous and DVHOP has been done, the metric of evaluation was the accuracy of localization, energy consumption and network overheard. Also, it’s shown for both algorithms cited that the accuracy of localization is inversely proportional to the energy consumed by the node. As we know, in a non-uniform network, we need more anchors. Hence, Amorphous outperforms DVHOP in terms of accuracy and energy consumption because Amorphous doesn’t require many anchors in its locating process. In [43], the authors use a genetic algorithm to improve DVHOP and they adopt PSO to refine the crossover step. The simulations realized in this research prove the efficiency of the ameliorated version of DVHOP in terms of precision by varying the percentage of anchors. In [44], the authors present Centroid, APIT, DVHOP and explain in detail the principles of functioning of each cited algorithm. In addition to that, they present DVHOPmax as an enhanced version of DVHOP that’s adjustable according to the topology of the network in order to reach a high level of accuracy. Then, a performance comparison has been done in terms of accuracy with the purpose of proving the efficiency of DVHOPmax in WSNs with non-uniform topology.

4. Traditional DVHOP algorithm

DVHOP is a distributed localization algorithm. It was invented by Niculescu and Nath [45] in 2003; it’s based on vector distance routing and consists of three different steps, as follows:
Step1: Flooding
Each unknown node knows the number of hops to their anchor by a mechanism of broadcast done by anchors.
Step2: Hop-size and distance calculation
After the flooding process, we can obtain the hop-size between anchors according to the formula (1)
hopsize i = ∑ j = 1   j # i n ( x i − x j ) 2 + y i − y j 2 ∑ j = 1 n h o p c o u n t i j
where (xi,yi), (xj,yj )represent respectively the coordinates of anchors i,j.
After obtaining hopsize, equation 2 is used to calculate the distance between anchor i and the unknown node.
du,i = hopsizei * hopcountu,i
Step3: Calculation of unknown node position
In this step, we specify the coordinates of all unknown nodes. For each unknown node, we apply the least square method to estimate its location.
(x,y) denotes the coordinates of the unknown nodes, (ai,bi) represents the location of the anchor node, where i = 1,2,..n and n is the number of anchors, thus the distance between unknown nodes and n anchors is expressed by the non-linear equations:
( x − a 1 ) 2 + ( x − b 1 ) 2 + ( z − c 1 ) 2 = d 1 2 . . ( x − a n ) 2 + ( x − b n ) 2 + ( z − c n ) 2 = d n 2
Then we find
x 2 − 2 a 1 x + a 1 2 + y 2 − 2 b 1 y + b 1 2 = d 1 2 . . x 2 − 2 a n x + a n 2 + y 2 − 2 b n y + b n 2   = d 1 2
(4) can be extendedto:
− 2 x ( a 1 − a n ) + a 1 2 − a n 2 − 2 y b 1 − b n + b 1 2 − b n 2 = d 1 2 . . − 2 x ( a n − 1 − a n ) + a n − 1 2 − a n 2 − 2 y b n − 1 − b n + b n − 1 2 − b n 2 = d n − 1 2
The solution of the system may be interpreted to the resolution of the equation Ax=b where
A = 2 ( a 1 − a n ) 2 ( b 1 − b n ) . . 2 ( a n − 1 − a n ) . . 2 ( b n − 1 − b n )
b = a 1 2 − a n 2 + b 1 2 − b n 2 + c 1 2 − c n 2 − d 1 2 . . a n − 1 2 − a n 2 + b n − 1 2 − b n 2 + c n − 1 2 − c n 2 − d n − 1 2
In the traditional DVHOP algorithm, the least square estimator done in the last step of the positioning process causes a huge error in locating the target node, which has a big influence on the accuracy of DVHOP. In our approach, we attempt to keep the two first steps of DVHOP and change the last step to an optimization problem. In detail, the proposed method is summarized in three steps: Each unknown node knows its number of hops to their anchors through a broadcast done by the anchors. Secondly, we calculate the distance between anchors and unknown nodes on the basis of the hop-size. Lastly, we select a specified meta-heuristic to minimize the sum of errors occurring in the multilateration process. Hence, the positioning problem may be interpreted to solve the minimization of the fitness function mentioned below:
f x , y =   1 n ∑ i = 1 n ǀ ( x − a i ) 2 + ( y − b i ) 2 − d i
where n is the number of anchors,
(ai,bi) are the coordinates of anchors, di is the distance between anchor i and unknown node.

5. The proposed approach for DVHOP improvement

In this part, we discuss three improved versions of the traditional DVHOP localization algorithm ameliorated by adopting two meta-heuristics (SA, PSO) and FMINCON solver dedicated to optimization under MATLAB. Our purpose is to enhance the precision of DVHOP. The two first steps in all enhanced algorithms are similar to the two first steps of DVHOP algorithm because these steps are the main reason for the high coverage of the localization of DVHOP. Hence, we leave these steps as they are and tackle our modifications in the last step of DVHOP. Moreover, we change the least square method adopted by the traditional algorithm to an optimization problem that can be resolved by each of the methods cited above. In the following, we shall cite in detail our improved versions of DVHOP.

5.1. DVHOP algorithm based simulated annealing

SA (simulated annealing) is a stochastic global search optimization that was introduced by kirkpatrick [46] in 1983. As a normal local search method, it uses a special strategy to avoid the local minima. This meta-heuristic is based on heating and cooling in order to obtain a flawless alloy. In detail, this method alternates the cycles of heating (or annealing) and cooling the metals slowly. In literature, there are different types of cooling schemes (logarithmic, arithmitic-geometric, adaptative) and SAbased on the linear cooling scheme is the best one because it makes the calculation in a short duration of time. Also, it can give precise results.
In general, the purpose of SA is to traverse the space of solutions in an iterative manner. We start with an initial solution S0 (generated randomly) which denotes the initial energy E0 and an initial temperature T0 that is generally high. We assume that an elementary change occurred in the solution at each iteration of the algorithm. This change causes a variation in the energy of the system that we denote ∆E. If ∆E is negative, the new solution is accepted because it improves the cost function. If ∆E is positive, the solution found maximizes the energy of the system. Hence, it’s considered worse than the previous solution. As a consequence, the new solution will be accepted with a probability P calculated according to the following Boltzman distribution:
P(E,T) = exp(-∆E/T)
where T denotes the temperature of the solid.
The choice of temperature is essential to guaranteeing the balance between intensification and diversification of solutions in the space of research. First, the choice of the initial temperature depends on the quality of the starting solution. Indeed, the initial value of the temperature must be relatively high. T is calculated iteratively as follows:
Tk+1← Tk . α
α ϵ[0,1], α is a parameter that expresses the decrease in temperature of the iteration. The decrease in temperature can also be carried out in stages. That is to say, the decrease only changes after a certain number of iterations. On the other hand, we can also raise the temperature when the search process seems blocked in a region of the search space. We can then consider a high increase in temperature as a process of diversification. while the decrease in temperature corresponds to an intensification process.
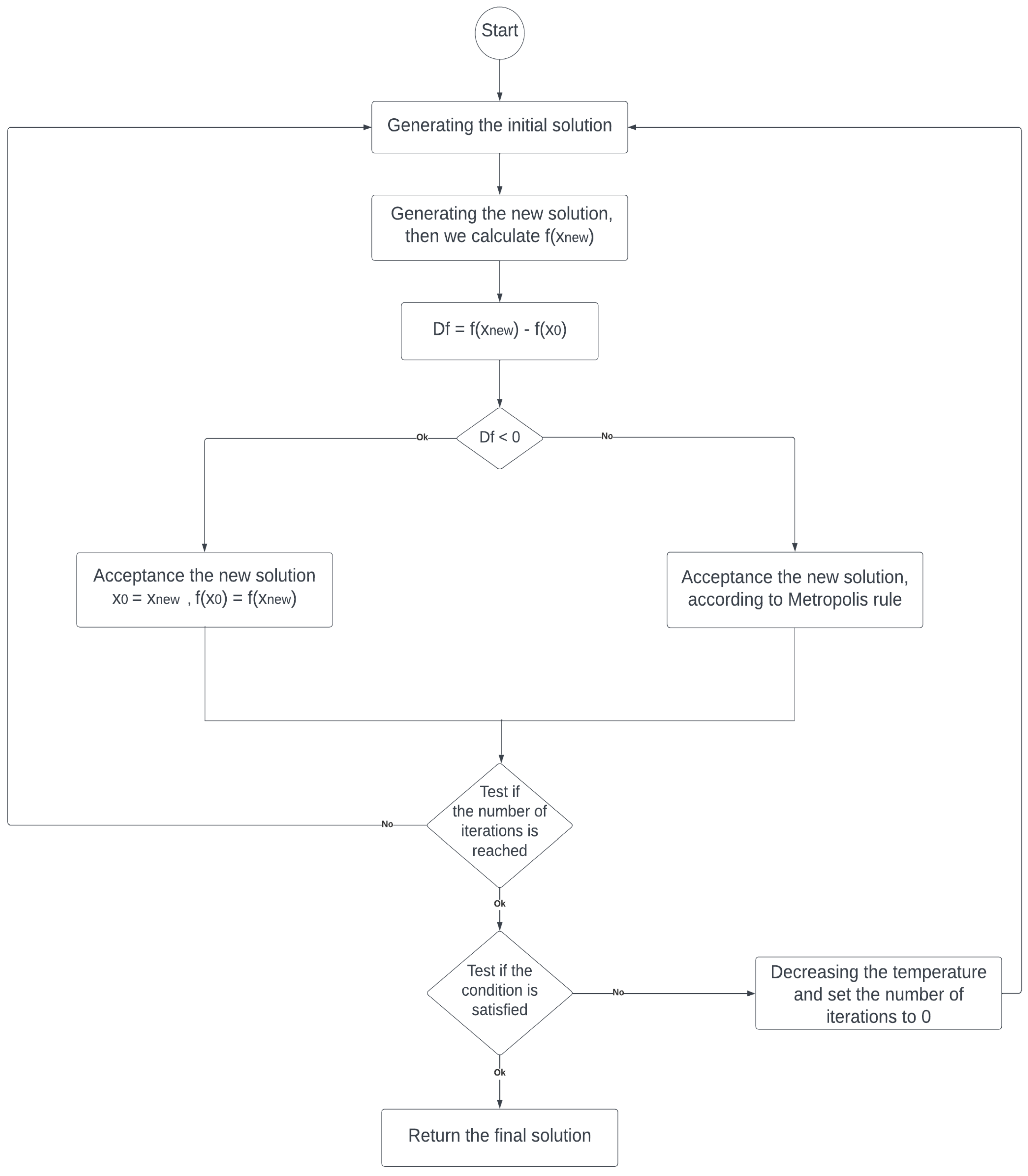
The flowchart mentioned below describes in detail the functioning of SA
Preprints 76628 g002
Figure 2. Flow chart of Simulated annealing algorithm.
Figure 2. Flow chart of Simulated annealing algorithm.
Preprints 76628 g002
The principle of SA-DVHOP is as follows: we execute simulated annealing algorithm inside the browsing of unknown nodes, more precisely after the distance calculation step. Indeed, for each solution extracted by simulated annealing algorithm, it will be assigned to an unknown node. The pseudo-code mentioned below describes the steps of SA-DVHOP algorithm.
Algorithm 1: SA-DVHOP algorithm
Initialization:
number of nodes =NB,
number of anchors=NA,
area of experimentation =1000*1000m2 ,
communication range=500m
1.calculation of hopcounti,j by finding the shortest path between nodes
2.hopsize calculation according (1)
3.calculate the positions of unknown nodes
for i=NA to NB
   4.distance calculation
   unknown_to_anchors_dist=hopsize(i)*shortest_path(i,1 to NA);
   5.fitness function f is calculated according (8)
   6.execution of Simulated annealing algorithm
   initialize the temperature T according to the cooling scheme (10)
   while (the end of the stage has not be reached)
    generate a random neighbor S' from S
    calculate ∆E = f(S') - f(S)
    if ∆E ≤ 0
      S←S'
    else
     accept S0 as the new solution with probability P(E,T) = exp(-∆E/T)
    end
    update T based on cooling scheme
   end
   return pbest
   6.assign the result of SA to an unknown node
   node.estmd(i,1to 2)=pbest;
end

5.2. DVHOP algorithm based particle swarm optimization

The optimization by particle swarm was invented by Kennedy and Eberhart in 1995. This method is based on the social behavior of animals living in swarms. Indeed, the particles are individuals and they move in order to search for a global solution, according to the following information:
  • Each particle has the ability to memorize the best point already passed and it attempts to return to this point.
  • Each particle is aware of the best point in its area and it will attempt to go towards this point.
PSO consists of a swarm of particles that fly throughout the space of solutions in order to reach the global solution. Analytically, in Rn, the particle i of the swarm (potential solution) is modeled by its position vector xi = (xi1, xi2, …, xin) and by its velocity vector vi = (vi1, vi2, …, vin). This particle remembers the ideal position that we noted pi = (pi1, pi2, …, pin) , the best position reached by all the particles of the swarm is noted by pg = (pg1, pg2, …, pgn). We can express the velocity vector using the following formula:
vi,j(t+1) = vi,j(t)+c1r1(pi,j(t) - xi,j(t)) + c2r2(pg,j(t) - xi,j(t))
c1, c2 are two constants called acceleration coefficients. r1, r2 are two random numbers that existed in the interval [0,1], vij(t) corresponds to the physical component of the displacement.
The position of particle i is then defined by
xi(t+1) =x i(t) + vi(t+1)
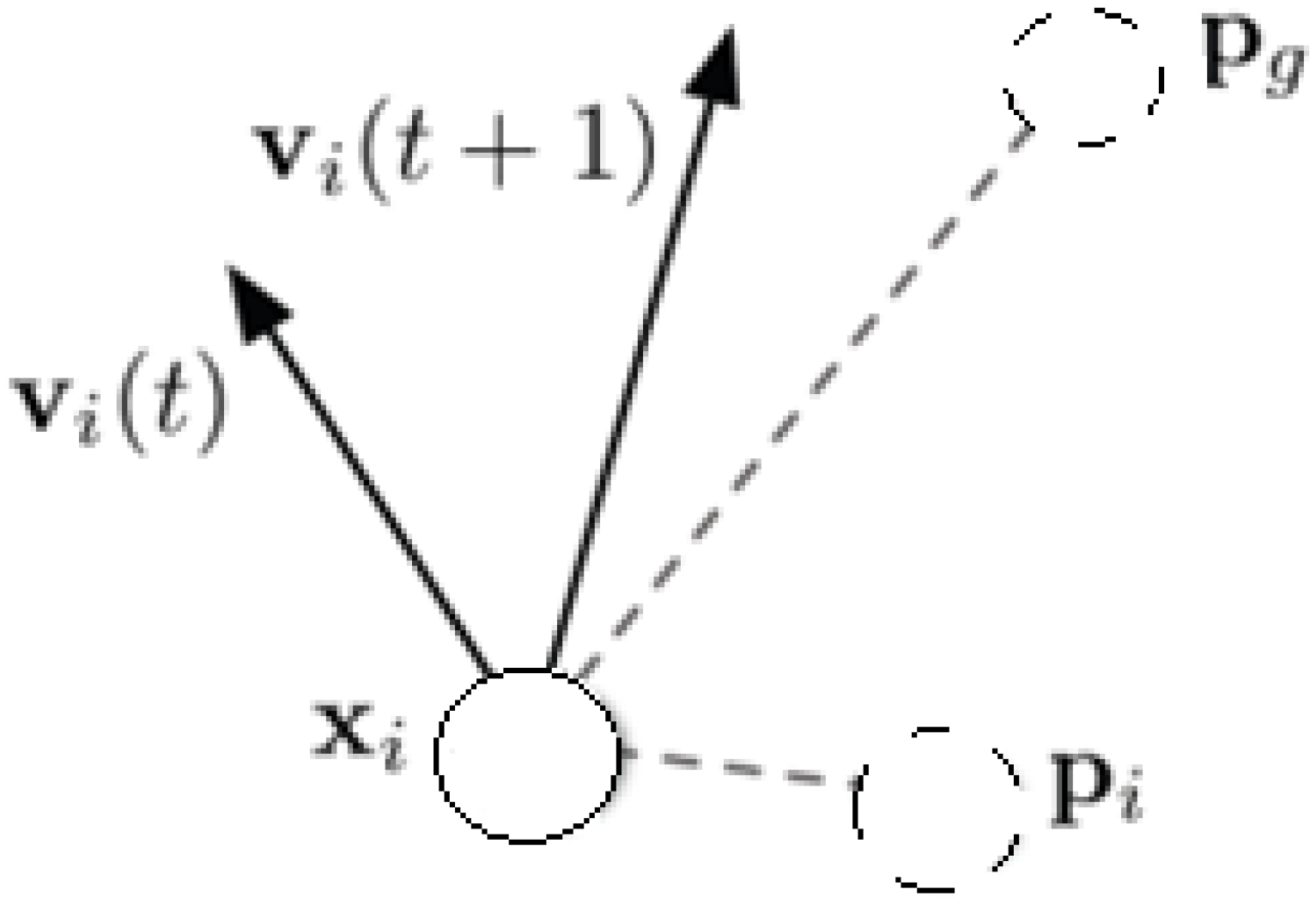
The particle swarm is usually represented by a geometric model, assuming that v is the velocity of the particle, x is the initial position of the particle and p is the optimal position of the particle. We also suppose that the particle swarm is composed of N particles. Briefly, in the process of finding the optimal solution, each particle modifies its position and velocity iteratively. That is to say, the updating of the position and velocity of the particle is based on its previous information and the previous best position found by the swarm. The geometric model illustrated in Figure 3 depicts the movement strategy of the particle.
The pseudo-code mentioned below describes the steps of PSO algorithm:
Algorithm 2: Particle swarm optimization algorithm
Randomly initialize Ps particles :Position and velocity
Assess particle position
while the stopping criterion is not reached
    for i=1,…,Ps
move the particles according (11) ,(12)
  if f(xi)<f(pi)
   pi= xi
if f(xi)<f(pg)
   pg= xi
end
end
end
end
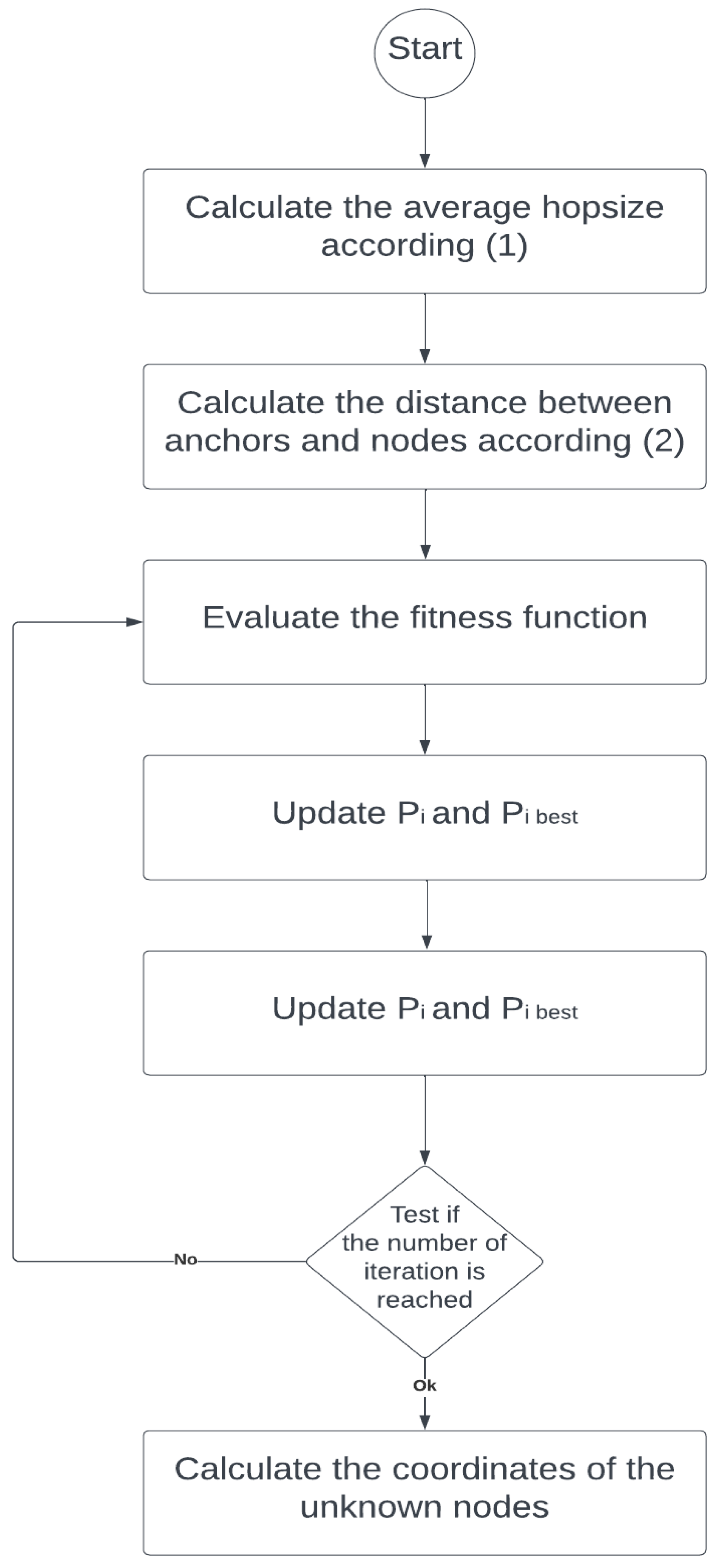
The flowchart mentioned below describes in detail the functioning of PSO-DVHOP:
Preprints 76628 g004
Figure 4. Flow chart of PSO-DVHOP algorithm.
Figure 4. Flow chart of PSO-DVHOP algorithm.
Preprints 76628 g004

5.3. DVHOP algorithm based FMINCON solver

FMINCON solver is presented among the solvers that belong to the library of optimization integrated in MATLAB. Moreover, this predefined function allows us to find the minimum of a constrained non-linear multi-variable function using the interior-point algorithm. However, when the user of MATLAB uses FMINCON, he must describe his problem precisely. Indeed, he specifies the cost function and all accompanying information, such as the initial point of the algorithm and the constraints. Indeed, the function to minimize is in the form of @objfun. Also, the constraints and bounds of constraints are represented by the adequate matrix.
There are two approaches for using FMINCON: either in a graphical mode presented by a window of MATLAB with different fields that allow the user to insert the required information (function, start point, constraints) or by calling FMINCON via the command window of MATLAB. In this case, the user must specify the cost function in script.m and we call the constraints and the initial point via command window. In both cases of utilization, when we run the solver, the results are shown, including the reason the algorithm terminated. Obviously, the results denote the final point reached.
In our case, we have used the solver via command window. However, our purpose was to resolve the optimization problem formulated as follows:
min ⁡ f x s u b j e c t t o A . x ≤ b A e q . x = b e q l b ≤ x ≤ u b
Seeing that, in the field of sensing, a sensor may be placed without any predefined condition, we haven’t set any constraints on our optimization problem. Also, we set the dimension of the problem at two because we do the localization in two dimensions. Hence, x is designed by [x(1) x(2)]. In addition to that, we refer the upper and lower values taken by x to the lower and upper abscissa and ordinate taken by a sensor in the sensing field. In our case, our field has 1000*1000 as a surface, so lb, ub take respectively the values [0,0] and [1000,1000].
Among the predefined solvers in MATLAB (linprog, ga, fminimax), we have implicitly opted for FMINCON because the latter may be set without gradient supply calculation. Hence, we avoid the additional complexity caused by the derivative calculation. Consequentially, FMINCON makes the optimization in a short period of time in comparison with their variants. Secondly, in both cases of utilization cited above (command window, graphical mode) this special function is simple to implement. Indeed, it just needs to assign each of their attributes properly. Thirdly, FMINCON solver is an efficient tool to avoid being trapped in premature convergence despite the multi-modality presented in our cost function dedicated to optimizing DVHOP.
The pseudo-code mentioned below describes the steps of FMINCON-DVHOP algorithm:
Algorithm 3: FMINCON-DVHOP algorithm
Initialization:
number of nodes =NB,
number of anchors=NA,
area of experimentation =1000*1000m2 ,
communication range=500m
1.calculation of hopcounti,j by finding the shortest path between nodes
for k=1 to NB
for i =1 to NB
for j=1 to NB
if(sh_path(i,k)+sh_path(k,j) < sh_path(i,j))
      sh_path(i,j)= sh_path(i,k)+sh_path(k,j);
end
end
end
end
2.hopsize calculation according (1)
3.calculate the positions of unknown nodes
for i=NA to NB
   4.distance calculation
   unknown_to_anchors_dist=hopsize(i)*sh_path(i,1 to NA);
   5.fitness function f is calculated according (6)
   A=[]; b=[]; Aeq=[]; beq=[]; x0=[0 0]; lb=[0 0]; ub=[1000 1000];
   6.assign for each unknown node the result of fmincon
node.estmd(i,1to 2)= fmincon(f,x0,A,b,Aeq,beq,lb,ub);
end

6. Results and discussions

In this section, we shall present the performance comparison of SA-DVHOP, PSO-DVHOP, FMINCON-DVHOP and DVHOP in WSN with random topology; all nodes are randomly distributed throughout the area of experimentation. Also, we have assessed our algorithms in grid topology. That is to say, the area of simulation is partitioned into grids and nodes and anchors are equally distributed throughout these grids. The criterion of comparison is ALE in order to select which localization algorithm is better in a specified configuration.

6.1. Simulations parameters

In order to ameliorate DVHOP, we have created three improved versions of the traditional DVHOP. The two tables mentioned below describe the parameter settings of SA-DVHOP and PSO-DVHOP.
Table 1. Parameter settings of SA-DVHOP.
Table 1. Parameter settings of SA-DVHOP.
Parameter Value
Dimension 2
Lower bound 0
Upper bound 1000
Number of iterations 10
Initial temperature 0.1
α 0.99
Population size 10
Number of neighbors per individual 5
Table 2. Parameter settings of PSO-DVHOP.
Table 2. Parameter settings of PSO-DVHOP.
Parameter Value
Population size 50
Number of iterations 100
c1 1.775
c2 2.8
Dimension 2
Lower bound 0
Upper bound 1000
To evaluate the performance of each localization algorithm in terms of accuracy of localization. The following metric has been considered:
Average localization error (ALE) which is the ratio of total localization error to the number of simple nodes. Indeed, ALE is used to assess the precision of each localization algorithm according to different parameters such as node density, anchor node ratio and shape of distribution. Indeed, a specified algorithm is more accurate if it has less ALE, ALE can be expressed as follows:
A L E = ( x t − x e ) 2 + ( y t − y e ) 2 n t − n h r
where ( x t ,   y t )   and ( x e , y e )   are the true and estimated coordinates of sensor nodes respectively.
nt denotes the total number of nodes.
nh presents the non localized nodes
r presents the communication range of a node.

6.2. Simulation results

To evaluate the performance of the cited algorithms, we split the simulation scenarios into two parts. Firstly, we make our comparison under a WSN with a grid topology and we vary the percentage of anchors and the number of nodes. In the second part, we remake the comparison with a random topology by varying the same metrics. It’s assumed that when we pass from grid topology to random topology, the error of localization increases because the calculation of hop-size by all the algorithms in grid topology is more accurate than that calculated in random topology.
We use the parameter settings listed in the following table:
Table 3. Parameter settings of simulations.
Table 3. Parameter settings of simulations.
Parameter Value
Area 1000*1000 m2
Total number of nodes 16-25-36-49-64-81
Topology uniform, irregular
Percentage of anchors 5%-10%-15%-20%-25%-30%
Communication range 300 m - 400 m - 500 m
Model of communication regular
In both cases of distribution (uniform, no-uniform) we followed the described strategy to make our evaluation: In the first step, we keep the number of nodes at 36 and the communication range at 400 m and we gradually vary the percentage of anchors. Secondly, we keep the percentage of anchors at 20% and we change the communication range accordingly. Then, we vary the number of nodes between 16 and 81.
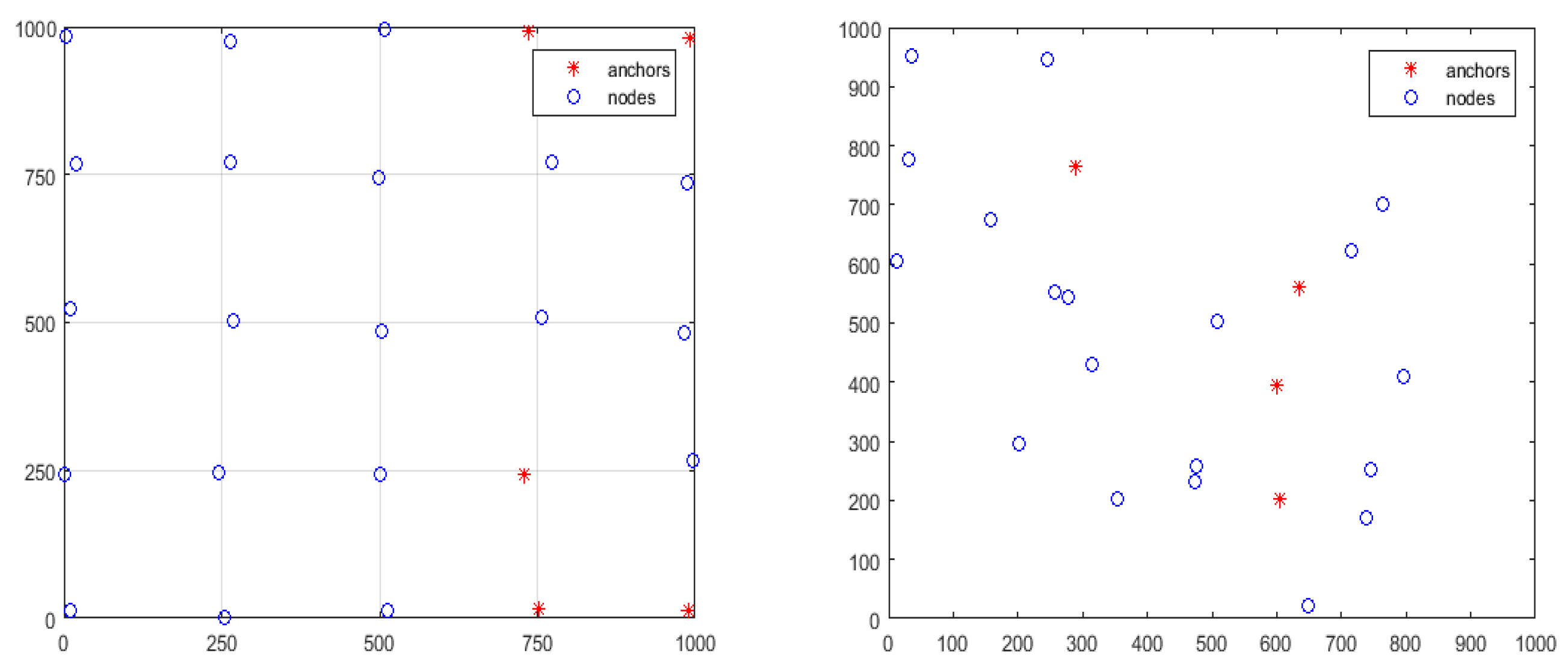
In Figure 5, we can see the initial deployment of nodes throughout the field of sensing with a total number of nodes equal to 25 (5 anchors and 20 unknown nodes). The percentage of anchors is expressed by the ratio of the number of anchors to the total number of nodes. In Figure 5a, we use a uniform distribution of nodes throughout an area whose surface is equal to 1000*1000 m2. In Figure 5b we keep the same parameters described in Figure 5a the only difference is that we change the topology of the network to a random topology.

6.2.1. The comparison under a uniform deployment of nodes

In this part, we shall establish a performance comparison of our algorithms by varying the percentage of anchors. We assume that the number of nodes is 36 and the communication range is set to 400 m.
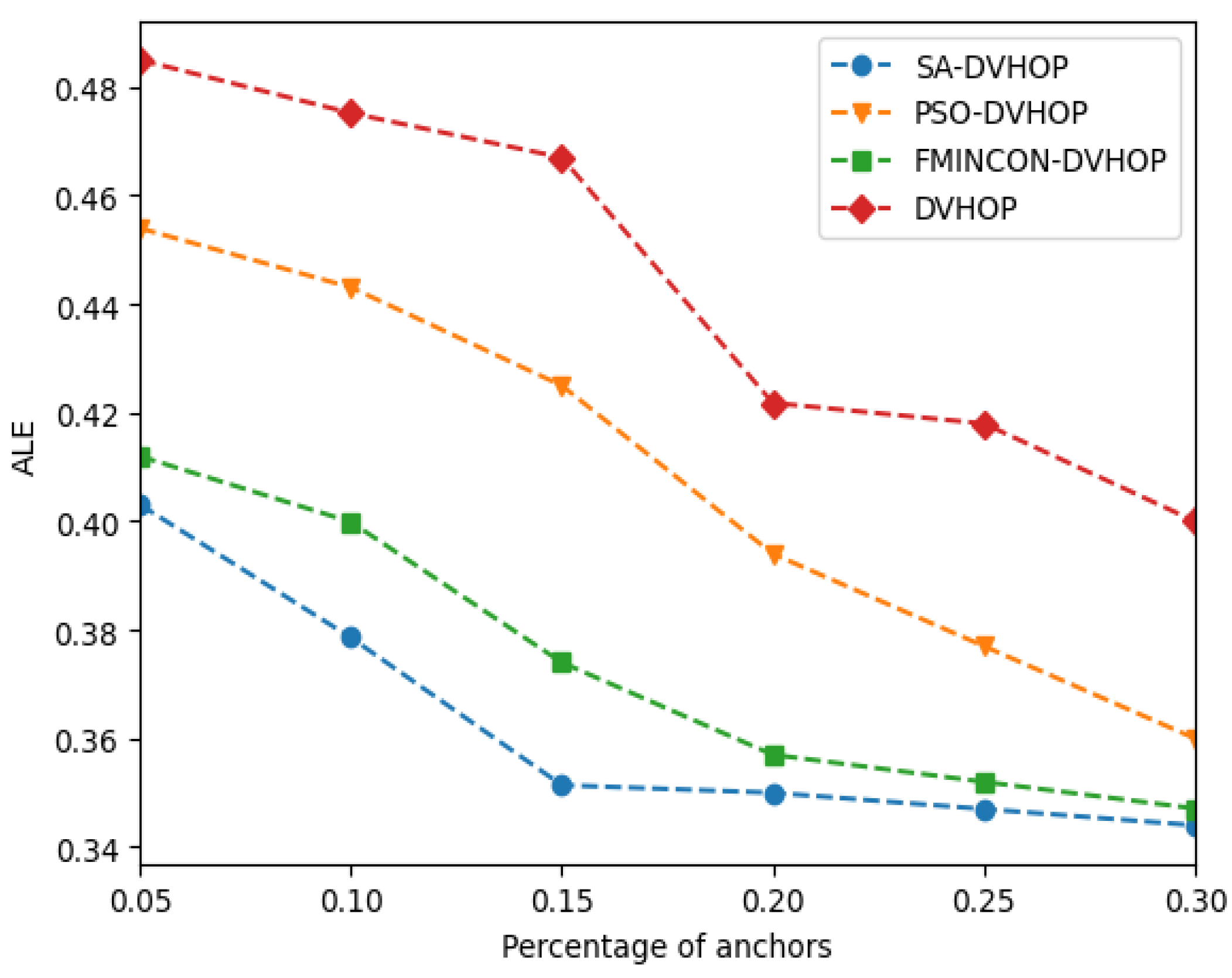
According to the results of Figure 6, it’s shown that DVHOP gives the worst result and its performance is increasing by varying the percentage anchors, because adding more anchors makes the multilateration done by DVHOP more precise. Consequently, DVHOP tends to locate the unknown nodes with great accuracy by increasing the number of anchor nodes.
On the other hand, it is evident that SA-DVHOP yields the most favorable outcomes, particularly due to its increasing accuracy within the 5% to 15% range of anchor percentage. However, in the 15% to 30% range, the precision of SA-DVHOP experiences a slight decrease. This can be attributed to the efficient cooling scheme employed by SA, wherein the atoms in the alloy are granted freedom of displacement. The temperature is gradually reduced until a static equilibrium of atoms is achieved. In cases where equilibrium is not reached, corrections are made by raising the temperature and slowly cooling the alloy. This process aligns with our cost function, resulting in solutions extracted by SA-DVHOP closely approximating the true solutions. Consequently, SA-DVHOP offers superior results compared to other algorithms. Additionally, both FMINCON-DVHOP and PSO-DVHOP also deliver commendable outcomes, with their accuracy continuing to improve as more anchors are incorporated.
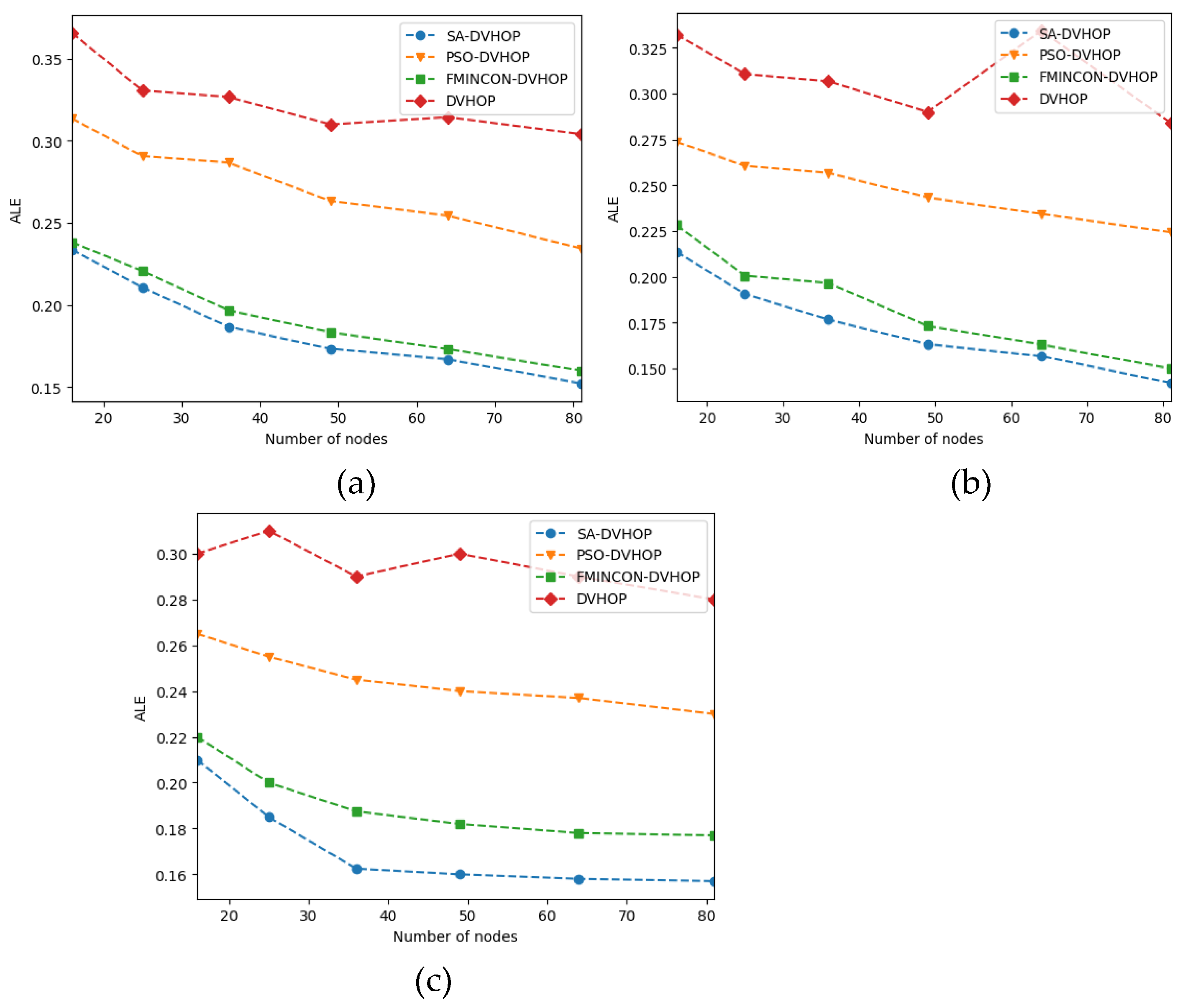
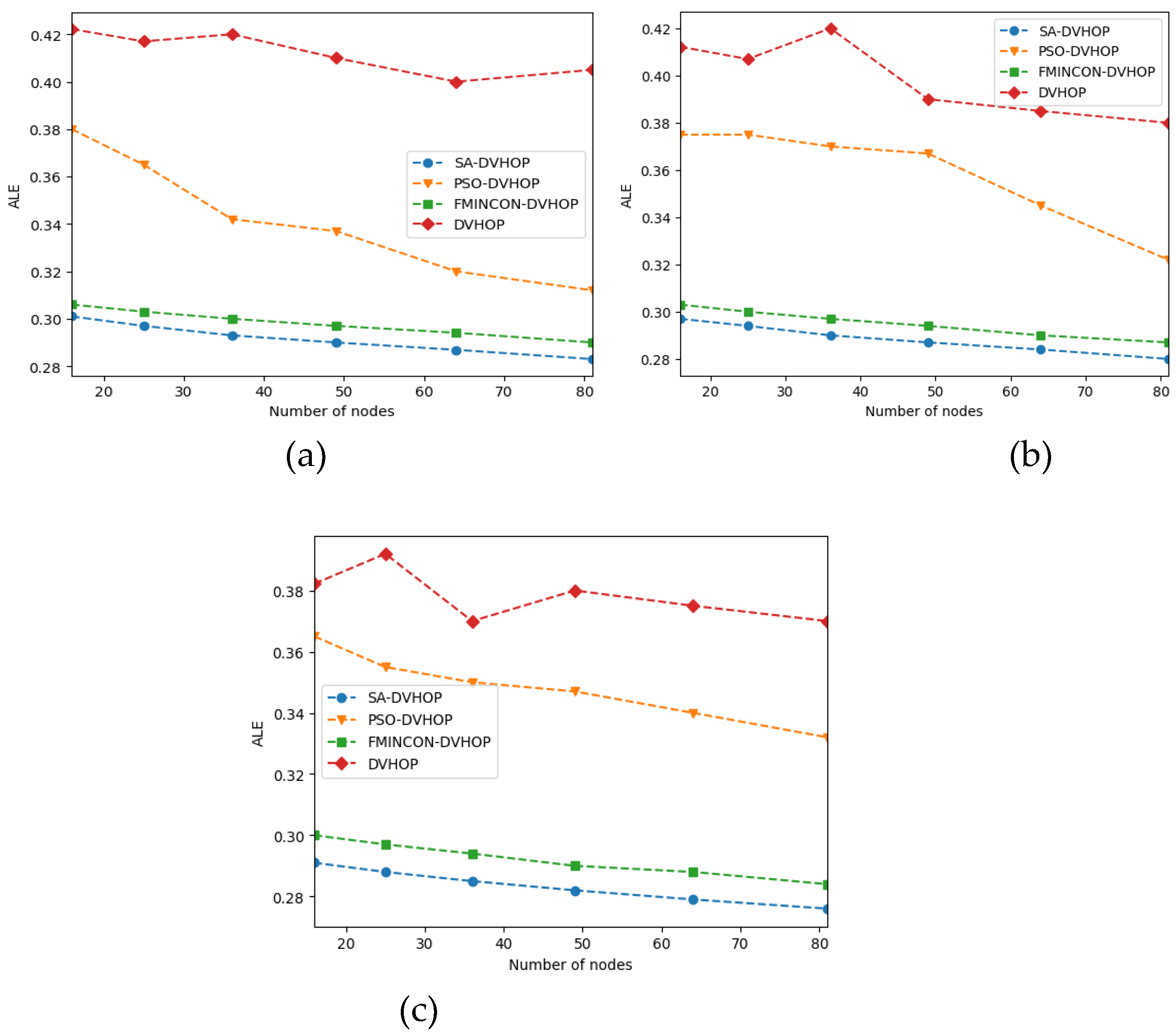
In the three configurations shown below, the communication range is set to 300 m, 400 m and 500 m, the percentage of anchors is set to 20% and we change the number of nodes between 16 nodes and 81 nodes. The results of the experiments are shown in Figure 7.
According to Figure 7, SA-DVHOP offers superior results compared to other algorithms when we increase the number of nodes. However, in the beginning, precisely within the 16–36 range of nodes, the precision of FMINCON-DVHOP and SA-DVOP experiences a significant decrease. However, in the 36–81 range, the variation of their accuracy shows a slight decrease because 36 nodes denote the number of nodes in which the cited algorithms perform better.
According to the three configurations shown, it’s observed that PSO-DVHOP gives a good result and its ALE keeps decreasing, but its performance remains less than that offered by the two mentioned algorithms. In addition to that, it’s clearly shown that DVHOP causes a huge error in estimating the position of unknown nodes and it’s observed different transitions in its performance variation. That reflects the non-stability in the calculation of least square adopted by the algorithm.
Finally, it’s concluded that in WSN with a uniform distribution of nodes, the optimization by the meta-heuristic methods has shown efficiency in enhancing the precision of the traditional DVHOP.

6.2.2. The comparison under a random distribution of nodes

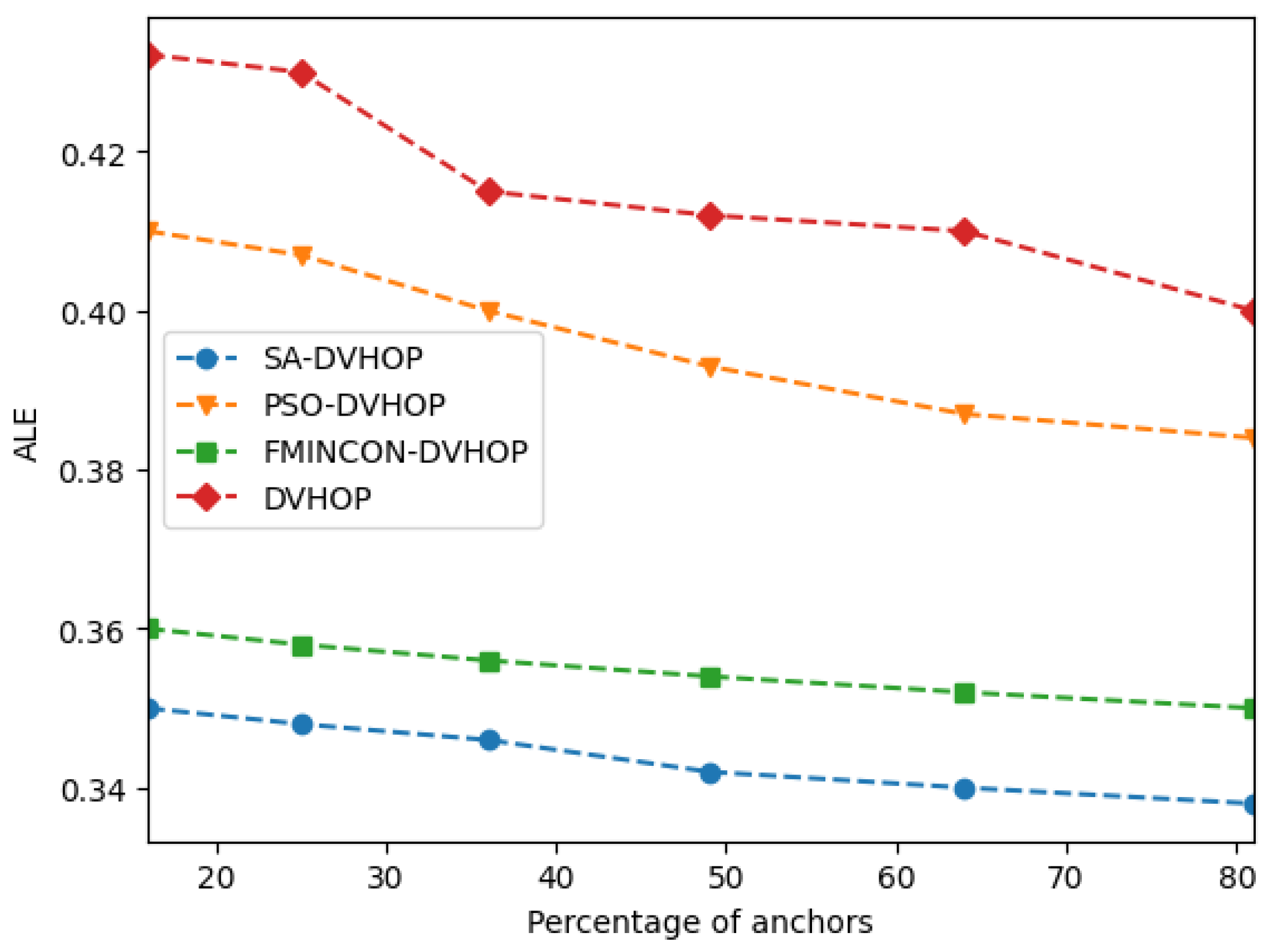
In this part, we research the impact of changing the number of anchors on the accuracy of each algorithm.Also, it’s noted that the number of nodes is 36 and the communication range is 400 m.
According to the results of Figure 8, it’s shown that our SA-DVHOP outperforms other localization algorithms when we increase the percentage of anchors because SA-DVHOP keeps the good properties of DVHOP in distance calculation. Additionally, SA-DVHOP shows better results due to the efficiency of SA for resolution purposes. Also, it’s noted that FMINCON-DVHOP gives a good result, which means FMINCON is an efficient tool to avoid being trapped in premature convergence. However, the precision offered by SA-DVHOP remains higher than that offered by FMINCON-DVHOP.
On the other hand, PSO-DVHOP is ranked in the third position, which means the exploration and exploitation adopted by PSO meta-heuristic suffer from a leak of balance that negatively impacts the resolution of the optimization problem. Consequently, this method doesn’t provide the same precise results as the mentioned algorithms. Finally, it’s observed that DVHOP gives the worst result when we vary the percentage of anchors.
In the three configurations shown below, the communication range is set to a 300 m, 400 m and 500 m, the percentage of anchors is set to 20% and we change the number of nodes between 16 nodes and 81 nodes. The results of the experiments are shown in Figure 9.
According to the results of Figure 9, it’s clearly observed that the accuracy of each algorithm increases with increasing communication range. Also, it’s shown that SA-DVHOP outperforms other algorithms. Besides that, it’s marked out that DVHOP gives the worst results. Indeed, in a random deployment of nodes, the algorithm is prone to imprecision in averaging the hop-size, which leads the algorithm to calculate imprecisely the distance between unknown nodes and anchors. Hence, the accuracy provided by DVHOP remains less than that offered by the improved algorithms.
On the other hand, the localization error of PSO-DVHOP decreases as the number of nodes increases because this algorithm uses a meta-heuristic technique to locate each node instead of adopting the least square method, which is judged to be the reason for the imprecision of DVHOP.
As shown in Figure 9c when the communication range is set to 500m, it’s clearly observed that both FMINCON-DVHOP and SA-DVHOP give the best results. and SA-DVHOP is more precise than FMINCON-DVHOP. That reflects the efficient cooling adopted by SA. The accuracy of SA-DVHOP is relatively not sensitive to the additional node for showing a satisfactory result. Consequently, SA-DVHOP is judged to be the most economical and precise algorithm among their variants.

7. Conclusions

The main goal of this work is the creation of an efficient localization algorithm in terms of accuracy. Although the first two steps of DVHOP contribute positively to locating the majority of nodes in the network and give the algorithm the reputation of high coverage. Nevertheless, the least square method adopted in its last step is judged to be the reason behind the imprecision of DVHOP. On the other hand, due to the importance of mathematical optimization and its ability to optimize DVHOP, we have chosen to formulate the resolution of non-linear equations as a meta-heuristic problem. Precisely, simmulated annealing, Particle swarm optimization and FMINCON were chosen for resolving the cited problem. Our simulation consists of comparing the performance of all the improved versions of DVHOP. The results prove that SA-DVHOP gives the best accuracy in comparison with DVHOP and the algorithms mentioned.
In reality, the communication occurred with irregular radio propagation. However, during our survey, we didn’t take this phenomenon into consideration. Hence, it’s suggested to search for a suitable localization algorithm in a field of sensing with irregular radio pattern as future works.

References

  1. Kanwar, V.; Kumar, A. DV-Hop localization methods for displaced sensor nodes in wireless sensor network using PSO, Wirel. Netw 2021, 27, 91–102. [Google Scholar]
  2. Li, M.; Liu, Y. Rendered path: Range-free localization in anisotropic sensor networks with holes. IEEE/ACM Transactions on Networking 2010, 18, 320–332. [Google Scholar]
  3. Cheikhrouhou, O.; Bhatti, G.; Alroobaea, R. A hybrid DV-hop algorithm using RSSI for localization in large-scale wireless sensor networks. Sensors 2018, 18, 1469. [Google Scholar] [CrossRef] [PubMed]
  4. Messous, S.; Liouane, H.; Liouane, N. Improvement of DV-Hop localization algorithm for randomly deployed wireless sensor networks. Telecommun. Syst. 2020, 73, 75–86. [Google Scholar] [CrossRef]
  5. He, T.; Huang, C.; M. Blum B.; A. Stankovic, J.; Abdelzaher, T. Range-Free Localization Schemes for Large Scale Sensor Networks. In Proceedings of the Ninth Annual International Conference on Mobile Computing and Networking, MOBICOM 2003, San Diego, CA, USA, 14 September -19 September 2003; pp. 81–95.
  6. Kumar, P.; Gupta, G.P. A weighted centroid localization algorithm for randomly deployed wireless sensor networks. J. King Saud-Univ.-Comput. Inf. Sci. 2019, 31, 82–91. [Google Scholar]
  7. Niculescu, D.; Nath, B. DV based positioning in Ad-hoc networks. In Proceedings of the IEEE INFOCOM 2003. Twenty-second Annual Joint Conference of the IEEE Computer and Communications Societies (IEEE Cat. No. 03CH37428), San Francisco, CA, USA, 30 March–3 April 2003; Volume 3, pp. 1734–1743. [Google Scholar]
  8. Messous, S.; Liouane, H. Online Sequential DV-Hop Localization Algorithm for Wireless Sensor Networks. Mob. Inf. Syst. 2020, 2020, 8195309. [Google Scholar] [CrossRef]
  9. Gui, L.; Huang, X.; Xiao, F.; Zhang, Y.; Shu, F.; Wei, J.; Val, T. DV-hop localization with protocol sequence based access. IEEE Trans. Veh. Technol. 2018, 10, 9972–9982. [Google Scholar] [CrossRef]
  10. Nagpal, R.; Shrobe, H.; Bachrach, J. Organizing a global coordinate system from local information on an ad hoc sensor network. In Information Processing in Sensor Networks; Springer: Berlin/Heidelberg, Germany, 2003; pp. 333–348. [Google Scholar]
  11. Yick, J.; Mukherjee, B.; Ghosal, D. Wireless sensor network survey, Computer Networks. 2008, 52, 267–280. [Google Scholar]
  12. Yu, K.; Guo, Y.J.; Hedley, M. TOA-based distributed localisation with unknown internal delays and clock frequency offsets in wireless sensor networks. IET Signal Process. 2009, 3, 106–118. [Google Scholar] [CrossRef]
  13. Niculescu, D.; Nath, B. Ad hoc positioning system (APS) using AOA. In Proceedings of the IEEE INFOCOM 2003. Twenty-second Annual Joint Conference of the IEEE Computer and Communications Societies (IEEE Cat. No. 03CH37428), San Francisco, CA, USA, 30 March–3 April 2003; Volume 3, pp. 1734–1743. [Google Scholar]
  14. Li, W.; Zhao, B. Analysis of TDOA Location Algorithm Based on Ultra-Wideband; Springer: Cham, Switzerland, 2020. [Google Scholar]
  15. Gou, P.; Li, F.; Jia, X.; Mao, G.; Sun, M. A Three-Dimensional DV-Hop Localization Algorithm Based on RSSI. In Proceedings of the 2018 3rd International Conference on Smart City and Systems Engineering (ICSCSE), Xiamen, China, 29–30 December 2018. [Google Scholar]
  16. Naranjo, P.; Shojafar, M.; Mostafaei, H.; Pooranian, Z.; Baccareli, E. P-SEP : A Prolong Stable Election Routing Algorithm for Energy-limited Heterogenous Fog-supported Wireless Sensor Networks. The journal of Supercomputing 2017, 73, 733–755. [Google Scholar] [CrossRef]
  17. Qichen, W. Research progress on wireless sensor network (WSN) security technology. J. Phys. Conf. Ser. 2022, 2256, 012043. [Google Scholar] [CrossRef]
  18. Romer, K.; Mattern, F. The design space of wireless sensor networks. IEEE Wirel. Commun. 2004, 11, 54–61. [Google Scholar] [CrossRef]
  19. Liang. W.; Li, K.-C; Long, J.; Kui, X.; Zomaya, A. An Industrial Network Intrusion Detection Algorithm based on Multi-Feature Data Clustering Optimization Model. IEEE Trans. Ind. Inform. 2019, 16, 2063–2071. [Google Scholar]
  20. Oğur, N.B.; Al-Hubaishi, M.; Çeken, C. IoT data analytics architecture for smart healthcare using RFID and WSN. ETRIJ 2022, 1, 135–146. [Google Scholar] [CrossRef]
  21. Liang, W.; Long, J.; Weng, T.-H.; Chen, X.; Li, K.-C.; Zomaya, A. TBRS: A trust based recommendation scheme for vehicular CPS network. Future Gener. Comput. Syst 2019, 92, 383–398. [Google Scholar] [CrossRef]
  22. Zhao, W.; Su, S.; Shao, F. Improved DV-hop algorithm using locally weighted linear regression in anisotropic wireless sensor networks. Wirel. Pers. Commun 2018, 98, 3335–3353. [Google Scholar] [CrossRef]
  23. Peng, B.; Li, L. An improved localization algorithm based on genetic algorithm in wireless sensor networks. Cogn. Neurodyn 2015, 9, 249–256. [Google Scholar] [CrossRef]
  24. Wang, Z.; Wang, X.; Liu, L.; Huang, M.; Zhang, Y. Decentralized feedback control for wireless sensor and actuator networks with multiple controllers. Int. J. Mach. Learn. Cybern. 2017, 8, 1471–1483. [Google Scholar] [CrossRef]
  25. Bhatti, G. Machine Learning Based Localization in Large-Scale Wireless Sensor Networks. Sensors 2018, 18, 4179. [Google Scholar] [CrossRef] [PubMed]
  26. Wang, J.; Ghosh, R.K.; Das, S. A survey on sensor localization. J. Control Theory Appl 2010, 8, 2–11. [Google Scholar] [CrossRef]
  27. Clark, J.A.; Jacob, J.L.; Stepney, S. The Design of S-Boxes by Simulated Annealing. In Proceedings of the 2004 Congress on Evolutionary Computation (IEEE Cat. No.04TH8753), Portland, OR, USA, 19–23 June 2004; Volume 2, pp. 1533–1537. [Google Scholar]
  28. Wang, J.; Zhu, Y.; Zhou, C.; Qi, Z. Construction Method and Performance Analysis of Chaotic S-Box Based on a Memorable Simulated Annealing Algorithm. Symmetry 2020, 12, 2115. [Google Scholar] [CrossRef]
  29. Giri, J.M. Simulated annealing and its applications to mechanical engineering: A review national conference on digital Souravlias, D.; Parsopoulos, K.E.; Meletiou, G.C. Designing Bijective S-Boxes Using Algorithm Portfolios with Limited Time Budgets. Appl. Soft Comput. 2017, 59, 475–486. [Google Scholar]
  30. Jain, M.; Saihjpal, V.; Singh, N.; Singh, S. An Overview of Variants and Advancements of PSO Algorithm. applied sciences 2022, 12, 8392. [Google Scholar] [CrossRef]
  31. Kowalczyk, L.; Elsner, W. Comparative analysis of optimisation methods applied to thermal cycle of a coal fired power plant. Archives of Thermodinamics 2013, 34, 4. [Google Scholar] [CrossRef]
  32. Srinivasan, K. ; K. Sinha, N.; J, U. Parametric optimization of high aspect ratio wing using surrogate model, IFAC –PapersOnLine 2018, 51, 231–236. [Google Scholar]
  33. Sertsoz, M.; Fidan, M. A comparison of PSO and Fmincon methods for finding optimum operating speed and time values in tram. International journal of Energy Applications and Technologies 2021, 8, 48–52. [Google Scholar] [CrossRef]
  34. Farjamnia, G.; Gasimov, Y.; Kazimov, C.; Hashemi, M. A survey of DV-Hop localization Methods in Wireless Sensor Networks. Journal of Communication Engineering 2020, 9, 359–398. [Google Scholar]
  35. Xue, D. Research on range-free location algorithm for wireless sensor network based on particle swarm optimization. Journal on Wireless Communications and Networking 2019, 2019, 221. [Google Scholar] [CrossRef]
  36. Kessentini, S.; Barchiesi, D. Particle Swarm Optimization with Adaptive Inertia Weight. International Journal of Machine Learning and Computing 5, 535. [CrossRef]
  37. Sharma, G.; Kumar, A. improved range-free localization for three dimensional wireless sensor networks using genetic algorithm. Computers & Electrical Engineering 2018, 72, 808–827. [Google Scholar]
  38. Phoemphon, S.; So-In, C.; Leelathakul, N. Optimized Hop Angle Relativity for DV-Hop Localization in Wireless Sensor Networks. IEEE Access 2018, 6, 78149–78172. [Google Scholar] [CrossRef]
  39. Zhang, D.; Zhang, X.; Qi, H. A new Location Sensing algorithm Based on DV-Hop and Quantum-Behaved Particle Swarm optimization in WSN. Asp transactions on pattern recognition and intelligent systems 2021, 1, 2. [Google Scholar] [CrossRef]
  40. Perdana, D.; Nugroho, A.; Dewanta, F. Performance Evaluation of DV-HOP and Amorphous Algorithms based on Localization Schemes in Wireless Sensor Networks TELKOMNIKA. 2013, 16, 1150–1157. [Google Scholar]
  41. Khadim, R.; Erritali, M.; Maaden, A. Rang-Free Localization Schemes for Wireless Sensor Networks. Indonesian Journal of Electrical Engineering and Computer 2015, 16, 323–332. [Google Scholar]
  42. Keshtgary, M.; Fasihy, M.; Ronaghi, Z. Performance Evaluation of Hop-Based Range-Free Localization Methods in Wireless Sensor Networks. ISRN Communications and Networking 2011, 2011, 485486. [Google Scholar] [CrossRef]
  43. Han, D.; Yu, Y.; Li, K.; Mello, R. Enhancing the Sensor Node Localization Algorithm Based on Improved DV-Hop and DE Algorithms in Wireless Sensor Networks. Sensors 2020, 20, 343. [Google Scholar] [CrossRef]
  44. Shakshuki, E.; Abu Elkhail, A.; Nemer, I.; Adam, M.; Sheltami, T. Comparative Study on Range Free Localization Algorithms, In The 10th International Conference on Ambient Systems, Networks and Technologies (ANT); Leuven, Belgium 2019; pp. 501–510.
  45. Pal Singh, S.; C. Sharma, S. Implementation of a PSO Based improved localization algorithm for Wireless Sensor Networks. IETE Journal of Research 2018, 65, 502–514. [Google Scholar] [CrossRef]
  46. Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1979, 220, 671–680. [Google Scholar] [CrossRef]
Preprints 76628 g001
Figure 1. Sensor nodes scattered in a field of sensing.
Figure 1. Sensor nodes scattered in a field of sensing.
Preprints 76628 g001
Preprints 76628 g003
Figure 3. Updating strategy of particle position.
Figure 3. Updating strategy of particle position.
Preprints 76628 g003
Preprints 76628 g005
Figure 5. The initial deployment of 25 nodes (percentage of anchors = 20%): (a) grid topology; (b) random topology.
Figure 5. The initial deployment of 25 nodes (percentage of anchors = 20%): (a) grid topology; (b) random topology.
Preprints 76628 g005
Preprints 76628 g006
Figure 6. Average localization error with variation in percentage of anchors.
Figure 6. Average localization error with variation in percentage of anchors.
Preprints 76628 g006
Preprints 76628 g007
Figure 7. Average localization error with variation in number of nodes with: (a) communication range = 300; (b) communication range = 400; (c) communication range = 500.
Figure 7. Average localization error with variation in number of nodes with: (a) communication range = 300; (b) communication range = 400; (c) communication range = 500.
Preprints 76628 g007
Preprints 76628 g008
Figure 8. Average localization error with variation in percentage of anchors.
Figure 8. Average localization error with variation in percentage of anchors.
Preprints 76628 g008
Preprints 76628 g009
Figure 9. Average localization error with variation in number of nodes in: (a) communication range = 300; (b) communication range = 400; (c) communication range = 500.
Figure 9. Average localization error with variation in number of nodes in: (a) communication range = 300; (b) communication range = 400; (c) communication range = 500.
Preprints 76628 g009
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated