Research on Multi-Sensor SLAM Technology for Complex Environment of Construction Machinery

Preprint

Article

Research on Multi-Sensor SLAM Technology for Complex Environment of Construction Machinery

Altmetrics

Downloads

130

Views

Comments

A peer-reviewed article of this preprint also exists.

Haoling Ren,

Yaping Zhao,

Tianliang Lin^*,Jiangdong Wu

Haoling Ren,

Yaping Zhao,

Tianliang Lin^*,Jiangdong Wu

This version is not peer-reviewed

Submitted:

15 June 2023

Posted:

16 June 2023

You are already at the latest version

Alerts

Abstract

Unmanned construction machinery vehicles mostly carry work in bridges, tunnels, and outdoor open spaces. Obtaining accurate pose estimation of the entire vehicle and establishing a map of the surrounding environment is of great significance for path planning and control in the later stage. Traditional simultaneous localization and mapping (SLAM) schemes, which mostly use a single sensor, but there are problems with localization drift and mapping failure in scenarios where there are few geometric features and the environment is prone to degradation. Currently, the multi-sensor fusion strategy has been proven to be an effective solution and widely used in the field of unmanned vehicle localization and mapping. This paper proposes a SLAM framework that tightly couples a LiDAR, IMU and camera to achieve accurate and reliable pose estimation. The framework is based on LiDAR-inertial system(LIS) and factor graph optimization theory. Texture information provided by vision is integrated into the LiDAR-inertial odometry to generate a new visual-inertial subsystem(VIS).The two subsystems, VIS and LIS, can assist each other and work jointly. Through real vehicle tests, the system can perform incremental, real-time state estimation, reconstruct dense 3D point cloud maps,and effectively solve the problems of localization drift and mapping failure in the lack of geometric features or challenging construction environments. Meanwhile, the system has a safety redundancy mechanism. When any subsystem fails, the system can also operate normally, to ensure the reliability and robustness of vehicle positioning.

Keywords:

Subject: Engineering - Mechanical Engineering

0. INTRODUCTION

Simultaneous Localization and Mapping(SLAM) technology aims to achieve positioning and mapping as two major goals, and has been widely used in the field of mobile robotics. The sensors widely used in SLAM technology include cameras, LiDARs, and IMUs. In simple scenarios, robot localization and mapping can be achieved using a single sensor. However, single sensor has defects. For monocular cameras, it is unable to observe the scale information of pixels, which can easily lead to localization drift and motion estimation bias in pure rotation motion. Although LiDARs can capture rich environmental information from a long distance, it has poor dynamic performance and degrades in environments with few geometric features.

In order to compensate for the deficiencies of single sensors, a SLAM framework that fuses multiple sensors has been proposed, combining the strengths of different sensors and complementing the detected information to better adapt to complex scenarios with poor lighting conditions or fast motion speeds, and to improve the robustness of localization and mapping. For example, V-LOAM [1] and DV-LOAM [2] are SLAM frameworks that fuse cameras, LiDARs, and IMUs. Detection information from vision was used to provide initial positional estimates for LiDAR odometry(LIO). However, LiDAR measurements are not jointly optimized with vision or inertial measurements, which belongs to loosely coupled SLAM. This makes map updating difficult, increases the computational and storage burden of the system, and is unsuitable for localization and mapping in dynamic environments. In order to avoid the drawbacks of loose coupling, subsequent multi-sensor fusion SLAM schemes mostly adopt tightly coupled methods, which can simultaneously consider all variables and have higher computational efficiency. There are examples such as LIC-fusion [3] and its extended version LIC-Fusion 2.0 [4], LVI-SAM [5], R2live [6], etc. R2LIVE consists of an odometry module based on a filtering approach and an optimization module based on a factor graph, and the LiDAR-inertial system is based on the FAST-LIO2 [7] framework, which incorporates sparse visual features and estimates the robot’s state in real-time by minimizing feature reprojection error, optimizing visual landmark points within the sliding window, and achieving good positioning accuracy and robustness in fast-moving environments with small LiDAR viewing angles. However, these multi-sensor fusion SLAM frameworks that use feature-based methods in the visual front-end require a lot of time to extract visual features from each frame of the image to estimate the robot’s pose, this leads to high computational complexity and low execution efficiency of the system.

Based on the studies of many predecessors, this paper proposes a multi-sensor tightly-coupled SLAM framework for addressing the problem of positioning and mapping failures that are prone to occur during autonomous operation of construction machinery in tunnels, mining areas, and open outdoor spaces. This framework ensures accurate and reliable pose estimation and mapping even in geometrically feature-poor and challenging environments. The framework is based on the existing LiDAR-inertial system and factor graph optimization theory, incorporates texture information provided by vision, and using direct method to establish matching relationships between adjacent image frames to execute visual-inertial odometry(VIO). The VIO and LIO subsystems can work together and assist each other. Additionally, the system has a safety redundancy mechanism. When any subsystem fails, the system can also operate normally, to ensure the reliability and robustness of vehicle positioning.

1. Overview of the system

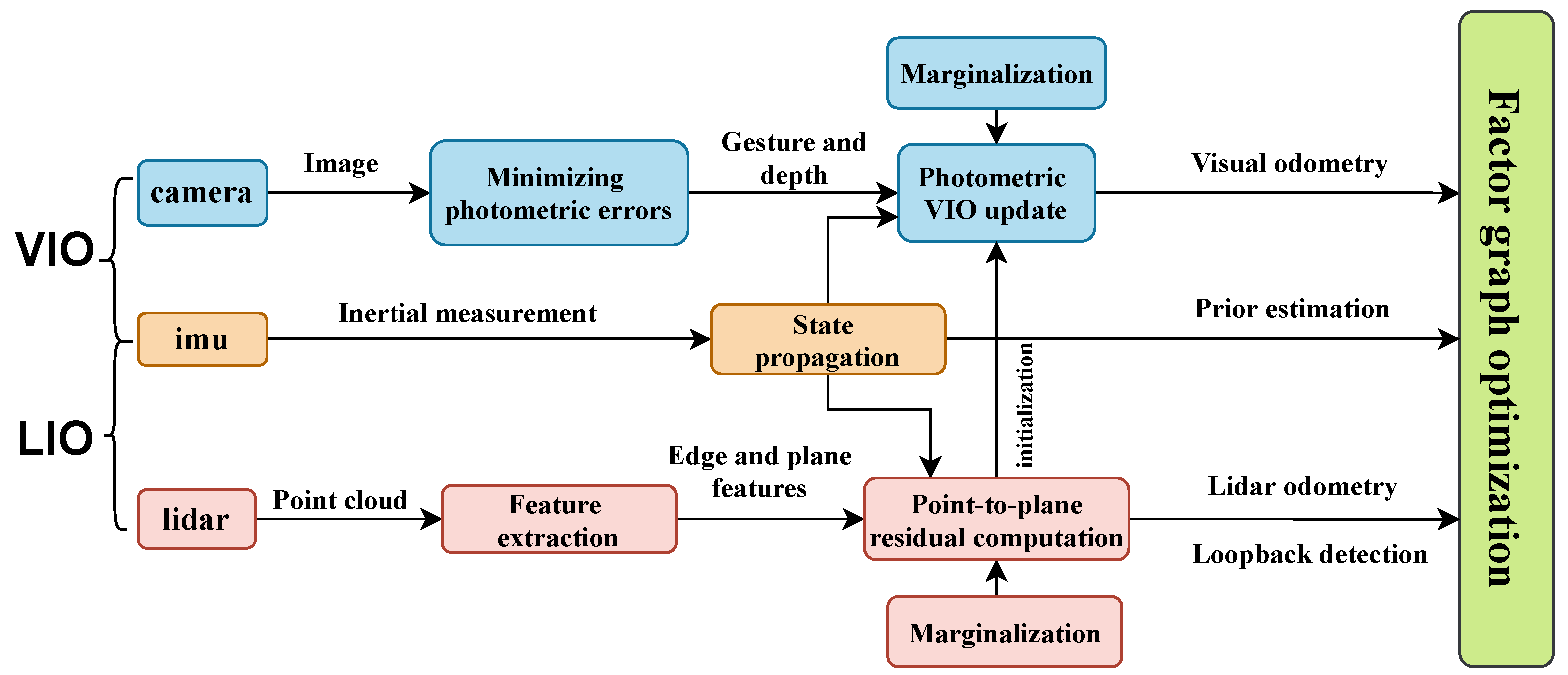
The framework of multi-sensor fusion SLAM technology proposed in this paper is shown in Figure 1, consisting of a LiDAR-inertial system and a visual-inertial system. LIO subsystem uses feature-based methods to detect edge and planar features of point cloud, matches the LiDAR key frames to the global map, estimates the state of the system by minimizing the point-to-plane residuals, executes LiDAR odometry, and constructs the geometric structure of the global map. To ensure the real-time and efficient performance of the system, the feature map maintains key frames in a sliding window. VIO system initializes using the state estimated by LIO system. The visual front-end of the system adopts direct methods, updates the system state by minimizing the photometric error from the frame to the map, performs visual odometry, and constructs the texture information of the map. Two subsystems are tightly coupled to jointly perform pose estimation. The whole system incorporates IMU preintegration constraint, visual odometry constraint, LiDAR odometry constraint and Loop closure detection constraint as factors into the factor graph to achieve global pose optimization.

2. LIDAR-inertial odometry

As early as 2005, the framework of LiDAR SLAM was initially determined, and many studies have been achieved later on LiDAR-based SLAM. For example, the early 2D LiDAR SLAM frameworks cartographer [8] and hector [9] can build environmental maps in a 2D plane, but the localization accuracy is poor. Later, 3D LiDAR SLAM was proposed, such as the LOAM series [10,11], which significantly improved the performance of localization and mapping. Pure LiDAR SLAM relies on simple scanning and matching methods, which has poor performance in dynamic and complex environments and cannot achieve reliable localization and mapping. Therefore, the SLAM framework with fusion of LiDAR and inertial measurement unit (IMU) is proposed. IMU can measure the acceleration and angular velocity of robots, and is not easily affected by external interference. The fusion of IMU can solve the problem of localization drift of pure LiDAR SLAM in fast motion scenarios. For example, Lego-LOAM [12] eliminates unreliable feature points based on LOAM, but adopts a loosely coupled approach to fuse IMU, which does not fully utilize sensor data. The later proposed LIOM [13], LIO-SAM [14], and FAST-LIO [15] are all tightly coupled LiDAR-inertial SLAM systems based on factor graph optimization, which does not require making Gaussian distribution assumptions compared to the traditional filtering method, by calculating the conditional probability between variables and passing the results to Bayesian trees [16] for posterior inference, it can efficiently handle large scale sparse matrices, improve the accuracy and robustness of the model, and has become the mainstream SLAM optimization method.

Table 1 shows the explanation of some important notations in this section. The LiDAR-inertial subsystem in this framework is based on the LIO-SAM, which has better localization and mapping effects. Assuming that the IMU coordinate frame is the same as the robot body coordinate frame, the state of the robot is defined

x = {[R^{T} p^{T} v^{T} b^{T}]}^{T}

(1)

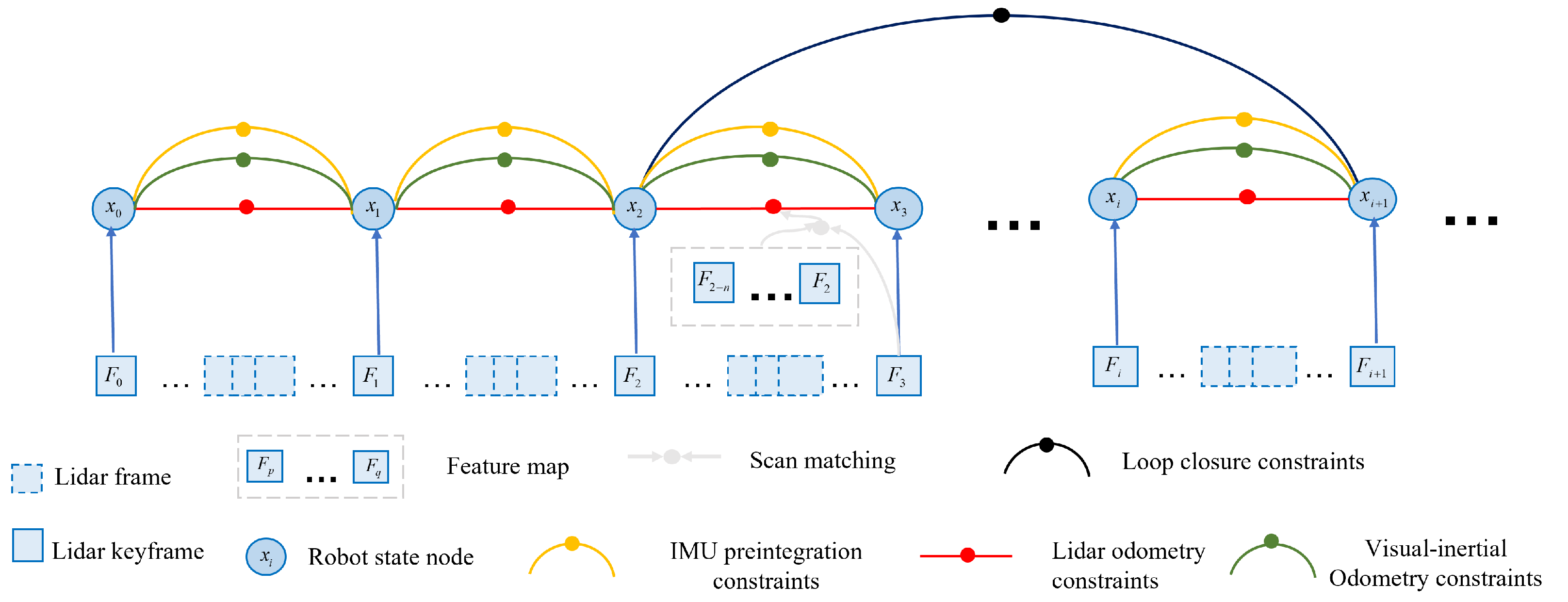
As shown in Figure 2, the factor graph of the LIO subsystem is composed of four constraints: IMU preintegration constraint, LiDAR odometry constraint, loop closure constraint, and robot state. The raw measurement data of IMU is used to estimate the sensor motion during LiDAR scanning. The estimated motion can be used not only to eliminate point cloud distortion, but also as the initial guess for LiDAR odometry optimization. The obtained initial guess can then be used to estimate the IMU bias and form a loop closure constraint through closed-loop detection. Finally, the relationships among all constraints are considered to achieve global factor graph optimization.

2.1. LiDAR odometry

The front-end of LIO subsystem is mainly processes sensor data. Following the methods of LOAM and Lego-LOAM. Firstly, the distorted point cloud is corrected, and then feature extraction is started to extract edge points and plane points by calculating the curvature of the point cloud in the frame.

F_{i}^{e}

and

F_{i}^{p}

are the sets of edge features and planar features extracted at moment i, respectively, and they together form the LiDAR frame sets

F_{i}

at moment i,

F_{i} = \{F_{i}^{e}, F_{i}^{p}\}

, where LiDAR frame F is represented under B. After obtaining the LIDAR frames, to avoid the factor graph being too large, which leads to data complexity and cumulative errors, each LIDAR frame extracted cannot be directly added to the factor graph as a factor. The widely used key frame strategy is used to select the most representative LiDAR frames at each moment as key frames. If the robot’s pose

x_{i}

exceeds the defined threshold at moment i , the LiDAR frame

F_{i + 1}

of the next moment will be used as the keyframe and the LiDAR frames between keyframes

F_{i}

and

F_{i + 1}

will be discarded to reduce the computational effort. The latest saved keyframe

F_{i + 1}

will be associated with the new robot state

x_{i + 1}

for data association. Then, the set

\{F_{i - n}, . . ., F_{i}\}

of n closest keyframes at moment i, also known as subkeyframes, are extracted and transformed to W through the corresponding transformation matrix set

\{T_{i - n}, . . ., T_{i}\}

. This results in a voxel map

M_{i}

consisting of a edge voxel map

M_{i}^{e}

and a planar voxel map

M_{i}^{p}

. The relationship between the LiDAR frame and voxel map is

M_{i} = {M_{i}^{e}, M_{i}^{p}}

(2)

M_{i}^{e} =^{'} F_{i}^{e} \cup^{'} F_{i - 1}^{e} \cup . . . \cup^{'} F_{i - n}^{e}

(3)

M_{i}^{p} =^{'} F_{i}^{p} \cup^{'} F_{i - 1}^{p} \cup . . . \cup^{'} F_{i - n}^{p}

(4)

In order to preserve the basic shape and geometric structure of the original point cloud as much as possible and improve the efficiency of voxel map processing, it is necessary to divide the map into several voxels and keep only one representative point in each voxel to realize the downsampling of point cloud data.

After filtering out the redundant point cloud features, the new keyframe set

F_{i + 1}

is feature-matched to the voxel map

M_{i}

that has already been created. Following the point to line and point to plane point cloud registration methods [17,18],

F_{i + 1}

is converted from B to W to obtain

^{'} F_{i + 1}

, and the distance equation from the point cloud feature to the corresponding edge or plane block is

d_{e_{k}} = \frac{|(P_{i + 1, k}^{e} - P_{i, u}^{e}) \times (P_{i + 1, k}^{e} - P_{i, v}^{e})|}{|P_{i, u}^{e} - P_{i, v}^{e}|}

(5)

d_{p_{k}} = \frac{|(P_{i + 1, k}^{p} - P_{i, u}^{p}) (P_{i, u}^{p} - P_{i, v}^{p}) \times (P_{i, u}^{p} - P_{i, w}^{p})|}{|(P_{i, u}^{p} - P_{i, v}^{p}) \times (P_{i, u}^{p} - P_{i, w}^{p})|}

(6)

where

k, u, v, w

denotes the index in the corresponding feature set. With the IMU preintegration factor (Section 2.2), frame-by-frame matching is not required, and the method of matching features from frame to local map is directly used, which saves processing time for global map and improves matching efficiency.

P_{i, u}^{e}

and

P_{i, v}^{e}

are the two points closest to the edge feature

^{'} P_{i + 1, k}^{e}

of the previous frame, which form the edge line.

P_{i, u}^{p}

P_{i, v}^{p}

, and

P_{i, w}^{p}

are the three points closest to the previous frame plane feature

^{'} F_{i + 1, k}^{p}

and not on the same line, which together form a plane block in

M_{i}^{p}

. Following the principle that edge features correspond to edge lines and plane features correspond to plane blocks, the equation for minimizing the positional transformation is

min_{T_{_{i + 1}}} \{\sum_{P_{i + 1, k}^{e} \in^{'} F_{i + 1}^{e}} d_{e_{k}} + \sum_{P_{i + 1, k}^{p} \in^{'} F_{i + 1}^{p}} d_{p_{k}}\}

(7)

Using the Gauss-Newton method to solve for the optimal pose transformation relationship of the robot at moments i and

i + 1

Δ T_{i, i + 1} = T_{i}^{T} T_{i + 1}

, and added to the factor graph as a LiDAR odometry factor.

2.2. IMU preintegration

During the optimization process of the factor graph, the robot’s state is inevitably adjusted continuously. Each adjustment requires a re-integration of the pose from the current moment and the previous moment, which can be very time-consuming. To avoid reintegration and make the IMU integration independent of the previous state, a preintegration strategy [19,20,21] is adopted.

Firstly, modeling the angular velocity and acceleration observed by IMU under B

{\hat{ω}}_{t} = ω_{t} + b_{t}^{w} + n_{t}^{w}

(8)

{\hat{a}}_{t} = R_{t}^{B W} (a_{t} - g) + b_{t}^{a} + n_{t}^{a}

(9)

where

{\hat{ω}}_{t}

and

{\hat{a}}_{t}

are the original measurements at moment t, and

R_{t}^{B W}

denotes the rotation matrix from W to B.

b_{t}

n_{t}

are the bias and white noise, respectively. g is the constant gravity vector under W. Assuming that

{\hat{ω}}_{t}

and

{\hat{a}}_{t}

in B remain unchanged, the motion of the robot is inferred from the measurement values of the IMU. The velocity v, pose p, and rotation q at moment

t + Δ t

are

v_{t + Δ t} = v_{t} + g Δ t + R_{t} ({\hat{a}}_{t} - b_{t}^{a} - n_{t}^{a}) Δ t

(10)

p_{t + Δ t} = p_{t} + v_{t} Δ t + \frac{1}{2} g Δ t^{2} + \frac{1}{2} R_{t} ({\hat{a}}_{t} - b_{t}^{a} - n_{t}^{a}) Δ t^{2}

(11)

R_{t + Δ t} = R_{t} exp (({\hat{ω}}_{t} - b_{t}^{ω} - n_{t}^{ω}) Δ t)

(12)

where

R_{t} = R_{t}^{W B} = R_{t}^{B W^{T}}

, here it is assumed that the angular velocity and acceleration of the B are constant during the integration process. The relative motion of the robot between moments i and j is calculated using the IMU preintegration, and the preintegrated measurements

Δ v_{i j}

Δ p_{i j}

, and

Δ R_{i j}

between these two moments are

Δ v_{i j} = R_{i}^{T} (v_{j} - v_{i} - g Δ t_{i j})

(13)

Δ p_{i j} = R_{i}^{T} (p_{j} - p_{i} - v_{i} Δ t_{i j} - \frac{1}{2} g Δ t_{i j}^{2})

(14)

Δ R_{i j} = R_{i}^{T} R_{j}

(15)

By using IMU preintegration, the poses of the robot can be jointly optimized using IMU bias and LiDAR odometry in the factor graph.

2.3. Loop closure detection

Loop closure detection [22] means that the robot can recognize the scenes it has reached before during its motion, forming loopback edges, and matching the map generated at this moment with the previous one to minimize the error between predicted and observed values. Using the closed-loop detection method proposed by Kaess et al. [23], the LiDAR odometry is used to determine whether there is a loop closure. Based on the latest keyframe, the keyframe within a distance of 15 m is searched for, and the timestamp difference between the two frames is greater than 30 s. Only when both conditions are satisfied, the corresponding loopback frame is considered to be found. After detecting loop closure, the ICP matching algorithm is used to calculate the Euclidean distance between the two key frames, iteratively update the matching relationship between them continuously to get the robot’s pose. The indexes of the two frames, inter-frame pose, and noise (ICP score) are added into the loop closure constraint. As shown in Figure 2, assuming that the latest state of the robot is

X_{i + 1}

, and

X_{2}

is the prior state detected by loop closure, the relative transformation of

F_{i + 1}

to the subkeyframe

\{F_{2 - m}, . . ., F_{2}, . . ., F_{2 + m}\}

is calculated as

Δ T_{2 i + 1}

3. Visual-inertial odometry

The SLAM systems that combining vision and IMU have also been widely studied. With the measurements and short-term motion constraints of IMU can assist visual odometry to recover scale information, and effectively solve the problem of localization drift in scenes with a lack of texture and fast motion. Currently, feature-based methods are commonly used in the front-end of visual-inertial SLAM, with adjacent frames detecting features for matching and estimating camera motion, such as the newer ORB-SLAM framework [24,25] and MonoSLAM [26]. There are also visual-inertial SLAM frameworks based on direct methods, such as LSD-SLAM [27], which directly estimate the motion of the camera using pixel information. Compared with feature-based methods, the direct method does not require feature extraction, data association, and minimization of feature reprojection errors. They are computationally more efficient and applicable to sparse, semi-dense, and dense point clouds.

The VIO subsystem in this paper, is a tightly coupled visual-inertial odometry based on the direct method. It estimates the camera pose and establishes the environment’s texture information by jointly minimizing the photometric error and IMU measurement error between image frames.The estimation is further optimized by factor graph optimization to obtain the best estimate state. In order to reduce the complexity of the system and to ensure that the nonlinear optimization problem is handled in a reasonable time range, this paper adopts marginalization technique [28], which continuously removes the old variables from the factor graph to optimize the latest state.

Table 2 shows the explanation of some important notations in this section, where gravity is defined as perpendicular to the negative Z-axis in the world coordinate frame. This system is based on nonlinear optimization, the camera’s pose and scene depth are estimated by continuously iteratively minimizing the energy function. Firstly, establish the minimum energy function

E_{a l l} = λ \cdot E_{p i c t u r e} + E_{i n e r t i a l}

(16)

where

E_{p i c t u r e}

denotes the photometric error and

E_{i n e r t i a l}

denotes the inertial error.

λ

denotes the balance coefficient, which is used to weigh the effects of photometric error and inertial error.

3.1. Visual odometry

The task of the VIO front-end is to execute visual odometry. Firstly, roughly estimating the camera pose by minimizing the photometric error. Assuming that there is a point p in the reference frame i,

p \in Ω_{i}

, which is also observable under another frame j, the photometric error of the two adjacent frames images is

E_{p j} = \sum_{p \in N_{p}} w_{p} {∥(I_{j} [p^{'}] - b_{j}) - \frac{t_{j} e^{a_{j}}}{t_{i} e^{a_{i}}} (I_{i} [p] - b_{i})∥}_{γ}

(17)

where

N_{p}

is the pixel around point p.

I_{i}

I_{j}

is the image of frame i and frame j.

t_{i}

t_{j}

is the exposure time of the image.

a_{i}

a_{j}

b_{i}

b_{j}

is the coefficient for correcting affine illumination variation.

γ

is the Huber parametric number.

ω_{p}

is the weight related to the gradient.

p^{'}

is the projection on

I_{i}

. Then the total photometric error is

E_{p i c t u r e} = \sum_{i \in F} \sum_{p \in P_{i}} \sum_{j \in o b s (p)} E_{p j}

(18)

where

F

is the set of keyframes to be optimized.

P_{i}

is the sparse set of points in the keyframes.

o b s (p)

is the set of keyframes where the point p is observed.

3.2. Inertial measurement and initialization

The frequency of IMU detection data is usually higher than that of the camera. In order to avoid the repetition of IMU integration, the VIO system still adopts preintegration method. The acceleration value

a_{i j}

and angular velocity value

ω_{i j}

measured by the IMU are added between two image frames

s_{i}

and

s_{j}

. The visual observations and inertial measurements are combined to further estimate the pose of the most nearest frame. According to the nonlinear dynamic model [28], establish the error term of speed and linear acceleration, and obtain the prediction

{\hat{s}}_{j}

and covariance

\overset{\land}{\sum_{s, j}}

. The inertial error function is

E_{inertial} (s_{i}, s_{j}) : = {(s_{j} ⊟ {\hat{s}}_{j})}^{T} s {\sum^{^}}_{s, j}^{- 1} (s_{j} ⊟ {\hat{s}}_{j})

(19)

Accurate initial values are crucial for guiding monocular systems. Monocular cameras cannot recover environmental scale information, but can use inertial data to obtain metric scale and gravity direction. However, there is inevitably bias in the IMU, so these quantities need to be properly initialized before processing in a tightly-coupled system. To address the issue that monocular visual-inertial systems cannot be immediately initialized during constant velocity or zero-acceleration motion, this paper treats scale and gravity direction as parameters of the system, and optimizes them together with pose to achieve initialization at any scale. The parameters that need to be initialized include the rough pose estimate between two frames, the average depth of nearby points, the initial gravity direction, velocity, scale, and IMU bias. Before initialization, the visual-inertial frame needs to be converted to the metric frame, with a transformation matrix of

T_{m_d} \in \{T \in S I M (3) | t r a n s l a t i o n (T) = 0\}

, where

ξ_{m_d} = log (T_{m_d}) \in s i m (3)

. The average depths are all normalized to 1, the gravity direction is calculated using acceleration measurements, the velocity and IMU bias are 0, and the scale is 1. Then, all variables and parameters at the initial frame are transformed into the world coordinate frame, and these values based on real scale will continue to be used in the VIO system.

3.3. Optimization of visual-inertial systems

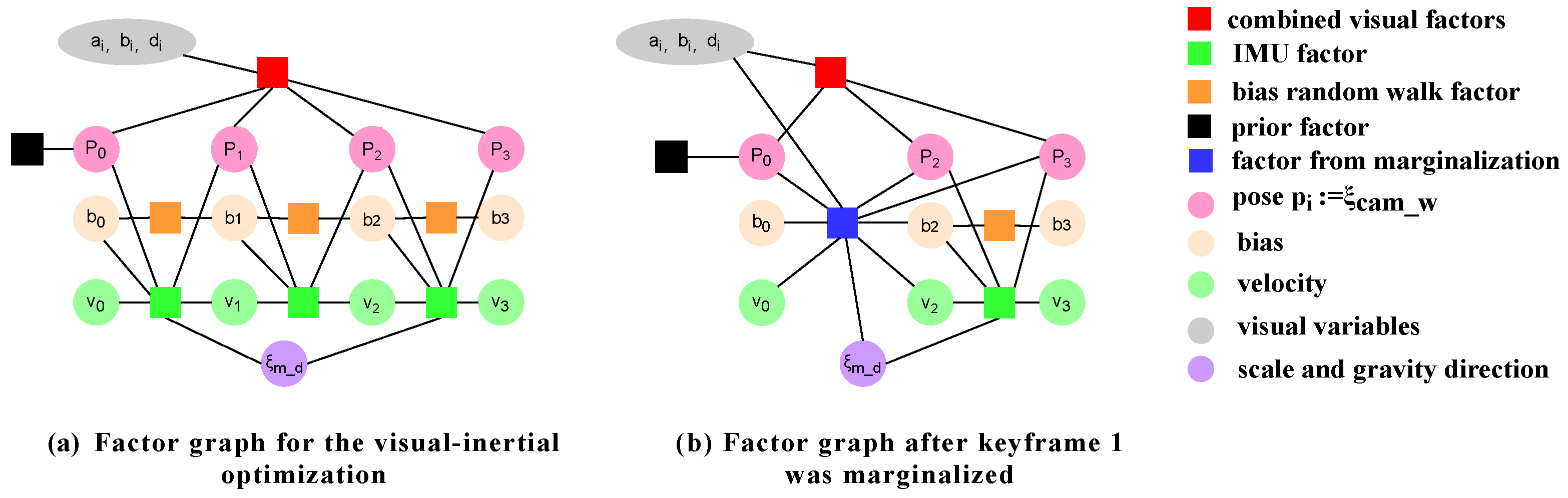
As shown in Figure 3, the poses of the keyframes, IMU bias, and velocity are combined as constraints to form a factor graph for global optimization of the visual-inertial system.The optimized keyframe poses are in the visual-inertial coordinate system and are not affected by environmental scale.The IMU factors are connected between two consecutive keyframes in the form of pre-integration as described in Section 2.2.The time interval threshold between two consecutive keyframes is set to 0.5 seconds to avoid errors in preintegration results due to long time intervals.

3.3.1. Position optimization

Based on the least squares problem, common optimization methods include Gaussian-Newton method, L-M method, and global nonlinear optimization method. To ensure computational efficiency and good convergence. In this paper, the Gauss-Newton method is used for positional optimization. Firstly, define the state vector of each effective key frame

s_{i} : = {[{(ξ_{c a m_ω}^{D})}^{T}, {v_{i}}^{T}, b_{i}^{T}, a_{i}, b_{i}, d_{i}^{1}, . . ., d_{i}^{m}]}^{T}

(20)

where

v_{i} \in R^{3}

denotes the velocity.

b_{_{i}} \in R^{6}

denotes the IMU bias.

a_{i}^{}

b_{i}

are the affine illumination coefficients.

d_{i}^{j}

is the inverse depth of the point in the key frame. The full state vector is established as

s = {[c^{T}, ξ_{m_d}^{T}, s_{1}^{T}, s_{2}^{T}, . . ., s_{n}^{T}]}^{^{T}}

(21)

where c denotes the geometric parameters of the camera and

ξ_{m_d}^{T}

denotes the rotational transformation from visual-inertial frames to metric frames.

Using stacked residual vector r to establish equation

J = \frac{d r (s ⊞ ϵ)}{d ϵ} |_{ϵ = 0}, H = J^{T} W J, b = - J^{T} W r

(22)

where W is the weight matrix. The photometric error term

E_{p i c t u r e}

and the inertial error term

E_{i m u}

have no common residual. The update equation is established as Equation (23), and the state vector of inertial residual in metric frame is defined as Equation (25)

δ = H^{- 1} b

(23)

H = H_{p i c t u r e} + H_{i m u}, b = b_{p i c t u r e} + b_{i m u}

(24)

{s^{'}}_{i} : = {[ξ_{w_i m u_{i}}^{M}, υ_{i}, b_{i}]}^{T}, s^{'} = {[{s_{1}^{'}}^{T}, {s_{2}^{'}}^{T}, . . ., {s_{n}^{'}}^{T}]}^{T}

(25)

The inertial residuals lead to

{H^{'}}_{_{i m u}} = {J_{i m u}^{'}}^{T} W_{i m u} {J^{'}}_{i m u}, {b^{'}}_{i m u} = - {J_{i m u}^{'}}^{T} W_{i m u} γ_{i m u}

(26)

To achieve the joint optimization of the data. Firstly, the values of

H_{i m u}

and

b_{i m u}

are calculated from Equation (21) , and

J_{r e l}

is calculated according to the method proposed by Von Stumberg et al. [29]

H_{i m u} = J_{r e l}^{T} \cdot {H^{'}}_{i m u} \cdot J_{r e l}

(27)

and

b_{i m u} = J_{r e l}^{T} \cdot {b^{'}}_{i m u}

(28)

3.3.2. Marginalization

As time goes on, there will be more and more landmark points and camera poses, leading to an increasing amount of computation. To achieve large-scale Gauss-Newton nonlinear optimization, the number of optimization variables needs to be limited. This paper uses the Schur-Complement method to marginalize out older keyframes and all variables related to that keyframe continuously. When marginalizing the visual factors between two keyframes, the method proposed by Engel et al. [30] is used. Firstly, all points in the keyframe are marginalized, and then remove the residual terms that affect the sparsity of the system. To maintain the consistency of the system, it is necessary to evaluate the Jacobian matrix for the marginal factors related variables and ensure that their values are the same. For visual factors, the Jacobian matrix can be evaluated at the linearized points. When computing the inertial factors, it is necessary to determine the evaluation points for all variables related to the marginal factors and evaluate their Jacobian matrices. As shown in Figure 3b, it can be intuitively understood how marginalization affects the connection between the factors.

4. Real vehicle experiments and results analysis

In order to verify the performance of the proposed system in real environment, a private dataset was self-made for real-vehicle experiments, and the public dataset M2DGR is used to compare this algorithm with several other mainstream LiDAR SLAM algorithms.

4.1. Establishment of experimental platform

The mobile robot experimental platform is shown in Figure 4. The electronically controlled crawler chassis can realize omnidirectional movement. Mobile power supply, display, on-board computing platform JETSON AGX ORIN (built-in ubuntu 20.04 OS), sensor equipment including ZED2i camera, 16-line LIDAR VLP-16 (vertical field of view of 30°, horizontal field of view of 360°), GUI-610GNSS combined navigation suite (positioning accuracy of 1cm+1ppm, attitude accuracy of 0.1°),and WHEELTEC N100 nine-axis IMU have been deployed on the car.

4.2. Collection of private datasets

In this paper, two groups of experimental datasets were collected to verify the performance of the system. The first group was an outdoor large-scale scene, as shown in Figure 5a, which collects a scene driving around a teaching building. It includes buildings, pedestrians, trees, and moving vehicles. The walking trajectory is shown as the green path in the bird’s-eye view satellite map in Figure 5b. The second group was a dimly-lit long corridor environment inside a teaching building, as shown in Figure 5c, the geometric features on the white walls on both sides of the corridor are lacking and the scene repeatability is high, which is in line with the degradation scenario. The experimental car was controlled to move in the above two scenarios and collect datasets.

4.3. Experimental results and analysis

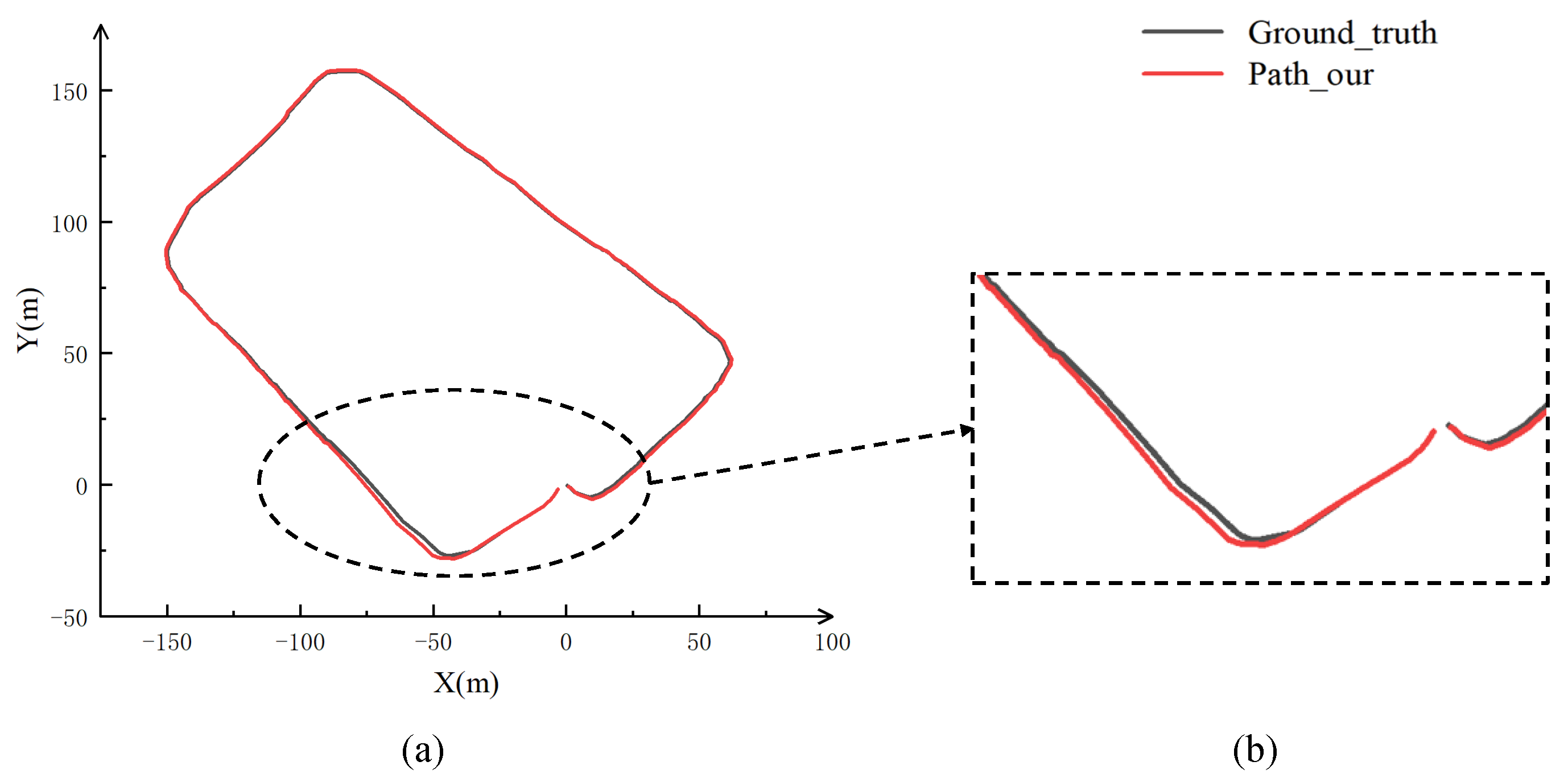
Conduct real vehicle experiments using the collected dataset. Figure 6 shows the positioning and mapping results obtained by the experimental car driving around the teaching building. The entire trajectory did not experience any drift, and a dense 3D environmental point cloud was reconstructed with a clear outline. To preliminarily verify the accuracy of the trajectory obtained by this algorithm, the GPS trajectory during the driving process was first obtained using combined inertial navigation as the true trajectory, and the two complete trajectories were compared, as shown in Figure 7. The two trajectories have a high degree of overlap except for a slight deviation in position shown in Figure 7b. Figure 8 shows the localization and mapping result of the indoor long corridor. In the face of this scene with insufficient features and easy degradation, there was no positioning tilt or displacement occurred, and the constructed map has distinct edges that reproduce the long corridor environment very well.

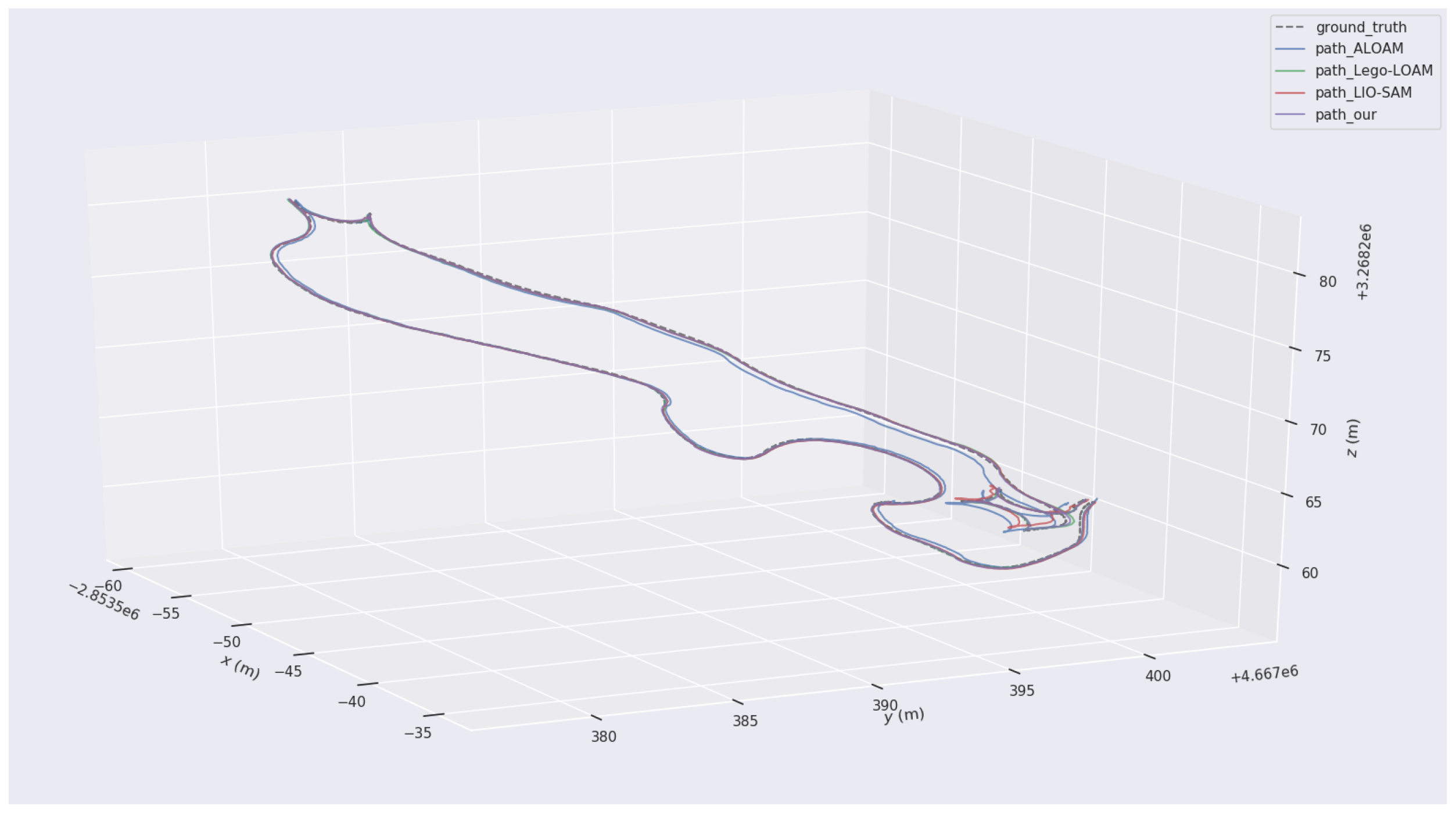
In order to evaluate the system’s performance using a better dataset, the high-quality public dataset M2DGR is adopted to compare this algorithm with several other mainstream LiDAR SLAM algorithms. The widely used M2DGR dataset is provided by Shanghai Jiaotong University, which contains rich sensor suites and diverse scenarios. Moreover, the speed of the ground robot in each test sequence is close to the actual speed in real environments, which helps to evaluate the effects of various SLAM algorithms more fairly. This paper chose sequence 1 of the M2DGR dataset for testing, with its scene being a relatively empty street and includes significant rotation during movement. Firstly, the trajectories of this algorithm, A-LOAM, Lego LOAM, and LIO-SAM are obtained. Then, the trajectory evaluation tool - evo is used to compare and analyze the obtained trajectories with the true value trajectories. 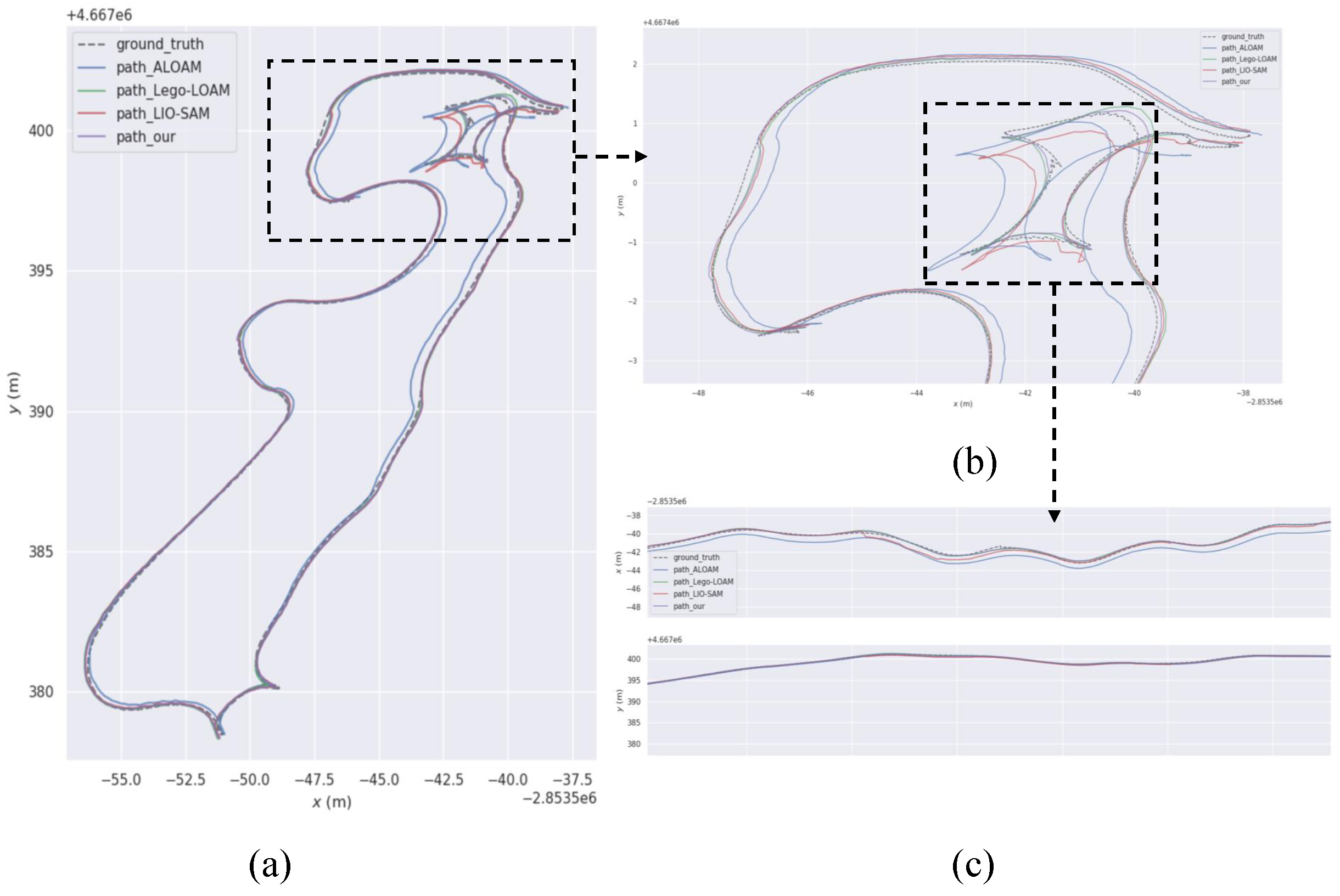Figure 9 shows the trajectory in a three-dimensional coordinate frame, and Figure 10 is the trajectory projected on the xy two-dimensional plane. It can be observed intuitively that compared to other algorithms, the localization trajectory obtained by this algorithm is generally closer to the ground truth trajectory, even in sections with significant shaking (Figure 10b), where it still performs well.

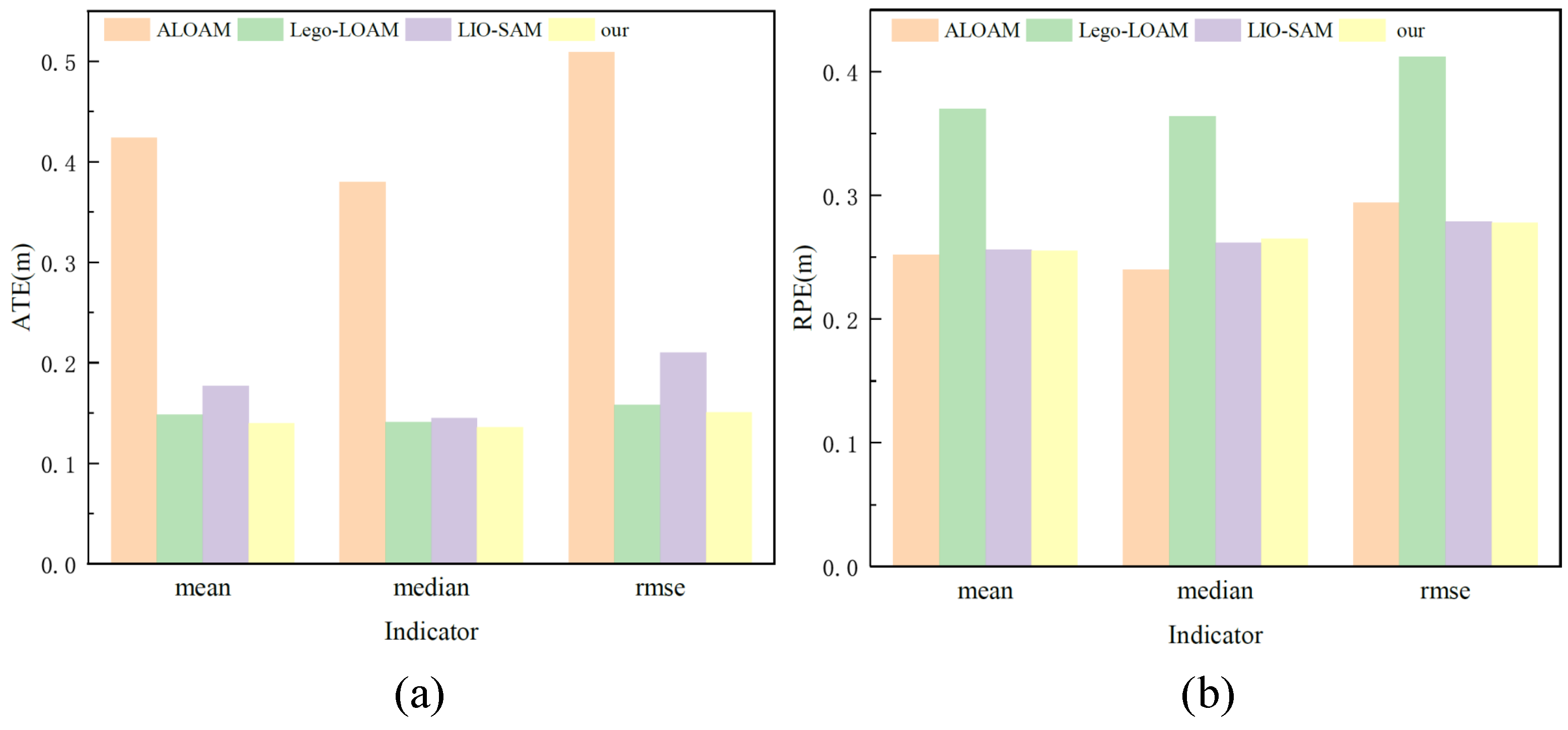
The positioning accuracy of each algorithm is further evaluated through absolute trajectory error (ATE) and relative trajectory error (RPE). The ATE is the direct difference between the estimated pose and the ground truth pose, which can intuitively reflect the overall accuracy of the algorithm in estimating poses and the global consistency of the estimated trajectory. The RPE is used to measure local accuracy and is suitable for evaluating the drift of the system. Table 3 and Table 4 show the ATE and RPE values obtained by the four algorithms in sequence 1. There are seven indicators used to measure the localization accuracy of a system, including maximum error (max), mean error (mean), median error (median), minimum error (min), root mean square error (rmse), sum of squared errors (sse), and standard deviation (std). The values of each indicator are inversely proportional to the localization accuracy. Among them, the most commonly used and representative indicator are mean, median, and rmse. Therefore, this section focuses on these three indicators. As shown in Figure 11, for absolute trajectory error, the three error values obtained by this algorithm are all the smallest. Since the backend of ALOAM is a grid-based map, the accumulated error after long-distance mapping is significant. However, Lego-LOAM incorporates a loop closure detection module, resulting in a significant reduction of the error. Compared with Lego-LOAM and LIO-SAM, the absolute positional error of this algorithm is reduced by about 4.6% and 24%, respectively. For relative pose error, Lego LOAM has the largest error. The three error values of this algorithm are very close to LIO-SAM, but there is still a decrease, and the rmse is also the smallest among the four algorithms. Compared to LOAM, Lego-LOAM and LIO-SAM, the relative positional errors of this algorithm are reduced by about 5.7%, 48% and 0.3%, respectively.

5. Conclusions

This paper proposes a multi-sensor fusion SLAM system for complex environments in construction machinery. The system integrates visual texture information into LiDAR-inertial odometry to generate a new visual-inertial subsystem. The visual odometry front end uses direct method to establish the matching relationship between adjacent frames for pose estimation. The LIO and VIO subsystems are tightly coupled to build multiple constraint items for factor graph optimization, ensuring the consistency of the global map. Through experiments on real vehicles and the M2DGR public dataset, this system achieves good localization and mapping results in both indoor long corridors and outdoor large scenes. Compared with the well-performing open-source frameworks Lego-LOAM and LIO-SAM, the absolute pose errors obtained by this algorithm are reduced by 4.6%, 24%, respectively , and the relative pose errors are reduced by 48% and 0.3%, respectively. This fully demonstrating that proposed system has better localization accuracy and can solve the problem of poor localization and mapping robustness of unmanned vehicles in environments with lack of geometric features and easy degradation.

Author Contributions

Investigation, Jiangdong Wu; Methodology, Yaping Zhao; Resources, Tianliang Lin; Software, Yaping Zhao; Validation, Yaping Zhao; Writing – original draft, Yaping Zhao; Writing – review & editing, Haoling Ren and Jiangdong Wu.

Funding

The authors declare that this study received funding from Fujian University industry university research joint innovation project plan (Grant NO. 2022H6007),Industry Cooperation of Major Science and Technology Project of Fujian Province(Grant NO. 2022H6028),and Xiamen Major Science and Technology Plan Projects(Grant NO. 3502Z20231013).The funder was not involved in the study design, collection, analysis,interpretation of data, the writing of this article or the decision to submit it for publication.

Conflicts of Interest

The authors declare no conflict of interest.

References

Ji Zhang and Sanjiv Singh. Visual-lidar odometry and mapping: Low-drift, robust, and fast. In 2015 IEEE International Conference on Robotics and Automation (ICRA), pages 2174–2181. IEEE, 2015. [CrossRef]
Wei Wang, Jun Liu, Chenjie Wang, Bin Luo, and Cheng Zhang. Dv-loam: Direct visual lidar odometry and mapping. Remote Sensing, 13(16):3340, 2021. [CrossRef]
Xingxing Zuo, Patrick Geneva, Woosik Lee, Yong Liu, and Guoquan Huang. Lic-fusion: Lidar-inertial-camera odometry. In 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pages 5848–5854. IEEE, 2019. [CrossRef]
Xingxing Zuo, Yulin Yang, Patrick Geneva, Jiajun Lv, Yong Liu, Guoquan Huang, and Marc Pollefeys. Lic-fusion 2.0: Lidar-inertial-camera odometry with sliding-window plane-feature tracking. In 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pages 5112–5119. IEEE, 2020. [CrossRef]
Tixiao Shan, Brendan Englot, Carlo Ratti, and Daniela Rus. Lvi-sam: Tightly-coupled lidar-visual-inertial odometry via smoothing and mapping. In 2021 IEEE international conference on robotics and automation (ICRA), pages 5692–5698. IEEE, 2021. [CrossRef]
Jiarong Lin, Chunran Zheng, Wei Xu, and Fu Zhang. R2 live: A robust, real-time, lidar-inertial-visual tightly-coupled state estimator and mapping. IEEE Robotics and Automation Letters, 6(4):7469–7476, 2021. [CrossRef]
Wei Xu, Yixi Cai, Dongjiao He, Jiarong Lin, and Fu Zhang. Fast-lio2: Fast direct lidar-inertial odometry. IEEE Transactions on Robotics, 38(4):2053–2073, 2022. [CrossRef]
Wolfgang Hess, Damon Kohler, Holger Rapp, and Daniel Andor. Real-time loop closure in 2d lidar slam. In 2016 IEEE international conference on robotics and automation (ICRA), pages 1271–1278. IEEE, 2016. [CrossRef]
Shubham Nagla. 2d hector slam of indoor mobile robot using 2d lidar. In 2020 International Conference on Power, Energy, Control and Transmission Systems (ICPECTS), pages 1–4. IEEE, 2020. [CrossRef]
Jiarong Lin and Fu Zhang. Loam livox: A fast, robust, high-precision lidar odometry and mapping package for lidars of small fov. In 2020 IEEE International Conference on Robotics and Automation (ICRA), pages 3126–3131. IEEE, 2020. [CrossRef]
Z. Ji and S. Singh. Loam: Lidar odometry and mapping in real-time. In Robotics: Science and Systems Conference, 2014. [CrossRef]
T. Shan and B. Englot. Lego-loam: Lightweight and ground-optimized lidar odometry and mapping on variable terrain. In 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2019. [CrossRef]
Zhong Wang, Lin Zhang, Ying Shen, and Yicong Zhou. D-liom: Tightly-coupled direct lidar-inertial odometry and mapping. IEEE Transactions on Multimedia, 2022. [CrossRef]
T. Shan, B. Englot, D. Meyers, W. Wang, and D. Rus. Lio-sam: Tightly-coupled lidar inertial odometry via smoothing and mapping. 2020. [CrossRef]
W. Xu and F. Zhang. Fast-lio: A fast, robust lidar-inertial odometry package by tightly-coupled iterated kalman filter. 2020. [CrossRef]
Kaess, Johannsson, Roberts, Ila, Leonard, JJ, and Dellaert. isam2: Incremental smoothing and mapping using the bayes tree. INT J ROBOT RES, 2012,31(2)(-):216–235, 2012. [CrossRef]
A. Segal, Dirk Hhnel, and S. Thrun. Generalized-icp. In Robotics: Science and Systems V, University of Washington, Seattle, USA, June 28 - July 1, 2009, 2009.
Ji Zhang and Sanjiv Singh. Low-drift and real-time lidar odometry and mapping. Autonomous Robots, 41:401–416, 2017. [CrossRef]
Q. Tong, P. Li, and S. Shen. Vins-mono: A robust and versatile monocular visual-inertial state estimator. IEEE Transactions on Robotics, PP(99):1–17, 2017. [CrossRef]
C. Forster, L. Carlone, F. Dellaert, and D. Scaramuzza. Imu preintegration on manifold for efficient visual-inertial maximum-a-posteriori estimation (supplementary material). Georgia Institute of Technology, 2015.
L. Carlone, Z. Kira, C. Beall, V. Indelman, and F. Dellaert. Eliminating conditionally independent sets in factor graphs: A unifying perspective based on smart factors. In 2014 IEEE International Conference on Robotics and Automation (ICRA), 2014. [CrossRef]
G. Kim and A. Kim. Scan context: Egocentric spatial descriptor for place recognition within 3d point cloud map. In 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2018. [CrossRef]
Raul Mur-Artal, Jose Maria Martinez Montiel, and Juan D Tardos. Orb-slam: a versatile and accurate monocular slam system. IEEE transactions on robotics, 31(5):1147–1163, 2015. [CrossRef]
R. Mur-Artal and JD Tardós. Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras. IEEE Transactions on Robotics, 2017. [CrossRef]
D Nistér, O. Naroditsky, and J. Bergen. Visual odometry. In IEEE, 2004. [CrossRef]
A. J. Davison, I. D. Reid, N. D. Molton, and O. Stasse. Monoslam: Real-time single camera slam. IEEE Computer Society, (6), 2007. [CrossRef]
Jakob Engel, Thomas Schps, and Daniel Cremers. Lsd-slam: Large-scale direct monocular slam. In European Conference on Computer Vision, 2014. [CrossRef]
R. Mur-Artal and J. D. Tardos. Visual-inertial monocular slam with map reuse. IEEE Robotics and Automation Letters, PP(99):796–803, 2016. [CrossRef]
L Von Stumberg, V. Usenko, and D. Cremers. Direct sparse visual-inertial odometry using dynamic marginalization. IEEE, 2018. [CrossRef]
J. Engel, V. Koltun, and D. Cremers. Direct sparse odometry. IEEE Transactions on Pattern Analysis & Machine Intelligence, pages 1–1, 2016. [CrossRef]

Figure 1. Framework diagram of the system.

Figure 2. Factor graph of the system.

Figure 3. Graph of visual-inertia optimization factor before and after marginalization.

Figure 4. Electric tracked chassis data acquisition platform.

Figure 5. Realistic environment of dataset collection.

Figure 6. Positioning and mapping results around the teaching building.

Figure 7. Comparison between the trajectory of this algorithm and the ground truth trajectory.

Figure 8. Positioning and mapping results of the long corridor inside the teaching building.

Figure 9. Schematic diagram of the trajectory in 3D space.

Figure 10. Schematic diagram of the trajectory in 2D plane frame system.

Figure 11. ATE and RPE of different algorithms.

Table 1. Notations and their Explanation.

Notation	Explanation
W	World coordinate frame
B	Robot body coordinate frame
R	Rotate the matrix, $R \in S O (3)$
p	Position vector, $P \in R^{3}$
v	Velocity
b	IMU Bias
T	Conversion matrix from B to W

Table 2. Notations and their Explanation.

Notation	Explanation
H	Matrix
x	Vector
$λ$	Scalar quantity
$T_{i - j} \in S E (3)$	Transformation between coordinate systems,using the equation $P_{i} = T_{i - j} P_{j}$ , points in the i coordinate frame can be converted to the j coordinate frame
$\hat{ξ} \in s e (3)$	Lie algebra elements, where $ξ \in R 6$ , and use them to apply small increments to the 6D pose ${ξ^{'}}_{i - j} = ξ_{i - j} ξ : = log {(e^{{\hat{ξ}}_{i - j}} . e^{\hat{ξ}})}^{\lor}$
$G 1 \cup G 2$	A factor graph containing all factors that are either in G1 or in G2
$T_{i - j} \in S E (3)$	The set of factors

Table 3. ATE values for different algorithms.

Algorithm	ATE
Algorithm	Max	Mean	Median	Min	Rmse	Sse	Std
ALOAM	1.231	0.424	0.380	0.038	0.509	226.777	0.282
Lego-LOAM	0.369	0.148	0.141	0.026	0.158	10.729	0.055
LIO-SAM	0.934	0.177	0.145	0.028	0.210	38.003	0.114
this paper	0.320	0.140	0.136	0.020	0.151	19.535	0.056

Table 4. RPE values for different algorithms.

Algorithm	RPE
Algorithm	Max	Mean	Median	Min	Rmse	Sse	Std
ALOAM	0.609	0.252	0.240	0.002	0.294	75.526	0.152
Lego-LOAM	0.909	0.370	0.364	0.004	0.412	72.903	0.182
LIO-SAM	0.806	0.256	0.262	0.001	0.279	66.935	0.111
this paper	0.561	0.255	0.265	0.001	0.278	66.434	0.110

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Research on Multi-Sensor SLAM Technology for Complex Environment of Construction Machinery

Abstract

0. INTRODUCTION

1. Overview of the system

2. LIDAR-inertial odometry

2.1. LiDAR odometry

2.2. IMU preintegration

2.3. Loop closure detection

3. Visual-inertial odometry

3.1. Visual odometry

3.2. Inertial measurement and initialization

3.3. Optimization of visual-inertial systems

3.3.1. Position optimization

3.3.2. Marginalization

4. Real vehicle experiments and results analysis

4.1. Establishment of experimental platform

4.2. Collection of private datasets

4.3. Experimental results and analysis

5. Conclusions

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe