Preprint
Article
Revealing the Genetic Code Symmetries through Computations Involving Fibonacci-like Sequences and Their Properties
Altmetrics
Downloads
149
Views
881
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
14 June 2023
Posted:
16 June 2023
You are already at the latest version
Alerts
Abstract
In this work, we present a new way to study the genetic code mathematical and chemical structure, based on the use of mathematical computations involving some few recently designed Fibonacci-like sequences, the “seeds” (“initial conditions”) of which are chosen according to the chemical and physical data of the three amino acids serine, arginine and leucine, playing a prominent role in a recent symmetry classification scheme of the genetic code. It appears that these mathematical sequences, of the same kind as the famous Fibonacci series, apart from their usual recurrence relations, are highly interwinned by many useful linear relationships. Using these sequences and also various sums or linear combinations of them, we derive several physical and chemical quantities of interest, as the number of total coding codons, 61, obeying various degeneracy patterns, the detailed number of hydrogen atoms, the detailed number of atoms (H/CNOS) and the integer molecular mass (or nucleon number), in the side chains of the 61 “amino acids”, also in various degeneracy patterns, in agreement with those described in the literature. Also, unexpectedly but interestingly, we find, as a by-product, an accurate description of the very chemical structure of the four ribonucleotides uridine monophosphate (UMP), cytidine monophosphate (CMP), adenosine monophosphate (AMP) and guanosine monophosphate (GMP), the building blocks of RNA whose groupings, in three units, constitutes the triplet codons. In summary, we find a full mathematical and chemical connection with the “ideal sextet’s classification scheme” mentioned above as well as with several others, notably, the Findley-Findley-McGlynn symmetrical classification. We organize the content of the text in such a way that, besides the presentation of several new research results, it has also an educational dimension. The paper could therefore be read and the computations easily worked out, also by non-experts with mathematical background.
Keywords:
Subject: Biology and Life Sciences - Biology and Biotechnology
1. Introduction
In this paper, we present a new way to study the genetic code and its symmetries, using mathematics, more precisely, a small set of brand new Fibonacci-like sequences and, occasionally, some (useful) well known elementary functions from number theory. Using these sequences, the whole and detailed chemical content of the set of amino acids, as structured by several well known symmetry patterns, including their degeneracy, is revealed. Also, several other original applications, using the above sequences, are carried out. Before presenting all these results, let us begin by giving a brief summary of the genetic code. This latter is the basis of life on Earth and was masterfully deciphered in the mid-sixties of the last century [1]. It is the great biological “dictionary” that translates the language of DNA/RNA, which transmit the inherited information located in the genes, to the language of proteins which carry out the biological constructions and functions. It is well known that the “alphabet” of the former language consists of four fundamental units, the nitrogenous bases T (thymine), C (cytosine), A (adenine) and G (guanine) for DNA and U (uracil), C, A and G for RNA. As for the “alphabet” of the second language, it comprises the set of 20 amino acids. In the process of translation between these two languages, in the ribosome for short, there are “words”, the codons, which are made of three nucleotides. In the standard genetic code, only 61 of such codons are translated into amino acids and three others serve as termination or stop codons. To a given codon, from the set of 61, corresponds one and only one amino acid. Now, it is well known that several codons could code for the same amino acid so that the genetic code is said degenerate and the 20 amino acids are organized into “multiplets”. These are as follows: 5 quartets, each, coded by four codons proline (P, Pro), alanine (A, Ala), threonine (T, Thr), valine (V, Val) and glycine (G, Gly); 9 doublets each coded by two codons phenylalanine (F, Phe), tyrosine (Y, Tyr), cysteine (C, Cys), histidine (H, His), glutamine (Q, Gln), glutamic acid (E, Glu) and aspartic acid (D, Asp), asparagines (N, Asn) and lysine (K, Lys); 3 sextets each coded by 6 codons serine (S, Ser), arginine (R, Arg) and leucine (L, Leu); 1 triplet coded by three codons isoleucine (I, Ile) and finally 2 singlets each coded by one codon methionine (M, Met) and tryptophane (W, Trp). In the parentheses, the one-letter and three-letter codes of the amino acids are indicated. Below, in Table 1, we show the genetic code table (the three stop codons are indicated in green color background).
In this work, the “anomalous” three amino acids serine, arginine and leucine, each coded by six codons, will play a prominent role. Contrary to all other 17 amino acids the codons of which share the same first base, the three mentioned amino acids have, each, their 6 codons distributed into two different family boxes. (There are 16 such family boxes and each one of them is a set of four codons having the same first and second base (see Table 1)). The structure of the three sextets is the following serine: {UCN, AGY}, arginine {CGN, AGR}, leucine {CUN, UUR} (N for any base, Y for pyrimidine U or C and R for purine A or G). There are more and more voices rising to underline or put emphasis on the singular nature of the three sextets and also to bring experimental data which tend to show it [3,4]. On the other side, people have always taken for granted that the number of amino acids encoded by the (standard) genetic code is 20. Yes, this is true but this view is evolving. Some few years ago, a published work, [5], claimed that this number has to be increased to 23 by considering that the quartet part and the doublet part of each one of the 3 sextets as distinct. In this work, the authors present a new “effective number of codons”, called , to characterize codon usage bias in the analyzes of protein-coding genes, which improves existing ones. Here, is shown to be a better predictor when its value is increased from 20 to 23 with, in particular, each 6-fold codon set (each sextet as it is called in this work) is considered to be composed of separate 4-fold and 2-fold parts. These six entities are which, added to the 17 remaining amino acids with no “degeneracy” at the first base position, as mentioned above, give a total of 23. This number, together with the remaining degenerate codons, 38, constitutes the pattern “” the importance of which not only has been established in our recent works (see [2] and the references therein) but is also again established all along the present work. One of these kind of approaches is particularly relevant to the present work, the “Ideal” symmetry classification scheme, introduced some few years ago in [6]. It will be summarized in Section 2.3 and we present its numerous links with the present work in Section 4.2. In Section 2, we summarize three important symmetries of the genetic code, including the above mentioned one. In Section 3, we present our new Fibonacci-like sequences and their properties, which are the main mathematical tools used in this paper. In Section 4, we apply these sequences to derive the degeneracy structure of the 61 amino acids, their hydrogen atom, atom and nucleon number content, as structured by the symmetries mentioned in Section 2 and various other remarkable patterns. In Section 5, still using some elements of our sequences, we make contact with the work by shCherbak, [7], concerning the singular structure of proline and derive, in a totally original way, the mathematical form of the shCherbak-Makukov “activation key, [8], which, as is well known, lead to many remarkable and beautiful nucleon number patterns comprising, in particular, those related to Rumer’s symmetry (see below about this latter). In Section 6, using the “seeds” of our Fibonacci-like sequences, that is their “initial conditions”, and only these, we find that they are capable, on their own, to provide the very hydrogen atom content of the 61 amino acids, derived in the various patterns considered in Section 4. We strongly recommend the reader, at this point, before going to the next sections and get a comfortable reading of them, to take a look at Appendix A, which summarizes the chemical data of all 20 amino acids, including also the degeneracies and Appendix B, where a few other mathematical tools, used in this paper, are defined with the visualization of some computation examples.
2. The symmetries of the genetic code
2.1. Rumer’s symmetry
The oldest known symmetry of the genetic code has been discovered by Rumer in 1966, [9]. This symmetry, which is defined by the transformation , divides the genetic code table into two equal halves of 32 codons each, we call them here and . The set (shown in grey background in Table 1) comprises 8 quartets of codons, each, having the same two first-bases and coding for the same amino acid, the third base being irrelevant. In this set, among the 8 quartets, 3 correspond to the quartet part of the 3 sextets serine, arginine and leucine. The set comprises group-I amino acids (2 singlets), group-II amino acids (9 doublets), group-III amino acid (1 triplet) and also 3 stops or termination codons (see Table 1). The point here, concerning symmetry, is that under Rumer’s transformation, performed on all three bases, the sets and are exchanged: ↔ .
2.2. The 3rd base symmetry classification
In 1982, Findley et al., [10], by viewing the genetic code as a relation, rather than a mapping, extracted a fundamental symmetry for the doubly degenerate codons (group-II). The 64-codons set is partitioned into four disjoint sub-sets and each one of them contains only codons having the same third base (see Table 2, below). These authors establish relations which define a one-to-one correspondence between one member of a doubly degenerate codon pair to the other member (see the reference above for details). These relations could be stated, in words, as follows: (i) if a codon for an amino acid has 3rd base U, then there is a codon for the same amino acid having 3rd base C and vice versa OR (ii) if a codon for an amino acid has 3rd base A, then there is a codon for the same amino acid having 3rd base G and vice versa. For a doubly degenerate codon pair (i) and (ii) are mutually exclusive. For order-4, or quartets, (i) and (ii) hold simultaneously. For order-6, the sextets, the quartet part obeys (i) AND (i) and, for the doublet part one has (i) OR (ii). For the odd-order degenerate codons (Ile, Met and Trp), however, there is a slight deviation from symmetry. Below, in Table 2, we show this classification
2.3. The weak/strong, purine/pyrimidine and keto/amino symmetries
The main idea behind the “ideal” symmetry classification scheme by Rosandić and Parr, [6], mentioned above, is to consider the three sextets serine, arginine and leucine, each encoded by six codons, as “initial generators” with serine playing the central role. This scheme divides the 64 codons table into two groups of 32 codons each, the “leading” group and the “nonleading” group and each one of them consists of A+U rich and G+C rich (equal) parts. The “ideal” classification scheme is generated by combining the six codons of serine, arginine and leucine in the following manner: serine, the “initial” generator with its six codons, arginine also with its six codons and leucine with only the quartet part of its six codons part define the “leading” group (with 32 codons). The remaining doublet part of leucine, on the other hand, constitutes a “seed” for the construction of the “nonleading” group (with 32 codons). The whole set is called by the above authors the “core”; its members are underlined in Table 3 below.
As explained, at length, by the authors, the genetic code table in this new scheme is created by codons sextets based on exact purine/pyrimidine symmetries (YR: (U, C, A, G) → (C, U, G, A)), A+U-rich/C+G-rich symmetries, strong/weak, or complementary, symmetries (SW: (U, C, A, G) → (A, G, U, C)) and keto/amino symmetries (KM: (U, C, A, G) → (G, A, C, U)) (see [6]). By starting with serine, the initial generator with its 6 codons, the whole “leading” group (32 codons) is created using transformations among those mentioned above and some mapping rules. In an analogous manner, starting from the two codons of leucine, as “seeds”, the whole “nonleading” group is constructed. There is also a simple relation between the “leading” group and the “nonleading” group (see the reference 6 mentioned above). We show, in Table 3, for visualization, these two groups by using our own format of the genetic code table (the “leading” group is shown in grey background). It is also interesting to note that, under Rumer’s transformation ,, the “leading” group remains globally invariant whether the transformation is applied to the first base , only, to the first two bases, only, or to all the three bases, and same for the “nonleading” group.
Below, in Section 4.2, we will show, that the three amino acids serine, arginine and leucine, will also play a prominent role, as mathematical (and chemically inspired) “seeds” to compute the chemical content of the twenty amino acids, including degeneracy.
3. A rich set of Fibonacci-like sequences and their properties
Let us introduce now, as stated in the introduction, four Fibonacci-like sequences which will prove resourse-rich and very interesting in their applications throughout this work. (Another fifth sequence, just as interesting, will be introduced later, in Equ.(26).) They are also called -Fibonacci sequences and are defined by the following common defining relation
where is the ordinary Fibonacci number. These four sequences differ only by the data of the numbers p and q which, here, play the role of “initial conditions” or “seeds”, as we will call them throughout this paper. Below, in the next section, we shall explain and justify the choice of these “seeds” but, for the moment, we introduce the four mentioned sequences by giving a name to each one of them and their “seeds”: (i) , (ii) , (iii) , (iv) . In Table 4 below, we give the first few terms
These sequences obey several linear relations, some of which will prove very interesting in view of their applications in this work. They are presented below, in Equ.(2), and could be easily checked
It is interesting to note here that the difference
gives the (slightly modified) Fibonacci sequence noted
in an unusual but interesting form: its “seeds” here are inverted with respect to the usual Fibonacci sequence. Also, the sum of any of its first members until a certain index gives a Fibonacci number, exactly, contrary to the usual Fibonacci sequence with seeds 0, 1 which always gives one unit less than a Fibonacci number. For example, in our case, for , we get . (Note that the indexing is here shifted but the recurrence relation is still valid.) There is also another relation linking the sequences and . It writes
For , the sequences and take the same value: . Also, for , and and their difference is 2. The case is also interesting, see below. These relations will have applications in the following sections. Importantly, the sequences in Table 4 together with the one defined in Equ.(26), below, display several numbers highly relevant in this work, either directly as members in Table 4 (shown in bold) or as sums to be evaluated in the following sections. We have also discovered that the above sequences, including the one defined in Equ.(26), can all be shown to exhibit a striking bilateral symmetry and other symmetry properties, in the line of thought of those established for the Fibonacci sequence by Edge, [11]. These findings will be reported elsewhere, in a forthcoming publication.
4. The symmetries of the genetic code revealed
4.1. The multiplet structure
Let us consider, in this section, the first sequence . Is is full of interesting numbers and sums. First, we have , and their sum . This is the number of codons in Rumer’s sets and , respectively. Second, we have . This is the pattern, “”, for 23 amino acids (the sextets counted two times) and 38 amino acids corresponding to 38 degenerate codons. This latter pattern will be mentioned, frequently, in this paper. In fact, the above relations will also let us to derive the detailed multiplet structure of the genetic code. As a matter of fact, consider the following sum, which will be used, occasionally, in this paper
It is the analog of the one for the Fibonacci sequence. For , we have . Grouping the first three terms, on the one hand, and the remaining two, on the other, we have by transferring the unit to the left
Using the sum mentioned above () and adding it to the preceding relation gives (by appropriately arranging the terms)
It appears that there are 15 amino acids and 14 degenerate codons in Rumer’s set while there are 8 amino acids and 24 degenerate codons in Rumer’s set . Let us now go into the details by examining, first, the set The number 15 could be partitioned in two ways. The first, consists in using the above sum for k=3 to get: . Using the second way, we can apply the useful -function and its properties (see below and Appendix B) to the number 15 (): which gives the same result as above where we have used the additivity property. Finally, the number 6, a perfect number, could be written as the sum of its proper divisors: , so that . Here, we have 1 triplet, 2 singlets, 3 doublet parts of the 3 sextets, and 9 doublets. On the other hand, for the degeneracy part, 14, which writes (see above), we can, again, write 6 as the sum of its divisors, arrange the terms and obtain Here, we have 3 degenerate codons for the 3 doublet parts of the 3 sextets, 2 degenerate codons for the triplet and 9 degenerate codons for the 9 doublets. For the set things are simpler. The degeneracy part from Equ.(8) above writes . As for the number of amino acids, 8, as a Fibonacci number, it could simply be written as . This is the structure of the set . The table below summarizes all these results for the two Rumer’s sets which are thus completely described using the Fibonacci-like sequence .
| M1 | multiplets | # amino acids | # degenerate codons | total |
| quartets | 5 | 15 | 20 | |
| quartet parts of the sextets | 3 | 9 | 12 | |
| total | 8 | 24 | 32 |
| M2 | multiplets | # amino acids | # degenerate codons | total |
| doublets | 9 | 9 | 18 | |
| doublet parts of the sextets | 3 | 3 | 6 | |
| triplet | 1 | 2 | 3 | |
| singlets | 2 | 0 | 3 | |
| total | 15 | 14 | 29 |
4.2. Hydrogen atom content and the symmetries
In this section, we examine the hydrogen atom content in each one of the symmetry cases summarized in Section 2: Rumer’s symmetry (Section 2.1), the 3rd base symmetry (Section 2.2) and the weak/strong, purine/pyrimidine and keto/amino symmetries (Section 2.3). Before developing these topics, let us consider, first, the hydrogen atom content in the 61 amino acids side chains, as partitioned by the degeneracy. (Please note that when we say, here and below, “61 amino acids”, we are of course taking into account the degeneracy of each one of the 20 amino acids.) From the table in the Appendix A, we have that the total number of hydrogen atoms in the 61 amino acids side chains is equal to . Let us note from the start that in this count, we take for the (singular) imino acid proline, as a special case, 5 hydrogen atoms in its side chain. We will return to this important point later, in Section 5, with brand new results. A quick look at Table 4 of our Fibonacci-like sequences, reveals that the number of hydrogen atoms, mentioned above, is showing itself in multiple instances. First, ostensibly, as the ninth member of the sequence ( Second, from the relation (viii) in Equ.(2) which, we recall, is valid for any n, in particular for : . Third, from the recurence relation of the sequence . Fourth, from the sum
This last equation will be considered in detail below as it has a great importance concerning the computation of the degeneracy of the genetic code, in various formats. By isolating the last term , we have
This relation is important and will play a prominent role is this section, and later (in Section 6); it gives the number of hydrogen atoms in the amino acids side chains, distributed into two parts: 139 hydrogen atoms in 23 amino acids (17 amino acids with no “degeneracy” at the first base position and the six entities , and ), on the one hand, and hydrogen atoms in the 38 remaining amino acids corresponding to the degenerate codons, on the other (see the introduction, below and also the Appendix A for the calculations). This is the pattern “”. Now, as we have from the recurrence relation of the sequence , we can cast the relation above as follows
This is the hydrogen atom in the usual pattern “ (20 amino acids and 41 degenerate codons). Note that 22 is the number of hydrogen atoms in serine, arginine and leucine, corresponding to one codon for each one of them (see the table in Appendix A). By restricting the sum in Equ.(10) as shown below, we have
This pattern corresponds to Rakocevic’s Cyclic Invariant Periodic System (CIPS) classification of the 20 amino acids where there are 133 (225) hydrogen atoms in the amino acids side chains in the secondary superclass (primary superclass), see [12] and [13]. The above hydrogen atom pattern, , is only one unit from another one which is twice relevant. By transferring the all first member of the sequence, , from the sum to the other factor, we get
First, this hydrogen atom pattern corresponds to 132 hydrogen atoms in the 3 sextets, on the one hand, and 226 hydrogen atoms in the remaining 17 amino acids, on the other (see below). Here, we see, the 3 sextets are set apart and this has, we think, a link with the subject of this section, see below. Second, this pattern describes also the partition of the 20 amino acids into 10 amino acids in the Class-I aminoacyl t-RNA synthetases (226 hydrogen atoms) and 10 amino acids in the Class-II aminoacyl t-RNA synthetases (132 hydrogen atoms), see [14]. Here, of course, the degeneracy is taken into account.
Now, in the following, we consider the hydrogen atom content for the three symmetry cases mentioned in Section 2.1, 2.2 and 2.3. As the case of Section 2.3, the “ideal” symmetry classification scheme, [6], occupies an important place in this work, inasmuch as it has a tight relation with our “seeds” of Fibonacci-like series, we begin by considering it, first. As mentioned and promised in the introduction, it is here the right place to explain and justify the choice of the “seeds”, or “initial conditions” of our Fibonacci-like sequences defined in Section 3, more precisely those of the sequences and . Concerning the former, the “seeds” are and (see Table 4). These are, respectively the number of hydrogen atoms in serine and arginine () and in leucine (9) and their sum, that is the recurrence relation, is the number of hydrogen atoms in the side chains of these three amino acids. As for the latter, the “seeds” are and , respectively the number of atoms in the side chains of arginine and leucine () and in the side chain of serine (). Here also, as for hydrogen, is the number of atoms in the side chains of these three amino acids. We show, below in this paper, using all the resources offered by our Fibonacci-like series and their properties, that these 3 sextets, more precisely, their hydrogen and atoms numbers, as “seeds”, will create the entire hydrogen atom, atom and even nucleon content of the whole set of amino acids, including the degeneracy, much like the creation of the 64 codons from the three sextets in the “ideal” symmetry scheme mentioned above, [6]. Let us, here in this section, begin with the hydrogen atom content. First, using the relation (v) in Equ.(2), we can derive the hydrogen atom content in the two sets: the “leading” group and the “nonleading” group. As a matter of fact, for (see Table 4), we have
It could be seen, from Table 3 and computed from the data in the table in Appendix A, that there are and hydrogen atoms in the”leading” group and in the “nonleading” group, respectively. Moreover, concerning the latter, we have that there are hydrogen atoms in the amino acids the codons of which have the same first two bases UU, CC, AA and GG (in the four corners of Table 3) and hydrogen atoms in the amino acids located in the four boxes in the center of the table which have as first two (different) bases UG, GU, AC and CA. The equation (14) above describes therefore, faithfully, this pattern. Now, we move further to describe accurately the hydrogen atom content involving the amino acids of the “core” comprising serine, arginine and leucine. To see this, we invoke the following two relations
It could be easily verified that they give the same result and both hold for any n. They can also be transformed into each other, using the relation (viii) in Equ.(2), . Now, for , they give and , respectively, with common value 358, the total number of hydrogen atoms in the 61 amino acids side chains. These are very interesting results for what follows. In the first case, as we have seen above, is the number of hydrogen atoms in the “leading” group and is the number of hydrogen atoms in the “nonleading” group. In the second case, is the number of hydrogen atoms in the part of the “core” belonging to the “leading” group (, ) and is the number of hydrogen atoms in the rest, comprising, in particular, the part of the “core” belonging to the “nonleading” group, that is, . The authors write in their paper “the sextets as initial building blocks for creation of their new scheme of the genetic code generate by themselves the patterns of A+U rich/C+G rich, purine/pyrimidine, weak-strong and amino-keto symmetries.” They also add that, in their approach, “the symmetries are a consequence of sextet’s dynamics”. Here, below, we can use our Fibonacci-like sequences to reveal the exact hydrogen atom content of the “core”, constituted by the 3 sextets. As mentioned above, the “core” has two parts: the one which belongs to the “leading” group and the other belonging to the “nonleading” group. Let us consider the former with 114 hydrogen atoms. Using Euler’s totient function ϕ and also so-called “reduced” totient function or Carmichael’s function λ(n), see Appendix B, we have for the number 114 and . Subtracting these from the number 114, we get and, rearranging, we get
This is the correct content of the part of the “core” in the “leading” group: hydrogen atoms () in arginine (), 36 hydrogen atoms in leucine () and 18 hydrogen atoms () in serine (). Let us, alternatively, add the above mentioned two functions to the number 114. We get
This is the number of hydrogen atoms in the “nonleading” group where the isolated number 18 is now re-interpreted as the number of hydrogen atoms in the “seed” of the “nonleading” group, that is, (see above). We have thus established the exact hydrogen atom content of the “ideal” symmetry scheme of the genetic code where the sextets play a prominent role. Note, finally, that, as has been used two times, one time as the number of hydrogen atoms in and one time as as the number of hydrogen atoms in , we can summarize all what has been said above by adding =18 to Equ.(17) and write the exact hydrogen atom structure of the entire “core” constituted by and , respectively. (The codons of the “core” are undelined in Table 3.) Of course, subtracting the number from the total sum , in Equ.(14) above, we are left with which is the number of hydrogen atoms in the other part of the 17 amino acids outside the “core”. We have seen above that the “seeds” of the sequences and are capable of creating the hydrogen atom structure of the “ideal” symmetry classification scheme. Now, what about the other sequences of Table 4 in this respect, that is the link to the “ideal” symmetry scheme? In fact, in turns out that they also house something interesting. Here, we consider only the sequence but more will be said later in Section 4.3 (Equs.(34-35)), concerning the sequence , defined below in Equ.(26). We have for the sequence , using Equ.(6): . First, from the Fibonacci relation with , we have or . Second, it could be easily shown that the sequence , in Equ.(4), is related to the Lucas sequence, so that, for , we have . Finally, we call, exceptionally, the term which also obeys the recurrence relation , that is or, equivalently, . Putting together all these results, we end up with . The last four terms could be easily interpreted as 1 triplet, 2 singlets, 5 quartets and 9 doublets, that is the 17 amino acids outside the “core”. As for the first two terms, in the parenthesis, they are just enough to describe the 5 entities and forming the part of the “core” belonging to the “leading” group, on the one hand, and 1 for , the part of the “core” belonging to the “nonleading” group, on the other.
As an interesting by-product of the results in this section, we have found, unexpectedly, a way to derive from the number of hydrogen atoms in the part of the “core” in the “leading” group, and in the rest, comprising the part of the “core” in the “nonleading” group (see above), and only from these, the very chemical structure of the building blocks of RNA; the four ribonucleotides uridine monophosphate (UMP), cytidine monophosphate (CMP), adenosine monophosphate (AMP) and guanosine monophosphate (GMP). As a matter of fact, using the functions and λ (see Appendix B), we have , and (see Appendix B where the details of the computations are given as examples). First, we have from these three quantities This is the total number of atoms in the four ribonucleotides, 56 in the four nucleotides U (12 atoms), C (13 atoms), A (15 atoms) and G (16 atoms) and 88 in the four identical “blocks” each with 22 atoms (see [12], for the details of the calculation, which includes also a mathematical derivation of the number 22 above which is part of the “condensation” equation for the assembly of a ribonucleotide from the three units a nucleotide, a ribose and a phosphate group with the release of two water molecules, also derived). Now, as there are 30 codons in the “leading” group (two stop codons not counted) and 31 codons in the “nonleading” group (one stop codon also not counted), see Table 3, we can use this decomposition for the number 61 above and finally write the relations above in the form . Note that the above decomposition of the number 61 could also be obtained another way, by using directly the properties of the sequence , see Table 4. We have , and so that by combining them, we get . The above computed quantities , , and are respectively the number of atoms in the four ribonucleotides UMP, CMP, AMP and GMP (see [14]).
Now, we return to the symmetries and examine the second case, Rumer’s symmetry (Section 2.1). Let us reconsider Equ.(10) and write it in the form
where we have used the recurrence relation of the sequence , to write the number as (see Table 4). Now, we have already mentioned in the examples following Equ.(5) that, for , one has or . Inserting, this quantity in the above equation results in
This is the hydrogen atom content in Rumer’s division: 186 hydrogen atoms in and 172 hydrogen atoms in where, in this latter, we have the correct partition into 84 hydrogen atoms in the 5 quartets and 88 hydrogen atoms in the 3 quartets of the 3 sextets. To get the details concerning the number of hydrogen atoms in , 186, we first isolate the sum of the first four numbers in the sum in Equ.(19), that is This is equal to the number of hydrogen atoms in the triplet isoleucine (see below). We are left, in the sum, with the three terms . Writing one time the number as from the relation (viii) in Equ.(2) with n=5 and two times as from the recurrence relation of the sequence we obtain finally
Here, and from the recurrence relation of the sequence . We have therefore, in the detail, the correct number of hydrogen atoms in : in the 9 doublets, in the doublets of the 3 sextets, in the triplet, in the singlet methionine and in the singlet tryptophane. Below, we consider the third and last case of symmetry. In Section 2.2, we explained that the authors extracted an inherent basic symmetry linked to the third base by portioning the 64-codons set into four pair-wise sub-sets where each one of them contains only codons having the same third base. In this way, a one-to-one correspondence between one member of a doubly degenerate codon pair to the other member. Here also, for this symmetry, we could describe the hydrogen atom content, using our Fibonacci-like series. Take the relation (v) in Equ.(2), the one we already considered above in Equ.(14)
This relation, as it is, is the pattern shown in Table 2 for the gross third-base division UC/AG. Here, we note that this relation already describes, nicely, the equality of the number of hydrogen atoms in the columns 3rd base U and 3rd base C where the amino acids are exactly the same (see the penultimate row in Table 2). In fact, we can do better by invoking two more relations. First, the relation (x) in Equ.(2): which, for , gives . Second, the relation , which also holds and gives, for , . Inserting the number , from the relation just above, in the second one, results in . Collecting these results in Equ.(22) above gives, finally
This last relation describes, therefore, completely, the hydrogen atom content pattern of Table 2. It is interesting that the 3rd base classification mentioned above can be supported by the following calculation. We know, from Section 2.2, that the doubly degenerate codons (group-II) obey a fundamental symmetry, so they must play a basic role including, we will show, in the hydrogen atom content too. As a matter of fact, we have, using the sequence
Subtracting this sum from Equ.(22) above, which gives the total number of hydrogen atoms in the 61 amino acids, we get by arranging
This is quite interesting as and are respectively the number of hydrogen atoms in the 9 doublets, on the one hand, and in the remaining 11 amino acids (5 quartets, 3 sextets, two singlets and 1 triplet), on the other, see below Equ.(21). In fact, this same relation could also be obtained, another way, from the relation mentioned in Section 4.1, and noting that the sum in Equ.(24) above is equal, in fact, to (recall , with k=9), we get back to our result: . Note also that and or which is nothing but the hydrogen atoms pattern of the present classification (see Equ.(22) and Table 2). (The function
is defined in Appendix B and the factor 2 which has been introduced is for “doubly” degenerate codons.)
4.3. The atom content and degeneracy
In the course of writing this paper, we have discovered one more Fibonacci-like sequence, tailor-made for the description of the number of atoms in the 61 amino acids (see Equ.(29) below). It is defined as follows
The first few terms are shown below
This sequence is related to the sequences and as follows
which holds for any n. The case is particularly interesting. As a matter of fact, we have
and we see that it gives the total number of atoms in the 61 amino acids distributed into 358 hydrogen atoms (see above) and 236 atoms (C/N/O/S), see the table in Appendix A (180 carbon atoms and 56 N/O/S atoms). Now, from the relation
which holds for any and is the analog relation for the sum of the first k Fibonacci numbers. For it gives or and, by inserting this latter in the above equation, we obtain
We have here the number of atoms in 23 amino acids, (the sextets with 35 atoms are counted two times) and is the number of atoms in the 38 amino acids corresponding to the 38 degenerate codons (see the table in Appendix A). Let us, at this stage, remember the sequence , especially its “seeds” and with sum . Let us also remember that these “seeds” were chosen, intentionally, as the sum of the number of atoms in and , on the one hand, and the number of atoms in , on the other. They are therefore, together, exactly the right thing to add and subtract from Equ.(31) above to obtain
which is the correct partition of the number of atoms: atoms in the 20 amino acids, on the one hand, and 390 atoms in the 41 amino acids corresponding to the 41 degenerate codons (see the table in Appendix A). Now, the use of the above sum in Equ(30), for , gives which number appears also doubly significant, see below. By subtracting this latter number from the total sum, , and arranging, we have
This partition of the number of atoms is interesting as is equal to the number of atoms in the six amino acids (sextets) and and is the number of atoms in the remaining 17 amino acids, of course, taking into account the degeneracy. It is striking that the first two recurrence relations of the sequence and , together, lead to the relation
which is in line with the above result for the atom numbers and also with the “ideal” symmetry scheme (as depicted below):
Finally, we could also derive the partition of the number of atoms for Rumer’s sets and . Consider, again, the equation above, , more precisely, the number 384 which was calculated from Equ.(30) with . By partitioning this sum in two parts, for and , we have , on the one hand, and , on the other. By gathering both terms in Equ.(33) and arranging, we obtain
This is the content of atoms 264 in and 330 in , see the table in Appendix A. We can also go to the details for the multiplets. Considering, first, , let us present the following (new) relation connecting the sequences and :
which, for gives . Using the recurrence relation for , we have and, by combining the above two relations, we get or . Multiplying this latter equality by any number does not change it, in particular by 4, having in mind that the 8 quartets composing the set have each 4 codons, and we have This is exactly the number of atoms in : in the 5 quartets and in the 3 quartet parts of the three sextets (see the table in Appendix A). The above equality, , which was used as an intermediate of the calculation above, could also be exploited for the set . As a matter of fact, consider Equ.(5), , for : . Inserting this difference in the above equality gives . Now, the following relation linking Fibonacci and Lucas numbers: is interesting as, for it gives . If, moreover, we use the recurrence relation for the Lucas number as , we get . This matches perfectly the number of atoms in the triplet isoleucine (), in the singlet methionine (11) and in the other singlet tryptophane (18), see the table in Appendix A. We showed above that there are atoms in the set . Subtracting the above number of atoms, 68, in the triplet and in the two singlets, we have atoms left. To get the right partition of these, it suffices to take the sum of the three first members of the sequence which appears to be the right number of atoms in the doublet parts of the three singlets. Adding and subtracting this latter from gives which is the number of atoms in the nine doublets, (see the table in Appendix A). In summary, we have
which is the very precise partition. Finally, let us note that the number , mentioned above (see below Equ.(32)), has also another relevant interpretation. As a matter of fact, it is equal to the number of atoms in the 20 amino acids, this time including to their side chains their 20 identical “blocks” with 9 atoms each:
4.4. Derivation of several nucleon number patterns
In this section, we use our Fibonacci-like series to derive several interesting patterns for the nucleon number (or integer molecular mass) content in the 61 amino acids. Before starting, let us make an important remark about the sequence (see Table 4).. In fact, there is a simple relation between the sequences and , the latter is simply five times the former: . One may wonder how the use of would bring something significant as it is simply related to ? In fact, it does and we will show that below. First, let us consider the following sum
It appears that this number, , is the number of nucleons, or integer molecular mass, contained in the 61 amino acids (see the table in Appendix A). This is nice but we could do more. Consider the “seeds” of the sequence 30 and 5 with sum 35, the number of atoms in the 3 sextets serine (5), arginine (17) and leucine (13). (It is not difficult to show, using the Zekendorf representation[1] of the number 30 () in terms of Fibonacci numbers and the fact that , that the sum of the “seeds” takes the form , i.e., the correct atom numbers in the three sextets, mentioned above.) Now, by isolating the sum of the above two “seeds” of from the third sum in Equ.(39) and include it in the two other sums, we get
Here also, we have another interesting result: there are nucleons in the 20 amino acids (see the table in Appendix A) and 2149 nucleons in the 41 amino acids corresponding to 41 degenerate codons. Let us now exploit the relation between the two sequences and (, mentioned above, and write the sum in Equ(39) as follows
Now, recall the sum , mentioned in Equ.(6) of Section 4.1. In our present case for its use in Equ.(41), we have for . By considering this latter relation in only one such sum in the first bracket of the above equation and transfer the unit, 1, to the second bracket, we obtain
One recognizes here the nucleon number in the pattern “ (see above and Appendix A): nucleons in the amino acids side chains and nucleons in the 38 amino acids side chains corresponding to the 38 degenerate codons (see above). As another, also interesting finding, we can, from the above relations, make contact with the “ideal” symmetry mentioned above in Section 4.2, at the level of the nucleon numbers. To do this, let us, first, remark that the number appears two times, one time as the number of hydrogen atoms in the “core” of the “ideal” symmetry scheme (see above) and one time as the number of nucleons in , see the table in Appendix A). This will prove significant in the following. Consider now the sum
The number by itself, is not very interesting but its ϕ-function is. As a matter of fact, we have and, adding to it two times the number gives This is the number of nucleons in the “core”: . Isolating one time the number 114 in the sum, that is gives us the partition of the nucleon numbers between the two parts of the “core”, in the “leading” group, on the one hand, and in the “nonleading” group, on the other:
In the following, we can also derive three more results by “watering three plants with one hose”, so to speak. As a matter of fact, consider again the sum in Equ.(39) and cut it as follows
Here, we have the nucleon number pattern of the 3rd-base classification of Section 2.2: nucleons in the U/C third-base division and nucleons in the A/G third-base division (see Table 2, last row). Now, by borrowing from the first bracket above the sum of the first three members of the sequence , the one we used earlier (see above Equ.(38)), to the benefit of the second bracket, we get[2]
Here, we recognize the number of nucleons in the “leading”group/”nonleading” group, and , respectively. Finally, we could also establish the nucleon number pattern corresponding to Rumer’s division. Consider again Equ.(39) by partitioning it as follows
It suffices now, analogously to what we did in Equ. (40) above, to subtract, one time, the sum of the “seeds” of the sequence in the bracket, that is, , and add it to the three terms in the parenthesis to obtain
We have, as promised above, nucleons in and 2072 nucleons in (see the table in Appendix A).
5. On proline’s singularity and a derivation of the shCherbak-Makukov “activation” key
In this section, we use our Fibonacci-like sequences to shed light, by giving concrete results, on a question relative to the special amino (more exactly imino) acid, proline, which is an exception among the set of 20 amino acids. As a matter of fact, it is the only amino acid where its side chain is connected to its block twice. shCherbak, [7], in order to “standardize” the common block of the amino acids, with 74 nucleons, proposed an imaginary “borrowing” of one nucleon (in fact one hydrogen atom) from the side chain of proline, which has only 73 nucleons in its block, to the benefit of its block, to reach 74, as the 19 other amino acids. In his next work with Makukov, [8], the above “borrowing”, or transfert of one nucleon, has been termed the “activation key”. Activating the key, i.e., standardizing, leads to an innumerable number of remarkable and beautiful arithmetical patterns. These authors say in their paper, [8], “Applied systematically without exceptions, the artificial transfer in proline enables holistic and arithmetically precise order in the code”. Here, in this section, we establish,, not only a mathematical version of the “activation key”, itself, but also its action on the (new) total hydrogen atom content, with simple possible extension to the atom and nucleon content. Let us begin by examining the action of the “activation key”). Consider, again, the sequence and the following sum
It could be easily shown and verified that the above relation holds for any k. For k=9, it gives As established and mentioned many times previously, is the number of hydrogen atoms in the 61 amino acids side chains, where the special amino acid proline has 5 hydrogen atoms in its side chain. If, instead, one considers that proline’s side chain has now 6 hydrogen atoms, at the cost of its block, i.e., no standardization made, or the “activation key” off (see below), and taking into account the number of its coding codons, which is 4, then we have now hydrogen atoms in the 61 amino acids side chains. Let us reconsider Equ.(10)) for the hydrogen atoms partition between 38 amino acids corresponding to the 38 degenerate codons and 23 amino acids () but, now, using the above relation ():
To get a correct partition, let us consider the perfect number 6 which is, as such, equal to the sum of its proper divisors: . These are just the right numbers we need. Inserting these in the above equation by selecting the odd divisors and 3 and shifting them to the left while leaving the even one, 2, to the right and finally arranging properly, we get
so that we have something quite correct: one more hydrogen atom in the 23 amino acids part (proline, a quartet, has now one more hydrogen atom in its side chain) and 3 more hydrogen atoms for its 3 degenerate codons. (Note that, the action of the “activation key” could easily be extended to the total number of atoms and the total number of nucleons, as it applies only to the hydrogen atom number content.) Taking a look at the 6th term in the sequence , , we have that it appears to be equal to the number of nucleons in proline side chain and block, see below about this latter sum. This number, 115, is invariant whether we make shCherbak’s “borrowing” of one nucleon or not. To get more insight, we consider another invariant number, the total number of hydrogen atoms in the 61 amino acids, including the blocks (with 4 hydrogen atoms in each), that is . Without borrowing one nucleon from the side chain of proline in favour of its block there are 362 hydrogen atoms in the 61 amino acids and 240 hydrogen atoms, , in the 61 blocks. Applying the “borrowing”, there are 358 hydrogen atoms in the 61 amino acids side chains and hydrogen atoms in the 61 blocks. Note, in passing, the following nice relations seemingly linking the two views: and . Now, let us examine the former point,, the derivation of the “activation key”. Considering the above mentioned invariant numbers, () and , we have, using their function (see Appendix B):
From which we deduce that which are seen to describe, fully and precisely, the two views: (“activation key” off) and (“activation key” on). From , where
is the sum of the divisors, we can also write . Also, from , we can also make contact with the sequence through the relation , mentioned above: . Moreover, we can, alternatively, exploit the number 75, itself. As a matter of fact, calling Legendre’s sum of three squares theorem[3], we have that the number 75 do not satisfy the theorem and can therefore be written as the sum of the following three squares: or . This latter form gives us again . Finally, using and the decomposition of the number as the sum of three squares, mentioned above, we can write, by allocating the two units in two ways: . This is, again, what we found above from Equs.(52-53).
6. A striking imprint in the “seeds”
We invite the reader, here, before starting this section, to remember what has been said about the three sextets in Section 4.2 when using the “seeds” of our fifth sequence . In the “ideal” symmetry classification scheme, mentioned in Section 2.3, the authors explain that, in their approach, the symmetries are a consequence of sextet’s dynamics and the whole set of amino acids is created starting from these three sextets where, serine, plays a prominent role. In our own approach, relying on the use of Fibonacci-like series, on the other hand, we have chosen, as already mentioned, for two of them, and , the hydrogen atom numbers and atom numbers of the three sextets (see Section 4.2) as “seeds”. It appears, while the writing of this paper goes to its end, that the “seeds” of, in fact, all the Fibonacci-like sequences used in this paper, and only these, by themselves, can “create”, strikingly and remarkably, the main hydrogen number patterns derived in this paper. As a matter of fact, the sum and product of the “seeds” of the sequence , alone, gives
One recognize here the number of hydrogen atoms in 20 amino acids, 117, augmented by the number of hydrogen atoms in the three sextets, 22. The total, 139, corresponds to 23 amino acids (the sextets counted two times). Now, let us compute the following expression, using the sum and product of the “seeds” of the sequence and only the sum of the “seeds” of the other three remaining sequences , and (the latter defined in Equ.(26). We have
Here, we have the number of hydrogen atoms in the 38 amino acids corresponding to the 38 degenerate codons. Equs.(54-55), together, constitute the “” hydrogen atom pattern established in Section 4.1). Now, taking the sum of the above equations and borrowing the number 22 from Equ.(54) to the benefit of Equ.(55) gives which corresponds to the other pattern “” (20 amino acids and 41 degenerate codons), see Equ.(11) in Section 4.1. Next, we arrange Equs.(54) and (55) as follows
Here, we have again the hydrogen atom content in Rumer’s division: 172 hydrogen atoms in and 186 hydrogen atoms in , see Section 4.2 Equ.(20). To get the other patterns, we call, exceptionally, the Fibonacci () and Lucas () series, which, as well known, are linked by the relation . For n=5, we have so that we can take this latter as the term in the above equations, arrange and get
This is the hydrogen atom pattern for (i) the 3rd base classification of Section 4.2, Equ.(14), and (ii) the “ideal” symmetry classification scheme in the same section, Equ. (22). Finally, we consider Zekendorf’s theorem (see footnote 1) and apply it to the number 117 giving . Writing , a Fibonacci number, as , we can rearrange the content of the second parenthesis in Equ.(57) above as and , so that which describes again the pattern . The fact of having used, here, the Fibonacci and Lucas sequences is all the more interesting in that it can, also, give us another remarkable result. As a matter of fact, adding the two “seeds” of the Fibonacci and Lucas sequences, and , respectively, to the above sum of Equs.(54) and (55) and arranging, we obtain
Conclusion
In this work, we have strayed a little off the beaten paths in the genetic code mathematical research. Starting with a handful of Fibonacci-like sequences, we have derived not only the degeneracy structure of the genetic code but also the hydrogen atom content, the atom number content and also the integer molecular mass (nucleon) content of the set of 20 amino acids as strutured in the 64-codon table. What made this possible is a judicious choice of the intial conditions, or “seeds”, of the above mentioned sequences. For two of these, they are chosen as the hydrogen atom numbers and atom numbers of the three enigmatic and intriguing amino acids serine, arginine and leucine. Our results, using these sequences, led us to reveal, as mentioned above, the elemental content of the 61 amino acids set as structured by various well-known symmetries, as Rumer’s symmetry, the “ideal” symmetry classification scheme and the basic symmetry associated to order-2 degeneracy. Moreover, as a by-product of our mathematical formalism, we derived the atomic (elemental) content of the building-blocks of RNA, the four ribonucleotides UMP, CMP, AMP and GMP. Also, still using the above mathematics, we bring, for the first time, an additional brick to shCherbak’s theory concerning the role of the special imino acid proline whose virtual “double” struture renders possible, via the use of the “activation key”, a large number of remarkable and beautiful arithmetical patterns. Let us stress, as a last word, that the content of this paper is, we believe, inovative. To the best of our knowledge, we have never seen such a kind of quantitative derivation of the chemical characteristics of the genetic code as structured by the degeneracy and also by several well known symmetries. Our main findings, as the total hydrogen atom content, the total atom content, the total molecular mass content of the 20 amino acids, including the degeneracy, as well as other relevant quantities related to the symmetries of the genetic code are found directly, either as ostensible members of the Fibonacci-like sequences or obtained from the summation properties of these latter. Other slighly more sophisticated quantities, also having something to do with the symmetries, are obtained with the help of some well known arithmetic functions.
Appendix A
In the table of this appendix, we give the detailed elemental composition of the side chains of the 20 amino acids. H stands for hydrogen, C for carbon, N for nitrogen, O for oxygen and S for sulfur. The calculated values of some important quantities, taking into account the degeneracies, are indicated in the last five rows; they are useful to know when reading the main text (those shown in bold, and others, are all mathematically derived in this paper). In the table, the first column, M, gives the number of codons which code for an amino acid (4 for a quartet, 6 for a sextet, 2 for a doublet, 3 for a triplet and 1 for a singlet). In column 6 we provide the number of atoms in the side chains and the number of nucleons (protons and neutrons), which is also the integer molecular mass of an amino acid, is displayed in column 7. Below the table, we offer hints for computing some of them. The table is in the “standardized” form, that is, proline has 5 hydrogen atoms in its side chain and all the twenty amino acids, including proline, have 74 nucleons in each of their blocks, see Section 5. The general chemical (linear) formula of an amino acid is
where R is the radical, also called the side chain, and the rest of the molecule constitutes what we call here the block. The carbon C, linked to R, is called α-carbon. In the special case of proline, its side chain from the α-carbon connects to the nitrogen N forming a pyrrolidine loop. (It is the side chain which gives an amino acid its specific functional properties.). To calculate, for example, the nucleon numbers, or the integer molecular mass of an amino acid, the molecular mass of the chemical elements are those of the most abundant isotopes: hydrogen (1), carbon (12), nitrogen (14), oxygen (16) and sulfur (32). From the formula above, one computes easily the integer molecular mass of the block: In the (unique) case of proline, as mentioned above, there is one less hydrogen atom in the block and the nucleon number is ; this is the non-standardized form (“activation key” off), (see Section 5).
| M | amino acid | # H | # C | # N/O/S | # atoms | # nucleons |
| 4 | Proline (P) | 5 | 3 | 0 | 8 | 41 |
| Alanine (A) | 3 | 1 | 0 | 4 | 15 | |
| Threonine (T) | 5 | 2 | 0/1/0 | 8 | 45 | |
| Valine (V) | 7 | 3 | 0 | 10 | 43 | |
| Glycine (G) | 1 | 0 | 0 | 1 | 1 | |
| 6 | Serine (S) | 3 | 1 | 0/1/0 | 5 | 31 |
| Leucine (L) | 9 | 4 | 0 | 13 | 57 | |
| Arginine (R) | 10 | 4 | 3/0/0 | 17 | 100 | |
| 2 | Phenylalanine (F) | 7 | 7 | 0 | 14 | 91 |
| Tyrosine (Y) | 7 | 7 | 0/1/0 | 15 | 107 | |
| Cysteine (C) | 3 | 1 | 0/0/1 | 5 | 47 | |
| Histidine (H) | 5 | 4 | 2/0/0 | 11 | 81 | |
| Glutamine (Q) | 6 | 3 | 1/1/0 | 11 | 72 | |
| Asparagine (N) | 4 | 2 | 1/1/0 | 8 | 58 | |
| Lysine (K) | 10 | 4 | 1/0/0 | 15 | 72 | |
| Aspartic Acid (D) | 3 | 2 | 0/2/0 | 7 | 59 | |
| Glutamic Acid (E) | 5 | 3 | 0/2/0 | 10 | 73 | |
| 3 | Isoleucine (I) | 9 | 4 | 0 | 13 | 57 |
| 1 | Methionine (M) | 7 | 3 | 0/0/1 | 11 | 75 |
| 1 | Tryptophane (W) | 8 | 9 | 1/0/0 | 18 | 130 |
| Total (20) | 117 | 67 | 20 | 204 | 1255 | |
| Total (23) | 139 | 76 | 24 | 239 | 1443 | |
| Total (38) | 219 | 104 | 32 | 355 | 1961 | |
| Total (61) | 358 | 180 | 56 | 594 | 3404 | |
| 172/186 | 264/330 | 1332/2072 | ||||
The get the results in the second of the last five rows from the first one, it suffices to count the values of the sextets two times. For the rest, to ease the calculations, one can use the following pre-calculated sums for the hydrogen atom content: 5 quartets 3 sextets 9 doublets 1 triplet 2 singlets . For the atom number: 5 quartets 3 sextets 9 doublets 1 triplet 13 2 singlets . For the nucleon numbers: 5 quartets 3 sextets 9 doublets 1 triplet 57 2 singlets .
In the calculations, the reader needs also to know what we mean by degeneracy. This latter is defined as the number of codons coding for an amino acid minus one. Therefore, for a quartet, the degeneracy is , for a doublet it is , for a triplet it is and for singlet it is . For the special case of the sextets, there are two possibilities, related to the two patterns mentioned several times in this paper: “ and . In the first case, the degeneracy is (3 for the quartet part and 2 for the doublet part whose two codons are considered both degenerate). In the second case, the quartet part and the doublet part of each sextet are considered as separate entities (ex. and so the degeneracy is equal to , 3 for the quartet part and 1 for the doublet part which is here considered as a doublet. In this way, we have for the number of amino acids and total number of coding codons , , in the first case, and , in the second one. With these definitions, it is not difficult to do the rest of the computations. Let us give some few examples from the table above for the number of hydrogen atoms for the pattern: , .
Appendix B
In this appendix, we mention some few other additional mathematical elements used in this paper. First, Euler’s totient function for an inger n, ϕ(n), which is extensively used in many scientific areas as cryptography and graph theory, as a few examples. It counts the number of positive integers less than or equal to n which are relatively prime to n (also called coprimes). For example 24 has 8 coprimes (1, 5, 7, 11, 13, 17, 19, 23): Second, Carmichael λ-function, also called reduced totient function, which is, in fact, used only one time in Section 4.2 where it appears to be very useful. It is defined as the smallest positive divisor of Euler’s totient function that satisfies Euler’s Theorem. For example (The reader could easily find good online calculators for these functions to check.) Next, the function which has been used, successfully, by us many times in our recent works on the genetic code, see for example [13]. It is define by
where is the sum of the prime factors, () of the integer n (written as (by the Fundamental Theorem of Arithmetic), including the multiplicities, is the Sum of the Prime Indices where PI(2)=1, PI(3)=2, PI(5)=3 and so on, also including the multiplicities and , so-called Big Omega function, is the number of the prime factors Consider, as an example, the number whose prime fctorization is . We have
The function enjoys also the useful additivity (“logarithmic”) property . Let us also give some few other illustration examples, taken from Section 4.2, concerning the computation of and . For the first, we have so that . For the second, we have . To get the result established in the end of Section 4.2, it makes sense to use the additivity property mentioned above: . This form, which sets apart the two factors 4 proved useful to reveal the structure of the four ribonucleotides (in Section 4.2).
References
- Nirenberg, M.; Leder, P.; Bernfield, M.; Brimacombe, R.; Trupin, J.; Rottman, F.; O’Neal, C.N.A. Codewords and Protein Synthesis, VII. On the General Nature of the RNA Code. Proc Nat. Acad Sci USA 1965, 53, 1161–1168. [Google Scholar] [CrossRef] [PubMed]
- Négadi, T. The genetic code degeneracy and the amino acids chemical composition are connected. NeuroQuantology 2009, 7, 181–187. [Google Scholar] [CrossRef]
- Inouye, M.; Takino, R.; Ishida, Y.; Inouye, K. Evolution of the genetic code; Evidence from codon use disparity in Escherichia coli. Proc Natl Acad Sci USA 2020, 117, 28572–28575. [Google Scholar] [CrossRef] [PubMed]
- Zwick, A.; Regier, J.C.; Zwickl, D. Resolving Discrepancy between Nucleotides and Amino Acids in Deep-Level Arthropod Phylogenomics: Differentiating Serine Codons in 21-Amino-Acid Models. PLoS ONE 2012, 7, e47450. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Yang, Q.; Xia, X. An improved implementation of effective number of codons. (Nc) Mol Biol Evol 2013, 30, 191–196. [Google Scholar] [CrossRef] [PubMed]
- Rosandić, M.; Parr, V. Codons sextets with leading role of serine create “ideal” symmetry classification scheme of the genetic code. Gene 2014, 543, 45–52. [Google Scholar] [CrossRef] [PubMed]
- shCherbak, V. The Arithmetical origin of the genetic code. In The codes of Life: The rules of Macroevolution. Barbieri, M.; Ed. New York: Springer Publishers, 2008; pp. 153–185. [Google Scholar]
- shCherbak, V.; Makukov, M. The “wow! Signal” of the terrestrial genetic code. Icarus 2013, 224, 228–242. [Google Scholar] [CrossRef]
- Rumer, Y. About systematization of the genetic code. Dok. Akad Nauk SSSR 1966, 167, 1393–1394. [Google Scholar]
- Findley, G.I.; Findley, A.M.; McGlynn, S.P.. Symmetry characteristics of the genetic code. Proceeding of the National Academy of Sciences of the United States of America, 79, 7061-7065.
- Edge, M. Symmetry in Fibonacci numbers. Symmetry: Culture and Science 2009, 20, 393–408. [Google Scholar]
- Rakocevic, M.M. Genetic Code: The unity of the stereochemical determinism and pure chance. 2009, arXiv:0904.1161v1 [q-bio.OT]. arXiv:0904.1161v1 [q-bio.
- Négadi, T. A Taylor-made arithmetic model of the genetic code and applications. Symmetry: Culture and Science 2009, 20, 51–76. [Google Scholar]
- Négadi, T. The genetic code invariance: when Euler and Fibonacci meet. Symmetry: Culture and Science 2014, 30, 261–262. [Google Scholar]
| 1 | The Zeckendorf theorem states that every positive integer can be represented uniquely as the sum of one or more non-consecutive Fibonacci numbers. |
| 2 | As an example of the computations, here is the one for the « nonleading » group which goes as follows: 31 × 6 + 57 × 4 + 100 × 6 + 15 × 4 + 59 × 2 +
73 × 2 + 107 × 2 + 57 × 3 + 75 = 1798, see Table 3 and the table in Appendix B. |
| 3 | This theorem states that a natural number n can be represented as a sum of three squares if and only if it is not of the form 4a(8b+7)
for a and b two positive integers. It could be easily verified that the number 75 cannot be written in this form so it can be represented as the sum of three squares. |
Table 1.
The genetic code table (format from Négadi, [2]).
Table 1.
The genetic code table (format from Négadi, [2]).
| UUU (F) | UUC (F) | UCU(S) | UCC(S) | CUU(L) | CUC(L) | CCU (P) | CCC (P) |
| UUA(L) | UUG(L) | UCA(S) | UCG(S) | CUA(L) | CUG(L) | CCA (P) | CCG (P) |
| UAU (Y) | UAC (Y) | UGU (C) | UGC (C) | CAU (H) | CAC (H) | CGU(R) | CGC(R) |
| UAA (stp) | UAG (stp) | UGA (stp) | UGG (W) | CAA (Q) | CAG (Q) | CGA(R) | CGG(R) |
| AUU (I) | AUC (I) | ACU (T) | ACC (T) | GUU (V) | GUC (V) | GCU (A) | GCC (A) |
| AUA (I) | AUG (M) | ACA (T) | ACG (T) | GUA (V) | GUG (V) | GCA (A) | GCG (A) |
| AAU (N) | AAC (N) | AGU(S) | AGC(S) | GAU (D) | GAC (D) | GGU (G) | GGC (G) |
| AAA (K) | AAG (K) | AGA(R) | AGG (R) | GAA (E) | GAG (E) | GGA (G) | GGG (G) |
Table 2.
The 3rd base classification of the 64 codons, [10].
Table 2.
The 3rd base classification of the 64 codons, [10].
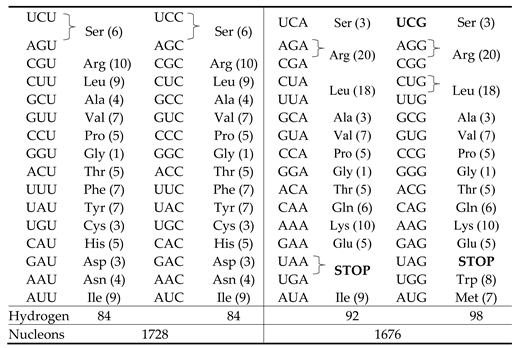
Table 3.
The “ideal” symmetry classification scheme, [6].
Table 3.
The “ideal” symmetry classification scheme, [6].
| UUU (F) | UUC (F) | UCU (S) | UCC (S) | CUU (L) | CUC (L) | CCU (P) | CCC (P) |
| UUA (L) | UUG (L) | UCA (S) | UCG (S) | CUA (L) | CUG (L) | CCA (P) | CCG (P) |
| UAU (Y) | UAC (Y) | UGU (C) | UGC (C) | CAU (H) | CAC (H) | CGU (R) | CGC (R) |
| UAA (stp) | UAG (stp) | UGA (stp) | UGG (W) | CAA (Q) | CAG (Q) | CGA (R) | CGG (R) |
| AUU (I) | AUC (I) | ACU (T) | ACC (T) | GUU (V) | GUC (V) | GCU (A) | GCC (A) |
| AUA (I) | AUG (M) | ACA (T) | ACG (T) | GUA (V) | GUG (V) | GCA (A) | GCG (A) |
| AAU (N) | AAC (N) | AGU (S) | AGC (S) | GAU (D) | GAC (D) | GGU (G) | GGC (G) |
| AAA (K) | AAG (K) | AGA (R) | AGG(R) | GAA (E) | GAG (E) | GGA (G) | GGG (G) |
Table 4.
The first few terms of the Fibonacci-like sequences , and .
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 6 | 1 | 7 | 8 | 15 | 23 | 38 | 61 | 99 | 160 | 259 | 419 | 678 | |
| 1 | 6 | 7 | 13 | 20 | 33 | 53 | 86 | 139 | 225 | 364 | 589 | 953 | |
| 13 | 9 | 22 | 31 | 53 | 84 | 137 | 221 | 358 | 579 | 937 | 1516 | 2453 | |
| 30 | 5 | 35 | 40 | 75 | 115 | 190 | 305 | 495 | 800 | 1295 | 2095 | 3390 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





