1. Introduction
This paper presents an optimization of thickness variation function of simply supported and cantilever beams, in terms of maximizing gaps between their chosen neighbouring frequencies. A method of optimization – sizing optimization – is a method of modifying dimensions or sizes of components in order to obtain the best structural performance. The beams are made of a homogeneous material. Analysed elements are considered in the framework of the Euler–Bernoulli theory.
There are a number of studies on the band-gap behaviour of structural elements. This phenomenon is of significant importance in various engineering applications. By controlling the band-gap characteristics, it is possible to alter the mechanical and vibrational properties of the structure, leading to improved performance and functionality. For example, in the field of materials engineering, the design of bandgap has become an essential tool in developing materials with specific properties, such as phononic crystals (PnC) and metamaterials [
1,
2,
3]. In the field of civil engineering, the band-gap characteristic of structural elements such as beams or plates is related to their dynamic response. Controlling their occurrence can affect the acoustic and vibrational insulation of the structure, which is crucial for the comfort and safety of the occupants. Therefore, the design and analysis of structural elements require a deep understanding of their band-gap behaviour, so it can lead to the development of lightweight, high-strength, and energy-efficient structures.
So far, many researchers have addressed the issue of optimization and analysis of structures with gaps between frequencies. One of the first publications in this area were presented by Olhoff et al. in 1970s and 1980s [
4,
5,
6]. The aim of first of these is to find a transversely vibrating beam that yields a maximum value of a higher natural frequency of specified order. The authors introduced a simple method of obtaining solutions corresponding to any higher value of the specified order using scaled optimal beam elements. In the second work, authors determined the optimal solution of a transversely vibrating, thin, elastic beam or rotating shaft, that maximizes the difference between two adjacent natural frequencies. The topic of vibrating beams or rotating shafts is also continued in the last of the mentioned papers. In all three works, the solution was derived by variational analysis and solved numerically by an iteration procedure based on a finite difference discretization. The more recent works of named researchers focus also on maximizing the gap between two adjacent eigenfrequencies but using other methods of topology optimization [
7]. In [
8,
9] the topology optimization problems were solved by the iterative procedure based on gradient-based algorithm.
Methods of solutions for the band-gap problem include also genetic algorithms (GAs) and other global heuristic approaches [
10]. However, most of the work in this area apply to topology optimization in terms of wave propagation [
11,
12] or phononic crystals and metamaterials optimization [
13,
14,
15,
16]. Therefore, the optimization mainly concerns the material structure and not the optimization by distribution of isotropic material in structural element with specific support conditions. In [
17] the authors have maximized the band gap size for bending waves in an infinite periodic Mindlin plate. They have also constructed a finite periodic plate using a number of the optimized base cells in a postprocessed version. Band gap optimization of infinite structures are also found in [
18], where the authors used generalized gradient ascent method for the optimization procedure. Shen et al. [
19] developed a two-stage GA with a floating mutation probability to design a two-dimensional (2D) PnC of a square lattice with the maximal absolute band gap. A similar topic was discussed in [
20], were Dong et al. maximized the relative widths of the gaps between the adjacent energy bands of the 2D PnC with a square lattice using finite element method (FEM) and a two-stage GA. A PnC unit cell optimization with GAs was also described in [
21], where thin plate composed of aluminium and epoxy resin was presented.
In the area of dynamics and vibrations, genetic algorithms are used for numerous optimization problems. Biswal et al. [
22] used GAs with FEM for design and analysis of nonprismatic piezolaminated cantilever beam for optimal vibration energy harvesting. GAs were also used for band-gap problem in periodic structures. Shi et al. [
23] considered the inverse problem of the flexural vibrational band gap of a periodically supported beam. Another GA optimization problems was presented in [
24] and [
25]. The former concerns a frequency response for locally resonant metamaterial beam and the latter presents a design method to optimize the material distribution of functionally graded beams with respect to some vibration and acoustic properties. GAs were also used to change the shape of the mechanical system under a nonlinear response for clamped-clamped beam [
26].
Genetic algorithms are also used in problems directly related to structural engineering, but under strength conditions, to minimalize material use, and consequently – the overall cost of the structural element. In [
27] authors used GA as an auxiliary tool for pre-dimensioning prestressed concrete beams. They optimized cross-section of the I-beam to develop an individual with the lowest cost of manufacturing that meets the SLS and ULS conditions. An attempt to optimize the cost of a prestressed concrete element was also presented by Aydın and Ayvaz [
28]. They determined the optimum span number and optimum cross-sectional properties of multi-span bridges using hybrid GA. Similar tools were also used to optimize structures of roofs like domes [
29] or steel trusses [
30,
31].
The goal of this work is to find the optimal thickness distribution of a linearly elastic beam. The design variable is the height of its cross-section, keeping its length, and width constant. The natural frequencies of the beams are computed using the finite element method. An optimizer based on the genetic algorithm is used to determine the optimal material distribution in terms of maximization the relative gap between two neighbouring frequencies.
The paper is outlined as follows. The theoretical background and fundamental equations as well as the methodology (finite element method and Genetic Algorithms) are presented in
Section 2.
Section 3 is a description of the research problem and studied cases. Discussion of the optimization process using genetic algorithms is briefly presented in
Section 4. In
Section 5, the results analysis and discussion are provided. The paper ends with general conclusions.
2. Fundamental Equations and Methods
2.1. Euler-Bernoulli Beam Theory
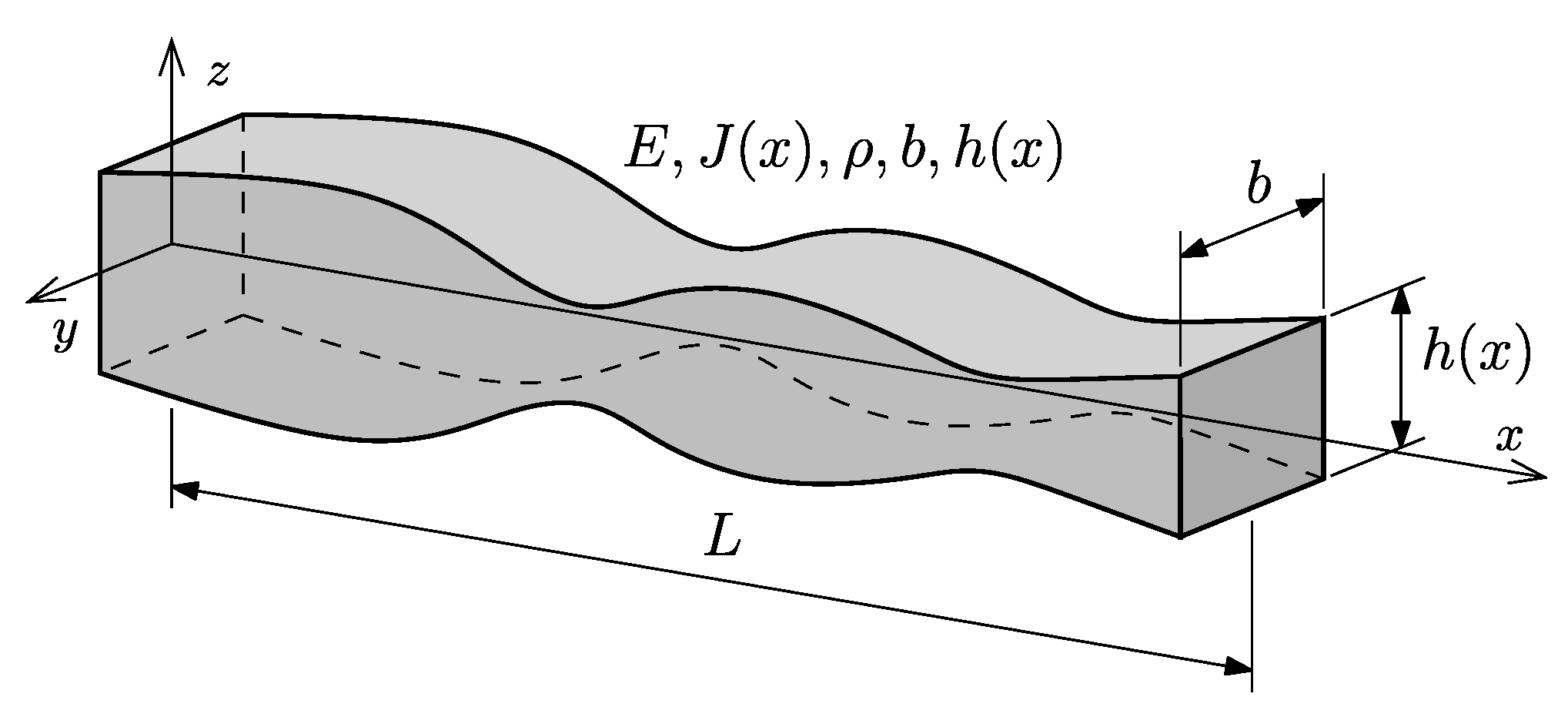
Analyzed element is a beam made of isotropic linear-elastic material of Young’s modulus
E, Poisson number
ν, and density
ρ. The geometry of the beam of a length
L, is described in an orthogonal Cartesian coordinate system
Oxyz. The
Ox axis coincides with the axis of the beam (
Figure 1). The cross-section of the beam is a rectangle with dimensions
b x
h(
x), which are parallel respectively to the
Oy and
Oz axes. The beam is represented by a model according to Euler-Bernoulli beam theory, which assumes that the segment straight and perpendicular to the beam
Ox axis before deformation remains straight and perpendicular after deformation. In this chapter variational formulation of fundamental equations for this problem is briefly introduced.
Let
be flexural stiffness,
be mass per unit and
be transverse deflection. Therefore, strain and kinetic energy are defined as follows:
The overdot stands for the derivative with respect to time
.
The action functional is given by:
where
V is the volume, and the Langragian is of the form:
Applying stationary-action principle and divergence theorem leads to:
After applying equations (2), (3) to (4) and performing transformations, the following formula was obtained:
Formula (5) can be also rewritten and presented as (6). It constitutes Euler-Lagrange equation for a free vibration Euler-Bernoulli beam:
2.2. Dynamics in Finite Element Method Approach
In problems of dynamics and free vibrations described by differential equations, finite element method (FEM) was used. The generalized equation of motion is given as:
where
M is mass matrix,
K is stiffness matrix,
C is damping matrix,
F is the external force vector, and
are displacement, velocity, and acceleration vectors respectively. The matrices of mass, stiffness and damping for entire structure can be defined as follows (the superscript
e denotes single finite element
e):
B(e) stands for linear strain matrix of elasticity of element
e,
D(e) is elasticity matrix of element
e,
N(e) is the shape functions vector of element
e, and
μ(e) is damping parameter of element
e. Here, the damping matrix has been defined so that the system could be considered as underdamped, i.e.:
In the case of forced harmonic vibrations, the external force can be expressed as:
Application of the multimodal approach for forced vibration analysis, leads to the following solution:
where parameter
ω is angular frequency, and coefficients
aC and
aS are defined as:
In this particular optimization problem, since we consider free vibrations, the damping matrix is equal to zero, and no external forces are involved. Thus, equation (8) takes the form of:
The solution and its second time derivative can be expressed as:
where
qa stands for eigenvector. It can be expressed as follows, where
m is number of degrees of freedom:
Assuming that eigenvalue
λ is equal to
ω2, the equation (13) can be written as:
Only the result where
qa ≠ 0 is considered, so to determine eigenvalues and eigenvectors, the following condition has to be met:
2.3. Genetic Algorythms
Genetic Algorithms are optimization techniques inspired by the principles of Darwin’s theory of natural selection and genetics. They are probabilistic algorithms that maintain a population of potential solutions. The solutions are subjected to genetic operations such as selection, crossover, and mutation, that mimic the process of biological evolution. In this section genetic operators and strategies are explained according to the following works [
32,
33,
34,
35]. The algorithms used in this work have been adapted to suit the requirements of the investigated problem. They were created using Python programming language ssupported mainly by following libraries: NumPy, SciPy and Matplotlib.
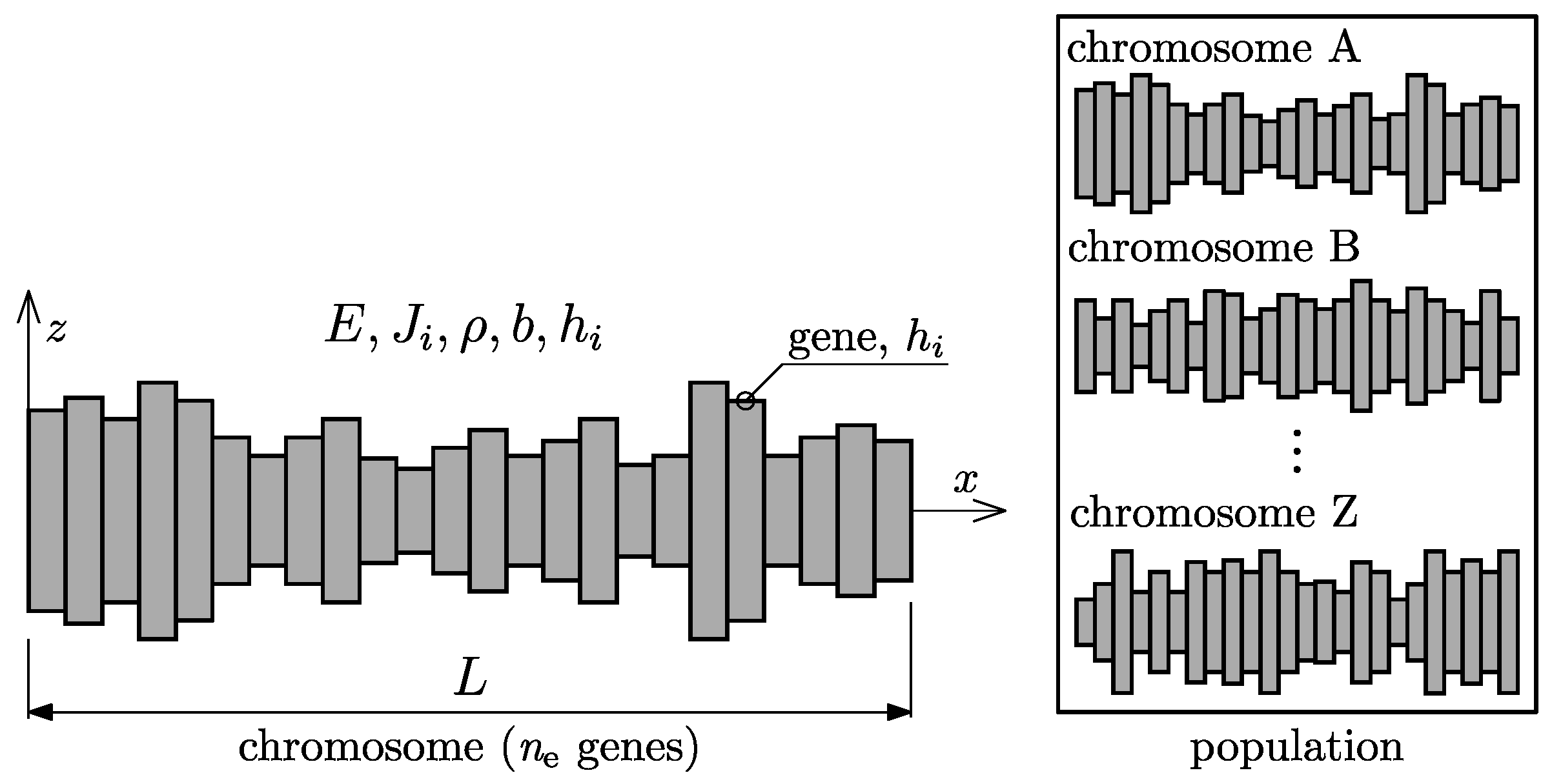
The beam was divided into
ne elements, each of them is of height
hi, and width
b, where
i = 1, 2, …,
ne. Each beam element is a single gene – the basic parameter (variable). The genes are represented by values corresponding to the height of the elements
hi and are joined into a string to form a chromosome. In the presented work, the chromosomes correspond to the individual input beams that constitutes a population.
Figure 2 illustrates the basic concepts behind optimization using presented GA.
The evolution starts with an initial population (population ‘0’). In this study it consists of np individuals (chromosomes). Population ‘0’ is randomly generated from a beta distribution and it is represented by matrix H with dimensions ne x np. The values of H are samples from beta distribution limited by minimum and maximum size of single element height: hmin = 0.5hi and hmax = 2hi, where hi = 10-2 m. The resulting values in H represent a random population of individual solutions for the optimization problem. Each column represents an individual, and each row represents an element with a given position.
The next step is the evaluation of created population. Population evaluation is performed in terms of the objective function which calculates relative difference between two adjacent frequencies. In this study, the objective function is defined as follows:
where
ω is natural frequency of optimized beams, and index
k represents number of natural vibration frequency.
To evaluate created population, it is necessary to determine the natural vibrations frequencies of each individual. The calculations were performed using own FEM procedure (described in previous subsection) built into the algorithm. The individuals of the initial population are assessed in terms of meeting the condition of the objective function maximalization and the best are then subjected to the genetic operators.
One of used operators is mutation. It is applied to all individuals except the best one among the left individuals. The mutation used in presented algorithm involves randomly selecting one gene (element) from the chromosome (beam) and modifying its value based on the chosen mutation type – addition or subtraction of specified value to the initial gene.
Then, the algorithm selects parents using the roulette wheel selection mechanism. It selects parents until their number reaches the desired value (npar). The parent selection algorithm ensures that a certain number of parents npar is selected for crossover by sampling from the cumulative probabilities. The first half of the selected parents is chosen based on their probabilities, while the second half is randomly chosen from the entire population, to avoid premature convergence. This can happen when similar chromosomes become dominant in a population. The algorithm then generates all possible pairs of selected parents for crossover using permutations. Value npar is determined using a mathematical equation based on the population size, the number of remaining individuals, and the number of obtained offspring, to ensure constant population size.
Offspring are created through crossover operations. The algorithm randomly chooses between one-point crossover (OPCX), blend crossover (BLXa) or two-point crossover (TPCX) based on predefined probabilities. OPCX operates on two parents A and B, and selects random point, where the chromosome separates. The first child is created by concatenating the first part of parent A with the second part of parent B. Similarly, the second child is created by concatenating the first part of B with the second part of A. BLXa also combines two parents A and B. It randomly generates new individuals by blending the genes within a specified range based on a defined blending factor. The last one, TPCX performs a two-point crossover between two parents. It selects two random crossover points and creates two children by combining the values before the first crossover point, between the two points, and after the second crossover point.
The resulting offspring are added to the population H. Population size is adjusted to selected value by removing any extra individuals created during crossover operations. Finally, the updated population H is returned by the algorithm, and described procedure is being repeated.
3. Problem Statement
We consider a beam of Young’s modulus E = 205 GPa, Poisson number ν = 0.3, and density ρ = 7850 kg/m3. It was assumed that the length of the beam is L = 1 m.
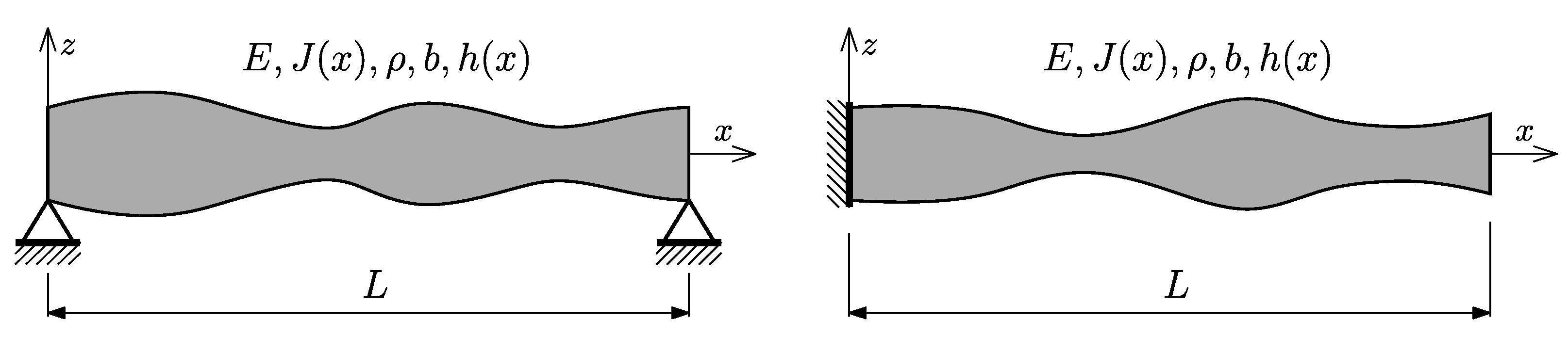
Two types of beam boundary conditions were considered (
Figure 3): simply supported at both ends (SS) and clamped-free (CF). Individuals were divided into
ne elements – 32 or 64. The number of individuals in each population was assumed as 320. The number of created populations (
npop) corresponds with number of elements – it is 200 for
ne = 32 and 300 for
ne = 64. The gaps between adjacent vibration frequencies were investigated in the range of
k from 1 to 8. Moreover, all cases were performed three times, and they differ only in automatically generated (random variable) parameters, to compare the influence on the GA solutions. As a result, the total number of cases subjected to optimization procedure, and then analyzed, is 96.
First, the presented genetic algorithm with integrated FEM-procedure for eigenproblem was used. The number of finite elements in the FEM procedure was equal to the number of genes for each individual n. Depending on the boundary conditions (BC or SS), a number of dynamic degrees of freedom (DOF) was defined, assuming that for each node it can be up to three.
In addition, forced vibration analysis was performed for optimized individuals. The maximum displacement
wmax was analyzed for both boundary conditions cases. The excitation force
F(
t) =
F0(
t) cos(
ωt) is located at the node closest to the support. The deflection has been investigated at the mid-span (for a SS beam) or at the end of the cantilever (for a CF beam). Described dynamic problem was presented in
Figure 4.
The obtained results (optimized individuals) were compared with reference individuals. Reference individual is a prismatic beam of rectangular cross-section b x href, where href was calculated as averaged height of optimized individual. As a result, both individuals – reference and optimized – have the same volume, but different material distribution.
4. Optimization Process Discussion
Here, examples of the optimization process in terms of eigenproblem is presented. The results are presented in plots only for selected cases as examples and briefly described.
Population "0" in each case consists of individuals with completely random genes, arranged without any specific order. The initial signs of individuals' fitness to the defined objective function in this problem start to appear as early as the 3
rd or 4
th population (for a division into
ne = 32 elements) or the 6
th or 7
th population (for a division into
ne = 64 elements). By the 10
th population, specific areas can be observed where each individual experiences a decrease or increase in thickness. With each subsequent population, these areas are more and more clearly marked. The evolution process for example cases is selectively presented in the
Figure 5,
Figure 6 and
Figure 7.
From the population of number about 150 (for ne = 32) and 200 (for ne = 64), the changes between individuals within a particular population as well as changes between neighboring populations are very slight. As a result, the best individuals selected from successive populations no longer differ significantly in terms of matching the fitness function. However, it can be noted that convergence is slowest for elements near the ends of the beam.
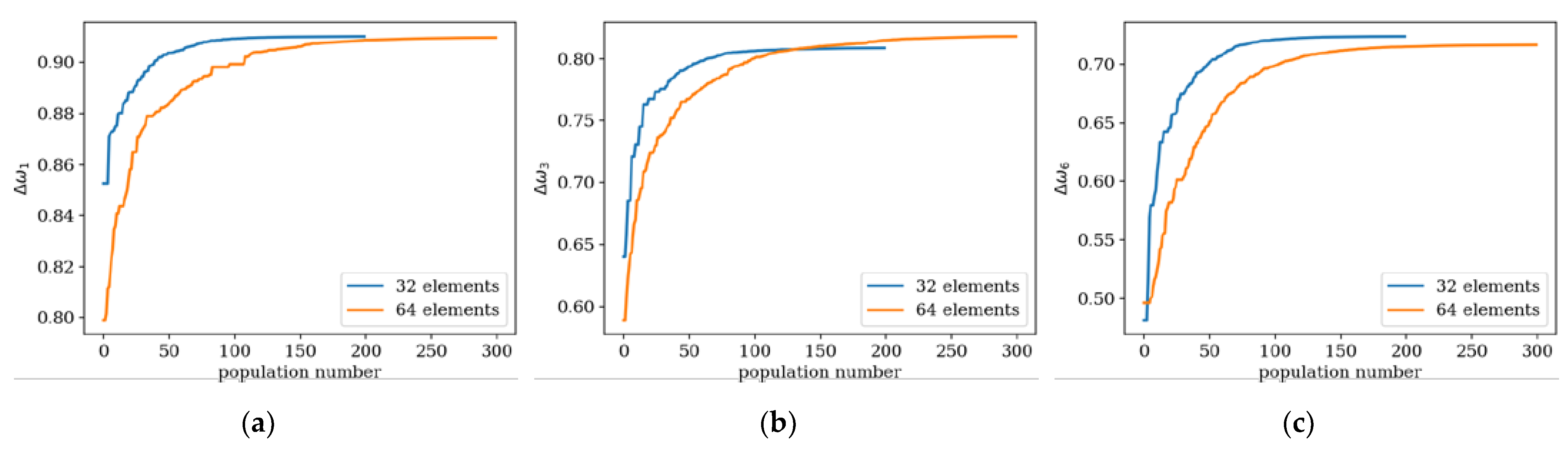
To investigate the influence of the number of elements
n, on the evolution and the final optimization result, additional plots, presented in
Figure 8,
Figure 9 and
Figure 10, were created. The largest differences are observed in the initial populations, reaching up to approximately 10% in the maximum objective function values achieved by the best individual. In the final populations, these differences decrease below 5%. This trend persists when the optimization is focused on values Δ
ω1 to Δ
ω6, corresponding to lower natural frequencies. However, for frequencies Δ
ω7 and Δ
ω8, these differences are higher – up to several percent.
Furthermore, individuals divided into
ne = 32 elements achieve slightly better results in the optimization process for differences in frequencies Δ
ω1 and Δ
ω2. On the other hand, for optimization targeting the highest frequencies Δ
ω7 and Δ
ω8, a division into
ne = 64 elements appears to be more advantageous. These observations apply to both SS and CF beams (
Figure 11).
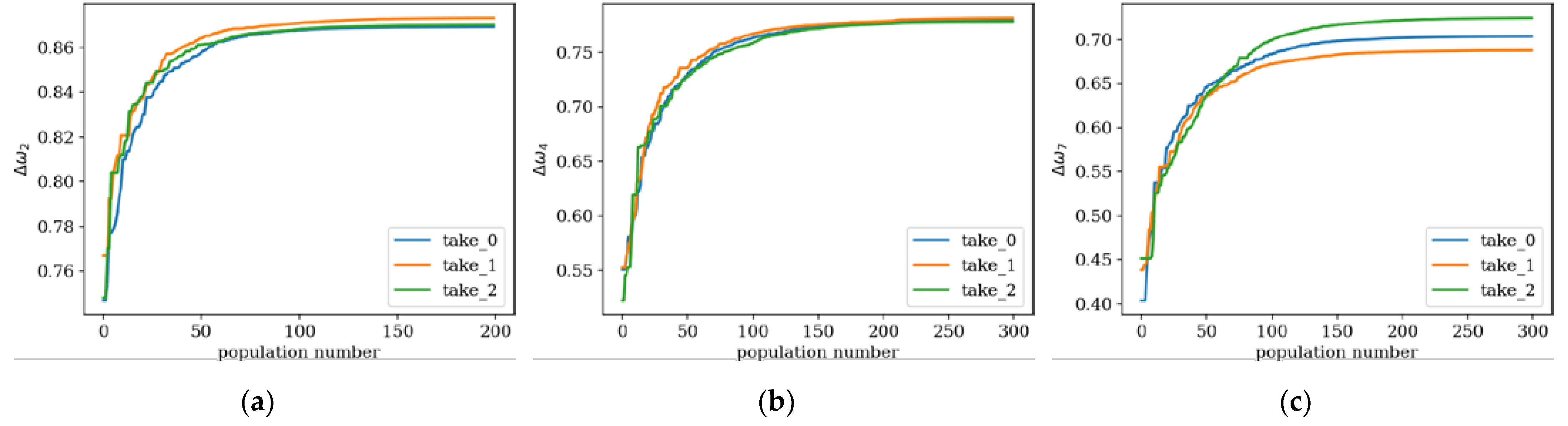
For each optimization case, three attempts were performed – marked as ‘take 0’, ‘take 1’ and ‘take 2’ – to compare random variable parameters’ influence on optimization algorithm results. In most cases the results are not differ significantly, up to 5% between the different approaches (
Figure 12a and 12b). In individual cases, the final optimization result is slightly different (around 7-8%,
Figure 11c), but the results still exhibit extremely strong convergence.
6. Summary and Conclusions
In presented paper, application of Genetic Algorithms for the optimization of simply supported and clamped-free beams was investigated, with a focus on maximizing the gaps between adjacent natural frequencies. The obtained results were analyzed to formulate following conclusions:
The application of GA proved to be effective in optimizing the beams for maximizing the gaps between natural frequencies. Optimized beam exhibited increased gaps between adjacent natural frequencies, according to defined fitness function.
Based on the conducted analyses, it can be concluded that for relatively low natural frequencies (Δω1, Δω2), a division into larger elements can be successfully applied. This will result in shorter computational time while maintaining satisfying results.
The randomness of parameters in the GA has a negligible influence on the final results. It was confirmed by the analysis of three independent approaches for each case. The ultimate results obtained from each approach for individual cases do not significantly differ.
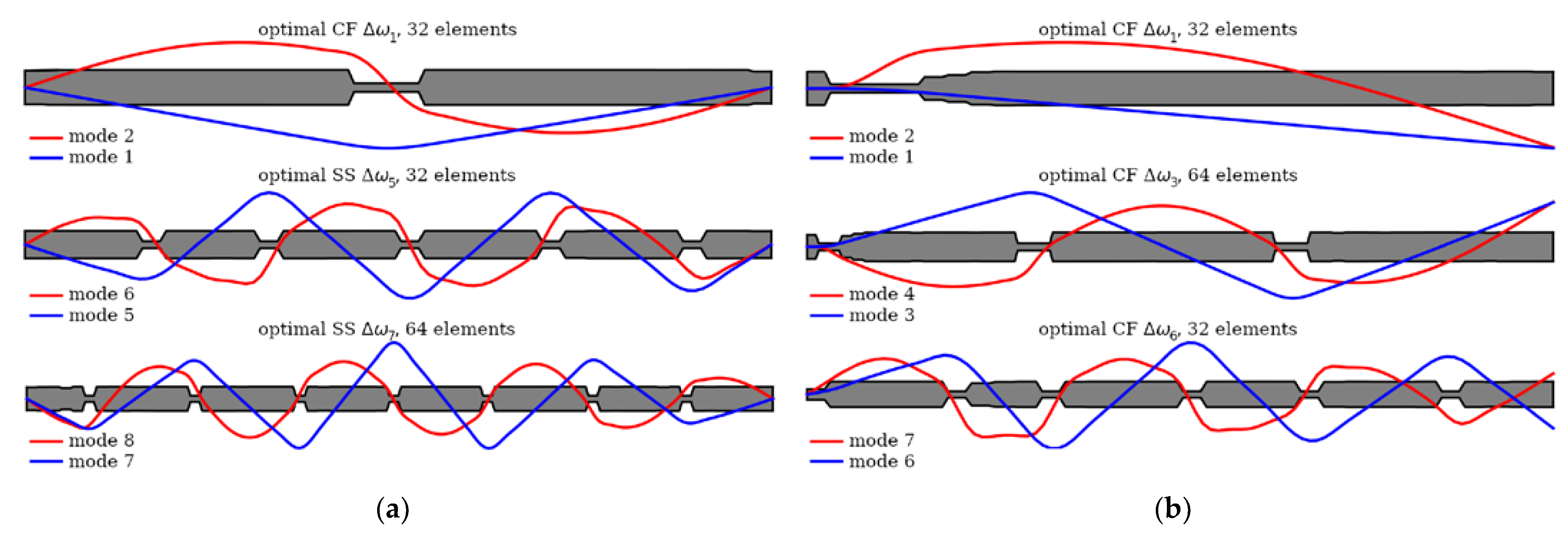
All optimized beams exhibit a periodic-like structure that is strongly correlated with the mode shape. Mass and stiffness reduction occurs at points where the lower mode shape of adjacent frequency k crosses the amplitude axis at 0 and the higher mode shape of frequency k+1 reaches an extreme value.
Both SS and CF optimized beams performed better than the reference beams at higher vibration frequencies.
The optimization aimed at improving the properties of beams related to natural vibrations also resulted in improved dynamic response, where the optimization process had a better impact on SS beams compared to CF beams.
Although the adopted objective function is convenient to use due to limited numerical values, it may, however, lead to solutions in which the absolute value of the gap is not the maximum.
It has to be stressed that in the GA algorithms, as a heuristic, stochastic search method, there is no proof that the solution is the global extreme. However, obtained results suggest that GA can be a valuable tool for engineers and researchers in optimizing beams with specific frequency requirements.
Further research could be directed into: applying more accurate beam models, such as Timoshenko-Ehrenfest thick beam theory, the use of finite elements with variable stiffness, imposing restrictions on the difference in the dimensions of adjacent elements. It would be also desirable to obtain experimental results for dynamics characteristics of optimized elements.
Figure 1.
Computational model of the beam.
Figure 1.
Computational model of the beam.
Figure 2.
Graphic representation of GA basics elements for presented problem.
Figure 2.
Graphic representation of GA basics elements for presented problem.
Figure 3.
Beams boundary conditions: left – simply supported, right – clamped-free.
Figure 3.
Beams boundary conditions: left – simply supported, right – clamped-free.
Figure 4.
Forced vibration analysis, left – SS beam, right – CF beam.
Figure 4.
Forced vibration analysis, left – SS beam, right – CF beam.
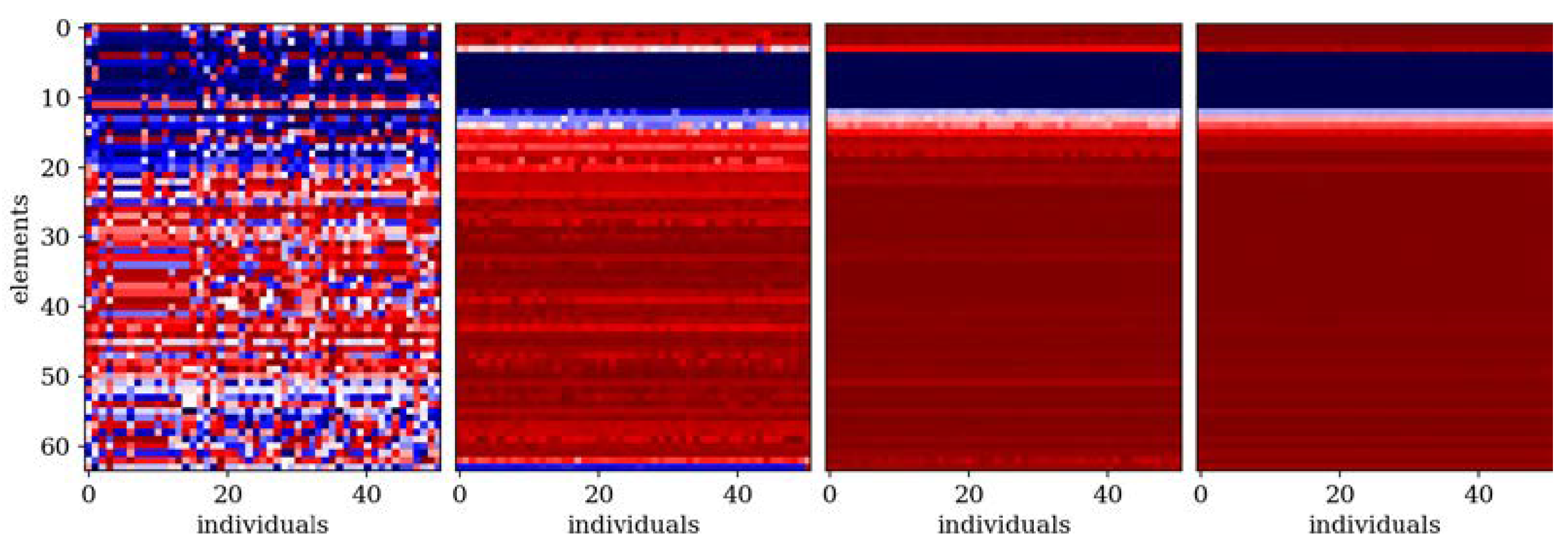
Figure 5.
Evolution of the example population; from left to right: population no 10, 100 and 190. Optimization in terms of Δω8 for SS beam, ne = 32.
Figure 5.
Evolution of the example population; from left to right: population no 10, 100 and 190. Optimization in terms of Δω8 for SS beam, ne = 32.
Figure 6.
Evolution of the example population; from left to right: population no 10, 100, 200 and 290. Optimization in terms of Δω1 for CF beam, ne = 64.
Figure 6.
Evolution of the example population; from left to right: population no 10, 100, 200 and 290. Optimization in terms of Δω1 for CF beam, ne = 64.
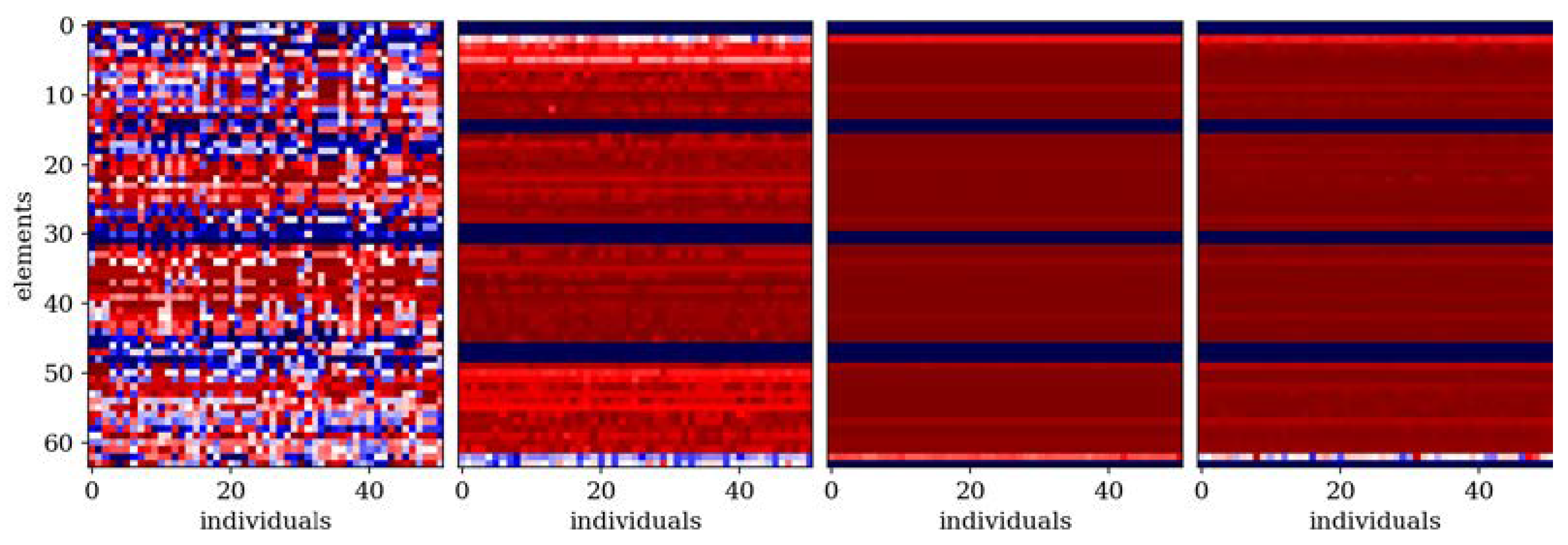
Figure 7.
Evolution of the example population; from left to right: population no 10, 100, 200 and 290. Optimization in terms of Δω4 for CF beam, ne = 64.
Figure 7.
Evolution of the example population; from left to right: population no 10, 100, 200 and 290. Optimization in terms of Δω4 for CF beam, ne = 64.
Figure 8.
Evolution of the best individuals from the example populations (starting with 10th population on the top); optimization for Δω1: (a) SS ne = 32; (b) SS ne = 64; (c) CF ne = 32; (d) CF ne = 64.
Figure 8.
Evolution of the best individuals from the example populations (starting with 10th population on the top); optimization for Δω1: (a) SS ne = 32; (b) SS ne = 64; (c) CF ne = 32; (d) CF ne = 64.
Figure 9.
Evolution of the best individuals from the example populations (starting with 10th population on the top); optimization for Δω4: (a) SS ne = 32; (b) SS ne = 64; (c) CF ne = 32; (d) CF ne = 64.
Figure 9.
Evolution of the best individuals from the example populations (starting with 10th population on the top); optimization for Δω4: (a) SS ne = 32; (b) SS ne = 64; (c) CF ne = 32; (d) CF ne = 64.
Figure 10.
Evolution of the best individuals from the example populations (starting with 10th population on the top); optimization for Δω7: (a) SS ne = 32; (b) SS ne = 64; (c) CF ne = 32; (d) CF ne = 64.
Figure 10.
Evolution of the best individuals from the example populations (starting with 10th population on the top); optimization for Δω7: (a) SS ne = 32; (b) SS ne = 64; (c) CF ne = 32; (d) CF ne = 64.
Figure 11.
Values of the fitness function for the best individuals depending on the population number for ne = 32 and 64 elements; optimization in terms of: (a) Δω1 for SS beam, (b) Δω3 for CF beam, (c) Δω6 for SS beam.
Figure 11.
Values of the fitness function for the best individuals depending on the population number for ne = 32 and 64 elements; optimization in terms of: (a) Δω1 for SS beam, (b) Δω3 for CF beam, (c) Δω6 for SS beam.
Figure 12.
Values of the fitness function for the best individuals from three trials; optimization in terms of: (a) Δω2 for CF beam, ne = 32; (b) Δω4 for CF beam, ne = 64; (c) Δω7 for SS beam, ne = 64.
Figure 12.
Values of the fitness function for the best individuals from three trials; optimization in terms of: (a) Δω2 for CF beam, ne = 32; (b) Δω4 for CF beam, ne = 64; (c) Δω7 for SS beam, ne = 64.
Figure 13.
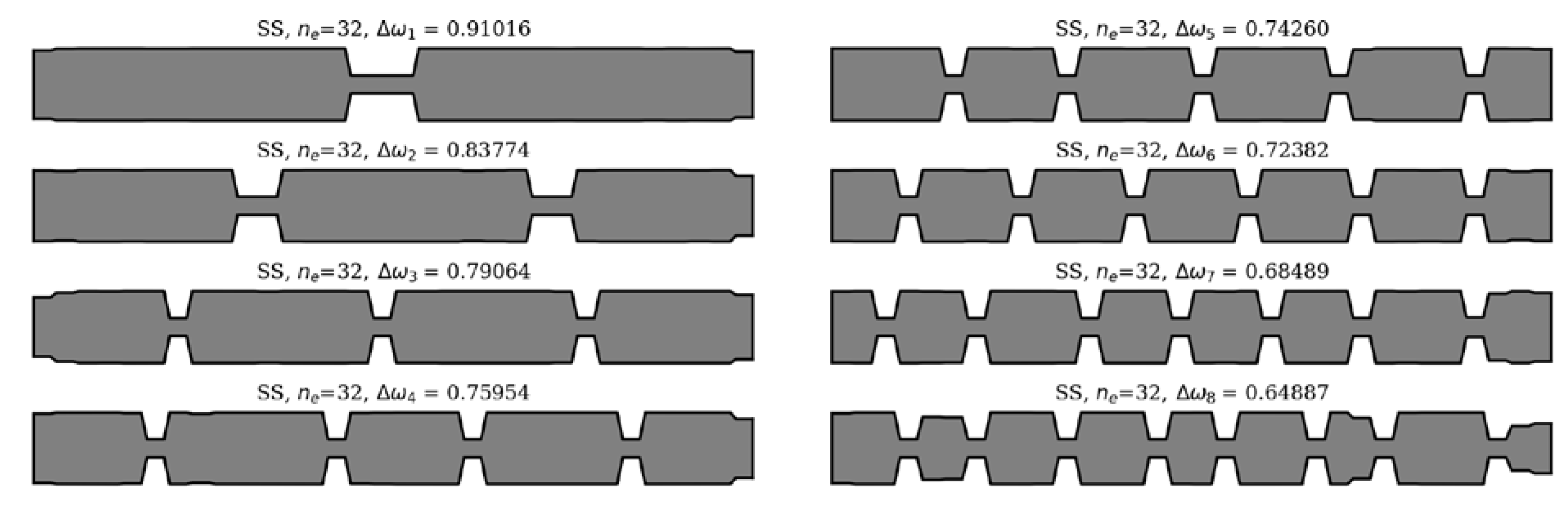
The winning individuals for SS beam, ne = 32.
Figure 13.
The winning individuals for SS beam, ne = 32.
Figure 14.
The winning individuals, for SS beam, ne = 64.
Figure 14.
The winning individuals, for SS beam, ne = 64.
Figure 15.
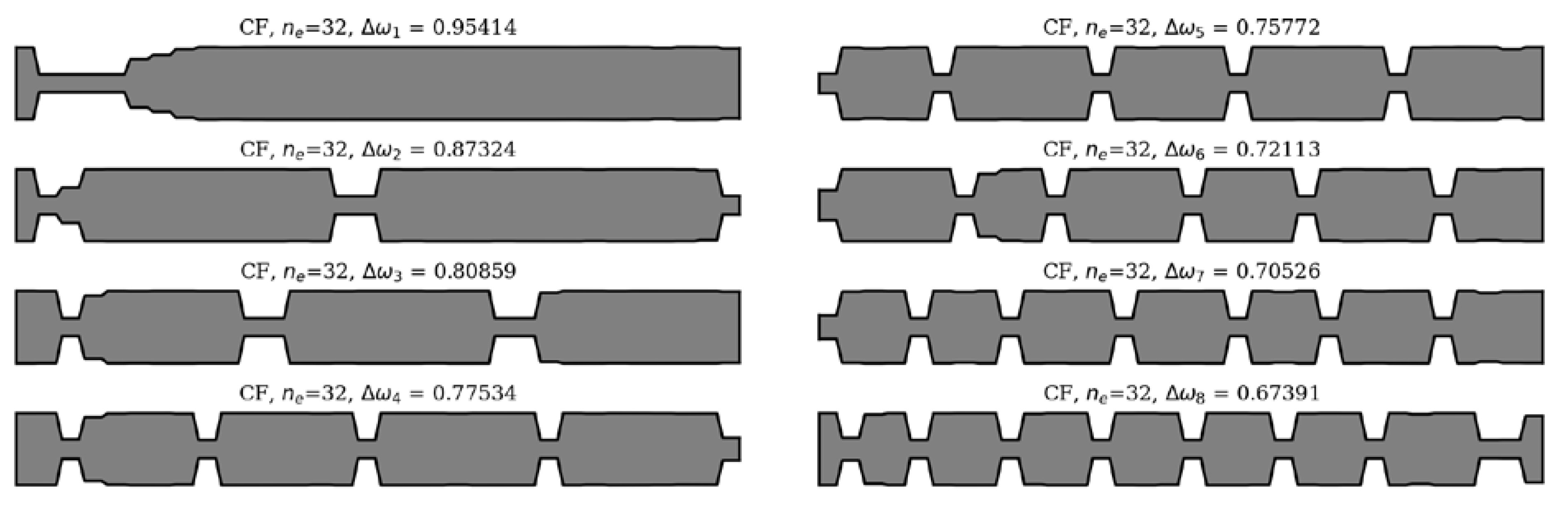
The winning individuals, for CF beam, ne = 32.
Figure 15.
The winning individuals, for CF beam, ne = 32.
Figure 16.
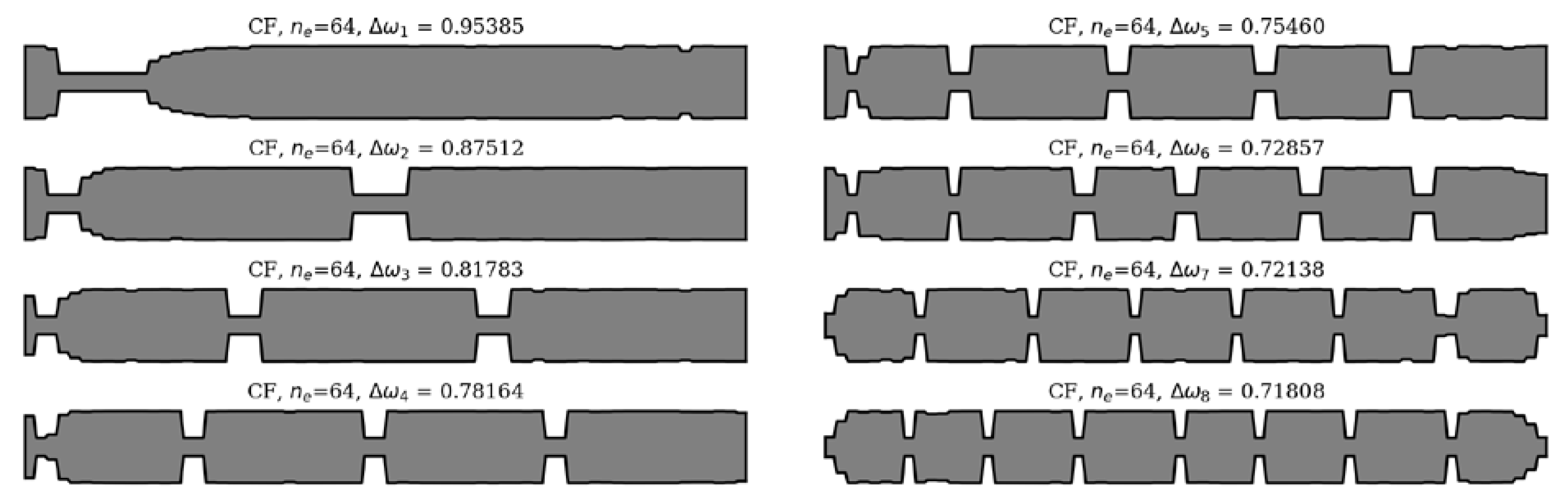
The winning individuals, for CF beam, ne = 64.
Figure 16.
The winning individuals, for CF beam, ne = 64.
Figure 17.
The relationship between the optimized beam cross-section and the mode shapes for chosen: (a) SS beams, (b) CF beams.
Figure 17.
The relationship between the optimized beam cross-section and the mode shapes for chosen: (a) SS beams, (b) CF beams.
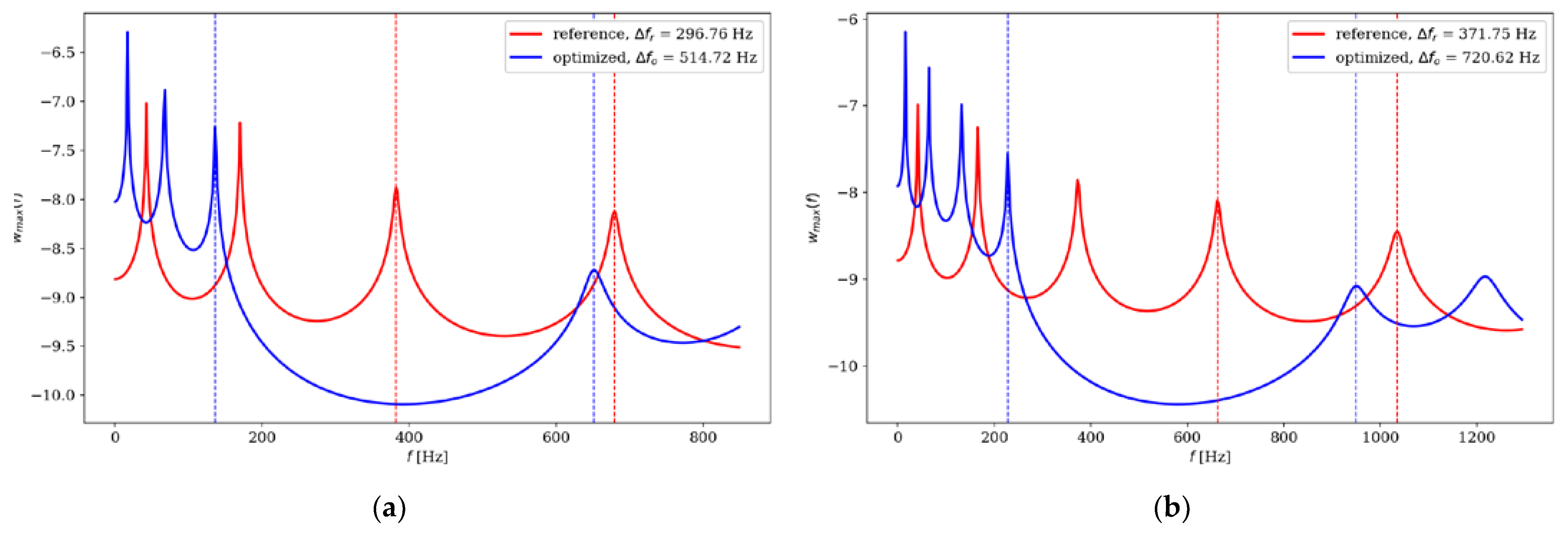
Figure 18.
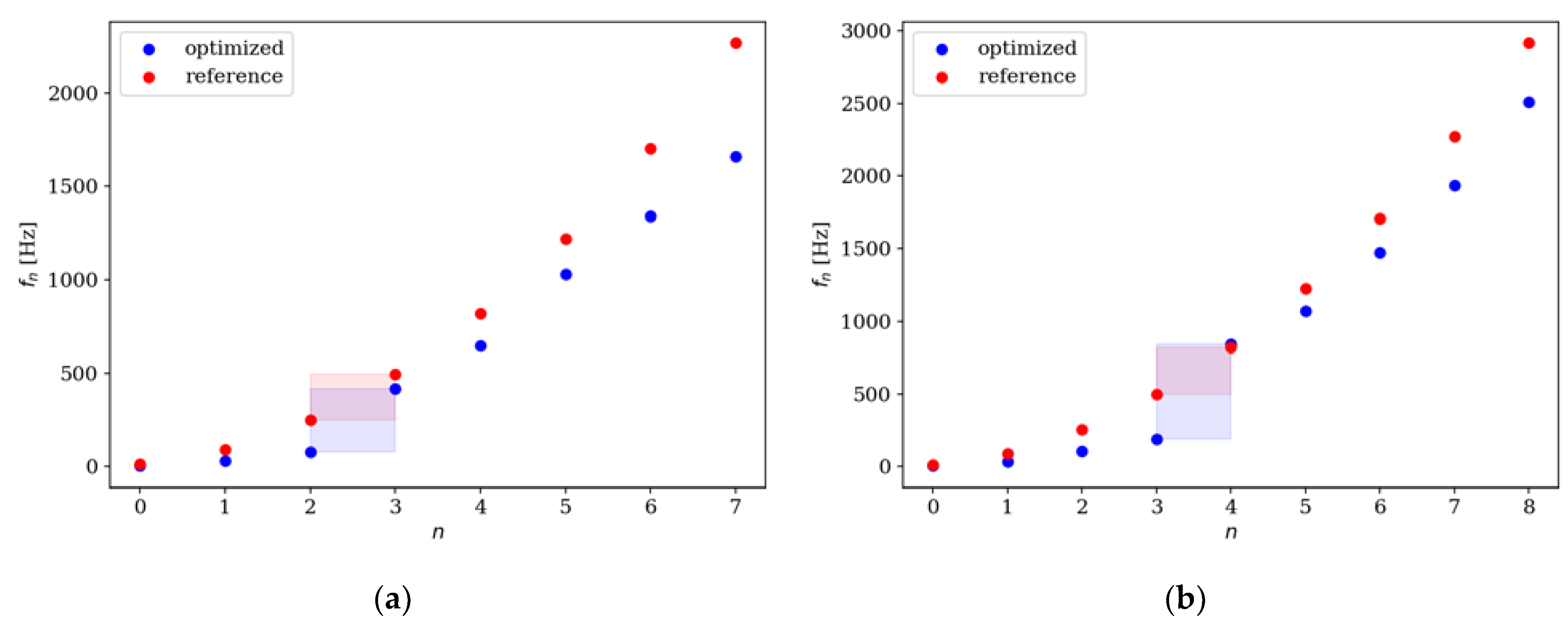
Comparison of the natural frequencies of reference and optimized beams for SS beam ne = 32; (a) Δω1; (b) Δω2.
Figure 18.
Comparison of the natural frequencies of reference and optimized beams for SS beam ne = 32; (a) Δω1; (b) Δω2.
Figure 19.
Comparison of the natural frequencies of reference and optimized beams for CF beam ne = 32; (a) Δω3; (b) Δω4.
Figure 19.
Comparison of the natural frequencies of reference and optimized beams for CF beam ne = 32; (a) Δω3; (b) Δω4.
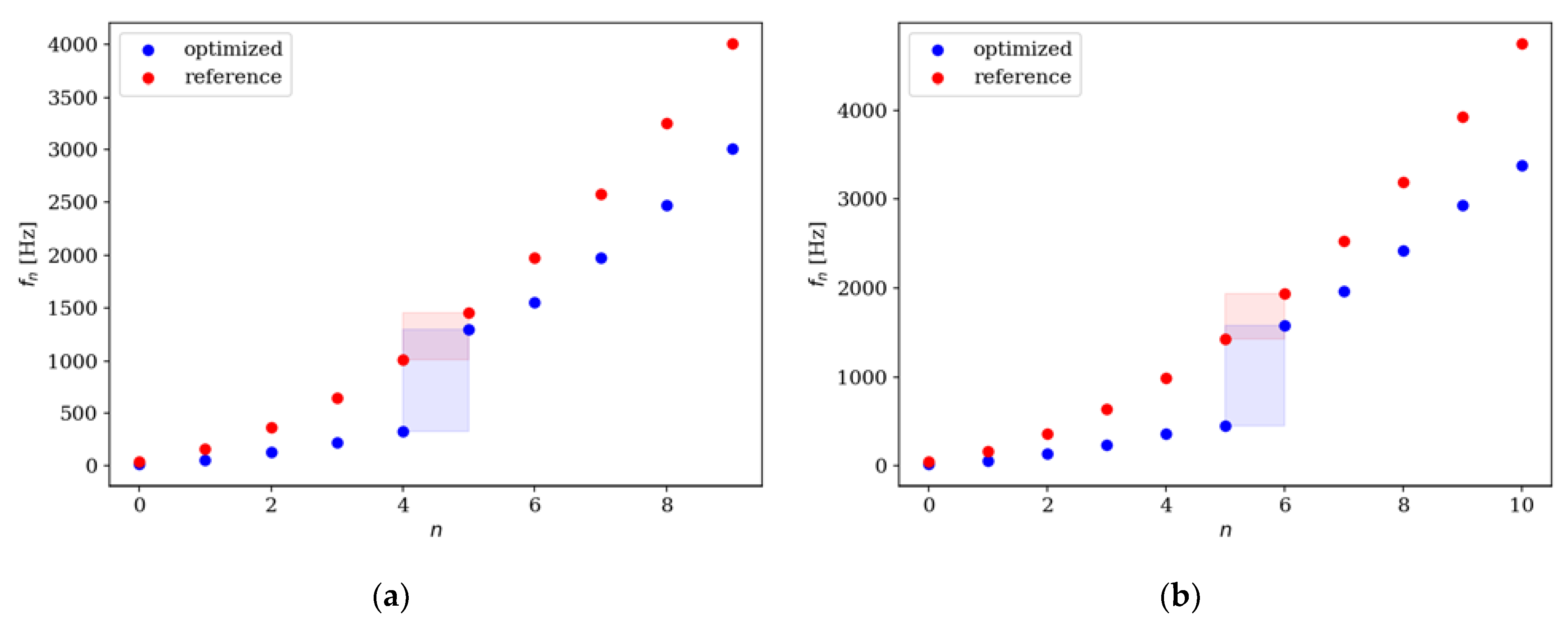
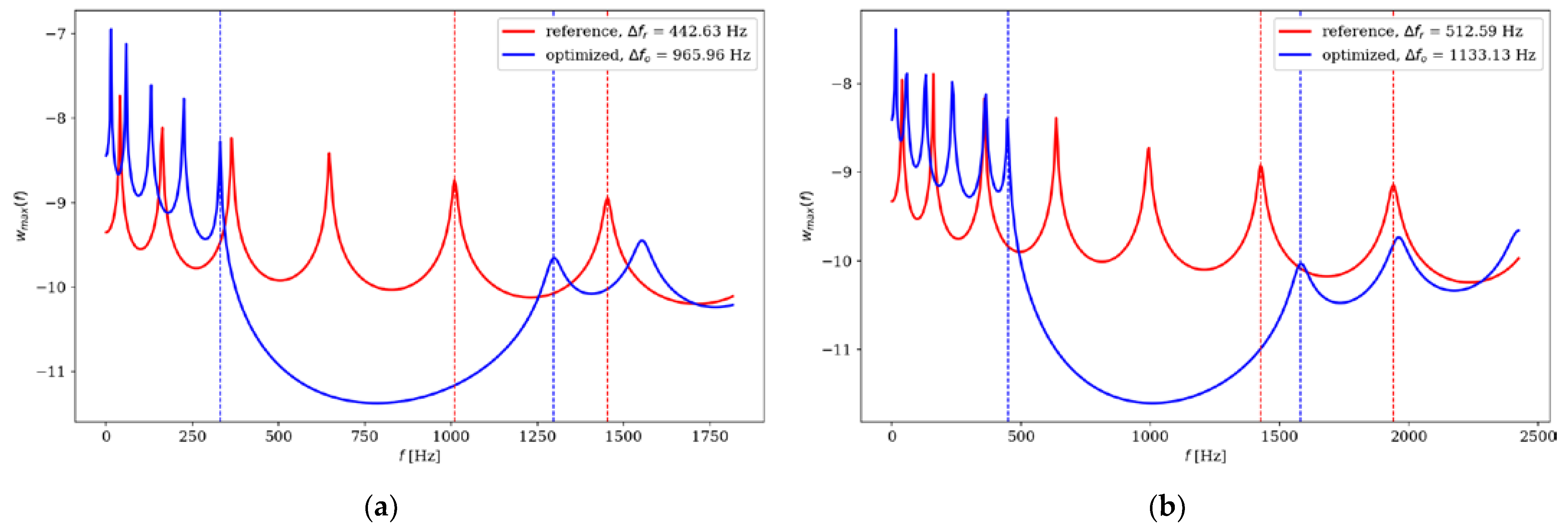
Figure 20.
Comparison of the natural frequencies of reference and optimized beams for SS beam ne = 64; (a) Δω5; (b) Δω6.
Figure 20.
Comparison of the natural frequencies of reference and optimized beams for SS beam ne = 64; (a) Δω5; (b) Δω6.
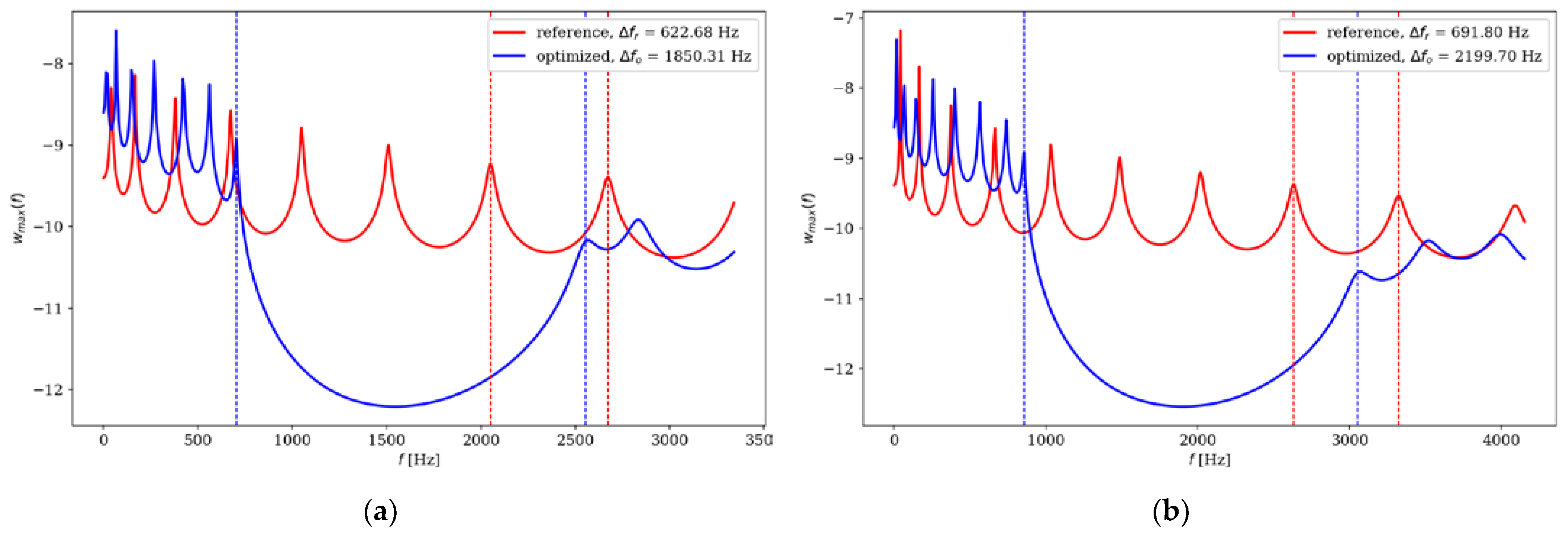
Figure 21.
Comparison of the natural frequencies of reference and optimized beams for CF beam ne = 64; (a) Δω7; (b) Δω8.
Figure 21.
Comparison of the natural frequencies of reference and optimized beams for CF beam ne = 64; (a) Δω7; (b) Δω8.
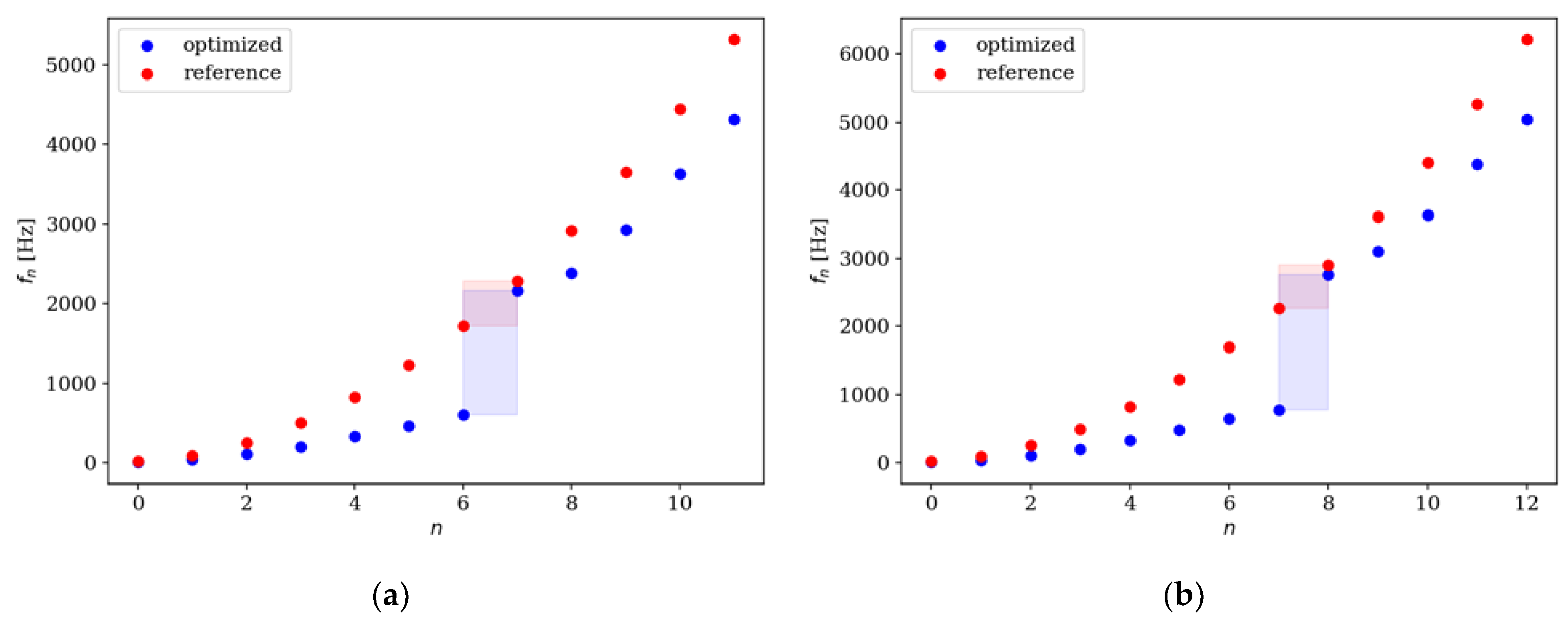
Figure 22.
Comparison of the amplitude response of reference and optimized beams for CF beam ne = 32; (a) Δω1; (b) Δω2.
Figure 22.
Comparison of the amplitude response of reference and optimized beams for CF beam ne = 32; (a) Δω1; (b) Δω2.
Figure 23.
Comparison of the amplitude response of reference and optimized beams for CF beam ne = 32; (a) Δω3; (b) Δω4.
Figure 23.
Comparison of the amplitude response of reference and optimized beams for CF beam ne = 32; (a) Δω3; (b) Δω4.
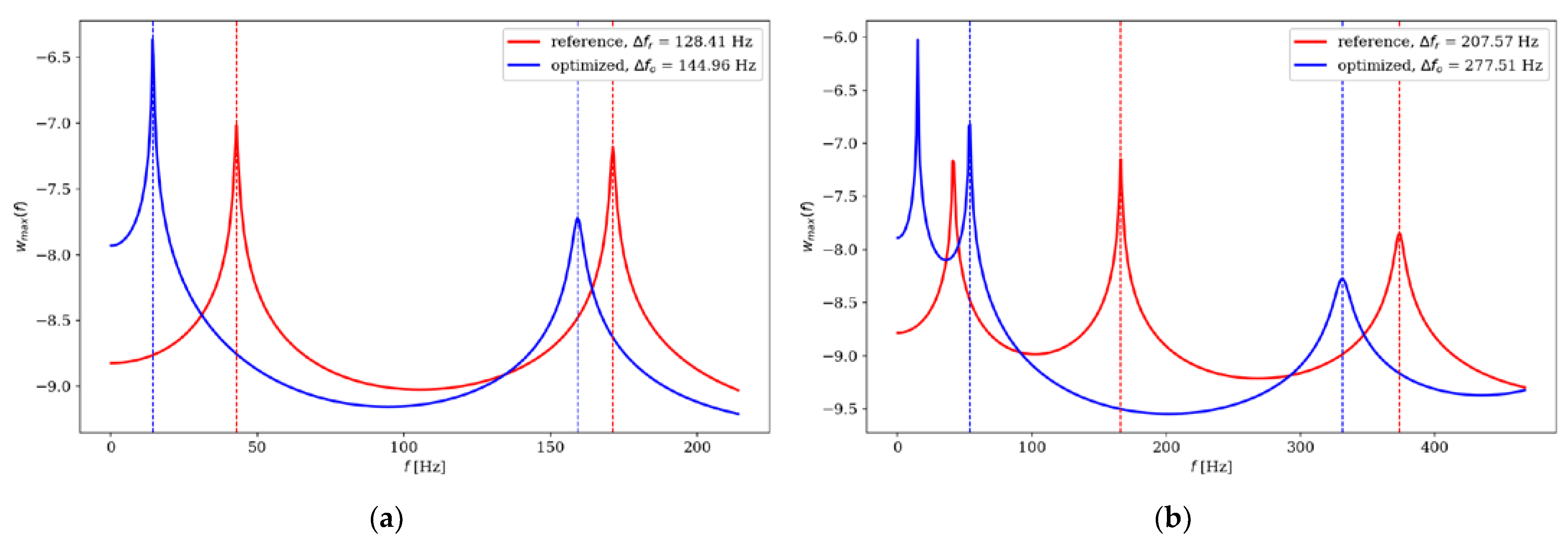
Figure 24.
Comparison of the amplitude response of reference and optimized beams for CF beam ne = 64; (a) Δω5; (b) Δω6.
Figure 24.
Comparison of the amplitude response of reference and optimized beams for CF beam ne = 64; (a) Δω5; (b) Δω6.
Figure 25.
Comparison of the amplitude response of reference and optimized beams for CF beam ne = 64; (a) Δω7; (b) Δω8.
Figure 25.
Comparison of the amplitude response of reference and optimized beams for CF beam ne = 64; (a) Δω7; (b) Δω8.
Table 1.
The differences between objective function values between beams divided into ne = 32 and ne = 64 elements.
Table 1.
The differences between objective function values between beams divided into ne = 32 and ne = 64 elements.
| k |
ne
|
SS beam |
CF beam |
| Δωk
|
Difference, % |
Δωk
|
Difference, % |
| 1 |
32 |
0,91016 |
0,05 |
0,95414 |
0,03 |
| 64 |
0,90969 |
0,95385 |
| 2 |
32 |
0,83774 |
0,04 |
0,87324 |
0,21 |
| 64 |
0,83743 |
0,87512 |
| 3 |
32 |
0,79064 |
0,31 |
0,80859 |
1,13 |
| 64 |
0,79311 |
0,81783 |
| 4 |
32 |
0,75954 |
0,76 |
0,77534 |
0,81 |
| 64 |
0,76539 |
0,78164 |
| 5 |
32 |
0,74260 |
0,32 |
0,75772 |
0,41 |
| 64 |
0,74499 |
0,75460 |
| 6 |
32 |
0,72382 |
1,00 |
0,72113 |
1,02 |
| 64 |
0,71665 |
0,72857 |
| 7 |
32 |
0,68489 |
5,45 |
0,70526 |
2,23 |
| 64 |
0,72434 |
0,72138 |
| 8 |
32 |
0,64887 |
9,92 |
0,67391 |
6,15 |
| 64 |
0,72036 |
0,71808 |
Table 2.
Comparison of the amplitude response of reference and optimized beams divided into ne = 32 elements.
Table 2.
Comparison of the amplitude response of reference and optimized beams divided into ne = 32 elements.
| k |
The individual |
SS beam |
CF beam |
| Δf
|
Difference, % |
Δf
|
Difference, % |
| 1 |
reference |
128,41 |
12,89 |
76,86 |
-17,60 * |
| optimized |
144,96 |
63,33 |
| 2 |
reference |
207,57 |
33,69 |
165,10 |
30,82 |
| optimized |
277,51 |
215,99 |
| 3 |
reference |
396,76 |
29,73 |
242,55 |
39,17 |
| optimized |
514,72 |
337,55 |
| 4 |
reference |
371,75 |
93,85 |
324,18 |
101,80 |
| optimized |
720,62 |
654,18 |
| 5 |
reference |
445,22 |
108,18 |
406,84 |
95,39 |
| optimized |
926,86 |
794,94 |
| 6 |
reference |
510,52 |
119,02 |
472,00 |
108,36 |
| optimized |
1118,15 |
983,48 |
| 7 |
reference |
570,74 |
123,02 |
533,87 |
119,57 |
| optimized |
1272,85 |
1172,22 |
| 8 |
reference |
603,70 |
137,95 |
574,00 |
130,03 |
| optimized |
1436,51 |
1320,39 |
Table 3.
Comparison of the amplitude response of reference and optimized beams divided into ne = 64 elements.
Table 3.
Comparison of the amplitude response of reference and optimized beams divided into ne = 64 elements.
| k |
The individual |
SS beam |
CF beam |
| Δf
|
Difference, % |
Δf
|
Difference, % |
| 1 |
reference |
126,86 |
13,86 |
76,42 |
-8,75 * |
| optimized |
144,44 |
69,73 |
| 2 |
reference |
206,89 |
34,07 |
166,26 |
16,47 |
| optimized |
277,38 |
193,65 |
| 3 |
reference |
285,49 |
62,88 |
242,55 |
39,13 |
| optimized |
465,01 |
337,45 |
| 4 |
reference |
370,80 |
94,92 |
247,30 |
47,54 |
| optimized |
722,76 |
364,87 |
| 5 |
reference |
442,63 |
118,23 |
331,71 |
82,80 |
| optimized |
965,96 |
606,36 |
| 6 |
reference |
512,59 |
121,06 |
405,86 |
101,58 |
| optimized |
1133,13 |
818,15 |
| 7 |
reference |
522,68 |
254,00 |
475,61 |
127,38 |
| optimized |
1850,31 |
1081,46 |
| 8 |
reference |
691,80 |
217,97 |
565,22 |
176,29 |
| optimized |
2199,70 |
1561,67 |