Submitted:
13 June 2023
Posted:
19 June 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Low–Frequency Oscillation and Overvoltage Characteristics of the Contact Line
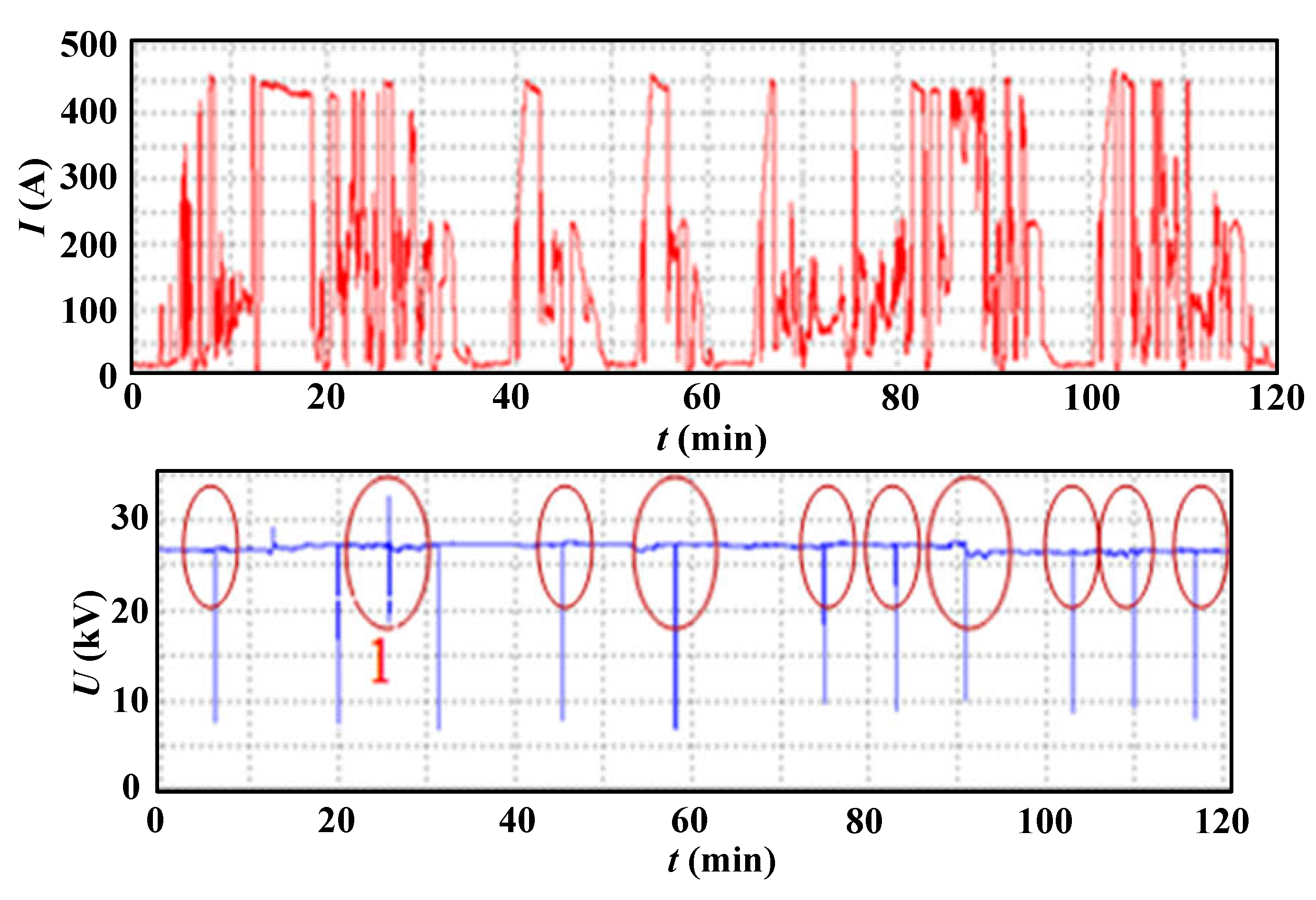
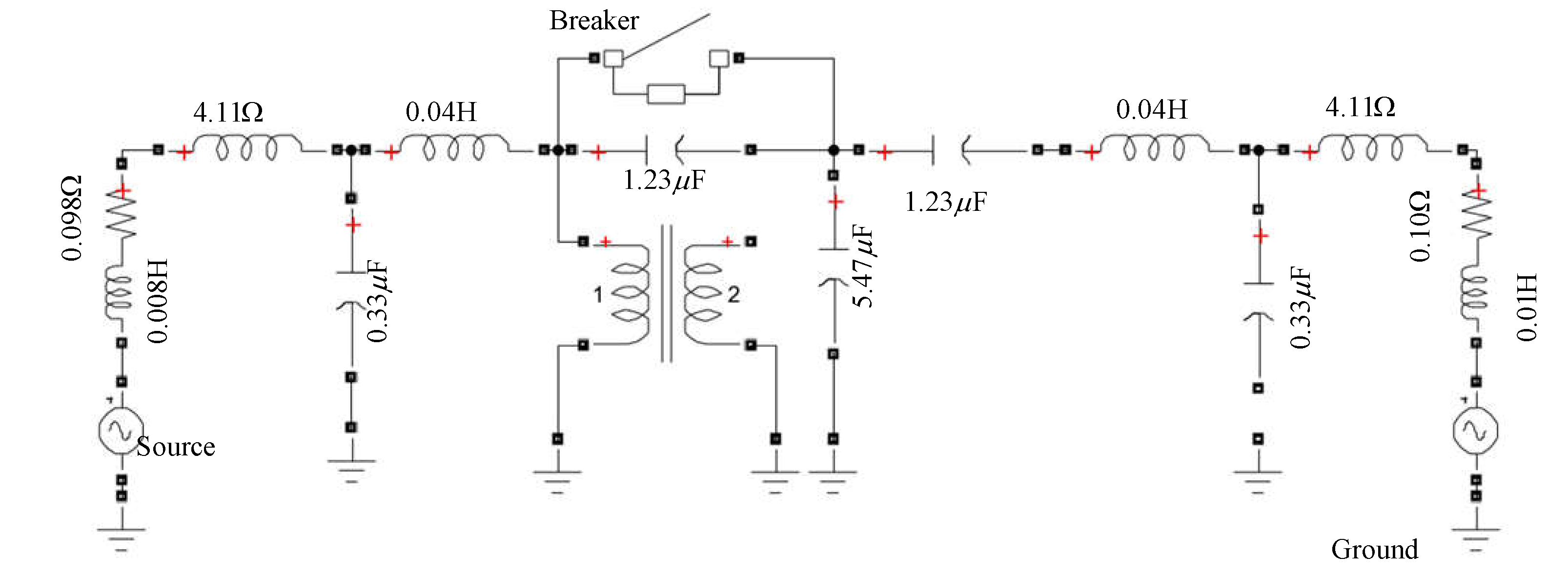
2.1. Test method and test process
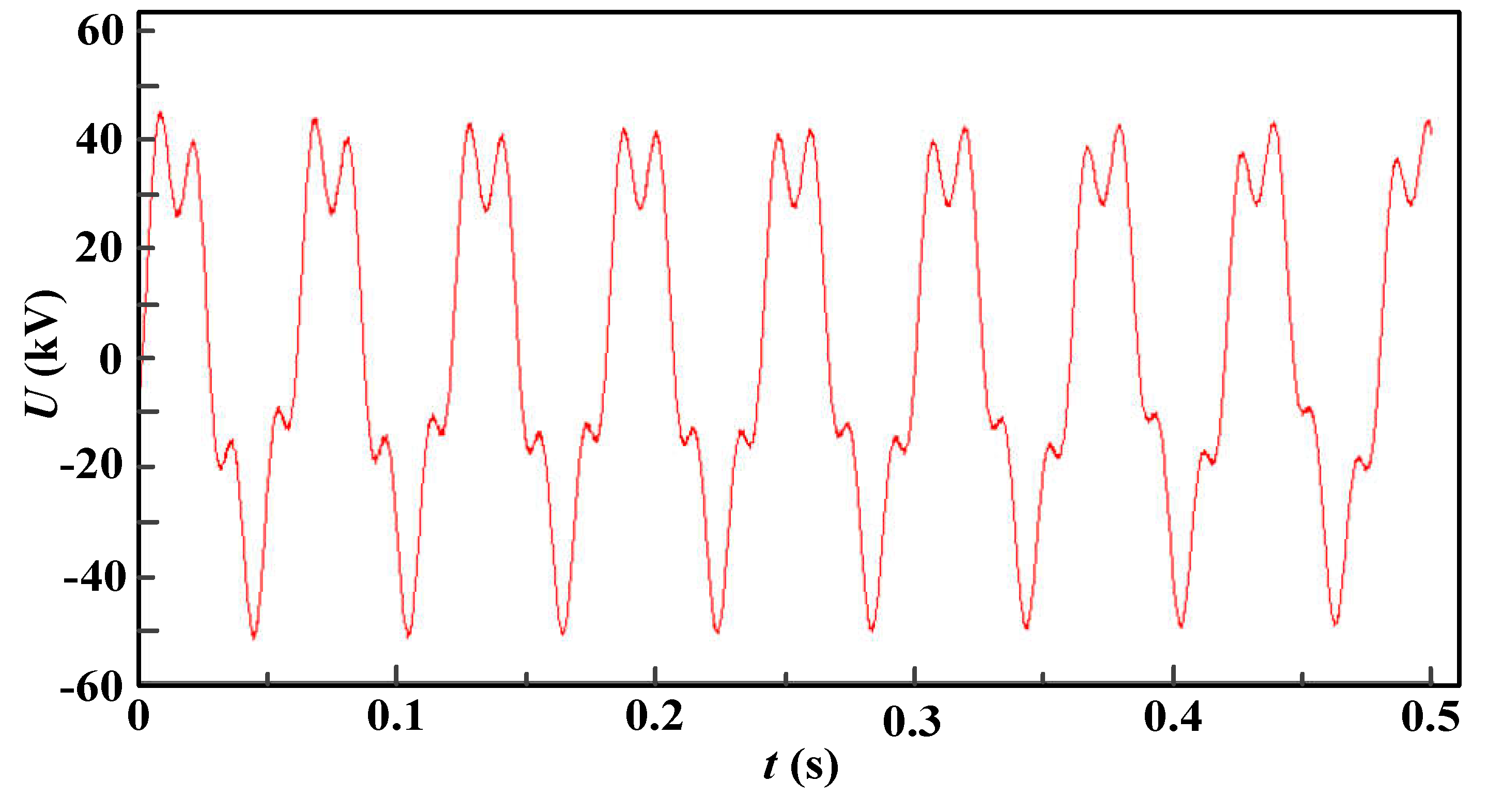
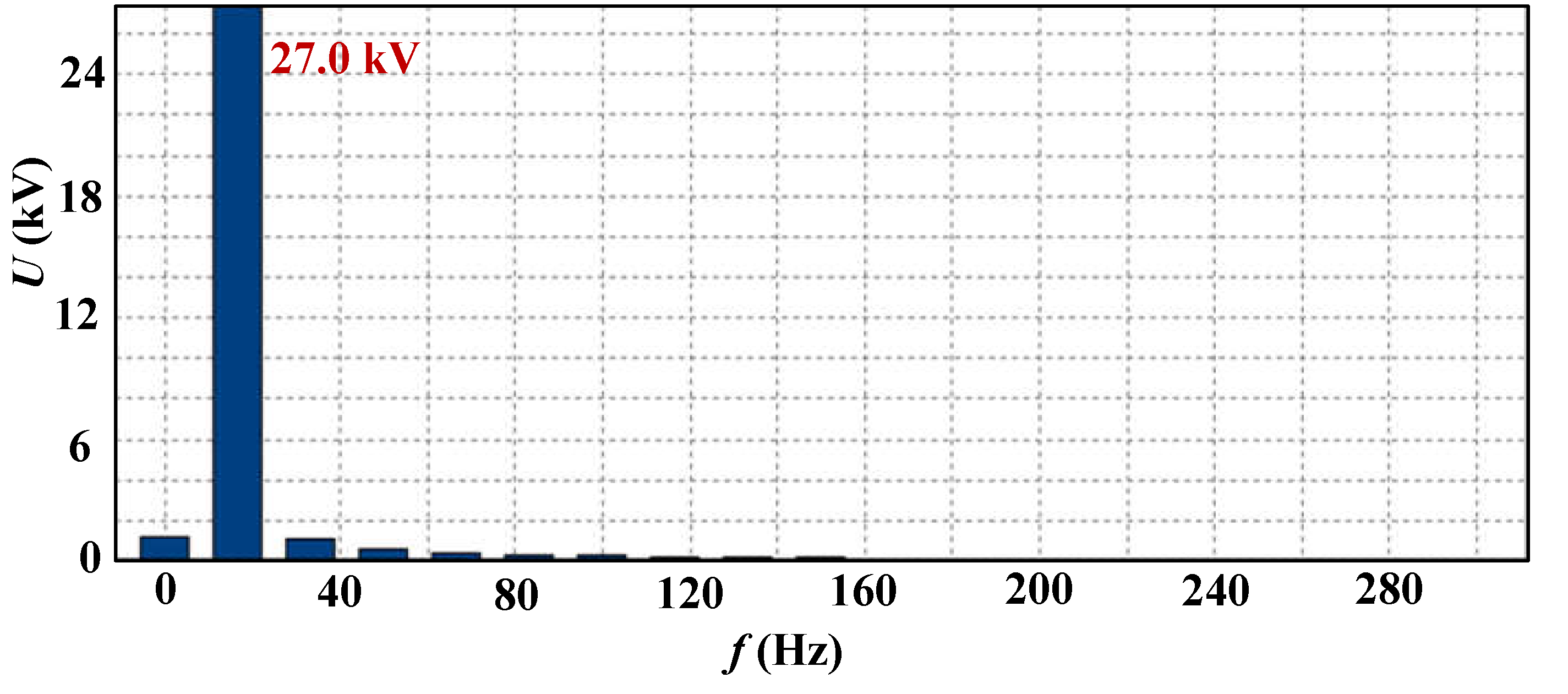
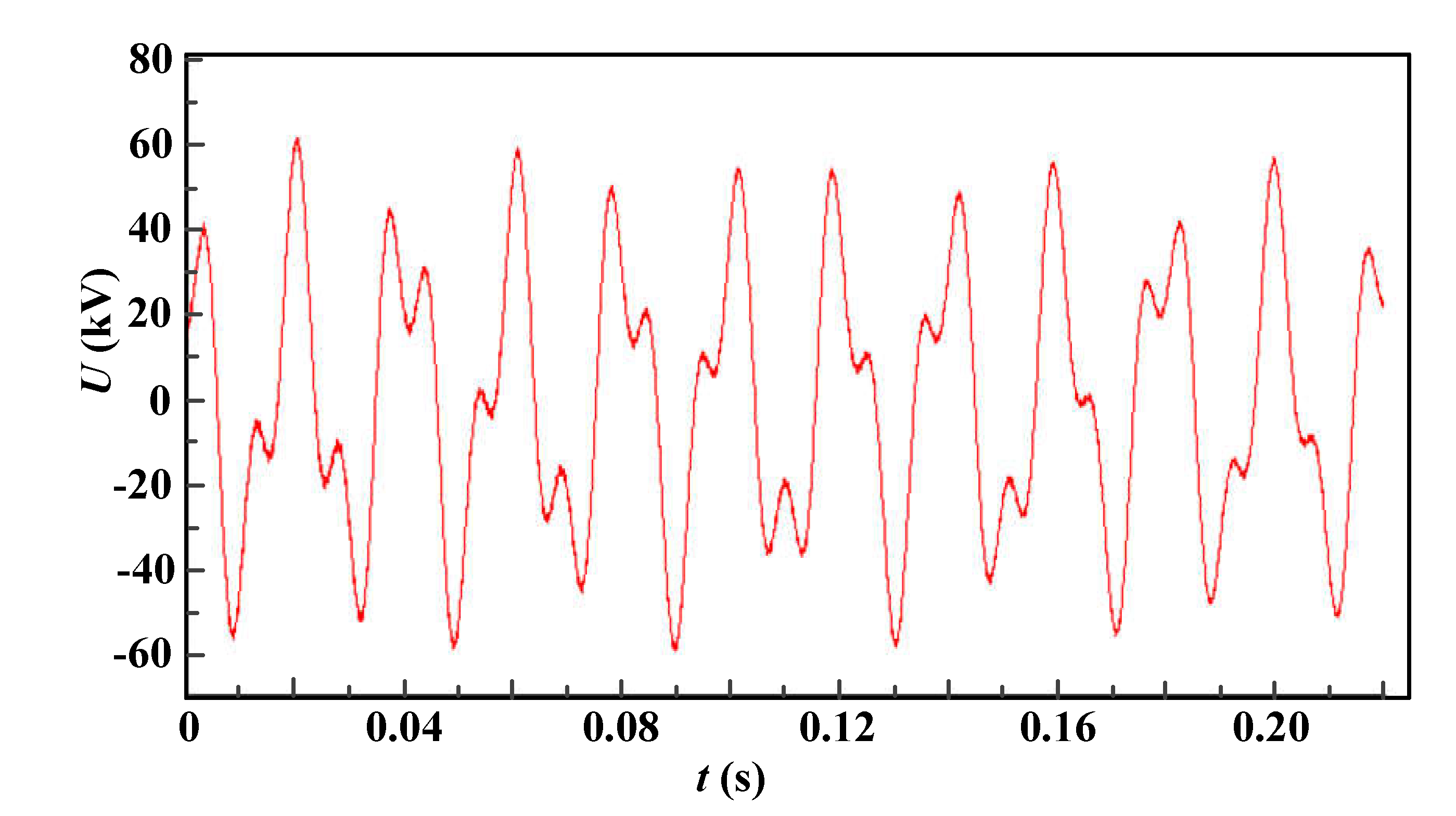
2.2. Wave characteristics and laws
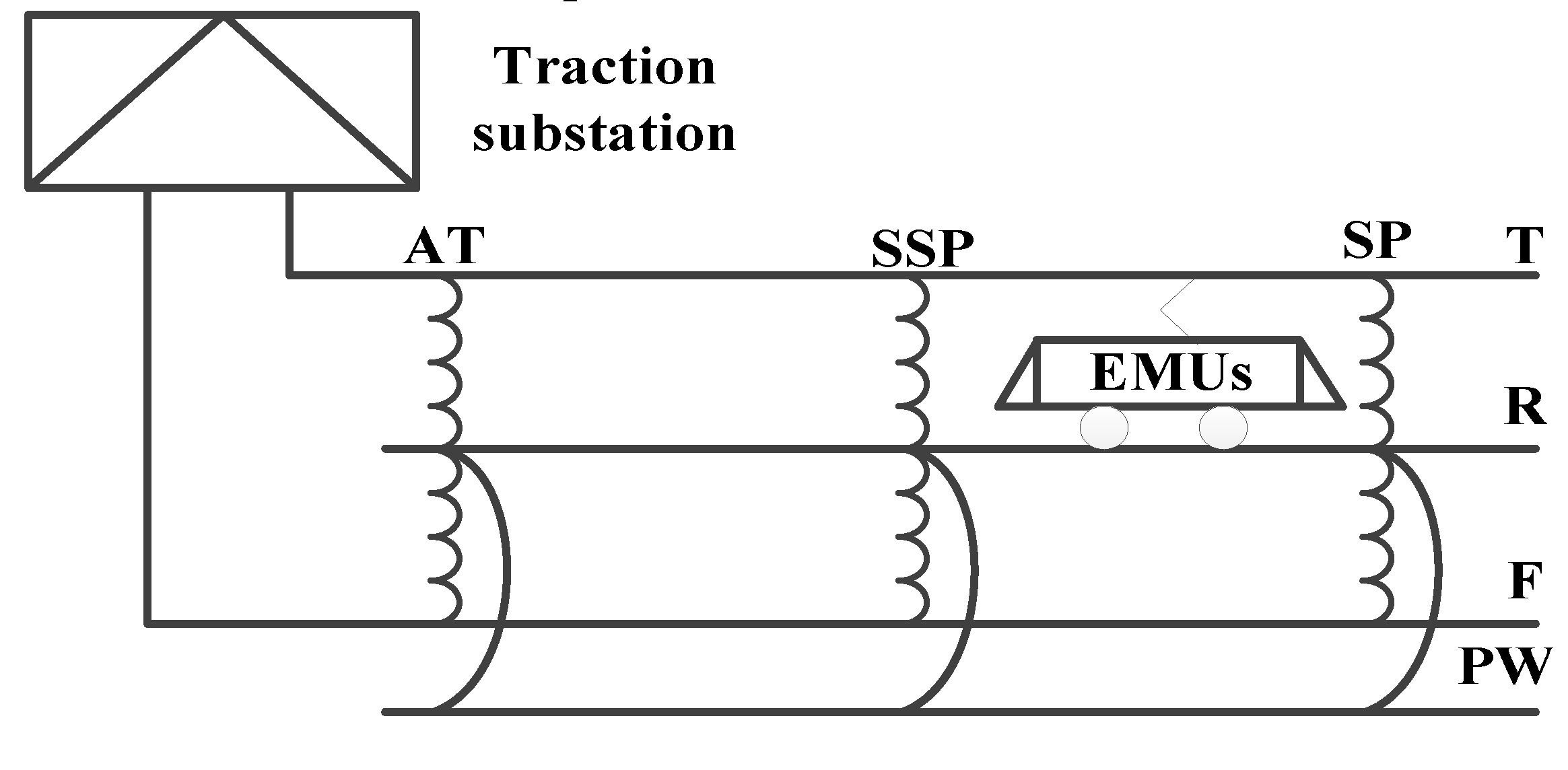
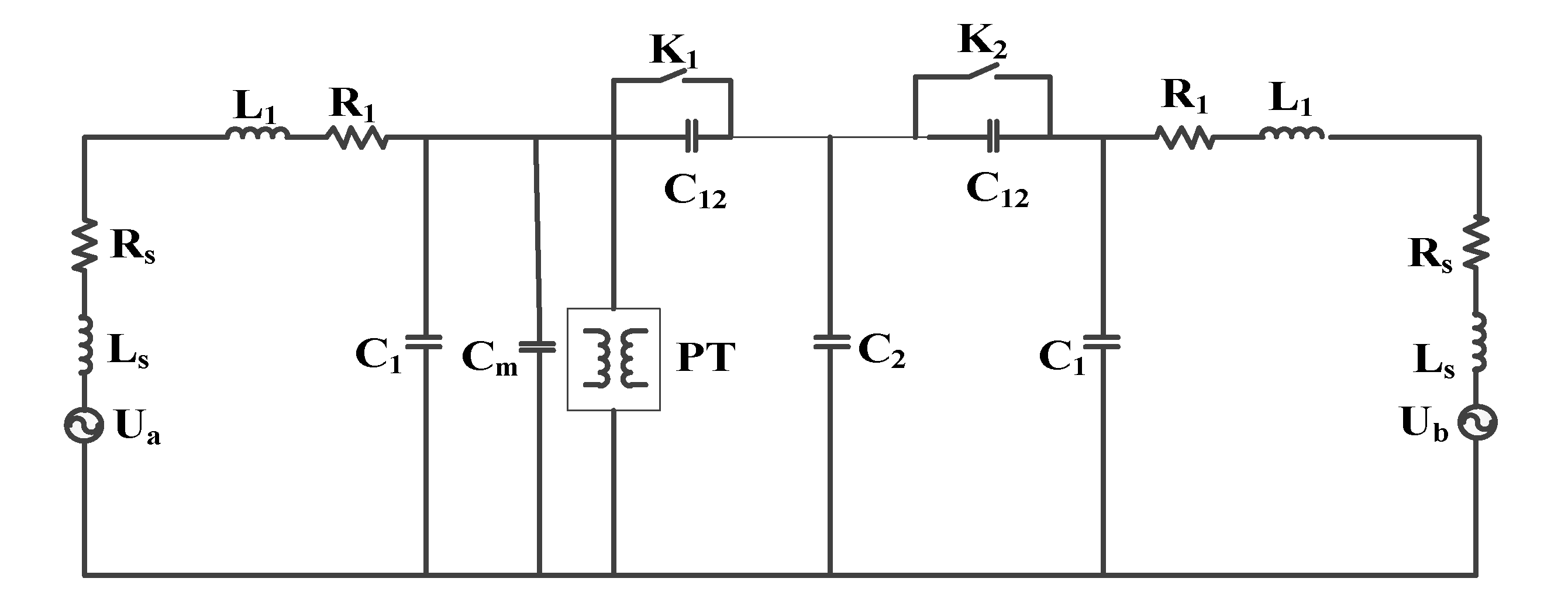
3. Vehicle–Line–Institute Model and Oscillation Characteristics
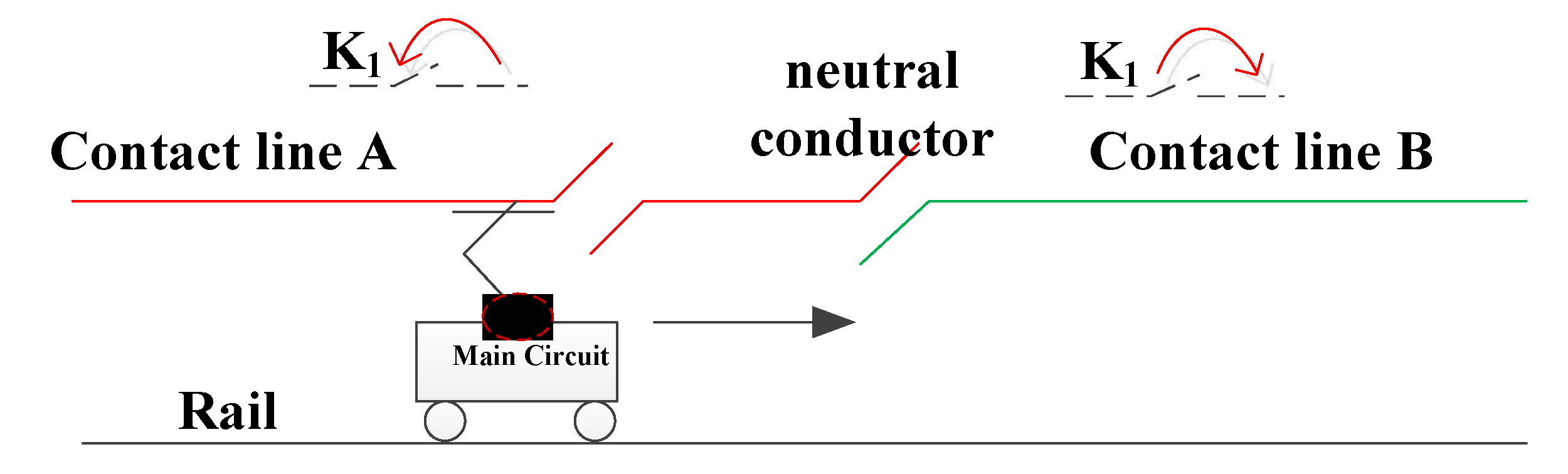
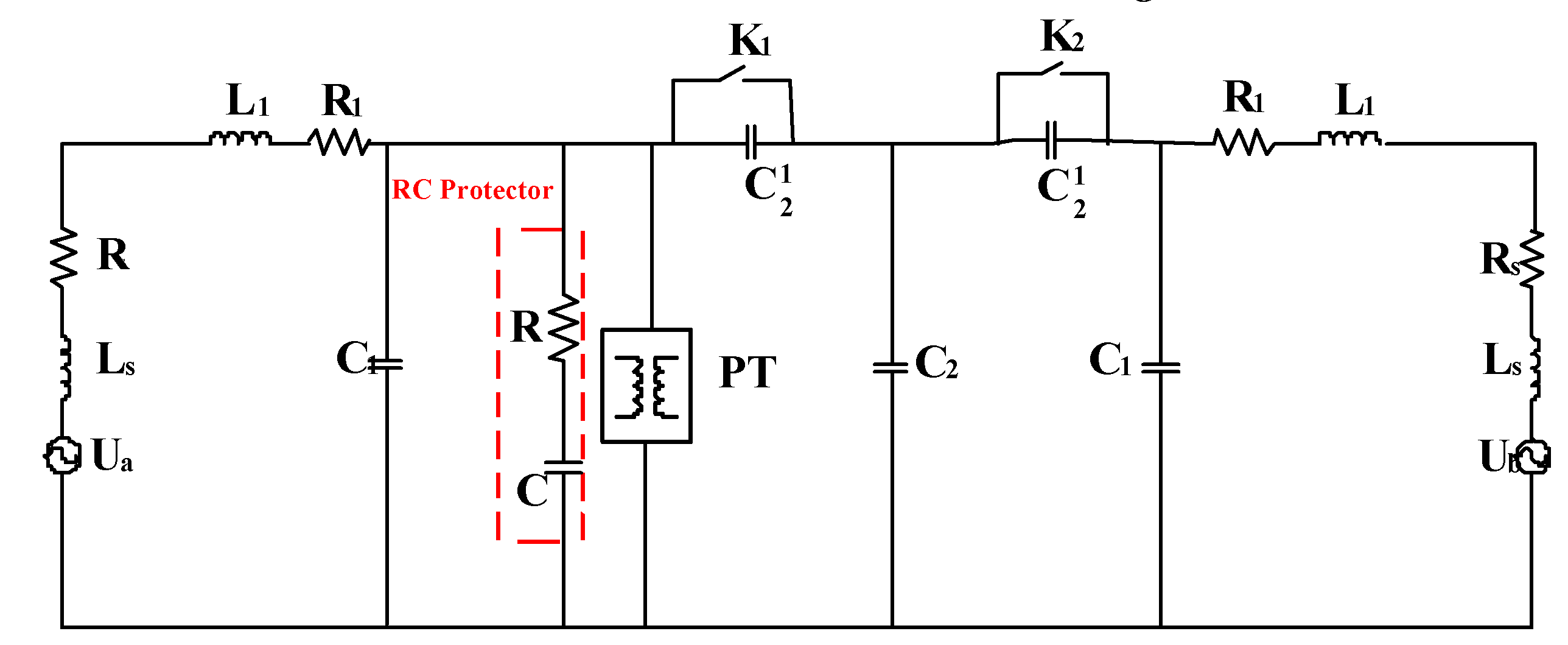
3.1. Research on the model of train passing through the neutral zone
| c | T1 | R1 | P1 | F1 | T2 | R2 | P2 | F2 |
|---|---|---|---|---|---|---|---|---|
| T1 | 13.12 | –0.83 | –1.74 | –2.04 | –2.00 | –0.41 | –0.36 | –0.56 |
| R1 | –0.83 | 20.12 | –0.63 | –0.23 | –0.41 | –0.44 | –0.12 | –0.09 |
| P1 | –1.74 | –0.63 | 8.42 | –1.12 | –0.36 | –0.12 | –0.08 | –0.11 |
| F1 | –2.04 | –0.23 | –1.12 | 8.28 | –0.56 | –0.09 | –0.11 | –0.26 |
| T2 | –2.00 | –0.41 | –0.36 | –0.56 | 13.12 | –0.83 | –1.74 | –2.04 |
| R2 | –0.41 | –0.44 | –0.12 | –0.09 | –0.83 | 20.12 | –0.63 | –0.23 |
| P2 | –0.36 | –0.12 | –0.08 | –0.11 | –1.74 | –0.63 | 8.42 | –1.12 |
| F2 | –0.56 | –0.09 | –0.11 | –0.26 | –2.04 | –0.23 | –1.12 | 8.28 |
| Serial Number | JDZXW5–25J | JDZXW5A –25J | JDZXW7–25D |
|---|---|---|---|
| EMU Type | CRH3X | CRH5X | CR400XF |
| Primary DC Resistance 20℃ | 43160Ω | 46488Ω | 43160Ω |
| Primary inductance | 11000H–12000H | 11000–12000H | 11000H–12000H |
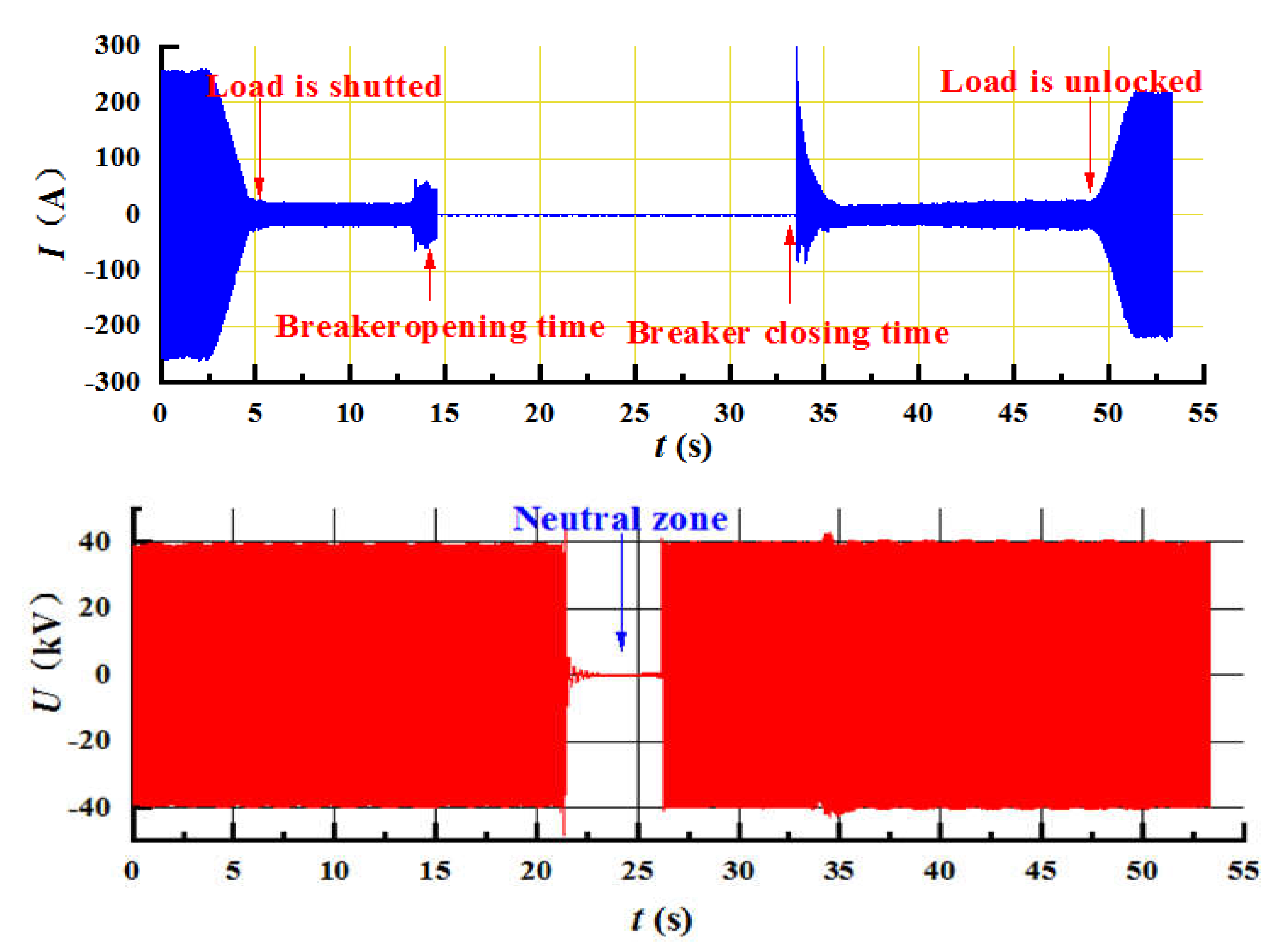
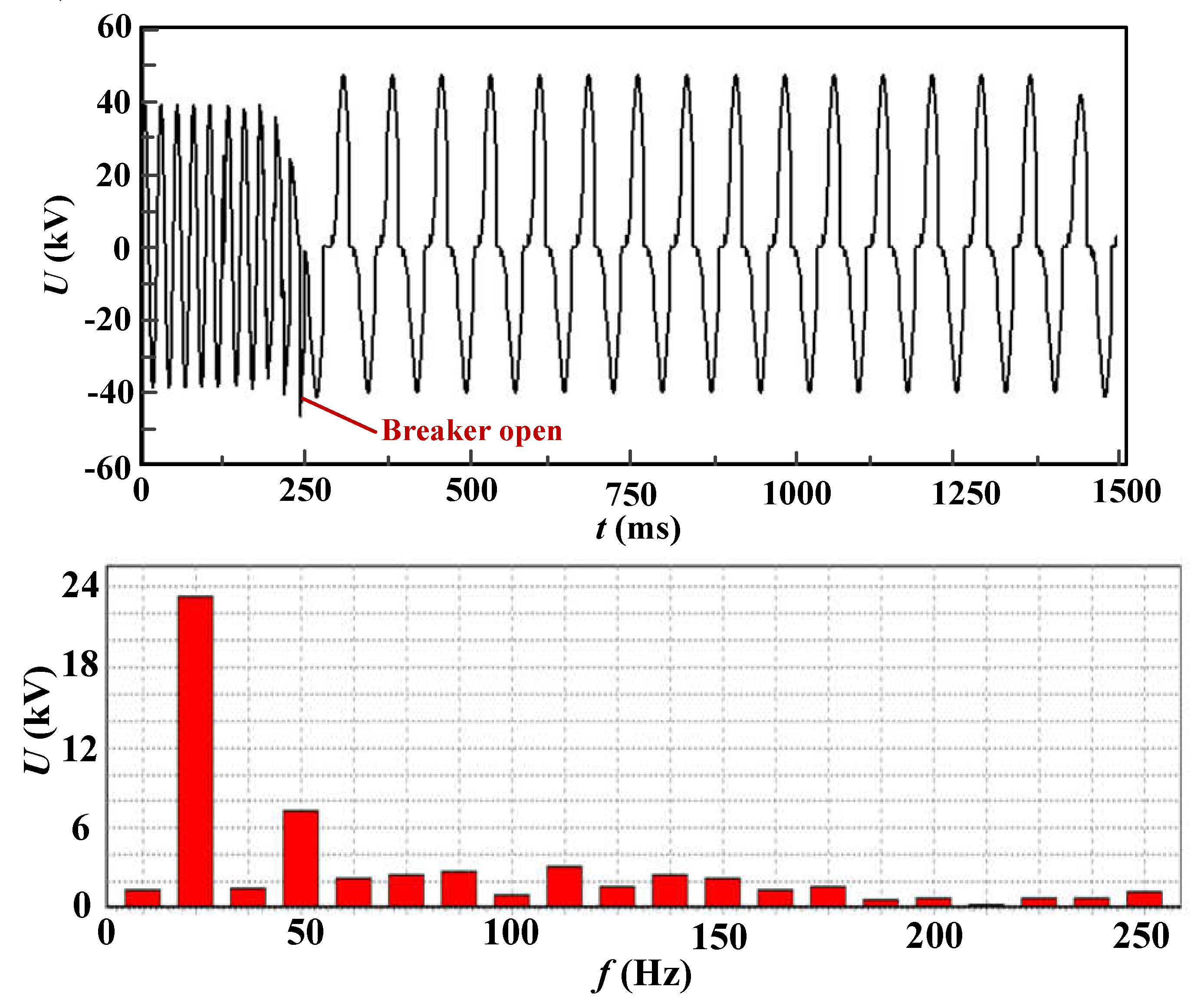
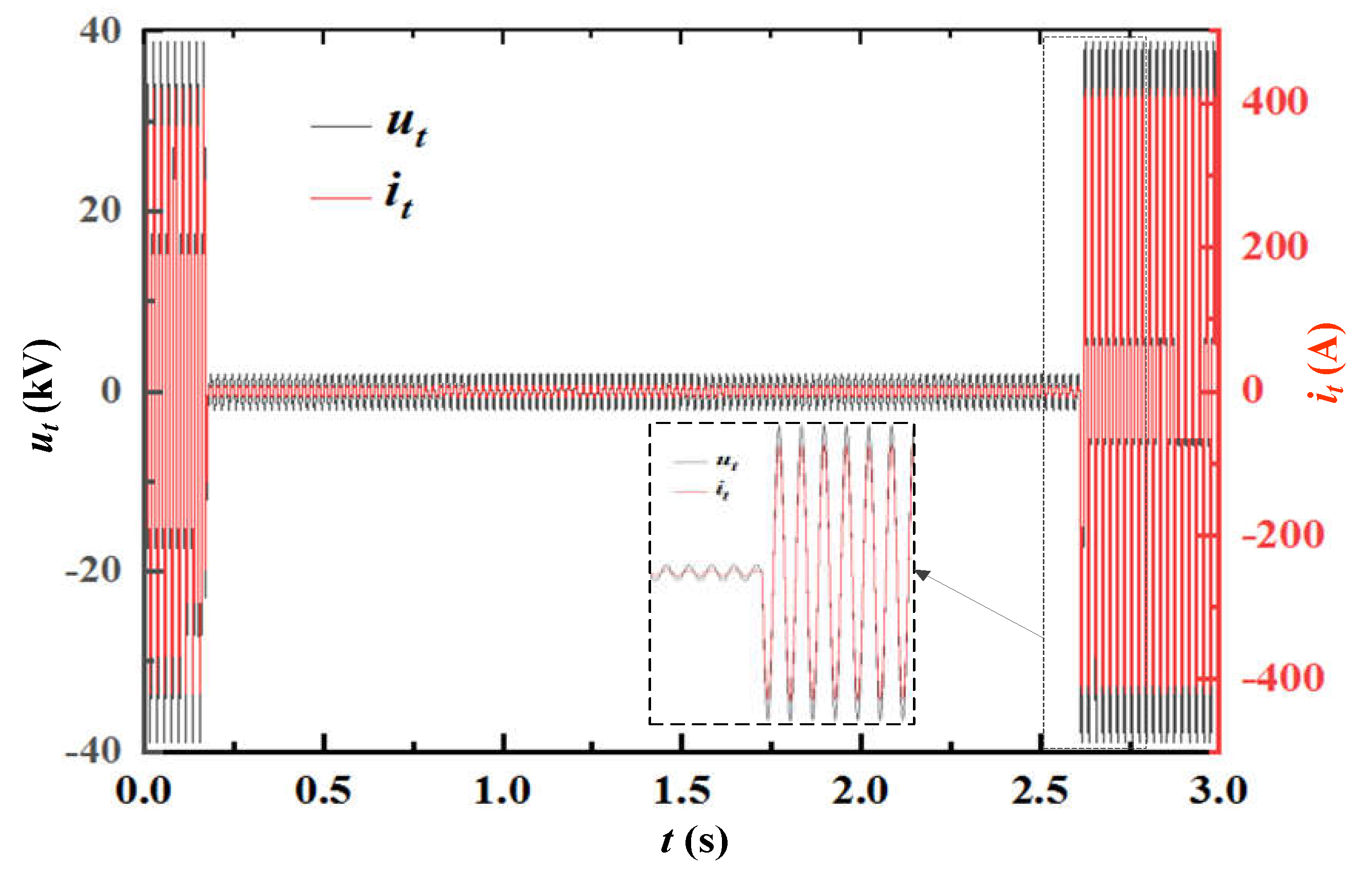
3.2. Oscillation process and overvoltage characteristics
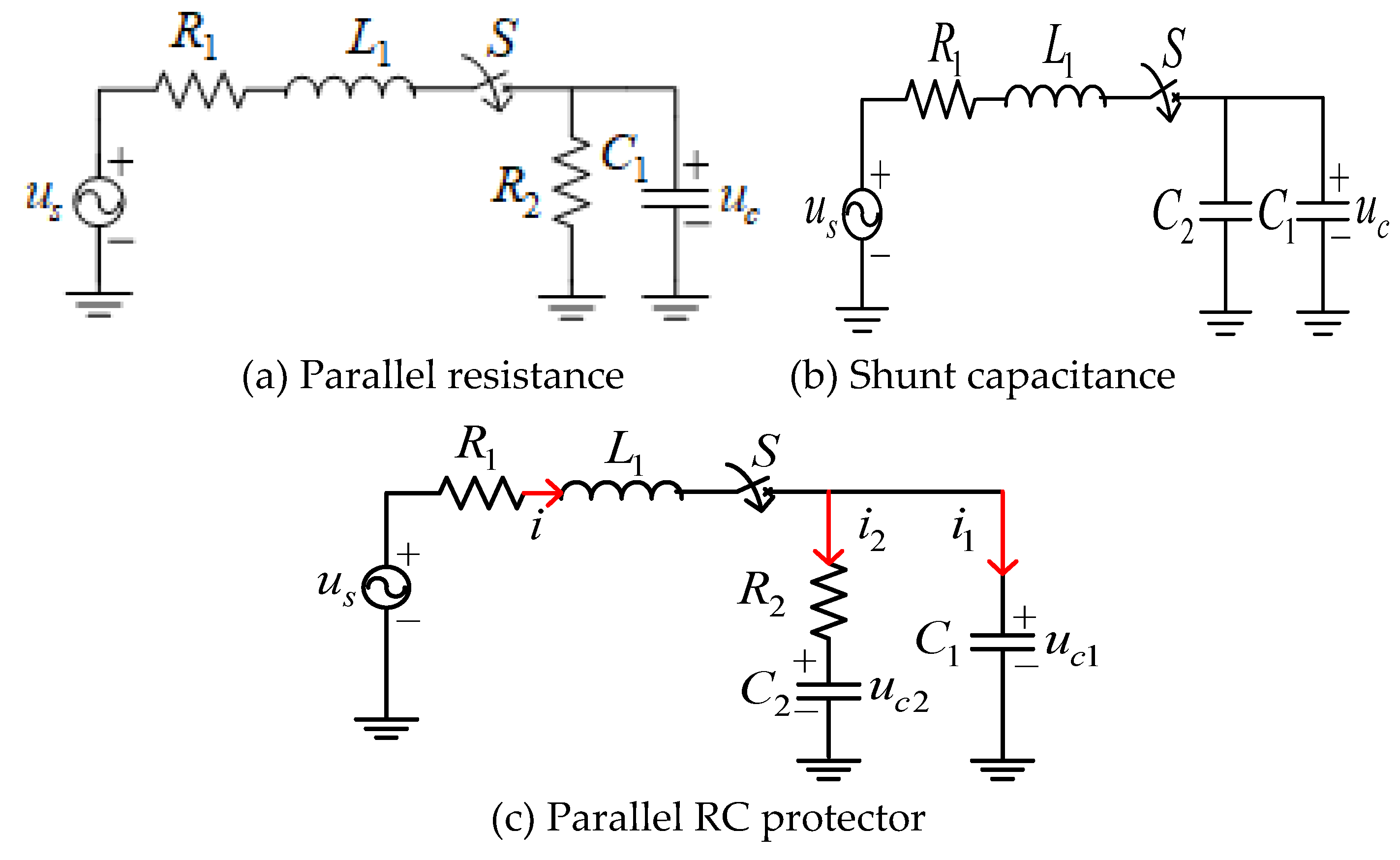
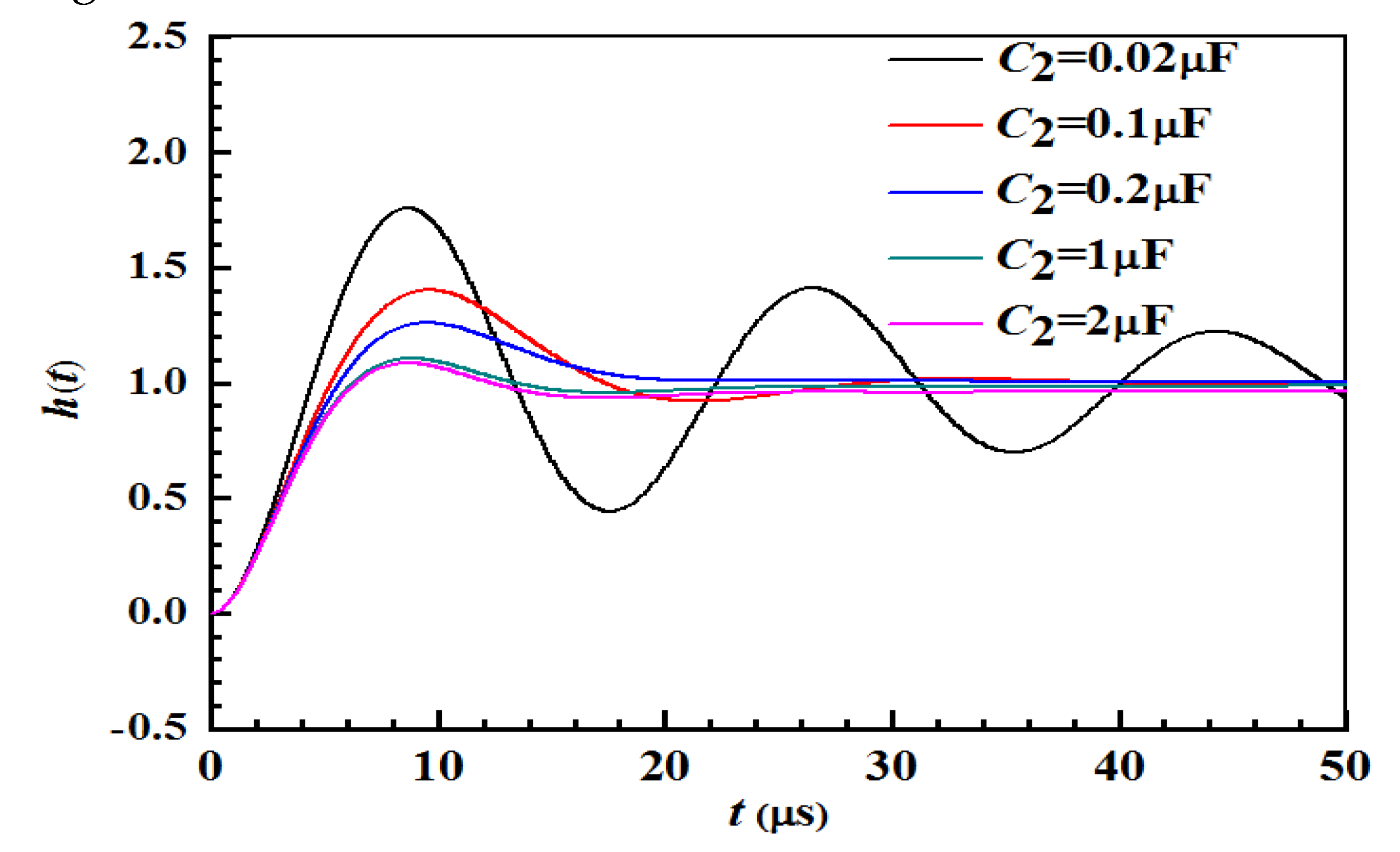
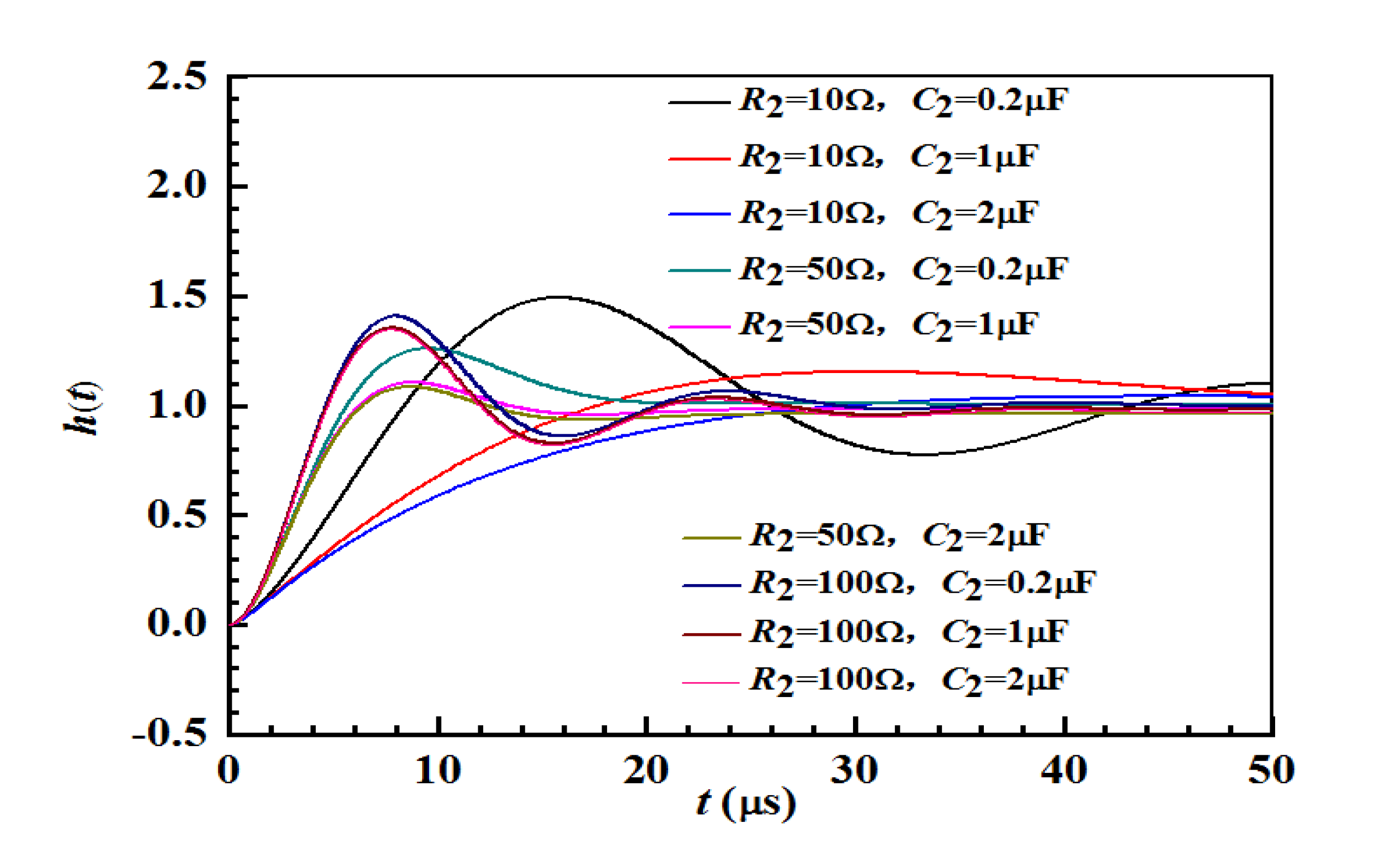
3.3. Methods of Suppressing Oscillation Process
4. Conclusions
- (1)
- Under normal operating conditions when the EMU enters the neutral zone, due to the opening and closing of the circuit breaker, the change of the equivalent circuit of the vehicle line leads to obvious operating overvoltage, while the neutral zone line voltage is very small. When there is an abnormal increase in the grid voltage in the neutral zone, the grid voltage waveform has obvious low frequency oscillation characteristics. When the amplitude of the oscillation voltage is obvious, it can reach 51.8kV, which is 1/3 power frequency low–frequency oscillation.
- (2)
- The voltage in the neutral zone of the EMU during the electrical separation is related to the power phase angle at the moment when the EMU enters the electrical neutral zone. When the phase angle of the power supply separation between the pantograph and the line is within the range of 60°~90° and 240°~270°, the voltage amplitude in the neutral zone is relatively large, and the maximum amplitude can reach 69.75kV. Low–frequency oscillation will also occur in the neutral zone. When low–frequency oscillation occurs, the contact line voltage in the neutral zone is mainly 1/3 power frequency (16.7 Hz).
- (3)
- After installing the RC suppression device in the neutral zone, when the EMU enters the electrical neutral zone, the absolute value of the voltage peak drops to below 20 kV. Compared with the case where the suppression device is not connected, the absolute value of the voltage peak is reduced by nearly 60%. And the low–frequency oscillation phenomenon can be effectively suppressed.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen L, Lu X, Min Y, et al. Optimization of governor parameters to prevent frequency oscillations in power systems. IEEE Transactions on Power Systems 2018, 33, 4466–4474. [Google Scholar] [CrossRef]
- Chen G, Tang F, Shi H, et al. Optimization strategy of hydro–governors for eliminating ultra–low frequency oscillations in hydro–dominant power systems. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 6, 1086–1094. [Google Scholar]
- Demello F P, Koessler R J, Agee J, et al. Hydraulic turbine and turbine control models for system dynamic studies. IEEE Transactions on Power Systems, 1992, 7, 167–179. [Google Scholar] [CrossRef]
- Yu X, Zhang J, Fan C, et al. Stability analysis of governor turbine hydraulic system by state space method and graph theory. Energy 2016, 114, 613–622. [Google Scholar] [CrossRef]
- Liu Z, Yao W, Wen J, et al. Effect analysis of generator governor system and its frequency mode on inter–area oscillations in power systems. Int J Elect Power Energy Syst, 2018, 96, 1–10. [Google Scholar] [CrossRef]
- Schleif F R, Martin G E, Angell R R, et al. Damping of system oscillations with a hydrogenerating unit. IEEE Transactions on Power Apparatus and Systems, 1967, 86, 438–442. [Google Scholar]
- Martinez JA, Mork BA. Transformer Modeling for Low– and Mid–Frequency Transients—A Review. IEEE Transactions on Power Delivery. 2005, 20, 1625–1632. [Google Scholar] [CrossRef]
- Leon F, Farazmand A, Joseph P. Comparing the T and pi Equivalent Circuits for the Calculation of Transformer Inrush Currents. IEEE Transactions on Power Delivery. 2012, 27, 2390–2398. [Google Scholar] [CrossRef]
- Jazebi S, Zirka SE, Lambert M, Rezaei–Zare A, Chiesa N, Moroz Y, et al. Duality Derived Transformer Models for Low–Frequency Electromagnetic Transients—Part I: Topological Models. IEEE Transactions on Power Delivery. 2016, 31, 2410–2419. [Google Scholar] [CrossRef]
- Mork BA, Gonzalez F, Ishchenko D, Stuehm DL, Mitra J. Hybrid Transformer Model for Transient Simulation—Part I: Development and Parameters. IEEE Transactions on Power Delivery. 2007, 22, 248–255. [Google Scholar] [CrossRef]
- Monteiro TC, Martinz FO, Matakas L, Komatsu W. Transformer Operation at Deep Saturation: Model. M: Transformer Operation at Deep Saturation.
- and Parameter Determination. IEEE Transactions on Industry Applications. 2012, 48, 1054–1063.
- Casoria S, Sybille G, Brunelle P. Hysteresis modeling in the MATLAB/Power System Blockset. Mathematics and Computers in Simulation. 2003, 63, 237–248. [Google Scholar] [CrossRef]
- Moses PS, Masoum MAS, Toliyat HA. Dynamic Modeling of Three–Phase Asymmetric Power Transformers With Magnetic Hysteresis: No–Load and Inrush Conditions, IEEE Transactions on Energy Conversion. 2010, 25, 1040–1047.
- Hassani V, Tjahjowidodo T, Do TN. A survey on hysteresis modeling, identification and control. Mechanical Systems and Signal Processing. 2014,49(1–2):209–233.
- Leite Jv, Benabou A, Sadowski N, da Luz Mvf. Finite Element Three–Phase Transformer Modeling Taking Into Account a Vector Hysteresis Model, IEEE Transactions on Magnetics. 2009, 45 (3): 1716 – 1719.
- Sun J, Mehrotra V. Orthogonal winding structures and design for planar integrated magnetics, In: Proc IEEE APEC; USA: Anaheim 2004, 933 – 938.
- Sun Y, Zheng W, Xu, W, A new method to model the harmonic generation characteristics of the thyristor controlled reactors, Proceedings of the Power Tech, Lausanne, 1–5 July, 2007, New York: IEEE, 2007, 1785–1790.
- TYLAVSKY D J, BROWN K A,MA T T Closed form solution for underground impedance calculations, Proceedings of the IEEE, 1986, 74, 1290–1292.
- TYLAVSKY D, J. Conductor impedance approximations for deep underground mines, IEEE Transactions on Industry Applications, 1987, 23, 723–730.
- WAITJR, Quasi–Static Limit for the Propagating Mode along a Thin Wire in a Circular Tunnel, IEEE Transactions on Antennas and Propagation, 1977, 25, 441–443.
- Zhou Hongyi,Liu Zhigang,Cheng Ye,et al.Extended black–box model of pantograph arcing considering varying pantograph detachment distance, Proceedings of 2017 IEEE Transportation Electrification Conference and Expo, Asia–Pacific. Harbin: IEEE, 2017.
- Liu Y J, CHang G W, Huang H M. Mayr’s equation–based model for pantograph arc of high–speed railway traction system, IEEE Transactions on Power Delivery, 2010, 25, 2025–2027.
- Qu Zhijian, Liu Yuxin, Zhou Min, et al. Over–voltage suppression of electric railway articulated neutral insulator, Advanced Materials Research, 2013, 791–793, 1837–1840.
- Wang Ying, Liu Zhigang, Mu Xiuqing, et al. Research on electromagnetic transient process in articulated split–phase insulator of high–speed railway considering viaduct’s electrical coupling, International Transactions on Electrical Energy Systems, 2017, 27, e2376.
- Zhang Ruifeng, Bai Yihui, Huang Ruyun, Fu Yu. Cause Analysis and preventive measures of low frequency oscillation in power supply side of power supply terminal, Guizhou Electric Power Technology. 2013, 16, 15–17.
- Wang Yun, Chang Peak, Chang Xi, Guo Xiaolong. Study on the key technology of identifying the type of low frequency oscillation and locating the disturbance source in power grid, Xinjiang Electric Power Technology. 2015,2:1–7.
- Li Yanghai, Pan Jian, Yang Tao, Huang Shuhong, Gao Wei. Status and development of low frequency oscillation monitoring and suppression technology in Power Grid. Hubei Electric Power. 2014, 38, 8–16. [Google Scholar]
- Zhang Xinyu, Chen Jie, Zhang Gang, Wang Lei, Qiu Ruichang, Liu Zhigang. An active oscillation compensation method to mitigate high–frequency harmonic instability and low–frequency oscillation in railway traction power supply system, IEEE. 6:70359–70367.
- Chen Feng, Yang Xiaonan, Liu Liang, Ma Xiaochen, Zhang Lei, Yu Yiping. Study on the influence of HVDC to low frequency oscillation in interconnected power system[C]. 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 2018, 1–5.
- Fan Lingling, Li Naihu, Wang Haifeng. Analysis of low frequency oscillation of damping power system with controllable series capacitor compensation device, Power Grid Technology, 1998, 22, 35–39.
- Zhang Fang, Fang Dazhong, Song Wennan, Chen Jiarong. Study on a novel two–stage control method for UPFC with damping tie–line low–frequency Oscillation. Proceedings of the twenty–one th annual conference of power system automation, 2005, 1039–1044.
- Li Hairong, Penk, Chen Yu, Nick Clegg, Allen Lee, Li Xialin. Analysis of low frequency oscillation mechanism of DC voltage control time scale in DC distribution system, High voltage technology, 2021, 1–16.
- Chen He, Huang He, Zhang Yong, Su Yinsheng. Researches on DC modulation to damp low frequency oscillation in China Southern Power Grid. IEEE Power & Energy Society General Meeting, 2015, 1–6.
- Gao Hongliang, Zhan Xisheng, Jiang Xiaowei, Wu Jie, Yang Qingsheng. Research on mechanism of power system low frequency oscillation based on damping coefficient, 2017 4th International Conference on Electrical and Electronics Engineering, 2017, 99–103.
- Yang Jie, Hu Haitao, Zhou Yi, Tao Haidong, Zhao Chaopeng, he zhengyou. Analysis of low frequency Oscillation suppression in Traction Power Supply System [ J ]. Electrified Railways, 2018, 29, 15–28. [Google Scholar]
- Zhou Yi, Hu Haitao, Yang Xiaowei, he zhengyou. Railway Electrification System, Chinese Journal of Electrical Engineering, 2017, 37, 72–80.
- Zha Wei, Yuan Yue. Mechanism of active–power–PSS low–frequency oscillation suppression and characteristic of anti–regulation[C]. 2011 Third International Conference on Measuring Technology and Mechatronics Automation, Shanghai, China, 2011, 538–541. 2011.
- Lu Shengyang, Zhang Wuyang, Wang Tong, Cai Yupeng, Li Huan, Zhu Tianyi, Gang Yining, Yu Yongliang. Parameter Tuning and simulation analysis of PSS function in excitation system with suppression of low frequency oscillation[C]. 2019 IEEE 8th International Conference on Advanced Power System Automation and Protection , Xi'an, China, 2019, 474–479.
- Pan Yiwei, Yang Yongheng, He Jinwei, Ariya Sangwongwanich, Frede Blaabjerg. Low–frequency oscillation suppressi–bregeon in series resonant dual–active–bridge converters under fault tolerant operation, 2019 IEEE energy conversion congress and exposition, Baltimore, MD, USA, 2019, 1499–1505.
- Zhou Yi, Hu Haitao, Lei Ke, Meng Zhaofei, he zhengyou. Low frequency constant amplitude oscillation mechanism of railway electrification system, Chinese Journal of Electrical Engineering, 2020, 1–13.
- Zhou Yi, Hu Haitao, Jiang Xiaofeng, he Zhengyou, Zhao Chaopeng. Study on voltage resonance of Low Frequency Power Supply Network for Traction Power Supply. Grid Technology, 2016, 40, 1830–1838. [Google Scholar]
- Yao Chao, Wang Xiaojun, Bi Chengjie, Zhang Yizhi, Jin Cheng. An approach to suppress low–frequency oscillation in electrification railway based on TCSC impedance control, 2018 IEEE 2nd International Electrical and Energy Conference (CIEEC), Beijing, China, 2018, 110–113.
- Bi Chengjie, Wang Xiaojin, Yao Chao, Pang Kexin, Jin Cheng. Analysis and evaluation of suppression methods on low–frequency oscillation in electric railways, 2018 IEEE 2nd International Electrical and Energy Conference (CIEEC), Beijing, China, 2018, pp. 56–63.
- Zhou Guohua, Tan Wei, Zhou Shuhan, Wang Yue, Ye Xin. Analysis of Pulse Train Controlled PCCM Boost Converter With Low Frequency Oscillation Suppression, IEEE, 2018, 6, 68795–68803.
| Serial number | Name | Model | Test standard, accuracy |
|---|---|---|---|
| 1 | Data acquisition | HS4 | 0.1%(12 bit) |
| 5 | Voltage probe | —— | 100V/2V,1% |
| 6 | Current Sensor | PQ5(U.S. Fluke) | 0~5A,40~2kHz,2% |
| Frequency (Hz) | Percentage (%) |
Frequency (Hz) | Percentage (%) |
|---|---|---|---|
| 0 | 6.04 | 133.33 | 13.36 |
| 16.67 | 100 | 150 | 6.86 |
| 33.33 | 6.29 | 166.67 | 10.89 |
| 50 | 31.34 | 183.33 | 9.81 |
| 66.67 | 9.53 | 200 | 6.12 |
| 83.33 | 10.73 | 216.67 | 6.88 |
| 100 | 12.07 | 233.33 | 2.81 |
| 116.67 | 4.60 | 250 | 3.17 |
| Phase angle(°) | Voltage (kV) | Phase angle (°) | Voltage (kV) | Phase angle (°) | Voltage (kV) |
|---|---|---|---|---|---|
| 0 | 46.70 | 120 | 51.78 | 240 | 69.75 |
| 10 | 52.25 | 130 | 48.37 | 250 | 68.85 |
| 20 | 56.15 | 140 | 45.10 | 260 | 67.61 |
| 30 | 58.80 | 150 | 40.53 | 270 | 64.44 |
| 40 | 60.64 | 160 | 41.80 | 280 | 62.25 |
| 50 | 62.30 | 170 | 45.39 | 290 | 61.29 |
| 60 | 66.22 | 180 | 50.11 | 300 | 57.81 |
| 70 | 66.12 | 190 | 55.04 | 310 | 53.40 |
| 80 | 64.11 | 200 | 59.57 | 320 | 48.50 |
| 90 | 64.98 | 210 | 62.00 | 330 | 44.55 |
| 100 | 59.25 | 220 | 65.17 | 340 | 43.84 |
| 110 | 57.01 | 230 | 67.84 | 350 | 42.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





