Preprint
Article
Structural Analysis and Lightweight Optimization of a Buoyant Rotor-Type Permanent Magnet Generator for a Direct-Drive Wind Turbine
Altmetrics
Downloads
112
Views
33
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
19 June 2023
Posted:
19 June 2023
You are already at the latest version
Alerts
Abstract
This study presents structural analysis and optimization for the lightweight design of a buoyant rotor-type permanent magnet (BRPM) generator, which was first presented in Bang (2010), and compares its structural performances to a conventional generator with a spoke arm-type rotor and stator. The main benefit of a BRPM is that it can be realized as a bearing-less drive system, free from the mechanical failure of rotor bearings, by using a buoyant rotor. Also, the deformation of a generator by blade vibration can be effectively suppressed using joint couplings between the blades and the rotor. For the design optimization, the objective is set as the mass of the rotor and the stator, and the maximum deformation of the airgap clearance between the rotor and the stator by external forces is constrained below 10% of the gap width. The commercial software Optistruct is used for the analysis and optimization. In this investigation, the analysis and optimization are conducted for a 10 MW wind turbine generator. However, the proposed methods can be extended to larger generator designs without requiring considerable modification. The mass of the opti-mized 10MW BRPM generator is 160.7 tons (19.3 tons for the rotor and 141.4 tons for the stator) while that of an optimized conventional spoke arm-type generator is obtained as 325.6 tons.
Keywords:
Subject: Engineering - Mechanical Engineering
1. Introduction
Direct-drive generators have attracted increasing interest for large-sized wind turbines due to the low structural failure ratio and ease of maintenance [1]. Stronger wind at higher altitudes for a large-sized wind turbine facilitates higher energy density per unit area. However, as the size of a wind turbine increases, the mass of the generator increases with a larger proportion. This is because the mass for the structural part of a generator is dominant over the active (or electromagnetic) part in a large-sized wind turbine. The larger mass of a generator requires stronger supporting structures in the nacelle and the tower, which results in a significant increase in the overall mass of a wind turbine structure. Thus, the lightweight design of a generator is important to lower the manufacturing and maintenance costs of large-sized wind turbines.
Much research has been conducted to achieve lightweight designs for permanent magnet direct drive generators. Jaen-Sola et al. [2] minimized the structural mass of the rotor and stator of a direct-drive wind turbine generator using topology optimization. Starting from a disk-type rotor (or stator) with no holes, the spiral-shaped (or circular-shaped) holes were removed from the disk through topology optimization for a mass-minimized design. They also optimized the thickness and topology of a conical rotor by considering dynamic responses as well as static stiffness for keeping the airgap clearance [3]. In Hayes et al. [4, 5], periodic repetitions of lattice structures manufactured by additive techniques were employed for a lightweight design of a 5MW generator. In their research, the geometric dimensions of the unit lattice of a stator and a rotor were optimized for a mass minimization problem while the structures had enough stiffness for radial, torsional, and axial directions.
Zavvos et al. [6, 7] used an analytical approach to minimize the mass of a permanent magnet direct drive generator by optimizing both the electromagnetic and structural dimension parameters simultaneously. They used a genetic algorithm for optimization and presented optimized designs for various diameter-to-axial-length ratios. In their works, elastic deformations of a generator due to the electromagnetic force, gravitational force, and angular acceleration are constrained during optimization, for which simplified equations for displacement calculations in [8] are used to deal with the heavy computational cost of the genetic algorithm. Grauers [9] reduced the cost of direct-drive wind turbines, which include structural parts, average losses, and active parts. Through the optimization, the size, efficiency, and weight of generators from 30kW to 3MW were presented. Shrestha et al. [10] proposed to employ a magnetic bearing for the support of the rotor, where the air gap between the rotor and the stator is maintained by the magnetic floating effect. The effectiveness of lightweight by use of the magnetic bearing support system was remarkable, 45% mass reduction in the case of a 5MW generator compared to a conventional direct-drive generator. However, it can be less reliable for a heavy dynamic load and needs more complex system configuration and higher manufacturing costs than conventional ones.
Lightweight designs can be also achieved by using effective structural system layouts. Alstom has been using the so-called pure torque concept to achieve a lightweight and reliable structural design; bending loads on blades imposed by wind are not transmitted to the rotor by using separate bearings and flexible couplings between the blade hub and the rotor [11]. In Bang [12], a bearing-less system with a buoyant rotor-type permanent magnet (BRPM) generator in Figure 1(a) that is buoyed by the fluid of the stator was presented. Note in Figure 1(a) that the rotor is completely enclosed by the stator and is connected to blades through joints without the use of support bearings. Seals should be employed on the stator to prevent fluid leakage through the joint connection.
In this investigation, the BRPM generator in Figure 1(a) is employed for the design of a 10MW direct-drive generator system. The advantages of the BRPM generator for the lightweight design of a large-sized generator are
1) Due to the bearingless drive, it is free from wear and fractures of the rotor bearing.
2) Joint couplings between blades and the rotor effectively prevent transmission of vibrations and impulsive forces of blades to the generator.
3) Smaller deformations are induced by the bending vibrations of the tower.
4) The lightweight of the rotor facilitates gap control.
To achieve mass-minimized designs, structural layouts and dimensions for a buoyant rotor and a stator will be determined by using CAE-based structural optimization methods. The plates of the stator on the blade side require disconnection for the joint connection, which significantly reduces the bending stiffness of the stator that supports the attractive magnetic force. To deal with this, an array of ribs (or reinforcing plates) will be introduced in the circumferential direction as stiffening members. Also, to maximize the stiffness-to-mass ratio of the ribs, topology optimization will be employed. By solving the optimization problem, the layout of the mass-minimized rib is designed while its stiffness satisfies a given constraint. For the design of a rotor, thickness optimization based on a surrogate model approach is used to determine plate thicknesses. The commercial software Optistruct [13] is used for the optimization.
To show the effectiveness of a BRPM generator from the structural viewpoint, the dynamic performances of the optimized BRPM generator will be calculated for external vibratory loads. Load cases for the blade vibration and the tower vibration will be analyzed by using a finite element analysis. The results of the optimized BRPM generator are compared with those of a conventional spoke arm-type generator which is also optimized by using the surrogate-model-based optimization method. The mass of the final design of the BRPM generator for a 10MW wind turbine is obtained as 160.7 tons (19.3 tons for a rotor and 141.4 tons for a stator), significantly lower than the mass of the optimized conventional generator, 325.6 tons (97.5 tons for a rotor and 228.1 tons for a stator).
2. Lightweight structural design of a BRPM generator
2.1. Design problem definition and load cases
Figure 2 shows the stator and rotor of a BRPM generator. The buoyancy of the fluid inside the stator supports the rotor without contacting it. Active parts for power generation are not illustrated in the figure. The vertical plates of the stator and rotor are under attractive magnetic force, by which bending deflection of plates arises as a dominant deformation. In Figure 2(a), denotes the width of the gap for a joint coupling between the rotor and the blades. In order to reinforce the bending stiffness of stator plates, ribs are employed in the circumferential direction of the stator as a circular array. The number of ribs and the depth (or thickness) of the rib will be determined through numerical tests.
The overall size of the rotor is determined by considering the design conditions in Table 1. In Figure 2(b), to determine the inner radius, , the height of the cross-section, , and the length, , the buoyancy of the rotor should be also considered (see [12] for more details). Once the size of the rotor is determined, the size of the cross-section of the stator should be designed such that it can contain a volume large enough to provide buoyancy for the rotor support. The width of the stator, in Figure 2(a), is given as
where and are thicknesses of active materials on the stator and the rotor, respectively. In Equation (1), is the gap width between the rotor and the stator, which is set as 8.9 mm in this study.
While the sizes of cross sections for the rotor and the stator can be calculated based on the generative power of the wind turbine, plate thicknesses such as , etc., and the layout of the ribs are not deterministic. Therefore, they should be optimized to obtain a mass-minimized rotor and stator while the generator has large enough stiffness against external loads. Table 2 lists whether each parameter in Figure 2 is treated as a design variable for optimization or not. It also lists which optimization method is employed for each design variable.
Structural topology and thickness optimizations will be performed by considering only static deformations of the rotor and the stator. After optimizations, the dynamic responses of the structures will be checked for verification purposes. A major deformation of the rotor and the stator is induced by the attractive magnetic force. As additional external loads, the hydrostatic force by the fluid inside the stator, the shear force by the fluid due to the rotation of the rotor, and the gravitational force are considered.
The attractive magnetic force is estimated as
where is the normal force density in the airgap, , magnetic flux density in the airgap, and , the permeability of air ( is calculated as 320kPa in this investigation).
The upper bound of the hydrostatic force by a fluid acting on the surface of the plates of the rotor and the stator is
where and are a fluid density and a gravitational acceleration, respectively. In the above, , the depth from the free surface of the fluid, is less than that is estimated using the dimensions in Table 2.
Due to the rotation of the rotor, shear stress is induced on the plates of the rotor and the stator. If the fluid is assumed Newtonian, the maximum shear stress is
where is the dynamic viscosity, , the rotor velocity and , the gap width between the rotor and the stator (8.9mm in this work). In Equation (4), the velocity, , is calculated by using the rated rotational speed and the radius of the rotor.
A gravitational force acting on the stator includes the weights of the rotor and the fluid as well as the weight of the stator. For comparison purposes, the total gravitational force is converted to a surface force by dividing the total weight by the inner surface area of the stator:
Because the masses of the rotor and stator are not determined, their estimated values by following [12] are used in Equation (5). A gravitational force acting on the rotor can be ignored due to the cancellation effect by the buoyancy.
Compared to the attractive magnetic force in Equation (2), the magnitudes of hydrostatic force in Equation (3) and the gravitational force of the stator in Equation (5) cannot be regarded as negligible. Thus, the static deformations of the BRPM generator by these three external loads are considered for problem formulations of structural topology and thickness optimizations. Dynamic responses by blade vibration and tower vibration are also checked for the final optimized design in Section 3.
2.2. Structural optimization of a stator
Because the bending deformation of stator plates by external loads is mainly supported by the ribs, the design of ribs is crucial to obtain a lightweight stator with high stiffness. An optimal rib layout is found by using topology optimization for the gray region in Figure 2(a). Topology optimization is a gradient-based optimization method that finds an optimum structural layout (or topology) under a limited resource of mass. Because topology optimization presents a totally new layout starting from a very simplified design domain, it can be efficiently applied to design problems with little previously known designs as in the present problem [14].
The gray region in Figure 2(a) is discretized by finite elements, each of which is parameterized with a design variable, , for optimization:
where is Young’s modulus for element i (i=1, 2, …, N; N: total number of elements in the gray region in Figure 2(a)), and is Young’s modulus for a rib material. In Equation (6), if the design variable is optimized as 1, the associated element is as stiff as a rib material, so the element is in a solid state. If the design variable is close to 0, the element has very little stiffness, i.e., in a void state. The exponent n in Equation (6) is a penalty parameter that pushes toward 0 or 1 during optimization (n=2.5 is used in this work). Because the design variable in Equation (6) is continuous, the maximum or minimum of the objective can be found fast by using a gradient information. In Figure 2(a), wall thicknesses, , , and , are set small as in Table 2. If thicker wall thicknesses are preferable, topology optimization would add more material around plates, resulting in thicker plates at the end of optimization.
The problem formulation for topology optimization of the rib is
where is the maximum displacement of the stator in the axial direction by external loads. The objective to be minimized in Equation (7a) is the mass of the rib, and the design constraint in Equation (7b) is to restrain the maximum axial displacement of the stator under a prescribed value .
Figure 3 shows the results of topology optimization. In Figure 3(a), the mass of the rib decreases as the optimization proceeds. Although there is a bump in the middle of Figure 3(a) due to the constraint violation in Figure 3(b), the topology shows stable convergence. The optimized rib layout consists of truss-like slender members, showing that the bending deformation of the stator plates is suppressed by high axial stiffness of truss-like members. Once the rib layout is obtained, through numerical tests, the depth (or thickness) of the rib and the number of ribs are determined. 120 ribs with 40mm depth positioned every 3 degrees in the circumferential direction of the stator are found to satisfy the design constraint. The stator with the optimized ribs has a mass of 141.4 tons (without active parts) and its maximum axial displacement is calculated 0.79mm (see Figure 3(c)).
2.3. Structural optimization of a rotor
The layout of the rotor in Figure 2(b) proposed in [12] has high stiffness for the attractive magnetic force so that the force can be efficiently supported by the axial stiffness of partitioning plates inside. Bang [12] also presented minimum thicknesses for partitioning plates by using the Euler beam theory. However, he did not consider the curvature effect of the rotor, and all the plates were modeled to have the same thickness. In this work, plate thicknesses of the rotor in Figure 2(b) are optimized separately by solving a two-dimensional elastic problem, for which axisymmetric shell elements are used for the finite element model. The problem formulation for the thickness optimization is
where and are the maximum axial displacement of the rotor and its constrained value, respectively. In Equation (8a), is a design variable shared by thicknesses of middle horizontal plates, , , …, . Because vertical plates in Figure 2(b) undergo bending deformation, their thicknesses are set larger than those of partitioning plates in Equation (8d).
The optimization problem in Equation (8) is solved by approximating the objective and constraint functions using Kriging surrogate models, for which sample points are selected following the CCD (Central Composite Design) [15]. All the optimization process is performed within the framework of Optistruct (Altair Inc., 2021). The optimized plate thicknesses are listed in Table 3, from which the mass of the optimized rotor is calculated as 19.3 tons. As a result, the total mass of the optimized generator without active parts is obtained as 160.7 tons (141.4 tons for the stator and 19.3 tons for the rotor). For the optimized stator and the rotor, the maximum deformation of the gap width is calculated as 0.873mm (0.786mm for the stator and 0.087mm for the rotor), which is less than the design constraint, 10% of the gap width (0.89mm).
3. Structural performance comparison between BRPM and conventional generators
Dynamic responses of the optimized BRPM generator are calculated for two scenarios: 1) axial vibration of the rotor induced by the blade vibration, and 2) axial vibration of the rotor and the stator by the tower vibration. Dynamic loads were not taken into account in the presented optimizations because their effect is not significant in the BRPM generator as will be shown in this section. For comparison, the dynamic stiffness of the conventional generator in Figure 1(b) is also calculated. The numerical analyses are conducted for the optimized BRPM generator and the conventional generator that is also optimized using surrogate models.
3.1. Deformation of the rotor by blade vibration
In Figure 1(b), the rotor of a conventional generator is directly connected to the blade hub, so external forces imposed on blades can be transmitted to the rotor without attenuation. Thus, the rotor of the generator should be designed such that it can have enough structural stiffness to deal with blade vibration or impulses as well as external static forces such as the attractive magnetic force and the gravitational force. In this work, the effect of the axial vibration of the blade hub on the deformation of the rotor is investigated. It is assumed that the hub bearing of blades undergoes a rigid body vibrating motion in the axial direction by the front wind. It is also assumed that the main shaft has little elastic deformation in the region between the hub bearing and rotor bearings. Therefore, contact surfaces of the rotor on rotor bearings vibrate synchronously with the hub bearing with the same amplitude.
Figure 4 illustrates the stator and rotor of a spoke arm-type generator whose dimensions are listed in Table 4. For the finite element analysis, the contact surface of the rotor indicated in Figure 4(b) is given a prescribed displacement in the axial direction, 5mm in this problem, and the harmonic analysis is performed with the frequency range from 0.1 Hz to 1 Hz with the increment of 0.001Hz. This frequency range is selected based on natural frequencies of blades of large-sized wind turbines [16]. The material for the generator is given as structural steel. For finite element discretization, 4-node shell elements are used (33,948 nodes for the rotor discretization).
The deformation of the rotor of the generator by the blade vibration is shown in Figure 5. Most deformation is observed as bending deformation in the members connecting the inner and outer flanges of the rotor. The maximum displacement is measured at point A in Figure 5. Figure 6 shows the maximum axial displacement of the rotor for the excitation frequency range, where the maximum deformation significantly increases at the frequency around 0.83 Hz. The peak in Figure 6 is 27.9 mm, 5.6 times larger than the displacement of the blade hub. This large deformation of the rotor can cause unstable electromagnetic operation of the generator and also can result in structural failure by inducing high stress on support bearings. Figure 7 shows the mode shapes of the rotor of the spoke arm-type generator. The first mode in Figure 7(a) has a natural frequency of 0.88 Hz, which is well matched with the peak frequency in Figure 6. Higher modes in Figure 7(b) and 7(c) do not seem to be easily excited by uniform axial vibration of blades.
In the case of the rotor of the BRPM generator, due to the usage of a bearingless drive, the vibration or impulsive forces of blades cannot be directly transmitted to the rotor from the blade hub. In Figure 1(a), the torque of the blades is transferred to the rotor through joint couplings. The joint is designed such that it acts as a rigid connector for the torsional rotation of blades so the rotor can rotate with the same angular speed as the blades. For axial vibration of blades, the joint acts as a disconnector so axial vibration or impulsive movement of blades cannot be transmitted to the rotor. Figure 8(a) shows an example of the proposed joint coupling. In the figure, shackles are used to allow free axial translational movement while they act as rigid connectors for rotational movement. However, the joint needs further design modification. It requires damping to remove blade vibration effect on the rotor. Nonetheless, it is obvious that the rotor of the BRPM generator takes no influence by the uniform axial vibration of blades.
3.2. Deformation of the rotor and the stator by tower vibration
By bending vibration of the tower of a large-sized wind turbine, a generator undergoes almost rigid-body translation with large displacement. The deformations of the BRPM and conventional generators under the vibration of the tower are analyzed by harmonically vibrating the generators 3,000mm in the axial direction. The frequency for the harmonic analysis is set as a low frequency range, 0.01-0.3Hz, which is determined based on natural frequencies of towers for existing large-sized wind turbines [17]. Connection surfaces of the generators with main shafts are excited by giving the axial displacement for the boundary condition.
Figure 9(a) shows deformation of a spoke arm-type generator when the tower is excited with the frequency of 0.3Hz. In the figure, bending deformations are noticeable in the outer flanges of the rotor and the stator. Because active parts are attached to the outer flanges, this deformation should be minimized for stable power generation. To this end, the cross-section of the outer flanges of the rotor and the stator should be designed to have large bending moments of inertia by using thicker plates, which might result in a large increase in the total mass of the generator. The displacements of the rotor and the stator in the radial direction on the nodes of line A and line B in Figure 9(a) are illustrated in Figs. 9(b) and 9(c), respectively. The increase (or decrease) of the gap width between the rotor and the stator is also plotted in the figures. In Figure 10, the maximum gap increase between the rotor and the stator is shown for the frequency range 0.01-0.3Hz. The maximum gap increase is calculated as 0.39mm at 0.3Hz, 4.4% of the total gap width. Considering that the upper bound of the design constraint for the gap increase is set as 10% of the total gap width in optimization problems in Equation (7) and Equation (8), this is not a small value.
Because the rotor of a BRPM generator is buoyant in the fluid, the gap width should be maintained by using the magnetic control force. Through this gap control, the deformation of the generator by external loads can also be simultaneously considered. It is worth mentioning that the gap control can be conducted by using the active parts for power generation and no additional system is required. This can be done by balancing the attractive forces that act on both sides of the airgap (see Figure 8(b) for the gap control).
In this study, the control force that is required to keep the gap width when the generator is under the condition of tower vibration is calculated by using finite element analysis. The control force can be indirectly calculated by constraining the deformation of the generator, and then calculating surface tractions required for this deformation constraint. The control force distribution is the same as the surface traction distribution. Because the gap is filled with fluid, the shear component of the surface traction can be ignored so the control force distribution is given opposite to the surface pressure with the same magnitude. To implement this in a finite element analysis, the fluid filled in the gap is modeled as an artificial material. To constrain the deformation of the gap, the elastic modulus of the artificial material is set very large, 1000 times larger than that of the generator. Other material properties of the artificial material are given the same as the fluid. A harmonic analysis for the frequency range 0.01-0.3Hz is conducted for the BRPM generator in Figure 11 whose dimensions are listed in Table 5. Figure 12 shows the control force distribution on the surfaces of active segments. Because the same set of active segments is positioned every 6 degrees as a circular array, results for one set of active segments are illustrated in the figure. The average control force (or surface pressure) is calculated as -24kPa on Segment 1, 72kPa on Segment 2, -85kPa on Segment 3, -55kPa on Segment 4, 114kPa on Segment 5 and 18kPa on Segment 6. Note that the directions of the control force are calculated opposite on Segment 1 and Segment 2 due to the disconnection for the seal. The maximum gap increase is calculated as 0.06mm, much smaller compared to that of the spoke arm-type generator in Figure 10.
Because deformations of the spoke arm-type generator by the blade vibration and tower vibration are large, the optimization for the spoke arm-type generator should additionally consider deformation constraints for these dynamic load cases. In Table 6, the performances of the optimized BRPM generator and the optimized spoke arm-type generator are compared. In the table, the displacement by a blade hub vibration is not compared because it cannot be calculated for a BRPM generator without considering the force control. The table shows that the BRPM generator has a similar deformation level to the spoke arm-type generator for dynamic excitation as well as static loads. However, noticeable difference can be observed in the total mass between the two optimized generators.
4. Conclusions
A lightweight generator for a 10MW wind turbine was designed by using a buoyant rotor-type permanent magnet (BRPM) direct drive system. The layout of a BRPM generator has inherent advantages over existing permanent magnet generators from a structural viewpoint: 1) it does not have rotor bearings, 2) due to joint couplings, blade vibrations are less transmitted to the rotor, and 3) smaller deformation is induced by the tower vibration through the gap width control. The structural effectiveness of a BRPM generator was shown by calculating static and dynamic deformations of a BRPM generator by finite element analyses and comparing the performances with those of a conventional spoke arm-type generator. To design a mass-minimized stator with high stiffness, the ribs of the stator were optimized by using topology optimization and plate thicknesses for the rotor were determined through thickness optimization. The attractive magnet force, the gravity, and the hydrostatic force by fluid were considered as dominant static loads for optimization. The final mass of the BRPM generator was obtained as 160.7 tons, 49.3% of the spoke arm-type generator with similar static and dynamic stiffness. Although a transverse flux type was employed in this investigation, the locations of permanent magnets can also be optimized for further mass reduction.
Author Contributions
Conceptualization, investigation, writing-review, editing and funding acquisition, Beok-Je Bang; methodology, writing and supervision, Gang-Won Jang; software, data curation, validation and visualization, Joon Ha Hwang.
Funding
This research was supported by Korea Institute of Energy Technology Evaluation and Planting (KETEP) grant funded by the Korea Government (MOTIE) (20228520020050).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bensalah, A.; Barakat, G.; Amara, Y. Electrical generators for large wind turbine: trends and challenges. Energies 2022, 15, 6700. [Google Scholar] [CrossRef]
- Jaen-Sola, P.; McDonald, A.S.; Oterkus, E. Design of direct-drive wind turbine electrical generator structures using topology optimization techniques, Journal of Physics: Conference Series 1618, 2020.
- Jaen-Sola, P.; Oterkus, E.; McDonald, A.S. Parametric lightweight design of a direct-drive wind turbine electrical generator supporting structure for minimizing dynamic response. Ships and Offshore Structures 2021, 16, 266–274. [Google Scholar] [CrossRef]
- Hayes, A.; Sethuraman, L.; Fingersh, L.J. Structural mass saving potential of a 5MW direct drive generator designed for additive manufacturing, International Conference on Future Technologies for Wind Energy, Boulder, Colorado, 2017.
- Hayes, A.; Sethuraman, L.; Dykes, K. Fingersh, L. J. Structural optimization of a direct-drive wind turbine generator inspired by additive manufacturing, Procedia Manufacturing 2018, 26, 740–752. [Google Scholar]
- Zavvos, A.; McDonald, A.S. Mueller, M. Optimisation tools for large permanent magnet generators for direct drive wind turbines, IET Renewable Power Generation 2013, 7, 163–171. [Google Scholar]
- Zavvos, A.; McDonald, A.S.; Mueller, M. Electromagnetic and mechanical optimization of direct-drive generators for large wind turbines, IET PEMD Conf., Brighton, UK, April 2010.
- McDonald, A.S. Structural analysis of low speed, high torque electrical generators for direct drive renewable energy converters, PhD Thesis, University of Edinburgh, 2008.
- Grauers, A.L. Design of direct-driven permanent-magnet generators for wind turbines, PhD Thesis, Chalmers University of Technology, 1996.
- Shrestha, G.; Polinder, H.; Bang, D.; Ferreira, J.A. Structural flexibility: a solution for weight reduction of large direct-drive wind-turbine generators. IEEE Transactions on Energy Conversion 2010, 25, 732–740. [Google Scholar] [CrossRef]
- Bergua, R.; Jové, J.; Echarte, J. Pure torque drivetrain design: a proven solution for increasing the wind turbine reliability, Brazil Windpower 2014 Conference and Exhibition, 2014.
- Bang, D.J. Design of Transverse Flux Permanent Magnet Machines for Large Direct-Drive Wind Turbines, PhD Thesis, Delft University of Technology, 2010.
- Altair Engineering Inc., Altair Optistruct User Guide, 2021.
- Bendsøe, M.P.; Sigmund, O. Topology Optimization: Theory, Method and Applications, Springer-Verlag Berlin Heidelberg New York, 2003.
- Wang, G.G.; Shan, S. Review of metamodeling techniques in support of engineering design optimization. Journal of Mechanical Design 2006, 129, 370–380. [Google Scholar]
- Bak, C.; Bitsche, R.; Yde, A.; Kim, T.; Hansen, M.H.; Zahle, F.; Gaunaa, M.; Blasques, J.; Døssing, M.; Heinen, J.J.W.; Behrens, T. Light rotor: the 10-MW reference wind turbine. In Proc 2012 EWEA Conference, Copenhagen, Denmark, 2012.
- Tricklebank, A.H.; Magee, B.; Halberstadt, P.H. Concrete towers for onshore and offshore wind farms: conceptual design studies, The Concrete Centre, 2007.
Figure 1.
Direct-drive permanent magnet generators: (a) a buoyant rotor-type (BRPM) generator in Bang (2010) and (b) a radial flux type generator (RFPM).
Figure 1.
Direct-drive permanent magnet generators: (a) a buoyant rotor-type (BRPM) generator in Bang (2010) and (b) a radial flux type generator (RFPM).
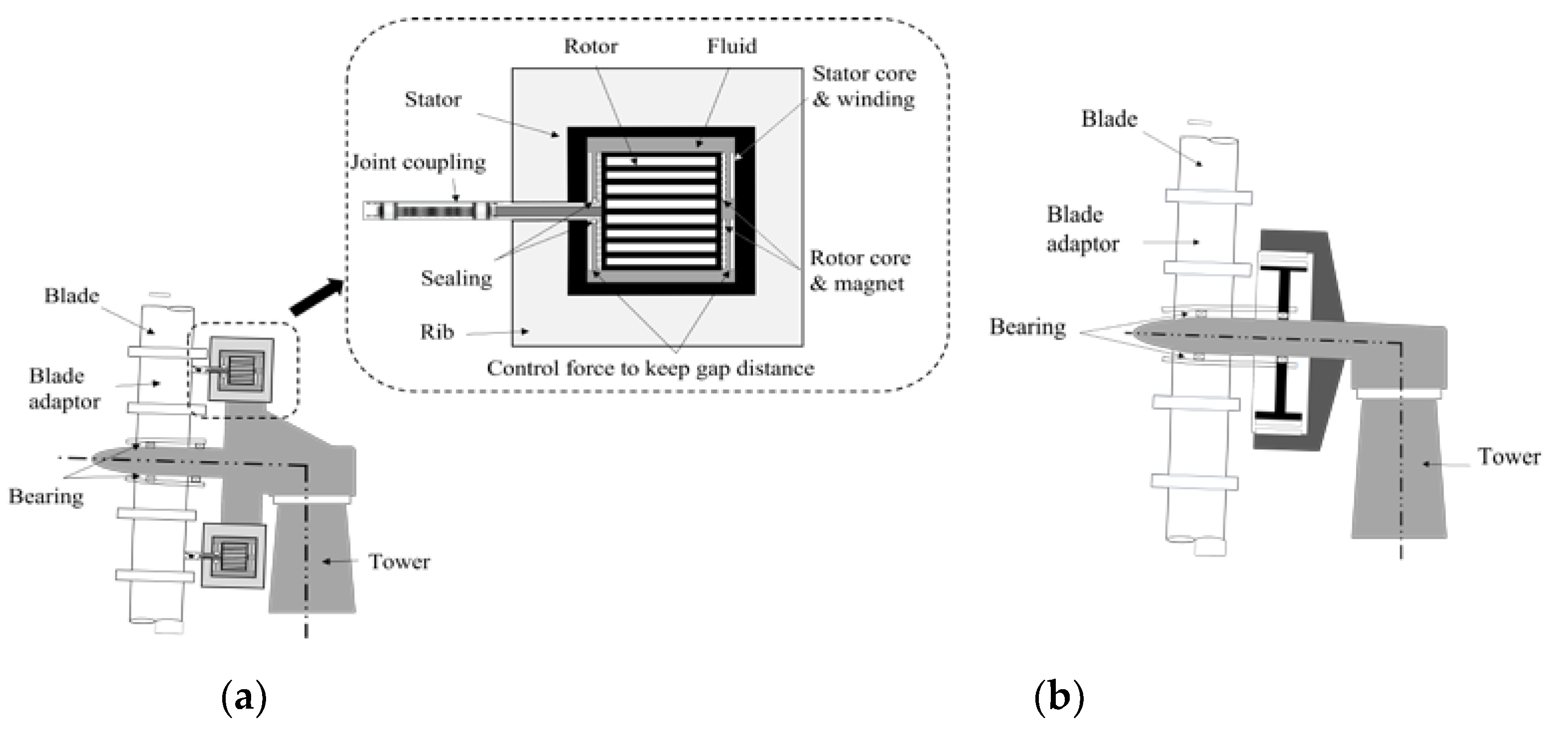
Figure 2.
Direct-drive permanent magnet generators: (a) a buoyant rotor-type (BRPM) generator in Bang (2010) and (b) a radial flux type generator (RFPM).
Figure 2.
Direct-drive permanent magnet generators: (a) a buoyant rotor-type (BRPM) generator in Bang (2010) and (b) a radial flux type generator (RFPM).
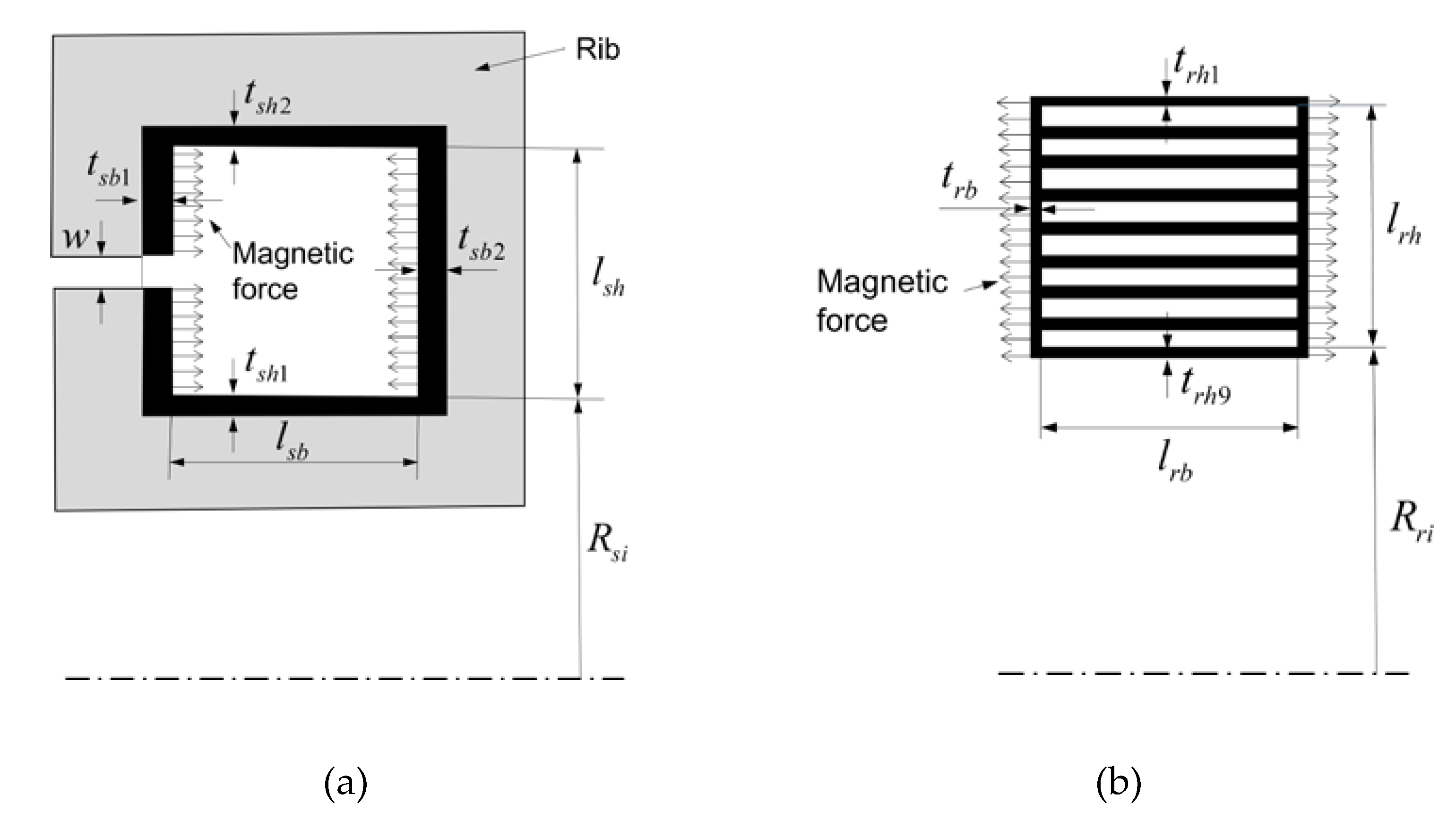
Figure 3.
Topology optimization of the rib for the stator: (a) convergence history for the objective, (b) convergence history for the constraint, and (c) deformed shape of the optimized stator.
Figure 3.
Topology optimization of the rib for the stator: (a) convergence history for the objective, (b) convergence history for the constraint, and (c) deformed shape of the optimized stator.
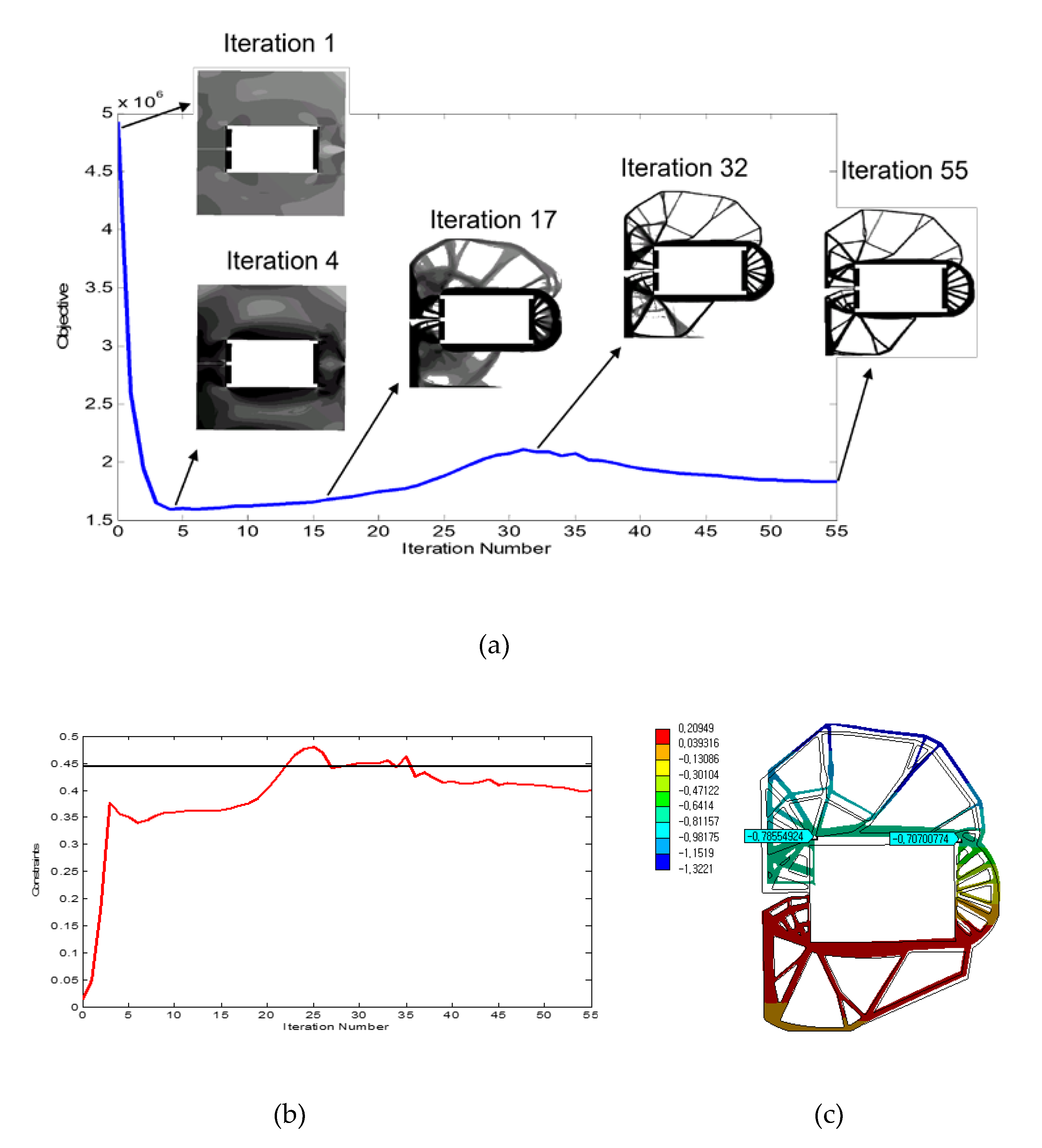
Figure 4.
RFPM generator: (a) a stator, and (b) a rotor.
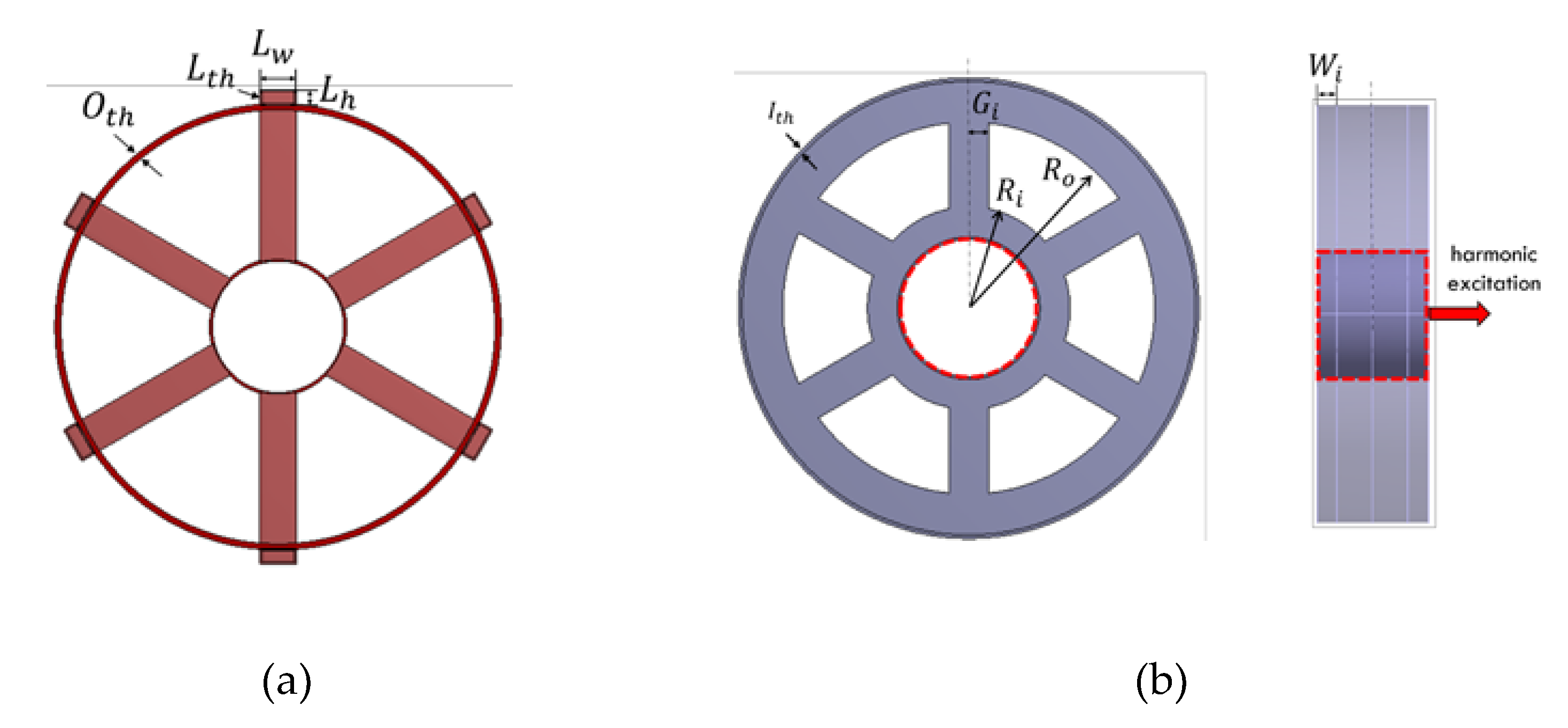
Figure 5.
Deformation of the rotor by the blade vibration.

Figure 6.
Maximum axial deformation of the rotor of the RFPM generator for the frequency range from 0.1 Hz to 1 Hz (The maximum displacement is measured at point A in Fig. 5.).
Figure 6.
Maximum axial deformation of the rotor of the RFPM generator for the frequency range from 0.1 Hz to 1 Hz (The maximum displacement is measured at point A in Fig. 5.).
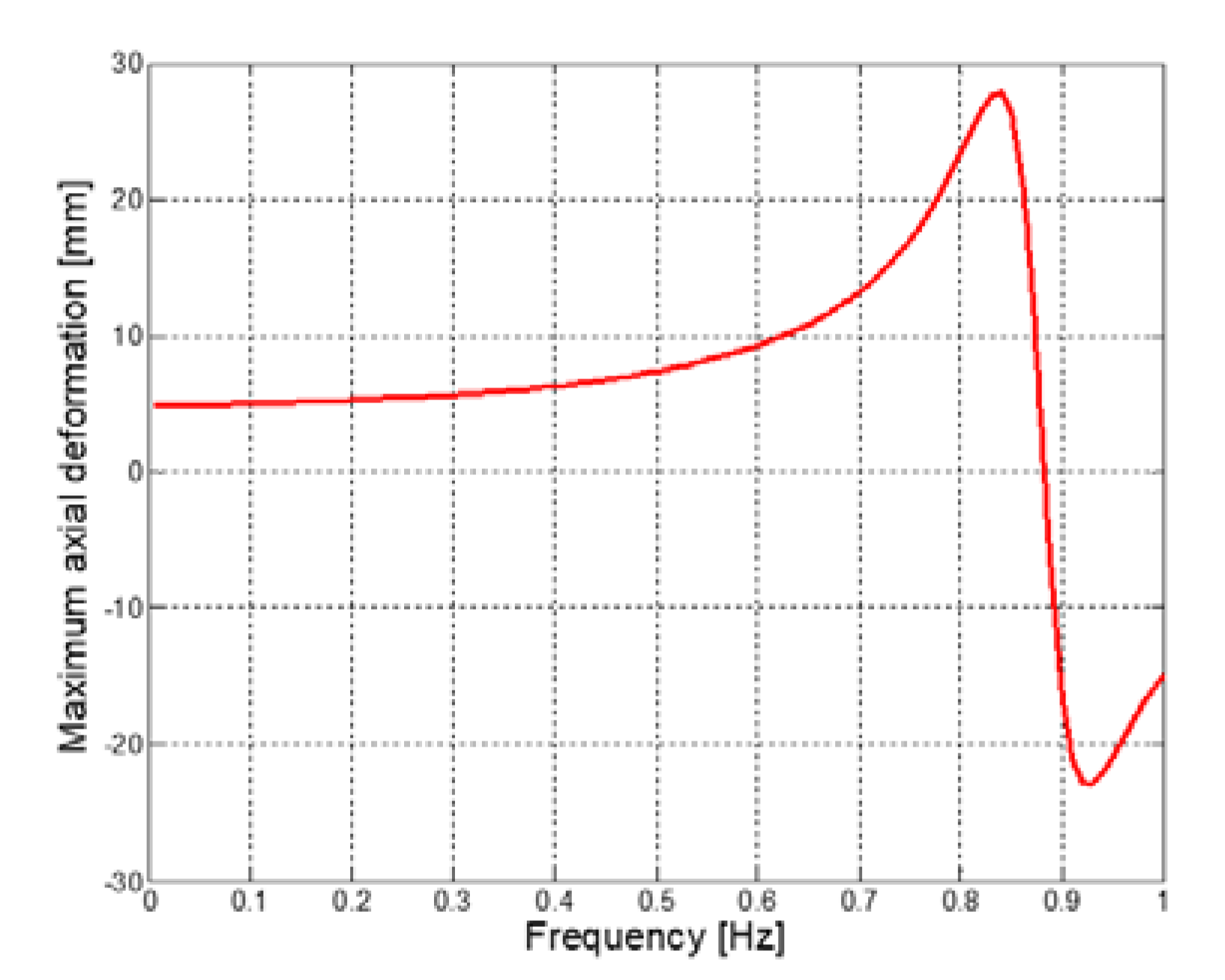
Figure 7.
RFPM generator: (a) a stator, and (b) a rotor.
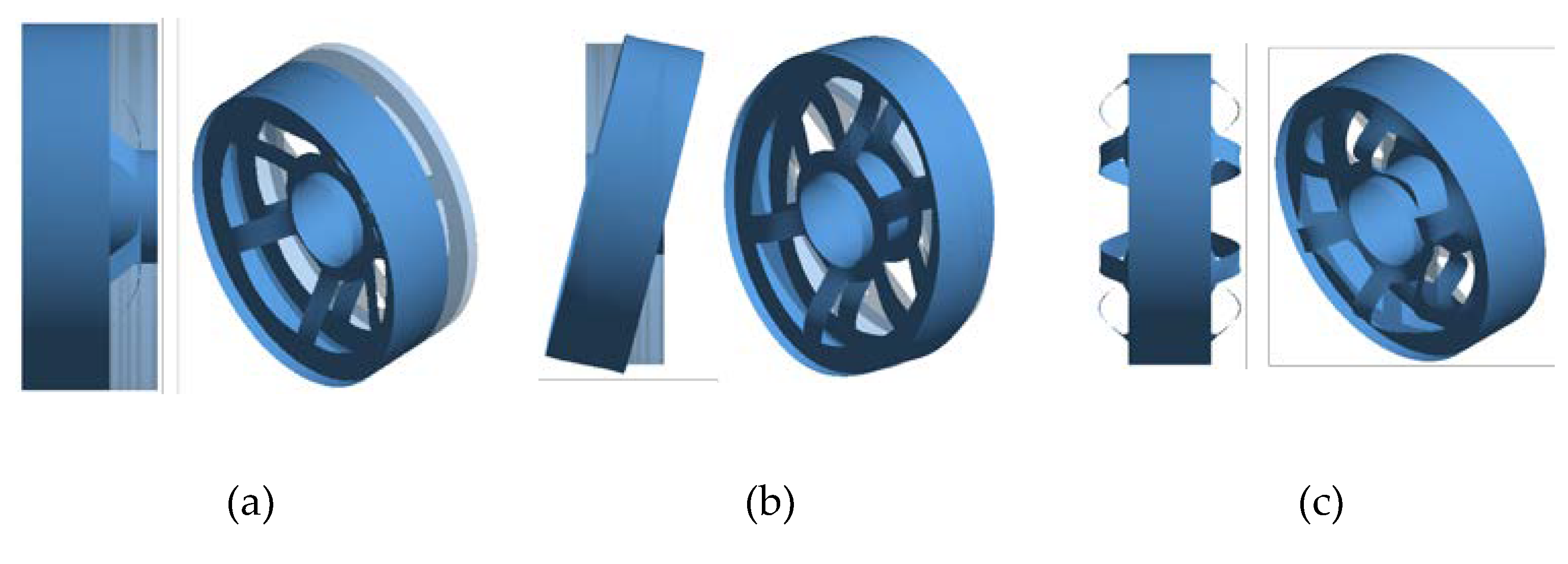
Figure 8.
(a) Experimental setup for axial vibration prevention and torque-only transfer verification, and (b) the airgap control.
Figure 8.
(a) Experimental setup for axial vibration prevention and torque-only transfer verification, and (b) the airgap control.
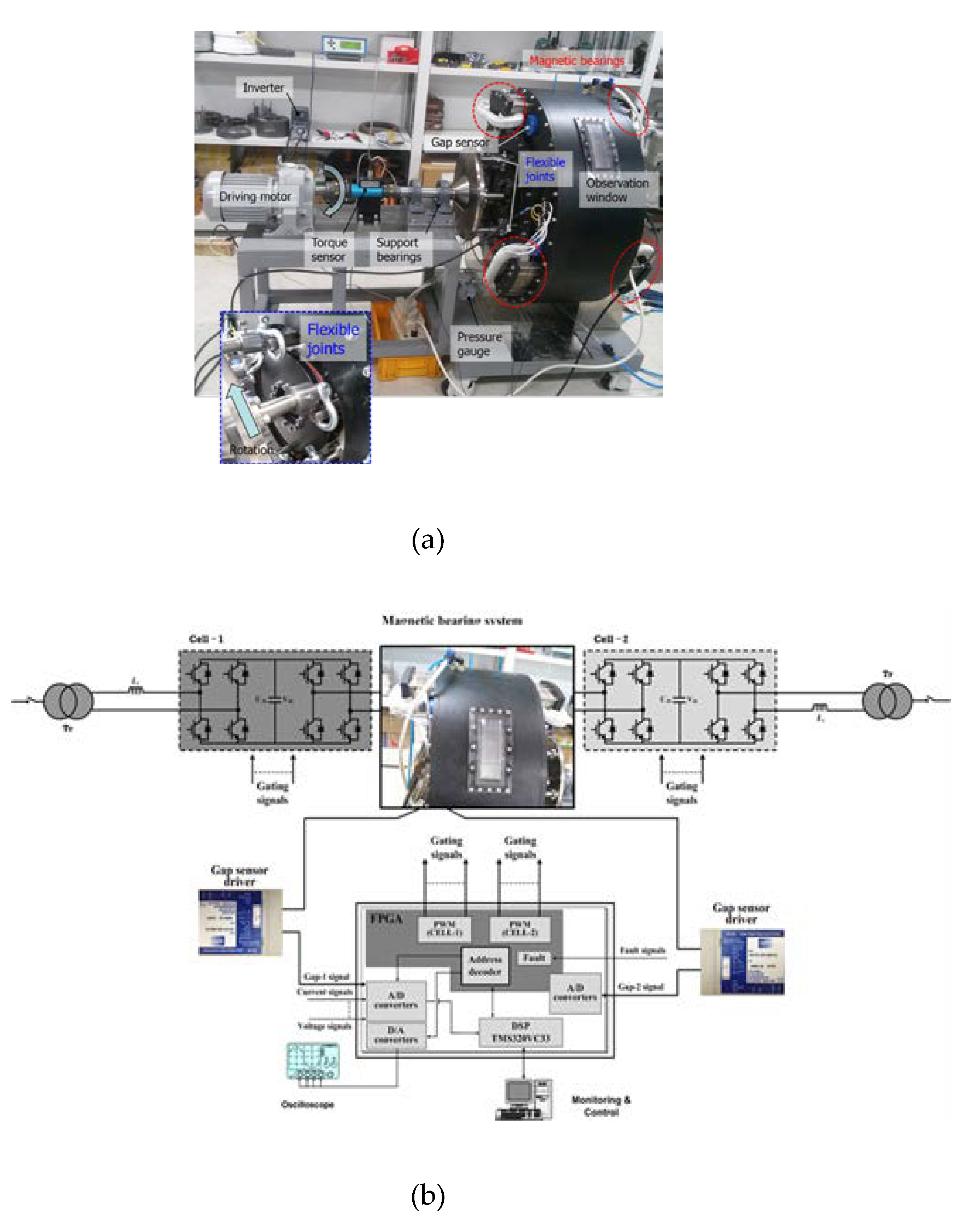
Figure 9.
Deformation of an RFPM generator by the tower vibration with an exciting frequency of 0.3Hz: (a) deformed shapes of the rotor and the stator, (b) radial displacements of the rotor and the stator and the gap increase on A, and (c) radial displacements of the rotor and the stator and the gap increase on B.
Figure 9.
Deformation of an RFPM generator by the tower vibration with an exciting frequency of 0.3Hz: (a) deformed shapes of the rotor and the stator, (b) radial displacements of the rotor and the stator and the gap increase on A, and (c) radial displacements of the rotor and the stator and the gap increase on B.
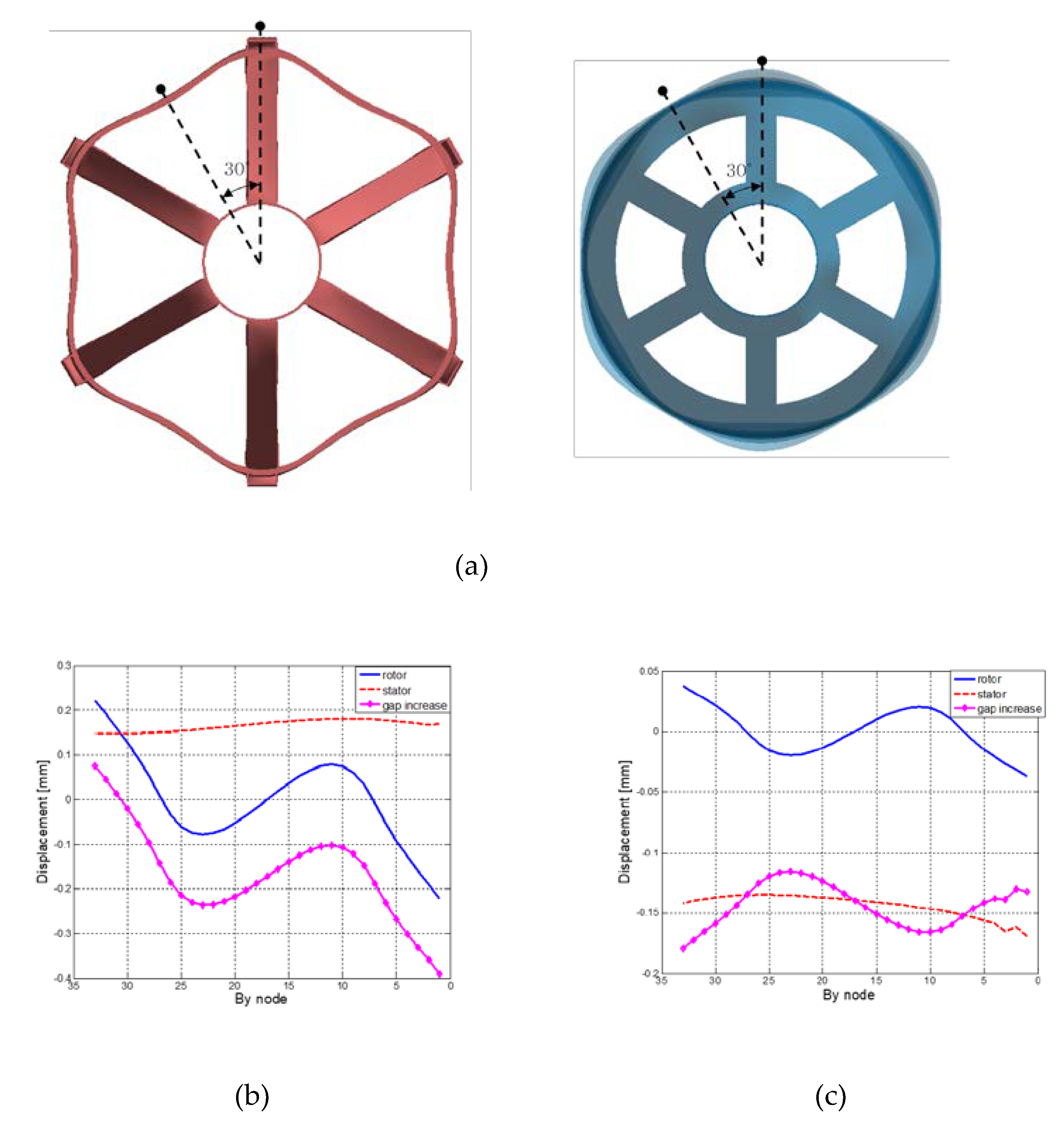
Figure 10.
Maximum gap increase between the rotor and the stator at the nodes on A and B in Fig. 9(a).
Figure 10.
Maximum gap increase between the rotor and the stator at the nodes on A and B in Fig. 9(a).
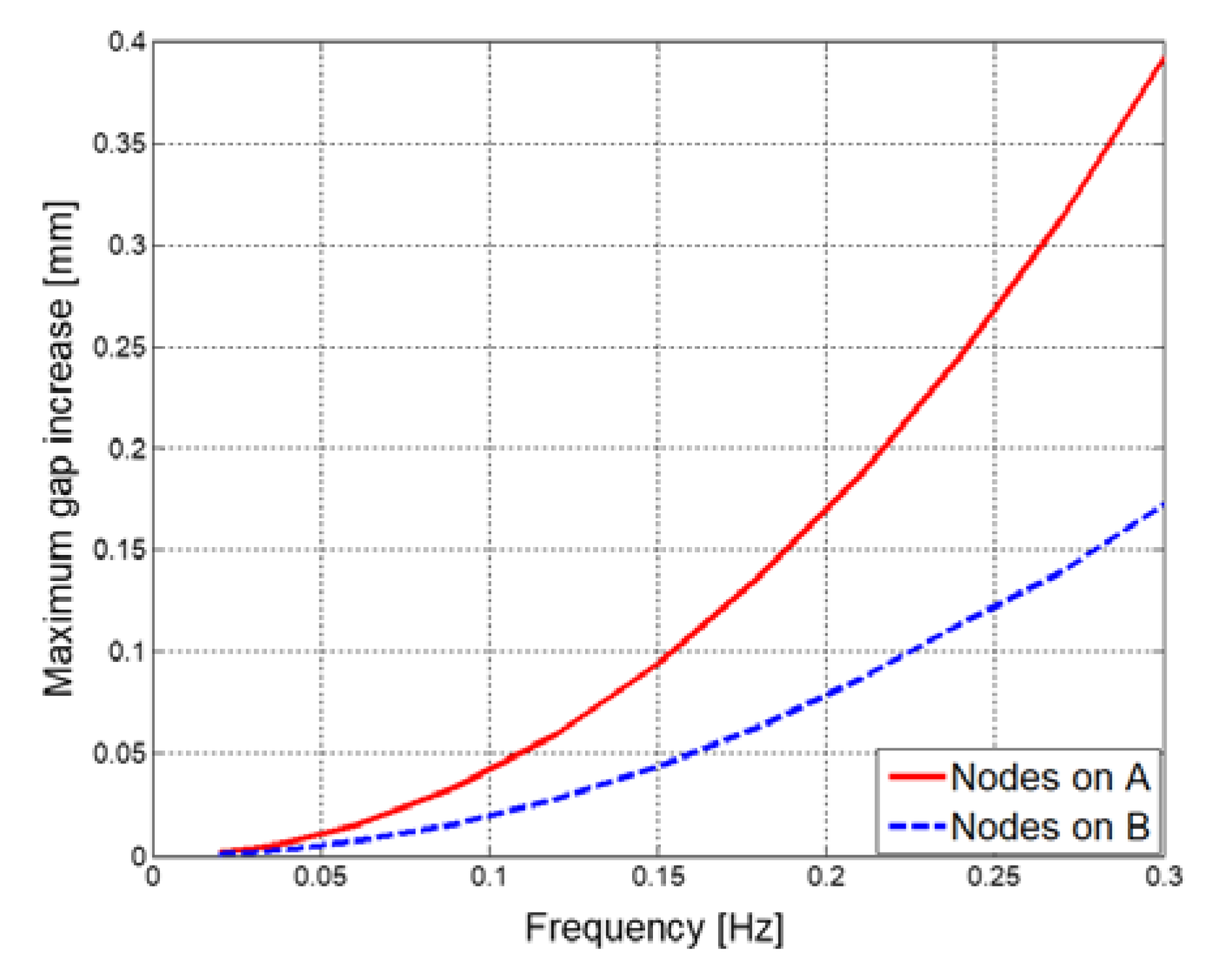
Figure 11.
Maximum gap increase between the rotor and the stator at the nodes on A and B in Fig. 9(a).
Figure 11.
Maximum gap increase between the rotor and the stator at the nodes on A and B in Fig. 9(a).
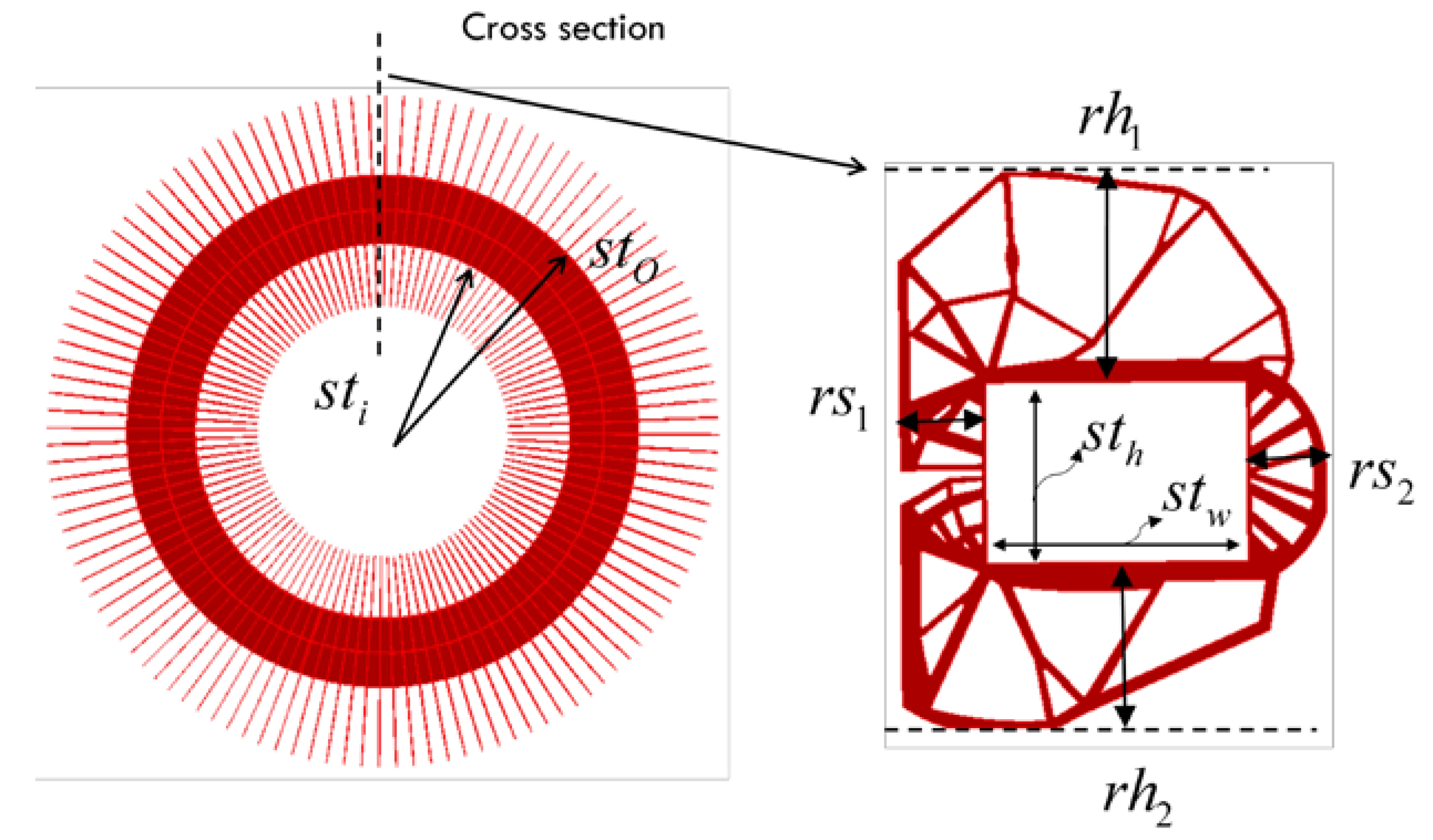
Figure 12.
Distribution of the control force on surfaces of active segments.
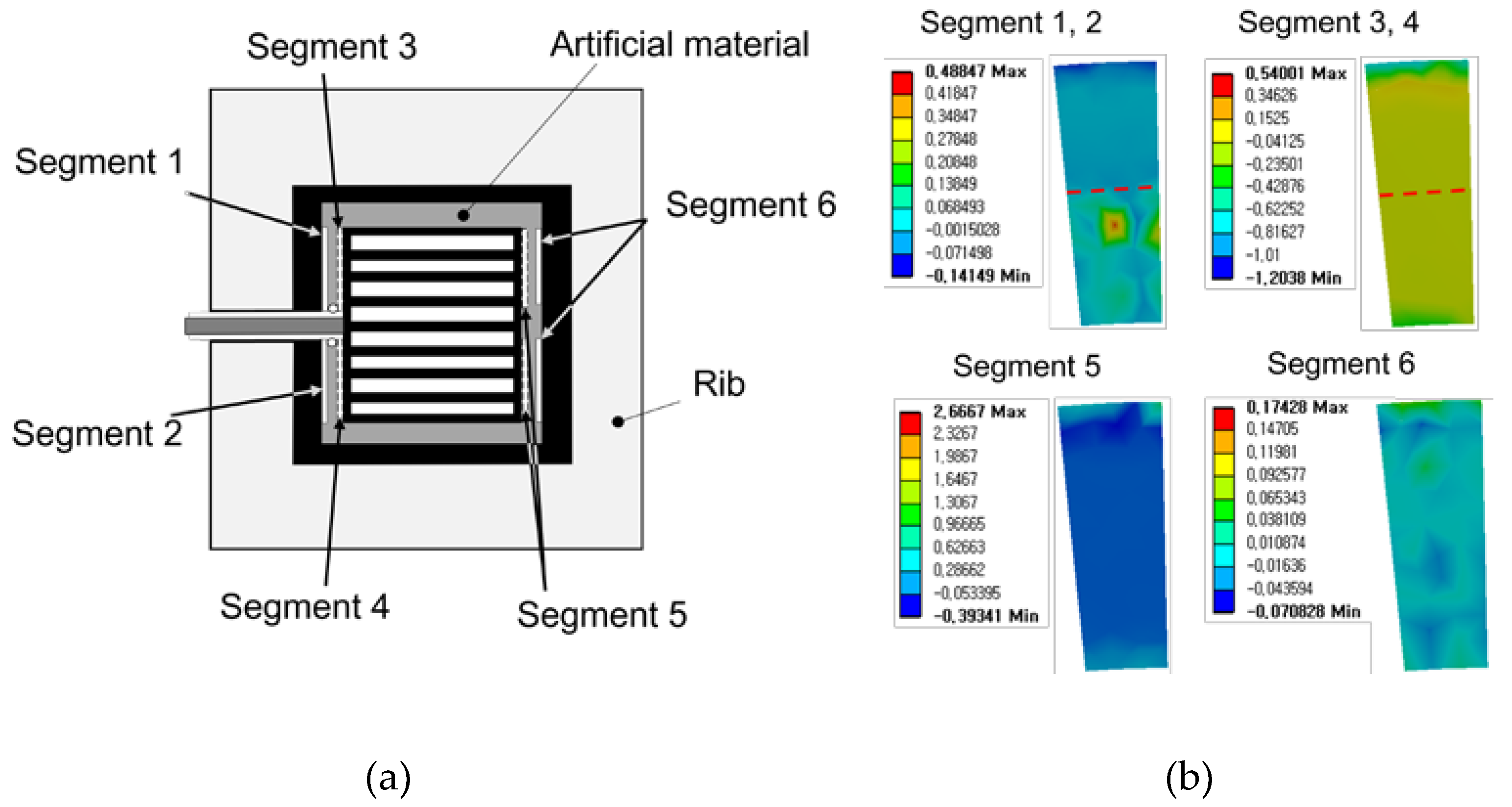
Table 1.
Design conditions of a BRPM generator.
| Principal factors | Values |
|---|---|
| Rated power | 10 MW |
| Rated wind speed | 12 m/sec |
| Rated rotational speed | 8.6 rpm |
| Maximum rotational speed | 8.6 rpm |
| Cut in wind speed | 3.2 m/sec |
| Cut off wind speed | 25 m/sec |
| Airgap size | 8.9 mm |
Table 2.
Parameters for the design of the BRPM generator in Fig. 2.
| Parameter | Value [mm] | Optimization | |
|---|---|---|---|
| Stator | 3757.3 | - | |
| 1365.4 | - | ||
| 1978.1 | - | ||
| 20 | - | ||
| 20 | - | ||
| 15 | - | ||
| 20 | - | ||
| Rib | Design domain | Topology optimization | |
| 10 | - | ||
| Rotor | 3846.1 | - | |
| 1187.8 | - | ||
| 1595.9 | - | ||
| Design variable | Thickness optimization | ||
| Design variable | Thickness optimization |
Table 3.
Results of thickness optimization for the rotor (unit: mm).
| Total mass [tons] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 15.6 | 7.3 | 2.7 | 2.7 | 2.7 | 2.7 | 2.7 | 2.7 | 2.7 | 6.2 | 19.3 | 0.087 |
Table 4.
Dimensions for the spoke arm-type generator in Fig. 4 (Dimensions are obtained by using the surrogate-model based optimization method which is also used for the rotor design of the BRPM generator.).
Table 4.
Dimensions for the spoke arm-type generator in Fig. 4 (Dimensions are obtained by using the surrogate-model based optimization method which is also used for the rotor design of the BRPM generator.).
| Stator parameter | Dimension [mm] | Rotor parameter | Dimension [mm] |
|---|---|---|---|
| 688 | 385 | ||
| 335 | 1970 | ||
| 38 | 3621 | ||
| 126 | 434 | ||
| 69 |
Table 5.
Dimensions for the BRPM generator in Fig. 11.
| Stator parameter | Dimension [mm] | Rotor parameter | Dimension [mm] |
|---|---|---|---|
| 3757.3 | 3846.1 | ||
| 5122.7 | 5033.9 | ||
| 1365.4 | 1187.8 | ||
| 1978.1 | 1596.0 | ||
| 1600 | 7.3 | ||
| 1500 | 2.7 | ||
| 550 | 6.2 | ||
| 550 | 15.6 |
Table 6.
Performance comparison between the optimized BRPM generator and the optimized spoke arm-type generator.
Table 6.
Performance comparison between the optimized BRPM generator and the optimized spoke arm-type generator.
| Maximum displacement [mm] | Mass [tons] | |||||
|---|---|---|---|---|---|---|
| Magnetic force | Tower vibration |
Rotor | Stator | Total | ||
| BRPM | Rotor | 0.078 | 0.12 | 19.3 | 141.4 | 160.7 |
| Stator | 0.340 | |||||
| Spoke arm-type generator | Rotor | 0.200 | 0.12 | 97.5 | 228.1 | 325.6 |
| Stator | 0.125 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





