Prerpints.org logo
Preprint
Article

LegoNet: Alternating Model Blocks for Medical Image Segmentation

Altmetrics

Downloads

101

Views

35

Comments

0

Submitted:

15 June 2023

Posted:

19 June 2023

You are already at the latest version

Alerts
Abstract
Since the emergence of convolutional neural networks (CNNs), and later vision transformers (ViTs), the standard paradigm for model development has been using a set of identical block types with varying parameters/hyper-parameters. To leverage the benefits of different architectural designs (e.g., CNNs and ViTs), we propose alternating structurally different types of blocks to generate a new architecture, mimicking how Lego blocks can be assembled. Using two CNN-based and one SwinViT-based blocks, we investigate three variations to the so-called LegoNet that apply the new block alternation concept for the segmentation task in medical imaging. We also study a new clinical problem that has not been investigated before – the right internal mammary artery (RIMA) and perivascular space segmentation from computed tomography angiography (CTA). It was proven to demonstrate a prognostic value to primary cardiovascular outcomes. We compare the model performance against popular CNN and ViT architectures using two large datasets (achieving 0.749 dice similarity coefficient (DSC) on the larger dataset). We also evaluate the model’s performance on three external testing cohorts, where an expert clinician corrected model-segmented results (DSC>0.90 for the three cohorts). To assess our proposed model for suitability in clinical use, we perform intra- and inter-observer variability analysis. Finally, we investigate a joint self-supervised learning approach to determine its impact on model performance.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

From the early U-Net [1] to the most recent vision transformer (ViT) models [2,3], deep learning (DL) segmentation architectures follow the typical style of an encoder and decoder network, where the encoder is usually made of a set of identically designed blocks with varying hyper-parameters. Other tasks, such as classification, detection, etc., are no exception to the segmentation encoder. Although this design choice has demonstrated excellent results on a wide range of applications, it is essential for the research community to investigate different design alternatives. That begs the question, “Does a deep learning encoder learn better representations when trained on identical or nonidentical blocks?”.
Several papers study the selection of architectures and various components, such as type and number of layers, hyperparameters, etc., under the umbrella of neural architecture search (NAS) [4,5,6]. With a pre-defined search space, NAS approaches investigate the automation of selection, which naturally means a considerable amount of time and resource consumption. In [7], the authors study the knowledge-transfer task for general-purpose model reuse. Again, such approaches heavily rely on intensive network/block search in the first phase and then use the selected network/blocks for model training. Additionally, these methods study the blocks that are from the same family e.g., only CNN-based blocks. Unlike these approaches, we handpick and study network stitching using structurally different neural blocks.
We study the behavior of harmonizing internally nonidentical blocks to perform segmentation of the right internal mammary artery (RIMA) and perivascular space from two types of imaging protocols, namely computed tomography coronary angiography (CTCA) and computed tomography pulmonary angiography (CTPA) scans. While several works focus on combining ViT and CNN encoders together [8,9], either side-by-side or sequentially, to the best of our knowledge, no work studied the block-level integration of different deep learning architectures. We propose to alternate structurally different yet compatible blocks with each other to build DL models. This new perspective opens many avenues on how to construct the model and what blocks to choose, and we test it using three different (two CNN-based and one SwinViT-based) blocks, providing three alternatives of the architecture. One can think of the approach as using compatible Lego blocks to assemble the structure, hence the name LegoNet. We assume that structurally varied blocks could learn different features that could be beneficial to learn more discriminative features, especially on complex problems such as medical image segmentation. Therefore, we aim to evaluate the proposed LegoNet on a unique and challenging problem.
RIMA is proven to be clinically valuable in several studies [10,11,12]. The inflammatory status of the entire vasculature can be represented by the inflammation in the RIMA and perivascular region given that atherosclerotic plaque does not affect it [11,12]. In recent work, Kotanidis et al. [10] studied the RIMA region by manually segmenting it to assess the vascular inflammatory signature of COVID-19 SARS-COV-2 viral infection on CTPA of 435 patients (The C19RS inflammatory signature). This C19RS signature extracted from the RIMA region is a novel non-invasive imaging biomarker that can help predict the in-hospital mortality of patients. The fact that it can provide homogeneous perivascular adipose tissue along its length allows us to extract reliable radiomic features from the perivascular region around it. Manual segmentation is highly time-consuming and labor-intensive, especially when the number of patients increases for better generalizability. When new cohorts of patients are to be segmented from the ORFAN study, for example, an automatic approach for RIMA segmentation is particularly beneficial. Localizing the RIMA region is challenging because it is a small rounded structure on the axial view but elongated vertically in the chest. Therefore, this work investigates the problem of segmenting the RIMA and perivascular space from CT angiography scans.
The main contributions of our work are as follows:
  • We propose a new concept of alternating different deep learning blocks to construct a unique architecture that demonstrates how the aggregation of different block types could help learn better representations.
  • We propose a joint self-supervised method of inpainting and shuffling as a pretraining task. That enforces the models to learn a challenging proxy task during pretraining, which helps improve the finetuning performance.
  • We introduce a new clinical problem to the medical image analysis community; i.e., the segmentation of the RIMA and perivascular space, which can be helpful in a range of clinical studies for cardiovascular disease prognosis.
  • Finally, we provide a thorough clinical evaluation on external datasets through intra-observer variability, inter-observer variability, model-versus-clinician analysis, and post-model segmentation refinement analysis with expert clinicians.

2. Materials and Methods

We propose a simple yet effective concept of alternating different blocks to construct a DL architecture. The concept is similar to how Lego blocks are constructed together to build a standing structure. The only constraint is the compatibility of structures with each other while assembling them. We explore the concept of building a DL network from nonidentical blocks to hopefully benefit from the strength of these different blocks. We propose to alternate two blocks in a single architecture, with three different types of blocks to choose from.

2.1. Building Blocks

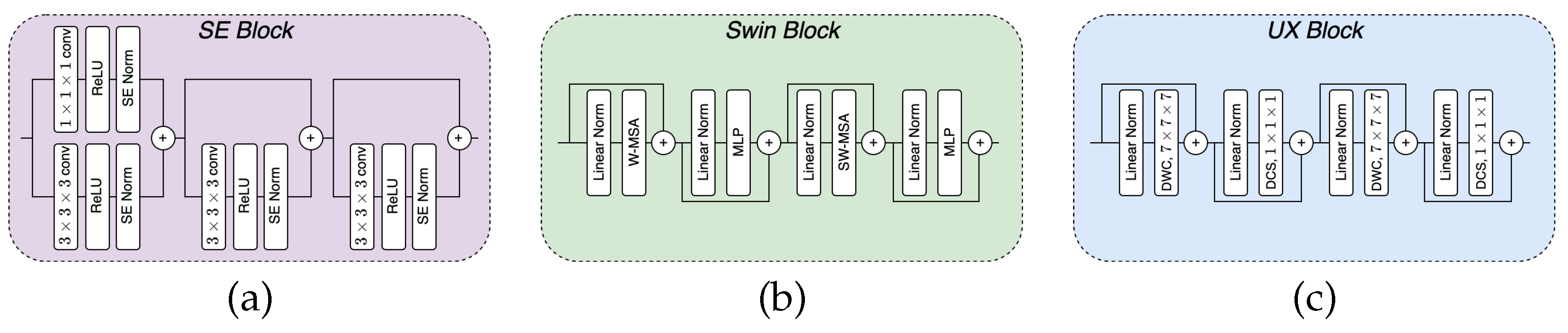
2.1.1. SE block

Squeeze-and-excitation (SE) block consists of stacks of a 3 × 3 × 3 convolutional block with residuals, a ReLU activation function, and a SE normalization (norm) module [13] within the layers. Figure 1(a) depicts the complete block. SE norm is similar to instance norm (IN) [14], but different in the parameters γ i and β i in Equation 1. IN treats them as fixed parameters, while in SE norm, they are modeled as functions of input [13].
y i = γ i x i ′ + β i
where x i ′ is the mean of a batch of input data X, and γ i and β i are the scale and shift normalization values.

2.1.2. Swin block

Swin transformer [15] with shifted windows boosted the performance of ViT-based models due to its ability to capture global and local information. We employ the Swin block to see its compatibility with other CNN-based blocks and how well it performs in conjunction. The block consists of a linear normalization, regular and window partitioning multi-head attention (W-MSA and SW-MSA, respectively), and MLP, with skip connections as shown in Figure 1(b) and Equation 2 (left).
Preprints 76798 g001
Figure 1. The figure shows the inner structure of each block type used for our model construction. (a) is the squeeze-and-excitation block; (b) is the Swin block; and (c) is the UX block.
Figure 1. The figure shows the inner structure of each block type used for our model construction. (a) is the squeeze-and-excitation block; (b) is the Swin block; and (c) is the UX block.
Preprints 76798 g001

2.1.3. UX block

The UX block, recently proposed in [16], is a convolution-based network block that relies on large kernel sizes and depth-wise convolutions. It mimics the Swin block in structure but uses depth-wise convolution (DWC) using 7 × 7 × 7 kernels, depth-wise convolutional scaling (DCS), and linear normalization as illustrated in Figure 1(c) and Equation 3 (right).
The outputs of the Swin and UX blocks, respectively, are computed in the sequential layers of l and l + 1 as:
z ^ l = W - MSA ( LN ( z l − 1 ) ) + z l − 1 ,
z l = MLP ( LN ( z ^ l ) ) + z ^ l ,
z ^ l + 1 = SW - MSA ( LN ( z l ) ) + z l ,
z l + 1 = MLP ( LN ( z ^ l + 1 ) ) + z ^ l + 1 ,
z ^ l = DWC ( LN ( z l − 1 ) ) + z l − 1 ,
z l = DCS ( LN ( z ^ l ) ) + z ^ l ,
z ^ l + 1 = DWC ( LN ( z l ) ) + z l ,
z l + 1 = DCS ( LN ( z ^ l + 1 ) ) + z ^ l + 1 ,
where z ^ l and z l are the outputs of the modules, W-MSA and SW-MSA denote regular and window partitioning multi-head self-attention modules, respectively, and DWC and DCS denote depthwise convolution (with kernel size starting from 7 × 7 × 7) and depthwise convolution scaling modules, respectively.

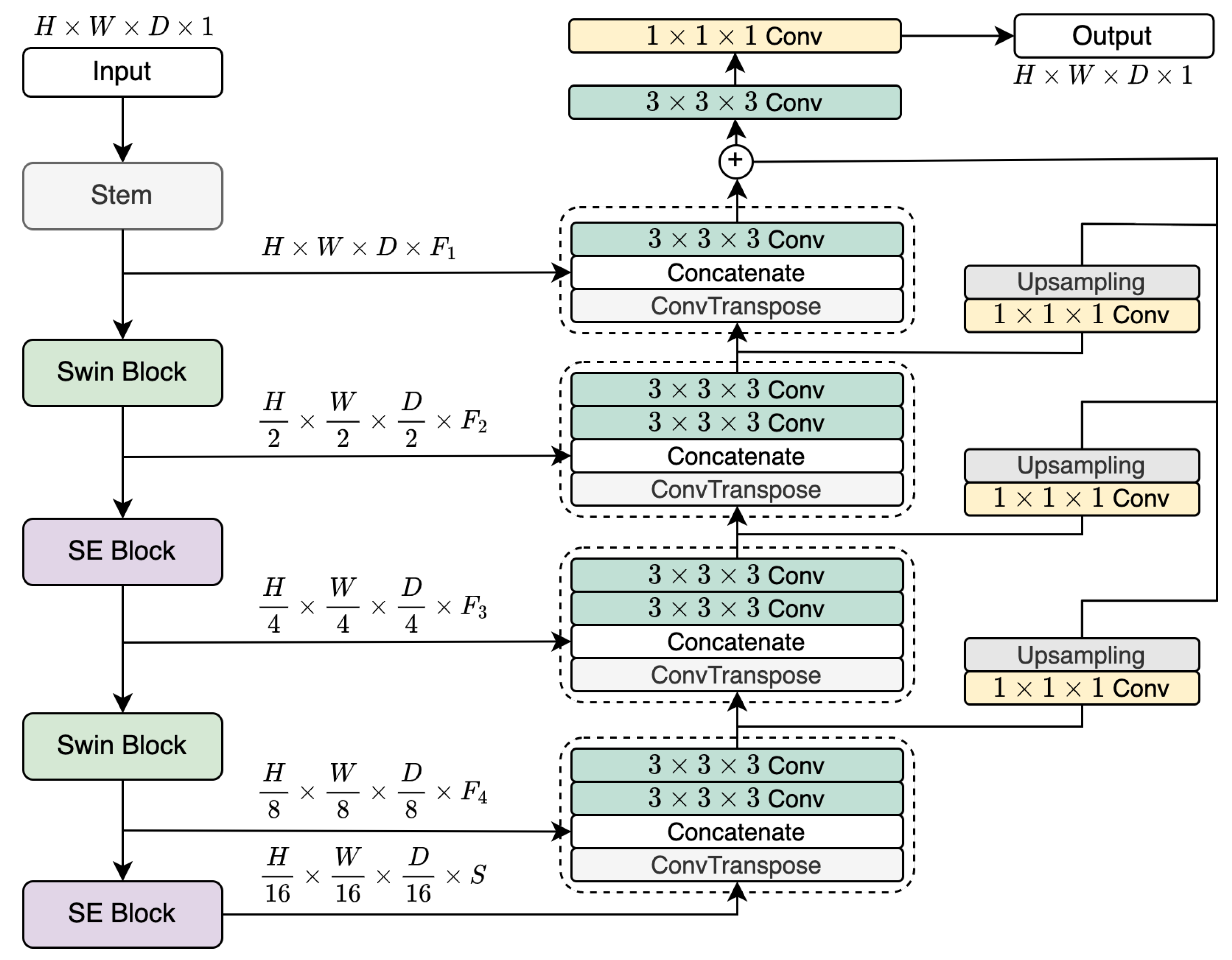
2.2. LegoNet Architecture

The proposed network uses combinations of the aforementioned blocks. The input in the size of X ∈ R H × W × D × C (where H, W, D and C correspond to dimensions and the number of channels, respectively) goes through a stem block, as shown in Figure 2. It is two 3 D convolutional blocks with 7 × 7 × 7 and 3 × 3 × 3 kernel sizes, respectively, which rearranges the input to the size of H × W × D × 24 . The concept of alternating the different blocks surfaces here, with two sets of blocks rotating with one another. Here, we propose three variations to the network as further detailed in Section 2.3. Depicted in Figure 2 is the second version with Swin and SE blocks. The first block (e.g. Swin) downsamples the data to H 2 × W 2 × D 2 × 48 . The next block (e.g. SE) reshapes the output to H 4 × W 4 × D 4 × 96 . The same two blocks will repeat the procedure to generate the representations with the sizes H 8 × W 8 × D 8 × 192 and H 16 × W 16 × D 16 × S , respectively, where S is the hidden size of the final block and is set to 768.

2.3. Alternating Composition of LegoNet

Although we believe that LegoNet as a concept is agnostic to the block type, we demonstrate the idea in three versions, with the difference being in the blocks chosen for the model construction, as listed in Table 1. The second version is depicted in Figure 2 with Swin and SE blocks alternating with each other. The other versions are structured in a similar manner, with SE and UX for the first version and Swin and UX for the third.

2.4. Joint SSL Pretraining

The proposed self-supervised learning (SSL) method reaps the benefits of inpainting [17] and jigsaw puzzle [18] approaches in the same pipeline, as shown in Figure 3. While the two approaches exist in the literature, the originality in this approach is the dual-task nature of pretraining that makes it ever so challenging. The initial scan is cut into N number of equal patches (set to 9) and shuffled randomly. Then, a portion of the shuffled image is masked (set to 40%), and the pretraining model is expected to regenerate the initial image, understanding the positional change and hidden information, which makes it a harder challenge.

3. Dataset and Preprocessing

The proposed concept was validated using two datasets and further verified with four external cohorts to exhaust the generalizability performance of the networks.

3.1. CTCA

The first dataset comprises 155 CTCA scans from three different centers from Oxford University Hospitals that is a substudy of the ORFAN study [10]. The manual segmentation is performed around the right internal mammary artery from the level of the aortic arch to 120mm caudally, and the perivascular space is calculated by taking one diameter of RIMA. The data acquisition and more details are described in [10]. Because the data is from multiple centers and the field of view for each patient is different, the dimensions, spacing, orientation, and direction of the scans are different. We preprocess the data to have the same direction, orientation, and isotropic spacing of 1 × 1 × 1 m m 3 , and as such, the dimensions are highly mismatched. To alleviate that issue, we resize the scans and corresponding masks to 96 × 96 × 96 during training, and the preserved data size is used to resize it back to the original sizes in the final stage.

3.2. CTPA

The second dataset consists of 112 CTPA scans coming from four different centers from Oxford University Hospitals from the same study as CTCA scans. Following the same procedure, we apply the resampling and resizing techniques on this dataset too. The scans were resized to 176 × 176 × 176 because they cover the whole body, and as such, the RIMA region is completely suppressed if we resize them to even lower dimensions. The common preprocessing for both datasets is normalizing the scans before feeding them into the network. We clip the CT scans between (-1024, 1024) and normalize them to (-1, 1).

3.3. External Datasets

Apart from the two above datasets used for training and comparison of models, we use several external datasets. For inter- and intra-observer variability analysis, a new cohort of 49 CTCA scans from the ORFAN study is used. Additionally, as external validation for the post-model agreement analysis, we used three cohorts of 40, 40, and 60 CTCA scans from different centers from the ORFAN study. These scans undergo the same preprocessing steps as above, including normalization and resampling.

4. Experimental Setup

A set of experiments are conducted on the CTCA and CTPA scans for a group of CNN and ViT networks. A single NVIDIA Tesla V100 GPU was utilized for the experiments. We evaluate our proposed method against a range of popular deep learning networks, including U-Net [19], SegResNet [20], UNETR [2], Swin UNETR [3], UX-Net [16], and UNesT [21]. All the experiments are trained for 100 epochs when started with random initialization. Pretraining performed for LegoNet is run for 300 epochs, and the model initialized with pretrained weights is finetuned for 100 epochs, with an early stopping method, having patience at 25 epochs to avoid overfitting. For LegoNet, AdamW optimizer with a learning rate of 1 e − 3 and weight decay of 1 e − 5 , and cosine annealing scheduler with minimum η of 1 e − 5 and T 0 at 25 are used. The loss function is calculated as the summation of Dice and Focal losses (Equation 4 and 5).
L D i c e = 2 ∑ i N y i ^ y i ∑ i N y i ^ 2 + ∑ i N y i 2 ,
L F o c a l = − ∑ i N ϵ y i ( 1 − y i ^ ) ψ l o g ( y i ^ ) − ( 1 − y i ) y i ^ ψ l o g ( 1 − y i ^ ) ,
L F i n a l = L D i c e + L F o c a l
where y ^ is the prediction of the model, y is the ground truth, ϵ is the weightage for the trade-off between precision and recall in the focal loss (empirically set to 1), ψ is focusing parameter (set to 2), and N is the sample size.
The primary metric of performance is the dice similarity coefficient (DSC), with an additional report of precision, recall, and 95% Hausdorff distance for further comparison. The reported results are the mean and standard deviation of 5-fold cross-validation for the training/validation data. To compare the complexity, we also report the number of learnable parameters and FLOPs for each model.

5. Results

5.1. CTCA

Table 2 shows the main results for the CTCA dataset and model complexities. The baseline CNN and ViT models respectively, U-Net and UNETR, show similar performance, with mean DSC of 0.686 and 0.690. UX-Net model achieves 0.695 in DSC, whereas UNesT performs poorly, outputting only 0.555. SwinUNETR yields better results, with 0.713 DSC. SegResNet demonstrates the highest performance compared to the other existing works. All three variations of the LegoNet outperform all the models in DSC as well as precision, recall, and HD95. LegoNetV2, that is, Swin and SE alteration, yields the highest DSC of 0.749, followed by the other two versions with 0.747 and 0.741 DSC, respectively. A similar trend is observed with precision, recall, and HD95 metrics, with LegoNet showing superior results to other networks.

5.2. CTPA

On the CTPA dataset, the performance is lower for all the models due to the large field of view of the pulmonary region that generally suppresses the RIMA and perivascular space, as visualized in Figure 4(c,d). As Table 3 shows, U-Net and UX-Net achieve similar mean DSC of 0.611 and 0.608, respectively, whereas UNETR performs poorly with 0.581 DSC. SegResNet again shows the best performance among the existing models, with 0.638 in DSC. LegoNet (version 1) shows superior performance with 0.642 mean DSC. The trade-off between precision and recall works for the benefit of SegResNet in precision (0.68) and LegoNet in recall (0.67) as the highest results.

5.3. Inter- and Intra-observer Variability

We explore the performance variability in terms of inter-observer, intra-observer, and model-versus-human agreement DSC. The model-vs-human agreement is calculated as the mean DSC of the three values for model prediction masks and the three manual segmentation masks. We use a new cohort of 49 CTCA scans for this set of experiments, which undergo the same preprocessing steps as the initial CTCA dataset. An expert radiologist performs segmentation twice on two occasions (with around 12 months difference) to assess intra-observer variability. A less senior radiologist segments the scans following the same protocol to evaluate inter-observer variability. The intra-clinician and inter-clinician variability reach 0.804 and 0.761 DSC, respectively. The model-vs-human variability for this cohort achieves 0.733 DSC.

5.4. External Cohorts

We validate the performance of our model on a set of external/unseen CTCA cohorts iteratively (40, 40, 60 scans), which are preprocessed in the same way. These cohorts are from a different center than the centers of the training data. The data acquisition protocol is the same for all the centers. An expert clinician analyzes and corrects the segmentation masks from the model, and then we calculate the post-model agreement in DSC. Table 4 (right) shows the total number of cases for three cohorts and their corresponding DSC values. The agreement in DSC between the model’s prediction and the clinician’s corrected masks are 0.935, 0.942, and 0.947 for the three cohorts, respectively.
Table 4. The left table shows the intra- and inter-observer variability and model-vs-human performance of the model on an unseen CTCA dataset. Years of XP refers to years of professional experience, specifically in cardiovascular medicine. The right table shows the count and performance of three unseen cohorts of CTCA scans for post-model agreement.
Table 4. The left table shows the intra- and inter-observer variability and model-vs-human performance of the model on an unseen CTCA dataset. Years of XP refers to years of professional experience, specifically in cardiovascular medicine. The right table shows the count and performance of three unseen cohorts of CTCA scans for post-model agreement.
Variability Years of XP DSC External Number of cases DSC
Intra 3 0.804 Cohort 1 40 0.935
Inter 1 0.761 Cohort 2 40 0.942
Model vs Human NA 0.733 Cohort 3 60 0.947
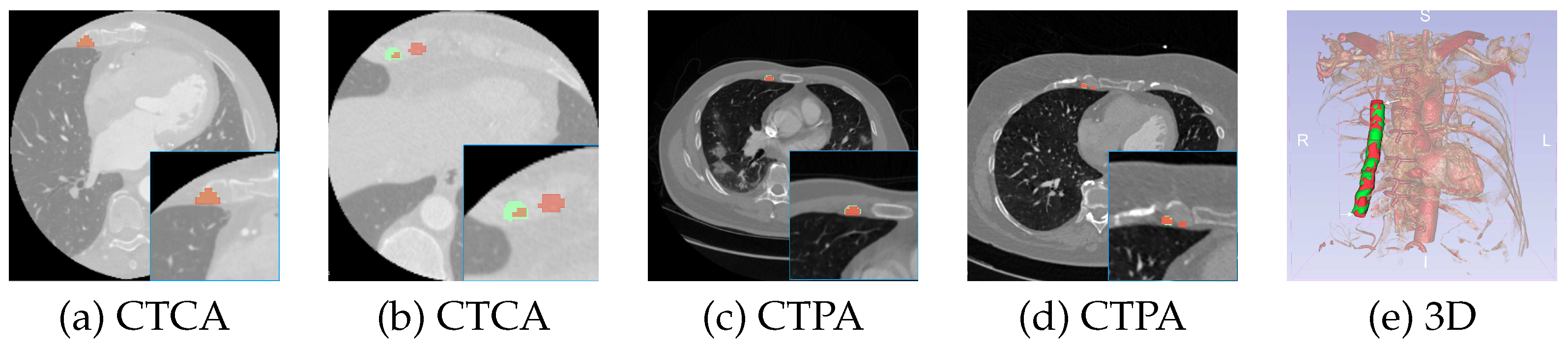
Preprints 76798 g004
Figure 4. The figure shows samples from the datasets and corresponding ground truth (in green) and prediction masks (in red) from LegoNet. (a) and (c) are well-predicted samples, and (b) and (d) are poorly predicted samples. (e) is a 3D visualization.
Figure 4. The figure shows samples from the datasets and corresponding ground truth (in green) and prediction masks (in red) from LegoNet. (a) and (c) are well-predicted samples, and (b) and (d) are poorly predicted samples. (e) is a 3D visualization.
Preprints 76798 g004

5.5. SSL

The pretraining is performed exclusively for LegoNet to analyze the benefit of using the approach instead of randomly initializing it. Note that this experiment is conducted to merely illustrate the effect of the proposed joint method rather than applying it to compare LegoNet with other models. The performance of LegoNetV2 on the CTCA dataset shows a marginal improvement from 0.749 (from Table 2) to 0.754 when initialized with the pretrained weights. HD95 also shows a positive trend, reaching the lowest of 2.08. Precision and recall are 0.75 and 0.78, respectively. These results only confirm the advantage of using an SSL approach over the model.

6. Discussion

While the performance of LegoNet is superior to other networks experimented with, there is a noticeable discrepancy between the cross-validation results (∼0.75 DSC) and the post-model agreement on external cohorts (∼0.90 DSC). It is primarily on account of the flexibility in the segmentation regions. That is, the clinician accepts the masks predicted by the model as representative of RIMA and perivascular space such that it can be used for patient diagnosis in [10], for example. With intra- and inter-observer and model-vs-human agreement analyses, we show that the results indeed reflect the cross-validation results.
Figure 4 illustrates samples for well-predicted (a and c) and poorly-predicted (b and d) masks from LegoNetV2 for CTCA and CTPA datasets. While most of the slices are well-predicted, beginning/ending slices are occasionally missegmented, which is observed as the most common mistake. The clinician, following a protocol, makes a judgment on which slice to start and which slice to end with to extract 120mm length (although RIMA is still visible in the next few slices). As long as RIMA is visible in the scan, the models continue to predict, going beyond 120mm, as is visualized in Figure 4(e). This behavior is commented by the clinician as negligible, and we will investigate the effect of the automatically segmented regions on the patient prognosis in the future.
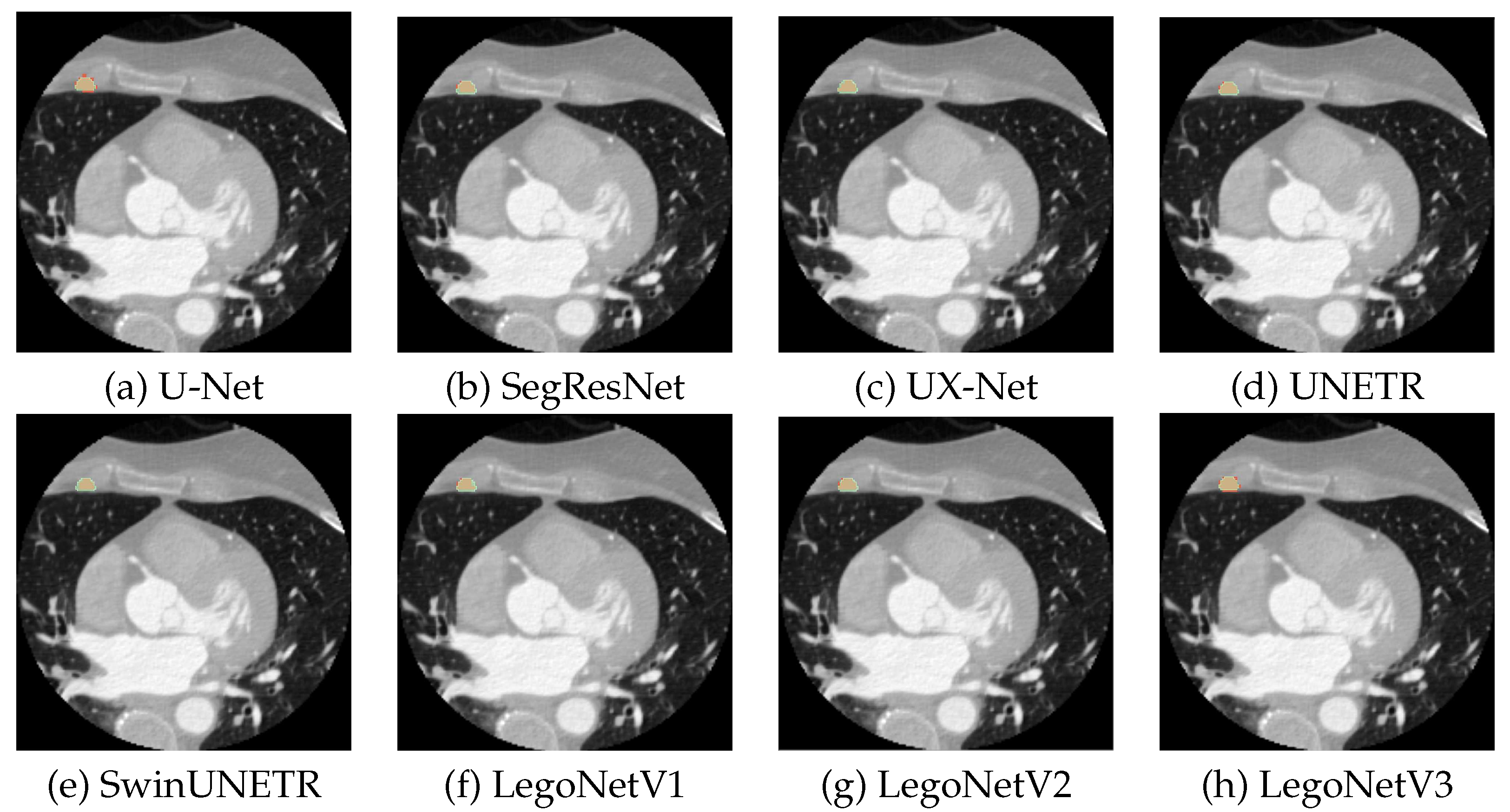
Figure 5 shows more qualitative results for each model for a random slice. The existing models show inferior predictions visually; U-Net under-segments the regions, and SwinUNETR and UX-Net over-segment them. LegoNet is more accurate with the contouring of the masks, which helps it outperform other models.
We attribute the superior performance of LegoNet to (i) structurally different blocks that are assumed to learn more discriminative features and (ii) the complexity of the model. Compared to CNN models, the complexity, both in parameters and FLOPs, is much higher. However, that is on par with ViT models, such as UNETR, SwinUNETR, and UNesT. The best-performing LegoNetV2, for example, stands at 50.71M parameters and 188.02G FLOPs, which is smaller than the three ViT-driven models.

7. Conclusion

The work proposes a new concept of alternating differently structured blocks to harmonize the benefits of different blocks to construct an architecture. This concept escapes the typical approach of building networks using the same blocks and shows that the dissimilar blocks can benefit model learning. Three variations of the LegoNet model that uses this concept are proposed for the segmentation of RIMA and perivascular space. RIMA has not been studied before; however, it is proven to provide clinical value for vascular inflammation and the prognosis of cardiovascular diseases. LegoNet performs superior to other leading CNN and ViT models on two CTA datasets, and we perform further validation on three external cohorts for the agreement in DSC between clinician and model prediction. We also study intra- and inter-observer variability as additional affirmation. As a limitation, the SSL method studies only the joint method of shuffling and masking and does not dive into the performance of the standalone methods. Finally, further assessment of different applications and tasks of the new novel LegoNet is needed.

Author Contributions

Conceptualization, I.S., C.X., M.S., P.P., C.K., H.W., K.C., S.N., C.A., and M.Y; methodology, I.S., C.X., M.S., P.P., C.K., H.W., K.C., S.N., C.A., and M.Y.; software, I.S., M.S., and M.Y.; validation, I.S., C.X., M.S., P.P., T.H., Z.F., C.K., H.W., K.C., S.N., C.A., and M.Y.; formal analysis, I.S., C.X., K.C., T.H., and Z.F.; investigation, I.S., M.S., C.X., K.C., T.H., Z.F.; resources, I.S., and C.X.; data curation, I.S., C.X., K.C., T.H., Z.F.; writing—original draft preparation, I.S., C.X., C.A., and M.Y.; writing—review and editing, I.S., C.X., M.S., P.P., T.H., Z.F., C.K., H.W., K.C., S.N., C.A, and M.Y.; visualization, I.S., C.X., and M.S., supervision, M.S., K.C., S.N., C.A., and M.Y.; project administration, I.S., and C.X.; funding acquisition, M.Y. All authors have read and agreed to the published version of the manuscript.’

Funding

M.Y. and I.S. were funded by MBZUAI research grant (AI8481000001). C.A. acknowledges support from the Oxford British Heart Foundation (CH/F/21/90009, TG/19/2/34831 and RG/F/21/110040), the Oxford BHF Centre of Research Excellence (RE/18/3/34214), the Oxford NIHR Biomedical Research Centre and Innovate UK.

Institutional Review Board Statement

This study was approved by the local research ethics committee of the University of Oxford, Oxford, UK (Oxford REC C 11/SC/0140). Detailed information on ethical approval and patient consent for the populations in the multiple study arms are given in the appendix (p 1) in [10].

Informed Consent Statement

Not applicable.

Data Availability Statement

The data used in this study can be accessible on request, by applying to the ORFAN Publications and Data Sharing Committee at https://oxhvf.com/the-orfan-study/.

Acknowledgments

Not applicable.

Conflicts of Interest

CA, KMC, and SN are Founders, Shareholders and Directors of Caristo Diagnostics LTD. MS and PP are employees of Caristo Diagnostics.

Abbreviations

The following abbreviations are used in this manuscript:
CNN Convolutional neural networks
CTA Computed tomography angiography
CTCA Computed tomography coronary angiography
CTPA Computed tomography pulmonary angiography
DCS Depth-wise convolutional scaling
DL Deep learning
DSC Dice similarity coefficient
DWC Depth-wise convolution
FLOPs Floating point operations
IN Instance normalization
MSA Multi-head self-attention
ORFAN The Oxford risk factors and non-invasive imaging study
ReLU Rectified linear activation unit
RIMA Right internal mammary artery
SE Squeeze-and-excitation
ViT Vision transformer

References

  1. Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: learning dense volumetric segmentation from sparse annotation. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2016: 19th International Conference, Athens, Greece, October 17-21, 2016, Proceedings, Part II 19. Springer, 2016, pp. 424–432.
  2. Hatamizadeh, A.; Tang, Y.; Nath, V.; Yang, D.; Myronenko, A.; Landman, B.; Roth, H.R.; Xu, D. Unetr: Transformers for 3d medical image segmentation. Proceedings of the IEEE/CVF winter conference on applications of computer vision, 2022, pp. 574–584.
  3. Hatamizadeh, A.; Nath, V.; Tang, Y.; Yang, D.; Roth, H.R.; Xu, D. Swin unetr: Swin transformers for semantic segmentation of brain tumors in mri images. Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries: 7th International Workshop, BrainLes 2021, Held in Conjunction with MICCAI 2021, Virtual Event, September 27, 2021, Revised Selected Papers, Part I. Springer, 2022, pp. 272–284.
  4. Liu, H.; Simonyan, K.; Yang, Y. Darts: Differentiable architecture search. arXiv preprint arXiv:1806.09055 2018.
  5. Tan, M.; Chen, B.; Pang, R.; Vasudevan, V.; Sandler, M.; Howard, A.; Le, Q.V. Mnasnet: Platform-aware neural architecture search for mobile. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2019, pp. 2820–2828.
  6. Zela, A.; Elsken, T.; Saikia, T.; Marrakchi, Y.; Brox, T.; Hutter, F. Understanding and robustifying differentiable architecture search. arXiv preprint arXiv:1909.09656 2019.
  7. Yang, X.; Zhou, D.; Liu, S.; Ye, J.; Wang, X. Deep model reassembly. Advances in neural information processing systems 2022, 35, 25739–25753. [Google Scholar]
  8. Chen, J.; Lu, Y.; Yu, Q.; Luo, X.; Adeli, E.; Wang, Y.; Lu, L.; Yuille, A.L.; Zhou, Y. Transunet: Transformers make strong encoders for medical image segmentation. arXiv preprint arXiv:2102.04306 2021.
  9. Zhang, Y.; Liu, H.; Hu, Q. Transfuse: Fusing transformers and cnns for medical image segmentation. Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Strasbourg, France, September 27–October 1, 2021, Proceedings, Part I 24. Springer, 2021, pp. 14–24.
  10. Kotanidis, C.P.; Xie, C.; Alexander, D.; Rodrigues, J.C.; Burnham, K.; Mentzer, A.; O’Connor, D.; Knight, J.; Siddique, M.; Lockstone, H.; others. Constructing custom-made radiotranscriptomic signatures of vascular inflammation from routine CT angiograms: a prospective outcomes validation study in COVID-19. The Lancet Digital Health 2022, 4, e705–e716. [Google Scholar] [CrossRef] [PubMed]
  11. Otsuka, F.; Yahagi, K.; Sakakura, K.; Virmani, R. Why is the mammary artery so special and what protects it from atherosclerosis? Annals of cardiothoracic surgery 2013, 2, 519. [Google Scholar] [PubMed]
  12. Akoumianakis, I.; Sanna, F.; Margaritis, M.; Badi, I.; Akawi, N.; Herdman, L.; Coutinho, P.; Fagan, H.; Antonopoulos, A.S.; Oikonomou, E.K.; others. Adipose tissue–derived WNT5A regulates vascular redox signaling in obesity via USP17/RAC1-mediated activation of NADPH oxidases. Science translational medicine 2019, 11, eaav5055. [Google Scholar] [CrossRef] [PubMed]
  13. Iantsen, A.; Jaouen, V.; Visvikis, D.; Hatt, M. Squeeze-and-excitation normalization for brain tumor segmentation. Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries: 6th International Workshop, BrainLes 2020, Held in Conjunction with MICCAI 2020, Lima, Peru, October 4, 2020, Revised Selected Papers, Part II 6. Springer, 2021, pp. 366–373.
  14. Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Instance normalization: The missing ingredient for fast stylization. arXiv preprint arXiv:1607.08022 2016.
  15. Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. Proceedings of the IEEE/CVF international conference on computer vision, 2021, pp. 10012–10022.
  16. Lee, H.H.; Bao, S.; Huo, Y.; Landman, B.A. 3D UX-Net: A Large Kernel Volumetric ConvNet Modernizing Hierarchical Transformer for Medical Image Segmentation. arXiv preprint arXiv:2209.15076 2022.
  17. Pathak, D.; Krahenbuhl, P.; Donahue, J.; Darrell, T.; Efros, A.A. Context encoders: Feature learning by inpainting. Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 2536–2544.
  18. Noroozi, M.; Favaro, P. Unsupervised learning of visual representations by solving jigsaw puzzles. Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, October 11-14, 2016, Proceedings, Part VI. Springer, 2016, pp. 69–84.
  19. Kerfoot, E.; Clough, J.; Oksuz, I.; Lee, J.; King, A.P.; Schnabel, J.A. Left-ventricle quantification using residual U-Net. Statistical Atlases and Computational Models of the Heart. Atrial Segmentation and LV Quantification Challenges: 9th International Workshop, STACOM 2018, Held in Conjunction with MICCAI 2018, Granada, Spain, September 16, 2018, Revised Selected Papers 9. Springer, 2019, pp. 371–380.
  20. Myronenko, A. 3D MRI brain tumor segmentation using autoencoder regularization. Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries: 4th International Workshop, BrainLes 2018, Held in Conjunction with MICCAI 2018, Granada, Spain, September 16, 2018, Revised Selected Papers, Part II 4. Springer, 2019, pp. 311–320.
  21. Yu, X.; Yang, Q.; Zhou, Y.; Cai, L.Y.; Gao, R.; Lee, H.H.; Li, T.; Bao, S.; Xu, Z.; Lasko, T.A.; others. UNesT: Local Spatial Representation Learning with Hierarchical Transformer for Efficient Medical Segmentation. arXiv preprint arXiv:2209.14378 2022.
Preprints 76798 g002
Figure 2. The figure shows LegoNetV2 architecture. F 1 − 4 indicate the feature size, which is set to { 24 , 48 , 96 , 192 } , and S is the hidden size, set to 768. This typical U-shaped architecture utilizes the block alternation concept, switching between Swin and SE blocks in the encoder in this example. The decoder is kept the same for all the variations of the model.
Figure 2. The figure shows LegoNetV2 architecture. F 1 − 4 indicate the feature size, which is set to { 24 , 48 , 96 , 192 } , and S is the hidden size, set to 768. This typical U-shaped architecture utilizes the block alternation concept, switching between Swin and SE blocks in the encoder in this example. The decoder is kept the same for all the variations of the model.
Preprints 76798 g002
Preprints 76798 g003
Figure 3. The figure shows the pipeline for SSL pretraining. Scans are first shuffled and then masked before feeding into the network with the objective of reconstructing the original scans.
Figure 3. The figure shows the pipeline for SSL pretraining. Scans are first shuffled and then masked before feeding into the network with the objective of reconstructing the original scans.
Preprints 76798 g003
Preprints 76798 g005
Figure 5. Prediction masks from different models for a sample scan from the CTCA dataset. Green corresponds to ground truth, and red indicates the prediction mask.
Figure 5. Prediction masks from different models for a sample scan from the CTCA dataset. Green corresponds to ground truth, and red indicates the prediction mask.
Preprints 76798 g005
Table 1. The table shows the different configurations for the network. These configurations can easily be changed in the code.
Table 1. The table shows the different configurations for the network. These configurations can easily be changed in the code.
Network Used blocks Hidden size Feature size
LegoNetV1 SE→UX→SE→UX 768 (24, 48, 96, 192)
LegoNetV2 SE→Swin→SE→Swin 768 (24, 48, 96, 192)
LegoNetV3 Swin→UX→Swin→UX 768 (24, 48, 96, 192)
Table 2. The table reports the mean and standard deviation of DSC, precision, recall, and HD95 for 5-fold cross-validation and the number of parameters and FLOPs of different models. The results are for the CTCA dataset. All the experiments in this table are trained with random initialization.
Table 2. The table reports the mean and standard deviation of DSC, precision, recall, and HD95 for 5-fold cross-validation and the number of parameters and FLOPs of different models. The results are for the CTCA dataset. All the experiments in this table are trained with random initialization.
Models DSC↑ Precision↑ Recall↑ HD95↓ Params (M)↓ FLOPs (G)↓
UNet [1,19] 0.686±0.03 0.72±0.04 0.69±0.03 2.70 3.99 27.64
SegResNet [20] 0.732±0.01 0.75±0.02 0.74±0.03 2.50 1.18 15.58
UX-Net [16] 0.695±0.03 0.73±0.06 0.70±0.01 3.17 27.98 164.17
UNETR [2] 0.690±0.02 0.72±0.03 0.69±0.03 3.00 92.78 82.48
SwinUNETR [3] 0.713±0.02 0.74±0.02 0.71±0.04 2.46 62.83 384.20
UNesT [21] 0.555±0.04 0.59±0.06 0.55±0.05 4.35 87.20 257.91
LegoNetV1 0.747±0.02 0.75±0.02 0.77±0.03 2.34 50.58 175.77
LegoNetV2 0.749±0.02 0.77±0.01 0.76±0.04 2.11 50.71 188.02
LegoNetV3 0.741±0.02 0.76±0.02 0.75±0.03 2.34 11.14 173.41
Table 3. The table reports the mean and standard deviation of DSC, precision, and recall for 5-fold cross-validation for different models for the CTPA dataset. All the experiments in this table are trained with random initialization.
Table 3. The table reports the mean and standard deviation of DSC, precision, and recall for 5-fold cross-validation for different models for the CTPA dataset. All the experiments in this table are trained with random initialization.
Models DSC↑ Precision↑ Recall↑
UNet [1,19] 0.611±0.10 0.66±0.10 0.61±0.10
SegResNet [20] 0.638±0.09 0.68±0.10 0.65±0.08
UX-Net [16] 0.608±0.08 0.65±0.10 0.62±0.06
UNETR [2] 0.581±0.10 0.62±0.12 0.61±0.07
LegoNetV1 0.642±0.08 0.66±0.11 0.67±0.07
* The complexity comparison of models is provided in Table 2.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated