Prerpints.org logo
Preprint
Article

Path for Near Room-Temperature Superconductivity in Q-carbon Related Materials

Altmetrics

Downloads

205

Views

87

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.pdf (90.55KB )

This version is not peer-reviewed

Submitted:

19 June 2023

Posted:

20 June 2023

Read the latest preprint version here

Alerts
Abstract
We present atomic structures and nonequilbrium synthesis of new class of materials, where the basic structural unit is a diamond tetrahedron. When units of one, two, and three tetrahedra are randomly packed, we create distinct phases of amorphous Q-carbon. Four tetrahedra in two adjacent layers lead to crystalline diamond lattice, which has four missing tetrahedra alternately. When these four missing tetrahedra are filled, we create subunit cell of crystalline Q-diamond. Theoretical calculations show that superconducting transition temperature (Tc) in 50 atomic % B-doped Q-diamond can reach near room temperature at ambient pressures. This is consistent with our earlier results using low-loss EELS measurements in 50 atomic % B-doped Q-carbon, which had mostly amorphous QB3 phase mixed with some crystalline Q-diamond phase. These EELS results showed that the Tc for these samples was in between 90K and 300K. Theoretical calculations of density of states, Eliashberg function, electron-phonon interaction parameter, and root-mean-square and logarithmic average of frequency in crystalline Q-diamond show Tc in the range of 268K to 300K, which is in a complete agreement with our EELS results in QB3.
Keywords: 
Subject: Engineering  -   Other

1. Introduction

The room-temperature superconductivity is the holy grail of solid-state physics and materials science, as it stands to revolutionize applications across the spectrum ranging from energy transmission and levitated trains to magnetic resonance imaging, nanosensing, and quantum computing [1,2]. The pursuit for room-temperature superconductivity at ambient pressures has intensified after considerable progress in metallic hydrogen based systems under extreme pressures [3]. While the superconductivity under extreme pressures may not lead to any practical applications, but we can learn a lot in terms of basic mechanism of Bardeen-Cooper-Schrieffer (BCS) superconductivity. However, our focus here is on BCS superconductivity at ambient pressures. These are also known as class-1 superconductors with a basic mechanism involving electron-phonon interaction [1]. Since the BCS mechanism of superconductivity, based upon electron phonon interaction, is well established, the path to high-temperature superconductivity is quite clear albeit very challenging. For the case of strong electron-phonon coupling (λ >1), Tc can be approximated by T c   = 0.2 [ λ < ω 2 > = ∑ i ɳ i / M i ] 0.5 , where λ depends upon the ratio of spring constants, ω is the averaged phonon frequency, M is the averaged atomic mass, and ɳ is the McMillan-Hopfield parameter having units of spring constant. This parameter is related to strength of electronic response near the Fermi surface to atomic perturbations. Using these guidelines, we have focused our search for enhanced Tc in strongly bonded sp3 and sp2 carbon related materials having appropriate dopants to provide free carriers and high density of states near the Fermi level.
The superconductivity was discovered by Kamerlingh Onnes in 1911 in mercury with the superconducting transition temperature (Tc) of 4.2K [4]. Since then, the progress has been slow in obtaining higher Tc at ambient pressures. This is particularly so for the BCS superconductivity at ambient pressures based upon electron-phonon interaction [5]. As shown in supplementary Figure S1, the Tc increased very slowly from 4.2K to 15K for V3Si, 18.3K for Nb3Sn and 23.2K for Nb3Ge, until 2001 with Tc = 39K in MgB2 at ambient pressures [6]. From theoretical considerations, MgB2 is an optimally doped superconductor, making Tc = 39K as the highest possible in this system [7]. More recently in 2017, B-doped Q-carbon was found to have Tc of 37K [8] and 57K [9] in B-doped Q-carbon at concentrations of 17at% and 25 at% B-doped, respectively, thus surpassing the MgB2 record of 39K at ambient pressures. From the critical current density and field measurements, the critical current density (Jc at 2T) in 17% B-doped Q-carbon at was estimated to be 4.3 × 107 Acm-2 at 21K. It was even more exciting to realize the possibility of Tc between 90 and 300K in 50% B-doped amorphous Q-carbon from low-loss EELS measurements [10,11,12].
Since the experimental discovery in 1911, theoretical developments were slow until 1957, when Bardeen, Cooper and Schrieffer developed a rather compete fundamental theory of superconductivity to relate the transition temperature (Tc) directly with Debye temperature and phonon spectrum, density of states near the Fermi level, and electron-phonon interaction [5]. The BCS framework laid out a clear albeit challenging path to obtain higher Tc by increasing Debye temperature, density of states near the Fermi level, and electron-phonon interaction parameter [1,13,14]. According to the BCS framework, Tc = ΘD exp [-1/N(0) V], where ΘD is the Debye temperature, N (0) is the density of states near the Fermi level, and V is the carrier (electron or hole) interaction potential. The N(0) V is the electron-phonon interaction parameter λ, which should be corrected for electron-electron repulsion parameter µ*, which is small ~0.115 in diamond related materials. This formulation is valid under weak electron-phonon coupling limit, λ <1. Under the strong electron-phonon coupling limit (λ > 1), Tc can be estimated by Tc = 0.183 < λ ωph2 >0.5, where ωph is averaged phonon frequency. The Tc can be also written as Tc = Σ (ɳ /M)0.5, M is averaged atomic mass, and ɳ is the McMillan-Hopfield parameter has units of spring constant, which is related to strength of electronic response near to atomic perturbations the Fermi surface [1].
Thus, materials with higher stiffness and lower mas should provide the best hope for higher transition temperatures in BCS superconducting systems [1]. This framework led us to diamond related materials with appropriate doping such as B and N to provide a direct path to high temperature superconductivity [8,9,10,11,12]. This is also consistent with the Debye temperature for diamond, which is the highest 2250K, compared to 443K for graphite and 276K for niobium. Despite this clear path to BCS high-temperature superconductivity in strongly bonded and light-mass carbon materials, the highest Tc of only 11K in B-doped diamond was achieved. It was realized that the transition temperature in diamond is limited primarily by the low value (2.0 at% B) of equilibrium (thermodynamic) solubility limit of boron concentration coupled with low dopant ionization efficiency [15]. Further enhancement in Tc is expected with increase in boron concentration much higher than the thermodynamic solubility limit. To achieve dopant concentrations higher than the thermodynamic solubility limits, we need to employ highly nonequilibrium methods. This should enhance the density of states as well as electron-phonon coupling. This challenge has been overcome by our discovery of melting of pure and doped carbon by nanosecond lasers in an undercooled state, which upon quenching turns into Q-carbon or diamond [8,9,10,11,12]. Using this technique, both Q-carbon and diamond can be doped with concentrations much higher than thermodynamic solubility limits. This involves the phenomenon of solute trapping during rapid quenching. When B-doped carbon layers are melted, carbon atoms get closely packed in molten state because of metallic bonding. It should be emphasized that higher B concentration in crystalline diamond lattice leads to internal strains which break Cooper pairs, and thus are not conducive to high-temperature superconductivity. This resulted in the Tc of only 17K was achieved in 17%B-doped crystalline carbon [16]. The amorphous structure of B-doped Q-carbon is more tolerant of internal strains, so the high-temperature superconductivity is not adversely affected to the same extent as in crystalline diamond [8,9,10,11,12].
This paper discusses the design and creation of novel covalently bonded carbon materials with Tc close to room temperature at ambient pressures. Since these carbon and diamond related materials are metastable at ambient pressures and temperatures, novel nonequilibrium processing methods are used to create these materials in a phase-pure form. We also address doping of these materials beyond the thermodynamic solubility limits and control of internal strains due to dopant size misfit with the host lattice to enhance Tc.

2. Design of Q-carbon and Diamond Related Materials:

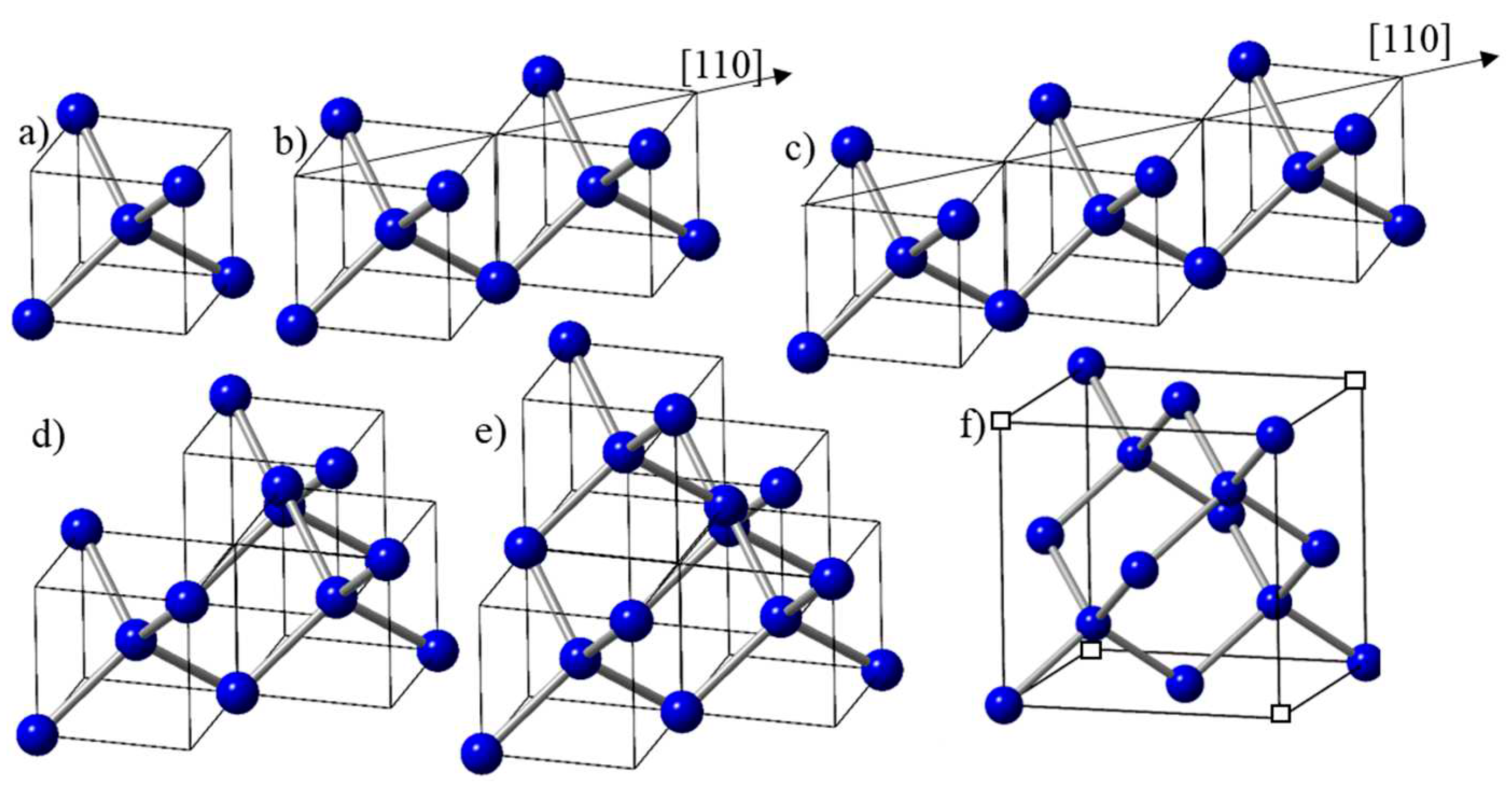
The electrons in the molten state of carbon are delocalized with metallic bonding. With undercooling, the localization of electrons starts and the formation of diamond tetrahedra begins. The formation of a tetrahedron can be correlated with the increase in carbon-carbon atom separation from 2r (close-packed metallic state with r = radius of carbon atom) to 3.26r (diamond tetrahedron) and covalent bonding. The basic unit in the design of new materials is diamond tetrahedron D1 (shown in Figure 1a, contained in one-eighth of diamond unit cell (a/2, a/2, a/2), where atoms are four-fold coordinated. With more time available in the undercooled state, two tetrahedra can grow along <110> direction and form a dimer, as shown in Figure 1b. With a further increase in time associated with reduced undercooling, three tetrahedra can grow along <110> direction, and form a trimer, (depicted in Figure 1c). The third tetrahedron can also join in <1-10> direction in the second plane to form the trimer (depicted in Figure 1d). This trimer is precursor to the formation of diamond unit cell, with the addition of fourth tetrahedron in the <1-10> direction, depicted in Figure 1e. In this framework, the diamond unit cell consists of four tetrahedra with effective number density of atoms of 16/a3, and four missing tetrahedra, giving an average of 8/a3. Here all the four carbon atoms are four-fold coordinated, and the four corner atoms contribute to net one atom (Figure 1f). In the diamond cubic unit cell of a 3-D structure, all the eight carbon atoms, including four missing atoms, indicated by empty squares, are shared by eight unit cells, resulting in one net atom.
By controlling the undercooling before quenching from a molten state, we can control the available time needed for the formation of clusters of one, two, three, and four tetrahedra. The available time for clustering increases with decreasing undercooling. With increasing undercooling, there is not enough time for these tetrahedra to organize into crystalline structures, so we create randomly packed amorphous Q-carbon phases. From the clusters of one, two, and three tetrahedra, we create distinct polymorphic phases of Q3, Q2, and Q1 of Q-carbon, respectively [10]. The formation of distinct allotropes or phases of Q-carbon depends upon the formation of clusters of one, two, or three tertrahedra before quenching. If there is enough time, the clustering of four tetrahedra in two different planes leads to the formation of diamond cubic lattice, where the crystallite size of nanodiamond is determined by the time of growth.
It is important to note that the addition of fourth tetrahedron along <1-10> direction in the second layer leads to the formation of diamond cubic unit cell, which can provide nucleation sites for diamond growth. This description of diamond unit cell is equivalent to two interpenetrating face-centered cubic (fcc) lattices, where the first one is displaced with respect to the other one by (a/4, a/4, a/4) along the diagonal. This framework has been generalized to cover other materials of zinc blende structures, notably Q-silicon with novel properties.
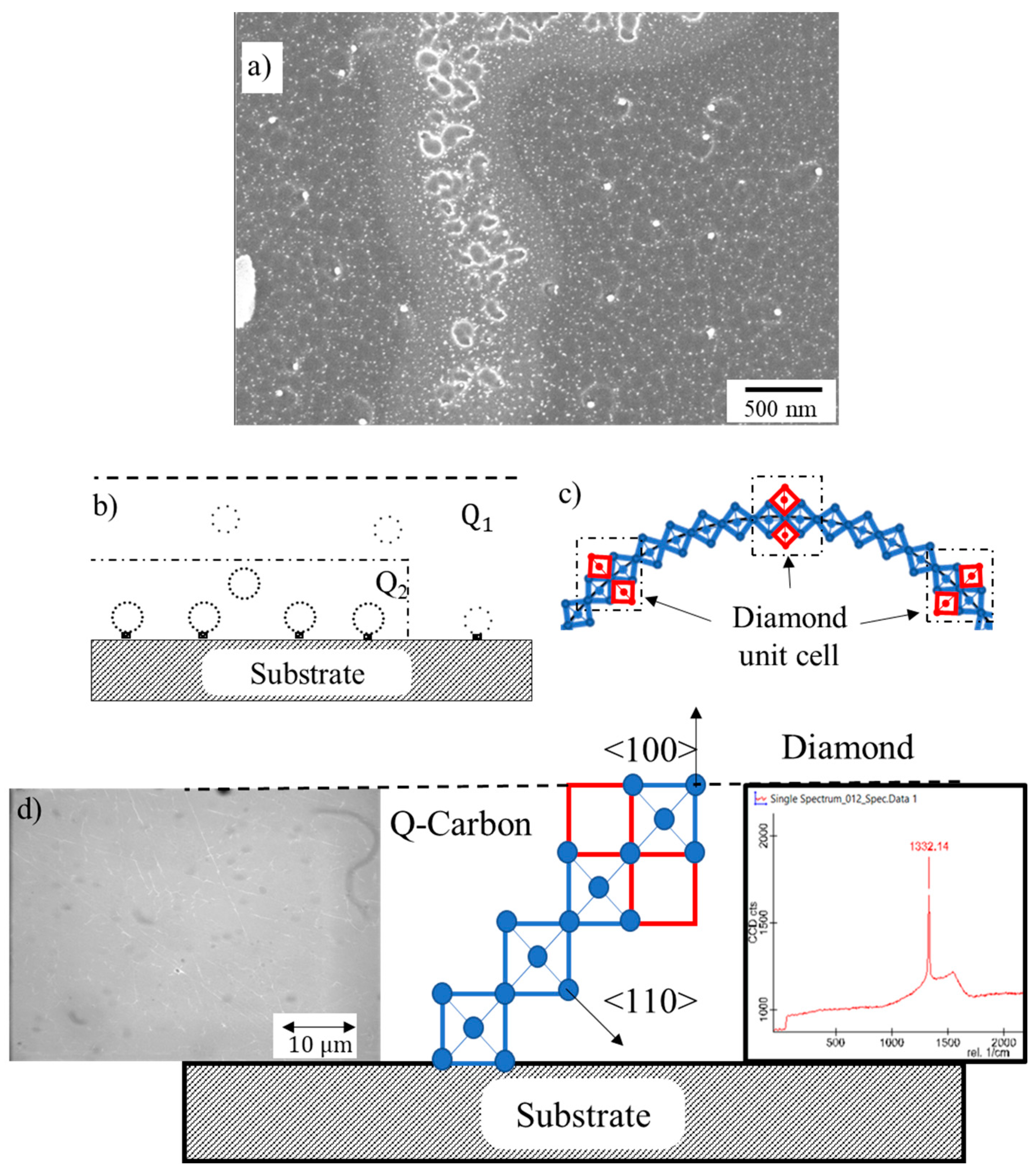
The growth of diamond tetrahedra along <110> direction, as shown in Figure 1b,c, can result in the formation of rings and strings, as depicted in Figure 2a. It should be noted that these tetrahedral are free pivot along the <001> edges and bend to form rings, provided there is enough time available before quenching. On these rings, diamond unit cell can nucleate (as shown in red), by attaching two tetrahedra in <1-10> direction. These unit cells grow and form nanodiamonds, whose size is determined by the growth time in the undercooled liquid before quenching. Figure 2b depicts the formation of nanodiamond rings in Q1 and Q2 phases, where number density nanodiamonds is much higher in Q2 phase than that in the Q1 phase. The schematic in Figure 2c depicts the formation of these ring structures attached with the substrate and the bulk. The nucleation at the substrate involves a heterogeneous nucleation with larger nanodiamonds, whereas in the bulk the nanodiamond size is smaller because of homogeneous nucleation. Using a thin layer of Q carbon and inducing nucleation only at the substrate, we are able grow epitaxial diamond, as shown in Figure 2d.
This cubic diamond unit cell having eight atoms and lattice constant of 0.356 nm has the highest (1.77x1023cm-3) number density of atoms, which leads to many unique properties, including highest stiffness (Young’s modulus) and hardness. Despite the highest number density of atoms, the atomic packing factor (APF) of diamond unit cell is the lowest of all the crystalline structures of only 34%, which means there is a lot of empty space (66%) in the diamond unit cell, compared to only 26% in FCC and HCP, and 32% in BCC crystal structures. This gives us a unique opportunity of creating new materials by incorporating more atoms to increase APF, while keeping the strong covalent bonding characteristics the same.

3. Design of Novel High-Temperature Superconducting Materials:

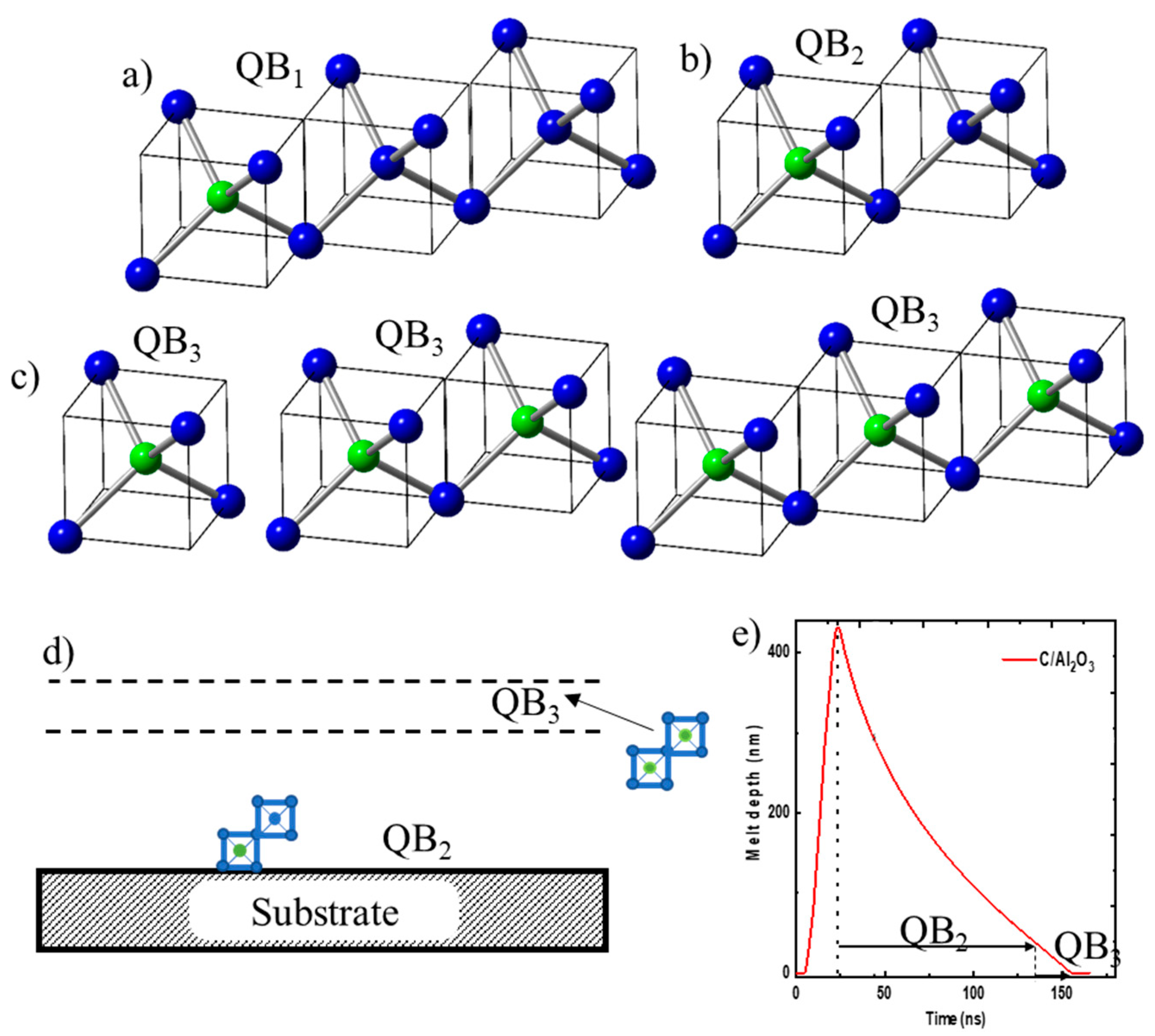
In designing Q-carbon and diamond based superconducting materials, we need to dope these materials to create free electrons or holes, which can form Cooper pairs for BCS superconductivity. The basic unit in the design of new materials is diamond tetrahedron D1 (depicted in Figure 1a, contained in one eighth of diamond unit cell (a/2, a/2, a/2). By replacing the central C by a dopant such as B, we can create 50% B-doped diamond tetrahedron. In the units of three tetrahedra, if the central atom in one of the three tetrahedra is replaced by a dopant, we can create 17% B-doped structures, named QB1, as shown in Figure 3a. These D1 tetrahedra can grow beyond three and create interesting ring and string structures of self-organized B-doped Q-carbon as well as diamond. If the central atom in one of these two tetrahedra is replaced by B, we create 25% B-doped structures, named QB2, as shown in Figure 3b. If B replaces the central atom in all of the tetrahedra (units of one, two or three), we create 50% B-doped structures, named QB3, as shown in Figure 3c. The PLA of thicker as-deposited carbon layers can create layers of QB2 and QB3 layers, where QB2 layer is formed near the substrate. This layer is followed by QB3 layer with increasing B concentration because of zone refining and segregation, as shown in Figure 3d. We also created Q-carbon doped with 17 at% B by pulsed laser annealing of alternate B and C layers, where thicknesses are adjusted to obtain desired QB1. Figure 3e shows calculation of melt depth versus time using SLIM code for 20ns ArF laser pulse having energy density of 0.6 Jcm-2. The surface starts to melt after a few nanoseconds, and melt front penetrates over 400 nm within 20 ns. This plot shows the time available for QB2 growth and the formation of QB3 near the surface where boron concentration increases to 50% because of zone refining. The details of this will be discussed below using high-resolution cross-sectional HAADF and EELS studies.
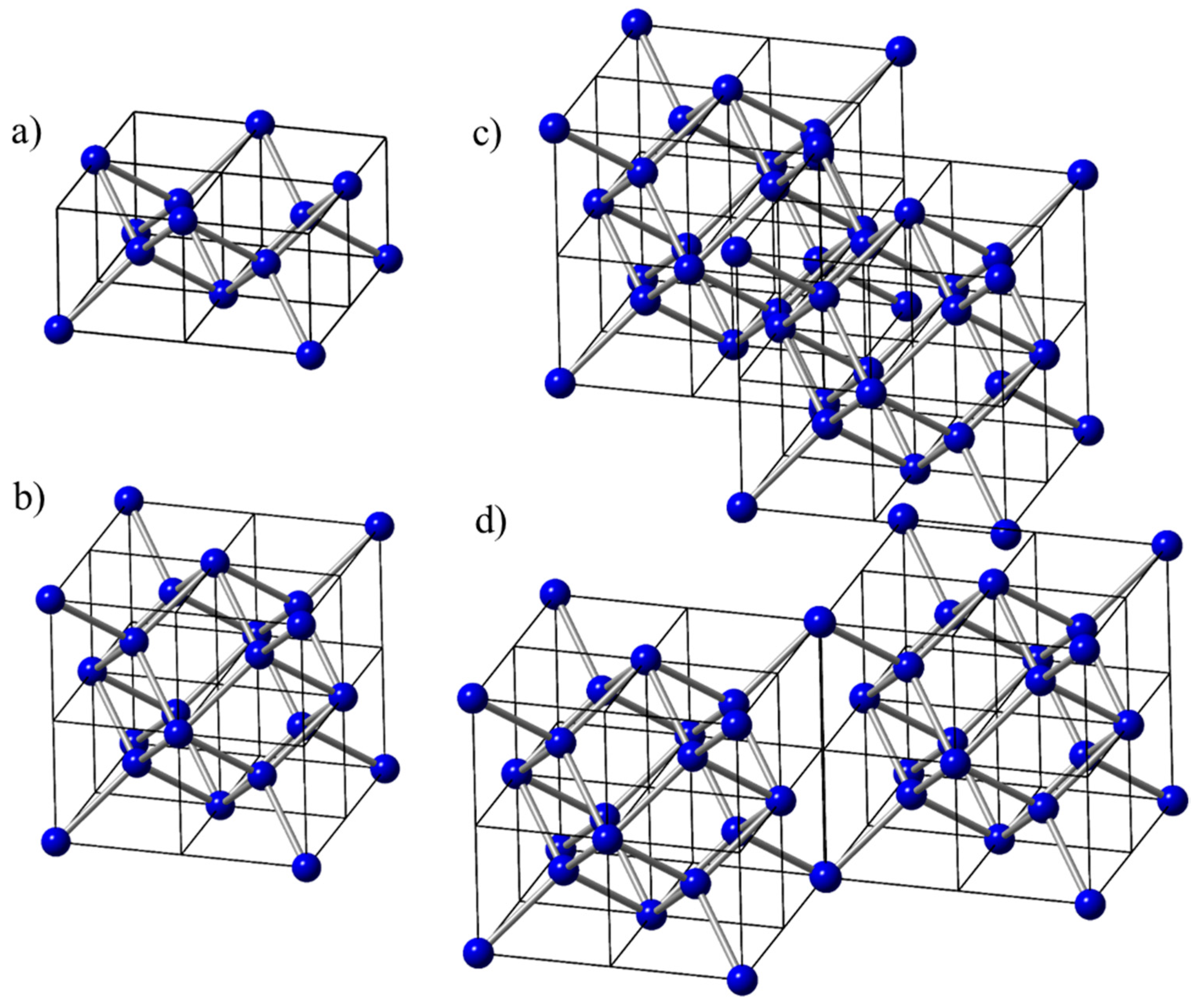
When four D1 tetrahedra are arranged in one plane (as shown in Figure 4a, we can create Q-diamond sheet with effective number density of atoms of 16/a3. With four D1 units in the second plane with a total of eight tetrahedra, we create Q-diamond subunit cell with net 16 atoms and number density of atoms as 16/a3, as shown in Figure 4b. By putting together four Q-diamond subunit cells, we create Q-diamond super unit cell, where there are two in <110> direction (Figure 4c) and two in <1-10> direction in the next plane (Figure 4d) with missing four neighboring subunit cells. Interestingly, this is quite similar to missing four tetrahedra in the diamond unit cell. By replacing central C atoms in these tetrahedra by B atoms selectively, 50% B-doped Q-diamond phase is created, having net 32 C and 32 B atoms arranged in two layers in the super unit cell.
In summary, using D1 subunit cell, which has twice the number density of diamond (16/a3 compared 8/a3 for diamond), we have created the following amorphous (randomly arranged) and crystalline structures. These materials with higher number density of atoms than diamond should have novel and improved properties.
(1)
Q3 and QB3 Structures: The D1 tetrahedra in Figure 1a and Figure 3c can be packed randomly with >80% atomic packing efficiency [19] and create Q3 and QB3 phases, respectively. These phases have number density of atoms of 12.8/a3, which is 60% percent higher than that of diamond. Since the HAADF contrast is directly proportional to number density of atoms, we can determine the density of Q-carbon by comparing with the contrast and density of diamond, as shown in HAADF cross-section in Figure S2. The APF of Q3 and QB3 is 51%, which is even lower than the simple cubic APF of 54%. By replacing the central carbon atom of the tetrahedra by appropriate dopants, we can create doped structures, such as 50% B-doped Q-carbon (QB3). These amorphous structures have covalent bonding (sp3) within the tetrahedra and some sp2 and dangling bonds between the tetrahedra. The dangling bonds between the tetrahedra provide the source for room-temperature ferromagnetism [20,21].
(2)
Q2 and QB2 Structures: When two D1 subunit cells attach along the <110> directions (as shown in Figure 1b and Figure 3b), we create D2 subunit cells. When D2 subunit cells are packed randomly, we create Q2 structures. If one of the two central atoms in D2 is replaced by boron, we create QB2 structure with 25% B. When D1 subunit cells grow along two perpendicular directions in a plane, we create two-dimensional platelet structures.
(3)
Q1 and QB1 Structures: When three D1 subunit cells attach, we create D3 subunit cell, as shown in Figure 1c and Figure 3a. When two D1 subunit cells attach along <110> and one along <1-10>, we create D3, as shown in Figure 1d. When D3 subunit cells are packed randomly, we create Q1 structures. If one of the three central atoms in D3 is replaced by boron, we create QB1 structure with 17% B.
(4)
Crystalline Q and QB diamond Structures: The D1 subunit cells can grow along <100> and <110> directions. Four D1 subunit cells in one plane create D14 subunit cell, as shown in Figure 4a. By putting eight of D1 subunit cells together in two planes, we create Q-diamond subunit cell, as depicted in Figure 4b. This unit cell has a total of fourteen atoms (eight atoms inside and six atoms on the unit cell faces), which are four-fold covalently bonded. In addition, 8 corner atoms are shared by four atoms, which gives net 2 atoms to the unit cell with a total of net 16 atoms. By replacing all of the inside carbon atoms by boron atoms (dopants), one can achieve dopant concentrations with increments (1/16) 6.25%. By replacing all of the central carbon atoms with boron atoms, we achieve a maximum concentration of 50%. Since the face atoms are already saturated, this unit cell cannot be repeated to obtain 3-D structures. However, these unit cells can grow along the <110> diagonal, as shown in Figure 4c. The second layer can grow with a 900 rotation. Thus, a super unit cell with four of these unit cells can be repeated to create 3-D structures. 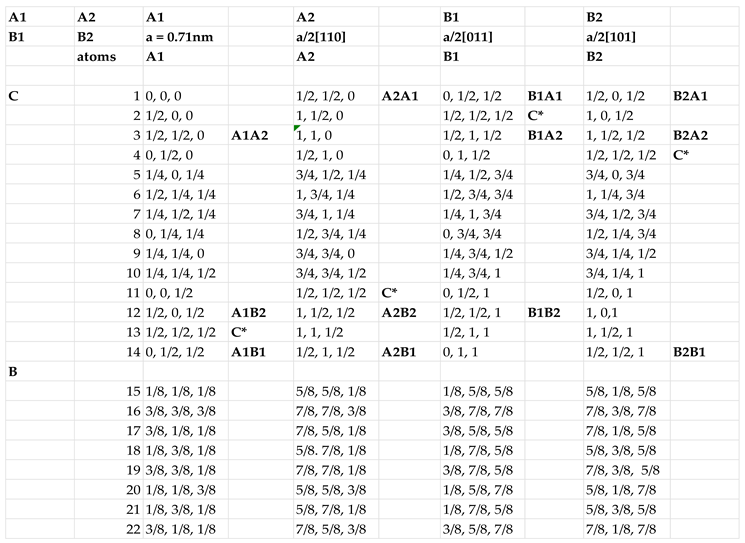This super unit cell has a total of 64 carbon atoms in Q-diamond structure, and 32 C+32B atoms in QB-diamond, as depicted in Figure 4c. The atomic coordinates of each carbon and boron atoms for Figure 4c are given in Table 1. The table shows the coordinates of all four (A1, A2, B1, and B2) subunit cells, where the common atom locations between different subunits are indicated.

4. Computational Method and Experimental Details:

Quantum ESPRESSO, based on DFT plane wave functions and pseudopotentials with local density approximation, was employed to perform electronic-structure calculations for Q-silicon super unit cell with atom coordinates of Table I. The cutoff energy for plane wave functions in Q-silicon is 120 Ry. The program uses Troullier-Martins norm-conserving psuedopotentials for the exchange correlation. The super unit cell consists of four subunit cells with 22 atoms each, which are arranged in <110> and <1-10> directions in two adjacent planes, making a total of 88 atoms. As shown in Table I, nine of these atoms are common, leaving 79 discrete lattice points. However, there are only 64 independent atoms per super unit cell with 16 each per subunit cell.
We synthesized QB1, QB2, and QB3 phases by depositing alternate layers of amorphous carbon and boron layers by pulsed laser deposition. The thickness ratios of carbon to boron layers were adjusted to obtain 17, 25 and 50 at% of boron. These C/B composite layers are melted by using nanosecond ArF laser pulses (wavelength 193nm, pulse duration 20ns, and energy density 0.6-0.8 Jcm-2). However, there is B zone refining as a function of solidification velocity, which changes the relative thicknesses of QB1, QB2, and QB3 composites. This zone refining process needs to be controlled to obtain thicker layers of QB3 (50 at% B). More details about the synthesis are provided in references [8,9].

5. Results and Discussion:

We focus on experimental results of QB3 amorphous structure and theoretical results of crystalline Q-diamond, where both have B-doped diamond tetrahedron as the base structural unit. The B-doped tetrahedron has central C atom replaced by B atom, giving a net 50% B concentration. The structure of Q-diamond is unique having the highest number density of atoms (3.54x1023atoms cm-3) in the subunit cells and empty spaces in-between. The subunit cell (as shown in Figure 4c) has 16 carbon atoms instead of eight as in diamond. When four of these subunit cells are arranged with four empty spaces in two layers, we generate a super unit cell with 64 net carbon atoms with lattice constant of 0.712 nm, which is twice that of diamond. Thus, while the number density of atoms in the subunit cell is twice that of diamond, the average density of atoms in the super unit cell is the same as that of diamond due to alternating empty spaces. This unique structure results because the face atoms in the subunit cells already saturated with four covalent bonds. It is envisaged that this unique structure has an optimum combination of phonon hardening (high frequency, optical phonons) within the subunit cells and phonon softening (low-frequency acoustic phonons) in between the subunit cells. This combination of phonon hardening, and phonon softening is critical to high superconducting transition temperature. The phonon softening (slow phonons) is more effective in enhancing electron-phonon interaction (λ), while phonon hardening enhances the Debye temperature.
In the BCS theory, Tc = ΘD exp [-1/N(0) V], where the density of states close to the Fermi level, N(0), is related to the doping, while the electron-phonon interaction, V, is determined by the lattice vibrations. As pointed out by Cohen [1] in most materials these two parameters cannot be separated, and often work against each other for enhancing Tc. However, in Q-diamond unit cell (Figure 3c) with all C atoms, the empty spaces can be filled with metal atoms such as K, Rb, Cs, Ti, Cu, and enhance N(0) independently, while preserving lattice vibrations responsible for pairing in the subunit cells, where the density of covalently bonded carbon atoms is twice that of diamond. In the case of B-doping, while the doping enhances N(0), but weaker C-B bonding may reduce lattice vibrational frequency somewhat needed for pairing.
By incorporating the electron-electron repulsive interaction parameter, µ*, the transition temperature for BCS superconductivity is given by [1],
Tc = θD Exp (-1/(λ - µ*)),
where θD is the Debye temperature, and λ takes into account the electron-phonon attractive interaction. This equation is applied to weak-coupling limit ( λ≤ 1). For strong-coupling limit (λ> 1), Tc is estimated by,
Tc = 0.183 [<ω2> λ]0.5,
where θD is replaced by the averaged phonon frequency 0.183 [<ω2>]0.5 and electron-phonon coupling Exp (-1/(λ - µ*) is replaced by [λ]0.5.
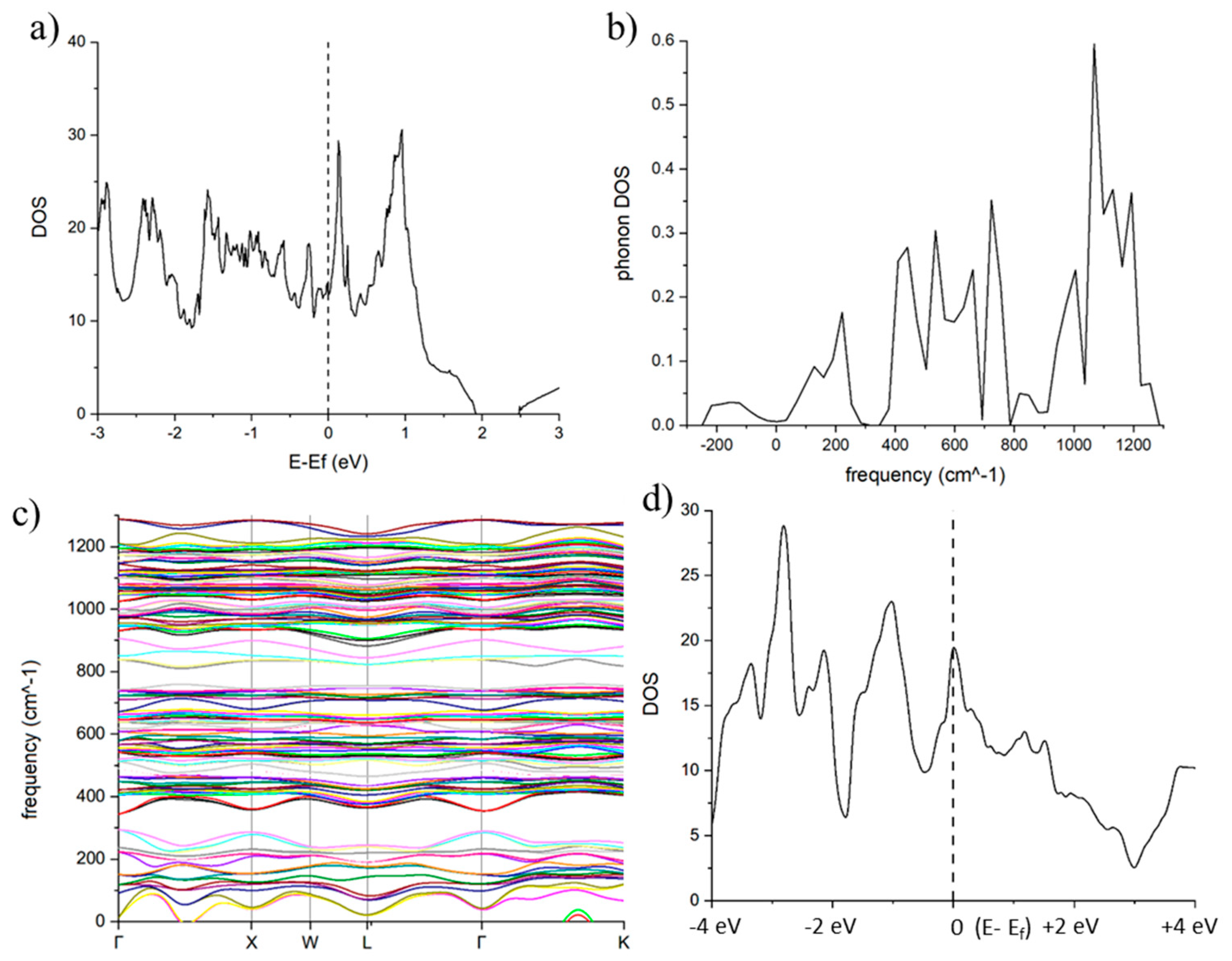
Since λ is given by λ = [(Ω2 – <ω2>)/<ω2>], where Ω is the bare phonon frequency corresponding to zero electron-phonon interaction, it can be estimated from the phonon density of states (DOS), phonon dispersion, and Eliashberg function calculations using Quantum Expresso.
Figure 5a shows DOS (eV per unit cell with 64 atoms) as function of distance from the Fermi level. It is should be noted that the DOS value in Q-diamond of 0.3 eV per atom is substantially higher than 0.1 eV per atom, calculated by Moussa and Cohen for doped diamond with 50% B [7]. Since λ (N(0) V) is directly proportional to the density of states close the Fermi level, we expect electron-phonon interaction in Q-diamond to substantially higher as much as by a factor of thee than that for B-doped diamond. The DOS plot (eV per atom) as function of frequency in Figure 5b shows the concentration of states around 200 cm-1 and 400-800 cm-1 (for acoustic phonons) and 900-1300 cm-1 for (optic phonons). The presence of a small fraction of negative DOS may be related to metastability aspects of crystalline Q-carbon. The crystalline Q-carbon structures have a deep local energy minimum but are metastable with respect to the global free-energy minimum of graphitic carbon. We have used standard coordinates (Table I) for these calculations, but the lattice location of face atoms, which are saturated already with four covalent bonds, may cause these negative frequencies. The plot in Figure 5c shows in detail the peak contributions around 200 cm-1, 400-800 cm-1, and 900-1300 cm-1. Figure 5d shows electronic density of states for 64 super unit cell as a function of Fermi energy. A high electronic DOS of 0.3 eV per atom shows metallic nature of Q-diamond and significant interaction with phonons to enhance the electron-phonon interaction parameter, λ.
From the Quantum Expresso calculations, averaged frequency [<ω2>]0.5 or ωph is estimated to be 750 cm-1 and λ = 2.0. This value is also consistent with λ = [(Ω2 – <ω2>)/<ω2>] = 2.004, where Ω = 1300 cm-1, which is the bare phonon frequency corresponding to λ = 0. Using this value of λ and the equation, Tc = 0.183 [<ω2> λ]0.5, we obtain Tc = 278K. The logarithmic averaging of frequency gives lower average values as it weighs in heavily the lower frequencies near zero, but higher λ. By using logarithmic average frequency ωlog = 600 cm-1 with corresponding λ = 3.694, we estimate Tc = 302K.
Using the McMillan formula based upon generalized Migdal-Eliashberg theory,
Tc = ((ΘD/1.45) exp - [1.04 (1+ λ)/{( λ – μ*(1 + 0.62 λ)}]
We obtain Tc = 259K, using λ = 2.004, μ* = 0.115, and ΘD = 2250K for diamond.
However, the Debye temperature for Q-diamond and QB3 are expected to be higher than diamond. The Debye temperature ΘD is given by, ΘD = h/(2πk) Vs(6π2Nv)1/3, where h is the Planck’s constant, k is the Boltzmann constant, Nv is the density of atoms per unit volume, and Vs is the velocity of sound given by (E/ρ)1/2, where E is the Young’s modulus and ρ is the mass density. Since Nv for QB3 was determined to be 60% higher than diamond, the ΘD for QB3 is estimated to be 2610K, compared to 2250K for diamond. For an estimated ΘD = 2610K for QB3, we obtain Tc =300K by using equation (3). These theoretical results are remarkably consistent with experimental results based upon low-loss EELS and transport measurements to be discussed below. The QE calculations from 2D structure show a much higher density of states per B atom in both unrelaxed and relaxed structures, compared to 3D bulk structure of Q-diamond. In addition, phonon frequency range in unrelaxed and relaxed 2D structures extends to 1800 cm-1 and 2300 cm-1, respectively. These characteristics lead to Tc estimates close to room temperature and higher. The details of all the above theoretical calculations will covered in another paper [22].

6. Experimental Results: High Temperature Superconductivity of QB3 (50% B):

We carried out a detailed study of the characteristics of bonding and the electronic structure in B-doped Q-carbon to understand the basic mechanism of high-temperature superconductivity in the BCS framework [23]. These studies were done using high-resolution electron-energy loss spectroscopy to probe energy-loss near edge structure (ELNES). Aberration-corrected STEM-FEI Titan 80-300 (fifth generation) was used to acquire HAADF images and EELS spectra. These studies provide a direct correlation between experimental results and theoretical calculations of the density of states close to the Fermi level, as illustrated in S3 for silicon. The peaks in ELNES directly correspond to the electronic density of states, which also correlate with phonon density of states. High-resolution HAADF imaging in cross-section showed the formation of distinct QB2 and QB3 phases/allotropes of carbon. After laser annealing heavily B-doped Q-carbon, the atomic fractions of B (from Figure 4c) in QB2 and QB3 phases were estimated as 25% and 50%, respectively. The detailed analysis of EELS data showed the presence sp3 bonded B with lattice location, consistent with the center of the tetrahedron, as presented in the earlier paper [12].
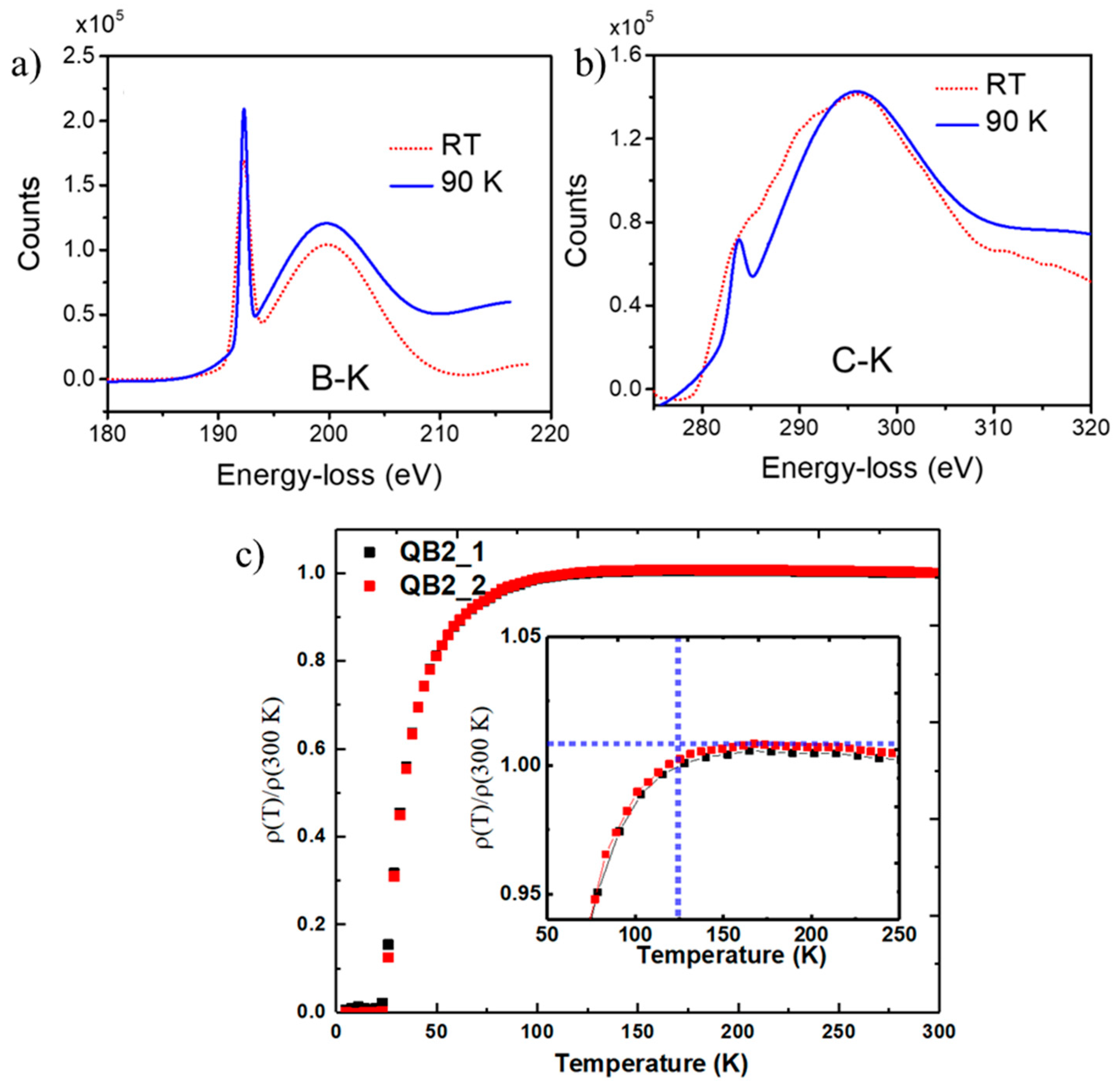
To probe the bonding characteristics and the electronic structure near Tc, we carried out EELS studies at 90K and compared the results at 300K. A comparison of B-K edge (at 192.9 eV) at 90 K and 300K in Figure 6a shows a substantial enhancement in π* and σ* peaks at 90K, indicating an enhancement in the density of states and presence of superconductivity. Similar enhancements in intensity for π* and σ* peaks for C-K edge (at 284 eV) are shown in Figure 6b, indicating Tc in between 90 and 300K. Similar studies from QB2 sample with Tc = 55K showed no changes in B-K and C-K edge EELS spectra at 90K and 300K. The electrical transport measurements were carried out as a function of temperature for a composite sample with 8 nm QB3 and 100 nm QB2, and the results are depicted in Figure 6c. The plot shows a drop in resistivity starting at 125K, as the thickness of QB3 is less than 10% of QB2 phase. Further experiments are continuing to create a thicker layer of only QB3 for transport and magnetic measurements.

7. Summary

The design of novel Q-phases is based upon diamond tetrahedron as the basic building block. These tetrahedra can be packed with a packing efficiency, which can exceed exceed 80 to 85%. If the central atom in the tetrahedron is replaced by B. This structure has B concentration, close to 50at% B, which has been named as QB3 phase. We have synthesized QB3 (10 nm thick QB3 on the top of thick QB2)) and carried out detailed analysis of atomic structure and bonding characteristics using cross-section TEM/STEM/HAADF. The synthesis of phase-pure QB3 phase and high-Tc transport measurements are continuing from thicker samples to obtain sharper Tc. The EELS and preliminary transport measurements provide a clear evidence for Tc over 125K. The EELS results on the changes of π*and σ*peaks at 300K and 90K show a significant enhancement in the density of states at 90K, indicating Tc to be considerably higher between 90K and 300K. Theoretical calculations for Q-diamond (crystalline form based upon diamond tetrahedra) using Quantum Expresso show ωph to be ~750 cm-1 and λ = 2.004. This value is also consistent with λ = [(Ω2 – <ω2>)/<ω2>], where Ω = 1300 cm-1, which is the bare phonon frequency corresponding to λ = 0. Using this value of λ and the equation, Tc = 0.183 [<ω2> λ]0.5, we obtain Tc = 278K. By using ωlog = 600 cm-1 from QE calculations and corresponding λ = 3.694, we obtain Tc = 302K. From the McMillan formula based upon generalized Migdal – Eliashberg theory and Debye temperature of QB3 of 2620K, we estimated the Tc value of 300K. By repeating the D12 subunit cell in one-dimension, we can form crystalline Q-diamond nanorod, which may have very high density of states close to the Fermi level. The density of states can be enhanced by doping with boron. By replacing central carbon atom with boron in each of these tetrahedra, we obtain a concentration of 50at% in different structures. By replacing central carbon atom with boron in alternate tetrahedra, we obtain dopant concentration of 25at%. Using D12 subunit cell, the Q-diamond super unit cell can be generated to form crystalline structures. This subunit cell cannot be repeated regularly as the face atoms are already four-fold coordinated. However, it can be repeated along the diagonal edges, leaving periodic holes and generating super unit cell structure presented in this paper. We have also obtained preliminary results on the formation of Q-silicon after nanosecond pulsed laser annealing of amorphous silicon. In fact, we expect the formation of Q-phases in all of the materials of zinc blende/diamond cubic crystal structures, which should exhibit novel functional properties.

Acknowledgments

We are pleased to acknowledge the support of National Science Foundation ( ), and the contributions of PhD students (Siba Sundar Sahoo, Minghao Pan, Pranay Kalakonda, Sumeer Khanna, Roger Sachan, Nayna Khosla, and Naveen Joshi) in drawing some of the figures.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. M. L. Cohen, Superconductivity in modified semiconductors and the path to higher transition temperatures, Supercond. Sci. Technol. 28 (2015) 043001. [CrossRef]
  2. Hebard and, G. Stewart, Progress in superconductivity, Physics Toady 72, 2 (2019) 44. [CrossRef]
  3. W. Pickett and M. Eremets, The quest for room-temperature superconductivity in hydrides, Physics Today, 72, 5 (2019) 52. [CrossRef]
  4. Gorter, C. J. Superconductivity until 1940 in Leiden and as seen from there. Reviews of modern physics. 1964, 36, 3. [Google Scholar] [CrossRef]
  5. J. Bardeen, L. N. Cooper, and J. R. Schrieffer, Phys. Rev. 106, 162 (1957); 108, 1175 (1957).
  6. Nagamatsu J, Nakagawa N, Muranaka T, et al. Superconductivity at 39 K in magnesium diboride. Nature [Internet]. Available online: http://www.ncbi.nlm.nih.gov/pubmed/11242039.
  7. Moussa, J. E.; Cohen, M. L. Two Bounds on the Maximum Phonon-Mediated Superconducting Transition Temperature. Phys. Rev. B 2006, 74, 94520. [Google Scholar] [CrossRef]
  8. Bhaumik, R. Sachan, J. Narayan, “High-Temperature Superconductivity in Boron-Doped Q-Carbon,” ACS Nano 11, 5351–5357 (2017). [CrossRef]
  9. Bhaumik, R. Sachan, S. Gupta, and J. Narayan, “Discovery of High-Temperature Superconductivity (Tc = 55 K) in B-Doped Q-Carbon,” ACS Nano, 11, 11915–11922 (2017). [CrossRef]
  10. J. Narayan, A. Bhaumik, R. Sachan, “High temperature superconductivity in distinct phases of amorphous B-doped Q-carbon,” J. Appl. Phys. 123, 135304 (2018). [CrossRef]
  11. J. Narayan et al, “Progress in Q-carbon and related materials with extraordinary properties,” Mater. Res. Lett. 6, 353 (2018). [CrossRef]
  12. J. Narayan, R. Sachan, and A. Bhaumik, Search for near room-temperature superconductivity in B-doped Q-carbon, Mater. Res. Lett. 7 (2019) 176-72. [CrossRef]
  13. Moussa, J. E.; Cohen, M. L. Constraints on Tc for Superconductivity in Heavily Boron-Doped Diamond. Phys. Rev. B - Condens. Matter Mater. Phys. 2008, 77, 64518 :. [Google Scholar] [CrossRef]
  14. Y. Sakai, J. Chelikowsky, amd M. Cohen,”Simulating the effect of boron doping in superconducting carbon,” Physical Rev. B 97, 054501 (2018). [CrossRef]
  15. Takano Y, Takenouchi T, Ishii S, et al. Superconducting properties homoepitaxial CVD diamond. Diam Relat Mater. 2007;16:911–914. [CrossRef]
  16. Bhaumik, A.; Sachan, R.; Narayan, J. Magnetic Relaxation and Three-Dimensional Critical Fluctuations in B-Doped Q-Carbon – a High-Temperature Superconductor. Nanoscale 2018, 10, 12665–12673. [Google Scholar] [CrossRef] [PubMed]
  17. J. Narayan et al. Formation of self-organized nano- and micro-diamond rings, Materials Research Letters 9, 300-307(2021). [CrossRef]
  18. Narayan, J; Khosla, N. Self-organization of amorphous Q-carbon and Q-BN nanoballs. Carbon. 2023. Available online: https://authors.elsevier.com/sd/article/S0008-6223(22)00168-3.
  19. Jaoshvili A, Esakia A, Porrati M, et al. Experiments on the random packing of tetrahedral dice. Phys Rev Lett. [Internet]. 2010 104:185501. Available online: https://link.aps.org/doi/10.1103/PhysRevLett.104 (accessed on 24 October 2017). [CrossRef]
  20. Bhaumik, A.; Nori, S.; Sachan, R.; Gupta, S.; Kumar, D.; Majumdar, A. K.; Narayan, J. Room-Temp Ferromagnetism and Extraordinary Hall Effect in Nanostructured Q-Carbon: Implications for Potential Spintronic Devices. ACS Appl. Nano Mater. 2018, 1, 807–819. [Google Scholar] [CrossRef]
  21. Sakai, Yuki; Chelikowsky, James R.; Cohen, Marvin L. Magnetism in amorphous carbon, PHYSICAL REVIEW MATERIALS Volume: ‏ 2 Article Number: 074403. [CrossRef]
  22. Pan, M. , Kim, K-W, and Narayan, J. Theoretical high Tc calculation in Q-diamond based materials, (to be published).
  23. Sachan, R.; Hatchtel, J.; Bhaumik, A.; Moatti, A.; Prater, J.; Idrobo, J.; and Narayan, J. Emergence of shallow energy levels in B-doped Q-carbon: A high-temperature superconductor. Acta Materialia 2019, 174, 153–159. [Google Scholar] [CrossRef]
  24. Narayan, J; Joshi, N.; Sahoo, S.; and Narayan, R. Synthesis and Novel Properties of Q-silicon, Materials Research Letters. [CrossRef]
Preprints 77052 g001
Figure 1. (a) Diamond tetrahedron D1 with central atom contained in (a/2, a/2, a/2) cube; (b) Two D1 tetrahedra connected along <110> direction; (c) Three D1 tetrahedra along <110>direction; (d) Three D1 tetrahedra: two in <110> direction (first layer) and one <1-10> direction (second layer); (e) Four D1 tetrahedra: two in <110> direction (first layer) and two <1-10> direction (second layer), this is the diamond unit cell with missing four neighboring tetrahedral; and (f) Diamond unit cell with missing four atoms from neighboring tetrahedra.
Figure 1. (a) Diamond tetrahedron D1 with central atom contained in (a/2, a/2, a/2) cube; (b) Two D1 tetrahedra connected along <110> direction; (c) Three D1 tetrahedra along <110>direction; (d) Three D1 tetrahedra: two in <110> direction (first layer) and one <1-10> direction (second layer); (e) Four D1 tetrahedra: two in <110> direction (first layer) and two <1-10> direction (second layer), this is the diamond unit cell with missing four neighboring tetrahedral; and (f) Diamond unit cell with missing four atoms from neighboring tetrahedra.
Preprints 77052 g001
Preprints 77052 g002
Figure 2. (a) Schematic of formation diamond tetrahedra along <110> direction and nucleation of diamond unit cell by addition of two tetrahedra in <1-10> direction in the second plane; (b) Schematic showing the formation of nanodiamond rings and larger nanodiamonds growing on the substrate epitaxially; (c) High-resolution SEM showing formation of nanodiamond rings in Q1 and Q2 phases, shaded region has layers and Q1 and Q2 phases; and (d) Mechanism of epitaxial growth of diamond mediated by Q-carbon.
Figure 2. (a) Schematic of formation diamond tetrahedra along <110> direction and nucleation of diamond unit cell by addition of two tetrahedra in <1-10> direction in the second plane; (b) Schematic showing the formation of nanodiamond rings and larger nanodiamonds growing on the substrate epitaxially; (c) High-resolution SEM showing formation of nanodiamond rings in Q1 and Q2 phases, shaded region has layers and Q1 and Q2 phases; and (d) Mechanism of epitaxial growth of diamond mediated by Q-carbon.
Preprints 77052 g002
Preprints 77052 g003
Figure 3. (a) Formation of QB1, when one central C atom is replaced by B in a three-unit (trimer) tetrahedra; (b) Formation of QB2, when one central C atom is replaced by B in a two-unit drimer) tetrahedral; (c) Formation of QB3, when one central C atom is replaced by B in a single tetrahedron, dimer and trimer tetrahedra; (d) Schematic of layers of QB2 and QB3 layers; and (e) SLIM calculation of melt depth versus time for 20ns ArF laser pulse having 0.6Jcm-2 of energy density. The plot shows times available for growth Q2 and Q3 phases.
Figure 3. (a) Formation of QB1, when one central C atom is replaced by B in a three-unit (trimer) tetrahedra; (b) Formation of QB2, when one central C atom is replaced by B in a two-unit drimer) tetrahedral; (c) Formation of QB3, when one central C atom is replaced by B in a single tetrahedron, dimer and trimer tetrahedra; (d) Schematic of layers of QB2 and QB3 layers; and (e) SLIM calculation of melt depth versus time for 20ns ArF laser pulse having 0.6Jcm-2 of energy density. The plot shows times available for growth Q2 and Q3 phases.
Preprints 77052 g003
Preprints 77052 g004
Figure 4. (a) Four D1 tetrahedra in one plane (D14); (b) Eight tetrahedtra in two planes, leading to formation of Q-diamond subunit cell with net 16 atoms; and (c) Formation of Q-diamond super unit cell with four subunit cells: two in <110> direction and two in <1-10> direction (d) with missing four neighboring subunit cells, similar to missing tetrahedra in the diamond unit cell. By replacing central C atoms in these tetrahedra by B atoms selectively, 50% B-doped Q-diamond phase is created, having net 32 C and 32 B atoms arranged in two layers.
Figure 4. (a) Four D1 tetrahedra in one plane (D14); (b) Eight tetrahedtra in two planes, leading to formation of Q-diamond subunit cell with net 16 atoms; and (c) Formation of Q-diamond super unit cell with four subunit cells: two in <110> direction and two in <1-10> direction (d) with missing four neighboring subunit cells, similar to missing tetrahedra in the diamond unit cell. By replacing central C atoms in these tetrahedra by B atoms selectively, 50% B-doped Q-diamond phase is created, having net 32 C and 32 B atoms arranged in two layers.
Preprints 77052 g004
Preprints 77052 g005
Figure 5. (a) Density of states (DOS) as a function of distance from the Fermi level; (b) DOS as a function of frequency, presence of negative frequencies is related to metastability of Q-carbon; (c) Detailed DOS distribution as function of frequency; and (d) Electronic DOS as a function of frequency.
Figure 5. (a) Density of states (DOS) as a function of distance from the Fermi level; (b) DOS as a function of frequency, presence of negative frequencies is related to metastability of Q-carbon; (c) Detailed DOS distribution as function of frequency; and (d) Electronic DOS as a function of frequency.
Preprints 77052 g005
Preprints 77052 g006
Figure 6. Cryo-EELS spectra from QB3 phase at 90K and RT of (a) B-K edge, (b) C-K for QB3 phase, and (c) corresponding resistivity vs T from QB3 phase with evidence of Tc = 90-300K.
Figure 6. Cryo-EELS spectra from QB3 phase at 90K and RT of (a) B-K edge, (b) C-K for QB3 phase, and (c) corresponding resistivity vs T from QB3 phase with evidence of Tc = 90-300K.
Preprints 77052 g006
Table 1. Atom coordinates for B-doped Q-carbon subunit cell and super unit cell. Four common atomic positions between different subunit cells are indicated by C* and common between A and B subunits.
Table 1. Atom coordinates for B-doped Q-carbon subunit cell and super unit cell. Four common atomic positions between different subunit cells are indicated by C* and common between A and B subunits.
Preprints 77052 i001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Path for Room-Temperature Superconductivity in Q-Carbon Related Materials

Jagdish Narayan

,

2023

Preliminary TC Calculations for Iron-Based Superconductivity in NaFeAs, LiFeAs, FeSe and Nanostructured FeSe/SrTiO3 Superconductors

Chi Ho Wong

et al.

,

2023

Boron Monochalcogenides; Stable and Strong Two-Dimensional Wide Band-Gap Semiconductors

Bohayra Mortazavi

et al.

,

2018

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated