Generating Robust Optimal Mixture Designs Due to Missing Observation Using a Multi-Objective Genetic Algorithm

Preprint

Article

Generating Robust Optimal Mixture Designs Due to Missing Observation Using a Multi-Objective Genetic Algorithm

Altmetrics

Downloads

124

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

19 June 2023

Posted:

20 June 2023

You are already at the latest version

Alerts

Abstract

Missing observation is a common problem in scientific and industrial experiments, particularly in a small-scale experiment. They often present significant challenges when experiment repetition is infeasible. In this research, we propose a multi-objective genetic algorithm as a practical alternative for generating optimal mixture designs that remain robust in the face of missing observation. Our algorithm prioritizes designs that exhibit superior D-efficiency while maintaining a high minimum D-efficiency due to missing observation. The focus on D-efficiency stems from its ability to minimize the impact of missing observations on parameter estimates, ensure reliability across the experimental space, and maximize the utility of available data. We study problems with three mixture components where the experimental region is an irregularly shaped polyhedral within the simplex. Our designs have proven to be D-optimal designs, demonstrating exceptional performance in terms of D-efficiency and robustness against missing observations. We provide a well-distributed set of optimal designs derived from the Pareto front, enabling experimenters to select the most suitable design based on their priorities using the desirability function.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

1. Introduction

Response surface methodology (RSM) is a collection of statistical and mathematical techniques utilized to develop new processes, enhance formulations, and optimize process performance. A mixture experiment is a special case of a response surface experiment, in which the components of the mixture cannot vary independently because their proportions must sum to a constant. The primary goal of a mixture design is to determine the optimal component proportion settings that maximize, minimize, or specify the response. Mixture experiments are frequently encountered in industries where product formulation is required, such as food and beverage processing, cosmetics, glass manufacturing, pharmaceutical drug production, cement production, polymer production and so on. For a detailed description of response surface methodology and mixture experiments, see [1,2].

In real-world situations, carefully planned experiments may encounter issues such as the failure to observe, the loss of responses for one or more runs during data collection, or dubious responses in certain circumstances, leading to missing observations. Responses or observations may be absent or unobservable for a variety of reasons. For instance, certain combinations of factors might create unstable conditions, resulting in implausible responses in chemical or biotechnical processes. Malfunctions or failures in equipment may lead to the destruction of some experimental units, thereby rendering the response unmeasurable. Additionally, in industrial experiments, responses may be unattainable or difficult to replicate at a design point due to extraneous factors often unrelated to the basic design structure, such as cost constraints, inefficiencies in time, technical unsatisfactoriness, transit issues, or other factors. The types of missing observations previously mentioned are commonly encountered during experiments aimed at developing new product. Extreme outliers might also be omitted and treated as missing observations in some experiments. Generally, these missing observations are treated as missing at random since they are not associated with one of the experimental factors of interest. Predicting which observation will be lost during an experiment is impossible, and all design points are equally likely to go missing. Numerous methods are available to address missing observations, including imputation using means, medians, k-nearest neighbor algorithms, deep learning, and so on. When missing observation occurs in the experimental design with a small number of runs, imputation techniques are often not utilized. They are deemed inappropriate due to their impractical nature in resolving such issues. The absence of responses negatively impacts statistical analysis results, specifically, the quality of the regression coefficient estimates, resulting in a poorly fitting model. Box and Draper [3] and Myers et al. [2] suggested that a robust experimental design should be robust against missing observation. Therefore, it is crucial to develop designs that are robust against missing observation.

In the field of experimental design, the robustness of design in the face of missing observations has been extensively studied, with a multitude of criteria and measures proposed to assess this robustness. Box and Draper [3] explored the impact of outliers or wild observations on fitted values, as obtained by least squares estimation in central composite designs. They also considered the relationship between the diagonal elements of the hat-matrix,

H

, and the robustness of a design. Herzberg and Andrews [4] introduced the concept of design breakdown probability and proposed the generalized variance and the minimization of the maximum variance criteria as the expected precision to assess design robustness. Andrews and Herzberg [5] proposed the average precision criterion based on the determinant of the information matrix to evaluate the robustness of designs against missing observations. Ghosh [6] pointed out that certain observations were more informative than others, implying that losing the most informative observation during an experiment incurred a more significant overall efficiency loss than losing a less informative one. Akhtar and Prescott [7] studied the effect of missing observations in central composite designs and developed a minimax loss criterion for missing observations based on the D-optimality criterion. Lal et al. [8] proposed utilizing the A-efficiency of the residual design to investigate design robustness against missing observations. Ahmad and Gilmour [9] considered the robustness of subset designs, a class of response surface designs, against missing observations based on the minimax loss criterion. They also noted that robustness came from the replication of points other than the center points. Yakubu et al. [10] examined the effect of missing observations on the predictive capability of response surface designs. They discovered that missing observations affected the estimation and predictive capability of central composite designs, with the most significant loss occurring in missing factorial points. Rashid et al. [11] employed the minimax loss criterion as well as the relative A, D, and G-efficiencies to investigate the robustness of augmented Box-Behnken designs against a missing observation.

The robustness against missing observations has been recognized in numerous experimental design studies. Many researchers have embarked on developing various algorithms to construct designs that remain robust in the face of missing data. Ahmad et al. [12] constructed augmented pairs minimax loss designs using the minimax loss criterion and assessed the impact of missing observations using a loss function criterion given by [7]. Ahmad and Akhtar [13] constructed the new second-order response surface designs, known as repaired resolution central composite designs, that are robust to missing observations under the minimax loss criterion. da Silva et al. [14] proposed exchange algorithms to generate optimal designs that satisfy compound criteria. They incorporated leverage uniformity into the compound design criterion and used a compound criterion to identify designs that are robust to missing runs when fitting a second-order model. Smucker et al. [15] introduced the truncated Herzberg–Andrews criterion to construct designs that perform comparably or better than classical designs when observations are missing. Chen et al. [16] suggested orthogonal-array-based composite minimax loss designs that are robust to missing data, considering D-efficiency and generalized scaled standard deviation for near-saturated, saturated, or supersaturated designs. Alrweili et al. [17] constructed minimax loss response surface designs, demonstrating robustness against missing design points in terms of the minimax loss criterion. Mahachaichanakul and Srisuradetchai [18] proposed the small optimal robust response surface designs generated by a genetic algorithm based on the minimum and median of D- and G-efficiency, exhibiting robustness to missing observations. Oladugba and Nwanonobi [19] constructed definitive screening composite minimax loss designs, demonstrating robustness to missing observations in terms of D-efficiency and generalized scaled standard deviation. Yankam and Oladugba [20] developed orthogonal uniform minimax loss (OUCM) designs, finding that the OUCM design outperforms the loss criterion and displays higher D-efficiency, A-efficiency, and T-efficiency.

The issue of missing observations is hard to avoid, even in well-designed experiments. Moreover, overlooking these missing observations can significantly impact statistical conclusions. Experimenters are often concerned about the robustness of their design when data collection encounters loss of some observations, especially when re-conducting the experiment is difficult or unfeasible. Therefore, they seek a design that remains robust to missing observation, while still enabling the estimation of model parameters with the least possible loss of efficiency. The D-efficiency is a widely used criterion in experimental design due to its association with the determinant of the information matrix. This determinant serves as a measure of the volume of the confidence ellipsoid, which in turn reflects the precision of the parameter estimates. A design that performs well in terms of D-efficiency might not perform as well when considering minimum D-efficiency due to missing observation. On the other hand, a design that maintains a high minimum D-efficiency due to missing observation may underperform in terms of D-efficiency. The objective of this research is to construct optimal robust mixture designs using a genetic algorithm. This algorithm is designed to generate mixture designs that perform effectively not just in terms of D-efficiency, but also in achieving a high minimum D-efficiency due to missing observation. Our proposed algorithm aims to simultaneously maximize both the D-efficiency and the minimum D-efficiency due to missing observation of mixture designs.

The Genetic Algorithm (GA) is widely recognized as one of the most popular metaheuristic algorithms for optimizing complex solution spaces. It has proven effective in generating high-quality solutions for various optimization problems. This algorithm was initially developed by Holland and his collaborators in the middle 1980s, drawing inspiration from Darwin's theory of natural evolution. In contrast to traditional search techniques, the genetic algorithm distinguishes itself in two key aspects. Firstly, it commences with an initial set of random solutions referred to as a population rather than a single solution. Secondly, it employs a fitness function to determine which solutions will survive to the next generation or be eliminated from the population, following the principle of “survival of the fittest” derived from Charles Darwin's theory of evolution. The goal of a single-objective genetic algorithm is to optimize one specific objective function. On the other hand, a multi-objective genetic algorithm aims to optimize multiple objective functions simultaneously. In real-world applications, it is common to encounter situations where several objectives need to be optimized simultaneously. A solution within a multi-objective genetic algorithm is deemed superior if it is better in at least one objective without falling short in the others. The outcome of a multi-objective genetic algorithm is frequently a set of Pareto-optimal solutions. These solutions represent the trade-offs between the different objectives, indicating that enhancements in one objective cannot be achieved without causing deterioration in another.

Over the past few decades, numerous studies have demonstrated successful applications of both single-objective and multi-objective genetic algorithms across diverse fields such as engineering and life sciences. Examples of designs generated using genetic algorithms based on a single objective function were presented in Borkowski [21], Heredia-Langner et al. [22,23], Park et al. [24], Limmun et al. [25,26], and Mahachaichanakul and Srisuradetchai [18]. Studies focusing on multi-objective genetic algorithms were well documented in Deb et al. [27], Konak et al. [28], and Long et al. [29]. Furthermore, research that concentrated on multi-objective optimal design can be found in Cook and Wong [30], Zhang et al. [31], and Lu et al. [32]. However, the literature appears to lack a comprehensive exploration of multi-objective genetic algorithms in the context of generating optimal designs for mixture experiments. In this study, we propose the use of multi-objective genetic algorithms to generate optimal designs that demonstrate robustness against missing observation.

The remainder of this paper is organized into nine sections. Section 2 provides the theoretical background for our research. Section 3 details the application of the leave-one-out optimality criteria as one of the objective functions in a genetic algorithm. The loss of efficiency in terms of the optimality criteria is explored in Section 4. Section 5 introduces the multi-objective functions adopted in this research. Our genetic algorithm, designed to address these multi-objective functions, is presented in Section 6. Section 7 outlines the methodology for examining the performance of the designs. Section 8 presents two illustrative experiments that demonstrate the performance of the proposed algorithm. Finally, Section 9 provides the conclusions and recommendations pertinent to this research.

2. Theoretical background

2.1. Notation and model

Mixture experiments involve combining two or more ingredients (components) to create an end product and then measuring the physical properties (response) of the end product. In a mixture experiment, the number of ingredients is denoted by

q

, and the proportion of each ingredient (component) is represented by

x_{1}, x_{2}, \dots, x_{q}

.The response variable in a mixture experiment depends solely on the relative proportions of the components. A defining characteristic of standard mixture experiments is that

\leq x_{i} \leq 1 a n d \sum_{i = 1}^{q} x_{i} = 1 .

(1)

These restrictions remove a degree of freedom from the component proportions and then each

x_{i}

can only lie on and inside a

(q - 1)

-dimensional regular simplex. The lower (

L_{i})

and/or upper

(U_{i})

bound constraints are commonly applied to the component proportions, which are referred to as single-component constraints (SCCs). The SCCs is given by

0 \leq L_{i} \leq x_{i} \leq U_{i} \leq 1 f o r i = 1,2, \dots, q .

(2)

Moreover, the linear multiple-component constraints (MCCs) are frequently found among the proportions of the form’s components

C_{j} \leq \sum_{i = 1}^{q} A_{i j} x_{i} \leq D_{j}; j = 1,2, \dots, h,

(3)

where

A_{i j}

are constants defining multivariate linear with

C_{j}

and

D_{j}

being the lower and upper bounds of the MCCs, respectively. In addition, the nonlinear multicomponent constraints are also possible, but they are less common and seldom addressed in the theoretical literature. If the single-component constraints (SCCs) and/or multiple-component constraints (MCCs) are imposed on the component proportions, the experimental region of interest changes from a simplex to an irregularly shaped polyhedron within the simplex. For the detailed review of mixture experiments, see Cornell [1] and Myers et al. [2].

There is a wide range of potential models that can be employed in mixture experiments. The Scheffé models are most commonly used for data derived from mixture experiments because of their ability to handle the natural restrictions in mixture experiments. The Scheffé mixture models include all components in the model and do not contain an intercept term due to the constraints on component proportions. In a mixture experiment with

q

-components

(x_{i}; i = 1,2, \dots, q)

, the Scheffé linear mixture model has the form,

y = \sum_{i = 1}^{q} β_{i} x_{i} + ε,

(4)

and the Scheffé quadratic mixture model can be expressed as

y = \sum_{i = 1}^{q} β_{i} x_{i} + \sum_{i = 1}^{q - 1} \sum_{j = i + 1}^{q} β_{i j} x_{i} x_{j} + ε,

(5)

where

y

represents the measured response variable; the coefficient

β_{i}

represents the expected response to the

i

th pure component; the coefficient

β_i j

represents the nonlinear blending between the

i

th and the

j

th components; and

ε

represents the error term accounting for random error. The error term is assumed to be independently and identically distributed as

N (0, σ^{2}) .

In this research, we make the assumption that the experimenter believes that the Scheffé quadratic mixture model can adequately approximate the true model. In matrix notation, the Scheffé mixture model can be written as

y = X β + ε,

(6)

where

y

is the

n

-dimensional vector of response,

X

is the

n \times p

model matrix containing the model expansions of the mixture component proportions (such as linear and cross-products terms) for each of the

n

runs of the experiment,

β

is the

p \times 1

vector of model parameters, and

ε

is the

n

-dimensional vector of random errors associated with natural variation of

y

around the underlying surface. The design matrix for the Scheffé quadratic model is defined as

X = (x_{1}, x_{2}, \dots, x_{q}, x_{1} x_{2}, x_{1} x_{3}, \dots, x_{q - 1} x_{q})'

. We assume that

ε

is independently and identically distributed, following a normal distribution with zero mean and variance

σ^{2} I_{n}

. Note that

σ^{2}

is an irrelevant constant; therefore, we set

σ^{2}

to one without the loss of generality when searching for an optimal design. The ordinary least-square estimator of

β

, which is equivalent to the maximum likelihood estimator under normal error, is

\hat{β} = {(X^{'} X)}^{- 1} X^{'} y

which has variance

V a r (\hat{β}) = σ^{2} {(X^{'} X)}^{- 1},

where

σ^{2}

is the error variance. The fitted model is given by

\hat{y} = X \hat{β} = {X (X^{'} X)}^{- 1} X^{'} y .

(7)

The variance-covariance matrix of the fitted values can be written as

V a r (\hat{y}) = σ^{2} [{X (X^{'} X)}^{- 1} X^{'}]

. The scaled prediction variance (SPV) of the response at a point

x_{0}

is given by

S P V = v (x_{0}) = \frac{n V a r (\hat{y} (x_{0}))}{σ^{2}} = n x_{0}^{'} {(X^{'} X)}^{- 1} x_{0},

(8)

where

x_{0}^{'}

is an expanded of a mixture components vector corresponding to the

p

terms in the model at the location

x_{0}

V a r (\hat{y} (x))

is the variance of the estimated response at

x_{0}

, and

σ^{2}

is the error variance. The SPV allows the experimenters to assess the precision of the predicted response per observation and penalizes larger designs over small designs. For further information on the mixture model, see Cornell [1].

2.2. Design optimality criteria

A design optimality criterion is a single-value generally used to summarize the effectiveness of a design and compare its quality against other designs. Optimal experimental designs are generated based on a particular optimality criterion and are typically optimal only for a specific model. Four commonly used alphabetic optimality criteria for evaluating design include the A-, D-, G-, and IV-criteria. The best-known among these that focus on precise parameter estimates are the A- and D-optimality criteria, while the G- and IV-optimality criteria emphasize precise prediction throughout the experimental region of interest. These criteria are defined based on the information matrix,

X' X

, also known as the Fisher information matrix. The information matrix is the proportional to the inverse of the ordinary least-squares estimator’s variance-covariance matrix. This information matrix not only quantifies the information that the experimental data provide about the unknown parameters but also serves to summarize the content of an experimental design with respect to the parameters of the model under consideration. Note that

X' X

is a function of experimental conditions only and the

σ^{2}

is a function of the response and experimental conditions.

The D-optimality criterion, a widely used optimality criterion, seeks to minimize the generalized variance of the parameter estimates

\hat{β}

, or equivalently, to maximize the determinant of the Fisher information matrix

|X^{'} X|

. The

|X^{'} X|

is inversely related to the volume of the

p

-dimensional confidence ellipsoid about the model coefficients. The larger

|X^{'} X|

, the better the estimation of the model parameters. The D-optimality criterion provides an assessment of the estimation quality for all

p

parameters and takes into account possible correlations among the parameter estimates in

\hat{β}

. The A-optimality criterion aims to minimize the trace of the inverse of the information matrix,

t r a c e {(X^{'} X)}^{- 1}

. The

t r a c e {(X^{'} X)}^{- 1}

equals the sum of the

p

elements on the main diagonal of the variance-covariance matrix of the ordinary least-squares estimator. Geometrically, this criterion minimizes the sum of the variances of the

p

parameter estimates in

\hat{β}

. The smaller the sum of the variances of the estimated coefficients, the more accurate the estimates of the model parameters. Note that D- and A-optimality criteria are defined solely as functions of the information matrix.

The G-optimality criterion seeks to minimize the maximum prediction variance over the experimental region of interest. This minimax-type design criterion is undifferentiable and requires solving at least two nested layers of optimization problems across the design space. The G-efficiency is approximated over a set of points from an extreme vertices design for finding the maximum scaled prediction variance. The boundary points, such as a vertex, face centroid, or edge centroid, typically yield the maximum scaled prediction variance. The IV-optimality criterion, on the other hand, aims to minimize the average prediction variance over the entire experimental region. This averaging-type design criterion focuses on minimizing the overall average prediction variance. According to Borkowski [33], the average prediction variance (APV) calculated using a random set of interior points is superior to that calculated using a fixed set of points. As the sample size of the random set of points increases, the estimators of this method provide an excellent approximation. In this research, we use an evaluation set of 5,000 points. For the optimal experimental design society, the IV-optimality criterion is often called the Q-, I- or Q-optimality criterion (see, for instance, Myers et al. [2], Goos et al. [34], and Atkinson et al. [35], respectively).

In this research, we used the D, A, G, and IV design optimality criteria to evaluate and select the design that best meets the specific objectives of the experiment. These criteria are defined as follows:

D - e f f i c i e n c y = \frac{100 {|X^{'} X|}^{1 / p}}{n},

(9)

A - e f f i c i e n c y = \frac{100 p}{t r a c e [n {(X^{'} X)}^{- 1}]},

(10)

G - e f f i c i e n c y = \frac{100 p}{\max_{xεχ} [n {x_{0}^{'} (X^{'} X)}^{- 1} x_{0}^{}]},

(11)

I V - e f f i c i e n c y = \frac{V}{\int_{χ}^{} n {x_{0}^{'} (X^{'} X)}^{- 1} x_{0}^{} d x_{1} x_{2} \dots x_{q}},

(12)

where

X

is the model matrix for a given design,

n

is the number of design points,

p

is the number of parameters,

x_{0}^{}

is a vector of a point in the design region expanded to model form,

χ

is the experimental design space, and

V

is the volume of the experimental design space

χ

. For example, if we consider the Scheffé quadratic model with

q

mixture components, then

x_{0}^{'} = (x_{1}, x_{2}, \dots, x_{q}, x_{1} x_{2}, x_{1} x_{3}, \dots, x_{q - 1} x_{q})

and matrix

X

has dimension

n \times (\frac{q (q + 1)}{2})

. In this research, a larger D-, A-, G- and IV- efficiency value indicates better performance. For further details regarding the motivations and applications of these optimality criteria, see Kiefer [36], Pukelsheim [37], and Atkinson et al. [35].

2.3. Genetic algorithms

Genetic algorithms are bio-inspired artificial intelligence tools modeled on the principles of genetics and natural selection in biology. They excel at finding optimal solutions in complex spaces, starting with an initial population of parent chromosomes. The genetic algorithm starts from an initial population of potential solutions, referred to as parent chromosomes. These chromosomes, randomly generated, are decoded to obtain the corresponding parameters, which they represent. Each chromosome contains a set of genes, and each gene holds dataset features, which serve as instructions for producing specific traits. After creating the parent chromosomes, a fitness (objective) function assesses each chromosome, assigning a fitness score to indicate how fit or suitable they are. The parent chromosomes then undergo evolution via evolutionary reproduction operators such as selection, crossover, and mutation, resulting in offspring chromosomes. The process of reproduction is focused on preserving the best chromosomes for the next generation. Subsequently, these offspring chromosomes are evaluated by the fitness (objective) function. The best parent and offspring chromosomes are transferred to subsequent generations following the survival of the fittest principle. The genetic algorithm continually evolves until it meets a pre-defined termination condition.

The selection operator aims to choose the fittest chromosomes for offspring reproduction based on a user-defined probability distribution. The chromosomes with higher objective function values have a higher likelihood of being selected for the reproduction process. The crossover operator combines two parent chromosomes to create two offspring chromosomes, again based on a user-defined probability distribution. Initially, a crossover location is chosen to segment the encoded chromosomes, then the traits of the selected parents beyond this location are swapped to generate two offspring. The mutation operator utilizes a user-defined probability distribution to optimize the effectiveness of the selected genes on a chromosome. This operator is crucial in preventing the creation of a uniform population incapable of further evolution. For an introduction and review of genetic algorithms, see Goldberg [38], Michalewicz [39], and Haupt and Haupt [40].

3. Leave- $m$ -out optimality criteria

The leave-

m

-out optimality criteria is a methodology used in experimental design to assess the robustness of an experiment against the loss of data points. This method allows experimenters to evaluate the sensitivity of their design’s optimality to missing or lost data. Generally, experimenters prefer smaller designs to conserve resources such as money and time. In many real-world situations, observations may be lost during an experiment for various reasons, and the experimenter might be unable to replicate those observations. By understanding the impact of lost data points on the experimental design, researchers strive to create designs that are robust against missing observations.

m

arbitrary design points in an experiment lack observations, the optimality of the design, which is specifically constructed based on a model and design size, may no longer hold for the given model. Throughout this research, the model under consideration is the Scheffé quadratic mixture model. Suppose that the complete information matrix

X^{'} X

n \times p

where

n

is the number of design points, and

p

is the number of parameters in the Scheffé quadratic mixture model. If

m

arbitrary design points have the missing observations, then the model matrix

X

is reduced by

m

rows. The model matrix

X

can be partitioned as

[X_{(r)}^{'} : X_{(m)}^{'}]'

where

X_{(r)}^{}

be the

n - m

remaining rows of the full model matrix

X

for the reduced design, excluding the missing observations and

X_{(m)}^{}

be the matrix of

m

rows corresponding to the

m

missing observations for some

1 \leq m \leq n

. For

m

missing observations, the complete information matrix can be expressed as

X^{'} X = X_{(r)}^{'} X_{(r)}^{} + X_{(m)}^{'} X_{(m) .}^{}

. Consequently, the information matrix for the reduced design differs from that of the complete design and can be defined as

X_{(r)}^{'} X_{(r)}^{} = X^{'} X - X_{(m)}^{'} X_{(m)}^{} .

Note that if the rank of the information matrix for the reduced design,

X_{(r)}^{'} X_{(r)}^{}

, is less than the number of parameters in the model, then the determinant for the reduced design,

|X_{(r)}^{'} X_{(r)}^{}|

, is zero, and the model parameters become unestimable. In real-world scenarios, it is impossible to predict which observations will be lost during an experiment. As such, all design points are equally likely to be missing. The D-, A-, G-, and IV-efficiency of omitting the m design points can be respectively defined as:

D_{(m^{-})} = \frac{100 {|X_{(r)}^{'} X_{(r)}|}^{1 / p}}{n - m},

(13)

A_{(m^{-})} = \frac{100 p}{t r a c e [(n - m) {(X_{(r)}^{'} X_{(r)})}^{- 1}]},

(14)

G_{(m^{-})} = \frac{100 p}{\max_{xεχ} [(n - m) {x_{0}^{'} (X_{(r)}^{'} X_{(r)})}^{- 1} x_{0}^{}]},

(15)

{I V}_{(m^{-})} = \frac{V}{\int_{χ}^{} (n - m) {x_{0}^{'} (X_{(r)}^{'} X_{(r)})}^{- 1} x_{0}^{} d x_{1} x_{2} \dots x_{q}} .

(16)

If a large number of observations are missing, it is likely that there are more fundamental issues that need to be addressed in an experiment. In this research, we focus on scenarios with a missing observation, where a missing observation is defined as an arbitrary design point. Consequently, we propose the leave-one-out D-, A-, G-, and IV-efficiency measures to protect against potential missing observations. Specifically,

m

will be replaced by 1 in our case. Suppose the

i

th design point is missing; the complete model matrix

X

will then be reduced by the

i

th row. The leave-one-out D-, A-, G-, and IV-efficiency can be calculated by substituting

m

with 1 in Equations. (13) to (16), respectively. The minimum values of leave-one-out efficiency occur when the observation with the most significant impact is missing from the experiment. These minimum values of leave-one-out D-, A-, G-, and IV-efficiency are referred to as the minimum D-, A-, G-, and IV-efficiency due to missing observation, respectively.

Numerous studies have highlighted the impact of missing observations. For example, Rashid et al. [11] found that the absence of a center point has a greater influence on the accuracy of model parameter estimates and relative A, D, and G-efficiencies than the loss of other design points. According to Ahmad et al. [9], robustness is greatly enhanced by replicating points other than the center ones, particularly by replicating axial points. However, it is unfeasible to identify the location of the missing observation in real-world situations. Losing the most sensitive observation in an experiment can be considered as the worst-case scenario, as a missing observation can lead to minimal design efficiency. Indeed, the minimum leave-one-out criterion represents the design efficiency under the worst-case scenario of losing an observation. If an experiment loses an observation, but the design still maintains a high minimum D-efficiency, it indicates that the design is robust against missing observations. In this research, we consider the minimum D-efficiency due to missing observation, identified as the worst-case scenario, as one of the objective functions.

4. Loss of efficiency in terms of the optimality criteria

The absence of observations can significantly influence the reliability and validity of the experimental outcomes. Therefore, understanding and evaluating the impact of missing observation becomes vital in designing robust and effective experiments. Loss of efficiency refers to a decrease in the precision or power of an experiment, a statistical test, or a model. It can be quantified as the percentage of the total criterion value that a design loses due to a missing observation. The minimax loss criterion is the most practical approach to mitigate the impact of missing observations from the design. This criterion seeks to minimize the worst-case scenario, that is, the maximum potential loss that could result from these missing observations. This criterion is based on the D-optimality. Herzberg and Andrews [4], Andrews and Herzberg [5] and Akhtar and Prescott [7] employed a criterion based on the relative loss of efficiency in terms of

|X' X|

, equivalent to the D-optimality criterion, to assess the impact of missing observations. The loss due to the absence of a set of

m

observations, as defined by Andrews and Herzberg [5] and Akhtar and Prescott [7], is denoted as

l_{i j \dots} = \frac{|X' X| - |X_{(r)}^{'} X_{(r)}^{}|}{|X' X|} = 1 - \frac{|X_{(r)}^{'} X_{(r)}^{}|}{|X^{'} X|},

(17)

where

X_{(r)}^{}

represent the

n - m

remaining rows of the full model matrix

X

due to

m

missing observations.

Given

n

design points, there are

(\begin{matrix} n \\ m \end{matrix})

possible subset designs having

m

missing observations. The loss of D-, A-, G-, and IV-efficiency due to

m

missing observations can be expressed as follows:

l_{D} (i, m) = 1 - \frac{D_{(m^{-})}}{D - e f f i c i e n c y},

(18)

l_{A} (i, m) = 1 - \frac{A_{(m^{-})}}{A - e f f i c i e n c y},

(19)

l_{G} (i, m) = 1 - \frac{G_{(m^{-})}}{G - e f f i c i e n c y},

(20)

l_{I V} (i, m) = 1 - \frac{{I V}_{(m^{-})}}{I V - e f f i c i e n c y},

(21)

where

i

represents the

i

th possible subset designs due to

m

missing observations for

i = 1,2, \dots, (\begin{matrix} n \\ m \end{matrix})

, and

D_{(m^{-})}, A_{(m^{-})}, G_{(m^{-})}

and

{I V}_{(m^{-})}

denote the leave-

m

-out D-, A-, G- and IV-efficiency, respectively. The loss of efficiency ranges from 0 to 1, and it is preferable to select a design that minimizes this loss. A loss of efficiency equal to 0 indicates no reduction in the determinant of the design’s information matrix due to missing observations. Conversely, a loss of efficiency equal to 1 signifies a complete breakdown of the design, rendering the model coefficients unestimable due to missing observations. A low value of efficiency loss signifies a minimal reduction in the determinant of the information matrix, and thus, less information is lost. The worst-case scenario, involving missing

m

observations, is characterized by the situation where the minimum leave-

m

-out criterion leads to the maximum efficiency loss. Hence, the maximum loss of D-, A-, G-, and IV-efficiency attributable to

m

missing observations can be represented as follows:

m a x l_{D} (i, m) = 1 - \frac{m i n D_{(m^{-})}}{D - e f f i c i e n c y},

(22)

m a x l_{A} (i, m) = 1 - \frac{m i n A_{(m^{-})}}{A - e f f i c i e n c y},

(23)

m a x l_{G} (i, m) = 1 - \frac{m i n G_{(m^{-})}}{G - e f f i c i e n c y},

(24)

m a x l_{I V} (i, m) = 1 - \frac{m i n {I V}_{(m^{-})}}{I V - e f f i c i e n c y},

(25)

where

m i n D_{(m^{-})}, m i n A_{(m^{-})}, m i n G_{(m^{-})}

and

m i n {I V}_{(m^{-})}

denote the minimum of leave-

m

-out D-, A-, G- and IV-efficiency, respectively. When substituting

m

with 1 in Eqations. (22) to (25), we obtain the maximum loss of efficiency due to missing observation based on D, A, G, and IV-efficiency, respectively. The principle of minimizing the maximum loss of efficiency is the idea behind the minimax loss criterion put forth by Akhtar and Prescott [7].

The effect of missing observations on parameter estimates directly correlates with the loss of D- and A-efficiency. The loss of D-efficiency quantifies the impact of missing observation on the volume of the joint confidence region for the vector of regression coefficients, while the loss of A-efficiency considers the effect of missing observation on the sum of the variances of the regression coefficients. In a mixture experiment, experimenters are more concerned with prediction variance than parameter estimation because the design points on the fitted surface represent predicted responses. The influence of missing observations on prediction variance directly correlates with the loss of G- and IV-efficiency. The effect of missing observation on the maximum variance of any predicted value over the experimental region is quantified by the loss of G-efficiency, whereas the impact of missing observation on the average variance of any predicted value over the experimental region is quantified by the loss of IV-efficiency. To mitigate the impact of a missing observation in an experiment, it is important for the experimenter to employ a design that is robust to missing observation and that performs well in unpredictable situations. Therefore, we propose assessing the fitness of each chromosome (design) in a genetic algorithm by using the maximum loss of D-, A-, G-, and IV-efficiency due to a missing observation.

5. Multi-objective functions

In many real-world problems, researchers often aim to optimize multiple objectives simultaneously. For example, they may need to optimize both taste and manufacturing cost or time in creating composite foods. The multi-objective optimization (MOO) is specifically designed to tackle these types of problems, wherein multiple objectives need to be optimized simultaneously. Unlike single-objective problems, multi-objective problems might not have the best (global) optimal solution that meets all objectives. Rather, they may yield a set of superior solutions within the search space, known as Pareto-optimal or non-dominated solutions. These Pareto-optimal solutions represent a trade-off among multiple objectives. The Pareto approach constructs a frontier of competitive designs, wherein no design can improve one criterion without compromising another. Once the Pareto optimal set is obtained, researchers often seek a single optimal solution or a reduced set of solutions from the Pareto optimal set to facilitate the decision-making process. Various methods exist for extracting a single optimal solution or a smaller subset from the Pareto optimal set. For more detail about multiple objectives function, see Deb [41] and Marler and Arora [42].

5.1. Non-dominated sorting

Non-dominated sorting is primarily used to sort solutions according to the Pareto dominance principle. The Pareto front represents the set of solutions for which no other solutions in the search space are superior across all objectives. A solution is considered non-dominated (or Pareto optimal) if (1) the solution

x^{(1)}

is as good as or superior to the solution

x^{(2)}

in all objectives and (2) the solution

x^{(1)}

is strictly superior to the solution

x^{(2)}

for at least one objective. In other words, a solution is Pareto optimal if no other solution dominates it and its corresponding objective vector is non-dominated.

Deb et al. [27] proposed the non-dominated sorting genetic algorithm II (NSGA-II), which employs non-dominated sorting and a crowded distance approach to identify a well-distributed set of solutions for multi-objective optimization problems. This algorithm is widely recognized as one of the most efficient and popular approaches for multi-objective optimization. The non-dominated sorting process in this research involves the following steps:

Compare each solution with all other solutions in the population. If a solution is not dominated by any other solution, it is a part of the first non-dominated Pareto front.
Remove the first non-dominated Pareto front from the population and repeat the process for the remaining solutions. The next set of solutions that are not dominated by any other solution are assigned to the second non-dominated Pareto front.
Repeat the process until all solutions are assigned to a Pareto front.

5.2. Thin a rich Pareto front based on ε-dominance

The

ε

-dominance method provides a reduced approximation of the full Pareto set. This method constructs a grid in the objective function space and accepts only one solution per grid cell. This grid creates an

ε

-box around each solution, and any new solution that falls within this

ε

-box is considered dominated and therefore discarded. A solution

x

is said to

ε

-dominace another solution

y

for some

ε > 0

if and only if

x_{j} + ε \geq y_{j}

for

i = 1, \dots, k

where

k

is the number of objective functions.

Laumanns et al. [43] proposed the concept of ε-dominance to address a problem encountered in earlier multi-objective evolutionary algorithms (MOEAs), regarding their convergence and distribution properties. The ε-dominance overcomes this problem and provably leads to MOEAs that exhibit both the desired convergence towards the Pareto front and a well-distributed set of solutions. Walsh et al. [44] extended the work of Laumanns et al. [43] to propose a thin rich Pareto front based on ε-dominance to improve convergence and diversity of Pareto front solutions for multi-objective evolutionary algorithms. The thinning a rich Pareto front based on

ε

-dominance method partitions the objective space into a series of hypercubes of length

ε

. Subsequently, the Euclidean distance to each hypercube’s Utopia point is minimized, enabling the selection of a smaller set of solutions from each hypercube containing

ε

-dominated solutions. The quantity of reduced solutions hinges on the selection of

ε

, in conjunction with the shape and diversity of the original Pareto front. For more details on thinning a rich Pareto front based on

ε

-dominance, see Walsh et al. [44]. In this research, we utilize the method proposed by Walsh et al. [44] to choose an appropriate design from the Pareto front.

5.3. Desirability functions

Desirability functions are particularly useful when optimizing a process with multiple objectives, as they enable prioritization of these objectives according to their importance. This methodology employs weights to represent different user priorities, allowing the researcher to select the best single solution based on these different weight values. The individual desirability score

(d_{i})

for each objective is combined into an overall desirability function

(D F)

, using either the arithmetic or geometric mean. Each objective function is converted into a desirability score

(d_{i})

that ranges from 0 to 1, with 1 indicating the most desirable outcome and 0 being completely undesirable. The desirability function based on the arithmetic mean can be mathematically represented as:

D F_{A r i} = \sum_{i = 1}^{m} w_{i} d_{i},

(26)

where

m

denotes the number of objective functions,

w_{i} \in [0,1]

is the selected weight for the

i

th objective function, and

d_{i}

is the desirability score of the

i

th objective function. The sum of all weights

, w_{i},

must equal one,

\sum_{i = 1}^{m} w_{i} = 1

. The desirability function based on the geometric mean can be mathematically represented as:

D F_{G e o} = d_{1}^{w_{1}} d_{2}^{w_{2}} \dots d_{m}^{w_{m}} .

(27)

In this research, the desirability function based on the geometric mean is adopted because if one of the objective functions has a desirability score close to zero, the geometric mean will be significantly affected, resulting in low overall desirability. This reflects the fact that a poor outcome in one objective function cannot be compensated for by better outcomes in other objective functions. For further details on the desirability function, see Derringer and Suich [45] and Myers et al. [2]. In this research, the

D F_{G e o}

is defined as

D F_{G e o} = D^{w} D_{1^{-}}^{1 - w},

(28)

where

D

and

D_{1^{-}}

are the scaled values of the D-efficiency and the minimum D-efficiency due to missing observation, respectively. We explore all regions of the Pareto front by considering the weight,

w_{i}

, in a sequence of (0, 0.1, 0.2, …, 0.9, 1). If the weight equals 0, the design will be deemed optimal based on the minimum D-efficiency due to missing observation. Conversely, if the weight equals 1, the design will be deemed optimal based on D-efficiency. For any other weight assignment, there are trade-offs between these two criteria. This method offers an alternative way to select the design based on aligning with the experimental priorities and considering the trade-offs between the two objective functions.

6. Genetic algorithms for generating optimal design

Genetic algorithms (GAs) are particularly effective in handling optimization problems in a large or complex design space. Their inherent parallel nature allows them to explore various potential solutions simultaneously, which is a valuable feature when dealing with both single-objective and multi-objective functions. GAs are also robust to changes in the problem setup and are not easily trapped in local optima. Therefore, they are suited to a variety of applications such as engineering, architecture, machine learning, and artificial intelligence, where optimal or near-optimal solutions are pursued.

The D-efficiency is a widely recognized optimality criterion for experimental design optimization. It is favored due to its ease of interpretation, flexibility, comprehensiveness, and computational efficiency. The D-efficiency serves as a measure of the quality of a design in a regression model, succinctly summarizing the information the design provides about the model parameters. The minimum D-efficiency due to a missing observation evaluates the worst-case scenario of the leave-one-out D-efficiency. This measurement determines how well a design can estimate the model parameters in the absence of an observation. As such, it provides the reliability of parameter estimates in the presence of missing data. In this research, both the minimum D-efficiency due to a missing observation and the D-efficiency are considered as the objective functions of the GA. It is important to note that a higher D-efficiency indicates a more informative design, leading to more precise parameter estimates. Similarly, a design with a high minimum D-efficiency due to a missing observation is preferred because it results in a lower loss of D-efficiency due to missing observation. Such a design demonstrates robustness to missing data and provides more reliable parameter estimates. In situations where a single missing observation is inevitable in an experiment, experimenters still need a design that remains robust against this absence, especially in smaller experimental settings. Our goal here is to generate designs robust against missing observation in small experiments using a genetic algorithm. These designs aim to preserve not just commendable D-efficiency, but also maintain a favorable minimum D-efficiency due to missing observation.

In this work, a chromosome is represented by the experimental design matrix, and a gene represents a row within this design matrix, or chromosome. Rather than using binary or other encoding methods, we employ real-value encoding with a precision of four decimal places for three reasons: (1) it is well-suited for optimization in a continuous search space, (2) it permits a wider range of possible values within smaller chromosomes, and (3) it is advantageous when addressing problems involving more complex values. As presented by Michalewicz [39], compared to binary encoding, real-valued encoding provides greater efficiency in terms of CPU time and offers superior precision for replications. A chromosome

C

with

n \times q

dimension represents a possible design where

n

denotes the number of the design points and

q

represents the number of mixture components. Each row of chromosome

C

represents a gene

x_{i} = [x_{i 1} x_{i 2} \dots x_{i q}]

for

i = 1,2, \dots n .

For example, if there are seven design points, a chromosome

C

consists of

(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}, x_{7})

In our work, we employ various genetic operators, including blending, between-parent crossover, within-parent crossover, extreme gene, and mutation operators, to maintain diversity in our genetic algorithm. Each of these operators has its own success probability, represented by the blending rate

(α_{b})

, the crossover rate

(α_{c b}, α_{c w})

, the extreme rate, and the mutation rate

(α_{m u})

. If a probability test is passed (PTIP), a genetic operator is executed, altering a gene or set of genes. A probability test follows a Bernoulli distribution with a success probability of

α_{i}

. Let

U

be a uniformly distributed random variable ranging from 0 to 1. If

0 \leq U \leq α_{i}

, a PTIP occurs and the operator is applied to a parent chromosome, generating an offspring chromosome.

The performance of the genetic algorithm can be improved by using success probabilities within the range

G_{i} \leq α_{i} \leq H_{i}

. The higher rates

(H_{i})

of the genetic parameter are utilized in the early iterations, followed by the lower rates

(G_{i})

in later iterations. This approach allows for substantial changes in the initial generations and subsequent convergence toward a more precise solution. The rate of these genetic parameters directly impacts the efficiency of the algorithm. We generate several sets to determine the optimal parameter values and select the one that yields the highest objective function values and maintains stability throughout the later iterations. The algorithm employed is based on the work of Limmun et al. [26]. The steps of our genetic algorithm are summarized as follows:

Step 1 Determine the genetic parameters, including the initial population size

(M)

, the number of iterations, the selection method, the blending rate

(α_{b})

, the crossover rate

(α_{c b}, α_{c w})

, the extreme rate

(α_{e})

, and the mutation rate

(α_{m u})

Step 2 Generate the initial population with an even number

M

chromosomes (mixture designs). We use the function of Borkowski and Piepel [46] to map randomly sampled points in a hypercube into a constrained mixture space. Encode each chromosome with real-value encoding rounded to four decimal places.

Step 3 Randomly select pairs from the

M

chromosomes for the reproduction process. Pairing chromosomes during reproduction is essential for promoting genetic diversity and ensuring population survival.

Step 4 Apply genetic operators, including blending, between-parent crossover, within-parent crossover, extreme gene, and mutation, to the parent chromosomes to produce offspring chromosomes. These operators are only applied to the parents if they pass the probability test. We have adapted the genetic operators proposed by Limmun et al. [26] in this research.

Step 5 Combine parent chromosomes of size

M

with offspring chromosomes of size

M

to form a new mixture population of size

2 M

Step 6 Calculate the minimum D-efficiency due to one missing observation and the D-efficiency as the objective functions for the entire new mixture population of size

2 M

, then construct and evaluate the Pareto fronts of this mixture population.

Step 7 Choose the best

M

chromosomes to form the new generation of the evolutionary population using the non-dominated sorting strategy. If the last allowed Pareto front contains more chromosomes than the number of required chromosomes, a random selection of chromosomes from this front will be included to fulfill the requirement.

Step 8 Repeat Steps 3 through 7 until the specified stopping criterion is satisfied, indicating convergence towards the optimal or near-optimal designs. The genetic algorithm will iteratively generate optimal or near-optimal, leading to the identification of highly efficient designs.

Step 9 Apply the blending operator to the optimal or near-optimal designs from Step 8 that have similar minimum D-efficiency due to a single missing observation and similar D-efficiency as they are considered to be the objective functions. This strategy aims to enhance these objective functions and protect against settling on local optima or sub-optimal solutions. Then, the non-dominated designs (chromosomes) appearing on the first Pareto front are selected and considered optimal designs.

Step 10 Select well-distributed set of optimal designs from the optimal designs in Step 9 using thinning a rich Pareto front based on

ε

-Dominance. This approach ensures broader coverage across all criteria values, providing a condensed but thorough depiction of the trade-off space.

7. Examining the performance of the competing designs

After identifying the competing optimal designs, the next step is to evaluate their performance. This involves understanding their strengths and assessing the trade-offs between different objectives, allowing us to more effectively match the designs to user priorities. In this research, we adopt the desirability function based on the geometric mean,

D F_{G e o},

as shown in Equation. (28), to evaluate the performance of individual designs. This approach aids in understanding the trade-offs inherent in each design, thus facilitating the alignment of designs with user priorities. Recall that a larger value is preferable.

For evaluating the performance of the design in this research, we adopt D-, A-, G-, and IV-efficiency. To assess the robustness of the designs in the presence of missing observations, we utilize the minimax loss efficiency based on the D-, A-, G-, and IV-criterion. If the maximum loss of efficiency is close to one, this indicates a higher loss of information due to missing observations. Conversely, if the maximum loss of efficiency is close to 0, it suggests minimal information loss due to missing observation. The breakdown of an experimental design in the case of missing observations occurs when the determinant of information matrix for the reduce design equals 0,

|X_{(r)}^{'} X_{(r)}^{}| = 0

. This situation becomes a serious problem because the matrix is singular and cannot be inverted. As a result, the model parameters become unestimable, or any estimates that are obtained could be highly sensitive and unreliable. The maximum number of missing observations can indeed be arbitrary. However, the prerequisite is that, even after losing these observations, the model matrix of the design must retain full rank. Furthermore, all model parameters should remain estimable under the assumed model to guarantee accurate parameter estimation. In the worst-case scenarios, we frequently find that

|X_{(r)}^{'} X_{(r)}^{}| = 0

when the number of missing observations in a small experiment exceeds 1, resulting in a loss efficiency of 1. Consequently, in this research, we have limited our consideration to cases where the number of missing observation equals 1.

We also use the fraction of design space (FDS) plot to assess the robustness of the design against missing observations. The FDS plot provides a visual depiction of the experimental region, demonstrating how prediction variance changes across different portions of the design space. We consider both the FDS curve of the complete design and the FDS curve of the design that excludes the most impactful point. These curves offer a manageable summary that facilitates the comparison of prediction variance performance. A design that maintains flatter and lower FDS curves for both the complete design and the design with missing observation across the design space is likely to exhibit good robustness properties. For a more detailed discussion on FDS plots, see Goldfarb et al. [47] and Ozol-Godfrey et al. [48].

8. Numerical examples

We addressed two mixture design problems that involved three mixture components where the experimental region was a polyhedral region within an irregular shape. The two illustrations we presented depicted distinct patterns of experimental regions: the first illustration displayed a region with four vertices, while the second illustration featured a region with six vertices. The full model under consideration in these cases was the Scheffé quadratic mixture mode, which is given by

E (y) = β_{1} x_{1} + β_{2} x_{2} + β_{3} x_{3} + β_{12} x_{1} x_{2} + β_{13} x_{1} x_{3} + β_{23} x_{2} x_{3} .

(29)

Note that this model contains six parameters. In both illustrations, the GA population consists of

M

=100 chromosomes. To evaluate performance efficiency, we compared the optimal designs derived from our process (referred to as GA designs) with those produced by Design-Expert 11 software (referred to as DX designs). The GA designs were generated using a MATLAB program developed by the author, whereas all DX designs were produced using the Design-Expert 11 software. The latter utilized the best search algorithm based on the D-criterion and supplemented by an additional model point option. This algorithm combined Point Exchange and Coordinate Exchange searches to explore the design space comprehensively.

8.1. Example 1: Sugar formulation

We examined this example from Spanemberg et al. [49] as an illustration. The objective of the experiment was to identify the optimal sugar formulation that maximized the shelf life and critical moisture content of hard candy. The sugar composition comprises three components: sucrose

(x_{1})

, high-maltose corn syrup

(x_{2})

, and 40 DE corn syrup

(x_{3})

. The range of constraints for the sugar mixture are presented below:

0.50 \leq x_{1} \leq 0.60; 0.00 \leq x_{2} \leq 0.50; 0.00 \leq x_{3} \leq 0.50 .

The boundary under consideration comprised four vertices. Prior to implementing the GA, we conducted a comprehensive investigation into the selection of GA parameter values and determined the suitable number of generations needed to achieve convergence. We set a limit of 1500 generations. Furthermore, we established the following ranges for the genetic parameter values :

0.05 \leq α_{b} \leq 0.25, 0.05 \leq α_{c b}, α_{c w} \leq 0.20, 0.005 \leq α_{e} \leq 0.15, 0.003 \leq α_{m u} \leq 0.20, 0.01 \leq σ \leq 0.10

where

α_{b}, α_{c b}, α_{c w}, α_{e}

and

α_{m u}

represent the blending rate, between-parent crossover rate, within-parent crossover rate, extreme rate, and mutation rate, respectively. The genetic parameter values were initially set to their maximum levels and then systematically reduced to lower levels after 400 generations.

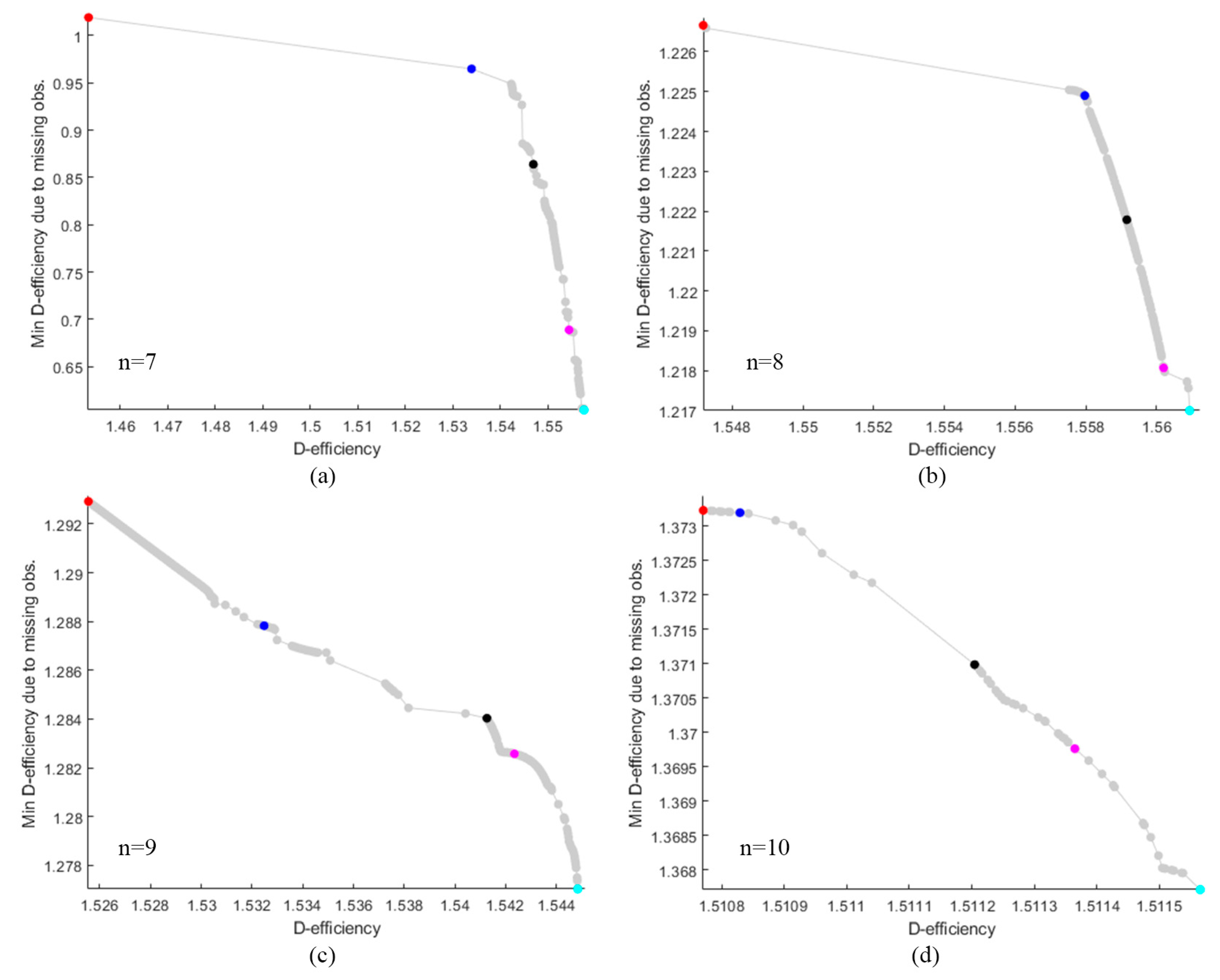
The performance of the competing designs was evaluated by considering those with 7 to 10 runs. Figure 1 illustrates the Pareto front, highlighted in gray, which showcases a well-distributed set of optimal GA designs derived from thinning a rich Pareto front using ε-dominance. The designs GA

n

.1, GA

n

.2, GA

n

.3, and GA

n

.4 are represented by red, blue, black, and magenta dots, respectively. For

n

=7, the gap between the highest and the lowest D-efficiency was approximately 0.0137, and the gap between the highest and lowest minimum D-efficiency due to a missing observation was around 0.008. However, this contrast was significantly reduced for

n

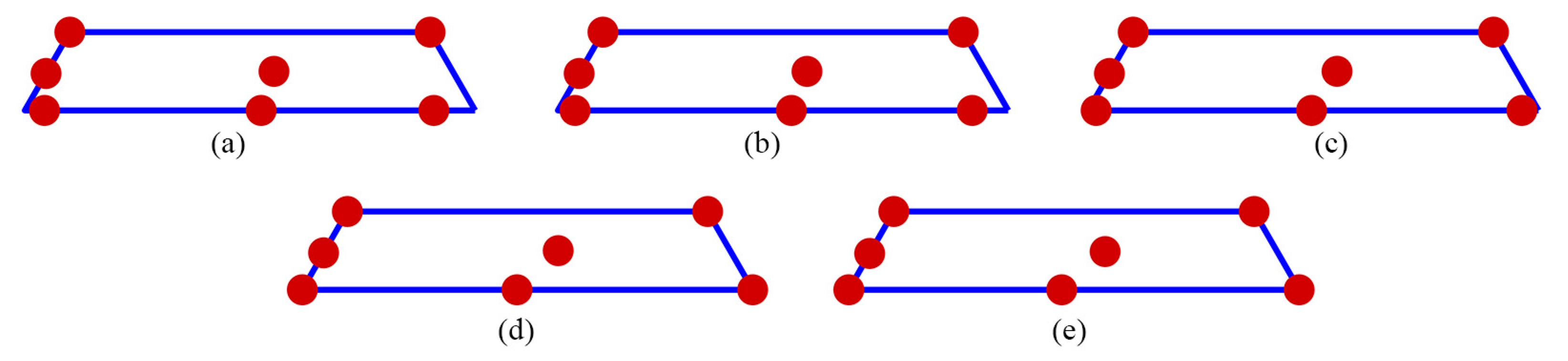
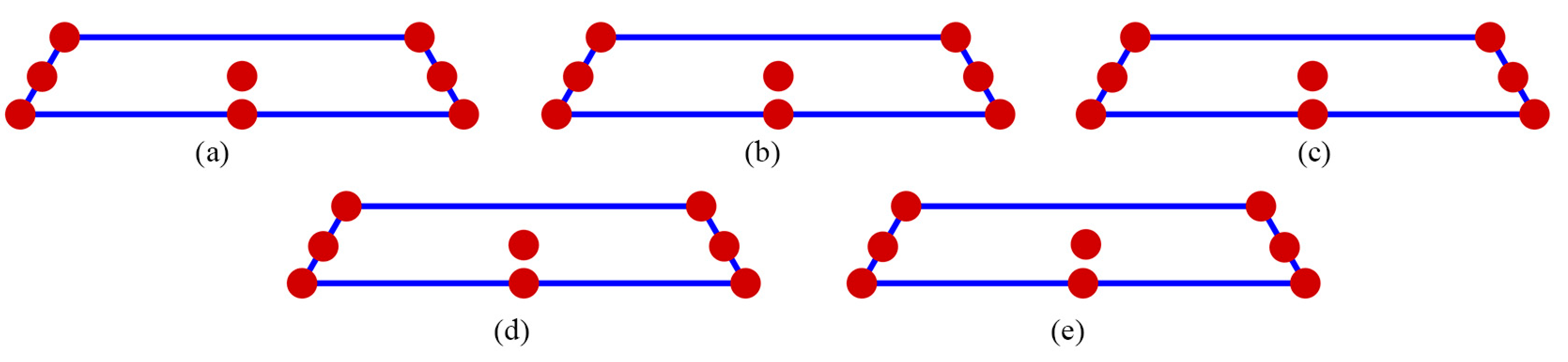
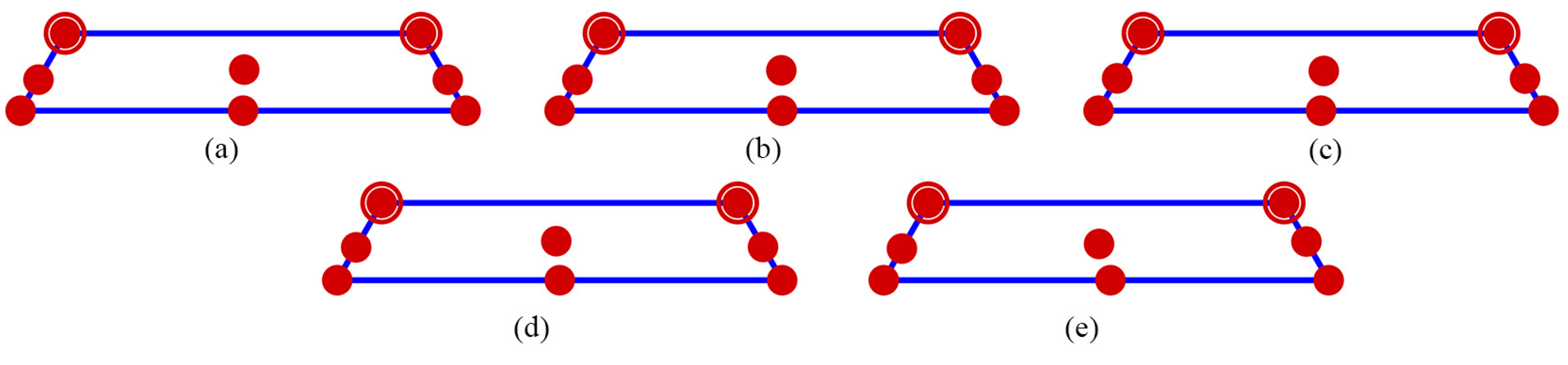
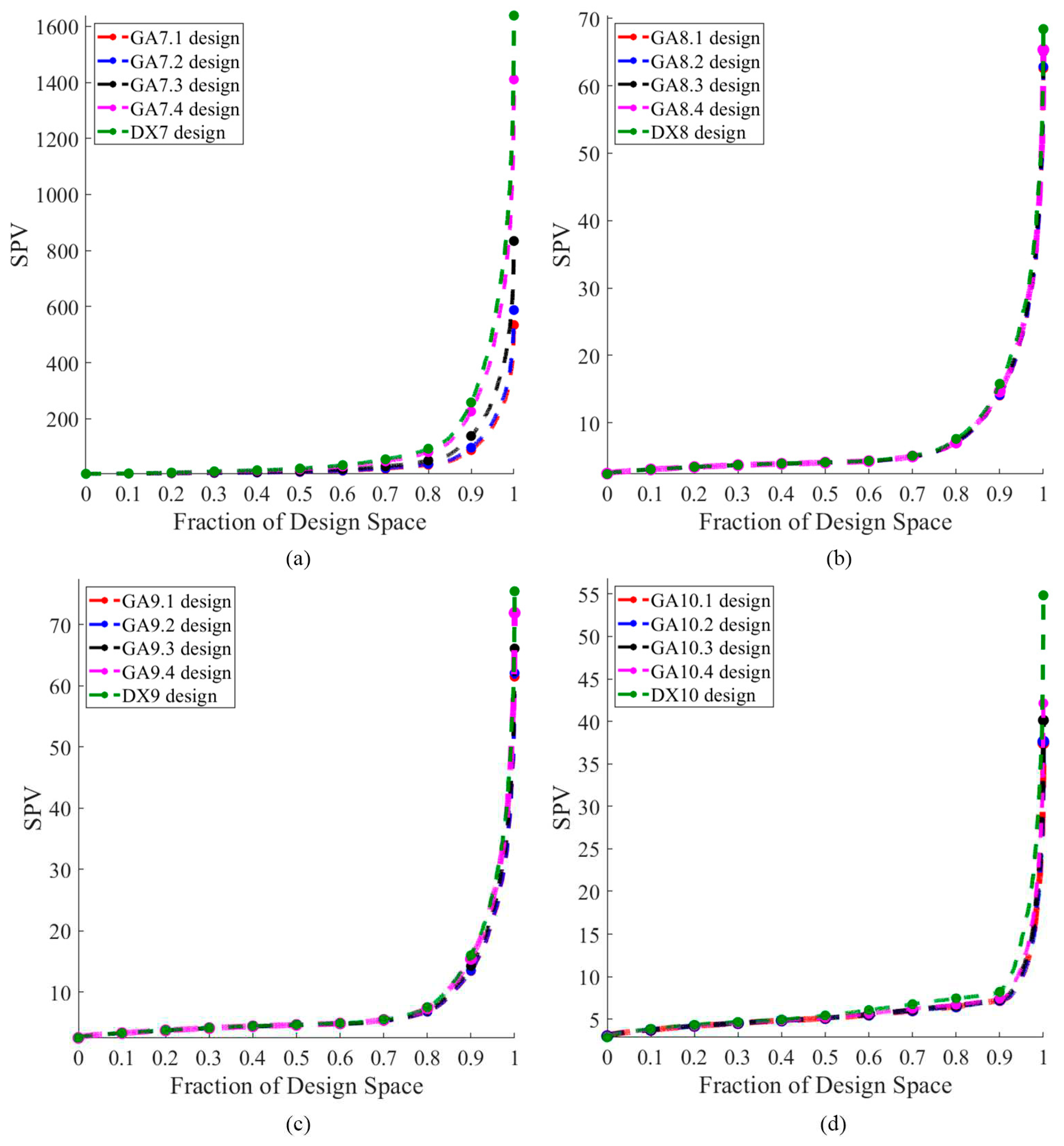
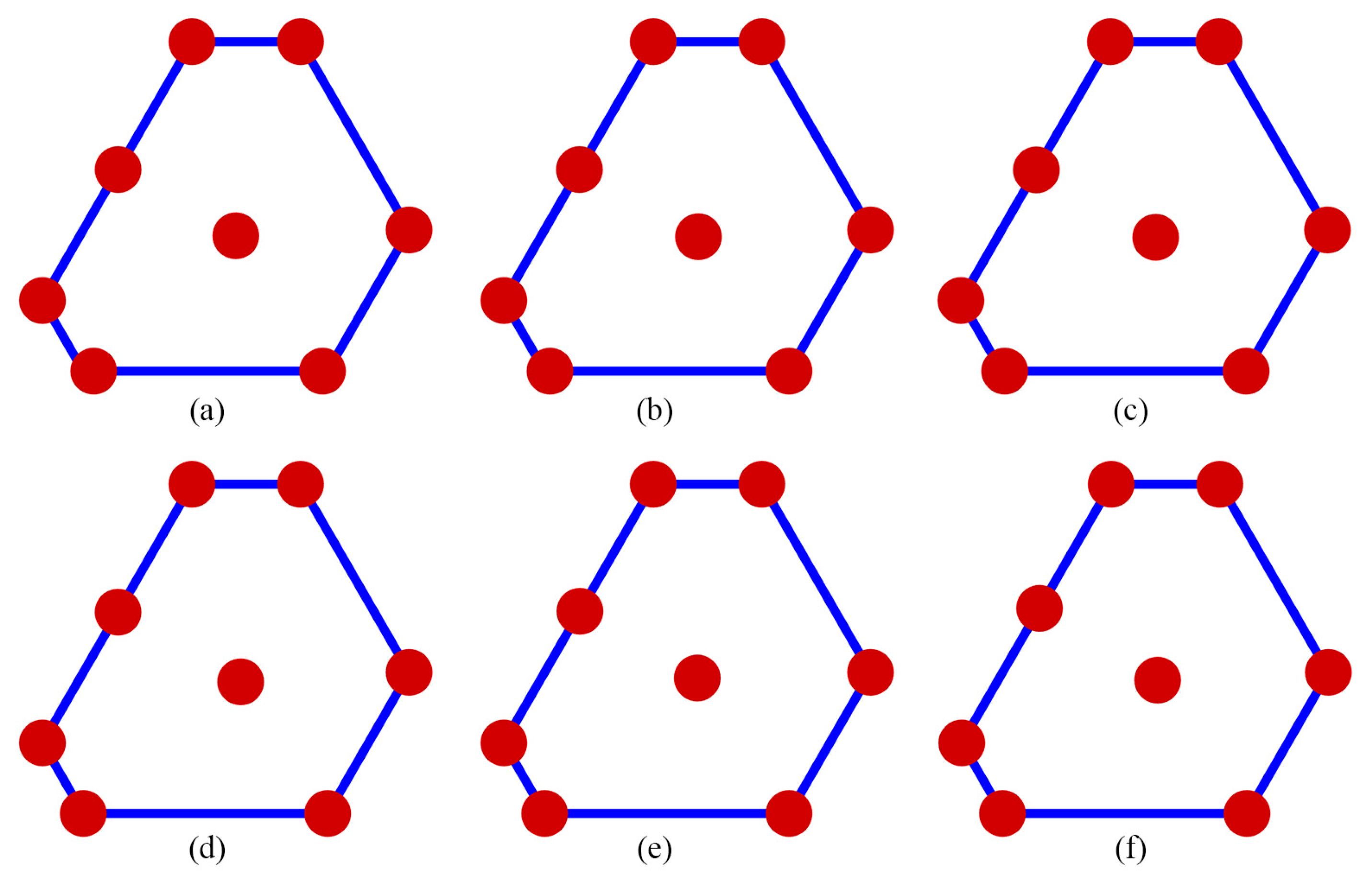
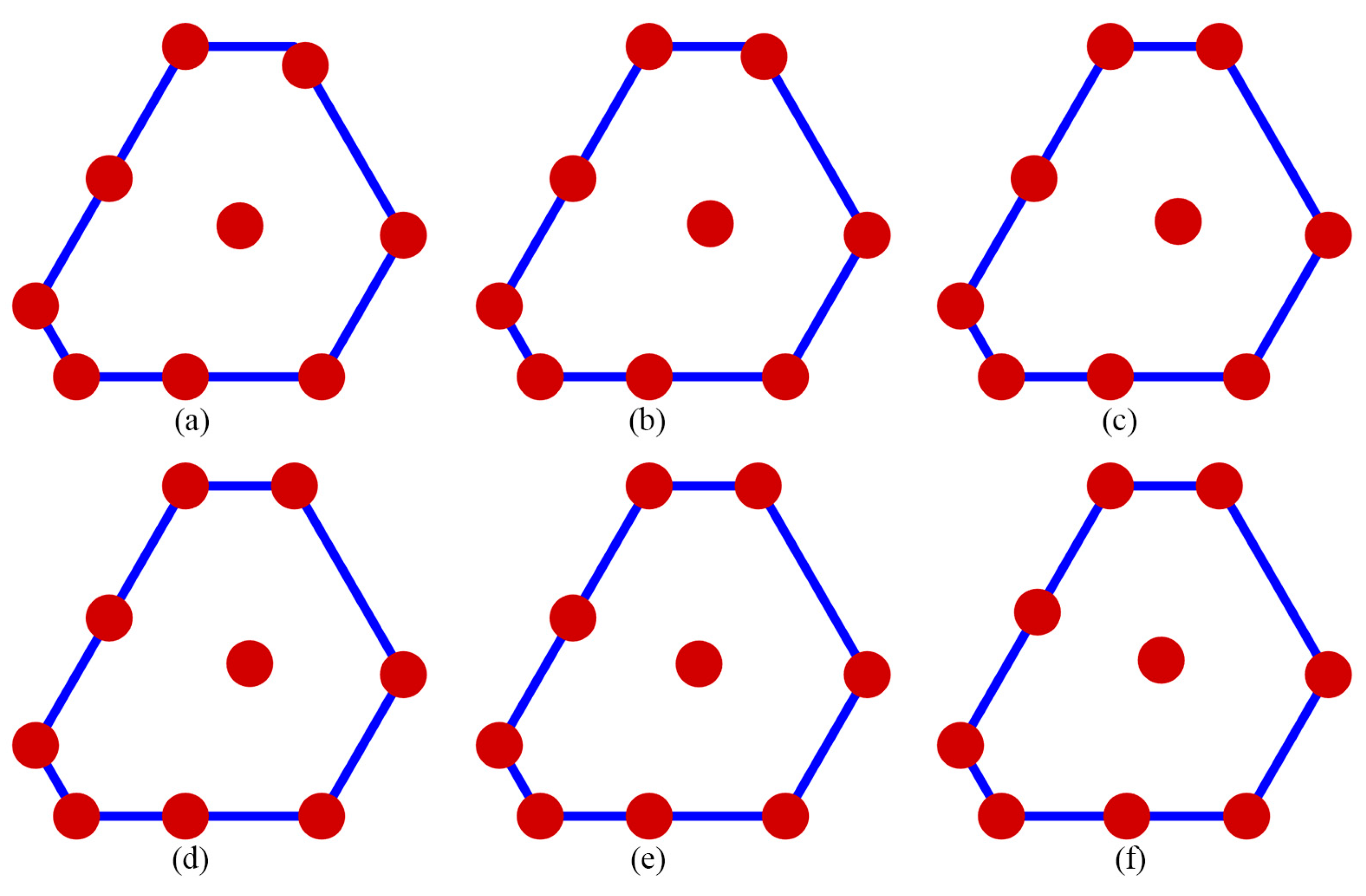
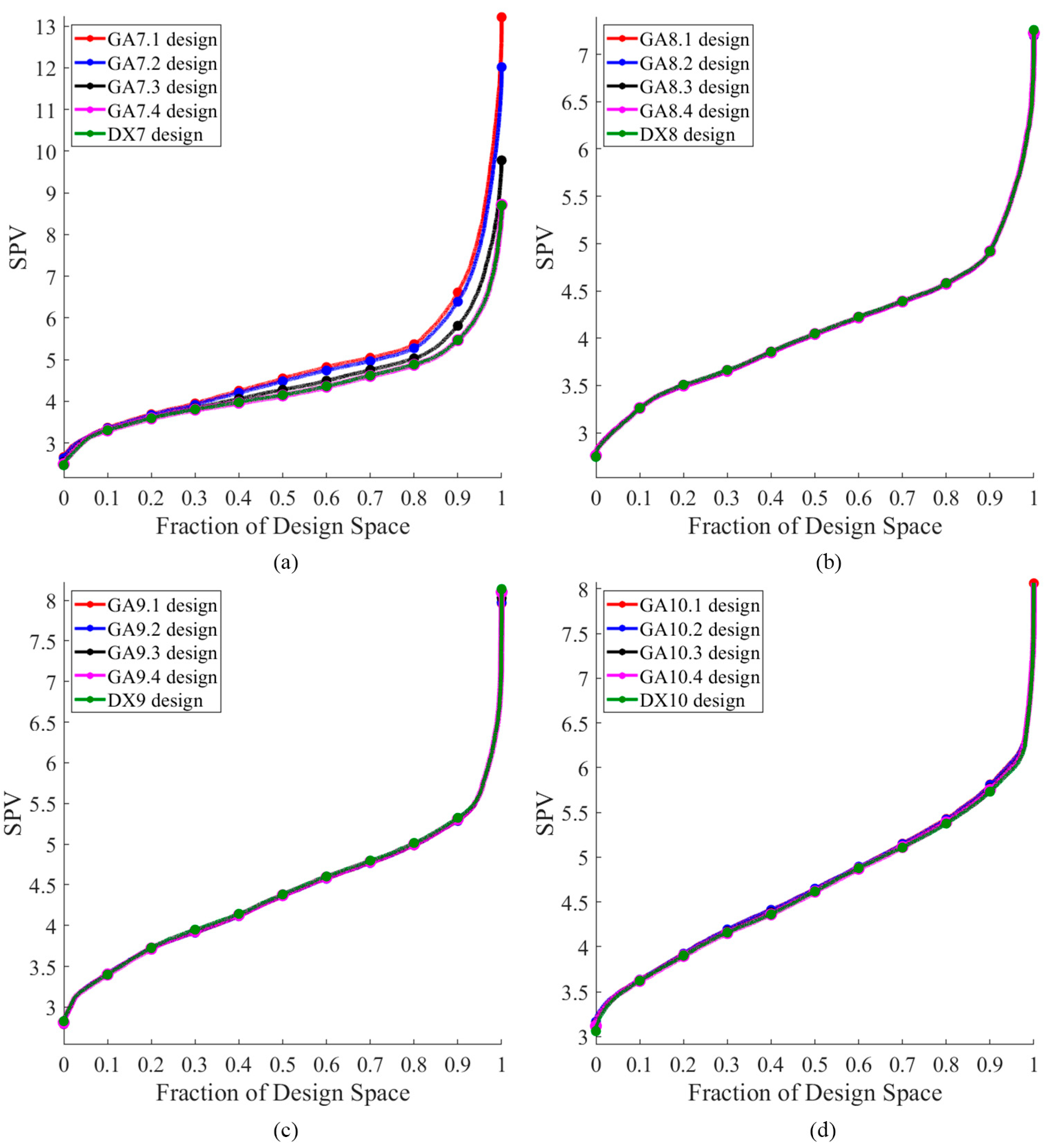
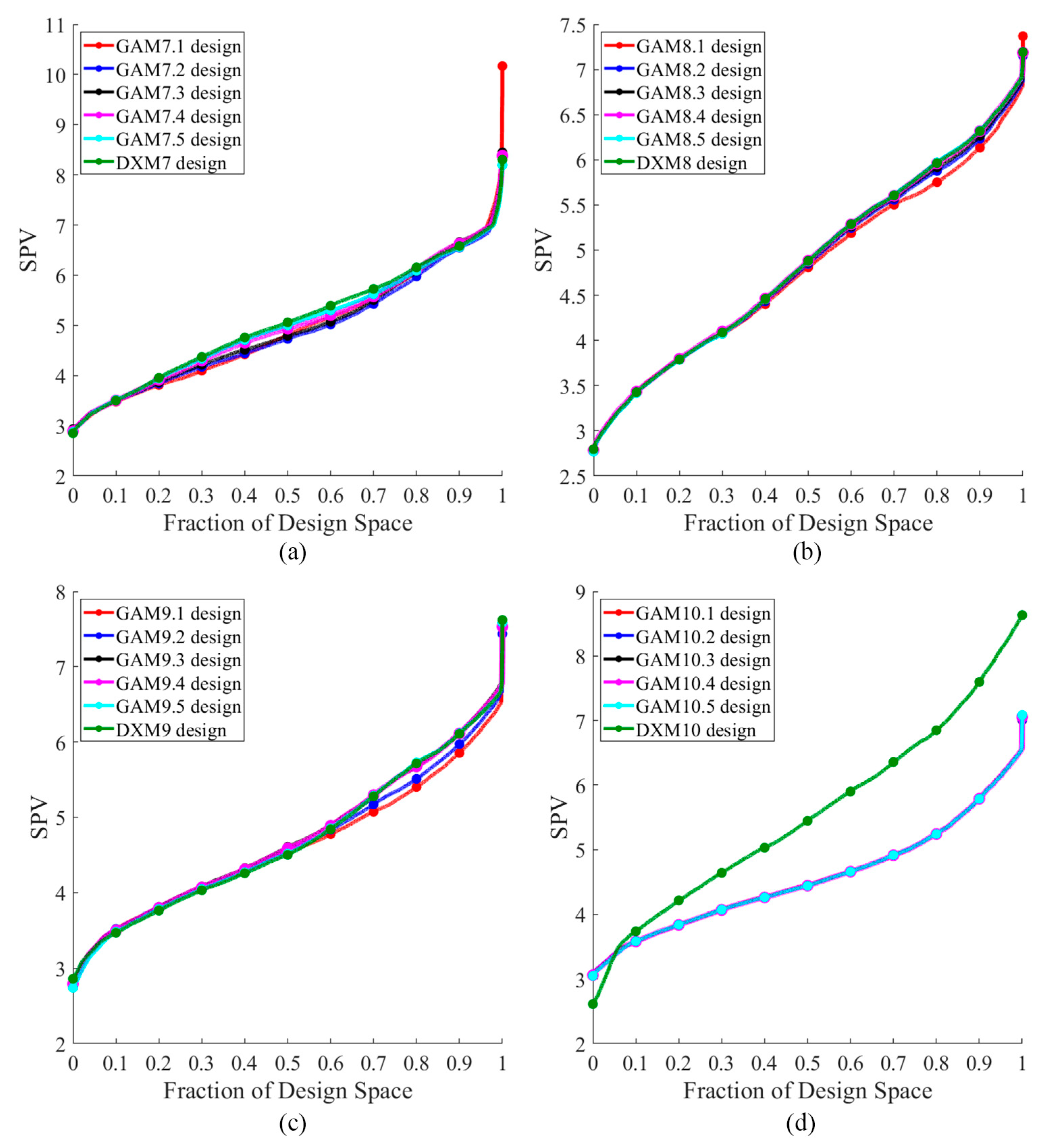
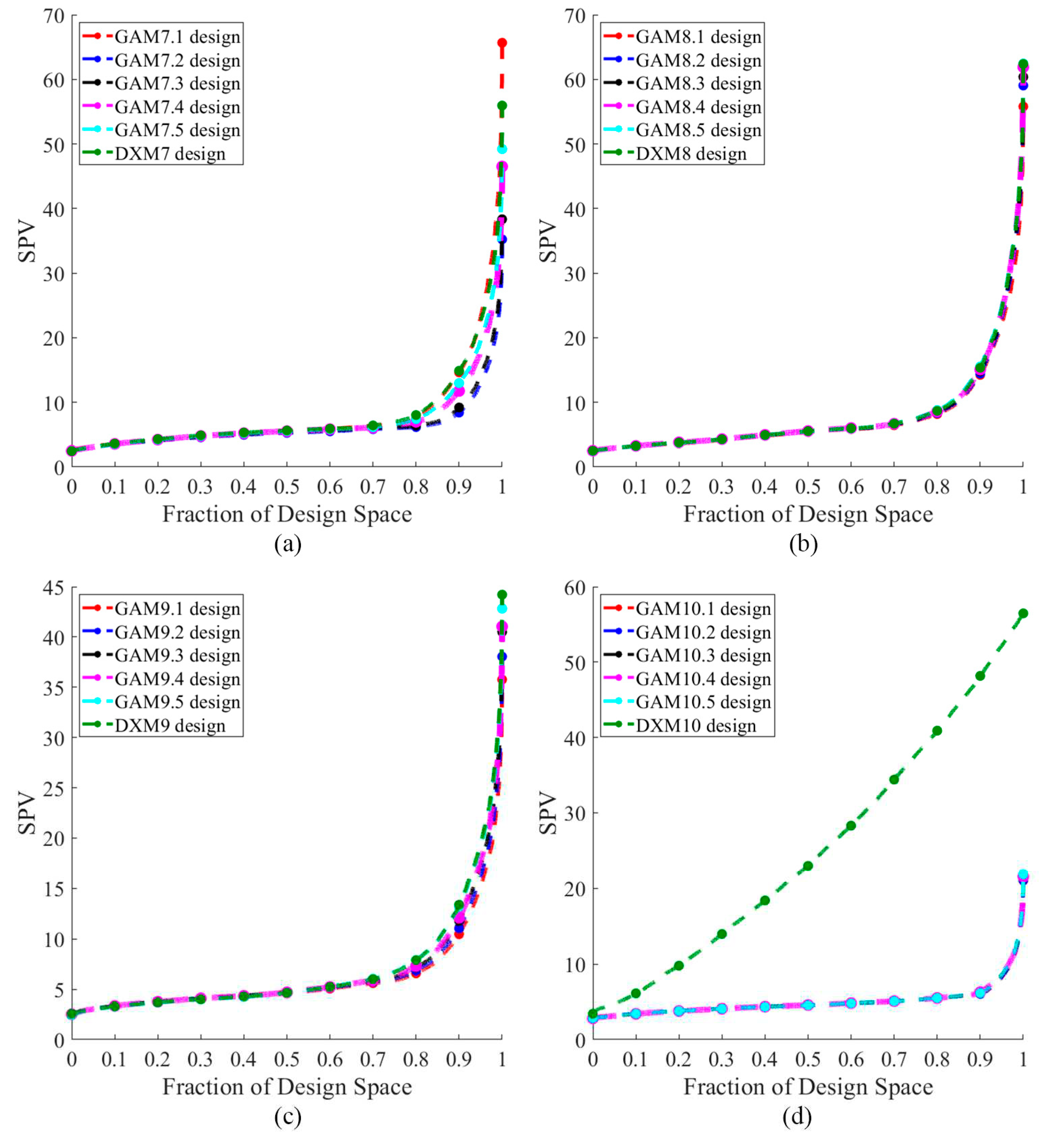
=8 to 10 where the gap between the highest and the lowest D-efficiency was less than 0.0001, and the gap between the highest and lowest minimum D-efficiency due to a missing observation was less than 0.002. Figures 2 to 5 display the distribution point patterns of all GA designs and the DX design for a range of design points from 7 to 10, respectively. Figure 6 illustrates the FDS plot for all GA designs and the DX design in the context of a complete design, whereas Figure 7 showcases the FDS plot for all GA designs and the DX design when the most impactful observation point was omitted. Table 1 shows the D, A, G, and IV-efficiency and the maximum loss of D, A, G, and IV-efficiency due to a single missing observation.

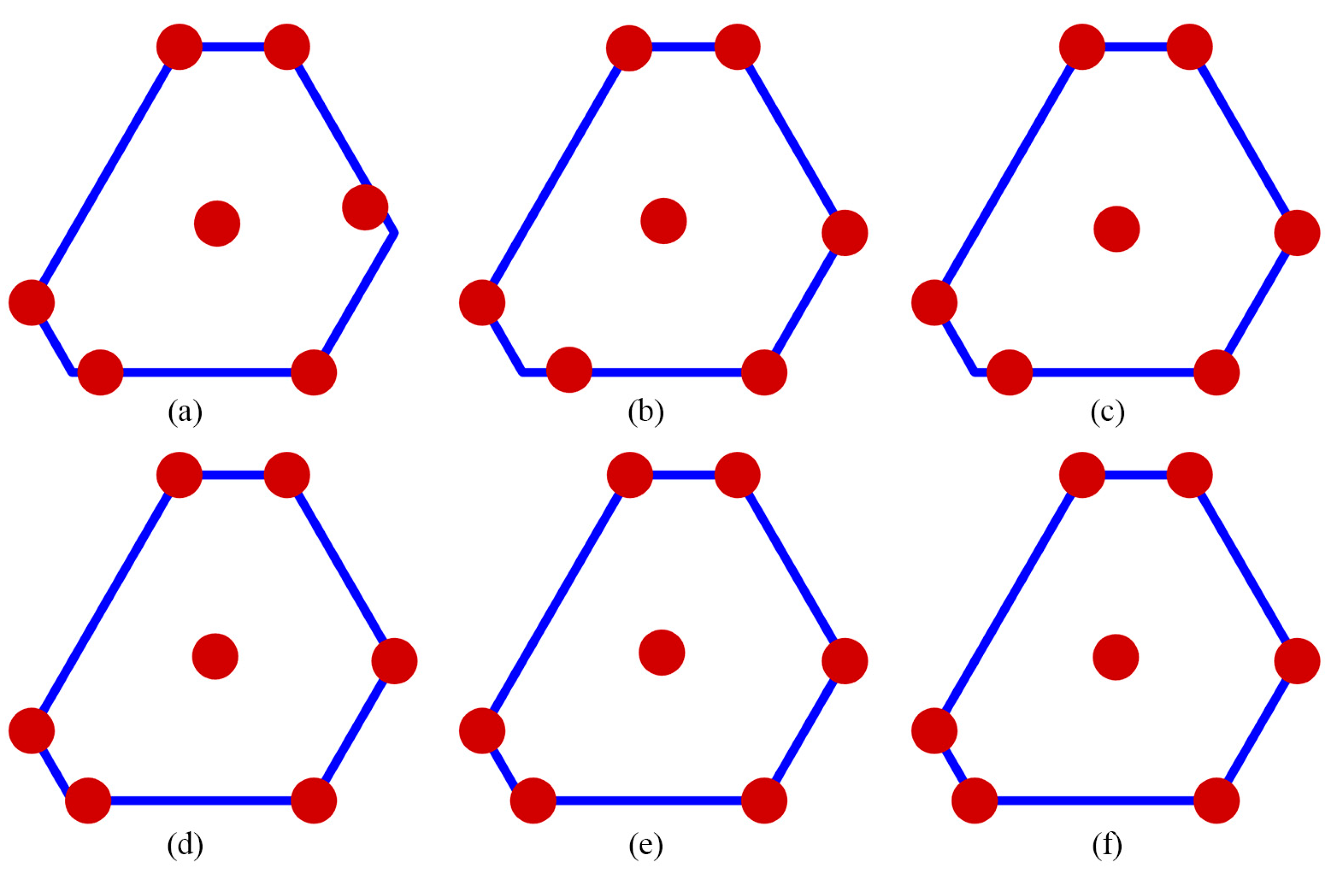
In Figure 2, for n=7, the distribution point patterns of all GA and DX designs tended to occupy all vertices or locations near them, as well as positions close to two edge centroid points and near the overall centroid. The distribution point patterns of GA7.1, GA7.2, and GA7.3 designs were distinct, and they differed from those of GA7.4 and DX7 designs. The GA7.4 and DX7 designs exhibited slight differences on the edge centroid points and overall centroid point, with other points being similar. As a result, the GA7.4 and DX7 designs showed similar performance in terms of D, A, G, and IV-efficiency and the maximum loss of D, A, G, and IV-efficiency due to a single missing observation, as shown in Table 1. Additionally, they had identical FDS curves for the complete design and demonstrated better performance in terms of prediction variance, as shown in Figure 6a. However, when considering the FDS plot that omits the most impactful observation point, as illustrated in Figure 7a, the FDS curves of the GA7.4 and DX designs were comparable, except at the boundary of the design region. As depicted in Figure 3, for n=8, the distribution point patterns of all GA and DX designs bore resemblance to those of n=7, but they tend to be closer to three edge centroid points, rather than two. 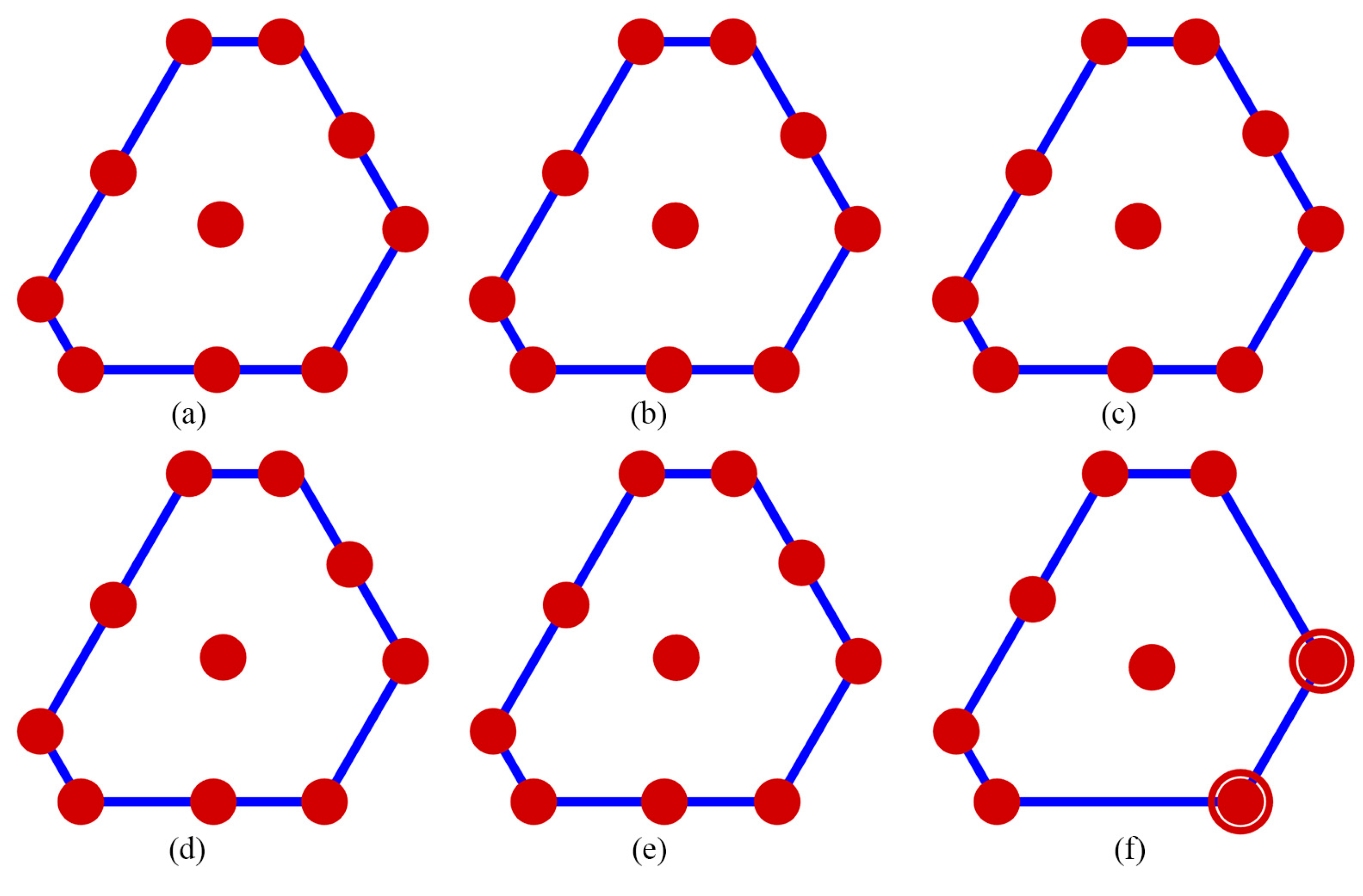In the case of n=9, as illustrated in Figure 4, the distribution point patterns of all GA and DX designs were similar to those for n=8, but with an additional replicated point at a vertex. Lastly, for n=10, the distribution point patterns of all GA and DX designs, as displayed in Figure 5, mirrored those for n=9, but with an added replicated point at two vertices. As a result, they demonstrate similar performance in terms of (1) D-, A-, G-, and IV-efficiency, and (2) the FDS curves for both the complete design and scenarios where the most impactful observation point is omitted, as indicated in Table 1 and Figure 6 and Figure 7. However, most GA designs outperformed the DX design when considering the maximum loss of D-, A-, G-, and IV-efficiency due to a single missing observation.

As indicated in Table 1, the GA7.3 design neither possessed the highest D-, A-, G-, and IV-efficiency nor did it have the lowest maximum loss of D-, A-, G-, and IV-efficiency due to a single missing observation. Instead, it maintained a middle level for all these values, which was considered desirable. As demonstrated in Figure 6a and Figure 7a, the GA7.3 design appeared to provide the greatest robustness against missing observations in terms of prediction variance. This was attributed to its FDS curves, which were markedly flatter and lower for both the complete design and scenarios involving the omission of more impactful observations. For

n

=8 to 10, the FDS curves for the complete design of all GA and DX designs were similar, as depicted in Figure 6. However, the FDS curves representing the omission of influential observations for the DX designs became less competitive at the boundary of the design region, particularly when

n

=10, as shown in Figure 7. The designs generated by our Genetic Algorithm (GA) seemed to exhibit robust properties against missing observation in terms of prediction variance. Our algorithm focused on creating robust designs that performed well not only in terms of D-efficiency but also in terms of minimum D-efficiency due to missing observation. Our GA designs successfully achieved these objectives. Furthermore, they also provided commendable A-, G-, and IV-efficiency, as well as manageable maximum losses of A-, G-, and IV-efficiency due to a single missing observation. However, we did not consider the maximum loss of efficiency due to two or more missing observations because the worst-case scenario would result in

|X_{(r)}^{'} X_{(r)}^{}| = 0

In this example, we provided four GA designs as a reference to help experimenters understand their performance and balance requirements. This assisted in assessing how well these designs aligned with user priorities and their robustness in handling missing observation. An assessment was performed using the desirability function based on the geometric mean,

D F_{G e o}

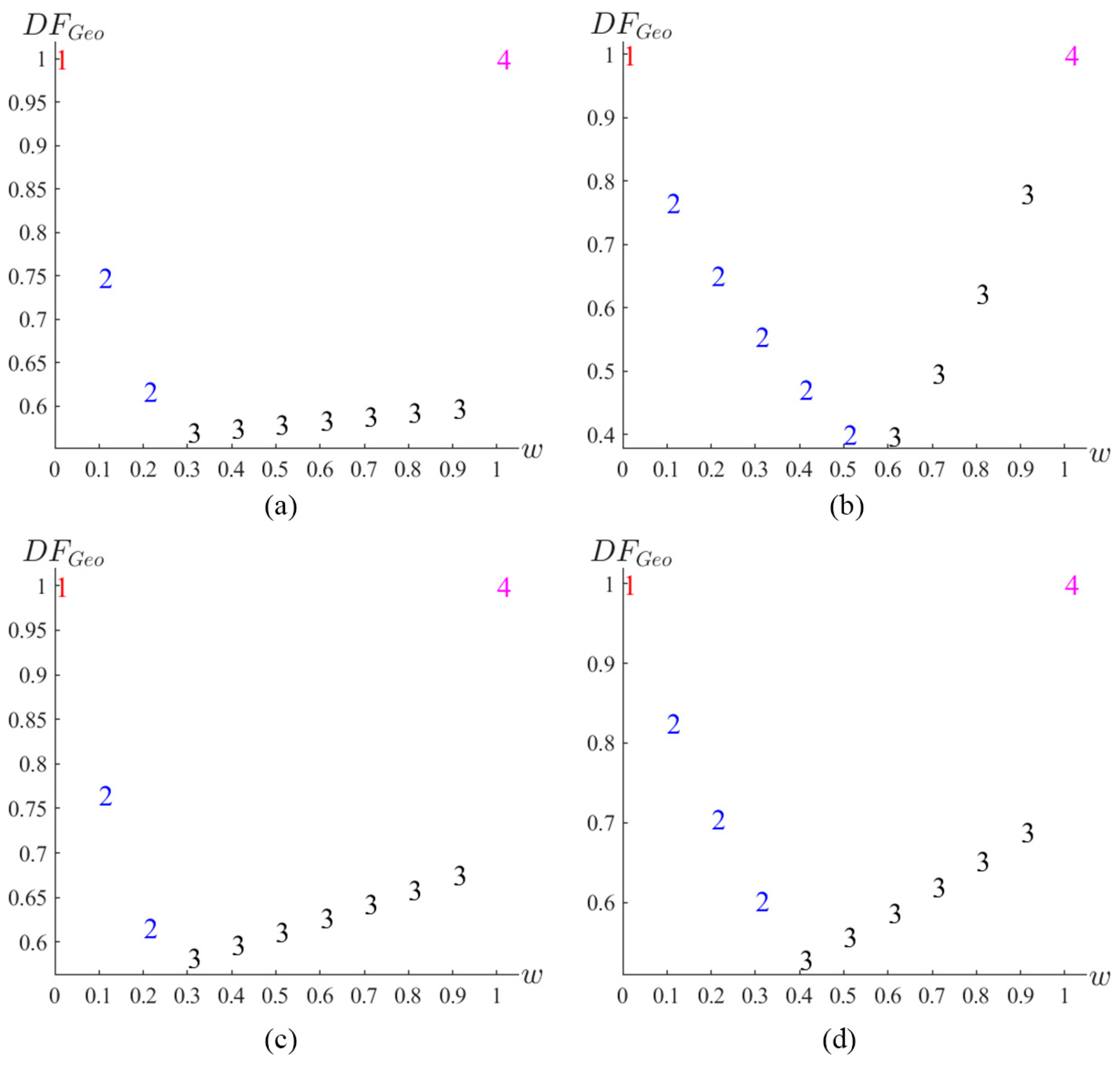
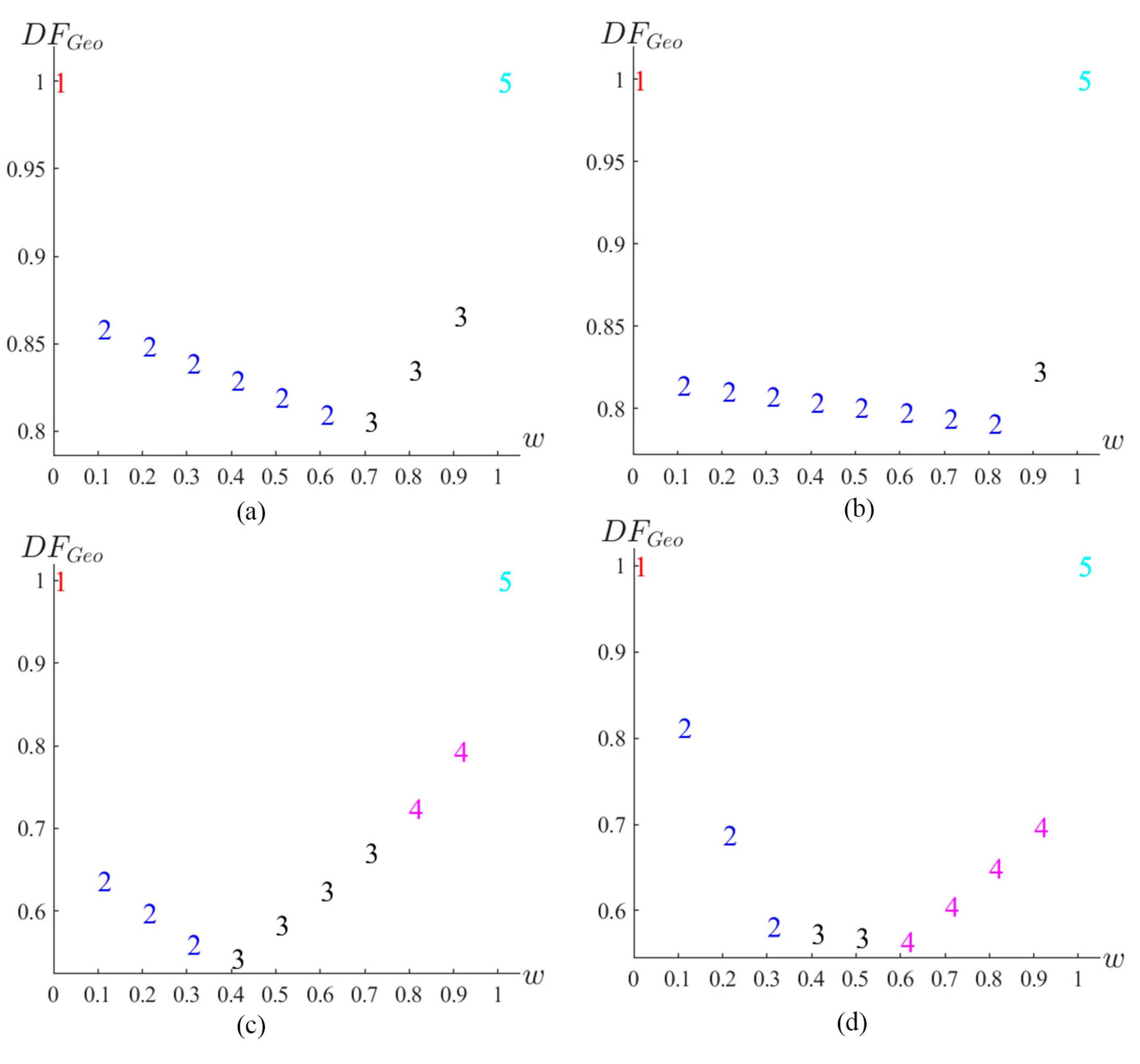
. Figure 8 showed the desirability function based on the geometric mean. The numbers displayed in Figure 8 corresponded to the numbers following the dots in the GA designs. The GA

n

.1 design was the optimal choice when the weight was 0, indicating that it was the optimal design based on the minimum D-efficiency due to missing observation. Conversely, the GA

n

.4 design was the optimal choice when the weight was 1, indicating that it was the optimal design based on the D-efficiency. The GA

n

.2 and GA

n

.3 designs became optimal when the weight ranged from 0.1 to 0.9, representing a trade-off between the minimum D-efficiency due to missing observations and the D-efficiency. As illustrated in Figure 8, for

n

=7 and 9, the GA

n

.2 design was the optimal choice when the weight fell between 0.1 and 0.2. However, the GA

n

.3 design became the optimal choice when the weight was in the range of 0.3 to 0.9. For

n

=8, the GA8.2 design was optimal when the weight ranged from 0.1 to 0.5, and the GA8.3 design was optimal when the weight ranged from 0.6 to 0.9. Interestingly, for

n

=9, the GA9.2 design was the optimal choice when the weight was between 0.1 and 0.3, while the GA9.3 design became optimal for weights from 0.4 to 0.9. The

D F_{G e o}

can serve as a tool, enabling experimenters to select the most robust optimal design based on their individual priorities. Therefore, in practice, if the primary focus of the experimenter was on minimizing the D-efficiency loss due to missing observation, the GA

n

.1 design would be preferred. However, if the emphasis was on the D-efficiency, the GA

n

.4 design would be more suitable. In cases where the experimenter wished to balance both criteria, the GA

n

.2 and GA

n

.3 designs would be the preferred choices.

8.2. Example 2: Mixture problem as presented in the Myers et al. (2016)

For our second example, we considered a mixture problem as presented by Myers et al. [2]. The lower and upper proportion constraints for this problem are as follows:

0.10 \leq x_{1} \leq 0.80; 0.00 \leq x_{2} \leq 0.75; 0.00 \leq x_{3} \leq 0.60 .

The boundary in this case consists of six vertices. Even though this example has the same number of components as the first example, the shape of the experimental region differs. Similar to the first example, we thoroughly examined the selection of GA parameter values before implementing the GA. We determined an appropriate number of generations for convergence, setting a limit of 1500 generations. Consequently, the genetic parameter values in this example differ from those in the first example. Furthermore, we established the following ranges for the genetic parameter values:

0.03 \leq α_{b} \leq 0.20, 0.03 \leq α_{c b}, α_{c w} \leq 0.20, 0.005 \leq α_{e} \leq 0.15, 0.005 \leq α_{m u} \leq 0.10, 0.01 \leq σ \leq 0.10

Initially, the genetic parameter values are set to their maximum levels, and then systematically decreased to lower levels after 500 generations. In this example, the performance of the competing designs, encompassing 7 to 10 runs, is demonstrated. Figure 9 features the Pareto front, emphasized in gray, and illustrates a well-distributed set of optimal GA designs. These designs resulted from the application of a thinning technique to a rich Pareto front using

ε

-dominance. The five GA designs chosen from the Pareto front, namely GAM

n

.1, GAM

n

.2, GAM

n

.3, GAM

n

.4, and GAM

n

.5, are denoted by red, blue, black, magenta, and cyan dots, respectively. As in the initial example, the gap between the highest and lowest D-efficiency, as well as the gap between the highest and lowest minimum D-efficiency due to a missing observation, was greater for

n

=7 compared to

n

=8 to 10. As depicted in Figure 10, for

n

=7, the distribution point patterns of all GA and DX designs tended to be positioned on or near all vertices, as well as close to the overall centroid. In the case of

n

=8, illustrated in Figure 11, the distribution point patterns of all GA and DX designs resembled those of

n

=7, but with an additional point near the edge centroid. For

n

=9, as shown in Figure 12, the distribution point patterns of all GA and DX designs mirrored those of

n

=8, but they were located near two edge centroid points instead of one. Finally, when

n

= 10, as depicted in Figure 13, the distribution point patterns of the GA and DX designs differed. The GA designs tended to be located on or near all vertices, close to three edge centroid points and the overall centroid point. On the other hand, the DX designs were positioned on or near all vertices, at two replicated vertices, near an edge centroid point and the overall centroid point.

Figure 14 presents the FDS plot for all GA designs and the DX design for a complete design, while Figure 15 depicts the FDS plot for all GA designs and the DX design when the most impactful observation point is omitted. Table 2 shows the D, A, G, and IV-efficiency as well as the maximum loss of D-, A-, G-, and IV-efficiency due to a single missing observation. The GA designs and DX design exhibited comparable performance in terms of prediction variance, with the exception of the GAM7.1 design, which showed inferior performance at the boundary, as illustrated in Figure 14a and Figure 15(a). Both the GAM7.2 and GMM7.3 designs demonstrated similar FDS curves in the complete design and when the most impactful observation point was omitted. Consequently, these designs appeared to possess robust properties against missing observation. The GAM7 and DXM7 designs were largely equivalent in terms of D-, A-, G-, and IV-efficiency, but the DXM7 design fell short when considering the maximum loss of D-, A-, G-, and IV-efficiency due to a single missing observation, as detailed in Table 2. For

n

=8 and 9, the FDS curves for both the complete design and when the most impactful observation point was omitted display a notable similarity. As a result, both the GA and DX designs seemed to exhibit robust properties in the face of missing observation. The GAM8.3, GAM8.4, GAM8.5, and DXM8 designs were quite comparable in terms of D-, A-, G-, and IV-efficiency, as well as the maximum loss of D, A, G, and IV-efficiency due to a single missing observation. Meanwhile, for

n

=9, the GAM9 and DXM9 designs showed a similar comparison in terms of D-, A-, G-, and IV-efficiency, and also in the maximum loss of these efficiencies due to a single missing observation. These observations highlight that even though designs might be comparable based on prediction variance, it did not necessarily imply comparability on other criteria. For

n

=10, as illustrated in Figure 14d and Figure 15d, the FDS curves of the GA designs outperformed the DX design for both the complete design and when the most impactful observation point was omitted. The GAM10 design outperformed in terms of D-, A-, G-, and IV-efficiency, and also showed a smaller maximum loss of these efficiencies due to a single missing observation. Consequently, the GAM10 designs appeared to possess strong robustness properties when faced with missing observation.

This example provided five GA designs as references, allowing experimenters to compare their performance and balance requirements. Figure 16 displays the desirability function based on the geometric mean, which helps assess how well these designs align with user priorities and their robustness in handling missing observations. The GAM

n

.1 design emerged as the optimal choice when the weight was 0, indicating its optimal performance based on the minimum D-efficiency due to missing observation. Conversely, the GAM

n

.5 design was the optimal choice when the weight was 1, signifying its superiority based on D-efficiency. The GAM7.2 design became optimal for weights ranging from 0.1 to 0.6, whereas the GAM7.3 design took precedence for weights between 0.7 and 0.9. The GAM8.2 design was optimal for weights ranging from 0.1 to 0.8, while the GAM8.3 design stood out when the weight was 0.9. For

n

=9, the GAM9.2 design was the optimal choice for weights between 0.1 and 0.3. The GAM9.3 design became optimal for weights between 0.4 and 0.7, and the GAM9.4 design excelled for weights between 0.8 and 0.9. Finally, for

n

=10, the GAM10.2 design was optimal for weights between 0.1 and 0.3. The GAM10.3 design took the lead for weights between 0.4 and 0.5, and the GAM10.4 design was optimal for weights ranging from 0.6 to 0.9. In practice, if an experimenter aims to balance both the D-efficiency and the minimum D-efficiency loss due to missing observations, the GA designs optimal for each weight may serve as good choices. This is because they can facilitate trade-offs between the two criteria and demonstrate robustness against missing observations. Their performance is measured based on prediction variance, optimality criteria, and loss of efficiency.

-dominance in the Myers et al. (2016) example.: (a) n=7; (b) n=8; (c) n=9; (d) n=10.

9. Conclusions

In real-world situations, even well-planned experiments can encounter missing observations. When it is infeasible to repeat experimental runs to fill in for these missing observations, experimenters often favor more robust designs to protect against potential information loss. In practice, it is impossible to predict which observations will be missing during the experiment, suggesting that any design point could potentially lack data. The loss of a particularly informative observation could be viewed as a worst-case scenario. Thus, during the planning stage, experimenters prefer designs that continue to perform well, even when faced with the loss of key data points. Because we focus on worst-case scenarios, we do not consider situations where more than one observation is missing during an experiment, resulting in

|X_{(r)}^{'} X_{(r)}^{}| = 0

. Therefore, we exclude such cases from the scope of this research.

In this paper, we propose a multi-objective genetic algorithm for generating optimal mixture designs that are robust against missing observation. When applying this genetic algorithm to solve multi-objective optimization, the evolutionary procedure favors chromosomes with both superior D-efficiency and minimum D-efficiency due to missing observation. Therefore, the trade-off between D-efficiency and minimum D-efficiency due to missing observation is considered within this algorithm. The emphasis on D-efficiency is due to several reasons: (1) if any observation is missed from a D-optimal design, the overall impact on the accuracy of the parameter estimates can be minimized (2) the loss of some observations does not disproportionately affect specific regions of the experimental space, thereby ensuring the reliability of the experimental results even when data is missing (3) a D-optimal design ensures that the remaining data is as informative as possible, maximizing the utility of the available data. We studied problems with three mixture components for generating optimal mixture designs when the experimental region is an irregularly-shaped polyhedron within the simplex. Our algorithm generates a well-distributed set of optimal mixture designs selected from the Pareto front through the thinning of a dense Pareto front based on

ε

-Dominance. The aim of this thinning process is to reduce the number of solutions while maintaining the trade-off relationship between objectives. This method ensures a balanced, diverse coverage of the Pareto front, offering a compact and comprehensive representation of the trade-off space.

Our algorithm is designed to generate mixture designs that not only perform well in terms of D-efficiency, but also maintain a high minimum D-efficiency due to missing observation. Consequently, this well-distributed set of optimal mixture designs has proven to be D-optimal designs. Our genetic algorithm stands apart from the general genetic algorithm in that it recruits points from a continuous design space. This results in our genetic algorithm having a higher upper bound for efficiencies compared to the general genetic algorithm. As for the distributional patterns of the GA designs, most of the design points are located at or close to the vertices, near the edge centroid points, and near the overall centroid point. Our results correspond to the findings of Rashid et al. [11] in that the point with the most significant effect on D-efficiency is the near over centroid point. When this point is missing, it has a greater impact on the accuracy of the model parameter estimates.

This research aims to create optimal mixture designs that simultaneously maximize both D-efficiency and minimum D-efficiency due to missing observation. Generally, a design might perform well in terms of D-efficiency but underperform when considering the loss of D-efficiency due to missing observation. Conversely, a design might maintain a low loss of D-efficiency due to missing observation, but fall short in D-efficiency. From the results, it is clear that (1) our algorithm can generate optimal mixture designs that perform well in both D-efficiency and the mitigated loss of D-efficiency, and (2) our algorithm can produce optimal mixture designs that demonstrate substantial robustness against missing observations. This robustness is substantiated by three key factors: (1) predictive variance, (2) D, A, G, and IV-efficiency, and (3) the loss of efficiency with respect to D-, A-, G-, and IV-efficiency. Furthermore, our GA design continues to perform well in terms of A-, G-, and IV-efficiency, and in minimizing the loss of efficiency based on these criteria. In fact, the GA designs perform as well as, if not better than, the DX designs when considering these three key factors.

Our algorithm not only generates designs that perform well in both optimality criteria and the minimization of efficiency loss due to missing observation, but it also provides a well-distributed set of optimal designs. This enables experimenters to understand the trade-offs between D-efficiency and minimum D-efficiency due to missing observation. Experimenters can select the optimal design for each weight using the desirability function from this comprehensive set of mixture designs. They can then choose a design that strikes an ideal balance between objective functions according to their priorities. Our method is flexible and can be easily adapted to other scenarios, such as when multiple component constraints exist, the number of components exceeds three, or when considering other optimality criteria.

In a mixture experiment with three mixture components, if we consider the Scheffé quadratic mixture model, there are six model parameters. When the experimental region has four vertices and the number of parameters exceeds the number of vertices, missing observations at either the near overall centroid point or the most impactful point still allows for accurate parameter estimation using certain optimal designs. However, in a scenario where the experimental region has six vertices and the number of parameters matches the number of vertices, missing observations at the near overall centroid point or the most impactful point can lead to insufficient information for accurately estimating all the model parameters using some optimal designs. Hence, it becomes crucial to consider optimal designs that possess robust properties against missing observation.

We propose our genetic algorithm as a practical alternative for generating optimal mixture designs that are robust due to missing experimental observation. Our algorithm offers a powerful strategy for creating designs that are resilient to potential information loss due to absent observations from an experiment. Our findings suggest that experimenters can have confidence in the proposed GA designs, as they perform comparably to, if not better than, the designs generated by another method in terms of robustness against missing observations. However, if protection against the worst-case scenario for parameter estimation is a priority, we recommend the proposed GA designs. Moreover, when the experiment is subject to resource constraints and missing observations are a frequent concern, a design robust against missing observation should be given serious consideration.

Author Contributions

Conceptualization, W.L., B.C. and J.J.B.; methodology, W.L., B.C. and J.J.B.; software, W.L. and J.J.B.; validation, W.L., B.C. and J.J.B.; formal analysis, W.L.; investigation, W.L., B.C. and J.J.B; writing—original draft preparation, W.L.; writing—review and editing, W.L., B.C. and J.J.B; visualization, W.L.; supervision, J.J.B.. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available upon reasonable request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

Cornell, J.A. Experiments with mixtures: designs, models, and the analysis of mixture data; 3rd ed.; John Wiley & Sons, 2002.
Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response surface methodology: process and product optimization using designed experiments; 4th ed.; John Wiley & Sons, Ltd.: Hoboken. NJ, USA, 2016.
Box, G.E.; Draper, N.R. Robust designs. Biometrika. 1975, 62, 347–352. [Google Scholar] [CrossRef]
Herzberg, A.M.; Andrews, D.F. Some considerations in the optimal design of experiments in non-optimal situations. J. R. Stat. Soc., B: Stat. Methodol, 1976, 38, 284–289.
Andrews, D.F.; Herzberg, A.M. The robustness and optimality of response surface designs. J Stat Plan Inference. 1979, 3, 249–257. [Google Scholar] [CrossRef]
Ghosh, S. Robustness of designs against the unavailability of data. Sankhya Ser B. 1982, 50–62. [Google Scholar]
Akhtar, M.; Prescott, P. Response surface designs robust to missing observations. Commun Stat Simul Comput. 1986, 15, 345–363. [Google Scholar] [CrossRef]
Lal, K.; Gupta, V.K.; Bhar, L. Robustness of designed experiments against missing data. J. Appl. Stat. 2001, 28, 63–79. [Google Scholar] [CrossRef]
Ahmad, T.; Gilmour, S.G. Robustness of subset response surface designs to missing observations. J Stat Plan Inference. 2010, 140, 92–103. [Google Scholar] [CrossRef]
Yakubu, Y.; Chukwu, A.U.; Adebayo, B.T.; Nwanzo, A.G. Effects of missing observations on predictive capability of central composite designs. Int. J. Comput. Sci. 2014, 4, 1–18. [Google Scholar] [CrossRef]
Rashid, F.; Akbar, A.; Arshad, H.M. Effects of missing observations on predictive capability of augmented Box-Behnken designs. Commun Stat Simul Comput. 2022, 51, 7225–7242. [Google Scholar] [CrossRef]
Ahmad, T.; Akhtar, M.; Gilmour, S.G. Multilevel augmented pairs second-order surface designs and their robustness to missing data. Commun Stat Theory Methods. 2012, 41, 437–452. [Google Scholar] [CrossRef]
Ahmad, T.; Akhtar, M. Efficient response surface designs for the second-order multivariate polynomial model robust to missing observation. J Stat Theory Pract. 2015, 9, 361–375. [Google Scholar] [CrossRef]
da Silva, M.A.; Gilmour, S.G.; Trinca, L.A. Factorial and response surface designs robust to missing observations. Comput Stat Data Anal. 2017, 113, 261–272. [Google Scholar] [CrossRef]
Smucker, B.J.; Jensen, W.; Wu, Z.; Wang, B. Robustness of classical and optimal designs to missing observations. Comput Stat Data Anal. 2017, 113, 251–260. [Google Scholar] [CrossRef]
Chen, X.P.; Guo, B.; Liu, M.Q.; Wang, X.L. Robustness of orthogonal-array based composite designs to missing data. J Stat Plan Inference. 2018, 194, 15–24. [Google Scholar] [CrossRef]
Alrweili, H.; Georgiou, S.; Stylianou, S. Robustness of response surface designs to missing data. Qual. Reliab. Eng. Int. 2019, 35, 1288–1296. [Google Scholar] [CrossRef]
Mahachaichanakul, S.; Srisuradetchai, P. Applying the median and genetic algorithm to construct D-and G-optimal robust designs against missing data. Appl. Sci. Eng. 2019, 12, 3–13. [Google Scholar] [CrossRef]
Oladugba, A.V.; Nwanonobi, O.C. Robustness of definitive screening composite designs to missing observations. Commun. Stat. - Theory Methods. 2021, 1-15.
Yankam, B.M.; Oladugba, A.V. Robustness of orthogonal uniform composite designs against missing data. Commun. Stat. - Theory Methods. 2021, 1-16.
Borkowski, J.J. A comparison of prediction variance criteria for response surface designs. J. Qual. Technol. 2003, 35, 70–77. [Google Scholar] [CrossRef]
Heredia-Langner, A.; Carlyle, W.M.; Montgomery, D.C.; Borror, C.M.; Runger, G.C. Genetic algorithms for the construction of D-optimal designs. J. Qual. Technol. 2003, 35, 28–46. [Google Scholar] [CrossRef]
Heredia-Langner, A.; Montgomery, D.C.; Carlyle, W.M.; Borror, C.M. Model-robust optimal designs: A genetic algorithm approach. J. Qual. Technol., 2004, 36, 263–279.
Park, Y.; Montgomery, D.C.; Fowler, J.W.; Borror, C.M. Cost-constrained G-efficient response surface designs for cuboidal regions. Qual. Reliab. Eng. Int., 2006, 22, 121–139.
Limmun, W.; Borkowski, J.J.; Chomtee, B. Weighted A-optimality criterion for generating robust mixture designs. Comput Ind Eng. 2018, 125, 348–356. [Google Scholar] [CrossRef]
Limmun, W.; Chomtee, B.; Borkowski, J.J. Using geometric mean to compute robust mixture designs. Qual. Reliab. Eng. Int. 2021, 37, 3441–3464. [Google Scholar] [CrossRef]
Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
Konak, A.; Coit, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
Long, Q.; Wu, C.; Wang, X.; Jiang, L.; Li, J. A multiobjective genetic algorithm based on a discrete selection procedure. Math. Probl. Eng. 2015. [Google Scholar] [CrossRef]
Cook, R.D.; Wong, W.K. On the equivalence of constrained and compound optimal designs. J Am Stat Assoc. 1994, 89, 687–692. [Google Scholar] [CrossRef]
Zhang, C.; Wong, W.; Peng, H. Dual-objective optimal mixture designs. Aust N Z J Stat. 2012, 54, 211–222. [Google Scholar] [CrossRef]
Lu, L.; Anderson-Cook, C.M.; Lin, D.K. Optimal designed experiments using a Pareto front search for focused preference of multiple objectives. Comput Stat Data Anal. 2014, 71, 1178–1192. [Google Scholar] [CrossRef]
Borkowski, J.J. A comparison of prediction variance criteria for response surface designs. J. Qual. Technol. 2003, 35, 70–77. [Google Scholar] [CrossRef]
Goos, P.; Jones, B.; Syafitri, U. I-optimal design of mixture experiments. J Am Stat Assoc. 2016, 111, 899–911. [Google Scholar] [CrossRef]
Atkinson, A.; Donev, A.; Tobias, R. Optimum experimental designs, with SAS. Oxford: Oxford University Press, 2007.
Kiefer, J. Optimum experimental designs. J R Stat Soc Series B Stat Methodol. 1959, 21, 272–304. [Google Scholar] [CrossRef]
Pukelsheim, F. Optimal design of experiments. Society for Industrial and Applied Mathematics, 2006.
Golberg, D.E. Genetic algorithms in search, optimization, and machine learning. Addison-Wesley, 1989.
Michalewicz, Z. Genetic algorithms+data structures=evolution programs. New York: Springer-Verlag, 1992.
Haupt, R.L.; Haupt, S.E. Practical genetic algorithms. John Wiley & Sons, 2004.
Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms. John Wiley & Sons, 2001.
Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct Multidiscipl Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
Laumanns, M.; Thiele, L.; Deb, K.; Zitzler, E. Combining convergence and diversity in evolutionary multiobjective optimization. Evol Comput. 2002, 10, 263–282. [Google Scholar] [CrossRef]
Walsh, S.J.; Lu, L.; Anderson-Cook, C.M. I-optimal or G-optimal: Do we have to choose? . Qual Eng. 2023, 1–22. [Google Scholar] [CrossRef]
Derringer, G.; Suich, R. Simultaneous optimization of several response variables. J. Qual. Technol., 1980, 12, 214–219.
Borkowski, J.J.; Piepel, G.F. Uniform designs for highly constrained mixture experiments. J. Qual. Technol. 2009, 41, 35–47. [Google Scholar] [CrossRef]
Goldfarb, H.B.; Anderson-Cook, C.M.; Borror, C.M.; Montgomery, D.C. Fraction of design space plots for assessing mixture and mixture-process designs. J. Qual. Technol. 2004, 36, 169–179. [Google Scholar] [CrossRef]
Ozol-Godfrey, A.; Anderson-Cook, C.M.; Montgomery, D.C. Fraction of design space plots for examining model robustness. J. Qual. Technol., 2005, 37, 223–235.
Spanemberg, F.E.; Korzenowski, A.L.; Sellitto, M.A. Effects of sugar composition on shelf life of hard candy: Optimization study using D-optimal mixture design of experiments. J. Food Process Eng. 2019, 42, e13213. [Google Scholar] [CrossRef]

Figure 1. The Pareto front of a well-distributed set of optimal GA designs derived from thinning a rich Pareto front using

ε

-dominance in the sugar example: (a) n=7; (b) n=8; (c) n=9; (d) n=10.

Figure 1. The Pareto front of a well-distributed set of optimal GA designs derived from thinning a rich Pareto front using

ε

-dominance in the sugar example: (a) n=7; (b) n=8; (c) n=9; (d) n=10.

Figure 2. The distribution point patterns of all competing designs for 7 runs in the sugar example: (a) GA7.1 design; (b) GA7.2 design; (c) GA7.3 design; (d) GA7.4 design; (e) DX7 design.

Figure 3. The distribution point patterns of all competing designs for 8 runs in the sugar example: (a) GA8.1 design; (b) GA8.2 design; (c) GA8.3 design; (d) GA8.4 design; (e) DX8 design.

Figure 4. The distribution point patterns of all competing designs for 9 runs in the sugar example: (a) GA9.1 design; (b) GA9.2 design; (c) GA9.3 design; (d) GA9.4 design; (e) DX9 design.

Figure 5. The distribution point patterns of all competing designs for 10 runs in the sugar example: (a) GA10.1 design; (b) GA10.2 design; (c) GA10.3 design; (d) GA10.4 design; (e) DX10 design.

Figure 6. The FDS plot for all competing designs in the context of a complete design in the sugar example: (a) n=7; (b) n=8; (c) n=9; (d) n=10.

Figure 7. The FDS plot for all competing designs when the most impactful observation point was omitted in the sugar example: (a) n=7; (b) n=8; (c) n=9; (d) n=10.

Figure 8. The Pareto front of a well-distributed set of optimal GA designs derived from thinning a rich Pareto front using

ε

-dominance in the sugar example: (a) n=7; (b) n=8; (c) n=9; (d) n=10.

Figure 8. The Pareto front of a well-distributed set of optimal GA designs derived from thinning a rich Pareto front using

ε

-dominance in the sugar example: (a) n=7; (b) n=8; (c) n=9; (d) n=10.

Figure 9. The Pareto front of a well-distributed set of optimal GA designs derived from thinning a rich Pareto front using ε-dominance in the Myers et al. (2016) example: (a) n=7; (b) n=8; (c) n=9; (d) n=10.

Figure 10. The distribution point patterns of all competing designs for 7 runs in the Myers et al. (2016) example: (a) GAM7.1 design; (b) GAM7.2 design; (c) GAM7.3 design; (d) GAM7.4 design; (e) DXM7 design.

Figure 11. The distribution point patterns of all competing designs for 8 runs in the Myers et al. (2016) example: (a) GAM8.1 design; (b) GAM8.2 design; (c) GAM8.3 design; (d) GAM8.4 design; (e) DXM8 design.

Figure 12. The distribution point patterns of all competing designs for 9 runs in the Myers et al. (2016) example: (a) GAM9.1 design; (b) GAM9.2 design; (c) GAM9.3 design; (d) GAM9.4 design; (e) DXM9 design.

Figure 13. The distribution point patterns of all competing designs for 10 runs in the Myers et al. (2016) example: (a) GAM10.1 design; (b) GAM10.2 design; (c) GAM10.3 design; (d) GAM10.4 design; (e) DXM10 design.

Figure 14. The FDS plot for all competing designs in the context of a complete design in the Myers et al. (2016) example: (a) n=7; (b) n=8; (c) n=9; (d) n=10.

Figure 15. The FDS plot for all competing designs when the most impactful observation point was omitted in the Myers et al. (2016) example.: (a) n=7; (b) n=8; (c) n=9; (d) n=10.

Figure 16. The Pareto front of a well-distributed set of optimal GA designs derived from thinning a rich Pareto front using

ε

Figure 16. The Pareto front of a well-distributed set of optimal GA designs derived from thinning a rich Pareto front using

ε

Table 1. The D-, A-, G-, and IV-efficiency and the maximum loss of D, A, G, and IV-efficiency due to single missing observation in the sugar example.

$n$	Design	D-eff	A-eff	G-eff	IV-eff	$\max l_{D}$	$\max l_{A}$	$\max l_{G}$	$\max l_{I V}$
7	GA7.1	0.1046	2.8844e-04	45.4001	0.1980	0.3946	0.8693	0.9753	0.8941
	GA7.2	0.1064	2.8896e-04	49.9959	0.2033	0.4119	0.8661	0.9796	0.9055
	GA7.3	0.1129	2.9015e-04	60.9705	0.2195	0.4696	0.8571	0.9882	0.9368
	GA7.4	0.1183	2.9248e-04	68.7810	0.2301	0.5307	0.8388	0.9938	0.9633
	DX7	0.1183	2.9272e-04	68.9232	0.2299	0.5423	0.8363	0.9947	0.9682
8	GA8.1	0.1188	3.8096e-04	83.3905	0.2419	0.2206	0.4536	0.8850	0.4198
	GA8.2	0.1188	3.8102e-04	83.3579	0.2419	0.2210	0.4539	0.8854	0.4210
	GA8.3	0.1188	3.8130e-04	83.0683	0.2418	0.2252	0.4566	0.8890	0.4321
	GA8.4	0.1188	3.8132e-04	83.0354	0.2418	0.2256	0.4569	0.8894	0.4333
	DX8	0.1188	3.8093e-04	82.6746	0.2417	0.2310	0.4636	0.8939	0.4389
9	GA9.1	0.1176	3.5533e-04	75.3398	0.2244	0.2153	0.4301	0.8705	0.3864
	GA9.2	0.1176	3.5525e-04	75.2591	0.2244	0.2164	0.4325	0.8716	0.3889
	GA9.3	0.1176	3.5556e-04	74.7365	0.2243	0.2237	0.4402	0.8785	0.4090
	GA9.4	0.1177	3.5575e-04	74.0821	0.2240	0.2334	0.4471	0.8874	0.4367
	DX9	0.1176	3.5303e-04	73.7343	0.2237	0.2389	0.4592	0.8922	0.4496
10	GA10.1	0.1178	3.2133e-04	74.4264	0.2105	0.1547	0.2762	0.7846	0.4118
	GA10.2	0.1178	3.2122e-04	74.3539	0.2106	0.1553	0.2751	0.7855	0.4125
	GA10.3	0.1179	3.2750e-04	73.4573	0.2114	0.1626	0.2799	0.7964	0.4049
	GA10.4	0.1179	3.3102e-04	72.8185	0.2119	0.1682	0.2823	0.8044	0.4006
	DX10	0.1177	3.3199e-04	69.8465	0.2115	0.1984	0.3021	0.8434	0.3955

Table 2. The D, A, G, and IV-efficiency and the maximum loss of D, A, G, and IV-efficiency due to single missing observation in the Myers et al. (2016) example.

$n$	Design	D-eff	A-eff	G-eff	IV-eff	$\max l_{D}$	$\max l_{A}$	$\max l_{G}$	$\max l_{I V}$
7	GAM7.1	1.4533	0.1937	59.0077	0.2012	0.2989	0.9025	0.9177	0.9023
	GAM7.2	1.5341	0.2157	71.8442	0.2038	0.3713	0.9494	0.9651	0.9505
	GAM7.3	1.5470	0.2166	71.0432	0.1995	0.4416	0.9751	0.9829	0.9757
	GAM7.4	1.5470	0.2166	71.0432	0.1995	0.4416	0.9751	0.9829	0.9757
	GAM7.5	1.5576	0.2148	73.2303	0.1983	0.6120	0.9972	0.9982	0.9972
	DXM7	1.5628	0.2149	72.2797	0.1973	0.9957	1.0000	0.8516	1.0000
8	GAM8.1	1.5470	0.2166	71.0432	0.1995	0.4416	0.9751	0.9829	0.9757
	GAM8.2	1.5470	0.2166	71.0432	0.1995	0.4416	0.9751	0.9829	0.9757
	GAM8.3	1.5592	0.2054	83.6974	0.2092	0.2164	0.7588	0.8812	0.7452
	GAM8.4	1.5602	0.2045	83.4824	0.2074	0.2193	0.7634	0.8839	0.7545
	GAM8.5	1.5609	0.2053	83.4081	0.2086	0.2203	0.7645	0.8848	0.7543
	DXM8	1.5607	0.2049	83.4166	0.2081	0.2202	0.7647	0.8847	0.7509
9	GAM9.1	1.5256	0.2034	79.3612	0.2173	0.1525	0.5556	0.7886	0.5307
	GAM9.2	1.5325	0.2021	80.6834	0.2167	0.1596	0.5680	0.8046	0.5444
	GAM9.3	1.5413	0.2007	79.8332	0.2135	0.1669	0.5811	0.8145	0.5651
	GAM9.4	1.5423	0.2016	79.6607	0.2128	0.1684	0.5831	0.8165	0.5640
	GAM9.5	1.5448	0.2039	79.1202	0.2147	0.1734	0.5878	0.8229	0.5658
	DXM9	1.5461	0.2027	78.7305	0.2159	0.1770	0.5887	0.8276	0.5639
10	GAM10.1	1.5108	0.1953	85.6790	0.2195	0.0910	0.4790	0.6670	0.4488
	GAM10.2	1.5109	0.1956	85.6238	0.2191	0.0913	0.4797	0.6675	0.4525
	GAM10.3	1.5112	0.1960	85.2596	0.2192	0.0928	0.4789	0.6708	0.4509
	GAM10.4	1.5114	0.1963	85.0476	0.2194	0.0937	0.4783	0.6728	0.4541
	GAM10.5	1.5116	0.1966	84.7067	0.2189	0.0952	0.4779	0.6759	0.4502
	DXM10	1.5446	0.1801	69.5099	0.1828	0.2017	0.7879	0.8471	0.7734

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Generating Robust Optimal Mixture Designs Due to Missing Observation Using a Multi-Objective Genetic Algorithm

Abstract

1. Introduction

2. Theoretical background

2.1. Notation and model

2.2. Design optimality criteria

2.3. Genetic algorithms

3. Leave- m -out optimality criteria

4. Loss of efficiency in terms of the optimality criteria

5. Multi-objective functions

5.1. Non-dominated sorting

5.2. Thin a rich Pareto front based on ε-dominance

5.3. Desirability functions

6. Genetic algorithms for generating optimal design

7. Examining the performance of the competing designs

8. Numerical examples

8.1. Example 1: Sugar formulation

8.2. Example 2: Mixture problem as presented in the Myers et al. (2016)

9. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

3. Leave- $m$ -out optimality criteria