Mathematical Modeling of Gas-Solid Two-Phase Flows: Problems, Achievements and Perspectives (A Review)

Preprint

Review

Mathematical Modeling of Gas-Solid Two-Phase Flows: Problems, Achievements and Perspectives (A Review)

Altmetrics

Downloads

194

Views

Comments

A peer-reviewed article of this preprint also exists.

Aleksey Yu. Varaksin,

Sergei V. Ryzhkov^*

Aleksey Yu. Varaksin,

Sergei V. Ryzhkov^*

This version is not peer-reviewed

Submitted:

20 June 2023

Posted:

20 June 2023

You are already at the latest version

Alerts

Abstract

Mathematical modeling is the most important tool for constructing the theory of different kinds of two-phase flows. The review is devoted to the analysis of the advent of the approach of mathematical modeling of two-phase flows, where solid particles act mainly as the dispersed phase. The main problems and features of the study of gas-solid two-phase flows are excluded. The main characteristics of gas flows with solid particles are given and the classification of two-phase flows is developed on their basis. The Lagrangian and Euler approaches to modeling the motion of a dispersed phase (particles) are described. Much attention is paid to the consideration of numerical simulation methods that describe descriptions of turbulent gas flow at different hierarchical levels (RANS, LES, DNS), different levels of description of interphase interactions (one-way coupling (OWC), two-way coupling (TWC) and four-way coupling (FWC)), as well as at different levels of interface resolution (partial-point (PP) and particle-resolved (PR)). Excluded are examples of some studies carried out on the basis of the identified approaches, as well as their exclusion for mathematical modeling of various classes of gas-solid two-phase flows.

Keywords:

Subject: Physical Sciences - Fluids and Plasmas Physics

Nomenclature

$d_{p}$	particle diameter, m
$η$	Kolmogorov length scale, m
$x_{p}$	particle radius vector, m
$u$	vector of actual velocity of gas, m/s
$v$	vector of actual velocity of particle, m/s
$u_{i}$ , $u_{j}$ , $u_{k}$	actual velocity components of gas, m/s
$v_{i}$ , $v_{j}$ , $v_{k}$	actual velocity components of particle, m/s
$U_{i}$ , $U_{j}$ , $U_{k}$	time-averaged velocity components of gas, m/s
$V_{i}$ , $V_{j}$ , $V_{k}$	time-averaged velocity components of particle, m/s
$u_{i}^{'}$ , ${u^{'}}_{j}$ , $u_{k}^{'}$	fluctuation velocity components of gas, m/s
$v_{i}^{'}$ , $v_{j}^{'}$ , $v_{k}^{'}$	fluctuation velocity components of particle, m/s
$ν$	kinematic viscosity of gas, m²/s
$a$	coefficient of thermal diffusivity, , m²/s
$τ$	time, s
$τ_{p}$	dynamic relaxation time of particle, s
$τ_{t}$	heat relaxation time of particle, s
$τ_{K}$	Kolmogorov time scale, s
$T_{f}$	characteristic time of gas in time-averaged motion, s
$T_{L}$	lagrangian integral time scale, s
$T_{p L}$	particle interaction time with energy-containing velocity fluctuations, s
$T_{p L t}$	particle interaction time with energy-containing temperature fluctuations, s
$t$	actual temperature of gas, К
$t_{p}$	actual temperature of particle, K
$T$	time-averaged temperature of gas, К
T_p	time-averaged temperature of particle, К
$t^{'}$	fluctuation temperature of gas, К
${t^{'}}_{p}$	fluctuation temperature of particle, K
$μ$	dynamic viscosity of gas, kg/(ms)
$ρ$	gas density, kg/m³
$ρ_{p}$	particle density, kg/m³
$p$	actual pressure of the gas, Pa
$P$	time-averaged pressure of the gas, Pa
$p^{'}$	fluctuation pressure of the gas, Pa
$C_{p}$	isobaric heat capacity of gas, J/(kg K)
$C_{p}_{p}$	heat capacity of material of particle, J/(kg K)
$φ$	actual volumetric concentration of the particles
$Φ$	time-averaged volumetric concentration of the particles
$φ^{'}$	fluctuation volumetric concentration of the particles
$M$	time-averaged mass concentration of the particles
${Re}_{p}$	particles Reynolds number
${Re}_{λ}$	Reynolds number by Taylor turbulence scale
${Re}_{τ}$	frictional Reynolds number
${Stk}_{f}$	Stokes number in time-averaged motion
${Stk}_{L}$	Stokes number in large-scale fluctuation motion
${Stk}_{K}$	Stokes number in small-scale fluctuation motion
Superscripts
$(...)^{'}$	fluctuation value
$\bar{(...)}$	time-averaged value
Subscripts
$p$	particle
$f$	fluid (gas)

1. Introduction

Continuum flows, that carry a dispersed admixture in the form of solid particles, occur in a number of natural phenomena [1,2,3,4]: sandstorms, tornadoes, volcanic eruptions, forest fires, precipitation in the form of hail, snow, etc. Examples of technical devices that use two-phase currents are paths of solid-fuel jet engines, devices for thermal preparation of coal in the schemes of energy-technological use of fuel, heat exchangers with two-phase working medium, devices for sand and shot blasting of various surfaces, pneumatic conveyors of bulk materials, dust collectors of various types and many others.

The review is devoted to the analysis of currently available approaches to mathematical modeling of two-phase flows, where mainly solid particles act as the dispersed phase. For anyone who is interested in direct numerical simulation (DNS) of turbulent flows with droplets and bubbles can be recommended a review [5].

The review is structured as follows. Section 2 describes the main problems and particularity of studying gas-solid two-phase flow. The main characteristics of gas flows with solid particles and the gas-solid two-phase flows classifications developed on their basis are discussed in Section 3. Section 4 describes Lagrangian and Eulerian approaches for modeling the motion of the dispersed phase and issues of mathematical modeling of the gas’s flow that carry particles. The final section 5 contains modern numerical modeling methods that describe the turbulent gas flow at different hierarchical levels, different levels of description of interphase interactions and different levels of resolution of the interphase boundary.

2. Main Problems and Specific Features of Two-Phase Flow Modeling

2.1. Main problems of two-phase flow modeling

Studies of two-phase (heterogeneous) flows are studied to solve two main classes of problems [6,7].

The first (or direct) task is to study the behavior of particles that are suspended in a carrier gas stream. The solution of this problem involves finding the characteristics of particles, exactly their sizes (in the case of polydisperse flow or the presence of phase and/or chemical transformations), the fields of their averaged and pulsation (quadratic averages) velocities and temperatures, concentrations, etc.

The second (or inverse) task is to study the inverse effect of particles on the characteristics of the gas flow that carry them. The solution of this problem involves finding the characteristics of a gas in the presence of particles, that is, fields of averaged and pulsation (mean quadratic) velocities and temperatures, coefficients of friction, heat transfer, etc.

The exceptional complexity of studying two-phase (multiphase) flows is probably related to two circumstances. From the one side, it is because of the theory of single-phase flows (especially turbulent ones) is in its development stage. From the other side, the addition of a dispersed impurity in the form of particles to the turbulent flow make the flow picture more complicated (see section 2.2). It is related to a wide variety of properties (first of all, inertia) and particle concentration, which leads to the implementation of numerous modes (classes) of two-phase flows (see section 3).

2.2. Specific features of two-phase flow modeling

In confirmation of the above, some features of the study of two-phase flows are given below.

2.2.1. Multiscale physics of two-phase flow

The inertia of particles (which is determined primarily by the size and density) can vary in a colossal range (many orders). One-phase flows are characterized by a number of space-time scales that are determined by the magnitude of their inherent flow velocity, flow regime (laminar, transient, turbulent), flow geometry, etc. For correct modeling of particle motion, it is necessary to consider their interaction at different scales that are determined by: 1) averaged movement, 2) wide-scale pulsation motion, 3) fine-scale pulsation motion, 4) different instabilities ( for example Tollmin-Schlichtings’ in boundary layers, Taylor–Gertlers’ in the pipes, Kelvin–Helmholtzs’ in pure shear layers) and etc.

2.2.2. Multiplicity of forces acting on particle

For the correct integration of the equations of particle’s motion, it is necessary to consider a large number of force factors (forces). Let 's list the main ones: 1) aerodynamic drag force, 2) gravity forces (Archimedes), 3) Safmans’ force, 4) Magnus’ force, 5) force of thermophoresis, 6) force of turbofreeze, 7) force of diffusiophoresis, 8) centrifugal force, 9) electrostatic force, 10) wall power.

It necessary to notice that many of these forces in one form or another contain the velocity of the carrier phase

u (τ)

that are a random variable in a turbulent flow. Therefore, the question often arises about the applicability of a particular expression that is obtained theoretically or empirically for other conditions for calculating the force ( for example for laminar flow or in the absence of velocity shift).

2.2.3. Multiplicity of modeling parameters

Mathematical or physical modeling of one-phase flows involves the calculation or measurement of a sufficiently large number of parameters (and their distributions in space).

In the case of a non-isothermal stationary turbulent one-phase flow, the main such parameters are: 1) three components of the average speed (U_i,

U_{j}

U_{k}

), 2) three components of the pulsation (rms) velocity (

{(\bar{{u_{i}^{'}}^{2}})}^{1 / 2}

{(\bar{{u_{j}^{'}}^{2}})}^{1 / 2}

{(\bar{{u^{'}}_{k}^{2}})}^{1 / 2}

), 3) average temperature (T), 4) pulsation (rms) temperature (

{(\bar{{t^{'}}^{2}})}^{1 / 2}

), 5) double correlations of various components of pulsation velocities (components of the Reynolds stress tensor) (

\bar{u_{i}^{'} u_{j}^{'}}

), 6)double correlations of pulsation velocity and pulsation temperature (

\bar{u_{i}^{'} t^{'}}

\bar{u_{j}^{'} t^{'}}

) and etc.

In the case of mathematical and physical modeling of two-phase flows with particles, the number of necessary parameters increases repeatedly. It is explained by the fact that similar parameters for the dispersed phase are added to the parameters that are pointed out above ( for example averaged (

V_{i}

V_{j}

, ) and pulsation velocities (

{(\bar{{v_{i}^{'}}^{2}})}^{1 / 2}

{(\bar{{v_{j}^{'}}^{2}})}^{1 / 2}

{(\bar{{v_{k}^{'}}^{2}})}^{1 / 2}

) and particle temperatures (

T_{p}

{(\bar{{t_{p}^{'}}^{2}})}^{1 / 2}

) and etc.), including its size, size distribution, averaged and pulsation (rms) concentration (

Φ

{(\bar{{φ^{'}}^{2}})}^{1 / 2}

) and parameters for the carrier phase ( in the presence of particles), the heat of phase transitions and many others.

2.2.4. Multiplicity of collision processes

In two-phase (multiphase) flows, various collision processes can take place [6,7]. These include: the interaction of dispersed inclusions with each other (particle–particle), the interaction of dispersed inclusions with a solid, a streamlined two–phase flow (particle–body), as well as the interaction of a dispersed impurity with walls limiting the two-phase flow (particle-wall). The first of these processes takes place in the case of collisions of dispersed inclusions that have dimensions of one order, the second – in the case when the dimensions of a solid are many orders larger, and the third – for the case when the size (radius of curvature) of a streamlined body tends to infinity, i.e. it "degenerates" into a flat wall.

Let's list the main reasons that contribute to the occurrence of collisions of particles with each other: 1) polydispersity that lead to a difference in the averaged velocities; 2) influence of the gradient of the averaged velocity of the carrier phase; 3) the influence of gravity (Archimedes); 4) turbulent transport effect that lead to the appearance of relative velocity between near particles; 5) the effect of clustering, i.e. an increase in the concentration of the dispersed phase in local regions of space; 6) electrostatic interaction; 7) Brownian motion.

It can be concluded that all the above-mentioned collision processes play an essential role in the formation of statistical characteristics of particle motion and, consequently, influence the characteristics of the continuous medium flow carrying them. As a result, the study of the role of contact interactions in the context of solving two main problems of studying two-phase flows seems extremely relevant.

2.2.5. Multiplicity of phase and chemical transformation

It is necessary to separately note the special role of various phase transformations in the fluid and gas dynamic and thermophysics of two-phase (multiphase) flows. The main phase transformations are well known: 1) condensation, 2) solidification, 3) melting, 4) evaporation (boiling), 5) sublimation. The presence of phase transformations often contributes to the "transformation" of an initially one-phase flow into a two-phase and vice versa, and also leads to the transition of a two-phase flow from one type to another.

Phase transformations are not considered because the subject of this review is gas flows with solid particles (gear-solid two-phase flow). However, for non-isothermal two-phase flows, particle melting may occur during interphase heat exchange. The melting of particles in the gas stream leads to the transition of a gas-solid two-phase flows into a gas-liquid two-phase flows. The subsequent process of crystallization (solidification) of droplets can cause the flow to "return" to its initial state.

Combustion occupies a special place among chemical transformations. The combustion processes of solid fuel particles and liquid droplets are important in a variety of technical applications.

2.2.6. Multiplicity of dimensionless parameters

The complexity and multiplicity of physical phenomena and processes occurring in two-phase flows predetermines the appearance of a large number of additional (compared to one-phase flows) dimensionless parameters (criteria) responsible for the presence and intensity of a process. An example of such parameters are the numerous Stokes numbers (see subsection 3.3) that characterize the inertia of the dispersed phase with ratio to various scales of the carrier gas; the Reynolds number of the particle, etc.

3. Main Characteristics of Two-Phase Flows

This section presents the main characteristics of gas flows with solid particles and the classifications of two-phase flows developed on their basis.

3.1. Particles concentration

An extensive physical characteristic of two-phase flows is the concentration of a dispersed impurity. Possible varieties of two-phase flows (classification) depending on the volume concentration of the dispersed phase Ф are given in [8,9]. There are three classes of two - phase flows: 1) dilute two-phase flow without the reverse effect of the dispersed phase; 2) dilute two-phase flow with the reverse effect of the dispersed phase; 3) dense two-phase flow with intense collisional interaction of particles with each other.

3.1.1. One-way coupling

For modeling the motion of particles in dilute two-phase streams (

Φ \leq 1 0^{- 6}

) that is, with a small volume concentration of the dispersed phase, the main attention is paid, as a rule, to establishing the characteristics (behavior) of particles during their interaction with turbulent vortices of the carrier flow. Such calculations are called "one-way coupling" (OWC), which means taking into account only the unidirectional impact of the carrier current on the particles suspended in it, which completely determines the features of their behavior.

3.1.2. Two-way coupling

With an increase in the concentration of particles (

10^{- 6} < Φ \leq 1 0^{- 3}

), they, in turn, begin to have the opposite effect on the characteristics (all without exception) of the carrier medium [10,11,12,13,14]. Taking into account the mutual influence of the dispersed and carrier phases significantly complicates the mathematical modeling of a two-phase flow. Such calculations are called "two-way coupling" (TWC).

3.1.3. Four-way coupling

A further increase in the concentration of particles (

Φ > 1 0^{- 3}

) leads to the need to take into account the contribution of interparticle interactions to the process of momentum and energy transfer of the dispersed phase [15,16,17,18]. The chaotic motion of particles during their interaction is called "pseudoturbulence" to distinguish from the actual turbulent pulsations of particle velocities associated with their involvement in the turbulent motion of the carrier flow. Pseudo-turbulent pulsations of particles can be caused by two reasons: 1) hydrodynamic interaction between particles by exchanging momentum and energy through random velocity and temperature fields of the carrier medium; 2) direct interaction through collisions. An increase in the concentration and size (inertia) of particles leads to the fact that the exchange of momentum and energy between particles as a result of collisions increases significantly compared to hydrodynamic interaction. In dense two-phase flows, interparticle collisions play a decisive role in the formation of the statistical properties of the dispersed phase. Taking into account paired (binary) particle collisions adds complexity to mathematical modeling. Such calculations are called "four-way coupling" (FWC).

Let’s note also that only in the case of very large (highly inertial) particles, the processes of interaction of particles with turbulent vortices of the carrier phase and interparticle collisions can be considered statistically independent. The relaxation time of such particles is much longer than the characteristic time of their interaction with turbulent vortices, so their motion is uncorrelated with turbulent pulsations of the carrier medium. In the other extreme case of small (low-inertia) particles, it is necessary to take into account the mutual influence of interparticle interactions and the particle-turbulence interaction.

It should be noted that in two-phase flows there is a clustering phenomenon, which consists in a sharp increase in the concentration of particles in local areas. This significant increase in the concentration of particles leads to an increase in the probability of particle collisions even in dilute two-phase flow.

From what has been said above, it is clear that in two-phase flows with a small mass content (concentration) of the dispersed phase, in which the particles do not undergo collisions and do not have a reverse effect on the flow of the carrier continuous medium, the phenomenon of clustering can lead to a qualitative restructuring of the flow. The formation of local areas of increased particle concentration was revealed experimentally or by calculation in various flows: homogeneous isotropic turbulence [19,20], shear flows in pipes (channels) [21,22], flows in the boundary layer [23], jet flows, traces behind streamlined bodies, flow around blunted bodies [24], free concentrated vortices [25,26,27].

3.2. Particles dynamic relaxation time

The behavior of particles in turbulent flows of the carrier medium and their inverse effect on the characteristics of the gas phase largely depend on their inertia. The inertia of solid particles moving in the flow is determined by their size (diameter)

d_{p}

and physical density

ρ_{p}

. The complex characteristic of the inertia of particles is the time of dynamic relaxation

τ_{p}

is represented in the following form

τ_{p} = τ_{p 0} / C ({Re}_{p}) = \frac{ρ_{p} d_{p}^{2}}{18 μ C ({Re}_{p})} .

(1)

Here

τ_{p 0}

– is the time of dynamic relaxation of the Stokes particle;

μ

– dynamic viscosity. Note that the relaxation time of a particle also depends on the dynamic viscosity of the medium in which its motion occurs. The correction function

C ({Re}_{p})

takes into account the effect of inertia forces on the relaxation time of a non-Stokes particle. In this way, in the case of moving of a non-Stokes particle, its inertia also depends on the Reynolds number

{Re}_{p}

of the particle, calculated from the relative velocity between the phases

W

and the diameter of the particles.

3.3. Stokes numbers

One-phase turbulent flows are characterized by a number of spatial and corresponding time scales. As a result, it is possible to construct a number of dimensionless criteria – Stokes numbers that determine the inertia of a dispersed impurity with ratio to certain flow scales, in the form of

{Stk}_{i} = \frac{τ_{p}}{T_{i}},

(2)

Where

T_{i}

– is some characteristic time of the carrier phase.

There are three main dimensionless criteria in [28,29]

{Stk}_{f}

{Stk}_{L}

and

{Stk}_{K}

– Stokes numbers in averaged, large-scale pulsation and small-scale pulsation movements, respectively.

3.3.1. Stokes number in time-averaged motion

In the case of particle motion in a continuous medium flow, where there is a gradient of the averaged velocity in the longitudinal direction

\partial U_{x} / \partial x \neq 0

(for example, during flow in nozzles, boundary layer or near streamlined bodies), as well as during acceleration in a flow with a constant value of the averaged velocity (

\partial U_{x} / \partial x = 0

), it is necessary to take into account the inertia of the dispersed phase when analyzing the relaxation process of the averaged phase velocities. To do this, we can use the Stokes number in the averaged motion, which we write as

{Stk}_{f} = \frac{τ_{p}}{T_{f}},

(3)

Where

T_{f}

– is the characteristic time of the carrier phase in the averaged motion.

3.3.2. Stokes number in large-scale fluctuation motion

The parameter of the dynamic inertia of the dispersed phase in large-scale pulsation motion is the Stokes number that has the following form

{Stk}_{f} = \frac{τ_{p}}{T_{L}},

(4)

Where

T_{L}

– is the characteristic time of the carrier gas in large–scale pulsation motion (time Lagrangian integral turbulence scale).

3.3.3. Stokes number in small-scale fluctuation motion

The inertia of particles in small-scale pulsation motion can be characterized by the Stokes number that we represent as

{Stk}_{f} = \frac{τ_{p}}{τ_{K}},

(5)

Where

τ_{K}

– is the Kolmogorov time scale of turbulence.

It should be noted that when considering non-isothermal two-phase flows, it is necessary to introduce appropriate dimensionless parameters characterizing the thermal inertia of particles with ratio to the corresponding characteristic time scales of changes in the temperature of the carrier medium.

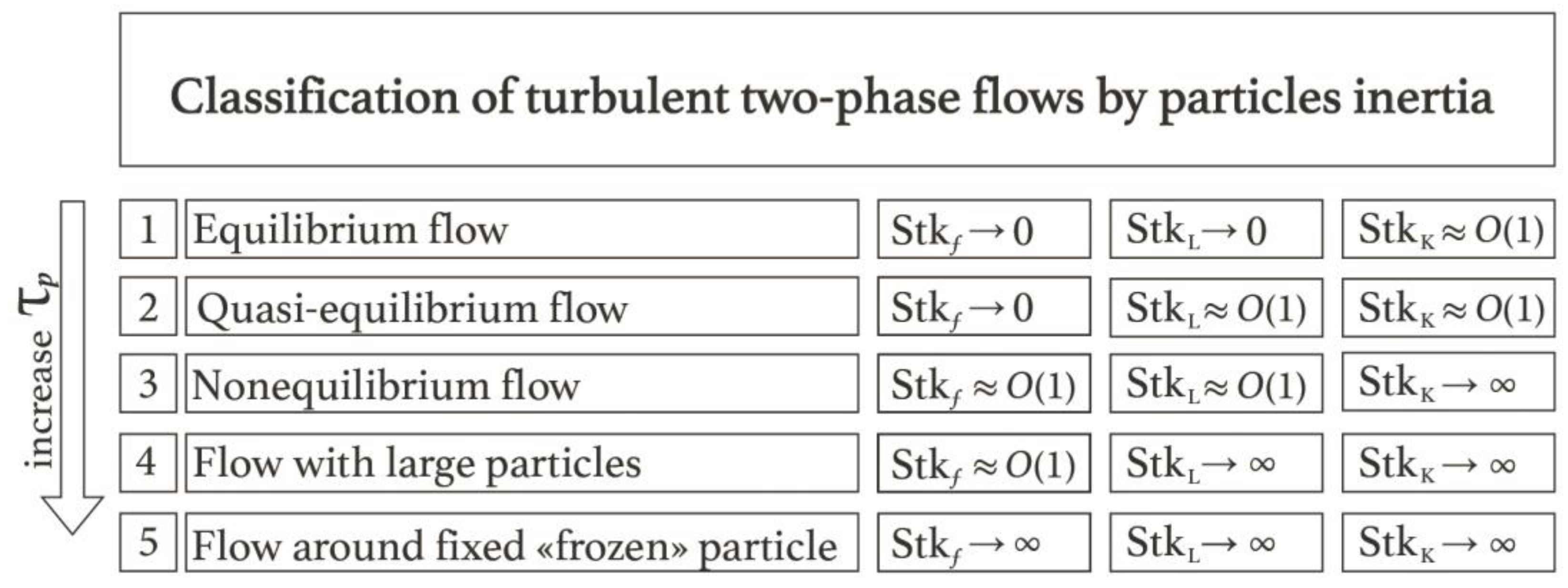
3.4. Classification of turbulent two-phase flows by particles inertia

Depending on the range of variation of the Stokes numbers in [28,29], several main classes of two-phase flows are distinguished (see Figure 1). We briefly describe them.

Equilibrium flow. A distinctive feature of this flow is the equality of the averaged (

U_{i, j, k} = V_{i, j, k}

) and pulsation (

u_{i, j, k}^{'} = v_{i, j, k}^{'}

) velocities of gas and particles and the following range of variation of the basic Stokes numbers: :

{Stk}_{f} \to 0

{Stk}_{L} \to 0

{Stk}_{K} \approx O (1)

Quasi-equilibrium flow. The peculiarity of such a flow is the equality of the averaged (

U_{i, j, k} = V_{i, j, k}

) and the difference in the pulsation (

u_{i, j, k}^{'} \neq v_{i, j, k}^{'}

) velocities of gas and particles, as well as the following range of variation of the basic Stokes numbers:

{Stk}_{f} \to 0

{Stk}_{L} \approx O (1)

{Stk}_{K} \approx O (1)

Nonequilibrium flow. When implementing this class of flow, there is a difference in both the averaged (

U_{i, j, k} \neq V_{i, j, k}

) and pulsation (

u_{i, j, k}^{'} \neq v_{i, j, k}^{'}

) velocities of gas and particles and the following range of changes in the basic Stokes numbers:

{Stk}_{f} \approx O (1)

{Stk}_{L} \approx O (1)

{Stk}_{K} \to \infty

Flow with large particles. The peculiarity of such a two-phase flow is the difference in the averaged (

U_{i, j, k} \neq V_{i, j, k}

) phase velocities, the complete inertia of the particles with ratio to the turbulent pulsations of the gas velocity (

v_{i, j, k}^{'} = 0

) and the following range of variation of the basic Stokes numbers:

{Stk}_{f} \approx O (1)

{Stk}_{L} \to \infty

{Stk}_{K} \to \infty

Flow around fixed “frozen” particle. In this case, the particles have an extremely large inertia, which is completely stationary and does not change its temperature. An analogue of such a hypothetical class of two-phase flows is a one-phase flow in heat exchangers, where fixed pipes act as such particles, through which the working fluid moves.

It should be noted that the sign "=" that is used above when comparing the velocities of particles and gas is conditional. It is clear that particles with inertia cannot fully track nither the averaged nor the pulsation movements of the gas. Therefore, for correctness, it can be assumed that the particle fully involved in the averaged (pulsation) motion of the gas is a particle whose averaged (pulsation) velocities differ by no more than 1% from the corresponding velocities of the carrier phase. Note that the case of inertia-free (with ratio to small-scale gas pulsations) particles is realized when

{Stk}_{K} \to 0

The above classes of two-phase flows will be further used in the description and analysis of methods for mathematical modeling of two-phase flows with particles.

Mathematical modeling methods play an important role in the study of the processes of motion of solid particles and their inverse effect on the characteristics of the carrier continuous gas medium. Numerous flow regimes of two-phase media that were tried to classify in section 3, have led to the creation of a significant number of mathematical models of such flows. For constructing models of two-phase flows of a wide variety of classes, researchers always face a choice. From the one side, it is necessary to take into account as many physical processes occurring in two-phase flows as possible that often leads to excessive complication of the mathematical formalization of the phenomena under consideration. From the other side, detailing a large number of processes in wich information about each individually is not always indisputable, can lead to a decrease in the reliability of the created model.

4. Lagrangian and Eulerian Modeling of Two-Phase Flows

The study of the features of the motion of the dispersed phase (cloud drops, raindrops, particles, fragments) in tornado-like vortices is of considerable interest due to several reasons.

4.1. Five reasons for considering of the two-phase nature of tornado

The variety of mathematical models developed to date can be divided into two large classes (types). First class models (Eulerian-Lagrangian, trajectory, stochastic) assume solution of equations of motion of the carrier gas phase in the usual Eulerian formulation, while motion of particles is described by Lagrangian equations, which are integrated along their trajectories. Second class models (Eulerian-Eulerian, continuum, two-liquid) describe the motion of the carrier phase and the motion of multiple particles based on the Eulerian continuum representation.

It is clear that the attempts of describing all the varieties of two-phase flows using models of both classes can hardly be justified. As a consequence, for certain classes of flows (see section 3), characterized primarily by the concentration of the dispersed phase and its inertia (Stokes numbers), models of one or another type should be preferred.

4.1. Lagrangian modeling

The system of equations for describing the translational and rotational motion of a single solid particle in a turbulent flow is given by (see, for example, [30]),

\frac{d x_{p}}{d τ} = v,

(6)

m_{p} \frac{d v}{d τ} = \sum_{i} F_{i} = F_{D} + F_{g} + F_{S} + F_{M} + ...,

(7)

I \frac{d ω_{p}}{d τ} = T,

(8)

where

x_{p}

is the position vector (radius vector) of the particle,

v

is the instantaneous velocity vector of the particle, ω_p is the angular velocity vector of the particle, ω_p is the mass of the particle, I is the moment of inertia of the particle. Equation (8) describes the change in angular velocity of the particle due to viscous interaction with the surrounding gas.

The right-hand side of equation (7) contains force factors that influence the motion of particles: F_D - aerodynamic drag force, F_g - gravitational force, F_S- Saffman force, and F_M- Magnus force. In addition to the forces described above, moving particles can also be affected by thermophoretic, turbophoretic, diffusiophoretic, centrifugal, electrostatic forces, etc. Due to the viscosity of the liquid, a moment of rotation T acts on a rotating particle.

4.2. Eulerian modeling

Let us briefly consider the current approaches to constructing continuum equations for the motion of dispersed impurity and analyze the features of describing their behavior for different classes of two-phase flows.

Equations describing the averaged motion and heat transfer of dispersed particles are written by analogy with well-known equations for continuous media (gas, liquid). The system of equations for the dispersed phase is also unclosed, as the equations contain second moments for velocity fluctuations

\bar{v_{i}^{'} v_{j}^{'}}

, as well as velocities and temperatures

\bar{v_{j}^{'} t_{p}^{'}_{}}

of particles, similar to Reynolds stresses and turbulent heat flux in gas. Using the accumulated experience of studying single-phase flows, various models are used to close the system of averaged equations of motion and impurity heat transfer. The most well-known models are algebraic and differential models.

Algebraic and differential models. There are two main approaches for determining velocity correlations of dispersed phases within algebraic models. According to the first approach, correlation moments are expressed directly through Reynolds stresses of the carrying flow [31,32],

\bar{v_{i}^{'} v_{j}^{'}} = A \bar{u_{i}^{'} u_{j}^{'}},

(9)

where A is the function of particle involvement in gas pulsation movement.

Equation (9) is valid for a relatively low-inertial dispersed phase (quasi-equilibrium flow) with a homogeneous distribution of the averaged velocity of the dispersed impurity in the flow.

The second way to determine turbulent stresses in the dispersed phase is to use gradient relations like the Boussinesq relations for single-phase flow [33],

\bar{v_{i}^{'} v_{j}^{'}} = - ν_{p} (\frac{\partial V_{i}}{\partial x_{j}}),

(10)

or in the form of [34,35],

\bar{v_{i}^{'} v_{j}^{'}} = - ν_{p} (\frac{\partial V_{i}}{\partial x_{j}} + \frac{\partial V_{j}}{\partial x_{i}} - \frac{2}{3} \frac{\partial V_{k}}{\partial x_{k}} δ_{i j}) + \frac{2}{3} k_{p} δ_{i j},

(11)

where ν_p is the turbulent viscosity coefficient of the dispersed phase. In literature different methods for determining the value of ν_p are described. [34,35].

In addition to algebraic models, differential models have recently become widespread for describing turbulent momentum and heat transfer in the dispersed phase. These models are based on using equations of balance of energy pulsations of the dispersed phase or second moments of velocity and temperature pulsations of particles.

Models based on kinetic equations for probability density function (PDF). The approach based on kinetic equations for probability density distributions of velocities, temperatures, and other characteristics of dispersed inclusions is the most consistent method for constructing continuum models (obtaining hydrodynamic and heat and mass transfer equations for the dispersed phase) [36]. The statistical approach based on distribution functions in phase space is a proven tool for constructing theoretical models in various areas of physics. Examples include the Boltzmann equation and the Bogolyubov-Born-Green-Kirkwood chain of equations in molecular kinetic theory of gases and liquids, the Fokker-Planck equation for describing the motion of Brownian particles, Vlasov kinetic equation in plasma physics, Smoluchowski-Muller equation in coagulation theory, etc. The statistical approach for describing pseudo-turbulent flow of the dispersed medium was first applied in [37]. The introduction of PDF allows obtaining a statistical description of a set of particles instead of a dynamic description of individual particles based on Langevin-type motion and heat transfer equations. In statistical modeling based on PDF, there is an obvious loss of information about the behavior of individual particles, which is obviously compensated by increasing the data on the statistical regularities of the movement and heat transfer of the entire set of particles. The use of a statistical method based on kinetic equations allows describing the interaction of particles with turbulent pulsations of the carrying gas, inter-particle collisions, particle-wall interaction, and other important processes.

The first method. Single-point kinetic equations for PDF of velocity and temperature distributions of particles in a turbulent flow, using a functional formalism based on the Furutsu-Donsker-Novikov formula for Gaussian random fields were obtained in the works [38,39,40,41,42,43,44,45,46,47].

According to this first method, to transform stochastic equations like the Langevin equation, which describes the instantaneous motion and heat exchange for a single particle (droplet), into a kinetic equation for a group of particles, a probability density function (PDF) is introduced that describes the coordinate _x, velocity ν, and temperature distribution of particles

t_{p}

P (x, v, t_{p}, τ) = \bar{δ (x - r_{p} (τ)) δ (v - v_{p} (τ)) δ (t_{p} - t_{p} (τ))},

(12)

where the averaging is not done over time, but over realizations of the random fields of the carrying gas flow.

Further, by differentiating (12) in time, taking into account the representation of gas velocity and temperature in the instantaneous equations of particle motion and heat exchange as sums of averaged and pulsation components, the equation for the probability density can be obtained.

The equation for the PDF is then used to derive equations for the averaged concentration, velocity, and temperature of particles, which have the following form [36]:

\frac{\partial Φ}{\partial τ} + \sum_{j} \frac{\partial Φ V_{j}}{\partial x_{j}} = 0,

(13)

\frac{\partial V_{i}}{\partial τ} + \sum_{j} V_{j} \frac{\partial V_{i}}{\partial x_{j}} = - \sum_{j} \frac{\partial \bar{v_{i}^{'} v_{j}^{'}}}{\partial x_{j}} + \frac{U_{i} - V_{i}}{τ_{p}} - \sum_{j} \frac{D_{p i j}}{τ_{p}} \frac{\partial \ln Φ}{\partial x_{j}},

(14)

\frac{\partial T_{p}}{\partial τ} + \sum_{j} V_{j} \frac{\partial T_{p}}{\partial x_{j}} = - \sum_{j} \frac{\partial \bar{v_{j}^{'} t_{p}^{'}}}{\partial x_{j}} + \frac{T - T_{p}}{τ_{t}} - \sum_{j} \frac{D_{p j}^{t}}{τ_{t}} \frac{\partial \ln Φ}{\partial x_{j}},

(15)

where

\bar{v_{i}^{'} v_{j}^{'}} = \frac{1}{Φ} \iint v_{i}^{'} v_{j}^{'} P d v d t_{p}

\bar{v_{j}^{'} t_{p}^{'}} = \frac{1}{Φ} \iint v_{j}^{'} t_{p}^{'} P d v d t_{p}

D_{p i j} = τ_{p} (\bar{v_{i}^{'} v_{j}^{'}} + g_{p} \bar{u_{i}^{'} u_{j}^{'}})

D_{p j}^{t} = τ_{t} \bar{v_{j}^{'} t_{p}^{'}} + τ_{p} g_{p t} \bar{u_{j}^{'} t^{'}}

g_{p} = T_{p L} / τ_{p} - 1 + e x p (- T_{p L} / τ_{p})

g_{p t} = T_{p L t} / τ_{p} - 1 + e x p (- T_{p L t} / τ_{p})

Here

T_{p L}

T_{p L t}

are the times of interaction between particles (droplets) and energy-intensive fluctuations of velocity and temperature, respectively. For non-inertial impurities

T_{p L} = T_{L}

and

T_{p L t} = T_{L t}

. Here

T_{L}

T_{L t}

are the time scales of velocity fluctuations and correlation of velocity and temperature fluctuations, respectively.

In the case of non-equilibrium flow, when the averaged and dynamic slip between the continuous and dispersed phases become significant, the interaction times with the fluctuations of the carrying flow become smaller than the corresponding scales of the continuous phase fluctuations.

The system of equations (13)-(15) is not closed, as the equations contain related to ue to particle involvement in fluctuating motion turbulent stresses

\bar{v_{i}^{'} v_{j}^{'}}

and turbulent heat flux

\bar{v_{j}^{'} t_{p}^{'}_{}}

in the dispersed phase, as well as turbulent diffusion of momentum and heat arising from non-uniform particle concentrations.

In [36], a mathematical description of momentum and heat transfer processes in the dispersed phase of varying complexity is developed. A closed system of equations is presented at the level of third moments. In this case, the fourth moments of pulsation characteristics present in the equations for third moments are approximately expressed through the sum of second moments [36]. To describe the hydrodynamics and heat exchange of the dispersed phase at the level of equations for second moments, triple correlations must be determined. For this purpose, equations for third moments are also used in [36], the simplification of which by neglecting small terms allows finding algebraic relationships for triple correlations containing only second moments. The simplification of the computational scheme can be associated with the use of one differential equation for the energy of pulsations of the dispersed phase velocity instead of equations for second moments, which has the following form [36]:

\frac{\partial k_{p}}{\partial τ} + \sum_{j} V_{j} \frac{\partial k_{p}}{\partial x_{j}} = - \frac{1}{Φ} \sum_{j} \frac{\partial Φ \bar{v_{i}^{'} v_{i}^{'} v_{j}^{'}}}{2 \partial x_{j}} - \sum_{j} \sum_{i} \bar{v_{i}^{'} v_{j}^{'}} \frac{\partial V_{i}}{\partial x_{j}} + \frac{2}{τ_{p}} (f_{u} k - k_{p})

(16)

where

k_{p} = \frac{1}{2} \sum_{i} \bar{v_{i}^{'} v_{i}^{'}}

is the energy of pulsations of the dispersed phase velocity.

In a stationary homogeneous flow or for small particles (quasi-equilibrium flow), from (16) we obtain

k_{p} = f_{u} k

, where

f_{u} = {(1 + {Stk}_{L})}^{- 1}

. In this case, equations (13), (14) with relation (11) provide a description of momentum transfer in the dispersed phase at the level of equations for first moments.

The second method. Another method for constructing kinetic equations for the PDF velocity of the dispersed phase is the method that uses the principle of invariance to random Galilean transformations [48] or summation of direct interactions by the Lagrangian method of renormalization perturbation theory [49]. The latter method allows for obtaining equations for joint PDF distributions of velocity and temperature of the dispersed impurity [50].

The third method. The third method is the construction of a closed kinetic equation based on the expansion of the characteristic functional into a series of cumulants [51,52].

It should be noted that when modeling turbulence with Gaussian random fields, all three mentioned above methods lead to the same kinetic equations for particles. However, the latter two methods are not limited to the case of Gaussian functions.

4.3. Advantages and limitations of Lagrangian and Eulerian modeling

Let us briefly consider the advantages and limitations of Euler-Lagrange and Euler-Euler models for describing the motion of flows of continuous media with solid particles, droplets, and bubbles [36].

The advantage of Euler-Lagrange (trajectory, stochastic) models is obtaining detailed statistical information about the motion of individual particles by integrating the equations of motion (heat transfer) of the dispersed phase in a known (pre-calculated) field of averaged velocities (temperatures) of the carrier phase. As for accounting for the random (pulsational) motion of dispersed inclusions, caused by their interaction with turbulent vortices of the carrier gas, in this case, it is necessary to integrate stochastic Langevin-type equations along the trajectories of individual particles (droplets) with subsequent averaging of solutions over the ensemble of initial data. This leads to a significant increase in the volume of calculations since to obtain statistically reliable information, it is necessary to use a sufficiently representative ensemble of realizations. With a decrease in the size of dispersed inclusions, the use of trajectory methods for calculating their motion also becomes more complicated. This is because to obtain correct information about the averaged characteristics of the dispersed phase, it is necessary to take into account the interaction of particles with turbulent vortices of the carrier phase of smaller and smaller sizes. The noted circumstance also greatly complicates the calculation process.

Trajectory Lagrangian description of the motion and heat transfer of the dispersed phase in a turbulent flow based on solving equations only for averaged quantities (without taking into account its interaction with random fields of velocity and gas temperature pulsations) will be correct in the case of inertial particles. Such particles (droplets) are not involved in the pulsational motion of the carrier phase since their relaxation time is much larger than the integral scale of turbulence. Such a description will be justified in the case of flow realization with large particles (see section 3).

It should be noted that with an increase in the concentration of the dispersed phase, there are also difficulties in using Euler-Lagrange models. Two circumstances can be distinguished. Firstly, an increase in concentration leads to a reverse influence of dispersed inclusions on the parameters of the carrier phase, and calculations have to be performed in several iterations, which complicates the computational procedure. Secondly, with an increase in concentration, the probability of collisions between particles increases, which leads to the entanglement of their trajectories.

The advantage of Euler-Euler (continuum, two-fluid) models is the use of equations of the same type to describe the motion of both the continuous and dispersed phases within the framework of mechanics of interpenetrating media. This allows for the use of a large body of experience in modeling single-phase turbulent flows and applying the same numerical methods to solve the entire system of equations. Describing the motion of highly non-inertial particles during the realization of equilibrium flow (see section 3) does not pose any significant difficulties. As the mass of the particle approaches zero, a limit transition to the problem of turbulent diffusion of passive (non-inertial) impurities is achieved. It should be noted that accounting for collisions between particles within two-fluid models does not lead to such a significant increase in calculations as in trajectory modeling.

The disadvantages of Euler-Euler models include some "loss" of information about the motion of individual particles, as well as difficulties in setting boundary conditions for the dispersed phase on flow-limiting surfaces. An attempt to combine the advantages of Lagrangian and Eulerian methods for describing the dispersed phase was made in [53], where a hybrid Lagrangian-Eulerian method was developed.

In general, Lagrangian and Eulerian methods for modeling the motion of the dispersed phase complement each other. Given the advantages and disadvantages of both methods described above, it is clear that each has its own areas of application. The Lagrangian method is applicable for describing flows characterized by significant dynamic (thermal) slip between phases. According to the classification of two-phase flows presented in section 3, such flows include non-equilibrium flow and flow with large particles. Obviously, the applicability of the Lagrangian method is also limited to flows with extremely low concentrations of the dispersed phase, i.e., weakly dusted flows (see section 3). The Eulerian method is applicable for equilibrium and quasi-equilibrium flows with high concentrations of the dispersed phase (heavily dusted flows).

As the concentration and inertial properties of the dispersed phase increase, choosing between the two types of two-phase flow models becomes a challenging task. The general trend is that as the concentration of impurities increases and their inertia decreases, the use of a continuum Eulerian representation to describe the dynamics of the dispersed phase becomes more preferable.

4.4. Description of the gas flow carrying the particles

With increasing volume fraction of the dispersed phase, it can affect the carrier medium (see section 3.1.2). Let us consider the motion of a continuous medium (gas) in the presence of particles when they begin to exert a reverse influence on its characteristics.

4.4.1. Actual equations

The continuity, motion and energy equations of the gas phase with relatively small volume fraction of particles (

φ ≪ 1

) in the absence of external mass forces have the form

\sum_{j} \frac{\partial u_{j}}{\partial x_{j}} = 0,

(17)

\frac{\partial u_{i}}{\partial τ} + \sum_{j} u_{j} \frac{\partial u_{i}}{\partial x_{j}} = - \frac{1}{ρ} \frac{\partial p}{\partial x_{i}} + ν \sum_{j} \frac{\partial^{2} u_{i}}{\partial x_{j} \partial x_{j}} - \frac{ρ_{p} φ}{ρ} \frac{(u_{i} - v_{i})}{τ_{p}},

(18)

\frac{\partial t}{\partial τ} + \sum_{j} u_{j} \frac{\partial t}{\partial x_{j}} = a \sum_{j} \frac{\partial^{2} t}{\partial x_{j} \partial x_{j}} - \frac{C_{p_{p}} ρ_{p} φ}{C_{p} ρ} \frac{(t - t_{p})}{τ_{t}},

(19)

The continuity equation (17) has a similar form to a single-phase flow equation. Equations (18) and (19) differ from the corresponding equations of motion and energy of a single-phase gas by the presence of terms in the right-hand side that take into account the dynamic and thermal effects of the dispersed phase on the carrier flow.

4.4.2. Time-averaged equations

Let us average equations (17)-(19) over time. Using a well-known method of averaging in the theory of variable-density single-phase flows [54], as well as based on the PDF method for constructing equations for the dispersed phase [36], we assume

\bar{φ^{'} v_{i}^{'}} = \bar{φ^{'} t_{p}^{'}}

. The resulting averaged continuity, motion and energy equations we will write as:

\sum_{j} \frac{\partial U_{j}}{\partial x_{j}} = 0,

(20)

\frac{\partial U_{i}}{\partial τ} + \sum_{j} U_{j} \frac{\partial U_{i}}{\partial x_{j}} = - \frac{1}{ρ} \frac{\partial P}{\partial x_{i}} + ν \sum_{j} \frac{\partial^{2} U_{i}}{\partial x_{j} \partial x_{j}} - \sum_{j} \frac{\partial (\bar{u_{i}^{'} u_{j}^{'}})}{\partial x_{j}} - \frac{ρ_{p} Φ}{ρ} \frac{(U_{i} - V_{i})}{τ_{p}} - \frac{ρ_{p} \bar{φ^{'} u_{i}^{'}}}{ρ τ_{p}},

(21)

\frac{\partial T}{\partial τ} + \sum_{j} U_{j} \frac{\partial T}{\partial x_{j}} = a \sum_{j} \frac{\partial^{2} T}{\partial x_{j} \partial x_{j}} - \sum_{j} \frac{\partial (\bar{u_{j}^{'} t^{'}})}{\partial x_{j}} - \frac{C_{p_{p}} ρ_{p} Φ}{C_{p} ρ} \frac{(T - T_{p})}{τ_{t}} - \frac{C_{p_{p}} ρ_{p} \bar{φ^{'} t^{'}}}{C_{p} ρ τ_{t}},

(22)

Equations (21) and (22) show that the reverse influence of particles on the gas motion and heat transfer is due to their averaged dynamic and thermal slip, as well as concentration pulsations. It should be noted that the contribution of the penultimate and last terms in the right-hand sides of equations (21) and (22) will be decisive for cases of flow with large particles and quasi-equilibrium two-phase flow, respectively (see section 3). In the case of non-equilibrium heterogeneous flow, where there is averaged and pulsating dynamic and thermal slip between phases, it is necessary to take into account the contribution of all the above-mentioned terms in the equations of motion and energy.

Let us consider the case when the distributions of averaged velocities and particle concentrations are known. To close the system of averaged equations, it is necessary to know the turbulent gas stresses

u_{i}^{'} u_{j}^{'}

and the turbulent heat flux

u_{j}^{'} t^{'}

, as well as correlations between particle concentration pulsations and gas velocity and temperature pulsations

φ^{'} u_{i}^{'}

and

φ' t^{'}

_, which can be represented as [55,56].

\bar{φ^{'} {u^{'}}_{i}} = - τ_{p} g_{p} \bar{u_{i}^{'} u_{j}^{'}} \frac{\partial Φ}{\partial x_{j}},

(23)

\bar{φ^{'} t^{'}} = - τ_{p} g_{p t} \bar{u_{j}^{'} t^{'}} \frac{\partial Φ}{\partial x_{j}},

(24)

g_{p} = T_{p L} / τ_{p} - 1 + \exp (- T_{p L} / τ_{p}), g_{p t} = T_{p L t} / τ_{p} - 1 + \exp (- T_{p L t} / τ_{p}) .

4.4.3. Equations for the Reynolds stresses

By subtracting equations (20)-(22) from equations (17)-(19), we can obtain the pulsation equations of continuity, motion, and energy of the gas in the presence of particles. The equation for the second moments of velocity pulsations of the carrier phase in the presence of particles can be easily obtained from the pulsation equation of motion. This equation has the following form:

\frac{\partial (\bar{{u^{'}}_{i} {u^{'}}_{j}})}{\partial τ} + \sum_{k} U_{k} \frac{\partial (\bar{{u^{'}}_{i} {u^{'}}_{j}})}{\partial x_{k}} = \sum_{k} \frac{\partial}{\partial x_{k}} [ν \frac{\partial (\bar{{u^{'}}_{i} {u^{'}}_{j}})}{\partial x_{k}} - \bar{{u^{'}}_{i} {u^{'}}_{j} {u^{'}}_{k}}] - \sum_{k} [(\bar{u_{j}^{'} {u^{'}}_{k}}) \frac{\partial U_{i}}{\partial x_{k}} + (\bar{u_{i}^{'} u_{k}^{'}}) \frac{\partial U_{j}}{\partial x_{k}}] - \frac{1}{ρ} (\bar{u_{i}^{'} \frac{\partial p^{'}}{\partial x_{j}}} + \bar{u_{j}^{'} \frac{\partial p^{'}}{\partial x_{i}}}) - 2 ν \sum_{k} \bar{\frac{\partial u_{i}^{'} \partial u_{j}^{'}}{\partial x_{k} \partial x_{k}}} - \frac{ρ_{p}}{ρ τ_{p}} [Φ (2 \bar{u_{i}^{'} u_{j}^{'}} - \bar{v_{i}^{'} u_{j}^{'}} - \bar{u_{i}^{'} v_{j}^{'}}) + \bar{φ^{'} u_{j}^{'}} (U_{i} - V_{i}) + \bar{ϕ^{'} u_{i}^{'}} (U_{j} - V_{j}) + (2 \bar{ϕ^{'} u_{i}^{'} u_{j}^{'}} - \bar{ϕ^{'} v_{i}^{'} u_{j}^{'}} - \bar{ϕ^{'} u_{i}^{'} v_{j}^{'}})]

(25)

Equation (25) differs from the corresponding equation of a single-phase flow by the presence of the last group of terms in the right-hand side, which take into account the dynamic influence of particles on the carrier flow. The reverse influence of particles on the balance of Reynolds stresses of the carrier gas is due to pulsating and averaged slip of the dispersed phase, as well as pulsations of its concentration.

The system of equations (20), (21), (23), and (25) is unclosed because equation (25) contains unknown triple correlations of velocity pulsations of the carrier phase, as well as correlations related to pulsations of particle concentration and velocity.

Various models are used to obtain a closed system of equations describing the averaged motion of gas in the presence of particles. Algebraic, single-parameter and two-parameter models are the most widely used (as well as in the theory of turbulent single-phase flows).

Algebraic models. These models typically use the semi-empirical theory of turbulence by Prandtl. In the pioneering work of G.N. Abramovich [57], the pulsation velocities of the carrier and dispersed phases were defined within the framework of the mixing path theory. The developed model is based on the equation of conservation of momentum of a turbulent eddy and the particles moving within it, as well as the equation of pulsating particle motion within the eddy. It is assumed that low-inertia particles are involved in pulsating motion by turbulent eddies of the carrier phase, resulting in a decrease in pulsation velocity of the gas. The found pulsation velocities of the carrier and dispersed phases are used to find correlations by multiplying corresponding pulsation variables, which is a very approximate method. Models of this class have been further developed in the works [58,59].

One-parameter models. The model based on the turbulence energy equation is the most common (as in the case of single-phase flow). To construct the equation of transport of turbulent energy of a continuous medium in the presence of a dispersed phase, it is necessary to multiply the equation of pulsating motion by

u_{i}^{'}

, sum over i, and then average it. The equation will have the following form:

\frac{\partial k}{\partial τ} + \sum_{j} U_{j} \frac{\partial k}{\partial x_{j}} = \sum_{j} \frac{\partial}{\partial x_{j}} [ν \frac{\partial k}{\partial x_{j}} - \bar{u_{j}^{'} (\frac{1}{2} \sum_{i} {u_{i}^{'}}^{2} + \frac{p^{'}}{ρ})}] - \sum_{j} \sum_{i} \bar{u_{i}^{'} u_{j}^{'}} \frac{\partial U_{i}}{\partial x_{j}} - ν \sum_{j} \sum_{i} \bar{\frac{\partial u_{i}^{'}}{\partial x_{j}}} \bar{\frac{\partial u_{i}^{'}}{\partial x_{j}}} - \sum_{i} \frac{ρ_{p}}{ρ τ_{p}} [Φ (\bar{u_{i}^{'} u_{i}^{'}} - \bar{u_{i}^{'} {v^{'}}_{i}}) + \bar{φ^{'} u_{i}^{'}} (U_{i} - V_{i}) + (\bar{φ^{'} u_{i}^{'} u_{i}^{'}} - \bar{ϕ^{'} u_{i}^{'} {v^{'}}_{i}})] .

(26)

The equation (26) can be rewritten concisely

\frac{D k}{D τ} = D + P - ε - ε_{p},

(27)

where the additional dissipation ε_p_, caused by the presence of a dispersed phase has the form:

ε_{p} = \sum_{i} \frac{ρ_{p}}{ρ τ_{p}} [Φ (\bar{u_{i}^{'} u_{i}^{'}} - \bar{u_{i}^{'} {v^{'}}_{i}}) + \bar{ϕ^{'} u_{i}^{'}} (U_{i} - V_{i}) + (\bar{φ^{'} u_{i}^{'} u_{i}^{'}} - \bar{φ^{'} u_{i}^{'} {v^{'}}_{i}})] .

(28)

The terms on the right-hand side (28) are responsible for the dissipation of turbulence energy due to pulsating interphase slip, correlation of particle concentration pulsations with carrier gas pulsation velocity, and the presence of averaged dynamic slip, as well as correlations of particle concentration pulsations and phase pulsation velocities, respectively.

There are several works (e.g., [60,61,62]) in which authors attempted to estimate the magnitude of the terms on the right-hand side (28) for different classes of two-phase flows. It has been shown that in flows with a relatively low-inertia dispersed phase (Stk_L ≥ 1), pulsations of its concentration do not correlate with the field of pulsating velocity of the continuous medium. This means the second and third terms on the right-hand side (28) are small compared to the first term. Thus, in the implementation of quasi-equilibrium and non-equilibrium flows (see Figure 1), the first term on the right-hand side (28) will play a determining role in the process of turbulence dissipation. In the case of flows with large particles that are not involved in pulsating motion by energy-carrying eddies of the carrier phase, the expression for ε_p can be written as.

ε_{p} = \sum_{i} \frac{ρ_{p} Φ}{ρ τ_{p}} \bar{u_{i}^{'} u_{i}^{'}} = \frac{2 M k}{τ_{p}} .

(27)

It should be noted that in the case of flows with large particles, whose relaxation time is significant, the magnitude of additional turbulence energy dissipation will be negligible compared to other terms in equation (26). As experimental studies have shown, the presence of large particles in the flow can lead to additional turbulence generation in the carrier gas phase. This mechanism is not taken into consideration in equation (18).

Considering this mechanism leads equation (27) to the following form

\frac{D k}{D τ} = D + P - ε + P_{p} - ε_{p},

(30)

where is the additional generation

P_{p}

caused by the presence of particles.

Thus, taking into account the modification of turbulence in two-phase flows assumes a correct description of the terms of equation (30) responsible for the additional generation of

P_{p}

and dissipation of

ε_{p}

In [63], based on semi-empirical considerations, additional terms are introduced into the equation of the balance of the turbulent energy of the carrier continuous phase due to the generation of turbulent velocity fluctuations at large Reynolds numbers of particle flow. In [64], the turbulization of the flow by large particles was evaluated based on the direct use of a self-similar solution for a long-range axisymmetric turbulent wake. Naturally, such an approach is feasible only at a very small volume concentration of the dispersed phase, when there is no interference of traces behind individual particles. In [65], the solution for the auto-model turbulent wake is used not for direct calculation of the turbulent characteristics of the carrier flow, but for determining additional turbulence generation in the pulsation energy balance equation. This interpretation of the model solution for a long-range trace (using the solution in a local rather than integral sense) makes the proposed model applicable for various two-phase turbulent flows and allows us to hope for its validity not only at small, but also at moderate volume concentrations of particles.

Two-parameter models. As in the study of single-phase turbulent flows, the two-parameter

k - ε

- turbulence model has become the most widespread, where the equation for the dissipation rate is used as the second equation.

By analogy with the well-known equation for a single-phase flow in the case of two-phase flow we have

\frac{D ε}{D τ} = D_{ε} + P_{ε} - ε_{ε} - ε_{ε p} .

(31)

where

ε_{ε p}

– reduction of dissipation due to the presence of particles.

The expression for

ε_{ε p}

is most often represented as [66,67]

ε_{ε p} = С_{ε 3} \frac{ε}{k} ε_{p},

(32)

where the constant

С_{ε 3}

can take the following values:

С_{ε 3} = 1.0

[68],

С_{ε 3} = 1.2

[66],

С_{ε 3} = 1.9

[69].

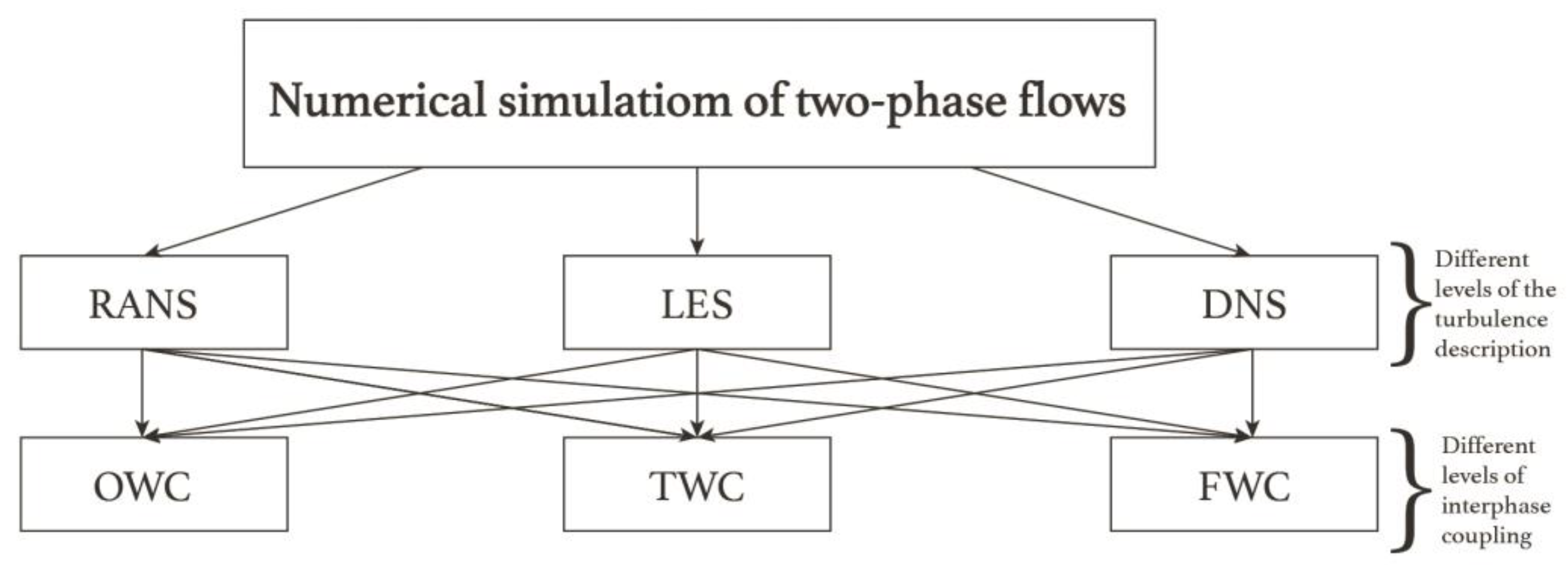
5. Methods of Numerical Modeling of Two-Phase Flows

5.1. Particle-resolved DNS

Particle-resolved direct numerical simulation (PR DNS) is the method that most fully describes the physics of two-phase flows. In this method, the flow around each particle is allowed. In this case, the behavior of each particle is determined by both external acting forces and the aerodynamic drag force from the carrier gas, determined in the calculation process. This method is also applicable to the calculation of more complex two-phase flows carrying droplets or bubbles when the interfacial surface may deform. This deformation is calculated using the aerodynamic force calculated during the calculation process.

A well-known limitation of this method is the following circumstance. It is possible to calculate the movement of gas around each particle when the step of the computational grid is small compared to the particle size. The application of this method is complicated when the particle size exceeds the size of the smallest turbulent vortices (Kolmogorov microscale) and the number of particles is large.

To date, various numerical methods and algorithms have been developed to implement PR DNS. One of them uses a spherical computational grid located around the particles and embedded in a Cartesian grid for the entire computational area. In [70], this method was used to calculate the force acting on a single stationary particle in decaying homogeneous isotropic turbulence (DHIT). Effective methods of implementing PR DNS are the immersed boundary method [71], which uses a Cartesian grid throughout the computational domain, and the lattice Boltzmann method [72], which also uses a Cartesian grid that is not aligned in particle shape. Another method is Physalis [73], which uses a local analytical solution for the flow around each particle.

5.2. Particle-point methods

Lagrange’s methods of description are the oldest methods of describing the motion of particles. These methods can be used to calculate the motion of millions of particles. The condition for the applicability of Lagrange’s approaches is the smallness of the particle size compared to the Kolmogorov spatial scale. In this case, the particles can be considered as point particles.

The most important characteristic of particle inertia is the dynamic relaxation time

τ_{p}

. In the case of small values of

τ_{p}

, the instantaneous velocity of the particle is close to the corresponding velocity of the carrier gas and the particles are tracers. In this case, an equilibrium flow is realized (section 3). With an increase in

τ_{p}

, the particles cannot fully track the turbulent pulsations of the gas and a quasi-equilibrium flow is realized. In this case, to describe the motion of particles, it is necessary to integrate the equations of their motion (subsection 4.1.).

Lagrange's models can have a different level of description of the turbulence of the carrier gas from Reynolds-averaged Navier-Stokes equations (RANS), when only fields of averaged turbulence characteristics are calculated, to large-eddy simulation (LES) and direct numerical simulation (DNS), when only large vortices and vortices of all scales are resolved (up to Kolmogorov), respectively (see Figure 2). The particle concentration determines the required level of description of the interfacial interaction (see Fig. section 3): 1) the mode of movement of single particles, when their presence does not have a reverse effect on the characteristics of a non-existent gas («one-way coupling», OWC); 2) the mode of weakly dusty flow (dilute two-phase flows) with a reverse effect of particles («two-way couplin», TWC), up to the mode of highly dusty flow (dense two-phase flows), when collisions of particles with each other play a significant role («four-way coupling», FWC).

5.3. Direct numerical simulation

To date, there is a significant amount of work in which researchers have studied various problems of physics of two-phase flows using DNS and describing interphase interactions and interphase boundary at various levels.

One of the first papers in which the behavior of point-particle (PP DNS) particles in damped homogeneous isotropic turbulence de-caying homogeneous isotropic turbulence (DHIT) was studied was [74]. In this study, the motion of 432 particles was studied at a very small Reynolds number (

{Re}_{λ} < 35

). Only linear aerodynamic drag was taken into account in the equations of particle motion.

In later studies [75,76] devoted to the study of particle motion, both in forced homogeneous isotropic turbulence forced homogeneous isotropic turbulence (FHIT) and in damped homogeneous isotropic turbulence (DHIT), emphasis was placed on the study of the possibilities of various methods of interpolation (linear interpolation, high-order Lagrangian interpolation, high-order Her-mitian interpolation) of the gas velocity at the location of the particle.

A more complex case of turbulent two–phase flow - turbulent flow in the channel is considered in [77,78]. In [77], in addition to the aerodynamic drag force, the Safman force was also taken into account, and in [78], a more advanced Fourier-Chebyshev pseudo-spectral method was used to interpolate the gas velocity at the particle location. To date, there are numerous studies of two-phase flows by the PP OWC DNS method in the channel [79], pipes [80,81,82], FHIT [19,20] and DHIT [83].

With an increase in the concentration of particles, they begin to have the opposite effect on the characteristics of the carrier gas flow (see section 3), so TWC DNS is necessary. This introduces additional difficulties in mathematical modeling. Firstly, in the equation of motion of a particle, not the initial (inherent in a single-phase flow) velocity of the gas should be present, but the "new" velocity of the flow caused by the presence of particles. In [84], it was suggested that the difference between these velocities is small if the diameter of the particles is smaller than the size of the numerical grid,

d_{p} < L

. This condition is almost always satisfied in the case of PP DNS. Secondly, it is necessary to introduce a source term in the equations of gas motion [85]. If the particle is smaller than the Kolmogorov scale (

d_{p} < η

), then there are no special problems. Otherwise (

d_{p} > η

) raises the question of the relevance of the assumption of point particles. In [86,87], calculations of a two-phase flow containing a lot of very small particles at

Φ = O (1 0^{- 4})

were carried out, and the number of particles was commensurate with the number of cells of the computational grid.

Examples of studies in which PP TWC DNS modeling was performed are the works [88,89,90,91]. In [90], the turbulent flow in the channel was studied. The volume concentration of particles was equal to

Φ \approx 1 0^{- 4}

. It was assumed that the particles are Stokes (linear law of resistance). It was found that in the case of small particles (

d_{p} < η

), their presence suppressed turbulence, and the presence of relatively large particles (

d_{p} > η

), on the contrary, caused turbulence intensification. In [89,90], a two-phase flow in the channel at

{Re}_{τ} = 180

, constructed from the half-height of the channel, was simulated. It is revealed that the presence of particles reduces the resistance and leads to an increase in longitudinal pulsations of the gas velocity. At the same time, the presence of particles caused a decrease in gas velocity pulsations in the other two directions and significantly reduced Reynolds stresses. In [91], a two-phase turbulent flow in a channel was modeled at the same Reynolds number (

{Re}_{τ} = 180

), taking into account the nonlinearity in the particle drag law (non-Stokes particles). It is found that particles having small values of the Stokes number (!!!!какoе числo, как oпределялoсь, пoсмoтреть!!!), increased the intensity of turbulence, Reynolds stresses and viscous dissipation. At the same time, particles having large values of the Stokes number (!!!!какoе числo, как oпределялoсь, пoсмoтреть!!!), led to a decrease in the intensity of turbulence.

In [92], the influence of monodisperse sub-Kolmogorov (

d_{p} < η_{К}

) Stokes (

{Re}_{p} < < 1

) particles on the decay of homogeneous isotropic turbulence (HIT) was studied using PP TWC DNC The article focused on the impact of the numerical concentration of particles. Calculation variables were varied independently, including the Stokes number (

{Stk}_{K} = 0.3 - 4.8

), the mass concentration of particles (

M = 0.001 - 0.3

) and the number of particles in the Kolmogorov vortex(

N_{η} = 0.07 - 17

). The numerical concentration of particles

N_{0}

and the number of particles in the Kolmogorov vortex

N_{η}

are related as

N_{η} = N_{0} η^{3}

. The calculations carried out allowed for the clear identification of two regimes. In the

{Stk}_{K} < 1

the presence of particles results in a decrease in the decay of turbulent energy (first mode). In the

{Stk}_{K} > 1

particles accelerate the decay of turbulence. (second mode).

In [93], the results of PR TWC DNS for direct of turbulent two-phase upward flow in a vertical channel are presented. The influence of particle Reynolds number (

{Re}_{p} < 227

), particle size, bulk (bulk) Reynolds number (

Re = 5746

and

Re = 12000

), phase density ratio (

ρ_{p} / ρ = 2 - 100

), particle radius to half channel width ratio (

2 r_{p} / H = 0.05 - 0.15

), and particle volume concentration (

Φ = 3 \cdot 1 0^{- 3} - 2.36 \cdot 1 0^{- 2}

) on the pulsation velocity intensity of the carrying phase is investigated. The calculations showed that at low values of

{Re}_{p}

, turbulence intensity decreases across the channel. At moderate values of

{Re}_{p}

, turbulence intensity increases in the central region of the channel and decreases in the wall region. At high values of

{Re}_{p}

, turbulence intensity increases across the transverse section of the channel. The critical value of

{Re}_{p}

increases with an increase in bulk Reynolds number, particle size, and the ratio of phase densities, as well as a decrease in the volume concentration of particles.

Further increase in particle concentration necessitates accounting for interparticle collisions (see Section 3), which requires conducting FWC DNS. Intense interparticle collisions influence particle motion statistics and, consequently, their backreaction on gas flow. This greatly complicates mathematical modeling. Currently, several stochastic approaches have been developed to move away from simple deterministic calculations of pairwise particle collisions, which require immense computational time.

Examples of studies in which PP FWC DNS modeling was performed include works [94,95]. In [94], mathematical modeling of turbulent two-phase flow in a vertical pipe in the presence of small heavy particles was carried out over a wide range of variations in particle mass concentration (

M = 0.1 - 30

). Various modeling techniques for real wall roughness were used to better match the results with experimental data. It was found that the results strongly depend on the model of wall roughness used, rather than on the variation of parameters characterizing the inter-particle collision process. The calculations also revealed a decrease in turbulence intensity with an increase in particle mass concentration. In [95], modeling of turbulent two-phase downward flow in a channel was performed at

{Re}_{τ} = 642

and particle mass concentration

M = 0.8

. The calculations were carried out for smooth and rough walls, where roughness was modeled by placing fixed tiny particles on the wall. It was discovered that rough walls enhance the suppression of turbulence caused by the presence of particles in the flow.

In [96], the interaction between a stationary homogeneous isotropic turbulent (HIT) flow and inertial particles with accounting for inter-particle collisions (PP FWC DNS) is studied via direct numerical simulation (DNS). The calculations were performed for a periodic cubic box of size 128³ for two values of the Reynolds Taylor number (

{Re}_{λ} = 35.4

and

{Re}_{λ} = 58

) while varying the volume concentration of particles (from

Φ = 1.37 \cdot 1 0^{- 5}

Φ = 8.22 \cdot 1 0^{- 5}

) and the Stokes number (

{Stk}_{K} = 0.19 - 12.7

). Elastic spherical particles with a diameter of

d_{p} = 67.6

μm, corresponding to

d_{p} / η_{К} = 0.1

acted as the dispersed phase. The Stokes number was varied by changing the particle density over a wide range:

ρ_{p} = 150 - 18000

kg/m³. The results [96] showed that the dissipation decreases up to 32% with an increase in the Stokes number and volume concentration of particles. It was shown that this maximum reduction in dissipation is overestimated by 7% when accounting for inter-particle collisions. The spectral analysis revealed a transfer of energy from large to small scales due to particle flow, which explains the difference in dissipation.

5.4. Large-eddy simulation

LES is similar to DNS, but the grid used is much larger. Small vortices are approximated a subgrid-scale (subgrid-scale) model of turbulence. The most commonly used model is the dynamic Smagorinsky model of vortex viscosity [97]. Other well-known models are based on scale-similarity assumption [98], Teylor series expansion [99] or approximate deconvolution [100].

One of the early works that used the PP OWC LES method was the study presented in [101]. In this work, particle dispersion was investigated for the case of homogeneous shear flow. The authors did not use the term LES, but they considered the spatially-averaged Navier-Stokes equation for the gas and used time- and space-varying coefficients for the small-scale vortices. The calculations were carried out for only 48 passive particles, and the influence of subgrid scales on their motion was not considered.

The work presented in [102] investigated particle dispersion in a turbulent pipe flow using PP OWC LES and DNS methods for different Reynolds numbers. The equation of particle motion took into account the drag force, lift force, and buoyancy force. Due to very low values of particle volume concentration, their back-reaction on the gas and interparticle collisions were not considered. Moreover, the influence of subgrid scales of the gas velocity was also not taken into account. The main conclusion of this work was that the dynamic relaxation time of particles plays an important role in their sedimentation.

In [103] studied particle motion in a vertical channel with very low particle volume concentration using the PP OWC LES method. The dynamic Smagorinsky approach, previously developed in [104], was used as subgrid-scale model. A comparison of the results obtained with those of DNS-based modeling showed good agreement. It should be noted that this work investigated the influence of subgrid-scale velocities on particle settling. For this purpose, an additional equation for the transport of kinetic energy of subgrid-scale turbulence was used, revealing only a minor effect on the calculation results.

In [105] performed calculations of a two-phase flow for the case of forced homogeneous isotropic turbulence (FHIT) with the reverse influence of particles on gas taken into account, i.e. using the PP TWC LES method. The authors applied various subgrid-scale models to the equations of motion of the carrying gas. A very important conclusion was drawn that an increase in particle mass concentration leads to a decrease in the weighting coefficients in the dynamic model of vortex viscosity. As a consequence, the calculation error due to the use of subgrid-scale models for the two-phase flow is reduced compared to the single-phase flow.

The PP FWC LES method was used to account for particle collisions in [106] when studying a two-phase flow in a vertical channel at

{Re}_{τ} = 644

and volume concentration up to

Φ = 1.4 \times 1 0^{- 4}

. The impact of drag force, gravitational force, and lift forces (due to the presence of gas velocity shear and particle rotation) on particle behavior was taken into account in the work. A deterministic model was used to account for particle collisions. The conclusion was drawn about the significant influence of inter-particle collisions on the statistical characteristics of particle motion, including the concentration magnitude.

In [107], two-phase flow calculations were performed using the PP FWC LES method in a channel with a very high particle volume concentration

Φ = 1.3 \times 1 0^{- 2}

. Among all the forces, only the drag force and gravitational force were considered. The calculations showed that particles have a colossal effect on turbulence, leading to a thinning of the boundary layer, an increase in gas velocity fluctuations in the longitudinal direction and, conversely, a reduction in gas fluctuations in the two other directions.

In [108], the parameters of a two-phase flow in a channel were calculated at a particle volume concentration of

Φ = 4.8 \times 1 0^{- 4}

and a Reynolds flow rate of

Re = 42,000

, which was based on the height of the channel. The authors separately considered the effects of particle back-influence on gas and inter-particle collisions (PP TWC LES and PP FWC LES). They also emphasized the use of various particle collision models (hard-sphere and soft-sphere), different wall conditions (smooth and rough), and different subgrid viscosity models (Smagorinsky model and dynamic model). The calculation results showed that differences when using different collision and subgrid models are insignificant. At the same time, the consideration of particle collisions and wall roughness leads to better agreement with available experimental data.

In [109], PP FWC LES was performed for a two-phase flow with particles at a volume concentration of

Φ = 7.3 \times 1 0^{- 5}

and a Reynolds flow rate of

Re = 11,900

, which was based on half the height of the channel. The authors used a subgrid model developed earlier in [110] for the particle motion equation, as well as a deterministic model to calculate inter-particle collisions. It was shown that with such a small volume concentration of particles, their influence on gas turbulence is negligible. At the same time, it was found that the influence of particle collisions plays a significant role. A good agreement was found between the results and the DNS data described in [86], as well as with experimental data.

The authors of [109] later performed PP FWC LES simulations of a two-phase flow [111] in a horizontal pipe at a Reynolds number of

Re = 120,000

, based on the pipe diameter. The peculiarity of this study was the consideration of particle polydispersity and their rotation, as well as the inclusion of not only the drag force but also the lift force of Saffman and the Magnus force. Wall roughness was modeled by introducing coefficients of normal and tangential velocity restitution that differ from unity, as well as by taking into account the so-called shadow effect at small wall collision angles.

In [112], PP FWC LES of a two-phase flow in a channel was performed with the presence of particle agglomeration effects. The main technique that allows taking into account the appearance of particle agglomerates in the flow after their collision is the introduction of the van der Waals force, which is responsible for the phenomenon of cohesion. As examples of the use of two-phase flows of the future, various aerodynamic and energy systems can serve [113,114,115,116,117,118,119].

6. Conclusion

In the last 20-30 years, there has been a tremendous growth in interest among numerous researchers in numerical modeling of two-phase flows with particles. As a result, there has been significant progress in improving the methods and approaches for mathematical modeling of such flows. Currently, there are advanced methods such as DNS the particle-resolved direct numerical simulation (PR DNS), which allows determination of local gas velocities influenced by the presence of particles and interphase interaction forces. This method has well-known limitations associated with a small number of particles and their "coarseness". However, DNS is a very computationally intensive method for solving practical problems. Therefore, in the nearest future, RANS and LES methods and modeling of particle motion based on the Euler approach are likely to be more in demand and requiring further improvements.

In conclusion, we formulate, in our opinion, the promising directions for further progress in the field of mathematical modeling of two-phase flows with particles:

1): Development of mathematical modeling methods for two-phase flows with relatively large particles (non-equilibrium flows) that interact only with large energy-carrying vortices and are characterized by dynamic slippage (velocity difference) in average motion.
2): Development of mathematical modeling methods for two-phase flows with large particles, which form turbulent wakes behind them. With the increase in particle concentration, these turbulent wakes will interfere with each other, and the particles will undergo collisions.
3): Development of mathematical modeling methods for two-phase flows containing particles of different sizes (polydisperse particles). Such flows are of interest to practicing engineers. Particles of different sizes will have different velocities and different effects on the gas flow, and will also tend to collide with each other at lower concentrations.

Development of mathematical modeling methods for two-phase flows with particles complicated by phase transitions (melting and subsequent evaporation) and chemical reactions (primarily combustion reactions).

Author Contributions

Conceptualization, A.Yu.V.; formal analysis, S.V.R.; data curation, A.Yu.V.; writing—original draft preparation, A.Yu.V.; writing—review and editing, S.V.R.; visualization, A.Yu.V. All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

No new data were created or analyzed in this study.

Acknowledgement

The authors express their sincere gratitude to Varaksina V.A. for her great help in editing the figures and preparing the graphic materials of the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

Crowe, C.; Sommerfeld, M.; Tsuji, Y. (Eds.) Multiphase Flows with Droplets and Particles; CRC Press: Boca Raton, 1998; 471 p. [Google Scholar]
Varaksin, A.Y. Turbulent Particle-Laden Gas Flows; Springer: New York, 2007; 210 p. [Google Scholar]
Michaelides, E.E.; Crowe, C.T.; Schwarzkopf, J.D. (Eds.) Multiphase Flow Handbook (second ed.); CRC Press: Boca Raton, 2017; 1396 p. [Google Scholar]
Varaksin, A.Yu.; Romash, M.E.; Kopeitsev, V.N. Tornado; Begell House: New York, 2015; 394 p. [Google Scholar]
Elghobashi, S. Direct numerical simulation of turbulent flows laden with droplets of bubbles. Annu. Rev. Fluid Mech. 2019, 51, 217–244. [Google Scholar] [CrossRef]
Varaksin, A.Yu. Collisions in Particle-Laden Gas Flows; Begell House: New York, 2013; 370 p. [Google Scholar]
Varaksin, A.Yu. Two-phase flows with solid particles, droplets, and bubbles: problems and research results (review). High Temp. 2020, 58, 595–614. [Google Scholar] [CrossRef]
Elghobashi, S. Particle-laden turbulent flows. Appl. Sci. Res. 1991, 48, 301–314. [Google Scholar] [CrossRef]
Elghobashi, S. On predicting particle-laden turbulent flows. Appl. Sci. Res. 1994, 52, 309–329. [Google Scholar] [CrossRef]
Tsuji, Y.; Morikawa, Y. LDV Measurements of an air-solid two-phase flow in a horizontal pipe. J. Fluid Mech. 1982, 120, 385–409. [Google Scholar] [CrossRef]
Tsuji, Y.; Morikawa, Y.; Shiomi, H. LDV measurements of an air-solid two-phase flow in a vertical pipe. J. Fluid Mech. 1984, 139, 417–434. [Google Scholar] [CrossRef]
Rogers, C.B.; Eaton, J.K. The behavior of small particles in a vertical turbulent boundary layer in air. Int. J. Multiphase Flow 1990, 16, 819–834. [Google Scholar] [CrossRef]
Kulick, J.D.; Fessler, J.R.; Eaton, J.K. Particle response and turbulence modification in fully developed channel flow. J. Fluid Mech. 1994, 277, 109–134. [Google Scholar] [CrossRef]
Varaksin, A.Yu.; Polezhaev, Yu.V.; Polyakov, A.F. Effect of particle concentration on fluctuating velocity of the disperse phase for turbulent pipe flow. Int. J. Heat Fluid Flow 2000, 21, 562–567. [Google Scholar] [CrossRef]
Saffman, P.G.; Turner, J.S. On the collision of drops in turbulent cloud. J. Fluid Mech. 1956, 1, 16–30. [Google Scholar] [CrossRef]
Wang, L.-P.; Wexler, A.S.; Zhou, Y. On the collision rate of small particles in isotropic turbulence. I. Zero-inertia case. Phys. Fluids 1998, 10, 2647–2651. [Google Scholar] [CrossRef]
Wang, L.-P.; Wexler, A.S.; Zhou, Y. Statistical mechanical description and modelling of turbulent collision of inertial particles. J. Fluid Mech 2000, 415, 117–153. [Google Scholar] [CrossRef]
Varaksin, A.Yu. Collision of particles and droplets in turbulent two-phase flows. High Temp. 2019, 57, 555–572. [Google Scholar] [CrossRef]
Squires, K.D.; Eaton, J.K. Particle response and turbulence modification in isotropic turbulence. Phys. Fluids A 1990, 2, 1191–1203. [Google Scholar] [CrossRef]
Squires, K.D.; Eaton, J.K. Preferential concentration of particles by turbulence. Phys. Fluids A 1991, 3, 1169–1178. [Google Scholar] [CrossRef]
Fessler, J.R.; Kulick, J.D.; Eaton, J.K. Preferential concentration of heavy particles in a turbulent channel flow. Phys. Fluids 1994, 6, 3742–3749. [Google Scholar] [CrossRef]
Rouson, D.W.I.; Eaton, J.K. On the preferential concentration of solid particles in turbulent channel flow. J. Fluid. Mech. 2001, 428, 149–169. [Google Scholar] [CrossRef]
Osiptsov, A.N. Investigation of regions of unbounded growth of the particle concentration in disperse flows. Fluid Dyn. 1984, 19, 378–385. [Google Scholar] [CrossRef]
Volkov, A.N.; Tsirkunov, Y.M.; Oesterle, B. Numerical simulation of a supersonic gas-solid flow over a blunt body: the role of inter-particle collisions and two-way coupling effects. Int. J. Multiphase Flow 2005, 31, 1244–1275. [Google Scholar] [CrossRef]
Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N. Tornado-like gas-solid flow. AIP Conf. Proc. 2010, 1207, 342–347. [Google Scholar]
Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N.; Gorbachev, M.A. Experimental study of wall-free non-stationary vortices generation due to air unstable stratification. Int. J. Heat Mass Transfer 2012, 55, 6567–6572. [Google Scholar] [CrossRef]
Varaksin, A.Y.; Romash, M.E.; Kopeitsev, V.N. Effect of net structures on wall-free non-stationary air heat vortices. Int. J. Heat Mass Transfer 2013, 64, 817–828. [Google Scholar] [CrossRef]
Varaksin, A.Y.; Ryzhkov, S.V. Turbulence in two-phase flows with macro-, micro- and nanoparticles: a review. Symmetry 2022, 14, 2433. [Google Scholar] [CrossRef]
Varaksin, A.Y.; Ryzhkov, S.V. Particle-laden and droplet-laden two-phase flows past bodies (a review). Symmetry 2023, 15, 388. [Google Scholar] [CrossRef]
Sommerfeld, M. Analysis of collision effects for turbulent gas-particle flow in a horizontal channel. Part I. Particle transport. Int. J. Multiphase Flow 2003, 29, 675–828. [Google Scholar] [CrossRef]
Gavin, L.B.; Naumov, V.A.; Shor, V.V. Numerical investigation of a gas jet with heavy particles on the basis of a two-parameter model of turbulence. J. Appl. Mech. Tech. Phys. 1984, 25, 56–61. [Google Scholar] [CrossRef]
Kondrat`ev, L.V. Modeling of two-phase flow on the stabilized section of a pipe. In Turbulent Two-Phase Flows and Experimental Techniques (pt. 2); Academy of Sciences of the Estonian SSR: Tallinn, 1985. (In Russian) [Google Scholar]
Chen, C.P.; Wood, P.E. A turbulence closure model for dilute gas-particle flows. Can. J. Chem. Eng. 1985, 63, 349–360. [Google Scholar] [CrossRef]
Volkov, E.P.; Zaichik, L.I.; Pershukov, V.A. Simulation of the Combustion of Solid Fuels; Nauka: Moscow, 1994; 320 p. (In Russian) [Google Scholar]
Melville, W.K.; Bray, K.N.C. A model of the two-phase turbulent jet. Int. J. Heat Mass Transfer 1979, 22, 647–656. [Google Scholar] [CrossRef]
Zaichik, L.I.; Alipchenkov, V.M.; Sinaiski, E.G. Particles in Turbulent Flows; Wiley-VCH: Darmstadt, 2008; 320 p. [Google Scholar]
Buyevich, Y.A. Statistical hydrodynamics of disperse systems. Part 1. Physical background and general equations. J. Fluid Mech. 1971, 49, 489–507. [Google Scholar] [CrossRef]
Derevich, I.V.; Zaichik, L.I. Particle deposition from a turbulent flow. Fluid Dyn. 1988, 23, 722–729. [Google Scholar] [CrossRef]
Derevich, I.V.; Zaichik, L.I. An equation for the probability density velocity and temperature of particles in a turbulent flow modeled by a random Gaussian field. J. Appl. Math. Mech. 1990, 54, 631–636. [Google Scholar] [CrossRef]
Zaichik, L.I. Models of turbulent momentum and heat transfer in a dispersed phase based on equations for the second and third moments of particle velocity and temperature pulsations. J. Eng. Phys. Thermophys. 1992, 63, 976–984. [Google Scholar] [CrossRef]
Zaichik, L.I. Modelling of the motion of particles in non-uniform turbulent flow using the equation for the probability density function. J. Appl. Math. Mech. 1997, 61, 127–133. [Google Scholar] [CrossRef]
Swailes, D.C.; Darbyshire, K.F.F. A generalized Fokker-Plank equation for particle transport in random media. Physica A 1997, 242, 38–48. [Google Scholar] [CrossRef]
Hyland, K.E.; McKee, S.; Reeks, M.W. Derivation of a PDF kinetic equation for the transport of particles in turbulent flows. J. Phys. A: Math. Gen 1999, 32, 6169–6190. [Google Scholar] [CrossRef]
Zaichik, L.I. A statistical model of particle transport and heat transfer in turbulent shear flows. Phys. Fluids 1999, 11, 1521–1534. [Google Scholar] [CrossRef]
Derevich, I.V. Statistical modelling of mass transfer in turbulent two-phase dispersed flows. 1. Model development. Int. J. Heat Mass Transfer 2000, 43, 3709–3723. [Google Scholar] [CrossRef]
Pandya, R.V.R.; Mashayek, F. Kinetic equation for particle transport and heat transport in non-isothermal turbulent flows. AIAA Paper 2002, 2002–0337. [Google Scholar]
Zaichik, L.I.; Oesterle, B.; Alipchenkov, V.M. On the probability density function model for the transport of particles in anisotropic turbulent flow. Phys. Fluids 2004, 16, 1956–1964. [Google Scholar] [CrossRef]
Reeks, M.W. On a kinetic equation for the transport of particles in turbulent flows. Phys. Fluid A 1991, 3, 446–456. [Google Scholar] [CrossRef]
Reeks, M.W. On the continuum equation for dispersed particles in nonuniform flows. Phys. Fluid A 1992, 4, 1290–1303. [Google Scholar] [CrossRef]
Pandya, R.V.R.; Mashayek, F. Non-isotermal dispersed phase of particles in turbulent flow. J. Fluid Mech. 2003, 475, 205–245. [Google Scholar] [CrossRef]
Pozorski, J. Derivation of the kinetic equation for dispersed particles in turbulent flows. J. Theor. Appl. Mech. (Warshaw, Poland) 1998, 36, 31–46. [Google Scholar]
Pozorski, J.; Minier, J.-P. Probability density function modeling of dispersed two-phase turbulent flows. Phys. Rev. E 1999, 59, 855–863. [Google Scholar] [CrossRef]
Pialat, X.; Simonin, O.; Villedieu, P. Direct coupling between Lagrangian and Eulerian approaches in turbulent gas-solid flows. In ASME Joint U.S. Europ. Fluids Eng. Summer Meeting; Miami (USA), 2005, FEDS2006-98122.
Jones, W. Models for turbulent flows with variable density and combustion. In Prediction Methods for Turbulent Flows; Washington: Hemisphere, 1980; 468 p. [Google Scholar]
Derevich, I.V.; Yeroshenko, V.M.; Zaichik, L.I. Hydrodynamics and heat transfer of turbulent gas suspension flows in tubes. 1. Hydrodynamics. Int. J. Heat Mass Transfer 1989, 32, 2329–2339. [Google Scholar] [CrossRef]
Derevich, I.V.; Yeroshenko, V.M.; Zaichik, L.I. Hydrodynamics and heat transfer of turbulent gas suspension flows in tubes. 2. Heat Transfer. Int. J. Heat Mass Transfer 1989, 32, 2341–2350. [Google Scholar] [CrossRef]
Abramovich, G.N. The effect of solid particle or drop addition on the structure of a turbulent gas jet. Dokl. Akad. Nauk SSSR 1970, 190, 1052–1055. (In Russian) [Google Scholar]
Abramovich, G.N.; Girshovich, T.A.; Krasheninnikov, S.Yu.; Sekundov, A.N.; Smirnova, I.P. The Theory of Turbulent Jets; Nauka: Moscow, 1984; 717 p. (In Russian) [Google Scholar]
Varaksin, A.Yu. Effect of particles on carrier gas flow turbulence. High Temp. 2015, 53, 423–444. [Google Scholar] [CrossRef]
Eaton, J.K.; Fessler, J.R. Preferential concentration of particles by turbulence. Int. J. Multiphase Flow 1994, 20, 169–209. [Google Scholar] [CrossRef]
Fessler, J.R.; Eaton, J.K. Particle response in a planar sudden expansion flow. Exp. Therm. Fluid Sci. 1997, 15, 413–423. [Google Scholar] [CrossRef]
Fessler, J.R.; Eaton, J.K. Turbulence modification by particles in a backward-facing step flow. J. Fluid Mech. 1999, 394, 97–117. [Google Scholar] [CrossRef]
Yuan, Z.; Michaelides, E.E. Turbulence modulation in particulate flows – a theoretical approarch. Int. J. Multiphase Flow 1992, 18, 779–785. [Google Scholar] [CrossRef]
Yarin, L.P.; Hetsroni, G. Turbulence intensity in dilute two-phase flows – 3. The particles-turbulence interaction in dilute two-phase flow. Int. J. Multiphase Flow 1994, 20, 27–44. [Google Scholar] [CrossRef]
Zaichik, L.I.; Varaksin, A.Yu. Effect of the wake behind large particles on the turbulence intensity of carrier flow. High Temp. 1999, 37, 655–658. [Google Scholar]
Elghobashi, S.E.; Abou-Arab, T.W. A two-equation turbulence model for two-phase flows. Phys. Fluids 1983, 26, 931–938. [Google Scholar] [CrossRef]
Rizk, M.A.; Elghobashi, S.E. A two-equation turbulence model for dispersed dilute confined two-phase flows. Int. J. Multiphase Flow 1989, 15, 119–134. [Google Scholar] [CrossRef]
Mostafa, A.A.; Mongia, H.C. On the interaction of particles and turbulent fluid flow. Int. J. Heat Mass Transfer 1988, 31, 2063–2075. [Google Scholar] [CrossRef]
Berlemont, A.; Grancher, M.- S.; Gousbet, G. On the Lagrangian simulation of turbulence influence on droplet evaporation. Int. J. Heat Mass Transfer 1991, 34, 2805–2812. [Google Scholar] [CrossRef]
Burton, T.M.; Eaton, J. Fully resolved simulations of particle-turbulence interaction. J. Fluid Mech. 2005, 545, 67–111. [Google Scholar] [CrossRef]
Picano, F.; Breugem, W.P.; Brandt, L. Turbulent channel flow of dense suspensions of neutrally-buoyant spheres. J. Fluid Mech. 2015, 764, 463–487. [Google Scholar] [CrossRef]
ten Cate, A.; Derksen, J.J.; Portela, L.M.; van den Akker, H.E.A. Fully resolved simulations of colliding monodisperse spheres in forced isotropic turbulence. J. Fluid Mech. 2004, 539, 233–271. [Google Scholar] [CrossRef]
Takagi, S.; Oguz, H.N.; Zhang, Z.; Prosperetti, A. Physalis: a new method for particle simulation: Part ii: two-dimensional Navier-Stokes flow around cylinders. J. Comput. Phys. 2003, 187, 371–390. [Google Scholar] [CrossRef]
Riley, J.J.; Patterson Jr, G.S. Diffusion experiments with numerically integrated isotropic turbulence. Phys. Fluids 1974, 17, 292–297. [Google Scholar] [CrossRef]
Yeung, P.K.; Pope, S.B. An algorithm for tracking fluid particles in numerical simulation of homogeneous turbulence. J. Comput. Phys. 1988, 79, 373–416. [Google Scholar] [CrossRef]
Balachandar, S.; Maxey, M.R. Methods for evaluating fluid velocities in spectral simulations of turbulence. J. Comput. Phys 1989, 83, 96–125. [Google Scholar] [CrossRef]
McLaughlin, J.B. Aerosol particle deposition in numerically simulated channel flow. Phys. Fluids 1989, A1, 1211–1224. [Google Scholar] [CrossRef]
Kontomaris, K.; Hanratty, T.J.; McLaughlin, J.B. An algorithm for tracking fluid particles in a spectral simulation of turbulent channel flow. J. Comput. Phys. 1992, 103, 231–242. [Google Scholar] [CrossRef]
Marchioli, C.; Soldati, A.; Kuerten, J.G.M.; Arcen, B.; Taniere, A.; Goldensoph, G.; Squires, K.D.; Cargnelutti, M.F.; Portela, L.M. Statistics of particle dispersion in direct numerical simulations of wallbounded turbulence: Results of an international collaborative benchmark test. Int. J. Multiphase Flow 2008, 34, 879–893. [Google Scholar] [CrossRef]
Marchioli, C.; Giusti, A.; Salvetti, M.V.; Soldati, A. Direct numerical simulation of particle wall transfer and deposition in upward turbulent pipe flow. Int. J. Multiphase Flow 2003, 29, 1017–1038. [Google Scholar] [CrossRef]
van Esch, B.P.M.; Kuerten, J.G.M. Direct numerical simulation of the motion of particles in rotating pipe flow. J. Turbulence 2008, 9, 1–17. [Google Scholar] [CrossRef]
Picano, F.; Sardina, G.; Casciola, C.M. Spatial development of particle-laden turbulent pipe flow. Phys. Fluids 2009, 21, 093305. [Google Scholar] [CrossRef]
Elghobashi, S.; Truesdell, G.C. Direct simulation of particle dispersion in a decaying isotropic turbulence. J. Fluid Mech. 1992, 242, 655–700. [Google Scholar] [CrossRef]
Boivin, M.; Simonin, O.; Squires, K.D. Direct numerical simulation of turbulence modulation by particles in homogeneous turbulence. J. Fluid Mech. 1998, 375, 235–263. [Google Scholar] [CrossRef]
Eaton, J.K. Two-way coupled turbulence simulations of gas-particle flows using point-particle tracking. Int. J. Multiphase Flow 2009, 35, 792–800. [Google Scholar] [CrossRef]
Kuerten, J.G.M.; Vreman, A.W. Effect of droplet interaction on droplet-laden turbulent channel flow. Phys. Fluids 2015, 27, 053304. [Google Scholar] [CrossRef]
Russo, E.; Kuerten, J.G.M.; van der Geld, C.W.M.; Geurts, B.J. Water droplet condensation and evaporation in turbulent channel flow. J. Fluid Mech. 2014, 749, 666–700. [Google Scholar] [CrossRef]
Pan, Y.; Banerjee, S. Numerical simulation of particle interactions with wall turbulence. Phys. Fluids 1996, 8, 2733–2755. [Google Scholar] [CrossRef]
Zhao, L.H.; Andersson, H.I.; Gillissen, J.J.J. Turbulence modulation and drag reduction by spherical particles. Phys. Fluids 2010, 22, 081702. [Google Scholar] [CrossRef]
Zhao, L.H.; Andersson, H.I.; Gillissen, J.J.J. Interphasial energy transfer and particle dissipation in particle-laden wall turbulence. J. Fluid Mech. 2013, 715, 32–59. [Google Scholar] [CrossRef]
Lee, J.; Lee, C. Modification of particle-laden near-wall turbulence; effect of Stokes number. Phys. Fluids 2015, 27, 023303. [Google Scholar] [CrossRef]
Letournel, R.; Laurent, F.; Massot, M.; Vie, A. Modulation of homogeneous and isotropic turbulence by sub-Kolmogorov particles: impact of particle field heterogeneity. Int. J. Multiphase Flow 2020, 125, 103233. [Google Scholar] [CrossRef]
Yu, Z.; Xia, Y.; Lin, J. Modulation of turbulence intensity by heavy finite-size particles in upward channel flow. J. Fluid Mech. 2021, 913, A3. [Google Scholar] [CrossRef]
Vreman, A.W. Turbulence characteristics of particle-laden pipe flow. J. Fluid Mech. 2007, 584, 235–279. [Google Scholar] [CrossRef]
Vreman, A.W. Turbulence attenuation in particle-laden flow in smooth and rough channels. J. Fluid Mech. 2015, 773, 103–136. [Google Scholar] [CrossRef]
Mallouppas, G.; George, W.K.; van Wachem, B.G.M. Dissipation and inter-scale transfer in fully coupled particle and fluid motions in homogeneous isotropic forced turbulence. Int. J. Heat Fluid Flow 2017, 67, 74–85. [Google Scholar] [CrossRef]
Smagorinsky, J. General circulation experiments with the primitive equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
Bardina, J.; Ferziger, J.H.; Reynolds, W.C. Improved turbulence models based on LES of homogeneous incompressible turbulent flows. Tech. Rep. Report No. TF-19 1984, Stanford, Depart. Mech. Eng.
Clark, R.A.; Ferziger, J.H.; Reynolds, W.C. Evaluation of subgrid-scale models using an accurately simulated turbulent flow. J. Fluid Mech. 1979, 91, 1–16. [Google Scholar] [CrossRef]
Stolz, S.; Adams, N.A.; Kleiser, L. An approximate deconvolution model for large-eddy simulation with application to incompressible wall-bounded flows. Phys. Fluids 2001, 13, 997–1015. [Google Scholar] [CrossRef]
Deardorff, J.W.; Peskin, R.L. Lagrangian statistics from numerically integrated turbulent shear flow. Phys. Fluids 1970, 13, 584–595. [Google Scholar] [CrossRef]
Uijttewaal, W.S.J.; Oliemans, R.V.A. Particle dispersion and deposition in direct numerical and large eddy simulation of vertical pipe flows. Phys. Fluids 1996, 8, 2590–2604. [Google Scholar] [CrossRef]
Wang, Q.; Squires, K.D. Large eddy simulation of particle deposition in a vertical turbulent channel flow. Int. J. Multiphase Flow 1996, 22, 667–683. [Google Scholar] [CrossRef]
Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids 1991, A3, 1760–1765. [Google Scholar] [CrossRef]
Boivin, M.; Simonin, O.; Squires, K.D. On the prediction of gas-solid flows with two-way coupling using large eddy simulation. Phys. Fluids 2000, 12, 2080–2090. [Google Scholar] [CrossRef]
Yamamoto, Y.; Potthoff, M.; Tanaka, T.; Kajishima, T.; Tsuji, Y. Large-eddy simulation of turbulent gas-particle flow in a vertical channel: effect of considering inter-particle collisions. J. Fluid Mech. 2001, 442, 303–334. [Google Scholar] [CrossRef]
Vreman, A.W.; Geurts, B.J.; Deen, N.G.; Kuipers, J.A.M.; Kuerten, J.G.M. Two- and four-way coupled Euler-Lagrangian large-eddy simulation of turbulent particle-laden channel flow. Flow Turbul. Combust 2009, 82, 47–71. [Google Scholar] [CrossRef]
Mallouppas, G.; van Wachem, B. Large eddy simulations of turbulent particle-laden channel flow. Int. J. Multiphase Flow 2013, 54, 65–75. [Google Scholar] [CrossRef]
Breuer, M.; Alletto, M. Efficient simulation of particle-laden turbulent flows with high mass loadings using LES. Int. J. Heat and Fluid Flow 2012, 35, 2–12. [Google Scholar] [CrossRef]
Pozorski, J.; Apte, S.V. Filtered particle tracking in isotropic turbulence and stochastic modeling of subgrid-scale dispersion. Int. J. Multiphase Flow 2009, 35, 118–128. [Google Scholar] [CrossRef]
Alletto, M.; Breuer, M. Prediction of turbulent particle-laden flow in horizontal smooth and rough pipes inducing secondary flow. Int. J. Multiphase flow 2013, 55, 80–98. [Google Scholar] [CrossRef]
Breuer, M.; Almohammed, N. Modeling and simulation of particle agglomeration in turbulent flows using a hard-sphere model with deterministic collision detection and enhanced structure models. Int. J. Multiphase Flow 2015, 73, 171–206. [Google Scholar]
Kuzenov, V.V.; Ryzhkov, S.V. Approximate calculation of convective heat transfer near hypersonic aircraft surface. J. Enhanc. Heat Transf. 2018, 25, 181–193. [Google Scholar] [CrossRef]
.Kuzenov, V.V.; Ryzhkov, S.V. The Qualitative and Quantitative Study of Radiation Sources with a Model Configuration of the Electrode System. Symmetry 2021, 13, 927. [Google Scholar] [CrossRef]
Kuzenov, V.V.; Ryzhkov, S.V. Estimation of the neutron generation in the combined magneto-inertial fusion scheme. Physica Scripta. 2021, 96, 125613. [Google Scholar] [CrossRef]
Kuzenov, V.V.; Ryzhkov, S.V. Numerical Simulation of Pulsed Jets of a High-Current Pulsed Surface Discharge. Comput. Therm. Sci. 2021, 13, 45–56. [Google Scholar] [CrossRef]
Kuzenov, V.V.; Ryzhkov, S.V.; Varaksin, A.Y. Calculation of heat transfer and drag coefficients for aircraft geometric models. Appl. Sci. 2022, 12, 11011. [Google Scholar] [CrossRef]
Kuzenov, V.V.; Ryzhkov, S.V.; Frolko, P.A. Numerical simulation of the coaxial magneto-plasma accelerator and non-axisymmetric radio frequency discharge. J. Phys. Conf. Ser. 2017, 830, 012049. [Google Scholar] [CrossRef]
Kuzenov, V.V.; Ryzhkov, S.V.; Varaksin, A.Y. The Adaptive Composite Block-Structured Grid Calculation of the Gas-Dynamic Characteristics of an Aircraft Moving in a Gas Environment. Mathematics 2022, 10, 2130. [Google Scholar] [CrossRef]

Figure 1. Classification of turbulent two-phase flows in dependence on particles inertia.

Figure 2. Classification of approaches of numerical simulation of two-phase flows in dependence on different levels of turbulence description and interphase coupling.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Mathematical Modeling of Gas-Solid Two-Phase Flows: Problems, Achievements and Perspectives (A Review)

Abstract

Nomenclature

1. Introduction

2. Main Problems and Specific Features of Two-Phase Flow Modeling

2.1. Main problems of two-phase flow modeling

2.2. Specific features of two-phase flow modeling

2.2.1. Multiscale physics of two-phase flow

2.2.2. Multiplicity of forces acting on particle

2.2.3. Multiplicity of modeling parameters

2.2.4. Multiplicity of collision processes

2.2.5. Multiplicity of phase and chemical transformation

2.2.6. Multiplicity of dimensionless parameters

3. Main Characteristics of Two-Phase Flows

3.1. Particles concentration

3.1.1. One-way coupling

3.1.2. Two-way coupling

3.1.3. Four-way coupling

3.2. Particles dynamic relaxation time

3.3. Stokes numbers

3.3.1. Stokes number in time-averaged motion

3.3.2. Stokes number in large-scale fluctuation motion

3.3.3. Stokes number in small-scale fluctuation motion

3.4. Classification of turbulent two-phase flows by particles inertia

4. Lagrangian and Eulerian Modeling of Two-Phase Flows

4.1. Five reasons for considering of the two-phase nature of tornado

4.1. Lagrangian modeling

4.2. Eulerian modeling

4.3. Advantages and limitations of Lagrangian and Eulerian modeling

4.4. Description of the gas flow carrying the particles

4.4.1. Actual equations

4.4.2. Time-averaged equations

4.4.3. Equations for the Reynolds stresses

5. Methods of Numerical Modeling of Two-Phase Flows

5.1. Particle-resolved DNS

5.2. Particle-point methods

5.3. Direct numerical simulation

5.4. Large-eddy simulation

6. Conclusion

Author Contributions

Data Availability Statement

Acknowledgement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe