General Quantum Gravity: A Pearl of Physics

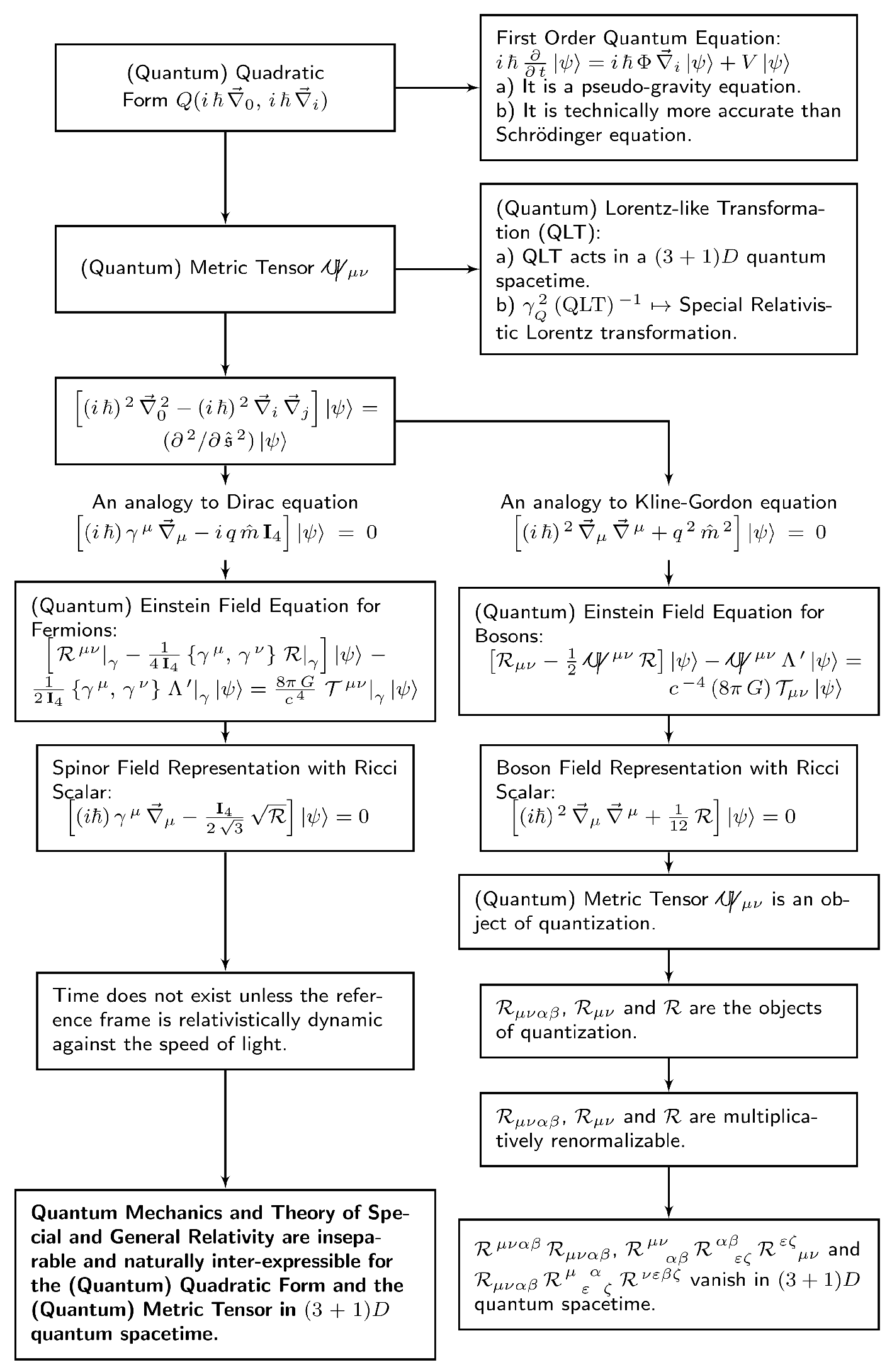
1. Introduction

The insuperable obstacle between gravity and quantum mechanics is their spacetimes. General Theory of Relativity is non-renormalizable, after quantization, and there is no very promising alternative [1]. One can suppose that, at very short distances and/or when the curvature becomes very large, gravitational phenomena must be described by some other theory that is extended compared to General Theory of Relativity [2]. For this purpose, by considering a (quantum) quadratic form $Q(i\hslash {\overrightarrow{\nabla }}_0,i\hslash {\overrightarrow{\nabla }}_i)$ on a state Hilbert space, we have developed a freely-falling inertial frame and a line element using a (quantum) metric tensor ${\mathrm{q}}_{\mu \nu }$. This inertial frame yields an analogy to Kline-Gordon equation, which is able to yield a spinor field representation analogous with Dirac equation. To make both of these analogies to be able to give us gravity, we developed one bosonic and one fermionic (quantum) Einstein field equations distinguishably out of them. The (quantum) metric tensor ${\mathrm{q}}_{\mu \nu }$ is found to be an object of quantization. Hence, the (quantum) Christoffel symbol ${\Gamma }_{\mu \nu }^k$, quantum Riemann tensor ${\mathcal{R}}_{\mu \nu \alpha \beta }$, quantum Ricci tensor ${\mathcal{R}}_{\mu \nu }$ and quantum Ricci scalar $\mathcal{R}$ are also reserved such quantization. For a real scalar field with a $\lambda {\phi }^4$ interaction, the (quantum) metric tensor ${\mathrm{q}}_{\mu \nu }$ becomes multiplicatively renormalizable in $(3+1)D$ quantum spacetime. Thus, the quantum forms ${\mathcal{R}}_{\mu \nu \alpha \beta }$, ${\mathcal{R}}_{\mu \nu }$ and $\mathcal{R}$ are evidently become multiplicatively renormalizable, too. Apparently, all divergences of the “dangerous” [3]${\mathcal{R}}^{\mu \nu \alpha \beta }{\mathcal{R}}_{\mu \nu \alpha \beta }$, ${\mathcal{R}}_{\alpha \beta }^{\mu \nu }{\mathcal{R}}_{\epsilon \zeta }^{\alpha \beta }{\mathcal{R}}_{\mu \nu }^{\epsilon \zeta }$ and ${\mathcal{R}}_{\mu \nu \alpha \beta }{\mathcal{R}}_{\epsilon \zeta }^{\mu \alpha }{\mathcal{R}}^{\nu \epsilon \beta \zeta }$ vanish in $(3+1)D$ quantum spacetime.

2. General Quantum Gravity

First of all, we must omit Schrödinger equation 1 as well as the spin connection throughout this work. Let a Hilbert state space $\mathcal{H}=L^2\left({\mathbb{R}}^n\right)$ is associated with any quantum system.

Definition 1 ((Quantum) Quadratic Form).

Let us postulate the existence of a single space-time M, on which all events occur, with no particular coordinates attached to it. Let us consider the differential operator $i\hslash {\overrightarrow{\nabla }}_{\mu }=\left(\left(i\hslash (\partial /\partial \left(ct\right)),-{\sum }_{i=1}^{3}i\hslash (\partial /\partial x^i)\right)\right)$ in $\mathcal{H}=L^2\left({\mathbb{R}}^{3,1}\right)$. For a diffeomorphism $\Phi :M\to L^2\left({\mathbb{R}}^{3,1}\right)$, let an event at a point $m\in M$, is occurred at $\Phi \left(m\right)$. Similarly, for another diffeomorphism $\Psi :M\to L^2\left({\mathbb{R}}^{3,1}\right)$, the same event is considered to be occurred at $\Psi \left(m\right)$. From inertial reference frames, the changing coordinates is then given by the map $F:\Psi \circ {\Phi }^{-1}:L^2\left({\mathbb{R}}^{3,1}\right)\to L^2\left({\mathbb{R}}^{3,1}\right)$. Let $Q:L^2\left({\mathbb{R}}^{3,1}\right)\to L^2\left(\mathbb{R}\right)$ be the (quantum) quadratic form defined by,

$$\begin{array}{c}\hfill Q(i\hslash {\overrightarrow{\nabla }}_0,i\hslash {\overrightarrow{\nabla }}_i)={\left(i\hslash \right)}^2{\displaystyle \frac{{\partial }^2}{\partial {\left(ct\right)}^2}}-\sum _{i,j=1}^3{\left(i\hslash \right)}^2{\displaystyle \frac{{\partial }^2}{\partial x^i\partial x^j}},\end{array}$$

(1)

so that, for the basic axiom of special relativity, F preserves Q, i.e., $Q\circ F=Q$.

Definition 2 ((Quantum) Metric Tensor).

Let us consider an infinite-dimensional complex vector space $\mathcal{V}\subset \mathcal{H}=L^2\left({\mathbb{R}}^{n-1,1}\right)$. Let $(M^n,\mathrm{q})$ is a smooth manifold, that is, $M^n$ is an n-dimensional differentiable manifold and $\mathrm{q}$ is a (quantum) metric tensor satisfying,

$$\begin{array}{c}\hfill {\mathrm{q}}_{\mu \nu }={\mathrm{q}}_{\alpha \beta }\left({\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\alpha }}{i\hslash {\overrightarrow{\nabla }}_{\mu }}}{\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\beta }}{i\hslash {\overrightarrow{\nabla }}_{\nu }}}\right)=g^{\alpha \beta }\left({\displaystyle \frac{\partial x^{\mu }}{\partial x^{\alpha }}}{\displaystyle \frac{\partial x^{\nu }}{\partial x^{\beta }}}\right)=g^{\mu \nu },\end{array}$$

(2)

when $g_{\mu \nu }=\mathrm{diag}[1,-1,\dots ,-1]$ is the n-dimensional Lorentz metric. This $\mathrm{q}$ is either a positive-definite section of the bundle of symmetric (covariant) 2-tensors $T^{*}M{\otimes }_S{T}^{*}M$ or a positive-definite bilinear maps, $\mathrm{q}\left({(i\hslash )}^{-1}x\right):T_{\left({(i\hslash )}^{-1}x\right)}M\times T_{\left({(i\hslash )}^{-1}x\right)}M\to \mathcal{V}$ for all ${(i\hslash )}^{-1}x\in M$. Here, the metric tensor ${\mathrm{q}}_{\mu \nu }$ is symmetric, i.e., ${\mathrm{q}}_{\mu \nu }={\mathrm{q}}_{\nu \mu }$, and $\det \left({\mathrm{q}}_{\mu \nu }\right)\ne 0$ . Components of its inverse matrix ${\mathrm{q}}^{-1}$ are themselves the components of matrix $\mathrm{q}$, namely, ${\mathrm{q}}_{\mu \nu }{\mathrm{q}}^{\mu \gamma }={\mathrm{q}}^{\gamma \mu }{\mathrm{q}}_{\mu \nu }={\delta }_{\nu }^{\gamma }$, where ${\delta }_{\nu }^{\gamma }$ is the Kronecker delta. The basic axiom of special relativity then ensures that F preserves $\mathrm{q}$.

Let the ‘energy-momentum four-vector’ operator ${\widehat{\mathcal{P}}}^{\mu }$ in $\mathcal{H}=L^2\left({\mathbb{R}}^{3,1}\right)$ for some state $\psi \in L^2\left({\mathbb{R}}^{3,1}\right)$, when ${\widehat{\mathcal{P}}}^{\mu }\to i\hslash {\overrightarrow{\nabla }}_{\mu }=\left(\left(i\hslash (\partial /\partial \left(ct\right)),-i\hslash (\partial /\partial x^i)\right)\right)=\left(c^{-1}\widehat{E},\widehat{\mathbf{p}}\right)$ with the energy operator 2$\widehat{E}\to i\hslash {\partial }_t$ and the three-momentum operator ${\widehat{\mathbf{p}}}^i\to -i\hslash {\overrightarrow{\nabla }}_i$ for $\mu =0,1,2,3$ and $i=1,2,3$. Consider next a freely-falling inertial frame (an orthonormal line operator) in the neighbourhood of a gravitating body in such a way that,

$$\begin{array}{ccc}\hfill Q(i\hslash {\overrightarrow{\nabla }}_0,i\hslash {\overrightarrow{\nabla }}_i)|\psi \rangle & \equiv & {\partial }_{\widehat{\mathfrak{s}}}^2|\psi \rangle ={\displaystyle \frac{{\partial }^2}{\partial {\widehat{\mathfrak{s}}}^2}}|\psi \rangle ={(i\hslash )}^2\left({\displaystyle \frac{{\partial }^2}{\partial {\left(ct\right)}^2}}-{\displaystyle \frac{{\partial }^2}{\partial x^i\partial x^j}}\right)|\psi \rangle \hfill \\ & \doteqdot & {(i\hslash )}^2{\mathrm{q}}_{\mu \nu }{\overrightarrow{\nabla }}_{\mu }{\overrightarrow{\nabla }}_{\nu }|\psi \rangle \equiv {\mathrm{q}}_{\mu \nu }{\widehat{\mathcal{P}}}^{\mu }{\widehat{\mathcal{P}}}^{\nu }|\psi \rangle ,\hfill \end{array}$$

(3)

using summation convention. Since $\mathcal{V}\subset \mathcal{H}=L^2\left({\mathbb{R}}^{3,1}\right)$, then (3) may yield a $(3+1)D$ quantum coordinate system $\left({(i\hslash )}^{-1}{x}^0,\dots ,{(i\hslash )}^{-1}{x}^{n-1}\right)$ for a point $p\in \mathcal{V}$, when ${(i\hslash )}^{-1}{x}^0={(i\hslash )}^{-1}\left(ct\right)$, so as it can get a line element $\mathrm{d}{\mathfrak{s}}^2$ in $\mathcal{V}$ as,

$$\begin{array}{c}\hfill \mathrm{d}{\mathfrak{s}}^2|\psi \rangle ={\mathrm{q}}^{\mu \nu }\mathrm{d}\left[{(i\hslash )}^{-1}{x}^{\mu }\right]\mathrm{d}\left[{(i\hslash )}^{-1}{x}^{\nu }\right]|\psi \rangle ={(i\hslash )}^{-2}{\mathrm{q}}^{\mu \nu }\mathrm{d}{x}^{\mu }\mathrm{d}{x}^{\nu }|\psi \rangle ,\end{array}$$

(4)

which can easily satisfy a (quantum) Lorentz-like transformation (QLT) originated from (3) (see Definition 3 below), though, this QLT will be in a quantum spacetime on contrary to the Special Relativistic Lorentz transformation. Let $(i\hslash ){\partial }_{\mu }^{\prime }|\psi \rangle =(i\hslash ){\Lambda }_{\mu }^{\nu }{\partial }_{\nu }|\psi \rangle +a_{\mu }|\psi \rangle$, where $\Lambda \equiv \left({\Lambda }_{\mu }^{\nu }\right)$ is a matrix with constant elements, and $a_{\mu }$ is a constant four-vector. Let (4) may yield a quantum factor ℘ as,

$$\begin{array}{ccc}\hfill {(i\hslash )}^4{\left({\displaystyle \frac{\mathrm{d}\mathfrak{s}}{\mathrm{d}\left(ct\right)}}\right)}^2|\psi \rangle & =& {(i\hslash )}^2{\mathrm{q}}^{\mu \nu }\left[{\displaystyle \frac{\mathrm{d}{x}^{\mu }}{\mathrm{d}\left(ct\right)}}{\displaystyle \frac{\mathrm{d}{x}^{\nu }}{\mathrm{d}\left(ct\right)}}\right]|\psi \rangle \hfill \\ & \equiv & {(i\hslash )}^2\left(1-{\displaystyle \frac{\left({\mathsf{v}}^i{\mathsf{v}}^j\right)}{c^2}}\right)|\psi \rangle \hfill \\ & =& {(i\hslash )}^2{\gamma }_Q^{-2}|\psi \rangle ={\wp }^{-2}|\psi \rangle ,\hfill \end{array}$$

(5)

where ${\mathsf{v}}^i$ is the velocity, which is accelerating in a curvilinear path for the quantum factor (in SI unit),

$$\begin{array}{c}\hfill \wp ={(i\hslash )}^{-1}{\gamma }_Q\doteqdot -ic{\left({\mathrm{q}}^{\mu \nu }{\mathsf{a}}^{\mu }{\mathsf{a}}^{\nu }\right)}^{-1/2}\mathrm{per}\left(\mathrm{kg}{\mathrm{m}}^2\right),\end{array}$$

(6)

where ${\mathsf{a}}^{\mu }$ is the acceleration whereas ${\mathsf{a}}^0$ is just a non-zero observation in the curvilinear path while c is always a physical constant (the Universality of the speed of light). Though ${\gamma }_Q$ is analogous to the Lorentz factor $\gamma ={\left(1-\left[\left({\mathsf{v}}^i{\mathsf{v}}^j\right)/c^2\right]\right)}^{-1/2}$, but ℘ is not Special Relativistic due to (6).

Definition 3 ((Quantum) Lorentz-like transformation (QLT)).

If we consider Λ matrix as

$$\begin{array}{c}\hfill \Lambda =\left(\begin{array}{cccc}(i\hslash )\wp & -(i\hslash ){\displaystyle \frac{c}{\mathsf{v}}}\wp & 0& 0\\ -(i\hslash ){\displaystyle \frac{c}{\mathsf{v}}}\wp & (i\hslash )\wp & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right),\end{array}$$

then a standard form of (Quantum) Lorentz-like transformation (QLT) is,

$$\begin{array}{ccc}\hfill (i\hslash ){\partial }_0^{\prime }|\psi \rangle =(i\hslash ){\gamma }_Q\left({\partial }_0-{\displaystyle \frac{c}{\mathsf{v}}}{\partial }_1\right)|\psi \rangle ,& & (i\hslash ){\partial }_1^{\prime }|\psi \rangle =(i\hslash ){\gamma }_Q\left({\partial }_1-{\displaystyle \frac{c}{\mathsf{v}}}{\partial }_0\right)|\psi \rangle ,\hfill \\ \hfill (i\hslash ){\partial }_2^{\prime }|\psi \rangle =(i\hslash ){\partial }_2|\psi \rangle ,& & (i\hslash ){\partial }_3^{\prime }|\psi \rangle =(i\hslash ){\partial }_3|\psi \rangle .\hfill \end{array}$$

(7)

Thus,

$$\begin{array}{c}\hfill {\gamma }_Q^2{\left(\mathrm{QLT}\right)}^{-1}\mapsto \mathrm{Special}\mathrm{Relativistic}\mathrm{Lorentz}\mathrm{transformation}.\end{array}$$

(8)

In $\mathcal{V}\subset \mathcal{H}=L^2\left({\mathbb{R}}^{3,1}\right)$ space, $(i\hslash ){\overrightarrow{\nabla }}_{\mu }={\displaystyle \frac{1}{2}}Tr\mathfrak{D}{\sigma }_{\mu }$, where ${\sigma }_0$ is the $2\times 2$ identity matrix and ${\sigma }_{1,2,3}$ are the Pauli spin matrices. So, the inner product would be given by ${(i\hslash )}^2\left(\overrightarrow{\nabla },\overrightarrow{\nabla }\right)=det\mathfrak{D}$. By considering the transformation $\mathfrak{D}\to A\mathfrak{D}{A}^{*}$ with A in $SL(2,C)$ and since $detA=1$, this transformation preserves ${(i\hslash )}^2\left(\overrightarrow{\nabla },\overrightarrow{\nabla }\right)$. Writing ${\mathfrak{D}}^{\prime }=A\mathfrak{D}{A}^{*}=(i\hslash ){\overrightarrow{\nabla }}_{\mu }^{\prime }{\sigma }_{\mu }$, we can see that there is a Lorentz-like transformation ${\Lambda }_A$ such that $(i\hslash ){\overrightarrow{\nabla }}^{\prime }=(i\hslash ){\Lambda }_A\overrightarrow{\nabla }$. It is clear that in this identification we must have ${\Lambda }_A={\Lambda }_{-A}$, so there is a two-to-one homomorphism of $SL(2,C)$ into $SO(3,1)$.

Let the operators $P_{\mu }$ and $J_{\alpha \beta }$ by the rule $P_{\mu }|\psi \rangle =i(i\hslash ){\partial }_{\mu }|\psi \rangle$, $J_{\alpha \beta }|\psi \rangle ={(i\hslash )}^{-1}\left({\eta }_{\alpha \nu }{x}^{\nu }{P}_{\beta }-{\eta }_{\beta \nu }{x}^{\nu }{P}_{\alpha }\right)$ $|\psi \rangle$, where $P_{\mu }$ and $J_{\alpha \beta }$ are called the generators of spacetime translations and the Lorentz rotations, respectively, then $P_{\mu }$ and $J_{\alpha \beta }$ define the Lie algebra of the Poincaré group [2]. Then there is a unitary representation $U(R,\alpha )$ of the Poincare group on $\mathcal{H}$, where $\alpha$ ranges over all spacetime translations and R ranges over all Lorentz boosts and spatial rotations, which fulfills ${\widehat{\mathcal{P}}}^0\ge 0$ and ${\left({\widehat{\mathcal{P}}}^0\right)}^2-{\widehat{\mathcal{P}}}^i{\widehat{\mathcal{P}}}^j\ge 0$ as well as a unique state ${\psi }_0$, called a vacuum, represented by a ray in $\mathcal{H}$, which is invariant under the action of the Poincaré group. For each test function f, defined on spacetime, there exists a set of operators ${\phi }_1\left(f\right),\dots ,{\phi }_n\left(f\right)$ (tempered distributions regarded as a functional of f) which, together with their adjoints defined on a domain D, are defined on a dense subset of $\mathcal{H}$, containing the vacuum ${\psi }_0\in D$. The Hilbert state space $\mathcal{H}$ is spanned by the field polynomials acting on the vacuum (cyclicity condition). The relation $U(R,\alpha ){\phi }_i\left(f\right)U{(R,\alpha )}^{-1}=\sum S_{ij}\left(R^{-1}\right){\phi }_j\left(\{R,\alpha \}f\right)$ is valid when each side is applied to any vector in domain D. Finally, if the supports of two fields are space-like separated, then the fields either commute or anticommute.

Over again, (5) yields,

$$\begin{array}{ccc}\hfill {(i\hslash )}^{-4}{\left[{\displaystyle \frac{{\partial }^2}{\partial {\left(ct\right)}^2}}\right]}^{-1}{\displaystyle \frac{{\partial }^2}{\partial {\widehat{\mathfrak{s}}}^2}}|\psi \rangle & =& {(i\hslash )}^{-2}{\gamma }_Q^2|\psi \rangle ,\hfill \\ \hfill \therefore {\displaystyle \frac{{\partial }^2}{\partial {\widehat{\mathfrak{s}}}^2}}|\psi \rangle ={(i\hslash )}^2{\gamma }_Q^2{\displaystyle \frac{{\partial }^2}{\partial {\left(ct\right)}^2}}|\psi \rangle & =& {(i\hslash )}^2{\gamma }_Q^2{\overrightarrow{\nabla }}_0^2|\psi \rangle ,\hfill \\ \hfill \mathrm{i}.\mathrm{e}.,{\gamma }_Q^{-2}{c}^2{\displaystyle \frac{{\partial }^2}{\partial {\widehat{\mathfrak{s}}}^2}}|\psi \rangle & =& {(i\hslash )}^2{\displaystyle \frac{{\partial }^2}{\partial t^2}}|\psi \rangle .\hfill \end{array}$$

(9)

So, (9) implies that the energy operator $\widehat{E}\to i\hslash {\partial }_t$ is now defining as $\widehat{E}\to {\gamma }_Q^{-1}c[\partial /\partial \widehat{\mathfrak{s}}]$ in $(3+1)D$ spacetime. Again, since relativistic mass $m=\gamma m_0$ for the Lorentz factor $\gamma ={\left(1-\left[\left({\mathsf{v}}^i{\mathsf{v}}^j\right)/c^2\right]\right)}^{-1/2}$, then we may assume analogously that the quantum relativistic mass is $\widehat{m}=(i\hslash )\wp {\widehat{m}}_0$ for $\wp ={(i\hslash )}^{-1}{\gamma }_Q$ of (6). Hence, the quantum relativistic mass $\widehat{m}$ is now behaving like as an operator.

Remark 1.

Inserting (9) ‘twice’ into the mass relation $\widehat{m}=(i\hslash )\wp {\widehat{m}}_0$, we may have, $\widehat{m}={(i\hslash )}^{-1}{\widehat{m}}_0{[\partial /\partial \left(ct\right)]}^{-1}[\partial /\partial \widehat{\mathfrak{s}}]={(i\hslash )}^{-1}{\widehat{m}}_0{[\partial /\partial \left(ct\right)]}^{-1}(i\hslash ){\gamma }_Q{\overrightarrow{\nabla }}_0$, so as, if $\Theta =(i\hslash ){\widehat{m}}_0^{-1}[\partial /\partial \left(ct\right)]$, then we have $\Theta \widehat{m}=(i\hslash ){\gamma }_Q{\overrightarrow{\nabla }}_0$. In natural units $\left[E\right]=\left[M\right]={\left[L\right]}^{-1}={\left[T\right]}^{-1}$ along with $\hslash =c=1$, this Θ becomes dimensionless, i.e., $\Theta =iq$, where q is a quotient number $q\in \mathbb{Q}$. The quantum rest mass ${\widehat{m}}_0$ is behaving like as another expression of the energy operator $\widehat{E}$, i.e., $\widehat{E}\to i\hslash {\partial }_t\doteqdot \Theta {\gamma }_Q^{-1}\widehat{m}c\equiv \Theta {\widehat{m}}_{0}c$ for $\widehat{m}=(i\hslash )\wp {\widehat{m}}_0={\gamma }_Q{\widehat{m}}_0$ with $\wp ={(i\hslash )}^{-1}{\gamma }_Q$.

Insertion of (9) in $\left[{(i\hslash )}^2{\overrightarrow{\nabla }}_0^2-{(i\hslash )}^2{\overrightarrow{\nabla }}_i{\overrightarrow{\nabla }}_j\right]|\psi \rangle =({\partial }^2/\partial {\widehat{\mathfrak{s}}}^2)|\psi \rangle$ of (3) yields,

$$\begin{array}{c}\hfill \left[{(i\hslash )}^2{\overrightarrow{\nabla }}_0^2-{(i\hslash )}^2{\overrightarrow{\nabla }}_i{\overrightarrow{\nabla }}_j\right]|\psi \rangle ={(i\hslash )}^2{\gamma }_Q^2{\overrightarrow{\nabla }}_0^2|\psi \rangle .\end{array}$$

(10)

Use of Rremark 1 into (10) yields a second order wave equation as,

$$\begin{array}{ccc}\hfill \left[{(i\hslash )}^2{\overrightarrow{\nabla }}_{\mu }{\overrightarrow{\nabla }}^{\mu }+{\left(i\Theta \widehat{m}\right)}^2\right]|\psi \rangle & =& 0,\hfill \\ \hfill \mathrm{i}.\mathrm{e}.,\left[{(i\hslash )}^2{\overrightarrow{\nabla }}_{\mu }{\overrightarrow{\nabla }}^{\mu }+q^2{\widehat{m}}^2\right]|\psi \rangle & =& 0\mathrm{for}\hslash =1,\hfill \end{array}$$

(11)

for the quotient number $q\in \mathbb{Q}$ and the construction $\psi =(\phi ,{\phi }_{\mu },{\phi }_{\mu \nu })$ when the spin of the particle is $(s=0,s=1,s=2)$ with the conditions ${\partial }^{\mu }{\phi }_{\mu }=0$, ${\partial }^{\mu }{\phi }_{\mu \nu }=0$, $g^{\mu \nu }{\phi }_{\mu \nu }=0$ and the total symmetrization of the indices as ${\phi }_{\mu \nu }\left(x\right)={\phi }_{\left(\mu \nu \right)}$. So, (11) is nothing but an analogy to Kline-Gordon equation, but unlike conventional Kline-Gordon equation, (11) must have to satisfy the $(3+1)D$ quantum coordinate system $\left({(i\hslash )}^{-1}{x}^0,\dots ,{(i\hslash )}^{-1}{x}^{n-1}\right)$ for (4); in addition, it is actually mass-independent due to $\Theta =(i\hslash ){\widehat{m}}_0^{-1}[\partial /\partial \left(ct\right)]$ and $(\widehat{m}/{\widehat{m}}_0)=(i\hslash )\wp ={\gamma }_Q$ as, $\left[{(i\hslash )}^2{\overrightarrow{\nabla }}_{\mu }{\overrightarrow{\nabla }}^{\mu }-{\partial }_{0\left(\tau \right)}^2\right]|\psi \rangle =0$ if ${\partial }_{0\left(\tau \right)}^2={\partial }^2/\partial {\left(c\tau \right)}^2$ when $\tau ={(i\hslash )}^{-1}{\gamma }_Q^{-1}t$ is the proper time. Technically, (11) is not a Kline-Gordon equation, though (11) has a close relation with General Theory of Relativity due to (6).

Now, (10), as well as (11), is able to yield a spinor field representation for Remark 1 for the gamma matrices ${\gamma }^{\mu }$ as,

$$\begin{array}{ccc}\hfill \left[(i\hslash ){\gamma }^0{\overrightarrow{\nabla }}_0+(i\hslash ){\gamma }^i{\overrightarrow{\nabla }}_i\right]|\psi \rangle & =& (i\hslash ){\gamma }_Q{\overrightarrow{\nabla }}_0{\mathbf{I}}_4|\psi \rangle ,\hfill \\ \hfill \therefore \left[(i\hslash ){\gamma }^{\mu }{\overrightarrow{\nabla }}_{\mu }-\Theta \widehat{m}{\mathbf{I}}_4\right]|\psi \rangle & =& 0,\hfill \\ \hfill \mathrm{i}.\mathrm{e}.,\left[(i\hslash ){\gamma }^{\mu }{\overrightarrow{\nabla }}_{\mu }-iq\widehat{m}{\mathbf{I}}_4\right]|\psi \rangle & =& 0\mathrm{for}\hslash =1,\hfill \end{array}$$

(12)

in terms of the Dirac tensor spinors $\psi ={\psi }_{{\mu }_1\dots {\mu }_n}$ for the construction $\psi =(\phi ,{\phi }_{\nu })$ when the spin of the particle is $(s=1/2,s=3/2)$ with ${\partial }^{\nu }{\phi }_{\nu }=0$ and ${\gamma }^{\nu }{\phi }_{\nu }=0$. So, (12) is analogous with Dirac equation, where ${\mathbf{I}}_4$ is the $4\times 4$ identity matrix. Though (12) also has a close relation with General Theory of Relativity for (6), but none of (11) and (12) are able to give us gravity yet. So, we need something additional to investigate further as follows.

On the first step, let us check our $(3+1)D$ quantum spacetime from the perspective of General Theory of Relativity [4].

Theorem 1.

Let $\left[{\mathcal{R}}_{\mu \nu }-{\displaystyle \frac{1}{2}}{\mathrm{q}}^{\mu \nu }\mathcal{R}\right]|\psi \rangle -{\mathrm{q}}^{\mu \nu }{\Lambda }^{\prime }|\psi \rangle =c^{-4}\left(8\pi G\right){\mathcal{T}}_{\mu \nu }|\psi \rangle$ is the non-vacuum (Quantum) Einstein field equation in $(3+1)D$ quantum spacetime, when ${\Lambda }^{\prime }$ is the ‘naive’ cosmological constant.

Proof. 

Let $(M^n,\mathrm{q})$ is a smooth manifold, that is, $M^n$ is an n-dimensional differentiable manifold and $\mathrm{q}$ is the quantum metric tensor satisfying (2), which is either a positive-definite section of the bundle of symmetric (covariant) 2-tensors $T^{*}M{\otimes }_S{T}^{*}M$ or a positive-definite bilinear maps, $\mathrm{q}\left({(i\hslash )}^{-1}x\right):T_{\left({(i\hslash )}^{-1}x\right)}M\times T_{\left({(i\hslash )}^{-1}x\right)}M\to \mathcal{V}$ for all ${(i\hslash )}^{-1}x\in M$. Here, $T^{*}M{\otimes }_S{T}^{*}M$ is the subspace of $T^{*}M\otimes T^{*}M$ generated by elements of the form $X\otimes Y+Y\otimes X$. Let ${\left\{{(i\hslash )}^{-1}{x}^{\mu }\right\}}_{\mu =1}^n$ be local coordinates in a neighborhood U of some point of M. In U the vector fields ${\left\{i\hslash {\overrightarrow{\nabla }}_{\mu }\right\}}_{\mu =1}^n$ form a local basis for $TM$ and the 1-forms ${\left\{{(i\hslash )}^{-1}\mathrm{d}{x}^{\mu }\right\}}_{\mu =1}^n$ form a dual basis for $T^{*}M$, that is, ${(i\hslash )}^{-1}\mathrm{d}{x}^{\mu }·(i\hslash ){\overrightarrow{\nabla }}_{\nu }={\delta }_{\nu }^{\mu }$. The metric may then be written in local coordinates as $\mathrm{q}={(i\hslash )}^{-2}{\mathrm{q}}_{\mu \nu }\mathrm{d}{x}^{\mu }\otimes \mathrm{d}{x}^{\nu }$, where ${\mathrm{q}}_{\mu \nu }\doteqdot \mathrm{q}\left(i\hslash {\overrightarrow{\nabla }}_{\mu },i\hslash {\overrightarrow{\nabla }}_{\nu }\right)$. Let ${\nabla }^{\mathrm{q}}$ denote the Levi-Civita connection of the metric $\mathrm{q}$. The Christoffel symbol is the components of the Levi-Civita connection and is defined in U by ${\nabla }_{\left(i\hslash {\overrightarrow{\nabla }}_{\mu }\right)}\left(i\hslash {\overrightarrow{\nabla }}_{\nu }\right)\doteqdot {\Gamma }_{\mu \nu }^k\left(i\hslash {\overrightarrow{\nabla }}_k\right)$, and for $\left[\left(i\hslash {\overrightarrow{\nabla }}_{\mu }\right),\left(i\hslash {\overrightarrow{\nabla }}_{\nu }\right)\right]=0$, we see that they are given by,

$$\begin{array}{c}\hfill {\Gamma }_{\mu \nu }^k|\psi \rangle ={\displaystyle \frac{1}{2}}{\mathrm{q}}_{k\ell }\left[\left(i\hslash {\overrightarrow{\nabla }}_{\mu }\right){\mathrm{q}}^{\nu \ell }+\left(i\hslash {\overrightarrow{\nabla }}_{\nu }\right){\mathrm{q}}^{\mu \ell }-\left(i\hslash {\overrightarrow{\nabla }}_{\ell }\right){\mathrm{q}}^{\mu \nu }\right]|\psi \rangle .\end{array}$$

(13)

Let the curvature $(3,1)$-tensor $\mathsf{Rm}$ is defined by,

$$\begin{array}{c}\hfill \mathsf{Rm}(X,Y)Z|\psi \rangle \doteqdot \left({\nabla }_X{\nabla }_{Y}Z-{\nabla }_Y{\nabla }_{X}Z-{\nabla }_{[X,Y]}Z\right)|\psi \rangle .\end{array}$$

Let the tensor $\mathsf{Rc}$ is the trace of $\mathsf{Rm}$ curvature tensor,

$$\begin{array}{c}\hfill \mathsf{Rc}(Y,Z)|\psi \rangle \doteqdot Tr\left(X\mapsto \mathsf{Rm}(X,Y)Z\right)|\psi \rangle .\end{array}$$

Its components are defined by ${\mathcal{R}}_{\mu \nu }|\psi \rangle \doteqdot \mathsf{Rc}\left(\left(i\hslash {\overrightarrow{\nabla }}_{\mu }\right),\left(i\hslash {\overrightarrow{\nabla }}_{\nu }\right)\right)|\psi \rangle$, thus, the Ricci tensor,

$$\begin{array}{c}\hfill {\mathcal{R}}_{\mu \nu }|\psi \rangle =\left[\left(i\hslash {\overrightarrow{\nabla }}_{\ell }\right){\Gamma }_{\mu \nu }^{\ell }-\left(i\hslash {\overrightarrow{\nabla }}_{\nu }\right){\Gamma }_{\mu \ell }^{\ell }+{\Gamma }_{k\ell }^{\ell }{\Gamma }_{\mu \nu }^k-{\Gamma }_{k\nu }^{\ell }{\Gamma }_{\mu \ell }^k\right]|\psi \rangle ,\end{array}$$

(14)

is purely Quantum Mechanical due to (13). Again, the scalar curvature $\mathsf{R}$ is the trace of $\mathsf{Rc}$ tensor: $\mathsf{R}|\psi \rangle \doteqdot {\sum }_{a=1}^n\mathsf{Rc}(e_a,e_a)|\psi \rangle$ where $e_a\in T_{\left({(i\hslash )}^{-1}x\right)}{M}^n$ is a unit vector spanning of a line $L\subset T_{\left({(i\hslash )}^{-1}x\right)}{M}^n$. Then, the non-vacuum quantum Einstein tensor $\mathsf{Rc}-{\displaystyle \frac{1}{2}}\mathrm{q}\mathsf{R}$ directly acts on a quantum spacetime. Thus, the non-vacuum quantum Einstein field equation, $\left[\mathsf{Rc}-{\displaystyle \frac{1}{2}}\mathrm{q}\mathsf{R}\right]|\psi \rangle ={\left(i\hslash \right)}^2(8\pi G/c^4)T|\psi \rangle$, is now ‘purely’ Quantum Mechanical for (13), where the rhs${\left(i\hslash \right)}^2$ comes from the energy-momentum tensor, for example, ${\mathcal{T}}_{\mu \nu }={\left(i\hslash \right)}^2{\partial }_{\mu }\varphi {\partial }_{\nu }\varphi -{\displaystyle \frac{1}{2}}{\left(i\hslash \right)}^2{g}_{\mu \nu }{\left(\partial \varphi \right)}^2-{\left(i\hslash \right)}^2\left(a/{\ell }^2\right){\varphi }^2{g}_{\mu \nu }={\left(i\hslash \right)}^2{T}_{\mu \nu }$, where ℓ is related to the cosmological constant $\Lambda$ as $\Lambda =-3/{\ell }^2$ and a is the (squared) Klein-Gordon mass [5]. 3 Again, the Ricci tensor is ${\mathcal{R}}_{\mu \nu }|\psi \rangle \doteqdot \mathsf{Rc}\left(\left(i\hslash {\overrightarrow{\nabla }}_{\mu }\right),\left(i\hslash {\overrightarrow{\nabla }}_{\nu }\right)\right)|\psi \rangle$$\doteqdot {\left(i\hslash \right)}^2\mathrm{Rc}\left({\partial }_{\mu },{\partial }_{\nu }\right)|\psi \rangle$, thus, the non-vacuum (Quantum) Einstein field equation in $(3+1)D$ quantum spacetime would become as,

$$\begin{array}{ccc}\hfill \left[{\mathcal{R}}_{\mu \nu }-{\displaystyle \frac{1}{2}}{\mathrm{q}}^{\mu \nu }\mathcal{R}\right]|\psi \rangle -{\mathrm{q}}^{\mu \nu }{\Lambda }^{\prime }|\psi \rangle & =& {\displaystyle \frac{8\pi G}{c^4}}{\mathcal{T}}_{\mu \nu }|\psi \rangle ,\hfill \\ \hfill \therefore {\left(i\hslash \right)}^2\left[{\mathrm{R}}_{\mu \nu }-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }\mathrm{R}\right]|\psi \rangle -g_{\mu \nu }{\Lambda }^{\prime }|\psi \rangle & =& {\left(i\hslash \right)}^2{\displaystyle \frac{8\pi G}{c^4}}{T}_{\mu \nu }|\psi \rangle ,\hfill \\ \hfill \mathrm{i}.\mathrm{e}.,\left[{\mathrm{R}}_{\mu \nu }-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }\mathrm{R}\right]|\psi \rangle +g_{\mu \nu }\Lambda |\psi \rangle & =& {\displaystyle \frac{8\pi G}{c^4}}{T}_{\mu \nu }|\psi \rangle ,\hfill \end{array}$$

(15)

where the Lorentz metric tensor $g_{\mu \nu }$ is satisfying (2) and the ‘naive’ cosmological constant (in SI unit) ${\Lambda }^{\prime }=1.112121717\times {10}^{-150}{\mathrm{J}}^2{\mathrm{s}}^2{G}^{-1}$, which yields the cosmological constant $\Lambda =-{\left(i\hslash \right)}^{-2}{\Lambda }^{\prime }$. □

The ‘−’ sign for the cosmological constant $\Lambda =-{\left(i\hslash \right)}^{-2}{\Lambda }^{\prime }$ is taken to make it clear that $\Lambda$ is always repulsive in nature.

The last line of (15) is Einsteinian and non-renormalizable, though, in the first line of (15), the mass dimension of gravitational constant G vanishes due to ${\mathcal{T}}_{\mu \nu }={\left(i\hslash \right)}^2{T}_{\mu \nu }$. So, not owing to the mass dimension of G, the perturbative version of the first line of (15) is renormalizable.

Theorem 2.

For $\left[{(i\hslash )}^2{\overrightarrow{\nabla }}_0^2-{(i\hslash )}^2{\overrightarrow{\nabla }}_i{\overrightarrow{\nabla }}_j\right]|\psi \rangle =({\partial }^2/\partial {\widehat{\mathfrak{s}}}^2)|\psi \rangle$ of (3), there exists a first order quantum equation in $(3+1)D$ as,

$$\begin{array}{c}\hfill i\hslash {\displaystyle \frac{\partial }{\partial t}}|\psi \rangle =i\hslash {\Phi }_i{\overrightarrow{\nabla }}_j|\psi \rangle +V|\psi \rangle ,\end{array}$$

while V is the external potential energy.

Proof. 

Let $\left[{(i\hslash )}^2{\overrightarrow{\nabla }}_0^2-{(i\hslash )}^2{\overrightarrow{\nabla }}_i{\overrightarrow{\nabla }}_j\right]|\psi \rangle ={(i\hslash )}^2{\gamma }_Q^2{\overrightarrow{\nabla }}_0^2|\psi \rangle$ for (10). Then the dynamics of the quantum state is possible to be defined as,

$$\begin{array}{ccc}\hfill i\hslash {\displaystyle \frac{\partial }{\partial \left(ct\right)}}|\psi \rangle & =& {(i\hslash )}^{-1}{\overrightarrow{\nabla }}_0^{-1}\left[{(i\hslash )}^2{\gamma }_Q^2{\overrightarrow{\nabla }}_0^2+{(i\hslash )}^2{\overrightarrow{\nabla }}_i{\overrightarrow{\nabla }}_j\right]|\psi \rangle \hfill \\ & =& (i\hslash )\left[{\gamma }_Q^2{\overrightarrow{\nabla }}_0+{\overrightarrow{\nabla }}_0^{-1}{\overrightarrow{\nabla }}_i{\overrightarrow{\nabla }}_j\right]|\psi \rangle \hfill \\ & =& (i\hslash )\left[{\gamma }_Q^2{\overrightarrow{\nabla }}_0+{\displaystyle \frac{c}{{\mathsf{v}}^i}}{\overrightarrow{\nabla }}_j\right]|\psi \rangle ,\hfill \end{array}$$

while ${\overrightarrow{\nabla }}_0^{-1}{\overrightarrow{\nabla }}_i={\left({\mathsf{v}}^i\right)}^{-1}c$. Therefore, by introducing external potential energy V and the Hamiltonian (or total energy) operator $\mathcal{H}$, we have a first order quantum equation in $(3+1)D$ as,

$$\begin{array}{c}\hfill i\hslash {\displaystyle \frac{\partial }{\partial t}}|\psi \rangle =i\hslash {\Phi }_i{\overrightarrow{\nabla }}_j|\psi \rangle +V|\psi \rangle \equiv \mathcal{H}|\psi \rangle ,\end{array}$$

(16)

where ${\Phi }_i={\left[(1-{\gamma }_Q^2){\mathsf{v}}^i\right]}^{-1}{c}^2$. □

Let (10) be rewritten as, $\left[{(i\hslash )}^2{\overrightarrow{\nabla }}_0^2-{(i\hslash )}^2{\overrightarrow{\nabla }}_i{\overrightarrow{\nabla }}_j\right]|\psi \rangle ={(i\hslash )}^2{\gamma }_Q^2{\overrightarrow{\nabla }}_0^2|\psi \rangle \doteqdot ({\partial }^2/\partial {\widehat{\mathfrak{s}}}^2)|\psi \rangle$ for (9), but as $({\partial }^2/\partial {\widehat{\mathfrak{s}}}^2)|\psi \rangle ={(i\hslash )}^2{\mathrm{q}}_{\mu \nu }{\overrightarrow{\nabla }}_{\mu }{\overrightarrow{\nabla }}_{\nu }|\psi \rangle$ for (3), then ${(i\hslash )}^2{\gamma }_Q^2{\overrightarrow{\nabla }}_0^2|\psi \rangle \doteqdot {(i\hslash )}^2{\mathrm{q}}_{\mu \nu }{\overrightarrow{\nabla }}_{\mu }{\overrightarrow{\nabla }}_{\nu }|\psi \rangle$ yields,

$$\begin{array}{ccc}\hfill {\mathrm{q}}_{\mu \nu }& =& \left({\displaystyle \frac{(i\hslash ){\gamma }_Q{\overrightarrow{\nabla }}_0}{(i\hslash ){\overrightarrow{\nabla }}_{\mu }}}{\displaystyle \frac{(i\hslash ){\gamma }_Q{\overrightarrow{\nabla }}_0}{(i\hslash ){\overrightarrow{\nabla }}_{\nu }}}\right)\equiv \left({\displaystyle \frac{\partial /\partial \widehat{\mathfrak{s}}}{i\hslash {\overrightarrow{\nabla }}_{\mu }}}{\displaystyle \frac{\partial /\partial \widehat{\mathfrak{s}}}{i\hslash {\overrightarrow{\nabla }}_{\nu }}}\right)\hfill \\ & \doteqdot & {\mathrm{q}}_{\alpha \beta }\left({\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\alpha }}{i\hslash {\overrightarrow{\nabla }}_{\mu }}}{\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\beta }}{i\hslash {\overrightarrow{\nabla }}_{\nu }}}\right)=g^{\mu \nu },\hfill \end{array}$$

(17)

hence it is a (quantum) metric tensor as like as (2). Additionally, a non-vacuum (Quantum) Einstein field equation exactly similar to (15) is also possible to exist for bosons. Thus, (15) is doubtlessly a non-vacuum bosonic (Quantum) Einstein field equation in $(3+1)D$ quantum spacetime.

Then the first order quantum equation (16) undoubtedly a pseudo-gravity equation for (17) ready to satisfy the non-vacuum bosonic (Quantum) Einstein field equation (15) in $(3+1)D$ quantum spacetime. So, the first order quantum equation (16) in $(3+1)D$ quantum spacetime is technically more accurate on the contrary to the second order Schrödinger equation in $3D$ (which has no relation with gravity at all).

In a similar way, due to the commutativity of partial derivatives, the first equation of (12) may yield,

$$\begin{array}{c}\hfill \left\{\left(i\hslash {\gamma }^{\mu }{\overrightarrow{\nabla }}_{\mu }\right),\left(i\hslash {\gamma }^{\nu }{\overrightarrow{\nabla }}_{\nu }\right)\right\}|\psi \rangle ={(i\hslash )}^2{\gamma }_Q^2{\overrightarrow{\nabla }}_0^2{\mathbf{I}}_4^2|\psi \rangle ,\end{array}$$

(18)

here and hereafter $\left\{,\right\}$ represents the anticommutator. Since ${(i\hslash )}^2{\gamma }_Q^2{\overrightarrow{\nabla }}_0^2{\mathbf{I}}_4^2|\psi \rangle \doteqdot ({\partial }^2/\partial {\widehat{\mathfrak{s}}}^2)|\psi \rangle$ for (9), then an orthonormal line operator is possible to be written in comparison to (3) as,

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\partial }^2}{\partial {\widehat{\mathfrak{s}}}^2}}|\psi \rangle & =& {\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^{\mu },{\gamma }^{\nu }\right\}\left(i\hslash {\overrightarrow{\nabla }}_{\mu }\right)\left(i\hslash {\overrightarrow{\nabla }}_{\nu }\right)+\right.\hfill \\ & & \left.+{\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^{\nu },{\gamma }^{\mu }\right\}\left(i\hslash {\overrightarrow{\nabla }}_{\nu }\right)\left(i\hslash {\overrightarrow{\nabla }}_{\mu }\right)\right]|\psi \rangle ,\hfill \end{array}$$

(19)

but if $({\partial }^2/\partial {\widehat{\mathfrak{s}}}^2)|\psi \rangle$ satisfies (19), where $\left\{,\right\}$ represents the anticommutator, which is satisfying the Clifford algebra as $\left\{{\gamma }^{\mu },{\gamma }^{\nu }\right\}={\gamma }^{\mu }{\gamma }^{\nu }+{\gamma }^{\nu }{\gamma }^{\mu }=2g^{\mu \nu }{\mathbf{I}}_4$, then for the commutativity of partial derivatives, the first equation of (12) yields:

Lemma 1.

If ${\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^{\mu },{\gamma }^{\nu }\right\}\equiv {\mathrm{q}}_{\mu \nu }=g^{\mu \nu }$, then it must satisfy,

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^{\mu },{\gamma }^{\nu }\right\}\left(i\hslash {\overrightarrow{\nabla }}_{\mu }\right)\left(i\hslash {\overrightarrow{\nabla }}_{\nu }\right)+{\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^{\nu },{\gamma }^{\mu }\right\}\left(i\hslash {\overrightarrow{\nabla }}_{\nu }\right)\left(i\hslash {\overrightarrow{\nabla }}_{\mu }\right)\right]|\psi \rangle \\ \hfill ={(i\hslash )}^2{\gamma }_Q^2{\overrightarrow{\nabla }}_0^2{\mathbf{I}}_4^2|\psi \rangle .\end{array}$$

Proof. 

In (19), the anticommutator relation ${\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^{\mu },{\gamma }^{\nu }\right\}$ must have to satisfy that,

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^{\mu },{\gamma }^{\nu }\right\}& =& {\displaystyle \frac{1}{2}}\left[\left({\displaystyle \frac{(i\hslash ){\gamma }_Q{\overrightarrow{\nabla }}_0{\mathbf{I}}_4}{(i\hslash ){\overrightarrow{\nabla }}_{\mu }}}{\displaystyle \frac{(i\hslash ){\gamma }_Q{\overrightarrow{\nabla }}_0{\mathbf{I}}_4}{(i\hslash ){\overrightarrow{\nabla }}_{\nu }}}\right)+\right.\hfill \\ & & \left.+\left({\displaystyle \frac{(i\hslash ){\gamma }_Q{\overrightarrow{\nabla }}_0{\mathbf{I}}_4}{(i\hslash ){\overrightarrow{\nabla }}_{\nu }}}{\displaystyle \frac{(i\hslash ){\gamma }_Q{\overrightarrow{\nabla }}_0{\mathbf{I}}_4}{(i\hslash ){\overrightarrow{\nabla }}_{\mu }}}\right)\right]\hfill \\ & =& {\displaystyle \frac{1}{2}}\left[\left({\displaystyle \frac{\partial /\partial \widehat{\mathfrak{s}}}{i\hslash {\overrightarrow{\nabla }}_{\mu }}}{\displaystyle \frac{\partial /\partial \widehat{\mathfrak{s}}}{i\hslash {\overrightarrow{\nabla }}_{\nu }}}\right)+\left({\displaystyle \frac{\partial /\partial \widehat{\mathfrak{s}}}{i\hslash {\overrightarrow{\nabla }}_{\nu }}}{\displaystyle \frac{\partial /\partial \widehat{\mathfrak{s}}}{i\hslash {\overrightarrow{\nabla }}_{\mu }}}\right)\right]\hfill \\ & \equiv & {\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^{\alpha },{\gamma }^{\beta }\right\}\left({\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\alpha }}{i\hslash {\overrightarrow{\nabla }}_{\mu }}}{\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\beta }}{i\hslash {\overrightarrow{\nabla }}_{\nu }}}\right)+\right.\right.\hfill \\ & & +\left.{\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^{\beta },{\gamma }^{\alpha }\right\}\left({\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\beta }}{i\hslash {\overrightarrow{\nabla }}_{\mu }}}{\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\alpha }}{i\hslash {\overrightarrow{\nabla }}_{\nu }}}\right)\right)+\hfill \\ & & +{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^{\beta },{\gamma }^{\alpha }\right\}\left({\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\beta }}{i\hslash {\overrightarrow{\nabla }}_{\nu }}}{\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\alpha }}{i\hslash {\overrightarrow{\nabla }}_{\mu }}}\right)+\right.\hfill \\ & & +\left.\left.{\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^{\alpha },{\gamma }^{\beta }\right\}\left({\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\alpha }}{i\hslash {\overrightarrow{\nabla }}_{\nu }}}{\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\beta }}{i\hslash {\overrightarrow{\nabla }}_{\mu }}}\right)\right)\right],\hfill \end{array}$$

for $\left\{{\gamma }^{\beta },{\gamma }^{\alpha }\right\}=-\left\{{\gamma }^{\alpha },{\gamma }^{\beta }\right\}$ and $(i\hslash {\overrightarrow{\nabla }}_{\beta })(i\hslash {\overrightarrow{\nabla }}_{\alpha })=-(i\hslash {\overrightarrow{\nabla }}_{\alpha })(i\hslash {\overrightarrow{\nabla }}_{\beta })$, etc., we have,

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^{\mu },{\gamma }^{\nu }\right\}& =& {\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^{\alpha },{\gamma }^{\beta }\right\}\left({\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\alpha }}{i\hslash {\overrightarrow{\nabla }}_{\mu }}}{\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\beta }}{i\hslash {\overrightarrow{\nabla }}_{\nu }}}\right)+\right.\hfill \\ & & \left.+{\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^{\beta },{\gamma }^{\alpha }\right\}\left({\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\beta }}{i\hslash {\overrightarrow{\nabla }}_{\nu }}}{\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\alpha }}{i\hslash {\overrightarrow{\nabla }}_{\mu }}}\right)\right],\hfill \end{array}$$

inputting ${\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^{\alpha },{\gamma }^{\beta }\right\}\equiv {\mathrm{q}}_{\alpha \beta }=g^{\alpha \beta }$, etc.,

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^{\mu },{\gamma }^{\nu }\right\}& \equiv & {\displaystyle \frac{1}{2}}\left[{\mathrm{q}}_{\alpha \beta }\left({\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\alpha }}{i\hslash {\overrightarrow{\nabla }}_{\mu }}}{\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\beta }}{i\hslash {\overrightarrow{\nabla }}_{\nu }}}\right)+{\mathrm{q}}_{\beta \alpha }\left({\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\beta }}{i\hslash {\overrightarrow{\nabla }}_{\nu }}}{\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\alpha }}{i\hslash {\overrightarrow{\nabla }}_{\mu }}}\right)\right]\hfill \\ & =& {\displaystyle \frac{1}{2}}\left[{\mathrm{q}}_{\alpha \beta }\left({\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\alpha }}{i\hslash {\overrightarrow{\nabla }}_{\mu }}}{\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\beta }}{i\hslash {\overrightarrow{\nabla }}_{\nu }}}\right)+{\mathrm{q}}_{\alpha \beta }\left({\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\alpha }}{i\hslash {\overrightarrow{\nabla }}_{\mu }}}{\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\beta }}{i\hslash {\overrightarrow{\nabla }}_{\nu }}}\right)\right]\hfill \\ & \doteqdot & {\mathrm{q}}_{\mu \nu }=g^{\mu \nu }.\hfill \end{array}$$

Hence, this gives the lemma. □

By the way, (19) also satisfies an equivalency as:

Theorem 3.

Let M be a spin manifold. If $\mathcal{R}$ is the quantum scalar curvature of M then,

$$\begin{array}{ccc}\hfill \left(i\hslash {\gamma }^{\mu }{\overrightarrow{\nabla }}_{\mu }\right)\left(i\hslash {\gamma }^{\nu }{\overrightarrow{\nabla }}_{\nu }\right)|\psi \rangle +{\displaystyle \frac{1}{4}}\mathcal{R}|\psi \rangle & =& {(i\hslash )}^2{\gamma }^{\mu }{\overrightarrow{\nabla }}_{\mu }{\gamma }^{\nu }{\overrightarrow{\nabla }}_{\nu }|\psi \rangle +{\displaystyle \frac{1}{4}}\mathcal{R}|\psi \rangle \hfill \\ & =& {(i\hslash )}^2{g}^{\mu \nu }{\overrightarrow{\nabla }}_{\mu }{\overrightarrow{\nabla }}_{\nu }|\psi \rangle \doteqdot {\displaystyle \frac{{\partial }^2}{\partial {\widehat{\mathfrak{s}}}^2}}|\psi \rangle ,\hfill \end{array}$$

yields,

$$\begin{array}{c}\hfill \left[{(i\hslash )}^2{\overrightarrow{\nabla }}_{\mu }{\overrightarrow{\nabla }}^{\mu }+{\displaystyle \frac{1}{12}}\mathcal{R}\right]|\psi \rangle =0,\end{array}$$

(20)

for the construction $\psi =(\phi ,{\phi }_{\mu },{\phi }_{\mu \nu })$ when the spin of the particle is $(s=0,s=1,s=2)$ with the conditions ${\partial }^{\mu }{\phi }_{\mu }=0$, ${\partial }^{\mu }{\phi }_{\mu \nu }=0$, $g^{\mu \nu }{\phi }_{\mu \nu }=0$ and the total symmetrization of the indices as ${\phi }_{\mu \nu }\left(x\right)={\phi }_{\left(\mu \nu \right)}$.

Proof. 

[Hints.] The laplacian □ on a spinor is usually yielded as [2],

$$\begin{array}{ccc}\hfill \square |\psi \rangle & =& \left(i\hslash {\gamma }^{\mu }{\overrightarrow{\nabla }}_{\mu }\right)\left(i\hslash {\gamma }^{\nu }{\overrightarrow{\nabla }}_{\nu }\right)|\psi \rangle +{\displaystyle \frac{1}{4}}\mathcal{R}|\psi \rangle \hfill \\ & =& {(i\hslash )}^2{\gamma }^{\mu }{\overrightarrow{\nabla }}_{\mu }{\gamma }^{\nu }{\overrightarrow{\nabla }}_{\nu }|\psi \rangle +{\displaystyle \frac{1}{4}}\mathcal{R}|\psi \rangle ={(i\hslash )}^2{g}^{\mu \nu }{\overrightarrow{\nabla }}_{\mu }{\overrightarrow{\nabla }}_{\nu }|\psi \rangle ,\hfill \end{array}$$

which again yields,

$$\begin{array}{ccc}\hfill {(i\hslash )}^2{g}_{\mu \nu }{g}^{\mu \nu }{\overrightarrow{\nabla }}_{\mu }{\overrightarrow{\nabla }}_{\nu }|\psi \rangle & =& {(i\hslash )}^2{g}_{\mu \nu }{\gamma }^{\mu }{\overrightarrow{\nabla }}_{\mu }{\gamma }^{\nu }{\overrightarrow{\nabla }}_{\nu }|\psi \rangle +{\displaystyle \frac{1}{4}}{g}_{\mu \nu }\mathcal{R}|\psi \rangle \hfill \\ & =& {(i\hslash )}^2{\gamma }_{\nu }{\overrightarrow{\nabla }}_{\mu }{\gamma }^{\nu }{\overrightarrow{\nabla }}_{\nu }|\psi \rangle +{\displaystyle \frac{1}{4}}{g}_{\mu \nu }\mathcal{R}|\psi \rangle \hfill \\ & =& 4{(i\hslash )}^2{\overrightarrow{\nabla }}_{\mu }{\overrightarrow{\nabla }}_{\nu }|\psi \rangle +{\displaystyle \frac{1}{4}}{g}_{\mu \nu }\mathcal{R}|\psi \rangle ,\hfill \end{array}$$

for ${\gamma }_{\nu }{\gamma }^{\nu }=4$, hence,

$$\begin{array}{ccc}\hfill g_{\mu \nu }\left[4{(i\hslash )}^2{\overrightarrow{\nabla }}_{\mu }{\overrightarrow{\nabla }}^{\mu }+{\displaystyle \frac{1}{4}}\mathcal{R}\right]|\psi \rangle & =& {(i\hslash )}^2{g}_{\mu \nu }{\overrightarrow{\nabla }}_{\mu }{\overrightarrow{\nabla }}^{\mu }|\psi \rangle ,\hfill \\ \hfill \therefore \left[{(i\hslash )}^2{\overrightarrow{\nabla }}_{\mu }{\overrightarrow{\nabla }}^{\mu }+{\displaystyle \frac{1}{12}}\mathcal{R}\right]|\psi \rangle & =& 0.\hfill \end{array}$$

This completes the proof of (20). □

Terms in (20) possess local conformal symmetry, while the fraction $1/12$ there in (20) is the nonminimal parameter. Evidently, (20) is not the Klein-Gordon equation emerged from spinor fields. Thus, the spinor field representation with quantum Ricci scalar would be,

$$\begin{array}{c}\hfill \left[(i\hslash ){\gamma }^{\mu }{\overrightarrow{\nabla }}_{\mu }-{\displaystyle \frac{{\mathbf{I}}_4}{2\sqrt{3}}}\sqrt{\mathcal{R}}\right]|\psi \rangle =0,\end{array}$$

(21)

for the construction $\psi =(\phi ,{\phi }_{\nu })$ when the spin of the particle is $(s=1/2,s=3/2)$ with ${\partial }^{\nu }{\phi }_{\nu }=0$ and ${\gamma }^{\nu }{\phi }_{\nu }=0$.

Remark 2.

In General Theory of Relativity, matter means everything that is not the gravitational field (metric), but in (20) as well as in its spinor field representation (21), we have replaced matter with quantum Ricci scalar $\mathcal{R}$ whereas General Relativistic Ricci scalar R never depicts such a possibility.

From $\widehat{m}=(i\hslash )\wp {\widehat{m}}_0$ and $\Theta \widehat{m}=(i\hslash ){\gamma }_Q{\overrightarrow{\nabla }}_0$ of Rremark 1, we get, ${\widehat{m}}_0=(i\hslash ){\Theta }^{-1}{\overrightarrow{\nabla }}_0$ for $\wp ={(i\hslash )}^{-1}{\gamma }_Q$. Combining, $\left[{(i\hslash )}^2{\overrightarrow{\nabla }}_{\mu }{\overrightarrow{\nabla }}^{\mu }+{\left(i\Theta \widehat{m}\right)}^2\right]|\psi \rangle =0$ and $\left[{(i\hslash )}^2{\overrightarrow{\nabla }}_{\mu }{\overrightarrow{\nabla }}^{\mu }+{\displaystyle \frac{1}{12}}\mathcal{R}\right]|\psi \rangle =0$ we get, $i\Theta \widehat{m}={\displaystyle \frac{1}{2\sqrt{3}}}\sqrt{\mathcal{R}}$, which yields for $\hslash =1$ as, $\widehat{m}=-q^{-1}{\displaystyle \frac{1}{2\sqrt{3}}}\sqrt{\mathcal{R}}$ since $\Theta =iq$, i.e., ${\widehat{m}}_0=-{\displaystyle \frac{1}{2\sqrt{3}}}{\left({\gamma }_{Q}q\right)}^{-1}\sqrt{\mathcal{R}}$.

Theorem 4

(Uncertainty Relations). For ${\widehat{m}}_0=(i\hslash ){\Theta }^{-1}{\overrightarrow{\nabla }}_0$ and/or ${\widehat{m}}_0={\displaystyle \frac{1}{2\sqrt{3}}}{\left(i\Theta {\gamma }_Q\right)}^{-1}\sqrt{\mathcal{R}}$, we have $\sqrt{\mathcal{R}}=i2\sqrt{3}{\gamma }_Q(i\hslash ){\overrightarrow{\nabla }}_0$, then we get the uncertainty relations as,

$$\begin{array}{c}\hfill \Delta {\widehat{m}}_0\Delta t\ge {\displaystyle \frac{\hslash }{2}},\mathrm{and}\Delta \sqrt{\mathcal{R}}\Delta t\ge {\displaystyle \frac{\hslash }{2}}.\end{array}$$

(22)

Proof. 

[Hints.] To quantify the precision of the rest mass and quantum Ricci scalar along with time, let us consider the standard deviation ${\sigma }_{\{{\widehat{m}}_0,\sqrt{\mathcal{R}},t\}}$. Let the variances of rest mass (${\sigma }_{{\widehat{m}}_0}$) and time (${\sigma }_t$), defined as,

$$\begin{array}{c}\hfill {\sigma }_{{\widehat{m}}_0}^2={\int }_{-\infty }^{\infty }{\widehat{m}}_0^2·|\psi \left({\widehat{m}}_0\right){|}^2\mathrm{d}{\widehat{m}}_0,{\sigma }_t^2={\int }_{-\infty }^{\infty }{t}^2·{\left|\phi \left(t\right)\right|}^2\mathrm{d}t.\end{array}$$

Evaluating the inverse Fourier transform through integration by parts, we get the theorem with equality if and only if ${\widehat{m}}_0$ and t are linearly dependent. A similar result would hold for the pair of conjugate variables $\sqrt{\mathcal{R}}$ and t. □

Theorem 5.

A fermionic analogy to quantum Christoffel symbol ${\left.{\Gamma }_{\mu \nu }^k\right|}_{\gamma }$ yields an antisymmetrized quantum Ricci tensor ${\left.{\mathcal{R}}_{\mu \nu }\right|}_{\gamma }$ along with a non-vacuum fermionic analogy to (Quantum) Einstein field equation.

Proof. 

Not considering the spin connection as our basic consideration as we have stated in the beginning line of the Section 2, let us consider,

$$\begin{array}{ccc}\hfill {\left.{\Gamma }_{\mu \nu }^k\right|}_{\gamma }|\psi \rangle & =& {\displaystyle \frac{1}{8{\mathbf{I}}_4}}\left\{{\gamma }^k,{\gamma }^{\ell }\right\}\left[\left(i\hslash {\overrightarrow{\nabla }}_{\mu }\right)\left\{{\gamma }_{\nu },{\gamma }_{\ell }\right\}+\right.\hfill \\ & & \left.+\left(i\hslash {\overrightarrow{\nabla }}_{\nu }\right)\left\{{\gamma }_{\mu },{\gamma }_{\ell }\right\}-\left(i\hslash {\overrightarrow{\nabla }}_{\ell }\right)\left\{{\gamma }_{\mu },{\gamma }_{\nu }\right\}\right]|\psi \rangle ,\hfill \end{array}$$

then,

$$\begin{array}{ccc}\hfill {\left.{\mathcal{R}}_{\mu \nu }\right|}_{\gamma }|\psi \rangle & =& {\displaystyle \frac{1}{2}}\left[\left\{\left(i\hslash {\overrightarrow{\nabla }}_{\ell }\right),{\Gamma }_{\mu \nu }^{\ell }\right\}-\left\{\left(i\hslash {\overrightarrow{\nabla }}_{\nu }\right),{\Gamma }_{\mu \ell }^{\ell }\right\}+\right.\hfill \\ & & +\left\{{\Gamma }_{k\ell }^{\ell },{\Gamma }_{\mu \nu }^k\right\}-\left\{{\Gamma }_{k\nu }^{\ell },{\Gamma }_{\mu \ell }^k\right\}]|\psi \rangle ,\hfill \end{array}$$

so, a non-vacuum fermionic analogy to (Quantum) Einstein field equation is,

$$\begin{array}{c}\hfill \left[{\left.{\mathcal{R}}^{\mu \nu }\right|}_{\gamma }-{\displaystyle \frac{1}{4{\mathbf{I}}_4}}\left\{{\gamma }^{\mu },{\gamma }^{\nu }\right\}{\left.\mathcal{R}\right|}_{\gamma }\right]|\psi \rangle -{\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^{\mu },{\gamma }^{\nu }\right\}{\left.{\Lambda }^{\prime }\right|}_{\gamma }|\psi \rangle \\ \hfill ={\displaystyle \frac{8\pi G}{c^4}}{\left.{\mathcal{T}}^{\mu \nu }\right|}_{\gamma }|\psi \rangle ,\end{array}$$

(23)

where the energy-momentum tensor ${\left.{\mathcal{T}}^{\mu \nu }\right|}_{\gamma }$ is, for example, generated by the energy-momentum tensor $T_{\alpha \beta }$ of the spinor field in such a way that ${\left.{\mathcal{T}}^{\mu \nu }\right|}_{\gamma }=g^{\mu \nu }{T}^{\alpha \beta }{T}_{\alpha \beta }$ according to the definition of (23), where, for example [2],

$$\begin{array}{ccc}\hfill T_{\alpha \beta }& =& {\displaystyle \frac{1}{2}}\left(i\hslash \right)\left[\overline{\psi }{\gamma }_{(\alpha }{\overrightarrow{\nabla }}_{\beta )}\psi -{\overrightarrow{\nabla }}_{(\alpha }\overline{\psi }{\gamma }_{\beta )}\psi \right]-\hfill \\ & & -{\displaystyle \frac{1}{2}}\left(i\hslash \right)g_{\alpha \beta }\left[\overline{\psi }{\gamma }^{\lambda }{\overrightarrow{\nabla }}_{\lambda }\psi -{\overrightarrow{\nabla }}_{\lambda }\overline{\psi }{\gamma }^{\lambda }\psi \right]+{\displaystyle \frac{{\mathbf{I}}_4}{2\sqrt{3}}}\sqrt{\mathcal{R}}\overline{\psi }\psi g_{\alpha \beta },\hfill \end{array}$$

for the mass-independent spinor field. □

So, not owing to the mass dimension of G in (23) for ${\left(i\hslash \right)}^2$ due to ${\left.{\mathcal{T}}^{\mu \nu }\right|}_{\gamma }$, the perturbative version of (23) is renormalizable.

Let us develop a first order quantum equation for fermions in $(3+1)D$ analogous to Theorem 2.

Theorem 6.

For (19), there exists a first order quantum equation for fermions in $(3+1)D$ as,

$$\begin{array}{c}\hfill i\hslash {\displaystyle \frac{\partial }{\partial t}}|\psi \rangle ={\displaystyle \frac{i\hslash }{2}}\left({\Phi }_i{\overrightarrow{\nabla }}_j+{\Phi }_j{\overrightarrow{\nabla }}_i\right)|\psi \rangle +V|\psi \rangle ,\end{array}$$

while V is the external potential energy.

Proof. 

Let (18) be written as,

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}}\left[\left({\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^0,{\gamma }^0\right\}{(i\hslash )}^2{\overrightarrow{\nabla }}_0^2+{\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^i,{\gamma }^j\right\}{(i\hslash )}^2{\overrightarrow{\nabla }}_i{\overrightarrow{\nabla }}_j\right)\right.+\\ \hfill \left.+\left({\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^0,{\gamma }^0\right\}{(i\hslash )}^2{\overrightarrow{\nabla }}_0^2+{\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^j,{\gamma }^i\right\}{(i\hslash )}^2{\overrightarrow{\nabla }}_j{\overrightarrow{\nabla }}_i\right)\right]|\psi \rangle \\ \hfill ={(i\hslash )}^2{\gamma }_Q^2{\overrightarrow{\nabla }}_0^2{\mathbf{I}}_4^2|\psi \rangle .\end{array}$$

Then the dynamics of the quantum state for fermions is possible to be defined as follows since ${\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^0,{\gamma }^0\right\}=1$, whereas ${\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^i,{\gamma }^j\right\}=g^{ij}$ and ${\displaystyle \frac{1}{2{\mathbf{I}}_4}}\left\{{\gamma }^j,{\gamma }^i\right\}=g^{ji}$ as $g^{ij}\equiv g^{ji}=[-1,-1,-1]$ for $i,j=1,2,3$,

$$\begin{array}{ccc}\hfill i\hslash {\displaystyle \frac{\partial }{\partial \left(ct\right)}}|\psi \rangle & =& {(i\hslash )}^{-1}{\overrightarrow{\nabla }}_0^{-1}\left[{(i\hslash )}^2{\gamma }_Q^2{\overrightarrow{\nabla }}_0^2{\mathbf{I}}_4^2+{\displaystyle \frac{1}{2}}\left({(i\hslash )}^2{\overrightarrow{\nabla }}_i{\overrightarrow{\nabla }}_j+{(i\hslash )}^2{\overrightarrow{\nabla }}_j{\overrightarrow{\nabla }}_i\right)\right]|\psi \rangle \hfill \\ & =& (i\hslash )\left[{\gamma }_Q^2{\overrightarrow{\nabla }}_0{\mathbf{I}}_4^2+{\displaystyle \frac{1}{2}}\left({\overrightarrow{\nabla }}_0^{-1}{\overrightarrow{\nabla }}_i{\overrightarrow{\nabla }}_j+{\overrightarrow{\nabla }}_0^{-1}{\overrightarrow{\nabla }}_j{\overrightarrow{\nabla }}_i\right)\right]|\psi \rangle \hfill \\ & =& (i\hslash )\left[{\gamma }_Q^2{\overrightarrow{\nabla }}_0{\mathbf{I}}_4^2+{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{c}{{\mathsf{v}}^i}}{\overrightarrow{\nabla }}_j+{\displaystyle \frac{c}{{\mathsf{v}}^j}}{\overrightarrow{\nabla }}_i\right)\right]|\psi \rangle ,\hfill \end{array}$$

while ${\overrightarrow{\nabla }}_0^{-1}{\overrightarrow{\nabla }}_i={\left({\mathsf{v}}^i\right)}^{-1}c$, etc. Therefore, by introducing external potential energy V and the Hamiltonian (or total energy) operator $\mathcal{H}$, we have a first order quantum equation for fermions in $(3+1)D$ as,

$$\begin{array}{c}\hfill i\hslash {\displaystyle \frac{\partial }{\partial t}}|\psi \rangle ={\displaystyle \frac{i\hslash }{2}}\left({\Phi }_i{\overrightarrow{\nabla }}_j+{\Phi }_j{\overrightarrow{\nabla }}_i\right)|\psi \rangle +V|\psi \rangle \equiv \mathcal{H}|\psi \rangle ,\end{array}$$

(24)

for $({\Phi }_i,{\Phi }_j)=\left({\left[(1-{\gamma }_Q^2{\mathbf{I}}_4^2){\mathsf{v}}^i\right]}^{-1}{c}^2,{\left[(1-{\gamma }_Q^2{\mathbf{I}}_4^2){\mathsf{v}}^j\right]}^{-1}{c}^2\right)$. □

The analogy between bosonic (15) and fermionic (23) (Quantum) Einstein field equations in $(3+1)D$, as well as the presence of relativistic effects in the bosonic (16) and fermionic (24) first order quantum equations in $(3+1)D$, and (20) as well as its spinor field representation (21) invoke us to name this formalism as General Quantum Gravity.

2.1. Renormalization [6]

Let $\varphi \left(x\right)$ is a field quantity or field operator or simply the field, which is the linear operator depending on a point ${(i\hslash )}^{-1}x$ in four-dimensional $\mathcal{V}\subset \mathcal{H}=L^2\left({\mathbb{R}}^{3,1}\right)$ space. Let there exists a non-singular matrix $\eta$ such that hermitian conjugation ${[\eta \Lambda (\partial )]}^{+}=\eta \Lambda (-\partial )$ with $\Lambda (\partial )$ is of the form $\Lambda (\partial )={\sum }_{\ell =0}^N{(i\hslash )}^{1,\dots ,\ell }{\Lambda }_{{\mu }_1\dots {\mu }_{\ell }}{\partial }_{{\mu }_1}\dots {\partial }_{{\mu }_{\ell }}$, where ${\Lambda }_{{\mu }_1\dots {\mu }_{\ell }}$ is symmetric in all pairs of indices and independent of ${(i\hslash )}^{-1}x$. Then (11) divisor exists such that $\Lambda (\partial )\mathrm{d}(\partial )=\mathrm{d}(\partial )\Lambda (\partial )={(i\hslash )}^2{\overrightarrow{\nabla }}_{\mu }{\overrightarrow{\nabla }}^{\mu }-{\Theta }^2{\widehat{m}}^2$. The field equation is Lorentz invariant and $[{\ell }_{\mu \nu },\Lambda (\partial )]=0$, where ${\ell }_{\mu \nu }$ is: ${\ell }_{\mu \nu }=x_{\mu }{\partial }_{\nu }-x_{\nu }{\partial }_{\mu }+i{S}_{\mu \nu }$, and $S_{\mu \nu }$ is defined by the transformation of $\varphi \left(x\right)$ under an infinitesimal Lorentz-like transformation, i.e., $\varphi \left(x\right)\to {\varphi }^{\prime }\left(x^{\prime }\right)=[1+(i/2)S_{\mu \nu }\delta {\omega }_{\mu \nu }]\varphi \left(x\right)$, when ${(i\hslash )}^{-1}{x}_{\mu }\to {(i\hslash )}^{-1}{x}_{\mu }^{\prime }={(i\hslash )}^{-1}({\delta }_{\mu \nu }+\delta {\omega }_{\mu \nu })x_{\nu }$ and $\delta {\omega }_{\mu \nu }+\delta {\omega }_{\nu \mu }=0$.

Now, with this background along with Section 2 of Chapter V in page 112 of [6], we can easily show that the operator ${\widehat{\mathcal{P}}}^{\mu }$ and the commutation relation of ${\varphi }_{\alpha }\left(x\right)$ so that $(i\hslash ){\overrightarrow{\nabla }}_{\mu }{\varphi }_{\alpha }\left(x\right)=\left[{\varphi }_{\alpha }\left(x\right),{\widehat{\mathcal{P}}}^{\mu }\right]\equiv \left\{\left[{\varphi }_{\alpha }\left(x\right),p^0\right],\left[{\varphi }_{\alpha }\left(x\right),{\widehat{\mathbf{p}}}^i\right]\right\}$, for $i=1,2,3$, is consistent with the equation $\Lambda (\partial )\varphi \left(x\right)=0$ or equivalently ${\Lambda }_{\alpha \beta }(\partial ){\varphi }_{\beta }\left(x\right)=0$.

Let the (quantum) metric tensor ${\mathrm{q}}_{\mu \nu }={\mathrm{q}}_{\alpha \beta }\left({\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\alpha }}{i\hslash {\overrightarrow{\nabla }}_{\mu }}}{\displaystyle \frac{i\hslash {\overrightarrow{\nabla }}_{\beta }}{i\hslash {\overrightarrow{\nabla }}_{\nu }}}\right)$ of (2) may transform as ${(i\hslash )}^2{\mathrm{q}}_{\mu \nu }{\overrightarrow{\nabla }}_{\mu }{\overrightarrow{\nabla }}_{\nu }={(i\hslash )}^2{\mathrm{q}}_{\alpha \beta }{\overrightarrow{\nabla }}_{\alpha }{\overrightarrow{\nabla }}_{\beta }\equiv {\partial }_{\widehat{\mathfrak{s}}}^2$ for (3). Then $(i\hslash ){\overrightarrow{\nabla }}_{\mu }\varphi \left(x\right)=\left[\varphi \left(x\right),{\widehat{\mathcal{P}}}^{\mu }\right]$ may yield (with the summation convention):

$$\begin{array}{ccc}\hfill \sum _{\mu ,\nu =0}^3{(i\hslash )}^2{\mathrm{q}}_{\mu \nu }{\overrightarrow{\nabla }}_{\mu }{\overrightarrow{\nabla }}_{\nu }\varphi {\left(x\right)}^2& \equiv & \sum _{\mu ,\nu =0}^3{\mathrm{q}}_{\mu \nu }{\widehat{\mathcal{P}}}^{\mu }{\widehat{\mathcal{P}}}^{\nu }\varphi {\left(x\right)}^2\hfill \\ & =& \sum _{\mu ,\nu =0}^3{\mathrm{q}}_{\mu \nu }\left[\varphi {\left(x\right)}^2,{\widehat{\mathcal{P}}}^{\mu }{\widehat{\mathcal{P}}}^{\nu }\right]\equiv \left[\varphi {\left(x\right)}^2,{\partial }_{\widehat{\mathfrak{s}}}^2\right].\hfill \end{array}$$

Thus (by omitting the summation convention),

$$\begin{array}{ccc}\hfill {\mathrm{q}}_{\mu \nu }\left[\varphi {\left(x\right)}^2,{\widehat{\mathcal{P}}}^{\mu }{\widehat{\mathcal{P}}}^{\nu }\right]& \equiv & {\mathrm{q}}_{\alpha \beta }\left[\varphi {\left(x\right)}^2,{\widehat{\mathcal{P}}}^{\alpha }{\widehat{\mathcal{P}}}^{\beta }\right],\hfill \\ \hfill \mathrm{i}.\mathrm{e}.,{\mathrm{q}}_{\mu \nu }& =& {\mathrm{q}}_{\alpha \beta }{\displaystyle \frac{\left[\varphi {\left(x\right)}^2,{\widehat{\mathcal{P}}}^{\alpha }{\widehat{\mathcal{P}}}^{\beta }\right]}{\left[\varphi {\left(x\right)}^2,{\widehat{\mathcal{P}}}^{\mu }{\widehat{\mathcal{P}}}^{\nu }\right]}}.\hfill \end{array}$$

(25)

Hence, the metric is an object of quantization. So as (13), as well as (14), is also an object of quantization for (25) in such a way,

$$\begin{array}{ccc}\hfill {\Gamma }_{\mu \nu }^k\varphi \left(x\right)& =& {\displaystyle \frac{1}{2}}{\mathrm{q}}_{k\ell }\left[\left[\varphi \left(x\right),{\widehat{\mathcal{P}}}^{\mu }\right]{\mathrm{q}}^{\nu \ell }+\left[\varphi \left(x\right),{\widehat{\mathcal{P}}}^{\nu }\right]{\mathrm{q}}^{\mu \ell }-\left[\varphi \left(x\right),{\widehat{\mathcal{P}}}^{\ell }\right]{\mathrm{q}}^{\mu \nu }\right],\hfill \\ \hfill {\mathcal{R}}_{\mu \nu }\varphi {\left(x\right)}^2& =& \left[\left[\varphi \left(x\right),{\widehat{\mathcal{P}}}^{\ell }\right]{\Gamma }_{\mu \nu }^{\ell }\varphi \left(x\right)-\left[\varphi \left(x\right),{\widehat{\mathcal{P}}}^{\nu }\right]{\Gamma }_{\mu \ell }^{\ell }\varphi \left(x\right)+\right.\hfill \\ & & +{\Gamma }_{k\ell }^{\ell }{\Gamma }_{\mu \nu }^k\varphi {\left(x\right)}^2-{\Gamma }_{k\nu }^{\ell }{\Gamma }_{\mu \ell }^k\varphi {\left(x\right)}^2].\hfill \end{array}$$

Thus, other two forms, i.e., quantum Riemann tensor ${\mathcal{R}}_{\mu \nu \alpha \beta }$ and quantum Ricci scalar $\mathcal{R}$ also reserve the similar theory.

For a real scalar field with a $\lambda {\phi }^4$ interaction and $\varphi \mapsto \phi$ (though, the following formalism must be true without considering this map), the renormalized Langrangian with (20) is ${\mathcal{L}}_R={\displaystyle \frac{1}{2}}\left(1+\delta z_1\right){\mathrm{q}}_{\alpha \beta }\left[{\phi }_R{\left(x\right)}^2,{\widehat{\mathcal{P}}}^{\alpha }{\widehat{\mathcal{P}}}^{\beta }\right]-{\displaystyle \frac{1}{24}}\left(1+\delta z_2\right)\mathcal{R}{\phi }_R^2-\left(1+\delta z_4\right){\lambda }_R{\phi }_R^4$. By denoting $z_1=1+\delta z_1$, $z_1{z}_{\mathcal{R}}=1+\delta z_2$ and $z_1^2{z}_{\lambda }=1+\delta z_4$, we get ${\mathcal{L}}_R={\displaystyle \frac{1}{2}}{z}_1{\mathrm{q}}_{\alpha \beta }\left[{\phi }_R{\left(x\right)}^2,{\widehat{\mathcal{P}}}^{\alpha }{\widehat{\mathcal{P}}}^{\beta }\right]-{\displaystyle \frac{1}{24}}{z}_1{z}_{\mathcal{R}}{\mathcal{R}}_R{\phi }_R^2-z_1^2{z}_{\lambda }{\lambda }_R{\phi }_R^4$. It is clear that the theory is multiplicatively renormalizable, and the renormalized Lagrangian ${\mathcal{L}}_R$ is related to the bare Lagrangian by the renormalization transformation $\phi =z_1^{1/2}{\phi }_R$, $\mathcal{R}=z_{\mathcal{R}}{\mathcal{R}}_R$ and $\lambda =z_{\lambda }{\lambda }_R$, where the renormalization constants $z_{1,\mathcal{R},\lambda }$ depend on the coupling constant ${\lambda }_R$ and on regularization parameters. Since ${\mathrm{q}}_{\mu \nu }\left[\phi {\left(x\right)}^2,{\widehat{\mathcal{P}}}^{\mu }{\widehat{\mathcal{P}}}^{\nu }\right]={\mathrm{q}}_{\alpha \beta }\left[\phi {\left(x\right)}^2,{\widehat{\mathcal{P}}}^{\alpha }{\widehat{\mathcal{P}}}^{\beta }\right]$, then, ${\mathcal{L}}_R$ could be written as,

$$\begin{array}{ccc}\hfill {\mathcal{L}}_R^{\prime }& =& {\displaystyle \frac{1}{2}}{z}_1{\left(z_1^{\prime }\right)}^{-1}{\mathrm{q}}_{\alpha \beta }{\displaystyle \frac{\left[{\phi }_R{\left(x\right)}^2,{\widehat{\mathcal{P}}}^{\alpha }{\widehat{\mathcal{P}}}^{\beta }\right]}{\left[{\phi }_R{\left(x\right)}^2,{\widehat{\mathcal{P}}}^{\mu }{\widehat{\mathcal{P}}}^{\nu }\right]}}-{\displaystyle \frac{1}{24}}{z}_1{\left(z_1^{\prime }\right)}^{-1}{z}_{\mathcal{R}}{\displaystyle \frac{{\mathcal{R}}_R}{\left[{\phi }_R{\left(x\right)}^2,{\widehat{\mathcal{P}}}^{\mu }{\widehat{\mathcal{P}}}^{\nu }\right]}}{\phi }_R^2-\hfill \\ & & -z_1^2{\left(z_1^{\prime }\right)}^{-1}{z}_{\lambda }{\displaystyle \frac{{\lambda }_R}{\left[{\phi }_R{\left(x\right)}^2,{\widehat{\mathcal{P}}}^{\mu }{\widehat{\mathcal{P}}}^{\nu }\right]}}{\phi }_R^4\hfill \\ & =& {\displaystyle \frac{1}{2}}{z}_1{\left(z_1^{\prime }\right)}^{-1}{\phi }_R{\mathrm{q}}_{\mu \nu }{\phi }_R-{\displaystyle \frac{1}{24}}{z}_1{\left(z_1^{\prime }\right)}^{-1}{z}_{\mathcal{R}}{\left[{\phi }_R{\left(x\right)}^2,{\widehat{\mathcal{P}}}^{\mu }{\widehat{\mathcal{P}}}^{\nu }\right]}^{-1}{\mathcal{R}}_R{\phi }_R^2-\hfill \\ & & -z_1^2{\left(z_1^{\prime }\right)}^{-1}{z}_{\lambda }{\left[{\phi }_R{\left(x\right)}^2,{\widehat{\mathcal{P}}}^{\mu }{\widehat{\mathcal{P}}}^{\nu }\right]}^{-1}{\lambda }_R{\phi }_R^4,\hfill \end{array}$$

(26)

where ${\mathcal{L}}_R^{\prime }={\left[{\phi }_R{\left(x\right)}^2,{\widehat{\mathcal{P}}}^{\mu }{\widehat{\mathcal{P}}}^{\nu }\right]}^{-1}{\mathcal{L}}_R$ and $z_1^{\prime }=1+\delta z_1^{\prime }$. Thus, (26) is multiplicatively renormalizable. So as (25), as well as quantum Ricci scalar $\mathcal{R}$, is multiplicatively renormalizable, too. Then, we can show that the quantum Christoffel symbol ${\Gamma }_{\mu \nu }^k$ is actually multiplicatively renormalizable in such a way that,

$$\begin{array}{ccc}\hfill {\mathcal{L}}_R^{(\Gamma )}& =& {\displaystyle \frac{1}{4}}{z}_1{\left(z_1^{\prime }\right)}^{-1}{\phi }_R{\mathrm{q}}_{k\ell }{\phi }_R\left[{\left(z_1^{\prime }\right)}^{1/2}{\phi }_R\left[{\phi }_R\left(x\right),{\widehat{\mathcal{P}}}^{\mu }\right]\left(z_1{\left(z_1^{\prime }\right)}^{-1}{\phi }_R{\mathrm{q}}^{\nu \ell }{\phi }_R\right)\right.+\hfill \\ & & +{\left(z_1^{\prime }\right)}^{1/2}{\phi }_R\left[{\phi }_R\left(x\right),{\widehat{\mathcal{P}}}^{\nu }\right]\left(z_1{\left(z_1^{\prime }\right)}^{-1}{\phi }_R{\mathrm{q}}^{\mu \ell }{\phi }_R\right)-\hfill \\ & & -\left.{\left(z_1^{\prime }\right)}^{1/2}{\phi }_R\left[{\phi }_R\left(x\right),{\widehat{\mathcal{P}}}^{\ell }\right]\left(z_1{\left(z_1^{\prime }\right)}^{-1}{\phi }_R{\mathrm{q}}^{\mu \nu }{\phi }_R\right)\right].\hfill \end{array}$$

Thus, the quantum forms ${\mathcal{R}}_{\mu \nu \alpha \beta }$, ${\mathcal{R}}_{\mu \nu }$ and $\mathcal{R}$ are evidently become multiplicatively renormalizable. Apparently, all divergences of the “dangerous” [3]${\mathcal{R}}^{\mu \nu \alpha \beta }{\mathcal{R}}_{\mu \nu \alpha \beta }$, ${\mathcal{R}}_{\alpha \beta }^{\mu \nu }{\mathcal{R}}_{\epsilon \zeta }^{\alpha \beta }{\mathcal{R}}_{\mu \nu }^{\epsilon \zeta }$ and ${\mathcal{R}}_{\mu \nu \alpha \beta }{\mathcal{R}}_{\epsilon \zeta }^{\mu \alpha }{\mathcal{R}}^{\nu \epsilon \beta \zeta }$ vanish in $(3+1)D$ quantum spacetime.

3. Conclusion

In this study of General Quantum Gravity, the Lorentz-like transformation (7), the interrelated (11), (12) and (16), as well as the bosonic (15) and fermionic (23) (Quantum) Einstein field equations, even the boson field representation with Ricci scalar (20) as well as its spinor field representation (21), are all emerged from the (quantum) quadratic form $Q(i\hslash {\overrightarrow{\nabla }}_0,i\hslash {\overrightarrow{\nabla }}_i)$ and the (quantum) metric tensor ${\mathrm{q}}_{\mu \nu }$ defined by (1) and (2), respectively. Thus, for (8) and for the bosonic (15) and fermionic (23) (Quantum) Einstein field equations, General Quantum Gravity yields that: Quantum Mechanics and Theory of Special and General Relativity are inseparable and naturally inter-expressible for the (quantum) quadratic form $Q(i\hslash {\overrightarrow{\nabla }}_0,i\hslash {\overrightarrow{\nabla }}_i)$ and the (quantum) metric tensor ${\mathrm{q}}_{\mu \nu }$ in $(3+1)D$ quantum spacetime.

From this work, we can determine an important unsolved fundamental problem: What is time? By comparing $\widehat{E}\to i\hslash {\partial }_t$ with $\widehat{E}\to c[\partial /\partial \left({\gamma }_Q\widehat{\mathfrak{s}}\right)]$ of (9), i.e., having $i\hslash {\partial }_t|\psi \rangle =c[\partial /\partial \left({\gamma }_Q\widehat{\mathfrak{s}}\right)]|\psi \rangle$, we can get the change of time for (4) while $t_0=0$ as,

$$\begin{array}{ccc}\hfill \mathrm{d}t|\psi \rangle & =& (i\hslash )c^{-1}\mathrm{d}\left({\gamma }_Q\widehat{\mathfrak{s}}\right)|\psi \rangle =c^{-1}{\gamma }_Q{\left({\mathrm{q}}^{\mu \nu }\mathrm{d}{x}^{\mu }\mathrm{d}{x}^{\nu }\right)}^{1/2}|\psi \rangle \hfill \\ & \doteqdot & c^{-1}{\gamma }_Q{\left(g_{\mu \nu }\mathrm{d}{x}^{\mu }\mathrm{d}{x}^{\nu }\right)}^{1/2}|\psi \rangle =c^{-1}{\gamma }_Q\mathrm{d}s|\psi \rangle ,\hfill \end{array}$$

(27)

for the (non-quantum) pure relativistic interval $\mathrm{d}s\ne \mathrm{d}\widehat{\mathfrak{s}}$, thus, time shifts itself from quantum frame to relativistic frame (Universality of time). Hence, time does not exist unless the reference frame is relativistically dynamic against the speed of light. On the other hand, at the speed of light, when ${\mathsf{v}}^{\mu }\to c$, the differentiation $dt$ becomes changeless, i.e., time freezes at the speed of light. As a result, photon’s rest mass becomes uncertain at ${\mathsf{v}}^{\mu }=c$ due to (22). Actually, (27) is the famous Einstein relation implying that a moving particle lives longer by a factor ${\gamma }_Q$. The classical direct experimental evidence for this phenomenon (see, for example, page 20 of [7]) justifies the validity of $\widehat{E}\to i\hslash {\partial }_t$ as well as $\widehat{E}\to c[\partial /\partial \left({\gamma }_Q\widehat{\mathfrak{s}}\right)]$, in other words, the validity of (3), so as the General Quantum Gravity, likewise.

We can also determine here another important unsolved fundamental problem: Why gravity is feeble against other fundamental forces? For fermionic (Quantum) Einstein field equation (23), we have considered the energy-momentum tensor ${\left.{\mathcal{T}}^{\mu \nu }\right|}_{\gamma }=g^{\mu \nu }{T}^{\alpha \beta }{T}_{\alpha \beta }$ generated by the energy-momentum tensor of the spinor field $T_{\alpha \beta }$. Taking the relative strength based on the strong force felt by a proton-proton pair as unity and omitting all additional conditions, it yields roughly that Approximate Relative Strength of$T^{\alpha \beta }\sim$Approximate Relative Strength of${\left({\left.{\mathcal{T}}^{\mu \nu }\right|}_{\gamma }\right)}^{1/2}\sim {10}^{-19}$. By adjusting the additional conditions, we may get the Approximate Relative Strength of electroweak force as $\sim {10}^{-13}$, which easily expresses that gravity is many orders of magnitude smaller than electroweak or strong interactions.