Modern cryptographic protocols such as zero-knowledge proofs and secure multi-party computation have increased the demand for a novel category of symmetric primitives. These primitives are not optimized for traditional platforms such as servers, microcontrollers, and desktop computers but rather for their ability to be implemented in arithmetic circuits. To enable efficient arithmetic operations, they define operations over larger finite fields and use low-degree invertible functions to construct their non-linear layers. Grendel is an arithmetization-oriented permutation that leverages the Legendre Symbol to enhance the growth of algebraic degrees in its non-linear layer. In this paper, we present a preimage attack on the sponge hash function instantiated with the full rounds of the Grendel permutation using algebraic methods. We introduce a technique that allows us to eliminate two full rounds of substitution permutation networks (SPN) in the sponge hash function with minimal or no additional cost. This method can be combined with univariate root-finding techniques and Gröbner basis attacks to break the number of rounds claimed by the designers. By utilizing this strategy, our attack achieves an improvement of two additional rounds compared to the previous state-of-the-art attack. While not breaking its security margin, it allows us to further understand the design and analysis of such cryptographic primitives.

Keywords:

Subject: Computer Science and Mathematics - Other

1. Introduction

Arithmetization-oriented primitives have recently been widely employed in advanced cryptographic protocols, including Fully Homomorphic Encryption (FHE) protocols, Multiparty Computation (MPC) protocols, and Zero-Knowledge (ZK) proofs. These advanced cryptographic protocols employ arithmetic to convert normal calculations into a sequence of finite field operations, such as addition and multiplication over a large finite field

F_{p}

, where p is a big prime integer, at least greater than or equal to

2^{63}

. In order to characterize these finite field operations, arithmetization-oriented primitives are created. The design criterion for arithmetic primitives is to lessen the multiplication complexity of cryptographic algorithms because the multiplication operation primarily consumes resources in advanced cryptographic protocols. Using the low-degree round function is an easy approach to accomplishing this objective.

There are many such arithmetization-oriented primitives, such as MiMC[1], GMiMC[2], HadesMiMC/Poseidon[3,4], Masta[5], Pasta[6], Ciminion[7], Chaghri[8] and Neptune[9]. These primitives directly use a low-degree round function as power maps

x \mapsto x^{d}

. More complex ones like Rescue use the low-degree power map

x \mapsto x^{3}

and its inverse

x \mapsto x^{1 / 3}

as round functions. A new arithmetization-oriented primitive Grendel[10] is designed for zero-knowledge proof systems. Grendel uses the Legendre symbol to enhance their round functions in combination with the SHARK-like construction. Let

χ_{p} (\cdot) : F_{p} \mapsto {- 1, 0, 1}

is defined as

χ_{p} (x) : = x^{\frac{p - 1}{2}} (mod p)

for the Legendre symbol. The application of the Legendre symbol in cryptography dates back to 1997. Mauduit and Sárközy introduced the Legendre symbol into the generation of pseudo-random bit sequences. Tóth [11] and Gyarmati et al.[12] introduce new measures of pseudorandomness (avalanche effect and cross-correlation) and assert that those values in the Legendre symbol sequence are high. Known as the Legendre symbol PRF,

x \mapsto χ_{p}^{k} (x) : = χ_{p} (x + k)

, k is the private key. In [13], Khovratovich developed a birthday-bound attack for the security analysis of the Legendre symbol PRF. This attack was later improved by Beullens et al. in [14] and Kaluderovic et al. in [15]. Key-recovery attacks against the Legendre symbol PRF may be converted into the solution of a certain set of multivariate quadratic equation systems over a prime field, according to more recent research by Seres et al. in [16].

In symmetric cryptographic schemes, to incorporate the Legendre symbol into a round function, it is necessary for the resulting non-linear layer to be invertible. In [17], it was first proposed to construct an invertible function using the Legendre symbol as follows:

x \mapsto x \cdot (χ_{p} (x) + α)

. This map is invertible when

χ_{p} (α^{2} - 1) = 1

. By combining the Legendre symbol with the power map, the map

x \mapsto x^{d} \cdot χ_{p} (x)

is obtained, which is invertible when

gcd (d + (p - 1) / 2, p - 1) = 1

. In [18], Grassi et al. further analyzed the generalization of

x \mapsto x \cdot (χ_{p} (x) + α)

x \mapsto x^{d} \cdot (χ_{p} (x) + α)

, building upon the foundations of [10,17]. They proposed new invertible functions that combine the Legendre symbol and analyzed their statistical and algebraic properties.

When operating on large finite fields, arithmetization-oriented ciphers are less susceptible to statistical attacks such as differential [19] and linear [20] attacks. However, they are more vulnerable to algebraic attacks. For example, the cipher Jarvis[21] was found to be vulnerable to Gröbner basis attacks. The high-order differential attack is also an effective method, as demonstrated in [22] for the high-order differential attack on GMiMC, and in [23] where Eichlseder et al. first applied the high-order differential attack on MiMC. Subsequently, Bouvier et al. [24] and Cui et al. [25] analyzed the upper bounds on the algebraic degrees of MiMC, reevaluating its security margin against high-order differentials using different approaches. In [26], Liu et al. proposed an innovative technique called the coefficient grouping technique, which reduces the evaluation of algebraic degrees to a well-structured optimization problem. They applied this technique to launch a high-order differential attack on Chaghri, a fully homomorphic encryption scheme. Exploring further the application of algebraic methods to analyze arithmetization-oriented ciphers remains an interesting avenue for future investigation.

Related works. In the original security analysis of the Grendel proposed by the designers in [10], the utilization of S-boxes based on the Legendre symbol was highlighted as a notable advantage. This choice allowed for achieving a higher algebraic degree within a relatively small number of rounds, providing resilience against high-order differential and interpolation attacks. Consequently, the focus of the analysis shifted towards the Gröbner basis attack, which presented two distinct approaches for constructing equation systems.

The first approach involves the attacker guessing all the Legendre symbols used in the scheme. Subsequently, they solve the resulting system of equations and verify the correctness of the guessed symbols based on the obtained solution. The complexity of this attack increases by approximately a factor of 2 for each correctly guessed symbol, considering the probability of accurate guessing is around $1 / 2$ .
On the other hand, the second approach avoids guessing the Legendre symbols and instead relies on the introduction of auxiliary variables to facilitate the establishment of the equation system. For more detailed information, please refer to [10].

Additionally, after guessing all Legendre symbols, the S-boxes in Grendel exhibit a low degree. As a result, it is not necessary to introduce intermediate variables in each round to mitigate the degree of growth. Instead, the attacker can directly solve a higher-degree system of equations. This alternative approach has already been used to attack the full hash function Grendel in [18]. In Section 3.1, we will provide a detailed description of their attack.

Our Contribution. In this paper, we further analyze the hash function Grendel on the basis of [10,18]. By introducing the Constrained Input/Constrained Output(CICO) problem and leveraging its solution to obtain preimages of the hash function Grendel, we can extend the previously proposed technique in [27] and enhance the preimage attack by bypassing two additional rounds of the SPN structure. By introducing the CICO problem, our attack is capable of attacking two additional rounds compared to the attack presented in [18], as shown in Table 1. Furthermore, we leverage the CICO problem to construct a system of multivariate equations for the hash function Grendel. By analyzing the introduction of intermediate variables and the main complexity of Gröbner basis attacks, we have further deepened our understanding of how to construct equation systems and conduct Gröbner basis attacks.

Table 1. For a security level of

s = 128

and a modulus

p = 2^{256}

, the number of rounds that can be attacked using the univariate root-finding method in different instances of the hash function Grendel.

Table 1. For a security level of

s = 128

and a modulus

p = 2^{256}

, the number of rounds that can be attacked using the univariate root-finding method in different instances of the hash function Grendel.

Instance $(d, n)$	Attacked Rounds in [10]	Attacked Rounds in [18]	Our result
(2,3)	28	25	27
(2,4)	21	20	22
(2,8)	11	12	14
(2,12)	7	8	10
(3,3)	22	22	24
(3,4)	16	18	20
(3,8)	8	11	13
(3,12)	6	8	10
(5,3)	16	19	21
(5,4)	12	16	18
(5,8)	6	10	12
(5,12)	4	7	9

2. Preliminaries

2.1. Notations

In the following, let p be a prime number, and

F_{p}

be a finite field with p elements. Let

F_{p}^{n}

denote a vector space with n elements, and each element in

F_{p}

. The notation

0^{u} \in F_{p}^{u}

is defined as having all u components equal to zero.

Let

F_{p}^{n}

be a vector space with standard basis

{e_{0}, e_{1}, \dots, e_{n - 1}}

. A vector subspace

V_{u}

F_{p}^{n}

can be represented as the span of a subset of a standard basis

{e_{0}, e_{1}, \dots e_{u - 1}}

, where

0 < u < n

Definition 1

(The Legendre Symbol). The Legendre symbol

χ_{p} (\cdot)

is a function

χ_{p} : F_{p} \mapsto {- 1, 0, 1}

defined as

\begin{matrix} χ_{p} (x) = \{\begin{matrix} 1 & if x is a nonzero quadratic residue modulo p, \\ - 1 & if x is a quadratic non - residue modulo p, \\ 0 & x = 0 . \end{matrix} \end{matrix}

2.2. CICO Problem

In the cryptanalysis of traditional symmetric schemes, the goal is to recover the key (or some subkeys) with complexity lower than

2^{k}

. However, the security of arithmetization-oriented hash functions such as the hash function Grendel is based on the infeasibility of solving the CICO problem.

Definition 2

(CICO Problem.). Let

F : F_{p}^{n} \to F_{p}^{n}

be a permutation, and let

0 < u < n

be an integer. For given

(a_{0}, \dots a_{n - u - 1}), (b_{0}, \dots, b_{n - u - 1}) \in F_{p}^{n - u}

, the CICO problem aims to find

(X_{0}, \dots, X_{u - 1}), (Y_{0}, \dots, Y_{u - 1}) \in F_{p}^{u}

such that

\begin{matrix} F (X_{0}, \dots, X_{u - 1}, a_{0}, \dots, a_{n - u - 1}) = (Y_{0}, \dots, Y_{u - 1}, b_{0}, \dots, b_{n - u - 1}) . \end{matrix}

A simpler version of the CICO problem is as follows: let

n = 2

and

u = 1

, then the CICO problem is to find

(X, Y) \in F_{p}^{2}

such that

F (X, 0) = (Y, 0)

. We observe that both the input and output of the permutation belong to the same vector subspace

V_{u}

. The CICO problem is highly relevant to the security of hash functions. Therefore, if the adversary has the ability to solve the problem with a complexity of less than

p^{n - u}

permutation calls, it is possible to find a preimage or collision of the hash function under the sponge structure. The CICO problem can usually be modelled as a system of equations and solved algebraically.

2.3. Solve the Systems of Algebraic Equations

Our attack is based on modelling cryptographic primitives as a system of polynomial equations. In this section, we present the methods and complexities of solving some univariate and multivariate equations, which are then used to attack the hash function Grendel.

We assume that the cryptographic primitive is represented as a well-defined system, a system of m polynomial equations consisting of n variables

X = (x_{0}, \dots, x_{n - 1}) \in F_{p}^{n}

\begin{matrix} \{\begin{matrix} F_{0} (x_{0}, \dots x_{n - 1}) = 0 \\ F_{1} (x_{0}, \dots x_{n - 1}) = 0 \\ ⋮ \\ F_{m - 1} (x_{0}, \dots x_{n - 1}) = 0 . \end{matrix} \end{matrix}

Then our purpose is to get the ordinary solution of the equation; then, we hope to get the round key of the encryption schemes or the preimage of the hash function.

2.3.1. Solve a System of Univariate Equations

A univariate equation has only one variable and an equation of

F (x) = 0

. Solving the given system is equivalent to find the roots of the univariate polynomial

F \in F_{p} [x]

with degree

D

of F. Since all operations are performed on the finite field

F_{p}

, the computational complexity is measured in terms of field operations.

Compute $G = x^{p} - x (mod F)$ .

The computation of $x^{p} (mod F)$ requires $O (D \cdot log (p) \cdot log (D) \cdot \log (log (D)))$ field operations with a double-and-add algorithm.
Compute $H = gcd (F, G)$ .

H has the same roots as F in $F_{q}$ since $H = gcd (F, x^{q} - x)$ , but its degree is likely much lower. This step [28] requires $O (D \cdot log {(D)}^{2})$ field operations.
Factor H.

In general, the polynomial H has only a few roots in $F_{p}$ . Thus, this step is negligible in complexity.

This root-finding approach using GCD computations is given in [28], and the final complexity of the algorithm is estimated by

\begin{matrix} O (M (D) log (D) log (D \cdot p)), \end{matrix}

(1)

where

M (D) : = 63.43 \cdot D log (D) log (log (D)) + O (D log (D))

is the complexity of multiplication of two polynomials of degree at most

D

over

F_{p}

2.3.2. Solve a System of Multivariate Equations

The Gröbner basis attack is a method to recover a secret from a system of polynomial equations. The first step is to convert the primitive into a system of multivariate equations. Then, a Gröbner basis is computed for the ideal generated by these polynomials. Finally, the Gröbner basis is utilized to compute the target variables in the given system. This attack method involves the following three phases.

To launch a Gröbner basis attack, the first step is to construct a set of polynomial equations describing the primitive. After that, a Gröbner basis for the ideal generated by these equations is computed, usually concerning the degrevlex ordering for better efficiency. The algorithm used for the computation of the Gröbner basis could be Buchberger’s algorithm [29], F4 [30] and F5 [31].
After computing the Gröbner basis for the given system of polynomial equations, the next step is to perform a change of term order to facilitate the computation of the elimination ideals and the elimination of variables. This is typically done by going from the degrevlex term order to the lex one, using an algorithm such as FGLM[32]. It is worth noting that in many applications, including those in cryptography, the systems of algebraic equations result in zero-dimensional ideals, meaning they have only finitely solutions.
The final step of a Gröbner basis attack is to solve the univariate equation for the last variable using a polynomial factoring algorithm. This allows us to obtain the specific value of the last variable, which can then be substituted into the remaining equations to obtain the full solution of the system. This step can use the algorithm given above to find the univariate equation system. Once the polynomial has been factored, we can easily find its roots, which correspond to the possible values of the last variable. By substituting each root into the remaining equations, we can obtain all possible solutions to the system of equations.

Cost of Gröbner basis Computation. For a system of m polynomial equations and n variables, there is

F_{0} (x_{0}, . . ., x_{n - 1}) = F_{1} (x_{0}, . . ., x_{n - 1}) = \dots = F_{m - 1} (x_{0}, . . ., x_{n - 1}) = 0,

where

F_{i} \in F_{p} [x_{0}, . . ., x_{n - 1}]

0 \leq i \leq m

. The complexity of computing a Gröbner basis in degrevlex term order [33] is

\begin{matrix} O ({(\binom{n + D_{r e g}}{D_{r e g}})}^{ω}) . \end{matrix}

(2)

In [34], another bound for the complexity of computing the Gröbner basis was provided as

\begin{matrix} O (n D_{r e g} \cdot {(\binom{n + D_{r e g} - 1}{D_{r e g}})}^{ω}), \end{matrix}

(3)

where

2 \leq ω < 2.3727

is the linear algebra constant representing the complexity of matrix multiplication and

D_{r e g}

is the degree of regularity. By further comparing these two complexities and computing their ratio, we can observe that

\begin{matrix} \frac{{(\binom{n + D_{r e g}}{D_{r e g}})}^{ω}}{n D_{r e g} \cdot {(\binom{n + D_{r e g} - 1}{D_{r e g}})}^{ω}} = \frac{(n + D_{r e g}^{ω})}{n^{ω + 1} \cdot D_{r e g}} . \end{matrix}

When n is small and

D_{r e g}

is large, the complexity calculation of Formula 3 provides a tighter bound. However, the authors in [18] found that when n is small, the complexity of computing the Gröbner basis is asymptotically smaller than the complexity of the FGLM algorithm. Therefore, for small values of n, the complexity of the Gröbner basis attack depends on the complexity of the FGLM algorithm. On the other hand, the Formula 2 becomes more restrictive when n has a comparatively larger value..

Cost of FGLM algorithm. Using the FGLM[32] algorithm, the complexity of converting the degrevlex order to lex order is:

\begin{matrix} O (n \cdot D_{I}^{3}), \end{matrix}

where n is the number of variables,

D_{I}

is the degree of the zero-dimensional ideal.

If the polynomial system is a regular system, we assume that there are n polynomials with the same degree

d_{i} = δ, i \in [1, n]

and n variables, then the

D_{r e g}

can be estimated by

1 + \sum_{i = 1}^{n} d_{i} - 1

. If the polynomial system is not a regular system, then its

D_{r e g}

is less than

1 + \sum_{i = 1}^{n} d_{i} - 1

, which is called Macaulay’s bound.

2.4. Description of Hash Function Grendel

The hash function Grendel is composed of the Grendel permutation combined with sponge structure. Let

p \geq 3

be a prime number and

n \geq 2

be an integral number. The Grendel permutation

P : F_{p}^{n} \to F_{p}^{n}

is obtained by iterating R rounds of the Grendel round function

F : F_{p}^{n} \to F_{p}^{n}

. The state size is n. Each round uses a different round constant. Each round function consists of three parts: a nonlinear layer, a linear layer, and adding round constants respectively denoted as

NL

L

, and

AC

The Nonlinear Layer: Let $X = (x_{0}, \dots, x_{n - 1}) \in F_{p}^{n}$ . $NL : F_{p}^{n} \to F_{p}^{n}$ consists of independent n identical S-boxes. $NL (X) = (S (x_{0}), S (x_{1}), \dots, S (x_{n - 1}))$ , where

$\begin{matrix} S (x) = x^{d} \cdot χ_{p} (x) . \end{matrix}$

$χ_{p}$ is the Legendre symbol, and $d \geq 2$ is an integer that satisfies $gcd (\frac{2 d + p - 1}{2}, p - 1) = 1$ .
The Linear Layer: The $L : F_{p}^{n} \to F_{p}^{n}$ is a $n \times n$ MDS matrix $M \in F_{p}^{n \times n}$ .
Adding Round Constants: Round constant $c_{j}^{i} \in F_{p}$ , where $0 \leq i \leq R - 1, 0 \leq j \leq n - 1$ .

The Grendel round function

F

consists of three parts and can be described as

F (\cdot) = AC \circ L \circ NL (\cdot)

. The Grendel permutation

P

is iterated R rounds by the

F

, which can be expressed as

P (\cdot) = {\underset{︸}{F \circ \dots \circ F (\cdot)}}_{R}

. The pseudocode describing the Grendel permutation is shown in Algorithm 1.

Algorithm 1:The Grendel Permutation

P

Input: $X = (X_{0}, X_{1}, \dots, X_{n - 1}) \in F_{p}^{n}$ ;
Output: $Y = (Y_{0}, Y_{1}, \dots, Y_{n - 1}) \in F_{p}^{n}$ .

1:: for $r = 0$ to $R - 1$ do
2:: for $i = 0$ to $n - 1$ do
3:: $X_{i} \leftarrow X^{d} \cdot χ_{p} (X_{i})$ ;
4:: end for
5:: $X \leftarrow M \cdot X$ ;
6:: for $i = 0$ to $n - 1$ do
7:: $X_{i} \leftarrow X_{i} + c_{i}^{r}$ ;
8:: end for
9:: end for
10:: $Y \leftarrow X$ ;
11:: return $Y$ ;

The sponge construction [35,36] is a cryptographic framework that utilizes an internal cryptographic permutation or function. It offers versatility in achieving different objectives, including encryption, authentication and hashing. The construction is based on the concept of a sponge, which consists of an internal permutation that operates on a fixed-sized state. By appropriately configuring the sponge, it can be adapted for various cryptographic applications, providing security and flexibility. In this paper, we slightly modify the original approach to operate on elements of

F_{p}

instead of

F_{2}

. Both the input and the output may be of arbitrary size. The state size is

n = r + c

, where r denotes the rate and c denotes capacity. To process a message m, which consists of elements from the field

F_{p}

, we utilize the following operations.

Padding. If the length of the message is already a multiple of r, no padding is necessary. However, if the length is not a multiple of r, we first append a $1 \in F_{p}$ to the message. Then, we pad the message with 0 until its length becomes a multiple of r.
Absorption. The message is divided into blocks of size r. Each block is added to the first r blocks of the state using the addition operation. Afterwards, the entire state is processed by applying the permutation function $P$ . Repeat the above operation until all the messages are absorbed.
Squeezing.In each iteration of the squeezing phase, a block of length r is squeezed out. The permutation function $P$ is applied to the entire state and the squeezed block is extracted. This process is repeated until the squeezing phase is completed.

Security.According to the proof presented in [36], when the inner permutation bears resemblance to a random permutation, the sponge construction is indistinguishable from a random oracle up to approximately

p^{c / 2}

queries. Equivalently, in order to provide s bits of security, we need

p^{c / 2} \geq 2^{s}

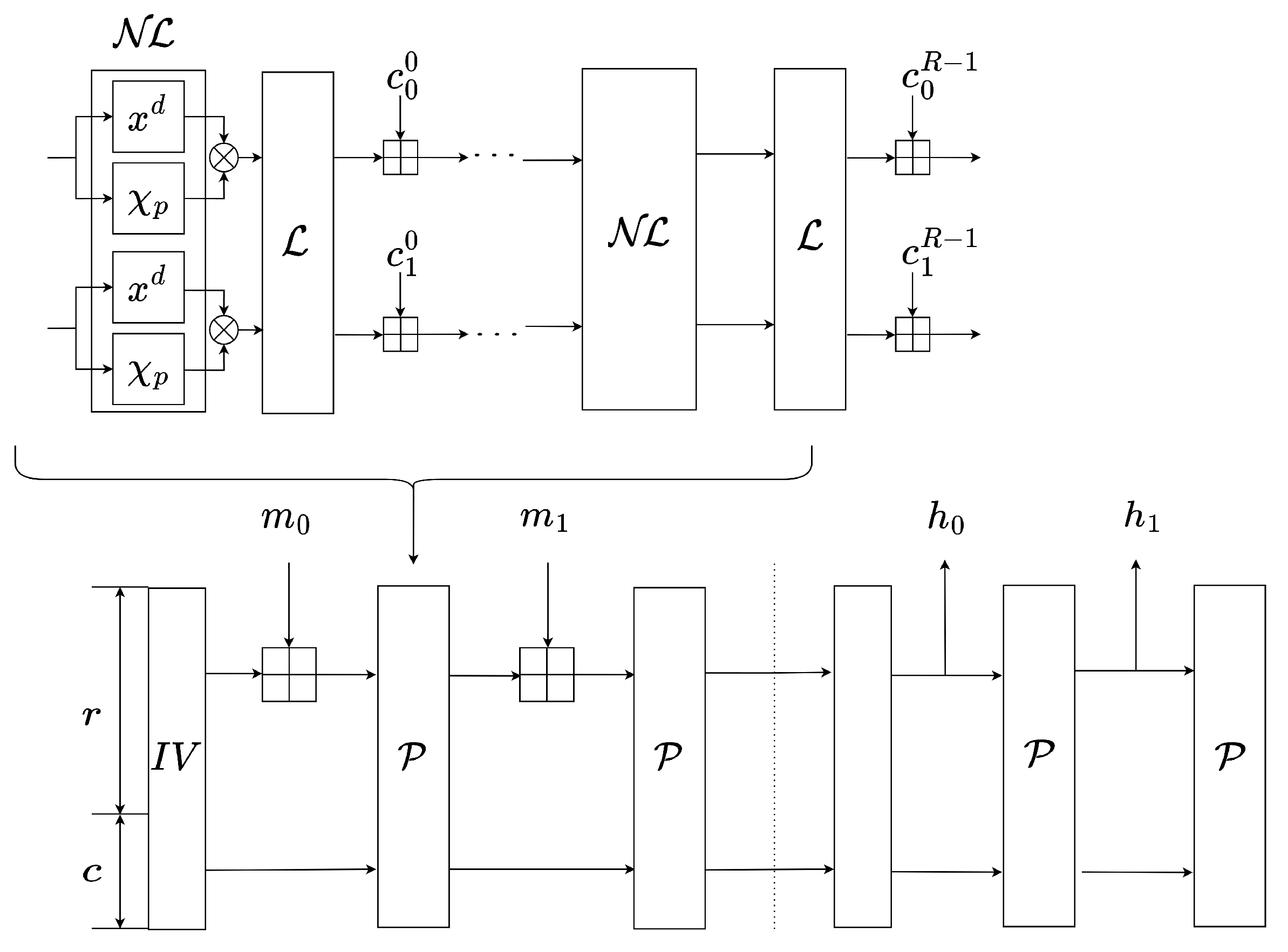
Figure 1. The above is an example of a Grendel permutation with a state size of 2. The following is an instance of the hash function Grendel with a sponge structure, which is built upon the Grendel permutation.

3. Algebraic Cryptanalysis of Hash Function Grendel

In this section, we simply review the preimage attack proposed by [18] on a sponge hash function instantiated with the Grendel permutation in Section 3.1. Then we introduce the CICO problem, and further analyze the security of the hash function Grendel.

3.1. Preimage Attack on Hash Function Grendel in [18]

Let s denote the security level and p represent the prime that defines the field. The authors in [18] focus on the case where

p \geq 2^{s}

, allowing for

r \geq 1

, r defines the rate of the sponge hash function. In this scenario, the hash function can output a single element from

F_{p}

, which aligns with common practice as p is typically chosen to be large.

Given a hash digest

h \in F_{p}

, the objective is to find a preimage. For cases where

r \geq 2

,18] begin by fixing

r - 1

input elements. Contrary to the analysis in [10], they refrain from introducing intermediate variables. Instead, the work in [18] with fixed Legendre symbol and employ polynomials of degree

d^{R}

, where R denotes the number of attacked rounds. In essence, the attack on R-round construction involves the following steps:

Iterating over all possible sets of Legendre symbols. The probability of a Legendre symbol being $\pm 1$ is approximately $\frac{1}{2}$ , while the probability of it being 0 is $\frac{1}{p}$ . Consequently, the probability that l Legendre symbols are different from zero can be calculated as ${(1 - \frac{1}{p})}^{l}$ . For a large number of rounds, if p is approximately $2^{32}$ , this probability exceeds $99.99 %$ . In their attack, $l = n R - (n - 1) = n (R - 1) + 1$ . In the first round, it is possible to compute $n - 1$ Legendre symbols deterministically because there is no linear layer before the initial application of the S-boxes.
Solving the resulting univariate equation to identify a preimage. They focus on the case in which the number of hash output elements is 1. By fixing all Legendre symbols, there are only a single unknown (the input variable) and a single equation of degree at most $d^{R}$ in the end. The equation system hence consists of only one univariate equation and can be solved by applying a root-finding algorithm to this equation.
Verifying if the solution obtained is a valid preimage. Furthermore, once the roots are discovered, they proceed to verify the validity of the obtained solution. They do this by comparing the computed Legendre symbols to the fixed ones for the given instance. If any inconsistency is found between the computed symbol using their solution and the fixed symbol, they promptly terminate the verification process, indicating that the trial is invalid. Considering that we only need to compute the first Legendre symbol in each instance with a probability of $50 %$ , the first two symbols with a probability of $25 %$ , and so on, we can expect to compute an average of 3 Legendre symbols for each trial before encountering an inconsistency.

3.2. Techniques to Skip SPN Rounds

In this section, we introduce a trick proposed by [27], which can help us skip two rounds without additional consumption when analyzing the permutation based on the SPN structure using the CICO problem.

Let permutation

P : F_{p}^{n} \to F_{p}^{n}

be s-secure against the CICO problem. We split it into two permutations

F_{0}

and

F_{1}

, i.e.,

P = F_{1} \circ F_{0} (\cdot)

V_{u}

is a vector subspace spanned by

{e_{0}, \dots, e_{u - 1}}

. We use

\begin{matrix} X = (X_{0}, X_{1}, \dots, X_{u - 1}, A_{0}, \dots, A_{n - u - 1}) \in V_{u}, \\ Z = (Z_{0}, Z_{1}, \dots, Z_{u - 1}, C_{0}, \dots, C_{n - u - 1}) \in V_{u} \end{matrix}

to be the input state and output state of

P

respectively, where

(A_{0}, \dots, A_{n - u - 1}) \in F_{p}^{n - u}

and

(C_{0}, \dots, C_{n - u - 1}) \in F_{p}^{n - u}

are fixed constants. According to the definition of CICO problem, if we can find

X

and

Z

such that

P (X) = Z

with a complexity smaller than

2^{s}

, then we may conclude that the permutation security margin is insufficient.

We denote

Y = (Y_{0}, Y_{1}, \dots, Y_{n - 1}) \in F_{p}^{n}

as the intermediate variable after

F_{0}

. If we can find

Y

so that it also belongs to the vector subspace

V_{u}

, then we can construct a polynomial system with

n - u

outputs through

F_{1}

. So we can find its root. Finally, we can get the value of

X

according to the value of

Y

, which is enough to solve the CICO problem. Then, to solve the CICO problem of permutation

P

, only the

F_{1}

part needs to be dealt with, not the whole permutation

P

In order to describe this technique in more detail, we assume that the permutation

P

is the Grendel permutation. We let

F_{0}

consist of two nonlinear layers, one linear layer and one round key addition in the Grendel round function.

F_{0}

can be expressed as

F_{0} (\cdot) = NL \circ AC \circ L \circ NL (\cdot)

, then

F_{1}

can be regarded as an

R - 2

round Grendel round function with a linear layer and a round key addition. S is denoted as the S-box, and

S^{- 1}

is the inverse of the S-box.

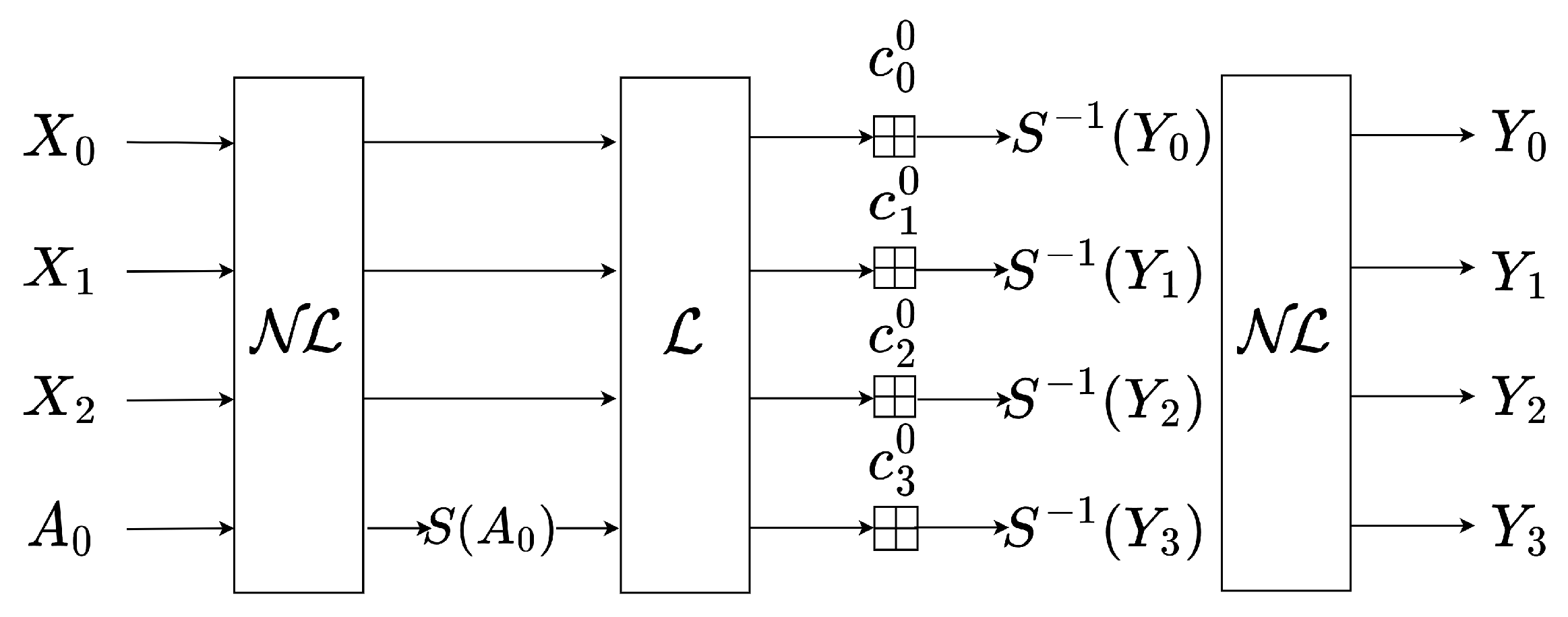
Figure 2. A detailed description of a specific trick with a state size of 4.

We need the S-box to satisfy the following property

\begin{matrix} S (A \cdot X) = S (A) \cdot S (X), \end{matrix}

(4)

where

A, X \in F_{p}

Let the linear layer MDS matrix

M

satisfy:

\begin{matrix} M^{- 1} = [\begin{matrix} m_{0, 0} & m_{0, 1} & m_{0, 2} & \dots & m_{0, n - 1} \\ m_{1, 0} & m_{1, 1} & m_{1, 2} & \dots & m_{1, n - 1} \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ m_{n - 1, 0} & m_{n - 1, 1} & m_{n - 1, 2} & \dots & m_{n - 1, n - 1} \end{matrix}] . \end{matrix}

Here

c_{j}^{i}

(

0 \leq i \leq R - 1, 0 \leq j \leq n - 1

) denotes the round constant. Next, we show how to construct univariate equations with the CICO problem. We always set

u = n - 1

in the following.

When $n = 3$ . We set

u = n - 1 = 2

, then

V_{u}

is a vector subspace spanned by

{e_{0}, e_{1}}

. Let the input states of

F_{0}

X = (X_{1}, X_{2}, A_{0}) \in V_{u}

, where

A_{0}

is a fixed constant. Let the states after

F_{0}

Y = (Y_{0}, Y_{1}, Y_{2}) \in F_{p}^{3}

. When passing through the first nonlinear layer of

F_{0}

, there is

\begin{matrix} S (A_{0}) & = m_{2, 0} (S^{- 1} (Y_{0}) - c_{0}^{0}) + m_{2, 1} (S^{- 1} (Y_{1}) - c_{1}^{0}) + m_{2, 2} (S^{- 1} (Y_{2}) - c_{2}^{0}) \\ = m_{2, 0} S^{- 1} (Y_{0}) + m_{2, 1} S^{- 1} (Y_{1}) + m_{2, 2} S^{- 1} - (m_{2, 0} c_{0}^{0} + m_{2, 1} c_{1}^{0} + m_{2, 2} c_{2}^{0}) . \end{matrix}

(5)

We fix

Y_{2}

to a constant value

B_{0} = S (m_{2, 2}^{- 1} (m_{2, 0} c_{0}^{0} + m_{2, 1} c_{1}^{0} + m_{2, 2} c_{2}^{0} + S (A_{0})))

. Then we can simplify the Equation 5 as

\begin{matrix} m_{2, 0} S^{- 1} (Y_{0}) + m_{2, 1} S^{- 1} (Y_{1}) = 0 \\ ⟺ & m_{2, 0} S^{- 1} (Y_{0}) = - m_{2, 1} S^{- 1} (Y_{1}) \\ ⟺ & S (m_{2, 0} S^{- 1} (Y_{0})) = S (- m_{2, 1} S^{- 1} (Y_{1})) \\ ⟺ & S (m_{2, 0}) Y_{0} = S (m_{2, 1}) Y_{1} . \end{matrix}

(6)

The S-box must satisfy the Formula 4, and the above Equation 6 can be established successfully. We found that

A_{0}

and

B_{0}

are fixed,

Y_{1}

can be represented by

Y_{0}

Y 1 = \frac{S (m_{2, 0})}{S (m_{2, 1})} Y_{0}

. Then we have

\begin{matrix} X = (X_{0}, X_{1}, A_{0}) \in V_{2}, \\ Y = Y_{0} (1, \frac{S (m_{2, 0})}{S (m_{2, 1})}, 0) + (0, 0, B_{0}) \in V_{2} . \end{matrix}

When $n = 4$ . We set

u = n - 1 = 3

, then

V_{u}

is a vector subspace spanned by

{e_{0}, e_{1}, e_{2}}

. Similar to

n = 3

, we denote the input and output states of

F_{0}

X = (X_{0}, X_{1}, X_{2}, A_{0}) \in V_{u}

and

Y = (Y_{0}, Y_{1}, Y_{2}, Y_{3}) \in F_{p}^{4}

respectively, where

A_{0}

are fixed constants. When passing through the first nonlinear layer of

F_{0}

, there is

\begin{matrix} S (A_{0}) & = m_{3, 0} (S^{- 1} (Y_{0}) - c_{0}^{0}) + m_{3, 1} (S^{- 1} (Y_{1}) - c_{1}^{0}) + m_{3, 2} (S^{- 1} (Y_{2}) - c_{2}^{0}) + m_{3, 3} (S^{- 1} (Y_{3}) - c_{3}^{0}) \\ = m_{3, 0} S^{- 1} (Y_{0}) + m_{3, 1} S^{- 1} (Y_{1}) + m_{3, 2} S^{- 1} + m_{3, 3} S^{- 1} (Y_{3}) \\ - (m_{3, 0} c_{0}^{0} + m_{3, 1} c_{1}^{0} + m_{3, 2} c_{2}^{0} + m_{3, 3} c_{3}^{0}) \\ = \sum_{i = 0}^{3} m_{3, i} S^{- 1} (Y_{i}) - \sum_{i = 0}^{3} m_{3, i} c_{i}^{0} . \end{matrix}

(7)

We fix

Y_{3}

to a constant denoted as

B_{0}

;

Y_{3}

satisfies

\begin{matrix} m_{3, 3} S^{- 1} (Y_{3}) = \sum_{i = 0}^{3} m_{3, i} c_{i}^{0} + S (A_{0}) . \end{matrix}

Then we can obtain

\begin{matrix} m_{3, 0} S^{- 1} (Y_{0}) + m_{3, 1} S^{- 1} (Y_{1}) + m_{3, 2} S^{- 1} (Y_{2}) = 0 . \end{matrix}

(8)

In order to simplify the equation, we set

(Y_{1}, Y_{2}) = (S (Q_{1}) Y_{0}, S (Q_{2}) Y_{0})

, and bring

(Y_{1}, Y_{2})

into Equation 8, then we get

\begin{matrix} S^{- 1} (Y_{0}) (m_{3, 0} + m_{3, 1} Q_{1} + m_{3, 2} Q_{2}) = 0 . \end{matrix}

Therefore, if

(Q_{1}, Q_{2})

and

Y_{3}

satisfy

\begin{matrix} \{\begin{matrix} m_{3, 0} + m_{3, 1} Q_{1} + m_{3, 2} Q_{2} = 0 \\ Y_{3} = S (m_{3, 3}^{- 1} (\sum_{i = 0}^{3} m_{3, i} c_{i}^{0} + S (A_{0}))), \end{matrix} \end{matrix}

we will have

\begin{matrix} X = (X_{0}, X_{1}, X_{2}, A_{0}) \in V_{3}, \\ Y = Y_{0} (1, Q_{1}, Q_{2}, 0) + (0, 0, 0, B_{0}) \in V_{3} . \end{matrix}

When $n \geq 4$ . In general, we set

u = n - 1

V_{n - 1}

is also a vector subspace spanned by

{e_{0}, e_{1}, \dots, e_{n - 2}}

. Similarly, the input and output states of

F_{0}

are in the form of

X = (X_{0}, X_{1}, \dots, X_{n - 2}, A_{0})

and

Y = (Y_{0}, Y_{1}, \dots, Y_{n - 1}) \in F_{p}^{n}

respectively. Let

A_{0} \in F_{p}

be a fixed constant. When passing through the first nonlinear layer of

F_{0}

, there is

\begin{matrix} S (A_{0}) = \sum_{i = 0}^{n - 1} m_{n - 1, i} (S^{- 1} (Y_{i}) - c_{i}^{0}) = \sum_{i = 0}^{n - 1} m_{n - 1, i} S^{- 1} (Y_{i}) - \sum_{i = 0}^{n - 1} m_{n - 1, i} c_{i}^{0} . \end{matrix}

(9)

We also fix

Y_{n - 1}

to a constant denoted as

B_{0}

, then

Y_{n - 1}

fulfills

\begin{matrix} m_{n - 1, n - 1} S^{- 1} (Y_{n - 1}) = \sum_{i = 0}^{n - 1} m_{n - 1, i} c_{i}^{0} + S (A_{n - 1}) . \end{matrix}

(10)

Just like

n = 3

and

n = 4

, we set

(Y_{1}, Y_{2}, \dots, Y_{n - 2}) = (S (Q_{1}) Y_{0}, S (Q_{2}) Y_{0}, \dots, S (Q_{n - 2}) Y_{0})

. By bringing

(Y_{1}, Y_{2}, \dots, Y_{n - 1})

and the constant

Y_{n - 1}

back into the Equation 9, then we can obtain

\begin{matrix} S^{- 1} (Y_{0}) (m_{n - 1, 0} + \sum_{i = 1}^{n - 1} m_{n - 1, i} Q_{i}) = 0 . \end{matrix}

Therefore, if

(Q_{1}, Q_{2}, \dots, Q_{n - 1})

and

Y_{n - 1}

satisfy

\begin{matrix} \{\begin{matrix} m_{n - 1, 0} + \sum_{i = 1}^{n - 1} m_{n - 1, i} Q_{i} = 0 \\ Y_{n - 1} = S (m_{n - 1, n - 1}^{- 1} (\sum_{i = 0}^{n - 1} m_{n - 1, i} c_{i}^{0} + S (A_{0}))), \end{matrix} \end{matrix}

we will have

\begin{matrix} X = (X_{0}, X_{1}, \dots, X_{n - 2}, A_{0}) \in V_{n - 1}, \\ Y = Y_{0} (1, Q_{1}, Q_{2}, \dots, Q_{n - 2}, 0) + (0^{n - 1}, B_{0}) \in V_{n - 1} . \end{matrix}

Let

Y

be the input to

F_{1}

, where only

Y_{0}

is the unknown variable. We define the output of

F_{1}

Z = (Z_{0}, Z_{1}, \dots, Z_{n - 2}, C_{0}) \in V_{n - 1}

C_{0} \in F_{p}

is a fixed constant. By considering the final position of the output from

F_{1}

, we construct a univariate equation with

Y_{0}

as its variable, which is in the form of

\begin{matrix} F (Y_{0}) = C_{0} . \end{matrix}

(11)

Given a valid

Y_{0}

, we can invariably infer an input

X

specifically tailored for the R-round permutation

P

that projects onto the vector subspace

V_{n - 1}

3.3. Application to Hash Function Grendel

In this section, we build upon the full-round preimage attack on the hash function Grendel presented in [18] by employing the trick described in the previous section to decrease the degree and complexity of the polynomial system. Let s be the security level, and let p be the prime that defines the field. We limit ourselves to focus on the case in which

p \geq 2^{s}

. The following are the details of our attack.

We first divide the Grendel permutation into two parts $F_{0}$ and $F_{1}$ as before. The Grendel permutation has R rounds. Consider the hash function Grendel with the following parameters: $n = r + c$ . The Grendel S-box, denoted as $S (x) : x \mapsto x^{d} \cdot χ_{p} (x)$ satisfies the Formula 4, which can be proven straightforwardly. Similarly, we set $u = n - 1$ , and the $V_{u}$ is a vector subspace. The Grendel permutation takes an input $X = (X_{0}, \dots, X_{r - 1}, 0^{c})$ where $X_{0}, \dots, X_{r - 1}$ represent the input messages, and it produces an output $Z = (Z_{0}, \dots, Z_{r - 1}, 0^{c})$ . The initial value IV of Grendel is set to all zeros, and the last c elements of the output $Z$ are also zeros. Consequently, after $X \in V_{u}$ passes through $F_{0}$ , it yields $Y = (Y_{0}, Y_{1}, \dots, Y_{n - 1}) \in V_{u}$ . As indicated in the previous section, we have $Y_{n - 1}$ and $(Q_{1}, \dots, Q_{n - 1})$ satisfy

$\begin{matrix} \{\begin{matrix} m_{n - 1, 0} + \sum_{i = 1}^{n - 1} m_{n - 1, i} Q_{i} = 0 \\ Y_{n - 1} = {(m_{n - 1, n - 1}^{- 1} (\sum_{i = 0}^{n - 1} m_{n - 1, i} c_{i}^{0}))}^{3} \cdot χ_{p} (m_{n - 1, n - 1}^{- 1} (\sum_{i = 0}^{n - 1} m_{n - 1, i} c_{i}^{0})) . \end{matrix} \end{matrix}$

Thus, for $F_{1}$ , there is only one unknown input variable $Y_{0}$ . Then we can process it similarly as in [18].
According to [18], it can be observed that when $p \geq 2^{32}$ , the probability of the Legendre symbol being $\pm 1$ is greater than $99.99 %$ . Therefore, we only consider guessing $\pm 1$ . Based on the previous step, $F_{1}$ has an input $Y$ with only one unknown variable $Y_{0}$ . The $F_{1}$ has $R - 2$ rounds; we must guess the number of Legendre symbols, given by $l = n (R - 3) + 1 = n R - 3 n + 1$ . Because only the Legendre symbol of $Y_{0}$ needs to be guessed in the first round of $F_{1}$ , and other values are constant, the Legendre symbol is known. Consequently, there are at most $2^{l} = 2^{n R - 3 n + 1}$ distinct sets of Legendre symbols to guess until the correct set of Legendre symbols is found.
After fixing the Legendre symbols, we can construct a polynomial with $Y_{0}$ as an unknown variable. The polynomial equation, as defined in Formula 11, has a degree of $D = d^{R - 2}$ . To determine the specific value of $Y_{0}$ , we can employ the root-finding algorithm in Section 2.3.1. The complexity $T_{1}$ of the root-finding algorithm is

$\begin{matrix} T_{1} = O (M (d^{R - 2}) log (d^{R - 2}) log (d^{R - 2} \cdot p)), \\ M (d^{R - 2}) = 63.43 \cdot d^{R - 2} log (d^{R - 2}) log (log (d^{R - 2})) + O (d^{R - 2} log (d^{R - 2})) . \end{matrix}$
Upon obtaining $Y_{0}$ ’s value, we need to verify its validity. This requires checking the correctness of each guessed Legendre symbol. According to [18], for each set of guessed Legendre symbols, we only need to verify three of them to exclude an invalid set. The complexity $T_{2}$ of computing a Legendre symbol [37] is evaluated as $O (σ {(log σ)}^{2} log (log (σ)))$ for $σ = log (p)$ . Therefore, the complexity of this step is $3 \cdot T_{2}$ .

As a result, when we obtain a valid

Y_{0}

, according to the CICO definition, we can always deduce the

X

such that they are mapped to the vector subspace

V_{u}

through the Grendel permutation. The overall complexity T of this attack is

\begin{matrix} T = (T_{1} + 3 \cdot T_{2}) \cdot 2^{n R - 3 n + 1} . \end{matrix}

Therefore, this particular instance is vulnerable to attack if

T \leq 2^{s}

. As shown in Table 1, for the case of security level

s = 128

, under different parameter settings, we can observe that we are able to perform two additional rounds of attack compared to the previous work [18]. However, we have not exceeded the new security margin set in [18].

In our investigation of the hash function Grendel, we ascertained that capitalizing on the CICO problem to devise a univariate equation is feasible solely under the conditions

u = r = n - 1

. This premise holds because, in this specific scenario, it enables the generation of an intermediate variable intimately associated with the vector subspace

V_{u}

and ensures that the hash output remains confined to this subspace.

3.4. The Gröbner Basis Attacks for Hash Function Grendel

In this section, we employ the CICO problem to construct a multivariate equation system for the hash function Grendel instantiation. Similarly, we consider the message absorption size to be r, resulting in r hash digests being squeezed out after a Grendel permutation. To further analyze the complexity, we utilize the Gröbner basis attack method described in Section 2.3.2 and incorporate insights gained from our experimental observations.

Building upon our previous assumption of guessing the Legendre symbols, we delve deeper into the analysis by considering the introduction of intermediate variables to reduce the degree of the polynomials. Based on the presence of intermediate variables, we categorize our attacks into two scenarios: one without the introduction of intermediate variables and the other with the introduction of intermediate variables in each round.

Considering the hash function Grendel with input messages

(X_{1}, X_{2}, \dots, X_{r - 1})

of size r and an IV set to all zeros, the Grendel permutation takes an input

X = (X_{1}, X_{2}, \dots, X_{r - 1}, 0^{c})

, where

0^{c}

denotes a vector of zeros with length c. The resulting output

Z = (Z_{0}, \dots, Z_{n - 1})

is subject to the CICO problem, where the input

X

belongs to the vector subspace

V_{r}

spanned by

{e_{0}, \dots, e_{r - 1}}

. To satisfy this condition, the last c positions of

Z

denoted as

C_{0}, \dots, C_{c - 1}

are fixed constants. In the following attacks, we always set

r = c = \frac{2}{n}

. Consequently, we can formulate a system of multivariate equations.

Without Intermediate Variables. Let

X

and

Z

be the input and output of the permutation. We don’t introduce any additional intermediate variables like

Y

. We can build an equation system with c variables and c equations.

\begin{matrix} \{\begin{matrix} F_{0} (X_{0}, X_{1}, \dots, X_{c - 1}) = C_{0} \\ F_{1} (X_{0}, X_{1}, \dots, X_{c - 1}) = C_{1} \\ ⋮ \\ F_{c - 1} (X_{0}, X_{1}, \dots, X_{c - 1}) = C_{c - 1} . \end{matrix} \end{matrix}

We obtain a system of equations with c equations and c variables, where each equation has a degree of

D_{i} = d^{R}, 0 \leq i \leq c - 1

. It is evident that the degree of the equations is much larger than the number of variables. Hence, we employ the Formula 3 to calculate the complexity of the Gröbner basis algorithm. In particular, by setting

d = 2

, we compare the complexities of computing the Gröbner basis and the FGLM algorithm. For a system of c equations where each equation having a degree of

2^{R}

, we can compute the upper bound on the regularity degree

D_{r e g}

of the equation system and the zero-dimensional ideal

D_{I}

as follows:

\begin{matrix} D_{r e g} \leq 1 + \sum_{i = 0}^{c - 1} (D_{i} - 1) = (2^{R} - 1) \cdot c + 1, & D_{I} \leq \prod_{i = 0}^{c - 1} D_{i} = 2^{R c} . \end{matrix}

Computing the Gröbner basis with respect to the grevlex term order using the Formula 3 exhibits asymptotic complexity:

\begin{matrix} T_{G} = n D_{r e g} \cdot {(\binom{n + D_{r e g} - 1}{D_{r e g}})}^{ω} \leq c \cdot ((2^{R} - 1) \cdot c + 1) \cdot (\binom{2^{R} \cdot c}{2^{R} \cdot c - c + 1 .}) \end{matrix}

Then, applying a fast variant of the FGLM algorithm to perform the change of term order exhibits asymptotic complexity:

\begin{matrix} T_{F} = {(D_{I})}^{ω} = 2^{R c ω} . \end{matrix}

By evaluating

T_{G}

and

T_{F}

for

c = 2

, there is

\begin{matrix} T_{G} = (2^{R + 2} - 2) \times (\binom{2^{R + 1}}{2^{R + 1} - 1}) = {(2^{R + 1})}^{ω} \times (2^{R + 2} - 2) \leq 2^{R w + w + r + 2}, \\ T_{F} = 2^{2 R w} . \end{matrix}

In this case, it is evident that

T_{F}

is greater than

T_{G}

, which indicates that FGLM algorithm becomes the bottleneck in the Gröbner basis attack.

Intermediate Variables. Directly using the input and output of the Grendel permutation are probably infeasible due to the maximum degree and dense polynomials involved. To address this challenge, one possible strategy is to introduce intermediate variables. This approach reduces the degrees in the equation system (and consequently reduces the number of monomials) but at the expense of introducing additional variables. For the Grendel permutation, we introduce new variables in each round to prevent the growth of degrees. Let

X

and

Y^{0} = (Y_{0}^{0}, \dots, Y_{n - 1}^{0}) \in F_{p}^{n}

represent the input and output of the first round’s nonlinear layer. The relationship between

X

and

Y^{0}

can be expressed through r equations of degree d and c equations of degree 1. Specifically,

Y_{0}^{0} = X_{0}^{d}

, in accordance with the definition of the S-box (excluding the consideration of the Legendre symbol, as it is determined based on the conjecture). Hence, we add n variables in each round. And we simply use the output values

C_{0}, \dots, C_{c - 1}

to construct the system of equations except for the last one. Then, we have

r + R n

variables and the same number of equations. Among these equations, there are

R n

equations with a degree of d and r equations with a degree of 1.

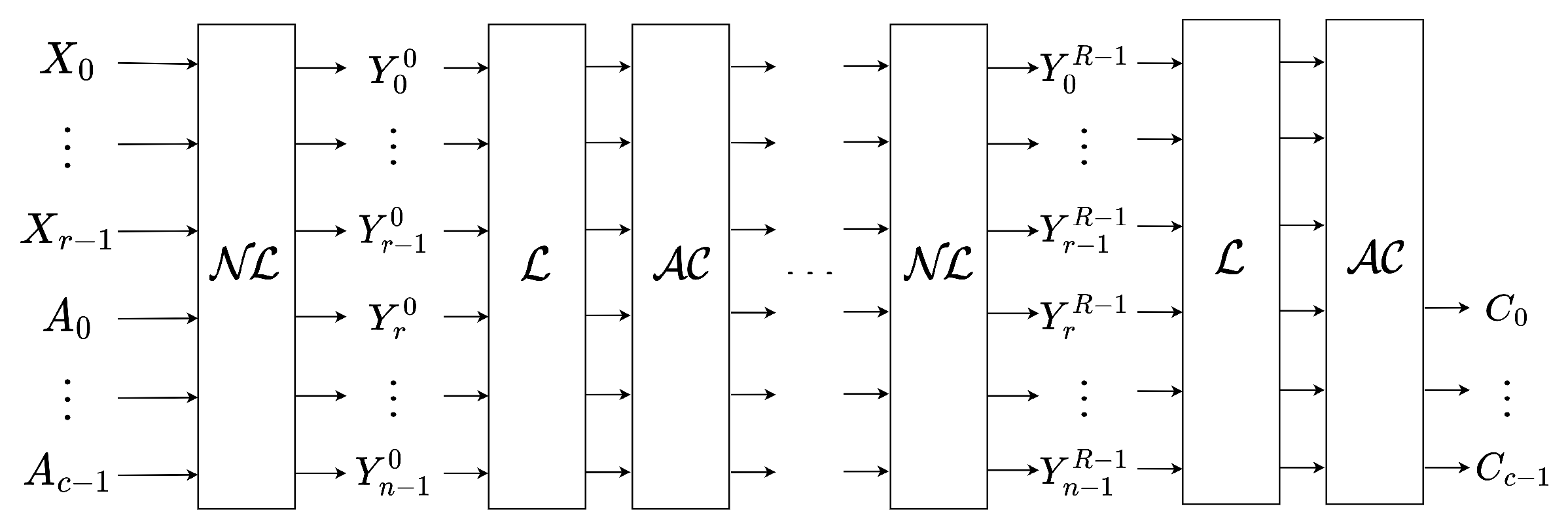
Figure 3. Overview of the introduction of intermediate variables in the Grendel permutation.

When n is large, indicating the presence of a greater number of intermediate variables, then

D_{r e g}

becomes relatively small. Therefore, we utilize the Formula 2 to evaluate the complexity of the Gröbner basis attack.

In summary, the complexity of the Gröbner basis attack on the hash function Grendel can be divided into three parts. The first part is the complexity of guessing the Legendre symbols, denoted as

T_{g u e s s}

. The second part is the complexity of the Gröbner basis attack, denoted as

T_{G B}

(with specific calculations selected from the various scenarios mentioned earlier). The third part is the complexity of verifying the Legendre symbols, denoted as

T_{v e r i f y}

. There is

\begin{matrix} T_{g u e s s} = 2^{(R - 1) n + c}, \\ T_{v e r i f y} = 3 \cdot O (σ {(log σ)}^{2} log (log (σ))) for σ = log (p) . \end{matrix}

The complete complexity of the Gröbner basis attack for the hash function Grendel can be evaluated by

\begin{matrix} (T_{G B} + T_{v e r i f y}) \cdot T_{g u e s s} . \end{matrix}

Table 2. For a security margin of

s = 128

and a modulus

p = 2^{256}

, by setting c = r = 2/n, we can evaluate the number of rounds that can be susceptible to Gröbner basis attacks with varying computational complexities.

Table 2. For a security margin of

s = 128

and a modulus

p = 2^{256}

, by setting c = r = 2/n, we can evaluate the number of rounds that can be susceptible to Gröbner basis attacks with varying computational complexities.

Instance $(d, n)$	Attacked Rounds with $T_{F}$	Attacked Rounds with $T_{G}$
(2,4)	16	21
(2,8)	8	10
(2,12)	5	7
(3,4)	12	17
(3,8)	6	8
(3,12)	4	5
(5,4)	9	14
(5,8)	4	7
(5,12)	3	4

4. Conclusion

In this paper, we propose a preimage attack on the sponge hash function implemented with full rounds of the Grendel permutation, utilizing algebraic approaches. By introducing the CICO problem, we address the construction of univariate and multivariate equation systems for the hash function Grendel and employ different algorithms to solve these equations, resulting in new analytical findings. This provides additional insights into the factors that designers should consider when developing arithmetization-oriented cryptographic primitives in response to the CICO problem. Moreover, We find that the choice of different algebraic methods for constructing equations can have an impact on the security analysis of cryptographic primitives. Therefore, it is worth exploring the possibility of combining different algebraic methods for the analysis of arithmetization-oriented cryptographic primitives.

Author Contributions

Conceptualization, J.N. and G.W.; methodology, J.Z.; validation, J.N.; formal analysis, R.L. and Y.S.; writing—original draft preparation, J.N.; writing—review and editing, R.L and Y.S.; supervision, G.W. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported by the National Key Research and Development Program of China (2022YFB2701900), the National Natural Science Foundation of China (No. 62072181), and Shanghai Trusted Industry Internet Software Collaborative Innovation Center.

Data Availability Statement

Data is contained within the article.

Acknowledgments

The authors would like to thank the anonymous reviewers for their helpful comments.

Conflicts of Interest

The authors declare no conflict of interest.

References

Albrecht, M.R.; Grassi, L.; Rechberger, C.; Roy, A.; Tiessen, T. MiMC: Efficient Encryption and Cryptographic Hashing with Minimal Multiplicative Complexity. Advances in Cryptology - ASIACRYPT 2016 - 22nd International Conference on the Theory and Application of Cryptology and Information Security, Hanoi, Vietnam, -8, 2016, Proceedings, Part I; Cheon, J.H.; Takagi, T., Eds., 2016, Vol. 10031, Lecture Notes in Computer Science, pp. 191–219. 4 December. [CrossRef]
Albrecht, M.R.; Grassi, L.; Perrin, L.; Ramacher, S.; Rechberger, C.; Rotaru, D.; Roy, A.; Schofnegger, M. Feistel Structures for MPC, and More. Computer Security - ESORICS 2019 - 24th European Symposium on Research in Computer Security, Luxembourg, -27, 2019, Proceedings, Part II; Sako, K.; Schneider, S.A.; Ryan, P.Y.A., Eds. Springer, 2019, Vol. 11736, Lecture Notes in Computer Science, pp. 151–171. 23 September. [CrossRef]
Grassi, L.; Lüftenegger, R.; Rechberger, C.; Rotaru, D.; Schofnegger, M. On a Generalization of Substitution-Permutation Networks: The HADES Design Strategy. Advances in Cryptology - EUROCRYPT 2020 - 39th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, -14, 2020, Proceedings, Part II; Canteaut, A.; Ishai, Y., Eds. Springer, 2020, Vol. 12106, Lecture Notes in Computer Science, pp. 674–704. 10 May. [CrossRef]
Grassi, L.; Khovratovich, D.; Rechberger, C.; Roy, A.; Schofnegger, M. Poseidon: A New Hash Function for Zero-Knowledge Proof Systems. 30th USENIX Security Symposium, USENIX Security 2021, -13, 2021; Bailey, M.; Greenstadt, R., Eds. USENIX Association, 2021, pp. 519–535. 11 August.
Ha, J.; Kim, S.; Choi, W.; Lee, J.; Moon, D.; Yoon, H.; Cho, J. Masta: An HE-Friendly Cipher Using Modular Arithmetic. IEEE Access 2020, 8, 194741–194751. [Google Scholar] [CrossRef]
Dobraunig, C.; Grassi, L.; Helminger, L.; Rechberger, C.; Schofnegger, M.; Walch, R. Pasta: A Case for Hybrid Homomorphic Encryption. IACR Transactions on Cryptographic Hardware and Embedded Systems 2023, 2023, 30–73. [Google Scholar] [CrossRef]
Dobraunig, C.; Grassi, L.; Guinet, A.; Kuijsters, D. Ciminion: Symmetric Encryption Based on Toffoli-Gates over Large Finite Fields. Advances in Cryptology - EUROCRYPT 2021 - 40th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, -21, 2021, Proceedings, Part II; Canteaut, A.; Standaert, F., Eds. Springer, 2021, Vol. 12697, Lecture Notes in Computer Science, pp. 3–34. 17 October. [CrossRef]
Ashur, T.; Mahzoun, M.; Toprakhisar, D. Chaghri - A FHE-friendly Block Cipher. Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security, CCS 2022, Los Angeles, CA, USA, -11, 2022; Yin, H.; Stavrou, A.; Cremers, C.; Shi, E., Eds. ACM, 2022, pp. 139–150. 7 November. [CrossRef]
Grassi, L.; Onofri, S.; Pedicini, M.; Sozzi, L. Invertible Quadratic Non-Linear Layers for MPC-/FHE-/ZK-Friendly Schemes over Fnp Application to Poseidon. IACR Trans. Symmetric Cryptol. 2022, 2022, 20–72. [Google Scholar] [CrossRef]
Szepieniec, A. On the Use of the Legendre Symbol in Symmetric Cipher Design. Cryptology ePrint Archive, Paper 2021/984, 2021. https://eprint.iacr.org/2021/984.
Tóth, V. Collision and avalanche effect in families of pseudorandom binary sequences. Period. Math. Hung. 2007, 55, 185–196. [Google Scholar] [CrossRef]
Gyarmati, K.; Mauduit, C.; Sárközy, A. The cross-correlation measure for families of binary sequences. In Applied Algebra and Number Theory; Larcher, G.; Pillichshammer, F.; Winterhof, A.; Xing, C., Eds.; Number Theory, Cambridge University Press, 2014; pp. 126–143. [CrossRef]
Khovratovich, D. Key recovery attacks on the Legendre PRFs within the birthday bound. Cryptology ePrint Archive, Paper 2019/862, 2019. https://eprint.iacr.org/2019/862.
Beullens, W.; Beyne, T.; Udovenko, A.; Vitto, G. Cryptanalysis of the Legendre PRF and Generalizations. IACR Trans. Symmetric Cryptol. 2020, 2020, 313–330. [Google Scholar] [CrossRef]
Kaluđerović, N.; Kleinjung, T.; Kostić, D. Cryptanalysis of the generalised Legendre pseudorandom function. Open Book Series 2020, 4, 267–282. [Google Scholar] [CrossRef]
Seres, I.A.; Horváth, M.; Burcsi, P. The Legendre Pseudorandom Function as a Multivariate Quadratic Cryptosystem: Security and Applications. Cryptology ePrint Archive, Paper 2021/182, 2021. Available online: https://eprint.iacr.org/2021/182.
Shallue, C.J. Permutation polynomials of finite fields. 2012; arXiv:math.NT/1211.6044]. [Google Scholar]
Grassi, L.; Khovratovich, D.; Rønjom, S.; Schofnegger, M. The Legendre Symbol and the Modulo-2 Operator in Symmetric Schemes over Fnp Preimage Attack on Full Grendel. IACR Trans. Symmetric Cryptol. 2022, 2022, 5–37. [Google Scholar] [CrossRef]
Biham, E.; Shamir, A. Differential Cryptanalysis of DES-like Cryptosystems. Advances in Cryptology - CRYPTO 1990, 10th Annual International Cryptology Conference, Santa Barbara, California, USA, -15, 1990, Proceedings; Menezes, A.; Vanstone, S.A., Eds. Springer, August 11-15, 1990, Vol. 537, Lecture Notes in Computer Science, pp. 2–21. [CrossRef]
Matsui, M. Linear Cryptanalysis Method for DES Cipher. Advances in Cryptology - EUROCRYPT 1993, Workshop on the Theory and Application of of Cryptographic Techniques, Lofthus, Norway, May 23-27, 1993, Proceedings; Helleseth, T., Ed. Springer, 1993, Vol. 765, Lecture Notes in Computer Science, pp. 386–397. [CrossRef]
Ashur, T.; Dhooghe, S. MARVELlous: a STARK-Friendly Family of Cryptographic Primitives. Cryptology ePrint Archive, Paper 2018/1098, 2018. Available online: https://eprint.iacr.org/2018/1098.
Beyne, T.; Canteaut, A.; Dinur, I.; Eichlseder, M.; Leander, G.; Leurent, G.; Naya-Plasencia, M.; Perrin, L.; Sasaki, Y.; Todo, Y.; Wiemer, F. Out of Oddity - New Cryptanalytic Techniques Against Symmetric Primitives Optimized for Integrity Proof Systems. Advances in Cryptology - CRYPTO 2020 - 40th Annual International Cryptology Conference, CRYPTO 2020, Santa Barbara, CA, USA, August 17-21, 2020, Proceedings, Part III; Micciancio, D.; Ristenpart, T., Eds. Springer, 2020, Vol. 12172, Lecture Notes in Computer Science, pp. 299–328. [CrossRef]
Eichlseder, M.; Grassi, L.; Lüftenegger, R.; ygarden, M.; Rechberger, C.; Schofnegger, M.; Wang, Q. An Algebraic Attack on Ciphers with Low-Degree Round Functions: Application to Full MiMC. Advances in Cryptology - ASIACRYPT 2020 - 26th International Conference on the Theory and Application of Cryptology and Information Security, Daejeon, South Korea, December 7-11, 2020, Proceedings, Part I; Moriai, S.; Wang, H., Eds. Springer, 2020, Vol. 12491, Lecture Notes in Computer Science, pp. 477–506. [CrossRef]
Bouvier, C.; Canteaut, A.; Perrin, L. On the algebraic degree of iterated power functions. Des. Codes Cryptogr. 2023, 91, 997–1033. [Google Scholar] [CrossRef]
Cui, J.; Hu, K.; Wang, M.; Wei, P. On the Field-Based Division Property: Applications to MiMC, Feistel MiMC and GMiMC. Advances in Cryptology - ASIACRYPT 2022 - 28th International Conference on the Theory and Application of Cryptology and Information Security, Taipei, Taiwan, December 5-9, 2022, Proceedings, Part III; Agrawal, S.; Lin, D., Eds. Springer, 2022, Vol. 13793, Lecture Notes in Computer Science, pp. 241–270. [CrossRef]
Liu, F.; Anand, R.; Wang, L.; Meier, W.; Isobe, T. Coefficient Grouping: Breaking Chaghri and More. Advances in Cryptology - EUROCRYPT 2023 - 42nd Annual International Conference on the Theory and Applications of Cryptographic Techniques, Lyon, France, April 23-27, 2023, Proceedings, Part IV; Hazay, C.; Stam, M., Eds. Springer, 2023, Vol. 14007, Lecture Notes in Computer Science, pp. 287–317. [CrossRef]
Bariant, A.; Bouvier, C.; Leurent, G.; Perrin, L. Algebraic Attacks against Some Arithmetization-Oriented Primitives. IACR Trans. Symmetric Cryptol. 2022, 2022, 73–101. [Google Scholar] [CrossRef]
von zur Gathen, J.; Gerhard, J. Modern Computer Algebra (3. ed.); Cambridge University Press, 2013.
Buchberger, B. A theoretical basis for the reduction of polynomials to canonical forms. SIGSAM Bull. 1976, 10, 19–29. [Google Scholar] [CrossRef]
Faugere, J.C. A new efficient algorithm for computing Gröbner bases (F4). Journal of pure and applied algebra 1999, 139, 61–88. [Google Scholar] [CrossRef]
Faugere, J.C. A new efficient algorithm for computing Gröbner bases without reduction to zero (F 5). Proceedings of the 2002 international symposium on Symbolic and algebraic computation, 2002, pp. 75–83.
Faugère, J.; Gianni, P.M.; Lazard, D.; Mora, T. Efficient Computation of Zero-Dimensional Gröbner Bases by Change of Ordering. J. Symb. Comput. 1993, 16, 329–344. [Google Scholar] [CrossRef]
Bettale, L.; Faugère, J.; Perret, L. Solving polynomial systems over finite fields: improved analysis of the hybrid approach. International Symposium on Symbolic and Algebraic Computation, ISSAC’12, Grenoble, France July 22 - 25, 2012; van der Hoeven, J.; van Hoeij, M., Eds. ACM, 2012, pp. 67–74. [CrossRef]
Bardet, M.; Faugère, J.; Salvy, B. On the complexity of the F5 Gröbner basis algorithm. J. Symb. Comput. 2015, 70, 49–70. [Google Scholar] [CrossRef]
Bertoni, G.; Daemen, J.; Peeters, M.; Van Assche, G. Sponge functions. ECRYPT hash workshop, 2007, Vol. 2007.
Bertoni, G.; Daemen, J.; Peeters, M.; Assche, G.V. On the Indifferentiability of the Sponge Construction. Advances in Cryptology - EUROCRYPT 2008, 27th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Istanbul, Turkey, April 13-17, 2008. Proceedings; Smart, N.P., Ed. Springer, 2008, Vol. 4965, Lecture Notes in Computer Science, pp. 181–197. [CrossRef]
Brent, R.P.; Zimmermann, P. An O(M(n) logn) Algorithm for the Jacobi Symbol. Algorithmic Number Theory, 9th International Symposium, ANTS-IX, Nancy, France, July 19-23, 2010. Proceedings; Hanrot, G.; Morain, F.; Thomé, E., Eds. Springer, 2010, Vol. 6197, Lecture Notes in Computer Science, pp. 83–95. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Algebraic Attacks against Grendel: An Arithmetization-Oriented Primitives with the Legendre Symbol

Abstract

1. Introduction

2. Preliminaries

2.1. Notations

2.2. CICO Problem

2.3. Solve the Systems of Algebraic Equations

2.3.1. Solve a System of Univariate Equations

2.3.2. Solve a System of Multivariate Equations

2.4. Description of Hash Function Grendel

3. Algebraic Cryptanalysis of Hash Function Grendel

3.1. Preimage Attack on Hash Function Grendel in [18]

3.2. Techniques to Skip SPN Rounds

3.3. Application to Hash Function Grendel

3.4. The Gröbner Basis Attacks for Hash Function Grendel

4. Conclusion

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe