Preprint
Article
Transient Dynamics in Counter-Rotating Stratified Taylor-Couette Flow
Altmetrics
Downloads
123
Views
58
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
20 June 2023
Posted:
21 June 2023
You are already at the latest version
Alerts
Abstract
Non-normal mode stability analysis has long been employed to study linear transient characteristics of wall bounded shear flows. However, the application of this approach to investigate shear flows with stratified thermal conditions (STCF) has received limited attention. This paper examines thermal effects on Taylor-Couette flow. The results in this study indicate the possibility of a subcritical bifurcation in stratified Taylor-Couette flow.
Keywords:
Subject: Computer Science and Mathematics - Mathematics
1. Introduction
The transition from laminar to turbulent fluid flow has been of interest for over a century. There are several states a fluid flow can exhibit beyond laminar before it becomes turbulent. These states have played a role in making significant contributions in industries such as automobile, civil, aerospace, and others. To address the instabilities arising from flow disturbances, a multitude of mathematical techniques have been developed within hydrodynamic stability theory [1,2].
Numerical and analytical methods, including bifurcation theory and other suitable approaches, have been employed to identify these flow patterns [3,4]. Among the various techniques, the transient growth method has gained extensive utilization in the exploration of subcritical transition in fluid flow, proving highly successful over several decades. This method has been invaluable in capturing and elucidating phenomena associated with stability problems in fluid flow that cannot be effectively addressed by linear stability theory alone [5,6,7,8,9].
The plane Couette flow and pipe Poiseuille flow are known to be stable for all Reynolds number within the theoretical mathematical framework of linear stability, but in practice these flows become turbulent for sufficiently large Reynolds number as accounted by Romanov[10], Davey[11], Drazin and Reid [12] and recent studies by others [13,14]. In practice the plane Poiseuille flow does exhibit an instability at a critical Reynolds number Rec ≈ 2300, but theoretically this phenomena is observed at a much larger Rec ≈ 5772 at which the so-called Tollmien-Schlichting wave depicting unstable mode appears[15,16]. The inconsistency in results has been attributed to the non-normality of the linearized Navier-Stokes operator. It is known that the non-normality is responsible for the spike (i.e. transient growth) in the growth rate within the linear regime that eventually trig- gers the transition of flow to turbulence. This behaviour is widely known as a subcritical transition or bypass transition[5,17,18]. The non-normal route to turbulence has raised many concerns in the literature by different schools of thought [7,19,20]. However, Reddy and Henningson[21] has objectively addressed the issues with insightful results for two and three dimensional plane Couette and Poiseuille flows. The utilization of the transient growth method for investigating subcritical bifurcations has witnessed widespread adop- tion and significant advancements over the last two decades with both theoretical and experimental justification[8,22,23,24].
The circular Couette flow often known as Taylor-Couette flow (TCF) has widely been studied experimentally and theoretically [25,26,27,28,29]. The TCF problem has been known to be one of the pioneering problems of hydrodynamic stability for several decades, since the early experimental and theoretical works of Taylor [30].
In 1965 Coles[31] experimentally investigated the transition of viscous flow in con- centric cylinders and reported that at certain Reynolds numbers where the linear theory predicted laminar flow, there exist spiral turbulence in the counter rotating flow [31]. In the following year, Van Atta [32] carried out similar experiments on the spiral transition of the flow and obtain related results. The result was also confirmed experimentally later in 1989 by Hegseth et al. [33]. In 2002 Prigent et al. [34] provided experimental results on spiral turbulence with agreement with Coles’[31] report.
Non-normality problem of the TCF linear operator was initially investigated by Greb- hardt and Grossmann in 1992 [26]. However, Hristova et al.[35] conducted a comprehensive investigation of this phenomenon using pseudospectral analysis. In 2002, Meseguer[36] examined the transient energy growth associated with the parametric regime reported by Coles[31] and observed significant amplification of transient energy in the counter-rotating regime, which aligned well with Coles’[31] experimental findings. It was discovered that the non-axisymmetric modes experience greater amplification and they could potentially trigger the subcritical transition to turbulence [19,36]. Maretzke et al.[37] further expanded on this perspective through numerical and analytical methods. The authors explored the transient energy growth across all TCF regimes and established a universal Re2/3 scaling. Additionally, it was established that the linear stability and transient growth remained un- affected by the ratio of cylinder rotation in the limits where there was no axial perturbation dependency.
However, there has been little attention regarding the application non-modal analysis to Stratified Taylor-Couette flow (STCF). Thus, the purpose of this work, is to extend the experimental work of Cole in the direction of thermal convection by means of non-modal analysis. We superimpose radial heating on the reported configuration of Coles[31] as given by Meseguer[36] and proceed with the investigation of the subcritical phenomena for the regime of the counter rotating flows.
This article is concerned with optimal transient growth in counter rotating stratified Taylor-Couette flow with non-axisymmetric perturbations. A brief description of the governing equations of the Taylor-Couette problem is presented in Section I. In Section II, the derived model is linearized. Section III describes the non-modal analysis method for computing the optimal energy growth. In section IV, a detailed discussion is presented for the results obtain in our investigation. Finally the paper is concluded in section V.
2. Mathematical Formulation
2.1. Model
We examine the behaviour of an incompressible fluid with kinematic viscosity, µ and a density, ρ = ρo + ρ′, which is contained between two concentric cylinders of infinite height. The inner cylinder has a radius, ri and rotates at an angular velocity, Ωi > 0, while the outer cylinder has a radius, ro and rotates at an angular velocity, Ωo < 0. Additionally, we assume a negative temperature gradient with inner temperature, Ti = + ∆T/2 and outer temperature, To = − ∆T/2, as depicted in Figure 1, where is the ambient temperature and ∆T is the temperature difference between the two cylinders. Thus, the model is governed by the incompressible Navier-Stokes equations for rapidly rotating flows, as described by Lopez et al. [38,39]:
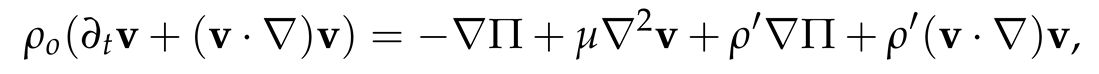

∂t T + (v · ∇)T = κ∇2 T,
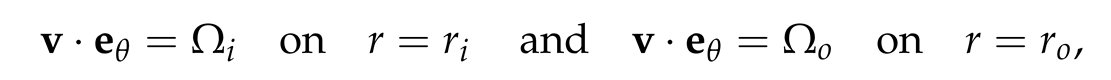
2.2. Boussinesq Approximation
We suppose the system is defined by a cylindrical coordinate system (r, θ, z). Thus, we proceed with the Boussinessq assumption by ignoring density variation in the flow, and keep only density contributions from the gravitational and centrifugal terms. Also, we assume a uniform gravitational acceleration, g in the vertical direction, z. Thus we have:
But ρ = ρo + ρ′ based on the assumption in defining (1) given by Lopez et al. [38]. Thus we have:
Now applying (6) to the buoyancy term in (1) and using Φ = gz, we have:
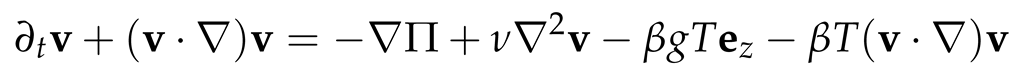 where β = −(1/ρo)∂ρ/∂T|ρ=ρo is the coefficient of thermal expansion.
where β = −(1/ρo)∂ρ/∂T|ρ=ρo is the coefficient of thermal expansion.
ρ = ρo (1 − βT)
ρ′ = −ρo βT
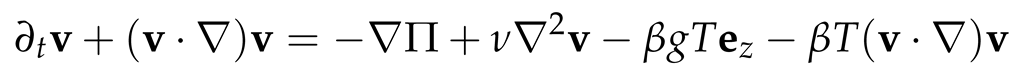
2.3. Nondimensionalization
In this section we proceed by converting Equations (2), (3) and (7) to dimensionless form by using ∆T, gap-width d = ro − ri, d2/ν, (ν/d)2 as the temperature, length, viscous time, and reduced pressure p/ρo scaling factors respectively. The inner ri and outer ro radius are expressed in dimensionless form as η/(1 − η) and 1/(1 − η) respectively. With these scaling factors we obtained new dimensionless parameters listed in Table 1 are obtained. Also, we introduce a dummy variable, Υ ∈ {0, 1} into the equation:
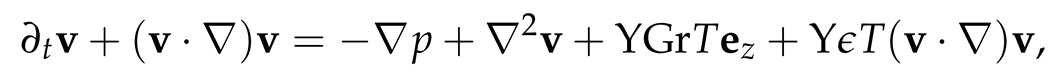
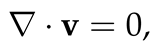
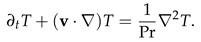 If Υ is 1, then (8) describes the STCF and if it is 0, then it becomes TCF without stratification. Thus, we use these parameters and the dimensionless Equations (8)–(10) in subsequent sections for our analysis and discussion.
If Υ is 1, then (8) describes the STCF and if it is 0, then it becomes TCF without stratification. Thus, we use these parameters and the dimensionless Equations (8)–(10) in subsequent sections for our analysis and discussion.
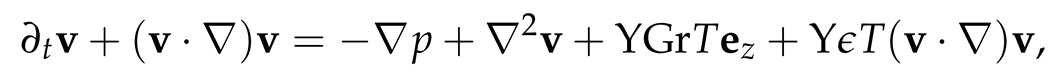
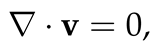
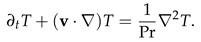
2.4. Basic Equations
Given the nondimensional equations, let the velocity be expressed as v = uer + veθ + wez in cylindrical coordinates, where u, v and w are the radial, azimuthal and axial components of the velocity, respectively, and er, eθ and ez are the unit vectors in the r, θ and z directions. The basic velocity U, becomes:
and the basic components of the velocity Ub, Vb and Wb, corresponds to the respective radial, azimuthal and axial basic profiles. Thus we proceed by deriving expression for the basic profiles by assuming that, U is independent of time t, azimuthal θ and axial z directions. In addition, in order to have a constant pressure gradient in the axial direction, we impose the zero mass flux constraint. That is,
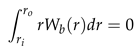 and thus, with these assumptions we obtain the following analytical solutions:
and thus, with these assumptions we obtain the following analytical solutions:
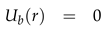
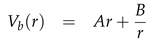
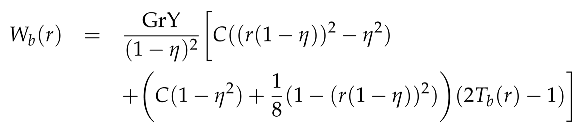
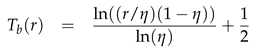 where Vb, Wb and Tb remain the same solutions introduced in related literature. The constants A, B and C are given by the expressions
where Vb, Wb and Tb remain the same solutions introduced in related literature. The constants A, B and C are given by the expressions
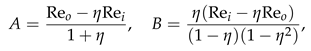 and
and
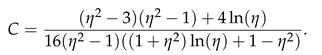
U = Uber + Vbeθ + Wbez
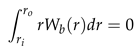
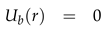
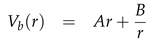
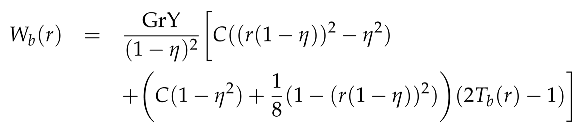
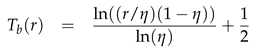
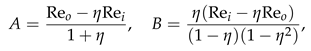
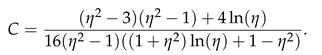
3. Linearization
Furthermore, we suppose that the basic state is subjected to an infinitesimal perturbation:
where δ is assumed to be a very small constant and is the residue (fluctuation) of the velocity. We substitute Equations (19)–(21), into the dimensionless governing equations (8)–(10). We then proceed by collecting the O(δ) terms and ignore higher order terms, including this term O(1) since they are simply the basic equations. Thus the linearized equations become:
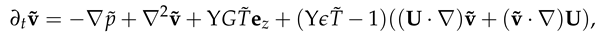
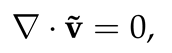
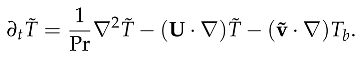
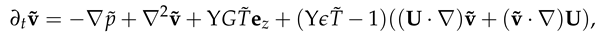
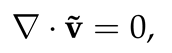
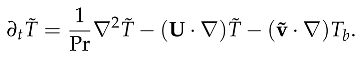
We suppose that the behaviour of the fluid exhibits inherent wave-like dynamics when it is in motion. Our objective is to describe the transition of Taylor-Couette flow form laminar to turbulent flow. In particular we seek to identify any differences between isothermal and stratified Taylor-Couette flow. To facilitate our analysis and expecting harmonic motion we utilize the Fourier transform in the azimuthal θ and axial z directions while we employ the Gauss-Lebatto collocation point Chebyschev polynomial expansion in the radial direction r, see Figure 1. Based on these considerations, we propose the following functional forms:
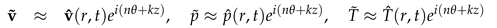 where the pressure , temperature and velocities , , and are functions of the radial, azimuthal, and axial coordinate directions. Also, n ∈ and k ∈ are the azimuthal and axial wavenumbers respectively. The frequencies of the disturbance are characterised by the wavenumbers. The wavelengths in the homogeneous directions, θ and z are Lθ = 2π/n and Lz = 2π/k respectively. Thus we proceed by substituting the above functional forms into the linearized Equations (22)–(24), and which after further simplification they become:
where the pressure , temperature and velocities , , and are functions of the radial, azimuthal, and axial coordinate directions. Also, n ∈ and k ∈ are the azimuthal and axial wavenumbers respectively. The frequencies of the disturbance are characterised by the wavenumbers. The wavelengths in the homogeneous directions, θ and z are Lθ = 2π/n and Lz = 2π/k respectively. Thus we proceed by substituting the above functional forms into the linearized Equations (22)–(24), and which after further simplification they become: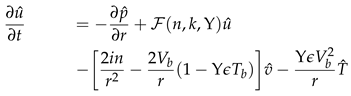
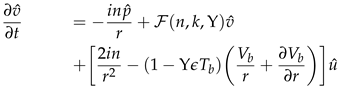
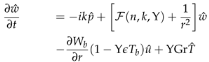
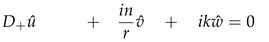
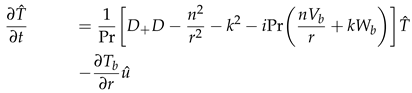
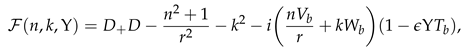
D = d/dr, and D+ = D + 1/r. Manipulating the Equations (25)–(29) we can represent the solenoidal system of equations in a compact form as an initial value problem:
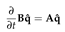 where A and B are defined in appendix B.
where A and B are defined in appendix B.
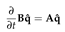
By assuming a solution of the form:
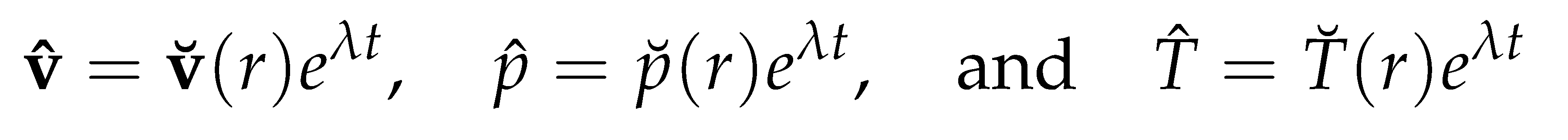 we transform the initial value problem to a generalized eigenvalue problem:
we transform the initial value problem to a generalized eigenvalue problem:
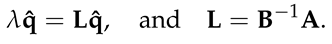 The scalar eigenvalue λ is complex and defines the temporal stability of the flow. That is if real part of λ is negative the flow is stable and the amplitude of the perturbations will decay in time. Also, if real part of λ is positive the flow is unstable and the amplitude of the perturbation will grow asymptotically in time. Further more, in order to define the boundary conditions, we assume that the perturbation of the velocity and temperature of the fluid motion must vanish at the walls:
The scalar eigenvalue λ is complex and defines the temporal stability of the flow. That is if real part of λ is negative the flow is stable and the amplitude of the perturbations will decay in time. Also, if real part of λ is positive the flow is unstable and the amplitude of the perturbation will grow asymptotically in time. Further more, in order to define the boundary conditions, we assume that the perturbation of the velocity and temperature of the fluid motion must vanish at the walls:
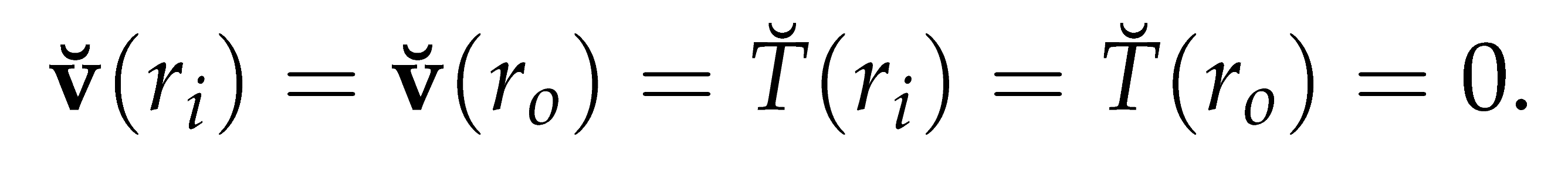 In other words, we impose homogeneous boundary condition for the velocity and tempera- ture perturbations at the respective walls of the cylinders.
In other words, we impose homogeneous boundary condition for the velocity and tempera- ture perturbations at the respective walls of the cylinders.
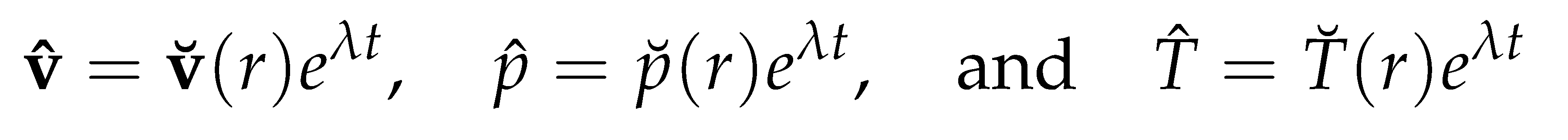
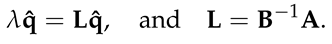
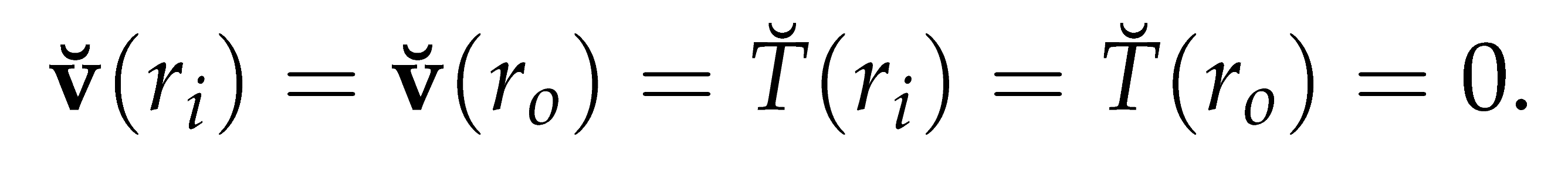
4. Numerical Results
The amplification factor, often denoted as G0, is a fundamental concept in the study of transient growth in fluid dynamics. It quantifies the maximum amplification of perturba- tions or disturbances in a given flow system over a certain time interval. Transient growth refers to the temporary amplification of perturbations in a flow before they eventually decay or become insignificant. This phenomenon is particularly relevant in subcritical transition to turbulence, where small disturbances can trigger the onset of turbulent behaviour. The amplification factor, G0, represents the maximum energy amplification that can be achieved by the optimal initial perturbations within a specified time frame. It characterizes the efficiency of energy transfer from the mean flow to the perturbations. A larger value of G0 indicates a higher potential for transient growth and the presence of strong amplification mechanisms in the flow. The computation of G0, as defined in Appendix A, involves solving an eigenvalue problem or performing a non-modal analysis, depending on the nature of the flow and the mathematical framework employed. By determining the optimal initial conditions and analyzing the linearized equations governing the flow, G0 can be evaluate. In addition, the structures and modes that contribute most significantly to the amplification can be identified. In our study, we employed well-established approaches from the literature to compute the amplification factor, G0. These approaches have been widely used and validated in previous research, providing reliable and effective methods for evaluating the maximum amplification of disturbances in fluid flows. By utilizing these established techniques, we ensure the accuracy and robustness of our calculations, allowing us to gain valuable insights into the transient growth and stability characteristics of the flow system under investigation [5,40,41].
The configuration is chosen so that our results can compare well with earlier studies of Taylor-Couette flow (TCF) without stratification [35,36,37]. Thereafter, we apply stratification to the problem to investigate the behaviour of the transient energy growth of the flow . Thus, we continue with equivalent configuration used by Meseguer[36] for the study of energy transient growth in TCF problem. We choose fixed values of η = 0.881, ϵ = 0.067, Pr = 68, various range of Gr and wavenumber pairs (n ∈ [0, 15], k ∈ [0, 15]). In addition, we consider specific counter rotating pairs of values for Rei and Reo from the set of significant pairs reported by the author for TCF. Furthermore, for proper justification of this investigation, we consider the symmetry introduce due to the periodic assumption made for the azimuthal (i.e. the SO(2)-symmetry because of the invariant of the system in respect of the azimuthal rotation about the center axis) and axial (i.e. the O(2)- symmetry because of the invariant of the system in respect of the reflections and translation of the axial axis) coordinate directions.
Due to the fact that no experimental work exists for the choice of configuration to which we can compare our results, we have introduced a parameter Υ in the governing dimensionless equation with values ranging from 0 to 1. The value of Υ is set to 0 in order to compare our findings with already existing results obtained for TCF (refs). The results as indicated in Figure 2 are in perfect agreement with the results reported by Hristova et al. [35], Meseguer [36], and recently by works of Maretzke et al. [37]. In addition, we verify that the eigenvalues of STCF is in perfect agreement with Lopez [38], and McFadden et al. [38].
The nondimensional scheme we used, is similar to Meseguer[36] and Maretzke et al.[37], but is slightly different from the scales used by Hristova et al.[35]. Thus, we made the conversions Rei = 2Rei and Reo = 2Reo /η in computing the results with those reported by Hristova et al.[35] and as done by others [36,37]. This is because, the authors used a scale of d/2 to non-dimensionalize the length and fix the angular rotation speed in defining the problem.
Meseguer[36] and Maretzke et al. [37] reported that close to the region where Rei = ηReo (i.e. the cylinders rotate at the same speed) no transient growth is observed. However, it is observed that the situation is different when the temperature increases beyond a certain threshold. There exists an amplification of the perturbation at specific times for different relative counter-rotating speeds in the presence of temperature variations. We continue by applying radial heating to the TCF problem and investigate the effect on the thermal stratification for various Grashof, Gr, numbers with specific counter rotating pairs Rei, Reo and wavenumbers. Figure 3 shows the amplification factor G against t for the four different configurations C1 to C4 for various values of Gr. We find that G has a minimum around Gr=3250 for configuration C1, around Gr=4800 for configuration C2, around Gr=5750 for configuration C3, and around Gr=7150 for configuration C4. These results are verified explicitly in Figure 4b. Figure 4 shows that as the temperature increases, the amplification of the perturbation monotonically decays, before reaching a turning point where it enters a new phase and begins increasing monotonically with temperature.
The growth rate shows a linear relationship with Gr in all configurations, as evident from the Figure 4a. The growth rate remains consistently low across all Gr values, indi- cating linear stability of the fluid within the considered range of flow and implying that buoyancy does not induce linear instability. Figure 4a clearly demonstrates an increase in the growth rate with higher Gr values, which aligns with the proportional relationship be- tween G0 and Gr as illustrated. We observe in Figure 4b that initially, there is an observable downward trend in the linear decay of G0 as Gr increases until it reaches a critical value Gr. Beyond this critical value, a linear increase in G0 is observed as Gr continues to rise. By examining the decay phase boundaries, the order of G0 for each configuration can be represented by the expression G0(C4) > G0(C3) > G0(C2) > G0(C1). Similarly, for the increasing phase, the order of G0 can be characterized as G0(C4) < G0(C3) < G0(C2) < G0(C1).
An intriguing observation depicted in Figure 4b is the relationship between C1 and the other configurations, namely C2, C3, and C4, with respect to their ratio and the magnitude of their growth rates. Notably, there is a bigger difference in the order of growth values between C1 and C2 when compared to the difference between C2 and C3 across all Gr values. The consistency in the proportionality of their speed ratio suggests that their growth rates should exhibit similar differences in the same order of magnitude. This observation could be due to the influence of buoyancy-induced contributions captured in the amplification reflected by G0.
The underlining behaviour of the fluid motion can be attributed to an internal sub-critical phenomena because of the induced thermal stratification on the dynamics of the disturbances.
During the decay phases of the amplification factor, it is evident that the combination of viscous and buoyancy influences the amplitude of the perturbations. In Figure 5, the amplification factor G is depicted to illustrate its growth as Gr increases. Each row in the sequence of plots represents the evolving behaviour of G as Gr increases. The first Gr = 2250, 3800, 3750, 5150 and last columns of each sequence represented by Gr = 4250, 5800, 7750, 9150 exhibit Gr values slightly distant from the turning point, Gr = 3250, 4800, 5750, 7150 showcasing a single peak with a certain amplitude. Additionally, the plots in the second and fourth columns demonstrate two distinct behaviors in the evolution. Notably, the second column plots display the emergence of a new crest on the wave front. This new crest continues to grow until it surpasses the initial crest in amplitude, eventually becoming the sole peak after the turning point for sufficiently high Gr values as depicted by the sequence. The third column has used a value of Gr where both crescents exhibit similar amplitudes. The initial crest gradually merges into the latter one, and with further increases in Gr, the former completely disappears due to induced buoyancy disturbances.
In Figure 6 we illustrate contour plots of the amplified perturbations in the radial velocity at the value of Gr when G = G0. The sequence of contour plots follows that of Figure 5 for C1 to C4. Notice t−2, t−1, t0, t1 and t2 follow an arithmetic progression, where t0 is defined as the time when G = G0. We see in Figure 6 that at G = G0 we have a reversal in the rotational direction of the perturbed flow.
5. Conclusion
Over the past twenty years, researchers have widely utilized non-normal analysis to investigate the linear transient characteristics of wall bounded flows, particularly shear flows. However, there has been a relatively limited focus on applying this approach to examine the behaviour of Stratified Taylor-Couette Flow (STCF).
This study aims to explore the dynamics of perturbations under different tempera- ture conditions and analyze their patterns of amplification. The research emphasizes the correlation between various flow configurations, highlighting their similarity in transient dynamics despite differing speed ratios. Additionally, it investigates the subcritical effects of thermal stratification on the dynamics of the disturbances. The interplay between viscous and buoyancy effects, counteracted by strong centrifugal forces, is found to influence the growth and decay of the amplification factor. As the temperature increases, beyond a turning point, buoyancy forces become dominant, leading to a linear increase in the ampli- fication factor. The findings of this study reveal that incorporating temperature into the analysis significantly alters the expected outcomes, deviating significantly from the results obtained by Meseguer[36] and Coles[31]. This supports the notion that buoyancy, induced by the stratification of temperature variation, plays a significant role. The transient analysis suggests the presence of complex dynamical phenomena specific to transient dynamics, which cannot be captured by solely focusing on the growth rate of the eigenvalue.
However, it is important to note that the occurrence of this phenomenon and its de- tectability through physical laboratory experiments are yet to be determined. Experimental verification would be beneficial to confirm these findings.
Author Contributions
Conceptualization, L.E. Godwin; methodology, L.E. Godwin; software, L.E. Godwin; validation, L.E. Godwin; formal analysis, L.E. Godwin; investigation, L.E.Godwin; resources, L.E. Godwin and S.C. Generalis; writing—original draft preparation, L.E. Godwin; writing—review and editing, L.E. Godwin, P.M.J. Trevelyan, T. Akinaga and S.C. Generalis; supervision, P.M.J. Trevelyan, S.C. Generalis; project administration, P.M.J. Trevelyan and S.C. Generalis; funding acquisition, L.E. Godwin and S.C. Generalis. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by RISE Horizon 2020 ATM2BT, Atomistic to Molecular Turbu- lence, Grant no 824022, TETFUND scholarship and DTI EPSRC grant, Aston University sponsorship.
Data Availability Statement
The Matlab sources codes used to generate the data in this study can be made available upon request.
Acknowledgments
We would like to thank Dr. Samesa Igirigi and Dr. Hart Abarasi for many fruitful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Energy Norm
In computing G0 not all eigenvalues and corresponding eigenvectors contribute to the evolution of the transient growth in respect to the non-normality of the matrix operator L. Thus in practise a subset of the eigenvalues and the corresponding eigenvectors are used in computing the transient growth. We suppose that, given the spectrum of L of the eigenmodes determined by the wavenumbers n and k, the linear subspace SN spanned by the corresponding eigenfunctions of the least stable N eigenvalues (λ1, λ2, ..., λN ) is defined as:
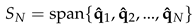 We expand the perturbation q ∈ SN as a linear combination in terms of the basis {} spanned by SN :
We expand the perturbation q ∈ SN as a linear combination in terms of the basis {} spanned by SN :
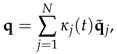 and κ is the time-dependent coefficient and the time evolution of (A2), becomes :
and κ is the time-dependent coefficient and the time evolution of (A2), becomes :
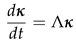 also, it follows that κ is an approximated eigenvalue solution, thus it admits the initial value solution of the form:
also, it follows that κ is an approximated eigenvalue solution, thus it admits the initial value solution of the form:
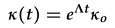 where,
where,
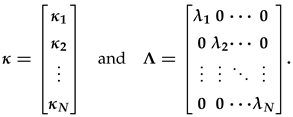 The matrix Λ is the linear evolution of the operator L projected unto the subspace SN and κ is the expansion coefficient. We proceed with the analysis of the initial value problem defined in the previous section. The evolution of the perturbation dynamics is described by transforming the perturbation q in to κ. This transformation is obtained by defining a scalar product and the corresponding energy norm. Thus we define the energy norm as the inner product of the perturbation, q:
The matrix Λ is the linear evolution of the operator L projected unto the subspace SN and κ is the expansion coefficient. We proceed with the analysis of the initial value problem defined in the previous section. The evolution of the perturbation dynamics is described by transforming the perturbation q in to κ. This transformation is obtained by defining a scalar product and the corresponding energy norm. Thus we define the energy norm as the inner product of the perturbation, q:
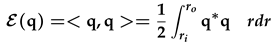 where q∗ is the complex conjugate of the perturbation q. Suppose we are given ∈ SN as the vectors of the inner product Mij, thus the energy norm can be expanded as:
where q∗ is the complex conjugate of the perturbation q. Suppose we are given ∈ SN as the vectors of the inner product Mij, thus the energy norm can be expanded as:
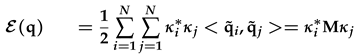 and M is Hermitian, positive definite Gramian matrix and can be decomposed by the Cholesky decomposition
where F∗ is the conjugate transpose of F. Thus we continue by expressing the energy norm of the perturbation in standard 2-norm (|| · ||2) on SN :
and M is Hermitian, positive definite Gramian matrix and can be decomposed by the Cholesky decomposition
where F∗ is the conjugate transpose of F. Thus we continue by expressing the energy norm of the perturbation in standard 2-norm (|| · ||2) on SN :
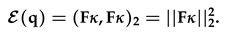
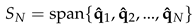
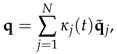
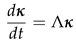
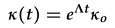
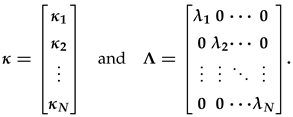
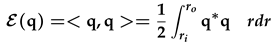
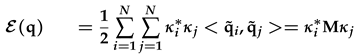
M = F∗ F
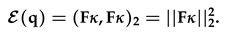
We seek to compute the maximum energy amplification factor G0(t), given an initial condition κo. Hence we proceed by defining the energy amplification factor g(t) as the ratio of the energy norm of the expansion coefficient κ(t) and its initial condition κo. The energy amplification factor g(t) is define mathematically as:
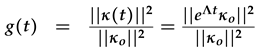 The optimal energy amplification G(t) is obtained by maximizing the g(t) for a given time t over all the initial conditions κo:
The optimal energy amplification G(t) is obtained by maximizing the g(t) for a given time t over all the initial conditions κo:
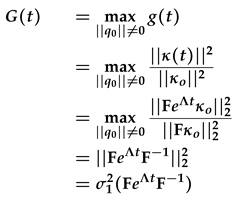 where σ1 is the principal singular value and it can be easily computed by widely available numerical softwares (i.e MATLAB). We compute G0 by maximizing G(t) for all values of the wavenumbers pair (k, n) and for fixed values of all of the other parameters Gr, Pr, Rei, Reo, η and ϵ.
where σ1 is the principal singular value and it can be easily computed by widely available numerical softwares (i.e MATLAB). We compute G0 by maximizing G(t) for all values of the wavenumbers pair (k, n) and for fixed values of all of the other parameters Gr, Pr, Rei, Reo, η and ϵ.
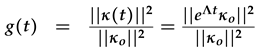
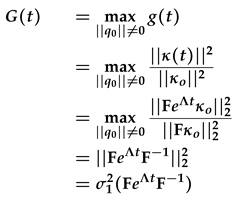
Appendix B. Definitions of matrices A and B

and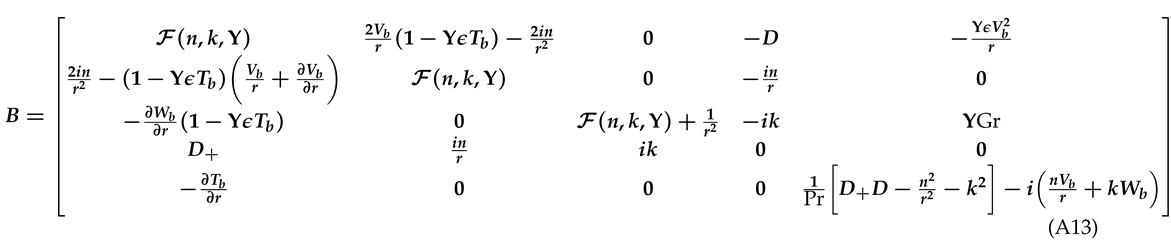
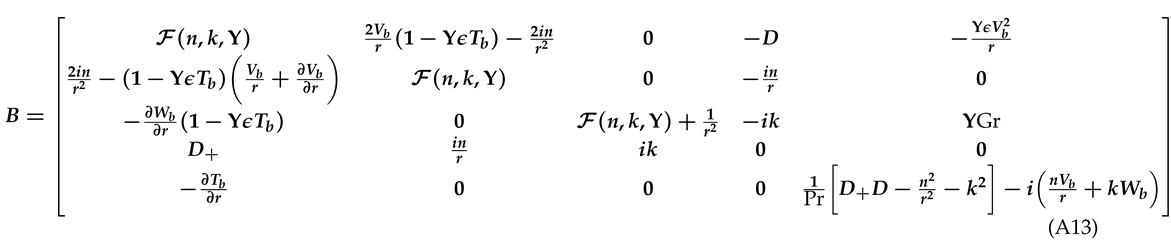
References
- Strogatz, S. In Nonlinear Dynamics and Chaos: with Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, USA, 2018.
- Richtmyer, R.D., Nonlinear Problems: Fluid Dynamics. In Principles of Advanced Mathematical Physics; Springer Berlin Heidelberg: Berlin, Heidelberg, 1978; pp. 364–408. [CrossRef]
- Drazin, P.G. Introduction to hydrodynamic stability; Vol. 32, Cambridge university press, 2002.
- Solomon, T.H., Non-linear Fluid Flow, Pattern Formation, Mixing and Turbulence. In Encyclopedia of Complexity and Systems Science; Meyers, R.A., Ed.; Springer New York: New York, NY, 2009; pp. 6195–6206. [CrossRef]
- Trefethen, L.N.; Trefethen, A.E.; Reddy, S.C.; Driscoll, T.A. Hydrodynamic stability without eigenvalues. Science 1993, 261, 578–584.
- Schmid, P.J.; Brandt, L. Analysis of Fluid Systems: Stability, Receptivity, Sensitivity: Lecture notes from the FLOW-NORDITA Sum- mer School on Advanced Instability Methods for Complex Flows, Stockholm, Sweden, 2013. Applied Mechanics Reviews 2014, 66, [https://asmedigitalcollection.asme.org/appliedmechanicsreviews/article-pdf/66/2/024803/6073896/amr_066_02_024803.pdf]. 024803. [CrossRef]
- Schmid, P.J.; Springer, D.S.H. Stability and Transition in Shear Flows, 2001. 556 pp. ISBN 0-387-98985-4. Journal of Fluid Mechanics 2003, 487, 377–379. [CrossRef]
- Karp, M.; Cohen, J. Tracking stages of transition in Couette flow analytically. Journal of Fluid Mechanics 2014, 748, 896–931. [CrossRef]
- Nayak, A.; Das, D. Transient growth of optimal perturbation in a decaying channel flow. Physics of Fluids 2017, 29, [https://pubs.aip.org/aip/pof/article-pdf/doi/10.1063/1.4985000/14808152/064104_1_online.pdf]. 064104. [CrossRef]
- Romanov, V.A. Stability of plane-parallel Couette flow. Functional analysis and its applications 1973, 7, 137–146.
- Davey, A. On the Stability of Plane Couette flow to Infinitesimal Disturbances. Journal of Fluid Mechanics 1973, 57, 369–380. [CrossRef]
- Drazin, P.G.; Reid, W.H. Hydrodynamic Stability. Journal of Fluid Mechanics 1981, 124. [CrossRef]
- Sano, M.; Tamai, K. A universal transition to turbulence in channel flow. Nature Physics 2016, 12, 249–253.
- Eckhardt, B. Transition to Turbulence in Shear Flows. Physica A: Statistical Mechanics and its Applications 2018, 504, 121–129. Lecture Notes of the 14th International Summer School on Fundamental Problems in Statistical Physics. [CrossRef]
- Orszag, S.A. Accurate solution of the Orr–Sommerfeld stability equation. Journal of Fluid Mechanics 1971, 50, 689–703.
- Baines, P.G.; Majumdar, S.J.; Mitsudera, H. The mechanics of the Tollmien-Schlichting wave. Journal of Fluid Mechanics 1996, 312, 107–124. [CrossRef]
- Andersson, P.; Berggren, M.; Henningson, D.S. Optimal disturbances and bypass transition in boundary layers. Physics of Fluids 1999, 11, 134–150.
- Kreilos, T.; Khapko, T.; Schlatter, P.; Duguet, Y.; Henningson, D.S.; Eckhardt, B. Bypass transition and spot nucleation in boundary layers. Physical Review Fluids 2016, 1, 043602.
- Meseguer, A.; Mellibovsky, F.; Avila, M.; Marques, F. Instability mechanisms and transition scenarios of spiral turbulence in Taylor-Couette flow. Physical Review E 2009, 80, 046315.
- Eckert, M. The troublesome birth of hydrodynamic stability theory: Sommerfeld and the turbulence problem. European Physical Journal H 2010, 35, 29–51. [CrossRef]
- Reddy, S.C.; Henningson, D.S. Energy growth in viscous channel flows. Journal of Fluid Mechanics 1993, 252, 209–238. [CrossRef]
- Heaton, C.J.; Peake, N. Transient growth in vortices with axial flow. Journal of Fluid Mechanics 2007, 587, 271–301. [CrossRef]
- Ha, K.; Chomaz, J.M.; Ortiz, S. Transient growth, edge states, and repeller in rotating solid and fluid. Phys. Rev. E 2021, 103, 033102. [CrossRef]
- Quintanilha, H.; Paredes, P.; Hanifi, A.; Theofilis, V. Transient growth analysis of hypersonic flow over an elliptic cone. Journal of Fluid Mechanics 2022, 935, A40. [CrossRef]
- Andereck, C.D.; Liu, S.; Swinney, H.L. Flow regimes in a circular Couette system with independently rotating cylinders. Journal of fluid mechanics 1986, 164, 155–183.
- Gebhardt, T.; Grossmann, S. The Taylor–Couette eigenvalue problem with independently rotating cylinders. Zeitschrift für Physik B Condensed Matter 1993, 90, 475–490.
- Bai, Y.; Latrache, N.; Kelai, F.; Crumeyrolle, O.; Mutabazi, I. Viscoelastic instabilities of Taylor-Couette flows with different rotation regimes. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2023, 381, 20220133, [https://royalsocietypublishing.org/doi/pdf/10.1098/rsta.2022.0133]. [CrossRef]
- Lopez, J.M.; Lopez, J.M.; Marques, F. Stably stratified Taylor-Couette flows. Philosophical Transactions of the Royal Society A: Mathe- matical, Physical and Engineering Sciences 2023, 381, 20220115, [https://royalsocietypublishing.org/doi/pdf/10.1098/rsta.2022.0115]. [CrossRef]
- Merbold, S.; Hamede, M.H.; Froitzheim, A.; Egbers, C. Flow regimes in a very wide-gap Taylor-Couette flow with counter-rotating cylinders. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2023, 381, 20220113, [https://royalsocietypublishing.org/doi/pdf/10.1098/rsta.2022.0113]. [CrossRef]
- Taylor, G.I. VIII. Stability of a viscous liquid contained between two rotating cylinders. Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character 1923, 223, 289–343, [https://royalsocietypublishing.org/doi/pdf/10.1098/rsta.1923.0008]. [CrossRef]
- Coles, D. Transition in circular Couette flow. Journal of Fluid Mechanics 1965, 21, 385–425.
- Van Atta, C. Exploratory measurements in spiral turbulence. Journal of Fluid Mechanics 1966, 25, 495–512.
- Hegseth, J.J.; Andereck, C.D.; Hayot, F.; Pomeau, Y. Spiral Turbulence and Phase Dynamics. Phys. Rev. Lett. 1989, 62, 257–260. [CrossRef]
- Prigent, A.; goire, G.G.; Chaté, H.; Dauchot, O.; van Saarloos, W. Large-Scale Finite-Wavelength Modulation within Turbulent Shear Flows. Physical Review Letters 2002, 89. [CrossRef]
- Hristova, H.; Roch, S.; Schmid, P.J.; Tuckerman, L.S. Transient growth in Taylor-Couette flow. Physics of Fluids 2002, 14, 3475–3484, [https://pubs.aip.org/aip/pof/article-pdf/14/10/3475/12764697/3475_1_online.pdf]. [CrossRef]
- Meseguer, A. Energy transient growth in the Taylor-Couette problem. Physics of Fluids 2002, 14, 1655–1660, [https://pubs.aip.org/ai pdf/14/5/1655/12586152/1655_1_online.pdf]. [CrossRef]
- Maretzke, S.; Hof, B.; Avila, M. Transient growth in linearly stable Taylor–Couette flows. Journal of Fluid Mechanics 2014, 742, 254–290.
- Lopez, J.M.; Marques, F.; Avila, M. The Boussinesq approximation in rapidly rotating flows. Journal of fluid mechanics 2013, 737, 56–77.
- Lopez, J.M.; Lopez, J.M.; Marques, F. Stably stratified Taylor–Couette flows. Philosophical Transactions of the Royal Society A 2023, 381, 20220115.
- Henningson, D.S.; Reddy, S.C. On the role of linear mechanisms in transition to turbulence. Physics of Fluids 1994, 6, 1396–1398.
- Schmid, P.J. Nonmodal stability theory. Annu. Rev. Fluid Mech. 2007, 39, 129–162.
Figure 1.
A schematic description of the system investigated in this paper. Here Ωi > 0, and Ωo < 0.
Figure 1.
A schematic description of the system investigated in this paper. Here Ωi > 0, and Ωo < 0.
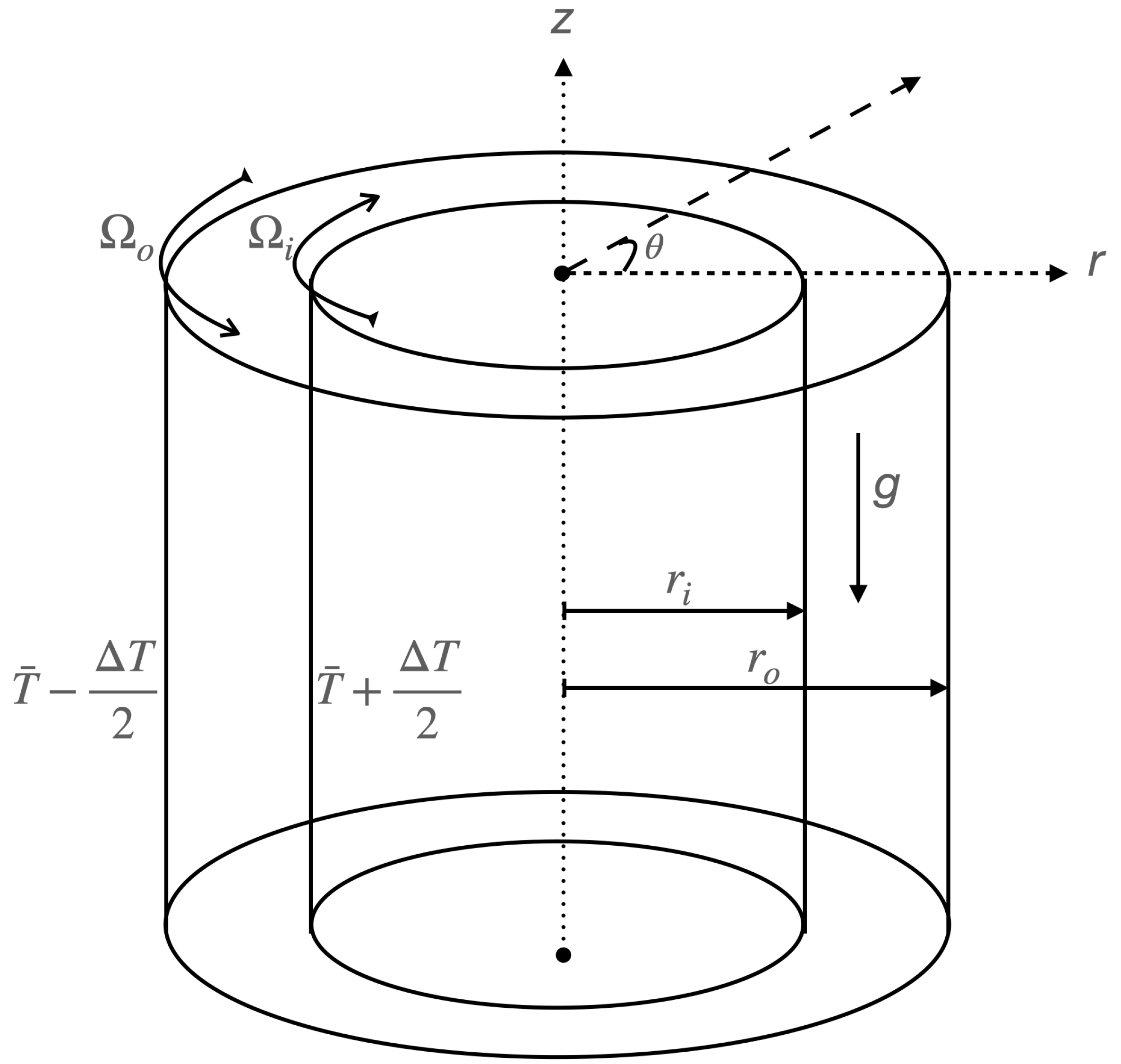
Figure 2.
Plots of the amplification factor for the same parameters values used by Meseguer [36] and Maretzke [37]. Rei = 240, Reo = −271.42, η = 0.881 and k = π for different values of (a) n = 1 and (b) k = 0. The corresponding results in Hristova et al. [35] are when Re= 120 and β = π/2 using the definitions in their paper.
Figure 2.
Plots of the amplification factor for the same parameters values used by Meseguer [36] and Maretzke [37]. Rei = 240, Reo = −271.42, η = 0.881 and k = π for different values of (a) n = 1 and (b) k = 0. The corresponding results in Hristova et al. [35] are when Re= 120 and β = π/2 using the definitions in their paper.
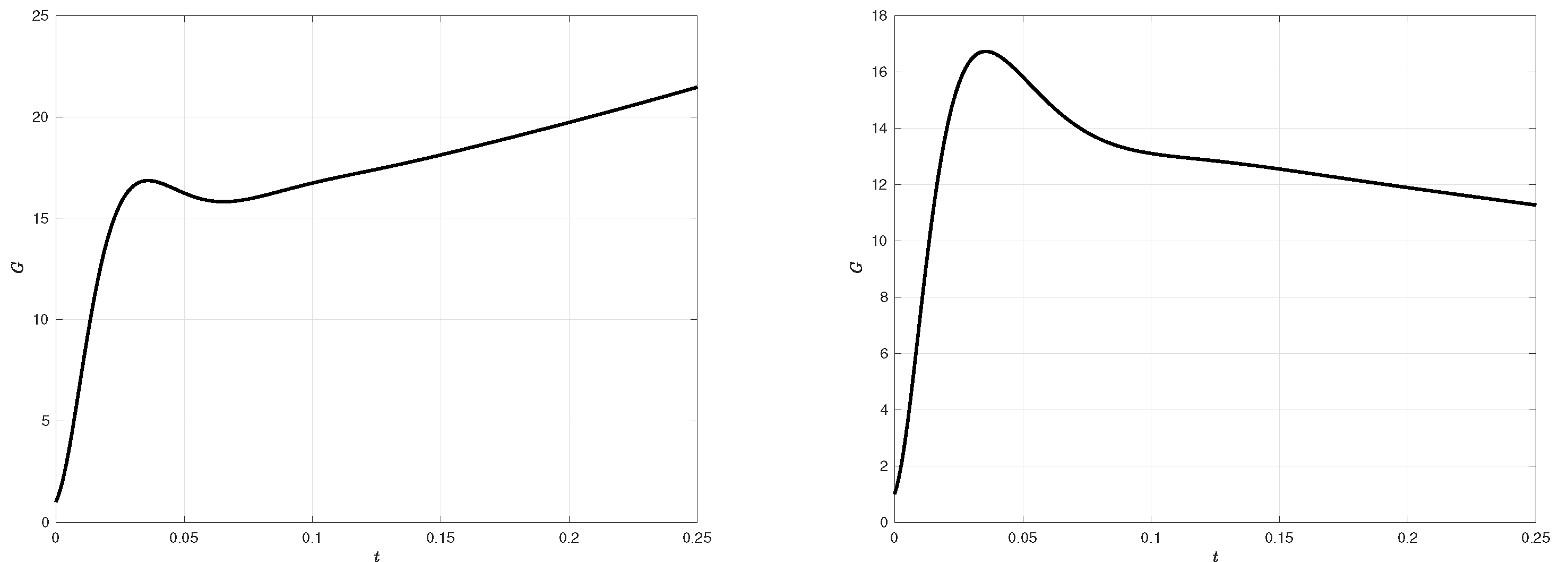
Figure 3.
The plots shows the transient growth for different Gr for each configuration C1, C2, C3 and C4 shown in Table 2), respectively, for a range of Gr ∈ [1000, 10000].
Figure 3.
The plots shows the transient growth for different Gr for each configuration C1, C2, C3 and C4 shown in Table 2), respectively, for a range of Gr ∈ [1000, 10000].
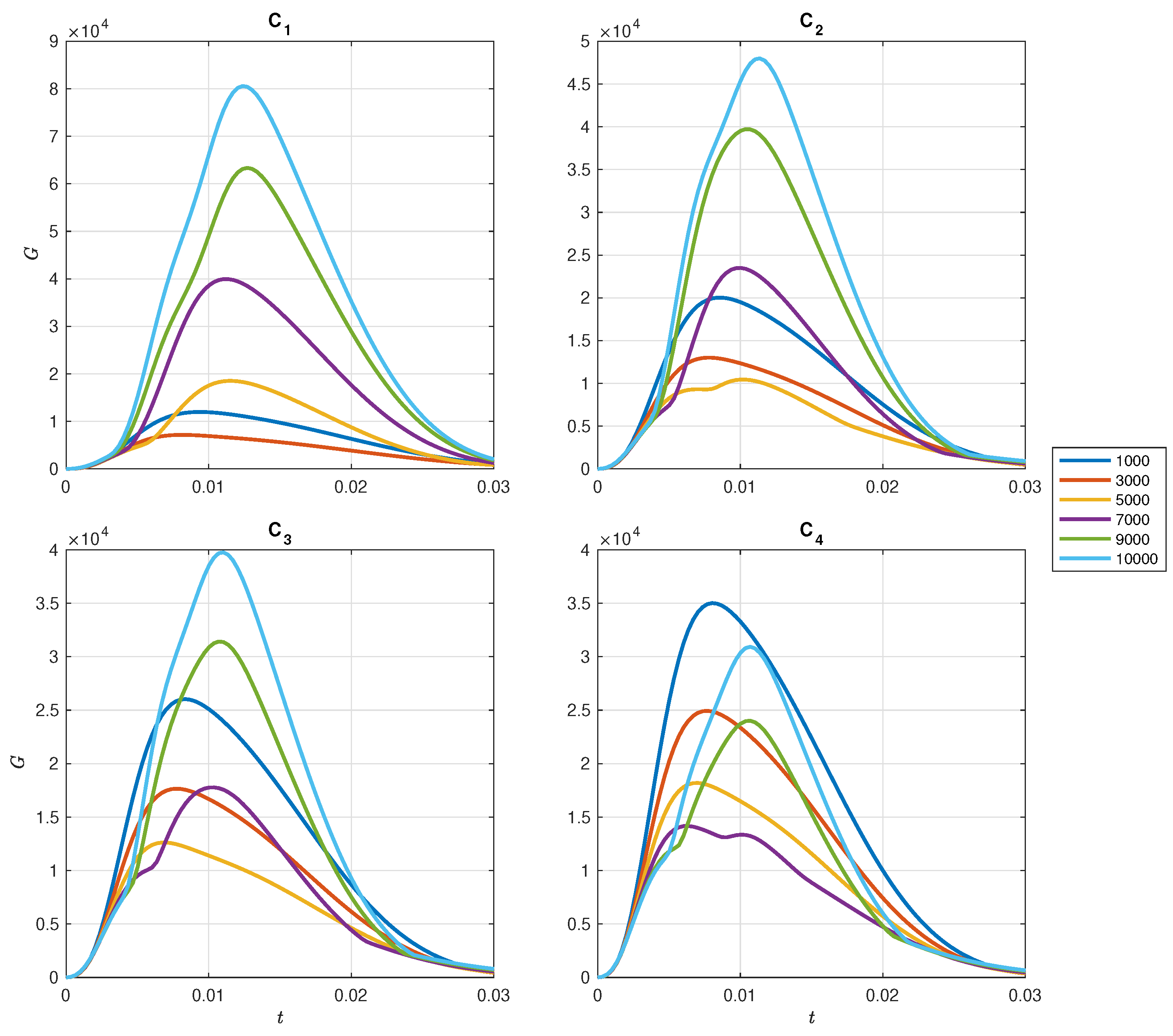
Figure 4.
The top plot is the growth rate with respect to Gr for each configuration. The bottom plot shows the optimal amplification factor G0 of the configurations C1 (solid), C2 (dotted), C3 (dot-dashed) and C4 (dashed) shown in Table 2 for a range of Gr ∈ [0, 10000].
Figure 4.
The top plot is the growth rate with respect to Gr for each configuration. The bottom plot shows the optimal amplification factor G0 of the configurations C1 (solid), C2 (dotted), C3 (dot-dashed) and C4 (dashed) shown in Table 2 for a range of Gr ∈ [0, 10000].
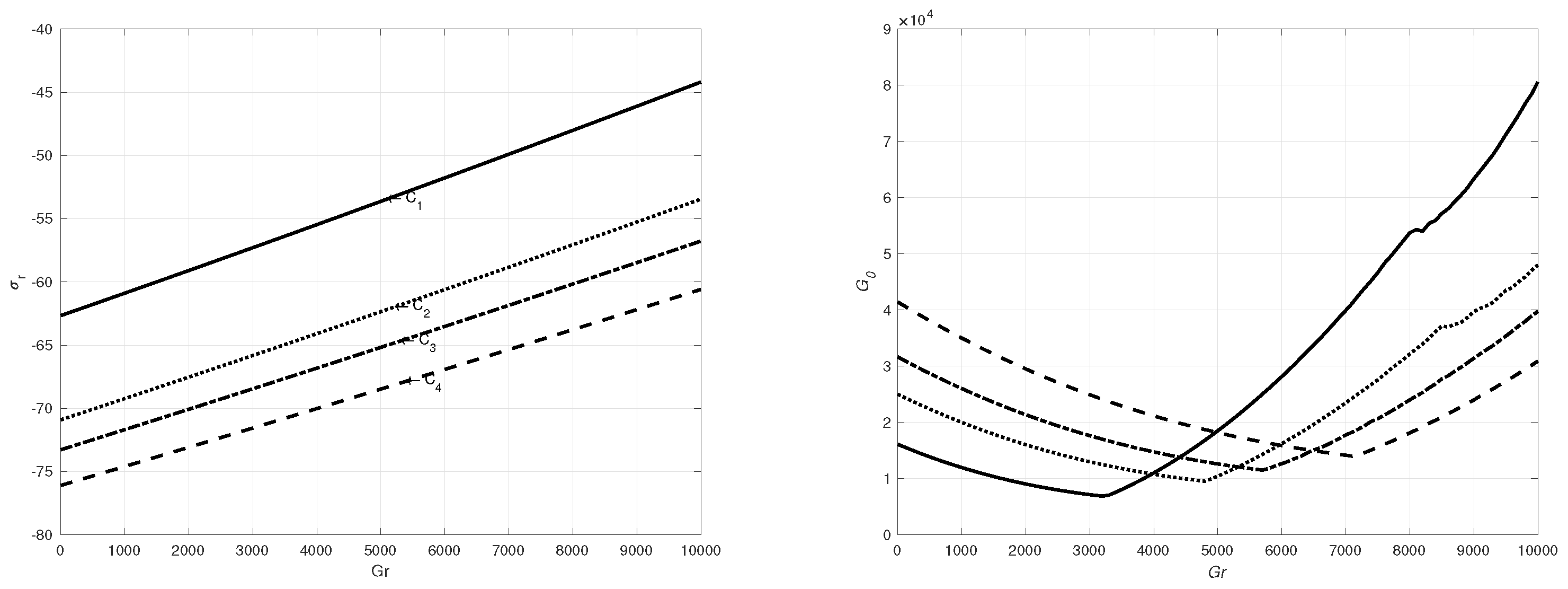
Figure 5.
Snapshots of transient growth factor G(t) for increasing Gr. The plots of the first to the last row represent C1, C2, C3, and C4 respectively. The numbers above each plot are their respective numerical values for Gr.
Figure 5.
Snapshots of transient growth factor G(t) for increasing Gr. The plots of the first to the last row represent C1, C2, C3, and C4 respectively. The numbers above each plot are their respective numerical values for Gr.
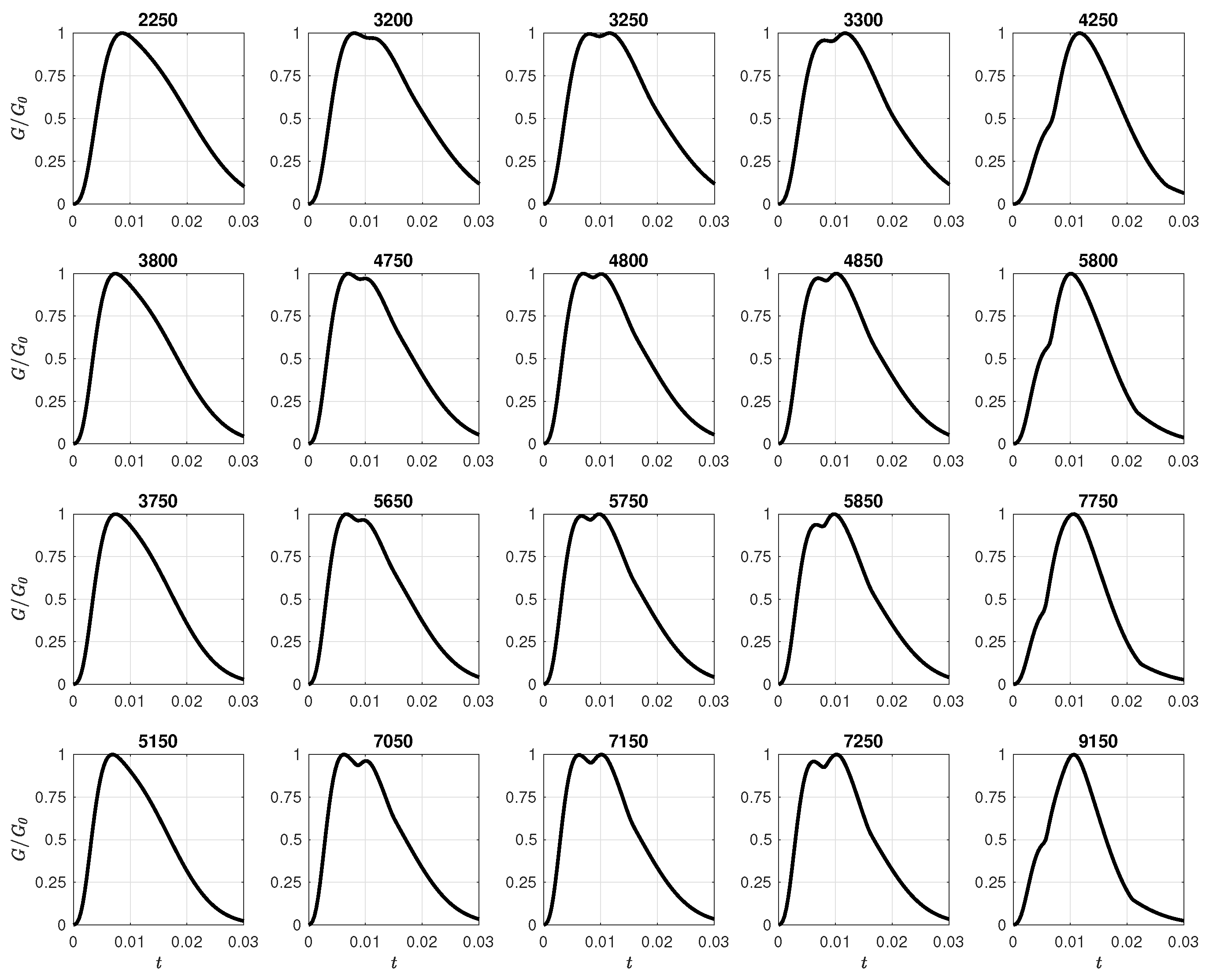
Figure 6.
Contour plots of the amplified perturbations in the radial velocity at the value of Gr when G = G0. The plots of the first to the last row represent C1, C2, C3, and C4, respectively.
Figure 6.
Contour plots of the amplified perturbations in the radial velocity at the value of Gr when G = G0. The plots of the first to the last row represent C1, C2, C3, and C4, respectively.
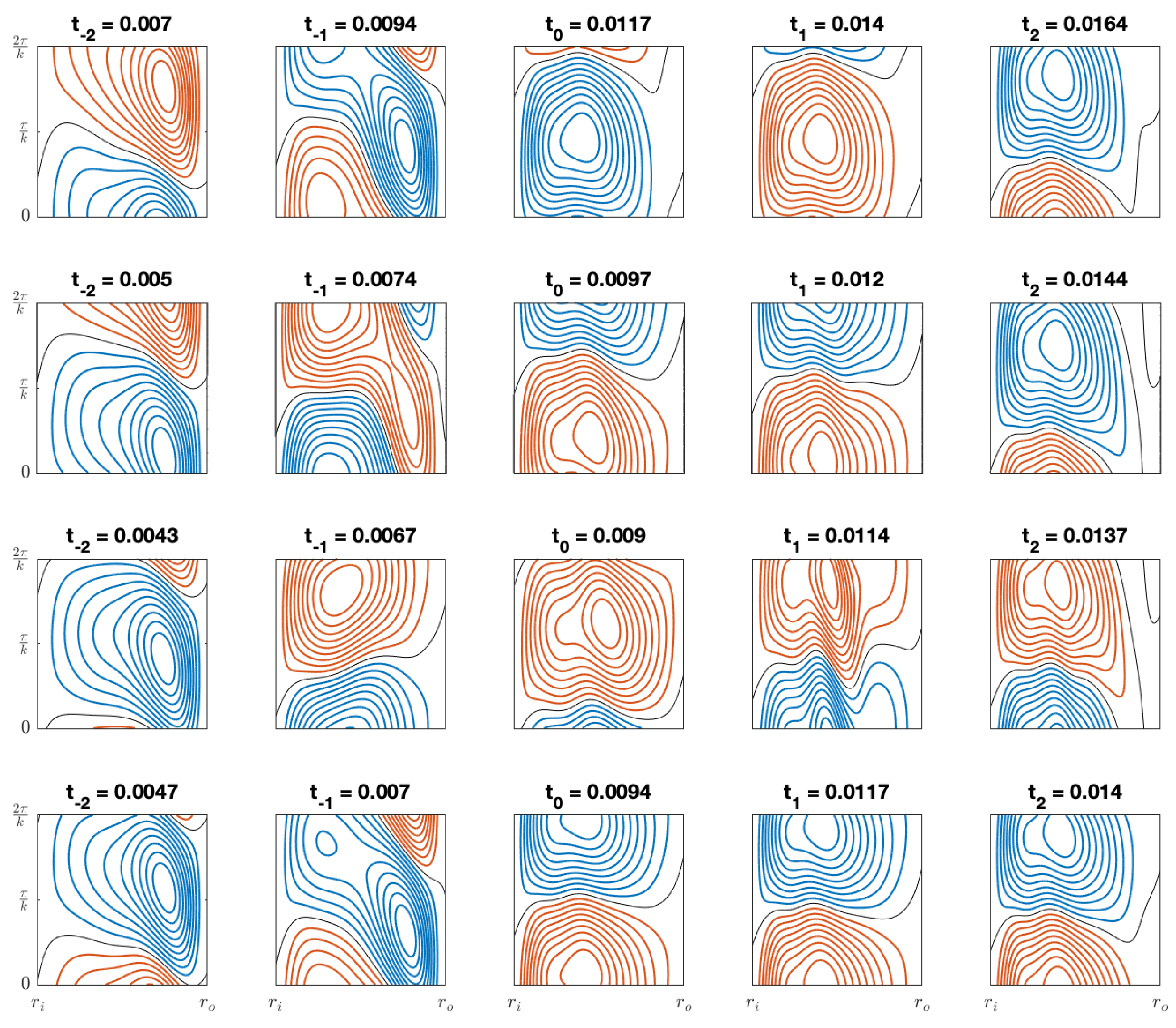
Table 1.
This table displays the dimensionless parameters that are created as a result of the scaling factors applied on the approximated governing equations.
Table 1.
This table displays the dimensionless parameters that are created as a result of the scaling factors applied on the approximated governing equations.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated


_Constantinou_Generalis.png)