Prerpints.org logo
Preprint
Article

Simplified Dynamic Strength Analysis of Cardboard Packaging Subjected to Transport Loads

Altmetrics

Downloads

119

Views

40

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

21 June 2023

Posted:

21 June 2023

You are already at the latest version

Alerts
Abstract
The article presents a simplified method for determining the strength of a corrugated board packaging subjected to dynamic transport loads. The proposed algorithm consists of several calculation steps: (1) a static analysis of the compressive strength of the package, (2) an analysis of random vibrations in the frequency domain, used to determine the resonance frequencies, and (3) a dynamic analysis of the package loaded with computed resonant frequencies. For this purpose, numerical models of the static compression test of the packaging before and after the dynamic analysis of the package subjected to general transport loads were developed. In order to validate the model, the laboratory packaging compression tests were also performed for samples of boxes with 3-layer cardboard. Thanks to this, it was possible to verify the results of numerical simulations of compression tests for several box geometries. Which, in turn, allowed for the development of a method based on dynamic and post-dynamic (static) numerical analysis, allowing to determine with high accuracy the resistance of selected packaging to vibrations and dynamic loads. The results of the (validated experimentally) numerical analysis prove the usefulness of the simplified method presented here for precise estimation of the load capacity of various packages dynamically loaded during transport.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Requirements of the cardboard packaging is strongly related to the transport conditions to which the box will be exposed. Different packaging specification will be required while ocean transport in containers, other in local domestic transport and other during long hours of heavy truck transport through the continent. Depending on the model of transport, the safety factors can range from 3 to even 8 [1]. Often such high values are roughly assumed with a large overestimation and it is not supported by reliable research or analysis of specific cases. Therefore, it is certainly an area to optimize the weight of the packaging, especially now when the industry is striving for sustainable development – zero waste, zero energy balance etc. First step to optimize the packaging should be understanding which factor plays a crucial role in determining strength of the packaging due to particular load mode [2,3,4].
It is worth emphasizing that transport loads are to a large extent not static but dynamic loads, hence high safety factors are used in such cases. In the corrugated packaging industry, the test known as vertical random vibration (VRV) test is the basic tool that allows to assess the resistance of a given packaging to dynamic loads [5]. It is particularly important to compare the load capacity of the packaging for static box compression test (BCT) before and after the vertical random vibration test. The great advantage of this approach is the possibility to confront the results for different types of packaging. These tests carried out even for only one type of packaging, allows for the elimination of a packaging design that would be defective in regard to dynamic loading.
However, for the company producing cardboard packaging, performing such tests in the factory, requires engaging special resources. This includes preparing many packaging samples with the necessary seasoning and performing the whole campaign of testing with many series of tests: BCTs of the packaging before the random vibration test, nominal VRV testing and BCTs of the packaging after the random vibration test.
Therefore, the use of modern numerical methods for the initial assessment of the suitability of the packaging design, obtaining insight for packaging prototype and/or cardboard grade selection seem to be very useful. The finite element method (FEM) is one of the most commonly used numerical methods for mechanical analysis of structures [6,7,8]. The effectiveness of this method is confirmed by many scientific works and industrial implementations, also in the cardboard packaging industry [9,10,11,12,13,14,15]. The finite element method requires the use of detailed/accurate packaging geometry in order to obtain reliable calculation results. For instance, in [16,17] it was shown that size/position of opening and perforation pattern in packaging play crucial role in determining the strength of the packaging, respectively. Moreover, reliable material data should be used, these data must reflect the mechanical properties of the cardboard from which the packaging is produced, and an adequate constitutive model must be adopted. Commercial products are available that enable the acquisition of such mechanical properties of cardboard and the implementation of FEM calculations [18]. As shown in the literature, the commonly used empirical approaches to model the compression strength are not enough in complex cases [19].
It should be emphasized that traditional dynamic analysis by using the finite element method to model VRV test in the time domain would be extremely computationally expensive. Therefore, in this paper, we propose to use a method combined with power spectral density (PSD) approach, which allows to solve a substitute dynamic problem in the frequency domain that finds a solution to the initial problem in the time domain. PSD approach is a method that allows to simplify the problem and is used effectively in many branches of mechanical engineering, including the automotive industry [20], aerospace [21], mechanics and machine construction [22], as well as biomedical engineering [23].
In the scientific literature, there are simplified methods for assessing the load capacity of packaging against static loads. An example of work on the static load capacity of packaging can be the paper of Garbowski et al. [19], in which the McKee formula and its extensions were considered and their effectiveness was compared with the numerical approach. Another example is an article on the effect of holes [17] or perforations [16] on the static load capacity of corrugated cardboard packaging. There are few studies that deal with the dynamic properties of packaging or corrugated boards [24,25], hence this work is of a particularly innovative/unique character.
Additionally, no papers on the use of the PSD method in estimating the strength in respect to VRV test of the cardboard packaging have been found in the literature. Such examples are available in the field of mechanics and machine construction, for example in the article on the reliability of wind power turbines [26]. Therefore in this work, a combination of static and dynamic test based on the PSD-VRV method was adopted to develop a fast and reliable algorithm for determining the strength of a corrugated box subjected to dynamic loads. To our knowledge, this has not been done before by other researchers, and therefore this work is a new contribution related to the effective estimation of the load capacity of cardboard packaging under dynamic loads.

2. Materials and Methods

2.1. Measurements of compressive strength of boxes

In order to receive reliable results of the numerical simulations the results must be validated with the experimental data. Here, the numerical results received from BCT were calibrated by comparing the outcome with the static compression tests of boxes conducted in the laboratory on the press machine. The nominal press force was 10 kN with an accuracy of 0.1 N. The accuracy of applying the displacement was 0.001 mm. The cardboard used for box samples was single-wall three-layered board with 400 g/m2 grammage, the B flute was used. The mean thickness of the cardboard was 2.85 mm. Three geometries of FEFCO code F201 boxes were tested, namely, 250 × 250 × 150 mm, 300 × 200 × 250 mm and 300 × 200 × 450 mm. Five samples were prepared for each geometry of the box to obtain a proper statistical representation. Selected box samples inside testing machine were presented in Figure 1.
Before the test the packaging were folded manually by one person, the top and bottom flaps were taped (see Figure 1). Packaging were conditioned according to the laboratory standard of TAPPI T402 [27] which determines the standard conditioning and testing atmospheres for paper, board, pulp handsheets, and related products. Therefore, the humidity of 50% and temperature of 23°C was set in the preconditioning chamber.

2.2. Measurements of vertical random vibration test of boxes

In order to determine and compare the performance of the packaging to environmental vibration during transportation the standard testing procedure is required. In this paper, the ISO 13355 standard was used [5]. The standard describes the method for testing the packaging in a vertical random vibration test. The method is more reliable and gives more realistic results than sinusoidal vibration tests described in ISO 2247 [28] and ISO 8318 [29].
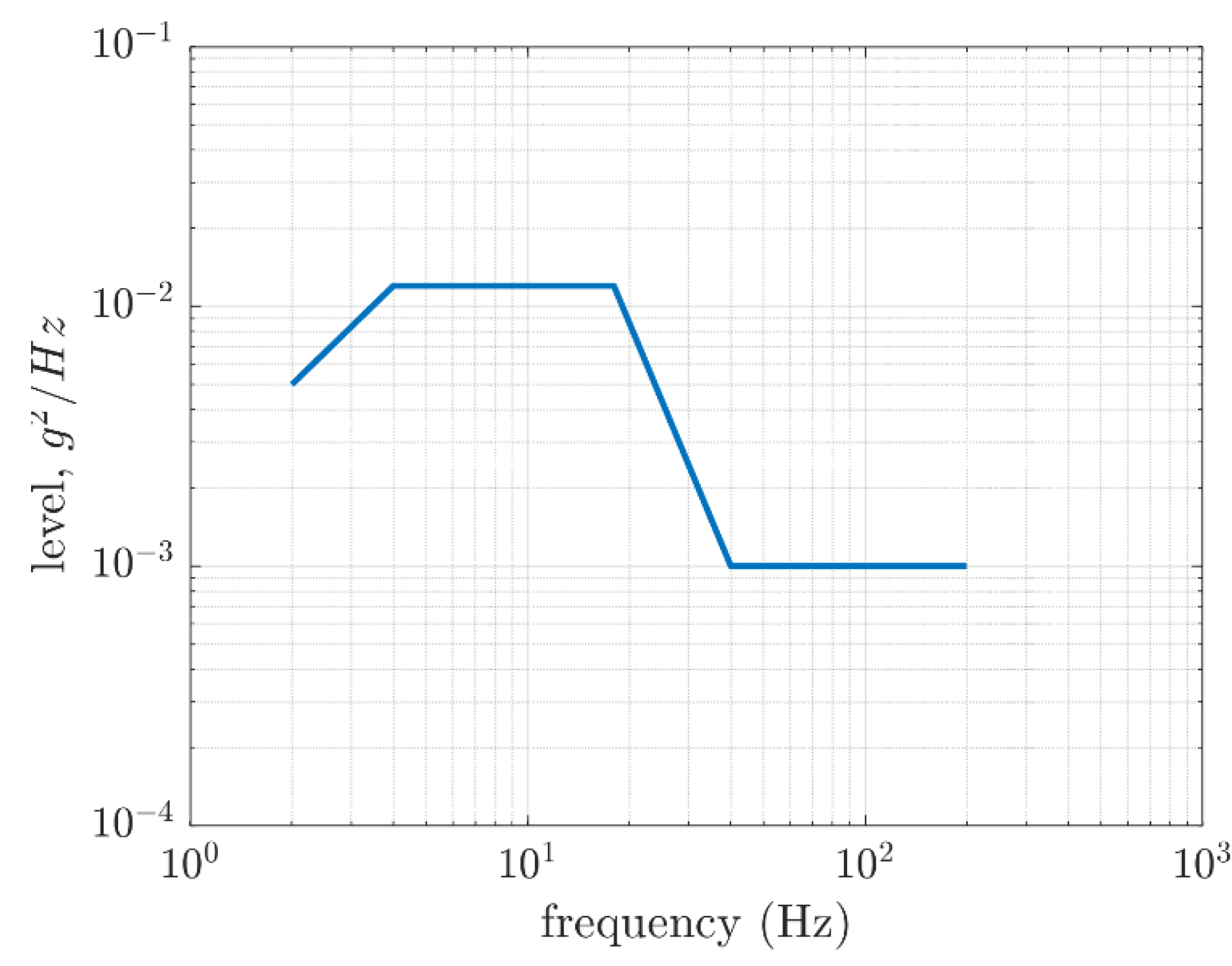
In ISO 13355 test, a vibrating table is excited for the effective frequency domain with a cardboard box sample placed on it. The setups of the test are predetermined, this applies, for example, to the duration of the test, the ambient temperature and humidity or acceleration of power spectral density. During the test the box sample cannot translate horizontally and must be closed. The vibration table must be stiff and the gravity center of the specimen must be positioned in the center of the table. According to ISO 13355, if the experimental data for reproducing the effects of transportation are absent, the test duration and power spectral density of the vibration table may be assumed as shown in Figure 2. Therefore, the data demonstrated in Figure 2 were used in the numerical study presented, as the representative data reproducing the environmental vibrations during transportation.

2.3. Numerical modelling of the resistance of the cardboard packaging due to transport loadings

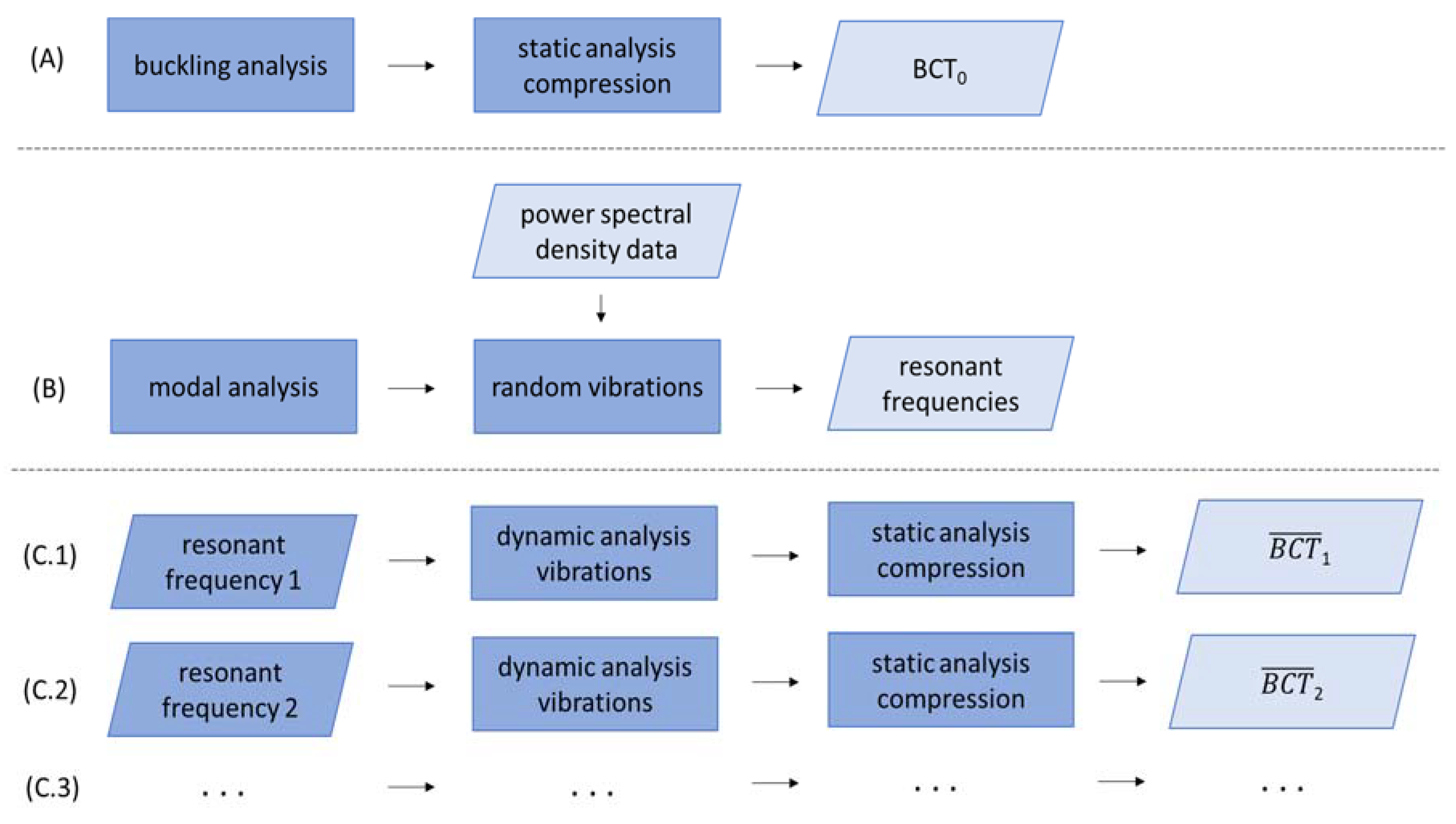
The overall aim of the paper is to derive the numerical tool for computing the change in the compression strength of particular box after representative environmental vibration during transportation. Therefore, as presented in Figure 3, first, the static finite element analysis of stress free state box is performed preceded by the buckling analysis to determine the numerical imperfection field, likewise in [3,4]. From this step B C T 0 is determined, i.e., the compression strength of the box before VRV test. Second, the modal analysis of the box is conducted and together with the power spectral density (PSD) data, they are used as the input for random vibrations analysis. Eigenmodes from eigenfrequency (modal) analysis are used to compute the response variables, such as stresses, strains or displacements. Numerical details on the method are available in [30,31,32]. In this step, the resonant frequencies, ω i are determined.
Third, the displacement boundary condition with particular i th resonant frequency, ω i , is applied to the bottom of the box in a dynamic analysis which simulates the vibrations with fixed frequency. Next, after selected number of cycles, the quasi-static compression test analysis is carried out numerically. From the last analysis, B C T i ¯ is determined, i.e., the compression strength of the box after VRV test in respect to i th resonant frequency, in which i depends on the number of determined resonant frequencies from random vibrations analysis.
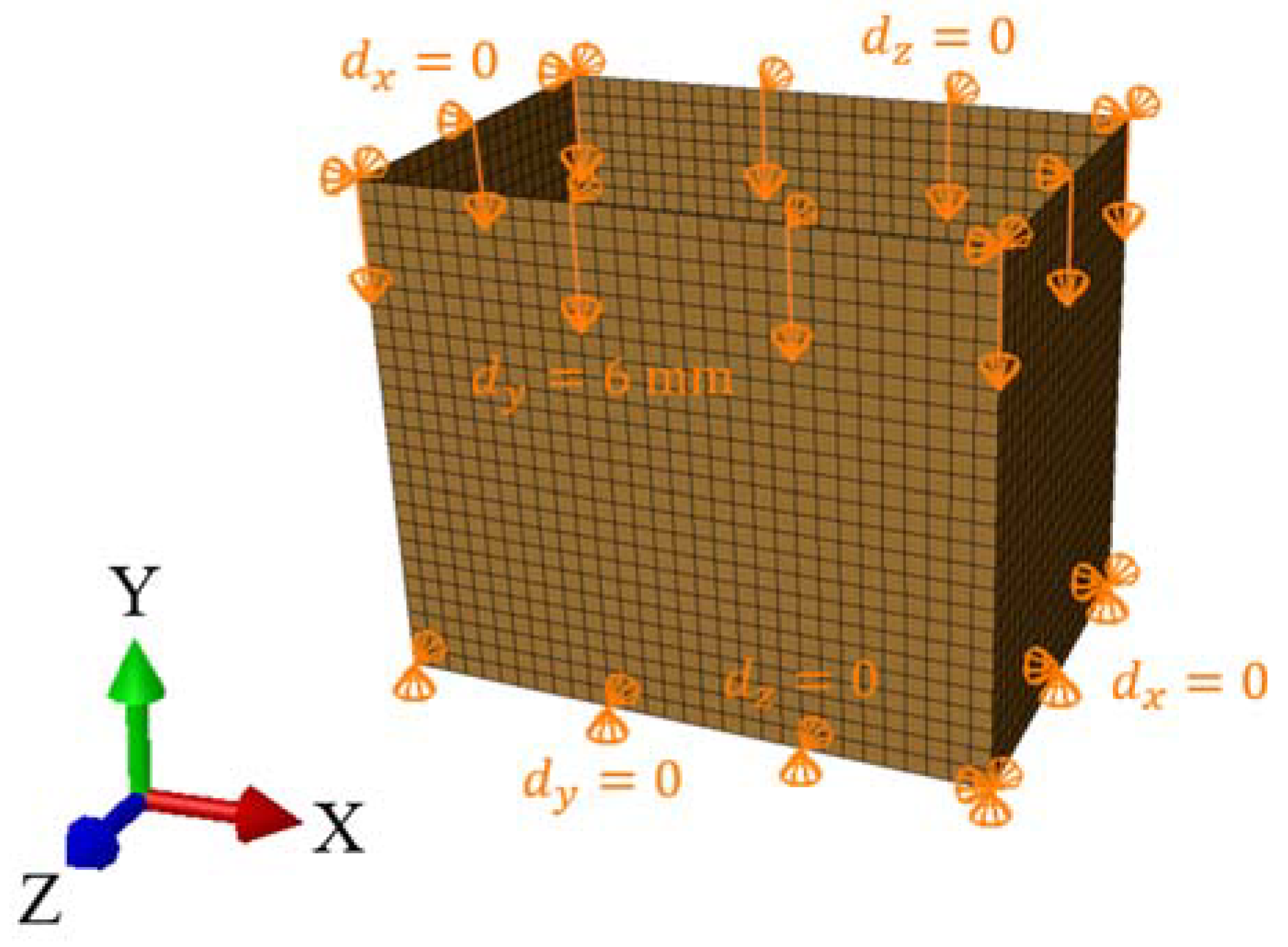
In the study, the static analysis of box compression, see Figure 3A, replicates the laboratory test conditions, likewise in [3,16,17]. In finite element method (FEM) analysis, only the load-bearing walls of the packaging were modeled (see Figure 4). Bottom and top flaps have been taken into account by applying appropriate boundary conditions. Out-of-plane displacements on the bottom and top edges of the sidewalls have been blocked. The box compression test was simulated by applying a vertical displacement to the top edges of the box. The other details on the finite element mesh and constitutive modelling will be described at the end of this section.
The study of vertical random vibrations in the time domain is a very dynamic process and easy to carry out in laboratory conditions. Vibration table and acceleration/displacement sensors are required to perform the test properly. On contrary, the numerical counterpart of such test modelled in time domain is not trivial to simulate due to extremely high nonlinear boundary conditions, which changes in time. Thus, if one would like to compute the structural response of any model in time domain, such boundary conditions would greatly decrease the numerical time step and made convergence difficult. Therefore, in the paper presented, the new approach for modelling VRV test of corrugated board packaging was used, in which the modal analysis is used to determine the resonant frequencies for later use in dynamic explicit finite element (FE) analysis with stable vibration frequency, see Figure 3B.
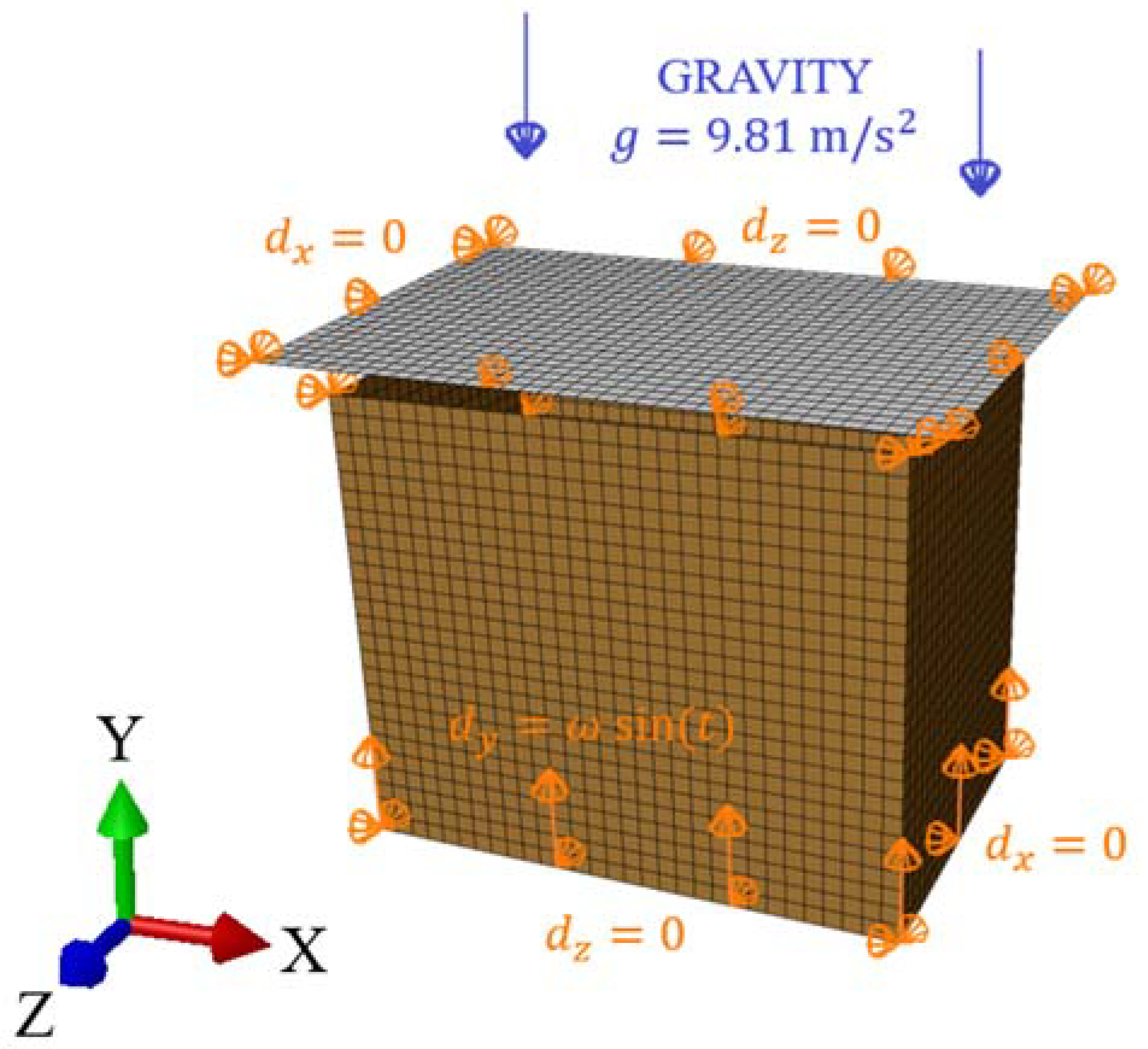
Compared to the static model, a rigid plate has been added to the dynamic explicit analysis to simulate the 8 kg load used in a real vertical random vibration test, see Figure 3C. The dynamic analysis consists of two computational steps. In the first step, the model is loaded with gravity ( g = 9.81   m / s 2 ), which causes the plate to fall onto the packaging. The packaging "holds" the rigid plate by applying contact between these two objects modeled. As in the case of static analysis, out-of-plane displacements of the bottom and top edges of the packaging were blocked. In-plane displacement of the plate was also blocked, see Figure 5. In the second step, the bottom of the box vibrates in time domain with an sinusoidal amplitude of 1 mm and frequency obtained from the modal analysis.
The static, modal and dynamic analyses were carried out for one grade of corrugated board. In each case, the constitutive model assumed was linear elastic orthotropic material with Hill plasticity [33]. In Table 1, the material constants used in the model to simulate the behavior of the 3B400 cardboard were presented. In Table 1, the first columns contain elastic constants, i.e., E 1 and E 2 are the modulus of elasticity, ν 12 is the Poisson's ratio, G 12 is the in-plane shear stiffness, G 13 and G 23 are the shear stiffnesses. In the last columns, the plastic constants of the material were presented, namely, σ 0 is the initial yield strength and R 11 is the yield strength factor in the machine direction of the corrugated board according to Hill potential [33].
Material data for 3B400 cardboard were determined by the BSE System from FEMAT [33]. In the system, the properties are determined based on four mechanical tests in cardboard machine and cross-machine directions. Corrugated board samples have been prepared in the laboratory and conditioned in a climatic chamber according to TAPPI standard T402 [27]. At least ten samples of cardboard were used for each test to obtain statistically representative material data.
In each case, 4-node quadrilateral shell elements with full integration scheme were used to model the corrugated board box. This type of element is labelled as S4 according to Abaqus FEA [33]. A global mesh sizes of 8-10 mm were assumed, which resulted in a different number of degrees of freedom for each geometry case. In 250 × 250 × 150 mm model, the number of elements was 2356 and the number of nodes was 2480. In 300 × 200 × 250 mm model, the number of elements was 2500 and the number of nodes was 2600. In 300 × 200 × 450 mm model, the number of elements was 4500 and the number of nodes was 4600. In dynamic analyses, the rigid plate was modelled discreetly with 864 finite S4 elements, the rigid body properties were assigned to the its elements.

3. Results

3.1. Static compressive strength of boxes

In this section, the outcome of the laboratory compression tests and its numerical counterpart is shown in order to validate the numerical model of the corrugated board packaging. Validation of the mathematical modelling is an intrinsic part of computational mechanics and allows trusting the results obtained.
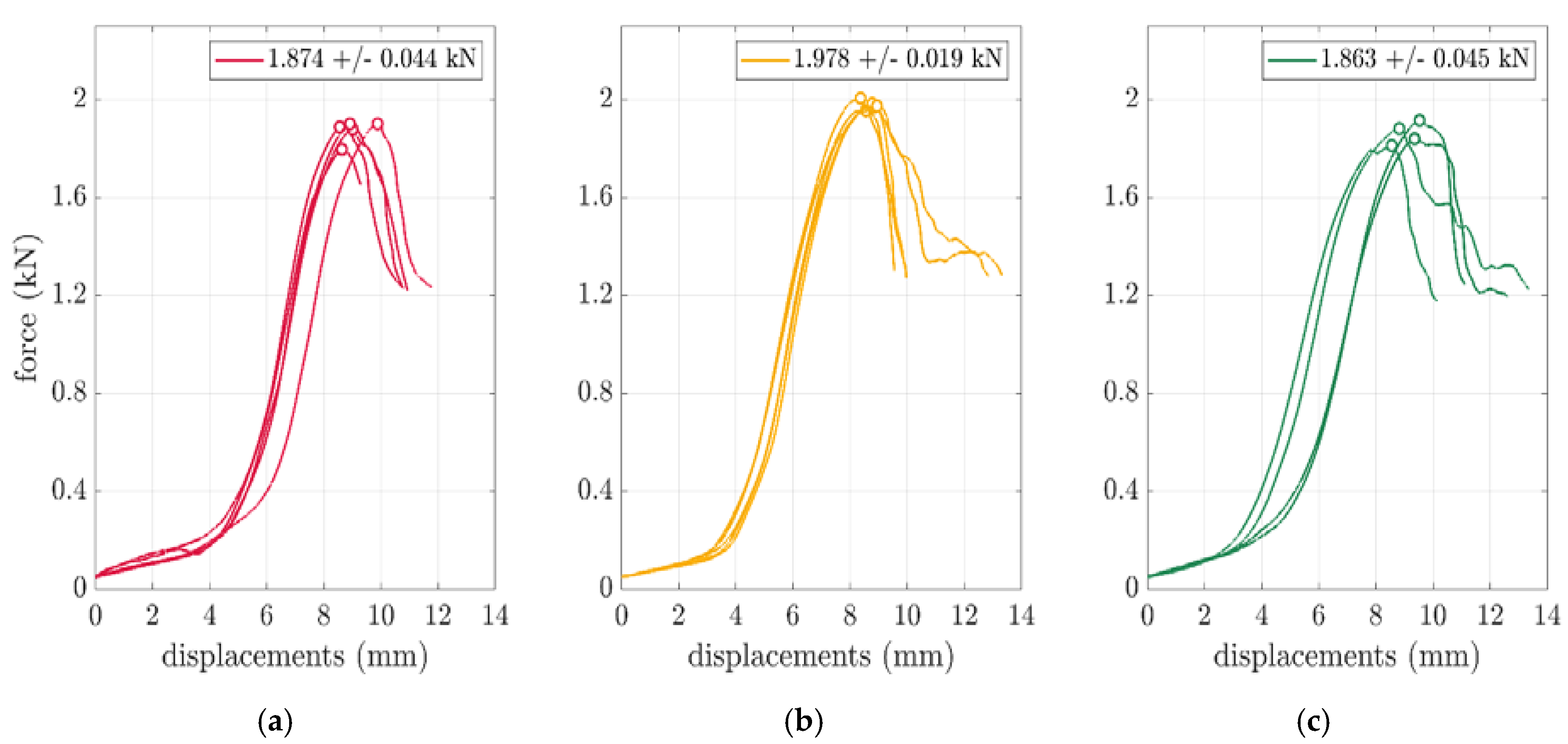
Therefore, in the Figure 6, the box compression test results were presented for selected boxes of FEFCO F201 with various dimensions. Force vs. displacement curves were obtained for all box samples used. The details of the testing procedure were described in Section 2.1. In the plots, the peak values were marked with circles. Relatively small spread of the maximal values may be observed. Individual and mean values with its standard deviations were presented in Table 2, see second and third column.
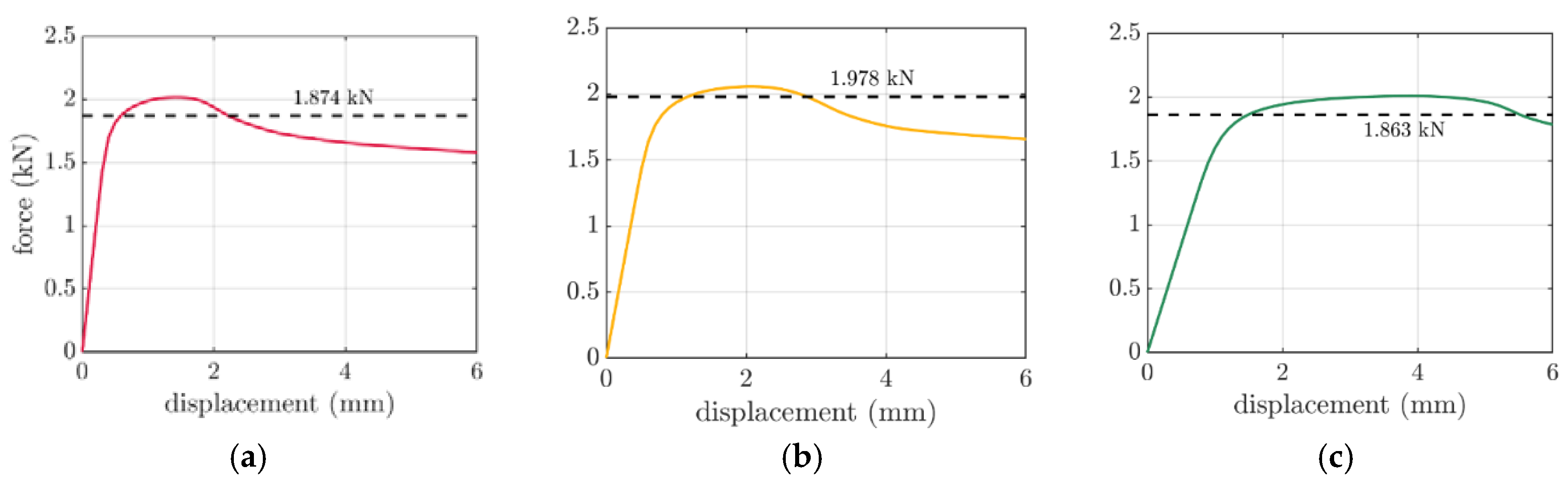
The counterpart cases were modelled through static linear analysis by utilizing the finite element method. The details of the numerical models were described in Section 2.3. In the Figure 7, the numerically derived curves from box compressions were presented for selected boxes of FEFCO F201 with various dimensions. The dashed lines present the mean level of the experimental values obtained. Box compression strengths from displacement control computations were presented in Table 2, see last column.

3.2. Vertical random vibrations of boxes

The workflow of the study and the dynamic analysis concept have been presented in Section 2.3. After static computations, the random response analyses have been conducted for three dimensions of boxes, i.e., 250 × 250 × 150 mm, 300 × 200 × 250 mm and 300 × 200 × 450 mm. Please note that for 250 × 250 × 150 mm case, the wider range of the frequency was considered because the resonant frequency falls on the boundary of the interval, approx. 200 Hz (the default power spectral density assumed was presented in Figure 2).
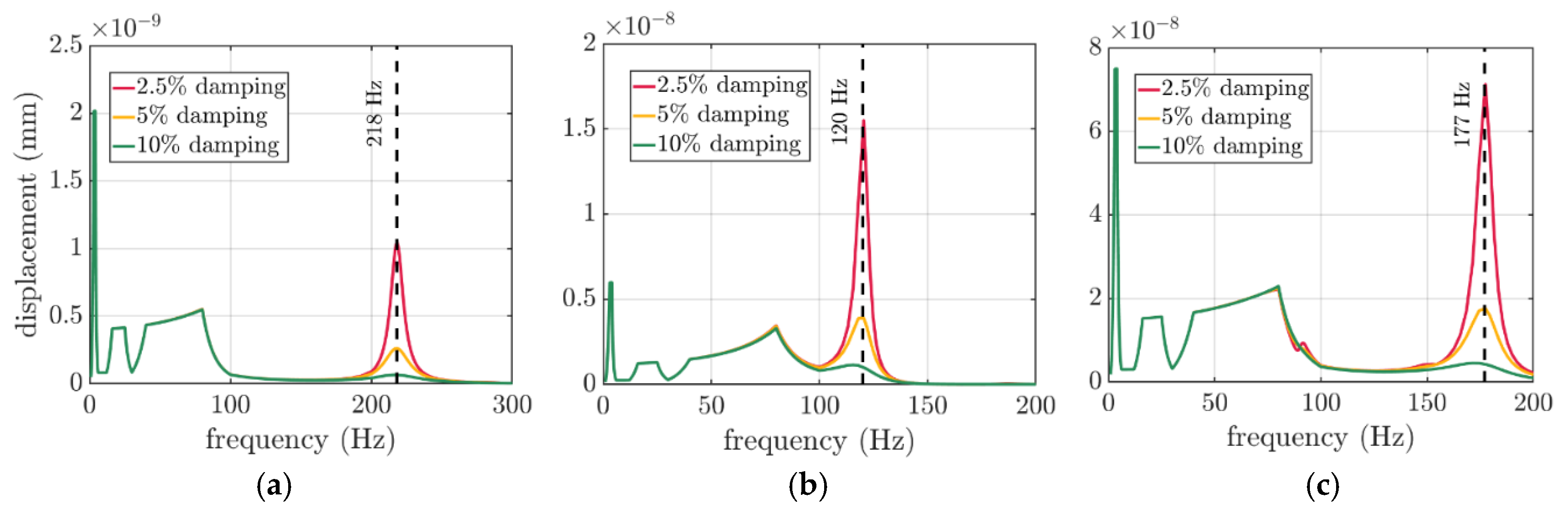
In random response analyses, three levels of damping were considered, i.e., 2.5 % , 5 % and 10 % The computational outcome due to modal analysis has been demonstrated in Figure 8. The change in the damping factor determines the activity of a particular frequency, which is identified as the resonant frequency, ω i . Therefore, for each case of the boxes three curves were presented in each subplot of Figure 8. 218 Hz, 120 Hz and 177 Hz were identified as the resonant frequencies for 250 × 250 × 150 mm, 300 × 200 × 250 mm and 300 × 200 × 450 mm boxes, respectively, see dashed vertical lines.
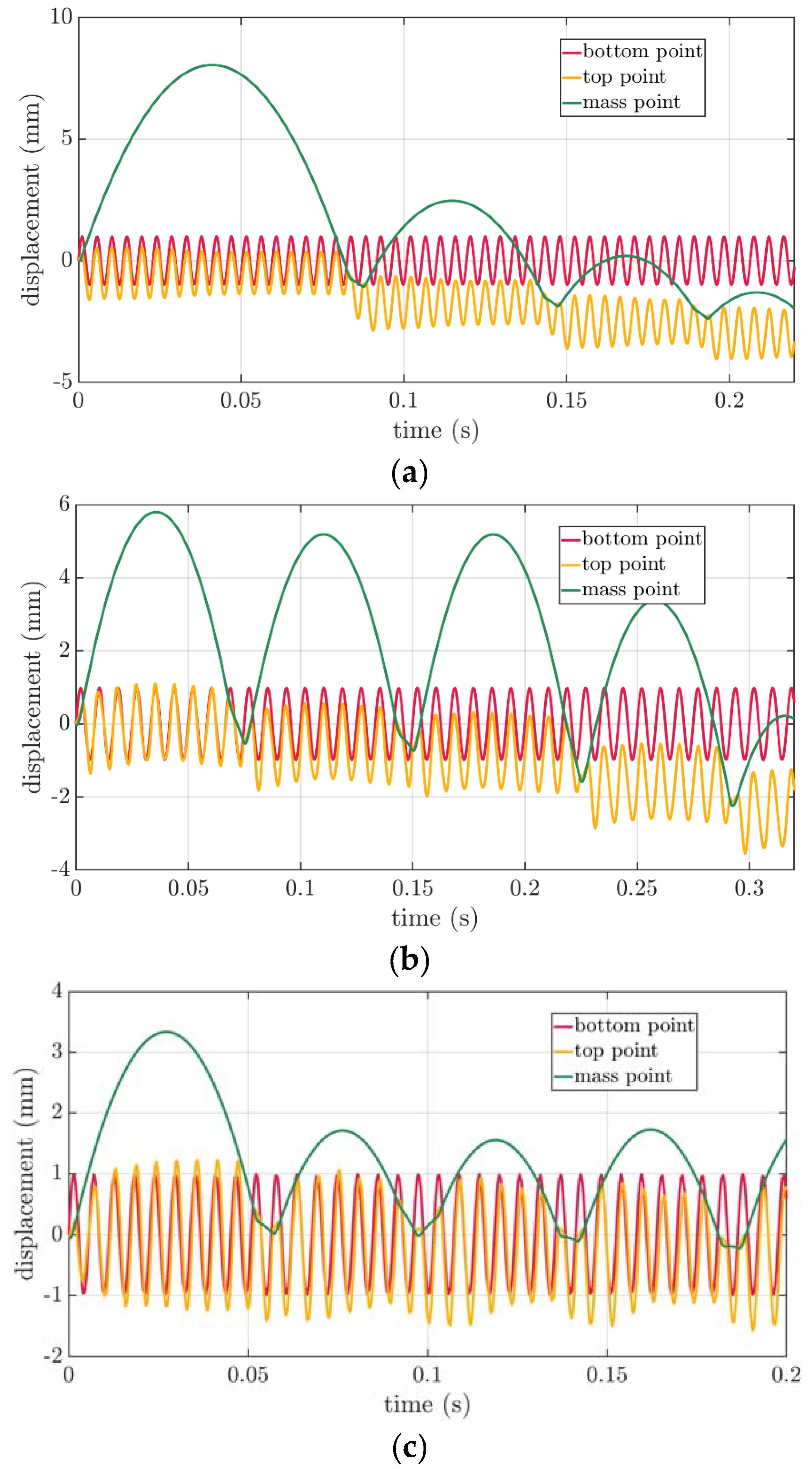
For each box, the resonant frequencies were used to apply the time-dependent boundary conditions of the bottom of the box in dynamic explicit FE analysis, see Section 2.3. In Figure 9, the results obtained were shown in time domain. Three types of curves were presented to represent the deformations of the packaging during VRV test, i.e., displacements of the bottom point of the packaging – red curve, displacements of the top point of the packaging – yellow curve, and displacement of the mass point of the rigid plate – green curve.

3.3. The change of load capacity of the box as a result of the random vibration test

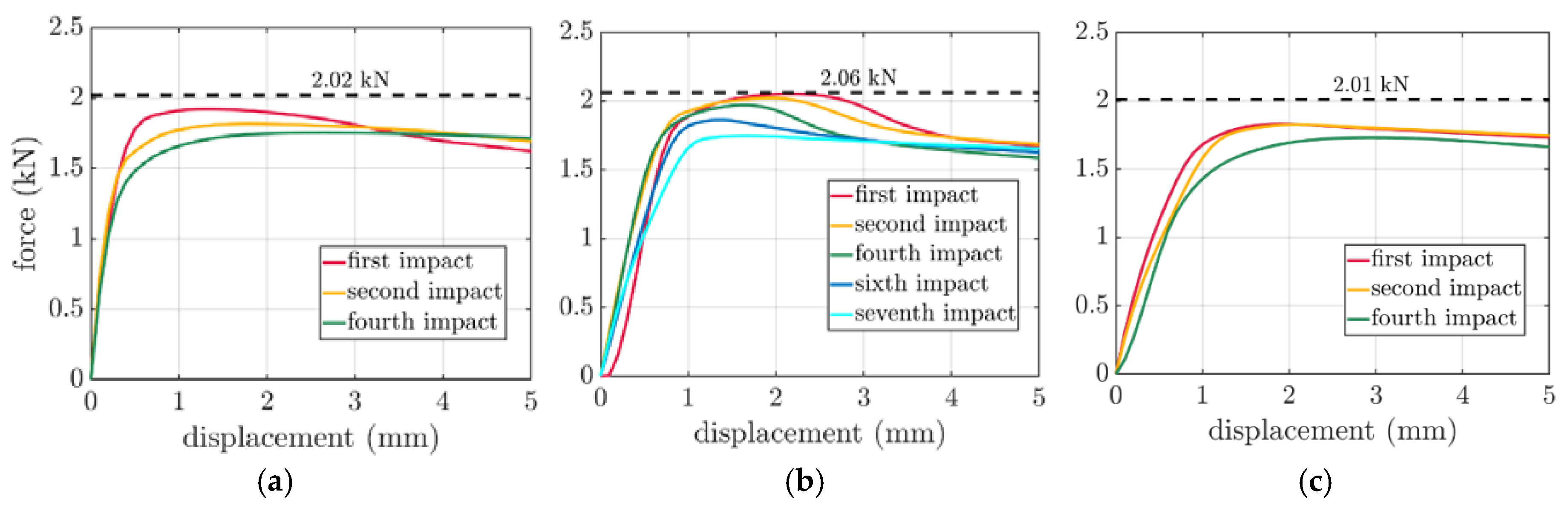
In the simplified method presented in the article, resonant frequencies ω i are determined, which excite vibrations of the bottom of the packaging with a regular sine amplitude. The vibrations accelerate the rigid plate at the top of the packaging and lift it up, the plate separates the packaging. The plate falls down and bounces off the packaging again and again. After each impact of the packaging, the compression strength of the box was verified computationally by static FE analysis taking into account the non-zero state of stress. Due to the accumulation of damage caused by plastic deformation inside the packaging, the box compression test curves differ from the outcome of the stress-free FEM static analysis.
The results of FEM computations after different number of impacts for boxes considered in the paper are presented in Figure 10 for 250 × 250 × 150 mm, 300 × 200 × 250 mm and 300 × 200 × 450 mm boxes. In each subplot, the dashed curve demonstrates the compression strength level from the stress-free FEM static analysis, while the colors represent selected force-displacement curves after particular number of impacts.
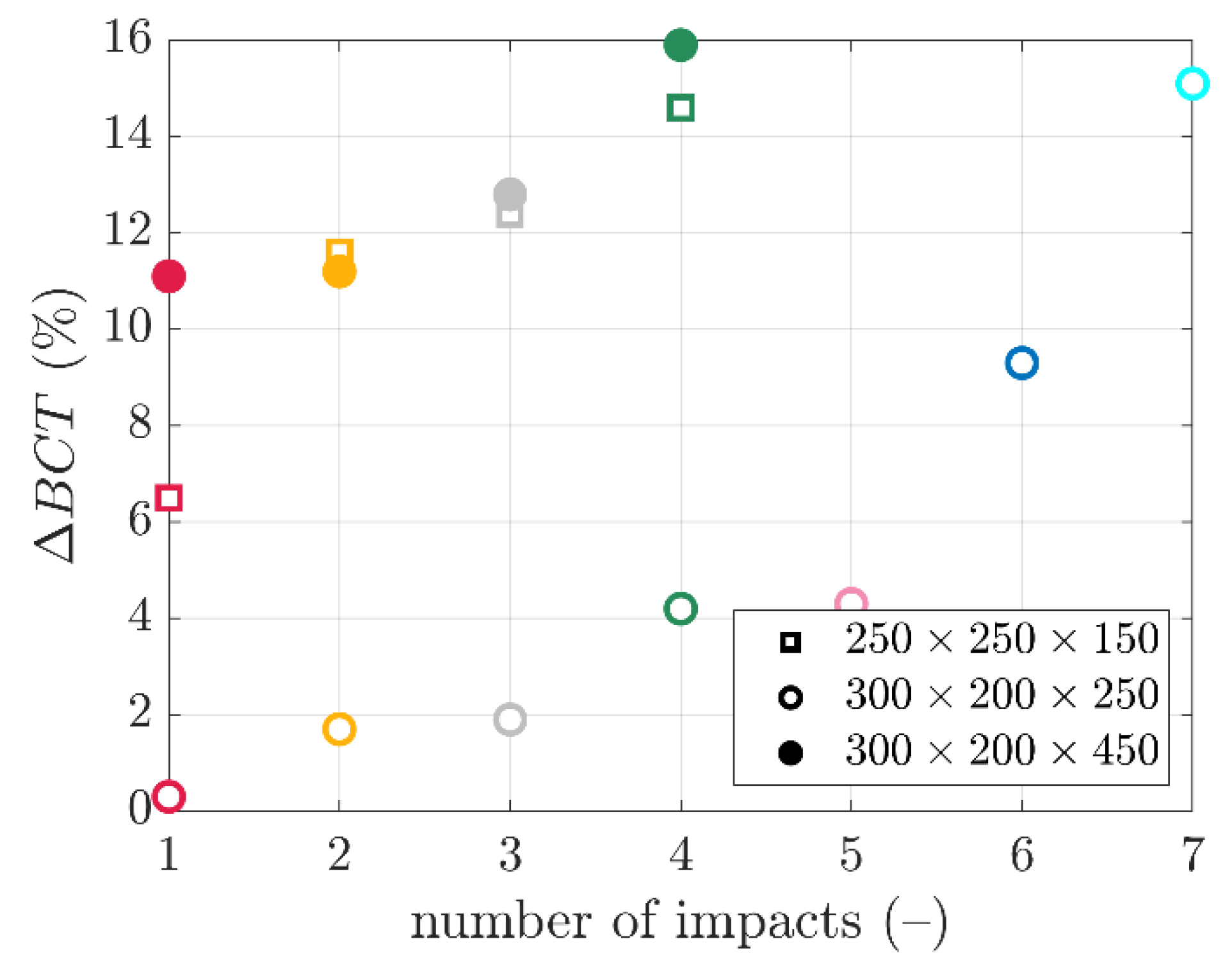
The data from Figure 10 were summarized and confronted each other in Figure 11. The peak values from Figure 10, i.e., the box compression strengths after dynamic analysis of the packaging subjected to transport loadings were divided by counterpart static strengths before VRV test simulation. Therefore, Δ B C T were computed for particular box and different number of impacts. Thus, the vertical axis represent Δ B C T , while horizontal axis expresses the number of impacts of the rigid plate with the packaging. Empty square markers demonstrates the results for 250 × 250 × 150 mm box. Filled circle markers summarizes the results for 300 × 200 × 250 mm box. Empty circle markers presents the results for 300 × 200 × 450 mm box.

4. Discussion

Validation of numerical calculations in comparison with the results of the performed test makes the results of the computations credible. Therefore, validation was carried out in the paper on the example of compression tests of the considered packaging. In Figure 6, the tests carried out on the hydraulic press showed a very low discrepancy, i.e. not less than 0.05   k N in relation to the values of 1.874   k N ,   1.978   k N , and 1.863 k N for 250 × 250 × 150 mm, 300 × 200 × 250 mm and 300 × 200 × 450 mm boxes, respectively. Moreover, in Figure 7, based on these results, the performed validation of numerical models showed a relatively low error. The errors of 6.6   % , 4.0   % and 7.9   % were obtained, as graphically presented in the Figure 7. Based on the above errors, it can be concluded that the computational approach have been verified. A successful validation allows to trust the rest of the results of the numerical calculation to a greater extent.
To compute the VRV response the resonant frequencies, ω , must have been computed. In Figure 8, the change in the damping factor determines the activity of a particular frequency, which is identified as the resonant frequency. The results in the graphs, from Figure 8a to Figure 8c, are consistently similar to each other (the same FEFCO code box), however, the change in the dimensions of the packaging determines the position of the resonant frequency for particular case.
One of the most interesting results are presented in Figure 9, which demonstrates the interactions between the reflecting rigid plate and induced vibrations in the packaging. In Figure 9a, the lowest box interaction was presented, i.e., 250 × 250 × 150 mm case. In this case, the rigid plate is initially raised relatively high, at about 8 mm. The first impact ( 0.08   s) and subsequent ones ( 0.15   s and 0.19   s) significantly deform the packaging because the top point of the plot (yellow curve) successively decreases its level after each bounce, similarly to the successive positions of the rigid plate (green curve).
In Figure 9b, the medium height box interaction was presented, i.e., 300 × 200 × 250 mm case. In this case, the plate is initially raised to a height of 6 mm. Here, after the first impact ( 0.075 s) the deformation is not so significant. Similarly with the next bounce ( 0.15 s) it may be noticed a slight lowering of the upper edge of the packaging (yellow plot). One notice significant increases in packaging deformation only in the third reflection ( 0.225 s) and the next one ( 0.29 s).
In Figure 9c, the highest box interaction was presented, i.e., 300 × 200 × 450 mm case. In this case, the first elevation of the plate is relatively small, about 3.3 mm. Each reflection is similar to each other and much smaller than the first plate elevation, about 1.6 − 1.8 mm. In this case, the deformation of the upper part of the packaging edge (yellow curve) is not so visible for the first four reflections ( 0.06 s, 0.095 s, 0.14 s and 0.18 s).
The compressive strength curves of boxes due to transport loading after each impact were summarized in Figure 10. The character of the curves compared for increasing number of impacts is different, they do not scale linearly. Also, there are no similarities between boxes, for instance compare Figure 10a and Figure 10c; both presents the strength curves after first, second and fourth impact. It may be observed that for the yellow and green curves the change of shapes is completely different.
The synthetic data from Figure 10 are shown in Figure 11, in which the trends in compressive strength drop due to transport loading may be observed for different number of impacts. Figure 11 demonstrates that the medium height packaging, 300 × 200 × 250 mm box, is the most resistant to BCT reduction due to the transport load, that is, Δ B C T s are the lowest for these cases (empty circles). From the first to the fifth impact, Δ B C T does not exceed 5 % . Only for sixth and seventh, the Δ B C T s equal to nearly 10 % and 15 % , respectively. Moreover, the lowest packaging, 250 × 250 × 150 mm box, demonstrates a relationship close to the linear decrease in BCT with the increasing number of impacts, the Δ B C T values range here from about 6 % to 14 % for impacts from first to fourth (empty squares). Moreover, for the highest packaging, i.e., 300 × 200 × 450 mm box, the values obtained are similar to those for the lowest packaging, although this packaging shows the highest Δ B C T values, for example, for the first impact we get already 11% (filled circles).
The summary plot in Figure 11 makes it possible to compare the resistance of the packaging to transport loads by comparing point graphs created due to the simplified computational method presented in the article. As shown earlier, a few analyzes of the impact of the plate against the packaging according to the presented method are enough to determine which packaging has the better resistance to the equivalent transport loads.

5. Conclusions

In this paper, a simplified method for calculating the resistance of corrugated card-board packaging to vertical vibrations during transport was presented. Three geometries of FEFCO F201 packaging, made of the same type of corrugated cardboard, were modelled. Dynamic analyses were carried out to check their resistance to vertical vibrations. The models created were validated using experimental results from static compression. In the first stage of the computations, the buckling analysis was carried out, and then the static load capacity was determined. In the second stage of the simulation, a modal analysis was performed, which allowed to determine the resonant frequency of the boxes. Then, a rigid plate was modeled, which was loaded with gravity force and set in motion by vibrations of the bottom edges of the packaging with resonant frequency. After each impact between plate and packaging, the compressive strength of the box was checked, which allowed to calculate the decrease in load capacity due to dynamic load.
Even though the boxes analyzed represent the same type of the box, the paper shows that each corrugated cardboard packaging reacts differently to vertical vibrations during transport. As expected, each successive impact of the rigid plate reduced the compression strength of the box, but depending the case the reduction varied. The BCT value in each case decreased by several percent. Based on the numerical method proposed, the alternative packaging designs may be verified in regard to its resistance to the generic transport loading. Moreover, in the numerical model, it is not required to take into consideration the time domain to identify the resonant frequency, but with the proposed surrogate problem, the resonant frequencies may be found in frequency domain which is much efficient and easier to be solved numerically.

Author Contributions

Conceptualization, T.G. (Tomasz Gajewski), T.G. (Tomasz Garbowski) and D.M. (Damian Mrówczyński); methodology, D.M. and T.G. (Tomasz Gajewski); software, D.M.; validation, D.M. and T.G. (Tomasz Garbowski); formal analysis, D.M.; investigation, D.M. and T.G. (Tomasz Gajewski); writing—original draft preparation, D.M., T.G. (Tomasz Gajewski); writing—review and editing, T.G. (Tomasz Gajewski) and T.G. (Tomasz Garbowski); visualization, D.M. and T.G. (Tomasz Gajewski); supervision, T.G. (Tomasz Garbowski) and T.G. (Tomasz Gajewski); project administration, T.G. (Tomasz Gajewski and T.G. (Tomasz Garbowski); funding acquisition, T.G. (Tomasz Garbowski) and T.G. (Tomasz Gajewski).

Funding

The authors also acknowledge the grant of the Ministry of Education and Science, Poland, from Poznan University of Technology for Young Researchers; grant number 0411/SBAD/0009.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

The authors thank AQUILA VPK Wrzesnia for providing samples of corrugated cardboard for the study. The authors also thank FEMat Sp. z o. o. for providing the laboratory equipment.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Motylewski, M.; Kurznik, J.; Szwarc, M.; Kolegov, P.; Luzan, S.; Rossier, S.; Bartnik, K. From fibre to corrugated board correlations between paper and corrugated board. Mondi Group, Margrafsen Publishing House, 2018.
  2. Mrówczyński, D.; Knitter-Piątkowska, A.; Garbowski, T. , Non-local sensitivity analysis and numerical homogenization in optimal design of single-wall corrugated board packaging. Materials 2022, 15, 720. [Google Scholar] [CrossRef] [PubMed]
  3. Mrówczyński, D.; Gajewski, T.; Garbowski, T. , Sensitivity Analysis of Open-Top Cartons in Terms of Compressive Strength Capacity. Materials 2023, 16, 412. [Google Scholar] [CrossRef] [PubMed]
  4. Garbowski, T.; Mrówczyński, D.; Grabski, J.K. , Modified Compression Test of Corrugated Board Fruit Tray: Numerical Modeling and Global Sensitivity Analysis. Materials 2023, 16, 1121. [Google Scholar] [CrossRef] [PubMed]
  5. ISO 13355:2016, Packaging — Complete, filled transport packages and unit loads — Vertical random vibration test. International Standard, 2016-08.
  6. Pająk, M.; Baranowski, P.; Janiszewski, J.; Kucewicz, M.; Mazurkiewicz, Ł.; Łaźniewska-Piekarczyk, B. Experimental testing and 3D meso-scale numerical simulations of SCC subjected to high compression strain rates. Constr Build Mater. 2021, 302, 124379. [Google Scholar] [CrossRef]
  7. Studziński, R.; Pozorski, Z. Experimental and numerical analysis of sandwich panels with hybrid core. J. Sandw. Struct. Mater. 2018, 20, 271–286. [Google Scholar] [CrossRef]
  8. Al-Rifaie, H.; Sumelka, W. Improving the blast resistance of large steel gates-numerical study. Materials 2020, 13, 2121. [Google Scholar] [CrossRef] [PubMed]
  9. Han, J.; Park, J.M. Finite element analysis of vent/hand hole designs for corrugated fibreboard boxes. Packag. Technol. Sci. 2007, 20, 39–47. [Google Scholar] [CrossRef]
  10. Hallbäck, N.; Korin, C.; Barbier, C.; Nygårds, M. Finite element analysis of hot melt adhesive joints in carton board. Packag. Technol. Sci. 2014, 21, 701–712. [Google Scholar] [CrossRef]
  11. Fadiji, T.; Coetzee, C.J.; Opara, U.L. Compression strength of ventilated corrugated paperboard packages: Numerical modelling, experimental validation and effects of vent geometric design. Biosyst. Eng. 2016, 151, 231–247. [Google Scholar] [CrossRef]
  12. Domaneschi, M.; Perego, U.; Borgqvist, E.; Borsari, R. An industry-oriented strategy for the finite element simulation of paper- board creasing and folding. Packag. Technol. Sci. 2017, 30, 269–294. [Google Scholar] [CrossRef]
  13. Fadiji, T.; Ambaw, A.; Coetzee, C.J.; Berry, T.M.; Opara, U.L. Application of finite element analysis to predict the mechanical strength of ventilated corrugated paperboard packaging for handling fresh produce. Biosyst. Eng. 2018, 174, 260–281. [Google Scholar] [CrossRef]
  14. Park, J.; Chang, S.; Jung, H.M. Numerical prediction of equivalent mechanical properties of corrugated paperboard by 3D finite element analysis. Appl. Sci. 2020, 10, 7973. [Google Scholar] [CrossRef]
  15. Park, J.; Park, M.; Choi, D.S.; Jung, H.M.; Hwang, S.W. Finite element-based simulation for edgewise compression behavior of corrugated paperboard for packing of agricultural products. Appl. Sci. 2020, 10, 6716. [Google Scholar] [CrossRef]
  16. Garbowski, T.; Gajewski, T.; Grabski, J.K. Estimation of the compressive strength of corrugated cardboard boxes with various perforations. Energies 2021, 14, 1095. [Google Scholar] [CrossRef]
  17. Garbowski, T.; Gajewski, T.; Grabski, J.K. Estimation of the compressive strength of corrugated cardboard boxes with various openings. Energies 2021, 14, 155. [Google Scholar] [CrossRef]
  18. FEMat Systems: BSE System. Available online: http://fematsystems.pl/bse-system_en/ (accessed on 19 June 2023).
  19. Garbowski, T.; Gajewski, T.; Grabski, J.K. The role of buckling in the estimation of compressive strength of corrugated cardboard boxes. Materials 2020, 13, 4578. [Google Scholar] [CrossRef]
  20. Wang, L.; Zhao, Y.; Li, L.; Ding, Z. Research on the vibration characteristics of the commercial-vehicle cabin based on experimental design and genetic algorithm. J. Vibroengineering 2016, 18, 4664–4677. [Google Scholar] [CrossRef]
  21. Sonnenberg, S.A.J.; Rocha, J.; Misol, M.; Rose, M. Experimental validation of an acceleration power spectral density aircraft panel model given different excitations. Can. Acoust. - Acoust. Can. 2018, 46, 19–30. [Google Scholar]
  22. Nguyen, T.Q.; Nguyen, T.A.; Nguyen, T.T. PSD characteristics for the random vibration signals used in bridge structural health monitoring in Vietnam based on a multi-sensor system. Int. J. Distrib. Sens. Netw. 2022, 18. [Google Scholar] [CrossRef]
  23. Duff, E.P.; Johnston, L.A.; Xiong, J.; Fox, P.T.; Mareels, I.; Egan, G.F. The power of spectral density analysis for mapping endogenous BOLD signal fluctuations. Hum. Brain Mapp. 2008, 29, 778–90. [Google Scholar] [CrossRef]
  24. Guo, Y.; Xu, W.; Fu, Y.; Zhang, W. Comparison studies on dynamic packaging properties of corrugated paperboard pads. Engineering 2010, 2, 378–386. [Google Scholar] [CrossRef]
  25. Osowski, P.; Piątkowski, T. Analysis of corrugated cardboard influence on the protective properties of complex packaging system. AIP Conference Proceedings 2017, 1822, 020011. [Google Scholar]
  26. Riva, R.; Cacciola, S.; Bottasso, C.L. Periodic stability analysis of wind turbines operating in turbulent wind conditions. Wind Energ. Sci. 2016, 1, 177–203. [Google Scholar] [CrossRef]
  27. TAPPI T402 sp-21, Standard conditioning and testing atmospheres for paper, board, pulp handsheets, and related products, Test Method TAPPI/ANSI T 402 sp-21, 2021.
  28. ISO 2247:2000, Packaging — Complete, filled transport packages and unit loads — Vibration tests at fixed low frequency. International Standard, 2000-03.
  29. ISO 8318:2000, Packaging — Complete, filled transport packages and unit loads — Sinusoidal vibration tests using a variable frequency. International Standard, 2000-03.
  30. Clough, R.W.; Penzien, J. Dynamics of Structures, McGraw-Hill, New York, 1975.
  31. Hurty, W.C.; Rubinstein, M.F. Dynamics of Structures, Prentice-Hall, Englewood Cliffs, New Jersey, 1964.
  32. Thompson, C.J. , Classical Equilibrium Statistical Mechanics, Oxford University Press, New York, 1988.
  33. Abaqus Unified FEA® Software. Available online: https://www.3ds.com/products-services/simulia/products/abaqus (accessed on 15 May 2023).
Preprints 77305 g001
Figure 1. Selected samples of the considered packaging in the BCT machine just before the compression test.
Figure 1. Selected samples of the considered packaging in the BCT machine just before the compression test.
Preprints 77305 g001
Preprints 77305 g002
Figure 2. Power spectral density profile in generic transportation from ISO 13355 [5] used in the paper.
Figure 2. Power spectral density profile in generic transportation from ISO 13355 [5] used in the paper.
Preprints 77305 g002
Preprints 77305 g003
Figure 3. The scheme of the procedure for calculating the decrease in load-bearing capacity of packaging due to random vertical transport loading.
Figure 3. The scheme of the procedure for calculating the decrease in load-bearing capacity of packaging due to random vertical transport loading.
Preprints 77305 g003
Preprints 77305 g004
Figure 4. Finite element mesh and boundary conditions in the static analysis.
Figure 4. Finite element mesh and boundary conditions in the static analysis.
Preprints 77305 g004
Preprints 77305 g005
Figure 5. Finite element mesh and boundary conditions in the dynamic analysis.
Figure 5. Finite element mesh and boundary conditions in the dynamic analysis.
Preprints 77305 g005
Preprints 77305 g006
Figure 6. Box compression test results for FEFCO F201 boxes: (a) 250 × 250 × 150 mm, (b) 300 × 200 × 250 mm and (c) 300 × 200 × 450 mm.
Figure 6. Box compression test results for FEFCO F201 boxes: (a) 250 × 250 × 150 mm, (b) 300 × 200 × 250 mm and (c) 300 × 200 × 450 mm.
Preprints 77305 g006
Preprints 77305 g007
Figure 7. Box compression test results for FEFCO F201 boxes from numerical analyses: (a) 250 × 250 × 150 mm, (b) 300 × 200 × 250 mm and (c) 300 × 200 × 450 mm.
Figure 7. Box compression test results for FEFCO F201 boxes from numerical analyses: (a) 250 × 250 × 150 mm, (b) 300 × 200 × 250 mm and (c) 300 × 200 × 450 mm.
Preprints 77305 g007
Preprints 77305 g008
Figure 8. The outcome of the random response analyses for three damping levels with marked resonant frequency for boxes: (a) 250 × 250 × 150 mm, (b) 300 × 200 × 250 mm and (c) 300 × 200 × 450 mm.
Figure 8. The outcome of the random response analyses for three damping levels with marked resonant frequency for boxes: (a) 250 × 250 × 150 mm, (b) 300 × 200 × 250 mm and (c) 300 × 200 × 450 mm.
Preprints 77305 g008
Preprints 77305 g009
Figure 9. Vertical displacements of the bottom and top of the packaging and the plate for FEFCO F201 boxes: (a) 250 × 250 × 150 mm, (b) 300 × 200 × 250 mm and (c) 300 × 200 × 450 mm.
Figure 9. Vertical displacements of the bottom and top of the packaging and the plate for FEFCO F201 boxes: (a) 250 × 250 × 150 mm, (b) 300 × 200 × 250 mm and (c) 300 × 200 × 450 mm.
Preprints 77305 g009
Preprints 77305 g010
Figure 10. Box compression test results after different number of impacts for: (a) 250 × 250 × 150 mm, (b) 300 × 200 × 250 mm and (c) 300 × 200 × 450 mm boxes.
Figure 10. Box compression test results after different number of impacts for: (a) 250 × 250 × 150 mm, (b) 300 × 200 × 250 mm and (c) 300 × 200 × 450 mm boxes.
Preprints 77305 g010
Preprints 77305 g011
Figure 11. The decrease in load-bearing capacity due to random vertical transport loading for different boxes dimensions and number of impacts with rigid plate.
Figure 11. The decrease in load-bearing capacity due to random vertical transport loading for different boxes dimensions and number of impacts with rigid plate.
Preprints 77305 g011
Table 1. Material constants used in the constitutive model of corrugated board of 3B400.
Table 1. Material constants used in the constitutive model of corrugated board of 3B400.
E 1 E 2 ν 12 G 12 G 13 G 23 σ 0 R 11
(MPa) (MPa) (–) (MPa) (MPa) (MPa) (MPa) (–)
1545.1 843.7 0.402 312.2 7.1 23.1 2.0 0.951
Table 2. Box compression test results for FEFCO F201 boxes with its numerical counterparts.
Table 2. Box compression test results for FEFCO F201 boxes with its numerical counterparts.
Tests Computations
Dimensions B C T 0 (kN) Mean   B C T 0 with standard deviation
(kN +/- kN)		 B C T 0 (error to exp.)
(kN)
250 × 250 × 150 1.797
1.902
1.888
1.879
1.902		 1.874 +/- 0.044 2.02 (6.6%)
300 × 200 × 250 1.956
2.006
1.970
1.984
1.974		 1.978 +/- 0.019 2.06 (4.0%)
300 × 200 × 450 1.840
1.882
1.813
1.915		 1.863 +/- 0.045 2.01 (7.9%)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated