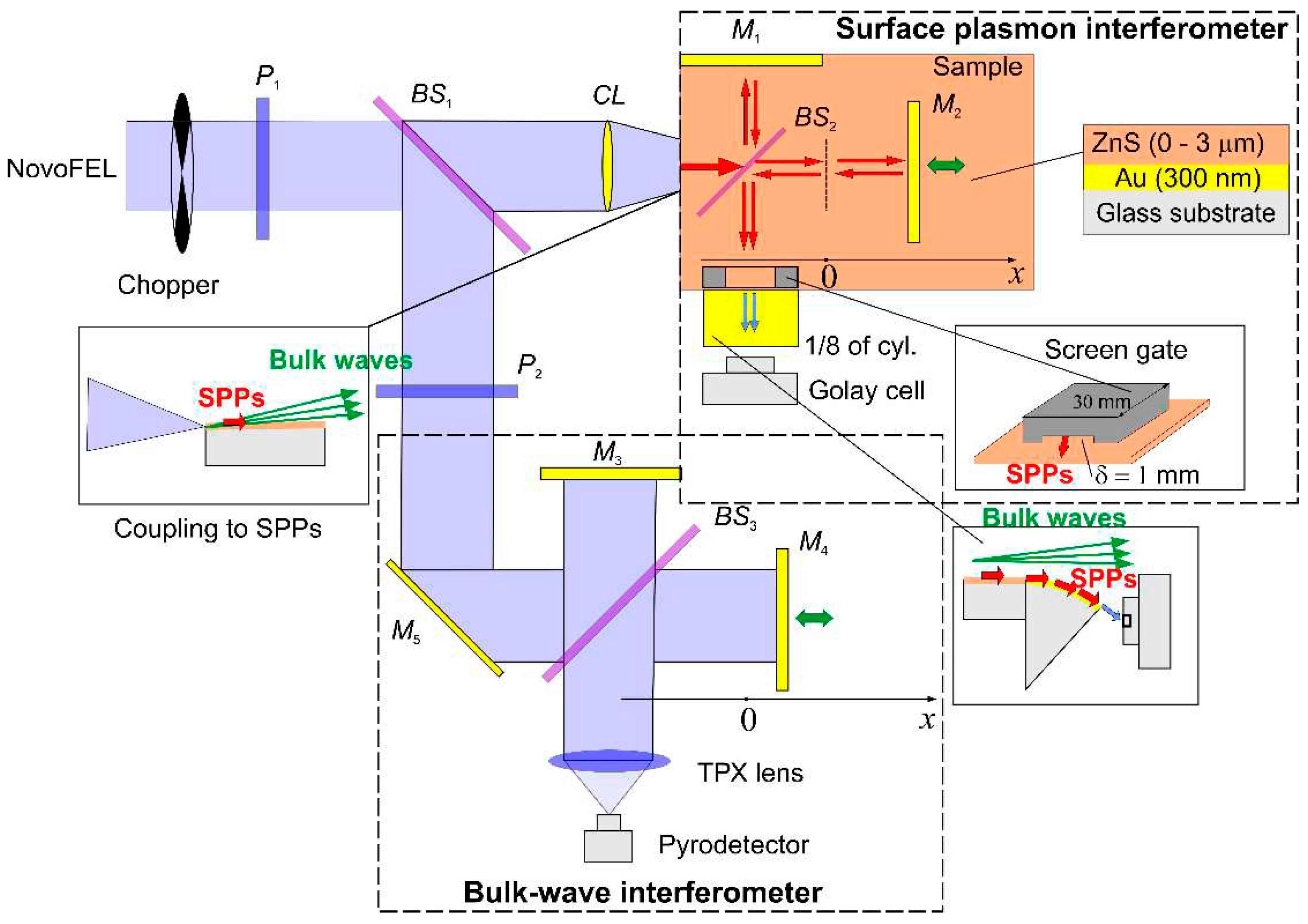
1. Introduction
The value of the dielectric permittivity of the surface of metal and metallized elements of optical circuits may differ significantly from that calculated by the Drude model, especially in the infrared (IR) and terahertz (THz) ranges, where the reflectivity of noble metals tends to 100%, and the anomalous skin effect manifests itself in a weak form [
1,
2]. In addition, in the THz range, the reflectivity of a metal surface (directly related to its dielectric constant) strongly depends on the quality and preparation of the mirror surface [
3,
4,
5]. Therefore, in order to model correctly operation of optical systems, it is necessary to use a measured value of the dielectric constant of the given reflective surface of metal (metallized) elements, not reference data.
For frequencies of the visible and near-IR ranges, a number of methods are known (reflectometry, polarimetry, conductometry, ellipsometry, Fourier spectroscopy, and calorimetry) for determination of the dielectric permittivity of thin-layer and bulk conducting samples [
6,
7]. However, since a weakly pronounced anomalous skin effect occurs in metals at THz frequencies [
8], their dielectric permittivity is no longer adequately described by the Drude model, and the results of its calculation by the above methods and Kramers-Kronig relations are of low reliability and in poor agreement [
2,
9]. For example, results of measurements of reflectivity coincide with calculations based on conductometric measurements and Kramers–Kronig transformations only for very pure metals with minimal roughness and without oxide layers [
3].
The waveguide method, in which a thin layer of metal under study is deposited onto a plate dielectric waveguide, has proved to be more reliable in the far IR range [
10]. However, in this method, the radiation interacts with the metal surface (within the skin layer, whose depth at THz frequencies does not exceed 100 nm [
4]), adjacent to the plate, not bordering with the environment.
New possibilities for the refractometry of metals have opened up with the proposal to use surface plasmon polaritons (SPPs) for this purpose. SPPs is a kind of surface electromagnetic waves, which exist at the interface between media, one of which (metal) contains conduction electrons and has a negative dielectric permittivity [
11]. The SPP characteristics (field distribution, attenuation coefficient, and phase velocity) are determined mainly by the optical constants of the metal and the ratio of the SPP frequency ω to the plasma frequency
ωp of the metal: the greater their difference (in the THz range,
ωp is about three orders of magnitude greater than ω), the lower the SPP decay and the closer the SPP phase velocity to the velocity of the corresponding plane wave in the medium adjoining the metal. This makes THz SPPs promising for use in high-speed lines for data transmission and processing [
12,
13,
14]. With the discovery of the ability of a structured (by holes, relief, or other ordered inhomogeneities) metal surface to direct THz SPPs with high attenuation and high field concentration in the near-surface region, it became possible to create both active and passive microdevices in which information is carried by SPPs [
15,
16,
17].
First, due to the attenuated total reflection (ATR) phenomenon, SPPs were applied to determination of the optical constants of metals with high conductivity in the visible range: both transparent metal layers [
18,
19,
20] and bulk samples [
21]. Later on, a similar technique was tested in the mid-IR range for a transparent layer of palladium (a transition metal with reflectivity of about 90%) [
22]. However, for noble metals, because of their high conductivity, this technique is not applicable, since the propagation length
Ls (the distance at which the wave intensity decreases by a factor of
e ≈2.718) of infrared SPPs reaches several centimeters, which leads to distortion of the reflected beam due to re-emission of SPPs into the ATR prism.
A fundamentally new method for SPP refractometry of metal surfaces in the IR range was proposed in [
23]. The method includes measurement of the propagation length of monochromatic SPPs over a bare metal surface (
L0) and the same surface containing a thin non-absorbing film (
L) of known thickness
d and refractive index
nlayer and then calculation of the optical constants of the metal using the
L0,
L,
d, and
nlayer values and the radiation wavelength
λ0 via simultaneous solution of the SPP dispersion equations for two- and three-layer structures [
11]. However, the reliability of the results obtained by such technique is low, since it implicitly assumes (in the derivation of the dispersion equations) that the observed attenuation of SPPs is due solely to the Joule losses in the metal, while in reality it also includes other significant mechanisms of dissipation of the SPP energy: scattering on the inhomogeneities and surface roughness, scattering on the granules of the near-surface layer of the metal, and heat losses due to the skin effect.
In the THz range, it was proposed to determine the dielectric permittivity of the surface of non-transparent metal objects from measured SPP characteristics such as the propagation length and depth of field penetration into the environment adjacent to the metal [
24]. However, this technique also does not take into account the influence of the SPP energy dissipation on inhomogeneities of a real surface on both measured quantities, which reduces the reliability of the results.
New prospects for the refractometry of metals seemed to appear in connection with the development in the early 1990s of the THz time-domain spectroscopy (THz TDS) [
25,
26]. A significant advantage of the TDS method in comparison with those mentioned above is in the measurement of not the power, but the amplitude and phase of the probing THz radiation in the form of a picosecond pulse. After interaction with the sample, the broadband THz radiation is strobed by femtosecond light pulses (for triggering of the THz radiation photodetector), which is to yield the time dependence of the photocurrent; the full inverse Fourier transform of this dependence makes it possible to obtain both the amplitude and phase spectrum of the reflected (transmitted) radiation in the entire THz range. The method has been tested for THz refractometry in a transmission/reflection geometry of transparent metal layers (up to 120 nm thick) on terahertz spectrometers with a wide dynamic range, with the use of reference dielectric plates [
27,
28]. Along with the advantages, which are impressive at first glance, the TDS method has a number of disadvantages: 1) the impossibility of studying metal samples with roughness, at which the reflected radiation is scattered; 2) strict requirements for the parallelism of the faces of the substrates; 3) long measurement time because of the need to average measurement results over a large number of pulses because of the stringent requirements for the synchronism and identity of THz and light pulses [
29].
There were attempts to combine the possibilities of SPP refractometry and TDS spectroscopy for study of the surface of metals and semiconductors in the THz range [
30,
31,
32]. A THz radiation pulse was converted into a pulse of broadband SPPs and, after they traveled a macroscopic distance over the sample, the SPPs were inversely converted into bulk radiation, which was detected, and the resulting photocurrent dependence on time was processed by the standard TDS method. However, test measurements have demonstrated the fundamental impossibility of integrating the capabilities of the SPP and TDS methods in real conditions. The main reason is parasitic radiation, both from the conversion (coupling) elements and from the SPP track (because of inhomogeneities on the real surface); as a result, the photodetector receives a “mixture” of bulk waves (BWs) from the conversion output element and BWs generated at the coupling input element and on surface inhomogeneities on the SPP track. As a result, the signal-to-noise ratio and measurement accuracy become very low [
32].
It is important to note that in all works we know on the refractometry of metal surfaces, the metal dielectric permittivity value
εm in the THz range, determined from analysis of the spectrum of radiation reflected from or transmitted through the studied metal layer, is two to three orders of magnitude greater than the εm values found from the characteristics of the SPPs for the same surface [
2]. The main reason for this difference is apparently the different length of interaction of the radiation with the sample under study. Indeed, in the transmission/reflection geometry, the interaction length is equal to the sample thickness (in the case of transmission, the thickness of metal films is up to 120 nm), which is several times greater than the skin layer thickness
δskin of metal (for gold,
δskin ≈ 40 nm). The grainy surface structure, inherent in an evaporated metal [
33,
34], as well as the roughness and small defects on optically polished substrates, forms an optically-inhomogeneous surface layer of the metal with a thickness comparable to
δs [
35]. The optical constants of such layer can differ significantly from the constants of the metal below it, composing the majority (in thickness) of the metal layer. Therefore, it is the metal under the transition layer that makes the main contribution to the transmission/reflection coefficient, and, consequently, the optical constants obtained from analysis of the transmission/reflection spectra are closer to the bulk metal constants, which are well described by the Drude model [
27,
28].
As for the THz SPP refractometry method, the field of the surface wave generated by the probing radiation penetrates into the metal only to the depth
δm ≈
δs [
36]. Therefore, the SPP characteristics are determined mainly by the optical properties of the transition layer of the metal. As a result, the effect of inhomogeneities and surface defects on the SPP characteristics exceeds that on the characteristics of the reflected probing radiation. In addition, taking into account the resonant enhancement of the field in the near-surface region during SPP-enhanced photon generation and the difference in the distribution of the fields of the SPPs and the reflected plane wave (the
δm value is slightly less than
δs) [
11], we can assume that the collisional frequency
ωτ of conduction electrons for SPPs exceeds this value for a plane wave of probing radiation incident on the metal.
Therefore, in our opinion, it can be stated that the value of the effective permittivity εm of the metal surface depends not only on the manufacturing and processing of the metal surface, but also on the method of its determination. More precisely, it depends on the nature of the interaction of the probing radiation with the object of study. Due to the intensive mastering of the THz range and the creation of THz plasmonic devices in recent years, the development of the THz SPP refractometry method is of particular relevance. In this paper, we consider the possibility of determining the effective (averaged over the surface layer) dielectric permittivity of metals and highly doped semiconductors (which provide a macroscopic SPP propagation length) at THz frequencies from the refractive index ns and absorption index κs for SPPs directed by this surface, measured with a plasmon Michelson interferometer (where is the SPP complex refractive index).
3. Results
The experiments were carried out with a set of samples with flat substrates containing non-transparent layers of sputtered gold coated with a ZnS layer of thickness
d =0 - 3000 nm.
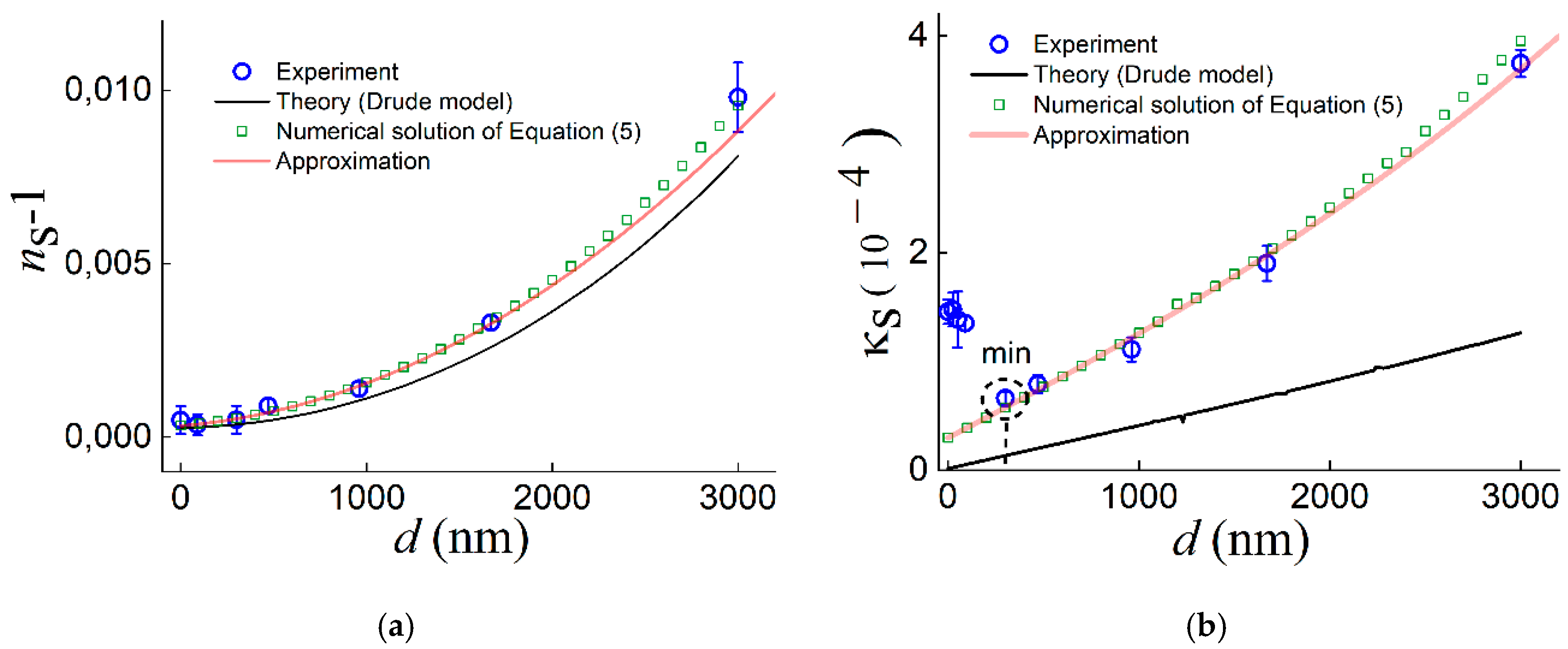
Figure 4a,b show the real part without unity
ns-1 and the imaginary part
κs of the SPP refractive index, respectively, found by the above methods, versus the
d value. In these figures, the black lines show the calculated dependences obtained by numerical solution of the dispersion equation for the “gold - ZnS layer - air” structure at
λ0 = 141 μm. In these calculations, the refractive index of ZnS was taken
[
52], and the gold permittivity
εm was calculated by the Drude model with the use of the reference values of plasma frequency
ωp = 1.37·10
16 s
-1 and frequency of collisions of conduction electrons
ωτ = 4.05·10
13 s
-1 [
53]:
where
ω = 2π
с/
λ0=1.34·10
13 s-1 (c is the speed of light in vacuum).
From
Figure 4a one can see that the value of
ns-1 monotonically increases with
d, all its experimental values lying above the calculated curve, which indicates that the real part Re(
εm) of the dielectric constant of the deposited gold is less than the value predicted by the Drude model —according to the SPP theory, decrease in Re(
εm) must be accompanied by increase in
ns.
Figure 4.
(a) Real part of SPP refractive index ns (without unity) and (b) imaginary part (SPP absorption index) κs vs. thickness d of ZnS layer on the gold surface: experiment (blue circles), approximation curves (red line), numerical solution of equation (5) for εm = -7000+i·3000 (green squares), and calculation by Drude model for εm = -104700+i·317180) (black line).
Figure 4.
(a) Real part of SPP refractive index ns (without unity) and (b) imaginary part (SPP absorption index) κs vs. thickness d of ZnS layer on the gold surface: experiment (blue circles), approximation curves (red line), numerical solution of equation (5) for εm = -7000+i·3000 (green squares), and calculation by Drude model for εm = -104700+i·317180) (black line).
Note that the determination errors for ns-1 for small thicknesses of ZnS (d ≤300 nm) and d = 3000 nm are noticeably larger than those for 300 nm < d < 3000 nm; the reason is the low intensity of the useful signal from the SPPs due to the low efficiency of SPP generation in the plasmon interferometer at such thicknesses of the dielectric layer.
The value of the SPP refractive index on uncoated gold was
ns≈ 1.0005, which corresponds to the SPP phase velocity
ϑph =
c/
ns ≈ 0.9995
c. Similar values of SPP phase velocities were also obtained for thick aluminum wire in experiments performed on a TDS spectrometer [
54], where
ϑph was determined from the time delay of a THz SPP pulse relative to a light pulse propagating in air.
As for the imaginary part
κs of the SPP refractive index, which characterizes the SPP decay, at increase in the thickness
d of the cover layer, the measured values (blue circles in
Figure 4b) first decrease, reach the minimum at
d ≈ 300 nm, and then grow monotonically. This behavior of
κs was explained in [
35] and is associated with the decrease in the radiative losses of SPPs at deposition of a dielectric layer onto the metal surface. At some
d =
d0 (300 nm in our case), the integral losses of SPPs reach the minimum, and at
d >
d0, their growth is due to the predominance of the Joule losses over the radiative losses because of the monotonic increase of the fraction of SPP field energy transferred into the metal with
d growth.
3.1. Determination of the permittivity of metal surface from the SPP characteristics on a set of samples with a dielectric layer of various thicknesses
In this section, we consider an approximation method for finding the metal permittivity, which uses the values found for a set of samples with ZnS coatings of various thicknesses.
To determine the effective permittivity
εm of a metal surface guiding the SPPs and containing a thin-layer coating of thickness
d with permittivity
εd from the found complex refractive index
of the SPPs, it is necessary to solve (with respect to
εm) the SPP dispersion equation for the three-layer structure “metal – dielectric layer – environment” [
55]:
where
εa is the permittivity of the environment.
Transcendental equation (5) can be solved numerically, but the solution is very sensitive to small variations in within the measurement error, which can result in a large error in determination of the metal permittivity εm. Therefore, we have developed an εm determination method based on the approximation of the (ns-1)(d) and κs(d) dependences measured for a series of samples with different ZnS coating thicknesses.
Since in the THz range
εm >>
εd,
εa, the
condition is met at
d<<
λ. Expanding both parts of equation (5) into a Taylor series with respect to a small correction to the refractive index
because of the dielectric coating on the metal, we obtain an approximate formula for calculating the surface impedance of the three-layer structure (see
Appendix A):
where
The dependences of
ns -1 and
κs on the ZnS layer thickness
d were found by formulas (6) and (7
) for the gold permittivity
εm calculated according to the Drude model (blue lines in
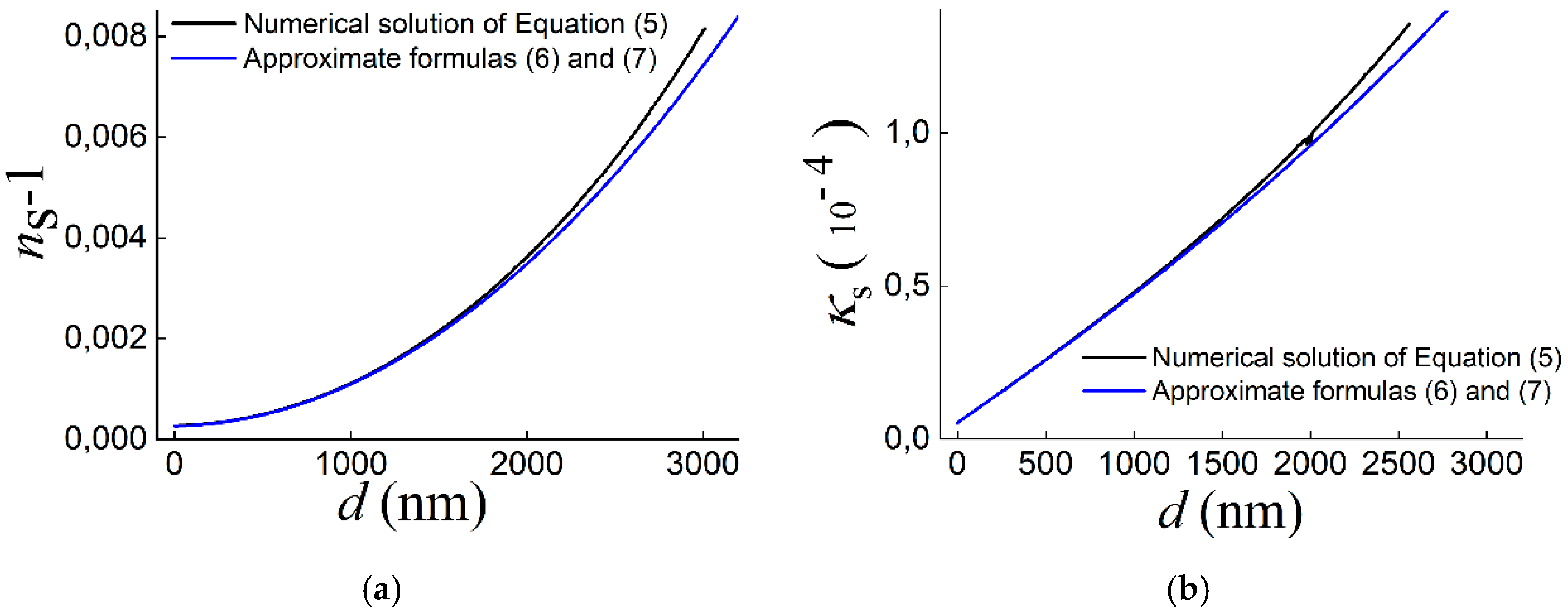
Figure 5). In the figure, the red lines show the results of the numerical solution of Eq. (5). It can be seen that at
d ≤ 1500 nm, the approximate and exact solutions practically coincide, and at 1500 nm <
d ≤ 3000 nm they differ by no more than 8%.
Figure 5.
Real part (without unity) ns and imaginary part κs of SPP refractive index in structure “gold – ZnS layer of thickness d – air” vs. d calculated by approximate formulas (6) and (7) (black lines) and by numerical solution of dispersion equation (5) (blew lines). Calculations used gold permittivity εm = -104700+i·317180, calculated by Drude model at λ0 =141 μm.
Figure 5.
Real part (without unity) ns and imaginary part κs of SPP refractive index in structure “gold – ZnS layer of thickness d – air” vs. d calculated by approximate formulas (6) and (7) (black lines) and by numerical solution of dispersion equation (5) (blew lines). Calculations used gold permittivity εm = -104700+i·317180, calculated by Drude model at λ0 =141 μm.
Then the experimental dependences (ns -1)(d ) and κs(d) were approximated by means of a Matlab program, using the least squares method to find the minimum deviations of the experimental values from the corresponding functions and (was found by formula (7)). The real and imaginary parts of the gold permittivity εm were varied as parameters. The search for the solution for both functions was performed in the range of ZnS layer thicknesses 300 nm ≤ d ≤ 1670 nm. The domain of the functions did not include small thicknesses (d < 300 nm), when the SPP decay is governed by the radiative losses, not taken into account by Eq. (5); at d = 3000 nm, the approximate formula gives noticeable deviations from the exact solution.
As a result of the approximation, the permeability of the deposited gold was found: the real part was Re(
εm) ≈ -7000±3000, and the imaginary was Im(
εm) ≈ 3000±1300. The approximation dependences (
ns-1)(
d) and
κs(
d) are shown by the gray lines in
Figure 4. The large errors (of up to 40%) in the determination of
εm by this method are due to the closeness of the refractive index
ns of the THz SPPs to the refractive index of air, which necessitates a higher accuracy in finding the
ns value.
In
Figure 4, the green squares show the results for the numerical solution of dispersion equation (5) by the downhill method [
56] at
εm = -7000+
i·3000. It can be seen that the results of the calculation at
d ≤ 1700 nm almost coincide with the curves obtained by approximate formula (7), which indicates the possibility of its effective application for evaluation calculations of the complex refractive index of THz SPPs in a three-layer structure in the presence of a dielectric coating layer of subwavelength thickness on the metal.
It was already noted above that the presence of a dielectric layer on the metal surface leads to increase in the fraction of SPP field energy transferred into the metal. In this case, the depth
δm of the penetration of the SPP field into the metal is practically independent of the coating thickness, as evidenced by the graphs in
Figure 6b, obtained from solution of equation (5) for the "gold - ZnS layer of thickness
d - air" structure. It can be seen that with the gold permeability found by the approximation method from the experimental results, the
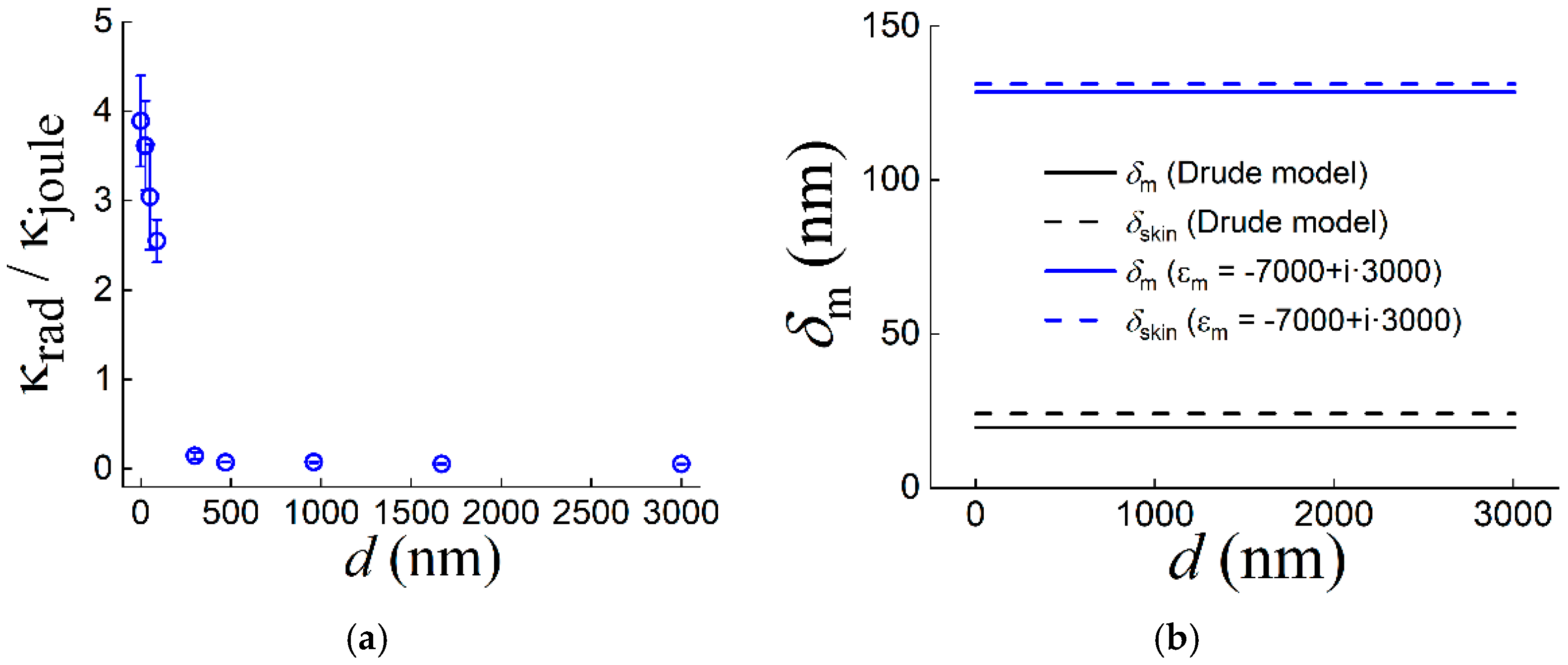
δm value is approximately six times greater than that for the permeability calculated by the Drude model. Therefore, for the deposited gold layer to be non-transparent for the THz SPP field (which excludes the effect of the substrate on the SPP characteristics), its thickness must be 150–200 nm at least.
From the plot of
κs(d) in
Figure 6a, it can be seen that at small thicknesses
d < 300 nm, the loss of SPPs in the experiment is much greater than the calculations predict. This is explained by the presence of radiative losses of SPPs, which are not taken into account either by the approximate formulas or by the dispersion equation; starting from
d ≈ 300 nm (where the minimum of the integral losses of SPPs is reached, and their radiative losses become relatively small compared with the Joule losses), the measured values of the absorption coefficient of SPPs approach the calculated dependence.
Figure 6.
(a) Ratio of radiative and Joule losses of SPPs, calculated by formula (8) at λ0 = 141 μm vs. thickness d of the ZnS layer in “deposited gold – ZnS layer – air” structure; (b) penetration depth δm (in terms of intensity) of SPP field into metal for "gold - ZnS layer with thickness d - air" structure at λ0 = 141 µm and gold permeability εm calculated according to Drude model (black line) and εm = -7000+i·3000, determined by approximation method from characteristics of SPPs (blew line). Dotted lines: corresponding values of skin layer thickness.
Figure 6.
(a) Ratio of radiative and Joule losses of SPPs, calculated by formula (8) at λ0 = 141 μm vs. thickness d of the ZnS layer in “deposited gold – ZnS layer – air” structure; (b) penetration depth δm (in terms of intensity) of SPP field into metal for "gold - ZnS layer with thickness d - air" structure at λ0 = 141 µm and gold permeability εm calculated according to Drude model (black line) and εm = -7000+i·3000, determined by approximation method from characteristics of SPPs (blew line). Dotted lines: corresponding values of skin layer thickness.
Based on this interpretation of the existence of minimum of the losses
κs(
d) and the assumption that other mechanisms of losses contribute negligibly to the total SPP decay, the SPP radiative losses can be estimated by the following formula:
where
κs is the total SPP losses measured in the experiment;
κJoule is the Joule SPP losses determined from the solution of equation (5).
Figure 6a shows the ratio of radiative losses estimated by formula (8) to Joule losses at different thicknesses
d of the ZnS layer, calculated from the solution of equation (5) with substitution of
εm = -7000+
i·3000 (found by the approximation method) into it. In this case, in the absence of a dielectric layer on the metal surface, the radiative losses exceed the Joule losses about four-fold. However, as
d grows, this ratio decreases monotonically to zero at
d ≥ 960 nm, when the SPP decay is determined mainly by losses in the metal.
3.2. Determination of the effective dielectric constant of metal surface from SPP characteristics on one sample
In
Section 3.1, we described an estimation of the dielectric permittivity of metal
εm via application of the approximation method to the measurements of the characteristics of THz SPPs on a set of samples with different thicknesses of dielectric layers on the metal surface. Despite its rather high reliability, this method is very laborious for a rapid assessment of the dielectric constant of metal (metallized) optical surfaces. Therefore, it is desirable (in view of practical applications) to have a method for determination of
εm from the complex refractive index
of THz SPPs, found from measurements of its real and imaginary parts on only one sample.
From equation (5), we obtained an approximate formula for calculating
εm from the measured characteristics of SPPs (see
Appendix A):
where the surface impedance
ξ is found from formula (6).
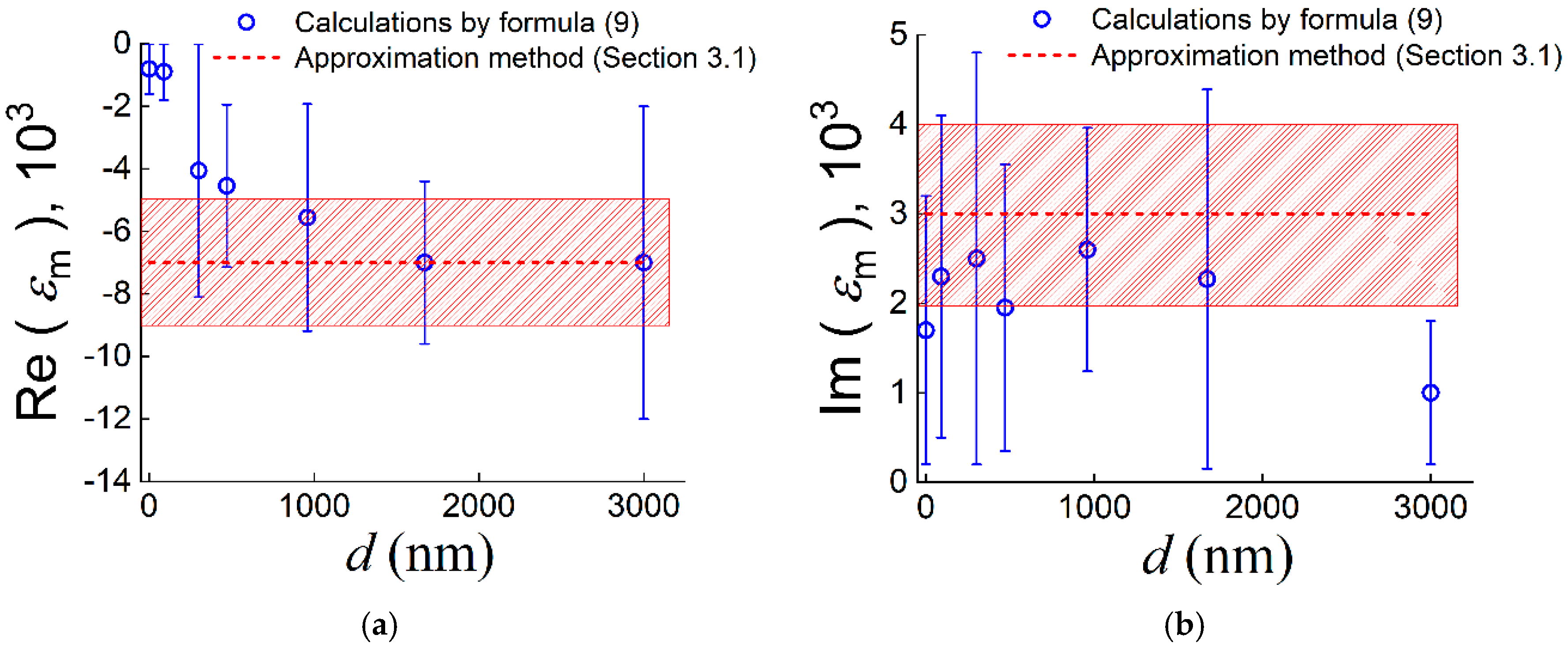
As was established above, radiative losses make a predominant contribution to the SPP decay on a metal without a dielectric coating layer, which leads to large errors in the determination of εm. Therefore, it is necessary to find a layer thickness d range in which the error in determination of εm is not so large. For this purpose, the permittivity εm of deposited gold was calculated by formula (9) with substitution of experimentally determined values of for samples with different thicknesses d of the ZnS layer into it.
The found values of the real Re(
εm) and imaginary Im (
εm) parts of the gold permittivity are shown by black circles in
Figure 7. The errors on the graphs correspond to the maximum permittivity deviations calculated in the ranges of experimental values
ns±Δ
ns and
κs±Δ
κs, where Δ
ns and Δ
κs are the corresponding measurement errors. It can be seen that the values of Re(
εm) and Im(
εm) at small thicknesses of the ZnS layer (
d < 300 nm) differ greatly from the approximation values, and at
d ≥ 300 nm, they approach the approximation values asymptotically (except for Im(
εm) at
d = 3000 nm, where already formula (9) gives insufficiently reliable results). This character of the dependence
εm(
d) can be explained by the fact that formula (9) does not take into account the radiative losses of SPPs; at larger thicknesses of the dielectric layer, when the radiative losses becomes much less than the thermal losses, formula (9) describes the experiment much better.
Figure 7.
(a) Real and (b) imaginary parts of gold permittivity
εm vs. thickness
d of ZnS layer (blew circles), calculated by formula (9) with
values found from results of measurements presented in
Figure 4. Red dotted lines: values of both parts of gold permeability, found by approximation method; rectangular areas filled with oblique red lines: corresponding standard deviation ranges.
Figure 7.
(a) Real and (b) imaginary parts of gold permittivity
εm vs. thickness
d of ZnS layer (blew circles), calculated by formula (9) with
values found from results of measurements presented in
Figure 4. Red dotted lines: values of both parts of gold permeability, found by approximation method; rectangular areas filled with oblique red lines: corresponding standard deviation ranges.
Note that according to the performed calculations, the real part Re(
εm) of the permittivity of gold without a ZnS coating layer (
d = 0) turned out to be equal to – 800 (see
Figure 7). This value of Re(
εm)
) is in agreement with the estimates given in earlier publications on THz SPP refractometry of deposited gold without a dielectric coating layer, implemented on a TDS spectrometer [
31] and with FEL radiation [
24]. However, as follows from the above, this value of Re(
εm) differs from its real value of -7000 almost 10 times. In our opinion, the erroneous estimation of Re(
εm) in previous works on THz SPP refractometry was because of the unaccounted significant radiative losses of SPPs on a metal surface free without a coating layer.
It is important to note that the obtained errors for metal effective permittivity (see
Figure 7) are very large (reach 50%). It is clear that its more reliable determination by the proposed method of SPP refractometry requires higher accuracy of finding the real part of the SPP refractive index from the recorded interferograms. For the accuracy of determination of the metal permittivity to be 20% (for thicknesses
d ≥ 500 nm), it is necessary to determine
ns with an error not worse than 10
-4 (with an actual error of 10% for
κs, which depends on the signal-to-noise ratio, adjustment, and stability of the intensity of NovoFEL radiation. For such accuracy for
ns, the stability of the radiation source in terms of wavelength during recording of interferogram must be not worse than 0.01 µm (for
λ0 = 141 µm), while the width of the generation line must be an order of magnitude smaller than 1.0 ÷1.5 µm in the normal operation mode. This can be achieved via reduction of the measurement time with faster and more sensitive detectors, as well as sources of coherent THz radiation that are more stable than FELs, such as gas lasers [
57], backward wave oscillators [
58], gyrotrons [
59], and quantum-cascade lasers [
60].
Note that it is possible to increase the stability of NovoFEL radiation to temporal variations in the radiation wavelength at operation in the mode of negative detuning of the electron bunch repetition rate from the repetition rate of light pulses inside the FEL optical resonator, accompanied by a decrease in the average radiation power [
61]. In operation in this mode, a stable single-mode generation regime was established, the linewidth of which reached the maximum possible narrow value (0.25%) [
49], while the wavelength shift in 15 minutes was not more than 0.1 of the width of the generated radiation spectrum (0.04 μm at λ
0 =141 µm), which is close to the desired accuracy. However, to achieve such a generation mode, a long and laborious adjustment of the NovoFEL parameters is necessary.