Prerpints.org logo
Preprint
Article

Parametric Iterative Method for Addressing an Embedded Steel Constitutive Model with Multiple Roots

Altmetrics

Downloads

117

Views

46

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

21 June 2023

Posted:

21 June 2023

You are already at the latest version

Alerts
Abstract
In this paper, an iterative procedure to find the solution of a nonlinear structural model is introduced. The model presents different multiplicities where parameters are randomly selected within a solvability region. To achieve this aim, a class of multipoint fixed-point iterative schemes for single roots is modified to find multiple roots, reaching the fourth order of convergence. Complex discrete dynamics techniques are employed to select the members with the most stable performance. The structural problem, as well as some academic problems involving multiple roots, are solved numerically to verify the theoretical analysis, robustness and applicability of the proposed scheme.
Keywords: 
Subject: Computer Science and Mathematics  -   Applied Mathematics

1. Introduction

Nonlinearity usually arise in structural models [1,2]. In particular, materials such as reinforced concrete (HCR) involve nonlinear stress-strain relationships in the mechanical model. The application of these model implementations usually calls for the application of numerical approaches to find solutions of the related nonlinear equations f ( x ) = 0 , where f : I ⊆ R → R , such as Newton-type methods [3]. The most appropriate algorithm for solving a nonlinear problem is usually a balance between computational cost and precision [4]. Nevertheless, in spite of the highly nonlinear character of the problem, it is however possible to increase the efficiency of the method by previously defining a solvability domain, which is derived by using algebraic procedures.
Newton’s method cannot be applied at a point where the first derivative cancels out. Graphically it means that the tangent line to the curve f ( x ) at this point is horizontal, and therefore it does not intersect the x-axis.
Let x * be a multiple root of f ( x ) = 0 with multiplicity m, then it is also a multiple root of f ′ ( x ) = 0 of multiplicity ( m − 1 ) , of f ″ ( x ) = 0 with multiplicity ( m − 2 ) , and so on [5]. The fact that the function does not change sign precludes the use of methods that use intervals. At multiple roots, not only f ( x ) , but also f ′ ( x ) approaches zero, which affects Newton’s method since its denominator includes the first derivative. In general, iterative procedures to solve nonlinear equations with single roots reduce their order of convergence when the equations have multiple roots ( m > 1 ), or even diverge.
Many authors have proposed modifications to Newton’s method. Two of the best-known are Rall’s method [6]
x k + 1 = x k − m f ( x k ) f ′ ( x k ) , k = 0 , 1 , 2 , …
and Schroder’s method [7]
x k + 1 = x k − f ( x k ) f ′ ( x k ) [ f ′ ( x k ) ] 2 − f ( x k ) f ″ ( x k ) , k = 0 , 1 , 2 , …
.
Most iterative methods for finding multiple roots require knowing the multiplicity m in advance. Despite m is not usually known, several authors have described different ways to estimate its value [8].
Based on the previous study [9] of the multipoint fixed point class of fourth-order iterative schemes
y k = x k − 2 3 f ( x k ) f ′ ( x k ) , x k + 1 = x k − G ( η ) f ( x k ) f ′ ( x k ) , k = 0 , 1 , 2 , … ,
where G ( η ) is a real function of variable η = f ′ ( y k ) f ′ ( x k ) that satisfies G ‴ ( 1 ) is bounded and G ″ ( 1 ) = 9 4 , G ′ ( 1 ) = − 3 4 and G ( 1 ) = 1 . We propose the iterative scheme for solving nonlinear equations with m > 1
y k = x k − a f ( x k ) f ′ ( x k ) , x k + 1 = x k − G ( η ) f ( x k ) f ′ ( x k ) , k = 0 , 1 , 2 , … ,
where a is a real parameter, and G ( η ) is the weight function of variable η = f ′ ( x k ) f ′ ( y k ) 1 m − 1 .
The manuscript is organized as follows. Section 2 introduces the steel constitutive model. Section 3 covers the convergence analysis of the introduced family (4). Section 4 carries out the stability analysis of the family. Finally, Section 5 verifies the applicability of the new family solving the steel constitutive model, and comparing the performance of the introduced methods with known ones that are present in the literature.

2. Resolvability of the steel model

Various authors [10,11,12] regard a steel reinforcement rigidified by the concrete adhered to it, also known as the "embedded bar model". Such approach, the named Refined Compression Field Theory (RCFT) [13], involves in the steel model an equilibrium constraint that accounts for the tensile stiffening action of the concrete between joints. As a consequence, a nonlinear equality is entered into the steel constitutive equation in terms of the apparent creep deflection. The later theory would predict the mean stress of an embedded bar as a dependence of the mean strain (i.e., as measured over a given span that included a variety of cracks) in the following way:
σ s , a v = f y − A c A s f c t 1 + 3.6 M ε s , a v , ε s , a v ≥ ε m a x , E s ε s , a v , ε s , a v < ε m a x ,
with
ε m a x = f y E s − f c t A c E s A s 1 + 3.6 M ε m a x ,
being E s the elastic modulus of steel, f y the yield point of steel, f c t the tensile resistance of concrete, s i g m a s , a v and s i g m a c t , a v the mean tensile stresses in the strengthening steel and in the concrete, respectively, A s is the cross-section of the steel bars, A c is the mean deformation in the reinforcing bar, A c is the surface area of concrete adhered to the bar which participates in the tensile stiffening action and M is a value that is dependent on the physical characteristics. The previous statement is based stress balance between a cracked section, where only reinforcement is contributing, and a general section, where both reinforcement and the surrounded concrete are participating. 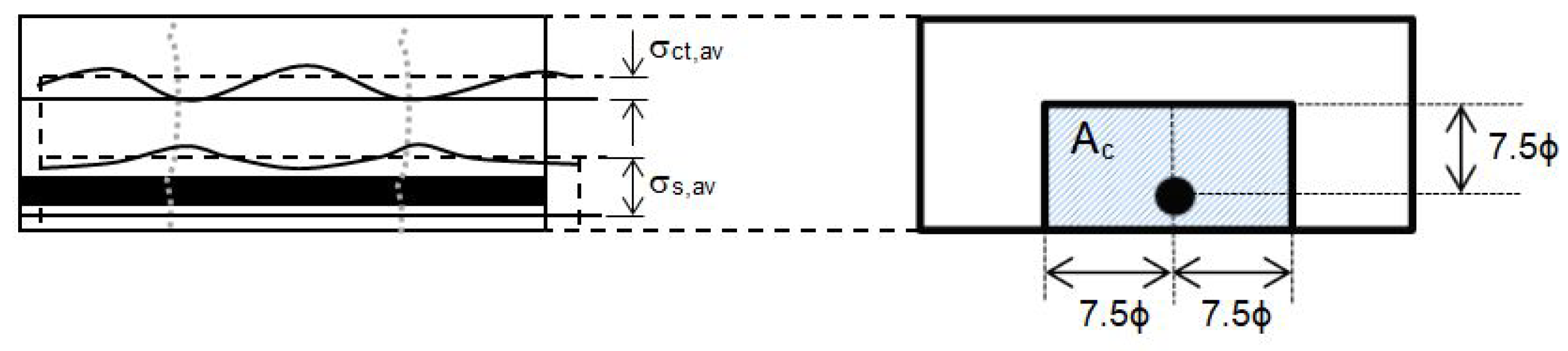Figure 1 represents the schematic.
Technical Codes [14] suggest a value for A c equal to the area surrounding the bar at a distance no greater than 7.5 from the center of the bar, being the diameter of the bar. It is found that for certain specimens (namely those with high values of the ratio f c t / ρ , where ρ is the reinforcing ratio) when this value is taken, it is not feasible to obtain a real positive solution for the effective yield stress ϵ m a x defined in (5). Furthermore, if the solvability analysis is stated in accordance with the variables f c t and m a x , and the area value A c is increased monotonically, beyond a given value of this area, the bijection is broken between f c t and m a x (uniqueness problem). Later, for higher area values of A c up to the prescribed values by the technical codes, one reaches the lack of real solution (existence problem) [15]. Thus, the internal stress equilibrium along the cracked element is not found.
In [15], we determine through algebraic methods the greatest value of the area A c for in which the constitutive model of the embedded steel has at least one real positive solution. In this regard, the greatest part of the tensile stiffening area which can be considered to maintain the solvability of the constitutive model (that is, to preserve the internal force equilibrium, so that by increasing the concrete involvement, the steel tension is reduced) is expressed by the coefficient
λ = A s f y A c f c t 2 3 + 1 + 10.8 M ϵ y 3 48.6 M ϵ y
where ϵ y = f y / E s is considered to be the deflection corresponding to the yield strength of the steel. Thus, the coefficient λ is the boundary of the solvability domain for the constitutive model of the embedded steel suggested by the RCFT. As this region is only derived from algebraic calculations, it can be applicable to any experimentally based approach to the tensile stiffening model of concrete.
The above limit, for some design cases, may be below the value required by the technical codes for the area A c , so therefore the region of resolubility is well within the design range required by the technical codes. In fact, various studies [13,16,17] indicate the appropriateness of correcting the tensile stiffening area to correct the shear performance of reinforced concrete elements, especially for high shear deformations, where technical codes underestimate the tensile stiffness of the concrete.

3. Convergence Analysis of the proposed class

In this section, the convergence analysis of family (4) is performed.
Theorem 1. 
Let us consider f : I ⊆ R → R be a differentiable enough function in an open interval I and let x * ∈ I be a multiple root of f ( x ) = 0 , with multiplicity m > 1 . Let also G ( η ) be a real function satisfying G μ = m , G ′ μ = − ( a − m ) 2 ( − 1 + m ) m a ( a − 2 m + a m ) , G ″ μ = m 4 ( 2 − 2 m − m 2 + m 3 ) 4 ( 2 + m ) , and | G ‴ μ | < + ∞ , being μ = m m − a . If a = 2 m 2 + m and x 0 is an initial guess close enough to x * , then the class of schemes (4) satisfies
e k + 1 = c 1 3 3 ( m − 1 ) 3 m 10 ( m + 2 ) 2 m 5 m 9 + 3 m 8 − m 7 − 11 m 6 + 6 m 5 + 8 m 4 − 42 m 3 + 36 m 2 + 48 m − 48 − 32 G ‴ ( μ ) ( m + 2 ) 2 − c 2 c 1 m + c 3 m ( m + 2 ) 2 e k 4 + O ( e k 5 ) .
has fourth-order of convergence, where η = f ′ ( x k ) f ′ ( y k ) 1 m − 1 , c k = m ! ( m + 1 ) ! f ( m + k ) ( x * ) f ( m ) ( x * ) , k = 2 , 3 , … , and e k = x k − x * .
Proof. 
Let x * be a multiple zero of f with multiplicity m. By hypothesis, f can be expanded using the Taylor series for f ( x k ) and f ′ ( x k ) about x * ,
f ( x k ) = f ( m ) ( x * ) m ! e k m ( 1 + e k c 1 + e k 2 c 2 + e k 3 c 3 + e k 4 c 4 ) + O ( e k 5 ) , f ′ ( x k ) = f ( m ) ( x * ) m ! e k m − 1 m + ( m + 1 ) e k c 1 + ( m + 2 ) e k 2 c 2 + ( m + 3 ) e k 3 c 3 + O ( e k 4 ) .
From these expressions, we get the expansion of first step
y k − x * = 1 − a m e k + a c 1 m 2 e k 2 + − a ( 1 + m ) c 1 2 + 2 a m c 2 m 3 e k 3 + a m 4 ( 1 + m ) 2 c 1 3 − m ( 4 + 3 m ) c 1 c 2 + 3 m 2 c 3 e k 4 + O ( e k 5 ) .
Expanding in Taylor’s series f ′ ( y k ) , around x * ,
f ′ ( y k ) = f ( m ) ( x * ) m ! y k m − 1 m + ( m + 1 ) y k − x * c 1 + ( m + 2 ) y k − x * 2 c 2 + ( m + 3 ) y k − x * 3 c 3 + O ( e k 4 ) ,
and then,
η = m m − a − a ( a − 2 m + a m ) c 1 ( a − m ) 2 ( − 1 + m ) m e k − a 2 ( a − m ) 3 ( m − 1 C ) 2 m 2 c 1 2 a 3 ( m + 1 ) 2 − 2 a 2 ( m + 1 ) 2 ( 2 m − 1 ) + a m 3 m 3 + 12 m 2 − 5 m − 6 − 6 m 2 m 2 − 1 − 2 c 2 ( m − 1 ) a 3 ( m + 2 ) − 4 a 2 m ( m + 2 ) + 3 a m 2 ( m + 4 ) − 6 m 3 e k 2 − a 6 ( m − 1 ) 3 m 4 ( a − m ) 4 6 c 3 ( m − 1 ) 2 m ( a − m ) 2 a 3 ( m + 3 ) − 4 a 2 m ( m + 3 ) + 6 a m 2 ( m + 3 ) − 12 m 3 − 6 c 2 c 1 ( m − 1 ) m a 5 m 2 + 3 m + 2 − 2 a 4 3 m 3 + 9 m 2 + 5 m − 2 + a 3 m 15 m 3 + 43 m 2 + 16 m − 20 − 2 a 2 m 2 8 m 3 + 30 m 2 + 3 m − 20 + 2 a m 3 3 m 3 + 22 m 2 + m − 20 − 4 m 4 3 m 2 + m − 4 + c 1 3 a 5 ( m + 1 ) 3 ( 2 m − 1 ) − 6 a 4 m ( m + 1 ) 2 2 m 2 + m − 2 + 3 a 3 m ( m + 1 ) 2 10 m 3 + 3 m 2 − 13 m + 2 − 2 a 2 m 2 16 m 5 + 52 m 4 − 21 m 3 − 50 m 2 − 5 m + 12 + 12 a m 3 m 5 + 7 m 4 − 3 m 3 − 10 m 2 + 2 m + 3 − 24 m 4 m 2 − 1 2 e k 3 + O ( e k 4 ) ,
that is, η tends to μ = m m − a when k → ∞ . We expand G ( η ) about μ = m m − a ,
G ( η ) ≈ G ( μ ) + G ′ ( μ ) η − μ + 1 2 G ″ ( μ ) η − μ 2 + 1 6 G ‴ ( μ ) η − μ 3 ,
and the error equations yields
e k + 1 = 1 − G ( μ ) m e k + G ( μ ) + a G ′ ( μ ) ( a − 2 m + a m ) ( a − m ) 2 ( − 1 + m ) c 1 m 2 e k 2 − 1 2 ( m − 1 ) 2 m 3 ( a − m ) 4 − a 2 c 1 2 G ″ ( μ ) ( a m + a − 2 m ) 2 + a G ′ ( μ ) ( a − m ) c 1 2 a 3 ( m + 1 ) 2 − 2 a 2 ( m + 1 ) 2 ( 2 m − 1 ) + a m 3 m 3 + 12 m 2 − 5 m − 6 − 6 m 2 m 2 − 1 − 2 c 2 ( m − 1 ) a 3 ( m + 2 ) − 4 a 2 m ( m + 2 ) + 3 a m 2 ( m + 4 ) − 6 m 3 − a c 1 2 G ″ ( μ ) ( a m + a − 2 m ) 2 + a G ′ ( μ ) ( a − m ) c 1 2 a 3 ( m + 1 ) 2 − 2 a 2 ( m + 1 ) 2 ( 2 m − 1 ) + a m 3 m 3 + 12 m 2 − 5 m − 6 − 6 m 2 m 2 − 1 − 2 c 2 ( m − 1 ) a 3 ( m + 2 ) − 3 a m 2 ( m + 4 ) − 6 m 3 − 2 G ( μ ) ( m − 1 ) 2 ( a − m ) 4 c 1 2 ( m + 1 ) − 2 c 2 m − 4 a c 1 2 G ′ ( μ ) ( m − 1 ) ( a m + a − 2 m ) ( a − m ) 2 e k 3 + O ( e k 4 ) .
To make null the coefficients of e k and e k 2 (and achieve third-order of convergence) the values of G ( μ ) and G ′ ( μ ) must satisfy
G ( μ ) = m , G ′ ( μ ) = − ( a − m ) 2 ( − 1 + m ) m a ( a − 2 m + a m ) .
In this case, the error equation depends on a and G ″ ( μ ) :
e k + 1 = 1 2 m 3 c 1 − 2 m 2 − a 2 G ″ ( μ ) ( a − 2 m + a m ) 2 ( m − 1 ) 2 ( a − m ) 4 + m ( m − 1 ) ( a − m ) ( a − 2 m + a m ) 6 a − 2 a 3 m − a 3 + 4 a 2 − 12 a m 3 + 2 a 2 + − a 3 + 6 a 2 + 5 a − 6 m 2 + ( 6 − 3 a ) m 4 + c 2 1 a − 2 m + a m − 2 − a 2 + 6 a − 2 m 2 + 4 a 2 m − 2 ( 3 a − 6 ) m 3 e k 3 − 1 6 ( m − 1 ) 3 m 4 ( m − a ) 6 ( a m + a − 2 m ) 6 c 3 ( m − 1 ) 3 m a 2 ( m + 3 ) − 3 a m ( m + 3 ) + 6 m 2 ( a − m ) 7 − 6 c 1 c 2 ( m − 1 ) ( a − m ) 2 a 7 ( m − 1 ) m ( m + 1 ) ( m + 2 ) + a 6 ( m + 2 ) G ″ ( μ ) ( m + 1 ) 2 − 8 m 4 − m 3 + 12 m 2 − 3 m + a 5 m ( ( m − 1 ) ( 25 m 4 + 87 m 3 + 48 m 2 − 40 m ) − G ″ ( μ ) ( m + 1 ) ( m + 2 ) ( 3 m + 7 ) ) + 2 a 4 m 2 ( G ″ ( μ ) ( 9 m 2 + 26 m + 19 ) − ( m − 1 ) m ( 2 m + 3 ) ( m ( 10 m + 27 ) − 19 ) ) + a 3 m 3 ( ( m − 1 ) ( 35 m 4 + 193 m 3 + 102 m 2 − 180 m ) − 12 G ″ ( μ ) ( 3 m + 4 ) ) + a 2 m 4 ( 24 G ″ ( μ ) − ( m − 1 ) m ( 16 m 3 + 129 m 2 + 87 m − 166 ) ) + 3 a m 6 m 4 + 14 m 3 + m 2 − 44 m + 28 − 6 ( m − 1 ) 2 m 7 ( m + 3 ) + c 1 3 a 9 ( m − 1 ) ( m + 1 ) 3 ( 2 m − 1 ) + a 8 ( m + 1 ) 2 3 G ″ ( μ ) ( m + 1 ) 2 + 7 m 3 + 10 m 2 + 17 m − 24 − a 7 ( m + 1 ) 2 3 G ″ ( μ ) ( m ( 5 m + 8 ) − 3 ) ( m + 1 ) + G ″ ( μ ) ( m + 1 ) 2 − 84 m 5 + 6 m 4 + 210 m 3 − 144 m 2 + 12 m + a 6 m ( m + 1 ) 2 ( 3 G ″ ( μ ) ( 7 m 3 + 40 m 2 + 17 m − 24 ) + 8 G ″ ( μ ) ( m + 1 ) − ( m − 1 ) m ( 196 m 3 + 275 m 2 − 497 m + 96 ) ) − a 5 m 2 3 G ″ ( μ ) ( 3 m 4 + 50 m 3 + 118 m 2 − 14 m − 77 ) ( m + 1 ) + 24 G ″ ( μ ) ( m + 1 ) 2 − 2 ( m − 1 ) ( 140 m 6 + 581 m 5 + 198 m 4 − 691 m 3 − 256 m 2 + 168 m ) + a 4 m 3 ( 6 G ″ ( μ ) ( m ( m ( m ( 9 m + 65 ) + 77 ) − 49 ) − 62 ) + 32 G ″ ( μ ) ( m + 1 ) − 3 ( m − 1 ) m ( 84 m 5 + 445 m 4 + 169 m 3 − 671 m 2 − 193 m + 222 ) ) + 2 a 3 m 4 ( − 6 G ″ ( μ ) ( m + 1 ) ( − 25 + 18 m + 9 m 2 ) − 8 G ″ ( μ ) + ( m − 1 ) m ( 70 m 5 + 499 m 4 + 264 m 3 − 959 m 2 − 248 m + 402 ) ) + a 2 ( m − 1 ) m 5 ( 24 G ″ ( μ ) ( 3 m + 4 ) − m ( 44 m 5 + 461 m 4 + 387 m 3 − 1141 m 2 − 331 m + 588 ) + 3 a ( m − 1 ) 2 m 7 ( 2 m 4 + 41 m 3 + 96 m 2 − 31 m − 80 ) − 6 ( m − 1 ) 3 m 8 ( m + 1 ) ( 2 m + 7 ) e k 4 + O ( e k 5 ) .
Solving the following system to get order of convergence four,
− 2 m 2 − a 2 G ″ ( μ ) ( a − 2 m + a m ) 2 ( m − 1 ) 2 ( a − m ) 4 + m ( m − 1 ) ( a − m ) ( a − 2 m + a m ) 6 a − 2 a 3 m − a 3 + 4 a 2 − 12 a m 3 + 2 a 2 + − a 3 + 6 a 2 + 5 a − 6 m 2 + ( 6 − 3 a ) m 4 = 0 , − 2 − a 2 + 6 a − 2 m 2 + 4 a 2 m − 2 ( 3 a − 6 ) m 3 = 0 , − 4 m 2 − 2 m ( − 6 m 3 + a 3 ( 2 + m ) − 4 a 2 m ( 2 + m ) + 3 a m 2 ( 4 + m ) ) ( a − m ) ( a − 2 m + a m ) = 0 ,
it results
G ″ ( μ ) = m 4 ( 2 − 2 m − m 2 + m 3 ) 4 ( 2 + m ) , a = 2 m 2 + m .
Therefore, the error equation of (4) is
e k + 1 = c 1 3 3 ( m − 1 ) 3 m 10 ( m + 2 ) 2 m 5 m 9 + 3 m 8 − m 7 − 11 m 6 + 6 m 5 + 8 m 4 − 42 m 3 + 36 m 2 + 48 m − 48 − 32 G ‴ ( μ ) ( m + 2 ) 2 − c 2 c 1 m + c 3 m ( m + 2 ) 2 e k 4 + O ( e k 5 ) .
□

4. Stability analysis

In this section, we carry out the study of stability, in the context of complex dynamics, we study the convergence of the family on polynomials with multiplicity different from one.

4.1. Basic Dynamical Concepts

In this section the dynamical performance of the iterative schemes described in (4) is analyzed. Previously, some concepts are recalled [18,19]. Let R : C ^ → C ^ be a rational function, where C ^ is the Riemann sphere. The orbit of a point z 0 ∈ C ^ is defined as the successive application of the operator R on that point, determined by the set { z 0 , R ( z 0 ) , R 2 ( z 0 ) , … , R n ( z 0 ) , … } , where R n ( z 0 ) refers to apply n times R to z 0 . In this case, R is calculated by applying the family of iterative schemes on p ( z ) , a low degree polynomial.
A fixed point z F ∈ C ^ of R is kept invariant after the application of the operator, satisfying R ( z F ) = z F .It should be noted that, while all roots of the quadratic polynomial are fixed points of the operator R, we can find fixed points of R being not roots of p ( z ) ; then, these points are called strange fixed points. Any fixed point is classified as
  • attracting, if | R ′ ( z F ) | < 1 ,
  • superattracting, if R ′ ( z F ) = 0 ,
  • repelling, if | R ′ ( z F ) | > 1 , or
  • parabolic or neutral, if | R ′ ( z F ) | = 1 .
In this context, R ′ ( z F ) is called the stability function of fixed points z F .
On the other hand, the attractor basins [20] define the final status of the orbit of any point in the complex plane after repeated application of the R operator. The basins of attraction of a attractive fixed point z F ∈ C ^ are then defined as the collection of pre-images of any order satisfying
A ( z F ) = { z 0 ∈ C ^ : R n ( z 0 ) → z F , n → + ∞ } .
Moreover, a point z c is called a critical point of R if R ′ ( z c ) = 0 . The asymptotical behavior of the critical points is a key fact for analyzing the stability of the method. Previous results [21] set that at least one critical point appears in each immediate basin of attraction, that is, in the connected component of the basin of attraction containing the attractor. Let us also remark that superattracting fixed points are indeed critical points. Moreover, those critical points that are not roots of p ( z ) are called free critical points.
The Fatou set of the rational function R, F ( R ) , is the set of points z ∈ C ^ which orbits are tending to an attractor . Its complementary set in z ∈ C ^ is the Julia set, J ( R ) . So that the basin of attraction of any fixed point pertains to the Fatou set and the boundaries of these basins of attraction pertain to the Julia set.
Henceforth, the dynamical behavior of fourth-order parametric family (4) on cubic polynomial p ( z ) = ( z − α ) 2 ( z − β ) , where α , β ∈ C , is analyzed. The weight function is
G ( η ) = m − ( a − m ) 2 ( − 1 + m ) m a ( a − 2 m + a m ) ( η − μ ) + m 4 ( 2 − 2 m − m 2 + m 3 ) 8 ( 2 + m ) ( η − μ ) 2 + G ‴ ( μ ) 6 ( η − μ ) 3 ,
where a = 2 m 2 + m and μ = m m − a .
A rational function O p ( z ) is obtained, depending on the parameter G ‴ ( μ ) of class (4), named from now on G 3 , and also on the roots α and β . To get a simpler operator, we use the conjugacy map [22] given by the Möbius transformation
M ( z ) = z − α z − β , M − 1 ( z ) = z β − α z − 1 ,
that satisfies
M ( ∞ ) = 1 , M ( α ) = 0 , M ( β ) = ∞ ,
yielding a rational function that does not longer depend on α and β , and it is conjugated to O G 3 ( z ) (and therefore, with equivalent dynamical behavior)
O G 3 ( z ) = M ∘ O p ∘ M − 1 z = z 4 P ( z , G 3 ) Q ( z , G 3 ) ,
where P ( z , G 3 ) = ( 312 − 8 G 3 + ( 1014 − 24 G 3 ) z + ( 1368 − 12 G 3 ) z 2 + ( 1050 + 16 G 3 ) z 3 + ( 546 + 6 G 3 ) z 4 + ( 198 − 6 G 3 ) z 5 + ( 42 + G 3 ) z 6 + 6 z 7 ) and Q ( z , G 3 ) = 768 + 2496 z + 2928 z 2 + 1140 z 3 − ( 726 + 8 G 3 ) z 4 − ( 1176 + 24 G 3 ) z 5 − ( 678 + 12 G 3 ) z 6 − ( 204 − 16 G 3 ) z 7 − ( 24 − 6 G 3 ) z 8 + ( 12 − 6 G 3 ) z 9 + G 3 z 10 .
Solving the O G 3 ( z ) = z equation yields the fixed points of the rational function: z = 0 and z = ∞ arise from the roots of the polynomial prior to the map of Möbius. The asymptotic behavior of all fixed points has a key role in the stability of the iterative methods involved since its convergence to fixed points other than the roots is a major disadvantage for an iterative approach.
A straightforward result of the Möbius map applied on this rational function is the inverse conjugation,
1 O G 3 ( z ) = O G 3 1 z .
Then:
  • If z F is a fixed point of O G 3 ( z ) , that is O G 3 ( z F ) = z F , then also its conjugate 1 / z F is, O G 3 ( 1 / z F ) = 1 / z F .
  • z = 1 is always an strange fixed point of O G 3 ( z ) , coming from the divergence of the original operator except maybe for some specific values of the parameters that simplify the operator.
  • Given two conjugate fixed points, both have the same character, since their stability function coincides as
    O G 3 ′ ( z F ) = 1 / O G 3 ′ ( z F ) .

4.2. Performance of the strange fixed points

The stability of strange fixed points depends on G 3 . Now, the stability of z = 1 is stated.
Theorem 2. 
The stability of the strange fixed point z = 1 is
  • attracting, if | G 3 − 168 | > 1152 ,
  • repelling, if | G 3 − 168 | < 1152 ,
  • parabolic, if | G 3 − 168 | = 1152 ,
  • not a fixed point, if G 3 = 168 .
Proof. 
z = 1 is an strange fixed point of O G 3 ( z ) if G 3 ≠ 168 . Fixed point z = 1 is attracting if
O G 3 ′ ( 1 ) = − 1152 − 168 + G 3 < 1 ↔ 1152 < − 168 + G 3 .
Finally, if G 3 satisfies | G 3 − 168 | < 1152 , then O G 3 ′ ( 1 ) > 1 and z = 1 is a repelling point. It is parabolic in O G 3 ′ ( 1 ) = 1 .
□
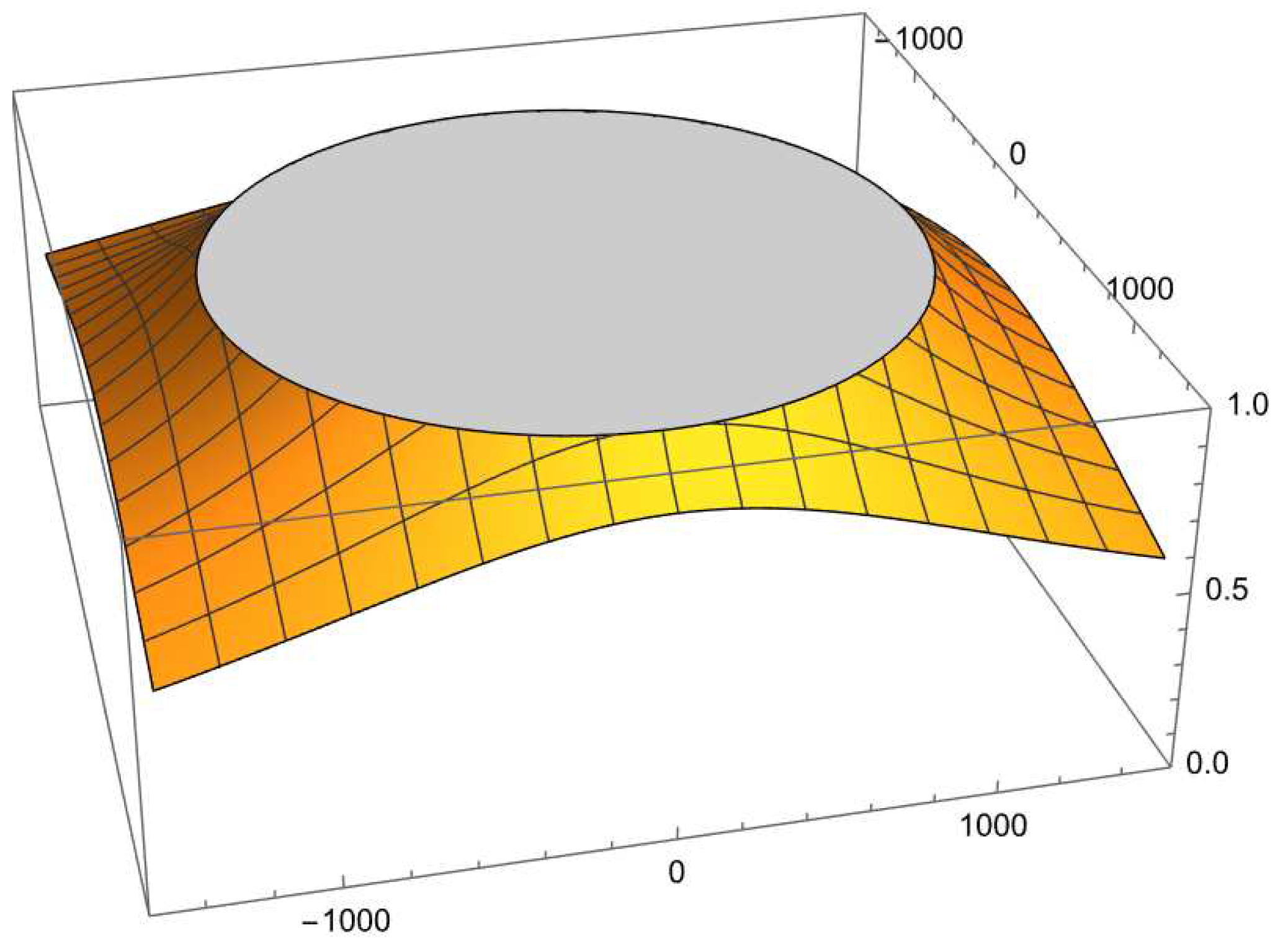
Theorem 3. 
The roots of T ( x ) = − 768 − 3264 x − 6192 x 2 + ( − 7020 − 8 G 3 ) x 3 + ( − 5280 − 24 G 3 ) x 4 + ( − 2736 − 12 G 3 ) x 5 + ( − 1008 + 16 G 3 ) x 6 + ( − 258 + 6 G 3 ) x 7 + ( − 36 − 6 G 3 ) x 8 + ( − 6 G 3 ) x 9 are strange fixed points of O G 3 ( z ) , different from z = 1 , and are denoted by f i ( G 3 ) , i=1,2,...,9. Moreover, four of them are superatracting for some values of G3 (and attracting around these values of G3):
  • f 1 ( G 3 ) is superattracting for values of G 3 ≈ { 1.49735 , 15.9586 , 1242.25 } ,
  • f 2 ( G 3 ) is superattracting for values of G 3 ≈ 1.10566 ± 0.31755 i ,
  • f 4 ( G 3 ) is superattracting for values of G 3 ≈ 1.11091 ± 0.314158 i ,
  • f 7 ( G 3 ) is superattracting for values of G 3 ≈ − 576.219 ± 61.5856 i and 1.10884 ± 0.315802 i , and
  • f 3 ( G 3 ) , f 5 ( G 3 ) , f 6 ( G 3 ) , f 8 ( G 3 ) and f 9 ( G 3 ) are repelling, with independence of the value of parameter G3.
In Figure 3, the stability function of O G 3 ( z ) is observed. Let us remark that complex values of G 3 inside region | G 3 − 168 | < 1152 define fourth-order iterative schemes whose numerical performance do not include divergence.
In addition, the existence of free critical points is essential for the stability of the family of iterative methods.

4.3. Critical points and parameter planes

To calculate the critical points, we get
O G 3 ′ ( z ) = R ( z , G 3 ) S ( z , G 3 ) ,
where R ( z , G 3 ) = 6 z 3 ( 4 + 5 z + 2 z 2 + z 3 ) 2 ( G 3 ( − 2 − 2 z + z 2 ) 2 ( − 64 − 108 z + 80 z 2 + 94 z 3 − 46 z 4 − 53 z 5 − 12 z 6 + z 7 ) + 6 ( 1664 + 6656 z + 10788 z 2 + 8583 z 3 + 2748 z 4 − 876 z 5 − 1404 z 6 − 741 z 7 − 192 z 8 − 14 z 9 + 4 z 10 ) ) and S ( z , G 3 ) = ( 768 + 2496 z + 2928 z 2 + 1140 z 3 − 2 ( 363 + 4 G 3 ) z 4 − 24 ( 49 + G 3 ) z 5 − 6 ( 113 + 2 G 3 ) z 6 + 4 ( − 51 + 4 G 3 ) z 7 + 6 ( − 4 + G 3 ) z 8 − 6 ( − 2 + G 3 ) z 9 + G 3 z 10 ) 2 .
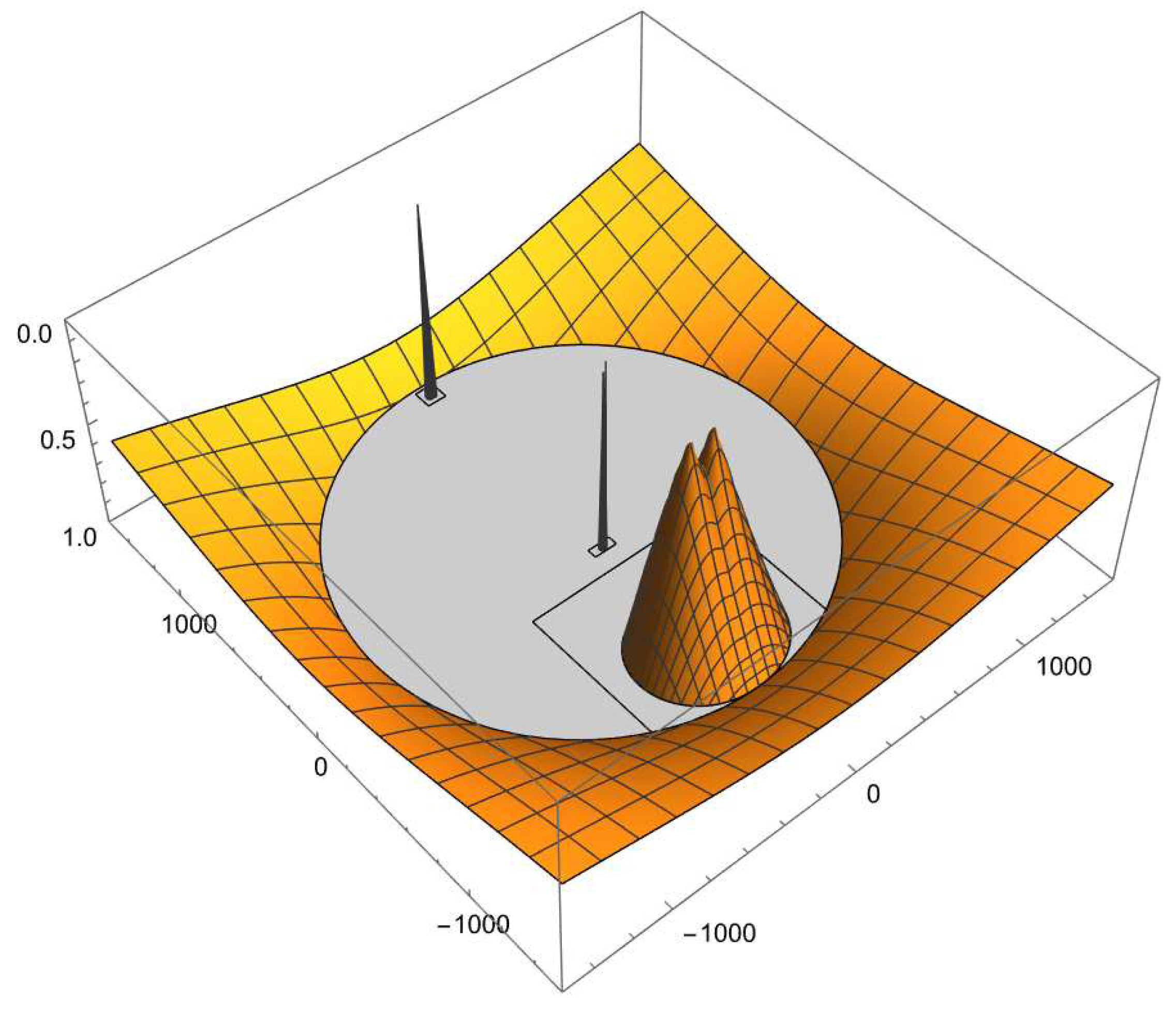
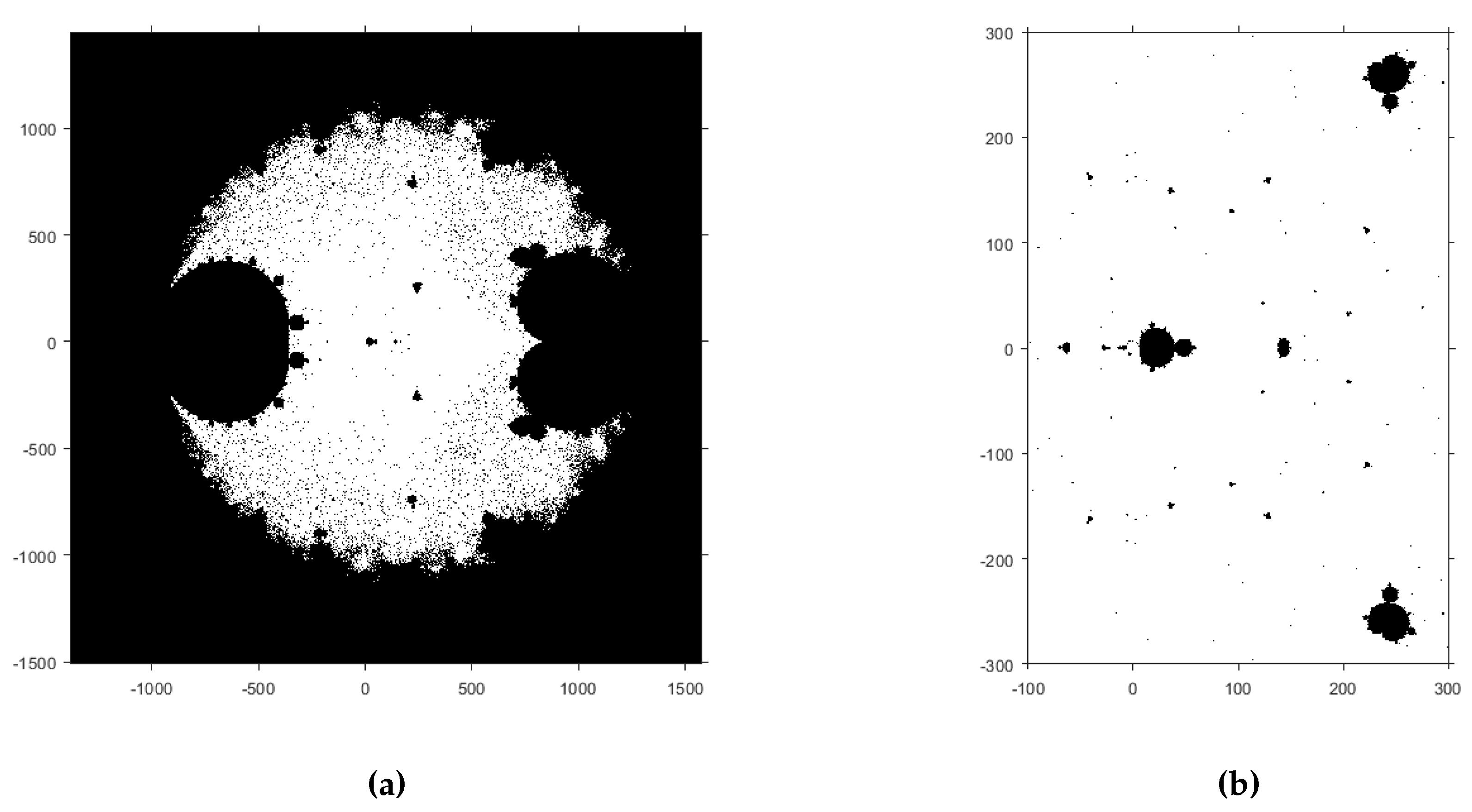
Since the order of the convergence of our iterative class of methods is greater than two, those fixed points from the original roots of p ( z ) , i.e., z = 0 and z = ∞ , are both critical points as well. In the next result, the remaining critical points, called free critical points, are also determined.
Theorem 4. 
The set of free critical points c r i , i = 1 , 2 , … , 13 , of fixed point operator O G 3 ( z ) is composed by c r 1 = − 1 , c r 2 = 1 2 ( − 1 + i 15 ) , c r 3 = 1 2 ( − 1 + i 15 ) which are preimages of the strange fixed point z = 1 and the roots of the polynomial t ( x ) = 9984 − 256 G 3 + ( 39936 − 944 G 3 ) x + ( 64728 − 544 G 3 ) x 2 + ( 51498 + 1272 G 3 ) x 3 + ( 16488 + 936 G 3 ) x 4 + ( − 5256 + 1008 G 3 ) x 5 + ( − 8424 − 768 G 3 ) x 6 + ( − 4446 + 186 G 3 ) x 7 + ( − 1152 + 174 G 3 ) x 8 + ( − 84 − 5 G 3 ) x 9 + ( 24 − 16 G 3 ) x 10 + G 3 x 11 .
Since c r 1 , c r 2 and c r 3 are preimages of z = 1 , only the parameter planes of c r i , i = 3 , 4 , … , 13 are obtained. The parameter plane represents if, taking an initial guess equal to the free critical point, its orbit converges or not. In this case, each point of the plane refers a value of G 3 ∈ C ^ , that is, a member of family (4). Instead of representing the 11 parameter planes, we just represent the unified parameter plane [21] for the sake of simplicity. White points represent convergence to any of the roots, while black points represent convergence to a different point or even divergence. The unified parameter plane is shown in Figure 4.
Let us remark the broad white region of Figure 4. Taking a white point guarantees the selection of a stable method.

5. Numerical performance

In this section, model (6) and different academic problems are solved by means of the iterative class (4), having the weight function described in (8) with G ‴ ( μ ) = 0 ,
y k = x k − 2 m 2 + m f ( x k ) f ′ ( x k ) , x k + 1 = x k − m + m 3 ( m − 1 ) 4 ( η − μ ) + m 4 ( 2 − 2 m − m 2 + m 3 ) 8 ( 2 + m ) ( η − μ ) 2 f ( x k ) f ′ ( x k ) , k = 0 , 1 , 2 , … ,
where μ = m + 2 m . The calculations have been performed in Matlab R2022b using variable precision arithmetics with 1000 digits of mantissa, on a computer equipped with a Intel ® Core™ i5-5200U CPU 2.20GHz. Tables that show the numerical performance collect the residuals | x k + 1 − x k | and | f ( x k + 1 ) | after convergence. Moreover, a computational estimation of the order of convergence ρ ˜ [23] is obtained as
p ≈ ρ ˜ = ln | f ( x k + 1 ) | / | f ( x k ) | ln | f ( x k ) | / | f ( x k − 1 ) | , k = 2 , 3 , …
When the components of vector ρ ˜ do not tend to any real value, it is marked as ’-’.

5.1. Model

To find the value of ε m a x of (6), the equation is rewritten as
f ( ε m a x ) = ε m a x − f y E s + f c t A c E s A s 1 + 3.6 M ε m a x .
The values of the parameters are in the ranges displayed in Table 1,
Table 2 shows the numerical performance of method (9) for solving the model (10). The stopping criterion is set when | f ( x k + 1 ) | < 10 − 16 , taking as initial guess the value x 0 = 9 4000 .
As deduced from Table 2, for initial guesses close to the solution, the results are successful. The method converges in 2 iterates to the solution for the used values of the parameters. The value of ρ ˜ can not be displayed since the number of iterates is lower than three.
Table 3 shows the effect of assuming an initial estimate further away from the root. In this case, x 0 = 1 100 and the stopping criterion remains as in the previous case.
The results of Table 3 show the good performance of the method, since it has converged to the solution in 3 iterates. The value of ρ ˜ differs from the theoretical one because in three iterations it has not been able to stabilize.

5.2. Academical problems

From now on, we are solving the following nonlinear equations with multiple roots:
  • Φ 1 ( x ) = e − x − 1 + x 5 3 , whose root is x * ≈ 4.9651 of multiplicity m = 3 , taking as initial guess x 0 = 26 ,
  • Φ 2 ( x ) = x 2 e x − sin ( x ) + x , whose root is x * = 0 of multiplicity m = 2 , taking as initial guess x 0 = 10 , and
  • Φ 3 ( x ) = ( x 2 − e x − 3 x + 2 ) 5 , whose root is x * ≈ 0.2575 of multiplicity m = 5 , taking as initial guess x 0 = − 6 .
The stopping criteria is set when | f ( x k + 1 ) | < 10 − 200 . The solution obtained with (9) is compared with the solutions applying Rall’s (1) and Schroder’s (2) methods, named O4, RA and SC, respectively. Table 4 collects the results, where "nc" denotes that the method does not converge.
The results of Table 4 illustrate how competitive method O4 is with respect to Rall’s and Schroder’s methods. In the three problems, the value of | f ( x k + 1 ) | and the number of iterations improve concerning the classical methods. Moreover, the ρ ˜ value matches the theoretical one.

6. Conclusions

In this paper, we have developed a parametric family of fourth-order numerical methods for solving a constitutive equation of reinforced concrete (6) with multiple roots. A dynamical analysis has been performed to select the best members of the family. For a particular method, its performance is compared with other known multiroot methods, obtaining the solution in fewer iterations with a higher order of convergence.

Author Contributions

Conceptualization, J.J.P. ; methodology, F.I.C..; software, A.C.and F.I.C.; formal analysis, J.R.T.; investigation, A.C. ; writing—original draft preparation, J.J.P. and A.M.H.; writing—review and editing, A.C. and J.R.T. All authors have read and agreed to the published version of the manuscript.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

References

  1. Hernández-Díaz, A.M.; Muñoz, A.; Jiménez-Alonso, J.F.; Sáez, A. Buckling design of submerged arches via shape parameterization. Computational and Mathematical Methods 2019, 1, e1057. [Google Scholar] [CrossRef]
  2. Jiménez-Alonso, J.F.; Pérez-Aracil, J.; Hernández Díaz, A.M.; Sáez, A. Effect of Vinyl flooring on the modal properties of a steel footbridge. Applied Sciences 2019, 9, 1374. [Google Scholar] [CrossRef]
  3. Galántai, A. The theory of Newton’s method. Journal of Computational and Applied Mathematics 2000, 124, 25–44. [Google Scholar] [CrossRef]
  4. Pérez-Aracil, J.; Camacho-Gómez, C.; Hernández-Díaz, A.M.; Pereira, E.; Camacho, D.; Salcedo-Sanz, S. Memetic coral reefs optimization algorithms for optimal geometrical design of submerged arches. Swarm and Evolutionary Computation 2021, 67, 100958. [Google Scholar] [CrossRef]
  5. Grewal, B.S. Numerical Methods in Engineering and Science: C,C++, and MATLAB.; Dulles: Mercury Learning and Information, 2011. [Google Scholar]
  6. Rall, L.B. Convergence of the Newton process to multiple solutions. Numerische Mathematik 1966, 9, 23–37. [Google Scholar] [CrossRef]
  7. Schröder, E.; Stewart, G. On infinitely many algorithms for solving equations. Technical report, 1998.
  8. Schröder, E. Über unendlich viele Algorithmen zur Auflösung der Gleichungen. Mathematische Annalen 1870, 2, 317–365. [Google Scholar] [CrossRef]
  9. Padilla, J.J.; Chicharro, F.I.; Cordero, A.; Torregrosa, J.R. Parametric Family of Root-Finding Iterative Methods: Fractals of the Basins of Attraction. Fractal and Fractional 2022, 6, 572. [Google Scholar] [CrossRef]
  10. Belarbi, A.; Hsu, T.T. Constitutive laws of concrete in tension and reinforcing bars stiffened by concrete. Structural Journal 1994, 91, 465–474. [Google Scholar]
  11. Pang, X.B.D.; Hsu, T.T. Behavior of reinforced concrete membrane elements in shear. Structural Journal 1995, 92, 665–679. [Google Scholar]
  12. Gil-Martín, L.M.; Hernández-Montes, E.; Aschheim, M.; Pantazopoulou, S. Refinements to compression field theory, with application to wall-type structures. American Concrete Institute Special Publication 2009, 265, 123–142. [Google Scholar]
  13. Palermo, M.; Gil-Martin, L.; Hernandez-Montes, E.; Aschheim, M. Refined compression field theory for plastered straw bale walls. Construction and Building Materials 2014, 58, 101–110. [Google Scholar] [CrossRef]
  14. Code, P. Eurocode 2: design of concrete structures-part 1–1: general rules and rules for buildings. British Standard Institution, London, 2005. [Google Scholar]
  15. Hernández-Díaz, A.; García-Román, M. Computing the refined compression field theory. International Journal of Concrete Structures and Materials 2016, 10, 143–147. [Google Scholar] [CrossRef]
  16. Palermo, M.; Gil-Martín, L.M.; Trombetti, T.; Hernández-Montes, E. In-plane shear behaviour of thin low reinforced concrete panels for earthquake re-construction. Materials and structures 2013, 46, 841–856. [Google Scholar] [CrossRef]
  17. España, R.M.; Hernández-Díaz, A.M.; Cecilia, J.M.; García-Román, M.D. Evolutionary strategies as applied to shear strain effects in reinforced concrete beams. Applied Soft Computing 2017, 57, 164–176. [Google Scholar] [CrossRef]
  18. Blanchard, P. Complex analytic dynamics on the Riemann sphere. Bull. AMS 1984, 11, 85–141. [Google Scholar] [CrossRef]
  19. Devaney, R.L. An Introduction to Chaotic Dynamical Systems; Addison-Wesley, 1986.
  20. Chicharro, F.I.; Cordero, A.; Torregrosa, J.R. Drawing dynamical and parameters planes of iterative families and methods. The Scientific World Journal 2013, 2013. [Google Scholar] [CrossRef] [PubMed]
  21. Chicharro, F.I.; Cordero, A.; Garrido, N.; Torregrosa, J.R. On the choice of the best members of the Kim family and the improvement of its convergence. Mathematical Methods in the Applied Sciences 2020, 43, 8051–8066. [Google Scholar] [CrossRef]
  22. Blanchard, P. ; others. The dynamics of Newton’s method. Proceedings of Symposia in Applied Mathematics. American Mathematical Society Providence, RI, USA, 1994, Vol. 49, pp. 139–154.
  23. Jay, L. A Note on Q-order of Convergence. BIT Numerical Mathematics 2001, 41, 422–429. [Google Scholar] [CrossRef]
Preprints 77268 g001
Figure 1. Profiles of average stresses ( s i g m a c t , a v and s i g m a s t , a v ) and area of prescribed tensile stiffening ( A c ) actually attached to the steel.
Figure 1. Profiles of average stresses ( s i g m a c t , a v and s i g m a s t , a v ) and area of prescribed tensile stiffening ( A c ) actually attached to the steel.
Preprints 77268 g001
Preprints 77268 g002
Figure 2. Stability region of z=1.
Figure 2. Stability region of z=1.
Preprints 77268 g002
Preprints 77268 g003
Figure 3. Regions of stability corresponding to f i ( G 3 ) , i=1,2,...,11.
Figure 3. Regions of stability corresponding to f i ( G 3 ) , i=1,2,...,11.
Preprints 77268 g003
Preprints 77268 g004
Figure 4. Unified parameter plane: (a) complete, (b) a detail in Re { G 3 } ∈ [ − 100 , 300 ] , Im { G 3 } ∈ [ − 300 , 300 ] .
Figure 4. Unified parameter plane: (a) complete, (b) a detail in Re { G 3 } ∈ [ − 100 , 300 ] , Im { G 3 } ∈ [ − 300 , 300 ] .
Preprints 77268 g004
Table 1. Ranges for input parameters of (10).
Table 1. Ranges for input parameters of (10).
Input Range
E s (GPa) 195 , 205
f y (MPa) 400 , 500
f c t (MPa) 25 , 50
A s (mm 2 ) 40 , 1200
A c (mm 2 ) 9000 , 52000
M (mm) 500 , 2800
Table 2. Numerical performance of problem (10) for x 0 = 9 4000 .
Table 2. Numerical performance of problem (10) for x 0 = 9 4000 .
| f ( x k + 1 ) | | x k + 1 − x k | Solution Iterations ρ ˜
2.95289e-19 0.0000138391 0.000635604 2 -
5.24395e-19 0.0000198302 0.000517161 2 -
1.46768e-19 0.0000207393 0.000446156 2 -
1.78237e-19 0.0000156739 0.000598853 2 -
5.2808e-19 0.0000151498 0.000600228 2 -
4.71609e-20 0.0000209598 0.000412874 2 -
1.09408e-19 0.000014158 0.000604944 2 -
2.25264e-19 0.0000205114 0.000525394 2 -
3.27036e-19 0.0000173992 0.000537687 2 -
1.94702e-19 0.0000180554 0.00045173 2 -
4.56095e-19 0.0000154389 0.000583336 2 -
1.24265e-19 0.0000190569 0.000542714 2 -
3.81289e-19 0.0000209862 0.000472623 2 -
1.46367e-19 0.0000150232 0.000568954 2 -
1.4193e-19 0.0000203555 0.000516532 2 -
Table 3. Numerical performance of problem (10) for x 0 = 1 100 .
Table 3. Numerical performance of problem (10) for x 0 = 1 100 .
| f ( x k + 1 ) | | x k + 1 − x k | Solution Iterations ρ ˜
2.9442e-19 0.00000168032 0.000635604 3 2.02379
4.70146e-19 0.00000684629 0.000517161 3 2.85371
4.27661e-20 0.00000803271 0.000446156 3 3.29596
1.81752e-19 0.00000260127 0.000598853 3 2.30058
5.25702e-19 0.00000220132 0.000600228 3 2.11224
1.78977e-19 0.00000883971 0.000412874 3 3.23475
1.0831e-19 0.00000160411 0.000604944 3 2.09545
1.45139e-19 0.00000858088 0.000525394 3 3.16438
3.3873e-19 0.00000347839 0.000537687 3 2.42474
2.15411e-19 0.00000336737 0.00045173 3 2.48239
4.59028e-19 0.00000223758 0.000583336 3 2.13696
9.06593e-20 0.00000589335 0.000542714 3 2.91293
2.69372e-19 0.00000885897 0.000472623 3 3.14682
1.48509e-19 0.00000182173 0.000568954 3 2.13834
2.15643e-19 0.00000799412 0.000516532 3 3.06402
Table 4. Numerical performance of problems Φ 1 ( x ) , Φ 2 ( x ) , and Φ 3 ( x ) .
Table 4. Numerical performance of problems Φ 1 ( x ) , Φ 2 ( x ) , and Φ 3 ( x ) .
Problem Method | f ( x k + 1 ) | | x k + 1 − x k | Iterations ρ ˜
Φ 1 ( x ) RA 5.067e-307 1.5112e-50 6 2
SC 4.4598e-315 6.8690e-52 6 2
O4 0 7.2526e-44 4 3.9991
Φ 2 ( x ) RA 2.0809e-311 2.7992e-78 15 2
SC nc nc nc -
O4 0 2.5147e-65 8 4.0000
Φ 3 ( x ) RA 6.3688e-289 2.5494e-29 14 2
SC 2.6371e-307 3.6995e-31 9 2
O4 0 1.2030e-40 8 4.0004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated