Prerpints.org logo
Preprint
Article

Compressed Sensing Techniques Applied to Medical Images Obtained With Magnetic Resonance

Altmetrics

Downloads

146

Views

37

Comments

0

Submitted:

21 June 2023

Posted:

22 June 2023

You are already at the latest version

Alerts
Abstract
The fast and reliable processing of medical images is of paramount importance to adequately generate data to feed machine learning algorithms that can prevent and diagnose health issues. Here we benchmark different compressed sensing techniques applied to magnetic resonance imaging as a means to reduce the acquisition time spent in the collection of data and signals that form the image. We show that by using these techniques, it is possible to reduce the number of signals needed and, therefore, substantially decrease the time to acquire the measurements. To this end, we have considered and compared different algorithms: the Iterative Re-Weighted Least Squares, the Iterative Soft Thresholding Algorithm, the Iterative Hard Thresholding Algorithm, the Primal Dual Algorithm and the Log-Barrier Algorithm. We have implemented such algorithms in different analysis programs that have been used to perform the reconstruction of the images and found that the Iterative Soft Thresholding Algorithm gives the optimal results. We found that the images obtained with this algorithm have less quality than the original ones, but the quality is good enough to distinguish each body structure and detect any health problems.
Keywords: 
Subject: Computer Science and Mathematics  -   Mathematics

1. Introduction

As the years go by and the scientific knowledge increases and refines, theories are updated and improved, giving rise to more reliable and efficient technological applications. For instance, within the field of signals processing, in the old days a camera with n pixels, needed n signals to form the image. In 1949, however, with the Shannon-Nyquist theorem [1], it was shown that it was possible to form the same image with fewer signals. This theorem states that it is feasible to recover a signal if it is uniformly sampled at a rate at least two times faster than its Fourier bandwidth, i.e. it allows to reconstruct a continuous signal with a discrete sequence of samples acquired. However, for some applications as radar imaging or different imaging modalities outside visible wavelengths, the needed sampling rate can be so high that for state-of-the-art samplers it is impossible to achieve such values. Also, because of the high number of samples collected, it is necessary to compress them [2]. In 2006, Donoho and the team composed by Romberg, Candès and Tao introduced the concept known as compressed sensing (CS) [3,4], which substantially simplified the acquisition process.
CS is an alternative technique to the Shannon-Nyquist sampling theorem. With this approach, it is possible to reconstruct a signal from a few random measurement by making use of some non linear techniques, provided that the original signal is compressible or sparse. A sparse signal has most of its coefficients null and only a few contain all the information. It is possible to obtain this kind of signal through a base transformation. For example, a sinusoidal signal of a given frequency obtained with a voltmeter as a function of time is not sparse. However, if the Fourier Transform is applied, the signal has a peak associated with that frequency. The rest of the values are zero. Therefore, in the Fourier domain, it is sparse [5].
The main objective of CS is to reduce the number of coefficients required to obtain the resolution and the desired quality for the representation of the object of interest. To achieve this, it uses a mathematical function called norm. The norm l p of a vector x (vectorial notation is shown in bold type) of length n is expressed as follows:
∥ x ∥ p = ∑ i = 1 n | x i | p 1 / p
In the case p = 0 , the l 0 norm consists of the number of non-zero elements in the vector x. The l 1 norm ( p = 1 ) gives as a result the sum of the elements of the vector. The l 2 norm is widely used to compute Euclidean distance [6].
The CS problem can be described as the reconstruction of the vector x, of dimension n, from the measurements y = A x , of dimension m, and the random measurement matrix A, known as sensing or measurement matrix, of dimensions mxn.
The solution to this problem depends on its typology, that is:
  • If m>n and rank(A)=n (purely overdetermined linear system), the linear system is solved via least squares:
    x = ( A T A ) − 1 A T y
    Besides, the reconstruction error of y: ∥ y − A x ∥ 2 is non-null.
  • In the purely underdetermined case (m<n and rank(A)=m) there are an infinite set of solutions that belong to a linear variety oriented by the null space of A. This is the typical case of under-sampling, that is, the number of samples in A (length of y) are less than the original size of x. In this case, the minimum l 2 norm solution writes:
    x MN = A T ( A A T ) − 1 y
    since it does not have components in the null space of A. This solution is sparse in the system of reference ( R n = Col A ⨁ Ker A ).
The sparse problem treated in this paper consists in finding the sparser solution in the l 0 norm, which is the same to impose sparsity in the canonic basis set of R n :
x = min ∥ x ∥ 0 subject to y = A x
Minimization in norm l 0 requires an exhaustive search over all possible sparse combinations. Since it requires a large computational cost, this minimization is replaced by the convex minimization problem in l 1 . This problem is determined as:
x = min ∥ x ∥ 1 subject to y = A x
and it is known as Basis Pursuit (BP). In more complex situations, the measurements obtained are corrupted by an unknown noise, which is denoted as e. Therefore, y = A x + e . The reconstruction problem is written as follows:
x = min ∥ x ∥ 1 subject to ∥ y − A x ∥ 2 ≤ ϵ ,
where ∥ e ∥ ≤ ϵ . This problem is known as BP Denoising (BPDN) [7].
This is equivalent to impose that the linear system y = A x is incompatible due to measurement noise. BPDN is a constrained problem whose solution can be approached by the following unconstrained optimization problem:
x = min x ∥ y − A x ∥ 2 2 + λ ∥ x ∥ 1
The parameters λ and ϵ are related but, generally, the relationship between them is not analytical and cannot be estimated [8].
CS technique has several applications in many fields, e.g. underwater imaging [9], wireless structural health monitoring [10] and 3D visualization of the iron oxidation state in FeO/Fe3O4 [11]. In this paper, CS is used in medical imaging; in particular, with images obtained by magnetic resonance imaging (MRI).
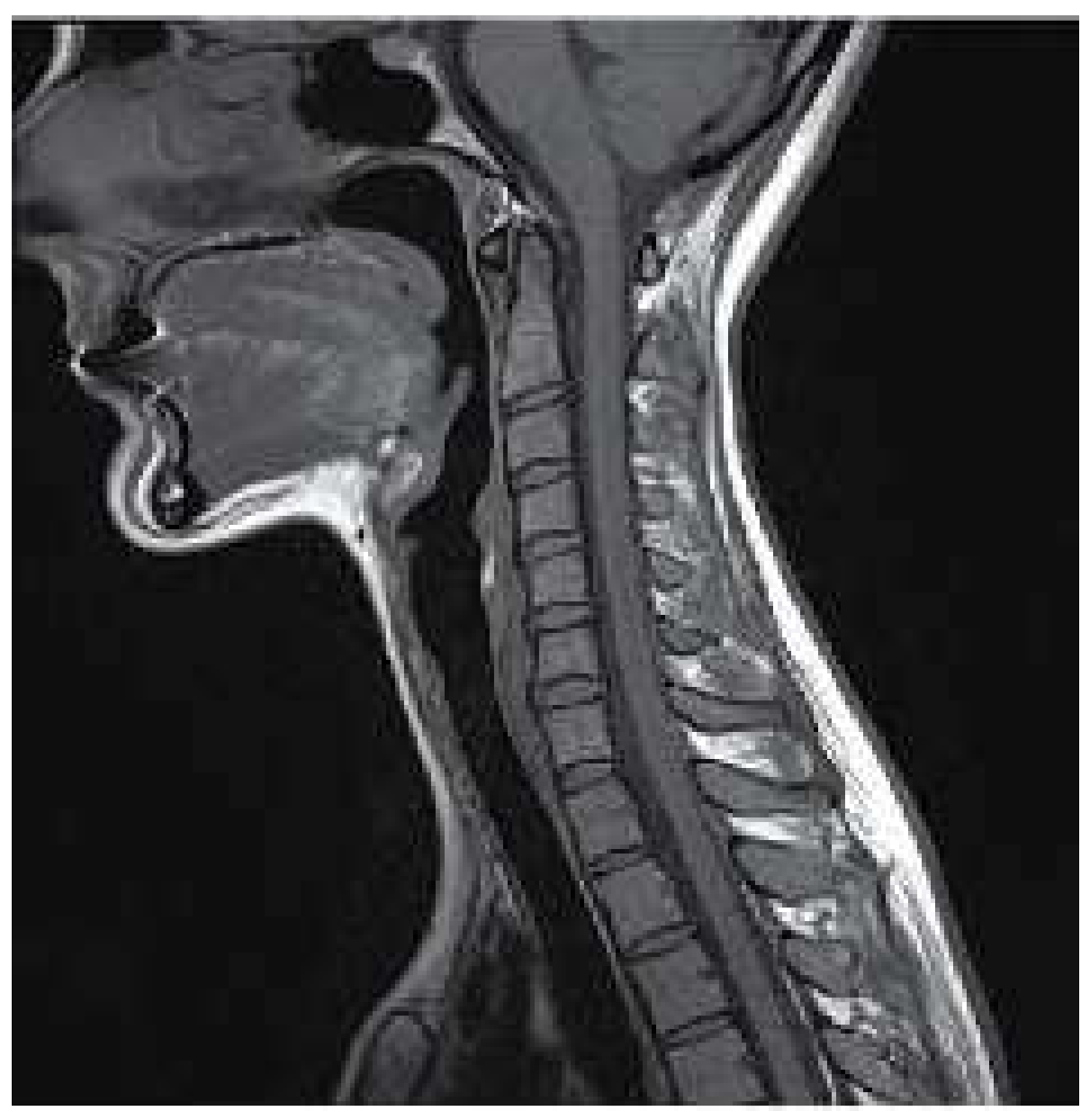
MRI is a non-invasive technique widely used in medicine to obtain medical images needed to make a later diagnosis. This technique is based on the physical phenomenon of resonance; it consist of the transition between different energy states when an atomic nucleus is introduced in an external magnetic field of a characteristic frequency. This frequency, known as Larmor frequency, corresponds to the precession frequency of the protons inside the nucleus. When a magnetic field is applied, the protons absorb the energy and promote to a higher level. Once the magnetic field is removed, the protons decay to the ground state. MRI measures the time and energy released from this last transition. Because of their surroundings, those two values will be different for each proton. Then, by applying the Inverse Fourier Transform to the obtained data it is created the image with different contrast for each component of the body [12], as shown in Figure 1.
This technique allows to distinguish different components of the human body, in particular soft tissues as muscles, tendons, ligaments, fats, etc. Not only that, it also makes it possible to differentiate between bones and organs [12]. The images can be in any direction or part and they can even be made of animals, for instance a mice [14]. Moreover, MRI can be used as an spectroscopy technique in biochemistry: it allows to know the three-dimensional and dynamic structure of biological molecules [15]. Additionally, its main advantage over other techniques, such as computed tomography or X-rays, is its lack of ionizing radiation, which makes MRI exams secure for the patient. Because of these reasons, its multiple uses and its high resolution imaging, MRI is known as the jewel in the crown in medical imaging [16].
Despite the many advantages mentioned before, MRI has some drawbacks: patients with pacemaker or with metal prostheses can be hurt by the strong magnetic field (up to 3T), so they can not be examined. Also, because of the reduced space and the high level of noise in the machine, it can generate stress or anxiety. In addition to these disadvantages, there are many more safety precautions that must be taken in consideration in order to perform an examination. In addition, maintenance of machine components and tests are very expensive. Finally, it takes a lot of time to acquire the data necessary to construct the image, approx. 40 minutes [17].
In this article we present a methodology to reduce the acquisition time of MRI by using three different CS algorithms. We consider different images of MRI of the head and reconstruct them with less measurements and, therefore, the acquisition time is reduced. In the algorithms, we introduced a number of data smaller than the real image and measure the time the algorithm takes on the reconstruction and the error committed. This study paves then the way for shorter exams in MRI.
The article is organized as follows: in Section 2 we describe the CS algorithms employed to reconstruct the image and how they can be applied in MRI. In Section 3, we present and discuss the results (reconstructed images, acquisition time and error). We finish with the conclusions.

2. Materials and Methods

MRI receives the data of proton relaxation and stores it in the frequency space, so that with the Inverse Fourier Transform it is possible to construct the image. The CS problem applied to this case can be written as:
y m × 1 = F m × n x n × 1 + η m × 1 η ∼ N ( 0 , σ 2 )
where y are the frequency samples collected by the machine, F is the Fourier measurement matrix x is the image to be constructed and η is the noise randomly distributed. We have to solve an inverse linear problem to recover the data that forms the image from the measurements; we use the measurement matrix which associates a frequency to a value in the grey scale. The object x can be an image in 2D or 3D but it is represented as a vector by concatenation.
In the ideal case in which enough measurements are taken ( n = m ), Eq. (8) can be solved by applying the Inverse Fourier Transform on the frequencies:
x = F − 1 y
To reduce the acquisition time, less measurements are taken. Therefore, Eq. (8) has infinite solutions which can be solved with minimization algorithms. In this article, to reconstruct the image we use five possible methods: Iterative Re-weighted Least Squares (IRLS), Iterative Soft Threshold (ISTA), Iterative Hard Threshold (IHTA), a primal dual algorithm (PD) and a log barrier algorithm (LB). The first three algorithms belong to the category of greedy algorithms. They have less accuracy in the reconstruction but is less expensive and simpler. PD and LB are convex algorithms; the error is minor but it takes a lot of computational resources [7]. All those algorithms shown below, are iterative because of the large storage size of A.

2.1. Iterative Re-weighted Least Squares

The first algorithm, IRLS, solves the minimization problem without restrictions, Eq.(7). To achieve this, it replaces the l 1 minimization with l 2 norm with a given weight represented by the diagonal matrix W In each iteration k. This matrix is updated by:
W ( k ) = diag ( | x i ( k ) | − 1 2 + γ )
where γ is the dumping factor which is reduced at each iteration. In order to obtain the reconstructed signal, the algorithm solves Eq.(11), obtained from the unconstrained lagrangian, until it reaches a certain number of iterations or the solution converges, i.e. ∥ y − A x ∥ 2 < ϵ where ϵ is the minimum error [8].
x ( k + 1 ) = ( W ( k ) ) − 1 A T ( A ( W ( k ) ) − 1 A T ) − 1 y

2.2. Iterative Soft Threshold Algorithm

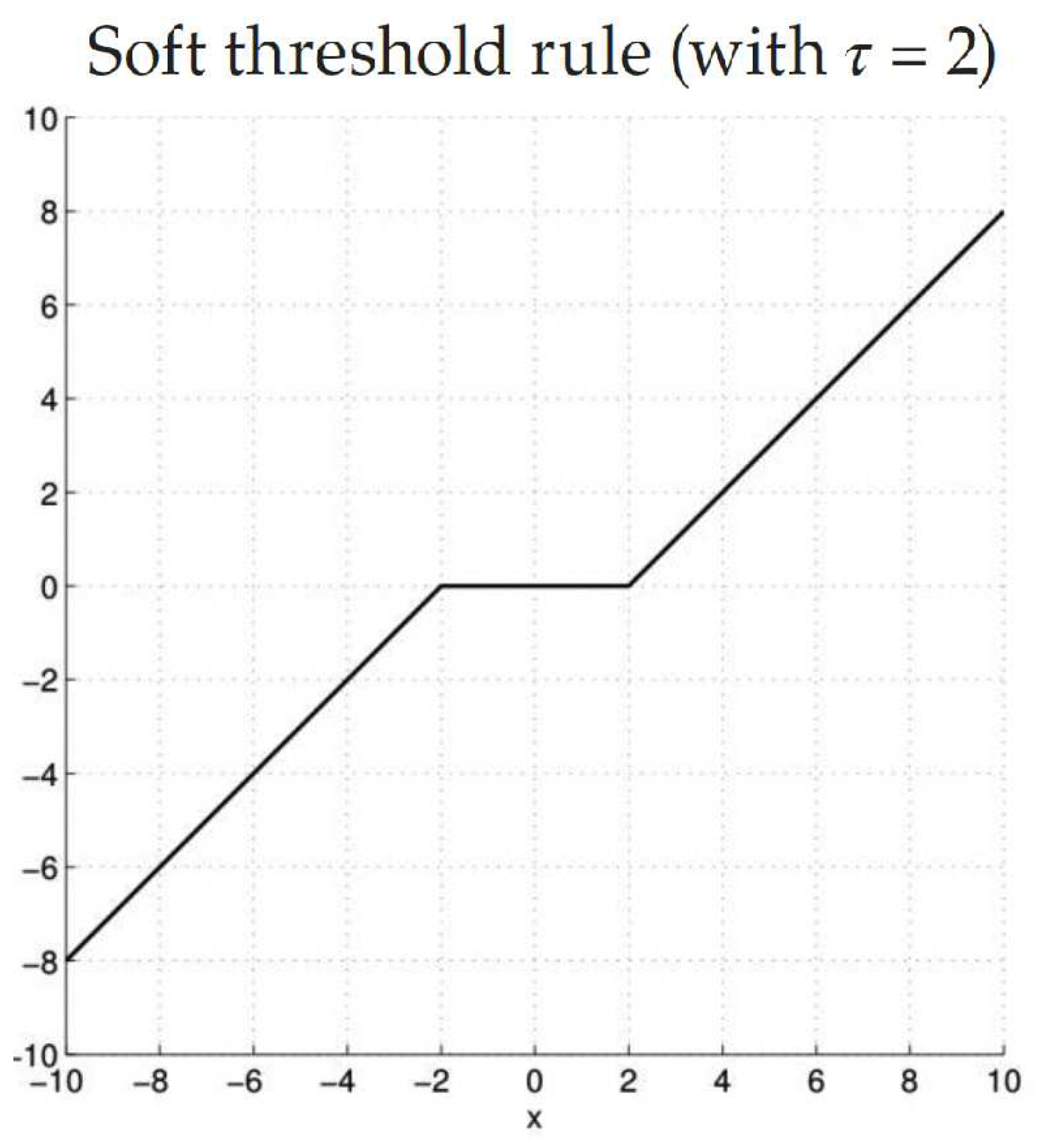
Next algorithm, ISTA, solves the same minimization problem as the previous algorithm (Eq.(7)). In this case, it is used the function called Soft Threshold:
soft ( x , τ ) = x + τ x < − τ 0 | x | ≤ τ x − τ x > τ
This, showed in Figure 2, tries to decrease the amplitude of the coefficients with noise. For example, if the amplitude of the signal is small, the noise and the number of data which provides information are of equal magnitude. The data contains little information and, therefore, the function returns 0. For larger amplitudes, the noise is very small compared to the intensity of the real signal, and thus the function subtracts the part associated with noise [18].
In order to obtain the reconstructed signal with this algorithm, it is necessary to calculate the Landweber Iteration, which is defined as:
b ( k ) = x ( k ) + 1 a A T ( y − A x ( k ) )
where a is the largest eigenvalue of the matrix A T A . The solution x k + 1 is calculated with the Soft Threshold rule, which is written in a more compacted way:
x ( k + 1 ) = signum ( b ( k ) ) max ( 0 , | b ( k ) | − λ 2 a )
In each iteration, the value of λ should be reduced in order to achieve convergence [8].
Over the years, ISTA have had a lot of improvements in order to reduce the adquisition time or to get a better resolution. For example, changing the thresholding function to equation Eq.(15), called p-thresholding function, the technique penalizes small coefficients and shrinks more values to zero. If p = 1 , the equation reduces to soft-thresholding (Eq.(12)) [19].
G τ , p ( x ) = sign ( x ) max ( 0 , | x | − τ | x | p − 1 )
Another algorithm which improves the convergence speed, which is ISTA’s main problem, is called fast ISTA (FISTA) which relies on the simplicity of the computation of the proximal map of l 1 norm. If the gradient algorithm is applied in Eq.(6, it is obtained the following iterative equations:
x ( k ) = x ( k − 1 ) − t ( k ) ∇ ( | | A x ( k − 1 ) − b ( k ) | | 2 )
where t ( k ) > 0 is the stepsize updated in each iteration. Using this idea with the unconstrained problem (Eq.(7)) it is obtained an iterative scheeme which can be seen as a proximal regularization of | | A x − b | | 2 . It is written as:
x ( k ) = min x 1 2 t ( k ) | | x − ( x ( k − 1 ) − t ( k ) ∇ ( | | A x ( k − 1 ) − b ( k ) | | 2 ) ) | | 2 + λ | | x | | 1
By using FISTA, the number of iterations required to obtain an optimal solution are less than ISTA as it improves the convergence rate [20]. However, there is no simple solution to the non-smooth part λ | | x | | 1 . In order to solve this, it is possible to approximate this term by its Moreau envelop, which is smooth [21]. This strategy is also used in projected ISTA (pISTA) and projected FISTA (pFISTA), in which the unconstrained model is converted into a much simpler form where the objective function can be separated and the orthogonal projection operator is introduced [22].
It is clear that it has been proposed many ways to optimize MRI and its different sequences that improves its stability, the memory consumption and the reconstruction time [23,24], but ISTA is still a good way for signal reconstruction because it stands out for its simplicity.

2.3. Iterative Hard Threshold Algorithm

As mentioned in Section 1, to solve the CS problem in the l 0 norm is very expensive. However, IHTA handles this problem if the data has noise, i.e.,
x = min x ∥ y − A x ∥ 2 2 + λ ∥ x ∥ 0
In this algorithm, it is defined the following function similar to ISTA:
hard ( x , τ ) = x | x | > τ 0 | x | ≤ τ
In this function, if the signal is of the same magnitude as the noise, it eliminates those values; otherwise, it does not alter the value [8]. In this algorithm the Landweber Iteration is also calculated by Eq.(13) and the solution is obtained by:
x ( k + 1 ) = HardThreshold ( | b ( k ) | , λ 2 a )

2.4. Primal Dual Algorithm

PD algorithms for linear programming are used to solve equation Eq.(5) among others. The standard form in linear programs is
min x 〈 c 0 , x 〉 subject to A x = y , f i ( x ) ≤ 0
where each of the f i = 1 , . . . , m is a linear functional f i ( x ) = 〈 c i , x 〉 + d i for c i ∈ R n and d i ∈ R . This algorithm finds the optimal x * and the dual vectors ν * ∈ R n , λ * ∈ R n , which satisfies the Karush-Kuhn-Tucker conditions, by solving this system of nonlinear equations with the Newton’s Method [25,26]:
c 0 + A T ν * + ∑ i λ i * c i = 0 λ i * f i ( z * ) = 0 , i = 1 , . . . , m A z * = y f i ( z * ) ≤ 0 , i = 1 , . . . , m
So in the inner loop of the PD algorithm, Newton’s Method is applied. Conjugate gradients are used in Eq.(22) in order to obtain the step direction Δ x . Then, update the solution by the next equation:
x ( k + 1 ) = x ( k ) − α Δ x

2.5. Log-Barrier Algorithm

The BPDN problem (Eq.(6)) can be modeled as Second-Order Cone Programs (SOCPs), i.e., it can be written as a linear program Eq.(21) where f i represents a second-order conic. This method consists of transforming the minimization problem into a series of linear problems in y:
min x 〈 c 0 , x 〉 + 1 τ k ∑ i − log ( − f i ( x ) ) subject to A x = y
Each one of this subproblems are solved with a high degree of accuracy with the Newton’s method to obtain x ( k ) . In each iteration k, τ k is updated so that τ k > τ k − 1 [26].

2.6. Application of the algorithms to MRI

The previous algorithms have been used to reduce the acquisition time of MRI. Since we were unable to access a MRI machine, we designed a code to read real MRI images, decompose the data and store it as a vector x. This code, also generates the measurement matrix A as a function to avoid memory problems due to the large size of the matrix. The measurements that would be obtained in MRI y are evaluated through A and x. The measurement matrix function calculates the Fourier Transform of x and randomly orders its coefficients. We apply the algorithms to y and obtain the signal and the reconstructed image x ^ . Our code also allows to obtain the time it takes to perform the algorithms and the error between the original and the reconstructed signal.
The aim of this article is to reduce the acquisition time and, therefore, the number of measurements taken must be less than the number needed to construct the original image. So, when the image is read, we randomly select a few values which will be stored in x. Then, y is obtained and the signal x ^ reconstructed.
We have analysed several images with the algorithms to obtain the parameters of time and error in function of the number of measures. With these results, we select the best algorithm to perform the reconstruction applied to MRI and the minimum number of measures needed to be able to distinguish all image components.

3. Results and discussion

This section presents the results after applying the CS algorithms on medical images obtained with MRI. We analysed several images of the head of the human body obtained from the database of the University of South Carolina [27].
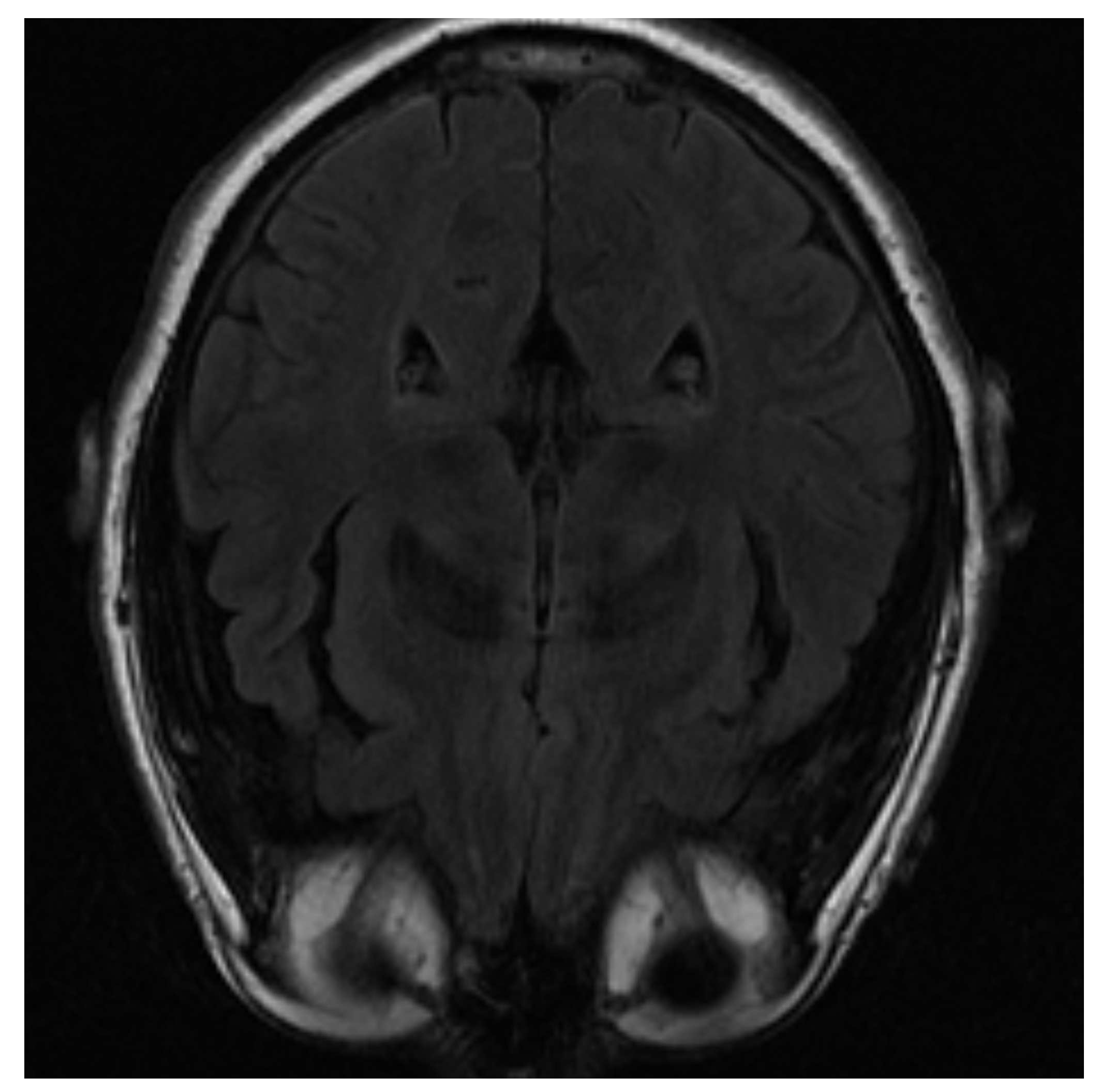
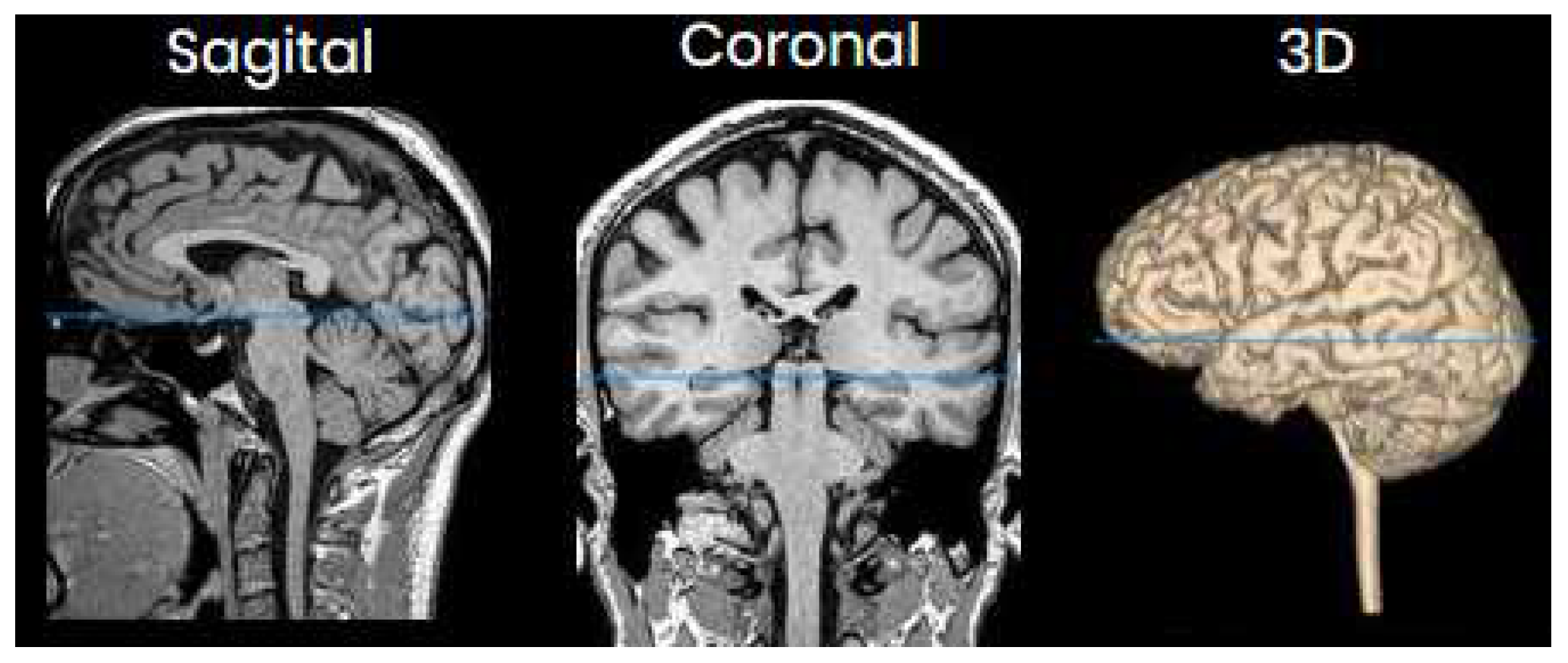
One of the images used in the simulations is shown in Figure 3 and corresponds to an axial slice of the brain in the plane marked by the blue lines in Figure 4. In it, the orbit of the eyes can be distinguished at the bottom. Fat appears with a very intense signal, while water and cerebrospinal fluid have a very low intensity.
The image is blurred in the left orbit, which is an example of an artifact. An artifact is a distortion in the image that has no relation to the subject of the region of the studied body. In this case, it has been generated due to the patient’s movement [28].
Next, we present the images and the parameters obtained from the reconstruction, time and error, for each algorithm as a function of the data taken from the original image.
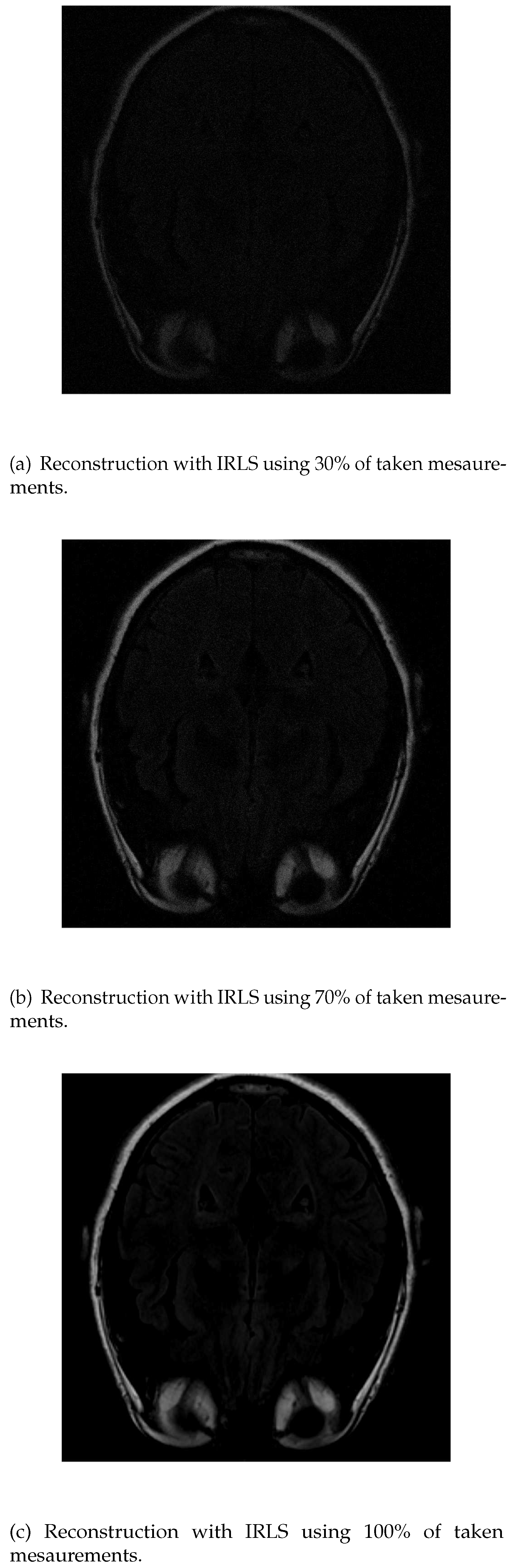
In the reconstruction by IRLS, only the outline of the head and orbits are detected in the first measurements, while the white matter is not distinguishable (Figure 5a). When 70% of the data is available (Figure 5b), the white matter can be distinguished, although it has little intensity. Also, the intensity of the orbits increases and the effect of the artifact starts to be noticed. If the algorithm is run with all the available data (Figure 5c), the resolution at the edges increases, but the intensity of the white matter signal is lost, which makes its identification more difficult.
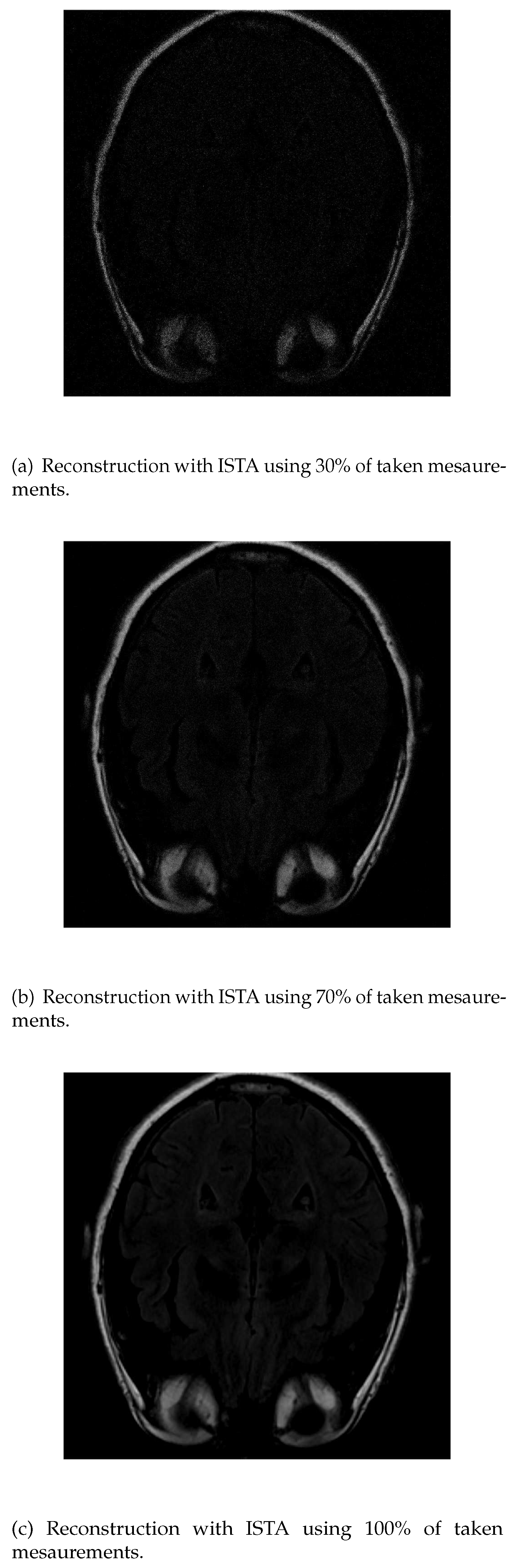
As in IRLS, the ISTA algorithm detects first the areas of highest intensity in the first measurements without distinguishing white matter (Figure 5a). If the number of input data is increased, the resolution of the edges increases but it is still difficult to differentiate the white matter (Figure 5b). Finally, the resolution increases until the shape of the fat is detected (Figure 5c).
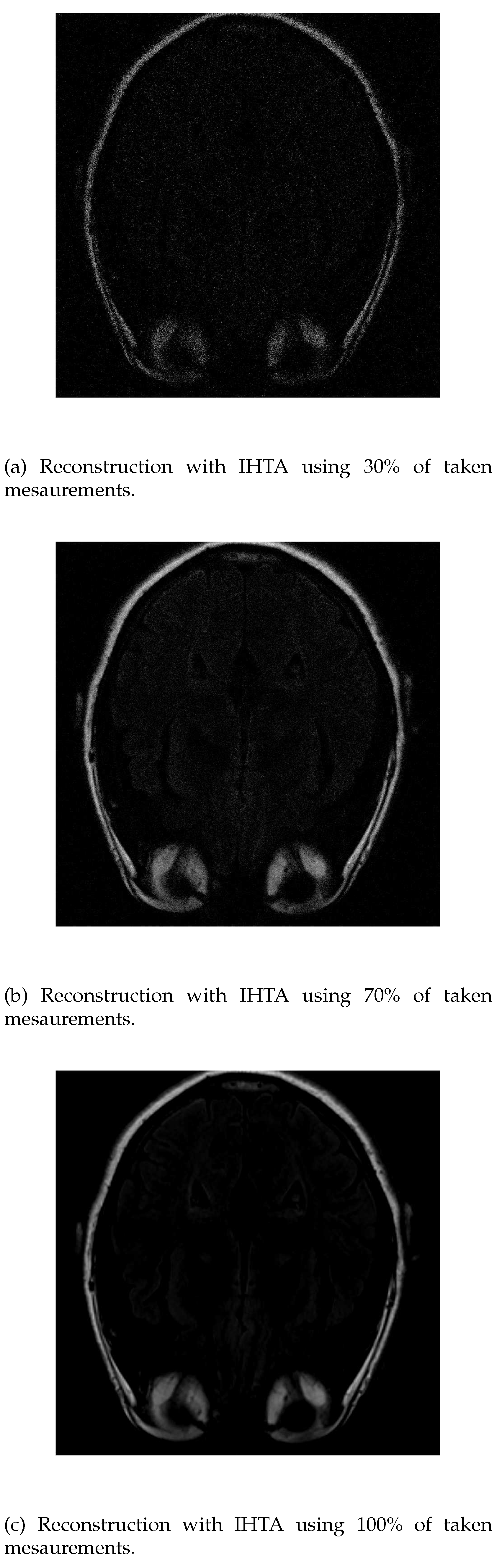
If it is employed IHTA for the reconstruction, when we use a 30% of the initial signal values (Figure 7a), much more noise is detected in the inner part of the head, where the white matter should be. In case of a 70% of measurements (Figure 7b), we obtain an image similar to the same case with ISTA, but the white has more intense signals, which allows to distinguish it better. The resolution increases as more data is added. However, when a 100% of data is reached Figure 7c), the white matter is not detected, it appears in black.
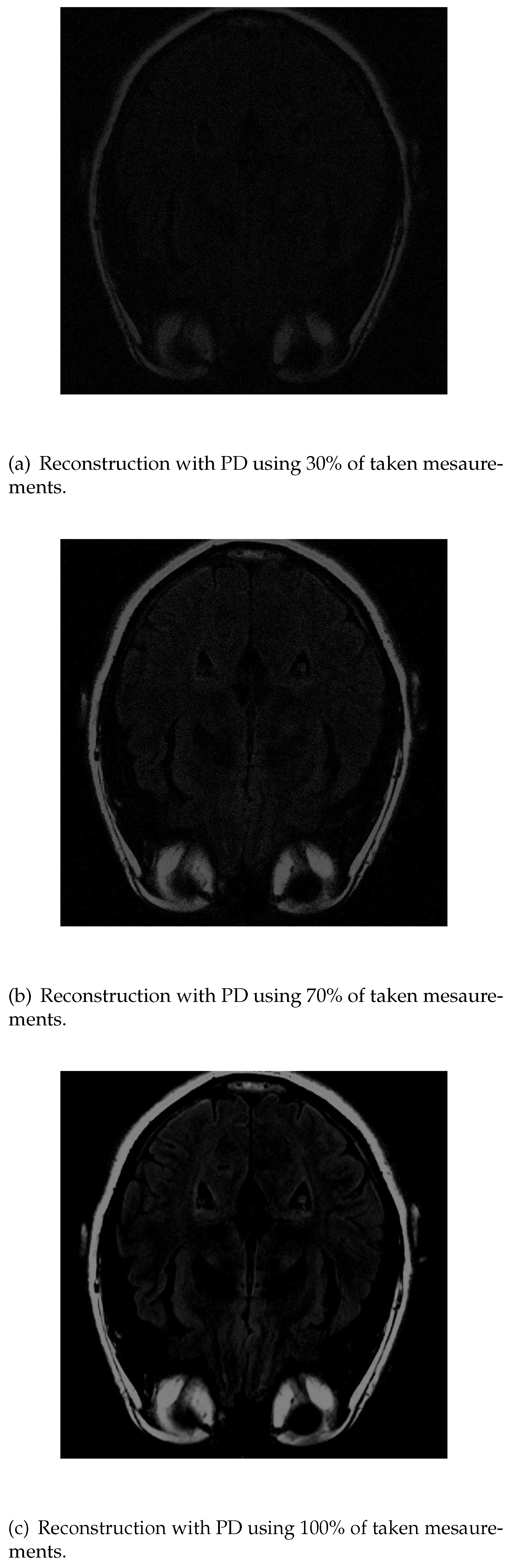
If we apply PD algorithm the object is much clearer with lower measurements. When it is used 30% of the initial values Figure 8a), the structure inside the head can be recognized and delimited, even though its low intensity. As the number of measurements is increased, the images get better resolution so when we have 70% Figure 8b), the image is similar to the original one. Finally, with 100% Figure 8c), the grey matter loses its intensity.
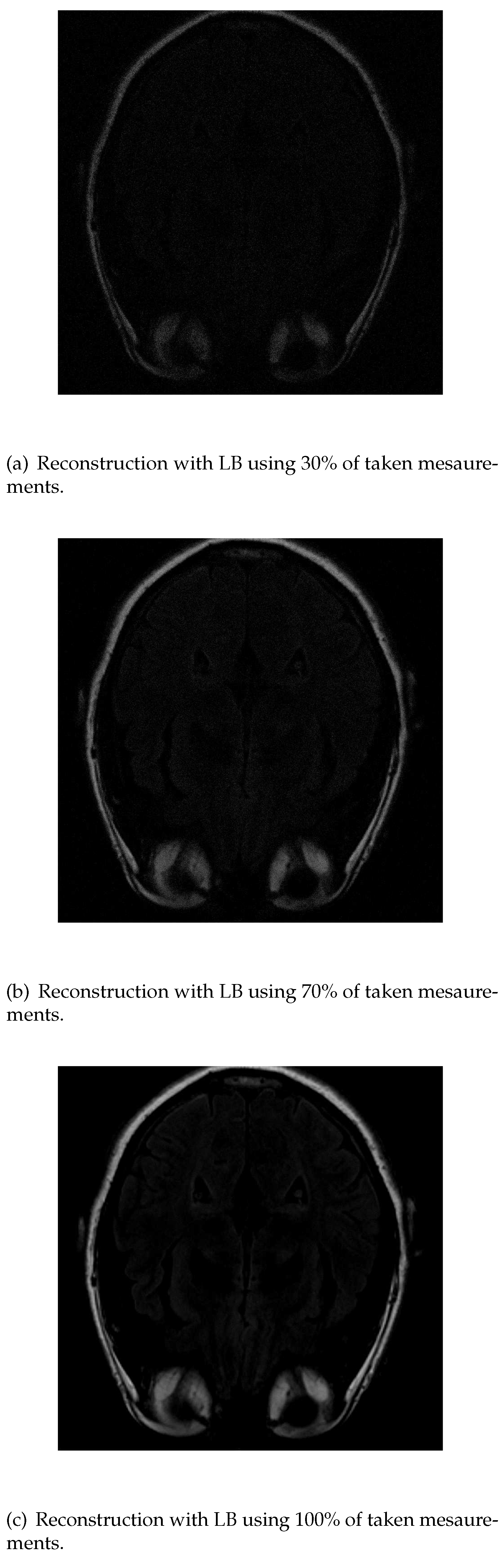
The images obtained with last algorithm, LB, are more blurred. With 30% of the measurements Figure 9a) it is not posible to distinguish the structures. It the algorithm works with 70% of the initial data Figure 9b), the image is reconstructed clearly. In the end, with all 100% of the data, the reconstruction is similar to the one obtained with PD algorithm.
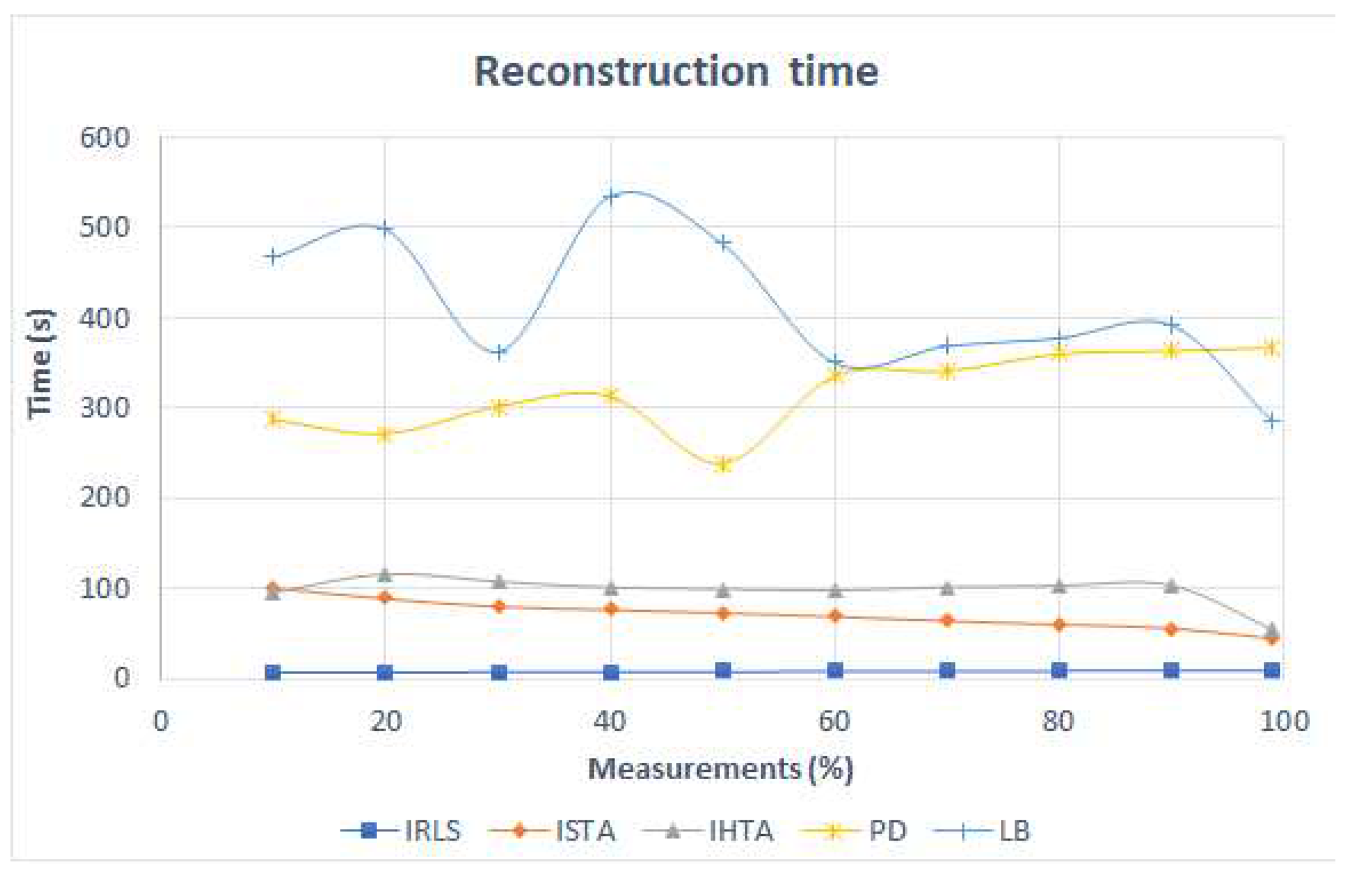
The graph in Figure 10 shows the time taken by the algorithms to reconstruct the image as a function of the number of entered data. The IRLS maintains a constant time of 8 s in all reconstructions. It solves the problem of reconstruction in the l 2 norm and it is the fastest one. In case of the ISTA algorithm, which employs a minimization in l 1 norm, the time decreases linearly from 100 s to approximately 50 s. The IHTA algorithm takes the longer time in the reconstructionas it can be predicted since it solves the minimization with l 0 norm. Also, two peaks are obtained at 20% and 90% of the measurements with IHTA. The convex algorithms, PD and LB, takes much more time than the greedy ones as expected. The reconstruction time for PD is higher as the number of measuremets increases. Its maximum value is 367 s. LB algorithm does not show a clear trend. It has three peaks, at 20%, 40% and 90%, the latter being the smoothest one. Finally, with 100% this time decreases to 285 s.
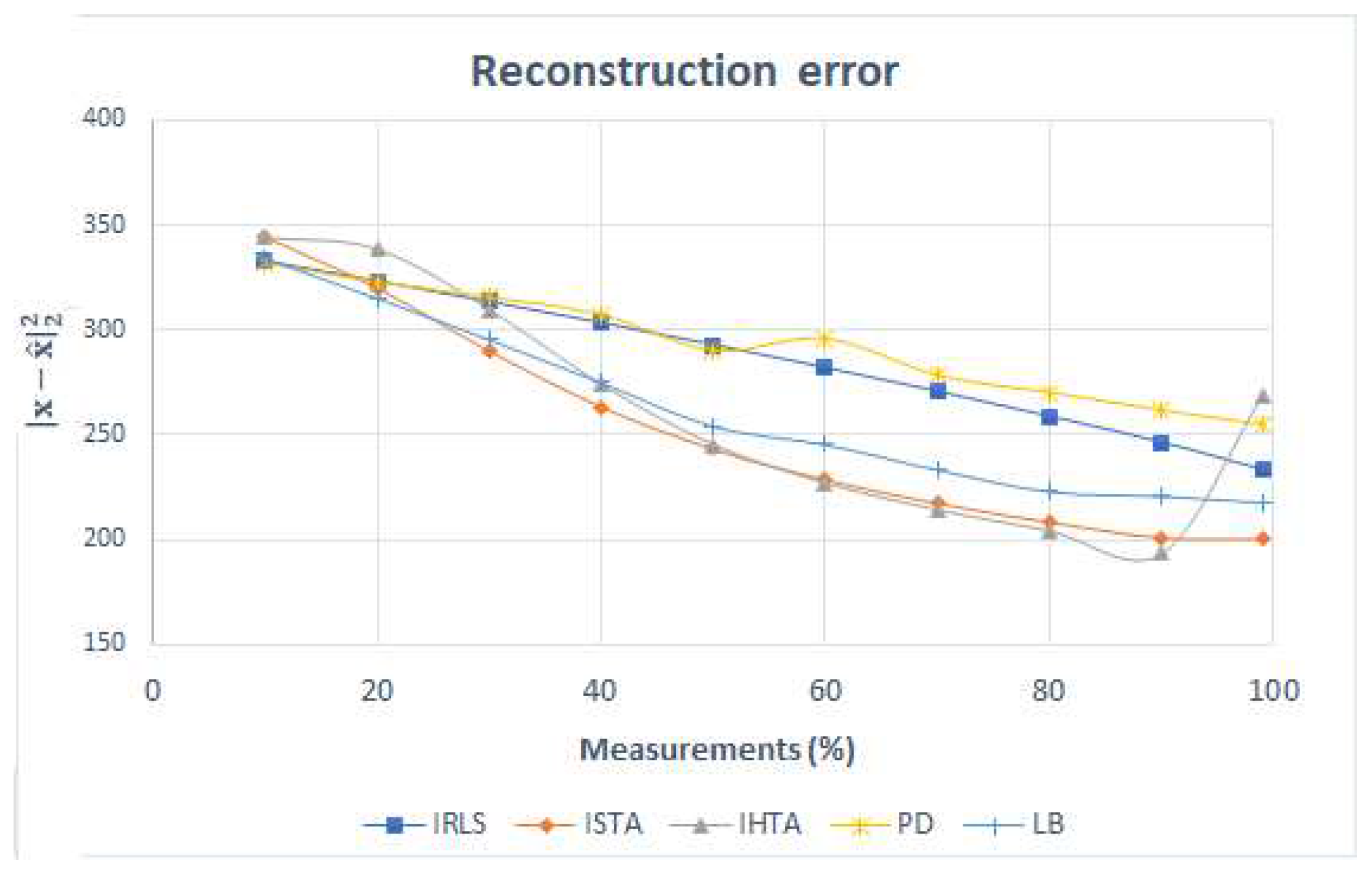
The error made in the reconstruction is found in the following Figure 11. The IRLS error decreases linearly. ISTA and IHTA are very similar: in both the error decreases with the number of measurements, except when 90% of the measurements are reached, where the error with IHTA increases abruptly. This is due to the fact that, as mentioned above, in this last reconstruction it does not detect the signal related to the white matter and, therefore, the error is very high. The error for PD and LB are higher than expected as they are convex algorithms and the images reconstructed were quite similar to the original. Both algorithms decrease the error similarly until 60%, where the error in PD is higher.

4. Conclusions

In this work, we have studied the CS techniques applied to images adquired with MRI. We have developed several programs that allowed us to quickly and clearly reconstruct an image. We started from a random signal with a smaller number of data than those needed to construct the original image in the conventional way. Then, we generated a similar image with a lower resolution. The algorithms chosen to perform this task were IRLS, ISTA, IHTA, PD and LB.
From the analysis of the images reconstructed with these algorithms it can be concluded that it is appropriate to use ISTA. Although it has an adequate computational time and in some cases it may not provide the best possible resolution, it allows to distinguish each component if 70% or more of the measurements are taken. Although the IHTA algorihtm has the highest resolution, it does not solve some images correctly and takes more time perform the reconstruction. The IRLS algorithm has the shortest computational time, but, like IHTA, it does not achieve enough accuracy. If there are less than 50% of the measurements, it should be used PD algorithm, since its images are clearer and it can recover the structures. LB algorithm takes too much time and does not give any improvement compared to the other algorithms.
These algorithms can be applied to different parts of the human body and with different MRI sequences as T 1 , T 2 or proton density. These sequences change the contrast of the images, allowing to draw a distinction between components of the human body. The images can also be reconstructed even if contrast agents were introduced.
The same CS technique studied in this article can be applied to other methods; for example, computed tomography or X-ray. Although the acquisition time of these is much shorter, it can still reduce the amount of radiation applied to the human body needed to obtain an image.

Author Contributions

EHA developed part of the mathematical formalism and performed the compressed sensing calculations. VMGS obtained the medical images and reviewed the article. JLFM developed the mathematical formalism.

Funding

The authors declare that no funds, grants, or other support were received during the preparation of this manuscript.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Shannon, C. Communication in the Presence of Noise. Proceedings of the IRE 1949, 37, 10–21. [Google Scholar] [CrossRef]
  2. Baraniuk, R.G.; Cevher, V.; Duarte, M.F.; Hegde, C. Model-Based Compressive Sensing. IEEE Transactions on Information Theory 2010, 56, 1982–2001. [Google Scholar] [CrossRef]
  3. Donoho, D. Compressed sensing. IEEE Transactions on Information Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
  4. Candès, E.; Romberg, J.; Tao, T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
  5. Rani, M.; Dhok, S.B.; Deshmukh, R.B. A Systematic Review of Compressive Sensing: Concepts, Implementations and Applications. IEEE Access 2018, 6, 4875–4894. [Google Scholar] [CrossRef]
  6. Geethanath, S.; Reddy, R.; Konar, A.; Imam, S.; Sundaresan, R.; Babu, D.R.R.; Vanketasan, R. Compressed Sensing MRI: A Review. Critical Reviews in Biomedical Engineering 2013, 41, 183–204. [Google Scholar] [CrossRef] [PubMed]
  7. Orovic, I.; Papic, V.; Ioana, C.; Li, X.; Stankovic, S. Compressive Sensing in Signal Processing: Algorithms and Transform Domain Formulations. Mathematical Problems in Engineering 2016, 2016, 1–16. [Google Scholar] [CrossRef]
  8. Majumdar, A. Compressed Sensing for Engineers; Taylor & Francis Group, 2019. [Google Scholar]
  9. Ouyang, B.; Dalgleish, F.R.; Caimi, F.M.; Giddings, T.E.; Shirron, J.J.; Vuorenkoski, A.K.; Nootz, G.; Britton, W.; Ramos, B. Underwater laser serial imaging using compressive sensing and digital mirror device. In Proceedings of the Laser Radar Technology and Applications XVI; Turner, M.D., Kamerman, G.W., Eds.; International Society for Optics and Photonics, SPIE, 2011; Volume 8037, pp. 67–77. [Google Scholar]
  10. Zou, Z.; Bao, Y.; Li, H.; Spencer, B.F.; Ou, J. Embedding Compressive Sensing-Based Data Loss Recovery Algorithm Into Wireless Smart Sensors for Structural Health Monitoring. IEEE Sensor Journal 2015, 15, 797–808. [Google Scholar]
  11. Torruella, P.; Arenal, R.; de la Peña, F.; Saghi, Z.; Yedra, L.; Eljarrat, A.; López-Conesa, L.; Estrader, M.; López-Ortega, A.; Salazar-Alvarez, G.; et al. 3D Visualization of the Iron Oxidation State in FeO/Fe3O4 Core–Shell Nanocubes from Electron Energy Loss Tomography. Nano Letters 2016, 16, 5068–5073. [Google Scholar] [CrossRef] [PubMed]
  12. Dance, D.; Christofides, S.; Maidment, A.; McLean, I.; Ng, K. Diagnostic Radiology Physics: A Handbook for Teachers and Students; IAEA, 2014. [Google Scholar]
  13. Costa, J.; Soria, J.A. Resonancia magnética dirigida a técnicos superiores en imagen para el diagnóstico; S.A. Elsevier España, 2015. [Google Scholar]
  14. The Centre for Phenogenomics. MICe Mouse Imaging Centre. 2004. Available online: http://www.mouseimaging.ca/index.html.
  15. López Larrubia, P. Aplicaciones de la resonancia magnética nuclear a la investigación biomédica. In Proceedings of the SEBBM Divulgación; 2009. [Google Scholar]
  16. Dawson, M. Paul Lauterbur and the Invention of MRI; The MIT Press, 2013. [Google Scholar]
  17. Martínez Guillamón, C. Aplicaciones Clínicas y Protocolos de Actuación en Resonancia Magnética; Galindo, S.L.; p. 2008.
  18. Mallat, S. A Wavelet Tour of Signal Processing, Third Edition: The Sparse Way, 3rd ed.; Academic Press, Inc.: USA, 2008. [Google Scholar]
  19. Elahi, S.; Kaleem, M.; Omer, H. Compressively sampled MR image reconstruction using generalized thresholding iterative algorithm. Journal of Magnetic Resonance 2018, 286, 91–98. [Google Scholar] [CrossRef] [PubMed]
  20. Beck, A.; Teboulle, M. A fast Iterative Shrinkage-Thresholding Algorithm with application to wavelet-based image deblurring. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing; 2009; pp. 693–696. [Google Scholar]
  21. Tan, Z.; Eldar, Y.; Beck, A.; Nehorai, A. Smoothing and Decomposition for Analysis Sparse Recovery. IEEE Transactions on Signal Processing 2014, 62, 1762–1774. [Google Scholar] [CrossRef]
  22. Liu, Y.; Zhan, Z.; Cai, J.; Guo, D.; Chen, Z.; Qu, X. Projected Iterative Soft-Thresholding Algorithm for Tight Frames in Compressed Sensing Magnetic Resonance Imaging. IEEE Transactions on Medical Imaging 2016, 35, 2130–2140. [Google Scholar] [CrossRef] [PubMed]
  23. Zibetti, M.; Helou, E.; Regatte, R.; Herman, G. Monotone FISTA With Variable Acceleration for Compressed Sensing Magnetic Resonance Imaging. IEEE Transactions on Computational Imaging 2019, 5, 109–119. [Google Scholar] [CrossRef] [PubMed]
  24. Zhang, G.; Deng, H.; Chen, Y. Investigating the stability of fast iterative shrinkage thresholding algorithm for MR imaging reconstruction using compressed sensing. In Proceedings of the 2015 12th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD); 2015; pp. 1296–1300. [Google Scholar]
  25. Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press, 2014. [Google Scholar]
  26. Candès, E.; Romberg, J. l1-MAGIC. Recovery of sparse signals via convex programming. Manuscript. 2004.
  27. of Neuro Imaging, L. LONI Image Data ARchive (IDA). 2021. Available online: https://ida.loni.usc.edu/login.jsp.
  28. Sartori, P.; Rozowykniat, M.; Siviero, L.; Barba, G.; Peña, A.; Mayol, N.; Acosta, D.; Castro, J.; Ortiz, A. Artefactos y artificios frecuentes en tomografía computada y resonancia magnética. Revista Argentina de Radiología 2015, 79, 192–204. [Google Scholar] [CrossRef]
Preprints 77303 g001
Figure 1. Example of MR image of the spinal column [13].
Figure 1. Example of MR image of the spinal column [13].
Preprints 77303 g001
Preprints 77303 g002
Figure 2. Soft Threshold rule with τ = 2 [8].
Figure 2. Soft Threshold rule with τ = 2 [8].
Preprints 77303 g002
Preprints 77303 g003
Figure 3. MRI image of an axial slice of the brain. In the area below are the eye orbits [27].
Figure 3. MRI image of an axial slice of the brain. In the area below are the eye orbits [27].
Preprints 77303 g003
Preprints 77303 g004
Figure 4. Images of a sagittal, coronal and 3D slice of the brain. The blue line shows the plane corresponding to the image Figure 3.
Figure 4. Images of a sagittal, coronal and 3D slice of the brain. The blue line shows the plane corresponding to the image Figure 3.
Preprints 77303 g004
Preprints 77303 g005
Figure 5. Reconstruction of the image in Figure 3 using IRLS with 30 % (a), 70 % (b) and 100 % (c) of taken measurements.
Figure 5. Reconstruction of the image in Figure 3 using IRLS with 30 % (a), 70 % (b) and 100 % (c) of taken measurements.
Preprints 77303 g005
Preprints 77303 g006
Figure 6. Reconstruction of the image in Figure 3 using ISTA with 30 % (a), 70 % (b) and 100 % (c) of taken measurements.
Figure 6. Reconstruction of the image in Figure 3 using ISTA with 30 % (a), 70 % (b) and 100 % (c) of taken measurements.
Preprints 77303 g006
Preprints 77303 g007
Figure 7. Reconstruction of the image in Figure 3 using IHTA with 30 % (a), 70 % (b) and 100 % (c) of taken measurements.
Figure 7. Reconstruction of the image in Figure 3 using IHTA with 30 % (a), 70 % (b) and 100 % (c) of taken measurements.
Preprints 77303 g007
Preprints 77303 g008
Figure 8. Reconstruction of the image in Figure 3 using PD with 30 % (a), 70 % (b) and 100 % (c) of taken measurements.
Figure 8. Reconstruction of the image in Figure 3 using PD with 30 % (a), 70 % (b) and 100 % (c) of taken measurements.
Preprints 77303 g008
Preprints 77303 g009
Figure 9. Reconstruction of the image in Figure 3 using LB with 30 % (a), 70 % (b) and 100 % (c) of taken measurements.
Figure 9. Reconstruction of the image in Figure 3 using LB with 30 % (a), 70 % (b) and 100 % (c) of taken measurements.
Preprints 77303 g009
Preprints 77303 g010
Figure 10. Reconstruction time of Figure 3 as a function of the number of measurements for each algorithm.
Figure 10. Reconstruction time of Figure 3 as a function of the number of measurements for each algorithm.
Preprints 77303 g010
Preprints 77303 g011
Figure 11. Error in the reconstruction of Figure 3 as a function of the number of measurements for each algorithm.
Figure 11. Error in the reconstruction of Figure 3 as a function of the number of measurements for each algorithm.
Preprints 77303 g011
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated