Prerpints.org logo
Preprint
Article

Numerical Simulation of Pore Pressure Change Caused by Hydrocarbon Generation in Chezhen Sag and Its Influence on Hydrocarbon Accumulation

Altmetrics

Downloads

121

Views

34

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

22 June 2023

Posted:

23 June 2023

You are already at the latest version

Alerts
Abstract
Pore fluid pressure is very important to the generation, migration and accumulation of petroleum. The previous studies indicate that the Chezhen sag region is typically characterized by pore fluid overpressure (the difference between pore fluid pressure and hydrostatic pressure). To date, the formation mechanism of pore overpressure and the accumulation regularity of “upper source-lower reservoir” type in this region remains unknown. In order to investigate these problems, a 2-D finite element model is established with regards to the fluid-solid coupling in Chegu 25 block of Chezhen depression, fully considering the existing seismic, logging data and regional tectonic stress environment. Meanwhile, we calculate the abnormal overpressure generated at the source rock during hydrocarbon generation and the process of hydrocarbon migration and accumulation along the faults, analyzing the dynamic conditions of hydrocarbon downward accumulation. The results show that overpressure can accelerate migration of hydrocarbon and improve the efficiency of hydrocarbon accumulation. However, when the overpressure is too large, tensile fractures and shear fractures may occur, resulting in hydrocarbon dissipation, and changing the results of oil and gas accumulation. The overpressure at the source rock is mainly caused by hydrocarbon generation, while the overpressure at the reservoir is primarily created by unbalanced compaction. As the dominant channel of hydrocarbon migration, overpressure will change the direction and path of hydrocarbon migration in the fault. Therefore, the “upper source-lower reservoir” hydrocarbon accumulation model is strongly explained by the high permeability of faults and the presence overpressure. In summary, the simulated overpressure results are in good agreement with the mud weight equivalent overpressure and the drill stem tests (DSTs).
Keywords: 
Subject: Environmental and Earth Sciences  -   Geophysics and Geology

1. Introduction

With the emergence of new technologies for petroleum exploration and development, as well as the large-scale exploitation of shallow petroleum resources, the deep basin reservoirs have gradually become the primary target strata of exploration [1,2]. The existing research and petroleum development practices indicate that, under the conventional basin hydrocarbon accumulation mode (under hydrostatic pressure), the hydrocarbon generated by the source rock mainly migrates and accumulates to the overlying stratum and accumulates under the action of buoyancy [3]. Especially, pore fluid pressure plays an important role in the generation, migration, and accumulation of hydrocarbons in sedimentary basins [4,5,6]. Overpressure, for instance, hinders the maturation of kerogen, alters the fluid movement path, and affects the hydrocarbon accumulation model [5,7,8]. Thus, under overpressure and other geological conditions, hydrocarbon can migrate downward from the upper source rock to the lower reservoir for accumulation [8]. Examples of this phenomenon include the Fuyang-Qingshankou petroleum system in the Songliao Basin [9,10], the Najmah-Marrat petroleum system in Kuwait, and the Macasty-Mingan-Romaine petroleum system in the Anticosti Basin in eastern Canada [9,11].
There are a lot of researches and explorations on the "upper source-lower reservoir" hydrocarbon accumulation model. They have found that continuous hydrocarbon generation from source rocks, sufficient overpressure, and a smooth hydrocarbon migration channel between the overlying source rock and underlying reservoir are the essential conditions for the hydrocarbon downward migration [12,13]. Additionally, these works also conduct a large number of numerical calculations to quantitatively analyze the mechanisms of overpressure formation, as well as hydrocarbon migration and accumulation [13,14,15,18]. Some studies, based on the principle of overpressure sealing, have suggested that overpressure is a crucial factor that affects the depth of downward hydrocarbon migration [13,14,16]. Besides, Zhuang et al. used the Bernoulli equation to describe the flow state of oil, and suggested that the permeability coefficient of rocks is another significant factor that greatly influences and determines the distance of hydrocarbon downward migration and the release rate of overpressure [17].
Nevertheless, it is clear that many studies have begun to pay attention to the evolutionary histories of hydrocarbon generation and overpressure in the basin and their influence on hydrocarbon migration and accumulation, due to advancements in basin simulation technology. Especially, Wang et al. proved the possibility of hydrocarbon downward migration through physical simulation experiments. They analyzed the differences in geological reserves of petroleum reservoirs formed by skeleton sand bodies and faults as migration pathways [19]. Luo et al. simulated a simplified model of sand-mudstone, and quantitatively studied the processes of overpressure formation and dissipation [20]. Guo, Wang, and Li et al. utilized basin modeling technology to examine the growth mechanism and evolution process of overpressure in the Bohai Bay Basin [21,22,23,24]. They believed that the main factors for the formation of overpressure in different regions of the basin would be different. For example, the primary cause for the formation of overpressure in the Dongying Depression is unbalanced compaction, and the main reason for the formation of overpressure in the Chexi area is hydrocarbon generation.
Overall, these works constructed a simplified geological model, while most researches only quantitatively consider the impact of a single dynamic factor (such as fluid overpressure or permeability coefficient) on the “upper source and lower storage” hydrocarbon accumulation model. Unfortunately, these studies have not comprehensively considered the influence of overpressure, rock permeability coefficient, or even the coupling of unbalanced compaction and hydrocarbon generation during overpressure generation and the pressure-stress coupling during overpressure evolution.
Based on the available data, we firstly calculate the overpressure generated by unbalanced compaction. We then systematically analyze and discuss the impact of this overpressure mechanism on the overall overpressure. Two overpressure-generation mechanisms of unbalanced compaction and hydrocarbon generation are coupled in the finite element model. In addition, we also evaluate the dynamic conditions of the “upper source-lower reservoir” hydrocarbon accumulation model, as well as the disparity of the simulated and observed overpressure values. This study helps people to better understand the mechanisms of hydrocarbon migration and accumulation, as well as the laws governing spatial distribution of hydrocarbons.

2. Geological background

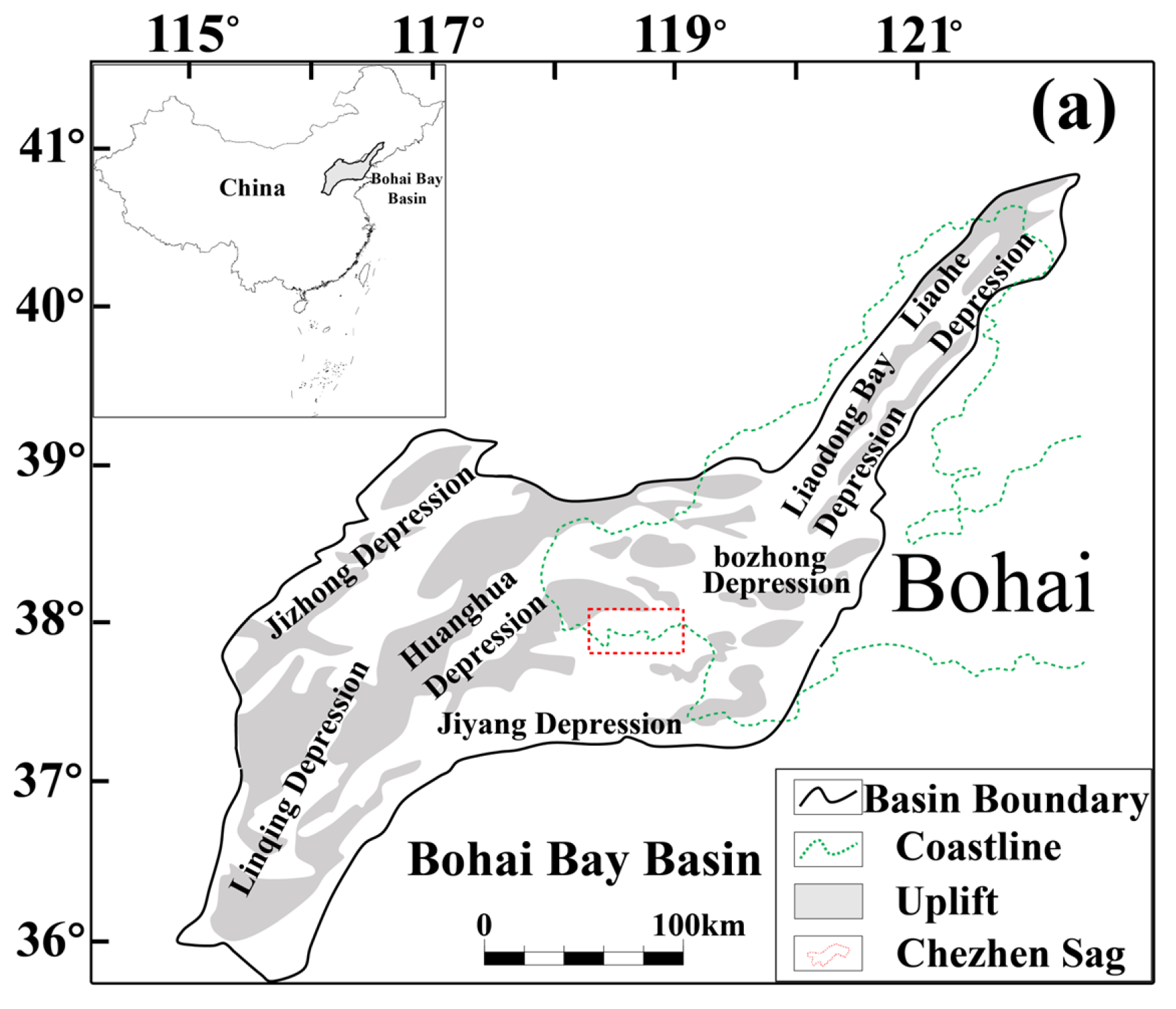
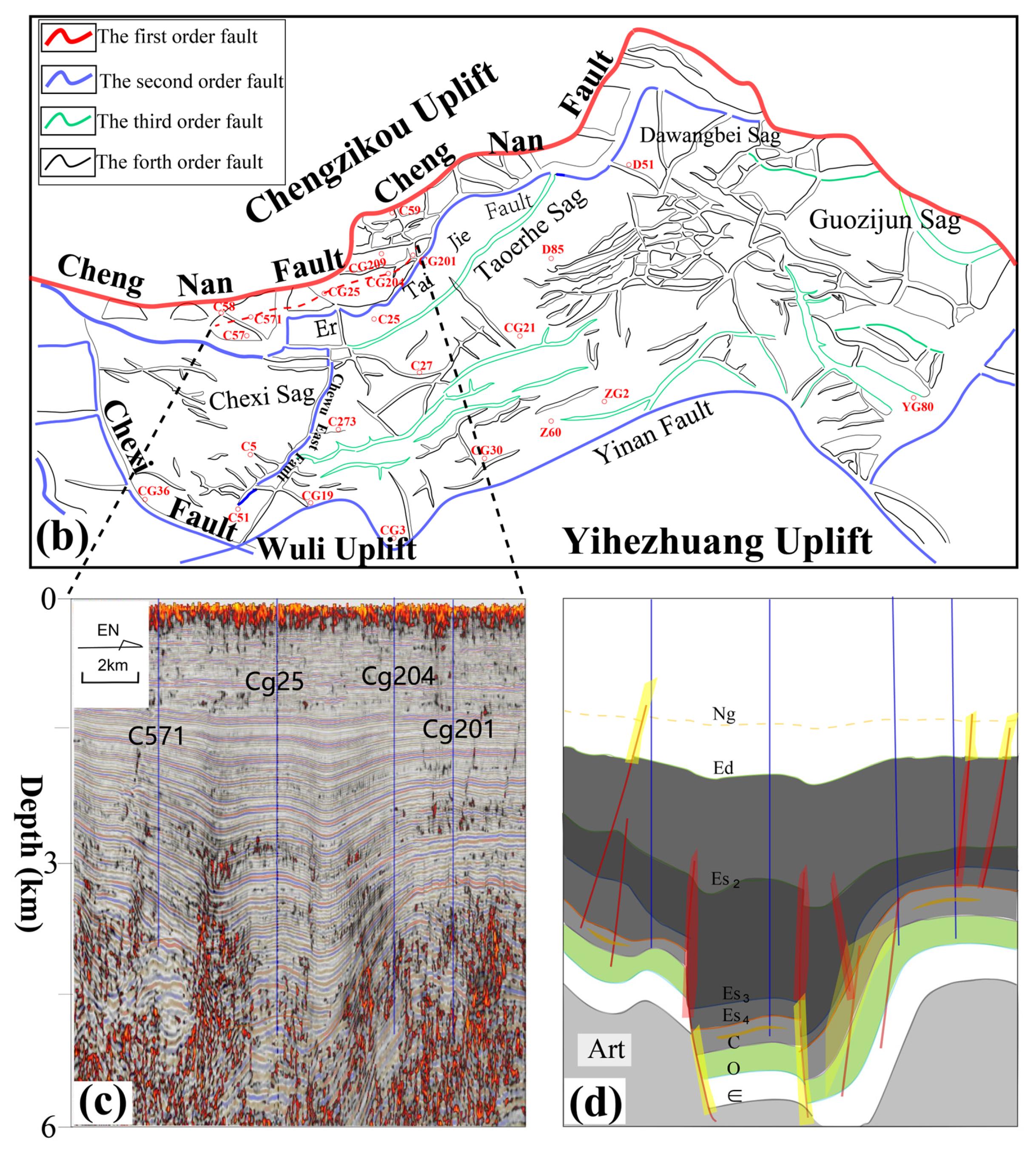
The Chezhen Sag, located in the Bohai Bay Basin, is a secondary sag within the Jiyang Depression (Figure 1a). It is a half-graben continental fault basin that is long along east-west direction but narrow along north-south direction, covering an area of about 2390 km2 (Figure 1a) [25]. It is surrounded by the Wudi uplift, Qingyun uplift, Chengzikou uplift, and Yihezhuang uplift in clockwise order from west to east (Figure 1b) [26]. Many faults have developed in the sag, and the tectonic units are highly segmented (Figure 1b). Three sub-depressions, Chexi, Dawangbei, and Guojuzi, have developed from west to east (Figure 1b) [25].
The northern part of the Chezhen Sag has experienced several strong regional tectonic movements [27]. During the early Yanshan Movement, the area experienced compression along the NE trend, resulting in the development of a local anticline [28]. In the late Yanshan Movement to the Himalayan Movement, the Chengnan faults and step faults began to become active [28]. Additionally, the prefabricated buried hill folds in the north of the Chezhen Sag underwent significant extension, leading to the formation of numerous secondary faults and fractures [29]. During the depositional period of the Shahejie Formation in the Paleogene, the buried hill structure was ultimately formed and subsequently cut into a series of complex fault blocks, which gave rise to buried hill hydrocarbon reservoirs [28,29].
The strata in Chezhen Depression include Paleogene Kongdian Formation (Ek), Shahejie Formation (Es) and Dongying Formation (Ed), Neogene Guantao Formation (Ng) and Minghuazhen Formation (Nm), and Quaternary Plain Formation (Qp) (Figure 1c, d) [24,30]. The Shahejie Formation consists of the Es1, Es2, Es3 and Es4. The Es3 is the main source rock and it is mature, while the source rock of the Es1 is still immature [31]. There are abundant caprocks in the entire stratigraphic column of the Chezhen sag, including Es4–Es3, Es1–Ed3 and Ng–Nm mudstone sections, all of which are regional seals with extremely low permeability. Guantao Formation and Minghuazhen Formation (Ng and Nm) show similar sedimentary sequences and strata throughout the Bohai Bay Basin [30].
The reservoir in this area consists of marine carbonate strata in the Lower Paleozoic, mainly including relatively dense limestone and dolomite, whose primary pores are not developed, and matrix porosity and permeability are generally low. Due to the transformation of tectonic movement and dissolution, faults in the Lower Paleozoic were very developed, and a large number of secondary genetic reservoir spaces were formed in the rocks [32]. The Yanshanian and Himalayan periods are two important periods, during which complex fault systems were finally formed, greatly enhancing the permeability of carbonate reservoirs [27].

3. Model settings

According to the drilling results, the petroleum in the lower Paleozoic buried hill in the study area basically comes from the Paleogene Shahejie Formation, while the Cambrian and Ordovician do not have the ability to generate hydrocarbons [34]. The middle and lower Es3 of the Shahejie Formation is the main source rock of the lower Paleozoic buried hill [35]. The reservoirs below the lower Es3 of the main source rock are rich in hydrocarbon resources and have great exploration potential [23].

3.1. Fault Sealing Properties

Two main types of migration systems between source rocks (Es3) and reservoirs (C), have been recognized by previous studies. One migration system is composed of small faults and micro-cracks that are difficult to be identified on the seismic profile, and in this case, the micro-crack is mainly caused by pore fluid overpressure fracturing the rock [14]. 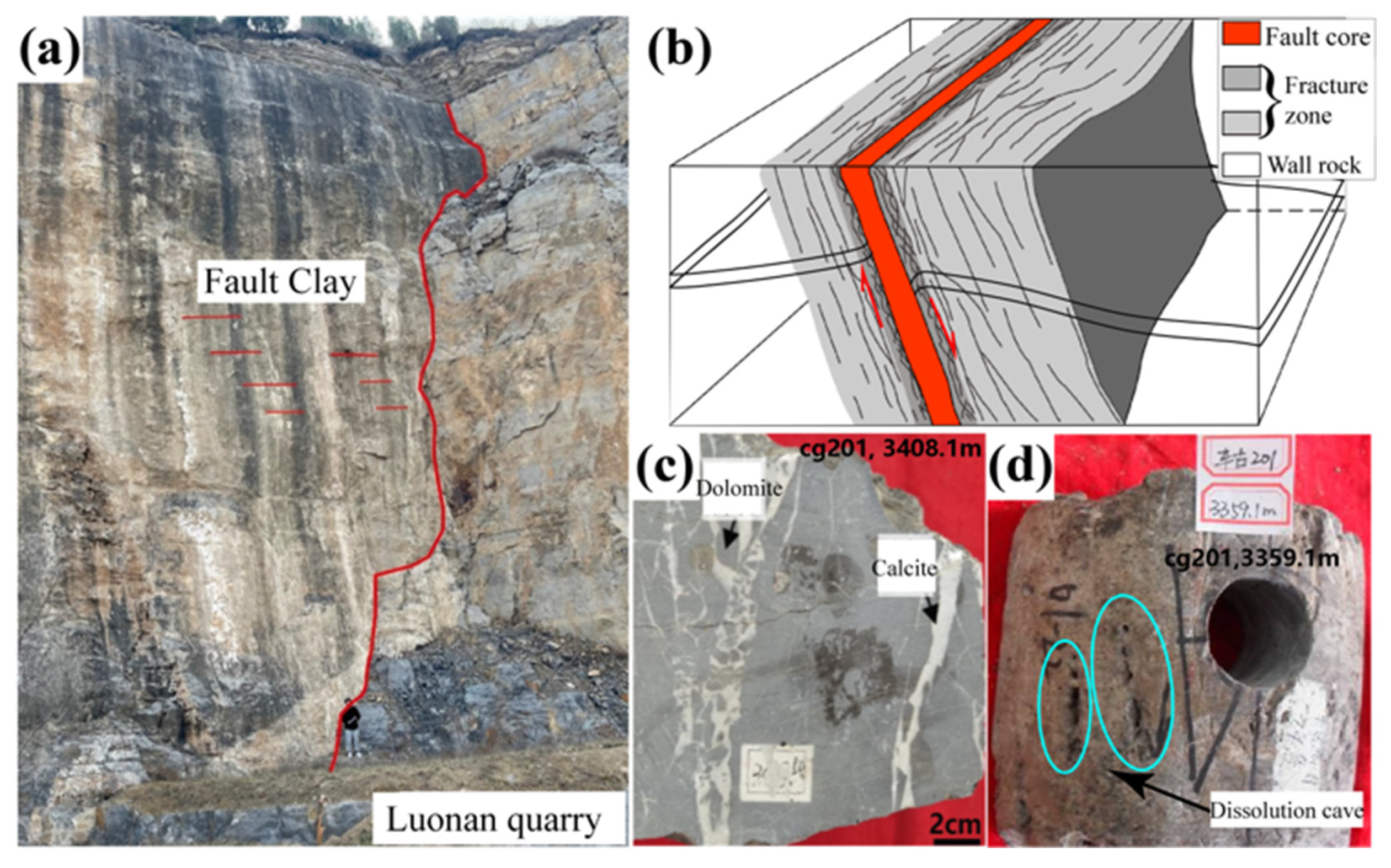The other migration system is the faults with a certain fault throw [15]. Considering the three-dimensional structure of the fault (not a single surface), it has a typical dual structure composed of fault core and fracture zone (Figure 2b) [36,37].
According to the carbonate rock field outcrops, reservoir core data, and permeability data from experimental results of rock samples in the fault zone (permeability data from personal communication with Zonghu Liao), the sealing properties of the two faults (Che 571 fault and Chegu 25 fault) in the study area can be explained. We find that the fractures of the fault core in this area are highly cemented and filled, primarily with calcite (Figure 2c). There are also muddy particles on the fault surface (Figure 2a). The fault core has low permeability, indicating that the lateral side of the fault effectively seals hydrocarbons. The fractures that are filled with calcite, are subsequently dissolved through corrosion, leading to the formation of dissolution cavities (Figure 2d) [27]. The fractures of the fault fracture zone are developed and its permeability is high, indicating that the fracture zone exhibits extensive fracturing and high permeability, suggesting that it provides convenient conditions for the vertical migration of hydrocarbons.
Furthermore, the seismic profile interpretation results show that the Che 571 fault and the Chegu 25 fault effectively cut the source rocks of the Shahejie Formation. Hence, we suggest that for hydrocarbon migration, these two faults are major channels (Figure 4), and micro-fractures are secondary channels.
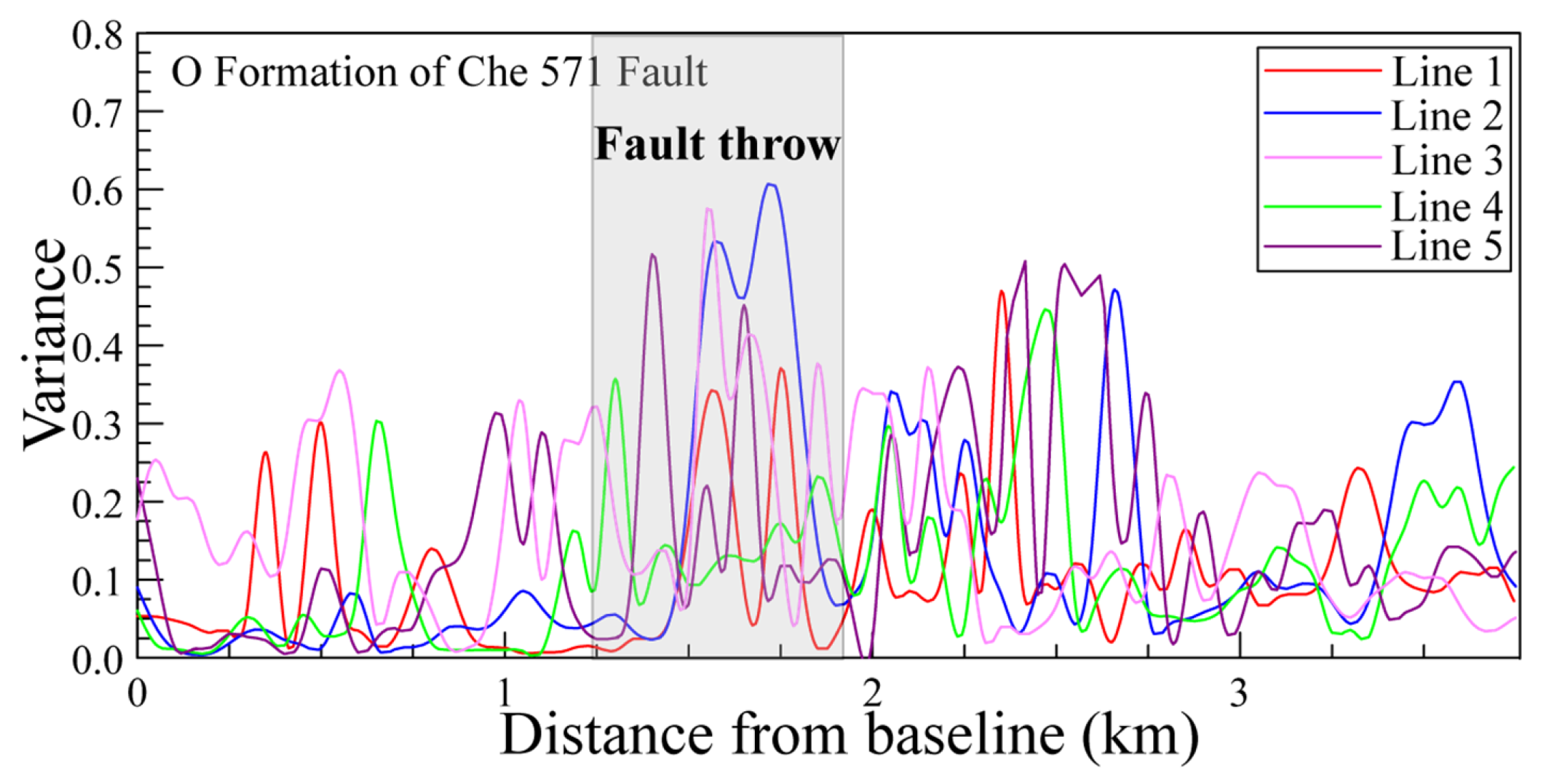
Preprints 77379 g003aPreprints 77379 g003b
Figure 3. Fault throws explained by fault coherence attributes.
Figure 3. Fault throws explained by fault coherence attributes.
Preprints 77379 g003aPreprints 77379 g003b
Preprints 77379 g004
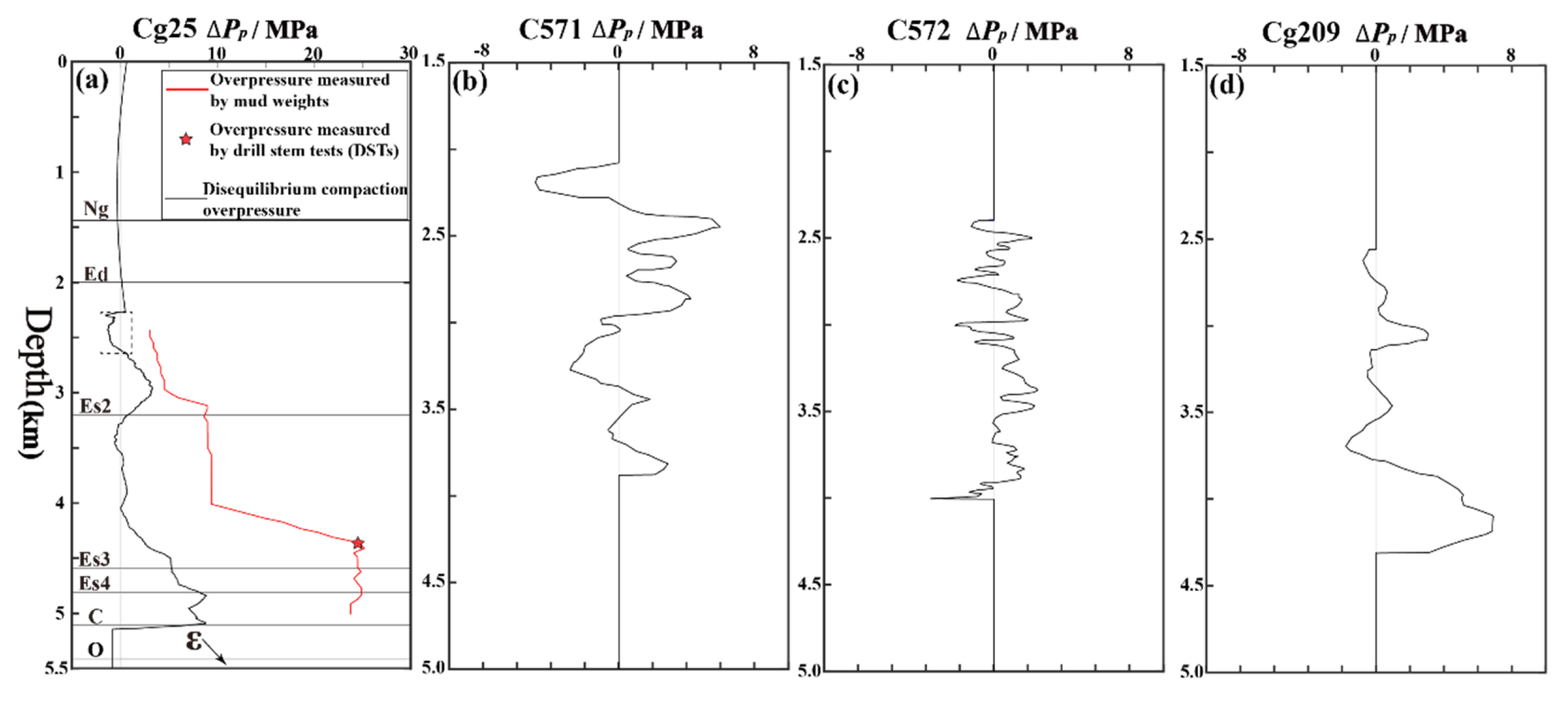
Figure 4. Overpressure caused by unbalanced compaction of four wells in the study area. (a) Overpressure of Chegu 25 well. (b) Overpressure of Che 571 well. (c) Overpressure of Che 572 well. (d) Overpressure of Chegu 209 well. The red solid curve represents the overpressure interpreted by mud weight data. The black solid curve represents the overpressure caused by unbalanced compaction interpreted by logging data. The asterisk indicates the overpressure interpreted by drill stem tests (DSTs). The results in (c) and (d) were modified from Wang, 2016 [23].
Figure 4. Overpressure caused by unbalanced compaction of four wells in the study area. (a) Overpressure of Chegu 25 well. (b) Overpressure of Che 571 well. (c) Overpressure of Che 572 well. (d) Overpressure of Chegu 209 well. The red solid curve represents the overpressure interpreted by mud weight data. The black solid curve represents the overpressure caused by unbalanced compaction interpreted by logging data. The asterisk indicates the overpressure interpreted by drill stem tests (DSTs). The results in (c) and (d) were modified from Wang, 2016 [23].
Preprints 77379 g004

3.2. Finite Element Model

We utilize the finite element software, Abaqus, to develop a poroelastic numerical model, and to simulate the evolution of overpressure resulting from the hydrocarbon generation process, which we call hydrocarbon generation overpressure. We assume that the faults on both sides of the Chegu 25 well are highly permeable. According to the results of fault throw interpreted by seismic coherence attributes, we determine that the average fault throw of Chegu 25 fault is 350 m, and the average fault throw of Che 571 fault is 800 m [41]. After some modelling experiments and comparison between modeling results and observation data, we select the average hydrocarbon generation rate of the model to be 10-13 m3/s. Our model domain is 8-km long and 6-km deep (Figure 5a). The upper boundary of the model is the displacement free boundary and the zero pore pressure boundary (drainage boundary). The left and right boundaries have the fixed normal displacement (zero) and hydrostatic pore pressure (drainage boundary, P H = ρ w g h ). The bottom boundary has the fixed normal displacement (zero) and the fixed pore pressure that equals hydrostatic pore pressure value at the depth (drainage boundary) (Figure 5a,b).
Permeability is related to lithology and effective stress. The commonly used permeability range in previous numerical simulation studies is 10-17 ~ 10-21 m2 [38,39]. Based on experimental results of permeability from rock samples in fault zone and previous research findings, it can be concluded that the third section of the Shahejie Formation (Es3) to the Carboniferous (C) consists mainly of sandstone. The permeability ranges from 1-5 × 10-18 m2 or 1-5 × 10-3 mD. The formations of Guantao Formation (Ng), Dongying Formation (Ed), and the second section of Shahejie formation (Es2), are used as caprocks, whose permeability is set to 1×10-19 m2 or 1×10-4 mD. The fracture zone has high permeability, up to 1 × 10-15 m2 (1 mD) (Table 1). The experimental results indicate that with the increase of effective pressure, the permeability decreases, and the decline can reach 2–4 orders of magnitude [40,41]. Thus, we set two permeability coefficients according to different depths of the fault, and the permeability coefficient of the shallow fault is larger (Table 1).
The primary period for hydrocarbon generation and overpressure formation, is from the end of uplift and denudation in the Neogene (14 Ma) to the present time [23]. At this stage, the tectonic activity has been weakened or even stopped, and the underground sedimentary environment was basically stable [27]. The sedimentary process before hydrocarbon generation in the study area can have formed an overpressure environment due to unbalanced compaction [33].
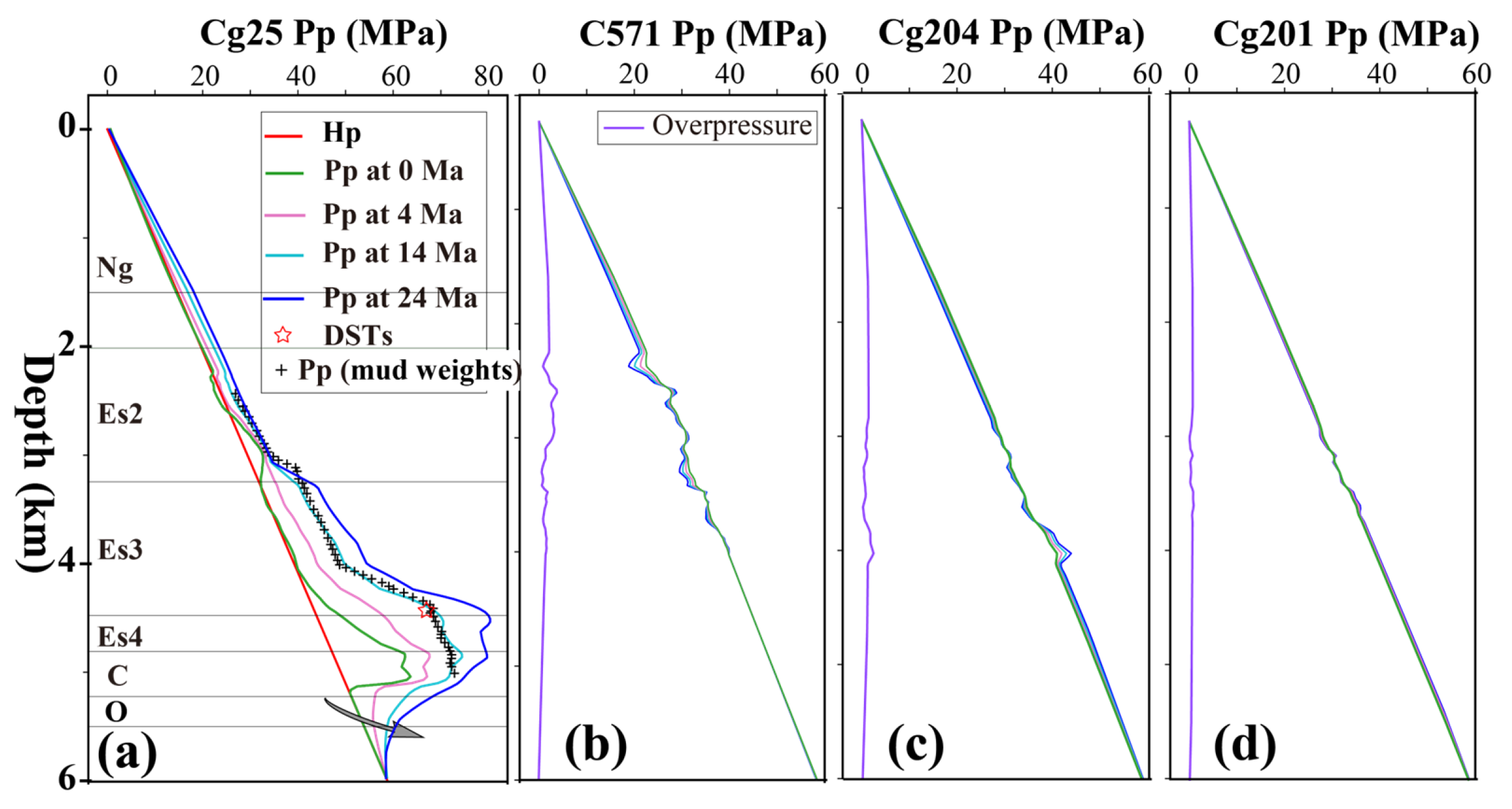
Of interest here is to find that this overpressure result can be calculated using logging data (mudstone porosity). Specifically, the calculation method and process are referred to in Appendix A. From the comparison between the overpressure caused by unbalanced compaction (later referred to as unbalanced compaction overpressure) and the overpressure measured by mud weight, we find that the unbalanced compaction overpressure could not reach the measured overpressure value (Figure 4a). Hence we conduct a finite element numerical simulation of the hydrocarbon generation process using the overpressure calculated from unbalanced compaction. The initial pore pressure field before hydrocarbon generation simulation (Figure 5c) is obtained by regional interpolation of the overpressure data from four wells near the study area (Figure 4).

3.3. Governing Equations

3.3.1. Equilibrium Equation

The equilibrium equation solved by the model is shown:
∂ σ i j ∂ x j + ρ g i = 0 ,
where, σ i j is the total stress tensor (i, j=1, 2, 3), and   ρ g i is the body force. In this study, the compressive stress is positive.

3.3.2. Principle of Effective Stress

An extended form of Terzaghi’s effective stress principle is used to calculate the effective stress state in Abaqus [45]. According to the improved effective stress law proposed by Nur and Byerlee [46], the effective stress is shown:
σ i j ′ = λ δ i j ε V + 2 G ε i j − δ i j α P p ,
where, λ = E v ( 1 + v ) ( 1 − 2 v ) and G = E 2 + 2 v . When i = j, δ i j = 1 , and when i ≠ j, δ i j = 0 . α is Biot constant, and equals   1 − K b K g , where K b is 'drainage' bulk modulus of rock and K g   is the bulk modulus of skeleton material [47]. When α = 0, the rock has no connected pores, and the pore pressure has no effect on the rock. When α = 1 , the pore pressure has the greatest impact on the rock. In this study, we assume that α equals one [39,48].

3.3.3. Constitutive Relations of Pore Fluids

The Darcy’s law is used to describe the relationship between fluid flow velocity (q) and pore fluid pressure ( P p ) [49]:
q = − k η w ∇ P p − ρ f g h ,
where, k is the permeability of sediments,   η w is the viscosity of pore fluid ( η w = 1.0 × 10 − 3 Pa s), h is the depth from the top of the model, and ∇ is the gradient sign.

3.3.4. Continuous Equation of Seepage

The seepage continuity equation is established according to the persistent condition that the amount of net outflow of water from the micro-element is equal to the variation of the micro-element volume at the same time [50]. In Abaqus, only the solid phase is meshed with finite elements, while pore water can flow in the meshes [51]. Therefore, for pore fluid, a continuous equation is needed to calculate the relationship between the growth rate of pore water quality at a point and the flow rate of pore water within a certain time increment.
The continuity equation at the non-source rock is as follows:
∂ ( S ρ f ϕ ) ∂ t + ∇ · ρ f q = 0 ,
where, t is time, S is saturation, and ϕ is porosity.
The continuity equation of the source rock is as follows:
∂ ( S ρ o i l ϕ ) ∂ t + ∇ · ρ o i l q = ρ o i l Q ,
where, Q is the flow velocity at the source (positive when the rocks serve as a source and negative when the rocks serve as a sink, kg/m3), and ρ o i l is the density of oil.

4. Model results

The first step of the model calculation is the geostatic stress step (in-situ stress equilibrium step). The pore fluid pressure field in this step is equal to the sum of hydrostatic pressure and unbalanced compaction overpressure.
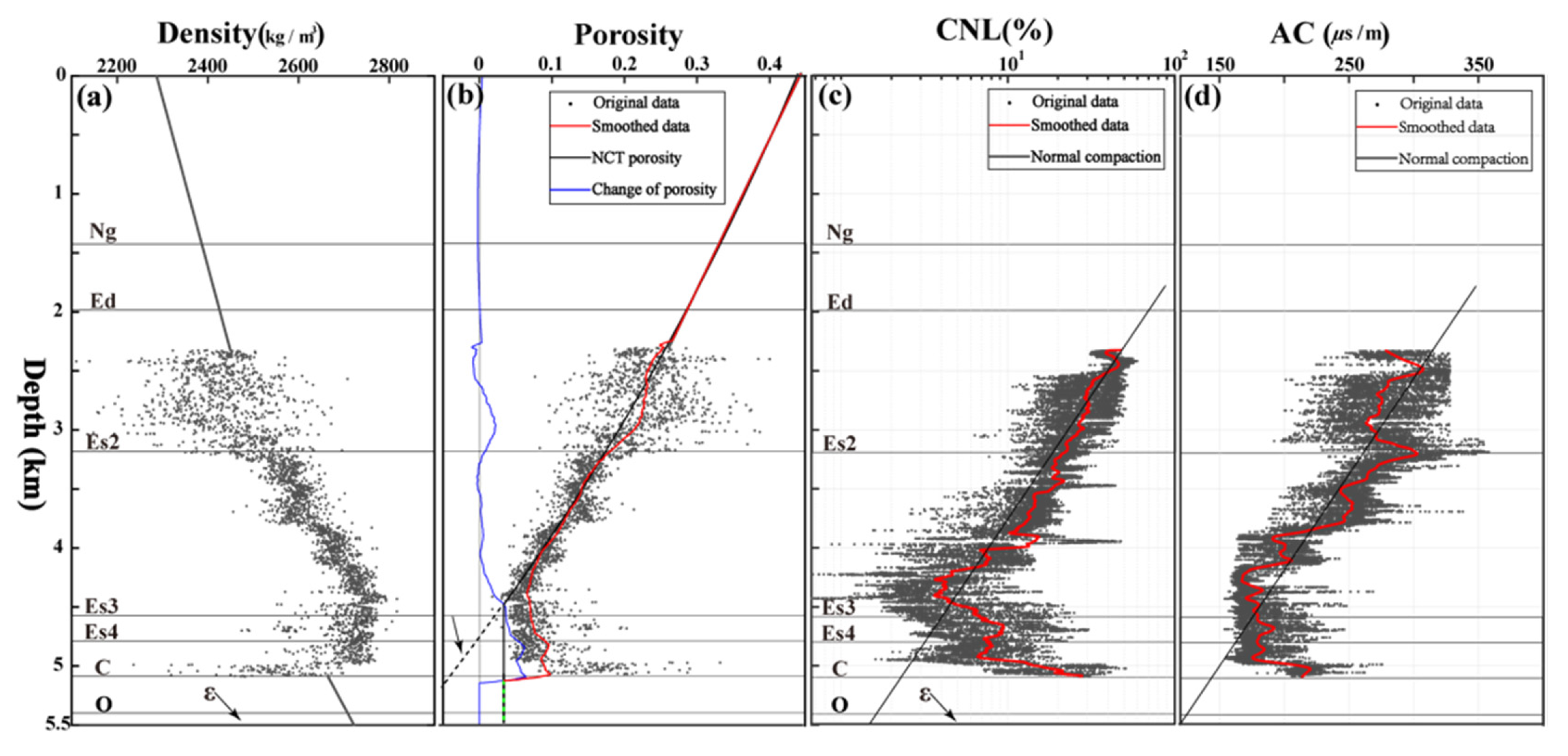
Considering the strike-slip tectonic stress environment in the study area, the ratio of the horizontal effective stress ( σ x x ′ ) to the vertical effective stress ( σ y y ′ ) in the initial state is 1.4, and the out-of-plane effective stress ( σ z z ′ ) to the vertical effective stress ( σ y y ′ ) is 0.7 [52]. The density and porosity data used in the model refer to Figure A1 in Appendix.
In the geostatic stress step, the pore fluid overpressure of the model is only caused by unbalanced compaction. In this step, the hydrocarbon generation process and its generated pore fluid pressure have not been included in the model. The goal of the geostatic stress step is to establish an initial pore fluid pressure field and an initial effective stress field for the following numerical simulation of the hydrocarbon generation process.
The second step of the modeling is to calculate the pore fluid pressure or overpressure caused by the hydrocarbon generation process since the Neogene (14 Ma). On the basis of the initial pore pressure field and the initial effective stress field obtained from the geostatic stress step simulation, we include the hydrocarbon generation and its resulting overpressure in the middle and lower sub-sections of the third and fourth members of the Shahejie Formation (see red dotted box in Figure 5) between the two faults in the study area in this step.
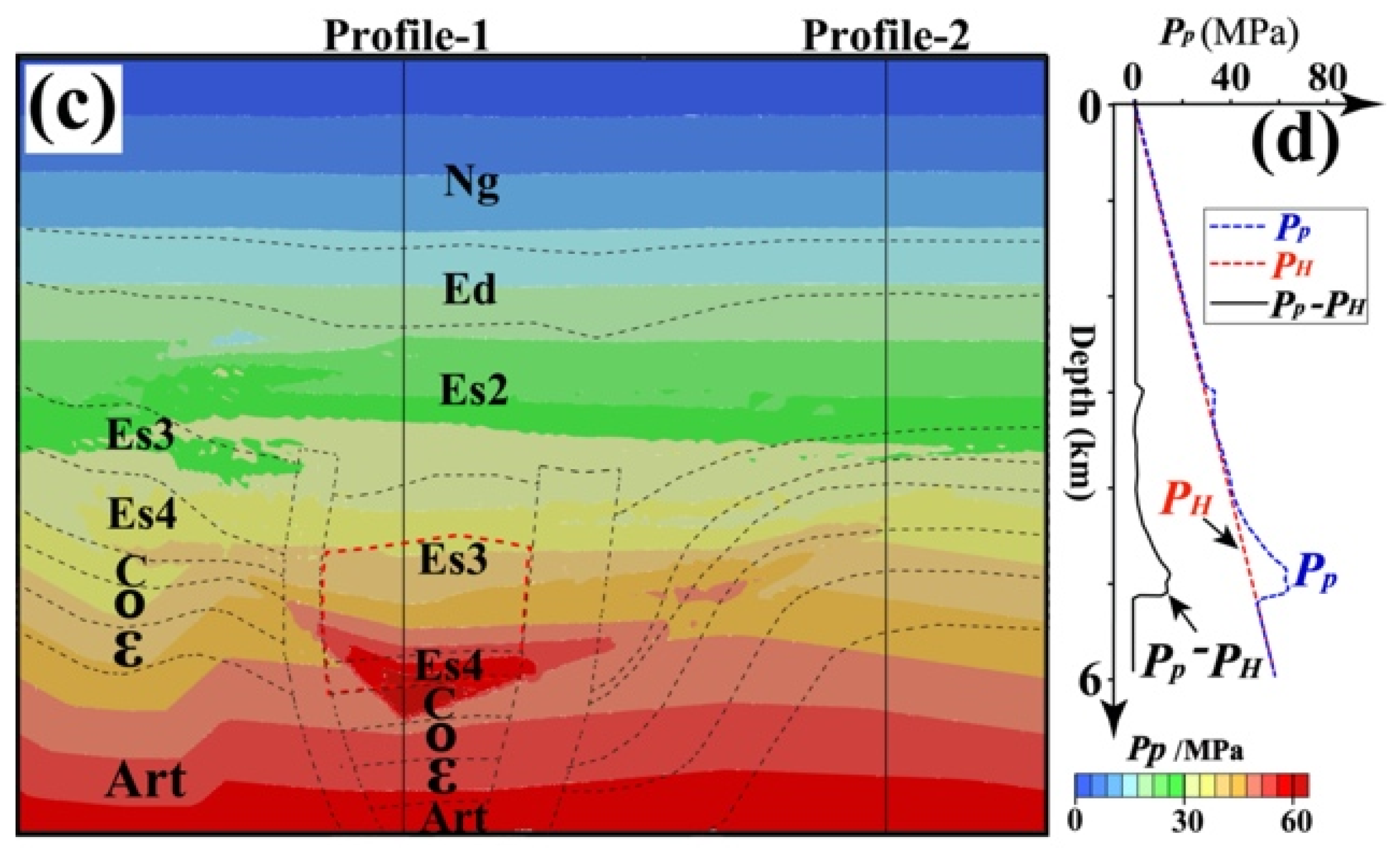
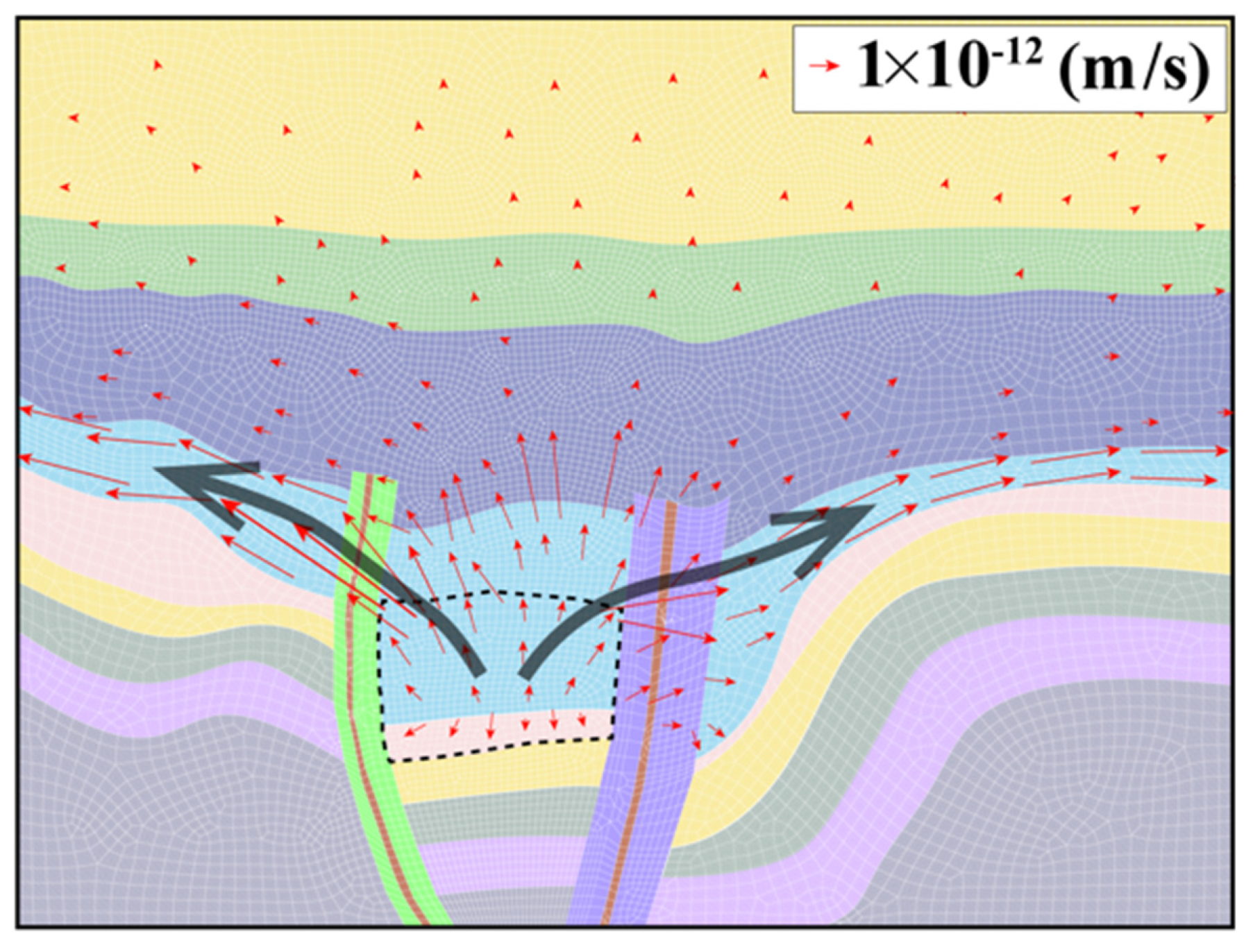
The simulated overpressure is mainly concentrated in the area between the two faults (Figure 6a), and the magnitude of overpressure decreases in the vertical direction. Due to its low permeability, the formation above Es2 acts as a seal for hydrocarbons and functions as a good cap rock. As a result, the overpressure in these formations is not significant. The maximum overpressure appears in the Es3 formation between the two faults, and the maximum value exceeds 30 MPa (Figure 6a).
Under the action of overpressure and buoyancy, the fluid flowing from Es3 and Es4 mainly flows along the fault to the shallow strata and the flow velocity is large (Figure 6b). Near Es2 formation, due to its sealing effect, the fluid cannot continue to move up and has to accumulate and change the flow direction, so a large downward flow velocity is generated at the top of the fault (Figure 6b). Because continuous hydrocarbon generation is still occurring and the lateral migration resistance is lower than the resistance through the caprock, the direction of fluid movement in the fault changes. It begins to migrate towards the strata on both sides of the fault, such as the velocity direction of the Es3 formation of Che 571 well, Chegu 204 well, and Chegu 201 well. Under the influence of pressure difference and high permeability of the fault, fluid can migrate from Es3 and Es4 to the Carboniferous formation (C) along the fault, leading to the overpressure accumulation (Figure 6b). Its flow rate is also lower than that of the upward migration fluid. Although overpressure can exist in the strata of Mantou Formation (ε) and Majiagou Formation (O), but the magnitude of overpressure is significantly reduced (Figure 6a). In addition, the overpressure area above the source rock is larger than that below it. This is because the fluid is difficult to continue to move down under the action of buoyancy, capillary resistance, and hydrodynamics [53].
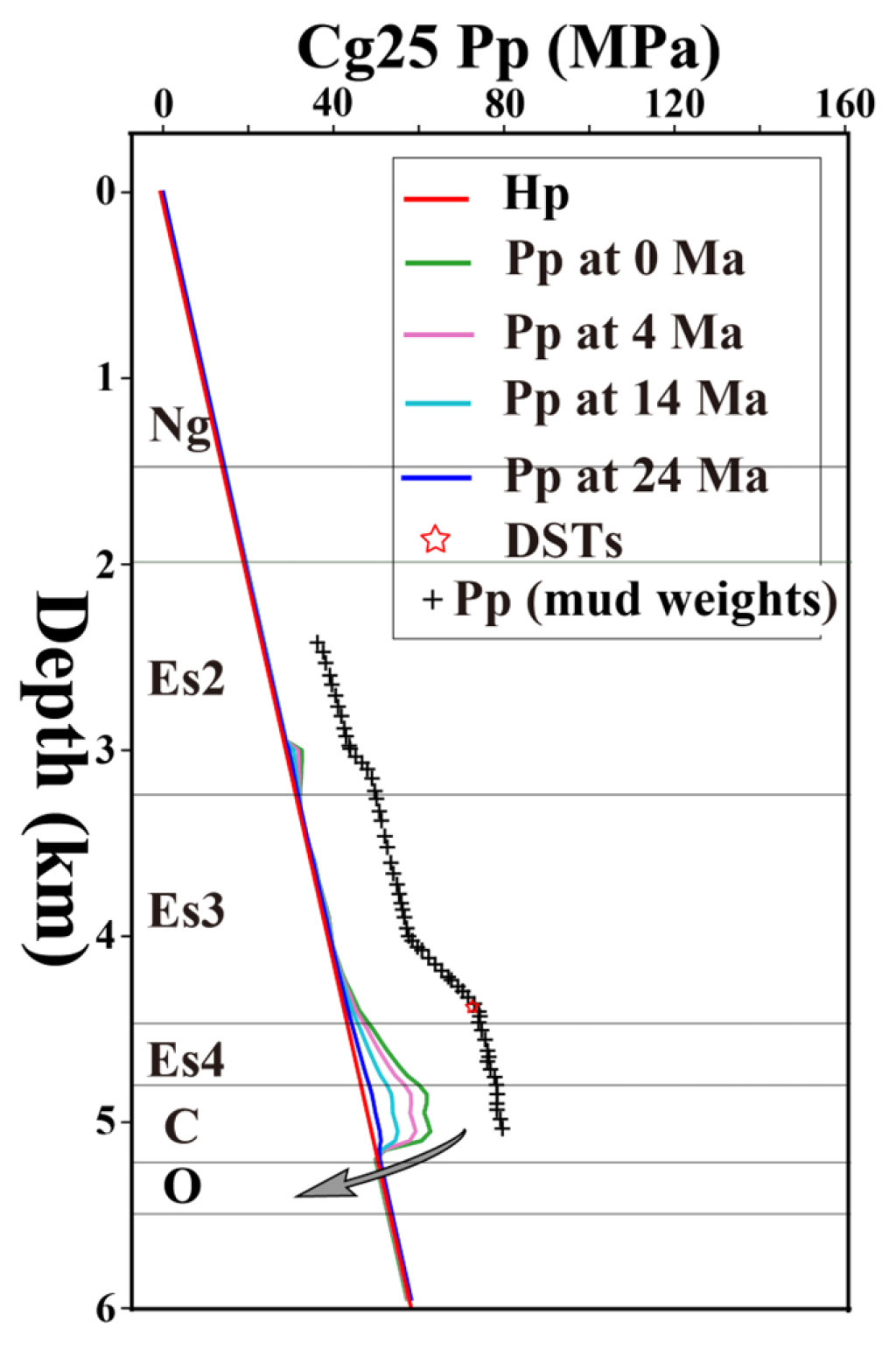
In order to further quantitatively verify the reliability of the model, we compare the simulation results of pore fluid pressure in Chegu 25 well with the overpressure measured by mud weight. We find that the simulated pore fluid pressure and mud weight equivalent pressure are in good agreement with the overall trend (Figure 7a). The simulated pore pressure agrees well with the mud weight equivalent pressure in Es2 and Es3 (Figure 7a). In Es3 and Es4, the simulated pore pressure is slightly higher than the mud weight equivalent pressure. The reservoir drilled in this well is a typical type of “upper source-lower reservoir”, but the reservoir drilled in Chegu 25 well only appears in a limited area between two faults. The overpressures of Wells K571, Chegu 204 and Chegu 201 do not change much during hydrocarbon generation (Figure 7b-d), and there is no accumulation condition for hydrocarbon to migrate downward. Because of the obvious overpressure at the deep source rock, the hydrocarbons in the reservoirs drilled by these three wells mainly come from the deep source rock and migrate upward along the fault or microfracture.
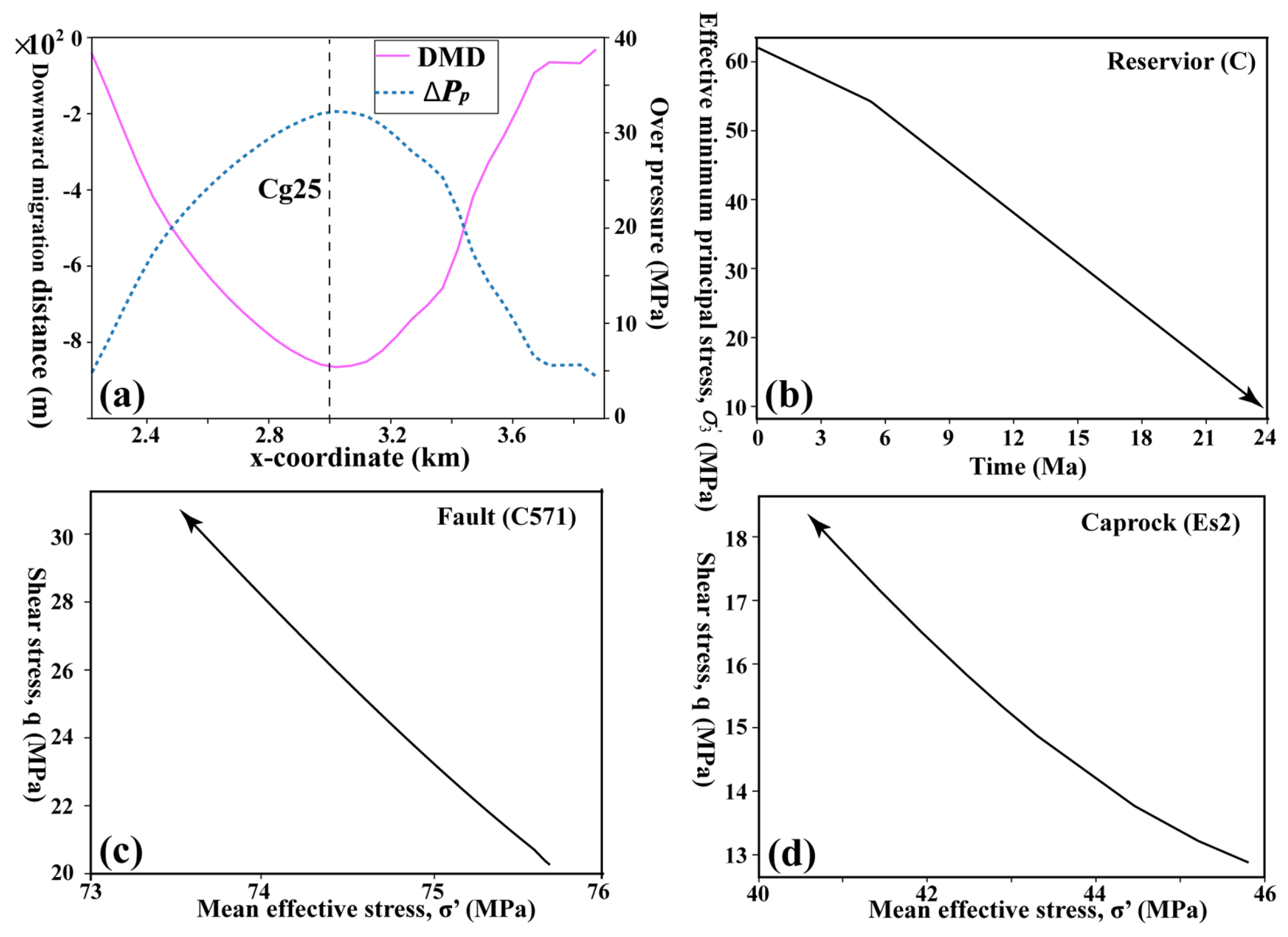
It is noteworthy that the distance or depth over which fluid overpressure is transmitted can be affected by various factors [18]. However, it can be determined that if the source rocks continue to generate hydrocarbons and the tectonic environment of the model area remains unchanged, overpressure may also occur in deeper strata (near the gray arrow of Figure 7a). By utilizing the overpressure results calculated by the model and referring to the previous maximum distance model of hydrocarbon migration [15], we can determine the maximum hydrocarbon downward migration distance near the maximum overpressure position of Chegu 25 well (Figure 5a red solid line and Figure 8a). Note that, it can be seen from the results that the maximum hydrocarbon migration distance is directly related to the overpressure. The greater the overpressure, the greater the distance of hydrocarbon migration. The maximum overpressure in Chegu 25 well is located in Es4 formation (corresponding depth is about 4800 m). The maximum hydrocarbon migration distance is more than 800 m (Figure 8a), and this distance decreases rapidly with the distance away from Chegu 25 well (Figure 8a).
During the process of increasing overpressure, hydraulic fracturing and shear fractures can occur in rocks, thus forming cracks or fracture systems [54,55]. Additionally, it can also re-activate or open the pre-existing faults [52]. Taking the stress state of point A in the Carboniferous (C) reservoir as an example (Figure 5 and Figure 8b), during the process of hydrocarbon generation (simulation time is 24 Ma), the pore fluid pressure of this point increases continuously, while the effective minimum principal stress ( σ 1 ′ ) decreases from 60 MPa to 10 MPa. As a result, the risk of rock tensile fracture rises. When the effective minimum principal stress decreases to the tensile strength of rock, it will lead to rock fracture. This also provides more channels for the propagation and dissipation of overpressure. In addition, we also analyzed the stress state of point B of C571 fault, and find that during the hydrocarbon generation process of 24 Ma, the mean effective stress ( σ m ′ = σ 1 ′ + σ 2 ′ + σ 3 ′ ) of this point decreases by about 2 MPa, and the shear stress (q= 1 / 2 ( σ 1 ′ − σ 2 ′ ) 2 + ( σ 1 ′ − σ 3 ′ ) 2 + ( σ 2 ′ − σ 3 ′ ) 2 ) increases by about 11 MPa (the direction indicated by the arrow in Figure 8c). This shows that the risk of shear failure of rocks near the fault increases. Similarly, the risk of shear failure of rock at point C at the caprock stratum (Es2) also increases (Figure 8d). Consequently, the overpressure in this area has an upper limit. When this limit is reached, the overpressure causes the rock to break and form new cracks, so that the overpressure is then reduced or dissipated.

5. Discussion

5.1. Effect of Fault Sealing on Hydrocarbon Accumulation

Hydrocarbon migration always moves from a high potential area to a low potential area, following the direction of minimum capillary resistance [53]. We have observed hydrocarbons migrating down the fault due to overpressure when the fault is open and serves as the primary pathway for migration. Studies have shown that the geometry of the basin, the characteristics of the reservoir, and the drainage layer (such as inclination and relative permeability) will affect the migration rate and direction of hydrocarbons [56,57]. It can be seen from Figure 9 that hydrocarbons are generated in Es3 and Es4 formations, and primarily migrate to both sides of the fault through the highly permeable Es3 formation. Due to its low porosity and low permeability, the flow rate of Es2 and Ed is significantly reduced, resulting in a noticeable sealing effect on fluid migration.

5.2. Influence of Formation Permeability on Hydrocarbon Accumulation

In order to investigate and compare the influence of formation permeability on the model results, we utilize a high permeability example (Table 1) to simulate the overpressure caused by the hydrocarbon generation process. During the continuous hydrocarbon generation process, there is no increase in overpressure, and overpressure dissipation occurs. When the simulation time reaches 24 Ma, the overpressure has essentially dissipated, and the pore fluid pressure has returned to almost the hydrostatic state (solid blue curve in Figure 10b). This result is inconsistent with the existing research findings on petroleum exploration and development in the region. Hence, the permeability parameters of rock are very important to the hydrocarbon generation overpressure.

5.3. Quantitative Comparison of Hydrocarbon Generation Overpressure and Unbalanced Compaction Overpressure

We compare the unbalanced compaction overpressure with the hydrocarbon generation overpressure of well Chegu 25, so as to assess the disparity in the contributions of hydrocarbon generation and unbalanced compaction to the overall overpressure in the formation. The results indicate that the overpressure value in the shallow strata (above 2800 m) is not big, typically less than 3 MPa. The total overpressure is mainly caused by hydrocarbon generation. The hydrocarbon generation overpressure in the Es3 and Es4 formations is much higher than the unbalanced compaction overpressure. The difference of overpressure generated by these two mechanisms even exceeds 10 MPa, as the formations (Es3 and Es4) are the main hydrocarbon generation positions. In the strata below the source rock, the fluid generated by hydrocarbon generation is difficult to migrate downward, resulting in a rapid decline in hydrocarbon generation overpressure. In the Carboniferous strata (C), the hydrocarbon generation overpressure is lower than the unbalanced compaction overpressure. In deeper formations, the unbalanced compaction overpressure cannot be accurately calculated because of the lack of logging data. Thus, the contribution of the two overpressure mechanisms to the total overpressure has not been discussed.
The comparison of hydrocarbon overpressure and unbalanced compaction in this study can offer a viable approach to analyze the composition of overpressure in strata through numerical simulation. However, this approach still has some limitations. Consequently, we utilize the normal compaction trend (NCT) method to calculate the overpressure resulting from unbalanced compaction, which calculates the overpressure by analyzing the relationship between the porosity and the vertical effective stress in sediments. Some previous studies pointed out that this method did not consider the effects of lateral deformation and shear-induced compaction when predicting pore pressure [38,58,59]. As a result, the calculated results would deviate from the actual overpressure (or pore pressure). In addition, this method has limitations in predicting overpressure in deep formations. The porosity in deep formations will be very small or even negative (Figure A1b), which does not align with reality. Therefore, this method requires modification or improvement.
Preprints 77379 g011
Figure 11. Comparison of hydrocarbon generation overpressure and unbalanced compaction overpressure in Chegu25 well section. The orange curve represents overpressure caused by hydrocarbon generation. The blue curve represents overpressure caused by unbalanced compaction.
Figure 11. Comparison of hydrocarbon generation overpressure and unbalanced compaction overpressure in Chegu25 well section. The orange curve represents overpressure caused by hydrocarbon generation. The blue curve represents overpressure caused by unbalanced compaction.
Preprints 77379 g011

6. Conclusions

In this study, the pore fluid pressure field and stress field near the Chegu 25 block in the Chezhen sag are investigated through numerical simulation, taking into account the two overpressure mechanisms of hydrocarbon generation and unbalanced compaction. Overall, the model evaluates the overpressure in different formations under these two mechanisms and verifies the accuracy of the simulation calculations by comparing them with the results of mud weight equivalent pressure and drill stem tests (DSTs). Additionally, in the process of simulating hydrocarbon generation, we analyze the variations in hydrocarbon accumulation modes for the four wells in the profile. This analysis provides evidence for the potential existence of the “upper source-lower reservoir” accumulation mode in the location of Chegu 25 well. Besides, we also analyze the necessary conditions for the existence of this accumulation mode. The simulation results show that:
(1) When a fault is open and has high permeability, it can serve as the major or dominant channel for hydrocarbon migration. Overpressure can then affect the direction and path of hydrocarbon migration. In the closed state of a fault, hydrocarbon migration is primarily driven by buoyancy, moving from deep source formations to shallow reservoirs where it eventually accumulates. This process is characteristic of conventional petroleum reservoirs. Under the condition of a fault opening, hydrocarbons can not only be trapped in conventional reservoirs but can also migrate downward along the fault and eventually accumulate. Although this condition is more strict, this situation can still exist.
(2) The overpressure can alter the direction and pathway of hydrocarbon migration, thereby promoting the migration of hydrocarbons and enhancing the efficiency of hydrocarbon accumulation. Excessive pore fluid overpressure, however, can lead to hydraulic fracturing or shear fractures of rocks, resulting in the formation of a fault system. This can cause the dissipation of hydrocarbons and prevent their accumulation.
(3) The permeability of rock plays an important role in the generation and maintenance of overpressure and the mechanism of accumulation mode. High permeability rocks allow for rapid flow of hydrocarbons and rapid dissipation of overpressure, and will not form overpressure in the formation. Low permeability rocks, on the contrary, impede the movement of hydrocarbons, causing them to accumulate slowly. This accumulation can lead to overpressure, which in turn promotes the downward migration and accumulation of hydrocarbons along faults.

Author Contributions

M.W. planned and designed the research work, writing—original draft preparation; G.L. software and methodology, writing—review and editing; F.Q., S.Z. and Z.L. writing—review and editing; N.Y. data processing. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Key R&D Program of the Ministry of Science and Technology of China with the Project “Integration Platform Construction for Joint Inversion and Interpretation of Integrated Geophysics (2018YFC0603500)”.

Acknowledgments

In this section, you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

In sedimentary basins, the porosity of sediments decreases regularly with depth as long as the pore fluid remains hydrostatic [60]. We call this decrease in porosity with depth the normal compaction trend. In this case, porosity is directly related to effective stress. When the unbalanced compaction produces overpressure, the variation curves of acoustic time difference and porosity with depth will deviate from the trend under normal compaction, which is manifested as the measured porosity is smaller than that under normal compaction [61,62,63].
The overpressure caused by unbalanced compaction can be expressed by the following formula [60]:
δ p z = δ ϕ ( z ) Φ 0 β − ∫ 0 z ρ m − ρ f g δ ϕ z ′ d z ′ ,
where, ρ f is fluid density that is related to water saturation S w and gas density ρ g . ρ f = S w ρ w + (1- S w ), where ρ w is water density. The organic matter type of source rocks in the middle and lower submembers of Es3 is type I, and the Ro value is 0.54% ~ 0.64%, which is kerogen with high oil yield [23,64]. In the model of this paper, we mainly focus on the formation mechanism of overpressure and its influence on hydrocarbon migration and accumulation. At the same time, in order to simplify the calculation, we only consider the phase state of water, the density of water instead of the density of oil, and do not consider the influence of gas on overpressure evolution and hydrocarbon migration and accumulation. Therefore, we take S w = 1, that is, ρ f = ρ w .
The porosity profile can be calculated by density logging [65]:
ϕ = ρ m − ρ ρ m − ρ f
In this study area, Chegu 25 well is normally compacted in the depth range below 3600 m, without abnormal pressure, and the overpressure occurs above 3600 m [24]. According to Formula (A3), the normal compaction curve of Chegu 25 well (Figure A1b) and the values of ϕ 0 and z c can be obtained by using the porosity data above 3600 m for nonlinear regression analysis [60]. From the compaction curve of Figure A1b, according to the trend of normal compaction curve below 4500 m, it can be observed that the porosity has a negative value (the green dotted line in Figure A1b), which contradicts the actual situation. André's unbalanced compaction pressure prediction model may have certain limitations, which prevent its use from predicting pressure in deep strata. Therefore, we simplify the porosity below 4500 m and standardize it to 0.03 (the green solid line in Figure A1b). Due to the strong discreteness of the original data, we smooth the porosity data (the red line Figure A1b).
Φ H z = 1 − 1 − Φ 0 exp ⁡ z z c ,
where, ϕ H is the "hydrostatic porosity" and the characteristic depth z c is defined as:
z c = 1 / Φ 0 β g ( ρ m − ρ f )
According to Formula (A4), the average compression coefficient β is calculated by using the average uncompacted porosity ϕ 0 and characteristic depth z c .
We use the logging data of Chegu 25 well to analyze the unbalanced compaction of strata. Figure A1 shows the results of density (DEN), acoustic time difference (AC) and neutron (CNL) logging data. The depth range of logging data is 2300–5100 m. The model assumes that the strata above 2000 m are the stress and pressure state of normal compaction. Based on the above data using formula (A1), we can obtain the pore pressure changes caused by unbalanced compaction (Figure A1e). The results embody that the overpressure produced by unbalanced compaction is relatively weak in Es2 (2700-3200m), and the value is generally less than 3 MPa. The larger overpressure is in the lower Es3 and below strata (4000–5100 m). The acoustic time difference, neutron and density logging data in this depth range are all greater than the normal compaction curve, and the maximum overpressure value is close to 10 MPa (Figure A1e).
Preprints 77379 g0a1
Figure A1. Logging data of well Cg25. (a) Density data. (b) Porosity data. (c) Neutron logging. (d) Acoustic time difference.
Figure A1. Logging data of well Cg25. (a) Density data. (b) Porosity data. (c) Neutron logging. (d) Acoustic time difference.
Preprints 77379 g0a1

References

  1. Krayushkin, V.A. The plutonic oil-gas fields (in Chinese). Xinjiang Pet. Geol. 2009, 30, 136–141. [Google Scholar]
  2. Jia, C.Z. Pang, X.Q., Jiang, F.J. Research status and development directions of hydrocarbon resources in China. Pet. Sci. 2016, 01, 2–23. [Google Scholar]
  3. Zou, C.N.; Tao, S.Z.; Bai, B.; Yang, Z.; Zhu, R.K.; Hou, L.H.; Yuan, X.J.; Zhang, G.S.; Wu, S.T.; Pang, Z.L.; et al. Differences and relations between unconventional and conventional Oil and Gas (in Chinese). China pet. Explor. 2015, 20, 1–16. [Google Scholar]
  4. Hunt, J M. Generation and migration of petroleum from abnormally pressured fluid compartments. AAPG. Bulletin 1990, 74, 1–12. [Google Scholar] [CrossRef]
  5. Hao, F.; Zou, H.Y.; Gong, Z.S.; Yang, S.G.; Zeng, Z.P. Hierarchies of overpressure retardation of organic matter maturation: Case studies from petroleum basins in China. AAPG Bulletin 2007, 91, 1467–1498. [Google Scholar] [CrossRef]
  6. Li, C.; Zhang, L.; Luo, X.R.; Wang, B.; Lei, Y.H.; Cheng, M.; Luo, H.M.; Wang, C.J.; Yu, L. Modeling of Overpressure Generation–Evolution of the Paleogene Source Rock and Implications for the Linnan Sag, Eastern China. Front. Earth Sci. 2022, 10, 1–22. [Google Scholar] [CrossRef]
  7. Chi, G.; Lavoie, D.; Bertrand, R.; Lee, M.K. Downward hydrocarbon migration predicted from numerical modeling of fluid overpressure in the Paleozoic Anticosti Basin, eastern Canada. Geofluids 2010, 10, 334–350. [Google Scholar] [CrossRef]
  8. Gao, C.W.; Luo, Q. A new plan for dividing source-reservoir-cap rock assemblage and its exploration meanings. Pet. Explor. Dev. 2022, 06, 29–31. [Google Scholar]
  9. Chi, Y.L.; Xiao, D.M.; Yin, J.Y. The Injection Pattern of Oil and Gas Migration and Accumulation in the Sanzhao Area of Songliao Basin (in Chinese). Acta. Geol. Sin. 2000, 74, 371–377. [Google Scholar]
  10. Lv, Y.F.; Li, J.M.; Fu, X.F.; Fu, G.; Wang, Y.G.; Xuan, C.J. Geologic conditions of oil gas downward discharging and exploration direction in the Sanzhao Sag, Songliao Basin (in Chinese). Chin. J. Geology 2009, 2, 525–533. [Google Scholar]
  11. Dubille, M.; Maury, G.; Al-Ali. S. A. K.; Alkhamiss, A. Downward Migration, Theory and Application to Najmah-Marrat Petroleum System. 79th EAGE Conference and Exhibition 2017. Eur. Assoc. Geoscientists & Engineers 2017, 1, 1–5. [CrossRef]
  12. Tóth, J.; Maccagno, M.D.; Otto, C.J.; Rostron, B.J. Generation and migration of petroleum from abnormally pressured fluid compartments: Discussion. AAPG Bulletin 1991, 75, 331–335. [Google Scholar] [CrossRef]
  13. Zou, C.N.; Jia, C.Z.; Zhao, W.Z.; Tao, S.Z.; Gu, Z.D.; Hou, Q.J.; Zhao, Z.Y.; Song, L.Z. Accumulation dynamics and distribution of lithostratigraphic reservoirs in South Songliao Basin. Pet. Explo. Dev. 2005, 32, 2. [Google Scholar]
  14. Fu, G.; Wang, Y.G. Migration horizons downward of oil from k1-qn source rock of F, Y oil layer in sanzhao depression and its significance (in Chinese). Acta. Sedimentologica Sin. 2008, 26, 355–360. [Google Scholar]
  15. Xiang, L.H.; Hao, X.F. Hydrocarbon “downward migration” mechanism and maximum migration distance estimation in Chexi Sag (in Chinese). Special Oil & Gas Reservoirs 2016, 23, 34–37. [Google Scholar]
  16. Feng, L.H. A method for upper and down expulsion hydrocarbon amount of overpressured sourcerock by interval transit time (in Chinese). J. Daqing Pet. institute 2007, 31, 22–24. [Google Scholar]
  17. Zhuang, J.C.; Zhang, S.W.; Wang, Y.S.; Lin, H.X. Pressure fall model of hydrocarbon conducted by fault (in Chinese). Pet. Geology Recovery Efficiency 2008, 15, 46–48. [Google Scholar]
  18. Shi, J.J.; Fu, G.; Li, L.L. The quantitative research of the downward migration distance and target horizons of K1 qn, oil and gas in Binbei area (in Chinese). Pet. Geology Recovery Efficiency 2009, 16, 26–29. [Google Scholar]
  19. Wang, Y.S.; Shan, Y.X.; Lao, H.G. Physical Simulation of Oil and Gas Backflow and Its Geological Significance (in Chinese). J. Southwest Pet. Univ. 2014, (Science & Technology Edition).
  20. Luo, X.; Vasseur, G. Overpressure dissipation mechanisms in sedimentary sections consisting of alternating mud-sand layers. Mar. Pet. Geology 2016, 78, 883–894. [Google Scholar] [CrossRef]
  21. Guo, X.; He, S.; Liu, K.; Song, G.; Wang, X.; Shi, Z. Oil generation as the dominant overpressure mechanism in the Cenozoic Dongying depression, Bohai Bay Basin, China. AAPG Bulletin 2010, 94, 1859–1881. [Google Scholar] [CrossRef]
  22. Li, C.; Zhang, L.; Luo, X.R.; Lei, Y.H.; Yu, L.; Cheng, M.; Wang, Y.S.; Wang, Z.L. Overpressure generation by disequilibrium compaction or hydrocarbon generation in the Paleocene Shahejie Formation in the Chezhen Depression: Insights from logging responses and basin modeling. Mar. Pet. Geology 2021, 133, 105258. [Google Scholar] [CrossRef]
  23. Wang, Y.L. Hydrocarbon migration dynamic conditions and accumulation models of lower Paleozoic in Chexi area (in Chinese) [Master]. China University Petroleum (East China): Qingdao, China, 2016.
  24. Li, C.; Luo, X.; Zhang, L.; Wang, B.; Guan, X.; Luo, H.; Lei, Y. Overpressure generation mechanisms and its distribution in the Paleocene Shahejie Formation in the Linnan sag, Huimin depression, eastern China. Energies 2019, 12, 3183. [Google Scholar] [CrossRef]
  25. Sun, Y.T.; Dong, L.F.; Liu, F.F.; Meng, T.; Zhang, B.; Shi, Q.Q. Tectonic evolution and dynamic origin mechanism in Chezhen Sag, Jiyang Depression (in Chinese). Chinese J. Geology 2022, 57, 427–438. [Google Scholar]
  26. Liu, L.J.; Lin, C.S. The control effect of sedimentary filling patterns and fault slope break zones of sha 3 member of shahejie formation in Chezhen Sag, Jiyang Depression (in Chinese). J. Yangtze Univ. (Natural Science Edition) 2020, 17, 10–17. [Google Scholar]
  27. Shang, L. Research on developing regularity of multiperiod structural fractures in Futai carbonate buried hill (in Chinese) [Doctor]. China University Petroleum (East China), Qingdao, China, 2014.
  28. Wang, Y.S. Detachment buried-hill oil-gas reservoir forming pattern in half-graben fault depression lake basin-taking Futai oil field as example (in Chinese). Pet. Geology Recovery Efficiency 2004, 11, 13–15. [Google Scholar]
  29. Liang, S.R. Geoburried-hills Reservoir characteristics and forming-mechanism in Chexi Are (in Chinese) [Doctor]. China University Petroleum (East China), Qingdao, China, 2007.
  30. Jin, S.; Cao, H.; Wang, H.; Chen, S. The Paleogene multi-phase tectono-sedimentary evolution of the syn-rift stage in the Nanpu Sag, Bohai Bay Basin, East China. Energy Explor. & Exploit, 2018; 36, 1519–1545. [Google Scholar] [CrossRef]
  31. Zhu, Y.G.; Jin, Q.; Zhang, Y.C.; Zhang, L.H.; Zhang, S.W.; Guo, C.C. Study on hydrocarbon generation system of Lower Tertiary Shahejie Formation in Chezhen depression (in Chinese). Nat. Gas Industry 2006, 26, 19–22. [Google Scholar]
  32. Zhang, J.Z.; Wang, Y.S.; Wang, X.J.; Cao, S.M.; Wang, X.F.; Bi, C.Q. Buried hill reservoir characteristic of the lower Palaeozoic in Futai oilfield. Pet. Geology Recovery Efficiency 2003, 4, 23–25+5. [Google Scholar]
  33. Zhang, J.L.; He, S.; Wang, Y.Q.; Hao, X.F.; Luo, S.Y.; Li, P.; Dang, X.W.; Yang, R.Z. Main mechanism for generating overpressure in the Paleogene source rock series of the Chezhen depression, Bohai Bay Basin. J. Earth Sci. 2019, 30, 775–787. [Google Scholar] [CrossRef]
  34. Ma, L.C.; Wang, Y.S.; Jing, A.Y. New understanding and discovery in exploration of Lower Paleozoic buried hills in Jiyang Depression, Bohai Bay Basin (in Chinese). Pet. Geology Recovery Efficiency 2021, 28, 10–16. [Google Scholar]
  35. Xue, H.T.; Lu, S.F.; Zhang, X.J.; Li, Z.; Shen, J.N. Evaluation of Lower Paleozoic carbonate source rocks in Jiyang depression. Geochem. 2006, 35, 609–614. [Google Scholar]
  36. Chester, F.M.; Evans, J.P.; Biegel, R.L. Internal structure and weakening mechanisms of the San Andreas fault. J. Geophys. Res-Solid Earth 1993, 98, 771–786. [Google Scholar] [CrossRef]
  37. Caine, J.S.; Evans, J.P.; Forster, C.B. Fault zone architecture and permeability structure. Geology 1996, 24, 1025–1028. [Google Scholar] [CrossRef]
  38. Liao, Z.H.; Liu, H.; Carpenter, B.M.; Marfurt, K.J.; Reches, Z.E. Analysis of fault damage zones using three-dimensional seismic coherence in the Anadarko Basin, Oklahoma. AAPG Bulletin 2019, 103, 1771–1785. [Google Scholar] [CrossRef]
  39. Gao, B.; Flemings, P.B. Pore pressure within dipping reservoirs in overpressured basins. Mar. Pet. Geology 2017, 80, 94–111. [Google Scholar] [CrossRef]
  40. Luo, G.; Flemings, P.B.; Hudec, M.R.; Nikolinakou, M.A. The role of pore fluid overpressure in the substrates of advancing salt sheets, ice glaciers, and critical-state wedges. J. Geophys. Res-Solid Earth 2015, 120, 87–105. [Google Scholar] [CrossRef]
  41. Chen, J.Y.; Yang, X.S.; Dang, J.X.; He, C.R.; Zhou, Y.S.; Ma, S.L. Internal structure and permeability of Wenchuan earthquake fault (in Chinese). Chinese J. Geophys. 2011, 54, 1805–1816. [Google Scholar]
  42. Duan, Q.B.; Yang, X.S.; Chen, J.Y. A preliminary experimental study on permeability of samples collected from Wenchuan earthquake fault zone. Prog. Earthquake Sci. 2012, 6, 55. [Google Scholar]
  43. Feng, J.; Qu, J.; Wan, H.; Ren, Q.Q. Quantitative prediction of multiperiod fracture distributions in the Cambrian-Ordovician buried hill within the Futai Oilfield, Jiyang Depression, East China. J. Struct Geology 2021, 148, 104359. [Google Scholar] [CrossRef]
  44. Wu, G.C.; Zhao, X.L.; Tang, J.; Du, Z.Y. First-order perturbation approximation for rock elastic moduli in transversely isotropic media. Sci. China Earth Sci. 2017, 60, 1645–1654. [Google Scholar] [CrossRef]
  45. Xia, Z.; Ma, H.Y.; Fang, K. Rock mechanical properties and fracability of continental shale in Zhanhua Sag, Bohai Bay Basin. Pet. Geology & Exp. 2019, 41, 134–141. [Google Scholar]
  46. Terzaghi, K. Theoretical soil mechanics, 1943. Published Online, 19.
  47. Nur, A.; Byerlee, J.D. An exact effective stress law for elastic deformation of rock with fluids. J. Geophys. Res. 1971, 76, 6414–6419. [Google Scholar] [CrossRef]
  48. Fjaer, E.; Holt, R.M.; Horsrud, P.; Raaen, A.M. Petroleum related rock mechanics (Vol. 33); Elsevier. 1992.
  49. Chang, C.; Luo, G.; Wang, M.W.; Sun, Y.Q. Near-salt perturbations of stresses and pore fluid pressures and their impacts on wellbore stability in the Kuqa depression of the Tarim Basin, China. Interpretation 2020, 8, SG33–SG49. [Google Scholar] [CrossRef]
  50. Joshua, P.E. Coupled fluid flow and geomechanical modeling of fault activated induced seismicity [Doctor]. Texas A&M University; 2018.
  51. Zhang, H.Y. Fluid mechanics; Beijing: Science Press, 2004. [Google Scholar]
  52. Simulia. Abaqus, a general purpose finite element analysis code: Dassault Systémes Simulia Corp. 2016. Available online: http://www.simulia.com (accessed on 18 December 2018).
  53. Yu, L.G. The FEM simulating of hydrocarbon migration in dongying depression (in Chinese) [Master]. China University Petroleum (East China), Qingdao, China, 2007.
  54. Xie, X.N.; Li, S.T.; Liu, X.F. Fluid Dynamics of Abnormal Pressure Basin; China University of Geosciences Press, 2006. [Google Scholar]
  55. Hubbert, M.K.; Willis, D.G. Mechanics of hydraulic fracturing. Transactions of the AIME 1957, 210, 153–168. [Google Scholar] [CrossRef]
  56. Osiptsov, A.A. Fluid mechanics of hydraulic fracturing: A review. J. Pet. Sci. Eng 2017, 156, 513–535. [Google Scholar] [CrossRef]
  57. Pratsch, J.C. Focused gas migration and concentration of deep-gas accumulations. Erdoel Kohle, Erdgas, Petrochem. Brennst. - Chem. 1982, (Germany, Federal Republic of), 35.
  58. Hindle, A.D. Petroleum migration pathways and charge concentration: A three-dimensional model. AAPG bulletin 1997, 81, 1451–1481. [Google Scholar] [CrossRef]
  59. Luo, G.; Hudec, M.R.; Flemings, P.B. Deformation, stress, and pore pressure in an evolving suprasalt basin. J. Geophys. Res-Solid Earth 2017, 122, 5663–5690. [Google Scholar] [CrossRef]
  60. Nikolinakou, M.A.; Heidari, M.; Flemings, P.B. Geomechanical modeling of pore pressure in evolving salt systems. Mar. Pet. Geology 2018, 93, 272–286. [Google Scholar] [CrossRef]
  61. Revil, A.; Pezard, P.A.; de Larouzière, F.D. 10. Fluid overpressures in western mediterranean sediments. SITES 974–979 1999. 48, 697–709. [CrossRef]
  62. Tingay, M.R.; Hillis, R.R.; Swarbrick, R.E.; Morley, C.K.; Damit, A.R. Origin of Overpressure and Pore-Pressure Prediction in the Baram Province, Brunei. AAPG Bulletin 2009, 93, 51–74. [Google Scholar] [CrossRef]
  63. Sharp, J.M. Momentum and Energy Balance Equations for Compacting Sediments. J. Int. Assoc. Math. Geology 1976, 98, 305–322. [Google Scholar] [CrossRef]
  64. Xiang, L.H.; Wang, X.J.; Hao, X.F.; Li, X.Y. The study of reservoir forming conditions about hc migration downward in chexi sag (in Chinese). Offshore oil 2013, 33, 42–47. [Google Scholar]
  65. Rubey, W.W.; Hubbert, M.K. Role of fluid pressure in mechanics of overthrust faulting, II. Overthrust Belt in geosynclinal area of western Wyoming in light of fluid-pressure hypothesis. AAPG Bulletin 1959, 70, 167–205. [Google Scholar]
  66. Ellis, D.V.; Singer, J.M. Well logging for earth scientists; Springer: Dordrecht, 2007. [Google Scholar]
Preprints 77379 g001aPreprints 77379 g001b
Figure 1. Geological map and seismic profile results of the study area. (a) Location of the Chezhen Sag. (b) Tectonic units, major fault, and well distribution of the Chezhen Sag. (c) Seismic profile results of the study area. (d) Results of seismic profile interpretation.
Figure 1. Geological map and seismic profile results of the study area. (a) Location of the Chezhen Sag. (b) Tectonic units, major fault, and well distribution of the Chezhen Sag. (c) Seismic profile results of the study area. (d) Results of seismic profile interpretation.
Preprints 77379 g001aPreprints 77379 g001b
Preprints 77379 g002
Figure 2. The dual structure of fault and fault sealing related data. (a) Buried hill carbonate outcrops. (b) The dual structure of fault. (c-d) Core data of fault zones.
Figure 2. The dual structure of fault and fault sealing related data. (a) Buried hill carbonate outcrops. (b) The dual structure of fault. (c-d) Core data of fault zones.
Preprints 77379 g002
Preprints 77379 g005aPreprints 77379 g005b
Figure 5. Finite element model setting of hydrocarbon generation process. (a) Finite element meshes and boundary conditions. The red dotted line area shows the location of hydrocarbon generating strata. (b) The left and right pore fluid pressure boundary of the model is the hydrostatic pore pressure boundary. (c) The initial pore fluid pressure field of the model.
Figure 5. Finite element model setting of hydrocarbon generation process. (a) Finite element meshes and boundary conditions. The red dotted line area shows the location of hydrocarbon generating strata. (b) The left and right pore fluid pressure boundary of the model is the hydrostatic pore pressure boundary. (c) The initial pore fluid pressure field of the model.
Preprints 77379 g005aPreprints 77379 g005b
Preprints 77379 g006
Figure 6. Simulation of the current pore fluid overpressure and fluid velocity field results. (a) Simulated present overpressure results; (b) Simulated current fluid velocity field results.
Figure 6. Simulation of the current pore fluid overpressure and fluid velocity field results. (a) Simulated present overpressure results; (b) Simulated current fluid velocity field results.
Preprints 77379 g006
Preprints 77379 g007
Figure 7. The pore pressure profiles of four wells in the study area. (a) Well Chegu 25 pore pressure simulation results. (b) Well Che 571 pore pressure simulation results. (c) Chegu 204 well pore pressure simulation results. (d) Well Chegu 201 pore pressure simulation results. The asterisk represents the pore pressure value obtained by the DSTs. The plus sign represents the pore pressure result interpreted by mud weight data, and the overpressure result is equal to the simulated pore fluid pressure minus the hydrostatic pore pressure.
Figure 7. The pore pressure profiles of four wells in the study area. (a) Well Chegu 25 pore pressure simulation results. (b) Well Che 571 pore pressure simulation results. (c) Chegu 204 well pore pressure simulation results. (d) Well Chegu 201 pore pressure simulation results. The asterisk represents the pore pressure value obtained by the DSTs. The plus sign represents the pore pressure result interpreted by mud weight data, and the overpressure result is equal to the simulated pore fluid pressure minus the hydrostatic pore pressure.
Preprints 77379 g007
Preprints 77379 g008
Figure 8. The simulation results of local pressure, stress and oil and gas backflow distance. (a) The maximum hydrocarbon downward migration distance near the maximum overpressure position (about 4800 m) of Chegu 25 well. DMD represents the downward migration distance. (b) The evolution of overpressure at point A with time. (c) The stress state change of point B at the fault. The arrow indicates the increase of simulation time. (d) The stress state change of point C at the caprock layer. The arrow pointing indicates the increase of simulation time. The location of the maximum overpressure area in Chegu 25 well and the three points of A, B, and C are shown in Figure 5a.
Figure 8. The simulation results of local pressure, stress and oil and gas backflow distance. (a) The maximum hydrocarbon downward migration distance near the maximum overpressure position (about 4800 m) of Chegu 25 well. DMD represents the downward migration distance. (b) The evolution of overpressure at point A with time. (c) The stress state change of point B at the fault. The arrow indicates the increase of simulation time. (d) The stress state change of point C at the caprock layer. The arrow pointing indicates the increase of simulation time. The location of the maximum overpressure area in Chegu 25 well and the three points of A, B, and C are shown in Figure 5a.
Preprints 77379 g008
Preprints 77379 g009
Figure 9. Flow velocity diagram of fault sealing model.
Figure 9. Flow velocity diagram of fault sealing model.
Preprints 77379 g009
Preprints 77379 g010
Figure 10. Pore fluid pressure change of Chegu 25 well. The asterisk represents the pore pressure value obtained by the DSTs. The plus sign represents the pore pressure result interpreted by the mud weight. The overpressure result is equal to the simulated pore fluid pressure minus the hydrostatic pressure.
Figure 10. Pore fluid pressure change of Chegu 25 well. The asterisk represents the pore pressure value obtained by the DSTs. The plus sign represents the pore pressure result interpreted by the mud weight. The overpressure result is equal to the simulated pore fluid pressure minus the hydrostatic pressure.
Preprints 77379 g010
Table 1. Material parameters of finite element model.
Table 1. Material parameters of finite element model.
Stratum Young's modulus (GPa) Poisson ratio Higher permeability (m2) Lower permeability (m2) [38,39]
Ng 30[43] 0.2543 1.5e-15 1.5e-20
Ed 32[43] 0.2543 1e-15 1e-20
Es2 32[43] 0.2543 1e-15 1e-20
Es3 35[44] 0.344 5e-15 5e-20
Es4 35[44] 0.344 3e-15 3e-20
C 35[42] 0.342 2e-15 2e-20
O 35[42] 0.342 1e-16 1e-21
∈ 35[42] 0.3542 1e-16 1e-21
Art 35 0.35 1e-16 1e-21
Fault-L-Es3 35 [27] 0.327 1e-12 1e-17
Fault-L-Es4 35 [27] 0.327 1e-13 1e-18
Fault-R-Es3 35 [27] 0.327 1e-12 1e-17
Fault-R-Es4 35 [27] 0.327 1e-13 1e-18
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated