You are currently viewing a beta version of our website. If you spot anything unusual, kindly let us know.
Preprint
Communication
Vortex Beam in Turbulent Kerr Medium
Altmetrics
Downloads
93
Views
19
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Abstract
The dynamics of the topological charge of a vortex optical beam propagating in a turbulent air with accounting for the cubic nonlinearity is theoretically considered. On a number of examples, we show that the optical beam self-focusing manifests itself ambiguously depending on optical wave power. At near-critical values of beam power, self-focusing leads to enhanced spatial localization of optical vortices and substantial suppression of vortex walk-off relative to the beam axis caused by air turbulence. However, with increasing of optical intensity the modulation instability imposed by cubic nonlinearity becomes significant and contributes jointly with medium turbulence to faster divergence of vortex beams.
Keywords:
Subject: Physical Sciences - Optics and Photonics
1. Introduction
The study of propagation of optical radiation with a non-zero topological charge in real turbulent atmosphere is an urgent task because such optical beams are considered as a basis for development of potentially stable communication links. The study of such vortex beams is devoted to a large number of works (see, e.g., [1-4]). Usually, when studying the propagation of vortex laser beams in turbulent medium air optical nonlinearity is not taken into account [1]. At the same time, the femtosecond atmospheric optics is currently actively developing and the question of vortex propagation beams are also actively studied in the context of high-power ultrafast optical communications [2-4]. As a rule, the researchers are interested in the influence of the topological charge on the propagation dynamics of a laser pulse, particularly, the effect of the topological charge on the stability and spatial energetic characteristics of optical radiation is studied or the manifestation of some specific effects which are characteristic for nonlinear femtosecond optics with random parameters [4].
At the same time, the topics on how optical medium nonlinearity affects the topological charge (TC) of a propagating laser radiation and the possibility of using TC as a communication channel are less explored to-date. Meanwhile, the vortex beam in a turbulent medium is known to be unstable [5-9], i.e. it splits upon propagation into several vortices with different TCs, while the character of their spatial distribution becomes chaotic which at realistic restrictions on the aperture of a receiver optics becomes a big challenge. This problem can be overcome to a greater or lesser degree by superimposing phase plates (including focusing of different types). Another possible method for the manipulation the optical vortex dynamics relies on the controlled use of nonlinear effects in the propagation medium [4]. The aim of this brief communication is answering the question on how the optical cubic nonlinearity affects the vortex beam propagation in a randomly inhomogeneous (turbulent) medium.
2. Materials and Methods
To find a solution to the problem considered, it is necessary to solve the nonlinear Schrödinger equation (NLSE) for an optical pulse envelope propagating in a nonlinear random medium. In this case, one should take into account not only the cubic (Kerr) nonlinearity, but also other physical effects associated with higher optical nonlinearities causing pulse transverse collapse arrest and the realization of pulse filamentation regime.
We consider the NLSE-type pulse propagation equation in the following form [2]:
Here, k0 is the wave number at the carrier wavelength (800 nm), εl and αl are the coefficients for the l-th order nonlinearity leading to the beam self-focusing arrest. These coefficients account for the physical effects stimulating wave refraction and nonlinear absorption in the self-induced electron plasma, respectively. In Eq. (1) the operator is introduced which is responsible for optical wave propagation in a cubic medium:
where εk is the coefficient for cubic medium nonlinearity (Kerr nonlinearity), and denotes the Laplace operator.
The turbulent phase screen εt is constructed in a regular way by the spectral method [10]. In this case, to simplify the calculations the spectral density function of turbulent inhomogeneities εt is modeled by a step-function: θ(k − kg)⋅τ. Here, kg is the upper cut-off spatial frequency of the pulse spectrum, and τ is a free parameter associated with the amplitude of the turbulence [11].
Next, it will be convenient to consider the problem in normalized coordinates: r → r/r0, z → z/Lr, U → U/A0. Here, r0 is the characteristic beam radius launching the medium, is the Rayleigh length representing the characteristic length of beam diffraction, and A0 is the initial electric field amplitude.
Let us first consider, for the purpose of primary analysis, a purely cubic medium. In cylindrical coordinates, the NLSE in normalized coordinates reads as
where, . The solution to this equation can be represented in the following form: , where m is integer. By substitution this in Eq. (3) one obtains
From this expression one can conclude that for a nonzero topological charge, the only physically meaningful is initial beam profile which approaches zero amplitude at the coordinate origin with power dependence greater than r2. By using other types of initial profiles as, e.g., in [3] where the initial optical field with TC m = 1 is taken as , lead to an error in the simulation since causes field instability and infinite amplitude on the beam axis.
For the problem considered of TC transmission over some distance in atmosphere, the issue on the existence of a (quasi-)soliton solution of Eq. (4) is of certain interest. This means that for such soliton the balance condition must be satisfied:
For m = 0, the solution to (5) is well-known as the Townes soliton [6]. However, a question is raised: Is there similar soliton solutions when m > 0? In the literature [7-9], only the approximate solutions for large m-values are known, but for the most practically important cases of small m apparently no such solutions are reported even in a numerical form.
Optical beams with small TC value are important because for large m the beam becomes highly unstable upon propagation and, therefore, for controlled TC transmission it is necessary considering an effective synthesized beam on a relatively large aperture comprised of subbeams carrying small TC. But even for small vortex beams their stability in turbulent medium is in question. Importantly, for the estimations of vortex beam propagation it is necessary to consider the behavior of the rms (effective) beam radius
where is optical power. Hence, the soliton balance condition (5) in accordance with the Virial theorem [12] can be presented in the following form:
This expression defines the lower limit of pulse power, so-called, critical self-focusing power, for each given beam profile. However, this condition is only the necessary criterion, even in a regular case of homogeneous medium. Particularly, in a turbulent atmosphere, the development of a local instability takes place leading to whole beam break-up into vortex-like filaments whose dynamics can be studied only numerically. Alternatively, this expression opens the way for partial compensation of beam diffraction by the optical nonlinearity that enables higher control over the spatial position of phase singularities in the beam profile carrying nonzero topological charge.
3. Results
Consider initial beam profile in the following form [3, 7]:
with two preset topological charges, m = 2 and 4. Vortex beams of such TCs are sufficiently stable in a regular cubic medium against to diffraction and are widely used in theoretical simulations. Initial beam radius is chosen as r0 = 1mm. The topological charge M measured on a finite aperture in the experiment can be calculated as a phase integral over a closed loop C in the beam profile, which covers the region of interest [7]:
Here, s denotes the Pointing vector normalized to the optical intensity:
The topological charge M derived according to (9) during beam propagation in the atmosphere generally can differ from the initial topological charge m, which on average should remain constant [10]. Besides, in the case of laser propagation in turbulent medium due to instability, the centers of phase singularities can walk-off the aperture boundaries.
Figure 1(a,b) show vortex beam profiles (a) at the beginning of a turbulent optical path and (b) after the 10m propagation in turbulent atmosphere.
As seen in Figure 1(b), the displacement of the singularity centers relative to the beam axis could be substantial. Thus, an undesirable situation is possible when working with a limited optical receiver aperture when one could not gather true information about the beam TC, because only part of the beam because only part of the beam will be on the receiver.
In Figure 2 we present the dynamics of M-value calculated within the receiver aperture with the size equal to initial beam radius (1 mm) for three cases: linear homogeneous medium without turbulence, turbulent air without cubic nonlinearity, and air with Kerr-nonlinearity and medium turbulence.
As seen, the effect of medium turbulence on the TC of propagating vortex beam manifests itself in TC changing and even vanishing if measured on the receiver. Moreover, TC can become fractional or even change its sign (negative). The addition of Kerr nonlinearity partially compensates for the turbulent changes of TC especially at the earlier stage of beam propagation.
4. Discussion
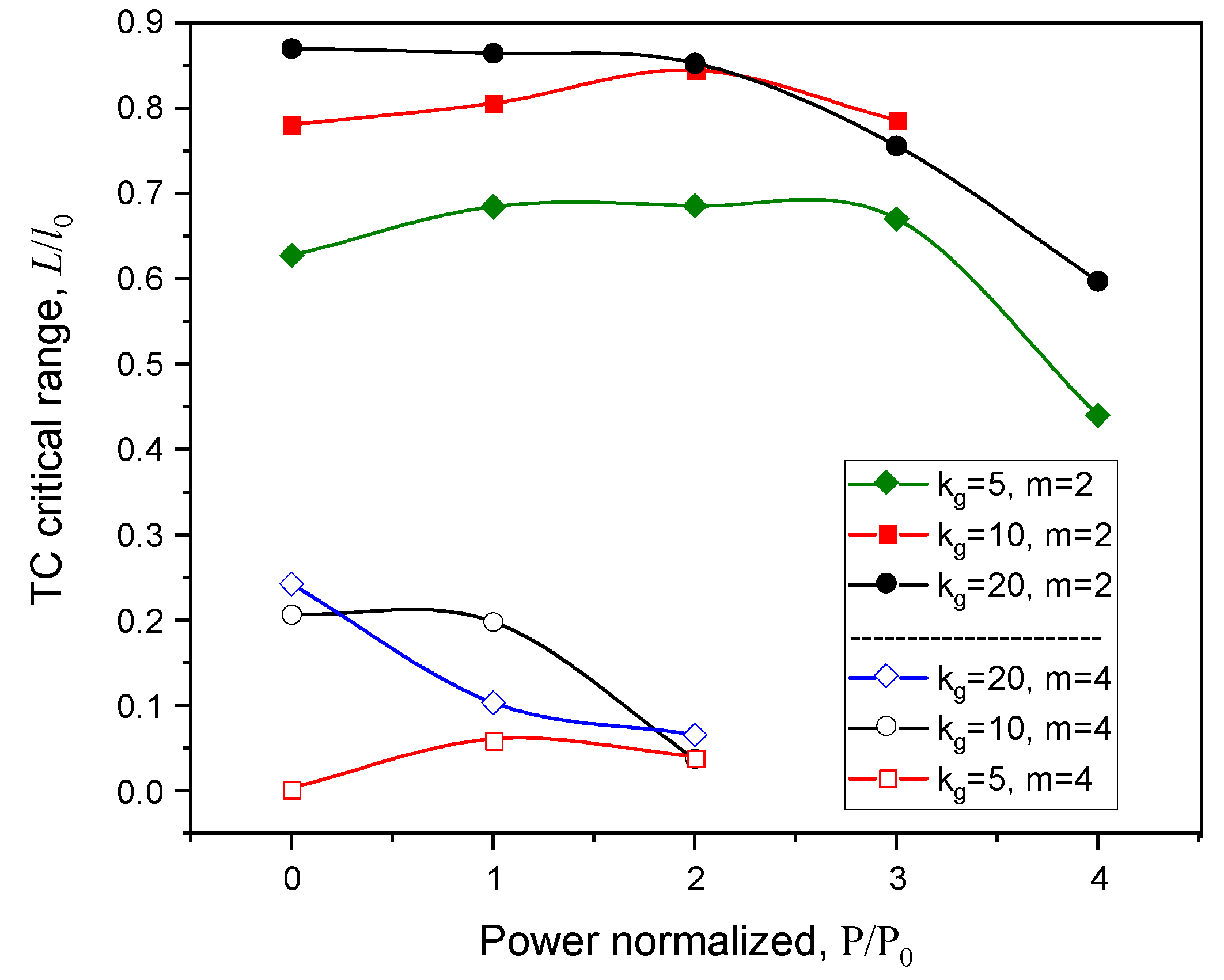
For revealing the TC statistical peculiarities, we varied several problem parameters, namely, pulse power, topological charge, and the turbulence spectrum represented by the cut-off wavevector kg. Worthwhile noting, larger kg values define smaller-scaled turbulence. The results of our simulations are summarized in Figure 3 for a specific distance L where the initial TC m of vortex beam becomes lost when measured within a fixed aperture (1 mm). All the results presented are statistically averaged on 12 independent realizations and normalized on similar TC range l0 in the case of beam propagation in homogeneous linear air.
Obviously, by varying the turbulence scale, laser pulse power, and the value of beam topological charge from Figure 3 one can reveal a general character of power dependence of TC critical distance exhibiting a primary increase and subsequent drop in the values of L measured on a limited receiver aperture. Meanwhile, the critical range increases with decreasing initial TC m of laser beam. At low pulse power, one can see a certain stabilization of singularity center positions near beam axis assisted by the self-focusing air nonlinearity. Here, for moderate m = 2, the distance L of TC detection in turbulent atmosphere is almost equal to the value in clean air (l0).
However, with pulse power increase the influence of air cubic nonlinearity becomes more prominent and the situation reverses which leads to walk-off of the singularities beyond the receiver aperture and L lowering. At the same time, the presence of a peak in the dependences in Figure 3 evidences the manifestation of the stabilizing action of cubic nonlinearity which essentially depends on the turbulence spectrum. Kerr-stabilization effect of phase singularity positions in a turbulent medium is most pronounced for smaller values of initial TC of a vortex beam.
5. Conclusions
In this paper, we consider the joint effect of medium turbulence and cubic nonlinearity on the possibility to capture on a finite receiver aperture the topological charge of a vortex optical beam propagating in a random inhomogeneous medium (air). By the numerical simulations we show, that the cubic nonlinearity at relatively moderate values of initial laser pulse power may be instructive for maintaining the regions of wave phase singularities near the beam axis (within receiver aperture) counteracting the turbulent divergence. At relatively high pulse power, the Kerr-nonlinearity begins to act along with the turbulence and causes faster beam transverse spreading upon pulse propagation.
Obviously, for a more realistic situations one should consider a broader range of pulse parameters including initial beam profile, phase distribution, type of spatial focusing, as well as larger beam scales in real atmospheric conditions. However, the constructive role of cubic nonlinearity makes it one of the promising mechanisms for high-power vortex radiation control for femtosecond atmospheric communications. For this purpose, it is necessary to implement the search for optimal profiles on a wider class of vortex beams and with a more realistic type of medium turbulence meeting to a real atmospheric condition.
Author Contributions
Conceptualization, Y.G. and A.B.; software, methodology, A.B.; validation, A.B., Y.G.; formal analysis and investigation, A.B.; data curation, I.G.; writing—original draft preparation, A.B.; writing—review and editing, Y.G. and I.G.; supervision, Y.G.; funding acquisition, Y.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Ministry of Science and Higher Education of the Russian Federation (V.E. Zuev Institute of Atmospheric Optics SB RAS).
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, F.; Liu, X.; Cai, Y. Propagation of partially coherent beam in turbulent atmosphere: a review (invited review). Progress in Electromagnetics Research. 2015, 150, 123–143. [Google Scholar] [CrossRef]
- Vinçotte, A.; Bergé, L. Femtosecond optical vortices in air. Phys Rev Lett. 2005, 95, 193901. [Google Scholar] [CrossRef]
- Yao, Gang; Yuhua Li and Rui-Pin Chen. Collapse Dynamics of Vortex Beams in a Kerr Medium with Refractive Index Modulation and PT-Symmetric Lattices Photonics. 2022, 9, 249. [CrossRef]
- Marcucci, G.; Danieli, C.; Conti, C. and Boyd, R. W. Vortex-beam Waveguide Lattices in Turbulent Kerr Media: Flat Bands, Anderson Localization of Light, and Topological Edge States OSA Nonlinear Optics 2021 , NM2A.2. [CrossRef]
- Yao, G.; Chew, K.H.; Wu, Y.; Li, Y.; Chen, R.P. Propagation dynamics of vector vortex beams in a strongly nonlocal nonlinear medium with parity-time-symmetric potentials. J. Opt. 2022, 24, 35606. [Google Scholar] [CrossRef]
- Porras, M.A.; Parola, A.; Faccio, D.; Couairon, A. and Trapani P.Di. Light-filament dynamics and the spatiotemporal instability of the Townes profile. Phys. Rev. A 2007. [Google Scholar] [CrossRef]
- Fibich, G. and Gavish, N. Theory of singular vortex solutions of the nonlinear Schrödinger equation Physica D: Nonlinear Phenomena 2008,237, 2696-2730. [CrossRef]
- Mizumachi, T. Discrete Instability of bound states for 2d nonlinear Schrödinger equations Contin. Dyn. Syst. 2005, 13, 413–428. [Google Scholar] [CrossRef]
- Mizumachi, T. Vortex solitons for 2d focusing nonlinear Schrödinger equation Differential Integral Equations 2007,12, 241–264. [CrossRef]
- Starikov, F.A.; Kochemasov, G. G.; Kulikov, S. M.; et al. Wavefront reconstruction of an optical vortex by a Hartmann-Shack sensor. Opt. Lett. 2007, 32, 2291–2293. [Google Scholar] [CrossRef]
- Kandidov, V. P. ; Kosareva, O. G.; Tamarov, M. P.; Brodeur, A.; Chin, S. L. Nucleation and random movement of filaments in the propagation of high-power laser radiation in a turbulent atmosphere Kvantovaya Elektronika 1999, 29, 73–77. [CrossRef]
- Apeksimov, D.V.; Bulygin, A.D.; Geints, Yu.E.; et al. Statistical parameters of femtosecond laser pulse post-filament propagation on a 65 m air path with localized optical turbulence. J. Opt. Soc. Am. B. 2022, 39, 3237–3246. [Google Scholar] [CrossRef]
Figure 1.
Amplitude profile (color surface) and vector field s (arrows) of the vortex beam with m = 2 (a) at optical path beginning and (b) after 10 m propagation in turbulent air. The circles mark the boundaries of singularities.
Figure 1.
Amplitude profile (color surface) and vector field s (arrows) of the vortex beam with m = 2 (a) at optical path beginning and (b) after 10 m propagation in turbulent air. The circles mark the boundaries of singularities.
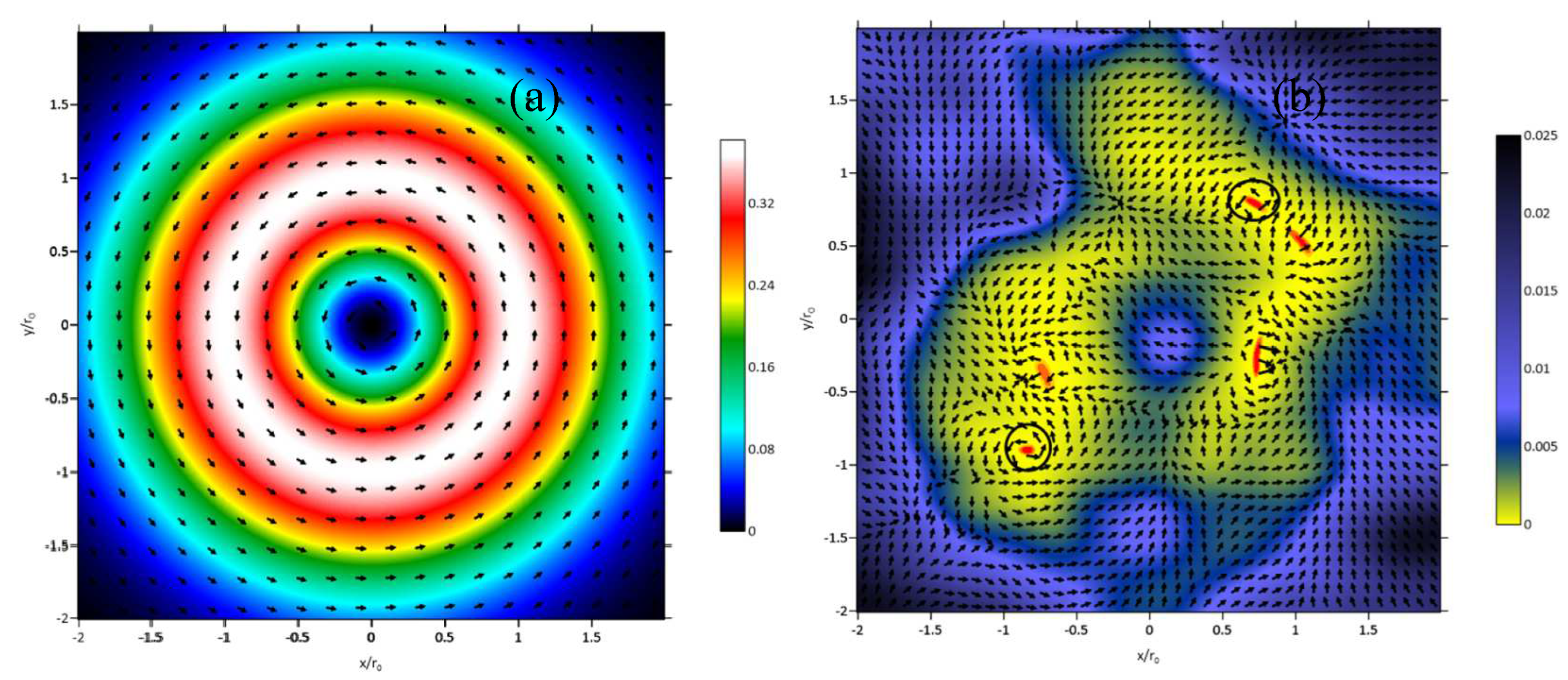
Figure 2.
Calculated intra-aperture topological charge M of a vortex beam with m = 2 propagating in air for different atmospheric situations.
Figure 2.
Calculated intra-aperture topological charge M of a vortex beam with m = 2 propagating in air for different atmospheric situations.
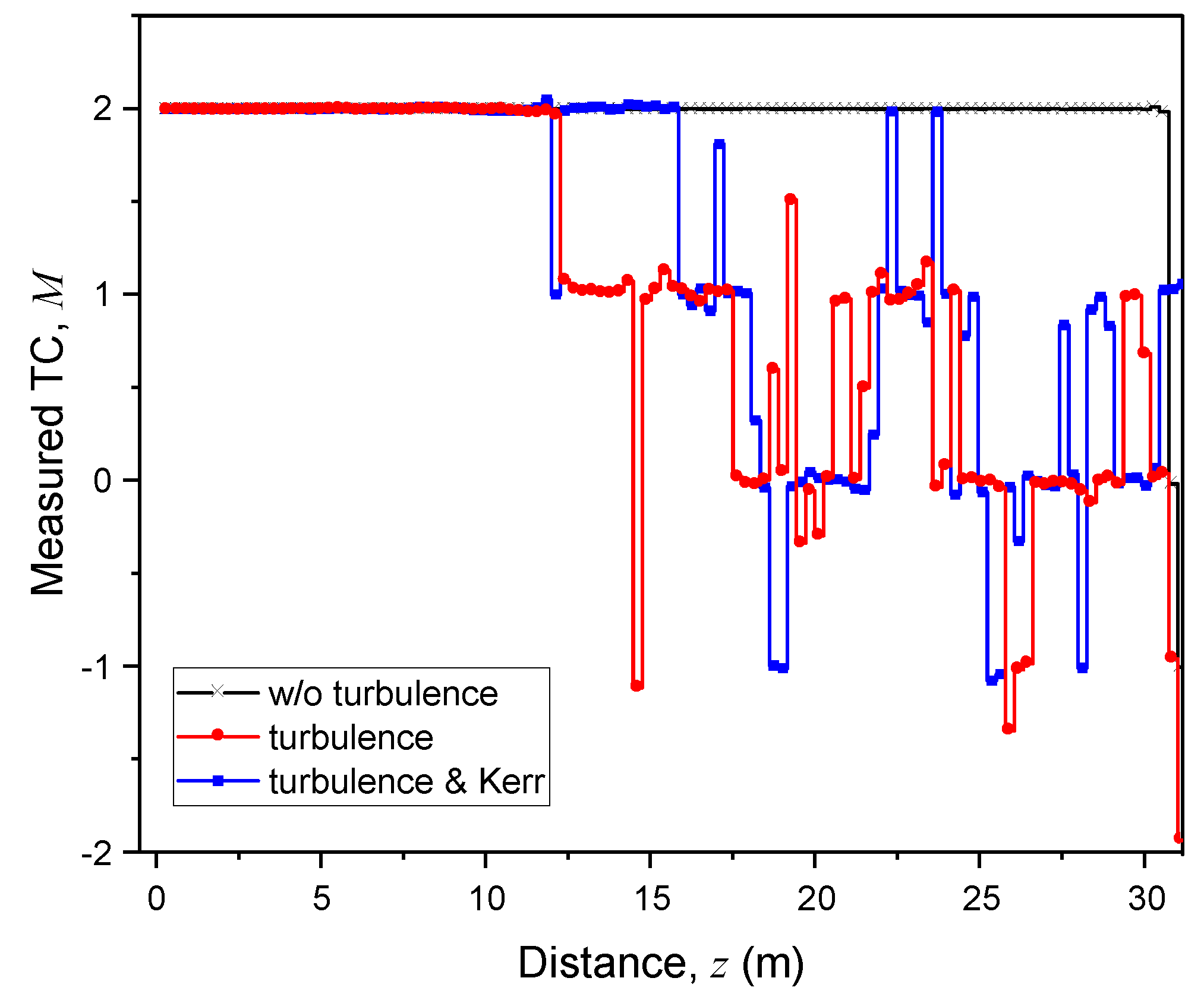
Figure 3.
Critical range (L) for initial beam TC loss relative to nonturbulent linear air (l0) at pulse power P0 = 3 GW (kg is given in cm-1).
Figure 3.
Critical range (L) for initial beam TC loss relative to nonturbulent linear air (l0) at pulse power P0 = 3 GW (kg is given in cm-1).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Submitted:
23 June 2023
Posted:
23 June 2023
You are already at the latest version
Alerts
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
23 June 2023
Posted:
23 June 2023
You are already at the latest version
Alerts
Abstract
The dynamics of the topological charge of a vortex optical beam propagating in a turbulent air with accounting for the cubic nonlinearity is theoretically considered. On a number of examples, we show that the optical beam self-focusing manifests itself ambiguously depending on optical wave power. At near-critical values of beam power, self-focusing leads to enhanced spatial localization of optical vortices and substantial suppression of vortex walk-off relative to the beam axis caused by air turbulence. However, with increasing of optical intensity the modulation instability imposed by cubic nonlinearity becomes significant and contributes jointly with medium turbulence to faster divergence of vortex beams.
Keywords:
Subject: Physical Sciences - Optics and Photonics
1. Introduction
The study of propagation of optical radiation with a non-zero topological charge in real turbulent atmosphere is an urgent task because such optical beams are considered as a basis for development of potentially stable communication links. The study of such vortex beams is devoted to a large number of works (see, e.g., [1-4]). Usually, when studying the propagation of vortex laser beams in turbulent medium air optical nonlinearity is not taken into account [1]. At the same time, the femtosecond atmospheric optics is currently actively developing and the question of vortex propagation beams are also actively studied in the context of high-power ultrafast optical communications [2-4]. As a rule, the researchers are interested in the influence of the topological charge on the propagation dynamics of a laser pulse, particularly, the effect of the topological charge on the stability and spatial energetic characteristics of optical radiation is studied or the manifestation of some specific effects which are characteristic for nonlinear femtosecond optics with random parameters [4].
At the same time, the topics on how optical medium nonlinearity affects the topological charge (TC) of a propagating laser radiation and the possibility of using TC as a communication channel are less explored to-date. Meanwhile, the vortex beam in a turbulent medium is known to be unstable [5-9], i.e. it splits upon propagation into several vortices with different TCs, while the character of their spatial distribution becomes chaotic which at realistic restrictions on the aperture of a receiver optics becomes a big challenge. This problem can be overcome to a greater or lesser degree by superimposing phase plates (including focusing of different types). Another possible method for the manipulation the optical vortex dynamics relies on the controlled use of nonlinear effects in the propagation medium [4]. The aim of this brief communication is answering the question on how the optical cubic nonlinearity affects the vortex beam propagation in a randomly inhomogeneous (turbulent) medium.
2. Materials and Methods
To find a solution to the problem considered, it is necessary to solve the nonlinear Schrödinger equation (NLSE) for an optical pulse envelope propagating in a nonlinear random medium. In this case, one should take into account not only the cubic (Kerr) nonlinearity, but also other physical effects associated with higher optical nonlinearities causing pulse transverse collapse arrest and the realization of pulse filamentation regime.
We consider the NLSE-type pulse propagation equation in the following form [2]:
Here, k0 is the wave number at the carrier wavelength (800 nm), εl and αl are the coefficients for the l-th order nonlinearity leading to the beam self-focusing arrest. These coefficients account for the physical effects stimulating wave refraction and nonlinear absorption in the self-induced electron plasma, respectively. In Eq. (1) the operator is introduced which is responsible for optical wave propagation in a cubic medium:
where εk is the coefficient for cubic medium nonlinearity (Kerr nonlinearity), and denotes the Laplace operator.
The turbulent phase screen εt is constructed in a regular way by the spectral method [10]. In this case, to simplify the calculations the spectral density function of turbulent inhomogeneities εt is modeled by a step-function: θ(k − kg)⋅τ. Here, kg is the upper cut-off spatial frequency of the pulse spectrum, and τ is a free parameter associated with the amplitude of the turbulence [11].
Next, it will be convenient to consider the problem in normalized coordinates: r → r/r0, z → z/Lr, U → U/A0. Here, r0 is the characteristic beam radius launching the medium, is the Rayleigh length representing the characteristic length of beam diffraction, and A0 is the initial electric field amplitude.
Let us first consider, for the purpose of primary analysis, a purely cubic medium. In cylindrical coordinates, the NLSE in normalized coordinates reads as
where, . The solution to this equation can be represented in the following form: , where m is integer. By substitution this in Eq. (3) one obtains
From this expression one can conclude that for a nonzero topological charge, the only physically meaningful is initial beam profile which approaches zero amplitude at the coordinate origin with power dependence greater than r2. By using other types of initial profiles as, e.g., in [3] where the initial optical field with TC m = 1 is taken as , lead to an error in the simulation since causes field instability and infinite amplitude on the beam axis.
For the problem considered of TC transmission over some distance in atmosphere, the issue on the existence of a (quasi-)soliton solution of Eq. (4) is of certain interest. This means that for such soliton the balance condition must be satisfied:
For m = 0, the solution to (5) is well-known as the Townes soliton [6]. However, a question is raised: Is there similar soliton solutions when m > 0? In the literature [7-9], only the approximate solutions for large m-values are known, but for the most practically important cases of small m apparently no such solutions are reported even in a numerical form.
Optical beams with small TC value are important because for large m the beam becomes highly unstable upon propagation and, therefore, for controlled TC transmission it is necessary considering an effective synthesized beam on a relatively large aperture comprised of subbeams carrying small TC. But even for small vortex beams their stability in turbulent medium is in question. Importantly, for the estimations of vortex beam propagation it is necessary to consider the behavior of the rms (effective) beam radius
where is optical power. Hence, the soliton balance condition (5) in accordance with the Virial theorem [12] can be presented in the following form:
This expression defines the lower limit of pulse power, so-called, critical self-focusing power, for each given beam profile. However, this condition is only the necessary criterion, even in a regular case of homogeneous medium. Particularly, in a turbulent atmosphere, the development of a local instability takes place leading to whole beam break-up into vortex-like filaments whose dynamics can be studied only numerically. Alternatively, this expression opens the way for partial compensation of beam diffraction by the optical nonlinearity that enables higher control over the spatial position of phase singularities in the beam profile carrying nonzero topological charge.
3. Results
Consider initial beam profile in the following form [3, 7]:
with two preset topological charges, m = 2 and 4. Vortex beams of such TCs are sufficiently stable in a regular cubic medium against to diffraction and are widely used in theoretical simulations. Initial beam radius is chosen as r0 = 1mm. The topological charge M measured on a finite aperture in the experiment can be calculated as a phase integral over a closed loop C in the beam profile, which covers the region of interest [7]:
Here, s denotes the Pointing vector normalized to the optical intensity:
The topological charge M derived according to (9) during beam propagation in the atmosphere generally can differ from the initial topological charge m, which on average should remain constant [10]. Besides, in the case of laser propagation in turbulent medium due to instability, the centers of phase singularities can walk-off the aperture boundaries.
Figure 1(a,b) show vortex beam profiles (a) at the beginning of a turbulent optical path and (b) after the 10m propagation in turbulent atmosphere.
As seen in Figure 1(b), the displacement of the singularity centers relative to the beam axis could be substantial. Thus, an undesirable situation is possible when working with a limited optical receiver aperture when one could not gather true information about the beam TC, because only part of the beam because only part of the beam will be on the receiver.
In Figure 2 we present the dynamics of M-value calculated within the receiver aperture with the size equal to initial beam radius (1 mm) for three cases: linear homogeneous medium without turbulence, turbulent air without cubic nonlinearity, and air with Kerr-nonlinearity and medium turbulence.
As seen, the effect of medium turbulence on the TC of propagating vortex beam manifests itself in TC changing and even vanishing if measured on the receiver. Moreover, TC can become fractional or even change its sign (negative). The addition of Kerr nonlinearity partially compensates for the turbulent changes of TC especially at the earlier stage of beam propagation.
4. Discussion
For revealing the TC statistical peculiarities, we varied several problem parameters, namely, pulse power, topological charge, and the turbulence spectrum represented by the cut-off wavevector kg. Worthwhile noting, larger kg values define smaller-scaled turbulence. The results of our simulations are summarized in Figure 3 for a specific distance L where the initial TC m of vortex beam becomes lost when measured within a fixed aperture (1 mm). All the results presented are statistically averaged on 12 independent realizations and normalized on similar TC range l0 in the case of beam propagation in homogeneous linear air.
Obviously, by varying the turbulence scale, laser pulse power, and the value of beam topological charge from Figure 3 one can reveal a general character of power dependence of TC critical distance exhibiting a primary increase and subsequent drop in the values of L measured on a limited receiver aperture. Meanwhile, the critical range increases with decreasing initial TC m of laser beam. At low pulse power, one can see a certain stabilization of singularity center positions near beam axis assisted by the self-focusing air nonlinearity. Here, for moderate m = 2, the distance L of TC detection in turbulent atmosphere is almost equal to the value in clean air (l0).
However, with pulse power increase the influence of air cubic nonlinearity becomes more prominent and the situation reverses which leads to walk-off of the singularities beyond the receiver aperture and L lowering. At the same time, the presence of a peak in the dependences in Figure 3 evidences the manifestation of the stabilizing action of cubic nonlinearity which essentially depends on the turbulence spectrum. Kerr-stabilization effect of phase singularity positions in a turbulent medium is most pronounced for smaller values of initial TC of a vortex beam.
5. Conclusions
In this paper, we consider the joint effect of medium turbulence and cubic nonlinearity on the possibility to capture on a finite receiver aperture the topological charge of a vortex optical beam propagating in a random inhomogeneous medium (air). By the numerical simulations we show, that the cubic nonlinearity at relatively moderate values of initial laser pulse power may be instructive for maintaining the regions of wave phase singularities near the beam axis (within receiver aperture) counteracting the turbulent divergence. At relatively high pulse power, the Kerr-nonlinearity begins to act along with the turbulence and causes faster beam transverse spreading upon pulse propagation.
Obviously, for a more realistic situations one should consider a broader range of pulse parameters including initial beam profile, phase distribution, type of spatial focusing, as well as larger beam scales in real atmospheric conditions. However, the constructive role of cubic nonlinearity makes it one of the promising mechanisms for high-power vortex radiation control for femtosecond atmospheric communications. For this purpose, it is necessary to implement the search for optimal profiles on a wider class of vortex beams and with a more realistic type of medium turbulence meeting to a real atmospheric condition.
Author Contributions
Conceptualization, Y.G. and A.B.; software, methodology, A.B.; validation, A.B., Y.G.; formal analysis and investigation, A.B.; data curation, I.G.; writing—original draft preparation, A.B.; writing—review and editing, Y.G. and I.G.; supervision, Y.G.; funding acquisition, Y.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Ministry of Science and Higher Education of the Russian Federation (V.E. Zuev Institute of Atmospheric Optics SB RAS).
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, F.; Liu, X.; Cai, Y. Propagation of partially coherent beam in turbulent atmosphere: a review (invited review). Progress in Electromagnetics Research. 2015, 150, 123–143. [Google Scholar] [CrossRef]
- Vinçotte, A.; Bergé, L. Femtosecond optical vortices in air. Phys Rev Lett. 2005, 95, 193901. [Google Scholar] [CrossRef]
- Yao, Gang; Yuhua Li and Rui-Pin Chen. Collapse Dynamics of Vortex Beams in a Kerr Medium with Refractive Index Modulation and PT-Symmetric Lattices Photonics. 2022, 9, 249. [CrossRef]
- Marcucci, G.; Danieli, C.; Conti, C. and Boyd, R. W. Vortex-beam Waveguide Lattices in Turbulent Kerr Media: Flat Bands, Anderson Localization of Light, and Topological Edge States OSA Nonlinear Optics 2021 , NM2A.2. [CrossRef]
- Yao, G.; Chew, K.H.; Wu, Y.; Li, Y.; Chen, R.P. Propagation dynamics of vector vortex beams in a strongly nonlocal nonlinear medium with parity-time-symmetric potentials. J. Opt. 2022, 24, 35606. [Google Scholar] [CrossRef]
- Porras, M.A.; Parola, A.; Faccio, D.; Couairon, A. and Trapani P.Di. Light-filament dynamics and the spatiotemporal instability of the Townes profile. Phys. Rev. A 2007. [Google Scholar] [CrossRef]
- Fibich, G. and Gavish, N. Theory of singular vortex solutions of the nonlinear Schrödinger equation Physica D: Nonlinear Phenomena 2008,237, 2696-2730. [CrossRef]
- Mizumachi, T. Discrete Instability of bound states for 2d nonlinear Schrödinger equations Contin. Dyn. Syst. 2005, 13, 413–428. [Google Scholar] [CrossRef]
- Mizumachi, T. Vortex solitons for 2d focusing nonlinear Schrödinger equation Differential Integral Equations 2007,12, 241–264. [CrossRef]
- Starikov, F.A.; Kochemasov, G. G.; Kulikov, S. M.; et al. Wavefront reconstruction of an optical vortex by a Hartmann-Shack sensor. Opt. Lett. 2007, 32, 2291–2293. [Google Scholar] [CrossRef]
- Kandidov, V. P. ; Kosareva, O. G.; Tamarov, M. P.; Brodeur, A.; Chin, S. L. Nucleation and random movement of filaments in the propagation of high-power laser radiation in a turbulent atmosphere Kvantovaya Elektronika 1999, 29, 73–77. [CrossRef]
- Apeksimov, D.V.; Bulygin, A.D.; Geints, Yu.E.; et al. Statistical parameters of femtosecond laser pulse post-filament propagation on a 65 m air path with localized optical turbulence. J. Opt. Soc. Am. B. 2022, 39, 3237–3246. [Google Scholar] [CrossRef]
Figure 1.
Amplitude profile (color surface) and vector field s (arrows) of the vortex beam with m = 2 (a) at optical path beginning and (b) after 10 m propagation in turbulent air. The circles mark the boundaries of singularities.
Figure 1.
Amplitude profile (color surface) and vector field s (arrows) of the vortex beam with m = 2 (a) at optical path beginning and (b) after 10 m propagation in turbulent air. The circles mark the boundaries of singularities.

Figure 2.
Calculated intra-aperture topological charge M of a vortex beam with m = 2 propagating in air for different atmospheric situations.
Figure 2.
Calculated intra-aperture topological charge M of a vortex beam with m = 2 propagating in air for different atmospheric situations.

Figure 3.
Critical range (L) for initial beam TC loss relative to nonturbulent linear air (l0) at pulse power P0 = 3 GW (kg is given in cm-1).
Figure 3.
Critical range (L) for initial beam TC loss relative to nonturbulent linear air (l0) at pulse power P0 = 3 GW (kg is given in cm-1).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Off-Axis Vortex Beam Propagation through Classical Optical System in Terms of Kummer Confluent Hypergeometric Function
Ireneusz Augustyniak
et al.
Photonics,
2020
The Effect of Air Turbulence on Vortex Beams in Nonlinear Propagation
Di Zhu
et al.
Sensors,
2023
Hall Effect at the Focus of an Optical Vortex with Linear Polarization
Victor Kotlyar
et al.
Micromachines,
2023
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






