Microscopic Mechanism of Ultrosonic Vibration Assisted Pressing WC-Co Powder by Simulation

The ultrasonic vibration assisted pressing process can improve the fluidity, the uneven distribution of density and particle size of WC-Co powder. However, the microscopic mechanism of ultrasonic vibration on the powder remains unclear. In this paper, WC and Co particles are simulated by three-dimensional spherical models of two particle sizes with the aide of the secondary development of Python. At the same time, the forming process of powder at mesoscale is simulated in the virtue of the finite element analysis software ABAQUS. The influence of vibration amplitude on the fluidity, the filling density and the stress distribution of WC-Co powder is investigated when the ultrasonic vibration is applied to the conventional pressing process. From simulation results, the ultrasonic vibration amplitude has great influences on the density of the compact. With the increase of the ultrasonic amplitude, the compact density also increases gradually. At the initial stage of the compaction, the particles move violently under the action of ultrasonic vibration, the fluidity is obviously enhanced, the arch bridge effect between particles is destroyed, the fine particles quickly fill the pores between the large particles, which increase the density, and the residual stress in the billet decreases after the compaction. From the experimental results, the size distribution of the billet is more uniform, the elastic aftereffect is reduced, the dimensional instability is improved, and the density curves obtained by experiment and simulation are within a reasonable error range.

Keywords:

Subject:

Chemistry and Materials Science - Materials Science and Technology

1. Introduction

WC-Co cemented carbide with high hardness, high toughness, high wear resistance and other excellent properties, is widely used in many fields, such as mining, aerospace, automobile manufacturing, oil drilling and so on [1,2].With the continuous improvement of social production level, the demand for cemented carbide in manufacturing industry is increasing. However, in the actual production process, the cemented carbide billet often appear various defects such as delamination, fracture, missing angle, etc. because of the poor powder fluidity, the uneven distribution of density and particle size, which greatly limits the application of its products in various fields[3]. Improving the uniformity of billet density and particle size distribution of cemented carbide can not only improve the hardness, bending strength, fracture toughness and other comprehensive mechanical properties, but also improve the physical properties of the material itself, such as electrical conductivity, thermal conductivity, permeability, thermal expansion coefficient, and high density powder metallurgy materials can also make parts have better machining performance and machining surface[4,5,6].

As a result, in order to improve the process of powder metallurgy, reduce the rejection rate and improve the comprehensive performance of products, domestic and foreign researchers have carried out a lot of research on the movement law of powder. The research shows that the particle will produce volume effect, surface effect and particle convection phenomenon under the ultrasonic vibration assisted pressing process [7,8]. Zhao Yanbo et al. [9]. studied the influence of vibration frequency and vibration amplitude on the filling effect of iron powder, and obtained the best parameters of filling effect. Zuo Miaomiao et al. [8]. analyzed the differences of internal contact force of granular medium, force chain, porosity and coordination number in the particle medium after the action of the ultrasonic vibration. Wang Wentao et al. [10] studied the effect of vibration on the dense packing of refractory powder, and obtained that the average porosity of powder first decreases and then increased with the increase of vibration time, and pointed out that the compaction effect caused by longitudinal vibration was better than that caused by transverse vibration. Sedaghat et al. [11] proposed a physics-based constitutive model to accurately describe the deformation behavior in the process of ultrasonic vibration assisted forming. At the same time finite element method was used to conduct numerical simulation of upsetting and progressive forming to evaluate the accuracy of the model. From results by considering the dislocation dynamics and acoustic energy transfer mechanism in the material under the ultrasonic vibration, the newly established ultrasonic constitutive equation could accurately predict the acoustic-plastic behavior of the material. Meanwhile, the application of ultrasonic vibration could significantly reduce the flow stress of the material, making it become soft during the forming process. The larger the amplitude, the smaller the inflow stress. Liu Bo et al. [12] used discrete element software to simulate the influence of Nd/Fe/B permanent magnet powder on the filling density at different vibration frequencies and vibration times. The results showed that the filling density reached its maximum when the vibration frequency was between 66 and 70 Hz, and the density first increased and then stabilized with the increase of vibration time. However, there were few studies on the pressing process of WC-Co cemented carbide by the ultrasonic vibration assisted pressing process.

This work proposes ABAQUS finite element software and Python co-simulation to simulate the pressing process of WC-Co powder with the aid of ultrasonic vibration. Compared with conventional pressing, the change is explored of vibration amplitude on the evolution of the fluidity, filling density and stress distribution of WC-Co powder after the ultrasonic vibration is applied, and the pressing experiment is compared with the simulation results.

2. Construction of the experiment Platform

An experiment platform is constructed to apply the axial ultrasonic vibration to the traditional pressing process, as shown in Figure 1. This platform is primarily made up of five parts: an automatic press, an ultrasonic transducer, an ultrasonic generator, a mold set and a piece of rubber cushion. The ultrasonic transducer is composed of a piezoelectric ceramic transducer, which can convert electrical energy into mechanical energy, an amplitude bar and a tool head. The vibration frequency is 20 kHz, the driving power is 2 kW, and the ultrasonic amplitude can be steplessly adjusted from 0% to 100%. It is mounted on the press with a flange whose pressure is transmitted directly to the transducer shell.

Firstly, a certain mass of mixture of WC-Co powder is weighed and poured into the mold. When the mold is filled with powder, the automatic press is started to make its indenter move slowly until it comes into contact with the powder. Then, the ultrasonic transducer is started and certain pressure is applied for the prepressure ultrasound for a few seconds. Finally, the pressure is applied slowly until the working pressure. In order to calculate the density, the mass, the height and the diameter of the pressed billet are measured, and the errors of the mass and size are ±1 mg and ±0.01 mm, respectively.

3. Construction of the mathematical model

The continuum theory and the discrete element method are commonly used in the numerical simulation of powder materials [13]. The continuum theory has made a lot of achievements in the research of powder impact forming, which mainly regards powder as a continuum to study the dynamic mechanical response of powder in the loading process [14]. Compared with the continuum theory, the discrete element method regards powder particles as independent discrete individuals, and each discrete individual has corresponding physical properties, so the discrete element method is more in line with the actual situation. In this paper, the numerical simulation of WC-Co powder pressing process is carried out based on the discrete element method, according to Newton's second law, so the equation of motion can be obtained as shown in Equation (1):

M \frac{d^{2} X}{d t^{2}} + C \frac{d X}{d t} + K X (t) = f (t)

(1)

M-the mass of particle, kg; X- the displacement of particle, m; C- the damping coefficient; K-the elastic coefficient; t-time, s; f-the unit load, N.

The role of the ultrasonic vibration assisted powder pressing process is to make the powder particles inside the mold have violent collision contact through high-frequency vibration, resulting in greater mobility, so that some smaller particles are evenly filled into the pores, so as to improve the density of the billet and reduce its porosity [8]. In order to better fit the actual situation and reduce the calculation amount, the soft ball model is used to calculate the contact force between particles. The model structure is shown in Figure 2. Particle i and particle j have contact slip under the external forces. The dotted line represents the particles just in contact, a represents the amount of overlap between the two particles in the normal direction, and b represents the tangential displacement of particle j.

According to the soft ball contact mechanics model, Figure 3 is a three-dimensional simplified model, which mainly introduces damping, spring and friction coefficient between the two particles [15], and its normal force (

F_{n i j}

) is shown in Equation (2).

F_{n i j} = - n [K_{n} a^{3 / 2} + C_{n} (V_{n i} - V_{n j}) n]

(2)

n- the unit vector of particle i and particle j; a- the normal overlap of two particles;

a = r_{i} + r_{j} - g_{i j}

;

g_{i j}

-the distance between two particle centers;

v_{n i}

and

v_{n j}

-the normal velocity of particle motion;

K_{n}

-the normal elastic coefficient;

C_{n}

- the normal damping coefficient. The unit vector of particle i and particle j (N), the normal elastic coefficient (

K_{n}

) and the normal damping coefficient (

C_{n}

) are shown in Equation (3), (4) and (5).

n = \frac{r_{i} - r_{j}}{| r_{i} - r_{j} |}

(3)

K_{n} = \frac{4}{3} E^{*} {(R^{*})}^{1 / 2}

(4)

C_{n} = 2 {(m K_{n})}^{1 / 2}

(5)

m- the mass of particle; E^*- the effective modulus of elasticity; R^*- the effective radius of particle; E* and R* can be obtained from equations (6) and (7)

E^{*} = \frac{E_{i} E_{j}}{E_{i} (1 - v_{i}^{2}) + E_{j} (1 - v_{j}^{2})}

(6)

R^{*} = \frac{r_{i} r_{j}}{r_{i} + r_{j}}

(7)

E_i and E_j are the elastic modulus of particle i and particle j, respectively, and v_i and v_j are the Poisson's ratios of particle i and particle j, respectively.

Tangential force (

F_{t i j}

) between particles is shown in Equation (8):

F_{t i j} = - (K_{t} b + C_{t} V_{t})

(8)

where, b is the tangential displacement;

V_{t}

is the particle contact point velocity;

K_{t}

and

C_{t}

are the tangential elastic coefficient and the damping coefficient, respectively. Where

K_{t}

and

C_{t}

can be obtained from equations (9) and (10):

K_{t} = 8 a^{1 / 2} G^{*} {(R^{*})}^{1 / 2}

(9)

C_{t} = 2 {(m K_{t})}^{1 / 2}

(10)

where, G* is the effective shear modulus, and its calculation formula is shown in Equation (11):

G^{*} = \frac{G_{i} (2 - v_{j}) + G_{j} (2 - v_{i})}{G_{i} G_{j}}

(11)

where, G_i and G_j are shear modulus of the particle i and the particle j, respectively.

4. Random generation of three-dimensional powder particles

In this paper, finite element simulation is carried out on the microscale particles to compare the mechanism of the particle rearrangement, deformation and interaction under the assisted pressing process of ultrasonic vibration. The entire simulation process is shown in Figure 4a. First, the electron microscopic images of WC with a particle size of 5 μm and Co powder particles with a particle size of 1.2 μm are obtained, as shown in Figure 4b,c. It can be seen from the figures that WC and Co particles are similar to spherical particles. Therefore, a three-dimensional spherical model of two particle sizes is adopted to simulate WC and Co particles.

Random generation of powder particles is performed through ABAQUS and Python secondary development. The main principles are as follows:

① To set the powder particle drop area, for example, randomly drop particles with radius R in a cube with length, width and height of 10, as shown in Figure 5, and their spherical coordinates (x,y,z) must be satisfied R≤x≤10-R, R≤y≤10-R and R≤z≤10-R.

② To determine whether the randomly generated balls overlap

Since two spherical particles of different particle sizes are generated, the radius of the two particle sizes is set to R₁ and R₂, respectively. The distance between the two spheres can be obtained by formula (12):

d = \sqrt{{(x_{i} - x_{j})}^{2} + {(y_{i} - y_{j})}^{2} + {(z_{i} - z_{j})}^{2}}

(12)

The distance between any two particles should meet the following conditions, as shown in equation (13) and (14):

d_{1} \geq 2 R_{1}

(13)

d_{2} \geq R_{1} + R_{2}

(14)

③ To set and control the number and density of particles generated.

5. Simulation model and parameter setting

5.1. Material attribute

The assignment of material properties is one of the essential steps of finite element simulation, and ABAQUS software has a dedicated material library containing most of the commonly used materials, so the user can call or enter parameters directly. At the same time, the matching of parameter units is extremely important, the main reason is that ABAQUS software has no fixed unit, so the user has to choose the corresponding matching unit for each quantity, and the unit of the final calculation result corresponds to the unit used. In this paper, the material properties of the corresponding parts are assigned, as shown in Table 1.

5.2. Analysis step setting and meshing

This work mainly studies the pressing process of WC-Co powder. The changes between powder particles are relatively complex, and there are multi-directional motion, rotation, collision, contact deformation, etc., in the moving process, so this process is a highly nonlinear problem. In order to improve the efficiency of finite element calculation and save the simulation time, this paper adopts the dynamic-display analysis step to carry out the finite element simulation of the conventional pressing process and the ultrasonic assisted pressing process.

In view of the complex particle movement in the powder pressing process, the mesh may be distorted, so the 4-node linear tetrahedral element mesh C3D4 in the dynamic-display analysis step is used in this paper. Since the parts have to repeat many times when performing material assignment and meshes in ABAQUS, the Python script is called to automate the material assignment and meshes, as shown in Figure 6.

5.3. Contact properties and boundary conditions

When the contact properties are defined, the powder particles are deformable, while the die and punch are set to rigid, compaction begins with the upper punch, and the die and lower punch are fixed. In the powder pressing process, the pressure is not all the deformation of the powder particles, and part of it is consumed by the friction between the particles, the particles and the mold wall, so the pressure is gradually decreasing from top to bottom.

Here, under conventional pressing conditions, the friction coefficient of WC-Co is 0.2. Under ultrasonic pressing conditions, due to the anti-friction effect of ultrasound, the friction coefficient will be reduced by about 50% according to Siegert's research [16,17,18], so the friction coefficient is 0.1.

This work adopts axial unidirectional pressing, and apply uniform downward displacement and sinusoidal vibration to the upper punch for a downward displacement 24 μm and the pressing time 1×10^-2 s, which displacement time curves are coupled. At the same ultrasonic frequency of 20 kHz, the amplitudes of 1, 2 and 3 μm are applied, respectively. The effects of different amplitudes on the fluidity, filling density and stress distribution of WC-Co powder are investigated. To speed up the simulation, the mold and powder filling ranges are scaled, while other physical quantities are adjusted accordingly [19].

6. Results

6.1. Analysis of the Particle Flow under the Conventional and the Ultrasonic Vibration-assisted Compression Processes

The fluidity characteristics of WC and Co particles are shown in Figure 7 under conventional and ultrasound-assisted compression conditions. In order to observe the particle fluidity more directly, a semi-sectional view is adopted. It can be seen from the figure that, without considering gravity, there are large pores between WC and Co particles in Figure 7a,e at the initial stage of compaction, and the contact force between particles is zero. When the upper punch moves down, the WC and Co particles near the upper punch first move to fill the pores, so the contact slip occurs between the particles. Compared with conventional compaction and ultrasound-assisted compaction, the particles move violently under the ultrasonic vibration, the particle fluidity is significantly enhanced, the arch bridge effect between particles is destroyed, and the fine particles quickly fill the pores between large particles in a short time to increase the density, and the uniformity of particle size distribution is also improved [19,20]. As the upper punch continues to move down, the compact becomes more and more dense, and the particles gradually change from the original collision and sliding flow to mutual extrusion deformation. At this time, the increase of the compact density is mainly due to the plastic deformation of the particles. At the end of pressing process, the height of the compact is significantly lower than that of conventional pressing process under the action of ultrasonic vibration.

6.2. Effects of ultrasonic vibration amplitudes on the compact density

The relationship curves between the ultrasonic amplitude and the compact density are obtained by the comparison with the conventional pressing process under ultrasonic amplitudes of 1, 2, and 3 μm, respectively, as shown in Figure 8. As can be seen from Figure 8, since the initial density increase is related to the particle displacement, the compact density increases slowly. When the pressure increases to a certain extent, the compact density increases rapidly under the combined action of the plastic deformation and the displacement of the powder particles [21]. After applying different ultrasonic amplitudes, the displacement between particles is accelerated, and smaller particles fill the pores, thus the compact density is significantly increased.

6.3. Effects of the Ultrasonic Vibration on the Stress Distribution of the Compact

The Mises stress distribution cloud of WC and Co particles is shown in Figure 9. under the conventional compression and different ultrasonic amplitudes. It can be found from the figure that the powder particles are deformed after pressing, because the contact between the particles will produce stress concentration, and the WC particles are harder, so the stress concentration is more obvious. However, after the ultrasonic vibration is applied, the stress at the contact between particles gradually decreases with the increase of ultrasonic amplitude, which indicates that ultrasonic vibration can change the stress distribution between particles and reduce the deformation stress between particles. Therefore, the ultrasonic vibration can reduce the stress concentration between particles during the powder pressing process, thereby reducing the residual stress in the compact after the powder pressing, reducing the elastic aftereffect [22], and improving the quality of the compact.

6.4. Experimental verification

Experiments are carried out through two kind of pressing processes to obtain the relationship between the pressing time and the compact density and the experimental results are compared with the simulation results, as shown in Figure 10. It can be seen from the figure that the experimental and simulated compact density errors are not large, and the errors in the forming process are both lower than 10%, indicating that the finite element simulation and experimental results are relatively consistent [23]. When the density is greater than 5 g/cm³, the error between the experimental value and the simulation value is greater than 6%, mainly because the finite element simulation regards the friction coefficient between the particles and between the particles and the mold as a fixed value during the particle forming process, while the friction coefficient between the particles and between the particles and the mold in the actual pressing process is a constantly changing process, especially the deformation and displacement of the particles in the middle and late pressing period are complicated. It is difficult for simulation to accurately reflect the forming process.

The cross-sectional microstructure of the compact under the two pressing conditions is observed and it is found that, as shown in Figure 11, the WC and Co particles are deformed correspondingly, and the particles change from the original approximately circular state to a flat state, which is more consistent with the simulation effect. By comparing the cross sections of conventional and ultrasonic pressing compacts, it is found that the particle size distribution is more uniform under the ultrasonic pressing process, which is related to the acceleration of particle flow rearrangement under the ultrasonic action [24].

When the pressure is withdrawn, the powder particles will slowly return to their original state, and the compact will rebound and expand along the direction of the pressing force during and after demoulding, and the compact size will increase. In order to characterize the size change after demoulding, Chuxuan Chen[25] Expressed as a percentage increase in the size of the compact after demoulding, as shown in equation (15).

δ = \frac{Δ H_{P}}{H_{P}}

(15)

H_p__the pressed size; ∆H_p_ the increased size after demoulding

Under the same pressing force for the conventional and ultrasonic vibration pressing processes, the dimensions of the compact after demoulding and the dimensions of the compact after standing for 15 minutes and 30 minutes are counted. Three different positions on the compact surface are measured for each dimension, and then the average value is taken to obtain the elastic after-effects of the compact after conventional pressing and ultrasonic vibration assisted pressing processes, as shown in Figure 12. The results show that the elastic after-effect of the compact is reduced and the dimensional instability is slightly improved, which is consistent with the simulation results in Figure 8, indicating that the residual internal stress is reduced due to the application of ultrasonic vibration during the pressing process [11].

7. Conclusions

In this paper, Python is used to randomly generate WC and Co particles, which are automatically run for material assignment and meshing to reduce the modeling time. Then, ABAQUS finite element simulation and experiments are conducted on the two pressing processes respectively, and the conclusions are as follows:

(1): The influence of ultrasonic vibration amplitude on the compact density is great, and the compact density increases gradually with the increase of ultrasonic amplitude. Especially in the early stage of particle deformation, the fluidity between particles is relatively intense, and the particles quickly fill the pores, so the filling density of the powder is significantly increased than that under conventional pressing conditions.
(2): The ultrasonic vibration in powder pressing can effectively reduce the deformation stress between particles, reduce the residual stress in the compact after pressing, reduce the elastic after-effect and improve the quality of the compact.
(3): The finite element simulation is consistent with the experimental results, but when the density is greater than 5 g/cm3, the error between the experimental value and the simulation value is greater than 6%, mainly because the finite element simulation regards the friction coefficient between particles and between particles and the mold as a constant value during the particle forming process, while the friction coefficient between particles and between particles and the mold is a constantly changing during the actual pressing process.

Author Contributions

Conceptualization, L.H. and J.X. experiment design, material preparation, and data collection, Y.W.; writing—original draft preparation, Y.C.; writing—review and editing, Y.C.; formal analysis, B.S.; investigation, Y.Y.; supervision, L.H. and J.X. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Natural Science Foundation of Jiangxi province (grant number 20171BAB206030), Key Resource and Development Program for Industrial Fields, and Innovative Leadership Program of Ganzhou Project (Kefa [2020] No. 60).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available from the corresponding author upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

References

Zhang, H.; Xiong, J.; Guo, Z.X.; Yang, T.E.; Yi, J.S.; Yang, S.D.; Liang, L. Influence of WC particle size on high temperature wear resistance of WC-Co cemented carbide. J. Hot working process 2022, 51, 21–24. [Google Scholar]
Wang, X.L.; Yong, W.; Peng Peng, H. Effect of Abrasive Material on Microstructure and Properties of WC-6% Co Cemented Carbide. J. Rare Metals and Carbides 2022, 50, 89–95. [Google Scholar]
Zhou, R.; Zhang, L.H.; He, B.Y.; Liu, Y.H. Numerical simulation of residual stress field in green power metallurgy compacts by modified Drucker–Prager Cap model. J. Transactions of Nonferrous Metals Society of China 2013, 23, 2374–2382. [Google Scholar] [CrossRef]
Ding, Q.; Zheng, Y.; Ke, Z.; Zhang, G.T.; Wu, H.; Xu, X.Y.; Lu, X.P.; Zhu, X.G. Effects of fine WC particle size on the microstructure and mechanical properties of WC-8Co cemented carbides with dual-scale and dual-morphology WC grains. J. International Journal of Refractory Metals and Hard Materials 2020, 87, 105166. [Google Scholar] [CrossRef]
He, R.; Li, B.; Ou, P.; Yang, C.H.; Yang, H.; Ruan, J.M. Effects of ultrafine WC on the densification behavior and microstructural evolution of coarse-grained WC-5Co cemented carbides. J. Ceramics International 2020, 46, 12852–12860. [Google Scholar] [CrossRef]
Zhou, H.S.; Lu, K.Z.; He, J.H.; Yang, H.H.; Liu, C.Z. Research progress of ultrasonic compaction powder forming technology. J. Acoustics Technology 2015, 34, 35–42. [Google Scholar]
Wang, X.; Qi, Z.; Chen, W. Study on constitutive behavior of Ti-45Nb alloy under transversal ultrasonic vibration-assisted compression. J. Archives of Civil and Mechanical Engineering 2021, 21, 1–15. [Google Scholar] [CrossRef]
Zuo, M.M. Study on dynamic characteristics of solid particles under high-frequency vibration D; Yanshan University: Yanshan, China, 2018. [Google Scholar]
Zhao, Y.B.; Ma, L.; Liu, B.; Shang, Z.X. Vibration filling density analysis of pure iron powder based on discrete element method. J. Powder Metallurgy Technology 2020, 38, 429–435. [Google Scholar]
Wang, W.T.; Wang, J.Y.; Duan, N.Q.; Du, W.H. Study on influencing factors of powder vibration dense packing based on discrete element method. J. Chinese Ceramics 2013, 49, 42–45. [Google Scholar]
Sedaghat, H.; Xu, W.; Zhang, L. Ultrasonic vibration-assisted metal forming: Constitutive modelling of acoustoplasticity and applications. J. Materials Processing Technology 2019, 265, 122–129. [Google Scholar] [CrossRef]
Liu, B.; Ma, L.; Liu, Q.Z.; Lu, Y. Effect of EDEM based vibration characteristics on the filling density of NdFeB permanent magnetic powder. J. China Powder Technology 2017, 23, 72–76. [Google Scholar]
Korim, N.S.; Hu, L. Study the densification behavior and cold compaction mechanisms of solid particles-based powder and spongy particles-based powder using a multi-particle finite element method. J. Materials Research Express 2020, 7, 056509. [Google Scholar] [CrossRef]
Wang, W.; Qi, H.; Liu, P.; Zhao, Y.B.; Chang, H. Numerical Simulation of Densification of Cu–Al Mixed Metal Powder during Axial Compaction. J. Metals 2018, 8, 537. [Google Scholar] [CrossRef]
Luo, X.L. Study on dynamic mechanical response of metal powder under impact loading based on three-dimensional discrete element method D; Ningbo University: Ningbo, China, 2018. [Google Scholar]
Jia, Q.; An, X.Z.; Zhao, H.Y.; Fu, H.Y.; Fu, H.T.; Zhang, H.; Yang, X.H. Compaction and solid-state sintering of tungsten powders: MPFEM simulation and experimental verification. J. Journal of Alloys and Compounds 2018, 750, 341–349. [Google Scholar] [CrossRef]
Ren, X.; Li, Z.; Zheng, Y.; Tian, W.; Zhang, K.C.; Cao, J.R.; Tian, S.Y.; Guo, J.L.; Wen, L.Z.; Liang, G.C. High Volumetric Energy Density of LiFePO4 Battery Based on Ultrasonic Vibration Combined with Thermal Drying Process. J. Journal of The Electrochemical Society 2020, 167, 130523. [Google Scholar] [CrossRef]
Siegert, K.; Ulmer, J. Influencing the Friction in Metal Forming Processes by Superimposing Ultrasonic Waves. J. Cirp Annals Manufacturing Technology 2001, 50, 195–200. [Google Scholar] [CrossRef]
Wang, W.T. Research on numerical simulation of iron powder molding based on discrete element method D; Central North University: Taiyuan, China, 2014. [Google Scholar]
Huang, P.Y. Principle of powder metallurgy M; Metallurgical Industry Press: Dongcheng, China, 1982. [Google Scholar]
Bo, H.Y. Meso simulation study on the influence of interface friction on iron powder compaction D; Hefei University of Technology: Hefei, China, 2009. [Google Scholar]
Ghafoor, S.; Li, Y.; Zhao, G.; Li, J.H.; Li, F.Y. Deformation characteristics and formability enhancement during ultrasonic-assisted multi-stage incremental sheet forming. J. Journal of Materals Research and Technology 2022, 18, 1038–1054. [Google Scholar] [CrossRef]
Cheng, Z.N. Research on deformation mechanism and microstructure evolution of ultrasonic assisted incremental forming materials D; Shandong University: Jinan, China, 2021. [Google Scholar]
Wang, W.; Xiao, J.; Ran, Z.; Zheng, X.T.; Fu, B. Improvement of density of energetic materials based on ultrasonic assisted isostatic pressing. J. Energetic materials 2021, 29, 521–529. [Google Scholar]
Chen, C.X. Quality control principle of cemented carbide M; Cemented Carbide Branch of China Tungsten Association: Zhuzhou, China, 2007. [Google Scholar]

Figure 1. The experiment platform of the ultrasonic vibration assisted pressing process.

Figure 2. The contact slip between particles.

Figure 3. The contact mechanics model of soft ball.

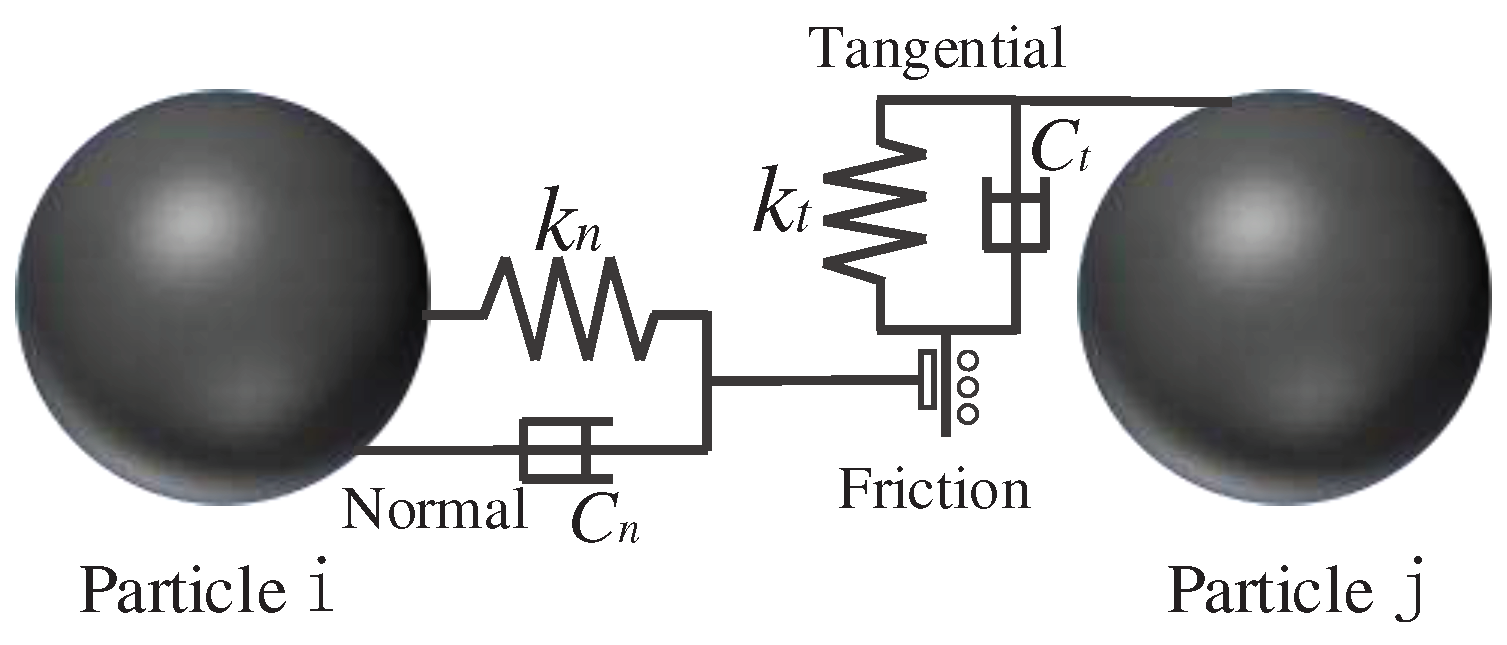
Figure 4. (a) the simulation flow chart; (b) the electron microscopic diagram of raw WC powder; (c) the electron microscopic image of raw Co powder.

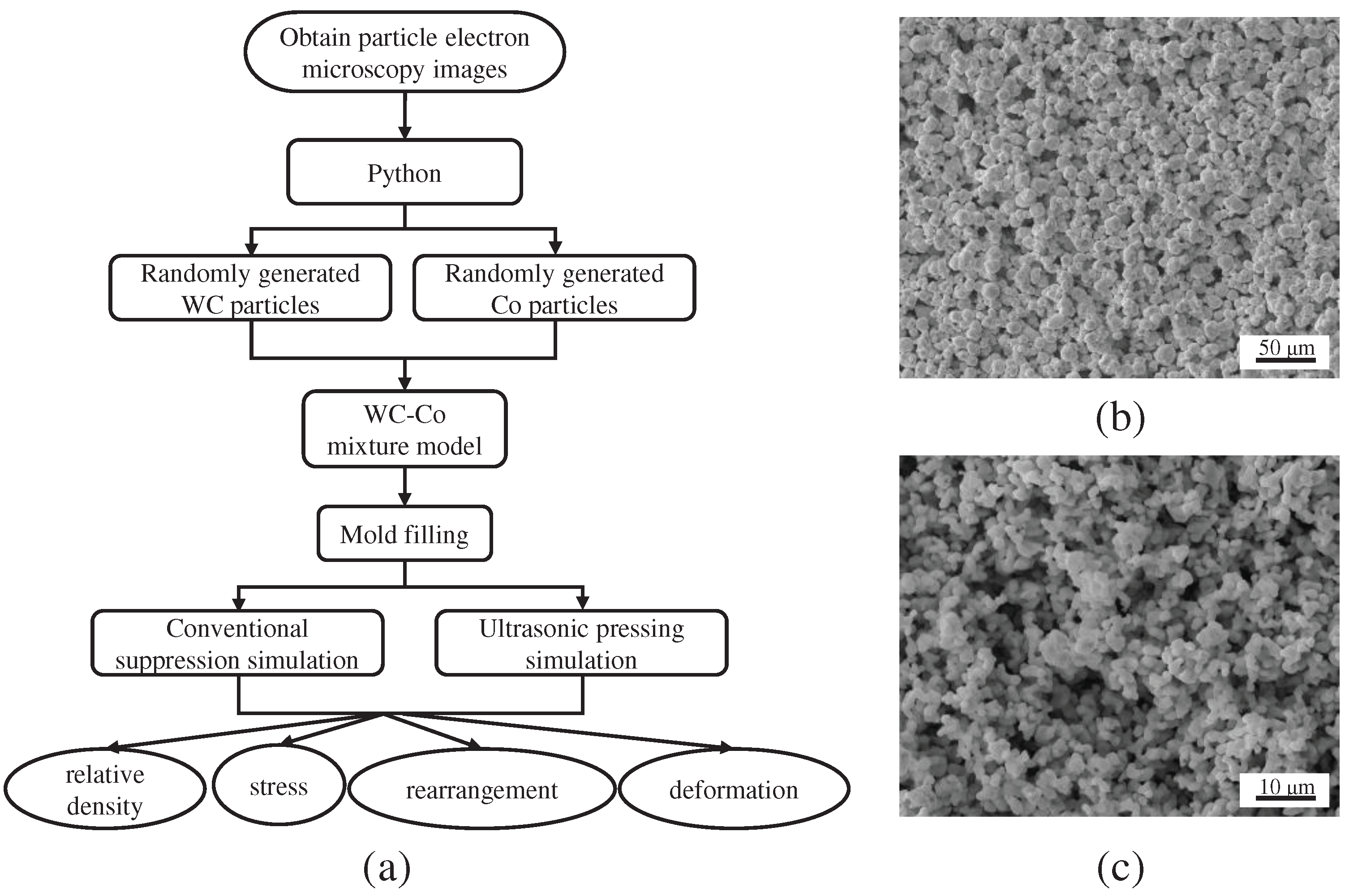
Figure 5. the schematic diagram of particle drop.

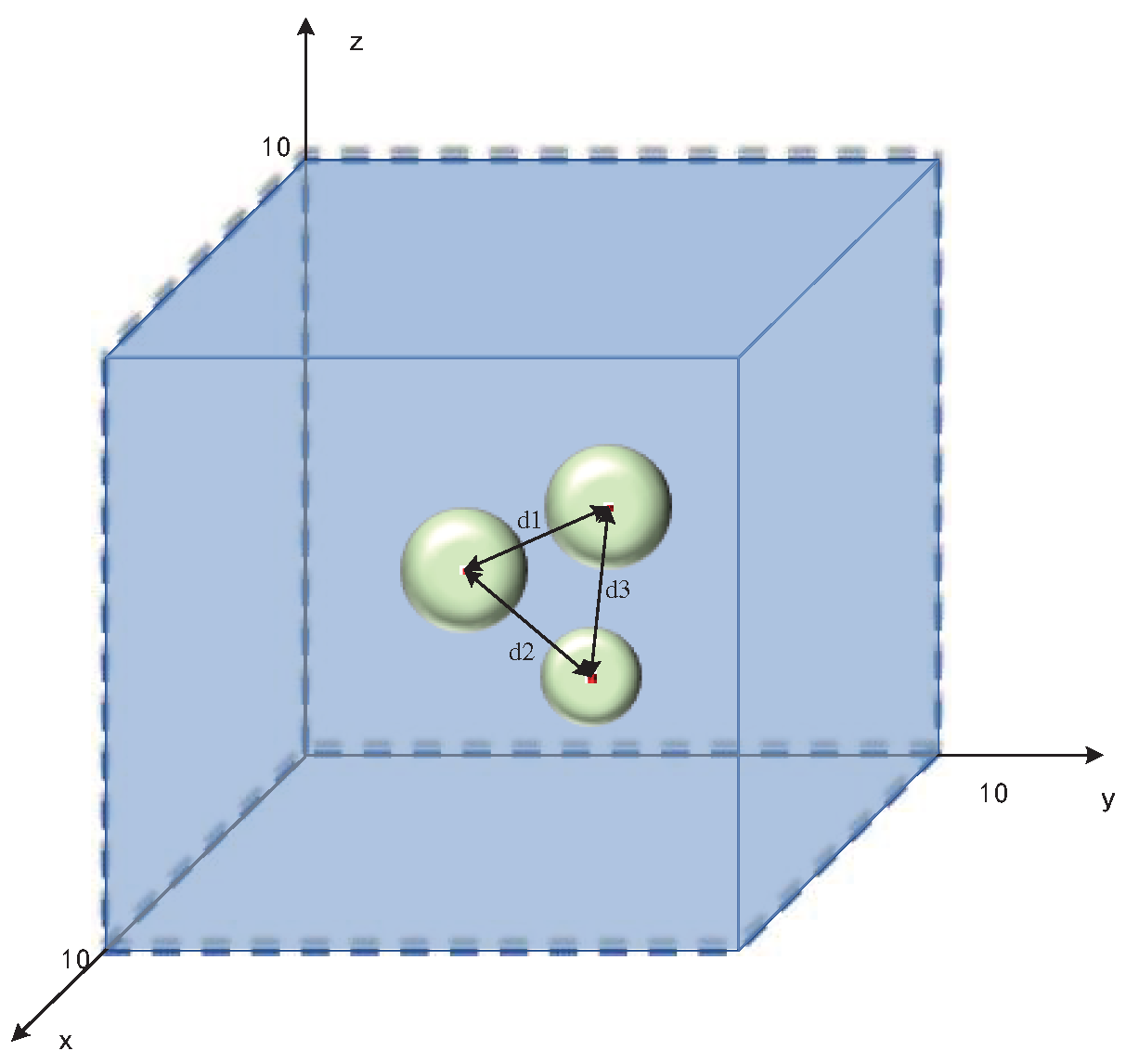
Figure 6. the WC-Co mixture and the press model meshing.

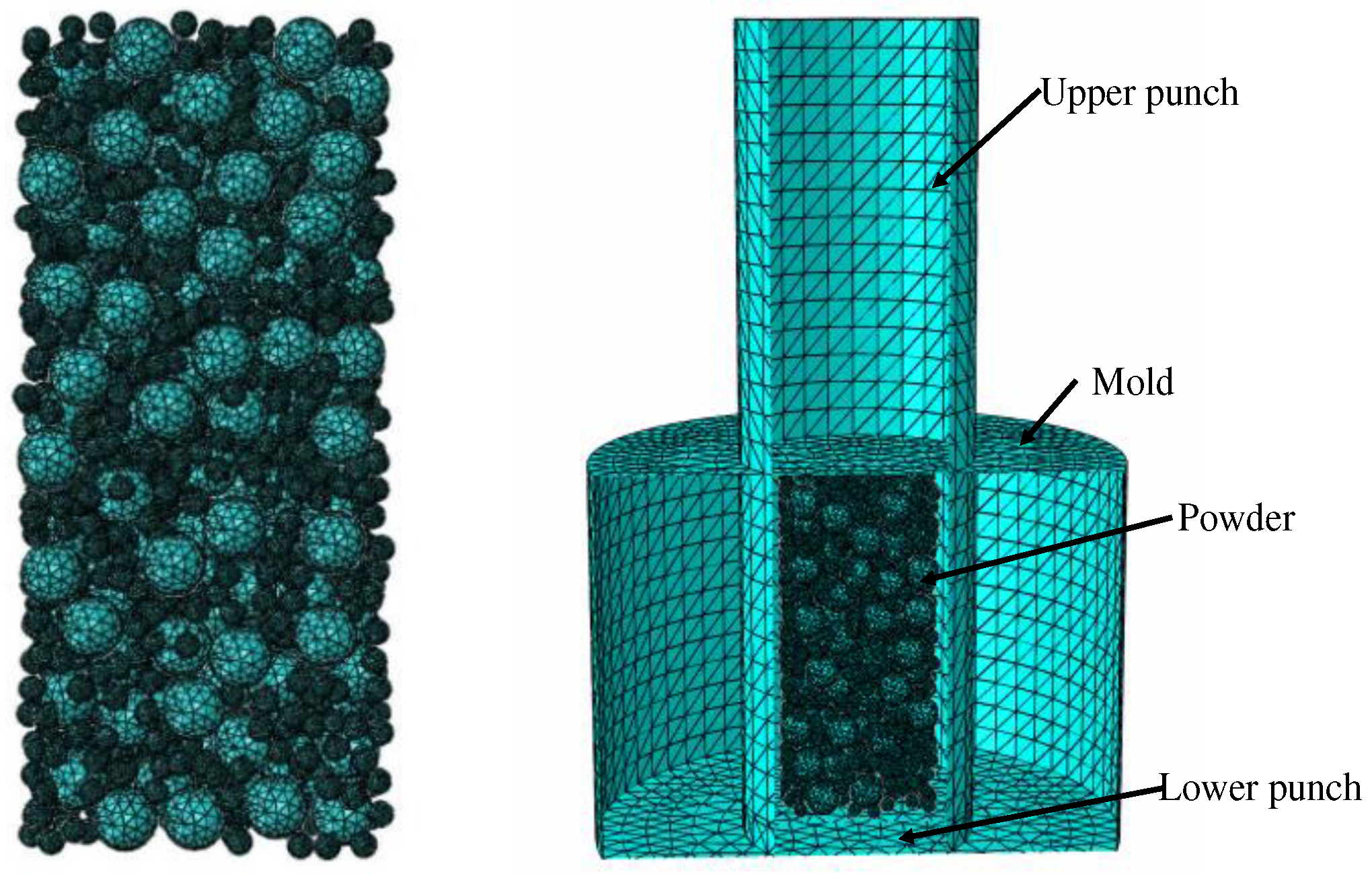
Figure 7. Displacement distribution cloud images at different times of conventional pressing and ultrasonic pressing processes.

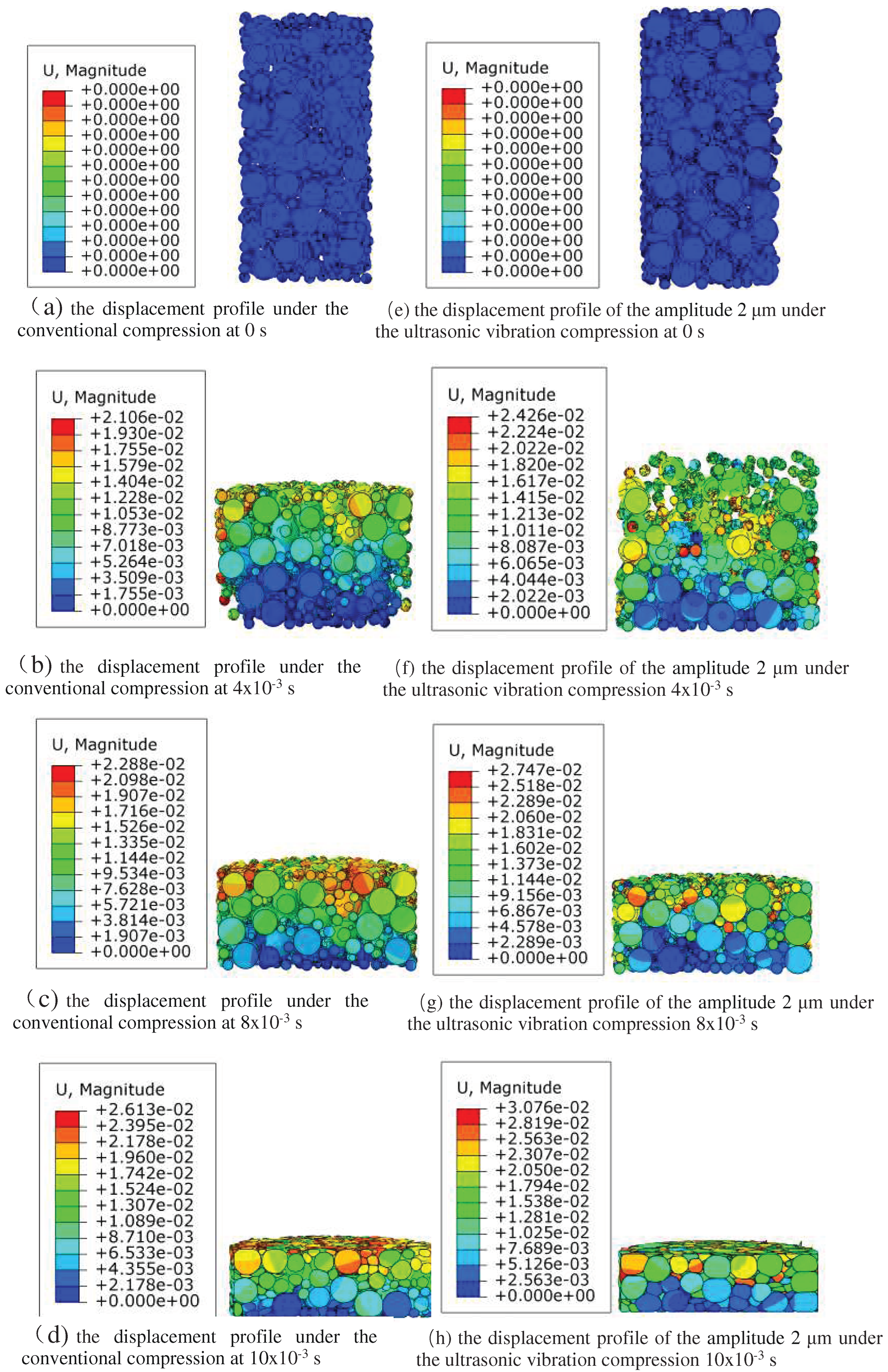
Figure 8. Effects of ultrasonic vibration amplitudes on the compact density.

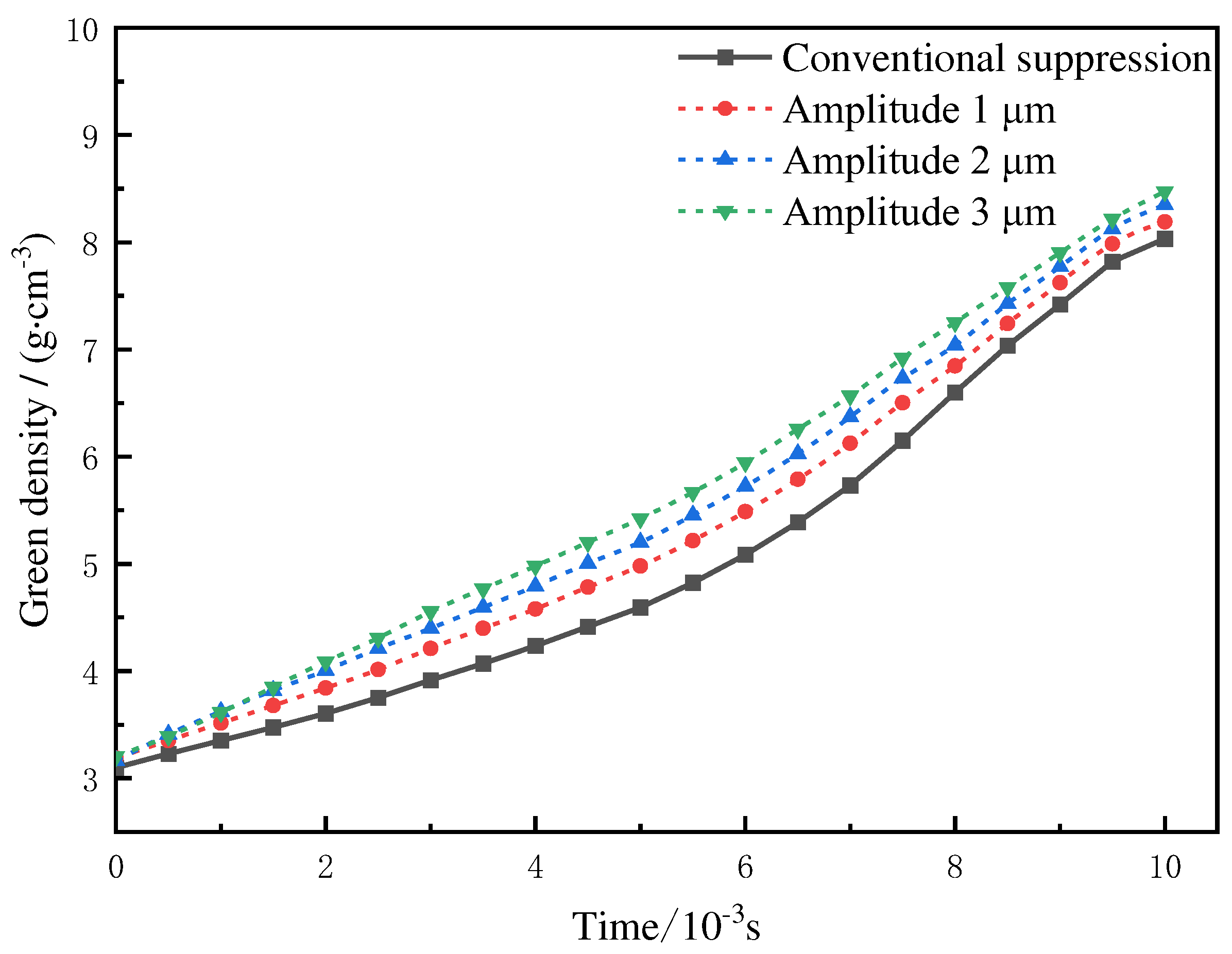
Figure 9. Mises stress distribution cloud image of WC and Co particles under the conventional compression and different ultrasonic amplitudes.

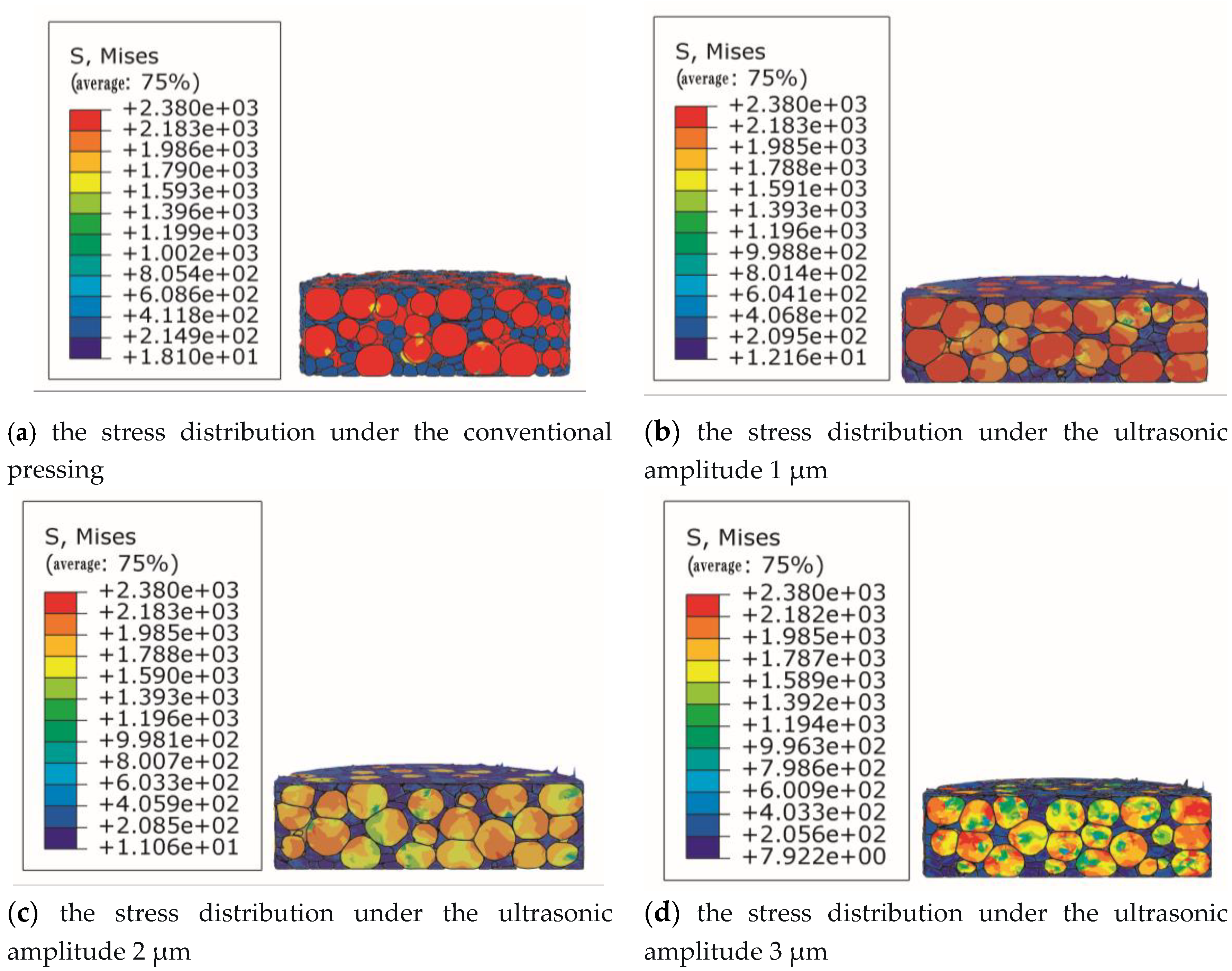
Figure 10. Results of the compression experiment and the simulation.

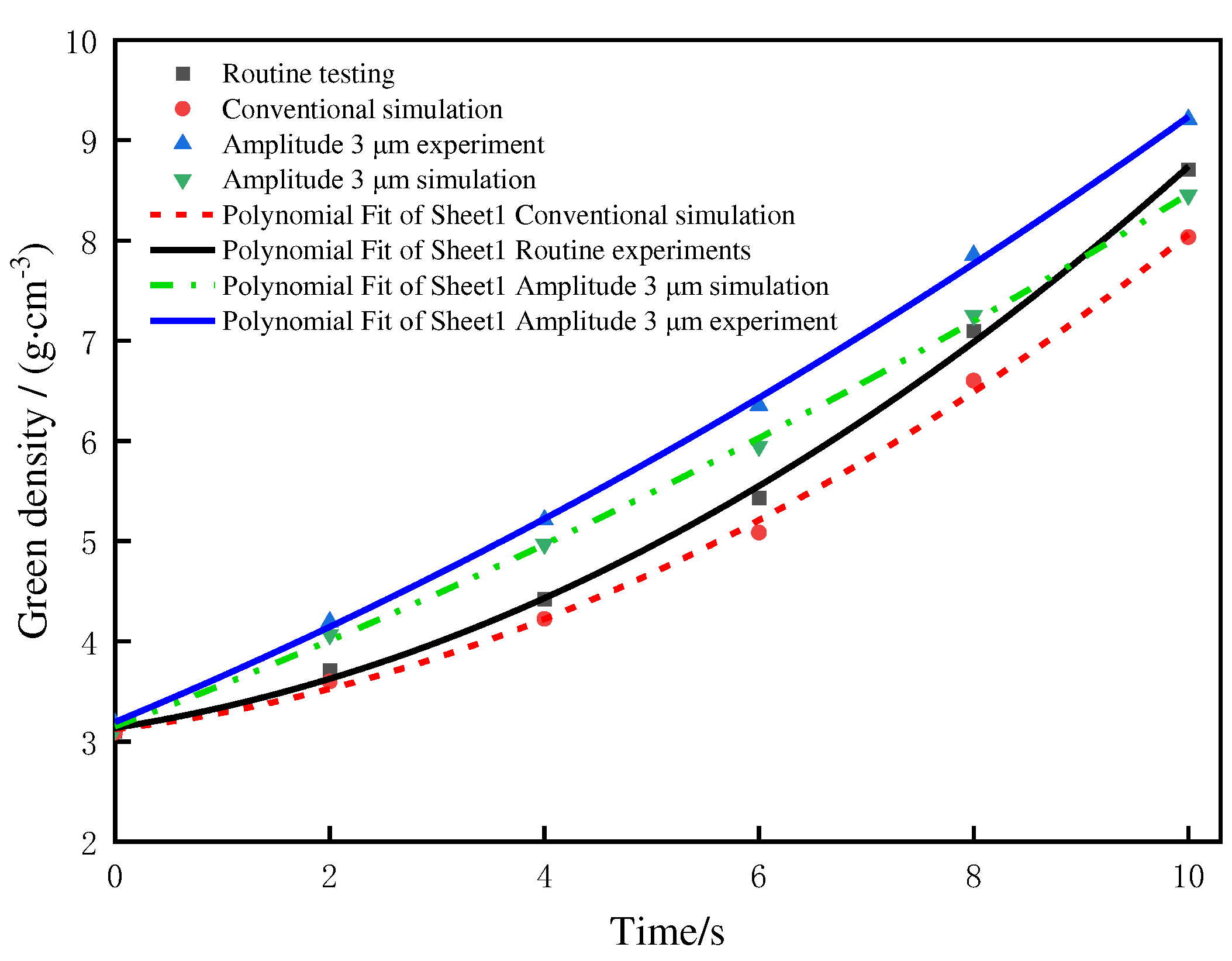
Figure 11. Scanning electron microscope image of longitudinal section of compacts.

Figure 12. changes of blank size after demoulding.

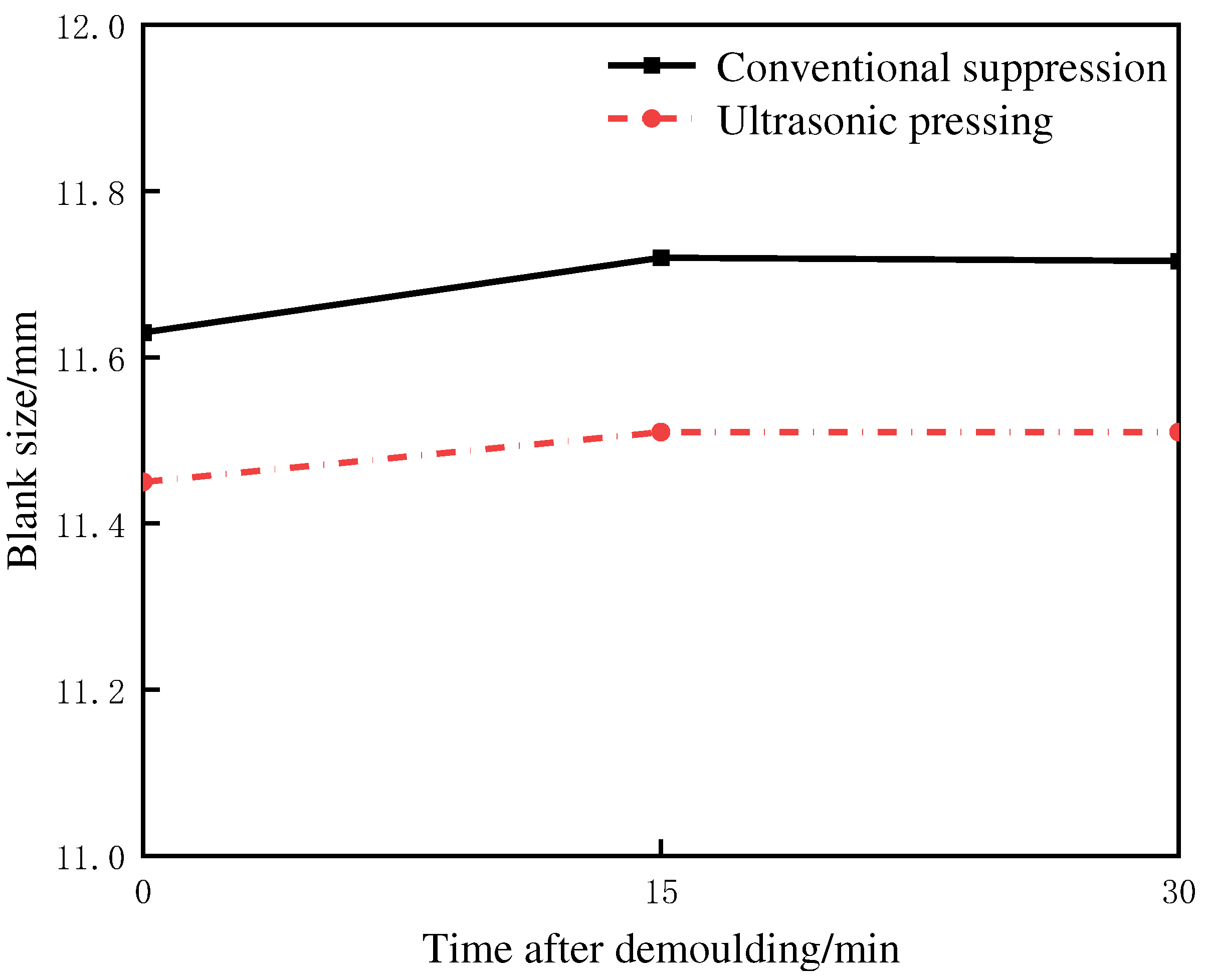
Table 1. the material properties of each component.

Performance parameter	ABAQUS unit	Mould	WC	Co
density	Tonne/mm³	7.89×10^-9	1.56×10^-9	7.9×10^-10
Modulus of elasticity	MPa	2.09×10⁵	7.14×10⁵	2.09×10⁵
Yield strength	MPa	no	2380	279
Poisson's ratio	no	0.269	0.19	0.3

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer