Prerpints.org logo
Preprint
Article

An Improved VMD-LSTM Model for Time-Varying GNSS Time Series Prediction with Temporally Correlated Noise

Altmetrics

Downloads

134

Views

50

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

24 June 2023

Posted:

25 June 2023

You are already at the latest version

Alerts
Abstract
GNSS time series prediction plays a significant role in monitoring crustal plate motion, landslide detection, and maintenance of the global coordinate framework. Long Short-Term Memory (LSTM), a deep learning model has been widely applied in the field of high-precision time series prediction especially when combined with Variational Mode Decomposition (VMD) to form the VMD-LSTM hybrid model. To further improve the prediction accuracy of the VMD-LSTM model, this paper proposes a dual variational modal decomposition long short-term memory (DVMD-LSTM) model to effectively handle the noise in GNSS time series prediction. This model extracts fluctuation features from the residual terms obtained after VMD decomposition to reduce the prediction errors associated with residual terms in the VMD-LSTM model. Daily E, N, and U coordinate data recorded at multiple GNSS stations between 2000 and 2022 are used to validate the performance of the proposed DVMD-LSTM model. The experimental results demonstrate that compared to the VMD-LSTM model, the DVMD-LSTM model achieves significant improvements in prediction performance across all measurement stations. The average RMSE is reduced by 9.86%, and the average MAE is reduced by 9.44%. Furthermore, the average accuracy of the optimal noise model for the predicted results is improved by 36.50%, and the average speed accuracy of the predicted results is enhanced by 33.02%. These findings collectively attest to the superior predictive capabilities of the DVMD-LSTM model, thereby enhancing the reliability of the predicted results.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Over the past three decades, with the rapid development of satellite navigation technology, a large number of GNSS continuously operating reference stations have been established worldwide. These stations provide important data sources for crustal plate motion monitoring [1,2,3], landslide detection [4], deformation monitoring of bridges or dams [5,6,7], and maintenance of regional or global coordinate frameworks [8]. By analyzing the long-term GNSS observation data time series from these stations, it is possible to predict the variation of coordinates at continuous time points, thereby providing important basis for determining motion trends. This has significant practical and theoretical value in geodesy and geodynamics research [9,10].
Time series prediction methods can be mainly categorized into two types: physical simulation and numerical simulation. Traditional physical and numerical simulation methods rely on geophysical theories, linear terms, periodic terms, and gap information to construct models [11]. However, these models face challenges in capturing complex nonlinear data and require manual selection of feature information and modeling parameters, leading to systematic biases and limitations [12]. In contrast, deep learning, as an emerging technology, can automatically extract information that is suitable for data features by constructing deep network structures. Deep learning exhibits strong learning capabilities and has advantages in handling large-scale and high-dimensional data. It has been widely applied in various fields such as image recognition [13], natural language processing [14], speech recognition [15], and time series prediction [16,17,18].
Long Short-Term Memory (LSTM), as an excellent variant of Recurrent Neural Networks (RNN), overcomes the issues of gradient vanishing, gradient exploding, and insufficient long-term memory in RNN [19,20]. Due to its significant advantages in long-range time series prediction, LSTM has been widely applied in various time series prediction domains such as electricity load forecasting [21] and wind speed prediction [22]. In recent years, the application of the LSTM algorithm in the GNSS domain has also become increasingly widespread. Kim et al. improved the accuracy and stability of absolute positioning solutions in autonomous vehicle navigation using a multi-layer LSTM model [23]. Tao et al. utilized a CNN-LSTM approach to extract deep multipath features from GNSS coordinate sequences, reducing the impact of multipath effects on positioning accuracy [24]. Xie et al. accurately predicted landslide periodic components using the LSTM model to establish a landslide hazard warning system [25].
Variational Mode Decomposition (VMD) is a signal processing method based on the principle of variational inference. It decomposes signals into various mode components (Intrinsic Mode Functions, IMF) with different frequencies through an optimization process, effectively extracting the time-frequency local features of signals and enabling efficient signal decomposition and analysis [26]. Currently, many researchers have combined VMD with LSTM to enhance the performance of LSTM in a range of fields. Huang et al. applied the VMD-LSTM model in the coal seam thickness prediction field, confirming that the predicted results closely matched the coal seam information obtained from existing boreholes [27]. Zhang et al. applied the VMD-LSTM model in the field of sports artificial intelligence, demonstrating its broad application prospects in predicting sports artificial intelligence directions [28]. Han et al. applied the VMD-LSTM model in the wind power prediction field, validating its high performance in multi-step and real-time predictions [29]. Xing et al. applied the VMD-LSTM model in predicting dynamic displacements of landslides and verified its high prediction accuracy using the case of the landslide in paddy fields in China [30].
The VMD-LSTM model has been widely adopted in various fields for time series prediction. However, most studies utilize VMD to decompose the original data, predict each Intrinsic Mode Function (IMF) and residual term separately, and then combine the predicted results to obtain the final prediction. Although this method yields good results for each IMF value, the fluctuation characteristics of the residual term are difficult to extract, leading to significant prediction errors in the model. Furthermore, existing research mainly focuses on the accuracy of the prediction results while neglecting the noise characteristics of the data itself [31,32,33]. Considering these factors, this paper proposes a dual VMD-LSTM (DVMD-LSTM) hybrid model that takes into consideration the characteristics of noise. By performing VMD decomposition on the residual components obtained from the initial VMD decomposition, the proposed model effectively extracts the fluctuation features within the residuals, enabling high-precision prediction of GNSS time series. By analyzing the RMSE and MAE of the predicted results in the E, N, and U directions across multiple measurement stations, the applicability and robustness of the proposed method are evaluated. Additionally, the quality of the predicted results is assessed by incorporating noise models and velocity evaluation.
The structure of this paper is as follows: Section 2 introduces the principles of VMD, LSTM algorithms, and accuracy evaluation metrics. The principles and specific processes of the DVMD-LSTM model are explained in detail. Section 3 describes the GNSS station data, presents data preprocessing strategies, and analyzes the reasons for the improved accuracy of the DVMD-LSTM model. Section 4 focuses on the prediction results and accuracy of both the single LSTM model and the hybrid model. The optimal noise model and velocity under each prediction model are compared and analyzed to evaluate the performance of the DVMD-LSTM model using different accuracy assessment metrics. Finally, Section 5 provides conclusions and analysis.

2. Principle and Method

2.1. Variational Modal Decomposition (VMD)

Variational Mode Decomposition (VMD) is an adaptive and fully non-recursive method for solving modal variational and signal processing problems [34]. GNSS time series exhibit inherent non-stationarity. Utilizing VMD to decompose the data effectively separates it into stationary signals, thereby extracting the fluctuation characteristics of the GNSS time series and providing a superior data foundation for model prediction. VMD iteratively searches for a variational model to decompose the original time series into distinct modal components. The specific decomposition process is outlined as follows [35,36]:
(1) For each modal component μ K ( t ) , the corresponding analytic signal is computed using the Hilbert transform, which allows obtaining its one-sided spectrum:
[ δ ( t ) + j π t ] ∗ μ K ( t )
In the equation, j 2 = − 1 , δ is the Dirac distribution.
(2) By introducing exponential terms in each mode, the center frequency e − j ω K t of each mode can be estimated, and the spectral components of each mode can be modulated to their respective fundamental frequency bands:
[ ( δ ( t ) + j π t ) ∗ μ K ( t ) ] e − j ω K t
(3) The bandwidth of ω K is estimated based on the smoothness of the demodulated signal's H1 Gaussian. This leads to a constrained variational problem:
min { μ K } , { ω K } { ∑ K ‖ d t [ ( δ ( t ) + j π t ) ∗ u K ( t ) ] e − j ω K t ‖ 2 2
s , t , ∑ K μ K = f
In the equation, f represents the original signal, { μ K } represents the decomposed mode functions, and { ω K } represents the corresponding center frequencies of each mode.
(4) On this basis, quadratic penalty factors α and Lagrange multiplier operator λ t are introduced to transform it into an unconstrained variational problem. The extended Lagrange expression is as follows:
L ( { μ K } , { ω K } , λ ) = α ∑ K ‖ ∂ t [ ( δ ( t ) + j π t ) ∗ μ K ( t ) ] e − j ω K t ‖ 2 2 + ‖ f ( t ) − ∑ K μ K ( t ) ‖ 2 2 + 〈 λ ( t ) , f ( t ) − ∑ K μ K ( t ) 〉
where α represents the quadratic penalty factor and λ t denotes the Lagrange multiplier operator. Subsequently, the alternating direction method of multipliers (ADMM) is employed to solve this unconstrained variational problem. By alternately updating μ K n + 1 , ω K n + 1 and λ   n + 1 the saddle point of the extended Lagrange expression, i.e., the optimal solution of the constrained variational model in Equation (3), is sought.
From the above analysis, it is evident that choosing an appropriate number of mode components, K, is crucial for obtaining high-quality decomposition results in VMD. An excessively large K may lead to over-decomposition, while a small K may result in under-decomposition of the data. To determine the optimal K value for the E, N, and U time series of different stations, this study adopts the method of comparing the signal-to-noise ratio (SNR) of the decomposed data to evaluate the quality of the decomposition results. A higher SNR indicates a clearer signal decomposition and better denoising effect. Through extensive experiments and based on empirical rules, this study restricts the K value to the range of 2 to 10 and selects the K value within this range that yields the highest SNR as the optimal K value for each time series. The definition of SNR is given as follows:
SNR = 10 lg ∑ i = 1 N f 2 ( i ) ∑ i = 1 N [ f ( i ) − g ( i ) ] 2
where f ( i ) represents the original signal, and g ( i ) represents the reconstructed signal.

2.2. Long Short Term Memory (LSTM)

LSTM is an improved type of recurrent neural network (RNN) that addresses the issue of long-term dependencies by utilizing memory cells, effectively mitigating the problems of vanishing and exploding gradients [37,38]. 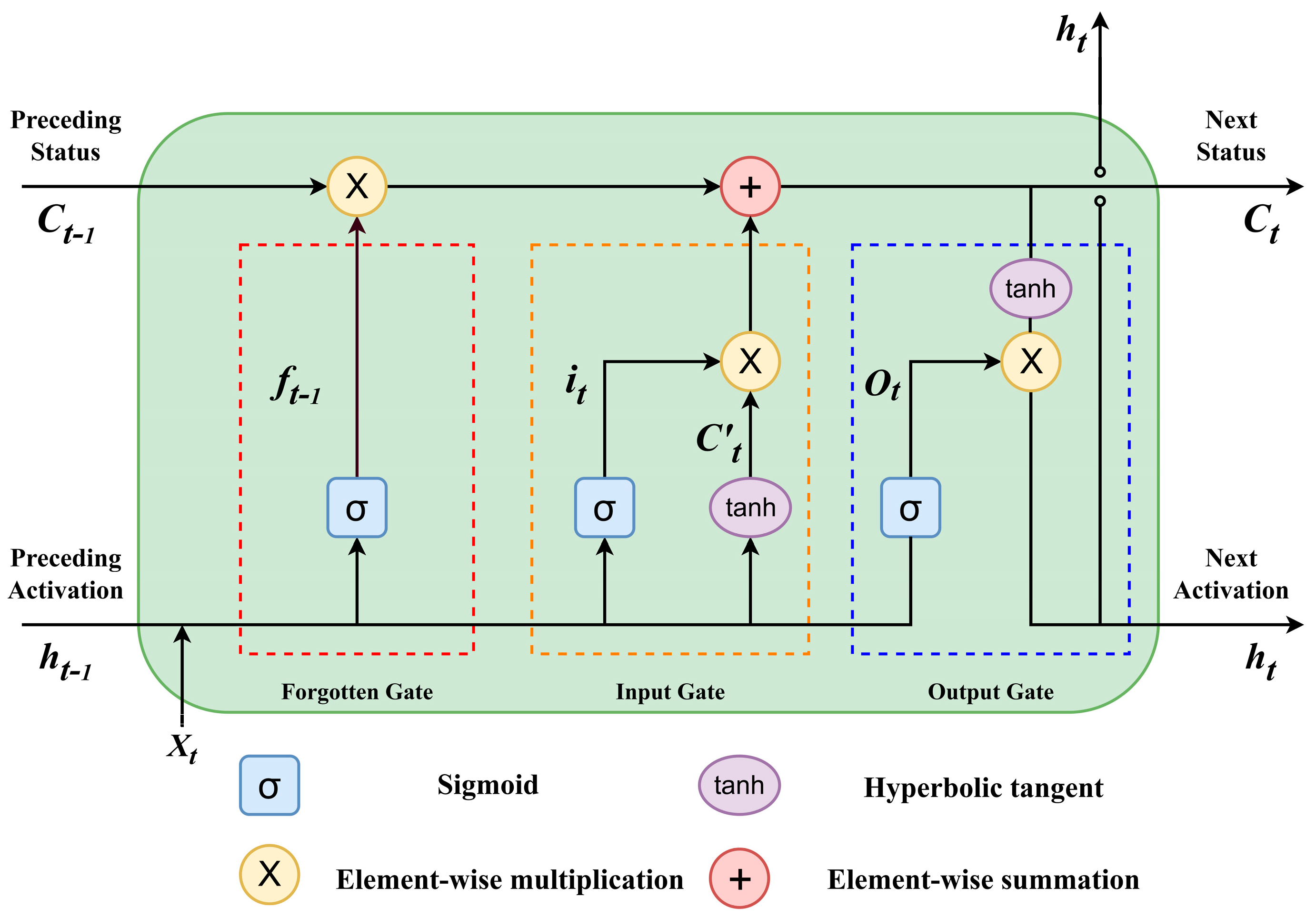Compared to traditional neural networks, LSTM demonstrates strong advantages in handling long-term sequence prediction tasks and has been widely applied in areas such as time series forecasting and fault detection [39,40]. The LSTM architecture consists of input layers, hidden layers, and output layers, where each hidden layer employs input gates, forget gates, and output gates to store and access data, as shown in Figure 1.

2.3. Dual variational mode decomposition long-short term memory network model (DVMD-LSTM)

The VMD-LSTM model, as a classical hybrid deep learning model, has been widely applied in time series prediction tasks such as load forecasting and wind speed prediction, demonstrating remarkable predictive accuracy [41,42]. This model utilizes the Variational Mode Decomposition (VMD) to decompose the original data into a set of Intrinsic Mode Functions (IMFs) and a residue component, denoted as "r." Subsequently, each IMF and the residue component "r" are individually predicted, and their predictions are cumulatively aggregated to obtain the final model's prediction. It is worth noting that the IMFs, being stationary signals, can achieve higher predictive accuracy when individually predicted, thus effectively enhancing the predictive performance of the VMD-LSTM model. The specific prediction process is shown on the left side of Figure 2, and the residual value is not decomposed. However, the residue component "r" remains unprocessed during the prediction process, leading to errors that can affect the model's predictive accuracy. Therefore, this paper proposes a hybrid deep learning model called Dual Variational Modal Decomposition - Long Short-Term Memory (DVMD-LSTM). In this model, the residue component "r" is further decomposed using VMD, and the decomposed modal components are fused for prediction. By replacing the predicted results of the original residue component "r" with the fused modal components, the DVMD-LSTM model eliminates irregular residue terms and enhances the predictive accuracy of the fused modal components, thereby improving the overall prediction accuracy. The specific workflow is illustrated in Figure 2.
The specific prediction process of the DVMD-LSTM model is as follows:
Step 1: Preprocess the GNSS time series data by removing outliers, performing interpolation, and other data preprocessing techniques. Then, input the preprocessed data into the Variational Mode Decomposition (VMD) for decomposition.
Step 2: Further decompose the residue component "r1" obtained from the VMD into individual modal components and another residue "r2" through another round of VMD.
Step 3: Add up the modal components obtained from the VMD decomposition of the residue component "r1" to form the fused Intrinsic Mode Function (Fuse-IMF). Use the Fuse-IMF as a feature for prediction in the LSTM model.
Step 4: Use the individual modal components obtained from the VMD decomposition of the original GNSS time series as features and input them separately into the LSTM model for prediction. Obtain K prediction results, where K represents the number of modal components.
Step 5: Add the K prediction results obtained in Step 4 with the prediction result of the Fuse-IMF to obtain the final prediction result of the DVMD-LSTM model.
Step 6: Calculate the RMSE and MAE of the prediction results and use them for evaluating the performance of the model under different noise models.

2.4. Precision evaluation index

To evaluate the prediction accuracy and noise characteristics of the hybrid model, this study employs Root Mean Square Error (RMSE) and Mean Absolute Percentage Error (MAPE) as evaluation metrics for model prediction accuracy [43,44]. Additionally, the Bayesian information criterion (BIC_tp) is used to determine the optimal noise model for the original GNSS time series and the predicted time series under each model, in order to evaluate whether the prediction results consider colored noise [45]. The definitions of the three evaluation metrics are as follows:
(1)
RMSE
R M S E = 1 n   ∑ i = 1 n ( y i − y ^ i ) 2
(2)
MAE
M A E = 1 n ∑ i = 1 n | ( y i − y ^ i ) |
In the above equations, y i represents the actual GNSS data values, y ^ i represents the predicted results of each model, and n denotes the number of GNSS data points. The values of RMSE and MAE are used as evaluation metrics for model prediction accuracy. Smaller values of RMSE and MAE indicate higher prediction accuracy of the model, while larger values indicate lower prediction accuracy.
(3)
BIC_tp
B I C _ t p = − 2 log ( L ) + log ( n 2 π ) v
To provide a visual assessment of the improvement achieved by the hybrid model on each evaluation metric, this study introduces the Improvement Ratio (I) to quantify the magnitude of improvement in each accuracy evaluation metric. By calculating the I value, the degree of improvement in accuracy achieved by the hybrid model can be accurately determined. The calculation formula for the Improvement Ratio is as follows:
I y y ^ = y - y ^ y
In the above equation, y and y ^ represent the evaluation metrics for accuracy, such as RMSE. The variable y represents the evaluation metric for the accuracy of the initial model's predictions, while y ^ represents the evaluation metric for the accuracy of the predictions made by the hybrid model. A larger value of I y y ^ indicates a greater improvement in the evaluation metric achieved by the hybrid model, and vice versa.

3. Data and experiments

3.1. Data Sources

To validate the applicability and robustness of the DVMD-LSTM model, daily coordinate time series data in the E, N, and U directions from eight stations, namely albh, burn, ceda, foot, gobs, rhcl, sedr, and smel, spanning the years 2000 to 2022, were selected as experimental data. The data for these stations were obtained from the International GNSS Service (IGS). The information for each station is presented in Table 1, and the distribution of the stations is depicted in Figure 3.

3.2. Data preprocessing

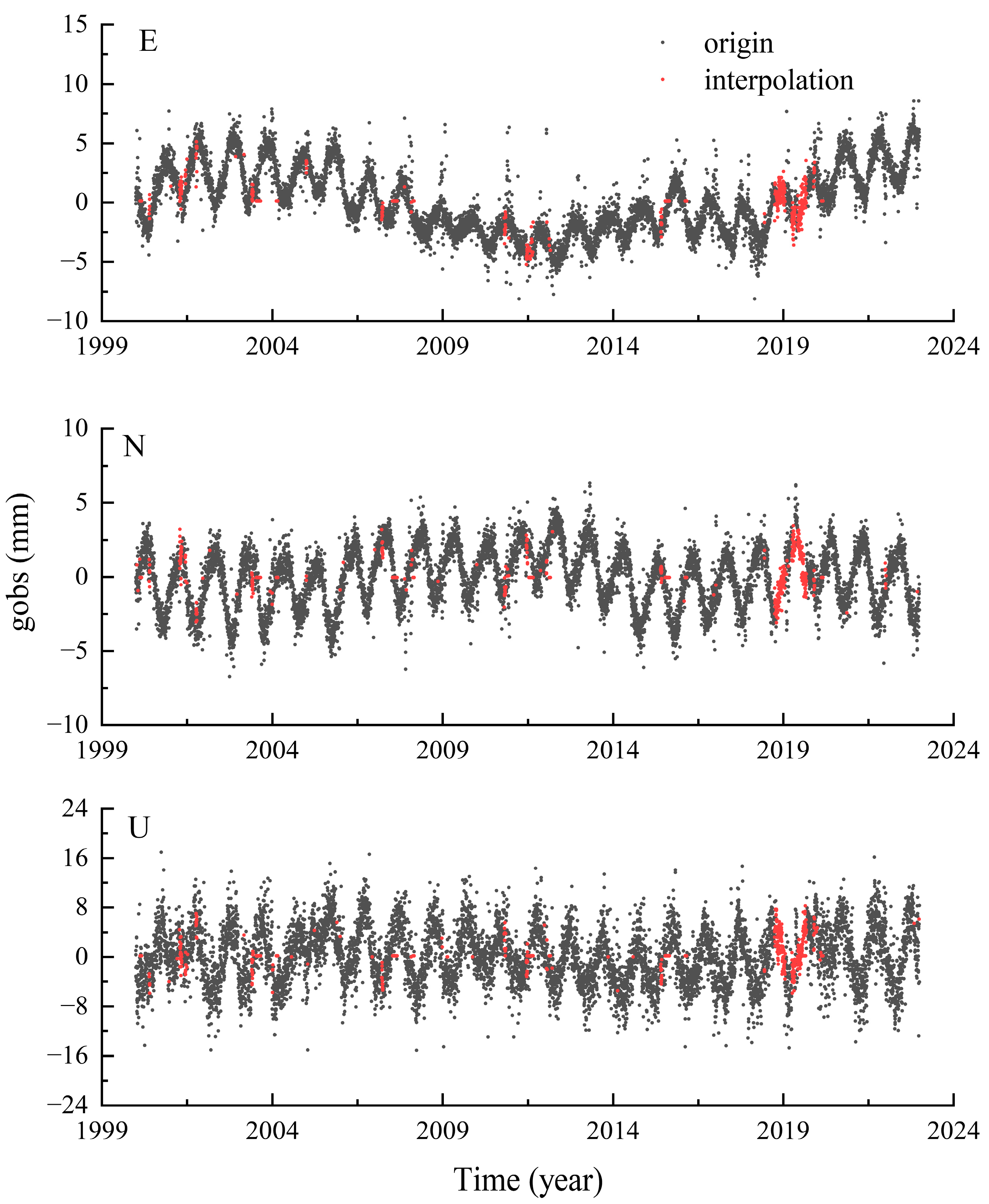
For data preprocessing, this study employed the Hector software to remove outliers and detect step discontinuities in the raw data [46]. After identifying the step discontinuities, they were corrected using the least squares fitting method. The corrected data was then subjected to interpolation using the Regularized Expectation Maximization (RegEM) algorithm. This method combines the Expectation Maximization (EM) algorithm with regularization techniques to simultaneously maximize the likelihood function and consider the smoothness of the model and noise reduction. It can effectively handle the interpolation problem of missing data [47,48]. Due to space limitations, only the comparison of interpolation results for the gobs station with the highest missing rate in the E, N, and U components is shown in Figure 4.
As shown in the figure, it can be observed that the RegEM method not only produces good interpolation results for scattered missing data but also maintains the trend of the sequence well in the presence of many continuous missing data. It successfully overcomes the limitation of poor interpolation performance of linear interpolation at locations with continuous missing data. Moreover, it provides high-quality continuous time series data for subsequent experiments.

3.3. DVMD-LSTM Reliability Analysis

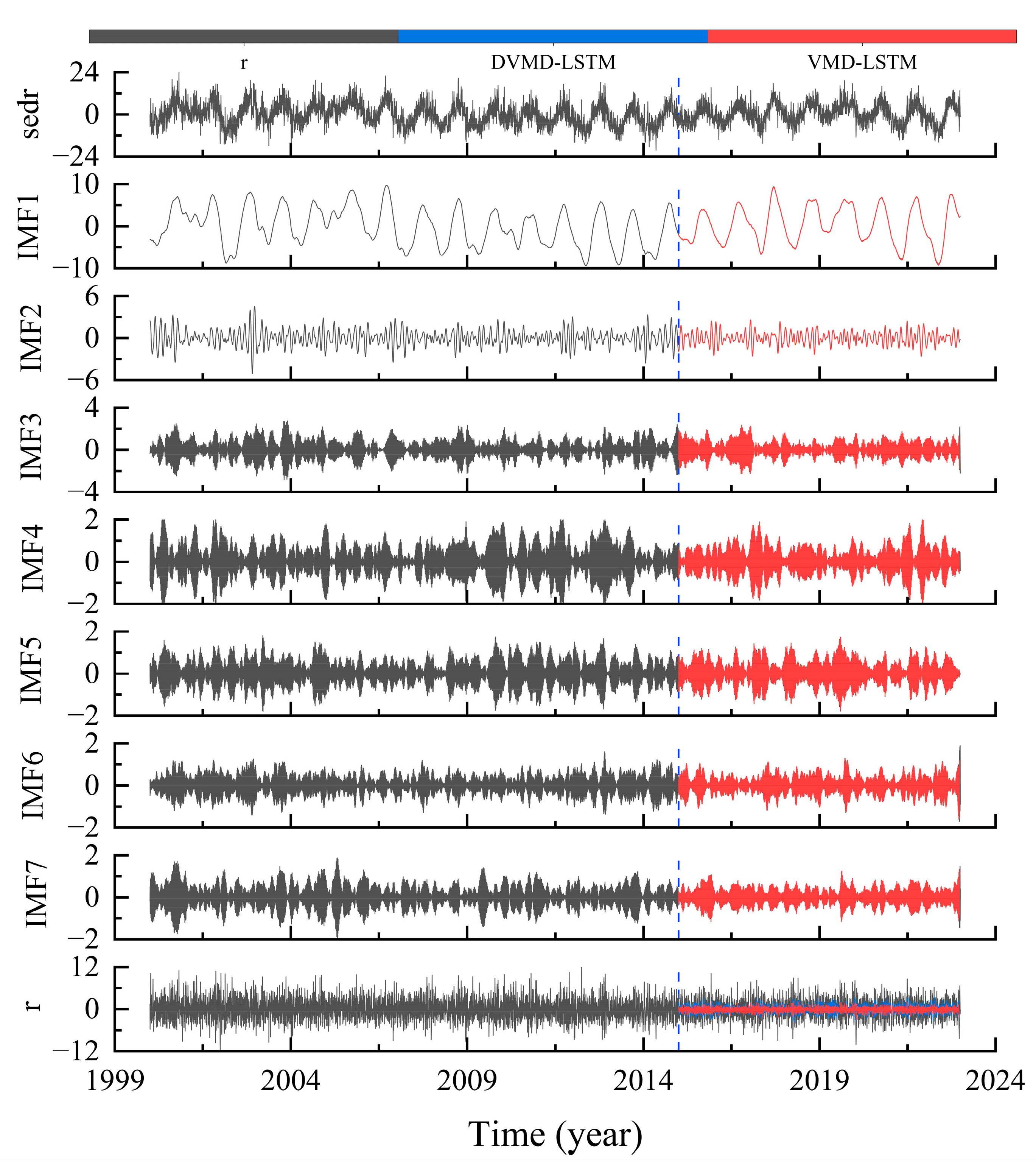
To investigate the reasons for the improved prediction accuracy of the DVMD-LSTM model compared to the VMD-LSTM model, this study utilized the signal-to-noise ratio (SNR) method to determine the value of K for VMD decomposition at each station (including E, N, and U directions). Subsequently, the decomposed IMF components and the residual term r were used as features in the LSTM model for prediction. Furthermore, a second VMD decomposition was performed on the residual term r, and the fused data were used as model features for prediction. Due to space constraints, this paper only presents the predicted results of the IMF components and residual after decomposition in the U direction of the sedr station. Please refer to Figure 5 for details.
According to Figure 5, the VMD-LSTM model demonstrates excellent predictive capability for each IMF component. However, due to the lack of apparent regularity in the residual term r, the VMD-LSTM model struggles to effectively capture its fluctuation characteristics, resulting in poor prediction performance and consequently affecting the overall prediction accuracy of the VMD-LSTM model. To address this issue, this study proposes the DVMD-LSTM model, which aims to maintain the same processing approach for each IMF component obtained from VMD decomposition while performing a secondary VMD decomposition specifically on the residual term r to further extract its fluctuation information. Through this step, the DVMD-LSTM model can more accurately predict the residual term r, leading to improved prediction performance, as discussed in Section 4.

4. Experimental results and analysis

4.1. DVMD-LSTM model prediction results and precision analysis

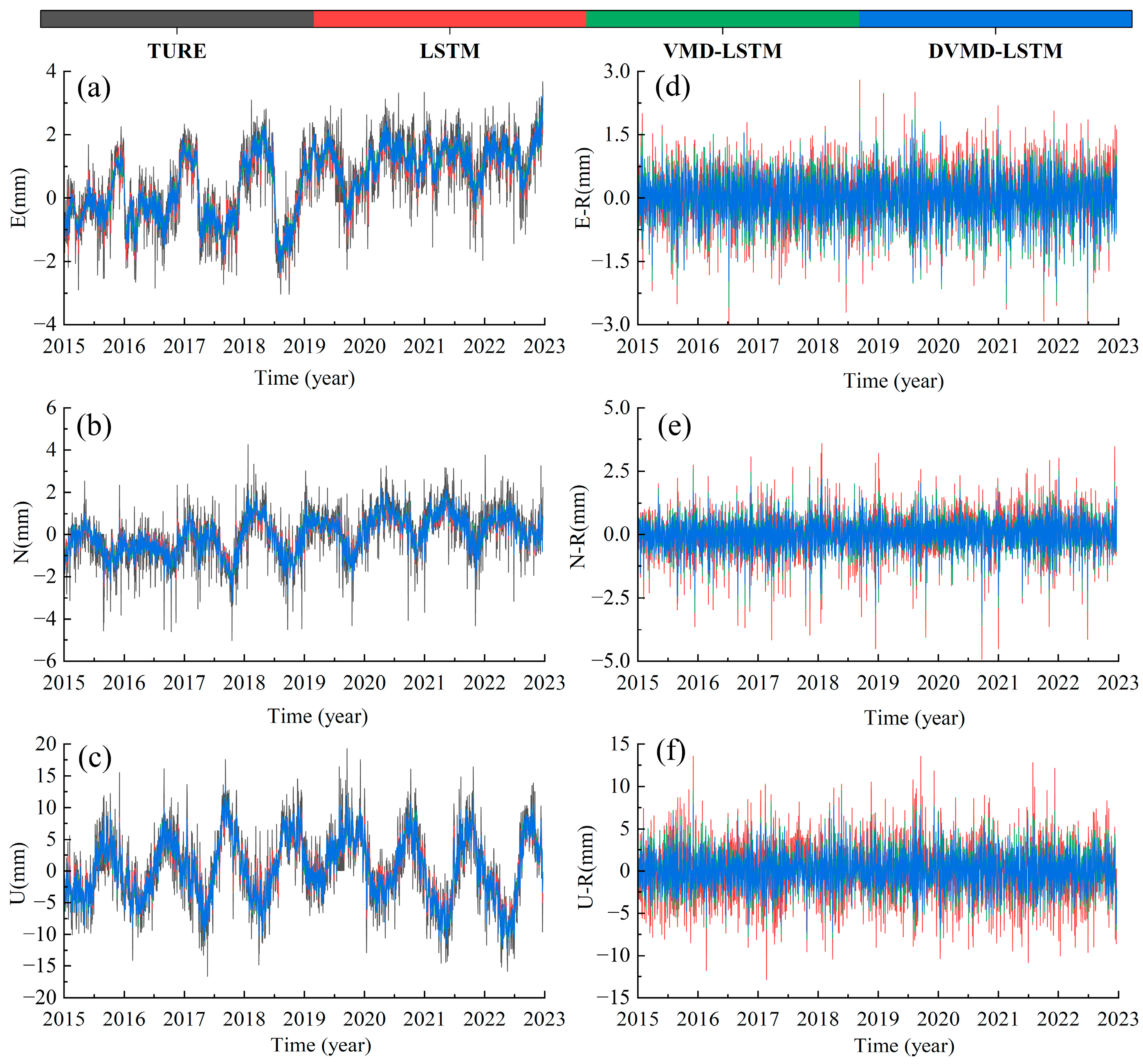
To compare the improvement in predictive accuracy of the DVMD-LSTM model and the VMD-LSTM model compared to the LSTM model under different fluctuation amplitudes, this study conducted experiments using datasets from different stations in three directions. The dataset was divided into a training set (from 2000 to 2011), a validation set (from 2012 to 2014), and a test set (from 2015 to 2022). The training set was used to train the model parameters and learn the data features. The validation set was used to fine-tune the model's hyperparameters and evaluate its performance. The test set was used for the final evaluation of the model's performance to assess its effectiveness in practical applications. The purpose of this dataset partitioning scheme was to ensure that the model had sufficient training data to fully learn the data features. Additionally, by obtaining sufficient prediction results on the test set, the optimal noise model for prediction accuracy could be evaluated. To better distinguish the prediction results, this study analyzed the prediction error R, which is the difference between the true values and the predicted results. Due to space limitations, this section only presents the prediction results of the sedr station in three directions for different models, as shown in Figure 6.
From Figure 6, it can be observed that as the fluctuation amplitude of the original data increases, the prediction errors of different models also increase to varying degrees, with the largest errors observed in the U direction. Compared to the LSTM model, the VMD-LSTM hybrid model better captures the fluctuation trends and amplitudes of the true values in the data, and exhibits smaller variations and extremities in the prediction error R. This indicates that after VMD decomposition, the VMD-LSTM model is able to capture the inherent fluctuation characteristics of the initial data more effectively, leading to more accurate predictions. Both the VMD-LSTM and DVMD-LSTM models exhibit similar prediction fluctuations and trends, but the DVMD-LSTM model has smaller prediction errors R. This suggests that the DVMD-LSTM model not only retains the advantages of the VMD-LSTM model in predicting fluctuation trends and amplitudes, but also achieves higher prediction accuracy.
To analyze the applicability and robustness of the DVMD-LSTM model, this study conducted predictions using the LSTM, VMD-LSTM, and DVMD-LSTM models in the E, N, and U directions for each GNSS station. The prediction accuracy and improvement achieved by each model are summarized in Table 2. Where “I” represents the degree of accuracy improvement of the hybrid model compared with the single LSTM model under different accuracy indexes.
Based on the findings presented in Table 2, it can be observed that the VMD-LSTM model demonstrates superior performance compared to the LSTM model in predicting the RMSE of the E direction by an average reduction of 19.77%, the N direction by an average reduction of 26.83%, and the U direction by an average reduction of 19.31%. Additionally, the VMD-LSTM model exhibits an average reduction of 20.31% in MAE for the E direction, 27.12% for the N direction, and 19.48% for the U direction. These results indicate that the VMD-LSTM model achieves improvements in prediction accuracy across all directional components for any given station, with the most significant enhancement observed in the N-direction.
Furthermore, the DVMD-LSTM model outperforms the LSTM model by achieving an average reduction of 29.48% in RMSE for the E direction, 35.67% for the N direction, and 30.33% for the U direction. Similarly, the average reduction in MAE for the DVMD-LSTM model is 29.48% for the E direction, 35.67% for the N direction, and 30.09% for the U direction, as compared to the VMD-LSTM model. Moreover, the DVMD-LSTM model demonstrates an average reduction of 9.71% in RMSE for the E direction, 8.84% for the N direction, and 11.02% for the U direction when compared to the VMD-LSTM model. Correspondingly, the average reduction in MAE is 9.17% for the E direction, 8.55% for the N direction, and 10.61% for the U direction. These findings highlight the significant improvement in prediction accuracy achieved by the DVMD-LSTM model through the modification of the treatment of the residual component. Notably, the improvement achieved by the DVMD-LSTM model is more substantial than that of the VMD-LSTM model relative to the LSTM model, and it demonstrates varying degrees of enhancement across different stations. The larger improvement in the U direction for the DVMD-LSTM model can be attributed to the significant presence of fluctuations in the time series. After VMD decomposition, the residual component becomes more prominent, and the VMD-LSTM model's inability to capture the fluctuation information leads to diminished prediction accuracy and greater room for improvement.
In summary, the DVMD-LSTM model preserves the advantages of the VMD-LSTM model in predicting fluctuation trends and frequencies while achieving higher prediction accuracy. The results of the predictions conducted across different directional components of various stations further validate the superiority of the proposed model. These experimental findings confirm the model's applicability and robustness, demonstrating its potential for broad utilization in the field of high precision time series forecasting.

4.2. Optimal Noise Model Research

4.2.1. Comparison of optimal noise models under each prediction model

To further investigate whether the DVMD-LSTM model can adequately consider the noise characteristics of different datasets during the prediction process, this study selected stations with the same optimal noise model as both the training and testing dataset. The optimal noise model represents the model that accurately describes and predicts noise under given data and problem conditions. Noise models are typically used to eliminate or reduce the impact of noise in data, thereby improving the performance and predictive capabilities of the models. The optimal noise models for the prediction results of each model were calculated, and the specific results are presented in Table 3.
According to Table 3, the optimal noise models differ among different stations, indicating the presence of inconsistent noise characteristics. Here is a brief introduction to the RWFNWN, PLWN, FNWN, and GGMWN noise models:
RWFNWN (Robust Wiener Filter with Nonlinear White Noise): RWFNWN is a common noise model in the real world. It combines long-memory (long-range dependence) fractional noise with independently and identically distributed white noise. PLWN (Poisson Log-Normal White Noise): PLWN assumes that the noise in the data follows a power-law distribution and incorporates independently and identically distributed white noise. Power-law distributions capture the self-similarity of data at different scales, where patterns exhibit similar statistical properties at both large and small scales. FNWN (Fractional Gaussian Noise): FNWN is a fractal noise model that describes the noise characteristics in data by combining fractional noise with white noise. Fractal noise exhibits self-similarity and scale invariance, allowing for a better description of coarse and fine-grained structures in the data. GGMWN (Generalized Gaussian-Mixture White Noise): GGMWN is a mixture of Gaussian noise model. It assumes that the noise in the data is composed of multiple components from Gaussian distributions, along with the addition of white noise. These noise models have different applicability in various data and problem domains. Selecting the appropriate noise model requires an evaluation and selection based on factors such as the characteristics of the data, the requirements of the problem, and the assumptions and complexities of the model.
The LSTM model exhibits significant differences between its prediction results and the optimal noise models of the original data, with an average accuracy of only 25% across all three directions. Additionally, the predominant optimal noise models are PLWN and GGMWN. This suggests that the LSTM model does not adequately consider the inherent noise characteristics of GNSS time series during prediction. In contrast, the VMD-LSTM model shows improved accuracy in capturing the optimal noise models, with an average accuracy of 42.67%. This indicates that the VMD decomposition effectively captures the noise characteristics within the IMF components, although the noise characteristics in the residual component r are not fully captured, resulting in relatively lower overall accuracy. Therefore, the proposed DVMD-LSTM model further enhances the noise characteristics in the residual component r by performing VMD decomposition once again. As a result, the DVMD-LSTM model achieves an impressive average accuracy of 79.17% in capturing the optimal noise models. In summary, the DVMD-LSTM model adequately considers the noise characteristics of the data during the prediction process by processing the original data and decomposed residual component.

4.2.2. Speed Estimation Impact Analysis

In order to further investigate the quality of the predicted results for each model, this study calculates the velocity of GNSS reference stations based on the predicted results. By comparing the velocity values obtained from the original data and the optimal noise model calculated under each prediction model, an assessment of the predicted results for each model is conducted. The specific results are presented in Table 4.
According to Table 4, in the E direction of each station, the average absolute error between the velocities predicted by the LSTM model and the velocities of the original data is 0.068 mm/year. In the N direction, it is 0.093 mm/year, and in the U direction, it is 0.078 mm/year. For the VMD-LSTM model, the average absolute error between the predicted velocities and the velocities of the original data is 0.031 mm/year in the E direction, 0.060 mm/year in the N direction, and 0.060 mm/year in the U direction. As for the DVMD-LSTM model, the average absolute error between the predicted velocities and the velocities of the original data is 0.016 mm/year in the E direction, 0.042 mm/year in the N direction, and 0.047 mm/year in the U direction. Compared to the LSTM model, the VMD-LSTM model shows an average improvement of 37.67% in velocity prediction accuracy, while the DVMD-LSTM model demonstrates an average improvement of 56.80%. Compared with VMD-LSTM, the speed prediction accuracy of DVMD-LSTM model is improved by 33.02% on average. Thus, both the VMD-LSTM and DVMD-LSTM models exhibit improved velocity prediction accuracy compared to the LSTM model, with the DVMD-LSTM model showing a greater improvement, further demonstrating its outstanding predictive performance.
In summary, this study evaluated the performance of various prediction models by analyzing their prediction accuracy, optimal noise models, and velocity results. The results indicate that the DVMD-LSTM model outperforms the others in multiple aspects, highlighting its potential for wide application in high-precision time series prediction with multiple noise characteristics.

5. Conclusion

Addressing the limitations of low prediction accuracy and inadequate consideration of noise characteristics in the VMD-LSTM model for time series forecasting, this paper proposes a high-precision GNSS time series prediction method based on DVMD and LSTM. The proposed method is comprehensively validated and tested on the daily time series data from eight North American regional GNSS stations, spanning the period from 2000 to 2022, in the E, N, and U directions. The experimental results demonstrate the following:
(1) The VMD-LSTM model shows good prediction results for each IMF value after VMD decomposition, but performs poorly in predicting the residual component. The proposed DVMD-LSTM model utilizes VMD decomposition to extract the fluctuation characteristics of the residual component, leading to a significant improvement in the prediction accuracy of the residual component and enhancing the overall prediction accuracy.
(2) Compared to the initial VMD-LSTM hybrid model, the DVMD-LSTM model exhibits significant improvements in prediction accuracy. The RMSE values for the DVMD-LSTM model are reduced by an average of 9.71% in the E direction, 8.84% in the N direction, and 11.02% in the U direction. Additionally, the MAE values are decreased by an average of 9.17% in the E direction, 8.55% in the N direction, and 10.61% in the U direction. Across all measurement stations, the DVMD-LSTM model consistently outperforms the VMD-LSTM model, indicating its superior predictive accuracy, adaptability, and robustness.
(3) Compared to the LSTM model, the DVMD-LSTM model achieves an average improvement of 36.50% in the accuracy of the average optimal noise model across all stations, reaching an overall accuracy of 79.17%. This demonstrates that the DVMD-LSTM model adequately considers the noise characteristics of the data during the prediction process and achieves superior prediction results. By calculating the velocities obtained from the optimal noise models, it is evident that the DVMD-LSTM model achieves an average improvement of 33.02% in velocity prediction accuracy compared to the VMD-LSTM model, further confirming the outstanding predictive performance of the DVMD-LSTM model.

Author Contributions

H. C and J. H, writing-original draft preparation; X. H and T. L and K. Y and X. M, methodology, reviewed and edited the manuscript; X. S and Z. H, data processing and figures plotting. All authors have read and agreed to the published version of the manuscript.

Funding

This work was sponsored by National Natural Science Foundation of China (42104023), Major Discipline Academic and Technical Leaders Training Program of Jiangxi Province (20225BCJ23014).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ohta, Y.; Kobayashi, T.; Tsushima, H.; Miura, S.; Hino, R.; Takasu, T.; Fujimoto, H.; Iinuma, T.; Tachibana, K.; Demachi, T.; et al. Quasi real-time fault model estimation for near-field tsunami forecasting based on RTK-GPS analysis: Application to the 2011 Tohoku-Oki earthquake (Mw 9.0). Journal of Geophysical Research: Solid Earth 2012, 117. [Google Scholar] [CrossRef]
  2. Serpelloni, E.; Faccenna, C.; Spada, G.; Dong, D.; Williams, S.D.P. Vertical GPS ground motion rates in the Euro-Mediterranean region: New evidence of velocity gradients at different spatial scales along the Nubia-Eurasia plate boundary. J. Geophys. Res. Solid Earth 2013, 118, 6003–6024. [Google Scholar] [CrossRef]
  3. Serpelloni, E.; Vannucci, G.; Pondrelli, S.; Argnani, A.; Casula, G.; Anzidei, M.; Baldi, P.; Gasperini, P. Kinematics of the Western Africa-Eurasia plate boundary from focal mechanisms and GPS data. Geophys. J. Int. 2007, 169, 1180–1200. [Google Scholar] [CrossRef]
  4. Cina, A.; Piras, M. Performance of low-cost GNSS receiver for landslides monitoring: test and results. Geomatics, Nat. Hazards Risk 2014, 6, 497–514. [Google Scholar] [CrossRef]
  5. Meng, X.; Roberts, G.W.; Dodson, A.H.; Cosser, E.; Barnes, J.; Rizos, C. Impact of GPS satellite and pseudolite geometry on structural deformation monitoring: analytical and empirical studies. J. Geodesy 2004, 77, 809–822. [Google Scholar] [CrossRef]
  6. Yi, T.-H.; Li, H.-N.; Gu, M. Experimental assessment of high-rate GPS receivers for deformation monitoring of bridge. Measurement 2013, 46, 420–432. [Google Scholar] [CrossRef]
  7. Xiao, R.; Shi, H.; He, X.; Li, Z.; Jia, D.; Yang, Z. Deformation Monitoring of Reservoir Dams Using GNSS: An Application to South-to-North Water Diversion Project, China. IEEE Access 2019, 7, 54981–54992. [Google Scholar] [CrossRef]
  8. Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef]
  9. Blewitt, G.; Lavallée, D. Effect of annual signals on geodetic velocity. J. Geophys. Res. Solid Earth 2002, 107, ETG 9–1. [Google Scholar] [CrossRef]
  10. Segall, P.; Davis, J.L. GPS APPLICATIONS FOR GEODYNAMICS AND EARTHQUAKE STUDIES. Annu. Rev. Earth Planet. Sci. 1997, 25, 301–336. [Google Scholar] [CrossRef]
  11. Wang, J.; Jiang, W.; Li, Z.; Lu, Y. A New Multi-Scale Sliding Window LSTM Framework (MSSW-LSTM): A Case Study for GNSS Time-Series Prediction. Remote. Sens. 2021, 13, 3328. [Google Scholar] [CrossRef]
  12. Klos, A.; Olivares, G.; Teferle, F.N.; Hunegnaw, A.; Bogusz, J. On the combined effect of periodic signals and colored noise on velocity uncertainties. GPS Solutions 2017, 22, 1. [Google Scholar] [CrossRef]
  13. He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition; 2016; pp. 770–778. [Google Scholar]
  14. Otter, D.W.; Medina, J.R.; Kalita, J.K. A Survey of the Usages of Deep Learning for Natural Language Processing. IEEE Trans. Neural Networks Learn. Syst. 2020, 32, 604–624. [Google Scholar] [CrossRef] [PubMed]
  15. Deng, L.; Platt, J.C. Ensemble deep learning for speech recognition. Interspeech 2014 2014. [Google Scholar] [CrossRef]
  16. Lim, B.; Zohren, S. Time-series forecasting with deep learning: a survey. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 2021, 379, 20200209. [Google Scholar] [CrossRef]
  17. Hua, Y.; Zhao, Z.; Li, R.; Chen, X.; Liu, Z.; Zhang, H. Deep Learning with Long Short-Term Memory for Time Series Prediction. IEEE Commun. Mag. 2019, 57, 114–119. [Google Scholar] [CrossRef]
  18. Sezer, O.B.; Gudelek, M.U.; Ozbayoglu, A.M. Financial time series forecasting with deep learning: A systematic literature review: 2005–2019. Appl. Soft Comput. 2020, 90, 106181. [Google Scholar] [CrossRef]
  19. Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Networks 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
  20. Graves, A. Supervised Sequence Labelling with Recurrent Neural Networks. 2012. [Google Scholar] [CrossRef]
  21. Gasparin, A.; Lukovic, S.; Alippi, C. Deep learning for time series forecasting: The electric load case. arXiv 2019, arXiv:1907.09207. [Google Scholar] [CrossRef]
  22. Yao, W.; Huang, P.; Jia, Z. Multidimensional LSTM Networks to Predict Wind Speed. 2018. [Google Scholar] [CrossRef]
  23. Kim, H.-U.; Bae, T.-S. Deep Learning-Based GNSS Network-Based Real-Time Kinematic Improvement for Autonomous Ground Vehicle Navigation. J. Sensors 2019, 2019, 1–8. [Google Scholar] [CrossRef]
  24. Tao, Y.; Liu, C.; Chen, T.; Zhao, X.; Liu, C.; Hu, H.; Zhou, T.; Xin, H. Real-Time Multipath Mitigation in Multi-GNSS Short Baseline Positioning via CNN-LSTM Method. Math. Probl. Eng. 2021, 2021, 1–12. [Google Scholar] [CrossRef]
  25. Xie, P.; Zhou, A.; Chai, B. The Application of Long Short-Term Memory(LSTM) Method on Displacement Prediction of Multifactor-Induced Landslides. IEEE Access 2019, 7, 54305–54311. [Google Scholar] [CrossRef]
  26. Wang, Y.; Markert, R.; Xiang, J.; Zheng, W. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system. Mech. Syst. Signal Process. 2015, 60–61, 243–251. [Google Scholar] [CrossRef]
  27. Huang, Y.; Yan, L.; Cheng, Y.; Qi, X.; Li, Z. Coal Thickness Prediction Method Based on VMD and LSTM. Electronics 2022, 11, 232. [Google Scholar] [CrossRef]
  28. Zhang, T.; Fu, C. Application of Improved VMD-LSTM Model in Sports Artificial Intelligence. Comput. Intell. Neurosci. 2022, 2022, 1–6. [Google Scholar] [CrossRef]
  29. Han, L.; Zhang, R.; Wang, X.; Bao, A.; Jing, H. Multi-step wind power forecast based on VMD-LSTM. IET Renewable Power Generation 2019, 13, 1690–1700. [Google Scholar] [CrossRef]
  30. Xing, Y.; Yue, J.; Chen, C.; Cong, K.; Zhu, S.; Bian, Y. Dynamic Displacement Forecasting of Dashuitian Landslide in China Using Variational Mode Decomposition and Stack Long Short-Term Memory Network. Appl. Sci. 2019, 9, 2951. [Google Scholar] [CrossRef]
  31. He, X.; Bos, M.S.; Montillet, J.-P.; Fernandes, R.; Melbourne, T.; Jiang, W.; Li, W. Spatial Variations of Stochastic Noise Properties in GPS Time Series. Remote. Sens. 2021, 13, 4534. [Google Scholar] [CrossRef]
  32. Nistor, S.; Suba, N.-S.; Maciuk, K.; Kudrys, J.; Nastase, E.I.; Muntean, A. Analysis of Noise and Velocity in GNSS EPN-Repro 2 Time Series. Remote. Sens. 2021, 13, 2783. [Google Scholar] [CrossRef]
  33. He, X.; Montillet, J.-P.; Fernandes, R.; Bos, M.; Yu, K.; Hua, X.; Jiang, W. Review of current GPS methodologies for producing accurate time series and their error sources. J. Geodyn. 2017, 106, 12–29. [Google Scholar] [CrossRef]
  34. Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE transactions on signal processing 2013, 62, 531–544. [Google Scholar] [CrossRef]
  35. Rehman, N.U.; Aftab, H. Multivariate Variational Mode Decomposition. IEEE Trans. Signal Process. 2019, 67, 6039–6052. [Google Scholar] [CrossRef]
  36. Wang, Z.; He, X.; Shen, H.; Fan, S.; Zeng, Y. Multi-source information fusion to identify water supply pipe leakage based on SVM and VMD. Inf. Process. Manag. 2021, 59, 102819. [Google Scholar] [CrossRef]
  37. Sherstinsky, A. , Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) Network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
  38. Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
  39. Sagheer, A.; Kotb, M. Time series forecasting of petroleum production using deep LSTM recurrent networks. Neurocomputing 2018, 323, 203–213. [Google Scholar] [CrossRef]
  40. Yadav, A.; Jha, C.K.; Sharan, A. Optimizing LSTM for time series prediction in Indian stock market. Procedia Comput. Sci. 2020, 167, 2091–2100. [Google Scholar] [CrossRef]
  41. Liao, X.; Liu, Z.; Deng, W. Short-term wind speed multistep combined forecasting model based on two-stage decomposition and LSTM. Wind. Energy 2021, 24, 991–1012. [Google Scholar] [CrossRef]
  42. Jin, Y.; Guo, H.; Wang, J.; Song, A. A Hybrid System Based on LSTM for Short-Term Power Load Forecasting. Energies 2020, 13, 6241. [Google Scholar] [CrossRef]
  43. Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)? – Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
  44. Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
  45. He, X.; Bos, M.S.; Montillet, J.P.; Fernandes, R.M.S. Investigation of the noise properties at low frequencies in long GNSS time series. J. Geodesy 2019, 93, 1271–1282. [Google Scholar] [CrossRef]
  46. Williams, S.D.P. CATS: GPS coordinate time series analysis software. GPS Solutions 2008, 12, 147–153. [Google Scholar] [CrossRef]
  47. Schneider, T. Analysis of Incomplete Climate Data: Estimation of Mean Values and Covariance Matrices and Imputation of Missing Values. J. Clim. 2001, 14, 853–871. [Google Scholar] [CrossRef]
  48. Christiansen, B.; Schmith, T.; Thejll, P. A Surrogate Ensemble Study of Climate Reconstruction Methods: Stochasticity and Robustness. J. Clim. 2009, 22, 951–976. [Google Scholar] [CrossRef]
Preprints 77542 g001
Figure 1. Basic structure of LSTM
Figure 1. Basic structure of LSTM
Preprints 77542 g001
Preprints 77542 g002
Figure 2. DVMD-LSTM Hybrid Model Prediction Process
Figure 2. DVMD-LSTM Hybrid Model Prediction Process
Preprints 77542 g002
Preprints 77542 g003
Figure 3. Distribution map of each GNSS station
Figure 3. Distribution map of each GNSS station
Preprints 77542 g003
Preprints 77542 g004
Figure 4. Three-direction interpolation comparison chart of GBOS station (Black represents the original data before interpolation, and red represents the interpolated data).
Figure 4. Three-direction interpolation comparison chart of GBOS station (Black represents the original data before interpolation, and red represents the interpolated data).
Preprints 77542 g004
Preprints 77542 g005
Figure 5. Prediction results of each IMF and residual under different models after VMD decomposition in U direction of sedr station.
Figure 5. Prediction results of each IMF and residual under different models after VMD decomposition in U direction of sedr station.
Preprints 77542 g005
Preprints 77542 g006
Figure 6. Comparison of prediction results and prediction error R in three directions of sedr station under different models ((a–c) are the prediction results of each model, and (d–f) are comparison diagrams of prediction error R of each model).
Figure 6. Comparison of prediction results and prediction error R in three directions of sedr station under different models ((a–c) are the prediction results of each model, and (d–f) are comparison diagrams of prediction error R of each model).
Preprints 77542 g006
Table 1. Information of each GNSS station.
Table 1. Information of each GNSS station.
Site Longitude   ( ° ) Latitude   ( ° ) Time span(year) Date missing rate
albh -123.49 48.39 2000-2022 0.61%
burn -117.84 42.78 2000-2022 1.27%
ceda -112.86 40.68 2000-2022 2.74%
foot -113.81 39.37 2000-2022 3.40%
gobs -120.81 45.84 2000-2022 3.65%
rhcl -118.03 34.02 2000-2022 1.79%
sedr -122.22 48.52 2000-2022 0.49%
smel -112.84 39.43 2000-2022 0.79%
Table 2. Comparison of the prediction results of each GNSS station in the three directions of E, N, and U under different models.
Table 2. Comparison of the prediction results of each GNSS station in the three directions of E, N, and U under different models.
Site ENU LSTM VMD-LSTM DVMD-LSTM
RMSE
(mm) 		MAE
(mm) 		RMSE
(mm) 		I/% MAE
(mm) 		I/% RMSE
(mm) 		I/% MAE
(mm)
albh E 0.89 0.65 0.76 13.91 0.55 14.03 0.67 24.56 0.49
burn 1.40 1.10 1.16 17.00 0.92 16.70 1.02 27.00 0.82
ceda 1.73 1.35 1.37 20.75 1.06 21.18 1.21 29.82 0.94
foot 0.58 0.44 0.51 12.91 0.38 13.51 0.45 22.12 0.34
gobs 1.00 0.70 0.86 13.74 0.58 16.08 0.77 23.53 0.52
rhcl 1.62 1.28 1.07 34.08 0.83 34.78 0.94 41.63 0.74
sedr 0.68 0.53 0.58 15.00 0.45 15.13 0.50 27.07 0.39
smel 0.57 0.44 0.40 30.80 0.30 31.08 0.34 40.11 0.26
albh N 0.73 0.57 0.55 24.53 0.43 24.23 0.49 32.77 0.38
burn 1.39 1.11 1.07 22.74 0.85 23.37 0.95 31.65 0.76
ceda 1.38 1.10 1.05 23.54 0.83 24.05 0.90 34.50 0.72
foot 0.59 0.43 0.39 33.45 0.29 31.81 0.34 41.35 0.26
gobs 0.86 0.63 0.63 26.95 0.46 26.60 0.56 34.86 0.41
rhcl 3.14 2.54 1.71 45.59 1.31 48.53 1.58 49.55 1.21
sedr 0.85 0.63 0.66 22.23 0.50 21.79 0.56 34.15 0.42
smel 0.55 0.42 0.47 15.62 0.35 16.54 0.41 26.53 0.30
albh U 3.38 2.60 2.89 14.57 2.25 13.77 2.51 25.74 1.96
burn 2.30 1.78 1.94 15.78 1.49 16.29 1.66 27.82 1.29
ceda 2.65 2.03 2.27 14.48 1.73 15.08 1.96 26.09 1.49
foot 2.39 1.83 1.87 21.89 1.43 22.23 1.60 32.94 1.23
gobs 2.92 2.22 2.28 22.17 1.72 22.48 1.99 32.04 1.53
rhcl 2.45 1.90 2.10 14.50 1.63 14.04 1.87 23.68 1.46
sedr 3.33 2.62 2.37 28.68 1.87 28.79 1.96 41.19 1.54
smel 2.36 1.87 1.84 22.38 1.43 23.12 1.58 33.17 1.24
Table 3. The optimal noise model of each station under different models in the three directions of E, N, and U.
Table 3. The optimal noise model of each station under different models in the three directions of E, N, and U.
Site ENU Optimal noise model
TURE LSTM VMD-LSTM DVMD-LSTM
albh E RWFNWN PLWN RWFNWN RWFNWN
burn RWFNWN PLWN PLWN RWFNWN
ceda RWFNWN PLWN PLWN RWFNWN
foot PLWN GGMWN FNWN PLWN
gobs RWFNWN PLWN RWFNWN RWFNWN
rhcl RWFNWN GGMWN PLWN RWFNWN
sedr RWFNWN PLWN PLWN RWFNWN
smel FNWN PLWN FNWN FNWN
albh N RWFNWN PLWN RWFNWN RWFNWN
burn FNWN PLWN PLWN PLWN
ceda RWFNWN PLWN PLWN RWFNWN
foot FNWN GGMWN FNWN FNWN
gobs RWFNWN PLWN RWFNWN RWFNWN
rhcl RWFNWN RWFNWN PLWN PLWN
sedr FNWN GGMWN RWFNWN FNWN
smel FNWN PLWN FNWN FNWN
albh U PLWN PLWN RWFNWN FNWN
burn PLWN GGMWN PLWN PLWN
ceda PLWN PLWN RWFNWN PLWN
foot PLWN PLWN FNWN FNWN
gobs PLWN GGMWN PLWN FNWN
rhcl FNWN PLWN RWFNWN FNWN
sedr PLWN PLWN PLWN PLWN
smel PLWN PLWN FNWN PLWN
Table 4. Velocity values obtained by each station under the optimal noise model.
Table 4. Velocity values obtained by each station under the optimal noise model.
Site ENU Trend(mm/year)
TURE LSTM VMD-LSTM DVMD-LSTM
albh E -0.041 0.020 0.055 -0.044
burn -0.108 -0.005 -0.051 -0.116
ceda -0.726 -0.528 -0.693 -0.736
foot 0.02 0.015 0.001 0.009
gobs 0.659 0.656 0.672 0.682
rhcl 0.811 0.666 0.805 0.783
sedr 0.354 0.341 0.378 0.313
smel 0.026 0.009 0.023 0.021
albh N 0.327 0.245 0.276 0.295
burn 0.124 0.08 0.116 0.13
ceda -0.065 -0.041 -0.227 -0.042
foot 0.009 0.029 -0.036 0.005
gobs 0.063 0.078 0.029 -0.02
rhcl 1.253 0.743 1.132 1.071
sedr 0.199 0.17 0.212 0.195
smel 0.02 -0.001 -0.025 0.017
albh U 0.383 0.204 0.131 0.268
burn 0.241 0.144 0.238 0.216
ceda 0.016 0.159 0.074 0.137
foot 0.194 0.125 0.194 0.202
gobs 0.301 0.278 0.283 0.262
rhcl 0.298 0.206 0.367 0.264
sedr 0.017 0.022 0.082 0.04
smel 0.195 0.182 0.206 0.183
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated